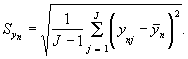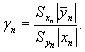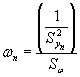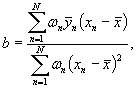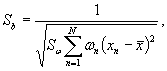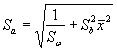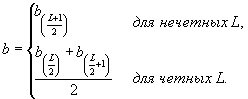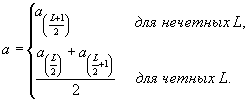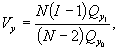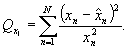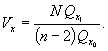|
МЕЖГОСУДАРСТВЕННЫЙ
СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ INTERSTATE
COUNCIL FOR STANDARDIZATION, METROLOGY AND CERTIFICATION |
|
|
РЕКОМЕНДАЦИИ |
РМГ 54- |
Государственная система обеспечения единства измерений
ХАРАКТЕРИСТИКИ ГРАДУИРОВОЧНЫЕ СРЕДСТВ ИЗМЕРЕНИЙ
СОСТАВА И СВОЙСТВ ВЕЩЕСТВ И МАТЕРИАЛОВ
Методика выполнения измерений
с использованием стандартных образцов
|
|
Москва Стандартинформ 2006 |
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-97 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены»
Сведения о рекомендациях
1 РАЗРАБОТАНЫ Уральским научно-исследовательским институтом метрологии (УНИИМ) Госстандарта России
2 ВНЕСЕНЫ Госстандартом России
3
ПРИНЯТЫ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол № 22 от 6 ноября
За принятие проголосовали:
|
Краткое наименование страны по МК (ИСО 3166) 044-97 |
Код страны по МК (ИСО 3166) 004-97 |
Сокращенное наименование национального органа по стандартизации |
|
BY |
Госстандарт Республики Беларусь |
|
|
Казахстан |
KZ |
Госстандарт Республики Казахстан |
|
Киргизия |
KG |
Кыргызстандарт |
|
Молдова |
MD |
Молдова-Стандарт |
|
Российская Федерация |
RU |
Госстандарт России |
|
Таджикистан |
TJ |
Таджикстандарт |
|
Туркменистан |
TM |
Главгосслужба «Туркменстандартлары» |
|
Узбекистан |
UZ |
Узстандарт |
|
UA |
Госпотребстандарт Украины |
4
Постановлением Государственного комитета Российской Федерации по стандартизации и метрологии от 26 января
5 ВВЕДЕНЫ ВПЕРВЫЕ
6
ПЕРЕИЗДАНИЕ. Май
Информация об изменениях к настоящим рекомендациям публикуется в указателе (каталоге) «Национальные стандарты», а текст этих изменений - в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящих рекомендаций соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»
Содержание
РЕКОМЕНДАЦИИ ПО МЕЖГОСУДАРСТВЕННОЙ СТАНДАРТИЗАЦИИ
|
Государственная система обеспечения единства измерений ХАРАКТЕРИСТИКИ ГРАДУИРОВОЧНЫЕ СРЕДСТВ ИЗМЕРЕНИЙ СОСТАВА И СВОЙСТВ ВЕЩЕСТВ И МАТЕРИАЛОВ Методика выполнения измерений с использованием стандартных образцов State system for ensuring the uniformity of
measurements. |
Дата введения - 2004-07-01
1 Область применения
Настоящие рекомендации содержат методику выполнения измерений (далее - МВИ) градуировочных характеристик (далее - ГХ) средств измерений состава и свойств веществ и материалов (далее - СИ).
ГХ СИ определяют по экспериментальным данным, полученным с использованием стандартных образцов (далее - СО).
МВИ, представленные в настоящих рекомендациях, применимы в случае, когда аттестованное значение СО и значение соответствующего сигнала СИ связаны линейной зависимостью либо когда зависимость между этими величинами может быть приведена к линейной.
Алгоритмы оценки ГХ СИ могут быть применимы при использовании для градуировки аттестованных смесей или градуировочных растворов.
2 Нормативные ссылки
В настоящих рекомендациях использована ссылка на следующий межгосударственный стандарт:
ГОСТ 8.315-97 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения
Примечание - При пользовании настоящими рекомендациями целесообразно проверить действие ссылочного стандарта по указателю «Национальные стандарты», составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящими рекомендациями следует руководствоваться измененным (замененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Общие положения
3.1 Градуировку СИ с помощью СО выполняют с целью установить зависимость между выходным сигналом СИ I и воспроизводимой СО аттестованной характеристикой А.
3.2 Для градуировки СИ используют комплекты СО, допущенные к применению в порядке, установленном ГОСТ 8.315.
Предпочтительно для градуировки использовать комплекты СО, число СО в которых N не менее пяти.
3.3 Аттестованные значения Ап экземпляров СО, входящих в комплект СО, должны быть распределены приблизительно равномерно в диапазоне измерения градуируемого СИ.
3.4 Диапазон аттестованных значений СО в комплекте должен совпадать с диапазоном измерения градуируемого СИ.
3.5 Состав и структура материала СО должны быть как можно более близкими к составу и структуре проб материала, контролируемого с использованием градуируемых СИ.
4 Подготовка к измерениям, условия их проведения и процедура
4.1 Подготовку проб СО и СИ к проведению измерений осуществляют в соответствии с описанием процедуры измерений с учетом требований инструкции по применению СО и эксплуатационных документов на градуируемое СИ.
4.2 Условия проведения измерений должны соответствовать нормальным условиям применения, установленным в эксплуатационных документах на СИ.
4.3 Стандартное отклонение значений выходного сигнала градуируемого СИ должно быть известно из эксплуатационных документов на СИ до проведения градуировки СИ либо значение входного сигнала должно быть оценено в процессе градуировки СИ.
4.4 Число единичных измерений (наблюдений) выходного сигнала I для каждого СО должно быть не менее пяти.
Если в процессе градуировки оценивают среднее стандартное отклонение значений выходного сигнала, то число измерений увеличивают до 10-15. Число измерений для всех экземпляров СО должно быть одинаково.
4.5 По результатам измерения значений выходного сигнала Inj - для каждого n-го СО вычисляют
среднеарифметическое значение выходного сигнала ![]() :
:
|
|
(1) |
где J - число измерений каждого n-го СО.
4.6 Полученные среднеарифметические значения выходных сигналов I и аттестованные значения СО А наносят на график и по методике в соответствии с приложением А выбирают вид преобразования исходных данных у = f(I) и х = g (А) для получения линейной ГХ.
5 Обработка результатов измерений
5.1 После выбора вида преобразования в соответствии с 4.6 вычисляют значения новых переменных:
|
xn = g (An), |
где g (An) - функция преобразования исходных данных аттестованного значения n-го СО;
|
ynj = f (Inj) |
(3) |
где f (Inj) - функция преобразования исходных данных выходного сигнала n-го СО.
5.2 Вычисляют стандартные отклонения ![]() величин хn по формуле
величин хn по формуле
где значения производной g' (А) берут при А = Аn
![]() погрешность аттестованного значения n-го СО.
погрешность аттестованного значения n-го СО.
5.3 Вычисляют среднеарифметические значения ![]() величин ynj по формуле
величин ynj по формуле
для n = 1,…, N
5.4 Если стандартное отклонение выходного сигнала СИ ![]() известно, то стандартное отклонение
известно, то стандартное отклонение ![]() величины у в n-й точке оценивают по формуле
величины у в n-й точке оценивают по формуле
|
|
(6) |
где значение производной ![]() берут при
берут при ![]() ;
;
![]() - стандартное отклонение выходного сигнала в n-й точке.
- стандартное отклонение выходного сигнала в n-й точке.
В случае, когда неизвестно стандартное отклонение величины I в n-й точке, ![]() оценивают по формуле
оценивают по формуле
|
|
(7) |
5.5 Записывают полученные результаты преобразования исходных данных и характеристики их погрешностей в таблицу по форме таблицы 1.
Таблица 1 - Исходные данные для построения ГХ
|
xn |
|
ynj |
|
|
γn |
|
x1 |
Sx1 |
y11, y12,….y1 I |
|
Sy1 |
γ1 |
|
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
|
xN |
SxN |
yN1, yN2,… yNi, |
|
SyN |
γN |
5.6 Для сравнения погрешностей исходных данных вычисляют отношения относительных стандартных отклонений γп по формуле
|
|
(8) |
Результаты вычислений записывают в последнюю колонку таблицы 1.
5.7 Вычисляют среднеарифметическое значение относительных стандартных отклонений ![]() по формуле
по формуле
|
|
(9) |
5.8 Выбирают в зависимости от соотношения погрешностей величин хп и уn т.е. в зависимости от значения, алгоритмы![]() , построения ГХ исходя из следующего:
, построения ГХ исходя из следующего:
- если γ ≤ 0,4, то ГХ определяют в соответствии с 6.2;
- в случае, когда имеются значимые погрешности измерения величин хп и уп, т.е. если ![]() > 0,4, то ГХ определяют в соответствии с 6.3.
> 0,4, то ГХ определяют в соответствии с 6.3.
6 Построение линейной ГХ
6.1 Построение линейной ГХ сводят к оценке коэффициентов a и b в уравнении вида
|
y = а + bx. |
Алгоритм оценки коэффициентов ГХ и вид ГХ выбирают в зависимости от соотношений погрешностей величин хп и уп по 5.8.
6.2 Построение ГХ методом наименьших квадратов
В случае, когда погрешности аттестованных значений СО (или переменной
x) незначимы по сравнению с погрешностями измерения выходных сигналов ![]() , ГХ строят в виде, задаваемом уравнением (10). Коэффициенты а и b и их погрешности вычисляют следующим образом.
, ГХ строят в виде, задаваемом уравнением (10). Коэффициенты а и b и их погрешности вычисляют следующим образом.
По исходным данным из таблицы 1 вычисляют сумму Sω обратных величин дисперсии преобразованного выходного сигнала
|
|
(11) |
и для каждого среднеарифметического значения ![]() его вес ωn
его вес ωn
Вычисляют среднеарифметические значения ![]() и
и ![]() по формулам:
по формулам:
|
|
(13) |
|
|
(14) |
ГХ определяют в виде уравнения (10).
Коэффициенты b и a вычисляют по формулам:
Стандартные отклонения Sb и Sа коэффициентов b и а вычисляют по формулам:
6.3 Построение ГХ методом усреднения оценок
В случае, когда имеются значимые погрешности измерения величин хп и уп ![]() , коэффициенты а и b в уравнении (10) оценивают следующим образом.
, коэффициенты а и b в уравнении (10) оценивают следующим образом.
Образуют из N точек таблицы 1 (х1, ![]() )... (xN,
)... (xN, ![]() ) все возможные пары различных точек (хi,
) все возможные пары различных точек (хi, ![]() ), [xj,
), [xj, ![]() (для i, j = 1, ... , N и i ¹ j)]. Число таких пар точек
(для i, j = 1, ... , N и i ¹ j)]. Число таких пар точек
![]()
Проводят через каждую пару точек прямую линию
|
y = aij + bij x. |
(19) |
Коэффициенты bij и aij определяют по формулам:
|
|
(20) |
|
aij = yi – bijxi. |
(21) |
Полученные по формулам (20) и (21) коэффициенты упорядочивают по возрастанию:
|
b(1) ≤ b(2) ... ≤ b(L), |
(22) |
|
a(1) ≤ a(2) ... ≤ a(L), |
(23) |
В качестве оценки коэффициента b в уравнении (10) принимают медиану ряда (22), вычисленную по формуле
Аналогично коэффициент а оценивают как медиану ряда (23)
2 Погрешности Δа и Δb коэффициентов а и b вычисляют по формулам:
|
|
(26) |
|
|
(27) |
где порядковые номера R и S членов рядов (23) и (22) определяют по формулам:
|
|
(28) |
|
S = L – R + 1. |
(29) |
7 Вычисление результатов измерений и оценка их погрешностей
7.1 При использовании ГХ для получения значения входной величины А по значению выходного сигнала I поступают следующим образом. Вычисляют по измеренному значению выходного сигнала I значение величины
|
y = f (I) |
(30) |
и по ГХ вычисляют значение величины х по формуле
|
|
(31) |
По значению величины х определяют значение величины А, используя обратное преобразование величины х.
|
A = g-1 (x) |
(32) |
где g-1 (x) функция, обратная функции х = g (А), использованная при преобразовании величины А в соответствии с 4.6.
7.2 Оценивают стандартное отклонение Sx величины х по формуле
|
|
(33) |
где Sy - стандартное отклонение величины у, оценивают в соответствии с 5.4, а значения стандартного отклонения величины а - Sa и стандартного отклонения величины b - Sb оценивают в зависимости от метода построения ГХ.
Если коэффициенты а и b были определены при построении ГХ методом наименьших квадратов в соответствии с 6.2, то Sa и Sb оценивают по формулам (18) и (17).
В случае, когда коэффициенты а и Ъ были определены при построении ГХ методом усреднения оценок в соответствии с 6.3, то Sa и Sb оценивают по формулам:
|
|
(34) |
|
|
(35) |
7.3 Стандартное отклонение SA измеряемой в соответствии с 7.1 величины А оценивают по формуле
|
|
(36) |
где значение производной g' взято при А, определенной по формуле (32), и значение Sx вычислено по формуле (33).
7.4 Погрешность ΔA измеряемой по ГХ величины А оценивают для заданной вероятности Р по формуле
|
ΔA = zP SA, |
(37) |
где zP - квантиль стандартного нормального распределения, соответствующий заданной вероятности Р.
8 Проверка линейности ГХ
8.1 Линейность ГХ предварительно проверяют на основе анализа расположения экспериментальных точек плоскости (х, у) относительно построенной ГХ у = а + bх.
Если отклонения от ГХ экспериментальных точек носят случайный характер, то выбор линеаризующих преобразований проведен правильно и полученная линейная ГХ адекватно отражает зависимость между величинами х и у.
Проверку случайности отклонений экспериментальных точек от ГХ (проверку линейности) проводят в случае, когда ГХ оценивают методом наименьших квадратов (6.2) в соответствии с критерием 8.2.
В случае оценки ГХ методом усредненных оценок (6.3) линейность ГХ проверяют в соответствии с критерием 8.3.
8.2 Проверку линейности ГХ, построенной методом наименьших квадратов по формулам (15) и (16), проводят следующим образом.
Вычисляют взвешенную сумму ![]() квадратов отклонения расчетных значений
квадратов отклонения расчетных значений ![]() , вычисленных по
формуле
, вычисленных по
формуле
|
|
(38) |
от средних значений ![]() , вычисленных по формуле (5),
, вычисленных по формуле (5),
|
|
(39) |
где коэффициенты ωn вычислены по формуле (12).
Вычисляют взвешенную сумму ![]() квадратов отклонений ynj от среднеарифметических значений
квадратов отклонений ynj от среднеарифметических значений ![]() .
.
|
|
(40) |
Вычисляют отношение средних квадратов отклонений Vy:
|
|
(41) |
где N - число точек при построении ГХ.
Сравнивают полученное значение Vy со значением квантиля F-распределения из таблицы Б.1 приложения Б со степенями свободы V1 = N - 2 и V2 = N (I - 1).
Если Vy ≤ F (V1, V2), то принимают гипотезу о линейности ГХ. В противном случае следует найти другое линеаризующее преобразование переменных.
8.3 Проверку линейности ГХ, построенной методом усреднения оценок по формулам (24) и (25), проводят следующим образом.
Если отклонения экспериментальных точек (хп, ![]() ) от ГХ изменяются закономерным образом, то
это дает основание считать выбор вида линейного преобразования не совсем удачным. Вычисляют
сумму
) от ГХ изменяются закономерным образом, то
это дает основание считать выбор вида линейного преобразования не совсем удачным. Вычисляют
сумму ![]() квадратов относительных отклонений расчетных значений
квадратов относительных отклонений расчетных значений ![]() , определенных по формуле
, определенных по формуле
|
|
(42) |
от значений хп
|
|
(43) |
Вычисляют сумму относительных стандартных отклонений ![]() :
:
|
|
(44) |
где ![]() определяют по формуле (4), а хп - по формуле (2).
определяют по формуле (4), а хп - по формуле (2).
Вычисляют отношение Vx квадратов стандартных отклонений:
|
|
(45) |
Сравнивают полученное значение Vx со значением квантиля F-распределения из таблицы Б.1 приложения Б со степенями свободы V1 = N - 2 и V2 = N.
Если Vx ≤ F (V1, V2), то принимают гипотезу о линейности ГХ. В противном случае следует найти другое линеаризующее преобразование переменных.
Приложение А
(рекомендуемое)
Виды преобразований для получения линейной зависимости
Из практики построения ГХ для СИ известны несколько наиболее распространенных преобразований переменных I и А, позволяющих сводить исходные монотонные нелинейные функции I = F (A) к нелинейной зависимости вида
|
y = a + bx, |
(A.1) |
где
|
y = а (I) |
(A.2) |
|
x = g (A) |
(A.3) |
Функции f (I) и g (A) выбирают из некоторого множества монотонных зависимостей таким образом, чтобы получить линейную зависимость
|
f (I) = a + b g (A) |
(A.4) |
хорошо согласующуюся с экспериментальными результатами.
Преобразования f (I) и g (А) называются линеаризующими.
В таблице А.1 указаны некоторые рекомендуемые виды таких линеаризующих преобразований.
Таблица А.1 - Виды исходных зависимостей I = F (A) и рекомендуемых линеаризующих преобразований
|
Исходная
зависимость |
Линеаризующее преобразование |
|
|
x = g (A) |
y = f (I) |
|
|
1 Дробно-линейные |
|
|
|
I = a + b/A |
x = 1/А |
у = I |
|
I = 1/(а + bА) |
х = А |
y = 1/I |
|
I = А/(а + bА) |
х = 1/А |
y = 1/I |
|
2 Показательные |
|
|
|
I = аеbA |
х = А |
y = ln I |
|
I = аеb/A |
х = 1/А |
y = ln I |
|
3 Степенная |
|
|
|
I = aAb, b < > 1 |
х = ln A |
y = ln I |
|
4 Логарифмическая |
|
|
|
I = a + b ln A |
х = ln A |
y = I |
В некоторых случаях можно применить следующую процедуру выбора линеаризующих преобразований. Откладывают в системе координат А и I точки с экспериментальными значениями ![]() , и через них приближенно
проводят от руки или с помощью лекала гладкую кривую
, и через них приближенно
проводят от руки или с помощью лекала гладкую кривую ![]() Выбирают две достаточно отдаленные опорные
точки А' и А ". Это могут быть крайние значения Ап либо средние значения, либо медианы крайних точек. Находят
по значениям А' и А" соответствующие значения I' и I". Например, если опорные точки А' и А" выбирают как
крайние (т.е. А' равно наименьшему, а А" - наибольшему значениям величин {Ап}), то I' и I" выбирают как
соответствующие им крайние значения из величин
Выбирают две достаточно отдаленные опорные
точки А' и А ". Это могут быть крайние значения Ап либо средние значения, либо медианы крайних точек. Находят
по значениям А' и А" соответствующие значения I' и I". Например, если опорные точки А' и А" выбирают как
крайние (т.е. А' равно наименьшему, а А" - наибольшему значениям величин {Ап}), то I' и I" выбирают как
соответствующие им крайние значения из величин ![]() .
.
Вычисляют по опорным точкам три вида средних:
-
арифметическое ![]()
-
геометрическое ![]()
-
гармоническое ![]()
Находят по построенной кривой ![]() в точках Аа, Аg,
Аh значения
в точках Аа, Аg,
Аh значения ![]() Вычисляют по формулам первой колонки таблицы А.2 значения разностей εi, которые приводят во второй колонке.
Вычисляют по формулам первой колонки таблицы А.2 значения разностей εi, которые приводят во второй колонке.
Таблица А.2 - Выбор вида ГХ и преобразования исходных данных
|
Формула для вычисления εi |
Значение εi* |
Вид ГХ |
Преобразование исходных данных |
|
|
|
x = g (A) |
y = f (I) |
||||
|
|
ε1 |
a + bx |
x = А |
y = I |
|
|
|
ε2 |
I = aebA |
х = А |
у = ln I |
|
|
|
ε3 |
1/(a + bA) |
х = А |
у =1/I |
|
|
|
ε4 |
a + b ln A |
х = ln A |
y = I |
|
|
|
ε5 |
aAb |
х = ln A |
у = ln I |
|
|
|
ε6 |
a + b/A |
x = 1/А |
y = I |
|
|
|
ε7 |
A/(a + bA) |
x = 1/А |
y = I |
|
|
* Индекс i означает номер преобразования исходных данных. |
|
||||
Из таблицы А.2 выбирают вид ГХ и преобразование исходных данных по номеру преобразования исходных данных i, для которого значение εi, оказалось наименьшим. Например, если наименьшим оказалось значение ε5, то выбирают вид ГХ аА6 и преобразование переменных х = ln A и у = ln I. Если имеется несколько значений εi, близких минимальному, то испытывают несколько видов ГХ, соответствующих этим значениям εi.
Приложение Б
(рекомендуемое)
Таблица Б.1 - Верхние доверительные границы F-распределения для Р = 0,95 (V2 - число степеней свободы числителя; V1 - число степеней свободы знаменателя)
|
V2 |
V1 |
|||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
|
|
5 |
5,51 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,77 |
4,74 |
4,62 |
4,56 |
|
6 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
3,94 |
3,87 |
|
7 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,64 |
3,51 |
3,44 |
|
8 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,35 |
3,22 |
3,15 |
|
9 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,14 |
3,01 |
2,94 |
|
10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,98 |
2,85 |
2,77 |
|
11 |
3,59 |
3,36 |
3,20 |
3,09 |
3,01 |
2,95 |
2,90 |
2,85 |
2,72 |
2,65 |
|
12 |
3,49 |
3,26 |
3,11 |
3,00 |
2,91 |
2,85 |
2,80 |
2,75 |
2,62 |
2,54 |
|
13 |
3,41 |
3,18 |
3,08 |
2,92 |
2,83 |
2,77 |
2,71 |
2,67 |
2,53 |
2,46 |
|
14 |
3,34 |
3,11 |
2,96 |
2,85 |
2,76 |
2,70 |
2,65 |
2,60 |
2,46 |
2,39 |
|
15 |
3,29 |
3,06 |
2,90 |
2,79 |
2,71 |
2,64 |
2,59 |
2,54 |
2,40 |
2,33 |
|
16 |
3,24 |
3,01 |
2,85 |
2,74 |
2,66 |
2,59 |
2,54 |
2,49 |
2,35 |
2,28 |
|
17 |
3,20 |
2,96 |
2,81 |
2,70 |
2,61 |
2,55 |
2,49 |
2,45 |
2,31 |
2,23 |
|
18 |
3,16 |
2,93 |
2,77 |
2,66 |
2,58 |
2,51 |
2,46 |
2,41 |
2,27 |
2,19 |
|
19 |
3,13 |
2,90 |
2,74 |
2,63 |
2,54 |
2,48 |
2,42 |
2,38 |
2,23 |
2,16 |
|
20 |
3,10 |
2,87 |
2,71 |
2,60 |
2,51 |
2,45 |
2,39 |
2,35 |
2,20 |
2,12 |
|
21 |
3,07 |
2,84 |
2,68 |
2,57 |
2,49 |
2,42 |
2,37 |
2,32 |
2,18 |
2,10 |
|
22 |
3,05 |
2,82 |
2,66 |
2,55 |
2,46 |
2,40 |
2,34 |
2,30 |
2,15 |
2,07 |
|
23 |
3,03 |
2,80 |
2,64 |
2,53 |
2,44 |
2,37 |
2,32 |
2,27 |
2,13 |
2,05 |
|
24 |
3,01 |
2,78 |
2,62 |
2,51 |
2,42 |
2,35 |
2,30 |
2,25 |
2,11 |
2,03 |
|
27 |
2,96 |
2,73 |
2,57 |
2,46 |
2,37 |
2,31 |
2,25 |
2,20 |
2,06 |
1,97 |
|
30 |
2,92 |
2,69 |
2,53 |
2,42 |
2,33 |
2,27 |
2,21 |
2,16 |
2,01 |
1,93 |
|
40 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,08 |
1,92 |
1,84 |
|
60 |
2,76 |
2,53 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1,84 |
1,75 |
|
120 |
2,68 |
2,45 |
2,29 |
2,17 |
2,09 |
2,02 |
1,96 |
1,91 |
1,75 |
1,66 |
|
∞ |
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,67 |
1,57 |
Ключевые слова: стандартные образцы, аттестованное значение СО, комплекты СО, градуировочная характеристика, линейная градуировочная характеристика, метод наименьших квадратов