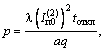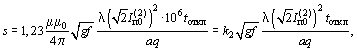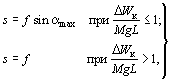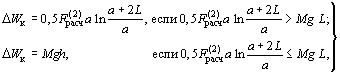РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ "ЕЭС РОССИИ"
ДЕПАРТАМЕНТ НАУЧНО-ТЕХНИЧЕСКОЙ ПОЛИТИКИ И РАЗВИТИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ПРОВЕРКЕ ГИБКИХ ПРОВОДНИКОВ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ И РАСПРЕДЕЛИТЕЛЬНЫХ УСТРОЙСТВ НА ВОЗМОЖНОСТЬ ИХ ОПАСНОГО СБЛИЖЕНИЯ И СХЛЕСТЫВАНИЯ ПРИ КОРОТКИХ ЗАМЫКАНИЯХ
РД 153-34.3-20.672-2002
Дата введения 2003-03-01
Разработано Московским энергетическим институтом (техническим университетом)
Исполнители проф., д.т.н. Б.Н. НЕКЛЕПАЕВ; проф., к.т.н. И.П. КРЮЧКОВ; проф., д.т.н. Е.П. КУДРЯВЦЕВ; вед. инж. М.В. ПИРАТОРОВ
Утверждено Департаментом научно-технической политики и развития РАО "ЕЭС России" 16.09.2002 г.
Начальник Ю.Н. КУЧЕРОВ
Введено впервые
Срок первой проверки настоящего РД -
Содержание
1 ОБЩИЕ ПОЛОЖЕНИЯ. НАЗНАЧЕНИЕ И ОБЛАСТЬ ПРИМЕНЕНИЯ
Методические указания предназначены для использования при выполнении расчетов по определению опасного сближения или схлестывания гибких проводников ВЛ и РУ при КЗ. Они являются руководящим документом для работников проектных, научно-исследовательских и эксплуатационных организаций при оценке смещений гибких проводников при КЗ.
Методические указания распространяются на расчеты колебаний при КЗ гибких проводников ВЛ и РУ всех классов напряжений.
Настоящие Методические указания основываются на положениях государственных
стандартов в области токов КЗ (ГОСТ
27514-87, ГОСТ Р 50254-92), Правил устройства электроустановок (ПУЭ 6-го изд.,
2 ВОПРОСЫ ТЕОРИИ
2.1 Модели проводников
В итоге многолетних исследований электродинамической стойкости гибких проводников, проведенных в разных странах мира, определились две расчетные модели таких проводников, наилучшим образом отвечающие задачам практики.
Одна из них представляет собой нерастяжимый стержень-маятник на жестком подвесе с массой, сосредоточенной в центре масс проводника в пролете. Вторая - гибкая нить с равномерно распределенной по длине массой, обладающая (в некоторых версиях не обладающая) конечной жесткостью на растяжение, изгиб и кручение.
Расчетная модель в виде маятника используется в упрощенных методиках расчетов, при этом не требуется обращение к ЭВМ. Расчетная модель в виде нити применена в разработанных в разных странах (в том числе и в СНГ) программах для расчетов электродинамической стойкости на ЭВМ. Расчетные модели, отличные от названных (как правило более сложные, чем схема-маятник), не нашли практического применения и далее подробно не рассматриваются.
2.2 Физические законы и зависимости, используемые в работе
Закон Ампера ![]()
Закон полного тока (закон Гаусса) ![]() .
.
Второй закон Ньютона MV = Ft.
Значение
кинетической энергии ![]() ,
,
![]() .
.
Значение потенциальной энергии Wпот = mgН,
![]() .
.
Уравнение Лагранжа ![]() .
.
3 ИНЖЕНЕРНАЯ МЕТОДИКА МЭИ
3.1 Расчетные условия
3.1.1 Общие расчетные условия
При проверке гибких проводников ВЛ и РУ на возможность их опасного сближения или схлестывания при КЗ необходимо правильно выбрать расчетные условия, т.е. наиболее тяжелые, но достаточно вероятные условия, при которых возможно опасное сближение или схлестывание проводников. К расчетным условиям относятся:
- расчетный вид КЗ;
- расчетная продолжительность КЗ.
Согласно Правилам устройства электроустановок расчетным видом КЗ является двухфазное КЗ. В качестве расчетной продолжительности КЗ может оказаться как суммарное время действия основной защиты электроустановки с гибкими проводниками и полное время отключения выключателя, так и суммарное время действия резервной защиты и полное время отключения выключателя.
3.1.2 Расчетные зоны динамики проводников
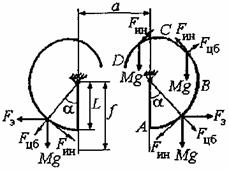
В период с момента возникновения КЗ и до его отключения расчетная модель гибкого проводника каждой фазы в виде жесткого стержня (рисунок 1) достаточно полно описывает его движение, и оценки смещений проводников на этом этапе движения оказываются весьма точными, что подтверждается опытными данными.
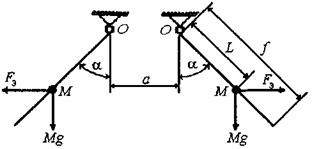
Рисунок 1 - Расчетная модель двух гибких проводников
На рисунке 1 и далее приняты следующие обозначения:
а - расстояние между осями проводников смежных фаз до КЗ, м;
М - масса проводника расчетного пролета, кг;
f - стрела провеса проводника в середине пролета, м;
L - расстояние от прямой, соединяющей точки крепления проводника одного пролета, до центра масс этого проводника (длина маятника), м;
a - угол отклонения проводника от вертикали, рад;
Fэ - электродинамическая сила, Н;
g - ускорение силы тяжести, м/с2.
После отключения КЗ проводники сначала движутся по инерции, преодолевая действие силы тяжести и сохраняя при этом в течение некоторого времени, пока имеет место натягивающая проводники сила, форму, близкую к форме плоской гибкой нити, загруженной собственным весом. На этом этапе движения проводников их поведение уже менее точно описывается принятой расчетной моделью, хотя и здесь оценки их смещения оказываются приемлемыми.
Тяжение в проводниках исчезает, когда центры масс проводников оказываются выше точек их крепления к опорам, и центробежные силы оказываются недостаточными для поддержания прежней формы проводников в виде гибкой натянутой нити. На этом этапе движения проводники подобны телам, падающим под действием инерционных сил и сил тяжести. Поэтому расчет смещений проводников с использованием модели в виде маятника здесь невозможен.
При КЗ проводники под действием электродинамических сил отталкиваются друг от друга, а их максимальное сближение имеет место после отключения КЗ, при колебаниях проводников вокруг исходного положения равновесия.
3.1.3 Баланс сил в расчетных зонах
При движении гибких проводников в результате возникшего на ВЛ или в РУ короткого замыкания расчетными нагрузками на расчетный маятник являются (рисунок 2):
а)
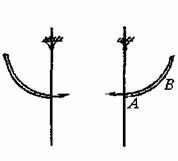
б)
а - траектории движения проводников (их центров масс) при большом кратковременном токе КЗ: АВ - участок траектории, который проходит проводник во время КЗ; ВС - участок траектории, который проходит проводник, натянутый действующими на него силами, после отключения тока КЗ; CD - участок траектории, где ненатянутый провод "падает" под действием силы тяжести и инерционных сил; б - траектории движения проводников при малом токе КЗ; Fцб - центробежная сила
Рисунок 2 - Траектории движения проводников при КЗ и после него
- сила тяжести Mg, направленная вертикально вниз и действующая постоянно на всех этапах движения проводников;
- электродинамическая сила Fэ, которая при двухфазном КЗ на линиях с проводниками, закрепленными в одной горизонтальной плоскости, направлена горизонтально и действует до момента отключения тока КЗ;
- инерционная сила Fин, направленная противоположно вектору окружного ускорения центра массы проводника в пролете и действующая в периоды, когда проводник натянут и его можно рассматривать как маятник;
- инерционные силы, свойственные телам, которые после воздействия нескольких сил двигаются в пространстве в поле силы тяжести: это имеет место на этапе движения гибких проводников, когда они не натянуты.
3.1.4 Принятые допущения
Принятие расчетной модели гибкого проводника в виде маятника, определение электродинамических сил по формулам, справедливым для параллельных бесконечно тонких и длинных проводников, оправданы многолетним опытом их использования. Эти гипотезы положены в основу рекомендаций МЭК по расчетам электродинамической стойкости электроустановок с гибкими проводниками. Целесообразность принятия этих гипотез подтверждена проведенными за рубежом достаточно обстоятельными экспериментами.
Упрощенный учет влияния отводов и гирлянд изоляторов, влияния нагрева проводников, отказ от учета деформаций растяжения проводников оправдываются сравнительными оценками, сделанными на базе многочисленных расчетов.
4 МЕТОДИКА РАСЧЕТА
Прежде чем приступать к расчету смещений гибких проводников при КЗ, вычисляется значение критерия, характеризующего степень опасности сближения проводников при КЗ. При значении этого критерия больше предельного, необходимо проводить расчет, в противном случае расчет не нужен.
Расчет выполняется в два этапа. На первом этапе вычисляется энергия, которую накапливают проводники пролета за время КЗ. Эта энергия равна работе электродинамических сил. На втором этапе по найденной энергии вычисляются горизонтальные смещения проводников в середине пролета.
Если продолжительность КЗ меньше 0,6 периода малых собственных колебаний расчетного маятника, то работа электродинамических сил за время КЗ вычисляется с помощью кривых, полученных путем решения уравнения вынужденных нелинейных колебаний расчетного маятника. Если же продолжительность КЗ больше 0,6 периода малых собственных колебаний расчетного маятника, то работа электродинамических сил за время КЗ вычисляется с помощью других кривых, построенных путем использования закона постоянства полной энергии потенциальной системы.
При кратковременных КЗ, когда их расчетная продолжительность не превышает так называемую предельную (см. ниже), смещение проводников оказывается возможным вычислять, не определяя работу электродинамических сил.
Упомянутый выше критерий, характеризующий степень опасности сближения проводников при КЗ, - параметр р, кА2×с/Н, определяется по формуле
|
|
(1) |
где ![]() - начальное
действующее значение периодической составляющей тока двухфазного КЗ, кА;
- начальное
действующее значение периодической составляющей тока двухфазного КЗ, кА;
tоткл - расчетная продолжительность КЗ, с;
q = mпог g - погонная сила тяжести проводника, Н/м;
mпог - погонная масса проводника, кг/м;
l - безразмерный коэффициент, учитывающий влияние апериодической составляющей электродинамической силы (график для его определения приведен на рисунке 3, где Та - постоянная времени затухания апериодической составляющей тока КЗ, с).
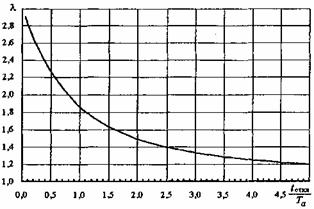
Рисунок 3 - Зависимость коэффициента l от tоткл/Та
При р £ 0,4 кА2×с/Н расчет смещений гибких проводников не нужен, так как опасности их чрезмерных сближений нет.
На рисунке 4 приведен график, связывающий параметры формулы (1) при l = 1. Кривые tоткл = f (![]() ) при aq = const ограничивают области параметров tоткл и
) при aq = const ограничивают области параметров tоткл и ![]() , при которых
расчет смещений проводников не нужен.
, при которых
расчет смещений проводников не нужен.
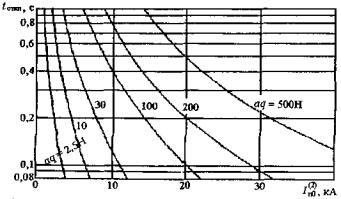
Рисунок 4 - Продолжительность КЗ, при которой р = 0,4
Если р > 0,4 кА2×с/Н, то сначала следует определить предельную продолжительность КЗ, с:
|
|
(2) |
где ![]() - частота малых собственных колебаний расчетного
маятника, 1/с, причем L = 2f/3, м;
- частота малых собственных колебаний расчетного
маятника, 1/с, причем L = 2f/3, м;
М = mпог l - масса проводника пролета, кг;
l - длина пролета, м;
![]() - расчетная электродинамическая сила при двухфазном КЗ, Н.
- расчетная электродинамическая сила при двухфазном КЗ, Н.
Последняя вычисляется по формуле:
|
|
(3) |
где ![]()
![]() -
постоянная составляющая электродинамической нагрузки на проводник в пролете при
двухфазном КЗ, Н;
-
постоянная составляющая электродинамической нагрузки на проводник в пролете при
двухфазном КЗ, Н;
m - относительная магнитная проницаемость воздушной среды (для воздуха m = 1);
m0 - магнитная проницаемость вакуума, Гн/м.
При tоткл £ tпред горизонтальное смещение проводника при КЗ, м, вычисляется по формуле
|
|
(4) |
где ![]()
В случае, если вычисленное по формуле (4) значение s оказывается больше стрелы провеса проводника в середине пролета, следует принимать s = f.
При tпред < tоткл £ 0,6 (2p/w0) горизонтальное смещение проводника при КЗ, м, вычисляется по одной из формул:
|
|
(5) |
где amax - угол максимального отклонения проводника от вертикали, рад:
|
amax = arccos (1 - DWк/Mg L) |
(6) |
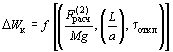 - энергия,
накопленная проводником пролета за время КЗ, Дж, и определяемая с
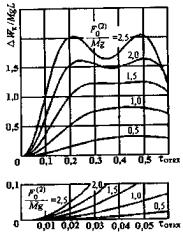
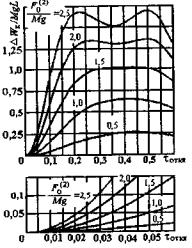
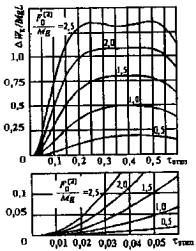
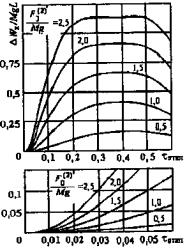
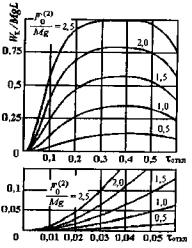
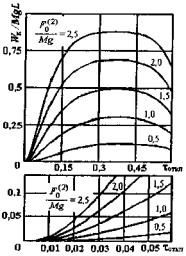
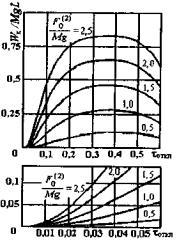
использованием графиков рисунка 5, где
tоткл = tоткл/T0 = tоткл w0/2p - относительная продолжительность КЗ в долях от периода собственных колебаний проводника в пролете.
- энергия,
накопленная проводником пролета за время КЗ, Дж, и определяемая с
использованием графиков рисунка 5, где
tоткл = tоткл/T0 = tоткл w0/2p - относительная продолжительность КЗ в долях от периода собственных колебаний проводника в пролете.
При tоткл > 0,6 (2p/w0) горизонтальное смещение проводника также вычисляется по формулам (5), однако входящая в формулы (5) и (6) энергия DWк, Дж, приближенно оценивается по одной из формул:
|
|
(7) |
где h - высота подъема проводника над его положением до КЗ, м, которая определяется с использованием рисунка 6.
|
|
|
|
а) при 2L/a = 0,5; |
б) при 2L/a = 1,1; |
|
|
|
|
в) при 2L/a = 2,1; |
г) при 2L/a = 3,1; |
|
|
|
|
д) при 2L/a = 4,l; |
е) при 2L/a = 5,1; |
|
|
|
|
ж) при 2L/a = 5,7 |
|
|
Рисунок 5 - Характеристики DWк/Mg L при двухфазном КЗ |
|
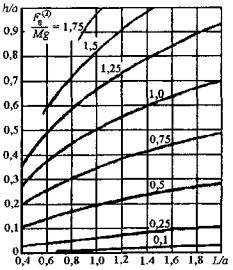
Рисунок 6 - Характеристики h/a при двухфазном КЗ
Максимальное сближение проводников (минимальное расстояние между проводниками) вычисляется по формуле
|
amin = а - 2 (s + rр) |
(8) |
где s - найденное максимальное горизонтальное смещение проводника в середине пролета от равновесного положения, а для расщепленных фаз - это горизонтальное смещение оси расчетного одиночного проводника с поперечным сечением, равным сумме сечений всех проводников фазы в середине пролета;
rр - радиус расщепления фазы, м.
Влияние гирлянд изоляторов можно приближенно учесть увеличением погонного веса и стрелы провеса проводников путем замены в приведенных выше формулах массы проводника М "приведенной" массой Мпр = Мg и стрелы провеса f "приведенной" стрелой провеса fпр = f + lг cos b, где g - коэффициент приведения массы (см. таблицу 1);
lг - длина гирлянды изоляторов, м;
b - угол отклонения натяжных гирлянд от вертикали до КЗ, рад.
Наличие отводов приближенно может также учитываться увеличением массы проводников. При этом приведенную массу проводника можно оценить по формуле
мпр = Мg + Мотв,
где Мотв - масса отводов в пролете, кг.
Таблица 1 - Коэффициент приведения массы g
|
fг/f |
Значение коэффициента приведения массы g при различных Мг/М |
||||||||
|
0,01 |
0,02 |
0,05 |
0,10 |
0,20 |
0,50 |
1,00 |
2,00 |
3,00 |
|
|
0,01 |
1,000 |
1,000 |
1,000 |
1,000 |
1,001 |
1,002 |
1,003 |
1,005 |
1,006 |
|
0,02 |
1,000 |
1,000 |
1,000 |
1,001 |
1,002 |
1,004 |
1,007 |
1,010 |
1,012 |
|
0,05 |
1,000 |
1,000 |
1,001 |
1,002 |
1,004 |
1,010 |
1,016 |
1,024 |
1,029 |
|
0,10 |
1,000 |
1,001 |
1,002 |
1,004 |
1,008 |
1,019 |
1,031 |
1,048 |
1,058 |
|
0,20 |
1,001 |
1,002 |
1,004 |
1,008 |
1,015 |
1,034 |
1,059 |
1,090 |
1,110 |
|
0,50 |
1,002 |
1,003 |
1,008 |
1,016 |
1,031 |
1,071 |
1,130 |
1,200 |
1,250 |
|
1,00 |
1,002 |
1,005 |
1,012 |
1,024 |
1,048 |
1,110 |
1,200 |
1,330 |
1,430 |
|
2,00 |
1,003 |
1,007 |
1,017 |
1,033 |
1,065 |
1,150 |
1,290 |
1,500 |
1,670 |
|
3,00 |
1,004 |
1,007 |
1,019 |
1,037 |
1,073 |
1,180 |
1,330 |
1,600 |
1,820 |
Примечание - Мг - масса гирлянд (суммарная масса двух натяжных гирлянд у двух опор проводников в пролете или масса одной гирлянды, если на опорах гирлянды подвесные); М - масса проводника в пролете; fг - провес гирлянд; f - стрела провеса проводника.
5 ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО СМЕЩЕНИЯ И МАКСИМАЛЬНОГО СБЛИЖЕНИЯ ПРОВОДНИКОВ ПРИ КЗ
Максимальное смещение гибких проводников при их раскачивании в условиях двухфазного КЗ определяется по выражению:
уmax = s.
Методика определения s дана выше.
Минимальное расстояние между гибкими проводниками при их сближении в условиях КЗ определяется по выражению:
amin = a - 2 уmax.
Необходимо соблюдать условие amin > amin доп,
где amin доп - минимально допустимое расстояние между проводниками фаз. Согласно ПУЭ (гл. 5) и исследованиям, проведенным в МЭИ, amin доп при разных номинальных напряжениях Uном составляют:
|
Uном, кВ |
amin доп, м |
|
35 |
0,2 |
|
110 |
0,45 |
|
150 |
0,6 |
|
220 |
0,95 |
|
330 |
1,4 |
|
500 |
2,0 |
|
750 |
3,3 |
|
1150 |
5,4 |
Обоснования указанных соотношений даны в настоящих Методических указаниях.
6 РЕКОМЕНДАЦИИ
При определении условий опасных сближений гибких проводников при КЗ
сначала следует по формуле (1) вычислить значение критерия р. Если р £ 0,4 кА2 × с/Н, то проводники находятся в неопасной зоне и могут нормально
эксплуатироваться; если же р > 0,4 кА2 × с/Н, то проводники находятся в опасной зоне, т.е. возможны пробои
изоляционных промежутков между ними и даже схлестывание. В этом случае
необходимо производить детальный расчет качаний проводников и воздействовать на
режимные параметры ![]() и tоткл в отдельности или совместно.
и tоткл в отдельности или совместно.
Приложение А
(справочное)
БАЗА ДАННЫХ ВЛ
Таблица А.1 - Параметры и характеристики элементов ВЛ
|
Номинальное напряжение, кВ |
Шифр опоры |
Схема расположения проводов |
Материал опоры |
Расстояние между проводами разных фаз на опоре, м |
Предельные марки проводов |
Район по гололеду и габаритные пролеты, м |
Погонная масса провода, кг/км |
Тип изолятора |
Количество изоляторов в гирлянде. шт. |
Длина гирлянды изоляторов с арматурой, м |
Масса изоляторов с арматурой, кг |
Расстояние от поверхности земли до ближайшего провода в месте его крепления, м |
||
|
А-В |
В-С |
С-А |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
35 |
П35-1 |
1 |
Сталь |
3,27 |
~5,22 |
~4,94 |
АС70/11-150/24 |
I:319-350; II:250-310 |
276-559 |
ПФ70-В ПС70-Б |
3 |
0,69 0,68 |
19 16 |
14,31 14,32 |
|
П35-2 |
2 |
Сталь |
3,27 |
3,27 |
6 |
АС70/11-150/24 |
I:295-335; II:235-290 |
276-559 |
ПФ70-В ПС70-Б |
3 |
0,69 0,68 |
19 16 |
13,31 13,32 |
|
|
ПБ35-1 |
1 |
Железобетон |
3,35 |
~3,42 |
~3,56 |
АС95/16-150/24 |
I:390-375; II:280-330 |
385-559 |
ПФ70-В ПС70-Б |
3 |
0,69 0,68 |
19 16 |
14,81 14,32 |
|
|
ПБ35-2 |
2 |
Железобетон |
3,09 |
3,09 |
6 |
АС95/16-150/24 |
I:275-265; II:230-255 |
385-559 |
ПФ70-В ПС70-Б |
3 |
0,69 0,68 |
19 16 |
11,81 11,82 |
|
|
ПД35-1 |
3 |
Дерево |
3 |
3 |
6 |
АС50/8-120/19 |
I:240-275; II:180-240 |
195-471 |
ПФ70-В ПС70-Б |
2 2 |
0,56 0,55 |
13 12 |
12,34 12,35 |
|
|
ПД35-3 |
3 |
Дерево |
3 |
3 |
6 |
АС150/24 |
I:275 II:265 |
559 |
ПФ70-В ПС70-Б |
2 2 |
0,56 0,55 |
13 12 |
12,34 12,35 |
|
|
ПД35-5 |
3 |
Дерево |
3 |
3 |
6 |
АС50/8-150/24 |
I:245-280; II:190-270 |
195-559 |
ПФ70-В ПС70-Б |
2 2 |
0,56 0,55 |
13 12 |
12,59 12,50 |
|
|
110 |
П110-1 |
1 |
Сталь |
4,52 |
~6,02 |
~5,6 |
АС70/11-95/16 |
I:386-375; II:300-305 |
276-385 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
18,75 17,65 |
|
П110-3 |
1 |
Сталь |
4,52 |
~6,22 |
~5,74 |
АС120/19-240/32 |
I:435-445-435; II:365-380 |
471-921 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
17,75 17,65 |
|
|
П110-2 |
2 |
Сталь |
4,52 |
4,52 |
8 |
АС70/11 |
I:380; II:300 |
276 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
17,75 17,65 |
|
|
П110-4 |
2 |
Сталь |
4,52 |
4,52 |
8 |
АС120/19-240/32 |
I:435-445-435; II:365-380 |
471-921 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
17,75 17,65 |
|
|
ПБ110-1 |
1 |
Железобетон |
3,35 |
~5,42 |
~4,94 |
АС70/11-150/24 |
I:295-330; II:235-300 |
276-959 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
13,25 13,15 |
|
|
ПБ110-3 |
1 |
Железобетон |
3,35 |
~5,42 |
~4,94 |
АС185/29; 240/32 |
I:330; 325; II:310; 315 |
728; 921 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
13,25 13,15 |
|
|
ПБ110-2 |
2 |
Железобетон |
3,35 |
3,35 |
6 |
АС70/11-120/19 |
I:276; 260-275; II:215; 235-250 |
276-471 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
12,25 12,15 |
|
|
ПБ110-4 |
2 |
Железобетон |
3,35 |
3,35 |
6 |
АС185/29; 240/32 |
I:275; II:275 |
728; 921 |
ПФ70-Б ПС70-Б |
7 8 |
1,25 1,35 |
38 36 |
12,25 12,15 |
|
|
110 |
ПД110-1 |
3 |
Дерево |
4 |
4 |
8 |
АС70/11-120/19 |
I:240-260; II:190-240 |
276-471 |
ПФ70-Б ПС70-Б |
6 7 |
1,1 1,2 |
33 32 |
10,9 10,8 |
|
ПД110-3 |
3 |
Дерево |
4 |
4 |
8 |
АС150/24; 185/29 |
I:260; 255; II:255; 230 |
559; 728 |
ПФ70-Б ПС70-Б |
6 7 |
1,1 1,2 |
33 32 |
10,9 10,8 |
|
|
ПД110-5 |
3 |
Дерево |
4 |
4 |
8 |
АС70/11-185/29 |
I:245-260 |
276-728 |
ПФ70-Б ПС70-Б |
6 7 |
1,1 1,2 |
33 32 |
12,05 11,95 |
|
|
150 |
П150-1 |
1 |
Сталь |
6,21 |
~6,72 |
~7,89 |
АС120/19-240/32 |
I:426-425-413; II:350-370 |
471-921 |
ПФ70-В ПС70-Б |
9 10 |
1,5 1,6 |
47 45 |
17,5 17,4 |
|
П150-2 |
2 |
Сталь |
6,21 |
~6,21 |
12 |
АС120/19-240/32 |
I:426-425-413; II:350-370 |
471-921 |
ПФ70-В ПС70-Б |
9 10 |
1,5 1,6 |
47 45 |
17,5 17,4 |
|
|
ПБ150-1 |
1 |
Железобетон |
4,27 |
~6,42 |
~6,34 |
АС120/19-240/32 |
I:290-270; II:245-270 |
471-921 |
ПФ70-В ПС70-Б |
9 10 |
1,5 1,6 |
47 45 |
12,0 11,9 |
|
|
ПБ150-2 |
2 |
Железобетон |
4,27 |
4,27 |
8 |
АС120/19-240/32 |
I:290-245; II:245-255-243 |
471-921 |
ПФ70-В ПС70-Б |
9 10 |
1,5 1,6 |
47 45 |
12,0 11,9 |
|
|
ПСБ150-1 |
3 |
Железобетон |
~5 |
~5 |
~1 |
АС120/19-240/32 |
I:385-380; II:325-360 |
471-921 |
ПФ70-В ПС70-Б |
9 10 |
1,5 1,6 |
47 45 |
16,0 15,9 |
|
|
220 |
П220-3 |
1 |
Сталь |
7 |
~9,92 |
~9,79 |
АС300/39; 400/51 |
I:520; 520; II:490; 475 |
1132; 1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
23,3 23,2 |
|
П220-2 |
2 |
Сталь |
6,22 |
6,96 |
12,02 |
АС300/39; 400/51 |
I:470; 465; II:440; 425 |
1132; 1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
20,3 20,2 |
|
|
ПБ220-1 |
1 |
Железобетон |
5,85 |
~7,52 |
~7,79 |
АС300/39; 400/51 |
I:310; II:310 |
1132; 1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
13,8 13,7 |
|
|
ПБ220-3 |
1 |
Железобетон |
5,85 |
~7,52 |
~7,79 |
АС300/39; 400/51 |
I:320; II:320 |
1132; 1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
15,3 15,2 |
|
|
ПСБ220-1 |
3 |
Железобетон |
~5,74 |
~5,74 |
~11,48 |
АС300/39; 400/51 |
I:350; II:345; 350 |
1132;1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
15,3 15,2 |
|
|
ПБ220-12 |
3 |
Железобетон |
~13,76 |
~13,76 |
~27,52 |
АС300/39; 400/51 |
I:430; II:410; 410 |
1132; 1490 |
ПФ70-В ПС70-Б |
13 14 |
2,2 2,3 |
72 67 |
19,0 18,9 |
|
|
ПД220-1 |
3 |
Дерево |
5,25 |
5,25 |
10,5 |
АС300/39-500/64 |
I:250-210; II:250-210 |
1132-1852 |
ПФ70-В ПС70-Б |
12 13 |
2,05 1,9 |
67 60 |
12,55 12,7 |
|
|
ПД220-3 |
3 |
Дерево |
5,25 |
5,25 |
10,5 |
АС300/39-500/64 |
I:250-210; II:250-210 |
1132-1852 |
ПФ70-В ПС70-Б |
12 13 |
2,05 1,9 |
67 60 |
12,55 12,7 |
|
|
330 |
П330-3 |
1 |
Сталь |
8,28 |
~14,02 |
~12,92 |
2хАС300/39; 2хАС400/51 |
I:495; II:470; 450 |
2x1132; 2x1490 |
ПФ70-В ПС70-Б ПС120-А |
19 21 17 |
3,0 3,2 3,1 |
118 111 130 |
22,5 22,3 22,4 |
|
П330-1 |
1 |
Сталь |
8,32 |
~15,92 |
~14,42 |
2хАС300/39 |
I:495; II:470 |
2x1132 |
ПФ70-В ПС70-Б ПС120-А |
19 21 17 |
3,0 3,2 3,1 |
118 111 130 |
22,5 22,3 22,4 |
|
|
П330-9 |
3 |
Сталь |
~8,46 |
~8,46 |
~16,92 |
2хАС300/39; 2хАС400/51 |
I:495; II:470; 450 |
2x1132; 2x1490 |
ПФ70-В ПС70-Б ПС120-А |
19 21 17 |
3,0 3,2 3,1 |
118 111 130 |
22,5 22,3 22,4 |
|
|
П330-2 |
2 |
Сталь |
8,45 |
7,24 |
14,02 |
2хАС300/39; 2хАС400/51 |
I:445; 425; II:415; 395 |
2x1132; 2x1490 |
ПФ70-В ПС70-Б ПС120-А |
19 21 17 |
3,0 3,2 3,1 |
118 111 130 |
19,5 19,3 19,4 |
|
|
ПБ330-7Н |
3 |
Железобетон |
~8,16 |
~8,16 |
~16,32 |
2хАС300/39; 2хАС400/51 |
I:450; II:425; 440 |
2x1132; 2x1490 |
ПФ70-В ПС70-Б ПС120-А |
19 21 17 |
3,0 3,2 3,1 |
118 111 130 |
20,0 19,8 19,9 |
|
|
500 |
ПБ-1 |
3 |
Сталь |
12 |
12 |
24 |
3хАС400/51; 3хАС500/64 |
II:460; II:425 |
3x1490 3x1852 |
ПФ120-А ПС120-А |
21 24 |
4,9 4,5 |
238 185 |
22,3 22,7 |
|
ПБ500-1 |
3 |
Железобетон |
~8,36 |
~8,36 |
~16,72 |
3хАС300/43; 3хАС400/51; 3хАС500/64 |
I:380; II:380 I:385; II:385 I:355; II:355 |
3x1255 3x1490 3x1852 |
ПФ120-А ПС120-А |
21 24 |
4,9 4,5 |
238 185 |
14,6 15,0 |
|
Примечание - Схема расположения проводов № 1 означает, что проводники двух фаз находятся на одинаковом расстоянии от поверхности земли, а проводник третьей фазы закреплен выше них; схема № 2 означает, что проводники разных фаз находятся на разном расстоянии от поверхности земли и закреплены на двухцепных опорах; схема № 3 означает, что проводники всех фаз находятся на одинаковом расстоянии от поверхности земли (так называемое горизонтальное расположение проводов).
Таблица А.2 - Основные расчетные характеристики сталеалюминиевых проводов марок АС, АСКС, АСКП, АпСКП, АпСКС
|
Номинальное сечение, мм2, алюминий/сталь |
Сечение, мм2 |
Масса, кг/км |
Модуль упругости Е, 103 Н/мм2 |
Допустимое напряжение s, Н/мм2 |
|||
|
Алюминий |
Сталь |
провода (без смазки) |
смазки для |
||||
|
АСКС, АпСКС |
АСКП, АпСКП |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
50/8 |
48,2 |
8,04 |
195 |
3,0 |
3,0 |
82,5 |
87 |
|
70/11 |
68,0 |
11,3 |
276 |
4,5 |
4,5 |
82,5 |
87 |
|
70/72 |
68,4 |
72,2 |
755 |
38 |
38 |
134 |
201 |
|
95/16 |
95,4 |
15,9 |
385 |
6,0 |
6,0 |
82,5 |
87 |
|
95/141 |
91,2 |
141 |
1357 |
69 |
69 |
146 |
228 |
|
120/19 |
118,0 |
18,8 |
471 |
11 |
35 |
82,5 |
87 |
|
120/27 |
114 |
26,6 |
528 |
14 |
37 |
89 |
99 |
|
150/19 |
148,0 |
18,8 |
554 |
12 |
42 |
77 |
81 |
|
150/24 |
149,0 |
24,2 |
599 |
14 |
44 |
82,5 |
87 |
|
150/34 |
147,0 |
34,3 |
675 |
18 |
48 |
89 |
99 |
|
185/24 |
187,0 |
24,2 |
705 |
14 |
51 |
77 |
81 |
|
185/29 |
181,0 |
29,0 |
728 |
16 |
52 |
82,5 |
87 |
|
185/43 |
185,0 |
43,1 |
846 |
23 |
61 |
89 |
99 |
|
185/128 |
187,0 |
128,0 |
1525 |
63 |
101 |
114 |
165 |
|
205/27 |
215,0 |
26,6 |
74 |
15 |
57 |
77 |
81 |
|
240/32 |
244,0 |
31,7 |
921 |
17 |
66 |
77 |
81 |
|
240/39 |
236,0 |
38,6 |
952 |
22 |
71 |
82,5 |
87 |
|
240/56 |
241,0 |
56,3 |
1106 |
30 |
78 |
89 |
99 |
|
300/39 |
301,0 |
38,6 |
1132 |
22 |
83 |
77 |
81 |
|
300/48 |
295,0 |
47,8 |
1186 |
27 |
87 |
82,5 |
87 |
|
300/66 |
288,5 |
65,8 |
1313 |
37 |
95 |
89 |
99 |
|
300/67 |
288,5 |
67,3 |
1323 |
37 |
95 |
89 |
99 |
|
300/204 |
298,0 |
204,0 |
2428 |
102 |
164 |
114 |
165 |
|
330/30 |
335,0 |
29,1 |
1152 |
12 |
112 |
... |
... |
|
330/43 |
332,0 |
43,1 |
1255 |
23 |
133 |
77 |
81 |
|
400/18 |
381,0 |
18,8 |
1199 |
12 |
131 |
... |
... |
|
401/22 |
394,0 |
26,6 |
1261 |
12 |
133 |
... |
... |
|
400/51 |
394,0 |
51,1 |
1490 |
28 |
134 |
77 |
81 |
|
400/64 |
390,0 |
63,5 |
1572 |
35 |
115 |
82,5 |
87 |
|
400/93 |
406,0 |
93,2 |
1851 |
53 |
133 |
89 |
99 |
|
450/56 |
434,0 |
56,3 |
1640 |
30 |
145 |
77 |
81 |
|
500/26 |
502,0 |
26,6 |
1592 |
15 |
158 |
... |
... |
|
500/27 |
481,0 |
26,6 |
1537 |
15 |
152 |
66,5 |
65 |
|
500/64 |
490,0 |
63,5 |
1852 |
33 |
163 |
77 |
81 |
|
500/204 |
496,0 |
204 |
2979 |
105 |
230 |
... |
... |
|
500/336 |
490,0 |
336 |
4005 |
168 |
270 |
114 |
165 |
Примечания
1 Значения допустимого напряжения указаны при среднегодовой температуре.
2 - ... - данные отсутствуют.
Приложение Б
(рекомендуемое)
ПРИМЕРЫ РАСЧЕТОВ ПО ИНЖЕНЕРНОЙ МЕТОДИКЕ МЭИ
Пример 1. Воздушная линия напряжением 110 кВ
Исходные данные:
длина пролета - l =
стрела провеса в середине пролета - f =
расстояние между фазами - а =
гирлянды подвесные, длина гирлянды - lг =
постоянная времени - Tа = 0,05 с,
погонная масса проводника - mпог = 1,3 кг/м,
масса гирлянды - Мг
=
начальное значение тока двухфазного КЗ - ![]() = 10 кА,
= 10 кА,
расчетная продолжительность КЗ - tоткл = 0,1 с.
Вычисляем приведенную стрелу провеса в середине пролета
fпр = f + fг = f + lг cos b = 10 + 1,5 × 1 =
Определяем
массу проводника М = mпогl =
1,3·200 =
Вычисляем параметр р. При tоткл/Tа = 0,1/0,05 = 2 по графику рисунка 3 находим l = 1,5, тогда 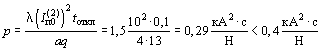 ,
поэтому расчет смещений проводников не нужен.
,
поэтому расчет смещений проводников не нужен.
Пример 1а. Произведем расчет смещений проводников этой же линии 110 кВ для случая, когда расчетная продолжительность КЗ составит tоткл = 0,3 с.
В этом случае tоткл/Tа = 0,3/0,05 = 6, по графику рисунка 3 находим l = 1, тогда 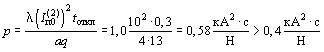 ,
в этом случае расчет смещений проводников необходим.
,
в этом случае расчет смещений проводников необходим.
Вычисляем параметры, необходимые для определения смещений: L = 2f/3 = 2·11,5/3 = ![]() .
.
По формуле (3) ![]() , поэтому предельная продолжительность КЗ составляет
, поэтому предельная продолжительность КЗ составляет ![]() .
.
Поскольку tоткл = 0,3 с < tпред = 1,336 с, расчет смещений проводников можно вести по формуле (4):
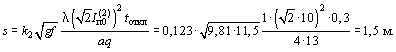
Минимальное расстояние между проводниками при их колебаниях после
отключения тока КЗ amin = a - 2уmах = a - 2s = 4 - 2 × 1,5 =
Пример 1б. Пусть теперь расчетная продолжительность КЗ составит tоткл = 2 с.
В этом случае tоткл/Tа = 2/0,05 = 40, по графику рисунка 3 находим l = 1, тогда 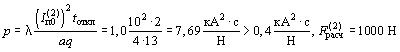 .
.
Находим ![]()
Поскольку tпред = 1,36 с < tоткл = 2 с < 0,6 (2p/w0) = 3,33 с, расчет смещений проводников следует вести по формуле (5).
Вычисляем нужные для расчета соотношения:
![]()
![]()
По графикам рисунка 5 при 2 L/a = 3,84, ![]() = 0,397 и tоткл = 0,36 находим DWк/Mg L = 0,1.
= 0,397 и tоткл = 0,36 находим DWк/Mg L = 0,1.
Максимальный угол отклонения расчетного маятника в соответствии с
формулой (6) amах= arccos (1 - DWк/Mg L) = arccos (1 - 0,1) = 0,45 рад. и смещение проводника s = f sin amax = 11,5 × sin 0,45 = 11,5 × 0,43 =
Пример 1в. Рассмотрим случай, когда начальное значение тока двухфазного КЗ составляет 6 кА, а расчетная продолжительность КЗ равна tоткл = 4 с.
В этом случае tоткл/Ta = 4/0,05 = 80, по графику рисунка 3 находим l = 1, тогда
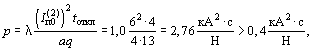 а
а
![]()
Поскольку tоткл = 4 с > 0,6 (2p/w0) = 3,33 с, расчет смещений проводников следует вести по формуле (5), а значение DWк определять по формуле (7).
Вычисляем нужные для расчета соотношения:
![]()
MgL = 265,2·9,81·7,67 = 19954 Дж.
Поскольку![]() < MgL = 19954 Дж, то энергия DWк, накопленная одним проводником при КЗ, равна DWк = Mgh.
< MgL = 19954 Дж, то энергия DWк, накопленная одним проводником при КЗ, равна DWк = Mgh.
Высоту подъема провода во время КЗ h определяем по графику
рисунка 5. При L/a = 7,67/4 = 1,92 и ![]() отношение h/a составит 0,04, поэтому h = 0,04×а = 0,04×4 =
отношение h/a составит 0,04, поэтому h = 0,04×а = 0,04×4 =
Минимальное расстояние между проводниками при их колебаниях после
отключения тока КЗ составит amin = a - 2ymax = a - 2s = 4 - 2 × 1,55 =
Пример 2. Распределительное устройство напряжением 330 кВ
Исходные данные:
длина пролета - l =
стрела провеса в середине пролета - f =
расстояние между фазами - а =
гирлянды натяжные, длина гирлянды - lг =
постоянная времени - Та = 0,05 с,
погонная масса проводника - mпог= 1,6 кг/м,
масса гирлянды - Мг =
начальное значение тока двухфазного КЗ - ![]() = 20 кА,
= 20 кА,
расчетная продолжительность КЗ - tоткл = 0,2 с.
Вычисляем провес гирлянд fг, рассматривая уравнения статики; результаты
вычислений представлены на рисунке Б.1. Приведенная стрела провеса в середине
пролета fпр = f + fг = 2,42 + 2,51 =
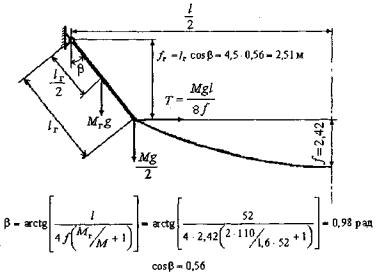
Рисунок Б.1 - К определению максимального расстояния между проводниками РУ 330 кВ
Определяем массу проводника М = mпог l = 1,6 × 52 =
При tоткл/Та = 0,2/0,05 = 4 по графику рисунка 3 находим l = 1,22, тогда
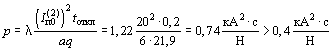 ,
поэтому расчет смещений проводников необходим.
,
поэтому расчет смещений проводников необходим.
Вычисляем параметры, необходимые для определения
смещений: L = 2f/3 = 2 × 4,93/3 = ![]() По формуле (3)
По формуле (3) ![]() 845,5 Н, поэтому предельная
продолжительность КЗ составляет
845,5 Н, поэтому предельная
продолжительность КЗ составляет ![]()
Поскольку tоткл = 0,2 с < tпред = 0,64 с, расчет смещений проводников можно вести по формуле (4):
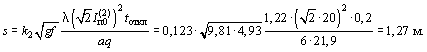
Минимальное расстояние между проводниками при их колебаниях после
отключения тока КЗ amin = a - 2уmах = a - 2s = 6 - 2 × 1,27 =
Пример 2а. Рассмотрим случай, когда расчетная продолжительность КЗ составляет tоткл = 2 с.
В этом случае tоткл/Ta = 2/0,05 = 40, по графику рисунка 3 находим l = 1, тогда
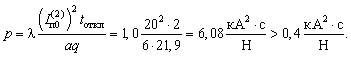
Находим 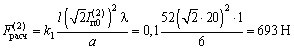 и
и
![]()
Поскольку tпред = 0,7 с < tоткл = 2 с < 0,6 (2p/w0) = 2,178 с, расчет смещений проводников следует вести по формуле (5).
Вычисляем нужные для расчета соотношения:
![]()
![]()
По графикам рисунка 5 при 2 L/a = 1,1, ![]() и tоткл = 0,55 находим DWк/Mg L = 0,25.
и tоткл = 0,55 находим DWк/Mg L = 0,25.
Максимальный угол отклонения расчетного маятника в соответствии с
формулой (6) amax= arccos (1 - DWк/Mg L) = arccos (1 - 0,25) = 0,72 рад. и смещение проводника s = f sin amax = 4,93 × sin 0,72 = 4,93 × 0,43 =
Ключевые слова: короткие замыкания, электродинамические силы, гибкие проводники, качания проводников, опасное сближение, схлестывание, смещение, угол отклонения, стрела провеса, воздушные линии, распределительные устройства, расчетная модель.