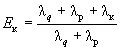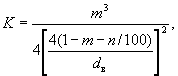Методическая документация в строительстве
Научно-исследовательский центр ОАО «Теплопроект»
МЕТОДИКА ОЦЕНКИ
ВЛИЯНИЯ ВЛАЖНОСТИ
НА ЭФФЕКТИВНОСТЬ ТЕПЛОИЗОЛЯЦИИ
ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ
МДС 41-7.2004
Москва
2004
СОДЕРЖАНИЕ
1 ВВЕДЕНИЕ
Одной из наиболее острых проблем развития топливно-энергетического комплекса России является проблема энергосбережения. От ее успешного решения во многом зависит жизнеспособность экономики страны.
Целевые установки программ энергосбережения России предусматривают экономию топлива и энергии в размере 500 - 600 млн т у.т. в 2010 г., что позволит также на 30 - 40 % сократить выбросы вредных веществ в атмосферу, которые достигают в настоящее время около 20 млн т в год, и стабилизировать выбросы парниковых газов.
Существенную роль в выполнении программы энергосбережения России призвана сыграть высокоэффективная тепловая изоляция, применяемая во всех областях промышленного производства и строительства. По приближенным оценкам повышение теплозащитных свойств теплоизоляционных конструкций промышленных сооружений, оборудования и трубопроводов, систем централизованного теплоснабжения и ограждений зданий в состоянии обеспечить в 2010 г. экономию энергоресурсов в объеме 40 млн т у.т.
Анализ состояния проблемы энергосбережения в строительстве и роли тепловой изоляции в ее решении показал, что в настоящее время потери теплоты объектами строительного комплекса России составляют:
через изолированные поверхности существующих промышленных сооружений, оборудования и трубопроводов - 356 млн Гкал/год, или 65 млн т у.т/год;
через изоляцию теплопроводов тепловых сетей - 324 млн Гкал/год, или 59,5 млн т у.т/год.
Затраты теплоты на отопление жилых, общественных и промышленных зданий, для восполнения потерь через изоляцию ограждающих конструкций достигают 1340 млн Гкал/год, или 240 млн т у.т/год. Таким образом, общие потери тепловой энергии объектами строительного комплекса составляют в настоящее время около 2 млрд Гкал/год, или 364,5 млн т у.т/год, т.е. около 20 % годового производства первичных топливно-энергетических ресурсов России.
Повышение производительности технологических установок, использующих теплоту, все более широкое применение в промышленности высоких температур и глубокого холода создают весьма сложные условия эксплуатации теплоизоляционных конструкций, промышленных сооружений и оборудования. Интенсивные процессы тепло- и влагообмена, возникающие при этом в теплоизоляции, оказывают существенное влияние на ее теплозащитные свойства и долговечность.
Влага, проникающая из окружающей среды в теплоизоляционные конструкции в процессе их эксплуатации, существенно изменяет условия теплообмена. Процессы совместного тепло- и влагообмена, возникающие при этом в изоляции, включая фазовые превращения влаги в пористой структуре теплоизоляционного слоя, приводят к значительному увеличению потерь теплоты по сравнению с расчетными, определенными без учета влагообмена. Известно, например, что потери теплоты теплоизолированными трубопроводами подземных тепловых сетей, работающих в условиях интенсивного воздействия грунтовой влаги, зачастую превышают расчетные в 1,5 - 2 раза. Накопление влаги в теплоизоляционных конструкциях низкотемпературного оборудования нередко приводит к столь значительному увеличению потерь холода, что необходима их полная замена.
Перенос влаги в теплоизоляции, работающей в условиях контакта с агрессивной средой (например, в теплоизоляции оборудования наружных установок и хранилищ промышленных предприятий, подземных трубопроводов бесканальных тепловых сетей, эксплуатируемых в условиях интенсивного воздействия влаги), во многом определяет интенсивность коррозионных процессов в конструкциях изолируемого оборудования и деструкцию теплоизоляции. Тем самым тепло- и влагообменные процессы в них являются одним из основных факторов, определяющих долговечность не только теплоизоляционных конструкций, но и изолируемого оборудования.
В связи с этим следует отметить, что в отличие от строительной теплофизики, где для оценки влияния тепло- и влагообменных воздействий окружающей среды на ограждающие конструкции зданий, вызывающих снижение их теплозащитных свойств, широко используются расчетные методы, разработанные в трудах О.Е. Власова, В.И. Богословского, В.М. Ильинского, В.Д. Мачинского, Ф.В. Ушкова, К.Ф. Фокина, А.У. Франчука и др., в отечественных (Н.М. Зеликсон, М.Г. Каганер, С.В. Хижняков, Е.П. Шубин) и зарубежных (И.С. Каммерер, Д.Ф. Меллой, Р. Каскет) монографиях и периодических публикациях, посвященных промышленной изоляции, вопросы совместного тепло- и влагопереноса и их влияние на теплозащитные свойства теплоизоляционных конструкций не рассматриваются.
К сожалению, методы строительной теплофизики в большинстве случаев не удается использовать для этих целей, поскольку температурно-влажностные условия, в которых эксплуатируется промышленная изоляция, существенно отличаются от условий эксплуатации теплоизоляции в ограждениях зданий. Достаточно отметить, что диапазон температур, в котором работают конструкции промышленной изоляции составляет от -180 до 600 °С, а теплоизоляция ограждений зданий - от -20 до 30 °С.
Вследствие интенсивных тепло- и влажностных воздействий окружающей среды, недостаточного учета влияния совместных тепло- и влагообменных процессов на теплозащитные свойства изоляции при проектировании и монтаже энергоэффективность теплоизоляционных конструкций промышленных сооружений в процессе эксплуатации снижается, что приводит к значительным сверхнормативным потерям тепловой энергии.
В настоящее время сверхнормативные тепловые потери через изолированную поверхность промышленных сооружений, оборудования, трубопроводов и тепловых сетей достигают 244 млн Гкал, или 44 млн т у.т. в год. Эксплуатационные тепловые потери через существующие теплоизоляционные конструкции значительно превышают расчетные, так в промышленной изоляции оборудования и трубопроводов они в 1,25 - 1,3 раза больше нормативных, а в тепловых сетях - в два раза.
Приведенные данные убедительно свидетельствуют о том, что для успешного решения проблемы энергосбережения в строительстве необходимо повышение энергоэффективности промышленной тепловой изоляции путем широкого внедрения в практику проектирования и строительства высокоэффективных теплоизоляционных материалов и конструкций на основе новых методов расчета, учитывающих влияние тепло- и влагообмена и обеспечивающих выбор оптимальных технологических, теплофизических и массообменных характеристик изоляции и проектных решений, гарантирующих стабильность теплозащитных свойств теплоизоляционных конструкций в процессе эксплуатации.
Исходя из изложенного в процессе выполнения настоящей работы предложены расчетные методы оценки влияния влажности на теплозащитные свойства теплоизоляции и предложения по нормированию расчетных значений ее теплопроводности в конструкциях.
2 ХАРАКТЕРИСТИКИ ВЛАЖНОСТНОГО СОСТОЯНИЯ ТЕПЛОИЗОЛЯЦИОННЫХ МАТЕРИАЛОВ
В капиллярно-пористой структуре теплоизоляционных материалов всегда содержится влага, количество которой определяется условиями эксплуатации и состоянием окружающей среды. Содержание влаги в материале определяют обычно высушиванием навески влажного материала Рвл при 105 °С (при этой температуре теплоизоляционные материалы практически не содержат влаги) до достижения постоянной массы Р0. Величина
U = (Рвл - Р0)/Р0 (1)
называется влагосодержанием материала и имеет единицу измерения - кг влаги/кг сухого материала. Влагосодержание, выраженное в процентах, называется относительной влажностью материала по массе или просто массовой влажностью W. Умножив влагосодержание U на плотность материала в сухом состоянии ρм, найдем влагосодержание материала по объему, кг/м3:
Uv = Uρм. (2)
В практике используют также понятие относительной влажности по объему, или объемной влажности
W = (Uρм)/ρж, (3)
где ρж - плотность воды.
Максимальное влагосодержание, которое достигается длительным выдерживанием материала в воде, называется влагосодержанием полного намокания Uт. Для зернистых и волокнистых материалов
Uт = т(ρж/ρм), (4)
для большинства ячеистых материалов
Uт < т(ρж/ρм), (5)
где т - пористость.
Свойства воды, содержащейся в теплоизоляционных материалах, ее подвижность при взаимодействии с окружающей средой характеризуются энергией связи влаги с поверхностью твердого вещества, образующего капиллярно-пористую структуру тела. По значению энергии этой связи различают физико-химически (сильная связь) и физико-механически (слабая связь) связанную воду.
Физико-химическая связь. Влага, связанная физико-химически, представляет собой пленку из молекул воды, адсорбированных на поверхности капиллярно-пористой структуры материала и удерживаемых на ней за счет силового поля на поверхности раздела твердое тело-газ, образующегося вследствие некомпенсированности молекулярных сил в поверхностном слое.
Толщина пленок жидкости, адсорбированных на поверхности пор и капилляров, колеблется от (3 - 5)·10-10 (мономолекулярный слой) до 1·10-7 м (полимолекулярный слой). Свойства адсорбционно-связанной воды из-за воздействия на нее мощного силового поля поверхностных молекулярных сил значительно отличаются от свойств свободной воды. Например, связанная вода не растворяет электролиты других растворимых веществ, обладает свойствами упругого тела, имеет повышенную плотность и пониженную теплоемкость (меньше единицы).
Физико-механическая связь. Влагой, физико-механически связанной со структурой, является жидкость, находящаяся в капиллярах, и жидкость смачивания. Капиллярная связь жидкости характеризуется коэффициентом поверхностного натяжения, равным силе, действующей вдоль поверхности жидкости и приложенной к единице длины линии, ограничивающей межфазную поверхность и капиллярное давление. Явления смачивания наблюдаются на границе раздела трех фаз, одна из которых обычно является твердым телом (фаза 3), а две другие - жидкостью (фаза 1) и газом (фаза 2).
При неполном смачивании жидкая поверхность раздела пересекает твердую поверхность по некоторой линии, называемой периметром смачивания, и образует с ней краевой угол θ, измеряемый в одной фазе. Косинус краевого угла является мерой смачивания В, связанной с коэффициентами поверхностного натяжения - межфазных границ s12; s31; s32 уравнением
B = соs θ = (s32 - s31)s12, (6)
которое показывает, что θ зависит только от молекулярной природы поверхностей раздела и не зависит от размеров капли или пузырька.
Возможны два случая смачивания: при 0 < В < +1 (s32 > s31), когда капля растекается по твердой поверхности, образуя равновесный угол θ < 90°, и при 0 > В > -1 (s32 > s31), когда капля воды на твердой поверхности образует угол θ > 90°.
При наличии искривленной границы между жидкой и газообразной фазами по обе стороны поверхности раздела имеется разность гидростатических давлений, обусловленная поверхностным натяжением и называемая лапласовым или капиллярным давлением. Капиллярное давление рs пропорционально средней кривизне С в рассматриваемой точке границы поверхности раздела двух фаз:
С = 1/r = 1/2 (1/r1 + 1/r2), (7)
где r - средний радиус кривизны;
r1 и r2 - радиусы кривизны двух главных сечений, т.е. сечений поверхности двумя взаимно перпендикулярными плоскостями, проходящими через нормаль к данной точке. Для шара
r = r1 = r2 и ps = 2s12С = 2s12/r. (8)
Из (8) видно, что капиллярное давление для плоской поверхности равно нулю, для выпуклой - оно положительно, для вогнутой - отрицательно (радиус кривизны считают положительным, когда он направлен в глубь жидкости).
Кривизна жидкой поверхности в капилляре определяется условиями смачивания. Для капиллярной трубки достаточно малого радиуса r0 мениск можно считать сферической поверхностью радиусом r0, определяемым по величине и по знаку.
r = r0/соs θ. (9)
Капиллярное давление, соответствующее такому мениску, равно
![]() (10)
(10)
Если рассмотреть равновесное состояние жидкости в U-образной трубке, одно колено которой достаточно большого диаметра (чтобы средняя часть мениска была плоской), а другое - капилляр, то при положительной смачиваемости стенок капилляра жидкостью (1 ³ соs θ > 0) она поднимается по отношению к уровню в широком колене, а при несмачиваемости (1 > cos θ ³ 0) опустится на величину
![]() (11)
(11)
где ρн - плотность насыщенного пара;
g - ускорение свободного падения.
Капиллярное давление обусловливает весьма важное для характеристики влажностного состояния капиллярно-пористых тел явление - капиллярную конденсацию. Благодаря капиллярному эффекту давление насыщенного пара над выпуклой поверхностью жидкости выше, а над вогнутой ниже, чем над плоской (закон Кельвина)
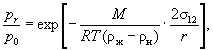 (12)
(12)
где М - относительная молекулярная масса;
R - универсальная газовая постоянная;
Т - абсолютная температура;
рr - давление насыщенного пара над вогнутой поверхностью;
Р0 - давление насыщенного пара над плоской поверхностью.
Таким образом, при контакте с насыщенным влажным воздухом сухое пористое тело, имеющее в своей структуре капилляры достаточно малых размеров, увлажняется за счет капиллярной конденсации в соответствии с (12). Например, при влажности воздуха j = 0,35 благодаря конденсации заполнятся все капилляры размером до 10-9 м, при j = 0,9 - все капилляры размером менее 10-8 м. При радиусе капилляра 10-7 м давление насыщения над мениском находящейся в нем жидкости практически равно давлению насыщения над плоской поверхностью. Это обстоятельство послужило одной из главных причин классификации пор размером больше 10-7 м как макрокапилляры, а пор меньше 10-7 м - как микрокапилляры.
В состоянии гигротермического равновесия с влажным воздухом температура тела равна температуре воздуха, давление пара во влажном воздухе, заключенном в капиллярно-пористой структуре, равно парциальному давлению пара в окружающем воздухе, а влагосодержание материала приобретает некоторое постоянное значение, называемое равновесным. Равновесное влагосодержание зависит от температуры и влажности окружающего воздуха и определяется формой связи влаги с материалом, которая, как отмечалось выше, может быть представлена в зависимости от парциального давления пара либо физико-химически, либо физико-механически связанной. Если материал при достижении равновесия поглощает влагу, этот процесс называется сорбцией, если отдает - десорбцией. Кривая, характеризующая зависимость между равновесным влагосодержанием материала и относительным парциальным давлением или влажностью j, %, при постоянной температуре, называется изотермой сорбции или десорбции. Влагосодержание материала при равновесии с насыщенным влажным воздухом (j = 100 %) называется максимальным гигроскопическим Uм.г.
Обычно изотерма сорбции изображается кривой в координатах: влагосодержание материала U, кг/кг (ось ординат), и парциальное давление пара во влажном воpдухе рп, Па (ось абсцисс).
Для большинства эффективных теплоизоляционных материалов изотермы сорбции указывают на две, достаточно четко выраженные области: 0 £ j £ 80 % - область адсорбционно-связанной влаги; 80 £ j £ 100 % - область капиллярно-связанной влаги. Причем для этих материалов в первой и во второй областях зависимость равновесного влагосодержания от влажности воздуха с достаточной для технических приближений точностью можно считать линейной. Это позволяет для построения приближенной изотермы сорбции экспериментально определять равновесное влагосодержание материала всего лишь при двух значениях влажности воздуха: при 80 и 100 %.
На основании экспериментальных данных о равновесном влагосодержании исследуемого материала при температуре воздуха 20 °С и влажности воздуха 80 и 100 % [u (j = 80 %); и = иmr] его сорбционная массоемкость (влагоемкость), кг/м·Па, определяется из выражений:
в область адсорбционно-связанной влаги:
в область капиллярно-связанной:
![]() (14)
(14)
где ![]() - парциальное давление насыщенного пара во влажном воздухе (j = 100 %),
Па;
- парциальное давление насыщенного пара во влажном воздухе (j = 100 %),
Па;
ρм - плотность изоляционного материала, кг/м3.
Промежуточные значения равновесного влагосодержания следует определять по формулам:
при 0 £ j < 80 %;
![]() (15)
(15)
при 80 % £ j £ 100 %,
При применении формул (13) - (16) следует использовать данные таблицы 1.
Таблица 1 - Характеристики пористости и равновесного влагосодержания теплоизоляционных материалов
|
Пористость общая т |
Равновесное влагосодержание, кг/кг, при t = 20 °С и влажности воздуха |
|||
|
открытая |
закрытая |
j = 80 % |
j = 100 % |
|
|
Волокнистые |
тo = 0,74m |
m3 = 0,26т |
0,01 |
0,05 |
|
Пенопласты |
mo = 0,98m |
m3 = 0,015m |
0,01 |
0,04 |
|
Пенокаучук |
тo = 0,985m |
т3 = 0,015m |
0,025 |
0,02 |
Приведенные выше соотношения позволяют определять равновесное влагосодержание теплоизоляционных материалов в зависимости от влажности окружающего воздуха при температуре 20 °С. Для определения по этим данным равновесного влагосодержания при любой другой температуре в диапазоне -60 £ t £ 60 °С следует применять приближенную формулу
U(t) = U(t = 20 °С; j) ´ [1 - 0,002(t - 20) ехр2,8 (1 - j)], (17)
где j - влажность воздуха в долях единицы.
Для оценки влажностного режима теплоизоляционных конструкций подземных сооружений, работающих в условиях контакта с массивом влажного грунта, например теплоизоляция подземных теплопроводов и др., введено понятие равновесного влагосодержания теплоизоляции Uгр, кг/кг, в системе теплоизоляция - влажный грунт, находящейся в условиях термодинамического равновесия. Значения этой величины для различных грунтов представлены в таблице 2.
Таблица 2 - Равновесное влагосодержание теплоизоляции V, кг/кг, в контакте с влажным грунтом
|
Грунт |
||||||||||||||||||||||||||
|
песчаный |
супесь |
суглинок |
глина |
|||||||||||||||||||||||
|
Влагосодержание грунта, кг/кг |
||||||||||||||||||||||||||
|
Пенопласты |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
|
0,14 |
0,17 |
0,18 |
0,20 |
0,24 |
0,28 |
0,32 |
0,07 |
0,12 |
0,15 |
0,18 |
0,20 |
0,24 |
0,30 |
0,035 |
0,06 |
0,08 |
0,12 |
0,15 |
0,18 |
0,24 |
0,01 |
0,03 |
0,04 |
0,06 |
0,10 |
|
|
Пенокаучуки |
0,10 |
0,12 |
0,13 |
0,14 |
0,17 |
0,2 |
0,23 |
0,05 |
0,90 |
0,11 |
0,13 |
0,14 |
0,17 |
0,21 |
0,025 |
0,042 |
0,56 |
0,09 |
0,10 |
0,12 |
0,18 |
0,008 |
0,02 |
0,03 |
0,04 |
0,07 |
|
Волокнистая |
0,40 |
0,60 |
0,07 |
1,0 |
1,25 |
1,40 |
1,50 |
0,1 |
0,21 |
0,40 |
0,60 |
1,00 |
1,25 |
1,30 |
0,01 |
0,03 |
0,05 |
0,20 |
0,40 |
0,80 |
1,1 |
0,01 |
0,02 |
0,05 |
0,10 |
0,15 |
3 УВЛАЖНЕНИЕ ТЕПЛОВОЙ ИЗОЛЯЦИИ В ПРОЦЕССЕ ЭКСПЛУАТАЦИИ
В предыдущем разделе приведены методы определения влажностных характеристик теплоизоляционных материалов в теплоизоляционных конструкциях, находящихся в условиях термодинамического равновесного состояния с окружающей средой. Ниже рассмотрены методы расчета динамики увлажнения теплоизоляционных конструкций за счет диффузии парообразной влаги в пористую структуру изоляции при контакте с влажным воздухом, а также процессов увлажнения капельной влагой при атмосферных осадках или контактах с массивом влажного грунта на основе закона изотермической диффузии влаги:
qm = -Dgraduv, (18)
где qт - плотность потока влаги
парообразной ![]() или капельной
или капельной ![]() , кг/(м2·ч),
обусловленная градиентом концентрации влаги uv, кг/м3,
в материале. В качестве расчетной схемы рассматривается изотермический влагоперенос в неограниченной пластине толщиной δ, м,
описываемый уравнением
, кг/(м2·ч),
обусловленная градиентом концентрации влаги uv, кг/м3,
в материале. В качестве расчетной схемы рассматривается изотермический влагоперенос в неограниченной пластине толщиной δ, м,
описываемый уравнением
с краевыми усилиями:
uv(τ = 0;
0 £ х £ δ) = ![]() ; (20)
; (20)
uv(0 £ τ £ ∞; х = δ) = ![]() ; (21)
; (21)
Решение
уравнения (19) с краевыми
усилиями (20) - (22) для
среднего влагосодержания по толщине пластины ![]() (τ) известно:
(τ) известно:
где Fот - массообменный критерий Фурье, равный:
Используя (23), среднее влагосодержание по толщине изоляции за время τувл можно определить из выражения:
![]() (τ) = θ·[uv(x = δ) - uv(τ
= 0)] + uv(τ = 0). (25)
(τ) = θ·[uv(x = δ) - uv(τ
= 0)] + uv(τ = 0). (25)
При расчете увлажнения изоляции, эксплуатируемой во влажном воздухе, определение безразмерного влагосодержания по (23) и среднего влагосодержания по толщине по (25) производится при значениях массообменного критерия Фурье, найденных по (25) с использованием коэффициента диффузии парообразной влаги Dп, м2/ч (таблица 3).
Таблица 3 - Характеристика диффузионного переноса парообразной влаги в теплоизоляционных материалах
|
Плотность, кг/м3 |
Пористость |
Диффузионная массопроводность (паропроницаемость) λм, мг/(м·ч·Па) |
Коэффициент диффузии пара Dп, м2/ч |
Коэффициент сопротивления диффузии μ |
|
|
Перлитобетон |
800 |
0,69 |
0,26 |
- |
3,04 |
|
|
600 |
0,77 |
0,30 |
- |
2,64 |
|
Пенобетон |
800 |
0,7 |
0,14 |
3,4·10-6 |
5,65 |
|
|
600 |
0,77 |
0,17 |
4,6·10-6 |
4,65 |
|
|
400 |
0,85 |
0,23 |
1,1·10-5 |
3,44 |
|
Минеральная вата |
150 |
0,93 |
0,47 |
- |
1,68 |
|
|
150 |
0,93 |
0,43 |
- |
1,84 |
|
|
150 |
0,93 |
0,41 |
- |
1,93 |
|
Минераловатная плита |
400 |
0,81 |
0,32 |
- |
2,47 |
|
на битумном связующем |
240 |
0,88 |
0,16 |
- |
4,94 |
|
Пенопласт: |
|
|
|
|
|
|
полистирольный ПСБ-С |
23 |
0,98 |
0,018 |
2,7·10-5 |
43,9 |
|
27 |
0,97 |
0,002 |
1,9·10 |
|
|
|
поливинилхлоридный |
59 |
0,96 |
0,002 |
2·10-7 |
395 |
|
75 |
0,95 |
0,001 |
0,8·10-7 |
791 |
|
|
фенолформальдегидный ФП-1 |
31 |
0,98 |
0,29 |
1,15·10-6 |
2,72 |
|
40 |
0,97 |
0,22 |
6·10-7 |
3,59 |
|
|
50 |
0,96 |
0,35 |
8,62·10-7 |
2,26 |
|
|
то же, ФП-5 |
52 |
0,96 |
0,13 |
1·10-6 |
6,1 |
|
69 |
0,95 |
0,094 |
8·10-7 |
8,4 |
|
|
полиуретановый ППУ-3С |
50 |
0,95 |
0,029 |
7·10-7 |
27,2 |
|
55 |
0,95 |
0,025 |
3·10-5 |
31,6 |
|
|
60 |
0,94 |
0,025 |
2,8·10-5 |
31,6 |
|
|
Пеностекло |
230 |
0,89 |
0,13 |
4,0 · 10-6 |
|
|
240 |
0,88 |
0,125 |
4,2 · 10-6 |
|
|
|
250 |
0,88 |
0,115 |
3,4 · 10-6 |
|
|
|
Вспученный перлит |
69 |
0,97 |
0,3 |
2·10-4 |
2,63 |
|
12 |
0,97 |
0,23 |
1,5·10-4 |
3,59 |
|
|
Стекловата на фенольном связующем |
50 |
0,98 |
0,54 |
5·10-4 |
1,5 |
|
Пенокаучук ВК |
89 |
0,92 |
1,26·10-4 |
6·10-9 |
6280 |
|
Пенокаучук ЕПДМ |
75 |
0,95 |
3,04·10-4 |
4·10-9 |
2600 |
|
Пенополиэтилен |
30 |
0,97 |
2,9·10-4 |
9·10-8 |
2728 |
Влагосодержание изоляции на наружной поверхности иv(х = δ) при заданной влажности воздуха j, %, определяется с помощью формул (15), (16).
При расчете увлажнения изоляции, работающей в контакте с капельной влагой, в качестве граничных условий (21) следует принимать значение влагосодержания полного намокания, а при контакте с массивом влажного грунта - равновесное влагосодержание Uгр по таблице 2. В этом случае определение массообменного критерия Фурье, используемого в (23) и (24), производится с использованием коэффициента D - коэффициента диффузии капельной влаги по таблице 4.
Таблица 4 - Коэффициент диффузии капельной влаги, м2/ч
|
Волокнистая |
Пенопласт |
Пенокаучук |
|
1,5·10-3 |
2·10-6 |
1,5·10-7 |
Для рассмотрения процессов влагопереноса в теплоизоляционных материалах во всем возможном диапазоне изменения влагосодержания, от нуля до максимального (область, включающая диффузионный и капиллярный перенос), когда влагосодержание теплоизоляции в конструкции изменяется от равновесного ир, соответствующего сорбционному, при заданной влажности воздуха до влагосодержания полного намокания, а обобщенный коэффициент диффузии влаги aтf(иv) в зависимости от влагосодержания может измениться на один-два порядка, вводится безразмерная величина относительного влагосодержания:
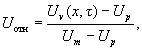 (26)
(26)
которая изменяется от 0 до 1.
Для описания поля влагосодержаний используется нелинейное уравнение влагопроводности
Анализ экспериментальных данных показал, что зависимость коэффициента диффузии влаги от влагосодержания гидрофильных материалов описывается уравнением
где ![]() - относительный коэффициент диффузии влаги, равный аm(Uv)/
- относительный коэффициент диффузии влаги, равный аm(Uv)/![]() ;
; ![]() - коэффициент
диффузии влаги при Uотн = 0.
- коэффициент
диффузии влаги при Uотн = 0.
Введением безразмерных переменных:
массообменного числа Фурье
![]() (29)
(29)
и относительной координаты
![]() (30)
(30)
уравнение (27) приводится к безразмерному виду:
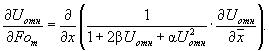 (31)
(31)
Для стационарных условий:
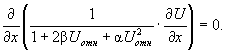 (32)
(32)
Решение (32) при
граничных условиях: ![]() = 0,
Uотн = 1,
= 0,
Uотн = 1, ![]() = 1, Uотн = 0 получено в
виде:
= 1, Uотн = 0 получено в
виде:
![]() (33)
(33)
где
![]() (34)
(34)
Для гидрофобных теплоизоляционных материалов зависимость коэффициента диффузии влаги от влагосодержания имеет качественно иной характер. Для ее описания предложено уравнение
![]() (35)
(35)
где относительный коэффициент диффузии
влаги ![]() в отличие от (28)
определяется как отношение коэффициента диффузии влаги при Uотн = 0
к коэффициенту диффузии влаги при Uотн = 1:
в отличие от (28)
определяется как отношение коэффициента диффузии влаги при Uотн = 0
к коэффициенту диффузии влаги при Uотн = 1:
![]() (36)
(36)
Решение
уравнения (28) в этом случае, при
тех же граничных условиях: Uотн(![]() = 0) = 1; Uотн(
= 0) = 1; Uотн(![]() = 1) = 0 выражается формулой
= 1) = 0 выражается формулой
![]() (37)
(37)
4 РАСЧЕТНЫЕ МЕТОДЫ ОЦЕНКИ ВЛИЯНИЯ УВЛАЖНЕНИЯ НА ТЕПЛОЗАЩИТНЫЕ СВОЙСТВА ТЕПЛОИЗОЛЯЦИИ
Передача теплоты в неувлажненных теплоизоляционных материалах является сложным процессом, включающим перенос теплоты кондуктивной теплопроводностью, излучением и конвекцией и осуществляется посредством:
теплопроводности твердого скелета, образующего пористую структуру материала;
теплопроводности газа, находящегося в порах и капиллярах;
излучения между стенками пор и капилляров;
конвективного переноса теплоты за счет конвективных токов газа в пористой структуре теплоизоляции.
Однако в целях упрощения тепловых расчетов для определения теплозащитных свойств теплоизоляционных конструкций используются расчетные зависимости, основанные на законе Фурье, справедливом, строго говоря, лишь для твердых тел, в которых перенос теплоты при наличии градиента температур происходит только за счет кондуктивной теплопроводности. Очевидно, что используемый при таком подходе коэффициент теплопроводности является обобщенной характеристикой проводимости теплоты в материале - эффективной теплопроводностью:
λэф = λq + λр + λк, (38)
где λq - коэффициент кондуктивной теплопроводности;
λр - коэффициент радиационной теплопроводности;
λк - коэффициент конвективной теплопроводности.
Наличие столь сложного характера составляющих в общем потоке теплоты в теплоизоляционных материалах и выражение этого процесса линейным уравнением переноса приводят к тому, что эффективная теплопроводность является сложной функцией не только температуры, но и давления, газа, заполняющего поры, степени черноты поверхности пор и капилляров, а также многих других факторов.
При разработке расчетного метода определения эффективной теплопроводности теплоизоляционных материалов для определения ее кондуктивной составляющей была использована модель О. Кришера. Как показали экспериментальные данные, она дает вполне удовлетворительные результаты при расчете теплопроводности легких высокоэффективных теплоизоляционных материалов, нашедших широкое применение в конструкциях промышленной изоляции (волокнистая изоляция, пенопласта, пенокаучуки и др.).
Расчетные формулы этой модели для определения кондуктивной теплопроводности материалов в сухом состоянии имеют вид:
![]() (40)
(40)
где а - экспериментально определяемый коэффициент, характеризующий структуру материала;
т - пористость материала в долях единицы;
λск - теплопроводность твердого скелета материала;
λг - теплопроводность газа, заполняющего пористую структуру материала.
Расчетные формулы для определения конвективной составляющей получены с помощью результатов численных решений систем линейных дифференциальных уравнений в частных производных, описывающих стационарный теплоперенос в пористых средах в условиях естественной конвекции в плоских и цилиндрических слоях. По результатам этих расчетов найдены критериальные уравнения, отражающие зависимость относительного коэффициента конвективной теплопроводности
от фильтрационного числа Релея - ![]() , которые для плоских и цилиндрических теплоизоляционных
слоев имеют вид:
, которые для плоских и цилиндрических теплоизоляционных
слоев имеют вид:
для плоского
горизонтального слоя при 40 < ![]() £ 100:
£ 100:
Ек = (![]() )0,05. (43)
)0,05. (43)
При ![]() £ 40, Ек =
1, конвективный
теплоперенос отсутствует, λк =
0.
£ 40, Ек =
1, конвективный
теплоперенос отсутствует, λк =
0.
Для плоского
вертикального слоя при 0 £ ![]() £ 100:
£ 100:
Ек = (![]() )0,035. (44)
)0,035. (44)
Для
цилиндрического слоя при 0 £ ![]() £ 100:
£ 100:
Eкц = 1 + 5,9·10-3[η(1 - η)]3/4
exp(-4,29η) ´ (![]() )2. (45)
)2. (45)
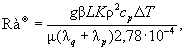 (46)
(46)
где 2,78·10-4 - коэффициент перевода размерности теплопроводности из ккал/(м·ч·°С), в ккал/(м·ч·°С);
μ - коэффициент динамической вязкости, кг/м·с;
g - ускорение силы тяжести, м/с2;
ρ - плотность, кг/м3;
b - коэффициент температурного расширения, 1/°С;
r - толщина слоя изоляции, м, для цилиндрического слоя L = r2 - r1;
r1 - радиус поверхности изолируемого трубопровода;
r2 - то же, поверхности изоляции;
К - коэффициент фильтрационной проницаемости изоляции, м2.
Предлагаемая расчетная методика определения эффективной теплопроводности волокнистых материалов реализуется следующим образом:
- расчет кондуктивной теплопроводности волокнистой изоляции выполняется по соотношениям (39) - (41), в которых в качестве теплопроводности скелета используется теплопроводность волокна (таблица 5), а газа - молекулярная теплопроводность воздуха (таблица 6).
Таблица 5 - Теплопроводность, Вт/(м·°С), и плотность волокна, кг/м3, структурные характеристики а волокнистых материалов
|
минеральное |
муллито-кремнеземистое |
базальтовое |
стекловолокно |
|
λв = 1,2 + 8,5·10-5(tт + 100) |
λв = 1,2 + 8,5·10-5(tт + 100) |
||
|
а = 0,69 |
а = 0,70 |
а = 0,70 |
а = 0,76 |
|
ρв = 1000 |
ρв = 1700 |
ρв = 1700 |
ρв = 1000 |
Таблица 6 - Теплопроводность полимерной матрицы пенопластов
|
Плотность матрицы, кг/м3 |
Теплопроводность, Вт/(м·°С), при нормальной температуре |
|
|
Полистирольный |
1050 |
0,20 |
|
Полиуретановый |
1250 |
0,25 |
|
Фенолформальдегидный |
1400 |
0,19 |
Конвективная составляющая эффективной теплопроводности волокнистых материалов определяется с использованием выражений (42) - (47), причем коэффициент фильтрационной проницаемости К, м2, входящий в (45), определяется по формуле
в которой п - содержание неволокнистых включений, %;
dв - диаметр волокна, м;
т - пористость волокнистой изоляции.
Радиационная теплопроводность волокнистых материалов определяется с помощью следующей зависимости:
![]() (48)
(48)
где σ - константа Больцмана, равная 4,965·10-8 ккал/(м2·ч·град);
Тm - средняя температура изоляции, К;
т - пористость;
dв - диаметр волокна, м;
Kосл - коэффициент ослабления, константа, определяемая для различных видов волокон по эмпирическим формулам:
муллитокремнеземистое волокно
Kосл = 25mdвTm + 5·10(1 - m)2/Tm; (49)
базальтовое волокно
Kосл = 70mdвTm + 5·103(1 - m)/Tm; (50)
минераловатное волокно
Kосл = 20mdвTm + 7·103(1 - m)3/Tm; (51)
стекловолокно
Kосл = 11,2·106mdвTm + 800(1 - m)2/Tm. (52)
В отличие от волокнистых материалов передача теплоты в пенопластах осуществляется в основном за счет кондуктивного переноса через газовую среду - 65 % и через полимерную матрицу - 25 - 27 %. На долю радиационной составляющей приходится не более 5 - 7 %. Конвективного переноса в них не наблюдается вообще, поскольку пенопласты практически не содержат сквозных пор, в отличие от волокнистой изоляции, где сквозная пористость является преобладающей. Коэффициент фильтрационной проницаемости пенопластов на 3 - 4 порядка меньше, чем у волокнистой изоляции.
Исходя из этих соображений для расчета эффективной теплопроводности пенопластов могут быть применены соотношения (39) - (41) с использованием в качестве структурных характеристик для фенолформальдегидных, поливинилхлоридных и пенополиуретановых пенопластов - 0,420, а для полистирольных - 0,20. Температурный коэффициент теплопроводности для всех пенопластов практически одинаков: b = 0,00015 Вт/м(°С)2, а коэффициенты теплопроводности полимерной матрицы приведены в таблице 6.
В процессе изготовления пористая структура пенопластов заполняется газами с теплопроводностью, значительно меньшей, чем у воздуха. В зависимости от принятой технологии этими газами могут быть углекислый, фреон, циклопентан и др. Поэтому теплопроводность свежеизготовленного пенопласта следует рассчитывать по (39) - (41), используя в качестве теплопроводности газа данные таблицы 7.
Таблица 7 - Теплопроводность газов в пористой структуре пенопластов
|
Теплопроводность, Вт/(м·°С) |
|
|
Воздух |
0,0257 [1 + 0,003(tm - 20)] |
|
Углекислый газ |
0,016 [1 + 0,0045(tm - 20)] |
|
Циклопентан |
0,013 [1 + 0,0051(tm - 20)] |
|
Фреон |
0,0081 [1 + 0,0054(tm - 20)] |
После изготовления теплоизоляционных конструкций в них происходит постепенное диффузионное замещение образовавшегося в порах пенопласта газа воздухом. При этом теплопроводность пенопластов увеличивается от начальных значений, определенных по (39) - (41) с учетом теплопроводности газа, до конечных, также определенных по (39) - (41), где в качестве теплопроводности газа принимается теплопроводность воздуха.
Известно, что при увлажнении изоляции теплопроводность ее увеличивается. В диапазоне изменения средних температур влажной изоляции 0 £ tср £ 25 °С увеличение эффективной теплопроводности происходит за счет повышения ее кондуктивной составляющей вследствие замещения воздуха в пористой структуре изоляции более теплопроводным компонентом - водой.
В этом случае
при определении эффективной теплопроводности влажной изоляции
(волокнистой и пенопластов) для расчета характеристики кондуктивного переноса
теплоты ![]() вместо выражений (39) - (41) используются зависимости:
вместо выражений (39) - (41) используются зависимости:
![]() (54)
(54)
где λж - теплопроводность воды;
W - относительная влажность по объему (3), остальные обозначения те же, что в (39) - (41).
Результаты экспериментальных исследований показали, что предложенная модель эффективной теплопроводности влажной изоляции удовлетворительно описывает теплоперенос при нормальных средних температурах. При повышенных средних температурах теплопроводность влажной изоляции превышает расчетные значения, определенные с помощью (53) - (55), в несколько раз. Объясняется этот факт явлением термовлагопроводности - возникновением потока влаги во влажном материале при его нагревании, направленного по потоку теплоты. В зависимости от характера пористой структуры, влагосодержания, градиента и уровня температур термовлагопроводность может быть вызвана различными физическими процессами:
под действием градиента поверхностного натяжения воды в менисках, в местах сужения пор и капилляров, вызванных градиентом температур, происходит термокапиллярное движение воды в сторону большего поверхностного натяжения, т.е. в сторону понижающихся температур;
в полностью увлажненных материалах перемещение жидкости против теплового потока может происходить за счет термоосмоса, обусловленного различием удельного теплосодержания жидкости в тонком слое у поверхности пор и капилляров в объеме;
парциальное давление пара в паровоздушной смеси, находящейся в пористой структуре теплоизоляционного материала, имеющего влагосодержание выше максимального гигроскопического, равно давлению насыщения при температуре тела;
при появлении градиента температур в нем возникает также градиент парциального давления насыщенного пара, который вызывает диффузионный перенос пара из мест с более высокой температурой в места с более низкой, сопровождающийся его конденсацией и повышением влагосодержания в холодной зоне.
Результаты проведенной численной оценки термоградиентных потоков влаги различной физической природы (термокапиллярный перенос, диффузия насыщенного пара с последующей конденсацией и др.) позволили заключить, что термовлагопроводность в конструкциях на основе эффективных теплоизоляционных материалов, обладающих высокой пористостью (волокнистые и пенопласты), преимущественно обусловлена диффузионным переносом.
Эффект увеличения теплопроводности влажного материала при его нагревании, обусловленный появлением при этом в его пористой структуре диффузионного потока пара, сопровождающегося испарением влаги в горячей зоне и конденсацией в холодной, предлагается учитывать введением дополнительного коэффициента теплопереноса, возникающего за счет термовлагопроводности λt, определяемого выражением
![]() (56)
(56)
где W - относительное влагосодержание изоляции по объему (3);
λм - коэффициент паропроницаемости изоляции, кг/(м·ч·Па) (таблица 3);
r - теплота фазового перехода влаги, ккал/кг;
tср - средняя температура материала, °С;
a = 2666 Па;
b = 0,046 1/°С.
В заключение следует отметить, что эффект резкого увеличения теплопроводности за счет термовлагопроводности при нагревании влажного материала проявляется только в начальный период прогрева влажной изоляции (в течение 5 - 10 ч) до установления стационарного температурного и влажностного режимов в теплоизоляционной конструкции, методика и алгоритм расчета которых для различных условий эксплуатации подробно рассмотрены в монографии В.Г. Петрова-Денисова, Л.А. Масленникова «Тепло- и влагообмен в промышленной изоляции» (М.: Энергоатомиздат, 1983).
5 ПРЕДЛОЖЕНИЯ ПО НОРМИРОВАНИЮ РАСЧЕТНЫХ ЗНАЧЕНИЙ ТЕПЛОПРОВОДНОСТИ ИЗОЛЯЦИИ В КОНСТРУКЦИЯХ
Теплозащитные свойства теплоизоляционных конструкций промышленных сооружений и трубопроводов, а также ограждений зданий, как показывает практика, снижаются в процессе эксплуатации. Так, например, за счет периодических тепловлажностных воздействий окружающей среды вследствие механических нагрузок, обусловленных вибрацией оборудования и ветровым напором переменного направления, волокнистая изоляция уплотняется, толщина ее уменьшается, а теплопроводность увеличивается. Теплоизоляционная конструкция изменяет свою форму («провисает»), внутри нее образуются полости с усиленной конвекцией в ней, воздуха. Все это приводит к снижению ее термического сопротивления. Температурно-влажностные деформации существенно изменяют пористую структуру теплоизоляционного слоя из пенопласта в процессе эксплуатации, до 80 % повышается содержание в нем открытых пор, что приводит к резкому увеличению лучистой составляющей в переносе теплоты, а также к повышению влагопроводности, что влечет за собой увеличение кондуктивной и общей теплопроводности теплоизоляционного слоя.
Снижение теплозащитных свойств теплоизоляционных конструкций в процессе эксплуатации определяет их долговечность. Как известно, долговечность технического объекта характеризуется сохранением его работоспособности до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Причем под работоспособностью понимается такое состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения определяющих их параметров в пределах, установленных нормативно-справочной документацией.
Событие, заключающееся в нарушении работоспособности, является отказом объекта, который может быть внезапным - практически мгновенный выход объекта из строя или постепенным, характеризующимся длительным выходом параметров, определяющих его работоспособность, за пределы нормативных допусков.
Рассматривая долговечность теплоизоляционных конструкций, следует считать, что их работоспособность характеризуется постепенным отказом и может быть представлена зависимостью:
в которой q(τ = 0) - тепловые потери в начале эксплуатации;
q(τ) - тепловые потери через τ лет эксплуатации.
Учитывая прямую пропорциональность между величинами тепловых потерь через теплоизоляционные конструкции и теплопроводностью используемого в них материала, найдем:
где λ(τ = 0) - теплопроводность теплоизоляционного материала в конструкции вначале;
λ(τ) - то же, через τ лет эксплуатации, Вт/(м·°С).
Выражение (57) с достаточной для практических целей точностью можно представить экспоненциальной зависимостью
где К - константа работоспособности, 1/год.
Используя (58) и (59), получим:
λ(τ) = λ(τ = 0)ехрKτ (60)
соотношение, определяющее динамику
снижения теплозащитных свойств теплоизоляционных конструкций за счет увеличения
теплопроводности изоляции в процессе эксплуатации. Для того чтобы обеспечить
требуемую нормированную плотность теплового потока через изолированную
поверхность оборудования трубопроводов систем инженерного оборудования зданий и
теплоснабжения за все время эксплуатации τ, лет, в качестве
расчетного значения коэффициента теплопроводности ![]() при определении
толщины изоляции предлагается использовать среднеинтегральную за τ лет
эксплуатации величину, значение которой на основании интегрирования (60) с учетом зависимости теплопроводности от температуры
определяется выражением
при определении
толщины изоляции предлагается использовать среднеинтегральную за τ лет
эксплуатации величину, значение которой на основании интегрирования (60) с учетом зависимости теплопроводности от температуры
определяется выражением
![]() (61)
(61)
где tт - средняя температура изоляции.
Значения константы работоспособности К, характеризующей динамику снижения теплоизоляционных свойств теплоизоляционных конструкций в процессе эксплуатации, определенные на основе результатов исследований, проведенных институтом «Теплопроект» совместно с институтами ВНИПИЭнергопром, АКХ им. Памфилова, НИИМосстрой, ВНИИСТ, а также работ Ю. Боброва, А. Дементьева, А. Дьячкова, Л. Невского, Дж. Барта, К. Холта, Дж. Келлнера, В. Диркса, приведены в таблице 8.
Таблица 8 - Константа работоспособности теплоизоляционных материалов К, 1/год
|
Условия прокладки |
||||||||||||
|
В отапливаемых помещениях |
В неотапливаемых подвалах, чердаках, подпольных каналах |
Надземная |
Подземная в проходных каналах |
Подземная в непроходных каналах |
Подземная бесканальная |
|||||||
|
Вид изоляции |
||||||||||||
|
пенокаучук** |
волокнистая |
пенопласты* |
пенокаучук** |
волокнистая |
пенопласты* |
волокнистая |
пенопласты* |
волокнистая |
армопенобетон |
пенополимербетон |
пенополиуретан*** |
|
|
Отопления и горячего водоснабжения |
- |
1,35·10-2 |
7·10-3 |
6,5·10-3 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Холодного водоснабжения |
4,2·10-3 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Централизованного теплоснабжения |
- |
1,35·10-2 |
7·10-3 |
- |
1,8·10-2 |
7·10-3 |
2,2·10-2 |
8·10-3 |
4,6·10-2 |
2,7·10-2 |
5·10-3 |
1,65·10-4 |
|
* Пенопласты с преимущественно закрытопористой структурой, пенополиуретан, пенополистирол и др. ** Пенокаучук типа Аэрофлекс, пенополиэтилен Экофлекс и др. *** Пенополиуретан в жесткой полиэтиленовой оболочке с дистанционным контролем влажности. |
||||||||||||