МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ДЕЛАМ
ГРАЖДАНСКОЙ ОБОРОНЫ, ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ
И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ СТИХИЙНЫХ БЕДСТВИЙ
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ «ВСЕРОССИЙСКИЙ ОРДЕНА "ЗНАК ПОЧЕТА" НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ПРОТИВОПОЖАРНОЙ ОБОРОНЫ» |
МЕТОДИКА ОПРЕДЕЛЕНИЯ УСЛОВИЙ
ТЕПЛОВОГО САМОВОЗГОРАНИЯ
ВЕЩЕСТВ И МАТЕРИАЛОВ
МОСКВА 2004
Методика позволяет определять условия теплового самовозгорания материалов на основании предварительных экспериментальных исследований. Приводятся способы расчета критических условий для скоплений вещества различной формы. Разработаны методы определения условий теплового самовозгорания, отложений материала, на поверхностях трубопроводов и другого технологического оборудования.
Методика предназначена для использования подразделениями ГПН и специализированными организациями. Она позволяет определять пожаробезопасные условия переработки транспортирования и хранения самовозгорающихся веществ (на основании критического размера скопления материала, критической температуры окружающей среды, времени индукции процесса теплового самовозгорания).
Разработана сотрудниками ФГУ ВНИИПО МЧС России: д.т.н., профессором Ю.Н. Шебеко; д.т.н., профессором В.И. Горшковым; к.т.н. И.А. Корольченко; А. С. Кухтиным; В.Л. Крыловым.
Согласована с ГУГПС МЧС России письмом № 18/2/848 от 02.04.2004 г. и утверждена ФГУ ВНИИПО МЧС России 21.04.2004 г.
ОГЛАВЛЕНИЕ
1. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
1.1. Аппаратура
Аппаратура для определения условий теплового самовозгорания включает в себя следующие элементы:
1.1.1. Термостат вместимостью рабочей камеры не менее 40 дм3 с терморегулятором, позволяющим поддерживать постоянную температуру от 60 до 500°С с погрешностью не более 2°С.
1.1.2.
Корзиночки кубической или цилиндрической формы высотой 15, 30, 35, 50, 70, 140
и
1.1.3.
Термоэлектрические преобразователи (термопары ТХА и ТХК) с максимальным
диаметром рабочего спая не более
1.1.4. Измеритель термоэлектродвижущей силы, позволяющий осуществлять визуализацию изменения температуры образца материала во времени с записью на бумажном или электронном носителе.
1.1.5.
Весы лабораторные с наибольшим пределом взвешивания
1.2. Подготовка и проведение испытаний
1.2.1. К
корзинкам крепят по три термоэлектрических преобразователя таким образом, чтобы
один конец одной термопары находился внутри корзинки в ее центре, а второй - на
расстоянии не более
1.2.2. Корзинки заполняют исследуемым веществом и взвешивают на весах. При испытаниях листового материала его набирают в стопку, соответствующую внутренним размерам корзинки. В образцах монолитных материалов предварительно высверливают до центра отверстие диаметром (7±5) мм для термоэлектрического преобразователя.
1.2.3.
Свободные концы термопреобразователей подсоединяют к измерителю
термоэлектродвижущей силы для регистрации изменения разности температур в
центре образца и температуры в рабочей камере термостата. За температуру
испытания принимают показания термоэлектрического преобразователя,
расположенного на расстоянии
1.2.4. Корзинку помещают в центр термостата, нагретого до заданной температуры (например, 200°С) и наблюдают за изменением температуры в центре образца.
1.2.5. Самовозгорание образца проявляется при резком увеличении разности температур, фиксируемой дифференциальной термопарой, до величины более 100°С или плавном росте температуры до величины, превышающей значение температуры самовоспламенения вещества.
1.2.6. Если при первом испытании самовозгорание не происходит в течение времени, указанного в табл. 1, то испытание с новым образцом материала того же размера проводят при температуре на 20°С больше заданной. Если самовозгорание произошло, то испытание проводят при температуре на 10°С меньше.
Таблица 1
|
Размер образца, мм |
Продолжительность испытаний, ч |
|
35 |
6 |
|
50 |
12 |
|
70 |
24 |
|
100 |
48 |
|
140 |
96 |
|
200 |
192 |
1.2.7. Испытания продолжают с образцами данного размера при различной температуре рабочего пространства термостата до достижения минимальной температуры, при которой образец самовозгорается. При уменьшении температуры ниже минимальной на 1°С самовозгорания не должно происходить. При этих температурах выполняют по два эксперимента. Минимальную температуру, при которой исследуемый материал самовозгорается, принимают за температуру самовозгорания образца данного размера.
1.2.8. Аналогичные испытания проводят с образцами исследуемого вещества в корзинках других размеров. Результаты испытаний оформляются в виде табл. 2.
Таблица 2
|
Размер образца, мм |
Температура самовозгорания |
|
|
°С |
К |
|
|
|
|
|
2. РАСЧЕТ УСЛОВИЙ ТЕПЛОВОГО ВЗРЫВА
2.1. Определение параметров кинетического уравнения реакции окисления
Исходными данными, для определения параметров кинетического уравнения реакции окисления, являются:
• данные табл. 2 для критической температуры самовозгорания T0 (К) образцов размером D, м;
• коэффициент теплопроводности материала λ, Вт/(м × К);
• теплоемкость исследуемого материала с, Дж/(кг × К);
• теплота реакции Q, Дж/кг.
Расчет предэкспоненциального множителя и энергии активации реакции окисления выполняется в следующем порядке.
2.1.1. Для каждого размера образца рассчитать число Рэлея по уравнению
где
g - ускорение силы тяжести, м/с2;
ν - кинематическая вязкость воздуха при температуре T0, м2/с;
а - температуропроводность воздуха при температуре T0, м2/с;
D - высота образца, м;
R - универсальная газовая постоянная, Дж/(моль × К);
T0 - температура рабочего пространства термостата, К;
Е - энергия активации реакции окисления. В первом приближении допускается принимать равной 100 кДж/моль.
Для облегчения расчетов зависимость комплекса g/νa от температуры в диапазоне T0=(350-800) К может быть рассчитана по формуле
2.1.2. Для всех размеров образцов вычислить коэффициенты теплоотдачи α по уравнениям:
при 5 × 102 < Ra < 2 × 107
при Ra > 2 × 107
где
σ =5,67 × 10-8 - постоянная Стефана-Больцмана, Вт/(м2 × К4).
Зависимость коэффициента теплопроводности воздуха от температуры может быть определена по формуле
2.1.3. По
величине ![]() , коэффициенту теплопроводности материала λ и
половине высоты r=D /2 вычисляют критерии Био для каждого образца:
, коэффициенту теплопроводности материала λ и
половине высоты r=D /2 вычисляют критерии Био для каждого образца:
2.1.4. Функцию φ(Bi), учитывающую интенсивность теплообмена образца с воздухом, определяют по уравнению
2.1.5. Рассчитывают параметры β и γ, характеризующие индивидуальные свойства реакции окисления:
где
с - теплоемкость материала, Дж/(кг × К),
a
Q - теплота реакции окисления, Дж/кг.
2.1.6. С учетом интенсивности теплообмена и особенностей реакции для каждого размера образца материала рассчитывают критическое значение параметра Франк-Каменецкого:
где
δ0 - критическая величина параметра δ при интенсивном теплообмене, равная 2,52 для образцов кубической формы и 2,76 для цилиндра с высотой, равной диаметру.
Результаты вычислений по формулам (1)-(10) сводят в табл. 3.
Таблица 3
|
Размер r, м |
То, К |
Ra |
α, Вт/(м2 · К) |
Bi |
φ(Bi) |
β |
γ |
δкр |
|
|
|
|
|
|
|
|
|
|
2.1.7. Зависимость критического значения параметра Франк-Каменецкого δкр от кинетических параметров реакции окисления
записывают в виде
где
ρ - плотность упаковки материала, кг/м3;
k0 - константа скорости реакции, 1/с.
2.1.8. По уравнению (13) для каждого размера образца рассчитывают величину М. С учетом значений М и N по уравнению (12) методом наименьших квадратов или программ обработки экспериментальных данных для персональных компьютеров Eureka, Curve Expert 1.3, Mathematica 3.0, Mathematica 4.0 и других определяют численные значения N и энергию активации Е.
2.1.9.
Вычисляют предэкспоненциальный множитель реакции окисления ![]() путем деления N на Е. Данные расчетов по
уравнениям (12)-(14) сводят в табл. 4.
путем деления N на Е. Данные расчетов по
уравнениям (12)-(14) сводят в табл. 4.
Таблица 4
|
Размер r, м
|
T0, К
|
М, |
N, |
Е, Дж/моль |
м · К/кг |
|
|
|
|
|
|
|
2.1.10. Если величина энергии активации, вычисленная в п. 2.1.8, отличается от ранее принятой и равной 100 кДж/моль более чем на 5%, расчеты по пп. 2.1.1-2.1.10 необходимо повторить с новым значением энергии активации. Процесс итераций необходимо выполнять до тех пор, пока энергии активации в начале и конце расчета не будут отличаться менее чем на 5%.
2.2. Расчет критической температуры
Исходными данными для расчета критической температуры при хранении и транспортировании веществ и материалов являются:
• форма и размеры упаковки материала;
• плотность упаковки материала, кг/м3;
• коэффициент теплопроводности материала λ, Вт/(м · К);
• теплоемкость исследуемого материала с, Дж/(кг · К);
• теплота реакции Q, Дж/кг;
• энергия активации Е реакции окисления, Дж/моль;
• предэкспоненциальный
множитель ![]() , м · К/кг.
, м · К/кг.
Расчет выполняется в следующем порядке.
2.2.1. Для заданной формы упаковки материала из табл. 5 выбрать или рассчитать в соответствии с прил. 1 величину критерия Франк-Каменецкого δ0
2.2.2. Подставив полученную величину в уравнение (11) вместо δкр и решив его относительно Т0, найти нулевое приближение для температуры самовозгорания.
2.2.3. По формуле (1) п. 2.1.1 вычислить значение критерия Рэлея для заданного размера упаковки материала.
2.2.4. Рассчитать коэффициент теплоотдачи по уравнению (4) и величину критерия Био по формуле (6).
2.2.5. Определить численное значение функции φ(Bi) по уравнению (7).
2.2.6. По формулам (8) и (9) найти величину параметров β и γ.
2.2.7. Рассчитать критическое значение параметра Франк-Каменецкого по уравнению (10).
2.2.8. Подставить величину δкр в уравнение (11) и найти новое значение температуры Т0.
2.2.9. Используя это значение Т0, повторить расчет параметров по пп. 2.2.2-2.2.8.
2.2.10. Указанную процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения температуры не будут отличаться друг от друга менее чем на 1°С. За критическую температуру принимается результат последнего расчета.
Таблица 5
|
Форма тела |
S0 |
|
Бесконечная пластина толщиной 2r Бесконечный цилиндр радиусом r Бесконечный квадратный стержень, сторона 2r Сфера радиусом r Цилиндр радиусом r высотой 2r Куб, высота 2r Тетраэдр, радиус
вписанной сферы r, сторона Полусфера |
0,88 2,00 1,70 3,32 2,76 2,52 2,23 6,27 |
Примеры расчетов приведены в прил. 2.
2.3. Расчет критического размера
Исходными данными для расчета критического размера упаковки при хранении и транспортировании веществ и материалов являются:
• энергия активации реакции окисления Е, Дж/моль;
• предэкспоненциальный
множитель ![]() , м · К/кг;
, м · К/кг;
• температура хранения, К;
• форма упаковки материала;
• плотность упаковки материала, кг/м3;
• теплоемкость исследуемого материала с, Дж/(кг · К);
• теплота реакции Q, Дж/кг.
Расчет выполняется в следующем порядке.
2.3.1. В соответствии с п. 2.2.1 определить величину параметра δ0.
2.3.2. Для заданной температуры хранения по формулам (8) и (9) вычислить параметры β и γ.
2.3.3. Рассчитать параметр δкр по формуле
2.3.4. В первом приближении минимальный размер найти из выражения
2.3.5. По уравнению (4) вычислить коэффициент теплоотдачи α.
2.3.6. Найти величину параметра Био по формуле (6) и рассчитать значение функции φ(Bi) по уравнению (7).
2.3.7. Определить величину параметра δкр по уравнению (10).
2.3.8. По формуле (16) вычислить новое значение размера упаковки материала.
2.3.9. Используя это значение r, повторить расчет параметров по пп. 2.3.5-2.3.9.
2.3.10. Процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения размеров будут отличаться друг от друга менее чем на 5%. За критический размер принимается результат последнего расчета.
2.4. Расчет времени индукции
Расчет времени индукции производится в том случае, когда хранение или перевозка материалов осуществляется при температуре окружающей среды больше критической.
Исходными данными для расчета являются:
• температура хранения или перевозки материала Т0 , К;
• критическая температура самовозгорания для заданного размера и формы упаковки материала Ткр;
• фактор формы упаковки материала j;
• размер упаковки r, м;
• плотность упаковки материала, кг/м3;
• коэффициент теплопроводности материала λ, Вт/(м · К);
• теплоемкость исследуемого материала с, Дж/(кг · К);
• теплота реакции Q, Дж/кг;
• энергия активации реакции окисления Е, Дж/моль;
• предэкспоненциальный
множитель ![]() , м · К/кг.
, м · К/кг.
Расчет выполняется в следующем порядке.
2.4.1. По температуре Т0 вычислить параметры β и γ с помощью формул (8) и (9).
2.4.2. По уравнению (4) определить коэффициент теплоотдачи α и найти величину параметра Био по формуле (6).
2.4.3. По формуле (11) рассчитать параметр δ, соответствующий температуре хранения T0 , и параметр δкр для критической температуры Ткр.
2.4.4. Вычислить относительное удаление от предела воспламенения
и функции
![]() ; (18)
; (18)
2.4.5. Рассчитать безразмерное время индукции с помощь уравнений (17)-(19) по выражению
![]() . (20)
. (20)
2.4.6. Определить размерное время индукции tИ (с) по формуле
 . (21)
. (21)
3. РАСЧЕТ КРИТИЧЕСКИХ УСЛОВИЙ ДЛЯ ОТЛОЖЕНИЙ ГОРЮЧИХ МАТЕРИАЛОВ
3.1. Критическая температура отложений на нагретой поверхности оборудования
Исходными данными для расчета критической температуры отложений на нагретой поверхности оборудования являются:
• температура среды, в которой образуются отложения, То, К;
• толщина отложений h, м;
• коэффициент теплопроводности материала λ, Вт/(м · К);
• теплоемкость исследуемого материала с, Дж/(кг · К);
• теплота реакции Q, Дж/кг;
• энергия активации реакции окисления Е, Дж/моль;
• предэкспоненциальный
множитель ![]() , м · К/кг.
, м · К/кг.
3.1.1. Принимая в первом приближении величину критерия Bi=4 и температуру нагретой поверхности оборудования ТГ на 200 К больше заданной температуры T0 , вычислить среднюю (между температурами холодной поверхности и газового пространства) температуру Тср по формуле
3.1.2. Рассчитать комплекс g/aν и коэффициент теплопроводности воздуха по уравнениям:
3.1.3. По найденным выше значениям определить другую величину критерия Био по выражению
где
С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз, и 0,54 для горизонтальной пластины, обращенной горячей стороной вверх.
3.1.4. Найденное в п. 3.1.3 значение Bi подставить в формулу (22) и по выражениям (23)-(25) найти новое значение критерия Био. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаться друг от друга менее чем на 10%.
3.1.5. Вычислить безразмерный температурный перепад
параметры
3.1.6. Для температуры ТГ определить параметры
![]() ;
;
![]()
и вычислить критическую величину δ по формуле
3.1.7. Подставить величину δкр в уравнение (11) и найти новое значение температуры ТГ.
3.1.8. Используя это значение ТГ, повторить расчет параметров по пп. 3.1.1-3.1.7.
3.1.9. Указанную процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения температуры не будут отличаться друг от друга менее чем на 1 К. За критическую температуру принимается результат последнего расчета.
3.2. Критическая температура для отложений материала на стенках трубопровода
Исходными данными для расчета критической температуры отложений на нагретой поверхности оборудования являются:
• температура среды снаружи трубопровода T0, К;
• толщина отложений h, м;
• скорость движения среды в трубопроводе V, м/с;
• коэффициент теплопроводности материала λ, Вт/(м · К);
• теплоемкость исследуемого материала с, Дж/(кг · К);
• энергия активации реакции окисления Е, Дж/моль;
• удельное тепловыделение Q, Дж/кг;
• предэкспоненциальный
множитель ![]() , м · К/кг.
, м · К/кг.
3.2.1. Принимая в первом приближении величину критерия Био на холодной стенке слоя Bix=4 и температуру среды внутри трубопровода ТГ на 200 К более T0, вычислить среднюю (между температурами холодной и горячей поверхностей слоя отложений) температуру Tср по формуле
3.2.2. Рассчитать комплекс g/aν и коэффициент теплопроводности воздуха по уравнениям (23) и (24).
3.2.3. По найденным выше значениям определить другую величину критерия Био на холодной стенке:
3.2.4. Найденное в п. 3.2.3 значение Bi подставить в формулу (30) и по выражениям (23), (24), (31) найти новое значение критерия Био. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаться друг от друга менее чем на 10%.
3.2.5. Определить значение кинематической вязкости воздуха по выражению
3.2.6. Вычислить величину критерия Био на горячей стенке слоя по выражению
3.2.7. Рассчитать безразмерный температурный перепад и параметр а по выражениям (26), (27).
3.2.8. Определить параметр δ по формуле
3.2.9. Для температуры ТГ определить параметры р и у; рассчитать критическую величину d по формуле (15).
3.2.10. Подставить величину dкр в уравнение (11) и найти новое значение температуры ТГ.
3.2.11. Используя это значение ТГ, повторить расчет параметров по пп. 3.2.1-3.2.10.
3.2.12. Указанную процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения температуры не будут отличаться друг от друга, менее чем на 1 К. За критическую температуру принимается результат последнего расчета.
3.3. Критический размер отложений на нагретой поверхности оборудования
Исходными данными для расчета критического размера отложений на нагретой поверхности оборудования являются:
• температура поверхности, на которой образуются отложения, ТГ, К;
• температура газовой среды около холодной поверхности слоя T0 , К;
• коэффициент теплопроводности материала l, Вт/(м × К);
• теплоемкость исследуемого материала с, Дж/(кг × К);
• теплота реакции Q, Дж/кг;
• энергия активации реакции окисления Е, Дж/моль;
• предэкспоненциальный множитель Qk0l, м × К/кг.
3.3.1. Принимая в первом приближении величину критерия Bi=5, в соответствии с пп. 3.1.1-3.1.2 определить температуру Tср, комплекс g/av и коэффициент теплопроводности воздуха.
3.3.2.
Принимая значение h равным
3.3.3. Найденное в п. 3.3.2 значение Bi подставить в формулу (22) и по выражениям (23)-(25) найти новое значение критерия Био. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаются друг от друга, менее чем на 10%.
3.3.4. В соответствии с пп. 3.1.5-3.1.6 вычислить безразмерный температурный перепад Q0, параметры а, d, b, g, dкр.
3.3.5. Подставить величину dкр в выражение
и найти новое значение толщины отложений h.
3.3.6. Используя это значение h, вычислить значение Bi в соответствии с пп. 3.1.3-3.1.4.
3.3.7. С учетом полученной величины Bi определить в соответствии с пп. 3.1.5-3.1.6 параметры d и dкр, рассчитать по формуле (35) значение h.
3.3.8. Указанную процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения толщины слоя не будут отличаться друг от друга менее чем на 5%. За критический размер принимается результат последнего расчета.
3.4. Критическая температура для отложений материала в технологическом оборудовании
Исходными данными для расчета критической температуры отложений на внутренней поверхности оборудования являются:
• температура среды в производственном помещении То, К;
• толщина отложений h, м;
• коэффициент теплопроводности материала А,, Вт/(м × К);
• теплоемкость исследуемого материала с , Дж/(кг × К);
• энергия активации реакции окисления Е , Дж/моль;
• удельное тепловыделение Q, Дж/кг;
• предэкспоненциальный множитель Qk0r /l, м × К /кг.
3.4.1. Принять в первом приближении величину критерия Био на холодной стенке BiX=2, значение критерия Био на горячей стенке BiГ=4, температуру среды в технологическом оборудовании ТГ на 200 К больше T0 . Вычислить среднюю (между температурами холодной поверхности и прилегающего газового пространства) температуру по формуле
где
![]() .
.
3.4.2. Рассчитать комплекс g/av и коэффициент теплопроводности воздуха около холодной стенки по уравнениям (23) и (24).
3.4.3. По найденным выше значениям определить другую величину критерия Био на холодной стенке по уравнению
где
С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз, и 0,54 для горизонтальной пластины, обращенной горячей стороной вверх.
3.4.4. Найденное в п. 3.4.3 значение BiX подставить в формулу (36) и по выражениям (23), (24) и (37) найти новое значение критерия Био. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаться друг от друга менее чем на 10%.
3.4.5. С учетом последних значений критерия Био вычислить среднюю (между температурами горячей поверхности и прилегающего газового пространства) температуру по формуле
где
![]() .
.
3.4.6. Рассчитать комплекс g/av и коэффициент теплопроводности воздуха около горячей стенки по уравнениям (23) и (24).
3.4.7. По найденным выше значениям определить другую величину критерия Био на горячей стенке по выражению
3.4.8. Найденное в п. 3.4.7 значение BiХ подставить в формулу (38) и по уравнениям (23), (24) и (39) найти новое значение критерия Био. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаться друг от друга менее чем на 10%.
3.4.9. Подставить последнее значение BiГ в формулу (36) и по уравнениям (23), (24) и (37) найти новое значение критерия BiХ. Процесс итераций продолжать до тех пор, пока последняя и предыдущая величины не будут отличаться друг от друга менее чем на 10%.
3.4.10. Рассчитать безразмерный температурный перепад, параметры а и d по выражениям (26), (27) и (34).
3.4.11. Для температуры ТГ определить параметры b и g, вычислить критическую величину d по формуле (15).
3.4.12. Подставить величину dкр в уравнение (11) и найти новое значение температуры ТГ.
3.4.13. Используя это значение ТГ, повторить расчет параметров по пп. 3.4.1-3.4.12.
3.4.14. Указанную процедуру расчета продолжать до тех пор, пока предыдущее и последующее значения температуры не будут отличаться друг от друга менее чем на 1 К. За критическую температуру, принимается результат последнего расчета.
ПРИЛОЖЕНИЕ 1
1. Расчет критерия Франк-Каменецкого d0 для некоторых форм упаковок материалов
1.
Вычисляют отношение квадрата характерного размера тела r2 (например, минимального размера тела по одной из осей
координат) к квадрату эквивалентной сферы Франк-Каменецкого ![]() по одному из
приведенных ниже соотношений.
по одному из
приведенных ниже соотношений.
Бесконечный прямоугольный стержень поперечным сечением 2а х 2b, р=b/а:
![]() . (П1)
. (П1)
Характерный размер r - половина наименьшей из трех сторон стержня а .
Бесконечный квадратный стержень (р=1):
Прямоугольный цилиндр радиусом r, высотой 2d, p=r/d:
 . (П3)
. (П3)
Круговой цилиндр с полусферическими днищами, радиус цилиндра r равен радиусу днищ, длина цилиндрической части 2d, p=r/d:
 . (П4)
. (П4)
Эллипсоид с полуосями а, b и с (а - наименьшая из полуосей):
![]() . (П5)
. (П5)
Усеченный эллипсоид вращения высотой 2d, радиусом r, радиус сечения эллипсоида плоскостью а:
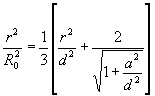 . (П6)
. (П6)
Если r/d ® 1 и а ® 0, поверхность усеченного эллипсоида преобразуется в сферу.
Многоугольный цилиндр высотой 2d, радиус вписанной окружности r, число сторон п, р=r/d:
![]() , (П7)
, (П7)
где
 .
.
Бесконечный многоугольный цилиндр, d/r ® ¥
![]() . (П8)
. (П8)
Тонкий многоугольный цилиндр, d/r ® ¥:
![]() (плоская плита
с полутолщиной d). (П9)
(плоская плита
с полутолщиной d). (П9)
Прямоугольный брус со сторонами 2а, 1b, 2с, р=b/a, q=с/а:
где
 .
.
Квадратный брус, а=с, q=1, b=pa:
из уравнения (П10):
 . (П11)
. (П11)
2. Находят радиус эквивалентной сферы Семенова по формуле
где
V - объем упаковки материала, м3;
S - ее внешняя поверхность, м2.
3. Определяют отношение квадратов радиуса эквивалентных сфер Франк-Каменецкого и Семенова:
4. Вычисляют фактор формы для заданной геометрии упаковки материала:
5. Находят функцию F(j) по формуле
6. Рассчитывают величину параметра Франк-Каменецкого с помощью формулы
2. Пример расчета параметра d0 для бесконечного квадратного стержня
1. Для квадратного стержня со стороной а в соответствии с формулой (П2)
2. Радиус эквивалентной сферы Семенова определим по формуле (П12):
![]() , или
, или ![]() . (П18)
. (П18)
3. Из выражения (П13) с учетом формул (П17) и (П18) найдем отношение квадратов радиусов эквивалентных сфер Франк-Каменецкого и Семенова:
4. Численную величину фактора формы для бесконечного квадратного стержня получим с помощью формул (П14) и (П19):
5. Вычислим функцию F(j) по уравнениям (П15) и (П20):
6. Величину параметра Франк-Каменецкого d0 для квадратного бесконечного стержня найдем с помощью формулы (П16) и значений функций (П17) и (П21):
![]() .
.
Точное значение этого параметра, полученное численным методом, равно 1,70.
ПРИЛОЖЕНИЕ 2
1. Пример расчета кинетических параметров реакции окисления
Рассчитать энергию активации и предэкспоненциальный множитель для реакции окисления хлопка по экспериментальным данным, приведенным в первых двух графах табл. П 2.1.
Коэффициент теплопроводности хлопка l=0,042 Вт/(м × К); теплоемкость с=1505 Дж/(кг × К); тепловой эффект реакции Q=1,75 × 107 Дж/кг; плотность упаковки материала r=80 кг/м3.
Расчет
проведем для образца размером D=
Данные для других размеров получим, повторяя приведенную ниже последовательность расчета.
1. По уравнениям (1) и (2) для каждого размера образца вычислим числа Рэлея.
Принимая в первом приближении энергию активации Е=100000 Дж/моль, для
образца размером D=
![]()
2. Коэффициент теплоотдачи a найдем по уравнению (3):
![]()
![]() Вт/(м2 × К),
Вт/(м2 × К),
где теплопроводность воздуха определена по формуле (5):
![]() Вт/(м ×
К).
Вт/(м ×
К).
3. Вычислим критерий Био, соответствующий размеру и коэффициенту теплоотдачи для каждого образца:
![]() .
.
4. Величина функции j(Bi), учитывающей интенсивность теплообмена образца с воздухом, для полученного значения Bi составит:
![]()
 .
.
5. Рассчитаем параметры b и g:
![]() ;
;
![]()
6. Критическое значение параметра Франк-Каменецкого будет равно:
![]()
![]() ,
,
где d0 - критическая величина параметра d, соответствующая интенсивному теплообмену, для образцов кубической формы равная 2,52. Результаты вычислений для всех образцов представлены в табл. П 2.1.
Таблица П 2.1
|
Размер r, м |
T0, К |
Ra |
a, Вт/(м2×К) |
Bi |
j(Bi) |
b×10-2 |
g×10-3 |
dкр |
|
0,0175 |
485 |
7978 |
31,4 |
13,1 |
0,863 |
4,00 |
1,68 |
2,34 |
|
0,025 |
475 |
24599 |
29,4 |
17,5 |
0,895 |
3,95 |
1,61 |
2,42 |
|
0,035 |
466 |
71161 |
27,6 |
23,0 |
0,918 |
3,87 |
1,55 |
2,48 |
|
0,05 |
456 |
260650 |
25,9 |
30,8 |
0,938 |
3,79 |
1,49 |
2,53 |
|
0,07 |
445 |
646034 |
24,0 |
40,0 |
0,952 |
3,70 |
1,42 |
2,56 |
|
0,10 |
436 |
2016710 |
22,4 |
53,3 |
0,964 |
3,62 |
1,36 |
2,59 |
7. По уравнению (13) для каждого размера образца рассчитаем величину М:
 .
.
8. С помощью этих значений и уравнения (12) методом наименьших квадратов определим численные значения N и энергию активации Е.
9. Вычислим предэкспоненциальный множитель реакции окисления Qk0/l, путем деления N на Е. Данные расчетов по пп. 7-9 сведем в табл. П 2.2.
Таблица П 2.2
|
Размер r, м |
T0, К |
М,
|
N,
|
Е, Дж/моль |
Qk0/l, |
|
м × К/кг |
|||||
|
0,0175 |
485 |
1,87 × 108 |
1,38 × 1022 |
128 980 |
1,07 × 1017 |
|
0,025 |
475 |
9,08 × 107 |
|||
|
0,035 |
466 |
4,57 × 107 |
|||
|
0,05 |
456 |
2,19 × 107 |
|||
|
0,07 |
446 |
1,08 × 107 |
|||
|
0,10 |
436 |
5,12 × 106 |
10. Повторяя расчет по пп. 1
- 9 с величиной энергии активации Е=128980, найдем новые значения энергии
активации Е=128950 Дж/моль и предэкспоненциального множителя Qk0/l=1,05 ×
2. Пример расчета критической температуры
Рассчитать
критическую температуру окружающей среды при транспортировании костной муки в
железнодорожных вагонах. Вагон представляет собой параллелепипед шириной
Исходными данными для расчета являются:
• плотность материала r=660 кг/м3;
• коэффициент теплопроводности материала l=0,14 Вт/(м × К);
• теплоемкость исследуемого материала с=780 Дж/(кг × К);
• теплота реакции Q=350 000 Дж/кг;
• энергия активации реакции окисления Е=50 740 Дж/моль;
• предэкспоненциальный множитель Qk0/l=2,46 ×
1. Для заданной формы и размеров вагона определим в соответствии с прил. 1 величину критерия Франк-Каменецкого d0.
2. Отношение квадратов полувысоты вагона к эквивалентной сфере Франк-Каменецкого рассчитаем как для прямоугольного бруса по выражению (П10):
 ,
,
где 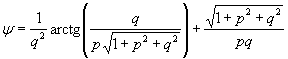 ;
;
a, b,c - половины сторон бруса, а - наименьшая сторона; р=b/a, q=с/а.
Подставляя р, q в эти равенства, получим:
![]() .
.
3. Средний радиус эквивалентной сферы Семенова равен:
![]() ,
,
где V, S - объем и поверхность грузового пространства вагона.
4. На основании (П19) и двух последних выражений отношение квадратов радиусов эквивалентных сфер Франк-Каменецкого и Семенова составит
![]() .
.
5. Фактор формы прямоугольного бруса по (П14) равен:
![]() .
.
6. Согласно (П15) функция F(j) будет равна:
![]() .
.
7. В соответствии с (П16) параметр d0 составит:
![]() .
.
8. Подставим полученную величину d0 в формулу
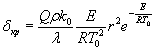
вместо dкр и, решив ее относительно Т0, получим нулевое приближение для этой температуры, равное 260 К.
9. С помощью полученной величины рассчитаем:
 - параметр, определяющий выгорание вещества;
- параметр, определяющий выгорание вещества;
![]() - параметр, характеризующий реакцию окисления.
- параметр, характеризующий реакцию окисления.
10. Так
как для размеров упаковок, превышающих
![]() .
.
11. Решив уравнение (11) относительно температуры, получим Т0=263 К (или -10°С). Следовательно, при перевозке костной муки в железнодорожных вагонах при температуре воздуха, превышающей -10°С, возможно самовозгорание транспортируемого продукта.
3. Пример расчета критического размера
Рассчитать минимальный безопасный размер насыпи при транспортировании костной муки в железнодорожных вагонах.
Расчет проведем для верхней границы диапазона климатического перепада температур воздуха в средней полосе России, равной 40°С, или 313 К.
Исходными данными для расчета критического размера являются:
• плотность упаковки материала r=660 кг/м3;
• коэффициент теплопроводности материала l=0,14 Вт/(м × К);
• теплоемкость исследуемого материала с=780 Дж/(кг × К);
• теплота реакции Q=350 000 Дж/кг;
• энергия активации реакции окисления Е=50 740 Дж/моль;
• предэкспоненциальный множитель Qk0/l=2,46 ×
1. Выполнив расчет в соответствии с пп. 1-7 предыдущего примера, найдем, что d0=1,78.
2. Для температуры Т0 =313 К вычислим параметры b и g по уравнениям (8) и (9):
![]() ;
;
 .
.
3. Считая j(Bi)=1, определим параметр dкр по формуле
![]() .
.
4. В первом приближении минимальный размер найдем из выражения (16):
 м.
м.
5. По уравнениям (1) и (2) для полученного размера вычислим число Рэлея:
![]() .
.
6. Коэффициент теплоотдачи a найдем по уравнению (4):
![]()
![]() Вт/(м ×
К).
Вт/(м ×
К).
где теплопроводность воздуха определена по формуле (5):
![]() Вт/(м ×
К).
Вт/(м ×
К).
7. Вычислим критерий Био, соответствующий размеру и коэффициенту теплоотдачи для каждого образца:
![]() .
.
8. Величина функции j(Bi), учитывающей интенсивность теплообмена образца с воздухом, для полученного значения Bi составит:
![]()
 .
.
9. Критическое значение параметра Франк-Каменецкого будет равно:
![]() .
.
10. По формуле (16) вычислим новое значение размера насыпи материала:
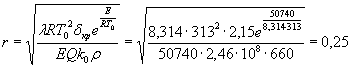 .
.
11. Сравнивая это значение r с его величиной, полученной в п. 5, видим, что учет интенсивности теплообмена практически не изменил значения критического размена. Перевозка костной муки в железнодорожных вагонах насыпью представляет опасность самовозгорания этого продукта.
4. Пример расчета времени индукции
Рассчитать время индукции при перевозке костной муки в вагоне при температуре 20°С (293 К).
Исходными данными для расчета являются:
• температура перевозки материала Т0=293 К;
• критическая температура самовозгорания для заданного размера и формы упаковки материала Ткр=263 К;
• фактор формы упаковки материала j=1,11;
• размер упаковки r=
• плотность упаковки материала r=660 кг/м3;
• коэффициент теплопроводности материала l=0,14 Вт/(м × К);
• теплоемкость исследуемого материала с=780 Дж/(кг × К);
• теплота реакции Q=350 000 Дж/кг;
• энергия активации реакции окисления Е=50 740 Дж/моль;
• предэкспоненциальныи множитель Qk0/l=2,46 ×
1. По температуре Т0 вычислим параметры b и g с помощью формул (8) и (9):
![]() ;
;
![]() .
.
2. По уравнениям (1) и (2) найдем число Рэлея:
![]() .
.
3. Коэффициент теплоотдачи a определим по уравнению (4):
![]()
![]() Вт/(м ×
К).
Вт/(м ×
К).
где теплопроводность воздуха определена по формуле (5):
![]() Вт/(м ×
К).
Вт/(м ×
К).
4. Вычислим критерий Био, соответствующий размеру и коэффициенту теплоотдачи для каждого образца:
![]() .
.
5. По формуле (11) рассчитаем параметр d, соответствующий температуре хранения Т0 , и параметр dкр

![]() ;
;
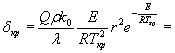
![]()
6. Вычислим относительное удаление от предела воспламенения:
![]()
и функции
![]()
![]()
![]() .
.
7. Рассчитаем безразмерное время индукции:
![]() .
.
8. Определим размерное время индукции tИ(с) по формуле
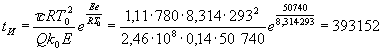 с=109,2 ч=4,55
суток.
с=109,2 ч=4,55
суток.
5. Пример расчета критической температуры нагретой поверхности оборудования для отложений веществ
Рассчитать
критическую температуру наружной поверхности электрооборудования для отложений
шламовой муки толщиной
Исходными данными для расчета критической температуры отложений на нагретой поверхности оборудования являются:
• температура среды, в которой образуются отложения, Т0=300 К;
• толщина отложений h=
• коэффициент теплопроводности материала l=0,055 Вт/(м × К);
• теплоемкость исследуемого материала с=1550 Дж/(кг × К);
• энергия активации реакции окисления Е =66 597 Дж/моль;
• удельное тепловыделение Q=349 637 Дж/кг;
• предэкспоненциальный множитель Qk0/l=2,55
×
1. Принимая в первом приближении величину критерия Bi=4 и температуру нагретой поверхности оборудования ТГ равной 500 К, вычислим среднюю (между температурами нагретой поверхности и газового пространства) температуру Тср по формуле (22):
![]() .
.
2. Рассчитаем комплекс g/av и коэффициент теплопроводности воздуха по уравнениям (23) и (24):
![]() ;
;
![]() .
.
3. По найденным выше значениям определим другую величину критерия Био по выражению (25):
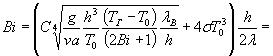

![]() ,
,
где С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз (принимаем в нашем случае как наиболее жесткий вариант).
4. Найденное в п. 3 значение Bi отличается от принятого в п. 1 более чем на 10%. Подставим последнее значение Bi в формулы (22)-(25) и получим величину Bi =1,15. Так как это значение отличается от предыдущего более чем на 10%, подставим последнее значение Bi в формулы (22)-(25) и получим величину Bi =1,14.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина Bi =1,14.
5. Произведем вычисления по формулам (26)-(28):
![]() ;
;
![]() ;
;
![]()
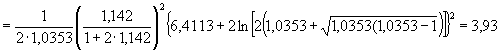 .
.
6. Для температуры ТГ определим параметры b, g и вычислим критическую величину d:
![]() ;
;
![]() ;
;
![]() .
.
7. Подставим величину dкр в уравнение (11) и найдем новое значение температуры: ТГ=544 К.
8. Используя это значение ТГ, повторим расчет параметров по пп. 1-7. Найдем новое значение температуры: ТГ=549 К.
Используя это значение ТГ, повторим расчет параметров по пп. 1-7. Найдем новое значение температуры: ТГ=549,5 К.
9. Так как предыдущее и последнее значения температуры отличаются друг от друга менее чем на 1°С, за критическую температуру примем результат последнего расчета.
6. Пример расчета критической температуры среды в воздуховоде для отложений материалов
Рассчитать
критическую температуру газовой среды внутри воздуховода для отложений шламовой
муки толщиной
Исходными данными для расчета критической температуры отложений на нагретой поверхности оборудования являются:
• температура внутренней поверхности воздуховода Т0=300 К;
• толщина отложений h=
• внутренний диаметр воздуховода D=
• скорость движения среды в воздуховоде V= 1 м/с;
• коэффициент теплопроводности материала l=0,055 Вт/(м × К);
• теплоемкость исследуемого материала с=1550 Дж/(кг × К);
• энергия активации реакции окисления Е== 66 597 Дж/моль;
• удельное тепловыделение Q=349 637 Дж/кг;
• предэкспоненциальный множитель Qk0r/l= 2,55 × 1013 К/м2.
1. Принимая в первом приближении величину критерия Био на холодной стенке слоя Bix=4 и температуру газовой среды внутри воздуховода ТГ равной 530 К, вычислим среднюю (между температурами холодной поверхности и газового пространства) температуру Тср по формуле (30):
![]() К.
К.
2. Рассчитаем комплекс g/аv и коэффициент теплопроводности воздуха по уравнениям (23) и (24):
![]() ;
;
![]() .
.
3. По найденным выше значениям определим другую величину критерия Био на холодной стенке по выражению (31):
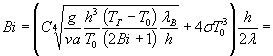

![]()
Найденное значение Bix отличается от принятого ранее более чем на 10%. Подставим последнее значение Bix в формулы (30), (23), (24), (31) и получим новую величину Bix=1,71. Найденное значение Bix отличается от принятого ранее более чем на10%. Подставим последнее значение Bix в формулы (29), (23), (24), (30) и получим новую величину Bix=1,69.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина Bix=1,69.
4. Определим значение кинематической вязкости воздуха по выражению (32):
![]()
![]() .
.
5. Вычислим величину критерия Био на горячей стенке слоя по формуле (33):

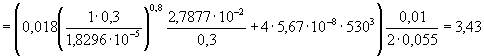 .
.
6. Произведем вычисления по формулам (26), (27) и (34):
![]() ;
;
![]() ;
;

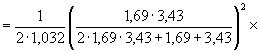
![]() .
.
7. Для температуры ТГ определим параметры b, g и вычислим критическую величину d:
![]() ;
;
![]() ;
;
![]() .
.
8. Подставим величину dкр в уравнение (11) и найдем новое значение температуры: ТГ=537 К.
9. Используя это значение ТГ, повторим расчет по пп. 1-8 и найдем новое значение температуры: ТГ=539 К.
Используя это значение ТГ, повторим расчет по пп. 1-8 и найдем новое значение температуры: ТГ=539,9 К.
Так как предыдущее и последнее значения температуры отличаются друг от друга менее чем на 1 К, примем последнее значение за критическую температуру.
7. Пример расчета критической температуры нагрева тепловой изоляции технологического трубопровода
Рассчитать
критическую температуру наружной поверхности технологического трубопровода для
теплоизоляции толщиной
Исходными данными для расчета критической температуры являются:
• температура окружающей среды Т0=300 К;
• скорость движения воздуха внутри трубопровода V= 1 м/с;
• толщина теплоизоляции h=
• коэффициент теплопроводности материала l=0,055 Вт/(м × К);
• теплоемкость исследуемого материала с=1550 Дж/(кг × К);
• энергия активации реакции окисления Е=66597 Дж/моль;
• удельное тепловыделение Q=349637 Дж/кг;
• предэкспоненциальный множитель Qk0r/l= 2,55 × 1013 К/м2.
1. Принимая в первом приближении величину критерия Био на холодной стенке слоя Bix=4 и температуру нагретой технологической трубы ТГ=500 К (равной температуре среды внутри трубопровода), вычислим среднюю (между температурами холодной и горячей поверхности слоя) температуру Тср по формуле (30):
![]()
2. Рассчитаем комплекс g/av и коэффициент теплопроводности воздуха по уравнениям (23) и (24):
![]() ;
;
![]() .
.
3. По найденным выше значениям определим другую величину критерия Био на холодной стенке слоя по выражению (31):


![]() .
.
Найденное значение Bix отличается от принятого ранее более чем на 10%. Подставим последнее значение Bix в формулы (30), (23), (24), (31) и получим новую величину Bix=2,28.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина Bix=2,28.
4. Определим значение кинематической вязкости воздуха по выражению (32):
![]()
![]() .
.
5. Вычислим величину критерия Био на горячей стенке слоя по формуле (33):
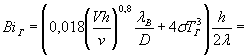
 .
.
6. Произведем вычисления по формулам (26), (27) и (34):
![]() ;
;
![]() ;
;
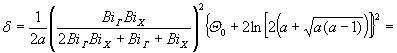
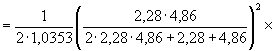
![]() .
.
7. Для температуры ТГ определим параметры b, g и вычислим критическую величину d:
![]() ;
;
![]() ;
;
![]() .
.
8. Подставим величину dкр в уравнение (11) и найдем новое значение температуры: ТГ=518 К.
9. Используя это значение ТГ, повторим расчет по пп. 1-8 и найдем новое значение температуры: ТГ=521 К.
Используя это значение ТГ, повторим расчет по пп. 1-8 и найдем новое значение температуры: ТГ=521 К.
Так как предыдущее и последнее значения температуры не отличаются друг от друга, принимаем последнее значение за критическую температуру.
8. Пример расчета критического размера отложений вещества на нагретой поверхности оборудования
Исходными данными для расчета критического размера отложений на нагретой поверхности оборудования являются:
• температура поверхности, на которой образуются отложения, ТГ=530 К;
• температура газовой среды около холодной поверхности слоя T0=300 К;
• коэффициент теплопроводности материала l=0,055 Вт/(м × К);
• теплоемкость исследуемого материала с=1550 Дж/(кг × К);
• теплота реакции Q=349637 Дж/кг;
• энергия активации реакции окисления Е=66597 Дж/моль;
• предэкспоненциальный множитель Qk0r/l= 2,55 × 1013 К/м2.
1. Принимая в первом приближении величину критерия Bi=4, в соответствии с формулами (22)-(24) определим температуру Тср, комплекс g/av и коэффициент теплопроводности воздуха:
![]() К;
К;
![]() ;
;
![]() .
.
2. Принимая значение h равным

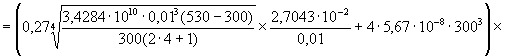
![]() ,
,
где С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз (принимаем в нашем случае как наиболее жесткий вариант в пространстве сушилки).
3. Найденное в п. 2 значение Bi отличается от принятого в п. 1 более чем на 10%. Подставим последнее значение Bi в формулу (22) и по выражениям (23)-(25) найдем другую величину Bi =1,17.
Найденное значение Bi отличается от предыдущего более чем на 10%. Подставим последнее значение Bi в формулу (22) и по выражениям (23)-(25) найдем другую величину Bi=1,157.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина Bi =1,157.
4. В соответствии с выражениями (26)-(28) вычислим безразмерный температурный перепад Q0, а также параметры a, d, b, g, dкр :
![]() ;
;
![]() ;
;
![]()
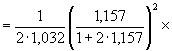
![]() .
.
5. Для температуры ТГ определим параметры b, g и вычислим критическую величину d:
![]() ;
;
![]() ;
;
![]() .
.
6. Подставим величину dкр в выражение (34):
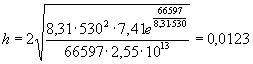 м.
м.
7.
Полученное значение толщины слоя более чем на 5% отличается от предыдущего.
Используя последнее значение h, производим вычисления по пп. 1-6 и определяем
следующее значение: h=
Так как предыдущее и последнее значения толщины слоя отличаются друг от друга менее чем на 5%, за критический размер принимается результат последнего расчета.
9. Пример расчета критической температуры для отложений веществ в технологическом оборудовании
Рассчитать
критическую температуру газовой среды внутри технологического аппарата для
отложений шламовой муки толщиной
Исходными данными для расчета критической температуры отложений на внутренней поверхности оборудования являются:
• температура среды в производственном помещении T0=300 К;
• толщина отложений h =0,01 м;
• коэффициент теплопроводности материала l=0,055 Вт/(м × К);
• теплоемкость исследуемого материала с=1550 Дж/(кг × К);
• энергия активации реакции окисления Е=66597 Дж/моль;
• удельное тепловыделение Q=349 637 Дж/кг;
• предэкспоненциальный множитель Qk0r/l= 2,55 × 1013 К/м2.
1. Принимая в первом приближении величину критерия Био на холодной стенке Bix=2, значение критерия Био на горячей стенке BiГ=4, температуру среды в технологическом оборудовании ТГ равной 500 К, вычислим среднюю (между температурами холодной поверхности и прилегающего газового пространства) температуру по формуле (36):
![]() К.
К.
2. Рассчитаем комплекс g/av и коэффициент теплопроводности воздуха около холодной стенки по уравнениям (23) и (24):
![]() ;
;
![]() .
.
3. По найденным выше значениям определим другую величину критерия Био на холодной стенке по выражению (37):

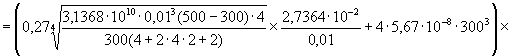
![]() ,
,
где С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз (принимаем в нашем случае как наиболее жесткий вариант в пространстве аппарата).
4. Найденное в п. 3 значение Bix отличается от принятого в п. 1 более чем на 10%. Подставим последнее значение Bix в формулу (36):
![]() ;
;
![]() ;
;
![]() ;
;


![]() .
.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина Bix=1,137.
5. С учетом последних значений критерия Био вычислим среднюю (между температурами горячей поверхности и прилегающего газового пространства) температуру по формуле (38):
![]()
 .
.
6. Рассчитаем комплекс g/аv и коэффициент теплопроводности воздуха около горячей стенки по уравнениям (23) и (24):
![]() ;
;
![]() .
.
7. По найденным выше значениям определим другую величину критерия Био на горячей стенке по выражению (39):

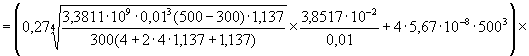
![]() ,
,
где С - коэффициент, равный 0,27 для горизонтальной пластины, обращенной горячей стороной вниз (принимаем в нашем случае как наиболее жесткий вариант в пространстве аппарата).
8. Найденное в п. 7 значение BiГ отличается от принятого в п. 1 более чем на 10%. Подставим последнее значение BiГ в формулу (38):
![]()
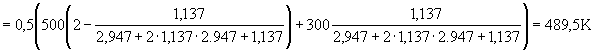 .
.
Рассчитаем комплекс g/av и коэффициент теплопроводности воздуха около горячей стенки по уравнениям (23) и (24):
![]() ;
;
![]() .
.
По найденным выше значениям определим другую величину критерия Био на горячей стенке по выражению (39):


![]() .
.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина BiГ=2,973.
9. Подставляем последнее значение BiГ в формулу (36):
![]() ;
;
![]() ;
;
![]() ;
;


![]() .
.
Так как последняя и предыдущая величины отличаются друг от друга менее чем на 10%, в дальнейших расчетах используется величина BiХ=1,131.
10. Произведем вычисления по формулам (26), (27), (34):
![]() ;
;
![]() ;
;

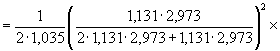
![]() .
.
11. Для температуры ТГ определим параметры
![]() ;
;
![]()
и вычислим критическую величину d:
![]() .
.
12. Подставим величину dкр в уравнение (11) и найдем новое значение температуры ТГ:
 ,
,
откуда ТГ=535 К.
13. Используя это значение ТГ, повторяем расчет параметров по пп. 1-12 и получаем новую величину: ТГ=540 К.
Используя это значение ТГ, повторяем расчет параметров по пп. 1-12 и получаем новую величину: ТГ=540,6 К.
Так как предыдущее и последнее значения температуры отличаются друг от друга менее чем на 1°С, принимаем последнюю величину за критическую температуру.

 .
.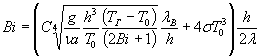 ,
, .
. .
.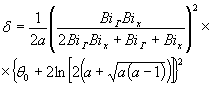 .
.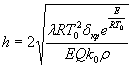 .
. .
. .
. .
.