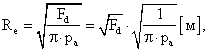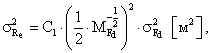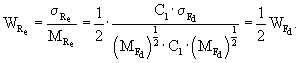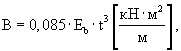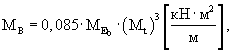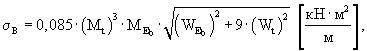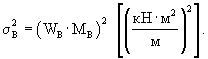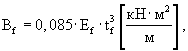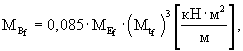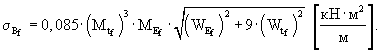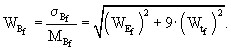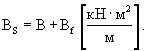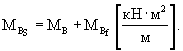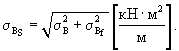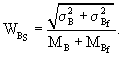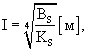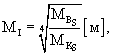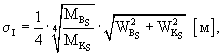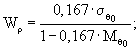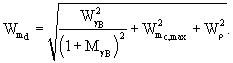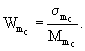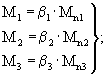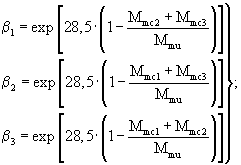МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Кафедра аэропортов
Утверждаю
Зав. кафедрой, профессор
___________ А.П. Степушин
15 апреля 2002 г.
В.Д. САДОВОЙ, В.А. ВИНОГРАДОВ
НАДЕЖНОСТЬ ЖЕСТКИХ АЭРОДРОМНЫХ ПОКРЫТИЙ
Методические указания
МОСКВА 2002
Методические указания содержат методику прогноза надежности проектируемых конструкций жестких покрытий аэродромов гражданской авиации, используемую при выполнении студентами курсового проекта по дисциплине «Экономико-математические методы проектирования аэропортов», изучаемой по специальности 291000 - Автомобильные дороги и аэродромы (специализация 291003 - Аэродромы), а также по дисциплине «Теория надежности и диагностика аэродромных сооружений», изучаемой по магистерской программе 550120 «Строительство и эксплуатация аэропортов и аэродромов».
Рассмотрено и рекомендовано на заседании кафедры «Аэропорты» и учебно-методического Совета факультета «Автомобильные дороги и аэродромы» МАДИ (ГТУ).
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
При проектировании аэродромных сооружений и конструкций процесс принятия инженерных решений сопряжен с необходимостью учета статистической изменчивости физико-механических характеристик материалов, с одной стороны, и силовых воздействий на сооружение - с другой. Поэтому обоснование оптимальных конструктивных параметров аэродромных сооружений и обеспечение их надежности возможно лишь на основе применения вероятностных методов. Цель методических указаний «Надежность жестких аэродромных покрытий» заключается в том, чтобы помочь инженеру или исследователю оценить уровень надежности принимаемого решения и степень экономического риска на стадии проектирования аэродромных покрытий.
Традиционный детерминированный подход к расчету конструкций аэродромных покрытий состоит, как известно, из двух этапов. На первом этапе определяют предельные значения внешних нагрузок и соответствующие параметры напряженно-деформированного состояния конструкции. На втором этапе сопоставляют вычисленные напряжения и деформации в конструкции с предельно допускаемыми значениями, вычисленными с учетом коэффициента условий работы. Будучи элементарным, второй этап расчета является в то же время весьма важным и ответственным. Именно на этом этапе косвенными методами решается вопрос о надежности и долговечности аэродромного покрытия.
Инженерная теория надежности аэродромных покрытий позволяет наряду с прогнозированием и регулированием процесса накопления повреждений в покрытии во время эксплуатации проводить сравнение и выбор оптимального варианта из ряда конкурирующих конструкций на стадии проектирования. Важным аспектом теории надежности является то, что она служит теоретической базой для обоснованного назначения численных величин расчетных параметров аэродромных покрытий и уточнения нормативного метода проектирования и эксплуатационной оценки несущей способности на различных этапах работы этих сооружений.
Целью курсового проекта (работы) является оценка надежности аэродромного покрытия жесткого типа на стадии проектирования и прогноз его технического состояния, которое характеризуется рядом качественных и количественных показателей:
- долговечность (характеризует предельный срок службы с момента ввода покрытия в эксплуатацию до момента наступления его предельного состояния);
- надежность (характеризует свойство сооружения сохранять долговечность на определенном интервале времени эксплуатации);
- работоспособность отдельной плиты или элемента площади покрытия - способность воспринимать воздействующие силовые факторы без разрушения или отказа определенного вида;
- отказ плиты или элемента площади покрытия характеризуется возникновением определенного вида повреждений или разрушений;
- отказ сооружения (покрытия в целом) - событие, когда невозможна дальнейшая эффективная и безопасная эксплуатация сооружения (предельное состояние покрытия по уровню повреждения);
- уровень повреждения покрытия - интегральная характеристика отказов плит (элементов) покрытия определенного вида;
- ресурс покрытия - характеристика объема (количества) движения воздушных судов, соответствующая предельному состоянию покрытия и сроку службы;
- ремонтопригодность - способность сооружения к восстановлению эксплуатационных качеств.
При определении надежности сооружения необходимо учитывать случайный характер воздействия эксплуатационных нагрузок, природно-климатических факторов, прочностных и деформационных характеристик материалов, а также геометрических параметров конструкций. При этом следует учитывать теоретические связи между перечисленными факторами, которые, как правило, имеют нелинейный вид в математическом смысле. Поэтому для определения статистических характеристик распределения значений расчетных параметров, характеризующих функциональное состояние сооружения или его элементов и зависящих от воздействующих факторов со случайной природой, приходится применять известный метод линеаризации нелинейных функций [1,2,8].
Сущность метода линеаризации нелинейной функции от нескольких случайных независимых аргументов состоит в том, чтобы разложить нелинейную случайную функцию в окрестности ее математического ожидания в ряд Тейлора, ограничив это разложение только линейными членами, т.е. представить нелинейную случайную функцию Z в виде:
|
|
(1) |
где φ(х1,х2,…) - нелинейная функция от независимых случайных аргументов х1,х2,…;
Мх1,Мх2,… - среднее значение (оценка математического ожидания) случайных аргументов х1,х2,…;
![]() и т.д. - значение частной производной первого
порядка функции φ
по аргументам х1,х2,… в области их средних значений.
и т.д. - значение частной производной первого
порядка функции φ
по аргументам х1,х2,… в области их средних значений.
На основании представления величины Z в виде (1) можно выразить статистические характеристики распределения ее случайных значений через соответствующие характеристики распределения случайных аргументов, а именно:
|
|
(2) |
где Mz, σz,Wz - соответственно среднее значение М, дисперсия σ2 и коэффициент вариации W величины Z;
Мх1,Мх2,…, σx1,σx2 - соответственно среднее значение М и стандарт разброса σ значений аргументов х1,х2,….
В курсовом проекте, посвященном прогнозу надежности проектируемых жестких аэродромных покрытий, широко применяются формулы (2). При этом, если специально не оговорено, символами М, σ, W обозначаются соответствующие статистические характеристики распределения случайных величин: среднее значение, стандарт и коэффициент вариации.
Проект включает выполнение следующих разделов:
- определение жесткостных характеристик покрытия;
- определение характеристик распределения транспортных и температурных нагрузок на аэродромное покрытие;
- определение характеристик напряженно-деформированного состояния покрытия;
- определение количества приложений самолетных нагрузок на разные участки покрытия;
- оценка уровня надежности и ресурса работы покрытия;
- заключение о расчетном уровне надежности проектируемого покрытия, прогноз технического состояния на проектный срок службы и рекомендации по оптимизации режима эксплуатации покрытия.
Оценка надежности конструкции аэродромного покрытия на стадии его проектирования может быть выполнена расчетно-теоретическим методом на основе исходной информации о статистических характеристиках распределения значений расчетных параметров. Всеобъемлющей и систематизированной такой информации к настоящему времени накоплено еще недостаточно, поэтому приходится довольствоваться в некотором смысле условными рекомендациями, построенными на обобщении известных данных нормативных документов по проектированию аэродромов [3,4], а также результатов исследований, выполненных по направлению работоспособности и срокам службы аэродромных покрытий [5-9].
Следует отметить, что для получения конкретных численных значений статистических характеристик расчетных параметров в настоящих методических указаниях использовано известное в математической статистике правило «трех сигм», что и определяет их некоторую условность. Вместе с тем, для решения поставленной задачи в учебных целях и, в особенности, для обеспечения ее многовариантности, в указаниях приведен в качестве ориентиров для исходных данных интервал изменения возможных значений характеристик статистической изменчивости расчетных параметров. При этом последовательность процедур или методика аналитического расчета надежности аэродромных покрытий сохраняется неизменной. В дальнейшем, по мере накопления надежной информации, поставляемой практикой строительства и эксплуатации аэродромных сооружений, исходные данные должны корректироваться.
Условные обозначения исходных данных
1. Группа участков покрытий аэродрома - А, Б, В.
2. Тип аэродромного покрытия - жесткое.
3. Коэффициент постели грунтового основания (Ks):
-
среднее значение 
- коэффициент вариации WKs=0,12…0,15.
4. Пескоцементное основание (tf,Ef,):
- средняя толщина Мtf=20…32 см;
- коэффициент вариации Wtf=0,016…0,012;
- средний модуль упругости МEf=3000…6000 МПа;
- коэффициент вариации WEf=0,135.
5. Армобетонное (цементобетонное) покрытие (t,Eb,Rtb):
- средняя толщина Мt=20…35 см;
- коэффициент вариации Wt=0,016…0,012;
- средний модуль упругости МЕb=3,04·104…3,24·104 МПа;
- коэффициент вариации WEb=0,08…0,10;
- средняя прочность бетона на растяжение при изгибе; МRtb=3,6…4,0 МПа;
- коэффициент вариации WRtb=0,135.
6. Суточная интенсивность движения ВС(N):
-
среднее значение 
-
коэффициент вариации ![]() ;
;
7. Характеристики нагрузки (КНН):
Таблица 1
|
Параметр |
|
I КНН (Ил-62, Ил-96-300, В-707-320, А-300) |
II КНН (Ил-86, Ил-76, В-737-200) |
III КНН (Ту-204, Ту-154, DC-10) |
|
Нормативная нагрузка на основную опору Fn. |
кН |
700 |
550 |
400 |
|
Число колес на опоре nk. |
шт |
4 |
4 |
4 |
|
Внутреннее давление воздуха в пневматиках колес ра. |
МПа |
1,00 |
1,00 |
1,00 |
|
Расстояния между колесами опоры х·у. |
см |
70·130 |
70·130 |
70·130 |
8. Расчетные коэффициенты:
- динамичности 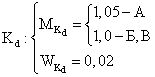
-
разгрузки ![]()
![]()
9. Номинальная амплитуда суточного колебания температуры воздуха А:
- среднее значение МA=4...6°С;
- коэффициент вариации WA=0,06.
10. Проектный срок службы покрытия Т, МT=12-16, лет.
РАЗДЕЛ 1
Статистические характеристики распределения самолетных нагрузок (КНН)
1. Средняя нагрузка на колесо стандартной опоры КНН
Расчетную нагрузку на колесо определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(3) |
|
|
где Fn - |
нормативная нагрузка на основную опору ВС, кН; |
|
|
nk - |
число колес на опоре, шт; |
|
|
Kd - |
коэффициент динамичности; |
|
|
γf - |
коэффициент разгрузки; |
|
|
Kd, γf - |
случайные величины; |
|
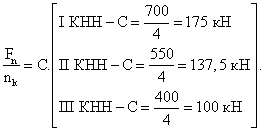
Для вычисления статистических характеристик распределения нагрузки на колесо применяют метод линеаризации.
Среднее значение расчетной нагрузки на колесо определяют по формуле:
|
|
(4) |
|
|
где MKd - |
среднее значение коэффициента динамичности; |
|
|
Mγf - |
среднее значение коэффициента разгрузки. |
|
Результаты расчетов значений MFd представляют отдельно для I-III КНН.
1.2. Стандарт и коэффициент вариации нагрузки на колесо
Дисперсию расчетной нагрузки на колесо определяют по формуле:
|
|
(5) |
|
|
где WKd - |
коэффициент вариации коэффициента динамичности, |
|
|
Wγf - |
коэффициент вариации коэффициента разгрузки. |
|
Результаты расчетов значений ![]() представляют отдельно
для I-III КНН.
Коэффициент вариации нагрузки на колесо определяют по формуле:
представляют отдельно
для I-III КНН.
Коэффициент вариации нагрузки на колесо определяют по формуле:
1.3. Средний радиус отпечатка колеса
Радиус круга, равновеликого площади отпечатка пневматика колеса, определяют по формуле:
|
|
(7) |
|
|
где Fd - |
расчетная нагрузка на колесо, кН; |
|
|
pa - |
внутреннее давление воздуха в пневматиках колес, МПа; |
|
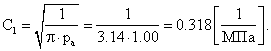
Среднее значение радиуса отпечатка колеса определяют по формуле:
Результаты расчетов значений MRe представляют отдельно для I-III КНН. Дисперсию радиуса отпечатка колеса определяют по формуле:
Результаты расчетов значений σRe представляют отдельно для I-III KHH.
1.4. Стандарт и коэффициент вариации значений радиуса отпечатка колеса
Стандарт разброса значений радиуса отпечатка колеса определяют по формуле:
Результаты расчетов значений σRe представляют отдельно для I-III KHH.
Коэффициент вариации радиуса отпечатка колеса определяют по формуле:
РАЗДЕЛ 2
Статистические характеристики распределения жесткости покрытия
Жесткость конструкции покрытия определяется суммарной жесткостью армобетонной плиты и пескоцементного основания в соответствии со СНиП 2.05.08-85 «Аэродромы».
2.1. Армобетонная (цементобетонная) плита
Жесткость армобетонной плиты определяют по формуле:
|
|
(12) |
|
|
где Eb - |
начальный модуль упругости бетона, МПа; |
|
|
t - |
толщина плиты, м. |
|
Среднее значение жесткости плиты определяют по формуле:
|
|
(13) |
|
|
где MEb - |
среднее значение начального модуля упругости бетона, МП; |
|
|
Mt - |
среднее значение толщины плиты, м. |
|
Дисперсию и стандарт разброса значений жесткости плиты определяют по формулам:
|
|
(14) |
|
|
|
(15) |
|
|
где WEb - |
коэффициент вариации начального модуля упругости бетона; |
|
|
Wt - |
коэффициент вариации толщины плиты. |
|
Коэффициент вариации жесткости плиты определяют по формулам:
2.2. Пескоцементное основание
Жесткость пескоцементного основания определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(18) |
|
|
где Ef - |
начальный модуль упругости п/ц, МПа; |
|
|
tf - |
толщина основания, м. |
|
Среднее значение жесткости основания определяют по формуле:
|
|
(19) |
|
|
где MEf - |
среднее значение начального модуля упругости п/ц, МПа; |
|
|
Mtf - |
среднее значение толщины основания, м. |
|
Дисперсию и стандарт жесткости пескоцементного основания определяют по формулам:
|
|
(20) |
|
|
|
(21) |
|
|
где WEf - |
коэффициент вариации начального модуля упругости п/ц, |
|
|
Wtf - |
коэффициент вариации толщины основания. |
|
Коэффициент вариации жесткости пескоцементного основания определяют по формуле:
2.3. Конструкция аэродромного покрытия
Суммарную жесткость конструкции аэродромного покрытия определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(23) |
Среднее значение суммарной жесткости покрытия определяют по формуле:
Дисперсию и стандарт разброса значений суммарной жесткости покрытия определяют по формулам:
Коэффициент вариации суммарной жесткости покрытия определяют по формуле:
2.4. Упругая характеристика конструкции аэродромного покрытия
Упругую характеристику покрытия определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(28) |
|
|
где KS - |
расчетный коэффициент постели однородного грунтового основания, MН/м3. |
|
Среднее значение упругой характеристики покрытия определяют по формуле:
Стандарт разброса значений упругой характеристики покрытия определяют по формуле :
Коэффициент вариации значений упругой характеристики покрытия определяют по формуле:
РАЗДЕЛ 3
Статистические характеристики распределения изгибающего момента в плите
покрытия от транспортной нагрузки
3.1. Параметр α
Параметр α определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(32) |
|
|
где Re - |
радиус круга, равновеликого площади отпечатка пневматика колеса, м; |
|
|
I - |
упругая характеристика плиты, м. |
|
Среднее значение параметра α определяют по формуле:
Результаты расчетов значений Мα представляют отдельно для I-III KHH.
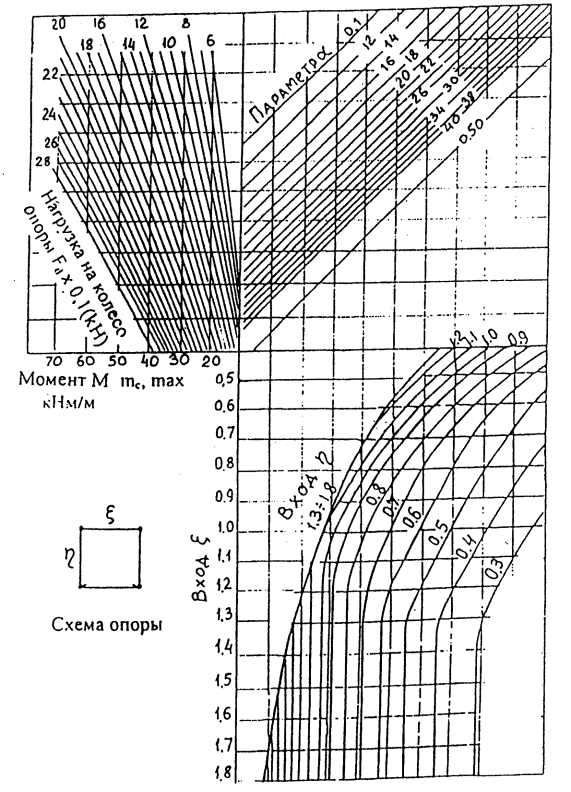
3.2. Максимальный центральный изгибающий момент mс,max
Для
определения среднего значения максимального центрального изгибающего момента ![]() в покрытии
рекомендуется использовать номограмму (см. рис. 1). Чтобы пользоваться этой
номограммой, необходимо вычислить следующие параметры:
в покрытии
рекомендуется использовать номограмму (см. рис. 1). Чтобы пользоваться этой
номограммой, необходимо вычислить следующие параметры:
|
|
(34) |
|
|
|
(35) |
|
|
где х,у - |
расчетные расстояния между колесами стандартной опоры. |
|
По номограмме (рис. 1) получают значения максимального
центрального изгибающего момента ![]() для I-III KHH.
для I-III KHH.
Коэффициент вариации максимального центрального изгибающего момента определяют по формуле:
Стандарт разброса максимального изгибающего момента определяют по формуле:
Результаты
расчетов значений ![]() и
и ![]() представляют отдельно
для I-III
KHH.
представляют отдельно
для I-III
KHH.
3.3. Расчетный изгибающий момент md
Вычисляют расчетные характеристики покрытия с учетом пескоцементного основания:
|
|
(38) |
|
|
(39) |
По
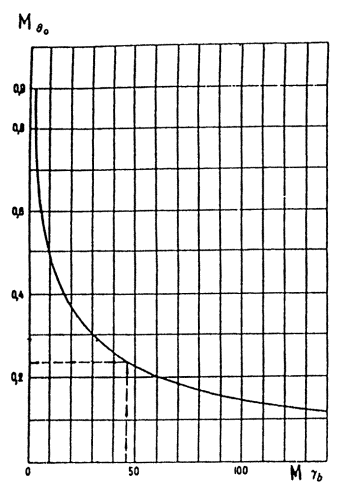
графику (рис. 2)
устанавливают значения параметра ![]() .
.
Далее определяют следующие параметры:
Рис.1 Номограмма для определения
момента ![]()
Рис.
2. График для определения ![]() .
.
Расчетный изгибающий момент в плите покрытия от расчетной нагрузки определяют согласно СНиП 2.05.08-85 "Аэродромы":
|
|
(44) |
Среднее значение расчетного изгибающего момента в покрытии определяют по формуле:
Результаты расчетов значений Mmd представляют отдельно для I-III КНН.
Коэффициент вариации расчетного изгибающего момента в покрытии определяют по формуле:
Стандарт разброса значений расчетного изгибающего момента определяют по формуле:
Результаты расчетов значений σmd представляют отдельно для I-III КНН.
РАЗДЕЛ 4
Статистические характеристики распределения температурного момента в плите
покрытия
Температурный момент в плите покрытия определяют по формуле:
|
|
(48) |
|
|
где A - |
номинальная амплитуда суточного колебания температуры воздуха, |
|
|
r - |
коэффициент, равный: 1,0 - для покрытий с длиной плиты 7,5 м и более, 0,5 - для покрытий с длиной плиты 5 м, а для промежуточных вариантов определяют интерполяцией. |
|
Среднее значение температурного момента в плите покрытия определяют по формуле:
Коэффициент вариации значений температурного момента в плите покрытия определяют по формуле:
Стандарт разброса значений температурного момента в плите покрытия определяют по формуле:
РАЗДЕЛ
5
Статистические характеристики распределения суммарного изгибающего момента в
плите покрытия
Суммарный изгибающий момент в плите покрытия определяют по формуле:
|
|
(52) |
Среднее значение суммарного изгибающего момента в плите покрытия определяют по формуле:
Результаты расчетов значений Мmс представляют отдельно для I-III KHH.
Стандарт разброса значений суммарного изгибающего момента в плите покрытия определяют по формуле:
Результаты расчетов значений smc представляют отдельно для I-III КНН.
Коэффициент вариации суммарного изгибающего момента в плите покрытия определяют по формуле:
Результаты расчетов значений Wmc представляют отдельно для I-III КНН.
РАЗДЕЛ
6
Статистические характеристики распределения несущей способности плиты покрытия
на изгиб
Предельный изгибающий момент в плите покрытия определяют по формуле:
|
|
(56) |
|
|
где KT - |
коэффициент нарастания прочности бетона во времени, зависящий от срока службы покрытия и равный:
|
|
|
Rtb - |
прочность бетона на растяжение при изгибе на 28 сутки, МПа. |
|
Среднее значение предельного изгибающего момента определяют по формуле:
Коэффициент вариации предельного изгибающего момента определяют по формуле:
Стандарт разброса значений предельного изгибающего момента определяют по формуле:
РАЗДЕЛ
7
Характеристики распределения количества нагружений покрытия транспортной
нагрузкой на проектный срок службы
Количество нагружений покрытия транспортной нагрузкой на проектный срок службы определяют по формуле:
|
|
(60) |
|
|
где ω - |
коэффициент, учитывающий разброс следов прохода колес опоры воздушного судна по ширине покрытия, принимаемый равным:
|
|
|
N - |
номинальная интенсивность движения ВС в сутки (взлет); |
|
|
T - |
срок службы покрытия, лет. |
|
Среднее значение количества нагружений покрытия транспортной нагрузкой на проектный срок службы определяют по формуле:
Стандарт разброса количества нагружений покрытия транспортной нагрузкой на заданный срок службы определяют по формуле:
Результаты расчетов значений Мn и σn представляют отдельно для I-III KHH.
РАЗДЕЛ 8
Оценка надежности покрытия по прочности и прогноз его технического состояния на
проектный срок службы
В основу методики оценки надежности работоспособности покрытия положены эмпирические закономерности изгибной усталости цементобетона [6] и рабочая гипотеза о линейном накоплении усталостных повреждений в структуре материала [1].
Надежность плиты (элемента) покрытия по условию прочности (трещинообразования) вычисляют по формуле:
|
|
(63) |
|
|
где Hтр(Т) - |
надежность по условию прочности элемента покрытия на конец срока службы Т, |
|
|
Ф(x) - |
значение интеграла вероятности (табл.2), |
|
|
x1,x2 - |
аргументы интеграла вероятности, которые необходимо определить по следующим формулам: |
|
|
|
(64) |
|
|
|
(65) |
|
|
|
(66) |
|
Вычисление значений параметров МΨ и σΨ производят на основе определенных в предыдущих разделах для каждой категории нагрузки (I-III KHH) значений следующих величин:
Мmс1, Мmс2, Мmс3, σ2mc1, σ2mc2, σ2mc3 - раздел 5;
Mmu, Wmu - раздел 6;
Мn1, Мn2, Мn3 - раздел 7.
Величины M1, М2, М3, представляющие собой суммарное приведенное количество воздействий нагрузки I, II и III KHH за срок службы покрытия, необходимо вычислить по следующим формулам:
После вычисления меры надежности работы плиты (элемента) покрытия по прочности (63) прогнозируют техническое состояние покрытия на проектный срок службы, точнее определяют уровень повреждения или процентное количество дефектной площади покрытия, имеющей следующие виды повреждений:
- сквозные поперечные, продольные и диагональные трещины
- сколы кромок плит в местах поперечных и продольных швов
|
|
(70) |
- шелушение поверхности плит
|
|
(71) |
- просадки поверхностей смежных плит в местах швов и трещин
|
|
(72) |
В квадратных скобках обозначены предельные значения уровня повреждений, требующие проведения капитального ремонта по частным видам повреждений покрытия.
Комплексная надежность работоспособности плиты (элемента) покрытия, учитывающая комплекс совместно возникающих на протяжении срока службы покрытия повреждений всех видов, определяется по формулам:
|
|
(73) |
|
|
или |
|
|
|
|
(74) |
|
|
|
(75) |
|
|
|
(76) |
|
|
где H(Т) - |
комплексная надежность покрытия, |
|
|
Т - |
срок службы, |
|
|
S - |
мера повреждения площади покрытия по видам (в процентах). |
|
На основании результатов вычислений по формулам (69)-(72) в случае необходимости оформляют фрагментарный чертеж прогноза технического состояния расчетного участка покрытия на заданный срок службы (в условных обозначениях). При определении поврежденной площади участка покрытия принимают во внимание следующее:
- условное расстояние между поперечными (продольными) сквозными трещинами, а также максимальный диаметр замкнутого контура области шелушения поверхности принимают равным 4 м;
- сколы кромок и просадки плит условно принимают сосредоточенными в районе поперечных швов и трещин;
- элемент площади бетонных покрытий определяется размерами отдельной плиты;
- элемент площади армобетонного покрытия имеет размеры 7×7(7,5) м.
В результате выполненного прогноза надежности покрытия делают вывод о наличии резерва в ресурсе работы или полном исчерпании ресурса работоспособности покрытия с определением предельного срока службы Тпр, соответствующего надежности работы элемента площади покрытия Нтр(Тпр)=0,5.
Таблица 2
Значения интеграла вероятности:
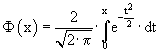
|
x |
Ф(х) |
x |
Ф(х) |
x |
Ф(х) |
x |
Ф(х) |
|
0,00 |
0,0000 |
0,60 |
0,4515 |
1,20 |
0,7699 |
1,80 |
0,9281 |
|
0,01 |
0,0080 |
0,61 |
0,4581 |
1,21 |
0,7737 |
1,81 |
0,9297 |
|
0,02 |
0,0160 |
0,62 |
0,4647 |
1,22 |
0,7775 |
1,82 |
0,9312 |
|
0,03 |
0,0239 |
0,63 |
0,4713 |
1,23 |
0,7813 |
1,83 |
0,9328 |
|
0,04 |
0,0319 |
0,64 |
0,4778 |
1,24 |
0,7850 |
1,84 |
0,9342 |
|
0,05 |
0,0399 |
0,65 |
0,4843 |
1,25 |
0,7887 |
1,85 |
0,9357 |
|
0,06 |
0,0478 |
0,66 |
0,4907 |
1,26 |
0,7923 |
1,86 |
0,9371 |
|
0,07 |
0,0558 |
0,67 |
0,4971 |
1,27 |
0,7959 |
1,87 |
0,9385 |
|
0,08 |
0,0638 |
0,68 |
0,5035 |
1,28 |
0,7995 |
1,88 |
0,9399 |
|
0,09 |
0,0717 |
0,69 |
0,5098 |
1,29 |
0,8029 |
1,89 |
0,9412 |
|
0,10 |
0,0797 |
0,70 |
0,5161 |
1,30 |
0,8064 |
1,90 |
0,9426 |
|
0,11 |
0,0876 |
0,71 |
0,5223 |
1,31 |
0,8098 |
1,91 |
0,9439 |
|
0,12 |
0,0955 |
0,72 |
0,5285 |
1,32 |
0,8132 |
1,92 |
0,9451 |
|
0,13 |
0,1034 |
0,73 |
0,5346 |
1,33 |
0,8165 |
1,93 |
0,9464 |
|
0,14 |
0,1113 |
0,74 |
0,5407 |
1,34 |
0,8198 |
1,94 |
0,9476 |
|
0,15 |
0,1192 |
0,75 |
0,5467 |
1,35 |
0,8230 |
1,95 |
0,9488 |
|
0,16 |
0,1271 |
0,76 |
0,5527 |
1,36 |
0,8262 |
1,96 |
0,9500 |
|
0,17 |
0,1350 |
0,77 |
0,5587 |
1,37 |
0,8293 |
1,97 |
0,9512 |
|
0,18 |
0,1428 |
0,78 |
0,5646 |
1,38 |
0,8324 |
1,98 |
0,9523 |
|
0,19 |
0,1507 |
0,79 |
0,5705 |
1,39 |
0,8355 |
1,99 |
0,9534 |
|
0,20 |
0,1585 |
0,80 |
0,5763 |
1,40 |
0,8385 |
2,00 |
0,9545 |
|
0,21 |
0,1663 |
0,81 |
0,5821 |
1,41 |
0,8415 |
2,05 |
0,9596 |
|
0,22 |
0,1741 |
0,82 |
0,5878 |
1,42 |
0,8444 |
2,10 |
0,9643 |
|
0,23 |
0,1819 |
0,83 |
0,5935 |
1.43 |
0,8473 |
2,15 |
0,9684 |
|
0,24 |
0,1897 |
0,84 |
0,5991 |
1,44 |
0,8501 |
2,20 |
0,9722 |
|
0,25 |
0,1974 |
0,85 |
0,6047 |
1,45 |
0,8529 |
2,25 |
0,9756 |
|
0,26 |
0,2051 |
0,86 |
0,6102 |
1,46 |
0,8557 |
2,30 |
0,9786 |
|
0,27 |
0,2128 |
0,87 |
0,6157 |
1,47 |
0,8584 |
2,35 |
0,9812 |
|
0,28 |
0,2205 |
0,88 |
0,6211 |
1,48 |
0,8611 |
2,40 |
0,9836 |
|
0,29 |
0,2282 |
0,89 |
0,6265 |
1,49 |
0,8638 |
2,45 |
0,9857 |
|
0,30 |
0,2358 |
0,90 |
0,6319 |
1,50 |
0,8664 |
2,50 |
0,9876 |
|
0,31 |
0,2434 |
0,91 |
0,6372 |
1,51 |
0,8690 |
2,55 |
0,9892 |
|
0,32 |
0,2510 |
0,92 |
0,6424 |
1,52 |
0,8715 |
2,60 |
0,9907 |
|
0,33 |
0,2586 |
0,93 |
0,6476 |
1,53 |
0,8740 |
2,65 |
0,9920 |
|
0,34 |
0,2661 |
0,94 |
0,6528 |
1,54 |
0,8764 |
2,70 |
0,9931 |
|
0,35 |
0,2737 |
0,95 |
0,6579 |
1,55 |
0,8789 |
2,75 |
0,9940 |
|
0,36 |
0,2812 |
0,96 |
0,6629 |
1,56 |
0,8812 |
2,80 |
0,9949 |
|
0,37 |
0,2886 |
0,97 |
0,6680 |
1,57 |
0,8836 |
2,85 |
0,9956 |
|
0,38 |
0,2961 |
0,98 |
0,6729 |
1,58 |
0,8859 |
2,90 |
0,9963 |
|
0,39 |
0,3035 |
0,99 |
0,6778 |
1,59 |
0,8882 |
2,95 |
0,9968 |
|
0,40 |
0,3108 |
1,00 |
0,6827 |
1,60 |
0,8904 |
3,00 |
0,99730 |
|
0,41 |
0,3182 |
1,01 |
0,6875 |
1,61 |
0,8926 |
3,10 |
0,99806 |
|
0,42 |
0,3255 |
1,02 |
0,6923 |
1,62 |
0,8948 |
3,20 |
0,99863 |
|
0,43 |
0,3328 |
1,03 |
0,6970 |
1,63 |
0,8969 |
3,30 |
0,99903 |
|
0,44 |
0,3401 |
1,04 |
0,7017 |
1,64 |
0,8990 |
3,40 |
0,99933 |
|
0,45 |
0,3473 |
1,05 |
0,7063 |
1,65 |
0,9011 |
3,50 |
0,99953 |
|
0,46 |
0,3545 |
1,06 |
0,7109 |
1,66 |
0,9031 |
3,60 |
0,99968 |
|
0,47 |
0,3616 |
1,07 |
0,7154 |
1,67 |
0,9051 |
3,70 |
0,99978 |
|
0,48 |
0,3688 |
1,08 |
0,7199 |
1,68 |
0,9070 |
3,80 |
0,99986 |
|
0,49 |
0,3759 |
1,09 |
0,7243 |
1,69 |
0,9090 |
3,90 |
0,99990 |
|
0,50 |
0,3829 |
1,10 |
0,7287 |
1,70 |
0,9109 |
4,00 |
0,99994 |
|
0,51 |
0,3899 |
1,11 |
0,7330 |
1,71 |
0,9127 |
4,417 |
1-10-5 |
|
0,52 |
0,3969 |
1,12 |
0,7373 |
1,72 |
0,9146 |
4,892 |
1-10-6 |
|
0,53 |
0,4039 |
1,13 |
0,7415 |
1.73 |
0,9164 |
5,327 |
1-10-7 |
|
0,54 |
0,4108 |
1,14 |
0,7457 |
1,74 |
0,9181 |
|
|
|
0,55 |
0,4177 |
1,15 |
0,7499 |
1,75 |
0,9199 |
|
|
|
0,56 |
0,4245 |
1,16 |
0,7540 |
1,76 |
0,9216 |
|
|
|
0,57 |
0,4313 |
1,17 |
0,7580 |
1,77 |
0,9233 |
|
|
|
0,58 |
0,4381 |
1,18 |
0,7620 |
1,78 |
.0,9249 |
|
|
|
0,59 |
0,4448 |
1,19 |
0,7660 |
1,79 |
0,9265 |
|
|
Пример прогноза надежности аэродромного покрытия
Исходные данные
1. Группа участков покрытия аэродрома - Б.
2. Тип аэродромного покрытия - жесткое.
3. Грунтовое основание: суглинок (Ks):
-
среднее значение ![]()
- коэффициент вариации WKs=0,14.
4. Пескоцементное основание (tf, Ef):
- средняя толщина Mtf=31 см;
- коэффициент вариации Wtf=0,015;
- средний модуль упругости МЕf=4·103 МПа;
- коэффициент вариации WEf=0,135.
5. Армобетонное покрытие (t, Eb, Rtb):
- размеры плиты в плане 7,5×1,5 м;
- средняя толщина Мt=30 см;
- коэффициент вариации Wt=0,016;
- средний модуль упругости МЕb=3,24·104 МПа;
- коэффициент вариации WEb=0,1;
- средняя прочность бетона на растяжение при изгибе MRtb=5 МПа;
- коэффициент вариации WRtb=0,135.
6. Суточная интенсивность движения ВС (N):
Таблица 3
|
I KHH |
II KHH |
III KHH |
|
MN=5 |
MN=20 |
MN=50 |
|
WN=0,07 |
WN=0,1 |
WN=0,1 |
7. Характеристики нагрузки:
Таблица 4
|
Параметр |
Ед. измерения |
I KHH |
II КНН |
III KHH |
|
Среднее значение МKd |
|
1,00 |
1,00 |
1,00 |
|
Коэффициент вариации WKd |
|
0,02 |
0,02 |
0,02 |
|
Среднее значение Мγf |
|
0,95 |
0,95 |
0,95 |
|
Коэффициент вариации Wγf |
|
0,02 |
0,02 |
0,02 |
8. Номинальная амплитуда суточного колебания температуры воздуха А:
- среднее значение МА=4°С;
- коэффициент вариации WA=0,06.
9. Проектный срок службы покрытия - 12 лет.
РАЗДЕЛ 1. Статистические характеристики распределения самолетных нагрузок
1.1. Средняя нагрузка на колесо
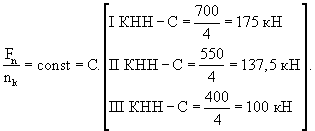
Среднее значение расчетной нагрузки на колесо определяют по формуле (4):
![]()
Результаты расчетов:
![]()
![]()
![]()
1.2. Дисперсия и коэффициент вариации нагрузки на колесо
Дисперсию расчетной нагрузки на колесо определяют по формуле (5):
![]()
Результаты расчетов:
![]()
![]()
![]()
Коэффициент вариации нагрузки на колесо определяют по формуле (6):
![]()
![]()
1.3. Средний радиус отпечатка колеса
Среднее значение радиуса отпечатка колеса определяют по формуле (8):
![]()
Результаты расчетов:
![]()
![]()
![]()
Дисперсию радиуса отпечатка колеса определяют по формуле (9):
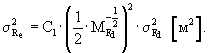
Результаты расчетов:
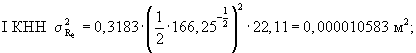
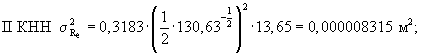
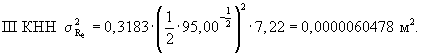
1.4. Стандарт и коэффициент вариации значений радиуса отпечатка колеса
Стандарт разброса значений радиуса отпечатка колеса определяют по формуле (10):
![]()
Результаты расчетов:
![]()
![]()
![]()
Коэффициент вариации значений радиуса отпечатка колеса определяют по формуле (11):
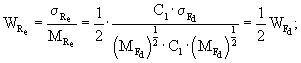
![]()
РАЗДЕЛ 2. Статистические характеристики распределения жесткости покрытия
Жесткость конструкции покрытия определяется суммарной жесткостью армобетонной плиты и пескоцементного основания.
2.1. Армобетонная плита
Среднее значение жесткости плиты определяют по формуле (13):
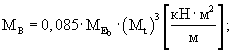
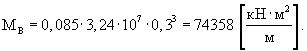
Стандарт разброса значений жесткости плиты определяют по формуле (15):
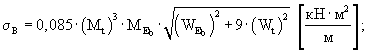
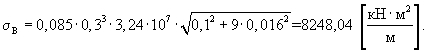
Коэффициент вариации жесткости плиты определяют по формуле (16):
![]()
![]()
Дисперсию разброса значений жесткости плиты определяют по формуле (17):
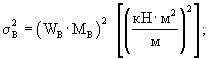
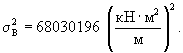
2.2. Пескоцементное основание
Среднее значение жесткости основания определяют по формуле (19):
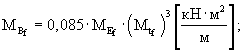
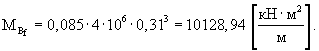
Стандарт распределения значений жесткости пескоцементного основания определяют по формуле (21):
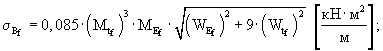
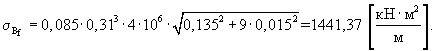
Коэффициент вариации жесткости пескоцементного основания определяют по формуле (22):
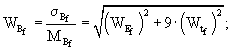
![]()
2.3. Конструкция аэродромного покрытия
Среднее значение суммарной жесткости покрытия определяют по формуле (24):
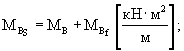
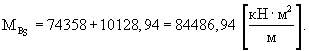
Стандарт разброса значений суммарной жесткости покрытия определяют по формуле (26):
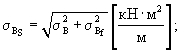
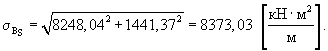
Коэффициент вариации суммарной жесткости покрытия определяют по формуле (27):
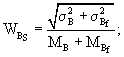
![]()
2.4. Упругая характеристика конструкции аэродромного покрытия
Среднее значение упругой характеристики покрытия определяют по формуле (29):
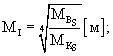
![]()
Стандарт разброса значений упругой характеристики покрытия определяют по формуле (30):
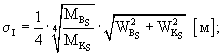
![]()
Коэффициент вариации упругой характеристики покрытия определяют по формуле (31):
![]()
![]()
РАЗДЕЛ 3. Статистические характеристики распределения изгибающего момента в плите покрытия от транспортной нагрузки
3.1. Параметр α
Среднее значение параметра α определяют по формуле (33):
![]()
Результаты расчетов:
![]()
![]()
![]()
3.2. Максимальный центральный изгибающий момент mс,max
Для
определения среднего значения максимального центрального изгибающего момента ![]() в покрытии рекомендуется
использовать номограмму (см. рис. 1).
Чтобы пользоваться этой номограммой, необходимо вычислить следующие параметры:
в покрытии рекомендуется
использовать номограмму (см. рис. 1).
Чтобы пользоваться этой номограммой, необходимо вычислить следующие параметры:
|
|
|
|
|
|
|
где х,у - |
расчетные расстояния между колесами стандартной опоры. |
Результаты расчетов:
![]()
![]()
По
номограмме (рис. 1) получают значения
максимального центрального изгибающего момента ![]() для I-III
KHH:
для I-III
KHH:
![]()
![]()
![]()
Коэффициент вариации максимального центрального изгибающего момента определяют по формуле (36):
![]()
![]()
Стандарт разброса максимального центрального изгибающего момента определяют по формуле (37):
![]()
Результаты расчетов:
![]()
![]()
![]()
3.3. Расчетный изгибающий момент md
Вычисляют расчетные характеристики покрытия с учетом пескоцементного основания:
![]()
![]()
![]()
![]()
По графику (рис. 2) устанавливают значения параметра:
![]()
Коэффициент вариации величины θ0 определяют по формуле (40):
![]()
![]()
Стандарт разброса величины е0 определяют по формуле (41):
![]()
![]()
По формулам (42) и (43) вычисляют параметры:
![]()
![]()
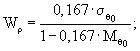
![]()
Среднее значение расчетного изгибающего момента в покрытии определяют по формуле (45):
![]()
Результаты расчетов:
![]()
![]()
![]()
Коэффициент вариации расчетного изгибающего момента в покрытии определяют по формуле (46):
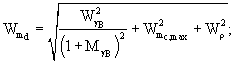
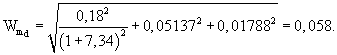
Стандарт разброса значений расчетного изгибающего момента определяют по формуле (47):
![]()
Результаты расчетов значений σmd:
![]()
![]()
![]()
РАЗДЕЛ 4. Статистические характеристики распределения температурного момента в плите покрытия
Среднее значение температурного момента в плите покрытия определяют по формуле (49):
![]()
![]()
Коэффициент вариации значений температурного момента в плите покрытия определяют по формуле (50):
![]()
![]()
Стандарт разброса значений температурного момента в плите покрытия определяют по формуле (51):
![]()
![]()
РАЗДЕЛ 5. Статистические характеристики распределения суммарного изгибающего момента в плите покрытия
Среднее значение суммарного изгибающего момента в плите покрытия определяют по формуле (53):
![]()
Результаты расчетов:
![]()
![]()
![]()
Стандарт разброса значений суммарного изгибающего момента в плите покрытия определяют по формуле (54):
![]()
Результаты расчетов:
![]()
![]()
![]()
Коэффициент вариации суммарного изгибающего момента в плите покрытия определяют по формуле (55):
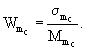
Результаты расчетов:
![]()
![]()
![]()
РАЗДЕЛ 6. Статистические характеристики распределения несущей способности плиты покрытия на изгиб
Среднее значение предельного изгибающего момента определяют по формуле (57):
![]()
![]()
Коэффициент вариации значений предельного изгибающего момента определяют по формуле (58):
![]()
![]()
Стандарт разброса значений предельного изгибающего момента определяют по формуле (59):
![]()
![]()
РАЗДЕЛ 7. Характеристики распределения количества нагружений покрытия транспортной нагрузкой на проектный срок службы
Среднее значение количества нагружения покрытия транспортной нагрузкой на проектный срок службы определяют по формуле (61):
![]()
Результаты расчетов:
![]()
![]()
![]()
Стандарт разброса количества нагружений покрытия транспортной нагрузкой на проектный срок службы определяют по формуле (62):
![]()
Результаты расчетов:
![]()
![]()
![]()
РАЗДЕЛ 8. Оценка надежности покрытия и прогноз его технического состояния на проектный срок службы
Вычисляют по формуле (68) коэффициенты приведения повторности воздействия нагрузок I-III КНН на покрытие:
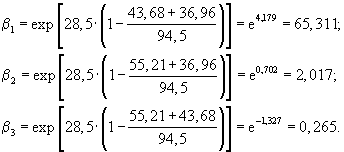
Вычисляют по формуле (67) приведенное суммарное количество воздействий нагрузок I-III КНН на покрытие:
![]()
![]()
![]()
![]()
Вычисляют по формулам (65) и (66) статистические характеристики распределения значений параметра Ψ:
![]()
![]()
Вычисляют по формулам (64) значения аргументов интеграла вероятности:
![]()
![]()
Вычисляют по таблице 2 значение интеграла вероятности Ф(х):
Ф(0,261)=0,206;
Ф(9,518)=1,0.
Вычисляют по формуле (63) надежность работоспособности элемента покрытия по условию трещинообразования на конец срока службы:
![]()
Прогнозируют техническое состояние покрытия в целом на срок службы по формулам (69)-(72), то есть определяют проектное количество дефектной площади покрытия, имеющей следующие виды повреждений:
- сквозные, поперечные, продольные и диагональные трещины:
STP(T=12л)=100%·(1-0,603)=39,7%;
- сколы кромок плит в местах поперечных и продольных швов и трещин:
SCK(T=12л)=0,8·39,7=31,8%;
- шелушение поверхности плит:
SШ(Т=12л)=0,6·39,7=23,8%;
- просадки поверхностей смежных плит в местах швов и трещин:
SПР(T=12л)=0,2·39,7=7,9%.
Вычисляют комплексную надежность работоспособности покрытия по формулам (73):
Н(Т=12л)=1-0,01·39,7-0,008·31,8-0,005·23,8-0,003·7,9=0,206.
Проверка
Н(Т=12л)=2·0,603-1=0,206.
Вывод: На заданный срок службы Т=12 лет армобетонное покрытие будет иметь некоторый резерв ресурса работоспособности, как в комплексном выражении, так и по частным видам дефектов. Таким образом, срок службы покрытия до предельного состояния составит более 12 лет.
Литература
1. Болотин В.В. Применение методов теории вероятностей и теории надежности в расчетах сооружений. - М.: Стройиздат, 1971.
2. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964.
3. Глава СНиП 32-03-96. Аэродромы. - М.: Минстрой РФ, 1996 .
4. Глава СНиП 2.05.08-85. - М.: Стройиздат, 1985.
5. Глушков Г.И., Носов В.П., Медников И.А. и др. Жесткие покрытия аэродромов и автомобильных дорог. - М.: Транспорт, 1994.
6. Садовой В.Д. Исследование некоторых вопросов надежности работы и эксплуатационной оценки прочности аэродромных покрытий. Автореф. дисс. к.т.н. - М.: МАДИ, 1975.
7. Степушин А.П. К обоснованию сроков службы жестких аэродромных покрытий из цементобетона. Проектирование, строительство и эксплуатация сооружений аэропортов. Сб. науч. тр. - М.: МАДИ, 2001.
8. Степушин А.П. Разработка вероятностно-статистического метода расчета прочности жестких покрытий аэродромов и автомобильных дорог. Автореф. дисс. д-ра техн. наук. - М.: Информавтодор, 1996.
9. Виноградов А.П. Надежность и сертификация прочности цементобетонных покрытий аэродромов. - М.: Ирмаст, 1994.