Министерство монтажных и специальных строительных работ СССР
Главное техническое управление
Всесоюзный научно-исследовательский институт по монтажным и специальным строительным работам
ТЕХНОЛОГИЯ МОНТАЖА РЕЗЕРВУАРОВ И ТРУБОПРОВОДОВ
Сборник научных трудов
Под редакцией д-ра техн. наук Б.В. Поповского, канд. техн. наук Р.И. Тавастшерны
Редакционно-издательский отдел
Москва 1985
СОДЕРЖАНИЕ
Технология монтажа резервуаров и трубопроводов. Сборник научных трудов. - М., ВНИИмонтажспецстрой, 1985.
В сборнике освещены результаты исследований процесс монтажа и работы конструктивных элементов стальных резервуаров, испытаний и применения пневматических укрытий на монтажных работах.
Рассматриваются вопросы прочности соединений трубопроводов из стали и пластмасс, расчета сопротивления сварного соединения и оценки несущей способности деталей трубопроводов под давлением.
Редакционная коллегия: Н.С. Станкевич (гл. редактор), Ю.В. Соколов, Б.В. Поповский, А.И. Алексеев, П.П. Алексеенко, И.С. Иоффе, М.С. Мазин, Н.Г. Малинина, В.М. Никиреев, Р.И. Тавастшерна, В.Я. Телегин, Н.А. Юхин, Н.Е. Марченко (секретарь).
ИССЛЕДОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПАРАМЕТРОВ ФОРМООБРАЗОВАНИЯ МОНТАЖНЫХ СТЫКОВ РУЛОНИРУЕМЫХ ПОЛОТНИЩ СТЕНОК РЕЗЕРВУАРОВ
Инженеры Г.А. Ритчик,
Л.В. Петрова, И.Н. Добрынина
С увеличением объемов и высоты резервуаров, сооружаемых с применением метода рулонирования, возрастают трудности, связанные с обеспечением правильной геометрической формы стенок в процессе монтажа.
В процессе изготовления сварных рулонированных полотнищ стенок на заводских установках основной металл претерпевает различные изгибные деформации. Заключительной операцией, определяющей его конечное напряженное состояние при изготовлении, является наворачнвание полотнища на каркас, диаметр которого по условиям железнодорожных перевозок принят равным 2660 мм. При этом полотнище испытывает чистый упруго-пластический изгиб со значительной глубиной проникновения пластики в сечение основного металла.
Полотнище стенки, свернутое в транспортабельный рулон и претерпевшее при этом упруго-пластический изгиб, на монтажной площадке после обрезки удерживающих планок распружинится до остаточного радиуса, который будет тем меньше, чем меньше высота упругого ядра сечения. Основной металл полотнища будет иметь при этом значительные остаточные напряжения. Для вертикальных цилиндрических резервуаров большого объема (10 - 50 тыс. м3) остаточный радиус нижних наиболее толстых поясов стенок будет равняться 2...4 м, что значительно меньше проектных радиусов резервуаров (14…30 м). Для придания таким полотнищам проектной кривизны необходим разгиб их путем принудительного разворачивания рулонов.
При разгибе полотнищ до проектного радиуса основной металл опять испытывает упруго-пластические деформации. Причем наружные волокна претерпевают пластические деформации противоположного знака по сравнению с деформациями при рулоннровании: волокна, на внешней поверхности стенки будут сжаты, а на внутренней растянуты. При принудительном разворачивании рулонов на монтажной площадке обеспечение проектной формы стенки производится приваркой нижней кромки к днищу, а верхней к щитам покрытия или наружной кольцевой площадке для резервуаров с плавающей крышей.
Закрепленное в проектном положении полотнище стенки находится в преднапряженном состоянии.
В особых условиях находятся при изготовлении и монтаже рулонированных стенок концевые участки полотнищ в зонах монтажных стыков, для придания которым проектной формы требуется развальцовка на проектный радиус (формообразование).
При рулонировании полотнищ на заводских установках условия закрепления начальной и конечной кромок не позволяют получать их изгиб на радиус сворачивания. В результате начальный участок полотнища шириной до 250 мм остается плоским, на следующем участке шириной до 500 мм происходит постепенное изменение радиуса кривизны от бесконечности до радиуса сворачивания.
Ширина этих участков зависит от плотности прилегания начальной кромки к кольцам каркаса в начальный момент рулонирования и конечной кромки к рулону при упаковке по завершении рулонирования.
При более плотном прилегании ширина прямолинейных участков уменьшается.
Характер изменения кривизны обоих концевых участков полотнища примерно одинаков, однако внутренний конец, который крепится к кольцам и заводится в специальные карманы, при неудачной конструкции карманов может получить перегиб в месте, где карман переходит в кривизну каркаса.
Исследование формы концевых участков рулонированных полотнищ было проведено на рулонах стенки резервуара объемом 20 тыс. м3. С помощью индикаторного кривизномера с базой 200 мм были замерены радиусы изгиба концевых участков всех поясов.
Как показали измерения, внутренний конец полотнища, закрепляемый на кольцах каркаса, имеет перегиб на расстоянии 750 мм от конца.
Форма внутреннего концевого участка полотнища стенки резервуара объемом 20 тыс. м3 была исследована также на различных этапах монтажа. Кривизна измерялась на нижнем поясе на расстоянии 100 мм от горизонтального шва с помощью индикаторного кривизномера на трех этапах монтажа:
а) после разворачивания рулона в свободном состояния концевого участка;
б) после правки концевого участка обратным изгибом на участке шириной до 3 м;
в) после сборки и сварки монтажного стыка.
Результаты замеров показали, что концевой участок шириной 750 мм и после правки остается плоским. Частично выправляется участок перегиба; проектную кривизну приобретает последующий участок шириной около 2 м.
После сборки и сварки монтажного стыка кривизна этой зоны характеризуется плоским участком у шва и небольшой обратной кривизной участков по обе стороны от места перегиба.
В целом зона монтажного стыка стенки принимает форму, близкую к проектной, и удовлетворяет требованиям, предъявляемым нормативными документами.
Особенности деформирования концевых участков рулонированных полотнищ при их изготовлении и монтаже обуславливают своеобразие напряженного состояния стенок больших резервуаров, смонтированных из нескольких рулонов. Основные серединные зоны полотнищ стенок, в которых имеют место значительные предварительные напряжения, превышающие в крайних волокнах предел текучести, переходят в зонах монтажных стыков в места с незначительными остаточными напряжениями (участки правки обратным изгибом шириной до 2 м) и, наконец, в уплощенные места (участки шириной до 750 мм по обе стороны от монтажного шва), где остаточные и предварительные напряжения основного металла отсутствуют.
Проведенные исследования геометрической формы концевых участков полотнищ с фиксированными кромками [1] позволили выявить необходимую протяженность зоны правки. Как показали результаты исследования, краевые прогибы концевых участков полотнищ затухают на протяжении 150 - 160 см. Этой зоной затухания можно руководствоваться при выборе необходимой зоны правки концевых участков полотнищ стенок резервуара объемом 50 тыс. м3. Для полотнищ стенок других резервуаров протяженность зоны правки можно определять из формулы:
![]() ,
,
где
Н - высота стенки;
R - проектный радиус резервуара;
δ - максимальная толщина стенки.
Анализ деформированного состояния рулонированных полотнищ стенок (в том числе концевых участков) в процессе изготовления и монтажа резервуаров позволяет определить основную принципиальную схему правки.
Правку концевых участков полотнищ наиболее целесообразно производить обратным изгибом на радиус, при котором упруго-пластические деформация полотнищ позволят получить остаточный радиус, равный проектному.
При этом начальный участок шириной до 500 -750 мм, который не вальцуется при рулонировании, и при обратном изгибе на монтажной площадке целесообразно оставить плоским, так как реализация на этом участке изгибающего момента вызовет серьезные затруднения.
Поэтому исследование параметров обратного изгиба велось для зоны (начинающейся на расстоянии 500 - 750 мм от кромок), которая претерпевает при рулонировании изгиб на. радиус сворачивания, а на монтаже подвергается правке до проектного радиуса резервуара,
Расчетная схема определения радиусов обратного изгиба для правки этой зоны концевых участков рулонированных полотнищ стенок представлена на рисунке. Она основана на рассмотрении частого упруго-пластического изгиба полосы из идеального упруго-пластического материала [2].
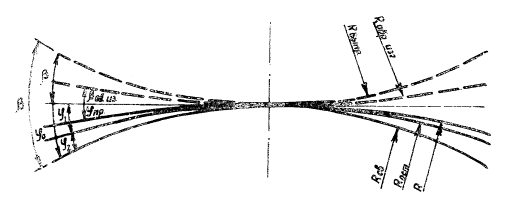
На рисунке приняты следующие обозначения:
![]() - радиус
сворачивания в рулон
- радиус
сворачивания в рулон
![]() - остаточный
радиус после рулонирования
- остаточный
радиус после рулонирования
![]() - радиус
обратного изгиба для получения проектного радиуса
- радиус
обратного изгиба для получения проектного радиуса
Последовательность расчета радиуса обратного изгиба [2]:
1. Определение остаточного радиуса после рулонирования
![]() ,
, ![]() :
:
где
![]() ,
, ![]()
2. Определение угла правки для получения плоского полотнища
![]() ;
; ![]()
3. Определение угла и радиуса обратного изгиба для получения проектной кривизны полотнища
![]()
![]() определяется по
таблице
определяется по
таблице
|
φ1 в долях к |
0-1к |
1к-2к |
2к-3к |
3к-4к |
4к-5к |
5к-6к |
|
βоб.из. рад/м |
β-1,43φпр |
β-1,18φпр |
β-1,11φпр |
β-1,1φпр |
β-1,08φпр |
β-φпр |
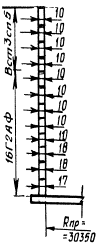
Экспериментальная проверка расчетов осуществлялась на образцах в виде полос размером. 500×100×δ мм из сталей, применяемых в стенках резервуаров. Полосы подвергались чистому изгибу в соответствии с различными операциями рулонирования полотнищ при изготовлении и монтаже. Исследования показали достаточно точное совпадение расчетных и экспериментальных результатов, так как стали марок ВСт3сп5, 09Г2С и 18Г2АФ, применяемые в стенках резервуаров, имеют ярко выраженную площадку текучести на диаграммах растяжения гагаринских образцов и хорошо отвечают предположению об идеальном упруго-пластическом материале.
Основные технологические параметры правки обратным изгибом - радиусы обратного изгиба и необходимые изгибающие моменты, полученные расчетным путем для стенки резервуара объемом 50 тыс. м3 представлены в таблице.
Радиусы обратного изгиба определялись по расчетной схеме, представленной на рисунке.
Единичный момент обратного изгиба полотнища для правки концевых участков (момент на единицу высоты пояса) определялся по формуле:
 кгс∙м/см
кгс∙м/см
где
σТ - предел текучести стали;
δ - толщина пояса;
![]() - коэффициент
упругой зоны при сворачивании полотнища в рулон;
- коэффициент
упругой зоны при сворачивании полотнища в рулон;
здесь Rсв - радиус сворачивания полотнища в рулон;
μ - коэффициент Пуассона;
E - модуль упругости стали;
![]() - отношение
радиуса сворачивания к радиусу обратного изгиба при правке.
- отношение
радиуса сворачивания к радиусу обратного изгиба при правке.
Основные параметры рулонирования и правки полотнищ стенки резервуара объемом 50 тыс. м3
Rcb. = 1340 мм
|
|
Марки стали |
16Г2АФ |
σТ = 50 кгс/мм2 |
ВСт3сп5 σТ = 28 кгс/мм: |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
δ, мм |
17 |
16 |
14 |
13 |
11 |
10 |
10 |
|
|
φо, рад/м |
0,75 |
0,75 |
0,75 |
0,75 |
0,75 |
0,75 |
0,75 |
|
|
φпр, рад/м |
0,33 |
0,033 |
0,033 |
0,033 |
0,033 |
0,033 |
0,033 |
|
|
к1 |
0,3401 |
0,3829 |
0,04177 |
0,4485 |
0,5301 |
0,578 |
0,3252 |
|
|
к 1/м |
0,1401 |
0,1488 |
0,1701 |
0,1832 |
0,2165 |
0,2381 |
0,1333 |
|
|
Rocт, мм |
2630 |
2800 |
3270 |
3830 |
4800 |
5840 |
2530 |
|
|
φ1, рад/м |
0,3802 |
0,3571 |
0,3058 |
0,278 |
0,2083 |
0,1712 |
0,3953 |
|
|
βо, рад/м |
1,1547 |
1,173 |
1,2207 |
1,249 |
1,321 |
1,369 |
1,1364 |
|
|
β, рад/м |
0,4047 |
0,423 |
0,4707 |
0,499 |
0,571 |
0,619 |
0,3864 |
|
|
βобр.изг., рад/м |
0,333 |
0,345 |
0,40 |
0,417 |
0,431 |
0,435 |
0,3125 |
|
|
Rобр.изг., мм |
3000 |
2900 |
2500 |
2400 |
2320 |
2300 |
3200 |
|
|
|
34,5 |
30 |
21,6 |
18,0 |
13,0 |
9,1 |
6,8 |
|
|
Моб.изг., т∙м |
5,2 |
4,5 |
3,25 |
2,7 |
2,0 |
4,1 |
4,12 |
|
|
МΣ, т∙м |
25,87 |
|
|
|
|
|
|
|
Результаты проведенных теоретических и экспериментальных исследований позволили сделать следующие основные выводы по технологическим параметрам правки концевых участков полотнищ:
а) ширина зоны правки от начальной или конечной кромок полотнища должна находиться в пределах 1600 - 2000 мм
б) для получения после правки остаточной кривизны близкой к проектной по всей высоте стенки, радиус обратного изгиба для различных поясов должен быть различен.
Этим технологическим требованиям должны удовлетворять применяемые способы и устройства по правке концевых участков. Наиболее идеальной схемой правки представляется правка с помощью сектора, оснащенного сменными дугами различной кривизны и длиной около 2 м.
Переставляя сектор с помощью крана на каждый пояс и используя сменные дуги соответствующей кривизны можно осуществить хорошую правку концевых участков шириной ~ 2 м на всю высоту стенки.
Опыт применения приспособления в виде каркаса с шаблонами постоянной кривизны, обеспечивающего обратный изгиб конца полотнища одновременно на всю высоту стенки, показывает возможность получения удовлетворительных результатов правки обратным изгибом на один радиус, соответствующий необходимому радиусу правки нижних поясов.
На основе этого опыта можно сделать вывод о том, что при правке обратным изгибом полотнищ переменной толщины можно ограничиться двумя-тремя радиусами обратного изгиба, что необходимо принимать во внимание при дальнейшем совершенствовании устройств для правки,
ЛИТЕРАТУРА
1. Никиреев В.М., Ритчик Г.А. К вопросу рулонирования полотнищ переменной толщины. - Сборник трудов ВНИИМСС. Исследование методов сварки. Процессы монтажа резервуаров, М., 1979.
2. Сахненко В.М. Холодная гибка и правка деталей. М., Машгиз, 1951.
КОНЦЕНТРАЦИЯ ДЕФОРМАЦИЙ В МОНТАЖНОМ СТЫКЕ СТЕНКИ ЦИЛИНДРИЧЕСКОГО РЕЗЕРВУАРА
Канд. техн. наук В.М. Никиреев
1. В стенках вертикальных цилиндрических резервуаров, выполненных из рулонных заготовок, встречаются монтажные стыки, у которых кольца соседних полотнищ соединены под небольшим углом. При заполнении резервуара в этих стыках возникают значительные местные напряжения и деформации. При большом количестве циклов налива и слива продукта в монтажных стыках, имеющих угловатость, наблюдаются случаи нарушения герметичности стенки в связи с малоцикловой усталостью металла. Для определения допустимого числа циклов налива и слива продукта необходимо установить зависимость коэффициента концентрации деформаций в упомянутом монтажном стыке от величины угла стыковки концов соединяемых полотнищ. В дальнейшем будем этот угол обозначать через 2 γ. Наиболее часто монтажные стыки имеют угловатость в средней зоне стенки - на уровне 3 - 6 поясов. В этой зоне мало сказываются влияния нижнего и верхнего уторных соединений стенки и поэтому при анализе деформаций в угловатых монтажных стыках будем пренебрегать влиянием уторов.
Рассмотрим замкнутую полосу единичной ширины толщиной δ, состоящей из п одинаковых круговых полос радиуса R, соединенных между собою под углом 2γ. Из условия равенства периметра кругового пояса цилиндрического резервуара проектного радиуса Ro и периметра упомянутой замкнутой полосы получим зависимость (рис. 1)
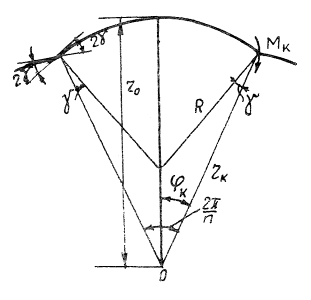
Рис. 1
![]()
Определим изгибные деформации этой полосы под воздействием внутреннего давления интенсивностью q.
Изгибающий момент М в поперечном сечении нагруженной полосы (рис. 2) и ее кривизна 1/ρ находятся из выражений [1]
![]() ; (1)
; (1)
![]() , (2)
, (2)
Точка 0 - начало полярной системы координат - совпадает с центром замкнутой полосы, Мо - изгибающий момент в середине круговой полосы (φ - 0).
Используя известную зависимость M = EJ(1/ρ - 1/R) и дважды интегрируя уравнения (1), (2) с учетом равенства ds2 = dr2 + (rdφ)2 и граничных условий (см. рис. 1), получим два уравнения для определения ro и rк
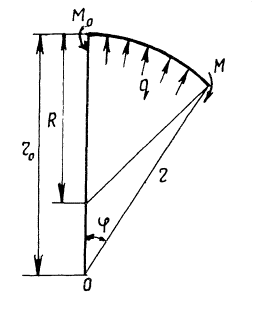
Рис. 2.
 ; (3)
; (3)
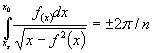 . (4)
. (4)
Здесь
![]() ; (5)
; (5)
![]() , (6)
, (6)
где
a = qR3/8EJ = 1,5(σo/E)(R/δ)2, σo = qR/δ, (7)
![]() . (8)
. (8)
Верхние знаки (+) берутся для угловатости типа "сердечко" (см. рис. 1); знаки (-) берутся для стыков, имеющих форму "домика". Ниже будем рассматривать угловатость типа "сердечко".
Так как подкоренное выражение x - f2(x) в интегралах уравнений (3) и (4) при х = хо равно нулю, то для получений численных результатов эти интегралы потребовали преобразования с выделением особенности функции x - f2(x) в окрестности х = хо.
После преобразований уравнения (3) и (4) приняли вид
 , (9)
, (9)
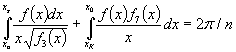 . (10)
. (10)
Здесь
![]() ,
,
![]() ,
,
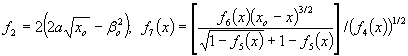 (11)
(11)
![]()
Первые интегралы этих уравнений выражаются через элементарные функции
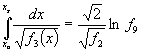 , (12)
, (12)
где
![]() ,
,
здесь ![]() ;
;
![]() (13)
(13)
где ![]() ,
,
![]() , (14)
, (14)
b = f1 - f2∙xo
При a ≥ 25 вторые интегралы в уравнениях (9) и (10) составляют менее 0,1 % соответственно от первых интегралов.
Это обстоятельство позволило для определяющей разности m = xo - xк получить простую зависимость
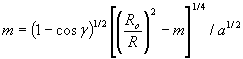 , (15)
, (15)
которая за 2 цикла решается простой интеграцией, если принять за начальное приближение
![]() . (16)
. (16)
Отметим, что при а ≥ 100 с погрешностью менее 1 % можно пользоваться формулой (18).
Изгибающий момент в угловом стыке определяется из выражения
![]() . (17)
. (17)
С учетом выражений (8) и (18) имеем
![]() . (18)
. (18)
При малых углах γ
≤ 8° и п ≤ 6, можно
принять (Ro/r)1/2
≈ 1, (1 - cosγ)1/2 = ![]() и тогда
получим изгибающий момент и наибольшие изгибные напряжения в стыке с
угловатостью, определяемые из линейной теории
и тогда
получим изгибающий момент и наибольшие изгибные напряжения в стыке с
угловатостью, определяемые из линейной теории
![]() ,
,
![]()
При γ = 2fyl/l, где fy - стрелка в угловатом стыке на базе l, будем иметь [2]
![]() .
.
Наибольшие суммарные напряжения находятся из формулы
![]() , (19)
, (19)
где σmax - коэффициент концентрация упругих напряжений. Полученный коэффициент концентрации получил экспериментальное подтверждение и является одной из основных характеристик, позволяющей по известной методике расчета конструкций на малоцикловую усталость [3] оценить долговечность цилиндрических резервуаров и сосудов в условиях циклического нагружения.
2. Расчеты цилиндрических резервуаров, выполненные по изложенной методике, показали, что действительная работа резервуаров, а следовательно их надежность, могут быть определены только на основе нелинейной теории оболочек. Для решения нелинейных дифференциальных уравнений применяется чаще всего метод конечного элемента или метод конечных разностей, позволяющий свести задачу к решению большой системы нелинейных алгебраических уравнений. Общих (универсальных) методов решения таких систем нет. В расчете оболочек получил распространение метод нагружения конструкции малыми ступенями (шагами) - аналог методу решения уравнений путем их дифференцирования по параметру.
Для таких тонкостенных конструкций, какими являются цилиндрические резервуары (R/δ - 2000 ÷ 3000 для стенки), величины ступеней нагрузок очень малы и для получения решения с удовлетворительной точностью число ступеней нагружения доходит до нескольких тысяч и более. В сообщении [4] описывался способ повышения сходимости метода последовательных нагружений путем использования экстраполяционных формул для предсказания приращений искомых функций. Ниже излагается обобщение этого способа, позволяющего существенно сократить число ступеней (шагов) нагружения.
Пусть
λqi = fi(w1…wN), i = 1, 2…N (20)
система нелинейных уравнений с параметром λ, изменяющимся от до 1, qi - заданные постоянные величины нагрузок, wi - искомые величины. Если параметр λ получает приращение Δλ то переменные wi также получают приращения Δwi. Используя ряд Тейлора, получим систему уравнений относительно Δwi.
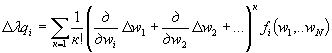 (21)
(21)
В методе исследовательного нагружения обычно ограничиваются первым членом ряда (К = 1). Решая полученную систему линейных уравнений, определяют Δwi. В работе [4] предложено учитывать квадратичные члены в разложении (21), исходя из линейной системы уравнений (i - 1, 2…N)
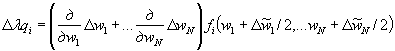 (22)
(22)
где Δwi - определяются по экстраполяционным формулам по известным Δwi из предыдущих шагов нагружения. При ![]() = Δwi система (22) (i = 1, 2... N) удовлетворяет выражению (21) до
квадратичных членов включительно. Обобщим систему (22) с целью повышения ее
точности исходя за выражения (21). Для этого функцию fi в (22) представим в виде
= Δwi система (22) (i = 1, 2... N) удовлетворяет выражению (21) до
квадратичных членов включительно. Обобщим систему (22) с целью повышения ее
точности исходя за выражения (21). Для этого функцию fi в (22) представим в виде
![]() , (23)
, (23)
здесь ![]() = 1 – С,
= 1 – С, ![]() = 1 - α, где
С и α - постоянные,
определяемые с учетом нелинейных членов до четвертого порядка включительно в
выражении (21).
= 1 - α, где
С и α - постоянные,
определяемые с учетом нелинейных членов до четвертого порядка включительно в
выражении (21).
Разложив функцию (23) в
ряд Тейлора и приравнивая подобные члены разложения в полученном выражении (при
![]() ) и в (21), придем к совместной системе уравнений
) и в (21), придем к совместной системе уравнений
![]() ,
,
![]() ,
,
![]() .
.
Корни этой системы ![]()
![]()
Функция, удовлетворяющая
системе (21): до нелинейных членов шестого порядка включительно, имеет вид (при
![]() = Δwi)
= Δwi)
![]()
![]()
где ![]() находятся из системы
четырех уравнений
находятся из системы
четырех уравнений
![]()
здесь п - 2, 3, 4, 5.
Корни этой системы ![]() ,
,
где ![]() - корни полинома
Лежандра.
- корни полинома
Лежандра.
![]() .
.
Оказывается, что корни α, С и β, μ, С равны абсциссам к коэффициентам квадратурной формулы Гаусса соответственно при двух и четырех узлах интерполяции интервала интегрирования. Отметим, что при трех узлах интерполяции требуемая точность не достигается из-за плохой аппроксимации членов, соответствующих смешанным производным выше третьего порядка в выражении (21). Только при четных узлах интерполяции достигается одинаковая точность аппроксимации всех нелинейных членов равных порядков, включая их смешанные произведения.
Для решения систем
нелинейных уравнений изложенным способом необходимо знать приращения искомых
неизвестных хотя бы на трех предыдущих шагах нагружения с целью определения ![]() для системы
(20). На начальных шагах нагружения это можно сделать следующим способам,
являющимся аналогом метода интегрирования Рунге-Кутта. Из-за громоздкости
доказательства приведем только последовательность этапов решения системы (20).
для системы
(20). На начальных шагах нагружения это можно сделать следующим способам,
являющимся аналогом метода интегрирования Рунге-Кутта. Из-за громоздкости
доказательства приведем только последовательность этапов решения системы (20).
1 этап - определяются ![]() из обычной системы
линейных уравнений, получаемой в методе последовательных нагружений (i =
1,2...N)
из обычной системы
линейных уравнений, получаемой в методе последовательных нагружений (i =
1,2...N)

2 и 3 этапы -
последовательно определяются ![]() из систем линейных
уравнений (j = 1 и 2)
из систем линейных
уравнений (j = 1 и 2)
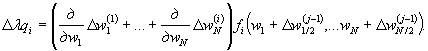
4 этап - определяются ![]() из системы линейных
уравнений
из системы линейных
уравнений
![]()
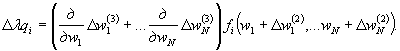
5 этап - определяются искомые приращения:
![]()
Полученные приращения ![]() будут удовлетворять
системе (21)
с точностью до нелинейных членов
четвертого порядка включительно.
будут удовлетворять
системе (21)
с точностью до нелинейных членов
четвертого порядка включительно.
Изложенный метод был применен для определения напряженно-деформированного состояния стенки цилиндрического резервуара (в средник поясах) в зоне монтажного стыка, имеющего угловатость, Задача решалась с учетом пластической работы стали. Так, для стали Ст3 было выявлено, что при угловатости 2γ = 5° происходит разное нарастание изгибных деформаций в монтажном стыке - с 0,4 % при 2γ = 4о до 3,3 % при 2γ = 6° с локализацией пластических деформаций в полосе монтажного стыка шириною всего 8 - 10 толщин стенки. Полученное затем аналитическое решение этой задачи подтвердило высокую точность изложенного выше метода.
ЛИТЕРАТУРА
1. Попов Е.Л. Нелинейные задачи статики тонких стержней. М., Гостехиздат, 1948.
2. Никиреев В.М. Приближенный метод проверки устойчивости цилиндрических резервуаров. Сб. научн. трудов ВНИИМСС. Исследования процесса монтажа трубопроводов и резервуаров. M., 1984.
3. Прочность конструкций при малоцикловом нагружении. Институт машиноведения им. А.А. Благонравова АН СССР. М., Наука, 1983.
4. Никиреев В.М. К решению систем нелинейных уравнений строительной механики методом последовательных нагружений. - Строительная механика и расчет сооружений. № 3, 1970.
ХАРАКТЕРИСТИКА НЕСУЩИХ ЭЛЕМЕНТОВ ДЛЯ ОБЛЕГЧЕННЫХ ПОКРЫТИЙ
Инж. Ю.В. Примаков
При сооружении покрытий для резервуаров и круглых силосов все большее распространение получают облегченные элементы, изготовленные как одно целое с настилом. Такая конструкция покрытия позволяет существенно снизить его массу (на 15 - 20 %) и уменьшить общую длину сварных соединений. При этом в 2 - 2,5 раза уменьшается номенклатура материалов для изготовления покрытий.
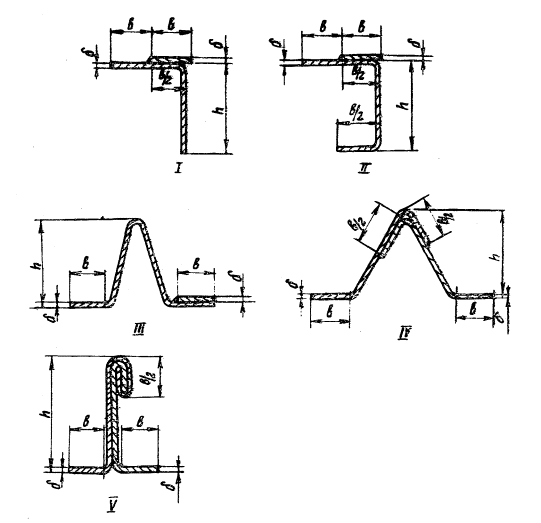
Рис 1. - Геометрические размеры несущих элементов
Во всех опытных или серийных покрытиях, где были использованы эти профили, применялась одна и та же схема радиально размещенных несущих элементов, которые при симметричном нагружении покрытия воспринимали изгибающие и сжимающие усилия. Это обстоятельство определило в данном случае способ сопоставления различных профилей по моменту сопротивления изгибу при равенстве площадей и толщин сравниваемых профилей.
В данной статье рассмотрены только те профили, которые были уже использованы в опытных или серийных покрытиях.
В связи с тем, что некоторые типы сечений весьма близки друг другу по конфигурации, было обращено особое внимание на одинаковость способа определения границ сечения и размеров включенной в расчетную формулу части оболочки. На рис. 1 представлены сечения тех профилей, которые рассмотрены в этой статье. При определении моментов инерции сечения в формулах были отброшены члены, имеющие небольшую величину и не влияющие на общий результат.
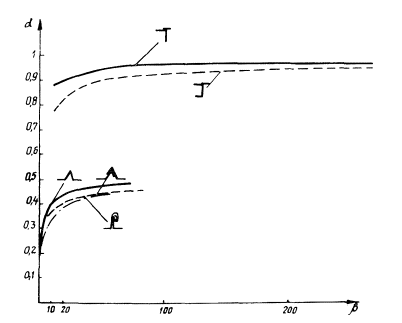
Рис. 2. Кривые геометрических характеристик различных элементов
Для сопоставления несущей способности гнутых профилей использовались коэффициенты α и β.
![]() ;
;
где h - высота профиля;
L - длина развертки;
![]()
где Jх - момент инерции сечения;
δ - толщина сечения.
На. рис. 2 представлены кривые изменения α и β в зависимости от длины развертки заготовки. На кривых видно, что в ряде случаев характеристики сходных по очертаниям элементов оказываются весьма близкими по значению. Это позволяет выбирать в каждой конструкции тот тип профиля, который наиболее соответствует условиям работы сооружения.
Примером может быть использование треугольных гофров, которые применялись в конструкциях крыш для резервуаров и зерновых силосов. Так как крыши для резервуаров, имеют небольшой угол подъема (около 7°), то целесообразно было использовать гофры типа III, которые позволяют применять упрощенную технологию изготовления и монтажа покрытия. Были выпущены проекты таких покрытий для резервуаров емкостью от 100 до 2000 м3. Сооружение и испытание таких покрытий на резервуарах емкостью 700 и 1000 м3 показали хорошее совпадение теоретических и экспериментальных данных, подтвердило правильность выбранной расчетной схемы.
Треугольный гофр типа IV более удобен для конических крыш, имеющих большой угол наклона, поэтому этот тип гофров был выбран для крыши металлического силоса с углом подъема крыши 30°. При таком конусе нужно было обеспечить удобство образования конической поверхности покрытия и стыковка гофров в зоне вершины гофра облегчает решение этой задачи. Крыши для силосов с треугольными гофрированными элементами имеют следующие особенности по сравнению с крышами для резервуаров:
1) на крыше имеется промежуточное кольцо, которое соединяется специальным натяжным устройством с радиальными гофрами, образуя жесткое соединение;
2) число гофров неодинаково в разных зонах, оно уменьшается по направлению к вершине конуса после пересечения опорного кольца.
Применение гофрированных элементов в покрытиях для силосов дало снижение массы покрытия на 25 % по сравнению с типовым проектом и позволило существенно сократить сроки возведения сооружения. Так же как и при испытаниях покрытия для резервуаров, совпадение теоретических и экспериментальных данных было удовлетворительное.
Из всех рассмотренных профилей, наиболее выгодны по соотношению α и β профили типа I и II. Этот тип профилей широко применяется в конструкциях, работающих на изгиб (например, панелях), он применялся в покрытиях для резервуаров как в СССР, так и за рубежом. Достоинствами такого профиля являются: большая жесткость при изгибных напряжениях, простота изготовления, экономичность. Недостатком - небольшая крутильная жесткость, что требует принятия дополнительных мер по сохранности заготовки в процессе транспортировки и монтажа.
Вариант сечения II более жесткий и более удобный при использовании в конструкции промежуточных колец или элементов, закрепляемых под крышей, на покрытии снизу.
Покрытия типа V разработаны болгарскими специалистами для зерновых силосов и напоминают аналогичные покрытия промышленных зданий, в которых несущим элементом является ужесточенный замковым соединением узел стыковки листов. Такое покрытие отличается от рассмотренных выше отсутствием сварки и может быть изготовлено из тонкого листа, имеющего антикоррозионное покрытие. Толщина покрытия определяется мощностью фальцезакатного приспособления и пластичностью материала настила. Опыт применения таких покрытий показал, что долговечность и сохранность антикоррозионного слоя зависит от устройства рабочего инструмента (роликов), которые должны быть либо гуммированные, либо изготавливаться из материалов, не повреждающих антикоррозионный слой. Недостатком конструкции крыши с такими элементами является необходимость создавать дополнительную систему конструкций дли установки термоподвесок.
Все эти профили уже применялись в различных покрытиях и поэтому имеется возможность сопоставить не только их геометрические характеристики, но и рассмотреть некоторые вопросы, связанные с практикой применения подобных несущих элементов. С точки зрения технологии изготовления монтажных заготовок подобные элементы могут быть условно разделены на две группы - первая состоит из несущих элементов, полностью образованных в процессе заводского изготовления, и вторая из элементов, которые приобретают проектные размеры и форму в процессе монтажа покрытия.
К первой группе относятся элементы типа I, II, III, ко второй типа IV и V. С точки зрения заводского изготовления монтажных заготовок и транспортировки между этими группами нет большой разницы, с точки зрения подгонки и сборки на монтаже, вторая группа удобнее. В то же время вторая группа увеличивает объем сварочных работ или требует специального оборудования для образования соединения на монтаже (типа фальцезакаточных станков). Выгибка гофров или других несущих элементов может при среднесерийном производстве производиться на листогибочных прессах, при крупносерийном производстве целесообразно использовать прокатное оборудование.
При транспортировке щитов покрытия, имеющих облегченные несущие элементы, необходимо принять, дополнительные меры предосторожности для обеспечения сохранности тонкостенного элемента. Особенно это необходимо для гнутых элементов открытого профиля типа I и II, а также для заготовок элементов типа V. Как показал опыт, наиболее эффективный способ сохранения заготовок от повреждений - упаковка в плотные пакеты с применением деревянных прокладок, вкладывая заготовки друг в друга. Полосы, ограничивающие щиты в узкой и в широкой части не привариваются. При этом существенно увеличивается объём сварочных работ на монтаже, но зато есть гарантия сохранности щитов при перевозках. Правка и подгонка поврежденных элементов - весьма трудоемкая операция, поэтому целесообразно пойти на некоторое увеличение объема сварочных работ на монтажной площадке.
Рассмотрение разных типов ужесточающих гнутых элементов, которые применяются в конструкции покрытий резервуаров и силосов, позволило сделать следующие выводы:
1) все рассмотренные типы гнутых элементов позволяют создать более экономичные по массе и по трудоемкости изготовлений покрытия, чем применявшиеся ранее профили горячего проката;
2) область рационального применения гнутых элементов каждого типа зависит от условий нагрузки и размеров перекрываемого пространства;
3) совершенствование технологии изготовления гнутых элементов, а также улучшение способов нанесения средств антикоррозионной защиты позволит расширить область применения экономичных конструкций.
ОПТИМИЗАЦИЯ ПАРАМЕТРОВ КОНСТРУКЦИЙ ИЗОТЕРМИЧЕСКИХ РЕЗЕРВУАРОВ
Канд. техн. наук А.З. Майлер
При проектировании изотермических резервуаров наряду с обеспечением надлежащей надежности конструкций ставится задача получения экономичных решений. Одним из центральных вопросов экономичного проектирования является создание рациональных конструктивных решений с учетом различных критериев качества, таких как минимальный расход материалов, технологичность изготовления и монтажа, сокращение эксплуатационных расходов и др. Традиционное проектирование предусматривает возможно более полный учет реальных требований, вливающих на экономичность решения на основе систематизации накопленного инженерного опыта.
Более строгая постановка указанной проблемы и методы ее решения имеют место в теории оптимального проектировании конструкций [1, 2], в рамках которой следует ставить вопросы оптимизации резервуарных конструкции часть которых уже получила практическое решение.
Проблема оптимизации параметров конструкций изотермических резервуаров может быть сформулирована в общей постановке следующим образом.
Приведенные затраты на сооружение изотермических резервуаров для хранения различных сжиженных газов в масштабе всего народного хозяйства должны быть минимизированы при условии полного удовлетворения спроса промышленности на газохранилища с использованием изотермических резервуаров.
Такая постановка задачи предусматривает оптимизацию всего параметрического ряда изотермических резервуаров с определением рациональных типов и объемов резервуаров, соответствующих спросу промышленности. При этом резервуар определенного типа и объема должен иметь оптимальные по приведенным затратам параметры, от которых зависят такие критерии качества, как расход материалов, технологичность изготовления, транспортировки и монтажа конструкций, в том числе металлических и железобетонных, фундаментов, теплоизоляции. К указанным критериям относятся и эксплуатационные затраты, в первую очередь энергетические, а также потери продукта, ремонтные расходы, противопожарные мероприятия и др.
Учитывая чрезвычайную сложность поставленной задачи ее решение возможно осуществить поэтапно исследованием ряда частных вопросов общей проблемы оптимизации параметров конструкций изотермических резервуаров.
В инженерной практике имеется опыт решения оптимизационных задач в области резервуарных конструкций. В основном это работы, относящиеся к резервуарам для хранения нефти и нефтепродуктов. Однако, учитывая близость конструкций резервуаров для хранения нефтепродуктов и сжиженных газов, работы по оптимизации нефтерезервуаров могут служить хорошей методической основой для анализа поставленной задачи.
Наиболее полно разработан вопрос оптимизации параметров резервуарных конструкций по расходу металла.
Впервые задачу определения наивыгоднейших значений высоты и диаметра резервуара решил В.Г. Шухов [3]. Формулы, предложенные в [3] были получены из условия минимума расхода металла и охватывали два варианта:
1) толщина стенки резервуара постоянна (малые объемы резервуаров)
![]() ;
; ![]() , (1)
, (1)
2) толщина стенки переменна
![]() ;
; ![]() , (2)
, (2)
где
V - объем резервуара,
t - толщина стенки;
λ - суммарная приведенная толщина крыши и днища;
T - допускаемое напряжение (при расчете по предельным состояниям - расчетное напряжение);
γ - объемная масса продукта.
При выводе приведенных формул были сделаны допущения, что суммарная приведенная толщина днища и крыши, а также толщина верхних поясов стенки постоянны и не зависят от изменения оптимизируемых высоты и диаметра резервуара. С увеличением объема резервуара указанные допущения значительно снижают точность результатов, так как приведенная толщина крыши и днища, а также толщина верхних поясов стенки резервуара существенно зависят от изменения его диаметра и высоты.
В связи с этим в [4] величина λ была выражена формулой:
![]() , (3)
, (3)
где λ и D в метрах. Соотношение (3) получено
на основе анализа имеющихся проектных решений. На этой же основе получен
диапазон изменения коэффициента ![]() , выражающего отношение средней толщины стенки к
максимальной, который изменяется в пределах от 0,59 до 0,71. Нижний предел
соответствует применению в нижних поясах стали с расчетным сопротивлением
порядка 210 МПа, верхний - порядка 400 МПа. В соответствии с (3) и значением а1 в [4]
предложены формулы для определения Нопт.
и Dопт.
, выражающего отношение средней толщины стенки к
максимальной, который изменяется в пределах от 0,59 до 0,71. Нижний предел
соответствует применению в нижних поясах стали с расчетным сопротивлением
порядка 210 МПа, верхний - порядка 400 МПа. В соответствии с (3) и значением а1 в [4]
предложены формулы для определения Нопт.
и Dопт.
В связи с тем, что и приведенная толщина λ, и средняя толщина tсp, являются функциями независимой переменной (либо Н, либо D), так как высота и диаметр связаны между собой при постоянном объеме резервуара), необходимо в оптимизационной задаче учесть эту функциональную связь. Для величины λ имеется выражение (3). На основе анализа применяемых в настоящее время проектов резервуаров в [5] для λ рекомендовано выражение:
λ = 0,0149∙D + 0,01044 (м), (4)
Использование постоянного
коэффициента ![]() , как это предложено в [4],
не отражает функциональной связи tср. с
оптимизируемыми параметрами. Указанная связь может быть получена путем
численного решения известного уравнения устойчивости замкнутой круговой
цилиндрической оболочки, подверженной одновременному действию осевых и
поперечных нагрузок относительно tср.
(см. например, СНиП II-23-81). Для удобства
использования в задаче оптимизации на основе численного решения функциональная
зависимость аппроксимируется, например, линейной функцией [6]:
, как это предложено в [4],
не отражает функциональной связи tср. с
оптимизируемыми параметрами. Указанная связь может быть получена путем
численного решения известного уравнения устойчивости замкнутой круговой
цилиндрической оболочки, подверженной одновременному действию осевых и
поперечных нагрузок относительно tср.
(см. например, СНиП II-23-81). Для удобства
использования в задаче оптимизации на основе численного решения функциональная
зависимость аппроксимируется, например, линейной функцией [6]:
tср. = 0,0213D + 0,001975 (м) (5)
Минимизация расхода металла является важным аспектом экономичного проектирования, однако не менее важным является учет затрат на сооружение фундаментов, теплоизоляции, а также энергозатрат при эксплуатации изотермических резервуаров.
Качественный анализ влияния указанных факторов на основные размеры резервуара показывает, что имеется тенденция к увеличению отношения Н/D. Известно, что цилиндр имеет минимальную поверхность при Н/D = 1. Чем меньше поверхность резервуара, тем меньше теплоприток в него из окружающей среды, тем меньше площадь изоляционного покрытия. Вертикальные цилиндрические резервуары для хранения нефтепродуктов объемом 20 тыс. м3 более имеют отношение Н/D от 0,4 до 0,2. В [5] показано, что для нефтерезервуаров указанные отношения целесообразно увеличить до 0,8…0,4. В изотермических резервуарах при увеличении высоты в соответствующем уменьшении диаметра сокращается площадь зеркала продукта и, как следствие, интенсивность его испарения, однако увеличивается нагрузка на теплоизоляционный слой между днищами и на фундамент резервуара. Сокращение площади теплоизоляционного слоя и фундамента с одновременным увеличением нагрузки приводит, по-видимому, к некоторому уменьшению их стоимости по аналогии с фундаментами нефтерезервуаров. Однако, этот вопрос требует специального исследования, так как затраты на сооружение фундаментов в значительной мере зависят от состояния основания, и в связи с этим их величина имеет большой разброс.
Учет эксплуатационных затрат требует включения в оптимизационную задачу характеристик всего комплекса по сжижению, хранению и регазификации продукта. Однако приближенная постановка [7] позволила получить практические результаты оптимизации на основе эксплуатационных ограничений, заключающихся в том, что толщина теплоизоляционного слоя и основные габариты резервуара должны соответствовать некоторому допускаемому теплопритоку в емкость,
В указанной работе задача была поставлена следующим образом.
![]() (6)
(6)
где П - приведенные затраты на сооружение изотермического резервуара;
D - оптимизируемый параметр - диаметр резервуара;
V, A, B. С - постоянные геометрические параметры - соответственно объем резервуара, расстояние между стенками, днищами и крышами.
В выражении приведенных затрат учтены затраты на сооружение наружного и внутреннего резервуаров, перлитной теплоизоляции, слоя пеностеклянных блоков между днищами и фундамента.
Эксплуатационное ограничение по теплопритоку имеет вид:
Q (D, V, A, B, C) ≤ Qдoп. (7)
где Qдоп - допускаемый теплоприток в емкость (ккал/ч).
В связи с необходимостью определения массы металла прочностной расчет конструкций входит составной частью в оптимизационную задачу. При этом величины приведенных толщин элементов получены аналогично (4) и (5).
В [7] представлены зависимости стоимости различных элементов и общих приведенных затрат на сооружение изотермического резервуара от отношения Н/D.
Область параметров, при которых суммарные затраты отличаются от оптимальных незначительно (в пределах 5 %), достаточно широка и отношение (Н/D)опт. колеблется от 0,54 до 1,03.
При значительном возрастании объемов строительства изотермических резервуаров и при переходе в ближайшем будущем на их серийное производство возрастает значение унификации элементов конструкций и методов их возведения. С этой проблемой тесно связана задача оптимизации параметрического ряда изотермических резервуаров по их типам и объемам. Методически указанная задача решена для нефтерезервуаров [8], и эта методика может быть модифицирована применительно к резервуарам для хранения сжиженных газов. При рассмотрении оптимизации параметрического ряда изотермических резервуаров, исходя из "Типовой методики оптимизации параметрического (типоразмерного) ряда" Госстандарта СССР, совокупностью изделий, отличающихся друг от друга числовыми значениями параметров, являются резервуары различной вместимости. Резервуары могут быть отнесены к объектам с ограниченной заменяемостью. Например, резервуар меньшей вместимости может быть заменен резервуаром большей вместимости, или больший - двумя малыми, однако, общая стоимость при таких решениях будет возрастать.
Оптимизация параметрического ряда в рассматриваемом случае заключается в нахождении совокупности резервуаров с такими значениями параметров (геометрических объемов), при которых заданные потребности в изделиях удовлетворяются с наименьшими суммарными приведенными затратами.
Потребность в резервуарах той или иной вместимости характеризуется "функцией спроса", которая задается как количество выпускаемых в год резервуаров определенной вместимости, необходимых народному хозяйству.
Связь между параметрами изделий и затратами на разработку, изготовление, монтаж и эксплуатацию определяется функцией затрат, которая задается как суммарные приведенные затраты резервуара определенной вместимости.
Для задания двух указанных функций на множестве возможных параметров изделий необходимо определить. дискретный ряд возможных вместимостей резервуаров, из которого можно "набирать" различные параметрические ряды.
В приближенном решении задачи могут быть использованы следующие предпосылки.
Определение "функции спроса" следует выполнять с помощью статистических методов прогнозирования, предусматривающих обобщение известных данных за определенный промежуток времени и экстраполяцию найденной закономерности на расчетный год. Множество возможных вместимостей необходимо определить таким образом, чтобы конструкция каждого резервуара была технологична в изготовлении, транспортировке и монтаже, а также рациональна по расходу материала. В условие технологичности целесообразно включить требование по унификации элементов конструкций. Рациональность конструкции по расходу материала должна обеспечиваться оптимальным отношением высоты и диаметра резервуара. Кроме того, при определении указанного отношения необходимо учитывать затраты на устройство фундаментов, сокращение площадей застройки, а также эксплуатационные затраты,
ЛИТЕРАТУРА
1. Рейтман М.И., Шапиро Г.С. Методы оптимального проектирования деформируемых тел, М., Наука, 1978.
2. Малков В.П., Угодчиков А.Г. Оптимизация упругих систем. М., Hayкa, Физматгиз, 1981.
3. Шухов В.Г. Избранные труды. Строительная механика. М., Наука, 1977.
4. Беляев Б.И. Оптимальные размеры вертикальных цилиндрических резервуаров. - Промышленное строительство. № 5, 1968.
5. Майлер А.З., Катанов А.А. Анализ рациональных конструктивных решений резервуаров с точки зрения расхода, металла, дифференцированного по прочности. Сб. научных трудов ВНИИмонтажспецстроя. Экономика механомонтажных работ. М., 1983.
6. Майлер А.З., Губадулина Е.В. Оптимизация параметров мультицилиндрических резервуаров вместимостью более 100 тыс. м3. Сб. научных трудов ВНИИмонтажспецстроя, Исследование процесса монтажа трубопроводов и резервуаров. М., 1984.
7. Майлер A.З., Поляков Д.В. Определение оптимальных параметров изотермических резервуаров с учетом технологических ограничений. Сб. научных трудов ВНИИмонтажспецстроя. Сооружение резервуаров и оболочек. Сварочные работы. М., 1982.
8. Майлер А.З., Катанов А.А., Поповский Б.В. Оптимизация параметрического ряда вертикальных цилиндрических резервуаров для хранения нефти и нефтепродуктов с учетом унификации конструкций. Сб. научных трудов ВНИИмонтажспецстроя. Монтаж и сварка резервуаров и технологических трубопроводов. M., 1983.
МЕТОДЫ ПОДОБИЯ И РАЗМЕРНОСТИ В ЗАДАЧЕ ОБТЕКАНИЯ МЯГКИХ ОБОЛОЧЕК ПОТОКОМ ВОЗДУХА
инж. В.П. Поляков,
канд. техн. наук Д.А. Бейлин,
инж. Ю.М. Гольберг
Обтекание мягких оболочек потоком воздуха наиболее полно исследуется на моделях с помощью аэромеханического эксперимента. При его проведении следует учитывать критерий геометрического, физического, кинематического и динамического подобия модели и натурной конструкции. Объектом экспериментов в аэродинамической трубе являлись модели воздухоопорных оболочек усеченной сферической формы, геометрически подобные реальным технологическим укрытиям с отношением Н/D = (0.3…0,82). Испытания проводились с соблюдением частичного подобия по механическим характеристикам материала оболочек, а также числам N, Eu и Re.
В процессе экспериментов изучались: распределение коэффициентов ветрового давлений, аэродинамические характеристики, изменение величины внутреннего избыточного давления, формы оболочки и реакции в опорном контуре в зависимости от скоростного напора потока. Для оценки распределения ветрового давлений поверхность оболочки была дренирована по трем меридиональным сечениям; определение аэродинамических характеристик осуществлялось с помощью шестикомпонентных весов, на которых устанавливались испытываемые модели. Перемещения точек поверхности оболочек замерялись по геодезическим координатам методом стереофотограмметрии с синхронным получением эпюры распределения давления.
В результате проведенных исследований установлено, что в принятых режимах обтеканий для оболочек, не имеющих одноосных областей, справедливы гипотезы плоских сечений и малых деформаций. Эпюры напряжений и перемещений соответствуют эпюре распределения давления на поверхности. Задавшись формой распределения напряжений в виде [1]
![]() ;
;
![]() , (1)
, (1)
получим натяжения в оболочке
![]() и
и ![]() (2)
(2)
где а, в, F - функции обобщенных аэродинамических характеристик и геометрии моделей; - угол срыва потока; ΔР - избыточное внутреннее давление; β - текущий угол, отсчитываемый от направления потока по широте; h - толщина оболочки.
По натяжениям Т1 и Т2 находим главные натяжения и определяем величину избыточного давления в оболочке, предшествующую появлению одноосных зон.
Экспериментальные исследования завершаются определением функциональной связи между критериями подобия в виде уравнения регрессии [2].
Перемещения точек поверхности модели являются функцией восьми параметров:
![]() (3)
(3)
где R, H и h - геометрические характеристики модели; Е, ρ - характеристики материала; p. q - силовые воздействия; t - время.
Анализ показателей степеней при параметрах дозволяет сделать вывод, что независимыми переменными являются безразмерные величины H/R, p/Е и q/E, в результате чего уравнение регрессии записывается в виде
 . (4)
. (4)
Обозначив ![]() и πi
- безразмерные комплексы, записанные в круглых скобках, получим:
и πi
- безразмерные комплексы, записанные в круглых скобках, получим:
πо = φ(π1, π2, π3) (5)
Представим регрессионное уравнение (5)с тремя переменными в форме:
![]() (6)
(6)
где Ао - согласующая постоянная; С1, С2 и C3 - неизвестные показатели степени. Логарифм согласующей постоянной и показатели степени (6) могут быть найдены из решения системы линейных уравнений вида:
y = Xс (7)
где y - опытные
значения отношения ![]() соответствующие
опытным коэффициентам (параметрам) матрицы Х.
соответствующие
опытным коэффициентам (параметрам) матрицы Х.
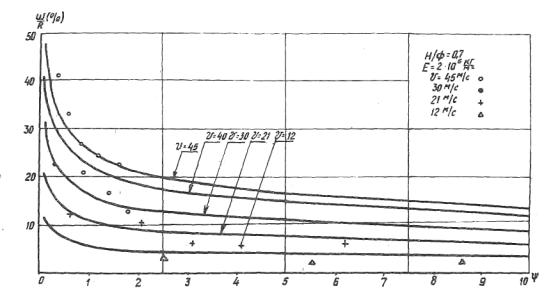
Рис. 1.

Рис. 2.
Соответственно величинам модуля упругости материала Е экспериментально были получены следующие значения параметров:
|
А0 |
С1 |
C2 |
С3 |
Е |
|
4,50 |
-2,47 |
-0,27 |
0,8 |
2∙106 |
|
5,71 |
-2,45 |
-0,27 |
0,8 |
2∙107 |
|
6,92 |
-2,47 |
-0,27 |
0,8 |
2∙108 |
Сопоставление экспериментальных значений и данных, полученных на основе предложенной модели, показано на рис. 1 и 2.
Результаты выполненных экспериментальных исследований позволяют оценить напряженно-деформированное состояние мягкой оболочки при обтекании потоком воздуха и определить величины внутреннего избыточного давления для различных форм оболочек и ветровых нагрузок
ЛИТЕРАТУРА
1. Поляков В.П., Бейлин Д.А., Гольберг Ю.М. О взаимодействии мягкой оболочки усеченной формы с потоком воздуха. В сб. трудов ВНИИмонтажспецстроя. Исследование процесса монтажа трубопроводов и резервуаров. М., 1984.
2. Седов Л.И. - Методы подобия и размерности в механике. М., "Наука", 1965.
СТАНДАРТНЫЕ ПОДПРОГРАММЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ДЛЯ РАСЧЕТА РЕЗЕРВУАРОВ
Инж. С.В. Волкова,
канд. физ-мат. наук Л.Л. Сабсович
Многие вопросы поведения резервуаров под нагрузкой приводят к решению задач теории упругости или теории оболочек. Как правило, аналитическое решение этих задач не представляется возможным. Поэтому приходится прибегать к численным методам решения.
Применив метод дискретизации к системе уравнений в частных производных, описывающей поведение изучаемого объекта в упругой или упруго-пластической стадии, можно получить систему линейных или нелинейных уравнений большего порядка относительно дискретных значений искомых функций.
Если система исходных уравнений была линейной, то система дискретных уравнений тоже будет линейной, однако матрица ее коэффициентов окажется слабо заполненной и будет носить ленточный характер. Если же исходная система была нелинейной, то ее тем или иным способом приходится линеаризовать и задача все равно сведется к решению ленточной системы линейных алгебраических уравнений большого порядка.
Решать такие системы можно только на ЭВМ, используя прямые или итерационные методы решения. Если система получалась не слишком большого порядка, то имеет смысл применять прямые методы решения. Учет ленточности системы позволяет значительно сократить требования кооперативной памяти ЭВМ, но и при этом обычно расположить всю матрицу в памяти ЭВМ не удается. Поэтому приходится прибегать к использованию памяти на внешних накопителях.
Существуют разные способы хранения матрицы системы на внешнем накопителе. В разработанных нами подпрограммах мы использовали два способа хранения матрицы: по строкам и по блокам.
Каждый из этих способов имеет свои преимущества и недостатки. Хранение по строкам часто (но не всегда) позволяет сократить ширину ленты, но требует более частого обращения к внешней памяти, что замедляет работу. Часто формирование блоков оказывается более простым, чем формирование отдельных строк, так как количество разных типов блоков много меньше, чем количество разных типов строк. При хранении матрицы по строкам легче применять более сильные варианты метода исключения Гаусса.
Нами разработаны две стандартные подпрограммы решения ленточных систем линейных алгебраических уравнений, матрица которых хранится на накопителях на магнитных дисках. Одна из них обрабатывает матрицу, хранящуюся по строкам, а вторая - по блокам. Обе подпрограммы используют метод последовательного исключения Гаусса (без выбора главного элемента).
Подпрограмма GSLD предназначена для решения систем, матрица которых хранится по строкам на диске в файле с прямым доступом. Порядок систем N, число верхних диагоналей, ρ, нижних - q, ширина ленты составляет L. = р + q + 1 количество столбцов правых частей m.
В оперативной памяти ЭВМ отводятся два массива - для хранения ведущей строки размером L и для хранения q строк нижних диагоналей размером q×L. Во втором массиве хранятся обрабатываемые строки. Верхняя строка этого массива по окончании очередной обработки становится ведущей и передается в первый массив, все строки второго массива перемещаются на одну строку выше, а нижняя строка заполняется очередной строкой из файла на диске. Использованная ведущая строка для проведения обратного хода пересылается обратно в файл на диске.
По окончании прямого хода выполняется обратный ход и на месте m столбцов правых частей (m ≥ 1) получаются решения системы.
Каждая запись строки в файле на диске имеет длину L.
Обращение к подпрограмме имеет вид;
CALL GSLD (NK, N, М, NP, NQ, BF, ВС, x, IER).
NK - логический номер канала, где хранится ленточная матрица на диске;
N - порядок матрицы;
M - количество столбцов правых частей;
NP - количество верхних диагоналей;
NQ - количество нижних диагоналей;
BF - рабочий массив из NQ×L элементов;
ВС - рабочий массив из L элементов;
x - массив из N×M элементов, где при обращении к подпрограмме должны находиться столбцы правых частей;
IER - служебная переменная: если в процессе решения выясняется, что на главной диагонали ведущей строки находится нулевой элемент, то переменной IER присваивается значение 1, решение прерывается и управление передается в программу, если же на главной диагонали ведущих строк нулевых элементов не окажется, то эта переменная будет иметь значение, равное 0.
Для увеличения быстродействия подпрограммы введен массив BF, который и определяет требования к оперативной памяти при использовании подпрограммы GSLD. Произведение NQ×L не должно превышать 7 - 8 тысяч для оперативной памяти в 64 Кбайт, а для оперативной памяти в 256 Кбайт оно может достигать 50 тысяч.
Для экономии оперативной памяти с диска можно было бы вызывать по одной строке и тогда массив BF, так же, как массив ВС, имел бы размерность L, однако, это во много раз увеличило бы время решения.
Подпрограмма GBLD использует хранение матрицы по блокам.
При сведении систем уравнений в частных производных первого и второго порядка к системе уравнений в конечных разностях в уравнениях, записанных для каждой точки, участвуют только по 3 смежных строки и столбца. Если формирование по блокам осуществлять по строкам, то в каждой строке уравнения системы будут участвовать переменные только трех смежных блоков, т.е. матрица будет иметь трехдиагональную блочную форму.
Однако вследствие наличия дифференциальных граничных условий верхняя и нижняя блочные строки будут иметь не по два блока, а по три, поэтому подпрограмма GBLD решает блочную систему порядка M вида
А11А12А13
A21A22A23
A32A33A34
А43А44А45
…
АМ-1, М-2АМ-1,М-1АМ-1,М
АМ,М-2АМ,М-1АМ,М
До обращения к подпрограмме следует записать все эти блоки в файл последовательного доступа по блочным строкам А11А12А13A21… Каждый блок записывается в память машины по столбцам, как это принято в фортране.
В подпрограмме допускается, что блоки не все одного размера. Размеры квадратных диагональных блоков задаются с помощью специального вектора N(M).
Минимальное количество блоков в оперативной памяти не может быть меньше трех (для двух сомножителей и результата произведения матриц). Однако для сокращения числа обращений к диску подпрограмма требует задания еще двух таких же массивов размером (max(N))2. Так что произведение 5 (max(N)) не должно превышать 7 - 8 тысяч для ЭВМ с оперативной памятью в 64 Кбайт.
Правая часть содержит только один столбец и задается в виде массива с числом элементов, равным порядку системы (N1 + N2 + …+ NМ).
По окончании работы подпрограммы результат содержится в специальном массиве. Файл исходных блоков и массив правых частей сохраняются.
Обращение к подпрограмме GBLD имеет вид:
CALL GBLD (M, N, KM, KZ, В, RD, RP, RL, RS, RV, XD, XP, XL, XS, DT, x)
Здесь
М - блочный порядок системы;
N - целый массив размерности М, определяющий размеры диагональных блоков;
КМ - логический номер канала - файла последовательного доступа, в котором размещены блоки системы;
KZ - логический номер канала - рабочего файла;
B - сектор правых частей, массив размерностью N1+Na+…NM, RD, RP} R, RS, RV - рабочие массивы, каждый размерностью (max N1, N2…NM))2
ХD, ХР, XL, XS - рабочие массивы, размерностью каждый max(N1, N2, NM);
DT - массив размерностью М для хранения значения детерминантов диагональных блоков;
X - массив размерностью N1+ N2+ NM для хранения результатов счета.
Обе эти подпрограммы использовались при расчетах напряженного состояния оболочки резервуара с отверстием и для расчета зоны "хлопуна" (зоны потери устойчивости) в оболочке резервуара.
СПОСОБ ИЗГОТОВЛЕНИЯ КРУТОИЗОГНУТЫХ ОТВОДОВ НЕПРЕРЫВНОЙ ПРОТЯЖКОЙ ТРУБНЫХ ЗАГОТОВОК ПО РОГООБРАЗНОМУ СЕРДЕЧНИКУ
Инж. Ю.Б. Шувалов,
канд. техн. наук В.А. Куренков,
инж. В.А. Кочнов
В отечественной и зарубежной практике наиболее распространенным способом заводского изготовления крутоизогнутых отводов является горячая протяжка трубных заготовок мерной длины по рогообразному сердечнику с последующими операциями горячей объемной правки и калибровки отводов. Широкое распространение данного способа объясняется тем, что он позволяет получать отводы с малым радиусом кривизны и равной по всему объему изделия толщиной стенки [1].
Существующий технологический процесс рассчитан на получение крутоизогнутых отводов из мерных труб-заготовок. Это приводит к многооперационной маршрутной технологии: врезка труб на мерные заготовки, горячая протяжка, горячая объемная правка, обработка присоединительных торцов под сварку и калибровка отводов по внутреннему диаметру. Прерывистость процесса и наличие стыков труб приводит к неустановившемуся пластическому деформированию, что вызывает искажение формы отвода, образование на торцах отвода "козырька", увеличивает вероятность брака (разрывы, гофры, смятие торцов изделий).
При данном способе происходит отход заготовок на наружной образующей сердечника. Отход заготовки от поверхности сердечника приводит к значительному искажению формы переднего торца отвода и увеличивает опасность разрыва и гофрообразования изделия. Раскрытие стыков заготовок приводит к неправильному формоизменению трубной заготовки на сердечнике, смятию торцов заготовок на внутренней образующей сердечника, так как усилие деформирования в этом случае передается каждой заготовке лишь частью площади торца предыдущей заготовки и увеличивает опасность гофрообразования заготовки. Таким образом, при горячей протяжке отводов из штучных трубных заготовок наблюдается значительный неисправимый брак в результате разрывов, гофрирования и смятия торцов заготовок. Полученные отводы имеют также значительные колебания радиусов кривизны и искажения диаметров отводов. Вследствие этого требуются дополнительные операции горячей объемной правки и калибровки отводов; а также дополнительной штамповой оснастки, интенсивное использование которой приводит к непоправимому браку: закусыванию и смятию отвода в штампе.
Этих недостатков лишен способ изготовления отводов непрерывной протяжкой длинномерной трубы по рогообразному сердечнику или из штрипса с резкой отвода на сходе сердечника [2]. Непрерывность процесса горячей протяжки отводов позволяет получать изделие без искажения его формы и "козырьков", а отсутствие стыков заготовок полностью устраняет брак по смятию, гофрированию и разрыву изделий.
Внедрение предложенного способа и соответствующего оборудования качественно меняет маршрутную технологию и устраняет парк станков для механической резки труб на мерные заготовки. Появляется возможность устранить операции горячей объемной правки и калибровки отводов и за счет этого соответственно сократить парк кузнечно-прессового оборудования.
Реализация данного способа и оборудования связана с протяжкой отводов из электросварных труб и исследованием их прочности, с разработкой технологии и устройства для резки отводов на сходе сердечника, с решением проблемы совмещения скоростей сварки труб и горячей протяжки отводов.
Для доказательства возможности изготовления отводов высокого качества из длинномерной трубы или штрипса были проведены экспериментальные исследования на лабораторной установке ВНИИМСС. В связи с тем, что существующие конструктивные решения по резке отводов на сходе сердечника (газовая резка, плазменная резка, резка кислородом) имеют сложное техническое исполнение, имитацию непрерывной протяжки на лабораторной установке проводили следующим образом (см. рисунок):
перед протяжкой трубных заготовок по рогообразному сердечнику, имеющему штангу 1, формообразующий участок 2 и калибрующий участок 3 с заданным радиусом кривизны, между трубными заготовками 4 создавали, например, сваркой перемычки 5 из сплошного металла, расположенные на одной линии, параллельной оси трубной заготовки. При этом а = 2∙S, где а - ширина этих перемычек; S - толщина стенки трубной заготовки.
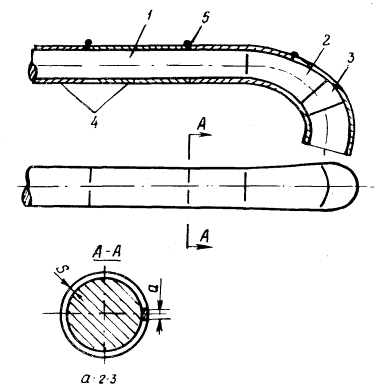
Схема процесса протяжки отводов на рогообразном сердечнике с использованием перемычек
Во время гибки трубных заготовок на рогообразном сердечнике эти перемычки ориентировали на наружной образующей сердечника и после протяжки отводов удаляли. При гибке заготовок на рогообразном сердечнике перемычки предотвращают раскрытие стыков заготовок и отход заготовки от поверхности сердечнике на наружной образующей сердечника. Происходит передача усилия протяжки всей площадью торца заготовки, что исключает смятие торцов заготовок на внутренней образующей сердечника и уменьшает опасность гофрообразования заготовки. При протяжке трубных, заготовок данным способом по рогообразному сердечнику происходит плотное прилегание заготовки к поверхности сердечника, что обеспечивает одновременную калибровку отвода по внутреннему диаметру на калибрующем участке сердечника и правильное формоизменение трубной заготовки на сердечнике. При этом не требуется дополнительная штамповая оснастка для горячей объемной правки и калибровки отводов.
Предложенный способ изготовления отводов [3] имеет преимущества перед способом изготовления отводов горячей протяжкой из длинномерной трубы или штрипса, так как не решен вопрос о способе резки отвода на сходе сердечника. Газовая резка, плазменная резка, резка кислородом имеют сложное техническое исполнение. Невозможно использование данного устройства при печном нагреве, который занимает значительный объем (80 - 90 %) при изготовления отводов горячей протяжкой в системе Минмонтажспецстроя. Необходимо создание технологии изготовления отводов непрерывной протяжкой с созданием перемычек между трубными заготовками, параметры и ориентация которых описаны выше (перемычки можно создавать либо недорезкой трубы на мерные заготовки, либо сваркой этих заготовок).
Преимущество предложенного способа изготовления крутоизогнутых отводов заключается в повышении точности изготовления отводов, повышения производительности труда и расширении технологических возможностей процесса,
ЛИТЕРАТУРА
1. Тавастшерна Р.И. Процесс изготовления крутоизогнутых отводов горячей протяжкой до рогообразному сердечнику. - Кузнечно-штамповочное производство. 1988, № 4, с. 18-22
2. Куренков В.А, Способ изготовления крутоизогнутых отводов из штрипса. - В кн. Изготовление и монтаж технологических трубопроводов. Труды ВНИИМСС, М., 1981.
3. Шувалов Ю.Б., Кочнов В.А. и др. Решение на выдачу авторского свидетельства от 25.09.84 г. на "Способ изготовления изогнутых отводов" государственной научно-технической экспертизой. Заявка № 3724592/25-27 (047752).
РАСЧЕТ СИЛОВЫХ ПАРАМЕТРОВ ДЛЯ ИЗГОТОВЛЕНИЯ ТОЛСТОСТЕННЫХ КРУТОИЗОГНУТЫХ ОТВОДОВ ГОРЯЧЕЙ ПРОТЯЖКОЙ
Инж. Ю.Б. Шувалов,
кандидаты техн. наук
Р.И. Тавастшерна, З.А. Куренков
Изготовление крутоизогнутых отводов горячей протяжкой труб по рогообразному сердечнику представляет собой высокопроизводительный способ, нашедший широкое распространение в серийном производстве отводов диаметром ДН 45…680 мм с толщиной стенки S - 2:5…8 мм при радиусах изгиба R - 1 Ду и 1,5 Ду из углеродистых и легированных сталей.
В связи с созданием в химической, нефтяной, газовой и других отраслях промышленности установок, работающих при высоких температурах, давлениях и агрессивных средах, выявилась острая потребность в изготовлении толстостенных отводов с относительной толщиной стенки S/D > 0,07.
Силовые условия процесса протяжки весьма сложны: схема деформирования не осесимметрична и в связи с этим напряжения на контактной поверхности сердечника сильно изменяются; процесс протяжки проводится при неравномерном нагреве трубы-заготовки в очаге деформации; неравномерно распределены силы нормального давления qn и трения qf (см. рисунок); труба-заготовка в процессе раздачи подвергается изгибу.
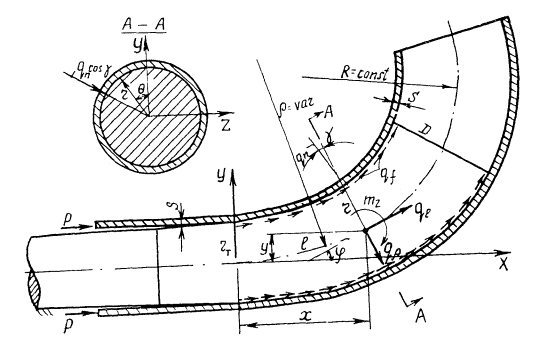
Схема процесса протяжки отвода на рогообразном сердечнике: r - радиус сечения сердечника вдоль средней линии; φ - угол между касательной к оси сердечника и осью X; θ - угол между r и осью У в поперечном сечении сердечника; l - длина оси сердечника от начала координат до рассматриваемой точки
Проведенные исследования силовых условий процесса и напряженного состояния рогообразного сердечника показали, что при горячей протяжке отводов в инструменте возникают значительные по величине нормальные растягивающие напряжения, особенно в сечении, расположенном в начале формообразующего участка сердечника [1], Таким образом, именно величина этих растягивающих напряжений будет определять прочность инструмента в целом (стойкость сердечника). Рассматривая сердечник как брус большой кривизны оси, величину максимальных растягивающих напряжений в сечении, расположенном в начале формообразующего участка, можно определить, используя теорию сопротивления материалов [2]:
![]() , (1)
, (1)
где
rT - внутренний радиус трубы-заготовки;
р - усилие протяжки отводов;
М - изгибающий момент в данном сечении.
Прочность металлов при высоких температурах характеризуется величиной предела длительной прочности σвд то есть таким напряжением при данной постоянной температуре, при действии которого в течение заданного промежутка времени в конце этого промежутка произойдет разрушение сердечника - либо потеря формы (изгиб), либо обрыв. Зная временные ресурсы работы сердечника, легко выразить его стойкость в количестве протянутых отводов, как это принято в практике:
![]() (2)
(2)
где
L - временная стойкость, сердечника, ч;
Пир – производительность пресса, ![]() ;
;
п - количество одновременно работающих сердечников.
Рассмотрим поверхность формообразующего участка сердечника, центральная ось которого - плоская кривая в системе ортогональных координат (см. рисунок).
Давление на сердечник qn в каждой точке может быть определено из уравнения для оболочки и в окончательном виде приведено в работе [2]:
![]() , (3)
, (3)
где
Тl. Тθ - внутренние усилия сжатия и растяжения в элементе протягиваемой трубы по направлениям главных кривизн;
Rl, Rθ - радиусы главных кривизн поверхности рогообразного сердечника, которые определяются в соответствии с положениями теории поверхностей.
В процессе протяжки между трубой-заготовкой и сердечником возникают значительные силы трения
qтр = f∙qn
где f - коэффициент трения.
Вследствие неравномерности деформации по сечению трубы величины нормальных давлений и сил трения принимают максимальные значения в области внутренней образующей сердечника (θ = 0) постепенно понижаясь по мере приближения к наружной образующей (θ - π). Это приводит к возникновению внешнего изгибающего момента mz. распределенного вдоль оси сердечника. Поверхностно распределенные силы qn и qf путем интегрирования в кольцевом направлении приводят к распределенным вдоль оси сердечника нагрузкам qρ. qe и mz (см. рисунок).
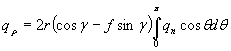 ;
;
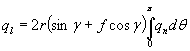 ; (4)
; (4)
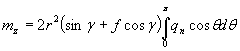
Определяем изгибающий момент в наиболее нагруженном сечении. Плечи сил ql, qp определяются из геометрии сердечника для каждой точки оси сердечника
![]() ;
;
![]() .
.
С учетом этих соотношений изгибающий момент определяется следующей формулой;
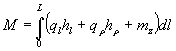 , (5)
, (5)
где L - длина средней линии формообразующего участка сердечника.
Определение усилия протяжки крутоизогнутых отводов на рогообразном сердечнике приведено в работе [3].
В общем виде усилие протяжки может быть записано в линейном виде:
P = K1∙S, (6)
где К1 – коэффициент, зависящий от условий протяжки и типоразмера протягиваемого отвода.
Интегрируя выражение (5) с учетом (3) и (4),получаем, что изгибающий момент также линейно зависит от толщины стенки трубы-заготовки:
M = K2∙S, (7)
где K2 - коэффициент, зависящий от тех же параметров.
Таким образом, преобразовывая выражение (1) относительно толщины стенки трубы получаем
![]() (8)
(8)
Эта формула является основоопределяющей для определенная условий протяжки крутоизогнутых толстостенных отводов.
Стойкость сердечника можно определить, зная характеристику длительной прочности материала сердечника при заданной температуре и возникающее в нем максимальное напряжение [1]. Согласно этой характеристике уровень максимально возникающих напряжений σ равен пределу длительной прочности материала на базе τ. Следовательно, долговечность сердечника из этого материала без учета на истирание поверхности инструмента равна τ2 работы. После этого происходит разрушение сердечника.
Вычисление максимального растягивающего напряжения при изготовлении отводов 76×3,5×100 мм из труб-заготовок 57×3,5 из стали 20 проводилось с использованием ЭВМ. Для расчета использованы следующие исходные данные:
S - 35 мм; L = 162 мм; f - 0,3; σS0 - 12 кг/мм2 (в начале очага деформации для температуры ТН - 880°С); σsк = 7 кг/мм2 (в конце очага деформации для температуры Тк = 900°С).
Получаем К1 – 2077,5; К2 = 31827,7 и σ =12,99 кг/мм2.
Следовательно,
долговечность сердечника при протяжке отводов 76×3,5×100 из стали 20 без учета истирания
поверхности инструмента равна 270 ч. Поэтому
согласно (2) с сердечника до выхода его из строя можно снять ![]() = 18810 отводов (209 шт./ч - производительность пресса
ПО926 при работе на сердечниках по данным Уральского завода монтажных изделий).
На основании статистических данных стойкость сердечника составляет 16 тыс.
штук, что полностью согласуется с полученным теоретическим результатом с учетом
истирания поверхности
инструмента.
= 18810 отводов (209 шт./ч - производительность пресса
ПО926 при работе на сердечниках по данным Уральского завода монтажных изделий).
На основании статистических данных стойкость сердечника составляет 16 тыс.
штук, что полностью согласуется с полученным теоретическим результатом с учетом
истирания поверхности
инструмента.
Задавая меньшие временные ресурсы работы сердечника согласно характеристике длительной прочности [1], получаем большие растягивающие напряжения в опасном сечении, которые соответствуют по формуле (8) более толстостенному отводу.
При протяжке более толстостенных отводов может понадобиться сердечник из другого материала с большим уровнем жаропрочности, например, литейный жаропрочный сплав на никелевой основе. Согласно [1] этот сплав обеспечивает повышение уровня жаропрочности по сравнению со сталью Х23Н18 при температуре 700°С в 4 - 7 раз и повышение стойкости сердечника в среднем в 25 раз. При изготовлении небольших партий особо толстостенных отводов возможно применение сердечника из серийного сплава ЖС6К, обеспечивающего повышенную стойкость сердечника.
ЛИТЕРАТУРА
1. Куренков В.А. Исследование технологии горячей протяжки отводов. Автореферат диссертации на соискание ученой степени кандидата технических наук. М. ВНИИМСС, 1975.
2. Бесман А.И., Куренков В.А., Тавастшерна Р.И. и др. Исследование прочности рогообразных сердечников для производства стальных отводов горячей протяжкой. - В кн.; Монтажные работы в строительстве. вып. 9, М., ВНИИмонтажспецстрой, 1973г., с. 132-145,
3. Шувалов Ю.Б., Тавастшерна Р.И. Определение усилия протяжки крутоизогнутых отводов на рогообразном сердечнике. - В кн.: Исследование процесса монтажа трубопроводов и резервуаров. М., ВНИИМСС, 1984.
РАЗРАБОТКА ДЕФОРМИРУЮЩЕГО ИНСТРУМЕНТА ПРИ ГОРЯЧЕЙ ПРОТЯЖКЕ КРУТОИЗОГНУТЫХ ОТВОДОВ
Инж. Ю.Б. Шувалов,
кандидаты техн. наук
В.А. Куренков, Р. И. Тавастшерна
При изготовлении и монтаже технологических трубопроводов большое применение находят крутоизогнутые отводы. В настоящее время способом горячей протяжки по рогообразному сердечнику изготавливают отводы диаметром 45 - 630 мм с толщиной стенки 2,5 - 18 мм при относительных радиусах изгиба R = 1 Ду и 1,5 Ду из углеродистых и легированных сталей.
Изготовление крутоизогнутых отводов диаметром более 600 мм в системе Минмонтажспецстроя СССР осуществляют в основном на месте монтажа трудоемким способом - сваркой из трубных секций. Заводское производство этих деталей налажено в системе Миннефтегазстроя и Мингазпрома штамповкой из листа половин отводов. Изготовление штампосварных отводов связано с большим расходом основных и вспомогательных материалов, топлива и энергии, требует больших людских затрат, особенно сварщиков высокой квалификации.
Технико-экономические расчеты, выполненные ВНИИмонтажспецстроем, показывают, что наиболее прогрессивным способом изготовления отводов в диапазоне диаметров Ду = 700 - 1200 мм является горячая протяжка - трубных заготовок по рогообразному сердечнику.
Одной из проблем при создании технологического процесса и оборудования для изготовления отводов является разработка новых и совершенствование существующих конструкций рогообразных сердечников.
Равнопрочный рогообразный сердечник
В настоящее время при протяжке отводов Ду = 40 - 600 мм применяются сердечники со сплошным сечением по всей длине. Однако, такие сердечники имеют большую массу, особенно для крупногабаритных отводов. Так, например, масса сердечника для изготовления отводов диаметром 250 мм равна 300 кг, а для отводов 600 мм - около 4000 кг. Получить крупногабаритное литье высокого качества (для отводов диаметром более 200 мм) весьма сложно, так как при литье сплошных, особенно крупногабаритных, отливок образуется крупнозернистая структура металла, сопряженная с образованием газовых раковин и пор.
В процессе эксплуатации сердечник подвергается действию значительных внешних силовых нагрузок и высокой температуры: до 1000°С при протяжке отводов из углеродистой и низколегированной сталей (сталь 20 и сталь 10Г2) и до 1200°С при протяжке отводов из нержавеющей стали (10Х18Н10Т). В результате этого сердечники выходят из строя, разрушаясь преимущественно по сечению, расположенному в зоне перехода направляющего участка в формообразующий. Это сечение является опасным, так как в нем возникают максимальные напряжения от действия внешних нагрузок. Во всех других сечениях формообразующего и калибрующего участков напряжения меньше, чем в опасном сечении, и практически снижаются до нуля в конце калибрующего участка [l]. Следовательно, неоправданно расходуются дорогостоящие жаропрочные стали и сплавы, из которых изготавливаются рогообразные сердечники со сплошным сечением по всей его длине.
Известны рогообразные сердечники для изготовления отводов, имеющие сквозную полость по всей длине сердечника (см., например, [2]).
Масса таких сердечников значительно меньше массы сердечников со сплошным сечением, но опасное сечение, расположенное в зоне перехода направляющего участка сердечника в формообразующий, ослаблено. Нормальное напряжение в этом сечении определяется по формуле (l);
![]() , (1)
, (1)
где
Р - усилие протяжки отводов;
М - изгибающий момент в сечении;
F0 - площадь опасного сечения;
К - константа, характеризующая конструкцию сердечника.
Таким образом, уменьшая площадь поперечного опасного сечения, мы тем самым пропорционально увеличиваем напряжение в этом сечении, и, следовательно, резко уменьшаем ресурс работы сердечника (стойкость сердечника определяется характеристикой длительной прочности материала сердечника [1]).
В связи с этим исключается возможность протяжки толстостенных отводов из углеродистой стали с относительной толщиной стенки S/ДН > 0,1 и из нержавеющей и легированных сталей, а протяжка отводов с относительной толщиной стенки S/ДН < 0,1 приведет к значительному сокращению срока службы рогообразного сердечника со сквозной полостью.
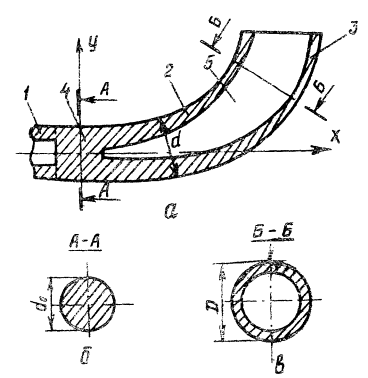
Рис 1. Конструкция равнопрочного рогообразного сердечника
а - общий вид рогообразного сердечника, б - сечение А-А по границе опасного сечения; в - сечение Б-Б по границе формообразующего и калибрующего участков
В связи с этим разработан равнопрочный рогообразный сердечник для протяжки отводов до Дн = 880 мм, в котором масса снижена на 40 - 50 %, и он не уступает по своим прочностным характеристикам сердечнику со сплошным сечением по всей длине.
Конструкция равнопрочного рогообразного сердечника представлена на рис. 1.
Рогообразный сердечник содержит направляющий участок 1, формообразующий 2 и калибрующих 3. На границе перехода направляющего участка в формообразующий (опасное сечение сердечника) симметрично относительно упомянутой границы расположена зона 4 сплошного сечения. Оставшийся формообразующий участок и весь калибрующий выполнены с внутренней полостью 5.
Проведенные исследования напряженного состояния сердечника с полостью, начинающейся от начала формообразующего участка, показали, что для создания равнопрочного сердечника необходимо, чтобы опасное сечение было сплошным, а толщина стенки формообразующего участка равномерно уменьшалась от dо/2 в начале участка до нуля в его конце. Из конструктивных соображений и из технологии литья полых заготовок толщина стенки калибрующего участка не может быть меньше dо/10 (dо - наружный диаметр направляющего участка). Из технологических условий процесса литья, а также для создания запаса прочности опасного сечения в зоне перехода направляющего участка в формообразующий должна быть зона сплошного сечения на длину не менее диаметра dо расположенная симметрично относительно упомянутой границы.
Предложенный сердечник является равнопрочным по всей длине и имеет массу на 40 – 50 % меньше, чем масса сердечника со сплошным сечением.
Рогообразный сердечник для заготовлений крупногабаритных отводов
Предварительные технико-экономические расчеты показывают, что наиболее прогрессивным способом изготовления крутоизогнутых отводов большого диаметра до 1020 мм является способ горячей протяжки электросварных труб по рогообразному сердечнику. Такой способ по сравнению с существующими обеспечивает значительную экономию металла, снижение трудоемкости и себестоимости изделий. Так, например, трудоемкость изготовления отводов 1020×10 мм методом горячей протяжки в 30 раз ниже, чем изготовление их секционными и в 15 раз ниже, чем в штампосварном варианте.
Некоторыми зарубежными фирмами организовано изготовление крупногабаритных отводов горячей протяжкой по рогообразному сердечнику: австрийская фирма "Эрне" осуществляет протяжку отводов диаметром до 1000 мм из бесшовных и электросварных труб; французская фирма "Валлурех", английская "Мунро и Миллер" осуществляют выпуск отводов подобным способом до 800 мм.
В настоящее время ВНИИмонтажспецстрой совместно с другими организациями разрабатывает технологию и оборудование для изготовления крупногабаритных отводов до 1200 мм методом горячей протяжки по рогообразному сердечнику.
В связи с этим встает вопрос о разработке основного деформирующего инструмента данной технологии - рогообразного сердечника.
Литой рогообразный сердечник со сплошным сечением по всей длине неприемлем при изготовлении крупногабаритных отводов, так как невозможно получить крупногабаритное литье рогообразных сердечников высокого качества. Масса таких сердечников весьма значительна: для отводов диаметром 1020 мм - около 25000 кг, а для отводов диаметром 1220 мм - около 35000 кг. Предполагается выпускать тонкостенные крупногабаритные отводы. В связи с этим необходимо изготавливать полые по всей длине рогообразные сердечники. При этом возможно снижение массы сердечника на 30 - 50 % по сравнению с сердечниками со сплошным сечением по всей длине. Однако и такие сердечники имеют значительную массу (от 10 до 20 т).
Известен полый рогообразный сердечник, который выполнен составным из отдельных частей, сваренных между собой в сечениях, нормальных к его оси.
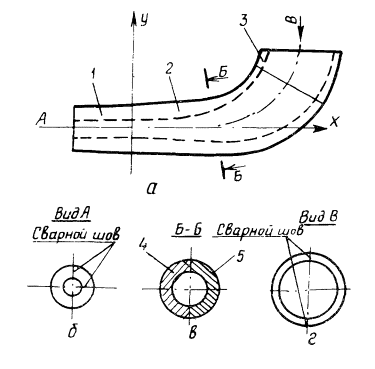
Рис. 2. Конструкция рогообразного сердечника для изготовления крупногабаритных отводов: а - общий вид рогообразного сердечника; б - вид А начала направляющего участка; в - сечение Б-Б формообразующего участка; г - вид В конца калибрующего участка
Изготовление отдельных частей сердечника связано с трудоемким и сложным процессом установки и крепления стержня при литье, в результате чего получается много брака. Наличие сварных швов по сечениям, нормальным к оси сердечника, которые работают на отрыв от изгибающего момента и усилия протяжки, резко снижает стойкость рогообразного сердечника, что выражается в снижении срока его службы.
В связи с этим разработан рогообразный сердечник для протяжки крупногабаритных отводов Дн = 720 - 1220 мм, который выполнен составным из отдельных частей, не требующих между собой сварки.
Конструкция рогообразного сердечника представлена на рис. 2.
Рогообразный сердечник содержит направляющий 1, формообразующий 2 и калибрующий участок 3 и выполнен составным из двух частей 4 и 5, симметричных относительно плоскости, проходящей через среднюю линию сердечника.
Выполнение сердечника составным сокращает технологию литья этих частей и изготовления сердечника. Каждая из симметричных половин не имеет полости и тем самым снимаются проблемы установки и крепления от смещения при литье длинномерного стержня внутри сердечника, а, следовательно, снижается вероятность брака.
Во время протяжки трубы-заготовки по рогообразному сердечнику на него действуют поверхностно распределенные силы нормального давления и трения. В любом сечении, нормальном к оси сердечника, эти силы симметричны относительно плоскости, проходящей через эту ось, и поэтому результирующая этих сил будет сжимать между собой указанные симметричные части сердечника и не давать смещаться им относительно друг друга. Следовательно, нет необходимости неразъемно соединять их между собой сваркой, и поэтому указанный рогообразный сердечник будет работать аналогично литому сердечнику. Отсутствие сварных швов резко увеличивает стойкость сердечника, что выражается в увеличении его срока службы.
Для исключения вероятности смещения симметричных частей сердечника относительно друг друга во время крепления их к штанге пресса возможна сварка этих частей в торцевых плоскостях (начало направляющего и конец калибрующего участков) (см. рис. 2 б, г).
Для получения высококачественного литья мелкозернистой структуры и в соответствии с технологией литья рогообразных сердечников площадь каждого последующего поперечного сечения сердечника от направляющего участка к калибрующему не превышает площади предыдущего поперечного сечения. Это улучшает качество литья и тем самым повышает стойкость сердечника.
Предложенный сердечник позволяет увеличить срок службы в 3 - 5 раз, улучшить качество и упростить технологию изготовления.
ЛИТЕРАТУРА
1. Овчинников А.Г., Куренков В.А. и др. Повышение прочности рогообразных сердечников.- В кн.: Монтажные работы в строительстве. Труды института. Вып. XI, М., 1974 г. (Минмонтажспецстрой, ВНИИмонтажспецстрой).
2. Авторское свидетельство СССР № 856615, кл. В21Д 8/12 от 1978 г.
3. Заявка № 8829865/25-27, по которой вынесено решение о выдаче авт. свид. от 27.03.85 г.
ОЦЕНКА НЕСУЩЕЙ СПОСОБНОСТИ ТРОЙНИКОВ, НАГРУЖЕННЫХ ВНУТРЕННИМ ДАВЛЕНИЕМ
Канд. техн. наук Г.М. Хажинский
Тройниковые соединение труб являются наиболее нагруженными элементами трубопровода и в значительной степени определяют его надежность при эксплуатации. В связи с этим большое внимание уделяется расчету на прочность тройников под действием внутреннего давлений. Однако известные методики подобного расчета и основанные на них способы выбора толщин стенок существенно различаются между собой. Свидетельством незавершенности этой проблемы является публикация многочисленных исследований по анализу прочности тройников. В настоящей работе сделана попытка разработать инженерный метод расчета, основанный на обобщении данных по экспериментальному и расчетному исследованию тройников. При этом основное внимание уделялось тому, чтобы данная методика обеспечивала возможность опенки напряжений в наиболее опасном сечении тройника как в пределах упругости, так и в условиях местного и развернутого пластического течения.

Рис. 1. Расчетная схема тройникового соединений трубопроводов
Как доказывают многочисленные экспериментальные данные, наиболее нагруженной является т. А в меридиональном сечении тройника (рис. 1). Именно в этой точке начинается пластическое течение. Гидравлические испытания тройников показали, что, как правило, в этой зоне появляется меридиональная трещина. Поэтому представляет интерес оценка локального напряженно-деформированного состояния тройника именно в этой точке. Такой подход получил достаточно широкое распространение и, по-видимому, оправдан. Как показало тензометрирование тройников [1] нагруженных внутренним давлением, в т. А (см. рис. 1) напряженное состояние основной оболочки и штуцера близко к осесимметричному. Это дает возможность использовать решения для осесимметричных оболочек при расчете тройниковых соединений.
Рассмотрим концентрацию напряжений у неподкрепленных отверстий в цилиндрических оболочках. При этом будем оценивать только окружные мембранные напряжения, которые достигают максимума в точке пересечения меридиональной плоскости симметрии с линией выреза. Решение для малого неподкрепленного выреза было впервые получено А.И. Лурье [2]:
 , (1)
, (1)
где ![]() - теоретический
коэффициент концентрации окружных мембранных напряжений на краю
неподкрепленного выреза;
- теоретический
коэффициент концентрации окружных мембранных напряжений на краю
неподкрепленного выреза;
![]() - радиус выреза;
- радиус выреза;
R, S - радиус и толщина стенки оболочки.
В дальнейшем это решение
было уточнено Н.П. Флейшманом, который показал, что при r2/RS → 0 значение ![]() = 2,9. Анализ формулы (1) показывает,
что величина
= 2,9. Анализ формулы (1) показывает,
что величина ![]() может быть представлена
в виде двух составляющих. Первая из них представляет собой коэффициент
концентрации мембранных напряжений основного состояния, а вторая определяет
краевой эффект в оболочке. Если воспользоваться решением для цилиндрической
оболочки, нагруженной на свободном конце перерезывающей силой
может быть представлена
в виде двух составляющих. Первая из них представляет собой коэффициент
концентрации мембранных напряжений основного состояния, а вторая определяет
краевой эффект в оболочке. Если воспользоваться решением для цилиндрической
оболочки, нагруженной на свободном конце перерезывающей силой ![]() , то
коэффициент концентрации напряжений может быть записан в виде:
, то
коэффициент концентрации напряжений может быть записан в виде:
![]() . (2)
. (2)
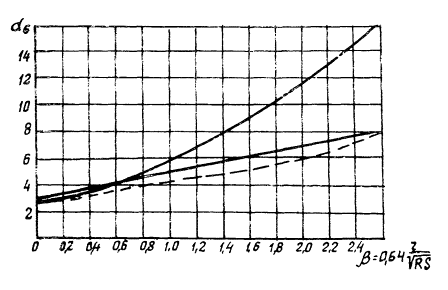
Рис. 2. Сравнение расчета по формуле (2) (сплошная линия) с экспериментальными данными Н.А. Флеровой [2] (штриховая линия) и решением для пологих оболочек [3] (штрихпунктирная линия)
На рис. 2 сплошной линией
показан расчет по формуле (2). Сопоставление с решением для пологих оболочек
[3] (штрихпунктирная линия), и экспериментальными данными Н.А. Флеровой [2]
(штриховая линия), полученных на оболочках с S/D = 0,0058, свидетельствуют о том, что при ![]() решение (2) дает
приемлемую точность.
решение (2) дает
приемлемую точность.
Переходя к отверстиям, подкрепленным штуцером, следует учитывать два фактора. С одной стороны должно уменьшиться первое слагаемое в формуле (2) за счет укрепляющего влияния односторонней накладки, которой является штуцер. С другой стороны, изменятся краевые условия для оболочки и при достаточно жестком штуцере на краю ее выполняются условия скользящей заделки. В последнем случае коэффициент 1,28 в формуле (2) должен быть заменен на 0,64 т.е. уменьшен вдвое. Наиболее просто можно учесть оба эти фактора, если записать выражение для теоретического коэффициента концентрации окружных мембранных напряжений в следующем виде:
![]() (3)
(3)
При φ = 1 (неукрепленное отверстие) формула (3) переходит в (2). При φ → 0, т.е. с увеличением эффекта подкрепления отверстия штуцером, величина 0,64 (1 + φ) будет стремиться к 0,84 и тем самым осуществится переход к новому виду закрепления края оболочки. Как показывают расчеты и результаты тензометрирования [2], величина φ зависит прежде всего от отношения S1/S, где S1 - толщина стенки штуцера. Представим φ в следующем виде:
![]() . (4)
. (4)
В табл. 1 представлены результаты расчета по формулам (3) и (4), а также экспериментальные значения ασ тройниковых соединений [2].
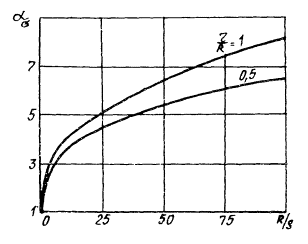
Рис. 3. Сравнение расчета по формулам (3) и (4) с результатами решения методом конечных элементов [4], [5]
Таблица 1
|
№ модели |
D, мм |
S, мм |
S1/S |
d/D |
|
|
|
|
1 |
1108 |
41 |
0,266 |
0,285 |
3,6 |
4,0 |
-10 |
|
2 |
1108 |
41 |
0,615 |
0,298 |
3,0 |
3,0 |
0 |
|
3 |
1108 |
41 |
1 |
0,313 |
2,6 |
2,6 |
0 |
|
4 |
1270 |
43 |
0,128 |
0,0425 |
2,9 |
2,7 |
7,4 |
|
5 |
1318 |
43 |
0,184 |
0,082 |
3,0 |
2,8 |
7,1 |
|
6 |
1263 |
106 |
0,184 |
0,161 |
3,0 |
2,9 |
3,4 |
|
7 |
1720 |
180 |
0,344 |
0,245 |
2,9 |
2,6 |
11,5 |
Дополнительно на рис. 3 показаны результаты сравнения расчета с численными данными, полученными с использованием оболочечных конечных элементов Ю.А. Куликовым и И.В. Стасенко [4 - 5]. Мембранные окружные напряжения в т. А получены осреднением значений на наружной и внутренней поверхностях основной трубы. Аналогичное сопоставление концентрации окружных мембранных напряжений согласно приближенному расчету и вычислениям методом конечных элементов [6] показала полное совпадение значений ασ. Был сосчитан вариант S1/S = α/D = 0,5, R/S = 50. В обоих случаях ασ - 5,4. Практически совпали результаты приближенного расчета при сопоставлении с экспериментальными данными Райли, приведенными в работе [7]. Райли было проведено тензометрирование тройника с d/D = 0,5, S1/S = 1, R/S = 115.
Для повышения несущей способности тройников иногда используются пропущенные патрубки. В табл. 2 сопоставлены расчетные значения ασ с экспериментальными, приведенными в работе [2] для тройников с пропущенными патрубками. Расчет выполнялся по формулам (3) и (4), причем для пропущенных патрубков величина S1 заменялась на S1экв = 2S1.
Проведенный анализ концентрации напряжений в пределах упругости свидетельствует о том, что приближенное решение для тройников обеспечивает точность около 12 %.
Рассмотрим условия начала пластического течения в т. А (см. рис 1). Для перехода от упругого деформирования в зоне концентратора к упругопластическому можно воспользоваться формулой Нейбера.
![]() , (5)
, (5)
где Кσ, Кε – коэффициенты концентрации напряжений и деформаций.
Выражение (5) получило достаточно широкое распространение в расчетной практике, однако оно приводит к систематической погрешности, на которую указано в работе [8]. В работе [9] показано, что при анализе концентрация напряжений лучшие результаты дает следующая связь:
![]() , (6)
, (6)
где Wmax, Wн - работа деформации в зоне концентратора и в сечении, принятом за номинальное.
Если принять, что Wmax соответствует остаточной деформации 0,2 %, то ее величина для идеально эластического материала равна
![]() . (7)
. (7)
Таблица 2
|
№ модели |
S1/S |
d/D |
|
|
|
|
1 |
0,435 |
0,052 |
2,2 |
2,3 |
-4,3 |
|
2 |
0,565 |
0,103 |
2,3 |
2,4 |
-4,2 |
|
3 |
0,630 |
0,153 |
2,5 |
2,7 |
-7,4 |
|
4 |
0,70 |
0,203 |
2,6 |
2,8 |
-7,1 |
|
5 |
0,70 |
0,054 |
1,8 |
1,8 |
0 |
|
8 |
0,89 |
0,105 |
1,9 |
1,9 |
0 |
|
7 |
0,98 |
0,155 |
2,0 |
2,0 |
0 |
|
8 |
1,11 |
0,205 |
2,0 |
2,1 |
-4,8 |
|
9 |
1,07 |
0,058 |
1,5 |
1,4 |
7,1 |
|
10 |
1,33 |
0,107 |
1,5 |
1,5 |
0 |
|
11 |
1,50 |
0,158 |
1,5 |
1,5 |
0 |
|
12 |
1,46 |
0,207 |
1,7 |
1,6 |
6,3 |
С другой стороны
![]() , (8)
, (8)
где σH номинальное (окружное) напряжение в основной трубе.
Подставляя (7) и (8) в (6), получим
![]() , (9)
, (9)
где
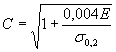
При выводе соотношения (9) не учитывалось влияние напряжений изгиба на начало пластического течения. Сопоставим расчет с экспериментальными данными.
В расчетной практике ФРГ получил распространение метод выбора толщины стенки по т.н. коэффициентам ослабления. Эта методика была разработана на основе исследований Зибеля, который предложил за начало текучести принимать момент, когда интенсивность остаточной деформации в т. А окажется равной 0,2 %. При этом расчетная величина давления начала текучести основной трубы определялась по формуле РТ - σ0,2S/R.
Обозначив через Р1 давление, соответствующее началу текучести в опасном сечении тройника, получим следующее выражение для V
![]() (10)
(10)
При σ0,2 = 220 МПа и Е = 2∙105 МПа величина С согласно (9) равна 2,2. Для этого случая построены зависимости V от параметра ![]() представленные на
рис. 4 сплошными линиями.
представленные на
рис. 4 сплошными линиями.
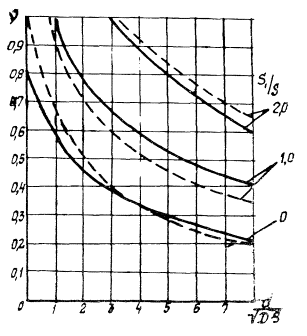
Рис. 4. Сравнение расчета коэффициентов ослабления по формуле (10) и Нормам [10]:
- - - - ADB9;
----- - расчет
Здесь же штриховыми показаны расчетные графики по нормам ФРГ ADB9 (1977 г.) [10], которые были построены на основе исследований Зибеля. При сравнении двух методик не учитывалась разница между внутренним и средним диаметрами штуцера.
Большая работа по анализу пластического деформирования тройников, нагруженных внутренним давлением, была проведена Родебау и Клаудом [11]. В этих экспериментах начало пластического течения определялось по индикатору в т. А (см. рис. 1). Такой метод определения начала текучести отличается от использованного Зибелем тензометрирования. Очевидно, что одна и та же величина относительного перемещения и деформации в т А будет достигнута при разных значениях внутреннего давления. В первом случае давление Р1 будет выше. Учитывая это, из выражения (10) получим
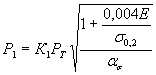 . (11)
. (11)
В табл. 3. представлены результаты сопоставления расчета при К1 = 1,2 с экспериментальными данными [1].
В работе [12]
приведены данные испытания двух тройниковых соединений, в которых начало
текучести определялось по 0,2 % остаточного перемещения в точке А. Геометрия
испытанных образцов: S1/S = 0,416 и 0,680; d/D = 0,5 и 1,0; D/S = 17,2. Соответственно Р1 ![]() - 0,87 и 0,90. Таким образом,
проведенный анализ условий начала текучести показал, что предлагаемая методика
обеспечивает достаточно надежное определение давления начала местной текучести.
- 0,87 и 0,90. Таким образом,
проведенный анализ условий начала текучести показал, что предлагаемая методика
обеспечивает достаточно надежное определение давления начала местной текучести.
Значительный практический интерес представляет оценка величины давления полного разрушения тройника. Обозначим через η отношение давления разрушения тройника (Р2) к величине разрушающего давления для основной трубы (Рв).
![]() . (12)
. (12)
Значение Рв может быть определено по формуле:
![]() , (13)
, (13)
где f(m) - функция показателя упрочнения m.
Обычно значение fm для сталей меняется в пределах от 1 до 0,9, причем меньшие значения соответствуют большим величинам m.
Давление разрушения тройника в зоне концентратора можно определить по формуле
![]() . (14)
. (14)
Таблица 3
|
№ модели |
D/S |
d/D |
S1/S |
ρТ, МПа |
|
ασ |
|
|
|
1 |
47 |
0,156 |
0,67 |
10,20 |
9,65 |
2,66 |
9,95 |
0,97 |
|
2 |
-"- |
0,212 |
0,67 |
9,93 |
9,14 |
2,87 |
9,00 |
1,02 |
|
8 |
-"- |
0,149 |
1,00 |
10,14 |
10,14 |
2,28 |
11,57 |
1,00* |
|
4 |
-"- |
0,269 |
0,67 |
9,93 |
9,10 |
3,08 |
8,38 |
1,09 |
|
5 |
-"- |
0,262 |
1,00 |
9,79 |
9,45 |
2,64 |
9,64 |
0,98 |
|
6 |
-"- |
0,206 |
1,00 |
10,14 |
10,00 |
2,46 |
10,72 |
0,99* |
|
7 |
-"- |
0,326 |
0,67 |
9,79 |
8,28 |
3,30 |
7,71 |
1,07 |
|
8 |
-"- |
0,319 |
1,00 |
10,28 |
9,52 |
2,81 |
9,52 |
1,00 |
|
9 |
-"- |
0,160 |
0,50 |
10,21 |
9,17 |
2,90 |
9,15 |
1,00 |
|
10 |
-"- |
0,216 |
0,50 |
10,28 |
8,69 |
3,14 |
8,52 |
1,02 |
|
11 |
-"- |
0,135 |
0,33 |
10,76 |
9,31 |
3,06 |
9,14 |
1,02 |
|
12 |
82 |
0,190 |
0,67 |
7,10 |
5,44 |
3,01 |
5,99 |
0,91 |
|
13 |
100 |
0,189 |
1,08 |
5,87 |
5,10 |
2,59 |
5,64 |
0,90 |
|
14 |
93 |
0,135 |
0,67 |
6,28 |
5,44 |
2,78 |
5,55 |
0,98 |
|
15 |
49 |
0,500 |
0,52 |
19,3 |
7,03 |
4,32 |
8,62 |
0,82 |
Примечание: Звездочкой обозначены случаи, когда разрушался основной цилиндр
Здесь
SК сопротивление разрыва образца при одноосном растяжении;
Кσf = коэффициент концентраций напряжений в момент разрыва.
Как показано в [8] на основе анализа разрушения в зоне различных концентраторов, величина Кσf является степенной функцией ασ. Соответствующий показатель степени может быть определен на основе обработки экспериментальных данных. Кроме того, используем эмпирическую связь между SK и σв, предложенную М.П. Марковцом [8]:
SK/σв = 1 + 1,4 ΨК, (15)
где ΨК - относительное сужение при разрыве.
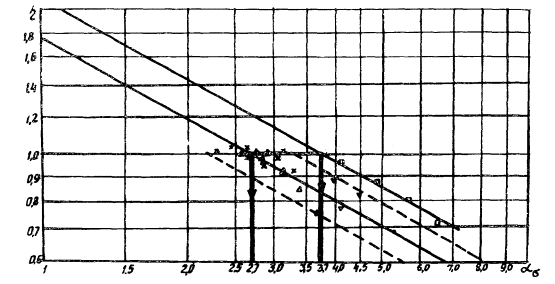
Рис. 5. Зависимость относительной несущей способности тройника от величины
ασ: * - данные
[11], ∆ - [13], □ - [14], ![]() - [15]
- [15]
Подставляя (13), (14),
(15) в (12) и учитывая, что ![]() получим
получим
![]() . (16)
. (16)
На рис. 5 показаны результаты обработки экспериментальных данных по разрушению тройников. Здесь представлены эксперименты, приведенные Родебау и Клаудом [11], А.В. Якупом [13], В.А. Фрейтагом и О.С. Суворовой [14], Блэаром [15]. В последних двух случаях величина η определялась по осредненной зависимости от d/D. При подсчете σв в [14] принималась средняя толщина стенки сосуда, равная 6 мм. Как видно из рис. 5, экспериментальные данные для углеродистых сталей легли в довольно широкую полосу разброса в отличие от данных работы [14] для тройников из нержавеющей стали. Уравнение для средних линий может быть представлено в виде:
![]() (17)
(17)
где B - 1,75 - для углеродистых сталей и 2,1- для нержавеющих.
Отметим, что значения B примерно соответствуют уравнению (16), в то время как значение l оказалось гораздо выше т для углеродистых сталей (0,46 по сравнению с 0,15 - 0,25). По-видимому, это связано с уже отмеченными выше отклонениями от формулы Нейбера за счет более жесткого характера нагружения в зоне концентратора. Точность подсчета η по изложенной методике составляет ±10 %. Из рис. 5 следует, что прочность тройников из углеродистой стали при ασ < 2,7 равна прочности прямой трубы. Аналогичный вывод можно сделать для труб из нержавеющей стали при ασ < 3,7. Таким образом, предложенная методика расчета тройников может быть использована при составлении "Норм расчета на прочность элементов трубопроводов". Для тройников из хрупких материалов оценка прочности должна производиться на основе теоретического коэффициента окружных мембранных напряжений ασ. При расчете по первому предельному состоянию (начало пластического течения в т. А) можно использовать формулу (10). При оценке второго предельного состояния (полное разрушение тройника) рекомендуется использовать формулу (17). Предложенная методика обеспечивает единый подход к расчету несущей способности тройниковых соединений под действием внутреннего давления.
ЛИТЕРАТУРА
1. Феденко Г.И. Концентрация напряжений и расчет элементов подкрепления отверстий в обечайках и днищах, работающих под внутренним давлением. Киев: Проблемы прочности, 1971, № 5, с.70-76.
2. Волошин А.А., Самсонов Ю.А. Расчет и конструирование пересекающихся оболочек сосудов. Л.: Машиностроение, 1968, 126 с.
3. Петерсон Р. Коэффициенты концентрации напряжений. М.: Мир, 1977, 302 с.
4. Куликов Ю.А., Стасенко И.В. Расчет тройникового соединения тонкостенных труб методом конечных элементов. - В кн.: Расчеты на прочность. Вып. 18. М.,: Машиностроение, 1977, с. 141-152.
5. Куликов Ю.А., Стасенко И.В. Напряженно-деформированное состояние тройниковых соединений тонкостенных труб. - В кн.: Расчеты на прочность. Вып. 20.: Машиностроение, 1979, с.229-237.
6. A.N. Gantayat, G.H. Powell. Finite element analysis of thin and thick-walled tubular joints. Nucl. Eng. and Des., 1978, V. 46, № 2, p.381-394.
7. Пэн, Бэкет. Расчет напряжений и смещений в месте пересечения оболочек. Труды американского общества инженеров-механиков. Конструирование и технология машиностроения. 1970, № 2, с.44-49.
8. Махутов Н.А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М.: Машиностроение, 272 с.
9. K. Molski, G. Glinka. A method pf elastic-plastic stress and strain calculation at a notch root. - Materials science and engineering. V. 50, № 1, p.93-100.
10. Стальные трубы. Справочник под редакцией Д. Шмидта -М., Металлургия, 1982, 535 с.
11. Родебау, Клауд. Оценка пластической прочности патрубков сосудов давления. Труды американского общества инженеров-механиков. Конструирование и технология машиностроения. 1968, № 4, с.126-136.
12. N.C. Lind, A.N. Sherbourne, F. Ellyin, J. Dainora. Plastic tests of two branch-pipe connections - Welding Research Council Bulletin, 1971; № 164, 7 p.
13. Яхун А.В. О прочности сварных тройниковых соединений. Вестник машиностроения, 1972, №; 1, с.22-23.
14. Фрейтаг В.А., Суворова О.С. Конструкция и несущая способность сварных крупногабаритных тройниковых соединений. - Химическое нефтяное машиностроение, 1988, № 5, с. 8-12.
15. Blair Y.S. Reinforcement of branch pieces-Engineering, 1946, V. 162, p.1-4, 217-221, 508-511, 529-533, 553-558, 577-581, 588, 805-606.
ОПРЕДЕЛЕНИЕ РАСЧЕТНО-ГРАФИЧЕСКИМИ МЕТОДАМИ ПРОЧНОСТИ СТЫКОВ ТРУБ ИЗ ПВХ-100
Инж. Ю.С. Бурбело,
канд. техн. наук С.Г. Радченко,
инж. Ю.А. Сндоренко
Киевским филиалом ВНИИМСС проводятся исследования по определению влияния на прочность шва труб из ПВХ-100, сваренного нагретым инструментом встык, различных параметров сварки, и определяются их оптимальные значения, а также разрабатываются практические рекомендации по определению прочности шва расчетно-графическими методами. При проведении экспериментов используются математические методы планирования эксперимента. */
*/ Материалы исследований по планированию эксперимента приведены в сборнике научных трудов ВНИИМСС "Монтаж технологического оборудования и трубопроводов и средства для его осуществления" М., 1982, стр. 183-173.
В рассматриваемом исследовании сварка проводилась плоским нагревательным инструментом без антиадгезионной защиты из фторопласта Ф4. После каждой операции рабочие поверхности нагревателя очищались от налипшего от предыдущей сварки материала трубы. Температура нагревателя регулировалась потенциометром типа ПСР-1. Сварка труб проводилась с помощью устройства, снабженного приспособлением для регулирования усилия сжатии труб. Оценка качества проводилась по полученным значениям предела прочности сваренных образцов на разрыв σв, сравниваемых с прочностью основного материала трубы. Для испытаний использовалась форма образцов, предусмотренная ГОСТ 11262-80. Чтобы разрушение происходило по сварке в месте шва, образец утонялся.
Анализ технологического процесса сварка нагретым инструментом труб из ПВХ-100 позволяет характеризовать его как многофакторный и сравнительно сложный. В формализованном виде его математическую модель можно представить следующим образом:
![]() ,
,
где
![]() - оценка
теоретического значения функции;
- оценка
теоретического значения функции;
х1…хк - факторы;
К - число факторов.
Ранее проведенными работами были установлены основные факторы, влияющие на прочность шва, а в результате предварительных исследований - область их изменений в проводимом эксперименте:
- температура нагревательного инструмента ТН, °С - 210 - 240;
- время оплавления свариваемых торцов tоп, с = 40 - 120;
- давление осадка Рос, кгс/см2 (МПа) 4,2…5,8 (0,42 - 0,58).
В соответствии с поставленными задачами, выбранным методом исследования, количественным характером управляемых факторов в качестве плана эксперимента был использован регулярный факторный план типа 33//27, который позволяет оценить взаимодействия более высокого порядка, чем в моделях второго порядка.
Выбор интервалов варьирования производился не формализовано, а исходя из имеющейся информации о степени влияния факторов на функцию.
Натуральные значения уровней варьирования факторов кодировались в линейные и квадратичные контрасты по формулам, приведенным в табл. 1.
В таблицах 2, 4 приведены матрица планирования, средние и расчетные значения результатов опытов. Полученные математические модели в ортогональных контрастах имеют следующий вид:
В кодированных значениях
![]() = 573,9 + 77,6 x2, - 14,1 z2 + 73,5 x1 - 24,7 Z1 + 15,3 x3 x1 + 7,9 z3xг - 6,2 z3 zг + 8,8 z3x4 - 4,3 z3 zi - 71 x2 xi + 24,4 x2 z1 + 18,8 zг x1 - 11,4 z2 z1 - 16,8 z3 x2 x1 +9,2 z3 x2 z1 + 12,3 z3 z2 x1 - 6,5 z3 z2 z1.
= 573,9 + 77,6 x2, - 14,1 z2 + 73,5 x1 - 24,7 Z1 + 15,3 x3 x1 + 7,9 z3xг - 6,2 z3 zг + 8,8 z3x4 - 4,3 z3 zi - 71 x2 xi + 24,4 x2 z1 + 18,8 zг x1 - 11,4 z2 z1 - 16,8 z3 x2 x1 +9,2 z3 x2 z1 + 12,3 z3 z2 x1 - 6,5 z3 z2 z1.
В натуральных значениях
![]() =
71963,119 + 17832,5229 ton + (-995,1407237)
=
71963,119 + 17832,5229 ton + (-995,1407237) ![]() + 62783,95420 ТH +
(-136,6565316)
+ 62783,95420 ТH +
(-136,6565316) ![]() + 2874981,517 Рос + (-25081,11773) РосТH
+ (-714,13729) Poc ton +
(-287526,8236)
+ 2874981,517 Рос + (-25081,11773) РосТH
+ (-714,13729) Poc ton +
(-287526,8236) ![]() + 7141,372978
+ 7141,372978 ![]() ton+
398,8703223 Pос
ton+
398,8703223 Pос ![]() + (-39,88703233),
+ (-39,88703233),
![]() + 2508,239204
+ 2508,239204 ![]() + 54,59194990 Poс
+ 54,59194990 Poс ![]() + (5,459194990)
+ (5,459194990) ![]()
TH + (-1555,475198) ton
TH + 3,385523015
ton ![]() + 8,679749879
+ 8,679749879 ![]() TH + (-0,01889050171)
TH + (-0,01889050171) ![]() + 622,9240462 Poc ton TH + (-62,29240462).
+ 622,9240462 Poc ton TH + (-62,29240462).
Poc ton
TH +
(-1,355792653) Poc ton ![]() + 0,0155792853
+ 0,0155792853 ![]() ton
ton
![]() + (-3,478877339) Poc
+ (-3,478877339) Poc ![]()
![]() TH + 0,347887339
TH + 0,347887339 ![]() TH + 0,000757106248.
TH + 0,000757106248.
Poc ![]()
![]() (-0,0007571062481)
(-0,0007571062481) ![]()
![]()
![]() .
.
Проверка гипотезы об адекватности полученной модели (табл. 3) проводилась с использованием F-критерия и показала, что модель адекватна (α = 0,05). Информативность модели устанавливалась путем вычисления множественного коэффициента корреляции R и проверки его значимости по F-критерию. Коэффициент множественной корреляции достаточно близок к 1, что свидетельствует о хорошем согласовании модельных и экспериментальных результатов и статистически значим при уровне значимости значительно меньшем, чем α = 0,01. Последний результат свидетельствует о том, что модель содержит полезную информацию о моделируемой функции.
В табл. 3 приняты
следующие обозначения: ![]() - дисперсия
воспроизводимости опыта; Sy - среднеквадратичная ошибка воспроизводимости опыта; fSy - число степеней
свободы дисперсии воспроизводимости опыта; Gрасч - расчетное
значение критерия Кохрена; Gтабл -
табличное значение критерия Кохрена; α
- уровень значимости; tтабл - табличное
значение критерия Стьюдента; Fрасч
- расчетное значение критерия Фишера; Fтабл - табличное значение критерия Фишера; fag - число
степеней свободы адекватности; R - множественный коэффициент
корреляции; fк - число степеней свободы для суммы
квадратов отклонения, связанной с К
коэффициентами модели; fост - число степеней свободы для суммы
квадратов отклонений остатков.
- дисперсия
воспроизводимости опыта; Sy - среднеквадратичная ошибка воспроизводимости опыта; fSy - число степеней
свободы дисперсии воспроизводимости опыта; Gрасч - расчетное
значение критерия Кохрена; Gтабл -
табличное значение критерия Кохрена; α
- уровень значимости; tтабл - табличное
значение критерия Стьюдента; Fрасч
- расчетное значение критерия Фишера; Fтабл - табличное значение критерия Фишера; fag - число
степеней свободы адекватности; R - множественный коэффициент
корреляции; fк - число степеней свободы для суммы
квадратов отклонения, связанной с К
коэффициентами модели; fост - число степеней свободы для суммы
квадратов отклонений остатков.
Натуральные и кодированные значения уровней варьирования факторов
|
Наименование и натуральное обозначение факторов |
Номер фактора |
Обозначение Xi в рабочей матрице |
уровни |
Формулы перехода от Хi к xi и Zi |
||
|
Fi |
xi |
zi |
||||
|
Температура нагревателя Тн |
1 |
210 |
0 |
-1 |
|
z1 = 3 |
|
225 |
1 |
0 |
-2 |
|||
|
240 |
2 |
1 |
1 |
|
||
|
Время оплавления свариваемых торцов труб |
2 |
40 |
0 |
-1 |
1 |
x2 =
3 |
|
80 |
I |
0 |
-2 |
|||
|
120 |
2 |
1 |
1 |
|||
|
Удельное давление осадки труб, Рос |
3 |
4,2 |
0 |
-1 |
1 |
z3 = 3 |
|
5,6 |
1 |
0 |
-2 |
|||
|
5,8 |
2 |
1 |
1 |
|||
Матрица планирования, уровни варьирования факторов
|
№ пп |
Кодированные значения уровней варьирования факторов |
Факторы |
контрасты |
|
|||||||||
|
|
|||||||||||||
|
натур. обозн. факт |
|
||||||||||||
|
ТН |
tоп |
Рос |
|
||||||||||
|
кодир. |
обозн. |
факт |
кодирован. обознач. контрастов |
|
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
1 |
F1 |
F2 |
F3 |
F1 |
F2 |
F3 |
x1 |
z1 |
x2 |
z2 |
x3 |
z3 |
|
|
2 |
0 |
0 |
0 |
210 |
40 |
4,2 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
|
|
3 |
1 |
1 |
1 |
225 |
80 |
5,0 |
0 |
-2 |
0 |
-2 |
0 |
-2 |
|
|
4 |
2 |
2 |
2 |
240 |
120 |
5,8 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
5 |
Опыт 1 |
Исп. 25 |
2 |
0 |
0 |
0 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
|
|
6 |
2 |
3 |
20 |
0 |
0 |
1 |
-1 |
1 |
-1 |
1 |
0 |
-2 |
|
|
7 |
3 |
5 |
21 |
0 |
0 |
2 |
-1 |
1 |
-1 |
1 |
1 |
1 |
|
|
8 |
4 |
8 |
25 |
0 |
1 |
0 |
-1 |
1 |
0 |
-2 |
-1 |
1 |
|
|
9 |
S |
2 |
18 |
0 |
1 |
1 |
-1 |
1 |
0 |
-2 |
0 |
-2 |
|
|
10 |
8 |
11 |
1 |
0 |
1 |
2 |
-1 |
1 |
0 |
-2 |
1 |
1 |
|
|
11 |
7 |
23 |
27 |
0 |
2 |
0 |
-1 |
1 |
1 |
1 |
-1 |
1 |
|
|
12 |
8 |
22 |
26 |
0 |
2 |
1 |
-1 |
1 |
1 |
1 |
0 |
-2 |
|
|
13 |
9 |
6 |
13 |
0 |
2 |
2 |
-1 |
1 |
1 |
1 |
1 |
1 |
|
|
14 |
10 |
12 |
9 |
1 |
0 |
0 |
0 |
-2 |
-1 |
1 |
-1 |
1 |
|
|
15 |
11 |
28 |
14 |
1 |
0 |
1 |
0 |
-2 |
-1 |
1 |
0 |
-2 |
|
|
16 |
12 |
18 |
19 |
1 |
0 |
2 |
0 |
-2 |
-1 |
1 |
1 |
1 |
|
|
17 |
13 |
21 |
5 |
1 |
1 |
0 |
0 |
-2 |
0 |
-2 |
-1 |
1 |
|
|
18 |
14 |
10 |
12 |
1 |
1 |
1 |
0 |
-2 |
0 |
-2 |
0 |
-2 |
|
|
19 |
15 |
7 |
4 |
1 |
1 |
2 |
0 |
-2 |
0 |
-2 |
1 |
1 |
|
|
20 |
18 |
4 |
10 |
1 |
2 |
0 |
0 |
-2 |
1 |
1 |
-1 |
1 |
|
|
21 |
17 |
24 |
7 |
1 |
2 |
1 |
0 |
-2 |
1 |
1 |
0 |
-2 |
|
|
22 |
18 |
8 |
6 |
1 |
2 |
2 |
0 |
-2 |
1 |
1 |
1 |
1 |
|
|
23 |
18 |
19 |
23 |
2 |
0 |
0 |
1 |
1 |
-1 |
1 |
-1 |
1 |
|
|
24 |
20 |
14 |
3 |
2 |
0 |
1 |
1 |
1 |
-1 |
1 |
0 |
-2 |
|
|
25 |
21 |
1 |
8 |
2 |
0 |
2 |
1 |
1 |
-1 |
1 |
1 |
1 |
|
|
26 |
22 |
17 |
18 |
2 |
1 |
0 |
1 |
1 |
0 |
-2 |
-1 |
1 |
|
|
27 |
23 |
20 |
17 |
2 |
1 |
1 |
1 |
1 |
0 |
-2 |
0 |
-2 |
|
|
28 |
24 |
27 |
11 |
2 |
1 |
2 |
1 |
1 |
0 |
-2 |
1 |
1 |
|
|
20 |
25 |
15 |
15 |
2 |
2 |
0 |
1 |
1 |
1 |
1 |
-1 |
1 |
|
|
30 |
26 |
13 |
22 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
0 |
-2 |
|
|
31 |
27 |
18 |
24 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Таблица 3
Результаты статистического анализа математической модели
|
Параметры статистического анализа |
Условные обозначения |
Значения параметров |
|
Проверка гипотезы о воспроизводимости результатов экспериментов |
|
848 |
|
Sy |
29,12 |
|
|
fSy |
27 |
|
|
Gрасч |
0,158 |
|
|
Gтабл |
0,32 |
|
|
α |
0,05 |
|
|
Табличное значение критерия Стьюдента |
tтабл |
2,05 |
|
Проверка гипотезы об адекватности полученной математической модели |
Fрасч |
0,69 |
|
Fтабл |
2,25 |
|
|
fag |
9 |
|
|
α |
0,05 |
|
|
Величина и значимость коэффициента множественной корреляции |
R |
0,9968 |
|
fк |
17 |
|
|
fост |
36 |
|
|
Fрасч |
30,4 |
|
|
Fтабл |
2,5 |
|
|
α |
0,01 |
Модель можно использовать в пределах изменения факторов, указанных в табл. 1. Фактические и расчетные (по модели) данные по прочности швов труб приведены в табл. 4.
Использование модели дает возможность контролировать и прогнозировать прочность сварного стыка при задаваемых параметрах сварки. Однако, она чрезмерно громоздка и неудобна для практических вычислений. Поэтому математическая модель была преобразована в номограмму (см. рисунок).
Номограмма построена для трех факторов:
х1 - температура нагревателя. °С;
х2 - время оплавления торцов, с;
х3 - давление стыковки труб при их сварке, кгс/см2 (МПа).
Порядок определения прочности стыков, сваренных на различных режимах (х1; х2; х3)s можно проследить по нанесенному на номограмму ключу. Например, требуется определить прочность сварного соединения труб, сваренных на следующих режимах:
- температура нагревателя 235°C
- время оплавления торцов 50 с;
- давление стыковки труб при их сварке 5,8 кгс/см2.
Для этого на оси х2 (правый верхний квадрат) из точки, соответствующей времени оплавления торцов (в данном случае 50 с), проводим прямую перпендикулярно оси х2 до пересечения с соответствующей выбранному давлению стыковки труб при сварке (5,6 кгс/см2) кривой х3. Из точки пересечения параллельно оси х2, проводим прямую до пересечения с линией, соответствующей выбранной температуре нагревателя х1 (в нашем случае 235°С). Из найденной точки опускаем перпендикуляр на промежуточную ось yc.
В левом верхнем квадранте проводим линию параллельно семейству линий ус, соответствующую полученному значению yc в правом верхнем квадранте.
В нижнем левом квадранте из точки 50°С на оси х2 строим перпендикуляр до пересечения с соответствующей значению 5,6 кгс/см2 линией х3. Из найденной точки пересечения параллельно оси х2 проводим прямую до пересечения с линией х1, соответствующей значению 235°С, и далее перпендикулярно оси х2, проводим прямую до пересечения с построенной линией ус в верхнем левом квадранте.
Значение точки пересечения определяем на промежуточной оси ус + yв. В соответствии с полученным значением проводим линию в правом нижнем квадранте параллельно семейству линий ус + yв. Аналогично предыдущим построениям на оси х2 (правый нижний квадрант) откладываем значение времени оплавления торцов, из этой точки проводим прямую перпендикулярно оси х2 до пересечения с соответствующей линией х3 и из полученной точки параллельно оси х2 проводим прямую до пересечения с ранее проведенной линией ус + yв. Перпендикуляр, опущенный из полученной точки на ось у, указывает искомую величину предела прочности при разрыве.
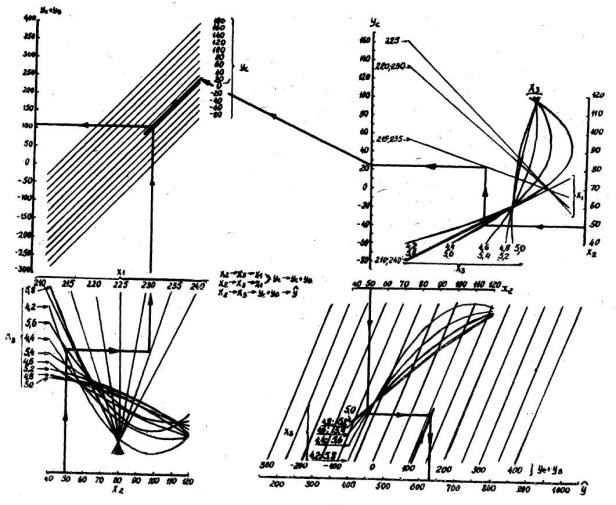
Номограмма для определения прочности при разрыве соединений труб ПВХ-100, свариваемых на различных режимах
Фактические и расчетные данные по прочности швов труб из ПВХ-100, выполненных сваркой нагретым инструментом встык
|
№ опытов |
Teмпература нагревателя, ТН |
Режимы сварки |
Предел прочноcти на разрыв, σв |
||
|
время оплавления ton |
давление осадки труб. Poc |
среднее значение по результатам проведенных опытов |
расчетные значения |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
210 |
40 |
4,2 |
219 |
202 |
|
2 |
210 |
40 |
5,0 |
400 |
402 |
|
3 |
210 |
40 |
5,8 |
157 |
171 |
|
4 |
210 |
80 |
4,2 |
612 |
616 |
|
5 |
210 |
80 |
5,0 |
489 |
491 |
|
6 |
210 |
80 |
5,8 |
593 |
586 |
|
7 |
210 |
120 |
4,2 |
638 |
616 |
|
8 |
210 |
120 |
5,0 |
611 |
613 |
|
9 |
210 |
120 |
5,8 |
565 |
585 |
|
10 |
225 |
40 |
4,2 |
641 |
629 |
|
11 |
225 |
40 |
5,0 |
550 |
552 |
|
12 |
225 |
40 |
5,8 |
620 |
629 |
|
13 |
225 |
80 |
4,2 |
599 |
601 |
|
14 |
225 |
80 |
5,0 |
614 |
616 |
|
15 |
225 |
80 |
5,8 |
605 |
601 |
|
16 |
225 |
120 |
4,2 |
658 |
666 |
|
17 |
225 |
120 |
5,0 |
650 |
652 |
|
18 |
225 |
120 |
5,8 |
676 |
666 |
|
18 |
240 |
40 |
4,2 |
580 |
573 |
|
20 |
240 |
40 |
5,0 |
575 |
577 |
|
21 |
240 |
40 |
5,8 |
600 |
604 |
|
22 |
240 |
80 |
4,2 |
641 |
626 |
|
23 |
240 |
80 |
5,0 |
624 |
626 |
|
24 |
240 |
80 |
5,8 |
644 |
657 |
|
25 |
240 |
120 |
4,2 |
649 |
636 |
|
26 |
240 |
120 |
5,0 |
636 |
638 |
|
27 |
240 |
120 |
5,8 |
656 |
667 |
О ПРОЧНОСТИ ПЕРЕХОДНЫХ ТРОЙНИКОВ ПЛАСТМАССОВЫХ ТРУБОПРОВОДОВ
Канд. техн. наук Э.В. Котенко,
инженеры Н.А. Цедюра,
Ю.А. Сидоренко
При монтаже пластмассовых трубопроводных систем применяются сварные переходные тройники, изготовленные из труб. Существует ряд конструкций этих деталей, отличающихся решением соединения магистрального участка и ответвления (рис. 1)

Рис. 1. Характерные конструкции сварных переходных тройников:
а - без усиления; б - усиленный наружным патрубком; в - то же внутренним патрубком; г - с формованной горловиной; д - то же с отбортованной горловиной
Литые тройники долговечнее, но в связи с отсутствием их производства для всех типоразмеров труб применение сварных тройников следует считать оправданным. Конструкция сварного тройника должна отвечать требованиям оптимальности по показателям прочности долговечности, трудоемкости в изготовлении и др.
В литературе не удалось обнаружить исследования по оптимизации конструкции переходных тройников, а судя по отдельным показателям, предпочтительны для применения в трубопроводных системах тройники с горловиной в магистральном участке [1] и усиленные патрубком с помощью приваренной втулки.*/ Первые более технологичны в изготовлении и имеют удовлетворительные гидравлические характеристики. Вместе с тем термопластическое деформирование материала при изготовлении горловин и предполагаемая опасность развития процессов старения в деформированном материале требуют проведения разносторонних исследований прочностных характеристик тройников.
*/ Разработать технологию изготовления переходных ответвлений в трубах из полиэтилена. Отчет НИР " гос. регистрация 72041210, Киев, 1972 г.
В настоящей работе делается попытка оценить прочностную сторону этой конструкции тройника. Рассматриваются две разновидности конструкции, отличающиеся технологическими особенностями изготовления горловины: вытяжкой (отбортовкой) и вытяжкой с принудительным формованием стенок горловины.
В качестве оценочных критериев приняты характеристики кратковременной и длительной прочности тройников при внутреннем гидростатическом давлении.
Общий вид образцов, применяющихся при исследованиях, приведен на рис.2. Несколько увеличенный размер деталей по сравнению с нормативным (ОСТ 36-55-81) обусловлен требованием к испытанию фасонных деталей трубопроводов внутренним давлением [2].
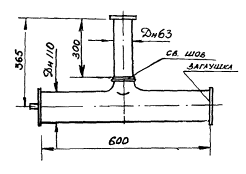 Для
изготовления тройников применялись полиэтиленовые трубы (ПНД) Дн 63 и Дн110 мм
тип "С" по ГОСТ 18599-73
производства Вильнюсского завода пластмассовых изделий. Вытяжка горловин
осуществлялась на лабораторном оборудовании Киф ВНИИМСС с соблюдением
технологических и геометрических параметров, приведенных в табл. 1.
Для
изготовления тройников применялись полиэтиленовые трубы (ПНД) Дн 63 и Дн110 мм
тип "С" по ГОСТ 18599-73
производства Вильнюсского завода пластмассовых изделий. Вытяжка горловин
осуществлялась на лабораторном оборудовании Киф ВНИИМСС с соблюдением
технологических и геометрических параметров, приведенных в табл. 1.
Рис. 2. Тройник с горловиной
Патрубки приваривались к горловинам контактно-тепловым способом встык. Сварка выполнялась в два этапа на режиме: Тсв = (220±10)°С; Ропл. начальное - 0,2 МПа; toпл = 55 с; Рос = 0,2 МПа. Остывание стыка под нагрузкой составляло 8 мин.
Детали контролировались внешним осмотром, измерялась толщина стенки элементов тройника и определялась ее минимальная величина. Прошедшие эти проверки на соответствие требованию ОСТ 36-56-81 тройники снабжались торцевыми затворами, выдерживались в воде при температуре испытания в течение двух часов, присоединялись к нагрузочному устройству и испытывались. Время между изготовлением деталей и началом их испытаний составляло не менее 24 ч.
Кратковременной нагрузкой испытывались детали при температуре +20°С на гидравлической установке ГНМ 720/100, оборудованной манометром МТП-160 (класс точности 1,5). В процессе испытания контролировалась величина максимального выдержанного образном давления и продолжительность испытания. Удовлетворительным считался результат в случае разрушений тройника в материале горловины, при этом продолжительность нагружения не должна превышать 30...60 с.
Испытание длительной гидростатической нагрузкой выполнялось при температуре 80°С на стенде длительных испытаний. Испытательный стенд обеспечивал постоянство температуры теплоносителя (воды) с точностью ±1°C, гидростатическое давление в образце с отклонением в пределах ±2 % и автоматическое фиксирование продолжительности испытания каждого образца.
Испытание выполнялось на двух уровнях нагрузки: 0,5 и 0,33 МПа согласно требованием к испытаниям сварных соединительных деталей, предусмотренным ТУ 6-19-213-83.
Результат испытания считался отрицательным, если разрушение тройника произошло за пределами зоны материала, деформируемого при изготовлении горловины. Такие результаты также включались в выборку, но исключались из рассмотрений при сопоставлении конструкций тройников.
Кратковременной нагрузкой было испытано 12 тройников, 9 из них имели горловины с формованной стенкой, а 3 - с отбортованной. Все образцы разрушились в местах соединения магистрального участка и ответвления. Прочность обеих конструкций оказалась практически одинаковой (табл. 2). По сравнению с прочностью других сварных конструкций переходных тройников [3] конструкций с горловиной оказалась предпочтительной.

Pиc. 3. Характерное разрушение тройников при испытании длительной гидростатической нагрузкой
Параметры режима и размеры отверстий, соблюдаемые при изготовлении горловин в трубах из ПНД, Дн 110 мм
|
Наружный диаметр горловины Дн, мм |
Размеры мм, отверстия, |
Высота горловины |
Температура разогрева материала, °С |
Усилие вытяжки, МПа |
|
|
вдоль оси трубы |
поперек оси трубы |
||||
|
63 |
45 |
20 |
10 |
13,5 ±5 |
40,0 |
Таблица 2
Результаты испытаний, сварных переходных тройников (110×63) из полиэтиленовых труб (ПНД) кратковременной гидростатической нагрузкой при температуре -+20°С
|
Конструкция тройников и технологические особенности их изготовления |
Средний наружный диаметр Дн, мм |
Минимальная толщина стенки S, мм |
Максимальное давление Р, МПа |
Максимальное тангенциальное напряжение МПа |
Характер и место разрушения- |
|
||
|
Магистральный участок |
Ответвление |
Магистральный участок |
ответвление |
|
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Переходной тройник без горловины, сваренный газовой прутковой сваркой [3] |
111,2 |
63,75 |
6,05 |
3,7 |
1,8 |
15,6 |
Вязкое разрушение по шву и по зоне термического влияния шва |
|
|
То же без горловины, сваренный контактным тепловым способом встык [3] |
111,3 |
63,85 |
6,00 |
3,7 |
2,3 |
18,7 |
Отрыв ответвления |
|
|
То же с горловиной с формованной стенкой и разогревом трубы горячим воздухом |
110,0 |
63,0 |
6,20 |
3,8 |
2,6 |
20,80 |
Вязкое разрушение по шву после значительной пластической деформации |
|
|
6,30 |
3,9 |
2,6 |
19,70 |
|
||||
|
6,20 |
3,7 |
_____2,5_____ |
____20,00____ |
|
||||
|
2,57 |
20,20 |
|||||||
|
То же, инфракрасным излучением |
110,0 |
63,0 |
6,2 |
3,8 |
2,70 |
21,00 |
Вязкое разрушение в материале горловины |
|
|
2,70 |
2150 |
|
||||||
|
_____2,70_____ |
____20,90____ |
|
||||||
|
2,70 |
21,10 |
|
||||||
|
То же, электронагревательным инструментом |
110,0 |
63,0 |
6,2 |
3,8 |
2,50 |
19,50 |
Вязкое разрушение в магистральном участке по материалу горловины |
|
|
3,9 |
2,60 |
19,70 |
|
|||||
|
3,8 |
_____2,67_____ |
____20,80____ |
|
|||||
|
2,59 |
20,00 |
|
||||||
|
Переходной тройник с отбортованной (без формования) горловиной с разогревом трубы для вытяжки горловины горячим воздухом |
110,0 |
63,0 |
6,2 |
3,8 |
2,60 |
20,8 |
Вязкое разрушение в материале горловины |
|
|
3,8 |
2,50 |
20,0 |
|
|||||
|
3,9 |
_____2,60_____ |
_____19,70____ |
|
|||||
|
2,57 |
20,2 |
|
||||||
Таблица 3
Результаты испытания переходных сварных тройников (110×63) из полиэтиленовых (ПНД) труб длительной гидростатической нагрузкой при температуре +80°С
|
Способ нагрева трубы перед вытяжкой горловины |
Вытяжка с принудительным формованием стенки |
Вытяжка без принудительного формования стенки |
||||||
|
Долговечность (ч) при нагрузке |
||||||||
|
№ обр. |
0,5 МПа |
№ обр. |
0,33 МПа |
№ обр. |
0,5 МПа |
№ обр. |
0,33 МПа |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Контактный (электронагревательным инструментом) |
1 |
10,3 |
11 |
55 |
19 |
17,9 |
28 |
38,7 |
|
2 |
12,5 |
12 |
50,5 |
20 |
10,2 |
29 |
48,2 |
|
|
3 |
25,7 |
13 |
27,5 |
21 |
34,2 |
30 |
20,8 |
|
|
4 |
15,1 |
14 |
91,7 |
22 |
15,5 |
31 |
36s3 |
|
|
5 |
14,3 |
15 |
26,8 |
23 |
19,1 |
32 |
32,5 |
|
|
Бесконтактный (горячим воздухом) |
6 |
11,5 |
18 |
37,5 |
24 |
13,6 |
33 |
76,0 |
|
7 |
9,6 |
17 |
28,1 |
25 |
18,8 |
34 |
139,9 |
|
|
8 |
17,5 |
18 |
30,2 |
26 |
14,8 |
35 |
74,0 |
|
|
9 |
17,8 |
|
|
27 |
11,7 |
36 |
191,2 |
|
|
10 |
6,2 |
|
|
|
|
37 |
191,5 |
|
Образцы № 10, 15, 17, 18, 23, 27, 29-32, 85, 87 разрушились за пределами деформируемой зоны.
Длительной нагрузкой испытано 37 тройников. Из общего количества этих деталей 18 имели горловину с формованной стенкой и 19 с отбортованной. Все образцы доведены до разрушения. Характерный вид разрушений приведен на рис. 3. Наблюдались также разрушения и в местах дефектов труб, преимущественно по царапине соединительного шва.
На основании полученных результатов (табл. 3) нельзя сделать заключение о работоспособности исследуемой конструкции в течение длительного срока. Полученный материал показывает, что тройники с отбортованной горловиной не уступают по долговечности тройникам с формованной горловиной. Обе конструкции имеют длительную прочность ниже нормативной величины этого показателя, установленной для литых деталей этого типа. Эффективным представляется использование сварных переходных тройников в трубопроводах из труб на тип ниже.
Заслуживают внимания изучение условий, способствующих старению материала горловин, и оценка влияния эффекта деформационного старения на работоспособность сварных переходных тройников с горловинами.
ЛИТЕРАТУРА
1. Трубопроводы пластмассовые. Детали соединительные сварные и формованные из полиэтиленовых и полипропиленовых труб для напорных трубопроводов. ОСТ 36-55-81. М., ЦБНТИ Минмонтажспецстроя СССР, 1981.
2. Rohrverbindungen und Rohrleitungs fur Druckrohrleitungen aus Polyathylen hart (PE hart). Typ. 1. Allgemeine Gutcanf-ordercungen Prufungen. Deutche Normen DIN 16 963 Teil 5. Juli 1997, 4S
3. В.И. Обвинцев, Э.В. Котенко, Н.А. Цедюра, Н.Г. Новиченко. Поиск способов усиления сварных деталей пластмассовых трубопроводов. Монтаж и сварка резервуаров и технологических трубопроводов. Сборник трудов ВНИИМСС, 1983 г.
ВЛИЯНИЕ РЕЖИМОВ ОТВЕРЖДЕНИЯ НА ПРОЧНОСТЬ КЛЕЕВЫХ СОЕДИНЕНИЙ БАНДАЖНОГО ТИПА
Канд. техн. наук В.С. Позднышев,
инженеры: Л.И. Жлуктова,
О.И. Филатова, Е.Б. Шумова
В лаборатории изготовления и монтажа технологических трубопроводов разработаны прогрессивные клеевые соединения бандажного типа. Технология их получения базируется на многослойной намотке на концы стыкуемых труб ленты из конструкционной стеклоткани с предварительно нанесенным на нее слоем эпоксидного клея. После отверждения клея на месте стыка образуется монолитный стеклотекстолитовый бандаж, имеющий прочную адгезионную связь с поверхностями труб, что обеспечивает надежное, герметичное и коррозионностойкое их соединение.
Выбор эпоксидных клеев холодного отверждения обоснован комплексом их ценных физико-химических, технологических и прочностных свойств. Они наиболее полно удовлетворяют требованиям строительно-монтажного производства, обладают высокой степенью монтируемости физико-механических и прочностных свойств в широком диапазоне температур, технологичны, достаточно жизнеспособны при нормальной температуре, практически не требуют устройств для создания давлений при склеивании, отверждаются как при обычных, так и при повышенных температурах; имеют малую усадку, стойки к комплексу климатических воздействий, обладают хорошей химстойкостыо к щелочам, углеводородам, некоторым кислотам и, что немаловажно, их составляющие компоненты наиболее доступны для приобретения монтажными организациями.
Номенклатура клеев на основе эпоксидных олигомеров, их технологические и прочностные характеристики наиболее подробно освещены в монографии Кардашова Д.А. [1].
Проведенный анализ ранее выполненных работ, а также результатов собственных исследований [2], позволил рекомендовать для склеивания стальных труб следующие составы клеевых композиций (см. таблицу).
Составы клеевых композиций
|
Компоненты |
Состав |
|
|
1 |
2 |
|
|
Эпоксидный олигомер ЭД,-20, масс. ч |
100 |
100 |
|
Дибутилфталат, масс. ч |
15 |
- |
|
Полиэтиленполиамин (ПЭПА), масс. ч. |
10 |
- |
|
Полиамидный низкомолекулярный. олигомер Л-18 (Л-20), масс. ч |
- |
40…50 |
|
Пудра алюминиевая ПАП-1 (ПАП-2), масс. ч. |
10 |
10 |
Следует отметить, что по сравнению с ПЭПА низкомолекулярные полиамиды обладают некоторыми преимуществами. Прежде всего они являются не только отвердителями, но и пластификаторами и более технологичны, так как при подготовке клеевых композиций соотношение смолы и полиамидов может выдерживаться не так строго, как при использовании ПЭПА. Наилучшие свойства клеевых соединений достигаются при содержании полиамидов от 40 до 50 %, Эти отвердители малотоксичны, они способствуют получению клеевых композиций с большей жизнеспособностью и лучшими эластическими свойствами, чем при использовании ПЭПА,
Введение в композицию пластификатора (в нашем случае дибутилфталата и полиамида Л-19), определяется необходимостью снижения начальной вязкости состава, что позволяет улучшить условия нанесения клея и формирования адгезионного контакта при смачивании клеем поверхности субстрата. Пластификатор снижает модуль упругости отвержденного клея и в то же время способствует снижению уровня концентрации напряжений и их релаксации с течением временя.
Нужные физико-механические свойства клеевых соединений во многом определяются природой наполнителя. Введение его в состав клеевой композиции повышает прочность клеевого соединения, снижает разность коэффициентов линейного расширения клея и склеиваемых материалов, что в конечном счете уменьшает внутренние напряжения в клеевой конструкции, расширяет диапазон рабочих температур и снижает их стоимость. Нарастание прочности при введении в составы наполнителей объясняется тем, что наполнители, обладая большой свободной поверхностью, являются носителями активных в отношении адгезии центров. В процессе отверждения происходят самоармирование олигомера. При этом прочность связи частиц наполнителя с ориентированной структурой макромолекул клея значительно выше когезионной прочности полимера. В конечном итоге повышается прочность клеевых соединений и тем больше, чем выше механическая прочность наполнителя.
При выборе наполнителя предпочтение было отдано наиболее технологичной алюминиевой пудре. Благодаря небольшой плотности и чешуйчатому строению она находится в клеевой композиции во взвешенном состоянии и не оседает в осадок при производстве работ. Ориентированное расположение чешуек алюминиевой пудры в пленке клея оказывает экранирующее действие и способствует повышению: эксплуатационных свойств соединений. Алюминиевая пудра - металлический наполнитель, поэтому она увеличивает теплопроводность композиции и тем самым снижает температурные напряжения.
Таким образом, клеевое соединение бандажного типа в стадии отверждения представляет собой сложную композиционную систему в которой взаимодействуют различные по природе материалы: металл трубы, эпоксидное связующее, отвердитель, пластификатор, наполнитель, алюминиевая пудра к армирующая стеклоткань. По имеющимся данным с таким сочетанием материалов клеевые соединения не исследовались. Прежде всего это относится к изучению влияния режимов отверждения на их прочность.
Анализ имеющихся работ показывает, что при холодном отверждении эпоксидных композиций (t =18 - 20°С) интенсивный рост прочности начинается после выдержки соединений в течение 3 - 5 ч., при этом по одним данным рост наблюдается без промежуточных пиков вплоть до максимума в течение 72 или 150 [3] а по другим - с промежуточным максимумом после 20 ч или 6 суток [4] с момента склеивания. Для интенсификации процесса отверждения и увеличения прочности соединений на клеях холодного отверждения их рекомендуется подвергать термообработке при температуре от 100 до 130°С.
Выше приведенное явилось основанием проведения экспериментальных исследований, направленных на изучение влияния режимов отверждения клея на прочностные свойства бандажных клеевых соединений. Для экспериментальных исследований были приняты трубчатые образцы из стали Ст3 (рис. 1) с размерами ДН×S = 57×3 мм, близкими к реальным типоразмерам труб, что позволило не рассматривать вопрос о влиянии масштабного фактора на результаты испытаний. Для намотки использовали ленты из конструкционной стеклоткани марки Т-13 (ГОСТ 19170-73) шириной l = ДН, количество слоев - 6. Поверхность образцов перед склеиванием подвергали механической обработке и обезжиривали.
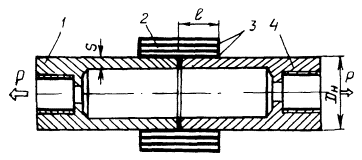
Рис 1. Схема образца клеевого соединения для исследования влияния режимов отверждения на прочность: 1, 4-стыкуемые части трубчатого образца; 2 - стеклоткань; 3 - клей. ДН - наружный диаметр трубы; S - толщина стенки трубы; l - длина нахлестки
Для устранения нежелательного влияния на результаты испытаний осевых смещений стыкуемых частей образца при сборке, а также с целью обеспечения его неподвижности при многослойной намотке стеклотканевой ленты и отверждении клея были использованы устройства для сборки труб конструкции ВНИИмонтажспецстроя.
Отверждение клея проводилось по трем режимам: холодное - при температуре 20 ± 2°С, горячее - при 120 ± 3°С и смешанное при указанных параметрах.
Результаты механических испытаний (сдвиг при растяжении) образцов клеевых соединений, отвержденных при различных режимах, представлены на рис. 2. Из рис. 2 видно, что при холодном отверждении максимальная прочность соединений с отвердителем полиэтиленполиамином в среднем на 8 % ниже, чем при использовании в качестве отвердителя полиамида Л-20. Характер кривых на рис. 2,а идентичен по форме, без промежуточных максимумов, при этом видно, что интенсивный рост значений прочности происходит при выдержке в течение первых суток. За этот промежуток времени прочность соединений с отвердителем ПЭПА составляет в среднем 92 % от достигнутой за время отверждения в течение 25 суток. Дальнейшее отверждение при нормальной температуре характеризуется уменьшением прироста прочности: за вторые сутки он составил в среднем 3 %, за третьи - до 2 %. Наличие роста значений прочности обнаруживается и при дальнейшей выдержке соединений в течение 25 суток, что свидетельствует о продолжительности процесса отверждения клеевых композиций и согласуется с выводами других исследователей, которые наблюдали изменение значений прочности в течение 1 - 6 месяцев, а в некоторых случаях и в течение 1 года [5].
Таким образом, исходя из данных эксперимента, минимальное время для холодного отверждения составляет не менее 48 ч. Наиболее целесообразна выдержка соединений при нормальной температуре в течение 3 суток.
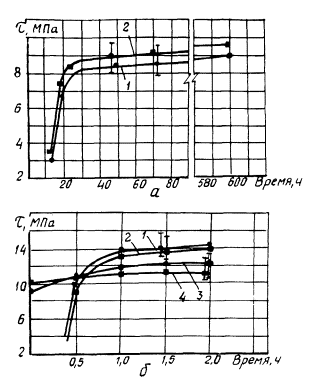
Рис. 2. Зависимость разрушающих напряжений сдвига от времени отверждения клеевых соединений: а - холодное отверждение при 20 ±3°С; б - горячее отверждение при 120 ±3°С (3, 4 - дополнительно после холодного отверждения в течение 24 ч); 1, 3 - композиции с полиэтиленполиамином, 2, 4 - композиции с полиамидным олигомером Л-20
Дополнительный часовой прогрев соединений, отвержденных в течение 24 ч при нормальной температуре увеличивает их прочность в среднем на 40 % для соединений с полиэтиленполиамином и на 32 % - с Л-20 (см. рис. 2, б). При этом кривые на графиках имеют пологий характер, без промежуточных максимумов.
Прогрев соединений свыше 1 ч незначительно сказывается на увеличении их прочности. Так, двухчасовый прогрев по сравнению с одночасовым прогревом обеспечивает рост значений прочности для состава с ПЭПА в среднем на 5 %, а для состава с Л-20 - на 3 %.
Прочность соединений горячего отверждения (время отверждения 1 - 1,5 ч) выше, чем прочность соединений холодного отверждения (время отверждения 72 ч) для клея с ПЭПА в среднем на 62 - 65 %, а для клея с Л-20 - на 44 - 48 %, Это можно объяснить тем, что при высокой температуре снижается вязкость композиции, а значит обеспечивается лучшая смачиваемость поверхностей склеивания, при этом повышается подвижность молекул олигомера и отвердителя, в результате чего ускоряется конверсия реакционноспособных групп и обеспечивается более высокое адгезионное сцепление.
При горячем отверждении наиболее интенсивный набор прочности происходит в течение первого часа.
Сопоставляя данные испытаний, можно сделать вывод, что соединения с полиамидным отвердителем менее чувствительны к высоким температурам отверждения, чем соединения отвердителем полиэтиленполиамином и пластификатором дибутилфталатом.
Следует отметить, что с увеличением времени холодного и горячего отверждения одновременно с ростом значений прочности наблюдается снижение вариационного коэффициента, при этом для состава с ПЭПА его значения уменьшаются от 18,6 до 7,4, а для состава с Л-20 - от 16,6 до 6,2. Приведенный порядок цифр характеризует разброс показателей прочности, поэтому можно сделать вывод, что состав с отвердителем Л-20 более однороден, чем состав с ПЭПА.

Рис. 3. Устройство для горячего отверждения клеевых соединений трубопроводов: 1 - ТЭНы; 2 – кожух; 3 - наборы сменных фланцев
Таким образом, установлено, что прочность соединений при горячем отверждении клея выше, чем при холодном в среднем на 62 - 65 % для клея с отвердителем полиэтиленполиамином и на 44 - 48 % для состава с отвердителем Л-20. Дополнительный часовой прогрев соединений, отвержденных при нормальной температуре, позволяет улучшить прочностные показатели в среднем на 30 - 40 %.
Для осуществления горячего отверждения клея в условиях строительно-монтажной площадки, а также повышения прочностных свойств клеевых соединений институтом разработано специальное устройство (рис. 3). Оно состоит из четырех ТЭНов мощностью 120 Вт каждый, заключенных в два полуцилиндра кожуха, шарнирно соединенных между собой. Устройство может работать от сети напряжением 36 и 220 В. Для закрепления устройства на трубах различных диаметров (Ду от 15 до 100 мм) оно снабжено набором сменных фланцев. Испытания устройства показали, что оно создает на поверхности стеклотекстолитового бандажа равномерное поле температур в заданных пределах (120 ± 3°С) и может быть использовано в реальных условиях монтажа.
ЛИТЕРАТУРА
1. Кардашов Д.А. Синтетические клеи. - М.: Химия, 1976, -508 стр.
2. Позднышев B.C. Тавастшерна Р.И. Склеивание - перспективный метод соединения стыков труб. Монтажные и специальные работы в строительстве. 1982, № 8.
3. Протасов B.H., Агапчев В.И. Исследование прочностных свойств клеевых соединений в клиновых задвижках. - Транспорт и хранение нефтепродуктов и углеводородного сырья. Научн.-техн. сб. 1971, № 6, с. 11 - 13,
4. Чернин И.З., Смехов Ф.И. Влияние условий отверждения на адгезию и прочность соединений. Вестник машиностроения. 1975, № 5, с. 59-61.
5. Фрейдин А.С. Прочность и долговечность клеевых соединений. -М.: Химия, 1971; 256 с.
ВОЗДЕЙСТВИЕ РАБОЧИХ ПАРАМЕТРОВ ТРУБОПРОВОДА НА СТОЙКОСТЬ КЛЕЕВЫХ СОЕДИНЕНИЙ
Канд. техн наук В.С. Позднышев,
инженеры Л.И. Жлуктова, С.И. Филатова
Технологические, прочностные и технико-экономические преимущества клеевых соединений определяют перспективы успешного их использования в практике монтажа стальных трубопроводов различного назначения.
Наиболее прогрессивны клеевые соединения бандажного типа, разработанные лабораторией изготовления и монтажа технологических трубопроводов ВНИИмонтажспецстроя [1, 2].
Новизна конструктивно-технологических решений бандажных клеевых соединений, а также актуальная потребность в них монтажных организаций обуславливает необходимость получения характеристик их работоспособности.
В связи с этим было получено аналитическое решение для качественной и количественной оценки напряженного состояния соединений при воздействии основных рабочих параметров трубопровода - внутреннего давления и температуры среды [3]; установлены экспериментальные зависимости, раскрывающие характер влияния геометрических размеров элементов соединений на несущую способность, а также выявлены условия оптимизации прочности соединений с учетом их реальной геометрии [4].
Однако широкое применение бандажных клеевых соединений сдерживается отсутствием данных об их работоспособности в условиях, приближенных к условиям монтажа и сдачи трубопроводов в эксплуатацию. Этому актуальному вопросу и посвящена данная статья.
Из всех существующих методов оценки работоспособности соединений наибольшее приближение к реальным условиям дают испытания трубчатых образцов и секций трубопроводов внутренним гидравлическим давлением. При этом следует учитывать, что в условиях эксплуатации трубопроводов возможно их многократное нагружение переменным давлением, например, при отключении трубопроводных систем, срабатывании запорной, регулирующей, предохранительной и контрольной арматуры, а также при пульсации давления от гидроприводов. Гидравлические насосы в режиме максимальной производительности создают пульсацию потока среды в пределах до 30 % от рабочего давления.
Соединения трубопроводов одновременно с гидравлическим давлением могут подвергаться температурному перепаду среды. В силу указанных обстоятельств кроме кратковременных гидравлических испытаний соединений до разрушения проводились испытания в условиях циклического нагружения, а также в условиях совместного действия давления, температуры и растягивающих усилий.
Для исследования кроме склеенных секций стальных труб применяли трубчатые образцы (рис. 1) из Ст3 с механической обработкой поверхности, характеризуемой RZ = 20 мкм, при этом их геометрические размеры были идентичны реальным типоразмерам труб (табл. 1), что позволило не рассматривать вопрос о влиянии масштабного фактора на результаты испытаний.
Анализ физико-механических и технологических характеристик эпоксидных конструкционных клеев, а также результаты собственных исследований позволили в качестве оптимальных принять следующие клеевые композиции: 1. Эпоксидный олигомер ЭД-20-100 масс. ч, пластификатор - дибутилфталат - 15 масc. ч, отвердитель полиэтиленполиамин - 10 масс. ч, наполнитель алюминиевая пудра - 10 масс. ч; 2. Эпоксидный олигомер ЭД-20 - 100 масс. ч, полиамидный олигомер Д-20 - 50 масс. ч., алюминиевая пудра - 10 масс. ч.


Рис 1. Испытание склеенных секций труб к образцов гидравлическим давлением: а - склеенные секции труб ДН×S = 57×4 мм; 1 - трубы; 2 – клеевой стык:8 - ручной насос; б – образцы в испытательной камере установки
Таблица 1
Образцы для испытаний
|
Виды испытаний |
Геометрические размеры образцов |
|||
|
наружный диаметр ДН, мм |
толщина стенки S, мм |
длина нахлестки бандажа l, мм |
количество слоев в бандаже, п |
|
|
Гидростатическая опрессовка |
|
|
|
|
|
- образцов при постоянной температуре (t = 18°С); |
30 |
2 |
15,21 |
5 |
|
30 |
6 |
15,21 |
5 |
|
|
90 |
3 |
45,63 |
5 |
|
|
90 |
6 |
45, 63 |
5 |
|
|
- секций труб при температуре воды от 12 до 90°С |
57 |
4 |
35 |
5 |
|
Воздействие внутреннего пульсирующего давления |
57 |
4 |
40 |
6 |
|
Совместное воздействие давления, температуры и растягивающих усилий |
38 |
2 |
25 |
6 |
Перед склеиванием наружные поверхности концов образцов и труб обезжиривали ацетоном. После многослойной намотки лент стеклоткани образцы отверждали в течение 24 ч при t = 22 ±2°С с последующей выдержкой на стенде в течение 7 суток.
Отсутствие дифференцированных требований к различным трубопроводным системам в части стойкости к пульсирующему давлению вызвало необходимость обоснования числа циклов испытаний. Обычно считают, что срок эксплуатации стальных трубопроводов не превышает 30 лет. Если допустить ежедневное включение и выключение трубопроводных систем, что значительно ужесточает реальные условия эксплуатации технологических и сантехнических трубопроводов, то база испытаний составит 104 циклов. Образцы нагружали давлением от qмин = 0 до qмакс = 2 МПа.
Для исследований соединений при нагружении внутренним пульсирующим давлением была использована специальная установка ВНИИмонтажспецстроя, отличающаяся от известных испытательных машин тем, что рабочей средой, заполняющей образцы, является вода, а не масло, работа с которым неэкономична и приносит целый ряд неудобств при обслуживании [5].
При испытаниях использовали гребенку из 5 образцов. После обнаружения течи в образцах каждый из них последовательно заглушался. Визуальное наблюдение за поведением образцов осуществлялось через смотровые окна испытательной камеры.
Моделирование длительных условий эксплуатации клеевых соединений трубопроводов производили на стенде (рис. 2). Образцы располагали на несущих полках стенда в вертикальном положении. В качестве коррозионно-активной среды использовалась горячая вода из системы отопления при параметрах: давление от 0,2 до 0,25 МПа, температура 85 ±5°С. Подвод и отвод воды осуществлялся через систему гибких шлангов. На каждый образец подвешивался груз массой 40 кг. Это дополнительно к составляющим нагрузки от воздействия давления и температуры создавало постоянные усилия сдвига в бандаже. Образцы подвергали воздействию нагрузок в течение 1,5 лет в суточном режиме цикличности: выдержка при рабочих параметрах в течение 8 ч и последующее отключение системы на 16 ч. В недельном цикле система водопитателя отключалась на 2 дня.

Рис. 2. Стенд для испытаний совместного действия гидравлического давления, температуры и растягивающих усилий: 1 - образец соединения; 2 - несущие полки стенда; 3, 4 - гибкие шланги для подачи воды; 5 - груз
После снятия со стенда образцы разрушали на разрывной машине, тем самым устанавливали изменение механической прочности.
Результаты гидравлических испытаний трубчатых образцов клеевых соединений при нормальной температуре приведены в табл. 2, из которой следует, что значения разрушающих давлений падают с увеличением диаметров и повышаются с увеличением толщин стенок труб. Так, например, для образцов малого диаметра (ДН = 30 мм) увеличение толщины стенки с 2 до 6 мм позволяет увеличить несущую способность в среднем в 2 раза (от 11,9 до 24,1 МПа). На больших диаметрах (ДН = 90 мм) идентичное увеличение толщин стенок увеличивает прочность соединений в меньшей степени, в среднем на 30 % (от 6,0 до 8,4 МПа). Увеличение относительной длины нахлестки стеклотекстолитового бандажа в клеевом соединении l/ДН от 0,5 до 0,7 повышает значение разрушающих гидравлических давлений; причем повышение более выражено для тонкостенных образцов (в среднем на 10 %).
Таблица 2
Величина разрушающих гидравлических давлений при опрессовке образцов клеевых соединений при нормальной температуре воды (t - 18°С)
|
Размеры труб ДН×S, мм |
Относительная длина нахлестки, l /ДН |
Среднее разрушающее давление, q, МПа |
Коэффициент вариации V, % |
|
30×2 |
0,5 |
11,9 |
7,3 |
|
30×2 |
0,7 |
12,9 |
7,1 |
|
30×6 |
0,5 |
23,7 |
7,9 |
|
30×6 |
0,7 |
24,1 |
9,1 |
|
90×3 |
0,5 |
6,0 |
6,8 |
|
90×3 |
0,7 |
6,6 |
6,8 |
|
90×6 |
0,5 |
8,0 |
6,6 |
|
90×6 |
0,7 |
8,4 |
7,6 |
С увеличением температуры воды от 12 до 90°С (рис. 3) значения разрушающих гидравлических давлений уменьшаются в среднем в 2 раза, при этом наиболее интенсивное падение происходит в диапазоне температур от 50 до 90°С.
Результаты испытаний показали (табл. 3), что клеевые соединения достаточно хорошо противостоят усталостному нагружению пульсирующим гидравлическим давлением: из 20 образцов, подвергавшихся испытаниям, только один образец с отвердителем Л-20 разрушился при базе испытаний около 104 циклов, а 7 образцов выдержали нагружение в 2∙104 циклов без нарушения герметичности.
Таблица 3
Результаты испытаний образцов клеевых соединений (ДН×S 57×4) пульсирующим гидравлическим давлением
|
Составы клеевых соединений |
Партии образцов |
Число циклов до разрушения образцов |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
1 |
а |
14210 |
20000 х) |
20000 х) |
14800 |
18900 |
|
б |
15140 |
20000 х) |
19200 |
16440 |
20000 х) |
|
|
2 |
а |
20000 х) |
16520 |
9630 |
12400 |
18000 |
|
б |
17220 |
20000 х) |
20000 х) |
12340 |
19230 |
|
х) образец не разрушился.
Таким образом, проведенные гидравлические испытания клеевых соединений с достаточной убедительностью свидетельствуют об их повышенной стойкости к кратковременным воздействиям статического и пульсирующего гидравлического давления, при этом при рабочем давлении до 1,0 МПа и температуре среды 90°С они могут работать с коэффициентом запаса по прочности, равным 4,2. При меньших температурах среды соединения могут работать при более высоких давлениях.
Результаты испытаний клеевых соединений после длительного (18 мес.) циклического воздействие горячей (t = 85 ± 5°С) воды под давлением q = 0,2 - 0,3 МПа и постоянной растягивающей нагрузки Р = - 0,4 кН приведены на рис. 4, из которого следует, что такого рода воздействия вызывают изменение их прочностных свойств с характерным максимумом в пределах 50 суточного воздействия (τмакс = 11,9 МПа).
За указанные периоды прочность образцов возросла в среднем на 10 %. Наличие максимума можно объяснить горячим доотверждением клеевых соединений, а также перераспределением напряжений в них вследствие развития релаксационных процессов.
При дальнейших испытаниях проявляется тенденция к снижению прочностных показателей, причем после воздействия указанных нагрузок в течение 1,5 лет значения статической прочности составили 81 - 85 % от контрольных.
Полученные закономерности воздействия рабочих параметров трубопровода позволили спрогнозировать их длительную работоспособность [6] методом экстраполяции кривых изменения кратковременной прочности в системе координат с полулогарифмическим масштабом на 1,0 - 1,5 порядка времени при продолжительности испытаний в пределах 2 - 5.107 с (рис. 5).

Рис. 3. Влияние температуры воды на величину разрушающего гидравлического давления
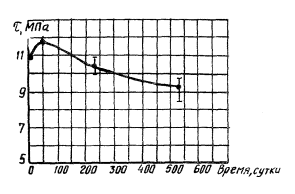
Рис. 4. Влияние совместного действия циклического гидравлического давления горячей воды и постоянной нагрузки на изменение статической прочности соединений
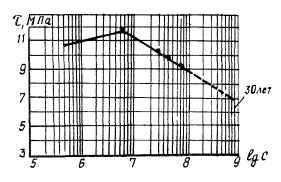
Рис. 5. Прогнозируемая долговечность клеевых соединений при циклическом воздействии гидравлического давления, горячей воды и постоянной нагрузки
Длительная прочность соединений при прогнозируемом сроке эксплуатации в течение 30 лет составит 55 % от кратковременной. Полученные способом прогнозирования данные о длительной работоспособности клеевых соединений трубопроводов хорошо согласуются с опытно-промышленными данными их внедрения. Так, в декабре 1974 г. один из стыков трубопровода (ДН = 57 мм) системы горячего водоснабжения лабораторного корпуса ВНИИмонтажспецстроя был соединен методом склеивания. В течение 9 лет клеевое соединение находится под воздействием внутреннего давления 0,3 - 0,4 МПа и температуры воды 90 ±5°С. За этот период разгерметизации не обнаружено. Метод склеивания апробирован при монтаже стояков горячего водоснабжения и отопления в одном из домов-новостроек (г. Москва, ул. Мещанская). При сдаче в эксплуатацию (сентябрь 1976 г.) системы были спрессованы при давлении 1,6 МПа и температуре 100 ± 5°С. За срок эксплуатации нарушений плотности не обнаружено.
Интересны данные о длительной эксплуатации клеевых соединений бандажного типа в системах воздушного отопления зданий пансионата "Клязьма" под Москвой.
Методом склеивания было соединено 200 прямолинейных стыков асбоцементных воздуховодов диаметром 400, 600, 800 мм, а также герметизированы узлы их сопряжений со стальными седловинами, к которым приваривались 5 - 10 отводных патрубков небольших диаметров. В течение 20 лет эксплуатации зданий клеевые соединения ни разу не вышли из строя [7].
Полученные результаты исследований позволили рекомендовать использование разработанной технологии склеивания при монтаже стальных трубопроводов диаметром до 108 мм, предназначенных для транспортирования под давлением до 1,0 МПа веществ с температурой от минус 60 до 90°С, к которым химически стоек стеклопластик на эпоксидном связующем.
ЛИТЕРАТУРА
1. Тавастшерна Р.И., Позднышев B.C., Жлуктова Л.И., Филатова О.И. Рекомендации по склеиванию стыков стальных трубопроводов. - М.: ЦБНТИ ММСС, 1980, 24 с.
2. Позднышев В.С., Тавастшерна Р.И. Склеивание - перспективный метод соединения стыков труб. Монтажные и специальные работы в строительстве. 1982, № 8, с. 7-8.
3. Кшнякин P.M., Позднышев В.С. Воздействие основных нагрузок на клеевые соединения труб с коррозионностойкими покрытиями. Строительство трубопроводов. 1982, № 6, с.30-32.
4. Позднышев B.C., Фрейдин А.С. Выбор оптимальных конструктивных параметров клеевых соединений трубопроводов. Вестник машиностроения. 1981, № 1, c.49-62.
5. Хажинский Г.М., Ташкинов А.В., Крупенин З.А., Давидовский Б.Г. Исследование прочности элементов и соединений трубопроводов на испытательной установке с пульсирующим внутренним давлением. Труды ВНИИМСС, Вып. 24, М., 1978.
6. Фрейдин А.С. Прочность и долговечность клеевых соединений. - М.: Химия, 1971, 258 с.
7. Позднышев B.C., Чистяков Н.Н., Фрейдин А.С. Клеевые соединения в санитарно-технических системах. Водоснабжение и санитарная техника. 1984, № 8, с, 15.
АННОТАЦИИ МАТЕРИАЛОВ, ПОМЕЩЕННЫХ В СБОРНИКЕ НАУЧНЫХ ТРУДОВ
Ритчик Г.А., Петрова Л.В., Добрынина И.Н. Исследование технологических параметров формообразования монтажных стыков рулонируемых полотнищ стенок резервуара. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.3.
Даны результаты исследования деформированного состояния зон монтажных стыков рулонируемых стенок резервуаров. Приводятся расчетная схема определения технологических параметров правки обратным изгибом концевых участков полотнищ на монтаже и результаты расчета для резервуара объемом 50 тыс. м3 с плавающей крышей. Даны рекомендации по способам правки концевых участков полотнищ в зонах монтажных стыков.
Никиреев B.M., Концентрация деформаций в монтажном стыке стенки цилиндрического резервуара. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 8.
Дано решение, определяющее напряжения и деформации в угловатом монтажном стыке стенки вертикальных цилиндрических резервуаров. Получена зависимость, позволяющая определять коэффициент концентраций упругих деформаций в зависимости от величины угловатости. Предложен метод, позволяющий улучшить сходимость шагового процесса решения нелинейных задач строительной механики. Метод использован при расчете монтажного стыка с угловатостью с учетом пластической работы стали.
Примаков Ю.В. Характеристика несущих элементов для облегченных покрытий. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.17.
В статье рассмотрены геометрические характеристики несущих элементов для покрытий, резервуаров и сплавов. Даны зависимости соотношений высоты профили к длине развертки и момента инерции к площади профиля.
Майлер А.З. Оптимизация параметров конструкций изометрических резервуаров - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.21.
Проанализированы вопросы оптимизации параметров изотермических резервуаров с учетом расхода материалов, технологичности и эксплуатационных затрат. Поставлена задача оптимизации параметрического ряда изотермических резервуаров на основе методики, разработанной для нефтерезервуаров.
Ползков В.П., Бейлин Д.А., Гольберг Ю.М. Методы подобия и размерности в задаче обтекания мягких оболочек потоком воздуха. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.27.
На основе теории размерностей и экспериментального исследования действительной работы мягких оболочек в потоке воздуха предложены формулы опенки напряженно-деформированного состояния оболочек.
Волкова C.B. Сабсович Л.Л. Стандартные подпрограммы решений систем линейных алгебраических уравнений для расчета резервуаров. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.30.
В статье приведены сведения о составленных во ВНИИмонтажспецстрое стандартных подпрограммах для решения систем линейных алгебраических уравнений, имеющих ленточную матрицу, с использованием накопителей на магнитных дисках.
Одна подпрограмма предполагает хранение матрицы по строкам, другая - в виде блоков. Обе подпрограммы используют метод прямого исключения Гаусса без выбора главного элемента (или блока). Подпрограмма, решающая систему в блочной запаса, рассчитана на решение 3-диагональной блочной системы специального вида.
Шувалов Ю.Б., Куренков В.А., Кочнов В.А. Способ изготовления крутоизогнутых отводов непрерывной протяжкой трубных заготовок по рогообразному сердечнику. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с.34.
В данной работе описан способ изготовлении отводов горячей протяжкой по рогообразному сердечнику с использованием перемычек из сплошного металла между трубными заготовками.
Шувалов Ю.Б., Куренков В.А., Тавастшерна Р.И. Расчет силовых параметров для изготовления толстостенных крутоизогнутых отводов горячей протяжкой. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 37.
В данной работе установлена зависимость напряженного состояния рогообразного сердечника от толщины стенки протягиваемого отвода, пользуясь которой можно установить стойкость сердечника в количестве протягиваемых отводов от толщины стенки отвода. Дано обоснование протяжки толстостенных отводов в условиях их заводского изготовления.
Шувалов Ю.Б., Куренков В.А. Разработка деформирующего инструмента при горячей протяжке крутоизогнутых отводов. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 42.
В работе изложены новые конструкции рогообразных сердечников для горячей протяжки отводов из трубных заготовок. Предложены: равнопрочный рогообразный сердечник для протяжки отводов ДУ - 4,0 - 600 мм, в котором масса сердечника снижена на 30 - 40 % и рогообразный сердечник для изготовления крупногабаритных отводов ДУ до 1200 мм, который выполнен составным из двух половин.
Хажинский Г.М. Оценка несущей способности тройников, нагруженных внутренним давлением. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 48.
На основе анализа расчетных и экспериментальных данных получено выражение для теоретического коэффициента концентрации мембранных окружных напряжений в точке пересечения оболочек и меридиональной плоскости симметрии. Рассмотрен случай нагружения тройникового соединения внутренним давлением. В основе полученного полуэмпирического выражения лежит допущение об осесимметричном характере напряженно-деформированного состояния оболочек в опасной точке. Исследовано упругое состояние, локальное пластическое течение и полное разрушение тройникового соединения. Расчеты сопоставлены с многочисленными экспериментальными данными, а также с результатами вычислений методом конечных элементов.
Бурбело Ю.С., Радченко С.Г., Сидоренко Ю.А. Определение расчетно-графическими методами прочности стыков труб из ПВХ-100. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 59.
Статья содержит методику, результаты опытов по сварке нагретым инструментом труб из поливинилхлорида (ПВХ-100) с целью получения математической модели процесса, отражающей зависимость прочности сварного стыка от переменных факторов режима сварки, а также построенную на базе модели номограмму и порядок пользования ею.
Котенко Э.В., Цедюра Н.А., Сидоренко Ю.А. О прочности переходных тройников пластмассовых трубопроводов. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 70.
Приведены характерные конструкции сварных переходных (неравнопроходных) тройников, изготавливаемых из пластмассовых труб. Описаны результаты сравнительной оценки различных тройников по показателям кратковременной и длительной прочности. Установлены наиболее уязвимые места конструкций переходных тройников. Показана перспективность применения конструкции тройника с горловиной в магистральном участке.
Позднышев В.С. Жлуктова Д.И., Филатова О.И., Шумова Е.Б. Влияние режимов отверждения на прочность клеевых соединений бандажного типа. - Сб. научных трудов. Технологий монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 77.
Приведены результаты экспериментальных исследований влияния режимов отверждения эпоксидных композиций на прочностные свойства клеевых соединений бандажного типа, рекомендованных для широкого применений при монтаже стальных трубопроводов различного назначения.
Позднышев B.C., Жлуктова Л.И., Филатовa O.И., Воздействие рабочих параметров трубопровода на стойкость клеевых соединений. - Сб. научных трудов. Технология монтажа резервуаров и трубопроводов. М., ВНИИмонтажспецстрой, 1985, с. 77.
Приведены результаты экспериментальных исследований работоспособности клеевых соединений в условиях совместного воздействия внутреннего давления, температуры и растягивающих усилий, моделирующих реальные условиях монтажа и сдачи трубопроводов в эксплуатацию.