А.М. ОСТРОВИДОВ, И.А. КУЗНЕЦОВ
ТАБЛИЦЫ
ДЛЯ ПРОЕКТИРОВАНИЯ МОСТОВ
НАУЧНО-ТЕХНИЧЕСКОЕ
ИЗДАТЕЛЬСТВО
АВТОТРАНСПОРТНОЙ ЛИТЕРАТУРЫ
МОСКВА 1959
Содержание
В справочнике приводятся основные данные для проектирования мостов и труб: таблицы по расчету отверстий, основные сведения о главнейших строительных материалах, таблицы для статического расчета конструкций, а также нормативные материалы по габаритам, расчетным нагрузкам, допускаемым напряжениям и пр.
Справочник рассчитан на инженеров, студентов вузов и техников, проектирующих мосты.
ПРЕДИСЛОВИЕ
Большой объем строительства мостов в Советском Союзе сопровождается широким развитием научно-исследовательских, изыскательских и проектных работ.
Основная масса мостов выполняется из железобетона. Среди них большое внимание уделяется новым прогрессивным конструкциям: тонкостенным, из легких бетонов, с каркасной и предварительно напряженной арматурой и др. Массовое применение получают сборные железобетонные конструкции и детали.
Из новых рациональных систем мостов больших пролетов получили широкое распространение металлические пролетные строения, объединенные для совместной работы с железобетонной плитой проезжей части. Создаются новые типы металлических мостов, основанные на идее предварительного напряжения конструкций, которые в ближайшие годы должны найти применение в большом масштабе.
Кроме железобетона и металла, в мостостроении используется дерево в области малых и средних мостов. Развитие строительства деревянных мостов идет по пути повышения его технического уровня и придания ему индустриального характера. Особого внимания заслуживают клеефанерные конструкции и клеестальные соединения, обладающие большой долговечностью и позволяющие создать эффективные сборные деревянные пролетные строения. Что касается каменных материалов, то применение их на строительстве мостов вытесняется бетоном и железобетоном.
Внедрение новых эффективных конструкций и рациональных схем в мостостроении требует от инженеров и техников конструкторов более полного использования этих новейших достижений передовой науки и техники. Обширный круг вопросов, с которыми приходится сталкиваться конструкторам в своей работе, требует самых разнообразных сведений из различных областей техники.
Цель издания справочных таблиц для проектирования мостов - дать основные сведения по расчету и конструированию, Которые охватывают вопросы повседневной практики проектирования мостов на автомобильных дорогах. Пользование такими справочными данными будет способствовать повышению производительности и облегчению труда проектировщиков.
Справочные таблицы отражают действующие ГОСТы, технические условия и нормы проектирования.
В таблицах, состоящих из четырех разделов, приведены сведения, относящиеся к гидрологии мостового перехода, расчету отверстий искусственных сооружений, основным строительным материалам, механическим характеристикам различных сечений, данным для статических расчетов, нормам допускаемых напряжений и прогибов, нагрузкам и габаритам. Раздел первый «Расчет отверстий мостов и регуляционных сооружений» составлен И.А. Кузнецовым, остальные разделы Л.М. Островидовым.
Справочные таблицы рассчитаны на инженеров и техников, занимающихся проектированием искусственных сооружении.
Авторы выражают глубокую благодарность кандидатам технических наук В.С. Кириллову и О.В. Андрееву, а также К.М. Ротштейну, М.Г. Ивянскому и другим инженерам Союздорпроекта за ряд ценных указаний, данных ими при подготовке книги к изданию.
РАЗДЕЛ ПЕРВЫЙ
РАСЧЕТ ОТВЕРСТИЙ МОСТОВ И РЕГУЛЯЦИОННЫХ СООРУЖЕНИЙ
Глава 1
РАСЧЕТ СТОКА ПОВЕРХНОСТНЫХ ВОД
§ 1. Общие указания
Министерством автомобильного транспорта и шоссейных дорог, Министерством путей сообщения и Министерством транспортного строительства в 1954 г. утверждены новые нормы расчета стока с малых бассейнов1, разработанные Союздорнии, ЦНИИС и Главтранспроектом.
1 Союздорнии. Нормы стока и инструкции по расчету стока и отверстий малых мостов и труб. Автотрансиздат, 1955.
Кроме новых норм, в практике проектирования часто применяются и другие методы. Ниже приводятся необходимые данные для расчета стока как по нормам 1954 г., так и по способам Соколовского и Протодьяконова - Лапина, получившим наибольшее распространение.
Основные положения норм 1954 г., принятые на автодорожном транспорте, сводятся к следующему.
Нормы стока воды надлежит применять для определения расчетных расходов и отверстий водопропускных искусственных сооружений на автомобильных дорогах при водосборной площади до 100 км2. В районах Черноморского побережья Кавказа, Карпат, Приморья, Дальнего Востока, Сахалина, Камчатки площадь эта может быть увеличена до 300 км2, но при параллельных натурных наблюдениях.
Нормы стока удовлетворяют следующим основным, положениям:
а) обеспечивают возможность определения расчетных расходов в любых климатических условиях при любой вероятности превышения паводков, устанавливаемой ТУ, а также предельно возможного максимального расхода для каждого бассейна - ММ (максимум-максиморум);
б) дают способ определения полного объема стока за время дождя и построения гидрографа для учета аккумуляции воды перед искусственными сооружениями;
в) удовлетворяют проверке объемов стока воды по общему балансу: в любой момент стока объем выпавших осадков (за вычетом потерь) должен равняться сумме объемов воды, имеющейся на склонах, в руслах, и воды, прошедшей через замыкающий створ бассейна;
г) слой стока (водоотдачи) определяется графическим путем как разность нарастающего слоя осадков и нарастающего слоя потерь в момент окончания дождя, при этом интенсивность водоотдачи может приниматься постоянной за период водоотдачи;
д) дают возможность вычислять расходы от дождей для проверки норм по фактически наблюдаемым осадкам и стоку.
Размеры отверстий мостов и труб определяются по расчетным расходам, вероятность превышения которых назначается по действующим ТУ на проектирование мостов и труб на автомобильных дорогах.
В нормах даны основные формулы и указания по двум видам стока: ливневому и смешанному.
Определение расхода производится для этих двух видов стока, и из полученных величин расходов для расчета отверстия следует принимать наибольшую.
В районе, для которого необходимо произвести расчеты стока ледникового, грунтового, маревого, селевого или какого-либо другого вида, отличного от ливневого и смешанного, надлежит разрабатывать специально обоснованные предложения о порядке расчета вида стока после производства соответствующих гидрологических изысканий.
Для бассейнов со значительным постоянным стоком грунтовых вод полный расход слагается из расхода, вычисленного по настоящим нормам, и грунтового стока, определенного по натурным данным. Грунтовым стоком менее 5% можно пренебречь.
Нормы применимы как при достаточном однообразии почвенных и топографических условий в пределах рассматриваемых бассейнов, так и при резком различии указанных условий. В последнем случае необходимо производить расчет для каждой части бассейна отдельно.
При составлении проектных заданий и технических проектов расчет всех малых сооружений на ливневый сток производится по упрощенной формуле Болдакова.
При рабочем проектировании рассчитываются вторично по точному методу Союздорнии:
а) все мосты отверстием более 10 м и прямоугольные трубы отверстием 2 м и более;
б) круглые трубы одноочковые и многоочковые, пропускающие расчетный расход после учета аккумуляции воды перед сооружением 10 м3/сек и более.
Определение расчетного расхода и объема смешанного стока может производиться путем суммирования расходов и объемов снегового и ливневого стока. Снеговой сток может определяться по методу Союздорнии (метод предельных интенсивностей).
Большинство максимальных расходов воды (объем воды, проходящей через определенный створ в единицу времени) на всех реках имеет дождевое происхождение.
Снеговые и смешанные расходы бывают больше дождевых в средней и северной частях Советского Союза и в Сибири.
Горно-ледниковые паводки в сочетании с дождями бывают во всех высокогорных районах, кроме Крайнего Севера.
Расчет на снеговой и смешанный сток является обязательным во всех районах, где имеется заметный снеговой покров.
§ 2. Ливневый (дождевой) сток
Ливневые районы
К ливневым районам относятся по инструкции:
Район № 1 - Белоруссия. Центральный район. Северная граница по водоразделу между р. Западной Двиной и р. Волгой. Череповец. Тотьма. Урал. Поволжье до Сталинграда. Воронеж. Орел. Брянск.
Район № 2 - Украина до Карпат и водораздела между р. Бугом и р. Днестром. Северная часть Крыма. Район с севера граничит с районом № 1.
Район № 3 - Карпаты, а также район к западу от водораздела между р. Бугом и р. Днестром.
Район № 4 - Черноморское побережье Кавказа. Южная часть Крыма.
Район № 5 - Прибалтика до устья р. Одера. Район Ленинграда с юга граничит с районом № 1.
Район № 6 - Северный Кавказ и район Главного Кавказского хребта - принимать по району № 2. Малый Кавказ, степи Кура-Араксинской низменности, Астраханские, Манычские, Сальские степи, Каспийское побережье от порта Ильича до Махачкалы - по району № 1. Каспийское побережье от Ленкорани до Астары и южнее - по району № 4.
Район № 7 - Пустыни Средней Азии и Монголии. Район предгорий для бассейнов с высотой водоразделов в 2 - 3 раза меньше главных хребтов (при этом для пустынь величина t - время водоотдачи - ограничивается 30 мин.). Принимать данные по району № 1. Район главных хребтов Средней Азии принимать при отметке водораздела до 3000 м по району № 2.
Район № 8 - Алтайский край. Целинные земли. Саяны. Забайкалье до Яблонового хребта.
Район № 9 - Центральная Сибирь и Южная Сибирь (принимать по району № 1).
Район № 10 - Приморье Дальнего Востока до бухты Де-Кастри. Бассейн Уссури до водораздела между р. Бикан и р. Хор и далее по хребту Сихотэ-Алинь. Горная часть Буреинского хребта. Юго-восточная часть Камчатки. Центральный и Южный Сахалин.
Для Приамурья до хребтов Яблонового, Кодар и Станового величина расхода и объем стока уменьшаются при грунтах I - III категорий на 10% и IV - VI - на 15 - 20%.
Упомянутые районы можно распространить:
район № 1 - на Польшу, кроме Прибалтийской части;
район № 2 - на Румынию, Болгарию, Албанию, Югославию, Чехословакию; в западной части Венгрии и далее, в районе Граца, максимальный расход может быть больше, чем по району № 3, в 1,5 - 3 раза;
район № 8 - на Монголию, при времени водоотдачи не более 30 мин.;
район № 10 - на Корею, Маньчжурию и часть Китайской Народной Республики в бассейне Желтого моря.
Определение расчетного расхода ливневого стока по нормам Союздорнии
Расчетный расход определяется по формуле:
Q = ωυ = ωmH2/3i1/2 м3/сек,
где ω - площадь живого сечения, м2;
υ - средняя скорость, м/сек (см. также табл. 16);
H - средняя глубина потока, м;
m - характеристика гидравлической шероховатости;
i - средний уклон главного лога.
Гидравлическая шероховатость m устанавливается в зависимости от характера лога и принимается равной:
ровное земляное ложе . . . . . . . . . . . . . 25
извилистое или заросшее ложе . . . . . 20
сильно заросшее ложе . . . . . . . . . . . . . 15
русло в завалах, валуны . . . . . . . . . . . 10
По упрощенной формуле Болдакова расчетный расход ливневого стока:
Q = ψ(h - z)3/2F2/3 м3/сек,
где h - слой стока в мм в зависимости от категории почв но впитыванию (табл. 1) при времени стока t = 30 мин. (табл. 2);
z - слой задержанного растительностью стока в мм, принимаемый для густой травы, редкого кустарника равным 5; среднего леса, кустарника 10; густого леса 15; тайги, завалов, мохового болота 20 - 40;
ψ - коэффициент, равный для бассейнов плоских 0,04, равнинных 0,06, холмистых 0,08, гористых 0,11, горных 0,14;
F - площадь бассейна, км2.
Объем стока в обоих случаях:
W = (h - z)F тыс. м3.
Категории почв по впитыванию (применительно к центральной территории Союза)
|
Наименование почв |
Категория почв |
|
Скала нетрещиноватая. Асфальт. Бетон |
I |
|
Глины. Солонцы суглинистые. Такыры |
II |
|
Суглинки. Неструктурные черноземы. Подзолистые почвы и серые лесные почвы |
III |
|
Чернозем структурный. Солонцы супесчаные. Задернованная супесь |
IV |
|
Супесь открытая |
V |
|
Развеваемые пески |
VI |
Слой стока h, мм (при z = 0 и t = 30 мин.)
|
Категория почв по впитыванию |
Вероятность превышения |
|||||||
|
1 2 |
1 5 |
1 10 |
1 25 |
1 50 |
1 100 |
1 500 |
ММ |
|
|
Слой стока h, мм |
||||||||
|
Район № 1 |
||||||||
|
I |
11 |
16 |
24 |
27 |
34 |
42 |
54 |
105 |
|
II |
6 |
11 |
18 |
22 |
29 |
35 |
46 |
100 |
|
III |
- |
- |
13 |
17 |
24 |
30 |
43 |
95 |
|
IV |
- |
- |
- |
13 |
20 |
27 |
39 |
91 |
|
V |
- |
- |
- |
- |
- |
13 |
23 |
75 |
|
VI |
- |
- |
- |
- |
- |
- |
9 |
60 |
|
Район № 2 |
||||||||
|
I |
17 |
22 |
26 |
32 |
40 |
51 |
77 |
164 |
|
II |
12 |
16 |
20 |
23 |
33 |
44 |
73 |
154 |
|
III |
7 |
11 |
10 |
19 |
28 |
39 |
66 |
150 |
|
IV |
- |
- |
7 |
18 |
27 |
37 |
63 |
130 |
|
V |
- |
- |
- |
- |
5 |
22 |
49 |
120 |
|
VI |
- |
- |
- |
- |
- |
- |
18 |
100 |
|
Район № 3 |
||||||||
|
I |
17 |
22 |
26 |
37 |
40 |
51 |
79 |
200 |
|
II |
12 |
16 |
20 |
23 |
33 |
44 |
73 |
195 |
|
III |
7 |
11 |
14 |
19 |
28 |
39 |
66 |
190 |
|
IV |
- |
- |
7 |
18 |
28 |
37 |
64 |
184 |
|
V |
- |
- |
- |
- |
5 |
22 |
49 |
171 |
|
VI |
- |
- |
- |
- |
- |
- |
22 |
155 |
|
Район № 4 |
||||||||
|
I |
15 |
23 |
38 |
46 |
55 |
60 |
76 |
140 |
|
II |
10 |
18 |
33 |
40 |
52 |
57 |
69 |
134 |
|
III |
5 |
13 |
28 |
36 |
45 |
52 |
64 |
129 |
|
IV |
- |
9 |
24 |
32 |
41 |
47 |
61 |
126 |
|
V |
- |
- |
- |
15 |
26 |
32 |
45 |
101 |
|
VI |
- |
- |
- |
- |
- |
15 |
28 |
95 |
|
Район № 5 |
||||||||
|
I |
16 |
21 |
25 |
29 |
32 |
38 |
44 |
80 |
|
II |
11 |
15 |
20 |
23 |
26 |
30 |
38 |
74 |
|
III |
7 |
11 |
15 |
19 |
22 |
27 |
34 |
70 |
|
IV |
- |
7 |
10 |
15 |
18 |
23 |
30 |
68 |
|
V |
- |
- |
- |
- |
- |
3 |
16 |
51 |
|
VI |
- |
- |
- |
- |
- |
- |
- |
35 |
|
Район № 8 |
||||||||
|
I |
8 |
15 |
t 20 |
27 |
35 |
40 |
55 |
100 |
|
II |
- |
10 |
15 |
22 |
30 |
37 |
49 |
93 |
|
III |
- |
5 |
13 |
20 |
29 |
33 |
46 |
92 |
|
IV |
- |
- |
- |
16 |
23 |
27 |
43 |
92 |
|
V |
- |
- |
- |
- |
- |
- |
26 |
76 |
|
VI |
- |
- |
- |
- |
- |
- |
- |
37 |
|
Район № 10 |
||||||||
|
I |
15 |
25 |
34 |
46 |
55 |
60 |
68 |
112 |
|
II |
12 |
20 |
31 |
38 |
45 |
54 |
64 |
110 |
|
III |
5 |
14 |
25 |
32 |
40 |
48 |
57 |
101 |
|
IV |
3 |
11 |
20 |
27 |
36 |
43 |
54 |
100 |
|
V |
- |
- |
7 |
15 |
21 |
28 |
37 |
87 |
|
VI |
- |
- |
- |
- |
8 |
12 |
22 |
66 |
Для других районов Советского Союза в категории почв по впитыванию нужно вносить следующие поправки:
лесные районы и лесостепь - без изменении,
степи - ниже на одну категорию,
пустыни - ниже на две категории,
муссонный климат - выше на одну категорию.
Категория почв бассейна определяется путем обследования выработок глубиной до 0,5 м. На 1 км2 бассейна нужно иметь не менее одной выработки при предварительных изысканиях и не менее двух при предпостроечных изысканиях.
При расстоянии центра тяжести площади бассейна до сооружения более 1 км расход и объем стока уменьшают за счет распластывания паводка путем умножения на коэффициент β (табл. 3).
Значение коэффициента β
|
Тип бассейна |
Длина блесен на, км |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
|
Коэффициент β |
||||||||
|
Плоский и холмистый |
1 |
0,95 |
0,90 |
0,85 |
0,80 |
0,75 |
0,70 |
0,60 |
|
Гористый и горный |
1 |
1 |
1 |
0,95 |
0,90 |
0,85 |
0,80 |
0,70 |
При бассейнах длиной или шириной более 5 км расход и объем стока уменьшают за счет неравномерности выпадения осадков путем умножения на коэффициент γ (табл. 4).
Значения коэффициента γ
|
Длина или ширина бассейна, км |
Коэффициент γ для районов |
|||
|
Украина, Кавказ, Средняя Азия |
центральные районы европейской части Союза, Сибирь |
северо-западные районы европейской части Союза |
зона муссонного климата |
|
|
5 |
0,9 |
0,9 |
1 |
|
|
10 |
0,8 |
0,9 |
1 |
1 |
|
25 |
0,7 |
0,9 |
0,9 |
0,9 |
|
35 |
0,6 |
0,8 |
0,8 |
0,8 |
Примечание. В зону муссонного климата входят Дальний Восток, Черноморское побережье Кавказа, Карпаты и Каспийское побережье Талышской низменности на участке Ленкорань-Астара и южнее.
Окончательно формулы Болдакова можно представить в следующем виде:
Q = βγψ(h - z)3/2F2/3;
W = βγ(h - z)F.
Следует иметь в виду, что вводить в эти формулы дополнительные поправки на заболоченность и озера не требуется, так как влияние заболоченности учитывается увеличенным для этого случая значением z, а от наличия озер пи расход, ни объем ливневого стока не изменяются.
При учете аккумуляции воды (что обычно делают, если можно ожидать снижения расхода на 20% и более) расчетный расход

где QA - уменьшенный расход в сооружении;
W - объем пруда перед сооружением;
α - см. табл. 6.
Остальные обозначения прежние.
Объем пруда подсчитывают по плану в горизонталях или по формуле:
![]()
где H- глубина пруда (до лотка сооружения), м;
b - ширина зеркала пруда в м (вдоль трассы) при глубине H;
i - средний уклон в тысячных выше сооружения в пределах пруда.
Для ориентировочных соображении объем пруда можно принимать по табл. 5.
Ориентировочный объем пруда W1
|
Глубина пруда H, м |
Характеристика бассейна у сооружения |
||||
|
плоский |
равнинный |
холмистый |
гористый |
горный |
|
|
Объем пруда W1, тыс. м3 |
|||||
|
1,0 |
15 |
5 |
2 |
- |
- |
|
1,5 |
45 |
15 |
5 |
2 |
- |
|
2,0 |
150 |
50 |
15 |
4 |
- |
|
2,5 |
500 |
140 |
40 |
10 |
- |
|
3,0 |
850 |
280 |
80 |
20 |
2 |
|
3,5 |
1400 |
400 |
150 |
30 |
3 |
|
4,0 |
2100 |
700 |
220 |
45 |
5 |
|
4,5 |
3000 |
1000 |
300 |
65 |
8 |
|
5,0 |
4000 |
1300 |
400 |
85 |
10 |
|
5,5 |
- |
1700 |
500 |
120 |
15 |
|
6,0 |
- |
2200 |
700 |
160 |
20 |
|
6,5 |
- |
3000 |
1000 |
220 |
25 |
|
7,0 |
- |
4000 |
1200 |
300 |
40 |
Значения коэффициента α в зависимости от отношения ![]()
|
|
α |
|
0 |
1,0 |
|
0,5 |
0,90 |
|
0,10 |
0,83 |
|
0,15 |
0,76 |
|
0,20 |
0,70 |
|
0,25 |
0,65 |
|
0,30 |
0,59 |
|
0,35 |
0,55 |
|
0,40 |
0,50 |
|
0,50 |
0,40 |
|
0,55 |
0,36 |
|
0,60 |
0,32 |
|
0,65 |
0,27 |
|
0,70 |
0,23 |
|
0,75 |
0,19 |
|
0,80 |
0,15 |
|
0,85 |
0,12 |
|
0,90 |
0,07 |
|
0,95 |
0,04 |
|
1,00 |
0 |
Пример. Автодорога III категории. Ливневый район № 10 (Южный Сахалин). Вероятность превышения расчетного паводка 1:n = 1:50. Почвы суглинистые (II категория по впитываемости). Район бассейна горный, переходящий у сооружения в гористый (ψ = 0,14). Площадь бассейна 3,5 км2. Залесенность небольшая (z = 10). Уклон лога у сооружения i = 15°/○○.
Слой стока (по табл. 2, район № 10, категория почвы II, 1:n = 1:50) h = 46 мм;
Q = 0,14(46 - 10)3/2 3,52/3 = 69 м3/сек;
W = (46 - 10)3,5 = 126 тыс. м3.
Глубина подпертой воды у сооружения Н = 3,3 м.
По табл. 5 (бассейн гористый, Н = 3,3 м):
W1 = 28 тыс. м3
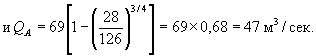
или по табл. 6
![]()
QA = 0,68×69 = 47 м3\сек.
Определение расчетного расхода ливневого стока по упрощенной формуле Соколовского
Максимальный расход дождевого паводка:
Q = BF1/2 м3\сек,
где F - площадь бассейна, км2;
B - районный коэффициент, принимаемый по табл. 7.
Значения коэффициента B
|
Зона |
F, км2 |
Обеспеченность, % |
|||
|
средняя |
10 |
2 - 3 |
1 |
||
|
Коэффициент B |
|||||
|
Лесная и лесостепная зона европейской части СССР |
- |
2 - 3 |
4 - 6 |
7 - 10 |
8 - 12 |
|
Степная зона (исключая ливнеопасную зону) |
Реки с F < 500 - 1000 км2 |
2 - 3 |
4 - 6 |
7 - 10 |
8 - 12 |
|
То же |
Прочие реки |
0,5 - 1 |
1 - 2 |
2 - 3 |
3 - 4 |
|
Предгорные районы (Урал) |
- |
3 - 5 |
6 - 8 |
10 - 14 |
12 - 18 |
|
Ливнеопасные районы: |
|
|
|
|
|
|
Дальневосточный край и Черноморское побережье Кавказа, горные реки Карпат |
- |
8 - 12 |
15 - 20 |
25 - 30 |
40 - 50 |
|
Западный Донбасс и Крым |
Реки с F < 500 - 1000 км2 |
5 - 8 |
10 - 20 |
15 - 25 |
30 - 40 |
|
То же |
Прочие реки |
0,5 - 1 |
1 - 2 |
2 - 3 |
3 - 4 |
Определение расчетного расхода ливневого стока по формуле Протодьяконова-Лапина
Расход дождевого стока по формуле Протодьяконова-Лапина, в интерпретации Е.В. Болдакова:
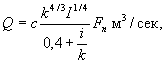
где c - коэффициент, зависящий от вероятности паводка (см. табл. 9);
k - климатический коэффициент, принимаемый для Севера 0,8, для Центрального района и Средней Сибири 1,0, для южной части Центрального района и Южной Сибири 1,2;
I - уклон дна лога, определяемый как отношение разности отметок водораздела у истоков водотока и дна лога у искусственного сооружения к длине лога;
F - площадь бассейна, км2;
n - показатель степени, принимаемый при F ≤ 10 км2 равным 3/4; при F > 10 км2 (но не более 100 км2) равным 2/3.
Вероятность паводка (расхода) по формуле Протодьяконова-Лапина-Болдакова
получается равной примерно ![]() .
.
Для перехода к другим вероятностям превышения можно пользоваться коэффициентами, приведенными в табл. 8.
Коэффициенты перехода от вероятности паводка ![]() к другим вероятностям
по Е.В. Болдакову
к другим вероятностям
по Е.В. Болдакову
|
Вероятность паводка |
Площадь бассейна F, км2 |
||
|
до 2 |
до 10 |
до 100 |
|
|
Значения коэффициентов перехода |
|||
|
1 10 |
0,36 |
0,44 |
0,54 |
|
1 25 |
0,56 |
0,62 |
0,68 |
|
1 50 |
0,72 |
0,75 |
0,81 |
|
1 100 |
0,88 |
0,89 |
0,92 |
|
1 200 |
1,0 |
1,0 |
1,0 |
|
1 300 |
1,1 |
1,1 |
1,1 |
|
1 1000 |
1,3 |
1,3 |
1,3 |
Значения коэффициента c
|
Вероятность паводка |
с |
Рассчитываются |
|
|
1 1000 |
7,8 |
Гребень плотины |
|
|
1 500 |
6,8 |
|
Бровка железнодорожной насыпи |
|
1 300
|
6,1
|
||
|
1 200 |
5,5
|
||
|
1 100 |
4,5 |
|
Отверстия мостов и бровка автодорожной насыпи |
|
1 50 |
3,6
|
||
|
1 25 |
2,9
|
||
|
1 10 |
1,8 |
|
Временные сооружения, нагорные канавы |
|
1 5 |
1,3
|
||
§ 3. Снеговой и смешанный сток
Районы снегового и смешанного стока
К районам снегового и смешанного стока по инструкции Союздорнии относятся:
Район № 1 - Северная граница: Рига, Великие Луки, Москва, Горький, Казань, Свердловск, Тюмень, Новосибирск. Южная часть Байкала. Район Яблонового и Станового хребтов и побережье Охотского моря. Камчатка. Южная граница европейской части Союза до зоны заметного снегового покрова, включая Полтаву, Сталинград. Далее, к востоку, южная часть Урала. Саяны. Алтай. Хамар-Дабан. Маньчжурия. Север Кореи.
Кроме того, по нормам района № 1 могут временно рассчитываться горные районы Карпат, Кавказа, Средней Азии.
Район № 2 - Северная граница до Северного Ледовитого океана. Южная граница до границы района № 1.
Район № 3 - Сальские и Астраханские степи. Южная Сибирь.
Определение расчетного расхода по нормам Союздорнии
Максимальный расход смешанного стока (за время интенсивного таяния в течение 10 час):
![]()
где W - объем смешанного стока, тыс. ж3;
τ - время наступления пика паводка после 14 час. (зависящее от времени формирования максимумов как склонового, так и руслового стекания), час.
Объем смешанного стока:
Wсм = Wсн + W тыс. м3
где Wсн - объем снегового стока, равный Wсн = WнF тыс. м3, причем Wн принимается по табл. 10;
W - объем ливневого весеннего стока, равный Wсн = hF тыс. м3, причем h (слой стока) принимается по табл. 11;
F - площадь бассейна, км2.
Время наступления пика паводка после 14 час.:
τ = 0,025τ1L0 час.,
где τ1 - время стекания потока по логу в мин. на каждый пикет (100 м) длины лога в зависимости от расхода Q и гидравлической шероховатости m принимается по табл. 12;
L0 - расстояние центра тяжести бассейна до сооружения, в пикетах.
Данные табл. 10 относятся к бассейнам длиной или шириной до 10 км.
Объем стока Wн, тыс. м3 с 1 км2
|
вероятность паводка |
Номер района снегового и смешанного стока |
||
|
1 |
2 |
3 |
|
|
Объем стока Wн |
|||
|
1:2 |
25 |
20 |
6 |
|
1:5 |
31 |
25 |
17 |
|
1:10 |
37 |
30 |
25 |
|
1:25 |
44 |
36 |
30 |
|
1:50 |
51 |
41 |
37 |
|
1:100 |
55 |
44 |
42 |
|
1:500 |
67 |
54 |
55 |
Слой стока h, мм
|
Район |
Род поверхности (почвы) |
h, мм |
|
1 |
Непроницаемая (асфальт, бетон) |
28 |
|
1 |
Все прочие |
9 |
|
2 |
Непроницаемая |
35 |
|
2 |
Все прочие |
14 |
|
3 |
Непроницаемая |
38 |
|
3 |
Все прочие |
14 |
Время стекания потока по логу τ1, в мин. на каждый пикет (100 м) длины лога
|
Q, м3/сек |
m |
Средним уклон в тысячных |
|||||||||||
|
1 |
2 |
3 |
5 |
7 |
10 |
15 |
20 |
30 |
40 |
60 |
100 |
||
|
Время стекания потока τ1 |
|||||||||||||
|
3 |
25 |
4,6 |
3,5 |
2,9 |
2,5 |
2,2 |
1,9 |
1,7 |
1,5 |
1,3 |
1,1 |
0,97 |
0,85 |
|
20 |
5,5 |
4,1 |
3,6 |
2,9 |
2,6 |
2,3 |
1,9 |
1,8 |
1,5 |
1,3 |
1,20 |
0,95 |
|
|
15 |
6,0 |
5,1 |
4,4 |
3,6 |
3,2 |
2,8 |
2,4 |
2,2 |
1,8 |
1,7 |
1,50 |
1,20 |
|
|
10 |
- |
6,9 |
6,0 |
4,9 |
4,3 |
3,8 |
3,3 |
3,0 |
2,5 |
2,3 |
2,0 |
1,6 |
|
|
5 |
25 |
4,1 |
3,1 |
2,6 |
2,2 |
1,9 |
1,7 |
1,5 |
1,3 |
1,1 |
1,0 |
0,85 |
0,75 |
|
20 |
4,8 |
3,6 |
3,2 |
2,6 |
2,3 |
2,0 |
1,7 |
1,6 |
1,3 |
1,2 |
1,0 |
0,80 |
|
|
15 |
5,9 |
4,5 |
3,9 |
3,2 |
2,8 |
2,5 |
2,2 |
1,9 |
1,6 |
1,5 |
1,3 |
1,0 |
|
|
10 |
- |
6,1 |
5,2 |
4,3 |
3,8 |
3,4 |
2,9 |
2,6 |
2,2 |
2,0 |
1,7 |
1,4 |
|
|
7 |
25 |
3,7 |
2,8 |
2,4 |
2,0 |
1,8 |
1,5 |
1,4 |
1,2 |
1,0 |
0,9 |
0,78 |
0,7 |
|
20 |
4,4 |
3,3 |
2,9 |
2,4 |
2,1 |
1,8 |
1,0 |
1,4 |
1,2 |
1,1 |
0,93 |
0,78 |
|
|
15 |
5,4 |
4,1 |
3,6 |
2,9 |
2,6 |
2,3 |
2,0 |
1,8 |
1,5 |
1,4 |
1,2 |
0,94 |
|
|
10 |
- |
5,6 |
4,8 |
3,9 |
3,5 |
3,1 |
2,7 |
2,4 |
2,0 |
1,8 |
1,6 |
1,2 |
|
|
10 |
25 |
3,4 |
2,6 |
2,2 |
1,8 |
1,6 |
1,4 |
1,3 |
1,1 |
0,93 |
0,84 |
0,7 |
0,63 |
|
20 |
4,0 |
3,0 |
2,6 |
2,2 |
1,9 |
1,5 |
1,4 |
1,3 |
1,1 |
0,97 |
0,85 |
0,71 |
|
|
15 |
5,0 |
3,7 |
3,3 |
2,7 |
2,4 |
2,1 |
1,8 |
1,6 |
1,4 |
1,2 |
1,1 |
0,86 |
|
|
10 |
- |
5,1 |
4,4 |
3,7 |
3,2 |
2,9 |
2,4 |
2,2 |
1,8 |
1,7 |
1,4 |
1,2 |
|
|
15 |
25 |
3,0 |
2,3 |
2,0 |
1,5 |
1,5 |
1,3 |
1,2 |
1,0 |
0,85 |
0,75 |
0,65 |
0,55 |
|
20 |
3,6 |
2,8 |
2,4 |
1,9 |
1,7 |
1,5 |
1,3 |
1,2 |
1,1 |
0,9 |
0,77 |
0,64 |
|
|
15 |
4,5 |
3,4 |
2,9 |
2,4 |
2,2 |
1,9 |
1,6 |
1,5 |
1,3 |
1,1 |
0,95 |
0,77 |
|
|
10 |
- |
4,6 |
3,9 |
3,3 |
2,9 |
2,6 |
2,2 |
2,0 |
1,7 |
1,5 |
1,3 |
1,1 |
|
|
20 |
25 |
2,8 |
2,1 |
1,9 |
1,5 |
1,4 |
1,2 |
1,1 |
0,93 |
0,79 |
0,70 |
0,60 |
0,5 |
|
20 |
3,4 |
2,6 |
2,2 |
1,8 |
1,6 |
1,4 |
1,2 |
1,1 |
0,94 |
0,84 |
0,72 |
0,58 |
|
|
15 |
4,2 |
3,2 |
2,7 |
2,2 |
2,0 |
1,7 |
1,5 |
1,4 |
1,2 |
1,0 |
0,88 |
0,74 |
|
|
10 |
5,6 |
4,3 |
3,6 |
3,1 |
2,7 |
2,4 |
2,0 |
1,8 |
1,6 |
1,4 |
1,2 |
1,0 |
|
|
50 |
25 |
2,2 |
1,7 |
1,5 |
1,2 |
1,1 |
0,94 |
0,85 |
0,75 |
0,60 |
0,55 |
0,46 |
0,40 |
|
20 |
2,7 |
2,1 |
1,8 |
1,4 |
1,3 |
1,1 |
0,95 |
0,86 |
0,75 |
0,65 |
0,56 |
0,45 |
|
|
15 |
3,3 |
2,5 |
2,2 |
1,8 |
1,6 |
1,4 |
1,2 |
1,1 |
0,9 |
0,82 |
0,66 |
0,57 |
|
|
10 |
4,4 |
3,4 |
2,8 |
2,5 |
2,2 |
1,9 |
1,6 |
1,4 |
1,3 |
1,1 |
0,96 |
0,82 |
|
|
100 |
25 |
1,9 |
1,4 |
1,2 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,45 |
0,4 |
0,34 |
|
20 |
2,3 |
1,8 |
1,5 |
1,2 |
1,1 |
0,94 |
0,82 |
0,72 |
0,62 |
0,55 |
0,46 |
0,3 |
|
|
15 |
2,7 |
2,1 |
1,9 |
1,5 |
1,4 |
1,2 |
1,0 |
0,9 |
0,8 |
0,7 |
0,57 |
0,5 |
|
|
10 |
3,7 |
2,8 |
2,4 |
2,1 |
1,8 |
1,6 |
1,4 |
1,2 |
1,1 |
0,95 |
0,82 |
0,67 |
|
|
200 |
25 |
1,5 |
1,2 |
1,0 |
0,86 |
0,77 |
0,67 |
0,53 |
0,52 |
0,44 |
0,4 |
0,35 |
0,29 |
|
20 |
1,9 |
1,4 |
1,3 |
1,0 |
0,91 |
0,79 |
0,68 |
0,61 |
0,52 |
0,47 |
0,4 |
0,31 |
|
|
15 |
2,3 |
1,8 |
1,6 |
1,3 |
1,1 |
0,97 |
0,84 |
0,76 |
0,64 |
0,58 |
0,5 |
0,41 |
|
|
10 |
3,2 |
2,4 |
2,1 |
1,7 |
1,5 |
1,3 |
1,2 |
1,0 |
0,9 |
0,79 |
0,68 |
0,55 |
|
|
500 |
25 |
1,1 |
0,96 |
0,85 |
0,69 |
0,62 |
0,54 |
0,46 |
0,41 |
0,36 |
0,31 |
0,23 |
0,23 |
|
20 |
1,2 |
1,1 |
1,0 |
0,81 |
0,73 |
0,65 |
0,56 |
0,49 |
0,43 |
0,38 |
0,33 |
0,26 |
|
|
15 |
1,7 |
1,4 |
1,3 |
1,0 |
0,88 |
0,78 |
0,69 |
0,6 |
0,53 |
0,46 |
0,4 |
0,33 |
|
|
10 |
2,3 |
2,0 |
1,4 |
1,4 |
1,2 |
1,1 |
0,22 |
0,82 |
0,7 |
0,62 |
0,54 |
0,45 |
|
|
1000 |
25 |
0,96 |
0,81 |
0,72 |
0,59 |
0,52 |
0,45 |
0,4 |
0,35 |
0,31 |
0,23 |
0,23 |
0,19 |
|
20 |
1,1 |
0,98 |
0,85 |
0,68 |
0,61 |
0,53 |
0,4,5 |
0,41 |
0,36 |
0,32 |
0,27 |
0,22 |
|
|
15 |
1,4 |
1,2 |
1,0 |
0,86 |
0,76 |
0,65 |
0,59 |
0,51 |
0,44 |
0,38 |
0,33 |
0,28 |
|
|
10 |
1,9 |
1,6 |
1,4 |
1,1 |
0,97 |
0,98 |
0,77 |
0,69 |
0,59 |
0,53 |
0,45 |
0,38 |
|
При больших бассейнах объем стока Wн надо умножать на коэффициенты:
|
при длине или ширине бассейна |
||
|
10 |
км |
1,0 |
|
12 |
" |
0,95 |
|
14 |
" |
0,90 |
|
16 |
" |
0,85 |
|
20 |
" |
0,80 |
На рис. 1 приведен гидрограф (ход изменения расхода воды во времени) снеготаяния на склонах и гидрограф стока у сооружения. По гидрографу можно учесть аккумуляцию воды перед сооружением при расчете отверстия, но с тем, чтобы опорожнение пруда происходило не позднее утра следующего дня, когда под влиянием солнечных лучей может начаться интенсивное снеготаяние.
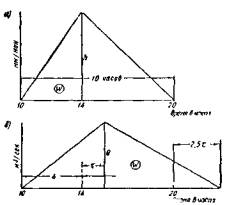
Рис. 1. Гидрографы:
а - накопление воды в бассейне при снеготаянии на склонах; б - расхода воды у
сооружения
Пример. F
= 33 км2; I
= 6%; L = 5 км =
50 пикетов; вероятность превышения ![]() район № 2; почва
проницаемая; m =
20.
район № 2; почва
проницаемая; m =
20.
Задаемся расходом Q = 50 м3/сек.
По табл. 12 (при Q = 50; m = 20; i = 6) τ1 = 1,35 мин. на пикет. Следовательно, τ = 0,025×1,35×50 = 1,7 часа.
По табл. 11 (для района № 2) h = 14 мм. Следовательно, W = 14×33 = 462 тыс. м3.
По табл. 10
(при вероятности превышения ![]() и районе № 2 Wн = 41 тыс. м3
с 1 км2. Следовательно, Wн = 41×33 = 1350 тыс. м3.
и районе № 2 Wн = 41 тыс. м3
с 1 км2. Следовательно, Wн = 41×33 = 1350 тыс. м3.
Отсюда
Wсм = 1350 + 462 = 1812 тыс. м3
и
![]()
(разница более 5 %).
Поэтому повторяем расчет при Q = 70 м3\сек. По табл. 12 τ1 = 1,27 мин., τ = 0,025×1,27×50 = 1,6 часа; остальные величины не меняются.
Расход ![]() т.е. не отличается от
принятого (70 м3\сек) более чем на 5 %. Этот расход и принимаем за
расчетный.
т.е. не отличается от
принятого (70 м3\сек) более чем на 5 %. Этот расход и принимаем за
расчетный.
Определение расчетного расхода по формуле Соколовского
Формула Соколовского применима как для малых, так и для больших бассейнов, хотя впервые была выведена для последних. Формула основана на том, что .если для интересующего пас водотока имеется река-аналог с достаточно большим рядом горизонтов, то можно расчетные расходы с этого бассейна перенести па новый переход, определив сначала коэффициент A на реке-аналоге.
Расход воды по Соколовскому:
Q = δδ'AF(1 - n) м3/сек,
где F - площадь бассейна, км2;
A - коэффициент, характеризующий сток весеннего половодья (определенный на основании непосредственных водомерных наблюдений в данном пункте - табл. 13);
n - показатель степени, принимаемый:
для F ≤ (20 - 50) км2 - равным 0,
для 100 > F > 50 км2 - равным 0,15,
для прочих водосборов равным 0,25;
δ - коэффициент уменьшения расхода за счет озер и заболоченности бассейна;
δ' - то же, за счет лесистости бассейна.
δ = 1 - 0,6lg(1 + α + 0,2β),
где α - площадь озер в процентах от общей площади бассейна;
β - площадь болот в процентах от общей площади бассейна.
δ' = 1 – λ(γ – γ1),
где γ - лесистость бассейна в долях от единицы
![]()
γ1 - средняя лесистость всего района;
λ - коэффициент, равный от 0,3 для лиственных лесов лесостепной зоны до 0,6 для таежных лесов Севера.
По последним данным, залесенность бассейна может уменьшать расход смешанного паводка только до тех пор, пока она не превысит 50 %. При дальнейшем увеличении залесенности расход вновь увеличивается. Поэтому коэффициенты δ и δ' рекомендуется принимать по Е.В. Болдакову (таблицы 14 и 15).
В результате расход, смешанного стока по Соколовскому будет:
при F ≤ (20 - 50) км2 Q = δδ'AF м3 /сек,
при 100 > F > 50 км2 Q = δδ'AF0,85 м3/cек,
для прочих водосборов Q = δδ'AF0,75 м3/cек,
где А - см. табл. 13;
δ - см. табл. 14;
δ' - см. табл. 15;
F - площадь бассейна, км2.
Пример.
Требуется определить максимальный расход с вероятностью превышения ![]() (1 % обеспеченности)
весеннего половодья р. Ваймуги (приток р. Ельца, бассейн р. Северной Двины) у
ст. Обозерская с площадью водосбора 340 км2. Озер в бассейне нет,
заболоченность и лесистость неизвестны.
(1 % обеспеченности)
весеннего половодья р. Ваймуги (приток р. Ельца, бассейн р. Северной Двины) у
ст. Обозерская с площадью водосбора 340 км2. Озер в бассейне нет,
заболоченность и лесистость неизвестны.
Значения коэффициента A по рекам Северного Края, выписанные из таблицы 13, приведены в следующей таблице.
Таблица "а"
|
Река |
Пункт |
Число лет наблюдений |
A |
|
Сев. Двина |
д. Абрамково |
59 |
1,94 |
|
" " |
с. Усть-Пинега |
60 |
2,35 |
|
Масляна |
д. Локтево |
11 |
1,99 |
|
Вычегда |
с. Сыктывкар |
16 |
1,87 |
|
Вымь |
с. Весляны |
26 |
2,33 |
|
Вага |
д. Власовская |
26 |
1,69 |
|
" |
д. Леховская |
23 |
1,86 |
|
Пинега |
с. Кулогоры |
22 |
2,87 |
Расходы воды в половодье рек (по Д.Л. Соколовскому)
|
№ п/п |
Река |
Пункт |
Площадь водосбора, км2 |
Число лет наблюдений |
Средний максимальный расход воды, м3/сек |
Коэффициенты |
Расходы воды A с 1 км2 площади бассейна, м3/сек |
||||
|
Cυ |
Cs |
Средний максимальный |
при вероятности превышения паводка |
||||||||
|
1 20 |
1 100 |
1 1000 |
|||||||||
|
|
|
Бассейн Баренцева и Белого морей |
|
|
|
|
|
|
|
|
|
|
1 |
Печора |
д. Якша |
9990 |
25 |
1394 |
0,15 |
2Cυ |
1,38 |
1,78 |
1,94 |
2,15 |
|
2 |
" |
д. Нижний Зауголок |
11660 |
15 |
1504 |
0,18 |
2Cυ |
1,34 |
1,75 |
1,96 |
0,22 |
|
3 |
" |
с. Троицко-Печорское |
35440 |
25 |
4002 |
0,24 |
2Cυ |
1,55 |
2,20 |
2,54 |
2,97 |
|
4 |
" |
с. Оксино |
317260 |
21 |
23052 25752 |
0,16 |
1,10 |
1,73 |
2,62 |
3,02 |
3,51 |
|
5 |
Волосница |
Волосницкий кордон |
304 |
15 |
62,8 |
0,54 |
1,85 |
0,86 |
1,78 |
2,80 |
3,54 |
|
6 |
Илыч |
д. Максимово |
9400 |
17 |
1745 2095 |
0,20 |
1,60 |
1,83 |
3,05 |
3,68 |
4,57 |
|
7 |
Уса |
с. Петрунь (Балабан) |
31240 |
19 |
6726 |
0,27 |
2Cυ |
2,87 |
4,23 |
4,96 |
5,88 |
|
8 |
Сула |
д. Коткина, в 2 км ниже устья р. Соймы |
8010 |
11 |
1069 |
0,16 |
2Cυ |
1,26 |
1,62 |
1,78 |
1,98 |
|
|
|
Реки между р. Печорой и р. Сев. Двиной |
|
|
|
|
|
|
|
|
|
|
9 |
Мезень |
д. Малонисогорская |
55590 |
20 |
5684 |
0,25 |
1,00 |
1,57 |
2,31 |
2,76 |
3,36 |
|
|
|
Бассейн р. Сев. Двины |
|
|
|
|
|
|
|
|
|
|
10 |
Сев. Двина |
д. Абрамково |
223200 |
59 |
12291 |
0,24 |
2Cυ |
1,20 |
1,69 |
1,94 |
2,26 |
|
11 |
" " |
с. Усть-Пинега |
350100 |
60 |
21918 |
0,21 |
2Cυ |
1,52 |
2,08 |
2,35 |
2,68 |
|
12 |
Сухона |
д. Рабанка |
15880 |
59 |
553 |
0,22 |
2Cυ |
0,39 |
0,55 |
0,62 |
0,71 |
|
13 |
" |
д. Камчуг |
38830 |
62 |
2221 |
0,28 |
2Cυ |
0,80 |
1,20 |
1,42 |
1,67 |
|
14 |
" |
д. Гремячево |
50150 |
54 |
3371 |
0,29 |
2Cυ |
1,00 |
1,54 |
1,82 |
2,16 |
|
15 |
Сусла |
Петровское |
147 |
10 |
5,83 8,04 |
0,88 |
2Cυ |
0,14 |
0,32 |
0,39 |
0,49 |
|
16. |
Масляна |
д. Локтево |
212 |
11 |
47,0 |
0,40 |
1,30 |
0,84 |
1,55 |
1,99 |
2,60 |
|
17 |
Вычегда |
с. Парч |
15690 |
15 |
1303 |
0,31 |
1,59 |
0,87 |
1,48 |
1,88 |
2,44 |
|
18 |
" |
с. Сыктывкар |
67800 |
16 |
4149 |
0,27 |
1,50 |
1,00 |
1,50 |
1,87 |
2,38 |
|
19 |
Вымь |
с. Бож-Ю-дор |
11200 |
9 |
1178 |
0,41 |
1,26 |
1,04 |
1,84 |
2,36 |
3,09 |
|
20 |
" |
с. Весляны |
19760 |
26 |
1862 |
0,33 |
1,40 |
1,08 |
1,83 |
2,33 |
3,00 |
|
21 |
Вага |
д. Власовская |
30340 |
26 |
2252 |
0,24 |
1,00 |
0,99 |
1,43 |
1,69 |
2,05 |
|
22 |
" |
д. Леховская |
42930 |
23 |
3185 |
0,24 |
1,10 |
1,06 |
1,55 |
1,86 |
2,26 |
|
23 |
Пинега |
с. Кулогоры |
37030 |
22 |
3644 |
0,35 |
1,20 |
1,36 |
2,25 |
2,87 |
3,67 |
|
|
|
Реки между р. Сев. Двиной и р. Онегой |
|
|
|
|
|
|
|
|
|
|
24 |
Нижняя Солза |
"Сухие пороги" (на 1,0 - 1,5 км ниже) |
1240 |
13 |
114 |
0,24 |
1,65 |
0,54 |
0,80 |
0,99 |
1,23 |
|
|
|
Бассейн р. Онеги |
|
|
|
|
|
|
|
|
|
|
25 |
Онега |
д. Надпорожский погост |
12690 |
55 |
375 |
0,35 |
1,15 |
0,32 |
0,52 |
0,66 |
0,83 |
|
26 |
Свида |
д. Горки |
5240 |
10 |
145 |
0,19 |
1,00 |
0,24 |
0,34 |
0,37 |
0,43 |
|
|
|
Реки между р. Онегой и р. Ковдой |
|
|
|
|
|
|
|
|
|
|
27 |
Сума |
Сумский посад (в 4 км выше) |
1970 |
10 |
61,9 |
0,28 |
1,30 |
0,21 |
0,32 |
0,40 |
0,50 |
|
28 |
Нижний Выг |
с. Надвоицы |
17440 |
14 |
399 |
0,27 |
1,70 |
0,26 |
0,40 |
0,51 |
0,65 |
|
29 |
" |
д. Фока (Крестовый остров) |
22720 |
13 |
551 |
0,25 |
1,40 |
0,30 |
0,44 |
0,54 |
0,68 |
|
30 |
Кемь |
с. Подужемье |
27920 |
17 |
720 |
0,26 |
1,30 |
0,33 |
0,49 |
0,61 |
0,77 |
|
|
|
Бассейн р. Ковды |
|
|
|
|
|
|
|
|
|
|
31 |
Ковда |
порог Лехми-Корва между порогами |
22 020 |
10 |
583 |
0,23 |
1,50 |
0,32 |
0,47 |
0,57 |
0,71 |
|
32 |
" |
Кузьмин и Семежье |
27950 |
16 |
723 |
0,24 |
1,50 |
0,34 |
0,49 |
0,60 |
0,75 |
|
33 |
Оланга |
д. Варталамбина |
6660 |
15 |
427 585 |
0,37 |
1,40 |
0,67 |
1,36 |
1,76 |
2,30 |
|
|
" |
Реки между р. Ковдой и р. Туломой |
|
|
|
|
|
|
|
|
|
|
34 |
Колвица |
д. Колвица |
1330 |
14 |
43,3 |
0,44 |
1,40 |
0,20 |
0,36 |
0,48 |
0,64 |
|
35 |
Умба |
исток из озера Умбозера |
2410 |
10 |
101 |
0,37 |
2,20 |
0,29 |
0,51 |
0,69 |
0,94 |
|
36 |
" |
порог Паялка |
6570 |
12 |
245 |
0,26 |
1,20 |
0,34 |
0,50 |
0,62 |
0,75 |
|
37 |
Териберка |
стойбище Териберка (в 3 км выше) |
2450 |
11 |
408 |
0,42 |
1,15 |
1,16 |
2,15 |
2,72 |
3,53 |
|
38 |
Кола |
1492-й км Кировской железной дороги |
3540 |
15 |
428 655 |
0,53 |
1,45 |
0,93 |
2,92 |
3,92 |
5,32 |
|
|
|
Бассейн р. Туломы |
|
|
|
|
|
|
|
|
|
|
39 |
Тулома |
Сигов-Ручей |
18770 |
15 |
1169 |
0,31 |
1,51 |
0,72 |
1,11 |
1,45 |
1,90 |
|
40 |
Печа |
д. Падун (в 3 км от устья) |
1690 |
11 |
158 |
0,40 |
1,20 |
0,60 |
1,06 |
1,35 |
1,75 |
|
|
|
Бассейн Балтийского моря. Северные притоки Финского залива |
1 |
|
|
|
|
|
|
|
|
|
41 |
Черная |
Дибуны пос. № 2 |
90 |
13 |
7,8 |
0,42 |
1,55 |
0,27 |
0,49 |
0,65 |
0,86 |
|
|
|
Бассейн р. Невы |
|
|
|
|
|
|
|
|
|
|
42 |
Тосна |
д. Рубежи |
1210 |
19 |
101 |
0,41 |
2Cυ |
0,50 |
0,89 |
0,11 |
1,40 |
|
|
|
Притоки Ладожского озера |
|
|
|
|
|
|
|
|
|
|
43 |
Видлица |
д. Аннюла |
1060 |
13 |
45,2 |
0,42 |
1,50 |
0,26 |
0,47 |
0,62 |
0,83 |
|
44 |
Олонка |
д. Чимилицы |
1070 |
16 |
125 |
0,39 |
1,55 |
0,67 |
1,18 |
1,55 |
2,06 |
|
45 |
Свирь |
с. Вознесенье |
59350 |
49 |
808 |
0,18 |
3Cυ |
0,21 |
0,28 |
0,32 |
0,36 |
|
46 |
" |
с. Мятусово |
66100 |
60 |
983 |
0,19 |
1,10 |
0,24 |
0,33 |
0,38 |
0,45 |
|
47 |
" |
с. Пиркиничи |
67300 |
49 |
1070 |
0,28 |
3Cυ |
0,26 |
0,39 |
0,47 |
0,57 |
|
48 |
Важинка |
д.Курлово |
2040 |
11 |
349 |
0,27 |
2Cυ |
1,18 |
1,75 |
2,07 |
2,45 |
|
49 |
Сясь |
д. Яхново |
6230 |
30 |
624 |
0,46 |
1,40 |
0,90 |
1,72 |
2,24 |
3,14 |
|
50 |
Тихвинка |
д. Горелуxa |
2030 |
61 |
187 |
0,38 |
1,20 |
0,61 |
1,06 |
1,36 |
1,75 |
|
51 |
Волхов |
прист. Гостинополье |
79630 |
46 |
1668 |
0,21 |
1,30 |
0,35 |
0,49 |
0,58 |
0,71 |
|
52 |
" |
д. Завод |
69000 |
11 |
1408 |
0,31 |
1,80 |
0,33 |
0,54 |
0,71 |
0,92 |
|
53 |
Горенка |
д. Горенка |
43 |
10 |
2,67 |
0,86 |
1,95 |
0,16 |
0,45 |
0,67 |
0,99 |
|
|
|
Притоки Онежского озера |
|
|
|
|
|
|
|
|
|
|
54 |
Шуя |
д. Нижний Бесовец |
9350 |
10 |
299 |
0,35 |
1,60 |
0,31 |
0,53 |
0,69 |
0,91 |
|
55 |
Суна |
б. Валазминский завод |
3430 |
15 |
84,5 |
0,33 |
1,65 |
0,19 |
0,31 |
0,40 |
0,53 |
|
56 |
" |
Водопад Пор-порог |
5870 |
23 |
203 |
0,44 |
1,50 |
0,30 |
0,56 |
0,75 |
0,99 |
|
57 |
" |
водопад Кивач |
6480 |
19 |
220 |
0,30 |
1,45 |
0,30 |
0,48 |
0,61 |
0,78 |
|
58 |
Ср. Лижма |
д. Кяппесельга |
524 |
16 |
9,85 |
0,42 |
1,60 |
0,08 |
0,16 |
0,22 |
0,29 |
|
|
|
Притоки оз. Ильмень |
|
|
|
|
|
|
|
|
|
|
59 |
Мети |
д. Бехово |
5100 |
41 |
202 |
0,38 |
1,25 |
0,33 |
0,60 |
0,78 |
1,01 |
|
60 |
" |
ниже устья р. Березайка |
8370 |
53 |
308 |
0,37 |
0,90 |
0,36 |
0,59 |
0,74 |
0,89 |
|
61 |
Мета |
ниже устья р. Уверь |
12330 |
54 |
554 |
0,32 |
1,00 |
0,44 |
0,72 |
0,89 |
1,11 |
|
62 |
" |
д. Большие Светицы |
16120 |
42 |
803 |
0,26 |
1,00 |
0,56 |
0,84 |
0,99 |
1,21 |
|
63 |
Березайка |
Березайский бейшлот |
2030 |
20 |
96,6 |
0,28 |
1,15 |
0,32 |
0,49 |
0,59 |
0,77 |
|
64 |
Полометь |
ст. Лычково |
2180 |
11 |
210 |
0,37 |
2Cυ |
0,66 |
1,14 |
1,36 |
1,67 |
|
65 |
Явонь |
д. Осинушка |
276 |
18 |
13,6 |
0,44 |
1,50 |
0,20 |
0,37 |
0,50 |
0,67 |
|
66 |
Ловать |
г. Великие Луки |
3060 |
12 |
177 |
0,56 |
1,45 |
0,43 |
0,90 |
1,22 |
1,67 |
|
67 |
" |
г. Холм |
14660 |
18 |
1060 |
0,39 |
1,80 |
0,79 |
1,41 |
1,87 |
2,54 |
|
63 |
Шелонь |
д. Заполье |
6820 |
17 |
622 |
0,35 |
1,55 |
0,86 |
1,39 |
1,82 |
2,36 |
|
|
|
Реки между р. Невой и р. Наровой |
|
|
|
|
|
|
|
|
|
|
69 |
Луга |
ст. Толмачево |
6320 |
24 |
343 |
0,50 |
1,94 |
0,49 |
1,00 |
1,40 |
1,98 |
|
70 |
" |
с. Киноши |
12640 |
15 |
663 |
0,42 |
1,85 |
0,56 |
1,02 |
1,38 |
1,80 |
|
71 |
Оредеж |
д. Моровино |
2890 |
12 |
116 170 |
0,52 |
2,30 |
0,30 0,43 |
0,67 0,87 |
0,86 1,27 |
1,26 1,85 |
|
72 |
Саба |
д. Райкова |
1290 |
10 |
68,2 |
0,48 |
2Cυ |
0,30 |
0,60 |
0,77 |
0,99 |
|
73 |
Долгая |
д. Пещерное |
184 |
10 |
10,8 |
0,58 |
2,15 |
0,22 |
0,46 |
0,67 |
0,98 |
|
74 |
" |
хут. Изотово |
697 |
12 |
39,0 |
0,35 |
1,60 |
0,30 |
0,48 |
0,63 |
0,83 |
|
|
|
Бассейн р. Нарови |
|
|
|
|
|
|
|
|
|
|
75 |
Плюсса |
колхоз "Красная Заря" |
265 |
12 |
19,9 |
0,39 |
1,30 |
0,36 |
0,53 |
0,68 |
0,89 |
|
76 |
" |
колхоз "Пограничники" |
6180 |
23 |
410 |
0,51 |
1,89 |
0,59 |
1,20 |
1,67 |
2,84 |
|
|
|
Притоки Чудско- Псковского озера |
|
|
|
|
|
|
|
|
|
|
77 |
Великая |
д. Пятоново |
20180 |
11 |
1049 |
0,56 |
1,90 |
0,62 |
1,36 |
1,85 |
2,62 |
|
78 |
Сороть |
д. Осинкино |
2960 |
16 |
202 |
0,35 |
1,60 |
0,51 |
0,85 |
1,05 |
1,44 |
|
79 |
Эма-Иеги (малый Эмбах) |
с. Теллисте |
1060 |
14 |
81 |
0,62 |
1,60 |
0,44 |
0,96 |
1,40 |
1,89 |
|
|
|
Реки между р. Наровой и р. Зап. Двиной |
|
|
|
|
|
|
|
|
|
|
80 |
Кейла |
г. Кейла |
668 |
15 |
41,3 |
0,78 |
2,15 |
0,31 |
0,81 |
1,21 |
1,81 |
|
81 |
Лейва |
д. Наюба |
84 |
14 |
6,87 |
1,03 |
2,68 |
0,25 |
0,76 |
1,38 |
2,02 |
|
82 |
Вазаллема |
хут. Урба |
383 |
10 |
27,1 |
0,56 |
2,20 |
0,31 |
0,66 |
0,97 |
1,54 |
|
83 |
Вихтерпалу |
д. Энглема |
468 |
11 |
29,3 |
0,65 |
1,78 |
0,29 |
0,67 |
0,95 |
1,35 |
|
84 |
Пярну |
с. Орекюла |
5180 |
14 |
466,7 |
0,75 |
2Cυ |
0,76 |
1,89 |
2,68 |
3,75 |
|
|
|
Бассейн р. Зап. Двины |
|
|
|
|
|
|
|
|
|
|
85 |
Зап. Двина |
д. Устье-Горяне |
16900 |
46 |
1068 |
0,35 |
1,20 |
0,72 |
1,20 |
1,51 |
1,93 |
|
86 |
" " |
г. Витебск |
27270 |
59 |
1675 |
0,33 |
1,00 |
0,62 |
1,27 |
1,57 |
1,95 |
|
87 |
" " |
д. Бояры |
41410 |
7 |
2166 |
0,36 |
1,07 |
0,73 |
1,23 |
1,55 |
1,96 |
|
88 |
Обша |
г. Белый |
1590 |
12 |
199 |
0,41 |
2Cυ |
0,79 |
1,39 |
1,73 |
2,18 |
|
89 |
Улла |
д. Промыслы |
3330 |
11 |
147 |
0,41 |
1,25 |
0,34 |
0,60 |
0,77 |
1,00 |
|
90 |
Усвиж Бук |
д. Мозолы |
156 |
10 |
19,5 |
0,68 |
2,10 |
0,44 |
1,05 |
1,56 |
2,26 |
|
91 |
Полота |
д. Янково 1-е |
618 |
12 |
34,8 |
0,58 |
1,80 |
0,28 |
0,60 |
0,85 |
1,20 |
|
92 |
Нача |
д. Горовцы |
212 |
13 |
16,7 |
0,72 |
2,00 |
0,30 |
0,73 |
1,07 |
1,59 |
|
|
|
Бассейн р. Немана |
|
|
|
|
|
|
|
|
|
|
93 |
Неман |
г. Столбцы |
3070 |
12 |
225 |
0,69 |
1,90 |
0,55 |
1,29 |
1,88 |
2,73 |
|
94 |
" |
г. Биоштаны |
43600 |
20 |
1082 |
0,45 |
2,00 |
0,36 |
0,68 |
0,94 |
1,31 |
|
95 |
" |
Шмаленингсн |
81230 |
12 |
2562 |
0,37 |
1,20 |
0,53 |
0,91 |
1,15 |
1,46 |
|
96 |
" |
|
91850 |
16 |
2695 |
0,37 |
1,30 |
0,51 |
0,87 |
1,12 |
1,63 |
|
97 |
Щара |
с. Щара |
6950 |
11 |
193 |
0,48 |
2Cυ |
0,24 |
0,48 |
0,62 |
0,80 |
|
98 |
Росс |
м. Росс |
964 |
10 |
28,4 |
0,68 |
2,10 |
0,16 |
0,39 |
0,57 |
0,84 |
|
99 |
Вилия |
г. Вильно |
14583 |
12 |
650 |
0,61 |
1,95 |
0,49 |
1,09 |
1,56 |
2,23 |
|
100 |
" |
м. Яново |
24630 |
19 |
921 |
0,45 |
1,45 |
0,49 |
0,88 |
1,18 |
1,56 |
|
101 |
Свента |
г. Укмерге |
5440 |
14 |
336 |
0,34 |
2Cυ |
0,54 |
0,86 |
1,03 |
1,28 |
|
102 |
Невяжа |
г. Кейданы |
3220 |
11 |
232 |
0,17 |
2Cυ |
0,54 |
0,71 |
0,78 |
0,90 |
|
103 |
Миния |
с. Картяна |
1230 |
14 |
144 |
0,31 |
1,95 |
0,68 |
1,12 |
1,46 |
1,95 |
|
|
|
Бассейн Черного и Азовского морей |
|
|
|
|
|
|
|
|
|
|
104 |
Днестр |
г. Николаев |
5470 |
16 |
329 |
0,64 |
1,40 |
0,52 |
1,15 |
1,60 |
2,20 |
|
105 |
" |
г. Галич |
14660 |
27 |
806 |
0,53 |
1,30 |
0,61 |
1,21 |
1,64 |
2,20 |
|
106 |
" |
г. Залещики |
24600 |
22 |
1050 |
0,67 |
1,70 |
0,54 |
1,25 |
1,78 |
2,53 |
|
107 |
" |
г. Бендеры |
66110 |
54 |
1084 |
0,42 |
1,00 |
0,26 |
0,48 |
0,61 |
0,78 |
|
|
|
Бассейн р. Южного Буга |
|
|
|
|
|
|
|
|
|
|
108 |
Южный Буг |
с. Подгуры |
24620 |
11 |
504 856 |
0,70 |
1,70 |
0,26 |
1,04 |
1,49 |
2,11 |
|
109 |
" " |
с. Богдановка-Александровка |
46200 |
16 |
1126 |
1,12 |
2Cυ |
0,36 |
1,16 |
1,85 |
2,86 |
|
110 |
Синюха |
с. Синюхин Брод |
16660 |
14 |
557 810 |
0,88 |
2Cυ |
0,41 0,53 |
1,22 1,48 |
1,56 2,16 |
2,27 3,19 |
|
|
|
Бассейн р. Днепра |
|
|
|
|
|
|
|
|
|
|
111 |
Днепр |
г. Орша |
6390 |
51 |
664 |
0,46 |
1,20 |
0,93 |
1,74 |
2,28 |
2,96 |
|
112 |
" |
г. Смоленск |
14080 |
59 |
857 |
0,39 |
1,30 |
0,66 |
1,18 |
1,52 |
1,96 |
|
113 |
Днепр |
г. Орша |
18010 |
56 |
946 |
0,33 |
1,20 |
0,61 |
1,05 |
1,34 |
1,74 |
|
114 |
" |
г. Речица |
58200 |
41 |
2247 |
0,43 |
1,25 |
0,60 |
1,09 |
1,41 |
1,85 |
|
115 |
" |
г. Киев |
327700 |
59 |
6869 |
0,58 |
1,56 |
0,50 |
1,07 |
1,49 |
2,04 |
|
116 |
" |
г. Кременчуг |
383000 |
53 |
7232 |
0,61 |
1,50 |
0,47 |
1,03 |
1,43 |
1,98 |
|
117 |
" |
г. Верхнеднепровск |
434000 |
52 |
7710 |
0,62 |
1,85 |
0,45 |
1,02 |
1,45 |
2,07 |
|
118 |
" |
г. Лоцманская-Каменка |
458620 |
52 |
7856 |
0,63 |
1,60 |
0,45 |
1,00 |
1,41 |
1,95 |
|
119 |
" |
г. Ильинское |
469650 |
6 |
9739 |
0,54 |
1,86 |
0,42 |
0,88 |
1,23 |
1,74 |
|
120 |
Березина |
г. Борисов |
5100 |
53 |
177 |
0,40 |
1,50 |
0,29 |
0,52 |
0,69 |
0,91 |
|
121 |
" |
г. Бобруйск |
20240 |
56 |
720 |
0,58 |
1,75 |
0,42 |
0,91 |
1,43 |
1,81 |
|
122 |
Ведрич |
хут. Бабичи |
438 |
11 |
17,0 |
0,78 |
1,82 |
0,18 |
0,45 |
0,59 |
0,93 |
|
123 |
Ивня |
д. Будки |
208 |
10 |
15,3 |
0,92 |
2,40 |
0,28 |
0,80 |
1,25 |
1,93 |
|
124 |
Сож |
д. Бахревка |
3020 |
42 |
445 |
0,62 |
1,60 |
1,09 |
2,41 |
3,38 |
4,72 |
|
125 |
" |
г. Славгород |
17660 |
43 |
1935 |
0,70 |
1,50 |
1,26 |
2,98 |
4,20 |
5,88 |
|
126 |
" |
г. Гомель |
38860 |
40 |
2377 |
0,67 |
1,50 |
0,87 |
1,99 |
2,78 |
3,88 |
|
127 |
Припять |
д. Мозырь |
97190 |
59 |
1770 |
0,65 |
1,70 |
0,32 |
0,74 |
1,05 |
1,40 |
|
128 |
Птичь |
д. Лучицы |
8770 |
37 |
296 |
0,62 |
1,65 |
0,33 |
0,76 |
1,02 |
1,45 |
|
129 |
Оресса |
д. Кутинки |
1780 |
10 |
95,7 |
0,72 |
1,92 |
0,35 |
0,84 |
1,23 |
1,80 |
|
130 |
" |
д. Андреевка |
3580 |
10 |
157 |
0,75 |
1,75 |
0,34 |
0,84 |
1,23 |
1,76 |
|
131 |
Уж |
г. Кагановичск |
5690 |
24 |
356 |
0,86 |
1,80 |
0,56 |
1,47 |
2,16 |
3,13 |
|
132 |
Ирша |
с. Пинязевичи |
2600 |
14 |
213 |
0,63 |
1,30 |
0,36 |
1,29 |
1,79 |
2,45 |
|
133 |
Десна |
с. Голубея |
4770 |
44 |
499 |
0,46 |
1,20 |
0,88 |
1,63 |
2,07 |
2,64 |
|
134 |
" |
г. Брянск |
13640 |
45 |
974 |
0,60 |
2Cυ |
0,77 |
1,68 |
2,24 |
2,92 |
|
135 |
" |
с. Вишенки |
37620 |
33 |
1461 |
0,62 |
1,35 |
0,54 |
1,19 |
1,63 |
2,22 |
|
136 |
" |
г. Чернигов |
81440 |
56 |
2242 |
0,81 |
2Cυ |
0,46 |
1,21 |
1,75 |
2,53 |
|
137 |
Судость |
д. Горица |
5780 |
13 |
440 |
0,37 |
1,15 |
0,47 |
1,13 |
1,43 |
1,83 |
|
138 |
Сейм |
с. Мутино |
25560 |
13 |
1335 |
0,65 |
1,70 |
0,66 |
1,51 |
2,13 |
3,02 |
|
139 |
Рось |
с. Карашин |
10300 |
11 |
428 |
0,90 |
2Cυ |
0,42 |
1,17 |
1,74 |
2,54 |
|
140 |
Супой |
с. Песчаное |
1900 |
12 |
307 |
1,09 |
2Cυ |
0,11 |
0,33 |
0,52 |
0,80 |
|
141 |
Сула |
г. Ромны |
4020 |
14 |
169 |
0,60 |
2Cυ |
0,31 |
0,72 |
0,97 |
1,30 |
|
142 |
" |
м. Снятин |
6540 |
11 |
246 |
0,68 |
2Cυ |
0,34 |
0,78 |
1,09 |
1,50 |
|
143 |
" |
с. Галицкое |
18700 |
13 |
417 |
0,88 |
2Cυ |
0,29 |
0,72 |
1,06 |
1,55 |
|
144 |
Псел |
с. Запселье |
22420 |
12 |
499 |
0,64 |
1,65 |
0,27 |
0,62 |
0,87 |
1,22 |
|
145 |
Хорол |
г. Миргород |
1920 |
20 |
103 |
0,81 |
2Cυ |
0,36 |
0,93 |
1,85 |
1,93 |
|
146 |
Орель |
м. Китай-город |
9450 |
14 |
281 |
0,92 |
2Cυ |
0,29 |
0,83 |
1,24 |
1,83 |
|
147 |
Волочья |
с. Васильковка |
11550 |
10 |
266 |
0,91 |
2Cυ |
0,24 |
0,67 |
1,00 |
1,43 |
|
148 |
Ингулец |
с. Могилевка |
9280 |
13 |
268 |
0,62 |
2Cυ |
0,28 |
0,62 |
0,85 |
1,17 |
|
|
|
Бассейн р. Дона |
|
|
|
|
|
|
|
|
|
|
149 |
Дон |
с. Гремячье |
59560 |
35 |
3890 |
0,39 |
2Cυ |
1,01 |
1,73 |
2,18 |
2,70 |
|
150 |
" |
ст. Лиски |
69130 |
53 |
3664 |
0,53 |
1,35 |
0,86 |
1,81 |
2,33 |
3,16 |
|
151 |
" |
ст. Казанская |
101800 |
51 |
3236 |
0,47 |
1,25 |
0,56 |
1,08 |
1,42 |
1,88 |
|
152 |
" |
хут. Хованский |
168800 |
46 |
4452 |
0,50 |
1,50 |
0,54 |
1,06 |
1,55 |
1,93 |
|
153 |
" |
г. Калач |
221600 |
64 |
5777 |
0,50 |
1,40 |
0,61 |
1,14 |
1,52 |
2,07 |
|
154 |
" |
ст-ца Мелеховская |
378400 |
55 |
5810 |
0,55 |
1,50 |
0,38 |
0,79 |
1,08 |
1,48 |
|
155 |
Хопер |
г. Балашов |
14330 |
18 |
808 |
0,54 |
1,50 |
0,62 |
1,31 |
1,94 |
2,34 |
|
156 |
" |
хут. Бесплемяновский |
44860 |
10 |
1015 |
0,75 |
2,15 |
0,33 |
0,82 |
1,15 |
1,85 |
|
157 |
Медведица |
ст. Себрякова |
31140 |
10 |
1118 |
0,60 |
1,40 |
0,48 |
1,04 |
1,41 |
1,85 |
|
158 |
" |
хут. Арчединский |
33730 |
12 |
872 |
0,80 |
2Cυ |
0,35 |
0,91 |
1,30 |
1,97 |
|
159 |
Карповка |
ст. Кривомузгинская |
1980 |
11 |
233 |
0,48 |
1,10 |
0,78 |
1,43 |
1,95 |
2,55 |
|
160 |
Чир |
Обливская |
8540 |
14 |
387 |
1,09 |
2Cυ |
0,43 |
1,53 |
2,39 |
3,80 |
|
161 |
Сев. Донец |
г. Змиев |
16630 |
12 |
774 |
0,48 |
2Cυ |
0,53 |
1,01 |
1,33 |
1,81 |
|
162 |
" " |
г. Лисичанск |
52440 |
35 |
1256 |
0,53 |
1,30 |
0,24 |
0,73 |
0,98 |
1,35 |
|
163 |
" " |
ст-ца Луганская (ниже устья р. Лугань) |
66780 |
12 |
1462 |
0,55 |
2,10 |
0,35 |
0,74 |
1,06 |
1,52 |
|
164 |
Оскол |
г. Купянск |
12720 |
12 |
870 |
0,66 |
1,30 |
0,73 |
1,65 |
2,26 |
3,08 |
|
165 |
Айдар |
хут. Передельский |
7350 |
10 |
211 |
0,55 |
2,00 |
0,27 |
0,54 |
0,79 |
1,13 |
|
166 |
Сал |
хут. Барабанщиков |
13730 |
16 |
404 |
0,84 |
2Cυ |
0,32 |
0,84 |
1,23 |
1,77 |
|
167 |
Западный Маныч |
Железнодорожный мост 169 км |
28290 |
10 |
86,8 |
1,44 |
2Cυ |
0,04 |
0,16 |
0,27 |
0,45 |
|
|
|
Бассейн Каспийского моря |
|
|
|
|
|
|
|
|
|
|
|
|
Бассейн р. Волги |
|
|
|
|
|
|
|
|
|
|
168 |
Волга |
Верхневолжский бейшлот |
3330 |
40 |
136 |
0,47 |
1,20 |
0,31 |
0,56 |
0,78 |
1,03 |
|
169 |
" |
с. Ельцы |
9130 |
45 |
404 |
0,42 |
2,00 |
0,43 |
0,79 |
1,09 |
1,51 |
|
170 |
" |
г. Ржев |
12210 |
17 |
943 |
0,45 |
1,60 |
0,80 |
1,50 |
1,91 |
2,42 |
|
171 |
" |
г. Старица |
21140 |
51 |
2100 |
0,35 |
1,20 |
1,20 |
2,20 |
2,52 |
3,25 |
|
172 |
" |
г. Калинин |
24140 |
61 |
2460 |
0,34 |
0,0 |
1,27 |
1,93 |
2,27 |
2,61 |
|
173 |
" |
устье р. Шоши |
38760 |
55 |
4080 |
0,30 |
0,0 |
1,48 |
2,21 |
2,51 |
2,84 |
|
174 |
" |
г. Ярославль |
154000 |
66 |
7052 |
0,29 |
0,0 |
0,91 |
1,35 |
1,53 |
1,72 |
|
175 |
" |
г. Кинешма |
187800 |
64 |
8485 |
0,24 |
0,70 |
0,94 |
1,35 |
1,58 |
1,87 |
|
176 |
" |
г. Чкаловск |
227900 |
61 |
10623 |
0,25 |
0,80 |
1,02 |
1,49 |
1,76 |
2,10 |
|
177 |
" |
г. Горький |
478700 |
59 |
19794 |
0,33 |
1,10 |
0,92 |
1,67 |
2,14 |
2,70 |
|
178 |
" |
с. Вязовые |
628600 |
36 |
22711 |
0,27 |
0,0 |
1,02 |
1,47 |
1,66 |
1,87 |
|
179 |
" |
г. Куйбышев |
1212000 |
62 |
36477 |
0,26 |
1,10 |
1,00 |
1,48 |
1,78 |
2,18 |
|
180 |
" |
г. Сталинград |
1353000 |
55 |
34618 |
0,23 |
1,00 |
0,87 |
1,24 |
1,47 |
1,78 |
|
181 |
Касня |
с. Тесово |
480 |
12 |
108 |
0,43 |
2Cυ |
1,05 |
1,90 |
2,44 |
3,14 |
|
182 |
Молога |
д. Ильицино |
500 |
10 |
31,1 39,2 |
0,26 |
1,20 |
0,29 |
0,55 |
0,68 |
0,84 |
|
183 |
" |
с. Спас-Забережье |
10240 |
10 |
479 637 |
0,33 |
1,40 |
0,47 |
1,00 |
1,28 |
1,68 |
|
184 |
" |
г. Устюжна |
19450 |
9 |
980 |
0,40 |
2,00 |
0,72 |
1,30 |
1,75 |
2,42 |
|
185 |
" |
г. Весьегонск |
31510 |
61 |
1848 |
0,40 |
1,10 |
0,78 |
1,37 |
1,74 |
2,23 |
|
186 |
Шексна |
посад Крохино |
13970 |
46 |
323 |
0,25 |
0 |
0,25 |
0,35 |
0,40 |
0,45 |
|
187 |
Суда |
д. Нелазский перевоз |
13830 |
10 |
1026 |
0,24 |
2,00 |
0,83 |
1,23 |
1,55 |
2,00 |
|
188 |
Андога |
хут. Ольховец |
2080 |
18 |
137 |
0,34 |
1,10 |
0,44 |
0,72 |
0,82 |
1,16 |
|
189 |
Унжа |
г. Макарьев |
18530 |
47 |
1495 |
0,24 |
0 |
0,94 |
1,32 |
1,47 |
1,64 |
|
190 |
Нея |
д. Буслаево |
5700 |
10 |
568 |
0,45 |
2Cυ |
0,86 |
1,59 |
2,02 |
2,57 |
|
191 |
Ока |
г. Орел |
4890 |
55 |
686 |
0,51 |
2Cυ |
1,18 |
2,30 |
3,05 |
3,93 |
|
192 |
" |
г. Белев |
17530 |
58 |
1960 |
0,49 |
1,30 |
1,30 |
2,51 |
3,36 |
4,40 |
|
193 |
" |
г. Калуга |
54930 |
66 |
5357 |
0,49 |
2Cυ |
1,50 |
2,90 |
3,90 |
4,80 |
|
194 |
" |
г. Кашира |
68730 |
56 |
6899 |
0,44 |
1,10 |
1,65 |
2,98 |
3,84 |
4,95 |
|
195 |
" |
г. Касимов |
130000 |
50 |
7849 |
0,39 |
1,30 |
1,16 |
1,98 |
2,40 |
3,16 |
|
196 |
" |
г. Муром |
187900 |
56 |
9302 |
0,39 |
1,10 |
1,03 |
1,81 |
2,26 |
2,91 |
|
197 |
Угра |
ст. Товарково |
15280 |
11 |
1728 |
0,48 |
2,20 |
1,25 |
2,30 |
3,26 |
4,55 |
|
198 |
Москва |
с. Макарово |
1420 |
15 |
280 |
0,44 |
1,40 |
1,21 |
2,25 |
2,88 |
4,03 |
|
199 |
" |
г. Звенигород |
5000 |
20 |
718 |
0,50 |
1,60 |
1,21 |
2,40 |
3,26 |
4,45 |
|
200 |
" |
с. Павшино |
7650 |
16 |
976 |
0,57 |
1,60 |
1,20 |
2,58 |
3,52 |
4,87 |
|
201 |
" |
Бабьегородская плотина |
8170 |
27 |
1284 |
0,36 |
1,45 |
1,50 |
2,56 |
3,29 |
4,27 |
|
202 |
Руза |
ст. Покров |
1270 |
17 |
206 |
0,47 |
1,36 |
0,96 |
1,84 |
2,43 |
3,24 |
|
203 |
" |
г. Руза |
2100 |
17 |
307 |
0,48 |
1,40 |
0,99 |
1,91 |
2,66 |
3,38 |
|
204 |
Истра |
с. Бужарово |
1010 |
14 |
168 |
0,74 |
1,90 |
0,94 |
2,35 |
3,42 |
4,99 |
|
205 |
" |
Павловская слобода |
1790 |
15 |
195 |
0,70 |
2,00 |
0,71 |
1,63 |
2,33 |
3,83 |
|
206 |
Пахра |
с. Макарово |
1760 |
15 |
227 |
0,43 |
1,20 |
0,84 |
1,53 |
1,96 |
2,57 |
|
207 |
Пехорка |
с. Кучино |
124 |
10 |
9,16 |
0,58 |
1,50 |
0,24 |
0,53 |
0,72 |
1,00 |
|
203 |
Цна |
с. Старый Спас |
717 |
12 |
83,7 |
0,56 |
1,60 |
0,60 |
1,25 |
1,73 |
2,38 |
|
209 |
Ушна |
д. Новлянская |
1210 |
16 |
68,7 130,7 |
0,90 |
2,10 |
0,34 |
0,94 |
1,47 |
2,04 |
|
210 |
Клязьма |
г. Городок |
5320 |
28 |
409 |
0,60 |
1,55 |
0,65 |
1,43 |
2,00 |
2,78 |
|
211 |
" |
с. Городище |
7900 |
16 |
594 |
0,42 |
1,10 |
0,70 |
1,28 |
1,64 |
2,12 |
|
212 |
" |
г. Владимир |
15190 |
23 |
915 |
0,59 |
1,90 |
0,67 |
1,45 |
2,06 |
2,94 |
|
213 |
" |
г. Ковров |
25830 |
48 |
1539 |
0,41 |
1,30 |
0,75 |
1,35 |
1,74 |
2,28 |
|
214 |
Поля |
с. Кривандино |
434 |
10 |
42,5 |
0,62 |
1,80 |
0,45 |
0,98 |
1,48 |
2,02 |
|
215 |
Ветлуга |
д. Дубники |
28590 |
38 |
1332 |
0,26 |
1,08 |
0,61 |
0,91 |
1,10 |
1,35 |
|
216 |
" |
с. Воскресенское |
35050 |
38 |
1418 |
0,24 |
1,10 |
0,55 |
0,80 |
0,95 |
1,14 |
|
217 |
Кама |
с. Волосницкое |
9770 |
62 |
952 |
0,30 |
0,95 |
0,95 |
1,48 |
1,81 |
2,22 |
|
218 |
" |
с. Гаинское |
27650 |
13 |
1269 |
0,22 |
0,90 |
0,58 |
0,83 |
0,97 |
1,16 |
|
219 |
" |
с. Бондюг |
45520 |
27 |
2305 |
0,34 |
1,10 |
0,74 |
1,21 |
1,51 |
1,91 |
|
220 |
" |
г. Березники |
83780 |
62 |
6070 |
0,26 |
0,90 |
1,23 |
1,83 |
2,13 |
2,64 |
|
221 |
" |
пристань Добрянская |
118200 |
57 |
7472 |
0,23 |
1,20 |
1,18 |
1,63 |
2,00 |
2,45 |
|
992 |
" |
г. Пермь |
167800 |
64 |
9547 |
0,27 |
1,05 |
1,15 |
1,74 |
2,11 |
2,59 |
|
223 |
" |
д. Myново |
340200 |
52 |
13275 |
0,23 |
1,00 |
0,94 |
1,35 |
1,60 |
1,93 |
|
224 |
" |
с. Сокольи Горы |
504400 |
60 |
18672 |
0,27 |
1,20 |
0,98 |
1,49 |
1,82 |
2,26 |
|
225 |
Вишера |
д. Писанная |
7480 |
10 |
1690 |
0,22 |
1,60 |
2,10 |
3,01 |
3,66 |
4,60 |
|
226 |
" |
д. Митраково (Вижайский завод) |
9020 |
42 |
1703 |
0,19 |
0,95 |
1,86 |
2,50 |
2,91 |
3,50 |
|
227 |
" |
д. Рябинин перевоз |
30820 |
10 |
3560 |
0,20 |
1,40 |
1,53 |
2,13 |
2,54 |
3,14 |
|
228 |
Колва |
д. Петрецово |
3530 |
15 |
416 |
0,33 |
1,40 |
0,92 |
1,50 |
1,89 |
2,44 |
|
229 |
" |
д. Подбобыка |
11930 |
13 |
1020 |
0,29 |
1,55 |
0,89 |
1.40 |
1,72 |
2,29 |
|
230 |
Березовская |
д. Болдырья |
2920 |
11 |
42 |
0,31 |
1,50 |
1,07 |
1,72 |
2,17 |
2,80 |
|
231 |
Вишерка |
д. Фадина |
3540 |
14 |
205 |
0,38 |
1,65 |
0,45 |
0,78 |
0,94 |
1,36 |
|
232 |
Чусовая |
ст. Перевал |
1500 |
11 |
76,3 |
0,64 |
1,90 |
0,32 |
0,81 |
1,10 |
1,50 |
|
233 |
" |
д. Харенки |
8370 |
11 |
619 |
0,56 |
2Cυ |
0,71 |
1,46 |
1,91 |
2,56 |
|
234 |
" |
д. Копчик |
11160 |
55 |
881 |
0,30 |
2Cυ |
0,78 |
1,26 |
1,50 |
1,78 |
|
235 |
" |
Чусовские Городки |
23900 |
62 |
2480 |
0,34 |
2Cυ |
1,26 |
2,08 |
2,52 |
3,08 |
|
236 |
Серебряная |
Серябрянский завод |
970 |
10 |
105 |
0,54 |
2Cυ |
0,60 |
1,23 |
1,61 |
2,12 |
|
237 |
Койва |
д. Федотовка |
1150 |
11 |
170 |
0,34 |
2,30 |
0,86 |
1,46 |
1,95 |
2,72 |
|
238 |
Усьва |
ст. Усьва |
2200 |
11 |
318 388 |
0,22 |
1,60 |
0,99 |
1,73 |
2,12 |
2,66 |
|
239 |
Вильва |
Курень Узких |
2930 |
10 |
429 |
0,42 |
1,80 |
1,03 |
1,98 |
2,66 |
3,64 |
|
240 |
Сылва |
Малебский завод |
3830 |
11 |
439 |
0,32 |
1,70 |
0,90 |
1,42 |
l,o9 |
2,04 |
|
241 |
" |
Суксунский завод |
6570 |
14 |
495 |
0,30 |
1,70 |
0,68 |
1,18 |
1,39 |
1,81 |
|
242 |
" |
с. Троицкое |
22270 |
11 |
1245 |
0,37 |
1,40 |
0,63 |
1,17 |
1,51 |
1,98 |
|
243 |
Бабка |
д. Балалы |
2020 |
10 |
209 |
0,44 |
1,90 |
0,69 |
1,32 |
1,73 |
2,46 |
|
244 |
Белая |
с. Бугоровка |
21000 |
24 |
1396 |
0,33 |
1,35 |
0,80 |
1,28 |
1,54 |
1,90 |
|
245 |
" |
г. Уфа |
100500 |
66 |
6208 |
0,45 |
1,40 |
1,10 |
2,07 |
2,74 |
3,61 |
|
246 |
" |
г. Бирск |
121300 |
62 |
6428 |
0,50 |
1,50 |
0,99 |
1,95 |
2,63 |
3,57 |
|
247 |
Большой Инзер |
хут. Серегина |
1020 |
12 |
145 |
0,33 |
1,45 |
0,78 |
1,26 |
1,51 |
1,83 |
|
248 |
Малый Инзер |
ст. Айгир |
930 |
11 |
207 238 |
0,28 |
1,20 |
1,10 |
2,00 |
2,66 |
3,30 |
|
249 |
Уфа |
с. Нязе-Петровск |
3800 |
13 |
262 |
0,54 |
1,55 |
0,54 |
1,12 |
1,52 |
2,09 |
|
250 |
" |
г. Красноуфимск |
14500 |
14 |
823 |
0,35 |
1,00 |
0,60 |
1,00 |
1,24 |
1,62 |
|
251 |
" |
пристань Шафеево |
36600 |
30 |
2180 |
0,45 |
1,20 |
0,82 |
1,53 |
2,00 |
2,61 |
|
252 |
" |
пос. Дудкинский |
52700 |
11 |
2452 |
0,31 |
1,10 |
0,71 |
1,12 |
1,39 |
1,72 |
|
253 |
Юрюзань |
д. Екатериновка |
1580 |
13 |
202 |
0,61 |
1,65 |
0,72 |
2,01 |
3,56 |
5,07 |
|
254 |
Дема |
с. Голумилино |
12400 |
10 |
273 |
0,66 |
1,75 |
0,24 |
0,54 |
0,76 |
1,09 |
|
255 |
Вятка |
г. Киров |
48300 |
65 |
2911 |
0,24 |
0 |
0,89 |
1,24 |
1,39 |
1,55 |
|
256 |
" |
д. Камень |
90400 |
37 |
3983 |
0,24 |
2Cυ |
0,77 |
1,11 |
1,24 |
1,48 |
|
257 |
" |
с. Вятские Поляны |
124400 |
25 |
4908 |
0,24 |
1,00 |
0,74 |
1,12 |
1,39 |
1,52 |
|
258 |
Корба |
с. Короткие |
3480 |
17 |
301 400 |
0,33 |
1,30 |
0,66 |
1,08 |
1,36 |
1,76 |
|
259 |
" |
с. Верхние Тюрюханы |
6700 |
14 |
464 |
0,18 |
1,10 |
0,64 |
0,84 |
0,98 |
1,15 |
|
260 |
Летка |
с. Казань |
3270 |
10 |
204 |
0,20 |
1,50 |
0,47 |
0,78 |
0,96 |
1,15 |
|
261 |
Чепца |
с. Полом |
5930 |
10 |
607 |
0,39 |
1,30 |
0,90 |
1,57 |
2,02 |
2,64 |
|
262 |
Быстрина |
с. Щипицино |
3540 |
16 |
485 |
0,42 |
1,30 |
1,05 |
1,90 |
2,49 |
3,25 |
|
263 |
Молома |
д. Щетиненки |
9700 |
17 |
738 944 |
0,23 |
1,50 |
0,76 |
1,49 |
1,86 |
2,38 |
|
264 |
Самра |
с. Елшанка |
22480 |
10 |
629 |
0,61 |
1,50 |
0,33 |
0,71 |
0,98 |
1,42 |
|
265 |
Бол, Кинель |
г. Бугуруслан |
6140 |
10 |
575 |
0,74 |
2Cυ |
0,83 |
2,02 |
2,86 |
4,04 |
|
266 |
" " |
с. Тимашево |
11960 |
11 |
528 |
0,89 |
1,90 |
0,45 |
1,28 |
1,90 |
2,80 |
|
267 |
Бол, Караман |
Советское (Мариенталь) |
3520 |
14 |
444 |
0,95 |
2Cυ |
0,93 |
2,80 |
4,25 |
6,38 |
|
|
|
Бассейн р. Урала |
|
|
|
|
|
|
|
|
|
|
268 |
Урал |
стан. Кизильская |
15920 |
13 |
475 |
1,19 |
2Cυ |
0,34 |
1,14 |
1,85 |
3,36 |
|
269 |
" |
г. Оренбург |
79610 |
17 |
1646 |
1,50 |
2Cυ |
0,35 |
1,40 |
2,46 |
4,20 |
|
270 |
" |
пос. Кушумский |
179500 |
30 |
3718 |
1,00 |
2Cυ |
0,43 |
1,23 |
2,02 |
3,11 |
|
271 |
Сакмара |
стан. Сакмарская |
27690 |
22 |
1907 |
0,67 |
2Cυ |
0,88 |
2,05 |
3,01 |
4,31 |
|
272 |
Большой Ик |
ст. Поляковка |
6020 |
10 |
641 |
0,54 |
2Cυ |
0,94 |
1,88 |
2,48 |
3,25 |
|
|
|
Бассейн Карского моря |
|
|
|
|
|
|
|
|
|
|
273 |
Обь |
г. Барнаул |
168500 |
20 |
5730 |
0,24 |
1,75 |
0,71 |
1,06 |
1,28 |
1,65 |
|
274 |
" |
г. Камень на Оби |
209500 |
46 |
5813 |
0,30 |
3,00 |
0,59 |
0,96 |
1,32 |
1,89 |
|
275 |
" |
г. Новосибирск |
246200 |
50 |
7860 |
0,30 |
1,15 |
0,71 |
1,11 |
1,38 |
1,74 |
|
276 |
" |
г. Могочин |
477100 |
50 |
15543 |
0,22 |
1,00 |
0,84 |
1,18 |
1,39 |
1,67 |
|
277 |
" |
г. Салехард |
2449000 |
15 |
35966 |
0,10 |
1,50 |
0,53 |
0,69 |
0,76 |
0,88 |
|
278 |
Бия |
г. Кебезень |
21900 |
10 |
1176 |
0,31 |
1,27 |
0,65 |
1,03 |
1,29 |
1,63 |
|
279 |
" |
Камболино |
25180 |
10 |
1460 |
0,24 |
1,05 |
0,73 |
1,03 |
1,29 |
1,56 |
|
280 |
" |
г. Бийск |
36870 |
51 |
2703 |
0,29 |
1,00 |
1,02 |
1,57 |
1,91 |
2,36 |
|
281 |
Томь |
улус Саркыш |
5970 |
13 |
1617 |
0,21 |
1,60 |
2,39 |
3,37 |
4,08 |
5,08 |
|
282 |
" |
г. Сталинск |
28230 |
50 |
6296 |
0,19 |
1,05 |
2,91 |
3,93 |
4,57 |
5,43 |
|
283 |
" |
Сю Крапивино |
42410 |
32 |
7680 |
0,16 |
1,10 |
2,60 |
3,38 |
3,90 |
4,54 |
|
284 |
" |
г Кемерово |
47090 |
13 |
8305 |
0,30 0,22 |
1,00 |
2,60 |
3,66 |
4,32 |
5,20 |
|
285 |
Кеть |
юрты Озерные |
36850 |
15 |
1147 |
0,21 |
1,40 |
0,42 |
0,60 |
0,73 |
0,89 |
|
286 |
" |
д Белоярка |
75780 |
10 |
1500 |
0,17 |
1,30 |
0,33 |
0,44 |
0,51 |
0,61 |
|
287 |
Урсул |
с. Онгудай |
3260 |
12 |
114,8 |
0,18 |
2,20 |
0,27 |
0,52 |
0,73 |
1,04 |
|
288 |
Чарыш |
с. Усть-Кумир |
3470 |
15 |
362,5 |
0,26 |
2,00 |
0,80 |
1,21 |
1,54 |
2,02 |
|
289 |
Кондома |
Кузедеево |
6940 |
10 |
2015 |
0,27 |
1,30 |
2,64 |
4,03 |
4,97 |
6,22 |
|
290 |
Средняя Терсь |
заимка Санникова |
1900 |
13 |
967 |
0,22 |
1,15 |
3,35 |
4,57 |
5,67 |
6,86 |
|
291 |
Иня (нижняя) |
д. Кайлы |
15720 |
14 |
532 |
0,36 |
1,40 |
0,38 |
0,64 |
0,82 |
1,07 |
|
292 |
Сев, Сосьва |
Культбаза |
54810 |
7 |
3131 |
0,22 |
1,42 |
0,86 |
1,24 |
1,48 |
1,84 |
|
293 |
Иртыш |
Усть-Каменогорское (зим. Булочное у устья р. Бол. Дьяконовка) |
146100 |
33 |
2073 |
0,24 |
1,10 |
0,27 |
0,41 |
0,54 |
0,59 |
|
294 |
" |
г. Тобольск |
955500 |
51 |
7044 |
0,31 |
1,35 |
0,24 |
0,37 |
0,46 |
0,60 |
|
295 |
" |
г. Усть-Ишим |
526800 |
45 |
3800 |
0,31 |
1,03 |
0,19 |
0,30 |
0,37 |
0,48 |
|
296 |
Кальджир |
с. Чумек |
1170 |
11 |
28,1 |
0,31 |
1,55 |
0,14 |
0,24 |
0,29 |
0,27 |
|
297 |
Тургусун |
Ниже выхода из гор |
1220 |
11 |
355 |
0,30 |
1,58 |
1,74 |
2,77 |
3,51 |
4,52 |
|
298 |
Ульба |
с. Белый Луг |
1240 |
11 |
264 |
0,42 |
1,60 |
1,26 |
2,30 |
3,05 |
4,10 |
|
299 |
Уба |
у устья реки Чесноковки |
1460 |
10 |
304 |
0,28 |
1,33 |
1,27 |
1,95 |
2,41 |
3,04 |
|
300 |
" |
в 1 км выше Большого Порога . |
3540 |
11 |
1102 |
0,37 |
1,35 |
2,18 |
3,25 |
3,96 |
4,90 |
|
301 |
Омь |
с. Качалинская |
47410 |
8 |
330 |
- |
- |
0,10 |
- |
- |
- |
|
302 |
Селеты |
с. Ильинское |
7260 |
8 |
170 |
|
|
0,22 |
|
|
|
|
303 |
Ишим |
г. Акмолинск |
7400 |
15 |
312 |
1,03 |
2,15 |
0,39 |
1,20 |
1,78 |
2,87 |
|
304 |
" |
г. Бузулук |
76600 |
12 |
632 |
1,9 |
4,0 |
0,14 |
0,66 |
1,26 |
1,73 |
|
305 |
Колутон |
Железнодорожный мост |
15300 |
8 |
477 |
1,59 |
2Cυ |
0,35 |
1,45 |
2,60 |
4,42 |
|
306 |
Тобол |
г. Курган |
136400 |
28 |
647 |
1,42 |
3,00 |
0,09 |
0,35 |
0,61 |
1,02 |
|
307 |
" |
г. Ялуторойск |
210400 |
35 |
650 |
1,28 |
3,20 |
0,07 |
0,24 |
0,42 |
0,71 |
|
308 |
" |
с. Липовское |
391700 |
45 |
2895 |
0,34 |
1,30 |
0,18 |
0,31 |
0,38 |
0,49 |
|
309 |
Исеть |
г. Свердловск (рейка выше водослива) |
935 |
11 |
23,3 |
1,00 |
2Cυ |
0,14 |
0,42 |
0,64 |
0,96 |
|
310 |
Миасс |
д. Ракаево |
2445 |
13 |
73,8 |
0,76 |
2Cυ |
0,21 |
0,62 |
0,79 |
1,03 |
|
311 |
Тура |
пос. Верхотурье |
4700 |
46 |
304 |
0,63 |
1,55 |
0,54 |
1,20 |
0,65 |
2,32 |
|
312 |
" |
г. Тюмень |
55250 |
46 |
866 |
0,43 |
1,20 |
0,23 |
0,42 |
0,57 |
0,75 |
|
313 |
Тагил |
с. Малыгино |
3800 |
11 |
141 |
0,38 |
1,15 |
0,28 |
0,50 |
0,64 |
0,82 |
|
314 |
Тагил |
с. Трошково |
7380 |
27 |
366 |
0,52 |
1,50 |
0,46 |
0,92 |
1,27 |
1,71 |
|
315 |
Пышма |
с. Богандинское |
18360 |
37 |
188 |
0,90 |
2,50 |
0,11 |
0,53 |
0,83 |
1,30 |
|
316 |
Тавда |
ст. Тавда |
82680 |
34 |
1765 |
0,37 |
1,25 |
0,36 |
0,62 |
0,79 |
1,00 |
|
317 |
Конда |
ст. Болгары |
49520 |
7 |
510 |
0,14 |
0,88 |
0,15 |
0,19 |
0,22 |
0,25 |
|
|
|
Бассейн реки Енисей |
|
|
|
|
|
|
|
|
|
|
318 |
Енисей |
с. Означенное |
180000 |
31 |
7261 |
0,33 |
1,55 |
0,82 |
1,35 |
1,73 |
2,26 |
|
319 |
" |
пос. Базаиха (г. Красноярск) |
299400 |
38 |
13246 |
0,27 |
1,40 |
1,02 |
1,56 |
1,93 |
2,43 |
|
320 |
Кизир |
с. Имисское |
9080 |
11 |
2160 |
0,22 |
1,40 |
2,32 |
3,33 |
4,00 |
4,97 |
|
321 |
Кан |
с. Ново-Смоленка |
23100 |
10 |
1312 |
0,35 |
1,80 |
0,71 |
1,20 |
1,58 |
2,11 |
|
322 |
Бирюса |
д. Сполох |
24020 |
12 |
2262 |
0,26 |
1,92 |
1,16 |
1,76 |
2,22 |
2,91 |
|
323 |
Уда (Тасеево) |
д. Михалево |
127400 |
9 |
4627 |
0,68 |
1,65 |
0,70 |
1,08 |
1,36 |
1,76 |
|
324 |
Илим |
д. Сотниково |
24700 |
11 |
1656 |
0,33 |
1,65 |
0,83 |
1,44 |
1,90 |
2,54 |
|
325 |
Курейка |
Графитов рудник |
38810 |
7 |
5300 |
0,30 |
1,00 |
1,87 |
2,94 |
3,59 |
4,48 |
|
326 |
Оленек |
с Сухона |
125500 |
8 |
12261 |
0,24 |
1,02 |
1,86 |
2,68 |
3,21 |
3,88 |
|
|
|
Бассейн моря Лаптевых |
|
|
|
|
|
|
|
|
|
|
327 |
Лена |
с. Качуг |
15930 |
26 |
646 |
0,58 |
1,55 |
0,46 |
0,98 |
1,35 |
1,85 |
|
328 |
" |
с. Грузновское |
43500 |
23 |
1425 |
0,43 |
1,10 |
0,47 |
0,84 |
1,05 |
1,83 |
|
329 |
" |
с. Усть-Кут |
76090 |
32 |
3166 |
0,42 |
1,20 |
0,63 |
1,22 |
1,58 |
2,10 |
|
330 |
" |
г. Киренск |
141000 |
21 |
6694 |
0,32 |
1,40 |
0,90 |
1,49 |
1,89 |
2,42 |
|
331 |
" |
г. Солянка |
773000 |
11 |
34118 |
0,23 |
1,25 |
1,30 |
1,89 |
2,27 |
2,79 |
|
332 |
Киренга |
д. Шорохова |
46680 |
15 |
3832 |
0,24 |
1,30 |
1,21 |
1,77 |
2,12 |
2,63 |
|
333 |
Витим |
г. Бодайбо |
185500 |
30 |
11745 |
0,25 |
0,90 |
1,31 |
1,90 |
2,25 |
2,72 |
|
334 |
Алдан |
г. Томмот |
46100 |
19 |
5807 |
0,29 |
1,25 |
1,84 |
2,82 |
3,50 |
4,48 |
|
335 |
" |
Охотский перевоз |
482300 |
17 |
28965 |
0,27 |
1,10 |
1,58 |
2,35 |
2,72 |
4,35 |
|
336 |
Тимптон |
пос. Нагорный |
1390 |
14 |
250,5 |
0,35 |
1,45 |
1,09 |
2,00 |
2,32 |
3,08 |
|
337 |
Вилюй |
с. Сунтар |
219300 |
17 |
8309 |
0,25 |
1,20 |
0,82 |
1,21 |
1,47 |
1,82 |
|
|
|
Бассейн Аральского моря и бессточных озер и рек Средней Азии |
|
|
|
|
|
|
|
|
|
|
|
|
Реки Центрального Казахстана |
|
|
|
|
|
|
|
|
|
|
338 |
Джаксы Сары-Су |
г. Сары-Су |
1080 |
11 |
19,3 |
1,05 |
2,20 |
0,10 |
0,28 |
0,48 |
0,74 |
|
339 |
Тантек |
с. Уч-Арал |
3330 |
13 |
265 |
0,56 |
2Cυ |
0,60 |
1,37 |
1,66 |
2,20 |
|
340 |
Нура |
с. Сергиопольский |
11280 |
11 |
258 |
1,00 |
2,02 |
0,24 |
0,71 |
1,08 |
1,62 |
|
341 |
" |
" |
11280 |
14 |
496 |
1,15 |
2Cυ |
0,45 |
1,50 |
2,42 |
3,76 |
|
342 |
" |
Романовское |
40600 |
9 |
419 |
- |
- |
0,15 |
- |
- |
- |
|
|
|
Бассейн оз. Балхаш |
|
|
|
|
|
|
|
|
|
|
343 |
Токрау |
с. Ак-Тумсук |
3890 |
10 |
15,3 |
1,23 |
2Cυ |
0,03 |
0,10 |
0,14 |
0,22 |
|
344 |
Лепса |
г. Лепсинск |
1170 |
12 |
107 |
0,42 |
1,60 |
0,54 |
0,87 |
1,30 |
1,75 |
|
345 |
" |
Ново-Антоновское |
2120 |
15 |
141 |
0,42 |
1,90 |
0,57 |
1,04 |
1,41 |
1,95 |
|
346 |
Чарын |
урочище Сары-Тогой |
7510 |
14 |
151 |
0,53 |
1,75 |
0,19 |
0,39 |
0,53 |
0,74 |
|
347 |
Каскелен |
с. Илийское |
3570 |
11 |
39 |
0,45 |
1,30 |
0,90 |
0,16 |
0,21 |
0,27 |
|
|
|
Бассейн оз. Иссык-Куль |
|
|
|
|
|
|
|
|
|
|
348 |
Джаргалап |
с. Лизогубовка |
234 |
14 |
36,1 |
0,34 |
1,50 |
0,60 |
1,00 |
1,29 |
1,68 |
|
|
|
Река Чу |
|
|
|
|
|
|
|
|
|
|
349 |
Кара-Ходжур |
с. Сары-Булак (ниже устья ручья) |
1380 |
10 |
58,9 |
0,50 |
2,20 |
0,25 |
0,52 |
0,74 |
1,11 |
|
|
|
Бассейн р. Сыр-Дарьи |
|
|
|
|
|
|
|
|
|
|
350 |
Сара-Супрова (Ходжа Ата-Сай) |
устье реки Тумаян |
206 |
11 |
17,9 |
0,26 |
1,60 |
0,33 |
0,50 |
0,62 |
0,79 |
|
351 |
Афлатун |
кишлак Афлатун |
772 |
11 |
40,4 |
0,25 |
1,40 |
0,28 |
0,41 |
0,50 |
0,63 |
|
352 |
Кугарт-Сай |
кишлак Джиргитал |
935 |
12 |
105 |
0,42 |
2,05 |
0,62 |
1,11 |
1,56 |
2,18 |
|
353 |
Кара-Упгур |
с. Воздвиженское |
1160 |
15 |
165 |
0,37 |
1,25 |
0,83 |
1,39 |
1,70 |
2,11 |
|
354 |
Майли-Су |
Зимовка-Боб |
579 |
15 |
39,6 |
0,47 |
1,70 |
0,34 |
0,64 |
0,86 |
1,15 |
|
555 |
Ангрен |
с. Турк |
1490 |
17 |
147 |
0,41 |
1,65 |
0,61 |
1,11 |
1,47 |
2,00 |
|
356 |
" |
пос. Самарский |
5270 |
18 |
197 |
0,42 |
1,70 |
0,32 |
0,58 |
0,78 |
1,06 |
|
|
|
Бассейн р. Арыс |
|
|
|
|
|
|
|
|
|
|
357 |
Арыс |
с. Мамаевка* |
6400 |
16 |
230 |
0,50 |
1,50 |
0,32 |
0,63 |
0,86 |
1,16* |
|
358 |
" |
железнодорожная ст. Тимур |
14470 |
22 |
167 |
0,45 |
1,40 |
0,13 |
0,24 |
0,31 |
0,42* |
|
359 |
Майдан-Тал |
Устье |
471 |
10 |
61,0 |
0,21 |
1,75 |
0,60 |
0,86 |
1,07 |
1,32* |
|
|
|
Бассейн р. Аму-Дарьи |
|
|
|
|
|
|
|
|
|
|
360 |
Каратаг-Дарья |
г. Каратаг |
684 |
13 |
130 |
0,24 |
2Cυ |
1,00 |
1,41 |
1,75 |
2,00 |
|
|
|
Бессточные реки между р. Сыр-Дарьей и р. Аму-Дарьей |
|
|
|
|
|
|
|
|
|
|
361 |
Кашка-Дарья |
кишлак Кайны |
468 |
15 |
53,3 |
0,71 |
2Cυ |
0,53 |
1,26 |
1,76 |
2,46 |
|
362 |
Кашка-Дарья |
г. Чиркачи |
2430 |
13 |
120 |
0,40 |
1,25 |
0,35 |
0,61 |
0,79 |
1,03 |
|
363 |
Кара-Су |
кишлак Улян |
132 |
10 |
8,08 |
0,48 |
1,85 |
0,24 |
0,40 |
0,57 |
0,78 |
|
364 |
Гузар-Дарьи |
" Яр-Тепе |
3170 |
11 |
59,7 |
0,62 |
1,85 |
0,14 |
0,32 |
0,45 |
0,64 |
|
365 |
Катта-Уру |
" Кошулуш |
1400 |
13 |
24,2 |
0,46 |
2,35 |
0,11 |
0,21 |
0,29 |
0,42 |
|
366 |
Кичик-Уру |
" Куль-Кишлак |
1660 |
14 |
19,6 |
0,70 |
1,90 |
0,08 |
0,15 |
0,26 |
0,38 |
|
|
|
Бессточные реки Мургаб и Теджен |
|
|
|
|
|
|
|
|
|
|
367 |
Мургаб |
с. Таш-Кепри |
46880 |
11 |
132 |
0,39 |
1,40 |
0,04 |
0,07 |
0,10 |
0,13 |
|
|
|
Бассейн р. Колымы |
|
|
|
|
|
|
|
|
|
|
368 |
Колыма |
в 0,5 км выше впадения р. Бахапчи |
60690 |
9 |
3570 |
0,62 |
2,18 |
0,92 |
2,04 |
3,02 |
4,41 |
|
369 |
" |
в 1,5 км выше пос. Усть-Средникан |
101800 |
8 |
7280 |
0,39 |
1,23 |
1,29 |
2,26 |
2,92 |
3,79 |
|
370 |
" |
г. Средне-Колымск |
361400 |
13 |
18346 |
0,18 |
1,38 |
1,24 |
1,68 |
1,97 |
2,36 |
|
371 |
Средникан |
в 3 км выше пос. Усть-Средникан |
1750 |
9 |
328 |
0,49 |
1,40 |
1,21 |
2,36 |
3,14 |
4,22 |
|
372 |
Бохапча |
в 5,4 км от устья |
14330 |
6 |
1560 |
- |
- |
1,19 |
- |
- |
- |
|
373 |
Таскан |
в 0,8 км выше пос. Таскан 2-й |
9540 |
6 |
907 |
- |
- |
0,94 |
- |
- |
- |
|
374 |
Берелех |
в 5,9 км выше впадения ключа Мальдяк |
5830 |
3 |
315 |
- |
- |
0,47 |
- |
- |
- |
|
375 |
Хатыннах |
в 0,7 км ниже впадения ключа Малого |
157 |
3 |
29,3 |
- |
- |
0,66 |
- |
- |
- |
* Сток искажен набором воды на орошение.
Учитывая маловодность последнего периода и в этой связи некоторую преуменьшенность средних максимумов расходов по этим створам, принимаем среднее значение A = 2,40 м3/сек. Тогда расход 1 % обеспеченности составит
Q = AF0,75 = 240×3400,75 = 190 м3/сек.
В том случае, если в районе перехода имеются небольшие реки-аналоги (не указанные, в табл. 13) с площадью бассейна до 1000 км2 (с достаточно большим рядом горизонтов на водомерном посту и гидрометрическими расходами), то можно расчетные расходы с этого бассейна перенести на новый переход, определив вначале параметр на реке-аналоге:
![]()
где Q и F - расход и площадь бассейна на реке-аналоге, а затем найти расход на новом переходе:
Q1 = AF10,75,
где Q1 и F1 - расход и площадь бассейна на новом переходе.
Значения коэффициента заболоченности δ
|
Процент заболоченности бассейна |
δ |
|
0 |
1 |
|
10 |
0,95 |
|
20 |
0,90 |
|
30 |
0,85 |
|
40 |
0,80 |
|
50 |
0,75 |
|
60 |
0,70 |
|
70 |
0,65 |
|
80 |
0,60 |
|
90 |
0,55 |
|
100 |
0,50 |
Значения коэффициента залесенности δ'
|
Процент залесенности бассейна |
δ' |
|
0 |
1 |
|
10 |
0,95 |
|
20 |
0,90 |
|
30 |
0,85 |
|
'10 |
0,80 |
|
50 |
0,75 |
|
Более 50 |
0,75 |
§ 4. Определение расхода, глубин и бытовых скоростей в подходящих руслах
Определение гидравлических характеристик подводящих русел производится следующим образом.
По живому сечению потока у сооружения ω и принятой гидравлической шероховатости лога m вычисляют (при разных, обычно трех-четырех, глубинах, через 0,5 - 1 м) бытовые скорости:
υ = mH2/3i1/2 м/сек
и расходы:
Q = ωυ м3/сек,
где H - глубина воды в логе, м;
i - уклон лога в тысячных;
m - гидравлическая шероховатость тога.
Скорость течения воды по логу можно принимать по табл. 16, в зависимости от сечения лога, уклона и глубины лога H1.
Скорости течения воды по логу
υ = mH2/3i1/2
|
H, м |
Уклон лога, % |
||||||||||
|
5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
Скорость течения воды υ, м/сек |
|||||||||||
|
Треугольное сечение главного лога |
|||||||||||
|
m = 10, H = 0,5H1 |
|||||||||||
|
0,25 |
0,17 |
0,25 |
0,35 |
0,43 |
0,50 |
0,56 |
0,61 |
0,66 |
0,71 |
0,75 |
0,79 |
|
0,50 |
0,28 |
0,40 |
0,56 |
0,69 |
0,80 |
0,90 |
0,98 |
1,06 |
1,13 |
1,20 |
1,26 |
|
0,75 |
0,37 |
0,52 |
0,73 |
0,90 |
1,04 |
1,16 |
1,27 |
1,37 |
1,47 |
1,56 |
1,64 |
|
1,0 |
0,44 |
0,63 |
0,89 |
1,09 |
1,26 |
1,41 |
1,54 |
1,66 |
1,78 |
1,89 |
1,98 |
|
1,25 |
0,51 |
0,73 |
1,02 |
1,26 |
1,46 |
1,64 |
1,79 |
1,93 |
2,07 |
2,19 |
2,30 |
|
1,50 |
0,58 |
0,82 |
1,16 |
1,42 |
1,64 |
1,84 |
2,01 |
2,16 |
2,32 |
2,46 |
2,58 |
|
1,75 |
0,65 |
0,91 |
1,28 |
1,57 |
1,82 |
2,04 |
2,30 |
2,40 |
2,56 |
2,73 |
2,87 |
|
2,00 |
0,71 |
1,00 |
1,41 |
1,73 |
2,00 |
2,24 |
2,45 |
2,64 |
2,83 |
3,00 |
3,15 |
|
2,25 |
0,77 |
1,08 |
1,52 |
1,87 |
2,16 |
2,42 |
2,65 |
2,85 |
3,06 |
3,24 |
3,40 |
|
2,50 |
0,82 |
1,16 |
1,64 |
2,01 |
2,32 |
2,60 |
2,84 |
3,05 |
3,28 |
3,48 |
3,65 |
|
2,75 |
0,88 |
1,25 |
1,76 |
2,16 |
2,50 |
2,80 |
3,05 |
3,30 |
3,54 |
3,75 |
3,94 |
|
3,00 |
0,93 |
1,31 |
1,85 |
2,27 |
2,62 |
2,98 |
3,21 |
3,46 |
3,71 |
3,93 |
4,13 |
|
3,50 |
1,03 |
1,45 |
2,04 |
2,50 |
2,90 |
3,25 |
3,55 |
3,83 |
4,10 |
4,35 |
4,57 |
|
4,00 |
1,13 |
1,59 |
2,24 |
2,75 |
3,18 |
3,56 |
3,90 |
4,20 |
4,50 |
4,77 |
5,01 |
|
4,50 |
1,21 |
1,71 |
2,41 |
2,96 |
3,42 |
3,83 |
4,19 |
4,51 |
5,13 |
5,13 |
5,39 |
|
5,00 |
1,31 |
1,84 |
2,59 |
3,18 |
3,68 |
4,12 |
4,51 |
4,86 |
5,21 |
5,52 |
5,80 |
|
5,50 |
1,39 |
1,96 |
2,76 |
3,39 |
3,92 |
4,39 |
4,80 |
5,17 |
5,55 |
5,88 |
6,17 |
|
6,00 |
1,48 |
2,08 |
2,93 |
3,60 |
4,16 |
4,66 |
5,09 |
5,49 |
5,88 |
6,24 |
6,55 |
|
Треугольное сечение главного лога |
|||||||||||
|
m = 15, H = 0,5H1 |
|||||||||||
|
0,25 |
0,25 |
0,37 |
0,57 |
0,64 |
0,75 |
0,84 |
0,91 |
0,99 |
1,06 |
1,07 |
1,19 |
|
0,50 |
0,42 |
0,60 |
0,84 |
1,04 |
1,20 |
1,35 |
1,47 |
1,59 |
1,69 |
1,80 |
1,89 |
|
0,75 |
0,55 |
0,78 |
1,00 |
1,35 |
1,56 |
1,74 |
1,90 |
2,06 |
2,20 |
2,34 |
2,46 |
|
1,00 |
0,66 |
0,95 |
1,33 |
1,64 |
1,89 |
2,11 |
2,31 |
2,49 |
2,67 |
2,83 |
2,97 |
|
1,25 |
0,76 |
1,09 |
1,53 |
1,89 |
2,19 |
2,46 |
2,68 |
2,90 |
3,10 |
3,28 |
3,45 |
|
1,50 |
0,87 |
1,23 |
1,74 |
2,13 |
2,46 |
2,76 |
3,01 |
3,24 |
3,48 |
3,69 |
3,87 |
|
1,75 |
0,97 |
1,36 |
1,92 |
2,36 |
2,73 |
3,06 |
3,45 |
3,60 |
3,84 |
4,10 |
4,30 |
|
2,00 |
1,06 |
1,50 |
2,11 |
2,59 |
3,00 |
3,36 |
3,67 |
3,96 |
4,25 |
4,50 |
4,73 |
|
2,25 |
1,15 |
1,62 |
2,28 |
2,80 |
3,24 |
3,63 |
3,98 |
4,27 |
4,59 |
4,85 |
5,10 |
|
2,50 |
1,23 |
1,74 |
2,46 |
3,01 |
3,48 |
3,90 |
4,26 |
4,60 |
4,91 |
5,23 |
5,48 |
|
2,75 |
1,32 |
1,87 |
2,62 |
3,24 |
3,75 |
4,20 |
4,59 |
4,95 |
5,30 |
5,63 |
5,90 |
|
3,00 |
1,39 |
1,96 |
2,77 |
3,40 |
3,93 |
4,40 |
4,82 |
5,19 |
5,56 |
5,90 |
6,20 |
|
3,50 |
1,54 |
2,17 |
3,05 |
3,75 |
4,35 |
4,88 |
5,33 |
5,75 |
6,15 |
6,53 |
6,85 |
|
4,00 |
1,69 |
2,38 |
3,36 |
4,14 |
4,78 |
5,35 |
5,85 |
6,30 |
6,75 |
7,15 |
7,51 |
|
4,50 |
1,81 |
2,56 |
3,62 |
4,45 |
5,13 |
5,75 |
6,29 |
6,76 |
7,70 |
7,70 |
8,08 |
|
5,00 |
1,91 |
2,76 |
3,88 |
4,78 |
5,52 |
6,17 |
6,76 |
7,30 |
7,82 |
8,28 |
8,70 |
|
5,50 |
2,09 |
2,94 |
4,14 |
5,08 |
5,88 |
6,58 |
7,20 |
7,75 |
8,33 |
8,82 |
9,25 |
|
6,00 |
2,22 |
3,12 |
4,30 |
5,40 |
6,34 |
7,00 |
7,64 |
8,24 |
8,82 |
9,35 |
9,83 |
|
Треугольное сечение главного лога |
|||||||||||
|
m = 20, H = 0,5H1 |
|||||||||||
|
0,25 |
0,34 |
0,50 |
0,70 |
0,86 |
1,00 |
1,12 |
1,22 |
1,32 |
1,42 |
1,50 |
1,58 |
|
0,50 |
0,50 |
0,80 |
1,12 |
1,38 |
1,60 |
1,80 |
1,96 |
2,12 |
2,26 |
2,40 |
2,52 |
|
0,75 |
0,74 |
1,04 |
1,46 |
1,80 |
2,08 |
2,32 |
2,54 |
2,74 |
2,94 |
3,12 |
3,28 |
|
1,00 |
0,88 |
1,26 |
1,78 |
2,18 |
2,52 |
2,82 |
3,08 |
2,32 |
3,56 |
3,78 |
3,96 |
|
1,25 |
1,02 |
1,46 |
2,04 |
2,52 |
2,84 |
3,28 |
3,58 |
3,86 |
4,14 |
4,38 |
4,60 |
|
1,50 |
1,16 |
1,64 |
2,32 |
2,84 |
3,28 |
3,68 |
4,02 |
4,32 |
4,64 |
4,92 |
5,16 |
|
1,75 |
1,30 |
1,82 |
2,56 |
3,14 |
3,64 |
4,08 |
4,60 |
4,80 |
5,12 |
5,46 |
5,74 |
|
2,00 |
1,42 |
2,00 |
2,82 |
3,46 |
4,00 |
4,48 |
4,90 |
5,28 |
5,66 |
6,00 |
6,30 |
|
2,25 |
1,54 |
2,16 |
3,04 |
3,74 |
4,32 |
4,84 |
5,30 |
5,70 |
6,12 |
6,48 |
6,80 |
|
2,50 |
1,64 |
2,32 |
3,28 |
4,02 |
4,64 |
5,20 |
5,68 |
6,12 |
6,56 |
6,96 |
7,30 |
|
2,75 |
1,76 |
2,50 |
3,52 |
4,32 |
5,00 |
5,60 |
6,12 |
6,60 |
7,08 |
7,50 |
7,88 |
|
3,00 |
1,86 |
2,62 |
3,70 |
4,54 |
5,24 |
5,86 |
6,42 |
6,92 |
7,42 |
7,86 |
8,26 |
|
3,50 |
2,06 |
2,90 |
4,08 |
5,00 |
5,80 |
6,50 |
7,10 |
7,66 |
8,20 |
8,70 |
9,14 |
|
4,00 |
2,26 |
3,18 |
4,48 |
5,50 |
6,36 |
7,12 |
7,80 |
8,40 |
9,00 |
9,54 |
10,0 |
|
4,50 |
2,42 |
3,42 |
4,82 |
5,92 |
6,84 |
7,66 |
8,38 |
9,02 |
10,3 |
10,3 |
- |
|
5,00 |
2,62 |
3,68 |
5,18 |
6,36 |
7,36 |
8,24 |
9,02 |
9,72 |
- |
- |
- |
|
5,50 |
2,78 |
3,92 |
5,52 |
6,78 |
7,84 |
8,78 |
9,60 |
10,3 |
- |
- |
- |
|
6,00 |
2,96 |
4,16 |
5,86 |
7,20 |
8,32 |
9,32 |
10,18 |
- |
- |
- |
- |
|
Треугольное сечение главного лога |
|||||||||||
|
m = 25, H = 0,5H1 |
|||||||||||
|
0,25 |
0,42 |
0,62 |
0,87 |
1,07 |
1,25 |
1,40 |
1,52 |
1,65 |
1,77 |
1,87 |
1,97 |
|
0,50 |
0,70 |
1,00 |
1,40 |
1,72 |
2,00 |
2,25 |
2,45 |
2,65 |
2,82 |
3,00 |
3,15 |
|
0,75 |
0,92 |
1,30 |
1,83 |
2,25 |
2,60 |
2,90 |
3,18 |
3,42 |
3,68 |
3,90 |
4,10 |
|
1,00 |
1,10 |
1,57 |
2,23 |
2,72 |
3,15 |
3,58 |
3,85 |
4,15 |
4,45 |
4,72 |
4,95 |
|
1,25 |
1,25 |
1,83 |
2,55 |
3,15 |
3,65 |
4,10 |
4,48 |
4,83 |
5,18 |
5,48 |
5,75 |
|
1,50 |
1,45 |
2,05 |
2,90 |
3,55 |
4,10 |
4,60 |
5,02 |
5,40 |
5,80 |
6,15 |
6,45 |
|
1,75 |
1,62 |
2,28 |
3,20 |
3,92 |
4,55 |
5,10 |
5,75 |
6,00 |
6,40 |
6,83 |
7,18 |
|
2,00 |
1,77 |
2,50 |
3,53 |
4,33 |
5,00 |
5,60 |
6,12 |
6,70 |
7,09 |
7,50 |
7,88 |
|
2,25 |
1,92 |
2,70 |
3,80 |
4,67 |
5,40 |
6,05 |
6,73 |
7,13 |
7,65 |
8,10 |
8,50 |
|
2,50 |
2,05 |
2,90 |
4,10 |
5,02 |
5,80 |
6,50 |
7,10 |
7,75 |
8,20 |
8,70 |
9,12 |
|
2,75 |
2,20 |
3,16 |
4,40 |
5,40 |
6,25 |
7,00 |
7,65 |
8,25 |
8,85 |
9,38 |
9,85 |
|
3,00 |
2,33 |
3,28 |
4,62 |
5,68 |
6,55 |
7,33 |
8,02 |
8,75 |
9,26 |
9,83 |
10,3 |
|
3,50 |
2,57 |
3,62 |
5,10 |
6,25 |
7,25 |
8,13 |
8,89 |
9,57 |
10,2 |
10,9 |
- |
|
4,00 |
2,82 |
3,98 |
5,60 |
6,88 |
7,95 |
8,90 |
9,75 |
10,5 |
- |
- |
- |
|
4,50 |
3,02 |
4,27 |
6,02 |
7,40 |
8,55 |
9,53 |
10,5 |
- |
- |
- |
- |
|
5,00 |
3,27 |
4,60 |
6,48 |
7,95 |
9,20 |
10,3 |
- |
- |
- |
- |
- |
|
5,50 |
3,48 |
4,90 |
6,90 |
8,48 |
9,80 |
- |
- |
- |
- |
- |
- |
|
6,00 |
3,70 |
5,20 |
7,33 |
9,00 |
10,4 |
- |
- |
- |
- |
- |
- |
|
Трапецеидальное сечение главного лога |
|||||||||||
|
m = 10, H = 0,6H1 |
|||||||||||
|
0,25 |
0,19 |
0,28 |
0,39 |
0,48 |
0,56 |
0,63 |
0,69 |
0,74 |
0,79 |
0,84 |
0,88 |
|
0,50 |
0,32 |
0,45 |
0,63 |
0,78 |
0,90 |
1,01 |
1,10 |
1,19 |
1,27 |
1,35 |
1,42 |
|
0,75 |
0,41 |
0,53 |
0,81 |
1,00 |
1,16 |
1,30 |
1,42 |
1,53 |
1,64 |
1,74 |
1,83 |
|
1,00 |
0,50 |
0,71 |
1,00 |
1,22 |
1,42 |
1,59 |
1,74 |
1,87 |
2,00 |
2,13 |
2,23 |
|
1,25 |
0,57 |
0,82 |
1,15 |
1,41 |
1,64 |
1,84 |
2,01 |
2,16 |
2,32 |
2,46 |
2,58 |
|
1,50 |
0,66 |
0,93 |
1,31 |
1,60 |
1,86 |
2,08 |
2,28 |
2,46 |
2,63 |
2,79 |
2,93 |
|
1,75 |
0,73 |
1,03 |
1,45 |
1,78 |
2,06 |
2,30 |
2,52 |
2,72 |
2,91 |
3,09 |
3,24 |
|
2,00 |
0,80 |
1,13 |
1,59 |
1,95 |
2,26 |
2,53 |
2,77 |
2,98 |
3,19 |
3,39 |
3,56 |
|
2,25 |
0,86 |
1,22 |
1,72 |
2,11 |
2,44 |
2,73 |
2,98 |
3,22 |
3,45 |
3,66 |
3,84 |
|
2,50 |
0,93 |
1,31 |
1,84 |
2,26 |
2,62 |
2,93 |
3,21 |
3,45 |
3,70 |
3,93 |
4,12 |
|
2,75 |
0,98 |
1,39 |
1,96 |
2,40 |
2,78 |
3,11 |
3,41 |
3,66 |
3,93 |
4,17 |
4,38 |
|
3,00 |
1,05 |
1,49 |
2,10 |
2,58 |
2,98 |
3,34 |
3,65 |
3,93 |
4,21 |
4,47 |
4,69 |
|
3,50 |
1,15 |
1,63 |
2,29 |
2,82 |
3,26 |
3,65 |
3,99 |
4,30 |
4,61 |
4,89 |
5,13 |
|
4,00 |
1,27 |
1,79 |
2,52 |
3,09 |
3,58 |
3,85 |
4,39 |
4,73 |
5,06 |
5,37 |
5,64 |
|
4,50 |
1,37 |
1,93 |
2,72 |
3,34 |
3,86 |
4,32 |
4,73 |
5,09 |
5,46 |
5,79 |
6,08 |
|
5,00 |
1,47 |
2,08 |
2,93 |
9,60 |
4,16 |
4,66 |
5,09 |
5,49 |
5,88 |
6,24 |
6,55 |
|
5,50 |
1,57 |
2,21 |
3,11 |
3,82 |
4,42 |
4,95 |
5,41 |
5,83 |
6,25 |
6,63 |
6,96 |
|
6,00 |
1,66 |
2,34 |
3,29 |
4,04 |
4,68 |
5,24 |
5,73 |
6,17 |
6,62 |
7,02 |
7,37 |
|
Трапецеидальное сечение главного лога |
|||||||||||
|
m = 15, H = 0,6H1 |
|||||||||||
|
0,25 |
0,29 |
0,42 |
0,59 |
0,72 |
0,84 |
0,95 |
1,03 |
1,11 |
1,18 |
1,26 |
1,32 |
|
0,50 |
0,48 |
0,68 |
0,95 |
1,17 |
1,35 |
1,51 |
1,65 |
1,78 |
1,90 |
2,03 |
2,13 |
|
0,75 |
0,61 |
0,87 |
1,22 |
1,50 |
1,74 |
1,95 |
2,13 |
2,30 |
2,46 |
2,61 |
2,74 |
|
1,00 |
0,75 |
1,06 |
1,50 |
1,83 |
2,13 |
2,39 |
2,61 |
2,82 |
3,00 |
3,19 |
3,34 |
|
1,25 |
0,86 |
1,23 |
1,73 |
2,11 |
2,46 |
2,76 |
3,01 |
3,24 |
3,48 |
3,69 |
3,87 |
|
1,50 |
0,99 |
1,39 |
1,96 |
2,40 |
2,79 |
3,12 |
3,42 |
3,70 |
3,95 |
4,18 |
4,40 |
|
1,75 |
1,09 |
1,54 |
2,18 |
2,67 |
3,09 |
3,45 |
3,78 |
4,08 |
4,36 |
4,64 |
4,85 |
|
2,00 |
1,20 |
1,69 |
2,39 |
2,93 |
3,39 |
3,79 |
4,16 |
4,48 |
4,79 |
5,09 |
5,34 |
|
2,25 |
1,29 |
1,83 |
2,58 |
3,17 |
3,66 |
4,10 |
4,47 |
4,83 |
5,17 |
5,50 |
5,75 |
|
2,50 |
1,39 |
1,96 |
2,76 |
3,39 |
3,93 |
4,39 |
4,81 |
5,17 |
5,55 |
5,90 |
6,18 |
|
2,75 |
1,47 |
2,08 |
2,94 |
3,60 |
4,17 |
4,66 |
5,11 |
5,49 |
5,90 |
6,25 |
6,57 |
|
3,00 |
1,57 |
2,23 |
3,15 |
3,87 |
4,47 |
5,01 |
5,47 |
5,90 |
6,31 |
6,70 |
7,02 |
|
3,50 |
1,73 |
2,44 |
3,44 |
4,23 |
4,89 |
5,47 |
5,99 |
6,45 |
6,91 |
7,33 |
7,68 |
|
4,00 |
1,91 |
2,69 |
3,78 |
4,63 |
5,37 |
5,78 |
6,58 |
7,10 |
7,59 |
8,05 |
8,45 |
|
4,50 |
2,06 |
2,90 |
4,08 |
5,01 |
5,79 |
6,48 |
7,09 |
7,63 |
8,20 |
8,68 |
9,10 |
|
5,00 |
2,20 |
3,12 |
4,40 |
5,40 |
6,24 |
6,99 |
7,64 |
8,24 |
8,82 |
9,35 |
9,82 |
|
5,50 |
2,36 |
3,32 |
4,66 |
5,73 |
6,63 |
7,42 |
8,11 |
8,75 |
9,37 |
9,80 |
10,0 |
|
6,00 |
2,49 |
3,51 |
4,94 |
6,06 |
7,02 |
7,86 |
8,59 |
9,25 |
9,92 |
10,0 |
- |
|
Трапецеидальное сечение главного лога |
|||||||||||
|
m = 20H = 0,6H1 |
|||||||||||
|
0,25 |
0,38 |
0,56 |
0,78 |
0,96 |
1,12 |
1,26 |
1,38 |
1,48 |
1,58 |
1,68 |
1,76 |
|
0,50 |
0,64 |
0,90 |
1,26 |
1,56 |
1,80 |
2,02 |
2,20 |
2,38 |
2,54 |
2,70 |
2,84 |
|
0,75 |
0,82 |
1,16 |
1,62 |
2,00 |
2,32 |
2,60 |
2,84 |
3,06 |
3,28 |
3,48 |
3,66 |
|
1,00 |
1,00 |
1,42 |
2,00 |
2,44 |
2,84 |
3,18 |
3,48 |
3,74 |
4,00 |
4,26 |
4,46 |
|
1,25 |
1,14 |
1,64 |
2,30 |
2,82 |
3,28 |
3,68 |
4,02 |
4,32 |
4,64 |
4,92 |
5,16 |
|
1,50 |
1,32 |
1,86 |
2,62 |
3,20 |
3,72 |
4,16 |
4,56 |
4,92 |
5,26 |
5,58 |
5,86 |
|
1,75 |
1,46 |
2,06 |
2,90 |
3,56 |
4,12 |
4,60 |
5,04 |
5,44 |
5,82 |
6,18 |
6,48 |
|
2,00 |
1,60 |
2,26 |
3,18 |
3,90 |
4,52 |
5,06 |
5,54 |
5,96 |
6,38 |
6,78 |
7,12 |
|
2,25 |
1,72 |
2,44 |
3,44 |
4,22 |
4,88 |
5,46 |
5,96 |
6,44 |
6,90 |
7,32 |
7,68 |
|
2,50 |
1,86 |
2,62 |
3,68 |
4,52 |
5,24 |
5,86 |
6,42 |
6,90 |
7,40 |
7,86 |
8,24 |
|
2,75 |
1,96 |
2,78 |
3,92 |
4,80 |
5,56 |
6,22 |
6,82 |
7,32 |
7,86 |
8,34 |
8,76 |
|
3,00 |
2,10 |
2,98 |
4,20 |
5,16 |
5,96 |
6,68 |
7,30 |
7,86 |
8,42 |
8,94 |
9,38 |
|
3,50 |
2,30 |
3,26 |
4,58 |
5,64 |
6,52 |
7,39 |
7,93 |
8,60 |
9,22 |
9,78 |
10,3 |
|
4,00 |
2,54 |
3,58 |
5,04 |
6,18 |
7,16 |
7,70 |
8,78 |
9,46 |
10,1 |
10,7 |
- |
|
4,50 |
2,74 |
3,86 |
5,44 |
6,68 |
7,72 |
8,64 |
9,46 |
10,2 |
- |
- |
- |
|
5,00 |
2,94 |
4,16 |
5,86 |
7,20 |
8,32 |
9,32 |
10,2 |
- |
- |
- |
- |
|
5,50 |
3,14 |
4,42 |
6,22 |
7,64 |
8,84 |
9,90 |
- |
- |
- |
- |
- |
|
6,00 |
3,32 |
4,68 |
6,58 |
8,08 |
9,36 |
10,48 |
- |
- |
- |
- |
- |
|
Трапецеидальное сечение главного лога |
|||||||||||
|
m = 25, H = 0,6H1 |
|||||||||||
|
0,25 |
0,43 |
0,70 |
0,97 |
1,20 |
1,40 |
1,57 |
1,72 |
1,85 |
1,97 |
2,10 |
2,20 |
|
0,50 |
0,80 |
1,12 |
1,53 |
1,95 |
2,25 |
2,52 |
2,75 |
2,98 |
3,18 |
3,38 |
3,55 |
|
0,75 |
1,02 |
1,45 |
2,02 |
2,50 |
2,90 |
3,25 |
3,55 |
3, 82 |
4,10 |
4,35 |
4,57 |
|
1,00 |
1,25 |
1,77 |
2,50 |
3,05 |
355 |
3,98 |
4,35 |
4,38 |
5,00 |
5,83 |
5,56 |
|
1,25 |
1,43 |
2,05 |
2,87 |
3,52 |
4,10 |
4,60 |
5,03 |
5,40 |
5,80 |
6,15 |
6,45 |
|
1,50 |
1,65 |
2,32 |
3,27 |
4,00 |
4,65 |
5,20 |
5,70 |
6,15 |
6,58 |
6,93 |
7,33 |
|
1,75 |
1,82 |
2,58 |
3,62 |
4,43 |
5,15 |
5,75 |
6,30 |
6,80 |
7,28 |
7,73 |
8,10 |
|
2,00 |
2,00 |
2,82 |
3,97 |
4,88 |
5,65 |
6,32 |
6,92 |
7,95 |
7,98 |
8,48 |
8,90 |
|
2,25 |
2,15 |
3,05 |
4,30 |
5,27 |
6,10 |
4,82 |
7,45 |
8,05 |
8,61 |
9,15 |
9,60 |
|
2,50 |
2,33 |
3,27 |
4,60 |
5,65 |
6,55 |
7,32 |
8,02 |
8,62 |
9,25 |
9,82 |
10,3 |
|
2,75 |
2,42 |
3,47 |
4,90 |
6,00 |
6,95 |
7,77 |
8,52 |
9,15 |
9,85 |
10,4 |
- |
|
3,00 |
2,62 |
3,72 |
5,25 |
6,45 |
7,45 |
8,35 |
9,13 |
9,83 |
10,5 |
- |
- |
|
3,50 |
2,88 |
4,07 |
5,72 |
7,05 |
8,15 |
9,13 |
9,98 |
10,7 |
- |
- |
- |
|
4,00 |
3,17 |
4,48 |
6,30 |
7,73 |
8,95 |
9,63 |
11,0 |
- |
- |
- |
- |
|
4,50 |
3,42 |
4,82 |
6,80 |
8,35 |
9,65 |
10,8 |
- |
- |
- |
- |
- |
|
5,00 |
3,67 |
5,20 |
7,33 |
9,00 |
10,4 |
- |
- |
- |
- |
- |
- |
|
5,50 |
3,92 |
5,52 |
7,76 |
9,55 |
- |
- |
- |
- |
- |
- |
- |
|
6,00 |
4,15 |
5,85 |
8,24 |
10,1 |
- |
- |
- |
- |
- |
- |
- |
|
Прямоугольное сечение главного лога |
|||||||||||
|
m = 10, H = H1 |
|||||||||||
|
0,25 |
0,282 |
0,396 |
0,559 |
0,685 |
0,79 |
0,89 |
0,97 |
1,04 |
1,12 |
1,19 |
1,24 |
|
0,50 |
0,447 |
0,630 |
0,890 |
1,08 |
1,26 |
1,41 |
1,54 |
0,66 |
0,78 |
1,89 |
1,98 |
|
0,75 |
0,583 |
0,820 |
1,16 |
1,40 |
1,64 |
1,84 |
2,01 |
2,16 |
2,32 |
2,46 |
2,58 |
|
1,00 |
0,710 |
1,00 |
1,41 |
1,73 |
2,00 |
2,24 |
2,45 |
2,64 |
2,83 |
3,00 |
3,15 |
|
1,25 |
0,82 |
1,16 |
1,64 |
2,01 |
2,32 |
2,60 |
2,84 |
3,06 |
3,28 |
3,48 |
3,65 |
|
1,50 |
0,93 |
1,31 |
1,85 |
2,26 |
2,62 |
2,94 |
3,22 |
3,46 |
3,71 |
3,93 |
4,12 |
|
1,75 |
1,03 |
1,45 |
2,04 |
2,51 |
2,90 |
3,25 |
3,56 |
3,82 |
4,10 |
4,35 |
4,56 |
|
2,00 |
1,34 |
1,59 |
2,24 |
2,75 |
3,18 |
3,56 |
3,90 |
4,20 |
4,50 |
4,77 |
5,00 |
|
2,25 |
1,22 |
1,72 |
2,42 |
2,98 |
3,44 |
3,85 |
4,21 |
4,54 |
4,87 |
5,16 |
5,41 |
|
2,50 |
1,31 |
1,84 |
2,60 |
3,18 |
3,68 |
4,13 |
4,51 |
4,85 |
5,21 |
5,52 |
5,79 |
|
2,75 |
1,39 |
1,96 |
2,75 |
3,40 |
3,92 |
4,40 |
4,80 |
5,17 |
5,55 |
5,88 |
6,17 |
|
3,00 |
1,49 |
2,08 |
2,93 |
3,60 |
4,16 |
4,66 |
5,10 |
5,50 |
5,89 |
6,24 |
6,55 |
|
3,50 |
1,63 |
2,30 |
3,24 |
3,98 |
4,60 |
5,15 |
5,65 |
6,08 |
6,51 |
6,90 |
7,24 |
|
4,00 |
1,79 |
2,52 |
3,55 |
4,35 |
5,04 |
5,64 |
6,18 |
6,65 |
7,14 |
7,56 |
7,98 |
|
4,50 |
1,93 |
2,72 |
3,98 |
4,70 |
5,44 |
6,10 |
6,67 |
7,18 |
7,70 |
8,16 |
8,56 |
|
5,00 |
2,08 |
2,93 |
4,14 |
5,07 |
5,86 |
6,55 |
7,20 |
7,74 |
8,30 |
8,79 |
9,23 |
|
5,50 |
2,21 |
3,11 |
4,39 |
5,38 |
6,22 |
6,96 |
7,63 |
8,20 |
8,80 |
9,33 |
9,79 |
|
6,00 |
2,34 |
3,30 |
4,65 |
5,70 |
6,60 |
7,39 |
8,1 |
8,70 |
9,34 |
9,90 |
10,4 |
|
Прямоугольное сечение главного лога |
|||||||||||
|
m = 15, H = H1 |
|||||||||||
|
0,25 |
0,423 |
0,594 |
0,839 |
1,03 |
1,19 |
1,35 |
1,45 |
1,56 |
1,68 |
1,78 |
1,86 |
|
0,50 |
0,670 |
0,945 |
1,33 |
1,62 |
1,89 |
2,11 |
2,31 |
2,49 |
2,67 |
2,84 |
2,97 |
|
0,75 |
0,875 |
1,23 |
1,74 |
2,10 |
2,45 |
2,76 |
3,02 |
3,24 |
3,48 |
3,69 |
3,83 |
|
1,00 |
1,06 |
1,50 |
2,12 |
2,59 |
3,00 |
3,32 |
3,68 |
3,95 |
4,25 |
4,50 |
4,71 |
|
1,25 |
1,23 |
1,74 |
2,46 |
3,02 |
3,48 |
3,90 |
4,26 |
4,60 |
4,93 |
5,23 |
5,48 |
|
1,50 |
1,39 |
1,96 |
2,78 |
3,39 |
3,93 |
4,41 |
4,80 |
5,19 |
5,57 |
5,90 |
6,18 |
|
1,75 |
1,54 |
2,17 |
3,05 |
8,77 |
4,35 |
4,88 |
5,34 |
5,73 |
6,15 |
6,53 |
6,85 |
|
2,00 |
1,69 |
2,38 |
3,36 |
4,13 |
4,77 |
5,35 |
5,85 |
6,30 |
6,75 |
7,15 |
7,50 |
|
2,25 |
1,83 |
2,58 |
3,63 |
4,48 |
5,16 |
5,77 |
6,31 |
6,80 |
7,31 |
7,74 |
8,12 |
|
2,50 |
1,96 |
2,66 |
3,90 |
4,78 |
5,52 |
6,20 |
6,77 |
7,28 |
7,82 |
8,29 |
8,69 |
|
2,75 |
2,08 |
2,93 |
4,14 |
5,10 |
5,88 |
6,60 |
7,20 |
7,75 |
8,33 |
8,82 |
9,27 |
|
3,00 |
2,23 |
3,12 |
4,40 |
5,40 |
6,24 |
6,98 |
7,65 |
8,25 |
8,85 |
9,36 |
9,84 |
|
3,50 |
2,44 |
3,46 |
4,86 |
5,97 |
6,90 |
7,73 |
8,49 |
9,12 |
9,78 |
10,3 |
10,8 |
|
4,00 |
2,68 |
3,78 |
5,33 |
6,53 |
7,56 |
8,46 |
9,27 |
9,98 |
10,7 |
- |
- |
|
4,50 |
2,89 |
4,08 |
5,97 |
7,05 |
8,15 |
9,15 |
10,0 |
10,8 |
- |
- |
- |
|
5,00 |
3,12 |
4,40 |
6,21 |
7,60 |
8,70 |
9,83 |
- |
- |
- |
- |
- |
|
5,50 |
3,31 |
4,67 |
6,59 |
8,09 |
9,33 |
10,4 |
- |
- |
- |
- |
- |
|
6,00 |
3,51 |
4,95 |
6,98 |
8,55 |
9,90 |
- |
- |
- |
- |
- |
- |
|
Прямоугольное сечение главного лога |
|||||||||||
|
m = 20, H = H1 |
|||||||||||
|
0,25 |
0,564 |
0,192 |
1,118 |
1,37 |
1,58 |
1,78 |
1,94 |
2,08 |
2,24 |
2,38 |
2,48 |
|
0,50 |
0,894 |
1,26 |
1,78 |
2,16 |
2,52 |
2,82 |
3,08 |
3,32 |
3,56 |
3,78 |
3,96 |
|
0,75 |
1,166 |
1,64 |
2,32 |
2,80 |
3,28 |
3,68 |
4,02 |
4,32 |
4,64 |
4,92 |
5,16 |
|
1,00 |
1,420 |
2,00 |
2,82 |
3,46 |
4,00 |
4,48 |
4,90 |
5,28 |
5,65 |
6,00 |
6,30 |
|
1,25 |
1,640 |
2,32 |
3,28 |
4,02 |
4,64 |
5,20 |
5,68 |
6,12 |
6,56 |
6,96 |
7,30 |
|
1,50 |
1,86 |
2,62 |
3,70 |
4,52 |
5,24 |
5,88 |
6,44 |
6,92 |
7,42 |
7,86 |
8,24 |
|
1,75 |
2,06 |
2,90 |
4,08 |
5,02 |
5,80 |
6,50 |
7,12 |
7,64 |
8,20 |
8,70 |
9,12 |
|
2,00 |
2,26 |
3,18 |
4,48 |
5,50 |
6,36 |
7,12 |
7,80 |
8,40 |
9,00 |
9,54 |
10,00 |
|
2,25 |
2,44 |
3,44 |
4,84 |
5,96 |
6,88 |
7,70 |
8,42 |
9,08 |
9,74 |
10,32 |
- |
|
2,50 |
2,62 |
3,68 |
5,20 |
6,36 |
7,36 |
8,26 |
9,02 |
9,70 |
10,42 |
- |
- |
|
2,75 |
2,78 |
3,92 |
5,52 |
6,80 |
7,84 |
8,80 |
8,60 |
10,34 |
- |
- |
- |
|
3,00 |
2,98 |
4,16 |
5,86 |
7,20 |
8,32 |
9,32 |
10,2 |
- |
- |
- |
- |
|
3,50 |
3,26 |
4,60 |
6,48 |
7,96 |
9,20 |
10,3 |
- |
- |
- |
- |
- |
|
4,00 |
3,58 |
5,04 |
7,10 |
8,70 |
10,18 |
- |
- |
- |
- |
- |
- |
|
4,50 |
3,86 |
5,44 |
7,96 |
9,40 |
- |
- |
- |
- |
- |
- |
- |
|
5,00 |
4,16 |
5,86 |
8,28 |
10,1 |
- |
- |
- |
- |
- |
- |
- |
|
5,50 |
4,42 |
6,22 |
8,78 |
- |
- |
- |
- |
- |
- |
- |
- |
|
6,00 |
4,68 |
6,60 |
9,30 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Прямоугольное сечение главного лога |
|||||||||||
|
m = 25, H = H1 |
|||||||||||
|
0,25 |
0,705 |
0,990 |
1,398 |
1,71 |
1,975 |
2,22 |
2,42 |
2,60 |
2,80 |
2,98 |
3,10 |
|
0,50 |
1,115 |
1,57 |
2,22 |
2,70 |
3,15 |
3,52 |
3,85 |
4,15 |
4,45 |
4,73 |
4,95 |
|
0,75 |
1,458 |
2,45 |
2,90 |
3,50 |
4,10 |
4,60 |
5,02 |
5,40 |
5,80 |
6,15 |
6,45 |
|
1,00 |
1,770 |
2,50 |
3,53 |
4,33 |
5,00 |
5,60 |
6,12 |
6,60 |
7,07 |
7,5 |
7,87 |
|
1,25 |
2,45 |
2,90 |
4,10 |
5,03 |
5,80 |
6,50 |
7,10 |
7,65 |
8,20 |
8,70 |
9,14 |
|
1,50 |
2,52 |
3,28 |
4,62 |
5,65 |
6,55 |
7,35 |
8,05 |
8,65 |
9,26 |
9,84 |
10,30 |
|
1,75 |
2,58 |
3,62 |
5,10 |
6,27 |
7,25 |
8,10 |
8,90 |
9,54 |
10,25 |
10,89 |
- |
|
2,00 |
2,82 |
3,98 |
5,60 |
6,88 |
7,95 |
8,90 |
9,75 |
10,50 |
- |
- |
- |
|
2,25 |
3,05 |
4,30 |
6,05 |
7,45 |
8,60 |
9,60 |
10,50 |
- |
- |
- |
- |
|
2,50 |
3,27 |
4,60 |
6,20 |
7,95 |
9,20 |
10,35 |
- |
- |
- |
- |
- |
|
2,75 |
3,48 |
4,90 |
6,90 |
8,50 |
9,80 |
- |
- |
- |
- |
- |
- |
|
3,00 |
3,73 |
5,20 |
7,34 |
9,00 |
10,4 |
- |
- |
- |
- |
- |
- |
|
3,50 |
4,07 |
5,75 |
8,10 |
9,95 |
- |
- |
- |
- |
- |
- |
- |
|
4,00 |
4,48 |
6,30 |
8,88 |
10,9 |
- |
- |
- |
- |
- |
|
- |
|
4,50 |
5,83 |
6,80 |
9,95 |
- |
- |
- |
- |
- |
- |
- |
- |
|
5,00 |
5,20 |
7,34 |
10,3 |
- |
- |
- |
- |
- |
- |
- |
- |
|
5,50 |
5,52 |
7,77 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
6,00 |
5,85 |
8,25 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Получив расходы, определяют по кривым H = f(Q) бытовые горизонты и скорости.
Зная расход, находят примерную бытовую глубину потока.
Сопоставляя полученные данные по наибольшей бытовой глубине поды с допускаемыми (неразмывающими) средними скоростями течения (таблицы 17, 18, 19, 20), устанавливают, будет ли происходить размыв русла при данном расходе.
Допускаемые неразмывающие средние скорости течения для несвязных грунтов
|
№ п/п |
Грунты и их характеристики |
Размеры частиц грунтов, мм |
Средние глубины потока, м |
||||||
|
наименование |
разновидности |
0,4 |
1 |
2 |
3 |
5 |
10 и более |
||
|
Средние скорости течения, м/сек |
|||||||||
|
1 |
Пыль и ил |
Пыль и ил с мелким песком; растительная земля |
0,005 - 0,05 |
0,2 |
0,3 |
0,4 |
0,4 |
0,5 |
0,6 |
|
2 |
Песок мелкий |
Песок мелкий с примесью среднего |
0,05 - 0,25 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
3 |
Песок средний |
Песок мелкий с глиной; песок средний с примесью крупного |
0,25 - 1,0 |
0,5 |
0,6 |
0,7 |
0,7 |
0,8 |
0,9 |
|
4 |
Песок крупный |
Песок крупный с примесью гравия; среднезернистый песок с глиной |
1,0 - 2,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
|
5 |
Гравий мелкий |
Гравий мелкий с примесью среднего |
2,5 - 5,0 |
0,8 |
0,8 |
1,0 |
1,1 |
1,2 |
1,5 |
|
6 |
Гравий средний |
Гравий крупный с песком и мелким гравием |
5,0 - 10 |
0,9 |
1,0 |
1,1 |
1,3 |
1,4 |
1,7 |
|
7 |
Гравий крупный |
Галька мелкая с песком и гравием |
10 - 15 |
1,1 |
1,2 |
1,3 |
1,5 |
1,6 |
2,0 |
|
8 |
Галька мелкая |
Галька средняя |
15 - 25 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
2,3 |
|
9 |
Галька средняя |
Галька крупная с примесью гравия |
25 - 40 |
1,5 |
1,8 |
2,1 |
2,3 |
2,4 |
2,7 |
|
10 |
Галька крупная |
Булыжник мелкий с галькой и гравием |
40 - 75 |
2,0 |
2,4 |
2,7 |
3,1 |
3,3 |
3,6 |
|
11 |
Булыжник мелким |
Булыжник средний с галькой |
75 - 100 |
2,4 |
2,8 |
3,2 |
3,5 |
3,8 |
4,2 |
|
12 |
Булыжник средний |
Булыжник средний с примесью крупного; булыжник крупный с мелкими примесями |
100 - 150 |
3,0 |
3,3 |
3,7 |
4,1 |
4,4 |
4,5 |
|
13 |
Булыжник крупный |
Булыжник крупный с примесью мелких валунов и гальки |
150 - 200 |
3,5 |
3,8 |
4,3 |
4,6 |
5,0 |
5,4 |
|
14 |
Валун мелкий |
Валуны средние с примесью гальки |
200 - 300 |
3,8 |
4,3 |
4,7 |
4,9 |
5,5 |
5,9 |
|
15 |
Валун средний |
Валуны с примесью булыжника |
300 - 400 |
- |
4,7 |
4,9 |
5,8 |
5,6 |
6,0 |
|
16 |
Валун особо крупный |
|
100 - 500 и более |
- |
- |
5,3 |
5,5 |
6,0 |
6,2 |
Примечание. Табличные значения скоростей не следует интерполировать. При промежуточных размерах частиц грунта и глубинах водотока значения скоростей течения принимаются по ближним табличным значениям размеров частиц и глубин водотока.
Допускаемые неразмывающие средние скорости течения для скальных грунтов
|
Наименование грунтов |
Средние глубины потока, м |
|||
|
0,4 |
1,0 |
2,0 |
3,0 |
|
|
Средние скорости течения, м/сек |
||||
|
Конгломерат, мергель, сланцы |
2 |
2,5 |
3 |
3,5 |
|
Пористый известняк, плотный конгломерат, слоистый известняк, известковый песчаник, доломитовый известняк |
3 |
3,5 |
4 |
4,5 |
|
Доломитовый песчаник, плотный не слоистый известняк, кремнистый известняк, мрамор |
4 |
5 |
6 |
6,5 |
|
Граниты, диабазы, базальты, андезиты, кварциты, порфиры |
15 |
18 |
20 |
22 |
Допускаемые неразмываемые скорости течении для связных грунтов
|
Наименование грунтов |
Содержание частиц, % |
Характеристика грунтов |
||||||||||||||||
|
менее 0,005 мм |
0,005 - 0,05 мм |
грунты малоплотные, коэффициент пористости 1,2 - 0.9; объемный вес грунтового скелета до 1,20 m/м3 |
грунты средней плотности, коэффициент пористости 0,9 - 0,6; объемный вес грунтового скелета 1,20 - 1,66 m/м3 |
грунты плотные, коэффициент пористости 0,6 - 0,3; объемный вес грунтового скелета 1,66 - 2,04 m/м3 |
грунты очень плотные, коэффициент пористости 0,3 - 0,2; объемный вес грунтового скелета 2,04 - 2,14 m/м3 |
|||||||||||||
|
Средние глубины потока, м/сек |
||||||||||||||||||
|
0,4 |
1 |
2 |
3 |
0,4 |
1 |
2 |
3 |
0,4 |
1 |
2 |
3 |
0,4 |
1 |
2 |
3 |
|||
|
Средние скорости течения, м/сек |
||||||||||||||||||
|
Глины |
30 - 50 |
50 - 70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суглинки |
10 - 30 |
70 - 90 |
0,35 |
0,40 |
0,45 |
0,50 |
0,70 |
0,85 |
0,95 |
1,1 |
1,0 |
1,2 |
1,4 |
1,5 |
1,4 |
1,7 |
1,9 |
2,1 |
|
Лёссовые грунты в условиях закончившихся просадок |
- |
- |
- |
- |
- |
- |
0,60 |
0,70 |
0,80 |
0,85 |
0,80 |
1,0 |
1,2 |
1,3 |
1,1 |
1,3 |
1,5 |
1,7 |
|
Супеси |
5 - 10 |
20 - 40 |
По табл. 17 в зависимости от крупности песчаных фракций |
|
|
|
|
|||||||||||
Допускаемые неразмывающие средние скорости течения для искусственных укреплении
|
№ п/п |
Тип укреплений |
Средние глубины потока, м |
|||
|
0,4 |
1,0 |
2,0 |
3,0 |
||
|
Средине скорости течения, м/сек |
|||||
|
1 |
Одерновка плашмя (на плотном основании) |
0,9 |
1,2 |
1,3 |
1,4 |
|
2 |
Одерновка в стенку |
1,5 |
1,8 |
2,0 |
2,2 |
|
3 |
Каменная наброска из булыжного или рваного камня в зависимости от его крупности |
По табл. 17 с коэффициентом 0,90 |
|||
|
4 |
Каменная наброска в два слоя в плетнях в зависимости от крупности камня |
По табл. 17 с коэффициентом 1,10 |
|||
|
5 |
Одиночное мощение на мху (слой мха не менее 5 см): |
|
|
|
|
|
а) из булыжника размером 15 см |
2,0 |
2,5 |
3,0 |
3,5 |
|
|
б) " " " 20 см |
2,5 |
3,0 |
3,5 |
4,0 |
|
|
в) " " " 25 см |
3,0 |
3,5 |
4,0 |
4,5 |
|
|
6 |
Одиночное мощение на щебне (слой щебня не менее 10 см): |
|
|
|
|
|
а) из рваного камня размером 15 см. |
2,5 |
3,0 |
3,5 |
4,0 |
|
|
б) " " " " 20 см |
3,0 |
3,5 |
4,0 |
4,5 |
|
|
в) " " " " 25 см |
3,5 |
4,0 |
4,5 |
5,0 |
|
|
7 |
Одиночное мощение с подбором лица и грубым приколом на щебне (слой щебня не менее 10 см): |
|
|
|
|
|
а) из камней размером 20 см |
3,5 |
4,5 |
5,0 |
5,5 |
|
|
б) " " " 25 см |
4,0 |
4,5 |
5,5 |
5,5 |
|
|
в) " " " 30 см |
4,0 |
5,0 |
6,0 |
6,0 |
|
|
8 |
Двойное мощение из рваного камня на щебне (слой щебня не менее 10 см): |
|
|
|
|
|
|
нижний слой из камней 15 см, верхний- из камней 20 см |
3,5 |
4,5 |
5,0 |
5,5 |
|
9 |
Хворостяная выстилка и хворостяные покрывала на плотном основании (для временных укреплений): |
|
|
|
|
|
- |
2,0 |
2,5 |
- |
||
|
б) при других толщинах выстилки |
По п. 9а с коэффициентом |
||||
|
10 |
Фашинные тюфяки: |
|
|
|
|
|
|
2,5 |
3,0 |
3,5 |
- |
|
|
|
б) при других толщинах тюфяков |
По п. 10а с коэффициентом |
|||
|
11 |
Габионы (размерами не менее 0,5×0,5×1,0 м) |
До 4,0 |
До 5,0 |
До 5,5 |
До 6,0 |
|
12 |
Бутовая кладка из камня известковых пород (с пределам прочности не менее 100 кг/см2 |
3,0 |
3,5 |
4,0 |
4,5 |
|
13 |
Бутовая кладка из камня крепких пород (с пределом прочности не менее 300 кг/см2) |
6,5 |
8,0 |
10 |
12 |
|
14 |
Бетон как одежда для креплений: |
|
|
|
|
|
|
марки 150 |
6,0 |
7,0 |
8,0 |
9,0 |
|
|
" 100 |
5,0 |
6,0 |
7,0 |
7,5 |
|
15 |
Бетонные лотки с гладкой поверхностью: |
|
|
|
|
|
|
бетон марки 150 |
12 |
14 |
16 |
18 |
|
|
" " 100 |
10 |
12 |
13 |
15 |
|
16 |
Деревянные лотки гладкие при надежном основании и течении вдоль волокон |
8 |
10 |
12 |
14 |
Примечания: 1. Табличные значения скоростей не следует интерполировать. При промежуточных глубинах водотока значения скоростей принимаются по глубинам, ближайшим к натурным.
2. Величина допускаемых скоростей течения при глубинах водотока больших 3 м (в случае отсутствия специальных исследований и расчетов) принимается по их значениям для глубины 3 м.
Глава 2
РАСЧЕТ ОТВЕРСТИИ МАЛЫХ РАВНИННЫХ СООРУЖЕНИИ
§ 5. Общие указания
К равнинным условно относят сооружения с уклоном лотка, равным или меньшим критического уклона, т.е. i ≤ iк.
При i ≥ 1,5 iк (обычно при i > 0,020) трубы и малые мосты рассчитывают как косогорные сооружения.
Расчет отверстия производят на пропуск расхода и объема стока с вероятностью их превышения согласно действующим ТУ.
Основными величинами при расчете являются:
1) отметка подпертого горизонта;
2) отверстие и вид сооружения;
3) высотное положение проектной линии дороги.
От горизонта воды зависят:
1) характер затопления разных угодий;
2) величина скоростей протекания воды в сооружении и на выходе, а также пропускная способность сооружения.
Трубы рассчитывают как безнапорные с зазором в трубе на входе в 1/6 высоты трубы для прямоугольных труб и 1/4 - для круглых и овоидальных труб, но не более 0,5 м для прямоугольных, 0,75 м для овоидальных и 0,25 м для круглых труб.
В мостах низ пролетного строения должен возвышаться над подпертым горизонтом по действующим ТУ.
Бровка полотна дороги должна возвышаться над подпертым горизонтом не менее чем на 0,5 м.
Допускается применение круглых полунапорных и напорных труб. При этом бровка полотна должна возвышаться над подпертым горизонтом не менее чем на 1 м.
Мосты рассчитывают как водослив с широким потоком.
По найденному расходу, задавшись расчетной скоростью или подпертым горизонтом воды и видом сооружения, определяют его отверстие или непосредственным расчетом или пользуясь таблицами 21 и 22 (см. ниже).
Таблица для расчета круглых труб
|
d, м |
0,75 |
0,90 |
1,00 |
1,25 |
1,50 |
2,00 |
||||||||||||||||
|
Оголовок |
I |
I |
II |
I |
II |
I |
II |
I |
II |
I |
II |
|||||||||||
|
Q, м3/сек |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
|
0,8 |
1,00 |
2,9 |
0,86 |
2,0 |
0,77 |
2,0 |
0,82 |
2,0 |
0,76 |
2,0 |
0,73 |
1,8 |
0,67 |
1,8 |
0,65 |
1,8 |
0,64 |
1,8 |
0,67 |
1,7 |
0,61 |
1,7 |
|
0,9 |
1,17 |
3,1 |
0,93 |
2,1 |
0,84 |
2,1 |
0,88 |
2,0 |
0,81 |
2,0 |
0,76 |
1,9 |
0,71 |
1,9 |
0,74 |
1,8 |
0,68 |
1,8 |
0,69 |
1,8 |
0,65 |
1,8 |
|
1,0 |
1,33 |
3,5 |
1,00 |
2,2 |
0,90 |
2,2 |
0,94 |
2,1 |
0,86 |
2,1 |
0,82 |
1,9 |
0,75 |
1,9 |
0,78 |
1,9 |
0,72 |
1,9 |
0,73 |
1,8 |
0,68 |
1,8 |
|
1,1 |
1,51 |
3,8 |
1,05 |
2,3 |
0,95 |
2,3 |
1,00 |
2,2 |
0,91 |
2,2 |
0,86 |
2,0 |
0,79 |
2,0 |
0,82 |
1,9 |
0,76 |
1,9 |
0,77 |
1,9 |
0,72 |
1,9 |
|
1,2 |
1,72 |
4,2 |
1,18 |
3,1 |
1,00 |
2,4 |
1,06 |
2,3 |
0,96 |
2,3 |
0,91 |
2,1 |
0,84 |
2,1 |
0,87 |
2,0 |
0,80 |
2,0 |
0,81 |
1,9 |
0,75 |
1,9 |
|
1,4 |
2,19 |
4,9 |
1,43 |
3,5 |
1,09 |
2,6 |
1,17 |
2,5 |
1,06 |
2,5 |
1,00 |
2,2 |
0,92 |
2,2 |
0,93 |
2,1 |
0,87 |
2,1 |
0,89 |
2,0 |
0,82 |
2,0 |
|
1,6 |
2,69 |
5,6 |
1,70 |
4,0 |
1,21 |
2,7 |
1,37 |
3,4 |
1,14 |
2,6 |
1,09 |
2,3 |
1,00 |
2,2 |
1,00 |
2,2 |
0,93 |
2,2 |
0,93 |
2,1 |
0,87 |
2,1 |
|
1,8 |
3,30 |
6,1 |
2,03 |
4,6 |
1,38 |
2,8 |
1,59 |
3,7 |
1,23 |
2,6 |
1,16 |
2,4 |
1,07 |
2,4 |
1,08 |
2,2 |
1,00 |
2,2 |
0,99 |
2,1 |
0,92 |
2,1 |
|
2,0 |
4,00 |
6,8 |
2,36 |
5,0 |
1,47 |
3,1 |
1,80 |
4,1 |
1,32 |
2,7 |
1,26 |
2,5 |
1,13 |
2,5 |
1,15 |
2,3 |
1,07 |
2,3 |
1,05 |
2,2 |
0,97 |
2,2 |
|
2,2 |
5,00 |
7,4 |
2,67 |
5,5 |
1,57 |
3,4 |
2,04 |
4,6 |
1,47 |
2,8 |
1,33 |
2,6 |
1,21 |
2,6 |
1,21 |
2,4 |
1,12 |
2,4 |
1,11 |
2,2 |
1,02 |
2,2 |
|
2,5 |
- |
- |
3,34 |
6,2 |
1,78 |
3,9 |
2,47 |
5,1 |
1,58 |
3,2 |
1,43 |
2,8 |
1,31 |
2,8 |
1,30 |
2,5 |
1,20 |
2,5 |
1,19 |
2,3 |
1,10 |
2,3 |
|
3,0 |
- |
- |
4,20 |
7,3 |
2,17 |
4,6 |
3,26 |
6,2 |
1,82 |
3,8 |
1,86 |
3,8 |
1,45 |
2,9 |
1,47 |
2,7 |
1,33 |
2,7 |
1,30 |
2,4 |
1,21 |
2,4 |
|
3,5 |
- |
- |
5,50 |
8,5 |
2,58 |
5,4 |
4,20 |
7,2 |
2,14 |
4,5 |
2,24 |
4,6 |
1,60 |
3,1 |
1,63 |
2,9 |
1,48 |
2,9 |
1,41 |
2,6 |
1,31 |
2,6 |
|
4,0 |
- |
- |
- |
- |
3,09 |
6,2 |
5,20 |
8,1 |
2,47 |
5,1 |
2,66 |
5,2 |
1,84 |
3,2 |
1,75 |
3,1 |
1,60 |
3,1 |
1,53 |
2,7 |
1,43 |
2,7 |
|
4,5 |
- |
- |
- |
- |
3,71 |
7,0 |
- |
- |
2,87 |
5,7 |
3,26 |
5,9 |
1,98 |
3,7 |
2,07 |
4,2 |
1,71 |
3,2 |
1,65 |
2,8 |
1,53 |
2,8 |
|
5,0 |
- |
- |
- |
- |
4,36 |
7,8 |
- |
- |
3,27 |
6,3 |
3,70 |
6,5 |
2,17 |
4,0 |
2,38 |
4,6 |
1,83 |
3,3 |
1,75 |
2,9 |
1,61 |
2,9 |
|
5,5 |
- |
- |
- |
- |
5,10 |
8,6 |
- |
- |
3,76 |
6,9 |
4,25 |
7,2 |
2,37 |
4,5 |
2,67 |
5,0 |
1,95 |
3,4 |
1,86 |
3,0 |
1,71 |
3,0 |
|
6,0 |
- |
- |
- |
- |
5,89 |
9,4 |
- |
- |
4,27 |
7,6 |
5,00 |
7,8 |
2,58 |
4,8 |
2,99 |
5,5 |
2,09 |
3,6 |
1,97 |
3,1 |
1,79 |
3,1 |
|
6,5 |
- |
- |
- |
- |
6,75 |
10 |
- |
- |
4,84 |
8,2 |
5,50 |
8,8 |
2,82 |
5,2 |
3,32 |
5,9 |
2,27 |
3,7 |
2,06 |
3,2 |
1,88 |
3,2 |
|
7,0 |
- |
- |
- |
- |
7,69 |
11 |
- |
- |
5,45 |
8,9 |
5,20 |
9,5 |
3,09 |
5,7 |
3,77 |
6,3 |
2,40 |
4,0 |
2,16 |
3,3 |
1,97 |
3,3 |
|
7,5 |
- |
- |
- |
- |
8,70 |
12 |
- |
- |
6,10 |
9,5 |
6,80 |
10 |
3,34 |
6,1 |
4,16 |
6,8 |
2,52 |
4,2 |
2,26 |
3,4 |
2,07 |
3,4 |
|
8,0 |
- |
- |
- |
- |
9,75 |
13 |
- |
- |
6,80 |
10 |
7,50 |
11 |
3,64 |
6,4 |
4,54 |
7,2 |
2,64 |
4,5 |
2,34 |
3,6 |
2,08 |
3,6 |
|
8,5 |
- |
- |
- |
- |
10,9 |
13 |
- |
- |
7,55 |
11 |
- |
- |
3,91 |
6,8 |
5,09 |
7,7 |
2,79 |
4,8 |
2,38 |
3,6 |
2,18 |
3,6 |
|
9,0 |
- |
- |
- |
- |
12,1 |
14 |
- |
- |
8,35 |
11 |
- |
- |
4,22 |
7,2 |
5,60 |
8,2 |
2,93 |
5,1 |
2,66 |
4,6 |
2,29 |
3,7 |
|
9,5 |
- |
- |
- |
- |
- |
- |
- |
- |
9,39 |
12 |
- |
- |
4,68 |
7,7 |
6,07 |
8,6 |
3,10 |
5,4 |
2,86 |
4,9 |
2,36 |
3,7 |
|
10 |
- |
- |
- |
- |
- |
- |
- |
- |
10,7 |
13 |
- |
- |
4,98 |
8,2 |
6,42 |
9,7 |
3,29 |
5,6 |
3,07 |
5,1 |
2,44 |
3,8 |
|
11 |
- |
- |
- |
- |
- |
- |
- |
- |
12,0 |
14 |
- |
- |
5,76 |
9,0 |
7,26 |
11 |
3,68 |
6,2 |
3,46 |
5,6 |
2,62 |
3,9 |
|
12 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
6,60 |
9,8 |
- |
- |
4,12 |
6,8 |
3,83 |
6,1 |
2,74 |
4,0 |
|
13 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,55 |
10 |
- |
- |
4,52 |
7,3 |
4,25 |
6,6 |
2,96 |
4,1 |
|
14 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,55 |
11 |
- |
- |
4,99 |
7,9 |
4,76 |
7,1 |
3,10 |
4,4 |
|
15 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9,63 |
12 |
- |
- |
5,51 |
8,4 |
5,29 |
7,6 |
3,28 |
4,7 |
|
16 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10,8 |
13 |
- |
- |
6,06 |
9,0 |
5,82 |
8,1 |
3,40 |
5,0 |
|
17 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11,9 |
14 |
- |
- |
6,70 |
9,6 |
6,47 |
8,7 |
3,60 |
5,4 |
|
18 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,33 |
10 |
7,08 |
9,2 |
3,80 |
5,7 |
|
19 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,00 |
11 |
7,81 |
9,8 |
4,04 |
6,0 |
|
20 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,70 |
11 |
8,40 |
11 |
4,27 |
6,4 |
|
21 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9,44 |
12 |
9,16 |
12 |
4,50 |
6,7 |
|
22 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10,2 |
12 |
9,94 |
12 |
4,74 |
7,0 |
|
23 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11,2 |
13 |
10,7 |
13 |
4,98 |
7,2 |
|
24 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11,8 |
14 |
11,5 |
13 |
5,28 |
7,6 |
|
25 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,55 |
8,0 |
|
26 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,85 |
8,3 |
|
27 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
6,14 |
8,6 |
|
28 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
6,45 |
8,9 |
|
-29 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
6,78 |
9,2 |
|
30 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,10 |
9,5 |
Обозначения:
Q - расход трубы, м3/сек; H - подпертый горизонт перед трубой; υ - скорость в
трубе, м/сек; d - диаметр трубы; I - необтекаемые оголовки; II - обтекаемые оголовки.
Таблица для расчета прямоугольных труб
|
Высота трубы hT, м |
1,00 |
1,50 |
2,00 |
2,50 |
3,00 |
3,50 |
4,00 |
|||||||||||||||||||||
|
Ого- |
I |
II |
I |
II |
I |
II |
I |
II |
I |
II |
I |
II |
I |
II |
||||||||||||||
|
q, м3/сек |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
H |
υ |
|
0,5 |
0,53 |
1,7 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
1,0 |
0,82 |
2,1 |
0,74 |
2,1 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
1,2 |
0,93 |
2,3 |
0,84 |
2,3 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
1,4 |
1,02 |
2,4 |
0,92 |
2,4 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
1,6 |
1,11 |
2,5 |
1,00 |
2,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
1,8 |
1,21 |
26 |
1,09 |
2,6 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
2,0 |
1,35 |
3,2 |
1,17 |
2,7 |
1,31 |
2,7 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
2,5 |
1,76 |
4,0 |
1,34 |
2,9 |
1,51 |
2,9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
3,0 |
2,27 |
4,8 |
1,51 |
3,0 |
1,68 |
3,1 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
3,5 |
2,88 |
5,5 |
1,69 |
3,5 |
1,93 |
3,8 |
1,55 |
3,3 |
1,88 |
3,3 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
4,0 |
3,56 |
6,4 |
1,90 |
4,0 |
2,23 |
4,3 |
1,82 |
3,4 |
2,05 |
3,4 |
- |
- |
- |
- |
- |
- |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
4,5 |
4,24 |
7,2 |
2,14 |
4,5 |
2,59 |
4,8 |
1,98 |
3,5 |
2,23 |
3,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
5,0 |
5,50 |
8,0 |
2,41 |
5,0 |
2,97 |
5,4 |
2,02 |
3,6 |
2,39 |
3,7 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
5,5 |
6,52 |
8,8 |
2,71 |
5,5 |
3,55 |
5,9 |
2,26 |
3,7 |
2,54 |
4,4 |
- |
- |
2,54 |
3,8 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
6,0 |
7,65 |
9,6 |
3,03 |
6,0 |
4,05 |
6,4 |
2,40 |
4,0 |
2,89 |
4,8 |
- |
- |
2,70 |
3,8 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
6,5 |
8,85 |
10 |
3,39 |
6,5 |
4,60 |
7,0 |
2,52 |
4,3 |
3,18 |
5,2 |
- |
- |
2,86 |
4,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
7,0 |
10,2 |
11 |
3,77 |
7,0 |
5,20 |
7,4 |
2,70 |
4,7 |
3,50 |
5,6 |
2,62 |
4,1 |
3,02 |
4,1 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
7,5 |
11,6 |
12 |
4,21 |
7,5 |
5,82 |
8,0 |
2,91 |
5,0 |
3,94 |
6,0 |
2,78 |
4,2 |
3,20 |
4,8 |
- |
- |
3,16 |
4,2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
6,0 |
13,1 |
13 |
4,15 |
8,0 |
6,50 |
8,5 |
3,11 |
5,3 |
4,33 |
6,4 |
2,92 |
4,3 |
3,41 |
5,2 |
- |
- |
3,30 |
4,2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
0,0 |
- |
- |
5,63 |
9,0 |
8,00 |
9,6 |
3,55 |
6,0 |
5,16 |
7,2 |
3,13 |
4,5 |
4,03 |
5,5 |
3,16 |
4,5 |
3,56 |
4,4 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
10 |
- |
- |
6,71 |
10 |
9,65 |
11 |
4,01 |
6,7 |
6,10 |
8,0 |
3,41 |
5,0 |
4,60 |
6,4 |
3,40 |
4,6 |
3,90 |
5,4 |
- |
- |
3,83 |
4,6 |
- |
- |
- |
- |
- |
- |
|
11 |
- |
- |
7,92 |
11 |
11,5 |
12 |
4,55 |
7,3 |
7,01 |
8,8 |
3,71 |
5,5 |
5,29 |
7,1 |
3,64 |
4,7 |
4,43 |
5,9 |
- |
- |
4,07 |
4,7 |
- |
- |
- |
- |
- |
- |
|
12 |
- |
- |
9,25 |
12 |
- |
- |
5,20 |
8,0 |
8,23 |
9,6 |
4,03 |
6,0 |
6,02 |
7,5 |
3,86 |
4,8 |
4,93 |
6,4 |
- |
- |
4,34 |
5,5 |
- |
- |
4,30 |
4,9 |
- |
- |
|
13 |
- |
- |
- |
- |
- |
- |
5,84 |
8,6 |
9,18 |
10 |
4,39 |
6,5 |
6,81 |
8,3 |
4,05 |
5,2 |
5,48 |
7,0 |
4,05 |
4,4 |
4,72 |
6,0 |
- |
- |
4,53 |
5,0 |
- |
- |
|
14 |
- |
- |
- |
- |
- |
- |
6,52 |
9,3 |
10,8 |
11 |
4,75 |
7,0 |
7,55 |
8,9 |
4,30 |
5,5 |
6,07 |
7,4 |
4,28 |
4,7 |
5,12 |
6,5 |
- |
- |
4,78 |
5,1 |
- |
- |
|
15 |
- |
- |
- |
- |
- |
- |
7,27 |
10 |
13,2 |
12 |
5,22 |
7,5 |
8,23 |
9,6 |
4,53 |
6,0 |
6,70 |
8,0 |
4,46 |
5,0 |
5,56 |
6,9 |
- |
- |
5,05 |
5,6 |
- |
- |
|
16 |
- |
- |
- |
- |
- |
- |
1,01 |
10 |
- |
- |
5,65 |
1,0 |
9,52 |
10 |
4,82 |
6,4 |
7,37 |
8,5 |
4,64 |
5,3 |
6,04 |
7,4 |
4,64 |
4,6 |
5,42 |
6,4 |
- |
- |
|
17 |
- |
- |
- |
- |
- |
- |
8,92 |
11 |
- |
- |
6,14 |
8,5 |
10,5 |
10 |
5,11 |
6,8 |
8,31 |
9,0 |
4,86 |
5,6 |
6,72 |
7,7 |
4,84 |
4,5 |
5,79 |
6,8 |
- |
- |
|
18 |
- |
- |
- |
- |
- |
- |
9,81 |
12 |
- |
- |
6,64 |
9,0 |
11,6 |
11 |
5,44 |
7,2 |
8,86 |
9,6 |
5,08 |
6,0 |
7,28 |
8,2 |
5,00 |
5,5 |
6,18 |
7,2 |
- |
- |
|
19 |
- |
- |
- |
- |
- |
- |
10,8 |
12 |
- |
- |
7,16 |
9,5 |
12,8 |
12 |
5,85 |
7,6 |
9,66 |
10 |
5,26 |
6,3 |
7,87 |
8,6 |
5,20 |
5,6 |
6,82 |
7,6 |
- |
- |
|
20 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,71 |
10 |
- |
- |
6,17 |
8,0 |
10,5 |
10 |
5,51 |
6,7 |
8,50 |
9,1 |
5,40 |
5,7 |
7,30 |
8,0 |
5,40 |
5,0 |
|
21 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,30 |
10 |
- |
- |
6,55 |
8,4 |
11,4 |
11 |
5,77 |
7,0 |
9,15 |
9,6 |
5,58 |
6,0 |
7,80 |
8,4 |
5,54 |
5,2 |
|
22 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,91 |
11 |
- |
- |
6,94 |
8,0 |
12,3 |
11 |
6,06 |
7,3 |
9,84 |
10 |
5,75 |
6,3 |
8,33 |
8,8 |
5,70 |
5,5 |
|
23 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9,54 |
11 |
- |
- |
7,34 |
8,4 |
13,3 |
12 |
6,34 |
7,6 |
10,5 |
10 |
5,96 |
6,5 |
8,89 |
9,2 |
5,88 |
5,7 |
|
24 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10,23 |
12 |
- |
- |
7,80 |
9,2 |
- |
- |
6,65 |
8,0 |
11,3 |
11 |
6,13 |
6,1 |
9,45 |
9,6 |
6,03 |
6,0 |
|
25 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10,93 |
12 |
- |
- |
8,22 |
10 |
- |
- |
6,96 |
8,8 |
12,0 |
11 |
6,41 |
7,1 |
9,93 |
10 |
6,24 |
6,2 |
|
25 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,70 |
10 |
- |
- |
7,28 |
8,6 |
12,9 |
12 |
6,65 |
7,4 |
10,6 |
10 |
6,40 |
6,5 |
|
27 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9,17 |
11 |
- |
- |
7,60 |
9,0 |
13,7 |
12 |
6,90 |
7,7 |
11,3 |
10 |
6,60 |
6,7 |
|
28 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,95 |
9,3 |
- |
- |
7,16 |
8,0 |
12,0 |
11 |
6,80 |
7,0 |
|
29 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,32 |
9,6 |
- |
- |
7,43 |
8,3 |
12,7 |
11 |
7,00 |
7,2 |
|
30 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,80 |
10 |
- |
- |
7,70 |
8,5 |
13,4 |
12 |
7,20 |
7,5 |
Обозначения:
q - расход на 1 пог. м
отверстия, м3/сек; H - подпертый горизонт; υ - скорость в
сооружении, м/сек; hТ - высота низа трубы или моста над лотком; I - необтекаемый оголовок в трубах и
мосты; II - обтекаемый оголовок в трубах.
В верхней части справа недостающие данные берут из соответствующих граф
при меньшей высоте трубы.
§ 6. Трубы
Водопропускная способность труб под насыпями дорог существенно зависит от режима работы труб.
Различают следующие режимы работы труб, положенные в основу их гидравлического расчета (рис. 2):
Рис. 2. Режимы работ труб:
а - безнапорный; б - полунапорный; в - напорный
а) безнапорный (ненапорный) режим, при котором поток на всем протяжении трубы имеет свободную поверхность (рис. 2, а);
б) полунапорный режим, при котором входное сечение трубы затоплено, а на остальном протяжении трубы поток имеет свободную поверхность (рис. 2, б);
в) напорный режим, при котором входное сечение трубы затоплено и труба на всем протяжении работает полным сечением (рис. 2, в).
Наибольшая водопропускная способность трубы наблюдается при напорном режиме.
Расчетные коэффициенты сжатия струй в полунапорных трубах ε приведены в табл. 23, коэффициенты скорости для полунапорных труб φ - в табл. 24.
Значения коэффициента сжатия ε струй в полунапорных трубах
|
Форма сечения труб |
ε |
|
Прямоугольная |
0,6 |
|
Круглая |
0,65 |
Значения коэффициента скорости φ для труб
|
Тип оголовка |
φ |
|
Необтекаемый |
0,85 |
|
Обтекаемый |
0,95 |
При проектировании и постройке автомобильных дорог применяют, как правило, типовые трубы со стандартными отверстиями, имеющими в поперечном сечении определенные очертания и размеры. Для всех типов труб и величин стандартных отверстий заранее подсчитан тот наибольший расход, который в состоянии пропустить труба, и вычислены все необходимые гидравлические элементы, соответствующие полному использованию пропускной способности трубы. Эти данные приведены в таблицах 21 и 22.
Трубы овоидальные, уширяющиеся книзу, а также с вертикальными стенками и сводом сверху рассчитывают как прямоугольные. Отверстие трубы, вводимое в расчет, считают равным ширине отверстия трубы понизу. Наименьшую высоту насыпи назначают по фактической конструкции трубы, а пропускную способность и положение подпертого горизонта рассчитывают по условной (расчетной) высоте трубы hТ, определение которой указано на рис. 3.
Рис. 3. Приведение площади сечения овоидальных труб к равновеликой прямоугольной
Нормированный зазор от горизонта воды на входе в трубу исчисляют в
размере ![]() от hТ до условного
потолка (см. рис. 3).
от hТ до условного
потолка (см. рис. 3).
Трубы с повышенным звеном прямоугольного типа являются плохо обтекаемыми. При затопленном входе их рассчитывают как полунапорные (пользуясь табл. 22 для труб с необтекаемыми оголовками), но при высоте трубы, равной высоте повышенного звена (рис. 4).
Рис. 4. Типы входных оголовков труб:
а - с повышенным прямоугольным (необтекаемым) звеном; б - с повышенным
обтекаемым (самозаряжающимся) звеном
Расчет отверстий безнапорных труб
Расчет отверстий безнапорных труб производят по допускаемому заполнению при входе по предельной степени наполнения:
![]()
где H - глубина воды перед трубой;
hТ - предельная глубина (высота) наполнения. Расчет ведется путем последовательных приближений или с помощью таблиц 21 и 22.
Пример расчета круглой трубы. Расход Q = 1,6 м3/сек. Уклон I = 0,01. Найти: глубину воды при входе H, глубину на выходе и скорость течения на выходе из трубы.
По табл. 21 выбираем круглую трубу d = 1,25 м (глубина при входе H = 1,09 м и скорость на входе υ = 2,3 м/сек).
Для определения глубины на выходе вычисляем модуль пропускной способности всего сечения трубы:
Kd = 24d8/3 = 24×1,258/3 = 43,2 м3/сек.
Необходимый модуль пропускной способности:
![]()
Отношение модулей:
![]()
По табл. 25
 откуда глубина
равномерного движения:
откуда глубина
равномерного движения:
h0 = 0,42d = 0,42×1,25 = 0,52 м.
Расчетные характеристики, характеристики скорости и значения критической функции для круглых труб
|
Степень наполнения |
Критическая функция |
Отношение расходных характеристик |
Отношение скоростных характеристик |
|
|
|
|
|
|
0,00 |
0,000 |
0,000 |
0,000 |
|
0,05 |
0,000 |
0,004 |
0,184 |
|
0,10 |
0,000 |
0,017 |
0,333 |
|
0,15 |
0,000 |
0,043 |
0,457 |
|
0,20 |
0,001 |
0,080 |
0,565 |
|
0,25 |
0,005 |
0,129 |
0,661 |
|
0,30 |
0,009 |
0,188 |
0,748 |
|
0,35 |
0,016 |
0,256 |
0,821 |
|
0,40 |
0,025 |
0,332 |
0,889 |
|
0,45 |
0,040 |
0,414 |
0,948 |
|
0,50 |
0,060 |
0,500 |
1,000 |
|
0,55 |
0,088 |
0,589 |
1,045 |
|
0,60 |
0,121 |
0,678 |
1,083 |
|
0,65 |
0,166 |
0,766 |
1,113 |
|
0,70 |
0,220 |
0,850 |
1,137 |
|
0,75 |
0,294 |
0,927 |
1,152 |
|
0,80 |
0,382 |
0,994 |
1,159 |
|
0,85 |
0,500 |
1,048 |
1,157 |
|
0,90 |
0,685 |
1,082 |
1,142 |
|
0,95 |
1,035 |
1,087 |
1,108 |
|
1,00 |
¥ |
1,000 |
1,000 |
Примечания: 1. Расход![]() Скорость
Скорость ![]()
2. Для заполненного сечения железобетонных труб Kd = 24d8/3 Wd = 30,5d2/3 (d в метрах).
Если бы уклон был I = 0, то на выходе установилась бы критическая глубина.
Критическая функция в этом случае равна:
![]()
По табл. 25
 откуда критическая
глубина на выходе
откуда критическая
глубина на выходе
hк = 0,55d = 0,55×1,25 = 0,69 м.
Сравниваем h0 с hк. Так как h0 = 0,52 м < hк = 0,69 м то уклон I = 0,01 больше критического.
По табл. 25
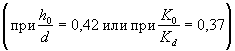
![]()
Так как
Wd
= 30,5d2/3
= 30,5×1,252/3 = 35,5 м/сек, то
W0 =
0,91Wd
= 0,91×35,5 = 32,3 м/сек.
Скорость на выходе:
![]()
что больше скорости на входе, равной 2,3 м/сек.
Пример расчета прямоугольной трубы. Расход Q = l,6 м3/сек. Уклон I = 0,015. Найти: глубину воды при входе H, глубину на выходе и скорость течения на выходе из трубы.
По табл. 22 выбираем прямоугольную трубу отверстием b = 1,00 м (глубина при входе H = 1,11 м и скорость на входе υ = 2,5 м/сек).
Расход воды на 1 м ширины трубы:
![]()
Критическая глубина:
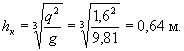
Модуль расхода:
![]()
Задаемся различными глубинами h и, определяя для них соответствующие ![]() подбираем такое
значение K',
которое будет соответствовать модулю расхода K. Нормальная глубина h0 будет
соответствовать равенству K'
= K.
подбираем такое
значение K',
которое будет соответствовать модулю расхода K. Нормальная глубина h0 будет
соответствовать равенству K'
= K.
Обозначения: ω - площадь живого сечения, м2;
p - подводный смоченный периметр (p = b + 2h);
R - гидравлический радиус
![]()
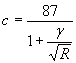 (по Базену), где γ - коэффициент
шероховатости - см. табл. 33.
(по Базену), где γ - коэффициент
шероховатости - см. табл. 33.
Примем в данном случае γ = 0,46. Расчет легче всего вести в табличной форме:
Таблица "б"
|
h |
ω |
p |
R |
|
c |
K' |
K |
|
0,50 |
0,50 |
2 |
0,25 |
0,5 |
45,3 |
11,4 |
|
|
0,55 |
0,55 |
2,10 |
0,26 |
0,51 |
45,7 |
13 |
|
|
0,60 |
0,60 |
2,20 |
0,27 |
0,52 |
46,1 |
14,5 |
14,6 |
|
0,64 |
0,64 |
2,28 |
0,28 |
0,53 |
46,5 |
15,8 |
|
Ближе всего к значению K = 14,6 подходит K' = 14,5.
Поэтому принимаем за глубину на выходе нормальную глубину h0 = 0,60 м.
Скорость на выходе:
![]()
что больше скорости на входе, равной 2,5 м/сек.
Если бы труба была расположена на уклоне, меньшем или равном критическому, то, в чем нетрудно убедиться, скорость на выходе была бы равна:
![]()
Расчет отверстий полунапорных труб
Полунапорное истечение наблюдается в трубах с необтекаемыми оголовками при глубине воды в логу перед трубой H ≥ 1,2hТ.
Расход:
![]()
где φ и ε - коэффициенты скорости и сжатия для полунапорных труб (см. таблицы 23 и 24);
ω - полная площадь сечения трубы, м2;
H - напор над дном входного сечения трубы, м.
Скорость на выходе определяют так же, как для безнапорных труб (см. предыдущие примеры расчета и таблицы 21 и 22).
Расчет отверстий напорных труб
Напорное протекание устанавливается только при обтекаемом входном оголовке и глубине потока перед трубой H ≥ 1,4hТ, а также при обязательном заполнении трубы водой на всем протяжении, что может иметь место при уклоне трубы, меньшем уклона трения, т.е. при
![]()
где ω2c2R = kd2 (kd - расходная характеристика трубы).
При обычной форме входного оголовка (необтекаемой) напорное протекание будет периодически срываться из-за подсоса воздуха в сжатое сечение потока (даже при H ≥ 1,4hТ и I < Iw). Такие трубы нужно рассчитывать как полунапорные, так как режим протекания в моменты срыва будет соответствовать полунапорному.
Если уровень воды в отводящем русле выше верха выходного сечения трубы на величину Δh, то необходимо учитывать, что уровень воды перед трубой увеличится на ту же величину (т.е. на Δh), но при условии, что:
![]()
где υ - скорость течения в трубе, м/сек;
υ1 - скорость течения в отводящем русле (нижнем бьефе трубы).
Расход:
![]()
где φ - коэффициент скорости (см. табл. 24);
ω - полная площадь поперечного сечения трубы, м2;
H - напор над дном входного сечения трубы.
Расчет ведут методом последовательных приближений или пользуясь таблицами 21 и 22. При этом (как указано выше) уклон трубы не должен превышать уклона трения.
Если уклон трубы окажется больше уклона трения, то глубина воды перед входом будет больше указанной в таблицах 21 и 22, и тогда она определяется по формуле:
H1 = H + l(Iw - I),
где H - табличное (см. таблицы 21 и 22) значение глубины H, соответствующее Iw = I;
l - длина трубы;
I - уклон трубы;
Iw - уклон трения.
Пример. Расход Q = 1,6 м3/сек. Уклон I = 0,01. Длина трубы l = 20 м.
По табл. 21 принимаем круглую трубу d = 0,75 м (H = 1,44 м, υ = 3,5 м/сек), так как
![]()
Труба большего диаметра (d = 1,00 м) с необтекаемым оголовком (H = 1,37 м; υ = 3,4 м/сек) будет пропускать расчетный расход при полунапорном режиме, так как
![]()
Таким образом, применение обтекаемого оголовка в данном случае позволяет сократить диаметр трубы с 1,00 м (при полунапорном режиме) до 0,75 м (при напорном режиме).
При этом подтопление насыпи при I = Iw возрастет всего лишь на 1,44 - 1,37 = 0,07 м.
Уклон трения для круглой трубы d = 0,75 м:
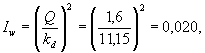
где
k = 24d8/3 = 24×0,758/3 = 11,15 м3/сек.
Уклон трубы должен быть не более I = Iw = 0,020.
При заданном уклоне I = 0,01 > Iw и длине трубы l = 20 м дополнительное повышение уровня воды перед трубой (в верхнем бьефе) будет:
l(Iw - I) = 20(0,02 - 0,01) = 0,20 м.
Глубина воды перед трубой будет:
H1 = H + l(Iw - I) = 1,44 + 0,20 = 1,64 м.
Скорость на выходе из напорной трубы d = 0,75 м получается всего на 0,10 м/сек больше скорости на выходе из полунапорной трубы d = 1,0 м (за счет лучшего использования поперечного сечения трубы).
Расчет высоты насыпи у трубы
Минимальная высота насыпи у безнапорной трубы:
Hmin = hТ + h1 + h2,
где h1 - толщина потолка трубы, м;
h2 - необходимая по ТУ толщина засыпки над трубой, м.
Минимальная высота насыпи у полунапорных и напорных труб:
Hmin = H + Δ,
где Δ - запас над уровнем воды перед трубой, назначаемый по ТУ.
§ 7. Мосты
В основу способа гидравлического расчета мостов положена классическая теория движения жидкости по водосливу с широким порогом (с широким порогом называют, водослив, с отношением длины порога к напору не более 2,5).
У водослива с широким порогом предполагается поверхность порога горизонтальной, сопротивление при входе на водослив и при протекании по нему незначительным и длина порога ограниченной.
Протекание воды под малым мостом может происходить по схемам свободного (незатопленный водослив, рис. 5) и несвободного (затопленный водослив, рис. 6) истечения.
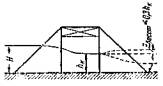
Рис. 5. Схема свободного протекания воды под мостом

Рис. 6. Схема несвободного протекания воды под мостом
При бытовой (естественной) глубине h ≤ hк установится свободное истечение; при h > hк истечение будет несвободным (hк - критическая глубина в подмостовом сечении1).
1
Критической называется такая глубина, при которой удельная энергия движущегося
по водосливу потока достигает минимума. Удельная энергия сечения определяется
выражением ![]() и будет минимальной
при h = hк
и будет минимальной
при h = hк
Стеснение водотока подходами к мосту допускается в том случае, если расчетная скорость потока под мостом больше скорости потока в бытовом состоянии при расчетном расходе.
Если русло укрепить нельзя и скорость течения повысить против бытовой также нельзя, то мостом следует перекрыть все зеркало потока при расчетном расходе; при этом отверстие не рассчитывают.
Свободное истечение
Отверстие рассчитывается по схеме свободного истечения (незатопленный водослив) в следующем порядке.
Назначается коэффициент сжатия ε (по табл. 26). Определяется допускаемая скорость vA по таблицам 17 - 20.
Значения коэффициента сжатия струй ε под мостами и коэффициента скорости φ для мостов
|
Форма устоев |
ε |
φ |
|
Обсыпные с конусами |
0,90 |
0,90 |
|
С откосными крыльями |
0,85 |
0,90 |
|
Выступающие из конуса |
0,80 |
0,85 |
Находится отверстие моста:
![]()
где b - принятое отверстие, м.
Определяется расход, приходящийся на 1 м ширины отверстия:
![]()
Находятся критическая глубина:
и критическая скорость:
![]()
Определяется напор H
= 1,5hк
(пренебрегая скоростным напором ![]() где υ0
- скорость подхода). Скоростью подхода можно пренебречь, если ω
> 3bH, где ω
- площадь живого сечения потока при подходе к мосту. Если ω ≤
3bH, то
скоростной напор учитывается, и тогда:
где υ0
- скорость подхода). Скоростью подхода можно пренебречь, если ω
> 3bH, где ω
- площадь живого сечения потока при подходе к мосту. Если ω ≤
3bH, то
скоростной напор учитывается, и тогда:
![]()
Высота низа конструкции моста над дном водотока с верховой стороны должна быть более hк + Δ (Δ - запас по ТУ).
Высота бровки полотна с верховой стороны должна быть более H200 + Δ.
Можно также пользоваться следующими приближенными формулами:
критическая глубина
![]()
напор
H = 1,6hк = 0,16υ2,
отверстие
![]()
погонный расход
![]()
скорость
![]()
Пример. Расчетный расход Q50 = 25 м3/сек. Глубина в нижнем бьефе h = 0,50 м. Высота насыпи 4,5 м. Дно укреплено двойной мостовой, υд = 3,5 м/сек. Коэффициент ε = 0,9.
![]()
Принимаем b = 7,00 м,
![]()

и, следовательно, водослив не затоплен.
Критическая скорость:
![]()
Возвышение низа конструкции:
hк + 0,50 = 1,09 + 0,50 = 1,59 м.
Максимальный расход:
Qм = 1,25, Q = 1,25×25 = 31,2 м3/сек,
![]()

![]()
Возвышение бровки полотна:
Hм + 0,50 = 2,14 + 0,50 = 2,64 м.
По приближенным формулам получим:
![]()
![]()
![]()
Возвышение низа конструкции:
hк + 0,50 = 1,16 + 0,50 = 1,66 м.
Скорость при максимальном расходе:
![]()
Hм = 0,16υ2 = 0,16×3,662 = 2,14 м.
Возвышение бровки полотна:
Нм + 0,50 = 2,14 + 0,50 = 2,64 м.
Несвободное истечение (h > hк)
Расчет ведется в следующей последовательности.
Назначаются коэффициенты ε и φ (по табл. 26).
Определяется hк по формуле свободного истечения (задаваясь υд по креплению русла), чтобы убедиться, что h > hк, и если это подтверждается, то принимают h = hк.
Находится отверстие:
![]()
Определяется расход на 1 м ширины отверстия:
![]()
скорость:
![]()
и напор:
![]()
(пренебрегая скоростным напором ![]() ).
).
При учете скоростного напора
Возвышение низа конструкции ≥ n + ∆ (∆ - запас по ТУ). Возвышение бровки полотна должно быть больше или равно H + ∆.
Можно пользоваться и приближенными формулами:
критическая глубина
![]()
напор
![]()
отверстие
![]()
погонный расход
![]()
скорость
![]()
Пример. Q = 20 м3/сек. h = 0,8 м. Высота насыпи 3 м. Высота пролетного строения 1 м. Дно - одиночная мостовая (υд = 2,5 м/сек), ε = 0,9 φ = 0.9.
Имеем:
![]()
![]()

и, следовательно, водослив затоплен (истечение несвободное).
Принимаем hк = h = 0,8 м. Следовательно:
![]()
Принимаем b = 12 м. Тогда:
![]()
![]()
![]()
Запас от низа конструкции до воды:
3,0 - 1,0 + 0,75-0,8 ≈ 2 м
(здесь 0,75 м - толщина балластного слоя на подходах к мосту).
Дальше надо сделать расчет на Qм = 1,25Q и определить запас от максимального подпорного горизонта до бровки полотна. Для краткости изложения этот расчет опущен (в результате получено Hм = 1,23 м).
По приближенным формулам получим:
![]()
![]()
и, следовательно, водослив затоплен. Поэтому:
![]()
Принимаем b = 12 м. Далее:
![]()
![]()
Qм = 1,25Q = 1,25×20 = 25 м3/сек
![]()
что допустимо, так как отверстие не поверяется на Qм (на этот расход поверяется только бровка полотна),
![]()
§ 8. Равнинные отводящие русла (при уклоне русла менее 0,20)
Расчет глубины размыва
Вследствие растекания потока на выходе из сооружения глубина воды уменьшается, а скорость увеличивается. Поэтому наибольшие скорости течения воды и наибольшие размывы дна наблюдаются не в выходном сечении моста или трубы, а в отводящем русле.
Различают три вида размывов:
1) из-за превышения фактической скорости потока v над допускаемой скоростью υд;
2) вызванного подмывом берега нисходящими струями при поперечной циркуляции потока;
3) вследствие перехода от бурного режима протекания к спокойному.
1-й случай. Фактическая скорость υ > υд.
Сечение узкого потока будет:
![]()
При широком русле (рис. 7) глубина воды после размыва:
![]()
глубина размыва
Δ = hp - h
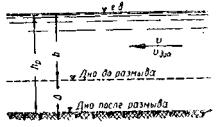
Размыв будет происходить по всей длине участка, где фактическая скорость превышает допускаемую.
2-й случай. Поток набегает на берег под углом а и берег может быть подмыт нисходящими струями (рис. 8).

Рис. 8. Схема подмыва берега нисходящими
струями при набеге струй потока под углом α:
а - поперечный разрез; б - план
Глубина дополнительного размыва (по данным ЦНИС МПС):
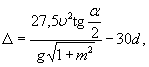
где υ - скорость потока на подходе к берегу, м/сек;
m - крутизна откоса;
α - угол между струей и берегом;
g - ускорение силы тяжести;
d - диаметр частиц грунта, мм (при мелкозернистых грунтах можно принимать d = 0).
3-й случай. В потоке происходит прыжок, что имеет место, если бытовая глубина больше критической глубины.
Наибольший размыв за прыжком (возникающим в укрепленном русле) наблюдается, когда прыжок расположен непосредственно у кромки крепления (рис. 9, а).
Рис. 9. Размыв за прыжком:
а - при недостаточной длине крепления дна; б - при достаточной длине крепления
дна
Если расстояние от прыжка до кромки крепления велико, то размыв уменьшается. При длинном креплении размыва может и не быть совсем (рис. 9, б), если:
![]()
и одновременно длина гладкого крепления ≥ 20h" или длина шероховатого крепления ≥ 8 h",
где h" - глубина прыжка;
hб - бытовая (естественная) глубина.
Расчет потока (по О.В. Андрееву).
Первый случай. Свободное растекание потока (рис. 10).
Рис. 10. Схема свободного растекания потока на выходе из сооружения
Растекание потока на всю ширину русла происходит в непосредственной близости от выходного отверстия сооружения.
Длина свободного растекания:
![]()
где Bp - ширина русла по зеркалу воды при бытовой глубине;
B - отверстие искусственного сооружения.
Глубина воды в сечении полного растекания (находится подбором):
![]()
где ![]() - энергия сечения
потока в месте полного растекания.
- энергия сечения
потока в месте полного растекания.
Скорость в сечении полного растекания:
![]()
Второй случай. Полусвободное растекание (рис. 11).
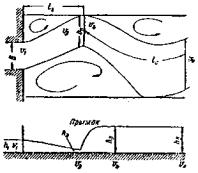
Рис. 11. Схема полусвободного растекания потока на выходе из сооружения
Растекание потока на всю ширину русла происходит на значительном протяжении.
Расчет ведется в следующем порядке.
Зная скорость υ1 и глубину h1 в выходном сечении сооружения, находят бытовую глубину потока в отводящем русле hб и бытовую скорость потока
![]()
Принимают hб за большую глубину прыжка в отводящем русле. Тогда меньшая глубина прыжка (по А.И. Шварцу):
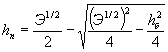
где ![]() - энергия сечения
потока перед прыжком (которую принимают равной энергии потока в выходном
сечении сооружения).
- энергия сечения
потока перед прыжком (которую принимают равной энергии потока в выходном
сечении сооружения).
Находят ширину прыжка:
![]()
Находят скорость потока перед прыжком:
![]()
и за прыжком:
![]()
Находят длину крепления до прыжка:
![]()
где ![]() - (см. 1-й случай);
- (см. 1-й случай);
![]() - глубина после
прыжка, если он возникает в выходном сечении сооружения;
- глубина после
прыжка, если он возникает в выходном сечении сооружения;
![]() - глубина после
прыжка, если он возникает в сечении полного растекания.
- глубина после
прыжка, если он возникает в сечении полного растекания.
Находят длину прыжка:
lпр = 5(hб - hп).
Находят (по Н.М. Бернадскому) длину растекания струи в водной массе до сечения, где скорость снижается до допускаемой (неразмывающей):
![]()
где hб - бытовая глубина в отводящем русле;
n- коэффициент шероховатости русла;
ln - символ натурального логарифма;
υ4 - скорость после прыжка;
υн - допускаемая скорость (υн ≥ υб).
Участки l2 и lпр (до прыжка и в пределах прыжка) укрепляют. За креплением допускают размыв.
Размыв за прыжком можно находить двумя способами:
1) делением прыжка на два вальца; тогда глубина размыва (по М.С. Вызго):
∆ = 0,85hб;
2) превышением фактической скорости за прыжком над допускаемой скоростью; тогда глубина размыва:
![]()
Если глубины размыва ∆ опасны для сооружения и крепления за ним, то отводящее русло нужно крепить дальше, рассчитывая размыв по уменьшающейся вниз по течению скорости в растекающейся струе; скорость эту определяют по интерполяции.
Рекомендации по конструкции укреплений отводящих русел
Длина укрепления отводящего русла (см. рис. 10) назначается такой, чтобы прыжок находился в пределах укрепления. Тогда:
l = l1+ l2 + l3.
где l1 - длина отгона прыжка (см. выше);
l2 - длина прыжка [l2 = (5¸20)]hб;
l3 = lс - расстояние от прыжка до кромки крепления.
Рекомендуется заканчивать укрепление предохранительным откосом (рис. 12, а) или «зубом» (рис. 12, б). Тогда участок l3 можно значительно сократить или даже исключить совсем, допустив сгон прыжка в размыв (в этом случае l = l1).
Рис. 12. Схема предохранительных укреплений на
выходе:
а - откос; б - «зуб»
Высота предохранительного откоса (или зуба):
![]()
Допустимая глубина потока за кромкой укрепления:
hр = 1,85kσh",
если в русле возможен размыв, или
hр = 1,85cσh",
если русло неразмываемое (бетон, камень).
Допустимая глубина за прыжком:
![]()
или
![]()
В этих формулах: σ = 1,35 - коэффициент сбойности течения (при полном сгоне прыжка в размыв);
k - коэффициент, учитывающий наклон потока к горизонту на угол φ (табл. 27) при c = 1;
c -
коэффициент (при k
= 1), зависящий от относительной длины укрепления ![]() (табл. 28);
(табл. 28);
hб - бытовая глубина.
Значение коэффициента k
|
φ |
0 |
12 |
25 |
40 |
50 |
75 |
90 |
|
tgφ |
0 |
0,213 |
0,466 |
0,840 |
1,190 |
3,730 |
|
|
k |
1 |
1,2 |
1,4 |
1,7 |
1,9 |
2,3 |
2,4 |
Значения коэффициента c
|
Относительная длина крепления |
c |
||||
|
1 |
0,89 |
0,76 |
0,65 |
0,54 |
|
|
Кирпич и бетон |
0 |
5 |
15 |
17 |
20 |
|
Мостовая |
0 |
2 |
6 |
7 |
8 |
Устраивать предохранительные откосы или зубья целесообразно и в тех случаях, когда прыжок не сгоняется с укрепления в размыв или когда глубина в отводящем русле меньше критической.
Размер камней в мощении:
![]()
Толщина крепления (мощения или бетона):
S = 0,6hк
§ 9. Фильтрующие насыпи
Фильтрующие насыпи бывают напорные, когда глубина воды перед насыпью превосходит высоту фильтрующей каменной наброски, и безнапорные, когда глубина воды перед насыпью не достигает верха фильтрующей каменной наброски.
Для напорных фильтрующих насыпей глубина воды перед насыпью равна:
![]()
где a - высота каменной фильтрующей прослойки;
l - длина по направлению течения (ширина насыпи понизу), м;
I - уклон каменной фильтрующей прослойки (обычно равен уклону лога);
I1 - гидравлический уклон, необходимый для фильтрации, определяемый по формуле:
![]()
где b - отверстие (ширина) фильтрующей прослойки, м;
k - коэффициент турбулентной фильтрации, зависящий от размеров и формы камня (табл. 29).
Значения коэффициента турбулентной фильтрации k, м/сек
|
Средний диаметр камней, приведенных к шару, см |
Коэффициент k для камней |
||
|
окатанных |
промежуточного типа |
рваных, остроугольных |
|
|
5 |
0,15 |
0,17 |
0,19 |
|
10 |
0,23 |
0,20 |
0,29 |
|
15 |
0,30 |
0,33 |
0,37 |
|
20 |
0,35 |
0,39 |
0,43 |
|
25 |
0,39 |
0,44 |
0,49 |
|
30 |
0,43 |
0,50 |
0,53 |
|
40 |
0,50 |
0,56 |
0,62 |
|
50 |
0,56 |
0,63 |
0,70 |
При безнапорных фильтрующих насыпях полагают, что уклон дна не влияет на условия протекания, и бытовой глубиной в отводящем русле пренебрегают. Тогда глубина воды перед насыпью будет:
![]()
где все обозначения - по предыдущему.
§ 10. Водоспуски
При устройстве между конусами моста глухой плотины с укрепленными откосами, через гребень которой пропускают паводок, напор на водосливе в м:
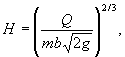
где Q - паводковый расход, м3/сек;
b - ширина водослива, м;
m = 0,35 - коэффициент расхода водослива (с толстой стенкой).
Глубина воды перед автодорожной насыпью равна H + h, где h - высота плотины, м.
При устройстве между конусами моста водосливной плотины с донным водоспуском, в начале которого делают водоприемный колодец, так называемый «монах», движение воды через кромку этого колодца при пропуске паводка происходит как через водослив с тонкой стенкой.
Если пропускная способность трубы (донного водоспуска) одинакова с пропускной способностью входного сечения водоприемного колодца, то напор в м над кромкой водослива:
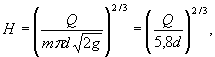
где Q - расчетный расход воды, м3/сек;
m = 0,42 - коэффициент расхода водослива с тонкой стенкой;
d - внутренний диаметр колодца, м;
и глубина воды перед откосом насыпи:
h = H + h1,
где h1 - высота колодца, м.
Если пропускная способность трубы под насыпью или плотиной меньше пропускной способности входного сечения водоприемного колодца, то расчет ведут по формуле полунапорного протекания. В этом случае напор над кромкой водослива:

где ε и φ - коэффициенты по таблицам 23 и 24, остальные обозначения прежние.
§ 11. Косогорные подводящие и отводящие русла (при уклоне русла более 0,20)
Искусственные русла на косогорах устраиваются в виде:
быстротоков - на любых уклонах, обычно с применением соответствующих гасителей энергии (искусственная шероховатость достигается постановкой поперечных ребер, шашек и пр.);
перепадов с водобойными колодцами - на значительных уклонах (перепады без водобойных колодцев практически могут применяться лишь на малых уклонах);
консольных водосбросов - для пропуска водотока над дорогой.
Быстротоки
Быстротоком называют искусственное русло с уклоном больше критического.
Поток вступает на быстроток с критической глубиной и дальше идет на спад, стремясь в пределе к нормальной глубине.
Характерной особенностью быстротоков является сравнительно
незначительная длина кривой спада и быстрое установление глубин, практически
весьма близких к нормальной глубине, являющейся наименьшей возможной глубиной.
Однако это может произойти лишь в том случае, если быстроток имеет достаточную
длину или уклон его дна очень крут. Тогда можно полагать, что глубина в конце
быстротока равна нормальной глубине h0 и, следовательно, скорость в конце быстротока ![]()
При очень больших уклонах (примерно, больше 0,4) струя может оторваться от дна в начале быстротока, и тогда глубину воды в конце быстротока следует находить из уравнения падения:
![]()
где q - расход воды на 1 пог. м отверстия;
φ - коэффициент скорости, принимаемый равным 0,85;
hс - глубина струи в сжатом сечении (в месте падения струи);
H0 - напор над гребнем водослива (H0 = 1,7hкр);
p - глубина падения (разность отметок дна начала и конца быстротока).
Сжатую глубину hс можно найти, пользуясь табл. 30.
Соотношение глубин при перепадах
|
|
|
|
|
2 |
0,70 |
0,80 |
|
2,2 |
0,63 |
1,0 |
|
2,4 |
0,58 |
1,2 |
|
2,6 |
0,56 |
1.3 |
|
2,8 |
0,52 |
1,5 |
|
3,0 |
0,50 |
1,6 |
|
3,2 |
0,48 |
1,7 |
|
3,4 |
0,46 |
1,8 |
|
3,6 |
0,45 |
1,0 |
|
3,8 |
0,43 |
2,0 |
|
4,0 |
0,42 |
2,0 |
|
4,2 |
0,41 |
2,07 |
|
4,4 |
0,40 |
2,10 |
|
4,6 |
0,39 |
2,15 |
|
4,8 |
0,38 |
2,18 |
|
5,0 |
0,37 |
2,20 |
|
5,2 |
0,36 |
2,20 |
|
5,4 |
0,35 |
2,30 |
|
5,6 |
0,35 |
2,30 |
|
5,8 |
0,34 |
2,30 |
|
6,0 |
0,33 |
2,30 |
|
6,2 |
0,31 |
2,30 |
Для этого находят энергию сечения Т0 =1,5hкрp, затем отношение ![]() и после этого по
табл. 30 -
отношение
и после этого по
табл. 30 -
отношение ![]()
Критическая глубина находится по формуле:

Колодезные перепады
Расчет сводится к определению длины и глубины каждого колодца, высоты водобойных стенок и скорости на выходе из сооружения.
Вход рассматривают как водослив с широким порогом (M = 1,42), водобойную стенку - как водослив с тонкой стенкой (M = 1,86).
Если колодец устраивается непосредственно за быстротоком (вертикальный уступ на быстротоке), то вместо напора над гребнем водослива следует принимать глубину струи на конце быстротока.
Расчет ведется в следующем порядке.
а) Расчет первого колодца: энергия сечения:
T0 = H + p;
по отношению ![]() пользуясь табл. 31, находят сжатую
глубину (до прыжка) hc
и глубину после прыжка h''c (глубина воды в
колодце 1,1h''c должна быть
меньше глубины колодца p,
т.е. 1,1h''c < p, так как иначе водослив
в начале колодца будет затоплен);
пользуясь табл. 31, находят сжатую
глубину (до прыжка) hc
и глубину после прыжка h''c (глубина воды в
колодце 1,1h''c должна быть
меньше глубины колодца p,
т.е. 1,1h''c < p, так как иначе водослив
в начале колодца будет затоплен);
напор перед водобойной стенкой (в конце колодца):
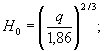
скорость подхода воды к водобойной стенке:
![]()
напор над водобойной стенкой:
![]()
высота водобойной стенки:
d = 1,1h''c - H;
длина водобойного колодца:
![]()
где
![]()
и

высота падения струи:
![]()
Данные для расчета водосливов
|
Характеристика порога водослива |
φ |
|
m |
|
|
Водослив с широким порогом |
|
|
|
|
|
При отсутствии потерь (идеальный случай) |
1 |
2/3 |
0,38 |
1,70 |
|
При хорошо округленной входной части водослива и весьма плавном подходе (трубы с откосными крыльями под углом 30° каждое) |
0,95 |
0,64 |
0,36 |
1,62 |
|
Порог с закругленным входным ребром |
0,92 |
0,63 |
0,35 |
1,55 |
|
Порог без закруглении входного ребра (обычные мосты и трубы с расходящимися откосными крыльями) |
0,85 |
0,59 |
0,32 |
1,42 |
|
Порог без закругления входного ребра и при неблагоприятных гидравлических условиях (неровный шероховатый вход) |
0,80 |
0,56 |
0,29 |
1,33 |
|
Водослив с тонкой стенкой |
0,90 |
- |
0,42 |
1,86 |
б) Расчет второго колодца:
энергия сечения
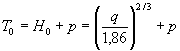
и далее расчет ведется так же, как и первого колодца.
в) Расчет третьего и последующих колодцев - ведется так же, как и второго колодца.
г) Расчет крепления на выходе:
За последним колодцем предусматривается крепление, которое может выдержать скорость, возникающую в сжатом сечении. Обычно па выходе делают рисберму.
Энергия сечения потока при наличии перед рисбермой водобойной стенки (в конце последнего колодца):
T0 = H0 + p0
(в этом случае p0 равно высоте стенки со стороны нижнего бьефа); при отсутствии перед рисбермой водобойной стенки:
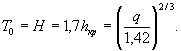
Далее по табл. 30 находится сжатая глубина hс.
Скорость в сжатом сечении ![]() Эта скорость не
должна превосходить допускаемую (неразмывающую) скорость υдоп,
для рисбермы (обычно 5 м/сек).
Эта скорость не
должна превосходить допускаемую (неразмывающую) скорость υдоп,
для рисбермы (обычно 5 м/сек).
Толщина рисбермы:
![]()
где
![]()
d - средний размер камня, см.
Если бы колодезный перепад устраивался непосредственно за быстротоком, то длина первого колодца была бы равна:
![]()
где υ0 - средняя скорость в конце быстротока;
i - уклон быстротока;
h - глубина струн в конце быстротока;
р - высота стенки падения.
При определении сжатой глубины hс и глубины за прыжком h''c за энергию потока в сечении в этом случае надо принять величину:
![]()
Если колодец устраивается за быстротоком без вертикального уступа, то длину колодца можно определить следующим путем. Допустим, что бытовая глубина в колодце:
hб = hкр.
Если глубина в конце быстротока h0, скорость в конце быстротока υ0, то большая глубина прыжка на выходе из быстротока будет:
![]()
Необходимая глубина колодца:
d = (1,1h2 + hб);
необходимая длина колодца:
l = 3(h2 - h0).
Расчет стенки состоит в определении ее высоты d и расстояния l от стенки падения до водобойной стенки. Если за стенкой получается отогнанный прыжок, то нужно ставить еще стенку и т. д.
Усиленная шероховатость
Если на быстротоке устроить небольшой высоты поперечные стенки из прямоугольных брусьев, то скорость протекания струи значительно уменьшится.
По данным С.В. Каплинского1, при прямоугольных ребрах высотой a = 15 см, размещенных друг от друга на расстоянии 6a = 6×15 = 90 см, и глубине воды над ребрами 3a > h > 5,5 м коэффициенты шероховатости n равны величинам, приведенным в табл. 32.
1 С.В. Каплинский. Водотоки усиленной шероховатости. Госэнергоиздат, 1950.
Значения коэффициента шероховатости n
|
Уклон дна водотока |
Ширина водотока, м |
|||
|
2 |
2,5 |
5 |
12 |
|
|
Коэффициент шероховатости n |
||||
|
0,06 |
0,027 |
0,028 |
0,032 |
0,037 |
|
0,09 |
0,028 |
0,0295 |
0,033 |
0,039 |
|
0,15 |
0,0285 |
0,0305 |
0,034 |
0,040 |
Опыты показали, что коэффициент шероховатости n возрастает с увеличением ширины русла, уклона и высоты ребра.
На автомобильных дорогах ширина быстротоков делается равной около 2 м. Более широкие быстротоки, порядка 12 м, почти не устраиваются.
В среднем значение n можно принимать для предварительных подсчетов равным n = 0,03 независимо от ширины быстротока и его уклона.
Скорость в быстротоке с усиленной шероховатостью в виде указанных ребер, по Каплинскому, равна:
![]()
где R - гидравлический радиус потока;
i - продольный уклон.
Пример. Быстроток с гладкими бетонными стенками (γ = 0,46) шириной 2 м должен пропустить расход Q = 4 м3/сек. Уклон быстротока i = 0,15. Допускаемая скорость υ = 5 м/сек.
Путем подбора находим бытовую глубину h0 = 0,27 м.
При этой глубине скорость в быстротоке
![]()
что превышает допускаемую, равную 5 м/сек.
Для уменьшения скорости устраиваем ребра высотой a = 15 см через 6a = 6×15 = 90 см.
Глубина воды над ребром h = 3a = 3×15 = 45 см.
Площадь живого сечения ω = 0,90 м2.
Смоченный периметр p = 2,90 м.
Гидравлический радиус R = 0,31 м.
По табл. 32 принимаем n = 0,0285.
Тогда скорость в быстротоке будет:
![]()
Консольные сбросы (лейки)
Обычно консоли устраивают в конце русла на участке сосредоточенного падения. Подводящее к консоли русло заканчивается водосливом с широким порогом. Далее вода течет по быстротоку, располагаемому над откосом на опорах. Лоток продолжается за последнюю опору, образуя горизонтальную консоль длиной 2 - 4 м.
Вода, падая с консоли, размывает грунт и образует воронку размыва. Воронка размыва углубляется падающей струей до тех пор, пока энергия струи не погасится.
С целью уменьшения размеров воронки размыва полезно консоль делать расширяющейся.
Подробные примеры расчетов косогорных сооружений различных типов приведены в Типовых проектах сооружений на автомобильных дорогах, выпуск 15. Автотрансиздат, 1955.
Глава 3
РАСЧЕТ ОТВЕРСТИЙ БОЛЬШИХ МОСТОВ
§ 12. Состав мостового перехода. Требования, предъявляемые к переходам
В основные инженерные сооружения мостового перехода входят:
подходы к мосту;
опоры и пролетные строения моста;
русловые струенаправляющие и укрепительные сооружения (непосредственно у моста);
выправительные пойменные регуляционные сооружения в районе перехода.
В зависимости от местных условий некоторые из указанных сооружений могут отсутствовать.
К каждому проектируемому большому мостовому переходу предъявляют следующие требования.
Пересекаемый участок реки должен обладать устойчивостью.
Поймы должны пересекаться в самом узком месте, а русло - в самом широком. Следует избегать пересечений рукавов, островов, а также мест, где могут образоваться ледяные зажоры.
Мост надо располагать по возможности нормально не только к руслу, но и к долине реки. Если такого участка нет, то надо выбрать наиболее пологую петлю реки, где такое совпадение имеется хотя бы на коротком участке. На небольших и средних реках в сложных случаях рекомендуется устраивать спрямление русел.
На судоходных и сплавных реках должны соблюдаться установленные подмостовые габариты.
При проектировании мостового перехода исходной величиной служит рабочая площадь живого сечения под мостом, которую определяют расчетом на пропуск расчетного паводка.
§ 13. Определение расчетных расходов
Общие указания
Определение расчетного расхода соды производится в следующей последовательности.
Находят одним из изложенных ниже способов бытовые расходы воды в реке.
Строят кривые расхода всего потока Q = f(H) и средней бытовой скорости русла υ = f(H). Среднюю скорость сопоставляют со скоростями на других участках реки и в особенности со скоростями под существующими мостами.
Устанавливают расход с требуемой вероятностью превышения для расчета отверстия моста и бровки полотна подходов.
Находят по кривой расходов на переходе соответствующие горизонты и среднюю скорость в русле.
Расчетный расход воды (в м3/сек) может быть определен:
на основе гидрометрических наблюдений в районе мостового перехода;
путем переноса расхода из другого места на реке, где он был определен с достаточной точностью;
по эмпирическим формулам гидравлики.
Надежнее всего определять расход с помощью гидрометрических наблюдений. Однако производство их сложно и дорого; кроме того, они дают достаточно ценный материал только тогда, когда их проводят при паводке выше среднемноголетнего, что бывает редко.
Определение расхода без наблюдений за проходом паводка производится по эмпирическим формулам гидравлики - морфологическим путем.
Эмпирические формулы гидравлики
Средняя скорость течения воды (в м/сек) определяется по формуле Шези:
![]()
где i - уклон потока;
R -
подводный радиус (![]() - м, где ω - площадь живого сечения, p - подводный периметр);
- м, где ω - площадь живого сечения, p - подводный периметр);
C - коэффициент, характеризующий сопротивление русла и пойм течению воды.
Для рек (кроме русел каньонного типа) R заменяют H (средняя
глубина, равная ![]() где b - ширина свободной
поверхности воды) и тогда
где b - ширина свободной
поверхности воды) и тогда
![]()
Величина C находится по эмпирическим формулам разных авторов, базировавшихся на наблюдениях за протеканием воды в руслах рек и канавах.
Для определения C при расчете мостов обычно пользуются формулой Базена:

где γ - коэффициент шероховатости.
Значения C для наиболее часто встречающихся случаев приведены в табл. 33.
Значения коэффициента C по формуле Базена
|
H |
γ |
|||
|
0,46 |
0,85 |
1,30 |
1,75 |
|
|
C |
||||
|
0,05 |
28,4 |
18,1 |
12,8 |
9,9 |
|
0,06 |
30,2 |
19,2 |
13,3 |
10,7 |
|
0,07 |
31,7 |
20,6 |
14,7 |
11,4 |
|
0,08 |
33,1 |
21,7 |
15,5 |
12,1 |
|
0,09 |
34,4 |
22,7 |
16,3 |
12,7 |
|
0,10 |
35,5 |
23,6 |
17,0 |
13,3 |
|
0,11 |
36,5 |
24,4 |
17,7 |
13,9 |
|
0,12 |
37,4 |
25,2 |
18,3 |
14,4 |
|
0,13 |
38,2 |
25,9 |
18,9 |
14,9 |
|
0,14 |
39,0 |
26,7 |
19,4 |
15,3 |
|
0,15 |
39,7 |
27,2 |
19,9 |
15,8 |
|
0,16 |
40,5 |
27,8 |
20,4 |
16,2 |
|
0,17 |
41,2 |
28,4 |
20,9 |
16,6 |
|
0,18 |
41,8 |
29,0 |
21,4 |
17,0 |
|
0,19 |
42,4 |
29,5 |
21,8 |
17,3 |
|
0,20 |
42,9 |
30,0 |
22,3 |
17,7 |
|
0,21 |
43,5 |
30,5 |
22,7 |
18,1 |
|
0,22 |
44,0 |
30,9 |
23,1 |
18,4 |
|
0,23 |
44,4 |
31,4 |
23,4 |
18,7 |
|
0,24 |
44,8 |
31,8 |
23,8 |
19,0 |
|
0,25 |
45,3 |
32,2 |
24,2 |
19,3 |
|
0,26 |
45,7 |
32,6 |
24,5 |
19,6 |
|
0,27 |
46,1 |
33,0 |
24,8 |
19,9 |
|
0,28 |
46,5 |
33,4 |
25,2 |
20,2 |
|
0,29 |
46,9 |
33,7 |
25,5 |
20,5 |
|
0,30 |
47,3 |
34,1 |
25,8 |
20,7 |
|
0,31 |
47,6 |
34,3 |
26,1 |
21,0 |
|
0,32 |
47,9 |
34,7 |
26,4 |
21,2 |
|
0,33 |
48,2 |
35,1 |
26,7 |
21,5 |
|
0,34 |
48,5 |
35,4 |
26,9 |
21,7 |
|
0,35 |
48,8 |
35,7 |
27,2 |
22,0 |
|
0,36 |
49,2 |
36,0 |
27,5 |
22,2 |
|
0,37 |
49,5 |
36,3 |
27,7 |
22,4 |
|
0,38 |
49,8 |
36,6 |
28,0 |
22,7 |
|
0,39 |
50,1 |
36,8 |
28,2 |
22,9 |
|
0,40 |
50,4 |
37,1 |
28,5 |
23,1 |
|
0,41 |
50,6 |
37,4 |
28,7 |
23,3 |
|
0,42 |
50,9 |
37,6 |
28,9 |
23,5 |
|
0,43 |
51,1 |
37,9 |
29,2 |
23,7 |
|
0,44 |
51,4 |
38,1 |
29,4 |
23,9 |
|
0,45 |
51,6 |
38,4 |
29,6 |
24,1 |
|
0,46 |
51,8 |
38,6 |
29,8 |
24,3 |
|
0,47 |
52,0 |
38,8 |
30,0 |
24,5 |
|
0,48 |
52,3 |
39,1 |
30,2 |
24,7 |
|
0,49 |
52,5 |
39,3 |
30,4 |
24,8 |
|
0,50 |
52,7 |
39,5 |
30,6 |
25,0 |
|
0,55 |
53,7 |
40,5 |
31,6 |
25,9 |
|
0,60 |
54,6 |
41,4 |
32,5 |
26,7 |
|
0,65 |
55,4 |
42,3 |
33,3 |
27,4 |
|
0,70 |
56,1 |
43,1 |
34,1 |
28,1 |
|
0,75 |
56,8 |
43,9 |
34,8 |
28,8 |
|
0,80 |
57,4 |
44,6 |
35,5 |
29,4 |
|
0,85 |
58,0 |
45,2 |
36,1 |
30,0 |
|
0,90 |
58,6 |
45,9 |
36,7 |
30,6 |
|
0,95 |
59,1 |
46,5 |
37,3 |
31,1 |
|
1,00 |
59,6 |
47,0 |
37,8 |
31,6 |
|
1,10 |
60,5 |
48,0 |
38,8 |
32,6 |
|
1,20 |
61,3 |
48,9 |
39,7 |
33,5 |
|
1,30 |
62,0 |
49,8 |
40,6 |
34,3 |
|
1,40 |
62,6 |
50,6 |
41,4 |
35,1 |
|
1,50 |
63,2 |
51,3 |
42,2 |
35,8 |
|
1,60 |
63,8 |
52,0 |
42,9 |
36,5 |
|
1,70 |
64,3 |
52,6 |
43,6 |
37,1 |
|
1,80 |
64,8 |
53,2 |
44,2 |
37,7 |
|
1,90 |
65,2 |
53,8 |
44,8 |
38,3 |
|
2,00 |
65,6 |
54,2 |
45,3 |
38,9 |
|
2,20 |
66,4 |
55,3 |
46,4 |
39,9 |
|
2,40 |
67,1 |
56,2 |
47,3 |
40,8 |
|
2,60 |
67,7 |
57,0 |
48,1 |
41,7 |
|
2,80 |
68,2 |
57,7 |
48,9 |
42,5 |
|
3,00 |
68,7 |
58,3 |
49,7 |
43,3 |
|
3,20 |
69,2 |
58,9 |
50,4 |
44,0 |
|
3,40 |
69,6 |
59,5 |
51,0 |
44,6 |
|
3,60 |
70,0 |
60,1 |
51,6 |
45,2 |
|
3,80 |
70,4 |
60,6 |
52,2 |
45,8 |
|
4,00 |
70,7 |
61,0 |
52,7 |
46,4 |
|
4,50 |
71,5 |
62,1 |
53,9 |
47,6 |
|
5,00 |
72,1 |
63,0 |
55,0 |
48,8 |
|
5,50 |
72,7 |
63,8 |
56,0 |
49,8 |
|
6,00 |
73,2 |
64,6 |
56,8 |
50,7 |
Можно также применять формулу Маннинга:
![]()
где n - коэффициент шероховатости.
Средняя скорость по Шези-Маннингу:
![]()
Значения коэффициентов шероховатости приведены в таблицах 34 и 35.
Коэффициенты шероховатости для русел и пойм рек
|
Характеристика потока |
По Базену |
По Маннингу |
|||
|
средние значения γ |
обычные колебания γ |
применительно к среднему значению |
|||
|
средняя глубина, м |
n |
||||
|
Ровное русло полугорных рек (галечно-гравийное ложе) |
1,2 |
0,8 - 1,5 |
|
2 4 6 10 |
0,024 0,023 0,023 0,023 |
|
Среднеизвилистое русло полугорных рек. Ровное русло равнинных рек (земляное ложе) |
1,5 |
1 - 2 |
|
2 4 6 10 |
0,026 0,025 0,025 0,024 |
|
Сильно извилистое русло полугорных рек, протоки и рукава. Среднеизвилистое русло равнинных рек |
2 |
До 2,5 |
|
2 4 6 10 |
0,031 0,029 0,029 0,028 |
|
Сильно извилистое русло равнинных рек, протоки и рукава. Русло горных рек (галечно-валунное ложе) |
2,5 |
2 - 3,5 |
|
2 4 6 10 |
0,035 0,033 0,032 0,030 |
|
Сильно извилистое русло равнинных рек с заросшими берегами. Русла рек с валунным ложем |
3,5 |
2,5 - 4 |
|
2 4 6 10 |
0,045 0,040 0,038 0,036 |
|
Порожистые участки рек с ровным течением. Незаросшие поймы |
5 |
3 - 7 |
|
2 4 6 10 |
0,060 0,058 0,051 0,048 |
|
Порожистые участки рек в средних условиях. Пойма, заросшая на 25 % |
7 |
5 - 9 |
|
2 4 6 10 |
0,092 0,077 0,065 0,060 |
Коэффициенты шероховатости для укреплений
|
Тип укрепления |
γ |
|
Одиночная мостовая |
1,30 |
|
Двойная мостовая |
1,30 |
|
Двойная мостовая из крупного рваного камня на цементном растворе |
1,30 |
|
Лоток из бутовой кладки с грубой поверхностью |
0,85 |
|
Лоток из бетона М-170 с устройством искусственной шероховатостей в виде поперечных ребер |
1,75 |
|
Железобетонная круглая труба, при высоте перепадов менее 10 см |
0,30 |
|
Железобетонная круглая труба, при высоте перепадов более 10 см |
0,46 |
|
Каменная труба, при высоте перепадов менее 20 см |
0,46 |
|
Каменная труба, при высоте перепадов более 20 см |
0,85 |
Поймы рек имеют обычно весьма большое, иногда решающее значение, так как при расчетных величинах паводков (с редкой вероятностью превышения) по поймам проходит большей частью 30 - 50%, а в отдельных случаях до 90% всего расхода. Поэтому Е.В. Болдаков рекомендует для рек пользоваться формулой:
υ = mH2/3i1/2 м/сек,
где m - характеристика шероховатости, одинаковая для русла и пойм (табл. 36).
Характеристика шероховатости m по Е.В. Болдакову (1955 г.)
|
Категории |
Морфологические признаки |
m |
|
|
среднее значение |
обычные колебания |
||
|
1 |
Русла земляные ровные. Русла полугорных рек в средних условиях. Незаросшие поймы |
30 |
22 - 40 |
|
2 |
Русла земляные, извилистые. Русла с галечно-валунным ложем. Ровное ложе суходолов. Земляные канавы при плохом содержании. Поймы, заросшие на 10 % |
25 |
20 - 30 |
|
3 |
Русла земляные сильно извилистые. Извилистое или заросшее ложе суходолов. Поймы, заросшие на 20 % |
20 |
15 - 25 |
|
4 |
Поймы, заросшие на 50 %. Сильно заросшее ложе суходолов, засоренное камнями |
15 |
10 - 20 |
|
5 |
Ложе суходола в завалах. Валуны. Селевой поток. Поймы, заросшие на 70 % |
10 |
6 - 15 |
|
6 |
Поймы, заросшие на 100 % |
5 |
0 - 8 |
Скорость в русле под мостом можно назначать и непосредственно по таблицам 37, 38 и 39.
Средние скорости по Е.В. Болдакову (1955 г.)
|
Глубина воды H, м |
υ, м/сек |
|
|
среднее значение |
обычные колебания |
|
|
5 |
0,6 |
0,4 - 1,0 |
|
6 |
0,8 |
0,5 - 1,1 |
|
7 |
0,9 |
0,6 - 1,2 |
|
8 |
1,0 |
0,7 - 1,3 |
|
9 |
1,1 |
0,8 - 1,3 |
|
10 |
1,2 |
0,9 - 1,4 |
|
11 |
1,3 |
1,0 - 1,5 |
|
12 |
1,4 |
1,1 - 1,6 |
|
14 |
1,5 |
1,2 - 1,8 |
|
16 |
1,6 |
1,7 - 1,9 |
|
18 |
1,8 |
1,6 - 2,1 |
|
20 |
2,0 |
1,8 - 2,2 |
Средние скорости по Д.Л. Соколовскому (1945 г.)
|
Характеристика рек |
υ, м/сек |
|
Реки заболоченные |
0,8 - 1,0 |
|
Реки обычные равнинные |
1,2 - 2,0 |
|
Реки полугорные или с холмистым рельефом |
2,0 - 2,5 |
|
Горные реки |
2,0 - 4,0 |
Средние скорости по Е.В. Болдакову (1939 г.)
|
Характеристика грунтов ложа рек: |
Средняя скорость воды под мостом υ, м/сек |
|
|
по геологическому строению |
по размываемости |
|
|
Ил, мелкий песок |
Слабый |
1,3 |
|
Крупный песок или глины с прослойками ила |
Средний |
1,6 |
|
Крупный песок с галькой, глина |
" |
1,8 |
|
Гравий |
Крепкий |
2,0 |
|
Галька |
" |
3,0 |
|
Булыжник |
" |
4,0 |
|
Грунт слабый или средний, но в глубокой части размыв достигает скалы; при длине размыва: |
|
|
|
в 20 % от ширины русла |
1,8 |
|
|
" 30 % " " " . |
2,0 |
|
|
" 40 % " " " . |
2,3 |
|
Для вычисления скоростей по формуле Шези ниже приводятся таблицы квадратных корней из величин уклонов и гидравлических радиусов.
Таблица 40
Значения квадратных корней из величин уклонов
|
Уклон i |
|
|
0,0001 |
0,0100 |
|
0,0002 |
0,0141 |
|
0,0003 |
0,0173 |
|
0,0004 |
0,0200 |
|
0,0005 |
0,0224 |
|
0,0006 |
0,0245 |
|
0,0007 |
0,0265 |
|
0,0008 |
0,0283 |
|
0,0009 |
0,0300 |
|
0,001 |
0,0316 |
|
0,0015 |
0,0387 |
|
0,002 |
0,0447 |
|
0,0025 |
0,0500 |
|
0,003 |
0,0548 |
|
0,0035 |
0,0592 |
|
0,004 |
0,0632 |
|
0,0045 |
0,0671 |
|
0,005 |
0,0707 |
|
0,0055 |
0,0742 |
|
0,006 |
0,0775 |
|
0,0065 |
0,0806 |
|
0,007 |
0,0837 |
|
0,0075 |
0,0866 |
|
0,008 |
0,0894 |
|
0,0085 |
0,0922 |
|
0,009 |
0,0949 |
|
0,0095 |
0,0975 |
|
0,01 |
0,1000 |
|
0,011 |
0,1049 |
|
0,012 |
0,1095 |
|
0,013 |
0,1140 |
|
0,014 |
0,1183 |
|
0,015 |
0,1225 |
|
0,016 |
0,1265 |
|
0,017 |
0,1304 |
|
0,018 |
0,1342 |
|
0,019 |
0,1378 |
|
0,020 |
0,1414 |
|
0,021 |
0,1449 |
|
0,022 |
0,1483 |
|
0,023 |
0,1517 |
|
0,024 |
0,1549 |
|
0,025 |
0,1581 |
|
0,026 |
0,1612 |
|
0,027 |
0,1643 |
|
0,028 |
0,1673 |
|
0,029 |
0,1703 |
|
0,03 |
0,1732 |
|
0,035 |
0,1871 |
|
0,04 |
0,2000 |
|
0,045 |
0,2121 |
|
0,05 |
0,2236 |
|
0,055 |
0,2345 |
|
0,06 |
0,2450 |
|
0,065 |
0,2550 |
|
0,07 |
0,2646 |
|
0,085 |
0,2915 |
|
0,09 |
0,3000 |
|
0,095 |
0,3082 |
|
0,10 |
0,3162 |
|
0,105 |
0,3240 |
|
0,11 |
0,3317 |
|
0,115 |
0,3391 |
|
0,12 |
0,3464 |
|
0,125 |
0,3536 |
|
0,13 |
0,3606 |
|
0,135 |
0,3674 |
|
0,14 |
0,3742 |
|
0,145 |
0,3808 |
|
0,15 |
0,3873 |
|
0,155 |
0,3937 |
|
0,16 |
0,4000 |
|
0,165 |
0,4062 |
|
0,17 |
0,4123 |
|
0,175 |
0,4182 |
|
0,18 |
0,4243 |
|
0,185 |
0,4301 |
|
0,19 |
0,4359 |
|
0,195 |
0,4416 |
|
0,20 |
0,4472 |
|
0,075 |
0,2739 |
|
0,08 |
0,2828 |
Таблица 41
Значения квадратных корней из величин гидравлических радиусов R
|
R |
|
|
0,100 |
0,316 |
|
0,105 |
0,324 |
|
0,110 |
0,332 |
|
0,115 |
0,339 |
|
0,120 |
0,346 |
|
0,125 |
0,353 |
|
0,130 |
0,360 |
|
0,135 |
0,367 |
|
0,140 |
0,374 |
|
0,145 |
0,381 |
|
0,150 |
0,387 |
|
0,155 |
0,394 |
|
0,160 |
0,400 |
|
0,165 |
0,406 |
|
0,170 |
0,412 |
|
0,175 |
0,418 |
|
0,180 |
0,424 |
|
0,185 |
0,430 |
|
0,190 |
0,436 |
|
0,195 |
0,442 |
|
0,200 |
0,447 |
|
0,210 |
0,458 |
|
0,220 |
0,469 |
|
0,230 |
0,480 |
|
0,240 |
0,490 |
|
0,250 |
0,500 |
|
0,270 |
0,520 |
|
0,280 |
0,529 |
|
0,290 |
0,539 |
|
0,300 |
0,548 |
|
0,310 |
0,557 |
|
0,320 |
0,566 |
|
0,330 |
0,574 |
|
0,340 |
0,583 |
|
0,350 |
0,592 |
|
0,360 |
0,600 |
|
0,370 |
0,608 |
|
0,380 |
0,616 |
|
0,390 |
0,624 |
|
0,400 |
0,632 |
|
0,420 |
0,648 |
|
0,440 |
0,663 |
|
0,460 |
0,678 |
|
0,480 |
0,693 |
|
0,500 |
0,707 |
|
0,520 |
0,721 |
|
0,540 |
0,735 |
|
0,51,0 |
0,748 |
|
0,580 |
0,762 |
|
0,600 |
0,775 |
|
0,620 |
0,787 |
|
0,640 |
0,800 |
|
0,660 |
0,812 |
|
0,680 |
0,825 |
|
0,700 |
0,837 |
|
0,720 |
0,849 |
|
0,740 |
0,860 |
|
0,760 |
0,872 |
|
0,780 |
0,883 |
|
0,800 |
0,894 |
|
0,820 |
0,905 |
|
0,840 |
0,916 |
|
0,860 |
0,927 |
|
0,880 |
0,938 |
|
0,900 |
0,949 |
|
0,920 |
0,959 |
|
0,940 |
0,970 |
|
0,960 |
0,980 |
|
0,980 |
0,990 |
|
1,000 |
1,100 |
|
1,025 |
1,010 |
|
1,050 |
1,025 |
|
1,075 |
1,04 |
|
1,100 |
1,05 |
|
1,125 |
1,06 |
|
1,150 |
1,07 |
|
1,175 |
1,08 |
|
1,200 |
1,10 |
|
1,225 |
1,11 |
|
1,250 |
1,12 |
|
1,275 |
1,13 |
|
1,300 |
1,14 |
|
1,325 |
1,15 |
|
1,350 |
1,16 |
|
1,375 |
1,17 |
|
1,400 |
1,18 |
|
1,425 |
1,19 |
|
1,450 |
1,20 |
|
1,475 |
1,21 |
|
1,500 |
1,22 |
|
1,550 |
1,24 |
|
1,600 |
1,26 |
|
1,650 |
1,28 |
|
1,700 |
1,30 |
|
1,750 |
1,32 |
|
1,800 |
1,34 |
|
1,850 |
1,36 |
|
1,900 |
1,38 |
|
1,950 |
1,40 |
|
2,000 |
1,41 |
|
2,050 |
1,43 |
|
2,100 |
1,45 |
|
2,150 |
1,47 |
|
2,200 |
1,49 |
|
2,250 |
1,50 |
|
2,300 |
1,52 |
|
2,350 |
1,53 |
|
2,400 |
1,55 |
|
2,450 |
1,57 |
|
2,500 |
1,58 |
|
2,550 |
1,60 |
|
2,600 |
1,61 |
|
2,650 |
1,63 |
|
2,700 |
1,64 |
|
2,750 |
1,66 |
|
2,800 |
1,67 |
|
2,850 |
1,69 |
|
2,900 |
1,70 |
|
2,950 |
1,72 |
|
3,000 |
1,73 |
|
3,100 |
1,76 |
|
3,200 |
1,79 |
|
3,300 |
1,82 |
|
3,400 |
1,85 |
|
3,500 |
1,87 |
|
3,600 |
1,90 |
|
3,700 |
1,92 |
|
3,800 |
1,95 |
|
3,900 |
1,97 |
|
4,000 |
2,00 |
Метод математической статистики
Расход заданной вероятности превышения определяется по формуле:
Q = Qcp(l + CvФ) м3/сек,
где Qср - средний максимальный
(многолетний паводочпын) расход, т.е. ![]() где ∑Q - сумма всех
максимальных расходов, n
- число лет наблюдений на водомерном посту;
где ∑Q - сумма всех
максимальных расходов, n
- число лет наблюдений на водомерном посту;
Cv -коэффициент вариации реки (коэффициент изменчивости паводков за ряд лет), зависящий от формы бассейна (при длинных бассейнах этот коэффициент, как правило, больше, чем при разветвленных);
Ф - поправочный коэффициент по табл. 42.
Коэффициент вариации реки:
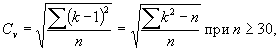

где ![]() т.е. отношение максимального
расхода каждого года, входящего в ряд, к среднему максимальному расходу.
т.е. отношение максимального
расхода каждого года, входящего в ряд, к среднему максимальному расходу.
Вычисления коэффициента вариации удобнее всего вести в табличной форме, как это указано в нижеследующем примере.
Пример определения коэффициента Cv (при числе лет непрерывных наблюдений n = 35, с 1887 по 1932 г. включительно).
Таблица „в"
|
№ п/п |
Год наблюдения |
Горизонты, м |
Максимальный расход, м3/сек |
|
(k - 1) |
(k - 1)2 |
|
|
+ |
- |
||||||
|
1 |
1887 |
155,50 |
500 |
0,73 |
- |
0,27 |
0,07 |
|
2 |
1888 |
156,40 |
1100 |
1,61 |
0,61 |
- |
0,37 |
|
3 |
1889 |
155,70 |
610 |
0,89 |
- |
0,11 |
0,01 |
|
4 |
1890 |
154,90 |
240 |
0,35 |
- |
0,65 |
0,42 |
|
5 |
1891 |
154,80 |
210 |
0,31 И т. д. |
- |
0,69 |
0,48 |
|
34 |
1931 |
155,10 |
900 |
1,32 |
0,32 |
- |
0,10 |
|
35 |
1932 |
155,90 |
780 |
1,14 |
0,14 |
|
0,02 |
|
|
|
∑Q = 23800 |
|
|
∑(k - 1)2 = 13,84 |
||
![]()
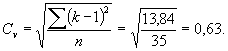
Для определения коэффициента Ф нужно предварительно найти коэффициент асимметрии C, характеризующий несимметричность распределения больших и малых расходов от среднего их значения.
Коэффициент асимметрии вычисляют по формуле:
![]()
или принимают по ГОСТ 3999-48 равным:
Cs = 2Cv при снеговых паводках
и
Cs = 4Cv при дождевых паводках.
Значения коэффициентов Cv и Cs для ряда рек Советского Союза указаны в табл. 13.
Далее по табл. 42 определяется коэффициент Ф.
При наличии, кроме непрерывного ряда годовых максимальных уровней и соответствующих им расходов, еще одного или нескольких значений особенно больших паводков, зафиксированных значительно ранее того, как были начаты непрерывные наблюдения, средний максимальный расход (по Е.В. Болдакову, С.Н. Крицкому и М.Ф. Менкелю):
![]()
где N - количество всех лет наблюдений;
s - количество отдельно зафиксированных больших расходов;
n - число непрерывно наблюденных расходов,
а коэффициент вариации реки
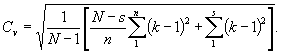
Поправочный коэффициент Ф при Сv = 1
|
Cs |
вероятность превышения паводка |
||||||||
|
1 1000 |
1 500 |
1 300 |
1 100 |
1 50 |
1 33 |
1 25 |
1 10 |
1 5 |
|
|
Значения коэффициента Ф |
|||||||||
|
0,0 |
3,1 |
2,9 |
2,7 |
2,3 |
2,0 |
1,9 |
1,8 |
1,3 |
0,8 |
|
0,1 |
3,3 |
3,0 |
2,8 |
2,4 |
2,1 |
1,9 |
1,8 |
1,3 |
0,8 |
|
0,2 |
3,4 |
3,1 |
2,9 |
2,5 |
2,1 |
1,9 |
1,8 |
1,3 |
0,8 |
|
0,3 |
3,5 |
3,2 |
3,0 |
2,6 |
2,2 |
1,9 |
1,8 |
1,3 |
0,8 |
|
0,4 |
3,7 |
3,3 |
3,1 |
2,6 |
2,2 |
2,0 |
1,8 |
1,3 |
0,8 |
|
0,5 |
3,8 |
3,5 |
3,3 |
2,7 |
2,3 |
2,0 |
1,9 |
1,3 |
0,8 |
|
0,6 |
4,0 |
3,6 |
3,3 |
2,8 |
2,3 |
2,1 |
1,9 |
1,3 |
0,8 |
|
0,7 |
4,1 |
3,7 |
3,4 |
2,8 |
2,4 |
2,1 |
1,9 |
1,3 |
0,8 |
|
0,8 |
4,2 |
3,8 |
3,5 |
2,9 |
2,4 |
2,1 |
2,0 |
1,3 |
0,8 |
|
0,9 |
4,3 |
3,9 |
3,7 |
3,0 |
2,4 |
2,1 |
2,0 |
1,3 |
0,8 |
|
1,0 |
4,5 |
4,1 |
3,7 |
3,0 |
2,5 |
2,2 |
2,0 |
1,3 |
0,8 |
|
1,1 |
4,7 |
4,2 |
3,8 |
3,1 |
2,5 |
2,2 |
2,0 |
1,3 |
0,7 |
|
1,2 |
4,8 |
4,3 |
3,9 |
3,1 |
2,6 |
2,2 |
2,1 |
1,3 |
0,7 |
|
1,3 |
5,0 |
4,4 |
4,0 |
3,2 |
2,6 |
2,3 |
2,1 |
1,3 |
0,7 |
|
1,4 |
5,1 |
4,6 |
4,1 |
3,3 |
2,7 |
2,3 |
2,1 |
1,3 |
0,7 |
|
1,5 |
5,2 |
4,7 |
4,2 |
3,3 |
2,7 |
2,3 |
2,1 |
1,3 |
0,7 |
|
1,6 |
5,4 |
4,8 |
4,3 |
3,4 |
2,8 |
2,4 |
2,1 |
1,3 |
0,7 |
|
1,7 |
5,5 |
4,9 |
4,4 |
3,4 |
2,8 |
2,4 |
2,2 |
1,3 |
0,7 |
|
1,8 |
5,7 |
5,0 |
4,5 |
3,5 |
2,8 |
2,4 |
2,2 |
1,3 |
0,6 |
|
1,9 |
5,8 |
5,1 |
4,5 |
3,5 |
2,8 |
2,4 |
2,2 |
1,3 |
0,6 |
|
2,0 |
5,9 |
5,2 |
4,6 |
3,6 |
2,9 |
2,5 |
2,2 |
1,3 |
0,6 |
|
2,1 |
6,0 |
5,3 |
4,8 |
3,6 |
2,9 |
2,5 |
2,2 |
1,3 |
0,6 |
|
2,2 |
6,2 |
5,4 |
4,9 |
3,7 |
2,9 |
2,5 |
2,2 |
1,3 |
0,6 |
|
2,3 |
6,4 |
5,5 |
4,9 |
3,7 |
2,9 |
2,5 |
2,2 |
1,3 |
0,6 |
|
2,4 |
6,5 |
5,7 |
5,0 |
3,8 |
3,0 |
2,5 |
2,2 |
1,2 |
0,5 |
|
2,5 |
6,6 |
5,8 |
5,0 |
3,8 |
3,0 |
2,5 |
2,2 |
1,2 |
0,5 |
|
2,6 |
6,7 |
5,8 |
5,1 |
3,9 |
3,0 |
2,5 |
2,2 |
1,2 |
0,5 |
|
2,7 |
6,9 |
5,9 |
5,2 |
3,9 |
3,0 |
2,5 |
2,2 |
1,2 |
0,5 |
|
2,8 |
7,0 |
6,0 |
5,3 |
3,9 |
3,0 |
2,5 |
2,2 |
1,2 |
0,5 |
|
2,9 |
7,1 |
6,1 |
5,4 |
4,0 |
3,1 |
2,5 |
2,2 |
1,2 |
0,5 |
|
3,0 |
7,2 |
6,3 |
5,4 |
4,0 |
3,1 |
2,5 |
2,2 |
1,2 |
0,4 |
|
3,2 |
7,5 |
6,5 |
5,5 |
4,1 |
3,1 |
2,5 |
2,3 |
1,1 |
0,4 |
|
3,5 |
7,9 |
6,8 |
5,8 |
4,2 |
3,2 |
2,5 |
2,3 |
1,1 |
0,3 |
Если имеется значение расхода и нужно определить его вероятность, то составляют указанным способом таблицу вероятностей превышения различных расходов и затем устанавливают, какой вероятности соответствует имеющийся расход.
Вероятность превышения любого расхода более значительный расходом можно определить по эмпирической формуле Н.Н. Чегодаева:
![]()
где m - количество расходов, больших или равных тому расходу, вероятность которого вычисляется;
n - число максимальных годовых расходов за весь период наблюдений.
При пользовании методом математической статистики следует учитывать, что максимальный сток является результатом совокупности различных естественных факторов (глубина промерзания почв, быстрота таяния снега, выпадение дождей во время снеготаяния, ледяные зажоры и проч.). Кроме того, надо учитывать хозяйственную деятельность человека, которая может повлиять на характер стока с бассейна (вырубка леса, мелиоративные мероприятия и др.).
Для предварительных соображений предельно возможный наибольший расход (ММ), вероятность превышения которого равна нулю, можно определить по формуле Е.В. Болдакова:
![]()
Эмпирическая формула Д.Л. Соколовского
По формуле Соколовского расход воды весеннего половодья (в м3/сек) равен:
Q = δδ'AF3/4
где A - расход в м3/сек с 1 км2 площади бассейна, принимаемый по табл. 13;
δ - коэффициент заболоченности бассейна (см. табл. 14);
δ' - коэффициент залесенности бассейна (см. табл. 15);
F - площадь бассейна, км2.
При пользовании вышеприведенной формулой необходимо тщательно изучить как рассматриваемый бассейн, так и бассейн-аналог, чтобы не ошибиться в выборе значения A. Для установления величины A нужно:
учитывать, при наличии резко расчлененного рельефа, ориентировку склонов и выбирать аналог, как правило, среди рек, имеющих ту же экспозицию;
принимать во внимание заболоченность и лесистость бассейнов рек и выбирать по возможности аналог с близкими в этом отношении условиями (тогда вводить значения δ и δ' не надо);
учитывать характер пойм рек для определения возможности значительного распластывания паводка в случае резкого расширения поймы реки и, следовательно, снижения величины A.
Связь между расходами, уровнями и средними скоростями
Связь между расходами и уровнями воды графически изображают в виде кривой расхода Q = f(H). Такую кривую строят по результатам определения расхода при различных горизонтах воды (рис. 13).

Аналогично строят кривую скорости υ = f(H).
Если в створе проектируемого перехода (пункт А) наблюдения за режимом реки кратковременны, а в другом створе той же реки (пункт Б), удаленном от створа перехода, велись достаточно долго, то для определения в пункте А максимальных уровней реки в годы, когда наблюдения здесь не производились, строят кривую связей уровней.
Для этого вычерчивают график (рис. 14) связи уровней, зафиксированных одновременно на обоих створах, и по его точкам проводят плавную кривую, которую при необходимости можно экстраполировать.
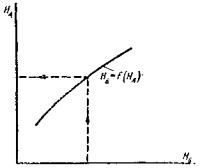
Если для пункта Б взять максимальную отметку уровня для года, в который наблюдения в пункте А не производились, то по кривой определится соответствующая отметка в пункте А.
В случае, когда наблюдения на месте перехода не велись совсем, также возможен перенос отметки со створа, где производились длительные наблюдения, но при условии отсутствия между этими створами значительных притоков.
Считая, что превышения максимума годовых уровней над меженью в обоих пунктах одинаковы, искомую отметку сносят по уклону реки.
§ 14. Расчет отверстий
Общие данные
В настоящее время отверстие моста получают по необходимой рабочей площади путем набора площади живого сечения под мостом, с учетом стеснения потока опорами, допускаемого размыва, величины предполагаемых срезок грунта на поймах реки, а также наличия, формы и размеров струенаправляющих дамб.
Поэтому для одного и того же места перехода возможны варианты моста с отверстиями различной величины. Окончательно величину отверстия моста назначают на основе технико-экономических соображений в соответствии с намеченной схемой сооружения.
Расчет отверстия моста производится в следующей последовательности:
определяют необходимую рабочую площадь под мостом;
устанавливают в зависимости от типа основания и геологического строения в месте перехода коэффициент размыва, а также величину и конфигурацию срезки;
набирают по данному створу рабочую площадь под мостом;
проверяют полученное подбором отверстие моста, принимая за искомую величину или среднюю скорость или коэффициент размыва;
строят линию среднего размыва, а также линию возможных местных размывов для определения наивысшей возможной отметки заложения опор.
Различают следующие случаи расчета отверстий мостов на больших реках: через равнинные реки, через предгорные блуждающие реки и через горные реки.
В общем случае рабочая площадь под мостом:
![]()
где Q - расчетный расход;
υ - средняя бытовая скорость течения;
μ - общий коэффициент сжатия.
По последним воззрениям мостовые отверстия пропускают единые русловые потоки жидкой фазы и наносов. Для равнинных рек, где активное русло перекрывают мостом полностью и где естественный русловой процесс выражен слабо, указанное обстоятельство вносит лишь небольшое уточнение по сравнению с прежними способами расчета отверстий. На реках блуждающего типа наносы значительно влияют на общий ход руслового потока и уточнение расчета в этом случае имеет существенное значение; главное же, такой расчет отражает существо происходящих в русле физических явлений.
Мосты на равнинных реках
Продольный профиль водной поверхности по оси потока (на прямолинейном участке) в естественном состоянии представляет собой наклонную линию. При наличии моста поток будет сжат подходами и очертание поверхности воды примет вид, показанный на рис. 15. Перед мостом возникает подпор и здесь могут отложиться наносы. Вследствие сжатия потока под мостом и непосредственно ниже его на этом участке может произойти значительный размыв дна.
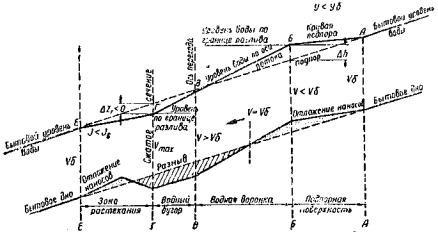
Рис. 15. Очертание водной поверхности на прямолинейном участке в районе мостового перехода
Дальше, ниже моста, поток начинает растекаться, скорости уменьшаются и происходит выпадение наносов.
Деформации дна (образование наносов и размывов), скорости и уклоны на отдельных участках потока зависят от относительных размеров отверстия моста, способа подведения потока к мосту и отвода его вниз по течению.
Различают два расчетных случая определения отверстия моста:
1-й случай - когда сжатое сечение совмещается с подмостовым сечением;
2-й случай - когда сжатое сечение потока образуется ниже моста.
1-й случай (основной). Сжатое (расчетное) сечение совмещается с подмостовым сечением. Это бывает при наличии струенаправляющих дамб рациональной формы или же, если, несмотря на отсутствие дамб (или их нерациональное очертание), сжатое сечение потока за мостом (где нет быков) больше или равно подмостовому сечению (где есть быки). Тогда
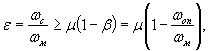
где ωс - сжатое сечение потока ниже продольной оси моста;
ωм - площадь подмостового сечения (между передними гранями устоев или конусами, включая площади вертикальных сечений быков), набираемая на продольном профиле перехода;
ε - коэффициент общего сжатия, зависящий от наличия и очертания в плане струенаправляющих дамб;
μ - коэффициент сжатия потока быками моста, зависящий от величины пролетов в свету (табл. 43);
![]() - коэффициент
стеснения; можно принимать
- коэффициент
стеснения; можно принимать ![]() где l - ширина быка по фасаду
моста, b -
расстояние между осями быков;
где l - ширина быка по фасаду
моста, b -
расстояние между осями быков;
ωоп - площадь поперечного сечения подмостового сечения, занятая речными опорами;
ωр =μ(1 - β)ωм = ωс,
где ωр - рабочая площадь подмостового сечения;
![]()
где Q - расчетный расход;
υ - расчетная скорость; при большом количестве наносов эта скорость равна бытовой, при малом количестве наносов она равна допускаемой (неразмывающей).
Значения коэффициента сжатия потока быками моста μ
|
Пролет моста в свету, м |
Коэффициент сжатия, μ |
|
|
уровень ледохода равен расчетному горизонту |
уровень ледохода не равен расчетному горизонту |
|
|
10 |
0,85 |
0,90 |
|
20 |
0,93 |
0,95 |
|
30 |
0,95 |
0,97 |
|
50 |
0,96 |
0,97 |
|
80 |
0,97 |
0,98 |
|
100 |
0,98 |
0,99 |
|
150 |
0,99 |
0,99 |
|
200 |
1,00 |
1,00 |
Расчетная величина υ (независимо от способа определения) должна соответствовать требованиям ТУ.
2-й случаи. Сжатое расчетное сечение (меньшее по площади, чем подмостовое) образуется ниже моста по течению. Этот случай бывает при отсутствии струенаправляющих дамб или при их нерациональной форме, а также, если нет конусов.
Тогда:

![]()
![]()
где Qп - расход, проходивший в бытовом состоянии по частям пойм, закрываемым насыпями подходов; остальные обозначения прежние.
Если динамическая ось потока не перпендикулярна оси перехода то при определении живого сечения необходимо учитывать косину и вводить поправку, определяя рабочую площадь из выражения:
![]()
где ωтр - расчетная площадь при нормальном пересечении;
α - острый угол между осью перехода и прямой, перпендикулярной оси потока.
При многопролетном косом мосту следует учитывать дополнительное стеснение опорами.
На судоходных реках надлежит проверять поверхностную скорость при расчетном судоходном горизонте:
![]()
где υ - средняя бытовая скорость при расчетном горизонте;
h - средняя глубина потока при том же горизонте,
![]()
L - отверстие моста;
i - уклон потока, который можно принимать равным уклону при расчетном высоком горизонте.
Поверхностная скорость в каждом судоходном пролете равна:
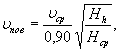
где υср - средняя скорость под мостом при расчетном судоходном горизонте;
Hh - средняя глубина в расчетном судоходном пролете;
Hср - средняя глубина под мостом при расчетном судоходном горизонте.
При наличии, кроме русла, хорошо развитых работающих проток в виде исключения допускается устройство на них дополнительных отверстий, но с тем, чтобы в дополнительное отверстие пропускалось не менее 20 % общего расчетного расхода воды, чтобы отверстие было рассчитано без размыва на скорость, допускаемую по грунту, и регуляционные сооружения обеспечивали соответствующее распределение расхода между отверстиями.
Если на пойме или при долинном ходе необходимо устройство малых отверстий для пропуска расходов ручьев и т. п., то такие отверстия должны иметь шандорные затворы на время половодья во избежание увеличения расхода в сооружении и прорыва насыпи.
Размыв под мостом и срезка грунта
Для уменьшения длины моста обычно допускают размыв дна и делают срезку грунта. Тогда в формулы для расчета площади вводят (вместо υ) скорость потока, соответствующую началу размыва:
υp = Pυ,
где P - коэффициент размыва, зависящий от типа основания и глубины заложения фундаментов опор.
Размыв русла вводят в расчет при прямом участке русла, а при криволинейном участке - только в средней части и со стороны вогнутой части русла. Со стороны выпуклой части размыв не учитывают.
Срезку учитывают при наборе площади подмостового сечения на профиле мостового перехода путем деления ωм на коэффициент Ср (лежащий в пределах):
1,25 ≥ Ср ≥ 1,
где
![]()
ωср - площадь срезки.
Срезку делают под уровень, при котором ее действительно можно сделать (на 0,5 - 1,0 м выше средней, но не низкой межени). Уклон срезки вдоль реки должен равняться уклону реки.
Общая площадь срезки и размыва не должна превышать 0,4 бытовой площади под мостом для судоходных рек и 0,5 для несудоходных рек. Размыв в пределах срезки допускают на общих основаниях, как в остальной части отверстия.
Срезку можно делать при прямом участке русла (длиной в 2 - 3 отверстия моста) и при криволинейном участке. В последнем случае срезка делается с вогнутой стороны реки, так как срезка, сделанная на выпуклой стороне, может заноситься в результате поперечной циркуляции потока и потому нерациональна.
Срезку делают не только под мостом, но и выше и ниже моста в виде широкого разворота, чтобы поток мог войти с расчетной средней скоростью и после беспрепятственно выйти, так как иначе срезка нормально работать не будет.
Средняя глубина после размыва (рис. 16, а):
hр = Ph,
где P - коэффициент размыва;
h - глубина до размыва.

Рис. 16. К расчету глубин после размыва под
мостом:
а - глубина после размыва; б - увеличение глубин после размыва к крайних частях
отверстия моста; в - глубины при наличии обнажений неразмываемых пластов грунта
или скалы; г - равномерный размыв; д - увеличение глубин при уменьшении радиуса
кривизны
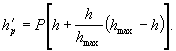
Максимальная возможная глубина после размыва на немеандрирующих реках (рис. 16, б):
Если в русле имеются обнажения коренных (неразмываемых) пород, то фактический коэффициент размыва (рис. 16, в):
![]()
где P1 - расчетный коэффициент размыва (см. выше);
ωм - необходимая подмостовая площадь;
ω1 - площадь размываемой части сечения до размыва;
ω2 - площадь остальной части сечения при предельном размыве.
Глубина после размыва (в размываемой части) может быть также определена из выражения:
![]()
где h и P - глубина до размыва и коэффициент размыва, определенные по предыдущему;
ω1 - площадь под мостом в размываемой части;
ω3- то же, в неразмываемой части.
Для рек со слабо работающим руслом (когда по поймам проходит не менее 80 % всего расхода и ширина скопления наносов в русле не превышает 20 % его полной ширины) общий размыв (рис. 16, г):
![]()
где q - расход на единицу длины рабочего отверстия моста;
L - длина моста;
υд - допускаемая скорость по грунту ложа;
β - часть площади, запятая опорами;
μ - коэффициент сжатия (см. табл. 43).
На меандрирующих реках (независимо от интенсивности работы пойм) надо учитывать возможное увеличение кривизны русла. Увеличение глубин от h1 до h2 при уменьшении радиуса кривизны от r1 до r2 (рис. 16, д) находят из выражения:
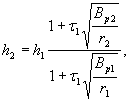
где h1 - глубина при радиусе кривизны излучины r1;
Bр1 - ширина русла при глубине h1;
h2 и Bр2 - то же, при радиусе r2;
τ1 и τ2 - коэффициенты, равные:
0,6 при r > 2,5Bр
2,5 при r = Bр
(промежуточные величины находят по интерполяции).
Максимальная глубина местного размыва у опоры по И.А. Ярославцеву:
![]()
где υ0 - средняя скорость течения у опоры, м/сек;
K1 - коэффициент, зависящий от формы лобовой грани опоры (см. табл. 44);
K2 - коэффициент, зависящий от расчетной ширины опоры b1 и скорости υ0 (рис. 17), причем расчетную ширину опоры b1 находят по табл. 44;
K3 - коэффициент, зависящий от глубины набегающего потока H (вне воронки размыва) и расчетной ширины опоры (рис. 18);
d - диаметр наиболее крупных фракций грунта (для песков d = 0).

Рис. 17. Коэффициент K2 в зависимости от расчетной ширины опоры b1 и скорости υ0
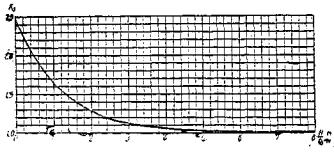
Рис. 18. Коэффициент K3 в зависимости от глубины набегающего потока H (вне воронки размыва) и расчетной ширины опоры
При пользовании указанной формулой надо иметь в виду, что на ряде периодических водотоков, а также на некоторых участках горных рек (обычно при υ0 > 5 - 6 м/сек) значение hв получается несколько завышенным.
Значения коэффициента K1 в зависимости от формы лобовой опоры
|
Форма опоры (схема) |
Значения коэффициента K1 |
Расчетная ширина опоры b1 |
|||||||||||||||||
|
|
При нормальном набегании потока K1 =0,87 При косом набегании потока K1 в зависимости от угла набегания α° |
При нормальном набегании потока b1 = b При косом набегании потока b1 = (l - b)sinα + b |
|||||||||||||||||
|
α° |
0° |
10° |
20° |
30° |
40° |
K1 для углов, равных или больших 20°, может быть взят по таблице при условии, что
|
|||||||||||||
|
K1 |
0,87 |
0,89 |
0,92 |
1,05 |
1,15 |
||||||||||||||
|
|
|||||||||||||||||||
|
|
K1 = 1,27 |
При нормальном набегании потока b1 = b При косом набегании потока b1 = lsinα + bcosα |
|||||||||||||||||
|
|
В зависимости от двугранного угла опоры β° |
При нормальной набегании потока b1 = b При косом набегании потока b1 @ (l - b)sinα + b |
|||||||||||||||||
|
β° |
120° |
80° |
60° |
||||||||||||||||
|
K1 |
1,25 |
1,0 |
0,76 |
||||||||||||||||
|
Указанные значения K1 справедливы лишь при небольших углах α° |
|||||||||||||||||||
|
|
В зависимости от величины |
При нормальном набегании потока
При косом набегании потока при b1 = (l - b)sinα + b0 где
при b1 = lsinα + b0cosα, где &о=Ь + (6ф-Ь) уу |
|||||||||||||||||
|
|
|
||||||||||||||||||
|
α° |
0 |
0,2 |
0,4 |
0,6 |
0,8 1,0 |
||||||||||||||
|
0 |
0,87 |
1,01 |
1,17 |
1,23 |
1,27 |
||||||||||||||
|
10 |
0,89 |
1,03 |
1,18 |
1,23 |
1,27 |
||||||||||||||
|
20 |
0,92 |
1,05 |
1,19 |
1,25 |
1.27 |
||||||||||||||
|
30 |
1,08 |
1,15 |
1,23 |
1,27 |
1,27 |
||||||||||||||
|
40 |
1,15 |
1,22 |
1,27 |
1,27 |
1,27 |
||||||||||||||
|
K1 для углов α°, равных или больших 20°, может быть взят по таблице при условии, что
|
|||||||||||||||||||
|
|
K1 = 1,27 |
При нормальном набегании потока
При косом набегании потока b1 = lsinα + b0cosα, где
|
|||||||||||||||||
|
|
K1= 1,02 |
b1 = b |
|||||||||||||||||
|
|
В зависимости от
величины |
При нормальном набегании потока b1 = b При косом набегании b1 = (l - b)sinα + b K1 для углов α, равных или больших 20°, может быть взят по таблице при условии, что |
|||||||||||||||||
|
α° |
|
||||||||||||||||||
|
0 |
2 |
4 |
8 |
12 |
|||||||||||||||
|
0 |
0,87 |
0,77 |
0,69 |
0,61 |
0,55 |
||||||||||||||
|
10 |
0,89 |
0,79 |
0,70 |
0,62 |
0,56 |
||||||||||||||
|
20 |
0,92 |
0,80 |
0,71 |
0,63 |
0,57 |
||||||||||||||
|
30 |
1,05 |
0,88 |
0,76 |
0,65 |
0,58 |
||||||||||||||
|
40 |
1,14 |
0,94 |
0,81 |
0,68 |
0,60 |
||||||||||||||
|
Следует проверить размыв у каждой сваи, рассматривая ее как цилиндрическую опору
|
|||||||||||||||||||
|
|
K1= 0,67 |
b1 = b |
|||||||||||||||||
По Е.В. Болдакову максимальная глубина при неравномерном (местном) сосредоточенном размыве у опор может быть определена по табл. 45.
Формулы местного размыва
|
Форма опоры |
Максимальная глубина размыва Л„, м |
|
Полуобтекаемая |
|
|
Прямоугольная |
|
|
При косине опоры > 10° |
|
где υ1 - средняя скорость течения, м/сек;
υ0 - допускаемая (неразмывающая) скорость для грунта ложа, м/сек.
Для первоначальных соображений и рекогносцировочных изысканий можно определить отверстие моста по М.Ф. Срибному:
![]()
где L - отверстие моста между заложениями оснований конусов;
a - при срезке принимается равным 1 - 1,1, а без срезки 1,2;
P0 - приведенный коэффициент размыва, определяемый следующим образом:
P принятый в расчете 1,4; 1,2 ; 1,0 и соответственно
P0 приведенный 1,3; 1,1 ; 1,0;
l1 - ширина русла;
l2 и l3 - ширина правой и левой пойм;
ρ2 и ρ3 - коэффициенты сопротивления пойм по табл. 46;
1,05 - коэффициент стеснения опорами (при мелких пролетах рекомендуется принимать 1,1).
Значения коэффициента сопротивления пойм
|
Характеристика пойм |
ρ |
|
Без растительности |
1,0 |
|
Залесенность равна 25 % площади |
0,8 |
|
" " 60 |
0,6 |
|
" " 75 |
0,4 |
|
" " 100 |
0,2 |
Мосты через предгорные блуждающие реки
В любом поперечном сечении русла блуждающих предгорных рек глубины распределяются неравномерно. Наибольшая глубина в меженной части русла больше средней глубины потока. В связи с быстрым перемещением русел на блуждающих реках, казалось бы, достаточно определить наибольшую глубину русла и назначить по ней глубину заложения всех опор моста. Однако расчетом, сделанным по натурным зависимостям, создавшимся на реке в течение ряда десятилетий, можно определить лишь «нормальные» характеристики сформированного подмостового русла, которые русло приобретает лишь в последующие годы. В ближайшие же годы после постройки моста в русле может произойти временное переуглубление, прежде всего из-за задержки наносов перед мостом для выработки нового продольного профиля реки в месте стеснения ее мостовым переходом.
Поэтому в расчете следует учитывать и временное переуглубление.
С учетом указанного временного переуглубления, по О.В. Андрееву и И.А. Ярославцеву, расчет производится по следующим формулам.
Площадь под мостом (рис. 19) в м2:
ω = hп(Bсж - bм) + bм(hм + А) = Bсжhcp,
где hп - глубина воды над побочнем;
Bсж - отверстие моста;
bм - ширина русла в межень;
А - амплитуда измерения горизонта воды от ГВВ до ГМВ;
hм - средняя меженная глубина;
hcp - средняя глубина в сечении.
Рис. 19. Схема сформированного русла предгорной блуждающей реки с учетом временного переуглубления
Глубина воды над побочнем в м:
![]()
Максимальная глубина воды в сформированном русле:
hmax = A + h'м,
где h'м - наибольшая глубина русла в межень.
Мосты через горные реки
Горные реки, как правило, текут в жестких неразмываемых границах. Обычно горные реки полностью перекрывают мостами или же пересекают их на участке конуса выноса, где река относится чаще всего к типу блуждающих.
Кроме указанных выше способов определения расходов воды, можно найти среднюю скорость потока по крупности отложенных камней, пользуясь табл. 47.
Средние скорости потока в зависимости от крупности отложенных камней
|
Наименование |
Средняя скорость горного потока, м/сек |
|||||||
|
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
6 |
|
|
Средний размер передвигаемого камня в открытых руслах, м |
0,15 |
0,25 |
0,35 |
0,5 |
0,6 |
0,75 |
1,0 |
1,4 |
Мосты в зоне подпора
Если мост устраивается в зоне подпора плотины или другой реки, то его отверстие рассчитывают на расход при расчетном горизонте воды и на горизонт подпора плотины или реки. Кроме этого, отверстие моста проверяют на дополнительный расход от слива подпертой воды.
Если расчетные горизонты воды на подпирающей и подпираемой реках по времени совпадают, то отверстие поверяют на собственный расход реки плюс расход от слива подпертой воды по формуле Е.В. Болдакова:
![]()
где 1,5 - коэффициент неравномерности спада;
ω - площадь зеркала воды (поверхность воды в пределах подпора выше моста), м2;
h - суточный спад в подпирающей реке, м;
86400 - число секунд в сутках.
Если такого совпадения по времени нет, то отверстие рассчитывают на собственный расход реки и поверяют на суммарный расход, равный расходу пересекаемого потока (при горизонте, совпадающем по времени с высоким горизонтом подпирающей реки) плюс расход от спада.
Отметка подпорного горизонта на переходе равна:
![]()
Дальность распространения подпора:
![]()
где Z - величина подпора на переходе (см. ниже), м.
Если мост проектируется в подпоре плотины, то его отверстие надо проверить на максимально возможный сброс воды плотиной.
Мост, расположенный ниже плотины (рассчитанной на вероятность превышения
расхода ![]() и реже), должен
рассчитываться на максимальный сброс воды плотиной. Если плотина рассчитана на
расход с вероятностью более частой, чем
и реже), должен
рассчитываться на максимальный сброс воды плотиной. Если плотина рассчитана на
расход с вероятностью более частой, чем ![]() то отверстие
рассчитывают на добавочный расход от прорыва плотины по формуле:
то отверстие
рассчитывают на добавочный расход от прорыва плотины по формуле:
![]()
где B - ширина водоема, м;
b - ширина прорыва, м;
H - величина подпора, м.
Деревянные мосты рассчитывают на прорыв плотины только в том случае,
если она рассчитана на расход с вероятностью превышения, равной или меньшей ![]()
Величина подпора перед мостом (от стеснения им реки):
![]()
где υ1 - средняя скорость под мостом до размыва при расчетном горизонте воды;
![]() - средняя
скорость нестесненного мостом потока
- средняя
скорость нестесненного мостом потока
Длину распространения подпора воды вдоль реки от плотины можно приближенно определить по формуле:
![]()
где i - средний продольный уклон реки в естественных условиях (при отсутствии подпора) в тысячных;
h - средняя глубина реки о естественных условиях, м;
∆ - подпор, м;
a - коэффициент, равный при д
|
|
5 |
2 |
1 |
0,5 |
0,3 |
0,2 |
0,1 |
0,005 |
|
a |
0,96 |
0,91 |
0,85 |
0,76 |
0,67 |
0,58 |
0,41 |
0,24 |
Все величины берутся из продольного профиля реки, а величина h + ∆ равна высоте плотины в метрах.
Величину нарастания горизонта за счет поперечного уклона воды вдоль насыпи на пойме можно принимать для первой трети
ширины поймы (считая от устоя моста) равной 0,0004, для средней трети - 0,0001 и для последней трети - 0,00007.
Отверстие мостов через зарегулированные реки и каналы назначают равным расстоянию между фиксированными урезами или набережными. Размыв и срезку дна в таких реках и каналах не допускают.
§ 15. Регуляционные сооружения
Регуляционные сооружения являются одной из основных частей комплекса сооружения мостового перехода.
Типы обычных регуляционных сооружений и виды мероприятий по регулированию потока у мостов приведены в табл. 48.
Типы обычных регуляционных сооружений
|
Задачи регулировании |
Название сооружений и мероприятий |
На каких реках применяются |
|
Плавное направление пойменных вод в мостовое отверстие во избежание местных русловых деформаций |
Незатопляемые пойменные криволинейные струе направляющие сооружения |
На меандрирующих и немеандрирующих равнинных реках |
|
Отжим мощных пойменных течении от устоя или конуса моста |
Незатопляемые поименные прямолинейные струеотжимающие сооружения |
То же |
|
Отжим мощных пойменных течений от насыпей подходов к мосту |
Незатопляемые пойменные траверсы |
То же |
|
Предотвращение прижима русла к устою моста или к регуляционным сооружениям, а также к территориям, на которых расположены хозяйственные объекты |
Закрепление берега речного русла. |
То же |
|
Спрямление русла |
На меандрирующих равнинных реках |
|
|
Предотвращение прижима русла к насыпям подходов к мосту |
Закрепление берега речной извилины или спрямление русла |
То же |
|
Устранение препятствий для перемещения скоплений наносов (без их разрушения и смены форм переноса насосов) |
Выправление границ русла планировкой и укреплениями берегов, затопляемыми продольными и поперечными русловыми сооружениями. |
На немеандрирующих равнинных реках |
|
|
Плавное ограничение ширины русловой зоны незатопляемыми продольными (оградительными) и поперечными (отбойными) русловыми сооружениями |
На блуждающих реках |
|
Плавное подведение к мостовому отверстию скоплений наносов и ограждение подходов к мосту от руслового потока |
Оградительные валы, постепенно стесняющие ширину русловой зоны |
На блуждающих реках |
|
Предотвращение смещения русловой зоны в новое, пониженное положение |
Оградительные валы, не меняющие обычную ширину русловой зоны |
То же |
|
Предотвращение прижима мощных водных рукавов к конусам моста и к регуляционным сооружениям |
Струеотбойные сооружения |
То же |
|
Пассивная защита откосов и подошвы откосов конусов, регуляционных сооружений и насыпей подходов к мосту от разрушения |
Укрепление откосов. Укрепление подошвы откосов |
На реках всех типов |
|
Изменение мощности и направления течения отдельных рукавов для уменьшения местных деформаций русла |
Средства оперативного регулирования перемещения наносов |
На немеандрирующих равнинных и блуждающих реках |
|
Прочие задачи регулирования (чаще всего по выправлению судового хода на мостовом переходе) |
Система сооружений в зависимости от характера задач регулирования |
- |
Наилучшая форма струенаправляющих дамб в плане:
с верховой стороны - плавная, криволинейная,
с низовой стороны - пологий раструб.
Прямые дамбы или вставки отжимают поток к противоположному берегу.
Расчет криволинейных дамб (по О.В. Андрееву) ведут в следующем порядке.
Определяют ориентировочный радиус кривизны дамбы (с точностью до 5 - 10 м):
R = kL,
где L - отверстие моста;
k - коэффициент, зависящий от отношения расхода поймы Qп ко всему расходу Q (табл. 49).
Коэффициент k в зависимости от отношения расхода пойми Qп ко всему расходу Q
|
Qп Q |
k |
|
0,60 |
0,25 |
|
0,50 |
0,20 |
|
0,40 |
0,15 |
|
0,30 |
0,10 |
|
0,20 |
0,05 |
|
0,15 |
0 |
Вычисляют, как указано на рис. 20, координаты головы верховой дамбы (поперек реки y = 1,438R; вдоль реки x = 2,350R, полагая, что центр координат находится на продольной оси перехода) и соответствующую точку наносят на план, внося необходимые поправки по ситуационным соображениям (т.е. изменяя, если нужно, величину R).

Рис. 20. Схема координат для разбивки оси дамбы
По окончательно подобранному радиусу R вычисляют (по табл. 50) координаты точек оси дамбы.
Координаты точек оси криволинейных дамб
|
Сооружение |
Кривая |
α° |
|
|
|
ε |
|
Верховое |
Кривая переменного радиуса |
90 |
2,350 |
1,438 |
|
3,0 |
|
80 |
2,336 |
1,262 |
0,175 |
2,75 |
||
|
70 |
2,288 |
1,087 |
0,182 |
2,5 |
||
|
60 |
2,207 |
0,914 |
0,191 |
2,25 |
||
|
50 |
2,084 |
0,740 |
0,216 |
2,0 |
||
|
40 |
1,909 |
0,566 |
0,246 |
1,75 |
||
|
30 |
1,657 |
0,391 |
0,375 |
1,50 |
||
|
20 |
1,276 |
0,216 |
0,425 |
1,25 |
||
|
15 |
1,000 |
0,132 |
0,279 |
1,0 |
||
|
Дуга круга |
10 |
0,672 |
0,058 |
0,337 |
1,0 |
|
|
5 |
0,336 |
0,015 |
0,337 |
1,0 |
||
|
0 |
0,000 |
0,000 |
0,337 |
1,0 |
||
|
Низовое |
5 |
-0,336 |
0,015 |
0,337 |
1,0 |
|
|
Прямая |
- |
-0,755 |
0,051 |
0,421 |
1,0 |
|
|
- |
-1,175 |
0,088 |
0,421 |
1,0 |
Примечание. Длина верхового и низового участка дамбы и полная ее длина выражаются формулами: Sн = 3,032R, Sн = 1,180R, S = 4,212R.
На переходе через блуждающие реки с поймами делают:
дамбы переменной кривизны, определяя величину x из выражения (рис. 21):
x = A(1,2 - φ),
где
![]()
ср - коэффициент (по табл. 51) в зависимости от величины ![]()
Рис. 21. Схемы регуляционных сооружений на
блуждающих реках:
а - создание с помощью заделанной в берег дамбы новой неразмываемой границы
берега; б - примыкание регуляционной дамбы к дамбе обвалования вдали от
русловой зоны (незатопляемых отметок вне русла нет, река течет в конусе
собственного выноса); в - продольная дамба, защищенная от размыва потоком и от
подмыва подошвы конуса; г - шпоры капитального типа для предохранения
размываемой дамбы или вала; д - рекомендуемое очертание верховых дамб для
создания условий протекании потока на всем участке с одним уклоном и глубиной.
Координаты точек оси дамбы
|
η |
φ |
1,2 - φ |
|
1,05 |
1,200 |
0,000 |
|
1,07 |
1,085 |
0,115 |
|
1,10 |
0,874 |
0,316 |
|
1,15 |
0,708 |
0,492 |
|
1,20 |
0,616 |
0,584 |
|
1,25 |
0,513 |
0,687 |
|
1,30 |
0,450 |
0,750 |
|
1,35 |
0,398 |
0,802 |
|
1,40 |
0,358 |
0,842 |
|
1,45 |
0,322 |
0,878 |
|
1,50 |
0,282 |
0,918 |
|
2,00 |
0,145 |
1,055 |
|
2,50 |
0,087 |
1,113 |
|
3,00 |
0,058 |
1,142 |
|
3,50 |
0,044 |
1,156 |
|
4,00 |
0,032 |
1,168 |
|
5,00 |
0,021 |
1,179 |
|
6,00 |
0,018 |
0,182 |
|
7,00 |
0,009 |
1,191 |
|
∞ |
0,000 |
1,200 |
Продольные валы с капитальными поперечными струеотбойными сооружениями (шпорами). На участках вблизи моста шпоры располагают перпендикулярно к течению, дальше - под углом до 30 - 40°. При больших углах наклона или малом расстоянии между шпорами им придают Г-образную форму (рис. 22, а) или крепят часть протяжения продольных валов у корней шпор с верховой стороны от них как указано на рис. 22, б. Расстояние между шпорами назначают по рис. 22, в.
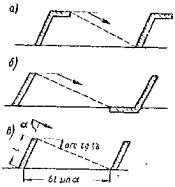
Рис. 22. Шпоры Г-образной формы для прикрытия защищаемого участка
На беспойменных блуждающих реках шпоры располагают по рис. 23.

Рис. 23. Расположение шпор на беспойменных блуждающих реках
Для защиты вогнутых берегов русла поименной равнинной реки (т.е. при затопляемой бровке берега) устраивают затопляемые сооружения (буны), которые работают:
при длительных низких горизонтах как шпоры,
при длительных высоких уровнях как донные направляющие.
Для спрямления русел меандрирующих рек устраивают каналы, перегораживая старое русло запрудой (в нижнем по течению участке петли) и оставляя в ней небольшое отверстие для быстрейшего заиления спрямленной излучины.
Глубина искусственного русла (капала):
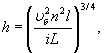
где υб - бытовая скорость в канале;
n - коэффициент шероховатости канала (принимается равным коэффициенту шероховатости русла реки);
l - длина канала;
L - длина спрямленной петли реки;
i - бытовой уклон излучины реки.
Скорость в канале определяют путем подбора из выражения:
![]()
Регуляционные сооружения, как правило, возводятся из местных материалов. Поперечному сечению сооружений (кроме водораздельных дамб и ограждающих валов) придают обычно форму трапеции по табл. 52.
Основные размеры регуляционных сооружений
|
Ширина поверху, м |
Крутизна откосов |
Глубина заложения подошвы укрепления, м |
|||||||||
|
тела |
голов |
тела |
голов |
Ниже линии размыва |
Во всех случаях не менее |
||||||
|
дамб |
шпор |
запруд |
дамб |
шпор |
дамб |
шпор |
запруд |
дамб |
шпор |
||
|
2 - 4 |
2 - 3 |
3 - 6 |
3 - 6 |
2 - 4 |
1:1,5 |
1:1,5 |
1:1 |
1:2 |
1:1,5 |
0,3 - 0,5 |
0,6 |
|
1:2,5 |
1:2 |
1:1,25 |
1:3 |
1:2 |
|||||||
Ширину основания водораздельных дамб и ограждающих валов па мостовых переходах, расположенных на конусах выноса, назначают с учетом возможности их работы на односторонний напор воды, равной:
для водонепроницаемых оснований - 5H + 4 м,
для водопроницаемых оснований - CH м, где H - напор, C = 12 для илистого грунта и C = 5 для галечных грунтов.
При назначении укреплений откосов регуляционных сооружений следует пользоваться соответствующими альбомами типовых конструкций.
Укрепление откосов регуляционных сооружений на воздействие льда и волн можно рассчитывать по следующим формулам.
Нормальное к откосу расчетное давление льда:
![]()
где υ - скорость льдины, м/сек;
δ - расчетная толщина льдины, м (обычно δ = 0,8 наблюденной толщины);
l, b - длина и ширина льдины, м;
β - угол наклона откоса к горизонту;
α - угол отклонения течения от касательной к сооружению.
Необходимая толщина укрепления, работающего в условиях навала льдин:
![]()
где σ - допускаемое давление на грунт под укреплением, т/м2.
Необходимая толщина верхнего слоя укрепления при воздействии волн:
t1 ≈ 0,25h м,
где h - высота волны в м, определяемая по формуле В.Г. Андреянова;
h = 0,0208W5/4D1/3,
где W - скорость ветра, м/сек;
D - длина разгона волны, км.
Длина волны:
λ = 0,304WD1/2, м.
Формула Андреянова применима при λ ≤ 2H, где H - критическая глубина по табл. 53.
Значения критической глубины H
|
|
H |
|
1:30 |
1,08h |
|
1:25 |
l,10h |
|
1:20 |
1,12h |
|
1:15 |
1,18h |
|
1:10 |
1,34h |
Если λ > 2H, то в расчет вводят λ = 2H, вычисляют фиктивную длину разгона волны D и по ней находят полную высоту волны.
Вес элемента (камень, массив) верхнего слоя покрытия откоса по Лупинскому:
Q = 11h3 кг,
где h - высота волны, м.
Второй (нижний) ряд наброски принимают из камней в 2 - 3 раза мельче камней первого ряда.
Под слоями камня делают подготовку в виде обратного фильтра. Толщина подготовки должна быть не менее 20 - 25 см.
Высота набега волны на откос (по Н.И. Джунковскому):
h1 = 3,2hktgα м,
где h - высота волны, м;
k = 1 - для гладких откосов;
k = 0,9 - для мощеных и одернованных откосов;
k = 0,77 - для каменной наброски и сплошных зарослей на откосе;
α - угол наклона откоса к горизонту.
Ширина рисбермы (в основании откоса):
![]()
где l - длина укрепления (по откосу), м;
t - толщина укрепления откоса, м;
h1 - толщина рисбермы, м, назначаемая по глубине местного размыва;
γ1 - объемный вес камней;
γ - объемный вес воды;
β - угол наклона откоса к горизонту;
f = 0,5 - коэффициент трения при подвижке укрепления по грунтовому откосу.
Ширину рисбермы не рассчитывают, если крутизна откоса больше 1:2.
Для защиты сооружений и укреплений берегов от подмыва рекомендуется применять тюфяки (из хвороста, из бетонных и железобетонных плит).
Толщина каменной наброски, которой пригружают хворостяной тюфяк:
t = 0,6t1,
где t1 - толщина хворостяного тюфяка (обычно не менее 0,6 м).
Крупность камня пригрузки:
![]()
где υ - фактическая скорость течения, м/сек;
m - коэффициент заложения откоса.
Общую глубину размыва у откосов струенаправляющих дамб принимают такой же, как и под мостом (см. нише).
Глава 4
ОПРЕДЕЛЕНИЕ РАСЧЕТНОГО СУДОХОДНОГО УРОВНЯ ВОДЫ (ПО НСП 103-52)
§ 16. Определение расчетного судоходного уровня воды для нешлюзованных рек
Устанавливается класс реки.
Составляется таблица из трех граф: в первой графе помещаются порядковые номера; во второй - наивысшие отметки уровня паводков по данным водомерных постов (отметки располагаются в нисходящем порядке, считая сверху вниз, начиная от самой высокой за весь период наблюдений); в третьей графе помещаются годы, в которые имели место эти отметки наивысшего уровня паводка.
Определяется расчетный порядковый номер N первой графы таблицы по формуле:
![]()
где a - коэффициент, принимаемый по табл. 54;
n - количество лет наблюдений на водомерном посту.
Значения коэффициентов a и k
|
Классы рек |
Величина коэффициентов |
|
|
a |
k |
|
|
I |
2 |
5 |
|
II |
3 |
6 |
|
III |
4 |
6 |
|
IV |
5 |
5 |
|
V |
5 |
3 |
|
VI |
4 |
2 |
|
VII |
4 |
2 |
Соответствующий расчетному порядковому номеру год (в третьей графе таблицы) является расчетным.
Определяется допустимая по классу реки продолжительность стояния уровней воды, которые были выше расчетного судоходного уровня в расчетном году, по формуле:
![]()
где m - фактическая продолжительность физической навигации (период, когда река свободна от льда и сала) в расчетном году, в сутках;
k - коэффициент, принимаемый по табл. 54.
По данным водомерных наблюдений в расчетном году устанавливается тот уровень воды, выше которого продолжительность стоянии высоких паводковых уровней составляет t суток.
Этот уровень принимается за расчетный судоходный уровень воды.
Пример определения расчетного судоходного уровня воды для нешлюзованной реки. Мост сооружается на реке III класса. Вблизи моста расположен водомерный пост, по которому имеются данные водомерных наблюдений за 41 год, помещенные в табл. «г».
|
№ п/п |
Наивысшие отметки уровня паводка, см |
Годы с наивысшими отметками уровни наводка |
|
1 |
1543 |
1908 |
|
2 |
1420 |
1926 |
|
3 |
1392 |
1917 |
|
4 |
1381 |
1931 |
|
5 |
1325 |
1937 |
|
6 |
1317 |
1029 |
|
7 |
1300 |
1913 |
|
8 |
1291 |
1900 |
|
9 |
1283 |
1924 |
|
10 |
1275 |
1904 |
Определяем расчетный порядковый номер N первой графы таблицы, принимая n = 41 и a = 4 (по табл. 54).
![]()
Принимаем N = 2 и за расчетный год - 1926, с наивысшей отметкой уровня паводка, равной 1420 см.
Фактическая продолжительность физической навигации в 1926 г. составила m = 187 суток; по табл. 54 принимаем k = 6. Тогда ![]() принимаем t = 11 суток.
принимаем t = 11 суток.
По материалам водомерных наблюдений устанавливаем, что в 1926 г. уровнем, выше которого уровни воды стояли в течение 11 суток, является уровень с отметкой 1065 см. Этот уровень и принимаем за расчетный судоходный уровень воды.
§ 17. Определение расчетного судоходного уровня воды для шлюзованных рек
Устанавливается класс реки.
Пели судоходство в половодье совершается через разборчатые плотины, то расчетный судоходный уровень определяется согласие вышеприведенным указаниям для нешлюзованных рек.
Если на реке в продолжение всей навигации имеется подпор, создаваемый плотиной, а паводок пропускается через плотину при отметках ниже нормального подпорного уровня, то мост располагается в одной из двух зон, указанных на рис. 24, а именно:
в первой зоне - когда отметки уровня пропуска паводка определенной вероятности превышения ниже отметок нормального подпорного уровня, с учетом кривой подпора;
во второй зоне - когда отметки уровня пропуска паводка определенной вероятности превышения выше отметок нормального подпорного уровня, с учетом кривой подпора.

Рис. 24. Зоны расположении мостов в шлюзованных реках
Если мост располагается в первой зоне, то за расчетный судоходный уровень воды принимается подпорный уровень водохранилища с учетом кривой подпора; при этом отметка расчетного судоходного уровня воды должна быть не менее чем на 0,5 м выше отметки нормального подпорного уровня водохранилища.
Если мост располагается во второй зоне, то определение расчетного судоходного уровня воды производится следующим образом.
1. По данным водомерных наблюдений или, если плотина и мост проектируются одновременно, по данным водохозяйственных расчетов из проекта плотины с водохранилищем, устанавливается отметка уровня воды при пропуске паводка, имеющего обеспеченность p%; процент обеспеченности наводка p принимается в зависимости от класса реки по табл. 55.
Значение коэффициентов k
|
Классы рек |
величины |
|
|
p% |
k |
|
|
I |
2 |
5 |
|
II |
3 |
6 |
|
III |
4 |
6 |
|
IV |
5 |
7 |
|
V |
5 |
7 |
|
VI |
5 |
6 |
|
VII |
5 |
6 |
2. По приведенной выше формуле вычисляется допустимая продолжительность t суток стояния уровней более высоких, чем расчетный судоходный уровень воды; при этом за расчетный год, для которого определяется продолжительность m суток физической навигации, принимается тот год, в который паводок имеет обеспеченность p%.
3. Для установления расчетного года по данным водомерных наблюдений или из проектных данных устанавливается тот уровень воды, выше которого продолжительность стояния высоких паводковых уровней составляет t суток. Этот уровень воды, увеличенный на 0,5 м, принимается за расчетный судоходный уровень, если он имеет отметку большую, чем отметка нормального подпорного уровня с учетом кривой подпора; если же этот уровень имеет отметку меньшую, чем отметка нормального подпорного уровня, то за расчетный судоходный уровень принимается отметка нормального подпорного уровня с учетом кривой подпора, увеличенная на 0,5 м.
Если паводок пропускается через плотину при отметках нормального подпорного уровня, то указанного выше деления на дне зоны не будет, в этом случае за расчетный судоходный уровень воды принимается отметка уровня воды при пропуске паводка обеспеченностью p%, соответствующей обеспеченности, указанной в табл. 55 (в зависимости от класса реки); эта отметка должна быть не менее чем на 0,5 м выше нормального подпорного уровня водохранилища.
Пример определения расчетного судоходного уровня воды для шлюзованной реки.
1-й случай. Мост сооружается на реке II класса в 14 км выше плотины, образующей водохранилище, обеспечивающее судоходство в продолжение всей навигации.
Нормальный подпорный уровень водохранилища равен 118,20 м; в месте сооружения моста отметка подпорного уровня с учетом кривой подпора равна 118,27 м. При пропуске через водосливные отверстия плотины паводка обеспеченностью 3 % (см табл. 55) отметка уровня воды в месте сооружения моста равна 116,45 м, т.е. ниже отметки нормального подпорного уровня. Следовательно, мост сооружается в первой зоне и за расчетный судоходный уровень воды должна быть принята отметка подпорного уровня с учетом кривой подпора, т.е. 118,27 м. Однако так как эта отметка меньше, чем отметка нормального подпорного уровне плюс 0,5 м, т.е. меньше чем 118,20 + 0,50 = 118,70 м, то за расчетный судоходный уровень воды принимаем уровень 118,70 м.
2-й случай. Мост сооружается на реке IV класса в 65 км выше плотины, которая образует водохранилище,
обеспечивающее судоходство в продолжение всей навигации. Нормальный подпорный
уровень водохранилища равен 18,35 м; в месте сооружения моста отметка
подпорного уровня с учетом кривой подпора равна 49,23 м. При пропуске через
водосливные отверстия плотины паводка обеспеченностью 5 % (см. табл. 55) отметка уровня воды
в месте сооружения моста равна 52,48 м, т.е. выше отметки нормального
подпорного уровня; следовательно, мост сооружается во второй зоне. Фактическая
продолжительность физической навигации в расчетном году (1931 г., когда имел
место паводок обеспеченностью p = 5 %) составляет по гидрологическим данным проекта
водохранилища 170 суток; по табл. 55 для реки IV класса k = 7. Отсюда ![]() Принимаем t = 12 суток.
Принимаем t = 12 суток.
По гидрологическим данным проекта водохранилища установлено, что в расчетном 1931 г. уровень воды, выше которого паводковые уровни стояли в течение 12 суток, имел отметку 50, 30 м. Так как эта отметка увеличена на 0,5 м против отметки нормального подпорного уровня с учетом кривой подпора (49,23 м), то за расчетный судоходный уровень принимаем 50,30 + 0,50 = 50,80 м.
3-й случай. Мост сооружается на реке III класса в 20 км выше плотины, образующей водохранилище, обеспечивающее судоходство в течение всей навигации. Нормальный подпорный уровень водохранилища равен 63,50 м; в месте сооружения моста отметка подпорного уровня с учетом кривой подпора равна 63,62 м. Паводок пропускается через плотину при нормальном подпорном уровне, что приводит в этот период к превышению отметок паводка над отметками нормального подпорного уровня; поэтому за расчетный судоходный уровень воды принимаем отметку уровня наводка.
При пропуске через водосливные отверстия плотины паводка обеспеченностью 4 % (см. табл. 55) отметка уровня воды в месте вооружения моста по гидрологическим данным проекта водохранилища равна 64,43 м. Так как этот уровень выше, чем отметка нормального подпорного уровня плюс 0,5 м (63,5 + 0,50 = 64,0 м) то за расчетный судоходный уровень воды принимаем 64,43 м.