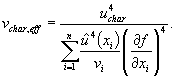ФЕДЕРАЛЬНОЕ
АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
рекомендации |
Р 50.2.058- 2007 |
Государственная система
обеспечения единства измерений
ОЦЕНИВАНИЕ
НЕОПРЕДЕЛЕННОСТЕЙ
АТТЕСТОВАННЫХ ЗНАЧЕНИЙ
СТАНДАРТНЫХ ОБРАЗЦОВ
|
|
Москва 2008 |
Предисловие
Сведения о рекомендациях
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием Уральским научно-исследовательским институтом метрологии Федерального агентства по техническому регулированию и метрологии
2 ВНЕСЕНЫ Управлением метрологии Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 декабря 2007 г. № 375-ст
4 ВВЕДЕНЫ ВПЕРВЫЕ
Информация о введении в действие (прекращении действия) настоящих рекомендаций, изменениях и поправках к ним, а также тексты изменений и поправок публикуются в информационном указа теле «Национальные стандарты»
Содержание
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная система обеспечения единства измерений
ОЦЕНИВАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ АТТЕСТОВАННЫХ ЗНАЧЕНИЙ СТАНДАРТНЫХ ОБРАЗЦОВ
Дата введения - 2008-08-01
1 Область применения
Настоящие рекомендации распространяются на стандартные образцы (далее - СО) состава и свойств веществ и материалов и устанавливают алгоритмы оценивания аттестованных значений СО и неопределенностей аттестованных значений СО.
2 Нормативные ссылки
В настоящих рекомендациях использованы нормативные ссылки на следующие нормативные документы:
ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Использование значений точности на практике
ГОСТ Р 50779.10-2000 (ИСО 3534.1-93) Статистические методы. Вероятность и основы статистики. Термины и определения
ГОСТ 8.315-97 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения
ГОСТ 8.531-2002 Государственная система обеспечения единства измерений. Стандартные образцы монолитных и дисперсных материалов. Способы оценивания однородности
ГОСТ 8.532-2002 Государственная система обеспечения единства измерений. Стандартные образцы состава веществ и материалов. Межлабораторная метрологическая аттестация. Содержание и порядок проведения работ
Р 50.2.031-2003 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Методика оценки характеристики стабильности
РМГ 53-2002 Государственная система обеспечения единства измерений. Стандартные образцы. Оценивание метрологических характеристик с использованием эталонов и образцовых средств измерений текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящими рекомендациями следует руководствоваться заменяющим (измененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
Примечание - При пользовании настоящими рекомендациями целесообразно проверить действие ссылочных нормативных документов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января
3 Термины, определения и обозначения
3.1 В настоящих рекомендациях применены термины по ГОСТ 8.315, ГОСТ Р 8.563, ГОСТ Р 50779.10, ГОСТ Р ИСО 5725-1, ГОСТ Р ИСО 5725-3, Р 50.2.031, а также следующие термины с соответствующими определениями:
неопределенность (измерения): Параметр, связанный с результатом измерения и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине [1].
стандартная неопределенность u: Неопределенность результата измерений, выраженная в виде стандартного отклонения [1].
суммарная стандартная неопределенность uс: Стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с зависимостью изменения результата измерений при изменении этих величин [1].
расширенная неопределенность U: Неопределенность, представляющая собой величину, определяющую интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине [1].
коэффициент охвата k: Коэффициент, используемый как сомножитель суммарной стандартной неопределенности для получения расширенной неопределенности [1].
Примечания
1 Расширенную неопределенность U вычисляют исходя из суммарной стандартной неопределенности и с и коэффициента охвата k по формуле
U = k uc
2 Выбор коэффициента k зависит от требуемого уровня достоверности. Для уровня достоверности приблизительно 0,95k = 2.
3 Следует всегда указывать коэффициент охвата к для того, чтобы можно было восстановить значение суммарной стандартной неопределенности измеряемой величины для использования в вычислениях суммарной стандартной неопределенности других величин, которые могут зависеть от этой величины.
оценивание типа А: Способ оценивания стандартной неопределенности, основанный на статистическом анализе серии наблюдений [1].
оценивание типа Б: Способ оценивания стандартной неопределенности, не основанный на статистическом анализе серии наблюдений [1].
способ аттестации стандартного образца: Метрологически обоснованная процедура установления аттестованного значения стандартного образца.
неопределенность аттестованного значения стандартного образца: Параметр, характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны аттестуемой характеристике стандартного образца.
стандартная неопределенность аттестованного значения стандартного образца: Неопределенность аттестованного значения стандартного образца, выраженная в виде стандартного отклонения.
расширенная неопределенность аттестованного значения стандартного образца: Неопределенность аттестованного значения стандартного образца, представляющая собой величину, определяющую интервал вокруг аттестованного значения стандартного образца, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны аттестуемой характеристике стандартного образца.
неопределенность от способа аттестации стандартного образца: Составляющая неопределенности аттестованного значения стандартного образца, обусловленная способом его аттестации.
Примечание - ИСО Руководством 35 [2] эта составляющая неопределенности трактуется как «неопределенность от характеризации» (uncertainty due to characterisation).
стандартная неопределенность от способа аттестации стандартного образца: Неопределенность от способа аттестации стандартного образца, выраженная в виде стандартного отклонения.
неопределенность от неоднородности материала стандартного образца: Составляющая неопределенности аттестованного значения стандартного образца, обусловленная различием значений аттестуемой характеристики стандартного образца в различных частях (пробах) материала стандартного образца.
стандартная неопределенность от неоднородности: Неопределенность от неоднородности, выраженная в виде стандартного отклонения.
неопределенность от нестабильности значения аттестуемой характеристики стандартного образца: Составляющая неопределенности аттестованного значения стандартного образца, обусловленная изменением значения аттестуемой характеристики стандартного образца в течение срока годности экземпляра стандартного образца.
стандартная неопределенность от нестабильности: Неопределенность от нестабильности, выраженная в виде стандартного отклонения.
входная величина: Величина, влияющая на значение аттестуемой характеристики стандартного образца.
рациональные методики выполнения измерений: Методики выполнения измерений, в соответствии с которыми единицы измерения величины не зависят от применяемого метода [3].
эмпирические методики выполнения измерений: Методики выполнения измерений, в соответствии с которыми единицы измерения величины зависят от применяемого метода [3].
3.2 В настоящих рекомендациях использованы следующие обозначения:
![]() - аттестованное значение СО;
- аттестованное значение СО;
хi - оценка i-й входной величины;
u - стандартная неопределенность;
uA - стандартная неопределенность при оценивании типа А;
uB - стандартная неопределенность при оценивании типа В;
u(хi) - стандартная неопределенность оценки i-й входной величины;
uс - суммарная стандартная неопределенность;
k - коэффициент охвата;
tp(v) - квантиль распределения Стьюдента для доверительной вероятности Р и числа степеней свободы v;
veff - эффективное число степеней свободы;
U - расширенная неопределенность;
UP - расширенная неопределенность для уровня доверия Р;
uс(![]() ) - суммарная
стандартная неопределенность аттестованного значения СО;
) - суммарная
стандартная неопределенность аттестованного значения СО;
UP (![]() ) - расширенная
неопределенность аттестованного значения СО для уровня доверия Р;
) - расширенная
неопределенность аттестованного значения СО для уровня доверия Р;
uchar - стандартная неопределенность от способа аттестации СО;
uh - стандартная неопределенность от неоднородности СО;
ustab - стандартная неопределенность от нестабильности СО.
4 Источники неопределенности аттестованного значения стандартного образца
4.1 Основными источниками неопределенности аттестованного значения СО являются:
- неоднородность материала СО (далее - неоднородность);
- нестабильность значений аттестуемой характеристики СО (далее - нестабильность);
- способ установления аттестованного значения СО (далее - способ).
4.2 На начальном этапе проводят анализ возможных влияний каждого источника неопределенности из 4.1 на значения аттестуемой характеристики СО.
В общем случае суммарную стандартную неопределенность аттестованного значения СО определяют из уравнения
![]() (4.1)
(4.1)
Примечание - В зависимости от типа материала СО и условий хранения экземпляров СО некоторые составляющие суммарной стандартной неопределенности аттестованного значения СО либо равны нулю, либо их вклад в неопределенность аттестованного значения СО может быть незначим.
5 Оценивание неопределенности от нестабильности
5.1 Способы оценивания неопределенности от нестабильности
При оценивании неопределенности от нестабильности применяют в зависимости от условий проведения измерений два способа:
- классическое исследование нестабильности [2] (измерения проводят в условиях промежуточной прецизионности);
- изохронное исследование нестабильности (измерения проводят в условиях повторяемости).
5.2 Классическое исследование нестабильности
5.2.1 Измерения при исследовании нестабильности проводят в условиях промежуточной прецизионности. Факторы, влияющие на расхождения результатов в данном случае:
а) время;
б) градуировка оборудования;
в) внешние условия;
г) нестабильность измерительной системы;
д) изменение значения аттестуемой характеристики;
е) повторяемость.
Факторы а) - д) варьируют за время проведения исследования стабильности. Рассеяние результатов под воздействием этих факторов характеризуют стандартным отклонением прецизионности (при различиях по фактору «время») σI/(Т).
5.2.2 Для оценивания неопределенности от нестабильности СО используют методики выполнения измерений (далее - МВИ), аттестованные в соответствии с ГОСТ Р 8.563. Предпочтительнее использовать МВИ с оцененным значением стандартного отклонения промежуточной прецизионности (при различиях по фактору «время») σI/(Т).
Стандартное отклонение промежуточной прецизионности σI/(Т) должно удовлетворять условию
![]() (5.1)
(5.1)
где Uдоп - допускаемое значение расширенной неопределенности аттестованного значения СО в соответствии с техническим заданием на разработку СО.
5.2.3 Продолжительность исследования нестабильности т должна быть более половины предполагаемого срока годности экземпляра СО.
Примечание - Продолжительность исследования нестабильности при ускоренном старении материала СО сокращается. Ее определяют исходя из предполагаемого срока годности экземпляра СО и известной или оцененной зависимости изменений аттестуемой характеристики от факторов нестабильности.
5.2.4 Для оценки неопределенности от нестабильности за период исследования нестабильности СО τ получают n результатов измерения значений аттестуемой характеристики хi (i = 1,2,..., n.)
5.2.5 Число измерений n определяют по таблице 5.1 в зависимости от отношения σI/(Т)/Uдоп.
Таблица 5.1 - Минимальное число измерений при исследовании нестабильности СО
|
σI/(Т) /Uдоп |
Минимальное число |
σI/(Т)/Uдоп |
Минимальное число |
|
2 |
68 |
1,2 |
25 |
|
1,8 |
55 |
1,0 |
18 |
|
1,6 |
44 |
0,8 |
11 |
|
1,4 |
34 |
0,5 |
4 |
Предпочтительно, чтобы в период исследования нестабильности СО т измерения были проведены через равные промежутки времени.
5.2.6 Отклонение результата измерения хi в i-й момент времени от первоначального значения х1 – di оценивают разностью
di = xi – x1, (5.2)
где xi - результат измерения значения аттестуемой характеристики СО в i-й момент времени;
х1 - первый результат, полученный в период исследования нестабильности СО.
5.2.7 С целью уменьшить влияние факторов промежуточной прецизионности проводят экспоненциальное сглаживание полученных значений d i по формуле
Di = αdi + (1 - α)Di-1, (5.3)
где Di - сглаженное значение разности результатов измерений в i-й момент времени (i = 2,.... n).
В качестве начального значения D 1 принимают d1 = 0.
Значение α выбирают из интервала от 0,1 до 0,3 в зависимости от значения отношения σI/(Т)/Uдоп по таблице 5.2.
Таблица 5.2 - Значения коэффициента α для экспоненциального сглаживания
|
σI/(Т) /Uдоп |
α |
|
До 0,7 |
0,3 |
|
От 0,7 до 0,9 |
0,25 |
|
От 0,9 до 1,2 |
0,20 |
|
От 1,2 до 1,5 |
0,15 |
|
Св. 1,5 |
0,10 |
5.2.8 Результаты контроля нестабильности записывают в форме таблицы 5.3.
Таблица 5.3 - Результаты исследования нестабильности СО
|
Номер измерения i |
di |
αdi |
(1-α)Di-1 |
Di |
Ri |
|
1 |
0 |
0 |
0 |
0 |
- |
|
2 |
d2 |
αd2 |
0 |
D2 |
R2 |
|
3 |
d3 |
αd3 |
(1-α)D2 |
D3 |
|
|
… |
… |
… |
… |
… |
|
|
n |
Dn |
αdn |
(1-α)Dn-1 |
Dn |
Rn |
5.2.9 По вычисленным значениям D i для i =2,3,..., n определяют скользящие размахи Ri по формуле
Ri = Di – Di-1 (5.4)
и вписывают полученные значения в последние столбец таблицы 5.3.
Вычисляют средний скользящий
размах ![]() по формуле
по формуле
![]() (5.5)
(5.5)
5.2.10 Предполагают следующую линейную модель изменения аттестуемой характеристики D в момент времени t
D = at, (5.6)
где а - скорость изменения значений аттестуемой характеристики результата в условиях промежуточной прецизионности.
Оцененное по результатам измерения изменение аттестуемой характеристики Di в момент времени ti представляют в виде
Di = ati + εi, (5.7)
где εi - отклонение i-го результата измерения в условиях промежуточной прецизионности.
5.2.11 Определяют коэффициент а в уравнении (5.7) по полученным значениям Di методом наименьших квадратов по формуле
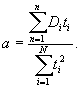 (5.8)
(5.8)
5.2.12 Определяют стандартное отклонение sa коэффициента а по формуле
 (5.9)
(5.9)
где sD - стандартное отклонение разностей результатов вычисляют
по среднему скользящему размаху ![]() по формуле
по формуле
![]() (5.10)
(5.10)
5.2.13 Стандартную неопределенность от нестабильности ustab в момент времени t оценивают по формуле
ustab = sat. (5.11)
Число степеней свободы ν для ustab оценивают по формуле
vu stab = n-1. (5.12)
5.2.14 Проверяют гипотезу об отсутствии тренда, т.е. гипотезу
Н0: а = 0. (5.13)
Для проверки
гипотезы Н0 вычисляют отношение ![]() по формуле
по формуле
![]() (5.14)
(5.14)
Сравнивают полученное значение ![]() с квантилем распределения Стьюдента t0,95(n-1) из
таблицы А.2 приложения А.
При выполнении неравенства
с квантилем распределения Стьюдента t0,95(n-1) из
таблицы А.2 приложения А.
При выполнении неравенства
![]() (5.15)
(5.15)
гипотезу об отсутствии тренда принимают. Статистически значимого изменения за период исследования стабильности не обнаружено. Но вклад неопределенности от нестабильности в суммарную неопределенность в этом случае следует оценивать исходя из назначенного срока годности экземпляра СО по формуле (5.11).
5.3 Изохронное исследование нестабильности
5.3.1 При изохронном методе исследования нестабильности применяют «метод ускоренного старения». Суть этого метода заключается в том, что в несколько раз усиливают воздействие факторов, вызывающих тренд аттестованной характеристики. Для обоснования метода ускоренного старения обычно применяют правило Вант-Гоффа для медленных реакций: скорость реакции при нагреве на 10°С увеличивается в 2-4 раза.
5.3.2 Материал СО, отобранный для исследования нестабильности, разделяют на две части. Одну из этих частей хранят в предполагаемых условиях хранения СО, другую - при повышенной температуре. При фиксированных значениях температуры хранения продолжительность исследования нестабильности τ оценивают по формуле
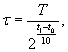 (5.16)
(5.16)
где T - предполагаемый срок годности экземпляра СО;
t0, t1 - предполагаемая температура хранения материала СО и температура хранения СО при ускоренном старении.
5.3.3 Получают в течение промежутка времени τ по n пар результатов измерений {х0i, х1i} в условиях повторяемости. Предпочтительно, чтобы в период исследования нестабильности СО τ измерения были проведены через равные промежутки времени.
Вычисляют отклонение результатов измерений di в i-й момент времени
di = x1i – x0i. (5.17)
5. 3.4 После выполнения всех измерений оценивают стандартное отклонение повторяемости sr
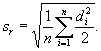 (5.18)
(5.18)
5.3.5 Предполагают (как и в случае классического метода исследования нестабильности в 5.2.10), что разность результатов di в момент времени ti можно представить в виде линейной зависимости
di = ati + εi (5.19)
5.3.6 Определяют коэффициент а в уравнении (5.19) по полученным значениям di методом наименьших квадратов по формуле
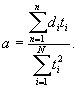 (5.20)
(5.20)
5.3.7 Определяют стандартное отклонение коэффициента a sa по формуле
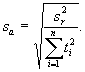
5.3.8 Стандартную неопределенность от нестабильности u stab в момент времени t и число степеней свободы vu stab оценивают по формулам (5.11) и (5.12).
5.3.9 Гипотезу об отсутствии тренда Н0 проверяют в соответствии с 5.2.14.
6 Оценивание неопределенности от неоднородности материала стандартного образца
6.1 Общие требования к оцениванию неоднородности материала стандартного образца
Общие требования к оцениванию неоднородности материала СО приведены в ГОСТ 8.531.
6.2 Оценивание неопределенности от неоднородности для дисперсных материалов стандартных образцов
6.2.1 От всей массы материала СО для оценивания неоднородности материала СО случайным образом отбирают N проб массой М0 каждая. Отбор проб проводят после приготовления материала СО. Масса каждой пробы М0 должна быть достаточной для проведения в соответствии с применяемой МВИ фиксированного числа измерений J.
Для определения числа отбираемых проб рассчитывают отношение Q:
Q = Uдоп /S мви, (6.1)
где Uдоп - допускаемое значение расширенной неопределенности;
Sмви - стандартное отклонение повторяемости или промежуточной прецизионности (при различиях по фактору «время»).
6.2.2 Число отбираемых проб N при фиксированном числе многократных измерений J находят по таблице 6.1 для значения Q, определенного по формуле (6.1).
Таблица 6.1 - Число отбираемых проб N для оценивания однородности
|
Интервал значений Q |
Число многократных измерений J |
||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
До 1,5 |
90 |
40 |
25 |
18 |
15 |
12 |
11 |
|
Св. 1,5 до 2,1 |
52 |
27 |
19 |
15 |
13 |
- |
- |
|
Св. 2,1 до 3,0 |
31 |
18 |
13 |
12 |
- |
- |
- |
|
Св. 3,0 до 4,2 |
19 |
12 |
11 |
- |
- |
- |
- |
|
Св. 4,2 |
12 |
- |
- |
- |
- |
- |
- |
6.2.3 В каждой из N проб J раз измеряют значение аттестуемой характеристики. Измерения выполняют либо в одной пробе массой М0 неразрушающим методом, либо в растворе, в который она переведена для обеспечения однородности.
6.2.4 Результаты измерений при оценивании характеристики однородности обрабатывают в следующем порядке.
Вычисляют среднеарифметические
значения ![]() всех NJ результатов
всех NJ результатов
![]() (6.2)
(6.2)
где xnj – j результат измерения в n -й пробе,
и N средних результатов ![]() для каждой пробы
для каждой пробы
![]() (6.3)
(6.3)
Вычисляют сумму квадратов отклонений SSe результатов измерений от средних значений для каждой пробы
![]() (6.4)
(6.4)
и сумму квадратов отклонений SS H средних результатов для каждой пробы от среднего арифметического всех результатов
![]() (6.5)
(6.5)
Вычисляют средние квадраты отклонений результатов измерений от средних значений для каждой пробы
![]() (6.6)
(6.6)
и между пробами
![]() (6.7)
(6.7)
Стандартную неопределенность от неоднородности материала СО оценивают по формуле
![]() (6.8)
(6.8)
Если ![]() <
< ![]() , то полагают
, то полагают
![]() (6.9)
(6.9)
где М - наименьшая представительная проба СО.
Число степеней свободы стандартной неопределенности u h , обозначаемое vu h = N - 1.
6.3 Оценивание неопределенности от неоднородности для монолитных материалов стандартных образцов
6.3.1 Оценивание неопределенности от неоднородности проводят после отработки технологии получения материала СО, исключающей регулярные изменения содержаний аттестуемого элемента, порядка приготовления материала СО и разделения его на экземпляры.
6.3.2 Из общего числа экземпляров СО отбирают случайным образом K (экземпляров СО (К ³ 25).
6.3.3 Подготовляют на каждом отобранном экземпляре СО аналитические поверхности в соответствии с методикой спектрального анализа, используемой для оценивания однородности.
6.3.4 На каждой аналитической поверхности выполняют два измерения со случайным выбором места возбуждения при оценивании однородности эмиссионным методом или два измерения без изменения положения СО - при оценивании однородности рентгенофлуоресцентным методом.
6.3.5 После проведения измерений разрезают каждый экземпляр СО по плоскости, параллельной аналитической поверхности. Положение плоскости разреза на каждом экземпляре СО определяют случайным образом на всей его длине (высоте). Подготовляют на срезах аналитические поверхности и проводят измерения в соответствии с 6.3.4.
6.3.6 По результатам измерений для каждого аттестуемого элемента вычисляют следующие суммы:
- сумму всех результатов S1
![]() (6.10)
(6.10)
- сумму квадратов средних результатов на аналитических поверхностях S2
 (6.11)
(6.11)
- сумму квадратов средних результатов на экземплярах СО S3
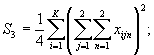 (6.12)
(6.12)
- сумму квадратов всех результатов S 4
![]() (6.13)
(6.13)
где i - номер экземпляра СО (i = 1, 2, ..., К);
j - номер аналитической поверхности n = 1, 2);
n - номер измерения ( n = 1, 2);
x ijn - результат n-го измерения на j-й поверхности i-го СО.
По суммам, определенным по формулам (6.10)-(6.13), вычисляют следующие суммы квадратов отклонений:
- средних результатов на экземплярах СО от среднего всех результатов SSBL
![]() (6.14)
(6.14)
- средних результатов на аналитических поверхностях от средних результатов на экземплярах СО SSBB
SSBB = S 2 - S 3; (6.15)
- результатов измерений от средних результатов на аналитических поверхностях SSW
SSW = S4 - S2; (6.16)
- результатов измерений от среднего всех результатов SST
![]() (6.17)
(6.17)
Для контроля правильности вычислений проверяют соотношение между суммами квадратов. Если вычисления проведены правильно, то должно быть выполнено равенство
SSBL + SSBB + SSW = SST. (6.18)
Если суммы квадратов удовлетворяют уравнению (6.18), вычисляют средние квадраты по соответствующим суммам квадратов отклонений, определенным по формулам (6.14)-(6.16):
MSBL = SSBL/(K - 1); (6.19)
MSBB = SSBB/K; (6.20)
MSW = SSW/(2K) (6.21)
и стандартное отклонение повторяемости результатов
![]() (6.22)
(6.22)
Величина SM характеризует неопределенность рентгенофлуоресцентного метода анализа в условиях повторяемости. При оценивании однородности эмиссионным методом SM характеризует суммарную неопределенность повторяемости метода и различие содержания аттестуемого элемента в аналитических объемах.
6.3.7 По средним квадратам, вычисленным по формулам (6.19)-(6.21), оценивают дисперсию внутриэкземплярной неоднородности SSмик и дисперсию межэкземплярной неоднородности SSмак по формулам:
SSмик = (MSBB - MSW)/2; (6.23)
SSмак = (MSBL - MSBB)/4. (6.24)
6.3.8 Оценки стандартного отклонения S мак, характеризующего межэкземплярную неоднородность, и Sмик, характеризующего внутриэкземплярную неоднородность, выполняют в зависимости от соотношений между средними квадратами MSW, MSBB и MSBL по формулам, приведенным в таблице 6.2. В таблице 6.2 через m обозначено число измерений для воспроизведения аттестованного значения СО эмиссионным методом.
Таблица 6.2 - Оценка стандартных отклонений Sмак и Sмик при различных соотношениях между средними квадратами MSW, MSBB, MSBL
|
Соотношение между средними |
Метод измерения |
|||
|
Рентгенофлуоресцентный |
Эмиссионный |
|||
|
Sмак |
Sмик |
Sмак |
Sмик |
|
|
MSW > MSBB > MSBL |
0 |
Sм |
0 |
|
|
MSW > MSBB, MSBB < MSBL |
|
Sм |
|
|
|
MSW > MSBB , MSBB > MSBL |
0 |
|
0 |
|
|
MSW < MSBB < MSBL |
|
|
|
|
6.3.9 Оценку стандартной неопределенности от неоднородности u h получают по формуле
![]() (6.25)
(6.25)
Число степеней свободы vuh стандартной неопределенности uh в зависимости от соотношений между средними квадратами MSW, MSBB и MSBL определяют по таблице 6.3.
Таблица 6.3 - Число степеней свободы при различных соотношениях между средними квадратами MSW, MSBB, MSBL
|
Соотношение между средними квадратами |
Число степеней свободы v u h |
|
MSW > MSBB > MSBL |
2K |
|
MSW > MSBB, MSBB < MSBL |
К - 1 |
|
MSW > MSBB, MSBB > MSBL |
К |
|
MSW < MSBB < MSBL |
К |
7 Оценивание неопределенности от способа установления аттестованного значения стандартного образца
7.1 Способы установления аттестованного значения стандартного образца
Алгоритм оценивания неопределенности способа установления аттестованного значения СО (далее - неопределенность способа) зависит от применяемого при аттестации СО способа установления аттестованного значения СО. В соответствии с ГОСТ 8.315 аттестованное значение СО устанавливают следующими способами:
а) межлабораторной аттестацией СО в соответствии с ГОСТ 8.532;
б) аттестацией СО в одной лаборатории:
- с использованием эталонов в соответствии с РМГ 53;
- с использованием МВИ, аттестованной в соответствии с ГОСТ Р 8.563;
- по процедуре приготовления в соответствии [4]).
7.2 Оценивание неопределенности от способа установления аттестованного значения стандартного образца при межлабораторной аттестации
7.2.1 Применяемые МВИ аттестуемой характеристики подразделяют по специфике измеряемой величины на следующие виды [2]:
а) единица измерения величины не зависит от применяемой МВИ (МВИ, основанные на различных физических и химических принципах измерения величины, - рациональные МВИ);
б) единица измерения величины определяется применяемой МВИ (эмпирические МВИ).
При межлабораторной аттестации МВИ измерения обычно проводят по нескольким рациональным МВИ и только по одной и той же эмпирической МВИ во всех лабораториях. Поэтому для оценивания неопределенности эмпирических и рациональных МВИ используют разные алгоритмы.
7.2.2 Требования к организации межлабораторной аттестации СО и подготовки материала СО приведены в ГОСТ 8.532.
7.2.3 Оценивание неопределенности от способа аттестации СО для эмпирических МВИ
7.2.3.1 Применяемая МВИ должна иметь характеристики прецизионности (стандартное отклонение повторяемости а Л и стандартное отклонение воспроизводимости σR), установленные в соответствии с ГОСТ Р ИСО 5725-2.
Примечание - При отсутствии характеристик прецизионности их оценки для использования в последующем могут быть получены по результатам межлабораторной аттестации СО по алгоритму, изложенному в ГОСТ Р ИСО 5725-2.
7.2.3.2 Для межлабораторной аттестации СО привлекают лаборатории, имеющие опыт использования применяемой МВИ.
Оптимальное число лабораторий р для получения достоверной оценки неопределенности от способа должно быть от 10 до 15.
7.2.3.3 Каждая i-я лаборатория выполняет в соответствии с МВИ в условиях повторяемости n измерений. В условиях повторяемости нецелесообразно проводить более четырех измерений. Протокол с результатами всех измерений (yi1 ,..., yin) в условиях повторяемости лаборатория направляет разработчику СО.
7.2.3.4 Разработчик СО оценивает приемлемость результатов в соответствии с разделом 5 ГОСТ Р ИСО 5725-6.
Вычисляют для каждой i-й лаборатории диапазон значений результатов ![]() , по формуле
, по формуле
![]() i
= yi, max
– yi,min (7.1)
i
= yi, max
– yi,min (7.1)
где yi,max
и yi,min
- наибольший и
наименьший результаты в i-й лаборатории. Сравнивают диапазон ![]() , с критическим диапазоном CR0,95 (n):
, с критическим диапазоном CR0,95 (n):
CR0,95 (n) = f (n) σr , (7.2)
где f(2) = 2,8; f(3) = 3,3; f(4) = 3,6.
При выполнении неравенства
![]() I
= ≤ CR0,95 (n) (7.3)
I
= ≤ CR0,95 (n) (7.3)
результаты i-й лаборатории принимают для дальнейшей обработки. В противном случае результаты i-й лаборатории исключают и предлагают данной лаборатории провести все измерения повторно.
7.2.3.5 Все результаты, оставленные после отбраковки по 7.2.3.4, обрабатывают следующим образом. Вычисляют:
- по результатам
каждой i-й лаборатории
среднее значение ![]()
![]() (7.4)
(7.4)
- общее среднее
значение по всем результатам ![]()
- стандартное отклонение повторяемости в i-й лаборатории si
![]() (7.6)
(7.6)
- оценку стандартного отклонения повторяемости sr
 (7.7)
(7.7)
- оценку
межлабораторной дисперсии ![]()
![]() (7.8)
(7.8)
Если по формуле (7.8) получено
отрицательное значение ![]() , то
принимают
, то
принимают ![]() i = 0.
i = 0.
7.2.3.6 По стандартным отклонениям воспроизводимости σ r и воспроизводимости σr , приписанным данной МВИ, определяют межлабораторную дисперсию
![]() (7.9)
(7.9)
7.2.3.7 Сравнивают
оценку межлабораторной дисперсии ![]() с дисперсией
с дисперсией ![]() по критерию
хи-квадрат, описываемому неравенством
по критерию
хи-квадрат, описываемому неравенством
![]() (7.10)
(7.10)
в котором x20,95(v) - квантиль x2 распределения сv = р - 1 степенями свободы, значения которого приведены в таблице А.1 приложения А.
Если неравенство (7.10)
выполнено, то межлабораторная дисперсия ![]() приемлема. Результаты всех лабораторий
в таком случае можно использовать для оценивания аттестованного значения СО и
стандартной неопределенности от способа в соответствии с 7.2.3.8.
приемлема. Результаты всех лабораторий
в таком случае можно использовать для оценивания аттестованного значения СО и
стандартной неопределенности от способа в соответствии с 7.2.3.8.
Если неравенство (7.10) не
выполнено, то межлабораторная дисперсия ![]() неприемлема вследствие плохой
воспроизводимости МВИ в одной или нескольких лабораториях. Оценивание
аттестованного значения СО и стандартной неопределенности от способа в этом
случае проводят в соответствии с 7.2.3.9.
неприемлема вследствие плохой
воспроизводимости МВИ в одной или нескольких лабораториях. Оценивание
аттестованного значения СО и стандартной неопределенности от способа в этом
случае проводят в соответствии с 7.2.3.9.
7.2.3.8 Оценивают аттестованное значение СО среднеарифметическим значением всех результатов, вычисленным по формуле (7.5):
![]() (7.11)
(7.11)
Стандартную неопределенность способа аттестации uchar оценивают по формуле
 (7.12)
(7.12)
7.2.3.9 При невыполнении условия (7.10) оценивают аттестованное значение СО средним взвешенным значением средних результатов лабораторий, вычисленным по формуле
![]() (7.13)
(7.13)
где W - сумма весовых коэффициентов wi
Весовые коэффициенты определяют следующим образом:
- средние результаты у, лабораторий располагают по возрастанию в ряд:
y(1) ≤ y(2) ≤ … ≤ y(i) ≤ … ≤ y(p), (7.14)
где (i) - номер результата в ряду по возрастанию;
р - общее число результатов;
- вычисляют медиану
результатов ![]() по формуле
по формуле
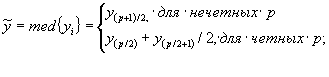 (7.15)
(7.15)
- вычисляют абсолютные отклонения результатов
измерений d0i от медианы ![]() по формуле
по формуле
![]() (7.16)
(7.16)
- вычисляют медиану абсолютных ненулевых отклонений по формуле
MAD0 = med {d0i} (7.17)
где med {d0i} определяют в зависимости от числа ненулевых значений d0i, по формуле, аналогичной формуле (7.15);
- для каждого результата y(i) вычисляют нормированное отклонение Ui от медианы по формуле
![]() (7.18)
(7.18)
где величины d0 i и MAD0 вычислены по формулам (7.16) и (7.17);
- весовые коэффициенты wi в зависимости от значений Ui вычисляют по формуле
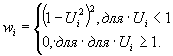 (7.19)
(7.19)
Для оценивания стандартной неопределенности от способа аттестации uchar вычисляют абсолютные отклонения результатов измерений от среднего взвешенного d2i по формуле
![]() (7.20)
(7.20)
и медиану абсолютных ненулевых отклонений MAD 2 по формуле
MAD2 = med {d2i} (7.21)
где med {d2i} определяют в зависимости от числа ненулевых значений d2i по формуле, аналогичной формуле (7.15).
Стандартную неопределенность от способа аттестации uchar определяют по формуле
uchar = 1,48 MAD2. (7.22)
Число степеней свободы uchar равно целой части суммы весовых коэффициентов W.
7.2.4 Оценивание неопределенности от способа аттестации СО для рациональных МВИ
7.2.4.1 В межлабораторной аттестации принимают участие p лабораторий, которые применяют q МВИ (q ≥ 2), основанных на различных физических или химических принципах. Если лаборатория применяет в межлабораторной аттестации несколько МВИ, то результаты этой лаборатории по каждой МВИ представляют как результаты отдельной лаборатории.
Предполагают, что каждая j-я МВИ имеет оцененные в соответствии с ГОСТ Р ИСО 5725-2 характеристики прецизионности (стандартное отклонение повторяемости σrj , стандартное отклонение воспроизводимости σRj и стандартное отклонение систематического смещения метода σс).
7.2.4.2 Разработчик СО оценивает приемлемость результатов в условиях повторяемости по процедуре, аналогичной 7.2.3.4.
7.2.4.3 Для каждой j-й МВИ определяют:
-
среднее значение в i-й лаборатории ![]() по j-й МВИ
по j-й МВИ
![]() (7.23)
(7.23)
где yjjk - k-й результат, полученный в i-й лаборатории по j-й МВИ;
-
общее среднее значение ![]() по всем результатам,
полученным по j-й МВИ,
по всем результатам,
полученным по j-й МВИ,
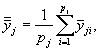 (7.24)
(7.24)
где p j - число лабораторий, представивших результаты по j-й МВИ;
- стандартное отклонение повторяемости в i-й лаборатории по j -й МВИ sji
 7.25)
7.25)
- оценку стандартного отклонения повторяемости для j -й МВИ srj
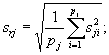 (7.26)
(7.26)
- оценку межлабораторного стандартного отклонения для j-й МВИ sLj
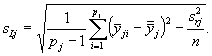 (7.27)
(7.27)
Если по формуле (7.27) получено отрицательное значение для s2Lj то принимают s2Lj = 0.
7.2.4.4 По характеристикам прецизионности, приписанным j -й МВИ, определяют межлабораторную дисперсию
![]() (7.28)
(7.28)
7.2.4.5 Сравнивают оценку межлабораторной дисперсии s2Lj с дисперсией σ2L по критерию хи-квадрат, описываемому неравенством
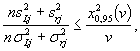 (7.29)
(7.29)
в котором x20.95(v) - квантиль x2-распределения с v = pj - 1 степенями свободы, значения которого при ведены в таблице А.1 приложения А.
7.2.4.6 При выполнении неравенства (7.29) межлабораторная дисперсия s2Lj приемлема. Результаты всех лабораторий в таком случае можно использовать для оценивания аттестованного значения СО и стандартной неопределенности способа.
Для j-й МВИ оценивают стандартную
неопределенность среднего значения ![]()
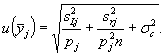 (7.30)
(7.30)
Число
степеней свободы vj стандартной неопределенности ![]() : vj = рj-1.
: vj = рj-1.
Если неравенство (7.29) не выполнено, то межлабораторная дисперсия s2Lj неприемлема вследствие плохой воспроизводимости j-й МВИ в одной или нескольких лабораториях. В этом случае возможны следующие варианты:
а) использовать критерий для выявления статистических выбросов [например, критерий Граббса в соответствии с ГОСТ Р ИСО 5725-2 (пункт 7.3.4)] и повторить процедуру проверки приемлемости результатов по 7.2.4.3-7.2.4.6;
б) забраковать все результаты при их малом числе.
7.2.4.7 После проверки приемлемости результатов проводят процедуру согласования средних значений, полученных по применяемым в межлабораторной аттестации МВИ, следующим образом:
- располагают все средние значения по МВИ по возрастанию в ряд
![]() (7.31)
(7.31)
- вычисляют отношение
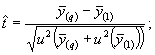 (7.32)
(7.32)
- сравнивают полученное значение ![]() с квантилем распределения Стьюдента
со степенями свободы veff
с квантилем распределения Стьюдента
со степенями свободы veff
![]() (7.33)
(7.33)
где veff оценивают по формуле
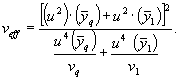 (7.34)
(7.34)
Значения квантилей распределения Стьюдента приведены в таблице А.2 приложения А.
7.2.4.8 При выполнении неравенства (7.33) для оценивания аттестованного значения СО принимают результаты, полученные по всем МВИ.
При невыполнении неравенства
(7.33) проводят проверку совместимости средних значений по 7.2.4.7 после
исключения из ряда (7.31) ![]() или
или ![]() .
.
7.2.4.9 В случае принятия положительного решения в соответствии с 7.2.4.7 аттестованное значение оценивают следующим образом:
- вычисляют для среднего значения результата j-й МВИ вес
![]() (7.35)
(7.35)
и сумму весов
![]() (7.36)
(7.36)
Аттестованное
значение СО ![]() оценивают средневзвешенным значением
оценивают средневзвешенным значением
![]() (7.37)
(7.37)
Стандартную неопределенность от способа аттестации uchar оценивают по стандартным неопределенностям средних значений по МВИ
![]() (7.38)
(7.38)
Определяют число степеней свободы uchar :
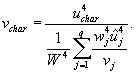 (7.39)
(7.39)
7.3 Оценивание неопределенности от способа установления аттестованного значения стандартного образца по методике выполнения измерений в одной лаборатории
7.3.1 Способы установления аттестованного значения стандартного образца в одной лаборатории
В соответствии с указанным в 7.1 можно выделить три способа установления аттестованного значения СО в одной лаборатории по результатам измерений:
- с использованием эталона;
- с использованием МВИ, аттестованной в соответствии с ГОСТ Р 8.563;
- косвенных (по процедуре приготовления).
7.3.2 Оценивание неопределенности от способа установления аттестованного значения стандартного образца по результатам измерений, полученным с помощью эталона
7.3.2.1 Эталоны,
используемые для аттестации СО, должны иметь действующие (непросроченные) сертификаты о калибровке, содержащие значения
расширенной неопределенности U(![]() ) с указанием коэффициента
охвата k для исключенных систематических эффектов и
стандартного отклонения результатов измерений в условиях повторяемости σг.
) с указанием коэффициента
охвата k для исключенных систематических эффектов и
стандартного отклонения результатов измерений в условиях повторяемости σг.
7.3.2.2 При выборе конкретных эталонов для определения аттестованных значений СО в общем случае следует руководствоваться соотношениями
U(![]() ) ≤ Uдоп и σr ≤ 1,2 Uдоп , (7.40)
) ≤ Uдоп и σr ≤ 1,2 Uдоп , (7.40)
где Uдоп - допускаемое значение расширенной неопределенности аттестованного значения СО в соответствии с техническим заданием на разработку СО.
7.3.2.3 Измерения при аттестационных исследованиях проводят согласно правилам выполнения измерений с помощью эталона или по МВИ, рекомендуемой разработчиком СО и учитывающей правила применения соответствующего эталона.
7.3.2.4 Для СО монолитных или дисперсных материалов предварительно оценивают стандартную неопределенность от неоднородности uh в соответствии с разделом 6. При поэкземплярной аттестации СО стандартную неопределенность от неоднородности не оценивают и в дальнейших расчетах принимают uh = 0.
7.3.2.5 Общее число измерений J , необходимых для оценки аттестованного значения СО методом многократных наблюдений, определяют следующим образом.
Определяют:
- допускаемое значение стандартного отклонения среднего значения результатов в условиях повторяемости sдоп
![]() (7.41)
(7.41)
- значения величин ξ и η
![]() (7.42)
(7.42)
- число измерений J по таблице 7.1 в зависимости от значений величин ξ и η.
Таблица 7.1 - Число измерений J при аттестации СО методом многократных наблюдений
|
η |
ξ |
|||||||
|
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
0,2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
|
0,3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
|
0,4 |
3 |
4 |
4 |
4 |
4 |
4 |
5 |
9 |
|
0,5 |
3 |
4 |
4 |
4 |
4 |
5 |
6 |
12 |
|
0,6 |
4 |
4 |
4 |
4 |
4 |
6 |
8 |
15 |
|
0,7 |
4 |
5 |
5 |
6 |
6 |
7 |
9 |
20 |
|
0,8 |
4 |
5 |
5 |
6 |
6 |
9 |
11 |
26 |
|
0,9 |
5 |
5 |
6 |
7 |
8 |
10 |
14 |
33 |
|
1,0 |
6 |
7 |
8 |
9 |
10 |
11 |
15 |
41 |
|
1,10 |
8 |
8 |
9 |
9 |
10 |
13 |
17 |
49 |
|
1,20 |
9 |
9 |
9 |
10 |
12 |
15 |
20 |
58 |
7.3.2.6 Аттестованное значение СО и стандартную неопределенность от способа оценивают следующим образом:
- получают в условиях повторяемости результаты n измерений (n ≥ J) х1 ,..., хn ;
- вычисляют среднее
значение результатов измерений ![]() и их стандартное отклонение s
и их стандартное отклонение s
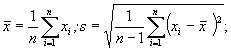 (7.43)
(7.43)
- сравнивают полученное значение стандартного отклонения со стандартным отклонением повторяемости по критерию хи-квадрат по неравенству
![]() (7.44)
(7.44)
где v = n-1, x20,95(v) - квантиль х2 распределения с v степенями свободы, значения которого приведены в таблице А.1 приложения А.
При выполнении неравенства (7.44) аттестованное значение СО оценивают средним значением
![]() (7.45)
(7.45)
и стандартную неопределенность от способа установления аттестованного значения СО оценивают по формуле
![]() (7.46)
(7.46)
Для стандартной неопределенности uchar число степеней свободы
vchar = n - 1. (7.47)
7.3.2.7 При невыполнении неравенства (7.44) полученные результаты бракуют и повторяют процедуру 7.3.2.6.
7.3.3 Оценивание неопределенности от способа установления аттестованного значения стандартного образца по результатам измерений с использованием аттестованной методики выполнения измерений
7.3.3.1 Для
установления аттестованного значения используют МВИ с известными
характеристиками неопределенности. Предварительно в процессе аттестации МВИ
определяют стандартную неопределенность повторяемости σг
стандартную неопределенность
систематического смещения результатов измерений по МВИ для данной лаборатории ![]() и стандартную
неопределенность промежуточной прецизионности σI() (в скобках - идентификация промежуточной ситуации в соответствии с ГОСТ
Р ИСО 5725-3).
и стандартную
неопределенность промежуточной прецизионности σI() (в скобках - идентификация промежуточной ситуации в соответствии с ГОСТ
Р ИСО 5725-3).
Составляющими систематического смещения могут быть систематическое смещение в результатах МВИ и систематическое смещение в результатах, полученных в лаборатории.
Стандартная неопределенность промежуточной прецизионности σI(), оцениваемая в соответствии с ГОСТ Р ИСО 5725-3, обусловлена различием между результатами, полученными :
- разными операторами;
- с использованием разного оборудования;
- в неодинаковых условиях окружающей среды;
- в разное время проведения измерений.
В лаборатории в зависимости от имеющихся условий могут быть проведены измерения по МВИ с изменением всех перечисленных факторов.
7.3.3.2 Измерения для установления аттестованного значения СО выполняют несколько операторов при различных уровнях промежуточной прецизионности.
Каждый оператор на одном уровне промежуточной прецизионности выполняет n измерений в условиях повторяемости. Оптимальное число результатов n находится в интервале от двух до четырех.
Результаты, полученные в условиях промежуточной прецизионности, обрабатывают следующим образом.
Вычисляют:
- для каждого j -го уровня среднее значение ![]() в условиях
повторяемости
в условиях
повторяемости
![]() (7.48)
(7.48)
- и оценку стандартного отклонения повторяемости sr для j-го уровня
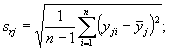 (7.49)
(7.49)
оценку стандартного отклонения повторяемости s r для всех уровней
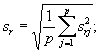 (7.50)
(7.50)
среднее значение ![]() по всем уровням
промежуточной прецизионности
по всем уровням
промежуточной прецизионности
![]() (7.51)
(7.51)
где р - число уровней промежуточной прецизионности;
- стандартное отклонение промежуточной прецизионности σI(о), обусловленное различием между операторами
 (7.52)
(7.52)
7.3.3.3 Сравнивают оценку стандартного отклонения повторяемости sr co стандартным отклонением повторяемости σг по критерию хи-квадрат, проверяя выполнение неравенства
![]() (7.53)
(7.53)
где число степеней свободы v = p(n - 1), x20,95(v) - квантиль x2-распределения с v степенями свободы, значения которых приведены в таблице А.1 приложения А.
При выполнении неравенства (7.53) повторяемость результатов для всех уровней промежуточной прецизионности удовлетворительна. Для дальнейшей обработки принимают результаты, полученные на всех уровнях. В противном случае выявляют уровни с наибольшими значениями стандартной неопределенности повторяемости и исключают результаты, полученные на этих уровнях. При необходимости проводят дополнительные измерения.
7.3.3.4 Сравнивают оценку стандартного отклонения промежуточной прецизионности sI(о) и стандартное отклонение промежуточной прецизионности σI(о) по критерию хи-квадрат
 (7.54)
(7.54)
где x20,95(v) - квантиль x2-распределения сv = p-1 степенями свободы, значения которых приведены в таблице А.1 приложения А.
7.3.3.5 При выполнении неравенства (7.54) стандартное отклонение s/(0) является приемлемым и результаты на всех уровнях можно использовать для оценивания аттестованного значения СО и стандартной неопределенности от способа.
При невыполнении неравенства (7.54) стандартное отклонение sI(o) неприемлемо. В этом случае возможны следующие варианты:
а) использовать критерий для выявления статистических выбросов [например, критерий Граббса в соответствии с ГОСТ Р ИСО 5725-2 (пункт 7.3.4)] и повторить процедуру проверки приемлемости результатов по 7.2.4.3-7.2.4.6;
б) забраковать все результаты при их малом числе.
7.3.3.6
При выполнении неравенства (7.54) аттестованное значение СО ![]() оценивают средним по всем результатам
оценивают средним по всем результатам ![]() , вычисленным
по формуле (7.51)
, вычисленным
по формуле (7.51)
![]() (7.55)
(7.55)
Стандартную неопределенность от способа установления аттестованного значения СО оценивают по формуле
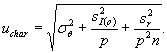 (7.56)
(7.56)
Для стандартной неопределенности u char эффективное число степеней свободы
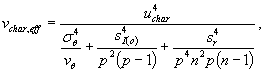 (7.57)
(7.57)
где ![]() - число степеней
свободы стандартного отклонения
- число степеней
свободы стандартного отклонения ![]() .
.
7.3.4 Оценивание неопределенности от способа установления аттестованного значения стандартного образца по результатам косвенных измерений
7.3.4.1 Результаты
косвенных измерений используют при аттестации по процедуре приготовления. В
соответствии с этим способом аттестации СО используют: при оценивании
аттестованного значения СО - оценки входных величин х i ; при оценивании стандартной неопределенности от способа аттестации -
оценки стандартных неопределенностей входных величин ![]() .
.
7.3.4.2 Аттестуемую
характеристику СО ![]() выражают в виде зависимости от входных
величин хi, где i = 1, 2, ..., n:
выражают в виде зависимости от входных
величин хi, где i = 1, 2, ..., n:
A = f (x1, x2 ,..., xn ); (7.58)
аттестованное значение СО А оценивают по оценкам входных величин хi используя зависимость (7.58):
![]() = f
(x1, x2 ,
..., xn ).
(7.59)
= f
(x1, x2 ,
..., xn ).
(7.59)
7.3.4.3 Стандартную неопределенность способа оценивают через стандартные неопределенности входных величин и их коэффициенты корреляции
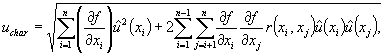 (7.60)
(7.60)
где r (xi , xj) - коэффициент корреляции входных величин хi и хj.
В случае статистической независимости входных величин uchar оценивают по формуле
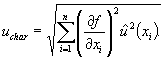 (7.61)
(7.61)
Эффективное число степеней свободы стандартной неопределенности uchar
7.3.4.4 Способы оценивания неопределенности входных величин определяют алгоритм вычисления их степеней свободы.
Если неопределенность входной величины x i оценена с помощью статистического анализа серии из n i измерений (оценивание типа А), то число степеней свободы
vi = ni – k , (7.63)
где k - число параметров, оцененных поданной серии измерений. В частности, если по серии результатов оценено только среднее значение (математическое ожидание), то k = 1 и vi = ni - 1.
Если неопределенность входной величины хi оценена иными способами кроме статистического анализа серии измерений (оценивание типа Б), то число степеней свободы устанавливают по имеющейся информации о неопределенности оценки стандартной неопределенности. В общем случае v , можно оценить по формуле [1]
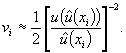 (7.64)
(7.64)
Если известно, что выходная величина с вероятностью, равной единице, принимает значения в известном интервале и результат оценивания типа Б стандартной неопределенности получен исходя из вида распределения (например, равномерного, треугольного), то число степеней свободы равно бесконечности (∞). В этом случае при расчете числа степеней свободы стандартной неопределенности
![]() по формуле (7.62)
принимают
по формуле (7.62)
принимают ![]()
7.3.4.5 Примеры получения оценок стандартных неопределенностей при оценивании типа Б для наиболее часто встречающихся распределений вероятностей приведены в приложении Б.
Пример оценивания стандартной неопределенности от способа установления аттестованного значения СО для СО, аттестуемого по процедуре приготовления, приведен в приложении В.
8 Оценивание суммарной стандартной и расширенной неопределенности аттестованного значения стандартного образца
8.1
Суммарную стандартную
неопределенность аттестованного значения СО ![]() оценивают по ее составляющим по
формуле
оценивают по ее составляющим по
формуле
![]() (8.1)
(8.1)
где составляющие uchar u h и u stab оценены в соответствии с разделами 7, 6 и 5.
Число эффективных степеней
свободы суммарной стандартной неопределенности ![]()
 (8.2)
(8.2)
8.2 Расширенную
неопределенность аттестованного значения СО ![]() для уровня доверия Р вычисляют по формуле
для уровня доверия Р вычисляют по формуле
![]() (8.3)
(8.3)
где tP(vc,eff) - квантиль распределения Стьюдента с эффективным числом степеней свободы vc,eff при доверительной вероятности Р . Значения квантилей распределения Стьюдента для доверительной вероятности 0,95 приведены в таблице А.2 приложения А.
8.3 Если вместо
неопределенности необходимо привести характеристику погрешности (границу
доверительного интервала для доверительной вероятности Р) ![]() , то ее
оценивают по формуле
, то ее
оценивают по формуле
![]() (8.4)
(8.4)
Приложение А
(справочное)
Статистические таблицы
Таблица А.1 - Квантили x2 -распределения x2 0,95(v)
|
v |
x20,95(v) |
v |
x20,95(v) |
v |
x20,95(v) |
|
1 |
3,841 |
11 |
19,675 |
22 |
33,924 |
|
2 |
5,991 |
12 |
21,026 |
24 |
36,415 |
|
3 |
7,815 |
13 |
22,362 |
26 |
38,885 |
|
4 |
9,488 |
14 |
23,685 |
28 |
41,337 |
|
5 |
11,070 |
15 |
24,996 |
30 |
43,773 |
|
6 |
12,592 |
16 |
26,296 |
32 |
46,194 |
|
7 |
14,067 |
17 |
27,587 |
34 |
48,602 |
|
8 |
15,507 |
18 |
28,869 |
36 |
50,998 |
|
9 |
16,919 |
19 |
30,144 |
38 |
53,384 |
|
10 |
18,307 |
20 |
31,410 |
40 |
55,758 |
Для v ≥ 41 значение x20,95(v) вычисляют по формуле
x20,95(v) = 1,36v + 10,8.
Таблица А.2 - Квантили распределения Стьюдента t0,95(v)
|
v |
x2 0,95(v) |
v |
x2 0,95(v) |
v |
x2 0,95(v) |
|
1 |
12,706 |
11 |
2,201 |
22 |
2,074 |
|
2 |
4,303 |
12 |
2,179 |
24 |
2,064 |
|
3 |
3,182 |
13 |
2,160 |
26 |
2,056 |
|
4 |
2,776 |
14 |
2,145 |
28 |
2,048 |
|
5 |
2,571 |
15 |
2,131 |
30 |
2,042 |
|
6 |
2,447 |
16 |
2,120 |
32 |
2,037 |
|
7 |
2,365 |
17 |
2,110 |
34 |
2,032 |
|
8 |
2,306 |
18 |
2,101 |
36 |
2,028 |
|
9 |
2,262 |
19 |
2,093 |
38 |
2,024 |
|
10 |
2,228 |
20 |
2,086 |
40 |
2,021 |
Для v ≥ 41 значение t0,95(v) вычисляют по формуле
![]()
Приложение Б
(справочное)
Оценивание стандартных неопределенностей по типу Б для некоторых общеизвестных
типов распределений
На следующих примерах различных общеизвестных типов распределений вероятностей показано, как могут быть получены оценки типа Б стандартной неопределенности по параметрам функций плотности распределения вероятностей.
Б.1 Равномерное распределение
Измеряемая величина с вероятностью 1 принимает значения в интервале [-а, +а] с одинаковой вероятностью для любой части интервала.
Функция плотности измеряемой величины
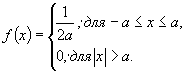 (Б.1)
(Б.1)
Оценка стандартной неопределенности по типу Б
![]() (Б.2)
(Б.2)
Функция плотности равномерного распределения на интервале [-1, +1] представлена на рисунке Б.1.
Рисунок Б.1 - Функция плотности равномерного распределения на интервале [-1, +1]
Примеры применения:
- в сертификате или другой сопроводительной документации даны пределы без указания доверительного уровня, без каких-либо оснований полагать, что какая-либо часть интервала более вероятна, чем другая;
- оценка дана в виде максимального диапазона (± а ), и форма распределения неизвестна.
Б.2 Треугольное распределение
Измеряемая величина с вероятностью 1 принимает значения в интервале [-а, +а]. Значения измеряемой величины в центре интервала более вероятны, чем вблизи его границ. Функция плотности измеряемой величины
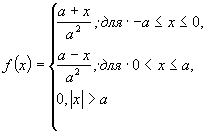 (Б.3)
(Б.3)
Оценка стандартной неопределенности типа Б
![]() (Б.4)
(Б.4)
Функция плотности треугольного распределения на интервале [-1, +1] представлена на рисунке Б.2.
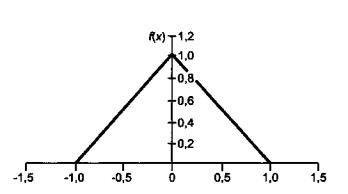
Рисунок Б.2 - Функция плотности треугольного распределения на интервале [-1, +1]
Примеры применения:
- значения измеряемой величины в центре интервала более вероятны, чем вблизи границ;
- оценка дана в виде максимального диапазона (± а), описываемого симметричным одномодальным распределением.
Б.3 Нормальное распределение
Функция плотности измеряемой величины
![]() ( Б.5)
( Б.5)
Функция плотности нормального распределения с параметрами σ = 1 и μ = 0 представлена на рисунке Б.3.

Рисунок Б.3 - Функция плотности нормального распределения
Примеры применения:
- неопределенность дана в виде стандартного отклонения s или σ. Стандартная неопределенность u(х) = s;
- неопределенность дана в виде относительного стандартного отклонения (s/x). Стандартная неопределенность u(х) = x(s/x);
-
неопределенность дана в виде коэффициента вариации Cv(%). Стандартная неопределенность ![]()
- неопределенность дана в виде 95 % -ного (или иного) доверительного интервала (х ± с). Стандартная неопределенность u(х) = с/2 (при 95 % ); u(х) = с/3 (при 99,7 % ).
Приложение В
(справочное)
Пример оценивания неопределенности от способа установления аттестованного
значения стандартного образца по результатам косвенных измерений
Материал СО состава раствора нитрата кадмия приготовлен с использованием ранее аттестованного СО состава металлического кадмия.
B .1 Приготовление материала стандартного образца
Мерную колбу (100 см3 ) взвешивают до и после внесения в нее навески металла. Для взвешивания применяют весы с разрешением 0,01 мг. Масса навески металла 0,10033 г. Предварительную очистку поверхности металла от загрязнения оксидами не проводили, поскольку материал СО находился в запаянной ампуле в инертной атмосфере аргона.
Аликвоту 4 см3 азотной кислоты (1:3) вносят в колбу для растворения находящейся в ней навески металлического кадмия. После растворения колбу заполняют неионизованной водой до метки, содержимое перемешивают, переворачивая колбу не менее 30 раз.
B .2 Расчет аттестованного значения стандартного образца
Аттестуемая характеристика СО - массовая концентрация кадмия в растворе, мг/дм3 . Массовую концентрацию кадмия в растворе CCd , мг/дм3 , рассчитывают по формуле
![]()
где 1000 - коэффициент пересчета из кубических сантиметров в кубические дециметры;
m - масса навески металла;
ω - степень чистоты металла, выраженная через массовую долю основного вещества - кадмия (сведения из паспорта на СО);
V - объем раствора, см 3.
Аттестованное значение CCd
![]()
B .3 Выявление и анализ источников неопределенности
Цель настоящего этапа процедуры состоит в том, чтобы перечислить все источники неопределенности для каждого из параметров - степени чистоты металлического кадмия и массы, а также объема его раствора, - влияющих на результат измерения.
Степень чистоты металлического кадмия, выраженная через массовую долю кадмия, указана в паспорте на СО (аттестованное значение массовой доли кадмия 0,9998, расширенная неопределенность аттестованного значения СО ±0,0001 для уровня доверия Р = 0,95).
Масса m металлического кадмия, из которого был приготовлен раствор кадмия, была измерена путем взвешивания мерной колбы до и после внесения в нее навески металла.
В документации изготовителя весов указаны три источника неопределенности при взвешивании в таре: повторяемость показаний, считываемость показаний (цифровое разрешение) и неопределенность, обусловленная градуировкой шкалы. Последний источник связан с изменениями чувствительности весов и градуировочной характеристикой. Неопределенностью, связанной с изменением чувствительности, можно пренебречь, поскольку разность масс получают на одних и тех же весах в очень узком диапазоне.
Примечание - Здесь не учтена поправка на выталкивающую силу воздуха, поскольку по соглашению все результаты приведены для взвешивания на воздухе. Остающиеся неопределенности слишком малы, чтобы их учет был оправдан.
Объем раствора, находящегося в мерной колбе, подвержен влиянию трех основных источников неопределенности: неопределенности указанного внутреннего объема колбы, т.е. неопределенности градуировки; отклонения при заполнении колбы до метки, т.е. неопределенности повторяемости; отличия температуры колбы и раствора от температуры, при которой была проведена градуировка.
B .4 Количественная оценка составляющих неопределенности
Вклад каждого выявленного источника неопределенности или измеряют непосредственно, или оценивают с использованием результатов предшествующих экспериментов, или выводят исходя из теоретических соображений.
Степень чистоты металлического кадмия, выраженная
через массовую долю кадмия, приведена в паспорте на СО и равна 0,9998 ± 0,0001.
Поскольку нет дополнительной информации, предполагается прямоугольное распределение.
Для получения стандартной неопределенности U(ω) значение 0,0001 следует разделить на ![]() (см. приложение Б).
(см. приложение Б).
![]()
Неопределенность, связанную с массой кадмия, оценивают, используя данные из свидетельства о поверке (калибровке) весов и документации изготовителя. В оценке неопределенности, составившей 0,05 мг, учтены доли трех ее источников, выявленных ранее (см. В.3).
Примечание - Подробные вычисления составляющих неопределенности массы могут быть очень сложными, поэтому целесообразно обращаться к рекомендациям изготовителя. В данном примере для упрощения эти вычисления опущены.
Неопределенность, зависящую от точности градуировки мерной посуды, оценивают следующим образом. Изготовителем мерной посуды указан объем колбы (100 ± 0,1) см 3 при температуре 20°С. Значение неопределенности приведено без указания доверительного уровня или вида распределения, поэтому необходимо какое-то дополнительное предположение. В данном случае стандартную неопределенность вычисляют исходя из предположения о треугольном распределении (приложение Б).
![]()
Примечание - Треугольное распределение выбрано потому, что в реальном процессе производства мерной посуды номинальные значения объема более вероятны, чем крайние значения. Получающееся в результате градуировки распределение вероятностей лучше аппроксимировать треугольным распределением, чем прямоугольным.
Неопределенность, выраженную отклонением при заполнении колбы, можно оценить экспериментально, определяя повторяемость результатов. Серия из 10 опытов по заполнению водой и взвешиванию мерной колбы вместимостью 100 см3 позволила установить стандартное отклонение, равное 0,02 см3 . Это значение можно использовать как значение стандартной неопределенности.
Неопределенность, обусловленную различием между температурой, при которой проводили градуировку, и температурой в лаборатории, можно оценить следующим образом.
По данным изготовителя мерной посуды градуировка колбы была проведена при температуре 20°С, в то время как температура в лаборатории колеблется в пределах ± 4°С. Неопределенность, вызванную этим эффектом, можно вычислить исходя из указанного диапазона температур и коэффициента объемного расширения. Объемное расширение жидкостей существенно больше, чем объемное расширение стекла, поэтому следует учитывать только первую составляющую. Коэффициент объемного расширения воды равен 2,1·10·-4°С-1 , что приводит к значениям границ:
±(100·4·2,1·10-4 ) = ±0,084.
Стандартную неопределенность рассчитывают исходя из предположения о прямоугольном распределении, т.е.
![]()
Значения неопределенностей, обусловленных градуировкой мерной колбы, повторяемостью и влиянием температуры, суммируют, получая суммарную стандартную неопределенность uc(V), см 3 ,объема V
![]()
В.5 Вычисление суммарной стандартной неопределенности
Значения влияющих факторов х, их стандартных неопределенностей u(х) и относительных стандартных неопределенностей u(х)/х представлены в таблице В.1.
Таблица В.1 - Значения влияющих факторов и их неопределенности
|
Фактор |
x |
u(х) |
u(х)/х |
|
Степень чистоты металла ω |
0,9998 |
0,000058 |
0,000058 |
|
Масса металла m |
100,33 мг |
0,05 мг |
0,0005 |
|
Объем раствора V |
100 см3 |
0,07 см3 |
0,0007 |
Поскольку ![]() , то в соответствии с 7.3.4.3 суммарную стандартную
неопределенность uc(CCd) выражают как
, то в соответствии с 7.3.4.3 суммарную стандартную
неопределенность uc(CCd) выражают как

![]()
![]()
![]()
то относительные стандартные неопределенности, связанные с каждой из составляющих, суммируют следующим образом:

Суммарная стандартная неопределенность uc(CCd), мг/дм 3 ,
uc(CCd) = C Cd ·0,0009 = 1003,1·0,0009 = 0,9.
Значение расширенной неопределенности U0,95(CCd), мг/дм3 , рассчитывают, умножая суммарную стандартную неопределенность на коэффициент охвата k = 2.
U0,95(CCd) = 2·0,9 = 1,8.
Библиография
|
[1] Guide to the expression of uncertainty in measurement. - ISO, Geneva, 1993. (Руководство по выражению неопределенности измерения /Пер. с англ.//Под ред. В.А. Слаева. - СПб: ВНИИМ, 1999) |
||
|
[2] ИСО/РЕМКО
Руководство 35 |
Стандартные образцы. Общие и статистические принципы аттестации (Reference materials. General and statistical principles for certification) |
|
|
[3] Guide: Quantifying uncertainty in analytical measurement, 2nd edition, 2000, Eurachem/ CITAC (Количественное описание неопределенности в аналитических измерениях. Руководство ЕВРАХИМ/СИТАК. - 2-е изд./ Пер. с англ.// Под ред. Л.А. Конопельке - СПб: ВНИИМ, 2002 |
||
|
Государственная система обеспечения единства измерений. Метрологическая аттестация стандартных образцов состава веществ и материалов по процедуре приготовления |
||
Ключевые слова: стандартный образец, аттестованное значение, неопределенность, стандартная неопределенность аттестованного значения стандартного образца