Краткие заметки
о расчете железобетонных
конструкций на действие поперечных сил
Москва
2008
В представленных заметках рассмотрены проблемы, связанные с расчетом железобетонных конструкций по наклонным сечениям при учете усилий в бетоне над наклонной трещиной, в продольной арматуре, пересекающей наклонную трещину, в поперечной арматуре, пересекающей наклонную трещину, и сил зацепления, действующих по берегам наклонной трещины.
Содержание
1. ОБЩИЕ СООБРАЖЕНИЯ
Проклятым вопросом железобетона назвал уважаемый профессор Порфирий Иванович Васильев проблему расчета железобетонных конструкций на действие поперечных сил или, по терминологии Запада, - расчета на срез.
Действительно, всю вторую половину прошлого столетия многие десятки и сотни ученых и специалистов в Советском Союзе и за рубежом пытались решить эту проблему. Было выдвинуто большое количество различных подходов и моделей. Перечисление их авторов и краткое описание предлагаемых методов расчета заняли бы много десятков и даже сотен страниц. Однако удовлетворительного решения этой проблемы до сих пор не найдено.
Вместо того чтобы дать описание, анализ и критику различных подходов, разумно обратиться к методам расчета, принятым в наиболее значимых нормативных документах, - нормах Советского Союза, Американских нормах и Международных Европейских нормативных документах.
2. РАСЧЕТ ПО НОРМАТИВНЫМ ДОКУМЕНТАМ
В нормах Советского Союза была принята методика расчета по предельным усилиям в наклонных сечениях. Предельные усилия в наклонном сечении включают предельную поперечную силу, воспринимаемую бетоном, и предельную поперечную силу, воспринимаемую поперечной арматурой, пересекающей наклонное сечение. Предельная поперечная сила, воспринимаемая бетоном в наклонном сечении, определяется по полуэмпирической зависимости, обратно пропорциональной длине проекции наклонного сечения на продольную ось элемента, предельная поперечная сила, воспринимаемая поперечной арматурой, определяется по полуэмпирической зависимости, прямо пропорциональной длине проекции наклонного сечения на продольную ось элемента.
Расчетные условия прочности на действие поперечных сил могут быть представлены в следующем виде:
для элементов без поперечной арматуры
Q ≤ Qb;
для элементов с поперечной арматурой
Q ≤ Qb + Qsw,
где Q - поперечная сила, действующая в наклонном сечении, другими словами, равнодействующая всех поперечных сил, действующих по одну сторону от рассматриваемого наклонного сечения;
Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении
![]()
Qsw - поперечная сила, воспринимаемая поперечной арматурой, пересекающей наклонное сечение
Qsw = φswqswc.
Здесь представлена только основная структура расчетных зависимостей.
Расчетные условия прочности бетона между наклонными сечениями и по наклонным сечениям на действие момента не рассматриваются.
В Американских нормах была принята методика по предельным усилиям на срез. Предельные усилия на срез включают предельную поперечную силу, воспринимаемую бетоном, и предельную поперечную силу, воспринимаемую поперечной арматурой. Предельная поперечная сила, воспринимаемая бетоном, определяется по эмпирической зависимости, связанной с соотношением поперечной силы и изгибающего момента от внешней нагрузки в нормальном сечении, рассматриваемом на срез, и относительным содержанием продольной растянутой арматуры в этом сечении. Предельная поперечная сила, воспринимаемая поперечной арматурой, определяется по полуэмпирической зависимости, принимая поперечную арматуру в пределах участка, равного рабочей высоте поперечного сечения по длине элемента.
Расчетные условия прочности на срез в обозначениях, принятых в отечественных нормативных документах, могут быть представлены в следующем виде:
для элементов без поперечной арматуры
Q ≤ Qb;
для элементов с поперечной арматурой
Q ≤ Qb + Qsw,
где Qb - усилие, воспринимаемое бетоном
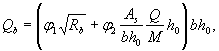
Qsw - усилие, воспринимаемое поперечной арматурой
Qsw = qswh0;
Q и M - поперечная сила и изгибающий момент в нормальном сечении.
Здесь также представлена только основная структура расчетной зависимости.
В Международных Европейских нормах расчет на действие поперечных сил (расчет на срез) был принят на основе стержневой модели, состоящей из наклонных растянутых и сжатых стержневых элементов. Предельные усилия в наклонных сжатых элементах, воспринимаемые бетоном, определяются по полуэмпирической зависимости, связанной с углом между сжатыми и растянутыми стержневыми элементами, предельные усилия в наклонных растянутых стержневых элементах, воспринимаемые поперечной арматурой, определяются по полуэмпирической зависимости, также связанной с углом между сжатыми и растянутыми стержневыми элементами. При этом поперечная сила от внешней нагрузки не должна превосходить как предельную поперечную силу, воспринимаемую сжатым стержневым элементом, так и предельную поперечную силу, воспринимаемую растянутым стержневым элементом.
Расчетное условие прочности в обозначениях, принятых в отечественных нормативных документах, может быть представлено в следующем виде:
для элементов без поперечной арматуры
Q ≤ Qb;
для элементов с поперечной арматурой
Q ≤ Qsw;
где Qb - усилие, воспринимаемое бетоном
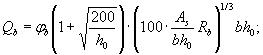
Qsw, усилие, воспринимаемое поперечной арматурой
Qsw = φswqswc;
Q - поперечная сила в нормальном сечении.
Здесь также представлена только основная структура расчетных зависимостей.
Расчет по сжатой наклонной полосе не рассматривается.
Из изложенного можно видеть, что методы расчета железобетонных конструкций на действие поперечных сил, представленные в наиболее значимых нормативных документах - в нормах Советского Союза (России), Американских нормах и в Международных Европейских нормативных документах, существенно отличаются друг от друга.
В нормах Советского Союза рассматривается модель наклонных сечений, между тем как в Международных Европейских нормативных документах, рассматривается стержневая модель.
В нормах Советского Союза и в Американских нормах предельная несущая способность по поперечной силе определяется как сумма предельных поперечных сил, воспринимаемых бетоном и поперечной арматурой, в то время как в Международных Европейских нормативных документах предельная несущая способность по поперечной силе оценивается независимо друг от друга по бетону и по поперечной арматуре.
В нормах Советского Союза предельная поперечная сила определяется в зависимости от проекции длины наклонного сечения на продольную ось элемента, в то время как в Американских нормах предельная поперечная сила, воспринимаемая бетоном, определяется в зависимости от соотношения поперечной силы и изгибающего момента, а также в зависимости от относительной величины продольной растянутой арматуры.
В нормах Советского Союза предельная поперечная сила, воспринимаемая поперечной арматурой, определяется на длине проекции наклонного сечения, в Американских нормах - на длине, равной рабочей высоте сечения, в Международных нормативных документах - на длине, связанной с углом между растянутыми и сжатыми стержневыми элементами.
Такое различие в методах расчета, очевидно, приводит и к различным результатам расчета, а также, очевидно, требует дальнейших усилий в направлении совершенствования методов расчета железобетонных элементов на действие поперечных сил.
3. ОБЩАЯ РАСЧЕТНАЯ МОДЕЛЬ
Разрушение железобетонных элементов от действия поперечных сил, как установлено многочисленными опытами, происходит по наклонному сечению, проходящему по наклонной трещине, при разрушении бетона над наклонной трещиной.
Казалось бы, самое простое - это выделить блок железобетонного элемента, отсеченного наклонным сечением, и рассмотреть равновесие внешних сил, действующих на выделенный блок, и внутренних усилий, действующих в наклонном сечении. Однако при определении усилий, действующих в наклонном сечении, возникает ряд трудноразрешимых проблем.
Рассмотрим блок, выделенный в элементе наклонным сечением и нормальным сечением, проходящем по нижнему, растянутому концу наклонного сечения, по которому действуют поперечные сила Q момент М и продольная сила N от внешних нагрузок (рис. 1).
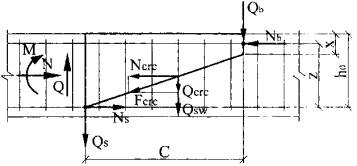
Рис. 1
Усилия, действующие в наклонном сечении (усилия в связях, соединяющих выделенный блок с остальным элементом), включают:
- усилия в бетоне над наклонной трещиной, которые можно представить в виде продольной и поперечной составляющих Nb и Qb
- усилия в поперечной арматуре Qsw,
- усилия в месте пересечения наклонного сечения и продольной растянутой арматуры, которые также можно представить в виде продольной и поперечной составляющих Ns и Qs;
- усилия, действующие по берегам наклонной трещины, которые также можно представить в виде продольной и поперечной составляющих Qcrc и Ncrc.
В результате может быть записана общая система уравнений равновесия, включающая уравнения равновесия внешних и внутренних поперечных сил, изгибающих моментов и продольных сил, действующих в наклонном сечении
∑Q = 0; Q = Qb + Qsw + Qs + Qcrc;
∑N = 0; N = Nb – Ns + Ncrc;
∑M = 0; M = Nbz – Qbc + Qswc/2.
Уравнение моментов здесь представлено как сумма моментов всех внешних и внутренних сил относительно точки пересечения наклонного сечения с продольной растянутой арматурой.
Теперь рассмотрим усилия, действующие в наклонном сечении.
4. УСИЛИЯ В БЕТОНЕ НАД НАКЛОННОЙ ТРЕЩИНОЙ
Бетон в зоне над наклонной трещиной находится в условиях плоского напряженного состояния. Если рассматривать сечения, проходящие от вершины наклонной трещины до грани элемента, то в этом сечении, очевидно, действуют нормальные и касательные напряжения. Предельные значения нормальных и касательных напряжений могут быть найдены из критерия прочности бетона при плоском напряженном состоянии, выраженного через главные взаимно перпендикулярные напряжения и сопротивления бетона по прочности на сжатие и сопротивления бетона по прочности на растяжение. Исходя из этого критерия, может быть установлено соотношение предельных нормальных и касательных напряжений, действующих в этом сечении.
Если принять приближенно равномерное распределение нормальных и касательных напряжений по высоте зоны бетона над наклонной трещиной, то мы получим соотношение поперечного и продольного усилий в этой зоне, отвечающее полученному соотношению нормальных и касательных напряжений. Однако сами величины продольного и поперечного усилий в зоне над наклонной трещиной остаются неизвестными, поскольку остается неизвестной высота зоны бетона над наклонной трещиной и к тому же соотношение между предельными значениями продольной и поперечной силы является переменной величиной.
Рассмотрим более подробно определение усилий, воспринимаемых бетоном над наклонной трещиной, Qb и Nb.
Критерий прочности бетона при плоском напряженном состоянии в области «сжатие-растяжение» и «сжатие-сжатие», получаемый непосредственно из экспериментальных данных, может быть представлен в виде криволинейного графика в координатах главных напряжений, сжимающих σ1 и растягивающих σ3 показанного на рис. 2. Однако такой криволинейный график достаточно сложен для дальнейшей интерпретации. Поэтому его целесообразно заменить более простыми и осторожными линейными графиками, показанными на рис. 3. Эти графики могут быть выражены простыми уравнениями:
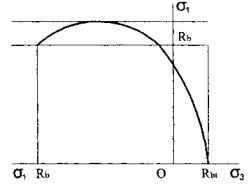
Рис. 2
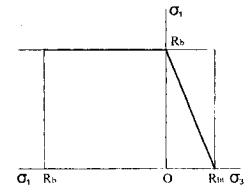
Рис. 3
для «сжатия-растяжения»
![]()
для «сжатия-сжатия»
![]()
Уравнения, выраженные через главные напряжения, можно с помощью известных соотношений теории упругости выразить через нормальные напряжения σb и касательные напряжения τb:
в области «сжатие-сжатие»
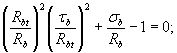
в области «сжатие-растяжение»
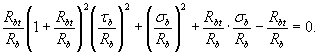
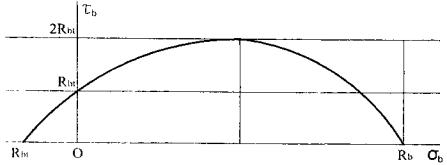
Рис. 4
Полученные уравнения можно представить в виде криволинейного графика в координатах нормальных и касательных напряжений, показанного на рис. 4. Можно видеть, что при нулевых значениях нормальных напряжений σb = 0 предельные касательные напряжения τb,ult равны прочности бетона на растяжение Rbt, далее с увеличением нормальных напряжений σb предельные касательные напряжения τb,ult вначале увеличиваются до некоторого максимума, примерно равного 2Rbt при нормальных напряжениях σb, примерно равных 0,5Rb, а затем уменьшаются до нуля при нормальных напряжениях σb, равных прочности бетона на сжатие Rb.
Использовать приведенные выше уравнения, связывающие предельные значения нормальных и касательных напряжений σb,ult и τb,ult достаточно сложно для дальнейшего анализа. Поэтому перейдем к дальнейшим упрощениям.
Предельные значения нормальных и касательных напряжений σb,ult и τb,ult можно принять независимыми друг от друга и равными их максимальным значениям, т.е. σb,ult = Rb и τb,ult = 2Rbt либо некоторым средним значениям, например, σb,ult = 0,5Rb, τb,ult = 1,5 Rbt.
Можно криволинейный график, отображающий связь между предельными значениями нормальных и касательных напряжений, заменить на линейный, например, показанный на рис. 5. Этот график выражается уравнением
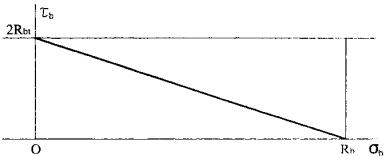
Рис. 5
В результате мы получаем зависимость, показывающую непрерывное линейное уменьшение предельных значений касательных напряжений с увеличением нормальных напряжений, т.е. достаточно простую зависимость, связывающую предельные нормальные и касательные напряжения. Понятно, эта зависимость завышает касательные напряжения при небольших нормальных напряжениях и занижает при больших значениях нормальных напряжений.
Распределение нормальных и касательных напряжений по высоте зоны бетона над наклонной трещиной имеет криволинейный характер. Можно принять, что вверху зоны бетона над наклонной трещиной касательные напряжения равны нулю, а нормальные напряжения достигают максимальных значений и напротив, у низа зоны бетона над наклонной трещиной касательные напряжения достигают максимальных значений. Поскольку определить фактическое распределение нормальных и касательных напряжений по высоте зоны бетона над наклонной трещиной достаточно сложно и, может быть, не имеет практического смысла, примем равномерное распределение нормальных и касательных напряжений по высоте зоны бетона над наклонной трещиной.
Принимая равномерное распределение нормальных и касательных напряжений по высоте х зоны бетона над наклонной трещиной и максимальные значения, не зависимые друг от друга, предельных нормальных и касательных напряжений, получим выражения для предельных поперечных и продольных усилий Qb и Nb, в бетоне над наклонной трещиной:
Qb = Qb,ult;
Nb = Nb,ult,
а принимая линейную связь между предельными касательными и нормальными напряжениями, получим выражение, определяющее зависимость между предельными значениями поперечных и продольных усилий в бетоне над наклонной трещиной
![]()
где
Qb,ult = 2Rbtbx, а Nb,ult = Rbbx.
Если обозначить величину 2Rbt через некоторое сопротивление бетона срезу Rb,sh, то приведенные усилия Qb,ult и Nb,ult запишутся в виде:
Qb,ult = Rb,shbx,
Nb,ult = Rbbx,
а уравнения - в виде:
в первом случае, когда усилия Qb и Nb определяются независимо друг от друга
Qb = Rb,shbx;
Nb = Rbbx,
и во втором случае, когда учитывается взаимосвязь между усилиями Qb и Nb
![]()
Очевидно, в предложенные зависимости могут быть введены соответствующие поправки на основе анализа экспериментальных данных, но тем не менее с большой долей условности нами получены, возможно, более простые выражения для предельных усилий в бетоне над наклонной трещиной.
Отметим, что имеется много других предложений по определению усилий в бетоне над наклонной трещиной, но мы здесь останавливаться на них не имеем возможности.
Учет неравномерности распределения напряжений по высоте зоны бетона над наклонной трещиной может быть осуществлен с помощью понижающих коэффициентов, вводимых на усилия Qb,ult и Nb,ult.
Остается только определить высоту бетона над наклонной трещиной х. Она, как будет дальше показано, может быть найдена из решения системы уравнений равновесия с привлечением деформационных зависимостей.
5. УСИЛИЯ, ВОСПРИНИМАЕМЫЕ ПОПЕРЕЧНОЙ АРМАТУРОЙ
Усилия, воспринимаемые поперечной арматурой, пересекающей наклонное сечение в пределах наклонной трещины, определить значительно легче. Опыты показывают, что при разрушении по наклонному сечению поперечная арматура, как правило, достигает предела текучести и поэтому напряжения в поперечной арматуре могут быть приняты равными расчетным сопротивлениям арматуры на растяжение. Правда, напряжения в поперечной арматуре подлине наклонной трещины распределяются достаточно неравномерно, однако если приближенно принять равномерное распределение напряжений с введением некоторого понижающего коэффициента, учитывающего эту неравномерность, то поперечное усилие в поперечной арматуре может быть установлено.
Принимая равномерное распределение напряжений в поперечной арматуре, пересекающей наклонную трещину, и равное сопротивлению арматуры растяжению, выражение для усилия в поперечной арматуре (вертикальной) Qsw может быть записано в виде
Qsw = qswc,
где qsw - интенсивность усилий в поперечной арматуре по длине элемента
![]()
с - длина проекции наклонного сечения на продольную ось элемента.
Здесь мы рассматриваем поперечную арматуру в виде арматурных стержней, расположенных нормально к продольной оси элемента.
6. СИЛЫ ЗАЦЕПЛЕНИЯ, ДЕЙСТВУЮЩИЕ ПО БЕРЕГАМ НАКЛОННОЙ ТРЕЩИНЫ
Значительно сложнее дело обстоит с определением сил зацепления, действующих по берегам наклонной трещины. Наличие этих сил, возникающих в результате взаимного смещения (сдвига) берегов наклонной трещины, установлено экспериментально и их величина составляет значительную долю в суммарном сопротивлении элемента по наклонному сечению.
Непосредственное определение сил зацепления встречает значительные трудности, поскольку они зависят от характера выступов и впадин по берегам наклонной трещины, ширины раскрытия наклонной трещины, формы наклонной трещины и распределяются неравномерно по длине наклонной трещины.
Если попробовать оценить силы, возникающие от сдвига берегов наклонной трещины, аналогично сопротивлению сдвига контактных швов сборно-монолитных конструкций с различной величиной шероховатости рабочих швов бетонирования, контакта арматуры периодического профиля с бетоном и тому подобных систем, то силы сдвига по берегам наклонной трещины можно выразить через расчетные сопротивления бетона растяжению с некоторым понижающим коэффициентом, равномерно распределенные (приближенно) подлине наклонного сечения в пределах наклонной трещины, опять-таки с некоторым понижающим коэффициентом.
Исходя из ориентировочных соображений выражение для усилия зацепления вдоль наклонного сечения может быть представлено в виде
Fcrc = kRbtblcrc,
а его вертикальная и горизонтальная составляющие
Qcrc = kRbtbc;
Ncrc = kRbtbh0.
Коэффициент k с осторожностью может быть принят 0,1.
Очевидно, что силы зацепления с увеличением ширины раскрытия наклонной трещины уменьшаются, однако ширина раскрытия по длине наклонной трещины остается не одинаковой, уменьшаясь у краев наклонной трещины.
7. УСИЛИЯ, ДЕЙСТВУЮЩИЕ В ПРОДОЛЬНОЙ АРМАТУРЕ
Оценка усилий, действующих в местах пересечения продольной растянутой арматуры и наклонного сечения, также содержит много трудностей и неопределенностей.
Многочисленные опыты показывают, что в месте пересечения с наклонной трещиной продольная арматура испытывает как растяжение, так и изгиб вследствие взаимного смещения частей элемента, разделенных наклонной трещиной, в результате чего в продольной арматуре в месте пересечения ее наклонным сечением возникает осевое продольное растягивающее усилие и поперечное, так называемое нагельное усилие, которое, в свою очередь, вызывает откол или раскалывание бетона защитного слоя.
Поперечное (нагельное) усилие в продольной арматуре может определяться исходя из предельного состояния при отрыве или раскалывании бетонного слоя, а также исходя из предельного состояния в арматурном стержне от действия изгибающего момента и растягивающей осевой продольной силы.
В первом случае поперечная сила может быть приближенно определена, принимая в плоскости отрыва бетонного слоя растягивающие напряжения в бетоне, равные расчетным сопротивлениям бетона растяжению, распространяющимся на некоторой длине вдоль продольной арматуры.
Во втором случае поперечная сила может быть найдена из расчета арматурного стержня как стального элемента на действие продольной растягивающей силы и изгибающего момента на некоторой длине изгиба от точки приложения поперечной силы.
Остановимся более подробно на определении усилий в продольной арматуре, пересекающей наклонную трещину.
Величину поперечной силы Qs, вызывающей отрыв бетонного слоя, определяем наиболее простым способом, принимая равномерное распределение растягивающих напряжений в плоскости отрыва на некоторой длине ls, равных сопротивлению бетона растяжению Rbt
Qs = Rbtbls,
Длина отрыва бетонного слоя ls на основании экспериментальных данных может быть принята равной примерно пятикратной толщине бетонного слоя (ls = 5hb).
После отрыва бетонного слоя продольная растянутая арматура, пересекающая наклонную трещину, находится под воздействием как растягивающих усилий Ns, так и поперечных усилий Qs, которые, в свою очередь, вызывают в продольной арматуре изгибающие моменты Ms = Qsls.
Таким образом, продольная растянутая арматура, пересекающая наклонную трещину, находится под воздействием продольной растягивающей силы Ns и изгибающего момента Ms.
Прочность арматурных стержней при действии продольной растягивающей силы Ns и изгибающего момента Ms может быть определена исходя из упругой или пластической работы арматуры.
При упругой работе прочность арматуры определяется уравнением
![]()
где N0s - предельная продольная сила, воспринимаемая арматурными стержнями при упругой работе;
M0s - предельный момент, воспринимаемый арматурными стержнями при упругой работе.
При пластической работе прочность арматуры определяется уравнением
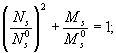
где N0s - предельная продольная сила, воспринимаемая арматурными стержнями при пластической работе;
M0s - предельный момент, воспринимаемый арматурными стержнями при пластической работе.
Продольные силы и моменты N0s и M0s определяются по известным формулам для стальных конструкций.
Выражая обратно изгибающий момент Ms через поперечную силу Qs, получим уравнение связи между предельной продольной силой Ns и предельной поперечной силой Qs при упругой и пластической работе продольной арматуры:
![]()
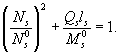
Длина изгиба продольной арматуры ls исходя из экспериментальных данных приближенно может быть принята равной пяти диаметрам арматуры (ls = 5ds).
8. ЭЛЕМЕНТ БЕЗ ПОПЕРЕЧНОЙ АРМАТУРЫ БЕЗ УЧЕТА НАГЕЛЬНЫХ СИЛ В ПРОДОЛЬНОЙ АРМАТУРЕ И СИЛ ЗАЦЕПЛЕНИЯ ПО НАКЛОННОЙ ТРЕЩИНЕ
Запишем уравнение равновесия для элементов без поперечной арматуры, подвергающихся действию только изгибающих моментов и поперечных сил. Силы зацепления по берегам наклонной трещины и нагельные (поперечные) силы в продольной растянутой арматуре в силу их недостаточной определенности не учитываются (рис. 6).
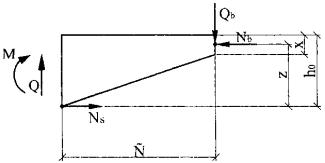
Рис. 6
Уравнение равновесия выглядит следующим образом:
Q = Qb;
Nb = Ns;
M + Qc = Nsz,
где уравнение равновесия моментов записано относительно точки приложения усилий в бетоне над наклонной трещиной.
Решение этой системы уравнений можно представить в следующем виде.
Из уравнения равновесия моментов определяем продольное усилие в арматуре
![]()
Из уравнения равновесия продольных сил Nb = Ns определяем продольное усилие в бетоне над наклонной трещиной, равное продольному усилию в арматуре
![]()
Из уравнения равновесия поперечных сил определяем поперечное усилие в бетоне над наклонной трещиной
Qb = Q.
Таким образом, мы определили усилия, действующие в наклонном сечении, через внешние усилия, приложенные к рассматриваемому блоку.
Выше мы установили соотношение между поперечной и продольной силами, воспринимаемыми бетоном над наклонной трещиной
![]()
Решая общую систему уравнений
Qb = Q;
![]()
![]()
получим уравнение прочности по бетону над наклонной трещиной
![]()
или выражение для предельной поперечной силы, воспринимаемой элементом, по прочности бетона над наклонной трещиной
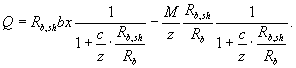
Условие прочности элемента по бетону над наклонной трещиной выражается в виде неравенств
![]()
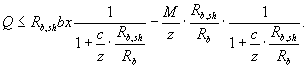
Условие прочности элемента по растянутой арматуре, полученное из уравнения равновесия, запишется в виде неравенства
М + Qc ≤ RsAsz.
Таким образом, для окончательного решения задачи необходимо определить высоту зоны бетона над наклонной трещиной х.
Для этого необходимо привлечь деформационную зависимость.
Имеется много предложений для схем деформирования железобетонного элемента по наклонному сечению. Мы выберем самую простую.
9. ДЕФОРМАЦИОННАЯ ЗАВИСИМОСТЬ
Деформационную зависимость запишем исходя из схемы поворота наклонного сечения относительно вершины наклонной трещины
![]()
Укорочение бетона на уровне середины зоны бетона над наклонной трещиной ΔbN в продольном направлении можно выразить через продольное усилие Nb и коэффициент податливости δbN
ΔbN = δbNNb,
а коэффициент податливости δbN можно представить в виде
![]()
Удлинение продольной растянутой арматуры в продольном направлении ΔsN, можно также выразить через продольное усилие Ns и коэффициент податливости δsN
ΔsN = δsNNs,
а коэффициент податливости δsN можно представить в виде
![]()
Соотношение ![]() имеет вид
имеет вид
![]()
Принимая из уравнения равновесия продольных сил в наклонном сечении Nb = Ns, получим
![]()
или, подставляя выражения для δbN и δsN
![]()
Согласно экспериментальным данным длина зоны деформирования бетона над наклонной трещиной примерно равна высоте этой зоны, то есть lbN = х, а длина зоны деформирования продольной арматуры примерно равна длине проекции наклонного сечения, то есть lsN = с.
Отсюда
![]()
Вернемся к исходному условию деформирования, которое учитывает сравнительно небольшую величину высоты зоны бетона над наклонной трещиной. Его можно упрощенно представить
![]()
Подставляя полученное соотношение ![]() в условие
деформирования, получим
в условие
деформирования, получим
![]()
Таким образом, мы получили зависимость высоты зоны бетона над наклонной трещиной от длины проекции наклонного сечения в виде обратной пропорции, то есть чем больше длина проекции наклонного сечения, тем меньше высота зоны бетона над наклонной трещиной, и наоборот. Такая зависимость в целом согласуется с экспериментальными данными.
В результате мы получили выражение для определения высоты зоны бетона над наклонной трещиной, которое можно подставить в приведенные выше условия прочности и получить законченное решение задачи.
10. АНАЛИЗ РАСЧЕТА
Подставив полученное выражение для высоты зоны бетона над наклонной трещиной х в приведенные выше уравнения и условия прочности по бетону над наклонной трещиной, получим окончательные зависимости для расчета прочности по наклонным сечениям.
Условие прочности, выраженное через поперечную силу, выглядит так
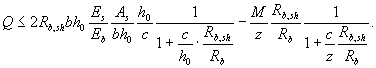
Таким образом, можно видеть, что величина
предельной поперечной силы, воспринимаемой бетоном над наклонной трещиной, а
значит, и величина предельной поперечной силы, воспринимаемой элементом в
целом, зависит от соотношения рабочей высоты и проекции наклонного сечения h0/с,
от относительного содержания продольной растянутой арматуры ![]() и от изгибающего
момента в нормальном сечении, проходящем через нижний растянутый конец
наклонного сечения М.
и от изгибающего
момента в нормальном сечении, проходящем через нижний растянутый конец
наклонного сечения М.
С увеличением соотношения h0/с предельная поперечная сила увеличивается,
также она увеличивается с увеличением относительного содержания продольной
арматуры ![]() и уменьшается с
увеличением момента М.
и уменьшается с
увеличением момента М.
Как видим, полученная расчетная зависимость включает основные параметры, присутствующие в расчетных зависимостях в приведенных выше нормативных документах.
Проанализируем полученное условие прочности при действии поперечной силы.
Если мы исключим из полученной расчетной зависимости выражение, учитывающее влияние изгибающего момента
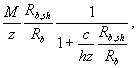
выражение, учитывающее соотношение между сопротивлением бетона срезу и сжатию
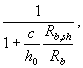
заменим выражение, учитывающее влияние продольной арматуры
![]()
некоторым коэффициентом, и выразим сопротивление бетона срезу Rb,sh через сопротивление бетона растяжению Rbt то получим зависимость, идентичную по своей структуре зависимости, принятой в российских нормах
![]()
Сравнительный анализ полученной расчетной зависимости и зависимости, принятой в российских нормах, показывает, какие факторы не учитываются в нормативной методике и каким образом их можно учитывать с помощью представленной расчетной модели. С другой стороны, этот анализ показывает, что нормативная методика в своей основе отражает сопротивление железобетонных элементов действию поперечных сил.
Очевидно, представленная общая зависимость получена при использовании весьма условных и приближенных подходов и приемов. Поэтому она требует дальнейшего исследования и анализа путем сопоставления с экспериментальными данными и введения корректив и численных коэффициентов.
Коррективы могут быть сделаны путем включения в расчетную модель нагельных (поперечных) сил в продольной арматуре, сил зацепления в наклонной трещине, уточнения параметров деформационной зависимости и усилий, действующих в бетоне над наклонной трещиной. Безусловно, это сделает расчетную зависимость еще более сложной и громоздкой по сравнению с уже полученной достаточно сложной и громоздкой зависимостью и тем более по сравнению с зависимостью, принятой в нормативных документах. Поэтому при дальнейших исследованиях следует стремиться к наиболее простой расчетной зависимости при сохранении основных принципов расчетной модели и наиболее значимых факторов, влияющих на несущую способность элемента при действии поперечных сил.
Другим путем, более логичным, является учет поперечных (нагельных) сил в продольной арматуре, Qs, которым в представленном анализе мы пренебрегали.
Отметим, что сравнение с действующими нормативными документами в данном случае является вполне оправданным, так как принятые в них эмпирические расчетные зависимости получены на основе анализа многочисленных экспериментальных данных.
11. ЭЛЕМЕНТ БЕЗ ПОПЕРЕЧНОЙ АРМАТУРЫ С УЧЕТОМ НАГЕЛЬНЫХ СИЛ В ПРОДОЛЬНОЙ АРМАТУРЕ
Запишем уравнения равновесия для элементов без поперечной арматуры, подвергающихся действию только изгибающих моментов и поперечных сил, с учетом влияния нагельных сил Qs. Силы зацепления по берегам наклонной трещины в силу их неопределенности не учитываем (рис. 7).
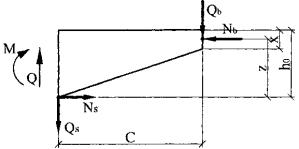
Рис. 7
Уравнения равновесия с уравнением равновесия моментов относительно точки приложения усилий в бетоне над наклонной трещиной имеют вид:
Q = Qb + Qs;
Nb = Ns;
М + Qc = Nsz + Qsc,
а уравнения равновесия с уравнением равновесия моментов относительно точки приложения усилий в месте пересечения наклонного сечения продольной арматурой имеют вид:
Q = Qb + Qs;
Nb = Ns;
М = Nbz + Qbc,
Дополнительно к уравнениям равновесия имеем уравнения связи между продольными и поперечными усилиями в бетоне Nb и Qb
![]()
и уравнение связи между продольными и поперечными усилиями в продольной арматуре
![]()
Расчет производим из совместного решения уравнений:
Q = Qb + Qs;
Nb = Ns;
М + Qc = Nsz + Qsc;
![]() ;
;
![]()
Решение системы уравнений производим следующим образом. Из уравнений равновесия поперечных сил и продольных сил выражаем усилия в бетоне над наклонной трещиной Nb и Qb
Qb = Q - Qs;
Nb = Ns;
и подставляем их в уравнение связи между усилиями Nb и Qb
![]()
Из совместного решения уравнения равновесия моментов и уравнения связи между поперечным и продольным усилиями в арматуре Ns и Qs
![]()
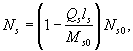
получим выражение для усилий Ns и Qs:
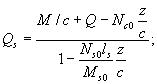
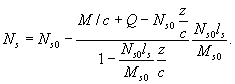
Подставив полученные выражения для усилий Ns и Qs в приведенное выше уравнение, получим уравнение прочности наклонного сечения элемента по бетону над наклонной трещиной
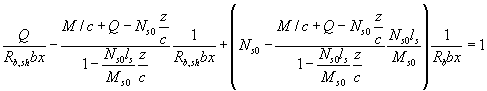
и соответствующее условие прочности в виде неравенства
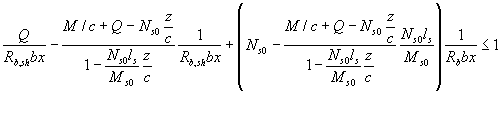
Как видим, получилось весьма громоздкое уравнение прочности по бетону над наклонной трещиной при всех упрощениях, вводимых в расчет. К тому же необходимо определять еще высоту зоны бетона над наклонной трещиной. При этом в деформационной зависимости необходимо будет учитывать податливость продольной арматуры не только в продольном, но и в поперечном направлении.
Расчет можно значительно упростить, если принять нагельную силу в момент отрыва бетонного слоя в виде постоянной независимой величины
Qs = Rbtbls.
В этом случае расчетное условие прочности по бетону над наклонной трещиной будет иметь вид
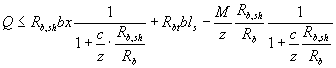
или после подстановки значения высоты зоны бетона над наклонной трещиной х из деформационной зависимости и приведенных выше упрощений
![]()
Принимая приближенно длину отрыва бетонного слоя ls равной пятикратной высоте бетонного слоя ls = 5hb и высоту бетонного слоя также приближенно равной 0,1 рабочей высоты поперечного сечения h0, hb = 0,1h0, получим ls = 0,5h0, и расчетное условие запишется в виде
![]()
то есть учет влияния нагельной силы в продольной арматуре компенсирует недостаточную величину поперечной силы, воспринимаемую бетоном над наклонной трещиной.
Анализ расчетного уравнения, связывающего продольное и поперечное усилия в продольной арматуре, показал, что поперечное усилие Qs приближенно можно выразить через продольное усилие Ns с помощью некоторого постоянного численного коэффициента k
Qs = kNs.
Величина этого коэффициента приближенно может быть принята равной 1/30.
Такой прием также позволит значительно упростить приведенные выше расчетные зависимости.
В этом случае расчетное условие прочности по бетону над наклонной трещиной имеет вид
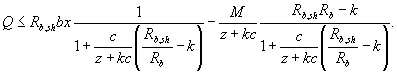
Условие прочности по растянутой продольной арматуре в первом случае имеет вид:
М + Qc - Rbtbh0c ≤ RsAsz,
а во втором случае
М + Qc ≤ RsAs (z + kc),
Таким образом, мы видим, что на основе общей расчетной модели, в принципе, можно учесть поперечную (нагельную) силу в продольной арматуре. Однако в результате получаются весьма громоздкие расчетные зависимости либо приходится в расчет включать весьма условные приемы.
12. ЭЛЕМЕНТЫ С ПОПЕРЕЧНОЙ АРМАТУРОЙ
Рассмотрим теперь изгибаемые железобетонные элементы с поперечной арматурой.
Следует отметить, что поперечная арматура, распределенная по длине элемента, воспринимает поперечные силы, возникающие в продольной арматуре при ее изгибе. В результате отдельная поперечная сила, воспринимаемая продольной арматурой, в расчетные уравнения равновесия могла бы не вводиться. Далее, наклонная трещина при наличии поперечной арматуры получает значительное раскрытие, что снижает силы зацепления, действующие по берегам наклонной трещины. В связи с этим в расчетные уравнения равновесия не вводим также силы зацепления в наклонной трещине (рис. 8).
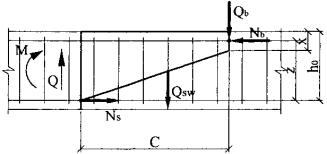
Рис. 8
В результате уравнения равновесия для изгибаемых элементов с поперечной арматурой приобретают вид:
Q = Qb + Qsw;
Nb = Ns;
М + Qc = Nsz + Qswc/2,
при моменте относительно точки приложения усилий в зоне бетона над наклонной трещиной и
Q = Qb + Qsw;
Nb = Ns;
М = Nbz – Qbc - Qswc/2,
при моменте относительно точки приложения усилий в месте пересечения продольной арматурой наклонного сечения.
Принимая усилие, воспринимаемое поперечной арматурой, известной величиной
Qsw = qswc
из уравнения равновесия поперечных сил определяется величина поперечной силы, воспринимаемой бетоном над наклонной трещиной
Qb = Q - Qsw = Q - qswc
и из уравнения равновесия моментов - величина продольной силы, воспринимаемой бетоном
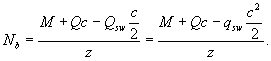
Если принять взаимосвязанные значения продольного и поперечного усилий в бетоне над наклонной трещиной
![]()
то из решения системы уравнений:
Qb = Q - Qswc;
![]()
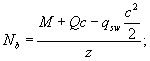
![]()
мы получим общее уравнение прочности наклонного сечения по бетону над наклонной трещиной
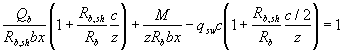
или выраженное через поперечную силу
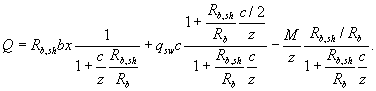
Условия прочности, соответственно, записываются в виде неравенств
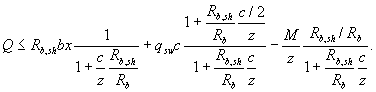
Остается подставить в это условие выражение для высоты зоны бетона над наклонной трещиной х, полученное из деформационной зависимости
![]()
Следует отметить, что в схеме деформирования следовало бы учитывать и податливость поперечной арматуры, однако это приводит к весьма сложным расчетным зависимостям.
При фиксированных, не зависимых друг от друга продольных и поперечных усилиях в бетоне над наклонной трещиной:
Qb = Rb,shbx;
Nb =Rbbx,
подставляя выражение для высоты зоны бетона над наклонной трещиной, полученное из деформационной зависимости
![]()
получим сразу выражение для предельной поперечной силы, воспринимаемой бетоном
![]()
а отсюда и предельную поперечную силу, воспринимаемую элементом по наклонному сечению
![]()
Условие прочности элемента по бетону записывается в виде
![]()
а условие прочности по арматуре - в виде
![]()
Таким образом, и для элементов с поперечной арматурой исходя из общей расчетной модели получаются достаточно простые расчетные зависимости.
13. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Очевидно, могло бы быть рассмотрено решение исходя только из уравнений равновесия без использования деформационной зависимости.
Например, для элементов без поперечной арматуры из уравнения равновесия моментов относительно равнодействующей усилий в бетоне над наклонной трещиной получим усилия в продольной арматуре
![]()
Из уравнения равновесия продольных сил получим продольное усилие в бетоне над наклонной трещиной
Nb = Ns.
Зная усилие х, можно определить высоту зоны бетона над наклонной трещиной
![]()
а зная высоту , можно определить предельную поперечную силу
Qb = Rb,shbx
и условие прочности
Q ≤ Rb,shbx.
Аналогичный расчет можно выполнить и для элементов с поперечной арматурой.
Альтернативой является полный учет деформаций укорочения, удлинения и сдвига в бетоне над наклонной трещиной, в арматуре, пересекающей наклонную трещину, и в самой наклонной трещине поперек и вдоль наклонного сечения.
Другим подходом к расчету является использование так называемой двухблочной или трехблочной модели, включающей блок, выделяемый наклонным сечением, блок, выделяемый нормальным сечением, проходящим через вершину наклонного сечения, и промежуточный блок, расположенный между наклонным и нормальным сечениями.
В целом расчет производится следующим образом.
Рассматриваются различные положения начала наклонного сечения по длине элемента с соответствующими значениями поперечной силы и момента в нормальном сечении, проходящем через начало наклонного сечения.
Для каждого положения начальной точки наклонного сечения рассматриваются различные положения наклонного сечения с различной длиной проекции наклонного сечения на продольную ось элемента.
Определяется наиболее опасное положение наклонного сечения по длине элемента и по длине проекции наклонного сечения, по которому оценивается прочность железобетонного элемента на действие поперечных сил и изгибающих моментов.
14. ЗАКЛЮЧЕНИЕ
Выше мы показали, что на основе общей расчетной модели, включающей уравнения равновесия моментов, продольных и поперечных сил с привлечением условия деформирования, в принципе, можно получить достаточно простые расчетные зависимости для оценки прочности железобетонных элементов по наклонным сечениям. Однако при этом, как было показано, приходится включить в расчет приближенные, достаточно условные приемы и подходы.
Полученная методика позволяет оценивать прочность железобетонных элементов по бетону над наклонной трещиной на действие поперечных сил и по растянутой продольной арматуре, пересекающей наклонную трещину, на действие момента для элементов без поперечной арматуры и с поперечной арматурой.
При расчете железобетонных элементов на
действие поперечных сил учитываются основные параметры, присутствующие в
приведенных выше нормативных документах: относительная длина проекции
наклонного сечения c/h0,
относительное содержание продольной арматуры ![]() относительная
величина момента M/z. Тем самым представленная модель
позволяет заменить эмпирические зависимости, присутствующие в различных
нормативных документах. Что касается эмпирической зависимости, присутствующей в
отечественных нормативных документах, выраженной через относительную длину
проекции наклонного сечения с/h0, то эта модель позволяет дополнить нормативную
зависимость влиянием относительного содержания продольной арматуры
относительная
величина момента M/z. Тем самым представленная модель
позволяет заменить эмпирические зависимости, присутствующие в различных
нормативных документах. Что касается эмпирической зависимости, присутствующей в
отечественных нормативных документах, выраженной через относительную длину
проекции наклонного сечения с/h0, то эта модель позволяет дополнить нормативную
зависимость влиянием относительного содержания продольной арматуры ![]() и относительного момента M/z, что в целом отвечает экспериментальным данным.
и относительного момента M/z, что в целом отвечает экспериментальным данным.
Безусловно, рассмотренная модель требует дальнейшего развития, уточнения и корректировки. В первую очередь она должна быть приведена в соответствии с экспериментальными данными путем уточнения прочности бетона над наклонной трещиной, высоты зоны бетона над наклонной трещиной, нагельного сопротивления продольной арматуры, сил зацепления по берегам наклонной трещины. Тем не менее эта модель, в силу своей простоты и физического содержания, является более привлекательной по сравнению с эмпирическими зависимостями, содержащимися в приведенных выше нормативных документах. Она может также служить обоснованием или показывать необходимость корректировки тех или иных эмпирических зависимостей.
Рассматривая представленную модель, можно также сделать вывод о нецелесообразности усложнения методики расчета железобетонных элементов на действие поперечных сил в силу невозможности точно оценить основные усилия, действующие в наклонном сечении.