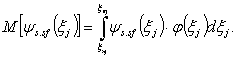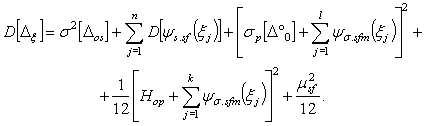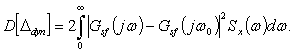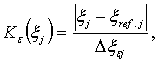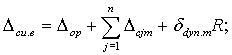РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
ХАРАКТЕРИСТИКИ ПОГРЕШНОСТИ
СРЕДСТВ ИЗМЕРЕНИЙ В РЕАЛЬНЫХ
УСЛОВИЯХ ЭКСПЛУАТАЦИИ.
МЕТОДЫ РАСЧЕТА
РД 50-453-84
СОДЕРЖАНИЕ
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Характеристики погрешности средств измерений Методы расчета |
РД Введены впервые |
Утверждены Постановлением Государственного комитета СССР по стандартам от 8 февраля 1984 г. № 448.
Постановлением Государственного комитета СССР по стандартам от 28 мая 1985 г. № 1501 срок введения установлен
с 01.01.86
Настоящие методические указания устанавливают методы расчета характеристик составляющей погрешности прямых однократных измерений - погрешности средства измерений (СИ) - по нормируемым в соответствии с ГОСТ 8.009-84 метрологическим характеристикам СИ, известным характеристикам влияющих величин и входного сигнала.
Методические указания предназначены для использования при разработке нормативно-технических документов по расчету погрешности измерений или соответствующих разделов других нормативно-технических документов; при разработке методик выполнения измерений, в частности, при выборе методов измерений и СИ, обеспечивающих заданные нормы точности измерений.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Методы, рекомендуемые данными МУ, позволяют рассчитать следующие характеристики погрешности СИ.
1.1.1. Математическое ожидание М[DСИ] и среднее квадратическое отклонение s[DСИ] погрешности СИ*.
* Список обозначений приведен в приложении 1.
1.1.2. Нижнюю DСИ.Н и верхнюю DСИ.В границы интервала, в котором с вероятностью Р находится погрешность СИ.
1.2. Для расчета характеристик погрешности СИ рекомендуется использовать один из методов, в зависимости от задач измерений, экономической целесообразности и доступной исходной информации.
1.2.1. Первый метод (п. 3.1) включает в себя расчет статистических моментов составляющих погрешности СИ и позволяет определить характеристики погрешности СИ как по п. 1.1.1, так и по п. 1.1.2.
Этот метод дает более рациональную (при числе составляющих погрешности СИ более трех) оценку погрешности СИ за счет пренебрежения редко реализующимися значениями погрешности, для чего назначается Р<1.
1.2.2. Второй метод (п. 3.2) включает в себя расчет наибольших возможных значений составляющих погрешности СИ и позволяет определить характеристики погрешности СИ только по п. 1.1.2 и только при Р=1. Этот метод дает грубую (при числе составляющих погрешности СИ более трех), хотя и надежную оценку погрешности СИ, включающую в себя редко реализующиеся значения погрешности.
Второй метод расчета целесообразно использовать, если:
хотя бы маловероятное нарушение требований к точности измерений может привести к серьезным отрицательным техническим или экономическим последствиям или связано с угрозой здоровью и жизни людей;
завышение требований к метрологическим характеристикам СИ, к которому ведет применение данного метода расчета при заданной норме точности измерений, и связанные с этим дополнительные затраты не препятствуют применению таких СИ.
1.3. В данных методических указаниях излагаются методы расчета, для которых в качестве исходных данных используются комплексы метрологических характеристик СИ, предусмотренные ГОСТ 8.009-84. В обоснованных случаях, в частности, для комплексов метрологических характеристик, отличающихся от предусмотренных ГОСТ 8.009-84, допускается применение других методов расчета характеристик погрешности СИ.
1.4. Характеристики погрешности СИ, рассчитанные в соответствии с настоящими методическими указаниями, в общем случае не следует отождествлять с характеристиками погрешности измерений. Помимо погрешности СИ погрешность измерений включает в себя методическую составляющую; составляющую от взаимодействия СИ с объектом измерений; составляющую, вносимую оператором при отсчете результатов измерений, методы расчета характеристик которых в данных методических указаниях не рассматриваются.
2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ХАРАКТЕРИСТИК ПОГРЕШНОСТИ СРЕДСТВА ИЗМЕРЕНИЙ
2.1. Для расчета характеристик погрешности СИ в реальных условиях эксплуатации необходимо располагать следующими исходными данными:
нормируемыми метрологическими характеристиками СИ (пп. 2.2.1 или 2.3.1);
характеристиками влияющих величин (пп. 2.2.2 или 2.3.2);
характеристиками входного сигнала (пп. 2.2.3 или 2.3.3);
2.2. В качестве исходных данных при расчете характеристик погрешности СИ первым методом (п. 3.1) используются следующие характеристики.
2.2.1. Нормируемые метрологические характеристики СИ:
математическое ожидание М[Dos] систематической составляющей основной погрешности СИ;
среднее квадратическое отклонение s[Dos] систематической составляющей основной погрешности СИ;
предел sр[D°os] допускаемого среднего квадратического отклонения случайной составляющей основной погрешности СИ;
предел Hop допускаемой вариации СИ при нормальных условиях;
номинальная цена msf единицы наименьшего разряда кода цифрового измерительного прибора (аналого-цифрового измерительного преобразователя);
номинальные функции влияния ys.sf(xj), j=1, 2...n на систематическую составляющую погрешности СИ;
номинальные функции влияния ys.sf(xj), j=1, 2...l на среднее квадратическое отклонение случайной составляющей погрешности СИ;
номинальные функции влияния yH.sf(xj), j=1, 2...k на вариацию СИ;
одна из полных динамических характеристик СИ: номинальная переходная характеристика hsf(t), номинальная импульсная переходная характеристика gsf(t), номинальная амплитудно-фазовая характеристика Gsf(jw), номинальная передаточная функция Gsf(S).
Примечания:
1. Перечисленные нормируемые метрологические характеристики указываются в нормативно-технической документации на СИ как характеристики любого экземпляра СИ данного типа. Вместо этих характеристик в качестве исходных данных могут использоваться индивидуальные метрологические характеристики СИ, определяемые в результате исследования конкретного экземпляра СИ:
наибольшая возможная по абсолютной величине Dsm неисключенная систематическая составляющая погрешности СИ;
среднее квадратическое отклонение s[D°] случайной составляющей погрешности СИ;
вариация H СИ;
цена единицы наименьшего разряда кода цифрового измерительного прибора (аналого-цифрового измерительного преобразователя);
функции влияния ys.sf(xj), j=1, 2...n на систематическую составляющую погрешности СИ;
функции влияния ys.sf(xj), j=1, 2...l на среднее квадратическое отклонение случайной составляющей погрешности СИ;
функции влияния yH.sf(xj), j=1, 2...k на вариацию СИ;
одна из полных динамических характеристик СИ: номинальная переходная характеристика h(t), номинальная импульсная переходная характеристика g(t), номинальная амплитудно-фазовая характеристика G(jw), номинальная передаточная функция G(S).
2. В п. 2.2.1 указаны только те метрологические характеристики СИ из числа вошедших в комплексы, предусмотренных в ГОСТ 8.009-84, которые необходимы для расчета характеристик погрешности СИ.
3. В исходные данные могут входить не все метрологические характеристики, перечисленные в и. 2.2.1 и примечании 1 к нему, если некоторые из них несущественны для СИ.
2.2.2. Характеристики влияющих величин xj.
2.2.2.1. Значения xj, j=1, 2 ... n (l, k) влияющих величин.
2.2.2.2. Математические ожидания М[xj], средние квадратические отклонения s[xj], наименьшие xнj и наибольшие xвj значения влияющих величин, соответствующие реальным условиям эксплуатации СИ, j=1, 2...n (l, k).
2.2.3. Характеристики входного сигнала x: спектральная плотность Sx(w) или автокорреляционная функция Rx(t) входного сигнала СИ, соответствующие реальным условиям эксплуатации СИ.
2.3. В качестве исходных данных при расчете характеристик погрешности СИ вторым методом (п. 3.2) используются следующие характеристики.
2.3.1. Нормируемые метрологические характеристики СИ:
предел Dор допускаемых значений основной погрешности СИ;
наибольшие допускаемые изменения eр(xj), j=1, 2 ... n погрешности СИ, вызванные изменением влияющих величин или неинформативных параметров входного сигнала (в дальнейшем, влияющих величин) xj в установленных пределах;
номинальная амплитудно-частотная характеристика Asf(w) СИ.
2.3.2. Характеристики влияющих величин xj.
2.3.2.1. Значения xj, j=1, 2 ... и влияющих величин.
2.3.2.2. Наименьшие xнj и наибольшие xвj, j= 1, 2 ... n значения влияющих величин, соответствующие реальным условиям эксплуатации СИ.
Примечание. Под реальными условиями эксплуатации СИ понимаются условия конкретного применения СИ, составляющие часть или, в частном случае, совпадающие с рабочими условиями, регламентированными в нормативно-технической документации на СИ.
2.3.3. Характеристики входного сигнала x: нижняя wн и верхняя wв границы спектра частот реального входного сигнала СИ.
2.4. Все исходные данные, используемые для расчета, должны быть приведены к одной и той же точке схемы измерений: входу или выходу СИ и выражены в единицах, обеспечивающих получение всех составляющих погрешности СИ в одних и тех же абсолютных или относительных (в долях или процентах от одного и того же значения измеряемой величины) единицах.
3. РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ В РЕАЛЬНЫХ УСЛОВИЯХ ЭКСПЛУАТАЦИИ
3.1. Первый метод расчета характеристик погрешности СИ в реальных условиях эксплуатации (примеры расчета см. в приложении 2).
3.1.1. Математическое ожидание М[Dx] статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
если исходные данные о влияющих величинах xj заданы в соответствии с п. 2.2.2.1, то
![]() (1)
(1)
если исходные данные о влияющих величинах xj заданы в соответствии с п. 2.2.2.2, то
Суммирование выполняется для п влияющих величин, для которых нормированы метрологические характеристики ys.sf(xj), j=1, 2...n СИ по п. 2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
3.1.1.1. Для линейных функций влияния ys.sf(xj)=Ks.sfj(xj-xref.j) значения M[ys.sf(xj)] вычисляются по формуле
3.1.2.1. Для вычисления M[ys.sf(xj)] нелинейной функции влияния ys.sf(xj) необходимы данные о законе распределения j(xj) влияющей величины xj
Приближенные значения M[ys.sf(xj)] нелинейных функций влияния вычисляются по формуле
Примечания:
1. Если для СИ нормирован предел Dosp допускаемых значений систематической составляющей основной погрешности без указания значения М[Dos] и если нет оснований предполагать несимметричность распределения указанной погрешности в пределах Dosp, то допускается для расчетов характеристик погрешности СИ пользоваться предположением М[Dos]=0.
2. Для СИ с индивидуальными метрологическими характеристиками (п. 2.2.1, примечание 1) для расчетов характеристик погрешности СИ принимается М[Dos]=0.
3. Если для j-й влияющей величины известны только ее наименьшее xнj и наибольшее xвj значения, соответствующие реальным условиям эксплуатации СИ, и нет оснований выделить области предпочтительных значений влияющей величины в границах от xнj до xвj, несимметрично расположенные относительно центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
M[xj]=0,5(xнj+xвj).
3.1.2. Дисперсия D[Dx] статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
если исходные данные о влияющих величинах xj заданы в соответствии с п. 2.2.2.1, то
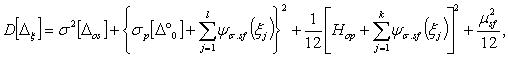 (6)
(6)
если исходные данные о влияющих величинах заданы в соответствии с п. 2.2.2.2, то
Для аналоговых СИ msf=0.
Суммирование выполняется для п, l и k влияющих величин, для которых нормированы метрологические характеристики ys.sf(xj), j=1, 2...n; ys.sf(xj), j=1, 2...l; yH.sf(xj), j=1, 2...k по п.2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
3.1.2.1. Для линейных функций ys.sf(xj)=Ks.sfj(xj-xref.j) значения D[ys.sf(xj)] вычисляется по формуле
3.1.2.2. Для вычисления D[ys.sf(xj)] нелинейной функции влияния ys.sf(xj) необходимы данные о законе распределения j(xj) влияющей величины xj
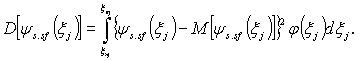 (9)
(9)
Приближенные значения D[ys.sf(xj)] для нелинейных функций влияния вычисляются по формуле
где M[ys.sf(xj)] - вычисляется в соответствии с (4), (5).
Примечания:
1. Если для СИ нормирован предел Dosp допускаемых значений
систематической составляющей основной погрешности без указания значения s[Dos] и если нет оснований предполагать несимметричность и
полимодальность распределения указанной погрешности в пределах Dosp, то допускается для расчетов характеристик погрешности СИ
пользовался предположением ![]() .
.
2. Для СИ с индивидуальными метрологическими
характеристиками (п. 2.2.1, примечание 1) для расчетов характеристик
погрешности СИ принимается ![]() .
.
3. Если для j-й влияющей величины известны только ее наименьшее xнj и наибольшее xвj значения, соответствующие реальным условиям эксплуатации СИ, и нет оснований выделить области предпочтительных значений влияющей величины в границах от xнj до xвj, за исключением, может быть, области вокруг центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
![]()
3.1.3. Дисперсия D[Ddyn] приведенной к выходу динамической составляющей погрешности аналогового СИ вычисляется по формуле
Примечания:
1. Если в качестве характеристики входного сигнала задана его автокорреляционная функция Rx(t) (п. 2.2.3), то предварительно вычисляется спектральная плотность входного сигнала по формуле
2. Если в качестве динамической характеристики нормирована передаточная функция Gsf(S) (п. 2.2.1), то предварительно заменой аргумента S на jw получают амплитудно-фазовую характеристику Gsf (jw).
3. Если в качестве динамической характеристики нормирована импульсная переходная характеристика gf(t), то предварительно вычисляют амплитудно-фазовую характеристику Gsf (jw) по формуле
![]() (13)
(13)
4. Если в качестве динамической характеристики нормирована переходная характеристика hsf(t), то предварительно вычисляют амплитудно-фазовую характеристику по формуле
![]() (14)
(14)
5. Рекомендуемые методы расчета динамической погрешности применимы для таких аналоговых СИ, которые могут рассматриваться как линейные.
6. Динамическая погрешность цифровых СИ рассчитывается в соответствии с рекомендациями РД 50-148-79 "Нормирование и определение динамических характеристик аналого-цифровых преобразователей мгновенного электрического напряжения и тока".
3.1.4. Определение характеристик погрешности СИ в реальных условиях его эксплуатации.
3.1.4.1. Характеристики погрешности СИ но п. 1.1.1 вычисляются по формулам
M[Dси]= M[Dx], (15)
3.1.4.2. Характеристики погрешности СИ по п. 1.1.2 вычисляются по формулам
Dси.н=M[Dси]-Ks[Dси], (17)
Dси.в=M[Dси]+Ks[Dси]. (18)
3.1.5. Значение К зависит от вида закона распределения погрешности Dси и выбранного значения вероятности Р. Приближенное значение К может быть найдено в соответствии с рекомендациями пп. 3.1.5.1 и 3.1.5.2.
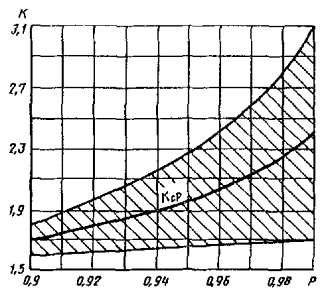
3.1.5.1. Если закон распределения погрешности Dси может быть отнесен к числу симметричных законов распределения с невозрастающей плотностью по мере удалений от центра распределения, то в качестве значения К может быть принято Кср. График зависимости Кср(P) приведен на рисунке.
Заштрихованная на рисунке область соответствует возможным значениям К. Разность между кривой Кср и любой из граничных кривых определяет погрешность коэффициента Кср (при Р = 0,95 эта погрешность лежит в границах ± 16%, при Р = 0,99 - в границах ± 30 %).
3.1.5.2. Для грубых, ориентировочных расчетов, если есть основания предполагать, что закон распределения погрешности Dси примерно удовлетворяет условиям п. 3.1.5.1, значение К может вычисляться по формуле
К=5(Р-0,5) для 0,8£Р<1 (19)
Эта формула дает значения К несколько завышенные по отношению Кср.
3.1.5.3. Если для закона распределения погрешности Dси, удовлетворяющего условиям п. 3.1.5.1, известна оценка параметра l, равного l=D/2s, где D - основание усеченной функции плотности распределения вероятностей (т. е. длина интервала погрешности, соответствующая Р=1), то значения коэффициента К могут выбираться по таблице, где также указана dК, % - наибольшая возможная относительная погрешность К.
|
Р |
Значения К (числитель) и dК, % (знаменатель) при l |
||||
|
2 |
3 |
4 |
5 |
6 |
|
|
0,90 |
1,6 7 |
1,7 25 |
1,5 40 |
1,2 65 |
- |
|
0,95 |
1,7 8 |
2,0 25 |
2,1 40 |
2,0 45 |
1,9 55 |
|
0,98 |
1,8 8 |
2,2 25 |
2,5 40 |
2,7 45 |
2,7 50 |
3.2. Второй метод расчета характеристик погрешности СИ в реальных условиях эксплуатации.
3.2.1. Наибольшее по абсолютной величине возможное значение Dсjm дополнительной погрешности СИ от j-й, влияющей величины вычисляется по формуле
Dсjm=eр(xj)Ke(xj), (20)
где
если диапазон изменения Dxej влияющей величины, для которого нормирована метрологическая характеристика eр(xj), равен диапазону рабочих условий применения СИ; или
если диапазон изменения Dxej влияющей величины, для которого нормирована метрологическая характеристика eр(xj), равен лишь части диапазона рабочих условий применения СИ, причем для любой части рабочих условий нормируется одно и то же значение eр(xj).
Примечание. Выражение (21) предполагает наихудший из всех возможных характер зависимости (ступенчатая функция) дополнительной погрешности СИ Dcj от xj в рабочей области значений влияющей величины. Если в результате исследования определена функция влияния конкретного экземпляра СИ, то расчет Dcjm может производиться с использованием этой функции влияния. Например, если в результате исследования установлен линейный характер зависимости Dcj от xj, то для расчета может использоваться выражение (22) вместо (21).
3.2.1.1. Если исходные данные о влияющих величинах xj заданы в соответствии с п. 2.3.2.1, то при определении значения Ke(xj) в соответствии с выражениями (21) и (22) в качестве xj используются конкретные значения влияющей величины.
3.2.1.2. Если исходные данные о влияющих величинах заданы в соответствии с п. 2.3.2.2, то при определении значения Ke(xj) в соответствии с выражениями (21) и (22) в качестве xj используется то из значений xнj или xвj, при котором Ke(xj) имеет наибольшее значение.
3.2.2. Оценка сверху относительного значения ddyn.m динамической погрешности для СИ с линейной фазово-частотной характеристикой вычисляется по формуле
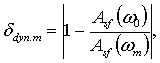 (23)
(23)
где Asf(w0) - номинальная амплитудно-частотная характеристика при нормальном значении w0 частоты;
Asf(wm) - номинальная амплитудно-частотная характеристика, наиболее отклоняющаяся на интервале wн£wm£wв (п. 2.3.3) от значения Asf(w0).
3.2.3. Нижняя Dси.н и верхняя Dси.в - границы интервала, в котором с вероятностью Р=1 находится погрешность СИ в реальных условиях эксплуатации (п. 1.1.2), вычисляются по формулам
где R - результат измерения.
Суммирование выполняется для n влияющих величин, для которых нормированы метрологические характеристики ep(xj), j= 1, 2 ... n СИ по п. 2.3.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
ПРИЛОЖЕНИЕ
1
Справочное
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Dси - погрешность СИ в реальных условиях эксплуатации;
Dси.н, Dси.в - нижняя и верхняя границы интервала, в котором с вероятностью Р находится погрешность СИ;
Dos - систематическая составляющая основной погрешности СИ;
Dsm - наибольшее возможное по абсолютной величине значение неисключенной систематической составляющей погрешности конкретного экземпляра СИ;
sp[D°0] - предел допускаемого среднего квадратического отклонения случайной составляющей основной погрешности конкретного экземпляра СИ;
Hop - предел допускаемой вариации СИ при нормальных условиях
msf - номинальная цена единицы наименьшего разряда кода цифрового измерительного прибора (аналого-цифрового измерительного преобразователя);
ys.sf(xj) - номинальная функция влияния j-й влияющей величины на систематическую составляющую погрешности СИ;
ys.sf(xj) - номинальная функция влияния j-й влияющей величины на среднее квадратическое отклонение случайной составляющей погрешности СИ;
yн.sf(xj) - номинальная функция влияния j-й влияющей величины на вариацию СИ;
eр(xj) - наибольшее допускаемое изменение погрешности СИ, вызванное отклонением j-й влияющей величины от нормального значения;
Dxej - приращение j-й влияющей величины, для которой нормирована метрологическая характеристика eр(xj);
Ks.sfj - номинальный коэффициент влияния j-й влияющей величины на систематическую составляющую погрешности СИ;
Ks.sfj - номинальный коэффициент влияния j-й влияющей величины на среднее квадратическое отклонение случайной составляющей погрешности СИ;
Kн.sfj - номинальный коэффициент влияния j-й влияющей величины на вариацию СИ;
Doр - предел допускаемой основной погрешности СИ;
hsf(t) - номинальная переходная характеристика СИ;
gsf(t) - номинальная импульсная переходная характеристика СИ;
Gsf(jw) - номинальная амплитудно-фазовая характеристика;
Gsf(S) - номинальная передаточная функция;
Asf(w) - номинальная амплитудно-частотная характеристика;
xj - j-я влияющая величина;
xнj, xвj - наименьшие и наибольшие значения j-й влияющей величины, соответствующие реальным условиям эксплуатации СИ;
xref.j - нормальное значение j-й влияющей величины;
j(xj) - закон распределения влияющей величины xj;
X - значение входного сигнала;
wн, wв - нижняя и верхняя границы спектра частот входного сигнала СИ;
Sx(w) - спектральная плотность входного сигнала СИ;
Rx(t) - автокорреляционная функция входного сигнала СИ;
Dx - статическая составляющая погрешность СИ при реальных значениях влияющих величин;
ys.sf(M[xj]) - номинальная функция влияния ys.sf(xj) при xj= M[xj];
y's.sf(M[xj]),
y''s.sf(M[xj]) - первая и вторая производные от номинальной функции влияния ys.sf(xj) при xj= M[xj];
yн.sfm(xj),
ys.sfm(xj) - наибольшие на интервале xнj£xj£xвj номинальные функции влияния yн.sf(xj), и ys.sfm(xj);
Ddyn - динамическая составляющая погрешности СИ;
K - коэффициент, используемый для вычисления интервальной оценки погрешности СИ по ее среднему квадратическому отклонению;
Dcjm - наибольшая возможная дополнительная погрешность СИ от j-й влияющей величины;
Ke(xj) - коэффициент, используемый для вычисления наибольшей возможной дополнительной погрешности СИ;
ddyn.m - оценка сверху относительной динамической погрешности СИ;
M[×] - символ математического ожидания;
D[×] - символ дисперсии;
s[×] - символ среднего квадратического отклонения.
ПРИЛОЖЕНИЕ
2
Справочное
ПРИМЕРЫ РАСЧЕТА ХАРАКТЕРИСТИК ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ В РЕАЛЬНЫХ УСЛОВИЯХ ЭКСПЛУАТАЦИИ
Пример 1. Расчет характеристик погрешности аналогового средства измерений мгновенных значений напряжения по первому методу (п. 3.1)
1.1. Исходные данные.
1.1.1. Нормируемые метрологические характеристики СИ:
предел допускаемой систематической составляющей основной погрешности Dosp=10 мB;
предел допускаемого среднего квадратического отклонения случайной составляющей основной погрешности sp[D°0]=5 мВ;
предел допускаемой вариации Hoр=6 мВ;
номинальные функции влияния на систематическую составляющую погрешности
ys.sf(x1)=Ks.sf1(x1-xref.1), ys.sf(x2)=Ks.sf1(x2-xref.2),
где Ks.sf1=0,5 мВ/°С; Ks.sf2=0,4 мВ/В - номинальные значения коэффициентов влияния температуры и напряжения питания на систематическую составляющую погрешности;
xref.1=20°C; xref.2=220 В - нормальные значения влияющих величин;
номинальные функции влияния на среднее квадратическое отклонение случайной составляющей погрешности
ys.sf(x1)=Ks.sf1(x1-xref.1), ys.sf(x2)=Ks.sf1(x2-xref.2),
где Ks.sf1=0,1 мВ/°С; Ks.sf2= 0,1 мВ/В - номинальные значения коэффициентов влияния температуры и напряжения питания на среднее квадратическое отклонение случайной составляющей погрешности;
номинальная амплитудно-фазовая характеристика
![]()
где Ksf=1 - номинальный коэффициент преобразования СИ при нормальном значении w0=0 частоты входного сигнала; T=5 мс - постоянная времени.
1.1.2. Характеристики влияющих величин.
xн1= 25°С, xв1=35°С, xн2=200 В, xв2=230 В.
1.1.3. Автокорреляционная функция измеряемого напряжения (характеристика входного сигнала) R(t)=DU×e-a|t|, где DU=0,1 В - дисперсия измеряемого напряжения;
a=0,2с-1.
1.2. Расчет математического ожидания и дисперсии статической составляющей погрешности СИ при значениях влияющих величин, отличающихся от нормальных значений.
1.2.1. Математическое ожидание М[Dx] статической составляющей погрешности СИ для заданных характеристик влияющих величин вычисляется по формулам п. 3.1.1.
Для случая, когда нет оснований предполагать несимметричность распределения значений систематической составляющей основной погрешности в интервале (-Dosp, Dosp) и значений влияющих величин x1, x2, в интервалах (xн1, xв1), (xн2, xв2)
М[Dos]=0, М[x1]=0,5(xн1+xв1)=0,5(25+35)=30°С, М[x2]=0,5(xн2+xв2)=0,5(200+300)=215В.
В соответствии с формулами (2), (3)
М[Dx]=M[Dos]+Ks.sf1(M[x1]-xref.1)+Ks.sf2(M[x2]-xref.2)=0,5×10-0,4×5=3мВ.
1.2.2. Дисперсия D[Dx] статической составляющей погрешности СИ для заданных характеристик влияющих величин вычисляется по формулам (7), (8)
D[Dx]=s2[Dos]+{sp[D°0]+Ks.sf1(xв1-xref.1)+Ks.sf2(xв2-xref.2)}2+K2s.sf1s2[x1]+K2s.sf2s2[x2]+H2op/12.
Для случая, когда нет оснований выделить область предпочтительных значений систематической составляющей основной погрешности в интервале (-Dosp, Dosp) и области предпочтительных значений влияющих величин x1, x2 в интервалах (xн1, xв1), (xн2, xв2)
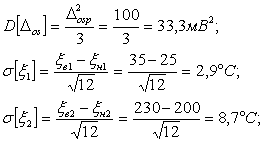
С учетом полученных значений средних квадратических отклонений
D[Dx]=33,3+(5+1,5+2)2+0,25×2,92+0,16×8,72+62/12=123 мВ2.
1.3. Расчет дисперсии D[Ddyn] динамической составляющей погрешности СИ производится по формулам (11), (12) п. 3.1.3. Предварительно по автокорреляционной функции измеряемого напряжения вычисляется спектральная плотность энергии измеряемого напряжения
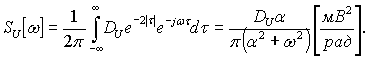
Дисперсия динамической составляющей погрешности, приведенной ко входу СИ, вычисляется по формуле
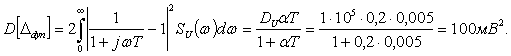
1.4. Расчет характеристик погрешности СИ в реальных условиях его эксплуатации.
1.4.1. Математическое ожидание и среднее квадратическое отклонение погрешности СИ вычисляется по формулам (15), (16) п. 3.1.4.
M[Dси]= M[Dx]=3 мВ;
![]()
1.4.2. Границы интервальной оценки погрешности СИ вычисляются по формулам (17), (18) п. 3.1.4.2. Если есть основания предполагать, что закон распределения погрешности Dси является симметричным, одномодальным и не более островершинным, чем нормальное распределение, то значение коэффициента Кcp можно определять по кривой, представленной на рисунке. Для значения Р=0,95 коэффициент Кcp составляет 1,95, тогда
Dси.н=M[Dси]-Кcps[Dси]=3-1,95×15=-26,3 мВ
Dси.в=M[Dси]+Кcps[Dси]=3+1,95×15=32,3 мВ
Пример 2. Расчет характеристик погрешности аналогового средства измерений мгновенных значений напряжения по второму методу (п. 3.2)
2.1. Исходные данные.
2.1.1. Нормируемые метрологические характеристики СИ:
предел допускаемых значений основной погрешности Dop=20 мВ;
наибольшее допускаемое изменение ep(x1) погрешности, вызванное отклонением температуры от нормального значения (20°С), составляет 5 мВ на каждые 10°С отклонения температуры;
наибольшее допускаемое изменение ep(x2) погрешности, вызванное отклонением напряжения питания от нормального значения (220 В) на ±10 %, составляет 10 мВ;
номинальная амплитудно-частотная характеристика
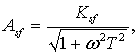
где Кsf=1 - номинальный коэффициент преобразования СИ при нормальном значении w0=0 частоты входного сигнала; Т= 5 мс - постоянная времени.
2.1.2. Характеристики влияющих величин
xн1= 25°С, xв1=35°С, xн2=200 В, xв2=230 В.
2.1.3. Спектр частот входного сигнала лежит в диапазоне 0-10 Гц (характеристика входного сигнала).
2.2. Расчет наибольших возможных значений дополнительных погрешностей (п. 3.2.1)
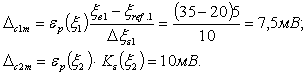
2.3. Расчет оценки сверху относительного значения динамической погрешности (п. 3.2.2)
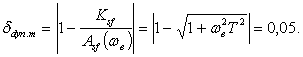
2.4. Расчет характеристик погрешности СИ в реальных условиях эксплуатации (п. 3.2.3).
Нижняя Dси.н и верхняя Dси.в границы интервала, в котором с вероятностью Р=1 находится погрешность СИ, вычисляется в соответствии с формулами (24), (25)
Dси.н=-(Dор+Dc1m+Dc2m+ddyn.mU)=-(20+7,5+10+0,05U)мВ=-(37,5+0,05U) мВ,
Dси.в=-Dси.н=(37,5+0,05U) мВ.
Для конкретного значения измеренного мгновенного напряжения U=0,6 В границы интервала погрешности составляют Dси.н=- 68 мВ, Dси.в=68 мВ.
Пример 3. Расчет характеристик погрешности аналого-цифрового преобразователя постоянного тока (п. 3.1)
3.1. Исходные данные.
3.1.1. Нормируемые метрологические характеристики АЦП:
предел допускаемых значений систематической составляющей основной погрешности Dosp=1мА;
предел допускаемых значений среднего квадратического отклонения случайной составляющей основной погрешности sp[D°0]= 0,3 мА;
номинальная функция влияния температуры на систематическую составляющую погрешности
ys.sf(x1)=Ks.sf1(x1-xref.1)2, ys.sf(x1)=0 при x1<<xref.1,
где Ks.sf1=0,001 мA/(°C), xref.1=20°C;
номинальная цена единицы наименьшего разряда кода msf=1 мА.
3.1.2. Характеристики влияющей величины:
xн1= 30° С, xв1=60°С.
3.2. Расчет математического ожидания и дисперсии статической составляющей погрешности АЦП при значениях влияющей величины, отличающихся от нормального значения.
3.2.1. Математическое ожидание М[Dx] статической составляющей погрешности для заданных характеристик влияющей величины вычисляется по формулам п. 3.1. Для случая, когда нет оснований выделить области предпочтительных значений систематической составляющей основной погрешности в интервале (-Dosp, Dosp) и области предпочтительных значений влияющей величины в интервале (xв1, xн1), несимметрично расположенные относительно центров указанных интервалов, получим
М[Dosp]=0, М[x1]=0,5(xн1+xв1)=0,5(30+60) =45°С.
В соответствии с формулами (2), (3), (5) и принятым способом представления нормированной основной погрешности АЦП
М[Dx]=M[Dosp]+Ks.sf1(M[x1]-xref.1)2+Ks.sf1s2(x1)=1×10-3(45-20)2+1×10-3(60-30)2/12=0,7 мА.
3.2.2. Дисперсия D[Dx] статической составляющей погрешности АЦП для заданных характеристик влияющей величины вычисляется по формулам (7), (8), (10)
D[Dx]=s2[Dosp]+{2Ks.sf1(M[x1]-xref.1)}2s2[x1]+1,6K2s.sf1s4[x1]+sp[D°0]+m2sf/12=
=0,33+(2×10-3)2(45-20)2 (60-30)2/12+1,6×1×10-6(60-30)4/12+0,09+0,083=0,7 мА2.
3.2.3. Расчет границ интервальной оценки погрешности АЦП производится по формулам (17), (18). Для случая, когда закон распределения погрешности может быть отнесен к числу симметричных законов распределения с невозрастающей плотностью по мере удаления от центра распределения, значение коэффициента Кср вычисляется по формуле (19). Для значения Р=0,9 коэффициент Кср равен 2, тогда
Dси.н=M[Dси]-Кcps[Dси]=0,7-1,7×0,84=-0,7 мА
Dси.в=M[Dси]+Кcps[Dси]= 0,7+1,7×0,84=2,1 мА