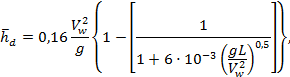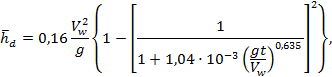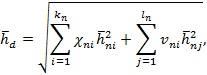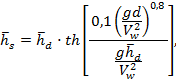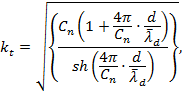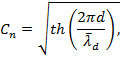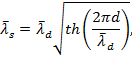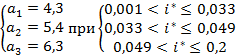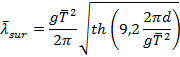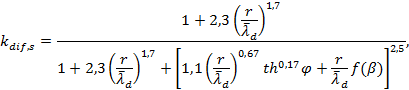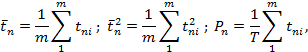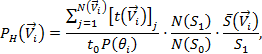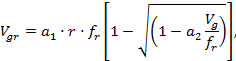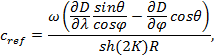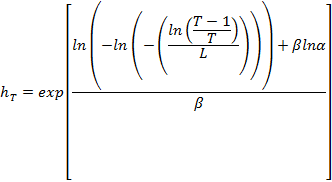МИНИСТЕРСТВО ПРИРОДНЫХ РЕСУРСОВ И ЭКОЛОГИИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральная служба по гидрометеорологии и мониторингу окружающей среды (Росгидромет)
РУКОВОДЯЩИЙ ДОКУМЕНТ	РД 52.10.865-2017

РУКОВОДСТВО ПО РАСЧЕТУ РЕЖИМНЫХ ХАРАКТЕРИСТИК
МОРСКОГО ВЕТРОВОГО ВОЛНЕНИЯ

Москва
2018

Предисловие

1 РАЗРАБОТАН Федеральным государственным бюджетным учреждением «Государственный океанографический институт имени Н.Н. Зубова» (ФГБУ «ГОИН»)

2 РАЗРАБОТЧИКИ И.М. Кабатченко, д-р геогр. наук (руководитель разработки), А.Р. Введенский, канд. техн. наук (ответственный исполнитель), Н.А. Дианский, д-р физ.-мат. наук, М.В. Резников, В.В. Фомин (ФГБУ «ГОИН»); Г.И. Литвиненко, д-р техн. наук, А.Г. Литвиненко (НПК «МорТрансНииПроект»), С.Н. Куличков, д-р физ.-мат. наук, В.Г. Полников, д-р физ.-мат. наук (ФГБУН «Институт физики атмосферы им. А.М. Обухова РАН»)

3 СОГЛАСОВАН:

с Управлением мониторинга загрязнения окружающей среды, полярных и морских работ (УМЗА) Росгидромета 07.07.2017:

с Федеральным государственным бюджетным учреждением «НПО «Тайфун» Росгидромета (ФГБУ «НПО «Тайфун») 23.06.2017

4 УТВЕРЖДЕН Руководителем Росгидромета 10.07.2017

ВВЕДЕН В ДЕЙСТВИЕ приказом Росгидромета от 08.08.2017 № 396

5 ЗАРЕГИСТРИРОВАН в ФГБУ «НПО «Тайфун» от 19.07.2017 за номером РД 52.10.865-2017

6 ВЗАМЕН «Методические указания. Расчет режима морского ветрового волнения. Вып. 42»

7 СРОК ПЕРВОЙ ПРОВЕРКИ 2023 год

ПЕРИОДИЧНОСТЬ ПРОВЕРКИ 5 лет

СОДЕРЖАНИЕ

 

РУКОВОДЯЩИЙ ДОКУМЕНТ

РУКОВОДСТВО ПО РАСЧЕТУ РЕЖИМНЫХ ХАРАКТЕРИСТИК МОРСКОГО ВЕТРОВОГО ВОЛНЕНИЯ

Дата введения - 2019-02-01

1 Область применения

Настоящий руководящий документ устанавливает порядок проведения расчетов и представления режимных характеристик морского ветрового волнения для основных типов морских акваторий.

Настоящий руководящий документ предназначен для:

- подразделений Росгидромета, производящих наблюдения и предоставление гидрометеорологической информации в прибрежных районах и морских акваториях;

- составителей региональных климатических справочников и пособий;

- организаций, ведущих научные изыскания для работ по освоению морского шельфа Российской Федерации, в том числе для проектирования, строительства и эксплуатации гидротехнических сооружений.

2 Нормативные ссылки

В настоящем руководящем документе использованы ссылки на следующие нормативные документы:

Р 31.3.07-01 Указания по расчету нагрузок и воздействия волн, судов и льда на морские гидротехнические сооружения

СП 38.13330.2012 Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов)

Примечание - При пользовании настоящим руководящим документом целесообразно проверять действие ссылочных нормативных документов.

Если ссылочный нормативный документ заменен (изменен), то при пользовании настоящим руководящим документом следует руководствоваться замененным (измененным) нормативным документом. Если ссылочный нормативный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем руководящем документе применены термины с соответствующими определениями:

3.1 ветровое волнение: Колебательное движение воды, вызванное ветром при его воздействии на свободную поверхность.

3.2 гидрометеорологическая помеха: Сочетание нескольких гидрометеорологических факторов (в том числе и параметров ветрового волнения), препятствующих работам в море в течение определенного промежутка времени.

3.3 главный профиль волны (профиль волны): Линия пересечения взволнованной поверхности с вертикальной плоскостью в направлении луча волны.

3.4 дифракция волн: Искривление фронтов и изменение высот бегущих волн, огибающих препятствия (сооружения, острова, мысы и др.).

3.5 длина волны: Горизонтальное расстояние по лучу волны между вершинами двух смежных гребней на волновом профиле.

3.6 длина разгона волн (разгон волн): Протяженность охваченной ветром акватории, измеренная по направлению ветра до расчетной точки.

3.7 критическая глубина: Глубина, при которой происходит обрушение волн.

3.8 луч волны: Линия, перпендикулярная фронту волны.

3.9 направление распространения волн: Направление перемещения волны, определяемое за короткий интервал времени порядка периода волны.

3.10 обеспеченность значения элемента волнения в режиме: Вероятность превышения порогового значения элементом волнения в один из сроков наблюдений или за указанный период времени.

3.11 обеспеченность значения элемента волн в системе: Вероятность превышения порогового значения элементом индивидуальной волны за период времени между сроками наблюдений.

3.12 окно погоды: Период времени с высотами волн ниже заданного уровня.

3.13 оперативные характеристики ветрового волнения: Сочетания параметров морского ветрового волнения, имеющие частую повторяемость.

Примечание - Такие характеристики также называют нормальными, фоновыми, эксплуатационными.

3.14 основные элементы волнения (элементы волны): Высота, длина, период, скорость, направление распространения волны.

3.15 период волны: Интервал времени между прохождением двух смежных вершин волн через фиксированную вертикальную плоскость.

3.16 период повторяемости: Статистически средний интервал повторения определенного события в течение длительного периода времени.

3.17 расчетные характеристики ветрового волнения: Сочетания параметров морского ветрового волнения, имеющие редкую повторяемость.

Примечание - Такие характеристики также называют экстремальными.

3.18 расчетный шторм: Шторм повторяемостью один раз в заданный период времени (например, 25, 50 или 100 лет) и характеризующийся максимальными за этот период высотами волн.

Примечание - Разным направлениям волн могут соответствовать различные расчетные штормы.

3.19 режимные характеристики морского ветрового волнения: Сочетания статистических параметров морского ветрового волнения с оценкой их повторяемости.

3.20 рефракция волн: Искривление фронтов и изменение высот бегущих волн под воздействием течений или обусловленное изменением глубины на мелководье.

3.21 скорость волны: Скорость перемещения в данной точке гребня волны вдоль луча волны.

3.22 трансформация волн: Изменение высоты и длины бегущих волн, искривление их фронтов под воздействием рельефа дна, препятствий, течений.

3.23 фронт волны: Линия на плане взволнованной поверхности, проходящая по вершинам волны.

3.24 шторм: Период времени с высотами волн выше заданного уровня.

3.25 штормовой нагон/сгон: Повышение/понижение уровня воды в акватории относительно среднего уровня, вызванные воздействием ветра и уменьшением атмосферного давления в шторме.

4 Расчет элементов волн в различных акваториях

4.1 Общие положения

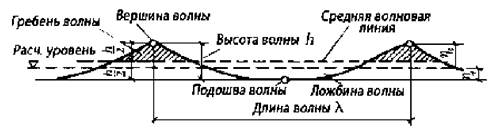
4.1.1 На рисунке 1 изображены главный профиль и элементы волны.

Рисунок 1 - Профиль и элементы волны

Расчетный уровень моря определяется с учетом сезонных и годовых колебаний, ветрового нагона и сгона, приливов и отливов.

Средняя волновая линия (см. рисунок 1) пересекает запись волновых колебаний так, что суммарные площади выше и ниже этой линии одинаковы.

4.1.2 Основными параметрами (статистическими характеристиками) морского ветрового волнения являются:

- средняя высота и высоты заданной обеспеченности;

- средняя длина и длины заданной обеспеченности;

- средний период и периоды заданной обеспеченности;

- направление распространения волн;

- средняя скорость распространения волн;

- средняя крутизна волн (отношение высоты волны к ее длине).

4.1.3 Статистические характеристики ветрового волнения в фиксированной точке акватории в каждый момент времени определяются распределением скорости и направления ветра над исследуемой акваторией, продолжительностью действия ветра, длиной разгона волн, глубиной места, рельефом и уклонами дна и конфигурацией береговой черты бассейна.

4.1.4 Расчеты элементов волн на открытых акваториях необходимо производить с учетом деления морей на акватории и зоны по уклонам дна и глубинам:

- глубоководная акватория - с глубиной d > 0,5λ, где дно не влияет на элементы волн, λ - средняя длина волн на глубокой воде;

- мелководная акватория - с глубиной d ≤ 0,5λ, с уклоном дна i* ≤ 0,001 или при практически горизонтальном дне;

- зона трансформации - область уменьшающихся глубин с уклонами дна i* > 0,001, по которой волны распространяются из глубоководной или мелководной акватории;

- прибойная зона - с глубинами от критической глубины d_cr до урезовой глубины d_cr,u, в пределах которой начинается и завершается разрушение волн;

- приурезовая зона - с глубиной менее d_cr,u, в пределах которой происходит накат волн на берег, т.е. поток от обрушенных волн периодически набегает на береговой откос или пляж;

- зона дифракции - акватория, огражденная одиночным молом, сходящимися молами, волноломом или комбинациями перечисленных типов сооружений.

4.1.5 Превышение вершины волны над расчетным уровнем η_с, м, (см. рисунок 1) для перечисленных акваторий и зон, исключая приурезовую, следует принимать согласно требованиям СП 38.13330.

4.1.6 Элементы волн на открытых глубоководных и мелководных акваториях, в зоне трансформации, прибойной зоне и на огражденных акваториях необходимо определять в соответствии с 4.2 - 4.6 и требованиями СП 38.13330.

4.1.7 Методы расчета скорости ветра, в том числе с использованием региональных моделей атмосферной циркуляции, приведены в приложении А. Расчет изменений уровня моря и описание моделей морской гидродинамики приведены в приложении Б. Применение моделей требует верификации результатов расчетов по данным натурных изысканий.

4.1.8 Методы определения параметров волнения с использованием моделей ветровых волн приведены в приложении В. Применение численных методов требует тестовой проверки по формулам (1), (2) и верификации результатов расчетов по данным натурных изысканий.

4.2 Элементы волн на глубоководной акватории

4.2.1 Среднюю высоту волны на глубоководной акватории , м, при простых условиях волнообразования (ветер постоянной скорости и направления, прямолинейный берег) необходимо определять с учетом скорости ветра, а также длины разгона или продолжительности действия ветра, согласно Р 31.3.07, по формулам

(1)

 

(2)

где V_w - скорость ветра, м/с, на высоте 10 м с осреднением 10 мин;

g - ускорение свободного падения, м/с²;

L - длина разгона, м;

t - продолжительность ветра, с.

Способы определения V_w приведены в А.1.3 (приложение А).

По значениям безразмерных параметров gL/V²_w и gt/V_w, следует вычислять значения  и принимать меньшую величину.

4.2.2 Средний период волн , с, и среднюю длину волны , м, следует определять по формулам

(3)

 

(4)

4.2.3 Высоту волны i %-й обеспеченности в системе волн h_i, м, необходимо определять по формуле

	(5)

где F_h - обеспеченность высоты волны (доли единицы);

d - фактическая глубина места, м;

k_i - коэффициент перехода к высоте волны i %-й обеспеченности.

4.2.4 При сложной конфигурации береговой черты среднюю высоту волны , м, необходимо определять по формуле

(6)

где , м, (при п = 1; ±2; ±3; ±4) - средние высоты волн, которые должны приниматься согласно формулам (1), (2), по расчетной скорости ветра и проекциям лучей L_n, м, на направление главного луча, совпадающего с направлением ветра. Лучи проводятся из расчетной точки до пересечения с линией берега с интервалом ±22,5° от главного луча. Конфигурация береговой черты считается сложной, если величина L_max/L_min ≥ 2, где L_max и L_min - наибольший и наименьший отрезки лучей, проведенных из расчетной точки в секторе ±45° от направления ветра до пересечения с подветренным берегом.

При наличии перед расчетным створом большого количества препятствий в виде островов с угловыми размерами менее 22,5° и суммой угловых размеров более 22,5° среднюю высоту волн в секторе п необходимо определять по формуле

(7)

где χ_ni, v_nj - соответственно угловые размеры i-го препятствия и j-го промежутка между соседними препятствиями, отнесенные к углу 22,5° (i = 1, 2, 3, ..., k_n; j = 1, 2, 3, …, l_n) в пределах n-го сектора, назначаемого в интервале ±11,25° от направления луча.

4.3 Элементы волн на мелководной акватории

4.3.1 Среднюю высоту волны на мелководной акватории, , м, с уклонами дна i* < 0,002 необходимо определять по формуле

(8)

где d - глубина воды в расчетной точке.

Параметр , и высоту волны , м, необходимо определять по формулам (1) и (2), при этом используют наименьшее значение.

4.3.2 Средний период  на мелководной акватории необходимо определять по формуле (3) с учетом вычисленных значений . Среднюю длину волны на мелководной акватории , м, необходимо определять по формуле (14) с учетом вычисленных значений .

4.3.3 Высоту волны i %-й обеспеченности в системе волн h_i необходимо определять по формуле (5).

4.4 Элементы волн в зоне трансформации

4.4.1 Высоту волн i %-й обеспеченности в зоне трансформации с уменьшающимися глубинами при уклонах дна i* ≥ 0,02 необходимо определять по формуле

(9)

где k_t - коэффициент трансформации;

k_r - коэффициент рефракции;

k_i - коэффициент перехода к высоте волны i %-й обеспеченности, определяемый по формуле (5);

 - исходная средняя высота волны на глубоководной акватории.

Коэффициент трансформации k_t, необходимо вычислять по формулам

(10)

 

(11)

Коэффициент рефракции должен определяться по формуле

(12)

где a_d - расстояние между смежными волновыми лучами в глубоководной зоне, м; а - расстояние между теми же лучами по линии, проходящей через заданную точку мелководной зоны, м.

Лучи волн на плане рефракции в глубоководной зоне необходимо принимать по заданному направлению распространения волн, а в мелководной зоне их следует продолжать в соответствии со схемой а и графиками б рисунка 2 согласно штриховой линии со стрелками.

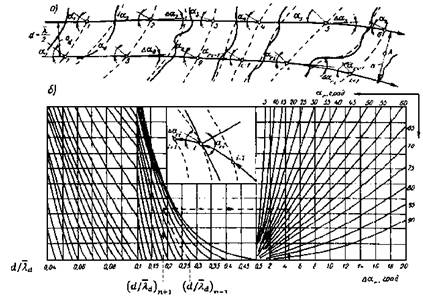
Рисунок 2 - Схема (а) и графики (б) для построения плана рефракции

Рефракцию участков дна со сложной топографией рекомендуется рассчитывать по численным моделям, приведенным в приложении В.

4.4.2 Высоту волн i %-й обеспеченности в зоне трансформации с уменьшающимися глубинами при уклонах дна 0,002 ≤ i* < 0,02 необходимо определять по формуле

(13)

где k_l - обобщенный коэффициент потерь.

Обобщенный коэффициент потерь k_l должен определяться по заданным значениям величины  и уклону дна i* в соответствии с таблицей 4.1. При i* ≥ 0,03 следует принимать k_l = 1.

Таблица 4.1 - Значения коэффициента потерь при различных уклонах дна

Коэффициент перехода k_i высоте волны заданной i %-й обеспеченности необходимо определять по формуле (5).

4.4.3 Длину волн , м, перемещающихся из глубоководной акватории в зону трансформации, необходимо определять по формуле

(14)

где  принимается по формуле (4).

4.5 Элементы волн в прибойной зоне

4.5.1 Глубину первого обрушения волн d_cr, м, в прибойной зоне при постоянном уклоне дна необходимо определять по формуле

(15)

где

4.5.2 Глубину последнего обрушения волн d_cr,u, м, начиная с которой происходит накат волн на берег, допускается при постоянном уклоне дна i* вычислять по формуле

(16)

Значение параметра k_n и число обрушений волн п необходимо определять по таблице 4.2.

Таблица 4.2 - Определение параметров обрушения

При уклонах дна 0,05 ≤ i* ≤ 0,2 и значении п = 1 критическая глубина d_cr = d_cr,u.

При уклонах дна 0,001 < i* < 0,01 необходимо принимать

dcr,u = 0,43dcr

(17)

4.5.3 Глубину последнего обрушения волн d_cr,u, м, при переменных уклонах дна допускается принимать по результатам последовательного определения глубин d_cr,u для участков с постоянными уклонами дна i*.

4.5.4 Высоту волн в прибойной зоне 1 %-й обеспеченности h_sur,1, м, при d_cr ≤ d ≤ d_cr,u необходимо определять по формуле

(18)

где коэффициент а_i, следует принимать в соответствии с 4.5.1.

4.5.5 Длину волны в прибойной зоне , м, следует вычислять по формуле

(19)

4.5.6 Высоту волны i %-й обеспеченности в прибойной зоне h_sur,i, м, необходимо определять по формуле

hsur,i = ki·hsur,1

(20)

Коэффициент перехода к высоте заданной обеспеченности k_i следует принимать по таблице 4.3.

Таблица 4.3 - Зависимость коэффициента перехода от значения обеспеченности

4.6 Элементы волн на огражденной акватории

4.6.1 Высоту дифрагированной волны h_dif, м, на огражденной акватории необходимо определять по формуле

hdif = kdif·hi

(21)

где k_dif - коэффициент дифракции волн;

h_i - высота исходной волны i %-й обеспеченностью перед входом на акваторию, м.

В качестве расчетной длины волны следует принимать исходную длину  на входе в акваторию.

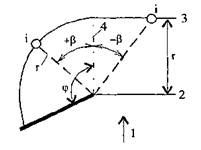
4.6.2 Коэффициент дифракции волн k_dif,s для акватории, огражденной одиночным молом, схема которой приведена на рисунке 3, следует вычислять по формуле

(22)

где

r - расстояние от головы мола до расчетной точки, м;

φ - угол между лучом исходной волны и осью мола в радианах;

β - угол между границей волновой тени и лучом, проведенным от головы мола в расчетную точку в радианах, в зоне волновой тени угол β считается положительным, вне зоны тени - отрицательным (см. рисунок 3).

4.6.3 Рекомендуется использовать численные модели (см. приложение В) для акваторий со сложной донной топографией для учета дифракции, отражения и интерференции волн у сооружений различных конструкций, в т.ч. проницаемых. При этом необходимо выполнять тестовую проверку моделей с использованием формулы (22).

1 - исходный луч; 2 - исходный створ; 3 - расчетный створ; 4 - граница волновой тени

Рисунок 3 - Схема акватории с одиночным молом

5 Режимные характеристики морского ветрового волнения

5.1 Общие положения

5.1.1 Определение режимных характеристик морского ветрового волнения (далее - режимные характеристики) проводится для средних высот, периодов и длин волн, генерального или среднего направления волнения, а также высот, периодов и длин волн i %-й обеспеченности в системе.

5.1.2 Для получения режимных характеристик используются многолетние ряды наблюдений за ветровым волнением на гидрометеорологических станциях или расчеты по полям ветра, используются 4- или 8-срочные данные наблюдений или расчетов.

5.1.4 Общая продолжительность наблюдений или расчетов должна охватывать период не менее 30 лет.

5.1.5 Режимные характеристики разделяют на 2 группы: частой повторяемости (далее - оперативные характеристики) и редкой повторяемости (далее - расчетные характеристики). К последним относятся, например, шторма или окна погоды, а также гидрометеорологические помехи.

При определении оперативных характеристик допустимо использовать 10-летние ряды наблюдений или расчетов.

5.1.6 При наличии льда длина разгона в формуле (1) рассчитывается не от кромки берега, а от границы неподвижного льда.

5.2 Оперативные характеристики морского ветрового волнения

5.2.1 Важнейшими оперативными характеристиками являются:

- обеспеченности F_X(y) = P(X ≥ y) высот h, периодов Т волн и длин λ волн;

- квантили высот h, периодов Т и длин λ волн с вероятностью появления до одного года включительно;

- условные (ассоциированные) Р(х|у) статистики волнения, определяемые как вероятность появления периодов волн при данном значении высот волн или направлений распространения волнения при данном значении высот волн.

5.3 Шторма и окна погоды

5.3.1 Шторма и окна погоды характеризуют синоптическую изменчивость ветрового волнения и могут быть представлены системой из четырех величин:

- продолжительность S шторма (положительного выброса траектории высоты волны h(t) за фиксированный уровень Z);

- продолжительность W окна погоды (отрицательного выброса траектории h(t) ниже фиксированного уровня Z);

- максимальное значение h⁺, м, высоты волны в шторме уровня Z;

- минимальное значение h^-, м, высоты волны в окне погоды уровня Z.

5.4 Гидрометеорологические помехи

5.4.1 Гидрометеорологическая помеха (далее - помеха) представляет собой набор гидрометеорологических факторов (включающих в себя ветровое волнение), препятствующих работам в море в течение определенного промежутка времени. Режимными характеристиками помех являются: средняя длительность  и средний квадрат длительности действия помех , а также вероятность их возникновения Р_n. Величины , , и Р_n получают по данным наблюдений (не менее 5 лет) за гидрометеорологическим режимом в акватории. Для этого:

а) определяются предельные значения скорости ветра, допустимой температуры воздуха и высоты волнения для данного типа работ. Строится совмещенный хронологический график скорости ветра, температуры воздуха и параметров волнения;

б) полученные значения наносятся на совмещенный график в виде прямых линий, параллельных оси времени;

в) интервалы времени, когда значение хотя бы одного гидрометеорологического фактора выходит за допустимые границы, проецируются на общую ось времени. Если в течение некоторого промежутка времени работы в море прерываются одним или несколькими гидрометеорологических факторами, то данный промежуток времени необходимо считать длительностью действия помехи;

г) по полученным значениям длительности помех рассчитываются величины , , и Р_n по формулам

(23)

где T - длительность рассматриваемого периода, сут;

t_ni - длительность i-й помехи, сут;

m - количество помех за период Т.

5.5 Расчетные характеристики морского ветрового волнения

5.5.1 Определение расчетных характеристик (редкой повторяемости) должны проводиться на основе данных многолетних наблюдений и/или решения численной гидродинамической задачи генерации и распространения ветрового волнения. Модель ветрового волнения должна учитывать известные процессы, влияющие на генерацию и распространение ветровых волн и зыби. К ним относятся: распространение и рефракция ветрового волнения, взаимодействие ветра и волн, нелинейные взаимодействия в спектре ветрового волнения, диссипация ветрового волнения, донное трение и обрушение ветрового волнения в приурезовой зоне. Исходные поля ветра задаются с учетом неоднородности и нестационарности ветрового потока над морем.

5.5.2 Расчетные режимные характеристики ветрового волнения в глубоководных и мелководных акваториях рассчитываются по вероятностным моделям, приведенным в приложении Г, на основании штормовых или годовых максимумов ветрового волнения.

5.5.3 Для мелководной акватории при глубине d ≤ 0,5λ и с уклонами дна i* < 0,002 допустимо определять предельно большую для данной акватории среднюю высоту волны по формуле

(24)

5.5.4 Расчетные характеристики в зоне трансформации, в прибойной зоне и на акваториях с ограждениями определяются по соответствующим расчетным характеристикам в глубоководных и мелководных акваториях. Данные характеристики используются как граничные условия с последующей трансформацией их процессами донного трения, рефракции, дифракции и обрушения волн в приурезовой зоне.

5.6 Расчетные характеристики в тропических циклонах

5.6.1 Повторяемость элементов ветровых волн в зонах действия тропических циклонов рассчитывают на основе повторяемостей направлений и скоростей ветра, формирующих эти волны.

5.6.2 Повторяемость направлений и скоростей ветра в зоне действия тропических циклонов  необходимо представлять в виде суммы двух составляющих: режима фоновых ветров и режима экстремальных ветров:

(25)

где  - повторяемость скоростей фоновых ветров;

 - повторяемость экстремальных скоростей ветра, формируемых тропическими циклонами.

5.6.3 Повторяемость направлений и скоростей фоновых ветров получают путем обработки многолетнего ряда наблюдений или типизации карт барической топографии, с последующим расчетом полей волн и присвоения им вероятностных характеристик соответствующих карт.

5.6.4 Повторяемость направлений и скоростей ветра, формируемых тропическими циклонами, рассчитывают на основе анализа траекторий тропических циклонов и карт барической топографии, соответствующих максимальному развитию каждого их тропических циклонов, за многолетний период по формуле

(26)

где N(S₁) - количество тропических циклонов, прошедших через зону S₁ за время t₀;

N(S₀) - количество тропических циклонов, прошедших через зону S₀ за время t₀;

 - средняя площадь области тропического циклона с данными скоростями и направлениями ветра;

t₀ - период наблюдений;

j - номер тропического циклона.

В качестве зоны S₀ следует принимать область океана, в которой зарождаются, достигают максимального развития и разрушаются тропические циклоны.

Зону S₁ следует принимать в виде квадрата размером 2,5°×2,5°, плотность траекторий тропических циклонов в котором за многолетний период может быть принята равномерной.

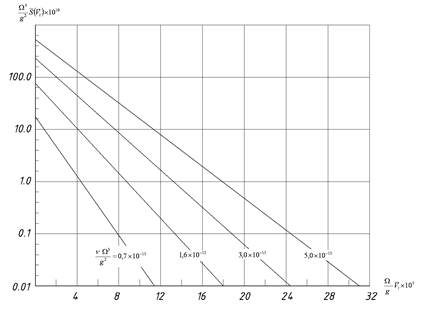
Значение средней площади области тропического циклона с данными скоростями и направлениями ветра  следует определять с помощью номограммы на рисунке 4.

Косые линии слева направо соответствуют широтам 15°, 20°, 25° и 30°,
 - скорость ветра, Ω - параметр Кориолиса, g - ускорение силы тяжести, v - кинематическая
вязкость воздуха,  - средняя площадь области тропического циклона с данными
скоростями и направлениями ветра.

Рисунок 4 - Зависимость безразмерной площади штормовой области тропического
циклона от безразмерной скорости ветра

6 Формы представления режимных характеристик морского ветрового волнения

6.1 Повторяемость высот волн

Повторяемость высот волн (3 %-й обеспеченности или значительных) по градациям, без учета направлений и с учетом направлений (8 румбов) по месяцам и/или за навигационный период представляется в виде таблицы 6.1.

Таблица 6.1 - Повторяемость высот волн

6.2 Совместная повторяемость высот и периодов волн

Совместная повторяемость высот и периодов волн строится для высот волн 3 %-й обеспеченности и средних периодов. Результаты представляются по интервалам высот и периодов волн, в виде таблицы 6.2. После разбиения на интервалы в таблице приводятся общая повторяемость и обеспеченность высот волн f(h) F(h) и периодов волн f(τ) F(τ), а также соответствующие теоретические значения обеспеченностей Ф(h) и Ф(τ), способ получения которых приведен в приложении Г.

Таблица 6.2 - Совместная повторяемость высот волн и средних периодов волн

6.3 Длительность штормов и окон погоды

Рассчитываются средние, среднеквадратические и максимальные значения длительности (в сутках) для волн, больших (для штормов) и меньших (для окон погоды) заранее заданных значений (1, 2, 3, 4, 5 м и т.д.).

Таблицы строятся для волн 3 %-й обеспеченности или значительных, отдельно для каждого месяца и навигационного периода в целом. Форма для заполнения представлена в таблице 6.3.

Таблица 6.3 - Длительность штормов и окон погоды

6.4 Роза волнения

Для построения розы волнения рассчитывается повторяемость волн по направлениям, %, всего 8 румбов. Представляется в графическом виде. Пример представлен на рисунке 5.

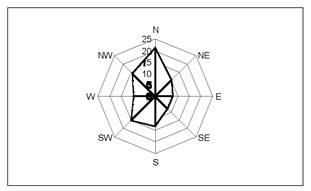
Обозначения румбов:
N, NE, E, SE, S, SW, W, NW - С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ, соответственно

Рисунок 5 - Роза волнения

6.5 Характеристики волн зыби

Рассчитывается повторяемость зыби, смешанного и ветрового волнения для выбранного периода времени. Результаты представляются в виде таблицы 6.4.

Таблица 6.4 - Повторяемость видов волнения по месяцам

В дополнение рассчитывается совместная повторяемость высот ветровых волн и волн зыби (используется высота волнения 3 %-й обеспеченности и/или значительная). После разбиения на интервалы в таблице приводятся общая повторяемость высот ветровых волн f(h_w3%) и высот волн зыби f(h_s3%). Результаты представляются в виде таблицы 6.5

Таблица 6.5 - Совместная повторяемость высот ветровых волн и зыби

6.6 Спектральные характеристики волнения

Для определения спектральных характеристик волнения рассчитываются средние за месяц, либо за выбранный период, моменты частотного спектра ветрового волнения: нулевой, первый, второй моменты. Результаты представляются в виде таблицы 6.6

Таблица 6.6 - Спектральные характеристики волнения

6.7 Угловое рассеяние волнения

Для определения углового рассеяния волнения рассчитывается среднее за месяц среднеквадратическое отклонение (в градусах) направления волнения относительно среднего направления. Результаты представляются в виде таблицы 6.7

Таблица 6.7 - Угловое рассеяние волнения

6.8 Статистические оценки высот волн

При определении статистических оценок высот волн учитывается их обеспеченность и период повторяемости. Определяются высоты волн: средние, 50 %-й, 13 %-й, 5 %-й, 3 %-й, 1 %-й и 0,1 %-й обеспеченности, возможные 1 раз в п лет, n = 1, 5, 10, 25, 50 и 100. Результаты статистических оценок представляются в виде таблицы 6.8

Таблица 6.8 - Статистические оценки высот волн

6.9 Сведения о достоверности оценок высот волн

В дополнение к статистическим оценкам высот волн приводятся сведения о достоверности оценок высот волн. Для этого находятся границы 95 %-го доверительного интервала высот волн: верхняя граница 2,5 %-й обеспеченности и нижняя граница 97,5 %-й обеспеченности для расчетных высот волн повторяемостью 1 раз в п лет.

Результаты представляются в виде таблицы 6.9

Таблица 6.9 - Высоты волн 95 %-го доверительного интервала

6.10 Оценка периодов, длин волн и придонных орбитальных скоростей

Определяются периоды, длины волн и придонные орбитальные скорости ветрового волнения, ассоциированные со средними высотами волн и высотами волн указанной обеспеченности. Оценки производятся для периодов различной (заданной) повторяемости n = 1, 5, 10, 25, 50 и 100 лет. Результаты представляются в виде таблиц 6.10 - 6.12

Таблица 6.10 - Период волн при заданной обеспеченности и повторяемости высот волн

Таблица 6.11 - Длина волн при заданной обеспеченности и повторяемости высоты волны

Таблица 6.12 - Придонная орбитальная скорость волн при заданной обеспеченности и повторяемости высоты волны

6.11 Оценки высот гребней волн

Определяются высоты гребней волн, соответствующих высотам волн 0,1 %-й обеспеченности, возможным 1 раз в п лет, n = 1, 5, 10, 25, 50 и 100. Результаты представляются в виде таблицы 6.13.

Таблица 6.13 - Высоты гребней волн

6.12 Волноопасные направления волн

Волноопасные направления волн - это наиболее вероятное направление прихода экстремальных волн. Для их определения анализируется не менее 10 наиболее сильных штормов, указываются направления волнения в момент наибольшего их усиления, о чем создается соответствующая запись.

6.13 Условные статистические характеристики волнения

Условные (ассоциированные) статистические характеристики волнения определяются в сочетании с волнообразующими факторами (например, «высота волны - скорость ветра», «высота волны - уровень моря»). Повторяемость сочетаний факторов приводится в виде таблиц 6.14 - 6.15.

Таблица 6.14 - Повторяемость, %, сочетаний высоты волн и скорости ветра

Таблица 6.15 - Повторяемость, %, сочетаний высоты волн и уровня моря

6.14 Характеристики гидрометеорологических помех

Характеристиками гидрометеорологических помех являются средняя длительность , средний квадрат длительности действия помех , а также вероятность их возникновения Р_п. Описание вида работы в море и характеристики помех, ограничивающих возможность проведения данного вида работ в море, представляются в виде таблицы 6.16.

Таблица 6.16 - Характеристики гидрометеорологических помех

Приложение А
(рекомендуемое)

Расчет скорости ветра и региональные модели атмосферной циркуляции

А.1 Расчет скорости ветра

А.1.1 Скорость ветра при длине разгона менее 100 км допускается определять по данным наблюдений на береговых станциях.

А.1.2 Скорость ветра над акваторией большой протяженности при длине разгона более 100 км следует определять по формулам (А.1) - (А.2), используя как исходную информацию синоптические карты.

А.1.3 Скорость ветра V_w, м/с, над водной поверхностью на горизонте Z = 10 м с осреднением 10 мин следует определять по градиенту атмосферного давления и вычислять по формуле

Vw = CgVgr,

(A.1)

где C_g - коэффициент трения, определяемый по А.1.9;

V_gr - скорость градиентного ветра, м/с.

А.1.4 Скорость градиентного ветра V_gr, м/с, при изобарах, проведенных на синоптических картах со стандартным «шагом» атмосферного давления р = 5 гПа, допускается вычислять по формулам

(А.2)

 

fr = 2ωlsinφ

(А.3)

где r - радиус кривизны изобар, м;

f_r - параметр Кориолиса, с^-1;

V_g - скорость геострофического ветра, м/с;

a₁ = 5,5·10⁴;

а₂ = 3,8·10^-5 м^-1;

ω_l = 7,29·10^-5 с^-1 - угловая скорость вращения Земли;

φ - широта в градусах.

При циклонах принимается r < 0, при антициклонах r > 0.

А.1.5 Скорость геострофического ветра V_g, м/с, при стандартном «шаге» атмосферного давления Δр = 5 гПа допускается определять, используя данные синоптических карт при изобарах, близких к прямолинейным (на границе циклона или антициклона), по формуле

(А.4)

где γ - расстояние между изобарами, м;

a₃ = 3,6·10^-3 м²/с².

А.1.6 Максимальную скорость градиентного ветра в антициклоне (r > 0) допускается определять по формуле

Vgr,max = a1rfr, при r ≤ rcr

(А.5)

А.1.7 «Критическое» значение радиуса кривизны изобар в антициклоне r_сr допускается вычислять по формуле

(А.6)

Если r > r_сr, то для расчета ветра в антициклоне следует использовать формулы (А.2) и (А.3).

А.1.8 Направление градиентного ветра в Северном полушарии необходимо принимать совпадающим с направлением изобар: в циклонах - против часовой стрелки, в антициклонах - по часовой стрелке. В Южном полушарии необходимо использовать противоположные направления.

А.1.9 Коэффициент трения C_g в формуле (А.1) допускается определять по данным таблицы А.1 при использовании значений скорости градиентного ветра V_gr, м/с, вычисленной по формулам (А.2), (А.3) и разницы температур воздуха и воды ΔТ, °С, для широт φ ≥ 35°.

Таблица А.1 - Определение коэффициента трения C_g

А.1.10 Направление ветра на горизонте z = 10 м определяется по углу поворота ветра α_т от направления градиентного ветра в сторону низкого давления; при этом для разницы температур воздуха и воды ΔТ = минус 2 °С; минус 1 °С; 0, допускается принимать углы поворота α_т = 0; 10°; 20°, соответственно.

А.2 Региональные модели атмосферной циркуляции

А.2.1 При расчете скорости и направления ветра для акваторий с пространственными масштабами более 100 км рекомендуется использовать мезомасштабные региональные модели атмосферы.

А.2.2 Используемая численная региональная модель атмосферы должна обеспечивать численное решение системы уравнений термо- и гидродинамики с использованием начальных и граничных условий. В общем виде систему уравнений можно выписать в виде:

	(A.7)
	(A.8)
	(A.9)
	(A.10)

где уравнение (А.7) расписывается для трех компонент скорости ветра , м/с,

р - давление, Па;

Т - температура воздуха, К;

ρ - плотность, кг/м³;

С_р = 7R/2;

Q - удельная влажность;

Θ = Т/π,

R - универсальная газовая постоянная.

Адвективные члены adv в уравнении (А.7) расписываются как  для трех направлений (х, у, z) для соответствующих компонент скорости ветра (u, v, w). С, Е - члены, описывающие конденсацию и испарение. При гидростатическом приближении уравнение (А.7) для вертикальной координаты z записывается в виде

(А.11)

А.2.3 В качестве начальных и граничных условий используются сведения из Мировых центров данных (массивы глобального реанализа), либо, если моделирование проводится методом вложенных сеток, данные с более грубым пространственным разрешением.

А.2.4 Пространственное разрешение численной модели должно выбираться с учетом аэрографических особенностей акватории. При достаточном обосновании допускается производить расчеты с шагом до 30 км. При выбранном разрешении выше 20 км допускается использование гидростатических региональных моделей атмосферы. При разрешении менее 20 км, а также в северных широтах, в зонах наличия ледников, необходимо использование негидростатических моделей атмосферы.

А.2.5 Граница области расчета характеристик скорости и направления ветра по региональной модели атмосферы должна быть максимально удалена от исследуемой акватории.

А.2.6 Шаг по времени должен составлять не более 6 ч.

А.2.7 Использованию модели должен предшествовать этап верификации в рамках сравнительного натурного эксперимента. Верификация должна производиться по данным с метеостанций, либо по данным, полученным в ходе проведения изыскательских работ.

Приложение Б
(рекомендуемое)

Расчет изменений уровня моря и модели морской гидродинамики

Б.1 Расчет изменений уровня моря

Б.1.1 При расчете уровня моря или фактической глубины необходимо учитывать изменения уровня моря, вызванные гидродинамическими причинами - ветровой нагон Δh_set, штормовой нагон η_s, волновой нагон η₀.

Б.1.2 При наличии рядов наблюдений уровень моря рекомендуется учитывать по данным ближайшего гидрометеорологического поста.

Б.1.3 При этом должны быть проведены натурные изыскания, подтверждающие репрезентативность данных измерений для всей исследуемой акватории.

Б.1.4 Высоту ветрового нагона Δh_set, м, в мелководной зоне акватории с постоянной глубиной d, м, допустимо определять по формулам

	(Б.1)
	(Б.2)

где α_w - угол между направлением ветра и нормалью к береговой черте в градусах;

V_w - расчетная скорость ветра, м/с;

L_m - длина разгона, м;

α₀ - коэффициент (α₀ = 0,85);

ρ_a/ρ_w - отношение плотности воды к плотности воздуха;

С₁₀ - коэффициент сопротивления, который допускается определять по формуле

(Б.3)

Б.1.5 Высоту ветрового нагона Δh_set, м, в прибрежной мелководной зоне с постоянным уклоном дна допустимо определять по формуле:

(Б.4)

где d₁ - глубина, отвечающая расстоянию L_m от расчетного створа до створа, в котором уровень соответствует исходному, м;

d - глубина в расчетной точке, м.

Глубину и положение створа в прибрежной зоне с уклоном дна i*, где уровень соответствует исходному, необходимо оценивать из условий:

	(Б.5)

Б.1.6 Высоту ветрового нагона в условиях больших глубин по отношению к высоте нагона (d > Δh_set) допускается определять:

- для постоянной глубины по формуле

(Б.6)

- для постоянного уклона дна по формуле

(Б.7)

Формулы (Б.6) и (Б.7) - упрощенный вариант формул (Б.1) и (Б.4). Расчеты по формулам (Б.1) и (Б.4) необходимо выполнять методом последовательных приближений, вычисляя первое приближение по формулам (Б.6) и (Б.7).

К конечному значению Δh_set необходимо вносить поправку на закон обратного барометра вида Δh_set = Δh_set - P_a/(ρ_wg), где Р_а - атмосферное давление. В случае приливного моря необходимо добавить также и приливную составляющую, выраженную в высоте прилива, определяемую согласно приливным таблицам на время расчета.

Б.1.7 Высоту штормового нагона η_s, м, в прибойной зоне d_cr < d < d_cr,u (d_cr - глубина первого обрушения и d_cr,u - глубина последнего обрушения волн) допускается определять по формуле

ηs = Δhset + η0

(Б.8)

где Δh_set - высота ветрового нагона, м;

η₀ - высота волнового нагона, м.

Высота ветрового нагона Δh_set, м, определяется в соответствии с Б.1.4 - Б.1.6.

Б.1.8 В случае плоского наклонного дна для произвольной точки внутренней прибойной зоны допустимо определять волновой нагон η₀ по формуле

η0 = G(γ)[dcr - d0],

(Б.9)

где d_cr - глубина первого обрушения,

d₀ - глубина в штилевую погоду.

Б.2 Модели морской гидродинамики

Б.2.1 При расчете подъемов уровня для акваторий со сложной донной топографией и в приливных морях рекомендуется использовать мезомасштабные модели морской гидродинамики.

Б.2.2 Течения и термодинамические поля температуры, солености формируются в результате сложных физических процессов, определяющих морскую циркуляцию под воздействием атмосферных факторов и приливов [1]. Необходимо отметить, что бароклинный радиус деформации Россби в морях средних и высоких широт имеет величины порядка 5 - 15 км. Эго значит, что значительный вклад в общую циркуляцию моря осуществляют бароклинные вихри с размером порядка двух радиусов Россби. Формирование мезомаштабных квазигеострофических вихрей происходит при активном взаимодействии течений и плотностной стратификации. Поэтому представляется необходимым и оправданным использование сложной и физически полной модели морской циркуляции высокого пространственного разрешения.

Б.2.3 Наибольшие колебания уровня происходят под действием гидрометеорологических факторов, которые вызывают сгонно-нагонные колебания уровня, достигающие в прибрежных районах моря 1 - 2 м и более.

Б.2.4 Модель морской гидродинамики должна воспроизводить приливную составляющую течений и уровня моря.

Б.2.5 При наличии морского льда в исследуемой акватории необходим его учет, так как это является необходимым условием воспроизведения циркуляции, близкой к натурной.

Б.2.6 Гидродинамическая модель должна быть адаптирована к условиям расчетной акватории. Наиболее перспективным подходом для этого является использование неравномерной пространственной сетки со сгущением в области исследуемого участка и удалением «жидких границ» от этого района. Таким образом, шаги по пространству в исследуемом районе могут составлять порядка 100 - 500 м, а при удалении от него сеточные шаги могут постепенно увеличиваться, достигая на периферии расчетной области 5 - 10 км. Использование неравномерного шага по пространству позволяет моделировать циркуляцию, уровень моря и термохалинные характеристики с высоким пространственным разрешением, но в то же время учитывать влияние крупномасштабной циркуляции в прилегающей области. Другим общепринятым подходом является технология моделирования на вложенных сетках, при использовании которой крупномасштабная циркуляция моделируется с грубым пространственным разрешением, а для исследуемой акватории моделирование проводится с требуемым пространственным разрешением. На жидкой границе сеточной области с высоким пространственным разрешением при таком подходе используются данные с крупномасштабной сеточной области.

Б.2.7 Модели морской циркуляции используются для расчета основных параметров морской гидротермодинамики:

- трехмерные поля зональной и меридиональной компонентов скорости течений;

- трехмерные поля температуры и солености;

- уровень моря;

- сплоченность и толщина морского льда, скорость дрейфа льда.

Б.2.8 Использованию модели должен предшествовать этап верификации в рамках сравнительного натурного эксперимента.

Б.2.9 Современные модели морской динамики основаны на системе уравнений гидротермодинамики океана, в которой, помимо приближений гидростатики и Буссинеска, используется предположение о постоянном радиусе Земли, а все уравнения записываются в цилиндрическом слое над сферой.

Б.2.10 В криволинейной ортогональной z-системе обобщенных координат (x, y, z) с базисной системой локальных базисных векторов , направленных вдоль соответствующих обобщенных координат (причем в каждой точке области океана базисный вектор  сонаправлен радиусу Земли), система уравнений (в приближениях гидростатики и Буссинеска, радиус Земли положен постоянным) имеет вид:

	(Б.10)
	(Б.11)
	(Б.12)
	(Б.13)
	(Б.14)
ρ = ρ(T, S, p),	(Б.15)

где  - вектор скорости течения, м/с, в точке (x, y, z) в координатах ;

Θ - потенциальная температура, °С;

S - соленость, шпс;

∇, ∇·, ∇× - соответственно операторы градиента, дивергенции и ротора;

[·]_h - оператор проекции на подпространство ;

 - сила Кориолиса;

Ω - угловая скорость вращения Земли;

, D^Θ и D^S - операторы параметризации маломасштабной физики (вязкости и диффузии);

р - давление, Па;

ρ₀ - фоновая плотность, кг/м³;

ρ - отклонение плотности от некоторого равновесного профиля;

R^Θ - внутренний источник тепла, обусловленный проникающей солнечной радиацией, Вт/м².

Здесь в общей форме записи не приводятся граничные условия для системы, поскольку их частный вид определяется видом турбулентных операторов , D^Θ и D^S.

Приложение В
(рекомендуемое)

Модели ветровых волн

В.1 Расчет элементов волн допускается выполнять, согласно [2], [3], в соответствии с разделом 4.

В.2 При сложных условиях волнообразования рекомендуется использование численных моделей ветрового волнения.

В.3 Использованию модели должен предшествовать этап ее верификации в рамках сравнительного натурного эксперимента с привлечением буйковых измерений.

В.4 Моделирование ветрового волнения [4] заключается в решении численным способом уравнения переноса двухмерного спектра волновой энергии F(ω, θ), м²с, или волнового действия n(ω, θ), м²·с², вида

(В.1)

где ω - частота, рад/с;

θ - направление распространения волнения.

В левой части уравнения полная производная по времени от двухмерного (частотно-углового) спектра волн ,  - групповая скорость, м/с, а правая часть есть так называемая функция источника модели ветровых волн Р. Функция Р содержит три основных слагаемых, являющихся составными частями общего механизма эволюции ветровых волн:

- скорость нелинейного переноса энергии по спектру, NL;

- скорость передачи энергии от ветра к волнам, IN;

- скорость потерь энергии волн, DIS.

В случае мелкой воды в левой части (В.1) могут присутствовать слагаемые, ответственные за эффекты рефракции и влияния мелководья.

В.5 В сферической системе координат, в наиболее широко распространенном представлении использования спектра волнового действия n(ω, θ), уравнение (В.1) имеет следующий вид [4] - [7]:

	(В.2)

где  - скорость ветра, м/с;

φ - широта, λ - долгота, º;

K - модуль волнового числа;

R - радиус земли, м;

с_λ - составляющая групповой скорости волнения в меридиональном направлении;

c_φ - составляющая в широтном направлении;

с_θ - скорость отклонения волнового луча от полюсов к экватору, вызванная сферичностью Земли;

с_ref - скорость поворота волнового луча вследствие рефракции;

Р - функция источников и стоков, включающая функцию взаимодействия волн и ветра (Р⁺), нелинейные взаимодействия в спектре ветровых волн (Р⁰) и диссипацию (Р^-).

В.6 Для задания члена взаимодействия волн с ветром Р⁺ рекомендуется использовать формулу Майлза

Р+ = βωn(ω, θ),

(В.3)

где для задания β допускается использование эмпирических выражений.

Для описания диссипации допускается использование полуэмпирических формул, ограничивающих рост спектральной плотности на высокочастотном участке спектра.

В.7 Для описания члена нелинейных взаимодействий в спектре ветрового волнения P_nl допускается использование его упрощенных представлений. Они учитывают разную степень полноты и детализации данного члена.

В.8 Допускается использование следующих способов упрощения кинетического интеграла [4] - [8]:

- интегрального (спектрально-параметрического);

- узконаправленного;

- дискретного.

В.9 Интегральные модели ветрового волнения основываются на интегрировании по волновым числам уравнения (В.1), которое может быть сведено к следующему виду:

(В.4)

где χ_т - значение элемента ветрового волнения,

 - интегральная групповая скорость ветрового волнения, она пропорциональна энергии ветрового волнения в степени 3/8,

Р₀ - интегральная функция источников и стоков.

В случае, если уравнение (В.4) записывается для нескольких элементов волнения, данный подход к моделированию ветрового волнения называется «спектрально-параметрическим».

В.10 «Узконаправленное» [9] приближение члена нелинейных взаимодействий рекомендуется использовать на акваториях, где легко можно выделить преобладающую систему волнения.

В рамках этого подхода от двухмерного спектра п(w, θ) переходят к двум интегральным функциям - спектру волновых чисел  и параметру узконаправленности Δ(k_х):

	(В.5)
	(В.6)
	(В.7)

где  - волновое число, K_у - координата в пространстве волновых чисел, перпендикулярная K_х, а направление K_х совпадает с генеральным направлением волнения. В этом случае функция источников и стоков может быть записана следующим образом:

	(В.8)
	(В.9)

где Р_п и Р_Δ - функции источников и стоков для  и Δ(K_х) соответственно,

В.11 Основным механизмом передачи волновой энергии в область больших периодов волн является механизм нелинейных взаимодействий в спектре ветрового волнения. Он описывается интегралом Хассельманна, который в прикладных моделях из-за своей алгебраической громоздкости не используется в явном виде. При практических расчетах используются упрощения данного интеграла, наибольшее распространение при расчете двухмерного спектра ветрового волнения из которых получило приближение «дискретных взаимодействий».

В.11.1 Приближение «дискретных взаимодействий» (DIA) используется для сокращения расчетов нелинейного слагаемого в функции источника, с сохранением физики этого процесса [4]. Оно получило широкое распространение во всех двухмерных спектральных волновых моделях.

В.11.2 Суть DIA заключается в том, что из всего разнообразия четверок взаимодействующих волн выбирается только одна. Ее характеристики в полярных координатах записываются следующим образом. Волновые числа  равняются волновому числу , которое характеризуется частотой ω и направлением θ. Волновое число , его частота определяется как ω₊ = ω(1 + j), а направление распространения как θ₊ = θ + Δθ₊. Волновое число , его частота находится из соотношения ω_- = ω(1 - j), а направление распространения из соотношения θ_ = θ - Δθ_. Здесь j равняется 0,25, Δθ₊ = 11,5°, Δθ_ = 33,6°. Член нелинейных взаимодействий определяется следующим образом:

(В.10)

где С = 3000.

В.11.3 Приближение Fast DIA позволяет ускорить расчет нелинейного слагаемого еще в 2 раза [10]. Суть Fast DIA заключается в том, что вместо строго резонанса четверок взаимодействия, требующего выполнения интерполяции спектра n(ω, θ) в фиксированные точки расчетной ω, θ - сетки, все вектора четверки взаимодействующих волн расположены именно на расчетной сетке, используемой в модели.

Для случая, когда расчетная сетка задана соотношениями

ω(i) = ω0·ei-1 (0 ≤ i ≤ I), θ(j) = -π + j·Δθ (0 ≤ j ≤ J)

(В.11)

При значениях е = 1,05 и Δθ = π/18 оптимальная конфигурация четверки взаимодействующих волн в версии Fast DIA задается следующими соотношениями:

а) по частотам
ω1 = ωe4,	ω2 = ωe5,	ω3 = ωe8,	(В.12)
б) по углам
θ1 = θ + 2Δθ,	θ2 = θ + 2Δθ,	θ3 = θ + 3Δθ,	(В.13)

при известных величинах ω и θ (по которым, как отмечено выше, устраивается расчетный цикл). В остальном, оценка NL[S(σ, θ)] определяется типичными соотношениями для DIA. Подгоночная константа С для оптимизированной версии Fast DIA в имеет значение 12000.

В.12 При моделировании ветрового волнения в мелководной зоне, зоне трансформации и обрушения волн уравнение (В.1) должно быть дополнено членами донного трения и обрушения волн. Член донного трения допустимо задавать в следующем виде:

(В.14)

где ,

f_w - параметр донного трения,

u_b - орбитальная волновая скорость у дна;

(В.15)

Обрушение волн допустимо учитывать в виде:

(В.16)

где D - эмпирическое выражение,

Е - полная энергия волнения.

В.13 На огражденной акватории скорости распространения изменяются под воздействием дифракции. Скорости распространения с учетом дифрагирования определяются следующим образом:

(В.17)

где

с и c_g - фазовая и групповая скорость соответственно.

Приложение Г
(рекомендуемое)

Методы расчета режимных характеристик морского ветрового волнения

Г.1 При исследовании режима ветрового волнения искомые характеристики рекомендуется разделять на 2 группы: частой повторяемости (оперативные, нормальные, фоновые, эксплуатационные) и редкой повторяемости (экстремальные, расчетные), возможные 1 раз в 5, 10, ..., 100 лет и более.

Г.2 При исследовании оперативных характеристик ветрового волнения (частой повторяемости) допустимо использовать 10-летний ряд расчетов/наблюдений.

Г.3 Метод расчета оперативных характеристик ветрового волнения по типовым картам атмосферного давления допустимо использовать при наличии 10-летнего 4-срочного ряда синоптических карт для выбранной акватории.

Г.3.1 Исходной информацией являются данные синоптических карт.

Г.3.2 Скорость ветра V_w, м/с, над водной поверхностью на горизонте Z = 10 м следует определять по формулам (A.1), (А.2) (приложение А).

Г.3.3 Расчет характеристик волнения ведется не для всех полей приземного давления за выбранный интервал времени, а лишь для тех, которые признаны типовыми.

Г.3.4 Выделение типовых полей давления состоит из нескольких этапов. На первом этапе проводится районирование всего моря. В каждом районе моря выделяют наиболее репрезентативную точку. По скорости и направлению ветра в данной точке все поля давления разделяют на типы и подтипы. В направлении ветра выделяют 8 румбов (С, СВ, В и т.д.), а скорость ветра разбивают на градации с шагом 5 м/с (0 - 5, 6 - 10, 10 - 15 м/с и т.д.). Сочетание каждого румба и градации называется типом. В соответствии со спецификой барического поля над всем морем в типах выделяют подтипы. Например, тип - северный ветер 0 - 5 м/с, подтип - циклон над северо-западной частью моря или подтип - гребень над центральной частью моря и т.д.

Г.3.5 В каждом типе (или подтипе, если они выделены) выбирается одна синоптическая карта (типовая), которой приписывается повторяемость всех карт, попавших в данный тип.

Г.3.6 Расчет элементов волнения следует определять в соответствии с 4.2 для глубоководных акваторий и 4.3 для мелководных акваторий.

Г.3.7 По полученным значения элементов волн и с учетом повторяемости типа/подтипа строят эмпирические распределения высот и периодов волн. Эмпирические распределения аппроксимируются распределением Вейбулла:

(Г.1)

где  - медианное климатическое значение средней высоты волны, м,

γ - параметр распределения.

Г.4 Метод определения оперативных характеристик ветрового волнения с использованием полей ветра, рассчитанных по региональным атмосферным моделям, допускается применять при наличии 10-летнего ряда рассчитанных полей ветра.

Г.4.1 Исходной информацией для метода, использующего региональные атмосферные модели, являются гидрометеорологические данные, хранящиеся в Мировых центрах данных.

Г.4.2 Эти данные являются входной информацией для моделей ветрового волнения в соответствии с формулой (В.1) (приложение В). По всем полям приземного ветра рассчитываются поля элементов волн.

Г.4.3 Для каждой точки сеточной области по полученным значениям элементов волн строят эмпирические распределения высот и периодов волн.

Г.4.3 Эмпирические распределения аппроксимируются теоретическими распределениями Вейбулла (Г.1) и логнормальным:

(Г.2)

Г.4.4 Для выбора предпочтительного распределения используется метод наименьших квадратов или метод моментов. Предпочтение отдается тому из теоретических распределений, которое дает наилучшую сходимость с эмпирическими распределениями элементов волн, в частности, с эмпирической режимной функцией высот волн.

Г.4.5 Лучшую сходимость с эмпирическими данными распределение Вейбулла дает при незначительном содержании зыби в волнении. Логнормальное распределение приводит к удовлетворительному согласию с данными наблюдений при волнении с большим вкладом зыби.

Г.5 Методы определения расчетных характеристик волнового режима (редкой повторяемости) используются при условии, что базовый период расчетов/наблюдений ветрового волнения должен быть не менее 30 лет.

Г.5.1 Рекомендуется использование региональной модели атмосферы в соответствии с формулами (А.7) - (А.10) (приложение А) и модели ветрового волнения в соответствии с формулой (В.1) (приложение В). Модель ветрового волнения должна учитывать все известные процессы, влияющие на генерацию и распространение ветровых волн и зыби.

Г.5.2 Для определения расчетных характеристик волнового режима по годовым максимумам в пределах каждого года находят наибольшее значение высоты h_мах, и для дальнейшего анализа принимается последовательность значений h_мах,i, i = 1, ..., N, где h_мах,i - наибольшая высота волн в i-том году, N - общее число отобранных лет.

Г.5.3 Используя методы порядковых статистик, строят эмпирическую функцию распределения годовых максимумов:

(Г.3)

где i - порядковый номер высоты волны в ранжированной выборке (номер 1 присваивается наибольшей высоте волны за весь период времени). Эмпирическое распределение аппроксимируют распределением Гумбеля:

(Г.4)

где α и β - параметры распределения Гумбеля. Высоту волны h_T с заданным периодом повторяемости Т находят из соотношения

(Г.5)

Г.6 Метод определения расчетных характеристик ветрового волнения по наиболее сильным штормам - Пики-Выше-Порога (ПВП) - рекомендуется использовать в условиях сильной изменчивости числа штормов за год. Иными словами, этот метод предпочтителен для акваторий, в которых легко можно выделить «штормовые» годы с большим числом штормов и длительные периоды времени, когда штормов не наблюдается совсем.

Г.6.1 В рамках метода ПВП расчет ведется для конкретной точки акватории. Если надо определить расчетные характеристики ветрового волнения для нескольких точек акватории, то процедуру следует повторить для каждой из них.

Г.6.2 На первом этапе производится отбор наиболее сильных штормов за весь базовый период расчетов/наблюдений для конкретной точки акватории. Отбор штормов осуществляется путем анализа прибрежных и судовых наблюдений за ветром и волнами, а также анализа исторических синоптических карт. Оптимальным числом штормов, по которому проводится расчет, является значение порядка 30 - 40.

Г.6.3 На втором этапе по модели ветрового волнения в соответствии с формулой (В.1) (приложение В) в каждом шторме рассчитывают элементы волн. В пределах каждого шторма находят наибольшее значение высоты, и для дальнейшего анализа принимается последовательность значений; i = 1, …, N, где h_мax,i - наибольшая средняя высота волн в i-том шторме, N - общее число отобранных штормов.

Г.6.4 Используя методы порядковых статистик, строят эмпирическую функцию распределения наибольших значений высот волн в штормах:

(Г.6)

где i - порядковый номер высоты волны в ранжированной выборке (номер 1 присваивается высоте волны в наиболее сильном шторме). Эмпирическое распределение рекомендуется аппроксимировать распределением Вейбулла (Г.1).

Г.6.5 Свертка полученной функции распределения наибольших высот волн в штормах с функцией числа сильных штормов за год есть функция распределения наибольших высот волн за год

Fy(hmax) = 1 - exp[-LFs(hmax)],

(Г.7)

где L - среднее число сильных штормов за год.

Высоту волны с заданным периодом повторяемости Т находят из соотношения

(Г.8)

Библиография

[1] Дианский Н.А. Моделирование циркуляции океана и исследование его реакции на короткопериодные и долгопериодные атмосферные воздействия. М.: Физматлит, 2013. - 272 с.

[2] Ветер, волны и морские порты. Ред. Ю.М. Крылов. Л.: Гидрометеоиздат, 1986. - 262 с.

[3] Лаппо Д.Д., Стрекалов С.С., Завьялов В.К. Нагрузки и воздействия ветровых волн на гидротехнические сооружения. Теория. Инженерные методы. Расчеты. ВНИИГ им. Б.Е. Веденеева. Л., 1990. - 432 с.

[4] The WAM Model - a third generation ocean wave prediction model. The WAMDI Group. - J.Phys.Ocean. - vol.18, 1988.

[5] Кабатченко И.М. Ветровое волнение. Курс Лекций. М.: Альтаир, 2015. - 98 с.

[6] Абузяров З.К., Нестеров Е.С., Лукин А.А., Давидан И.Н., Кабатченко И.М., Дымов В.И., Вражкин А.Н. Режим, диагноз и прогноз ветрового волнения в океанах и морях. М.: Информполиграф, 2013. - 292 с.

[7] Проблемы исследования и математического моделирования ветрового волнения. Ред. И.Н. Давидана. C.-П.: Гидрометеоиздат, 1995. - 472 с.

[8] Лаврёнов И.В. Математическое моделирование ветрового волнения в пространственно-неоднородном океане. C.-П.: Гидрометеоиздат, 1998. - 500 с.

[9] Захаров В.Е., Манаков С.В., Новиков С.П., Питаевский Л.П. Теория солитонов: Метод обратной задачи. М.: Наука, 1980. - 320 с.

[10] Полников В.Г. Нелинейная теория случайного поля волн на воде. М.: Ленанд, 2007. - 408 с.

Ключевые слова: руководство, метод, расчет, ветровое волнение, море, элементы волн, режим волнения, статистические характеристики, моделирование

Лист регистрации изменений