Методические указания
по расчету радиационной обстановки в окружающей среде и ожидаемого облучения
населения при кратковременных выбросах радиоактивных веществ в атмосферу МПА-98
(утв. приказом Министра РФ по атомной энергии 30 декабря 1998 г.)
Введены впервые
Введение
Настоящие «Методические указания по расчету радиационной обстановки в окружающей среде и ожидаемого облучения населения при кратковременных выбросах радиоактивных веществ в атмосферу» разработаны в соответствии с Законами Российской Федерации «Об охране окружающей природной среды», «О санитарно-эпидемиологическом благополучии населения», «Об использовании атомной энергии» и «Об экологической экспертизе», «Нормами радиационной безопасности НРБ-96».
Концепция документа построена с учетом требований отечественных нормативных документов и рекомендаций международных организаций (МКРЗ, МАГАТЭ и ВОЗ), мирового опыта и практики, терминов и определений. Документ в первую очередь ориентирован на действующую в Российской Федерации нормативную базу, но вместе с тем содержит формулы, позволяющие производить расчеты как в терминах эффективных, так и эквивалентных доз. Табличный же материал, в соответствии с НРБ-96, представлен дозовыми коэффициентами перехода в терминах эффективных доз.
Документ содержит рекомендации по расчету радиационной обстановки на местности и ожидаемых доз облучения населения в результате разовых выбросов в атмосферу в произвольные, заранее не запланированные моменты времени. Предполагается, что выброс может произойти в любой, самый неблагоприятный для формирования доз облучения момент времени, поэтому предложенная методология позволяет получить максимально возможные оценки.
Термин «максимально возможная оценка» предполагает не запредельную величину выброса. Он означает, что из всех возможных условий формирования радиационной обстановки выбирается наихудший вариант, приводящий к наибольшим дозам облучения. При этом, конкретные условия формирования доз (прежде всего условия рассеяния выброса), приводящие к таким экстремальным оценкам, для разных точек местности могут быть различными. Так, в непосредственной близости от источника выброса наиболее опасны штилевые условия. На сравнительно небольшом удалении - конвективные (неустойчивые) условия. На большем расстоянии - стабильные категории погоды.
В настоящем документе аварийные поля концентраций в воздухе и выпадений на местности предложено представлять функционалом, являющимся максимально возможной реализацией этих характеристик при всех возможных условиях рассеяния выбросов, связанных с погодными условиями. Ранее, для оценки воздействия проектных повышенных выбросов обычно использовали расчет только одного (и часто не самого тяжелого) сценария рассеяния выбросов. Например, предполагали, что в момент выброса реализовалась категория F рассеяния выбросов. В лучшем случае дополнительно рассматривали еще 1 - 2 сценария. Но такой подход не позволял судить о возможных неблагоприятных последствиях на всей окружающей территории. Нужна экстремальная «огибающая» всех возможных сценариев рассеяния, представляющая наихудшие последствия в каждой точке местности. Методология нахождения такой «огибающей» и является предметом данного документа.
Область применения Методических указаний ограничивается выбросами, не сопровождающимися большими тепловыделениями, приводящими к подъему облака на большую высоту за пределы пограничного слоя атмосферы. Такие выбросы возникают при проектных авариях и инцидентах небольшого масштаба по системе классификации аварий МАГАТЭ, во время дезактивации оборудования, при планово-предупредительных и разного рода ремонтных работах. Их отличительной особенностью является то, что они не планируются заранее, а могут произойти неожиданно, в любой момент времени.
Практически все нормативные документы США, Канады, Англии, ФРГ и других стран, а также документы МАГАТЭ при расчетах последствий небольших аварий, связанных с выбросом радионуклидов в атмосферу и не приводящих к выбросам больших объемов газо-воздушной смеси и тепла, при проектных расчетах последствий проектных аварий рекомендуют использовать хорошо проверенную на практике гауссову модель атмосферной диффузии надлежащей (наилучшим образом подходящей для данных условий) модификации. Имеющееся изобилие более сложных моделей рассеяния аварийных выбросов в атмосфере (различные градиентные модели переноса, лагранжевы модели, 3-х мерные боксовые и иные модели диффузии) возможно могут быть полезны при управлении реальной аварией, но они малопригодны для проектных расчетов и при авариях малого масштаба, так как менее достоверны и требуют большего числа трудно измеряемых параметров. Гауссова же модель для проектных расчетов подходит идеально.
В число решаемых с помощью данных Методических указаний задач, наряду с прямыми расчетами последствий проектных выбросов, входят также задачи расчета разнообразных зон планирования, а возможно и санитарно-защитных зон.
Наибольшие уровни воздействия на окружающую среду (правда на небольших расстояниях от источника выброса) возникают при штилях и слабом ветре. Слабым при этом считается такой минимальный ветер, когда вместо сносимой по ветру струи в районе источника выброса образуется штилевое облако накапливающихся в воздухе загрязняющих веществ. Расчет диффузии при штилевых условиях в научной литературе представлен весьма скудно. Имеются лишь описания возможных подходов к решению задачи на основе той или другой теории диффузии. Главная трудность связана с тем, что при штилях не применима гипотеза Френкеля о пренебрежимости продольной диффузии по сравнению с переносом ветром. В настоящем документе представлены оригинальные аналитические формулы и схемы, пригодные для практических расчетов.
Документ содержит все необходимые формулы, значения и описание всех используемых параметров. Он может быть использован при «ручном счете», но основное назначение документа - служить основой разработки программного обеспечения расчетов на ЭВМ.
Глава 1. Общие положения
1.1. Цель создания, задачи и назначение Методических указаний
Цель создания настоящего документа - методическое обеспечение расчетов, позволяющих ответить на вопрос: какая радиационная обстановка может сложиться на местности в результате разового выброса радиоактивных веществ в атмосферу, если заранее неизвестно когда он (выброс) произойдет? Имеются ввиду не усредненные оценки, характерные, например, для задач вероятностного анализа безопасности, и не оценки последствий реального разового аварийного выброса с целью принятия решений. Предмет документа - возможные экстремальные оценки, используемые на разных стадиях проектирования (включая обоснование выбора места размещения предприятия); для разработки различных зон аварийного планирования, обоснования размеров санитарно-защитных зон и в других подобных случаях.
В число решаемых задач входят:
- расчеты возможных экстремальных значений факторов разбавления в атмосфере для разовых выбросов с учетом всех процессов очищения атмосферы и накопления дочерних радионуклидов, динамического и теплового подъема облака выброса по траектории, влияния рельефа местности и аэродинамической тени экранирующего здания для низких выбросов при ветреных условиях;
- расчеты возможных экстремальных значений интегралов концентрации радионуклидов выброса (материнских и образовавшихся во время переноса дочерних) в атмосферном воздухе на различных расстояниях от источника разового выброса с учетом возможности реализации как ветреных условий, так и штилей;
- расчеты возможных экстремальных значений интегральных выпадений на поверхность земли выброшенных радионуклидов (и их продуктов распада) на местности с учетом ветреных условий и штилей;
- расчет миграции выпавших радионуклидов по наземным пищевым цепочкам, производимый с учетом местных особенностей фенологии растений и рациона питания населения с целью получения экстремальных оценок коэффициента перехода «выпадение из атмосферы - поступление в организм человека» в случае выпадения в наиболее опасный момент вегетации растений;
- расчеты возможных экстремальных значений ожидаемых доз облучения населения от разовых радиоактивных выбросов в атмосферу.
Предлагаемая методология позволяет также получать экстремальные оценки разовых концентраций примеси в приземном слое атмосферы при наиболее неблагоприятных условиях рассеяния непрерывных выбросов при работе предприятий в номинале (при непрерывных выбросах).
Документ содержит формулы и таблицы исходных данных, необходимые как для упрощенных экстремальных оценок интегралов концентрации радионуклидов выброса в воздухе, выпадений их на почву и ожидаемых доз облучения в точке максимума их реализации, так и полный набор формул, позволяющих сделать полноценные расчеты перечисленных характеристик в различных точках местности с учетом характерных метеоусловий (устанавливаемых по циклу наблюдений не менее 3-х лет) и других особенностей формирования радиационной обстановки и доз облучения населения, включая ветреные и штилевые условия рассеяния выбросов.
Упрощенные оценки характеристик радиационной обстановки в точке максимума их реализации возможны только для ветреных условий. Они проводятся методом «ручного счета». Для штилей же простых формул расчета рассеяния примеси в атмосфере не существует.
Проведение уточненных расчетов с учетом всех особенностей рассеяния выбросов и формирования доз облучения населения ориентировано на применение ЭВМ. Объем представленного в настоящем документе материала достаточен для разработки полноценных программ расчета по всем аспектам рассматриваемой здесь проблемы, а также для проведения сертификации создаваемого программного обеспечения расчетов.
1.2. Область применения
Настоящие методические указания могут применяться для:
- анализа последствий разовых выбросов при планово-предупредительных работах, связанных, например, с дезактивацией основного оборудования и помещений, или в других похожих штатных ситуациях, предусмотренных регламентом работы, при которых производятся разовые выбросы радиоактивных веществ в атмосферу;
- оценки радиационной обстановки на местности, которая может сложиться при проектных авариях;
- проектирования защитных сооружений и установок, достаточных для ограничения проектных выбросов уровнями, при которых аварийными планами не предусматривается проведение каких-либо защитных мероприятий, или если таковые установлены, то непревышение пределов доз для МПА (максимальных проектных аварий);
- обоснования размера и конфигурации санитарно-защитной зоны вокруг предприятия;
- обоснования размеров и конфигурации зон аварийного планирования для аварийных выбросов, не сопровождающихся большими выбросами тепла и объема газо-воздушной смеси, которые могут привести к подъему облака выброса за пределы пограничного слоя атмосферы;
- для решения иных задач обоснования безопасности воздействия на окружающую среду проектируемых или реконструируемых предприятий (т.н. проблемы ОВОС).
1.3. Ограничения
Настоящие методические указания не предназначены для решения задач управления произошедшей аварией. В этих целях следует применять другие методы и модели оценки ситуации в реальном масштабе времени, учитывающие действительную траекторию распространения облака аварийного выброса и конфигурацию формируемого следа выпадений, период года (с точки зрения момента вегетации растений) и другие факторы влияния.
Действие методических указаний не распространяется и на так называемые «горячие» выбросы, сопровождающиеся большими тепловыделениями и(или) объемами выбрасываемой газо-воздушной смеси, которые приводят к быстрому подъему облака выброса за пределы пограничного слоя атмосферы. Формулы, позволяющие оценить границу применимости и идентифицировать такие выбросы, в методических указаниях приводятся.
Расстояние от места выброса, где репрезентативны результаты расчетов по приведенным в методических указаниях формулам, не превосходит 30 км.
Приведенные в Приложении 1 формулы расчета коэффициентов перехода «разовые выпадения из атмосферы - поступление в организм человека» дают экстремальные оценки этих коэффициентов в любые моменты года, включая и наиболее «опасные» периоды вегетации кормовых и пищевых растений. Поскольку целью Методических указаний является получение экстремальных оценок, приведенные в Приложении 1 формулы не применимы в случае, если выброс и выпадения произошли вне вегетативного периода года, когда действующим путем загрязнения растений является только корневое усвоение выпавших радионуклидов. Приведенные в Приложении 1 формулы можно использовать только для целей прогнозирования максимально возможных последствий аварийных выбросов.
Глава 2. Принятая концепция расчета доз при кратковременных выбросах
2.1. Общая постановка задачи
Области применения настоящих методических указаний отличаются тем, что для них сценарием событий момент осуществления выброса не планируется. Он (выброс) может произойти в любой момент времени. Это прежде всего относится к разного рода авариям и инцидентам, которые происходят внезапно. Но к тому же классу относятся и разовые выбросы, производящиеся при разного рода ремонтных и планово-предупредительных работах. Даже если они предусмотрены регламентом, время их осуществления обычно определяется производственной необходимостью, а не погодными условиями.
При оценке возможных последствий таких выбросов необходимо ориентироваться на наихудшие условия их рассеяния в атмосфере и миграции в окружающей среде, то есть - на экстремальные (из совокупности возможных) условия формирования ожидаемых дозовых нагрузок на население.
Что касается миграции выпавших радионуклидов во внешней среде, то она существенно зависит от момента выпадения в течение года. Наиболее сильно зависимость от момента выпадения проявляется для пищевых цепочек, которые в большинстве случаев являются критическими путями облучения. Коэффициенты перехода Ks, м2, «выпадение из атмосферы - поступление в организм человека с пищевыми продуктами», определяемый отношением (5.21) зависит от стадии вегетации растений в момент выпадения радионуклидов. Причем, для разных растений максимум этого коэффициент достигается в различные моменты выпадения (обычно это момент сбора урожая, который различен для разных культур). Физический смысл коэффициентов перехода Ks - интеграл перорального поступления данного радионуклида в организм человека (Бк) при разовом его выпадении плотностью 1 Бк/м2.
Возможны два подхода к расчету миграции:
1) оценка максимально возможных значений коэффициента перехода Ks «выпадения из атмосферы - пероральное поступление в организм человека» для каждой отдельно взятой пищевой цепи с последующим суммированием полученных таким образом экстремальных оценок для всех цепочек, не взирая на то, что для каждой из них максимумы реализации могут приходится на различные моменты времени выпадения;
2) расчет суммарного по всем пищевым цепочкам коэффициента перехода Ks в зависимости от момента выпадения в течение вегетативного периода года и поиск его максимума для совокупности всех характерных для данной местности пищевых путей.
Первый подход более прост, но практически всегда дает завышенные оценки.
Второй способ дает более реальные оценки, но более сложен и неоднозначен. Трудность в том, что для различных радионуклидов моменты выпадения, дающие максимальные оценки перорального поступления, могут быть разными. Например, для короткоживущих радионуклидов критической цепочкой обычно является поступление с листовыми овощами (салатом, зеленым луком, щавелем и т.п.), которые потребляются «с грядки», и максимум потребления которых приходится на начало лета. Долгоживущие же нуклиды накапливаются в наибольшей степени в долго созревающих растениях, урожай которых собирается в конце лета. При этом, для переменного состава выпадений максимальные оценки совокупного для всех радионуклидов выброса и получаемого по всем пищевым цепочкам внутреннего облучения могут оказаться неопределенными. Поэтому, для практических задач предпочтительным является 1-й подход к оценке миграции по пищевым цепям, который дает хотя и завышенные, но зато определенные оценки пероральных поступлений и ожидаемых доз.
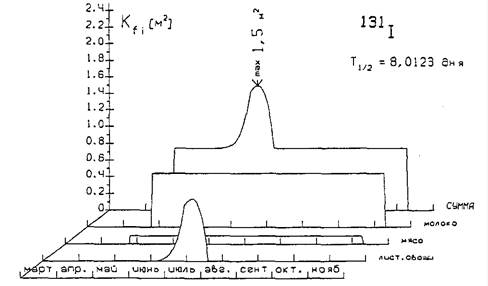
Ситуацию иллюстрируют рис. 1, 2 и 3, на которых изображены зависимости коэффициентов перехода «выпадение из атмосферы - поступление в организм человека» с основными дозообразующими пищевыми продуктами» Ks, м2, от времени выпадения для 131I, 137Cs и 106Ru. Они рассчитаны по формулам Приложения 1. Разница между максимумами их реализации для приведенных радионуклидов достигает 1,5 месяцев.
Рис. 1. Зависимость коэффициента перехода Ks, м2, от момента выпадения 131I для основных дозообразующих продуктов питания (по Московской области)
Рис. 2. Зависимость коэффициента перехода Ks, м2, от момента выпадения 137Cs для основных дозообразующих продуктов питания (по Московской области)
Рис. 3. Зависимость коэффициента перехода Ks, м2, от момента выпадения 106Ru для основных дозообразующих продуктов питания (по Московской области)
Приведенные коэффициенты для животных цепочек (молока и мяса) рассчитаны с учетом как пастбищного, так и стойлового периодов содержания животных, когда потребляется корм, загрязненный в вегетативный период года.
На рассеяние примеси в атмосфере и формирование следа выпадений на земле влияют следующие факторы:
1) высота и продолжительность выброса;
2) скорость ветра и термическая стратификация атмосферы (т.н. категория устойчивости атмосферы);
3) траектория подъема облака выброса, которая зависит от объема и «перегрева» по отношению к окружающему атмосферному воздуху выбрасываемой газо-воздушной смеси;
4) для «низких» выбросов - высота и эффективное сечение здания с которого осуществляется выброс (его аэродинамическая тень);
5) дисперсность выброшенных аэрозолей, а также наличие в момент выброса, тип и интенсивность осадков.
Последний фактор на небольших расстояниях от места выброса существенно влияет только на формирование следа выпадений. В частности, при наличии осадков, максимум выпадений может сформироваться непосредственно под местом выброса, даже если выброс был «приподнятым» и приземные концентрации примеси под ним были равны нулю.
Из прочих факторов на рассеяние весьма существенно влияет третий. Обычно его влияние недооценивают. Используя понятие «эффективная высота подъема облака», игнорируют таким образом траекторию подъема облака выброса. Особенно ее влияние существенно для неустойчивых (конвективных) условий рассеяния примеси, при которых, строго говоря, понятие «эффективная высота подъема облака выброса» вообще неприемлемо. При таких условиях «теплые» выбросы поднимаются до ближайшего слоя инверсии профиля температуры воздуха, который может быть очень высок (т.н. инверсионной крышки). «Холодные» же выбросы (перегрев которых по отношению к окружающему атмосферному воздуху отрицателен) в этом случае опускаются до уровня земли.
Всевозможные условия действия всех перечисленных факторов приводят к тому, что на разных расстояниях от точки выброса «опасными» могут быть различные их реализации. Так, в непосредственной близости от места выброса наиболее опасны штилевые условия. На больших расстояниях - устойчивые условия при холодной погоде, при которых перегрев выбрасываемой газо-воздушной смеси максимален. На малых расстояниях - неустойчивые условия рассеяния выбросов.
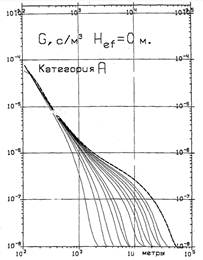
На рис. 4 в качестве примера представлена серия кривых, представляющих зависимость фактора разбавления от расстояния от эпицентра выброса через трубу высотой 100 м 150000 м3/час нагретой до 22 °С газо-воздушной смеси. Выброс экранировался 60 м зданием эффективным сечением 6000 м2. Каждая кривая здесь представляет собой реализацию разового фактора разбавления в атмосфере G, с/м3, (отношения временного интеграла приземной концентрации к величине выброса примеси), для одного наблюдения. Весь набор кривых рассчитан по 3-х годичному циклу наблюдений на одной из метеостанций Управления гидрометеослужбы России по стандартной 8-срочной (8 раз в сутки) сетке наблюдений по формулам настоящих указаний. Разнообразие кривых обусловлено не только различными реализациями скоростей ветра и категорий устойчивости атмосферы. Сильно также влияние разнообразия температуры атмосферного воздуха, которое приводит к значительному разбросу теплового подъема (или наоборот, опускания) облака выброса. Вблизи от эпицентра выброса куполообразные профили фактора разбавления обусловлены штилями разной продолжительности, во время которых происходит накопление выбрасываемой примеси вокруг источника без переноса ее ветром.
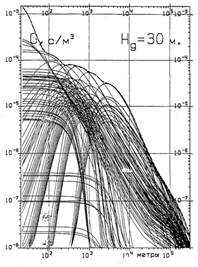
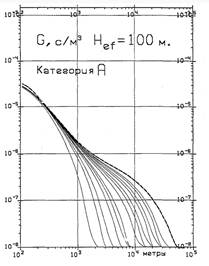
На рис. 5 приводится аналогичная серия кривых при выбросе на высоте 30 м, при прочих условиях формирования предыдущей серии кривых, включая экранирование зданием. При этом, несмотря на влияние аэродинамической тени за зданием, удаленные максимумы возникают из-за теплового подъема выбросов.
На обоих рисунках видно, что реализующееся многообразие условий рассеяния образует ограниченную сверху совокупность кривых фактора разбавления в атмосфере, что существует общая огибающая семейства таких кривых, представляющая их верхнюю грань и ограничивающая область возможной реализации этого параметра, а следовательно и доз облучения. Установление вида такой экстремальной огибающей поверхности фактически решает все поставленные в данном документе задачи. По существу это и является главной целью настоящих методических указаний.
На рис. 4 и 5 собраны кривые для всех направлений ветра. Различие между ними не делалось. Если же построить аналогичные серии кривых для отдельных секторов направления ветра, то их «огибающие» могут оказаться разными. Это обусловлено тем, что ветры разных направлений связаны с различными воздушными массами и отличаются разными условиями рассеяния. Так, северный ветер как правило связан с более холодным воздухом. Для него характерны более устойчивые категории рассеяния и более выраженный тепловой подъем выбросов (но вместе с тем ограниченный сравнительно низким предельным подъемом облака).
Рис. 4. Диапазон реализаций разового фактора разбавления для приподнятого (100 м) выброса, рассчитанный по 3-х годичной статистике метеонаблюдений
Южные ветра приводят к более интенсивному перемешиванию атмосферного воздуха. Неустойчивые условия рассеяния для них более часты. Это находит отражение и для статистики экстремальных условий, формирующих экстремальные «огибающие» семейств кривых рассеяния выбросов для разных направлений. В результате на плоскости формируются экстремальные «огибающие» поверхности, являющиеся верхней границей всех реализовавшихся за срок наблюдения характеристик рассеяния и ожидаемых доз облучения.
Рис. 5. Диапазон реалeизаций разового фактора разбавления для низкого (30 м) выброса, рассчитанный по 3-х годичной статистике метеонаблюдений
Если имеется несколько возможных источников разовых выбросов, то при оценки возможных радиационных последствий необходимо строить общую для всех таких источников (и возможных «сценариев» формирования разовых выбросов для каждого из них) экстремальную поверхность характеристик загрязнения и ожидаемых доз облучения. С учетом вышесказанного она может оказаться весьма разнообразной.
На рис. 6 и 7 в качестве примера приведены оценки распределения ожидаемых эквивалентных доз на щитовидную железу взрослого человека от выбросов трех расположенных вблизи друг от друга источников высотой по 100 м (на рис. 6) и 30 м (на рис. 7), с прочими условиями выброса, соответствующими кривым рис. 4 и 5. Разовые выбросы в обоих случаях для 3-х источников приняты равными 1, 1.3 и 0.8 Ки 131I. Дозы рассчитаны для всех путей облучения, включая пищевые цепочки. Утолщенными линиями проведены изодозы 1,5 сЗв (бэр), соответствующие пределу годовой дозы на щитовидную железу отдельного лица из населения согласно рекомендациям МКРЗ N 61.
Расчет миграции по пищевым путям проводился по 1-му консервативному варианту оценок, описанному на стр. 3 настоящих указаний. Согласно ему искались оценки экстремальных значений коэффициентов перехода «выпадения из атмосферы - пероральное поступление в организм человека» Ks, м2, для каждой отдельно взятой пищевой цепи с последующим суммированием таким образом полученных оценок для всех продуктов питания. Масштаб изображенных на рисунках карт, несмотря на записи в угловых штампах, произвольно изменен, но длинна стороны ячейки сетки условных координат соответствует на местности 2 км. Ориентация карт по вертикали с юга (низ карты) на север (ее верх).
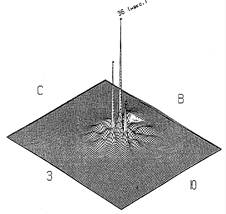
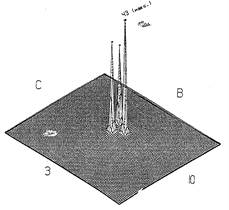
На рис. 8 и 9 даны трехмерные сеточные изображения поверхности экстремально возможных оценок ожидаемых эквивалентных доз, соответствующие рис. 7 и 8. Резкие пики в точках выброса обусловлены дозами, реализующимися при штилевых условиях. Причем при наихудших из возможных условий их реализации: при жаркой погоде, когда на предприятии работают кондиционеры и охлаждающие калориферы, и температура выбрасываемой газо-воздушной смеси имеет максимальный отрицательный перепад температуры по отношению к нагретому окружающему атмосферному воздуху.
Задача оценки радиационной обстановки на местности, которая может сложиться в результате разового радиоактивного выброса в атмосферу, в настоящем документе ставится так: для каждой точки местности среди возможных условий рассеяния выброса и формирования ожидаемых доз облучения ищутся те, которые приводят к максимальным значениям последних. При этом, в разных точках местности полученные результаты могут соответствовать различным, но обязательно наиболее «опасным» условиям.
Такие экстремальные оценки при разовых выбросах можно получать следующими способами:
1) расчетом «огибающей» по реальному ряду наблюдений за длительный срок;
2) на основе статистических (по интервалу доверительной вероятности) оценок возможных экстремальных реализаций параметров, влияющих на рассеяние выбросов в атмосфере и формирование доз облучения;
3) методом «ручного счета» на основе упрощенных формул оценки максимумов факторов разбавления, коэффициентов перехода и других характеристик.
Первый способ оценки проиллюстрирован предыдущими рисунками. Согласно ему в течение какого-либо, достаточно продолжительного периода последовательно перебирают все реализовавшиеся условия рассеяния, и с учетом всех факторов влияния для каждой точки местности ищется максимальная реализация искомой характеристики (интеграла концентрации в воздухе, выпадения на землю, ожидаемых доз облучения).
Рис. 6. Распределение на местности экстремально возможных оценок ожидаемых эквивалентных доз на щитовидную железу взрослого человека от разового выброса 1, 1.3 и 0.8 Ки 131I, произведенного на высоте 100 м
Рис. 7. Распределение на местности экстремально возможных оценок ожидаемых эквивалентных доз на щитовидную железу взрослого человека от разового выброса 1, 1.3 и 0.8 Ки 131I, произведенного на высоте 30 м (с учетом экранирования зданием размерениями 60×100 м).
Рис. 8. Изомерия экстремальной поверхности ожидаемых доз, изображенной на рис. 6
Рис. 9. Изомерия экстремальной поверхности ожидаемых доз, изображенной на рис. 7
Это абсолютный подход, и за длительный срок наблюдения, достаточный, чтобы все реализовавшиеся условия можно было считать генеральной совокупностью, он дает точную оценку искомой экстремальной «огибающей» поверхности распределения рассматриваемых характеристик на местности. Вопрос лишь в том, какой срок наблюдения достаточен. При решении этого вопроса следует иметь ввиду, что практически все редкие экстремальные метеоусловия, статистика которых обычно рассматривается при проектировании предприятий, такие как ураганы, смерчи и др. не приводят к экстремальным оценкам радиационной обстановки в районе расположения источника выброса. Наоборот, условия рассеяния при них наиболее благоприятны в том смысле, что дают минимальные дозы. С точки зрения формирования радиационной обстановки на местности «опасными» следует считать экстремальные оценки температуры атмосферного воздуха и продолжительность штиля, во время которого происходит накопление выбрасываемой примеси вблизи места выброса.
Оценки воздействия экстремумов температуры не очень существенны. Для низких температур атмосферного воздуха перепад температуры для выбрасываемой газо-воздушной смеси максимален, что приводит к быстрому тепловому подъему облака выброса, а следовательно и к более низким дозам облучения. Но обычно такие условия реализуются зимой во время устойчивых категорий рассеяния, когда подъем «теплого» облака выброса ограничен отрицательной работой сил плавучести. Для предельно же высоких температур атмосферного воздуха летом характерны «холодные» выбросы, при которых перепад температур выбрасываемой газо-воздушной смеси и окружающего атмосферного воздуха отрицателен. Обычно в это время в атмосфере формируются неустойчивые (конвективные) условия рассеяния, которые приводят к быстрому опусканию облака выброса до уровня земли. При этом больший отрицательный перепад температур приводит только к увеличению скорости этого процесса. Поэтому начиная с какой-то величины, дальнейшее увеличение отрицательного «перегрева» выбрасываемой смеси не приводит к ухудшению условий рассеяния. Опуститься ниже земли облако выброса не может. Что касается продолжительности штилевых условий, то влияние этого фактора на временной интеграл концентрации в воздухе вблизи источника выбросов значимо. Оно ограничено только процессами очищения атмосферы (т.н. «истощения» облака выброса).
Исходя из вышесказанного и проведенных нами численных экспериментов с рядами наблюдений разной продолжительности, можно сделать вывод, что для реализации предлагаемого способа достаточна 3-х годичная стандартная 8-срочная статистика метеонаблюдений. Исключение возможно составляет оценка наибольшей продолжительности штилевых условий. Следует заметить, что годовая статистика наблюдений может оказаться недостаточной, так как в случае холодного лета не будут реализованы наихудшие условия, связанные с «холодными» выбросами при жаркой погоде.
Второй подход к экстремальным оценкам предполагает, что используется статистика наблюдений входных параметров, влияющих на условия рассеяния выбросов. По ней определяются такие их характеристики, как дисперсия и среднее, находятся максимальные значения, соответствующие установленному доверительному порогу вероятности их реализации (например 5 % за 30 лет и т.п.). Затем по найденным экстремальным значениям параметров производятся оценки «огибающих». Это перспективный, но к настоящему времени еще не разработанный метод.
В принципе такой подход может быть более экономичным с точки зрения объема вычислений, чек оценки «огибающей» по описанному выше 1-му способу. Главная трудность в том, что параметров влияющих на формирование радиационной обстановки много, а для разных точек местности их «опасный» набор может быть различен. Так, например, на близких расстояниях от источника опасны неустойчивые погодные категории, на удалении же наоборот - устойчивые. Увеличение температуры окружающего воздуха для неустойчивых условий может привести к наиболее опасным приземным концентрациям выбрасываемой примеси, а для устойчивых этот фактор несущественен и т.д. Поэтому в настоящее время второй подход может быть реализован (лишь частично, в комбинации с другими способами, при оценки лишь отдельных параметров. Например, таких, как продолжительность штилевых условий. Или, например, можно рассчитать единую «огибающую» для всех расстояний, как это сделано на рис. 4 и 5, и распространить ее на все направления ветра. Тогда вместо сложных конфигураций «огибающей» поверхности рис. 6 и 7 получится упрощенная, еще более «экстремальная», имеющая запас по некоторым направлениям, но с изодозами в виде концентрических крутов, поверхность. Зато объем вычислений будет меньше. Кроме того, за счет образовавшегося запаса будет меньше вероятность «недооценки» рассчитываемой характеристики для секторов с наименьшей повторяемостью направлений ветра, статистика наблюдений для которых может оказаться недостаточной.
Последний способ предполагает использование упрощенных формул. Их набор невелик и ограничивается только ветреными условиями. Как правило они дают оценки в точке максимума приземной концентрации, часто умалчивая, где этот максимум реализуется. Точность оценок по упрощенным формулам обычно лежит в пределах порядка величины. Наиболее полезное применение таких формул - это экспертиза разного рода работ, в которых были использованы оригинальные модели рассеяния.
2.2. Предположения и допущения
Предполагается, что:
- выброс кратковременный и его продолжительность настолько мала, что за время реализации условия рассеяния выбрасываемой примеси не меняются;
- оценки всех характеристик радиационной обстановки в каждой точке местности являются максимально возможными для совокупности разнообразных условий рассеяния выброса и формирования ожидаемых доз;
- имеется начальное разбавление
выброса, приводящее к тому, что удельная активность выбрасываемой
газо-воздушной смеси ![]() , Бк/м3, ограничена. Обычно
это означает, что вышедшая из оборудования активность изначально перемешивается
с воздухом внутри какого-либо помещения здания объемом Vo, м3. Последний можно определить по формуле
, Бк/м3, ограничена. Обычно
это означает, что вышедшая из оборудования активность изначально перемешивается
с воздухом внутри какого-либо помещения здания объемом Vo, м3. Последний можно определить по формуле
где Qo - интегральная величина выброса, Бк. По формуле (2.1) можно проводить и обратный расчет: удельной активности выбрасываемой смеси по объему помещения, где первоначально локализуются выбросы;
- выброс газо-воздушной смеси происходит не мгновенно, хлопком, а с некоторой конечной скоростью V, м3/сек. Возможны следующие варианты:
- выброс происходит через исправную штатную вентсистему. В этом случае объемная скорость выхода газо-воздушной смеси постоянна;
- выброс происходит не штатно, через проемы здания. При этом объемная скорость истечения газо-воздушной смеси V(t), м3/сек, уменьшаясь изменяется со временем. В этом случае, при расчетах высоты подъема облака предполагается, что объемная скорость выброса неизменна, равна ее значению в момент начала выброса и продолжается эффективное время
|
|
(2.2) |
где V(0) - скорость истечения в начальный момент выброса t = 0, м3/сек.
- термический подъем облака выброса происходит по
траектории. Его предельная величина при устойчивых условиях ограничена
рассчитываемой максимальной высотой подъема облака (в некоторых моделях ее
называют «эффективной высотой выброса»). Для неустойчивых и нейтральных условий
постепенный подъем облака выброса происходит до высоты слоя перемешивания
атмосферы ![]() (фактически - до границы пограничного
слоя атмосферы);
(фактически - до границы пограничного
слоя атмосферы);
- во время движения облака выброса и миграции выпавших радионуклидов во внешней среде происходит распад материнских нуклидов и накаливание дочерних изотопов;
- вертикальная дисперсия облака
ограничена максимальной величиной ![]() , связанной с высотой слоя
перемешивания атмосферы
, связанной с высотой слоя
перемешивания атмосферы ![]() формулой
формулой
|
|
(2.3) |
- след выпадений на почву формируется как за счет сухого осаждения выброшенных радиоактивных аэрозолей, так и при вымывания их осадками. Последнее приводит к значимым выпадениям под приподнятым источником выброса;
- наряду с тепловым и динамическим подъемом облака выброса происходит «проседание» центра масс его аэрозольной компоненты со скоростью гравитационного оседания аэрозолей Vs. Если дисперсность аэрозолей велика, то за счет этого эффекта и разных скоростей осаждения происходит расслоение облака - «тяжелые» аэрозоли больших размеров осаждаются на более близком расстоянии и быстрее легкой мелкодисперсной компоненты облака;
- при расчетах ожидаемых доз на территории промплощадки возможно только внешнее облучение от облака выброса и следа выпадений на землю, и внутреннее облучения от вдыхания радионуклидов во время прохождения облака выброса;
- при расчете ожидаемых доз в санитарно-защитной зоне в числе прочих следует учитывать и пищевой путь поступления радионуклидов при потребления местных продуктов питания, выращивание которых в санитарно-защитной зоне санитарными правилами ОСП-72/87 допускается.
Глава 3. Расчет экстремальных оценок рассеяния кратковременных выбросов в атмосфере и формирования следа выпадений при ветреных условиях
3.1. Общие формулы расчета рассеяния
Для решения круга задач, очерченных данным документом, наилучшей является гауссова модель атмосферной диффузии - наиболее популярная и чаще всего используемая модель в мире. Она рекомендована для практического применения всеми Международными организациями, включая: Всемирную метеорологическую организацию (ВМО), Международное агентство по атомной энергии (МАГАТЭ), Научный комитет по действию атомной радиации (НКДАР) ООН, Всемирную организацию здравоохранения (ВОЗ) и др. Нашла применение гауссова модель и в отечественных рекомендациях. Преимущество гауссовой модели атмосферной диффузии перед другими заключается в объеме использованного экспериментального материала и апробированности ее практически во всех районах мира. По степени надежности гауссова модель вне конкуренции. Положение таково, что фактически гауссова модель в области ее применимости стала эталонной при сравнительных расчетах по другим моделям диффузии примеси. Она удобна также сравнительной простотой и возможностью учитывать практически все факторы влияния. В ее оригинальном виде гауссова модель мало подходит для целей управления конкретной, уже случившейся аварией в реальном масштабе времени, так как является эйлеровой моделью. Например, она не позволяет учесть движение облака по траектории. Но для проектных расчетов на небольших расстояниях от источника выброса она подходит идеально.
Зависимость от времени приземной
концентрации (объемной активности) ![]() , Бк/м3, выбрасываемого
радионуклида r в атмосфере на оси траектории движения облака на
расстоянии х от точечного источника мгновенного (хлопком) выброса
рассчитывается по формуле
, Бк/м3, выбрасываемого
радионуклида r в атмосфере на оси траектории движения облака на
расстоянии х от точечного источника мгновенного (хлопком) выброса
рассчитывается по формуле
где Qo,r - величина мгновенного выброса радионуклида r, Бк; G'o,r - так называемый фактор разбавления мгновенного выброса в атмосфере, м-3. Его можно рассчитать по формуле
где h(x) - высота центра облака выброса над поверхностью земли на расстоянии x от точки выброса, м; u - скорость ветра на высоте выброса, м/с; Fr(x) - так называемый фактор истощения облака выброса для радионуклида r на расстоянии x по ветру (безразмерная величина, описывающая изменение интегрального количества выброшенного количества радионуклида r с расстоянием от места выброса, уменьшающегося за счет радиоактивного распада, сухого осаждения и вымывания его из облака осадками); σx, σy и σz - зависящие от расстояния дисперсии облака выброса в направлении движения облака по ветру х, в горизонтальном направлении поперек ветра у и в вертикальном направлении z. Это основные параметры гауссовой модели диффузии. Эмпирические формулы и более подробное описание их будет приведено ниже.
Формулы (3.1) и (3.2) дают динамику изменения приземной концентрации в точке x, расположенной на траектории движения центра облака выброса. Для оценки же радиационных последствий прохождения такого облака (интеграла ингаляционного поступления в организм человека, выпадений на почву, дозы от внешнего излучения прошедшего облака) необходимо знать временной интеграл концентрации в этой точке. Его находят, интегрируя формулу (3.1) по времени t. В результате, вместо формул (3.1) и (3.2) для временного интеграла концентрации Cv,r(x), Бк ∙ с/м3, получим следующие формулы
где
- временной интеграл от мгновенного фактора разбавления, с/м3, называемый также разовым фактором разбавления. Формулы (3.3) и (3.4) дают максимально возможные в данных условиях значения интеграла концентрации на расстоянии x от места выброса (на оси траектории движения, облака выброса).
Как будет показано в разделе 3.5, вымывание на землю
примеси, содержащейся в облаке выброса, во время выпадения осадков, зависит не
от приземной концентрации, а от ее интегрального содержания в столбе воздуха,
«промываемого» осадками на всем пути движения капель (или снежинок) через толщу
облака выброса. Поэтому для учета этого фактора требуется знание не приземной
концентрации примеси, а интеграл по вертикальному профилю ее распределения в
облаке ![]() , с/м2.Чтобы вычислить эту
величину, необходимо знать вертикальный профиль концентрации (или фактора
разбавления) в воздухе. Его можно получить из предыдущих формул, сделав замену
, с/м2.Чтобы вычислить эту
величину, необходимо знать вертикальный профиль концентрации (или фактора
разбавления) в воздухе. Его можно получить из предыдущих формул, сделав замену
где z - высота точки-рецептора (где ищутся концентрации) над уровнем земли, м.
Подставив (3.5) в формулу (3.4) и проинтегрировав по z от 0 (уровня земли) до ∞, получим искомую формулу для интеграла от разового фактора разбавления по вертикальной координате z
где Go,r(x,z) - разовый фактор разбавления концентрации на высоте z над уровнем земли, с/м3. Следует заметить, что вертикальные профили концентрации гауссовой модели, даваемые формулой (3.5), как правило не являются хорошими приближениями к реальным профилям. Но интеграл фактора разбавления по вертикальной координате (3.6) верен. Это особенность гауссовой модели диффузии.
Имеется одна особенность формулы (3.6): непосредственно под точечным источником (при х
= 0) дисперсия σy равна нулю, то
есть формула (3.6) в эпицентре выброса
дает для ![]() (и следовательно, для выпадений)
бесконечность.
(и следовательно, для выпадений)
бесконечность.
Для приподнятого выброса, когда h ≠ 0, значение разового фактора безопасности Go,r(0),
а вместе с ним и приземная концентрация примеси согласно формуле (3.4) под точкой выброса равны нулю. Иная
картина наблюдается, если рассмотреть наземный выброс, когда h = 0. В
этом случае мы также имеем бесконечность. Эта особенность связана с тем, что
понятие точечный источник абстрактно. Оно в частности предполагает, что в
момент выброса концентрация примеси в источнике равна бесконечности. В реальных
же случаях выброс всегда осуществляется с некоторой начальной концентрацией
(удельной активностью) ![]() .
.
Для учета этого эффекта наиболее
эффективен «метод виртуального источника», согласно которому предполагается,
что выброс осуществляется не точно в источнике, а на некотором начальном
расстоянии xb с подветренной стороны. Таком, чтобы к моменту прихода
центра облака выброса к источнику, концентрация примеси в центре облака была
точно равна ее первоначальной концентрации в выбрасываемой газо-воздушной
смеси. При этом рассеяние на начальном участке не показывается, а в формулы (3.1) - (3.6)
вместо x подставляется величина x + xb.
При этом, в точке x = 0, мы будем иметь значения Go,r(xb) и ![]() . Причем концентрация примеси в точке
выброса будет точно равна начальной концентрации в выбрасываемой смеси согласно
определения величины xb.
Величину «виртуального» сдвига xb находят решая трансцендентное уравнение, полученное
из (3.1) при x, t и h,
равных нулю, заменяя σx = σy.
. Причем концентрация примеси в точке
выброса будет точно равна начальной концентрации в выбрасываемой смеси согласно
определения величины xb.
Величину «виртуального» сдвига xb находят решая трансцендентное уравнение, полученное
из (3.1) при x, t и h,
равных нулю, заменяя σx = σy.
|
(2π)3/2 ∙ σy(xb)2 ∙ σz(xb) = Vo, |
(3.7) |
где Vo - некоторый объем, м3,
в котором еще до момента выброса изначально перемешивается вышедшая из
оборудования радиоактивность. Обычно это объем какого либо помещения, куда
выходит радиоактивность и из которого осуществляется выброс. Если оно не
известно, то этот параметр можно рассчитать по формуле (2.1) предыдущей главы, зная начальную концентрацию ![]() , Бк/м3, с которой начал
осуществляться выброс.
, Бк/м3, с которой начал
осуществляться выброс.
3.2. Расчет выпадений из облака на поверхность земли
Разовые выпадения на поверхность земли радионуклида r на расстоянии x от источника выброса рассчитываются по формуле
где Qo,r - величина разового выброса радионуклида r, Бк; Vg,r - его скорость сухого
осаждения на поверхность земли, м/с; Λr - постоянная вымывания примеси из атмосферы осадками, c-1; Go,r(x)
- разовый фактор разбавления примеси в приземном слое воздуха для r-го
радионуклида на расстоянии x/см. формулу (3.4)/, с/м3; ![]() - интеграл по вертикальной координате z
от зависящего от высоты разового фактора разбавления примеси для r-го
радионуклида, вычисляемого на расстоянии x по формуле (3.6). Методы расчета Vg,r и Λr будут
изложены в разделе 3.6.
- интеграл по вертикальной координате z
от зависящего от высоты разового фактора разбавления примеси для r-го
радионуклида, вычисляемого на расстоянии x по формуле (3.6). Методы расчета Vg,r и Λr будут
изложены в разделе 3.6.
В отдельных приложениях используются понятия факторов сухого и влажного осаждения, м, которые соответственно определяются равенствами
|
Ψr(x) = Vg,r ∙ Go,r(x), |
(3.9) |
|
|
(3.10) |
При этом формула (3.8) принимает вид
|
Cs,r(x) = Qo,r ∙ [Ψr(x) + Ψr(x)]. |
(3.11) |
При наличии значимого вклада образующихся при переносе дочерних радионуклидов, вместо формулы (3.8) расчеты разовых выпадений радионуклида r надлежит проводить по следующей формуле, справедливой при любом распределении радионуклидов в атмосфере
где ![]() - временной интеграл концентрация
радионуклидов r в приземном слое атмосферы на расстоянии x от
источника, Бк ∙ с/м3, рассчитываемый по аналогичной (3.3) и (3.4) формуле
- временной интеграл концентрация
радионуклидов r в приземном слое атмосферы на расстоянии x от
источника, Бк ∙ с/м3, рассчитываемый по аналогичной (3.3) и (3.4) формуле
|
|
(3.13) |
а ![]() - интеграл по вертикальной координате z
от распределенной по высоте (вертикальному профилю) концентрации в точке x.
Последний рассчитывается аналогично (3.6)
по формуле
- интеграл по вертикальной координате z
от распределенной по высоте (вертикальному профилю) концентрации в точке x.
Последний рассчитывается аналогично (3.6)
по формуле
|
|
(3.14) |
В этих формулах Qo,r - интеграл содержания в облаке выброса на расстоянии x радионуклида r, рассчитанного с учетом истощения облака, а если это дочерний нуклид, то и накопления за время движения облака при распаде его материнских предшественников. Методы расчета этой величины будут изложены в разделе 3.5. Применяя последние формулы можно учесть вклад короткоживущих дочерних нуклидов, находящихся в равновесии с их материнскими предшественниками. Например, короткоживущих гамма-излучающих криптонов и 138Xe.
3.3. Расчет коэффициентов дисперсии σy и σz
Существующие способы оценки коэффициентов дисперсии σy и σz, входящие в формулы предыдущих разделов, определяются в конечном счете путем сопоставления результатов измерения объемных активностей примеси в воздухе от реальных источников с расчетами по теоретическим формулам гауссовой модели атмосферной диффузии на основе той или иной системы классификации погодных условий. Происходит постепенное накопление данных. Более поздние разработки обычно учитывают предшествующий экспериментальный материал, который сохраняется в международных и национальных информационных банках данных. В настоящих указаниях используется оригинальная аппроксимация наиболее часто используемых формул Смита-Хоскера (для σz) и Бриггса (для σy), согласно которой поперечную σy и вертикальную σz дисперсии при кратковременных выбросах рассчитывают по следующей общей формуле, предложенной Эйри
|
|
(3.15) |
где х - расстояние от источника выброса, м;
![]()
a1(P) = Pα1 + α2 ∙ P + α3 ∙ P2;
α2(Р) = β1 + β2 ∙ P + β3 ∙ P2.
b(z0,P) = 10b1(P) + b1(P) ∙ lg(100 ∙ z0) + b1(P) ∙ [lg(100 ∙ z0)]2;
b1(P) = γ1 + γ2 ∙ P + γ3 ∙ P2;
b2(P) = δ1 + δ2 ∙ P + δ3 ∙ P2;
b3(P) = b3;
P - параметр устойчивости Смита, значения которого для разных категорий устойчивости атмосферы приведены в табл. 3.1;
z0 - т.н. высота шероховатости подстилающей поверхности (параметр, зависящий от величины сил трения воздуха о поверхности земли, представленный в табл. 3.2). В формулах имеет размерность см.
Значения остальных параметров для расчета σy(x) и σz(x) представлены в табл. 3.3.
Формула (3.15) достаточно универсальна и учитывает особенности рассеяния над местностями с различными типами поверхности земли.
При расчетах σz(x) следует учесть, что ее величина ограничена предельной
величиной ![]() , зависящей от толщины слоя
перемешивания атмосферы, различной для разных категорий устойчивости. Значения
, зависящей от толщины слоя
перемешивания атмосферы, различной для разных категорий устойчивости. Значения ![]() даны в табл. 3.4.
даны в табл. 3.4.
Таблица 3.1. Соотношение между категориями устойчивости атмосферы и значениями параметра Смита Р
|
Категории устойчивости |
А |
В |
С |
D |
Е |
F |
G |
|
Интервал изменения Р |
0 - 1 |
1 - 2 |
2 - 3 |
3 - 4 |
4 - 5 |
5 - 6 |
6 - 7 |
|
Характерные значение Р для категорий устойчивости |
0,5 |
1,5 |
2,5 |
3,5 |
4,5 |
5,5 |
6,5 |
Таблица 3.2. Высота шероховатости z0 для различных типов подстилающей поверхности
|
Микрорельеф поверхности |
z0, см |
|
Снег, газон высотой до 1 см |
0,1 |
|
Скошенная и низкая трава до 15 см |
0,6 - 2 |
|
Высокая трава до 60 см |
4 - 9 |
|
Неоднородная поверхность с чередующимися участками травы, кустарника и т.п. |
10 - 20 |
|
Парк, лес высотой до 10 м |
20 - 100 |
|
Городские постройки |
400 |
Таблица 3.3. Значения параметров для расчета σy(x) и σz(x)
|
Параметр |
Значения параметров |
|
|
для расчета σy(x) |
для расчета σz(x) |
|
|
a0 |
70,6 |
145 |
|
α1 |
0,521 |
1,03 |
|
α2 |
0,340 |
-0,0766 |
|
α3 |
2,47 ∙ 10-3 |
0,0502 |
|
β1 |
-0,295 |
-0,272 |
|
β2 |
-0,0556 |
-0,0117 |
|
β3 |
-9,18 ∙ 10-3 |
-2,91 ∙ 10-3 |
|
γ1 |
-3,14 |
-2,44 |
|
γ2 |
0,343 |
0,481 |
|
γ3 |
0,0107 |
0,0153 |
|
δ1 |
0,307 |
-8,79 ∙ 10-3 |
|
δ2 |
-0,0557 |
-0,0269 |
|
δ3 |
-9,14 ∙ 10-3 |
1,27 ∙ 10-3 |
|
b3 |
0. |
-7,04 ∙ 10-3 |
Таблица 3.4. Значения верхней границы ![]() для различных категорий
устойчивости
для различных категорий
устойчивости
|
Категория устойчивости |
|
Категория устойчивости |
|
|
А |
1600 |
Е |
250 |
|
B |
1200 |
F |
200 |
|
С |
800 |
G |
160 |
|
D |
500 |
|
|
Достоинством формулы (3.15) расчета дисперсий σy и σz является:
- непрерывная зависимость σy(x) и σz(x) от высоты шероховатости z0;
- в аппроксимация (3.15) включены параметризации Бриггса для σy(x) над городской застройкой;
- непрерывная зависимость от параметра устойчивости Смита Р, что позволяет получить непрерывный переход между категориями устойчивости;
- представление (3.15) позволяет получить аналитические формулы для расчета разового фактора разбавления при штиле и слабом ветре (см. Приложение 2).
3.4. Условия выброса: учет влияния зданий
Влияние зданий существенно только при ветреных условиях. Оно выражается в искажении ветрового потока вблизи них и образования зоны циркуляции воздуха за зданием (так называемой аэродинамической тени). При этом какая-то часть или вся выбрасываемая примесь может попадать в зону тени, перемешиваться там и быстро достигать поверхности земли. В результате за зданием образуется объемный источник. Степень вовлечения выбрасываемой примеси в зону тени зависит от места и высоты расположения устья трубы по отношению к зданию. Если источник выброса настолько высок, что линии тока, проходящие через точку выброса не попадают в зону влияния здания, то перенос примеси не искажается, и выбросы не будут вовлечены в зону аэродинамической тени. При более низких источниках часть примеси окажется вовлеченной в зону тени, а часть переносится по неискаженной траектории. Выбросы из фонарей, отдушин, шахт, расположенных на крыше зданий, из окон и других проемов обычно полностью попадают в зону тени за зданием.
Выбросы из высоких труб. Высокими считают трубы, выбросы из которых проходят выше зоны смещения потока воздуха зданием. Для таких выбросов влияние зданий не существенно. В качестве грубого приближения высокими можно считать трубы, устье которых выше, чем двойная высота наиболее высокого из ближайших зданий.
Выброс на уровне крыши зданий. При выбросе из фонарей и шахт, расположенных на крыше, из окон и других проемов здания, расположенных на разных уровнях, или из расположенных в непосредственной близости с подветренной стороны от него других источников выброса, высота которых ниже высоты здания, примесь будет попадать в зону аэродинамической тени, перемешиваться в турбулентной струе, создаваемой потоком воздуха при обтекании здания и быстро достигать поверхности земли.
Аналогичная картина будет наблюдаться, если выбросы осуществляются из низкой трубы, но облако встречает расположенное вблизи высокое здание. В результате формируется объемный источник мощностью Vb, м3/с,
|
Vb = Cb ∙ Sb ∙ u, |
(3.16) |
где u - скорость ветра, м/с; Sb - площадь сечения здания перпендикулярно направлению ветра, м2; Cb - безразмерный коэффициент распределения примеси, учитывающий условия обтекания и форму здания. Последний коэффициент отражает распределение примеси в зоне смещения потока воздуха за зданием. Он определяется при модельных экспериментах в аэродинамической трубе. Для практических расчетов можно принять консервативную оценку Cb = 1,0.
Расчет приземных концентраций в этом случае проводится по методу виртуального источника, используя для расчета «виртуального» сдвига xb следующую формулу, аналогичную формуле (3.7)
|
π ∙ σy(xb) ∙ σz(xb) ∙ u = Vb, |
(3.17) |
где u - скорость ветра, м/с; Vb - мощность объемного источника в зоне аэродинамической тени (за зданием), м3/с; σy(x) и σz(x) - зависящие от расстояния дисперсии облака выброса в поперечном и вертикальном направлениях. Если имеется начальное разбавление в момент выброса, то для него отдельно по уравнению (3.7) рассчитывается свой «виртуальный» сдвиг xb, который сравнивается со сдвигом, рассчитанным по уравнению (3.17). Выбирается наибольшее значение. Но как правило, величина «виртуального» сдвига, рассчитанная по формуле (3.17) оказывается большей.
Выброс из низких труб. Низкими считаются трубы, высота которых меньше, чем высота зоны возмущения Hiz, образующейся в результате взаимодействия воздушного потока и близко расположенного здания. Расчет для таких труб проводится по смешанной модели, согласно которой доля 1 - Kb от общего количества выброса рассчитывается как выброшенный из высокой трубы, а доля примеси равная Kb, поступает в зону аэродинамической тени, где формируется объемный источник Vb. Принимается, что все выбросы из проемов здания и других, расположенных вблизи него источников, высота которых ниже здания, попадают в зону его аэродинамической тени.
Значения Kb в зависимости от приведенной
высоты здания ![]() приведены в табл. 3.5. Приведенную высоту здания
приведены в табл. 3.5. Приведенную высоту здания ![]() , зависящую от взаимного расположения
здания и трубы, рассчитывают по формуле
, зависящую от взаимного расположения
здания и трубы, рассчитывают по формуле
|
|
(3.18) |
где hg - геометрическая высота источника выброса от поверхности земли, м; Hb - высота здания, м; Hiz - расстояние от уровня земли до верхней границы зоны смещения потока воздуха за зданием, м:
|
|
(3.19) |
где b - ширина перпендикулярного направлению ветра сечения здания, м.
Таблица 3.5. Доля выбросов Kb, попадающая в зону аэродинамической тени за зданием при низком выбросе в зависимости от безразмерной приведенной высоты здания
|
Приведенная высота здания, |
Доля выброса, попадающая в зону аэродинамической тени за зданием, Kb |
Приведенная высота здания, |
Доля выброса, попадающая в зону аэродинамической тени за зданием, Kb |
|
0 |
1 |
0,6 |
0,338 |
|
0,05 |
0,984 |
0,7 |
0,192 |
|
0,1 |
0,960 |
0,8 |
0,094 |
|
0,2 |
0,906 |
0,9 |
0,040 |
|
0,3 |
0,808 |
0,95 |
0,014 |
|
0,4 |
0,662 |
1,0 |
0 |
|
0,5 |
0,5 |
|
|
3.5. Учет траектории подъема облака выброса
Подъем облака выброса учитывается при расчете рассеяния выбросов высоких труб и той части выброса низких, которая реализуется в неискаженной форме. Выбросы, попадающие в зону аэродинамической тени, ни тепловой, ни динамический подъем не испытывают. Подъем облака над землей рассчитывается по формуле
|
H = hg + ΔH - ΔHv - C, |
(3.20) |
где hg - геометрическая высота трубы от ее основания; ΔH - динамический (скоростной) и тепловой подъем облака над устьем источника; С - поправка на скос траектории облака при слабом ветре от влияния аэродинамической тени самой трубы; ΔHv = Vs ∙ x / u - «проседание» центра масс облака примеси за счет эффекта гравитационного оседания, Vs - скорость гравитационного оседания аэрозолей (значимая лишь для тяжелой, быстро оседающей примеси), м/с; u - скорость ветра на высоте выброса, м/с, равная
|
u = uf ∙ (Hg / Hf)ε. |
(3.21) |
Здесь Hg - геометрическая высота выброса, м; Hf - высота флюгера (~10 м); uf - скорость ветра на высоте флюгера, м/с. Значения параметра ε приведены в табл. 3.6.
Таблица 3.6. Значения параметра ε, используемого для расчета изменения скорости ветра с высотой по формуле (3.21)
|
Категория устойчивости |
z0 = 1 см |
z0 = 10 см |
z0 = 100 см |
z0 = 400 см |
|
А |
0,05 |
0,08 |
0,16 |
0,27 |
|
В |
0,06 |
0,09 |
0,17 |
0,28 |
|
С |
0,06 |
0,11 |
0,20 |
0,31 |
|
D |
0,12 |
0,16 |
0,27 |
0,37 |
|
Е |
0,34 |
0,32 |
0,38 |
0,47 |
|
F |
0,53 |
0,54 |
0,61 |
0,69 |
|
G |
0,70 |
0,71 |
0,79 |
0,81 |
Заметим, что в случае холодных выбросов или тяжелой быстро оседающей примеси величина Р не может быть отрицательной. На больших расстояниях сохраняется достигнутое значение H = 0. Случаи, когда наблюдается не подъем, а опускание облака выброса до уровня земли нередки. Обычно это характерно для жаркой погоды летом, когда помещения охлаждаются кондиционерами или калориферами.
Поправку С на скос траектории облака от влияния аэродинамической тени трубы вычисляют по формулам
|
|
(3.22) |
где u - скорость ветра на уровне устья трубы, м/с; w0 - скорость истечения выбрасываемых газов, м/с; d - диаметр устья трубы, м.
При расчете подъема облака выброса ΔH над устьем от скоростного напора и плавучести выбросов необходимо учитывать, что он происходит постепенно, образуя траекторию подъема облака до некоторой предельной высоты ΔHmax, которая при неустойчивых условиях определяется высотой до ближайшего, достаточно мощного слоя инверсии (обычно на верхней границе слоя перемешивания), а при устойчивых - предельной высотой подъема, называемой эффективной высотой выброса, или, если ниже этой высоты имеется мощный слой инверсии - высотой до его нижней границы. Последняя рассчитывается по формуле
|
|
(3.23) |
Значения ![]() приводятся в табл. 3.4. Наиболее существенное влияние оказывает подъем
облака по траектории при неустойчивой стратификации атмосферы.
приводятся в табл. 3.4. Наиболее существенное влияние оказывает подъем
облака по траектории при неустойчивой стратификации атмосферы.
Траектория подъема струи ΔH(x) для всех погодных условий вычисляется по модифицированным формулам Неттервилла:
- для категории D (безразличной стратификации атмосферы) -
- для категорий А, В и С (условиях неустойчивости) -
|
|
(3.25) |
для категорий E, F и G (устойчивых условиях) -
где х - расстояние от основания трубы, м; t = u / x - время движения облака по ветру до расстояния х, с; u - скорость ветра на высоте выброса, м/с; β - безразмерная константа переноса; f = 0,7 ∙ 10-2 - характерная частота спектра турбулентности при нейтральной атмосфере, c-1;
параметр устойчивости атмосферы, c-1; g = 9,8 - ускорение свободного падения, м/с2; To - абсолютная температура атмосферного воздуха, °К; dθ / dz - градиент потенциальной температуры (разница измеренного и адиабатического градиента температуры), °К/м. Значения параметров s и β для различных категорий устойчивости атмосферы приведены в табл. 3.7.
Таблица 3.7. Значения параметра устойчивости атмосферы s и константы переноса β, используемых при расчете траектории подъема струи по формулам (3.24) - (3.26)
|
|
А |
В |
С |
D |
Е |
F |
G |
|
s, c-1 |
2 ∙ 10-2 |
1,7 ∙ 10-2 |
1,47 ∙ 10-2 |
0 |
2,32 ∙ 10-2 |
3,3 ∙ 10-2 |
3,83 ∙ 10-2 |
|
β |
0,25 |
0,35 |
0,45 |
0,45 |
0,25 |
0,25 |
0,25 |
|
|
(3.28) |
начальный радиус струи с поправкой Ханны, м; w0 - скорость истечения выброса, м/с; d - диаметр устья трубы, м;
величина, пропорциональная потоку кинетической энергии истекающей струй выброса, м4/с;
величина, пропорциональная потоку сил плавучести, м4/с3; ΔT = T - Tc - - разность температур выбрасываемого T0 и атмосферного Т воздуха, °К.
Зная тепловую мощность источника выбросов Qr, Дж/с, величину F0 можно рассчитать также по формуле
|
|
(3.31) |
где 1000 (°С ∙ м3)/Дж - размерный коэффициент пропорциональности.
Член (3.29) учитывает динамический подъем струи выброса в результате скоростного напора выброса, член (3.30) - плавучий подъем вследствие перегрева выбрасываемого воздуха. В отдельные периоды перегрев может быть ΔT < 0.
3.6. Учет радиоактивных превращений и истощения облака выброса
Выведение примеси из облака выбросов происходит за счет трех процессов очищения атмосферы: радиоактивного распада, сухого осаждения примеси и вымывания ее атмосферными осадками (дождем, снегом). Оно учитывается фактором истощения Fr(x), который представляет собой долю от потока примеси через вертикальное сечение, перпендикулярное траектории движения облака в точке выброса, остающейся в облаке к моменту достижения его центром точки наблюдения, или что то же самое - долю от интегрального содержания примеси в выброшенном облаке, которая останется в нем в точке наблюдения. Вид и характеристики функции Fr(x) зависят от радионуклида r категории устойчивости атмосферы, скорости ветра и распределения аэрозолей по размерам.
Функция истощения облака выброса в результате радиоактивного распада дается формулой
|
Fr(x) = exp(-λr ∙ x / u), |
(3.32) |
где λr - постоянная радиоактивного распада r-го радионуклида, c-1; u - скорость ветра в центральной точке облака. Заметим, что (x / u) = t - время движения примеси до заданной точки.
Функция истощения вследствие сухого осаждения дается интегралом
|
|
(3.33) |
где h - эффективная высота выброса, м; σz(x) - зависимость вертикальной дисперсии распределения примеси в облаке выброса от расстояния x, м; Vg - скорость сухого осаждения, м/с. На больших расстояниях, где высота слоя перемешивания (а следовательно и σz(x) достигает своего максимального значения, справедлива формула
|
|
(3.34) |
где ![]() - максимальная высота слоя
перемешивания, м; xm
- расстояние, на котором σz(x) достигает
максимума.
- максимальная высота слоя
перемешивания, м; xm
- расстояние, на котором σz(x) достигает
максимума.
Скорость сухого осаждения Vg, м/с - это эмпирический параметр, характеризующий взаимодействие примеси с поверхностью. Она определяется отношением
|
|
(3.35) |
и не является скоростью в кинематическом смысле. Ее величину определяют как гравитационное оседание аэрозолей, так и механизмы захвата и адсорбции примеси на поверхности. Для частиц с размерами большими 10 мкм определяющим является гравитационное оседание Vs. Для аэрозолей меньших размеров и газов - механизмы адсорбции.
После выброса промышленные аэрозоли активно взаимодействует с естественной пылью, преципитируя на ней. Если выброс не является грубо дисперсным и в весовом отношении не велик (что обычно характерно для предприятий атомной промышленности и энергетики), то выброшенная примесь в результате взаимодействия с естественной атмосферной пылью приобретает ее свойства. В этом случае значения скорости осаждения Vg можно принимать согласно табл. 3.8. В частности, приведенные там значения характерны для атомных станций.
Таблица 3.8. Значения скорости сухого осаждения для выброшенной примеси, по размерам подобной атмосферной пыли
|
Вещество |
Vg, см/с |
|
Элементарный йод |
2 |
|
Органические соединения йода |
0,1 |
|
Аэрозоли |
0,8 |
Если происходит выброс грубодисперсной примеси, то значения Vg необходимо рассчитывать по размерам аэрозолей, используя данные табл. 3.8, где приведены значения скоростей гравитационного оседания частиц в зависимости от их аэродинамического диаметра. Зная распределение частиц по размерам ni и используя табл. 3.8, можно вычислить эффективную скорость осаждения Vg,ef по формуле
|
|
(3.36) |
где ni - распределение оседающей примеси по скоростям осаждения Vg,i.
При определении Vg,ef как правило недопустимо использовать единственное значения АМАД. Расчет надо производить по группам, пользуясь формулой (3.36). Для этого необходимо знать распределение аэрозолей выброса по размерам. В случае представимости такого распределения логнормальным законом, достаточно знать АМАД и логнормальную дисперсию β.
Таблица 3.8. Зависимость скорости гравитационного оседания капель влаги от их аэродинамического диаметра
|
Диаметр частиц, мкм |
Vg, см/с |
|
0,1 |
8 ∙ 10-6 |
|
1,0 |
4 ∙ 10-3 |
|
10,0 |
0,3 |
|
100,0 |
25 |
Для пылевых частиц значения скорости гравитационного оседания необходимо корректировать, умножая значения Vs, взятые из табл. 3.8, на множитель P / P0, где P - плотность пылевых частиц, P0 - плотность воды.
При практических расчетах следует также иметь в виду, что дисперсный состав выброшенного аэрозоля в процессе переноса может существенно изменяться. Так, тяжелая примесь оседает вблизи от места выброса, мелкодисперсная - способна переносится на большие расстояния. В результате неоднородного выведения аэрозолей разного размера из облака выброса значение Vg,ef как правило изменяется с расстоянием до тех пор, пока аэрозоли выброса в результате взаимодействия с естественной атмосферной пылью не примут ее свойства.
Функция истощения облака в результате процессов влажного выведения, обусловленного захватом аэрозолей каплями осадков или снежинками, дается формулой
|
F(x) = exp[-Λ ∙ x / u], |
(3.37) |
где Λ - постоянная вымывания осадками, c-1. Она зависит от типа осадков, спектра дождевых капель и интенсивности осадков. Ее величину вычисляют по формуле
|
Λ = kr ∙ k0 ∙ I, |
(3.38) |
где I - интенсивность осадков, мм/ч; kr - стандартная величина абсолютной вымывающей способности дождя (для всех нуклидов, кроме инертных газов, принимается kr = 10-5 ч/(мм ∙ с), характерная для дождя интенсивностью I = 1 мм/ч); k0 - относительная вымывающая способность осадков других типов, приведенная в табл. 3.9.
Таблица 3.9. Относительные вымывающие способности различных типов осадков
|
Тип осадков |
k0 |
Тип осадков |
k0 |
|
Дождь |
1,0 |
Снег |
3,0 |
|
Дождь с грозой |
1,1 |
Морось |
4,5 |
|
Снег с дождем |
2,4 |
Туман |
5,0 |
|
Ливень |
2,8 |
|
|
Полная функция истощения облака рассчитывается перемножением дифференциальных функций истощения за счет всех трех процессов.
При наличии цепочек радиоактивного распада формулы (3.32) - (3.38) строго говоря не пригодны. Для практических расчетов рекомендуется следующее приближение
где Fr(x) - функция истощения для r-го радионуклида цепочки; постоянные Rk,r даются рекуррентными формулами, удобными для программной реализации расчетов на ЭВМ
|
|
(3.40) |
ar, c-1 - константы
где λr, Λr, Vg,r - постоянная радиоактивного распада, постоянная вымывания осадками и скорость сухого осаждения для r-го радионуклида соответственно. В общем случае все эти параметры могут различаться для разных нуклидов. При наличии разветвленных изобарных цепочек в формулы (3.39) - (3.41) вводятся коэффициенты ветвления.
Заметим, что истощение облака выбросов под действием атмосферных осадков вблизи от места выброса малозначимо. Так, для умеренного дождя характерен коэффициент вымывания Λ = 10-5 c-1. Если допустить движение облака со скоростью 2 м/с, то на расстоянии 10 км за счет вымывания дождем из облака будет выведено на землю не более 5 % примеси. Поэтому истощением облака за счет вымывания осадками на расстояниях по крайней мере до 10 км можно пренебречь.
Однако из этого вовсе не следует, что влажным осаждением можно пренебрегать при расчете выпадений на землю. В некоторых точках оно может даже превалировать. Такая ситуация возникает, например, под приподнятой траекторией облака выбросов вблизи от источника. При этом складывается на первый взгляд парадоксальная ситуация: истощение облака незначительно, а выпадения велики. Это объясняется тем, что вблизи от источника облако выброса еще компактно, и значения вертикального интеграла фактора безопасности Gz велики.
Таким образом вблизи от места выброса значимым обычно является лишь один путь очищения атмосферы - сухое осаждение. В разных местах оно происходит с разной интенсивностью.
3.7. Вторичный ветровой подъем осевшей на землю примеси
Вторичное поднятие (дефляция) выпавшей на поверхность земли примеси для большинства радионуклидов связано с пылеобразованием. Лишь для отдельных нуклидов оно обусловлено действием других причин. Например, для йода характерен подъем вследствие прямой возгонки, для трития - испарения. Пылеобразование может быть обусловлено действием ветра и деятельностью человека: движением транспорта, строительными и сельскохозяйственными работами и т.п. Антропогенный фактор слабо исследован и в каждом случае специфичен. Здесь учтены лишь процессы ветрового пылеобразования.
Вторичный подъем радионуклидов в приземный слой воздуха оценивают с помощью коэффициента дефляции Ka, м-1:
|
|
(3.42) |
Динамику изменения значений коэффициента дефляции за счет ветрового подъема рассчитывают по формуле
|
|
(3.43) |
где t - время с момента
образования отложения; λ1 - постоянная уменьшения
коэффициента дефляции для быстрой фазы, c-1;
λ2 - постоянная его более продолжительного уменьшения, c-1; λ - постоянная радиоактивного
распада, c-1; ![]() = 10-5;
= 10-5;
![]() = 10-9 м-1;
λ1 и λ2 равны 1,46 ∙ 10-7
и 2,2 ∙ 10-10 с-1. Последние соответствуют периодам
полувыведения 55 суток и 100 лет.
= 10-9 м-1;
λ1 и λ2 равны 1,46 ∙ 10-7
и 2,2 ∙ 10-10 с-1. Последние соответствуют периодам
полувыведения 55 суток и 100 лет.
Относительный вклад во временной интеграл приземной объемной активности в воздухе за счет вторичного пылеобразования равен
|
|
(3.44) |
где ![]() - временной интеграл объемной
активности радионуклида в приземном слое воздуха (его приземной концентрации)
вследствие вторичного ветрового подъема, Бк/м3;
- временной интеграл объемной
активности радионуклида в приземном слое воздуха (его приземной концентрации)
вследствие вторичного ветрового подъема, Бк/м3; ![]() - интеграл объемной активности
радионуклида в воздухе при отсутствии ветрового подъема (за время прохождения
облака выброса), Бк/м3; Vg, Λ и
- интеграл объемной активности
радионуклида в воздухе при отсутствии ветрового подъема (за время прохождения
облака выброса), Бк/м3; Vg, Λ и ![]() - скорость сухого осаждения,
постоянная вымывания осадками и толщина атмосферного слоя перемешивания.
Максимальное значение этого отношения для нуклидов с периодом полураспада
больше 1 года, при принятых значениях
- скорость сухого осаждения,
постоянная вымывания осадками и толщина атмосферного слоя перемешивания.
Максимальное значение этого отношения для нуклидов с периодом полураспада
больше 1 года, при принятых значениях ![]() и
и ![]() и Vg = 1 см/с может достигать 73
%. Для большей скорости осаждения величина отношения пропорционально
увеличивается. Следует заметить, что загрязнение воздуха за счет дефляции
формируется после прохождения облака и воздействует длительное время. Его
следует учитывать только при расчете поступления в организм человека путем вдыхания.
На загрязнение почвы оно не влияет, так как с нее и идет формирование
вторичного облака пыли. Упрощенно можно сказать: что поднялось в воздух - то и
осело обратно. Перенос за пределы следа выпадений незначителен.
и Vg = 1 см/с может достигать 73
%. Для большей скорости осаждения величина отношения пропорционально
увеличивается. Следует заметить, что загрязнение воздуха за счет дефляции
формируется после прохождения облака и воздействует длительное время. Его
следует учитывать только при расчете поступления в организм человека путем вдыхания.
На загрязнение почвы оно не влияет, так как с нее и идет формирование
вторичного облака пыли. Упрощенно можно сказать: что поднялось в воздух - то и
осело обратно. Перенос за пределы следа выпадений незначителен.
3.8. Расчет поправок на рельеф местности
Точные расчеты деформации воздушного течения рельефом местности в рамках гауссовой модели невозможны, но масштаб ее влияния может быть оценен «методом потенциальных течений». Метод состоит в построении математических формул для невязкого потенциального (ламинарного) течения в области с криволинейной границей. На основе этого подхода в нормативном документе ОНД-86 разработаны упрощенные практические рекомендации по учету влияния отдельных форм рельефа (гряды, ложбины и уступа). Они не дают профиль искажения потока. На их основе можно получить только оценки максимально возможного влияния рельефа путем расчета поправки к приземному фактору разбавления в направлении румба n по формуле
|
Rn = 1 + φ1 ∙ (ηm - 1), |
(3.45) |
где ηm определяют по табл. 3.10; безразмерные величины n1 = hg / h0 и n2 = a0 / h0; hg - геометрическая высота источника; h0 - высота (в случае ложбины - глубина) препятствия, a0 - полуширина гряды, ложбины или склона уступа; x0 - расстояние от источника до середины препятствия в случае гряды и ложбины, или до верхней кромки склона в случае уступа.
Таблица 3.10. Значения коэффициента ηm в формуле (3.45) от параметров n1 и n2, для расчетов поправки на рельеф местности
|
n1 |
n2 |
|||||||||||
|
Ложбина (впадина) |
Уступ |
Гряда (холм) |
||||||||||
|
4 - 5 |
6 - 9 |
10 - 15 |
16 - 20 |
4 - 5 |
6 - 9 |
10 - 15 |
16 - 20 |
4 - 5 |
6 - 9 |
10 - 15 |
16 - 20 |
|
|
<0,5 |
4,0 |
2,0 |
1,6 |
1,3 |
3,5 |
1,8 |
1,5 |
1,2 |
3,0 |
1,5 |
1,4 |
1,2 |
|
0,6 - 1,0 |
3,0 |
1,6 |
1,5 |
1,3 |
2,7 |
1,5 |
1,3 |
1,2 |
2,2 |
1,4 |
1,3 |
1,0 |
|
1,1 -2,9 |
1,8 |
1,5 |
1,4 |
1,1 |
1,6 |
1,4 |
1,2 |
1,1 |
1,4 |
1,3 |
1,2 |
1,0 |
|
3,0 - 5,0 |
1,4 |
1,3 |
1,2 |
1,0 |
1,3 |
1,2 |
1,1 |
1,0 |
1,2 |
1,2 |
1,1 |
1,0 |
|
>5 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
Зависимость функции φ1 от отношения |x0| / a0 представлена в табл. 3.11. Если источник расположен на верхнем плато уступа, то при определении φ1 следует брать отрицательное значение |x0| / a0.
При аппроксимации реального рельефа рассмотренными простейшими элементами (уступом, грядой или ложбиной) из трех элементарных форм практическое значение имеют лишь гряда и ложбина.
Для оценки максимально возможных значений Rn разработан алгоритм представления реального рельефа элементарными формами. Согласно ему реализуется следующая последовательность действий:
- строится рельеф для выбранного азимутального сечения местности, проходящего через трубу;
- ищется самая глубокая точка долины;
- по обе стороны от этой точки находят все вершины (локальные максимумы);
- для каждой вершины ищется условный минимум высоты поверхности земли относительно линии, соединяющей самую глубокую точку долины с вершиной;
- через найденную точку условного минимума проводится отрезок, соединяющий рассматриваемую вершину с горизонтальной линией, проведенной через самую глубокую точку долины;
- через вершину проводится горизонтальный луч, в результате чего все эти построения образуют идеализированный уступ;
- для полученного уступа по формуле (3.45) вычисляется поправочный множитель Rn;
- эта процедура повторяется для всех вершин сечения, расположенных по обе стороны от трубы;
- для каждого n-го азимутального сечения местности выбирается максимальное значение, которое присваивается поправочному коэффициенту Rn;
- при этом, если два найденных по обе стороны от самой глубокой точки долин максимальных значения не совпадут с точностью не менее 95 %, то по этим двум вершинам строится стилизованная схема ложбины с центром между ними и отыскивается новое значение Rn для геометрии ложбины;
- процесс повторяется для других азимутальных сечений.
Таблица 3.11. Функция φ1(|x0| / a0) влияния рельефа на распределение примеси [см. формулу (3.45)]
|
Отношение |x0| / a0 |
Функция φ1 |
Отношение (|x0| / a0 |
Функция φ1 |
||
|
Гряда |
Ложбина |
Гряда |
Ложбина |
||
|
-1,4 |
-0,063 |
|
1,2 |
0,932 |
-0,090 |
|
-1,2 |
-0,069 |
|
1,4 |
0,678 |
-0,125 |
|
-1,0 |
-0,068 |
0,018 |
1,6 |
0,421 |
-0,127 |
|
-0,8 |
-0,080 |
0,231 |
1,8 |
0,310 |
-0,128 |
|
-0,6 |
-0,070 |
0,5 |
2 |
0,233 |
-0,124 |
|
-0,4 |
-0,068 |
0,751 |
2,2 |
0,186 |
-0,108 |
|
-0,2 |
-0,067 |
0,943 |
2,4 |
0,14 |
-0,103 |
|
0 |
-0,036 |
0,992 |
2,6 |
0,122 |
-0,084 |
|
0,2 |
0,047 |
0,943 |
2,8 |
0,099 |
|
|
0,4 |
0,277 |
0,751 |
3 |
0,086 |
|
|
0,6 |
0,523 |
0,5 |
3,2 |
0,070 |
|
|
0,8 |
0,857 |
0,231 |
3,4 |
0,067 |
|
|
1 |
1,008 |
0,018 |
3,6 |
0,068 |
|
3.9. Упрощенные формулы
Приближенная оценка разового
фактора разбавления в точке максимальной его реализации ![]() , с/м3, может быть получена
по упрощенной формуле
, с/м3, может быть получена
по упрощенной формуле
где h - высота центра облака в точке xmax реализации максимума разового фактора разбавления, м; σy(x) и σz(x) - горизонтальная и поперечная дисперсии облака выброса на расстоянии xmax от источника выброса, рассчитываемые по формуле (3.15) с учетом начального разбавления, учитываемого «виртуальным» сдвигом xb [см. формулу (3.7)], то есть фактически на расстоянии xmax + xb; u - скорость ветра на высоте выброса, м/с; Fr(xmax) - значение фактора разбавления на расстоянии xmax от источника выброса. Последний фактор имеет значение только для короткоживущих радионуклидов r. Для радионуклидов с периодом полураспада час и более в точке максимума Fr(xmax) = 1. Формула (3.46) получена из формулы (3.4) путем варьирования параметра σz(x) в предположении постоянства отношения (σz(xmax) / σy(xmax)) = const.
Значения xman можно определить, решая трансцендентное уравнение
|
|
(3.47) |
Его решения для разных категорий устойчивости и различных высот облака выброса h приведены в табл. 3.12.
Таблица 3.12. Зависимость расстояния до точки максимума приземной концентрации xmax от категории устойчивости атмосферы и высоты центра облака выброса h
|
Высота облака, м |
Расстояние до максимума концентрации xmax, метры |
|||||
|
А |
В |
С |
D |
Е |
F |
|
|
5 |
26 |
33 |
43 |
58 |
98 |
180 |
|
10 |
51 |
68 |
93 |
130 |
220 |
450 |
|
15 |
74 |
105 |
146 |
210 |
360 |
790 |
|
20 |
98 |
140 |
200 |
290 |
510 |
1200 |
|
25 |
120 |
180 |
260 |
380 |
670 |
1660 |
|
30 |
145 |
220 |
320 |
470 |
850 |
2200 |
|
35 |
170 |
260 |
380 |
560 |
1030 |
2800 |
|
40 |
190 |
300 |
440 |
660 |
1200 |
3400 |
|
45 |
215 |
340 |
500 |
770 |
1400 |
4200 |
|
50 |
240 |
390 |
570 |
870 |
1650 |
5000 |
|
60 |
280 |
470 |
700 |
1100 |
2100 |
6800 |
|
70 |
330 |
560 |
840 |
1340 |
2700 |
9100 |
|
80 |
380 |
650 |
990 |
1600 |
3200 |
11800 |
|
90 |
425 |
740 |
1140 |
1850 |
3900 |
15100 |
|
100 |
470 |
835 |
1300 |
2100 |
4600 |
19000 |
Табл. 3.12 позволяет выполнить оценки фактора (σz(xmax) / σy(xmax)) формулы (3.46) в зависимости от высоты облака h. Оценки этого фактора приведены в табл. 3.13. В зависимости от категории устойчивости и высоты выброса они изменяются от 0,8 до 0,14.
Для совсем простых и быстрых консервативных опенок, при счете «в уме», пренебрегая последним фактором, а также высотой подъема облака, расчет максимально возможного при ветре u фактора разбавления от приподнятого разового выброса можно сделать по следующей, еще более упрощенной формуле, не требующей даже знания категории устойчивости
|
|
(3.48) |
где u - скорость ветра, м/с; hg - геометрическая высота выброса, м, е = 2,73 - основание натурального логарифма. Точность таких оценок составляет порядок величины. Причем как правило в сторону завышения, то есть расчеты по формуле (3.48) дадут в конечном счете завышенные, но не более, чем на порядок величины, оценки ожидаемых доз.
Таблица 3.13. Зависимость фактора (σz(xmax) / σy(xmax)) формулы (3.46) от высоты центра облака разового выброса h
|
Высота облака, м |
Фактор (σz(xmax) / σy(xmax)) |
|||||
|
А |
В |
С |
D |
Е |
F |
|
|
5 |
0,62 |
0,68 |
0,74 |
0,77 |
0,60 |
0,50 |
|
10 |
0,64 |
0,65 |
0,70 |
0,69 |
0,54 |
0,40 |
|
15 |
0,65 |
0,63 |
0,67 |
0,65 |
0,50 |
0,35 |
|
20 |
0,66 |
0,62 |
0,65 |
0,62 |
0,47 |
0,31 |
|
25 |
0,67 |
0,61 |
0,63 |
0,60 |
0,45 |
0,29 |
|
30 |
0,67 |
0,61 |
0,62 |
0,58 |
0,44 |
0,27 |
|
35 |
0,67 |
0,60 |
0,61 |
0,56 |
0,42 |
0,25 |
|
40 |
0,68 |
0,39 |
0,60 |
0,55 |
0,41 |
0,24 |
|
45 |
0,68 |
0,59 |
0,59 |
0,54 |
0,39 |
0,23 |
|
50 |
0,68 |
0,58 |
0,58 |
0,53 |
0,38 |
0,22 |
|
60 |
0,69 |
0,57 |
0,57 |
0,51 |
0,36 |
0,20 |
|
70 |
0,69 |
0,57 |
0,56 |
0,49 |
0,35 |
0,19 |
|
80 |
0,69 |
0,56 |
0,54 |
0,48 |
0,33 |
0,18 |
|
90 |
0,70 |
0,56 |
0,54 |
0,47 |
0,32 |
0,17 |
|
100 |
0,70 |
0,55 |
0,53 |
0,46 |
0,31 |
0,16 |
Глава 4. Расчет экстремальных оценок рассеяния кратковременных выбросов в атмосфере и формирования следа выпадений при штилях
4.1. Общие формулы расчета рассеяния при штилях
Понятие «штилевые условия» в синоптической метеорологии и микрометеорологии (теории атмосферной диффузии) не совпадают. В первой штилевыми считаются условия, когда скорость ветра ниже чувствительности прибора. Применительно к наблюдениям на сетевых метеостанциях Управления гидрометеослужбы (УГМС) России тогда, когда скорость ветра меньше 1 м/с, так как точность сетевых измерений УГМС ±0,5 м/с. Во втором случае штилем считается состояние, когда турбулентная диффузия примеси опережает перенос ветром. В этом случае разовые выбросы принимают форму облака, зависающего вблизи трубы, а не сносимого по ветру. Слабый ветер, не превышающий 0,5 м/с, лишь искажает форму штилевого облака, накапливающегося вокруг источника выбросов, деформируя и вытягивая его в направлении ветра.
К сожалению точных аналитических формул расчета рассеяния примеси при штилях не существует. Временной интеграл концентрации (объемной активности) выброшенной примеси Cv,r, Бк ∙ с/м3, рассчитывается также по формуле (3.3) предыдущей главы, но интеграл по времени t, пришедшего после выброса вычисляется не в бесконечных пределах, а до момента Δt, где Δt - продолжительность конкретного штиля.
В Приложении 2 приводятся приближенные аналитические формулы расчета, хорошо аппроксимирующие точные значения интеграла при определенных, приемлемых для практических расчетов условиях приближения. Здесь же будет изложен метод, основанный на численных расчетах с применением ЭВМ. Он проверен на практике и реализован программно. Согласно ему вместо разового фактора разбавления Go,r(x), используемого при ветреных условий, в формулу (3.3) следует подставлять зависящий от продолжительности штилевых условий разовый фактор разбавления при штиле и слабом ветре G(x,Δt), с/м3, рассчитываемый по формуле
где ![]() , с/м3 - фактор разбавления
при полном штиле (u = 0):
, с/м3 - фактор разбавления
при полном штиле (u = 0):
![]() , с2/м5 -
поправочный фактор для учета деформации облака слабым ветром u:
, с2/м5 -
поправочный фактор для учета деформации облака слабым ветром u:
2σy(t) и 2σz(t) - зависящие от времени (считая от момента выброса) поперечная и вертикальная дисперсии облака выброса; F(t) - зависящая от времени функция истощения облака за счет радиоактивного распада, сухого и влажного осаждения примеси, a Δt - продолжительность штиля. При расчете необходимо иметь в виду, что x - величина алгебраическая, и с наветренной стороны источника принимает отрицательные значения.
Второй член формулы (4.1), учитывающий слабый ветер практического применения не имеет, так как измерить с необходимой точность среднюю составляющую скорости слабого ветра, при котором справедливо приближение (4.1) на фоне всегда присутствующих пульсаций ветра, связанных со структурой турбулентности, затруднительно. В табл. 4.1 для разных категорий устойчивости приведены нижние пределы скорости ветра, являющихся пределом применимости приближения (4.1) при штилевых условиях рассеяния примеси.
Таблица 4.1. Скорости ветра на высоте стандартной метеомачты hm, при которой его можно считать слабым, а условия рассеяния - штилевыми
|
Высота метеомачты, м |
Верхний предел слабого ветра, при котором условия еще могут считаться штилевыми, м/с |
|||||
|
А |
В |
С |
D |
Е |
F |
|
|
10 |
0,45 |
0,35 |
0,3 |
0,23 |
0,15 |
0,1 |
Используемые же на метеостанциях и метеопостах наблюдательной метеосети России приборы из-за своей инерционности и влияния трения не позволяют проводить измерения слабых ветров с достаточной точностью. Архивных данных нет.
Коэффициенты дисперсии штилевого облака σy(t) и σz(t) зависят от структуры турбулентности в момент штиля. Вопрос о их виде еще не имеет окончательного решения. Для практических расчетов рекомендуется использовать зависимость (3.15), делая замены переменных x = t ∙ uc,j, где uc,j - скорость ветра, характерная для j-й категории устойчивости при ветреной погоде. Для различных категорий приведенные в табл. 4.2.
Таблица 4.2. Скорости ветра uc,j, м/с, характерные для разных категорий устойчивости, применяемые при представлении дисперсий размеров облака Гауссовой модели σy(t) и σz(t), как функций времени, прошедшего после выброса t
|
Характерные для разных категорий устойчивости атмосферы скорости ветра uc,j, м/с |
||||||
|
А |
B |
С |
D |
Е |
F |
G |
|
1 |
1,5 |
3 |
4 |
2 |
1,5 |
1 |
Формула (4.1) является Тейлоровским разложением в ряд по малой
величине ![]() фактора разбавления
фактора разбавления ![]() мгновенного выброса, связывающего
разовый выброс с зависящей от времени t, прошедшего после выброса,
мгновенной приземной концентрацией примеси на расстоянии x от места
выброса [см. формулу (3.2)]. Интегрируя
далее двучленное разложение мгновенного фактора разбавления в ряд Тейлора,
получают вышеприведенные формулы для разового фактора разбавления при штиле.
мгновенного выброса, связывающего
разовый выброс с зависящей от времени t, прошедшего после выброса,
мгновенной приземной концентрацией примеси на расстоянии x от места
выброса [см. формулу (3.2)]. Интегрируя
далее двучленное разложение мгновенного фактора разбавления в ряд Тейлора,
получают вышеприведенные формулы для разового фактора разбавления при штиле.
4.2. Расчет выпадений из штилевого облака выброса
Расчет сухих и влажных (во время
выпадения осадков) выпадений во время штиля производят также по формулам (3.8) предыдущей главы, куда вместо
разового фактора разбавления Go,r(x),
используемого при ветреных условий, подставляют штилевой фактор разбавления (4.1), а вместо ![]() - интеграл по вертикальной координате z
от распределения по высоте (вертикальному профилю) штилевого фактора
разбавления
- интеграл по вертикальной координате z
от распределения по высоте (вертикальному профилю) штилевого фактора
разбавления
|
|
(4.4) |
где
и
4.3. Условия выброса
4.3.1. Учет подъема облака выброса
При штилях также происходит тепловой и динамический подъем облака выбросов. Понятия траектории подъема при этом не существует, а время подъема из-за быстротечности подъема не существенно. Значение имеет только предельная высота подъема, рассчитываемая по формуле
|
H = hg + ΔHmax, |
(4.7) |
где hg - геометрическая высота выброса (например, трубы от ее основания); ΔHmax - динамический (скоростной) и тепловой предельный подъем облака над устьем источника.
Для неустойчивых и нейтральных условий величина ΔHmax определяется высотой до нижней границы ближайшего, запирающего дальнейшее рассеяние вверх слоя инверсии. При антициклональных штилях запирающие слои как правило особенно мощны. Это так называемые инверсии оседания.
Для устойчивых условий при штиле предельную высоту подъема (опускания) центра облака рассчитывают по формуле
|
ΔHmax = 5,1 ∙ Ф1/4 ∙ s-3/8, |
(4.8) |
где s - параметр устойчивости атмосферы, вычисляемый по формуле (3.27) и приведенный в табл. 3.7.
4.3.2. Учет начального разбавления выброса
Речь о том, что примесь выбрасывается с некоторой начальной концентрацией. Не учет этого фактора, как и в случае ветреной погоды, может дать при расчетах по вышеприведенным формулам бесконечные интегралы концентрации примеси в воздухе и интегральных выпадений под источником выброса. Избежать этого можно применив метод «виртуального» источника, аналогично тому, как это было сделано в конце раздела 3.1 предыдущей главы. Отличается он только тем, что при штилях отыскивают не «виртуальный» сдвиг расстояния xb, как при ветреных условиях, а первоначальный «виртуальный» сдвиг времени tb по формуле
|
(2π)3/2 ∙ σy(tb)2 ∙ σz(tb) = V0, |
(4.9) |
где V0
- некоторый объем помещения, м3, в котором еще до момента выброса
изначально перемешивается вышедшая из оборудования радиоактивность [см.
пояснения к формуле (3.7) предыдущей главы];
σy(t)
и σz(t)
- зависящие от времени (считая от момента выброса) поперечная и вертикальная
дисперсии облака выброса. При этом все интегралы в предыдущих формулах данной
главы ![]() следует заменит на интегралы вида
следует заменит на интегралы вида ![]() то есть интегрирование начинать не с
нуля, с начального «виртуального» сдвига времени tb.
то есть интегрирование начинать не с
нуля, с начального «виртуального» сдвига времени tb.
4.4. Учет радиоактивных превращений и истощения eштилевого облака выброса
Для учета накопления дочерних радионуклидов, возникающих за
время существования штилевого облака, в формулы (4.2), (4.3), (4.5) и (4.6)
вместо фактора истощения F(t)
подставляют значения интегрального содержания r-го нуклида радиоактивной
цепочки Qr(t), рассчитываемое по формулам (3.39) - (3.41).
При этом, вместо факторов разбавления и их интегралов по высоте z
получают значения временных интегралов от приземных концентраций Cv,r(x), Бк ∙ с/м3,
и от интегралов концентрации по вертикали ![]() в штилевом облаке выбросов. Расчеты
выпадений
в штилевом облаке выбросов. Расчеты
выпадений ![]() на землю, Бк ∙ с/м3,
при этом производят по формуле (3.12).
на землю, Бк ∙ с/м3,
при этом производят по формуле (3.12).
Результаты расчетов профиля
разового фактора разбавления ![]() для штилевого облака выброса в
зависимости от расстояния x и продолжительности штиля Δt приведены на рис. 10
- 15. Все кривые соответствуют выбросу
примеси с начальным разбавлением объемом V0
= 104 м3 и скоростью сухого осаждения Vg =
0,8 см/с при отсутствии теплового и динамического подъема выбросов для
категорий устойчивости А (неустойчивые условия), D (нейтральные условия) и F
(устойчивые условия). Первые три кривые рассчитаны для выброса на высоте 0 м, а
остальные для высоты выброса 100 м.
для штилевого облака выброса в
зависимости от расстояния x и продолжительности штиля Δt приведены на рис. 10
- 15. Все кривые соответствуют выбросу
примеси с начальным разбавлением объемом V0
= 104 м3 и скоростью сухого осаждения Vg =
0,8 см/с при отсутствии теплового и динамического подъема выбросов для
категорий устойчивости А (неустойчивые условия), D (нейтральные условия) и F
(устойчивые условия). Первые три кривые рассчитаны для выброса на высоте 0 м, а
остальные для высоты выброса 100 м.
Рис. 10. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36 час, 2, 3, 4, 6, 8 и 30 сут
для выброса на высоте 0 м при категории устойчивости А
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36 час, 2, 3, 4, 6, 8 и 30 сут
для выброса на высоте 0 м при категории устойчивости А

Рис. 11. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 0 м при категории
устойчивости D
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 0 м при категории
устойчивости D

Рис. 12. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36 час, 2, 3, 4, 6, 8 и 30 сут
для выброса на высоте 0 м при категории устойчивости F
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36 час, 2, 3, 4, 6, 8 и 30 сут
для выброса на высоте 0 м при категории устойчивости F

Рис. 13. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости F
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости F

Рис. 14. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости D
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости D
Рис. 15. Зависимость штилевого фактора разбавления ![]() , с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости F
, с/м3, от расстояния x и продолжительности штиля Δt = 1, 2, 3, 4, 6, 12, 24, 36
час, 2, 3, 4, 6, 8 и 30 сут для выброса на высоте 100 м при категории
устойчивости F
Глава 5. Расчет ожидаемых доз облучения от кратковременных выбросов в атмосферу
5.1. Общие положения
Для разовых выбросов в атмосферу расчет ожидаемых доз целесообразно проводить по «методу коэффициентов накопления», обеспечивающему получение оценок ожидаемых доз облучения за время жизни человека в рассматриваемой точке местности. Строго говоря вычисляются полувековые ожидаемые дозы. Это обычно принимаемое допущение. При этом для короткоживущих или быстро выводящихся радионуклидов полное накопление ожидаемой дозы может наступать задолго до конца жизни человека. Для долгоживущих радионуклидов учитывается не только радиоактивный распад, но и другие процессы выведения нуклидов в окружающей среде.
![]() - есть ожидаемая эффективная или
эквивалентная доза, создаваемая в различных органах или тканях j у лица
возрастной группы а, вызванную радионуклидами r по пути воздействия р.
Для внешнего облучения дозы гамма- и бета-излучения рассчитывают с учетом всех
процессов выведения, а не только радиоактивного распада.
- есть ожидаемая эффективная или
эквивалентная доза, создаваемая в различных органах или тканях j у лица
возрастной группы а, вызванную радионуклидами r по пути воздействия р.
Для внешнего облучения дозы гамма- и бета-излучения рассчитывают с учетом всех
процессов выведения, а не только радиоактивного распада.
Для внутреннего облучения указанная величина представляет собой полувековую ожидаемую эквивалентную дозу для взрослых (эффективную или на отдельный орган или ткань) или соответствующие дозы за время жизни от момента поступления до 70 лет для детей и подростков.
Эффективные и/или эквивалентные дозы на органы или ткани представимы суммой доз, вызванных различными радионуклидами по различным путями облучения
|
|
(5.1) |
где Ha,j - ожидаемая эффективная или эквивалентная доза на орган или ткань j лица возрастной группы а, Зв;
![]() - ожидаемая эффективная или
эквивалентная доза на орган или ткань j лица возрастной группы а,
вызванная радионуклидом r по пути воздействия р, Зв.
- ожидаемая эффективная или
эквивалентная доза на орган или ткань j лица возрастной группы а,
вызванная радионуклидом r по пути воздействия р, Зв.
Различают прямые и непрямые (для пищевых цепочек) пути воздействия выбросов. Прямые пути зависят от места нахождения человека на местности. К ним относят:
- внешнее облучение от нахождения в облаке выброса и на следе выпадений на местности;
- внутреннее облучение за счет ингаляционного пути поступления радионуклидов.
Дозы по пищевым цепочкам определяются не местом нахождения жителей на местности, а территориальным распределением посевных площадей и других сельскохозяйственных угодий.
5.2. Расчет ожидаемых доз по прямым путям облучения
5.2.1. Внешнее облучение от облака
Приведенные ниже формулы для расчета доз внешнего облучения получены в пренебрежении самоэкранированием органов и тканей, и не учитывают различия в возрастных группах. При этом, величина ошибки в значении эффективной дозы, вносимая принятым упрощением, не превышает % 50 %. По мере увеличения расстояния от трубы форма струи может изменяться от линейного (цилиндрического) источника до источника в форме полубесконечного пространства.
Для полубесконечного облака
где ![]() - ожидаемая доза от радионуклида r
в различных органах и тканях j за счет излучения от проходящего облака
выброса, рассчитанная в предположении применимости геометрии полубесконечного
пространства с удельной активностью воздуха, равной приземной концентрации
радионуклида r в рассматриваемой точке х, Зв;
- ожидаемая доза от радионуклида r
в различных органах и тканях j за счет излучения от проходящего облака
выброса, рассчитанная в предположении применимости геометрии полубесконечного
пространства с удельной активностью воздуха, равной приземной концентрации
радионуклида r в рассматриваемой точке х, Зв;
Cv,r(x) - интеграл приземной концентрации (объемной активности) радионуклида r в рассматриваемой точке x, Бк ∙ с/м3.
![]() - дозовые факторы конверсии
(коэффициенты перехода «концентрация в воздухе - мощность дозы») при облучении
от полубесконечного облака для радионуклидов r и различных органов и
тканей j, Зв ∙ м3/(с ∙ Бк). Значения дозовых
коэффициентов
- дозовые факторы конверсии
(коэффициенты перехода «концентрация в воздухе - мощность дозы») при облучении
от полубесконечного облака для радионуклидов r и различных органов и
тканей j, Зв ∙ м3/(с ∙ Бк). Значения дозовых
коэффициентов ![]() для полевой дозы гамма-излучения
приводятся в табл. 5.1 и 5.2;
для полевой дозы гамма-излучения
приводятся в табл. 5.1 и 5.2;
![]() - коэффициент защищенности зданиями
для радионуклида r распределенного в полубесконечном пространстве,
учитывающий также время пребывания человека на открытой местности. Его значения
приведены в табл. 5.3.
- коэффициент защищенности зданиями
для радионуклида r распределенного в полубесконечном пространстве,
учитывающий также время пребывания человека на открытой местности. Его значения
приведены в табл. 5.3.
Для гамма-излучения коэффициент ![]() - с достаточной для практических
расчетов точностью представим полевой дозой. При этом ошибка в сторону
завышения дозы на органы или ткани в самых неблагоприятных случаях не
превзойдет +50 %. С такой точностью коэффициент
- с достаточной для практических
расчетов точностью представим полевой дозой. При этом ошибка в сторону
завышения дозы на органы или ткани в самых неблагоприятных случаях не
превзойдет +50 %. С такой точностью коэффициент ![]() можно оценивать по формуле лучевого
равновесия
можно оценивать по формуле лучевого
равновесия
|
|
(5.3) |
где ![]() - энергетический выход фотонов,
Мэв/расп.
- энергетический выход фотонов,
Мэв/расп.
Для бета-излучения полевую дозу можно рассчитывать также по формуле (5.3), если вместо Er подставлять значение средней энергии бета-частиц.
Для гамма-излучения формулу (5.2) можно применять фактически уже за зоной максимума приземной концентрации. Для бета-излучения она справедлива на любых расстояниях, что обусловлено сравнительно небольшой длинной свободного пробега бета-частиц в воздухе. Следует только помнить, что формула (5.2) для бета-излучения дает дозу для открытой, незащищенной одеждой поверхности кожи.
Для условий применимости линейного источника (под проходящим облаком вблизи от источника приподнятого выброса, где приземные концентрации близки к нулю) следует использовать формулу
|
|
(5.4) |
суммирование проводится по n группам энергетического спектра En излучения радионуклида r;
Qo,r - разовый выброс радионуклида r, Бк;
u - скорость ветра, м/с;
![]() - дифференциальная керма-постоянная в
воздухе для гамма-излучения энергии En, Гр ∙ м2/(с ∙ Бк);
- дифференциальная керма-постоянная в
воздухе для гамма-излучения энергии En, Гр ∙ м2/(с ∙ Бк);
rδ - фактор конверсии от поглощенной дозы в воздухе к поглощенной дозе в биологической ткани, Зв/Гр. Для широкого спектра энергий фотонов
![]() и
и ![]() - массовые
коэффициенты поглощения энергии фотонов в биологической ткани и воздухе
соответственно, м2/кг;
- массовые
коэффициенты поглощения энергии фотонов в биологической ткани и воздухе
соответственно, м2/кг;
![]() - функция излучения линейного
источника в воздухе на высоте h для энергии фотонов En, м-1.
- функция излучения линейного
источника в воздухе на высоте h для энергии фотонов En, м-1.
где BD(Enμnhef) - дозовый фактор накопления рассеянного излучения для точечного изотропного источника с энергией фотонов En дл толщины экранирующего слоя воздуха μnhef;
hef - эффективная высота струи, м.
Значения функции излучения ![]() в воздухе для бесконечного линейного
источника для различных эффективных высот hef и энергий
фотонов En
приведены в табл 5.4.
в воздухе для бесконечного линейного
источника для различных эффективных высот hef и энергий
фотонов En
приведены в табл 5.4.
В промежуточной зоне, где не действуют приближения линейного источника и полубесконечного облака, для практических оценок можно использовать экстраполяционную формулу расчета дозы внешнего облучения Hr(x) в следующей форме
|
|
(5.7) |
где ![]() - доза, рассчитанная по формуле (5.2) для облака радионуклидов r в
форме полубесконечного пространства, Зв.
- доза, рассчитанная по формуле (5.2) для облака радионуклидов r в
форме полубесконечного пространства, Зв.
Доза ![]() , Зв, создаваемая под бесконечным
линейным источником высотой hef для радионуклида r
рассчитывается по формуле
, Зв, создаваемая под бесконечным
линейным источником высотой hef для радионуклида r
рассчитывается по формуле
|
|
(5.8) |
Здесь ![]() - доза от бесконечного линейного
источника, рассчитанная с использованием формул (5.5) и (5.6) со
спектром излучения En,
характерным для радионуклида r;
- доза от бесконечного линейного
источника, рассчитанная с использованием формул (5.5) и (5.6) со
спектром излучения En,
характерным для радионуклида r;
K(х) - множитель, учитывающий приподнятость струи над землей. Он определяется отношением приземных концентраций
![]()
где h - высота выброса, м.
Для гауссовой модели:
|
|
(5.9) |
где h - высота облака в точке детектирования, м;
![]() - вертикальная дисперсия струи, м.
- вертикальная дисперсия струи, м.
При необходимости более точного расчета мощности дозы гамма-излучения от радиоактивного облака сложной формы необходимо моделировать его в виде последовательных небольших объемных источников и производить численное интегрирование по всем источникам, используя общую формулу
|
|
(5.10) |
где ![]() - тот же дозовый фактор конверсии при
облучении от облака для радионуклидов r и различных органов и тканей j,
что и в формуле (5.2), Зв ∙ м3/(Бк
∙ с);
- тот же дозовый фактор конверсии при
облучении от облака для радионуклидов r и различных органов и тканей j,
что и в формуле (5.2), Зв ∙ м3/(Бк
∙ с);
BD - дозовый фактор накопления в воздухе;
![]() - распределение объемной активности
радионуклида r в воздухе, Бк/м3;
- распределение объемной активности
радионуклида r в воздухе, Бк/м3;
μ - линейный коэффициент ослабления излучения в воздухе, м-1;
d - расстояние от детектора до элементарного, объема dV, м.
5.2.2. Внешнее облучение от загрязненной нуклидами поверхности земли
Ожидаемая эффективная или эквивалентная доза, Зв, от радионуклида r на различные органы и ткани j, формируемая гамма- или бета-излучением от загрязненной поверхности земли, рассчитывается по формуле
где Cs,r(x) - интегральные выпадения радионуклида г в рассматриваемой точке x, Бк/м2;
![]() - дозовый фактор конверсии
(коэффициент перехода «поверхностная активность - мощность дозы») при облучении
от поверхности почвы для радионуклидов r для различных органов и тканей j,
для полевой дозы гамма-излучения приведенный в табл. 5.2, Зв ∙ м2/(Бк ∙ с);
- дозовый фактор конверсии
(коэффициент перехода «поверхностная активность - мощность дозы») при облучении
от поверхности почвы для радионуклидов r для различных органов и тканей j,
для полевой дозы гамма-излучения приведенный в табл. 5.2, Зв ∙ м2/(Бк ∙ с);
![]() - коэффициент, учитывающий время
нахождения (проживания) на местности
- коэффициент, учитывающий время
нахождения (проживания) на местности
|
|
(5.12) |
λef - постоянная уменьшения уровня излучения от одномоментно загрязненной почвы за счет радиоактивного распада и экранирования ее верхним слоем при диффузии радионуклидов вглубь почвы, с-1;
t1 - время проживания человека на загрязненной поверхности земли, с. Для практических расчетов рекомендуется t1 = 50 лет;
![]() - коэффициент защищенности зданиями
для радионуклида r распределенного по поверхности почвы, учитывающий
также время пребывания человека на открытой местности, приведенный в табл. 5.3.
- коэффициент защищенности зданиями
для радионуклида r распределенного по поверхности почвы, учитывающий
также время пребывания человека на открытой местности, приведенный в табл. 5.3.
Строго говоря, формула (5.11) дает полевую дозу. При этом ослабление излучения за счет экранирования телом человека не учитывается. Однако расчеты показывают, что такое упрощение оправдано, так как величина ошибки от замены истинной дозы на органы или ткань полевой дозой в самом худшем случае не превзойдет коэффициента 2. Причем в сторону завышения, то есть в запас расчета.
5.2.3. Внутреннее облучение от вдыхания радионуклидов в облаке
Эффективная или эквивалентная ожидаемая доза, Зв, в различных органах и тканях j от радионуклида r за счет ингаляции во время прохождения облака для лица возрастной группы а, рассчитывается по формуле
|
|
(5.13) |
Здесь ![]() - дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при ингаляции радионуклидов r
для полувековой ожидаемой дозы (эффективной или эквивалентной для различных
органов и тканей j) для лица возрастной группы а, Зв/Бк:
- дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при ингаляции радионуклидов r
для полувековой ожидаемой дозы (эффективной или эквивалентной для различных
органов и тканей j) для лица возрастной группы а, Зв/Бк:
|
|
(5.14) |
где ![]() - дозовый фактор конверсии при
ингаляции радионуклидов r для полувековой ожидаемой дозы (эффективной
или эквивалентной для различных органов и тканей j для взрослых, Зв/Бк.
Его значения для эффективной дозы, взятые из НРБ-96 приведены в табл. 5.5;
- дозовый фактор конверсии при
ингаляции радионуклидов r для полувековой ожидаемой дозы (эффективной
или эквивалентной для различных органов и тканей j для взрослых, Зв/Бк.
Его значения для эффективной дозы, взятые из НРБ-96 приведены в табл. 5.5;
![]() - безразмерный поправочный коэффициент
для возрастной группы а, радионуклида r, органов и тканей j, для
ингаляционного пути поступления. Значения поправочных коэффициентов приведены в
табл. 5.6 и 5.7;
- безразмерный поправочный коэффициент
для возрастной группы а, радионуклида r, органов и тканей j, для
ингаляционного пути поступления. Значения поправочных коэффициентов приведены в
табл. 5.6 и 5.7;
![]() - интегральное поступление
радионуклида r за счет ингаляции для лиц возрастной группы а, Бк:
- интегральное поступление
радионуклида r за счет ингаляции для лиц возрастной группы а, Бк:
|
|
(5.15) |
где ![]() - временной интеграл концентрации
радионуклида r в приземном слое воздуха в рассматриваемой точке х,
Бк ∙ с/м3;
- временной интеграл концентрации
радионуклида r в приземном слое воздуха в рассматриваемой точке х,
Бк ∙ с/м3;
![]() - интенсивность вдыхания для лиц
возрастной группы а, м3/с, приведенные в табл. 5.8.
- интенсивность вдыхания для лиц
возрастной группы а, м3/с, приведенные в табл. 5.8.
5.2.4. Внутреннее облучение от потребления питьевой воды
Ожидаемая доза облучения (эффективная или эквивалентная в различных органах и тканях j от радионуклида r за счет потребления питьевой воды лицами возрастной группы а, Зв, равна
|
|
(5.16) |
Здесь ![]() - дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при заглатывании радионуклидов r
для ожидаемой дозы (эффективной или эквивалентной в различных органах и тканях j)
у лиц возрастной группы а, Зв/Бк:
- дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при заглатывании радионуклидов r
для ожидаемой дозы (эффективной или эквивалентной в различных органах и тканях j)
у лиц возрастной группы а, Зв/Бк:
где ![]() - дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при заглатывании радионуклидов r
для ожидаемой дозы (эффективной или эквивалентной в различных органах и тканях j)
у взрослых, Зв/Бк. Его значения для эффективной дозы, взятые из НРБ-96,
приведены в табл;
- дозовый фактор конверсии
(коэффициент перехода «поступление - доза») при заглатывании радионуклидов r
для ожидаемой дозы (эффективной или эквивалентной в различных органах и тканях j)
у взрослых, Зв/Бк. Его значения для эффективной дозы, взятые из НРБ-96,
приведены в табл;
![]() - поправочный коэффициент для
возрастной группы а, радионуклида r, органов и тканей j, для
перорального пути поступления, приведенные в табл. 5.6 и 5.7;
- поправочный коэффициент для
возрастной группы а, радионуклида r, органов и тканей j, для
перорального пути поступления, приведенные в табл. 5.6 и 5.7;
![]() - интегральное поступление
радионуклида r с питьевой водой для лиц возрастной группы а, Бк:
- интегральное поступление
радионуклида r с питьевой водой для лиц возрастной группы а, Бк:
|
|
(5.18) |
где ![]() - временной интеграл концентрации
радионуклида r в питьевой воде, Бк ∙ с/л;
- временной интеграл концентрации
радионуклида r в питьевой воде, Бк ∙ с/л;
![]() - годовое потребление питьевой воды
лицом возрастной группы а, приведенное в табл. 5.8, л/год.
- годовое потребление питьевой воды
лицом возрастной группы а, приведенное в табл. 5.8, л/год.
5.3. Расчет ожидаемых доз по наземным пищевым цепочкам
Эффективная или эквивалентная ожидаемая доза в различных органах и тканях j от радионуклида r при пероральном поступлении однократно выпавших радионуклидов до полного их выведения из окружающей среды у лиц возрастной группы а, Зв, рассчитывается по формуле
Здесь ![]() - тот же фактор конверсии, что и в
формуле (5.17);
- тот же фактор конверсии, что и в
формуле (5.17);
Fp - доля продуктов р, выращиваемых в зоне загрязнения, и входящая в рацион местных жителей, или жителей других районов, куда перевозятся продукты питания местного производства. При консервативных оценках полагают Fp = 1. Для некоторых продуктов, таких, как молоко, листовые овощи, фрукты и ягоды с индивидуальных участков - это достаточно реалистичное предположение;
![]() - интеграл перорального поступления
радионуклида r с продуктами р для лиц возрастной группы а,
вычисляемое при условии, что все потребляемые продукты р производятся в районе
расположения предприятия - источника выброса, Бк:
- интеграл перорального поступления
радионуклида r с продуктами р для лиц возрастной группы а,
вычисляемое при условии, что все потребляемые продукты р производятся в районе
расположения предприятия - источника выброса, Бк:
где ![]() - интеграл выпадения радионуклида r
в рассматриваемой точке x за счет сухого осаждения, Бк/м2;
- интеграл выпадения радионуклида r
в рассматриваемой точке x за счет сухого осаждения, Бк/м2;
![]() - интеграл выпадения радионуклида r в рассматриваемой точке x за счет вымывания
осадками, Бк/м2. Коэффициент 0,2 учитывает смывание «влажных»
отложений примеси с вегетативных частей растений в момент выпадения осадков;
- интеграл выпадения радионуклида r в рассматриваемой точке x за счет вымывания
осадками, Бк/м2. Коэффициент 0,2 учитывает смывание «влажных»
отложений примеси с вегетативных частей растений в момент выпадения осадков;
![]() - коэффициент перехода «выпадение из
атмосферы - поступление в организм человека» радионуклида r с продуктами
питания р для лиц возрастной группы а по воздушному (стеблевому) пути
загрязнения растений, м2;
- коэффициент перехода «выпадение из
атмосферы - поступление в организм человека» радионуклида r с продуктами
питания р для лиц возрастной группы а по воздушному (стеблевому) пути
загрязнения растений, м2;
![]() - коэффициент перехода «выпадение из
атмосферы - поступление в организм человека» радионуклида r с продуктами
питания р для лиц возрастной группы а по корневому пути загрязнения растений, м2.
- коэффициент перехода «выпадение из
атмосферы - поступление в организм человека» радионуклида r с продуктами
питания р для лиц возрастной группы а по корневому пути загрязнения растений, м2.
Коэффициенты ![]() и
и ![]() представляют собой долю от интеграла
выпадения на единицу площади сельскохозяйственных угодий активности
радионуклида r, поступающей за 50 лет проживания на загрязненной
выпадениями после разового выброса территории с пищевыми продуктами р в
организм человека возрастной группы а соответственно по воздушному и корневому
путям при условии равновесного накопления радионуклидов во внешней среде
представляют собой долю от интеграла
выпадения на единицу площади сельскохозяйственных угодий активности
радионуклида r, поступающей за 50 лет проживания на загрязненной
выпадениями после разового выброса территории с пищевыми продуктами р в
организм человека возрастной группы а соответственно по воздушному и корневому
путям при условии равновесного накопления радионуклидов во внешней среде
Формулы для расчета коэффициентов перехода по пищевым цепочкам приведены в Приложении 1.
5.4. Учет особенностей миграции трития и 14C
Миграция во внешней среде и пути загрязнения продуктов питания в случае выбросов трития Т (3H) в форме тритиевой воды НТО и 14C в виде углекислого газа CO2 имеет свои особенности.
Главным путем загрязнения
продуктов питания тритием является влагообмен в атмосфере, содержащей НТО в форме
пара. Процессы обмена протекают быстро, и в результате достигается равновесное
накопление трития в разных средах. Внутреннее облучение в этом случае
рассчитывают также по формуле (5.19),
где под ![]() подразумевается интеграл перорального
поступления трития в форме НТО
подразумевается интеграл перорального
поступления трития в форме НТО ![]() , которое рассчитывают по формуле
, которое рассчитывают по формуле
|
|
(5.22) |
где 86400 - число секунд в сутках;
![]() - временной интеграл объемной
активности в приземном слое воздуха тритиевой воды НТО в рассматриваемой точке
x, Бк ∙ с/м3;
- временной интеграл объемной
активности в приземном слое воздуха тритиевой воды НТО в рассматриваемой точке
x, Бк ∙ с/м3;
![]() - абсолютная влажность атмосферного
воздуха, г/м3, (среднее за вегетативный период значение
- абсолютная влажность атмосферного
воздуха, г/м3, (среднее за вегетативный период значение ![]() можно принять равным 0,009 кг/м3);
можно принять равным 0,009 кг/м3);
Uw,p - суточное потребление связанной влаги в составе пищевых продуктов, кг/сут (референтное значение Uw,p составляет 0,7 кг/сут);
Kw - безразмерный коэффициент фракционирования, равный отношению удельной активности трития в воде продуктов, выраженной в единицах Бк/г, к удельной активности трития в атмосферной влаге.
Коэффициент фракционирования Kw нe всегда достигает равновесного значения. Однако, имея ввиду, что в продуктах питания, выращенных и произведенных в данной местности, тритий может содержаться также в органически связанной форме, для оценок можно принять Kw = 1.
Консервативные оценки ожидаемых доз от трития, содержащегося в атмосферном воздухе в форма НТО можно производить по следующей упрощенной формуле, предполагающей равенство удельной активности трития в воде тканей человека и в атмосферной влаге,
|
|
(5.23) |
где ![]() - временной интеграл объемной
активности НТО в приземном слое воздуха в рассматриваемой точке х, Бк ∙ с/м3;
- временной интеграл объемной
активности НТО в приземном слое воздуха в рассматриваемой точке х, Бк ∙ с/м3;
![]() - абсолютная влажность атмосферного
воздуха,
- абсолютная влажность атмосферного
воздуха, ![]() , (среднее за вегетативный период
значение
, (среднее за вегетативный период
значение ![]() можно принять равным 0,009 кг/м3;
можно принять равным 0,009 кг/м3;
![]() - среднее содержание влаги в тканях
человека; (для стандартного человека
- среднее содержание влаги в тканях
человека; (для стандартного человека ![]() = 614 г/кг);
= 614 г/кг);
![]() - дозовый фактор конверсии для расчета
ожидаемой дозы от трития в тканях человека
- дозовый фактор конверсии для расчета
ожидаемой дозы от трития в тканях человека ![]() .
.
Радиоактивный углерод 14С
обычно поступает в атмосферу в виде углекислого газа или других, быстро
окисляющихся до CO2, соединений. Углекислый
газ поглощается растениями в процессе фотосинтеза, что для 14C является практически единственным значимым путем
облучения населения. Поэтому и в этом случае расчет доз облучения проводится
также по формуле (5.19), где под ![]() подразумевается интеграл перорального
поступления радиоуглерода
подразумевается интеграл перорального
поступления радиоуглерода ![]() . Последний рассчитывают по формуле
. Последний рассчитывают по формуле
|
|
(5.24) |
где ![]() - временной интеграл объемной
активности 14C в виде углекислого
газа в приземном слое воздуха в рассматриваемой точке х, Бк/м3;
- временной интеграл объемной
активности 14C в виде углекислого
газа в приземном слое воздуха в рассматриваемой точке х, Бк/м3;
Fp - доля продуктов р, выращиваемых в зоне загрязнения, и входящая в рацион местных жителей или жителей других районов, куда перевозятся продукты питания местного производства;
![]() - дозовый фактор конверсии для 14C в воздухе, Зв ∙ м3/(с
∙ Бк).
- дозовый фактор конверсии для 14C в воздухе, Зв ∙ м3/(с
∙ Бк).
Последний рассчитывается по следующим формулам:
- для растительных пищевых продуктов
|
|
(5.25) |
- для молока
|
|
(5.26) |
- для мяса
|
|
(5.27) |
где 86400 - число секунд в сутках;
![]() - доля углерода в общей массе
продуктов (равная: для мяса - 0,2, для молока - 0,05, для продуктов
растительного происхождения - 0,11);
- доля углерода в общей массе
продуктов (равная: для мяса - 0,2, для молока - 0,05, для продуктов
растительного происхождения - 0,11);
![]() - содержание природного углерода в
воздухе, кг/м3 (в среднем
- содержание природного углерода в
воздухе, кг/м3 (в среднем ![]() кг/м3);
кг/м3);
Ub - потребление кормов животными, кг/сут;
Um,p - потребление продуктов вида р человеком, кг(л)/сут;
![]() - дозовый фактор конверсии при
поступлении радиоуглерода 14C перорально для полувековой ожидаемой эквивалентной дозы
(эффективной или для различных органов и тканей j) взрослых. Его
значения для эффективной дозы, взятые из НРБ-96, для различных
радионуклидов приведены в табл. 5.5,
Зв/Бк;
- дозовый фактор конверсии при
поступлении радиоуглерода 14C перорально для полувековой ожидаемой эквивалентной дозы
(эффективной или для различных органов и тканей j) взрослых. Его
значения для эффективной дозы, взятые из НРБ-96, для различных
радионуклидов приведены в табл. 5.5,
Зв/Бк;
![]() и
и ![]() - коэффициенты перехода «корм -
молоко» и «корм - мясо» для 14C равные
- коэффициенты перехода «корм -
молоко» и «корм - мясо» для 14C равные ![]() = 0,012 и
= 0,012 и ![]() = 0,031, сут/кг(л).
= 0,031, сут/кг(л).
Таблица 5.1. Дозовые коэффициенты ![]() изотопов Аr, Кr и Хе для расчета
облучения тела человека гамма-излучением радиоактивного облака в форме
полубесконечного пространства
изотопов Аr, Кr и Хе для расчета
облучения тела человека гамма-излучением радиоактивного облака в форме
полубесконечного пространства
|
Нуклид |
Зв/с Бк/м3 |
бэр/с Kи/м3 |
Нуклид |
Зв/с Бк/м3 |
бэр/с Kи/м3 |
|
41Ar |
8,67 ∙ 10-14 |
0,321 |
131mXe |
1,18 ∙ 10-14 |
|
|
85mKr |
1,06 ∙ 10-14 |
0,0393 |
133mXe |
2,78 ∙ 10-14 |
0,0103 |
|
85Kr |
1,51 ∙ 10-14 |
133Xe |
3,24 ∙ 10-14 |
0,012 |
|
|
87Kr |
5,24 ∙ 10-14 |
0,194 |
135mXe |
2,86 ∙ 10-14 |
0,106 |
|
89Kr |
1,39 ∙ 10-14 |
0,516 |
137Xe |
1,25 ∙ 10-14 |
0,0464 |
|
90Kr |
1,22 ∙ 10-14 |
0,451 |
138Xe |
7,24 ∙ 10-14 |
0,268 |
|
91Kr |
4,94 ∙ 10-14 |
0,183 |
139Xe |
2,97 ∙ 10-14 |
0,11 |
|
92Kr |
4,62 ∙ 10-14 |
0,171 |
140Xe |
1,22 ∙ 10-14 |
0,451 |
|
135Xe |
1,65 ∙ 10-14 |
0,081 |
|
|
|
Таблица 5.2. Дозовые коэффициенты
пересчета ![]() для гамма-излучающих радионуклидов
для гамма-излучающих радионуклидов
|
Нуклид |
T1/2 |
E, Мэв/расп. |
|
|
|
|
|
|
18F |
1,83 ч |
0,988 |
5,70 |
4,09 ∙ 10-17 |
6,68 ∙ 10-14 |
5,14 ∙ 10-16 |
4,88 ∙ 10 |
|
22Na |
2,062 года |
2,20 |
11,8 |
8,50 ∙ 10-17 |
1,49 ∙ 10-13 |
1,07 ∙ 10-15 |
1,1 ∙ 10 |
|
24Na |
15,0 ч |
4,12 |
18,1 |
1,30 ∙ 10-16 |
2,78 ∙ 10-13 |
1,64 ∙ 10-15 |
1,27 ∙ 10 |
|
28Mg |
20,91 ч |
1,38 |
7,81 |
5,60 ∙ 10-17 |
9,34 ∙ 10-14 |
7,04 ∙ 10-16 |
7,65 ∙ 10 |
|
38Cl |
37,21 мин |
1,49 |
6,81 |
4,88 ∙ 10-17 |
1,01 ∙ 1013 |
6,14 ∙ 10-16 |
1,98 ∙ 10 |
|
42K |
12,36 ч |
0,276 |
1,35 |
9,70 ∙ 10-18 |
1,86 ∙ 10-14 |
1,22 ∙ 10-16 |
7,83 ∙ 10 |
|
46Sc |
83,83 дня |
2,01 |
10,8 |
7,73 ∙ 10-17 |
1,36 ∙ 10-13 |
9,71 ∙ 10-16 |
1,0 ∙ 10 |
|
48V |
16,238 дня |
2,92 |
15,5 |
1,11 ∙ 10-16 |
1,97 ∙ 10-13 |
1,40 ∙ 10-15 |
2,82 ∙ 10 |
|
51Cr |
27,704 дня |
0,0326 |
0,176 |
1,26 ∙ 10-18 |
2,20 ∙ 10-15 |
1,59 ∙ 10-17 |
5,46 ∙ 10 |
|
52Mn |
5,591 дня |
3,40 |
18,0 |
1,29 ∙ 10-16 |
2,30 ∙ 10-13 |
1,62 ∙ 10-15 |
1,13 ∙ 10 |
|
54Mn |
312,5 дня |
0,836 |
6,61 |
3,31 ∙ 10-17 |
5,65 ∙ 10-14 |
4,16 ∙ 10-16 |
1,54 ∙ 10 |
|
56Mn |
2,5785 ч |
1,68 |
8,47 |
6,08 ∙ 10-17 |
1,14 10-13 |
7,64 ∙ 10-16 |
1,02 ∙ 10-11 |
|
59Fe |
44,529 дня |
1,19 |
6,18 |
4,43 ∙ 10-17 |
8,03 10-14 |
5,57 ∙ 10-16 |
3,07 ∙ 10-9 |
|
58Co |
70,8 дня |
1,21 |
6,72 |
4,82 ∙ 10-17 |
8,20 ∙ 10-14 |
6,06-10-16 |
5,29 ∙ 10-9 |
|
60Co |
5,271 года |
2,50 |
12,8 |
9,22 ∙ 10-17 |
1,69 ∙ 10-13 |
1,16 ∙ 10-15 |
2,13 ∙ 10-7 |
|
65Ni |
2,52 ч |
0,596 |
3,01 |
2,16 ∙ 10-17 |
4,02 ∙ 10-14 |
2,76 ∙ 10-16 |
3,55 ∙ 10-12 |
|
64Cu |
12,701 ч |
0,198 |
1,13 |
8, ∙ 10-18 |
1,33 ∙ 10-14 |
1,02 ∙ 10-16 |
6,7 ∙ 10-12 |
|
65Zn |
243,9 дня |
0,582 |
3,06 |
2,19 ∙ 10-17 |
3,93 ∙ 10-14 |
2,71 ∙ 10-16 |
8,07 ∙ 10-9 |
|
88Rb |
17,8 мин |
0,686 |
3,16 |
2,27 ∙ 10-17 |
4,64 ∙ 10-14 |
2,85 ∙ 10-16 |
4,40 ∙ 10-13 |
|
89Rb |
15,2 мин |
2,32 |
11,4 |
8,15 ∙ 10-17 |
1,57 ∙ 10-14 |
1,02 ∙ 10-15 |
1,35 ∙ 10-12 |
|
95Nb |
35,15 дня |
0,764 |
4,27 |
3,06 ∙ 10-17 |
5,16 ∙ 10-14 |
3,85 ∙ 10-16 |
1,68 ∙ 10-9 |
|
95Zr |
63,98 дня |
0,736 |
4,12 |
2,96 ∙ 10-17 |
4,97 ∙ 10-14 |
3,72 ∙ 10-16 |
2,93 ∙ 10-9 |
|
97Zr/97mNb |
16,9 ч |
0,874 |
4,88 |
3,50 ∙ 10-17 |
5,91 ∙ 10-14 |
4,40 ∙ 10-16 |
3,86 ∙ 10-11 |
|
99Mo/99mTe |
66 ч |
0,277 |
1,68 |
1,20 ∙ 10-17 |
1,87 ∙ 10-14 |
1,51 ∙ 10-16 |
5,18 10-11 |
|
103Ru/103mRh |
39,28 дня |
0,493 |
2,98 |
2,14 ∙ 10-17 |
3,33 ∙ 10-14 |
2,69 ∙ 10-16 |
1,31 ∙ 10-9 |
|
105Ru/105mRh |
4,44 ч |
0,794 |
4,68 |
3,36 ∙ 10-17 |
5,36 ∙ 10-14 |
4,22 ∙ 10-16 |
9,72 ∙ 10-12 |
|
106Ru/106Rh |
371,6 дня |
0,203 |
1,15 |
8,27 ∙ 10-18 |
1,37 ∙ 10-14 |
1,04-10-16 |
4,54 ∙ 10-9 |
|
110mAg/110Ag |
249,76 дня |
2,84 |
15,4 |
1,10 ∙ 10-16 |
1,92 ∙ 10-13 |
1,39 ∙ 10-15 |
4,16 ∙ 10-8 |
|
132Te/132I |
78,2 ч |
0,226 |
1,76 |
1,26 ∙ 10-17 |
1,52 ∙ 10-14 |
1,56 ∙ 10-16 |
6,45 ∙ 10-11 |
|
129I |
1,57 107лет |
0,0246 |
0,633 |
4,54 ∙ 10-18 |
1,66 ∙ 10-15 |
5,71 ∙ 10-17 |
4,50 ∙ 10-8 |
|
131I |
8,0213 дня |
0,380 |
2,16 |
1,55 ∙ 10-17 |
2,57 ∙ 10-14 |
1,94 ∙ 10-16 |
1,94 ∙ 10-10 |
|
132I |
2,30 ч |
2,28 |
12,6 |
9,04 ∙ 10-17 |
1,54 ∙ 10-13 |
1,14 ∙ 10-15 |
1,36 ∙ 10-11 |
|
133I |
20,9 ч |
0,592 |
3,36 |
2,41 ∙ 10-17 |
4,0 ∙ 10-14 |
3,03-10-16 |
3,29 ∙ 10-11 |
|
134I |
52,6 мин |
2,57 |
13,9 |
9,98 ∙ 10-17 |
1,74 10-13 |
1,25 ∙ 10-15 |
5,71 ∙ 10-12 |
|
135I/135mXe |
6,61 ч |
1,66 |
8,44 |
6,06 ∙ 10-17 |
1,12 10-13 |
7,61 ∙ 10-16 |
2,61 ∙ 10-11 |
|
134Cs |
2,062 года |
1,55 |
8,72 |
6,26 ∙ 10-17 |
1,05 10-13 |
7,87 ∙ 10-16 |
6,60 ∙ 10-8 |
|
136Cs/136mBa |
13,1 дня |
2,14 |
11,6 |
8,32 ∙ 10-17 |
1,44 ∙ 10-13 |
1,04 ∙ 10-15 |
1,70 ∙ 10-9 |
|
137Cs/137mBa |
30,14 года |
0,565 |
3,24 |
2,33 ∙ 10-17 |
3,82 ∙ 10-14 |
2,92 ∙ 10-16 |
1,46 ∙ 10-7 |
|
138Cs |
32,2 мин |
2,26 |
11,2 |
8,01 ∙ 1017 |
1,53 ∙ 10-13 |
1,01-10-15 |
2,80 ∙ 10-12 |
|
140Ba |
12,74 дня |
0,176 |
1,14 |
8,21 ∙ 10-18 |
1,19 10-14 |
1,03-10-16 |
1,64 ∙ 10-10 |
|
140La |
40,272 ч |
2,28 |
11,5 |
8,24 ∙ 10-17 |
1,54 ∙ 10-13 |
1,04-10-15 |
2,16 ∙ 10-10 |
|
141Ce |
32,501 дня |
0,0774 |
0,433 |
3,11 ∙ 10-18 |
5,23 ∙ 10-15 |
3,90 ∙ 10-17 |
1,57 ∙ 10-10 |
|
143Се |
33 ч |
0,264 |
1,70 |
1,22 ∙ 10-17 |
1,78 ∙ 10-14 |
1,54 ∙ 10-16 |
2,63 ∙ 10-n |
|
144Ce/144Pr |
285,8 дня |
0,0193 |
0,129 |
9,26 ∙ 10-19 |
1,30 ∙ 10-15 |
1,16 ∙ 10-17 |
3,96 ∙ 10-10 |
|
144Pr |
17,28 мин |
0,0290 |
0,141 |
1,01 ∙ 10-18 |
1,96 ∙ 10-15 |
1,27 ∙ 10-17 |
1,90 ∙ 10-14 |
|
152Eu |
13,33 года |
1,16 |
6,28 |
4,51 ∙ 10-17 |
7,80 ∙ 10-14 |
5,67 ∙ 10-16 |
1,94 ∙ 10-7 |
|
154Eu |
8,8 года |
1,22 |
6,54 |
4,69 ∙ 10-17 |
8,26 ∙ 10-14 |
5,90 ∙ 10-16 |
1,56 ∙ 10-7 |
|
155Eu |
4,96 года |
0,0713 |
0,394 |
2,83 ∙ 10-18 |
4,82 ∙ 10-15 |
3,55 ∙ 10-17 |
6,23 ∙ 10-9 |
|
156Еu |
15,19 дня |
1,33 |
6,48 |
4,65 ∙ 10-17 |
8,99 ∙ 10-14 |
5,84 ∙ 10-16 |
1,10 ∙ 10-9 |
|
156Np |
2,355 дня |
0,160 |
0,794 |
5,70 ∙ 10-18 |
1,08 ∙ 10-14 |
7,16 ∙ 10-17 |
2,10 ∙ 10-11 |
Примечания:
- E = ∑niЕi - полная
энергия фотонов, Мэв/расп.; Г - гамма-постоянная, Р ∙ см2/(ч
∙ мКи); Гδ - керма-постоянная, Гр ∙ м2/с
∙ Бк); rδ = 1,09 -
переходный множитель от поглощенной дозы в воздухе к поглощенной (или
эквивалентной) дозе в биологической ткани, Зв/Гр; ![]() -
дозовый коэффициент, равный мощности эквивалентной дозы на внешней поверхности
незащищенного тела от фотонного излучения радионуклидов, содержащихся в
полубесконечном облаке, Зв ∙ м3/(с ∙ Бк);
-
дозовый коэффициент, равный мощности эквивалентной дозы на внешней поверхности
незащищенного тела от фотонного излучения радионуклидов, содержащихся в
полубесконечном облаке, Зв ∙ м3/(с ∙ Бк); ![]() -
дозовый коэффициент, равный мощности эквивалентной дозы от поверхностного
загрязнения с косинусоидальным распределением фотонного излучения на высоте 1
м, Зв ∙ м3/(с ∙ Бк);
-
дозовый коэффициент, равный мощности эквивалентной дозы от поверхностного
загрязнения с косинусоидальным распределением фотонного излучения на высоте 1
м, Зв ∙ м3/(с ∙ Бк); ![]() -
ожидаемая доза, Зв ∙ м2/Бк, от поверхностно загрязненной
почвы, нормированная на начальную поверхностную активность Cs
= 1 Бк/м2 в момент выпадения.
Здесь λef =
0,693 / Tef определена с
учетом постоянной радиоактивного распада
-
ожидаемая доза, Зв ∙ м2/Бк, от поверхностно загрязненной
почвы, нормированная на начальную поверхностную активность Cs
= 1 Бк/м2 в момент выпадения.
Здесь λef =
0,693 / Tef определена с
учетом постоянной радиоактивного распада ![]() и
постоянной «экологического» выведения λe = 0,04 года-1.
и
постоянной «экологического» выведения λe = 0,04 года-1.
-
Дозовый коэффициент ![]() , Зв ∙
м3/(с ∙ Бк), может быть использован также при оценочных
расчетах доз на живой организм, погруженный в воду, загрязненную радиоактивными
веществами, если табличное значение этого коэффициента увеличить в два раза
(этим учитывается 4π геометрия облучения).
, Зв ∙
м3/(с ∙ Бк), может быть использован также при оценочных
расчетах доз на живой организм, погруженный в воду, загрязненную радиоактивными
веществами, если табличное значение этого коэффициента увеличить в два раза
(этим учитывается 4π геометрия облучения).
Таблица 5.3. Коэффициенты экранирования
зданиями гамма-излучения от радиоактивного облака ![]() и от загрязненной почвы
и от загрязненной почвы ![]() , равные отношению мощности дозы
внутри помещения и вне его
, равные отношению мощности дозы
внутри помещения и вне его
|
Сооружение или местонахождение |
От облака, |
От почвы, |
|
На 1 м выше уровня почвы |
1 |
0,7 |
|
Кирпичный дом |
0,6 |
0,05 - 0,3 |
|
Небольшое многоэтажное здание: |
|
|
|
- подвал |
- |
0,01 |
|
- земляной пол или 1-й этаж |
- |
0,5 |
|
Большое многоэтажное здание: |
|
|
|
- подвал |
0,2 |
0,005 |
|
- верхний этаж |
- |
0,01 |
Примечание: Значения коэффициента экранирования приведены
относительно мощности дозы гамма-излучения на высоте 1 м от источника в форме
полубесконечного облака или поверхностно загрязненной почвы. Для многоэтажных
зданий значения коэффициента даны в местах, расположенных вдали от окон и
дверей. Видно, что коэффициент экранирования меняется в широких пределах от 0,01
до 0,6. Рекомендуется принимать усредненное значение ![]() , в
котором учтены эффекты экранирования и неполного пребывания человека на
открытой местности.
, в
котором учтены эффекты экранирования и неполного пребывания человека на
открытой местности.
Таблица 5.4. Нормированная на единичную линейную активность
мощность полевой дозы на местности от расположенного над поверхностью почвы
линейного бесконечного источника излучения ![]() со спектром фотонов, характерным
для радионуклида r, пЗв ∙ м/(с ∙ МБк)*
со спектром фотонов, характерным
для радионуклида r, пЗв ∙ м/(с ∙ МБк)*
|
Нуклид |
Высота линейного бесконечного источника в воздухе над почвой, метры |
||||||||
|
10 |
30 |
60 |
100 |
120 |
150 |
200 |
300 |
500 |
|
|
41Ar |
14,1 |
4,3 |
1,87 |
0,92 |
0,693 |
0,476 |
0,276 |
0,107 |
0,0211 |
|
85mKr |
1,98 |
0,608 |
0,23 |
0,0866 |
0,056 |
0,0302 |
0,0114 |
1,87 ∙ 10-3 |
6,5 ∙ 10-5 |
|
85Kr |
0,0281 |
8,48 ∙ 10-3 |
3,43 ∙ 10-3 |
1,49 ∙ 10-3 |
1,05 ∙ 10-3 |
6,44 ∙ 10-3 |
3,05 10-4 |
7,79 ∙ 10-5 |
6,5 ∙ 10-5 |
|
87Kr |
8,23 |
2,48 |
1,05 |
0,499 |
0,37 |
0,248 |
0,139 |
0,0536 |
0,0116 |
|
88Kr |
18,8 |
5,65 |
2,46 |
1,22 |
0,92 |
0,637 |
0,375 |
0,154 |
0,0352 |
|
99Kr |
21,4 |
6,46 |
2,77 |
1,34 |
1 |
0,681 |
0,390 |
0,153 |
0,0333 |
|
90Kr |
20 |
6,08 |
2,59 |
1,23 |
0,911 |
0,61 |
0,341 |
0,127 |
0,0244 |
|
91Kr |
8,18 |
2,48 |
1,03 |
0,473 |
0,344 |
0,224 |
0,12 |
0,0422 |
8 ∙ 103 |
|
92Kr |
7,78 |
2,36 |
1 |
0,475 |
0,351 |
0,234 |
0,13 |
0,0472 |
8,6 ∙ 10-3 |
|
131mXe |
0,857 |
0,176 |
0,0373 |
7,05 ∙ 10-3 |
3,39 ∙ 10-3 |
1,26 ∙ 10-3 |
3,09 10-4 |
3,36 ∙ 10-5 |
8,1 ∙ 10-7 |
|
133mXe |
1,15 |
0,26 |
0,0683 |
0,0189 |
0,0112 |
5,56 ∙ 10-3 |
2 ∙ 10-3 |
3,34 ∙ 10-4 |
1,2 ∙ 10-5 |
|
133Xe |
1,08 |
0,274 |
0,0779 |
0,0211 |
0,0118 |
5,25 ∙ 10-3 |
1,5 ∙ 10-3 |
1,47 ∙ 10-4 |
1,9 ∙ 10-6 |
|
135mXe |
5,6 |
1,67 |
0,667 |
0,29 |
0,204 |
0,125 |
0,0597 |
0,0154 |
1,3 ∙ 10-3 |
|
135Xe |
3,2 |
0,965 |
0,371 |
0,147 |
0,0976 |
0,055 |
0,0226 |
4,38 ∙ 10-3 |
2,2 ∙ 10-4 |
|
137Xe |
2,25 |
0,677 |
0,276 |
0,122 |
0,0869 |
0,0545 |
0,0272 |
8,11 ∙ 10-3 |
1,1 ∙ 10-3 |
|
138Xe |
11,4 |
3,44 |
1,46 |
0,692 |
0,513 |
0,345 |
0,195 |
0,075 |
0,0157 |
|
139Xe |
5,61 |
1,7 |
0,659 |
0,265 |
0,178 |
0,103 |
0,0442 |
9,64 ∙ 10-3 |
7 ∙ 10-3 |
|
140Xe |
21,4 |
6,43 |
2,7 |
1,27 |
0,932 |
0,618 |
0,337 |
0,119 |
0,0202 |
|
219Rn |
0,712 |
0,214 |
0,0838 |
0,034 |
0,023 |
0,0133 |
5,67 ∙ 10-3 |
1,18 ∙ 10-3 |
6,5 ∙ 10-5 |
|
220Rn |
4,89 ∙ 10-3 |
1,47 ∙ 10-3 |
5,99 ∙ 10-3 |
2,64 ∙ 10-3 |
1,86 ∙ 10-4 |
1,16 ∙ 10-4 |
5,57 ∙ 10-5 |
1,48 ∙ 10-5 |
1,3 ∙ 10-6 |
|
222Rn |
5,07 ∙ 10-3 |
1,53 ∙ 10-3 |
6,18 ∙ 10-3 |
2,69 ∙ 10-4 |
1,89 ∙ 10-4 |
1,16 ∙ 10-4 |
5,46 ∙ 10-5 |
1,39 ∙ 10-5 |
1,1 ∙ 10-6 |
|
7Be |
0,628 |
0,189 |
0,0759 |
0,0327 |
0,0228 |
0,0138 |
6,45 ∙ 10-3 |
1,59 ∙ 10-3 |
1,2 ∙ 10-4 |
|
22Na |
25,8 |
7,82 |
3,29 |
1,54 |
1,13 |
0,742 |
0,401 |
0,139 |
0,0234 |
|
24Na |
38,8 |
11,7 |
5,15 |
2,59 |
1,97 |
1,38 |
0,832 |
0,354 |
0,0856 |
|
26Al |
29,1 |
8,80 |
3,74 |
1,78 |
1,32 |
0,886 |
0,496 |
0,186 |
0,0372 |
|
46Sc |
23,4 |
7,11 |
3,04 |
1,46 |
1,09 |
0,732 |
0,407 |
0,146 |
0,0241 |
|
44Ti |
1,89 |
0,609 |
0,214 |
0,069 |
0,041 |
0,0193 |
5,81 ∙ 10-3 |
5,79 ∙ 10-4 |
6,8 ∙ 10-6 |
|
51Cr |
0,317 |
0,119 |
0,0471 |
0,0191 |
0,0129 |
7,43 ∙ 10-3 |
3,15 ∙ 10-3 |
6,4 ∙ 10-4 |
3,2 ∙ 10-5 |
|
52Mn |
39,7 |
12 |
5,13 |
2,45 |
1,82 |
1,22 |
0,675 |
0,243 |
0,0425 |
|
54Mn |
10,1 |
3,07 |
1,29 |
0,608 |
0,446 |
0,293 |
0,157 |
0,0517 |
7,1 ∙ 10-3 |
|
59Fe |
13,3 |
4,06 |
1,76 |
0,857 |
0,643 |
0,438 |
0,250 |
0,0948 |
0,0176 |
|
58Co |
11,9 |
3,61 |
1,51 |
0,699 |
0,508 |
0,33 |
0,173 |
0,055 |
7,2 ∙ 10-3 |
|
60Co |
27,7 |
8,43 |
3,66 |
1,8 |
1,35 |
0,927 |
0,534 |
0,206 |
0,0397 |
|
64Cu |
2,34 |
0,722 |
0,293 |
0,128 |
0,0903 |
0,0556 |
0,0266 |
6,96 ∙ 10-3 |
6,3 ∙ 10-4 |
|
65Zn |
6,52 |
2,02 |
0,872 |
0,424 |
0,317 |
0,215 |
0,121 |
0,0449 |
7,9 ∙ 10-3 |
|
75Se |
4,74 |
1,49 |
0,577 |
0,226 |
0,149 |
0,0831 |
0,0334 |
6,14 ∙ 10-3 |
2,7 ∙ 10-4 |
|
89Sr |
1,0110-3 |
3,0610-4 |
1,30 ∙ 10-4 |
6,18 ∙ 10-5 |
4,56 ∙ 10-5 |
3,03 ∙ 10-5 |
1,65 ∙ 10-5 |
5,66 ∙ 10-6 |
8,5 ∙ 10-7 |
|
91Sr |
8,27 |
2,51 |
1,06 |
0,503 |
0,371 |
0,246 |
0,133 |
0,0457 |
7 ∙ 10-3 |
|
91mYа |
6,72 |
2,02 |
0,825 |
0,364 |
0,258 |
0,160 |
0,0775 |
0,0207 |
1,8 ∙ 10-3 |
|
91Y |
0,0406 |
0,0124 |
5,36 ∙ 10-3 |
2,62 ∙ 10-3 |
1,97 ∙ 10-3 |
1,35 ∙ 10-3 |
7,74 ∙ 10-4 |
2,96 ∙ 10-4 |
5,6 ∙ 10-5 |
|
95Zr |
9,14 |
2,76 |
1,15 |
0,531 |
0,385 |
0,25 |
0,13 |
0,0405 |
5 ∙ 10-3 |
|
95mNb |
1,04 |
0,237 |
0,0899 |
0,0349 |
0,021 |
0,0127 |
5,0110-3 |
8,74 ∙ 10-4 |
3,2 ∙ 10-5 |
|
95Nb |
9,44 |
2,85 |
1,19 |
0,553 |
0,403 |
0,262 |
0,137 |
0,0435 |
5,5 ∙ 10-3 |
|
99Mo |
1,88 |
0,562 |
0,231 |
0,104 |
0,0744 |
0,0474 |
0,0241 |
7,31 ∙ 10-3 |
8,8 ∙ 10-4 |
|
103Ru |
5,96 |
1,8 |
0,726 |
0,315 |
0,221 |
0,135 |
0,0638 |
0,0162 |
1,3 ∙ 10-3 |
|
103mRh |
0,0926 |
5,62 ∙ 10-3 |
3,03 ∙ 10-4 |
2,45 ∙ 10-5 |
1,10 ∙ 10-5 |
4,14 ∙ 10-6 |
9,59 ∙ 10-7 |
5,89 ∙ 10-6 |
2,6 ∙ 10-10 |
|
106Ru+ 106mRh |
2,51 |
0,757 |
0,31 |
0,139 |
0,0989 |
0,0623 |
0,031 |
8,9 ∙ 10-3 |
10-3 |
|
105Rh |
0,990 |
0,298 |
0,116 |
0,0471 |
0,0317 |
0,0182 |
7,72 ∙ 10-3 |
1,56 ∙ 10-3 |
7,7 ∙ 10-5 |
|
110mAg |
32,5 |
9,84 |
4,16 |
1,96 |
1,44 |
0,951 |
0,514 |
0,175 |
0,0271 |
|
125mTe |
2,16 |
0,347 |
0,0543 |
7,12 ∙ 10-3 |
2,88 ∙ 10-3 |
8,26 ∙ 10-4 |
1,3 ∙ 10-4 |
6,0410-4 |
6 ∙ 10-8 |
|
127mTe |
0,669 |
0,108 |
0,0165 |
2,12 ∙ 10-3 |
8,62 ∙ 10-4 |
2,58 ∙ 10-4 |
5,13 ∙ 10-5 |
6,43 ∙ 10-6 |
5,1 ∙ 10-7 |
|
129mTe |
0,876 |
0,191 |
0,0577 |
0,0223 |
0,0157 |
9,86 ∙ 10-3 |
5,0210-3 |
1,52 ∙ 10-3 |
1,8 ∙ 10-4 |
|
131mI |
16,5 |
4,96 |
2,08 |
0,968 |
0,710 |
0,466 |
0,251 |
0,0853 |
0,0132 |
|
132Te |
3,96 |
1,05 |
0,353 |
0,126 |
0,0809 |
0,0437 |
0,0168 |
2,84 ∙ 10-3 |
10-4 |
|
130I |
26,5 |
7,98 |
3,29 |
1,49 |
1,07 |
0,682 |
0,346 |
0,103 |
0,0119 |
|
131I |
4,89 |
1,46 |
0,576 |
0,240 |
0,165 |
0,0982 |
0,0441 |
0,0102 |
7,3 ∙ 10-4 |
|
132I |
27,1 |
8,20 |
3,43 |
1,59 |
1,16 |
0,757 |
0,399 |
0,129 |
0,0181 |
|
133I |
7,52 |
2,27 |
0,930 |
0,415 |
0,296 |
0,186 |
0,0923 |
0,0264 |
3 ∙ 10-3 |
|
134I |
30,4 |
9,22 |
3,90 |
1,84 |
1,36 |
0,899 |
0,488 |
0,168 |
0,0262 |
|
133I |
16,9 |
5,14 |
2,22 |
1,08 |
0,813 |
0,555 |
0,318 |
0,123 |
0,0240 |
|
134Cs |
19,2 |
5,81 |
2,41 |
1,10 |
0,799 |
0,514 |
0,265 |
0,0814 |
0,01 |
|
136Cs |
25,7 |
7,79 |
3,28 |
1,53 |
1,12 |
0,741 |
0,4 |
0,137 |
0,0213 |
|
137Cs+ |
7,54 |
2,26 |
0,932 |
0,421 |
0,303 |
0,193 |
0,0975 |
0,0286 |
3,1 ∙ 10-3 |
|
137mBa |
|
|
|
|
|
|
|
|
|
|
140Ba |
2,44 |
0,722 |
0,281 |
0,119 |
0,0826 |
0,05 |
0,0234 |
5,88 ∙ 10-3 |
4,7 ∙ 10-4 |
|
140La |
25,2 |
7,64 |
3,27 |
1,58 |
1,18 |
0,8 |
0,454 |
0,174 |
0,035 |
|
141Ce |
1,07 |
0,323 |
0,116 |
0,0409 |
0,0256 |
0,0132 |
4,65 ∙ 10-3 |
6,55 ∙ 10-5 |
1,6 ∙ 10-5 |
|
143Ce |
4,02 |
1,16 |
0,439 |
0,176 |
0,12 |
0,0709 |
0,0323 |
8,16 ∙ 10-3 |
7,8 ∙ 10-4 |
|
144Ce |
0,336 |
0,0994 |
0,034 |
0,0112 |
6,86 ∙ 10-3 |
3,41 ∙ 10-3 |
1,15 ∙ 10-3 |
1,54 ∙ 10-4 |
3,6 ∙ 10-6 |
|
144mPr |
0,346 |
0,0972 |
0,0278 |
7,16 ∙ 10-3 |
3,87 ∙ 10-3 |
1,63 ∙ 10-3 |
4,51 ∙ 10-4 |
6,65 ∙ 10-5 |
6,5 ∙ 10-6 |
|
144Pr |
0,336 |
0,102 |
0,0435 |
0,0211 |
0,0158 |
0,0107 |
6,09 ∙ 10-3 |
2,34 ∙ 10-3 |
4,7 ∙ 10-4 |
|
182Ta |
14,8 |
4,52 |
1,92 |
0,909 |
0,673 |
0,452 |
0,253 |
0,0939 |
0,0172 |
|
181W |
0,594 |
0,201 |
0,0687 |
0,021 |
0,0121 |
5,48 ∙ 10-3 |
1,53 ∙ 10-3 |
1,32 ∙ 10-4 |
1,2 ∙ 10-6 |
|
182W |
7,59 ∙ 10-4 |
2,48 ∙ 10-4 |
8,93 ∙ 10-5 |
3 ∙ 10-5 |
1,83 ∙ 10-5 |
9 ∙ 10-6 |
2,94 ∙ 10-6 |
3,58 ∙ 10-7 |
7,2 ∙ 10-9 |
___________
Таблица 5.5. Численные значения дозовых
факторов конверсии (коэффициент перехода «поступление - доза») при ингаляции ![]() заглатывании
заглатывании ![]() радионуклидов r для полувековой
ожидаемой эффективной дозы для взрослых, Зв/Бк (по НРБ-96)
радионуклидов r для полувековой
ожидаемой эффективной дозы для взрослых, Зв/Бк (по НРБ-96)
|
Радионуклид |
Период полураспада |
Класс* ингаляции |
Дозовый фактор |
Дозовый фактор |
|
3H |
12,3 лет |
|
1,8 ∙ 10-11 |
4,2 ∙ 10-11 |
|
7Be |
53,3 сут |
П |
4,9 ∙ 10-11 |
2,8 ∙ 10-11 |
|
|
|
М |
5,3 ∙ 10-11 |
|
|
14C |
5730 |
|
5,8 ∙ 10-10 |
5,8 ∙ 10-10 |
|
22Na |
2,60 лет |
Б |
1,3 ∙ 10-9 |
3,2 ∙ 10-9 |
|
24Na |
15,0 час |
Б |
3 ∙ 10-10 |
4,3 ∙ 10-10 |
|
26Al |
7,16 ∙ 10+5 лет |
Б |
1,1 ∙ 10-8 |
3,5 ∙ 10-9 |
|
|
|
П |
1,8 ∙ 10-8 |
|
|
32Si |
450 лет |
Б |
3 ∙ 10-11 |
5,6 ∙ 10-10 |
|
|
|
П |
1,5 ∙ 10-11 |
|
|
|
|
М |
8 ∙ 10-11 |
|
|
32P |
14,3 сут |
Б |
8 ∙ 10-10 |
2,4 ∙ 10-9 |
|
|
|
П |
3,2 ∙ 10-10 |
|
|
33P |
25,4 сут |
Б |
9,6 ∙ 10-11 |
2,4 ∙ 10-10 |
|
|
|
П |
1,4 ∙ 10-9 |
|
|
35S |
87,4 сут |
Б |
5,4 ∙ 10-10 |
1,1 ∙ 10-10 |
|
|
|
П |
1,3 ∙ 10-9 |
|
|
36Cl |
3,01 ∙ 10 лет |
Б |
3,4 ∙ 10-10 |
9,3 ∙ 10-10 |
|
|
|
П |
6,9 ∙ 10-9 |
|
|
40K |
1,28 10+9 лет |
Б |
2,1 ∙ 10-9 |
6,2 ∙ 10-9 |
|
45Ca |
165 сут |
П |
2,1 ∙ 10-9 |
1,6 ∙ 10-10 |
|
41Ca |
4,53 сут |
П |
1,8 ∙ 10-9 |
1,6 ∙ 10-9 |
|
46Sc |
83,8 сут |
М |
6,5 ∙ 10-9 |
1,5 ∙ 10-9 |
|
41Sc |
3,35 сут |
М |
1 ∙ 10-10 |
5,5 ∙ 10-10 |
|
48Sc |
1,82 сут |
М |
1,1 ∙ 10-9 |
1,1 ∙ 10-9 |
|
44Ti |
47,3 лет |
Б |
6,1 ∙ 10-8 |
5,8 ∙ 10-9 |
|
|
|
П |
4 ∙ 10-8 |
|
|
48V |
16,2 сут |
Б |
1,1 ∙ 10-9 |
2 ∙ 10-9 |
|
|
|
П |
2,3 ∙ 10-9 |
|
|
49V |
330 сут |
Б |
2,1 ∙ 10-11 |
1,9 ∙ 10-11 |
|
|
|
П |
3,2 ∙ 10-11 |
|
|
51Cr |
27,7 сут |
Б |
|
3,8 ∙ 10-11 |
|
|
|
П |
3,1 ∙ 10-11 |
|
|
|
|
М |
3,6 ∙ 10-11 |
|
|
52Mn |
5,59 сут |
Б |
9,9 ∙ 10-10 |
1,8 ∙ 10-9 |
|
|
|
П |
1,4 ∙ 10-9 |
|
|
53Mn |
3,1 ∙ 10+6 лет |
Б |
2,9 ∙ 10-11 |
3 ∙ 10-11 |
|
|
|
П |
5,2 ∙ 10-11 |
|
|
54Mn |
312 сут |
Б |
8,1 ∙ 10-10 |
1,1 ∙ 10-10 |
|
|
|
П |
1,5 ∙ 10-9 |
|
|
55Fe |
2,70 лет |
Б |
1,1 ∙ 10-10 |
3,3 ∙ 10-10 |
|
|
|
П |
3,1 ∙ 10-10 |
|
|
59Fe |
44,5 сут |
Б |
2,2 ∙ 10-9 |
1,8 ∙ 10-9 |
|
|
|
П |
3,5 ∙ 10-9 |
|
|
56Co |
78,7 сут |
П |
4,6 ∙ 10-9 |
2,5 ∙ 10-9 |
|
|
|
М |
6,4 ∙ 10-9 |
|
|
51Co |
271 сут |
П |
5,2 ∙ 10-10 |
2,1 ∙ 10-10 |
|
|
|
М |
9,4 ∙ 10-10 |
|
|
58Co |
70,8 сут |
П |
1,5 ∙ 10-9 |
1,4 ∙ 10-10 |
|
|
|
М |
2 ∙ 10-9 |
|
|
60Co |
5,27 сут |
П |
9,6 ∙ 10-9 |
3,4 ∙ 10-9 |
|
|
|
М |
2,9 ∙ 10-9 |
|
|
59Ni |
7,5 ∙ 10+4 лет |
Б |
1,8 ∙ 10-10 |
6,3 ∙ 10-11 |
|
|
|
П |
1,3 ∙ 10-10 |
|
|
65Zn |
244 сут |
|
2,9 ∙ 10-9 |
3,9 ∙ 10-9 |
|
67Ga |
3,26 сут |
Б |
6,8 ∙ 10-11 |
1,9 ∙ 10-10 |
|
|
|
П |
2,3 ∙ 10-10 |
|
|
68Ge |
288 сут |
Б |
2,8 ∙ 10-11 |
1,3 ∙ 10-9 |
|
|
|
П |
5,1 ∙ 10-11 |
|
|
71Ge |
11,8 сут |
Б |
5 ∙ 10-12 |
1,2 ∙ 10-11 |
|
|
|
П |
10-11 |
|
|
73As |
80,3 сут |
П |
9,3 ∙ 10-10 |
2,6 ∙ 10-10 |
|
74As |
17,8 сут |
П |
2,1 ∙ 10-9 |
1,3 ∙ 10-9 |
|
76As |
1,10 сут |
П |
7,4 ∙ 10-10 |
1,6 ∙ 10-9 |
|
77As |
1,62 сут |
П |
3,8 ∙ 10-10 |
4 ∙ 10-10 |
|
75Se |
120 сут |
Б |
10-9 |
2,6 ∙ 10-9 |
|
|
|
П |
1,4 ∙ 10-9 |
|
|
82Br |
1,47 сут |
Б |
3,7 ∙ 10-10 |
5,4 ∙ 10-10 |
|
|
|
П |
|
|
|
86Rb |
18,6 сут |
Б |
9,6 ∙ 10-10 |
2,8 ∙ 10-9 |
|
85Sr |
64,8 сут |
Б |
3,9 ∙ 10-10 |
5,6 ∙ 10-10 |
|
89Sr |
50,5 сут |
Б |
10-9 |
2,6 ∙ 10-9 |
|
90Sr |
29,1 сут |
Б |
2,4 ∙ 10-8 |
2,8 ∙ 10-8 |
|
88Y |
107 сут |
П |
3,9 ∙ 10-9 |
1,3 ∙ 10-9 |
|
|
|
М |
4,2 ∙ 10-9 |
|
|
90Y |
2,67 сут |
П |
1,4 ∙ 10-9 |
2,7 ∙ 10-9 |
|
|
|
М |
1,5 ∙ 10-9 |
|
|
91Y |
58,5 сут |
П |
6,7 ∙ 10-9 |
2,4 ∙ 10-9 |
|
|
|
М |
8,4 ∙ 10-9 |
|
|
93Zr |
I,53 ∙ 10 лет |
Б |
2,5 ∙ 10-8 |
1,1 ∙ 10-9 |
|
|
|
П |
9,6 ∙ 10-9 |
|
|
|
|
М |
3,1 ∙ 10-9 |
|
|
95Zr |
64 сут |
Б |
2,5 ∙ 10-9 |
9,5 ∙ 10-10 |
|
|
|
П |
4,5 ∙ 10-9 |
|
|
|
|
М |
5,5 ∙ 10-9 |
|
|
93mNb |
13,6 лет |
П |
4,6 ∙ 10-10 |
1,2 ∙ 10-10 |
|
|
|
М |
1,6 ∙ 10-9 |
|
|
94Nb |
2,03 ∙ 10 лет |
П |
10-8 |
1,7 ∙ 10-9 |
|
|
|
М |
4,5 ∙ 10-8 |
|
|
95Nb |
35,1 сут |
П |
1,4 ∙ 10-9 |
5,9 ∙ 10-10 |
|
|
|
М |
1,6 ∙ 10-9 |
|
|
99Mo |
2,75 сут |
Б |
2,3 ∙ 10-10 |
6 ∙ 10-10 |
|
|
|
М |
9,1 ∙ 10-10 |
|
|
96Tc |
4,28 сут |
Б |
6 ∙ 10-10 |
1,1 ∙ 10-9 |
|
|
|
П |
1,1 ∙ 10-10 |
|
|
97Tc |
2,6 ∙ 10+6 лет |
Б |
4,6 ∙ 10-11 |
6,8 ∙ 10-11 |
|
|
|
П |
2,1 ∙ 10-10 |
|
|
97mTc |
87 сут |
Б |
2,8 ∙ 10-10 |
5,5 ∙ 10-10 |
|
|
|
П |
3,1 ∙ 10-9 |
|
|
98Tc |
4,2 ∙ 10+6 лет |
Б |
10-9 |
2 ∙ 10-9 |
|
|
|
П |
8,1 ∙ 10-9 |
|
|
99Tc |
2,13 ∙ 10+5 лет |
Б |
2,9 ∙ 10-10 |
6,4 ∙ 10-10 |
|
|
|
П |
3,9 ∙ 10-9 |
|
|
97Ru |
2,90 сут |
Б |
6,1 ∙ 10-11 |
1,5 ∙ 10-10 |
|
|
|
П |
1,1 ∙ 10-10 |
|
|
|
|
М |
1,1 ∙ 10-10 |
|
|
103Ru |
39,3 сут |
Б |
4,9 ∙ 10-10 |
1,3 ∙ 10-10 |
|
|
|
П |
2,3 ∙ 10- 9 |
|
|
|
|
М |
2,8 ∙ 10- 9 |
|
|
106Ru |
1,01 года |
Б |
8 ∙ 10-9 |
1 ∙ 10-9 |
|
|
|
П |
2,6 ∙ 10-8 |
|
|
|
|
М |
6,2 ∙ 10-8 |
|
|
105Rh |
1,47 сут |
Б |
8,8 ∙ 10-11 |
3,1 ∙ 10-10 |
|
|
|
П |
3,1 ∙ 10-10 |
|
|
|
|
М |
3,4 ∙ 10-10 |
|
|
103Pd |
17 сут |
Б |
9 ∙ 10-11 |
1,9 ∙ 10-10 |
|
|
|
П |
3,8 ∙ 10-11 |
|
|
|
|
М |
4 ∙ 10-10 |
|
|
107Pd |
6,5 ∙ 10+6 лет |
Б |
2,6 ∙ 10-11 |
3,1 ∙ 10-11 |
|
|
|
П |
8 ∙ 10-11 |
|
|
|
|
М |
5,5 ∙ 10-10 |
|
|
105Ag |
41 сут |
Б |
5,5 ∙ 10-10 |
4,7 ∙ 10-10 |
|
|
|
П |
7 ∙ 10-10 |
- |
|
|
|
М |
7,9 ∙ 10-10 |
|
|
110mAg |
250 сут |
Б |
5,5 ∙ 10-9 |
2,8 ∙ 10-9 |
|
|
|
П |
7,3 ∙ 10-9 |
|
|
|
|
М |
1,2 ∙ 10- 8 |
|
|
111Ag |
7,45 сут |
Б |
4,1 ∙ 10-10 |
1,3 ∙ 10-9 |
|
|
|
П |
1,5 ∙ 10- 9 |
|
|
|
|
М |
1,7 ∙ 10-9 |
|
|
109Cd |
1,27 лет |
Б |
8,1 ∙ 10-9 |
2 ∙ 10-9 |
|
|
|
П |
6,2 ∙ 10-9 |
|
|
|
|
М |
8,8 ∙ 10-9 |
|
|
115Cd |
2,23 сут |
Б |
3,7 ∙ 10-10 |
1,4 ∙ 10-9 |
|
|
|
П |
9,7 ∙ 10-10 |
|
|
|
|
М |
1,1 ∙ 10-9 |
|
|
115mCd |
44,6 сут |
Б |
5,3 ∙ 10-9 |
3,3 ∙ 10-9 |
|
|
|
П |
5,9 ∙ 10-9 |
|
|
|
|
М |
7,3 ∙ 10-9 |
|
|
111In |
2,83 сут |
Б |
1,3 ∙ 10-10 |
2,9 ∙ 10-10 |
|
|
|
П |
2,3 ∙ 10-10 |
|
|
114mIn |
49,5 сут |
Б |
9,3 ∙ 10-9 |
4,1 ∙ 10-9 |
|
|
|
П |
5,9 ∙ 10-9 |
|
|
113Sn |
115 сут |
Б |
5,4 ∙ 10-10 |
7,4 ∙ 10-10 |
|
|
|
П |
2,5 ∙ 10-9 |
|
|
119mSn |
293 сут |
Б |
2,9 ∙ 10-10 |
3,4 ∙ 10-10 |
|
|
|
П |
2 ∙ 10-9 |
|
|
123Sn |
129 сут |
Б |
1,2 ∙ 10-9 |
2,1 ∙ 10-9 |
|
|
|
П |
7,7 ∙ 10-9 |
|
|
125Sn |
9,64 сут |
Б |
9,2 ∙ 10-10 |
3,1 ∙ 10-9 |
|
|
|
П |
3 ∙ 10-9 |
|
|
122Sb |
2,70 сут |
Б |
3,9 ∙ 10-10 |
1,7 ∙ 10-9 |
|
|
|
П |
10-9 |
|
|
124Sb |
60,2 сут |
Б |
1,3 ∙ 10-9 |
2,5 ∙ 10-9 |
|
|
|
П |
6,1 ∙ 10- 9 |
|
|
125Sb |
2,77 лет |
Б |
1,4 ∙ 10- 9 |
1,1 ∙ 10-9 |
|
|
|
П |
4,5 ∙ 10- 9 |
|
|
121Te |
17 сут |
Б |
2,5 ∙ 10-10 |
4,3 ∙ 10-10 |
|
|
|
П |
3,9 ∙ 10-10 |
|
|
121mTe |
154 сут |
Б |
1,8 ∙ 10-9 |
2,3 ∙ 10-9 |
|
|
|
П |
4,3 ∙ 10-9 |
|
|
125mTe |
58 сут |
Б |
5, 2 ∙ 10-10 |
8,7 ∙ 10-10 |
|
|
|
П |
3, 3 ∙ 10-9 |
|
|
127mTe |
109 сут |
Б |
1,6 ∙ 10-9 |
2,3 ∙ 10-9 |
|
|
|
П |
7,2 ∙ 10-9 |
|
|
129mTe |
33,6 сут |
Б |
1,3 ∙ 10-9 |
3 ∙ 10-9 |
|
|
|
П |
6,3 ∙ 10-9 |
|
|
131mTe |
1,25 сут |
Б |
8,8 ∙ 10-10 |
1,9 ∙ 10-9 |
|
|
|
П |
1,1 ∙ 10-9 |
|
|
132Te |
3,26 сут |
Б |
1,8 ∙ 10-9 |
3,7 ∙ 10-9 |
|
|
|
П |
2,2 ∙ 10-9 |
|
|
125I |
60,1 сут |
Б |
5,3 ∙ 10-9 |
1,5 ∙ 10-8 |
|
126I |
13 сут |
Б |
10-8 |
2,9 ∙ 10-8 |
|
129I |
1,57 ∙ 10+7 лет |
Б |
3,7 ∙ 10-8 |
1,1 ∙ 10-7 |
|
131I |
8,04 сут |
Б |
7,6 ∙ 10-9 |
2,2 ∙ 10-8 |
|
131Cs |
9,69 сут |
Б |
2,9 ∙ 10-11 |
5,8 ∙ 10-11 |
|
134Cs |
2,06 лет |
Б |
6,8 ∙ 10-9 |
1,9 ∙ 10-8 |
|
135Cs |
2,3 ∙ 10 лет |
Б |
7,1 ∙ 10-10 |
2,2 ∙ 10-9 |
|
136Cs |
13,1 сут |
Б |
1,3 ∙ 10-9 |
3,1 ∙ 10-9 |
|
137Cs |
30 лет |
Б |
4,9 ∙ 10-9 |
1,3 ∙ 10-8 |
|
131Ba |
11,8 сут |
Б |
2,3 ∙ 10-10 |
4,5 ∙ 10-10 |
|
133Ba |
10,7 лет |
Б |
1,5 ∙ 10-9 |
1,5 ∙ 10-9 |
|
140Ba |
12,7 сут |
Б |
10-9 |
2,6 ∙ 10-9 |
|
140La |
1,68 сут |
Б |
6 ∙ 10-10 |
2 ∙ 10-9 |
|
|
|
П |
1,1 ∙ 10-9 |
|
|
139Ce |
138 сут |
П |
1,6 ∙ 10-9 |
2,6 ∙ 10-10 |
|
|
|
М |
1,8 ∙ 10-9 |
|
|
141Ce |
32,5 сут |
П |
3,1 ∙ 10-9 |
7,1 ∙ 10-10 |
|
|
|
М |
3,6 ∙ 10-9 |
|
|
143Ce |
1,38 сут |
П |
7,4 ∙ 10-10 |
1,1 ∙ 10-9 |
|
|
|
М |
8,1 ∙ 10-10 |
|
|
144Ce |
284 сут |
П |
3,4 ∙ 10-8 |
5,2 ∙ 10-9 |
|
|
|
М |
4,9 ∙ 10-8 |
|
|
143Pr |
13,6 сут |
П |
2,1 ∙ 10-9 |
1,2 ∙ 10-9 |
|
|
|
М |
2,3 ∙ 10- 9 |
|
|
147Nd |
11 сут |
П |
2 ∙ 10-9 |
1,1 ∙ 10-9 |
|
|
|
М |
2,3 ∙ 10-9 |
|
|
147Pm |
2,62 года |
П |
4,7 ∙ 10-9 |
2,6 ∙ 10-10 |
|
|
|
М |
4,6 ∙ 10-9 |
|
|
149Pm |
2,21 сут |
П |
6,6 ∙ 10-10 |
9,9 ∙ 10-10 |
|
|
|
М |
7,2 ∙ 10-10 |
|
|
151Sm |
90 лет |
П |
3,7 ∙ 10-9 |
9,8 ∙ 10-11 |
|
153Sm |
1,95 сут |
П |
6,1 ∙ 10-10 |
7,4 ∙ 10-10 |
|
152Eu |
13,3 года |
П |
3,9 ∙ 10-9 |
1,4 ∙ 10-9 |
|
154Eu |
8,8 лет |
П |
5 ∙ 10-8 |
2 ∙ 10-9 |
|
155Eu |
4,96 лет |
П |
6,5 ∙ 10-9 |
3,2 ∙ 10-10 |
|
151Gd |
120 сут |
Б |
7,8 ∙ 10-10 |
2 ∙ 10-10 |
|
|
|
П |
8,1 ∙ 10-10 |
|
|
153Gd |
242 сут |
Б |
2,1 ∙ 10-9 |
2,7 ∙ 10-10 |
|
|
|
П |
1,9 ∙ 10-9 |
|
|
160Tb |
72,3 сут |
П |
6,6 ∙ 10-9 |
1,6 ∙ 10-9 |
|
161Tb |
6,91 сут |
П |
1,2 ∙ 10-9 |
7,2 ∙ 10-10 |
|
166Dy |
3,4 сут |
П |
1,8 ∙ 10-9 |
1,6 ∙ 10-9 |
|
166Ho |
1,12 сут |
П |
6,6 ∙ 10-10 |
1,4 ∙ 10-9 |
|
169Er |
9,3 сут |
П |
9,8 ∙ 10-10 |
3,7 ∙ 10-10 |
|
170Tm |
129 сут |
П |
6,6 ∙ 10-9 |
1,3 ∙ 10-9 |
|
171Tm |
1,92 года |
П |
1,3 ∙ 10-9 |
1,1 ∙ 10-10 |
|
169Yb |
32 сут |
П |
2,4 ∙ 10-9 |
7,1 ∙ 10-10 |
|
|
|
М |
2,8 ∙ 10-9 |
|
|
177Lm |
6,71 сут |
П |
10-9 |
5,3 ∙ 10-10 |
|
|
|
М |
1,2 ∙ 10-9 |
|
|
175Hf |
70 сут |
Б |
7,2 ∙ 10-10 |
4,1 ∙ 10-10 |
|
|
|
П |
1,1 ∙ 10-9 |
|
|
181Hf |
42,4 сут |
Б |
1,4 ∙ 10-9 |
1,1 ∙ 10-9 |
|
|
|
П |
4,7 ∙ 10-9 |
|
|
182Ta |
115 сут |
П |
7,2 ∙ 10-9 |
1,5 ∙ 10-9 |
|
|
|
М |
9,8 ∙ 10-9 |
|
|
181W |
121 сут |
Б |
2,8 ∙ 10-11 |
7,6 ∙ 10-11 |
|
185W |
75,1 сут |
Б |
1,4 ∙ 10-10 |
4,4 ∙ 10-10 |
|
184Re |
38 сут |
Б |
4,6 ∙ 10-10 |
10-9 |
|
|
|
П |
1,8 ∙ 10-9 |
|
|
186Re |
3,78 сут |
Б |
5,3 ∙ 10-10 |
1,5 ∙ 10-9 |
|
|
|
П |
1,1 ∙ 10-9 |
|
|
191Os |
15,4 сут |
Б |
2,5 ∙ 10-10 |
5,7 ∙ 10-11 |
|
|
|
П |
1,5 ∙ 10-9 |
|
|
|
|
М |
1,8 ∙ 10-9 |
|
|
193Os |
1,25 сут |
Б |
1,7 ∙ 10-10 |
8,1 ∙ 10-10 |
|
|
|
П |
4,7 ∙ 10-10 |
|
|
|
|
М |
5,1 ∙ 10-10 |
|
|
190Ir |
12,1 сут |
Б |
7,9 ∙ 10-10 |
1,2 ∙ 10-9 |
|
|
|
П |
2 ∙ 10-9 |
|
|
|
|
М |
2,3 ∙ 10-9 |
|
|
192Ir |
74 сут |
Б |
1,8 ∙ 10-9 |
1,4 ∙ 10-9 |
|
|
|
П |
4,9 ∙ 10-9 |
|
|
|
|
М |
6,2 ∙ 10-9 |
|
|
191Pt |
2,8 сут |
Б |
1,1 ∙ 10-10 |
3,4 ∙ 10-10 |
|
193mPt |
4,33 сут |
Б |
|
|
|
195Au |
183 сут |
Б |
7,1 ∙ 10-11 |
2,6 ∙ 10-10 |
|
|
|
П |
10-9 |
|
|
|
|
М |
1,6 ∙ 10-9 |
|
|
198Au |
2,69 сут |
Б |
2,3 ∙ 10-10 |
10-9 |
|
|
|
П |
7,7 ∙ 10-10 |
|
|
|
|
М |
8,4 ∙ 10-10 |
|
|
197Hg |
2,68 сут |
Б |
6 ∙ 10-11 |
2,3 ∙ 10-10 |
|
|
|
П |
2,9 ∙ 10-10 |
|
|
203Hg |
46,6 сут |
Б |
4,7 ∙ 10-10 |
1,9 ∙ 10-9 |
|
|
|
П |
2,3 ∙ 10-9 |
|
|
200Tl |
1,09 сут |
Б |
1,4 ∙ 10-10 |
2 ∙ 10-10 |
|
201Tl |
3,04 сут |
Б |
4,7 ∙ 10-11 |
9,5 ∙ 10-11 |
|
202Tl |
12,2 сут |
Б |
2 ∙ 10-10 |
4,5 ∙ 10-10 |
|
204Tl |
3,78 лет |
Б |
4,4 ∙ 10-10 |
1,3 ∙ 10-9 |
|
203Pb |
2,17 сут |
Б |
9,1 ∙ 10-11 |
2,4 ∙ 10-10 |
|
210Pb |
22,3 года |
Б |
8,9 ∙ 10-7 |
6,8 ∙ 10-7 |
|
205Bi |
15,3 сут |
Б |
4 ∙ 10-10 |
9 ∙ 10-10 |
|
|
|
П |
9,2 ∙ 10-10 |
|
|
206Bi |
6,24 сут |
Б |
7,9 ∙ 10-10 |
1,9 ∙ 10-9 |
|
|
|
П |
1,7 ∙ 10-9 |
|
|
207Bi |
38 лет |
Б |
5,2 ∙ 10-10 |
1,3 ∙ 10-9 |
|
|
|
П |
5,3 ∙ 10-9 |
|
|
210Bi |
5,01 сут |
Б |
1,1 ∙ 10-9 |
1,3 ∙ 10-9 |
|
|
|
П |
8,4 ∙ 10-8 |
|
|
210Po |
138 сут |
Б |
6 ∙ 10-7 |
1,2 ∙ 10-6 |
|
|
|
П |
3 ∙ 10-6 |
|
|
223Ra |
11,4 сут |
П |
6,9 ∙ 10-6 |
10-7 |
|
224Ra |
3,66 сут |
П |
2,9 ∙ 10-6 |
6,5 ∙ 10-8 |
|
225Ra |
14,8 сут |
П |
5,8 ∙ 10-6 |
9,6 ∙ 10-8 |
|
226Ra |
1600 лет |
П |
1,6 ∙ 10-5 |
2,8 ∙ 10-7 |
|
228Ra |
5,75 лет |
П |
2,6 ∙ 10-6 |
6,2 ∙ 10-7 |
|
225Ac |
10 сут |
Б |
8,2 ∙ 10-2 |
2,4 ∙ 10-8 |
|
|
|
П |
6,9 ∙ 10-6 |
|
|
|
|
М |
2,9 ∙ 10-8 |
|
|
227Ac |
21,8 лет |
Б |
5,4 ∙ 10-4 |
1,1 ∙ 10-6 |
|
|
|
П |
2,1 ∙ 10-4 |
|
|
|
|
М |
6,6 ∙ 10-5 |
|
|
227Th |
18,7 сут |
П |
2,8 ∙ 10-6 |
8,9 ∙ 10-9 |
|
|
|
М |
9,6 ∙ 10-6 |
|
|
228Th |
1,91 года |
П |
3,1 ∙ 10-5 |
2 ∙ 10-8 |
|
|
|
М |
3,9 ∙ 10-5 |
|
|
229Th |
7340 лет |
П |
9,9 ∙ 10- 5 |
4,8 ∙ 10- 2 |
|
|
|
М |
6,5 ∙ 10- 5 |
|
|
230Th |
2,2 ∙ 10+4 лет |
П |
4 ∙ 10-5 |
2,1 ∙ 10- 2 |
|
|
|
М |
1,3 ∙ 10- 5 |
|
|
231Th |
1,06 сут |
П |
3 ∙ 10-10 |
3,4 ∙ 10-10 |
|
|
|
М |
3,2 ∙ 10-10 |
|
|
232Th |
1,4 ∙ 10+10 лет |
П |
4,2 ∙ 10- 5 |
2,3 ∙ 10- 2 |
|
|
|
М |
2,3 ∙ 10- 5 |
|
|
234Th |
24,1 сут |
П |
6,3 ∙ 10-9 |
3,4 ∙ 10-9 |
|
|
|
М |
2,3 ∙ 10-5 |
|
|
230Pa |
17,4 сут |
П |
5,2 ∙ 10-2 |
9,2 ∙ 10-10 |
|
|
|
М |
2,1 ∙ 10-2 |
|
|
231Pa |
3,22 ∙10+4 лет |
П |
1,3 ∙ 10-4 |
2,1 ∙ 10-2 |
|
|
|
М |
3,2 ∙ 10-5 |
|
|
233Pa |
27 сут |
П |
3,1 ∙ 10-9 |
8,8 ∙ 10-10 |
|
|
|
М |
3,2 ∙ 10-9 |
|
|
230U |
20,8 сут |
Б |
3,6 ∙ 10-2 |
5,4 ∙ 10-8 |
|
|
|
П |
1,3 ∙ 10-5 |
|
|
|
|
М |
1,5 ∙ 10-5 |
|
|
232U |
72 года |
Б |
3,5 ∙ 10-6 |
2,9 ∙ 10-2 |
|
|
|
П |
|
|
|
|
|
М |
3,5 ∙ 10-5 |
|
|
233U |
1,58 ∙ 10+5 лет |
Б |
5,7 ∙ 10-7 |
5 ∙ 10-8 |
|
|
|
П |
3,2 ∙ 10-6 |
|
|
|
|
М |
8,7 ∙ 10-6 |
|
|
234U |
2,44 ∙ 10+5 лет |
Б |
5,5 ∙ 10-7 |
4,9 ∙ 10-8 |
|
|
|
П |
3,1 ∙ 10-6 |
|
|
|
|
М |
8,5 ∙ 10-6 |
|
|
235U |
7,04 ∙ 10+8 лет |
Б |
5,1 ∙ 10-7 |
4,6 ∙ 10-8 |
|
|
|
П |
2,8 ∙ 10-6 |
|
|
|
|
М |
7,7 ∙ 10-6 |
|
|
236U |
2,37 ∙ 10-7 лет |
Б |
5,2 ∙ 10-7 |
4,6 ∙ 10-8 |
|
|
|
П |
2,9 ∙ 10-6 |
|
|
|
|
М |
7,9 ∙ 10-6 |
|
|
238U |
4,47 ∙ 10-9 лет |
Б |
4,9 ∙ 10-7 |
4,4 ∙ 10-8 |
|
|
|
П |
2,6 ∙ 10-6 |
|
|
|
|
М |
7,3 ∙ 10-6 |
|
|
237Np |
2,14 ∙ 10+6 лет |
П |
2,1 ∙ 10-5 |
1,1 ∙ 10-7 |
|
239Np |
2,36 сут |
П |
9 ∙ 10-10 |
8 ∙ 10-10 |
|
238Pu |
87,7 лет |
П |
4,3 ∙ 10-5 |
2,3 ∙ 10-7 |
|
|
|
М |
1,5 ∙ 10-5 |
|
|
239Pu |
2,41 ∙ 10+4 лет |
П |
4,7 ∙ 10-5 |
2,5 ∙ 10-7 |
|
|
|
М |
1,5 ∙ 10- 5 |
|
|
240Pu |
6540 лет |
П |
4,7 ∙ 10-5 |
2,5 ∙ 10-7 |
|
|
|
М |
1,5 ∙ 10-5 |
|
|
241Pu |
14,4 года |
П |
8,5 ∙ 10-7 |
4,7 ∙ 10-9 |
|
|
|
М |
1,6 ∙ 10-7 |
|
|
242Pu |
3,76 ∙ 10+5 лет |
П |
4,5 ∙ 10-6 |
2,4 ∙ 10-7 |
|
|
|
М |
1,4 ∙ 10-5 |
|
|
244Pu |
8,26 ∙ 10+7 лет |
П |
4,4 ∙ 10-5 |
2,4 ∙ 10-7 |
|
|
|
М |
1,3 ∙ 10-5 |
|
|
245Cm |
432 года |
П |
3,9 ∙ 10-5 |
2 ∙ 10-7 |
|
241mAm |
152 года |
П |
3,5 ∙ 10-5 |
1,9 ∙ 10-7 |
|
243Am |
7380 лет |
П |
3,9 ∙ 10-5 |
2 ∙ 10-7 |
|
242Cm |
163 сут |
П |
4,9 ∙ 10-6 |
1,3 ∙ 10-8 |
|
243Cm |
28,5 лет |
П |
3,9 ∙ 10-5 |
2 ∙ 10-7 |
|
244Cm |
18,1 года |
П |
3,2 ∙ 10-5 |
1,6 ∙ 10-7 |
|
245Cm |
8500 лет |
П |
5,5 ∙ 10-5 |
3 ∙ 10-7 |
|
246Cm |
4730 лет |
П |
5,5 ∙ 10-5 |
2,9 ∙ 10-7 |
|
247Cm |
1,56 ∙ 10+7 лет |
П |
5,1 ∙ 10-5 |
2,7 ∙ 10-7 |
|
248Сm |
3,39 ∙ 10+5 лет |
П |
2 ∙ 10-4 |
1,1 ∙ 10-6 |
|
249Bk |
320 сут |
П |
1,5 ∙ 10-7 |
9,7 ∙ 10-10 |
|
249Cf |
350 лет |
П |
6,6 ∙ 10-5 |
3,5 ∙ 10-7 |
|
250Cf |
13,1 года |
П |
3,2 ∙ 10-5 |
1,6 ∙ 10-7 |
|
251Cf |
898 лет |
П |
6,7 ∙ 10-5 |
36 ∙ 10-7 |
|
252Cf |
2,64 года |
П |
1,8 ∙ 10-5 |
9 ∙ 10-8 |
|
253Cf |
17,8 сут |
П |
1,2 ∙ 10-6 |
1,4 ∙ 10-9 |
|
254Cf |
60,5 сут |
П |
3,7 ∙ 10-5 |
4 ∙ 10-7 |
|
253Es |
20,5 сут |
П |
2,5 ∙ 10-6 |
6,1 ∙ 10-9 |
|
254Es |
276 сут |
П |
8 ∙ 10-6 |
2,8 ∙ 10-8 |
|
254mEs |
1,64 сут |
П |
4,4 ∙ 10-7 |
4,2 ∙ 10-9 |
________________
* Классы ингаляции: Б - быстро выводящиеся соединения, М - медленно выводящиеся соединения, П - промежуточное время выведения вдыхаемых аэрозолей.
Таблица 5.6. Коэффициенты кратности
превышения эффективных доз у молодых ![]() и взрослых
и взрослых ![]() людей
людей ![]() при
поступлении в организм одинаковой активности ингаляционным и пероральным путями
(рассчитаны с учетом особенностей метаболизма радионуклидов в организме молодых
людей)
при
поступлении в организм одинаковой активности ингаляционным и пероральным путями
(рассчитаны с учетом особенностей метаболизма радионуклидов в организме молодых
людей)
|
Радионуклид |
Путь поступления (класс транспортабельности) |
R(t) |
||
|
Возраст, годы |
||||
|
1 - 8 |
8 - 12 |
12 - 20 |
||
|
51Cr г |
Вдыхание (Б) |
3,51 |
2,42 |
1,63 |
|
Вдыхание (М) |
3,32 |
1,99 |
1,30 |
|
|
|
Заглатывание |
2,38 |
1,36 |
1,15 |
|
52Mn |
Вдыхание (М) |
2,74 |
1,75 |
1,23 |
|
|
Заглатывание |
2,09 |
1,36 |
1,14 |
|
54Mn |
Вдыхание (М) |
3,11 |
2,11 |
1,33 |
|
|
Заглатывание |
1,96 |
1,43 |
1,13 |
|
58Co |
Вдыхание (М) |
1,89 |
1,18 |
1,08 |
|
|
Заглатывание |
2,12 |
1,22 |
1,09 |
|
60Co |
Вдыхание (М) |
3,56 |
2,31 |
1,36 |
|
|
Заглатывание |
1,85 |
1,39 |
1,16 |
|
103Ru |
Вдыхание (Б) |
3,80 |
2,35 |
1,48 |
|
|
Вдыхание (М) |
4,32 |
2,57 |
1,49 |
|
|
Заглатывание |
2,66 |
1,34 |
1,13 |
|
106Ru |
Вдыхание (Б) |
4,61 |
3,03 |
1,66 |
|
|
Вдыхание (М) |
5,03 |
2,98 |
1,56 |
|
|
Заглатывание |
3,76 |
1,64 |
1,24 |
|
129I |
Вдыхание (Б) |
4,85 |
2,47 |
2,09 |
|
|
Заглатывание |
4,10 |
2,26 |
2,04 |
|
131I |
Вдыхание (Б) |
8,59 |
3,61 |
2,20 |
|
|
Заглатывание |
7,35 |
3,35 |
2,17 |
|
134Cs |
Вдыхание (Б) |
1,92 |
4,76 |
1,33 |
|
|
Заглатывание |
1,63 |
1,62 |
1,29 |
|
137Cs |
Вдыхание (Б) |
2,68 |
2,22 |
1,49 |
|
|
Заглатывание |
2,28 |
2,03 |
1,45 |
Таблица 5.7. Коэффициенты кратности
превышения эффективных доз у молодых ![]() и взрослых
и взрослых ![]() людей
людей ![]() при
поступлении в организм одинаковой активности ингаляционным и пероральным
путями. Учтен лишь геометрический фактор роста. Особенности метаболизма
радионуклидов в организме детей не учитывались (приняты как у взрослых)
при
поступлении в организм одинаковой активности ингаляционным и пероральным
путями. Учтен лишь геометрический фактор роста. Особенности метаболизма
радионуклидов в организме детей не учитывались (приняты как у взрослых)
|
Нуклид |
R(t) |
Нуклид |
R(t) |
||||
|
Возраст, годы |
Возраст, годы |
||||||
|
1 - 8 |
8 - 12 |
12 - 17 |
1 - 8 |
8 - 12 |
12 - 20 |
||
|
3H |
4,10 |
2,47 |
1,62 |
89Sr |
4,52 |
2,74 |
1,36 |
|
14C |
4,67 |
2,34 |
1,36 |
90Sr |
2,18 |
1,32 |
1,05 |
|
22Na |
3,16 |
1,96 |
1,27 |
90 |
3,71 |
2,44 |
1,70 |
|
24Na |
3,34 |
2,03 |
1,29 |
95Zr |
3,72 |
2,38 |
1,29 |
|
32 p |
4,65 |
2,59 |
1,38 |
95Nb |
3,41 |
2,24 |
1,29 |
|
35S |
4,54 |
2,30 |
1,35 |
W5Ru |
3,73 |
2,10 |
1,35 |
|
45Ca |
4,49 |
2,52 |
1,25 |
110mAg |
3,70 |
2,26 |
1,56 |
|
59Fe |
3,12 |
1,92 |
1,30 |
l44Ce |
2,62 |
1,77 |
1,24 |
|
64Cu |
3,87 |
2,15 |
1,37 |
144Pr |
2,51 |
1,80 |
1,38 |
|
65Zn |
2,81 |
1,77 |
1,19 |
154Eu |
2,15 |
1,40 |
1,08 |
Таблица 5.8. Количество воздуха, вдыхаемого стандартным человеком и детьми (м3/сут) и потребление воды (л/сут)
|
Условия |
Взрослый мужчина |
Взрослая женщина |
Ребенок 10 лет |
ребенок до 1 года |
Новорожденный |
|
Покой |
3,6 (8) |
2,9 (8) |
2,3 (8) |
1,3 (14) |
0,69 (23) |
|
Легкая деятельность |
9,6 (8) |
9,1 (8) |
6,24 (8) |
2,5 (10) |
0,09 (1) |
|
Профессиональная деятельность |
9,6 (9) |
9,1 (8) |
6,24 (8) |
- |
- |
|
Всего за сутки |
23 |
21 |
|
3,8 |
0,8 |
|
потребление питьевой воды, л/сут |
1,0 |
|
0,7 |
0,5 |
|
Примечание: В скобках дано время осуществления данной деятельности (часов в сутки).
Приложение П1
к
Методическим указаниям по расчету и
радиационной обстановки в окружающей среде и
ожидаемого облучения населения при кратковременных
выбросах радиоактивных веществ в атмосферу
П1.1. Общие положения
В настоящем Приложении
приводятся формулы для расчета коэффициентов перехода радионуклидов по пищевым
цепочкам ![]() и
и ![]() для случаев кратковременных выпадений
при аварийных выбросах радиоактивных веществ в атмосферу /см. формулы (5.19) и (5.20) основной части Методических указаний/. Оба эти
коэффициента представляют собой доли от кратковременного выпадения на единицу
площади сельскохозяйственных угодий активности радионуклида r,
поступающей в организм постоянно проживающего в данной местности человека
возрастной группы а за все время его жизни с пищевыми продуктами р
соответственно по воздушному и корневому путям загрязнения растений
для случаев кратковременных выпадений
при аварийных выбросах радиоактивных веществ в атмосферу /см. формулы (5.19) и (5.20) основной части Методических указаний/. Оба эти
коэффициента представляют собой доли от кратковременного выпадения на единицу
площади сельскохозяйственных угодий активности радионуклида r,
поступающей в организм постоянно проживающего в данной местности человека
возрастной группы а за все время его жизни с пищевыми продуктами р
соответственно по воздушному и корневому путям загрязнения растений
|
|
(П1.1) |
При этом предполагается, что все
потребляемые продукты питания имеют местное происхождение. Такая оценка дает
максимально возможные в данных условиях дозы. Они практически всегда превышают
реальные, так как местные продукты в рационе населения обычно составляют лишь
долю от привозимых «чистых» продуктов. Однако для некоторых местных продуктов,
например молока, листовых овощей, фруктов и ягод с индивидуальных участков,
такие оценки могут быть близкими к реальным. Для воздушных путей поступления
используется обозначение ![]() , для корневых -
, для корневых - ![]() . Коэффициент
. Коэффициент ![]() значим только при выпадениях в период
вегетации растений, коэффициент же
значим только при выпадениях в период
вегетации растений, коэффициент же ![]() может быть значим и при выпадениях в
невегетативные периоды года. Это связано с поступлением достаточно долгоживущих
радионуклидов сначала на поверхность почвы, а затем переносом активности в ее
нижележащие слои и постепенным корневым усвоением растениями.
может быть значим и при выпадениях в
невегетативные периоды года. Это связано с поступлением достаточно долгоживущих
радионуклидов сначала на поверхность почвы, а затем переносом активности в ее
нижележащие слои и постепенным корневым усвоением растениями.
Коэффициенты ![]() для данного радионуклида рассчитывают
по формуле
для данного радионуклида рассчитывают
по формуле
|
|
(П1.2) |
где ![]() - площадь сельскохозяйственных угодий,
требующаяся для производства продуктов питания данного вида р,
потребляемых отдельным индивидуумом возрастной группы а, м2;
- площадь сельскохозяйственных угодий,
требующаяся для производства продуктов питания данного вида р,
потребляемых отдельным индивидуумом возрастной группы а, м2;
![]() - безразмерный коэффициент.
Представляет собой долю от общего количества радионуклидов, выпавших на занятую
посадками данной культуры площадь, которая сохранится в произведенных продуктах
к моменту употребления их в пищу.
- безразмерный коэффициент.
Представляет собой долю от общего количества радионуклидов, выпавших на занятую
посадками данной культуры площадь, которая сохранится в произведенных продуктах
к моменту употребления их в пищу.
Значения коэффициента ![]() различаются для разных радионуклидов,
продуктов питания, местных климатических условий, типа почвы, агротехнических
приемов ее обработки, условий выпадения (кратковременных или непрерывных). В
случае кратковременных выпадений важен также момент их реализации в течение
вегетативного периода.
различаются для разных радионуклидов,
продуктов питания, местных климатических условий, типа почвы, агротехнических
приемов ее обработки, условий выпадения (кратковременных или непрерывных). В
случае кратковременных выпадений важен также момент их реализации в течение
вегетативного периода.
Параметр ![]() рассчитывают для конкретных лиц по
следующим формулам:
рассчитывают для конкретных лиц по
следующим формулам:
- для продуктов растительного происхождения
|
|
(П1.3) |
где ![]() - годовая урожайность рассматриваемого
вида растений р в данной местности, кг/(м2 ∙ год);
- годовая урожайность рассматриваемого
вида растений р в данной местности, кг/(м2 ∙ год);
![]() - годовое
потребление этого вида растений лицом возрастной группы а, кг/год;
- годовое
потребление этого вида растений лицом возрастной группы а, кг/год;
- для продуктов животного происхождения
|
|
(П1.4) |
где ![]() - годовое
потребление мяса или молока лицом возрастной группы а, кг(л)/год;
- годовое
потребление мяса или молока лицом возрастной группы а, кг(л)/год;
Р - годовая продуктивность одного животного (среднегодовой привес мяса в расчете на одно животное или его удойность), кг(л)/год;
![]() - площадь k-й кормовой
культуры, приходящаяся на одно животное (в число которых входят площади пастбищ
и сенокосов, которые должны рассматриваться раздельно), м2.
- площадь k-й кормовой
культуры, приходящаяся на одно животное (в число которых входят площади пастбищ
и сенокосов, которые должны рассматриваться раздельно), м2.
Последний параметр может быть определен исходя из общей площади сельскохозяйственных угодий и числа животных, или более точно по формуле
|
|
(П1.5) |
где ![]() - годовая урожайность k-й
кормовой культуры, кг/(м2 ∙ год);
- годовая урожайность k-й
кормовой культуры, кг/(м2 ∙ год);
![]() - ее годовое
потребление одним животным, кг/год.
- ее годовое
потребление одним животным, кг/год.
Значения параметра ![]() могут ра зличаться для жителей не
только разных республик, краев, областей, но и одного поселка. Для грубых
оценок среднее значение этого параметра можно получить из статистических
данных, деля площади, занятые под данную культуру, на число потребителей в
области, регионе или республике.
могут ра зличаться для жителей не
только разных республик, краев, областей, но и одного поселка. Для грубых
оценок среднее значение этого параметра можно получить из статистических
данных, деля площади, занятые под данную культуру, на число потребителей в
области, регионе или республике.
В дальнейшем тексте мы будем опускать индексы г и р, подразумевая, что все характеристики относятся к конкретному радионуклиду и продукту питания, а дозы облучения находят путем суммирования доз, вычисленных для каждого нуклида и всего набора продуктов.
Для суммы всех пищевых цепочек коэффициент накопления Kfi вычисляют по общей формуле
где ∏ - произведение коэффициентов накопления между смежными звеньями отдельной пищевой цепочки;
∑ - суммирование распространяется на все пищевые цепочки;
Kmn - коэффициенты перехода между последовательными звеньями m и n отдельной цепочки.
Соотношение (П1.6)
дает способ разложения сложных сетей миграции на отдельные неразветвленные
цепочки, которые дальше рассматриваются раздельно. При построении приводимых
ниже формул расчета Kfi использована общая схема миграции радионуклидов во внешней
среде, приведенная на рис. П1. Индексы при коэффициентах перехода соответствуют
маркировке схемы. Например, коэффициент Kfa относится к переходу F →
A. Реально он обозначает долю всех выпадений,
поступающую в рацион сельскохозяйственных животных. При разложении общей сети
миграции на отдельные неразветвленные цепочки различают воздушный и корневой
(почвенный) пути поступления радионуклидов в растения и фураж. Для воздушных
путей поступления будет использоваться обозначение ![]() ,а для корневых -
,а для корневых - ![]() . Различаются также: миграция по
молочной и мясной цепочкам, учитывается период выпаса скота и период его
стойлового содержания, в течение которого животные потребляют запасенный на
зиму корм.
. Различаются также: миграция по
молочной и мясной цепочкам, учитывается период выпаса скота и период его
стойлового содержания, в течение которого животные потребляют запасенный на
зиму корм.
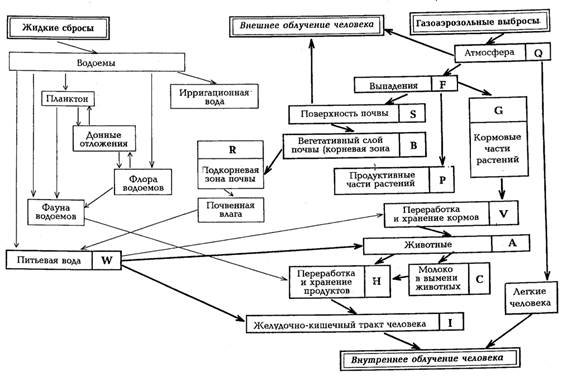
Рис. П1. Расчет безразмерных коэффициентов перехода по пищевым цепочкам Kfi при кратковременных выпадениях радионуклидов на почву
П1.2. Расчет безразмерных коэффициентов перехода по пищевым цепочкам Kfi при кратковременных выпадениях радионуклидов на почву
П1.2.1. Молочная цепочка - воздушный путь загрязнения
Здесь К - дифференциальные коэффициенты перехода радионуклидов по молочной цепочке. Коэффициенты, индексы которых состоят только из строчных букв, безразмерны. Коэффициенты, в индексы которых входит хотя бы одна прописная буква, как правило имеют размерность. Ниже приводятся формулы для расчета их значений.
Безразмерный коэффициент перехода Kfg представляет собой долю от всех выпадений, которая достигает продуктивной части фитомассы травы. В период вегетации травы или нахождения животных на пастбищах Kfg = 1. В остальное время года Kfg = 0.
Коэффициент перехода KgG, м2 ∙ сут/кг, связывает выпадения радионуклидов с временным интегралом концентрации их в траве пастбищ и сенокосов, вычисленным соответственно за время поедания травы животными и время сенокошения. Пастбища характеризуются равновесием между приростом фитомассы травы и ее убыванием от потравы пасущимися животными. Его расчет проводят по следующей формуле, не зависящей от момента выпадения в вегетативный период года
|
|
(П1.8) |
где ![]() - средний за время вегетации травы
коэффициент первоначального задержания приведенный в табл. П1.1, м2/кг (коэффициент 2 учитывает
разницу между средним и максимальным значением коэффициента первоначального
задержания);
- средний за время вегетации травы
коэффициент первоначального задержания приведенный в табл. П1.1, м2/кг (коэффициент 2 учитывает
разницу между средним и максимальным значением коэффициента первоначального
задержания);
λ - постоянная радиоактивного распада, сут-1;
λα - постоянная полевых потерь, сут-1.
При установившемся равновесии между приростом и потравой растений животными, последняя величина численно равна постоянной потерь от потравы. Можно принять λa = 0,05 сут-1, что соответствует периоду полувыведения около 14 суток.
Для сенокосов, в отличие от пастбищ, нет строго равновесия между накоплением и убыванием фитомассы травы. Накопление фитомассы травы происходит непрерывно до очередного сенокошения. В различных климатических зонах режимы сенокошения бывают 2-х и 3-х укосными. В средней полосе обычно применяют 2-х укосное сенокошение. Коэффициент KgG в этом случае зависит от момента выпадения активности во время роста травы. Он равен
где t - промежуток времени между началом весеннего роста травы или предыдущего сенокошения и моментом выпадения радиоактивности, сут;
Tha,i - продолжительность очередного, i-го сенокошения, сут;
Tv,i - время роста фитомассы травы от (i - 1) до i-го сенокошения, сут.
Суммарное время вегетации травы в течение года (до последнего сенокоса) равно
|
|
(П1.10) |
Если выпадение произошло во время сенокоса, то тогда при равномерном перемешивании всего урожая сена будет справедлива формула
|
|
(П1.11) |
где η - доля площади всех сенокосов, остававшихся неубранной к моменту выпадения радиоактивности. Ее можно оценить по фактическим данным или рассчитать по формуле
|
|
(П1.12) |
где τ - время, прошедшее с начала i-го сенокоса до момента выпадения активности, сут.
Коэффициент перехода KGv описывает процедуру «сбора» урожая травы. Она различна для пастбищ и сенокосов, но в обоих случаях коэффициент KGv, (м2 ∙ сут), по смыслу представляет собой интенсивность сбора травы с единицы площади. Для пастбищ коэффициент KGv не зависит от времени выпадения в период вегетации травы. Он равен
|
|
(П1.13) |
где Pγ - годовая урожайность фитомассы травы с единицы площади, кг/м2;
Tpa - продолжительность выпаса животных в течение года, сут;
Ka - доля от выраженной в сут-1 постоянной «полевых потерь» λa, связанная с поеданием пастбищной травы животными. По разным данным реальные значения Ka близки к 0,5.
Справедлива также следующая формула, полученная в предположении равновесия на пастбище между приростом фитомассы травы и поеданием ее животными
|
|
(П1.14) |
где ![]() - средняя равновесная плотность
фитомассы травы на пастбищах, кг/м2;
- средняя равновесная плотность
фитомассы травы на пастбищах, кг/м2;
λa - постоянной «полевых потерь», связанная с поеданием и вытаптыванием пастбищной травы животными, сут-1.
Для сенокосов коэффициенты KGv описывают сбор урожая, приготовление сена или других кормов и хранение их до начала потребления осенью, после перехода на стойловое содержание животных. При кратковременных выпадениях радионуклидов между (i - 1) и i-м сенокосом справедлива формула
где Tw,i - промежуток времени между i-м укосом травы, загрязненной выпадениями, и моментом перевода животных на стойловое содержание (началом потребления запасенных на зиму кормов), сут;
Tha,i - продолжительность i-го сенокоса, сут;
Py,i - накос травы с единицы площади за i-й сенокос, кг/м2.
Приведенные формулы для пастбищного периода справедливы при
содержании животных только на подножном корму. Однако летом их часто
докармливают свежими зелеными кормами. Существуют также хозяйства, где животные
весь год находятся в стойлах, а свежий зеленый корм доставляется животным. В
этих случаях справедливы формулы для стойлового содержания животных (П1.9) и (П1.15) при i = 1, где Tw,i = 0, a ![]() и другие параметры относятся к
рассматриваемой кормовой культуре.
и другие параметры относятся к
рассматриваемой кормовой культуре.
Безразмерные коэффициенты Kva - это доля нуклидов, попавших на траву и другие кормовые культуры, которая в конечном счете поступит в желудочно-кишечный тракт животных. В период выпаса животных Kva = 1.
При стойловом содержании учитывается распад за время хранения сена и кормов
|
|
(П1.16) |
где Tc - время потребления кормов из хранилищ (длительность периода стойлового содержания животных), сут.
Коэффициенты KaC,сут/л, связывают поступление радионуклидов в желудочно-кишечный тракт молочных животных с их содержанием в молоке в момент доения. Многие радионуклиды способны накапливаться в организмах коров и постепенно переходить в молоко (в первую очередь это относится к остеотропным нуклидам).
При консервативных оценках (для старого животного, которое «поглотило» радионуклид в молодом возрасте и давало вклад в ожидаемую дозу потребляющего ее молоко человека в течение всего времени жизни коровы) этот коэффициент можно рассчитать по формуле
где ![]() - коэффициент накопления стабильного
изотопа рассматриваемого радионуклида в молоке, сут/л. Рекомендуемые значения
этих коэффициентов приводятся в табл. П1.2.
Для аномальных местных условий их можно рассчитать по формуле
- коэффициент накопления стабильного
изотопа рассматриваемого радионуклида в молоке, сут/л. Рекомендуемые значения
этих коэффициентов приводятся в табл. П1.2.
Для аномальных местных условий их можно рассчитать по формуле
|
|
(П1.18) |
T1 - продолжительность жизни молочного животного, сут;
ΔT - промежуток времени между двумя доениями коров, сут;
R(τ) - так называемая функция ретенции рассматриваемых радионуклидов для организма животного, безразмерна.
Последняя определяется как доля от одномоментно введенной в организм животного активности, которая остается через время т после введения. Для всех радионуклидов, кроме изотопов щелочноземельных элементов (Са, Ва, Sr и Ra) принято использовать одно-экспоненциальную модель выведения
|
R(τ) = exp[-(λ + λb)τ]. |
(П1.19) |
где λ - постоянная радиоактивного распада, сут-1;
λb - постоянная биологического выведения радионуклида из организма животного, сут;
![]() - эффективный период выведения
стабильного изотопа данного радионуклида r, сут:
- эффективный период выведения
стабильного изотопа данного радионуклида r, сут:
|
|
(П1.20) |
Rst(τ)
- функция ретенции стабильного элемента. Для экспоненциальной модели![]() . C физической точки зрения это время,
в течение которого содержание стабильных нуклидов уменьшится в 2,73 раза.
. C физической точки зрения это время,
в течение которого содержание стабильных нуклидов уменьшится в 2,73 раза.
Интеграл в формуле (П1.17) в этом случае имеет вид
|
|
(П1.21) |
Рекомендуемые значения эффективного
времени выведения ![]() для разных химических элементов
приведены в табл. П1.2.
для разных химических элементов
приведены в табл. П1.2.
Для щелочноземельных элементов
экспоненциальная модель выведения не применима, поэтому значения ![]() для них не указаны. Для них
используется модель выведения Маршалла. Согласно ей
для них не указаны. Для них
используется модель выведения Маршалла. Согласно ей
|
|
(П1.22) |
где λ - постоянная радиоактивного распада, сут-1.
Значения остальных параметров приведены в табл. П1.3.
Коэффициент перехода KCh, л/сут, связывает содержание радионуклидов в молоке в момент доения с поступлением в товарное молоко, идущее в торговую сеть или на переработку. Он может быть рассчитан по формуле
|
|
(П1.23) |
где Pc - удойность молочных животных, л/сут;
Tch - время хранения и перевозки молока на молокозаводы, сут (для свежего молока Tch = 0).
Безразмерный коэффициент Khi учитывает потерю радионуклидов во время переработки молока. Для свежего молока Khi = 1.
П1.2.2. Мясная цепочка - воздушный путь загрязнения
|
|
(П1.24) |
Величины Kfg, KgG, KGv, Kva аналогичны таким же величинам в формуле (П1.7) и рассчитываются также.
Коэффициент KaA, сут/кг, связывает поступление радионуклидов в желудочно-кишечный тракт животных с их содержанием в мясе. Формулы для него получены при тех же предположениях, что и для (П1.17). Для консервативных оценок в случае кратковременных выпадений имеем
|
|
(П1.25) |
где ![]() - коэффициент накопления стабильного
изотопа данного радионуклида в мясе, сут/кг:
- коэффициент накопления стабильного
изотопа данного радионуклида в мясе, сут/кг:
|
|
(П1.26) |
Значения ![]() приведены в табл. П1.2. При их вычислении были взяты осредненные данные,
которые могут быть использованы для приближенных оценок. Коэффициенты
приведены в табл. П1.2. При их вычислении были взяты осредненные данные,
которые могут быть использованы для приближенных оценок. Коэффициенты ![]() различаются для разных стран и климатических
условий.
различаются для разных стран и климатических
условий.
Коэффициент перехода KAh, кг/сут, связывает содержание радионуклидов в мягких тканях сельскохозяйственных животных с выходом их в товарное мясо. Он рассчитывается по формуле
|
|
(П1.27) |
где Pm - масса животного в момент забоя, кг;
T1 - продолжительность его жизни, сут;
Tah - время выдержки мясных туш до переработки или поступления в продажу, сут.
Коэффициент Khi учитывает потери радионуклидов во время кулинарной обработки мяса. Обычно принимают Khi = 1.
П1.2.3. Растительная цепочка - воздушный путь загрязнения
Культурные растения условно подразделяются на два класса: к первому классу относят растения с продолжительным периодом созревания продуктивных частей и сравнительно коротким временем сбора урожая. Такими являются зерновые, зернобобовые, корне- и клубнеплодные, капуста, помидоры, фрукты и т.п. К второму классу принадлежат растения с малым временем роста и созревания продуктивных частей и продолжительным периодом сбора урожая. Например огурцы, салат, зеленый лук, шпинат, некоторые ягоды и др. Для обоих классов:
|
|
(П1.28) |
Различие заключается в способах расчета коэффициентов Kpp и KPh.
Безразмерный коэффициент перехода Kfp (также, как и Kfg для травы) представляет собой долю выпадений из атмосферы, которая попадает на растения. Для кратковременных выпадений в вегетационный период Kfp = 1. В остальное время года Kfp = 0.
Коэффициент Kpp связывает выпадения радионуклидов с временным интегралом их концентрации в продуктивных частях растений за время сбора урожая. Его величина существенно зависит от момента выпадения. В случае кратковременных выпадений на растения, относящихся к первому классу (с периодом цветения большим времени сбора урожая), коэффициент Kfp(t) дается формулой
где значения параметров A и В выбирают в зависимости от момента выпадения активности согласно условиям
|
|
(П1.30) |
|
|
(П1.31) |
t - момент выпадения активности, считая с начала цветения растений, сут;
Tfl - длительность периода цветения растений данного вида, сут;
Tv - период загрязнения продуктивных частей данного растения (интервал времени c начала цветения до начала сбора урожая), сут;
Tha - продолжительность периода сбора урожая, сут.
Формула (П1.29) справедлива для всех растений, кроме озимых зерновых культур. Для них следует использовать следующие формулы:
- при выпадении весной, после начала вегетации
|
|
(П1.32) |
- при выпадении осенью, после сева
|
|
(П1.33) |
- при выпадениях в период зимней паузы роста Kpp.
В двух последних формулах Tw - продолжительность зимней паузы роста растений, сут.
Если выпадение произошло в момент сбора урожая, то для всех культур справедлива формула
|
|
(П1.34) |
где η - доля площади посадок данной культуры, оставшаяся неубранной к моменту выпадения активности. Ее можно оценить по формуле (П1.12), где τ - время, прошедшее с начала сбора урожая.
Для культур, относящихся к второму классу, характерно, что на растениях находятся «плоды» различной степени зрелости, которые собирают по мере их созревания продолжительное время. В этом случае весь период вегетации плодовых частей можно разделить на три этапа, различающихся картиной накопления активности в урожае:
1) начальный период цветения и образования завязей, пока на поле еще нет созревших плодовых частей;
2) период, когда продолжается цветение и образование новых завязей, но уже начат сбор созревших «плодов». На этом этапе на поле присутствуют «плоды» всех степеней зрелости и можно говорить о равновесии между сбором «плодов» и образованием новых завязей;
3) период, когда закончилось образование новых завязей, но еще продолжается сбор поспевающих «плодов», образовавшихся на предыдущем этапе.
При кратковременных выпадениях для всех трех этапов коэффициент перехода, м2 ∙ сут/кг, можно рассчитывать по общей формуле
|
|
(П1.35) |
где ![]() - среднее значение коэффициента
первоначального задержания для рассматриваемой культуры (см. табл. П1.1), м2/кг;
- среднее значение коэффициента
первоначального задержания для рассматриваемой культуры (см. табл. П1.1), м2/кг;
Tha - продолжительность периода сбора урожая, сут;
Tv - время загрязнения растений (считая с начала цветения до начала сбора урожая), сут;
Tb и Te - в зависимости от момента выпадения t выбираются из условий
|
|
(П1.36) |
|
|
(П1.37) |
где t - момент выпадения активности, считая с начала периода цветения, сут;
Tv - время вегетации одного продуктивного «плода» с момента образования завязи до созревания, сут;
tfl,n и tfl,k - моменты начала и окончания периода цветения рассматриваемой культуры, сут.
При выпадении до цветения или после сборе урожая Kpp = 0.
Для озимых зерновых культур вместо Tv следует подставлять (Tv - Tw), где Tw - продолжительность зимней паузы роста, сут.
Коэффициент перехода KPh связывает содержание радионуклида в продуктивных частях растений в момент сбора урожая с моментом поступления их на хранение и переработку. При непрерывных и одномоментных выпадениях для всех растений коэффициент KPh, кг/(м2 ∙ сут), можно рассчитывать по общей формуле
|
KPh = (Py/Tha)exp(-λTs), |
(П1.38) |
где Py - урожайность данной культуры, кг/м2;
Tha - продолжительность периода сбора урожая, сут;
Ts - промежуток времени между сбором урожая и поступлением в хранилища продуктов или на переработку, сут.
Потери при кулинарной обработке для некоторых нуклидов приводятся в табл. П1.4.
П1.2.4. Молочная, мясная и растительная цепочки - корневой путь загрязнения
Для культурных растений, выращиваемых на пахотных землях, справедливы следующие формулы:
- молочная цепочка
|
|
(П1.39) |
- мясная цепочка
|
|
(П1.40) |
- растительная цепочка
|
|
(П1.41) |
Коэффициент Kfs в трех последних формулах - это доля выпавших нуклидов, которая достигает поверхности почвы. Процесс отложения нуклидов на почву конкурирует с фиксацией на растениях. Для грубых оценок можно положить Kfs = 1.
Более точно, для пастбищ при выпадении в период выпаса коров
|
|
(П1.42) |
где ![]() - средний за время вегетации травы
коэффициент первоначального задержания приведенный в табл. П1.1, м2/кг;
- средний за время вегетации травы
коэффициент первоначального задержания приведенный в табл. П1.1, м2/кг;
Р - плотность фитомассы травы на пастбищах, кг/м2.
В остальное время года Kfs = 1.
Для сенокосов при выпадении во время роста травы i-го укоса
|
|
(П1.43) |
где индексом i помечены величины, относящиеся к периоду роста травы i укоса;
t - промежуток времени между началом весеннего роста травы или предыдущего сенокошения и моментом выпадения радиоактивности, сут;
Tv,i - промежуток времени между (i - 1) - м укосом травы, загрязненной выпадениями, и моментом выпадения радионуклидов, сут;
Py,i - накос травы с единицы площади за i-й сенокос, кг/м2.
Для остального времени года Kfs = 1.
Для растительных продуктов коэффициент Kfs можно рассчитать по формуле
|
Kfs=1 - Kp - Kv, |
(П1.44) |
где Kp - доля от всей выпавшей активности, фиксировавшаяся на продуктивных частях растений;
Kv - доля выпавшей активности, отложившаяся на вегетативных частях растений и убранная с поля во время сбора урожая.
Заметим, что с поля может убираться не вся вегетативная масса растений, некоторая часть остается на поле.
Коэффициент Kp равен
|
|
(П1.45) |
где t - промежуток времени между началом весеннего роста продуктивных частей рассматриваемой культуры и моментом выпадения радиоактивности, сут;
![]() - среднее значение коэффициента
первоначального задержания на продуктивных частях рассматриваемой культуры, м2/кг
(см. табл. П6.1);
- среднее значение коэффициента
первоначального задержания на продуктивных частях рассматриваемой культуры, м2/кг
(см. табл. П6.1);
Py - урожайность данной культуры, кг/м2;
Tv - время роста (с начала цветения до начала сбора продуктивных частей растения), сут.
Коэффициент Kv равен
|
|
(П1.46) |
где t - промежуток времени между началом весеннего роста вегетативной массы рассматриваемой культуры и моментом выпадения радиоактивности, сут;
![]() - среднее значение коэффициента
первоначального задержания на вегетативной массе рассматриваемой культуры, м2/кг;
- среднее значение коэффициента
первоначального задержания на вегетативной массе рассматриваемой культуры, м2/кг;
Py,v - поверхностная плотность вегетативной массы данного вида растений к моменту сбора урожая, кг/м2;
Tv,v - продолжительность роста вегетативной массы данного вида растений, сут.
Для невегетативного периода года Kfs = 1.
Безразмерный коэффициент Ksb - это доля нуклидов, которая в момент весенней пахоты переходит с поверхности почвы вглубь пахотного слоя. Для разового выпадения он рассчитывается по формуле
|
Ksb = exp(-λΔτ), |
(П1.47) |
где λ - постоянная радиоактивного распада, сут-1;
Δτ - интервал времени между одномоментным выпадением радионуклидов и весенней пахотой, сут.
При выводе формул для Ksb предполагалось, что вся отложившаяся активность находится до весенней пахоты на поверхности почвы.
Коэффициент KbB, м2 ∙ сут/кг, связывает поступление активности в толщу почвы в момент весенней пахоты с ее содержанием в пахотном слое
|
|
(П1.48) |
где λ - постоянная радиоактивного распада, сут-1:
Λr - постоянная выведения нуклидов из пахотного слоя процессами диффузии вглубь почвы и вследствие уноса их с урожаем, сут-1;
Hb - толщина пахотного слоя, м;
Pb - плотность почвы, кг/м3.
Коэффициенты накопления KBP или KBG связывают содержание радионуклидов в пахотном слое почвы в момент весенней пахоты с содержанием их в культурных растениях или траве в момент сбора урожая. При непрерывных и одномоментных выпадениях они рассчитываются по одинаковым формулам:
- Для культурных пастбищ
|
|
(П1.49) |
где 365 - число дней в году;
Tpa - продолжительность выпаса коров в течение года, сут;
tb,pa - момент начала выпаса коров, считая с начала года, сут;
tpl - момент весенней пахоты лугов, считая с начала года, сут;
![]() - безразмерный коэффициент,
характеризующий накопление стабильных изотопов рассматриваемого радионуклида в
траве
- безразмерный коэффициент,
характеризующий накопление стабильных изотопов рассматриваемого радионуклида в
траве
|
|
(П1.50) |
где Gst и Bst - равновесные концентрации стабильных изотопов рассматриваемых радионуклидов соответственно в траве и в почве, г/кг.
- Для сенокосов
|
|
(П1.51) |
где Nm - число укосов травы на сено в течение одного года;
Tpl,n - время от весенней пахоты до начала n-го сенокоса, сут;
Tv,n - продолжительность вегетации травы до n-го сенокоса, сут.
- Для растительных культур
|
|
(П1.52) |
где Tpl - время между весенней пахотой и началом вегетации продуктивных частей растений, сут;
Tv - продолжительность вегетации продуктивных частей, сут;
Wp и Wv - содержание сухого вещества в продуктивных частях и вегетативной массы растений соответственно;
![]() - безразмерный коэффициент,
характеризующий накопление стабильных элементов в растениях
- безразмерный коэффициент,
характеризующий накопление стабильных элементов в растениях
|
|
(П1.53) |
Pst и Bst - равновесные концентрации стабильных изотопов рассматриваемых радионуклидов в растениях и в почве, г/кг.
Рекомендуемые значения ![]() приведены в табл. П1.2. При их расчете были использованы осредненные
данные, которые нуждаются в конкретных условиях в уточнении. Они могут быть
использованы лишь для приблизительных оценок. Для конкретных местных условий
требуются уточнения.
приведены в табл. П1.2. При их расчете были использованы осредненные
данные, которые нуждаются в конкретных условиях в уточнении. Они могут быть
использованы лишь для приблизительных оценок. Для конкретных местных условий
требуются уточнения.
Для тех радионуклидов, миграция
которых в биосфере проходит на фоне обмена сродственных химических элементов,
можно применять добавляемый к коэффициенту перехода ![]() коэффициент дискриминации DF,
который, например, для изотопов Sr по отношению к природному Са определяется
как
коэффициент дискриминации DF,
который, например, для изотопов Sr по отношению к природному Са определяется
как
|
|
(П1.54) |
Коэффициент KPh рассчитывают по формуле (П1.38). Все остальные коэффициенты рассчитываются по формулам предыдущих разделов.
П1.2.5. Молочная и мясная цепочки - поступление радионуклидов при водопое сельскохозяйственных животных
- Молочная цепочка
|
|
(П1.55) |
- мясная цепочка
|
|
(П1.56) |
где KWi - коэффициент перехода «объемная активность воды в водоеме - поступление в организм человека», л/сут /произведение KWi на интеграл объемной активность воды Av, Бк ∙ сут/л, равно интегральному поступлению радионуклидов в организм человека U, Бк/;
Um - годовое потребление молока (мяса) одним человеком, л(кг)/год;
Pa - средняя годовая продуктивность одного животного (удойность коров или нарастание мясной массы животного), л(кг)/год;
KWa - коэффициент, связывающий содержание радионуклидов в воде с поступлением их в желудочно-кишечный тракт животных, л/сут. В простейшем случае водопоя непосредственно из водоемов KWa = Pw, где Pw - количество воды, потребляемое одним животным, л/сут.
Ориентировочные значения различных параметров, входящих в формулы настоящего раздела, приведены в табл. П1.5 и П1.6. Приведенные там значения носят иллюстративный характер. Они характерны для Центра Европейской части России и отличаются (в первую очередь рационами питания) для различных регионов и этнических групп населения.
Таблица П1.1. Коэффициенты первоначального
задержания активности или массы на продуктивных частях растений ![]() , усредненные за время вегетации Tv растений и даты сева, характерные для средней полосы
Европейской части России
, усредненные за время вегетации Tv растений и даты сева, характерные для средней полосы
Европейской части России
|
Вид растения |
|
Tv, сут |
Дата сева |
|
Озимые: рожь, пшеница |
0,16 |
300 |
5 сентября |
|
Яровая пшеница |
0,16 |
85 |
25 апреля |
|
Капуста |
0,014 |
150 |
|
|
|
|
(70 - 200) |
20 апреля |
|
Томаты |
0,025 |
30 |
1 июня |
|
|
|
(50 - 70) |
|
|
Огурцы |
0,04 |
10 |
10 мая |
|
Яблоки |
0,01 |
120 |
- |
|
Картофель |
0,004 |
100 |
25 апреля |
|
|
|
(70 - 150) |
|
|
Свекла |
0,004 |
130 |
1 мая |
|
Листовые овощи |
0,35 |
10 |
20 апреля |
|
Трава |
0,35 |
100* |
|
__________________
* Относится к сенокосам (время вегетации до последнего укоса травы).
Таблица П1.2. Коэффициенты перехода
стабильных нуклидов для цепочек «корм - мясо» ![]() , «корм - молоко»
, «корм - молоко» ![]() «, почва - растение»
«, почва - растение» ![]() и
и ![]() (безразмерные) и период
биологического полувыведения химического элемента из организма коровы Tb =
0,693 ∙ Tr
(безразмерные) и период
биологического полувыведения химического элемента из организма коровы Tb =
0,693 ∙ Tr
|
Химический элемент |
Коэффициент перехода |
Период полувыведения из организма коровы Tb, сут |
||
|
Корм - мясо |
Корм - молоко |
Почва - растение |
||
|
Н |
0,013 |
0,01 |
- |
- |
|
С |
0,031 |
0,012 |
- |
- |
|
Li |
0,013 |
0,05 |
8,3 ∙ 10-4 |
11 |
|
Be |
1,3 ∙ 10-3 |
10-4 |
4,2 ∙ 10-4 |
2,7 |
|
Na |
0,038 |
0,05 |
0,052 |
17 |
|
Mg |
6,2 ∙ 10-3 |
0,01 |
0,13 |
180 |
|
Al |
1,9 ∙ 10-3 |
5 ∙ 10-4 |
1,8 ∙ 10-4 |
550 |
|
Si |
5 ∙ 10-5 |
10-4 |
1,5 ∙ 10-4 |
6 ∙ 10+5 |
|
P |
0,057 |
0,03 |
1,1 |
257 |
|
S |
0,12 |
0,018 |
0,6 |
90 |
|
CI |
0,1 |
0,05 |
0,5 |
35 |
|
К |
0,015 |
0,01 |
0,37 |
58 |
|
Ca |
5 ∙ 10+3 |
0,01 |
0,036 |
- |
|
Sc |
0,02 |
5 ∙ 10-6 |
1,1 ∙ 10-3 |
1,4 ∙ 10+3 |
|
Ti |
0,039 |
5 ∙ 10-6 |
5,4 ∙ 10-5 |
32 |
|
V |
2 ∙ 10-3 |
10-3 |
1,3 ∙ 10-3 |
42 |
|
Cr |
3 ∙ 10-3 |
2,2 ∙ 10-3 |
2,5 ∙ 10-4 |
616 |
|
Mn |
10-3 |
2,5 ∙ 10-4 |
0,03 |
17 |
|
Fe |
0,05 |
1,2 ∙ 10-3 |
6,6 ∙ 10-4 |
800 |
|
Co |
0,017 |
10-3 |
9,4 ∙ 10-3 |
9,5 |
|
Ni |
6,7 ∙ 10-3 |
6,7 ∙ 10-3 |
0,019 |
667 |
|
Cu |
0,01 |
0,014 |
0,12 |
80 |
|
Zn |
0,038 |
0,039 |
0,4 |
933 |
|
Ga |
0,017 |
5 ∙ 10-5 |
6 |
|
|
Ge |
0,25 |
5 ∙ 10-4 |
0,1 |
930 |
|
As |
2,5 ∙ 10-3 |
6 ∙ 10-3 |
0,01 |
280 |
|
Se |
0,019 |
0,045 |
1,3 |
55 |
|
Br |
0,033 |
0,05 |
0,76 |
14 |
|
Rb |
0,038 |
0,03 |
0,13 |
80 |
|
Sr |
6 ∙ 10-4 |
2 ∙ 10-3 |
0,017 |
- |
|
Y |
5,8 ∙ 10-3 |
10-5 |
2,6 ∙ 10-3 |
1,4 ∙ 10+4 |
|
Zr |
0,04 |
5 ∙ 10-6 |
1,7 ∙ 10-4 |
450 |
|
Nb |
0,35 |
2,5 ∙ 10-3 |
9,4 ∙ 10-3 |
760 |
|
Mo |
0,01 |
7,5 ∙ 10-3 |
0,012 |
100 |
|
Tc |
0,05 |
0,02 |
0,25 |
30 |
|
Ru |
0,05 |
5 ∙ 10-6 |
0,05 |
73 |
|
Rh |
1,9 ∙ 10-3 |
0,01 |
10 |
10 |
|
Pd |
5 ∙ 10-3 |
0,01 |
5 |
5 |
|
Ag |
0,022 |
0,05 |
0,15 |
52 |
|
Cd |
6,7 ∙ 10-4 |
1,2 ∙ 10-4 |
0,3 |
200 |
|
In |
0,01 |
10-4 |
0,25 |
48 |
|
Sn |
0,1 |
2,5 ∙ 10-3 |
2,5 ∙ 10-3 |
200 |
|
Sb |
5 ∙ 10-3 |
1,5 ∙ 10-3 |
0,011 |
38 |
|
Те |
9,6 ∙ 10-3 |
10-3 |
1,3 |
25 |
|
I |
0,01 |
0,02 |
0,02 |
50 |
|
Cs |
6 ∙ 10-3 |
0,014 |
0,01 |
30 |
|
Ba |
4 ∙ 10-3 |
6 ∙ 10-4 |
5 ∙ 10-3 |
- |
|
La |
2,5 ∙ 10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
500 |
|
Ce |
1,5 ∙ 10-3 |
10-5 |
2,5 ∙ 10-3 |
563 |
|
Pr |
5,9 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
750 |
|
Nd |
4,7 ∙ 10-3 |
5 ∙ 10-6 |
2,4 ∙ 10-3 |
655 |
|
Pm |
6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
655 |
|
Sm |
6,2 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
655 |
|
Eu |
6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
635 |
|
Gd |
4,5 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
550 |
|
Tb |
5,6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
670 |
|
Dy |
6,7 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
700 |
|
Ho |
5,6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
750 |
|
Er |
5 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
670 |
|
Tm |
5,6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
675 |
|
Yb |
5 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
685 |
|
Lu |
5,6 ∙ 10-3 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
750 |
|
Hf |
0,05 |
5 ∙ 10-6 |
1,7 ∙ 10-4 |
563 |
|
Та |
0,2 |
2,5 ∙ 10-3 |
6,3 ∙ 10-3 |
240 |
|
W |
0,017 |
5 ∙ 10-4 |
0,018 |
100 |
|
Re |
0,02 |
0,025 |
0,25 |
14 |
|
Os |
0,05 |
5 ∙ 10-3 |
0,05 |
80 |
|
Ir |
1,9 ∙ 10-3 |
5 ∙ 10-3 |
13 |
20 |
|
Pt |
5 ∙ 10-3 |
5 ∙ 10-3 |
0,5 |
24 |
|
Au |
0,01 |
0,025 |
2,5 ∙ 10-3 |
120 |
|
Hg |
3,35 ∙ 10-3 |
3,8 ∙ 10-4 |
0,38 |
100 |
|
Tl |
0,05 |
2,2 ∙ 10-5 |
0,25 |
25 |
|
Pb |
3,7 ∙ 10-4 |
6,2 ∙ 10-4 |
0,069 |
1460 |
|
Bi |
0,01 |
5 ∙ 10-4 |
0,15 |
58 |
|
Po |
0,012 |
3 ∙ 10-4 |
1 |
30 |
|
At |
0,05 |
0,05 |
0,25 |
57 |
|
Fr |
0,055 |
0,05 |
0,01 |
70 |
|
Ra |
0,043 |
0,01 |
1,4 ∙ 10-3 |
- |
|
Ac |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
2,4 ∙ 10+4 |
|
Th |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
5,7 ∙ 10+4 |
|
Ра |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
4,1 ∙ 10+4 |
|
U |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
100 |
|
Np |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
3,9 ∙ 10+4 |
|
Pu |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
6,5 ∙ 10+4 |
|
Am |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
2 ∙ 10+4 |
|
Bk |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
2,4 ∙ 10+4 |
|
Cf |
10-4 |
5 ∙ 10-6 |
2,5 ∙ 10-3 |
6,5 ∙ 10+4 |
Примечания:
1) Приведенные в таблице коэффициенты перехода получены из соотношений:
![]() =
[мг/кг мяса (влажная масса)] / [мг/сут рацион корма (влажная масса)];
=
[мг/кг мяса (влажная масса)] / [мг/сут рацион корма (влажная масса)];
![]() = [мг/л
молока] / [мг/сут рацион корма (влажная масса)];
= [мг/л
молока] / [мг/сут рацион корма (влажная масса)];
![]() [мг/кг
растений (влажная масса)] / [мг/кг почвы (сухая масса)].
[мг/кг
растений (влажная масса)] / [мг/кг почвы (сухая масса)].
2) Для щелочноземельных элементов экспоненциальная модель выведения неприменима, поэтому для них следует применять модель Маршалла (П1.22).
Таблица П1.3. Параметры формулы Маршалла (П1.22) для функции ретенции R(t) щелочноземельных элементов
|
Параметр |
Единица измерения |
Са |
Sr |
Ва |
Ra |
|
ρ |
безразмерный |
0,79 |
0,6 |
0,62 |
0,821 |
|
m |
сут-1 |
0,1 |
0,25 |
0,75 |
0,4 |
|
ε |
сут |
0,76 |
0,2 |
0,007 |
0,12 |
|
b |
безразмерный |
0,1 |
0,18 |
0,237 |
0,415 |
|
β |
безразмерный |
0,532 |
0,555 |
0,564 |
0,608 |
|
r |
безразмерный |
0,826 |
0,949 |
0,991 |
0,997 |
|
λr |
сут-1 |
7,93 ∙ 10-8 |
7,93 ∙ 10-8 |
1,27 ∙ 10-7 |
4,64 ∙ 10-8 |
|
σ |
безразмерный |
4 |
4 |
4 |
4 |
Таблица П1.4. Доля радионуклидов, остающаяся в пищевых продуктах после переработки и кулинарной обработки
|
Продукт |
короткоживущие нуклиды |
90Sr |
Йод |
137Cs |
U, Pu |
|
Зерно (хлеб) |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
|
Овощи: |
|
|
|
|
|
|
плодовые |
0,7 |
0,8 |
0,7 |
0,8 |
0,7 |
|
листовые |
0,6 |
0,7 |
0,6 |
0,7 |
0,6 |
|
корнеплоды |
0,3 |
0,5 |
0,3 |
0,5 |
0,3 |
|
Картофель |
|
0,8 |
0,7 |
0,8 |
0,8 |
Таблица П1.5. Параметры, необходимые для расчетов коэффициентов перехода радионуклидов по пищевым цепочкам, характерные для Центра Европейской части России
|
Обозначение |
Параметр |
Значение |
|
P |
Средняя плотность травяного покрова пастбищ (сырая масса) |
0,242 |
|
λa |
Постоянная «полевых» потерь на траве пастбищ при выпасе скота |
0,05 сут |
|
Ka |
Доля от постоянной «полевых» потерь λa, связанная с поеданием травы животными (доля, равная 1 - Ka связана с вытаптыванием травы животными, смыванием дождем и т.п.) |
0,5 |
|
Py |
Урожай вегетативной массы однолетних* растений (включая траву) |
72 ц/га |
|
Pw |
Среднее содержание сухого вещества в вегетативной массе растений и траве |
25 % |
|
Tpa |
Продолжительность сезона выпаса коров |
185 сут/год |
|
|
Принятая дата начала выпаса коров |
20 апреля |
|
Pc |
Средняя удойность коров |
2500 л/год |
|
ΔT |
Промежуток времени между двумя доениями коров |
8 часов |
|
Pm |
Масса «мясных» быков к моменту забоя |
300 кг |
|
Ia |
Кормовой рацион коров |
40 кг/сут |
|
Pa |
потребление воды коровой |
60 л/сут |
|
Tl |
Продолжительность жизни скота: |
|
|
|
мясные быки |
1,5 года |
|
|
молочные коровы |
15 лет |
|
Tah |
Время выдержки от момента забоя скота до начала потребления мяса |
14 сут |
|
Hb |
Глубина вспахивания почвы |
0,25 м |
|
Pb |
Плотность почвы |
1800 |
|
λr |
Постоянная метаболического выведения нуклидов из корневого слоя почвы |
0,02 год |
|
|
Потребления мяса взрослым человеком |
80 кг/год |
|
|
Потребление молока взрослым (с учетом молока на производство молокопродуктов) |
1 л/сут |
|
|
Потребление молока ребенком до 1 года |
0,7 л/сут |
|
Tw |
Продолжительность зимней паузы роста растений |
165 дней |
|
|
Принятая дата начала зимней паузы роста |
1 ноября |
|
|
Распределение кормовых угодий: |
|
|
|
мясной скот - пастбища |
37 % |
|
|
сенокосы |
36 % |
|
|
молочный скот - пастбища |
14 % |
|
|
сенокосы |
13 % |
________________
* Значение остальных параметров для вегетативной массы растений совпадает с данными для травы, приведенными в табл. П1.1.
Таблица П1.6. Параметры, зависящие от вида растений, характерные для Центра Европейской части России
|
Обозначение |
Параметр |
Зерно яровой пшеницы |
Зерно озимой ржи |
Картофель |
Капуста |
Томаты |
Огурцы |
Яблоки |
Листовые овощи |
|
|
Среднее значение коэффициента первоначального задержания, |
0,16 |
0,16 |
0,004 |
0,014 |
0,025 |
0,04 |
0,01 |
0,35 |
|
Tv |
Время роста продуктивных частей растений, сут |
85 |
300 |
100 |
150 |
30 |
10 |
120 |
10 |
|
Tfl |
Продолжительность периода цветения, сут |
10 |
10 |
10 |
10 |
20 |
30 |
10 |
- |
|
Tha |
Продолжительность сбора урожая, сут |
7 |
7 |
20 |
20 |
20 |
30 |
90 |
10 |
|
Wp |
Содержание сухого вещества в продуктивных частях растений |
90 % |
90 % |
25 % |
25 % |
10 % |
5 % |
25 % |
25 % |
|
Ts |
Время начальной выдержки от момента сбора урожая до начала потребления, сут |
90 |
90 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Ta |
Продолжительность потребления продуктов одного урожая, сут |
365 |
365 |
365 |
365 |
30 |
1 |
180 |
1 |
|
Py |
Урожайность культур (сырая масса), ц/га |
15 |
20 |
120 |
230 |
150 |
50 |
100 |
70 |
|
|
Сроки сева |
25.04 |
05.09 |
25.04 |
20.04 |
01.06 |
10.05 |
- |
20.04 |
|
Ua |
Рекомендуемое потребление продуктов питания работников, занятым физическим трудом средней тяжести, кг/год |
90 |
73 |
120 |
73 |
36 |
18 |
55 |
8 |
Приложение П2
к
Методическим указаниям по расчету
радиационной обстановки в окружающей среде и
ожидаемого облучения населения при кратковременных
выбросах радиоактивных веществ в атмосферу
П2.1. Общие положения
Разовый фактор разбавления при штиле и слабом ветре G(x,Δt), с/м3, вычисляется как интеграл по времени от мгновенного фактора разбавления G'o,r(x, t), м-3, на интервале, равном продолжительности штилевых условий Δt
|
|
(П2.1) |
где
|
|
(П2.2) |
где t - время, прошедшее после мгновенного выброса клуба примеси, с;
h(x) - высота центра облака выброса над поверхностью земли на расстоянии х от точки выброса, м;
u - скорость ветра на высоте выброса, м/с;
vs - скорость гравитационного оседания примеси в атмосфере, м/с;
Fr(x) - так называемый фактор истощения облака выброса для радионуклида r на расстоянии х по ветру (безразмерная величина, описывающая изменение интегрального количества выброшенного количества радионуклида r с расстоянием от места выброса, уменьшающегося за счет радиоактивного распада, сухого осаждения и вымывания его из облака осадками);
σx, σy и σz - зависящие от расстояния дисперсии облака выброса в направлении движения облака по ветру х, в горизонтальном направлении поперек ветра у и в вертикальном направлении z. Это основные параметры гауссовой модели диффузии. Эмпирические формулы и более подробное описание их будет приведено в разделе 3.3 основной части Методических указаний.
Функция истощения облака выброса в результате радиоактивного распада и вымывания примеси из атмосферы осадками дается формулой
|
|
(П2.3) |
где λr - постоянная радиоактивного распада r-го радионуклида, с-1;
Λ - постоянная вымывания r-го радионуклида осадками, с-1;
u - скорость ветра в центральной точке облака.
Функция истощения вследствие сухого осаждения дается интегралом
|
|
(П2.4) |
где h - эффективная высота выброса, м;
σz(x) - зависимость вертикальной дисперсии распределения примеси в облаке выброса от расстояния х, м;
Vg - скорость сухого осаждения, м/с.
Совместное действие обоих факторов истощения описывается их произведением.
Заметим, что (х / u) = t - время движения примеси до заданной точки. Поэтому можно говорить о функции истощения, зависящей от времени движения облака выброса t, равного. Для этого в предыдущих выражениях достаточно сделать замену переменных
|
|
(П2.5) |
где uc,j - скорость ветра, характерная для j-й категории устойчивости при наличии ветра.
Для различных категорий uc,j приведены в табл. П2.1
Таблица П2.1. Скорости ветра uc,i, м/с, характерные для разных категорий устойчивости, применяемые при представлении дисперсий размеров облака Гауссовой модели σy(t) и σz(t), как функций времени, прошедшего после выброса t
|
Характерные для разных категорий устойчивости атмосферы скорости ветра uc,i, м/с |
||||||
|
А |
В |
С |
D |
Е |
F |
G |
|
1 |
1,5 |
3 |
4 |
2 |
1,5 |
1 |
П2.2. Расчет факторов разбавления при штилях и слабом ветре
Получены следующие приближенные формулы вычисления разового фактора разбавления при штиле и слабом ветре.
|
|
(П2.6) |
где ![]() - приближенное значение G(x,Δt),
- приближенное значение G(x,Δt),
|
|
(П2.7) |
|
|
(П2.8) |
|
|
(П2.9) |
|
|
(П2.10) |
|
|
(П2.11) |
|
|
(П2.12) |
|
|
(П2.13) |
|
|
(П2.14) |
|
|
(П2.15) |
|
|
(П2.16) |
ay(z0, P), by(z0, P), az(z0, P), bz(z0, P) определяются общими выражениями:
![]()
![]()
a2(P) = β1 + β2 ∙ P + β3 ∙ P2;
a2(P) = β1 + β2 ∙ P + β3 ∙ P2;
![]()
b1(P) = γ1 + γ 2 ∙ P + γ3 ∙ P2;
b2(P) = δ1 + δ2 ∙ P + δ3 ∙ P2;
![]()
P - параметр устойчивости Смита;
z0 - т.н. высота шероховатости подстилающей поверхности (параметр, зависящий от величины сил трения воздуха о поверхности земли), имеет размерность см;
Ф(x) - интеграл вероятности.
Значения остальных параметров для расчета σy(x) и σz(x) представлены в табл. П2.1.
Таблица П2.1. Значения параметров для расчета σy(x) и σz(x)
|
Параметр |
Значения параметров |
|
|
для расчета σy(x) |
для расчета σz(x) |
|
|
a0 |
70,6 |
145 |
|
α1 |
0,521 |
1,03 |
|
α2 |
0,340 |
-0,0766 |
|
α3 |
2,47 ∙ 10-3 |
0,0502 |
|
β1 |
-0,295 |
-0,272 |
|
β2 |
-0,0556 |
-0,0117 |
|
β3 |
9,18 ∙ 10-3 |
-2,91 ∙ 10-3 |
|
γ1 |
-3,14 |
-2,44 |
|
γ2 |
0,343 |
0,481 |
|
γ3 |
0,0107 |
0,0153 |
|
δ1 |
0,307 |
-8,79 ∙ 10-3 |
|
δ2 |
-0,0557 |
-0,0269 |
|
δ3 |
-9,14 ∙ 10-3 |
1,27 ∙ 10-3 |
|
b3 |
0. |
-7,04 ∙ 10-3 |
П2.3. Аналитические представление функции истощения
Функция истощения облака вследствие сухого оседания примеси при H ≠ 0 представима следующей приближенной формулой
|
|
(П2.17) |
где H - эффективная высота выброса, м;
σz(x) - зависимость вертикальной дисперсии распределения примеси в облаке выброса от расстояния х, м;
Vg - скорость сухого осаждения, м/с;
u - скорость ветра, м/с;
Ф(x) - интеграл вероятности;
|
Министр
Российской Федерации |
Е.О. Адамов |
Содержание