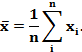Положения настоящей рекомендации распространяются на алгоритмы и программы обработки данных, которые выделены как самостоятельные объекты и существуют обособленно (в частности, могут использоваться на различных вычислительных устройствах) и рекомендуются для использования в измерительной практике.

Настоящая рекомендация устанавливает основные положения аттестации алгоритмов и программ, предназначенных для обработки данных при измерениях физических величин.

Положения настоящей рекомендации могут быть использованы при разработке алгоритмов и программ обработки данных при измерениях, исследовании их свойств и обосновании целесообразности их применения для решения измерительных задач, а также при разработке нормативно-технических документов, регламентирующих обработку данных при измерениях, и методик выполнения измерений (МВИ).

Определения основных терминов, используемых в рекомендации - по справочному приложению 1

2 ОБЩИЕ ПОЛОЖЕНИЯ

2.1 Алгоритм обработки экспериментальных данных, полученных при измерении (результатов наблюдений), представляет собой последовательность арифметических и логических операций, производимых над полученными экспериментальными данными (с учетом априорной информации) с целью определения результата измерения и характеристик его погрешности.

2.1.1 Алгоритмы, применяемые для обработки данных при измерениях, должны сопровождаться алгоритмами оценивания характеристик погрешностей результатов измерений.

2.1.2 Алгоритм может быть задан различными способами, в том числе, представлен в явном виде (конечной последовательностью арифметических и логических операций), или в виде рекуррентной вычислительной процедуры.

2.2 Программа обработки данных при измерении представляет собой самостоятельный объект, являющийся конкретной программной реализацией алгоритма обработки данных. Свойства программы существенно завесят от конкретной программной и аппаратной среды, в которой она работает.

Примечание. Программа как самостоятельный объект, может использоваться на нескольких ЭВМ, совместимых либо на программном, либо на аппаратном уровне.

2.3 Аттестация алгоритма (программы) обработки данных - исследование свойств алгоритма (программы) на моделях исходных данных, в результате которого определяют свойства и оценивают количественные характеристики алгоритма (программы), с последующей регистрацией полученных характеристик в свидетельствах об аттестации или разделах других документов (с указанием использованных моделей).

Модели исходных данных для аттестации выбираются в соответствии с положениями разд. 5.

2.3.1 Рекомендуется выполнять аттестацию для следующих объектов:

· алгоритмов обработки данных, представляющих собой самостоятельные объекты использования;

· программ обработки данных, реализующих выбранный алгоритм обработки и представляющих собой самостоятельные программные продукты;

· алгоритмов и программ обработки данных в составе прикладного программного обеспечения конкретных измерительных устройств, ИВК, ИИС, ИУС, МВИ.

2.3.2 Аттестация программы должна выполняться после ее отладки, верификации и тестирования.

2.3.3 При выполнении аттестации программы целесообразно использовать результаты аттестации исходного алгоритма (проверяя соответствие характеристик алгоритмов и программ, а также используемых моделей исходных данных).

Примечание. Аттестация алгоритма может представлять собой первый этап аттестации программы.

2.4 Аттестация алгоритмов и программ рассматривается в двух аспектах: общая (исследовательская) и конкретная (метрологическая).

2.4.1 Если алгоритм (программа) рассматривается как самостоятельный объект и может применяться для обработки исходных данных с различными свойствами, то выполняется общая (исследовательская) аттестация алгоритма (программы).

2.4.2 Если алгоритм (программа) рассматривается как составная часть прикладного программного обеспечения конкретных измерительных устройств, ИВ К, ИИС, ИУС, МВ И, и имеется значительная априорная информация об исходных данных, то выполняется конкретная (метрологическая) аттестация.

2.5 Общая (исследовательская) аттестация алгоритма (программы) -исследование внутренних свойств алгоритма (программы) с целью последующего обоснования его применения в конкретных задачах.

В результате общей аттестация алгоритма (программы) получают оценки характеристик точности, устойчивости и сложности алгоритма (программы), при различных моделях исходных данных.

2.6 Метрологическая аттестация алгоритма (программы) - это исследование точностных свойств алгоритма (программы) в рамках конкретной измерительной задачи или МВИ с целью оценивания характеристик составляющих погрешностей результатов измерений.

В результате метрологической аттестации получают оценки характеристик составляющих погрешностей результатов обработки.

2.7 Результаты аттестации алгоритма (программы) следует использовать при обосновании его (ее) выбора и применения.

2.7.1 Общую аттестацию нового алгоритма (программы) следует выполнять на заключительном этапе разработки алгоритма (программы) прежде, чем рекомендовать его для практического применения.

При применении ранее разработанного и аттестованного алгоритма используют результаты его аттестации с обязательной проверкой соответствия перечня характеристик алгоритма и моделей исходных данных требованиям, которые предъявляются к алгоритму при его применении.

2.7.2 Метрологическая аттестация алгоритма (программы) проводится при выборе алгоритма (программы) для решения конкретной измерительной задачи, при разработке МВИ, проектировании ИВК шли ИИС, при аттестации МВИ, ИВК или ИИС.

3 ОБЩАЯ СХЕМА АТТЕСТАЦИИ АЛГОРИТМОВ (ПРОГРАММ)

3.1 При выполнении аттестации алгоритма (программы) рекомендуется придерживаться следующего порядка действий:

3.1.1 Установить набор основных .характеристик алгоритма (программы), которые следует оценивать: П₁ …, П_n.

3.1.2 Установить набор моделей исходных данных, поступающих на обработку u₁ …, u_m.

3.1.3 Вычислить (оценить) значения характеристик алгоритма (программы) П_i, на выбранных типовых моделях u_j:

π_ij(a) = П_i(a, u_j).

3.1.4 Оформить свидетельство об аттестации алгоритма (программы), включающее матрицу характеристик π_ij(a).

3.2 При выполнении общей аттестации целесообразно выделить (описать) группу однородных алгоритмов, предназначенную для решения одной задачи обработки и содержащую исследуемый алгоритм.

Примечание. Рабочая классификация алгоритмов обработки, полезная для целей аттестации приведена в справочном приложении 2.

3.3 В рамках приведенной единой схемы аттестации (п. 3.1) задачи общей и метрологической аттестации алгоритмов (программ) различаются:

· по целям их выполнения и способам использования полученных результатов;

· по используемым наборам характеристик алгоритмов (см. разд. 4);

· по используемым типовым моделям исходных данных, поступающих на обработку (см. разд. 5).

3.4 Характеристики алгоритмов (программ) устанавливают с учетом целей аттестации и свойств группы алгоритмов.

3.4.1 При общей аттестации характеристики устанавливают лак, чтобы они достаточно полно отражали свойства алгоритмов и позволяли сопоставлять их в рамках выделенной группы однородных алгоритмов, предназначенных для решения одной из типовых измерительных задач (при одинаковых вариантах условий, определяющих возможные случаи применения).

Указанные наборы характеристик приводятся в разделах НТД, регламентирующих обработку данных для соответствующих задач.

3.4.2 При метрологической аттестации характеристики устанавливают с целью оценивания составляющих погрешностей результатов обработки а конкретной измерительной задаче (или МВИ) и приводят в соответствующей МВИ, свидетельстве об аттестации алгоритма или программной документации.

3.5 Набор типовых моделей исходных данных, поступающих на обработку, устанавливают, исходя из конкретных целей аттестации, с учетом следующих требований:

· модели должны быть не очень сложными;

· число моделей в наборе должно быть небольшим;

· модели должны в совокупности достаточно полно описывать свойства возможных исходных данных.

Выбранные модели должны, по возможности, соответствовать наихудшим вариантам (с точки зрения искомых характеристик алгоритма или программы).

3.5.1 При общей аттестации набор моделей устанавливают на основе предварительных представлений и накопленных сведений о свойствах данных так, чтобы наиболее полно выявить свойства алгоритма.

3.5.2 При метрологической аттестации набор моделей устанавливают на основе анализа априорной информации о конкретной измерительной задаче (выявления источников погрешностей и анализа их свойств) с целью наибольшего приближения к свойствам реальных данных.

3.5.3 При переходе от обшей к метрологической аттестации число используемых моделей, как правило, уменьшается, а вид моделей уточняется (в том числе, усложняется).

3.6 Получаемые при аттестации значения характеристик на типовых моделях p_ij(а) представляют собой зависимости соответствующих характеристик алгоритмов (программ) от параметров, описывающих модели исходных данных.

Примечания:

1 Основные способы оценивания (вычисления) указанных зависимостей приведены в разд. 6.

2 Основные формы представления зависимостей приведены в разд. 7.

3 Примеры аттестации алгоритмов обработки данных при прямых многократных измерениях приведены в рекомендуемом приложении 3.

4 РЕКОМЕНДАЦИИ ПО ВЫБОРУ ХАРАКТЕРИСТИК
АЛГОРИТМОВ И ПРОГРАММ ПРИ ПРОВЕДЕНИИ АТТЕСТАЦИИ

4.1 При общей аттестации алгоритмов (программ) установлены следующие группы характеристик:

· характеристики точности, предназначенные для оценивания погрешностей результатов измерений, получаемых при использовании алгоритма (программы);

· характеристики устойчивости (надежности), которые задают область работоспособности алгоритма (программы);

· характеристики сложности, которые отражают трудоемкость вычислений или вычислительные затраты при однократном применении алгоритма (программы).

4.2 К характеристикам точности алгоритмов (программ) относятся:

· основные характеристики точности, предназначенные для оценивания составляющих погрешностей результатов обработки на моделях исходных данных;

· вспомогательные характеристики точности - параметры погрешностей результатов обработки, полезные при сопоставлении алгоритмов (программ), но отличные от основных характеристик точности.

4.2.1 При аттестации алгоритмов оценивают характеристики составлявших погрешностей результатов обработки, в том числе:

· методической погрешности, обусловленной неидеальностью метода обработки;

· трансформированной погрешности, обусловленной погрешностями исходных данных и их преобразованиями при обработке.

4.2.2 К основным характеристикам точности алгоритмов (программ) относятся:

· границы методической составляющей погрешности;

· границы систематических составляющих трансформированной погрешности результата измерения;

· СКО случайной составляющей трансформированной погрешности.

4.2.3 При метрологической аттестации программ, реализующих алгоритмы, необходимо оценивать характеристики точности (СКО и границы погрешностей) с учетом дополнительных составляющих погрешностей результатов, обусловленных особенностями работы программы в конкретной вычислительной среде, в том числе:

· округлением промежуточных результатов;

· ограниченностью разрядной сетки;

· дискретизацией по аргументу;

· конечным чистом итераций;

· использованием конечных разложений в ряд, и др.

4.3 К характеристикам устойчивости алгоритмов (программ) относятся:

· допустимое число или доля данных, которые могли бы содержать промахи (большие погрешности), не нарушая работоспособности алгоритма;

· границы интервалов (областей) значений параметров исходных данных, в которых алгоритм работает без сбоев (грубых ошибок).

4.4 Основными характеристиками сложности алгоритмов являются показатели вычислительной сложности, определяемые числом типовых операций (арифметических и логических), необходимых для однократного вычисления по данному алгоритму.

4.5 К основным характеристикам сложности программ обработай данных относятся:

· временная сложность, определяемая как время работы ЭВМ при однократном выполнении программы;

· объемная сложность, определяемая как объем памяти ЭВМ (отдельно долговременной и оперативной), необходимой для работы программы.

4.6 При метрологической аттестации алгоритмов (программ) используют основные характеристики точности по п. 4.2.

Примечание. По согласованию с заказчикам при метрологической ammecmaцuu могут использоваться также некоторые вспомогательные характеристики точности, а также характеристики устойчивости и сложности.

5 РЕКОМЕНДАЦИИ ПО ВЫБОРУ МОДЕЛЕЙ ИСХОДНЫХ ДАННЫХ
ПРИ АТТЕСТАЦИИ АЛГОРИТМОВ И ПРОГРАММ

5.1 Модели исходных данных при аттестации формируются как сочетания моделей полезных сигналов и моделей погрешностей исходных данных.

5.1.1 Если данные, поступают на обработку в аналоговом виде, то модели исходных данных представляют в виде случайных или детерминированных функций непрерывного аргумента.

5.1.2 Если данные поступают на обработку в дискретном виде, то модели исходных данных представляют в виде случайных или детерминированных последовательностей.

5.2 Модели полезных сигналов формируют на основе постановки измерительной задачи, используя уравнения измерений, сведения о свойствах входных сигналов средства измерений (СИ) и его метрологических характеристиках.

5.3 Модели погрешностей формируют отдельно для случайных и систематических составляющих, учитывая сведения по п. 5.2. а также сведения о возможных помехах на входе и выходе СИ.

5.4 Для случайных составляющих погрешностей исходных данных принимают модели в виде случайных функций или последовательностей, имеющих определенные распределения и корреляционные функции.

В пп. 5.4.1 и 5.4.2 приведены примеры распределений и корреляционных функций, наиболее часто применяемых при аттестации. Вместо них ши в дополнение к ним можно использовать другие распределения и корреляционные функции, вид которых обоснован спецификой исследуемого алгоритма и условий его применения.

5.4.1 При выполнении аттестации можно использовать следующие распределения (существенно различные по свойствам):

· гауссовское,

· равномерное,

· двойное экспоненциальное.

Для исследования поведения алгоритмов при небольших отклонениях распределений погрешностей от гауссовского используют засоренное гауссовское распределение, имеющее плотность вида:

f(x) = (1 - c)⋅g(x) + c(x)⋅b(x),

где g и h - плотности гауссовского и засоряющего распределений, с > 0.

5.4.2 При проведении аттестации можно использовать следующие корреляционные функции:

· δ -функцию (соответствующую белому шуму),

· стационарную корреляционную функцию вида

R(t) = s⋅exp(-a⋅t)⋅cos(b⋅t), a > 0,

· стационарную корреляционную функцию с заданной дробно-рациональной спектральной плотностью,

· нестационарную корреляционную функцию вида

R(t, v) = s⋅min(t, v), t, v > 0

5.5 Для систематических составляющих погрешностей возможны модели в виде детерминированных функций или последовательностей. Например, в виде следующих функций:

· постоянной,

· линейной,

· синусоидальной.

Примечание. В отбельных случаях для неисключенных систематических погрешностей принимают статистические модели (чаще всего - с равномерным распределением).

6 СПОСОБЫ ОЦЕНИВАНИЯ ХАРАКТЕРИСТИК АЛГОРИТМОВ И ПРОГРАММ

6.1 Выделяются три основных подхода к определению (оцениванию) характеристик алгоритмов (программ) на моделях исходных данных:

· аналитический подход;

· численные расчеты показателей точности;

· математическое моделирование (прежде всего, статистическое).

6.2 При аналитическом подходе выражения p_ij(а) находят в виде явных функций от параметров исходных данных, в том числе, характеристик погрешностей исходных данных и объема данных; при этом используют точные или приближенные аналитические методы в рамках принятых (точных) моделей исходных данных. Зависимости могут быть представлены в различных формах (см. п. 7.3).

6.3 При использовании численных методов выделяются два основных варианта.

6.3.1 Принимают упрощенные типовые модели данных и приближенно оценивают характеристики алгоритма (программы) как функции от параметров моделей данных. В результате получают приближенные аналитические зависимости характеристик от параметров моделей.

6.3.2 задают конкретные значения параметров моделей исходных данных и приближенно оценивают значения характеристик алгоритма (программы), соответствующих выбранным значениям. В результате получают оценки характеристик для конкретных значений параметров.

6.4 При использовании статистического моделирования выполняют следующие операции:

· задают конкретные значения параметров моделей исходных данных;

· моделируют (многократно) наборы исходных данных, поступающих на вход алгоритма (программы) обработки;

· применяя исследуемый алгоритм (программу) к полученным наборам данных, получают серию результатов вычислений;

· путем дополнительной обработки полученной серии результатов вычислений, оценивают искомые характеристики алгоритма (программы).

5.4.1 При использовании моделирования для каждого набора значений параметров исходных данных С получают конкретное значение характеристики π_ij(a, С) т.е. i-я характеристика представляется в виде таблицы f_ij = n_ij(a, С).

5.4.2 При реализации процедуры статистического моделирования, как правило, используют ЭВМ. При анализе результатов аттестации необходимо учитывать свойства процедуры моделирования, в том числе, используемых датчиков случайных чисел.

6.5 При аттестации сложных алгоритмов целесообразно комплексно использовать указанные подходы. В частности, целесообразно приближенно оценивать асимптотическое поведение показателей в аналитическом виде; а затем, более точно, - оценивать показатели путем статистического моделирования.

7 ОФОРМЛЕНИЕ И ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ АТТЕСТАЦИИ

7.1 Результаты обшей аттестации алгоритмов (программ) могут быть представлены:

· в свидетельствах об аттестации алгоритмов (программ);

· в справочных материалах, содержащих типовые алгоритмы обработки данных при прямых, косвенных, совместных и совокупных измерениях и результаты их аттестации;

· в разделах НТД, посвященных вопросам обработки данных для отдельных групп измерений (в том числе, НТД по методам обработки данных).

7.2 Результаты метрологической аттестации алгоритмов (программ) могут быть представлены:

· в разделах НТД, связанных с вопросами обработки данных при конкретных видах измерений (в том числе, МВИ или аттестатов МВИ);

· в разделах свидетельств об аттестации ИВК или ИИС.

7.3 При представлении результатов аттестации алгоритма (программы) в документах по пп. 7.1, 7.2 должны быть указаны следующие данные:

· перечень характеристик П₁,.... П_n., значения которых оценивались при аттестации;

· перечень моделей исходных данных u_i …, u_ij, при которых определялись (оценивались) значения характеристик;

· способы оценивания характеристик на указанных моделях;

· зависимости π_ij(a) характеристик от параметров моделей исходных данных, вычисленные (оцененные) на указанных моделях данных.

7.4 Зависимости π_ij(а) характеристик алгоритма (программы) от параметров моделей исходных данных, полученные в ходе аттестации, могут быть представлены в форме:

· аналитического выражения (формулы), задающего π_ij(а) как явную функцию от параметров моделей исходных данных c₁ c₂, …

π_ij(а) = f_ij(c₁ c₂, …);

· таблицы значений показателей π_ij(а) при конкретных значениях параметров моделей исходных данных c₁ c₂, …;

· комбинированной, когда некоторые параметры входят в зависимость аналитически, а другие - задаются конкретными значениями;

· графиков зависимостей значений показателей π_ij(а) от отдельных параметров моделей исходных данных:

π_ij(а, c_k) = f_ij(c_k)

7.5 Расчет значений характеристик алгоритма (программы) на типовых моделях исходных данных выполняется:

· разработчиком алгоритма (программы) - если предлагается новый алгоритм (программа);

· пользователем алгоритма (программы) - если отсутствуют данные о его аттестации:

· разработчиком МВИ - при метрологической аттестации алгоритма обработки данных, входящего в состав МВИ, и отсутствии данных об аттестации алгоритма;

· разработчиком ИВК, ИИС, ИУС или измерительного устройства - при метрологической аттестации алгоритмов (программ), входящих в состав прикладного программного обеспечения перечисленных систем и отсутствии данных об их предварительной аттестации.

Приложение 1
Справочное

ОСНОВНЫЕ ИСПОЛЬЗУЕМЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

1 Алгоритм - однозначное описание последовательности операций над исходными данными (из некоторой совокупности возможных исходных данных), направленной на получение результата, полностью определяемого этими исходными данными.

2 Программа - самостоятельный объект, являющийся конкретной реализацией алгоритма обработки данных, предназначенной для исполнения на ЭВМ.

3 Методическая погрешность результата измерения, обусловленная неидеальностъю алгоритма обработки данных - составляющая погрешности результата измерения, которая получается при применении алгоритма к точным исходным данным (не содержащим погрешностей) при условии точного выполнения всех арифметических и логических операций.

Пример. Погрешность, обусловленная использованием квадратурной формулы при вычислении интеграла.

4 Трансформированная погрешность - составляющая погрешности результата измерения, обусловленная наличием погрешности исходных данных, поступающих на обработку, и их преобразованием с помощью алгоритма (программы).

5 Верификация программы - проверка (доказательство) логической непротиворечивости программы.

Приложение 2
Справочное

КЛАССИФИКАЦИЯ АЛГОРИТМОВ ОБРАБОТКИ ДАННЫХ ПРИ ИЗМЕРЕНИЯХ

1 Рабочая классификация алгоритмов обработки данных при измерениях, полезная для целей аттестации алгоритмов, использует четыре основных признака, соответствующих структурным элементам алгоритмов:

а) вид оцениваемой характеристики;

б) вид вычислительной процедуры;

в) вид исходных данных;

г) форма представления результатов.

1.1 Наиболее существенными являются первые два признака, связанные с описанием основных объектов алгоритма. Последние два признака связаны с формой представления основных объектов.

1.2 Для каждого из основных признаков классификации выделяют подчиненные ему частные признаки и конкретные варианты признаков, и далее формируют основные группы алгоритмов при разбиении по данным признакам.

2 При классификации алгоритмов по оцениваемым характеристикам в качестве частных признаков классификации принимают:

а) конкретный смысл характеристики в рамках определенной математической модели;

б) размерность характеристики, число аргументов или параметров;

в) функциональный вид зависимости (в частности, линейность), а также свойства гладкости (или непрерывности).

3 При классификации алгоритмов по виду вычислительных процедур в качестве частных признаков принимают:

а) подход, принятый при построении алгоритма;

б) структурные особенности построения алгоритма.

3.1 В соответствии с первым частным признаком выделяют три основные группы алгоритмов:

· оптимальные алгоритмы (при определенных модели и критерии);

· устойчивые (робастные) алгоритмы, которые имеют высокую эффективность на более широких моделях;

· эвристические алгоритмы, которые имеют широкую область применения (хотя и не столь высокую точность).

3.2 При классификации алгоритмов по второму частному признаку учитывают, прежде всего:

· способ управления порядком выполнения действий;

· зависимость параметров процедуры от исходных данных;

· способ задания алгоритма;

· наличие определенных типовых блоков (подалгоритмов) в составе алгоритма.

Краткая классификация алгоритмов по вычислительным процедурам представлена в таблице П2.1, помещенной в конце настоящего приложения.

4 При классификации алгоритмов по виду исходных данных выделяют следующие частные признаки:

· форму представления данных (дискретная или аналоговая);

· режим поступления данных;

· объем массива данных;

· размерность данных;

· зависимость между исходными данными.

5 При классификации по формам представления результатов обработки данных учитывают как формы представления результатов измерений, так и формы представления погрешностей измерений.

Данная классификация тесно связана с классификацией по первому признаку.

6 В соответствии с классификацией по видам оцениваемых характеристик выделяются однородные группы алгоритмов обработки, предназначенных для решения одинаковых измерительных задач.

7 Для целей аттестации алгоритмов основной является классификация по видам вычислительных процедур, которая выполняется в рамках однородных групп алгоритмов.

Таблица П2.1

Классификация алгоритмов обработки данных
при прямых измерениях по виду вычислительных процедур

Признаки классификации	Группы алгоритмов обработки
	Оптимальные	Устойчивые	Эвристические
Подход при построении алгоритма	Максимального правдоподобия в том числе, средние арифметические Байесовские Оценки Питмена	Усеченные средние М - оценки, в том числе, Хубера, Тьюки, Андерса 1^Р - оценки, 0 < р < 2	Медиана Основанные на порядковых статистиках Основанные на рангах или метках
Зависимость вычислительной процедуры от данных	Линейные алгоритмы Разветвляющиеся алгоритмы Циклические алгоритмы Адаптивные алгоритмы
Способ задания вычислительной процедуры	Явное выражение Неявное выражение Итерационная процедура Процедура численной оптимизации Неформальное описание

Приложение 3
Рекомендуемое

ПРИМЕР ОБЩЕЙ АТТЕСТАЦИИ АЛГОРИТМОВ ОБРАБОТКИ ДАННЫХ ПРИ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЯХ

Рассматриваются два простых алгоритма обработки данных при прямых многократных измерениях:

1) x̄(0,25) - усеченное среднее, полученное при отбрасывании в упорядоченном наборе исходных данных для обработки

x′₁ < … < х′_n

по 25 % наименьших и наибольших результатов и усреднении остальных данных;

2) медиана med(x), т.е. среднее значение x′_{k + 1} (при n = 2⋅k + 1) или полусумма средних (при n = 2⋅k) в упорядоченном наборе данных.

При общей аттестации алгоритмов обработай данных при прямых многократных измерениях принимают следующие основные метрологические характеристики точности:

П₁(а) = S(a) - CKO случайной погрешности результата измерения;

П₂(а) = θ(a) - границу систематической погрешности результата измерения.

Приведенные алгоритмы естественно сопоставлять с наиболее распространенным на практике алгоритмом - средним арифметическим данных:

Поэтому удобно представлять указанные характеристики в приведенной форме (отнесенные к соответствующим характеристикам погрешностей среднего арифметического):

В качестве показателя устойчивости алгоритма принимают точку срыва П_r = δ^²(a) - допустимую долю выбросов в данных (результатов, содержащих большие погрешности), наличие которых не приводит к нарушению работоспособности алгоритма.

При общей аттестации алгоритмов обработки данных при прямых многократных измерениях принимают следующие модели данных:

u₁: x₁, …, х_n - независимые случайные величины со средним А и дисперсией S, имеющие гауссовские распределения;

u₂: x₁, …, х_n - независимые случайные величины, имеющие равномерные распределения на интервале (-L, L);

u₃: x₁, …, х_n - независимые случайные величины, имеющие двустороннее экспоненциальное распределение с плотностью

средним А и дисперсией s;

u₄: x₁, …, х_n - независимые случайные величины, имеющие засоренное гауссовское распределение с плотностью

f(x) = 0,95⋅g(x) + 0,05⋅h(x),

где g(x) - плотность гауссовского распределения со средним А и дисперсией s; h(x) - плотность гауссовского распределения со средним А и дисперсией 9⋅s;

u₅: x₁, …, х_n - линейно изменяющаяся последовательность со средним значением А и углом наклона b;

u₆: x₁, …, х_n - постоянная последовательность вида А + с;

u₇: x₁, …, х_n - последовательность, изменяющаяся по синусоидальному закону:

x_k = А + c⋅sin(k⋅ω + q).

В результате аттестации алгоритма получается таблица значений показателей алгоритма, вычисленных (оцененных) на типовых моделях исходных данных

П_ij(a) = |π_ij(a)| = |П_ij(a, u)|

Значения перечисленных характеристик на приведенных моделях исходных данных могут быть вычислены аналитическими методами. Полученные значения характеристик приведены в сводной таблице П3.1, помещенной на следующей странице.

Таблица П3.1

Значения характеристик алгоритмов усеченного среднего и медианы

Типовые модели погрешностей	Значения характеристик алгоритмов
	(0,25)			med(x)

u₁	1,20		0,25	1,57		0,5
u₂	2,00		0,25	3,00		0,5
u₃	0,61		0,25	0,50		0,5
u₄	0,92		0,25	1,20		0,5
u₅		0,5			0,5
u₆		1			1
u₇		4/n			1

1 ОБЛАСТЬ ПРИМЕНЕНИЯ

2 ОБЩИЕ ПОЛОЖЕНИЯ

3 ОБЩАЯ СХЕМА АТТЕСТАЦИИ АЛГОРИТМОВ (ПРОГРАММ)

4 РЕКОМЕНДАЦИИ ПО ВЫБОРУ ХАРАКТЕРИСТИК АЛГОРИТМОВ И ПРОГРАММ ПРИ ПРОВЕДЕНИИ АТТЕСТАЦИИ

5 РЕКОМЕНДАЦИИ ПО ВЫБОРУ МОДЕЛЕЙ ИСХОДНЫХ ДАННЫХ ПРИ АТТЕСТАЦИИ АЛГОРИТМОВ И ПРОГРАММ