РУКОВОДСТВА ПО БЕЗОПАСНОСТИ
в области использования
атомной энергии
РАСЧЕТНЫЕ СООТНОШЕНИЯ И МЕТОДИКИ
РАСЧЕТА ГИДРОДИНАМИЧЕСКИХ И ТЕПЛОВЫХ
ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ И ОБОРУДОВАНИЯ
ЯДЕРНЫХ ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
С ЖИДКОМЕТАЛИЧЕСКИМ ТЕПЛОНОСИТЕЛЕМ
РБ-075-12
ФБУ«НТЦ ЯРБ»
|
ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ЭКОЛОГИЧЕСКОМУ, |
|
УТВЕРЖДЕНО |
РУКОВОДСТВО ПО БЕЗОПАСНОСТИ
РАСЧЕТНЫЕ СООТНОШЕНИЯ И МЕТОДИКИ РАСЧЕТА
ГИДРОДИНАМИЧЕСКИХ И ТЕПЛОВЫХ ХАРАКТЕРИСТИК
ЭЛЕМЕНТОВ И ОБОРУДОВАНИЯ ЯДЕРНЫХ ЭНЕРГЕТИЧЕСКИХ
УСТАНОВОК С ЖИДКОМЕТАЛИЧЕСКИМ ТЕПЛОНОСИТЕЛЕМ
(РБ-075-12)
|
Введено в действие |
|
с 31 августа 2012 г. |
Москва 2012
Руководство по безопасности «Расчетные соотношения и методики расчета гидродинамических и тепловых характеристик элементов и оборудования ядерных энергетических установок с жидкометаллическим теплоносителем» носит рекомендательный характер и не является нормативным правовым актом.
Настоящее руководство по безопасности содержит рекомендации Федеральной службы по использованию расчетных соотношений и методик расчета гидродинамических и тепловых характеристик элементов и оборудования ядерных энергетических установок с жидкометаллическим теплоносителем.
Выпускается впервые 1.
___________
1 Разработано коллективом авторов в составе И.Р. Уголева (ФБУ «НТЦ ЯРБ»), В.П. Бобков и И.П. Смогалев (ФГУП «ГНЦ - РФ ФЭИ»)
I. Общие положения
1. Настоящее руководство по безопасности «Расчетные соотношения и методики расчета гидродинамических и тепловых характеристик элементов и оборудования ядерных энергетических установок с жидкометаллическим теплоносителем» (далее - Руководство по безопасности) разработано в соответствии со статьей 6 Федерального закона от 21 ноября 1995 г. № 170-ФЗ «Об использовании атомной энергии» и содержит рекомендации по выполнению требований федеральных норм и правил в области использования атомной энергии «Требования к содержанию отчета по обоснованию безопасности АС с реакторами на быстрых нейтронах», утвержденных постановлением Федеральной службы по экологическому, технологическому и атомному надзору от 2 декабря 2005 г. № 9 (Зарегистрировано Минюстом России 26 января 2006 г. № 7413).
2. Руководство по безопасности распространяется на элементы и оборудование жидкометаллических циркуляционных контуров ядерных энергетических установок.
3. В руководстве по безопасности приводятся расчетные соотношения и методики расчета основных гидродинамических и тепловых характеристик элементов и оборудования ядерных энергетических установок с жидкометаллическим теплоносителем (далее - ЯЭУ), включая:
коэффициенты гидравлического сопротивления трения и местных касательных напряжений, расходов;
коэффициенты теплоотдачи и температуры поверхностей теплообмена;
параметры тепломассообмена при конденсации и теплоотдачи при кипении теплоносителя а также погрешности этих характеристик.
Для режимов без кипения теплоносителя приводятся рекомендации, относящиеся только к стационарным процессам. Рекомендации даны для случаев течения и теплообмена «чистых» (практически без примесей) теплоносителей при хорошем смачивании и отсутствии на поверхности теплообмена каких-либо наслоений или контактных слоев.
4. Рекомендации, содержащиеся в настоящем руководстве по безопасности, предназначены для использования специалистами организаций, при создании, верификации и экспертизе программных средств (далее - ПС), применяемых при проектировании, испытании и эксплуатации ЯЭУ, а также для обоснования и/или обеспечения их безопасности.
5. Настоящее руководство по безопасности содержит проверенные и обоснованные соотношения и методы расчета гидродинамических и тепловых характеристик активных зон, элементов и оборудования циркуляционных контуров ЯЭУ.
6. В руководстве по безопасности применяется единая терминология и система обозначений, а также Международная система единиц СИ.
7. Для расчетных соотношений и методик расчета, приведенных в главах II и III настоящего Руководства по безопасности, указываются погрешности расчетных параметров, такие как:
D (в % или абсолютных величинах) - среднеарифметическая погрешность описания данной методикой использованного массива экспериментальных данных;
σ (в % или абсолютных величинах) - среднеквадратичная погрешность описания данной методикой использованного массива экспериментальных данных;
δ (± δ в % или абсолютных величинах) - максимальное отклонение рекомендованной методики от использованного массива экспериментальных данных.
8. Для расчетных соотношений и методик расчета, приведенных в главах II и III настоящего Руководства по безопасности, указываются пределы применимости по определяющим параметрам в использованном массиве экспериментальных данных, а также из общефизических соображений.
9. В случае использования других соотношений и методик, чем те, которые указаны в настоящем Руководстве по безопасности, должно быть показано, что расчет теплогидравлических параметров выполнен с погрешностями, дающими возможность сделать обоснованные заключения о безопасности ЯЭУ.
II. Расчет гидродинамических параметров
10. Гидравлическая система первого контура ЯЭУ состоит из каналов активной зоны, насосов, трубопроводов, коллекторов, каналов парогенератора и предназначена для прокачки теплоносителя и передачи тепла от твэлов реактора ко второму жидкометаллическому контуру и далее к воде и водяному пару в парогенераторах (при трехконтурной схеме) или сразу к воде и водяному пару (при двухконтурной схеме). Дополнительными устройствами, входящими в гидравлическую систему, являются теплообменные аппараты, арматура, дроссельные и сепарирующие устройства. Замкнутая гидравлическая система подводящих и отводящих трубопроводов, распределительных устройств внутри корпуса реактора и каналов (кассет) с тепловыделяющими элементами называется циркуляционным контуром.
11. Большинство гидродинамических расчетов в ядерной энергетике связано с течениями в каналах. Главными задачами при расчете таких течений являются определение гидравлических сопротивлений каналов различной геометрии и местных сопротивлений, расчет распределения по каналам расходов, скоростей и касательных напряжений. Основными целями расчета являются: определение потерь давления в каналах и на элементах контура, затрат мощности на прокачку теплоносителя, а также и цели, связанные, в частности, с расчетом эрозии, коррозии, массопереноса.
12. При проведении гидравлических расчетов используются следующие величины, характеризующие поток в каналах: геометрические параметры канала (например площадь поперечного сечения, гидравлический диаметр, длина, абсолютная шероховатость), скорость, плотность и вязкость среды. Средняя плотность среды определяется по средней температуре среды в канале на данном участке.
13. Все теплоносители, используемые в атомной энергетике, включая жидкие металлы, являются ньютоновскими жидкостями и, таким образом, подчиняются общим закономерностям в области гидродинамики.
14. Режимы однофазного течения.
1) Режимы течения в каналах с безотрывным обтеканием.
Ламинарный или слоистый режим течения характеризуется отсутствием пульсаций гидродинамических величин. Критическое число Рейнольдса Reкр, (Re = wd/v), при достижении которого происходит потеря устойчивости и разрушение ламинарного режима течения в трубах круглого поперечного сечения, обычно принимается равным 2300. За счет устранений возмущений на входе в канал можно существенно затянуть существование ламинарного режима течения до Reкр = (5 ÷ 7)·104. Наличие шероховатости на стенках трубы уменьшает значение критического числа Рейнольдса. Неизотермичность потока также влияет на критическое число Рейнольдса. При совпадении направлений свободного и вынужденного движений у стенки критическое число Рейнольдса возрастает в зависимости от величины числа Релея (Ra = g·b·l3·Dt/va) (таблица № 1).
Таблица № 1
Зависимость критического числа Рейнольдса от числа Релея при совпадении направлений свободного и вынужденного движений в круглой гладкой трубе
|
Ra · 10-6 |
0 |
1,6 |
4,7 |
11,6 |
15,8 |
|
Reкр |
2300 |
3500 |
5200 |
6200 |
7100 |
При противоположном направлении естественной конвекции и вынужденного движения у стенки критическое число Рейнольдса уменьшается, снижаясь при Ra = 105 до значения Reкр = 103.
Критическое число Рейнольдса для каналов некруглого поперечного сечения имеет примерно такое же значение, как и для круглой трубы (таблица № 2). Для каналов с узкими угловыми областями критическое число Рейнольдса является условной величиной, поскольку турбулентность сначала возникает в широкой части канала, а затем распространяется на узкую.
Таблица № 2
Критическое число Рейнольдса для каналов различной геометрии при продольном обтекании
|
Reкр |
|
|
Кольцевой |
2000 ÷ 2800 |
|
Прямоугольный |
2000 ÷ 2300 |
|
Треугольный с amin > 45° |
≈ 2000 |
|
Сборки стержней различной упаковки |
≈ 2000 |
В змеевиках и других криволинейных каналах, где возникают значительные центробежные силы, граница перехода к турбулентному режиму течения сдвигается в область более высоких значений чисел Рейнольдса.
Критическое число Рейнольдса (граница перехода ламинарного течения в турбулентное) в змеевиках рассчитывается по формуле:
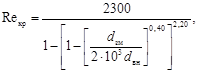 (1)
(1)
где dзм - диаметр змеевиков, м;
dвн - внутренний диаметр трубы змеевика, м.
Критическое число Рейнольдса в спирально-навитых (витых) трубах диаметром dсн, меньшим их внутреннего диаметра (рис. 1), и в локально-навитых трубах, у которых навитые участки чередуются с прямолинейными длиной L, рассчитывается по формуле:
где dсн = dцп - dвн, м.
Пределы применимости формулы (2): S/dсн = 12 ÷ 40; 0,2 < dвн/dцп < 0,7.
Рис. 1. Геометрия спирально-навитых труб:
а - спирально-навитая труба;
б - локально спирально-навитая труба;
dцп = диаметр цилиндрической поверхности, описанной около спирально-навитой трубы, м;
dвн - внутренний диаметр исходной гладкой трубы, м;
dн - наружный диаметр исходной гладкой трубы, м;
S - шаг навивки трубы, м
Переходный к турбулентному режим течения характеризуется чередованием областей с ламинарным и турбулентным течениями. На величину чисел Рейнольдса, в диапазоне изменения которых наблюдается указанный режим течения, сильно влияют шероховатость поверхности, интенсивность турбулентности потока на входе в канал, которые сдвигают начало переходного режима течения в область более низких чисел Рейнольдса, и величина температурного фактора, определяющая взаимодействие между вынужденной и естественной конвекциями.
При переходном режиме течения возникают низкочастотные пульсации параметров потока и наблюдается резкое изменение интенсивности переноса тепла и импульса с возрастанием числа Рейнольдса.
Принимается, что переход от ламинарного режима течения к турбулентному в трубах происходит при Re = (5 ÷ 7)·103, а в сборках стержней треугольной и квадратной упаковок - при Re = (10 ÷ 15)·103.
Турбулентный режим течения характеризуется наличием интенсивных пульсаций параметров потока (например скорости, плотности, температуры), что связано с существованием вихрей, имеющих широкий диапазон пространственных и временных масштабов. Особенностью турбулентного режима течения является также наличие вязкого подслоя у стенки (при надежном смачивании), в котором происходит затухание пульсаций. При плохом смачивании возможно проскальзывание жидкости относительно стенки. Эти случаи весьма редки и в настоящем Руководстве по безопасности не рассматриваются.
2) Режимы течения в каналах с отрывным обтеканием.
Структура течения в каналах с повышенной шероховатостью стенок, с турбулизирующими поток вставками, с поперечным расположением труб и в засыпках определяется характером развития и отрыва пограничных слоев, которые формируются на стенках обтекаемых тел. Процесс отрыва сопровождается возникновением турбулентных вихрей и интенсификацией теплообмена. Наличие по ходу потока большого количества дискретных элементов (например, выступов шероховатости, впадин, песчинок.) приводит к постоянному чередованию зон отрыва и областей, где происходит восстановление пограничного слоя, и препятствует образованию структуры течения (ламинарная, турбулентная).
Ламинарное (безотрывное) течение в таких каналах имеет место при более низких числах Рейнольдса. Относительная величина шероховатости, начиная с которой проявляется ее влияние на переход к турбулентному течению в трубах, рассчитывается по формуле:
![]() (3)
(3)
При течении среды в трубах с интенсификаторами теплосъема критическое число Рейнольдса в зависимости от степени шероховатости изменяется в пределах 500 ÷ 2000. Особо низкие значения (Rе ≈ 50) наблюдаются при поперечном обтекании труб и в засыпках.
При числах Рейнольдса, больших критического, имеет место течение со смешанной структурой пограничных слоев. Например, при поперечном обтекании труб в диапазоне чисел Рейнольдса 2·103 < Re < 2·105 на фронтальной части трубы образуется ламинарный пограничный слой, а на тыловой - турбулентный.
3) Гидравлическое сопротивление каналов при течении однофазной среды.
Расчет гидравлических сопротивлений проводится для определения полного перепада давления в теплообменном аппарате и затрат мощности на прокачку теплоносителей.
Общий перепад давления между двумя сечениями канала, в котором движется однофазный стационарный поток, складывается из потерь давления на трение DPтр, потерь давления, возникающих при движении потока через местные сопротивления DPм, нивелирного напора DPнив и перепада давления, связанного с ускорением потока DPуск.
Общий перепад давления, таким образом, рассчитывается по формуле:
DP = DРтр + DРм + DРнив + DPуск. (4)
Сопротивление трения при стационарном течении однофазного потока в трубах, каналах различного сечения, при продольном обтекании пучков труб для изотермического и неизотермического потоков при практически применяемых величинах температурного напора рассчитывается по формуле:
![]() (5)
(5)
где ξ - коэффициент гидравлического сопротивления трения, зависящий от геометрии канала, числа Рейнольдса и относительной шероховатости поверхности D/dг;
L - длина канала, м;
dг - гидравлический диаметр канала, м;
ρ - плотность среды, кг/м3;
![]() - средняя скорость теплоносителя в канале, м/с.
- средняя скорость теплоносителя в канале, м/с.
Потеря давления на местном сопротивлении рассчитывается по формуле:
![]() (6)
(6)
где ξм - коэффициент местного гидравлического сопротивления;
![]() - средняя скорость потока, к которой отнесен
коэффициент местного гидравлического сопротивления, м/с.
- средняя скорость потока, к которой отнесен
коэффициент местного гидравлического сопротивления, м/с.
Местные сопротивления возникают при резком изменении поперечного сечения канала или направления движения теплоносителя и считаются сосредоточенными.
Нивелирный напор на данном участке рассчитывается по формуле:
DPнив = ρgh, (7)
где ρ - среднее значение плотности среды, кг/м3;
h - высота канала (расстояние по вертикали в случае наклонного канала), м;
g - ускорение силы тяжести, м/с2.
Потеря напора на ускорение потока рассчитывается по формуле:
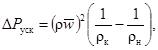 (8)
(8)
где ρк, ρн - плотности среды в конце и начале канала, кг/м3.
Погрешность δ расчета общего гидравлического сопротивления по формуле (4) определяется, в основном, погрешностью расчета гидравлического сопротивления трения и местного сопротивления и составляет ± (10 ÷ 25) %.
Конкретные формулы для расчета коэффициентов гидравлического сопротивления трения и местного сопротивления приведены в следующих разделах.
15. Однофазные ламинарные течения.
1) Ламинарные стабилизированные течения в каналах.
В разделе приведены формулы для расчета коэффициентов гидравлического сопротивления трения, распределения скоростей и касательных напряжений при ламинарном течении в каналах разной геометрии.
Теплофизические характеристики, если особо не оговаривается, относятся к средней массовой температуре потока в заданном сечении канала. Формулы получены как результат точных решений и аппроксимации этих решений формулами.
а) Ламинарное течение в трубах.
Коэффициент гидравлического сопротивления трения при ламинарном течении в трубе круглого поперечного сечения рассчитывается по формуле:
ξ = ξo = 64/Re, (9)
где ![]() (
(![]() - средняя по сечению скорость, η -
кинематическая скорость).
- средняя по сечению скорость, η -
кинематическая скорость).
Пределы применимости формулы (9): Re £ 2300.
Погрешность δ расчета ξ составляет ± 5 %.
Распределение скорости при ламинарном течении в трубе круглого поперечного сечения подчиняется параболическому закону и рассчитывается по формуле:
Пределы применимости формулы (10): Re £ 2300.
Погрешность D расчета w составляет ± 1,0 %.
Касательное напряжение на стенке трубы круглого поперечного сечения при ламинарном течении (tст) рассчитывается по формуле:
Пределы применимости формулы (11): Re £ 2300.
Погрешность D расчета tст составляет ± 1,0 %.
Коэффициент гидравлического сопротивления трения при ламинарном течении между двумя плоскими параллельными пластинами бесконечных размеров (плоская труба) рассчитывается по формуле:
где ![]() (H
- расстояние между пластинами, м). Определяющий размер при расчете числа Re
- расстояние между пластинами.
(H
- расстояние между пластинами, м). Определяющий размер при расчете числа Re
- расстояние между пластинами.
Пределы применимости формулы (12): Re £ 2300.
Погрешность δ расчета ξ, составляет ± 1 %.
Распределение скорости при ламинарном течении в плоской трубе рассчитывается по формуле:
где y - расстояние по нормали от оси трубы до рассматриваемой точки.
Пределы применимости формулы (13): Re £ 2300,
где ![]() ; dг = 4F/П
(dг -
гидравлический диаметр, м;
; dг = 4F/П
(dг -
гидравлический диаметр, м;
4F - четыре площади поперечного сечения;
П - смоченный периметр, м).
Погрешность δ расчета w составляет ± 10,0 %. Эта погрешность обусловлена погрешностью задаваемых геометрических и режимных параметров.
Коэффициент гидравлического сопротивления трения при ламинарном течении в трубе эллиптического поперечного сечения рассчитывается по формуле:
где ![]() ; dг = 4F/П
; dг = 4F/П
b1, b2 - большая и малая полуоси эллипса, м. Определяющий размер при расчете числа Re - гидравлический диаметр.
Пределы применимости формулы (14): Re £ 2300.
Погрешность D расчета ξ, составляет ± 5 %.
Распределение скорости при ламинарном течении в трубах эллиптического поперечного сечения рассчитывается по формуле:
где y - координата точки от центра эллипса вдоль оси b1
z - координата точки от центра вдоль оси b2.
Пределы применимости формулы (15): Re £ 2300.
Погрешность δ расчета w составляет ± 5,0 %.
Коэффициент гидравлического сопротивления трения при ламинарном течении в трубах прямоугольного поперечного сечения определяется по таблице № 3.
Таблица № 3
Коэффициент гидравлического сопротивления трения при ламинарном течении в трубах прямоугольного поперечного сечения
|
b/h |
1,00 |
1,25 |
1,50 |
2,00 |
2,50 |
3,00 |
4,00 |
5,00 |
10,00 |
∞ |
|
ξRe |
56,90 |
57,47 |
58,82 |
62,14 |
64,00 |
68,35 |
72,90 |
76,29 |
84,61 |
96,00 |
В таблице: b, h - стороны прямоугольника. Определяющий размер при расчете числа Re - гидравлический диаметр.
Погрешность δ определения ξ по таблице составляет ± 5 %. Данные таблицы со среднеквадратичной погрешностью 0,6 % описываются формулой:
ξRe = 95,9 - 123,31x + 135,14x2 - 50,89x3, (16)
где x = h/b.
Пределы применимости формулы (16): Re £ 2300.
Коэффициент гидравлического сопротивления трения при ламинарном течении в трубах с поперечным сечением в форме равнобедренного треугольника рассчитывается по формуле:
где b - половина угла при вершине равнобедренного треугольника;
В - параметр, который рассчитывается по формуле:
![]() (17а)
(17а)
Определяющий размер при расчете числа Re - гидравлический диаметр.
Пределы применимости формулы (17): Re £ 2300.
Погрешность δ расчета ξ, составляет ± 5 %.
Для равностороннего треугольника, если b = 30°, то ξRe = 53,33.
Для прямоугольного равнобедренного треугольника, если b = 45°, то ξRe = 52,71.
Погрешность δ расчета ξ, составляет ± 5 %.
б) Ламинарное течение в кольцевых каналах.
В разделе приведены формулы для расчета коэффициентов гидравлического сопротивления трения и распределения скорости при ламинарном течении в концентрических кольцевых каналах.
Для эксцентрических кольцевых каналов даны приближенные формулы расчета коэффициентов гидравлического сопротивления трения и касательных напряжений.
Коэффициент гидравлического сопротивления трения при ламинарном течении в кольцевых каналах определяется числом Re и отношением радиусов кольцевого канала θ = R1/R2, где R1 - внутренний радиус зазора кольцевого канала, м; R2 - наружный радиус зазора кольцевого канала, м.
Коэффициент гидравлического сопротивления трения при ламинарном течении в концентрических кольцевых каналах рассчитывается по формуле:
ξ · Re = 64Кф, (18)
где Кф - коэффициент формы, который рассчитывается по формуле:
Определяющий размер при расчете числа Re - гидравлический диаметр кольцевого канала dг = d2 - d1.
Пределы применимости формулы (19): Re £ 2300.
Погрешность δ расчета ξ, составляет ± 5 %.
Распределение скорости при ламинарном течении в концентрических кольцевых каналах рассчитывается по формуле:
где R - текущий радиус зазора кольцевого канала, R1 < R < R2.
Пределы применимости формулы (20): Re £ 2300.
Погрешность δ расчета ξ, составляет ± 10 %.
Коэффициент гидравлического сопротивления трения при ламинарном течении в эксцентрических кольцевых каналах рассчитывается по формуле:
где A = 3 - 4,5(1 - θ) + 2(1 - θ)2;
е - относительный эксцентриситет кольцевого канала, который равен: e = a/(R2 - R1);
a - эксцентриситет кольцевого канала, м;
ξo - коэффициент гидравлического сопротивления трения при ламинарном течении в трубах, рассчитывается по формуле (9). Определяющий размер при расчете числа Re - гидравлический диаметр эксцентрического кольцевого канала.
Пределы применимости формулы (21): Re £ 2300; 0,3 < 0,1 + 0,5e < θ.
Погрешность δ расчета ξ, составляет ± 8 %.
Схема поперечного сечения эксцентричного кольцевого канала приведена на рис. 2.
Распределение касательных напряжений по периметру внутренней и внешней стенок эксцентрического кольцевого канала при ламинарном течении рассчитывается по формуле:
где при i = l:
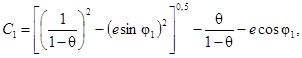 (23)
(23)
при i = 2:
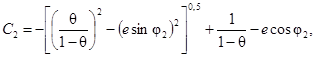 (24)
(24)
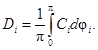 (25)
(25)
Индексы i = l, 2 относятся к внутренней и внешней поверхностям кольцевого канала соответственно. Углы j1 и j2 отсчитываются от узкой части эксцентричного кольцевого канала (рис. 2).
Пределы применимости формулы (22): Re £ 2300.
Погрешность δ расчета ti составляет ± 10 %.
Рис. 2. Схема поперечного сечения эксцентричного кольцевого канала
в) Ламинарное продольное течение в сборках стержней.
В разделе рассматриваются правильные упаковки стержней. Стержни (твэлы) располагаются по вершинам равностороннего треугольника или квадрата. Соответственно такие системы называются треугольными или квадратными упаковками стержней. Схемы ячеек показаны на рис. 3.
Рис. 3. Схемы треугольной и квадратной упаковки стержней:
dн - диаметр твэла; S - расстояние между осями твэла
Коэффициент гидравлического сопротивления трения при ламинарном течении в сборках стержней треугольной и квадратной упаковок рассчитывается по формуле:
где ![]()
ξ* - относительный радиус эквивалентной окружности, которой заменяется шестигранная или квадратная граница ячейки вокруг стержней, рассчитываемый по формуле:
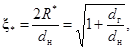 (26a)
(26a)
где R* - радиус эквивалентного по площади сектора круга, м;
dн - наружный диаметр стержня, м;
dг - гидравлический диаметр сборки стержней, м, который рассчитывается:
для треугольной упаковки стержней по формуле:
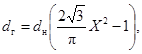 (26б)
(26б)
для квадратной упаковки стержней по формуле:
где Х - относительный шаг расположения стержней в решетке.
Определяющий размер при расчете числа Re - гидравлический диаметр сборки стержней.
Пределы применимости формулы (26): Re £ 2000; X = S/dн > 1,40 (рис. 3.)
Погрешность δ расчета ξ, составляет ± 8 %.
Коэффициенты гидравлического сопротивления трения для сборок стержней треугольной и квадратной упаковок с погрешностью, большей чем по формуле (26), рассчитываются по формуле:
ξRe = 64Кф, (27)
где Кф - коэффициент формы, значения которого приведены в таблице № 4.
Таблица № 4
Коэффициент формы для сборок стержней треугольной и квадратной упаковок
|
1,00 |
1,02 |
1,05 |
1,10 |
1,20 |
1,30 |
1,40 |
1,50 |
2,00 |
|
|
Треугольная упаковка стержней |
0,407 |
0,663 |
0,966 |
1,274 |
1,560 |
1,715 |
1,834 |
1,940 |
2,462 |
|
Квадратная упаковка стержней |
0,406 |
0,518 |
0,679 |
0,913 |
1,264 |
1,510 |
1,699 |
1,858 |
2,518 |
Пределы применимости формулы (27): Re £ 2000; S/dн = 1,0 ÷ 2,0.
Погрешность δ расчета ξ по формуле:
при S/dн = 1,0 ÷ 1,4 составляет ± 12 %;
при 1,4 < S/dн < 2,0 составляет ± 8 %.
Оценочные расчеты коэффициентов гидравлического сопротивления трения в сборках стержней допускается проводить по формуле (27), если принять:
для треугольной упаковки стержней:
![]() (28)
(28)
для квадратной упаковки стержней:
![]() (29)
(29)
В этом случае погрешность δ расчета ξ составляет ± 15 %.
2) Нестабилизированное ламинарное течение на входном участке каналов.
Под влиянием трения о стенки гидродинамические характеристики ламинарного потока в прямолинейных каналах изменяются на некоторой длине, называемой входным или начальным участком. Развитие характеристик потока сопряжено с дополнительными затратами энергии на прокачку жидкости через канал.
При расчете теплообменных аппаратов с малой относительной длиной представляется целесообразным учитывать особенности течения жидкости на начальном участке по сравнению с участком стабилизированного течения.
Длина входного участка и профиля гидродинамических характеристик в его различных сечениях зависят от конфигурации входных устройств.
Формирование профиля скорости на гидродинамическом входном участке осуществляется через молекулярный механизм обмена. Это приводит к тому, что длина входного участка при выбранной конфигурации входного устройства не зависит от характеристик поверхности каналов, т.е. для каналов с гладкими или шероховатыми стенками длина входных участков практически одинакова при фиксированном числе Рейнольдса.
а) Нестабилизированное ламинарное течение на входном участке круглой трубы.
Длина входного участка - это расстояние от входа до сечения, где скорость потока на оси канала (трубы) устанавливается с точностью не менее 5 %, а касательное напряжение - с точностью не менее 1 %.
Длина входного участка (участка стабилизации потока) при ламинарном течении в круглых трубах с плавным профилированным входом рассчитывается по формуле:
где Lст - длина входного участка, м.
Пределы применимости формулы (30): Re £ 2300.
Погрешность δ расчета Lст составляет ± 10 калибров трубы.
Падение давления по длине входного участка круглой трубы вызывается поверхностным трением и изменением количества движения потока жидкости.
Перепад давления на участке между входным и произвольными поперечными сечениями входного участка трубы рассчитывается по формуле:
где X = x/(Redвн) - безразмерное расстояние между входным и произвольным поперечными сечениями входного участка трубы;
ρ - плотность, кг/м3,
w - скорость, м/с.
Пределы применимости формулы (31): Re £ Reкр.
Погрешность δ расчета ![]() составляет ± 5 %.
составляет ± 5 %.
Перепад давления на всей длине входного участка трубы рассчитывается по формуле:
При стабилизированном ламинарном течении перепад давления на длине трубы, равной длине входного участка, равен:
средняя скорость задается.
Из отношения перепадов давления, найденных по формулам (32) и (33), следует, что на всей длине входного участка затраты энергии на прокачку ламинарного потока жидкости в 1,33 раза больше, чем на соответствующей длине стабилизированного ламинарного течения.
Пределы применимости формул (32) и (33): Re £ Reкр.
Погрешность δ расчета DPвх составляет ± 6 %.
Профиль скорости при ламинарном течении жидкости на входном участке круглой трубы (u) рассчитывается в пограничном слое по формуле:
где ![]() -
относительная толщина пограничного слоя, зависящая от продольной координаты х,
м;
-
относительная толщина пограничного слоя, зависящая от продольной координаты х,
м;
Y - расстояние от стенки трубы, м;
δпс - толщина пограничного слоя; в центральной части трубы за пределами пограничного слоя по формуле:
Пределы применимости формул (34) и (35): Re £ Reкр.
Погрешность δ расчета u составляет ± 10 %.
Толщина пограничного слоя при заданном числе Рейнольдса связана с продольной координатой зависимостью:
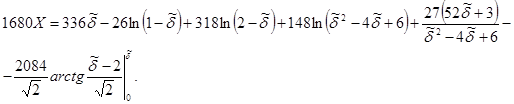 (36)
(36)
При фиксированных расстояниях x и числе Рейнольдса толщина пограничного слоя находится итерационно.
б) Нестабилизированное ламинарное течение на входном участке плоской трубы.
Плоская труба - канал, образованный двумя плоскими параллельными пластинами бесконечных размеров. Плоская труба является предельным случаем кольцевого канала.
Длина входного гидродинамического участка в плоских трубах с гладкой и шероховатой поверхностями (Lст) рассчитывается по формуле:
где Н - расстояние между параллельными пластинами, характерный размер при расчете числа Рейнольдса Re = 2wH/v.
Пределы применимости формулы (37): пластины с регулярной шероховатостью в форме выступов прямоугольного поперечного сечения; относительная высота элементов шероховатости изменяется от 0 до Н/3; Re £ Reкр.
Погрешность δ расчета Lст составляет ± 10 H.
16. Однофазные турбулентные течения.
Помимо ламинарного наблюдаются также следующие режимы течения (рис. 4). Различие этих течений определяется величиной приведенной шероховатости k+ = kv*/v,
где k - средняя
величина выступов шероховатости; ![]()
![]() - динамическая скорость, м/сек; tо -
касательное напряжение на стенке, H.
- динамическая скорость, м/сек; tо -
касательное напряжение на стенке, H.
1-турбулентный режим без проявления шероховатости при k+ £ 5. В этом режиме гидравлическое сопротивление такое же, как и в гладких трубах.
2-переходный режим при 5 < k+ £ 70. В этом режиме течения гидравлическое сопротивление зависит от Re и отношения dвн/k.
3-автомодельный режим при k+ > 70, при котором коэффициент гидравлического сопротивления не зависит (или слабо зависит) от Re и зависит от отношения dвн/k.
Трубы с неравномерной шероховатостью
считаются гладкими, если D/dг < 15/Re,
где D - эквивалентная абсолютная шероховатость, м; ![]() .
.
Значения D для различных материалов приведено в таблице № 5.
Таблица № 5
Значения D для различных материалов
|
Значение D, м |
|
|
Нержавеющая сталь |
1 · 10-5 |
|
Алюминий |
1,5 · 10-5 |
|
Углеродистая сталь: |
|
|
новые трубы при тщательной очистке воды; |
8 · 10-5 |
|
трубы для насыщенного пара или воды с незначительной коррозией; |
2 · 10-4 |
|
водопроводы, находящиеся в эксплуатации. |
2 · 10-3 |
Все рекомендации раздела получены для изотермического течения или случаев слабой зависимости теплофизических свойств от температуры. Теплофизические свойства, если особо не оговаривается, относятся к средней массовой температуре потока в заданном сечении канала.
Рис. 4. Изменение коэффициента сопротивления при течении в трубах с искусственной песочной шероховатостью (1, 2, 3 - расчет по формулам Пуазейля, Блазиуса и Прандтля)
1) Стационарное стабилизированное турбулентное течение в «гладких» каналах,
а) Стационарное стабилизированное турбулентное течение в трубах.
В разделе приведены соотношения для расчета коэффициентов гидравлического сопротивления трения, касательных напряжений и полей скорости.
Коэффициент гидравлического сопротивления трения при турбулентном течении в круглой трубе рассчитывается по формуле:
где ![]()
Пределы применимости формулы (38): Re = 4·103 ÷ 108.
Погрешность δ расчета ξ составляет ± 5 %.
Касательное напряжение на стенке трубы круглого поперечного сечения при турбулентном течении рассчитывается по формуле:
Пределы применимости формулы (39): Re = 4·103 ÷ 108.
Погрешность δ расчета tст составляет ± 10 %.
Распределение скорости при турбулентном течении в трубе круглого поперечного сечения рассчитывается по формулам универсального закона (рис. 5):
и+=у+ при y+ < 5; (40)
где и+ = w/v*; у+ = y·v/v*; ![]()
у - расстояние от стенки трубы, м.
Пределы применимости формул (40), (41), (42): Re = 4·103 ÷ 108.
Погрешность δ расчета по формулам составляет ± 5 %.
Рис. 5. Универсальный профиль скорости в трехслойной модели Кармана
Распределение скорости в трубе круглого поперечного сечения может также рассчитываться по единой по всем диапазонам изменения у+ формуле:
где ![]()
Пределы применимости формулы (43): Re = 4·103 ÷ 108.
Погрешность δ расчета по формуле составляет +3 % + -5 %.
Отношение средней скорости к максимальной при турбулентном течении в трубе круглого поперечного сечения рассчитывается по формулам:
Пределы применимости формул (44) и (45): Re = 4·103 ÷ 108.
Погрешность δ расчета по формуле составляет ± 10 %.
Коэффициент турбулентного переноса количества движения.
Коэффициент турбулентного переноса количества движения ev обычно необходим при расчетах касательных напряжений или переноса тепла в моделях, использующих уравнения Рейнольдса для турбулентного движения, при турбулентном течении в трубе круглого поперечного сечения он рассчитывается по формуле:
где ![]() ;
;
wmax - максимальная скорость потока;
Y = y/rвн - относительное расстояние от стенки трубы, м;
rвн - внутренний радиус трубы, м.
Распределение скорости рассчитывается по ранее приведенным формулам.
Пределы применимости формулы (46): Re = 4·104 ÷ 105.
Погрешность δ расчета ev составляет ± 20 %.
Пульсации скорости в трех взаимоперпендикулярных направлениях характеризуются величиной интенсивности.
Интенсивность пульсаций скорости при турбулентном течении в трубе круглого поперечного сечения рассчитывается по формуле:
где i = l, 2, 3 - индексы, обозначающие направление пульсаций:
i = l - вдоль среднего движения,
i = 2 - перпендикулярно стенке,
i = 3 - в тангенциальном направлении;
A1 = 0,95; A2 = 0,40; A3 = 0,60;
B1 = 1,48; B2 = 0,77; B3 = 1,17;
wmax - максимальная скорость потока;
Y = y/rвн - относительное расстояние от стенки трубы, м;
rвн - внутренний радиус трубы, м;
w - рассчитывается по формулам (42) и (43).
Пределы применимости формулы (47): Re = 7,5 · 103 ÷ 2,5 · 105; y+ > 10.
Погрешность δ расчета Gi составляет ± 10 %.
б) Стационарное стабилизированное турбулентное течение в концентрических кольцевых каналах.
В раздел включены соотношения для расчета коэффициентов гидравлического сопротивления трения, касательных напряжений и полей скорости при турбулентном течении в гладких кольцевых каналах. Схема кольцевого канала приведена на рис. 6.
Коэффициент гидравлического сопротивления трения при турбулентном течении в кольцевых каналах рассчитывается по формуле:
где θ = R1/R2;
ξo - коэффициент гидравлического сопротивления трения круглой трубы диаметром, равным гидравлическому диаметру кольцевого канала. ξo рассчитывается по формуле (38).
Пределы применимости формулы (48): Re = 2,3·103 ÷ 4·106; θ = 0,06 ÷ 1,00.
Погрешность δ расчета ξ составляет ± 8 %.
Для приближенных расчетов в диапазоне θ = 0,1 ÷ 0,80 можно использовать формулу:
![]() (49)
(49)
Касательное напряжение на стенках концентрического кольцевого канала при турбулентном течении рассчитывается:
на внутренней стенке по формуле:
на наружной стенке по формуле:
где ξ рассчитывается по формуле (48).
Пределы применимости формул (50) и (51): Re = 2,3·103 ÷ 4·106; θ = 0,06 ÷ 1,00.
Погрешность ξ расчета t1 и t2 по формулам составляет ± 10 %.
Рис. 6. Схема кольцевого канала
Распределение скорости при турбулентном течении в кольцевом канале при R1/R2 > 0,50 рассчитывается по формулам (40) ÷ (43) для круглой трубы. Линия максимальной скорости при этом условии считается равноудаленной от стенок кольцевого канала.
Положение линии максимальной скорости в кольцевых каналах при θ < 0,50 рассчитывается по формуле:
![]() (52)
(52)
где ro - радиус линии максимальной скорости, м.
в) Стационарное стабилизированное турбулентное течение в эксцентрических кольцевых каналах.
Коэффициенты гидравлического сопротивления трения при турбулентном течении в эксцентрических кольцевых каналах рассчитываются по формуле:
где ξo рассчитывается по формуле (9);
B = 0,577 - 0,866(1 - θ) + 0,46(1 - θ)2;
f = 1 + 0,35е·(1 - θ)4;
e = a/(R2 - R1) (a - эксцентриситет, м).
Пределы применимости формулы (53): Re = 6·103 ÷ 2,5·105; θ > (0,1 + 0,5e) >0,3.
Погрешность расчета ξ составляет ± 8 %.
Относительное распределение касательного напряжения на стенках кольцевого канала с эксцентриситетом рассчитывается по формуле:
где i = l для внутреннего и i = 2 для внешнего периметров кольцевого зазора;
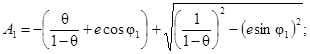 (55)
(55)
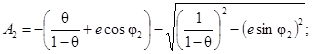 (56)
(56)
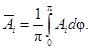 (57)
(57)
Пределы применимости формулы (54): θ = 0,25 ÷ 1,00.
Погрешность δ расчета ti составляет ± 15 %.
Средние по периметру касательные напряжения на стенках кольцевого канала с эксцентриситетом рассчитываются по формулам:
где ξ рассчитывается по формуле (53),
![]() - средняя скорость среды в канале.
- средняя скорость среды в канале.
Пределы применимости формул (58) и (59): θ = 0,25 ÷ 1,00; ![]() - для внешней стенки кольцевого канала.
- для внешней стенки кольцевого канала.
Погрешность δ расчета ![]() составляет ± 15 %.
составляет ± 15 %.
Средние по радиусу кольцевого канала с эксцентриситетом локальные скорости рассчитываются по формуле:
где ξ рассчитывается по формуле (48);
ξo рассчитывается по формуле (53).
Пределы применимости формулы (60): Re = 6·103 ÷ 2,5·105; θ ³ 0,1 + 0,5e ³ 0,3,
где e - значение эксцентриситета, 0 £ e £ 1.
Погрешность δ расчета ![]() составляет ± 20 %.
составляет ± 20 %.
г) Стационарное стабилизированное турбулентное течение в сборках стержней треугольной упаковки.
В раздел включены соотношения для расчета коэффициентов гидравлического сопротивления трения, касательных напряжений и полей скорости при турбулентном стабилизированном течении вдоль сборок гладких цилиндрических стержней треугольной упаковки. Так как гидродинамика жидких металлов и воды одинакова, то формулы для жидких металлов справедливы и для воды.
Стержни сборки треугольной упаковки образуют три типа ячеек (рис. 7).
Рис. 7. Расположение ячеек внутри сборки гладких стержней треугольной упаковки:
1 - центральная ячейка; 2 - боковая ячейка; 3 - угловая ячейка.
Коэффициент гидравлического сопротивления трения при турбулентном течении в сборках гладких стержней треугольной упаковки рассчитывается по формуле:
где ξo = 0,210/Re0,25, ![]() . Определяющий
размер при расчете числа Re - гидравлический диаметр треугольной упаковки
стержней, рассчитывается по формулам пункта 15, подпункт 1
настоящего документа:
. Определяющий
размер при расчете числа Re - гидравлический диаметр треугольной упаковки
стержней, рассчитывается по формулам пункта 15, подпункт 1
настоящего документа:
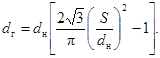
Пределы применимости формулы (61): S/dн = 1,0 ÷ 1,5; Re = 6·103 ÷ 105.
Погрешность δ расчета ξ, составляет ± 6 %.
Соотношения для ξ сборок стержней, выраженные через ξo для трубы и через пористость сборки, рассчитываются:
для треугольных сборок:
ξ/ξo = 0,57 + 0,8(e - 0,091)0,33; (61а)
для квадратных сборок:
ξ/ξo = 0,59 + 0,67(e - 0,091)0,5, (61б)
где ξ/ξo - коэффициент сопротивления для круглой трубы при том же числе Re (формула (38));
e - пористость сборки.
Среднее по периметру стержня в сборке гладких стержней касательное напряжение рассчитывается по формуле:
где ξ рассчитывается по формуле (61).
Пределы применимости формулы (62): S/dн = 1,0 ÷ 1,5; Re = 6·103 ÷ 105.
Погрешность δ расчета ![]() составляет ± 10 %.
составляет ± 10 %.
Распределение касательных напряжений по периметру стержня центральной ячейки рассчитывается по формуле:
где j - угол, отсчитываемый от узкого сечения центральной ячейки в радианах. Коэффициенты А1 ÷ А4 приведены в таблице № 6.
Пределы применимости формулы (63): S/dн = 1,0 ÷ l,5; Re = 6·103 ÷ 105.
Погрешность δ расчета tj составляет ± 15 %.
Таблица № 6
Значения коэффициентов A1 ÷ A4 в формуле (63)
|
S/dн |
A1 |
A2 |
A3 |
A4 |
|
1,00 |
-1,0073 |
-0,1059 |
0,0991 |
0,0318 |
|
1,05 |
-0,2522 |
0,0043 |
-0,0410 |
-0,0002 |
|
1,10 |
-0,1277 |
-0,0098 |
0,0028 |
0,0014 |
|
1,20 |
-0,0143 |
0 |
0 |
0 |
|
1,25 |
0 |
0 |
0 |
0 |
Сводка корреляций для расчета коэффициентов гидравлического сопротивления в пучках стержней приведена в таблице № 7.
Таблица № 7
Сводка корреляций для расчета коэффициентов гидравлического сопротивления в пучках стержней
|
Корреляции |
|
|
Ламинарный режим течения |
|
|
Пучок гладких стержней |
где значения коэффициента формы kL приводятся в таблице № 8 |
|
Пристенные каналы и пучок стержней в целом |
где χL - геометрический параметр, значения которого даются в таблице № 9 |
|
Пучок оребренных стержней |
где 1,125 £ s/d £ 1,417; l £ Re £ 2·103; 8,3 £ h/d £ 50 |
|
Формула Марклея |
где 2 £ Re < 400; 1,067 £ S/d £ 1,32; h/d ≈ 8 |
|
Пучок стержней с дистанционированием «ребро по ребру» |
(ξp/ξ)1 ≈ 1 + [1,8/(h/d)], где S/d = 1,13 - 1,15; h - шаг закрутки ребер |
|
Переходный режим течения от ламинарного к турбулентному |
|
|
Пучок гладких стержней в треугольной упаковке |
lgξ = 5,2Re-0,22+0,145((s/d)-1) - 2,35, где для диапазона параметров 10 £ Re £ 2·105; 1,0 £ S/d £ 1,5 точность описания составляет ± 20 % |
|
При расположении стержней по квадрату |
где 1,0 £ S/d £ 2,0; 104 £ Re £ 5·105 |
|
Пучок оребренных стержней |
где 2 £ Re £ 500; 1,067 £ S/d £ 1,32; h/d ≈ 8 |
|
Турбулентный режим течения |
|
|
Пучок гладких стержней |
ξ = 0,21/Re0,25[l + ((s/d) - 1)0,32], где 1,0 £ s/d £ 1,5; 6·103 £ Re £ 2·105. Уравнение согласуется с экспериментальными данными с точностью ± 10 % |
|
Пристенные каналы и пучок стержней в целом |
где χm - геометрический параметр. Экспериментально установлено, что параметры χL и χm связаны друг с другом соотношением: χm = (l + 3χL)/4, где 0,25 < χl < 1,25 и 0,45 < χm < 1,2 |
|
Пристенные каналы и пучок стержней в целом |
При расчете
числа Рейнольдса (
где n - номер ряда стержней |
|
Пучок стержней с треугольной упаковкой и дистанционированием «ребро по стержню» |
где 1,0 £ s/d £ 1,5; 104 £ Re £ 2·105; 8,0 £ h/d £ 50. Уравнение с точностью ± 15 % согласуется с экспериментальными данными |
|
Для более точных расчетов при меньшем диапазоне изменения параметра h/d |
где 1,0 £ s/d £ 1,5; 8,0 < h/d £ 25; 6·103 £ Re < 2·105; значение ξ рассчитывается для пучка гладких стержней. Уравнение с точностью ± 10 % согласуется с данными экспериментальных исследований при указанных диапазонах изменения параметров |
|
Формула Новендстерна |
где 1,06 £ s/d £ 1,42; 2,6·103 £ Re £ 2·105; 8,0 £ h/d £ 96. Точность уравнения равна ± 30 %, по крайней мере, при больших числах Re |
|
Формула Марклея |
ξp = 0,48/Re0,25,3 где Re > 5000; 1,067 £ s/d £ 1,32; h/d ≈ 8 |
|
Пучки стержней типа БН-600 |
ξp = 0,117(D/dh + 68/Re)0,25,3 где D - эквивалентная шероховатость поверхности твэлов |
|
Пучок стержней с дистанционированием «ребро по ребру» |
где 2 £ n £ 4 (n - число заходов ребер); 1,05 £ s/d £ 1,25; h/d ³ 5(h - шаг навивки ребер); Re = 104 + 2·105 |
Таблица № 8
Значения фактора kL для ламинарного течения в пучках стержней
|
Относительный шаг, S/d |
|||||||||
|
1,0 |
1,02 |
1,05 |
1,10 |
1,20 |
1,30 |
1,40 |
1,5 |
2,0 |
|
|
Треугольный |
0,407 |
0,663 |
0,966 |
1,274 |
1,56 |
1,715 |
1,834 |
1,940 |
2,46 |
|
Квадратный |
0,406 |
0,518 |
0,679 |
0,913 |
1,264 |
1,510 |
1,699 |
1,858 |
2,51 |
Таблица № 9
Значения параметров χL и χр в формулах в таблице № 9
|
Число стержней |
χL |
χр |
|
|
1 |
7 |
0,774 |
0,830 |
|
2 |
9 |
0,982 |
0,987 |
|
3 |
37 |
1,059 |
1,044 |
|
4 |
61 |
1,098 |
1,073 |
|
5 |
91 |
1,120 |
1,090 |
|
6 |
127 |
1,135 |
1,101 |
|
7 |
169 |
1,145 |
1,109 |
|
8 |
217 |
1,152 |
1,114 |
|
9 |
271 |
1,158 |
1,119 |
|
10 |
331 |
1,163 |
1,122 |
|
11 |
397 |
1,166 |
1,125 |
Коэффициенты межканального обмена.
Расчет расходов в элементарных ячейках между стержнями производится по методу «изобарных сечений». Более точные методы учитывают обмен массой и количеством движения между ячейками стержневой сборки. Для этого вводят коэффициенты межканального обмена.
Коэффициент межканального обмена массой представляет собой отношение расхода теплоносителя через единицу длины зазора между стержнями к продольному расходу теплоносителя. Коэффициент межканального обмена количеством движения указывает, какую долю от разности количества движения в двух смежных ячейках составляет поперечный поток количества движения, отнесенный к единице длины зазора между ячейками. Показано, что коэффициент межканального обмена массой равен коэффициенту межканального обмена количеством движения, если оперировать лишь средними скоростями потока в ячейках. В дальнейшем не делается различия между этими двумя коэффициентами межканального обмена.
Межканальный обмен осуществляется за счет молекулярного и турбулентного переноса, а также за счет направленной конвекции, поэтому суммарный коэффициент межканального обмена представляется в виде:
![]() (64)
(64)
Коэффициент межканального обмена количеством движения за счет молекулярных и турбулентных процессов для сборок гладких стержней треугольной упаковки рассчитывается по формуле:
где ![]()
Отношение между средними скоростями теплоносителя в боковой и центральной ячейках сборки гладких стержней треугольной упаковки при турбулентном течении рассчитывается по формуле:
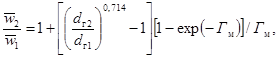 (66)
(66)
где ![]() ;
;
ξ = 0,316Re-0,25;
![]() dг = 4ω/P -
гидравлический диаметр ячейки, м;
dг = 4ω/P -
гидравлический диаметр ячейки, м;
ω - площадь проходного сечения ячейки, м;
P - смоченный периметр ячейки, м;
![]() - коэффициент межканального обмена количеством
движения, рассчитывается по формуле (65).
- коэффициент межканального обмена количеством
движения, рассчитывается по формуле (65).
Скорость в заданной точке внутри ячейки рассчитывается по соотношениям для круглых труб (формулы 40 ÷ 43) с использованием локальных масштабов:
![]() (67)
(67)
где ![]() ;
;
![]() ;
;
![]() ;
;
tj рассчитывается по формуле (63);
yi - координата по нормали к стенке.
Отношение средней скорости к максимальной в ячейке сборки гладких стержней треугольной упаковки при турбулентном течении рассчитывается по формуле:
где ![]()
dн - наружный диаметр стержней, м.
Пределы применимости формулы (68): Re = 4 · 103 ÷ 105.
Погрешность δ расчета ![]() составляет
± 10 %.
составляет
± 10 %.
д) Стационарное стабилизированное турбулентное течение в сборках стержней квадратной упаковки.
Коэффициент гидравлического сопротивления трения при турбулентном течении в сборках гладких стержней квадратной упаковки рассчитывается по формуле:
где b = 10(S/dн - 1);
ξо - коэффициент гидравлического сопротивления трения при турбулентном течении в трубе, внутренний диаметр которой равен гидравлическому диаметру сборки стержней квадратной упаковки; ξо рассчитывается по формуле (38).
Определяющий размер при расчете числа Re по формуле - гидравлический диаметр сборки стержней квадратной упаковки, который рассчитывается по формуле (26в).
Пределы применимости формулы (69): (х = S/dн).
Погрешность δ расчета ξ составляет ± 10 %.
ж) Стационарное стабилизированное турбулентное течение внутри трубы змеевика.
Коэффициент гидравлического сопротивления трения при турбулентном течении внутри трубы змеевика рассчитывается по формуле:
ξ = ξo · Kф, (70)
где ξo - коэффициент гидравлического сопротивления трения в прямой трубе того же внутреннего диаметра, что и труба змеевика;
Kф - коэффициент формы змеевика, рассчитывается по формуле:
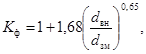 (71)
(71)
где dвн - внутренний диаметр трубы змеевика, м (рис. 8.);
dзм - диаметр навивки змеевика, м.
Пределы применимости формулы (70): ![]() .
.
Погрешность δ расчета ξ составляет ± 10 %.
Коэффициент гидравлического сопротивления
при течении внутри труб змеевиков с большим радиусом гиба 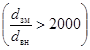 рассчитывается по
зависимостям для прямых труб.
рассчитывается по
зависимостям для прямых труб.
Рис. 8. Основные геометрические характеристики трубного пучка
з) Местные гидравлические сопротивления при стационарном турбулентном течении в каналах.
Разные формы канала. Местные сопротивления связаны либо с резким изменением формы канала (например, из-за сужения, расширения, вентилей, клапанов, задвижек), либо с изменением направления потока (например, из-за изгибов, тройников).
Места, где наблюдаются наибольшие местные потери давления в реакторах, перечислены ниже.
Местные гидравлические сопротивления в корпусе реактора:
от холодной петли до нижней камеры корпуса реактора;
вход в нижнюю камеру;
вход в активную зону;
дистанционирующие решетки;
выход из активной зоны;
верхняя камера корпуса до горячей петли;
байпасы:
нижняя камера до активной зоны;
байпас активной зоны до верхней камеры;
нижняя камера - горячая петля;
нижняя камера - верхние головки тепловыделяющей сборки (ТВС);
верхние головки - верхняя камера (непосредственно);
верхние головки ТВС - приводы контрольных стержней;
приводы стержней - верхняя камера (разные линии).
Местные гидравлические сопротивления в первом контуре:
горячая петля до входного (горячего) коллектора парогенератора;
повороты главного трубопровода;
вход в трубы горячего коллектора;
выход из труб в холодный коллектор;
главный трубопровод от холодного коллектора до насоса;
вход в насос;
гидравлическое сопротивление насоса;
выход из насоса.
Потери давления на местном сопротивлении рассчитываются по формуле:
![]() (72)
(72)
где ξм - коэффициент местного сопротивления;
![]() - средняя скорость потока, к которой отнесен
коэффициент местного сопротивления, м/с.
- средняя скорость потока, к которой отнесен
коэффициент местного сопротивления, м/с.
Обычно это скорость в наименьшем проходном сечении канала, где ξм - коэффициент местного сопротивления, определяется по формуле:
ξм = A/Re + ζкв, (73)
где А, ζкв - постоянные для данной формы местного сопротивления;
ξкв - коэффициент местного сопротивления для турбулентного течения (Re > 104) в области квадратичного сопротивления. В таблице № 10 даны постоянные значения для нескольких видов сопротивлений.
Таблица № 10
Значения А и ζкв для некоторых местных сопротивлений
|
А |
ζкв |
|
|
Внезапное расширение трубопровода (выход трубы в большой резервуар) |
30 |
1 |
|
Пробочный кран |
150 |
0,40 |
|
Вентиль: |
||
|
обыкновенный; |
3000 - 5000 |
2,5 - 5,0 |
|
Косва |
900 |
2,5 |
|
Угловой вентиль |
400 |
0,8 |
|
Шаровой клапан |
5000 |
45 |
|
Угольник: |
||
|
90° |
400 |
1,4 |
|
135° |
600 |
0,4 |
|
Колено 90° |
130 |
0,2 |
|
Тройник |
150 |
0,3 |
|
Задвижка: |
||
|
n*) = 1 |
75 |
0,15 |
|
п = 0,75 |
350 |
0,2 |
|
n = 0,5 |
1300 |
2 |
|
n = 0,25 |
3000 |
20 |
|
Диафрагма: |
||
|
п = 0,64 |
70 |
1 |
|
п = 0,40 |
120 |
7 |
|
n = 0,16 |
500 |
70 |
|
n = 0,05 |
3200 |
800 |
|
______________ *) n - степень открытия задвижки или соотношение сечения отверстия диафрагмы к сечению канала |
||
Коэффициенты местного сопротивления в квадратичной области при резком изменении сечения канала можно определить по таблице № 11, где рассмотрены наиболее простые случаи.
Местные гидравлические сопротивления возникают при резком изменении поперечного сечения канала и направления движения потока теплоносителя и считаются сосредоточенными.
Коэффициент местного сопротивления при течении турбулентного потока через дистанционирующие решетки и решетки-интенсификаторы теплосъема в сборках при равномерном распределении расхода по ячейкам проходного сечения активной зоны рассчитывается по формуле:
где ![]() - коэффициент
сужения;
- коэффициент
сужения;
f - площадь проходного сечения канала, м2;
fp - площадь проходного сечения дистанционирующей решетки, м2,
![]()
wp - скорость потока через отверстие решетки, м/с;
dг - гидравлический диаметр решетки, м;
Lp - высота решетки, м;
kш - абсолютная шероховатость материала решетки-интенсификатора, м.
Пределы применимости формулы (74): Re = 105 ÷ l06.
Погрешность δ расчета ξм составляет ± 10 %.
Таблица № 11
Коэффициенты местного гидравлического сопротивления для частных случаев
|
Схема |
Формула или таблица |
|||||||||||
|
Резкое сужение сечения |
|
ξ = 0,5(1-(ωм/ωб)); (75) |
||||||||||
|
при Re > 104 ξ, зависит только от отношения ωм/ω6; |
||||||||||||
|
при Re < 104 ξ = f · Re |
||||||||||||
|
Резкое расширение сечения |
|
ξ = 1,1[(1-(ωм/ωб)]2; (76) |
||||||||||
|
при Re > 104 ξ, зависит только от ωм/ω6; |
||||||||||||
|
при Re < 104 ξ = f · Re, причем с уменьшением Re ξ увеличивается |
||||||||||||
|
Вход в трубу с выступающими кромками |
|
δ/d |
b/d |
ξ |
||||||||
|
|
0,2 |
1,0 |
||||||||||
|
|
0,05 - 0,2 |
0,85 |
||||||||||
|
> 0,04 |
0,5 |
|||||||||||
|
Вход в трубу с закругленными кромками |
\ |
r/d |
ξ |
Примечание |
||||||||
|
0,05 |
0,4 |
При выступающих кромках. |
||||||||||
|
0,05 |
0,25 |
При кромках заподлицо со стенкой. |
||||||||||
|
0,10 |
0,12 |
|||||||||||
|
0,20 |
0 |
|||||||||||
|
Вход в трубу с закругленными кромками от плоской стены |
|
При h/d > 0,3 ξ ≈ 0,05; |
||||||||||
|
при
h/d = 0,25 |
||||||||||||
|
Вход в трубу через решетку или диафрагму |
|
ξ = [1,707((ωм/ωб)-1)]2; (77) |
||||||||||
|
Вход в трубу через боковые отверстия (n - число отверстий) |
|
ωм/ωб |
ξ |
|||||||||
|
n = 1 |
n = 2 |
|||||||||||
|
0,2 |
65 |
65 |
||||||||||
|
0,3 |
30 |
36,5 |
||||||||||
|
0,4 |
14,9 |
17,0 |
||||||||||
|
0,5 |
9,0 |
12,0 |
||||||||||
|
0,6 |
6,3 |
8,7 |
||||||||||
|
0,7 |
4,5 |
6,9 |
||||||||||
|
0,8 |
3,5 |
5,5 |
||||||||||
|
0,9 |
2,7 |
4,5 |
||||||||||
|
1,0 |
2,3 |
3,8 |
||||||||||
|
1,2 |
1,6 |
2,8 |
||||||||||
|
1,4 |
- |
2,0 |
||||||||||
|
Выход из трубы через решетку или диафрагму |
|
|
||||||||||
|
Выход из трубы через боковые отверстия (п - число отверстий) |
|
ωм/ωб |
ξ |
ωм/ωб |
||||||||
|
n = 1 |
n = 2 |
|||||||||||
|
0,2 |
66 |
68 |
||||||||||
|
0,3 |
30 |
33 |
||||||||||
|
0,4 |
16 |
16 |
||||||||||
|
0,5 |
10 |
12 |
||||||||||
|
0,6 |
7,3 |
8,5 |
||||||||||
|
0,7 |
5,5 |
6,8 |
||||||||||
|
0,8 |
4,5 |
5,9 |
||||||||||
|
0,9 |
3,7 |
5,0 |
||||||||||
|
1,0 |
3,2 |
4,4 |
||||||||||
|
1,2 |
2,4 |
3,5 |
||||||||||
|
Решетка или диафрагма внутри трубы (отверстия с острыми краями) |
|
|
||||||||||
|
Поворот на угол j |
|
j° |
R/d |
|||||||||
|
1 |
1,5 |
2 |
3 |
4 |
5 |
|||||||
|
60 |
0,32 |
0,25 |
0,21 |
0,18 |
0,16 |
0,15 |
||||||
|
90 |
0,41 |
0,34 |
0,30 |
0,24 |
0,22 |
0,20 |
||||||
|
120 |
0,50 |
0,40 |
0,34 |
0,27 |
0,24 |
0,22 |
||||||
|
180 |
0,60 |
0,48 |
0,40 |
0,32 |
0,28 |
0,26 |
||||||
|
Круглый диффузор при |
|
a° |
5 |
10 |
15 |
20 |
25 |
30 |
||||
|
wб /wм = 2 ÷ 9; |
j |
0,05 |
0,13 |
0,27 |
0,40 |
0,60 |
0,72 |
|||||
|
j = Dр/Dрр, |
a° |
35 |
40 |
|||||||||
|
Dрр - сопротивление при внезапном расширении |
j |
0,9 |
1,0 |
|||||||||
Коэффициент местного гидравлического сопротивления при течении турбулентного потока через дистанционирующие решетки и решетки-интенсификаторы теплосъема с неравномерным распределением расхода по ячейкам рассчитывается по формуле:
где ξ1 рассчитывается по формуле (74);
dгi - гидравлический диаметр i-й ячейки, м;
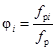 - доля проходного сечения i-ой
ячейки в общем проходном сечении дистанционирующей решетки;
- доля проходного сечения i-ой
ячейки в общем проходном сечении дистанционирующей решетки;
![]()
![]() - средняя скорость потока в канале, м/с;
- средняя скорость потока в канале, м/с;
dго - гидравлический диаметр канала, м.
Пределы применимости формулы (80): Re = 105 ÷ 106.
Погрешность δ расчета ξм составляет ± 10 %.
Гидравлическое сопротивление при турбулентном течении потока в поворотах рассчитывается по формуле:
где DP - Па;
ξм = 0,73kN;
ξтр - коэффициент гидравлического сопротивления трения о стенки гиба, рассчитывается по формулам раздела 15;
L - длина гиба, м;
dвн - внутренний диаметр трубы гиба, м;
k - коэффициент, зависящий от угла поворота потока в канале, определяется по рис. 9;
N - коэффициент, зависящий от относительного радиуса закругления гиба r, определяется по рис. 10.
Пределы применимости формулы (81): Re = 10 ÷ 106.
Погрешность δ расчета DP составляет ± 20 %.
Рис. 9. Зависимость коэффициента k от угла поворота
Эта кривая со среднеквадратичной погрешностью 0,5 % описывается формулой:
k = -1 - 0,393074 · 104/(δ - 0,139532 · 104) - 0,170774 · 103/(δ + 0,934155 · 102).
Эта же кривая со среднеквадратичной погрешностью 0,9 % описывается формулой:
N = 0,05684 + 0,364/(r/d + 0,4925).
Рис. 10. Зависимость коэффициента N от относительного радиуса закругления гиба
и) Взаимное влияние местных сопротивлений.
Коэффициенты местных сопротивлений относятся к течению сред с установившимся на входе распределением скоростей. В практике местные сопротивления иногда размещаются близко одно к другому и профиль скорости не успевает выравниваться, так как вихри, возникающие при проходе среды через первое сопротивление, влияют на распределение скоростей на значительном расстоянии вниз по течению. При больших числах Рейнольдса это расстояние может быть более (30 ÷ 40)d.
Суммарный коэффициент местного сопротивления нескольких близко расположенных местных сопротивлений может быть больше или меньше суммы соответствующих коэффициентов отдельных сопротивлений в зависимости от их конфигураций и длины участка между ними. Отсутствие общих закономерностей требует отдельных исследований каждой из комбинаций местных сопротивлений.
Уменьшение суммарного коэффициента сопротивления можно объяснить тем, что поток после первого сопротивления не успевает выровняться и потеря напора, которая затрачивается на это выравнивание, «экономится». В качестве примера приводим рис. 11, где показана зависимость суммарного коэффициента сопротивления двух поворотов от расстояния между ними. Величина ξ для одного поворота (l/d = 0) на 90° равна 1,2. При увеличении l/d величина ξ уменьшается, достигая минимума при l/d ~ 2, затем возрастает до значения 0,47, соответствующего удвоенному значению ξ для одного поворота под углом 45°.
На рис. 12 приведена характерная зависимость поправочного коэффициента, учитывающего влияние сопротивлений (ξ1 ξ2) друг на друга в соответствии с формулой ξполн = (ξ1 + ξ2)(1 + k). Минимальное значение k наблюдается при l/d = 0. Максимальное - при l/d ≈ 5. Это характерно для «тонких» шайб, каждая из которых имеет большой коэффициент сопротивления, а при их сложении получается одна «толстая» шайба, имеющая меньший коэффициент сопротивления.
Рис. 11. Зависимость коэффициента суммарного сопротивления двух поворотов от расстояния между ними
Рис. 12. Зависимость взаимного влияния двух последовательно расположенных сопротивлений от длины прямого участка между ними
2) Нестабилизированное турбулентное течение на входных участках каналов.
а) Нестабилизированное турбулентное течение на входном участке трубы.
Длина входного участка при турбулентном течении в круглых гладких трубах с плавным профилированным входом рассчитывается по формуле (стабилизация поля скорости 1 % в ядре потока):
где ![]() .
.
Погрешность в определении Lст при плавном входе в круглую трубу составляет ± 7 калибров трубы.
Схема развитого пограничного слоя при течении жидкости на начальном участке круглых труб с плавным входом приведена на рис. 13.
Рис. 13. Схема развитого пограничного слоя при течении жидкости на начальном участке круглых труб с плавным входом
Длина входного участка при турбулентном течении в круглых гладких трубах с турбулизирующими входными устройствами (например, внезапное сужение, конфузор, диффузор, диафрагмирующие шайбы) рассчитывается по формуле:
Из сравнения формул (82) и (83) следует, что гидродинамические возмущения турбулентного потока на входе в круглые трубы значительно уменьшают длину входного участка.
Пределы применимости формул (82) и (83): Re = 5 · 103 ÷ 106.
Погрешность δ в определении Lст составляет ± 3 калибра трубы.
При турбулентном течении жидкости энергия на перестройку гидродинамических характеристик потока затрачивается, в основном, на первой половине входного участка круглой трубы.
Падение давления на длине DL = 0,5Lст при турбулентном течении в трубах с плавным профилированным входом рассчитывается по формуле:
где wст - скорость на оси трубы при стабилизированном турбулентном течении.
Величина ![]() зависит от числа Рейнольдса и
вычисляется по формулам (44 и 45).
зависит от числа Рейнольдса и
вычисляется по формулам (44 и 45).
Пределы применимости формулы (84): Re = 104 ÷ 105.
Погрешность δ расчета DPвх составляет ± 20 %.
б) Нестабилизированное турбулентное течение на входном участке стержневых сборок.
Длина входного участка зависит от конструктивного оформления входа в стержневую сборку. Максимальная относительная длина входного участка принимается (стабилизация определяется по величине касательного напряжения на стенке с точностью 5 %):
при плавном профилированном входе в сборку:
при остроугольном входе (входе из большого объема):
при наличии трубной решетки на входе в стержневую сборку:
Пределы применимости формул (85), (86), (87): S/dн = 1; Re = l,5 · 104 ÷ 7,5 · 104.
Погрешность δ определения Lст составляет ± 5dг.
3) Турбулентное течение в каналах с шероховатыми стенками.
а) Турбулентное течение в трубах с регулярной шероховатостью стенки.
Падение давления при турбулентном течении в трубе с регулярно расположенными на стенке элементами шероховатости (выступы прямоугольного сечения, рис. 14) рассчитывается по формуле:
![]() (88)
(88)
где dэ - эффективный внутренний диаметр трубы с регулярной шероховатостью стенки, который рассчитывается с учетом объема вихревых зон потока при обтекании элементов шероховатости;
![]() - средняя эффективная скорость потока;
- средняя эффективная скорость потока;
ξэ - эффективный коэффициент сопротивления.
Эффективный внутренний диаметр рассчитывается:
при ![]() :
:
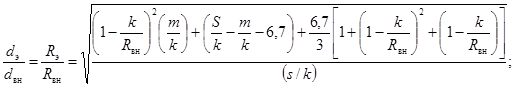 (89)
(89)
при ![]() :
:
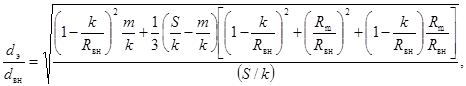 (90)
(90)
где 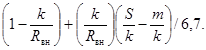
Средняя эффективная скорость потока в трубе с регулярной шероховатостью стенки рассчитывается по формуле:
![]() (91)
(91)
где M - массовый расход жидкости, кг/с;
ρ - средняя на длине DL плотность, кг/м3.
Эффективное число Рейнольдса при турбулентном течении в трубе с регулярной шероховатостью стенки рассчитывается по формуле:
![]() (92)
(92)
Рис. 14. Линейные размеры трубы и элемента регулярной шероховатости.
Характеристики турбулентного потока. D = dвн - внутренний диаметр трубы без выступов, м; т - продольный размер выступа, м; k - высота выступа, м; S - шаг расположения элементов регулярной шероховатости, м; dэ - эффективный диаметр трубы с регулярной шероховатостью стенки, м; Dпр = dпр - приведенный диаметр трубы с регулярной шероховатостью стенки, м
Эффективный коэффициент гидравлического сопротивления трения при турбулентном течении в трубе с регулярной шероховатостью стенки рассчитывается по формуле:
где ξв - вихревой коэффициент гидравлического сопротивления трения;
DLв - длина трубы, занятая вихревыми зонами; DLв = 1,7k - до элемента шероховатости, DLв = 5k после элемента шероховатости;
![]()
ξо - коэффициент гидравлического сопротивления трения при турбулентном течении в гладкой трубе внутренним диаметром dэ, рассчитывается по формуле (38).
Вихревой коэффициент гидравлического сопротивления трения рассчитывается по формуле:
где 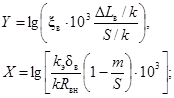
A = l,19, когда 0,3 < X < 1,8;
A = -0,52X + 1,34, когда -2,7 < X < 0,3;
kэ - эффективная высота шероховатости; kэ = k - (Rвн - Rэ);
![]() - средний масштаб вихрей при
турбулентном течении в трубе с регулярной шероховатостью стенки:
- средний масштаб вихрей при
турбулентном течении в трубе с регулярной шероховатостью стенки:
![]()
Rnp - приведенный радиус трубы с регулярной шероховатостью стенки:
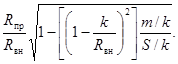
Пределы применимости формулы (94):
Reэ > 104;
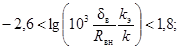 0,016
< k/Rвн <
0,22.
0,016
< k/Rвн <
0,22.
Погрешность δ расчета DP составляет ± 25 %.
При расчете профиля скорости труба внутренним диаметром dвн с регулярной шероховатостью стенки условно заменяется на трубу с гладкими стенками с внутренним диаметром dэ.
Профиль скорости в шероховатых каналах.
Профиль скорости при турбулентном течении в трубе с внутренним диаметром dэ рассчитывается по формуле:
U+ = 2,5lnηэ + C, (95)
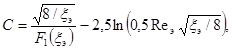 (96)
(96)
где соотношение между средней эффективной и максимальной скоростями турбулентного потока в трубе с регулярной шероховатостью стенки рассчитывается по формуле:
F1(ξэ) = 0,8925 - 0,2325lg(100ξэ), (97)
ξэ рассчитывается по формуле (93);
w = u+ v*;
уэ = ηэ v/υ* - для безразмерных расстояний по нормали от стенки трубы диаметром dэ, которые измеряются в пределах:
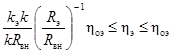 (98)
(98)
или 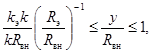 (99)
(99)
где ηэ - безразмерное расстояние от стенки трубы диаметром dэ, которое рассчитывается по формуле:
![]()
где ![]() - скорость трения на
стенке трубы диаметром dэ,
- скорость трения на
стенке трубы диаметром dэ,
tо - касательное напряжение трения на стенке трубы диаметром dэ, которое рассчитывается по формуле:
![]()
yэ - расстояние от стенки трубы диаметром dэ.
ηоэ - безразмерный эффективный радиус трубы с регулярной шероховатостью стенки рассчитывается по формуле:
Пределы применимости формулы (100):
Reэ > 104; 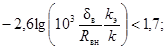
![]() ;
;
![]()
Погрешность δ расчета локальных скоростей w составляет ± 10 %.
б) Турбулентное течение в кольцевых каналах с регулярной шероховатостью стенок.
Коэффициент гидравлического сопротивления трения при турбулентном течении в кольцевых каналах с регулярной шероховатостью (прямоугольные выступы, рис. 15) на поверхности внутреннего стержня рассчитывается по формуле:
ξ = (0,053 + 1,85k/dэ)Re-0,07, (101)
где k - высота прямоугольного выступа, м;
dэ = d2 - d1 - эквивалентный диаметр зазора кольцевого канала, м (рис. 15);
d1 - внутренний диаметр зазора кольцевого канала с учетом шероховатости;
dэ - определяющий размер при расчете числа Рейнольдса.
Пределы применимости формулы: Re = 5 · 103 ÷ 105; k/dэ = 0,0028 ÷ 0,021; k/b = 0,3 ÷ 0,8 (b - ширина выступа); S/k = 10; d1/d2 = 0,40.
Погрешность δ расчета ξ составляет ± 4 %.
Рис. 15. Линейные размеры кольцевого канала и элементов регулярной шероховатости
а - прямоугольные выступы; б - закругленные трапецеидальные выступы
Коэффициенты гидравлического сопротивления трения при турбулентном течении в кольцевых каналах с регулярной шероховатостью (закругленные трапецеидальные выступы, рис. 15) на поверхности внутреннего стержня рассчитываются по формуле:
ξ = (0,063 + 5k/dэ)Re-0,11, (102)
где k - высота закругленного трапецеидального выступа;
dэ = d2 - d1 - эквивалентный диаметр кольцевого канала (рис. 15);
dэ - определяющий размер при расчете числа Рейнольдса.
Пределы применимости формулы (102):
Re = 5 · 103 ÷ 105; k/dэ = 0,0028 ÷ 0,021; k/b = 0,3 ÷ 0,8; S/k ~ 10; d1/d2 ~ 0,40.
Погрешность δ расчета ξ составляет ± 4 %.
4) Турбулентное течение в трубах с песочной и технической шероховатостями.
а) Турбулентное течение в трубе с песочной шероховатостью стенки.
Коэффициент гидравлического сопротивления трения при турбулентном течении в трубе с песочной шероховатостью стенки рассчитывается по формуле:
где ks - абсолютный размер песочной шероховатости, м;
Rпр - приведенный внутренний радиус трубы с песочной шероховатостью стенки, определяющий размер при расчете числа Рейнольдса (рис. 16):
Предел применимости формулы (104): Re > 6000.
Погрешность δ расчета ξ составляет ± 7 %.
б) Турбулентное течение в трубе с технической шероховатостью стенки.
Песочная шероховатость стенок в теплотехнических и гидротехнических устройствах реализуется редко. На практике имеют место случаи нерегулярной шероховатости стенок, которая является следствием либо технологической обработки материала, либо появляется в процессе эксплуатации из-за осаждения на стенках твердых примесей потока, коррозии, эрозии материалов. Такую шероховатость называют технической. Размеры технической шероховатости определить достаточно сложно. В связи с этим вводится величина шероховатости, эквивалентная песочной шероховатости технического канала. Эквивалентная шероховатость устанавливается в опытах из равенства гидравлических сопротивлений технического канала и канала с песочной шероховатостью.
Рис. 16. Схема песочной и технической шероховатости стенки трубы
Коэффициент гидравлического сопротивления трения при турбулентном течении в трубе с технической шероховатостью стенки (рис. 16) рассчитывается по формуле:
где ks/Rпр - техническая шероховатость, эквивалентная песочной;
Rпр - приведенный внутренний диаметр трубы с технической шероховатостью стенки, определяющий размер при расчете числа Рейнольдса.
Пределы применимости формулы (105): Re > 6000.
Погрешность δ расчета ξ из-за неопределенностей в классификации характера поверхности составляет ± 25 %.
Профиль скорости при турбулентном течении в трубе с песочной и технической шероховатостями рассчитывается по формулам (95) ÷ (97), в которых ξэ рассчитывается по формуле (103).
При расчетах принимается Rэ = Rпр, что для случаев песочной и технической шероховатостей стенок трубы не вносит заметной погрешности в результаты расчета скорости.
5) Поперечное обтекание турбулентным потоком цилиндрических тел и пучков труб.
а) Поперечное обтекание турбулентным потоком цилиндрических тел.
Полное гидравлическое сопротивление при поперечном обтекании изотермическим турбулентным потоком цилиндрических тел равно сумме равнодействующей сил трения и давления, приложенных к поверхности тел.
Безразмерный коэффициент полного гидравлического сопротивления рассчитывается по формуле:
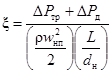 (106)
(106)
или ξ = ξтр + ξд, (107)
где DPд - потери давления, обусловленные неполным восстановлением давления,
wнп - скорость набегающего потока, м/с;
dн - наружный диаметр трубы, цилиндра, м;
L - длина трубы, цилиндра, м.
Коэффициент гидравлического сопротивления трения при поперечном обтекании потоком круглого цилиндра в диапазоне Re = 30 ÷ 104 рассчитывается по формуле:
ξ = 4Re-0,5, (108)
где ![]() .
.
Коэффициент полного гидравлического сопротивления при поперечном обтекании турбулентным потоком (Re = 104 ÷ 2 · 105) круглого цилиндра составляет:
ξ = 1,20; (109)
эллиптического цилиндра вдоль большой оси (отношение величины большой оси к величине малой < 5):
ξ = 0,7; (110)
эллиптического цилиндра вдоль малой оси (отношение величины большой оси к величине малой <5):
ξ = 1,7. (111)
При Re > 103 основной вклад в коэффициент полного гидравлического сопротивления вносит коэффициент сопротивления давления, на который влияют степень турбулентности потока Tu, загромождение канала kзгр и шероховатость обтекаемых тел.
Коэффициент сопротивления давления при обтекании потоком одиночного цилиндра:
при Ret = 40 ÷ 103 составляет:
ξд = 1,09, (112)
где Ret = Re · Tu - турбулентное число Рейнольдса;
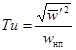 - степень турбулентности, доли единицы при расчетах;
- степень турбулентности, доли единицы при расчетах;
![]() - интенсивность пульсаций скорости, рассчитывается,
например, по формуле (47);
- интенсивность пульсаций скорости, рассчитывается,
например, по формуле (47);
при Ret = 103 ÷ 104, Tu = (0,3 ÷ 10) % определяется по формуле:
![]() (113)
(113)
при Ret = 4 · 103 ÷ 105, Tu = (0,3 ÷ 12) %, kзгр = 0,25 составляет:
![]() (114)
(114)
при Ret = 104 ÷ 2 · 105, kзгр = 0 ÷ 0,90 определяется по формуле:
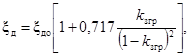 (115)
(115)
где ξдо - коэффициент сопротивления давления при поперечном обтекании цилиндра безграничным потоком, определяется по формуле при Ret = 105 ÷ 106, kзгр = 0,3 ÷ 0,7:
Значения констант формулы (116) приведены в таблице № 12.
Погрешность δ расчета составляет ± 10 %.
Шероховатость поверхности влияет на коэффициент сопротивления давления при поперечном обтекании потоком цилиндрических тел в случае, если ее высота превышает безразмерную критическую величину, которая рассчитывается по формуле kкр · и*/v и равна 15 для ламинарного пограничного слоя и 70 - для турбулентного пограничного слоя.
Таблица № 12
Значения констант формулы (116) для расчета коэффициента сопротивления давления при поперечном обтекании турбулентным потоком одиночного цилиндра
|
kзгр |
Ao |
A1 |
B1 |
C1 |
A2 |
B2 |
C2 |
|
0 |
0,10 |
1,11 |
1,80 |
3,95 |
0,25 |
0,80 |
6,00 |
|
0,30 |
0,22 |
1,58 |
2,50 |
2,06 |
0,30 |
1,10 |
4,50 |
|
0,50 |
0,88 |
1,62 |
5,80 |
1,78 |
1,50 |
1,20 |
4,30 |
|
0,70 |
2,25 |
4,80 |
6,00 |
1,58 |
1,90 |
1,22 |
4,20 |
б) Поперечное обтекание турбулентным потоком пучков труб.
Схема расположения труб и обозначение геометрических параметров для коридорных и шахматных пучков приведены на рис. 17.
Рис. 17. Схема расположения труб в шахматном и коридорном пучках труб:
S1 - поперечный шаг пучка; S2 - продольный шаг пучка.
Гидравлическое сопротивление многорядных (для рядов, начиная с номера 4 и далее) коридорных и шахматных пучков гладких, наклонных и шероховатых труб при поперечном обтекании их турбулентным потоком рассчитывается по формуле:
где ξ1 = (ξ/χ) - коэффициент гидравлического сопротивления одного глубинного ряда коридорных и шахматных пучков труб при поперечном обтекании;
(ξ/χ) для коридорных пучков труб определяется по рис. 18 в зависимости от продольного относительного шага b и числа Рейнольдса, b = s2/dн;
(ξ/χ) для шахматных пучков труб определяется по рис. 18 в зависимости от поперечного относительного шага a и числа Рейнольдса, a = s1/dн;
χ для коридорных и шахматных пучков труб определяется по вспомогательным графикам на рис. 18;
![]() - средняя скорость в минимальном проходном сечении
пучка, используется для расчета числа Рейнольдса;
- средняя скорость в минимальном проходном сечении
пучка, используется для расчета числа Рейнольдса;
z - количество рядов в пучке труб;
cz - коэффициент, учитывающий зависимость гидравлического сопротивления от числа рядов пучка; значения сz, для малорядных коридорных и шахматных пучков труб определяются по рис. 19; принимается, что cz = l при z ³ 3;
cb - коэффициент, учитывающий уменьшение гидравлического сопротивления пучка вследствие уменьшения угла атаки; значения cb определяются по рис. 20;
сk - коэффициент, учитывающий увеличение гидравлического сопротивления из-за шероховатости труб пучка; значения ск для шахматных пучков труб определяются по рис. 21.
При расчете гидравлического сопротивления
за определяющую температуру потока принимается средняя на глубине пучка
температура, за определяющую скорость - средняя скорость в наименьшем проходном
сечении пучка, за определяющий размер - наружный диаметр трубы пучка, т.е. ![]()
Пределы применимости формулы (117) определяются по рис. 18, 19.
Погрешность δ расчета DP составляет ± 20 %.
Рис. 18. Номограммы для определения коэффициентов гидравлического сопротивления коридорных и шахматных пучков труб при поперечном обтекании их турбулентным потоком:
а) - коридорные пучки труб; б) - шахматные пучки труб
Рис. 19. Поправочные коэффициенты для расчета гидравлического сопротивления малорядных коридорных и шахматных пучков труб при поперечном обтекании их турбулентным потоком:
а) коридорные пучки труб; б) шахматные пучки труб
Рис. 20. Поправочный коэффициент cb для расчета гидравлического сопротивления шахматных и коридорных пучков труб при «косом» обтекании их турбулентным потоком:
1 - шахматные пучки труб; 2 - коридорные пучки труб
Рис. 21. Поправочный коэффициент ck для расчета гидравлического сопротивления шахматных пучков труб при поперечном обтекании их турбулентным потоком:
k/dн - относительная высота элементов шероховатости
Коэффициент гидравлического сопротивления одного ряда при поперечном обтекании турбулентным потоком шахматных пучков шероховатых труб рассчитывается:
при Re = 102 ÷ 2 · 105, a = S1/dн = 1,25 ÷ 2,00; b = S2/dн ³ 0,395; k/dн = 6 · 10-3 ÷ 40 · 10-3 по формуле:
ξ1ш = 14,4(a - 1)-0,40 · Re-0,30 · (k/dн)0,15, (118)
где ![]()
при Re = 2 · 105 ÷ 107, a = 1,25 ÷ 2,00; b = 1,25 ÷ 2,00; k/dн = 10-3 ÷ 8 · 10-3 по формуле:
ξ1ш = 0,450(a - 1)-0,45 · (k/dн)0,07, (119)
где k - высота элементов шероховатости, м;
dн - наружный диаметр трубы пучка, несущей шероховатость, м.
При расчете ξ1ш за определяющую температуру принимается средняя
температура жидкости, за определяющую скорость - средняя скорость в наименьшем
проходном сечении пучка, за определяющий размер - наружный диаметр трубы пучка,
т.е. ![]() .
.
Погрешность δ расчета ξ1ш составляет ± 10 %.
Коэффициент гидравлического сопротивления одного глубинного ряда шахматных пучков оребренных труб (спиральное оребрение) при поперечном обтекании их турбулентным потоком рассчитывается:
при Re = 102 ÷ 103; e = 1,5 ÷ 6,0; a = 1,13 ÷ 2,00; b = 1,06 ÷ 2,00 по формуле:
ξ1op = 135,2e0,50 ·Re-0,70 · a-0,55 · b0,50, (120)
где e - коэффициент оребрения (отношение полной внешней поверхности оребренной трубы к наружной поверхности трубы без оребрения);
при Re = 103 ÷ 105; e = 1,9 ÷ 6,0; a = 1,60 ÷ 4,13; b = 1,20 ÷ 2,35 по формуле:
ξ1op = 6,4e0,50 ·Re-0,25 · a-0,55 · b0,50; (121)
при Re = 105 ÷ 1,4 · 106; e = 1,9 ÷ 16,0; a = 1,60 ÷ 4,13; b = 1,20 ÷ 2,35 по формуле:
ξ1op = 0,36e0,50 ·a-0,55 · b0,50 (122)
Погрешность δ расчета ξ1op составляет ± 10 %.
Коэффициент гидравлического сопротивления одного глубинного ряда коридорных пучков оребренных труб (спиральное и круглое оребрение) при поперечном обтекании их турбулентным потоком рассчитывается по формуле:
ξ1op = 0,136e0,50η-0,40, (123)
где η = (a - 1) · (b - 1).
Пределы применимости формулы (123): Re = 103 ÷ 105; e = 1,9 ÷ 16,3; a = 2,38 ÷ 3,13; b = 1,20 ÷ 2,35.
Погрешность δ расчета ξ1op составляет ± 10 %.
6) Турбулентное течение в каналах с интенсификаторами теплосъема
а) Турбулентное течение в трубах с интенсификаторами теплосъема
Коэффициент гидравлического сопротивления при турбулентном течении однофазной среды в одиночных трубах с поперечными кольцевыми гофрами (рис. 22) рассчитывается:
при dвн/Dвн = 0,90 ÷ 0,97; t/Dвн = 0,5 ÷ 10 по формуле:
при dвн/Dвн = 0,88 ÷ 0,98; t/Dвн = 0,50 по формуле:
при dвн/Dвн = 0,90 ÷ 0,98; t/Dвн = 0,25 по формуле:
где ![]() - при расчетах по формуле (124), n
= 1/3 при нагревании жидкостей; ξгл = 0,185Re-0,20 - коэффициент
гидравлического сопротивления в гладкой трубе при расчетах по формулам (125) и
(126).
- при расчетах по формуле (124), n
= 1/3 при нагревании жидкостей; ξгл = 0,185Re-0,20 - коэффициент
гидравлического сопротивления в гладкой трубе при расчетах по формулам (125) и
(126).
Пределы применимости формул (124) ÷ (126): ![]() ; υ рассчитывается по среднемассовой температуре потока; w - скорость потока в гладкой трубе, м/с.
; υ рассчитывается по среднемассовой температуре потока; w - скорость потока в гладкой трубе, м/с.
Погрешность δ расчета ξ составляет ± 12 %.
Рис. 22. Труба с поперечными кольцевыми гофрами-интенсификаторами теплосъема:
Dвн - внутренний диаметр гладкой трубы; dвн - внутренний диаметр трубы с кольцевыми гофрами; dн - наружный диаметр трубы с кольцевыми гофрами; h - высота кольцевой гофры; t - шаг расположения кольцевых гофр
Коэффициент гидравлического сопротивления трения при стабилизированном течении газов внутри одиночной витой трубы (рис. 1, п. 15) рассчитывается по формуле:
где dг - гидравлический диаметр витой трубы, м;
D - диаметр кривизны канала, м.
Пределы применимости формулы (127):
![]() S/dов = 6,2 ÷ 12,2;
S/dов = 6,2 ÷ 12,2;
![]()
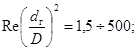 dов/D = 1,7
dов/D = 1,7
Погрешность δ расчета ξ составляет ± 15 %.
Коэффициент гидравлического сопротивления трения при турбулентном течении внутри одиночной спирально-навитой трубы (рис. 1, п. 15) рассчитывается по формуле:
где dсн = dцп - dвн, м;
dцп - диаметр цилиндрической поверхности, описанной около спирально навитой трубы, м;
dвн - внутренний диаметр исходной трубы, м.
Пределы применимости формулы (128):
Reкр < Re £ 8 · 104; S/dсн = 12 ÷ 40; dсн/dвн = 0,2 ÷ 0,7;
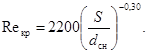
Погрешность δ расчета ξ составляет ± 15 %.
Коэффициент гидравлического сопротивления трения при турбулентном течении внутри одиночной локально-спирально-навитой трубы (рис. 1) рассчитывается по формуле:
![]() (129)
(129)
где ξо рассчитывается по формуле (127).
Пределы применимости формулы те же, что и формулы (128), L/S = 2 ÷ 5.
Погрешность δ расчета ξ составляет ± 15 %.
Коэффициент гидравлического сопротивления трения при турбулентном течении внутри трубы с трехзаходным внутренним спиральным оребрением рассчитывается по формуле:
где ξо - коэффициент гидравлического сопротивления трения исходной гладкой трубы;
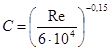 ,
,
![]() ,
,
![]() - скорость потока в исходной гладкой трубе,
- скорость потока в исходной гладкой трубе,
dвн - внутренний диаметр исходной трубы;
h - высота оребрения, м;
S - шаг оребрения, м.
Пределы применимости формулы (130):
![]() ;
; ![]() ;
;
![]()
Погрешность δ расчета ξ составляет ± 15 %.
б) Турбулентное течение в кольцевых каналах с интенсификаторами теплосъема.
Коэффициент гидравлического сопротивления трения при турбулентном течении в кольцевых каналах с внутренней спирально-навитой трубой (рис. 24) рассчитывается:
при S/dцп = 3 ÷ 5 по формуле:
при S/dцп > 5 по формуле:
где ![]() , dн - наружный диаметр исходной гладкой трубы, м.
, dн - наружный диаметр исходной гладкой трубы, м.
Пределы применимости формул (131), (132):
Re = Reкр ÷ 5·104; Reкр = 2000(S/dсн)-0,30; dсн = dцп - dн; θ = 0,5 ÷ 0,95.
Погрешность δ расчета ξ составляет ± 15 %.
Коэффициент гидравлического сопротивления трения при турбулентном течении в кольцевых каналах с внутренней локально спирально-навитой трубой (рис. 24) рассчитывается по формуле:
![]() (133)
(133)
где ξ0 рассчитывается по формулам (131), (132).
Пределы применимости формулы: S/dцп = l,2 ÷ l,6; L/S = 2 ÷ 5.
Погрешность δ расчета ξ составляет ± 15 %.
Рис. 24. Кольцевой канал с внутренней спирально-навитой трубой:
а) кольцевой канал с внутренней спирально-навитой трубой; б) кольцевой канал с внутренней локально спирально-навитой трубой
в) Турбулентное течение в пучках труб с интенсификаторами теплосъема.
Коэффициент гидравлического сопротивления при турбулентном продольном течении среды в межтрубном пространстве шахматных пучков труб с поперечными кольцевыми гофрами (рис. 22) рассчитывается:
при Re < 3,1 · 103 по формуле:
при Re = 3,1 · 103 ÷ 2 · 104 по формуле:
при Re = 2 · 104 ÷ 105 по формуле:
где
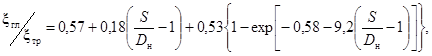
![]() - коэффициент гидравлического сопротивления
трения в гладкой трубе исходного
диаметра.
- коэффициент гидравлического сопротивления
трения в гладкой трубе исходного
диаметра.
Пределы применимости формул (134), (135), (136): S/Dн = 1,02 ÷ 10.
Погрешность δ расчета ξ составляет ± 15 %.
Коэффициент гидравлического сопротивления при продольном стабилизированном течении однофазной среды в межтрубном пространстве теплообменников из витых труб (рис. 23) рассчитывается:
при Frм > 100 по формуле:
при Frм < 100 по формуле:
где Frм -
модифицированное число Фруда, характеризующее соотношение между инерционными и
центробежными силами; ![]() для пучка витых труб;
для пучка витых труб;
Re рассчитывается по среднемассовой скорости потока в рассматриваемом сечении; S - шаг закрутки витых труб, м.
Пределы применимости формул (137), (138): Re = 3 · 103 ÷ 5 · 104; S/dов = 6 ÷ 12; tст/tж = 11,42; dов/D = 1,7.
Погрешность δ расчета ξ составляет ± 15 %.
Рис. 23. Схема пучка из витых труб:
S - шаг закрутки витой трубы: dов - максимальный размер овала; D - толщина витой трубы; dн - наружный диаметр исходной гладкой трубы
г) Поперечное обтекание турбулентным потоком пучков труб с интенсификаторами теплосъема.
Гидравлическое сопротивление пучков поперечно-омываемых витых труб (рис. 24):
при Re = 103 ÷ 4,7·103; S/dов = 12,2 рассчитывается по формуле:
при Rе = 4,7·103 ÷ 3·104; S/dов = 12,2 рассчитывается по формуле:
при Rе = 103 ÷ 3,7·103; S/dов = 6,1 составляет:
при Rе = 3,7·103 ÷ 3·104; S/dов = 6,1 рассчитывается по формуле:
ξ = 5,78Re-0,13, (142)
где Z - число рядов в пучке витых труб;
![]()
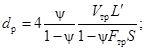
ψ - пористость пучка витых труб по теплоносителю (отношение объема пространства между трубами к полному объему);
Vтр - объем витой трубы, м3;
F - поверхность витой трубы, м2;
L' - половина периметра витой трубы;
S - шаг закрутки витой трубы;
![]() - определяющая скорость, м/с;
- определяющая скорость, м/с;
w0 - скорость набегающего потока, м/с.
Пределы применимости соотношений (139), (140), (141): tст/tж = 1,1 ÷ 1,5.
Погрешность δ расчета DP составляет ± 25 %.
Коэффициент гидравлического сопротивления при поперечном обтекании шахматных пучков плоско-овальных спирально-оребренных труб (рис. 25) рассчитывается по формуле:
ξ = 20,8Re-0,42(δ/ δ2)-0,65 · Z, (143)
где ![]() ,
,
![]() ;
;
w - скорость в сжатом сечении пучка, м/с;
Z - число рядов в пучке;
f - площадь сжатого сечения (задается), м2;
L - глубина пучка (задается), м;
Fп - площадь теплоотдающей поверхности пучка, м2;
![]() S1 - поперечный
шаг пучка, м;
S1 - поперечный
шаг пучка, м;
![]() S2 - продольный шаг
пучка, м, d1, d2 - параметры
плоско-овальной трубы (рис. 25).
S2 - продольный шаг
пучка, м, d1, d2 - параметры
плоско-овальной трубы (рис. 25).
Пределы применимости формулы (143): Re = 4·102 ÷ 4·103; δ1/δ2 = 1,5 ÷ 2,5; Sp = 2,0 мм; hр = 2,9 мм; d1·d2 = 5,5´13,5 мм.
Погрешность δ расчета ξ составляет ± 10 %.
Рис. 25. Геометрические характеристики плоско-овальных спирально-оребренных труб
7) Нестационарные течения.
Движение жидкости или газа с переменными во времени скоростями и давлениями называется нестационарным или неустановившимся. Нестационарные гидравлические процессы делятся на периодические и переходные. Периодические процессы называются затухающими, если с течением времени наблюдаемые величины приближаются к стационарным значениям. Если устанавливаются незатухающие колебания, амплитуда и частота которых не зависит от величины начального возмущения, то такой процесс называется автоколебательным. Особенности перечисленных выше процессов обусловлены в первую очередь влиянием нестационарности течения на турбулентный перенос.
Неустановившееся ламинарное движение жидкости вызывается возмущениями, сопровождается изменением профиля скорости, что может влиять на возникновение турбулентности. Переход ламинарного течения в турбулентное может происходить при числах Re, отличающихся от Reкр, для установившегося течения. Возможны переходные режимы с временным появлением турбулентности на отдельных участках потока.
На практике в большинстве случаев наибольший интерес представляют турбулентные нестационарные процессы. В ядерной энергетике рассмотрение аварийных и переходных процессов играет большую роль в вопросах безопасности.
Влияние сжимаемости среды в нестационарных гидравлических процессах неоднозначно. В одних случаях сжимаемость существенно влияет на процесс, в других влияние незначительно. Сжимаемость жидкостей возрастает при наличии в них нерастворенного газа. В этом случае, а также для газов, вследствие их большой сжимаемости, этот эффект рекомендуется учитывать.
При истечении газов через дроссельные устройства возникают режимы, при которых изменение давления после дроссельного устройства не приводит к изменению массового расхода газа (критическое истечение).
Основная сложность математических моделей нестационарного движения среды связана с их многомерностью и нелинейностью. Усреднение переменных величин по сечению потока должно выполняться с учетом нестационарности их распределения. Подходы, в которых неустановившееся движение жидкости изучается в предположении квазистационарной структуры потока, с современной точки зрения некорректны.
В нестационарных турбулентных потоках происходит деформация поля скоростей (рис. 26.). При ускорении потока (¶w/(¶t > 0) профиль скорости становится более вытянутым, а при замедлении потока (¶w/(¶t < 0) - более плоским по сравнению с квазистационарным. Изменяется также турбулентная вязкость и распределение касательных напряжений по сечению канала. В сложных нестационарных течениях, при переходе от ускоренного течения к замедленному и обратно, деформация профиля скорости происходит более сложным образом.
Уравнение Бернулли для нестационарного течения несжимаемой жидкости в канале имеет вид:
где
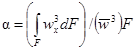 - коэффициент коррекции кинетической энергии,
учитывающий неравномерность распределения скорости по сечению. При ламинарном
течении a = 2, при турбулентном a = 1,22 ÷ 1,02;
- коэффициент коррекции кинетической энергии,
учитывающий неравномерность распределения скорости по сечению. При ламинарном
течении a = 2, при турбулентном a = 1,22 ÷ 1,02;
![]() - потери на трение при нестационарном
течении;
- потери на трение при нестационарном
течении; ![]() - коэффициент
гидравлического сопротивления трения при таком течении;
- коэффициент
гидравлического сопротивления трения при таком течении;
![]() - потери напора за счет инерции потока;
- потери напора за счет инерции потока;
![]() - часть
инерционного напора, затрачиваемого на разгон жидкости или торможение;
- часть
инерционного напора, затрачиваемого на разгон жидкости или торможение;
![]() - часть
инерционного напора, затрачиваемого на перестройку профиля скорости;
- часть
инерционного напора, затрачиваемого на перестройку профиля скорости;
l - длина канала;
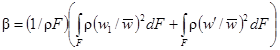 -
коэффициент коррекции количества движения;
-
коэффициент коррекции количества движения;
w1 - усредненная скорость по элементарному (dF) кольцу круглого канала;
w' - пульсации скорости в элементе dF;
![]() - средняя скорость в канале;
- средняя скорость в канале;
![]() - потери напора за счет i-го
местного сопротивления;
- потери напора за счет i-го
местного сопротивления;
![]() -коэффициент местного сопротивления трения при
нестационарном течении.
-коэффициент местного сопротивления трения при
нестационарном течении.
Поскольку ![]() , то вторым членом в выражении для b можно пренебречь, поэтому
, то вторым членом в выражении для b можно пренебречь, поэтому 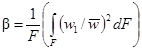 .
.
Рис. 26. Профиль скорости w (y), турбулентная вязкость (νт) и касательное напряжение (t) в пристенном слое: --- стационарный режим; --- нестационарный;
а) ускорение потока; б) замедление потока
а) Гидравлические сопротивления.
Для несжимаемой жидкости в канале постоянного сечения из (144) при z1 = z2 и в предположении, что давление во всех точках сечения канала имеет одинаковое значение, получаем:
Другие уравнения можно получить из рассмотрения объема несжимаемой среды V, записывая баланс изменения количества движения и сил (без учета массовых сил) в проекции на ось OX:
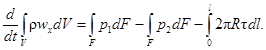 (146)
(146)
Полагая давление одинаковым в пределах одного сечения и вычисляя интегралы, находим:
Уравнения (145) и (147) различаются тем, что первое получено на основании теоремы об изменении кинетической энергии объема жидкости, второе - на основании теоремы об изменении количества движения того же объема; t - среднее касательное напряжение на стенке. Коэффициент гидравлического сопротивления для нестационарных условий имеет вид:
Разделив (147) на ![]() , получаем коэффициент нестационарного поверхностного трения:
, получаем коэффициент нестационарного поверхностного трения:
Для установившегося течения (![]() ; db/dt = 0) соотношения (148) и (149)
дают известное в гидравлике равенство стационарных значений коэффициента
гидравлического сопротивления ξ0 и коэффициента поверхностного
трения Сf0
Касательное напряжение на стенке трубы в стационарных условиях рассчитывается:
; db/dt = 0) соотношения (148) и (149)
дают известное в гидравлике равенство стационарных значений коэффициента
гидравлического сопротивления ξ0 и коэффициента поверхностного
трения Сf0
Касательное напряжение на стенке трубы в стационарных условиях рассчитывается:
![]() (150)
(150)
Для нестационарного течения это соотношение несправедливо.
![]() (151)
(151)
Таким образом, для стационарного течения Cf = ξ, (или C0 = ξ0).
Экспериментальное определение Cf проще,
чем ξ, поскольку для нахождения ξ, кроме (р1 - p2), ![]() , надо еще
знать b и db/dt. Последние две величины не могут быть определены без
измерения мгновенных скоростей в нестационарном потоке. В связи со сложностью
таких измерений обычно измеряют Cf, а не ξ,
но при обсуждении результатов не всегда на это обращается внимание. Связь между
этими двумя величинами вычисляется по формуле:
, надо еще
знать b и db/dt. Последние две величины не могут быть определены без
измерения мгновенных скоростей в нестационарном потоке. В связи со сложностью
таких измерений обычно измеряют Cf, а не ξ,
но при обсуждении результатов не всегда на это обращается внимание. Связь между
этими двумя величинами вычисляется по формуле:
Cf = ξ + De, (152)
где De ~ 0,01 - 0,03. Общей характеристикой нестационарности течения принято считать параметры:
![]() (153)
(153)
![]() (154)
(154)
где ξ0 = C0 - квазистационарный коэффициент гидравлического сопротивления, который равен коэффициенту сопротивления поверхностного трения.
Экспериментальные данные для условий постоянного ускорения (замедления) описываются формулой:
где а = 0,098 для ускоренного течения (K > 0); а = 0,75 для замедленного течения (K < 0).
Выражение (155) относится только к
случаю постоянных ускорений ![]() . Если
же -
. Если
же - ![]() , то, как
показывают эксперименты, необходимо учитывать влияние второй производной
скорости на процесс с помощью безразмерного параметра:
, то, как
показывают эксперименты, необходимо учитывать влияние второй производной
скорости на процесс с помощью безразмерного параметра:
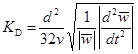 (156)
(156)
или 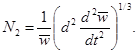 (157)
(157)
Особенно важен учет этих критериев при больших значениях N1, то есть при весьма быстро протекающих нестационарных процессах. Аппроксимирующая зависимость коэффициента трения от параметров K и KD получена в виде:
где C0 определяется по (155), см. также рис. 27. Здесь K и KD рассчитаны по несколько видоизмененным формулам:
где ξ0 - квазистационарный эффективный коэффициент гидравлического сопротивления, учитывающий сопротивление трубы и местные сопротивления на входе и выходе;
Q - объемный расход;
F0 - сечение трубы.
Расчет переходных процессов с использованием формулы (159) проводится по уравнению движения несжимаемой жидкости:
![]() (160)
(160)
где w = Q/F - средняя по сечению трубы мгновенная скорость;
(p1 - p2) - разность давлений перед входом в трубу и после выхода из нее;
Cf определяется по формуле (158) или по графику (рис. 27.).
Рис. 27. Относительный коэффициент сопротивления в зависимости от параметров KD и K
Ниже приводится ряд других
формул для коэффициента гидравлического сопротивления
в канале (![]() ). Выражение для отношения
нестационарного коэффициента гидравлического сопротивления в канале ξ к
квазистационарному ξ0 в предположении, что профиль скорости в
ядре потока подчиняется степенному закону, выглядит так:
). Выражение для отношения
нестационарного коэффициента гидравлического сопротивления в канале ξ к
квазистационарному ξ0 в предположении, что профиль скорости в
ядре потока подчиняется степенному закону, выглядит так:
![]()
где п = f(Re);
п = 7 при Re < 105;
п = 10 при Re = 3,2 · 106.
Окончательное выражение имеет вид:
![]() (161)
(161)
где K измеряется в см.
|
n |
7 |
8 |
9 |
10 |
|
A |
0,449 |
0,391 |
0,346 |
0,310 |
Данные Дэйли, полученные при течении воды в вертикальной трубе (l/d = 21; Re < 5 · 105) и при -0,3 < (2K) < 0,3, обобщаются формулой:
![]() (162)
(162)
где C = 0,01 для ускорения; C = 0,62 при замедлении потока.
По данным Лийва ξ определяется для ускоренного и замедленного потока воды в трубе:
d = 0,075 м; l/d
= 53; Remax = 1,65 · 106;
![]() изменялось
от -1,25 до 0,8.
изменялось
от -1,25 до 0,8.
Результаты обобщены формулой:
![]() (163)
(163)
Для течения с ускорением можно воспользоваться также соотношением Денисова:
![]() (164)
(164)
где ![]()
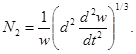
Формула проверена для диапазонов: N1 = 0,04 ÷ 0,43; N2 = 0,12 ÷ 0,86.
Турбулентный поток можно считать квазистационарным при N1 Re < 0,16.
Эффектами нестационарности
можно пренебречь лишь при ![]() , где
, где 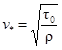 - динамическая скорость.
- динамическая скорость.
б) Пульсирующие (автоколебательные) течения.
Рассматриваются течения, в
которых средняя по сечению скорость изменяется во времени по закону ![]() , соответственно
, соответственно
Re = Rem [1 + A sin(ωt)].
Существуют три характерных режима взаимодействия турбулентности с осредненным потоком: режим квазистационарной турбулентности, режим «замороженной» турбулентности и промежуточный режим. В первом - период колебаний (T) расхода больше характерного времени турбулентных пульсаций (t), т.е. (T > t) и колебания расхода не оказывают влияния на турбулентность. В режиме «замороженной» турбулентности (t >> Т) она не успевает измениться за период высокочастотных колебаний расхода.
Границы этих областей можно
приближенно оценить по турбулентному числу Стокса:
![]() ,
где
,
где ![]() -
число Стокса; ξ0 - коэффициент сопротивления трения при
стационарном течении для Re0. При St < 0,1 - режим квазистационарной турбулентности;
при St > 1 - режим «замороженной» турбулентности.
-
число Стокса; ξ0 - коэффициент сопротивления трения при
стационарном течении для Re0. При St < 0,1 - режим квазистационарной турбулентности;
при St > 1 - режим «замороженной» турбулентности.
В квазистационарной области в каждый момент времени коэффициент сопротивления трения можно вычислить по стационарным зависимостям - по формуле (38).
В других областях касательное напряжение на стенке (tс), а, следовательно, и коэффициент сопротивления изменяется по закону:
![]() где
где 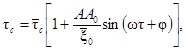 (165)
(165)
здесь ![]() -
среднее по периоду колебаний касательное напряжение на стенке, которое
приближенно вычисляется по стационарным зависимостям;
-
среднее по периоду колебаний касательное напряжение на стенке, которое
приближенно вычисляется по стационарным зависимостям;
![]() ;
;
A0 = 16S/Re0 - относительная амплитуда колебаний для области замороженной турбулентности; для этой области j = p/4.
В промежуточной области расчет значительно сложнее и здесь не приводится.
В общем случае квазистационарный метод расчета гидравлических потерь использовать неправомерно. Так как границы применимости квазистационарного метода для всех случаев в настоящее время не установлены, он может использоваться лишь тогда, когда при нестационарном течении большая доля общих потерь приходится на инерционные составляющие и когда относительное значение потерь на трение невелико.
III. Расчет тепловых характеристик
1) Общие подходы к расчету параметров конвективного теплообмена.
Основная цель теплового расчета реактора или теплообменника, или другого узла атомной энергетической установки - получить распределение температуры по всему объему узла или в наиболее опасной зоне при определенных значениях исходных данных. Причем необходимо знание максимальных значений температур и неравномерностей температуры в наиболее напряженных областях. Максимальная температура - это сумма нескольких слагаемых: температуры входа - tвх, подогрева теплоносителя от входа до данного сечения - Dtп, среднего перепада температур между стенкой и средней жидкости - Dta, среднего перепада температур на оболочке твэла - Dtо, среднего перепада температур на «среде» между оболочкой и топливным сердечником - Dtср и среднего перепада температур на топливном сердечнике - Dtтс:
tмак = tвх + Dtп + Dta + Dtо + Dtср + Dtтс.
В ряде случаев при обосновании работоспособности установки необходимо знание локальных полей и, иногда, градиентов температуры, в частности при расчете термонапряжений и в задачах термодиффузии.
Наиболее универсальный метод расчета температурного поля при течении в каналах произвольного поперечного сечения основан на решении системы дифференциальных уравнений переноса, которая включает в себя дифференциальные уравнения переноса тепла, массы и количества движения в потоке жидкости и уравнения переноса тепла в охлаждаемом (или нагреваемом) этой жидкостью твердом теле (например, твэле). Система уравнений переноса тепла (например, для двумерной задачи) представлена ниже. Необходимо также знание полей скорости, которые рассчитываются по соотношениям главы II.
Теплоотдача определяется не только формой канала и режимом течения теплоносителя, но и степенью чистоты металла. На границе стенки с жидким металлом может присутствовать слой, вызывающий дополнительное термическое сопротивление теплоотдаче (Rk). Причинами этого термического сопротивления могут быть:
окисные или интерметаллические пленки на теплоотдающей поверхности, которые могут либо исчезать, либо образовываться во время работы;
осаждение примесей из потока металла при охлаждении последнего и образование неподвижного слоя примесей (в этом случае Rk, не зависит от скорости и предсказать его величину не представляется возможным);
образование подвижного слоя примесей в случае нагрева металла.
Свойства жидких металлов слабо зависят от температуры. Кроме того, перепады температуры в потоке обычно невелики. Поэтому нет необходимости при расчетах теплоотдачи жидких металлов учитывать зависимость их свойств от температуры потока.
Высокая теплопроводность и сравнительно низкая удельная теплоемкость на единицу массы приводят к тому, что в условиях активных зон реакторов, охлаждаемых жидкими металлами, температура оболочек твэлов определяется, главным образом, подогревом жидкого металла, а не интенсивностью теплообмена. Отношение подогрева Dtп к температурному напору Dta (стенка - жидкость), например для реакторов типа БН-600, составляет Dtп/Dta = 4l · Nu/dг · Re ~ 20. Поэтому температурное поле твэла и теплоносителя очень чувствительно к «геометрии» ТВ С и всех ее элементов, а по периметру твэлов возникают неравномерности температуры, которые играют более значительную роль, чем температурные напоры «стенка - жидкость».
а) Дифференциальные уравнения теплообмена
Двумерные уравнения для прямоугольной системы координат
Уравнение для температуры потока теплоносителя в данном сечении:
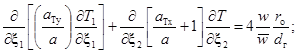 (166)
(166)
уравнение для температуры оболочки твэла (без тепловыделения):
![]() (167)
(167)
уравнение для температуры зоны с топливом:
![]() (168)
(168)
где Qv - плотность распределенных в объеме источников тепловыделения;
![]()
![]()
![]()
tо - температура теплоносителя в точке с координатами ξ1 = l и ξ2 = 0;
rо - характерный размер (наружный радиус твэла);
a - коэффициент температуропроводности, м2/с;
aту, aтх - коэффициенты турбулентного переноса тепла во взаимно-перпендикулярных направлениях.
Двумерные уравнения для цилиндрической системы координат.
Уравнение для температуры потока теплоносителя в данном сечении:
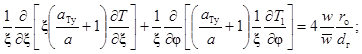 (169)
(169)
уравнение для температуры оболочки твэла (без тепловыделения):
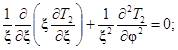 (170)
(170)
уравнение для температуры зоны с топливом:
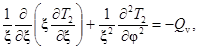 (171)
(171)
где ![]() j - рад;
j - рад; ![]() .
.
Граничные условия к системам уравнений задаются в зависимости от конкретных условий теплообмена по периметру канала. Условия сшивки на границе теплообмена между жидкостью и стенкой принимаются как:
равенство температур жидкости и стенки в любой точке периметра канала;
равенство тепловых потоков со стороны жидкости и стенки в любой точке периметра канала.
Для расчета коэффициентов турбулентного переноса тепла в каналах произвольного поперечного сечения канал разбивается на элементарные гидродинамические ячейки (рис. 28). Каждая элементарная ячейка ограничена стенкой (теплоотдающей поверхностью), линией максимальной скорости и нормалью, проведенной на стенку из самой удаленной от поверхности теплообмена точки.
б) Коэффициенты турбулентного переноса тепла.
Коэффициенты турбулентного переноса тепла в двух взаимоперпендикулярных направлениях в сечении каналов рассчитываются по формулам:
по нормали к поверхности:
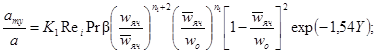 (172)
(172)
в тангенциальном (перпендикуляром в данном сечении) направлении:
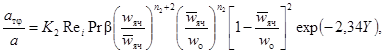 (173)
(173)
где K1 = 0,16; K2 = 0,36; n1 = 4; п2 = 1; ![]() ;
;
![]() ;
;
![]() - максимальное
расстояние по нормали от стенки до линии максимальной скорости;
- максимальное
расстояние по нормали от стенки до линии максимальной скорости;
y - расстояние по нормали от стенки до данной точки.
Числа Re, значения
![]() , wо
рассчитываются в предположении гидродинамической изолированности ячейки, wо - максимальная
скорость в ячейке.
, wо
рассчитываются в предположении гидродинамической изолированности ячейки, wо - максимальная
скорость в ячейке.
В случае неизолированных ячеек (рис. 28) учет турбулентного взаимодействия между ними осуществляется при помощи функции влияния n-ой ячейки на m-ую:
![]() (174)
(174)
где ![]() ;
; ![]() ;
;
Ln, Lm - расстояние вдоль периметра от границы ячейки (от главной нормали, ограничивающей ячейку) до i-той точки периметра;
L - суммарная длина теплоотражающего периметра во взаимодействующих ячейках (двух соседних).
Значения коэффициентов находятся из условий:
равенства aтi на границе между ячейками:
![]()
неизменности среднего по
периметру значения ![]() в двух взаимодействующих ячейках:
в двух взаимодействующих ячейках:
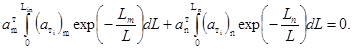 (175)
(175)
При большом числе неизолированных ячеек производится сшивка для любых двух соседних ячеек, затем для этих ячеек (которые рассматриваются как единая ячейка) со следующей ячейкой и так далее.
Рис. 28. Схемы разбиения сечения каналов на элементарные ячейки
При ламинарном течении турбулентные члены переноса обращаются в нули.
в) Параметр приближенного теплового моделирования твэлов.
Для описания теплообмена в сборках необходимо иметь значения параметра приближенного теплового моделирования. Этот параметр (e) рассчитывается по основной гармонике разложения температурного поля твэла в ряд Фурье (K = 6 и 4 для треугольной и квадратной решеток соответственно). Он особенно важен для тесных решеток твэлов ((s/d) < 1,1), когда следует ожидать большие неравномерности температуры по периметру твэлов. При очень низкой эквивалентной теплопроводности твэла (e → 0) угловые растечки тепла весьма малы или вообще отсутствуют. Неравномерности температуры по периметру твэла значительны (велики перегревы в узких местах ячейки). Коэффициенты теплоотдачи минимальны (Nu → Numin), что соответствует условию q = const по периметру твэла. При очень высокой эквивалентной теплопроводности твэла (e → ∞) неравномерности температуры по периметру твэла отсутствуют (Nu → Numax), что соответствует условию: Tw - const по периметру твэла. Параметр e для цилиндрических твэлов находят (схемы тепловыделяющих элементов изображены на рис. 29) из следующих выражений (для треугольной решетки твэлов):
для твэла без оболочки (рис. 29 а):
e = λт/λf; (176)
для твэла с одной оболочки (рис. 29 б):
e = (λо/λf) · (1 - m1R1)/(1 + m1R1), (177)
где т1 = (λт - λо)/(λт + λо);
R1 = (r1/rо)2k, R2 = (r2/rо)2k;
для твэла с двумя оболочками (слоями) (рис. 29 в):
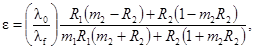 (178)
(178)
где т1 = (λт - λ0)/(λт + λ0);
m2 = (λ1 - λ0)/(λ1 + λ0);
R1 = (r1/r0)2k, R2 = (r2/r0)2k;
для твэла с тремя оболочками (слоями) (рис. 29 г):
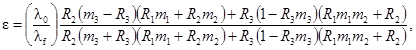 (179)
(179)
где т1 = (λт - λ0)/(λт + λ0);
m2 = (λ1 - λ0)/(λ1 + λ0);
m3 = (λ2 - λ1)/(λ2 + λ1);
R1 = (r1/rо)2k, R2 = (r2/rо)2k; R3 = (r3/r0)2k
для твэла с оболочкой и контактным термическим сопротивлением Ф (рис. 29 д):
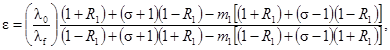 180)
180)
где т1 = (λт - λ0)/(λт + λ0);
R1 = (r1/r2)2k, s = kλ1Ф/r1;
для твэла с отверстием радиусом r* с оболочкой и контактным термическим сопротивлением Ф (рис. 29 е):
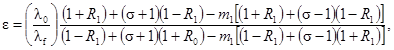 (181)
(181)
где т1 = (λ0 - λт)/(λ0 + λт);
m2 = (λ1 - λ0)/(λ1 + λ0);
R0 = (r*/r0)2k, R1 = (r1/r0)2k;
s = kλ0Ф/r1;
λ0 - коэффициент теплопроводности соответствующего слоя;
Ф - контактное термическое сопротивление на границе стенка - жидкость.
Рис. 29. Схемы тепловыделяющих элементов для вычисления параметра теплового подобия:
а - твэл без оболочки; б - твэл с оболочкой; в - твэл с двумя оболочками; г - твэл с тремя оболочками (слоями); д - твэл с оболочкой и контактным термическим сопротивлением на границе; е - кольцевой твэл с оболочкой и контактным термическим сопротивлением на границе
В вышеприведенных соотношениях параметр эквивалентной теплопроводности твэлов для треугольных сборок рассчитывается по шестой (k = 6), для квадратных сборок - по четвертой (k = 4) гармонике разложения температурного поля твэла в ряд Фурье.
Ниже приведены инженерные соотношения для чисел Нуссельта и температурных неравномерностей при течении в типичных каналах ЯЭУ.
2) Теплообмен при ламинарном течении в каналах.
Задачи теплообмена при ламинарном течении рассматриваются в предположении, что:
течение и теплообмен стационарны;
жидкость несжимаема, ее теплофизические свойства не зависят от температуры;
течение жидкости гидродинамически стабилизировано;
во входном сечении теплообменного участка температура жидкости постоянна по сечению;
на поверхности теплообмена задана постоянная плотность теплового потока;
в потоке отсутствуют внутренние источники тепла;
изменение плотности теплового потока вдоль оси за счет теплопроводности мало по сравнению с изменением плотности вдоль оси, обусловленным конвекцией.
Интенсивность конвективной теплоотдачи жидкостей и газов при ламинарном течении определяется коэффициентом теплоотдачи, который, как правило, относится к разнице температур стенки и средней температуры среды: a = q/(tст - tж). Коэффициент теплоотдачи обычно определяется через число Нуссельта: a = Nuλ/dг, где dг - гидравлический диаметр канала.
Теплофизические свойства относятся, как правило, к среднемассовой температуре потока в данном сечении. При вычислении среднего по длине коэффициента теплоотдачи свойства относят к средней температуре потока: tж = (tвх + tвых)/2.
а) Теплообмен при ламинарном течении в трубах.
Теплообмен при ламинарном течении в трубах при постоянном тепловом потоке на стенке рассчитывается по соотношению (для Re < Reкр):
Nu = 4,36. (182)
Погрешность D расчета Nu практически равна нулю.
Теплообмен в плоских щелях при постоянном тепловом потоке с двух сторон рассчитывается по соотношению (для Re < Reкр):
Nu = 8,24. (183)
Теплообмен в плоских щелях при постоянном тепловом потоке с одной стороны рассчитывается по соотношению (для Re < Reкр):
Nu = 5,36. (184)
Погрешность расчета Nu практически равна нулю.
б) Теплообмен при ламинарном течении в кольцевых каналах.
Теплообмен при ламинарном течении в кольцевых каналах при двухстороннем постоянном по длине тепловом потоке (или с одной стороны - подвод тепла, а с другой - отвод, или наоборот) с произвольным отношением плотностей тепловых потоков q1 и q2 рассчитывается по формулам:
для внутренней поверхности:
![]() (185)
(185)
для наружной поверхности:
![]() (186)
(186)
где Q = q2/q1;
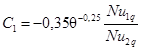 ;
;
C2 = -0,35θ0,75;
![]() ;
;
![]() - число Нуссельта для внутренней
поверхности кольцевого зазора при отсутствии теплового потока на
противоположной поверхности, рассчитывается по формуле:
- число Нуссельта для внутренней
поверхности кольцевого зазора при отсутствии теплового потока на
противоположной поверхности, рассчитывается по формуле:
Nu1q = 4,25 + l,13θ-0,083. (187)
Пределы применимости формулы (187): θ = 0,1 ÷ 1,0.
Погрешность δ расчета Nu1q составляет ± 2 %.
![]() - число Нуссельта для внешней поверхности зазора
кольцевого канала при отсутствии теплового потока на внутренней;
- число Нуссельта для внешней поверхности зазора
кольцевого канала при отсутствии теплового потока на внутренней;
Пределы применимости формулы (188): θ = 0 ÷ 1,00.
Погрешность δ расчета Nu2q составляет ± 5 %.
в) Теплообмен при ламинарном течении в сборках стержней с треугольной упаковкой.
Теплообмен в центральных зонах ТВС. Числа Нуссельта зависят от двух параметров: относительного шага расположения стержней (s/d) и от параметра моделирования e. Расчет теплоотдачи ведется при х = s/d = 1 по формуле:
Nuл = 1,25[1 - 3,6(4,2 + 2,5e0,86)-1], (189)
определяющий размер для правильной
решетки: 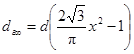 ,
,
определяющая скорость w - средняя по сечению скорость в пучке.
Пределы применимости формулы (189): Pe = 14 ÷ 4000;
e > 10-2 - параметр теплового подобия при K0 = 6; х = s/d = 1,0 ÷ 2,0.
При x = 1 ÷ 1,2
Nuл = [7,55х - 6,3x-17х(х-0,81)]{1 - 3,6x[x20(1 + 2,52e0,86) + 3,2)-1}. (190)
При х = 1,2 ÷ 2
Nuл = 7,55х - 20х-13. (191)
Зависимость числа Нуссельта при ламинарном течении Nuл от параметров показана на рис. 30.
Погрешность D расчета Nuл по формулам: (189), (190), (191) составляет ± 20 %.
Рис. 30. Числа Нуссельта при ламинарном течении в треугольных решетках твэлов
3) Теплообмен при турбулентном течении в каналах,
а) Теплообмен при турбулентном течении в трубах.
Дифференциальное уравнение для поля температуры в потоке имеет вид:
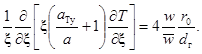
Решение уравнения при постоянном по длине тепловом потоке в широком диапазоне параметров (Re = 2300 ÷ 5·105, Рr = 0 ÷ 100) позволило получить следующее соотношение для чисел Нуссельта:
Nu = Nu0 + b·Re0,87·Prn
или Nu = (7 - 3,6/lgRe) + 0,008Re0,87·Prn, (192)
где b = 0,0096; n = 0,4 + 0,45/(2Рr + 1).
Погрешность описания экспериментальных данных для чистых условий не превышает ± 10 %.
Теплообмен при турбулентном течении (Рr = 0,004 ÷ 0,05) в круглых трубах в реальных условиях рассчитывается по эмпирической формуле:
при Ре < 104, Re = 104 ÷ 105
Nu = 5 + 0,025Pe0,80; (193)
или с учетом предельного перехода на ламинарный режим течения при q = const по формулам:
при Ре = 300 ÷ 104
Nu = 7,5 + 0,005Ре; (194)
при Ре < 300
Nu = 4,36 + 0,016Рe. (194а)
Погрешность D расчета Nu по формулам (193), (194), (194а) составляет ± 20 %.
Теплообмен при турбулентном течении жидких металлов в коротких трубах рассчитывается по формуле:
Nu = Nu0 · eL, (195)
где Nu0 рассчитывается по формулам (182) ÷
(184);
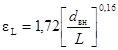 .
.
Пределы применимости формулы (195): Ре = 300 ÷ 2000; L/dвн = 2 ÷ 20.
Погрешность D расчета Nu составляет ± 20 %.
Длина входного теплового участка при турбулентном течении жидких металлов в трубах рассчитывается по формуле:
![]() (196)
(196)
Погрешность D расчета Lст составляет ± 20 %.
В реальных не контролируемых условиях по чистоте теплоносителя на границе стенки с жидким металлом может присутствовать слой, вызывающий дополнительное термическое сопротивление (Rк) теплоотдаче. Причинами возникновения термического сопротивления являются:
окисные или интерметаллические пленки на теплоотдающей поверхности, которые могут либо исчезать, либо образовываться во время работы;
осаждение примесей из потока металла при его охлаждении; в этом случае термическое сопротивление Rк не зависит от скорости и предсказать его величину не представляется возможным;
образование подвижного слоя примесей в случае нагрева металла; в этом случае величина термического сопротивления рассчитывается по формуле:
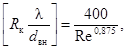 (197)
(197)
где λ - коэффициент теплопроводности термического сопротивления, Вт/(м·°C).
Минимальное число Нуссельта в условиях нагрева при наличии термического сопротивления рассчитывается по формуле:
где Nu рассчитывается по формулам (193), (194), (194 а).
Пределы применимости формулы (198) определяются пределами применимости формул (193), (194), (194 а).
Погрешность D расчета Numin составляет ± 20 %.
Приближенно теплообмен при турбулентном течении в трубах жидких металлов, загрязненных примесями, оценивается: по формуле:
Nu = 3 + 0,014Pe0,80; (199)
или при Ре = 102 ÷ 104 по формуле:
Nu = 4,36 + 0,0021Ре. (200)
Погрешность оценочного расчета Nu составляет ± 25 %.
Безразмерное распределение температуры в потоке при турбулентном течении чистых жидких металлов в круглой трубе рассчитывается по эмпирическим зависимостям:
при 0 < y++ < 1 по формуле:
T+ = y++; (201)
при 1 < у++ < 11,7 по формуле:
T+ = 1,87(lny++ + 1) + 0,065y++ - 0,36; (202)
при y++ > 11,7 по формуле:
T+ = 2,5lny++ - 1, (203)
где у++ = у+·Pr;
![]() -
безразмерное расстояние от стенки трубы;
-
безразмерное расстояние от стенки трубы;
![]()
![]() - масштаб температуры, К;
- масштаб температуры, К;
Тст - температура стенки трубы, К;
Tж - среднемассовая температура в заданном сечении трубы, К;
υ* - масштаб скорости, м/с;
![]() ;
;
ξ рассчитывается по формулам раздела II.
В формулах: q - Вт/м2;
![]() - м/с; y - координата по нормали к
стенке, м; v - м2/с; cр - удельная теплоемкость, Дж/(кг · К).
- м/с; y - координата по нормали к
стенке, м; v - м2/с; cр - удельная теплоемкость, Дж/(кг · К).
Погрешность D расчета Т+ составляет ± 15 %.
б) Теплообмен при турбулентном течении в кольцевых каналах.
Теплообмен при турбулентном течении в кольцевых каналах при теплообмене только на одной из стенок кольцевого канала рассчитывается по соотношениям, полученным с учетом экспериментальных и расчетных данных: на внутренней стенке зазора кольцевого канала по формуле:
![]() (204)
(204)
или более подробно:
![]() (205)
(205)
на наружной стенке зазора кольцевого канала по формуле:
![]() (206)
(206)
или более подробно:
![]() (207)
(207)
где θ = d1/d2 (не менее 0,1 до 1,0);
n = 0,4 + 0,45/(2Pr + 1). (208)
Для двухстороннего теплообмена целесообразно воспользоваться соотношениями, в которых используется понятие безразмерной разности температур вместо числа Нуссельта (DT = 1/Nu = λ/(ad)). Данный подход существенно удобнее тем, что позволяет не иметь дело с величинами чисел Нуссельта, равными бесконечности или отрицательными, имеющими место при некоторых соотношениях параметров. Приведенные ниже соотношения справедливы в следующих диапазонах параметров: 5000 < Re < 100000; 0 < Pr < 100; -100 < Q < +100; 0,1 < θ < 1,0, где θ = d1/d2, Q = q2/q1.
Разности температур на обогреваемых стенках при одностороннем обогреве:
![]() (209)
(209)
![]() (210)
(210)
Разности температур на противоположных адиабатных стенках при одностороннем обогреве:
![]() где
где ![]() (212)
(212)
Эти разности температур на адиабатных стенках имеют отрицательные значения (разность температуры поверхности и потока на противоположной стороне имеет обратный знак по отношению к разности на теплопередающей поверхности).
Для двустороннего теплообмена
(теплоподвода или теплоотвода) полученные соотношения разности температур ![]() и
и ![]() имеют вид:
имеют вид:
![]() (213)
(213)
![]() (214)
(214)
где ![]() - безразмерная разность
температур для первой стенки q1 (внутренней) при наличии теплового потока q2 на противоположной
стенке;
- безразмерная разность
температур для первой стенки q1 (внутренней) при наличии теплового потока q2 на противоположной
стенке;
и ![]() - безразмерная разность температур для
второй стенки (q2) при
наличии теплового потока (q1) на
первой стенке. Далее можно рассчитать температуры поверхностей при заданных
тепловых потоках с учетом знаков:
- безразмерная разность температур для
второй стенки (q2) при
наличии теплового потока (q1) на
первой стенке. Далее можно рассчитать температуры поверхностей при заданных
тепловых потоках с учетом знаков:
при подводе тепла - знак (+), ![]() ; (215)
; (215)
где λ - теплопроводность теплоносителя.
Пределы применимости формул (211) ÷ (216): θ = d1/d2 = 0,1 ÷ l,0; Ре = 300 ÷ 4000; Q = q2/q1 = от -10 ÷ 10.
Погрешность s расчета составляет не выше 15 %.
Теплообмен при турбулентном течении жидких металлов в эксцентрических кольцевых каналах является неравномерным по углу и длине. Стабилизация теплообмена при больших значениях Ре иногда совсем не наступает, что указывает на слабое перемешивание теплоносителя. Определенную роль играет толщина стенки канала и ее теплопроводность.
Максимальная неравномерность температуры при турбулентном течении жидких металлов в кольцевом канале с эксцентриситетом рассчитывается (оценочные расчеты) по формуле:
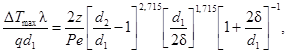 (217)
(217)
где ![]() - безразмерная координата
вдоль оси кольцевого канала;
- безразмерная координата
вдоль оси кольцевого канала;
δ - расстояние между стенками кольцевого канала по нормали к внутренней поверхности, м;
х - расстояние между центрами окружностей кольцевого канала.
![]() , К;
, К;
q - Вт/м2;
λ - теплопроводность жидкого металла, Вт/(м, K);
d1 - м; d2 - м.
Погрешность D расчета DTmax составляет ± 20 %.
Экспериментальные формулы для частных случаев кольцевых каналов.
Можно пользоваться более простыми, но менее точными соотношениями (102 £ Re £ 105, Pr ≈ 10-2; d1/d2 > 05):
односторонний стабилизированный теплообмен:
Nu = 4,9 + 0,0175Pe08; (218)
двусторонний стабилизированный теплообмен:
Nu = 10 + 0,025Pe0,8. (219)
Для нахождения коэффициента теплоотдачи на начальном участке теплообмена длиной l в кольцевом зазоре при l/(Pe·dг) < 0,0357 в случае одностороннего обогрева коэффициент теплоотдачи следует умножить на поправочный коэффициент:
el = 0,194[(Pe · dr)/l]0,49, (220)
где dг - гидравлический диаметр канала;
l - расстояние от начала обогрева.
в) Теплообмен при турбулентном течении в сборках стержней с треугольной упаковкой.
Теплообмен в стандартных ячейках сборок.
В реакторах с жидкометаллическим охлаждением применяют стержневые твэлы, располагаемые в виде правильных треугольных или квадратных решеток. Геометрия ячеек является причиной неравномерности температуры по периметру твэла, что приводит к дополнительным термическим напряжениям, локальным перегревам и, таким образом, снижает надежность твэла.
Поле температуры в твэле зависит не только от геометрических параметров, но и от теплопроводности теплоносителя, оболочки и материала сердечника. Задача о теплообмене пучков твэлов является, в итоге, сопряженной.
В шестигранных кассетах, которые типичны для реакторов с жидкометаллическим охлаждением, различают центральные, боковые и угловые твэлы (рис. 31). Из анализа дифференциальных уравнений, описывающих перенос тепла в сборках цилиндрических твэлов, получены следующие критериальные соотношения:
Nu = Nu(Re; Pr; s/d0; e), (221)
DTw = DTw(Re; Pr; s/d0; e), (222)
где DТw - разность температур в точке максимума и средней температуры теплоносителя в данном сечении;
s - шаг расположения твэлов;
d0 - диаметр твэлов;
Re - число Рейнольдса;
Pr - число Прандтля;
e - параметр приближенного теплового моделирования твэла (см. ниже).
Для расчета теплообмена центральных твэлов при турбулентном течении жидких металлов в сборках стержней с треугольной упаковкой рекомендован метод, наиболее обоснованный как теоретическими расчетами, так и экспериментальными данными. Основное соотношение для числа Нуссельта в широком диапазоне чисел Re и Pr имеет вид:
Nu = Nu0 + bRe0,87 · Prn, (223)
где Nu0 - предельное значение числа Нуссельта, имеющее место при данном числе Рейнольдса, для данной сборки (d, s, e), но при стремлении числа Прандтля к 0. Оно описывается соотношением:
![]() (224)
(224)
Для b дано соотношение:
где E = e[1+4/(1+10Pr)], n = 0,4+1/(2Pr + 1).
Пределы применимости метода расчета числа Нуссельта в треугольных сборках (223)÷(225) следующие: Re = 2300 ÷ 5·105; Pr = 0 ÷ 100; s/d - от 1 до 1,5; e - от 0,1 до 100; Nu > 1,0.
Погрешность описания экспериментальных данных не превышает ± (5 ÷ 40) %.
Для расчета величины максимальной неравномерности температур вдоль периметра теплообмена рекомендуется аппроксимирующее соотношение:
![]() (226)
(226)
где C = l + 10(s/d - l);
Nu - число Нуссельта при данном e;
Nut - число Нуссельта при e → ∞. Величина ψ для жидкометаллических теплоносителей принимается равной 1.
Эмпирические соотношения для чисел Нуссельта в сборках.
Далее приводятся экспериментально полученные соотношения для чисел Nu для разных частных случаев.
Теплообмен в стандартных ячейках, эмпирические соотношения (см. рис. 31).
Рис. 31. Расположение центрального (а), бокового (б) и углового (в) твэлов:
dн - наружный диаметр стержня, м; dв - диаметр вытеснителя, м; d1 = 2R1; d2 = 2R2
Для X = s/dн = 1 используется эмпирическое соотношение:
Nu = A1 + B1 · Pe0,56, (227)
где ![]() ;
; ![]() .
.
Для Х = 1 ÷ 1,2 используется эмпирическое соотношение:
![]() (228)
(228)
где ![]() ;
;
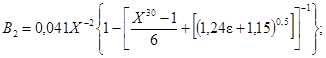 n2 = 0,56 + 0,19X - 0,1X80.
n2 = 0,56 + 0,19X - 0,1X80.
Для Х = 1,2 ÷ 2 используется эмпирическое соотношение:
где A3 = 7,55Х - 20Х13; B3 = 0,041X2; n3 = 0,56 + 0,19X
В соотношениях (227) ÷ (229): определяющий размер ![]() ;
определяющая скорость
;
определяющая скорость ![]() - средняя по сечению скорость в сборке
стержней; X = s/dн -
относительный шаг расположения стержней; e - параметр
приближенного теплового моделирования твэла; e
рассчитывается по формулам пункта 17, подпункт 1) в).
- средняя по сечению скорость в сборке
стержней; X = s/dн -
относительный шаг расположения стержней; e - параметр
приближенного теплового моделирования твэла; e
рассчитывается по формулам пункта 17, подпункт 1) в).
Пределы применимости формул (227) ÷ (229): Pe = 1 ÷ 4000; Pr < 0,04; e > 10-2.
Погрешность s расчета Nu составляет 30 %.
Теплообмен боковых твэлов (рис. 31) при турбулентном течении жидких металлов в сборках стержней треугольной упаковки рассчитывается:
в шестигранной кассете без вытеснителей по формуле:
где a1 = 4,69Х - 4,131; b1 = 0,577X - 0,566; m1 = 3,53X2 - 8,71X + 5,79;
в шестигранной кассете с вытеснителями по формуле:
где a2 = 4,81X - 3,348; b2 = 1,381X - 1,376; m2 = l,26X2 - 3,35X + 2,74.
Пределы применимости формул (230), (231): dв/dн = 0,16 +
0,26; Pe = 30 + 3000; Х = 1,06 ÷
1,30; ![]() (рис.
31).
(рис.
31).
Погрешность s расчета Nu составляет ± 20 %.
Теплообмен угловых твэлов (рис. 31) при турбулентном течении жидких металлов в сборках стержней треугольной упаковки рассчитывается: в шестигранной кассете без вытеснителей по формуле:
где C = 7,13X + 6,792; d1 = 0,331X - 0,342; к1 = 5,27X2 - 13,12Х + 8,83;
в шестигранной кассете с вытеснителями по формуле:
где C2 = 3,59X - 3,189; d2 = l,324X - l,363; к2 = 14,88 - 32,98X + 25,43X2 - 6,573.
Пределы применимости формул (232), (233):
Х = 1,06 ÷
1,30; Pe = 30 ÷ 3000; ![]() (рис. 31); dв/dн = 0,16 ÷ 0,26.
(рис. 31); dв/dн = 0,16 ÷ 0,26.
Погрешность s расчета Nu составляет 15 %.
В формулах (230) ÷
(233):
определяющий размер ![]() ; определяющая скорость
; определяющая скорость ![]() w -
средняя по сечению сборки стержней.
w -
средняя по сечению сборки стержней.
Неравномерность температуры по периметру стержневого твэла зависит от геометрических размеров, шага расположения стержней, теплопроводности материала стержня, его оболочек и теплоносителя, а также от характеристик последнего.
В сборках стержней треугольной упаковки при X ³ 1,15 максимальные неравномерности температуры по периметру стержня невелики.
При меньших относительных шагах безразмерная максимальная неравномерность температуры по периметру центрального стержня рассчитывается по формуле:
где ![]() ;
;
DTmax - безразмерная неравномерность температуры;
Tст - температура наружной оболочки стержня, К;
Rн - наружный радиус стержня, м;
λ - коэффициент теплопроводности, Вт/(м·К);
![]() - Вт/м2;
- Вт/м2;
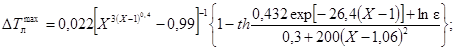
g = 8·10-3 + 2,4·10-4e;
b = 0,65 + 51X20·lgX;
e рассчитывается по формулам пункта 17, подпункт 1) в).
Пределы применимости формулы (234): X = 1 ÷ 1,15; Ре = 1 ÷ 2000; e ³ 0,20.
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность
температуры боковых твэлов при турбулентном течении жидких металлов в сборках
стержней треугольной упаковки зависит от параметра ![]() , объединяющего шаг
сборки стержней и зазор D3 между
обечайкой и периферийными твэлами, и рассчитывается по формуле:
, объединяющего шаг
сборки стержней и зазор D3 между
обечайкой и периферийными твэлами, и рассчитывается по формуле:
DТmax = A + B · ψ + С· exp(-D · ψ), (235)
где ![]() - безразмерная
неравномерность температуры;
- безразмерная
неравномерность температуры;
dн - наружный диаметр стержня, м;
Tст - К;
![]() - Вт/м2;
- Вт/м2;
λ - Вт/(м · К);
Значения коэффициентов А, В, С, D формулы приведены в таблице № 13.
Пределы применимости формулы (235): Pe = 200 ÷ 700; L/dг ³ 200; ψ = 0,2 ÷1,0; X = 1,04 ÷ 1,21; dв/dн = 0,16 ÷ 0,25, где dв - диаметр вытеснителя, м.
Погрешность s расчета DTmax составляет 15 %.
Таблица № 13
Значения коэффициентов А, В, С, D в формуле (235)
|
А |
В |
С |
D |
|
|
Кассеты неоребренных твэлов без вытеснителей |
||||
|
Pe = 700 |
0,100 |
0,400 |
0,630 |
15,000 |
|
Pe = 400 |
0,210 |
0,410 |
0,890 |
12,500 |
|
Pe = 200 |
0,470 |
0,820 |
1,300 |
10,000 |
|
Кассеты оребренных твэлов без вытеснителей |
||||
|
Pe = 700 |
0,020 |
0,480 |
0 |
0 |
|
Pe = 400 |
0,270 |
0,310 |
0 |
0 |
|
Pe = 200 |
0,520 |
0,620 |
0 |
0 |
|
Кассеты неоребренных твэлов с вытеснителями |
||||
|
Pe = 700 |
0,214 |
0,083 |
1,030 |
4,150 |
|
Pe = 400 |
0,330 |
0,120 |
1,170 |
5,050 |
|
Pe = 200 |
0,400 |
0,500 |
3,660 |
5,070 |
|
Кассеты оребренных твэлов с вытеснителями |
||||
|
Pe = 700 |
0,053 |
0,160 |
1,330 |
7,250 |
|
Pe = 400 |
0,132 |
0,170 |
2,250 |
6,720 |
|
Pe = 200 |
0,450 |
0,190 |
4,080 |
5,900 |
Характер температурных полей угловых твэлов при турбулентном течении жидких металлов в сборках стержней более сложен, чем боковых. Он сильно зависит от геометрических особенностей угловой зоны, представляющей собой более затесненный канал, чем зона бокового твэла.
Возможны различные соотношения между неравномерностями температуры боковых и угловых твэлов, но в большинстве случаев максимальные неравномерности температуры по периметру угловых твэлов значительно меньше, чем боковых твэлов. Поэтому оценочные расчеты максимальных неравномерностей температуры по периметру угловых твэлов проводятся по формуле (235).
г) Неравномерности температуры по периметру твэла в деформированных сборках стержней треугольной упаковки.
При использовании в реакторах на быстрых нейтронах натрия в качестве теплоносителя имеют место большие подогревы теплоносителя по каналам. Разность подогревов теплоносителя вокруг твэлов вызывает большие неравномерности температуры по периметру твэлов, особенно если твэлы окружены ячейками различной конфигурации.
Допуски на геометрические размеры кассет твэлов реакторов на быстрых нейтронах, имеющих малые диаметры твэлов и относительно тесные решетки, соизмеримы по величине с поперечными размерами ячеек, окружающих твэлы, что обусловливает заметный эффект от смещения и прогибов твэлов даже при использовании на твэлах дистанционирующих проволочных навивок. Особую важность эти вопросы приобретают для периферийных твэлов, на которых навивается проволока в два раза меньшего диаметра, чем на центральных твэлах. Это создает возможности смещения периферийных твэлов вдоль обечайки, по крайней мере, на половину зазора между твэлами.
Основными параметрами деформации решеток являются направление смещения твэла θ и относительное смещение s, характеризующееся отношением величины смещения e в данном направлении к максимально возможному смещению в данном направлении.
Под деформацией решетки понимается смещение одиночного твэла или группы твэлов по всей высоте активной зоны за счет изменения межцентрового расстояния между твэлами.
Максимальная безразмерная неравномерность температуры по периметру бокового оребренного твэла (рис. 32) в деформированной сборке стержней треугольной упаковки без вытеснителей в периферийной зоне при турбулентном течении жидких металлов в случае, если деформация решетки вызвана смещением бокового или углового твэлов вдоль обечайки, рассчитывается по формуле:
DTmax = 60,9Pe-0,813, (236)
где ![]() - безразмерная
неравномерность температуры по периметру бокового
твэла;
- безразмерная
неравномерность температуры по периметру бокового
твэла;
![]()
dг - гидравлический диаметр недеформированной сборки стержней, м;
![]() - средняя
скорость потока в сборке, м/с;
- средняя
скорость потока в сборке, м/с;
Тcm - К;
λ - Вт/(м · К);
q - Вт/м2.
Пределы применимости формулы (236): е = 0,5(S - dн); L/dг - 220; Pe = 50 ÷ 550; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,50,5(S - dн), где е - величина смещения твэла, м; S - шаг недеформированной решетки, м; D3 - зазор между стенкой обечайки и твэлами периферийной зоны, м.
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру бокового оребренного твэла (рис. 32) в деформированной сборке стержней треугольной упаковки без вытеснителей в периферийной зоне, когда деформация сборки вызвана смещением бокового или углового твэлов вдоль обечайки, a L/dг = 410, рассчитывается по формуле:
DTmax = 150/Pe-0,93. (237)
В формуле (237) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (237): e = 0,5(S - dг); L/dн = 410; Pe = 50 ÷ 550; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет ± 15 %.
Максимальная безразмерная неравномерность температуры по периметру бокового оребренного твэла (рис. 33) в деформированной сборке стержней треугольной упаковки с вытеснителями в периферийной зоне, когда деформация сборки вызвана смещением бокового или углового твэлов вдоль обечайки, рассчитывается по формуле:
DТmax = 557Pe-1,23. (238)
В формуле (238) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (238): е = 0,5(S - dн); L/dг = 220; Ре = 50 ÷ 550; dв/dн = 0,24, где dв - диаметр вытеснителя, м.
Погрешность s расчета DTmax составляет ± 15 %.
Максимальная безразмерная неравномерность температуры по периметру бокового твэла при dв/dн = 0,27 и тех же условиях, что и для формулы (238), рассчитывается по формуле:
DTmax = 112,5 Ре-1,028. (239)
Пределы применимости формулы (239): e = 0,5(S - dн); L/dг = 220; dв/dн = 0,27, Pe = 50 ÷ 550; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного бокового твэла в деформированной сборке стержней треугольной упаковки с вытеснителями в периферийной зоне (рис. 34), когда деформация вызвана смещением бокового или углового твэлов вдоль обечайки, рассчитывается по формуле:
DTmax = 585Pe-1,23. (240)
В формуле (240) обозначения и размерности величин такие же, как и формуле (239).
Пределы применимости формулы (240): e = 0,5(S - dн); L/dг = 185; dв/dн = 0,27; Pe = 100 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 34), когда деформация вызвана смещением бокового или углового твэлов вдоль обечайки, рассчитывается по формуле:
DTmax = 47Ре-0,47. (241)
В формуле (241) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (241): e = 0,5(S - dн); L/dг ≈ 220; Pe = 60 ÷ 700; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру оребренного углового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 36), когда деформация вызвана смещением углового твэла вдоль обечайки, рассчитывается:
при L/dг ≈ 220 по формуле:
DTmax = 164Ре-0,953; (242)
при L/dг ≈ 410 по формуле:
DTmax = 430Ре-1,065. (243)
В формулах (242) и (243) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формул (242), (243): e = 0,5(S - dн); Pe = 50 ÷ 550; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру оребренного углового твэла в деформированной сборке стержней треугольной упаковки с вытеснителями (рис. 37), когда деформация вызвана смещением углового твэла вдоль обечайки, рассчитывается:
при dв/dн ≈ 0,24 по формуле:
DTmax = 469Ре-1,347; (244)
при dв/dн ≈ 0,27 по формуле:
DTmax = 112,5Ре-1,028. (245)
В формулах (244) и (245) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формул (244), (245): e = 0,5(S - dн); L/dг ≈ 220; Ре = 50 ÷ 550; e = 0,20; S/dн = 1,17 ÷ 1,18; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Рис. 32. Схема смещения бокового твэла без вытеснителей
1 - тепловыделяющий элемент;
2 - дистанционирующая проволока;
3 - стенка шестигранной обечайки
Рис. 33. Схема смещения оребренного бокового твэла деформированной сборки с вытеснителями
1 - тепловыделяющий элемент;
2 - дистанционирующая проволока;
3 - стенка шестигранной обечайки;
4 - вытеснители
Рис. 34. Схема смещения неоребренного бокового твэладеформированной сборки с вытеснителями
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки;
3 - вытеснители
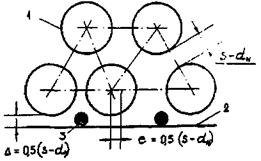
Рис. 35. Схема смещения неоребренного бокового твэла деформированной сборки без вытеснителей
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки
Рис. 36. Схема смещения оребренного углового твэла деформированной сборки без вытеснителей
1 - тепловыделяющий элемент;
2 - дистанционирующая проволока;
3 - стенка шестигранной обечайки
Рис. 37. Схема смещения оребренного углового твэла деформированной сборки с вытеснителями
1 - тепловыделяющий элемент;
2 - дистанционирующая проволока;
3 - вытеснители;
4 - стенка шестигранной обечайки
Максимальная безразмерная неравномерность температуры по периметру неоребренного углового твэла в деформированной сборке стержней треугольной упаковки с вытеснителями (рис. 38), когда деформация вызвана смещением углового твэла вдоль обечайки, рассчитывается по формуле:
DTmax = 100Ре-0,708. (246)
В формуле (246) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (246): e = 0,20; S/dн = 1,17 ÷ 1,18; e = 0,5(S - dн); L/dг = 185; dв/dн = 0,27; Ре = 100 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного углового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 39), когда деформация вызвана смещением углового твэла вдоль обечайки, рассчитывается по формуле:
DTmax = 100Ре-0,708. (247)
В формуле (247) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (247): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 185; Ре = 20 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного бокового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 42), когда деформация вызвана смещением бокового элемента по нормали к стенке обечайки до касания с двумя стержнями, рассчитывается по формуле:
DTmax = 3,00 + 6,97Ре-0,0079. (248)
В формуле (248) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (248): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 210; Ре = 20 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного бокового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 40), когда деформация вызвана смещением бокового элемента по нормали к стенке шестигранной обечайки до касания с ней, рассчитывается по формуле:
DTmax = 0,88 + 30Ре-1,054. (249)
В формуле (249) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (249): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 210; Ре = 20 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного бокового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей (рис. 41), когда деформация вызвана смещением бокового элемента по нормали к стенке шестигранной обечайки на величину e = 0,45(S - dн), рассчитывается по формуле:
DTmax = 0,90 + 25,4Ре-1,099. (250)
В формуле (250) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формулы (250): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 210; Ре = 20 ÷ 700; D3 = 0,5(S - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру неоребренного центрального твэла в деформированной сборке стержней треугольной упаковки (рис. 43), когда деформация вызвана смещением центрального твэла по линии, соединяющей центры твэлов, рассчитывается:
при e = 0,5(S - dн); L/dr = 185; Ре = 100 ÷ 700
по формуле:
DTmax = 39,7Ре-0,83; (251)
при e = S - dн; L/dr = 210; Ре = 60 ÷ 700
по формуле:
DTmax = 185Ре-0,75. (252)
В формулах (251) и (252) обозначения и размерности величин такие же, как и формуле (236).
Пределы применимости формул (251), (252): e = 0,20; s/dн = 1,17 ÷ 1,18; D3 = 0,5(s - dн).
Погрешность s расчета DTmax составляет 15 %.
Максимальная безразмерная неравномерность температуры по периметру твэла в деформированной сборке стержней треугольной упаковки, с учетом влияния величины зазора между твэлами и обечайкой, когда деформация вызвана смещением элемента вдоль обечайки, рассчитывается по формуле:
DTmax = b[A + Bψ – Cexp(-Dψ)], (253)
где b - поправочный коэффициент, зависящий от вида деформации сборки;
![]() - параметр, объединяющий шаг сборки
стержней и зазор между обечайкой и твэлами;
- параметр, объединяющий шаг сборки
стержней и зазор между обечайкой и твэлами;
А, В, С, D, b - коэффициенты, значения которых приведены в таблице № 14.
Пределы применимости формулы (253): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 210; Ре = 20 ÷ 700.
Погрешность s расчета DTmax составляет 20 %.
Таблица № 14
Значения коэффициентов А, В, С, D, b в формуле (253)
|
A |
B |
C |
D |
b |
|
|
Сборка неоребренных твэлов без вытеснителей |
|||||
|
700 |
0,10 |
0,40 |
0,63 |
15,00 |
5,40lgPe -7,52 |
|
400 |
0,21 |
0,41 |
0,89 |
12,50 |
|
|
200 |
0,47 |
0,82 |
1,30 |
10,00 |
|
|
Сборка неоребренных твэлов с вытеснителями |
|||||
|
700 |
0,214 |
0,083 |
1,030 |
4,150 |
6,86 - 1,95 lgPe |
|
400 |
0,330 |
0,120 |
1,770 |
5,050 |
|
|
200 |
0,400 |
0,500 |
3,660 |
5,070 |
|
|
Сборка оребренных твэлов без вытеснителей |
|||||
|
700 |
0,02 |
0,48 |
- |
- |
0,28lgPe + 0,396 |
|
400 |
0,27 |
0,31 |
- |
- |
|
|
200 |
0,52 |
0,62 |
- |
- |
|
|
Сборка оребренных твэлов с вытеснителями |
|||||
|
700 |
0,053 |
0,160 |
1,330 |
7,250 |
0,34lgPe + 0,783 |
|
400 |
0,132 |
0,170 |
2,250 |
6,720 |
|
|
200 |
0,450 |
0,190 |
4,080 |
5,900 |
|
Максимальная безразмерная неравномерность температуры по периметру твэла в деформированной сборке стержней треугольной упаковки, с учетом влияния величины зазора между твэлами и обечайкой, когда деформация вызвана смещением элемента по нормали к стенке обечайки, рассчитывается по формуле:
DTmax = g[A + Bψ - Cexp(-Dψ)], (254)
где А, В, С, D - коэффициенты, значения которых приведены в таблице № 14,
g = 3,50lgPe - 6,85 - при касании боковым твэлом стенки шестигранной обечайки (рис. 40);
g = 7,75lgPe - 11,8 - при касании боковым твэлом двух соседних центральных твэлов (рис. 42).
Пределы применимости формулы (254): e = 0,20; s/dн = 1,17 ÷ 1,18; L/dг = 10 ÷ 410; Ре = 200 ÷ 700.
Погрешность s расчета DTmax составляет 20 %.
Рис. 38. Схема смещения неоребренного углового твэла деформированной сборки с вытеснителями
1 - тепловыделяющий элемент;
2 - вытеснители;
3 - стенка шестигранной обечайки.
Рис. 39. Схема смещения неоребренного углового твэла деформированной сборки стержней треугольной упаковки без вытеснителей
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки.
Рис. 40. Схема смещения неоребренного бокового твэла деформированной сборки без вытеснителей
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки
Рис. 41. Схема смещения неоребренного бокового твэла в деформированной сборке стержней треугольной упаковки без вытеснителей
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки.
Рис. 42. Схема смещения неоребренного бокового твэла деформированной сборки без вытеснителей
1 - тепловыделяющий элемент;
2 - стенка шестигранной обечайки.
Рис. 43. Схема смещения неоребренного центрального твэла деформированной сборки
Максимальная неравномерность температуры по периметру твэлов в деформированной сборке стержней треугольной упаковки, когда деформация вызвана групповым смещением твэлов, смещением двух твэлов до соприкосновения с третьим с образованием канала плотной упаковки, рассчитывается по формуле:
где:
![]()
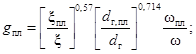
![]()
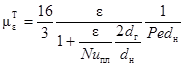
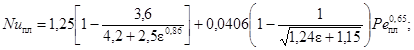
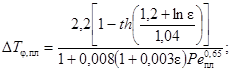
![]()
В формуле (255):
dг - гидравлический диаметр недеформированной сборки стержней, м;
dпл - гидравлический диаметр сборки стержней плотной упаковки, м;
ξ - коэффициент гидравлического сопротивления трения недеформированной сборки стержней;
ξпл - коэффициент гидравлического сопротивления трения сборки стержней плотной упаковки, который рассчитывается по формуле (61);
L - длина участка тепловыделения, м;
ω - площадь проходного сечения недеформированной сборки стержней, м2;
ωпл - площадь проходного сечения сборки стержней плотной упаковки, м2;
tст - температура оболочки, °C;
dн - м;
q - Вт/м2;
λ - Вт/(м·°C);
![]() - коэффициент обмена теплом между каналами за счет
теплопроводности твэлов, 1/м;
- коэффициент обмена теплом между каналами за счет
теплопроводности твэлов, 1/м;
![]() - для недеформированной сборки стержней;
- для недеформированной сборки стержней;
![]() -
для сборки стержней плотной упаковки;
-
для сборки стержней плотной упаковки;
w - м/с;
а - м2/с;
e - параметр теплового моделирования твэлов, который рассчитывается по формулам пункта 17 подпункта 1) в).
Пределы применимости формулы (255): e = 0,20; S/dн = 1,17 ÷ 1,18; L/dг = 210 ÷ 410; Ре = 200 ÷ 700.
Погрешность s расчета Dtmax составляет 20 %.
Максимальная температура оболочки твэлов, образующих канал плотной упаковки при групповом смещении твэлов, рассчитывается по формуле:
В формуле (256) обозначения и размерности величин такие же, как и формуле (255).
Пределы применимости формулы (256): e = 0,20; s/dн = 1,17 ÷ 1,18; L/dг = 210 ÷ 410; Ре = 200 ÷ 700.
Погрешность D расчета tст,max составляет ± 20 %.
4) Межканальный обмен теплом и массой в сборках стержней.
Межканальный обмен теплом в сборках активных зон реакторов необходимо знать при определении уровня температур в каждом твэле тепловыделяющей сборки. Подогрев температур в каждой ячейке разный и зависит от расходов по ячейкам, от радиальной и аксиальной неравномерности энерговыделения и других факторов. Температуры в твэле определяются и уровнем температур теплоносителя в окружающих ячейках.
Зазоры между твэлами, связывающие каналы в единую систему, обеспечивают обмен массой, импульсом и энергией между каналами. Обмен осуществляется посредством механизмов конвективного переноса, турбулентной диффузии и молекулярного (электронного в жидких металлах) переноса.
Конвективные поперечные потоки массы, сопровождающиеся переносом импульса и энергии, обусловлены, как правило, дистанционирующими проволочными навивками на твэлах или связаны с разбалансом давления в теплоносителе в смежных каналах. Турбулентный и молекулярный потоки импульса и энергии возникают при разности скорости и температуры теплоносителя в смежных каналах. Неравномерность распределения температуры теплоносителя в каналах, окружающих твэлы, приводит к перераспределению плотности теплового потока по периметру твэлов, создавая эффект обмена теплом между каналами за счет теплопроводности твэлов.
Интенсивность межканального обмена определяется геометрическими и режимными параметрами, теплофизическими свойствами теплоносителя и материалов твэла и характеризуется коэффициентом межканального обмена массой, импульсом и энергией (теплом).
Коэффициент межканального обмена массой µм определяется как отношение поперечного потока массы на единицу длины зазора между каналами Gij к полному продольному потоку теплоносителя в канале тепловыделяющей сборки Gi.
µм = Gij/Gi. (257)
Коэффициент межканального обмена импульсом µг определяется как поперечный поток импульса на единице длины зазора между каналами Pij, отнесенный к разности потоков импульса в смежных каналах:
µг = Pij/[Gi(wi - wi)], (258)
где wj - средние скорости теплоносителя в каналах i и j.
Далее предполагается, что всегда µг = µм.
Коэффициент межканального обмена теплом определяется как поперечный поток тепла на единицу длины зазора между каналами Qij отнесенный к разности потоков тепла в смежных каналах:
µт = Gij/[Gi(ii - ij], (259)
где, ii, ij - удельная энтальпия теплоносителя в каналах i и j.
Коэффициент межканального обмена теплом показывает, какой долей от разности полных энтальпий теплоносителя обмениваются два смежных канала на единицу длины зазора между каналами.
Коэффициенты межканального обмена необходимы для замыкания системы уравнений баланса массы, количества движения и энергии. Точность проводимых теплогидравлических расчетов в значительной степени определяется точностью расчетных соотношений для коэффициентов межканального обмена.
Межканальный тепломассообмен снижает температуру в области «горячих пятен» и уменьшает неравномерности распределения температуры, возникающие за счет перекосов энерговыделения и наличия каналов разной конфигурации. Тем самым он способствует форсированию мощности ядерных реакторов.
Эффективный (суммарный) коэффициент межканального обмена представляет собой сумму составляющих.
Для обмена импульсом это конвективный и турбулентный перенос:
![]() (260)
(260)
Для обмена теплом это конвективный, молекулярный, турбулентный обмен и обмен за счет теплопроводности твэлов:
![]() (261)
(261)
Коэффициенты межканального обмена массой при дистанционировании твэлов «ребро в оболочке» рассчитываются:
локальный (поток массы из i в j - канал через единицу длины зазора, отнесенный к продольному расходу теплоносителя в канале) по формуле:
средний по длине зазора по формуле:
где: фг(s/dн) = 2,57s/dн - 3,57ехр[-119(s/dн - 1)2,12]+1;
ψ(Re) = 1,085 - 0,754ехp(-0,132·10-3Re);
h - шаг проволочной навивки, м;
aij - фаза вхождения проволочной навивки в j-канал из i-канала;
dн - наружный диаметр твэла, м;
![]()
Пределы применимости формул (262), (263): s/dн = 1,01 ÷ 1,40; h/dн = 2 ÷ 50; Rе = 2·103 ÷ 2·105.
Погрешность s расчета ![]() составляет 15 %.
составляет 15 %.
Средний по длине зазора коэффициент межканального обмена массой при дистанционировании твэлов «ребро по ребру» рассчитывается по формуле:
где ![]() ψ(Re)
= 1,085 - 0,754ехp(-0,132·10-3Re);
ψ(Re)
= 1,085 - 0,754ехp(-0,132·10-3Re); ![]()
Пределы применимости формулы (264): s/dн = 1,01 ÷ 1,40; h/dн = 5 ÷ 65; Rе = 5·103 ÷ 105.
Погрешность s расчета ![]() составляет 15 %.
составляет 15 %.
При дистанционировании твэлов разнонаправленными навивками межканальный обмен является более интенсивным, чем в случае однонаправленного оребрения твэлов (рис. 44). Более высокие значения коэффициентов межканального обмена обусловлены тем, что поперечная составляющая скорости не меняет своего знака по длине зазоров.
При чередовании гладких и оребренных твэлов с противонаправленными навивками интенсивность обмена через зазор между твэлами с противонаправленными навивками в два раза больше, чем через два других зазора (между гладкими и оребренными твэлами).
При дистанционировании твэлов противонаправленными по рядам твэлов навивками коэффициенты межканального обмена массой в двух зазорах канала в два раза больше, чем в третьем зазоре (рис. 44).
Различие в коэффициентах межканального обмена массой по зазорам не случайно: в зазоре с повышенной интенсивностью обмена направленный поток теплоносителя создается двумя ребрами, а в зазоре с пониженной интенсивностью - одним ребром.
Локальный коэффициент межканального обмена теплом (конвективная составляющая) для однонаправленных навивок «ребро по ребру» или «ребро по оболочке» рассчитывается по формуле:
где b ≈ 0,70;
![]() - рассчитывается по формулам (263) и (264).
- рассчитывается по формулам (263) и (264).
Пределы применимости формулы (265) и погрешности расчета остаются такими же, как и для формул (263) и (264).
Средний по длине зазора коэффициент межканального обмена теплом (конвективная составляющая) для однонаправленных навивок «ребро по оболочке» рассчитывается по формуле:
где b ≈ 0,70;
![]() рассчитывается по формуле (263).
рассчитывается по формуле (263).
Пределы применимости формулы (266): s/dн = 1,01 ÷ 1,40; h/dн = 2 ÷ 50; Rе = 2·103 ÷ 2·105.
Погрешность s расчета ![]() составляет 15 %.
составляет 15 %.
Средний по длине зазора коэффициент межканального обмена теплом (конвективная составляющая) для однонаправленных навивок «ребро по ребру» рассчитывается по формуле:
где b ≈ 0,70;
![]() рассчитывается по формуле (264).
рассчитывается по формуле (264).
Пределы применимости формулы (266): s/dн = 1,01 ÷ 1,40; h/dн = 5 ÷ 65; Rе = 5·103 ÷ 105.
Погрешность s расчета ![]() составляет 15 %.
составляет 15 %.
Коэффициент межканального обмена теплом (конвективная составляющая) при дистанционировании твэлов разнонаправленными навивками с чередованием гладких и оребренных твэлов рассчитывается: для зазоров с пониженной интенсивностью обмена - по формуле (267), для зазоров с повышенной интенсивностью теплообмена - по формуле (266) с последующим умножением результатов на два, для каждого из трех зазоров с равнораспределенным обменом - по формуле (266).
Рис. 44. Схема винтовых оребрений твэлов и направления поперечных потоков теплоносителя в зазорах 1, 2, 3 канала i
(а); «ребро по ребру» б); на противонаправленных навивках по рядам (в) и при чередовании гладких и оребренных твэлов (г)
Коэффициент межканального обмена теплом (конвективная составляющая) при дистанционировании твэлов противонаправленными по рядам твэлов навивками рассчитывается: для зазоров с пониженной интенсивностью обмена и для зазоров с повышенной интенсивностью обмена - по формуле (266) с последующим увеличением полученного результата в два раза.
Одинаковая по периметру чехла ориентация проволочной навивки в зазорах между чехлом тепловыделяющей сборки и периферийными твэлами обусловливает однонаправленность поперечного конвективного потока массы через зазоры.
Коэффициент конвективного межканального обмена массой для зазоров между чехлом и периферийными твэлами рассчитывается по формуле:
где ψ(Re) = l - 0,696exp(-0,132·10-3Re);
D3 - ширина зазора между чехлом и периферийными твэлами, м;
dн - наружный диаметр стержня (твэла), м;
h - шаг навивки, м;
![]()
Пределы применимости формулы (268): (dh + D3)/dн =1,00 ÷ 1,25; h/dн = 7,6 ÷ 52,0; Re = 0,6·103 ÷ 2,9 · 104.
Погрешность s расчета ![]() составляет
15 %.
составляет
15 %.
Коэффициент конвективного межканального обмена теплом для зазоров между чехлом и периферийными твэлами рассчитывается по формуле:
где ![]() рассчитывается
по формуле (268).
рассчитывается
по формуле (268).
Пределы применимости формулы (269): (dн + D3)/dн = 1,00 ÷ 1,25; h/dн = 7,6 ÷ 52,0; Re = 0,6·103 ÷ 7·104.
Погрешность s расчета ![]() составляет
15 %.
составляет
15 %.
Коэффициент межканального гидродинамического молекулярно-турбулентного обмена массой рассчитывается по формуле:
Пределы применимости формулы (270): s/dн = 1,05 ÷ 1,060; Re = 104 ÷ 2·105.
Погрешность s расчета ![]() составляет
20 %.
составляет
20 %.
Коэффициент межканального молекулярного обмена теплом для сборки неоребренных твэлов треугольной упаковки рассчитывается по формуле:
Пределы применимости формулы (271): s/dн = 1,10 ÷ 1,40; Ре = 70 ÷ 1500.
Погрешность s расчета ![]() составляет
20 %.
составляет
20 %.
Коэффициент межканального турбулентного обмена теплом для сборки неоребренных твэлов треугольной упаковки рассчитывается по формуле:
![]() (272)
(272)
Пределы применимости формулы (271): s/dн = 1,13 ÷ 1,32; Rе = 4·103 ÷ 5·104.
Погрешность s расчета ![]() составляет
20 %.
составляет
20 %.
Коэффициент межканального молекулярно-турбулентного обмена теплом для сборки неоребренных твэлов треугольной упаковки рассчитывается по формуле:
Пределы применимости формулы (273): s/dн = 1,10 ÷ 1,40; Ре = 70 ÷ 1500.
Погрешность s расчета ![]() составляет
20 %.
составляет
20 %.
В случае неоднородного подогрева теплоносителя в каналах, окружающих твэл, наблюдается неравномерность распределения плотности теплового потока по периметру твэла, которая определяет эффект обмена теплом между каналами за счет теплопроводности твэлов.
Коэффициент межканального обмена теплом за счет теплопроводности твэлов рассчитывается по формуле:
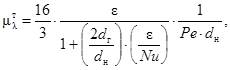 (274)
(274)
где e - параметр теплового моделирования твэлов, рассчитывается по формулам пункта 17, подпункт 1) в). Число Nu рассчитывается по формулам (227) ÷ (233).
Погрешность s расчета ![]() составляет
20 %.
составляет
20 %.
5) Теплообмен при турбулентном течении в каналах сложного поперечного сечения.
а) Продольное течение в каналах сложного профиля.
Для расчета теплообмена при турбулентном течении жидких металлов в каналах сложного поперечного сечения канал разбивается на элементарные гидродинамические ячейки. Каждая элементарная ячейка ограничена стенкой (теплоотдающей поверхностью), линией максимальной скорости и нормалью, проведенной на стенку из самой удаленной от поверхности теплообмена точки (рис. 28).
Средний по длине теплообмен в каждой элементарной ячейке рассчитывается по формуле:
где ![]()
![]()
![]() - гидравлический диаметр элементарной
ячейки, м;
- гидравлический диаметр элементарной
ячейки, м;
![]() - средняя
по сечению элементарной ячейки скорость потока, м/с;
- средняя
по сечению элементарной ячейки скорость потока, м/с;
![]() - среднее расстояние от
поверхности теплообмена до линии максимальной скорости;
- среднее расстояние от
поверхности теплообмена до линии максимальной скорости;
![]()
yi - расстояние по нормали от стенки до линии максимальной скорости;
Lni - периметр элементарной ячейки, м;
lx - координата вдоль периметра элементарной ячейки;
![]() (276)
(276)
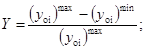
e - параметр теплового моделирования, рассчитывается по формулам пункта 17, подпункт 1) в).
Пределы применимости формулы (275): Re = 5·103 ÷ 105; Pr = 0,005 ÷ 0,050.
Погрешность s расчета Nui составляет 25 %.
б) Поперечное обтекание плоских пластин, сфер и пучка труб.
При ламинарном обтекании жидким металлом плоской пластины расчет локальной теплоотдачи на расстоянии x от начала обтекания производится по формуле:
![]() (277)
(277)
где Nux = ах/λ;
Рех= wx/a;
для средней теплоотдачи на длине:
![]() (278)
(278)
где ![]()
Ре = wl/a;
при турбулентном течении в пограничном слое:
![]() (279)
(279)
Теплоотдача при обтекании одиночной сферы жидким металлом рассчитывается по формуле:
![]() (280)
(280)
где C = 1,13 для Tw = const и С = 1,29 для q = const. В диапазоне Ре = 102 ÷ 103 справедлива формула:
Nu = 2 + 0,386Pe0,5. (281)
Обтекание ряда сфер рассчитывается по формулам:
![]() (для Tw = const); (282)
(для Tw = const); (282)
Nu = Pe0,5S0,5 (для q = const). (283)
Значения S = f(p/d) приведены в таблице № 15 (p - шаг расположения сфер; d - диаметр сфер).
Таблица № 15
Значения S в соотношениях (292) и (293)
|
p/d |
1,0 |
1,1 |
1,2 |
1,3 |
1,5 |
2,0 |
2,4 |
2,8 |
3,5 |
5 |
10 |
|
S |
1,564 |
1,644 |
1,710 |
1,762 |
1,837 |
1,928 |
1,957 |
1,973 |
1,986 |
1,992 |
2,00 |
Теплоотдача при поперечном обтекании жидким металлом пучков труб (шахматное и коридорное расположение) определяется при Ре = 10 ÷ 1300 по формуле:
Nu = 2Pe0,5. (284)
Погрешность D расчета Nu составляет ± 30 %.
Здесь число Pe определено по скорости набегающего потока и наружному диаметру труб, коэффициент теплоотдачи рассчитывается по среднему тепловому потоку и среднему температурному напору.
Теплоотдача при обтекании пучков труб под углом j = 30 ÷ 90° при Pe = 10 ÷ 600 и Pe = 0,007 ÷ 0,03 определяется по формуле:
Nuj = Nusin0,4j, (285)
где Nu - число Нуссельта, определенное по формуле (284);
j - угол между направлением потока и осью трубы (j < 90°).
При j < 30° теплоотдача при обтекании пучков труб определяется по зависимостям для продольного обтекания или по формуле:
Nuj = Nu[sinj + sin2j]0,5[1 + sin2j], (286)
которая приближенно справедлива и для j < 90°.
в) Переменное энерговыделение и начальные тепловые участки.
Для пересчета температурного поля, полученного при постоянном энерговыделении, используется интеграл Дюамеля, построенный на принципе суперпозиции, вытекающем из факта линейности уравнения энергии относительно температуры:
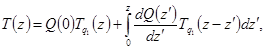 (287)
(287)
где Q(z) - функция распределения теплового потока по длине канала,
Tq1(z) - распределение температуры по длине канала при единичном скачке энерговыделения (функция влияния);
Q(0) - начальное энерговыделение (в точке z = 0), постоянное по длине канала (начальный скачок).
Удобным и простым соотношением для учета переменного энерговыделения, вытекающем из интеграла Дюамеля, является соотношение для температурного напора «стенка - жидкость»:
где q(z - L) - переменное по z энерговыделение;
L - длина релаксации, связанная с длиной начального теплового участка соотношением L = lнт/3;
a - коэффициент теплоотдачи при постоянном по длине канала энерговыделении. Использование (288) предполагает знание длин начальных тепловых участков lнт при q = const no длине z.
Для треугольной решетки твэлов данные по lнт получены из численного решения задачи о температурном поле в характерной ячейке «бесконечной» решетки твэлов при турбулентном, стержневом и ламинарном течениях теплоносителя (стабилизированные условия).
Длина lнт определялась в предположении, что число Нуссельта на начальном участке отличается от стабилизированного значения не более чем на 2 %.
Изменение коэффициентов теплоотдачи и неравномерностей температуры по периметру твэлов на начальных участках решеток твэлов, обтекаемых турбулентным, стержневым и ламинарным потоками теплоносителя, описывается универсальной формулой:
где F(x) - значение функций ![]() и
и ![]() на начальном участке;
на начальном участке;
F - значение функций F1(x) и F2(x) в стабилизированной области теплообмена;
![]() - безразмерная длина
начального теплового участка по числу Нуссельта;
- безразмерная длина
начального теплового участка по числу Нуссельта;
![]() - безразмерная длина
начального теплового участка по максимальной неравномерности температуры;
- безразмерная длина
начального теплового участка по максимальной неравномерности температуры;
![]() - средний по периметру твэла тепловой поток на поверхности твэла;
- средний по периметру твэла тепловой поток на поверхности твэла;
R - радиус твэла;
![]() - число Пекле (
- число Пекле (![]() );
);
d = 2R - диаметр твэла;
![]() - средняя в
ячейке скорость теплоносителя;
- средняя в
ячейке скорость теплоносителя;
р(e, s/d) - функции e и s/d;
![]() - безразмерная продольная координата.
- безразмерная продольная координата.
Диапазон применимости формулы (289) для турбулентного течения: 1,02 £ s/d £ 2,0; 0,01 £ e £ 10; 100 £ Ре £ 2500.
Значения xнт по Nu и неравномерностям температуры, а также функции р(e, s/d) берутся по соответствующим графикам, приведенным в документе «Методические указания и рекомендации по теплогидравлическому расчету активных зон быстрых реакторов» (руководящий технический материал РТМ 1604.008-88, утвержден и введен в действие 13.10.1988, № ГЖ-6627/19, ГНЦ РФ ФЭИ, 1988 г.). Формулу (289) представляют в виде переходной функции для температурного напора стенка - жидкость:
а значения lNu/dг аппроксимируют формулой:
![]() (291)
(291)
где 1,25 £ s/d £ 1,7; 0,1 < e < 10; 100 £ Ре £ 2500;
Гидродинамически нестабилизированное течение.
Длина начальных тепловых участков по коэффициентам теплоотдачи рассчитывается по соотношению:
где 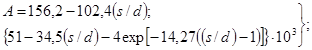 (294)
(294)
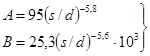 для 1,2 £ s/d £ 1,7. (295)
для 1,2 £ s/d £ 1,7. (295)
Пределы применимости формулы (293):
по параметру e6: 0,4 £ e £< 1,0 при 1,0 £ s/d £ 1,10; 0,4 £ e £ 1,6 при 1,2 £ s/d £ 1,7;
по числу Пекле: 15 £ Pe £ 800 для s/d = 1,0; 50 £ Ре £ 3000 для 1,10 £ s/d £ 1,7.
Для «тесных» решеток высокотеплопроводных
твэлов (s/d £ 1,1; ![]() ) длину
начального теплового участка, определенную по формуле (293), уменьшают на 30 - 40 %.
) длину
начального теплового участка, определенную по формуле (293), уменьшают на 30 - 40 %.
Расчет длин начальных тепловых участков по неравномерностям температуры проводится по формуле:
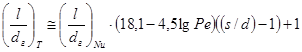 (296)
(296)
где 1,0 £ s/d £ 1,2;
500 £ Ре £ 2000;
0,4 £ e £ 1,0.
Для раздвинутой квадратной решетки твэлов s/d ³ 1,3 в условиях гидродинамически стабилизированного течения по методу эквивалентного кольца пересчитываются данные для треугольной решетки по формуле:
![]() (297)
(297)
вытекающей из предположения о равенстве гидравлических диаметров треугольной и квадратной ячеек твэлов.
где
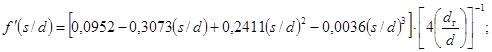 (299)
(299)
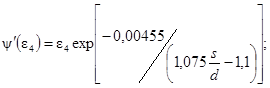 (300)
(300)
![]() , j(Pe) - см. (292).
, j(Pe) - см. (292).
Переходная функция для температурного напора «стенка - жидкость» θ(z) определяется по (290) при использовании (298) для lнт/dг и (301) для p'.
Для гидродинамически нестабилизированного течения начальные тепловые участки описываются формулой:
![]() (302)
(302)
где 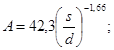
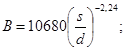 100 £ Ре £ 2000; 1,28 £ s/d £ 1,46.
100 £ Ре £ 2000; 1,28 £ s/d £ 1,46.
Переходная функция для безразмерного перепада температуры «стенка - жидкость» при q = const выглядит:
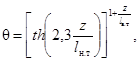 (303)
(303)
где 1,28 £ s/d £ 1,46; 300 £ Ре £ 1000.
г) Перегревы твэлов под ребрами.
Увеличение температуры оболочки под ребрами происходит наиболее заметно у твэлов с малой эквивалентной теплопроводностью (делящийся материал - двуокись урана, оболочка - нержавеющая сталь, теплоноситель - натрий), определяемой параметром e. Для твэлов активных зон и экранов быстрых реакторов значения e составляют около 0,05 - 0,3.
Влияние оребрения на неравномерности температуры центральных твэлов в тесных и раздвинутых решетках твэлов проявляется по-разному и обусловливается размерами ребер. В тесных решетках твэлов при малых размерах ребер (s/d = l,04) распределение температуры по периметру центральных твэлов зависит, в основном, от конфигурации каналов. При ориентации ребер в узкие части каналов происходит дополнительное повышение неравномерности температуры под ребрами:
для оребренных твэлов:
![]() (304)
(304)
для гладких твэлов:
![]() (304a)
(304a)
где s/d = 1,04; s = 0,27; 20 £ Pe £ 300.
В относительно раздвинутых решетках твэлов (s/d = l,15) размеры ребер существенно больше, чем в тесных решетках: температурное поле центральных твэлов характеризуется местными повышениями температуры стенки под ребрами.
Перегревы оболочек твэлов под ребрами в случае однозаходной проволочной навивки или трехзаходных ребер примерно одинаковы и рассчитываются по формуле:
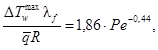 (305)
(305)
где 1,15 £ s/d £ 1,20; 40 £ Ре £ 700; ![]() - перегрев оболочки твэла под ребром;
- перегрев оболочки твэла под ребром;
R -
радиус оболочки. Для более тесных решеток (![]() ) с
дистанционированием твэлов «ребро по ребру» рекомендуется формула:
) с
дистанционированием твэлов «ребро по ребру» рекомендуется формула:
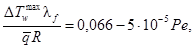 (306)
(306)
где 40 £ Ре £ 400.
д) Сборки стержней в квадратной упаковке.
Для расчета теплообмена центральных твэлов при турбулентном течении жидких металлов в сборках стержней в квадратной упаковке рекомендован метод, наиболее обоснованный как теоретическими расчетами, так и экспериментальными данными. Основное соотношение для числа Нуссельта в широком диапазоне чисел Re и Pr имеет вид:
Nu = Nu0 + bRe0,87Prn, (307)
здесь Nu0 - предельное значение числа Нуссельта, имеющее место при данном числе Рейнольдса, для данной сборки (d, s, e), но при стремлении числа Прандтля к 0. Оно описывается формулой:
![]() (308)
(308)
Для b дано соотношение:
![]() (309)
(309)
где E = e[1 + 4/(1 + 10Pr)]; n = 0,4 + 1/(2Pr + 1). (310)
Этот метод справедлив при l,0 £ s/d £ 2,0; 10 £ Pe £ 2500; Re
> 5000; ![]() . Параметр эквивалентной
теплопроводности твэлов e4 для
квадратных сборок рассчитывается по четвертой (k0 = 4) гармонике разложения температурного поля твэла в
ряд Фурье (см. выше).
. Параметр эквивалентной
теплопроводности твэлов e4 для
квадратных сборок рассчитывается по четвертой (k0 = 4) гармонике разложения температурного поля твэла в
ряд Фурье (см. выше).
Для числа Нуссельта рекомендовано также соотношение:
![]() (311)
(311)
где
A = 0,007; B = 0,64 +
0,246(s/d), l,20 £
(s/d) £ l,50; 10 £ Pe £ 2500; ![]() . Число
Пекле рассчитывается по гидравлическому диаметру «бесконечной» ячейки
квадратной решетки твэлов
. Число
Пекле рассчитывается по гидравлическому диаметру «бесконечной» ячейки
квадратной решетки твэлов ![]() и скорости теплоносителя в этой ячейке.
и скорости теплоносителя в этой ячейке.
Для более широкой области s/d решеток твэлов 1,0 £ s/d £ 1,5, но при фиксированном
значении параметра ![]() справедливо соотношение, стыкующееся с
данными для s/d = 1,20 ÷ 1,5:
справедливо соотношение, стыкующееся с
данными для s/d = 1,20 ÷ 1,5:
![]() (312)
(312)
где ![]()
![]()
Максимальная неравномерность температуры
по периметру твэлов рассчитывается по формуле (1,20 £ s/d £ 1,35; 1 £ Pe < 2000; ![]() ):
):
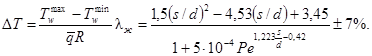 (313)
(313)
Числитель этой формулы есть значение DTл для ламинарного режима течения при указанных s/d и e = 1,4. Для других s/d и e значения DTл берутся из номограммы (рис. 45).
Отклонение распределения температуры от косинусоидального распределения оценивается по номограмме (рис. 46).
19. Теплоотдача при естественной и смешанной конвекциях.
1) Естественная конвекция.
При естественной (свободной) конвекции движение жидкости полностью определяется процессом теплообмена. В жидких металлах влияние молекулярной (электронной) теплопроводности распространяется далеко за область гидродинамического пограничного слоя, где поле скорости определяется не молекулярной вязкостью, а турбулентной. В таком случае Nu = f(GrPr2),
где ![]()
![]()
Для горизонтального цилиндра при ламинарном течении, где GrPr = 10 ÷ 104, теплоотдача рассчитывается по формуле:
Nu = 0,53(GrPr)1/4. (314)
Для более широкого диапазона чисел Gr рекомендуется зависимость:
Nu = C[GrPr2/(1 + Pr)], (315)
где C = 0,67; n = 1/4 при Gr = 102 ÷ 108; C = 0,35; n = 1/3 при Gr > 108.
Для вертикального цилиндра высотой H и радиусом r теплоотдача рассчитывается по формуле:
где Nuн = aH/X; Raн = GrнPr = gbDTH3/va.
Пределы применимости формулы (316): Raнr/H = 1,6·106 ÷ 4·107; r/Н = 0,39 ÷ 1,50.
Рис. 45. Зависимость
максимальной неравномерности температуры по периметру твэлов от параметра e при различных относительных шагах квадратных решеток
твэлов при ламинарном течении теплоносителя (х = s/d,
![]()
![]() )
)
Рис. 46. Номограмма для
определения параметра ![]() в квадратной решетке твэлов при
ламинарном течении теплоносителя
в квадратной решетке твэлов при
ламинарном течении теплоносителя
Теплопередача в среде жидкого металла между вертикальными пластинами для чисел Ралея Ra = 4·104 ÷ 9,4·109 рассчитывается по формуле:
Nu = 0,028Ra0,355 (317)
или для RaNu = 8·104 ÷ 1012:
Nu = 0,0714(RaNu)0,262. (318)
Теплоотдача в плоском зазоре между двумя поверхностями, расположенными под различными углами наклона к горизонтали, рассчитывается для Ra = 5· 104 ÷ 7,2·108 по формуле:
Nu = C(j)Ra1/3Pr0,074, (319)
где значения C(j):
|
j, град |
0 |
30 |
45 |
60 |
90 |
|
C |
0,069 |
0,065 |
0,059 |
0,057 |
0,049 |
2) Смешанная конвекция.
Теплообмен при параллельной смешанной конвекции в вертикальных круглых трубах описывается для q = const соотношением:
Nu = (0,373 ÷ 6,67 Pr)Z4 ± 25 %, (320)
где ![]()
Пределы применимсти формулы (320): l/d > 5; Pe = 3 ÷ +150; Z = 5 ÷ 30; Pr = 0,005 ÷ 0,02.
Оценку теплоотдачи при параллельной смешанной конвекции в плотной упаковке стержней можно провести по формуле:
где Nu0 - число Нуссельта для чисто вынужденной конвекции числа Ре при тех же условиях.
Пределы применимости формулы (321): CrPr = 0 ÷ 500; Ре = 30 ÷ 1000.
Встречная смешанная конвекция (ВСК) в жидких металлах характеризуется большими пульсациями температур, связанными с неустойчивостью потока.
При низких числах Пекле в коротких трубах опытные данные описываются зависимостью:
Nup = 0,27Pe1,1d/l, (322)
где Nup = adг/λ; Pe = 3 ÷ 300; l/d < 5.
К формуле (322) необходимы некоторые пояснения. Пусть необходимо рассчитать теплообменник «труба в трубе», где имеет место встречная смешанная конвекция. Ход температур в таком теплообменнике показан на рис. 47.
Рис. 47. Расчет теплообмена при встречной смешанной конвекции
Известны температура входа теплоносителей Т0, T1 геометрия, теплоемкости C1 = C2 = C. Нужно найти температуры теплоносителей на выходе и мощность теплообменника. По формуле (322) находим aр. Затем находим термические сопротивления стенки и теплоотдачу с другой стороны:
![]()
![]() j = fw·λw/f2·λ2; χ = f1·λ1/f2·λ2,
j = fw·λw/f2·λ2; χ = f1·λ1/f2·λ2,
где f - поперечное сечение, индексы: w - стенка; 1 - вспомогательный канал; 2 - канал с ВСК.
Далее находим расчетный коэффициент теплопередачи:
1/kp = 1/λp + Rwр + R1р. (323)
Имея три уравнения: Q = kpF(T3 - T0); Q = С(Т0 - Т); Q = С(Т3 - T1), определяем Q, Т2, Т3: Q = kpF(T0 - T1)/(1 + kpF/C). Здесь F - поверхность теплообменника, м2; C - расходная теплоемкость, Дж/(с·К).
20. Теплоотдача при кипении.
Перегревы жидкого металла перед закипанием. Перегрев перед закипанием жидких металлов является функцией более 15-ти определяющих параметров и различные теоретические расчеты оказываются мало полезными для практики. Поэтому все рекомендации основаны на экспериментальных данных.
Для натрия при давлениях до 0,2 МПа и числах Re ~ 105 следует считаться с возможностью перегрева порядка 100 °C.
1) Пузырьковое кипение металлов в большом объеме.
Существуют различные режимы кипения в большом объеме. Участок кривой кипения, соответствующий теплообмену путем естественной конвекции для жидких металлов, имеет значительно большую протяженность, чем для обычных жидкостей. При постепенном увеличении плотности теплового потока реализуются условия, когда теплообмен внезапно переходит из режима естественной конвекции в режим пузырькового кипения с меньшим перегревом стенки.
При низких давлениях и малых плотностях тепловых потоков может возникнуть неустойчивое пузырьковое кипение, при котором коэффициент теплообмена колеблется между значением для свободной конвекции и значением для пузырькового кипения.
Средние значения коэффициентов теплообмена при неустойчивом кипении ниже, чем при установившемся режиме пузырькового кипения. Колебания температуры поверхности в этом режиме могут оказывать неблагоприятные влияния на конструкции.
Формула для расчета теплоотдачи при пузырьковом кипении разных металлов имеет вид:
a = Aqmpn, (324)
где q - плотность теплового потока, Вт/м2;
р - давление, МПа.
Значения коэффициентов А, т, п для разных металлов приведены в таблице № 16. Там же указаны диапазоны применения формул.
Таблица № 16
Коэффициенты в формуле (335)
|
А |
т |
п |
Диапазон давления, МПа |
Точность, % |
|
|
Натрий |
21,4 |
0,67 |
0,4 |
5 - 30 |
25 |
|
Натрий |
7,55 |
0,67 |
0,1 |
30 - 150 |
25 |
|
Натрий |
7,32 |
0,7 |
0 |
15 - 127 |
30 |
|
Калий |
4,44 |
0,7 |
0,15 |
30 - 200 |
20 |
|
Калий |
6,35 |
0,67 |
0,1 |
10 - 200 |
20 |
|
Цезий |
24,5 |
0,67 |
0,4 |
2 - 10 |
20 |
|
Цезий |
6,1 |
0,67 |
0,1 |
10 - 320 |
20 |
|
Ртуть |
3,14 |
0,7 |
0 |
6 - 310 |
25 |
|
Ртуть и магниевые амальгамы |
5,88 |
0,7 |
0,3 |
7 - 1100 |
25 |
|
5,52 |
0,67 |
0 |
100 - 1200 |
25 |
|
|
7,67 |
0,67 |
0 |
100 - 1200 |
25 |
Обобщение эмпирических формул для расчета теплоотдачи при развитом кипении натрия, калия и цезия приводит к формулам:
для p/pсг = 4·10-5 ÷ 10-3:
![]() (325)
(325)
для p/pсг = 10-3 ÷ 2·10-2:
![]() (326)
(326)
где q - Вт/м2;
r - Дж/кг;
s - Н/м = Дж/м2;
λ - Вт/(м · К);
ρ - кг/м3;
Ts - температура насыщения, К;
р - давление, МПа;
pсг - критическое давление, МПа.
Удовлетворительные результаты расчета теплоотдачи при развитом кипении металлов дает также критериальная формула:
![]() (327)
(327)
где Nu = a·d/λ';
Ре = (q/r·р")с·ρ'·l/λ';
![]() ;
;
![]() ;
;
λ', Ts, ρ' - параметры на линии насыщения;
ρ" - плотность насыщенного пара.
2) Кризис теплообмена при кипении металлов в большом объеме.
Основные отличия между характеристиками кризиса теплообмена в жидких металлах и обычных жидкостях связаны с различием коэффициентов теплопроводности и углов смачивания.
Большую роль (по сравнению с обычными жидкостями) играет кризис, наступающий в области неустойчивого кипения, которое характерно для малых приведенных давлений (р/рсг). В жидких металлах при пузырьковом кипении значительная доля тепла отводится от поверхности за счет теплопроводности и конвекции.
Для щелочных металлов и ртути критические тепловые нагрузки при кипении в большом объеме могут быть оценены по формуле:
или для щелочных металлов по формуле:
где B = 1,203,
C = 4,50 для развитого устойчивого пузырькового кипения;
B = 1,203,
C = 1,80 для неустойчивого пузырькового кипения.
В формулах (328), (329): r - кДж/кг; g - м/с2; ρ - кг/м3; s - Н/м; р, рсг - МПа; qсг - МВт/м2.
Среднеквадратичная s погрешность расчета qсг составляет 15 %.
3) Пленочное кипение.
Тепловой поток при пленочном кипении
может быть представлен в виде суммы двух составляющих: q
= qcon + qи, где
![]() ,
qcon - конвективная составляющая;
,
qcon - конвективная составляющая; ![]() - составляющая, связанная с излучением
через паровую пленку (рассчитывается по формулам теплообмена излучения).
- составляющая, связанная с излучением
через паровую пленку (рассчитывается по формулам теплообмена излучения).
Конвективная составляющая рассчитывается по соотношению:
![]() (330)
(330)
где
Nu = a/λ";
![]()
![]()
![]()
![]() - эффективная теплота парообразования
(разность между теплосодержанием пара при средней температуре Тf
= (Tw
+ Ts)/2
и теплосодержанием жидкости при Ts); l
- характерный размер, длина Лапласа; А = 0,42 ÷ 0,72 по данным разных авторов.
- эффективная теплота парообразования
(разность между теплосодержанием пара при средней температуре Тf
= (Tw
+ Ts)/2
и теплосодержанием жидкости при Ts); l
- характерный размер, длина Лапласа; А = 0,42 ÷ 0,72 по данным разных авторов.
4) Кипение металлов в каналах.
При кипении металлов в каналах уже при
паросодержаниях в несколько процентов наступает дисперсно-кольцевой режим. Это
является следствием низких приведенных давлений - p/pсг. Фазовый переход в этом
случае, как правило, осуществляется испарением металла с поверхности пристенной
пленки без образования пузырьков пара на стенке. Это связано с малой толщиной и
высокой теплопроводностью жидкой пленки. Эффективные коэффициенты теплообмена
при этом достигают сотен кВт/м2·К.
Влияние массовой скорости и массового паросодержания невелико. В неустойчивых
(пульсирующих) потоках металлов коэффициенты теплообмена ниже, чем в
стационарных. Различают четыре области теплоотдачи при кипении металлов в
каналах: 1) область перегрева жидкости (она может отсутствовать!); 2) область
развитого кипения (интенсивного теплообмена), 0 < х < xlim; 3)
переходная область, ![]() ; 4) область ухудшенного теплообмена
(закризисная область),
; 4) область ухудшенного теплообмена
(закризисная область), ![]() .
.
Область перегрева жидкости. Наличие перегрева связано с отсутствием на поверхности действующих центров парообразования. Для их активации необходим перегрев поверхности. Степень перегрева может быть оценена по формуле:
![]() (331)
(331)
где ![]() -
перегрев стенки по отношению к температуре насыщения;
-
перегрев стенки по отношению к температуре насыщения;
ps - давление насыщения в Н/м2;
r - теплота парообразования в Дж/кг;
s - поверхностное натяжение в Н/м2;
dm - диаметр впадины шероховатости, м.
Область развитого кипения
(интенсивного теплообмена). Область
развитого кипения охватывает паросодержание от нуля до ![]() . Чтобы расчитать
коэффициент теплоотдачи при кипении металлов в трубах можно воспользоваться
формулами, полученными для случая кипения металлов в большом объеме. Для
расчета теплового потока и паросодержания на границе между областью
интенсивного теплообмена и переходной областью получены зависимости:
. Чтобы расчитать
коэффициент теплоотдачи при кипении металлов в трубах можно воспользоваться
формулами, полученными для случая кипения металлов в большом объеме. Для
расчета теплового потока и паросодержания на границе между областью
интенсивного теплообмена и переходной областью получены зависимости:
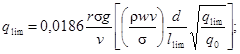 (332)
(332)
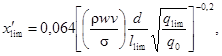 (333)
(333)
где q0 - тепловой поток при х = 0, Вт/м2;
llim - длина зоны развитого кипения;
ρw - массовая скорость.
Другой метод расчета интенсивности теплообмена при кипении в каналах основывается на определении DТa = q/a = DTпл + DTф. Здесь DTпл ≈ q·d(1 - j)/4λ', - перепад температуры в пленке, где (1 - j) находится по зависимостям соответствующих разделов; DTф - разность температур, обусловленная фазовым переходом при испарении:
![]()
где М - молекулярная масса;
b - коэффициент испарения;
R - универсальная газовая постоянная.
Переходная область. Предполагается, что в переходной области часть поверхности
(ω) омывается жидкостью, а остальная часть (1 - ω) - паром, ![]() , где х
- текущее массовое паросодержание;
, где х
- текущее массовое паросодержание; ![]() -
массовое паросодержание в начале переходной области;
-
массовое паросодержание в начале переходной области; ![]() - массовое
паросодержание в конце переходной области:
- массовое
паросодержание в конце переходной области:
![]() (334)
(334)
Коэффициент теплоотдачи находят по формуле:
где a' - коэффициент теплоотдачи в
начале переходной области при ![]() ;
;
a" - коэффициент теплоотдачи к влажному пару;
q - тепловой поток в соответствующем сечении;
λw - коэффициент теплопроводности материала стенки;
s = 3,2 · 10-3 м - эмпирическая величина.
Закризисная область (область ухудшенного теплообмена). Коэффициент теплоотдачи в закризисной зоне с некоторым запасом (то есть он будет несколько занижен) рассчитывается по формуле для сухого насыщенного пара:
Nu" = 0,023(Re")8 · (Pr")0,4, (336)
где все физические свойства относятся к сухому насыщенному пару.
Для парокалиевой смеси, текущей в змеевиковых трубах, при давлениях 0,1 ÷ 0,3 МПа рекомендуется формула:
Nu" = 0,017(Reсм)0,8 · (Prw)0,8 · Y, (337)
где ![]()
![]() для ρ/ρ" < 450;
для ρ/ρ" < 450;
Y = 1 + 70(1 - х) для ρ/ρ" > 450.
5) Кризис теплоотдачи при кипении металлов в трубах.
Основные различия между характеристиками кризиса теплоотдачи в жидких металлах и обычных жидкостях связаны с различием коэффициентов теплопроводности и степени смачиваемости. Большую роль по сравнению с обычными жидкостями играет кризис теплоотдачи, возникающий в области неустойчивого кипения, которое характерно для небольших приведенных давлений P/Pк.
В жидких металлах при пузырьковом кипении значительная доля тепла отводится от теплоотдающей поверхности за счет теплопроводности и конвекции.
Критическая плотность теплового потока при кипении в трубах калия рассчитывается по формуле:
где qкр - МВт/м2;
pw - кг/(м2·с);
L - м;
dвн - м;
хвх - относительная энтальпия калия на входе.
Пределы применимости формулы (338): P = 0,013 ÷ 0,41 МПа; L/dвн = 30 ÷ 100; ρw = 20 ÷ 325 кг/(м2·с).
Среднеквадратичная D погрешность расчета qкр составляет ± 15 %.
Критическая плотность теплового потока при кипении в трубах натрия, калия и цезия рассчитывается по формуле:
где qкр - МВт/м2;
r - кДж/кг;
ρ - кг/м3;
ρw - кг/(м2·с);
P - МПа;
L - м;
dвн - м.
Пределы применимости формулы (339): P/Pкр = (0,1 ÷ 8,3) 10-; ρw = 20 ÷ 1530 кг/(м2·с); L/dвн = 25 ÷ 150.
Среднеквадратичная а погрешность расчета qкр составляет 15 %.
6) Кризис теплоотдачи при кипении жидких металлов в кольцевых каналах.
Критическая плотность теплового потока при кипении натрия, калия и цезия в кольцевых каналах рассчитывается по формуле:
![]() (340)
(340)
где FП - полная смоченная поверхность кольцевого канала, м2;
FT - поверхность теплоотдачи кольцевого канала, м2;
dг - гидравлический диаметр кольцевого канала, м;
r - кДж/кг;
ρ - кг/м3;
ρw - кг/(м2·с);
dг - м;
Р - МПа;
qкр - МВт/м2.
Пределы применимости формулы: P/Pкр = (0,1 ÷ 8,3) ·10-2; ρw = 20 ÷ 1530 кг/(м2·с); L/dвн = 25 ÷ 150.
Среднеквадратичная s погрешность расчета qкр составляет 15 %.
7) Кризис теплоотдачи при испарении жидких металлов из капиллярных структур.
Капиллярные структуры тепловых труб и паровых камер разделяются на две группы:
капиллярные структуры, которые работают только в испарительном режиме;
капиллярные структуры, которые работают в испарительном режиме и в режиме кипения.
К кризисным явлениям (недопустимый перегрев или пережог теплопередающей стенки) в капиллярных структурах первой группы приводят: капиллярное ограничение, ограничение из-за уноса жидкости потоком пара и вскипание теплоносителя.
К кризисным явлениям в капиллярных структурах второй группы приводят: капиллярное ограничение, ограничение из-за уноса жидкости потоком пара, а также процессы, связанные с кипением теплоносителя.
Критическая плотность теплового потока при свободномолекулярном и промежуточных режимах испарения натрия из прямоугольных канавок (Kn > 0,10) рассчитывается по формуле:
![]() T0 = Ts(P0); T
= Ts(P);
T0 = Ts(P0); T
= Ts(P);
Пределы применимости формулы (341): ![]() .
.
Погрешность D расчета qсг составляет:
при Kn > 1 - ± 30 %;
при 0,1 < Kn < 1,0 - ± 50 %.
Критическая плотность теплового потока при сплошном режиме испарения натрия из прямоугольных канавок (Kn < 1) рассчитывается по формуле:
Пределы применимости формулы (342): ![]()
Погрешность D расчета qсг составляет ± 50 %.
В формулах этого раздела:
Kn = L/Rпор - число Кнудсена, где L - средняя длина свободного пробега молекул, м, которая рассчитывается по формуле:
![]()
где К - постоянная Больцмана, Дж/кг;
µ" - динамическая вязкость пара, Нм;
m - масса молекулы, кг;
Р - давление паров теплоносителя над капиллярной структурой, Па;
T - температура теплоносителя над капиллярной структурой, К;
Т0 - температура поверхности испаряющей жидкости, К;
![]() - суммарные потери давления в контуре циркуляции
теплоносителя;
- суммарные потери давления в контуре циркуляции
теплоносителя;
DРs - капиллярное давление в мениске, Па;
Rпор - радиус поры капиллярной структуры, м;
b - половина ширины канавок, м;
d - ширина выступов канавок, м;
константы а и b приведены в таблице № 17.
Результаты опытных данных для кипения натрия и калия в трубах описываются зависимостью:
![]() (343)
(343)
где (ρw) = 50 ÷ 800 кг/(м2·с);
паросодержание на входе xin = Cp(Ts - Tin)/r;
-0,4 < xin < 0;
l/d = 30 ÷ 166,
r - теплота испарения, Дж/кг.
Таблица № 17
Константы a, b
|
a |
b |
|
|
Трубы |
0,216 |
0,807 |
|
Пучки с дистанционирующими решетками |
0,209 |
0,746 |
|
Пучки с дистанционированием витой проволокой |
0,224 |
0,766 |
Обобщение опытных данных разных исследователей для кризиса теплообмена в трубах, кольцевых каналах для натрия, калия, цезия позволяет рекомендовать зависимость:
где Fт - поверхность теплообмена;
Fп - полная смоченная поверхность;
qcr - МВт/м2;
(ρw) - кг/(м2·с);
r - кДж/кг.
Пределы применимости формулы (344): l/d = 25 ÷ 150; G = 20 ÷ 1530 кг/(м2·с); p/pк = (0,1 ÷ 8,3)10-2.
21. Теплообмен при конденсации.
Интенсивность теплообмена паров металлов мало зависит от характера течения пленки конденсата из-за высокой теплопроводности металлов. Определяющую роль в этом случае играют два эффекта:
- преобладающим является термическое сопротивление фазового перехода (при относительно малых температурах и давлениях насыщенного пара коэффициент конденсации b < 1);
- наличие в парах неконденсирующихся газов, что очень трудно учесть.
Поток пара к поверхности (кг·м-2·с-1) определяется соотношением:
![]() (345)
(345)
где j - масса пара, конденсирующаяся в единицу времени на единице поверхности;
b - безразмерный коэффициент конденсации, равный отношению числа сконденсировавшихся молекул к числу всех молекул пара, падающих на поверхность жидкости;
рs и Ts - давление и температура насыщенного пара в объеме;
р - давление на линии насыщения, соответствующее температуре поверхности пленки Т;
Ri - индивидуальная газовая постоянная.
Тепловой поток через поверхность рассчитывается: q = rj. Соотношение для коэффициента теплообмена имеет вид:
![]() (346)
(346)
где pw - давление насыщенного пара при температуре стенки Tw.
При p < 103
Па коэффициент конденсации f = 1.
С увеличением давления коэффициент конденсации падает по закону: ![]() .
.
1) Теплоотдача при пленочной конденсации чистых паров металлов на твердой поверхности.
Теплоотдача при пленочной конденсации чистых паров металлов на твердой поверхности рассчитывается по формуле:
![]() (347)
(347)
где aф - коэффициент теплоотдачи фазового перехода, который для любых конфигураций поверхности конденсации рассчитывается по формуле:
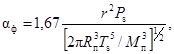 (348)
(348)
или
где f - коэффициент конденсации, равный единице для жидких металлов при низком давлении;
Rп - газовая постоянная пара, Дж/(кгК);
Мп - безразмерный молекулярный вес пара,
aпл - коэффициент теплоотдачи собственно при пленочной конденсации паров металлов.
Погрешность D расчета aф составляет ± 30 %.
Средний по поверхности коэффициент теплоотдачи при пленочной конденсации чистых паров металлов на вертикальной поверхности (ламинарное течение пленки конденсата, Reпл = 4G/µ' < 1600) рассчитывается:
при постоянном по высоте конденсатора температурном напоре по формуле:
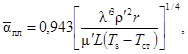 (350)
(350)
где L - высота поверхности конденсата, м.
Погрешность D расчета ![]() составляет
± 20 %.
составляет
± 20 %.
при постоянной по высоте конденсатора плотности теплового потока по формуле:
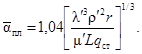 (351)
(351)
Погрешность D расчета ![]() составляет
± 20 %.
составляет
± 20 %.
Средний коэффициент теплоотдачи при пленочной конденсации чистых паров металлов на внешней поверхности горизонтальных труб (ламинарное течение пленки конденсата, Reпл - 4G/µ' < 1600) рассчитывается:
при постоянном по длине конденсатора температурном напоре по формуле:
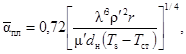 (352)
(352)
где dн - наружный диаметр трубы, м.
Погрешность D расчета ![]() составляет
± 20 %;
составляет
± 20 %;
при постоянной по длине конденсатора плотности теплового потока по формуле:
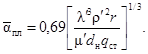 (353)
(353)
Погрешность D расчета ![]() составляет
± 20 %.
составляет
± 20 %.
Средний коэффициент теплоотдачи при пленочной конденсации чистых паров металлов на плоской поверхности под действием быстродвижущегося конденсирующегося пара рассчитывается:
при ламинарном течении пленки конденсата (Reпл = 4G/µ' < 1600) по формуле:
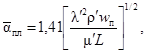 (354)
(354)
где L - длина поверхности конденсации, м;
wп - скорость пара, м/с.
Погрешность D расчета ![]() составляет
± 40 %;
составляет
± 40 %;
при турбулентном течении пленки конденсата (Reпл = 4G/µ' > 1600) по формуле:
где ![]()
![]()
![]()
Погрешность D расчета ![]() составляет ± 40 %.
составляет ± 40 %.
В формулах (349) ÷ (355): a - Вт/(м2·К); λ - Вт/(м·К); ρ - кг/м3; µ - кг/(с·м); r - кДж/кг; q - Вт/м2; g - м/с2; v - м2/с; G - массовый расход конденсата на единицу ширины конденсатора, кг/(с·м).
2) Тепломассообмен при пленочной конденсации на твердой поверхности смеси из паров металлов и неконденсирующихся газов.
Интенсивность теплообмена при конденсации паров металлов сильно зависит от чистоты паров. Даже малые примеси газов к парам приводят к резкому снижению теплоотдачи. Это связано с тем, что вблизи поверхности теплообмена образуется слой с повышенной концентрацией газа в паре. Распределение концентраций в таком слое при отсутствии движения пара вдоль поверхности конденсации определяется законами диффузии.
Средний по поверхности коэффициент массоотдачи при конденсации на плоской поверхности неподвижной смеси из паров металлов и неконденсирующихся газов (конвекция в парогазовой смеси отсутствует) рассчитывается по формуле:
где ![]() - приведенная толщина слоя
неконденсирующегося газа у поверхности конденсации, м;
- приведенная толщина слоя
неконденсирующегося газа у поверхности конденсации, м;
![]() - коэффициент массоотдачи, кг/с;
- коэффициент массоотдачи, кг/с;
Dп - коэффициент взаимной диффузии, м2/с;
![]()
где
|
п = 1,80; |
с = 1,60 |
- для смеси калий-аргон; |
|
п = 1,80; |
с = 2,30 |
- для смеси калий-азот; |
|
п = 1,90; |
с = 3,30 |
- для смеси калий-гелий; |
|
п = 1,90; |
с = 3,80 |
- для смеси калий-водород; |
|
Т - К; |
Р - Па. |
В формуле (356): Mп - безразмерный молекулярный вес пара; Mг - безразмерный молекулярный вес газа; Rп - газовая постоянная пара, Дж/(кг·К); Rг - газовая постоянная газа, Дж/(кг·К); mг - масса конденсирующегося газа, кг; Т - среднеарифметическая температура парогазового слоя, К; F - площадь поверхности конденсации, м2.
Погрешность D расчета ![]() составляет ± 30 %.
составляет ± 30 %.
Средний коэффициент массоотдачи при конденсации парогазовой смеси, движущейся внутри труб (поток на входе гидродинамически стабилизирован), рассчитывается по формуле:
где 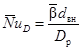 ;
;
![]() - коэффициент диффузии,
отнесенный к градиенту парциального давления пара;
- коэффициент диффузии,
отнесенный к градиенту парциального давления пара;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В формуле: q - Вт/м2; dвн - м; P - Па; Тп - температура пара, К; Pг - парциальное давление газа, Па; wсм - м/с; µ - кг/(с·м); v - м2/с; ρ - кг/м; r - кДж/кг; Rп - газовая постоянная пара, Дж/(кг·К); Рсм - давление парогазовой смеси, Па.
Пределы применимости формулы (357): eг = 0,01 ÷ 0,75; ПD = 3 ÷ 35; Reсм = 850 ÷ 1700; PrD = 0,13 ÷ 0,70; L/dвн = 1 ÷ 24; Rп/Rг = 0,1 ÷ 1,0.
Погрешность D расчета ![]() составляет ±
30 %.
составляет ±
30 %.
Средний коэффициент массоотдачи при конденсации парогазовой смеси с небольшим содержанием паров металла, движущегося внутри труб, рассчитывается по формуле:
где с = 0,017 - для смеси калий - азот, калий - аргон;
с = 0,022 - для смеси цезий - аргон.
В формуле (358) критерии подобия, величины и размерности величин те же, что в формулах (356), (357).
Пределы применимости формулы (358): ![]() ; Reсм = 1000 ÷ 11300; Pп - парциальное давление пара, Па.
; Reсм = 1000 ÷ 11300; Pп - парциальное давление пара, Па.
Погрешность D расчета ![]() составляет
± 30 %.
составляет
± 30 %.
3) Тепломассообмен при капельной конденсации паров металлов.
Коэффициент теплоотдачи при капельной конденсации неподвижного чистого ртутного пара на поверхности из нержавеющей стали рассчитывается по формуле:
где ![]() - термическое сопротивление фазового
перехода;
- термическое сопротивление фазового
перехода;
![]() - термическое сопротивление жидкого конденсата;
- термическое сопротивление жидкого конденсата;
![]() - добавочное термическое
сопротивление, обусловленное локальным подводом тепла к стенке конденсатора
только через капли;
- добавочное термическое
сопротивление, обусловленное локальным подводом тепла к стенке конденсатора
только через капли;
![]() - усредненное отношение поверхности капель к
поверхности конденсатора.
- усредненное отношение поверхности капель к
поверхности конденсатора.
Комплексы, входящие в формулу (359) имеют следующие значения:
при капельной конденсации ртутного пара на вертикальной поверхности из нержавеющей стали, окисленной при комнатной температуре:
![]()
![]()
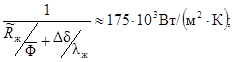
при капельной конденсации ртутного пара на вертикальной поверхности из нержавеющей стали, окисленной при температуре 550 °C:
![]()
![]()
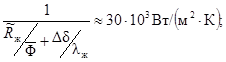
при капельной конденсации ртутного пара на горизонтальной поверхности из нержавеющей стали, окисленной при комнатной температуре:
![]()
![]()
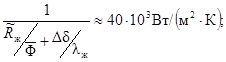
В формулах раздела: aкк - Вт/(м2·К); λ - Вт/(м·К).
Погрешность D расчета aкк составляет ± 40 %.
СОДЕРЖАНИЕ
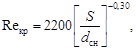
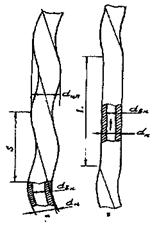
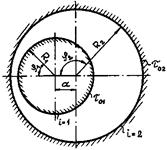
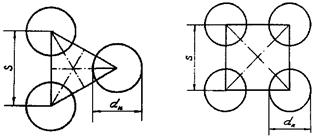
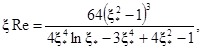 (26)
(26)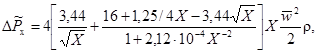
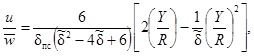
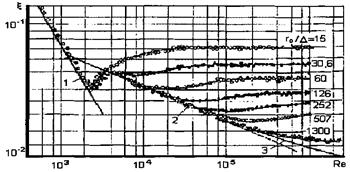
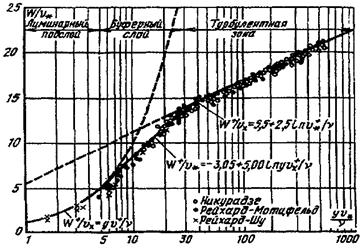
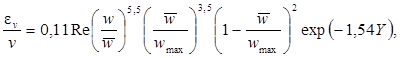
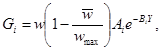
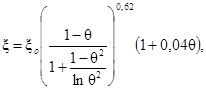 (48)
(48)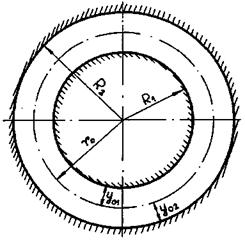
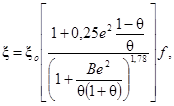
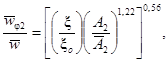
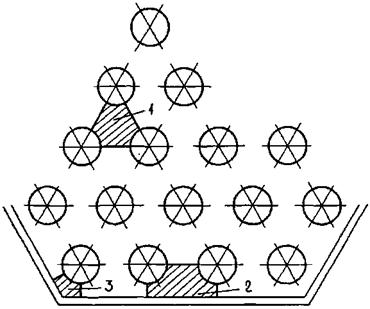
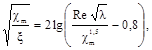
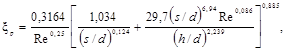
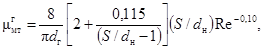 (65)
(65)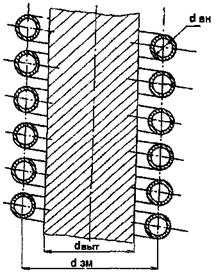
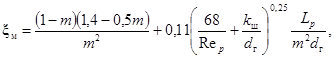
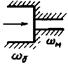
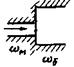
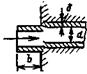
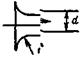
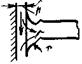
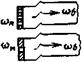
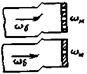
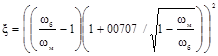 (78)
(78)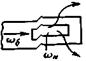
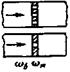
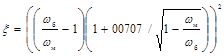
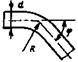
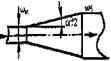
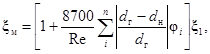
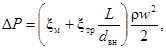
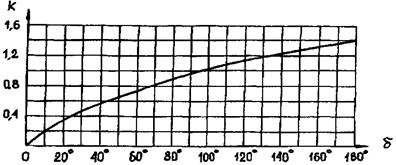
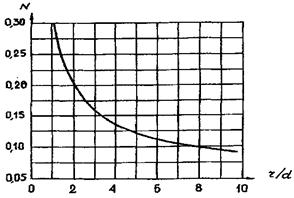
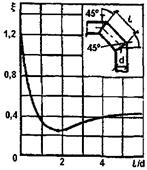
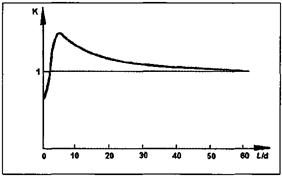
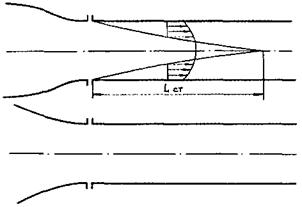
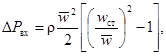
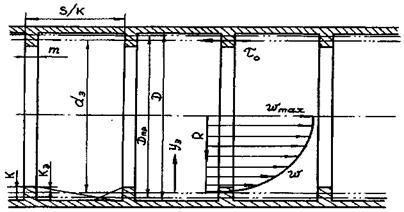
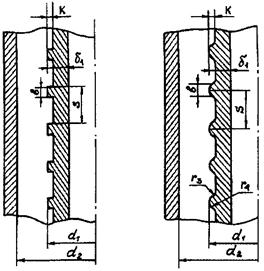
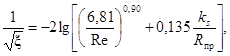 (103)
(103)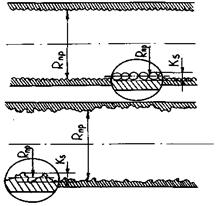
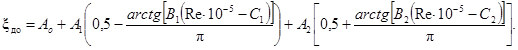 (116)
(116)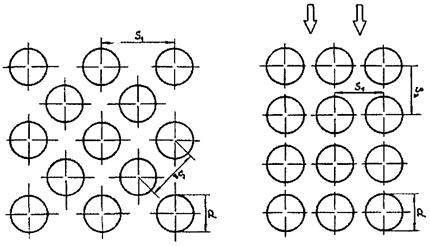
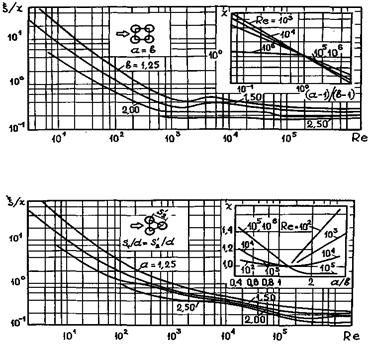
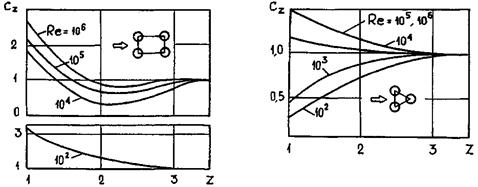
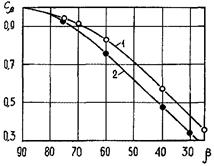
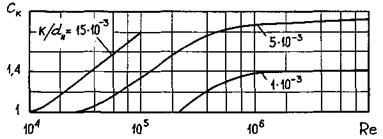
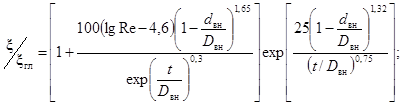
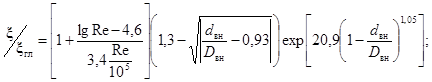
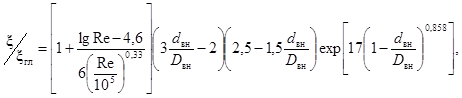
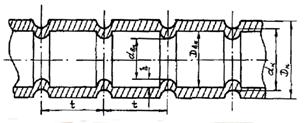
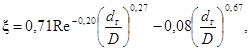 (127)
(127)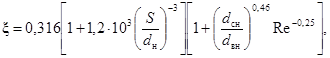 (128)
(128)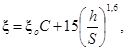 (130)
(130)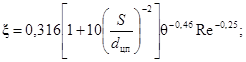 (131)
(131)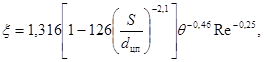
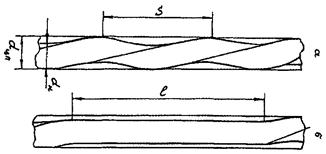
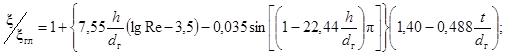
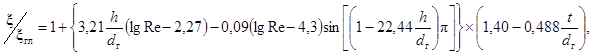
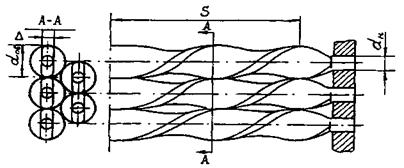
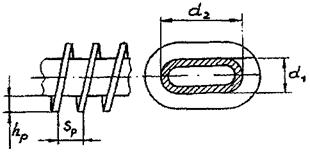
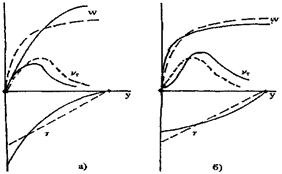
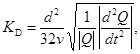 (159)
(159)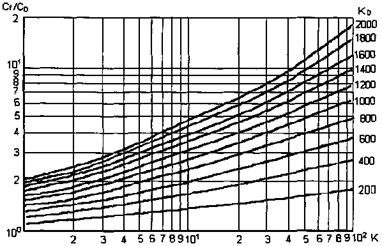
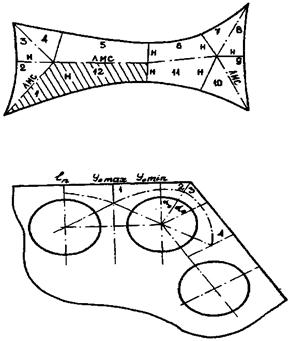
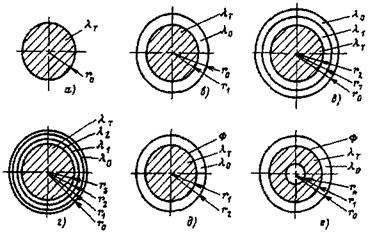
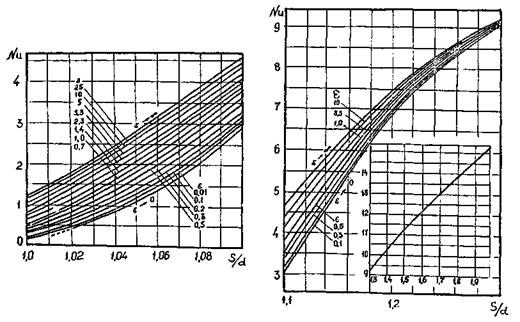
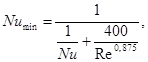 (198)
(198)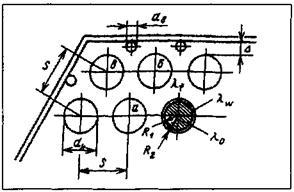
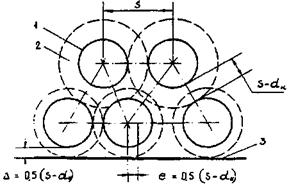
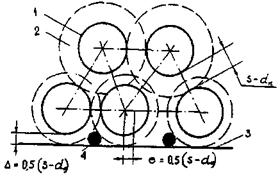
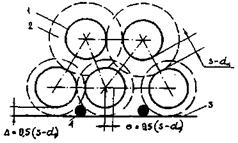
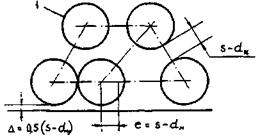
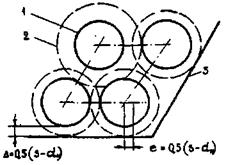
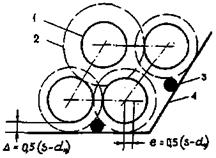
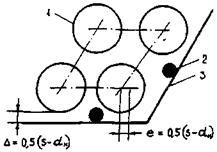
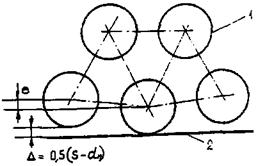
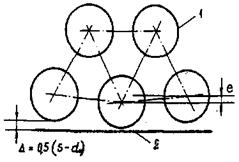
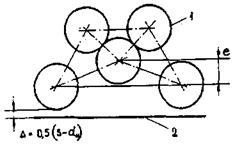
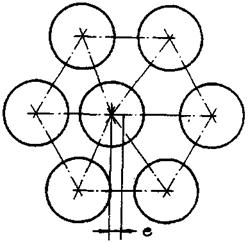
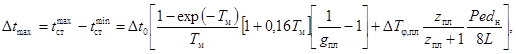 (255)
(255)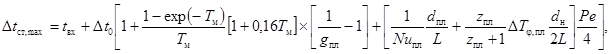 (256)
(256)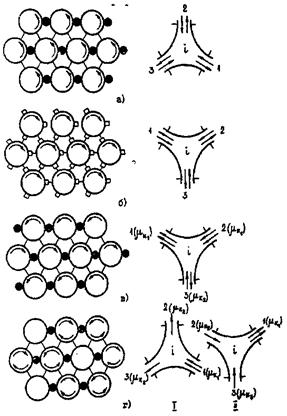
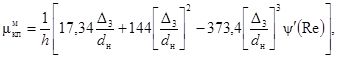 (268)
(268)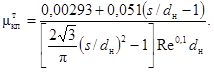
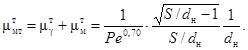
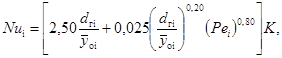
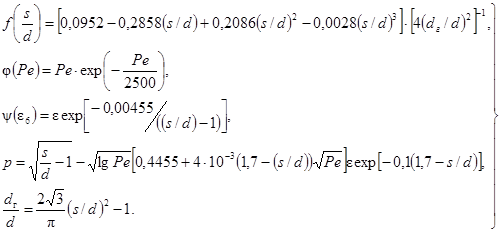 (292)
(292)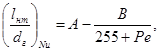 (293)
(293)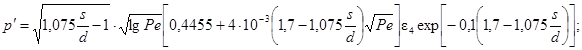
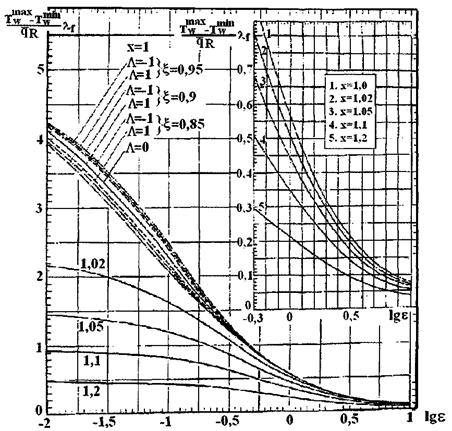
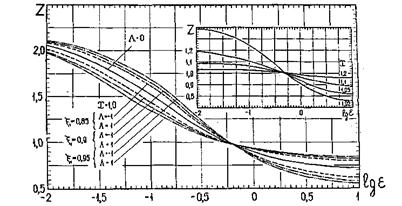
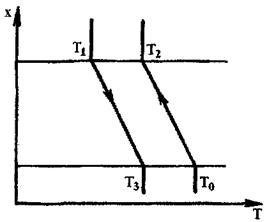
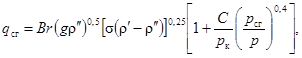
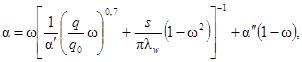 (335)
(335)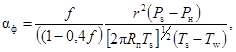
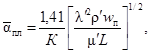 (355)
(355)