Государственная система обеспечения
единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ МНОГОКРАТНЫЕ

Методы обработки результатов измерений.
Основные положения

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о стандарте

1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ им. Д.И. Менделеева») Федерального агентства по техническому регулированию и метрологии

2 ВНЕСЕН Управлением метрологии Федерального агентства по техническому регулированию и метрологии

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 декабря 2011 г. № 1045-ст

4 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

СОДЕРЖАНИЕ

Государственная система обеспечения единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ МНОГОКРАТНЫЕ

Методы обработки результатов измерений.
Основные положения

Дата введения - 2013-01-01

1 Область применения

Настоящий стандарт распространяется на прямые многократные независимые измерения и устанавливает основные положения методов обработки результатов этих измерений и вычисления погрешностей оценки измеряемой величины.

В настоящем стандарте учтены требования, предъявляемые к методам и результатам измерений в соответствии с ГОСТ Р 5725-1, ГОСТ Р 5725-2, ГОСТ Р 5725-3, ГОСТ Р 5725-4, ГОСТ Р 5725-5, ГОСТ Р 5725-6.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения

ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений

ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений

ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений

ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями.

3.1

3.2 неисправленный результат измерений величины: Результат измерений величины, полученный до введения в него поправки в целях устранения систематических погрешностей.

3.3 исправленный результат измерений величины: Результат измерений величины, полученный после введения поправки в целях устранения систематических погрешностей в неисправленный результат измерений величины.

3.4 неисправленная оценка измеряемой величины: Среднее арифметическое значение результатов измерений величины до введения в них поправки в целях устранения систематических погрешностей.

3.5 исправленная оценка измеряемой величины: Среднее арифметическое значение результатов измерений величины после введения поправки в целях устранения систематических погрешностей в неисправленную оценку измеряемой величины.

3.6 группа результатов измерений величин: Несколько результатов измерений (не менее четырех, п ³ 4), полученных при измерениях одной и той же величины, выполненных с одинаковой тщательностью, одним и тем же средством измерений, одним и тем же методом и одним и тем же оператором.

3.7 погрешность измерения: Разность между результатом измерения величины и действительным (опорным) значением величины.

3.8 случайная погрешность измерения; случайная погрешность: Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

3.9 систематическая погрешность измерения; систематическая погрешность: Составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

3.10 неисключенная систематическая погрешность измерения: Составляющая погрешности измерения, обусловленная погрешностью оценивания систематической погрешности, на которую введена поправка, или систематической погрешностью, на которую поправка не введена.

3.11 грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей.

4 Общие положения

4.1 Необходимость выполнения прямых многократных измерений устанавливают в конкретных методиках измерений.

Примечание - Под многократными измерениями понимают не менее четырех измерений.

4.2 При статистической обработке группы результатов прямых многократных независимых измерений выполняют следующие операции:

- исключают известные систематические погрешности из результатов измерений;

- вычисляют оценку измеряемой величины;

- вычисляют среднее квадратическое отклонение результатов измерений;

- проверяют наличие грубых погрешностей и при необходимости исключают их;

- проверяют гипотезу о принадлежности результатов измерений нормальному распределению:

- вычисляют доверительные границы случайной погрешности (доверительную случайную погрешность) оценки измеряемой величины;

- вычисляют доверительные границы (границы) неисключенной систематической погрешности оценки измеряемой величины;

- вычисляют доверительные границы погрешности оценки измеряемой величины.

4.3 Проверку гипотезы о том, что результаты измерений принадлежат нормальному распределению, проводят с уровнем значимости q от 10 % до 2 %. Конкретные значения уровней значимости должны быть указаны в конкретной методике измерений.

4.4 Для определения доверительных границ погрешности оценки измеряемой величины доверительную вероятность Р принимают равной 0,95.

В случаях, когда измерение не представляется возможным повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99.

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается кроме доверительной вероятности Р = 0,99 указывать более высокую доверительную вероятность.

4.5 В настоящем стандарте изложены требования к методам обработки результатов измерений и к оцениванию точности измеряемой величины посредством погрешностей.

5 Оценка измеряемой величины и среднее квадратическое отклонение

5.1 Оценку измеряемой величины , за которую принимают среднее арифметическое значение исправленных результатов измерений, вычисляют по формуле

                                                            (1)

где х_i - i-й результат измерений;

п - число исправленных результатов измерений.

Примечание - Если во всех результатах измерений содержится постоянная систематическая погрешность, ее допускается исключить после вычисления среднего арифметического значения неисправленных результатов измерений.

5.2 В целях удобства вычислений формулу (1) допускается записать в виде

                                                       (2)

где а - близкое к  значение, удобное для расчета;

у_i = х_i - а.

5.3 Среднее квадратическое отклонение S группы, содержащей п результатов измерений, вычисляют по формуле

                                                      (3)

Примечание - Наличие случайных погрешностей вызывает рассеяние результатов измерений. В качестве основной числовой характеристики случайного рассеяния результатов измерений принята дисперсия D = σ² или стандартное отклонение σ. Ограниченное число результатов измерений позволяет получать лишь оценки этих характеристик (S² и S). Математическое ожидание оценки S² равно дисперсии (M[S²] = σ²), однако математическое ожидание оценки S отлично от σ, так как оценка S смещена.

Несмещенную оценку S допускается вычислять по упрощенной формуле

В этом случае смещение оценки S не более 1 %.

5.4 Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины)  вычисляют по формуле

                                                          (4)

6 Исключение грубых погрешностей

6.1 Для исключения грубых погрешностей используют критерий Граббса. Статистический критерий Граббса исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению. Для этого вычисляют критерии Граббса G₁ и G₂, предполагая, что наибольший х_mах или наименьший x_min результат измерений вызван грубыми погрешностями:

                                           (5)

Сравнивают G₁ и G₂ с теоретическим значением G_T критерия Граббса при выбранном уровне значимости q. Таблица критических значений критерия Граббса приведена в приложении А.

Если G₁ > G_T, то x_max исключают как маловероятное значение. Если G₂ > G_T, то x_min исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонения ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.

Если G₁ £ G_T, то х_mах не считают промахом и его сохраняют в ряду результатов измерений. Если G₂ £ G_T, то x_min не считают промахом и его сохраняют в ряду результатов измерений.

7 Доверительные границы случайной погрешности

7.1 Доверительные границы случайной погрешности оценки измеряемой величины в соответствии с настоящим стандартом устанавливают для результатов измерений, принадлежащих нормальному распределению.

При невыполнении этого условия методы вычисления доверительных границ случайной погрешности должны быть указаны в методике измерений.

7.2 При числе результатов измерений п £ 15 принадлежность их к нормальному распределению не проверяют. При этом вычисление доверительных границ случайной погрешности оценки измеряемой величины по методике, предусмотренной настоящим стандартом, допускается только в том случае, если заранее известно, что результаты измерений принадлежат нормальному распределению.

Примечание - Если не известно распределение погрешностей оценки искомой величины, способы нахождения доверительных границ случайной погрешности могут быть указаны в методике измерений с учетом того, что подобные измерения повторяют.

7.3 При числе результатов измерений 15 < п £ 50 для проверки принадлежности их к нормальному распределению предпочтителен составной критерий, приведенный в приложении Б.

7.4 При числе результатов измерений п > 50 для проверки принадлежности их к нормальному распределению предпочтителен один из критериев: χ² К. Пирсона или ω² Мизеса-Смирнова. Критерий К. Пирсона χ² приведен в приложении В, критерий ω² Мизеса-Смирнова - в приложении Г.

7.5 Доверительные границы ε (без учета знака) случайной погрешности оценки измеряемой величины вычисляют по формуле

                                                                 (6)

где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов измерений п находят по таблице, приведенной в приложении Д.

8 Доверительные границы неисключенной систематической погрешности

8.1 Неисключенная систематическая погрешность (далее - НСП) оценки измеряемой величины образуется из составляющих, в качестве которых могут быть приняты НСП:

- метода;

- средства измерений;

- вызванные другими источниками.

В качестве границ составляющих НСП принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

8.2 Границу НСП Θ_Σ оценки измеряемой величины при наличии менее трех (т < 3) НСП, каждая из которых представлена границами Θ_i, оценивают по формуле

                                                     (7)

8.3 При наличии трех и более составляющих НСП распределение внутри границ этих составляющих (погрешности средств измерений каждого типа, погрешности поправок и т.д.) рассматривают как распределение случайных величин. При отсутствии данных о виде распределения случайных величин их распределения принимают равномерными.

8.4 При числе составляющих НСП более или равном трем (т ³ 3) доверительные границы НСП Θ_Σ (Р) оценки измеряемой величины вычисляют путем построения композиции НСП. При равномерном распределении НСП доверительные границы Θ_Σ (Р) допускается вычислять по формуле

                                                    (8)

где Θ_i - граница i-й НСП;

k - коэффициент, определяемый принятой доверительной вероятностью, числом составляющих НСП и их соотношением между собой.

Для доверительной вероятности Р = 0,95 коэффициент k пренебрежимо мало зависит от числа составляющих НСП и их соотношения, поэтому при указанной доверительной вероятности коэффициент k принимают равным 1,1.

Для доверительной вероятности Р = 0,99 коэффициент k принимают равным 1,4, если число суммируемых НСП более четырех (т > 4). Если же число суммируемых НСП равно четырем или менее четырех (m £ 4), то коэффициент k определяют по графику зависимости k = f(m, l), приведенному на рисунке 1, где ось абсцисс соответствует значениям отношения  На рисунке 1 кривая 1 соответствует т = 2; кривая 2 - m = 3; кривая 3 - т = 4.

При трех или четырех суммируемых НСП в качестве Θ₁ принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве Θ₂ следует принять ближайшую к Θ₁ составляющую.

Рисунок 1 - Зависимость k = f(m, l)

8.5 Если НСП появляется в результате исключения систематической погрешности от воздействия влияющей величины Y на измеряемую величину X, то при исключении систематической погрешности, возникающей из-за изменения этой влияющей величины, необходимо определить зависимость измеряемой величины от влияющей величины [например, Х = f(Y)]. В этом случае при вычислении границ НСП оценки измеряемой величины необходимо учитывать коэффициент влияния , получаемый при разложении функции влияния в ряд Тейлора.

При наличии одной НСП, представленной границами, и второй НСП, представленной с коэффициентом влияния, формула (7) будет иметь вид

                                                  (9)

При суммировании не более трех НСП (т £ 3), полученных от воздействия влияющих величин (и при отсутствии НСП, возникающих при непосредственном влиянии систематической погрешности на измеряемую величину), формула (7) будет иметь вид

                                                    (10)

При наличии числа μ НСП, представленных границами, и числа т - μ НСП, полученных от воздействия влияющих величин и представленных с коэффициентами влияния, формула (8) будет иметь вид

                                       (11)

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.

9 Доверительные границы погрешности оценки измеряемой величины

9.1 Доверительные границы погрешности оценки измеряемой величины находят путем построения композиции распределений случайных погрешностей и НСП, рассматриваемых как случайные величины в соответствии с 8.3. Если доверительные границы случайных погрешностей найдены в соответствии с разделом 7, границы погрешности оценки измеряемой величины Δ (без учета знака) вычисляют по формуле

Δ = KS_Σ,                                                             (12)

где К - коэффициент, зависящий от соотношения случайной составляющей погрешности и НСП.

Суммарное среднее квадратическое отклонение S_Σ оценки измеряемой величины вычисляют по формуле

                                                     (13)

где S_Θ - среднее квадратическое отклонение НСП, которое оценивают в зависимости от способа вычисления НСП по формуле

                                                           (14)

где Θ_Σ - границы НСП, которые определяют по одной из формул (7), (9), (10) или

                                                       (15)

где Θ_Σ(Р) - доверительные границы НСП, которые определяют по одной из формул (8), (11);

k - коэффициент, определяемый принятой доверительной вероятностью Р, числом составляющих НСП и их соотношением между собой.

Коэффициент К для подстановки в формулу (12) в зависимости от числа НСП определяют по эмпирическим формулам соответственно

                                           (16)

10 Форма записи оценки измеряемой величины

10.1 Оформление записи оценок измеряемых величин проводят в соответствии с правилами по межгосударственной стандартизации [2].

10.2 Округление при обработке результатов измерений выполняют в соответствии с приложением Е.

10.3 При симметричных доверительных границах погрешности оценку измеряемой величины представляют в форме

                                                             (17)

где  - оценка измеряемой величины.

Числовое значение оценки измеряемой величины должно оканчиваться цифрой того разряда, что и значение погрешности Δ.

10.4 При отсутствии данных о виде функций распределений составляющих погрешности оценки измеряемой величины и необходимости дальнейшей обработки результатов измерений или анализа погрешностей оценки измеряемой величины представляют в форме

                                                            (18)

В случае когда границы неисключенной систематической погрешности вычисляют в соответствии с 8.5, следует дополнительно указывать доверительную вероятность Р.

Примечание - Оценки  и Θ могут быть выражены в абсолютной и относительной формах.

Приложение А
(справочное)

Критические значения для критерия Граббса

Таблица А.1 - Критические значения G_T для критерия Граббса

Приложение Б
(справочное)

Проверка гипотезы о нормальности распределения результатов измерений при числе результатов измерений 15 < п £ 50

При числе результатов измерений п £ 50 нормальность их распределения проверяют с помощью составного критерия.

Б.1 Критерий

Вычисляют отношение

                                                    (Б.1)

где S^* - смещенное среднее квадратическое отклонение, вычисляемое по формуле

                                               (Б.2)

Результаты измерений в ряду считают распределенными нормально, если

d_1-q/2 <  £ d_q/2,                                                    (Б.3)

где d_1-q/2 и d_q/2 - квантили распределения, получаемые из таблицы Б.1 по n, q₁/2 и (1 - q₁/2), причем q₁ - заранее выбранный уровень значимости (1 %, 5 %, 99 % или 95 %).

Таблица Б.1 - Квантили d_q/2 и d_1-q/2 распределения

Б.2 Критерий 2

Считают, что результаты измерений принадлежат нормальному распределению, если не более т разностей  превысили значение z_p/2 × S,

где S - среднее квадратическое отклонение, вычисляемое по формуле (3);

z_P/2 - верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности Р/2.

Значения вероятности Р определяют из таблицы Б.2 по выбранному уровню значимости q₂, %, и числу результатов измерений п. Зависимость z_p/2 от Р приведена в таблице Б.3.

При уровне значимости, отличном от предусмотренных в таблице Б.2, значение Р находят путем линейной интерполяции.

При несоблюдении хотя бы одного из критериев считают, что распределение результатов измерений группы не соответствует нормальному.

Таблица Б.2 - Значения Р для вычисления z_P/2

Таблица Б.3 - Значения z_P/2

Приложение В
(справочное)

Проверка гипотезы о нормальности распределения результатов измерений
при числе измерений п > 50

В.1 При числе результатов измерений п > 50 для проверки критерия согласия теоретического распределения с практическим чаще всего используют критерий К. Пирсона. Рекомендуемые числа интервалов r в зависимости от числа результатов измерений приведены в таблице В.1. Вычисления сводят в таблицу В.2, в которой приведен алгоритм вычислений для проверки гипотезы о нормальности распределения результатов измерений. При этом группируют результаты измерений. Группирование - разделение результатов измерений от наименьшего x_min до наибольшего х_mах на r интервалов.

Таблица В.1 - Рекомендуемые числа интервалов в зависимости от числа результатов измерений

Таблица В.2 - Вспомогательная таблица для проверки распределения результатов измерений

Ширину интервала h выбирают постоянной и вычисляют по формуле

                                                    (B.1)

B.2 Установив границы интервалов, подсчитывают число результатов измерений , попавших в каждый интервал. Далее вычисляют: середины интервалов х_i0, среднее арифметическое  и среднее квадратическое отклонение результатов измерений S. Определяют число результатов измерений п_i, которое должно было бы находиться в интервале, если бы распределение результатов измерений было нормальным, по формуле

                                                                   (B.2)

где φ - плотность нормального распределения ;

 - вероятность попадания результатов измерений в i-й интервал.

B.3 Для каждого интервала вычисляют критерий К. Пирсона . Просуммировав  по всем r интервалам, получают 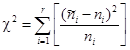 с определенным числом степеней свободы f. Для нормального распределения f = r - 3.

B.4 Выбрав уровень значимости q по таблицам распределения χ², находят нижнее χ_H² и верхнее χ_B² (значения q-процентных точек для распределения χ² приведены в таблице В.3).

Выбрав уровень значимости критерия, определяют квантили χ_H² и χ_B². Квантиль χ², вычисленный по результатам измерений, должен находиться между χ_H² и χ_B².

Таблица В.3 - Значения q-процентных точек χ_q² для распределения χ²

Приложение Г
(справочное)

Проверка гипотезы о нормальности распределения результатов измерений
при числе измерений n ³ 50, критерий ω²

Г.1 Критерий Мизеса-Смирнова ω² использует статистику, имеющую вид

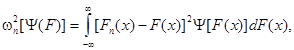
где F(x) - теоретическая функция распределения;

F_n(x) - эмпирическая функция распределения;

ψ[F(x)] - весовая функция, область определения которой представляет собой область значений функции F(x).

Конкретный вид статистики ω_п² (или, точнее, п ω_п²) зависит от вида весовой функции. Как правило, используют весовые функции двух видов: ψ(F) = 1, при которой все значения функции распределения обладают одинаковым весом, и , при которой вес результатов измерений увеличивается на «хвостах» распределений. В приведенном критерии использована весовая функция второго вида, поскольку на практике различия между распределениями наиболее отчетливы в области крайних значений. Однако почти всегда малое число результатов измерений имеется как раз в области крайних значений. Поэтому целесообразно придать этим результатам больший вес.

Если принять весовую функцию второго вида, то статистика п ω_п² после выполнения интегрирования имеет вид

    (Г.1)

где F(x_j) - значение функции теоретического распределения при значении аргумента, равном х_j (j = 1, ..., п);

х₁ £ х₂ £ ... £ х_п - результаты измерений, упорядоченные по значению.

Результаты измерений х_j рекомендуется свести в таблицу, аналогичную таблице Г.1 расчетного примера применения критерия ω², а соответствующие им значения F(x_j) внести в третий столбец таблицы, аналогичной таблице Г.2 этого же примера.

Статистика nω_n² подчиняется асимптотическому (при n → ∞) распределению

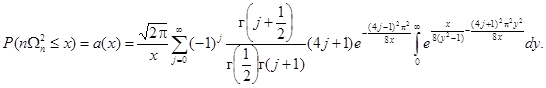
Значения функции распределения а(х) для 0 £ х < 2,6 с шагом 0,01 приведены в таблице Г.3.

Г.2 Применение критерия ω² требует выполнения большого объема вычислительных операций, но этот критерий более мощный, чем критерий Пирсона χ². Число результатов измерений при использовании этого критерия должно быть более 50.

Г.3 При использовании критерия ω² вычисления проводят в следующем порядке:

Г.3.1 Вычисляют значение статистики nω_n² по формуле (Г.1).

Промежуточные вычисления по формуле (Г.1) рекомендуется сводить в таблицу, аналогичную таблице Г.2 примера. После заполнения таблицы суммируют значения, внесенные в ее последний столбец. Значение величины nω_n² находят, подставляя полученную сумму в формулу (Г.1).

Г.3.2 По таблице Г.3 находят значение функции распределения а(х) для х, равного вычисленному значению nω_n².

Г.3.3 Задают уровень значимости α. Рекомендуется выбирать значение α, равное 0,1 или 0,2.

Г.3.4 Если а ³ (1 - α), то гипотезу о согласии эмпирического и теоретического распределений отвергают, если а < (1 - α), то гипотезу принимают.

Пример применения критерия ω²

Пример составлен при малом количестве данных в целях иллюстрации сложного вычислительного процесса при использовании критерия ω².

Результаты измерений приведены в таблице Г.1.

Таблица Г.1 - Результаты измерений

Требуется проверить гипотезу о том, что группа результатов измерений не противоречит нормальному распределению. Среднее арифметическое значение и среднее квадратическое отклонение результатов измерений, представленных в таблице Г.1, равные соответственно  = 25,4087 и S = 4,3241, приняты в качестве параметров нормального распределения, значения функции распределения которого F(x_j) представлены в третьем столбце таблицы Г.2.

Результаты дальнейших вычислений также приведены в таблице Г.2.

Таблица Г.2 - Результаты промежуточных вычислений значения статистики nω_n² по формуле (Г.1)

Сумма значений, приведенных в столбце 10 таблицы Г.2, равна минус 7,61478. Тогда результат вычисления по формуле (Г.1) будет nω_n² = -n - 2(-7,61478) = 0,229554 ≈ 0,23. Значение функции а(х), в соответствии с таблицей Г.3, для х = nω_n² = 0,23 равно 0,016. Это значение достаточно мало (0,016 < 0,8 < 0,9), следовательно, в соответствии с Г.4, гипотеза о том, что выборка принадлежит нормально распределенной генеральной совокупности, не может быть отвергнута.

Таблица Г.3 - Значения функции а(х)

Приложение Д
(справочное)

Значения коэффициентов t для случайной величины Y,
имеющей распределение Стьюдента с n - 1 степенями свободы

Таблица Д.1 - Значения коэффициентов Стьюдента t

Приложение Е
(обязательное)

Правила округления при обработке результатов измерений

Е.1 Точность результатов измерений и точность вычислений при обработке результатов измерений должны быть согласованы с требуемой точностью получаемой оценки измеряемой величины.

Е.2 Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами.

Две значащие цифры в погрешности оценки измеряемой величины сохраняют:

- при точных измерениях;

- если первая значащая цифра не более трех.

Е.3 Число цифр в промежуточных вычислениях при обработке результатов измерений должно быть на две больше, чем в окончательном результате.

Е.4 Погрешность при промежуточных вычислениях должна быть выражена не более чем тремя значащими цифрами.

Е.5 Сохраняемую значащую цифру в погрешности оценки измеряемой величины при округлении увеличивают на единицу, если отбрасываемая цифра неуказываемого младшего разряда больше либо равна пяти, и не изменяют, если она меньше пяти.

Библиография