НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ
СТРОИТЕЛЬНОЙ ФИЗИКИ (НИИСФ)
ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО КОМПЛЕКСНОМУ
ОПРЕДЕЛЕНИЮ
ТЕПЛОФИЗИЧЕСКИХ
ХАРАКТЕРИСТИК
СТРОИТЕЛЬНЫХ
МАТЕРИАЛОВ
![]()
МОСКВА СТРОЙИЗДАТ 1987
Рекомендовано к изданию решением секции № 4 научно-технического совета НИИСФ Госстроя СССР.
Описаны методика и измерительная аппаратура для комплексного определения теплофизических характеристик материалов импульсным методом. Изложены физические концепции метода, причины появления и способы компенсации систематических ошибок. Для обработки полученных результатов приведена программа для ЭВМ.
Для инженерно-технических работников научно-исследовательских и строительных организаций, занимающихся исследованием теплофизических свойств и долговечности строительных материалов.
ПРЕДИСЛОВИЕ
В НИИСФ проведен комплекс теоретических и экспериментальных исследований, связанных с физическим обоснованием импульсного метода комплексного определения теплофизических характеристик строительных материалов, выявлением систематических ошибок измерений, их оценкой и уравновешиванием. Метод позволяет применять стандартную измерительную аппаратуру в совокупности с несложной дополнительной оснасткой. Для обработки получаемого массива экспериментальных данных на ЭВМ разработана программа NNK1, составленная на языке Фортран-IV, а также для работы в режиме диалога с ЭВМ на языке Бейсик-II.
Рекомендации предназначены для экспрессного определения тепловой активности, температуропроводности, теплопроводности и объемной теплоемкости строительных материалов на образцах или изделиях без их разрушения и при одностороннем доступе.
Рекомендации разработаны в лаборатории долговечности ограждающих конструкций НИИСФ канд. техн. наук Ю.Д. Ясиным и инж. Н.Н. Кузнецовой и содержат конкретные указания по использованию методики и аппаратуры.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. К основным теплофизическим характеристикам материалов, определяемым импульсным методом, относятся:
сg - объемная теплоемкость, Дж/(м3×К);
а - коэффициент температуропроводности, м2/с;
l - коэффициент теплопроводности, Вт/(м×К);
b - коэффициент тепловой активности, Дж/(м2×с1/2×К).
Для нахождения этих характеристик достаточно определить только две любые из них, остальные рассчитывают с помощью известных уравнений связи
l = асg; ![]()
1.2. Строительные материалы относятся, как правило, к влажным капиллярно-пористым материалам. Определение их теплофизических характеристик является сложной метрологической задачей, поскольку в таких материалах осуществляется взаимосвязанный перенос тепла и влаги при наличии источников (стоков) тепла, обусловленных фазовыми превращениями влаги. При определении искомых характеристик в этом случае необходимо либо расчетным путем оценивать влияние только кондуктивной составляющей потока тепла, либо экспериментальным путем сводить к минимуму влияние конвективной составляющей и источников (стоков) тепла. Последнее практически более целесообразно, но накладывает ряд ограничений на метод определения.
1.3. Импульсные методы определения имеют неоспоримые преимущества перед другими известными методами, поскольку в пределах определенного интервала времени с момента создания теплового импульса с заданными параметрами возмущение температурного поля практически не вызывает изменения исходного влажностного состояния и, следовательно, возникновения конвективной составляющей и дополнительных источников (стоков) тепла, обусловленных фазовыми превращениями влаги.
1.4. Известные импульсные методы комплексного определения теплофизических характеристик, однако, предполагают наличие датчиков температуры либо внутри, либо на противоположной от импульсного источника стороне исследуемого образца, изделия. Эти обстоятельства существенно ограничивают возможности таких методов.
1.5. Разработанные НИИСФ способ и устройство для определения теплофизических характеристик строительных материалов1 обладают рядом неоспоримых преимуществ. Они позволяют экспрессно и комплексно определять теплофизические характеристики твердых, в том числе влажных капиллярно-пористых строительных материалов на образцах или изделиях без их нарушения и при одностороннем доступе к ним.
_____________
1 А.с. № 1122956 (СССР). Способ определения теплофизических характеристик материалов конструкций / Ю.Д. Ясин, Н.Н. Кузнецова. Опубл. в Б. И., 1984, № 41.
А.с. № 1107036 (СССР). Устройство для определения теплофизических характеристик материалов конструкций / Ю.Д. Ясин, Н.Н. Кузнецова. Опубл. в Б. И., 1984, № 29.
2. ОСНОВЫ ИМПУЛЬСНОГО МЕТОДА ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
2.1. Метод основан на частном решении теплофизической задачи об изменении избыточной температуры во времени в центре плоского импульсного источника тепла центральносимметричной формы и конечных размеров, расположенного в плоскости соприкосновения двух (эталонного и исследуемого) полубесконечных тел. Это решение получено в виде
где Dt(t) - изменяющаяся во времени избыточная температура в центре плоского импульсного источника тепла, К;
Q - количество тепла, выделенное единицей площади импульсного источника, Дж/м2;
R - радиус плоского кругового импульсного источника, эквивалентного источнику центральносимметричной формы, м; индексы «э» и «м» относятся к эталонному и исследуемому телам соответственно.
2.2. Для значений времени, соответствующих начальному периоду развития теплового процесса, решение (1) совпадает с решением аналогичной теплофизической задачи с плоским импульсным источником бесконечных размеров
2.3. Практически выражения (1) и (2) равны, если невязка в значениях избыточных температур, рассчитанных по ним, не превышает предельной абсолютной погрешности измерения температуры Dt, величина которой определяется по паспортным данным измерительного прибора. В предельном случае при t = tкр это может быть, представлено следующим образом:
Таким образом, tкр - момент времени, исчисляемый с момента возникновения импульса и разграничивающий время действия рассматриваемого теплового процесса на два интервала: t < tкр и t > tкр, т.е., когда этот процесс описывается выражениями (2) и (1) соответственно.
2.4. Значение tкр определяют из уравнения (3), например, методом последовательных приближений
где i = 1 ... n - номер
итерации; n определяется из условия ![]() , где Dt - предельная абсолютная погрешность
измерения t, которая определяется по паспортным
данным измерительного устройства.
, где Dt - предельная абсолютная погрешность
измерения t, которая определяется по паспортным
данным измерительного устройства.
2.5. Расчетные формулы, полученные из выражений (1), (2) с учетом (4), имеют вид:
для коэффициента тепловой активности
для коэффициента температуропроводности
В выражении (6) используют значение bм, найденное предварительно по формуле (5).
2.6. Коэффициент теплопроводности и объемную теплоемкость с использованием уже найденных коэффициентов тепловой активности в температуропроводности определяют по формулам:
3. ОЦЕНКА СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОТКЛОНЕНИЙ
ОБЩИЕ ПРИНЦИПЫ
3.1. Согласно общим принципам теории ошибок измерений для косвенного метода, в котором определяемый параметр в области возможных изменений описывается непрерывно дифференцируемой функцией
y = f(x1, ..., хп),
где x1, ..., хп - независимые аргументы (они же измеряемые параметры), предельная абсолютная ошибка определяемого параметра может быть выражена через предельные абсолютные ошибки измеряемых параметров по формуле
3.2. В общем случае предельная абсолютная ошибка может включать в себя систематическую и случайную составляющие:
|Ey| = |qy| + |Dy|, ![]()
Поскольку систематические ошибки смещают оценки измеряемых и определяемого параметров, они подлежат устранению. Для этого устанавливают физическую сущность каждой значимой систематической ошибки и, введением соответствующих поправок, исключают их влияние.
3.3. После устранения систематических ошибок выражение (9) имеет вид
Оно используется при априорной оценке предельной абсолютной ошибки определяемого параметра в косвенном методе, при этом значения предельных абсолютных ошибок измеряемых параметров выбирают по паспортным данным соответствующих измерительных устройств.
3.4. Кроме выражения (10) для априорных оценок могут быть использованы выражения:
или
![]() (12)
(12)
Здесь eу = Dy/у
- предельная относительная
ошибка параметра; ![]() - его среднее значение в определяемом
диапазоне изменения; sy,
- его среднее значение в определяемом
диапазоне изменения; sy, ![]() - среднеквадратические
отклонения, D = 3s.
- среднеквадратические
отклонения, D = 3s.
ПРИРОДА СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ И ИХ УСТРАНЕНИЕ
3.5. Расчетные выражения (5), (6) получены на основе решения идеализированной математической модели. Это может быть причиной образования ряда систематических ошибок, наиболее важные из которых предопределены:
толщиной и теплофизическими свойствами плоского нагревателя;
отсутствием идеального теплового контакта между плоскостями нагревателя и исследуемого материала;
фактической длительностью теплового импульса;
конечными размерами соприкасающихся тел и т.д.
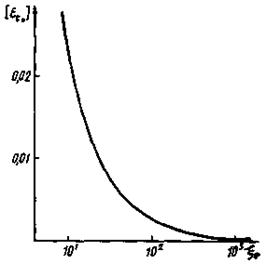
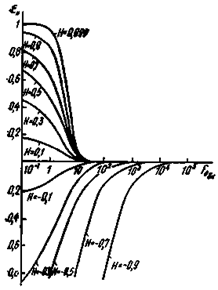
Рис. 1. Зависимость
относительной ошибки eн, обусловленной влиянием толщины и
теплофизических характеристик нагревателя от величин Н = (bм - bн)/(bм + bн),
![]()
3.6. Влияние толщины и теплофизических характеристик плоского нагревателя на значение избыточной температуры в его центре можно оценить, пользуясь известным решением симметричной относительно плоскости расположения источника тепла задачи о распространении мгновенного теплового импульса в системе, состоящей из двух полубесконечных тел и бесконечной пластины нагревателя толщиной 2dн, размещенной между ними.
где Н = (bм - bн)/(bм + bн); н - индекс принадлежности нагревателю.
Пренебрегая наличием нагревателя, т.е. полагая bн = bм = b, из выражения (13) получим
Относительная ошибка eн, обусловленная наличием нагревателя, определяется с учетом (13) и (14) по формуле
где ![]()
3.7. Графическая зависимость ![]() представленная
на рис. 1, позволяет выбрать время
измерения или подбирать параметры нагревателя таким образом, чтобы ошибка,
обусловленная его влиянием, не превышала наперед заданной величины.
представленная
на рис. 1, позволяет выбрать время
измерения или подбирать параметры нагревателя таким образом, чтобы ошибка,
обусловленная его влиянием, не превышала наперед заданной величины.
Пример. Нагреватель выполнен из фольги толщиной 2dн = 2 × 10-4 м, теплофизические характеристики которой в принятых единицах измерений находятся в диапазонах: 15 < l < 160; 5 × 10-5 < а < 1 × 10-4; 7 × 103 < b < 25 × 103. Этим условиям удовлетворяют металлы с большим удельным сопротивлением (Ом), которые и целесообразно использовать при изготовлении нагревателей. Для такого нагревателя относительная ошибка eн, монотонно убывая, уже через 2 с после подачи импульса становится меньше 2 × 10-2.
3.8. Отсутствие идеального теплового контакта, вызванное непараллельностью плоскостей нагревателя и исследуемого материала, а также наличием на его поверхности выступов и впадин, являются причиной появления систематических ошибок.
3.9. Влияние воздушных зазоров можно свести до минимума путем их заполнения консистентной смазкой с известными теплофизическими свойствами1, наличие которой в виде дополнительного слоя учитывают используя решение
где Н = (bм - bсм)/(bм + bсм);
![]()
Относительная ошибка eсм, обусловленная наличием дополнительного слоя смазки толщиной dсм, с учетом (2), (15) и (16), определяется по формуле
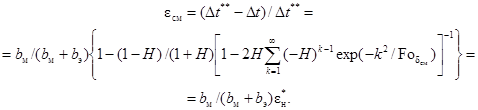 (17)
(17)
Здесь ![]() определяют по
формуле (15) либо из графической
зависимости, представленной на рис. 1,
при этом вместо теплофизических характеристик нагревателя принимают
соответствующие характеристики смазок.
определяют по
формуле (15) либо из графической
зависимости, представленной на рис. 1,
при этом вместо теплофизических характеристик нагревателя принимают
соответствующие характеристики смазок.
3.10. Поскольку значения тепловой активности консистентных смазок (солидол, графитная и контактная смазка, унитол, литол и др.)1 находятся в диапазоне 500 - 800 Дж/(м×с1/2×К) и близки к значениям тепловой активности большинства строительных материалов, относительная ошибка, обусловленная наличием слоя смазки, будет, как правило, незначительна.
_____________
1 Фройштетер Г.В., Трилиский К.К., Ищук Ю.А., Ступак П.П. Реологические и теплофизические свойства пластичных смазок. - М.: Химия, 1980.
Пример. При исследовании керамзитобетонов с
коэффициентом тепловой активности 450 < bм
< 7501 с использованием в качестве заполнения воздушных прослоек
солидола (bсм = 559 Дж/(м×с1/2×К),
согласно графической зависимости, представленной на рис. 1, для |H| <
0,15, (что соответствует рассматриваемому случаю) величина относительной ошибки
eсм и будет меньше 3 × 10-2 ¸ 5
× 10-2, начиная с ![]() или при толщине слоя смазки 2 × 10-4 (м) и температуропроводности асм
= 7 × 10-8 (м2/с),
начиная с момента времени t = 6 с.
или при толщине слоя смазки 2 × 10-4 (м) и температуропроводности асм
= 7 × 10-8 (м2/с),
начиная с момента времени t = 6 с.
______________
1 Глава СНиП II-3-79*. Строительная теплотехника. - М.: Стройиздат, 1982.
3.11. Когда относительная
ошибка eсм превышает допустимое значение, a ![]() и H > 0, коэффициент тепловой активности
материала с учетом влияния смазки рассчитывают по формуле
и H > 0, коэффициент тепловой активности
материала с учетом влияния смазки рассчитывают по формуле
bм = bсм(1 + H)/(1 - H). (18)
Здесь значение Н определяют из выражения
![]()
которое получено из (16) при учете одного члена ряда.
3.12. В математической модели, лежащей в основе метода, использовалось понятие мгновенного источника тепла. Это обязывает оценить и, если необходимо, учесть влияние длительности теплового импульса на измеряемый параметр - избыточную температуру нагревателя.
3.13. С физической точки зрения воздействие импульсного источника можно представить следующим образом: в неограниченной среде в момент времени t = 0 начал действовать плоский источник тепла постоянной мощности, затем в заданный момент t* выделение тепла источником прекращается.
3.14. Математически это можно выразить как включение в момент времени t* дополнительного отрицательного источника (стока) тепла равной (по абсолютной величине) мощности.
Избыточная температура нагревателя изменяется во времени под действием источника постоянной мощности по выражению
![]()
где q - удельная мощность нагревателя, Вт/м2.
То же, но с учетом воздействия отрицательного источника той же мощности, включенного в момент времени t*,
![]()
Рис. 2.
Зависимость относительной ошибки ![]() , обусловленной фактической
длительностью импульса, от параметра x0 = t/t*
, обусловленной фактической
длительностью импульса, от параметра x0 = t/t*
Последнее выражение таким образом описывает изменение избыточной температуры плоского нагревателя под действием импульсного источника тепла с фактической длительностью импульса t*.
3.15. Относительная ошибка обусловленная фактической длительностью импульса, определяется по формуле
![]()
где изменение избыточной температуры нагревателя под действием мгновенного источника тепла определяется выражением
![]()
откуда следует, что для t < t* ![]() а для t > t* ошибка
определяется выражением
а для t > t* ошибка
определяется выражением
где x0 = t/t*.
Зависимость (19) графически представлена на
рис. 2. С помощью последнего можно
получить представление о том интервале времени, в котором предельная относительная
ошибка ![]() не
будет превышать заданной величины.
не
будет превышать заданной величины.
3.16. Используемое в методе решение для системы полубесконечных тел будет справедливо в течение некоторого времени t < tмакс - времени сохранения условия полубесконечности исследуемого образца. Эти условия определяют, используя известное решение, описывающее распределение избыточной температуры в толще материала по нормали к плоскости нагревателя
где Qм - количество
тепла, выделенное единицей площади импульсного источника в тело исследуемого
материала, Дж/м2. Путем решения уравнения Dt¢(t) = 0 при z = zм находят
значение ![]() ,
соответствующее появлению
максимального значения температуры в плоскости z = zм
,
соответствующее появлению
максимального значения температуры в плоскости z = zм
![]()
где zм - толщина исследуемого образца или максимальная глубина проникновения импульса.
Полагая в (20), что при t = tmax
< ![]() в
плоскости z = zм
уровень полезного сигнала Dt не
превышает порога чувствительности прибора Dt, получим уравнение, определяющее условия полубесконечности
исследуемого образца
в
плоскости z = zм
уровень полезного сигнала Dt не
превышает порога чувствительности прибора Dt, получим уравнение, определяющее условия полубесконечности
исследуемого образца
решая которое относительно неизвестного параметра, можно определить его требуемое значение.
Пример. Определить время tmax, в
течение которого удовлетворяется условие полубесконечности для облицовки из
декоративного камня толщиной zм = 0,015 м с коэффициентами тепловой
активности bм = 1000 Дж/(м×с1/2×К) и температуропроводности ам
= 4 × 10-7 м2/с при
нагревателе размером R
= 0,02 м, выделяющем единицей
площади количество тепла Qм = 800 Дж/м2, при ошибке
измерения температуры Dt =
0,01 К. Искомая величина tmax с учетом условий задачи и расчетной
формулы (22) равна 98 с (с округлением
до целой секунды), что удовлетворяет условию полубесконечности, поскольку ![]() ,
вычисленное по формуле (21), разно
156 с.
,
вычисленное по формуле (21), разно
156 с.
СЛУЧАЙНЫЕ ОТКЛОНЕНИЯ И АПРИОРНАЯ ОЦЕНКА ТОЧНОСТИ
3.17. После того, как значимые систематические ошибки выявлены, проведена их оценка и показаны возможности их уравновешивания, ошибка метода будет определяться случайной составляющей, предельное значение которой можно оценить априорно, как это показано в пп. 3.3 и 3.4.
3.18. Следуя (11), выражение для нахождения предельной относительной ошибки определения коэффициента тепловой активности исследуемого материала с учетом (5) будет иметь вид
где ![]() ,
, ![]() - предельные относительные ошибки
определения коэффициентов тепловой активности исследуемого и «эталонного»
материала соответственно;
- предельные относительные ошибки
определения коэффициентов тепловой активности исследуемого и «эталонного»
материала соответственно;
et, et - предельные относительные ошибки измеряемых параметров: температуры и времени соответственно.
3.19. В свою очередь предельная относительная ошибка определения коэффициента тепловой активности «эталонного» материала с учетом (5), в котором положено bм = bэ, может быть найдена из выражения
С учетом (24) выражение (23) преобразуется к виду
![]() (25)
(25)
3.20. Поскольку избыточная температура нагревателя изменяется во временном интервале tн £ t £ tкр, ее среднее значение рассчитывается по выражению

тогда предельная относительная ошибка определяется по формуле
Формула для определения предельной относительной ошибки ½et½, полученная аналогичным образом, имеет вид
3.21. Вводя безразмерное время x1 = tкр/tн в выражения (26) и (27), получим, соответственно:
для предельной относительной
ошибки ![]()
![]() (28)
(28)
для предельной относительной
ошибки ![]()
![]() (29)
(29)
Здесь
![]()
и
![]()
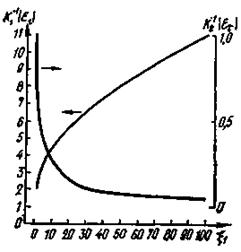
Рис. 3.
Зависимость ![]() и
и ![]() от параметра x = tкр/tн.
от параметра x = tкр/tн.
3.22. Исходя из характера
изменения предельных относительных ошибок ![]() и
и ![]() (рис. 3) их суммарная ошибка
(рис. 3) их суммарная ошибка ![]() =
= ![]() +
+ ![]() будет иметь минимум, который можно
определить исходя из условия
будет иметь минимум, который можно
определить исходя из условия ![]() Учитывая последнее, будем иметь уравнение
Учитывая последнее, будем иметь уравнение
![]() (30)
(30)
решая которое относительно x, например, итерационным методом при заданных значениях K1 и K2 можно определить оптимальное отношение tкр/tн.
3.23. Поскольку количество тепла, выделенное единицей площади импульсного источника Q, определяется из выражения
Q = Wнt*/Sн = I2rнt*/Sн = IUt*/Sн, (31)
где Wн - мощность
нагревателя, Вт; U - напряжение на клеммах нагревателя, В; I - сила тока, протекающего через
нагреватель, А; Sн - площадь нагревателя, м2; rн -
сопротивление нагревателя, Ом, предельная относительная ошибка ![]() в соответствии с измеряемыми параметрами определяется по формулам
в соответствии с измеряемыми параметрами определяется по формулам
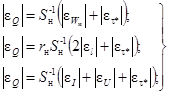 (32)
(32)
3.24. Предельная относительная ошибка определения коэффициента температуропроводности эталонного материала, согласно уравнению (1), в котором положено bм = bэ, ам = аэ, может быть определена по формуле
где
Lэ = {1 - ехр[R2/(4аэt)]}4аэt/R2.
Предельная относительная ошибка определения коэффициента температуропроводности исследуемого материала с учетом (33) может определяться из выражения
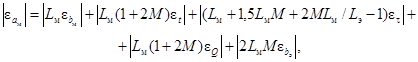 (34)
(34)
где
![]()
![]()
4. ПРОГРАММА ДЛЯ ЭВМ ПО ОБРАБОТКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
4.1. Программа NNK1 предназначена для комплексного
вычисления теплофизических характеристик строительных материалов (тепловой
активности ![]() температуропроводности
температуропроводности ![]() теплопроводности
теплопроводности
![]() объемной
теплоемкости
объемной
теплоемкости ![]() на основе импульсного неразрушающего
метода по экспериментальным данным - значениям температуры Dt½T½, измеряемой в фиксированные моменты
времени t½TAU½ в центре импульсного источника тепла, расположенного в
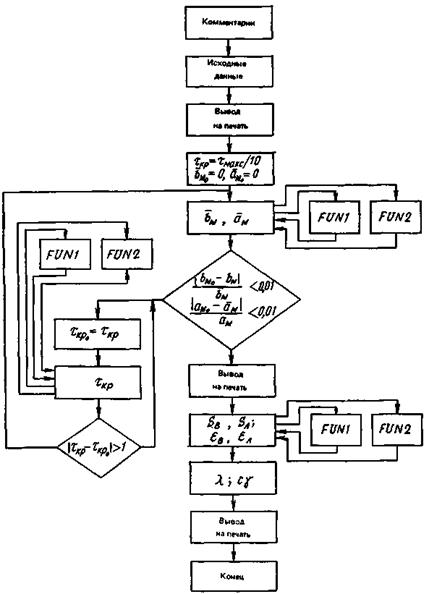
плоскости соприкосновения эталонного и исследуемого материалов. Блок-схема
программы приведена на рис. 4.
на основе импульсного неразрушающего
метода по экспериментальным данным - значениям температуры Dt½T½, измеряемой в фиксированные моменты
времени t½TAU½ в центре импульсного источника тепла, расположенного в
плоскости соприкосновения эталонного и исследуемого материалов. Блок-схема
программы приведена на рис. 4.
4.2. Программа снабжена соответствующими комментариями, включающими описание исходных данных (измеряемые параметры и параметры устройства) и определяемых характеристик с указанием единиц измерения.
4.3. Программа работает
следующим образом. После ввода исходных данных, в качестве первого приближения
назначается величина tкр, соответствующая 0,1tmax, начиная с tн,
и задаются начальные средние значения ![]() и
и ![]() . Затем для фиксированных
избыточных температур нагревателя и соответствующих моментов времени по
формулам (5) и (6) вычисляют значения bм, ам
и их средние
. Затем для фиксированных
избыточных температур нагревателя и соответствующих моментов времени по
формулам (5) и (6) вычисляют значения bм, ам
и их средние ![]() ,
, ![]() . Полученные
значения сравниваются с их первым или последующими приближениями
. Полученные
значения сравниваются с их первым или последующими приближениями ![]() и
и ![]() и, если
условия
и, если
условия
не выполняются, то происходит уточнение
значений tкр по итерационной формуле (4) в цикле, выход из которого осуществляется по условию ![]() где
где ![]() присваивается значение предыдущего приближения tкр. Таким же образом значениям
присваивается значение предыдущего приближения tкр. Таким же образом значениям ![]() и
и ![]() присваиваются
значения
присваиваются
значения ![]() и
и
![]() .
.
4.4. В случае выполнения
условий (35), значения ![]() и
и ![]() выводятся
на печать и вычисляются их среднеквадратические отклонения и относительные
ошибки. Далее по формулам (7) и (8) определяются значения l и сg. Все вычисленные значения также выводятся
на печать.
выводятся
на печать и вычисляются их среднеквадратические отклонения и относительные
ошибки. Далее по формулам (7) и (8) определяются значения l и сg. Все вычисленные значения также выводятся
на печать.
Электрическая принципиальная схема таймера (к прил. 2)
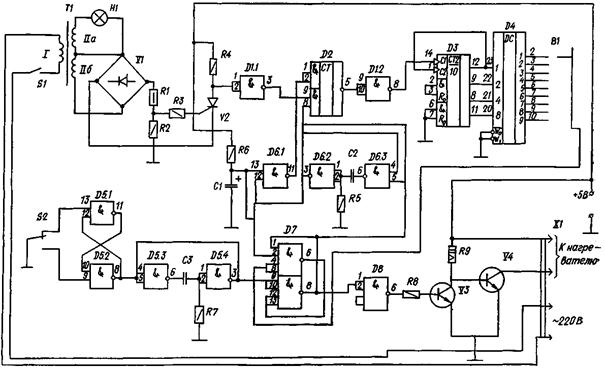
Рис. 4. Блок-схема программы NNK1
4.5. С целью более компактной записи программы использованы две подпрограммы-функции FUN1 и FUN2, реализующие общие части выражений (4), (5) и (6).
Программа NNK1, написанная на языке Фортран-IV, приведена в прил. 1.
5. ОБОРУДОВАНИЕ, ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА, ОСНАСТКА
5.1. Для комплексного определения теплофизических характеристик необходимы: первичный преобразователь и вторичные устройства для создания теплового импульса и для измерения и регистрации изменения во времени избыточной температуры нагревателя первичного преобразователя.
5.2. Для измерения и регистрации температуры может быть использован ампервольтомметр Ф30К, в комплект которого входят измерительный прибор, транскриптор и цифропечатающая электроуправляемая машина. Аналогичное устройство можно собрать из отдельных приборов, например вольтметра универсального В7-21, транскриптора Ф5033 и цифропечатающей машины ЭУМ-23Д. Возможны и другие комбинации и замены аналогичных приборов.
5.3. Устройство для создания теплового импульса состоит из стабилизированного источника питания, например Б5-21, и таймера, задающего временной интервал нагрева. В качестве таймера может быть использовано устройство, разработанное Ройфе В.С., принципиальная электрическая схема которого и перечень основных элементов к этой схеме представлены в прил. 2.
5.4. Первичный преобразователь состоит из эталонного тела (тела преобразователя), плоского нагревателя круговой или другой центральносимметричной формы и термопары, размещенной в центре нагревателя. Плоский нагреватель изготавливают из проволоки или фольги. Мощность нагревателя и его размеры, а также толщину тела первичного преобразователя выбирают исходя из представлений, изложенных выше. Для широкого круга строительных материалов характерный линейный размер плоского нагревателя можно назначить исходя из условия
где ![]() - относительная ошибка измерения температуры в момент времени tкр.
- относительная ошибка измерения температуры в момент времени tкр.
Пример. Определить параметры первичного
преобразователя для исследования материала с априорно заданными
характеристиками а = 4 ×
10-7 (м2/с), b =
1000 Дж/(м2·с1/2×К). Материалом для тела первичного преобразователя выбран
полистирол со следующими теплофизическими
характеристиками: аэ = 3 × 10-7 (м2/с), bэ =
200 Дж/(м2×с1/2×К). Измерение избыточной температуры в
центре нагревателя производят измерительно-регистрирующим устройством, например
Ф30К, с ее регистрацией через 5 с. При проведении эксперимента необходимо
обеспечивать, с одной стороны - представительность экспериментального массива
для статистической оценки искомых характеристик, а с другой - минимизировать
время эксперимента, что обусловлено требованием экспрессности метода, а также
условиями сохранения полубесконечности исследуемого образца и тела первичного
преобразователя. С этой целью выбираем количество измерений N = 30, а tmax = 150 с. Поскольку значения тепловой
активности определяются с большей надежностью, принимаем tкр = 50, что обеспечивает десять результатов измерений Dt(t) для
вычисления коэффициента bм и двадцать результатов измерений для вычисления коэффициента
температуропроводности ам. Наконец, для получения достоверных
характеристик при абсолютной ошибке измерения температуры Dt = 0,01 К, потребуем, чтобы относительная
ошибка et не превышала 1 × 10-2, при t = tкр и 2 × 10-2 при t = tmax.
Радиус нагревателя оценим по формуле (36),
при этом получим R = 2 × 10-2 м. Далее, с учетом заданных значений Dt, et(tmax), ам, bм, R по формуле (1)
найдем значения Q, обеспечивающие соответствующие точности измерения et(tкр) £ 1 × 10-2 и et(tmax) £ 2 × 10-2:
![]() = 15128 Дж/м2 и
= 15128 Дж/м2 и ![]() = 15816 Дж/м2. Положим Q = 16000 Дж/м2 и по
итерационной формуле (4) уточним
значение tкр = 56 с. Чтобы убедиться в сохранении
условий полубесконечности исследуемого образца при заданных параметрах,
предварительно оценим по формуле (20)
при z = 0 и t = tmax Qм - количество
тепла, выделенное единицей площади нагревателя в тело материала, которое
составит 13400 Дж/м2, а также определим по формуле (21)
= 15816 Дж/м2. Положим Q = 16000 Дж/м2 и по
итерационной формуле (4) уточним
значение tкр = 56 с. Чтобы убедиться в сохранении
условий полубесконечности исследуемого образца при заданных параметрах,
предварительно оценим по формуле (20)
при z = 0 и t = tmax Qм - количество
тепла, выделенное единицей площади нагревателя в тело материала, которое
составит 13400 Дж/м2, а также определим по формуле (21) ![]() - время наступления
максимального значения температуры в плоскости z = 0,05 м, равное 1122 с. Затем, пользуясь выражением (22), получим время, в течение
которого сохраняются условия полубесконечности образца - tmax = 778 с, превышающее предполагаемое в
эксперименте (tmax = 150 с).
- время наступления
максимального значения температуры в плоскости z = 0,05 м, равное 1122 с. Затем, пользуясь выражением (22), получим время, в течение
которого сохраняются условия полубесконечности образца - tmax = 778 с, превышающее предполагаемое в
эксперименте (tmax = 150 с).
Для определения толщины эталонного тела первичного преобразователя воспользуемся уравнением (22), заменив в нем индексы материала (м) на индексы эталона (э) и приняв Qэ = Q - Qм и определим глубину проникновения импульса в тело эталона за время tmax = 150 с, которая составит zэ = 0,026 м.
С целью расширения
возможностей разрабатываемого первичного преобразователя выберем zэ = 0,05 м, тогда в этой плоскости время наступления ![]() составит
1496 с, а величина Dtmax не будет превышать
Dt, что обеспечит сохранение условий полубесконечности при любом t.
составит
1496 с, а величина Dtmax не будет превышать
Dt, что обеспечит сохранение условий полубесконечности при любом t.
6. ПОДГОТОВКА И ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА. ОБРАБОТКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
6.1. Для определения коэффициентов тепловой активности bм и температуропроводности ам эталонного тела первичного преобразователя последний устанавливают на поверхности образца из того же материала, что и тело первичного преобразователя так, как это схематически показано на рис. 5. При этом плоский нагреватель с датчиком температуры и поверхность исследуемого образца должны иметь тепловой контакт.
6.3. Поскольку в данном случае исследуемый образец имеет те же теплофизические характеристики (bм = bэ, ам = аэ), расчетные формулы, полученные из выражений (1), (2) с учетом (4), имеют вид:
для коэффициента тепловой активности
для коэффициента температуропроводности
при этом в выражении (38) используют значения bэ, найденные предварительно по формуле (37).
Остальные теплофизические характеристики lэ и (сg)э рассчитывают по формулам (7) и (8).
6.4. Для определения теплофизических характеристик исследуемого материала (общий случай) производят испытание образца или изделия согласно пп. 6.1 и 6.2. Затем полученный массив экспериментальных данных обрабатывают на ЭВМ по программе NNK1.
Рис. 5. Блок-схема устройства для комплексного определения теплофизических характеристик материалов образцов и изделий
6.5. Исходный массив экспериментальных данных набивают на стандартных перфокартах в следующей последовательности:
на первой карте - численное значение экспериментального массива N форматом I3, равное количеству измерений избыточной температуры нагревателя, проведенных с начала подачи импульса;
на второй карте - значения Q, AE, BE, DT, DTAU, R;
на последующих картах - массивы значений Т и TAU по семь значений на каждой карте, причем начало массива совмещают с на чалом новой карты. Значения на второй и последующих картах набивают форматом Е11.4.
6.6. Результаты расчета представляются на дисплее или, в виде распечатки ЭВМ, снабжены соответствующими заголовками, обозначениями и не требуют дополнительных разъяснений.
Пример. Результаты расчета на ЭВМ.
Исходные данные
|
N = 30 |
|||||
|
Q = 0.3898E04 |
AE = 0.2307E-06 |
ВЕ = 0.1372Е 03 |
|||
|
DT = 0.5000Е-02 |
DTAU = 0.1000Е-01 |
R = 0.1000Е-01 |
|||
|
1 |
2 |
3 |
4 |
||
|
Т = 0.9500Е 00 |
0.6700Е 00 |
0.5400Е 00 |
0.4600Е 00 |
||
|
TAU = 0.5000Е 01 |
0.1000Е 02 |
0.1500Е 02 |
0.2000Е 00 |
||
|
5 |
6 |
7 |
8 |
||
|
Т = 0.3900Е 00 |
0.3500Е 00 |
0.3100Е 00 |
0.2700Е 00 |
||
|
TAU = 0.2500E 02 |
0.3000Е 02 |
0.3500Е 02 |
0.4000Е 00 |
||
|
9 |
10 |
11 |
12 |
||
|
Т = 0.2400Е 00 |
0.2200Е 00 |
0.2000Е 00 |
0.1900Е 02 |
||
|
TAU = 0.4500Е 02 |
0.5000Е 02 |
0.5500Е 02 |
0.6000Е 02 |
||
|
13 |
14 |
15 |
16 |
||
|
Т = 0.1700Е 00 |
0.1600Е 00 |
0.1500Е 00 |
0.1400Е 00 |
||
|
TAU = 0.6500Е 02 |
0.7000Е 02 |
0.7500Е 02 |
0.8000Е 00 |
||
|
17 |
18 |
19 |
20 |
||
|
Т = 0.1300Е 00 |
0.1200Е 00 |
0.1100Е 00 |
0.1000Е 00 |
||
|
TAU = 0.8500E 02 |
0.9000Е 02 |
0.9500Е 02 |
0.1000Е 03 |
||
|
21 |
22 |
23 |
24 |
||
|
Т = 0.9000Е-01 |
0.9000Е-01 |
0.8000Е-01 |
0.8000Е-01 |
||
|
TAU = 0.1050E 03 |
0.1100Е 03 |
0.1150Е 03 |
0.1200Е 03 |
||
|
25 |
26 |
27 |
28 |
||
|
Т = 0.8000Е-01 |
0.7000Е-01 |
0.7000Е-01 |
0.7000Е-01 |
||
|
TAU = 0.1250E 03 |
0.1300Е 03 |
0.1350Е 03 |
0.1400Е 03 |
||
|
29 |
30 |
||||
|
Т = 0.7000Е-01 |
0.6000Е-01 |
||||
|
TAU = 0.1450E 03 |
0.1500Е 03 |
||||
Расчетные данные
|
AMSR = 0.3958E-06 |
BMSR = 0.8995E 03 |
SBM = 0.1913E 01 |
|
EPSBM = 0.2127E 00 |
SAM = 0.2425E-07 |
EPSAM = 0.6128E 01 |
|
DLAMB = 0.5659E 00 |
CGAM = 0.1430E 07 |
6.7. Необходимо регулярно проводить опытную проверку метода и устройства на образцовых мерах, согласно пп. 6.1 и 6.2, расчет их теплофизических характеристик, согласно п. 6.4.
Проверку согласия между
имеющимися значениями теплофизических характеристик образцовых мер и
соответствующими установленными значениями осуществляют с помощью ![]() -критерия по
формуле
-критерия по
формуле
![]() (39)
(39)
при
![]() (40)
(40)
где ![]() ,
, ![]() - средние значения
сравниваемых (известной и экспериментально определенной) теплофизических
характеристик, образцовой меры соответственно;
- средние значения
сравниваемых (известной и экспериментально определенной) теплофизических
характеристик, образцовой меры соответственно; ![]() ,
, ![]() - их выборочные дисперсии; n1, n2 - количество измерений; v - число степеней свободы.
- их выборочные дисперсии; n1, n2 - количество измерений; v - число степеней свободы.
Полученное значение ![]() сравнивают
с
сравнивают
с ![]() при
принятом уровне значимости и производят оценку согласия.
при
принятом уровне значимости и производят оценку согласия.
Пример. Провести опытную проверку метода и устройства, используя в качестве образцовых мер:
стекло ЛК-5 ![]() = 1,17
Вт/(м×К);
= 1,17
Вт/(м×К);
оптическое стекло ![]() = 0,91
Вт/(м×К);
= 0,91
Вт/(м×К);
оргстекло ![]() = 0,196 Вт/(м×К);
= 0,196 Вт/(м×К);
коэффициент теплопроводности которых представлен метрологической службой. Из-за отсутствия других статистических характеристик образцовых мер положим S1 = 0 и n1 = ∞. Средние значения тепло-физических характеристик этих материалов, экспериментально полученных предлагаемым методом на устройстве, представлены в таблице, где, кроме того, даны среднеквадратические отклонения и объем выборок.
Таблица
|
|
|
|
|
|
|
|
|
|
Вт/(м×К) |
кДж/(м3×К) |
кДж/(м×с1/2×К) |
м2/с |
||||
|
Стекло ЛК-5 (n = 8) |
|||||||
|
1,15 |
0,06 |
1960 |
120 |
1,500 |
0,028 |
5,9 |
0,48 |
|
Стекло оптическое (n = 6) |
|||||||
|
0,92 |
0,05 |
2200 |
132 |
1,420 |
0,026 |
4,2 |
0,34 |
|
Оргстекло (n = 7) |
|||||||
|
0,198 |
0,017 |
1600 |
135 |
0,563 |
0,011 |
0,23 |
0,11 |
Проверка согласия
между имеющимися по данным метрологической службы значениями теплопроводности
образцовых мер и соответствующими значениями, полученными по методу и на
устройстве, показала, что сравниваемые значения статистически неразличимы,
поскольку ![]() -критерий оказался меньше
-критерий оказался меньше ![]() при общепринятом уровне значимости р = 0,05.
при общепринятом уровне значимости р = 0,05.
ПРИЛОЖЕНИЕ 1
Программа NNK1
С
С КОМПЛЕКСНОЕ ВЫЧИСЛЕНИЕ ТЕПЛОФИЗИЧЕСКИХ
С ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
С С ИСПОЛЬЗОВАНИЕМ ИМПУЛЬСНОГО
С НЕРАЗРУШАЮЩЕГО МЕТОДА/А.С. № 1107036,
С № 1122956/ПО ЗНАЧЕНИЯМ ТЕМПЕРАТУРЫ Т,
С ИЗМЕРЯЕМОЙ В ФИКСИРОВАННЫЕ МОМЕНТЫ
С ВРЕМЕНИ TAU В ЦЕНТРЕ НАГРЕВАТЕЛЯ,
С РАСПОЛОЖЕННОГО В ПЛОСКОСТИ
С СОПРИКОСНОВЕНИЯ ЭТАЛОННОГО
С И ИССЛЕДУЕМОГО МАТЕРИАЛОВ.
С
С ИСХОДНЫЕ ДАННЫЕ
С
С ИЗМЕРЯЕМЫЕ ПАРАМЕТРЫ
С Т - ИЗБЫТОЧНАЯ ТЕМПЕРАТУРА (ГРАД),
С TAU - ВРЕМЯ (С),
С N - КОЛИЧЕСТВО ИЗМЕРЕНИЙ,
С
С ПАРАМЕТРЫ УСТРОЙСТВА
С R, Q - РАДИУС (М) И МОЩНОСТЬ
С НАГРЕВАТЕЛЯ (ДЖ/(М**2)),
С АЕ, BE - ТЕМПЕРАТУРОПРОВОДНОСТЬ (М**2/С)
С И ТЕПЛОВАЯ АКТИВНОСТЬ (ДЖ/(M**2*SQRT(C)**
С ГРАД)) ЭТАЛОНА,
С DT, DTAU - ТОЧНОСТИ ИЗМЕРЕНИИ ТЕМПЕРАТУРЫ
С И ВРЕМЕНИ,
С ОПРЕДЕЛЯЕМЫЕ ПАРАМЕТРЫ
С AM - ТЕМПЕРАТУРОПРОВОДНОСТЬ (М**2/С),
С ВМ - ТЕПЛОВАЯ АКТИВНОСТЬ (ДЖ/(М**2 SQRT
С (С)* ГРАД)),
С DLAMB - ТЕПЛОПРОВОДНОСТЬ (ВТ/(М*ГРАД)),
С CGAM - ОБЪЕМНАЯ ТЕПЛОЕМКОСТЬ (ДЖ/(М**2*ГРАД)).
С SAM, SBM - СРЕДНЕКВАДРАТИЧЕСКИЕ ОТКЛОНЕНИЯ
С AM, BM,
С EPSAM, EPSBM - ОТНОСИТЕЛЬНЫЕ ОШИБКИ
С ОПРЕДЕЛЕНИЯ AM, BM.
С INTEGER N,INDEX(300)
С REAL Q, АЕ, BE, DT, TAU, R,
С IT (300), TAU (300)
С READ (5,51) N
51 FORMAT(1 3)
WRITE (6, 61) N
61 FORMAT(5X, ИСХОДНЫЕ ДАННЫЕ/
13X, ¢N =¢, 13)
READ (5,52) Q, AE, BE, DT, DTAU, R
52 FORMAT (7E11.4)
WRITE (6,62) Q, AE, BE, DT, DTAU, R
62 FORMAT (3X, ¢Q =¢, E11.4, 1X, ¢AE =¢,
E11.4, 1X, ¢BE =¢, E11.4,/
23X, ¢DT =¢, E11.4, 1X, ¢DTAU =¢, E11.4, 1X, ¢R =¢, E11.4)
READ(5, 52) (T(I), I = 1, N)
DO 10 I = 1, N
INDEX(I) = I
10 CONTINUE
DO 11 L1 = 1, N, 5
L2 = L1 + 4
IF(N.LT.L2) L2 = N
WRITE(6,70) (INDEX(I), I = LI, L2)
70 FORMAT (10I12)
WRITE(6,71) (T(I), I = L1, L2)
71 FORMAT(3X, ¢T =¢, 10Е12.4)
WRITE (6,72) (TAU(I) I = I1, L2)
72 FORMAT(3X, ¢TAU =¢, 10E12.4)
11 CONTINUE
RR = -R*R/4.0
Q = Q*0.5642
TAUKR = TAU(N)/10.0
BMSRO = 0.0
AMSRO = 0.0
100 CONTINUE
BMSUM = 0.0
K = 0
DO 12 I = 1, N
IF(TAU(I).GE.TAUKR) GO TO 15
K = K + 1
BM = FUN2(T(1).Q.TAU(1)) - BE
BMSUM = BMSUM + BM
12 CONTINUE
15 CONTINUE
AK = FLOAT(K)
BMSR = BMSUM/AK
AMSUM = 0.0
L = 0
K1 = K + 1
DO 16 I = K1, N
L = L + 1
AM = RR/(TAU(I)*ALOG(1.0 - BMSR/(FUN2(
IT(I), Q, TAU(I)) - FUN1(AE, BE, RR, TAU(I)))))
AMSUM = AMSUM + AM
16 CONTINUE
AL = FLOAT(L)
AMSR = AMSUM/AL
A1 = ABS(BMSRO - BMSR)/BMSR
A2 = ABS(AMSRO - AMSR)/AMSR
IF(A1.LE.0.01.AND.A2.LE.0.01) GO TO 101
17 CONTINUE
TAUKRO = TAUKR
P2 = 1.0/(BE + BMSR) - 1.0/FUN2(DT.Q.TAUKRO))
P1 = 1.0 - BMSR/(P2 - FUN1(AE, BE, RR, TAUKRO))
TAUKR = RR/(AMSR ALOG(P1))
IF (ABS(TAUKRO).GT.1.0) GO TO 17
AMSRO = AMSR
BMSRO = BMSR
GO TO 100
101 CONTINUE
WRITE(6,65) AMSR, BMSR
65 FORMAT (5Х, ¢РАСЧЕТНЫЕ ДАННЫЕ¢/
13X, ¢AMSR =¢, E11.4,1X, ¢BMSR =¢, E11.4)
K = 0
SB = 0
DO 22 I = 1, N
IF(TAU(I).GE.TAUKR) GO TO 25
K = K + 1
В = FUN2(T(1), Q, TOU(1)) - BE - BMSR
B = B*B
SB = SB + B
22 CONTINUE
25 CONTINUE
P = K - 1
X = 0.0
IF(P.EQ.O.O) GO TO 55
OB = SQRT(SB/P)
X = 1.0
EPSBM = OB*100.0/BMSR
55 CONTINUE
L = 0
SA = 0
K1 = K + 1
DO 26 I = K1, N
IF(TAU(I).LE.TAUKR) GOTO 27
L = L + 1
A = RR/(TAU(I)*ALOG(1.0 - BMSR/(FUN2(T(I), Q, TAU(I))
1 - FUN1(AE, BE, RR, TAU(I))))) - AMSR
A = A*A
SA = SA + A
26 CONTINUE
27 CONTINUE
P = L - 1
Y = 0.0
IF(P.EQ.O.O) GO TO 57
OA = SQRT(SA/P)
Y = 1.0
EPSAM = OA*100.0/AMSR
57 CONTINUE
IF(X.EQ.O.O.OR.Y.EQ.O.O.) GO TO 85
DLAMB = BMSR*SQRT(AMSR)
CGAM = BMSR/SQRT(AMSR)
WRITE (6,67) OB, EPSBM
67 FORMAT(3X, ¢SBM =¢, E11.4, 1X, ¢EPSBM =¢, E11.4)
WRITE (6,68) OA, EPSAM
68 FORMAT(3X, ¢SAM =¢, E11.4, 1X, ¢EPSAM =¢, E11.4)
WRITE (6,78) DLAMB, CGAM
78 FORMAT (3X, ¢DLAMB =¢, E11.4, 1X, ¢CGAM =¢, E11.4)
85 CONTINUE
STOP
END
FUNCTION FUN1(AE, BE, RR, TAUI)
REAL AE, BE, RR, TAUI
FUN1 = BE/(1.0 - EXP(RR/AE/TAUI))
RETURN
END
FUNCTION FUN2(TDT, Q, TAUI)
REAL TDT, Q, TAUI
FUN2 = Q/(TDT*SQRT(TAUI))
RETURN
END
Приложение 2
Перечень элементов к электрической принципиальной схеме таймера
(см. рис. на с. 16 - 17)
|
Обозначение на схеме |
Элементы |
||
|
наименование |
тип |
номинал |
|
|
R1 |
Резистор |
МЛТ-0,5 |
200 Ом |
|
R2 |
» |
МЛТ-0,125 |
100 Ом |
|
R3 |
» |
» |
620 Ом |
|
R4 |
» |
» |
2 кОм |
|
R5 |
» |
» |
240 Ом |
|
R6 |
» |
» |
1 кОм |
|
R7 |
» |
» |
240 Ом |
|
R8 |
» |
» |
100 Ом |
|
R9 |
» |
ПЭВ-7 |
10 Ом |
|
С1 |
Конденсатор |
К53-16 |
10 мкФ |
|
С2 |
» |
клс |
0,1 мкФ |
|
С3 |
» |
То же |
0,1 мкФ |
|
V1 |
Диодная сборка |
КД-9068 |
|
|
V2 |
Тиристор |
КУ10.1А |
|
|
V3 |
Транзистор |
КТ 801Б |
|
|
V4 |
» |
КТ 803А |
|
|
D1 |
Микросхема интегральная |
К155ЛА3 |
|
|
D2 |
То же |
К155 ИЕ1 |
|
|
D3 |
» |
К155 ИЕ2 |
|
|
D4 |
» |
К155 ИЕ3 |
|
|
D5 |
» |
К155 ЛА3 |
|
|
D6 |
» |
К155 ЛА6 |
|
|
D7 |
» |
К155 ЛА1 |
|
|
D8 |
» |
К155 ЛА6 |
|
|
Т1 |
Трансформатор |
220В/(2´98) |
|
|
X1 |
Разъем |
2РМ-145-4И-161 |
|
|
S1 |
Тумблер |
ТВ-1 |
|
|
S2 |
Кнопка |
МАЗ |
|
|
В1 |
Переключатель галетный |
11 положений |
|
СОДЕРЖАНИЕ
 (1)
(1)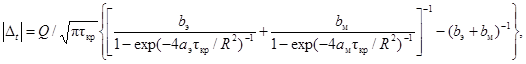 (3)
(3)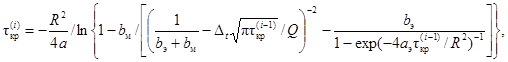 (4)
(4)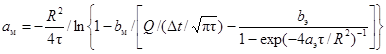
 (15)
(15)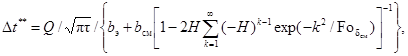 (16)
(16)