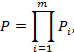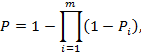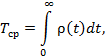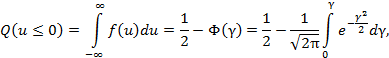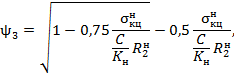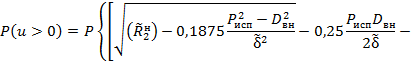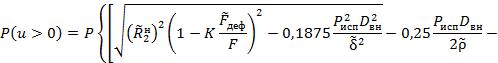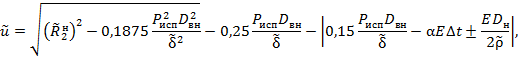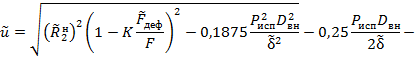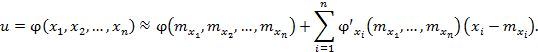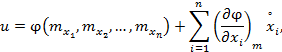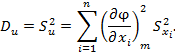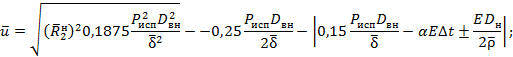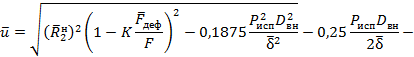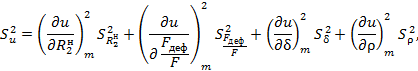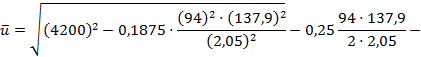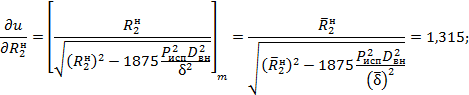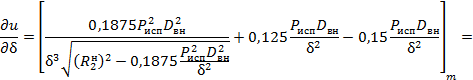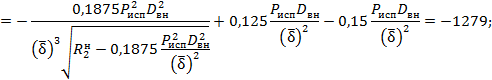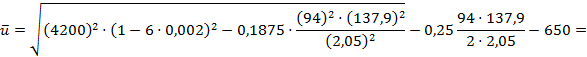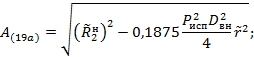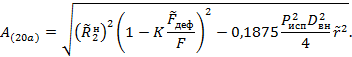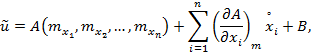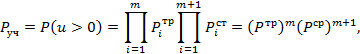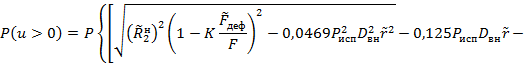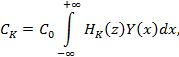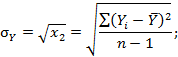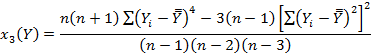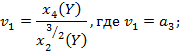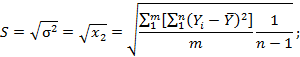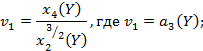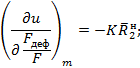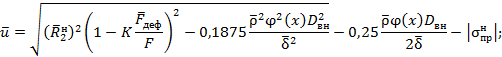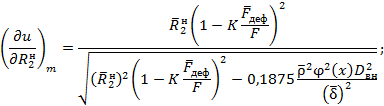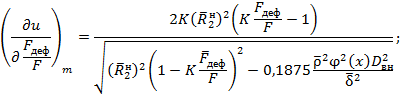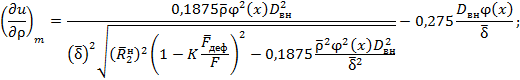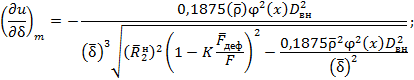МИНИСТЕРСТВО
СТРОИТЕЛЬСТВА ПРЕДПРИЯТИЙ
НЕФТЯНОЙ И ГАЗОВОЙ ПРОМЫШЛЕННОСТИ
ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ПО СТРОИТЕЛЬСТВУ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
ВНИИСТ
РУКОВОДСТВО
ПО ИНЖЕНЕРНОЙ ОЦЕНКЕ
И ПРОГНОЗИРОВАНИЮ ФАКТИЧЕСКОЙ
КОНСТРУКТИВНОЙ НАДЕЖНОСТИ
МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
Р 301-77
Москва 1978
«Руководство по инженерной оценке и прогнозированию фактической конструктивной надежности магистральных трубопроводов» посвящено вопросам использования вероятностных методов для оценки и прогнозирования конструктивной надежности при сооружении магистральных трубопроводов.
Разработка Руководства - первый этап работы над созданием практических вероятностных методов расчета конструктивной надежности трубопроводов.
В руководстве рассмотрен наиболее распространенный способ прокладки трубопроводов - подземная прокладка в обычных грунтовых условиях.
Применение настоящего Руководства имеет целью апробацию предложенных методов оценки фактической конструктивной надежности трубопроводов.
Руководство разработано в лаборатории надежности конструкций трубопроводов кандидатами техн. наук:
В.В. Рождественским, В.Д. Шапиро, Н.Я. Пономаревой, старшим инженером Л.Г. Холстовой и руководителем группы лаборатории математических методов исследования Г.А. Шацкой.
|
Внесено ВНИИСТом (ЛНК) |
Утверждено
ВНИИСТом |
Разработано впервые |
СОДЕРЖАНИЕ
|
ВНИИСТ |
Руководство
по инженерной оценке |
Р 301-77 |
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Под конструктивной надежностью магистрального трубопровода в соответствии [1] следует понимать его свойство сопротивляться внешним и внутренним нагрузкам и воздействиям, сопутствующим перекачке продукта, без нарушений герметичности и оговоренных предельных состояний при соблюдении правил эксплуатации, технического обслуживания и ремонта.
1.2. Под отказом трубопровода следует подразумевать любое нарушение герметичности трубопровода или нарушение любого из оговоренных СНиП II-45-75 предельных состояний.
1.3. Основными задачами повышения конструктивной надежности являются:
уменьшение количества отказов на единицу длины трубопровода в единицу времени иначе - повышение безотказности трубопровода);
повышение долговечности, т.е. срока службы трубопровода.
1.4. Повышение конструктивной надежности магистральных трубопроводов во многом способствует повышению их функциональной надежности, т.е. повышению эффективности нефте- и газоснабжения.
1.5. Трубопровод как конструктивная система должен включать элементы, выполняющие только конструктивные и конструктивно-технологические функции: трубы, сварные соединения, компенсаторы, опоры под трубопроводы (при надземной прокладке), кривые вставки, изоляцию, арматуру и др. Элементы, выполняющие только технологическую роль и влияющие только на процесс перекачки продукта (промысловое оборудование, газо- или нефтеперекачивающие агрегаты и т.д.), из рассмотрения конструктивной надежности магистрального трубопровода исключают. Вопросы конструктивной надежности технологического оборудования, наземных сооружений и других объектов, входящих в нефте- или газотранспортную систему, должны изучаться самостоятельно.
1.6. Надежность* трубопровода определяется надежностью всех перечисленных выше конструктивных элементов. При рассмотрении однониточного трубопровода его надежность определяется как надежность системы с последовательным соединением зависимых элементов [2]. При рассмотрении многониточного трубопровода или трубопровода, включающего резервные нитки, лупинги, его надежность должна определяться как надежность системы с последовательно-параллельным (смешанным) соединением зависимых элементов.
________
*Здесь и далее под «надежностью» подразумевается конструктивная надежность.
1.7. Учет взаимной зависимости элементов трубопроводов при оценке надежности системы имеет важное значение. Между последовательно соединенными элементами трубопровода существует определенная зависимость: на все его элементы или участки одновременно воздействуют одни и те же факторы: температура, внутреннее давление, упругий изгиб - проектный или случайный, собственная масса, масса вышележащих слоев и отпор грунта, что в соответствии с теорией надежности делает все элементы трубопровода более надежными, чем если бы все эти нагрузки и воздействия каждый из элементов испытывал вне связи с другими элементами. С точки зрения строительной механики указанный факт объясняется перераспределением усилий, характерным для любого участка трубопровода как статически неопределимой конструкции.
2. ПУТИ ОБЕСПЕЧЕНИЯ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ
ПРИ СТРОИТЕЛЬСТВЕ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
2.1. Задачи повышения надежности конструкций трубопроводов можно подразделить (рис. 1) на:
задачи обеспечения требуемого уровня надежности в предэксплуатационный период, т.е. в процессе изготовления материалов, труб и деталей для трубопроводов, выполнения проектно-изыскательских работ, при транспортировке труб, строительстве, предэксплуатационных испытаниях;
задачи поддержания должного уровня надежности при эксплуатации.
В настоящем руководстве рассматриваются задачи обеспечения требуемого уровня надежности.
2.2. Имеются два пути решения задач обеспечения конструктивной надежности в предэксплуатационный период (см. рис. 1).
Первый (практический)путь включает:
тщательнее расследование специальными межотраслевыми комиссиями отказов, происходящих при испытаниях и эксплуатации трубопроводов;
установление причин отказов (которые могут быть, например, металлургического, строительного, эксплуатационного характера);
воздействие на эти причины и их учет в дальнейшем, т.е. при проектировании, изготовлении труб, сооружении новых трубопроводов. Сюда же следует отнести и непосредственную корректировку технологических процессов (металлургических, листо- и трубопрокатных, сварочных и других ) на основании сигналов, поступающих от исполнителей текущих или последующих операций в процессе производства и контроля качества. Такие сигналы, указывая на допущенные дефекты, отклонения, нарушения СНиП и ТУ на данном или предыдущем этапах производства, помогают восстанавливать на этих этапах нормальный ход технологических процессов, что способствует правильному формированию надежности трубопроводов.
2.3. Если определить причины возникновения тех или иных отказов или дефектов затруднительно, к анализу причин должны подключаться специализированные лаборатории научно-исследовательских организаций (см. рис. 1).
2.4. По своему содержанию практический путь обеспечения надежности, нося межотраслевой характер, должен вместе с тем быть целенаправленным, иметь единый координирующий центр.
2.5. Для решения задач количественной оценки и оптимизации уровня надежности важно развитие и применение научного, или прогнозного (теоретического, экспериментального)пути обеспечения надежности магистральных трубопроводов (см. рис. 1). Ито даст возможность определять, каким должен быть в каждом конкретном случае уровень надежности, устанавливать целесообразные способы его достижения.
2.6. Порядок разработки, назначения, обеспечения и контроля количественных показателей надежности трубопроводов целесообразно определять по табл. 1. Главными этапами прогнозного пути обеспечения надежности являются (см. табл. 1):
разработка и выдача эксплуатирующими или проектными организациями требований к надежности и долговечности (количественных оценок надежности) трубопроводов;
обеспечение проектными и строительными организациями этих требований путем прогнозных расчетов надежности выбранных конструктивных решений с учетом принятых методов и фактического качества строительства.
2.7. Развитие научного (прогнозного) пути обеспечения надежности требует в первую очередь разработки расчетного аппарата числовой оценки уровня конструктивной надежности, достаточно полно учитывающего основные специфические факторы, влияющие на формирование надежности при строительстве трубопроводов. Настоящее Руководство является первой попыткой разработки аппарата числовой оценки надежности конструкций трубопроводов.
Общий порядок разработки, назначения, обеспечения и контроля показателей надежности трубопроводов
|
Стадии, на которых производится разработка, назначение и контроль показателей надежности магистральных трубопроводов |
Разработка и назначение показателей надежности |
Контроль и обеспечение показателей надежности |
Примечание |
||||
|
Организации осуществляющие |
Наименование контролируемых показателей надежности |
||||||
|
Организации, осуществляющие назначение показателей надежности |
Наименования назначаемых показателей надежности |
Обеспечение показателей надежности |
контроль показателей надежности |
||||
|
Проектирование |
Проектное задание |
Мингазпром, Миннефтепром |
Р1, Р2, …, Pi, P Р |
- |
- |
- |
|
|
Рабочее проектирование |
- |
- |
Проектная организация |
Проектная организация (самоконтроль) |
Р1, Р2, …, Pi, P Р |
Р1, Р2, …, Pi - надежности (вероятности безотказной работы) элементов трубопровода (прямых участков переходов и т.д. |
|
|
Экспертиза проекта |
Мингазпром, Миннефтепром, Миннефтегазстрой |
Уточнение значений Р1, Р2, …, Pi, P с учетом реальных условий строительства |
Проектная организация (корректировка технических решений) |
Мингазпром, Миннефтепром |
Р1, Р2, …, Pi, Р |
Р - надежность (вероятность безотказной работы) трубопровода как системы |
|
|
Подготовительный период |
|||||||
|
Транспортировка, складирование, приемка труб и материалов |
Миннефтегазстрой (Госинспекция по качеству строительства, отраслевые НИИ) |
Рс |
Снабженческие органы Миннефтегазстроя, транспортные организации |
Строительные организации Миннефтегазстроя, представитель заказчика |
Рс |
Рс - сохраняемость труб и материалов (вероятность сохранить в процессе транспортировки исправное состояние) |
|
|
Процесс строительства |
Миннефтегазстрой (отраслевые НИИ) |
Уточнение значений Р1, Р2, …, Pi, P с учетом реального качества строительства |
Строительные организации Миннефтегазстроя |
Проектная организация, представитель заказчика, а также отраслевые НИИ Миннефтегазстроя |
Р1, Р2, …, Pi, P |
|
|
|
Строительство |
Предэксплуатационные испытания |
Миннефтегазстрой (Госинспекция по качеству строительства, отраслевые НИИ) |
P0, p0, mp, σp |
Строительные организации Миннефтегазстроя |
Представитель заказчика, Инспекция по качеству строительства Миннефтегазстроя |
P0, p0, mp, σp |
P0, p0, mp, σp - соответственно, функция, плотность и числовые характеристики распределения относительного числа отказов при испытаниях по испытуемым участкам трубопровода |
|
Приемка |
Миннефтегазстрой (Госинспекция по качеству строительства) |
Тгар, уточнение значений Р1, Р2, …, Pi, P, с учетом проведения контроля, разбраковки и ремонта |
- |
Представитель заказчика |
Р1, Р2, …, Pi, P, Рс, P0, p0, mp, σp |
Тгар - гарантийный срок |
|
|
Эксплуатация |
Мингазпром, Миннефтепром |
τср, Kт.и., ω, Тср, P(t) |
Эксплуатирующие организации Мингазпрома и Миннефтепрома |
Государственная газовая инспекция, Мингазпром, Миннефтепром |
τср, Kт.и., ω, Тср, P(t) |
τср - средняя наработка на отказ Kт.и. - коэффициент технического использования трубопровода ω - количество отказов в год на 1000 км (параметр потока отказов) Тср - средняя долговечность трубопровода P(t) - вероятность безотказной работы трубопровода до момента t |
|
Рис. 1. Принципиальная схема обеспечения надежности при строительстве магистральных трубопроводов
3 ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО РАСЧЕТУ
НА НАДЕЖНОСТЬ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
3.1. ОСНОВНЫЕ ПРИНЦИПЫ РАСЧЕТА
3.1.1. Расчет трубопроводов на конструктивную надежность может включать:
оценку безотказности (в том числе начальной безотказности) трубопроводов (прогнозирование отказов);
оценку долговечности трубопроводов с учетом их ремонтопригодности;
оценку сохраняемости трубопроводов и их элементов.
3.1.2. Оценивать надежность трубопровода, прогнозировать отказы можно только с определенной вероятностью. Это объясняется тем, что большинство факторов, влияющих на его надежность в процессе эксплуатации: внешние и внутренние нагрузки и воздействия, радиусы упругого изгиба прокладываемого трубопровода, физико-механические свойства применяемых материалов труб, прочность и сплошность сварных соединений и др., являются статистически изменчивыми.
3.1.3. Важнейшей характеристикой надежности является функция надежности P(t), определяемая согласно [3] как вероятность безотказной работы, т.е. вероятность пребывания трубопровода (или его элемента) в области допустимых состояний в течение определенного интервала времени эксплуатации. Обратная ей в вероятностном смысле характеристика Q(t) = 1 - Р(t) характеризует вероятность отказа.
Примечание. В дальнейшем показатель вероятности безотказной работы условимся обозначать буквой Р, например Р(t), а вероятность отказа - буквой например Q(t).
3.1.4. Расчетная (прогнозная) оценка вероятности отказа [4] - величина относительная и зависит от степени подробности описания рассматриваемой системы (трубопровода) и ее элементов, действующих на нее нагрузок и воздействий. Поэтому оценки надежности, определяемые для одного и того же элемента при различных исходных расчетных предпосылках, несопоставимы.
3.1.5. Наиболее простыми являются расчеты оценок надежности, при которых свойства материалов, действующие на трубопровод нагрузки и воздействия рассматриваются на уровне случайных величин. При этом факт развертывания вероятностных свойств нагрузок во времени условно заменяется понятием статистической изменчивости нагрузок. Поэтому данный подход называют подходом, не учитывающим фактор времени, хотя это и не вполне правильно: при замене случайных процессов случайными величинами фактор времени также учитывается, но приближенно (упрощенно). Оценки надежности при таком подходе (без учета фактора времени) характеризуют вероятность нарушения (или, наоборот, ненарушения) какого-либо (каких-либо) из предельных состояний, оговоренных в СНиП II-45-75 при применении упрощенной вероятностной модели функционирования трубопровода.
3.1.6. В настоящем Руководстве выбран упрощенный метод оценки надежности без учета фактора времени.
При данном подходе назначение директивного (нормативного) уровня надежности при эксплуатации производится путем расчета надежности по излагаемой в Руководстве методике при условии изменения указанных выше случайных величин в пределах действующих норм.
3.1.7. Учитывая повторяемость отказов, характерную для восстанавливаемых систем, помимо теоретических (прогнозных) оценок надежности для магистральных трубопроводов в периоды предпусковых испытаний и эксплуатации возможно нахождение оценок фактической надежности на основе обработки сведений об отказах при испытаниях или эксплуатации. Эти оценки могут быть использованы как ориентировочные, базовые оценки надежности при назначении требуемого (нормативного) уровня конструктивной надежности аналогичных строящихся трубопроводов соответственно на момент испытаний или какой-либо момент эксплуатации.
3.1.8. При оценке надежности проектируемого или строящегося трубопровода на момент предпусковых испытаний в качестве контрольного (поверочного) норматива следует использовать показатель H(l) среднеожидаемого количества отказов при предпусковых испытаниях на участке трубопровода длиной l, связанный с показателем вероятности отказа Q(l) при испытаниях участка трубопровода известной двусторонней оценкой [5]:
В этом случае, производя прогнозный расчет показателя Q(l), следует учитывать случайную величину внутреннего давления как детерминированную, равную испытательному давлению.
3.1.9. Найденный при использовании соображений в п. 3.1.6 или 3.1.8 нормативный уровень конструктивной надежности в общем может не быть оптимальным. Вопросы оптимизации уровня надежности требуют привлечения экономических подходов [6 - 8], учитывающих размеры ущербов от вероятных отказов, эти вопросы требуют самостоятельной проработки применительно к трубопроводному строительству. Тем не менее использование уровня надежности, найденного при ориентации на нормативные значения допусков или же на минимальное желаемое количество отказов при испытании, является (при отсутствии оценок оптимальной надежности) вполне целесообразным.
3.1.10. При назначенном или установленном по пп. 3.1.6 и 3.1.8 уровне нормативной надежности на период испытания и эксплуатации целесообразен следующий порядок действий по обеспечению трубопроводу необходимой надежности в процессе проектирования и сооружения:
на стадии предпроектных проработок: расчет и сравнение по критерию надежности всех вариантов конструктивных решений в схем прокладки трубопровода;
при выбранных конструктивном решении и трассе трубопровода: прогнозный расчет показателей конструктивной надежности (при строгом учете статистической изменчивости факторов, в том числе качества сооружения и укладки, учитывая предыдущий опыт проектирования и строительства) всех элементов трубопровода; анализ структурной схемы надежности (схемы соединения элементов) трубопровода (или его проектируемого участка) и степени зависимости между элементами; оценка конструктивной надежности трубопровода (или его проектируемого участка) как системы; сравнение с нормативным уровнем надежности; обеспечение ( путем необходимых изменений в конструкции и технологии производства работ) требуемой расчетной надежности всех элементов и трубопровода в целом (или его проектируемого участка).
3.1.11. В соответствии с принятым в настоящем Руководстве подходом к оценке надежности при практическом применении данной методики несколько изменяется и указанный в табл. 1 порядок разработки, назначения, обеспечения и контроля показателей надежности. При применении настоящего Руководства последовательность этапов обеспечения надежности будет соответствовать табл. 2.
3.2. ОБЩАЯ
СХЕМА РАСЧЕТА ТРУБОПРОВОДОВ
НА НАДЕЖНОСТЬ (БЕЗОТКАЗНОСТЬ), ВКЛЮЧАЯ
НАЧАЛЬНУЮ НАДЕЖНОСТЬ
3.2.1. Основные этапы для расчетов безотказности на всех предэксплуатационных стадиях следующие:
А. Анализ структурной схемы формирования надежности трубопровода, т.е. анализ типов соединения его элементов. Оценку надежности системы [9] с последовательным соединением независимых элементов определяют по теореме умножения вероятностей:
где i - номер элемента (i - m);
m - количество элементов, а оценку надежности системы из параллельно соединенных независимых элементов определяют как:
Упрощенная схема разработки, назначения, обеспечения и контроля показателей надежности сооружаемого трубопровода
|
Стадии, на которых осуществляются разработка, назначение, обеспечение и контроль показателей надежности магистральных трубопроводов |
Разработка и назначение показателей надежности |
Контроль и обеспечение показателей надежности |
Примечания |
|||||
|
Организации, осуществляющие |
Наименование разрабатываемых (назначаемых) показателей надежности |
Организации, осуществляющие |
Наименование контролируемых показателей надежности |
|||||
|
разработку показателей |
назначение показателей надежности |
обеспечение показателей надежности |
контроль показателей надежности |
|||||
|
Проектирование |
Проектное задание |
Проектная организация |
Мингазпром, Миннефтепром (выбор и утверждение вариантов) |
P1, P2, …Pi P1, P2, …Pi P1, P2, …Pi |
- |
- |
- |
P1, P2, …Pi - надежности (вероятности безотказной работы) элементов трубопровода, рассчитанные без учета фактора времени |
|
Рабочее проектирование |
Проектная организация |
- |
P, H(l) и уточненные значения P1, P2, …Pi |
- |
- |
- |
P - надежность (вероятности безотказной работы трубопровода) как системы, рассчитанная без учета фактора времени |
|
|
Экспертиза проекта |
- |
- |
- |
- |
Мингазпром, Миннефтепром, Миннефтегазстрой |
P, H(l), P1, P2, …Pi |
H(l) - среднеожидаемое количество отказов при испытании трубопровода или его участков l |
|
|
Подготовительный период |
||||||||
|
Транспортировка, складирование и приемка труб и материалов |
|
|
По таблице 1 |
|
|
|
|
|
|
Строительство |
Процесс строительства |
ГИКС, отраслевые НИИ Миннефтегазстроя |
Корректировка с учетов качества строительства и согласование с проектной организацией и заказчиком значений P, H(l), P1, P2, …Pi |
Строительные организации Миннефтегазстроя |
Госинспекция по качеству строительства Миннефтегазстроя (ГИКС) |
P, H(l), P1, P2, …Pi, Pc |
|
|
|
Предэксплуатационные испытания |
- |
- |
- |
Строительные организации Миннефтегазстроя |
|
|
|
|
|
Приемка |
ГИКС, Миннефтегазстрой |
Миннефтегазстрой |
Тгар |
- |
Представитель заказчика |
P, Pc, H(l), P1, P2, …Pi, |
|
|
|
Эксплуатация |
|
|
Таблица 1 |
|
|
|
|
|
где Р1, Р2, …, Pi, Pm - надежность отдельных элементов;
Π - знак перемножения вероятностей;
i - номер элемента (i = 1 ÷ m);
m - количество элементов системы.
Линейная часть магистрального трубопровода представляет собой систему с зависимыми элементами, поэтому формулы (2) и (2а), справедливые только для систем с независимыми элементами, использовать нельзя. Для двух зависимых случайных событий А и В [2] должно иметь место выражение
|
P(AB) = P(A)⋅P(B) + r(A, B), |
(3) |
где r(A, B) - коэффициент корреляции.
Последовательное соединение в системе с зависимыми элементами сохраняет тот же смысл, что и в системе с независимыми элементами, однако понятие «элемент» здесь является значительно более сложным и неопределенным. Поэтому для линейного участка трубопровода как системы, состоящей из набора отдельных последовательно соединенных труб и сварных соединений, количество элементов же будет соответствовать количеству составляющих ее труб и сварных соединений. Из формулы (3) применительно к трубопроводам видно: если оценки надежности подсчитывают для двух сечений по длине трубопровода, то, чтобы привести рассматриваемую систему к системе с независимыми элементами и использовать формулу (2а), нужно сечения А и В выбрать настолько далеко друг от друга, чтобы r(A, B) = 0. Таким образом, чтобы оценить надежность участка трубопровода с учетом его длины, используя простое соотношение (2а), нужно предварительно определить длину зоны взаимной корреляции оценок надежности по длине.
При таком подходе количество условных элементов для подсчета надежности участка трубопровода по формуле (2а) будет m + 1, где m - число зон корреляции оценок надежности по сечениям исследуемого участка. Принципы расчета длины зоны взаимной корреляции освещены в разд. 4 настоящего Руководства.
В связи с невозможностью установить число условных элементов трубопровода как системы, не рассчитав предварительно надежность, на стадии первичного анализе структурной схемы надежности трубопровода числом этих элементов, очевидно, нужно задаваться (c учетом предыдущего опыта оценки надежности). После расчета надежности это число может быть уточнено и в случае ошибки оценка надежности пересчитана с учетом фактического числа условных элементов.
Б. Определение, если имеется возможность, ориентировочного значения требуемой (нормативной) надежности трубопровода и его участков для стадий испытания и эксплуатации.
На момент испытаний это возможно с использованием формулы (1), если установлено некоторое минимальное допустимое число отказов при испытании трубопровода или его участков.
На период эксплуатации это возможно при выполнении любого из условий:
определен оптимальный уровень надежности трубопровода и его участков;
произведена оценка надежности с учетом фактора времени и имеется фактическая статистика отказов при эксплуатации аналогичных трубопроводов;
имеется опыт расчета показателей надежности аналогичных трубопроводов или их участков;
на предыдущих стадиях формирования надежности уже получены соответствующие оценки, которые можно принять за ориентировочные значения требуемой надежности.
В. Расчет требуемых нормативных значений надежности элементов трубопроводов:
при заданном нормативном уровне надежности трубопровода или его участка как системы расчет производят, исходя из заданной для всего трубопровода или его участка (как системы) оценки надежности и структурной схемы соединения элементов с предварительным назначением ориентировочного числа условных элементов системы по п. 3.2.1, А;
при отсутствии заданного нормативного уровня надежности трубопровода (или его участка) как системы расчет производят с ориентацией на нормативные значения допусков, оговоренных СНиП для всех учитываемых расчетных изменчивых параметров.
Г. Оценка фактической надежности элементов трубопровода:
подготовка исходных данных: выбор расчетного элемента или сечения (по основному металлу, сварному шву и т.д.); привязка выбранного элемента или сечения к соседним перекачечным станциям; подготовка характеристик трассы на расчетном участке и т.д.;
выбор расчетной модели, отвечающей поставленной цели;
сбор и обработка статистической информации об изменчивых факторах, входящих в выбранную расчетную модель;
насыщение расчетной модели необходимой статистической информацией;
отыскание и применение способа расчетного определения вероятности отказа, скрытой в выбранной расчетной модели, т.е. непосредственная расчетная оценка надежности элемента трубопровода или конкретного сечения.
Д. Сопоставление полученной фактической оценки надежности элементов с требуемым уровнем надежности (если этот уровень определен) и вывод о соответствии или несоответствии каждого из элементов выдвигаемым требованиям к их надежности.
Е. Подбор новых материалов, конструкций, методов прокладки и проведение других мероприятий, направленных на повышение надежности оказавшихся ненадежными элементов (для стадии проектирования).
Ж. Вновь оценка фактической поэлементной надежности и сопоставление с требованиями, и так до обеспечения требуемой надежности всем элементам трубопровода.
З. Оценка фактической надежности трубопровода (или его участка) как системы с зависимыми элементами.
И. Расчет (прогнозирование) среднеожидаемого количества отказов при испытаниях трубопровода и его участков по вычисленным вероятностным характеристикам надежности (для стадии строительства) и сопоставление данного расчетного показателя с фактическим количеством отказов при испытаниях.
3.2.2. Анализ статистических данных об отказах на магистральных трубопроводах показывает, что большая часть их происходит не по причине недостаточной долговечности применяемых конструкций и материалов, а из-за пониженного уровня безотказности трубопроводов к началу эксплуатации. Это снижение связано с недостаточно высоким качеством исходных материалов, дефектами монтажных , сварочных и других работ, нарушениями проекта при укладке трубопроводов, недостатками проектно-изыскательского характера. В этих случаях отказы происходят, как правило, в процессе предэксплуатационных испытаний или же в первые годы эксплуатации, по мере повышения рабочего давления и выхода трубопроводов на проектный режим перекачки.
3.2.3. Уровень надежности, приобретаемый трубопроводом к моменту предпусковых испытаний и выявляемый в процессе этих испытаний путём опрессовки участков трубопровода испытательным давлением, называется уровнем начальной надежности или начальной базотказностью трубопровода. Показатель уровня начальной безотказности трубопровода является условным и характеризует уровень надежности, сформировавшийся на предэксплуатационных этапах: инженерных изысканий, проектирования, изготовления, доставки, сооружения, а также в процессе контроля качества строительства (за счет сопутствующего ремонта) - по отношению к детерминированной величине испытательного давления.
3.2.4. С позиций расчетного прогнозирования отказа оценка начальной надежности эквивалентна расчету надежности (безотказности) трубопровода без учета фактора времени с представлением фактора внутреннего давления как детерминированной величины, равной испытательному давлению.
3.2.5. В разд. 4 настоящего Руководства приведена методика оценки начальной надежности (безотказности) магистральных трубопроводов.
3.3. ОЦЕНКА НАДЕЖНОСТИ ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
3.3.1. В связи с тем что магистральный трубопровод испытывают отдельными участками различной длины, удобным показателем надежности при этом является распределение относительного числа отказов на единицу длины (например, на 1 км). Числовые характеристики этого распределения - средневероятное число отказов и его дисперсия - являются важнейшими прогнозируемыми показателями, на которые, как указывалось выше, ориентированы расчеты начальной надежности.
3.4. СВЯЗЬ
НАЧАЛЬНОЙ НАДЕЖНОСТИ С КОНТРОЛЕМ
КАЧЕСТВА СТРОИТЕЛЬСТВА ТРУБОПРОВОДОВ
3.4.1. Повышение уровня начальной надежности обусловливается проведением ремонтов и отбраковки труб, прибывающих к месту строительства, осуществлением ремонта и отбраковки дефектных монтажных сварных соединений после неразрушающего контроля и других подобных мероприятий.
3.4.2. Правильная организация приемочного контроля качества способствует повышению уровня начальной надежности [10]. Если, например, в процессе проведения выборочного приемочного контроля (и связанного с ним ремонта) монтажных сварных соединений доля дефектных сварных соединений снизилась от величины q до так называемого приемочного, т.е. допустимого в условиях выборочного контроля уровня qn, то вероятность отказа любого произвольно взятого стыка контролируемой партии снизится от величины qQ до величины
|
qnQ < qQ, |
где Q - вероятность отказа одного дефектного стыка.
3.4.3. Наиболее эффективен для повышения начальной надежности сплошной контроль, снижающий в результате сопутствующего ему ремонта величину q до нуля. Снижение уровня (доли) дефектности путем выборочного контроля даже при наибольшем по нормам проценте контроля (25 %) незначительно. Оно характеризуется формулой:
|
|
где qвх, qвых - доля дефектных изделий (в данном случае - дефектных стыков) в партии соответственно до проведения контроля (и ремонта) и после;
N, n -
соответственно объем партии и выборки (количество стыков в партии и выборке),
т.е. ![]() - процент контроля.
- процент контроля.
3.5.
РАСЧЕТ ТРУБОПРОВОДОВ НА ДОЛГОВЕЧНОСТЬ С УЧЕТОМ
ИХ РЕМОНТОПРИГОДНОСТИ
3.5.1. Оценка долговечности магистрального трубопровода как системы - задача вероятностно-экономического характера. Долговечность трубопровода при решении данной задачи определяется как экономически оптимальный срок его эффективной службы в условиях роста эксплуатационных затрат и снижения коэффициента технического использования в связи с увеличением параметра потока отказов в «период старения» трубопровода.
3.5.2. Под долговечностью трубопровода как системы понимается время Т работы трубопровода от начала эксплуатации до момента прекращения его эксплуатации или остановки с целью полной замены в связи с нерентабельностью его дальнейшей эксплуатации из-за резкого снижения коэффициента технического использования (частых отказов и ремонтов), сопровождающегося ростом эксплуатационных затрат. То же определение относят и к отдельным ниткам или большим участкам трубопровода, рассматриваемым как подсистемы.
3.5.3. Долговечность, рассматриваемая вне экономических соображений, - величина случайная и, так же как безотказность, выражается через функцию надежности. Так, для любых элементов трубопровода, работающих до первого отказа (невосстанавливаемых элементов), подлежащих замене (а не ремонту) после отказа (это характерно для любых отказов, сопровождающихся разрывом, а не утечкой), выражение для средней долговечности Тср будет иметь вид [3]:
|
|
где t - время (наработка на отказ).
Показатель долговечности играет важную роль при исследовании вероятностно-экономических вопросов прогнозирования и назначения срока службы трубопроводов.
3.5.4. В общем случае последовательность расчета трубопровода на долговечность должна быть следующей:
а) определение (методом ускоренных испытаний на надежность) или назначение из предшествующего опыта статистических характеристик (среднего значения, дисперсии) долговечности всех элементов трубопровода определенной выбранной конструкции при конкретных условиях эксплуатации (т.е. при наличии конкретных данных о коррозионной активности грунтов в районах прокладки трубопровода, возможном характере и частоте колебаний внутреннего давления во времени и т.д.);
б) назначение (нормирование) среднего срока службы (средней долговечности) трубопровода как системы, исходя из средней долговечности труб*, т.е. долговечности основных, наиболее массовых элементов, с учетом оптимизации эксплуатационных затрат. При этом под долговечностью труб в конкретных условиях эксплуатации следует понимать их наименьшую долговечность по отношению к различным действующим на них нагрузкам и воздействиям;
________
*При оценке долговечности по критерию их коррозионной стойкости трубы рассматривают совместно с изоляционным покрытием выбранной конструкции.
в) определение периодичности проведения, объемов, стоимости и трудоемкости плановых ремонтов элементов, обладающих долговечностью ниже нормированной средней долговечности трубопровода как системы;
г) сопоставление полученных экономических показателей с нормативами эксплуатационных затрат и вывод о сохранении или изменении конструктивного решения трубопровода и соответственно назначенного (нормативного) срока службы трубопровода;
д) перерасчет трубопровода новой конструкции (в случае изменения конструктивного решения) на измененные экономические показатели.
3.5.5. В связи с постоянно возрастающими объемами капитальных ремонтов магистральных трубопроводов при их проектировании и сооружении необходимо наряду с долговечностью оценивать и ремонтопригодность различных вариантов конструктивных решений.
3.5.6. Под ремонтопригодностью [1] подразумевается свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения его отказов, повреждений и устранению их последствий путем проведения ремонтов и технического обслуживания.
Различные конструктивные решения трубопроводов обладают различной степенью ремонтопригодности, что связано с различным заглублением трубопроводов, разной приспособленностью к очистке старой изоляции, степенью сложности ремонта равнинных участков, переходов и т.д. Различна и обеспеченность трубопроводов устройствами для фиксации дефектов, утечек, отказов.
3.5.7. Оценивать ремонтопригодность того или иного трубопровода следует по совокупности показателей стоимости и трудоемкости ремонта с учетом приспособленности к техническому обслуживанию и обеспеченности средствами технической диагностики.
3.6. СОХРАНЯЕМОСТЬ ТРУБОПРОВОДОВ И ИХ ЭЛЕМЕНТОВ
3.6.1. Под сохраняемостью [1] следует понимать свойство трубопровода, его участков, элементов или материалов, применяемых для его сооружения, непрерывно сохранять исправность и приспособленность к работе в течение и в результате транспортировки, хранения, монтажа, а также в течение (или к окончанию) срока пребывания трубопровода или его участка в состоянии ненагруженного резерва.
3.6.2. Сохраняемость материалов, труб, элементов или участков трубопровода количественно измеряется показателями двух типов:
показателем времени безотказного хранения, т.е. случайной величиной срока, в течение которого на рассматриваемом этапе (при хранении труб или сварочных материалов, пребывании участка трубопровода в состоянии ненагруженного резерва и т.д.) данные материалы, элементы или участки трубопровода в тех или иных условиях находятся в исправном состоянии. Числовой характеристикой сохраняемости в данном случае, помимо показателя, «наработки» t, является, например, вероятность безотказного хранения к моменту t, обозначаемая Рс(t);
показателем вероятности безотказного хранения (или транспортировки и т.д.) к концу рассматриваемого периода. При таком подходе вместо случайного параметра времени t свойство сохраняемости трубопровода оценивают по параметрам исправности, например в виде случайной величины доли исправных элементов к общему их количеству на момент окончания рассматриваемого этапа, случайной величины количества повреждений на каждый транспортируемый элемент к окончанию этапа транспортировки и т.д. При этом понятие «отказ» заменяется аналогичным понятием нарушения исправности. Соответственно критерий вероятности отказа заменяется критериев вероятности нарушения исправности или обратным (в вероятностном смысле) критерием вероятности нахождения трубопровода или его элементов в исправном состоянии.
3.6.3. Сохраняемость элементов трубопровода можно оценивать как на отдельных этапах строительства, так и к окончанию совокупности этих этапов, например к окончанию строительства, пребывания участка трубопровода в резерве.
3.7. СБОР И ОБРАБОТКА СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ
3.7.1. Необходимые этапы при оценке надежности трубопроводов и их элементов - сбор и обработка статистической информации об отказах и характеристиках изменчивых факторов, влияющих на формирование надежности.
3.7.2. Статистическую информацию об отказах следует обрабатывать и хранить с использованием перфокарт.
3.7.3. Источником первичной статистической информации об отказах являются акты расследования отказов, заполняемые специальной комиссией на месте отказа в соответствии с [11].
3.7.4. Статистическую информацию об изменчивых факторах, влияющих на формирование надежности, следует представлять:
для случайных величин:
числовыми характеристиками (математическим ожиданием, дисперсией, а для асимметричных распределений также коэффициентами асимметрии и эксцесса);
плотностью (или функцией) распределения, удовлетворительно согласованной с фактической статистикой;
для случайных функций и процессов:
функцией математического ожидания;
корреляционной функцией или спектральной плотностью.
3.7.5. Статистическую информацию следует обрабатывать с помощью ЭВМ, для чего целесообразно использовать программу «ООК», данную в настоящем Руководстве.
4. ОЦЕНКА
НАЧАЛЬНОЙ КОНСТРУКТИВНОЙ
НАДЕЖНОСТИ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
4.1. СВЯЗЬ ВЕРОЯТНОСТНОЙ ОЦЕНКИ НАДЕЖНОСТИ
С НОРМАТИВНЫМИ РАСЧЕТАМИ ТРУБОПРОВОДОВ
4.1.1. Безотказная работа любой конструкции или ее элемента характеризуется набором условий типа:
|
ui = Ri - Si > 0, |
(4) |
где u - функция надежности (например, запас прочности в конструкции);
S - расчетный показатель (например, усилие в конструкции);
R - предельное значение этого показателя (например, прочность этого элемента);
i - номер (тип) предельного состояния, принятого в качестве условия отказа.
Неравенство (4) является основополагающим при инженерной оценке конструктивной надежности. Оно, например, может означать, что отказ не произойдет, если усилие в конструкции не превысит несущую способность этой конструкции.
4.1.2. В данном разделе задача инженерной
оценки начальной конструктивной надежности магистральных трубопроводов
понимается как отыскание вероятности безотказной работы трубопровода при его
предпусковых испытаниях, т.е. вероятности выполнения неравенства (4), в котором фактор ![]() является случайным, т.е. относится к
категории случайных величин или случайных функций, а фактор S - детерминированной величиной, равной испытательному
давлению.
является случайным, т.е. относится к
категории случайных величин или случайных функций, а фактор S - детерминированной величиной, равной испытательному
давлению.
Примечание. В дальнейшем случайные величины условимся обозначать
одной волнистой чертой, например ![]() , а
случайные функции - двумя, например
, а
случайные функции - двумя, например ![]() .
.
4.1.3. Вероятностная оценка надежности является относительной величиной и зависит от вида расчетной модели, положенной в основу неравенства (4), и подробности описания рассматриваемого объекта как в части его свойств, так и в части нагрузок.
4.1.4. В настоящем Руководстве в качестве расчетных моделей рассматриваются условия предельных состояний, заложенные в СНиП II-45-75 для расчетов трубопроводов на прочность и деформативность.
4.1.5. Нормативные расчеты трубопроводов на прочность, деформативность и устойчивость осуществляются с обязательным введением в расчетные формулы дифференцированного коэффициента запаса, т.е. с введением различных расчетных коэффициентов (перегрузки, безопасности по материалу, условий работы, надежности). Введение в расчет таких коэффициентов отражает статистическую природу изменчивых факторов, входящих в расчетные соотношения. Использование коэффициентов необходимо на случай реализации неблагоприятных значений изменчивых факторов: низких прочностных характеристик металла, повышенных значений рабочего давления и др. Поэтому нормативный расчет с вероятностной точки зрения ведут не на среднестатистические значения изменчивых факторов, а на некоторые условные (большие или меньшие, чем среднестатистические, в зависимости от характера данного фактора), лимитируемые расчетными коэффициентами.
4.1.6. В связи с тем что вероятностный расчет оперирует статистическими распределениями расчетных факторов, потребность во введении расчетных коэффициентов в рассматриваемую модель явления при вероятностных расчетах отпадает. Поэтому в основу вероятностных моделей в настоящем руководств положены нормативные расчетные соотношения, лишенные расчетных коэффициентов.
4.2.
ПРИМЕР ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ФУНКЦИИ
НАДЕЖНОСТИ ДЛЯ СЛУЧАЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
4.2.1. Наиболее простое условие
для оценки начальной надежности можно получить, исходя из формулы расчета
кольцевых напряжений в стенке трубопровода ![]() :
:
|
|
(5) |
представив ее в виде, аналогичном (4):
где ![]() - случайная величина какой-либо
характеристики прочности трубы, достижение которой принято за предельное
состояние, например случайная величина временного сопротивления металла
растяжению;
- случайная величина какой-либо
характеристики прочности трубы, достижение которой принято за предельное
состояние, например случайная величина временного сопротивления металла
растяжению;
Рисп - детерминированная величина испытательного давления;
Dвн - внутренний диаметр трубы, вводимый в расчет как детерминированная величина, в связи с тем что эта величина обладает малой статистической изменчивостью;
![]() - случайная величина толщины стенка
трубы.
- случайная величина толщины стенка
трубы.
4.2.2. Исходя из условия (5а), функцию надежности, т.е. вероятность безотказной работы в процессе испытания, определяют из выражения
4.2.3. Выражение (6) легко представить в виде линейной комбинации случайных
факторов, если в качестве второй случайной величины брать величину, обратную
δ, т.е. ![]() . Тогда выражение (6) примет линейный вид
. Тогда выражение (6) примет линейный вид
где ![]() - случайная величина, обратная
- случайная величина, обратная ![]() ;
;
![]() - постоянный
(детерминированный ) коэффициент.
- постоянный
(детерминированный ) коэффициент.
4.2.4. Статистические наблюдения
показывают, что распределения случайных величин ![]() и
и ![]() (а следовательно, и
(а следовательно, и ![]() , т.е.
, т.е. ![]() ) являются нормальным или достаточно
близки к нормальным, т.е. имеют малую асимметрию. Поэтому решение по условию (7) можно получить методом А.Р. Ржаницына [6, 12],
в соответствии с правилом: если распределения при линейной композиции случайных
величин являются нормальными, то распределение их разности также является
нормальным. Поэтому математическое ожидание
) являются нормальным или достаточно
близки к нормальным, т.е. имеют малую асимметрию. Поэтому решение по условию (7) можно получить методом А.Р. Ржаницына [6, 12],
в соответствии с правилом: если распределения при линейной композиции случайных
величин являются нормальными, то распределение их разности также является
нормальным. Поэтому математическое ожидание ![]() и дисперсия Du или квадрат стандарта
и дисперсия Du или квадрат стандарта ![]() , распределения
, распределения ![]() (с учетом некоррелированности
(с учетом некоррелированности ![]() и
и ![]() ) выразятся:
) выразятся:
|
|
(8) |
|
|
(8a) |
где ![]() - математические ожидания
соответствующих случайных величин, обозначаемые одной прямой (в отличие от
самих случайных величин, обозначаемых волнистой) чертой;
- математические ожидания
соответствующих случайных величин, обозначаемые одной прямой (в отличие от
самих случайных величин, обозначаемых волнистой) чертой;
Su, SR, Sr - стандарты (квадратные корни из дисперсий Du, DR, Dr) соответствующих случайных величин. Обозначения буквой S стандартов Приняты в отличие от распространенных обозначений стандартов буквой σ для того, чтобы не смешивать их с обозначением напряжений.
Величина γ, равная:
|
|
(8б) |
при принятом
подходе является характеристикой безопасности по А.Р. Ржаницыну и представляет
собой количество стандартов, на которое отстоит среднее значение ![]() нормального распределения случайной
величины
нормального распределения случайной
величины ![]() от значения u = 0.
от значения u = 0.
4.2.5. Учитывая нормальность
распределения ![]() , вероятность отказа Q(u) при испытаниях для найденной величины γ составит:
, вероятность отказа Q(u) при испытаниях для найденной величины γ составит:
где Φ - табулированный интеграл вероятностей Ф*(γ) [13].
4.2.6. Вероятность безотказной работы при испытаниях соответственно будет составлять:
|
|
(10) |
4.2.7. В соответствии с формулой (1) по найденной оценке вероятности отказа можно определить среднеожидаемое количество отказов при предпусковых испытаниях.
4.3. ОЦЕНКА НАЧАЛЬНОЙ НАДЕЖНОСТИ ДЛЯ НЕКОТОРОЙ ТОЧКИ
(СЕЧЕНИЯ) ПО ДЛИНЕ ТРУБОПРОВОДА
4.3.1. Для прямолинейных и упруго изогнутых участков магистральных трубопроводов оценивать начальную конструктивную надежность в каком-либо сечении следует, исходя из условий прочности, деформативности и устойчивости в соответствии со СНиП II-45-75.
В настоящем Руководстве приведена только методика оценки начальной надежности трубопровода с использованием (в качестве условия отказа) условия предельного состояния по деформативности, имеющего в соответствии со СНиП II-45-75 вид:
|
|
где ![]() определяется из соотношения:
определяется из соотношения:
в котором факторы ![]() и
и ![]() учтены как случайные величины. Здесь
ψ3, С, Kн,
α, Δt, Dн,
ρ - по СНиП II-45-75.
учтены как случайные величины. Здесь
ψ3, С, Kн,
α, Δt, Dн,
ρ - по СНиП II-45-75.
Как отмечалось в п. 4.1.6, вероятностный расчет должен производиться при отсутствии дифференцированного коэффициента запаса, поэтому указанное выше предельное неравенство должно иметь вид
или, если понимать его как условие сохранения надежности:
4.3.2. Методы оценки начальной надежности по условиям прочности и устойчивости будут аналогичны рассматриваемым и в настоящем руководстве не приведены.
4.3.3. В условия (11),
(12), (12а) наряду с толщиной стенки δ и показателем
механической прочности металла ![]() входит другой существенно изменчивый
фактор - радиус упругого изгиба
входит другой существенно изменчивый
фактор - радиус упругого изгиба ![]() , благодаря которому оценка начальной
надежности, вычисляемая по условиям (11),
(12), (12а), будет зависеть от местоположения расчетного
сечения трубопровода по отношению к соседним компрессорным (КС) или насосным
(НС) станциям. Для получения сначала упрощенного решения допустим, что радиус
упругого изгиба является не случайной функцией по длине трубопровода, а
случайной величиной.
, благодаря которому оценка начальной
надежности, вычисляемая по условиям (11),
(12), (12а), будет зависеть от местоположения расчетного
сечения трубопровода по отношению к соседним компрессорным (КС) или насосным
(НС) станциям. Для получения сначала упрощенного решения допустим, что радиус
упругого изгиба является не случайной функцией по длине трубопровода, а
случайной величиной.
4.3.4. Так как ставится задача оценки начальной надежности, по-прежнему полагаем, что фактор внутреннего давления Р - детерминированная величина, равная испытательному давлению.
4.3.5. Фактор температурного перепада ![]() при испытании участка трубопровода
можно принять детерминированной величиной, равной при гидравлических испытаниях
разности между температурой грунта и температурой замыкания участка
трубопровода. При испытании газом вместо температуры грунта следует взять
температуру закачиваемого газа с учетом его остывания на момент подъема
давления до заданного испытательного.
при испытании участка трубопровода
можно принять детерминированной величиной, равной при гидравлических испытаниях
разности между температурой грунта и температурой замыкания участка
трубопровода. При испытании газом вместо температуры грунта следует взять
температуру закачиваемого газа с учетом его остывания на момент подъема
давления до заданного испытательного.
4.3.6. Разрешая условия (11), (12), (12а) относительно вероятности безотказной работы трубопровода при испытании, имеем:
в котором выражение
для ![]() берется„по модулю вне зависимости от
его знака, а факторы
берется„по модулю вне зависимости от
его знака, а факторы ![]() ,
, ![]() и
и ![]() учтены как случайные величины.
учтены как случайные величины.
4.3.7. Если при оценке начальной надежности расчетное сечение выбирают по металлу сварного шва (а не по основному металлу), следует учесть еще один статистически изменчивый фактор - несплошность металла сварного шва, т.е. статистически учесть влияние сварочных дефектов.
Для этого можно воспользоваться приведенной в работе [14] эмпирической зависимостью уменьшения прочности сварного шва от площади дефектов с учетом вида этих дефектов:
|
|
(14) |
или приближенно:
где ![]() - нормативное сопротивление металла
дефектного сварного стыка на разрыв из условия достижения предела текучести;
- нормативное сопротивление металла
дефектного сварного стыка на разрыв из условия достижения предела текучести;
![]() - суммарная
площадь дефектов шва в сечении, нормальном к оси трубы;
- суммарная
площадь дефектов шва в сечении, нормальном к оси трубы;
K - коэффициент влияния вида дефекта;
F - площадь сечения сварного шва (брутто).
4.3.8. С учетом формулы (15) функция надежности по сварному соединению при испытании трубопровода выразится соотношением
4.3.9. В условиях (13)
и (16) помимо случайных величин ![]() имеется еще
одна случайная величина - коэффициент
имеется еще
одна случайная величина - коэффициент ![]() . Данный коэффициент в соответствии со СНиП II-45-75
при растягивающих продольных напряжениях, т.е. при
. Данный коэффициент в соответствии со СНиП II-45-75
при растягивающих продольных напряжениях, т.е. при ![]() (иначе, когда выражение, берущееся по
модулю в условиях (13) и (16), имеет знак плюс), принимают равным единице. Для
этого случая условия (13) и (16) будут иметь прежний вид, где ψ3
= 1. Для случая сжимающих продольных напряжений, т.е. для
(иначе, когда выражение, берущееся по
модулю в условиях (13) и (16), имеет знак плюс), принимают равным единице. Для
этого случая условия (13) и (16) будут иметь прежний вид, где ψ3
= 1. Для случая сжимающих продольных напряжений, т.е. для ![]() (иначе, когда выражение, берущееся по
модулю в условиях (13) и (16), имеет знак минус), значение ψ3
определяют по формуле
(иначе, когда выражение, берущееся по
модулю в условиях (13) и (16), имеет знак минус), значение ψ3
определяют по формуле
|
|
в которой ![]() , а следовательно, и ψ3
есть случайные величины.
, а следовательно, и ψ3
есть случайные величины.
4.3.10. Коэффициенты C и Kн в соответствии с п. 4.1.6 при вероятностном решении задачи должны быть опущены.
Поэтому условие (13) при оценке начальной надежности по основному металлу
для случая ![]() после простых преобразований примет
вид:
после простых преобразований примет
вид:
Соответствующее условие при оценке надежности по сварному стыку
для случая ![]() примет вид:
примет вид:
4.3.11. Чтобы реализовать оценку надежности по условиям (13), (17) и (16), (18), т.е. определить статистические характеристики функции надежности (среднее значение, дисперсию), а следовательно, найти характеристику безопасности γ, вероятность отказа Q = Q(u ≤ 0) и среднеожидаемое количество отказов при испытании, следует прибегнуть [6, 12, 15] к способу линеаризации функции нескольких случайных переменных, для чего каждая из функций надежности по условиям (13), (17):
рассматривается в
достаточно малой окрестности точки ![]() или
или ![]() - для (18), т.е. в окрестности математического ожидания каждое
из этих функций.
- для (18), т.е. в окрестности математического ожидания каждое
из этих функций.
Так как в достаточно малой окрестности функция является почти линейной, ее приближенно можно заменить линейной. Это означает, что в разложении функции u в ряд Тейлора в окрестности математического ожидания можно сохранить только члены первого порядка, а все высшие отбросить, т.е. (перейдя к другим обозначениям) представить каждую из функций в виде [13]:
|
|
Следовательно, и зависимость между случайными величинами можно приближенно заменить линейной зависимостью:
|
|
где ![]() - математические ожидания аргументов;
- математические ожидания аргументов;
![]() - частные производные аргументов;
- частные производные аргументов;
знак m при частных производных означает, что в выражения, получаемые в результате дифференцирования, следует подставлять математические ожидания;
![]() - центрированные случайные аргументы.
- центрированные случайные аргументы.
4.3.12. К линейной функции нескольких некоррелированных, а в нашем случае - и независимых случайных аргументов применимы простые правила определения числовых характеристик линейных функций случайных аргументов, а именно:
а) математическое ожидание линейной функции равно той же
линейной функции от математических ожиданий аргументов. Кроме того, известно,
что центрированные аргументы ![]() имеют математические ожидания, равные
нулю;
имеют математические ожидания, равные
нулю;
б) дисперсия линейной функции некоррелированных (а тем более независимых) случайных величин равна сумме произведения квадратов коэффициентов (частных производных) на дисперсии соответствующих аргументов, т.е.
4.3.13. Таким образом, для случая (17) можно записать: для математического ожидания функции надежности u:
для дисперсии функции надежности:
где знак m при частных производных ![]() по-прежнему означает, что в выражения,
получаемые в результате дифференцирования, следует подставлять математические
ожидания;
по-прежнему означает, что в выражения,
получаемые в результате дифференцирования, следует подставлять математические
ожидания;
![]() - стандарты
соответствующих случайных величин.
- стандарты
соответствующих случайных величин.
4.3.14. Аналогичные выражения для математического ожидания и дисперсии можно записать и для условий (16) и (18):
|
(24) |
|
|
|
(24a) |
|
(25) |
где ![]() - стандарт случайной величины
- стандарт случайной величины ![]() .
.
4.3.15. Известно [13], что при композиции достаточно большого (4 - 5 и более) числа практически произвольных законов распределения, обладающих дисперсиями одного порядка*, суммарный закон оказывается сколь угодно близок к нормальному независимо от того, каковы были законы распределения слагаемых. В рассмотренных выше случаях количества случайных слагаемых (3 и 4) могут оказаться недостаточными для получения нормально распределенной композиции, поэтому в разд. 6 настоящего Руководства разработана программа обработки на ЭВМ статистических данных, учитывающая такую возможность.
________
*Статистические наблюдения
показывают, что исходные случайные величины обладают изменчивостью одного
порядка:![]() .
.
Цель примененного в данной программе метода - получение нормальных распределений при исходных случайных распределениях любого (в том числе асимметричного) вида. Для получения нормальных распределений каждое распределение случайной величины заменяется распределением среднего по подвыборкам, на которые разбивается каждая совокупность наблюдений за случайной величиной. Как известно, критерий среднего по подвыборке распределен асимптотически нормально. Более подробное пояснение данного приема приведено в разд. 6 настоящего руководства.
4.3.16. Заменяя в формулах (22), (22a), (23), (24), (24а), (25) дисперсии самих случайных аргументов на дисперсии случайных аргументов в подвыборках (средние значения остаются прежними), мы, очевидно, мало изменяя смысл задачи, можем считать нормальным распределение композиции. Определив по указанным выше формулам числовые характеристики нормально распределенной функции надежности u, можно найти характеристику безопасности γ, затем по таблицам функции нормального распределения, учитывая формулу (9), найти вероятностную обеспеченность для значения u = 0, т.е. оценку вероятности отказа Q = Q(u ≤ 0). Такая оценка при одних и тех же объемах подвыборок n имеет одно и то же смещение и как мера надежности является вполне пригодной при решении многих практических задач.
4.3.17. В табл. 3
сведены все описанные выше формулы, а также выражения для соответствующих
частных производных для определения характеристик случайной величины ![]() функции надежности в сечении
трубопровода (с применением линеаризации этой функции).
функции надежности в сечении
трубопровода (с применением линеаризации этой функции).
4.3.18. Методы оценки начальной надежности в сечении трубопровода с ориентацией на другие предельные состояния аналогичны проведенному, поэтому в настоящем Руководстве не приводятся.
Таким образом, после проведения расчетов начальной надежности в сечении трубопровода с использованием в качестве условий отказа условий прочности, деформативности и устойчивости по СНиП II-45-75 должны быть получены три вероятностных оценки надежности, которые в совокупности должны характеризовать надежность в какой-либо точке (в сечении) трубопровода при его испытаниях.
4.4. ПРИМЕР ОЦЕНКИ НАЧАЛЬНОЕ НАДЕЖНОСТИ В СЕЧЕНИИ
ИСПЫТУЕМОГО УЧАСТКА МАГИСТРАЛЬНОГО ТРУБОПРОВОДА
4.4.1. Требуется оценить начальную надежность в некотором сечении проложенного упругим изгибом участка газопровода 1-й категории диаметром 1420 мм, с толщиной стенки δ = 20,5 мм, предназначенного для работы под давлением ρ = 75 кгс/см2 и испытываемого газом при давлении Рисп = 1,25⋅75 = 94 кгс/см2.
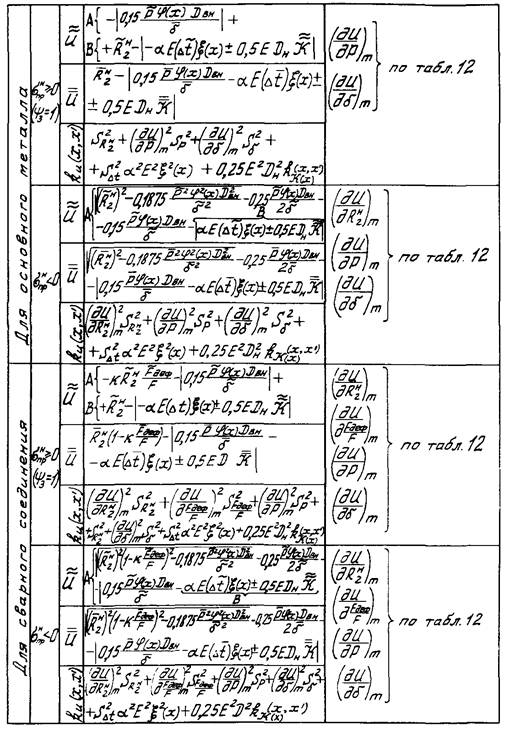
Формулы для определения характеристик
случайной функции эксплуатационной
надежности ![]() способом ее частичной минерализации
способом ее частичной минерализации
Температурный перепад (для предстоящих испытаний с учетом остывания газа в процессе подъема испытательного давления) составляет Δt = +40 °С.
Средние значения случайных величин, определяющих надежность
труб и сварных соединений, составляют: ![]() = 4200 кгс/см2;
= 4200 кгс/см2; ![]() = 20,5 мм;
= 20,5 мм; ![]() = 3000 м;
= 3000 м; ![]() = 0,002 (после 100-процентного
контроля сварных соединений просвечиванием и ремонта, при условии соблюдения СНиП
III-Д.10-72 в части требования, чтобы глубина
оставшихся дефектов не превышала допустимых значений, т.е. 10 % от толщины
стенки трубы или 1 мм).
= 0,002 (после 100-процентного
контроля сварных соединений просвечиванием и ремонта, при условии соблюдения СНиП
III-Д.10-72 в части требования, чтобы глубина
оставшихся дефектов не превышала допустимых значений, т.е. 10 % от толщины
стенки трубы или 1 мм).
Стандарты случайных величин и соответствующие значения
стандартов среднего по выборке составляют: ![]() = 500 и 167 кгс/см2; Sδ = 0,2 и 0,07
см; Sρ =
400 и 133 м;
= 500 и 167 кгс/см2; Sδ = 0,2 и 0,07
см; Sρ =
400 и 133 м; ![]() = 0,003 и 0,001.
= 0,003 и 0,001.
Коэффициент K влияния вида дефектов назначается из условия, что в дефектных сварных соединениях преобладают непровары. При таких дефектах, в соответствии с [14] для δ = 20 мм, K = 6.
4.4.2. По формуле (11):
|
|
Так как выражение для ![]() (принимаемое по модулю) имеет знак
минус, то для определения статистических характеристик функции надежности u
используем выражения (22a),
(23), (24а), (25).
(принимаемое по модулю) имеет знак
минус, то для определения статистических характеристик функции надежности u
используем выражения (22a),
(23), (24а), (25).
4.4.3. Оценка надежности элементов (труб);
|
|
Для определения дисперсии в соответствии с табл. 3 найдем частные производные функции (19а) по всем случайным аргументам:
|
|
Примечание. Для случая ![]() и
использования условия (22) выражения для
частных производных в соответствии с табл. 3
составили бы:
и
использования условия (22) выражения для
частных производных в соответствии с табл. 3
составили бы:
|
|
Подставляя полученные значения в формулу (23) получим значения дисперсии и стандарта средних по выборке:
|
|
Теперь можно определить значение стандарта по всему массиву реализации случайной величины u, т.е. Su, так как известие, что
|
|
где n - число наблюдений в выборке (допустим, что при определении выборочных стандартов генеральные совокупности разбивались на группы по n = 5 наблюдений). Тогда:
|
|
Характеристика безопасности γ составляет:
|
|
Вероятность отказа при этом из предположения нормального распределения по таблицам Φ*(γ) составит Qэл = 0,0005, т.е. надежность каждого элемента (трубы) будет равна Рэл = 0,9995, что в общем удовлетворяет требованиям к надежности ответственных конструкций, для которых, согласно [16], рекомендуются значения начальной надежности в пределах от Р = 0,999 (из расчета на постепенные отказы) до Р = 0,9999 (из расчета на внезапные отказы).
4.4.4. Оценка надежности элементов (сварных соединений) определяется следующим образом:
|
|
частная производная ![]() для функции (20б) в соответствии с
табл. 3 будет составлять:
для функции (20б) в соответствии с
табл. 3 будет составлять:
|
|
Примечание. Для случая ![]() и
использования функции (20) с выражениями
(24а) и (25) частные производные
и
использования функции (20) с выражениями
(24а) и (25) частные производные ![]() и
и ![]() равнялись бы (в соответствии с табл. 3):
равнялись бы (в соответствии с табл. 3):
|
|
Другие частные производные функции (20а) в соответствии с табл. 3 будут иметь вид, аналогичный найденным выше для функции (19a):
|
|
Подставляя полученные значения в выражение (25), получим значения дисперсии и стандарта средних значений по выборке:
|
|
Значение генерального стандарта составит:
|
|
Характеристика безопасности γ составит:
|
|
Вероятность отказа сварного стыка при этом из предположения нормального распределения по таблицам Φ*(γ) составит: Qэл = 0,0016, а надежность Рэл = 1 - 0,0016 = 0,9984, что несколько ниже указанных в п. 4.4.3 значений, рекомендуемых в [16] для ответственных конструкций.
Так как процент контроля сварных стыков по условию равен 100 % и после него проводился соответствующий ремонт сварных соединений, следует считать, что стыки с дефектами, превышающими допустимые по СНиП III-Д.10-72, отсутствуют. Поэтому найденное выше значение вероятности отказа Qэл не нужно понижать как при выборочном контроле умножением на величину приемочного уровня качества qп. При этом найденное значение Qэл присуще каждому из стыков данного участка.
4.5. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК
СЛУЧАЙНОЙ ВЕЛИЧИНЫ ФУНКЦИИ НАДЕЖНОСТИ
ПУТЕМ ЕЕ ЧАСТИЧНОЙ ЛИНЕАРИЗАЦИИ
4.5.1. Выше был приведен приём
определения числовых характеристик функции ![]() нескольких случайных аргументов с
помощью линеаризации выражения, характеризующего эту функцию. Можно несколько
упростить процедуру нахождения числовых характеристик функции надежности
нескольких случайных аргументов с
помощью линеаризации выражения, характеризующего эту функцию. Можно несколько
упростить процедуру нахождения числовых характеристик функции надежности ![]() , если разбить каждое из условий (19), (19а),
(20) на две части:
, если разбить каждое из условий (19), (19а),
(20) на две части:
|
|
которые символизируют нелинейную (А) и линейную (В) части каждого из этих условий.
4.5.2. Чтобы усилить линейную часть В каждого из условий (19), (19а),
(20), следует, как это было выполнено в
п. 4.2.3., рассматривать и
вводить в указанные условия не случайные величины ![]() и
и ![]() , а обратные им случайные величины
, а обратные им случайные величины ![]() и
и ![]() т.е. случайную кривизну.
т.е. случайную кривизну.
4.5.3. Это сразу позволит считать функцию надежности (19а) для основного металла при ψ3 = 1 линейной относительно входящих в ее выражение случайных аргументов и весьма просто выразить числовые характеристики функции надежности в этом условии по правилам определения числовых характеристик линейных функций случайных аргументов:
|
|
(26) |
|
|
(27) |
4.5.4. Для остальных условна (19), (19а), (20) мы можем подвергнуть линеаризации только оставшиеся нелинейными части А, т.е.
для условия (19б):
|
|
(28) |
для условия (20а)
|
|
(29) |
для условия (20б):
|
|
(30) |
4.5.5. В результате такой частичной линеаризации мы получим приближенные зависимости следующего вида:
|
|
где ![]() - математические ожидания аргументов,
т.е.
- математические ожидания аргументов,
т.е. ![]() и т.д.
и т.д.
В - линейная часть выражения для ![]() .
.
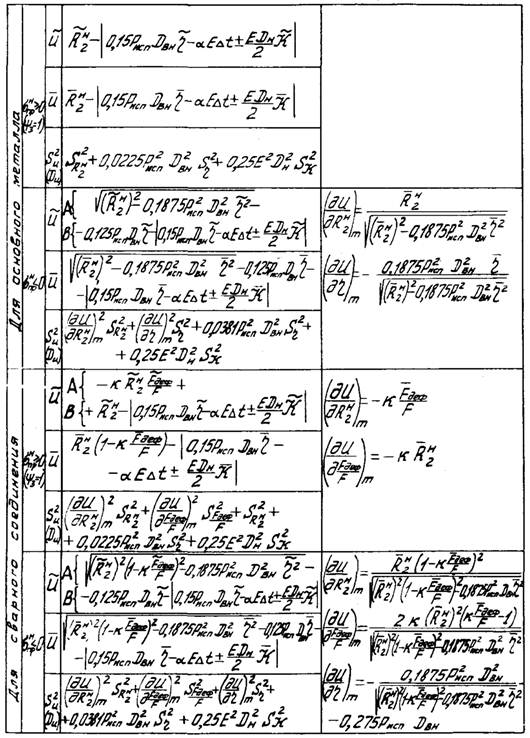
4.5.6. Применяя к линейным функциям (типа указанной в п. 4.5.5) правила, указанные в п. 4.3.12, получим выражения для
числовых характеристик функции надежности ![]() (табл. 4).
(табл. 4).
4.5.7. Некоторыми недостатками указанного способа
определения числовых характеристик ![]() можно считать необходимость
превращения при статистической обработке случайных величин
можно считать необходимость
превращения при статистической обработке случайных величин ![]() и
и ![]() в обратные им величины, а также большую
сложность подсчета погрешностей линеаризации, чем в п. 4.3.
в обратные им величины, а также большую
сложность подсчета погрешностей линеаризации, чем в п. 4.3.
Формулы для определения характеристик случайной величины ![]() (функции начальной надежности)
способом ее частичной линеаризации
(функции начальной надежности)
способом ее частичной линеаризации
4.6. УЧЕТ
УПРУГОГО ИЗГИБА ТРУБОПРОВОДА КАК СЛУЧАЙНОЙ
ФУНКЦИИ. ОЦЕНКА НАЧАЛЬНОЙ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ
ДЛЯ УЧАСТКА ТРУБОПРОВОДА
4.6.1. В разд. 4.3 приведена методика определения характеристик начальной надежности для сечений трубопровода.
Эти оценки начальной надежности могут быть отнесены к любой точке (любому сечению) испытуемого участка трубопровода, поскольку характеризуются идентичным преобразованием одних и тех же случайных величин. Однако описанный упрощенный подход к оценке надежности с представлением всех случайных аргументов, в том числе и радиуса упругого изгиба в виде случайных величин, не дает возможности перейти от оценки начальной надежности в сечении трубопровода к оценке начальной надежности всего рассматриваемого участка трубопровода на момент его предпусковых испытаний. Это объясняется тем, что в соответствии с п. 3.2.1 при данном подходе не может быть четко определено понятие «элемент» при рассмотрении участка трубопровода как системы. Можно показать, что, например, для случая, когда в качестве элементов системы принимаются последовательно соединенные трубы и соединяющие их сварные стыки, оценка надежности всего участка является чрезвычайно заниженной.
Например, для условий 4.4 испытуемый участок трубопровода имеет длину 30 км. Весь участок выполнен неповоротной сваркой. Общее количество стыков составляет m + 1 = 2700 шт. (из расчета 90 стыков на 1 км трассы). Тогда начальную надежность всего участка Руч в соответствии с нашим предположением следует вычислять по формуле
где Ртр - надежность каждой отдельной трубы;
Рст - надежность каждого отдельного сварного стыка;
m - число труб на участке;
(m + 1) - число сварных стыков на участке.
Принимая значения Ртр и Рст из примера 4.4, т.е. присваивая выбранным элементам оценки надежности для сечений трубопровода, получим:
|
|
Сомножители вычисляем с помощью логарифмирования:
|
|
Таким образом, оценка начальной надежности участка составит:
|
|
Это означает, что при достаточно высокой надежности элементов (точнее, оценок надежности в сечении трубопровода) мы приходим к исчезающе малому значению надежности даже сравнительно короткого участка трубопровода, что явно противоречит смыслу и условиям задачи, в которой в качестве исходных данных принимались вполне реальные значения характеристик случайных факторов.
Перейти от оценки надежности в сечении трубопровода к оценке начальной надежности всего испытуемого участка становится возможным, если рассматривать радиус упругого изгиба в соответствии с действительной природой этого случайного фактора в виде случайной функции [13, 17, 18] по длине трубопровода.
4.6.2. При выборе такой статистической модели сам трубопровод является динамической системой, в которой силовые воздействия преобразуются в напряжения. Поэтому для этой системы должен быть прежде всего определен оператор L, преобразующий силовые воздействия υ в напряжения:
где x - текущая координата расчетного сечения по оси трубопровода;
![]() - обозначения
соответствующих случайных функций*.
- обозначения
соответствующих случайных функций*.
________
*Случайную функцию в отличие от случайной величины в соответствии с примечанием к п. 4.1.2 будем обозначать двумя волнистыми чертами.
4.6.3. В принятой модели силовым воздействием является упругий изгиб трубопровода, поэтому в качестве входного случайного процесса следует рассматривать радиус упругого изгиба ρ(х) или кривизну K(х), т.е. вторую производную в уравнении упругой оси трубопровода fʹʹ(x)
|
|
где ![]() - случайная функция кривизны оси
трубопровода.
- случайная функция кривизны оси
трубопровода.
4.6.4. В качестве оператора будем в соответствии со СНиП II-45-75 использовать последнее слагаемое в условии (11) расчета максимальных продольных напряжений с учетом изгиба при упругой работе металла труб (при прокладке трубопровода упругим изгибом).
4.6.5. Таким образом, оператор L в условии (32), преобразующий упругий изгиб в напряжения, будет в соответствии с условием (11) иметь вид:
или, если сбор статистических данных о случайных значениях радиуса упругого изгиба ведется через координаты упругой оси трубопровода:
Примечание. В формуле (34)
L является оператором двойного дифференцирования. Поэтому здесь
несколько сложнее, чем в случае (33),
осуществлять преобразование характеристик входной случайной функции f(x)
в характеристики выходной случайной функции напряжений ![]() . А
именно: учитывая линейность и однородность оператора L в выражении (34), для определения математического
ожидания выходной случайной функции
. А
именно: учитывая линейность и однородность оператора L в выражении (34), для определения математического
ожидания выходной случайной функции ![]() следует
тот же оператор (т.е. в данном случае двойное дифференцирование и умножение на
постоянный множитель
следует
тот же оператор (т.е. в данном случае двойное дифференцирование и умножение на
постоянный множитель ![]() )
применить к математическому ожиданию входной случайной функции f(x).
Для определения корреляционной функции выходной случайной функции
)
применить к математическому ожиданию входной случайной функции f(x).
Для определения корреляционной функции выходной случайной функции ![]() следует
(также учитывая личейность и однородность оператора L) дважды применить
тот же оператор к корреляционной функции исходной случайной функции f(х).
следует
(также учитывая личейность и однородность оператора L) дважды применить
тот же оператор к корреляционной функции исходной случайной функции f(х).
4.6.6. По свойству линейных однородных операторов постоянный множитель можно вынести за знак операторе:
Аналогично для условия (34) имеем:
|
|
(36) |
где L есть оператор двойного дифференцирования.
4.6.7. Из условия (35)
видно, что при рассмотрении случайной функции в форме для кривизны входная
случайная функция упругого изгиба преобразуется в случайную функцию напряжений
лишь умножением на постоянный коэффициент ![]() . Поэтому для упрощения последующих
выводов примем за основу более простое условие (35), поскольку методы для натурного сбора статистических
сведений о входной случайной функции в представления их как через координаты
упругой оси, так и непосредственно через кривизну имеются.
. Поэтому для упрощения последующих
выводов примем за основу более простое условие (35), поскольку методы для натурного сбора статистических
сведений о входной случайной функции в представления их как через координаты
упругой оси, так и непосредственно через кривизну имеются.
4.6.8. В соответствии с правилами определения характеристик случайных функций математическое ожидание выходной случайной функции выразится как
а корреляционная функция -
|
|
(38) |
т.е. как произведение квадрата постоянного коэффициента на корреляционную функцию входной случайной функции.
Здесь характеристики случайных функций (математическое ожидание,
корреляционная функция) будут являться уже не числами, а неслучайными
функциями, поэтому в формуле (37)
неслучайная функция математического ожидания случайной Функции ![]() обозначена двумя чертами
обозначена двумя чертами ![]() . Такого обозначения будем
придерживаться и в дальнейшем.
. Такого обозначения будем
придерживаться и в дальнейшем.
4.6.9. Так как входной случайной функцией является
пространственное положение координаты упругой оси трубопровода, справедливо
считать, что на вход подаются две независимые (точнее, некоррелированные) случайные
функции ![]() или
или ![]() , описывающие изменение радиуса
упругого изгиба (или кривизны) оси трубопровода в горизонтальной у и
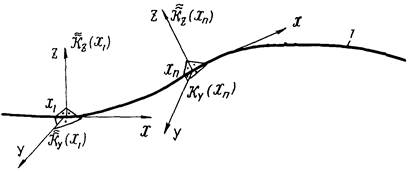
вертикальной z плоскостях (рис. 2).
, описывающие изменение радиуса
упругого изгиба (или кривизны) оси трубопровода в горизонтальной у и
вертикальной z плоскостях (рис. 2).
Суммарный изгибающий момент МΣ в любом сечении трубопровода будет составлять среднее геометрическое моментов, действующих в координатных плоскостях [19]:
|
|
где Мy, Мz - изгибающие моменты, действующие в соответствующих координатных плоскостях.
Так как М = σW; Му = σуW; Мz = σzW, то:
|
|
где М - изгибающий момент;
W - момент сопротивления;
σy, σz - напряжения от изгиба в соответствующих координатных плоскостях, т.е. наибольшие (суммарные) продольные напряжения от изгиба составят:
|
|
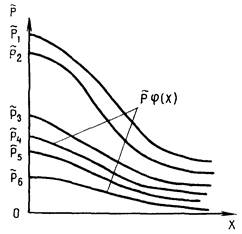
Рис. 2. Представление случайной функции ![]() как результата
как результата
действия двух случайных функций - ![]() , действующих
, действующих
в горизонтальной и вертикальной плоскостях:
Ky(x1);
Ky(xn),
Kz(x1);
Kz(xn)
- соответственно
значения случайных функций ![]() ;
;
1 - пространственное положение упругой оси трубопровода
Так как в нашей задаче σ, σу,
σz - случайные функции, т.е. ![]() ; иначе:
; иначе:
можно видеть, что оператор преобразования
функций ![]() и в функцию
и в функцию ![]() не является линейным. Поэтому, чтобы
избежать преобразования случайных функций нелинейным оператором, целесообразно
уже на стадии сбора и обработки статистических сведений о кривизне трубопровода
в двух плоскостях для каждого i-го сечения, в котором производятся
измерения
не является линейным. Поэтому, чтобы
избежать преобразования случайных функций нелинейным оператором, целесообразно
уже на стадии сбора и обработки статистических сведений о кривизне трубопровода
в двух плоскостях для каждого i-го сечения, в котором производятся
измерения ![]() , сразу находить значение наибольшей
кривизны Ki:
, сразу находить значение наибольшей
кривизны Ki:
Эти значения Ki в будут исходными статистическими наблюдениями наибольшей кривизны в каждом сечении, при этом формула (39) будет записываться в прежнем виде (35), т.е.
|
|
а оператор преобразования по-прежнему останется линейным.
4.6.10. При сборе статистических
данных о кривизне или радиусе упругого изгиба трубопровода важно учитывать
следующее обстоятельство. В каждое фактическое наблюденное значение радиуса
упругого изгиба входит случайная ρсл и неслучайная ρпр
составляющие, причем неслучайной составляющей ρпр является
проектное значение радиуса упругого изгиба. Поэтому, определяя по формуле (40) i-е значение наибольшей кривизны
в i-м сечении трубопровода, мы под значением ![]() должны подразумевать сумму случайного
должны подразумевать сумму случайного ![]() и проектного
и проектного ![]() значений кривизны в данном сечении:
значений кривизны в данном сечении:
|
|
(41) |
а под значением ![]() - сумму:
- сумму:
|
|
(41a) |
Отдельно подсчитывать напряжения ![]() от случайной составляющей наибольшей
кривизны
от случайной составляющей наибольшей
кривизны ![]() и напряжение σпр от
неслучайной составляющей проектной кривизны
и напряжение σпр от
неслучайной составляющей проектной кривизны ![]() нельзя, так как они характеризуют
напряжения в разных точках сечения и должны суммироваться геометрически, что
опять-таки приведет к появлению нелинейного оператора.
нельзя, так как они характеризуют
напряжения в разных точках сечения и должны суммироваться геометрически, что
опять-таки приведет к появлению нелинейного оператора.
4.6.11. С учетом формулы (35) формула для функции надежности будет иметь вид:
4.6.12. Разрешая условие (42) относительно вероятности безотказной работы, имеем соответственно для основного металла и сварного стыка:
4.6.13. С учетом случайной природы коэффициента ψ3, аналогично формам (13) и (15), условия (43) и (43а) распадаются на две пары следующих условий:
а) для основного металла:
б) для сварного стыка:
4.6.14. Случайная функция надежности ![]() в условии (42) является линейной относительно составляющих
напряжения и может быть записана в виде:
в условии (42) является линейной относительно составляющих
напряжения и может быть записана в виде:
|
|
(46) |
где случайная
величина прочности ![]() и каждая составляющая напряжения
и каждая составляющая напряжения ![]() соответствуют своему выражению в
условии (42) и являются либо неслучайной
величиной, либо случайной величиной, либо случайной функцией. Поэтому выходную
случайную функцию надежности
соответствуют своему выражению в
условии (42) и являются либо неслучайной
величиной, либо случайной величиной, либо случайной функцией. Поэтому выходную
случайную функцию надежности ![]() , линейно составленную из неслучайных и
случайных аргументов, можно выразить в соответствии с правилами сложения
случайных функций со случайными и неслучайными величинами:
, линейно составленную из неслучайных и
случайных аргументов, можно выразить в соответствии с правилами сложения
случайных функций со случайными и неслучайными величинами:
для математического ожидания:
для корреляционной функции:
где ![]() - соответственно математическое
ожидание и корреляционная функция случайной функции надежности;
- соответственно математическое
ожидание и корреляционная функция случайной функции надежности;
DR, Dr - соответственно дисперсии случайных величин
4.6.15. Выражение (47)
и (48) для характеристик выходной
случайной функции ![]() были бы справедливыми, если бы и
выражения (44), (44а), (45), (45а) были линейными относительно всех
входящих в них случайных аргументов. Однако указанные функции не являются
линейными, но, как и в разд. 4.5, могут
быть подвергнуты частичной линеаризации. Поэтому характеристики случайной
функции, т.е. неслучайная функция математического ожидания
были бы справедливыми, если бы и
выражения (44), (44а), (45), (45а) были линейными относительно всех
входящих в них случайных аргументов. Однако указанные функции не являются
линейными, но, как и в разд. 4.5, могут
быть подвергнуты частичной линеаризации. Поэтому характеристики случайной
функции, т.е. неслучайная функция математического ожидания ![]() и корреляционная функция Ru(x, xʹ) будут приближенно выражаться соотношениями,
представленными в табл. 5.
и корреляционная функция Ru(x, xʹ) будут приближенно выражаться соотношениями,
представленными в табл. 5.
4.6.16. Характеристики случайной функции ![]() для исследуемого участка трубопровода
следует находить отдельно для входящих в этот участок прямолинейных и
упругоизогнутых по проекту отрезков, а затем, определив длину условного
элемента рассматриваемой системы, по формуле (2)
оценки надежности системы с последовательным соединением элементов переходить к
оценке начальной надежности всего участка.
для исследуемого участка трубопровода
следует находить отдельно для входящих в этот участок прямолинейных и
упругоизогнутых по проекту отрезков, а затем, определив длину условного
элемента рассматриваемой системы, по формуле (2)
оценки надежности системы с последовательным соединением элементов переходить к
оценке начальной надежности всего участка.
4.6.17. Знание корреляционной функции Ru(x, xʹ) выходной
случайной функции ![]() дает возможность:
дает возможность:
определить длины условных элементов участка трубопровода как системы;
определить дисперсию случайной функции надежности Du(x);
установить, является ли случайная функция ![]() стационарной; при условии ее стационарности
вычисление характеристик надежности очень упрощается, так как для стационарной
случайной функции u(x) = const и Du(z)
= const;
стационарной; при условии ее стационарности
вычисление характеристик надежности очень упрощается, так как для стационарной
случайной функции u(x) = const и Du(z)
= const;
установить (если функция ![]() стационарна), что в точках наблюдения
значений случайной кривизны, по которым оценивается дисперсия, наблюдаемые
значения не являются коррелированными.
стационарна), что в точках наблюдения
значений случайной кривизны, по которым оценивается дисперсия, наблюдаемые
значения не являются коррелированными.
Формулы для определения характеристик случайной
функции начальной надежности ![]() способом ее
способом ее
частичной линеаризации
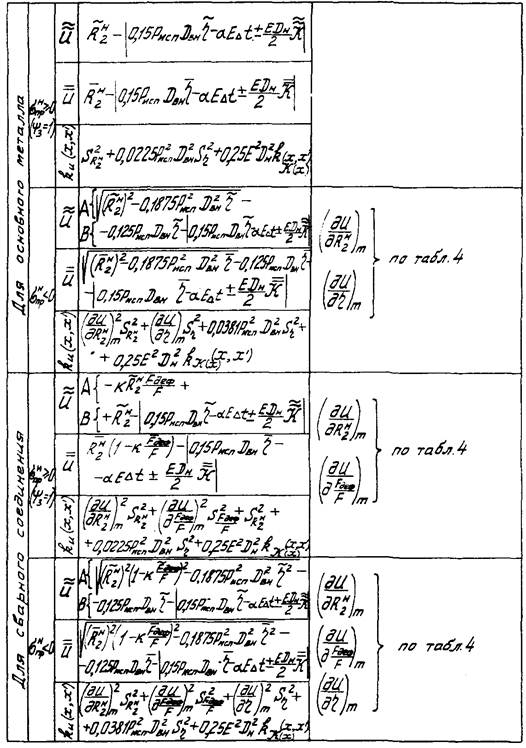
4.6.18. Дисперсию случайной функции надежности Du(х) определяют по найденной корреляционной функции Ru(х, xʹ) при x = x1, т.е. как
|
Du(х) = Ru(х, xʹ). |
(49) |
4.6.19. Получить выражения для
характеристик исходной случайной функции ![]() в результате натурных наблюдений за
реализациями данной функции кривизны оси трубопровода можно следующим образом
(пп. 4.6.20 - 4.6.35) [13].
в результате натурных наблюдений за
реализациями данной функции кривизны оси трубопровода можно следующим образом
(пп. 4.6.20 - 4.6.35) [13].
4.6.20. Для нахождения характеристик
математического ожидания ![]() , дисперсии
, дисперсии ![]() и корреляционной функции
и корреляционной функции ![]() случайной функции рассматривают ряд из
10 - 12 равноотстоящих друг от друга сечений x1,
x2, x3,
…, xn (например,
при х = 50 или 100 м, рис. 3).
случайной функции рассматривают ряд из
10 - 12 равноотстоящих друг от друга сечений x1,
x2, x3,
…, xn (например,
при х = 50 или 100 м, рис. 3).
Рис. 3. Схема опытного определения характеристик случайной
функции ![]()
4.6.21. В каждом из этих сечений измеряют значения K в горизонтальной и вертикальной плоскостях, по которым в соответствии с формулой (40) определяют случайное значение наибольшей кривизны в сечении. При этом вероятностный анализ для прямолинейных и упругоизогнутых по проекту участков необходимо производить раздельно.
4.6.22. Полученные случайные значения ![]() наибольшей кривизны в сечениях наносят
на график (рис. 4), они представляют собой
одну из реализаций
наибольшей кривизны в сечениях наносят
на график (рис. 4), они представляют собой
одну из реализаций ![]() случайной функции
случайной функции ![]() .
.
4.6.23. Выделять для упругоизогнутых участков проектную
составляющую в каждом из наблюдаемых значений случайной кривизны не следует,
так как в конечном счете требуется определить характеристики функции надежности
и значение начальной надежности, для чего требуется знание истинной кривизны в
каждой точке, включая и неслучайную составляющую. Такой подход не исказит
истинных характеристик случайной функции кривизны, а лишь повлияет на значение
математического ожидания ![]() .
.
4.6.24. Далее с такими же интервалами по длине трубопровода или на некоторых расстояниях от предыдущего участка наблюдений на исследуемом участке трубопровода производят еще m таких же серий измерений, также наносимых на график (см. рис. 4) и представляющих собой m других реализаций - K2(x), K3(x), …, Km(x) случайной функции.
4.6.25. Зарегистрированные значения Ki(x) заносят в таблицу, каждая строка которой соответствует определенной реализации случайной функции, а число строк соответствует числу наблюденных ее реализаций m (табл. 6). Таким образом, в таблице в i-й строке помещены значения случайной функции, наблюденной в i-й реализации при значениях аргумента х, равных x1, х2, …, xn. Обозначим через Ki(xj) значение, соответствующее i-й реализации в точке xj.
4.6.26. Полученный материал легко представить себе как результат m наблюдений над системой из n случайных величин. Поэтому характеристики случайной функции в сечении трубопровода х будут определяться из следующих соотношений:
математические ожидания ![]()
дисперсии DK(xj):
Форма представления натурных наблюдении
для случайной функции ![]()
|
x |
x1 |
x2 |
… |
xj |
… |
xl |
… |
xn |
|
K(x) |
||||||||
|
K1(x) |
K1(x1) |
K1(x2) |
… |
K1(xj) |
… |
K1(xl) |
… |
K1(xn) |
|
K2(x) |
K2(x2) |
K2(x2) |
… |
K2(xj) |
… |
K2(xl) |
… |
K2(xn) |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
Ki(x) |
Ki(x2) |
Ki(x2) |
… |
Ki(xj) |
… |
Ki(xl) |
… |
Ki(xn) |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
Km(x) |
Km(x2) |
Km(x2) |
… |
Km(xj) |
… |
Km(xl) |
… |
Km(xn) |
корреляционные моменты RK(xj, xl):
4.6.27. Отделив по формуле (50) значения математических ожиданий ![]() можно приближенно оценить зависимость
математического ожидания от координаты х (табл. 7), которую можно нанести на график (рис. 4).
можно приближенно оценить зависимость
математического ожидания от координаты х (табл. 7), которую можно нанести на график (рис. 4).
4.6.28. Далее можно найти оценки для элементов корреляционной матрицы - оценки дисперсий и корреляционных моментов. Дисперсии можно вычислять по формуле (51), но удобнее - через начальные моменты:
Рис. 4. Определение характеристик случайной функции ![]() из
из
опыта: K1(x),
K2(x),
K3(x),
K4(x),
K5(x),
K6(x),
K7(x),
K8(x),
K9(x)
- реализации случайной функции ![]()
4.6.29. Корреляционные моменты также удобнее вычислять не по формуле (52), а через начальные моменты:
4.6.30. Для удобства расчета по формулам (53) и (54) в случае упругоизогнутого по проекту участка целесообразно перенести начале отсчета ближе к математическому ожиданию, уменьшая каждое наблюденное значение максимальной случайной кривизны в сечении Ki и значения математических ожиданий на величину проектного радиуса упругого изгиба. При этом корреляционная функция не изменится.
4.6.31. Совокупность полученных
значений дисперсий и корреляционных моментов является элементами корреляционной
матрицы системы случайных величин, иначе - значениями корреляционной функции RK(x, xʹ). Например, при расстоянии между точками
наблюдения кривизны х = 100 м матрица значений RK(x, xʹ) будет
выглядеть, как показано в табл. 8, где по
главной диагонали стоят оценки дисперсий. Если по найденным значениям дисперсий
найти соответствующие им значения стандартов ![]() (табл. 9),
то, анализируя табл. 7 и 9, можно сделать заключение о стационарности случайной
функции
(табл. 9),
то, анализируя табл. 7 и 9, можно сделать заключение о стационарности случайной
функции ![]() . Известно, что условиями
стационарности случайной функции является постоянство математического ожидания
и дисперсии по аргументу случайной функции (в нашем случае по координате х):
. Известно, что условиями
стационарности случайной функции является постоянство математического ожидания
и дисперсии по аргументу случайной функции (в нашем случае по координате х):
|
|
4.6.32. Если найденные значения математических ожиданий в табл. 7 будут приблизительно равны между собой и значения дисперсий в табл. 8 также окажутся достаточно близкими друг к другу, можно сделать вывод, что исследуемая случайная функция стационарна. В этом случае отпадает необходимость наблюдать случайную кривизну по всей дайне исследуемого участка, что существенно упростит задачу оценки надежности.
4.6.33. Если случайная функция не вполне стационарна, следует привести ее к стационарному виду, осреднив полученные значения математических ожиданий и дисперсий:
Изменение математического ожидания по координате x.
|
x |
x1 |
x2 |
… |
xj |
… |
xl |
xn |
|
|
|
|
… |
|
… |
|
|
Значения корреляционной функции RK(x, xʹ)
корреляционная матрица системы случайных величин)
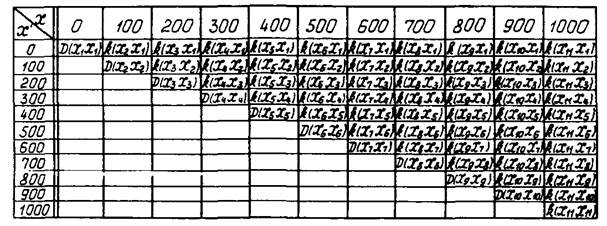
Изменение стандарта па координате x
|
x |
x1 |
x2 |
… |
xj |
… |
xl |
… |
xn |
|
SK(x) |
SK(x1 x1) |
SK(x2 x2) |
… |
SK(xjj) |
… |
SK(xl xl) |
… |
SK(xn xn) |
Значения нормированной корреляционной функции rK(x, xʹ)
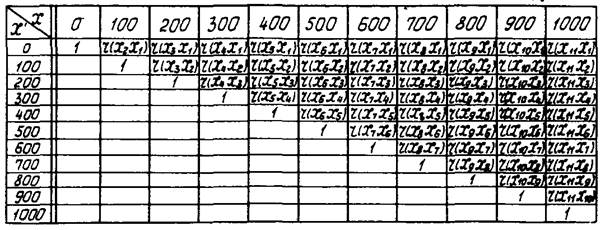
4.6.34. Теперь можно по формуле
|
|
(55) |
(поделив значения в табл. 8 на произведения соответствующих стандартов) получить таблицу значений нормированной корреляционной функции rK(х, хʹ) (табл. 10).
4.6.35. Если случайная функция оказалась стационарной, по табл. 10 можно легко построить ее нормированную корреляционную функцию. Известно, что корреляционная функция (в том числе и нормированная) стационарной случайной функции зависит только от Δх = хʹ - x, поэтому при постоянном Δx она должна быть постоянной. В табл. 10 постоянному Δx соответствуют: главная диагональ (Δx = 0) и параллели главной диагонали (Δx = 100, Δx = 200…) средняя оценки нормированной корреляционной функции вдоль этих параллелей, получим значения нормированной корреляционной функции стационарной случайной функции, обозначаемой через ρK(Δx), необходимые для ее графического построения и (если это нужно) для дальнейшей аналитической аппроксимации. Вид ρK(Δx) представлен на рис. 5.
4.6.36. Если случайная функция ![]() оказалась стационарной, легко
установить длину зоны автокорреляции l значений наблюдаемого
параметра кривизны по длине трубопровода, т.е. в соответствии с п. 3.2.1 длину условного элемента
системы. Эта зона будет равна длине участка затухания нормированной
корреляционной функции ρK(Δx) (см. рис. 5),
которая по определению и является коэффициентом корреляции в формуле (3).
оказалась стационарной, легко
установить длину зоны автокорреляции l значений наблюдаемого
параметра кривизны по длине трубопровода, т.е. в соответствии с п. 3.2.1 длину условного элемента
системы. Эта зона будет равна длине участка затухания нормированной
корреляционной функции ρK(Δx) (см. рис. 5),
которая по определению и является коэффициентом корреляции в формуле (3).
4.6.37. Если случайная функция
кривизны ![]() окажется стационарной (есть основание
предполагать, что на практике она стационарна, поскольку отклонения кривизны
оси трубопровода от проектного положения в любую сторону для каждой из
наблюдаемых плоскостей, т.е. для горизонтальной и вертикальной плоскостей,
очевидно, равновероятны), то вычисление характеристик выходной случайной
функции
окажется стационарной (есть основание
предполагать, что на практике она стационарна, поскольку отклонения кривизны
оси трубопровода от проектного положения в любую сторону для каждой из
наблюдаемых плоскостей, т.е. для горизонтальной и вертикальной плоскостей,
очевидно, равновероятны), то вычисление характеристик выходной случайной
функции ![]() и далее характеристик начальной
надежности резко упрощается. В этом случае
и далее характеристик начальной
надежности резко упрощается. В этом случае ![]() также будет стационарной,если учесть
ее линейную связь по формулам табл. 5 с
входной функцией (как для
также будет стационарной,если учесть
ее линейную связь по формулам табл. 5 с
входной функцией (как для ![]() ), так и для Du(х)),и
будет иметь
), так и для Du(х)),и
будет иметь ![]() . Подставляя в формулы для
. Подставляя в формулы для ![]() и Ru(х,
хʹ) по табл. 5 значения
и Ru(х,
хʹ) по табл. 5 значения ![]() и RK(х,
хʹ) = DK(х)
осредненные значения математического ожидания и дисперсии входной случайной
функции
и RK(х,
хʹ) = DK(х)
осредненные значения математического ожидания и дисперсии входной случайной
функции ![]() , вычисленные по формулам (54a), (54б), находим постоянные по x значения
, вычисленные по формулам (54a), (54б), находим постоянные по x значения ![]() и Du начальной надежности в сечении. При пересчете по формулам
табл. 5 дисперсии случайных величин
заменены дисперсиями средних по подвыборкам, поэтому и значение дисперсии
случайного процесса Du следует
вводить в расчет, уменьшая до величин
и Du начальной надежности в сечении. При пересчете по формулам
табл. 5 дисперсии случайных величин
заменены дисперсиями средних по подвыборкам, поэтому и значение дисперсии
случайного процесса Du следует
вводить в расчет, уменьшая до величин
|
|
где n - число наблюдений в подвыборках, группируемых при обработке случайных величин, входящих в формулы табл. 5. При этом дисперсию выходной случайной функции также следует скорректировать:
|
|
4.6.38.
Определив вероятностные характеристики функции надежности ![]() для одного условного элемента системы,
т.е. надежность в сечении x, можно найти и оценку начальной надежности
исследуемого участка трубопровода как системы из последовательно соединенных
условных элементов. При использовании формул (21),
(31) следует иметь в виду, что
надежности прямых и упругоизогнутых но проекту участков следует определять
отдельно, поэтому надежность участка, включающего как прямые, так и
упругоизогнутые составляющие, должна определяться перемножением вероятностей,
найденных для всех этих частей участка. Учитывая, что условная длина элемента
определялась длиной зоны автокорреляции только нагрузки, модель самого элемента
не меняется. Поэтому под условным элементом мы будем подразумевать участок
трубопровода без кольцевых швов, равный по длине зоне автокорреляции нагрузки и
ограниченный по концам сварными соединениями.
для одного условного элемента системы,
т.е. надежность в сечении x, можно найти и оценку начальной надежности
исследуемого участка трубопровода как системы из последовательно соединенных
условных элементов. При использовании формул (21),
(31) следует иметь в виду, что
надежности прямых и упругоизогнутых но проекту участков следует определять
отдельно, поэтому надежность участка, включающего как прямые, так и
упругоизогнутые составляющие, должна определяться перемножением вероятностей,
найденных для всех этих частей участка. Учитывая, что условная длина элемента
определялась длиной зоны автокорреляции только нагрузки, модель самого элемента
не меняется. Поэтому под условным элементом мы будем подразумевать участок
трубопровода без кольцевых швов, равный по длине зоне автокорреляции нагрузки и
ограниченный по концам сварными соединениями.
4.6.39. С учетом этих замечаний формулы для расчетной оценки начальной надежности участка трубопровода к моменту его предпусковых испытаний при условии стационарности случайной функции упругого изгиба будут иметь вид:
а) для случая неповоротной сварки всего участка, состоящего из прямой и упругоизогнутой по проекту частей:
Рис. 5.
Характерный вил нормированной корреляционной функции
стационарной случайной функции ![]() :
:
l - длина зоны автокорреляции (длина условного
элемента)
где n, n1 - число условных элементов системы, т.е. число участков, равных по длине зоне автокорреляции, укладывающихся на исследуемом участке трубопровода (или же соответственно на его прямой и упругоизогнутой частях);
[…]пр, […]из - надежности, соответственно прямой и упругоизогнутой составляющих исследуемого участка;
![]() - надежности в сечении соответственно
трубы и сварного стыка;
- надежности в сечении соответственно
трубы и сварного стыка;
б) для случая неповоротной сварки трехтрубных секций того же участка:
|
|
(57) |
где ![]() - надежности в
сечении соответственно неповоротного и поворотного стыков.
- надежности в
сечении соответственно неповоротного и поворотного стыков.
4.6.40. Для
условий примера 4.4 при длине
испытуемого участка трубопровода 30 км, выполненного неповоротной сваркой, и
прямолинейного (проектный упругий изгиб отсутствует) получены данные о
стационарности случайной функции кривизны оси трубопровода. Установлено, что
протяженность зоны затухания корреляционной функции, принимаемая за длину
условного элемента системы, составляет 1 км. Определив, что при этом ![]() , найдем по формуле (56) оценку начальной надежности участка:
, найдем по формуле (56) оценку начальной надежности участка:
|
|
Вычисление сомножителей проводим, как и в п. 4.6.1, с помощью логарифмирования:
|
|
Таким образом, оценка надежности участка к моменту его испытания составит:
|
|
что, в общем, ниже ориентировочных «нормативных» оценок (Р = 0,95 ÷ 0,99), рекомендуемых в [16] для массового элемента статически неопределимой конструкции, отказ которого не влечет внезапного разрушения системы (если допустить, что испытуемый участок трубопровода является элементом статически неопределимой системы, не разрушающейся при испытании участка).
Теперь по формуле (1) найдем среднеожидаемое количество отказов при
испытании, учитывая, что ![]()
|
|
т.е. для условий примера 4.4. на испытуемом участке наверняка не возникнет ни одного отказа.
4.6.41. Если входная, а следовательно, и выходная случайные
функции окажутся нестационарными (что маловероятно ) для определения
вероятностных характеристик надежности ![]() для всех
сечений участка трубопровода требуется определение
для всех
сечений участка трубопровода требуется определение ![]() и Du(х)по всем значениям реализаций
входной случайной функции по табл. 7 и 8 (в нашем случае через каждые 100 м). При
этом число реализаций случайной функции mдолжно
составлять
и Du(х)по всем значениям реализаций
входной случайной функции по табл. 7 и 8 (в нашем случае через каждые 100 м). При
этом число реализаций случайной функции mдолжно
составлять ![]() , где z - длина всего исследуемого участка, h - шаг
наблюдений (см. рис. 3) за случайной
функцией. Сценки характеристик случайной функции для прямых и упругоизогнутых
по проекту участков по-прежнему следует производить раздельно, объединяя в
соответствии с п. 4.6.38.
, где z - длина всего исследуемого участка, h - шаг
наблюдений (см. рис. 3) за случайной
функцией. Сценки характеристик случайной функции для прямых и упругоизогнутых
по проекту участков по-прежнему следует производить раздельно, объединяя в
соответствии с п. 4.6.38.
Примечание. Так как на данном этапе наблюдения на фактическим характером случайной функции кривизны оси трубопровода отсутствуют, то, считаясь с возможной фактической нестационарностью случайной функция кривизны (хотя такая возможность мала), при натурном исследовании кривизны оси трубопровода соседние реализации следует выбирать не подряд, как показано на рис. 3, а с таким расчетом, чтобы 10 - 12 реализаций были распределены по всему изучаемому участку (или, если участок имеет и прямую, и упругоизогнутую составляющие, соответственно - по каждому из этих участков в отдельности).
4.6.42. Очевидно, что в случае нестационарной функции ![]() ее корреляционная функция не будет
постоянной по Δх для любых сечений по длине трубопровода: для одних
и тех же значений Δх в разных местах по длине участка трубопровода
значения корреляционной функции будут различны. Это не позволит четко установить
единую длину условного элемента системы, поэтому расчет надежности для участка
по указанной выше методике в случае нестационарной функции
ее корреляционная функция не будет
постоянной по Δх для любых сечений по длине трубопровода: для одних
и тех же значений Δх в разных местах по длине участка трубопровода
значения корреляционной функции будут различны. Это не позволит четко установить
единую длину условного элемента системы, поэтому расчет надежности для участка
по указанной выше методике в случае нестационарной функции ![]() выполнить невозможно. В связи с этим
надежность испытуемого участка трубопровода в случае нестационарной функции
выполнить невозможно. В связи с этим
надежность испытуемого участка трубопровода в случае нестационарной функции ![]() следует характеризовать совокупностью
оценок надежности в сеченияк трубопровода, расчет которых следует производить
по-прежнему в соответствии с формулами табл. 5,
с использованием всех найденных значений
следует характеризовать совокупностью
оценок надежности в сеченияк трубопровода, расчет которых следует производить
по-прежнему в соответствии с формулами табл. 5,
с использованием всех найденных значений ![]() и всех элементов корреляционной
матрицы.
и всех элементов корреляционной
матрицы.
4.6.43. Кривизну (вернее, координаты оси трубопровода с последующим, расчетным переходом к кривизне или радиусу кривизны) оси трубопровода по длине исследуемого участка измеряют [20] после укладки участка трубопровода в траншею до ее засыпки.
В горизонтальной плоскости измерения производят теодолитом путем установки его на трубу (с закреплением его штатива на гибкой проволочной рамке) и последовательной съемки в точках с интервалами, равными шагу наблюдения за случайной функцией. Съемку производят при горизонтальном расположении рейки на трубе. В нижней части рейка должна быть снабжена горизонтальным (т.е. перпендикулярным самой рейке) упорным элементом, который фиксирует ее положение на трубе. Съемку ведут теодолитным ходом - с одновременным измерением горизонтальных углов в точках измерений.
В вертикальной плоскости измерения производят нивелиром с установкой его рядом с траншеей и с последовательным перемещением рейки по трубе по тем же точкам отсчета.
Таким образом, съемку в каждой точке производят дважды (теодолитом и нивелиром) при горизонтальном и вертикальном расположении рейки на трубе.
Результаты геодезической съемки, обеспечивающие знание координат пространственного положения оси трубопровода, обрабатывают на ЭВМ по стандартной программе для получения значений кривизны в соответствующих точках.
5. ОЦЕНКА ЭКСПЛУАТАЦИОННОЙ КОНСТРУКТИВНОЙ
НАДЕЖНОСТИ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
5.1. В основу прогнозной оценки эксплуатационной надежности, т.е. вероятности безотказной работы трубопровода, его участка или элемента под действием эксплуатационных нагрузок и воздействий, по-прежнему будут положены условия (11), (12), (12а). Как указывалось, в настоящем Руководстве выбран упрощенный метод оценки надежности - без учета фактора времени. Такая оценка в соответствии с п. 3.1.5 характеризует вероятность ненарушения какого-либо (каких-либо) из предельных состояний, оговоренных в СНиП II-45-75 (в нашем случае - условия деформативности), при применении упрощенной модели функционирования трубопровода.
5.2. В условия (11),
(12), (12а) наряду с радиусом упругого изгиба ![]() , толщиной стенки
, толщиной стенки ![]() и показателем механических свойств
металла
и показателем механических свойств
металла ![]() входят другие существенно изменчивые
факторы - рабочее давление
входят другие существенно изменчивые
факторы - рабочее давление ![]() и температурный перепад Δt,
благодаря которым оценка надежности, полученная на основе данных формул, будет
зависеть от местоположения расчетного сечения трубопровода по отношению к
соседним компрессорным (КС) или насосным (НС) станциям.
и температурный перепад Δt,
благодаря которым оценка надежности, полученная на основе данных формул, будет
зависеть от местоположения расчетного сечения трубопровода по отношению к
соседним компрессорным (КС) или насосным (НС) станциям.
Факторы ![]() и Δ
и Δ![]() упрощенно можно представить как
элементарные случайные функции, т.е. как случайные величины, но изменяющиеся по
длине трубопровода между соседними перекачечными станциями по определенному и
при этом неслучайному закону.
упрощенно можно представить как
элементарные случайные функции, т.е. как случайные величины, но изменяющиеся по
длине трубопровода между соседними перекачечными станциями по определенному и
при этом неслучайному закону.
5.3. Применительно к случайному фактору внутреннего давления
![]() реализацию элементарного процесса
можно представить как некоторое полученное у предыдущей перекачечной станции
случайное значение ρ, которое затем, по мере движения продукта по трубе к
следующей станции, падает по определенному неслучайному закону. На рис. 6 показана совокупность реализаций такого
случайного процесса, которая может быть получена простым изменением масштаба по
оси ординат.
реализацию элементарного процесса
можно представить как некоторое полученное у предыдущей перекачечной станции
случайное значение ρ, которое затем, по мере движения продукта по трубе к
следующей станции, падает по определенному неслучайному закону. На рис. 6 показана совокупность реализаций такого
случайного процесса, которая может быть получена простым изменением масштаба по
оси ординат.
Форма записи элементарного случайного процесса для фактора внутреннего давления следующая:
|
|
(58) |
или для температурного перепада, как показано на рис. 7:
|
|
(59) |
где φ(х), ξ(х) - обычные (неслучайные) функции;
x - текущая координата по длине трубопровода с началом x = 0 у предыдущей перекачечной станции и концом x = l - у последующей.
5.4. Разрешая условия (11), (12) относительно вероятности безотказной работы, можно записать соотношение;
где Рэ
или Рэ(u >
0) - эксплуатационная надежность, в котором факторы ![]() учтены как
элементарные случайные процессы, а факторы
учтены как
элементарные случайные процессы, а факторы ![]() - как
случайные величины.
- как
случайные величины.
Рис. 6a. Представление фактора внутреннего давления ![]() как элементарного случайного процесса:
как элементарного случайного процесса:
![]() - возможные значения случайной
величины
- возможные значения случайной
величины
внутреннего давления в трубопроводе на выходе из перекачечной станции
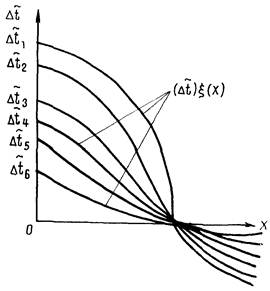
Рис. 6б. Представление фактора температурного перепада ![]() как элементарного случайного процесса:
как элементарного случайного процесса:
![]() - возможные
значения случайной величины
- возможные
значения случайной величины
температурного перепада трубопровода на выходе из перекачечной станции
5.5. Если при оценке надежности расчетное сечение выбирается по металлу сварного шва, условие (57б) примет вид:
5.6. Повторяя рассуждения пп. 4.3.11 - 4.3.20, приходим к формулам
(и выражениям частных производных) для определения характеристик случайной
величины ![]() (функции надежности в сечении
трубопровода х) путем ее линеаризации (табл. 11) или, что несколько проще, методом ее частичной
линеаризации (табл. 11).
(функции надежности в сечении
трубопровода х) путем ее линеаризации (табл. 11) или, что несколько проще, методом ее частичной
линеаризации (табл. 11).
5.7. В отличие от оценки начальной
надежности, в данном случае количество случайных аргументов достаточно
велико, что дает основание считать определяемые по табл. 11 и 11
характеристики ![]() и Su параметрами
нормально распределенной функции
и Su параметрами
нормально распределенной функции ![]() . Это дает возможность в данном случае
не обязательно использовать прием «искусственной нормализации» исходных
распределений аргументов. Однако обработку статистической информации и в этом
случае удобно производить на ЭВМ с помощью достаточно универсальной программы
«ООК», приведенной в разд. 6.
. Это дает возможность в данном случае
не обязательно использовать прием «искусственной нормализации» исходных
распределений аргументов. Однако обработку статистической информации и в этом
случае удобно производить на ЭВМ с помощью достаточно универсальной программы
«ООК», приведенной в разд. 6.
5.8. Поскольку в условия (60)
и (61) входят только случайные величины
и элементарные случайные функции (радиус упругого изгиба ρ в данном случае
тоже рассматривается как случайная величина), функция надежности ![]() (для сечения, находящегося на
расстоянии x от перекачечной станции) также будет выражаться в виде
элементарной случайной функции:
(для сечения, находящегося на
расстоянии x от перекачечной станции) также будет выражаться в виде
элементарной случайной функции: ![]() , в которой, согласно п. 5.7, распределение
, в которой, согласно п. 5.7, распределение ![]() будет нормальным.
будет нормальным.
Формулы для определения характеристик
случайной величины ![]() (функции эксплуатационной надежности)
(функции эксплуатационной надежности)
путем ее линеаризации
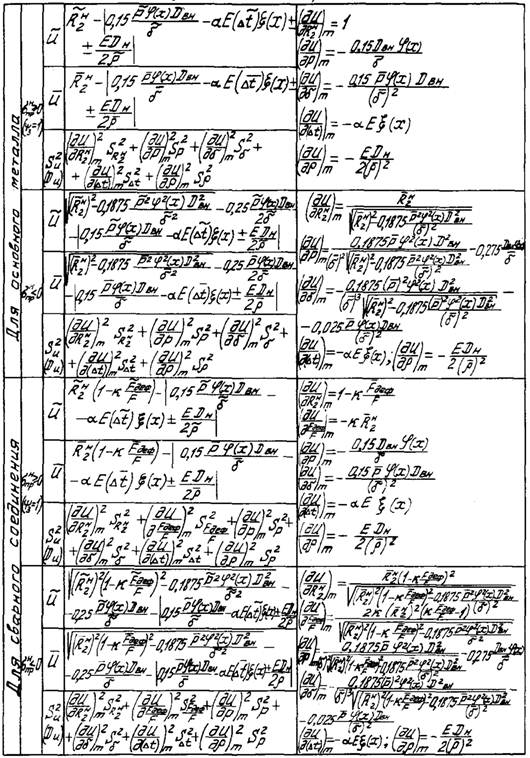
Формулы для определения характеристик
случайной величины ![]() (функции эксплуатационной надежности)
(функции эксплуатационной надежности)
способом ее частичной линеаризации
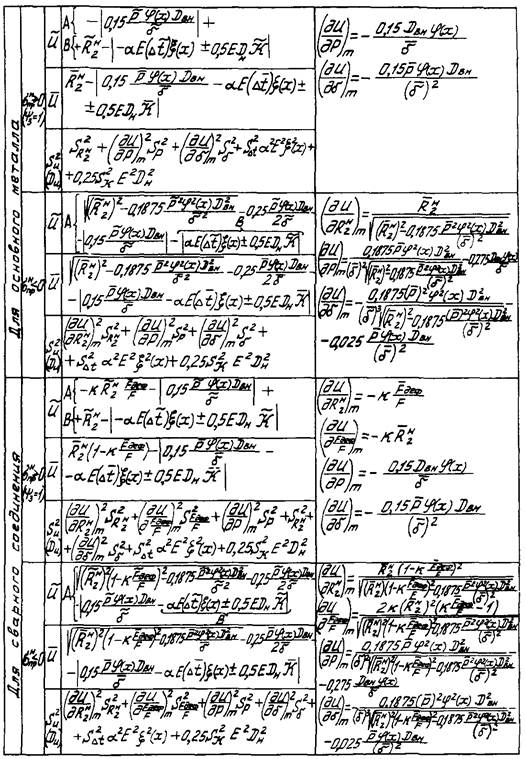
Таким образом, по табл. 11
и 12 можно найти оценку эксплуатационной
надежности в любом сечении трубопровода между соседними перекачечными
станциями, причем в различных сечениях эти оценки (в силу рассмотрения факторов
![]() и Δ
и Δ![]() как элементарных случайных функций)
будут различны.
как элементарных случайных функций)
будут различны.
Определение оценки надежности участка трубопровода при
данном подходе, как и при подходе к ![]() как к случайной величине, невозможно в
силу неопределенности при принятой расчетной модели понятия элемента системы.
как к случайной величине, невозможно в
силу неопределенности при принятой расчетной модели понятия элемента системы.
5.9. При рассмотрении упругого изгиба трубопровода как
случайной функции по координате x, сначала рассмотрим вариант, когда
случайная функция кривизны оси трубопровода ![]() стационарна (что, очевидно, и имеет
место на практике). Повторяя рассуждения пп. 4.6.1 - 4.6.18,
получаем формулы для определения характеристик случайной функции
стационарна (что, очевидно, и имеет
место на практике). Повторяя рассуждения пп. 4.6.1 - 4.6.18,
получаем формулы для определения характеристик случайной функции ![]() эксплуатационной надежности в сечении
трубопровода х (табл. 13).
эксплуатационной надежности в сечении
трубопровода х (табл. 13).
5.10. Из формул (табл. 11)
для корреляционной функции Ru(х,
хʹ) очевидно, что выходная случайная функция ![]() надежности не будет стационарной, так
как значения корреляционной функции RK(х,
хʹ) входной случайной функции при подстановке в выражения Ru(х, хʹ) непрерывно изменяются
в связи с изменением по координате Других случайных функций, учитываемых
расчетом. Однако это не является препятствием к определению расчетной длины
условного элемента при рассмотрении участка трубопровода как системы (здесь под
системой может подразумеваться участок трубопровода между двумя перекачечными
станциями или любая его часть), так как длина условного элемента принимается в
соответствии с п. 4.6.36 на
основе рассмотрения нормированной корреляционной функции входной случайно
функции. Таким образом, если входная случайная функция
надежности не будет стационарной, так
как значения корреляционной функции RK(х,
хʹ) входной случайной функции при подстановке в выражения Ru(х, хʹ) непрерывно изменяются
в связи с изменением по координате Других случайных функций, учитываемых
расчетом. Однако это не является препятствием к определению расчетной длины
условного элемента при рассмотрении участка трубопровода как системы (здесь под
системой может подразумеваться участок трубопровода между двумя перекачечными
станциями или любая его часть), так как длина условного элемента принимается в
соответствии с п. 4.6.36 на
основе рассмотрения нормированной корреляционной функции входной случайно
функции. Таким образом, если входная случайная функция ![]() стационарна, оценку надежности участка
трубопровода определяют по-прежнему в соответствии с п. 4.6.38.
стационарна, оценку надежности участка
трубопровода определяют по-прежнему в соответствии с п. 4.6.38.
5.11. Если случайная функция ![]() окажется нестационарной, единую длину
условного элемента системы установить нельзя, поэтому надежность участка
трубопровода, как и в п. 4.6.40,
следует характеризовать совокупностью оценок надежности в сечениях данного
участка трубопровода.
окажется нестационарной, единую длину
условного элемента системы установить нельзя, поэтому надежность участка
трубопровода, как и в п. 4.6.40,
следует характеризовать совокупностью оценок надежности в сечениях данного
участка трубопровода.
Формулы
для определения характеристик
случайной величины ![]() (функции начальной надежности)
(функции начальной надежности)
путем ее линеаризации
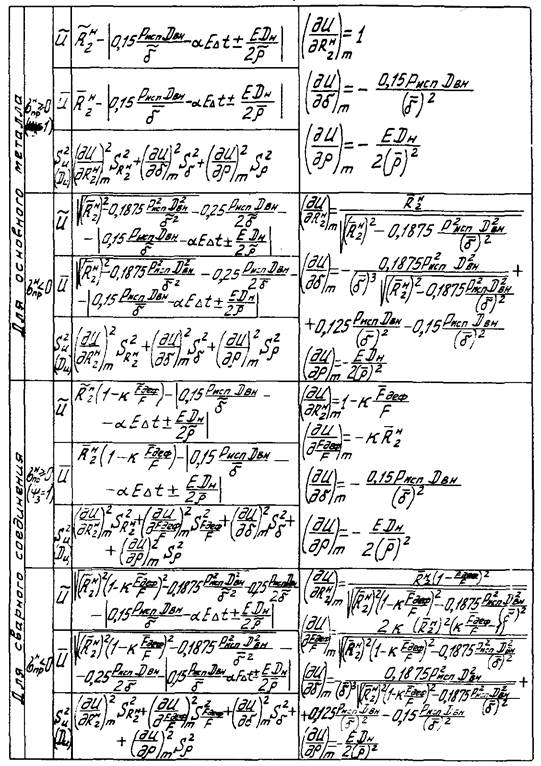
6. ПРОГРАММА ДЛЯ
СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ СТАТИСТИЧЕСКИ
ИЗМЕНЧИВЫХ ПАРАМЕТРОВ ПО МЕТОДУ КРИВЫХ
ГРАМА - ШАРЛЬЕ НА ПРИМЕРЕ ДЕФЕКТОВ СВАРКИ
(ПРОГРАММА «ООК»)
6.1. Программа определения ординаты для кривой Грама - Шарлье написана на языке АЛГОЛ с применением условных обозначений входного языка транслятора «МЭИ-3» для ЭВМ «Минск-22», «Минск-32», которые приведены в табл. 14.
Условные обозначения
|
Принятое обозначение в формуле |
Идентификатор |
Наименование параметров и массивов |
|
K |
K |
Количество наблюдений случайной величины |
|
Y |
Y |
Значение случайной величины (длина дефекта) |
|
x1 |
x1[1:M, 1:K] |
Значение случайной величины (ширина дефекта) |
|
x2 |
x2[1:M, 1:K] |
Значение случайной величины (глубина дефекта) |
|
n |
N |
Число точек в группе |
|
m |
M |
Число групп |
|
Ky |
KY |
Количество интервалов гистограммы для Y |
|
|
KX1 |
То же для x1 |
|
|
KX2 |
То же для x2 |
|
|
DY |
Среднее значение по всему количеству K наблюдений случайной величины |
|
|
DX1 |
То же для x1 |
|
|
DX2 |
То же для x2 |
|
|
SIσMAY |
Стандарт распределения средних |
|
yi |
yi[1:KY] |
Значение середины интервалов гистограммы Y |
|
x1i |
x1i[1:KX1] |
То же для x1 |
|
x2i |
x2i[1:KX1] |
То же для x2 |
|
x4 x2 x3 |
|
K - статистики Фишера (несмещенные оценки куммуляторов) |
|
S |
S |
Стандарт распределения случайной величины |
|
v1 |
NU1 |
Коэффициент асимметрии генеральной совокупности (v1 = a3) |
|
N2 |
NU2 |
Коэффициент, аналогичный коэффициенту эксцесса генеральной совокупности (v2 = a4 - 3) |
|
N1(Y) |
NU1Y |
Коэффициент асимметрии средних |
|
N2(Y) |
NU2Y |
Коэффициент, аналогичных коэффициенту эксцесса средних |
|
Z |
Z |
Отклонение от среднего в единицах стандартного отклонения |
|
f(z) |
f(z) |
Ордината плотности нормированного отклонения |
|
f3(z) |
F3Z |
Третья производная f(z) |
|
C3 C4 |
C3 C4 |
Коэффициенты уравнения кривой Грама - Шарлье |
|
C3f3(z) |
C3F3Z |
Второй член уравнения кривой Грама - Шарлье (поправка на асимметрию) |
|
φ4(z) |
FI4Z |
Ордината кривой Грама - Шарлье, согласованной по асимметрии и эксцессу |
|
Y0 |
Y0 |
Коэффициент для проверки согласия с фактическими данными |
|
Y0⋅φ4(z) |
Y0FI4Z |
Ордината при поверке согласия |
|
φ3(z) |
FI3Z |
Ордината кривой Грама - Шарлье, согласованной только по асимметрии |
|
f4(z) |
F4Z |
Четвертая производная от f(z) |
|
C4⋅f4(z) |
C4F4Z |
Третий член уравнения кривой Грама - Шарлье (поправка на эксцесс) |
6.2. ПРИНЦИП
ОПИСАНИЯ СТАТИСТИЧЕСКИХ СВЕДЕНИЙ
КРИВОЙ ГРАМА - ШАРЛЬЕ
6.2.1. В основу статистического описания изменчивых параметров в настоящем Руководстве положен метод построения кривых [21] Грама - Шарлье. Кривые распределения Грама - Шарлье Являются обобщением нормальной кривой на случай асимметричных кривых [22]. Любую функцию Y(х) можно разложить в ряд по ортогональным полиномам [23] Чебышева-Эрмита:
|
|
6.2.2. Коэффициенты СK определяют по формулам:
|
|
где HK(z) - полином Чебышева:
|
|
![]() - значение нормированного отклонения
от среднего случайной величины x.
- значение нормированного отклонения
от среднего случайной величины x.
6.2.3. Коэффициенты СK просто выражаются через центральные моменты кривой у(х), в результате чего получается ряд Грама - Шарлье:
Первый член ряда представляет собой кривую Гаусса, второй дает поправку на асимметрию кривой, третий - на эксцесс (крутизну) кривой. В результате имеем для плотности распределения f(z) выражение [22]:
где f3(z), f4(z) соответственно 3-я и 4-я производные от плотности нормального распределения f(z) называемые полиномами Эрмита:
|
f3(z) = (3z - z3)f(z); f4(z) = (3 - 6z2 + z4)f(z); |
![]() - коэффициент
асимметрии;
- коэффициент
асимметрии;
![]() - коэффициент эксцесса.
- коэффициент эксцесса.
6.2.4. Таким образом, для определения ординат кривой Грама - Шарлье и соответствующих статистических характеристик необходимо иметь:
1) ![]() - третий центральный момент;
- третий центральный момент;
2) ![]() - четвертый центральный момент;
- четвертый центральный момент;
3) ![]() - стандартное отклонение в выборке;
- стандартное отклонение в выборке;
4) значения полиномов Эрмита:
а) ![]() ;
;
б) ![]()
и значение
плотности нормированного нормального распределения f(z) при всех ![]() .
.
6.2.5. В результате статистической аппроксимации должны быть получены:
а) ординаты кривой распределения изучаемой случайной величины (ординаты кривой Грама - Шарлье);
б) числовые характеристики распределения исследуемой случайной величины и распределения критерия средних значений этой случайной величины по выборкам.
6.3.
АЛГОРИТМ РАСЧЕТА ОРДИНАТ КРИВЫХ ГРАМА - ШАРЛЬЕ
И ПОЛУЧЕНИЯ ЧИСЛОВЫХ ХАРАКТЕРИСТИК СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
6.3.1. Программа «ООК» предназначена для расчета ординат кривых распределения случайных величин и систем случайных величин, а также для получения соответствующих числовых характеристик распределения.
6.3.2.. Алгоритм расчета ординат кривых распределения разрабатывали на примере случайных величин размеров дефектов сварки трубопроводов. Статистической обработке подвергали полученную на основании анализа результатов неразрушающего радиографического контроля статистическую информацию о конфигурации сварочных дефектов определенного типа. Дефект сварки определенного типа представлялся в виде системы трех случайных величин: длины дефекта Y, ширины дефекта x1 и глубины дефекта x2. Указанные величины предполагались некоррелированными. Контрольный экземпляр программы «ООК» хранится в лаборатории математических методов исследования (ЛММИ) ВНИИСТа*.
________
*Программа корреляционно-регрессионного анализа «КРА», дополняющая программу «ООК» в случаях необходимости обработки системы коррелированных случайных величия, разработана ЛММИ по алгоритму ЛНК ВНИИСТа. Контрольный экземпляр программы «КРА» хранится в ЛММИ ВНИИСТа.
Описание алгоритма расчета ординат кривых распределения будем производить для одной из случайных величия системы, например для Y, имея в виду, что алгоритм обработки других случайных величин x1, x2 системы идентичен.
6.3.3. Для получения ординат плотности распределения случайной величины Y следует:
А. Найти коэффициенты С3, С4 следующем порядке:
определить среднее значение Y случайной величины по формуле
|
|
определить несмещенную оценку дисперсии по выборке (иначе, несмещенную оценку куммулянты x2):
|
|
определить стандартное отклонение случайной величины Y от центра;
|
|
определить K - статистики Фишера, иначе несмещенные оценки куммулянтов x4 и x3:
|
|
определить оценки коэффициентов v1 и v2 аналогичных коэффициентам a3, a4 асимметрии и эксцесса:
|
|
определить коэффициенты С3 и С4 в уравнении (62а):
|
|
Б. Найти значения плотности нормированного нормального распределения f(z) и значения ее 3-й и 4-й производной в следующем порядке:
разбить все поле возможных значений случайной величины Y на Kу интервалов (K = 10 ÷ 20 интервалов в зависимости от размаха наблюденных значений Yi);
зафиксировать Kу значений середины интервалов Yi;
определить Kу
значений отклонений от среднего значения ![]() ;
;
определить Kу значений отклонений от среднего значений отклонений z от среднего в единицах стандартного отклонения:
|
|
определить Kу значений ординат плотности нормированного нормального распределения:
|
|
вычислить Kу значений полиномов Эрмита:
|
|
вычислить Kу значений 3-й и 4-й производных f(z):
|
|
определить ординаты плотности распределения φ(z) как ординаты кривой Грама - Шарлье по уравнению (62).
6.3.4. Однако если наблюденная совокупность значений случайной величины явно асимметрична, то мало оснований для применения в указанной форме ряда Грама - Шарлье, основанного на симметричном нормальном распределении. При большой асимметрии генеральной совокупности определение ординат и построение кривой Грама - Шарлье целесообразно осуществлять на основе разбиения всего массива наблюденных значений случайной величины на ряд n подвыборок. В этом случае распределение случайной величины заменяется распределением средних значений в подвыборках, которые, как известно из математической статистики, приближаются к нормальному с возрастанием объема выборки, но в то же время отражают (хотя и в меньшей степени) асимметрию и эксцесс распределения исходной случайной величины. Трактовка вероятности для распределения такого критерия несколько меняется. Например, понятие вероятности превышения случайной величиной некоторой величины α будет заменяться понятием вероятности превышения средним значением в подвыборке (из n значений случайной величины) величины α.
6.3.5. В более общем виде алгоритм определения ординат кривой Грама-Шарлье для статистических данных с любой асимметрией будет иметь несколько иной вид в сравнении с приведенным выше. Статистические характеристики среднего дисперсии, асимметрии, эксцесса в этом случае будут вычислять не по всему массиву наблюдений случайной величины, а по m подвыборкам (группам) по n значений в каждой. Только после этого уже по этим m подвыборкам вычисляют межгрупповые, т.е. общие характеристики.
6.3.6. Таким образом, более общий алгоритм расчета ординат кривых Грама - Шарлье по статистическим данным рекомендуется следующий:
А. Определение коэффициентов С3 и С4:
весь массив значений случайной величины Y разбить на m подвыборок (групп) по n = 5 ÷ 10, но не менее четырех значений в каждой группе;
в каждой подвыборке (группе)
определить среднее значение ![]() случайной величины по формуле
случайной величины по формуле
|
|
где n - число значений случайной величины в каждой подвыборке (группе);
определить несмещенную оценку дисперсии как среднее по значениям тех же дисперсий в подвыборках (группах), а также стандартное отклонение случайной величины от центра;
|
|
определить стандартное отклонение среднее по выборкам;
|
|
определить R - статистики Фишера, т.е. несмещенные оценки куммулянтов x4 и x2 как средние по m значениям тех же статистик в подвыборках (группах):
|
|
определить оценки коэффициентов v1 и v2 совокупности, аналогичные коэффициентам a3, a4 и эксцесса:
|
|
определить коэффициенты v1(Y) и v2(Y) для распределения средних:
|
|
определить коэффициенты С3, С4 в уравнении (62а):
|
|
Б. Найти значения плотности нормированного нормального распределения f(z) и значения ее 3-й и 4-й производной в следующем порядке:
разбить все поле возможных значений случайной величины Y на Ky интервалов (Ky = 10 ÷ 20 интервалов в зависимости от размаха наблюденных значений Yi);
найти Ky значений середины интервалов Yi;
определить Ky
значений отклонений от среднего значения ![]() ;
;
определить Ky значений отклонения (z) от среднего в единицах стандартного отклонения по выборкам:
|
|
определить Ky значений ординат плотности нормированного нормального распределения:
|
|
значений Ky полиномов Эрмита:
|
|
вычислить Ky значений 3-й и 4-й производных f(z):
|
|
определить ординаты плотности распределения φ(Y) как ординаты кривой Грама - Шарлье по уравнению (62).
6.3.7. Как указывалось выше, алгоритм обработки других случайных величин (x1, x2) системы в точности соответствует изложенному для случайной величины Y.
6.3.8. Методом кривых Грама - Шарлье можно пользоваться и при построении самой функции надежности [16].
6.4. ЗАДАНИЕ ВХОДНОЙ ИНФОРМАЦИИ
Исходные данные для расчета по программе «ООК» задают в виде
целых десятичных чисел (для K, N, KY, ![]() ,
, ![]() ) и реальных чисел (для всех остальных
данных). Они записываются массивами, каждый из которых заключается в границы
ввода.
) и реальных чисел (для всех остальных
данных). Они записываются массивами, каждый из которых заключается в границы
ввода.
Реальные числа могут бить записаны либо в виде числа с плавающей запятой (мантисса 7 цифр, знак порядка и порядок - 2 цифры), либо в виде числа с кодовой запятой (например , +100,0). В этом случае порядок числа не задается.
Представление реальных чисел в виде целого числа (без запятой) не допускается.
Задаются следующие исходные данные:
в 1-м массиве - K, n;
во 2-м - KY, ![]() ,
, ![]() ;
;
в 3-м - Y (K чисел);
в 4-м - х1 (K чисел);
в 5-м - х2 (K чисел);
в 6-м - Y - (KY чисел);
в 7-м - x1i
(![]() чисел);
чисел);
в 8-м - х2i (![]() чисел).
чисел).
6.5. ПЕРФОРАЦИЯ ИСХОДНЫХ ДАННЫХ
Исходные данные набивают массивами на одной перфоленте в цифровом коде «Минск-22». Все числа десятичные.
6.6. ПЕЧАТЬ РЕЗУЛЬТАТОВ
Результаты расчета по программе «ООК» печатаются на БПМ и АЦПУ.
После ввода исходных данных, перед началом расчета, на БПМ печатаются все исходные данные в том порядке, в каком они записываются и набиваются на перфоленту.
Затем печатаются на АЦПУ ![]() ,
, ![]() ,
, ![]() ; на БПМ (узкая печать) печатается следующая
информация сначала для массива
; на БПМ (узкая печать) печатается следующая
информация сначала для массива ![]() , x4,
x3, S,
v1, v2,
σ(Y), v1(Y), v2(Y), C3, C4, Y0,
z, f(z), f3(z), f4(z), Y0φ4(z); причем начиная с K информация повторяется Kу
раз, затем на АЦПУ печатается C3⋅f3(z),
φ3(z), C4⋅f4(z),
φ4(z) соответственно Kу раз.
, x4,
x3, S,
v1, v2,
σ(Y), v1(Y), v2(Y), C3, C4, Y0,
z, f(z), f3(z), f4(z), Y0φ4(z); причем начиная с K информация повторяется Kу
раз, затем на АЦПУ печатается C3⋅f3(z),
φ3(z), C4⋅f4(z),
φ4(z) соответственно Kу раз.
Аналогичная выходная информация печатается для массива x1 и x2
лишь с той разницей, что для x1 информация повторяется ![]() раз, а для x2
-
раз, а для x2
- ![]() раз.
раз.
6.7. РЕШЕНИЕ ПО ПРОГРАММЕ «ООК»,
ЗАПИСАННОЙ НА МАГНИТНУЮ ЛЕНТУ
6.7.1. Установить магнитную ленту с программой «ООК» на лентопротяжный механизм (ЛПМ).
6.7.2. На пишущей машинке набрать задание для ЭВМ.
ВЫ-ААААА; ПМ ◊↑ ААААА ↑ М22 ![]() 0000010А10
0000ВА◊.
0000010А10
0000ВА◊.
6.7.3. Закоммутировать ЛПМ на (0,0) в соответствии с указанием ЭВМ, подтвердив выполнение действий директивой *↑◊. ЭВМ напечатает ресурс и будет ждать следующих директив.
6.7.4. Набрать директиву: ![]()
6.7.5. Поставить перфоленту «Считывание рабочей программы «ООК» с магнитной ленты» на фотоввод (УВВЛ).
6.7.6. Набрать директиву: ВЛЦ◊ (должен быть ввод перфоленты).
6.7.7. Поставить на УВВА перфоленту с исходными данными.
6.7.8. Набрать директиву: ПУ-0◊ (происходит считывание программы с магнитной ленты, ввод варианта и начало решения).
По окончании решения должен быть останов 17636.
6.8. ПРОГРАММА «ООК»




6.9. КОНТРОЛЬНЫЙ ПРИМЕР
6.9.1. Исходные данные

6.9.2. Результаты расчета



7. ПРОГРАММА ДЛЯ ОЦЕНКИ КОНСТРУКТИВНОЙ
НАДЕЖНОСТИ ДЛЯ НЕКОТОРОЙ ТОЧКИ (СЕЧЕНИЯ)
МАГИСТРАЛЬНОГО ТРУБОПРОВОДА (ПРОГРАММА «ОНК»)
7.1. Программа для оценки конструктивной надежности магистральных трубопроводов написана на языке АЛГОЛ с применением условных обозначений входного языка транслятора «МЭИ-3» для ЭВМ «Минск-22» и «Минск-32». Условные обозначения приведены в табл. 15.
Условные обозначения
|
Принятые обозначения в формуле |
Идентификатор |
Наименование, ед. измерения |
|
|
SLG |
Суммарные продольные напряжения от средних значений нагрузок и воздействий, кгс/см2 |
|
σ1 |
SIG1 |
То же, случай растягивающих напряжений |
|
σ2 |
SIG2 |
То же, случай сжимающих напряжений |
|
|
P |
Среднее значение (математическое ожидание) случайной величины рабочего давления в трубопроводе на выходе перекачечной станции, кгс/см2 |
|
φ(x) |
FIX |
Неслучайная функция изменения (падения) давления в трубопроводе по его длине на участке между соседними перекачечными станциями (безразмерная величина) |
|
Dвн |
DVN |
Внутренний диаметр трубы, см |
|
|
DEL |
Среднее значение (математическое ожидание) случайной величины толщины стенки трубы, см |
|
α |
ALPHA |
Коэффициент линейного расширения металла трубы, град-1 |
|
E |
E |
Модуль упругости металла, кгс/см2 |
|
|
Dt |
Среднее значение (математическое ожидание случайной величины) температурного перепада (принимаемого положительным при нагревании) на выходе перекаченной станции. Равно разности между средним значением случайной величины температуры стенок трубы при эксплуатации на выходе перекачечной станции и температурой фиксации расчетной схемы трубопровода, °С |
|
ε(х) |
KSI |
Неслучайная функция изменения (уменьшения) температурного перепада по длине трубопровода на участке между соседними перекачечными станциями (безразмерная величина) |
|
Dн |
DN |
Наружный диаметр трубы, см |
|
|
KR |
Среднее значение (математическое ожидание) случайной величины кривизны оси трубопровода при упругом изгибе или же постоянная величина функции математического ожидания стационарной случайной функции кривизны, см-1 |
|
|
- |
Среднее значение (математическое ожидание) случайной величины функции надежности (несущей способности) в сечении трубопровода или значение функции математического ожидания случайной функции надежности в сечении трубопровода, кгс/см2 |
|
- |
|
То же, для случая |
|
- |
|
То же, для случая |
|
|
RH |
Среднее значение случайной величины предела текучести металла труб, кгс/см2 |
|
|
FDF |
Среднее значение отношения случайной величины суммарной площади дефектов в сечении монтажного сварного соединения к площади его сечения (безразмерная величина) |
|
K |
KV |
Коэффициент влияния вида дефекта (безразмерная величина) |
|
|
SRH |
Стандарт случайной величины |
|
|
SFDF |
Стандарт случайной величины |
|
S𝜌 |
SP |
Стандарт случайной величины |
|
Sδ |
SD |
Стандарт случайной величины |
|
SΔt |
SDT |
Стандарт случайной величины |
|
SK |
SKR |
Стандарт случайной величины |
|
|
SU |
Дисперсия случайной величины функции надежности |
7.2.
АЛГОРИТМ РАСЧЕТА ХАРАКТЕРИСТИК НАДЕЖНОСТИ
ТРУБОПРОВОДОВ
|
|
(63) |
где ![]() , φ(х), Dвн,
, φ(х), Dвн, ![]() , α, E,
, α, E,
![]() , ξ(x),
Dн,
, ξ(x),
Dн, ![]() задаются.
задаются.
В результате расчета по данной формуле получаем два значения
![]() .
.
Б. Используя полученные значения ![]() , рассчитать характеристики
, рассчитать характеристики ![]() и
и ![]() .
.
1. Если полученные два значения ![]() будут одного и того же знака, то для дальнейшего
расчета принимается значение, большее по абсолютной величине.
будут одного и того же знака, то для дальнейшего
расчета принимается значение, большее по абсолютной величине.
При этом:
а) если полученное расчетное
значение ![]() , то значения
, то значения ![]() и
и ![]() вычисляют по формулам:
вычисляют по формулам:
где ![]() ,
, ![]() , S𝜌, Sδ, SΔt, SK задаются;
, S𝜌, Sδ, SΔt, SK задаются;
![]() , K,
, K, ![]() - и указанные
в п. А величины задаются;
- и указанные
в п. А величины задаются;
![]() - модуль (абсолютная величина)
найденного выше, в п. А, значения
- модуль (абсолютная величина)
найденного выше, в п. А, значения ![]() ;
;
|
|
б) если полученное расчетное значение ![]() , то значения
, то значения ![]() и
и ![]() вычисляются по формулам:
вычисляются по формулам:
|
|
(66) |
где ![]() и др. задаются (см. выше);
и др. задаются (см. выше);
![]() - см.выше;
- см.выше;
![]() и другие
задаются (см. выше);
и другие
задаются (см. выше);
|
|
2. Если полученные два значения ![]() будут иметь разные знаки, то для
дальнейшего расчета принимаются оба (положительное и отрицательное) значения.
При этом обе пары значений
будут иметь разные знаки, то для
дальнейшего расчета принимаются оба (положительное и отрицательное) значения.
При этом обе пары значений ![]() и
и ![]() вычисляют в соответствии с указаниями
в п. 7.2.Б.1.
вычисляют в соответствии с указаниями
в п. 7.2.Б.1.
Выводить на печать:
значения ![]() со своими знаками (по п. 7.2.А);
со своими знаками (по п. 7.2.А);
значения ![]() и
и ![]() (или две пары этих значений, если
значения
(или две пары этих значений, если
значения ![]() получились разных знаков).
получились разных знаков).
Примечание. Описанный в данном задании расчет проводить для вариантов:
1) при K = 0; φ(х)
= 1; ξ(х) = 1; S𝜌 = 0 (иначе для ![]() - неслучайная величина); SΔt = 0 (иначе для
- неслучайная величина); SΔt = 0 (иначе для ![]() = Δt - неслучайная
величина).
= Δt - неслучайная
величина).
Это случай начальной надежности, расчет для основного металла;
2) при K ≠
0 задается: φ(х) = 1; ξ(х) = 1; S𝜌 =
0 (иначе для ![]() - неслучайная величина); SΔt = 0 (иначе для
- неслучайная величина); SΔt = 0 (иначе для ![]() = Δt - неслучайная
величина).
= Δt - неслучайная
величина).
Это случай начальной надежности, расчет для сварного соединения;
3) при K ≠
0, φ(х) ≠ 1 задается; ξ(х) ≠ 1 задается; ![]() и задаются.
и задаются.
Это случай эксплуатационной надежности, расчет для основного металла;
4) при K ≠
0 задается, φ(х) ≠ 1 задается; ξ(х) ≠ 1
задается; ![]() задаются.
задаются.
Это случай эксплуатационной надежности, расчет для сварного соединения.
7.3.
ЗАДАНИЕ ВХОДНОЙ ИНФОРМАЦИИ ДЛЯ ПРОГРАММЫ «ОНК»
ПРОИЗВОДИТСЯ СЛЕДУЮЩИМ ОБРАЗОМ
Исходные данные для расчета по программе «ОНК» задаются в виде реальных десятичных чисел, которые записываются массивами, каждый из которых заключается в границы ввода.
Реальные числа могут быть записаны либо в виде числа с плавающей запятой (мантисса - 7 цифр, знак порядка и порядок - 2 цифры), либо в виде числа с кодовой запятой.
В 1-м массиве задаются следующие исходные данные: ρ, Δt, φ(x), ξ(x), K, Dвн, δ, α;
во 2-м массиве E, DN, K, ![]() ,
, ![]() ;
;
в 3-м массиве ![]() ,
, ![]() , Sρ, Sδ, SΔt, SK.
, Sρ, Sδ, SΔt, SK.
7.4. ПЕРФОРАЦИЯ ИСХОДНЫХ ДАННЫХ (см. п. 6.5).
7.5. ПЕЧАТЬ РЕЗУЛЬТАТОВ
После ввода исходных данных, перед началом расчета на БПМ печатаются все исходные данные в том порядке, в каком они записываются и набиваются на перфоленту. Затем печатаются σ1, σ2, а далее, в зависимости от их знаков, могут быть два случая:
1-й случай, когда σ1 и σ2
имеют разные знаки, тогда печатается следующая выходная информация: u1, ![]() ,
, ![]() , u2,
, u2,
![]() ,
, ![]()
2-й случай, когда σ1 и σ2
имеют одинаковые знаки, тогда печатается следующая информация: σ, u, Su, ![]() .
.
7.6. РЕШЕНИЕ ПО ПРОГРАММЕ «ОНК», ЗАПИСАННОЙ
НА МАГНИТНУЮ ЛЕНТУ
Инструкция для оператора при решении по программе «ОНК» соответствует инструкции, изложенной в п. 6.7 с той разницей, что для выполнения п. 6.7.5 необходимо иметь перфоленту «Считывание рабочей программы «ОНК» с магнитной ленты».
Эта перфолента выводятся на перфоратор при трансляция исходной программы «ОНК» с помощью транслятора МЭИ-3. По окончании решения должен быть останов.
7.7. ТЕКСТ ПРОГРАММЫ «ОНК»


7.8. КОНТРОЛЬНЫЙ ПРИМЕР
Инструкция по запуску контрольного примера для программы «ОНК» соответствует инструкции, приведенной в п. 7.6.
Результаты контрольного примера выдаются на БПМ в следующем виде:
Исходные данные
|
+9399999 + 02P +4000000 + 02Δt +1000000 + 01φ(x) +1000000 + 01ξ(х) +6000000 + 01K |
+ 1378999 + 03Dвн + 2050000 + 01 + 1200000 - 04α +2099999 + 07E + 1240000 + 03Dн |
+ 3333333 - 05
+ 1999999 - 02 + 1670000 + 03 + 9999999 - 03 |
|
|
+0000000 + Sρ +6999999 - 01Sδ +0000000 + 00SΔt +3333330 - 05SK |
|
Результаты расчета
|
+4374828 + 03σ1 -5565170 + 03σ2 +3712117 + 04u1 +5252772 + 03 +1771148 + 04u2 |
+3073786 + 06 +5544174 + 04 |
8. ЗАКЛЮЧЕНИЕ
8.1. Разработка настоящего Руководства является первый вагон на пути создания вероятностных методов расчета трубопроводов на надежность. Поэтому настоящий документ в своей практической части может быть использован лишь при решении некоторых частных случаев оценки надежности, а именно: оценки фактической конструктивной надежности на момент испытания трубопровода (оценка начальной надежности) и оценки фактической эксплуатационной надежности (безотказности) трубопровода при использовании упрощенной расчетной модели функционирования трубопровода.
8.2. Используя настоящее Руководство, можно получить оценку надежности в каком-либо (каких-либо) сечении или оценку надежности конечного участка трубопровода, например участке, подвергаемого предпусковым испытаниям.
8.3. Оценку фактической конструктивной надежности по изложенной методике можно производить не только к моменту окончания строительства, т.е. не только для подготовленного к испытаниям или эксплуатации трубопровода или участка. Такая оценка возможна и при проектировании, экспертизе проекта, в процессе строительства - при наличии информации о вероятностно-статистических характеристиках изменчивых параметров, полученной ранее, по трубопроводам, аналогичным проектируемому в части материалов, нагрузок, условий и качества сооружения.
8.4. Изложенная в Руководстве методика оценки конструктивной надежности при использовании ее для сравнения конкурирующих проектных решений по критерии надежности требует развития в части применения других расчетных условий отказа, характеризующих соответствующие предельные состояния. В частности, к изложенной методике необходимо присоединить условие для оценки надежности заводских сварных соединений, условие для оценки надежности основного металла при наличии в нем внутренних дефектов и механических повреждений и т.д. При сравнении по критерию надежности, например подземной и наземной прокладок трубопровода, при оценке надежности трубопровода с учетов его взаимодействия с грунтом и ряде других случаев также следует подбирать соответствующие расчетные условия, отличающиеся от используемых в Руководстве.
8.5. Дальнейшими задачами в области исследования и разработки методов расчета на надежность магистральных трубопроводов являются следующие:
представление исходных расчетных соотношений в виде, позволяющем учитывать действительные условия работы трубопровода во всем их многообразии;
развитие работ по сбору и обработке первичной статистической информации об отказах и параметрах качества строящихся и эксплуатируемых трубопроводов, нагрузках, а также параметрах качества исходных материалов;
расширение спектра используемых приемов и методов расчета вероятностных оценок надежности по статистической информации об отказах и изменчивых параметрах трубопроводов, в частности учет фактора времени;
исследование взаимосвязи между прямыми и косвенными оценками надежности, т.е. между оценками вероятности разрушения, полученными на основе использования тех или иных расчетных моделей, и характеристиками, не фигурирующими в вероятностных расчетах, но отражающими те или иные важные свойства материалов и конструкций, такими, как ударная вязкость, процент волокна в изломе и др.;
оптимизация конструктивной надежности трубопроводов исходя из экономических соображений и требуемой функциональной надежности, т.е. надежности нефте- и газоснабжения.
ЛИТЕРАТУРА
1. ГОСТ 13377-75 «Надежность в технике. Термины и определения». М., «Госстандарт», 1975.
2. Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. М., «Советское радио», 1975.
3. Болотин В.В. Применение методов теории вероятностей и теории надежности в расчетах сооружений. М., Стройиздат, 1971.
4. Болотин В.В. К статистической интерпретации норм расчета строительных конструкций. «Строительная механика и расчет сооружений», 1977, № 1.
5. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. М., «Наука», 1965.
6. Ржаницын А.Р. К проблеме расчетов сооружений на безопасность. Сб. «Вопросы безопасности и прочности строительных конструкций», ЦНИПС, М., Госстройиздат, 1952.
7. Снарскис Б.И. К статистическо-экономическому обоснованно несущей способности конструкций. Труды АН Литовской ССР, сер. Б, № 2 (29), 1961.
8. Рекомендации по применению экономико-статистических методов при расчете сооружений с чисто экономической ответственностью. М., ЦНИИСК, 1972.
9. Болотин В.В. Статистические методы в строительной механике. М., Стройиздат, 1965.
10. Руководство по методике статистического контроля и учета качества сварки магистральных трубопроводов (Р 194-75). М., ВНИИСТ, 1975.
11. Руководство по техническому расследованию отказов линейной части магистральных трубопроводов (Р 227-76). М., ВНИИСТ, 1976.
12. Ржаницын А.Р. Статистическое обоснование расчетных коэффициентов. В сб.: «Материалы к теории расчета по предельному состоянию», вып. 2. Под ред. В.М. Келдыша, М., Стройиздат, 1949.
13. Вентцель Е.С. Теория вероятностей. М., «Наука», 1969.
14. Ангресс Я. Теоретические основы оценки качества сварных швов. Перевод № 2508 (70/20905). Киев, 1969.
15. Ржаницын А.Р. Статистический метод определения допускаемых напряжений при продольном изгибе. Научное сообщение ЦНИПС, вып. 3. М., Стройиздат, 1951.
16. Рекомендации по оценке надежности строительных конструкций. Уральский Промстройниипроект. Свердловск, 1974.
17. Пугачев В.С. Введение в теории вероятностей. М., «Наука», 1968.
18. Пугачев В.С. Теория случайных функций и ее применение в задачах автоматического управления. М., Физматгиз, 1962.
19. Беляев Н. М. Сопротивление материалов. М., «Наука», 1976.
20. Закатов П.С. и др. Инженерная геодезия. М., «Недра», 1976.
21. Митропольский А.К. Техника статистических вычислений. М., «Наука», 1971.
22. Коуден Д. Статистические методы контроля качества. М., Физматгиз, 1961.
23. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лаг.-ласа. М., Физматгиз, 1959.
РАБОТАТЬ
ВЫСОКОПРОИЗВОДИТЕЛЬНО,
БЕЗ ТРАВМ И АВАРИЙ
(из опыта работы бригады Героя Социалистического Труда
А.Д. Басова)
1. Не только знать, но и строжайше соблюдать все норны, правила и инструкции по технике безопасности.
2. Работы проводить в строгом соответствии с проектом организации работ (планом, нарядом-допуском или нарядом-заказом).
3. В обязательном порядке пользоваться всеми предписанными индивидуальными средствами защиты (касками, противогазами, спецобувью, защитными очками, рукавицами и др.).
4. Вести самоконтроль и взаимный контроль всех членов бригады за соблюдением правил техники безопасности.
5. Воспитывать личную и коллективную ответственность за обеспечение работы на производственном участке.
6. Активно участвовать в смотрах, конкурсах и соревнованиях за высокую культуру производства.
7. Опытные рабочие должны следить за работой молодых и вновь поступивших рабочих.
8. Совершенствовать обучение всего обслуживающего персонала.
9. Планировать мероприятия по улучшению условий труда и технике безопасности.
10. Совершенствовать технологические процессы, своевременно заменять устаревшее оборудование.
11. Повышать роль общественного инспектора.
12. Осуществлять 3-ступенчатый метод контроля за безопасностью на производстве.
13. Постоянно проводить профилактическую работу по выявлению нарушений правил техники безопасности.
14. Осуществлять контроль за своевременным выполнением профилактических мероприятий по предупреждению производственного травматизма, аварий и заболеваний.
САМОДИСЦИПЛИНА, САМОКОНТРОЛЬ, БЕЗУСЛОВНОЕ ВЫПОЛНЕНИЕ ПРАВИЛ И НОРМ ТЕХНИКИ БЕЗОПАСНОСТИ - ВОТ ОСНОВА МЕТОДА РАБОТЫ БЕЗ ТРАВМ И АВАРИЙ.