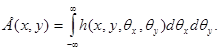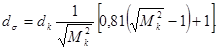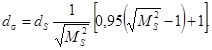ФЕДЕРАЛЬНОЕ
АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ |
ГОСТ Р ИСО/ТО |
ЛАЗЕРЫ И ЛАЗЕРНЫЕ УСТАНОВКИ (СИСТЕМЫ)
Методы измерений ширин, углов расходимости и
коэффициентов распространения лазерных пучков
Часть 3
Собственная и геометрическая классификация лазерных
пучков, специфика их распространения и методики
измерений
ISO/TR 11146-3:2004 Lasers and laser-related
equipment -
Test methods for laser beam widths, divergence angles
and beam propagation ratios - Part 3: Intrinsic and
geometrical laser beam classification, propagation and
details of test methods
(IDT)
|
|
Москва |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт оптико-физических измерений» (ФГУП «ВНИИОФИ») на основе собственного аутентичного перевода международного стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением метрологии Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 25 декабря 2008 г. № 763-ст
4 Настоящий стандарт идентичен международному стандарту ИСО/ТО 11146-3:2004 «Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 3: Собственная и геометрическая классификация лазерных пучков, специфика их распространения и методики измерений» (ISO/TR 11146-3:2004 «Lasers and laser-related equipment - Test methods for laser beam widths, divergence angles and beam propagation ratios. Part 3: Intrinsic and geometrical laser beam classification, propagation and details of test methods»)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
Предисловие
к международному
стандарту ИСО/ТО 11146-3:2005 «Лазеры и лазерные установки (системы).
Методы
измерений ширин, углов расходимости и коэффициентов распространения лазерных
пучков. Часть 3: Собственная и геометрическая классификация лазерных пучков,
специфика
их распространения и методики измерений»
ИСО (Международная организация по стандартизации) - Всемирная федерация национальных органов по стандартизации (членов ассоциации). Разработкой международных стандартов обычно занимаются технические комитеты. Каждый член ассоциации, заинтересованный в тематике, для которой создан технический комитет, имеет право быть представленным в этом комитете. Международные организации, правительственные и неправительственные, связанные с ИСО, также принимают участие в работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов разрабатывают в соответствии с правилами, изложенными в директивах ИСО/МЭК, часть 2.
Проекты международных стандартов, принятые техническими комитетами, рассылают членам ассоциации для голосования. Публикация в качестве международного стандарта требует одобрения, по крайней мере, 75 % членов ассоциации, принявших участие в голосовании.
При определенных обстоятельствах, когда техническим комитетом собраны данные и сведения, отличающиеся от опубликованных в международных стандартах (например, описание предмета), может быть решено простым голосованием членов технического комитета опубликовать технический доклад (ТД). Доклад носит информативный характер и не подлежит обсуждению или пересмотру, пока не будет установлено, что содержащаяся в нем информация является правильной и полезной.
Международный стандарт ИСО/ТО 11146-3 подготовлен подкомитетом ПК 9 «Электрооптические системы» технического комитета ИСО/ТК 172 «Оптика и фотоника».
Данное издание ИСО/ТО 11146-3 является первым совместным с ИСО/ТО 11146-1 изданием, выпущенным взамен ИСО 11146:1999, содержание которого с точки зрения технических аспектов пересмотрено и расширено.
Стандарты ИСО под общим наименованием «Лазеры и лазерные устройства (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков» состоят из следующих трех частей:
- часть 1: Стигматические (гомоцентрические) и слабоастигматические пучки;
- часть 2: Астигматические пучки;
- часть 3: Собственная и геометрическая классификация лазерных пучков, специфика их распространения и методики измерений.
Введение
к международному
стандарту ИСО/ТО 11146-3:2005 «Лазеры и лазерные установки (системы).
Методы
измерений ширин, углов расходимости и коэффициентов распространения лазерных
пучков. Часть 3: Собственная и геометрическая классификация лазерных пучков,
специфика
их распространения и методики измерений»
Свойства, характеризующие процесс распространения каждого пучка лазерного излучения, описаны десятью независимыми параметрами, теоретической основой которых служит метод определения моментов второго порядка. Однако в силу достаточно высокой степени симметрии большинства лазерных пучков, получивших широкое распространение во множестве приложений, для их полного описания требуется меньшее число параметров. Конструкции резонаторов большинства практически используемых лазеров формируют на выходе стигматические (гомоцентрические) пучки или пучки со слабым астигматизмом.
Теоретическое описание структуры лазерных пучков и параметров, характеризующих процессы их распространения в пространстве, также, как и классификационные признаки, основано на определении моментов второго порядка распределения Вингера, приведенного в данной части ИСО 11146.
Методики измерений, описанные в ИСО 11146-1 и ИСО 11146-2, в основном (но необязательно) базируются на определении с помощью матричного приемника излучения (энергии) распределений плотности мощности в поперечном сечении пучка, например, с применением ПЗС-камер. Точность результатов измерений с применением упомянутой методики сильно зависит от уровня предварительной обработки полученных экспериментальных данных, а именно, от вычитания распределения фона и коррекции смещения базисной линии. Настоящий стандарт также содержит детальное описание процедур предварительной обработки данных.
В некоторых случаях точность результатов измерений, выполняемых с применением матричных приемников излучения, может оказаться недостаточной либо такие приемники по каким-либо причинам недоступны. Выходом из этого положения является применение косвенных методов определения диаметров пучков или их ширин в качестве альтернативных, но при условии получения сопоставимых по точности результатов измерений. Некоторые альтернативные методы измерений представлены в данной части ИСО 11146.
Международная организация по стандартизации (ИСО) обращает внимание на тот факт, что вследствие использования данного документа может быть задействован патент относительно установления измерений параметров распространения пучка вдоль каустики, сформированной промежуточной линзой, при условии, что перетяжка пучка точно локализована или зона ее расположения искусственно формируется оптической системой, как описано в 5.5.
ИСО не дает никаких заключений относительно достоверности, подтверждения, компетентности этого патента.
Владелец этого патента (U.S. № 5,267,012) заверил ИСО, что он заключит лицензионные соглашения на разумные и приемлемые сроки и условия с желающими во всем мире. Это заявление владельца данного патента подтверждено и заверено с ИСО. Информацию можно получить по адресу:
Coherent Inc.
5100 Patrick Henry Drive
Santa Clara, CA 95056-0980
USA
Следует обратить внимание на возможность того, что некоторые части настоящего стандарта могут быть предметом патентирования другими, которые не указаны выше. ИСО не несет ответственности за любые подобные договоры или патенты.
Введение
к национальному
стандарту Российской Федерации ГОСТ Р ИСО/ТО 11146-3-2008 «Лазеры
и лазерные установки (системы). Методы измерений ширин, углов расходимости и
коэффициентов распространения лазерных пучков. Часть 3: Собственная и
геометрическая
классификация лазерных пучков, специфика их распространения и методики
измерений»
Целью настоящего стандарта является прямое применение в Российской Федерации международного стандарта ИСО/ТО 11146-3:2005 «Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 3: Собственная и геометрическая классификация лазерных пучков, специфика их распространения и методики измерений» как основы для изготовления и поставки объекта стандартизации по договорам (контрактам) на экспорт.
ГОСТ Р ИСО/ТО 11146-3-2008 представляет собой полный аутентичный текст ИСО/ТО 11146-3:2005.
Для удобства чтения и восприятия к термину «стигматические» пучки в скобках приведен принятый термин «гомоцентрические» пучки.
ГОСТ Р ИСО/ТО 11146-3-2008
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЛАЗЕРЫ И ЛАЗЕРНЫЕ УСТАНОВКИ (СИСТЕМЫ)
Методы измерений
ширин, углов расходимости и коэффициентов распространения
лазерных пучков
Часть 3
Собственная и
геометрическая классификация лазерных пучков, специфика
их распространения и методики измерений
Lasers
and laser-related equipment. Test methods for laser beam widths, divergence
angles and beam propagation
ratios. Part 3. Intrinsic and geometrical laser beam classification,
propagation and details of test methods
Дата введения - 2010-01-01
1 Область применения
Настоящий стандарт разработан в развитие стандарта ИСО 11146-1 [1] на методы измерений ширин (диаметра) пучка, углов расходимости и коэффициентов распространения пучков лазерного излучения. Настоящий стандарт содержит теоретическое описание характеристик пучка, базирующееся на моментах второго порядка распределения Вигнера, включая геометрические и специфичные именно для лазерного излучения характеристики пучка, а также предложения по имеющей важное значение процедуре корректировки (путем вычитания) результатов воздействия фонового излучения на приемно-усилительное устройство с входной ПЗС-матрицей. В настоящем стандарте также представлены альтернативные способы описания и определения параметров стигматических или слабоастигматических пучков, пригодные в случаях недоступности матричных первичных измерительных преобразователей или получения неудовлетворительных результатов.
2 Описание параметров лазерного пучка методом моментов второго порядка распределения Вигнера
2.1 Область применения
Почти любой пучок когерентного или частично когерентного лазерного излучения может быть представлен максимум десятью независимыми параметрами - так называемыми моментами второго порядка распределения Вигнера. Лазерные пучки, обладающие некоторого типа симметрией, стигматизмом или слабым (простым) астигматизмом, могут быть охарактеризованы меньшим числом параметров. Знание этих параметров позволяет прогнозировать характер распространения пучка за пределами любой безаберрационной оптической системы.
Здесь и далее в настоящем стандарте термин «распределение плотности мощности» Е (х, у, z) относится к непрерывным лазерам и может быть заменен термином «распределение плотности энергии» Н (х, у, z) применительно к импульсным лазерам. Более того, в принятой системе координат ось z практически параллельна (коллинеарна) направлению распространения пучка, а оси х и у служат горизонтальной и вертикальной осями соответственно.
2.2 Распределение Вигнера
Распределение
Вигнера ![]() является общим и
полным описанием узкополосных когерентных и частично когерентных лазерных
пучков в измеряемом поперечном сечении. Вообще, это распределение отображает
суммарную мощность пучка, проходящую сквозь измеряемое поперечное сечение с
горизонтальным θx и вертикальным
θy параксиальными
углами относительно оси z, как показано на рисунке 1.
является общим и
полным описанием узкополосных когерентных и частично когерентных лазерных
пучков в измеряемом поперечном сечении. Вообще, это распределение отображает
суммарную мощность пучка, проходящую сквозь измеряемое поперечное сечение с
горизонтальным θx и вертикальным
θy параксиальными
углами относительно оси z, как показано на рисунке 1.
Примечание - Распределение Вигнера представляет собой функцию от аксиальной координаты z, т.е. распределение Вигнера одного и того же лазерного пучка различно для его сечений с разными координатами z. Следовательно, значения величин (параметров), полученные с использованием распределения Вигнера также, вообще говоря, являются функциями от z. В настоящем стандарте эта зависимость от z может быть исключена из рассмотрения, а само распределение Вигнера соотнесено с произвольно выбранным значением z, соответствующим координате по аксиальной оси поперечного сечения пучка, именуемого «плоскостью измерений» (или «измерительной плоскостью»).
В соответствии с вигнеровским распределением для распределения плотности мощности Е (х, у) в плоскости измерений справедливо выражение
Примечание - Пределы интегрирования в уравнении (1) практически ограничены максимальными углами отклонения параксиальных лучей в лазерном пучке; в зависимости от условий постановки задачи они могут быть распространены до бесконечности.
х, у - координаты в плоскости измерений;
θx, θy - соответствующие угловые координаты
Рисунок 1 - Координаты распределения Вигнера
2.3 Моменты первого и второго порядков распределения Вигнера
Моменты первого порядка:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
где Р - мощность излучения в пучке, описываемая выражением:
![]() (6)
(6)
или с учетом уравнения (1)
![]() (7)
(7)
«Пространственные» моменты <x> и <y> отображают положение центроида пучка в плоскости измерений, а «угловые» моменты (θx и θy) - направление его распространения.
Центрированные моменты второго порядка описываются выражением
![]() (8)
(8)
где к, l, m и п - неотрицательные целые числа, а к + l + т + п = 2. Общее число различных моментов второго порядка равно десяти.
Три
«пространственных» момента второго порядка <x2>, <y2> и <xy> характеризуют
поперечную протяженность распределения плотности мощности в плоскости
измерений; три «угловых» момента ![]() - расходимость
пучка, а четыре смешанных момента
- расходимость
пучка, а четыре смешанных момента ![]() - его фазовые
характеристики в той же плоскости.
- его фазовые
характеристики в той же плоскости.
«Пространственные» моменты первого и второго порядков могут быть непосредственно получены при известном распределении плотности мощности Е (х, у).
Из уравнения (1) следует:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Для определения остальных моментов второго порядка необходимо измерить «пространственные» моменты в других сечениях (плоскостях измерений) пучка и применить описываемое далее правило распространения моментов второго порядка.
Примечание - Подробное описание процедуры определения всех десяти моментов второго порядка приведено в ИСО 11146-2 [2].
2.4 Матрица пучка
Десять моментов второго порядка образуют симметричную 4×4 матрицу пучка:
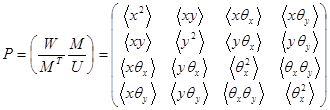 (14)
(14)
с симметричной подматрицей «пространственных» моментов
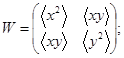 (15)
(15)
с симметричной подматрицей «угловых» моментов
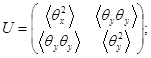 (16)
(16)
и подматрицей смешанных моментов
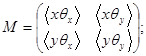 (17)
(17)
2.5 Распространение излучения сквозь безаберрационные оптические системы
Безаберрационные оптические системы характеризуются системой 4×4 матриц S, формируемых в соответствии с основными положениями геометрической оптики. Распространение моментов второго порядка сквозь такую систему описывается уравнением
![]() (18)
(18)
где Рin и Pout - матрицы пучка во входной и выходной плоскостях оптической системы, соответственно.
Примеры матриц системы приведены в приложении А.
2.6 Соотношения моментов второго порядка и физических параметров пучка
Десять моментов второго порядка тесно связаны с хорошо известными физическими параметрами пучка.
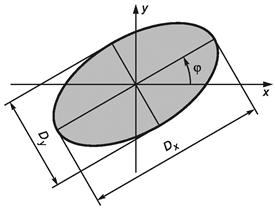
Три «пространственных» момента описывают поперечную протяженность распределения плотности мощности пучка в плоскости измерений. Направления минимальной и максимальной протяженностей, именуемые главными осями, всегда взаимно ортогональны. Любое распределение плотности мощности характеризуется протяженностями вдоль его главных осей и ориентациями последних. Ширина пучка вдоль главной оси, ближней к оси х лабораторной системы координат, описывается выражением
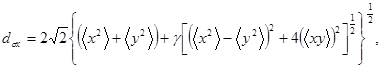 (19)
(19)
а вдоль ближней к оси у - выражением
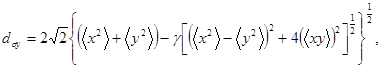 (20)
(20)
где
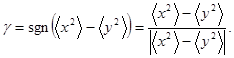 (21)
(21)
Если
главные оси образуют угол «+» или «-» π/4 с осями х или у,
когда ![]() , то dσx по условию
является большей из обеих ширин пучка:
, то dσx по условию
является большей из обеих ширин пучка:
![]() (22)
(22)
![]() (23)
(23)
Азимутальный угол между главной осью, ближней к оси х, и самой осью х равен:
φ = 1/2arctan(2<xy>/(<x2>) - <y2>)), что справедливо при
![]() (24)
(24)
при
![]()
![]() (25)
(25)
где
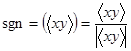 (см. рисунок 2) (26)
(см. рисунок 2) (26)
Рисунок 2 - Азимутальный угол и ширины пучка вдоль главных осей распределения плотности мощности
Аналогично тремя «угловыми» моментами описывается расходимость пучка, характеризуемая взаимно ортогональными направлениями максимальной и минимальной протяженностей. Эти направления называются «главными осями расходимости пучка» и могут не совпадать с главными осями распределения плотности мощности в плоскости измерений. Расходимость пучка вдоль направления главной оси, ближней к оси х лабораторной системы координат, описывается выражением
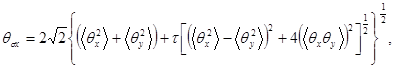 (27)
(27)
а вдоль ближней к оси у - выражением
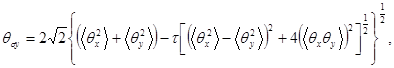 (28)
(28)
где
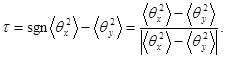 (29)
(29)
Если
главные оси расходимости пучка образуют угол «+» или «-» π/4 с осями х
или у, когда ![]() то θσx по условию
является большей из обеих расходимостей пучка:
то θσx по условию
является большей из обеих расходимостей пучка:
![]() (30)
(30)
![]() (31)
(31)
Азимутальный угол расходимости между главной осью, ближней к оси х, и самой осью х равен φθ = 1/2arctan(2<θxθy>/(<θx2>) - <θy2>)), что справедливо при
![]()
![]() (32)
(32)
при
![]()
![]() (33)
(33)
где
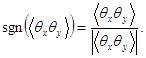 (34)
(34)
Четыре смешанных момента описывают усредненные фазовые характеристики пучка в плоскости измерений. Наилучшая аппроксимация этих характеристик достигается с использованием фазового параболоида с взаимно ортогональными направлениями максимальной и минимальной кривизны.
Обе эти кривизны могут иметь нулевые или отрицательные значения вдоль главных осей, причем независимо друг от друга. Направления максимальной и минимальной кривизны, именуемые главными осями фазового параболоида, могут не совпадать ни с главными осями распределения плотности мощности в плоскости измерений, ни с главными осями расходимости пучка. Для согласования азимутального угла этих главных осей с радиусами кривизны усредненного фазового фронта вдоль них вычисляют матрицу С кривизны:
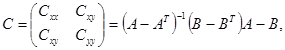 (35)
(35)
где
![]() (36)
(36)
![]() (37)
(37)
Радиус кривизны усредненного фазового фронта вдоль направления главной оси, ближайшей к оси х лабораторной системы координат, вычисляют по формуле
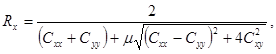 (38)
(38)
а вдоль главной оси, ближайшей к оси у, - по формуле
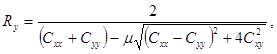 (39)
(39)
где
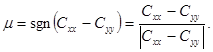 (40)
(40)
Если главные оси усредненной фазовой крутизны составляют с осями х и у угол «+» или «-» π/4, т.е. когда Cxx = Cyy, то Rx оказывается большим из двух главных радиусов (с учетом знака):
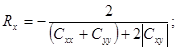 (41)
(41)
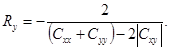 (42)
(42)
Азимутальный угол кривизны фазы между главной осью, ближайшей к оси х, и осью х равен φp = 1/2arctan(2cxy/(Cxx - Cyy) что справедливо при
![]() (43)
(43)
при ![]()
φp = sgn(cxy)π/4, (44)
где
 (45)
(45)
Другой физический параметр пучка, связанный с поведением фазы и именуемый «параметром закручивания» t, определяют по формуле
![]()
Параметр закручивания пропорционален орбитальному угловому моменту пучка и является инвариантом при распространении излучения сквозь стигматические оптические системы.
2.7 Инварианты распространения
Из закона распространения матрицы пучка вытекает инвариантность двух не зависящих друг от друга параметров:
эффективного (действующего) коэффициента распространения пучка
![]() (46)
(46)
и собственно астигматизма (истинного астигматизма)
![]() (47)
(47)
Первый из них характеризует фокусируемость пучка.
Примечание - В более широком понимании M2eff служит обобщенной мерой расширения пучка или его локализации в ближней и дальней зонах поля его распространения.
У стигматического (гомоцентрического) пучка действительный коэффициент распространения равен просто коэффициенту распространения пучка:
![]() (48)
(48)
У
слабоастигматических пучков, обладающих коэффициентами распространения ![]() действительный
коэффициент распространения пучка равен среднегеометрическому коэффициентов
распространения по обеим главным осям пучка:
действительный
коэффициент распространения пучка равен среднегеометрическому коэффициентов
распространения по обеим главным осям пучка:
![]() (49)
(49)
Собственно (истинный) астигматизм характеризует как видимый, так и скрытый астигматизм пучка. Применительно к стигматическим пучкам собственно (истинный) астигматизм а теряет смысл и поэтому его принимают равным нулю. Собственно (истинный) астигматизм пучков со слабым астигматизмом (слабоастигматичных пучков) описывают формулой
![]() (50)
(50)
Эти формулы инвариантны лишь при распространении пучка в безаберрационных (без потерь) оптических системах. Применительно к другим системам они требуют видоизменения. Любые сочетания этих инвариантов также являются инвариантами.
2.8 Геометрическая классификация
Пучки могут быть классифицированы по их поведению при прохождении (распространении) в стигматических или слабоастигматических оптических системах. Стигматической является оптическая система, реализуемая только на основе идеальных сферических линз. Слабоастигматическая система может быть реализована с использованием идеальных цилиндрических линз одинаковой ориентации.
Геометрическая классификация пучков базируется на симметрии распределений плотности мощности в сечениях распространяющегося пучка. Термин «симметрия» рассматривается в контексте метода моментов второго порядка. Распределение плотности мощности классифицируют как циркулярное (круговое), если отношение минимальной ширины пучка к максимальной, измеренных в сечениях вдоль главных осей, более 0,87. В противном случае распределение плотности мощности классифицируют как эллиптическое.
Примечание - В этом смысле даже распределение плотности мощности с плоской вершиной, имеющее форму квадрата, считают циркулярным.
Эллиптическое распределение плотности мощности характеризуется его направленностью, числовым выражением которой является азимутальный угол φ. При распространении пучка в свободном пространстве распределение плотности мощности по всей его трассе может быть либо полностью циркулярным или эллиптическим, либо на ее отдельных участках циркулярным или эллиптическим.
Пучок считается стигматическим (гомоцентрическим), если во всех его поперечных сечениях по трассе распространения излучения в свободном пространстве распределения плотности мощности сохраняют циркулярность, а при прохождении сквозь цилиндрическую линзу произвольной ориентации все эллиптические распределения плотности мощности по выходе излучения из линзы ориентированы в том же или ортогональном направлении, что и ось, параллельная цилиндрической поверхности линзы.
Пучок считается слабоастигматическим, если все эллиптические распределения плотности мощности в сечениях по трассе распространения пучка в свободном пространстве имеют одинаковую (или ортогональную) азимутальную ориентацию (направленность), а при прохождении сквозь цилиндрическую линзу той же ориентации (направленности), что и пучок, все эллиптические распределения плотности мощности на выходе излучения из линзы имеют ту же или ортогональную ей ориентацию, что и цилиндрическая линза.
Все остальные пучки считаются астигматическими.
Геометрическая классификация пучка базируется на соотношениях, вытекающих из анализа матрицы пучка. Если все три субматрицы W, М и U примерно пропорциональны единичной матрице, то пучок считают стигматическим (гомоцентрическим). Пучок считают слабоастигматическим и растянутым вдоль осей х и у, если субматрицы W, М и U диагональны. Пучок также считается слабоастигматическим, но повернутым на азимутальный угол φ, если субматрица М приблизительно симметрична, т.е. отсутствует параметр закручивания t, а главные оси распределения плотности мощности в плоскости измерений, главные оси расходимостей пучка и фазового параболоида практически совпадают:
φ = φθ ≈ φp. (51)
Все остальные пучки согласно геометрической классификации считаются астигматическими.
2.9 Классификация истинных пучков
Геометрическая классификация пучка может претерпеть изменения после прохождения его через оптическую систему. Однако не любой пучок при этом может быть преобразован в стигматический (гомоцентрический). Возможность пучка быть преобразованным в стигматический называется истинным стигматизмом. Следовательно, слабоастигматический и даже астигматический пучки могут быть классифицированы как истинно стигматические (гомоцентрические).
Пучок классифицируется как истинно стигматический при соблюдении условия:
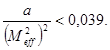 (52)
(52)
Примечание - Пороговое значение 0,039 находится в полном соответствии с порогом циркулярности 0,87 распределений плотности мощности. Эти пороговые уровни гарантируют идентичность геометрически стигматического пучка и истинно стигматического пучка.
3 Корректировка влияния фона и смещения базисной линии
3.1 Общие сведения
Сигналы, регистрируемые приемно-усилительным устройством в качестве результата измерений распределения плотности мощности (энергии) Emeas(x, у) или Hmeas(x, у), могут быть разделены на две части: «истинное» распределение плотности мощности (энергии) Е (х, у) или Н (х, у), генерируемой источником пучка лазерного излучения, и вероятное неоднородное фоновое распределение ЕВ (х, у), порождаемое сторонними источниками (например, излучение фона или шумы приемно-усилительного устройства):
![]() (53)
(53)
где фоновый сигнал в свою очередь может быть разделен на однородную (гомогенную) компоненту EB,offset(x, y) (например, сдвиг базовой линии), неоднородную (негомогенную) компоненту EB,inh(x, y) (например, наклон базовой линии) и высокочастотные шумовые компоненты EB,noise(x, y):
Примечание - Обычно третий компонент формулы (54) не только не может быть скорректирован, но в этом просто нет необходимости. Благодаря процессу интегрирования при вычислении параметров пучка шумовая составляющая является источником случайных погрешностей и влияет лишь на воспроизводимость результатов измерений, в то время как две других компоненты порождают систематические погрешности.
Пространственное распределение фонового излучения характеризуется усредненным значением плотности мощности EB,offset и его стандартным отклонением EB,σ. Если изменения порождаемого фоновым излучением выходного сигнала приемника излучения, характеризуемые разностями усредненных значений с выходов локальных участков чувствительной поверхности приемника и общим усредненным значением, менее ER,σ, то фоновое излучение, попадающее в приемник, можно считать однородным (см. 3.4).
Перед проведением оценки параметров пучка необходимо выполнить процедуры корректировки влияния фона во избежание появления составляющих сигналов помех в крыльях распределения, которые нельзя было бы отделить от полезного сигнала при проведении операций интегрирования. Первый шаг - это грубая корректировка путем вычитания из полученных результатов измерений распределения плотности мощности в сечении пучка либо известного («картированного») пространственного распределения фонового излучения, либо его усредненного распределения. При наличии приемника излучения с постоянным уровнем шума по всей его чувствительной площадке можно ограничиться корректировкой путем вычитания усредненного уровня фона. Во всех других случаях необходима коррекция путем вычитания «картированного» (т.е. определенного заранее пространственного распределения) плотности фонового излучения.
Оба вида этих корректировок (см. 3.2 и 3.3) приводят к снижению уровня вызываемой смещением погрешности в лучшем случае до 0,1 значащей цифры младшего разряда, но не всегда обеспечивают корректировку влияния смещения базовой линии от ее нулевого положения.
По причине стохастической природы фонового шума (сдвиг базовой линии определяют путем усреднения всех не подвергшихся облучению элементов (пикселей) приемника излучения), порождаемого флуктуациями окружающих источников излучения, рассеянным излучением или другими источниками некогерентного излучения лазера (например, флуоресценцией и/или остаточным потоком лампы накачки), достаточно точное определение сдвига базовой линии достигается измерениями распределения плотности мощности в поперечном сечении пучка. Даже небольшие сдвиги базовой линии от ее нулевого положения могут порождать значительные погрешности при оценке параметров, характеризующих измеренное распределение плотности мощности. Следовательно, особенно для малоразмерных пучков, когда их ширины не превышают четверти поперечного размера чувствительной площадки приемника излучения, необходимо выполнение дополнительных процедур, описанных в 3.4.
При надлежащей корректировке путем вычитания фонового излучения должны существовать отрицательные шумовые составляющие в корректируемом распределении плотности мощности. Их необходимо включать в последующие оценки для компенсации положительных шумовых составляющих.
3.2 Грубая корректировка путем вычитания распределения фона («картированного» распределения фонового излучения)
Перед постановкой основного эксперимента по измерению «карты» распределения плотности мощности («карты сигналов») необходимо зарегистрировать «темновое изображение» («карту фона»), представляющее собой распределение плотности фонового излучения при перекрытом пучке непрерывного лазера или выключенной схеме задержки (запуска) импульсного лазера.
Усредненная «карта фона» является усредненным результатом, по крайней мере, не менее 10 измерений (п > 10) распределения плотности фонового излучения:
После корректировки с использованием формулы (55) истинное распределение плотности мощности («карта сигналов») описывают выражением
![]()
![]() (56)
(56)
При попадании на приемник излучения флуктуирующих во времени нескорректированных остаточных излучений фона, вызывающих искажения результатов измерений, необходимо выполнить непосредственно следующие друг за другом эксперименты по регистрации «карты фона» и «карты сигналов». Для импульсных лазеров или непрерывных лазеров с быстродействующим затвором это может быть выполнено цикличными включениями приемно-усилительного устройства с выполняемыми в режиме «on-line» вычитаниями «карты фона» (см. 3.4).
3.3 Грубая корректировка путем вычитания усредненного распределения фонового излучения
Для приемно-усилительных устройств с неизменным (постоянным) уровнем фонового излучения, распределенного по чувствительной поверхности приемника, может быть применена корректировка измеренных распределений путем вычитания усредненного уровня фона.
Усредненный по чувствительной поверхности приемника гомогенный уровень фонового излучения EB,offset определяют регистрацией и усреднением по площади этой поверхности результатов, по крайней мере, не менее 10 измерений (п > 10) распределения фона:
![]() (57)
(57)
где т - общее число индивидуальных (х, у) регистрируемых приемником точек.
Вычитание усредненного уровня фона приводит к скорректированному распределению
![]() (58)
(58)
Вычитание усредненного уровня фона из «карты сигналов» не всегда позволяет скорректировать смещение базовой линии от ее нулевого положения. Даже небольшие смещения базовой линии могут порождать значительные погрешности оценки параметров, характеризующих измеренное распределение плотности мощности. Поэтому должны быть приняты меры по минимизации погрешностей, порождаемых смещением базовой линии (см. 3.4).
Процедуры, описанные в 3.2 и 3.3, в большинстве случаев позволяют снизить погрешности за счет смещения базовой линии до уровня менее 0,1 значащей цифры младшего разряда. Для малоразмерных пучков (с ширинами пучка менее 0,25 входной апертуры приемника излучения) необходима дополнительная, более тонкая процедура корректировки влияния смещения базисной линии, описываемая в 3.4.
3.4 Тонкая корректировка влияния смещения базисной линии
3.4.1 Общие сведения
Обоснование необходимости измерений распределения плотности мощности для точного определения смещения базовой линии от ее нулевого положения приведено в 3.1. В недавнем прошлом для точного определения смещения базовой линии по результатам измерений распределения плотности мощности использовали четыре группы методов:
- преобразования Фурье;
- гистограмм;
- статистических (стохастических);
- аппроксимации.
Две последние группы методов относительно просты (см. 3.4.2 и 3.4.3).
3.4.2 Статистический (стохастический) метод
Распределение фона характеризуется его средним значением EB,offset и стандартным отклонением EB,σ. Приблизительно (предположительно) оцениваемые смещения базовой линии EB,offset и уровень шума EB,σ могут быть извлечены при анализе либо необлученного изображения, либо необлученной части внутри измеренного распределения (см. 3.4.3). Все пиксели, чьи уровни Ei,j по шкале серости соответствуют неравенству
![]() (59)
(59)
при 2 < пT < 4, считают облученными и должны быть учтены при расчетах ширины пучка. Остальные пиксели считают необлученными. Усреднение их выходных сигналов определяет значение смещения базовой линии, которое следует вычесть из результатов измерений. Поскольку измеренное распределение плотности мощности всегда представлено в цифровом виде, эта процедура непосредственно неприменима для обработки результатов измерений. Поэтому осуществляется двухразмерная (по плоскости, двухкоординатная) свертка (усреднением субматриц из n · m пикселей
![]()
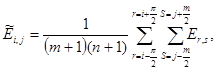 (60)
(60)
а для определения облученных пикселей должно быть соблюдено условие
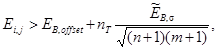 (61)
(61)
где 2 < пT < 4.
Смещение линии, которое подлежит вычитанию из измеренного изображения, в результате определяют по усредненному числу необлученных пикселей. Обычно значения m и n составляют от двух до пяти процентов размера изображения. Свертку изображения используют только для определения числа необлученных пикселей. Последующие вычисления распространяются на измеренное изображение со скорректированным смещением.
Примечание - Описанная процедура распространяется на обработку пороговых изображений. В противоположность традиционным методам обработки пороговых сигналов и изображений, когда пороговый уровень может быть установлен лишь для целых чисел, описанная процедура не приводит ни к появлению дополнительных погрешностей измерений, ни к потере информации.
3.4.3 Метод аппроксимации
Метод аппроксимации позволяет не только учесть приблизительные (предположительно) оцениваемые при статистической (стохастической) обработке величины, но и обеспечить во многих случаях достаточную точность коррекции влияния смещения.
Примечание - Распределение плотности мощности недифрагировавшего лазерного пучка быстро уменьшается по мере удаления от его центра. Следовательно, в случаях, когда ширина пучка не превышает половины поперечного размера чувствительной площадки приемника излучения, обычно существуют участки в пределах измеряемого распределения, которые не подвергаются облучению лазерным пучком (чаще всего это угловые зоны изображения).
Определение смещения базовой линии усреднением выборки из N необлученных точек (например, матрицы из n · m пикселей в каждой из четырех угловых зон изображения) внутри изображения позволяет непосредственно определить смещение, которое необходимо вычесть из измеренного распределения. При этом оценивают и вносимую этим смещением неопределенность измерений.
Пример - Использование обычной ПЗС-камеры с уровнем шума в одну цифру наименьшего значащего разряда при п = т = 50 обеспечивает измерения с нескорректированным остатком неопределенности за счет смещения базовой линии порядка 1/100 этой цифры.
Обычно т и п составляют от 2 % до 5 % размера изображения. Корректность этого метода должна быть проверена сравнением смещения базовой линии измеренного распределения со смещением, полученным для темнового изображения при одинаковых зонах (площадях) усреднения:
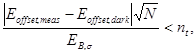 (62)
(62)
причем nt должно быть менее четырех.
Если это соотношение не выполнено, то либо влияет значительный уровень остаточного излучения не устраненного перекрытием пучка, либо поперечные размеры последнего слишком велики по сравнению с поперечными размерами приемника излучения и поэтому угловые зоны изображения оказались облученными.
В этом случае необходимо:
a) применить формирующую пучок оптическую систему с минимально возможным рассеянием;
b) переформировать пучок с меньшим расширением или выбрать приемник излучения с увеличенным поперечным размером;
c) повысить уровень защищенности приемно-усилительного устройства от воздействия внешнего излучения и некогерентного излучения лазерного резонатора.
4 Альтернативные методики измерений ширины пучка
4.1 Общие сведения
Если измерительная аппаратура с достаточно высокими отношением сигнал - шум и разрешающей способностью недоступна, можно воспользоваться описываемыми в настоящем разделе альтернативными методиками. С помощью достаточно простой аппаратуры они обеспечивают точность измерений диаметра или ширины пучка, приемлемую для многих применений лазеров.
Описываемые ниже методики не базируются на определении моментов второго порядка функции пространственного распределения плотности мощности, необходимых для соблюдения требований формализма законов распространения лазерного излучения.
Соотношение между значениями диаметра пучка, полученными с применением метода на основе моментов второго порядка и альтернативной методики, сильно зависит от формы распределения плотности мощности [4]. Однако, как видно из таблицы 1, существует корреляция между значениями коэффициента распространения пучка, полученными одной из альтернативных методик, и классическим методом, описанным в настоящем стандарте.
Корреляция подтверждается следующей формулой
где Mi2 - коэффициент распространения пучка, полученный i-й альтернативной методикой;
сi - коэффициент корреляции между значениями М2, полученными альтернативной методикой, и стандартным методом моментов второго порядка.
Таблица 1 - Альтернативные методики - коэффициенты корреляции
|
ci |
|
|
Варьируемой диафрагмы (см. 4.2) |
1,14 |
|
Движущегося резкого края (ножа Фуко) |
0,81 |
|
Перемещаемой щели |
0,95 |
|
Примечание - Эти значения справедливы для газовых лазеров с устойчивым резонатором, мощностью до 10 Вт (для СО2 лазеров до 1 кВт) и с M2 до четырех для стигматических (гомоцентрических) пучков. Для больших значений М2 (М2 > 4) и лазеров других типов значения коэффициента корреляции требуют подтверждения. |
|
Из соотношения (63) следует формула для вычисления диаметров (ширин) пучка:
![]() (64)
(64)
где di - диаметр или ширина пучка, определяемые i-й альтернативной методикой.
4.2 Методика варьируемой диафрагмы
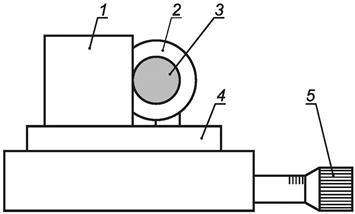
4.2.1 Принцип измерений
Варьируемую диафрагму, размещаемую в плоскости измерений, применяют для определения части мощности пропущенного сквозь нее пучка в зависимости от диаметра отверстия (см. рисунок 3). Нескорректированное (ориентировочное) значение диаметра пучка равно минимальному диаметру отверстия в диафрагме, сквозь которое проходит 86,5 % суммарной мощности измеряемого пучка излучения. Диаметр пучка рассчитывают по формуле, приведенной в 4.2.5.
Методика применима лишь для пучков, у которых отношение главных осей поперечного сечения не более 1,15:1.
4.2.2 Приемник излучения
Приемник излучения должен соответствовать требованиям разделов 3 и 4 МЭК 61040 [3]. Кроме того:
- необходимо подтверждение (по данным сертификата производителя или путем измерений) линейности зависимости выходной величины приемника излучения (например, электрического напряжения или ЭДС) от входной. Зависимость от длины волны излучения, нелинейность, неоднородность распределения чувствительности по приемной площадке (зонная характеристика) должны быть минимизированы или скорректированы путем калибровки всего приемно-усилительного устройства;
- необходимо убедиться в достаточности лучевой стойкости приемной поверхности чувствительного элемента во избежание ее повреждений при чрезмерных облученностях, уровнях мощности (энергии);
- зонная характеристика должна быть достаточно равномерной, чтобы приемник не реагировал на смену позиционирования пучка, попадающего в открытое отверстие диафрагмы;
- размер приемной площадки чувствительного элемента должен быть выбран таким, чтобы приемником воспринималось более 99 % суммарной мощности пучка лазерного излучения.
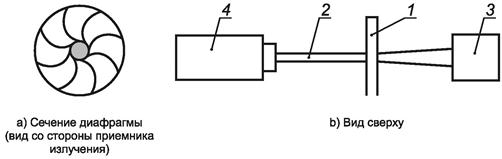
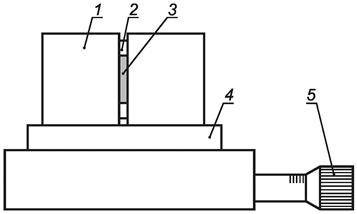
1 - варьируемая диафрагма; 2 - пучок; 3 - приемник излучения; 4 - лазер
Рисунок 3 - Схема измерений ширины пучка по методике варьируемой диафрагмы
4.2.3 Диафрагмы/отверстия
Используют набор диафрагм со ступенчатым изменением диаметров отверстий в них, чтобы при смене очередной диафрагмы пропускаемая следующей диафрагмой мощность пучка сокращалась не более чем на 5 %. Допускается использование ирисовых диафрагм с калиброванными по размерам отверстиями.
Конструкция диафрагмы должна обеспечивать сохранение неизменными во время измерений геометрической формы пучка и коэффициента поглощения его мощности (энергии) (т.е. допустимо использование водяного охлаждения, отражателей или ослабителей в соответствии с ИСО 11146-1 [1]).
4.2.4 Методика измерений
Следует убедиться в том, что плоскости диафрагмы и входной апертуры перпендикулярны к оптической оси. Затем необходимо провести юстировку приемника излучения с целью его центрирования относительно оптической оси с погрешностью не более 0,1 ширины измеряемого пучка. Дальнейшая процедура центрирования сводится к уменьшению отверстия в диафрагме сначала до достижения уровня пропускаемой ею мощности порядка 80 % номинальной, а затем - к перемещению ее в плоскости измерений до достижения максимального уровня проходящей сквозь отверстие мощности.
Проверку попадания всей измеряемой мощности на чувствительный элемент приемника выполняют введением диафрагмы коаксиально пучку на приемной площадке чувствительного элемента так, чтобы она перекрывала до 30 % площади периферийной части приемной площадки. При этом не должно возникнуть заметных изменений уровня измеряемой мощности.
Регистрируют значение суммарной мощности Р0, после чего ступенчато уменьшают площади отверстия диафрагмы так, чтобы при каждой вариации этой площади (диаметра) измеряемая мощность уменьшалась не более чем на 5 %. Регистрируют значения ближайшего наибольшего d1 и ближайшего наименьшего d2 диаметров отверстия диафрагмы, при которых уровень пропускаемой ею мощности достигает 86,5 % первоначального отсчета. Одновременно регистрируют соответствующие этим диаметрам значения мощности P1, P2 или энергии Q1, Q2.
4.2.5 Вычисления
Вычисления нескорректированного (ориентировочного) значения диаметра пучка d86,5 выполняют по формуле линейной интерполяции в промежутке между известными размерами отверстий d1 и d2 и соответствующими им зарегистрированными значениями мощности Р1, Р2 около уровня 86,5 %:
![]() (65)
(65)
При ограничениях, приведенных в 4.1, вычисляют диаметр (ширина) пучка:
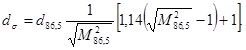 (66)
(66)
4.3 Методика движущегося резкого края (ножа Фуко)
4.3.1 Принцип измерений
Нож Фуко используют для пересечения пучка непосредственно перед приемной поверхностью достаточно большой площади чувствительного элемента смонтированного приемника излучения, в результате чего измеряют прошедшую мощность в зависимости от положения резкого края ножа (см. рисунок 4). Нескорректированная (ориентировочная) ширина пучка равна расстоянию между двумя положениями резкого края, в одном из которых приемник воспринимает 84 %, а в другом - 16 % пропускаемой мощности. Ширину пучка рассчитывают по формулам (67) и (68). При измерениях эллиптических пучков направление движения резкого края должно совпадать с двумя главными осями пучка.
1 - резкий край (нож Фуко); 2 - приемник излучения; 3 - пучок; 4 - механизм перемещения ножа; 5 - микрометр
Рисунок 4 - Схема измерений ширины пучка по методике движущегося резкого края (ножа Фуко)
4.3.2 Приемник излучения
Требования к приемнику излучения и к приемно-усилительному устройству в целом совпадают с изложенными в 4.2.2. Длина резкого края должна, по крайней мере, перекрывать диаметр приемной поверхности чувствительного элемента.
4.3.3 Методика измерений для стигматических (гомоцентрических) пучков
Регистрируют значение мощности пучка с выведенным за его пределы ножом Фуко. Механизмом 4 (см. рисунок 4) нож смещают по горизонтальной оси х до тех пор, пока резкий край не сократит измеряемую лазерным ваттметром мощность до уровня 84 % первоначального, при этом фиксируется положение x1. Перемещение продолжают до положения х2, при котором уровень измеряемой мощности достигает 16 % первоначального.
4.3.4 Вычисления
Нескорректированную (ориентировочную) ширину пучка в данном сечении dk определяют по формуле
При ограничениях, приведенных в 4.1, соответствующее значение ширины (диаметра) пучка dϭ определяют по формуле
4.3.5 Методика измерений для слабоастигматических пучков
Для определения ширин пучков dσx и dσy необходимы перемещения резкого края вдоль двух главных осей сечения пучка. Методика измерений (испытаний) и формулы вычислений те же, что в 4.3.3 и 4.3.4. Положения главных осей могут быть найдены следующим образом:
a) определением двух ортогональных направлений, в которых нескорректированные (ориентировочные) ширины пучка одинаковы;
b) поворотом этих двух ортогональных направлений на 45° до совпадений с главными осями.
4.4 Методика перемещаемой щели
4.4.1 Принцип измерений
Щель, монтируемую на механизме перемещения, используют для вырезания «полосы» из сечения пучка перед фиксированным приемником излучения с большой площадью приемной поверхности так, чтобы измерять зависимость прошедшей сквозь щель мощности излучения от ее положения (см. рисунок 5). Нескорректированная (ориентировочная) ширина пучка равна расстоянию между двумя положениями щели, в которых пропущенная сквозь щель мощность равна 13,5 % ее максимального значения. Ширину пучка вычисляют по формуле (69). При измерениях эллиптических пучков направления движения щели должны совпадать с двумя главными осями пучка.
Примечание - При использовании ленточного приемника излучения, перемещаемого вместе со щелью, лучших результатов измерений достигают для пучков больших диаметров.
1 - перемещаемая щель; 2 - приемник излучения; 3 - пучок; 4 - механизм перемещения щели; 5 - микрометр
Рисунок 5 - Схема измерений ширины пучка по методике перемещаемой щели
4.4.2 Приемник излучения
Требования к приемнику излучения и к приемно-усилительному устройству в целом совпадают с изложенными в 4.2.2.
Длина щели должна по крайней мере перекрывать диаметр приемной поверхности чувствительного элемента.
4.4.3 Щель
Длина щели должна не менее чем в два раза превышать примерную ширину измеряемого пучка. Ширина щели должна быть не более 1/20 примерной ширины измеряемого пучка.
4.4.4 Методика измерений для стигматических (гомоцентрических) пучков
Щель вне пучка устанавливают перпендикулярно к оси его распространения и измеряют суммарную мощность, воспринимаемую приемником излучения при открытом входном отверстии приемно-усилительного устройства (отсчет № 1). Затем щель перемещают в плоскости измерений в направлении, перпендикулярном к оси распространения, пока пропускание сквозь нее в одном конце сечения не достигнет 13,5 % суммарной мощности, зарегистрированной при отсчете № 1. При этом фиксируют положение х1 щели. То же повторяют при дальнейшем перемещении щели до положения х2, соответствующего ее пропусканию 13,5 % суммарной мощности на другом конце сечения пучка.
4.4.5 Вычисления
Расстояние между положениями х2 и х1 х2 - х1 является нескорректированной (ориентировочной) шириной пучка ds.
При ограничениях, приведенных в 4.1, соответствующее значение ширины (диаметра) пучка dσ вычисляют по формуле
4.4.6 Методика измерений для слабоастигматических пучков
Для определения ширин пучков dσx и dσy необходимо выполнить два измерения вдоль главных осей сечения пучка. Методика измерений и формулы вычислений те же, что в 4.4.4 и 4.4.5. Положения главных осей могут быть найдены следующим образом:
a) определением двух ортогональных направлений, в которых нескорректированные (ориентировочные) ширины пучка одинаковы;
b) поворотом этих двух ортогональных направлений на 45° до совпадений с главными осями.
Приложение А
(справочное)
Матрицы оптических систем
Безаберрационные оптические системы характеризуются 4×4-форматными матрицами. Закон распространения излучения, приведенный в 2.5, базируется на этих матрицах и легко может быть использован для оценки свойств пучка. В настоящем приложении представлены матрицы, характеризующие большинство наиболее важных и распространенных оптических элементов, и описана процедура вычисления матриц для состоящих из них оптических систем.
Матрицу, характеризующую распространение пучка на расстояние L в свободном пространстве, описывают выражением
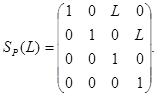 (А.1)
(А.1)
Тонкую сферическую линзу с фокусным расстоянием дописывают матрицей
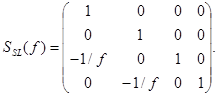 (А.2)
(А.2)
Одиночную тонкую цилиндрическую линзу описывают матрицей
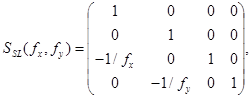 (А.3)
(А.3)
где fx и fy - фокусные расстояния в горизонтальном и вертикальном направлениях соответственно.
Цилиндрическую
линзу, повернутую на угол ![]() вокруг
оптической оси, описывают матрицей
вокруг
оптической оси, описывают матрицей
![]() (А.4)
(А.4)
где
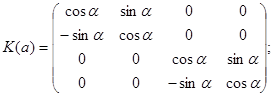 (А.5)
(А.5)
R(α)T - транспонированная матрица R(α).
Матрицу оптической системы или схемы, состоящей из нескольких оптических элементов, формируют в виде произведения матриц, характеризующих отдельные элементы оптической системы. Например, матрица оптической схемы в виде сферической линзы с фокусным расстоянием f, расстоянием L1 от входной (передней) плоскости линзы и расстоянием L2 от выходной ее плоскости равна
![]() (А.6)
(А.6)
Библиография
|
Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 1: Стигматические (гомоцентрические) и слабоастигматические пучки |
|
|
Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 2: Астигматические пучки |
|
|
Измерительные преобразователи, приборы и установки для измерений лазерного излучения |
|
|
«Choice of clip levels for beam width measurements using knife edge techniques», IEEE Journal of Quantum Electronics Vol. 27 p. 1098 - 1104 (1991) |
|
|
[5] Siegman A.E. |
«Defining the effective radius of curvature for a nonideal optical beam», IEEE Journal of Quantum Electronics Vol. 27 p. 1146 - 1148 (1991) |
|
[6] Nemes G. |
«Synthesis of general astigmatic optical systems, the detwisting procedure, and the bean quality factors for general astigmatic laser beams», Laser Beam Characterization, H. Weber, N. Reng, J. Ludtke, and P. M. Mejias, eds., Technical University Berlin, Institutes of Optics, StraSSe des 17. Juni 135, 10623 Berlin, Germany, p. 93 - 104 (1994) |
|
[7] Nemes G. |
Intrinsic and geometrical beam classification and the beam identification after measurement, SPIE Proc. 4932, p. 624 - 636 (2003) |
Ключевые слова: лазер, лазерное излучение, мощность, энергия, распределение плотности мощности (энергии), диаметр пучка, расходимость пучка, коэффициент распространения пучка