ОТРАСЛЕВОЙ СТАНДАРТ
|
СИСТЕМА ЕДИНСТВА ИЗМЕРЕНИЙ Аппроксимация градуировочных характеристик |
ОСТ 100108-73Взамен 922АТ |
Распоряжением Министерства от 27 декабря 1973 г. № 087-16 дата введения 1 июля 1974 г.
Настоящий стандарт устанавливает метод определения числа измерений при градуировке, оценки коэффициентов полинома, правильность выбора его степени для измерительных преобразователей, используемых при летных испытаниях летательных аппаратов.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Градуировочная характеристика средства измерений, используемая при обработке результатов летных испытаний, должна иметь вид степенного полинома:
x = a0 + a1y + a2y2 + ... + aкyк,
где х - входной сигнал средства измерений;
у - выходной сигнал средства измерений;
к - максимальная степень полинома, которым выражена градуировочная характеристика рассматриваемого средства измерений.
1.2. Градуировочная характеристика определяется оценкой неизвестных коэффициентов полинома a0, а1, ..., ак по методу наименьших квадратов на основании имеющихся значений x и y.
1.3. Оценка градуировочной характеристики производится при условии, что результаты прямых измерений входной величины имеют погрешности не более 0,3 от погрешности выходной величины.
Проверку соответствия результатов градуировки проводят на стадии аттестации средств измерений.
1.4. Максимальная степень полинома к определяется по результатам аппроксимации градуировочных характеристик 5 - 10 однотипных средств измерений.
1.5. При определении максимальной степени полинома градуировка производится для значений входной величины x, равномерно расположенных по диапазону измерения этой величины.
Число точек измерения принимается не менее 20.
1.6. При каждом значении входной величины x производится одно измерение выходной величины y.
1.7. Пример определения максимальной степени аппроксимирующего полинома приведен в справочном приложении 1 к настоящему стандарту.
1.8. Число измерений при построении индивидуальной градуировочной характеристики определяется по формуле:
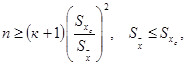
где ![]() - среднеквадратическая погрешность
средства измерений;
- среднеквадратическая погрешность
средства измерений;
![]() - среднеквадратическая погрешность аппроксимации.
- среднеквадратическая погрешность аппроксимации.
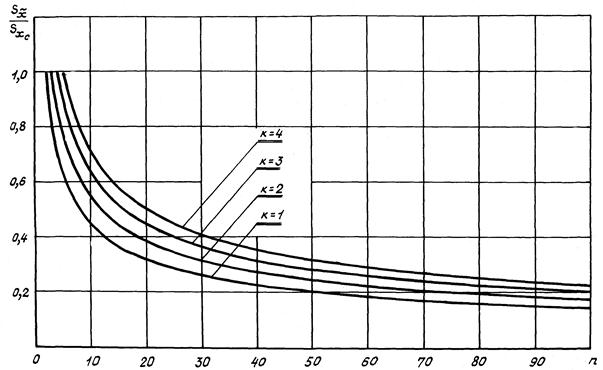
1.9. График зависимости отношения ![]() от числа
измерений для полиномов различных степеней приведен в справочном приложении 2 к
настоящему стандарту.
от числа
измерений для полиномов различных степеней приведен в справочном приложении 2 к
настоящему стандарту.
1.10. Градуировочные точки располагаются равномерно по рассматриваемому диапазону.
1.11. Погрешность оценки характеристик уменьшается, если градуировка производится в (к + 1) точках и при таких значениях xj, для которых значения yj определяется по формуле:
![]()
где tj -
значения корней полинома, представляющего собой коэффициент при Zк в разложении ![]() по степеням Z.
по степеням Z.
Величина tj для к = j = 2 + 6 принимает следующие значения:
t1 = -1; t2 = 1;
t1 = -1; t2 = 0; t3 = 1;
t1 = -1; t2 = -0,4472; t3 = 0,4472; t4 = 1;
t1 = -1; t2 = -0,6550; t3 = 0; t4 = 6550; t5 = 1;
t1 = -1; t2 = -0,7650; t3 = - 0,2852; t4 = 2852; t5 = 0,7650; t6 = 1;
При каждом значении xj или при близком к нему значении производился одно или более повторных измерений выходной величины y. Кроме того, для контроля правильности функционирования средства измерений в промежуточных точках производится несколько дополнительных измерений.
2. АППРОКСИМАЦИЯ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК
2.1. Аппроксимация градуировочной характеристики для постоянной по диапазону погрешности рассматриваемого средства измерений
2.1.1. Расчет ведется на основе имеющихся значений x1, x2, ..., xn и y1, y2, ..., yn, а также абсолютного значения среднеквадратической погрешности Sx градуировочных точек.
2.1.2. Значения исходных величин x и y приводятся (нормализуются) к диапазону измерения [0, 1] по формулам:
![]()
где ![]() и
и ![]() - нормализованные значения
величин xj и yj.
- нормализованные значения
величин xj и yj.
2.1.3. Среднеквадратическая погрешность нормализуется по формуле:
![]()
2.1.4. Определение коэффициентов полинома
![]() для
нормированных
для
нормированных ![]() и
и
![]() производится
по формуле:
производится
по формуле:
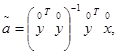
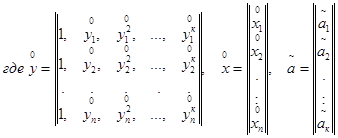
Примечание: Символ Т означает транспонирование матриц, а символ «- 1» - их обращение.
2.1.5. Нормализованное
значение погрешности ![]() определения величины xj по полученной в
результате аппроксимации градуировочной характеристике при заданном нормализованном значении
определения величины xj по полученной в
результате аппроксимации градуировочной характеристике при заданном нормализованном значении ![]() находится по
формуле:
находится по
формуле:
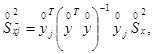
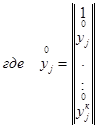
2.2. Аппроксимация градуировочной характеристики для изменяющейся по диапазону погрешности рассматриваемого средства измерения
2.2.1. Расчет ведется на основе имеющихся значений x1, x2, ..., xn и y1, y2, ..., yn, а также абсолютных значений среднеквадратических погрешностей Sx1, Sx2, ..., Sxn градуировочных точек.
2.2.2. Определение коэффициентов полинома
![]() производится
по формуле:
производится
по формуле:
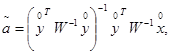
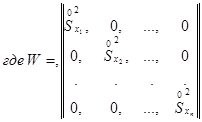
2.2.3. Нормализованное значение
погрешности определения величины xj по полученной оценке градуировочной характеристики при
заданном нормализованном значении ![]() находится по формуле:
находится по формуле:
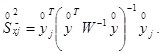
2.3. Определение степени полинома производится проверкой неравенства:
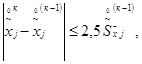
где ![]() - оценки по полиномам степени
к и (к - 1) значений величины
- оценки по полиномам степени
к и (к - 1) значений величины ![]() при заданном
при заданном ![]() ;
;
![]() - нормализованное
значение среднеквадратической погрешности определения величины xj по полиному
степени (к - 1).
- нормализованное
значение среднеквадратической погрешности определения величины xj по полиному
степени (к - 1).
Первоначальное значение степени к не должно быть менее 7. Если неравенство не выполняется, то в качестве аппроксимирующего принимается полином степени к.
Если неравенство выполняется, то степень полинома уменьшается на единицу и неравенство проверяется для следующей пары полиномов, т.е. полиномов степени (к - 1) и (к - 2) и т.д.
2.3.1. Проверка прекращается, как только неравенство в какой-либо точке не выполнится. В качестве действительного принимается полином, степень которого в сравниваемой паре высшая.
2.3.2. Неравенство следует проверять в пяти-десяти точках характеристики, равномерно расположенных по диапазону выходной величины y.
2.4. Пересчет полученных коэффициентов полинома к значениям, соответствующим не нормализованным значениям величин x и y, осуществляется по формулам:
![]()
где ![]()
Пример определения коэффициентов a0, a1, ..., a4 для полинома 4-й степени приведен в справочном приложении 3 к настоящему стандарту.
2.5. Характеристикой рассеяния градуировочных точек относительно полученного аппроксимирующего полинома служит значение среднеквадратического отклонения, которое в единицах измерения входной величины определяется по формуле
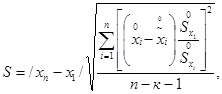
где ![]() - нормализованное значение входной
величины x, полученное при градуировании;
- нормализованное значение входной
величины x, полученное при градуировании;
![]() -
нормализованное значение входной величины x, оцененное по полиному.
-
нормализованное значение входной величины x, оцененное по полиному.
2.6. Пример оценки индивидуальной градуировочной характеристики средств измерений приведен в справочном приложении 4 к настоящему стандарту.
ПРИЛОЖЕНИЕ
1
Справочное
Пример определения максимальной степени аппроксимирующего полинома
Для определения максимальной степени полинома градуировочная характеристика задана 21 парой значений x и y. Градуировочные точки располагались равномерно по диапазону величины x. Результаты полученных измерений приведены в табл. 1.
Таблица 1
|
Значение входной величины x |
Значение выходной величины y |
Номер измерения |
Значение входной величины x |
Значение выходной величины y |
|
|
1 |
0,00 |
0,144 |
12 |
5,52 |
0,656 |
|
2 |
0,51 |
0,192 |
13 |
6,02 |
0,693 |
|
3 |
1,01 |
0,228 |
14 |
6,52 |
0,756 |
|
4 |
1,51 |
0,275 |
15 |
7,03 |
0,795 |
|
5 |
2,02 |
0,317 |
16 |
7,53 |
0,858 |
|
6 |
2,52 |
0,365 |
17 |
8,03 |
0,894 |
|
7 |
3,03 |
0,408 |
18 |
8,53 |
0,950 |
|
8 |
3,53 |
0,464 |
19 |
9,04 |
0,989 |
|
9 |
4,03 |
0,498 |
20 |
9,54 |
1,017 |
|
10 |
4,53 |
0,554 |
21 |
10,04 |
1,061 |
|
11 |
5,03 |
0,595 |
В результате аттестации было установлено, что для средства измерений рассматриваемого типа погрешность постоянна по диапазону, а значение среднеквадратической погрешности градуировочных точек равно 0,06 ед.
В результате обработки данных было установлено, что рассматриваемая градуировочная характеристика может быть аппроксимирована полиномом 3-й степени со следующими значениями коэффициентов:
а0 = -2,110; а1 = 15,366; а2 = -8,686; а3 = 4,667.
Значение среднеквадратического отклонения равно 0,073 ед.
Степень полинома выбиралась на основании данных, приведенных в табл. 2.
Таблица 2
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
|
dj, 7 - 6 % |
1,324 |
0,586 |
0,548 |
0,558 |
0,603 |
1,305 |
|
dj, 6 - 5 % |
1,370 |
0,687 |
0,678 |
0,694 |
0,700 |
1,349 |
|
dj, 5 - 4 % |
1,122 |
0,660 |
0,508 |
0,512 |
0,678 |
1,081 |
|
dj, 4 - 3 % |
0,425 |
0,164 |
0,263 |
0,281 |
0,164 |
0,384 |
|
dj, 3 - 2 % |
-0,641 |
-0,343 |
-0,054 |
-0,096 |
-0,397 |
-0,610 |
|
dj, 2 - 1 % |
0,293 |
0,449 |
0,166 |
0,160 |
0,433 |
0,308 |
Здесь ![]() -
нормализованное значение выходной величины y в точке j;
-
нормализованное значение выходной величины y в точке j;
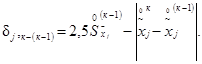
Приложение 2
Справочное
График зависимости отношения 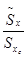 от числа измерений для
полиномов различных степеней
от числа измерений для
полиномов различных степеней
ПРИЛОЖЕНИЕ
3
Справочное
Пример определения коэффициентов для полинома 4-й степени
Для полинома 4-й степени коэффициенты определяются по формулам:
![]()
![]()
![]()
![]()
![]()
ПРИЛОЖЕНИЕ 4
Справочное
Пример оценки индивидуальной градуировочной характеристики
Градуировочные характеристики рассматриваемого типа средств измерений представляются полиномами с максимальной степенью, равной 3.
При построении индивидуальной
градуировочной характеристики должно быть произведено не менее четырех
измерений величин x и y
(при ![]() ).
).
Градуировочная характеристика была задана 21 точкой. Точки равномерно расположены по диапазону величины x. Результаты градуировки приведены в табл. 1.
Таблица 1
|
Значение входной величины x |
Значение выходной величины y |
Номер измерения |
Значение входной величины x |
Значение выходной величины y |
|
|
1 |
0,00 |
0,139 |
12 |
5,52 |
0,646 |
|
2 |
0,50 |
0,179 |
13 |
6,02 |
0,689 |
|
3 |
0,99 |
0,228 |
14 |
6,52 |
0,744 |
|
4 |
1,50 |
0,273 |
15 |
7,02 |
0,782 |
|
5 |
2,00 |
0,310 |
16 |
7,53 |
0,846 |
|
6 |
2,50 |
0,364 |
17 |
8,03 |
0,886 |
|
7 |
3,01 |
0,398 |
18 |
8,53 |
0,934 |
|
8 |
3,51 |
0,452 |
19 |
9,03 |
0,976 |
|
9 |
4,01 |
0,494 |
20 |
9,52 |
1,004 |
|
10 |
4,51 |
0,551 |
21 |
10,03 |
1,045 |
|
11 |
5,00 |
0,584 |
Погрешность рассматриваемого средства измерений постоянна по всему диапазону, а величина среднеквадратической погрешности градуировочных точек равна 0,06 ед.
В результате обработки данных получены следующие значения коэффициентов полинома:
а0 = -1,943; а1 = 14,590; а2 = -7,343; а3 = 4,094.
Значение среднеквадратического отклонения равно 0,071 ед.
СОДЕРЖАНИЕ