ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р МЭК |
Надежность в технике
МЕТОДЫ СРАВНЕНИЯ
ПОСТОЯННЫХ
ИНТЕНСИВНОСТЕЙ ОТКАЗОВ И ПАРАМЕТРОВ ПОТОКА
ОТКАЗОВ
IEC
61650:1997
Reliability
data analysis techniques - Procedures for
comparison of two constant failure rates and two constant
failure (event) intensities
(IDT)
|
|
Москва Стандартинформ 2008 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН ТК 119 «Надежность в технике»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2007 г. № 580-ст
4 Настоящий стандарт идентичен международному стандарту МЭК 61650:1997 «Методы анализа надежности. Методы сравнения постоянных интенсивностей отказов и параметров потока отказов» (IEC 61650:1997 «Reliability data analysis techniques - Procedures for comparison of two constant failure rates and two constant failure (event) intensities»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении D
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
Введение
На практике часто возникает необходимость сопоставить характеристики надежности систем и компонентов, когда есть технические или другие причины предполагать, что они различны. Например, сравнить надежность объектов, изготовленных одним и тем же предприятием в различные промежутки времени или произведенных различными предприятиями.
Интенсивность отказов и параметр потока отказов часто используют в качестве показателей надежности. Настоящий стандарт описывает методы сравнения двух наборов наблюдений, соответствующих постоянной интенсивности отказов/постоянному параметру потока отказов. В стандарте приведены примеры, иллюстрирующие применение методов на практике.
Для проверки предположения о постоянстве интенсивности отказов/параметра потока отказов рекомендуется применять ГОСТ Р МЭК 60605-6 «Надежность в технике. Критерии проверки постоянства интенсивности отказов и параметра потока отказов».
В приложении А приведены необходимые для применения стандарта таблицы. Математическое обоснование метода приведено в приложении В, а примеры применения стандарта - в приложении С.
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Надежность в технике МЕТОДЫ
СРАВНЕНИЯ ПОСТОЯННЫХ ИНТЕНСИВНОСТЕЙ ОТКАЗОВ И Reliability in
techniques. Procedures for comparison of constant failure rates and constant |
Дата введения - 2008-06-01
1 Область применения
Настоящий стандарт устанавливает методы сравнения двух наблюдаемых:
- интенсивностей отказов;
- параметров потока отказов;
- интенсивностей/параметров потока событий.
Методы позволяют установить, можно ли считать статистически существенными различия между двумя наборами наблюдений.
Предполагается, что интервалы времени до отказов, событий (между отказами, событиями) независимы и подчиняются экспоненциальному распределению в течение периода наблюдений (суммарного времени испытаний).
Примечание - Это предположение подразумевает, что интенсивность отказов/параметра потока отказов постоянны.
Кроме того, предполагается, что имеются технические или иные причины возможных различий (улучшение или ухудшение) между наблюдаемыми характеристиками надежности двух сравниваемых наборов объектов. Некоторые примеры применения описанных методов приведены в 5.4.
Разработанные методы являются методами проверки гипотез (с заданным уровнем значимости) о принадлежности двух наборов наблюдений к одной и той же совокупности или одному и тому же процессу, т.е. гипотезы о совпадении значений истинного среднего (математического ожидания) для этих двух наборов.
Примечание - Интенсивность отказов соответствует невосстанавливаемым объектам и характеризует наработки до отказа. Параметр потока отказов соответствует только восстанавливаемым объектам и характеризует процесс, описывающий последовательность событий; например наработки между отказами.
Приведенные в настоящем стандарте методы не ограничиваются сравнением интенсивностей параметров потока отказов. Они могут быть применены к двум наборам наблюдений любых событий, для которых выполняются вышеупомянутые предположения.
Примечание - Два набора наблюдений могут содержать элементы одной и той же совокупности или описывать объект в различных условиях (окружающая среда, нагрузка) или только сопоставимые наборы событий (например, автомобильные аварии на дороге).
В настоящем стандарте приведены числовые методы и графические процедуры. Периоды наблюдений, соответствующие двум наборам, не обязательно должны быть равны, но если они совпадают, методы сильно упрощаются.
2 Нормативные ссылки
В настоящем стандарте использована ссылка на следующий стандарт:
МЭК 60050-191:1990 Международный электротехнический словарь. Глава 191. Надежность и качество услуг
3 Термины и определения
В настоящем стандарте применены термины по МЭК 60050-191.
4 Условные обозначения
4.1 Перечень обозначений
α - расчетный уровень значимости;
α0 -заданный уровень значимости;
λi - истинная интенсивность отказов для i-го набора;
Ф(и) - интегральная функция нормированного нормального распределения, Ф(иα) = α;
i - индекс набора наблюдений, принимает значения 1 или 2;
f - статистика F-распределения;
fc - критическое значение статистики F-распределения для заданного уровня значимости;
F1-α(v1, v2) - квантиль уровня (1 - α) F-распределения с v1 и v2 степенями свободы;
р - отношение, р = T1*/(T1* + Т2*);
r - общее количество отказов, r = r1 + r2;
ri - количество отказов i-го набора;
Ti* - суммарная наработка i-го набора;
и - статистика нормированного нормального распределения;
иα - квантиль уровня α нормированного нормального распределения;
ис - критическое значение для заданного уровня значимости, полученное для нормированного нормального распределения;
w - истинное значение интенсивности/параметра потока отказов (см. 4.2).
Примечание - Значение w в общем случае неизвестно;
![]() - оценка
интенсивности/параметра потока отказов для i-го набора,
- оценка
интенсивности/параметра потока отказов для i-го набора, ![]()
zi - истинное значение параметра потока отказов для i-го набора.
4.2 Преобразование обозначений
Поскольку методы настоящего стандарта применимы к различным показателям надежности, в стандарте использован общий символ w для интенсивности отказов и параметра потока отказов.
Следовательно,
- для интенсивности отказов w = λ;
- для параметра потока отказов w = z.
5 Предположения
5.1 Предположения
Критерий проверки гипотез основан на предположении, что наработки до отказов (между отказами) независимы и подчиняются экспоненциальному распределению в течение периода наблюдений (суммарной наработки). Это предположение подразумевает, что интенсивность отказов и соответственно параметр потока отказов постоянны.
Поскольку предполагается, что имеются технические или иные причины возможных различий (улучшение или ухудшение) между характеристиками надежности, соответствующими двум наборам сравниваемых наблюдений, для проверки гипотез использованы односторонние критерии.
5.2 Восстанавливаемые объекты
Методы применимы для сравнения параметров потока отказов на основе наблюдений восстанавливаемых объектов при условии выполнения в пределах каждого периода следующих предположений:
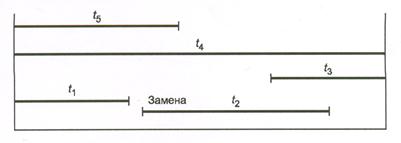
- время испытаний вычисляют как наработку в процессе испытаний, исключая время ремонта и других простоев (см. рисунок 1);
- восстановленные объекты можно считать новыми.
Рисунок 1 - Пример вычисления Тi* для одного восстанавливаемого объекта (Тi* = t1 + t2 + t3 + t4)
5.3 Невосстанавливаемые объекты
Методы применимы для сравнения интенсивностей отказов на основе наблюдений за невосстанавливаемыми объектами при условии выполнения в пределах каждого периода следующих предположений:
- время испытаний вычисляют как сумму наработок до отказа и, при отсутствии отказа, наработок неотказавших объектов за время наблюдений (см. рисунок 2);
- все объекты принадлежат к одной и той же совокупности.
Рисунок 2 - Пример вычисления Тi* для пяти невосстанавливаемых объектов (Тi* = t1 + t2 + t3 + t4 + t5)
5.4 Примеры объектов применения
Объектами применения описанных методов являются следующие: все виды интенсивностей отказов компонентов и монтажных плат; параметры потока отказов оборудования, объектов, систем, перезапусков и т.п. Можно проводить сравнение наблюдений одного и того же объекта в течение различных периодов времени, объектов одного вида различных производителей или работающих в различных условиях, объектов до и после модернизации.
Примечание - Способность статистики обнаруживать различия между двумя интенсивностями отказов, параметрами потока отказов (событий) возрастает вместе с количеством наблюдаемых событий.
6 Требования к исходным данным
Для применения методов необходимы следующие данные:
- наблюдаемое количество отказов в течение двух периодов наблюдений r1 и r2;
- суммарные наработки Т1* и Т2*, соответствующие этим двум периодам;
- заданный (выбранный) уровень значимости α0 (если требуется).
Если необходимы дополнительные исследования статистических предположений, то потребуются данные о времени возникновения каждого отказа.
7 Методы
7.1 Общая схема
Нулевая гипотеза - интенсивности отказов (параметры потока отказов) равны или Н0: w1 = w2. Альтернативная гипотеза - w1, меньше w2 или Н1: w1 < w2.
Соответственно в 7.2 описаны точные и в общем случае применимые методы проверки этих гипотез. Для расчетов допускается использовать биномиальное распределение (при расчетах на компьютере) или таблицы F-распределения, приведенные в приложении А.
Самый общий случай, когда время испытаний для двух наборов наблюдений одинаково (Т1* = Т2*), рассмотрен в 7.3. Результат может быть получен графическими методами без вычислений или в количественном виде посредством очень простых и точных формул.
Метод применим в случаях Т1* = Т2* и Т1* ≠ Т2*.
7.2.1 Использование биномиального распределения
a) Определяют r1 так, чтобы
![]()
b) Вычисляют r:
r = r1 + r2.
c) Вычисляют р:
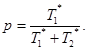
d) Вычисляют уровень значимости α, используя биномиальное распределение:
где ![]()
e) Принимают решение в соответствии с критериями, приведенными в таблице 1 для заданного уровня значимости α0.
Если уровень значимости α0 не задан, то для относительно малых значений α, например α = 0,05 (5 %), принимают решение - w1 < w2.
Чем меньше α, тем меньше вероятность того, что это заключение может быть неверным.
Примечание - Уровень значимости можно также определить, используя таблицы или кривые для биномиального распределения с применением интерполяции.
Таблица 1 - Критерии принятия решения на основе биномиального распределения
|
Результат сравнения α и α0 |
Решение |
|
α < α0 |
w1 < w2 |
|
α > α0 |
w1 = w2 |
7.2.2 Использование F-распределения
Эквивалентный формуле (1) альтернативный метод вычисления α состоит в следующем:
a) Вычисляют f:
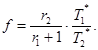
b) Находят fc по таблицам F-распределения. Для (1 - α0) = 0,90 используют таблицу А.1 (приложение А), а для (1 - α0) = 0,95 - таблицу А.2 (приложение А).
![]()
где v1 = 2(r1 + 1);
v2 = 2r2.
c) Принимают решение в соответствии с критериями, приведенными в таблице 2.
Таблица 2 - Критерий принятия решения на основе F-распределения
|
Результат сравнения f и fc |
Решение |
|
f > fc |
w1 < w2 |
|
f < f c |
w1 = w2 |
Обычно рекомендуются уровни значимости α0 = 5 % или 10 %, соответствующие квантилю уровня (1 - α0) (0,95 или 0,90) F-распределения.
7.3 Методы, применяемые в случае T1* = T2*
7.3.1 Графический метод r ≤ 250
a) Определяют r1 так, чтобы r1 < r2;
b) Вычисляют r = r1 + r2;
c) Определяют положение точки (r = r1) на рисунке А.1 (если 4 ≤ r ≤ 130) или на рисунке А.2 (если 110 ≤ r ≤ 250) приложения А и отмечают положение точки (выше или ниже) относительно кривой для установленного уровня значимости α0;
d) Принимают решение в соответствии с критериями, приведенными в таблице 3.
Таблица 3 - Критерии решения на основе рисунков А.1, А.2 (приложение А)
|
Взаимное расположение точки (r, r1) и кривой α0 |
Решение |
|
Точка (r, r1) ниже кривой α0 |
w1 < w2 |
|
Точка (r, r1) выше кривой α 0 |
W1 = w2 |
Примечание - Фактический уровень значимости может быть приближенно оценен с применением интерполяции между кривыми.
7.3.2 Приближенный метод, применяемый в случае r > 8
a) Определяют r1 так, чтобы r1 < r2;
b) Вычисляют u:
где ![]()
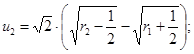
c) Принимают решение в соответствии с критерием, приведенным в таблице 4, используя uс из таблицы 5.
Таблица 4 - Критерий решения на основе нормированного нормального распределения
|
Решение |
|
|
u > uс с уровнем значимости α0 |
w1 < w2 |
|
u < uс с уровнем значимости α0 |
w1 = w2 |
Таблица 5 - Уровни значимости (односторонние) при использовании нормированного нормального распределения
|
0,1 |
0,25 |
0,5 |
1,0 |
2,5 |
5,0 |
10,0 |
|
|
Критическое значение uс |
3,09 |
2,81 |
2,58 |
2,33 |
1,96 |
1,65 |
1,28 |
Примечание - Фактический уровень значимости может быть определен с помощью нормированного нормального распределения.
Приложение А
(справочное)
Таблицы F-распределения.
Таблицы и графики для сравнения двух интенсивностей отказов
или параметров потоков отказов в случае T1*
= T2*
Примечание - Данное приложение относится к 7.2.2 и 7.3.
Таблица А.1 - Квантили F-распределения уровня 0,90 [F0,90 (v1, v2)]
|
v2 |
v1 |
||||||||||
|
2 |
4 |
6 |
8 |
10 |
20 |
30 |
40 |
60 |
120 |
00 |
|
|
2 |
9,00 |
9,24 |
9,33 |
9,37 |
9,39 |
9,44 |
9,46 |
9,47 |
9,47 |
9,48 |
9,49 |
|
4 |
4,32 |
4,11 |
4,01 |
3,95 |
3,92 |
3,84 |
3,82 |
3,80 |
3,79 |
3,78 |
3,76 |
|
6 |
3,46 |
3,18 |
3,05 |
2,98 |
2,94 |
2,84 |
2,80 |
2,78 |
2,76 |
2,74 |
2,72 |
|
8 |
3,11 |
2,81 |
2,67 |
2,59 |
2,54 |
2,42 |
2,38 |
2,36 |
2,34 |
2,32 |
2,29 |
|
10 |
2,92 |
2,61 |
2,46 |
2,38 |
2,32 |
2,20 |
2,16 |
2,13 |
2,11 |
2,08 |
2,06 |
|
12 |
2,81 |
2,48 |
2,33 |
2,24 |
2,19 |
2,06 |
2,01 |
1,99 |
1,96 |
1,93 |
1,90 |
|
14 |
2,73 |
2,39 |
2,24 |
2,15 |
2,10 |
1,96 |
1,91 |
1,89 |
1,86 |
1,83 |
1,80 |
|
16 |
2,67 |
2,33 |
2,18 |
2,09 |
2,03 |
1,89 |
1,84 |
1,81 |
1,78 |
1,75 |
1,72 |
|
18 |
2,62 |
2,29 |
2,13 |
2,04 |
1,98 |
1,84 |
1,78 |
1,75 |
1,72 |
1,69 |
1,66 |
|
20 |
2,59 |
2,25 |
2,09 |
2,00 |
1,94 |
1,79 |
1,74 |
1,71 |
1,68 |
1,64 |
1,61 |
|
30 |
2,49 |
2,14 |
1,98 |
1,88 |
1,82 |
1,67 |
1,61 |
1,57 |
1,54 |
1,50 |
1,46 |
|
40 |
2,44 |
2,09 |
1,93 |
1,83 |
1,76 |
1,61 |
1,54 |
1,51 |
1,47 |
1,42 |
1,38 |
|
60 |
2,39 |
2,04 |
1,87 |
1,77 |
1,71 |
1,54 |
1,48 |
1,44 |
1,40 |
1,35 |
1,29 |
|
120 |
2,35 |
1,99 |
1,82 |
1,72 |
1,65 |
1,48 |
1,41 |
1,37 |
1,32 |
1,26 |
1,19 |
|
∞ |
2,30 |
1,94 |
1,77 |
1,67 |
1,60 |
1,42 |
1,34 |
1,30 |
1,24 |
1,17 |
1,00 |
Таблица А.2 - Квантили F-распределения уровня 0,95[F0,95(v1, v2)]
|
v2 |
v1 |
||||||||||
|
2 |
4 |
6 |
8 |
10 |
20 |
30 |
40 |
60 |
120 |
00 |
|
|
2 |
19,00 |
19,25 |
19,33 |
19,37 |
19,40 |
19,45 |
19,46 |
19,47 |
19,48 |
19,49 |
19,50 |
|
4 |
6,94 |
6,39 |
6,16 |
6,04 |
5,96 |
5,80 |
5,75 |
5,72 |
5,69 |
5,66 |
5,63 |
|
6 |
5,14 |
4,53 |
4,28 |
4,15 |
4,06 |
3,87 |
3,81 |
3,77 |
3,74 |
3,70 |
3,67 |
|
8 |
4,46 |
3,84 |
3,58 |
3,44 |
3,35 |
3,15 |
3,08 |
3,04 |
3,01 |
2,97 |
2,93 |
|
10 |
4,10 |
3,48 |
3,22 |
3,07 |
2,98 |
2,77 |
2,70 |
2,66 |
2,62 |
2,58 |
2,54 |
|
12 |
3,89 |
3,26 |
3,00 |
2,85 |
2,75 |
2,54 |
2,47 |
2,43 |
2,38 |
2,34 |
2,30 |
|
14 |
3,74 |
3,11 |
2,85 |
2,70 |
2,60 |
2,39 |
2,31 |
2,27 |
2,22 |
2,18 |
2,13 |
|
16 |
3,63 |
3,01 |
2,74 |
2,59 |
2,49 |
2,28 |
2,19 |
2,15 |
2,11 |
2,06 |
2,01 |
|
18 |
3,55 |
2,93 |
2,66 |
2,51 |
2,41 |
2,19 |
2,11 |
2,06 |
2,02 |
1,97 |
1,92 |
|
20 |
3,49 |
2,87 |
2,60 |
2,45 |
2,35 |
2,12 |
2,04 |
1,99 |
1,95 |
1,90 |
1,84 |
|
30 |
3,32 |
2,69 |
2,42 |
2,27 |
2,16 |
1,93 |
1,84 |
1,79 |
1,74 |
1,68 |
1,62 |
|
40 |
3,23 |
2,61 |
2,34 |
2,18 |
2,08 |
1,84 |
1,74 |
1,69 |
1,64 |
1,58 |
1,51 |
|
60 |
3,15 |
2,53 |
2,25 |
2,10 |
1,99 |
1,75 |
1,65 |
1,59 |
1,53 |
1,47 |
1,39 |
|
120 |
3,07 |
2,45 |
2,18 |
2,02 |
1,91 |
1,66 |
1,55 |
1,49 |
1,43 |
1,35 |
1,25 |
|
∞ |
3,00 |
2,37 |
2,10 |
1,94 |
1,83 |
1,57 |
1,46 |
1,39 |
1,32 |
1,22 |
1,00 |
Линейная интерполяция для промежуточных значений является достаточно точной.
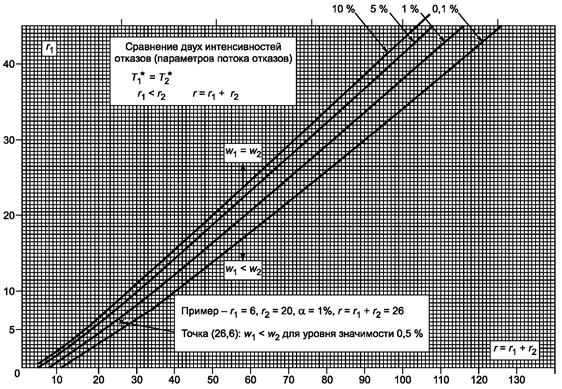
Рисунок А.1 -
Сравнение двух интенсивностей отказов (параметров потока отказов)
для T1* = T2*. Уровни
значимости 10 %; 5 %; 1 %; 0,1 %; 4 ≤ r ≤ 130
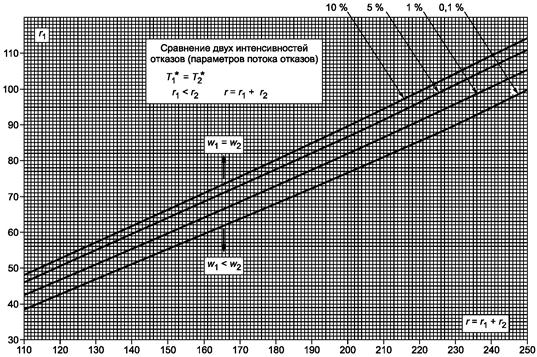
Рисунок А.2 -
Сравнение двух интенсивностей отказов (параметров потока отказов)
для T1* = T2*. Уровни
значимости 10 %; 5 %; 1 %; 0,1 %; 110 ≤ r ≤ 250
Приложение В
(справочное)
Математическое обоснование
B.1 Гипотезы и расчетные формулы для общего случая (T1* = T2* или T1* ≠ T2*)
Гипотезы Н0: w1 = w2 и H1: w1 < w2. Критерий является односторонним биномиальным критерием в соответствии с формулой (1) 7.2.1 (см. [1]).
В случае двустороннего критерия Н0: w1 = w2 и H1: w1 ≠ w2. В этом случае вместо (1) необходимо использовать следующую формулу
![]() (1a)
(1a)
B.2 Гипотезы и расчетные формулы для T1* = Т2*
Гипотезы Н0: w1 = w2 и H1: w1 < w2. Уравнения (2) в 7.3.2 основаны на [1] и [2]. Для r > 10 приближение является достаточно точным.
Кривые на рисунках А.1 и А.2 (приложение А) представляют собой решение уравнения (2) относительно
r1 = r1(u, r).
Решение имеет вид:
![]()
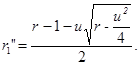
На рисунках А.1 и А.2 изображен график функции r1(r):
![]()
для фиксированных значений u = uс, соответствующих фиксированным значениям α0 (см. 7.3.2 таблицу 5).
Для двустороннего критерия значения α0 являются удвоенными значениями по отношению к значениям, приведенным в таблице 5, и изменяются от 0,2 % до 20,0 %.
Приложение С
(справочное)
Примеры
С.1 Пример 1. Применение 7.2
Наблюдения. Для восстанавливаемого оборудования типа А суммарное время испытаний T1* = 1 год, количество отказов r1 = 1.
Для восстанавливаемого оборудования типа В суммарное время испытаний T2* = 2 года, количество отказов r2 = 9.
Вопрос. Значительно ли ниже параметр потока отказов для оборудования типа А, чем для оборудования типа В при уровне значимости 5 % (α0 = 0,05).
Ответ. Вычисления:
![]()
r = r1 + r2 = 1 + 9 = 10,
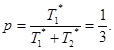
Применение уравнения (1) дает
α = 0,104= 10,4 %.
Поскольку α = 0,104, α0 = 0,05 и α > α0 в соответствии с таблицей 1 можно заключить, что
w1 = w2 или z1 = z2.
Таким образом, оборудование типа А не имеет более низкого параметра потока отказов, чем оборудование типа В при уровне значимости 5 %.
Тот же самый результат может быть получен с использованием квантиля F-распределения уровня (1 - 0,05) = 0,95 [см. таблицу А.2 (приложение А)].
Вычисление f:
![]()
Вычисление fc:
fc = F1-α(v1, v2) = 2,93,
где v1 = 2(1 + 1) = 4;
v2 = 2 · 9= 18;
1 - α = 0,95.
В соответствии с таблицей 2 гипотеза w1 = w2 или z1 = z2 не может быть отклонена, поскольку f = 2,25, fc = 2,93 и f < fc при уровне значимости 5 %.
С.2 Пример 2. Применение 7.3.1 (см. пример, представленный на рисунке А.1)
С.3 Пример 3. Применение 7.3.2
Наблюдения. T1* = T2*; r1 = 1; r2 = 7.
Вопрос. Существует ли значимое различие между w1 и w2 при уровне значимости α0 = 5 %.
Вычисления:
![]()
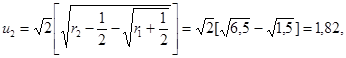
![]()
Ответ. При уровне значимости 5 % в соответствии с таблицей 5uc = 1,65. Поскольку u > uс, в соответствии с таблицей 4 можно сделать вывод, что
w1 < w2.
Фактический уровень значимости α:
α = Ф(uα) = 3,44 % (точное значение α = 3,52 %).
С.4 Пример 4. Применение 7.3.2 (см. пример, представленный на рисунке А.1)
Ниже приведены вычисления, соответствующие графическому примеру.
Наблюдения. Компоненты непрерывного производства (1000 шт.) подвергнуты испытаниям при высокой температуре в течение 1000 ч. Из них 20 отказавших компонентов были немедленно заменены.
1000 компонентов, изготовленных при более высоком качестве производства, подвергнуты таким же испытаниям при высокой температуре в течение 1000 ч, шесть отказавших компонентов были немедленно заменены.
Таким образом, T1* = T2* = 106 часов; r1 = 6; r2 = 20.
Вопрос. Обеспечивает ли новое производство значительно более высокую безотказность компонентов при уровне значимости α = 1 %.
Вычисления: u1 = 2,55; u2 = 2,64; u = 2,59 > uc = 2,33.
Ответ. При уровне значимости 1 % в соответствии с таблицей 4 можно сделать вывод, что
w1 < w2 или λ1 < λ2.
Это означает, что новое производство существенно повышает безотказность компонентов. Фактический уровень значимости α:
α = Ф(иα) = 0,47 % (точное значение α = 0,468 %).
Приложение D
(справочное)
Сведения о соответствии национального стандарта
Российской Федерации
ссылочному международному стандарту
Таблица D.1
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта Российской Федерации |
|
МЭК 60050-191:1990 |
* |
|
* Соответствующий национальный стандарт отсутствует. Поскольку языки МЭК 60050-191 включают русский, рекомендуется непосредственное применение МЭК 60050-191. |
|
Библиография
|
Сох, D.R. and Lewis, P.A., The statistical analysis of series of events, pp. 223 - 228. Methuen, London, 1966 |
|
|
Hald, A., Statistical theory with engineering applications, pp. 672 - 726. John Wiley and Sons, Inc., New York, London, Sydney, 1952 |
Ключевые слова: интенсивность отказов, параметр потока отказов, суммарная наработка, проверка гипотез, уровень значимости