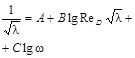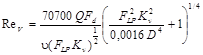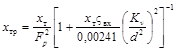Государственный
ордена Трудового Красного
Знамени проектный институт
ПРОЕКТМОНТАЖАВТОМАТИКА
РУКОВОДЯЩИЙ МАТЕРИАЛ
Расчет и
применение регулирующих органОВ
в системах автоматизации технологических
процессов
РМ4-163-77
Срок введения 1 апреля 1978 г.
|
Главный инженер |
Антонов |
|
Начальник отдела |
Хакимов |
|
Гл. специалист |
Абросимов |
1977
Настоящий руководящий материал составлен взамен следующих руководящих материалов:
Р-73002, Расчет смесительных клапанов (1959 г.);
Р-73003, Расчет регулирующих дроссельных органов (1961 г.);
РМ4-91-71, Расчет регулирующих органов, за которыми происходит парообразование (1971 г.);
РМ4-119-71, Расчет регулирующих органов (1971 г.).
Данный материал является руководством по расчету и применению дроссельных регулирующих органов в системах автоматизации технологических процессов. При пользовании этим материалом следует иметь в виду, что он не заменяет собой каталогов, правил и других нормативных и информационных документов, содержащих указания по выбору и применению трубопроводной арматуры. Поэтому при выполнении расчетов и выборе регулирующих органов в каждом конкретном случае необходимо выяснять (по каталогам и другим действующим информационным материалам) возможность применения принимаемого в процессе расчета регулирующего дроссельного органа.
СОДЕРЖАНИЕ
1. НАЗНАЧЕНИЕ
Настоящий руководящий материал составлен в развитие ГОСТ 16443-70 «Устройства исполнительные. Методы расчета пропускной способности, выбора условного прохода и пропускной характеристики» и является руководством по расчету и применению регулирующих дроссельных органов в системах автоматизации технологических процессов. При его разработке была использована часть проекта Публикации 534 «Регулирующие дроссельные органы для управления технологическими процессами» Международной электротехнической комиссии, а такие другие материалы (см. перечень использованных документов и литературы).
Выбор нужного регулирующего органа производится в процессе выполнения расчета, т.е. из ряда серийно изготавливаемых регулирующих органов выбирается конкретный типоразмер, имеющий необходимый диаметр условного (присоединительного) прохода, нужную пропускную способность и пропускную характеристику. Пригодность принимаемого регулирующего органа по другим характеристикам (рабочему давлению и температуре, материалу деталей, соприкасающихся с протекающей средой и т.п.) должна выявляться по каталогам и другим действующим информационным материалам и правилам.
При выполнении расчетов может возникнуть необходимость в переходе от одних единиц измерения к другим. Соотношения между различными единицами измерения даны в приложении 1.
В приложении 2 приведены формулы пересчета объема и плотности газов.
Данный материал не регламентирует объем и формы исполнения расчетов, так как они определяются особенностями проектируемых систем автоматизации и достоверностью и полнотой исходных данных, имеющихся в распоряжения проектировщиков.
В руководящем материале приняты следующие основные условные обозначения;
|
Условное обозначение |
|
|
Внутренний диаметр трубопровода |
D |
|
Присоединительный (условный) диаметр регулирующего органа |
d |
|
Площадь прохода D |
|
|
Площадь прохода d |
|
|
Коэффициент формы проточной части регулирующего органа |
Fd |
|
Поправочный коэффициент |
FF |
|
Коэффициент восстановления давления жидкости |
FL |
|
Коэффициент восстановления давления и влияния входного патрубка |
FLP |
|
Поправка на влияние переходных патрубков |
FP |
|
Поправка на влияние вязкости |
FR |
|
Поправка на показатель адиабаты |
Fæ |
|
Ускорение свободного падения |
g |
|
Коэффициент начала кавитации |
Kc |
|
Пропускная способность регулирующего органа |
Kv |
|
Длина трубопровода |
L |
|
Относительный ход регулирующего органа |
l |
|
Отношение условной пропускной способности регулирующего органа к пропускной способности трубопровода |
n |
|
Абсолютное давление (общее обозначение) |
P |
|
Абсолютное давление в начале гидравлической цепи |
Po |
|
Абсолютное давление в конце гидравлической цепи |
PK |
|
Абсолютное давление перед регулирующим органом (перед входным переходным патрубком) |
P1 |
|
Абсолютное давление после регулирующего органа (после входного переходного патрубка) |
P2 |
|
Абсолютное давление в наименьшем сечении |
Pнс |
|
Абсолютное давление насыщенных паров |
Pнп |
|
Перепад давления (общее обозначение) |
ΔP |
|
Потери давления на местных сопротивлениях |
ΔPм |
|
Потери давления на прямых участках трубопровода |
ΔPп |
|
Располагаемый напор гидравлической цепи |
ΔPc |
|
Общее обозначение расхода |
Q |
|
Число Рейнольдса потока |
ReD |
|
Число Рейнольдса регулирующего органа |
ReV |
|
Температура среды перед регулирующим органом |
t |
|
Скорость |
V |
|
Относительный перепад давления |
x = ΔP/Р1 |
|
Относительный критический перепад давления воздуха |
xт |
|
Относительный критический перепад давления с учетом входного патрубка |
хтр |
|
Коэффициент расхода |
α |
|
Поправка на изменение плотности |
ε |
|
Коэффициент местного сопротивления (общее обозначение) |
ς |
|
Коэффициент сопротивления входного переходного патрубка без учета потерь от изменения скорости |
ς1 |
|
Коэффициент потерь напора во входном патрубке |
ςв1 |
|
Коэффициент сопротивления выходного патрубка без учета потерь от изменения скорости |
ς2 |
|
Коэффициент потерь напора в выходном патрубке от изменения скорости |
ςв2 |
|
Коэффициент трения |
λ |
|
Показатель адиабаты |
æ |
|
Динамическая вязкость |
μ |
|
Кинематическая вязкость |
υ |
|
Плотность |
ρ |
2. ЗАДАЧА РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА
В системах автоматизации технологических процессов, как правило, применяются серийно изготавливаемые регулирующие органы. Выбор конкретного типоразмера регулирующего органа производится по каталогам и другим материалам в процессе выполнения расчета, выявляющего пригодность выбираемого органа в тех или иных конкретных условиях эксплуатации. При этом должны учитываться как свойства и рабочие параметры протекавшей через регулирующий орган среды, так и другие условия и требования, являющиеся следствием общих требований, предъявляемых к системе автоматизации и к объекту управления в целом.
В отличие от трубопроводной арматуры серийные регулирующие органы характеризуются следующими дополнительными показателями:
- условной пропускной способностью Kvy;
- пропускной характеристикой, которая может быть линейной или равнопроцентной.
Таким образом в результате расчета производится выбор конкретного типоразмера регулирующего органа, характеризуемого величиной Kvy, пропускной характеристикой и другими показателями (условным давлением, условным диаметром и т.д.), предусмотренными стандартами на регулирующие органы. Так как условная пропускная способность однозначно определяет расход через регулирующий орган только в квадратичной области турбулентного режима движения жидкости через регулирующий орган, установленный в трубопроводе, имеющим внутренний диаметр, равный условному проходу регулирующего органа, то в случаях работы регулирующих органов в других условиях возникает необходимость в дополнительных характеристиках. К числу таких характеристик относятся:
FL - коэффициент восстановления давления жидкости за регулирующим органом;
FP - поправка на влияние переходных патрубков, через которые регулирующий орган встраивается в трубопровод;
xт - относительный критический перепад давления воздуха для регулирующего органа.
Применение характеристик FL, FP и xт повышает достоверность определения необходимой пропускной способности регулирующего органа Kv в тех случаях, когда он работает не в квадратичной области турбулентного движения среды и установлен через переходные конические патрубки.
В тех случаях, когда в каталогах и других информационных материалах не указаны величины этих характеристик, их ориентировочные значения можно принимать по приложениям данного материала.
Заметим, что повышение достоверности расчета вследствие учета поправок FL, FP и др. будет иметь место только в том случае, когда исходные данные для расчета (расход, перепад давления и др.) достаточно точно определяют фактические условия работы регулирующего органа.
3. ВИДЫ И ОБЛАСТЬ ПРИМЕНЕНИЯ РЕГУЛИРУЮЩИХ ОРГАНОВ
Большое разнообразие используемых в народном хозяйстве жидкостей, паров и газов с различными свойствами и параметрами обусловило множество видов, конструкций и исполнений регулирующих органов, применяемых в промышленности. Всякий регулирующий дроссельный орган состоит из двух основных частей: неподвижного корпуса и перемещаемого относительно корпуса затвора. Пропускная способность регулирующего органа зависит от положения затвора в корпусе.
До роду движения затвора различает регулирующие органы с вращательным движением затвора (заслоночные регулирующие органы, краны и т.д.) и поступательным (односедельные и двухседельные регулирующие органы). По виду потребляемой исполнительными механизмами регулирующих органов энергии различают регулирующие органы с гидравлическими, пневматическими и электрическими исполнительными механизмами.
Выбор регулирующих органов должен производиться исходя из свойств технологических сред, их температуры и давления, в соответствия с указаниями заводов-изготовителей по каталогам и другим информационным материалам. В табл. 1 указаны основные достоинства и недостатки некоторых имеющих широкое применение регулирующих органов.
|
Достоинства |
Недостатки |
|
|
Проходной односедельный |
Коэффициент восстановления давления FL близок к единице, что обеспечивает большой критический перепад давления. Может быть изготовлен плотнозапорным |
Необходимы исполнительные механизмы с большим усилием или крутящим моментом. Мало пригодны для управления потоками суспензий. |
|
Проходной двухседельный |
Гидродинамические силы, воздействующие на плунжер, частично уравновешены, что позволяет использовать исполнительные механизмы малой мощности |
Не может быть выполнен плотнозапорным |
|
Заслоночный (поворотная заслонка) |
Низкая стоимость, большая пропускная способность при малых перепадах давления, простая конструкция |
Малая величина коэффициента восстановления FL обуславливает небольшой критический перепад давления. Склонен к кавитация |
|
Угловой |
Корпус полностью опорожняем при сливе жидкости из трубопровода |
Высокая стоимость |
|
Мембранный (с мембранным затвором) |
Может быть плотнозапорным, конструктивно прост, большая пропускная способность |
Рабочие давление и температура сравнительно невелики |
4. РЕГУЛИРУЮЩИЙ ОРГАН КАК ЭЛЕМЕНТ ГИДРАВЛИЧЕСКОЙ ЦЕПИ ОБЪЕКТА АВТОМАТИЗАЦИИ
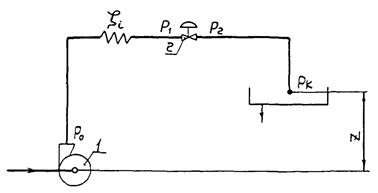
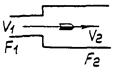
Всякий регулирующий дроссельный орган является изменяемым управляющим гидравлическим сопротивлением гидравлической цепи объекта автоматизации, определяющим расход через эту линию (рис. 1).
Располагаемый напор ΔPс или суммарные потери давления в гидравлической цепи (включая перепад давления на регулируемом органе) определяют по следующей формуле
где Po - давление в начале гидравлической цепи, кгс/м2;
PK - давление в конце гидравлической цепи, кгс/м2;
z - разность уровней начала и конца гидравлической цепи, м;
ρ - плотность протекающей среды, кг/м3.
Величину zρ принимают со знаком плюс, если источник напора расположен на верхней отметке и минус, если источник напора расположен на нижней отметке. Для газа и пара, как правило, величина zρ пренебрежимо мала.
Потери давления на трубопроводе и технологических аппаратах ΔPт (без учета перепада давления на регулирующем органе) равны
где ΔPп - потери давления на прямых участках трубопровода, кгс/м2;
ΔPм - потери давления на местных сопротивлениях и технологических аппаратах гидравлической цепи, кгс/м2.
Рис. 1. Гидравлическая цепь с регулирующим органом:
1 - насос; 2 - регулирующий орган
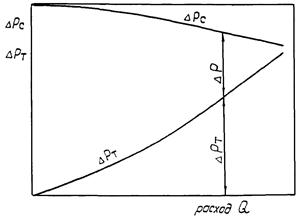
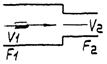
Рис. 2. Гидравлические характеристики:
ΔPс = f1(Q) - источника напора; ΔPт = f2(Q) - гидравлической цепи (без регулирующего органа)
Перепад давления (рис. 2) на регулирующем органе ΔP будет равен
где ΔPс - определяется по формуле (1), а ΔPт - по формуле (2).
Уравнение (3) и график на рис. 2 показывают, что перепад давления на регулирующем органе для заданной величины расхода Q является для каждой гидравлической цепи вполне определенной величиной, зависящей как от источника напора, так и от гидравлической цепи и не может приниматься произвольно.
Зависимость располагаемого напора ΔPс от расхода через гидравлическую цепь Q, ΔPс = f(Q), является характеристикой источника напора, (например, насоса).
Величины ΔPп и ΔPм определяются по следующим уравнениям
![]() (4)
(4)
![]() (5)
(5)
где λ - коэффициент трения для прямых участков трубопровода (величина безразмерная);
L - длина трубопровода диаметром D, м;
D - внутренний диаметр трубопровода длиной L, м;
V - скорость среды в рассматриваемом участке трубопровода, м/с;
g = 9,81 м/с2, ускорение свободного падения;
ρ - плотность протекающей среды кг/м3;
ς - коэффициент местного сопротивления.
Знак Σ обозначает, что величины ΔPп и ΔPм получаются суммированием по участкам трубопровода, имеющим разные L, D, λ и ς.
В зависимости от того, куда будут отнесены потери от трения по длине сопротивления величину ΔPп + ΔPм можно рассматривать двояко:
а) в первом случае под ΔPт можно понимать падение давления только на соединительных трубопроводах, L - суммарная длина трубопровода, а ΔPм включают в себя потери давления от трения на длине местных сопротивлений;
б) во втором случае под ΔPт следует понимать падение давления как на соединяющих трубопроводах, так и на длине местных сопротивлений. Во втором случае L - сумма длин трубопровода диаметром D и длин местных сопротивлений по их средней линии, а ΔPм - потери давления от изменения направления и скорости потока, не включающие в себя потери от трения на длине местных сопротивлений.
В данном руководящем материале принят второй способ вычисления потерь давления и в приведенных в приложениях 3 и 4 коэффициентах сопротивления ς потери от трения на длине местных сопротивлений не учтены.
При определении потерь давления необходимо различать два режима движения потока: ламинарный и турбулентный. Критерием, определяющим режим движения потока в трубопроводе, служит неравенство
ReD >< ReK,
где ReD - число Рейнольдса потока, отнесенное к внутреннему диаметру трубопровода D;
ReK - критическое значение числа Рейнольдса, отнесенное к D.
Для круглых труб
![]()
где V - средняя скорость, м/с;
D - внутренний диаметр трубопровода, м;
υ - кинематическая вязкость среды, м2/с.
Общепринятая величина ReK = 2320.
Таким образом, если ReD > 2320, поток в трубе будет турбулентным, если ReD < 2320 - поток в трубе можно принимать ламинарным.
Формулы для определения числа Рейнольдса потока в круглых трубах приведены в приложении 5.
Для некруглых труб уравнение (6) примет вид
![]() (7)
(7)
где DЭ - эквивалентный диаметр трубопровода, м. Остальные величины и размерности те же, что и в формуле (6).
![]() (8)
(8)
где R - гидравлический радиус, м;
F - площадь живого сечения потока, м2;
П - смоченный периметр, м.
Уравнение (4) справедливо как для ламинарного, так и для турбулентного потоков. Коэффициент трения λ зависит от режима движения потока.
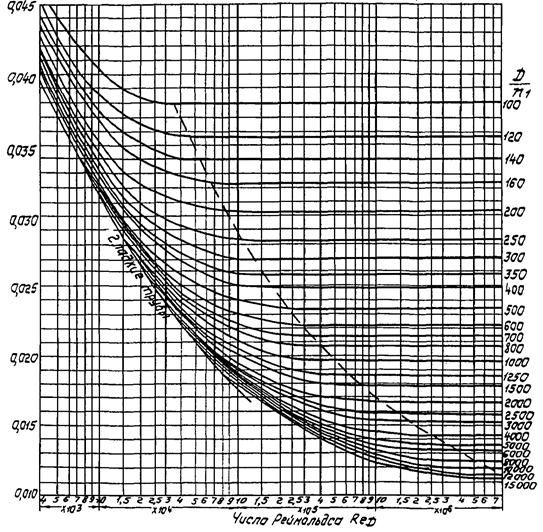
Определение λ см. приложение 6. Для некруглых трубопроводов в уравнения приложения 5 необходимо подставлять ReD и DЭ, определяемые по формулам (7) и (8).
Коэффициент трения λ трубопровода некруглого сечения при ламинарном режиме движения (ReDЭ < 2320) равен
![]()
где K1 - коэффициент формы.
Для прямоугольного сечения с отношением сторон b/a величина K1 равна
|
b/a |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,7 |
1,0 |
|
K1 |
1,5 |
1,32 |
1,2 |
1,1 |
1,03 |
0,97 |
0,91 |
0,80 |
Коэффициент местного сопротивления ς в уравнении (5) при турбулентном режиме движения принято считать постоянной, не зависящей от ReD величиной. При ламинарном движении ς ≠ const.
Общая потеря давления на местных сопротивлениях равна арифметической сумме потерь на каждом сопротивлении при условии, что эти сопротивления разделены прямыми участками длиной не менее 5D. Непосредственное последовательное соединение местных сопротивлений, как правило, повышает потери давления.
Коэффициенты сопротивления технологических аппаратов (или зависимости потерь давления на них от расхода) следует получать у проектировщиков технологической части объекта автоматизации. Для всех местных сопротивлений необходимо указывать сечение (или скорость), к которому отнесена величина ς.
Значения ς для некоторых видов местных сопротивлений приведены в приложении 3. Кроме этого, при определении падения давления на местных сопротивлениях ΔPм рекомендуется использовать книгу: Идельчик И.Е. Справочник по гидравлическим сопротивлениям, М., 1960.
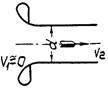
5. ЗАВИСИМОСТЬ РАСХОДА ЧЕРЕЗ ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ОТ ПЕРЕПАДА ДАВЛЕНИЯ НА НЕМ
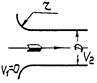
Зависимость между скоростью жидкости в суженном сечении перехода f гидравлического сопротивления Vf и перепадом давления на нем ΔP при турбулентном движении жидкости выражается следующим уравнением
![]() (9)
(9)
где α - коэффициент расхода гидравлического сопротивления, отнесенный к скорости Vf;
g - ускорение свободного падения;
ρ - плотность жидкости.
Зависимость между скоростью жидкости перед гидравлическим сопротивлением Vf и перепадом давления на нем ΔP также может быть записана в следующем виде
![]() (10)
(10)
где ς - коэффициент сопротивления, отнесенный к средней скорости перед гидравлическим сопротивлением Vf.
Напишем уравнение неразрывности струи для площади поперечного сечения входного прохода сопротивления F и площади прохода в его наименьшем сечении f
VF · F = Vf · f.
Согласно этому выражению скорость потока перед гидравлическим сопротивлением будет равна
![]()
Подставив найденное значение VF в уравнение (10), получим
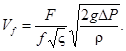 (11)
(11)
Из сравнения уравнений (9) и (11) следует, что
![]() (12)
(12)
или
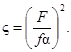 (13)
(13)
Заметим, что выражения (12) и (13) справедливы только в том случае, когда ς отнесено к F, а α к f. Площади F и f должны быть выражены в одинаковых единицах измерения.
Умножив уравнения (9) и (11) на f, получим выражения для объемного расхода жидкости через гидравлическое сопротивление
![]() (14)
(14)
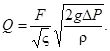 (15)
(15)
Уравнения (14) и (15) справедливы для следующих единиц измерения:
Q - м3/с; ΔР - кгс/м2;
f и F - м2; ρ - кг/м3.
g - м/с2;
Уравнение (14) можно записать следующим образом
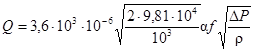
или
![]() (16)
(16)
где Q - м3/ч;
f - мм2;
ΔP - кгс/см2;
ρ - г/см3.
Коэффициент расхода гидравлического сопротивления α есть величина безразмерная.
Аналогично, уравнение (15) примет вид
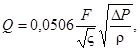 (17)
(17)
где F также в мм2, ς - величина безразмерная. Размерности остальных величин такие же, как в уравнении (16).
Для круглых сечений f и F, равных
![]() и
и ![]()
получим
![]() (18)
(18)
и
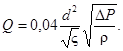 (19)
(19)
Уравнениям (18) и (19) можно придать следующий вид
![]() (20)
(20)
где
или
![]() (22)
(22)
Напоминаем, что в выражениях (21) и (22) α отнесен к сечению, имеющему диаметр d1, а ς к сечению с диаметром d. Уравнения (21) и (22) справедливы для d1 и d в мм.
Величина Kv называется пропускной способностью. Из уравнения (20) следует, что Kv численно равна количеству жидкости в м3/ч, имеющей плотность 1 г/см3 и протекающей через гидравлическое сопротивление (регулирующий орган) при перепаде давления на нем 1 кгс/см2. Уравнение (20) является основным уравнением расхода через регулирующий дроссельный орган. Оно справедливо, когда ΔP выражено в кгс/см2, ρ в г/см3, а Q в м3/ч.
6. ВЛИЯНИЕ ПЕРЕХОДНЫХ ПАТРУБКОВ НА РАСХОД ЧЕРЕЗ РЕГУЛИРУЮЩИЙ ОРГАН В РАБОЧИХ УСЛОВИЯХ
Так как регулирующие дроссельные органы выбираются не по условному проходу трубопровода D, а по пропускной способности регулирующего органа, то, как правило, условный (присоединительный) диаметр регулирующего органа d < D. Это делает необходимым встраивать регулирующий орган в трубопровод через переходные патрубки. Эти патрубки также являются гидравлическими сопротивлениями, соединенными последовательно с гидравлическим сопротивлением регулирующего органа.
Перепад давления, измеренный непосредственно у регулирующего органа ΔPv, равен
ΔPv = ΔP - ΔPp, (23)
где ΔP = P1 - P2 - общий перепад давления на регулирующем органе и патрубках;
ΔPp - суммарный перепад давления на переходных патрубках (без регулирующего органа);
P1 - давление на входе входного переходного патрубка;
P2 - давление на выходе выходного переходного патрубка.
Согласно уравнению (20) перепады давления ΔPv, ΔPp и ΔP равны
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
где Kp - пропускная способность переходных патрубков;
Ko - общая пропускная способность регулирующего органа с переходными патрубками;
ΔPp - суммарный перепад давления на переходных патрубках (без регулирующего органа);
P1 - давление на входе входного переходного патрубка;
P2 - давление на выходе выходного переходного патрубка.
Поскольку перепад давления ΔPv < ΔP, то при установке регулирующих органов через переходные патрубки возникает необходимость увеличить Kv (по сравнению с Kv в случае установки клапана в трубопроводе D = d).
По этой причине формула (20) примет вид
![]() (27)
(27)
где Fp - поправка на влияние переходных патрубков.
Из уравнения (27) с учетом уравнения (20), найдем
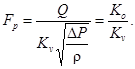 (28)
(28)
Откуда
![]() (29)
(29)
Подставив уравнения (24), (25) и (26) в (23), получим
![]() (30)
(30)
Суммарная пропускная способность переходных патрубков согласно (22) равна
![]() (31)
(31)
где ς - суммарный коэффициент сопротивления патрубков.
Из уравнения (31) получим
![]() (32)
(32)
Подставив уравнение (32) в (30), получим
![]() (33)
(33)
Умножив полученное выражение на Kv2, с учетом уравнения (29) получим:
![]()
Откуда
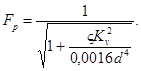 (34)
(34)
В уравнении (34) суммарный коэффициент сопротивления патрубков равен
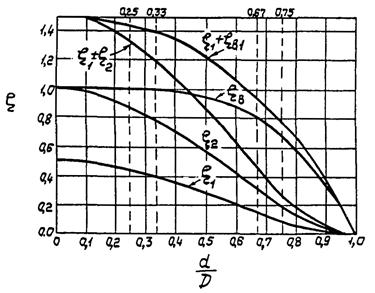
где ς1 - коэффициент сопротивления входного патрубка без потерь от изменения скорости;
ςв1 - коэффициент потерь напора во входном патрубке от изменения скорости;
ς2 - коэффициент сопротивления выходного патрубка без потерь от изменения скорости;
ςв2 - коэффициент потери напора в выходном патрубке от изменения скорости.
Если внутренние диаметры технологического трубопровода до регулирующего органа и после него равны, т.е. D1 = D2 = D, то ςв1 = ςв2 и эти коэффициенты в уравнении (35) взаимно уничтожаются. Если же D1 ≠ D2, то эти коэффициенты вычисляются по формуле
![]() (36)
(36)
где d - диаметр условного прохода (присоединительный) регулирующего органа;
D - внутренний диаметр технологического трубопровода.
В уравнение (36) подставляется внутренний диаметр трубопровода перед регулирующим органом D1 при вычислении ςв1 и внутренний диаметр трубопровода после регулирующего органа D2 при вычислении ςв2.
При отсутствии надежных экспериментальных данных для конкретных конструкций переходных патрубков необходимые значения коэффициентов ς1 и ς2 можно вычислить по следующим формулам:
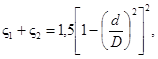 (37)
(37)
если оба патрубка одинаковы;
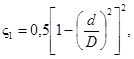 (38)
(38)
если применяется только входной патрубок;
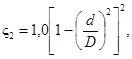 (39)
(39)
если применяется только выходной патрубок.
Коэффициенты трения и потерь на переходных патрубках могут приниматься по графику приложения 7, рассчитанного по формулам (36) - (38).
Влияние переходных патрубков на расход через регулирующий орган при критическом движении жидкости через регулирующий орган рассматривается в разделе 9.
7. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ ЧЕРЕЗ РЕГУЛИРУЮЩИЙ ОРГАН
Полученное в разделе 6 уравнение (27), определяющее взаимосвязь между пропускной способностью регулирующего органа (в общем случае - гидравлического сопротивления)
![]()
справедливо только при однофазном турбулентном движении жидкости, когда имеет место прямая пропорциональность между квадратом средней скорости и перепадом давления. Поэтому при выполнении расчета и выборе регулирующего органа необходимо выявлять режим движения среды через регулирующий орган и, если он не является однофазным турбулентным, то это должно быть учтено введением соответствующего поправочного коэффициента.
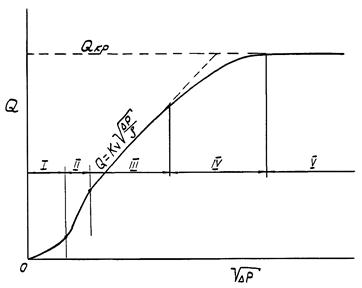
На рис. 3 показан график зависимости объемного расхода жидкости через регулирующий орган от квадратного корня из перепада давления. График разбит на области, в каждой из которых справедлива своя закономерность между расходом и перепадом давления. Уравнение (27) справедливо в области квадратичного сопротивления III (см. рис. 3).
Рис. 3. Расход жидкости через регулирующий орган Q в зависимости от квадратного корня из
перепада давления ![]() (для положения «открыто»):
(для положения «открыто»):
I - область ламинарного движения; II - переходная область; III - турбулентное однофазное движение в квадратичной области; IV - область кавитации; V - критическое течение двухфазной смеси
8. ТУРБУЛЕНТНОЕ ОДНОФАЗНОЕ ДВИЖЕНИЕ В КВАДРАТИЧНОЙ ОБЛАСТИ
Согласно вышеизложенному, при турбулентном однофазном движении в квадратичной области справедливо уравнение (27)
![]()
где Fp - поправка на влияние переходных патрубков (величина безразмерная);
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69;
ΔP - перепад давленая на регулирующем органе, измеренный до и после переходных патрубков, кгс/см2;
ρ - плотность жидкости в рабочих условиях, г/см3.
Если для применяемых конструкций переходных патрубков величина поправки Fp неизвестна, то ее приближенное значение может быть найдено по формуле (34) раздела 6. Если переходные патрубки до и после клапана одинаковы, то есть диаметр трубопровода до и после регулирующего органа один и тот же, то величина Fp может быть найдена по приложению 8.
Так как до недавнего времени поправка на влияние переходных патрубков не применялась, то целесообразно проиллюстрировать влияние переходных патрубков на расход через различные виды регулирующих органов примерами. В табл. 2 приведены ориентировочные сведения для некоторых видов регулирующих органов при двух отношениях диаметра присоединения регулирующего органа d к диаметру трубопровода D.
|
Вид регулирующего органа |
Уменьшение расхода в % |
|
|
при d/D = 0,67 |
при d/D = 0,5 |
|
|
Проходной полнопроходной регулирующий клапан |
3 |
5 |
|
Поворотная заслонка, открытая на 60° |
8 |
10 |
|
Поворотная заслонка, открытая на 90° |
18 |
32 |
Из таблицы следует, что влияние переходных патрубков проявляется в наибольшей мере для регулирующих органов, имеющих малое гидравлическое сопротивление в положении «открыто».
9. КАВИТАЦИЯ И ВСКИПАНИЕ
При увеличении перепада давления на регулирующем органе ΔP (уменьшении давления после органа P2) расход Q возрастает и, как показано на рис. 3, поток попадает в область кавитации IV. Условие начала кавитации имеет вид
где ΔPнк - перепад давления на регулирующем органе, соответствующий началу кавитации;
Kc - коэффициент начала кавитации (приложение 9);
P1 - абсолютное давление перед регулирующим органом;
Pнп - давление насыщенных паров при рабочей температуре.
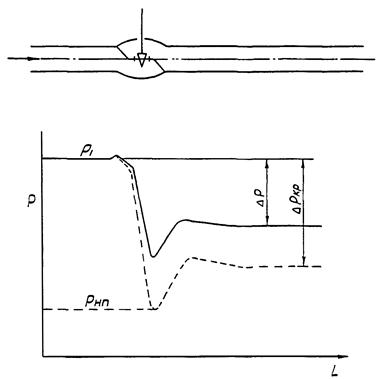
Дальнейшее увеличение ΔP приводит поток в область критического течения двухфазной (парожидкостной) смеси (область V на рис. 3). На рис. 4 сплошной линией показана эпюра распределения давления по длине регулирующего органа и прилегающих к нему участков труб для однофазного потока в квадратичной области III (см. рис. 3). Там же штриховой линией показана эпюра распределения давления в том случае, когда давление в наименьшем сечении струи Pнс стало равно давлению насыщенных паров Pнп жидкости, протекающей через регулирующий орган. При Pнс = Pнп в потоке образуются пузырьки пара, которые, при дальнейшем движении, попадают в область более высокого давления и схлопываются.
Образование и схлопывание пузырьков пара называется кавитацией. Схлопывание пузырьков пара сопровождается шумом, который усиливается по мере уменьшения давления P2 за регулирующим органом. При этом пузырьки становятся крупнее, а шум возрастает, что обычно сопровождается вибрациями и эрозионным разрушением внутренней поверхности регулирующего органа. При дальнейшем уменьшении давления P2 до величины менее Pнп пузырьки не схлопываются и образуют с жидкостью двухфазную смесь, то есть происходит вскипание жидкости при прохождении ее через регулирующий орган. При этом расход достигает предельного значения, которое остается неизменным при дальнейшем уменьшении P2 (увеличении ΔP). Этот наибольший (предельный) расход определяется перепадом
Рис. 4 Распределение давления Р по длине регулирующего органа и трубопровода L
Отсюда следует необходимость уметь определять давление жидкости в наименьшем сечении струи в регулирующем органе Pнс, что позволит выявить режим движения жидкости и определить критическое значение перепада давления ΔPкр, ограничивающее расход жидкости через регулирующий орган.
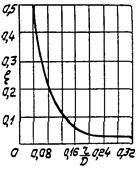
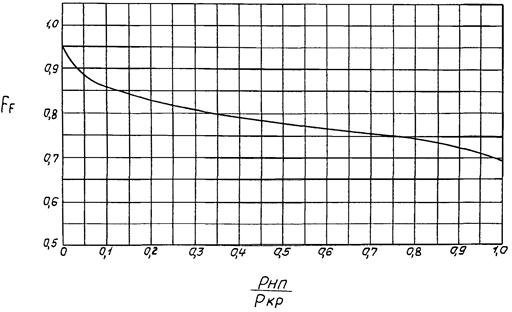
Отношение абсолютного давления в наименьшем сечении струи Pнс при наибольшем (предельном) расходе к давлению насыщенного пара Pнп обозначим
![]()
Откуда
где FF - поправочный коэффициент, определяемый по графику приложения 10, в зависимости от отношения давления насыщенного пара Pнп протекающей через регулирующий орган жидкости к ее критическому давлению Pкр.
Подставив в уравнение (41) величину давления в наименьшем сечении струи за регулирующим органом из уравнения (42), получим уравнение критического перепада на регулирующем органе для жидкости
Перепад ΔP'кр измерен между входом регулирующего органа и местом наименьшего сечения струи.
Уравнение прямого наклонного участка графика на рис. 3 в случае установки регулирующего органа без переходных патрубков в трубопроводе D = d имеет вид
![]() (20)
(20)
Уравнение горизонтального участка на рис. 3 имеет вид
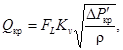 (44)
(44)
где FL - коэффициент восстановления давления жидкости, учитывающий геометрию проточной части регулирующего органа;
Qкр - критический (предельный) расход.
Записав уравнение (20) для Qкр и приравняв его выражению (44) получим
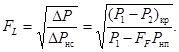 (45)
(45)
Коэффициент восстановления давления FL является характеристикой регулирующего органа и должен, наряду с Kv, определяться экспериментально при разработке регулирующего органа. Ориентировочные значения FL приведены в приложении 9.
Из уравнения (45) получим уравнение критического перепада давления ΔPкр, измеренного между входным и выходным патрубками регулирующего органа
ΔPкр = (P1 - P2)кр = FL2(P1 - FFPнп). (46)
Уравнение (46) позволяет выявить наличие или отсутствие критического режима движения жидкости через регулирующий орган.
При
ΔP = P1 - P2 < Kc(P1 - Pнп) (47)
расход через регулирующий орган при турбулентном квадратичном режиме движения жидкости будет определяться уравнением
![]() (27)
(27)
Если же
ΔP = P1 - P2 > FL2(P1 - FFPнп), (48)
то будет иметь место критическое течение двухфазной смеси и расход будет определяться уравнением
![]() (49)
(49)
Уравнение (49) справедливо при установке регулирующего органа в трубопроводе D = d, т.е. без конических переходных патрубков, когда Fp = 1. Если же регулирующий орган установлен через входной переходной патрубок, то необходимо учесть снижение давления перед регулирующим органом за счет влияния этого патрубка. В этом случае уравнение примет вид
![]() (50)
(50)
где FLP - коэффициент восстановления давления и влияния входного переходного патрубка.
Коэффициент восстановления давления и влияния входного переходного патрубка FLP является функцией коэффициента восстановления давления FL, отношения условного (присоединительного) диаметра регулирующего органа d к внутреннему диаметру трубопровода D и конструкции входного переходного патрубка.
Найдем выражение для определения FLP. Для регулирующего органа, установленного через входной переходный патрубок (так как расход при критическом режиме определяется перепадом давления ΔPнс, измеренным между входом регулирующего органа и местом наименьшего сечения струи, то выходной патрубок в данном случае на расход не влияет), FL = FLP, и уравнение (45) примет вид
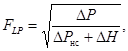 (51)
(51)
где ΔP - перепад давления на регулирующем органе и переходных патрубках;
ΔH - разность давлений скоростных напоров на входном патрубке.
Уравнение (19)
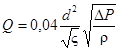 (19)
(19)
при ς = 1 позволяет определить скоростной напор или соответствующее ему давление в круглом сечении диаметром d.
Применив уравнение (19) к сечениям, имеющим диаметры d и D, найдем разность давлений на входном патрубке
![]() (52)
(52)
ρQ2 = Kv2ΔP, (53)
Записав пропускную способность Kv в виде
![]() (55)
(55)
подставим выражения (54) и (55) в (53) и найдем
![]() (56)
(56)
Подставив выражение (56) в (52), получим
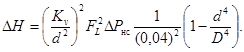 (57)
(57)
Возведем уравнение (51) в квадрат и подставим в него значения ΔP и ΔH из уравнений (54) и (57)
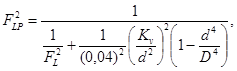
откуда
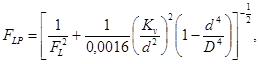 (58)
(58)
где
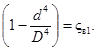 (36)
(36)
Для того, чтобы учесть также потери от трения во входном коническом переходе, вместо ςв1 подставим ςвх,
и получим искомое выражение для FLP
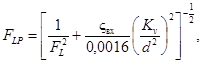 (60)
(60)
где FLP - коэффициент восстановления давления и влияния входного патрубка (величина безразмерная);
FL - коэффициент восстановления давления (величина безразмерная);
ςвх = ς1 + ςв1 (величина безразмерная);
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69;
d - присоединительный (условный) диаметр регулирующего органа, мм.
10. ПЕРЕХОДНЫЙ РЕЖИМ И ЛАМИНАРНЫЙ ПОТОК
10.1. Общие положения
Турбулентное движение жидкости через регулирующий орган, как правило, имеет место для сравнительно маловязких жидкостей, таких как вода, спирт и т.д. При протекании через регулирующий орган более вязких или медленно текущих жидкостей зависимость между расходом и перепадом давления будет отличаться от (27), так как в этом случае регулирующий орган будет работать либо в переходной области, либо в области ламинарного движения.
На рис. 3 показано, что области турбулентного движения жидкости предшествует переходная область II и область ламинарного движения I, в которой расход прямо пропорционален перепаду давления.
Для правильного выбора пропускной способности регулирующего органа необходим способ соотнесения конкретных условий, в которых будет работать регулирующий орган, с параметрами, характеризующими этот орган (Kv, d, FL и т.п.), найденными экспериментально в процессе его разработки. Одним из способов соотнесения рабочих условий с параметрами регулирующего органа состоит в использовании числа Рейнольдса
![]() (61)
(61)
где Q - объемный расход, м3/ч;
υ - кинематическая вязкость, сСт;
dЭ - характерный размер, мм.
В качестве характерного размера dЭ целесообразно принять размер, который однозначно характеризовал бы протекающий через регулирующий орган поток. В регулирующем органе максимальная скорость имеет место в наименьшем сечении струи за дроссельным отверстием регулирующего органа. Эту скорость и соответствующий ей эквивалентный диаметр наименьшего сечения струи (полагая ее сечение круглым) можно использовать для построения формулы для определения числа Рейнольдса регулирующего органа ReV.
Искомый эквивалентный диаметр наименьшего сечения струи можно выразить через пропускную способность Kv и коэффициент восстановления давления FL. Для каждого конкретного регулирующего органа удобно иметь одну и ту же величину этого диаметра, независимо от режима движения жидкости через регулирующий орган. Поэтому этот диаметр целесообразно применять для некоторых фиксированных условий: турбулентное движение воды при комнатной температуре. Допустимость такого подхода можно обосновать следующим образом. Известно, что для расходомерной диафрагмы отношение диаметра наименьшего сечения струи после нее к диаметру отверстия диафрагмы практически постоянно, если поток турбулентный. Это дает возможность по известному диаметру наименьшего сечения струи определить диаметр отверстия. Диаметр отверстия не зависит от режима движения жидкости. Распространив такой подход на регулирующий орган, придем к тому, что эквивалентный диаметр наименьшего сечения струи за дроссельным отверстием регулирующего органа также может рассматриваться как приблизительно неизменная величина, которой соответствует некоторый эквивалентный (воображаемый) диаметр дроссельного отверстия регулирующего органа, не зависящий от условий течения жидкости.
Так как отношение эквивалентных диаметров струи и отверстия практически неизменно, то в качестве характерного размера можно принять любую из этих величин. Для упрощения расчетов в качестве характерного размера удобно принять эквивалентный диаметр наименьшего сечения струи dЭ.
Площадь сечения струи Fc равна объемному расходу Q, разделенному на среднюю скорость струи Vc в ее наименьшем сечении
![]() (62)
(62)
где Q - мм3/с;
Vc - мм/с;
dЭ - мм.
Расход через регулирующий орган равен
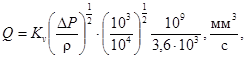 (63)
(63)
где ΔP - кгс/см2;
ρ - г/см3.
Скорость струи в ее наименьшем сечении можно выразить через напор, измеренный между входом переходного патрубка и местом наименьшего сечения струи, следующим образом
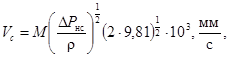 (64)
(64)
где ΔРнс - кгс/м2;
ρ - кг/м3;
M - поправка, учитывающая изменение скорости перед регулирующим органом из-за наличия переходного конического патрубка перед регулирующим органом
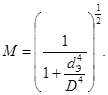 (65)
(65)
Подставив уравнения (63) и (64) в (62), получим
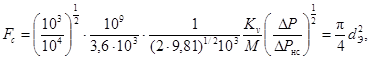 (66)
(66)
где 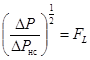 - коэффициент восстановления давления для регулирующего органа, установленного без
конических переходных патрубков, т.е. при d
= D.
- коэффициент восстановления давления для регулирующего органа, установленного без
конических переходных патрубков, т.е. при d
= D.
Подставив уравнение (65) в (66), найдем
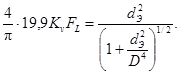 (67)
(67)
Возведя уравнение (67) в квадрат и сделав необходимые преобразования, получим
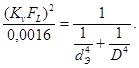
Откуда
![]()
или
что дает
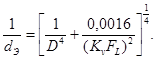 (68)
(68)
Подставив уравнение (68) в (61), получим
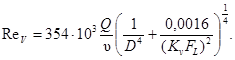 (69)
(69)
Умножив и разделив уравнение (69) на 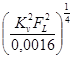 найдем
найдем
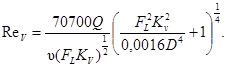 (70)
(70)
Для регулирующего органа, установленного в конических переходных патрубках FL = FLP.
Число Рейнольдса является безразмерным критерием, справедливым при соблюдении механического подобия проточных частей регулирующих органов. Поскольку проточные части регулирующих органов отличаются большим разнообразием, то это учитывается коэффициентом формы проточной части регулирующего органа Fd. Для односедельных проходных регулирующих органов Fd = 1,0; для двухседельных проходных регулирующих органов и поворотных заслонок Fd = 0,71.
С учетом вышеизложенного, формула для определения числа Рейнольдса регулирующего органа примет вид
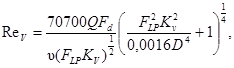 (71)
(71)
где Q - объемный расход, м3/ч;
υ - кинематическая вязкость, сСт;
D - внутренний диаметр трубопровода, мм,
FLP - коэффициент восстановления давления и влияния входного переходного патрубка (см. уравнение (60));
Fd - коэффициент формы проточной части регулирующего органа (см. выше);
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69.
При работе регулирующего органа в переходной области уравнение расхода (27) принимает вид
![]() (72)
(72)
где FR - поправка на влияние вязкости (величина безразмерная);
FP - поправка на влияние переходных патрубков (величина безразмерная);
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69;
ΔP - перепад давления, кгс/см2;
ρ - плотность жидкости перед регулирующим органом, г/см3.
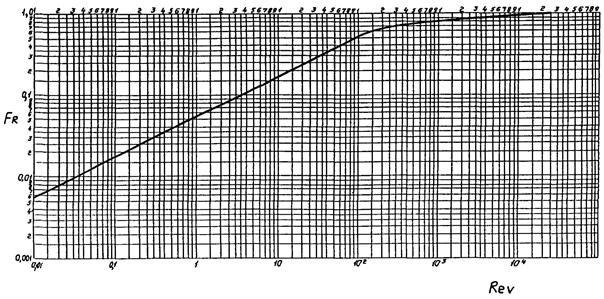
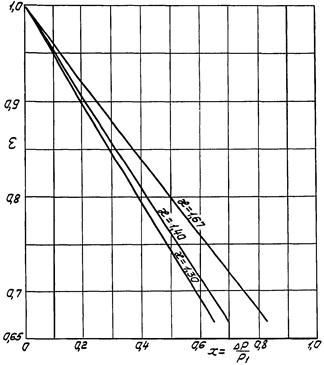
На графике приложения 11 показана зависимость поправки на влияние вязкости FR от числа Рейнольдса регулирующего органа ReV.
Из графика следует, что при ReV > 33000 поток турбулентен (FR = 1). При числе Рейнольдса ReV < 100 поток ламинарен и расход через регулирующий орган прямо пропорционален перепаду давления. При 100 < ReV < 33000 имеет место промежуточный режим течения жидкости.
10.2. Уравнение расхода для ламинарного движения через регулирующий орган
Уравнение (72) справедливо как для промежуточной, так и для ламинарной областей. Для того, чтобы использовать это уравнение необходимо число Рейнольдса ReV, определяемое по уравнению (71). Громоздкость уравнения (71) и необходимость предварительно задаваться пропускной способностью Kv и условным (присоединительным) диаметром d для вычисления ReV, для того чтобы определить поправку FR по графику приложения 11, затрудняет использование уравнения (72) для расчета регулирующих органов. Поэтому целесообразно преобразовать уравнение (72) таким образом, чтобы отпала необходимость пользоваться уравнением (71) для определения ReV. Это оказалась возможным для области ламинарного движения жидкости. В этой области зависимость поправки на влияние вязкости FR от числа Рейнольдса ReV выражается следующей эмпирической формулой
или
FR2 = 28,1 · 10-4ReV. (74)
Возведя уравнение (72) в квадрат и подставив в него (74), получим
![]() (75)
(75)
Подставив уравнение (71) в (75) и выполнив необходимые преобразования, получим
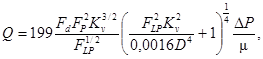 (76)
(76)
где μ = ρυ - динамическая вязкость, сП.
Найденное выражение удобно записать следующим образом
![]() (77)
(77)
где
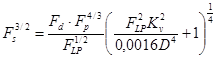
или
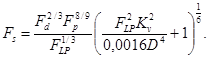 (78)
(78)
Так как Fp8/9 ≈ Fp, то выражению (78) удобно придать следующий вид
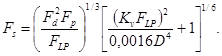 (79)
(79)
Поскольку FLP < 1, то FLP < FLP8/9, что целесообразно учесть, увеличив коэффициент в выражении (77). Приняв среднее значение FLP ≈ 0,65 (с некоторым запасом), найдем необходимым увеличить коэффициент в уравнении (77) на 8 %. При этом уравнение (77) примет вид
![]() (80)
(80)
где ΔP - перепад давления, кгс/см2;
μ - динамическая вязкость, сП;
Fs - по формуле (79);
Kv - пропускная способность по ГОСТ 14691-69.
10.3. Расчет регулирующих органов с учетом влияния вязкости
Полученное в разделе 6 уравнение (27)
![]()
позволяет определять потребную пропускную способность регулирующего органа Kv в квадратичной области турбулентного движения жидкости через регулирующий орган, когда FR = 1,0.
Уравнение (80)
![]()
дает возможность определить пропускную способность Kv в области ламинарного движения жидкости. Однако без ответа остались два вопроса:
- как выявить режим движения жидкости без вычисления числа Рейнольдса ReV по уравнению (71);
- как определить величину поправки на влияние вязкости FR, если окажется, что имеет место переходный режим движения жидкости через регулирующий орган.
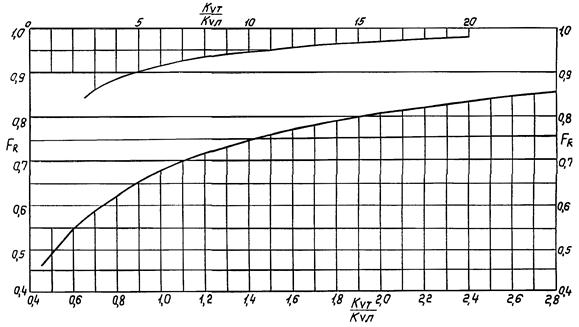
Так как нам уже известны уравнения (27) и (80), дающие возможность определить необходимые значения в квадратичной области турбулентного движения и в области ламинарного движения, то имеется возможность выявить область работы регулирующего органа в конкретном случае методом исключения следующим образом:
- определить пропускную способность регулирующего органа Kvт, полагая поток турбулентным;
- определить пропускную способность регулирующего органа Kvл, полагая поток ламинарным;
- найти отношение ![]() (или
(или ![]() ) и по найденному отношению
определять режим движения жидкости через регулирующий орган.
) и по найденному отношению
определять режим движения жидкости через регулирующий орган.
Если найденное отношение больше 20, то имеет место движение в квадратичной области турбулентного движения или других областях, для которых FR = 1,0.
Если же найденное отношение меньше 0,46, то поток ламинарный. Переходный режим движения жидкости через регулирующий орган имеет место в том случае, когда
![]() (81)
(81)
В случае переходного режима движения жидкости через регулирующий орган поправка FR определяется по графику приложения 12. Сводка уравнений для расчета регулирующих органов, управляющих потоками жидкости, приведена в приложении 13.
11. РЕЖИМЫ ДВИЖЕНИЯ ГАЗА ИЛИ ПАРА ЧЕРЕЗ РЕГУЛИРУЮЩИЙ ОРГАН
В отличие от жидкостей, газы и пары при движении их через регулирующие органы, расширяются и, следовательно, их плотность уменьшается. Это уменьшение плотности влияет на величину расхода и поэтому оно должно учитываться при определении потребной пропускной способности регулирующего органа Kv.
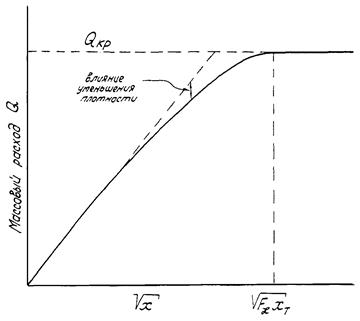
На рис. 5 сплошной линией показан график массового расхода газа или пара через регулирующий орган в зависимости от квадратного корня из относительного перепада давления, то есть от
![]() (82)
(82)
где P1 - абсолютное давление перед регулирующим органом;
Р2 - абсолютное давление после регулирующего органа.
При увеличении перепада давления на регулирующем органе ΔP (уменьшении давления Р2 при P1 = const) расход Q возрастает до предельного (критического) значения Qкр, когда скорость в наименьшем сечении струи за дроссельным отверстием регулирующего органа становится равной скорости звука. При дальнейшем увеличении ΔP расход остается неизменным и равным Qкр и может быть увеличен только увеличением давления перед органом P1, что эквивалентно увеличению плотности.
На рис. 5 штриховой линией показана теоретическая зависимость между расходом и перепадом давления для несжимаемой жидкости. Разность ординат между штриховой и сплошной линиями представляет влияние уменьшения плотности газа или пара при прохождении его через регулирующий орган. Из рисунка видно, что квадратичная зависимость между расходом и перепадом давленая для газов и паров при их турбулентном движении через орган соблюдается лишь приблизительно. Для газов и паров, как и для жидкостей, возможно движение в переходном и ламинарном режимах (на рис. 5 это не показано).
Рис. 5. Массовый расход газа или пара через регулирующий орган Q в зависимости от
квадратного корня из относительного перепада давления ![]()
Уравнение расхода газа или пара через регулирующий орган при турбулентном режиме движения имеет вид
![]() (83)
(83)
где ε - поправка на изменение плотности газа или пара (величина безразмерная);
Fp - поправка на влияние переходных патрубков (величина безразмерная);
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69;
![]() - относительный
перепад давления;
- относительный
перепад давления;
P1 - абсолютное давление перед регулирующим органом;
ΔP - перепад давления, кгс/см2;
ρ - плотность газа или пара перед регулирующим органом (в рабочих условиях), кг/м3.
Так как плотность газов и паров принято измерять в кг/м3, то это учтено коэффициентом 31,6.
Поправка на изменение плотности ε определяется по уравнению
![]() (84)
(84)
где x - относительный перепад давления на регулирующем органе;
xт - критический относительный перепад давления для выбираемого регулирующего органа;
Fæ - поправка на показатель адиабаты газа или пара.
Величина xт является константой каждого конкретного типа регулирующего органа. В тех случаях, когда эта величина в каталогах не указана, она может приниматься по приложению 14.
Поправка на показатель адиабаты газа или пара определяется по формуле
![]() (85)
(85)
где æ - показатель адиабаты газа для пара (см. приложение 15).
Если регулирующий орган устанавливается в трубопровод через конические переходные патрубки, то в уравнение (84) вместо xт следует подставлять xтр. Величина xтр определяется следующим уравнением
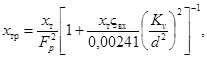 (86)
(86)
где Fp - поправка на влияние переходных патрубков;
ςвх - коэффициент сопротивления входного патрубка, определяемый по формуле (59) или по графику приложения 7;
Kv - пропускная способность регулирующего органа по ГОСТ 14691-69;
d - условный (присоединительный) диаметр регулирующего органа, мм.
Как следует из рис. 5 уравнение (83) определяет расход через регулирующий орган только при условии
![]() (87)
(87)
так как при
имеет место критическое движение и расход через регулирующий орган при P1 = Const не зависит от ΔP. Поэтому во всех случаях, когда имеет место условие (88) вместо x в уравнение (83) следует подставлять x = Fæxт или, если регулирующий орган установлен через конические патрубки, x = Fæxтр.
Ламинарный переходный режимы движения газа через регулирующие органы встречаются сравнительно редко (при малых абсолютных давлениях и высоких температурах газов). Расчет регулирующих органов в таких случаях можно выполнять по методике, изложенной в разделе 10 (с учетом поправки на расширение ε).
Уравнение расхода газа или пара для ламинарного режима движения получим из уравнения (80)
![]() (89)
(89)
где ε - поправка на расширение.
Остальные обозначения см. уравнение (80). Сводка уравнений для расчета регулирующих органов, управляющих потоками газа или пара, приведена в приложении 16.
Для управления потоками газа низкого давления применяются нестандартизированные заслоночные органы (поворотные заслонки). Пропускные способности некоторых видов нестандартизированных заслоночных органов могут быть определены по приложению 17.
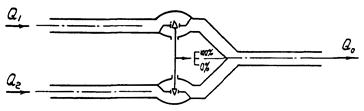
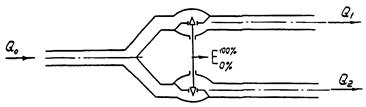
12. ТРЕХХОДОВЫЕ РЕГУЛИРУЮЩИЕ ОРГАНЫ
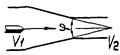
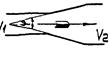
Трехходовые регулирующие органы предназначены для управления смешением (смесительные органы) или распределением (распределительные органы) потоков жидкостей. Оба вида трехходовых регулирующих органов схематично можно представить в виде двух проходных регулирующих органов, соединенных так, как показано на рис. 6 и 7 и управляемых таким образом, что сумма проходов при любом положении затвора остается приблизительно неизменной.
Трехходовые регулирующие органы обычно изготавливаются с линейной пропускной характеристикой каждого канала (прохода).
В соответствии с рис. 6 и 7 расчет трехходового регулирующего органа можно рассматривать как расчет двух взаимосвязанных проходных регулирующих органов. Перепады давления на каждом канале определяются по формуле (3) раздела 4. Необходимые пропускные способности каждого канала в открытом положении определяются в зависимости от режима движения жидкости, по формулам разделов 8 или 10. Если пропускная способность одного из каналов оказывается чрезмерно большой для найденного перепада давления на рассматриваемом канале, то перепад давления на этом канале можно уменьшить установкой в трубопроводе гасящего дросселя или вентиля.
Рис. 6. Схема смесительного регулирующего трехходового органа
Рис. 7. Схема распределительного регулирующего трехходового органа
13. ПРОПУСКНЫЕ ХАРАКТЕРИСТИКИ РЕГУЛИРУЮЩИХ ОРГАНОВ
13.1. Общие положения
Характеристики регулирующих органов удобно разбивать на две категории: пропускные и рабочие расходные.
Пропускная характеристика регулирующего органа представляет собой зависимость между положением затвора S и соответствующим этому положению пропускной способностью Kv.
Рабочая расходная характеристика регулирующего органа представляет собой зависимость между положением затвора S и соответствующим этому положению расходом через регулирующий орган в рабочих условиях.
Наиболее широкое применение в промышленности имеют следующие пропускные характеристики: линейная и равнопроцентная. Кроме этих двух следует также рассмотреть характеристику клапана с тарельчатым затвором.
13.2. Линейная пропускная характеристика
Если между положением затвора S регулирующего органа и соответствующей этому перемещению пропускной способностью Kv имеет место прямая пропорциональность, то регулирующий орган имеет линейную пропускную характеристику
![]() (90)
(90)
где Kv100 - максимальная (при полном открытии) пропускная способность;
Kv0 - начальная (в момент открытия) пропускная способность.
13.3. Равнопроцентная пропускная характеристика
Этой характеристике свойственно то, что равным изменениям положения затвора соответствует одно и то же процентное изменение пропускной способности Kv для всех участков хода затвора. Теоретически регулирующие органы с равнопроцентной пропускной характеристикой не имеют положения «закрыто», но так как из практических соображений такое положение необходимо, то в положении, близком к закрытому характеристика преднамеренно отклоняется от теоретической. Уравнение равнопроцентной характеристики таково:
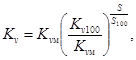 (91)
(91)
где Kvм - минимальная пропускная способность, при которой еще соблюдается теоретическая равнопроцентная характеристика;
Kv100 - максимальная пропускная способность (в положении «открыто»);
S100 - полный ход затвора;
S - ход затвора (текущее значение).
13.4. Пропускная характеристика регулирующего органа с тарельчатым затвором
Эта характеристика обеспечивает быстрое изменение Kv в начале хода затвора, считая от положения «закрыто». Такие регулирующие органы обычно применяются для управления периодическими или циклическими процессами, когда необходимо быстрое перемещение затвора из положения «открыто» в положение «закрыто» или обратно.
13.5. Выбор пропускной характеристика
Наиболее целесообразная пропускная характеристика в каждом конкретном случае определяется статическими и динамическими характеристиками объекта автоматизации. Поэтому выбор пропускной характеристики, как правило, должен производиться в процессе анализа динамики объекта автоматизации и расчета его системы управления. По этой причине без анализа динамики объекта правильно выбрать необходимую пропускную характеристику регулирующего органа удается только в простейших случаях, указанных в табл. 3.
|
Пропускная характеристика |
||
|
при ΔP/ΔPc ≥ 0,25 |
при 0,05 < ΔP/ΔPc < 0,25 |
|
|
Регулирование расхода газа или жидкости: |
||
|
расход измеряется сужающим устройством |
с тарельчатым затвором или линейная |
линейная |
|
расход измеряется ротаметром (или сужающим устройством и устройством извлечения квадратного корня) |
линейная |
равнопроцентная |
|
Регулирование давления в емкости |
линейная |
равнопроцентная |
|
Регулирование уровня в емкости |
линейная |
равнопроцентная |
В разделе 15 приводятся дополнительные указания по выбору пропускных характеристик регулирующих органов с помощью ЭВМ.
14. РЕКОМЕНДУЕМЫЙ ПОРЯДОК РАСЧЕТА
14.1. Исходные данные
Для расчета регулирующего органа необходимо нижеследующее:
- чертежи размещения трубопроводов, запорной арматуры и технологических аппаратов гидравлической цепи с размерами и координатами. Из этих чертежей берутся необходимые размеры (D, L и т.п.) для определения коэффициентов гидравлических сопротивлений;
- максимальный (технологический) расход через регулирующий орган;
- абсолютные давления в начале и конце гидравлической цепи, где устанавливается регулирующий орган;
- температура протекающей через орган среды;
- плотность протекающей через регулирующий орган среды при температуре и давлении перед органом;
- вязкость протекающей через регулирующий орган среды при температуре и давлении перед органом;
- характеристика источника напора
Po = f(Q).
14.2. Порядок расчета
Расчет регулирующего органа целесообразно выполнять в следующем порядке:
- определить недостающие данные, необходимые для выполнения расчета (плотность в рабочих условиях, перепад давления на регулирующем органе и т.п.);
- выявить режим движения среды через регулирующий орган (если это неизвестно) и вид регулирующего органа;
- определить необходимую пропускную способность регулирующего органа.
15. ОБ ИСПОЛЬЗОВАНИИ ЭВМ ДЛЯ РАСЧЕТА РЕГУЛИРУЮЩИХ ОРГАНОВ
Необходимость применения метода проб и ошибок, задаваясь пропускной способностью регулирующего органа и его диаметром условного прохода, а также громоздкость уравнений (60) и (71), существенно затрудняют выполнение расчетов вручную и вынуждают прибегать к обходным методам, как это было сделано в подразделе 10.2. Использование ЭВМ позволяет решать задачи расчета регулирующих органов непосредственно по сложным уравнениям, не прибегая к оценкам по таблицам и к обходным приемам.
Особо следует отметить целесообразность использования ЭВМ для выявления (выбора) необходимой пропускной характеристики регулирующего органа. Определив по уравнению (3) перепады давления на регулирующем органе для максимального, минимального и нескольких промежуточных значений расхода, можно определить пропускные способности, соответствующие этим расходам и найденным перепадам давления. Так как пропускная характеристика регулирующего органа представляет собой зависимость пропускной способности от перемещения затвора регулирующего органа, то по известной пропускной характеристике выбираемого регулирующего органа можно определить положение затвора, соответствующие вычисленным пропускным способностям и, следовательно, тем значениям расхода, для которых были вычислены пропускные способности.
Построив графики зависимостей расхода от хода затвора (расходные характеристики) для приведенных в каталогах или других информационных материалах пропускных характеристик, следует выбрать регулирующий орган с той пропускной характеристикой, которой соответствует наиболее приемлемая форма расходной характеристики (с точки зрения теории автоматического регулирования).
В тех случаях, когда в информационных материалах не приводятся графики пропускных характеристик, эти характеристики можно принимать по ГОСТ 16443-70. На черт. 1 и 2 приложения 3 этого стандарта приведены зависимости относительного расхода от относительного хода затвора. Пропускным характеристикам соответствуют кривые для n = 0, где n - отношение условной пропускной способности регулирующего органа к пропускной способности трубопровода.
В частном случае, когда располагаемый напор ΔPc = Const, выявление приемлемой расходной характеристики удобно производить по указанным чертежам ГОСТ 16443-70. Искомая расходная характеристика (в относительных единицах) в этом случае определяется кривой для фактического значения отношения условной пропускной способности регулирующего органа к пропускной способности трубопровода.
Следует подчеркнуть, что использование ЭВМ для расчета регулирующих органов, как правило, целесообразно лишь в случае наличия достаточно достоверных исходных данных.
16. ПРИМЕР РАСЧЕТА ПЕРЕПАДА ДАВЛЕНИЕ НА РЕГУЛИРУЮЩЕМ ОРГАНЕ
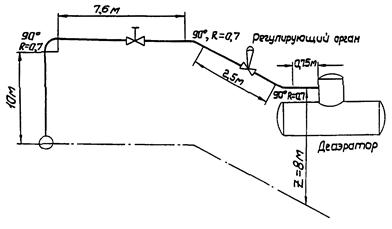
Данные для расчета
1. Наименование протекающей среды - водяной пар
2. Максимальный расход пара Q = 10000 кг/ч
3. Абсолютное давление пара в магистрали Po = 5 кгс/см2
4. Абсолютное давление в деаэраторе Pк = 1,2 кгс/см2
5. Температура пара t = 210 ºС
6. Удельный объем пара при Po и t v = 0,4433 м3/кг
7. Динамическая вязкость при Po и t μ = 1,68 · 10-6 (кгс · с)/м2
8. Внутренний диаметр паропровода D = 250 мм
Дополнительные данные см. рис. 8
Расчет
1. Определим число Рейнольдса потока при максимальном расходе
![]()
2. Найдем условие гидравлической гладкости паропровода (приложение 6)
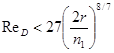
r = 125 мм; n1 = 0,1 мм
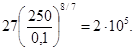
Условие гидравлической гладкости не соблюдено.
Рис. 8. Гидравлическая цепь системы регулирования давления в деаэраторе
3. Так как трубы в данном случае нельзя считать гидравлически гладкими, то определение λ произведем по графику приложения 6
D/n1 = 250/0,1 = 2500;
λ = 0,016.
4. Суммарная длина паропровода (рис. 8)
L = 10 + 7,6 + 2,5 + 0,75 + 3p/4 · 2 · 0,7 = 24,15 м.
5. Средняя скорость в паропроводе при максимальном расходе
Q = 10000 кг/ч равна
![]()
Q = 10000/3600 = 2,78 кг/с;
F = 0,785D2 = 0,785 · 0,252 = 0,0491 м2;
![]()
6. Определим потери давления на прямых участках паропровода при Q = 10000 кг/ч
![]()
ΔPп = 0,011 кгс/см2.
7. Определим потери давления в местных сопротивлениях трубопровода при Q = 10000 кг/ч
![]()
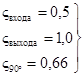 по приложению 3
по приложению 3
ςзадв = 0,08 по приложению 4
![]()
ΔPм = 0,026 кгс/см2.
8. Определим потери давления на трубах и местных сопротивлениях (без регулирующего органа)
ΔPт = ΔPп + ΔPм = 0,011 + 0,026 = 0,037 кгс/см2.
9. Определим располагаемый напор гидравлической цепи
ΔPс = Po - Pк = 5 - 1,2 = 3,8 кгс/см2.
10. Определим перепад давления на регулирующем органе при Q = 10000 кг/ч
ΔP = ΔPc - ΔPт = 3,8 - 0,037 = 3,76 кгс/см2.
Очевидно, что при малых расходах перепад давления на регулирующем органе практически будет равен располагаемому напору
ΔP ≈ ΔPc = 3,8 кгс/см2,
т.е. практически перепад давления на регулирующем органе будет постоянным. Регулирующий орган в данном случае следует принять с линейной пропускной характеристикой.
17. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ЖИДКОСТИ (ТУРБУЛЕНТНЫЙ РЕЖИМ)
Данные для расчета
1. Наименование протекающей среды рассол
2. Максимальный расход Q = 340 м3/ч
3. Плотность жидкости ρ = 1,2 г/см3
4. Давление перед регулирующим органом P1 = 5,3 кгс/см2
5. Давление после регулирующего органа P2 = 4,6 кгс/см2
6. Диаметр трубопровода D = 200 мм
Расчет
1. Определим произведение FpKv
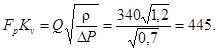
2. Зададимся двухседельным регулирующим органом, имеющим Kvy = 630 и Dy = d = 150 мм
![]()
![]()
По приложению 8 поправка на влияние переходных патрубков Fp = 0,94. Следовательно
![]()
Приняв коэффициент запаса 1,2, найдем
Kv = 1,2×474 = 568.
Примем регулирующий орган, имеющий Kvy = 630 мм и Dy = 150 мм.
18. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ЖИДКОСТИ (ЛАМИНАРНЫЙ РЕЖИМ)
Данные для расчета
1. Наименование протекающей среды продукт
2. Максимальный расход Q = 11 м3/ч
3. Плотность жидкости ρ = 0,9 г/см3
4. Давление перед регулирующим органом Р1 = 6 кгс/см2
5. Давление после регулирующего органа P2 = 4,6 кгс/см2
6. Динамическая вязкость μ = 20000 сП
7. Температура жидкости t = 20 °С
8. Диаметр трубопровода D = 150 мм
Расчет
1. Определим произведение FpKv, полагая поток турбулентным
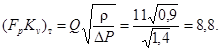
2. Определим произведение FpKv, полагая поток ламинарным
![]()
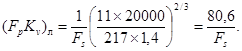
3. Определим отношение найденных величин
![]()
Из таблицы приложения 9 видно, что величина 0,11Fs для всех видов регулирующих органов менее 0,46, что указывает на ламинарное движение жидкости через регулирующий орган. Задавшись заслоночным регулирующим органом, имеющим при открытии 60° условную пропускную способность Kvg = 160 и Dy = d = 80 мм по таблице приложения 9 найдем
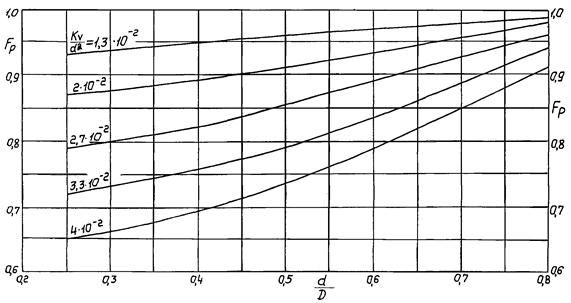
Fs = 0,92 и Kv/d2 = 2,3×10-2.
Следовательно
FpKv = 80,6/Fs = 80,6/0,92 = 87,6.
Фактическое значение Kv/d2 = 160/802 = 2,5×10-2, т.е. близко к табличному 2,3×10-2.
4. По приложению 8 найдем поправку на влияние переходных патрубков
d/D = 80/150 = 0,53;
Fp = 0,88.
То же значение Fp можно получить по формуле (34)
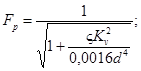
ς = ς1 + ς2
= 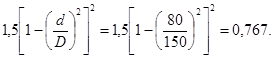
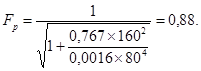
Величина ς = ς1 + ς2 также может быть определена по графику приложения 7.
5. Определим необходимую величину Kv
![]()
Приняв коэффициент запаса 1,2, найдем
Kv = 1,2×100 = 120.
Примем заслоночный регулирующий орган, имеющий при открытии 60º условную пропускную способность Kvy = 160 и Dy = 80 мм.
19. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ЖИДКОСТИ (ПЕРЕХОДНЫЙ РЕЖИМ)
Данные для расчета
1. Наименование протекающей среды продукт
2. Максимальный расход Q = 40 м3/ч
3. Плотность жидкости ρ = 1,10 г/см3
4. Давление перед регулирующим органом P1 = 5,2 кгс/см2
5. Давление после регулирующего органа P2 = 4,4 кгс/см2
6. Динамическая вязкость μ = 2000 сП
7. Диаметр трубопровода D = 100 мм
Расчет
1. Определим произведение FpKv, полагая поток турбулентным
![]()
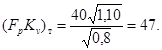
2. Определим произведение FpKv, полагая поток ламинарным
![]()
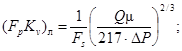
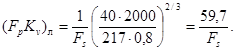
3. Определим отношение найденных величин
![]()
Задавшись заслоночным регулирующим органом открытым на 60º и имеющим условную пропускную способность Kvy = 100 и D = d = 65 мм, по приложению 9 найдем Fs = 0,92. Тогда
![]()
Так как условие
![]()
соблюдено, то имеет место переходный режим движения жидкости через регулирующий орган.
4. По приложению 12 определим поправку на влияние вязкости
FR = 0,60.
Определим произведение FpKv для переходного режима движения жидкости через регулирующий орган
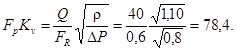
6. По приложению 8 найдем поправку на влияние переходных патрубков
d/D = 60/100 = 0,65;
Kv/d2 = 100/652 = 2,4×10-2;
Fp = 0,92.
7. Определим необходимую величину Kv
![]()
8. Приняв коэффициент запаса 1,2, найдем
Kv = 1,2×85 = 102.
Примем заслоночные регулирующий орган, имеющий при открытии 60° условную пропускную способность Kvy = 100 и Dy = 65 мм.
20. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ЖИДКОСТИ (КАВИТАЦИЯ ИЛИ ВСКИПАНИЕ)
Данные для расчета
1. Наименование протекающей среды вода
2. Максимальный расход Q = 17 м3/ч
3. Температура воды t = 164 °С
4. Давление перед регулирующим органом P1 = 8,1 кгс/см2
5. Давление после регулирующего органа P2 = 5,6 кгс/см2
6. Давление насыщенного пара Pнп = 7,0 кгс/см2
7. Критическое давление Pкр = 225,6 кгс/см2
8. Плотность воды ρ = 0,9042 г/см3
9. Диаметр трубопровода D = 40 мм
Расчет
1. Задавшись двухседельным регулирующим органом с пробковым затвором, для которого согласно таблице приложения 9 коэффициент начала кавитации Kc = 0,70, а коэффициент восстановления давления жидкости FL = 0,85, определим перепады давления, соответствующие началу кавитации и вскипанию
ΔP = Kc(P1 - Pнп) = 0,70(8,1 - 7,0) = 0,77 кгс/см2 < P1 - P2
ΔPкр = FL2(P1 - FFPнп).
Поправочный коэффициент FF по приложению 10 равен
![]()
FF = 0,925;
ΔPкр = 0,852(8,1 - 0,925×7,0) = 1,15 кгс/см2 < P1 - P2.
Так как P1 - P2 = 2,5 кгс/см2 > 1,15 кгс/см2, то в регулирующем органе будет иметь место вскипание и после него будет двухфазная парожидкостная смесь.
Орган целесообразно установить таким образом, чтобы свести к минимуму длину участка трубопровода после него. Сечение трубопровода после регулирующего органа должно быть увеличено так как парожидкостная смесь имеет больший объем, чем вода.
2. Определим произведение FLPKv
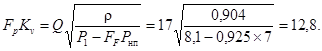
3. Зададимся двухседельным регулирующим органом с Dy = 40 мм = d, имеющим Kvy = 25, и имеющим, согласно таблице приложения 9, коэффициент восстановления давления жидкости FL = 0,85. Так как Dy = d = D = 40 мм, то FLP = FL = 0,85.
Определим необходимую пропускную способность
![]()
Приняв коэффициент запаса 1,2 найдем
Kv = 1,2×15,1 = 18,1.
Примем двухседельный регулирующий орган с Dy = 40 мм и Kvy = 25.
21. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ГАЗЕ (ТУРБУЛЕНТНЫЙ РЕЖИМ)
Данные для расчета
1. Наименование газа инертный
2. Максимальный расход Q = 9000 кг/ч
3. Плотность раза в рабочих условиях ρ = 45,1 кг/м3
4. Давление перед регулирующим органом P1 = 8 кгс/см2
5. Давление после регулирующего органа P2 = 3,8 кгс/см2
6. Показатель адиабата газа æ = 1,14
7. Диаметр трубопровода D = 50 мм
Расчет
1. Определим относительный перепад давления
![]()
2. Определим поправку на показатель адиабаты
Fæ = æ/1,40 = 1,14/1,40 = 0,81.
3. Задавшись двухседельным регулирующим органом с пробковым затвором, по приложению 9 найдем его относительный критический перепад давления xт = 0,70.
4. Определим режим движения газа через регулирующий орган
Fæxт = 0,81×0,70 = 0,568 > x = 0,525.
Так как имеет место условие x < Fæxт, то движение газа через регулирующий орган турбулентное некритическое.
5. Определим поправку на изменение плотности ε
![]()
6. Определим произведение FpKv
![]()
7. Зададимся регулирующим органом, имеющим Kvy = 40 и Dy = d = 50 мм.
В этом случае Fp = 1,0 так как переходные патрубки не нужны.
Приняв коэффициент запаса 1,2, найдем
Kv = 1,2×30 = 36.
Приняв окончательно двухседельный регулирующий орган с пробковым затвором, имеющий
Kvy = 40 и Dy = 50 мм.
Так как существуют двухседельные регулирующие органы, имеющие Kvy = 40 и Dy = 40 мм, то целесообразно проверять возможность использования такого органа в данном случае.
8. Определим поправку на влияние переходных патрубков
![]()
d/D = 40/50 = 0,80.
По приложению 8 найдем Fp = 0,97.
9. Определим относительный критический перепад давления с учетом входного патрубка
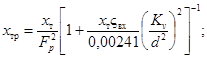
ςвх = ς1 + ςв1 = 0,66 (по приложению 7)
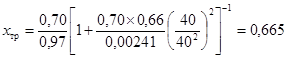
10. Определим режим движения газа через регулирующий орган с учетом переходных патрубков
Fæxтр = 0,81×0,665 = 0,54 > 0,525 (движение некритическое турбулентное).
11. Определим новую поправку на изменение плотности
![]()
12. Определим необходимую пропускную способность регулирующего органа с Dy = 40 мм
![]()
Приняв коэффициент запаса 1,2, найдем
Kv = 1,2×31,5 = 37,8.
Расчет показывает, что регулирующий орган, имеющий Kvy = 40 и Dy = 40 мм, также может быть использован в данном случае.
22. ПРИМЕР РАСЧЕТА РЕГУЛИРУЮЩЕГО ОРГАНА НА ГАЗЕ (КРИТИЧЕСКОЕ ТЕЧЕНИЕ)
Данные для расчета
1. Наименование сернистый
2. Максимальный расход Q = 84000 кг/ч
3. Плотность газа при 20 °С и Р = 1,033 кгс/см2 ρн = 2,73 кг/м3
4. Коэффициент сжимаемости газа K = 0,98
5. Показатель адиабаты газа æ = 1,25
6. Температура газа t = 157 °С
7. Абсолютное давление перед регулирующим органом P1 = 2,1 кгс/см2
8. Абсолютное давление после регулирующего органа P2 = 1,2 кгс/см2
9. Диаметр трубопровода D = 500 мм
Расчет
1. Определим плотность газа в рабочих условиях
![]()
2. Определим относительный перепад давления
![]()
3. Определим поправку на показатель адиабаты
![]()
4. Задавшись заслоночным регулирующим органом, открытым на 60°, по приложению 9 найдем его относительный критический перепад давления xт = 0,38.
5. Определим режим движения газа через регулирующий орган
Fæxт = 0,89×0,38 = 0,34 < x = 0,43.
Так как имеет место условие x > Fæxт, то движение газа через регулирующий орган критическое.
6. Определим поправку на изменение плотности ε
![]()
Так как ε не может быть меньше 0,67, то примем εкр = 0,67.
7. Определим произведение FpKv
![]()
8. Зададимся заслоночным регулирующим органом, имеющим в открытом на 60° положении Kvy = 3600 и Dy = d = 400 мм.
![]()
d/D = 400/500 = 0,8.
По приложению 8 найдем Fp = 0,97.
9. Определим относительный критический перепад давления с учетом входного патрубка
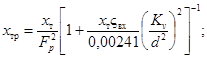
ςвх = ς1 + ςв1 = 0,66 (по приложению 7)
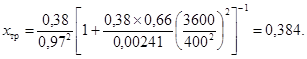
Так как практически xтр = xт = 0,38, то дальнейший расчет для определения уточненного значения Kv не нужен.
Приняв коэффициент запаса 1,2, найдем
![]()
Примем заслоночный регулирующий орган, имеющий в открытом на 60° положении Kvy = 3600 и Dy = 400 мм.
Приложение 1
Соотношения между различными единицами измерения
Соотношения между единицами давления
|
Па |
бар |
мм вод. ст. |
мм рт. ст. |
кгс/см2 |
|
|
Па |
1 |
10-5 |
0,102 |
7,5024 · 10-3 |
1,02 · 10-5 |
|
бар |
105 |
1 |
1,02 · 104 |
7,5024 · 102 |
1,02 |
|
мм вод. ст. |
9,8067 |
9,8067 · 10-5 |
1 |
7,35 · 10-2 |
10-4 |
|
мм рт. ст. |
1,33 · 102 |
1,33 · 10-3 |
13,6 |
1 |
1,36 · 10-3 |
|
кгс/см2 |
9,8067 · 104 |
0,98067 |
104 |
7,35 · 102 |
1 |
Соотношения между единицами кинематической вязкости
|
м2/с |
Ст |
сСт |
м2/ч |
ft2/s |
|
|
м2/с |
1 |
104 |
106 |
3600 |
10,76 |
|
Ст |
10-4 |
1 |
100 |
0,36 |
1,076 · 10-3 |
|
сСт |
10-6 |
0,01 |
1 |
3,6 · 10-3 |
1,076 · 10-5 |
|
м2/ч |
2,778 · 10-4 |
2,778 |
277,8 |
1 |
2,99 · 10-3 |
|
ft2/s |
9,29 · 10-2 |
929 |
9,29 · 104 |
334,5 |
1 |
Соотношения между единицами динамической вязкости
|
Паскаль-секунда |
пуаз |
кгс · с/м2 |
lbf · s/ft2 |
|
|
Паскаль-секунда |
1 |
10 |
0,102 |
2,09 · 10-2 |
|
Пуаз |
0,1 |
1 |
1,02 · 10-2 |
2,09 · 10-6 |
|
кгс · с/м2 |
9,81 |
98,1 |
1 |
0,205 |
|
lbf · s/ft2 |
47,88 |
478,8 |
4,88 |
1 |
Пересчет вязкости в градусах Энглера в м2/сек можно производить по формуле
![]()
Приложение 2
Формулы пересчета объема и плотности газов
|
Входящие в формулу величины |
Примечание |
||
|
Обозначение |
Наименование |
||
|
|
Vн |
Объем газа при давлении и температуре, принятых за нормальные |
1. Величины Рн, Р1 и Тн, Т1 должны иметь, соответственно, одинаковую размерность 2. Абсолютное давление равно сумме избыточного и атмосферного давлений 3. Коэффициент сжимаемости газа равен отношению объемного веса газа при Р1Т1, подсчитанного по законам идеального газа, к реальному удельному весу газа при Р1Т1,
|
|
V1 |
Объем газа при рабочих давлении и температуре |
||
|
ρн |
Плотности газа при давлении и температуре, принятых за нормальные |
||
|
ρ |
Плотность газа при рабочих давлении и температуре |
||
|
Pн1) 2) |
Абсолютное давление, принятое за нормальное |
||
|
P11) 2) |
Абсолютное рабочее давление |
||
|
Tн1) |
Абсолютная температура, принятая за нормальную |
||
|
Т11) |
Абсолютная рабочая температура |
||
|
K3) |
Отнесенный к Рн коэффициент сжимаемости газа при рабочих давлении и температуре |
||
Приложение 3
Коэффициент сопротивления некоторых местных сопротивлений
|
Изображение |
Коэффициент сопротивления, ς |
К какой скорости отнесен ς |
Примечание |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Выход из трубы в резервуар больших размеров |
ς = 1,0 |
V1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вход в трубу (Входная кромка скруглена радиусом 1) |
V2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вход в трубу (входная кромка по лемнискате) |
ς = 0,02 |
V2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дроссельные органы (сужающие устройства) расходомеров переменного перепада |
- |
Потери давления на сужающих устройствах расходомеров и длины участков, на которых эти потери измеряются, см. руководящий материал № Р26002 «Расчет сужающих устройств расходомеров» |
- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
внезапное расширение |
ς = (F2/F1 - 1)2;
|
V2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
внезапное сужение |
ς = 0,5(1 - F2/F1);
|
V2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Конические переходы |
Конффузор |
|
V2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Диффузор |
|
V1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Резкий поворот трубы на угол α |
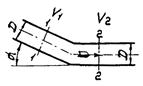
круглая труба |
|
V1 = V2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прямая труба |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Плавный поворот трубы на угол α |
Круглая труба |
ς = F(α) · ς" где ς см. табл. 1, а F(α) см. табл. 2
Таблица 2
|
V1 = V2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приложение 4
Коэффициент сопротивления полностью открытой арматуры
|
Изображение |
Коэффициент сопротивления ς |
Примечание |
|||||||||||||||||||||||||
|
Вентиль стандартный с вертикальными делительными стенками |
|
||||||||||||||||||||||||||
|
Вентиль стандартный с делительными стенками под углом 45° |
|
||||||||||||||||||||||||||
|
Вентиль «Рей» |
ς = 3,4 |
||||||||||||||||||||||||||
|
Вентиль «Косва» с полным сечением седла |
|
||||||||||||||||||||||||||
|
Вентиль «Косва» с суженным сечением седла |
|
||||||||||||||||||||||||||
|
Вентиль прямоточный |
|
Re ≥ 1 · 104 |
|||||||||||||||||||||||||
|
Задвижка типа «Лудло» в цилиндрической трубе |
|
Приложение 5
Сводная таблица формул для определения числа Рейнольдса потока
|
Величины, входящие в формулу |
|||
|
Обозначение |
Единицы измерения |
Наименование |
|
|
|
μ |
кгс · с/м2 |
Динамическая вязкость |
|
υ |
М2/с |
Кинематическая вязкость |
|
|
|
Q0 Qн |
м3/ч Нм3/ч |
Объемный часовой расход То же |
|
|
G ρ |
кг/ч кг/м3 |
Массовый расход Плотность |
|
|
ρн |
кг/нм2 |
Объемный вес в нормальных условиях |
|
|
D |
мм |
Внутренний диаметр трубы |
|
|
υ |
см2/с(Ст) |
Кинематическая вязкость |
|
Q |
м3/ч |
Объемный часовой расход |
|
|
|
G |
кг/ч |
Весовой часовой расход |
|
ρ |
кг/м3 |
Плотность |
|
|
D |
мм |
Внутренний диаметр трубы |
|
|
|
μ |
кг/м · ч |
Динамическая вязкость |
|
Q |
м3/ч |
Объемный часовой расход |
|
|
|
Qн |
Нм3/ч |
То же |
|
G |
кг/ч |
Массовый часовой расход |
|
|
ρ |
кг/м3 |
Объемный вес |
|
|
|
ρн |
кг/Нм3 |
Прочность в нормальных условиях |
|
D |
мм |
Внутренний диаметр трубы |
|
|
|
μ |
мкПз |
Динамическая вязкость |
|
Q0 |
м3/ч |
Объемный часовой расход |
|
|
|
Qн |
Нм3/ч |
То же |
|
G |
кг/ч |
Весовой часовой расход |
|
|
ρ |
кг/м3 |
Объемный вес |
|
|
|
ρн |
кг/Нм3 |
Объемный вес в нормальных условиях |
|
D |
мм |
Внутренний диаметр трубы |
|
Приложение 6
Коэффициент трения λ круглых трубопроводов
|
Трубы |
Область применения формулы |
Формула |
Примечания |
|||||||||||||||||||||||||
|
Ламинарный |
Гладкие и шероховатые |
ReD < 2320 |
|
1. Удовлетворяющие условию 2. ReD - число Рейнольдса 3 Коэффициенты универсального уравнения Никурадзе
4. ω - относительная шероховатость (отношение высоты выступов шероховатости, п1 к радиусу трубопровода r). Для цельнотянутых железных и стальных, а также оцинкованных труб высота выступов шероховатости 0,1 мм, для новых чугунных труб - 0,3 мм, для цельнотянутых стальных и железных труб после нескольких лет эксплуатации и при отсутствии особых источников загрязнения и внутренней коррозии - 0,2 мм, для железных и стальных труб, сильно загрязненных и подвергшихся значительной внутренней коррозии - от 0,5 до 2 мм. 5. Универсальное уравнение Никурадзе решается методом последовательных приближений. |
||||||||||||||||||||||||
|
Турбулентный |
Гладкие и гидравлически1) гладкие |
2320 < ReD < 1 · 105 |
(уравнение Блазиуса) |
|||||||||||||||||||||||||
|
1 · 105 < ReD < 1 · 108 |
(уравнение Никурадзе для гладких труб) |
|||||||||||||||||||||||||||
|
Шероховатые |
ReD > 2320 См. примечания 3 - 5 |
(универсальное уравнение Никурадзе) |
Коэффициенты трения «λ» круглых трубопроводов λ = f(ReD, D/п1) стальных труб по данным В.Т.И.
|
n, мм |
|
|
Трубопроводы из новых труб, в том числе станционные паропроводы перегретого пара |
0,06 |
|
Теплофикационные паропроводы перегретого пара и водяные теплопроводы при наличии деаэрации и химчистки подпиточной воды |
0,1 |
|
Паропроводы насыщенного пара и водяные теплопроводы при незначительных утечках воды (до 0,5 %) и деаэрации подпитка |
0,2 |
|
Паропроводы, работающие периодически (с простоями), и конденсатопроводы с открытой системой возврата конденсата |
0,5 |
|
Воздухопроводы сжатого воздуха от поршневых турбокомпрессоров |
0,8 |
|
Конденсатопроводы, работающие периодически, и водяные теплопроводы при отсутствии деаэрации и химочистки подпиточной воды и при больших утечках из сети (до 1,5 ÷ 3 %). |
1,0 |
Приложение 7
Коэффициенты ς и ςв для одинаковых конических переходных патрубков (внезапные расширения)
Приложение 8
Поправка на влияние переходных патрубков Fp
Приложение 9
Ориентировочные значения коэффициентов для расчета регулирующих органов
|
Вид регулирующего органа |
Направление потока |
Установка в трубе |
Установка в трубе |
||||||||
|
Kv/d2 |
FL |
xт |
Fd |
Fs |
Kc |
Kv/D2 |
FLP |
xтр |
Fs |
||
|
Односедельный проходной: |
|||||||||||
|
- с пробковым затвором; |
под затвор |
1,5 · 10-2 |
0,90 |
0,72 |
1,0 |
1,05 |
0,65 |
0,36 · 10-2 |
0,85 |
0,73 |
1,04 |
|
- с пробковым затвором; |
на затвор |
1,5 · 10-2 |
0,80 |
0,55 |
1,0 |
1,09 |
0,58 |
0,36 · 10-2 |
0,76 |
0,57 |
1,08 |
|
- с цилиндрическим затвором с профильными окнами |
оба |
1,2 · 10-2 |
0,90 |
0,75 |
1,5 |
1,38 |
-*) |
0,3 · 10-2 |
0,86 |
0,75 |
1,36 |
|
Двухседельный проходной: |
|||||||||||
|
- с пробковым затвором |
- |
1,7 · 10-2 |
0,85 |
0,70 |
0,71 |
0,85 |
0,70 |
0,4 · 10-2 |
0,79 |
0,71 |
0,84 |
|
- с цилиндрическим затвором с профильными окнами |
- |
1,7 · 10-2 |
0,90 |
0,75 |
0,71 |
0,84 |
-*) |
0,4 · 10-2 |
0,83 |
0,75 |
0,83 |
|
Угловой полнопроходный с пробковым затвором |
под затвор |
2,3 · 10-2 |
0,90 |
0,72 |
1,0 |
1,08 |
0,64 |
0,57 · 10-2 |
0,78 |
0,73 |
1,04 |
|
на затвор |
2,7 · 10-2 |
0,80 |
0,65 |
1,0 |
1,12 |
0,53 |
0,66 · 10-2 |
0,69 |
0,68 |
1,08 |
|
|
Заслоночный, открытый на 60º |
- |
2,3 · 10-2 |
0,68 |
0,38 |
0,71 |
0,92 |
0,3 |
0,56 · 10-2 |
0,63 |
0,43 |
0,91 |
|
Заслоночный, открытый на 90º |
- |
> 4 · 10-2 |
0,55 |
0,20 |
0,71 |
1,01 |
-*) |
> 1 · 10-2 |
0,45 |
0,33 |
0,97 |
*) сведения отсутствуют
Приложение 10
Поправочный коэффициент FF
Приложение 11
Поправка на влияние вязкости FR
Приложение 12
Поправка на влияние вязкости FR для переходного режима движения жидкости
Приложение 13
Уравнения для расчета регулирующих органов, управляющих потоками жидкости
|
Режим движения |
Уравнение |
Величины, входящие в уравнения |
|
||
|
Обозначения |
Ед. изм. |
Наименование |
|
||
|
Турбулентное однофазное в квадратичной области, ΔP < Kc(P1 - Pнп) |
|
D |
мм |
Внутренний диаметр трубы |
|
|
Fd |
- |
Коэффициент формы |
|
||
|
FF |
- |
Поправочный коэффициент |
|
||
|
FL |
- |
Коэффициент восстановления давления жидкости |
|||
|
Кавитация и вскипание, ΔP > FL2(P - FFPнп) |
|
||||
|
FLP |
- |
Коэффициент восстановления давления и влияния входного патрубка |
|
||
|
Fp |
- |
Поправка на влияние переходных патрубков |
|||
|
FR |
- |
Поправка на влияние вязкости |
|||
|
Ламинарный |
|
||||
|
Kc |
- |
Коэффициент начала кавитации |
|
||
|
Kv |
- |
Пропускная способность |
|
||
|
P1 |
кгс/см2 |
Абсолютное давление перед регулирующим органом |
|
||
|
Переходный |
FR - см. приложение 12 |
Pнп |
кгс/см2 |
Абсолютное давление насыщенных паров |
|
|
ΔP |
кгс/см2 |
Перепад давления |
|
||
|
Q |
м3/ч |
Объемный расход |
|
||
|
- |
|
ReV |
- |
Число Рейнольдса регулирующего органа |
|
|
μ |
сП |
Динамическая вязкость |
|
||
|
υ |
сСт |
Кинематическая вязкость |
|
||
|
ρ |
г/см3 |
Плотность |
|
||
Приложение 14
Критический относительный перепад давления с учетом влияния переходных патрубков хтр
|
Kv/d2 |
1,3 · 10-2 |
2 · 10-2 |
2,7 · 10-2 |
3,3 · 10-2 |
4 · 10-2 |
||||||||||||||||
|
xт |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,40 |
0,50 |
0,60 |
0,70 |
0,20 |
0,30 |
0,40 |
0,50 |
0,15 |
0,20 |
0,25 |
|
d/D |
xтр |
xтр |
xтр |
xтр |
xтр |
||||||||||||||||
|
0,80 |
0,40 |
0,49 |
0,59 |
0,69 |
0,78 |
0,40 |
0,49 |
0,58 |
0,67 |
0,75 |
0,39 |
0,48 |
0,56 |
0,64 |
0,21 |
0,30 |
0,39 |
0,47 |
0,17 |
0,21 |
0,26 |
|
0,75 |
0,40 |
0,50 |
0,59 |
0,69 |
0,78 |
0,40 |
0,49 |
0,58 |
067 |
0,75 |
0,40 |
0,49 |
0,57 |
0,65 |
0,22 |
0,31 |
0,40 |
0,48 |
0,18 |
0,23 |
0,27 |
|
0,67 |
0,40 |
0,50 |
0,60 |
0,69 |
0,78 |
0,41 |
0,50 |
0,59 |
0,68 |
0,76 |
0,42 |
0,51 |
0,59 |
0,67 |
0,24 |
0,33 |
0,43 |
0,51 |
0,19 |
0,25 |
0,30 |
|
0,60 |
0,41 |
0,51 |
0,60 |
0,70 |
0,79 |
0,42 |
0,52 |
0,61 |
0,69 |
0,78 |
0,43 |
0,53 |
0,61 |
0,69 |
0,25 |
0,36 |
0,45 |
0,54 |
0,21 |
0,27 |
0,32 |
|
0,50 |
0,41 |
0,52 |
0,61 |
0,71 |
0,80 |
0,44 |
0,53 |
0,63 |
0,71 |
0,79 |
0,46 |
0,55 |
0,64 |
0,72 |
0,28 |
0,39 |
0,49 |
0,58 |
0,24 |
0,30 |
0,36 |
|
0,40 |
0,42 |
0,52 |
0,62 |
0,71 |
0,80 |
0,44 |
0,55 |
0,65 |
0,74 |
0,82 |
0,49 |
0,58 |
0,67 |
0,75 |
0,30 |
0,42 |
0,53 |
0,62 |
0,26 |
0,33 |
0,40 |
|
0,33 |
0,43 |
0,53 |
0,62 |
0,72 |
0,81 |
0,46 |
0,56 |
0,66 |
0,75 |
0,83 |
0,50 |
0,60 |
0,69 |
0,78 |
0,31 |
0,44 |
0,55 |
0,64 |
0,27 |
0,34 |
0,40 |
|
0,25 |
0,44 |
0,53 |
0,63 |
0,73 |
0,83 |
0,48 |
0,58 |
0,67 |
0,76 |
0,85 |
0,52 |
0,62 |
0,71 |
0,79 |
0,33 |
0,46 |
0,57 |
0,67 |
0,27 |
0,37 |
0,44 |
Приложение 15
Поправка на изменение плотности ε для двухседельных регулирующих органов с пробковым затвором (хт = 0,70)
Значения показателя адиабаты æ
Приложение 16
Уравнения для расчета регулирующих органов, управляющих потоками газа или пара
|
Режим движения |
Уравнение |
Величины, входящие в уравнения |
||
|
Обозначения |
Ед. изм. |
Наименование |
||
|
Турбулентное, x ≤ Fæxт |
|
d |
мм |
Присоединительный диаметр регулирующего органа |
|
Fp |
- |
Поправка на влияние переходных патрубков |
||
|
Fæ |
- |
Поправка на показатель адиабаты |
||
|
Критическое, x > Fæxт |
|
P1 |
кгс/см2 |
Абсолютное давление перед регулирующим органом |
|
Р2 |
кгс/см2 |
Абсолютное давление после регулирующего органа |
||
|
ΔP |
кгс/см2 |
Перепад давления |
||
|
Переходный режим |
|
Q |
кг/ч |
Массовый расход |
|
x |
- |
Относительный перепад давления |
||
|
xт |
- |
Относительный критический перепад давления воздуха |
||
|
xтр |
- |
То же, с учетом входного патрубка |
||
|
- |
|
ε |
- |
Поправка на изменение плотности |
|
εкр |
- |
То же, в критическом режиме |
||
|
ςвх |
- |
Коэффициент сопротивления входного патрубка |
||
|
æ |
- |
Показатель адиабаты |
||
|
ρ |
кг/м3 |
Плотность |
||
Приложение 17
Пропускные способности нестанартизованных заслоночных регулирующих органов
|
Общий вид и основные размеры |
Пропускная способность при открытии 60º |
|
|
Круглая поворотная заслонка с плоским крылом, без упоров |
d = 0,995D, δ = 0,01D |
Kv = 2,2 · 10-2d2 |
|
Круглая поворотная заслонка с плоским крылом, с упорами |
d = 0,95D, δ = 0,02D |
Kv = 1,9 · 10-2d2 |
|
Квадратная поворотная заслонка с плоским крылом, без упоров |
а = 0,995A |
Kv = 2,8 · 10-2a2 |
|
Квадратная поворотная заслонка с плоским крылом, с упорами |
а = 0,98A, δ = 0,005A |
Kv = 3 · 10-2a2 |
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННЫХ ДОКУМЕНТОВ И ЛИТЕРАТУРЫ
1. Технические документы
|
Устройства исполнительные для систем автоматического регулирования. Термины. |
|
|
ГОСТ 16443-70 |
Устройства исполнительные. Методы расчета пропускной способности, выбора условного прохода и пропускной характеристики |
|
IEC draft Publication 534-2 Section one |
Control Valve Sizing Equations for Incompressible Fluid Flow under Installed Conditions |
|
ISA-S39.1 (1972) (Instrument Society of America) |
Control Valve Sizing Equations for Incompressible Fluids |
|
ISA-S39.3 (1973) |
Control Valve Sizing Equations for Compressible Fluids |
2. Литература
1. Арзуманов Э.С. Расчет и выбор регулирующих органов автоматических систем, М., 1971.
2. Казинер Ю.Я. и Слободкин М.С. Арматура систем автоматического управления, М., 1977.
3. Driskell L. Control Valve Sizing with ISA. Formulas. How to Apply the New Standarts, Instrumentation Tecnology, July, 1974, Pp. 33 - 48.
4. Baumann H.D. Effects of Pipe Reducers on Valve Capacity, Instruments and Control Systems, December, 1968, pp. 99 - 102.
5. McCutcheen E.B. A Reynolds Number for Control Valves, in «Flow: its Measurement and Control in Science and Industry», vol. 1, part 3, 1974 (ed. Dowdell R.B.).
6. Driskell L.R. Philosophy of Control Valve Sizing Instrumentation Technology, January, 1975, pp. 33 - 34.
7. Chalfin S. Specifying Control Valve, Chemical Engineering, October 14, 1974, pp. 105 - 114.
8. Buckley P.S. and Mariam P.L. Solving Instrumentation Problems with a Programmable Calculator, Instrumentation Technology, February, 1975, pp. 31 - 37.
9. de Filippis, L. Control Valve Flow Theory and Sizing, ISA Transactions, vol. 13, No. 4, 1974, pp. 347 - 368.