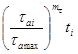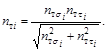РЕКОМЕНДАЦИИ
РАСЧЕТЫ И ИСПЫТАНИЯ НА ПРОЧНОСТЬ.
РАСЧЕТЫ НА ПРОЧНОСТЬ ВАЛОВ И ОСЕЙ
Р 50-83-88
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
МОСКВА
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
|
РАСЧЕТЫ И ИСПЫТАНИЯ НА ПРОЧНОСТЬ РАСЧЕТ НА ПРОЧНОСТЬ ВАЛОВ И ОСЕЙ |
Р 50-83-88 |
Дата введения 01.07.89
В настоящих рекомендациях стандартизованы общие положения расчета на прочность валов и осей при статических и циклических нагрузках, наличии или отсутствии концентрации напряжений с учетом заданной вероятности разрушения и масштабного фактора.
Рекомендации распространяются на стальные валы и оси, подвергаемые термической, термохимической обработкам и (или) поверхностному упрочнению и предназначены для работников научно-исследовательских институтов, конструкторских бюро и заводских лабораторий, занимающихся их проектированием и расчетами на прочность.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. В ряде справочников, учебников и учебных пособий расчет на сопротивление усталости валов и осей рекомендуется производить в предположении регулярности режима нагружения по формулам Серенсена - Кинасошвили.
В валах и осях регулярные напряжения, как правило, не встречаются.
В связи с этим основное внимание уделено методам расчета валов и осей на сопротивление усталости при нерегулярном нагружении, в частности при случайном и блочном.
Методы основаны на сведении случайного нагружения к блочному путем схематизации случайных процессов по методам полных циклов или дождя и приведении амплитуд асимметричных циклов к эквивалентным амплитудам симметричного цикла по ГОСТ 25.101.
Накопление усталостных повреждений при блочном нагружении учитывается путем применения корректированной линейной гипотезы суммирования (2). Как показано в ряде работ путем обобщения многочисленных экспериментальных данных, опубликованных в мировой литературе, корректированная гипотеза дает в статистическом смысле существенно более точные результаты в оценке долговечности, чем линейная гипотеза без корректировки (1, 2, 5).
Расчетная оценка медианных значений и коэффициентов вариации пределов выносливости валов и осей осуществляется по ГОСТ 25.504.
Основное внимание в настоящих рекомендациях уделено методам расчета функций распределения долговечности (ФРД) валов и осей, представляющих собой зависимость вероятности разрушения от наработки (долговечности) в условиях эксплуатации. Эти функции являются основной характеристикой надежности и долговечности деталей, определяют медианные и гамма-процентные ресурсы, задаваемые в технических условиях на проектируемую машину. Расчёт ФРД на стадии проектирования и доводки опытного экземпляра машины позволяет оценить удовлетворение требований по надежности, найти оптимальные конструктивно-технологические решения, получить исходные данные для расчета объема выпуска запасных частей и решать другие практические задачи. Расчет ФРД осуществляется вероятностными методами, разработанными в ИМАШ АН СССР (2), изложенными в методических указаниях РД 50-607 Госстандарта СССР.
Изложенные вероятностные методы расчета усталостной долговечности используются в ряде отраслей машиностроения, а также получили отражение в многочисленной справочной, монографической и учебной литературе. Опыт промышленного применения этих методов показал их эффективность и прогрессивность.
Пример 1 (приложение 9) показывает,
как с помощью этих методов может быть оценен эффект от применения тех или иных
конструктивно-технологических мероприятий в смысле повышения надежности и
долговечности деталей. Так, медианная долговечность вала с прямобочными шлицами
составляет ![]() ≈ 2,5
года, а долговечность, соответствующая вероятности разрушения 10 %
(гамма-процентная долговечность Lγ при γ
= 90 %) Lv ≈ 1 год, (кривая 1,
черт. 10), что явно
недостаточно. Введение эвольвентных шлиц (кривая 2) повышает
≈ 2,5
года, а долговечность, соответствующая вероятности разрушения 10 %
(гамма-процентная долговечность Lγ при γ
= 90 %) Lv ≈ 1 год, (кривая 1,
черт. 10), что явно
недостаточно. Введение эвольвентных шлиц (кривая 2) повышает ![]() до 10 лет (т.е.
в 4 раза), a
Lγ
до 3,5 лет (т.е. в 3,5 раза). Введение дополнительной обкатки шлиц повышает
медианный ресурс неограниченно, а гамма-процентный ресурс Lγ до 15 лет, то
есть в 15 раз по сравнению с исходным вариантом.
до 10 лет (т.е.
в 4 раза), a
Lγ
до 3,5 лет (т.е. в 3,5 раза). Введение дополнительной обкатки шлиц повышает
медианный ресурс неограниченно, а гамма-процентный ресурс Lγ до 15 лет, то
есть в 15 раз по сравнению с исходным вариантом.
Таким образом расчеты показали, что введение 2 недорогостоящих мероприятий: замена прямобочных шлиц эвольвентными и наклеп поверхности накаткой приводит к резкому повышению надежности и долговечности. Так как при этом получаются количественные оценки долговечности по параметру вероятности разрушения, то это позволит дать технико-экономические оценки целесообразности применения различных конструктивно-технологических мероприятий. Точность расчета ФРД зависит от объема исходной экспериментальной информации. Опыт применения этих методов в промышленности показывает, что при используемых в настоящее время объемах экспериментальной информации по нагруженности и прочности расчетные ФРД находятся в удовлетворительном соответствии с эмпирическими ФРД, найденными по статистическим данным об отказах в эксплуатации.
В случае ограниченного количества экспериментальной информации расчет валов и осей на сопротивление усталости может быть выполнен по коэффициентам запаса прочности с использованием понятий эквивалентных напряжений (разд. 3).
1.2. Термины и обозначения, применяемые в методических указаниях:
относящиеся к геометрии и кинематике зубчатых передач - по ГОСТ 16530, ГОСТ 16531, ГОСТ 19325, ГОСТ 18498;
относящиеся к прочностным расчетам - по ГОСТ 21354, ГОСТ 23207, ГОСТ 25.502, ГОСТ 25.504, ГОСТ 25.101, ГОСТ 25.507, РД 50-607, MP 206.
Перечень основных обозначений, применяемых в методических указаниях, приведен в приложении 1.
1.3. Силы, действующие на валы и оси, при составлении расчетных схем подразделяют на:
силы, меняющие положение относительно вала или оси и вызывающие в волокнах знакопеременные напряжения;
силы, не меняющие положение относительно вала или оси, т.е. вращающиеся вместе с валом или осью и вызывающие в волокнах постоянные по знаку напряжения.
Формулы для определения усилий, действующих на валы и оси со стороны зубчатых колес, приведены в табл. 2.
1.4. Характеристики сопротивления усталости валов и осей определяются по ГОСТ 25.504 и методическим рекомендациям MP 206.
1.5. Экспериментальное определение характеристик сопротивления усталости лабораторных образцов, моделей и натурных валов и осей - по ГОСТ 25.502 и ГОСТ 25.507.
1.6. Статистическая обработка данных измерений эксплуатационной нагруженности валов и осей и представления результатов - по ГОСТ 25.101, MP 75, MP 55.
1.7. Расчет усталостной долговечности валов и осей по параметру вероятности разрушения - по методическим указаниям РД 50-607.
1.8. Перед проведением расчета прочности валов и осей необходимо:
выполнить чертеж вала или оси с сопрягаемыми деталями;
разбить вал или ось на ступени с различной геометрической характеристикой поперечных сечений, границы ступеней обозначить арабскими цифрами по возрастанию слева направо;
проставить линейные размеры длин ступеней вала или оси, их диаметров, а также расстояний между силами, действующими на вал или ось с учетом установочных баз подшипников, определяемых по приложению 3;
проставить поля допусков вала или оси, переходные радиусы и их допуски между ступенями вала или оси, а также другие геометрические параметры источников концентрации напряжений.
1.9. Геометрические характеристики поперечных сечений определяются по формулам п. 2.6 и табл. 5, 6 приложения 4.
1.10. Методы конструктивного упрочнения вала или оси в местах посадки подшипников приведены в приложении 5.
1.11. Коэффициенты Кυ влияния технологических методов поверхностного упрочнения на пределы выносливости приведены в приложении 6.
1.12. Эффективные коэффициенты концентрации напряжений Кσ, Кτ для валов и осей приведены в приложении 7.
1.13. Таблица функции нормального распределения приведена в приложении 8.
1.14. Примеры расчета приведены в приложении 9.
2. РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
2.1. Статическую прочность рассчитывают по максимальным внешним нагрузкам, действующим на вал или ось - крутящему моменту Тmах (в случае вала), сосредоточенным и распределенным силам, изгибающим моментам (в случае вала и оси).
2.2. Максимальный момент Тmах за срок службы определяют с учетом специфики машины (по моменту опрокидывания электродвигателя, по предельному моменту при наличии предохранительных элементов, с учетом инерционных моментов при внезапном торможении без предохранительных элементов и т.п.).
Для выявления максимального за срок службы крутящего и изгибающего моментов следует выполнить анализ режимов работы машины, узла или детали, режимов нагружения сечений вала или оси и выбрать расчетные режимы и расчетные сечения.
2.3. Опорные реакции определяют в двух
взаимно перпендикулярных плоскостях отдельно от сил, меняющих ![]() ,
, ![]() меняющих
меняющих ![]() ,
, ![]() положение
относительно вала, с учетом всех сил и моментов, действующих на вал.
положение
относительно вала, с учетом всех сил и моментов, действующих на вал.
2.4. Определяют максимальные осевые силы Fmax растяжения (сжатия), действующие в рассматриваемых поперечных сечениях вала, соответствующие Тmax.
2.5. Определение изгибающих и крутящих моментов и построение эпюр
2.5.1. Определяют составляющие изгибающих
моментов отдельно от сил, меняющих ![]() ,
, ![]() и не меняющих
и не меняющих ![]() положение
относительно вала, в плоскостях zox и yох для сечений, в
которых приложены сосредоточенные силы (внешние силы и опорные реакции) и в
местах изменений сечений вала, а также суммарный момент
положение
относительно вала, в плоскостях zox и yох для сечений, в
которых приложены сосредоточенные силы (внешние силы и опорные реакции) и в
местах изменений сечений вала, а также суммарный момент ![]() от сил, не меняющих
положение относительно вала (ось х совпадает с осью вала или оси, оси y и z лежат в
плоскости, перпендикулярной к оси вала).
от сил, не меняющих
положение относительно вала (ось х совпадает с осью вала или оси, оси y и z лежат в
плоскости, перпендикулярной к оси вала).
2.5.2. Определяются изгибающие моменты Мп и Мл справа и слева от сечения в местах приложения осевых сил, смещенных относительно оси вала.
2.5.3. Суммарные изгибающие моменты ![]() от сил,
меняющих положение относительно вала, определяют по формуле
от сил,
меняющих положение относительно вала, определяют по формуле
![]()
где i - индекс сечения.
2.5.4. Максимальные изгибающие моменты Mmaxi определяют по формуле
![]()
2.5.5. Строятся эпюры изгибающих моментов Мм и Мн раздельно для сил меняющих и не меняющих положение относительно вала.
2.5.6. Строятся эпюры результирующих изгибающих моментов путем арифметического суммирования ординат эпюр для сил, меняющих и не меняющих положение относительно вала.
2.5.7. Строится эпюра крутящего момента Тmax
2.5.7.1. В шпоночном соединении за точку приложения силы, создающей крутящий момент, принимается середина минимальной длины площадки контакта шпонки с сопрягаемыми деталями.
2.5.7.2. В шлицевом соединении за точку приложения крутящего момента принимается середина длины площади контакта сопрягаемых деталей. Если длина контакта больше диаметра впадин шлицев, то эпюра крутящего момента принимается по закону треугольника с вершиной у края шлицев.
2.6. Геометрические характеристики поперечного сечения:
момент сопротивления при изгибе Wи,
момент сопротивления при кручении Wк,
площадь поперечного сечения А - вычисляются по нетто-сечению по формулам:
для валов с одной шпоночной канавкой
для валов с двумя противоположными шпоночными канавками
для валов с прямобочными шлицами
Для валов с эвольвентными шлицами и для вала-шестерни в сечении по зубьям геометрические характеристики поперечного сечения даны в табл. 1 и 2 приложения 4.
Для валов с треугольными шлицами
![]()
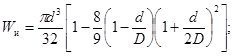
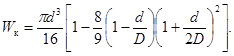 (3)
(3)
Здесь b - ширина шпонки или шлица;
z - число шлиц;
h - высота шпонки;
D, d - наружный и внутренний диаметры шлицевого вала;
d - диаметр вала со шпоночным пазом.
Для валов диаметром d с поперечным отверстием диаметром а
![]()
![]()
![]() (4)
(4)
2.7. Нормальное σi и касательное τi напряжения в рассматриваемом i сечении вала определяют по формулам
![]() (5)
(5)
![]() (6)
(6)
2.8. Частные запасы прочности по нормальным
![]() и
касательным
и
касательным ![]() напряжениям определяют по формулам
напряжениям определяют по формулам
Пределы текучести материала σт и τт определяются на стандартных образцах, вырезанных из заготовок такого же диаметра, что и у рассчитываемого вала или оси. Если предел текучести определяется на образцах, вырезанных из прутков диаметром 10 - 20 мм (обозначенный σ'т), то расчетный предел текучести σт для материала вала или оси диаметром d находится по формуле
где для легированных сталей
К1 = 0,74 для d > 150 мм;
К1 = 1 для углеродистых сталей.
2.9. Общий коэффициент запаса прочности по пределу текучести nт при совместном действии нормальных и касательных напряжений определяется по формуле
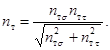 (10)
(10)
Данная формула соответствует расчету по гипотезе прочности максимальных касательных напряжений.
2.10. Статическая прочность считается обеспеченной, если
nт ≥ [nт],
где [пт] - минимально допустимое значение общего коэффициента запаса по пределу текучести.
Значение [пт] принимается в диапазоне [пт] = 1,3 - 2,0 в зависимости от ответственности конструкции и последствий разрушения вала, от принятой точности определения нагрузок и напряжений, от уровня технологии изготовления и контроля, от однородности и стабильности свойств материала и от других факторов. Нормативное значение [пт] устанавливается на основе опыта расчетов и наблюдений за поведением машины в эксплуатации с учетом отмеченных факторов в нормативных документах отрасли или предприятия применительно к определенным типам машин и деталей.
3. РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
3.1. Определение расчетных характеристик сопротивления усталости валов и осей
Величины пределов выносливости валов и осей в опасных сечениях определяют в соответствии с ГОСТ 25.504 по формулам:
![]()
![]() (11)
(11)
![]() - медианные
значения пределов выносливости материала, определенные на лабораторных
образцах, изготовленных из прутков диаметром 10 - 20 мм;
- медианные
значения пределов выносливости материала, определенные на лабораторных
образцах, изготовленных из прутков диаметром 10 - 20 мм;
![]() - медианные
значения пределов выносливости материала, определенные на лабораторных образцах,
изготовленных из заготовок таких же поперечных сечений, что и у рассчитываемой
детали;
- медианные
значения пределов выносливости материала, определенные на лабораторных образцах,
изготовленных из заготовок таких же поперечных сечений, что и у рассчитываемой
детали;
К1 - определяется по формуле (9).
При отсутствии
экспериментальных данных значения ![]() и
и ![]() ориентировочно определяют следующими
соотношениями:
ориентировочно определяют следующими
соотношениями:
![]()
![]() (13)
(13)
где σв в МПа.
Значения коэффициентов влияния качества обработки поверхности определяют по формулам:
при изгибе
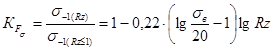 при Rz > 1 мкм; (15)
при Rz > 1 мкм; (15)
![]() =1 при Rz ≤ 1 мкм
=1 при Rz ≤ 1 мкм
при кручении
Значения коэффициентов влияния поверхностного упрочнения оцениваются по табл. 8 - 10 приложения 6.
Для валов с
геометрическими источниками концентрации напряжений (канавки, переход от одного
сечения к другому по галтели, отверстия и т.п.) отношения Кσ/![]() ,
характеризующие
влияние
концентрации напряжений и масштабного фактора, определяют по ГОСТ
25.504.
,
характеризующие
влияние
концентрации напряжений и масштабного фактора, определяют по ГОСТ
25.504.
Для валов с
напрессованной деталью отношение Кσ/![]() рассчитывается
по формуле (для случая, в котором через напрессованную деталь передается
изгибающий момент и сила)
рассчитывается
по формуле (для случая, в котором через напрессованную деталь передается
изгибающий момент и сила)
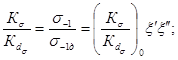 (17)
(17)
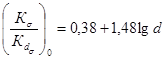 при d < 150 мм; (18)
при d < 150 мм; (18)
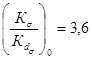 при d ≥ 150 мм;
при d ≥ 150 мм;
(σв в МПа)
![]() = 0,65 +
0,014р при р ≤ 25 МПа;
= 0,65 +
0,014р при р ≤ 25 МПа;
где р - давление посадки, которое при напрессовке кольца на вал может быть подсчитано по формуле Лямэ.
Аналогичное отношение при кручении определяют по формуле
Значения эффективных коэффициентов концентрации напряжений при изгибе и кручении для валов со шпонками, шлицами, резьбой, валов с отверстием приведены на черт. 2 - 7 приложения 7.
Коэффициенты
влияния абсолютных размеров поперечного сечения ![]() ,
, ![]() , определяют по
формулам:
, определяют по
формулам:
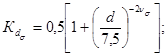 (22)
(22)
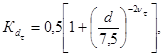 (23)
(23)
где d - диаметр вала или оси в мм.
Параметры уравнения подобия усталостного разрушения vσ, vτ определяют или экспериментально по методике, изложенной в MP 206, или по корреляционным формулам:
(σв в МПа).
Уравнение кривой усталости принимается в форме
N = ∞ при ![]()
Показатель наклона левой ветви кривой усталости в случае отсутствия прямых экспериментальных данных определяют по уравнению
а К - определяется по уравнению (14).
Величину NG можно принять равной NG = 2 × 106.
Значения коэффициентов влияния асимметрии цикла на предельные амплитуды ψσ, ψτ для лабораторных образцов определяют по формуле
ψσ = 0,02 + 2 × 10-4 × σв; (29)
ψτ = 0,5 ψσ,
где σв в МПа.
То же для деталей
где К определяют по уравнению (14).
Характеристики сопротивления усталости для наиболее ответственных валов и осей, повреждения которых связаны с угрозой безопасности людей или серьезными экономическими потерями, рекомендуется определять испытаниями на усталость натурных деталей (при диаметрах d < 300 мм) или достаточно крупных моделей (d = 100 - 200 мм), с осуществлением экстраполяции на натурные размеры на основе теории подобия усталостного разрушения.
3.2. Определение расчетных характеристик нагруженности
По эпюрам изгибающих и крутящих моментов в опасных сечениях находятся амплитуды нормальных σаi и касательных τаi напряжений для ступеней блока нагружения (i = 1, 2, ..., r), а также числа циклов действия амплитуд нормальных viσ и касательных viσ напряжений каждого i-го уровня (I = 1, 2..., r) в блоке нагружения.
Формирование блока нагружения по результатам тензометрирования в тех случаях, когда оно производилось, осуществляется по ГОСТ 25.101.
Коэффициент вариации уровня нагруженности υε определяется на основе результатов ряда повторных измерений эксплуатационной нагруженности с варьированием нерегламентируемых факторов (например для автомобиля состояние дороги в пределах определенной регламентируемой группы дорог, квалификация водителя, экземпляр машины, состояние погоды и пр.) по методике, изложенной в (1).
3.3. Расчет коэффициентов запаса прочности
3.3.1. Вычисляют корректирующие коэффициенты аpσ и аpτ.
Из блока нагружения исключают амплитуды aai < 0,5σ-1g; оставшееся число ступеней обозначают r1σ и вычисляют параметр ξσ
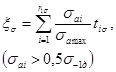 (31)
(31)
где ![]()
![]() - число циклов
в укороченном блоке нагружения.
- число циклов
в укороченном блоке нагружения.
Вычисляют корректирующий коэффициент а
Если по формуле получится значение аpσ < 0,1, то следует принять аpσ = 0,1;
Аналогично
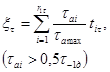 (33)
(33)
где ![]()
![]()
3.3.2. Расчет коэффициентов запаса прочности по нормальным nσ и касательным nτ напряжениям производится по формулам:
![]()
![]() (35)
(35)
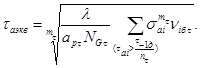 (37)
(37)
λ - количество блоков нагружения за расчетную наработку.
Определение σаэкв и τаэкв производится последовательным приближением: задаваясь значением п'σ и n'τ находят σаэкв, τаэкв, после чего находят пσ и nτ по (35); в случае существенного расхождения заданных и полученных коэффициентов запаса (более 10 %), вычисления повторяют.
3.3.3. Вычисляют общий коэффициент запаса прочности по формуле:
Прочность считается обеспеченной в случае
где [n] = 1,5 - 2,5 - нормативное минимально допустимое значение коэффициента запаса прочности. Конкретное значение [п] из данного диапазона устанавливается применительно к конкретным деталям определенных типов машин на основе опыта предшествующих расчетов в КБ и наблюдением за поведением машин в эксплуатации с учетом ответственности конструкции и других факторов, отмеченных ранее.
3.4. Расчет функции распределений усталостной долговечности при нерегулярном нагружении
Функцией распределения усталостной долговечности называют зависимость между долговечностью детали (наработкой в часах, пробегом в километрах и т.п.) и вероятностью появления усталостной трещины. Эта функция является важнейшей характеристикой безотказности и долговечности детали и служит для решения многих практически важных задач (оценка медианного и γ-процентного ресурса, установление срока службы между капитальными ремонтами, определение объема выпуска запасных частей и т.д.).
Последовательность расчета функции распределения долговечности сводится к следующему:
3.4.1. Вычисляется коэффициент aσ для нормальных напряжений по формуле (32).
3.4.2. Проводится расчет зависимости
относительной долговечности D от коэффициента относительного
уровня нагруженности 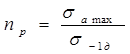 (в предположении действия только
нормальных напряжений)
(в предположении действия только
нормальных напряжений)
Вычисление производится для ряда значений пр в диапазоне 1 - 2,5.
3.4.3. Для каждого из значений пр, выбранного в п. 3.4.2, вычисляют коэффициенты
![]()
![]() (41)
(41)
и квантиль нормального распределения иР по формуле
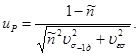 (42)
(42)
Коэффициенты
вариации пределов выносливости валов и осей ![]() определяют по ГОСТ
25.504, коэффициенты вариации уровня нагруженности υεσ - по методике (2).
определяют по ГОСТ
25.504, коэффициенты вариации уровня нагруженности υεσ - по методике (2).
3.4.4. По квантилю иР находится
вероятность разрушения Р %, соответствующая данному nP а следовательно и относительной
долговечности ![]() . По данным парам
чисел
(Р % и
. По данным парам
чисел
(Р % и ![]() ) строят функцию
распределения долговечности в координатах (Р, λσ) или
(Р, Lσ), где Lσ = lσλσ (λσ - число блоков
нагружения до появления усталостной трещины в предположении действия только
нормальных напряжений).
) строят функцию
распределения долговечности в координатах (Р, λσ) или
(Р, Lσ), где Lσ = lσλσ (λσ - число блоков
нагружения до появления усталостной трещины в предположении действия только
нормальных напряжений).
Табличная форма расчета поясняется в примере (см. приложение 9). Аналогично проводится расчет функции распределения долговечности в предположении действия только касательных напряжений, т.е. зависимости Р % от λτ.
3.4.5. Расчет функции распределения долговечности с учетом действия нормальных и касательных напряжений
По функциям распределения величин λσ и λτ, найденным в п. 3.4.4, определяются медианные долговечности λσ, λτ (соответствующие вероятности разрушения Р = 50 %).
Медианную
долговечность ![]() , соответствующую
одновременному действию нормальных и касательных напряжений, определяют по
формуле
, соответствующую
одновременному действию нормальных и касательных напряжений, определяют по
формуле
где ![]()
Среднее квадратическое отклонение случайной величины lg λ определяется по формуле
Величины ![]() и
и ![]() определяют по
формулам:
определяют по
формулам:
![]() (45)
(45)
![]() (46)
(46)
Предполагается, что распределение усталостной долговечности подчиняется логарифмически нормальному закону распределения. В этом случае число блоков нагружения λP соответствующее вероятности разрушения Р %, определяется из уравнения
![]() (47)
(47)
где up - квантиль нормального распределения;
![]() определяется по
уравнению (43), S lgλ - по (44).
определяется по
уравнению (43), S lgλ - по (44).
Наработка LP (в часах, километрах, единицах операций и т.д.) до появления усталостной трещины с вероятностью Р % определяется по формуле
где lб - наработка, соответствующая одному блоку нагружения.
Формула (47) определяет функцию распределения усталостной долговечности вала при совместном действии нормальных и касательных напряжений.
ПРИЛОЖЕНИЕ 1
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
А - площадь поперечного сечения, м2;
a - корректирующий коэффициент при расчетах по корректированной линейной гипотезе суммирования повреждений;
D = Nсум/NG - относительная долговечность;
d - диаметр сплошного вала, м;
Fmax - максимальное осевое усилие растяжения (сжатия), соответствующее Tmax, Н;
К - коэффициент снижения предела выносливости;
Кσ и Kτ - эффективные коэффициенты концентрации напряжений при изгибе и кручении, равные отношению пределов выносливости образцов без концентрации напряжений к пределу выносливости образцов с концентрацией напряжений;
Kdσ, Kdτ - коэффициенты влияния абсолютных размеров поперечного сечения (диаметра вала или оси), равные отношению пределов выносливости образцов без концентрации напряжений диаметром d к пределу выносливости гладких лабораторных образцов диаметром d0 = 7,5 мм при изгибе с вращением;
КFσ, КFτ - коэффициенты влияния шероховатости поверхности, равные отношению пределов выносливости образцов с данным качеством поверхности к пределу выносливости гладкого лабораторного полированного образца;
Kυ - коэффициент влияния поверхностного упрочнения, равный отношению предела выносливости упрочненной детали К пределу выносливости неупрочненной детали;
L - ресурс вала (оси), измеренный в тех же единицах, что и lσ;
Lб - протяженность периода эксплуатации вала, соответствующая одному блоку нагружения и измеряемая в часах работы, днях и других единицах;
К - коэффициент, учитывающий снижение механических свойств (σв, σт, σ-1, τт, τ-1) с ростом размеров заготовок;
![]() ,
, ![]() - изгибающие
моменты от сил, меняющих положение относительно вала в плоскостях zох и уох, где
i
-
индекс сечения, н∙м;
- изгибающие
моменты от сил, меняющих положение относительно вала в плоскостях zох и уох, где
i
-
индекс сечения, н∙м;
Мн - изгибающий момент от сил, не меняющий положение относительно вала, н∙м;
Мп, Мл - изгибающие моменты, действующие справа и слева от данного сечения, н∙м;
![]() - суммарный
изгибающий момент от сил, меняющих положение относительно вала, н∙м;
- суммарный
изгибающий момент от сил, меняющих положение относительно вала, н∙м;
![]() - суммарный
изгибающий момент от сил, не меняющих положение относительно вала, н∙м;
- суммарный
изгибающий момент от сил, не меняющих положение относительно вала, н∙м;
Мmax i - максимальный
изгибающий момент, равный сумме ![]() и
и ![]() н∙м;
н∙м;
mσ, mτ - показатель угла наклона левой ветви кривой усталости;
N - число циклов нагружения;
NG - абсцисса точки перелома кривой усталости;
Nсум - суммарное число циклов действия всех амплитуд за срок службы;
![]() -
коэффициент, характеризующий относительный уровень переменной
нагруженности;
-
коэффициент, характеризующий относительный уровень переменной
нагруженности;
nτσ - запас прочности по пределу текучести при изгибе и растяжении (сжатии);
nтτ - запас прочности по пределу текучести при кручении;
nт - запас прочности по пределу текучести при совместном действии нормальных и касательных напряжений;
nσ, nτ - запасы прочности по пределам выносливости при изгибе и кручении соответственно;
п - общий коэффициент запаса прочности по пределу выносливости при совместном действии нормальных и касательных напряжений;
S lgλσ, S lgλτ - средние квадратические отклонения логарифмов случайных величин λσ и λτ;
Тmax - максимальный крутящий момент, н∙м;
![]() - относительное
число повторения амплитуд τai в укороченном
блоке нагружения;
- относительное
число повторения амплитуд τai в укороченном
блоке нагружения;
![]() - относительное
число повторения амплитуд τai в укороченном
блоке нагружения;
- относительное
число повторения амплитуд τai в укороченном
блоке нагружения;
![]() ,
, ![]() -
составляющие опорных реакций вдоль осей z и у от
сил, меняющих положение относительно вала, Н;
-
составляющие опорных реакций вдоль осей z и у от
сил, меняющих положение относительно вала, Н;
Rн - опорные реакции от сил, не меняющих положение относительно вала, Н;
r - число ступеней в блоке нагружения;
uР - квантиль нормального распределения, соответствующая вероятности разрушения Р;
υσ-1д, υτ-1д - коэффициенты вариации пределов выносливости вала при изгибе и кручении;
υεσ, υετ - коэффициенты вариации уровней нагруженности при действии нормальных а и касательных напряжений;
Wк, Wи - моменты сопротивления поперечного сечения при кручении и изгибе, м3;
λσ, λτ - число блоков нагружения до появления усталостной трещины в предположении действия только нормальных и только касательных напряжений соответственно;
![]() ,
, ![]() - медианные
значения λσ и λτ;
- медианные
значения λσ и λτ;
![]() - медианная
долговечность, выраженная числом блоков нагружения при совместном действии нормальных
и касательных напряжений;
- медианная
долговечность, выраженная числом блоков нагружения при совместном действии нормальных
и касательных напряжений;
vσ, vτ - постоянные для данного металла величины, определяющие чувствительность к концентрации напряжений и влиянию абсолютных размеров поперечного сечения при изгибе и кручении, являющиеся параметрами уравнения подобия усталостного разрушения;
![]() - общее число
циклов нормальных напряжений в блоке нагружения;
- общее число
циклов нормальных напряжений в блоке нагружения;
![]() - общее число
циклов касательных напряжений в блоке нагружения;
- общее число
циклов касательных напряжений в блоке нагружения;
νiбσ, νiбτ - число циклов повторения амплитуд соответственно σаi и τаi в блоке нагружения;
![]() - число циклов
нормальных напряжений в блоке нагружения после отбрасывания ступеней с σai < 0,5σ-1д;
- число циклов
нормальных напряжений в блоке нагружения после отбрасывания ступеней с σai < 0,5σ-1д;
![]() - число циклов
касательных напряжений в блоке нагружения после отбрасывания ступеней с τаi < 0,5τ-1д;
- число циклов
касательных напряжений в блоке нагружения после отбрасывания ступеней с τаi < 0,5τ-1д;
![]() ,
, ![]() -
поправочные
коэффициенты;
-
поправочные
коэффициенты;
σi, τi - нормальные и касательные напряжений в i-м сечении вала, МПа;
σаi, τаi - амплитуды нормальных и касательных напряжений i-й ступени блока нагружения, эквивалентного по повреждающему действию реальному случайному процессу нагружения, МПа;
σa max, τa max - максимальные амплитуды нормальных и касательных напряжений в блоке нагружения, МПа;
![]() ,
, ![]() - средние
значения σa max, τa max, МПа;
- средние
значения σa max, τa max, МПа;
![]() ,
, ![]() - медианные
значения пределов выносливости вала при изгибе и кручении на множестве всех
плавок металла данной марки и возможных отклонений размеров и технологий изготовлений
в пределах допусков, выраженные в номинальных напряжениях, МПа;
- медианные
значения пределов выносливости вала при изгибе и кручении на множестве всех
плавок металла данной марки и возможных отклонений размеров и технологий изготовлений
в пределах допусков, выраженные в номинальных напряжениях, МПа;
![]() ,
, ![]() -
соответственно при изгибе и кручении медианные значения пределов выносливости
на совокупности всех плавок металла данной марки гладких лабораторных образцов
диаметром d0 = 7,5 мм,
изготовленных из заготовок диаметром d равным абсолютному
размеру рассчитываемой детали, МПа;
-
соответственно при изгибе и кручении медианные значения пределов выносливости
на совокупности всех плавок металла данной марки гладких лабораторных образцов
диаметром d0 = 7,5 мм,
изготовленных из заготовок диаметром d равным абсолютному
размеру рассчитываемой детали, МПа;
![]() ,
, ![]() - соответственно
при изгибе и кручении медианные значения пределов выносливости гладких
лабораторных образцов диаметром d0 = 7,5 мм,
изготовленных из заготовок металла данной марки размерами 10 - 20 мм, МПа;
- соответственно
при изгибе и кручении медианные значения пределов выносливости гладких
лабораторных образцов диаметром d0 = 7,5 мм,
изготовленных из заготовок металла данной марки размерами 10 - 20 мм, МПа;
σВ - временное сопротивление (предел прочности) стали данной марки при растяжении, МПа;
σа экв, τа экв - эквивалентные напряжения при изгибе и кручении, МПа;
σа, τа - амплитуды напряжений циклов при изгибе и кручении, МПа;
ψа, ψа - коэффициенты чувствительности к асимметрии цикла напряжений.
ПРИЛОЖЕНИЕ 2
СИЛЫ НА РАБОЧИХ ЭЛЕМЕНТАХ МУФТ И В ЗАЦЕПЛЕНИИ ЗУБЧАТЫХ И ЧЕРВЯЧНЫХ ПЕРЕДАЧ
Неуравновешенная
составляющая Fнt окружной силы ![]() на рабочих
элементах муфт
на рабочих
элементах муфт
|
Расчет вала на статическую прочность и усталость |
Расчет подшипников качения на долговечность |
|
|
Кулачковая |
|
|
|
Пальцевая |
|
|
|
Цепная |
|
|
|
Зубчатая |
|
|
|
Гидромуфта |
|
|
Окружная сила на
рабочих элементах муфт ![]() , где dм - диаметр
начальной окружности муфты
, где dм - диаметр
начальной окружности муфты
Силы в зацеплении зубчатых и червячных передач
|
Силы |
||||
|
окружные |
радиальные |
осевые |
||
|
Зубчатая цилиндрическая |
прямозубая |
|
|
|
|
косозубая |
|
|
||
|
шевронная |
|
|||
|
Зубчатая коническая |
прямозубая |
|
|
|
|
Червячная |
Колесо |
|
|
|
|
Червяк |
|
|
|
|
Силы в зацеплении конических зубчатых передач с круговыми зубьями (ГОСТ 19326)
|
Силы, возникающие в передаче (ведущий элемент-шестерня), |
||
|
осевые |
радиальные |
|
|
(при Fx > 0 усилие направлено от вершины делительного конуса шестерни) |
(усилие направлено к оси шестерни) |
|
|
(усилие направлено от вершины делительного конуса колеса) |
(при Fr>0 усилие направлено к оси колеса) |
|
|
(усилие направлено от вершины делительного конуса шестерни) |
(при Fr>0 усилие направлено к оси шестерни) |
|
|
(при Fx>0 усилие направлено от вершины делительного конуса колеса) |
(усилие направлено к оси колеса) |
|
Примечание. Если в передаче ведущий элемент - колесо, то условия для него определяются по строке «шестерня», а для шестерни - по строке «колесо».
ПРИЛОЖЕНИЕ 3
Формулы для определения установочных баз подшипников
|
Формула |
||
|
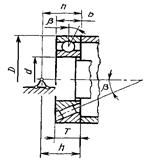
Радиальные. Радиально-упорные 2- и 4-рядные. Радиально-упорные сдвоенные, когда углы контакта β направлены в разные стороны |
|
|
|
Радиальные подшипники, поставленные по два на опоре |
|
|
|
Радиально-упорные однорядные
Роликовые подшипники конические однорядные |
или
|
|
|
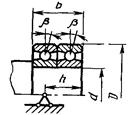
Радиально-упорные сдвоенные, когда углы контакта направлены в одну сторону |
|
|
|
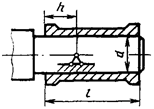
Подшипники скольжения. |
h=0,3 l, но не более 0,5 d |
|
ПРИЛОЖЕНИЕ 4
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ ВАЛОВ С ЭВОЛЬВЕНТНЫМИ ШЛИЦАМИ И ВАЛА-ШЕСТЕРНИ
Геометрические характеристики поперечных сечений валов с эвольвентными шлицами по ГОСТ 6033
|
D × m × z, мм |
Wи, см3 |
Wк, см3 |
I, см4 |
А, см2 |
D × m × z, мм |
Wи, см3 |
Wк, см3 |
I, см4 |
А, см2 |
|
|
20×1,25×14 |
0,579 |
1,159 |
0,572 |
2,657 |
120×3×38 |
150,0 |
300,0 |
895,3 |
105,9 |
|
|
25×1,25×18 |
1,201 |
2,403 |
1,487 |
4,298 |
120×5×22 |
138,3 |
276,6 |
823,0 |
101,3 |
|
|
30×1,25×22 |
2,161 |
4,322 |
3,215 |
6,331 |
130×3×42 |
192,7 |
385,3 |
1246 |
125,0 |
|
|
30×1,25×26 |
3,532 |
7,065 |
6,138 |
8,757 |
130×5×24 |
178,6 |
357,2 |
1152 |
119,9 |
|
|
35×2×16 |
3,198 |
6,397 |
5,533 |
8,275 |
130×8×15 |
160,7 |
321,4 |
1032 |
112,8 |
|
|
40×1,25×30 |
5,389 |
10,78 |
10,71 |
11,58 |
140×3×45 |
242,5 |
485,0 |
169,0 |
145,6 |
|
|
40×2×18 |
4,921 |
9,841 |
9,743 |
11,00 |
140×5×26 |
226,1 |
452,2 |
15,71 |
140,1 |
|
|
45×1,25×34 |
7,804 |
16,61 |
17,46 |
14,79 |
150×3×48 |
300,3 |
600,5 |
2243 |
167,7 |
|
|
50×1,25×38 |
10,85 |
21,70 |
26,99 |
18,39 |
150×8×17 |
255,9 |
511,9 |
1899 |
153,5 |
|
|
50×2×24 |
10,10 |
20,21 |
25,06 |
17,69 |
160×3×52 |
366,8 |
733,6 |
2923 |
191,5 |
|
|
55×2×26 |
13,69 |
27,37 |
37,36 |
21,60 |
160×5×З0 |
344,9 |
689,8 |
2742 |
185,2 |
|
|
55×3×17 |
12,57 |
25,13 |
84,18 |
20,58 |
170×5×32 |
417,4 |
834,8 |
3527 |
210,1 |
|
|
60×2×28 |
18,00 |
36,01 |
53,65 |
25,90 |
170×8×20 |
384,3 |
768,6 |
3236 |
200,6 |
|
|
60×3×18 |
16,61 |
33,21 |
49,32 |
24,75 |
180×3×58 |
527,4 |
1055 |
4731 |
243,7 |
|
|
65×2×31 |
23,20 |
46,41 |
74,95 |
30,62 |
180×5×34 |
499,4 |
989,9 |
4470 |
236,6 |
|
|
65×3×20 |
21,55 |
43,11 |
69,40 |
29,39 |
190×5×36 |
591,6 |
1183 |
5591 |
264,7 |
|
|
70×2×34 |
29,29 |
58,57 |
101,9 |
35,72 |
190×8×22 |
548,6 |
1097 |
5168 |
253,8 |
|
|
70×3×22 |
27,36 |
54,73 |
94,95 |
34,40 |
190×10×17 |
520,7 |
1041 |
4895 |
246,4 |
|
|
75×2×36 |
36,36 |
72,71 |
135,6 |
41,32 |
200×5×38 |
694,5 |
1389 |
6910 |
294,3 |
|
|
75×3×24 |
34,10 |
68,20 |
126,9 |
39,78 |
220×5×42 |
934,7 |
1869 |
10230 |
358,2 |
|
|
80×2×38 |
44,45 |
88,89 |
176,9 |
47,08 |
240×5×46 |
1225 |
2450 |
14640 |
428,5 |
|
|
80×3×25 |
41,87 |
83,75 |
166,2 |
45,56 |
260×5×50 |
1370 |
3139 |
20330 |
505,0 |
|
|
85×3×27 |
50,78 |
101,6 |
214,3 |
51,75 |
300×5×58 |
2442 |
4883 |
36500 |
676,9 |
|
|
85×5×15 |
45,26 |
90,52 |
190,1 |
48,48 |
340×8×41 |
3439 |
6878 |
58190 |
854,0 |
|
|
90×3×28 |
60,76 |
121,5 |
271,6 |
58,28 |
380×8×46 |
4859 |
9718 |
91930 |
1074 |
|
|
90×5×16 |
54,57 |
109,1 |
242,8 |
54,85 |
400×8×48 |
5694 |
11390 |
113400 |
1193 |
|
|
95×3×30 |
72,14 |
144,3 |
340,5 |
65,27 |
440×8×54 |
7649 |
15300 |
167700 |
1450 |
|
|
95×5×18 |
65,29 |
130,6 |
306,9 |
61,69 |
480×8×58 |
10000 |
20000 |
239200 |
1733 |
|
|
100×3×32 |
84,81 |
169,6 |
421,5 |
72,63 |
500×8×61 |
11340 |
22690 |
282700 |
1884 |
|
|
100×5×18 |
76,88 |
153,8 |
380,6 |
68,76 |
|
|
|
|
|
|
|
110×3×35 |
114,3 |
228,7 |
625,5 |
88,51 |
|
|
|
|
|
|
|
110×5×20 |
104,6 |
209,2 |
570,1 |
84,24 |
|
|
|
|
|
|
Геометрические характеристики вала-шестерни в сечении по зубьям
|
Формулы |
|
|
Момент инерции при расчетах на жесткость |
где δI - коэффициент, учитывающий коэффициент смещения и количество зубьев вала-шестерни, принимается по графику (черт. 1); d - диаметр делительной окружности; d0 - диаметр центрального отверстия; d и d0 - принимаются по графику |
|
Момент сопротивления при расчете на изгиб |
где da - диаметр вершин зубьев |
|
Момент сопротивления при расчете на кручение |
Wк=2Wи |
|
Площадь сечения при расчете на растяжение (сжатие) |
где δS - коэффициент, учитывающий коэффициент смещения и количество зубьев, принимается по графику (черт. 1) |
Примечание. Для косозубых валов-шестерен расчет по данным формулам будет идти в запас прочности.
Графики для определения коэффициентов δI, δS
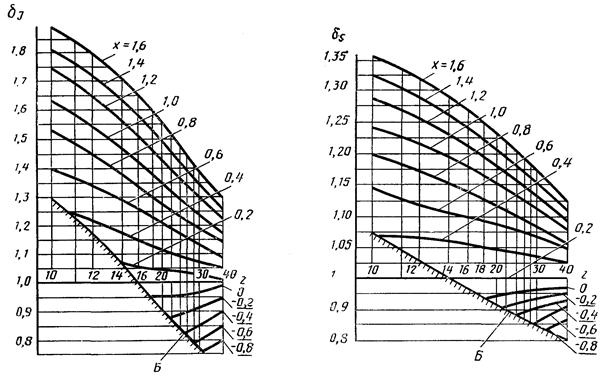
Б - блокирующая линия из условия отсутствия подрезания зубьев
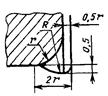
ПРИЛОЖЕНИЕ 5
МЕТОДЫ КОНСТРУКТИВНОГО УПРОЧНЕНИЯ ВАЛОВ В МЕСТАХ ПОСАДКИ ПОДШИПНИКОВ
Несущая способность многих валов машин ограничена в связи с большими значениями эффективного коэффициента концентрации напряжений у края напрессованной детали (в частности внутреннего кольца подшипника качения).
Во всех таких случаях несущая способность вала может быть существенно увеличена, если в указанной зоне концентрации напряжений выполнить проточку по одному из способов, указанных ниже.
Следует иметь в виду, что после разгрузки зоны концентрации напряжений у края внутреннего кольца подшипника опасным и недостаточно прочным может оказаться другое сечение в случае, если не будет проявляться фреттинг-коррозия.
Эффективный коэффициент концентрации напряжений для проточки определяется, как обычно, по наименьшему радиусу профиля проточки.
|
Метод конструктивного упрочнения |
Эскиз |
|
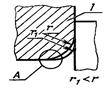
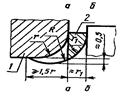
1. Случай отсутствия разгрузки зоны А концентрации напряжений у края детали 1 |
|
|
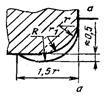
2. Случай разгрузки концентратора с помощью проточки, очерченной радиусом R с сохранением галтели радиуса r1 |
|
|
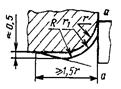
3. Торец уступа оставлен на месте (а-а), проточка радиуса R сопрягается с галтелью радиуса r1 |
|
|
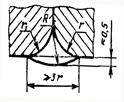
4. Торец уступа оставлен на месте (а-а), проточка радиуса r сопрягается с конусным переходом |
|
|
5. Проточка на стыке двух деталей (двух подшипников) |
|
|
6. Проточка для случая, когда деталь (подшипник) не граничит с уступом вала |
ПРИЛОЖЕНИЕ 6
КОЭФФИЦИЕНТЫ Kυ ВЛИЯНИЯ ТЕХНОЛОГИЧЕСКИХ МЕТОДОВ ПОВЕРХНОСТНОГО УПРОЧНЕНИЯ НА ПРЕДЕЛЫ ВЫНОСЛИВОСТИ.
Поверхностная закалка с нагревом токами высокой частоты (изгиб с вращением, глубина закаленного слоя 0,9 - 1,5 мм)
|
Кυ для образцов диаметром |
||
|
7 - 20 мм |
30 - 40 мм |
|
|
Без концентрации напряжений |
1,3 - 1,6 |
1,2 - 1,5 |
|
С концентрацией напряжений |
1,6 - 2,8 |
1,5 - 2,5 |
Химико-термическая обработка
|
Вид образца |
Кυ для образцов диаметром |
||
|
8 - 15 мм |
30 - 40 мм |
||
|
Азотирование при глубине слоя 0,1 - 0,4 мм, твердости слоя НВ 730 - 970 |
Без концентрации напряжений |
1,15 - 1,25 |
1,10 - 1,15 |
|
С концентрацией напряжений (поперечное отверстие, надрез) |
1,90 - 3,00 |
1,30 - 2,00 |
|
|
Цементация при глубине слоя 0,2 - 0,6 |
Без концентрации напряжений |
1,20 - 2,10 |
1,10 - 1,50 |
|
С концентрацией напряжений |
1,50 - 2,50 |
1,20 - 2,00 |
|
|
Цианирование при глубине слоя 0,2 мм |
Без концентрации напряжений |
1,80 |
- |
Поверхностный наклеп
|
Вид образца |
Кυ для образцов диаметром |
||
|
7 - 20 мм |
30 - 40 мм |
||
|
Обкатка роликом |
Без концентрации напряжений |
1,20 - 1,40 |
1,10 - 1,25 |
|
С концентрацией напряжений |
1,50 - 2,20 |
1,30 - 1,80 |
|
|
Обдувка дробью |
Без концентрации напряжений |
1,10 - 1,30 |
1,10 - 1,20 |
|
С концентрацией напряжений |
1,40 - 2,50 |
1,10 - 1,50 |
|
ПРИЛОЖЕНИЕ 7
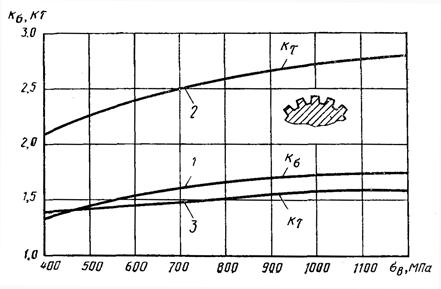
ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ Кσ и Кτ ДЛЯ РАЗЛИЧНЫХ КОНСТРУКТИВНЫХ ЭЛЕМЕНТОВ
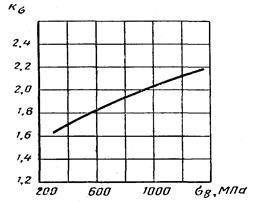
Эффективные коэффициенты концентрации напряжений для валов с поперечным отверстием (для нетто-сечений) при изгибе
![]()
![]()
![]()
![]()
(σв в МПа)
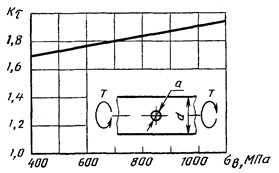
Эффективные коэффициенты концентрации напряжений для валов с поперечным отверстием (для нетто сечений) при кручении
Кτ = 0,363×10-3 σв + 1,54 (σв в МПа)
Эффективные коэффициенты концентрации напряжений для валов с отверстием при растяжении-сжатии
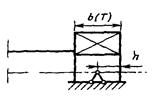
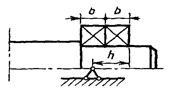
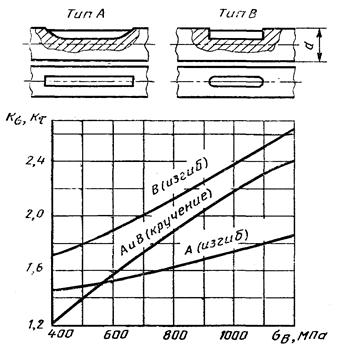
Коэффициенты Кσ, Кτ для валов со шпоночными пазами типа А и В
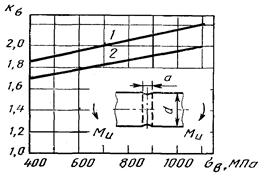
Эффективные коэффициенты концентрации напряжений при изгибе Кσ и кручении Кτ для валов со шлицами
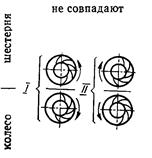
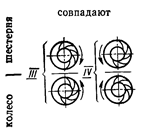
1 - прямобочные и эвольвентные шлицы; 2 - прямобочные шлицы; 3 - эвольвентные шлицы
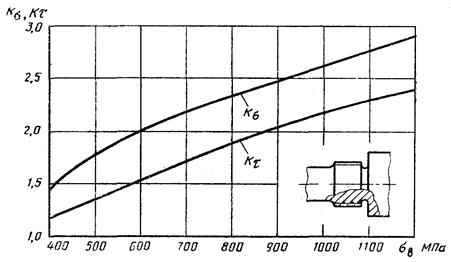
Эффективные коэффициенты Кσ и Кτ для валов с выточками
ПРИЛОЖЕНИЕ 8
ЗНАЧЕНИЯ ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ Ф И КВАНТИЛИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ иР
Функция нормального распределения
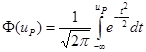
|
Ф(иР) |
иР |
Ф(иР) |
иР |
Ф(иР) |
иР |
Ф(иР) |
иР |
Ф(иР) |
|
|
0,00 |
0,5000 |
1,00 |
0,8413 |
2,00 |
0,97725 |
3,00 |
0,92865 |
4,00 |
0,94683 |
|
0,05 |
0,5199 |
1,05 |
0,8531 |
2,05 |
0,97982 |
3,05 |
0,92885 |
4,05 |
0,94743 |
|
0,10 |
0,5398 |
1,10 |
0,8643 |
2,10 |
0,98214 |
3,10 |
0,93032 |
4,10 |
0,94793 |
|
0,15 |
0,5596 |
1,15 |
0,8749 |
2,15 |
0,98422 |
3,15 |
0,93184 |
4,15 |
0,94834 |
|
0,20 |
0,5793 |
1,20 |
0,8849 |
2,20 |
0,98510 |
3,20 |
0,93313 |
4,20 |
0,94866 |
|
0,25 |
0,5987 |
1,25 |
0,8943 |
2,25 |
0,98777 |
3,25 |
0,93423 |
4,25 |
0,94893 |
|
0,30 |
0,6179 |
1,30 |
0,9032 |
2,30 |
0,98928 |
3,30 |
0,93517 |
4,30 |
0,95146 |
|
0,35 |
0,6368 |
1,35 |
0,9115 |
2,35 |
0,99061 |
3,35 |
0,93596 |
4,35 |
0,95319 |
|
0,40 |
0,6554 |
1,40 |
0,9192 |
2,40 |
0,99180 |
3,40 |
0,93663 |
4,40 |
0,95459 |
|
0,45 |
0,6736 |
1,45 |
0,9265 |
2,45 |
0,99286 |
3,45 |
0,93720 |
4,45 |
0,95571 |
|
0,50 |
0,6915 |
1,50 |
0,9332 |
2,50 |
0,99379 |
3,50 |
0,93767 |
4,50 |
0,95660 |
|
0,55 |
0,7088 |
1,55 |
0,9394 |
2,55 |
0,99461 |
3,55 |
0,93807 |
4,55 |
0,95732 |
|
0,60 |
0,7257 |
1,60 |
0,9452 |
2,60 |
0,99534 |
3,60 |
0,93841 |
4,60 |
0,95789 |
|
0,65 |
0,7422 |
1,65 |
0,9505 |
2,65 |
0,99597 |
3,65 |
0,93869 |
4,65 |
0,95834 |
|
0,70 |
0,7580 |
1,70 |
0,9554 |
2,70 |
0,99653 |
3,70 |
0,93892 |
4,70 |
0,95870 |
|
0,75 |
0,7734 |
1,75 |
0,9599 |
2,75 |
0,99702 |
3,75 |
0,94116 |
4,75 |
0,95898 |
|
0,80 |
0,7881 |
1,80 |
0,9641 |
2,80 |
0,99744 |
3,80 |
0,94274 |
4,80 |
0,96207 |
|
0,85 |
0,8023 |
1,85 |
0,9678 |
2,85 |
0,99781 |
3,85 |
0,94409 |
4,85 |
0,96383 |
|
0,90 |
0,8159 |
1,90 |
0,9713 |
2,90 |
0,99813 |
3,90 |
0,94519 |
4,90 |
0,96521 |
|
0,95 |
0,8289 |
1,95 |
0,9744 |
2,95 |
0,99841 |
3,95 |
0,94609 |
4,95 5,00 5,05 5,09 |
0,96629 0,96713 0,96779 0,96821 |
Примечание: определение Ф(ир) для отрицательных ир производится по формуле Ф(ир) = 1 - Ф(-иР).
Пример: пусть требуется найти Ф(иР = -1);
по таблице находим Ф(-иР) = Ф(1) = 0,8413.
Следовательно Ф(иР = - 1) = 1 - 0,8413 = 0,1587. В правой части таблицы приняты сокращенные записи: 0,95660 = 0,99999660; то есть цифра, стоящая сверху у девятки, означает число девяток после запятой.
Значения квантили иР нормального распределения
|
Р % |
иР |
Р % |
иР |
Р % |
иР |
|
50 |
0 |
80 |
0,842 |
98 |
2,054 |
|
54 |
0,126 |
85 |
1,036 |
99 |
2,326 |
|
60 |
0,253 |
90 |
1,282 |
99,50 |
2,576 |
|
65 |
0,385 |
95 |
1,645 |
99,80 |
2,878 |
|
70 |
0,524 |
97 |
1,881 |
99,90 |
3,090 |
|
75 |
0,674 |
97,5 |
1,960 |
99,99 |
3,719 |
Примечание. и1-Р = -иР; например, и0,40 = - и0,60 = - 0,253, где и0,40 - квантиль, соответствующая вероятности 40 %.
ПРИЛОЖЕНИЕ 9
ПРИМЕРЫ РАСЧЕТА
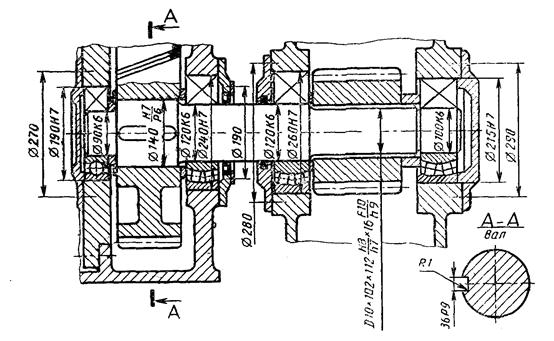
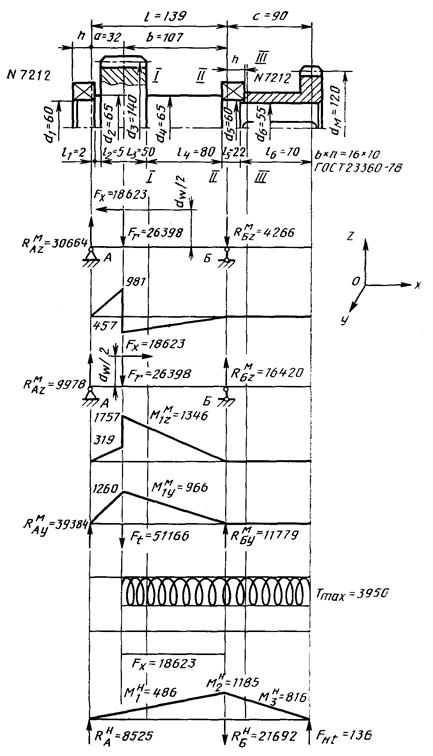
Пример 1. Расчет вертикального вала редуктора механизма поворота портального крана
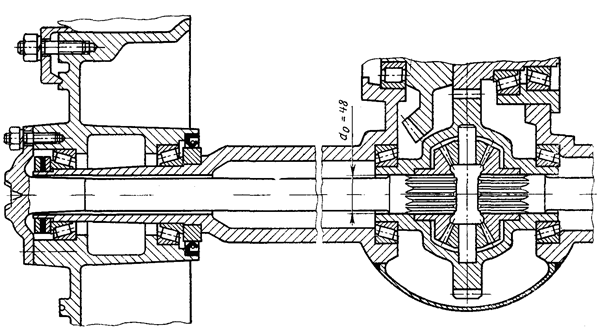
Чертеж вала
редуктора механизма поворота портального крана представлен на черт. 8. Вал изготовлен из стали 45 с
медианным значением предела прочности ![]() = 735 МПа, твердость 220 НВ. Вал
укреплен в 4 подшипниках качения, так что при изгибе представляет собой дважды
статически неопределимую систему. Вал подвергался тензометрированию в условиях
эксплуатации. Датчики были наклеены в средней части вала между подшипниками.
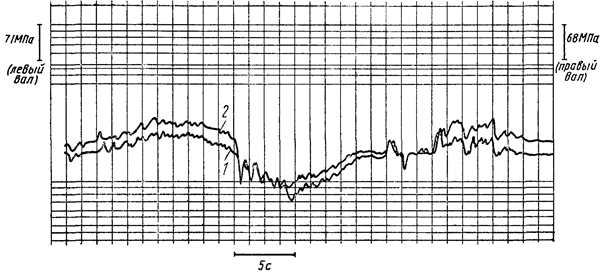
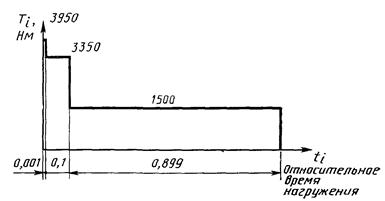
Осциллограммы изменения крутящего момента на валах левого (1) и правого (2)
редукторов механизма поворота крана представлены на черт. 9.
= 735 МПа, твердость 220 НВ. Вал
укреплен в 4 подшипниках качения, так что при изгибе представляет собой дважды
статически неопределимую систему. Вал подвергался тензометрированию в условиях
эксплуатации. Датчики были наклеены в средней части вала между подшипниками.
Осциллограммы изменения крутящего момента на валах левого (1) и правого (2)
редукторов механизма поворота крана представлены на черт. 9.
Построение эпюр изгибающих моментов и вычисление амплитуд нормальных напряжений от изгиба, а также данные тензометрирования показали, что эти напряжения весьма малы и их можно не учитывать при оценке накопления усталостных повреждений. Поэтому прочность вала определяется амплитудами касательных напряжений от кручения, которые имеют наибольшее значение в месте посадки правой шестерни на шлицевое сечение вала Ø 112 мм с прямобочными шлицами.
Вал редуктора механизма поворота портального крана
Осциллограммы изменения крутящего момента на левом и правом валах редуктора
1. Расчет характеристик сопротивления усталости вала
Медианные значения пределов выносливости стали подсчитываем по формулам (13)
![]() = (0,55 -
0,0001 ×
= (0,55 -
0,0001 × ![]() ) ×
) × ![]() = (0,55 - 0,0001 × 735)
- 735 = 350 МПа;
= (0,55 - 0,0001 × 735)
- 735 = 350 МПа;
![]() = 0,55
= 0,55![]() = 0,55 × 350 =
193 МПа.
= 0,55 × 350 =
193 МПа.
Определение предела выносливости шлицевого вала Ø 112 мм с напрессованной деталью производим вначале по формуле (21).
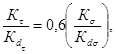
где Кσ/Кdσ определяется по формулам (17)-(20). Для данного вала имеем:
d = 112 мм; ![]() = 735 МПа;
р > 25 МПа;
= 735 МПа;
р > 25 МПа;
По (18) имеем:
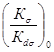 =
0,38 + 1,48 lg∙d = 0,38 + 1,48∙lg 112 = 3,41.
=
0,38 + 1,48 lg∙d = 0,38 + 1,48∙lg 112 = 3,41.
По (19):
ξ' = 0,305 + 0,00139σв = 0,305 + 0,00139 × 735 = 1,327.
По (20): ξ" = 1 для р > 25 МПа.
По (17):
![]() =
=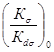 ξ' ξ"
= 3,41 × 1,327 × 1 = 4,53.
ξ' ξ"
= 3,41 × 1,327 × 1 = 4,53.
По (21): ![]() =
=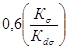 =0,6 ×
4,53=2,72.
=0,6 ×
4,53=2,72.
Далее по черт. 6 находим для вала с прямобочными шлицами
для ![]() =
735 МПа: Кτ = 2,50;
=
735 МПа: Кτ = 2,50;
для определения Кdτ по формуле (23)
необходимо найти значение ντ для данной стали.
По (24) имеем:
vσ = 0,19 -
0,000125 × σв = 0,19 - 0,000125 × 735 =
0,098 ![]() 0,1.
0,1.
По (25): vτ = 1,5 × νσ = 1,5 × 0,1 = 0,15;
По (23): 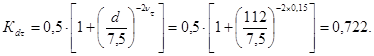
Значение Кτ/Кdτ равняется
![]()
Принимаем из двух значений последнее, как наибольшее. Шероховатость поверхности шлицев составляет Rz = 25 мкм. По (15) определяем коэффициент влияния качества обработки поверхности при изгибе
KFσ = 1 - 0,22∙(lg![]() - 1)∙lg Rz = 1 - 0,22∙(lg
- 1)∙lg Rz = 1 - 0,22∙(lg ![]() )∙lg 25,0 = 0,824.
)∙lg 25,0 = 0,824.
По (16) имеем
KFτ = 0,575 × KFσ + 0,425 = 0,575 × 0,824 + 0,425 = 0,899.
Коэффициент К, характеризующий влияние всех факторов на предел выносливости, находим по (14) при Kυ = 1
![]()
Предел выносливости данного вала в рабочем сечении при кручении составляет
![]() МПа.
МПа.
При изгибе для вала с напрессовкой уже было подсчитано
![]()
для вала с прямобочными шлицами по черт. 6 Кσ = 1,62; значение Кdσ находим по формуле (22)
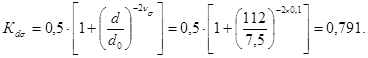
![]()
Таким образом, при изгибе преобладающее значение имеет напрессовка и
![]()
![]()
Предел выносливости шлицевого вала с напрессовкой при изгибе равен
![]() МПа.
МПа.
Рассчитаем теперь предел выносливости вала с эвольвентнымн шлицами и напрессовкой. Для вала с эвольвентными шлицами по черт. 5 находим Кτ = 1,5; значение Кdτ = 0,722; следовательно
![]() - по шлицам. По
условию прочности прессового соединения ранее имели
- по шлицам. По
условию прочности прессового соединения ранее имели
![]() Из этих двух
значений принимаем наибольшее
Из этих двух
значений принимаем наибольшее
![]()
Далее по (14):
![]()
Предел выносливости вала с эвольвентными шлицами без упрочнения составляет
![]() МПа.
МПа.
При введении наклепа поверхности шлиц и впадин предел выносливости может быть повышен в 1,2 - 1,5 раза (приложение 6, табл. 10).
Примем Кυ = 1,3. В этом случае предел выносливости вала с эвольвентными шлицами и наклепом составит
τ-1д = 68,2 × 1,3 = 88,7 МПа.
Параметры кривой усталости могут быть приняты следующими:
m = 3,5; NG = 2 × 106 циклов, коэффициент вариации υσ-1д = 0,1.
2. Расчет функции распределения усталостной долговечности вала
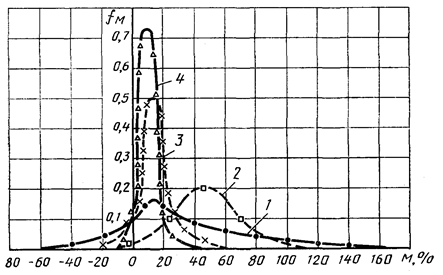
Осциллограммы (черт. 9) обрабатывались по методу полных циклов (ГОСТ 25.101). Ступенчатая аппроксимация функции распределения амплитуд касательных напряжений от кручения представлена в табл. 13. В качестве блока нагружения выбраны одни сутки работы крана. Общее число циклов в блоке с учетом коэффициента средней временной загрузки портальных кранов составляет νδ = 6474 цикла.
Вследствие небольшой длины вала и наличия 4 подшипников изгибные напряжения оказались весьма малыми. По результатам тензометрирования получалась наибольшая амплитуда нормальных напряжений от изгиба σа max = 28 МПа, что меньше половины предела выносливости вала в шлицевом сечении при изгибе (σ-1д = 73,8 МПа, как следует из предыдущего расчета). Так как при расчете усталостной долговечности амплитуды σаi < 0,5σ-1д отбрасываются, как не влияющие на накопление усталостных повреждений, то амплитуд σаi > 0,5σ-1д не остается, и расчет усталостной долговечности при изгибе производить не следует. Поэтому производим расчет только на кручение.
Вначале рассчитываем вал с прямобочными шлицами, примененный в редукторе, для которого τ-1д = 54,1 МПа.
Находим 0,5 × τ-1д = 0,5 × 54,1 = 27,0 МПа и отбрасываем амплитуды τаi < 27,0 МПа, как показано в табл. 13. Суммируя величины viб от i = 1 до i = 8 находим число циклов в укороченном блоке (9-я и 10-я ступени отброшены)
![]()
Далее находим ![]() и произведения
и произведения ![]() (6-я строка),
суммируя которые по i, находим ξ по формуле (33):
(6-я строка),
суммируя которые по i, находим ξ по формуле (33):
![]()
Это число записано в последней графе сумм в 6-й строке. По формуле (34) находим корректирующий коэффициент ар
![]()
Подсчет
усталостной долговечности выполняется по формуле (40) и сведен в табл. 15.
Предварительно находим значения сумм, стоящих в знаменателе (40), для
чего вычисляем (τai/τa max)m при m=3,5 (7-я
строка) и произведения (τai/τa max)m![]() стоящие в 8-й
строке.
стоящие в 8-й
строке.
Для расчета
долговечности по параметру вероятности разрушения задаемся несколькими
значениями nР (nР = 2,0; 1,5; 1,2
при τ-1д = 54,1 МПа), записанными
в табл. 16.
Далее находим 1/пр, ![]() и значения сумм ∑:
и значения сумм ∑:
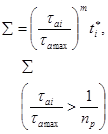
записанных в 1-й, 2-й и 3-й строках табл. 16 соответственно.
Например, при
nР = 2 необходимо
просуммировать числа 8 строки табл. 13, соответствующие ![]() = 0,5, то есть
числа для i, равного от 1 до
6:
= 0,5, то есть
числа для i, равного от 1 до
6:
∑ = 0,0541 + 0,0547 + 0,0223 + 0,0430 + 0,0061 + 0,0062 = 0,186
(ибо для i ≥ 7,
![]() ).
).
Далее вычисляются по (40) значения относительных долговечностей
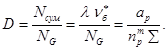
Эти величины записаны в 4-й строке табл. 16. Например, при nР = 2 имеем
![]()
Далее вычисляются долговечности в числе блоков нагружения
![]()
Так при пр = 2 имеем
![]()
(5-я строка), lg λ = 2,33 (9-я строка).
Для подсчета вероятностей разрушения по формуле (42) примем:
![]() = 54,1 МПа;
= 54,1 МПа; ![]() = 85 МПа;
= 85 МПа; ![]() = 0,1;
= 0,1; ![]() = 0,15.
= 0,15.
По (41)
находим ![]() и
и
![]() записанные в 6-й
строке табл. 16.
записанные в 6-й
строке табл. 16.
Далее, по (42)
находим квантили нормального распределения up,
соответствующие вероятности разрушения Р %; так для пр
= 2 имеем: ![]() = 1,273 и
= 1,273 и
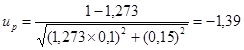 (7-я
строка).
(7-я
строка).
По данному значению up по таблице нормального распределения путем линейной интерполяции находим вероятность разрушения
Р = Ф(-1,39) = 1-Ф(1,39) = 0,08226
или Р = 8,2 % (8-я строка табл. 16).
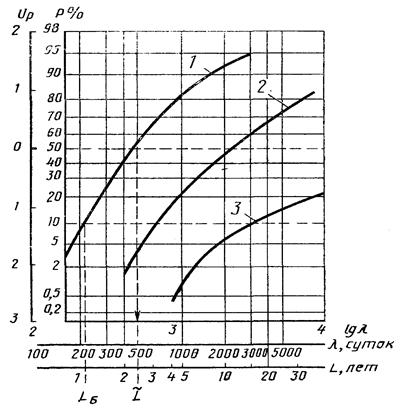
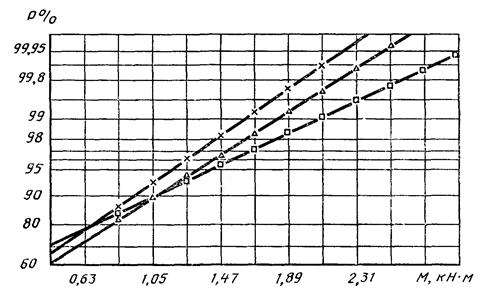
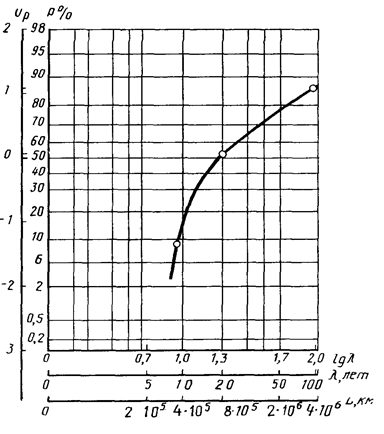
На черт. 10 на
логарифмически нормальной вероятностной бумаге построена подсчитанная указанным
образом для τ-1д = 54,1 МПа
функция распределения усталостной долговечности вала (линия 1). По оси абсцисс
отложена усталостная долговечность λ в числе блоков нагружения (в данном
случае - в числе суток работы, так как за блок приняты одни сутки), а также в
годах работы
L = ![]() лет, в
предположении, что портовый кран работает 210 суток в году. По оси ординат
отложены квантили up в равномерном
масштабе и соответствующие им вероятности разрушения Р % в масштабе,
вытекающем из нормального закона распределения (связь между up и Р %
дается таблицами нормального распределения). Пунктирная линия, проходящая на
уровне up = 0, Р
=
50 %, пересекает линию 1 в точке, абсцисса которой равна медианной
долговечности
лет, в
предположении, что портовый кран работает 210 суток в году. По оси ординат
отложены квантили up в равномерном
масштабе и соответствующие им вероятности разрушения Р % в масштабе,
вытекающем из нормального закона распределения (связь между up и Р %
дается таблицами нормального распределения). Пунктирная линия, проходящая на
уровне up = 0, Р
=
50 %, пересекает линию 1 в точке, абсцисса которой равна медианной
долговечности ![]() = 500 суток или
= 500 суток или ![]() = 2,4 года
эксплуатации. Горизонтальная линия на уровне Р = 10 % определяет
γ-процентный ресурс вала (при вероятности безотказной работы γ = 1 - Р
= 90 %), а именно Lγ = 1 год. Эти
цифры означают, что в среднем можно ожидать поломки, примерно, 10 % работающих
валов наработки в эксплуатации 1 год и поломки половины валов наработки ~ 2,5
года. Эти цифры подтверждаются большим числом поломок валов после указанных
наработок.
= 2,4 года
эксплуатации. Горизонтальная линия на уровне Р = 10 % определяет
γ-процентный ресурс вала (при вероятности безотказной работы γ = 1 - Р
= 90 %), а именно Lγ = 1 год. Эти
цифры означают, что в среднем можно ожидать поломки, примерно, 10 % работающих
валов наработки в эксплуатации 1 год и поломки половины валов наработки ~ 2,5
года. Эти цифры подтверждаются большим числом поломок валов после указанных
наработок.
Так как
долговечность и надежность вала, оцениваемая вероятностью безотказной работы до
заданной наработки, недостаточны, необходимо предусмотреть меры их повышения.
Из черт. 6
следует, что существенного снижения эффективных коэффициентов концентрации Кτ
шлицевого вала можно добиться заменой прямобочных шлиц на эвольвентные. Из
предыдущего расчета следует, что предел выносливости вала с эвольвентными
шлицами и напрессовкой составляет τ-1д = 68,2 МПа.
Расчет функции распределения усталостной долговечности вала с эвольвентными
шлицами дан в табл. 14 и 15. В этом случае из исходного
блока нагружения отброшены амплитуды τаi ≤ 0,5τ-1д = 0,5 × 68,2 = 34,1 МПа, то есть
оставлены амплитуды для i от 1 до 7. Число циклов в
укороченном блоке ![]() = 829. Подсчитывается новое значение
ξ=0,660 и ар = 0,432;
= 829. Подсчитывается новое значение
ξ=0,660 и ар = 0,432; ![]() Далее вычисления ведутся как
и в предыдущем случае
(табл.
14
и 15).
Функция распределения усталостной долговечности для вала с эвольвентными шлицами
представлена линией 2 на черт. 10. Видно, что медианная долговечность
Далее вычисления ведутся как
и в предыдущем случае
(табл.
14
и 15).
Функция распределения усталостной долговечности для вала с эвольвентными шлицами
представлена линией 2 на черт. 10. Видно, что медианная долговечность ![]() = 10 лет,
гамма-процентная долговечность Lγ = 3,5 года (при γ = 90 %. Р =
1 - γ
=10
%). Таким образом, получено существенное увеличение долговечности и надежности
однако и оно может быть признано недостаточным.
= 10 лет,
гамма-процентная долговечность Lγ = 3,5 года (при γ = 90 %. Р =
1 - γ
=10
%). Таким образом, получено существенное увеличение долговечности и надежности
однако и оно может быть признано недостаточным.
Дальнейшее
повышение долговечности может быть достигнуто путем применения поверхностного
упрочнения наклепом. Предел выносливости при кручении вала с эвольвентными
шлицами и наклепом составляет τ-1д = 88,7 МПа, как было вычислено
ранее. Подсчет усталостной долговечности для этого вала представлен
в табл. 16.
В данном случае в блоке нагружения остается 6 ступеней, ![]() = 560; ар =
0,515;
= 560; ар =
0,515; ![]() Функция
распределения долговечности представлена линией 3 на черт. 10, из
которого имеем Lγ = 15 лет. Медианная
долговечность становится неограниченно большой, как следует из процедуры
вычислений, ибо n < 1. Таким образом введение
эвольвентных шлиц и наклепа поверхности позволит увеличить γ-процентный
ресурс в 15 раз, а медианную долговечность на много порядков, что вполне
обеспечивает надежную работу вала без увеличения его габаритов и веса.
Функция
распределения долговечности представлена линией 3 на черт. 10, из
которого имеем Lγ = 15 лет. Медианная
долговечность становится неограниченно большой, как следует из процедуры
вычислений, ибо n < 1. Таким образом введение
эвольвентных шлиц и наклепа поверхности позволит увеличить γ-процентный
ресурс в 15 раз, а медианную долговечность на много порядков, что вполне
обеспечивает надежную работу вала без увеличения его габаритов и веса.
Функции распределения усталостной долговечности вала
1 - τ-1д = 54,1 МПа; 2 - 68,2 МПа; 3 - 88,7 МПа
Данные к расчету функций распределения долговечности вала при τ-1д = 54,1 МПа
|
Номер графы |
Сумма |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
1 |
τаi МПа (R = -1) |
85 |
77 |
69 |
61 |
53 |
45 |
37 |
29 |
21 |
13 |
|
|
2 |
ti |
0,0115 |
0,0165 |
0,0098 |
0,0294 |
0,0066 |
0,0124 |
0,0415 |
0,0861 |
0,229 |
0,557 |
1,0 |
|
3 |
τаi/τamax |
1 |
0,906 |
0,812 |
0,718 |
0,624 |
0,529 |
0,435 |
0,341 |
0,247 |
0,153 |
|
|
4 |
νiб |
75 |
107 |
64 |
190 |
44 |
80 |
269 |
557 |
1482 |
3606 |
6474 |
|
5 |
|
0,0541 |
0,0772 |
0,0462 |
0,1371 |
0,0317 |
0,0577 |
0,1941 |
0,4019 |
- |
- |
1,0 |
|
6 |
|
0,0541 |
0,0699 |
0,0375 |
0,0984 |
0,0198 |
0,0305 |
0,0844 |
0,1370 |
- |
- |
0,532 |
|
7 |
|
1 |
0,708 |
0,482 |
0,314 |
0,192 |
0,108 |
0,0543 |
0,0232 |
- |
- |
|
|
8 |
|
0,0541 |
0,0547 |
0,0223 |
0,0430 |
0,0061 |
0,0062 |
0,0105 |
0,0093 |
- |
- |
|
|
9 |
νiбλ=νiб∙500 |
37500 |
53500 |
32000 |
95000 |
22000 |
40000 |
134500 |
278500 |
|
|
|
|
10 |
|
0,0904 |
0,1291 |
0,0772 |
0,2292 |
0,0531 |
0,0965 |
0,3245 |
|
|
|
|
|
11 |
|
0,1339 |
0,1910 |
0,1143 |
0,3393 |
0,0786 |
0,1429 |
|
|
|
|
|
|
12 |
|
0,1339 |
0,1730 |
0,0928 |
0,2436 |
0,0490 |
0,0756 |
|
|
|
|
|
Данные к расчету функции распределения долговечности вала при τ-1д = 68,2 МПа
|
Номер графы |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1 |
τai МПа |
85 |
77 |
69 |
61 |
53 |
45 |
37 |
|
2 |
νiб |
75 |
107 |
64 |
190 |
44 |
80 |
269
|
|
3 |
|
1 |
0,906 |
0,812 |
0,718 |
0,624 |
0,529 |
0,435 |
|
4 |
|
0,0905 |
0,1291 |
0,0772 |
0,2292 |
0,0531 |
0,0965 |
0,3245; 1,000 |
|
5 |
|
0,0905 |
0,1170 |
0,0627 |
0,1646 |
0,0331 |
0,0510 |
0,1412 ξ = 0,660 |
|
6 |
|
1 |
0,708 |
0,482 |
0,314 |
0,192 |
0,108 |
0,0543 |
|
7 |
|
0,0905 |
0,0914 |
0,0372 |
0,0720 |
0,0102 |
0,0104 |
0,0176 |
Данные к расчету функции распределения долговечности
вала при τ-1д = 88,7 МПа
|
Номер графы |
Сумма |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|||
|
1 |
τai МПа (R= - 1) |
85 |
77 |
69 |
61 |
53 |
45 |
|
|
2 |
νiб |
75 |
107 |
64 |
190 |
44 |
80 |
|
|
3 |
|
1 |
0,906 |
0,812 |
0,718 |
0,624 |
0,529 |
|
|
4 |
|
0,1339 |
0,1911 |
0,1143 |
0,3393 |
0,0786 |
0,1429 |
1,000 |
|
5 |
|
0,1339 |
0,1731 |
0,0928 |
0,2436 |
0,0490 |
0,0756 |
ξ=0,768 |
|
6 |
|
1 |
0,708 |
0,482 |
0,314 |
0,192 |
0,108 |
|
|
7 |
|
0,1339 |
0,1353 |
0,0551 |
0,1065 |
0,0151 |
0,0154 |
|
Расчет функции распределения усталостной долговечности вала механизма поворота крана
|
τ-1д |
||||
|
54,1 |
68,2 |
88,7 |
||
|
0 |
nр |
2,0 1,5 1,2 |
1,8 1,5 1,2 |
1,7 1,4 1,1 |
|
1 |
|
0,500 0,667 0,833 |
0,555 0,667 0,833 |
0,588 0,714 0,909 |
|
2 |
|
11,31 4,133 1,893 |
7,824 4,133 1,893 |
6,406 3,247 1,396 |
|
3 |
∑ |
0,186 0,174 0,109 |
0,3013 0,2911 0,1819 |
0,4459 0,4308 0,1339 |
|
4 |
|
0,149 0,437 1,522 |
0,183 0,359 1,255 |
0,180 0,368 2,755 |
|
5 |
λ |
215 631 2196 |
441 866 3028 |
643 1314 9839 |
|
6 |
|
1,273 0,955 0,764 |
1,445 1,204 0,963 |
1,775 1,461 1,148 |
|
7 |
uР |
-1,39 0,25 1,40 |
-2,14 -1,06 0,21 |
-3,33 -2,20 -0,78 |
|
8 |
P % |
8,2 59,9 91,9 |
1,6 14,5 58,3 |
0,04 1,4 21,8 |
|
9 |
Lg λ |
2,33 2,80 3,34 |
2,64 2,94 3,48 |
2,81 3,12 3,99 |
3. Расчет по эквивалентным напряжениям
Расчет проводился по формулам (35) и (37). Пусть пτ = 2,0, тогда
![]() МПа.
МПа.
В табл. 13 отбрасываем ступени 9 и 10, значения ξ и ар вычислены (ξ = 0,532; ар = 0,314), νб = 1386.
Задаемся временем работы редуктора 2 года. С учетом времени навигации получаем, что за этот период вал отработает примерно 500 сут. Значения пiτ для каждой ступени даны в табл. 13 (строка 9).
Величина τэкв, определенная по формуле (37), будет = 55,7 МПа.
По выражению (35)
![]()
Заданный и полученный коэффициент запаса имеют существенные различия, поэтому вычисления повторяем.
Задаемся пτ = 1,5. Тогда ![]() МПа. В табл. 13
отбрасываем 8, 9 и 10 ступени. Число циклов в укороченном блоке равно
МПа. В табл. 13
отбрасываем 8, 9 и 10 ступени. Число циклов в укороченном блоке равно ![]() = 829. Значения
= 829. Значения
![]() даны в табл. 13,
строка 10. Новое значение ξ = 0,660 и ap=0,501.
Определяем эквивалентные напряжения, оставив время работы вала 2 года.
даны в табл. 13,
строка 10. Новое значение ξ = 0,660 и ap=0,501.
Определяем эквивалентные напряжения, оставив время работы вала 2 года.
Значения τэкв в этом случае будет τэкв =48,1 МПа.
Тогда пτ = 1,12.
Задаемся новым значением пτ = 1,25, тогда
![]() МПа.
МПа.
отбрасываем 7,
8, 9, 10-й графы в табл. 13. Тогда новое ![]() =560. Значения
=560. Значения ![]() и
и ![]() даны в табл. 13 в
строках 11 и 12. В этом случае ξ = 0,768; ар=0,659.
Эквивалентное напряжение равно τэкв = 43,7. Вычисленное
значение
даны в табл. 13 в
строках 11 и 12. В этом случае ξ = 0,768; ар=0,659.
Эквивалентное напряжение равно τэкв = 43,7. Вычисленное
значение ![]() Таким образом,
принимаем значение запаса равным 1,25.
Таким образом,
принимаем значение запаса равным 1,25.
Это значение
характеризует недостаточную прочность вала и соответствует тому, что по линии 1
на черт. 10
при L![]() 2 года
вероятность разрушения Р = 40 %. Таким образом расчет функций распределения
долговечности дает более полную и объективную картину по сравнению с расчетом
по эквивалентным
напряжениям.
2 года
вероятность разрушения Р = 40 %. Таким образом расчет функций распределения
долговечности дает более полную и объективную картину по сравнению с расчетом
по эквивалентным
напряжениям.
4. Расчет по номинальным напряжениям
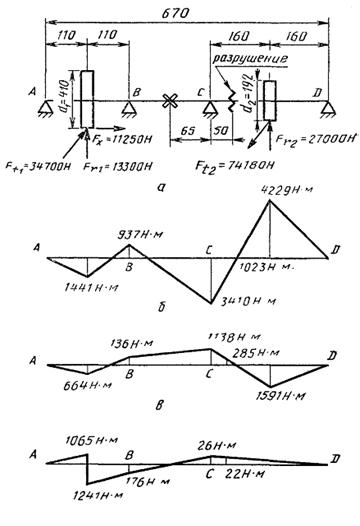
Номинальные напряжения, действующие на вертикальном валу, определяем по потребляемой мощности электродвигателя. Момент на вертикальном выходном валу трехступенчатого редуктора определяем по мощности (1,9 кВт) и угловой скорости (ω1 = 102,1 с-1) электродвигателя с учетом передаточного отношения всех трех ступеней (и∑ = 50,4) и коэффициента полезного действия редуктора (η = 0,885). Вычисленный крутящий момент на валу Т4 = 7120 нм. Рассматривая вал, как балку на 4 опорах, строим методом трех моментов эпюры изгибающих моментов в горизонтальной и вертикальной плоскостях. Силы, действующие в зацеплении, размеры вала и эпюры моментов даны на черт. 11. Силы, действующие в зацеплении зубчатых колес, определены по известным формулам (приложение 2). Моменты сопротивления вала в зоне разрушения Wи = 0,1315 × 10-3 м3; Wк = 0,263 × 10-3 м3 (d = 0,102 м).
Эквивалентный изгибающий момент равен:
![]() Н∙м
Н∙м
Амплитуда напряжений изгиба:
![]() МПа.
МПа.
Касательные напряжения на вертикальном валу от действия крутящего момента:
![]() МПа.
МПа.
Схема вала и эпюры изгибающих моментов
а - схема нагружения вала; б - эпюра изгибающего момента в горизонтальной плоскости от сил Ft1, Ft2; в - эпюра изгибающего момента в вертикальной плоскости от сил Fr1, Fr2 - эпюра изгибающего момента в вертикальной плоскости от силы Fх
Коэффициенты запаса прочности по нормальным и касательным напряжениям равны:
![]()
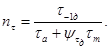
Значение ψτд определяем по ГОСТ 25.504
![]()
ψτ=0,01 + 10-4×σв=0,01 + 10-4×735=0,0835.
![]()
Значение σ-1д = 73,8 МПа определено ранее. Тогда
![]()
![]()
Суммарный коэффициент запаса равен:
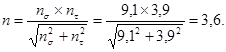
Полученный коэффициент запаса по номинальным напряжениям значительно больше, чем коэффициент запаса, рассчитанный по эквивалентным напряжениям. Анализ опыта эксплуатации указанных валов свидетельствует, что коэффициент запаса п = 3,6 не согласуется с многочисленными случаями разрушения валов в эксплуатации.
Это
несоответствие связано с тем, что расчет напряжений по номинальной мощности
двигателя не учитывает динамических явлений, вследствие чего полученное
касательное напряжение τа = 13,5 МПа соответствует
стационарному основному длительно действующему режиму (10-я ступень табл. 13), в
то время
как
пиковые перегрузки превышают это значение в ![]() 6,3 раз, как показывают
результаты тензометрирования (сравнение 1-й и 10-й ступеней в табл. 13).
Таким образом для получения более точных оценок долговечности и надежности валов
и осей необходимо проводить тензометрирование в условиях эксплуатации или
делать расчет напряжений более точными методами с учетом динамических явлений.
6,3 раз, как показывают
результаты тензометрирования (сравнение 1-й и 10-й ступеней в табл. 13).
Таким образом для получения более точных оценок долговечности и надежности валов
и осей необходимо проводить тензометрирование в условиях эксплуатации или
делать расчет напряжений более точными методами с учетом динамических явлений.
Пример 2. Вероятностный расчет усталостной долговечности полуоси грузового автомобиля
1. Исходные данные для расчета
Полуось
изображена на черт. 12. Деталь
изготовлена из поковки. Материал сталь 40Х. Временное сопротивление ![]() = 800 МПа,
коэффициент вариации временного сопротивления
= 800 МПа,
коэффициент вариации временного сопротивления ![]() = 0,06. Расчетное сечение -
шлицевая часть полуоси. Минимальный диаметр полуоси равен d = 48 мм.
= 0,06. Расчетное сечение -
шлицевая часть полуоси. Минимальный диаметр полуоси равен d = 48 мм.
Задний мост грузового автомобиля
Коэффициент влияния поверхностного упрочнения Кυ = 1,0, коэффициент анизотропии КА = 1. Чистота поверхности Rz = 3,2 мкм. Шлицы эвольвентные.
Полуось разгружена
от изгиба и работает только на кручение. Функция распределения напряжений
рассчитана по формуле (8) на основании результатов исследования
нагруженности полуосей автомобилей в различных условиях дорожного движения.
Исходные данные о нагруженности представлены в табл. 17, где напряжения полуоси
грузового автомобиля для различных условий эксплуатации определены выборочным
средним значением ![]() , коэффициентом вариации
, коэффициентом вариации ![]() амплитуд
процесса и числом циклов vστ, на
определенном отрезке пути (блоке нагружения), который в данном случае равен 200
км. В табл. 18
представлены нагрузочные режимы (уровни нагружения и соответствующие им числа
циклов (графы 2, 3, 4, 5, 6, 7)). На основании этих режимов получен смешанный
(обобщенный) режим (графа 8) с распределением напряжений для уровней τаi, соответствующий
одному блоку (λ = 1) при условии, что 50 % пробега по асфальтовым дорогам
пересеченной местности, 25 % - городские условия, асфальт, 15 % - булыжное
шоссе, 10 % - грунтовые дороги (5 % - разбитые грунтовые дороги, 5 % -
грунтовые дороги в хорошем состоянии). Общий пробег, при этом (λ = 1)
составляет L = 40000 км, что
равняется в среднем пробегу грузового автомобиля за один год эксплуатации.
амплитуд
процесса и числом циклов vστ, на
определенном отрезке пути (блоке нагружения), который в данном случае равен 200
км. В табл. 18
представлены нагрузочные режимы (уровни нагружения и соответствующие им числа
циклов (графы 2, 3, 4, 5, 6, 7)). На основании этих режимов получен смешанный
(обобщенный) режим (графа 8) с распределением напряжений для уровней τаi, соответствующий
одному блоку (λ = 1) при условии, что 50 % пробега по асфальтовым дорогам
пересеченной местности, 25 % - городские условия, асфальт, 15 % - булыжное
шоссе, 10 % - грунтовые дороги (5 % - разбитые грунтовые дороги, 5 % -
грунтовые дороги в хорошем состоянии). Общий пробег, при этом (λ = 1)
составляет L = 40000 км, что
равняется в среднем пробегу грузового автомобиля за один год эксплуатации.
Коэффициент
вариации амплитуд полученного процесса нагружения ![]() = 0,2. На черт. 13 и 14 для
наглядности приведены графики, характеризующие распределение амплитуд крутящего
момента на полуоси грузового автомобиля при движении по различным дорогам (8).
= 0,2. На черт. 13 и 14 для
наглядности приведены графики, характеризующие распределение амплитуд крутящего
момента на полуоси грузового автомобиля при движении по различным дорогам (8).
Распределение крутящего момента на полуосях автомобиля
(в относительных координатах) в зависимости от условий эксплуатации
1 - дорога с твердым покрытием в плохом состоянии (выбитое булыжное шоссе);
2 - плохая грунтовая дорога с участками бездорожья (песок, рыхлый снег);
3 - грунтовая дорога в
удовлетворительном состоянии; 4 - шоссе с асфальтобетоннымпокрытием ![]()
Функции распределения амплитуд нагрузки на полуось грузового автомобиля грузоподъемностью 5,5 т при движении по различным дорогам
× - асфальтированное шоссе по равнинной местности;
∆ - асфальтированное шоссе по пересеченной местности;
- разбитая грунтовая дорога
Экспериментальные данные об эксплуатационной нагруженности обработаны двухпараметрическим методом размахов, откуда и получено однопараметрическое распределение приведенных к симметричному циклу амплитуд процесса.
2. Расчет характеристик сопротивления усталости
Медианные значения предела выносливости гладкого лабораторного образца диаметром d = 7,5 мм, изготовленного из испытываемой марки стали, определяются по формулам (13):
![]() = (0,55 - 0,0001σв)σв =
(0,55-0,0001-800) 800=376 МПа,
= (0,55 - 0,0001σв)σв =
(0,55-0,0001-800) 800=376 МПа,
![]() =0,5
=0,5![]() =0,5×376=188
МПа
=0,5×376=188
МПа
Параметр уравнения подобия определяется по формулам (24) и (25):
νσ
= 0,19 - 0,000125![]() = 0,19 -
0,000125×800 = 0,09;
= 0,19 -
0,000125×800 = 0,09;
ντ = 1,5 νσ = 1,5×0,09 = 0,14.
Значение эффективного коэффициента концентрации напряжений Кτ определяется по черт. 6 для полуоси с эвольвентными шлицами:
для ![]() = 800 МПа Кτ
= 1,5.
= 800 МПа Кτ
= 1,5.
Коэффициент влияния абсолютных размеров поперечного сечения Кdτ определяется по (23):
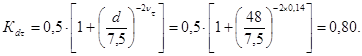
Отношение ![]() равняется:
равняется:
![]()
Коэффициент влияния качества обработки поверхности определяется по формулам (15) и (16):
![]()
![]() =0,575
=0,575![]() +0,425=0,575×0,93+0,425=0,96.
+0,425=0,575×0,93+0,425=0,96.
Коэффициент К, характеризующий влияние всех факторов на предел выносливости, определяется по формуле (14) при Kυ = 1:
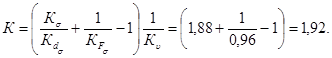
Предел выносливости полуоси при симметричном цикле нагружения равен по формуле (11):
![]() МПа.
МПа.
Показатель наклона левой ветви кривой усталости определяется по формуле (27)
![]()
где коэффициент С равен (28)
![]()
По результатам стендовых испытаний полуосей при симметричном цикле получены следующие характеристики (8) τ-]д = 90 МПа, NGτ = 6 × 106 циклов; тτ = 3,3; υτ-1 = 0,08. Кривая усталости материала полуоси типа 1.
Исходные данные для расчета полуоси грузового автомобиля
|
Условия эксплуатации |
|
νστ, циклы (на 200 км пробега) |
υτa |
|
Улицы городов |
41 |
484 |
0,185 |
|
Асфальтированное шоссе, пересеченная местность |
33,5 |
722 |
0,086 |
|
Разбитое булыжное шоссе |
39 |
45161 |
0,209 |
|
Грунтовая дорога хорошего качества |
39 |
3423 |
0,204 |
|
Развитая грунтовая дорога |
44 |
88006 |
0,225 |
Нагрузочные режимы полуоси грузового автомобиля для различных условий эксплуатации
|
Пробег, км |
|||||||
|
200 |
200 |
200 |
200 |
200 |
40000 |
||
|
i |
τai (МПа) |
Условия эксплуатации |
|||||
|
Городские условия, асфальт |
Асфальтовое шоссе, пересеченная местность |
Разбитое булыжное шоссе |
Разбитая грунтовая дорога |
Грунтовая дорога хорошего качества |
Смешанный (обобщенный) нагрузочный режим |
||
|
Число циклов нагружения на уровнях, νiбτ |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
138 |
|
|
25 |
100 |
|
1750 |
|
2 |
122 |
|
|
55 |
150 |
|
3150 |
|
3 |
106 |
|
|
100 |
250 |
10 |
5600 |
|
4 |
90 |
|
|
150 |
600 |
20 |
10700 |
|
5 |
74 |
10 |
|
350 |
1800 |
30 |
29300 |
|
6 |
58 |
16 |
4 |
800 |
4300 |
60 |
68800 |
|
7 |
48 |
36 |
6 |
1500 |
20800 |
180 |
257200 |
|
8 |
43 |
180 |
10 |
10181 |
34000 |
390 |
659330 |
|
9 |
38 |
170 |
44 |
20000 |
15000 |
2100 |
783900 |
|
10 |
33 |
46 |
630 |
10500 |
8000 |
480 |
465100 |
|
11 |
28 |
26 |
28 |
1500 |
3006 |
153 |
80690 |
|
Суммарное число циклов
нагружения |
484 |
722 |
45161 |
88006 |
3423 |
2365520 |
|
|
Выборочное среднее значение амплитуды нагружения
|
41 |
33,5 |
39 |
44 |
39 |
40,8 |
|
|
Коэффициент вариации амплитуд нагружения, υτa |
0,185 |
0,086
|
0,209 |
0,225 |
0,204 |
0,2 |
|
3. Расчет коэффициента запаса прочности по касательным напряжениям
Исходными данными для расчета являются полученные экспериментальные значения τ-1д, NGτ и тτ, а также данные из табл. 19, в которой смешанная функция распределения напряжений (графы 1, 2 и 4) приведена из табл. 18 (графа 8) с учетом повреждающих напряжений для рассчитываемой полуоси. Взяты семь уровней напряжений от τа1 = 138 МПа до τа7 = 48 МПа (τа7 > 0,5τ-1д). Уровни напряжений τаi < 0,5τ-1д в расчет не взяты.
Приведенные в таблице значения напряжений τа и соответствующие им числа циклов viσ подверглись предварительной обработке.
Получены для
каждого из уровней напряжений i значения ![]() - (графа 3),
- (графа 3), ![]() - (графа
5),
- (графа
5), ![]() -
(графа 6),
-
(графа 6), 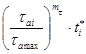 - (графа 7) и
- (графа 7) и ![]() - (графа 8). В
графах 4, 5, 6 произведено суммирование и получены параметры:
- (графа 8). В
графах 4, 5, 6 произведено суммирование и получены параметры:
![]()
![]()
![]()
![]()
Коэффициент запаса прочности равен (35)
![]()
где эквивалентные касательные напряжения определялись по формуле (37)
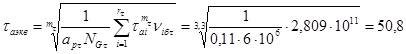 МПа.
МПа.
Корректирующий коэффициент арτ равен (34)
![]()
параметр ξτ (см. табл. 19) равен (33)
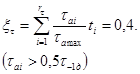
Значение τэкв
определялось последовательным приближением при различных значениях пτ,
путем подстановки и выражение (37) различных значений сумм ![]() до совпадения
значений пτ и τэкв по выражениям
(35)
и (37). В данном случае
суммирование велось до 7-й ступени включительно (столбец 8), т.е. до совпадения
значений
до совпадения
значений пτ и τэкв по выражениям
(35)
и (37). В данном случае
суммирование велось до 7-й ступени включительно (столбец 8), т.е. до совпадения
значений
![]() МПа;
МПа;
![]()
4. Расчет функции распределения усталостной долговечности при нерегулярном нагружении
Функция распределения усталостной долговечности определена зависимостью между долговечностью полуоси в километрах пробега и вероятностью разрушения (см. черт. 15).
Относительные долговечности определялись по формуле (40) при значениях относительного уровня переменной нагруженности пр = 2; пр = 1,5; пр = 1,2.
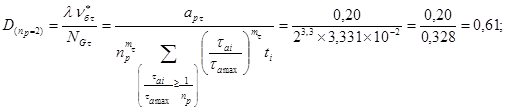
![]()
![]()
Суммирование 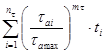 в формуле (40) при пр
= 2 велось до 5-й
ступени
включительно, т. к.
в формуле (40) при пр
= 2 велось до 5-й
ступени
включительно, т. к. ![]() а
а ![]() на 5-й ступени
составляет 0,536. Суммирование при пр = 1,5 велось до 4-й
ступени включительно, а при пр =1,2 до 2-й.
на 5-й ступени
составляет 0,536. Суммирование при пр = 1,5 велось до 4-й
ступени включительно, а при пр =1,2 до 2-й.
Долговечности λ, выраженные в числах блоков нагружения, определены для значений пр = 2; пр = 1,5; пр = 1,2 по формуле:
![]()
![]()
![]()
Пробег, соответствующий полученному числу блоков λ равен:
![]() км;
км;
![]() км;
км;
![]() км;
км;
Квантили нормального распределения up для каждого из значений пр равны (42):
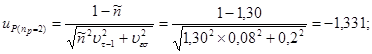
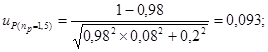
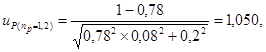
где ![]()
![]()
![]()
![]()
По таблицам значений квантили нормированного нормального распределения от уровня Р определены вероятности разрушения:
![]()
![]()
![]()
На черт. 15 приведен график функции распределения усталостной долговечности полуоси грузового автомобиля, построенный по результатам расчета. Из графика определен гамма-процентный ресурс (при γ = 90 %, Р = 10 %) полуоси, который равен Lγ = 90° = 4,00 × 105 км, что соответствует долговечности грузового автомобиля в эксплуатации.
Функция распределения усталостной долговечности полуоси грузового автомобиля
Данные к расчету функции распределения долговечности полуоси грузового автомобиля
|
|
|
|
|
|
|
|
|
|
1 |
138 |
1,000 |
0,175×104 |
4,648×10-3 |
4,648×10-3 |
4,648×10-3 |
2,017×1010 |
|
2 |
122 |
0,884 |
0,315×104 |
8,367×10-3 |
7,396×10-3 |
5,570×10-3 |
2,417×1010 |
|
3 |
106 |
0,768 |
0,560×104 |
1,487×10-2 |
1,142×10-2 |
6,225×10-3 |
2,702×1010 |
|
4 |
90 |
0,652 |
1,070×104 |
2,842×10-2 |
1,853×10-2 |
6,928×10-3 |
3,009×1010 |
|
5 |
74 |
0,536 |
2,930×104 |
7,782×10-2 |
4,171×10-2 |
9,939×10-3 |
4,318×1010 |
|
6 |
58 |
0,420 |
6,880×104 |
1,827×10-1 |
7,675×10-2 |
1,044×10-2 |
4,538×1010 |
|
7 |
48 |
0,348 |
25,72×104 |
6,831×10-1 |
2,377×10-1 |
2,098×10-2 |
9,086×1010 |
|
∑ |
|
|
|
А =1,000 |
ξ = 0,4 |
|
2,809×1011 |
Пример 3. Расчет вала на прочность
1. Исходные данные для расчета.
Вал изображен на черт. 16. Материал - сталь, имеющая следующие характеристики сопротивления усталости и статической прочности:
предел прочности при растяжении σв = 1100 МПа;
предел текучести при изгибе σr = 850 МПа;
предел текучести при кручении τт = 550 МПа;
предел выносливости при изгибе σ-1 = 480 МПа;
предел выносливости при кручении τ-1 = 270 МПа;
коэффициенты чувствительности к асимметрии цикла ψσ = 0,2 и ψτ = 0,1;
абсцисса точки перелома кривой усталости NG = 2× 106 циклов.
Вал подвергнут цементации, Кυ = 1,4.
Максимальный крутящий момент Тmах = 3950 Н∙м, частота вращения вала поб = 0,406 с-1, расчетный срок службы Тр = 5000 ч. Циклограмма нагружения приведена на черт. 17.
Минимально допускаемые запасы прочности и выносливости приняты [пт] = 1,9 и [п] = 1,9
2. Определение внутренних силовых факторов и расчет на статическую прочность
2.1. Определение размеров на длине вала
Установочную базу подшипников определяем согласно приложению 3.
![]() мм,
мм,
где Т = 24 мм, d = 60 мм, D = 100 мм и β = 13° - данные для подшипника № 7212. Принимаем h = 22 мм.
Остальные размеры приняты в соответствии с конструкцией нагружающего устройства.
Данные для шестерни и зубчатой муфты.
Для шестерни: модуль зубьев m = 10 мм, число зубьев zм = 14; угол наклона зуба β = 20°, угол зацепления косозубой цилиндрической передачи atω = 25,865°; диаметр начальной окружности dω = 154,4 мм.
Для муфты: модуль зубьев m = 5 мм, число зубьев zм = 24, диаметр делительной окружности dм = mм × zм = 5 × 24 = 120 мм.
2.2. Определение внешних сил, действующих на вал от зубчатого зацепления шестерни с колесом
Окружное, радиальное и осевое усилия, действующие на вал, определяем согласно приложению 2.
![]() Н;
Н;
![]() Н;
Н;
![]() Н.
Н.
Определяем неуравновешенную составляющую окружной силы на рабочих элементах муфты
![]() Н.
Н.
Ft, Fr, Fх - силы, меняющие положение относительно вала. Сила Fнt не меняет положение относительно вала.
Циклограмма нагружения
2.3. Построение эпюр внутренних силовых факторов
Определяем реакции опор от сил, меняющих положение относительно вала.
При направлении осевой силы Fx к опоре А:
![]() Н;
Н;
![]() Н;
Н;
![]() Н;
Н;
![]() Н.
Н.
При направлении осевой силы Fх к опоре Б:
![]() Н;
Н;
![]() Н.
Н.
Определяем реакции опор от сил, не меняющих положение относительно вала
![]() Н;
Н;
![]() Н.
Н.
Эпюры внутренних силовых факторов приведены на черт. 16.
Анализ эпюр внутренних силовых факторов и несущей способности сечений вала показал, что опасными сечениями являются сечения:
I-I - место перехода от шестерни к валу диаметром 65 мм;
II-II - место прессовой посадки правого подшипника на вал;
III-III - шпоночное соединение при посадке муфты на вал при направлении осевой силы Fx в сторону опоры Б.
Для сечения I-I:
![]() Н∙м.
Н∙м.
![]() Н∙м.
Н∙м.
![]() Н∙м.
Н∙м.
![]() Н∙м.
Н∙м.
Для сечения II-II:
![]()
![]() Н∙м.
Н∙м.
Для сечения III-III:
![]()
![]() Н∙м.
Н∙м.
2.4. Определение геометрических характеристик опасных сечений вала
Сечение I-I:
![]() м3;
м3;
![]() м3;
м3;
![]() м2.
м2.
Сечение II-II:
![]() м3;
м3;
![]() м3;
м3;
![]() м2.
м2.
Сечение III-III:
![]() м3;
м3;
![]() м3;
м3;
|
I-I |
II-II |
III-III |
|||
|
Момент Н∙м |
изгибающие |
|
1657 |
0 |
0 |
|
|
486 |
1185 |
816 |
||
|
|
2143 |
1185 |
816 |
||
|
крутящий |
Тmaxi |
3950 |
3950 |
3950 |
|
|
Осевая сила, Н |
Fzi |
18623 |
18623 |
0 |
|
|
Момент сопротивления, м3 |
Wиi |
26,96×10-6 |
21,2×10-6 |
14,51×10-6 |
|
|
Wкi |
53,92×10-6 |
42,4×10-6 |
30,85×10-6 |
||
|
Площадь сечения, м2 |
Ai |
3,32×10-3 |
2,83×10-3 |
- |
|
|
Напряжение, МПа |
изгиб с растяжением (сжатием) |
|
85,1 |
62,4 |
56,2 |
|
кручение |
|
73,3 |
93,2 |
128 |
|
|
Запас прочности |
изгиб с растяжением (сжатием) |
|
9,99 |
13,6 |
15,1 |
|
кручение |
|
7,5 |
5,9 |
4,3 |
|
|
общий |
|
6,0 |
5,4 |
4,1 |
|
2.5. Расчет вала на статическую прочность
Статическая прочность обеспечена; во всех случаях птi > [пт] = 1,9.
3. Расчет вала на сопротивление усталости по коэффициентам запаса прочности
3.1. Определение характеристик сопротивления усталости вала.
Сечение I-I. Согласно формуле (11)
![]()
![]()
По формуле (14) при изгибе и растяжении - сжатии
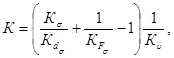
где 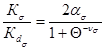 (по ГОСТ
25.504).
(по ГОСТ
25.504).
Теоретический коэффициент концентрации напряжений для ступенчатого вала находим по ГОСТ 25.504 (приложение 3).
Для радиуса галтели ρ = 6,5 мм, диаметра вала d = 65 мм и диаметра шестерни по впадинам
![]() мм
мм
ασ = 1,75.
По формуле (24)
vσ = 0,19 - 0,000125 σв = 0,19 - 0,000125 × 1100 = 0,053.
По ГОСТ 25.504 рассчитываем относительный градиент первого главного напряжения в зоне концентрации при изгибе:
![]() мм.
мм.
Определяем относительный критерий подобия усталостного разрушения по ГОСТ 25.504:
![]()
Отсюда:
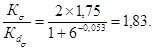
Коэффициент влияния шероховатости поверхности определяем по (16) для Rz = 20 мкм
![]()
Коэффициент снижения предела выносливости при Kυ = 1,4 равен:
![]()
Отсюда предел выносливости при изгибе вала для сечения I-I
![]() МПа.
МПа.
По (14) при кручении
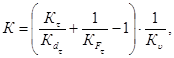
где 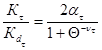 (по ГОСТ
25.504).
(по ГОСТ
25.504).
Согласно (25):
ντ = 1,5νσ = 1,5 × 0,053 = 0,080;
ασ = 1,45 (ГОСТ 25.504);
![]() мм;
мм;
![]()
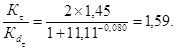
По (16) определяем коэффициент влияния шероховатости поверхности
![]() = 0,575
= 0,575![]() + 0,425 = 0,575
× 0,79 + 0,425 = 0,88.
+ 0,425 = 0,575
× 0,79 + 0,425 = 0,88.
Коэффициент влияния поверхностного упрочнения как и в случае изгиба Кυ= 1,4.
Коэффициент снижения предела выносливости при кручении равен
![]()
Отсюда предел выносливости при кручении вала для сечения I-I:
![]() МПа.
МПа.
Сечение II-II. По формулам (17) - (20) при d = 60 мм и р > 25 МПа находим
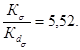
Согласно формуле (21)
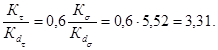
Приняв параметр
шероховатости поверхности Rz = 10 мкм, по (15) и (16) находим ![]() = 0,91.
= 0,91.
Коэффициент снижения предела выносливости при кручении равен
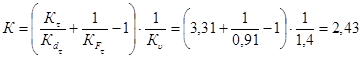
Отсюда, предел выносливости при кручении для сечения II-II:
![]() МПа.
МПа.
Сечение III-III. По (17) - (20) при d = 55 мм и р = 20 МПа определяем
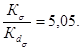
По формуле (21)
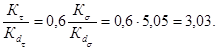
По формуле (14) при ![]() = 0,91
рассчитываем коэффициент снижения предела выносливости при кручении:
= 0,91
рассчитываем коэффициент снижения предела выносливости при кручении:
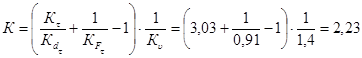
Отсюда:
![]() МПа.
МПа.
Определяющим источником концентрации напряжений для сечения III-III является посадка муфты на вал. Как показывают расчеты, коэффициенты снижения пределов выносливости в этом сечении для галтели и шпонки несколько меньше.
3.2. Расчет вала на сопротивление усталости по коэффициентам запаса.
Принимаем наработку, соответствующую одному блоку нагружения, равной расчетному сроку службы вала lб = Tр = 500 ч. В этом случае число блоков нагружения λ = 1.
Определяем количество циклов, приходящееся на каждую из трех ступеней нагружения (черт. 17):
ν1σ = t1 × n об × 3600 × Tр = 0,001 × 0,406 × 3600 × 5000 = 7,3 × 103;
ν 2σ = t2 × n об × 3600 × Tр = 0,1 × 0,406 × 3600 × 5000 = 7,3 × 105;
ν 3σ = t3 × n об × 3600 × Tр = 0,899 × 0,406 × 3600 × 5000 = 6,57 × 106;
Сечение I-I. Показатель наклона левой ветви кривой усталости определяем по (27) и (28)
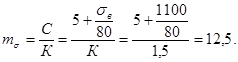
Корректирующий коэффициент ар принимаем равным ар = 0,25; NG = 2 × 106 циклов.
Определяем σаi (эквивалентные амплитуды напряжений симметричных циклов, равноценные по своему повреждающему действию асимметричному циклу с параметрами σа и σm)
![]()
где ![]()
Для первой ступени нагружения находим:
![]() МПа;
МПа;
![]() МПа.
МПа.
![]() МПа.
МПа.
Для остальных ступеней полагаем, что амплитуды напряжений пропорциональны крутящим моментам
![]() МПа;
МПа;
![]() МПа.
МПа.
Расчет коэффициента запаса проводим по формулам (35) и (36). Задаемся пσ = 6. По (36):
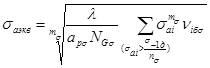
Суммирование
проводим по ![]() МПа.
МПа.
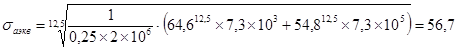 МПа.
МПа.
По (35):
![]()
Полученное значение пσ не имеет существенного расхождения с заданным. Принимаем пσ = 6.
При расчете по касательным напряжениям принимаем
mτ = mσ = 12,5;
арτ = 0,25;
NGτ = 2,106.
Полагаем, что при кручении вал работает по пульсирующему циклу, а касательные напряжения на каждой ступени нагружения, также как и нормальные, пропорциональны крутящим моментам.
Находим приведенные амплитуды касательных напряжений по формуле:
![]()
По (30):
![]()
Для первой ступени нагружения
![]() МПа;
МПа;
Для остальных ступеней нагружения
![]() МПа;
МПа;
![]() МПа.
МПа.
Расчет коэффициента запаса по касательным напряжениям проводим по формулам (35), (37).
Задаемся пτ = 6
По (37):
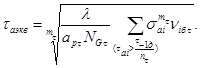
где ![]() МПа.
МПа.
Получаем
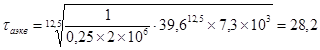 МПа.
МПа.
По (35):
![]()
Полученное значение пτ отличается от заданного, поэтому повторяем вычисления при пτ = 6,6.
Суммирование в формуле (37) проводим по
![]() МПа.
МПа.
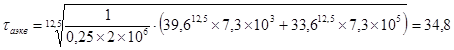 МПа.
МПа.
![]() МПа.
МПа.
Принимаем пτ = 6,6.
Определяем общий коэффициент запаса прочности при одновременном действии нормальных и касательных напряжений (38):
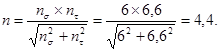
Сечение II-II. Расчет проводим по касательным напряжениям, так как циклические нормальные напряжения в этом сечении отсутствуют. По (27) и (28):
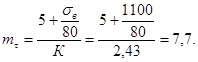
Для первой ступени нагружения
![]() МПа.
МПа.
По (30):
![]()
![]() МПа.
МПа.
Для остальных ступеней
![]() МПа;
МПа;
![]() МПа.
МПа.
Задаемся пτ = 2,5.
По формуле (37), учитывая только
![]() МПа.
МПа.
получаем τаэкв = 28 МПа.
По (35):
![]()
Вычисления повторяем, задаваясь пτ = 2,8.
Получаем τаэкв = 43,4.
![]()
Принимаем пτ = 2,8.
Сечение III-III.
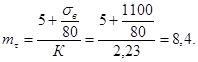
Для первой ступени нагружения
![]() МПа.
МПа.
По (30):
![]()
![]() МПа.
МПа.
Для остальных ступеней получаем
τ а2 = 56,8 МПа
τ а3 = 25,4 МПа.
Задаемся пτ = 2,2.
Суммируя в (37) слагаемые с
![]() МПа.
МПа.
получаем τаэкв = 59,7 МПа
![]()
Полученное значение пτ не имеет существенного расхождения с заданным. Принимаем пτ = 2,2.
Таким образом прочность при циклических нагрузках также обеспечена, во всех случаях п > [п] = 1,9.
СПИСОК ЛИТЕРАТУРЫ
1. Серенсен С.В., Громан М.Б., Когаев В.П., Шнейдерович Р.М. Валы и оси. Конструирование и расчет. М.: Машиностроение, 1970, 320 с.
2. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М.: Машиностроение, 1977, 232 с.
3. Бойцов Б.В. Прогнозирование долговечности напряженных конструкций. М.: Машиностроение, 1985, 232 с.
4. ГОСТ 25.504-82. Расчеты и испытания на прочность. Методы расчета характеристик сопротивления усталости. М.: Изд-во стандартов, 1982; 80 с.
5. Когаев В.П., Махутов Н.А., Гусенков А.П. Расчеты деталей машин и конструкций на прочность и долговечность. М.: Машиностроение, 1985, 224 с.
6. Степнов М.Н. Статистические методы обработки результатов механических испытаний. М.: Машиностроение, 1985, 232 с.
7. ОСТ 12.44.097-83. Валы и оси. Расчет на прочность и жесткость. М.: Изд-во стандартов, 1983, 88 с.
8. Гольд Б.В., Оболенский Е.П., Стефанович Ю.Г., Трофимов О.Ф. Прочность и долговечность автомобиля. М.: Машиностроение, 1974, 328 с.
9. Лукинский В.С., Котиков Ю.Г., Зайцев Е.И. Долговечность деталей шасси автомобиля. Л.: Машиностроение, 1984, 231 с.
СОДЕРЖАНИЕ
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНЫ
Институтом машиноведения АН СССР, Институтом горного дела АН СССР, Межотраслевым научно-техническим комплексом «Надежность машин», Государственным комитетом СССР по стандартам, Министерствами высшего и среднего специального образования СССР и РСФСР, Министерством автомобильной промышленности СССР, Министерством тяжелого, энергетического и транспортного машиностроения СССР, Министерством угольной промышленности СССР, Министерством речного флота РСФСР, Министерством сельскохозяйственного и тракторного машиностроения СССР, Министерством строительного, дорожного и коммунального машиностроения СССР
ИСПОЛНИТЕЛИ
В.П. Когаев, А.П. Гусенков, Б.В. Бойцов, Е.И. Тавер, С.С. Дмитриченко, Е.И. Степанычев, М.Н. Степнов, П.В. Семенча, А.А. Попов, А.И. Семин, Б.Ф. Хазов, Э.Н. Никольская, О.В. Леонова, В.В. Солодухин (руководители темы), В.Б. Стрекалов, И.М. Петрова, Л.Л. Смирнова, И.В. Гадолина, С.Г. Лебединский, М.А. Алимов, А.Ю. Марцинкевич, Е.Е. Власова, Е.В. Гиацинтов, А.С. Серегин, Б.И. Селезнев, А.Н. Постнов, Л.В. Ногаева, Н.С. Костин, А.Л. Иванов, Г.П. Кравченко, В.Л. Спасский, В.И. Артемьев, Т.И. Арсенькина, А.И. Вашунин, Ю.А. Шухмин, В.А. Полев, М.П. Толубаева, Л.А. Васина, С.В. Солод, Ю.А. Зислин, В.А. Мостаков, Д.Б. Баттаков, С.Ф. Бедрин, Б.Р. Григорян, В.В. Спиченков, Ю.В. Шумаков
2. УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 29.09.88 № 3349
3. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Номер пункта, приложения |
|
|
ГОСТ 18 498-73 |
|
|
ГОСТ 21 354-75 |
|
|
ГОСТ 23 207-73 |
|
|
РД 50-607-86 |
|
|
MP 55-82 |
|
|
MP 75-85 |
|
|
MP 206-86 |
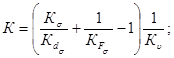
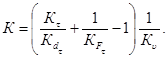 (
(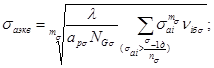 (
(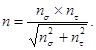 (
(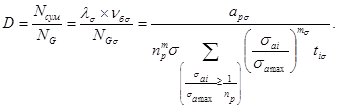 (
(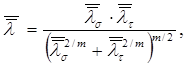 (
(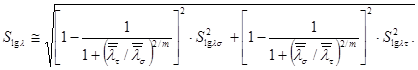 (
(