ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
(ГОССТАНДАРТ СССР)
ВСЕСОЮЗНЫЙ НАУНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ПО НОРМАЛИЗАЦИИ В МАШИНОСТРОЕНИИ
(ВНИИМАШ)
Утверждены
Приказом ВНИИМАШ
№ 65 от 14.03.1988 г.
РАСЧЕТЫ И ИСПЫТАНИЯ НА ПРОЧНОСТЬ
МЕТОД И ПРОГРАММА РАСЧЕТА НА ЭВМ
УСТОЙЧИВОСТИ ОБОЛОЧЕК СЛОЖНОЙ
ФОРМЫ
РЕКОМЕНДАЦИИ
Р 50-54-59-88
МОСКВА 1988
Рекомендации
|
Р 50-54-59-88 Разработаны и введены впервые |
Настоящие рекомендации (Р) разработаны в соответствии с Программой работ по стандартизации в области надежности, прочности, износостойкости, эксплуатации и ремонта техники на 1986 - 1990 гг.
Предназначены для численного исследования устойчивости и напряженно-деформированного состояния элементов оболочечных конструкций сложной формы, в том числе составных, с разрывными геометрическими параметрами, ребристых, с отверстиями и вырезами, ограниченными координатными линиями, взаимодействующих с упругой средой. Учитываются физическая и геометрическая нелинейности. Рекомендуемая методика разработана впервые и реализована в пакете прикладных программ «МЕКРИС».
Р могут применяться для расчетов при проектировании оболочечных конструкций изделий машиностроения и строительства, отвечающих современным требованиям надежности и обеспечения материалоемкости.
Введение
Предлагаемые рекомендации распространяются на методы, алгоритмы и программы расчета на ЭВМ в двумерной постановке напряженно-деформированного состояния и устойчивости оболочек сложной формы. Р разработаны для применения в расчетной практике при проектировании оболочечных конструкций машиностроения, отвечавших современным требованиям надежности и снижения материалоемкости.
Рекомендуемая методика численного исследования устойчивости оболочек базируется на применении новой схемы метода конечных разностей - метода криволинейных сеток [1, 2, 6 - 8]. Одно из основных преимуществ МКС по сравнению со многими другими методами дискретизации состоит в улучшении скорости сходимости решений за счет исключения отрицательного эффекта жестких смещений. Кроме того, составная оболочечная конструкция может рассматриваться целиком, без разделения ее на отдельные элементы, в связи с чем исключается необходимость введения дополнительных уравнений, описывающих условия сопряжения элементов. При этом на границах расчетного фрагмента отсутствуют законтурные узлы, разностные соотношения остаются справедливыми и в местах излома срединной поверхности оболочки.
В качестве исходных при построении методики приняты уравнения классической теории тонких оболочек в инвариантной форме [21] с учетом геометрической нелинейности и пластичности материала. Геометрическая нелинейность уравнений обусловлена учетом изменения кривизны срединной поверхности в процессе нагружения и изменением ориентации векторов внутренних усилий и внешнего воздействия относительно системы координат, связанной со срединной поверхностью недеформированной оболочки, а также учетом квадратичного члена в выражениях компонент тензора мембранных деформаций. Учет пластичности материала основан на использовании соотношений теории малых упруго-пластических деформаций (деформационная теория) [14]. С помощью метода продолжения по параметру в сочетании с методом Ньютона-Канторовича решение нелинейной задачи сводиться к решению последовательности линеаризованных краевых задач [5]. Для решения системы конечноразностных уравнений выбран блочный метод Гаусса.
Рекомендуемая методика реализована в комплексе программ «МЕКРИС-2» [8], являющимся эффективным инструментом исследования нелинейного деформирования и устойчивости оболочечных элементов машин и конструкций. Объектами исследования могут быть:
1) тонкие оболочки сложной формы, в том числе и составные, с постоянной или переменной толщиной. Элементы составной оболочки могут иметь произвольную аналитически заданную форму, стык может быть как гладким, так и с изломом поверхности по линии сопряжения;
2) оболочки, подкрепленные ребрами в одном или обоих направлениях. Ребра принимаются в расчет дискретно и могут быть центрально расположенными относительно срединной поверхности оболочки, с эксцентриситетом или односторонними;
3) оболочки, ослабленные отверстиями или вырезами, контуры которых совпадают с координатными линиями на поверхности;
4) оболочки в упругой среде, моделируемой винклеровским основанием, с односторонними или двусторонними связями.
Рекомендуемый комплекс программ «МЕКРИС-2» имеет определенные преимущества, к числу которых можно отнести:
- высокую скорость сходимости численных решений, позволяющую в сочетании с быстродействующим алгоритмом решения системы уравнений значительно сократить время счета и повысить эффективность использования ЭВМ;
- возможность раздельного и совместного учета различных факторов нелинейности - конечных углов поворота, изменения формы и физических свойств материала оболочки;
- при решении задач устойчивости возможность построения траекторий нагружения и нахождения на них предельных точек и точек бифуркации, исследования характера перестройки равновесных форм и анализа закритических состояний;
- учет симметричности в структуре исследуемой конструкции при описании расчетной схемы;
- возможность варьирования шага разности сетки на отдельных участках объекта, что позволяет подвергать детальному анализу наиболее напряженные зоны без увеличения числа неизвестных;
- автоматическое сгущение сетки;
- проведение вычислений с обычной и удвоенной точностью;
- возможность восстановления и продолжения вычислительного процесса в случае сбоя оборудования, а также в случае вынужденного прерывания счета;
- незамкнутость по отношению к новым классам решаемых задач;
- компактность и простоту задания исходных данных.
Подлинник комплекса программ «МЕКРИС-2» хранится в Киевском ордена Трудового Красного Знамени Инженерно-строительном институте и подвергается дальнейшему совершенствованию. Один из вариантов сдан в Государственный и Республиканский фонды алгоритмов и программ [8].
Предназначены для работников научно-исследовательских институтов, конструкторских бюро и заводских лабораторий, занимающихся расчетами на прочность и устойчивость оболочечных изделий машиностроения.
1. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
МКС - метод криволинейных сеток;
НДС - напряженно-деформированное состояние;
МД - магнитный диск (том прямого доступа);
АЦПУ - алфавитно-цифровое печатающее устройство;
МЛ - магнитная лента;
Е - модуль упругости материала оболочки;
G - модуль сдвига;
G1 - модуль упрочнения;
n - коэффициент Пуассона;
aт - коэффициент температурного линейного расширения;
XYZ - декартова система координат;
xa - система координат, связанная со срединной поверхностью недеформированной оболочки;
![]() ,
, ![]() - векторы
основного и взаимного локальных базисов;
- векторы
основного и взаимного локальных базисов;
Ñ - символ ковариантного дифференцирования;
![]() - вектор
перемещений;
- вектор
перемещений;
Ud - ковариантные компоненты перемещений;
![]() -
контрвариантный вектор внутренних усилий;
-
контрвариантный вектор внутренних усилий;
![]() - контрвариантные
компоненты внутренних усилий;
- контрвариантные
компоненты внутренних усилий;
![]() - контрвариантный
вектор внутренних моментов;
- контрвариантный
вектор внутренних моментов;
Мab - контрвариантные компоненты внутренних моментов;
а - фундаментальный определитель поверхности;
![]() -
коэффициенты преобразования компонент ректоров из основного базиса в точке (i, j) в компоненты
взаимного локального базиса в точке (i ± 0,5, j ± 0,5);
-
коэффициенты преобразования компонент ректоров из основного базиса в точке (i, j) в компоненты
взаимного локального базиса в точке (i ± 0,5, j ± 0,5);
Cab - ковариантные компоненты
дискриминантного тензора (С11 = С22 = 0; ![]() );
);
Cab -
контрвариантные компоненты дискриминантного тензора (С11 = С22
= 0; ![]() );
);
eab - компоненты тензора мембранных деформаций;
ei - интенсивность деформаций;
eт - деформации текучести;
eiт - интенсивность деформаций текучести;
K - модуль объемной деформации;
mab - компоненты тензора изгибных деформаций;
![]() - вектор
углов поворота малой окрестности точки срединной поверхности оболочки;
- вектор
углов поворота малой окрестности точки срединной поверхности оболочки;
Va - компоненты вектора углов поворота;
sab - контрвариантные компоненты тензора напряжений;
si - интенсивность напряжений;
sт - предел текучести материала;
siт - интенсивность напряжений текучести;
![]() -
интегральные характеристики жесткости оболочки (m
= 0, 1, 2);
-
интегральные характеристики жесткости оболочки (m
= 0, 1, 2);
![]() -
интегральные характеристики жесткости ребер (m =
0, 1, 2);
-
интегральные характеристики жесткости ребер (m =
0, 1, 2);
Здесь и ниже латинские индексы принимают значения 1, 2, 3; греческие - 1, 2.
2. ПОСТАНОВКА ЗАДАЧИ
Рассматривается пространственная тонкостенная конструкция, представляющая собой некоторую композицию из произвольно набранных оболочечных фрагментов.
Предполагается, что на конструкцию действует система произвольных внешних нагрузок и температура.
Задача состоит в определении напряженно-деформированного состояния, исследовании процесса деформирования и анализе устойчивости рассматриваемой конструкции в геометрически и физически нелинейной постановке.
2.1. Геометрически нелинейные соотношения теории тонких оболочек
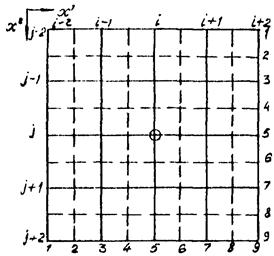
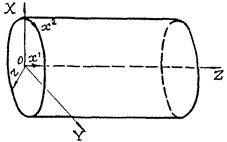
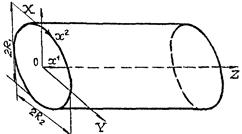
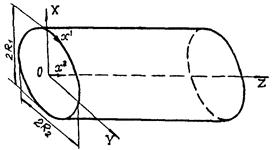
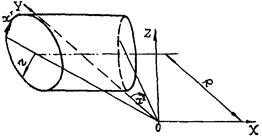
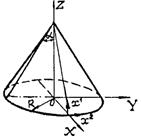
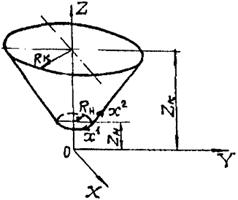
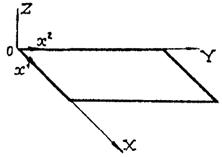
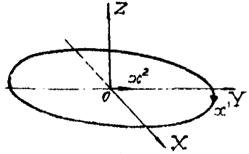
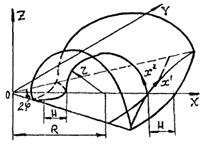
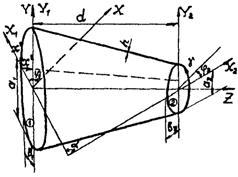
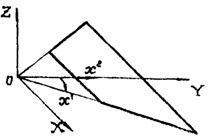
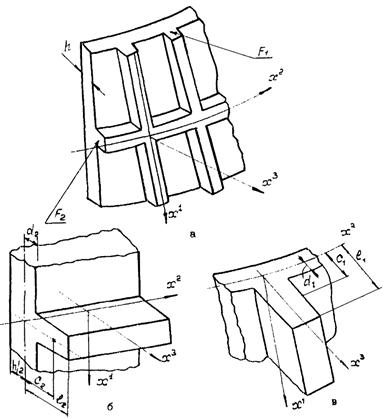
Исследование процесса деформирования тонких оболочек в пределах конечных деформаций удобно проводить с использованием подхода Лагранжа. При этом за систему отсчета принимается декартова система координат XYZ, а индивидуализация точек срединной поверхности оболочки осуществляется при помощи вектор-функции
где параметры х1,
х2 определяют неподвижные, в общем случае косоугольные,
криволинейные координаты, связанные с недеформированной срединной поверхностью
оболочки (рис. 2.1). Проекции вектор-функции ![]() точек
срединной поверхности в пределах элемента оболочки в системе отсчета XYZ задаются непрерывными однозначными функциями
точек
срединной поверхности в пределах элемента оболочки в системе отсчета XYZ задаются непрерывными однозначными функциями
Х = Х(х1, х2), Y = Y(х1, х2), Z = Z(х1, х2). (2.2)
Векторы
направленные по касательным к координатным линиям х1, х2, и вектор
совпадающий с ортом нормали к срединной поверхности, представляют собой основной локальный базис точек срединной поверхности оболочки.
Коэффициенты аab первой квадратичной формы
определяющие внутреннюю метрику срединной поверхности оболочки и представляющие собой дважды ковариантные компоненты метрического тензора, выражаются зависимостью
а фундаментальный определитель метрического тензора имеет вид
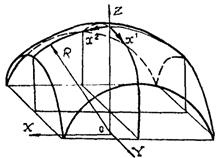
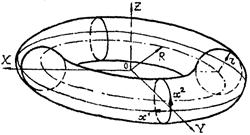
Системы декартовых и криволинейных координат
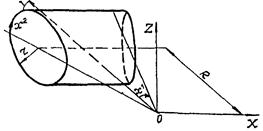
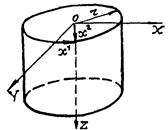
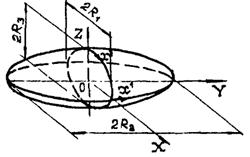
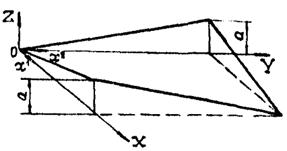
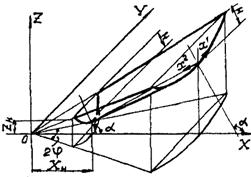
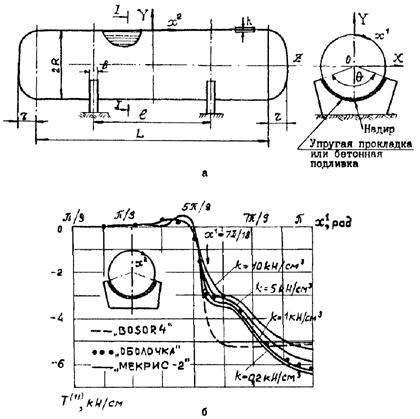
Положительные направления внутренних усилий, компонент нагрузки и внутренних моментов, действующих на элемент срединной поверхности
Векторы взаимного локального базиса криволинейных косоугольных координат х1, х2 связаны с векторами основного локального базиса соотношениями
Описание деформирования срединной поверхности оболочки осуществляется уравнениями, определяющими вектор перемещения ее точек
При этом уравнение деформированной поверхности принимает вид
а касательные векторы основного локального базиса деформированной срединной поверхности определяются выражением
Компоненты основного метрического тензора деформированной срединной поверхности оболочки в соответствии с (2.6) и с учетом (2.11) выражаются соотношением
Выражения компонент тензора мембранных деформаций получаются из соотношения (2.12) вариацией компонент основного метрического тензора
При деформировании тонких оболочек изменение коэффициентов первой квадратичной формы значительно более энергоемко по сравнению с изменением коэффициентов второй квадратичной формы, что выражается в существенном изменении ориентации локальных базисов при незначительном изменении их длин. Исходя из этого, в выражениях компонент мембранных деформаций для их упрощения уместно сохранить произведение величин углов поворота, определяющих изменение внешней метрики, и пренебречь произведением величин изменения длин базисных векторов, а также произведением величин изменения длин базисных векторов на величины углов поворота. В соответствии с этим выражение для компонент мембранных деформаций преобразуется к виду
![]() (2.14)
(2.14)
Изменение ориентации элементов срединной поверхности оболочки в пространстве вследствие ее деформирования описывается вектором углов поворота
где V1
и V2 определяют углы поворота нормали
вокруг касательных векторов взаимного локального базиса ![]() и
и ![]() соответственно,
Wn
выражает средний угол поворота малой окрестности точки срединной поверхности
оболочки вокруг нормали, Сab - компоненты дважды контрвариантного
тензора, принимающего в зависимости от сочетания индексов следующие значения
соответственно,
Wn
выражает средний угол поворота малой окрестности точки срединной поверхности
оболочки вокруг нормали, Сab - компоненты дважды контрвариантного
тензора, принимающего в зависимости от сочетания индексов следующие значения
С11 = С22
= 0, ![]() .
.
Связь углов поворота нормали с вектором перемещений выражается соотношением
Изменение кривизны оболочки вследствие деформирования определяется изгибными деформациями
где Сbg - компоненты дважды ковариантного дискриминантного тензора, принимающие в зависимости от сочетания индексов следующие значения
С11 = С22
= 0, ![]() .
.
Для приведения трехмерной задачи теории упругости к двухмерным соотношениям теории оболочек используются гипотеза недеформируемых нормалей Кирхгофа-Лява и допущение, состоящее в том, что нормальными напряжениями в направлении, перпендикулярном к срединной поверхности оболочки, можно пренебречь ввиду их малости по сравнению с основными напряжениями.
Компоненты тензоров внутренних тангенциальных усилий и внутренних моментов выражаются через компоненты тензоров мембранных и изгибных деформаций зависимостями, следующими из закона состояния линейной теории упругости, при условии равенства нулю напряжений, нормальных к срединной поверхности, приведенными в работе [21]:
где ![]() , а с учетом пренебрежения
влиянием мембранных деформаций на изменение кривизны
, а с учетом пренебрежения
влиянием мембранных деформаций на изменение кривизны
Условие равенства нулю главного вектора всех сил, действующих на элемент срединной поверхности оболочки, формулируется в виде
где ![]() ,
, ![]() - контрвариантные векторы
внутренних усилий с компонентами Т1k,
Т2k;
- контрвариантные векторы
внутренних усилий с компонентами Т1k,
Т2k; ![]() - вектор
внешней поверхностной нагрузки.
- вектор
внешней поверхностной нагрузки.
Условие равенства нулю главного момента всех сил и моментов, приложенных к элементу срединной поверхности оболочки, приводит к соотношению
Контрвариантные векторы внутренних усилий можно разложить по векторам основного локального базиса деформированной срединной поверхности
где Tab - дважды контрвариантные компоненты тензора внутренних усилий, характеризующие мембранные внутренние усилия оболочки;
Ta3 - выражают перерезывающие силы.
Контрвариантные векторы внутренних моментов удобно представлять в виде разложения по векторам взаимного локального базиса недеформированной срединной поверхности
где Mab - компоненты разложения, означающие величины внутренних моментов, Cab - дважды ковариантные компоненты дискриминантного тензора.
Перерезывающие силы Ta3 определяются из соотношения (2.21), выражающего равенство нулю главного момента всех сил и моментов, действующих на элемент оболочки
Вектор
внешней нагрузки ![]() в зависимости от характера нагружения
можно раскладывать по базисным векторам как недеформированной, так и
деформированной поверхностей. Если в процессе деформирования оболочки вектор
внешней нагрузки изменяет свое направление, как это имеет место в случае
гидростатического давления, то его следует представлять в виде разложения по
базисным векторам деформированной поверхности
в зависимости от характера нагружения
можно раскладывать по базисным векторам как недеформированной, так и
деформированной поверхностей. Если в процессе деформирования оболочки вектор
внешней нагрузки изменяет свое направление, как это имеет место в случае
гидростатического давления, то его следует представлять в виде разложения по
базисным векторам деформированной поверхности
Если направление вектора внешней нагрузки не изменяется в процессе деформирования, например, в случае действия собственного веса, то его удобно представлять в виде разложения по базисным векторам исходной поверхности
![]() (2.26)
(2.26)
На рис. 2.2 показаны положительные направления компонент внутренних усилий, моментов и внешней нагрузки, действующих на элемент срединной поверхности оболочки.
Подстановка в физические соотношения (2.18) мембранных (2.14) и изгибных (2.19) деформаций, выраженных через компоненты вектора перемещений, приводит к выражению компонент мембранных усилий и моментов через составляющие вектора перемещений. Перерезывающие силы Ta3 определяются через компоненты вектора перемещений посредством подстановки в соотношения (2.24) выражений внутренних моментов через компоненты вектора перемещений. Подставив выражения внутренних усилий в уравнение равновесия и спроектировав его на векторы взаимного локального базиса, можно получить систему трех скалярных дифференциальных уравнений в перемещениях.
Эта система
уравнений совместно с граничными условиями представляет собой полную систему
разрешающих уравнений. Учет нелинейных зависимостей компонент тензора
мембранных деформаций от компонент вектора перемещений вместе с учетом
изменения направления действия векторов внутренних усилий деформированной
поверхности, а в случае следящей нагрузки и изменения направления действия
вектора нагрузки ![]() , делает систему разрешающих уравнений
нелинейной.
, делает систему разрешающих уравнений
нелинейной.
2.2. Учет дискретно расположенных ребер в соотношениях теории тонких оболочек
При расчете ребристых оболочек в уравнения равновесия (2.20), сформулированные для узлов, через которые проходят ребра, необходимо добавить члены, учитывающие внутренние усилия ребер, а в выражениях перерезывающих сил (2.24) - члены, характеризующие внутренние моменты ребер.
Выражения внутренних усилий и моментов ребер получаются интегрированием напряжений по высоте ребер. Вследствие одноосного напряженного состояния ребер напряжения в ребрах, ориентированных вдоль координатных линий х1, принимают вид
а для ребер, ориентированных в направлении х2, -
где Е1, Е2 - модули упругости материала ребер первого и второго направлений.
Внутренние усилия и моменты в ребрах выражаются соотношениями
Здесь i = 1 - для ребер первого направления, i = 2 - второго направления; Fi и Ji0 - площади поперечных сечений ребер первого и второго направлений и их собственные осевые моменты инерции; Сi - эксцентриситеты ребер относительно срединной поверхности оболочки.
2.3. Учет влияния температуры
Для учета температурного воздействия на напряженно-деформированное состояние ребристой оболочки необходимо члены внутренних усилий и моментов, обусловленные температурным воздействием, перенести с противоположным знаком в правую часть уравнений равновесия. Решив систему уравнений равновесия с правой частью в виде суммы добавок от внутренних усилий и моментов, можно получить температурные деформации и усилия ребристой оболочки.
Выражение для напряжений, учитывавшее температурные деформации, имеет вид:
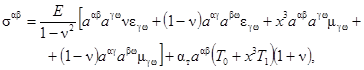 (2.30)
(2.30)
где aт - коэффициент температурного линейного расширения материала; Т0 = Т0(х1, х2) - Функция распределения температуры на срединной поверхности оболочки; Т1 = Т1(х1, х2, х3) - функция распределения температуры по толщине.
Выделив из выражения (2.30) температурный член и обозначив его sтab, получим:
Интегрируя по толщине оболочки напряжения (2.31), найдем выражения для температурных членов во внутренних усилиях и моментах оболочки:
где h - толщина оболочки.
Температурные слагаемые в выражениях для напряжений в ребрах имеют вид
где ![]() ,
, ![]() - температурные члены в
выражениях напряжений ребер первого и второго направлений соответственно; aт1, aт2 - коэффициенты температурного линейного
расширения материалов соответствующих ребер.
- температурные члены в
выражениях напряжений ребер первого и второго направлений соответственно; aт1, aт2 - коэффициенты температурного линейного
расширения материалов соответствующих ребер.
Интегрируя по высоте ребер напряжения (2.33), получаем температурные члены внутренних усилий и моментов ребер
2.4. Учет влияния пластичности материала
При исследовании напряженно-деформированного состояния тонких оболочек за пределами упругости необходимо знать зависимости компонентов напряжений от компонентов деформации, которые устанавливаются в теории пластичности.
В основу исследований НДС и устойчивости оболочек за пределом упругости положены соотношения теории малых упруго-пластических деформаций (деформационная теория) [14]. Основные положения этой теории являются обобщением закона Гука для неодноосного напряженного состояния в предположении, что в каждой точке тела путь нагружения является прямым. Широкая практика использования деформационной теории показала, что она дает хорошие результаты и для путей нагружения малой кривизны [17].
В теории малых упруго-пластических деформаций соотношения между напряжениями и деформациями имеют такой же вид, как и в упругой стадии, однако величины Ес, nс, Gс зависят от деформированного состояния в точке и вида функции s1 = Ф(ei). Модуль растяжения и коэффициент поперечного сжатия связаны с модулями Gc и объемной деформации K формулами
![]()
![]() (2.35)
(2.35)
Модуль объемной деформации K не зависит от деформированного состояния и выражается через модуль упругости E и коэффициент Пуассона n упругой стадии деформирования, модуль сдвига Gс в деформационной теории определяется формулой
и связан с модулем упругости в упруго-пластической стадии деформирования соотношением
Будем рассматривать два способа представления зависимости интенсивности напряжений si от интенсивности деформаций ei.
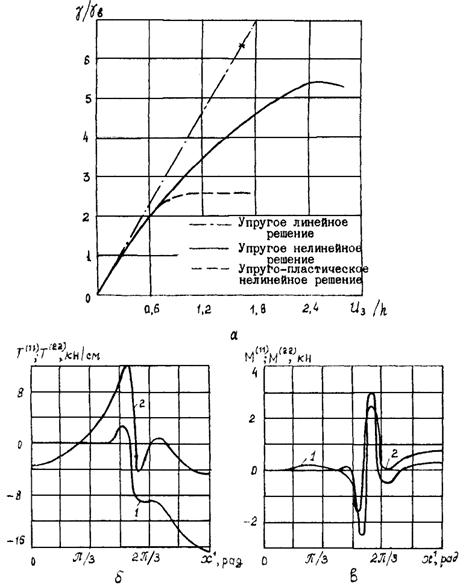
Идеально упруго-пластическое тело (рис. 2.3, а) характеризуют формулами
si = 3Gei при ei < eiт;
Соотношение si = sт представляет собой критерий пластичности Мизеса.
Из соотношений (2.38) и (2.36) следует
Gс = G при ei < eiт;
Упруго-пластическое тело с линейным упрочнением (рис. 2.3, б) обычно задают соотношениями
si = 3Gei при ei < eiт;
si = 3Gei + 2Gт(ei - eiт) при ei ³ eiт, (2.40)
где Gт - модуль упрочнения, 3Geiт = sт. При Gт = 0 из (2.40) получаем выражения (2.38). Из формул (2.40) находим секущий модуль сдвига:
Gс = G при ei < eiт;
В приведенных формулах секущий модуль сдвига вычисляется по значению интенсивности деформаций и зависимости si(ei), а затем, используя (2.35), определяются секущие модуль упругости Ес и коэффициент Пуассона nс.
Диаграммы деформирования материала
а - упруго-пластическое тело; б - упруго-пластическое тело с линейным упрочнением
Для построения идеализированных диаграмм деформирования материала, представленных на рис. 2.3, используем в качестве базисной диаграмму одноосного растяжения sx × lx. Для этого напряженного состояния при
s11 = sх; s22
= s33 = s12 = s13 = 0, l11
= lx, l12
= l13 = l23
= 0 и ![]() получим
получим
Последнему выражению в (2.42) можно придать различные формы записи, например:
где ![]() .
.
Формулы (2.42) и (2.43) позволяют по диаграмме одноосного растяжения построить диаграмму деформирования sх - eх. При известных значениях предела текучести sт и деформации текучести eт, при одноосном растяжении соответствующие им значения интенсивностей напряжений и деформаций определяем по формулам:
Если принять условие несжимаемости материала, то диаграммы деформирования материала (см. рис. 2.3) совпадут с диаграммами одноосного растяжения.
Зависимости между напряжениями и деформациями в оболочке, работающей в упруго-пластической стадии, при достигнутой интенсивности деформаций ei формально сохраняют такой же вид, как и в упругой оболочке
Здесь модуль упругости Ес и коэффициент Пуассона nс зависят не только от координат х1 и х2 на поверхности оболочки, но и изменяются по толщине оболочки. Их значения определяются по формулам (2.35) и диаграмме деформирования материала в зависимости от значения интенсивности деформаций ei в рассматриваемой точке тела оболочки.
В тонкой оболочке, для которой справедливы гипотезы Кирхгофа-Лява, деформации lab выражаются через мембранные eab и изгибные деформации mab срединной поверхности по формулам:
Выполнив после подстановки (2.46) в обобщенный закон Гука (2.45) интегрирование по толщине оболочки, получим выражения для усилий и моментов в физически нелинейно-упругой оболочке:
Здесь коэффициенты ![]() (m = 0, 1, 2) представляют собой интегральные
характеристики жесткости оболочки в точке с криволинейными координатами x1, x2:
(m = 0, 1, 2) представляют собой интегральные
характеристики жесткости оболочки в точке с криволинейными координатами x1, x2:
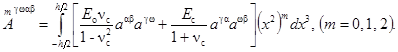 (2.48)
(2.48)
Уравнения равновесия элемента оболочки, выражения мембранных и изгибных деформаций через перемещения ее срединной поверхности для оболочки, работающей в упруго-пластической стадии, сохраняют такой же вид, как и для упругой оболочки.
При совместной работе оболочки и ребер в уравнения равновесия, сформулированные для узлов, через которые проходят ребра, необходимо добавить члены, характеризующие внутренние усилия ребер, а в выражения поперечных сил - члены, характеризующие внутренние моменты ребер. Выражения внутренних усилий и моментов ребер получаем интегрированием по высоте и ширине ребер функций, описывающих напряжения.
Вследствие одноосного напряженно-деформированного состояния ребер принимаем:
1) напряжения в ребрах, расположенных вдоль координатных линий х1, имеют вид
где Ec1 - секущий модуль упругости материала ребра первого направления.
Интегрируя выражения напряжений (2.49) по ширине и высоте сечения ребра, получаем выражения усилии и моментов в ребрах первого направления
2) напряжения в ребрах, расположенных вдоль координатных линий х2, имеет вид:
где Ес2 - секущий модуль упругости материала ребра второго направления.
Интегрируя, как и выше, выражения (2.51), получим выражения для внутренних усилий и моментов ребер второго направления:
![]()
![]() (2.52)
(2.52)
В выражениях
(2.50)
и (2.52)
коэффициенты ![]() представляют собой интегральные
характеристики жесткости ребер, проходящих черев узел разностной сетки с
координатами х1, х2:
представляют собой интегральные
характеристики жесткости ребер, проходящих черев узел разностной сетки с
координатами х1, х2:
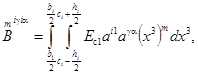 (m = 0, 1, 2; по i не
суммировать), (2.53)
(m = 0, 1, 2; по i не
суммировать), (2.53)
где hi, bi, ci - соответственно ширина, высота сечения ребра i-го направления и его эксцентриситет относительно срединной поверхности.
В узлах разностной сетки, через которые проходят подкреплявшие ребра, жесткостные характеристики (2.48) и (2.53) суммируются.
3. МЕТОДЫ И АЛГОРИТМЫ РЕШЕНИЯ
3.1. Метод криволинейных сеток
При
использовании метода конечных разностей и метода конечных элементов для
дискретизации дифференциальных соотношений теория оболочек имеет место
неудовлетворительная сходимость речений ряда задач упругого деформирования
оболочек. По этой причине при построении дискретной математической модели
континуальной задачи приходится вводить неоправданное видом разрешающих функций
большое количество степеней свободы. Это обстоятельство сопряжено со
значительным расходом ресурсов ЭВМ, что может привести к непреодолимым
трудностям при решении задач нелинейной устойчивости оболочек в двумерной
постановке. Причиной неудовлетворительной сходимости численных решений с
использованием метода конечных разностей является существенное влияние жестких
смещений на погрешность конечноразностной аппроксимации ковариантных
производных компонент разрешавших вектор-функций. Так, вектор-функцию ![]() , от
компонент которой вычисляются ковариантные производные, можно представить в
окрестности точки дискретизации в виде суммы постоянной вектор-функции
, от
компонент которой вычисляются ковариантные производные, можно представить в
окрестности точки дискретизации в виде суммы постоянной вектор-функции ![]() и
переменной вектор-функции
и
переменной вектор-функции ![]()
![]() (3.1)
(3.1)
Аналитическое выражение ковариантной производной имеет вид
Ковариантную
производную (3.2)
компонент вектор-функции ![]() выразим в виде суммы ковариантных
производных компонент составлявших вектор-функции
выразим в виде суммы ковариантных
производных компонент составлявших вектор-функции ![]() и
и ![]() . Поскольку значение
ковариантной производной от компонент постоянной поставлявшей вектор-функции
. Поскольку значение
ковариантной производной от компонент постоянной поставлявшей вектор-функции ![]() равно нулю,
значение ковариантной производной компонент
равно нулю,
значение ковариантной производной компонент ![]() равно значению ковариантной
производной компонент переменной составляющей вектор-функции
равно значению ковариантной
производной компонент переменной составляющей вектор-функции ![]() . При
переходе от аналитического выражения ковариантной производной (3.2) к
ее конечноразностному аналогу получаем численное выражение ковариантной
производной от компонент постоянной составлявшей вектор-функции
. При
переходе от аналитического выражения ковариантной производной (3.2) к
ее конечноразностному аналогу получаем численное выражение ковариантной
производной от компонент постоянной составлявшей вектор-функции ![]()
где Dх1 - длина ячейки разностной сетки в
направлении координатной линии х1. При неизменяемости
вектор-функции ![]() ее компоненты на криволинейных сетках
являются переменными функциями, в силу чего правая часть (3.3)
имеет погрешность разностной аппроксимации, пропорциональную модулю
ее компоненты на криволинейных сетках
являются переменными функциями, в силу чего правая часть (3.3)
имеет погрешность разностной аппроксимации, пропорциональную модулю ![]() . При
больших значениях малоизменяющихся вектор-функций
. При
больших значениях малоизменяющихся вектор-функций ![]() погрешность разностной
аппроксимации ковариантной производной компонент постоянной составлявшей
вектор-функции
погрешность разностной
аппроксимации ковариантной производной компонент постоянной составлявшей
вектор-функции ![]() в виде (3.3) может стать соизмеримой с
вычисляемым значением ковариантной производной компонент переменной
составляющей вектор
в виде (3.3) может стать соизмеримой с
вычисляемым значением ковариантной производной компонент переменной
составляющей вектор ![]() . В этом проявляется отрицательное
влияние жестких смещений на сходимость численных решений метода конечных
разностей на криволинейных сетках.
. В этом проявляется отрицательное
влияние жестких смещений на сходимость численных решений метода конечных
разностей на криволинейных сетках.
Предложенная
Е.А. Гоцуляком модификация метода сеток (метод криволинейных сеток), являвшаяся
обобщением метода конечных разностей для случая дискретизации векторных
дифференциальных соотношений в системе криволинейных координат, полностью
исключает погрешность аппроксимации ковариантной производной компонент
постоянной составляющей вектор-функции ![]() . Суть ее состоит в следующем, для
дискретизации дифференциальных соотношений теории упругих тонких оболочек
методом криволинейных сеток используется аналитическое выражение ковариантной
производной в виде
. Суть ее состоит в следующем, для
дискретизации дифференциальных соотношений теории упругих тонких оболочек
методом криволинейных сеток используется аналитическое выражение ковариантной
производной в виде
При конечноразностной аппроксимации (3.4) в точке (i; j) разностной аналог ковариантной производной принимает вид
Значение
конечноразностного аналога (3.5) ковариантной производной компонент
постоянной составляющей вектор-функции ![]() точно равно нулю. Таким образом в
методе криволинейных сеток исключается погрешность обусловленная жесткими
смещениями.
точно равно нулю. Таким образом в
методе криволинейных сеток исключается погрешность обусловленная жесткими
смещениями.
Исключение погрешности аппроксимации ковариантных производных компонент постоянных составляющих вектор-функции дифференциальных соотношений теории тонких оболочек приводит к существенному улучшению сходимости численных решений метода криволинейных сеток в сравнении со сходимостью решений традиционного метода конечных разностей. Улучшенная сходимость метода криволинейных сеток позволяет получать желаемую точность численного решения при уменьшенном количестве степеней свободы, что приводит к более экономному расходованию ресурсов ЭВМ и позволяет эффективно решать задачи теории оболочек в двумерной постановке.
3.2. Дискретизация дифференциальных соотношений теории тонких оболочек
Для дискретизации континуальной задачи теории оболочек используем метод криволинейных сеток. На срединной поверхности S оболочки строим координатные линии недеформированной системы координат i, j. Определяя вектор внутренних усилий на линиях между узлами разностной сетки, преобразуем уравнение равновесия (2.20) в узле (i; j) к разностному виду:
В целях
улучшения сходимости на геометрически неравномерных сетках, а также на линиях
стыков сопрягаемых оболочек выполним усреднение функции ![]() и нагрузки в
конечноразностных ячейках, примыкающих к узлу (i;
j). В этом случае (3.6) принимает вид:
и нагрузки в
конечноразностных ячейках, примыкающих к узлу (i;
j). В этом случае (3.6) принимает вид:
Проецируя конечноразностное векторное уравнение равновесия элемента оболочки (3.7) с центром в узле (i; j) на векторы взаимного локального базиса в этом узле, получаем систему трех скалярных уравнений равновесия:
Здесь введены обозначения для величин, представляющих собой коэффициенты преобразования координат базиса в точке (i ± 0,5; j ± 0,5) к координатам базиса в точке (i; j)
Выражения перерезывающих усилий Ta3, входящих в уравнения равновесия (3.8), получаем из (2.24)
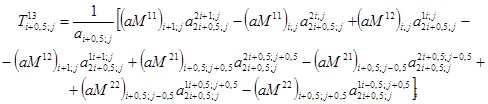 (3.10)
(3.10)
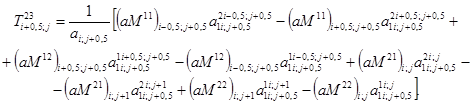 (3.11)
(3.11)
В разностном уравнении равновесия (3.8) мембранные усилия T1a необходимо определять в точках между узлами на линиях x1, T2a - между узлами координатных линий x2. В соответствии с этим для применения соотношений (2.18) находимо иметь все компоненты мембранных деформаций между узлами на координатных линиях.
В результате дискретизации дифференциальных соотношений (2.14) получаем разностные выражения компонент тензора мембранных деформаций
![]() (3.13)
(3.13)
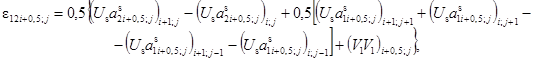 (3.14)
(3.14)
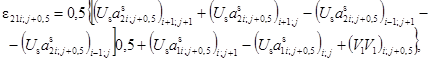 (3.15)
(3.15)
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
Внутренние моменты, входящие в выражения перерезывающих сил (2.24), определяются как в узлах, так и в центрах ячеек разностной сетки, поэтому для применения зависимостей (2.18) необходимо иметь компоненты тензора изгибных деформаций в узлах и центрах разностной сетки, дискретные выражения которых имеют вид:
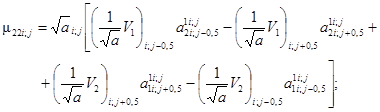 (3.19)
(3.19)
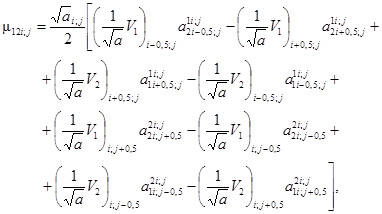 (3.20)
(3.20)
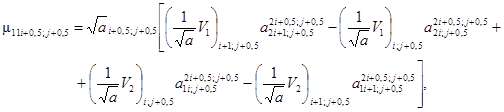 (3.21)
(3.21)
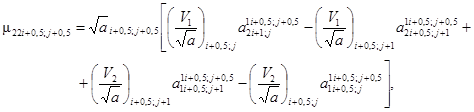 (3.22)
(3.22)
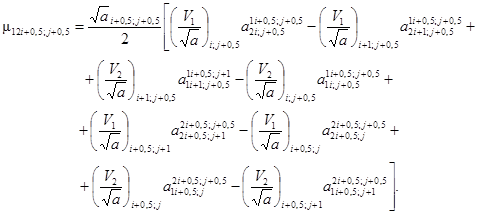 (3.23)
(3.23)
Компоненты вектора углов поворота окрестности оболочки, входящие в дискретные выражения деформаций (3.12) - (3.23), получим между узлами на линиях разностной сетки
Последовательная подстановка соотношений (3.24) - (3.27), (3.18) - (3.23), (3.12) - (3.17), (2.18), (3.10) - (3.11) в (3.8) позволяет перейти от рассмотрения дифференциального векторного уравнения равновесия к системе алгебраических уравнений в перемещениях. Разрешающая система уравнений краевой задачи строится последовательным обходом углов сеточной области, наложенной на рассчитываемый объект.
3.3 Граничные условия
Разностные уравнения, описывающие равновесие углов дискретной модели, должны быть дополнены условиями на границах. В методе криволинейных сеток реализованы граничные условия свободного края, подвижного и неподвижного шарнирного опирания, скользящей и жесткой заделки, симметрии и косой симметрии поля перемещений.
Приведем граничные условия для контурных линий сеточной области (i1 £ i £ im; j1 £ j £ jn).
Для свободного края, расположенного вдоль линии i = i1 справедливы соотношения
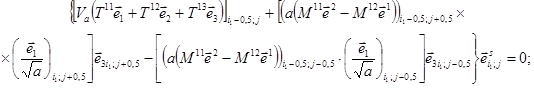
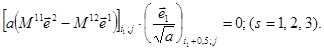
На свободном крае вдоль линии i = im в приведенных выражениях меняются индексы i1 на im, i1 - 0,5 на im + 0,5 и i1 + 0,5 на im - 0,5.
Для свободного края, расположенного вдоль линии j - j1 справедливы аналогичные равенства
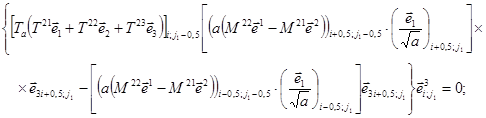
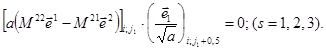
На свободном крае по линии j = jn в приведенных выражениях меняются индексы j1 на jn, j1 - 0,5 на jn + 0,5 и j1 + 0,5 на jn - 0,5. Программная реализация условий свободного края осуществляется посредством исключения на разностного уравнения (3.6) той его части, которая по условиям данного края равна нулю, что приводит к исключению неизвестных в законтурных узлах сетки на стадии формирования системы разрешающих уравнений. В основу физической интерпретации граничных условий свободного края может быть положено то обстоятельство, что в местах отсутствия материала оболочки отсутствует и воздействие внутренних усилий. В случае ортогональной равномерной сетки предельный переход в описанных соотношениях приводит к классическому виду граничных условий свободного края
![]()
![]()
В узле (i1, j1), расположенном на пересечении двух контурных линий с условиями свободного края, из разностного уравнения исключаются две группы членов, равные нулю согласно приведенным соотношениям. Таким образом шаблон коэффициентов усекается с двух сторон, что приводит к исключению неизвестных во всех законтурных узлах. Аналогичная операция исключения производится и в трех остальных углах (i1, in), (im, j1), (im, jn).
Различные
варианты шарнирного опирания и защемления реализуются посредством замены одного
или нескольких приведенных выше соотношений на одно или нескольких
соответствующих кинематических условий вида ![]() (s
= 1, 2, 3);
(s
= 1, 2, 3); 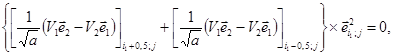
справедливых для линии i = i1. Для контурной линии j = j1 аналогичная замена производится с использованием равенств
![]() (s = 1, 2, 3);
(s = 1, 2, 3);
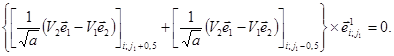
В контурной линии i = i1, расположенной на плоскости симметрии, исключение неизвестных, определяющих перемещения в законтурных узлах, осуществляется с помощью равенств
![]()
![]()
![]() (k = 1, 2)
(k = 1, 2)
В случае косой симметрия используются равенства
![]()
![]()
![]() (k = 1, 2)
(k = 1, 2)
3.4. Построение решения задач о нелинейном деформировании и устойчивости оболочек
Задачи о нелинейном деформировании механических систем поддаются аналитическим методам решения лишь в простейших случаях. Поэтому при решении нелинейных задач теории оболочек, описываемых дифференциальными уравнениями с частными производными и переменными коэффициентами, возникает необходимость в привлечении численных методов.
Для решения систем нелинейных дифференциальных уравнений применен метод дифференцирования по параметру с коррекцией невязкой метода Ньютона [5], суть которого состоит в том, что нелинейное функциональное уравнение порядка k
F(Х) = 0, X = [x1, ..., xk, p)T, (3.28)
описывающее равновесное состояние оболочки, дополняется уравнением
описывающим величину выбранного ведущего параметра, что приводит к функциональному уравнению
Ф(Х) = lЕ, Е = [e, ..., ek+1]; ei = 0 (i = 1, ..., k), Gk+1 = 1.
Это уравнение можно приближенно записать в виде разложения в ряд Тейлора с сохранением двух его членов
[Ф(Х)]z+1 » [Ф(Х)]z + [Ф¢(Х)]z[DX]z+1 » (lz + Dlz+1)E. (3.30)
Отсюда получается выражение приращения вектора неизвестных на z + 1 шаге приращения ведущего параметра
[DX]z+1 = [Ф¢(Х)]z-1{Dlz+1E + lzE - [Ф(Х)]z}, (3.31)
где последние два члена в фигурных скобках представляют собой накопленную невязку метода Ньютона от предыдущих шагов приращения ведущего параметра.
Такой подход позволяет реализовать на ЭВМ пошаговый процесс, сводящий решение нелинейной краевой задачи к последовательности решений линеаризованных краевых задач, заменяющих процедуры построения операторов [Ф¢(Х)]z-1.
Перепишем соотношение (3.31) в виде
[Ф¢(Х)]z[DX]z+1 = Dlz+1E + lzE - [Ф(Х)]z, (3.32)
которое представляет собой
линеаризованное в окрестности состояния уравнение равновесия, составленное с
учетом накопленных в оболочке мембранных усилий ![]() и углов поворота Va*.
и углов поворота Va*.
Поскольку нелинейные уравнения теории оболочек сформулированы в исходной недеформированной метрике, линеаризацию соотношений (2.14), (3.8) производим с учетом изменения векторов локального базиса.
Учитывая специфику деформирования тонких оболочек, проявляющуюся в существенном изменении ориентации базисных векторов при незначительном изменении их длин, представим выражения векторов деформированной поверхности в виде
В соответствии с предположением о неизменяемости в процессе деформирования модулей базисных векторов выражения приращений векторов основного локального базиса будут иметь вид
![]() (3.34)
(3.34)
Исходя из
уравнений равновесия (3.8) и вводя в рассмотрение значения базисных
векторов (3.35)
и накопленных усилий ![]() , представим линеаризованные уравнения
равновесия тонкой оболочки в виде
, представим линеаризованные уравнения
равновесия тонкой оболочки в виде
где s = 1, 2, 3 определяет номер уравнения.
Пренебрегая
членами, содержащими накопленные значения перерезывающих сил ![]() , как это
принято в теории устойчивости тонких оболочек, представим линеаризованные
уравнения равновесия в окончательном виде
, как это
принято в теории устойчивости тонких оболочек, представим линеаризованные
уравнения равновесия в окончательном виде
В уравнении (3.37) члены, определяющие внешнее воздействие, сформулированы для нагрузки, которая в процессе деформирования не меняет своего направления. В случаях, когда в процессе изменения формы оболочки нагрузка изменяет ориентацию, как при действии гидростатического давления, грузовые члены уравнений равновесия носят нелинейный характер. Для такой следящей нагрузки линеаризованные уравнения равновесия должны быть дополнены членами, полученными линеаризацией нелинейной нагрузки
Линеаризованные выражения мембранных деформаций (2.14) имеют вид
В соотношениях (3.36), (3.39) звездочками обозначены значения накопленных величин в окрестности линеаризованного состояния, соответствующие переменные без звездочек обозначают приращение этих величин.
Используя (3.37), (3.38), (3.39), (3.10), (3.11). (2.19), (3.12) - (3.23), (3.24) - (3.27), (3.8) в процедуре (3.31), получим последовательность линеаризованных разрешающих уравнений напряженно-деформированного состояния оболочек, коэффициенты которых на k + 1 шаге алгоритма (3.32) вычисляются с использованием характеристик состояния предыдущего k-го шага.
При построении линеаризованных систем разрешающих уравнений на каждом шаге алгоритма (3.31) производится последовательное формирование конечноразностного шаблона коэффициентов при неизвестных в каждом узле сеточной области, связанной со срединной поверхностью оболочки. Для этого во всех узлах формируются массивы шаблонов жесткостей оболочки и ребер, температур, компонент векторов локальных базисов и корней квадратных из фундаментальных определителей поверхности. После формирования шаблона конечноразностных коэффициентов производится их рассылка в коэффициенты матрицы разрешающих уравнений. По мере формирования блок-строки матрицы происходит ее преобразование методом Гаусса, что позволяет хранить в оперативной памяти лишь те блоки, которые участвуют в преобразованиях. Остальные блоки хранятся в файле прямого доступа на МД. Алгоритм построения матрицы разрешающих уравнений учитывает ее ленточную структуру, что позволяет избежать лишних арифметических операций в методе Гаусса с нулевыми блоками матрицы и сократить время счета. При переходе от шага к шагу алгоритма (3.31) матрица системы линеаризованных разрешающих уравнений и ее определитель претерпевают изменения. Смена знака определителя свидетельствует о наличии на кривой нагружения особой точки в интервале параметра нагружения, ограниченного его значениями, соответствующими предыдущим двум шагам нагружения. Если смена знака определителя сопровождается сменой знака параметра нагрузки или перемещений, то особая точка является предельной; если смены знака параметра нагрузки или перемещений не наблюдается, то особая точка является бифуркационной. Вблизи особой точки происходит постепенное вырождение матрицы разрешающих уравнений, для регуляризации задачи и получения возможности продолжения решения в закритической области производится перестройка системы уравнений посредством смены ведущего параметра нагружения. Для построения ответвляющегося (бифуркационного) решения необходимо как можно ближе подойти к точке бифуркации с уменьшенным шагом нагружения и на шаге, предшествующем смене знака определителя, задать оболочке такие перемещения, которые бы привели к ветвлению решения в точке бифуркации.
Решение упруго-пластических и пластических задач сопряжено со значительными трудностями, и многие задачи расчетов за пределами упругости до сих пор не имеют решений. Поэтому в теории пластичности еще в большей степени, чем в теории упругости, имеют значение приближенные методы решения. При этом стремятся построить такой алгоритм, чтобы до минимума сократить выполнение большего числа операций при численном интегрировании по толщине оболочки в выражениях (2.48). Обычно предпочтение отдается различным способам линеаризации, позволяющим уменьшить количество вычислений и свести нелинейную задачу к последовательности линейных, методом упругих решений, дополнительных нагрузок и переменных параметров упругости и другим разновидностям метода Ньютона.
Идея решения физически нелинейных задач механики твердого деформируемого тела в виде последовательности решений линейно-упругих задач с некоторыми дополнительными условиями принадлежит А.А. Ильюшину. Им был предложен процесс последовательных приближения с дополнительными объемными и поверхностными нагрузками, позволяющими создать равные деформации в упругом и упруго-пластическом телах. Этот итерационный процесс решения называется методом упругих решений (МУР). Позже И.А. Биргер предложил еще два варианта итерационного процесса, основой которого на шаге нагружения является линейно-упругая задача либо с переменными параметрами упругости, либо с дополнительными деформациями.
При разработке программы по расчету оболочек с учетом упруго-пластических свойств материала в геометрически линейной и в геометрически нелинейной постановках использовано сочетание на каждом шаге нагружения метода переменных параметров упругости и метода дополнительных нагрузок А.А. Ильюшина.
На k-ом шаге нагружения
принимаются переменные параметры упругости и дополнительные
нагрузки, обусловленные накопленным уровнем деформаций в оболочке, решается
упругая задача, в результате чего определяется усилия, моменты и деформации k-го приближения. По этим величинам в каждой точке
разностной сетки оболочки и семи точках по толщине оболочки подсчитываются интенсивности
деформаций ![]() . В координатах si - ei
диаграмм деформирования (см. рис. 2.3)
для каждой рассматриваемой точки тела оболочки определяется величина
. В координатах si - ei
диаграмм деформирования (см. рис. 2.3)
для каждой рассматриваемой точки тела оболочки определяется величина ![]() , равная
отношению интенсивности напряжений
, равная
отношению интенсивности напряжений ![]() , соответствующей интенсивности
деформаций
, соответствующей интенсивности
деформаций ![]() . По величине
. По величине ![]() определяем также
параметры
определяем также
параметры ![]() и
и
![]() .
Секущие параметры
.
Секущие параметры ![]() ,
, ![]() ,
, ![]() будут различными не только на
поверхности оболочки, но и по толщине оболочки. На основе вычисленных упругих
констант k-го шага нагружения по (2.48) и (2.53) вычисляем интегральные жесткостные
характеристики
будут различными не только на
поверхности оболочки, но и по толщине оболочки. На основе вычисленных упругих
констант k-го шага нагружения по (2.48) и (2.53) вычисляем интегральные жесткостные
характеристики ![]() и
и ![]() для речения задачи на (k + 1) шаге нагружения. Далее при составлении системы
разрежающих уравнений вычисляются дополнительные нагрузки, которые будут
приложены при решении упругой задачи на (k + 1) шаге
нагружения, и решается упругая линейная задача этого шага нагружения.
для речения задачи на (k + 1) шаге нагружения. Далее при составлении системы
разрежающих уравнений вычисляются дополнительные нагрузки, которые будут
приложены при решении упругой задачи на (k + 1) шаге
нагружения, и решается упругая линейная задача этого шага нагружения.
Расчет продолжается до достижения заданного уровня нагружения или до потери несущей способности оболочки. Для тонких оболочек возможна потеря устойчивости до появления развитых пластических зон в оболочке. При реализации шагового процесса необходимо первый шаг выбрать таким, чтобы максимальные напряжения в оболочке достигли предела текучести, а все последующие шаги нагружения выбрать минимальными.
4. ОПИСАНИЕ ПРОГРАММЫ
4.1. Общие сведения, функциональное назначение и используемые технические средства
Символическое обозначение программы - «МЕКРИС-2», наименование комплекс программ по расчету напряженно-деформированного состояния и устойчивости оболочек сложной формы. Функционирует в виде библиотек исходных модулей SYS2.T.MKC2, загрузочных модулей SYS2.T.MKCP и набора тестовых примеров расчета SYS2.T.TEST с библиотечной организацией.
Комплекс программ «МЕКРИС-2» предназначен для решения на ЭВМ в двумерной постановке статических задач определения НДС и исследования устойчивости ребристых оболочек сложной формы, ослабленных отверстиями или вырезами, с учетом геометрической и физической нелинейностей. Срединная поверхность оболочки может быть составлена из ряда аналитических поверхностей. Стык может быть как гладким, так и с изломом поверхности по линии сопряжения. Ребра принимаются в расчет дискретно и могут быть центральными или эксцентричными относительно срединной поверхности оболочки, а также прерывистыми или непрерывными. На границах расчетного фрагмента возможно задание произвольной комбинации различных граничных условий.
Решение задач можно получать при произвольных статических силовых воздействиях и произвольных температурных воздействиях, задаваемых в виде двух независимых функций: распределения температуры в срединной поверхности и перепада температуры по толщине оболочки.
Область применения комплекса ограничивается классом тонких пластинок и оболочек. Сочленение фрагментов составных оболочек допустимо только по координатным линиям. Контуры отверстий и вырезов должны совпадать с координатными линиями на поверхности оболочки. Ограничения на объемы решаемых задач диктуются, как правило, ресурсами ЭВМ.
В состав комплекса входят:
- программа по решении задач о НДС и устойчивости оболочек с учетом геометрической нелинейности, она позволяет определять общее напряженно-деформированное состояние, исследовать характер перестройки равновесных форм рассматриваемых систем, строить траектории нагружения, находить на них предельные точки и точки бифуркации, анализировать закритические состояния. Включает также возможность анализа НДС геометрически линейной постановке (первый шаг решения нелинейной задачи);
- программа по решению задач упруго-пластического деформирования оболочек. Она позволяет исследовать процесс деформирования оболочек с учетом соотношений теории малых упруго-пластических деформаций.
В качестве языков программирования при написании программ использованы ФОРТРАН-IV и АССЕМБЛЕР. На языке АССЕМБЛЕР реализованы модули, определяющие быстродействие вычислительного процесса. Использование алгоритмического языка ФОРТРАН-IV делает программирование эффективным и многосторонним, что позволяет пользователю легко пополнить подпрограммы вновь разработанными блоками.
Функционирование комплекса «МЕКРИС-2» базируется на ЭВМ серии ЕС с объемом оперативной памяти не менее 512 Кбайт под управлением ОС ЕС версии 6.1. При этом запросы программ на оперативную память в зависимости от объема решаемых задач составляют от 200 до 600 Кбайт. Программный комплекс состоит из 6 тысяч операторов. При эксплуатации программ комплекса используется файл прямого доступа FT08F001 на МД, размер которого определяется объемом решаемой задачи.
В качестве устройства ввода информации могут использоваться перфокарточные устройства ввода, МД или МЛ, устройства вывода - АППУ, МД или МЛ. Для транспортировки программ применяется магнитная лента. Копирование библиотечных наборов осуществляется утилитой IEHMOVE операционной системы ОС ЕС.
Эксплуатация комплекса программ «МЕКРИС-2» не требует специальной подготовки системных программистов и обслуживающего персонала ЭВМ, так как использует стандартное системное математическое обеспечение ОС ЕС. Основной режим работы - пакетный.
Высокий уровень автоматизации всех этапов вычислительного процесса и компактность задания исходной информации позволяют специалистам в области прочностных расчетов конструкций освоить работу с комплексом в минимальные сроки без изучения теоретических основ метода. Их подготовка может производиться в процессе передачи и освоения комплекса.
4.2. Основные характеристики
4.2.1. Краткая характеристика используемых методов и сведения об их эффективности
Методы решения задач о НДС и устойчивости оболочек, описанные в разделе 3, позволили разработать вычислительный алгоритм, пригодный для исследования широкого круга задач теории оболочек в геометрически и физически нелинейных постановках, реализованный в комплексе «МЕКРИС-2». Используемый метод дискретизации разрешавших соотношений теории оболочек (МКС) обладает высокой скоростью сходимости благодаря полному исключению погрешности аппроксимации функций жестких смешений. Для решения систем алгебраических уравнений, являющихся дискретным математическим аналогом континуальных задач, используется блочный метод Гаусса, учитывающий ленточную структуру матрицы решаемой системы уравнений. Примененный для решения нелинейных задач метод продолжения по параметру с пошаговой коррекцией решения методом Ньютона при относительно небольших затратах машинного времени позволяет не только строить траектории нагружения и находить на них особые точки, но и исследовать закритическое поведение оболочки с достаточной для инженерной практики точностью.
Эффективность метода криволинейных сеток иллюстрируется на решении тестовых задач, приведенных в приложении 1.
4.2.2. Временные характеристики.
Для решения задачи о напряженно-деформированном состоянии оболочки на ЭВМ ЕС-1050 необходимо при разностной сетке 9´9 узлов - 4 мин. и сетке 13´13 - 7 мин. Время, необходимое для решения геометрически нелинейной задачи устойчивости, например при сетке 9´9 узлов и 10 шагах вычислительного процесса, составит 42 минуты. С увеличением или уменьшением количества шагов время счета соответственно увеличивается или уменьшается пропорционально количеству шагов.
При исследовании упруго-пластического деформирования оболочек временные характеристики одного шага вычислительного процесса на ЭВМ ЕС-1050 следующие: для сетки 9´9 узлов - 5 мин., для сетки 13´13 узлов - 8 минут.
Следует отметить, что при одинаковом общем количестве узлов разностной сетки и прочих равных условиях меньше машинного времени необходимо для расчета оболочки, имеющей минимальное число узлов в направлении координатной линии х1.
4.2.3. Средства контроля правильности выполнения программы.
Правильность работы алгоритмов программ комплекса проверяется путем решения контрольного примера, описанного в приложении 1. Контроль за работой программ в процессе решения задачи (проверка некоторых вводимых величин, оценка качества решения системы уравнений) осуществляется с помощью информационных и диагностических сообщений.
Предусмотрены средства восстановления и продолжения вычислительного процесса, которые могут оказаться полезными в следующих ситуациях:
- время решения задачи достаточно велико, и существует опасность сбоев ЭВМ;
- выделяемое время меньше требуемого, и задача может быть решена только в несколько приемов;
- частичное изменение исходных данных (например, параметров нагружения), позволявшее продолжить счет с определенного места.
Для хранения промежуточных и окончательных результатов решения задачи используется файл прямого доступа FT08F001, организованный на МД.
4.2.4. Иллюстрация возможностей.
Возможности комплекса программ «МЕКРИС-2» иллюстрируются примерами расчета, приведенными в приложении 2.
4.3. Описание логической структуры
Весь программный комплекс условно можно разбить на несколько функциональных блоков: блок управления решениям задачи о нелинейном деформировании и устойчивости; блок решения системы линеаризованных алгебраических уравнений равновесия; блок построения конечноразностного шаблона коэффициентов при неизвестных; блок построения массивов проекций векторов локальных базисов и шаблонов жесткостных характеристик оболочки и ребер.
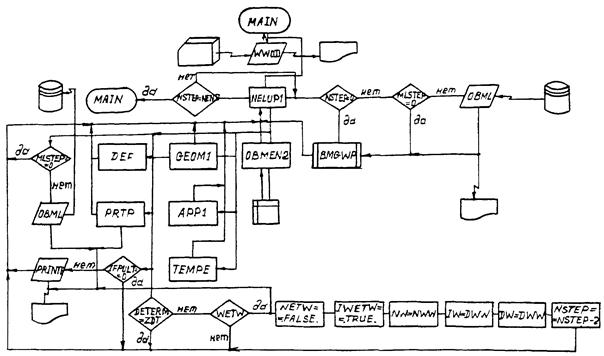
4.3.1. Блок управления решением задачи
Блок управления решением задачи (рис. 4.1) включает головную программу MAIN, которая вызывает подпрограмму WWOD для ввода и распечатки исходных и преобразованных данных задачи. После этого вызывается управляющая подпрограмма NELUP1 (при решении задачи в упругой постановке) или NENUP2 (при решении задачи в упруго-пластической постановке).
В числе формальных параметров управляющих подпрограмм имеются имена подпрограмм, осуществляющих: выбор оператора левой части (OPERLE - в упругой постановке, OPERLN - в упруго-пластической постановке); решение алгебраических систем уравнений по блочной схеме Гаусса (BMGWP - при использовании одинарной точности для обменов с МД, DBMGWP - при использовании двойной точности); формирование блоков системы уравнений (BMS - при нормировании блоков с элементами одинарной точности или DBMS - при нормировании с двойной точностью); формирование компонентов вектора нагрузки (OPERP - имя подпрограммы для конкретного вида нагружения); формирование проекций касательных векторов основного локального базиса поверхности точек сеточного шаблона (GEOM - имя подпрограммы для конкретного вида поверхности или подпрограмма SOSTAV для составных оболочек). Имена подпрограмм, выступающих в качестве фактических параметров при обращении к управляющим подпрограммам NELUP1 или NELUP2, должны быть задекларированы внешними оператором EXTERNAL в головной программе МА. Здесь же оператором DEFINT FILE декларируются параметры файл прямого доступа № 8, который предназначен для обменов промежуточными результатами преобразования исходной матрицы в прямом ходе блочного метода Гаусса и для хранения результатов счета необходимого числа последних шагов решения алгоритма дифференцирования по параметру с целью сохранения возможности возобновления счета с любого из них. При обменах с файлом прямого доступа информация передается в бесформатном виде, размер записи составляет 900 слов по 4 байта при использовании подпрограммы BMGWP или 1800 слов при использовании DBMGWP. Общий размер файла прямого доступа, выраженный числом записей, состоит из: числа записей MBLOK, необходимых для обменов в алгоритме Гаусса; числа записей KZ2, необходимых для хранения результатов счета требуемого числа шагов решения задачи нелинейного деформирования или устойчивости. Значение MBLOK зависит от размеров сеточной области МО, NО, количества правых частей KOLPCH и числа МВ листов памяти оперативного запоминающего устройства, выделенных задаче, и вычисляется в операторах
KFINIS = (MO ´ NO ´ KOLFOB - 1)/30 + 1
LFINIS = KFINIS + KOLPCH/30 + 1
MBLOK = (((4 ´ MO + 3) ´ KOLFOB - 1)/60 + 1 + (LFINIS + KFINIS)) ´ KFINIS - MB,
где KOLFOB - количество разрешающих функций в узле. Значение KZ2 зависит от параметра NHR, определяющего число шагов решения, которые необходимо сохранить для возможности возобновления счета с любого из них, и от размеров сеточной области MO, NO:
KZ2 = NHR ´ ((13 ´ MO ´ NO + 6)/900 + 2).
Таким образом, размер файла прямого доступа, выраженный числом записей по 900 или 1800 слов, равняется
KФ8 = MLSTEP + KZ2,
где MLSTEP - номер записи файла прямого доступа, начиная с которой осуществляется запись сохраняемых результатов счета NHP шагов вычислительного процесса (MLSTEP ³ MBLOK).
Блок-схема управления решением задачи о нелинейном деформировании и устойчивости оболочек
В целях экономии оперативной памяти для загрузки программного комплекса в программе MAIN следует позаботиться о размерностях массивов PDEF из COMMON/SDEF/, SX из COMMON/SX/, OZU из COMMON/COZU/ и RMX из COMMON/RB/.
Размерность массивов SX и RMX должна равняться наименьшему числу, кратному 900 и большему, чем KOSX = KRMX = 3 × MO × NO × 6. При KRMX < 2700 необходимо размерность массивы RMX задать равной RMX (2700).
Размерность массива PDEF определяется аналогично, но должна быть при решении задач в упругой постановке больше KPDEF = MO × NO × 10, при решении задач в упруго-пластической постановке - больше KPDEF = MO × NO × 13.
Первая размерность массива OZU должна равняться размеру записи файла прямого доступа 900 или 1800, а вторая размерность значению KOZ, задаваемому в исходных данных параметром MB.
Заданные в головной программе размерности перечисленных массивов присваиваются соответственно параметрам KOSX, KRMX, KPDEF и KOZ из COMMON/OST/, служащими для получения информационных сообщений.
Размерность двумерного массива QSTR из COMMON/QSTR/ равна 30´78. При использовании подпрограммы DBMS данный массив необходимо декларировать с двойной точностью, а при использовании BMS этой декларации производить не следует.
Управляющие подпрограммы NELUP1 (NELUP2) (см. рис 4.1) имеют формальные параметры, которыми служат имена подпрограмм, определяющих конфигурацию программного комплекса. Они были рассмотрены выше. Режимы работы управляющих подпрограмм определяются на уровне задания исходных данных, переменными:
- NBEGIN - номер шага, с которого начинается (возобновляется) счет;
- NEND - номер шага, которым счет оканчивается (прерывается);
- NEL - логическая переменная, при истинном значении которой решается задача с учетом изменения формы срединной поверхности оболочки в процессе деформирования, в противном случае учет изменения формы производиться не будет;
- NELDEF - логическая переменная, при истинном значении которой задача решается с учетом нелинейной связи компонентов тензора мембранных деформаций и компонентов вектора перемещений, при её ложном значении реализуется линейная зависимость;
- WETW - логическая переменная, при истинном значении которой автоматически производится перевод на ответвляющееся решение при смене знака определителя;
- NWW переменная, определяющая номер компоненты вектора перемещений, служащей ведущим параметром ответвляющегося решения;
- IWW, JWW - переменные, определяющие целочисленные координаты узла ведущего параметра ответвляющегося решения;
- DWW - значение приращения ведущего параметра ответвляющегося решения;
- NW - переменная, определяющая номер компоненты вектора перемещения или нагрузки, выбранной в качестве ведущего параметра основной ветви решения;
- IW, JW - переменные, определяющие целочисленные координаты узла ведущего параметра основной ветви решения;
- DW - значение приращения ведущего параметра перемещения основной ветви решения;
- DP - значение приращения ведущего параметра нагрузки основной ветви решения;
- MLSTEP - номер записи в файле прямого доступа, начиная с которой осуществляется запись и хранение результатов последних NHR шагов решения.
В процессе решения анализируется обусловленность матрицы и знакопостоянство её определителя. Смена знака определителя свидетельствует о наличии особой точки на кривой нагружения в окрестности рассматриваемого состояния. Если при этом WETW = .TRUE., то осуществляется возврат к предыдущему шагу и смена ведущего параметра, т.е. автоматически реализуется переход на ответвляющееся решение.
После завершения каждого шага нагружения в зависимости от значений элементов массива IFPULT, задаваемых в исходных данных, печатаются поля накопленных физических значений перемещений, внутренних усилий и моментов, координат узлов сеточной области, накопленных мембранных деформаций и узлов поворота и напряжений. Кроме того печатается номер шага вычислительного процесса, значение определителя и его десятичного порядка, значения переменных NW, IW, JW, DW. При MLSTEP > 0 производится запись в файл прямого доступа значений накопленных перемещений, номера шага, накопленной нагрузки, IW, JW, NW, DW, знака определителя, а также накопленных значений деформаций и углов поворота.
В том случае, когда ведущим параметром выбрана одна из компонент вектора перемещений, по найденным значениям этих компонент определяются координаты узла с максимальным значением выбранной компоненты, которые присваиваются переменным IW, JW, определяющим на следующих шагах нагружения узел ведущего параметра.
4.3.2. Блок решения системы линеаризованных уравнений равновесия
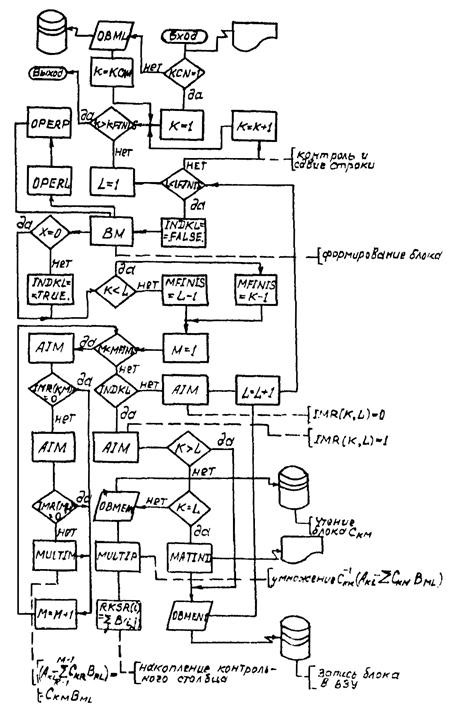
Блок решения системы линеаризованных уравнений равновесия (рис. 4.2) состоит из подпрограммы BMGWP (DBMGWP), реализующей алгоритм компактной схемы блочного метода Гаусса, и BMS (DBMS), управляющей формированием блоков исходной матрицы размерностью 30´30. Достоинства блочного метода Гаусса при решении задач теории оболочек:
- возможность решения задачи при однократном порождении исходной матрицы без необходимости её хранения;
- соответствие блочного строения матрицы системы уравнений листовой структуре данных файла прямого доступа, упрощающее организацию обмена информацией с МД;
- возможность решения с несколькими правыми частями, соответствующими различным вариантам загружения оболочки (при решении задач о НДС в линейной постановке);
- возможность параллельного вычисления определителя исходной матрицы.
Преобразование исходной матрицы А по компактной схеме Гаусса равносильно разложению её на сомножители С и В:
![]() (K ³ L).
(K ³ L).
![]() (K < L).
(K < L).
Здесь блоки AKL, CKL, BKL представляют собой квадратные субматрицы из K-ой блок-строки и L-того блок-столбца матриц А, С и В. Фиксированный порядок КВС = 30 субматриц связан с размером записи файла прямого доступа 302.
Матрицы-сомножители С и В имеют соответственно верхнюю и нижнюю треугольную структуру. Диагональ матрицы В составляется из единичных блоков BMM. Такой вид матрицы С и B позволяет вычислять определитель det//A// перемножением определителей диагональных субматриц СMM.
Схема алгоритма при прямом ходе метода Гаусса
Для алгоритмов, требующих многократного решения систем уравнений с одинаковой матрицей А, хранение нижней треугольной матрицы С выполняется по условию .NOT.STATIC.
Наряду с возможностью обработки матриц общего вида в подпрограммах заложен алгоритм, учитывающий аффективное преобразование малозаполненных матриц и матриц ленточной структуры. Это достигается введением индикаторной матрицы, идентифицируемой массивом IMF с поразрядным хранением информации.
Подпрограммы BMGWP и DBMGWP используются при решении линейных и нелинейных задач устойчивости методом дифференцирования по параметру. При шаговом алгоритме этого метода на каждом шаге решается задача в приращениях, при этом к числу неизвестных добавляется параметр однопараметрической нагрузки, а правой частью системы уравнений является вектор невязки. Решение линеаризованной задачи методом Гаусса в окрестности особой точки, в которой матрица становится близкой к вырожденной, оказывается малоэффективным. Поэтому вблизи особых точек производится регуляризация матрицы уравнений посредством введения дополнительного неизвестного и нового дополнительного уравнения. Дополнительное уравнение, вводимое при регуляризации, представляет собой уравнение задания приращения одной из компонент вектора перемещений узла, в котором эта компонента имеет максимальное значение. При этом матрица перестает быть вы рожденной, но ее главный минор, являющийся определителем нерегуляризованной матрицы, по-прежнему остается нулевым, что не позволяет использовать метод Гаусса. Для устранения равенства нулю главного минора регуляризованной матрицы производится перестановка местами строки введенного уравнения и строки уравнения для перемещения, которое выбрано новым ведущим параметром при регуляризации.
Подпрограммы BMGWP и DBMGWP вызывают следующие подпрограммы:
- OBMB с дополнительным входом OBML, осуществляет обмен информацией с МД;
- AIM осуществляет поразрядный обмен с МО37;
- OBMEN1 с дополнительным входом OBMEN2, осуществляет обмен информацией с МД;
- BMS или DBMS осуществляет построение блоков исходной матрицы;
- PRINBL осуществляет отладочную печать блоков исходной и преобразованной матрицы;
- MULTDM осуществляет умножение двух блоков с вычитанием их произведения;
- MULTDP осуществляет умножение двух блоков со сложением их произведения;
- MATIND обращает блок матрицы.
Результатом работы подпрограмм BMGWP и DBMGWP являются векторы решений, которые блоками по 30 неизвестных хранятся на МД на местах последних блоков преобразованной матрицы.
При построении блоков исходной матрицы подпрограммами BMS и DBMS вызывается подпрограмма OPEPLE или OPERLN, которая в зависимости от кода оператора узла разностной сетки и от его граничных условий осуществляет вызов подпрограммы построения конечноразностного шаблона коэффициентов OPERС1 или OPERCN при наличии зон пластических деформаций, и подпрограммы вычисления коэффициентов однопараметрической нагрузки.
Посредством обращения к подпрограмме DBUND осуществляется исключение неизвестных в законтурных узлах за плоскостями симметрии и косой симметрии.
4.3.3. Блок построения разностного шаблона коэффициентов при неизвестных
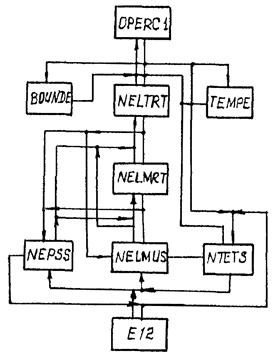
Блок построения разностного шаблона коэффициентов при неизвестных (рис. 4.3) состоит из ряда подпрограмм, моделирующих основные этапы вывода разрешавших уравнений теории оболочек, осуществляя последовательное накопление значений элементов массива конечноразностных коэффициентов U(75) в COMMON/QKOEF/.
Построение скалярных уравнений равновесия моделирует подпрограмма OPERC1 или OPERCN при наличии зон пластических деформаций, вызывая подпрограммы NELTRT или NEKTFN при упруго-пластической работе материала оболочки, NTETS, BOUNDE. Она накапливает значения разностных коэффициентов U(75), полученных от вклада каждого из усилий, с последующим умножением их на множители, с которыми эти усилия входят в каждое из трех уравнений равновесия.
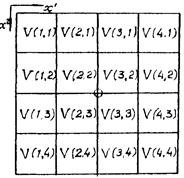
Коэффициенты, с которыми входят усилия в уравнения равновесия, определяются на основе элементов массивов Е(1458) и SQA(9,9) из COMMON/METR/, заполняемых подпрограммой GEOM1. Элементы массива SQA представляют собой значения квадратных корней из фундаментальных определителей поверхности в узлах вспомогательного сеточного шаблона 9´9 (рис. 4.4). Массив Е(1458) можно представить в виде E(K, N, IP, JP), где K = 1, 2, 3 - номер компоненты векторов локальных базисов в декартовой системе координат; N = 1, 2 ..., 6 - номер вектора локального базиса (1 2, 3 - соответствуют трем векторам основного базиса, а 4, 5, 6 - векторам взаимного базиса); IP, JP - номера узлов вспомогательного сеточного шаблона 9´9, в которых определены локальные базисы.
Принадлежность узла, для которого строится шаблон коэффициентов, к контурным или предконтурным узлам свободного или шарнирно опертого края определяется значениями элементов массива логических переменных Y(4, 4) из COMMON/BECA/, полученными в результате работы подпрограммы анализа поля признаков APP1. Истинные значения элементов этого массива свидетельствуют о наличии соответствующей ячейки (рис. 4.5), а ложные - о её отсутствии. При отсутствии двух смежных ячеек, на общей линии которых определено некоторое усилие или угол поворота, вызов подпрограммы накопления коэффициентов шаблона от выражения этого усилия или угла поворота не осуществляется.
Схема блока построения шаблона конечноразностных коэффициентов линеаризованных уравнений равновесия
Вспомогательный сеточный шаблон 9´9 для узла (i; j)
Шаблон логических переменных, определяющих наличие материала в ячейках шаблона 5´5 узла (i; j)
Подпрограммы NELTRT, NELTFN, выполняющие
накопление значений коэффициентов разностного шаблона при неизвестных
линеаризованных уравнений равновесия в приращениях от внутренних усилий,
состоят из самостоятельных блоков, каждый из которых реализует подключение в
уравнения равновесия выражения соответствующей компоненты тензора внутренних
усилий Tat (a = 1, 2; t = 1, 2, 3). Обращение к этим блокам осуществляется по
именам дополнительных входов ENTRY. Объединение
самостоятельных блоков в одну подпрограмму обусловлено общностью их декларативных
операторов и функционального назначения. Количество этих блоков в подпрограмме NELTR равно шести: ENTRY T11 реализует подключение выражения компоненты ![]() ; ENTRY T12 - компоненты
; ENTRY T12 - компоненты ![]() ; ENTRY T22 - компоненты
; ENTRY T22 - компоненты ![]() ; ENTRY T21 - компоненты
; ENTRY T21 - компоненты ![]() ; ENTRY T1N - компоненты
; ENTRY T1N - компоненты ![]() ; ENTRY T2N - компоненты
; ENTRY T2N - компоненты ![]() .
.
В подпрограмме NELTFN аналогичные функции реализуют блоки ENTRY N11, ENTRY N12, ENTRY N22, ENTRY N21, ENTRY Q1N, ENTRY Q2N.
Блоки подпрограммы NELTRT производят подстановку в линеаризованные уравнения равновесия в приращениях физических соотношений теории оболочек для мембранных усилий и соотношений между перерезывающими пилами и внутренними моментами, подпрограммы NELTFN - постановку в уравнения равновесия в зависимости от достигнутых значений интенсивности деформаций физических соотношений теории оболочек, либо упругого деформирования, либо упруго-пластической работы материала.
По элементам логического массива V(4, 4) анализируется положение точки определения усилия относительно свободного или шарнирно опертого края. Если точка находится на свободном или шарнирно опертом крае, в расчет принимается половинная жесткость, если нет, то полная жесткость оболочки.
Признаком наличия ребра в точке определения внутренних усилий служит ненулевое значение соответствующего элемента массивов жесткостей на сжатие EF1 и EF2 для ребер направления х1 и х2 соответственно.
При работе подпрограммы NELTFN осуществляется обращение к подпрограмме RINK7, в которой происходит вычисление максимального значения интенсивности деформаций EIM в рассматриваемой точке сеточной области. Если это значение не превышает заданной интенсивности деформаций пластичности EIPL, то происходит передача управления к построению шаблона коэффициентов соответствующих усилий по физическим соотношениям упругого деформирования.
При достижении максимального значения интенсивности деформаций EIM на данном шаге нагружения значения EIPL в подпрограмме PINK7 вычисляются интегральные жесткостные характеристики оболочки путем интегрирования по толщине оболочки семиточечной формулой Ньютона-Котеса и заполняют массивы жесткостных характеристик RZ0(9), RZ1(9), RZ2(9) в COMMON/RIP1/. Для точек сеточной области, находящихся в упруго-пластической области при EIM > EIPL, шаблон коэффициентов строится с использованием выражений для усилий, уже содержащих интегральные характеристики жесткостей оболочки с учетом развития зон пластичности.
При функционировании подпрограмм NELTRT, NELTFN осуществляется обращение к блокам подпрограмм NEPSS, NELMUS, NELMRT или NELMFN при наличии зон пластических деформаций, работа которых заключается в накоплении коэффициентов разностного шаблона от выражений мембранных и изгибных деформаций и выражений внутренних моментов соответственно.
В блоках подпрограмм NELTRT, NELTFN используются для построения коэффициентов массивы шаблонов геометрических характеристик оболочки, ребер и шаблонов температур.
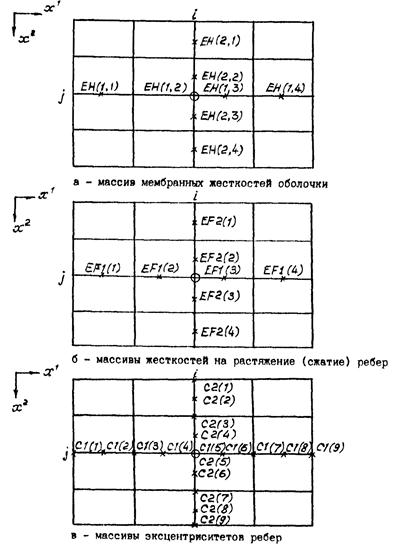
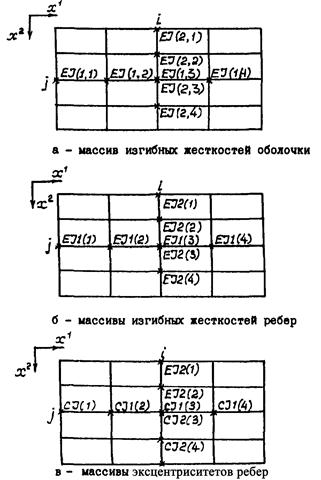
Массив EH(2, 4) из COMMON/EH/, заполняемый подпрограммой GEOM1, содержит значения мембранных жесткостей оболочки в различных точках сеточного шаблона 5´5. На рис. 4.6, а приведены точки сеточного шаблона с элементами массива EH, в которых содержатся значения мембранных жесткостей оболочек в этих точках.
Массивы EF1(4), EF2(4), CF1(4) и CF2(4) из COMMON/REB/, заполняемые подпрограммой REBRA, содержат значения жесткостей на сжатие-растяжение и эксцентриситетов ребер первого и второго направлений в точках определения соответствующих усилий. На рис. 4.6, б приведены точки сеточного шаблона и элементы массивов EF1 и EF2, в которых содержатся значения жесткостей ребер в этих точках. На рис. 4.6, в внесены точки с соответствующими элементами массивов значений эксцентриситетов C1 и С2 ребер первого и второго направлений.
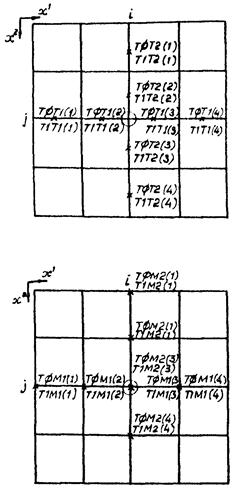
Через COMMON/TEMP/ подпрограммы NELTRT, NELTFN из подпрограммы TEMPE
передаются переменные ALFAT, ALFAT1, ALFAT2,
определяющие значения коэффициентов температурного расширения материала
оболочки и ребер в направлении х1 и х2
соответственно, а также массивы шаблонов компонент температур Т0Т1(4),
Т0Т2(4), Т1Т1(4), Т1Т2(4) элементы
которых содержат компоненты температуры точек пяточного шаблона ![]() и
и ![]() как
показано на рис. 4.7.
как
показано на рис. 4.7.
Накопление температурного члена уравнения равновесия производится в переменной RT, занимающей место 77-го коэффициента массива шаблона коэффициентов.
Подпрограммы NELTRT, NELTFN, осуществляющие накопление значений коэффициентов разностного шаблона при неизвестных линеаризованных уравнений равновесия в приращениях от выражения внутренних моментов, состоят из самостоятельных блоков, каждый из которых реализует подключение выражения соответствующей компоненты тензора внутренних моментов Mab (a, b = 1, 2) при определении перерезывающих сил. Обращение к этим блокам производится по именам дополнительных входов ENTRY. Объединение блоков в одну подпрограмму обусловлено общностью их декларативных операторов и функционального назначения.
Каждый из блоков со своим дополнительным
входом осуществляет следующую функцию: ENTRY M11 или ENTRY H11 - реализует подключение выражения компоненты ![]() в выражении
Т13; ENTRY M11N или ENTRY H11N - компоненты
в выражении
Т13; ENTRY M11N или ENTRY H11N - компоненты ![]() в выражения
Т23; ENTRY M22
или ENTRY H22 -
компоненты
в выражения
Т23; ENTRY M22
или ENTRY H22 -
компоненты ![]() в выражении Т23; ENTRY M22N или ENTRY H22N - компоненты
в выражении Т23; ENTRY M22N или ENTRY H22N - компоненты ![]() в выражении
Т13; ENTRY M12
или ENTRY H12 -
компоненты
в выражении
Т13; ENTRY M12
или ENTRY H12 -
компоненты ![]() в выражении Т13; ENTRY M21 или ENTRY H21 - компоненты
в выражении Т13; ENTRY M21 или ENTRY H21 - компоненты ![]() в выражении
Т23; ENTRY M12N или ENTRY H12N - компоненты
в выражении
Т23; ENTRY M12N или ENTRY H12N - компоненты ![]() и
и ![]() в выражении
Т13 и Т23.
в выражении
Т13 и Т23.
Схема определения соответствия параметров массивов геометрических характеристик сечений оболочки и ребер точкам сеточного шаблона 5´5 узла (i; j)
В зависимости от положения точки относительно свободного или шарнирно опертого края физические соотношения, реализуемые блоками подпрограмм NELTRT, NELTFN, либо вообще не реализуются, что свидетельствует о нулевом значении момента на краю, либо реализуются с половинной жесткостью. Так, например, выражения М11 и М12 на левом и правом свободных краях равны нулю, а М21 и М22 здесь включаются с половинной жесткостью. Положение точки определения моментов относительно свободного или шарнирно опертого краев анализируется по значениям элементов логического массива V(4) из COMMON/BECA/, заполняемого при работе подпрограммы анализа поля признаков AРР1.
В случае ребристой оболочки моменты подсчитываются с учетом жесткостей ребер. Наличие ребра в точке определения соответствующих моментов характеризуется ненулевым значением жесткости массивов жесткостей на сжатие EF1 и EF2 для ребер первого и второго направлений.
При работе подпрограммы NELMFN в различных точках сеточного шаблона происходит обращение к подпрограмме RINK7, вычисляющей в этих точках максимальное значение интенсивности деформаций FIM. При FIM £ EIPL происходит передача управления на формирование коэффициентов при неизвестных при использовании физических уравнений упругой задачи. Если FIM > EIPL, в подпрограмме RINK7 для данной точки сеточной области путем интегрирования по формуле Ньютона-Котеса для 7 точек по толщине оболочки вычисляются жесткостные характеристики оболочки в упруго-пластической стадии и заполняются массивы RZ0(9), RZ1(9), RZ2(9) в COMMON/RIPL/, которые используются затем для формирования коэффициентов при неизвестных от внутренних моментов для точек поверхности оболочки, находящихся в упруго-пластической зоне.
Схема соответствия элементов массивов температуры точкам сеточного шаблона
При работе подпрограмм NELMRT, NELMFN осуществляется также обращение к дополнительным входам подпрограмм NELMUS и NELPSS, работа которых заключается в накоплении коэффициентов разностного шаблона от выражений изгибных и мембранных деформаций соответственно.
В блоках подпрограмм NELMRT, NELMFN используется для построения коэффициентов при значениях изгибных и мембранных деформаций массивы геометрических характеристик оболочки и ребер, а также массивы температур.
Массив EJ(2, 4) из COMMON/EH/, заполняемый подпрограммой GEOM1, содержит значения изгибных жесткостей оболочки в различных точках сеточного шаблона 5´5. На рис. 4.8, а приведены точки сеточного шаблона и соответствующие им элементы массива EJ, в которых содержится значения изгибных жесткостей оболочки в этих точках.
Массивы EJ1(4), EJ2(4), CJ1(4) и CJ2(4) из COMMON/REB/, заполняемые подпрограммой REBRA, содержат значения изгибных жесткостей и эксцентриситетов ребер первого и второго направлений. На рис. 4.8, б приведены точки сеточного шаблона и соответствующие им элементы массивов EJ1 и EJ2, в которых содержатся значения изгибных жесткостей ребер в этих точках. На рис. 4.8, в помещены точки сеточного шаблона и соответствующие им элементы массивов эксцентриситетов CJ1 и CJ2.
Через COMMON/TEMP/ из подпрограммы TEMPE передаются переменные ALFAT, ALFAT1, ALFAT2, определяющие значения коэффициентов температурного расширения материала оболочки и ребер соответственно, а также массивы шаблонов компонентов температуры T0M1(4), T0M2(4), T1M1(4), T1M2(4), элементы которых содержат значения температуры в точках сеточного шаблона в соответствии с рис. 4.7.
Накопление температурного члена производится в переменной RT, занимающей место 77-го коэффициента массива шаблона коэффициентов.
Подпрограмма NEPSS, осуществляющая накопление коэффициентов разностного шаблона при неизвестных линеаризованных уравнений равновесия в приращениях от выражений мембранных деформаций, состоит из самостоятельных блоков, каждый из которых реализует подключение выражения соответствующей компоненты тензора мембранных деформаций в выражениях внутренних усилий и моментов. Обращение к этим блокам осуществляется по именам дополнительных входов в подпрограмму NEPSS: ENTRY EPS11 осуществляет подключение выражения компоненты e11i±0,5;j; ENTRY EPS11N - компоненты e11i;j±0,5; ENTRY EPSS22 - компоненты e22i;j±0,5; ENTRY EPS22N - компоненты e22i±0,5;j; ENTRY EPS12 - компоненты e22i±0,5;j; ENTRY EPS21 - компоненты e21i;j±0,5.
Схема определения соответствия элементов массивов шаблонов геометрических характеристик сечений оболочки и ребер точкам сеточного шаблона 5´5 узла (i; j)
Если логические переменные NEL и NELDEF из COMMON/NEL/ имеют истинные значения, то блоками подпрограммы реализуются нелинейные выражения для мембранных деформаций, если хотя бы одна из этих переменных имеет ложное значение, то реализуются линейные выражения.
При работе блоков EPS12 и EPS21 осуществляется обращение к подпрограмме E12, которая реализует выражение e12i±0,5;j±0,5 в центрах ячеек, примыкающих к точкам определения e12i±0,5;j и e21i;j±0,5. Блоки EPS12 и EPS21 реализуют выражения e12i±0,5;j и e21i;j+0,5 посредством усреднения значений e12i+0,5;j±0,5.
Посредством анализа элементов логического массива V(4, 4) из COMMON/BECA/ исключаются значения коэффициентов разностного шаблона при неизвестных законтурных узлов.
Для построения коэффициентов разностного шаблона используются значения элементов массива Е(1458) из COMMON/METR/, формируемого подпрограммой GEOM1.
Накопление значений коэффициентов разностного шаблона осуществляется в элементах массивов U1(5, 5), U2(5, 5), W(5, 5), передаваемых через COMMON/QKOEF/.
Подпрограмма NELMUS, выполняющая накопление коэффициентов разностного шаблона при неизвестных линеаризованных уравнений равновесия от выражений компонент нагибных деформаций, состоит из самостоятельных блоков, каждый из которых реализует подключение выражения соответствующей компоненты тензора нагибных деформаций в выражениях внутренних усилий и моментов. Обращение к этим блокам осуществляется по именам дополнительных входов: ENTRY MU11 производит подключение выражения компоненты m22i;j; ENTRY MU22N - компоненты m11i±0,5;j±0,5; ENTRY MU22 - компоненты m22i;j; ENTRY MU11N - компоненты m22i±0,5;j±0,5; ENTRY MU12 - компоненты m12i;j; ENTRY MU12N - компоненты m12i±0,5;j±0,5.
При работе подпрограммы NELMUS осуществляется обращение к дополнительным входам подпрограммы NTETS, работа которых заключается в накоплении коэффициентов разностного шаблона от выражений компонент тензора углов поворота.
Посредством анализа элементов логического массива V(4, 4) из COMMON/BECA/ исключаются значения коэффициентов разностного шаблона при неизвестных законтурных узлов.
Для построения общих множителей при коэффициентах разностного шаблона от выражений изгибных деформаций используются массивы E(1458), SQA(9, 9) из COMMON/METR/, формируемые в подпрограмме GEOM1.
Подпрограмма NTETS, осуществляющая накопление коэффициентов разностного шаблона при неизвестных линеаризованных уравнений равновесия от выражений углов поворота нормали, состоит из самостоятельных блоков, каждый из которых реализует подключение выражения соответствующего угла поворота. Обращение к этим блокам производится по именам дополнительных входов: ENTRY TET1 реализует подключение выражения v1i±0,5;j; ENTRY TET1N - выражения v1i;j±0,5; ENTRY TET2 - выражения v2i;j±0,5; ENTRY TET2N - выражения v1i;j±0,5.
Посредством анализа элементов логического массива V(4, 4) из COMMON/BECA/ исключаются значения коэффициентов разностного шаблона при неизвестных законтурных узлов.
Для построения коэффициентов разностного шаблона используются значения элементов массива E(1458) из COMMON/METR/, а массивы шаблонов значений накопленных мембранных деформаций и углов поворота REPS11(5, 5), REPS12(5, 5), REPS22(5, 5), RTETA1(5, 5), RTETA2(5, 5), REPS1N(5, 5), REPS21(5, 5), REPS2N(5, 5), RTET1N(5, 5), RTET2N(5, 5) из COMMON/STABIL/ при построении невязки.
Накопление значений коэффициентов разностного шаблона осуществляется в элементах массивов U1(5, 5), U2(5, 5), W(5, 5) из COMMON/QKOEF/.
Подпрограмма E12 выполняет накопление коэффициентов разностного шаблона при неизвестных линеаризованных уравнений равновесия от выражений сдвиговых мембранных деформаций в центре ячейки.
Для построения коэффициентов разностного шаблона используются значения элементов массива Е(1458) из COMMON/METR/, заполняемых в подпрограмме GEOM1.
Накопление значений коэффициентов разностного шаблона осуществляется в элементах массивов.
4.3.4. Блок построения шаблонов геометрических параметров и жесткостных характеристик
Блок построения массива компонент ректоров локальных базисов, массива корней квадратных из фундаментального определителя, массивов жесткостей оболочки и ребер включает подпрограммы GEOM1, EHJ, REBRA и подпрограммы для конкретного вида поверхностной или подпрограмму SOSTAV для составных поверхностей.
Подпрограмма GEOM1 реализует построение массивов Е(1458) и SQA(9, 9) из COMMON/METR/, заполнение переменных X, Y, Z из COMMON/XYZ/ координат узлов сеточной области, заполнение массивов жесткостей оболочки EH(2, 4) на растяжение (сжатие), EJ(2, 4) - на изгиб из COMMON/EH/.
Структуру
массива E(1458) удобно представить для четырехмерного
массива E(3, 6, 9, 9). Значения первого индекса
определяет номера трех проекций базисного вектора на оси декартовой системы
координат x, y, z. Значения второго индекса определяют номера 1, 2 ... 6
векторов локальных базисов поверхности в узлах сеточного шаблона 9´9 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно.
Значения третьего и четвертого индексов определяют целочисленные координаты
узлов вспомогательного сеточного шаблона 9´9, для которых вычисляются компоненты базисных векторов.
соответственно.
Значения третьего и четвертого индексов определяют целочисленные координаты
узлов вспомогательного сеточного шаблона 9´9, для которых вычисляются компоненты базисных векторов.
Массив SQA(9, 9) в своих элементах содержит значения корня квадратного из фундаментального определителя поверхности, узла сеточного шаблона 9´9.
Формальными при обращении к подпрограмме GEOM1 являются следующие параметры:
- GEOM - имя подпрограммы геометрии, которая обеспечивает построение массивов Х1, X2, X3, Y1, Y2, Y3 из COMMON/BAZIS/ (задается в головной программе);
- ITCH, JTCH - координаты узла сеточной области объекта в направлении x1 и x2 соответственно;
- MO, NO - количество разностных узлов на рассчитываемом фрагменте в направлении х1, х2 соответственно.
Вызов подпрограммы GEOM1 осуществляется: а) при построении матрицы разрешающих уравнений из подпрограммы OPERLE или OPERLN; б) из подпрограммы NELUP1 или NELUP2 при подготовке к печати результатов счета.
Обращение к подпрограмме GEOM1 в вызывающих подпрограммах производится в циклах, реализующих обход сеточной области по узлам сначала в направлении х1, затем в направлении х2. Поэтому при построении массивов E и SQA в узлах, для которых ITCH ¹ 1, используется часть элементов этих массивов, определенных для предыдущего узла. Для формирования недостающей части массивов E и SQA реализуется усеченный цикл по номерам узлов сеточного шаблона 9´9 во втором направлении с обращением к подпрограмме, имя которой передано через формальный параметр GEOM. В узлах с номером ITCH = 1 в направлении x1 эти массивы строятся заново полностью посредством обхода всех узлов сеточного шаблона 9´9.
Исходными данными для построения массивов E и SQA служит переменные x1, x2, x3, y1, y2, y3 из COMMON/BAZIS/, формируемые подпрограммой GEOM. Эти массивы представляют собой значения проекции касательных векторов основного локального базиса точки на оси глобальной декартовой системы координат.
В подпрограмме GEOM1 вызываются подпрограммы EHJ и REBRA, осуществляющие заполнение массивов жесткостных характеристик сечений оболочки и ребер.
Если рассчитываемый объект представляет собой оболочку, срединная поверхность которой является гладкой аналитической поверхностью, то следует подключить только ту подпрограмму, которая предназначена для построения касательных векторов основного локального базиса этой аналитической поверхности. В тех случаях, когда рассчитываемый объект представляет собой оболочку, срединная поверхность которой составлена из различных аналитических поверхностей, необходимо подключить подпрограмму SOSTAV, которая осуществляет построение шаблона проекций касательных векторов основного базиса для составных поверхностей.
Составной оболочкой в смысле работы SOSTAV считается оболочка, на отдельных участках которой, ограниченных координатными линиями, имеют место различия поверхностей, и (или) физических параметров материала и (или) шага разностной сетки. При этом в исходных данных переменной KGEO присваивается число, равное количеству таких участков, а для каждого из них задаются: в массиве KOORG(5, 10) из COMMON/KOORG/ исходные координаты левого верхнего, правого нижнего узлов участка и номер подпрограммы геометрии в таблице SOSTAV; в массиве FPAR(7, 25) из COMMON/FPAR/ - физические параметры материала и толщина оболочки; в массиве GPAR(19, 25) из COMMON/GPAR/ - физические пределы изменения координат x1 и x2, константы параметрических уравнений поверхности, угла поворота и координаты начала декартовой системы координат, в которой сформулированы параметрические уравнения поверхности, относительно глобальной декартовой системы координат.
Заказанные в подпрограмме SOSTAV вторые размерности массивов KOORG, FPAR, GPAR, равные 25, обеспечивают работу с составными оболочками, количество участков которых меньше или равно 25. Если необходимо рассчитывать оболочку с большим числом участков, необходимо привести в соответствие количество участков с вторыми размерностями перечисленных массивов не только в подпрограмме SOSTAV, но и в подпрограмме WWOD, где эти массивы заполняются посредством считывания исходных данных задачи.
Формальными при вызове подпрограммы SOSTAV являются следующие параметры:
- ITCH, JTCH - целочисленные координаты узла сеточной области, который служит центром вспомогательного сеточного шаблона 9´9;
- MO, NO - переменные, значения которых определяют размеры сеточной области;
- M, N - целочисленные координаты узлов вспомогательного сеточного шаблона 9´9, для которых строится основной локальный базис.
Подпрограмма SOSTAV в зависимости от принадлежности узла вспомогательного сеточного шаблона, для которого строится основной локальный базис, к той или другой поверхности вызывает соответствующую этой поверхности подпрограмму. Если узел вспомогательного сеточного шаблона лежит на стыке двух или четырех участков, то в этом узле строится усредненный базис.
Если в исходных данных, при описании участков сеточной области допущена ошибка, в результате которой какая-либо точка оказалась неописанной, подпрограммой печатается сообщение: «... не определена геометрия точки ITCH, JTCH, М, N». При этом задание снимается.
При обращении к подпрограммам, реализующим конкретные виды аналитических поверхностей, в подпрограмму SOSTAV посредством COMMON/BAZIS/ передаются массивы шаблонов проекций касательных векторов основного локального базиса в декартовой системе координат, в которой сформулированы уравнения поверхности. С использованием значений углов поворота эти проекции пересчитываются для глобальной декартовой системы координат, после чего массивы из COMMON/BAZIS/ заполняются переопределенными проекциями, и в таком виде попадают в подпрограмму GEOM1 в качестве исходных данных для построения массива проекций всех векторов как основного, так и взаимного базисов узлов вспомогательного сеточного шаблона 9´9.
Таблица подпрограмм поверхностей конкретного вида (табл. 4.1) в подпрограмме SOSTAV реализуется вычисляемым оператором GOTO, который в зависимости от значения NGEO отсылает на метку оператора вызова соответствующей номеру NGEO подпрограммы. Эта таблица при необходимости может меняться и дополнятся.
Таблица 4.1
|
Имя подпрограммы, уравнение и вид поверхности, содержимое области COMMON/GEPAR/ |
||
|
1 |
2 |
|
|
1 |
CIL X = rcosx2, Y = rsinx2, Z = x1. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, z |
||
|
2 |
CILELS X = R1cosx2, Y = R2sinx2, Z = x1. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R1, R2 |
||
|
3 |
CILSKO X = (R + rcosx2)tgx1, Y = R + zcosx2, Z = rsinx1. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R, z |
||
|
4 |
CILV X = r × sinx1, Y = r × cosx1, Z = x2. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, z |
||
|
5 |
CILELV X = R1cosx1, Y = R1sinx1, Z = x2. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R1, R2 |
||
|
6 |
CILSKV X = (R + rcosx1)tgx2, Y = R + zcosx1, Z = r × sinx1. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R, z |
||
|
7 |
ELSOID X = R1cosx1sinx2, Y = R2sinx1sinx2, Z = R3cosx2. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R1, R2, R3 |
||
|
8 |
GIPAR X = x1, Y = x2,
|
|
|
/GEPAR/ xн1, xк1, xн2, xк2, a |
||
|
9 |
KONUS X = (R - x1 × sina)cosx2, Y = (R - x1 × sina)sinx2, Z = x1cosa. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R, a |
||
|
10 |
KONV X = (R + x2 × cosa)sinx1, Y = (R + x2 × cosa)cosx1, Z = x2sina + Zн. |
|
|
/GEPAR/ xн1, xк1, Zн, Zк, Rн, Rк |
||
|
11 |
PLAST X = x1, Y = x2, Z = 0. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2 |
||
|
12 |
PLAS X = x2 × sinx1, Y = x2 × cosx1, Z = 0. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2 |
||
|
13 |
TORTSP X = B(1 - C)cosx2 + Dsinx1, Y = Dsinx1, Z = B(1 - C)sinx2 + r × sinx2, B = (R2sin2j + H2)/2H, D = R + rcosx2, C = cos(arcsin(Dsinx1/B)), H = 0,8. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R, r, j |
||
|
14 |
SFERAK X = Rsinx2, Y = Rsinx1,
|
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R |
||
|
15 |
TOR X = (R + rcosx2)sinx1, Y = (R + rcosx2)cosx1, Z = r × sinx2. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, R, r |
||
|
16 |
KONTSP X = B(1 - C)cosa + Dcosx1, Y = Dsinx1, Z = B(1 - C)sina + A,
B = (D2sin2j + H2)/2H, C = cos(arcsin(Dsinx1/B)),
H = 0,8. |
|
|
/GEPAR/ xн1, xк1, xн2, xк2, Xн, Zн, j |
||
|
17 |
TORS1 X = [b1cosx1cosj1(d - x2) + b2cosgcosj2x2]/d, Y = [a1rsinx1(d - x2) - a2singx2]/d, Z = [-b1cosx1sinj1(d - x2) + (d - b2cosgsinj2)x2]/d. |
|
|
/GEPAR/ d, b1, a1, j1, b2, a2, j2 |
||
|
18 |
TRAPLA X = x2tgx1, Y = x2, Z = 0. /GEPAR/ xн1, xк1, xн2, xк2 |
|
4.3.4.1. Общие положения составления подпрограмм, описывающих поверхности конкретного вида.
Подпрограммы, описывающие различные поверхности, осуществляют построение массивов касательных векторов основного локального базиса в узлах вспомогательного сеточного шаблона 9´9 для конкретного вида поверхности. В комплексе «МЕКРИС-2» имеется ряд подпрограмм (см. табл. 4.1), подключение которых обеспечивает решение задачи для поверхности соответствующего вида. Если возникает необходимость в описании поверхности, для которой нет соответствующей подпрограммы, то её надо составить, пользуясь описанными ниже рекомендациями.
Радиус-вектор любой поверхности имеет вид:
![]()
где ![]() ,
, ![]() ,
, ![]() - орты декартовой системы
координат Х = Х(х1, х2), Z = Z(z1,
z2), Y
= Y(y1,
y2) - параметрические уравнения
поверхности.
- орты декартовой системы
координат Х = Х(х1, х2), Z = Z(z1,
z2), Y
= Y(y1,
y2) - параметрические уравнения
поверхности.
Касательные векторы основного локального базиса получаются дифференцированием радиус-вектора по целочисленным координатам сеточной области:
![]()
![]()
где i, j - целочисленные координаты сеточной области; d1 = d1(x1), d2 = d2(x2) - физические значения изменения параметров x1 и x2 между соседними узлами разностной сетки.
Формальными при обращении к подпрограммам, описывающим поверхности, являются следующие параметры:
- ITCH, JTCH - целочисленные координаты узла сеточной области;
- M, N - координаты узлов вспомогательного сеточного шаблона 9´9 с центром в узле ITCH, JTCH;
- MO, NO - размеры сеточной области.
Для их работы из подпрограммы WWOD или SOSTAV через COMMON/GEPAR/ передаются 7 величин, необходимых для построения касательных базисов векторов, первые 4 из которых X1N, X1K, X2N, X2K представляют начальные и конечные значения параметров x1 и x2, остальные 3 используются произвольно для передачи значений констант, необходимых для построения параметрических уравнений.
Идентификаторами величин изменения параметров x1 и x2 между узлами разностной сетки d1 и d2 служат переменные D1 и D2, которые всегда вычисляются операторами:
D1 = (x1k - x1N)/(MO - 1);
D2 = (x2k - x2N)/(NO - 1).
Значения параметров x1 и x2 в узлах сеточного вспомогательного шаблона 9´9 с координатами M, N идентифицируются переменными AR1 и AR2, которые вычисляются операторами:
AR1 = D1 × (ITCH - 1 + 0,5 + (M - 5)) + x1N;
AR2 = D2 × (JTCH - 1 + 0,5 + (N - 5)) + x2N.
В элементы
массивов Х1, Y1, Z1,
Х2, Y2, Z2
с индексами M и N засылаются значения компонент касательных векторов основного
локального базиса в узлах шаблона с координатами (М, N) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно.
Эти массивы передаются через COMMON/BAZIS/ в вызывающую программу.
соответственно.
Эти массивы передаются через COMMON/BAZIS/ в вызывающую программу.
На средней линии вспомогательного шаблона при N = 5 подсчитываются координаты узлов, лежащих на этой линии, которые записываются в массивы ХМ, YM, ZM, передаваемые через COMMON/XYZ/ в вызывающие программы для подсчета координат центра шаблона.
4.3.4.2. Общие положения составления подпрограмм, заполняющих массивы жесткостей оболочки.
Комплекс «МЕКРИС-2» может быть использован для решения задач теории оболочек как с постоянной толщиной, так и с переменной. При решении задач для оболочек постоянной толщины используется подпрограмма EHJ, загрузочный модуль которой подключается автоматически при разрешении внешних ссылок на шаге редактирования связей. Для расчета оболочки переменной толщины пользователю «МЕКРИС-2», необходимо составить подпрограмму с тем же именем EHJ, которая бы обеспечивала построение массивов шаблонов жесткостей EH и EJ оболочки с переменной толщиной, и ввести её во входной поток шага FORT процедуры FORTGCLG.
Подпрограмма EHJ должна иметь следующие формальные параметры:
- ITCH, JTCH - целочисленные координаты узла сеточной области, для которого строится шаблон жесткостей;
- MO, NO - размеры сеточной области.
В подпрограмме должны быть определены значения модуля упругости и коэффициента Пуассона, которые можно передать через COMMON/FIZPAR/.
Значения элементов шаблонов жесткостей нужно передавать через COMMON/EH/.
На рис. 4.6, а и 4.8, а показаны схемы соответствия элементов шаблонов мембранных жесткостей EH и изгибных жесткостей EJ точкам сеточного шаблона 5´5 узла (i, j). В подпрограмме идентификаторы ITCH и JTCH соответствуют целочисленным координатам узла сеточной области i и j.
4.3.4.3. Общие положения составления подпрограмм, заполняющих массивы местностей ребер.
Комплекс программ «МЕКРИС-2» может быть использован для исследования напряженно-деформированного состояния и устойчивости оболочек, подкрепленных набором ребер, расположенных как в направлении х1, так и в направлении х2. Для расчета оболочек с ребрами постоянного сечения имеется подпрограмма REBRA, которая для таких ребер строит массивы шаблонов жесткостей EF1, EF2, EJ1, EJ2, и массивы шаблонов эксцентриситетов CF1, CJ1, CF2, CJ2, элементы которых содержат соответственно жесткости на растяжение-сжатие, изгибные жесткости и значения эксцентриситетов ребер, расположенных в направлении х1 и х2 для точек сеточного шаблона 5´5 узла с координатами (ITCH, JTCH). На рис. 4.6 и рис. 4.8 приведены схемы соответствия элементов массивов жесткостей и эксцентриситетов ребер точкам сеточного шаблона 5´5.
При необходимости расчета оболочек с ребрами переменного сечения пользователю «МЕКРИС-2» необходимо написать подпрограмму REBRA, которая обеспечивала бы построение массивов жесткостей и эксцентриситетов для таких ребер и ввести её во входной набор шага FORT процедуры FORTGCLG.
Подпрограмма REBRA должна иметь следующие формальные параметры:
- ITCH, JTCH - целочисленные координаты узла сеточной области, для которого строятся шаблоны жесткостей и эксцентриситетов ребер;
- MO, NO - размеры сеточной области.
Массивы жесткостей и эксцентриситетов необходимо передавать через общую область /REB/ в виде
COMMON/REB/ER1, EF1(4), EJ1(4), GS1(4), GI1(4), GF1(4), CJ1(4), HPF1(4), HPJ1(4), HMJ1(4), ER2, EF2(4), EJ2(4), GS2(4), GI2(4), GF2(4), GJ2(4), HPF2(4), HPJ2(4), HMF2(4), HMJ2(4),
через которую передаются переменные и массивы в следующей последовательности:
- ER1 - модуль упругости материала ребра направления x1;
- EF1(4) - массив элементов шаблона местностей ребра направления x1 на растяжение-сжатие;
- GS1(4) - массив элементов шаблона жесткостей ребра направления x1 на сдвиг;
- GI1(4) - массив элементов шаблона жесткостей ребра направления x1 на кручение;
- GF1(4) - массив элементов шаблона эксцентриситетов ребра направления x1 в точках определения, совпадающих с точками определения элементов EF1(4);
- СJ1(4) - массив элементов шаблона эксцентриситетов ребра направления x1 в точках определения, совпадающих с точками определения элементов EJ1(4);
- HPF1(4) - массив элементов шаблона максимальных значений крайних волокон ребер направления x1 в точках определения, совпадающих с точками определения элементов массива EF1(4);
- HPJ1(4) - массив элементов шаблона максимальных значений x2 крайних волокон ребер направления x1 в точках определения, совпадающих с точками определения элементов массива EJ1(4);
- HMF1(4) - массив элементов шаблона минимальных значений крайних волокон ребер направления x1 в точках определения, совпадающих с точками определения элементов массива EF1(4);
- HMJ1(4) - массив элементов шаблона минимальных значений крайних волокон ребер направления x1 в точках определения, совпадающих с точками определения элементов массива EJ1(4);
- EР2 - модуль упругости материма ребер направления x2;
- EF2(4) - массив элементов шаблона жесткостей ребра направления x2 на растяжение-сжатие;
- GS2(4) - массив элементов шаблона жесткостей ребра направления x2 на сдвиг;
- GI2(4) - массив элементов шаблона жесткостей ребра направления x2 на кручение;
- GF2(4) - массив элементов шаблона эксцентриситетов, ребра направления x2 с точками, совпадающими с точками определения элементов EF2(4);
- CJ2(4)- массив элементов шаблона эксцентриситетов ребра направления x2 в точках, совпадавших с точками определения элементов EJ2(4);
- HPF2(4) - массив элементов шаблона максимальных значений x крайних волокон ребер направления x2 в точках определения, совпадавших с точками определения элементов массива EF2(4);
- HPJ2(4) - массив элементов шаблона максимальных значений x1 крайних волокон ребер направления x2 в точках определения, совпадающих с точками определения элементов массива EJ2;
- HMF2(4) - массив элементов шаблона минимальных значений x3 крайних волокон рёбер направления x2 в точках определения, совпадающих с точками определения элементов массива EF2(4);
- HMJ2(4) - массив элементов шаблона минимальных значений x3 крайних волокон ребер направления x2 в точках определения, совпадающих с точками определения элементов массива EJ2(4).
4.3.5. Общие положения доставления подпрограмм, определяющих внешние воздействия
В комплексе программ «МЕКРИС-2» имеется ряд подпрограмм (табл. 4.2), подключение каждой из которых в программу обеспечивает решение задачи от нагрузки соответствующего вида. Если возникает необходимость решения задачи при силовом воздействии, для которого еще нет соответствующей подпрограммы, вычисляющей коэффициенты матрицы от нагрузки, то надо написать такую подпрограмму, дав ей уникальное имя, пользуясь описанными ниже рекомендациями.
Формальные параметры подпрограммы в порядке их следования в операторе SUBROUTINE следующие:
AРР - не используется;
GEOM - имя подпрограммы геометрии;
ITCH, JTCH - целочисленные координаты узла сеточной области, для которого строится разностное уравнение;
MO, NО - размеры сеточной области;
QN - массив элементов разностного шаблона, дополненный коэффициентами от нагрузки и невязки; NQN - первая размерность массива QN;
KOLFOB - количество разрешающих функций в узле разностной сетки.
Массив QN в подпрограмме должен декларироваться с двойной точностью.
Через общую область /WP/ в подпрограмму должны передаваться параметры нагружения: NW, IW, JW, DW, DP, SDP. Поскольку подпрограмма строится с таким расчетом, чтобы она была пригодна для продолжения решения как по параметру нагрузки, приращение которого равно DP, так и по параметру перемещения с приращением DW, в комплекс «МЕКРИС-2» введен признак, в соответствий с которым при DW ¹ 0 продолжение решения осуществляется по параметру перемещения, а при DW = 0 - по параметру нагрузки. При продолжении решения по параметру перемещения DW переменные NW, IW, JW определяют номер компоненты вектора перемещения, выбранной ведущим параметром, и целочисленные координаты узла приложения ведущего параметра и направлении х1 и х2. При продолжении решения по параметру нагрузки DP переменные NW, IW, JW могут применяться программистом по собственному усмотрению. В переменной SDP накапливается значение параметра нагрузки, используемое при подсчете коэффициентов невязки QN(16, NUR), где NUR - номер уравнения.
|
Имя подпрограммы |
Вид воздействия |
|
|
1. |
OPERP1 |
Нагружение в виде смещения края, для которого ITCH = 1, вдоль координаты x1 на величину DU1, задаваемую в исходных данных параметром DP. |
|
2. |
OPERP2 |
Нагружение в виде смещения края, для которого JTCH = 1, вдоль координаты x2 на величину DU2, задаваемую в исходных данных параметром DP. |
|
3. |
OPERP3 |
Нагружение сосредоточенной силой в узле (ITCH = IW, JTCH = JW), направленной вдоль вектора основного локального базиса в этой точке. |
|
4. |
OPERP4 |
Нагружение распределенным по краю ITCH = 1 усилием, направленным вдоль x1. Физическое значение которого задается в исходных данных параметром DP. |
|
5. |
OPERP5 |
Нагружение равномерным нормальным давлением, физическое значение которого задается в исходных данных параметром DP. |
|
6. |
OPERP6 |
Нагружение собственным весом, действующим вдоль оси X декартовых координат, физическое значение которого задается в исходных данных параметром DP. |
|
7. |
OPERP7 |
Нагружение неравномерным нормальным давлением. |
|
8. |
OPERP8 |
Воздействие гидростатическим давлением. |
При построении в уравнениях равновесия коэффициентов от нагрузки производится усреднение значений векторов нагрузки, определенных в центрах ячеек, прилегающих к узлу, равновесие которого рассматривается. Поэтому через общую область /NAGR/ в подпрограмму должен передаваться массив P(5, 5, 3, 3), элементы которого представляют собой четверть произведения величины квадратного корня из фундаментального определителя поверхности на коэффициенты преобразования единичных компонентов векторов нагрузки, определенных в центрах ячеек сеточного шаблона 5´5, при сведении их к центру шаблона для каждого из трех уравнений равновесия. Первые два индекса массива определяют номера левого верхнего узла ячейки в сеточном шаблоне 5´5, в центре которой обозначены компоненты вектора нагрузки; третий индекс означает номер уравнения, для которого вычисляется коэффициент от нагрузки; четвертый индекс определяет номер контравариантной компоненты вектора нагрузки.
Для того, чтобы не производить вычислений коэффициентов матрицы от нагрузки в тех уравнениях, где неизвестные заданы, для каждого уравнения необходимо произвести анализ закреплений. Информацию для этого анализа содержит первый разряд элементов массива KODUR(6) из COMMON/PP/, индекс которого определяет номер уравнения. Если первый разряд соответствующего элемента равен нулю, то построение коэффициента нагрузки и невязки производить не следует. Этот анализ производится в цикле, осуществляющем обход по индексу номера уравнения оператором
IF(MOD(KODUR(NUR), 10).EQ.0)GO_TO_n,
где NUR - индекс номера уравнения; n - метка оператора CONTINUE, являющегося последним оператором цикла.
Если приращение вектора внешней нагрузки принять в виде
![]()
где А1, А2, А3 служат функциями от х1, х2, то группа операторов, вычисляющих коэффициенты нагрузки и невязки, будет иметь вид:
⊔⊔⊔⊔⊔ DO m2 NUR = 1,3
⊔⊔⊔⊔⊔ IF (MOD(KODUR(NUR), 10).EQ.0) GO TO m2
⊔⊔⊔⊔⊔⊔ DO ⊔ m1 ⊔ I = 2,3
⊔⊔⊔⊔⊔⊔ DO ⊔ m1 ⊔ J = 2,3
⊔⊔⊔⊔⊔⊔ AR1 = ...
⊔⊔⊔⊔⊔⊔ AR2 = ...
⊔⊔⊔⊔⊔⊔ A(1) = ...
⊔⊔⊔⊔⊔⊔ A(2) = ...
⊔⊔⊔⊔⊔⊔ A(3) = ...
⊔⊔⊔⊔⊔⊔ DO ⊔ m1 ⊔ K = 1,3
⊔⊔⊔⊔ m1 ⊔ QN(77, NUR) = QN(77, NUR) + P(I, J, NUR, K) ´ A(K)
⊔⊔⊔⊔⊔⊔ QN(76, NUR) = -QN(76, NUR) - (SDP + DP) ´ QN(77, NUR)
⊔⊔⊔⊔ m2 ⊔ CONTINUE.
Здесь в правой части операторов AR1 и AR2 должны быть выражения, определяющие значения координат х1 и х2 центра ячейки с левым верхним узлом, имеющим координаты в сеточном шаблоне 5´5 (I; J); в правой части операторов, заполняющих элементы массива A1 - выражения функций А1, А2, А3 от координат х1 и х2.
Для идентификации подпрограммы на листинге выдачи программы целесообразно включать в подпрограмму информационную печать, содержащую имя подпрограммы и вид вектора нагрузки, который она реализует. Для того, чтобы такая печать производилась лишь раз, при первом входе в подпрограмму, оператором DATA присваивается некоторое значение переменной NVH; печать следует осуществлять по условию, когда NVH будет равно числу, присвоенному в DATA. После печати переменной NVH присвоить значение, отличное от первоначального. При последующих входах в подпрограмму, условие, по которому осуществляется печать, выполняться не будет.
4.3.6. Общие положения составления подпрограмм, заполняющих массивы температуры
Комплекс
программ «МЕКРИС-2» может использоваться для исследования
напряженно-деформированного состояния и устойчивости оболочек, подверженных
тепловому воздействию. Для решения таких задач пользователю программы
необходимо составить подпрограмму TEMPE, которая
бы обеспечивала построение массивов шаблонов температуры для теплового
воздействия с конкретным распределением ![]() и
и ![]() по сеточной области, и ввести
ее во входной набор шага FORT процедуры FORTGCLC. В противном случае автоматически подключается
подпрограмма TEMPE, осуществляющая обнуление
массивов шаблонов температур.
по сеточной области, и ввести
ее во входной набор шага FORT процедуры FORTGCLC. В противном случае автоматически подключается
подпрограмма TEMPE, осуществляющая обнуление
массивов шаблонов температур.
Подпрограмма TEMPE должна иметь в качестве формальных параметры ITCH и JTCH, которые определяют целочисленные координаты узла, являющегося центром сеточного шаблона 5´5.
Результатом работы пользовательской подпрограммы TEMPE должны стать заполненные массивы шаблонов температуры T0T1(4), T0T2(4), T0M1(4), T0M2(4), T1T1(4), T1T2(4), T1M1(4), T1M2(4), для элементов которых на рис. 4.7 приведены схемы соответствия точек их определения в сеточном шаблоне 5´5. Передача массивов шаблонов температур должна осуществляться через общую область /TEMP/ в виде
COMMON/TEMP/ ALFAT, ALFAT1, ALFAT2, T0T1(4), T0T2(4), TOM1(4), TOM2(4), T1T1(4), T1T2(4), T1M1(4), T1M2(4),
где ALFAT, ALFAT1, ALFAT2 - соответственно коэффициенты температурного линейного расширения материалов оболочки и ребер направления х1 и х2.
4.4. Исходные данные
Подготовка комплекса «МЕКРИС-2» к расчету заключается: в составлении головной программы; в подготовке исходной информации; в формировании стартового пакета.
4.4.1. Головная программа определяет вариант расчета, конфигурацию используемой программы и требуемые ресурсы оперативной памяти ЭВМ. Она имеет следующую структуру:
DEFINE FILE 8 (KÆ8, ![]() , U, I)
, U, I)
EXTERNAL ![]() ,
, ![]() ,
, ![]() ,
, 
COMMON/COZU/OZU (![]() , N1)
, N1)
COMMON/SDEF/PDEF (N3)/SX/SX (N2)
DOUBLE PRECISION QSTR
COMMON/QSTR/QSTR (30, 78)
COMMON/OST/KOSX, KPDEF, KOZ, KRMX
COMMON/RB/X (900), RMX (N4)
KOZ = N1,
KOZX = N2,
KPDEF = N3,
KRMX = N4,
CALL WWOD
CALL ![]() ,
, ![]() ,
, 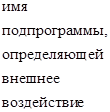 ,
, ![]() ,
, ![]() ,
, 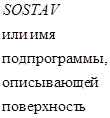
STOP
END
Рекомендации по составлению головной программы приведены в пункте 4.3.1.
4.4.2. Исходная информация, необходимая для работы программ комплекса, подразделяется на числовые входные данные и данные, задаваемые с помощью подпрограмм. К данным второго типа относятся массивы жесткостей оболочки и ребер, массивы касательных векторов основного локального базиса в узлах сеточного шаблона, величины температурных воздействий и компоненты внешней нагрузки, описанные в пунктах 4.3.4 - 4.3.6.
Содержание и структура числовых входных данных описывается на примере подготовки информации для составной оболочки, изображенной на рис. 4.9 [7], состоящей из 12 цилиндрических секций. Система координат XYZ является глобальной, система координат Х0Y0Z0 - местной для цилиндрических секций. Исходя из симметрии объекта, в качестве расчетного фрагмента принимается часть цилиндрической секции, ограниченная плоскостями симметрии X0Y, X00Y0 и плоскостью косого среза (см. рис. 4.9, в). На расчетный фрагмент накладывается сетка 9´37 узлов (9 узлов в направлении координатной линии x1, 37 - в направлении линии x2). С целью наложения неравномерной сетки в направлении координатной линии x2 рассчитываемый фрагмент разбивается на два элемента (I, II). На первый элемент в направлении x2 накладывается 12 разностных делений (0 £ x2 £ p/2), на второй - 24 деления (p/2 £ x2 £ p). Так как в местах стыка цилиндрических секций поверхность оболочки терпит разрыв, для определения компонент локального базиса за контуром расчетного фрагмента дополнительно необходимо задать участок, состоящий также из двух элементов (III, IV).
Геометрические и физические параметры оболочки соответственно равны: модуль упругости Е = 2 × 106 кг/см2; коэффициент Пуассона n = 0,3; толщина h = 0,07 см; радиус цилиндрической секции z = 25,8 см; радиус тороидальной оболочки R = 55 см. Для рассчитываемого фрагмента х1 меняется от 0 до p/12 рад, х2 - от 0 до p рад.
а, б - общий вид оболочки; в - расчетный фрагмент оболочки
Составная тороидальная оболочка
Последовательность составления пакета числовых входных данных:
- на первой перфокарте по формату 715 задаются параметры MO, NO, KOLFOB, KOLPCH, MSGU, NSGU, INDZAM, где MO - число узлов на рассчитываемом фрагменте в направлении координаты x1; NO - то же в направлении x2; KOLFOB - количество разрешающих функций; KOLPCH - количество правых частей в матрице разрешающих уравнений; MSGU - параметр автоматического сгущения сетки в направлении координаты x1; NSGU - то же в направлении x2; INDZAM - характеризует замкнутость рассматриваемого фрагмента.
Область задаваемых значений: MO, NO - целые положительные числа ³ 5; KOLFOB - принимается равным 3; KOLPCH - для задач НДС и устойчивости принимается равным 3; MSGU, NSGU - целые положительные числа (при MSGU и NSGU, равных 0 или 1, сгущение сетки не происходит); INDZAM - для замкнутого расчетного фрагмента принимается равным 1, для незамкнутого - 0.
Пример задания этих параметров применительно к рассматриваемой задаче (с учетом сгущения сетки):
⊔⊔⊔⊔5⊔⊔⊔13⊔⊔⊔⊔3⊔⊔⊔⊔3⊔⊔⊔⊔2⊔⊔⊔⊔3⊔⊔⊔⊔0;
- вторая перфокарта содержит параметр IEX, служащий признаком для продолжения счета в случае вынужденного прерывания на этапе прямого хода метода Гаусса (подсчета определителей и миноров блок-строк матриц). IEX = K (K = 1, 2, 3; ..., N, где N - общее число миноров блок-строк матриц) - решение задачи может быть продолжено с указанного значения минора блок-строки матрицы. При K > N решение задачи начинается с подсчета первого минора.
Вводится по формату 15;
- третья
перфокарта содержит величины ABKRIT и OTKRIT, служащие критериями контроля абсолютной и
относительной погрешностей преобразования исходной матрицы по схеме Гаусса, а
также переменную RKR, задающую значение
отношения ![]() ,
при котором возможно пренебрежение косоугольностью разностной сетки. В
большинстве задач ABKRIT и OTKRIT
принимаются равными соответственно 102 и 103, RKR = 10-5.
,
при котором возможно пренебрежение косоугольностью разностной сетки. В
большинстве задач ABKRIT и OTKRIT
принимаются равными соответственно 102 и 103, RKR = 10-5.
Формат задания - 3EI0.3;
- в четвертой перфокарте по формату 415 задаются переменные MB, ML, INDOUB, NBMGZ, где MB - характеризует количество записей (по 900 слов каждая) оперативного запоминающего устройства, выделяемых для записи промежуточных результатов в процессе решения задачи; ML - определяет число записей (по 900 или 1800 слов каждая) памяти внешнего запоминающего устройства (магнитный диск), выделяемых для хранения промежуточных результатов счета; INDOUB - обусловливает точность (обычная или двойная), с которой выполняются обмены с внешней памятью; NBMGZ - определяет кратность записи миноров блок-строк матриц на МД. Значение переменной МВ должно соответствовать значению второй размерности массива OZU, декларируемого оператором COMMON/COZU/ головной подпрограмме MAIN. Минимально допустимое значение для МВ равно 2. Значение, присваиваемое переменной МL, должно равняться количеству записей (второй параметр) в операторе DEFINE FILE задаваемому в головной подпрограмме. Нулевое значение INDOUB характеризует обычную, единичное значение - двойную точность обменов с внешней памятью. При NBMGZ = 0 запись миноров блок-строк матриц на МД не производится, а параметр IEХ принимается равным 1;
- с пятой по восьмую перфокарты задают значения элементам массивов MPRINC(4) и MPRINR(4), управляющих печатью блоков соответственно исходной и преобразованной матриц. Первый и второй элементы каждого из массивов определяют номера строки и столбца первого, а третий и четвертый элементы - последнего блока части матрицы, выводимой на печать. Если номер строки или столбца первого блока больше номеров соответственно строки и столбца последнего блока, то печать отсутствует.
Формат задания - 215;
- в девятой перфокарте задается значение параметру LITR, определявшему число строк в поле признаков, т.е. число перфокарт, необходимых для его описания. Формат задания параметра LITR - 15;
- очередные несколько перфокарт (число их равно LITR) описывают поле признаков (кодовый массив LITRPEG(7, LITR)), содержащее информацию о граничных условиях узлов сеточной области. Строка в поле признаков задается по формату 413, 316, первое и третье числа характеризуют номера начального и конечного узлов в направлении координатной линии х1, второе и четвёртое - номера начального и конечного узлов в направлении координатной линии х2 участка сеточной области, характеризующегося одинаковыми признаками. Последующие три числа соответственно для функций U1, U2 и U3 задают информацию о кинематических и статических условиях узлов этого участка.
При составлении воля признаков следует различать два случая:
а) первый соответствует рассмотрению сеточной области с граничными условиями типа жесткого защемления, плоскости симметрии или косой симметрии и их комбинаций;
б) второй случай - рассмотрению сеточной области с граничными условиями типа свободного края, шарнирного опирания или скользящего шарнирного опирания и их комбинаций.
Кодирование участков сеточной области с граничными условиями типа свободного края
|
Вид границы сеточной области |
Значения кодов в узлах, отмеченных звездочками |
|||||||||||||||||||
|
U1 |
U2 |
U3 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
|||
|
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
||
|
2 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
||
|
3 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
||
|
4 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
||
|
5 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
||
|
6 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
||
|
7 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
||
|
8 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
||
|
9 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
||
|
ИЛИ |
||||||||||||||||||||
|
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
|||
|
10 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
||
|
ИЛИ |
||||||||||||||||||||
|
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
7 |
0 |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
|||
|
11 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
||
|
ИЛИ |
||||||||||||||||||||
|
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
5 |
0 |
0 |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
|||
|
12 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
6 |
0 |
0 |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
||
|
ИЛИ |
||||||||||||||||||||
|
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
8 |
0 |
⊔ |
⊔ |
⊔ |
1 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
1 |
|||
|
13 |
7 |
0 |
5 |
0 |
0 |
1 |
7 |
0 |
5 |
0 |
0 |
1 |
7 |
0 |
5 |
0 |
0 |
1 |
||
|
14 |
7 |
0 |
6 |
0 |
0 |
1 |
7 |
0 |
6 |
0 |
0 |
1 |
7 |
0 |
6 |
0 |
0 |
1 |
||
|
15 |
8 |
0 |
5 |
0 |
0 |
1 |
8 |
0 |
5 |
0 |
0 |
1 |
8 |
0 |
5 |
0 |
0 |
1 |
||
|
16 |
8 |
0 |
6 |
0 |
0 |
1 |
8 |
0 |
6 |
0 |
0 |
1 |
8 |
0 |
6 |
0 |
0 |
1 |
||
|
17 |
7 |
0 |
6 |
0 |
0 |
1 |
8 |
0 |
5 |
0 |
0 |
0 |
⊔ |
⊔ |
⊔ |
⊔ |
⊔ |
0 |
||
Правила задания информации об узлах в первом случае несколько отличаются от аналогичных правил во втором случае.
В первом случае каждый узел сетки характеризуется следующими признаками:
- местоположением (угловой, контурный, внутренний);
- ориентацией для контурных рядов (верхний, правый, нижний, левый);
- условием закрепления для контурных рядов (защемление, симметрия или косая симметрия);
- типом используемого оператора.
Эта информация для каждой из функций кодируется шестиразрядным десятичным числом. Первые два разряда определяют, является ли данная функция известной или ее необходимо определить (задают тип оператора), третий разряд - условие закрепления узла, расположенного в верхнем или нижнем контурном ряде, четвертый разряд - принадлежность узла верхнему или нижнему контурному ряду. В пятом и шестом разрядах кодового числа соответственно записывается условие закрепления узла, расположенного в левом или правом контурном ряде, и определяется принадлежность его левому или правому контурному ряду.
Значения кодов, определяющих ориентацию контурных узлов, приняты следующие: 5 - верхний, 6 - нижний, 7 - левый, 8 - правый контурный узел. Коды 1, 2 характеризую условия закрепления контурных узлов: 1 - плоскость симметрии или защемление, 2 - косая симметрия.
Для определения типа оператора используются коды 00 и 01, где 00 означает, что функция в данном узле известна, 01 - что функция в этом узле является неизвестной и ее необходимо определить.
Во втором случае при кодировании сеточной области с граничными условиями типа свободного края, шарнирного опирания или скользящего шарнирного опирания каждый узел сетки характеризуется следующими признаками:
- местоположением (угловой, контурный, внутренний);
- ориентацией (угловой - верхний левый, верхний правый, нижний правый, нижний левый; контурный - верхний, правый, нижний, левый);
- видом угла сеточной области (входной, выходной);
- наличием материала в ячейке сетки (верхней правой, верхней левой, нижней правой, нижней левой);
- типом используемого оператора.
Описанная информация кодируется в кодовых числах первой и второй функций шестиразрядным десятичным числом (табл. 4.3). Первые два разряда каждого из кодовых чисел задают условие, которое отражает, является данная функция известной или ее необходимо определить, т.е. задают тип оператора. Коды, выражающие тип используемого оператора, аналогичны кодам первого случая: код 00 означает, что функция известна в данном узле, 01 - то, что функция неизвестна и подлежит определению.
В кодовом числе первой функции значение третьего и четвертого разрядов, равное 50, характеризует принадлежность узла к верхнему краю и отсутствие левой верхней ячейки, а равное 60 - принадлежность узла к нижнему краю и отсутствие левой нижней ячейки. Значение пятого и шестого разрядов, равное 70, характеризует принадлежность узла левому краю и отсутствие левой верхней ячейки, равное 80 - принадлежность узла к правому краю и отсутствие правой верхней ячейки.
В кодовом числе второй функции значение третьего и четвертого разрядов, равное 50, выражает принадлежность узла верхнему краю и отсутствие правой верхней ячейки, а равное 60 - принадлежность узла нижнему краю и отсутствие правой нижней ячейки. Значение пятого и шестого разрядов, равное 70, характеризует принадлежность узла левому краю и отсутствие левой нижней ячейки, а равное 80 - принадлежность узла правому краю и отсутствие правой нижней ячейки.
В кодовом числе третьей функции первые два разряда, как и в кодовых числах первой и второй функций, отражают тип используемого оператора. Последующие разряды кодового числа определяют, является угол поворота в контурном узле сеточной области известным (нулевое значение разрядов) или неизвестным: значение третьего и четвертого разрядов, равное 50, характеризует принадлежность данного узла к верхнему краю, а равное 60 - принадлежность узла к нижнему краю. Значение пятого и шестого разрядов, равное 70, означает, что угол поворота является неизвестным в узле, принадлежащем левому краю, а равное 80 - угол поворота будет неизвестным в узле, принадлежащем правому краю сеточной области.
При кодировке сеточной области необходимо соблюдать следующую очередность. В первую очередь описываются угловые точки области. Затем наносят узлы контурных линий, включая угловые. Завершается кодирование описанием узлов исключенных подобластей в результате наличия вырезов и внутренних узлов сеточной области, включая углы контурных линий. Следует отметить, что при повторном описании одних и тех же узлов преимуществом обладает первое, т.е. данным узлам присваиваются коды по первому описанию.
Для рассматриваемой оболочки (см. рис. 4.9, в) с учетом сгущения сетки поле признаков имеет вид:
⊔⊔⊔⊔⊔9
⊔⊔1⊔⊔1⊔⊔1⊔⊔1215100715100715101
⊔⊔5⊔⊔1⊔⊔5⊔⊔1815100815100815101
⊔⊔5⊔13⊔⊔5⊔13816100816100816101
⊔⊔1⊔13⊔⊔1⊔13716100716100716101
⊔⊔1⊔⊔1⊔⊔5⊔1⊔⊔5101⊔⊔5100⊔⊔5101
⊔⊔5⊔⊔1⊔⊔5⊔13810000810001810001
⊔⊔1⊔13⊔⊔5⊔13⊔⊔6101⊔⊔6100⊔⊔6101
⊔⊔1⊔⊔1⊔⊔1⊔13710000710001710001
⊔⊔1⊔⊔1⊔⊔5⊔13⊔⊔⊔⊔⊔1⊔⊔⊔⊔⊔1⊔⊔⊔⊔⊔1;
- после отрок поля признаков на (n + 1)-й перфокарте (n = 9 + LITR) по формату 15 задается переменная KGEO, определяющая число элементов, образующих составную оболочку;
- следующие несколько групп перфокарт (по четыре каждая) описывают геометрические и физические параметры элементов, число которых задается переменной KGEO. Каждая из групп описывает информацию об элементе:
а) первая перфокарта - массив KO, определяющий для каждого из элементов начальный и конечный номера узлов в направлениях координатной линии x1 (первый и третий элементы массива) и координатной линии x2 (второй и четвертый элементы массива), а также код соответствующей поверхности. Код принимается равным номеру вызываемого в подпрограмме SOSTAV соответствующего модуля, вычисляющего геометрические характеристики данной поверхности. При этом в головной подпрограмме должен присутствовать оператор EXTERNAL-SOSTAV и при обращении к управляющей подпрограмме в качестве формального параметра должно быть указано имя SOSTAV. Пересчет первых четырех параметров массива KO с учетом сгущения сетки выполняется автоматически. При KGEO = 1 (рассматривается простая оболочка) код поверхности (пятый параметр массива KO) можно не задавать. Для этого случая вид поверхности рассматриваемой оболочки определяется модулем, описанным в головной подпрограмме, посредством оператора EXTERNAL. Формат задания параметров массива KO(5) - 515;
б) вторая перфокарта определяет значения массива FIZPAR(7) элементы которого в порядке следования характеризуют модуль упругости материала (E), толщину (h), коэффициент Пуассона (n), предел текучести материала (sт), коэффициент температурного линейного расширения (a), интенсивность деформаций пластичности (eiт) и степень упрочнения материала, которая принимается равной утроенному значению модуля сдвига (G) в зоне упрочнения.
Описанные величины вводятся по формату 7Е10.4;
в) третья перфокарта описывает значения величин геометрических параметров элемента оболочки, содержание и последовательность задания которых определяют в COMMON/GEPAR/ соответствующей подпрограммы, вычисляющей проекции векторов основного локального базиса поверхности оболочки, данные величины вводятся по формату 7E10.4;
г) четвертая перфокарта задает значения шести параметрам, определяющим положение местной декартовой системы координат рассматриваемого элемента (в местной декартовой системе координат описывается поверхность элемента) относительно общей для составной оболочки декартовой системы координат. Первые три параметра отражают соответственно координаты X, Y, Z начала местной системы координат в общей системе координат. Последующие три параметра задают эйлеровы углы поворота местной системы координат относительно общей: первый параметр характеризует угол поворота в радианах относительно оси X, второй - угол поворота относительно оси Y, третий - угол поворота относительно оси Z. Угол является положительным, если его вектор совпадает с направлением оси, вокруг которой проводится вращение. Эти данные вводятся по формату 6Е10.4. Образец задания описанной модной информации для рассматриваемой составной тороидальной оболочки (см. рис. 4.9, в) следующий:
⊔⊔⊔⊔7⊔⊔⊔⊔1⊔⊔⊔⊔5⊔⊔⊔⊔5⊔⊔⊔⊔7
⊔.2000E⊔07⊔1.0700E⊔00⊔3000E⊔00
⊔.0000E⊔00⊔.2618E⊔00⊔.0000E⊔00⊔.1571E⊔01⊔.5500E⊔02⊔.2580E⊔02
⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.2618E⊔00
⊔⊔⊔⊔1⊔⊔⊔⊔5⊔⊔⊔⊔5⊔⊔⊔⊔13⊔⊔⊔⊔1
⊔.2000E⊔07⊔.0700E⊔00⊔.3000E⊔00
⊔.0000E⊔00⊔.2618E⊔00⊔.1571E⊔01⊔.3146E⊔01⊔.5500E⊔02⊔.2580E⊔02
⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.2618E⊔00
⊔⊔⊔⊔5⊔⊔⊔⊔1⊔⊔⊔⊔9⊔⊔⊔⊔5⊔⊔⊔⊔1
⊔.2000E⊔01⊔.0700E⊔00⊔.3000E⊔00
-.2618E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.1571E⊔01⊔.5500E⊔02⊔.2580E⊔02
⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00-2618E⊔00
⊔⊔⊔⊔5⊔⊔⊔⊔5⊔⊔⊔⊔9⊔⊔⊔⊔13⊔⊔⊔⊔1
⊔.2000E⊔07⊔.0700E⊔00⊔.3000E⊔00
-.2618E⊔00⊔.0000E⊔00⊔.1511E⊔01⊔.3146E⊔07⊔.5500E⊔02⊔.2580E⊔02
⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00⊔.0000E⊔00-.2618E⊔00
- по формату 15 на следующих двух перфокартах ((n + 4m + 2)-й и (n + 4m + 3)-й, где m = KGEO) вводятся параметры, определявшие начальный (NBEGIN) и конечный (NEND) номера шагов вычислительного процесса. Параметр NBEGIN принимается равным 1 или задается равным последующему номеру шага в случае, если результаты предыдущего шага считываются из файла прямого доступа;
- (n + 4m + 4)-я перфокарта описывает данные MLSTEP, NHR, где MLSTEP определяет начальный номер записи результатов решения, с которой начинается запись в файл прямого доступа, NHR - число шагов, результаты которых будут подряд записываться в файл на магнитный диск. При MLSTEP = 0 запись результатов решения в файл не производится.
Формат задания - 215;
- в (n + 4m + 5)-й перфокарте вводятся переменные WETW, NWW, IWW, JWW, DWW, используемые при построении ответвляющегося решения. Здесь логическая переменная WETW служит признаком для анализа знака определителя системы разрешающих уравнений и ветвления решения; NWW, IWW и JWW характеризуют ведущий параметр перемещения - соответственно номер компоненты перемещения (U1, U2 или U3) и координаты узла (IWW, JWW) сеточной области, в котором задается значение этого перемещения; DWW - задает величину приращения ведущего параметра.
Область значений: логической переменной WETW присваивается .TRUE. или .FALSE.. Если WETW = .TRUE., то при решении задачи автоматически производится анализ знака определителя и при его смене - переход на ответвляющуюся ветвь решения. При WETW = .FALSE. - анализ знака определителя не производится, ответвляющееся решение не строится; NWW принимается равным 1, 2 или 3 (NWW обычно задается равным 3, так как для тонких оболочек перемещение U3 является основным по отношению к U1 и U2); IWW, JWW - могут принимать значения соответственно от 1 до МО и от 1 до NO; DWW обычно принимается равным 1/4 + 1/6 толщины оболочки.
Описанные данные вводятся по формату L5, 315, Е10.4;
- в (n + 4m + 6)-й перфокарте по формату 1711 задается массив IFPULT(17), управляющий печатью полей перемещений, усилий, моментов, деформаций, напряжений и координат X, Y, Z узлов разностной сетки. Каждому элементу массива IEP присваивается 1 или 0: 1 - включить печать, 0 - выключить печать.
Печати тех или иных полей напряженно-деформированного состояния поставлены в соответствие следующие элементы массива IFPULT:
U1, U2, U3 - 1, 2, 3 элементы; T13, T23 - 10, 11 элементы;
T11, T12, T22 - 4, 5, 6 элементы; X, Y, Z - 12, 13, 14 элементы.
М11, М12, М22 - 7, 8, 9 элементы;
Шестнадцатый элемент массива IFPULT управляет печатью полей напряжений s11, s12, s22, семнадцатый - объединенной печатью полей деформаций и углов поворота нормали e11, e12, e22, v1, v2, e11n, e12n, e22n, v1n, v2n, IFPULT(17) не используется;
- в (n + 4m + 7)-я перфокарта вводится по формату 2L5 и задает значения логическим переменным NEL, NELDEF. При решении геометрически нелинейной задачи NEL = .TRUE., при решении линейной задачи NEL = .FALSE..
Если NELDEF = .TRUE., то задача решается с учетом нелинейных соотношений между компонентами тензора мембранных деформаций и вектора перемещений, если NELDEF = .FALSE., то соответствующие соотношения линейны;
- следующие две перфокарты задают значения параметрам DW, DP((n + 4m + 8)-я перфокарта) и переменным NW, IW, JW, NREBR((n + 4m + 9)-я перфокарта), где DW, NW, IW и JW характеризуют ведущий параметр при построении основного решения и имеют назначения, аналогичные параметрам DWW, NWW, IWW, JWW; DP - определяет величину приращения нагрузки для случая, когда ведущим параметром является нагрузка; NREBR - задает суммарное число ребер.
Область значения: параметр NW принимается равным 1, 2 или 3 (обычно принимается равным 3); IW - может принимать значения от 1 до МО, JW - от 1 до NO; DW обычно задается равным 1/5 - 1/10 толщины оболочки; NREBR принимается равным числу ребер, а в случае их отсутствия - равным 0.
При задании параметру DP ненулевого значения, DW, NW, IW, JW принимаются равными нулю и наоборот: при DP = 0.0., DW, NW, IW ¹ 0.
Формат чтения - 2Е10.4/415;
- следующая группа перфокарт (от (n + 4m + 10)-й до (n + 4m + k)-й, где k = 9 + NREBR ´ 2) задает геометрические параметры ребер, общее число которых определяется переменной NREBR. Содержание и структура входных данных о ребрах описывается на примере подготовки информации для фрагмента составной тороидальной оболочки (см. рис. 4.9, в), подкрепленного одним ребром в направлении координатной линии х2 (ребро проходит по узлам сетки с координатами ITCH = 5, JTCH = от 1 до 37, где ITCH - номер узла в направлении x1, JTCH - в направлении х2) и нерегулярной системой из шести ребер в направлении координатной линии x1 (ребра проходят по узлам сетки с координатами:
первое - ITCH = 5, JTCH от 1 до 37;
второе - JTCH = 8, ITCH от 1 до 9;
третье - JTCH = 13, ITCH от 1 до 9;
четвертое - JTCH = 20, ITCH от 1 до 9;
пятое - JTCH = 25, ITCH от 1 до 9;
шестое - JTCH = 31, ITCH от 1 до 9.
Фрагмент ребристой оболочки показан на рис. 4.10, где приняты следующие обозначения: F1, F2 - площади поперечных сечений; С1, С2 - расстояния от центров тяжести поперечных сечений ребер до срединной поверхности оболочки; l1, l2 - максимальные расстояния до крайних волокон ребер; d1, d2 - минимальные расстояния до крайних волокон ребер. Числовые значения описанных параметров, а также собственные осевые моменты инерции J для рассматриваемых ребер приведены в таблице 4.4. Модуль упругости материала ребер (ER) принят равным 19,8 МН/см2. При решении задач упруго-пластического деформирования оболочек дополнительно задаются предел текучести материала ребер (SIGMT), интенсивность деформаций пластичности (EPST) и степень упрочнения материала (TALF), которая принимается равной утроенному значению модуля сдвига в зоне упрочнения.
Фрагмент ребристой оболочки
а - схема расположения ребер; б, в - геометрические параметры ребер
|
от ITCH |
от JTCH |
до ITCH |
до JTCH |
F |
J |
C |
l |
d |
|
|
1 |
5 |
1 |
5 |
37 |
3,0 |
1,0 |
1,035 |
2,035 |
0,035 |
|
2 |
1 |
5 |
9 |
5 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
|
3 |
1 |
6 |
9 |
8 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
|
4 |
1 |
13 |
9 |
13 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
|
5 |
1 |
20 |
9 |
20 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
|
6 |
1 |
25 |
9 |
25 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
|
7 |
1 |
31 |
9 |
31 |
0,6 |
0,05 |
0,535 |
1,035 |
0,035 |
Каждая из перфокарт группы (от (n + 4m + 10)-й до (n + 4m + k)-й) описывает информацию об одном ребре:
а) массив KOR(4, NREBR), определяющий начальный и конечный номера узлов в направлениях координатной линии x1 (первый и третий элементы массива) и координатной линии х2 (второй и четвертый элементы массива);
б) массив GREB(11, NREBR), элементы которого в порядке следования характеризуют модуль упругости материала (ER), предел текучести материала (SIGMT), интенсивность деформаций пластичности (EPST), степень упрочнения материала (TALF), площадь поперечного сечения (F), собственный момент инерции (J), координату центра тяжести поперечного сечения ребра в локальной системе координат срединной поверхности оболочки (С), максимальную (l) и минимальную (d) координаты крайних волокон поперечного сечения, фиктивную площадь поперечного сечения при сдвиге (SR) и фиктивный момент инерции поперечного сечения при кручении (RIR). Положительные значения координат С, l и d совпадают с направлением линии x3.
Описанные величины вводятся по формату 415, 4E10.4/7Е10.4.
Образец задания описанной входной информации для рассматриваемой ребристой оболочки (см. рис. 4.10) следующий:
⊔⊔⊔⊔5⊔⊔⊔⊔1⊔⊔⊔⊔5⊔⊔⊔⊔37⊔.1980Е + 7
⊔.3000E + 01⊔1000Е + 01⊔.1035E + 01⊔.2035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔5⊔⊔⊔⊔9⊔⊔⊔⊔5⊔.1980Е + 07
⊔.6000E + 00⊔0500Е + 00⊔.5350 + 00⊔.1035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔8⊔⊔⊔⊔9⊔⊔⊔⊔8⊔.1980Е + 07
⊔.6000E + 00⊔0500Е + 00⊔.5350Е + 00⊔.1035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔13⊔⊔⊔⊔9⊔⊔⊔⊔13⊔.1980Е + 01
⊔.6000E + 00⊔0500Е + 00⊔.5350Е + 00⊔.1035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔20⊔⊔⊔⊔9⊔⊔⊔⊔20⊔.1980Е + 07
⊔.6000E + 00⊔0500Е + 00⊔.5350Е + 00⊔.1035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔25⊔⊔⊔⊔9⊔⊔⊔⊔25⊔.1980Е + 07
⊔.6000E + 00⊔0500Е + 00⊔.5350Е + 00⊔.1035E + 01⊔.0350E + 00
⊔⊔⊔⊔1⊔⊔⊔⊔31⊔⊔⊔⊔9⊔⊔⊔⊔31⊔.1980Е + 07
⊔.6000E + 00⊔0500Е + 00⊔.5350Е + 00⊔.1035E + 01⊔.0350E + 00
При NREBR = 0 входная информация о ребрах не задается.
Описанные в этом пункте входные данные задаются посредством операторов READ в подпрограмме WWOD и могут вводиться с перфокарт во входном потоке задания, либо назначением на шаге GO вводного файла на библиотечный раздел, в котором они записаны.
4.4.3. Стартовый пакет для расчета на ЭВМ формируется на языке управления заданиями с использованием процедуры FORTGCLG (FORTHCLG или FORECLG). При этом во входной поток шага FORT необходимо поместить головную программу, а на шаге LKED набор данных SYSLMOD дополняется библиотечным набором SYS2.L.MKC2, включающим загрузочные модули с неразрешенными ссылками подпрограмм комплекса «МЕКРИС-2». Во входной поток шага GO подается числовая исходная информация и описывается файл прямого доступа FT08F001:
//GO.FT08F001 и DD⊔DSN⊔ = имя набора, UNIT = SYSDA, DISP = (NEW, KEEP),
//⊔VOL = SER = имя тома, DCB = (RECFM = FB, DSORGE = DA,
BLKSIZE = ![]() ,
,
//⊔SPASE = (![]() , Kфв).
, Kфв).
4.5. Получаемые результаты
Выходные данные, получаемые в результате работы программ комплекса, подразделяются на две группы. К первой группе относится задаваемая с помощью перфокарт исходная информация о задаче, второй - результаты решения задачи. Печать выходных данных осуществляется по группам в перечисленной последовательности.
Распечатка исходной информации о задаче и результатов ее преобразования осуществляется операторами PRINT в подпрограмме WWOD. В последовательности, аналогичной их заданию, осуществляется печать числовых данных. Дополнительно приводится распечатка кодового массива LITREG (поле признаков) и массивов KO, KOR, сформированных для конкретной постановки с учетом заданных параметров сгущения разностной сетки MSGU, NSGU, а также информационных сообщения. Формат печати данных аналогичен формату их ввода.
Печать результатов решения задачи осуществляет подпрограмма NELUP1 (для задач НДС и устойчивости оболочек с учетом геометрической нелинейности) или NELUP2 (для задач упруго-пластического деформирования оболочек).
Управление печатью производится в соответствии с массивом IFPULT(17), каждому элементу которого при задании входных данных присваивается значение 1 или 0.
Под заголовком НОМЕР СТРОКИ ОПРЕДЕЛИТЕЛЬ МИНОР на печать выдаются номера блок-строк матрицы коэффициентов разрешающих уравнений и значения соответствующих миноров.
Затем следует печать заданных (в случае присвоения соответствующему элементу массива IFPULT значения 1) компонент напряженно-деформированного состояния. Результаты печатаются в табличной форме, т.е. для каждого узла или между узлами сеточной области. Табличные значения выдаются на печать в виде целых чисел, для которых указывается один общий десятичный порядок.
Под заголовками ПЕРЕМЕЩЕНИЯ U1, ПЕРЕМЕЩЕНИЯ U2, ПЕРЕМЕЩЕНИЯ U3 печатаются узловые физические значения соответственно перемещений ПЕРЕМЕЩЕНИЯ U1, U2 и U3. Под названием УСИЛИЯ Т11, УСИЛИЯ Т12, УСИЛИЯ Т22 печатаются поля мембранных усилий Т(11), Т(12) и Т(22). Физические значения для Т(12) и Т(11) выдаются на печать между узлами из координатной линии х1, для Т(22) - между узлами на линии х2.
Под заголовками УСИЛИЯ М11, УСИЛИЯ М12, УСИЛИЯ М22 печатаются поля изгибных М(11), М(12) и крутящего М(22) моментов. Физические значения внутренних моментов печатаются в узлах сеточной области.
Под заголовками УСИЛИЯ Т1N, УСИЛИЯ Т2N печатаются поля перерезывающих сил (T(13), T(23)). Физические значения T(13) выдаются на печать между узлами на линии x1, а T(23) - между узлами линии x2.
Координаты узлов разностной сетки относительно основной декартовой системы координат X, Y, Z печатаются соответственно под заголовками КООРДИНАТЫ УЗЛОВ X, КООРДИНАТЫ УЗЛОВ Y и КООРДИНАТЫ УЗЛОВ Z.
Под
заголовками НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ G1P, НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ G1M, НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ G2P, НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ G2M на печать выдаются физические значения напряжений ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Под
заголовками КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ GKP,
КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ GKM на печать выдаются
физические значения напряжений ![]() ,
, ![]() .
.
Для узлов сеточной области оболочки значения нормальных и касательных напряжений подсчитываются по формулам:
![]()
![]()
![]()
В узлах, совпадающих с ребрами, значения нормальных напряжений в крайних волокнах поперечных сечений ребер рассчитывают по формулам:
![]()
![]()
![]()
![]()
где l, d - максимальные и минимальные координаты крайних волокон поперечных сечений ребер; Ep1, Ep2 - модули упругости ребер первого и второго направлений.
Под заголовками ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙ GIP и ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙ GIM на печать выдаются значения интенсивности напряжений на лицевых поверхностях оболочки.
Значения интенсивности напряжений подсчитываются по формуле
![]()
где TI и TII - инварианты тензора напряжений
TI(s) = aabsab; TII(s) = sabsab;
Поля деформаций и углов поворота нормали e11, e12, e22, v1, v2, e11n, e21n, e22n, v1n, v2n печатаются без заголовков в перечисленной последовательности. Физические значения для e11, e12, v1, v2n и e22n выдаются на печать между узлами на линии х1, для e11n, e21n, e22, v2 и v1n - между узлами на линии х2.
После перечисленных выше компонент напряженно-деформированного состояния печатаются номер шага вычислительного процесса (ШАГ), накопленная величина нагрузки (НАКОПЛЕННАЯ НАГРУЗКА), величина приращения ведущего параметра нагрузки DP (ПРИРАЩЕНИЕ НАГРУЗКИ), значение мантиссы определителя системы разрешающих уравнений (DETERN) и его десятичный порядок (IED), номер ведущего параметра перемещения (NW) и координаты узла, в котором задается значение этого перемещения (IW, JW), а также величина приращения ведущего параметра перемещения (DW).
ПРИЛОЖЕНИЯ
Приложение 1
ПРИМЕРЫ РЕШЕНИЯ ТЕСТОВЫХ ЗАДАЧ
Правомерность использования и надежность новых численных методов обычно демонстрируются на тестовых задачах, для которых в литературе имеются точные решения или экспериментальные данные. Важным показателем эффективности любого численного метода является скорость сходимости численного решения к точному при увеличении числа степеней свободы дискретной модели рассматриваемой задачи.
Для проверки эффективности рекомендуемого комплекса программ «МЕКРИС-2», базирующегося на методе криволинейных сеток, выбраны три тестовые задачи, в которых отрицательное влияние жестких смещений на сходимость вычислений является заметным. Четвертый пример, описанный в данном приложении, предназначен для контроля работоспособности комплекса программ.
1. Деформирование свободной цилиндрической оболочки под действием двух диаметрально направленных сил
Рассмотрена задача о деформировании свободной цилиндрической оболочки (рис. 1, а), нагруженной двумя диаметрально противоположно направленными самоуравновешенными сосредоточенными силами Р. Так как торцевые края оболочки свободны и нагрузка не имеет осевой симметрии, то её деформации сводятся, в основном, к изгибу. С учетом этой особенности в работе [19] с удовлетворительной точностью аналитически определена величина укорочения диаметра, вдоль которого действуют сосредоточенные силы. Решение этой задачи методом конечных элементов, как показано в работах [15, 18, 20], оказалось весьма чувствительным к отрицательному влиянию жестких смещений. Авторами этих работ для проверки эффективности метода приведены результаты исследования сходимости численных решений с различными типами интерполирующих полиномов.
Расчетные схемы оболочек к тестовым задачам
а - свободная цилиндрическая оболочка, нагруженная сосредоточенными силами; б - цилиндрическая оболочка с прямоугольными отверстиями
Значения прогибов цилиндрической оболочки в точках приложения сосредоточенных сил
|
Метод конечных элементов |
МКС |
|||||||
|
Билинейные кубические [20] |
То же, плюс жесткие смещения [15] |
Трехмерные полилинейные КЭ (моментная схема) [18] |
||||||
|
К-во ур-ний |
Смещение |
К-во ур-ний |
Смещение |
К-во ур-ний |
Смещение |
К-во ур-ний |
Смещение |
|
|
4´4 |
150 |
0,6 |
150 |
2,86 |
150 |
2,61 |
60 |
2,98 |
|
4´8 |
270 |
1,41 |
270 |
2,88 |
270 |
2,88 |
116 |
2,95 |
|
8´8 |
486 |
1,48 |
486 |
2,89 |
486 |
2,90 |
222 |
2,94 |
При расчете методом криволинейных сеток, как и в работах [15, 18, 20], рассмотрена оболочка, длина которой L = 0,263 м, радиус кривизны R = 0,126 м, толщина h = 0,00238 м. Модуль упругости материала оболочки E = 72 ГПа, коэффициент Пуассона n = 0,3125. Величина сосредоточенных сил Р = 4,43 кН. При таких параметрах оболочки и нагрузки значение прогиба в точках приложения сил, полученное по методике [19], составляет 0,028 м.
Благодаря симметрии напряженно-деформированного состояния относительно плоскостей, проходящих через линию действия сил в продольном направлении и в поперечном направлении, а также плоскости, проходящей через ось оболочки, нормалью к которой является линия действия сил, для расчета выделен фрагмент, представляющий собой восьмую часть оболочки. Координата х1 на поверхности ориентирована в продольном направлении, х2 - в окружном направлении. На границах х1 = L/2, х2 = 0, х2 = p/2 приняты условия симметрии вектора перемещений; на границе х1 = 0 - условия свободного края.
В табл. 1 приведены значения прогиба в точке приложения сил, полученные методом криволинейных сеток с различной густотой разностной сетки и, для сравнения, результаты, найденные методом конечных элементов в работе [15, 18, 20]. Сравнение приведенных результатов свидетельствует о высокой скорости сходимости МКС и его достаточной точности.
2. НДС цилиндрической оболочки с прямоугольными отверстиями
Рассмотрено напряженно-деформированное состояние цилиндрической оболочки с четырьмя большими прямоугольными отверстиями (см. рис. 1, б) при осевом сжатии. Исследована сходимость численного решения метода криволинейных сеток. Результаты сопоставлены с решениями [10], [11], полученными по методу конечных разностей без учета жестких смещений и по методу конечных элементов с различными типами аппроксимирующих полиномов.
В работе [10] отмечено, что решение задачи, достигнутое на основе соотношений теории пологих оболочек с использованием метода конечных разностей, имеет неудовлетворительную сходимость. Там же приведено решение этой задачи, базирующееся на технической теории оболочек и применении метода конечных элементов. Матрица жесткости конечных элементов получена с использованием двух типов полиномов, аппроксимирующих компоненты вектора перемещений с 24-мя неопределенными параметрами, что соответствует 6-ти обобщенным неизвестным в узле. Показано, что при использовании полиномов первого типа, составленных без учета жестких смещений, сходимость численного решения не достигалась. В полиномах второго типа, в отличие от первого, использованы функции формы цилиндрической поверхности элемента, что позволило избавиться от отрицательного влияния жестких смещений. Использование таких полиномов в расчетах с различной густотой сетки, хотя и не привело к достижению сходимости численного решения при сетке 24´5, т.е. при 594 неизвестных, однако выявило тенденцию асимптотического сближения результатов по мере увеличения количества неизвестных. Полученные при этом данные обнаружили концентрацию напряжений в углу отверстия. В работе [II] эта же задача решена методом конечных элементов с использованием полиномов, учитывающих жесткие смещения, на основе разрешающих соотношений теории оболочек В.В. Новожилова. Показано, что в этом случае сходимость численного решения достигнута при сетке 11´16 (422 неизвестных).
Для сравнения с результатами приведенных выше работ рассчитана оболочка высотой H = 28 см, радиусом R = 12,5 см, толщиной h = 0,028125 см, длиной выреза в окружном направлении l2 = 7p см и в осевом направлении l1 = 12 см, т.е. при значениях отношений h/R = 0,00225, H/R = 2,24, l1/H = 3/7, l2/H = p/4 принятых в работах [10, 11]. Коэффициент Пуассона материала оболочки принят равным 0,3.
Наличие плоскостей симметрии оболочки позволило выделить для расчета фрагмент, представляющий собой 1/8 часть в окружном и 1/2 часть в осевом направлении. На контурах, принадлежащих плоскостям симметрии, приняты условия симметрии вектора перемещений. На торцевом контуре заданы условия подвижного в осевом направлении шарнирного опирания и учтено действие осевой нагрузки интенсивностью q. На контурах отверстия приняты условия свободного края.
С целью
исследования сходимости результатов, полученных методом криволинейных сеток,
проведены расчеты при различной густоте разностной сетки, нанесенной на
фрагмент оболочки. В табл. 2 приведены значения относительных прогибов ![]() и
относительных осевых внутренних усилий
и
относительных осевых внутренних усилий ![]() для характерных точек оболочки,
обозначенных на рис. 1, б буквами А, В, С, D, E. Здесь же для
сравнения представлены результаты расчетов, полученных методом конечных
элементов [10,
11]
и методом конечных разностей [10].
для характерных точек оболочки,
обозначенных на рис. 1, б буквами А, В, С, D, E. Здесь же для
сравнения представлены результаты расчетов, полученных методом конечных
элементов [10,
11]
и методом конечных разностей [10].
Анализ результатов позволяет сделать вывод, что сходимость решения по методу криволинейных сеток достигнута при менее густой сетке по сравнению со случаем применения метода конечных элементов с использованием наилучшей аппроксимации. Количественное расхождение результатов можно объяснить более жесткой дискретной моделью метода конечных элементов по сравнению с моделью метода криволинейных сеток. Неудовлетворительные результаты метода конечных разностей, приведенные в работе [10], можно объяснить как непригодностью теории пологих оболочек для решения такой задачи, так и плохой сходимостью традиционного метода конечных разностей.
Результаты расчета цилиндрической оболочки с четырьмя прямоугольными отверстиями
|
Сетка |
К-во ур-ний |
Перемещения |
Усилия |
|||||||||
|
А |
B |
С |
Д |
Е |
А |
B |
С |
Д |
Е |
|||
|
МКЭ без учета жестких смещений [10] |
4´5 |
104 |
-0,464 |
0,140 |
0,359 |
0,468 |
0,447 |
0 |
-1,476 |
-0,560 |
-1,361 |
-0,555 |
|
12´5 |
300 |
-1,988 |
0,656 |
1,226 |
1,577 |
1,461 |
0 |
-3,736 |
0,015 |
-3,222 |
0,054 |
|
|
24´5 |
594 |
-3,973 |
1,528 |
1,738 |
2,829 |
2,119 |
0 |
-8,046 |
0,409 |
-5,577 |
0,595 |
|
|
МКЭ с учетом жестких смещений [10] |
4´5 |
104 |
-3,112 |
0,710 |
1,917 |
1,446 |
2,351 |
0 |
-2,861 |
0,299 |
-2,794 |
0,783 |
|
12´5 |
300 |
-7,405 |
3,555 |
1,434 |
5,614 |
1,779 |
0 |
-6,592 |
0,484 |
-5,320 |
0,764 |
|
|
24´5 |
594 |
-8,325 |
4,167 |
1,313 |
6,822 |
1,638 |
0 |
-10,320 |
0,479 |
-7,497 |
0,745 |
|
|
То же [11] |
11´16 |
422 |
-9,021 |
4,111 |
2,189 |
7,006 |
2,844 |
0 |
-6,256 |
0,548 |
-4,965 |
0,922 |
|
МКР без учета жестких смещений [10] |
12´16 |
307 |
-5,640 |
2,197 |
2,093 |
4,097 |
2,571 |
0 |
-5,457 |
0,605 |
-4,737 |
0,864 |
|
МКС |
6´7 |
112 |
-9,866 |
4,980 |
1,455 |
7,941 |
2,011 |
0 |
-5,146 |
0,355 |
-4,288 |
0,705 |
|
12´7 |
214 |
-11,122 |
5,457 |
1,951 |
9,436 |
2,607 |
0 |
-7,416 |
0,517 |
-5,250 |
0,965 |
|
|
18´14 |
671 |
-11,108 |
5,449 |
2,110 |
9,488 |
2,798 |
0 |
-8,352 |
0,588 |
-5,286 |
0,995 |
|
3. Устойчивость бесконечной цилиндрической оболочки при действии внешнего равномерно распределенного давления
Среди задач устойчивости оболочек наиболее изучены задачи устойчивости цилиндрических оболочек. Задача об устойчивости бесконечной круговой цилиндрической оболочки при действии внешнего равномерно распределенного давления, благодаря однородности напряженно-деформированного состояния в до и послекритическом состоянии в направлении образующей, сводится к задаче устойчивости кольца, имеющей аналитическое решение, хорошо согласующееся с экспериментальными данными
qкр = h2EJ/R3,
где q - значение интенсивности внешнего давления, n - количество волн функции прогиба в послекритическом состоянии, E - модуль упругости материала, J - осевой момент инерции поперечного сечения, R - радиус оболочки.
При использовании различных численных методов для определения величины критического равномерно распределенного внешнего давления на кольцо отмечается низкая сходимость результатов, обусловленная погрешностью аппроксимации функций жестких смещений. Как показано в работе [9], относительная погрешность критической величины равномерного внешнего давления для кольца, полученной обычным методом конечных разностей, выражается соотношением
![]()
где m - количество разностных делений в окружном направлении. Из приведенной формулы видно, что при увеличении количества разностных делений погрешность убывает, но скорость убывания зависит от квадрата отношения радиуса оболочки к ее толщине.
При помощи комплекса программ «МЕКРИС-2» решена задача устойчивости кольца с отношением R/h = 100. При этом для определения минимальной критической нагрузки, соответствующей количеству волн функции прогиба в закритическом состоянии n = 2, в качестве расчетного фрагмента в осевом направлении выделена часть цилиндрической поверхности, ширина которой выбиралась из условия равенства сторон разностных ячеек, зависящая от количества разностных делений в окружном направлении. В этом направлении размер расчетного фрагмента составил четверть окружности. На всех границах фрагмента приняты условия симметрии вектора перемещений. Задача решена с наложением разностных сеток 4´4, 4´6, 4´12, 4´16.
Результаты исследования сходимости численного решения приведены в табл. 3 в виде значений относительных погрешностей численного определения величины критического давления при различной густоте разностной сетки.
|
4´4 |
4´8 |
4´12 |
4´16 |
|
|
Погрешность, % |
5,78 |
1,39 |
0,61 |
0,36 |
Из таблицы видно, что величина погрешности определения критического давления по мере сгущения разностной сетки в окружном направлении достаточно хорошо следует квадратичной зависимости от величины конечно-разностного деления.
4. Устойчивость цилиндрической панели в упруго-пластической области деформирования
На основе метода криволинейных сеток и теории малых упруго-пластических деформаций с учетом сжимаемости материала выполнено исследование устойчивости при внешнем равномерном давлении прямоугольной в плане цилиндрической панели (рис. 2, а). Граничные условия панели соответствуют шарнирно-неподвижному закреплению кромок.
Данная задача была рассмотрена в работе [16], где для ее решения использованы нелинейные дифференциальные уравнения изгиба пологих оболочек в смешанной форме и применен метод конечных разностей (вследствие симметрии поверхности и внешней нагрузки рассматривалась четверть панели и наносилась сетка 10´10 узлов). В основу алгоритма решения нелинейных разностных уравнений, учитывающих геометрическую и физическую нелинейность, положен общий метод итерации, разработанный авторами работы [16].
Геометрические характеристики панели при расчете приняты следующими: размеры в плане 2а´2в = 0,4´0,2 м; толщина h = 0,01 м; радиус кривизны R = 0,25 м. Принятые размеры соответствуют параметру пологости k = 16 [16].
Материал панели подчиняется диаграмме деформирования с линейным законом упрочнения и имеет следующие характеристики: модуль упругости Е = 196 ГПа; коэффициент Пуассона n = 0,3; интенсивность деформаций текучести eiт = 4,28 × 10-3; модуль сдвига при упрочнении G1 = 14,8 ГПа.
На рис. 2, б приведены полученные в [16] кривые зависимостей «нагрузка-прогиб». Штриховая кривая соответствует нелинейному упругому решению, упруго-пластическое деформирование показано штриховой кривой с крестиками. Верхняя критическая нагрузка упруго-пластического решения в 1,8 раза меньше, чем для упругого решения.
Рис. 2. Устойчивость цилиндрической панели
а - общий вид; б - кривые зависимостей прогиба в центре панели от равномерно распределенной нагрузки
Решение упругой и упруго-пластической задач устойчивости цилиндрической панели по методу криволинейных сеток выполнено при разностной сетке 13´13 узлов. Полученные зависимости нагрузки от прогиба в центре панели представлены на рис. 2, б, где упругое решение показано сплошной линией, упруго-пластическое - сплошной линией с крестиками.
Анализ показывает, что значения верхних критических нагрузок упругого и упруго-пластического решений практически совпадают с полученными в работе [16]. Расхождение в значениях нижних критических нагрузок обусловлено тем, что в [16] использованы упрощенные разрешающие уравнения теории пологих оболочек, не учитывающие всех нелинейных факторов исходных геометрически-нелинейных уравнений теории оболочек. Кроме того, в смешанной форме уравнений, использованных в [16], нельзя точно удовлетворить граничным условиям шарнирного опирания. Равенство нулю сдвигающих усилий выполняется здесь в интегральном смысле, на что указывает автор работы [3]. Эти обстоятельства приводят к тому, что оболочка оказывается более жесткой.
Приложение 2
ПРИМЕРЫ РАСЧЕТА СОСТАВНЫХ ОБОЛОЧЕК
В данном приложении приводятся примеры расчета, иллюстрирующие возможности предлагаемой методики и комплекса программ «МЕКРИС-2» применительно к расчету на устойчивость оболочечных конструкций сложной формы.
1. Упруго-пластическое деформирование горизонтального цилиндрического сосуда
В различных отраслях промышленности для хранения жидкости широко применяются тонкостенные горизонтальные сосуды, опирающиеся на две седловины. При этом вблизи опор в сосуде возникают высокие окружные напряжения, которые значительны в двух зонах, а именно, в верхней зоне контакта с седловиной, известной под наименованием рог, и в крайней нижней части, надире, при неприкрепленной седловине. Указанные напряжения в ряде случаев определяют конструкцию сосуда вблизи опор, а наличие сжатой зоны при неприкрепленной седловине не исключает возможности существования в этой зоне местного выпучивания.
С применением комплекса программ «МЕКРИС-2» в геометрически и физически нелинейной постановке выполнен расчет горизонтального цилиндрического сосуда с эллипсоидальными крышками, опирающегося на пару одинаковых жестких седловин, которые не сварены с сосудом и расположены на удалении от его концов (рис. 1, а). Исследовано напряженно-деформированное состояние и неустойчивое поведение сосуда вблизи опор, наполненного жидкостью, но не подвергаемого пригрузкой внутренним давлением. Значение гравитационной нагрузки на стенку сосуда от жидкого содержимого определяется произведением gН, где g - удельный вес жидкости; Н - высота столба жидкости (0 £ Н £ 2R), R - радиус цилиндра.
Упруго-пластический расчет горизонтального цилиндрического сосуда
а - геометрия сосуда; б - распределение тангенциального усилия Т(11) по центру профиля седловины сосуда
Для расчета выбран сосуд со следующими значениями геометрических параметров (см. рис. 1, а): R = 1,3 м; r = 0,65 м; L/R = 6,46; 2R/h = 325; l/R = 3,23; b = 0,2 м; Q = 2,44 рад. Жесткость упругой прокладки между сосудом и опорами варьируется и принимается равной k = 10; 5; 1; 0,2 кН/см3. Материал оболочки сосуда - сталь с модулем упругости E = 206 ГПа, коэффициентом Пуассона n = 0,3 и диаграммой деформирования без упрочнения при пределе текучести sт = 240 МПа и интенсивности деформаций текучести eiт = 10-3.
Учитывая, что напряженно-деформированное состояние сосуда при действии гравитационной нагрузки от жидкого содержимого обладает симметрией относительно плоскостей X0Y и Y0Z, для расчета была выделена четвертая часть поверхности сосуда. Координата x1 на поверхности сосуда ориентирована в окружном направлении, x2 - в направлении образующей. На границах выделенного для расчета фрагмента приняты условия симметрии вектора перемещений.
На расчетный фрагмент была нанесена неравномерная разностная сетка с числом делений в направлении координаты x1, равным 18, в направлении x2, равным 42. При этом фрагмент в окружном направлении разбивался на 2 участка, в продольном - на 4 участка, на которые накладывалась сетка различной густоты. На участке, включающем опору, использовалась разностная сетка с ячейками длиной 7,8 см и шириной 0,1396 рад. Дальнейшее сгущение разностной сетки не приводило к повышению точности результатов расчета.
В результате анализа напряженно-деформированного состояния сосуда вначале было получено распределение реакций по поверхности взаимодействия седловины с сосудом для случая гидравлического испытания (т.е. при заполнении посуда водой). Значение радиального давления в надире на линии симметрии профиля седловины хорошо согласуется с приведенным в работе [22] и оказывается на 13 ¸ 20 % выше, чем полученное в предположении равномерного распределения контактного давления по поверхности взаимодействия седловины и сосуда.
На рис. 1, б показаны графики распределения окружного мембранного усилия T11 (сплошные линии) по центру профиля седловины при различной жесткости опоры. Приведенные значения усилия T(11) можно сравнить с аналогичными величинами усилий, полученными авторами работы [22] с применением программ «SHELL» (рис. 1, б, точки) и «BOSOR4» (рис. 1, б, штриховая кривая). Следует отметить, что «МЕКРИС-2» и «SHELL» прогнозируют несколько более высокие значения T(11) надире (» на 5 ¸ 15 %), чем соответствующие значения согласно «BOSOR4» при допущении о равномерном распределении контактного давления между сосудом и опорой. Согласно программам «МЕКРИС-2» и «SHELL» наибольшие T(11) находятся в надире, а при применении равномерно распределенного контактного давления согласно «BOSOR4» - в 0,8726 рад от надира.
Значения продольного мембранного усилия T(22) в надире по оси симметрии профиля седловины, полученные с помощью «МЕКРИС-2», также сжимающие, но меньше, чем T(11), в 3,1 ¸ 3,8 раз.
В таблице приведены значения нормальных напряжений на линии симметрии профиля седловины в надире и роге. Максимальные значения напряжений s(11), s(22) находятся в роге и отличаются от соответствующих значений в надире на 25 ¸ 45 %. Напряжения s(11) как в надире, так и в роге получены в 1,5 ¸ 3 раз больше s(22). С увеличением жесткости упругой прокладки значения нормальных напряжений уменьшаются.
|
k, кН/см3 |
Значения напряжений на линии симметрии профиля седловины, кН/см2 |
|||
|
в надире |
в роге |
|||
|
s(11) |
s(22) |
s(11) |
s(22) |
|
|
0,2 |
-8,689 |
-4,944 |
-11,43 |
-6,978 |
|
1 |
-8,395 |
-4,465 |
-11,14 |
-6,396 |
|
5 |
-7,590 |
-3,363 |
-10,590 |
-5,239 |
|
10 |
-6,592 |
-2,066 |
-9,649 |
-3,666 |
Предварительный анализ выпучивания сосуда в зоне опор выполнен в геометрически линейной постановке. Было применено распределение давления по радиальной поверхности взаимодействия сосуда с опорой, полученное при k = 1 кН/см3, что дало удельный вес выпучивания, равный 6,33. Это число означает, что выпучивание произойдет, если жидкость в сосуде окажется в 6,33 раз тяжелее воды. При этом было обнаружено, что форма выпучивания локализована вблизи опор как продольно, так и по окружности. Для вычисления критического удельного веса выпучивания на ЭВМ ВС-1060 потребовалось около 2 часов процессорного времени.
Определенную таким образом величину критического удельного веса можно сравнить с аналогичными значениями 4,25 и 5,78, полученными по программе «NASTRAN» [22] при использовании элементов длиной 20 см с 0,1745 рад по окружности. Первое значение критического удельного веса найдено для случая распределения давления по радиальной поверхности взаимодействия сосуда с опорой, прогнозируемого программой «SHELL», упомянутой выше, второе - при условии равномерного распределения давления по поверхности взаимодействия. Расход процессорного времени на ЭВМ VAX 782 при вычислениях по «NASTRAN» составил около 30 часов.
Расхождений между значениями критического удельного веса, полученными по «МЕКРИС-2» и «NASTRAN», вызвано, в основном, несоответствием принятых расчетных моделей, а также вследствие недостаточной точности сходимости решений по «NASTRAN». При анализе выпучивания по «МЕКРИС-2» рассматривается четверть сосуда, включая и фрагмент эллипсоидальной крышки, а при анализе по «NASTRAN» в качестве расчетной модели принят цилиндр бесконечной длины на симметрично расположенных седловинных опорах с расстоянием между ними, равным половине действительной длины сосуда.
При расчетах было принято, что вблизи седловины сосуд нагружен способом, допускающим нестесненные перемещения. Эти несколько нереальные граничные условия предполагают наличие прогибов, больших толщины оболочки. Однако в действительной конструкции перемещения стеснены вследствие сохранения с помощью седловин круглой формы, поэтому большие прогибы не возникают, и картина выпучивания ограничена.
Анализ устойчивости сосуда, выполненный в геометрически нелинейной постановке, позволил получить критический удельный вес выпучивания, равный 5,42, который на 14 % меньше результата линейного расчета. Однако и это значение критического удельного веса свидетельствует, что определяющим критерием несущей способности для рассмотренного сосуда является развитие пластических деформаций.
В результате решения геометрически и физически нелинейной задачи определено значение предельного удельного веса жидкости, равное gпр = 2,58 × gв, где gв - удельный вес воды. Полученная зависимость относительного удельного веса жидкости от относительного прогиба в надире на линии симметрии профиля седловины представлена на рис. 2, а штриховой кривой. Штрихпунктирная линия соответствует линейному упругому решению, сплошная - упругому нелинейному деформированию. Для построения кривой нагружения упруго-пластического деформирования сосуда потребовалось около 3 часов процессорного времени на ЭВМ ЕС-1060.
На рис. 2 приведены эпюры мембранных усилий T(11), T(22) и изгибающих моментов M(11), M(22) в наиболее напряженном поперечном сечении, принадлежащем плоскости симметрии профиля седловины, при значении gпр. Здесь линии 1 соответствуют усилию T(11) и моменту M(11), линии 2 - усилию T(22) и моменту M(22).
Таким образом установлено, что несущая способность сосуда исчерпывается в результате развития пластических деформаций при значении удельного веса жидкости, значительно меньшем, чем полученном при упругом нелинейном решении. В упруго-пластической области работают небольшие участки поверхности сосуда, расположенные в зоне опор. За счет пластических деформаций в этих местах существенно возрастают прогибы оболочки.
Анализ несущей способности цилиндрического сосуда
а - графили зависимостей «нагрузка-прогиб»; б, в - характер распределения усилий T(11), T(22) и моментов M(11), M(22) по центру профиля седловины сосуда
2. Устойчивость составной тороидальной оболочки с ломаной образующей
В геометрически нелинейной постановке исследовано упругое деформирование и устойчивость при действии равномерного внешнего давления составной тороидальной оболочки (рис. 3, а), поверхность которой набрана из двух цилиндрических, четырех конических фрагментов и двух кольцевых пластин [12]. Оболочка в окружном направлении конструктивно разбита на 4 секции, соединенные фланцами.
Учитывая, что напряженно-деформированное состояние оболочки при действии равномерно распределенного давления обладает циклической симметрией и симметрией относительно плоскости центров поперечных сечений, для расчета была выделена четверть секции, ограниченной соединительными фланцами. Координата x1 на поверхности оболочки ориентирована в окружном направлении, x2 - в направлении меридиана от плоскости симметрии с внутренней стороны к плоскости симметрии с наружной стороны. На границах выделенного для расчета фрагмента приняты условия симметрии вектора перемещений.
При расчете были приняты следующие значения геометрических параметров (рис. 3, б): R1 = 1,25 м; R2 = 1,52 м; R3 = 1,92 м; R4 = 2,1 м; a = 1,0964 м; b = 1,72 м; c = 1,18 м; h = 1 см. Материал оболочки - сталь с модулем упругости E = 196 ГПа и коэффициентом Пуассона n = 0,3.
Фланцы, соединяющие секции оболочки, учитывались как односторонне расположенные с внешней стороны ребра толщиной bр = 3,3 см, высотой hр = 4 см и эксцентриситетом относительно срединной поверхности оболочки ср = 2,5 см.
Составная тороидальная оболочка с ломаной образующей
а - общий вид оболочки; б - расчетный фрагмент; в - характер распределения перемещения U3, усилий Т(11), Т(22) и моментов М(11), М(22) вдоль координатной линии х2; г - графики зависимостей «нагрузка-прогиб»
На выделенный для расчета фрагмент была нанесена разностная сетка с числом делений в окружном направлении x1 - MО = 8 и в направлении меридиана x2 - NО = 24. Величина критического давления при расчете с сеткой 8´24 получена в пределах 686 кПа < qкр < 784 кПа с числом волн формы потери устойчивости в окружном направлении внешней цилиндрической поверхности n/4 = 4 на одной секции, ограниченной соединяющими фланцами. При этом на одну волну функции прогиба в окружном направлении приходится 4 разностных интервала.
Для проверки сходимости вычислений был проведен расчет с разностной сеткой 12´24. При этом значение критического давления оказалось в пределах 688 кПа < qкр < 723 кПа. Картина послекритического формообразования характеризуется наличием на поверхности внешней цилиндрической части n/4 = 4 волн в окружном направлении на одной секции, что согласуется с результатами расчета при сетке 8´24 и свидетельствует о его достоверности.
На рис. 3, в представлены эпюры функции U3, внутренних нормальных усилий и изгибающих моментов вдоль меридиана посредине секции при величине внешнего давления 723 кПа. В напряженное состояние рассматриваемой оболочки вносят наибольший вклад окружные нормальные усилия, в распределении которых вдоль меридиана имеют место зоны краевого эффекта в окрестностях линий сопряжения составляющих поверхностей.
На рис. 3, г для двух характерных точек, одна из которых находится на кольцевой пластине и имеет сеточные координаты (1; 13) в области 12´24, другая - на внешней цилиндрической поверхности с сеточными координатами (6; 25), представлены графики зависимостей «нагрузка-прогиб». Несущая способность оболочки определена устойчивостью внешнего цилиндрического пояса. Оценку критического давления для этого фрагмента можно выполнить по формуле
![]()
полученной для шарнирно опертых по торцам цилиндрических оболочек [3]. При этом закритическое формообразование характеризуется числом волн
![]()
В формулах было принято Е = 196 ГПа, h = 0,01 м, L = a = 1,0964 м, R = R4 = 2,1 м.
По-видимому, повышение критической нагрузки рассматриваемой составной оболочки по сравнению с критической нагрузкой для шарнирно опертой цилиндрической оболочки обусловлено, главным образом, наличием ребер, которые препятствуют развитию послекритического формообразования с количеством волн n = 14, соответствующим минимальной критической нагрузке для шарнирно опертой цилиндрической оболочки при действии внешнего равномерного давления.
3. Несущая способность криволинейного участка трубопровода за пределом упругости
Наиболее нагруженными элементами в конструкциях трубопроводных систем, применяющихся в различных отраслях, являются кривые трубы, используемые в местах излома осей трубопроводов и при создании компенсаторов температурных деформаций, так как в них обычно возникают максимальные изгибающие моменты. В качестве сопрягающих элементов пересекающихся цилиндрических труб традиционно используются секторы тороидальных оболочек, обеспечивающие снижение жесткости узла сопряжения и его гидравлического сопротивления. Анализ напряженно-деформированного состояния трубопроводов показывает, что пластические деформации начинают развиваться прежде всего в сопрягающих элементах кривых труб. Для практики важно знать не только напряженно-деформированное состояние криволинейного участка трубопровода, но и при каких значениях нагрузки исчерпывается его несущая способность.
Несущая способность криволинейного участка трубопровода
а - график зависимости нагрузки P от сближения торцов оболочки A; б, в - характер распределения усилия T(22) и момента M() в наиболее напряженном поперечном сечении участка
Для исследования был выбран криволинейный участок трубопровода, представляющий собой сложную оболочку, состоящую из пересекающихся под прямым углом цилиндрических элементов, сопряженных сектором тороидальной оболочки (рис. 4, а). На концах криволинейного участка трубопровода приложены системы сил, главные векторы которых (Р) проходят через центры краевых сечений и взаимно уравновешиваются друг другом. Материал тороидального и цилиндрических элементов - сталь с модулем упругости E = 208 ГПа, коэффициентом Пуассона n = 0,3 и диаграммой деформирования без упрочнения при текучести sт = 240 МПа и интенсивности деформаций текучести xiт = 10-3. Толщина цилиндрических элементов hц = 6,22´10-3 м, тороидального элемента hт = 4,85´10-3 м. Длина цилиндрических элементов B = 0,96 м. Радиусы поперечных сечений тороидальной и цилиндрической секций rц = rт = 0,155 м. Радиус кривизны оси тороидального элемента R = 0,46 м.
Исходя из симметрии напряженно-деформированного состояния рассматриваемой составной оболочки, в качестве расчетного выбран фрагмент, ограниченный плоскостью оси трубы и плоскостью нормального поперечного сечения посредине тороидального участка. Система гауссовых криволинейных координат на поверхности расчетного фрагмента выбрана следующим образом: координата x1 направлена в окружном направлении от внешнего контура к внутреннему; координата x2 направлена вдоль трубы от наружного контура к контуру в плоскости симметрии. На границах фрагмента, принадлежащих плоскости симметрии, приняты условия симметрии вектора перемещений, на границах действия системы распределенных сил заданы внутренние усилия
![]()
![]()
Кроме того, для исключения подвижности расчетного фрагмента вдоль линии пересечения плоскостей симметрии наложена соответствующая связь на точку с нулевой гауссовой кривизной на контурной линии тороидального участка.
В результате решения геометрически и физически нелинейной задачи определена предельная нагрузка Pпр = 187 кН (см. рис. 4, а). Эта нагрузка определялась по зависимости нагрузки P от сближения торцов оболочки D и получена за 24 шага нагружения при разностной сетке 12´12. Сходимость упругих решений при различной густоте разностной сетки исследована в работе [13]. На рис. 4, б представлены эпюры внутреннего усилия T(22), а на рис. 4, в - эпюры внутреннего момента M(11) в наиболее напряженном поперечном сечении, принадлежащем плоскости симметрии, при значении нагрузки P = 150 кН. Здесь штриховыми линиями представлены эпюры, соответствующие упругому решению при различной густоте разностной сетки, а сплошными - упруго-пластическому деформированию трубы.
Анализ полученных результатов показывает, что для достижения сходимости численного решения достаточно наложения на рассчитываемый фрагмент оболочки разностной сетки 12´12. Точками на рис. 4, б обозначены результаты эксперимента [23], выполненного в упругой стадии деформирования, при нагрузке P = 150 кН. Установлено, что в упруго-пластической области работают небольшие участки поверхности оболочки, расположенные вдоль линий нулевой гауссовой кривизны. За счет пластических деформаций в этих местах существенно уменьшаются экстремальные значения изгибающих моментов, а прогибы оболочки возрастают в 1,8 раза по сравнению с упругим решением.
Литература
1. Баженов В.А., Гуляев В.И., Гоцуляк Е.А. и др. Методические рекомендации по применению метода криволинейных сеток и программ расчета на ЭВМ устойчивости оболочек сложной формы. - Киев: КИСИ. 1986. - 72 с.
2. Баженов В.А., Гуляев В.И., Гоцуляк Е.А. и др. Расчет на устойчивость оболочек сложной формы. - Киев: КИСИ, 1987. - 134 с.
3. Вольмир А.С. Устойчивость деформируемых систем. - М.: Наука, 1967. - 984 с.
4. Григолюк Э.И., Кабанов В.В. Устойчивость оболочек. - М.: Наука, 1978. - 360 с.
5. Гуляев В.И., Баженов В.А., Гоцуляк Е.А. Устойчивость нелинейных механических систем. - Львов: Вища школа, 1982. - 255 с.
6. Гоцуляк Е.А., Ермишев В.Н., Жадрасинов Н.Т. Сходимость метода криволинейных сеток в задачах теории оболочек//Сопротивление материалов и теория сооружений. - Киев, 1981. - Вып. 39. - С. 80 - 84.
7. Гоцуляк Е.А., Ермишев В.Н. Напряженно-деформированное состояние и устойчивость многоугольной тороидальной камеры//Сопротивление материалов и теория сооружений. - Киев, 1984. - Вып. 45. - С. 9 - 12.
8. Гоцуляк Е.А., Ермишев В.Н., Оглобля А.И., Мельниченко Г.И. Комплекс программ по расчету напряженно-деформированного состояния и устойчивости оболочек сложной формы (МЕКРИС-2). - Киев: КИСИ, 1986. - 410 с./Деп. в ГосФАП СССР 21.11.86 г., № 50870000816.
9. Гоцуляк Е.А., Пемсинг К. Об учете жестких смещений при решении задач теории оболочек методом конечных разностей//Численные методы решения задач строительной техники. - Киев, 1978. - С. 93 - 98.
10. Длугач М.И., Ковальчук Н.В. Метод конечных элементов в применении к расчету цилиндрических оболочек с прямоугольными отверстиями//Прикладная механика. - 1973. - Т. 9, вып. 11. - С. 35 - 41.
11. Длугач М.И., Ковальчук Н.В. Исследование напряженного состояния ребристых цилиндрических оболочек с прямоугольными отверстиями методом конечных элементов//Прикладная механика. - 1974. - Т. 10, вып. 10. - С. 22 - 30.
12. Ермишев В.Н., Малков А.А., Оглобля А.И. Устойчивость тороидальных оболочек сложной формы//Сопротивление материалов и теория сооружений. - Киев, 1987. - Вып. 50. - С. 22 - 25.
13. Ермишев В.Н. Исследование напряженно-деформированного состояния криволинейного участка трубопровода. - Киев: КИСИ, 1985. - 20 с/Рук. деп. в УкрНИИНТИ 2.10.85 г., № 2430-Ук85.
14. Ионов В.И., Огибалов П.М. Прочность пространственных конструкций. Ч. 1. Основы механики сплошной среды. - М.: Высшая школа, 1978. - 382 с.
15. Кантин Г., Клауф Р.В. Искривленный конечный элемент цилиндрической оболочки//Ракетная техника и космонавтика. - 1968. - № 6. - С. 82 - 87.
16. Корнишин М.С., Дедов Н.И., Столяров Н.Н. Изгиб и устойчивость при внешнем давлении гибких пластин и пологих оболочек в упругопластической области с учетом сжимаемости материала, разгрузки и цикличности нагружения: Теория оболочек и пластин. - Л.: Судостроение, 1975. - 394 с.
17. Королев В.И. Упруго-пластические деформации. - М.: Машиностроение, 1971. - 304 с.
18. Сахаров А.С., Соловей Н.А. Исследование устойчивости оболочек методом конечных элементов в задачах пластин и оболочек//Пространственные конструкции зданий и сооружений. - М.; Стройиздат, 1977. - Вып. 3. - С. 10 - 15.
19. Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. - М.: Наука, 1966. - 635 с.
20. Фондер Г.А., Клауф Р.В. Явное добавление смещений тела как жесткого целого в криволинейных конечных элементах//Ракетная техника и космонавтика. - 1973. - № 3. - С. 62 - 72.
21. Черных К.Ф. Линейная теория оболочек. В двух частях. - Л.: ЛГУ, 1962. - Ч. 1. - 274 с; - 1985. - Ч. 11. - 395 с.
22. Kendricks., Tooth A.S. The behaviors of a horizontal vessel on loose saddles - a buckling assessment of the support region//J. Strain Analysis. - 1986. - Vol. 21. - N.1. - P.P. 45 - 50.
23. Gross N., Ford H. The Flexibility of short-radius Pipe-bends//Proc. of Inst. Mech. Engs. Series B. - 1952 - 1953. Vol. 1. - P.P. 480 - 491.
РАЗРАБОТАНЫ: Киевским ордена Трудового Красного Знамени Инженерно-строительным институтом
РУКОВОДИТЕЛИ РАЗРАБОТКИ: В.А. Баженов, В.И. Гуляев, Е.А. Гоцуляк
ИСПОЛНИТЕЛИ: В.Н. Ермишев, Г.И. Мельниченко, А.И. Оглобля
ОДОБРЕНЫ научно-методической комиссией по стандартизации методов расчета и испытаний элементов машин и конструкций на устойчивость секции «Расчеты и испытания на прочность» НТС Госстандарта СССР
УТВЕРЖДЕНЫ к изданию Приказом ВНИИНМАШ № 65 от 14.03.1988 г.
СОДЕРЖАНИЕ
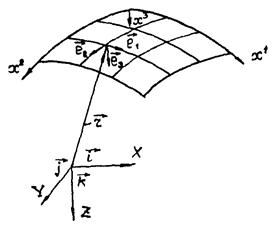
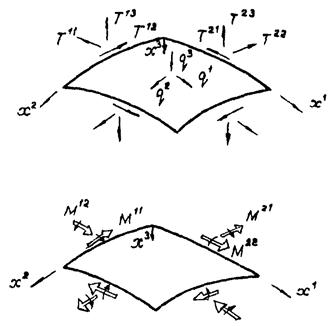
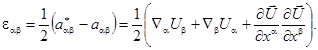 (
(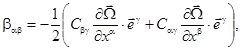 (
(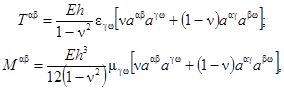 (
(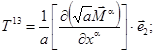
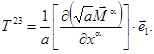 (
(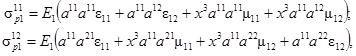 (
(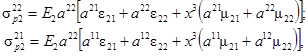 (
(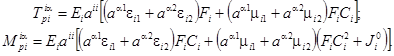 (
(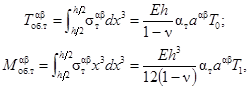 (
(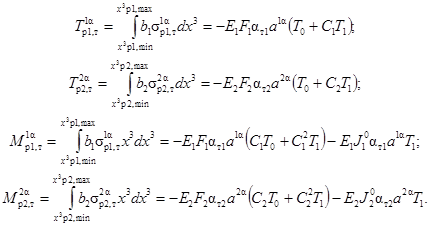 (
(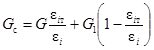 при
при 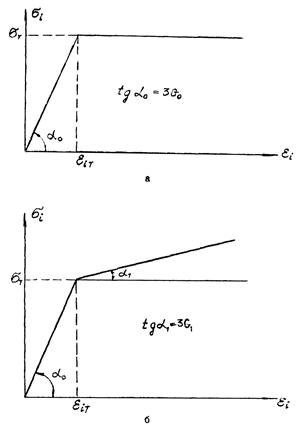
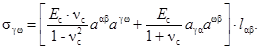 (
(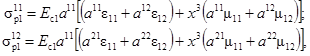 (
(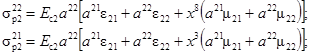 (
(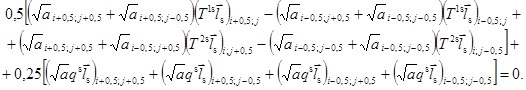 (
(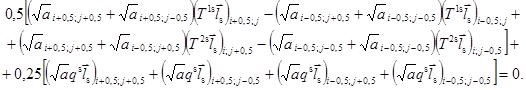 (
(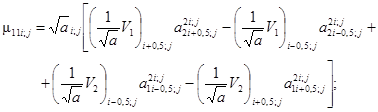 (
(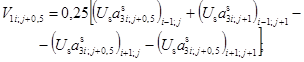 (
(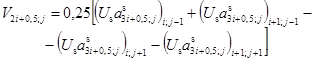 (
(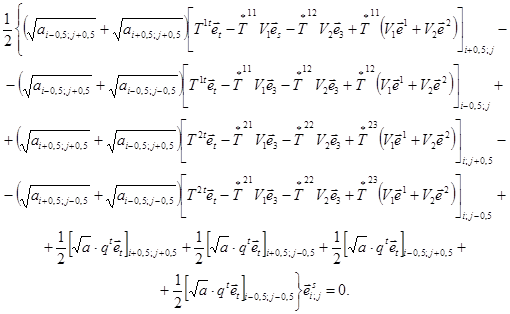 (
(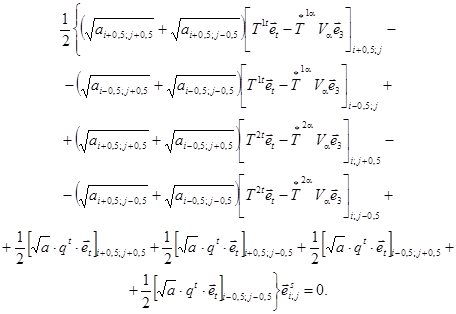 (
(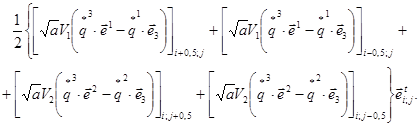 (
(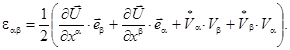 (
(