МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ЦЕПИ РАЗМЕРНЫЕ
ОСНОВНЫЕ ПОНЯТИЯ. МЕТОДЫ РАСЧЕТА
ЛИНЕЙНЫХ И УГЛОВЫХ ЦЕПЕЙ
РД 50-635-87
РУКОВОДЯЩИЙ ДОКУМЕНТ ПО СТАНДАРТИЗАЦИИ
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Цепи размерные Основные понятия Методы расчета линейных и угловых цепей |
РД 50-635-87 |
Дата введения 01.07.88
Настоящие методические указания распространяются на изделия машиностроения и приборостроения и являются методической основой при разработке межотраслевой и отраслевой нормативно-технической документации в области расчета размерных цепей.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
Размерные цепи отражают объективные размерные связи в конструкции машины, в технологических процессах изготовления ее деталей и сборки, при измерении.
Эти связи возникают в соответствии с условием и принятым решением конструкторской, технологической задачи или задача измерения.
Свойства и закономерности размерных цепей отражаются системой понятий и аналитическими зависимостями, позволяющими производить расчет номинальных размеров, допусков, координат середин полей допусков и обеспечивать наиболее экономичным путем точность изделий при конструировании, изготовлении, ремонте и во время эксплуатации.
Методические указания содержат:
термины и определения, раскрывающие сущность размерной цепи и ее структуру;
соотношения между элементами размерной цепи;
виды размерных цепей;
связи между размерными цепями;
методы достижения точности изделий при помощи размерных цепей;
методику построения размерных цепей;
методику расчета плоских размерных цепей;
примеры расчета размерных цепей.
2. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
2.1. Основные понятия
2.1.1. Размерная цепь - совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур.
Обозначение: прописная буква русского или строчная буква греческого (кроме букв α, δ, ξ, λ, ω) алфавитов без индексов.
Примеры.
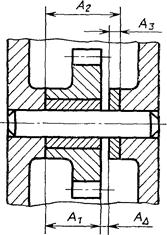
Задача: обеспечить совпадение оси заднего центра токарного станка с осью переднего центра в вертикальной плоскости.
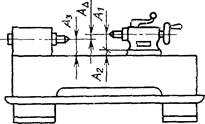
Размерная
цепь А, определяющая расстояние АD
между осями заднего и переднего центров
токарного станка в вертикальной плоскости
Черт. 1
Задача: получить в результате обработки требуемый размер радиуса валика.
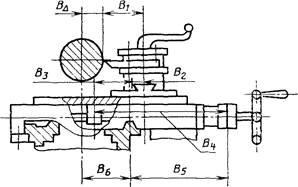
Размерная
цепь В, определяющая размер ВD
радиуса валика, изготовляемого на токарном станке.
Черт. 2
2.1.2. База - поверхность или выполняющее ту же функцию сочетание поверхностей, ось, точка, принадлежащая заготовке или изделию и используемая для базирования.
2.1.3. Звено размерной цепи - один из размеров, образующих размерную цепь.
Обозначение: прописная буква русского или строчная буква греческого (кроме букв α, δ, ξ, λ, ω) алфавитов с индексом. На схемах размерных цепей звенья условно обозначаются:
а) линейные размеры - двусторонней стрелкой
![]()
б) параллельность - односторонней стрелкой с направлением острия к базе
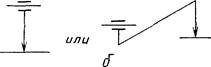
в) перпендикулярность - односторонней стрелкой с направлением острия к базе
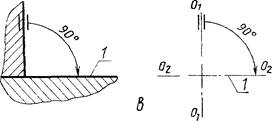
1 - база
Черт. 3
2.1.4. Схема размерной цепи - графическое изображение размерной цепи.
2.2. Звенья размерных цепей
2.2.1. Замыкающее звено - звено размерной цепи, являющееся исходным при постановке задачи или получающееся последним в результате ее решения.
Обозначение: прописная буква русского или строчная буква греческого (кроме букв α, δ, ξ, λ, ω) алфавитов с индексом D.
Примеры.
а) задача (конструкторская): исходя из служебного назначения механизма, установить номинальный размер и предельные отклонения зазора АD, обеспечивающие свободное вращение шестерни.
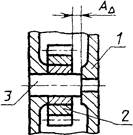
АD - замыкающее звено;
Черт. 4
б) задача (технологическая): в процессе изготовления деталей и сборки обеспечить получение заданной конструктором величины зазора АD.
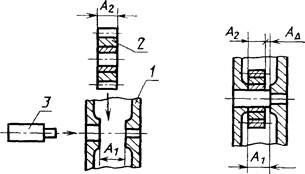
АD - замыкающее звено.
Черт. 5
2.2.2. Составляющее звено - звено размерной цепи, функционально связанное с замыкающим звеном.
Обозначение: прописная буква русского или строчная буква греческого (кроме букв α, δ, ξ, λ, ω) алфавитов с индексом, соответствующим порядковому номеру составляющего звена.
2.2.3. Увеличивающее звено - составляющее звено размерной цепи, с увеличением которого замыкающее звено увеличивается.
2.2.4. Уменьшающее звено - составляющее звено размерной цепи, с увеличением которого замыкающее звено уменьшается.
Пример.
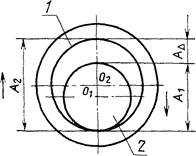
1 - втулка; 2
- вал: АD -зазор;
![]() -
уменьшающее звено;
-
уменьшающее звено; ![]() -
увеличивающее звено.
-
увеличивающее звено.
Черт. 6
2.2.5. Компенсирующее звено - составляющее звено размерной цепи, изменением значения которого достигается требуемая точность замыкающего звена.
Обозначается соответствующей буквой, заключенной в прямоугольник.
Пример.
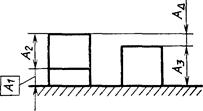
A1 - компенсирующее звено.
Черт. 7
2.2.6. Общее звено - звено, одновременно принадлежащее нескольким размерным цепям.
Обозначение формируется из обозначений звеньев размерных цепей, в которые входит данное звено со знаком равенства между ними.
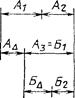
A3 = B1 - общее звено размерных цепей А и Б.
Черт. 8
2.3. Виды размерных цепей
2.3.1. Основная размерная цепь - размерная цепь, замыкающим звеном которой является размер, обеспечиваемый в соответствии с решением основной задачи.
2.3.2. Производная размерная цепь - размерная цепь, замыкающим звеном которой является одно из составляющих звеньев основной размерной цепи.
Пример.
Задача: обеспечить требуемую величину зазора (АD) между роликами 1 и 2.
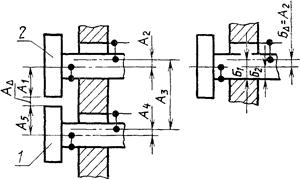
А - основная размерная цепь; Б - одна из производных
размерных цепей
(БD = А2, где А2 -
одно из звеньев основной размерной цепи).
Черт. 9
2.3.3. Конструкторская размерная цепь - размерная цепь, определяющая расстояние или относительный поворот между поверхностями или осями поверхностей деталей в изделии.
2.3.4. Технологическая размерная цепь - размерная цепь, обеспечивающая требуемое расстояние или относительный поворот между поверхностями изготавливаемого изделия при выполнении операции или ряда операций сборки, обработки, при настройке станка, при расчете межпереходных размеров.
Пример.
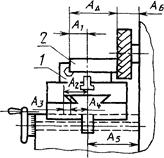
1 - приспособление; 2 - заготовка;
АD - размер, полученный в результате обработки.
Черт. 10
2.3.5. Измерительная размерная цепь - размерная цепь, возникающая при определении расстояния или относительного поворота между поверхностями, их осями или образующими поверхности изготавливаемого или изготовленного изделия.
2.3.6. Линейная размерная цепь - размерная цепь, звеньями которой являются линейные размеры.
2.3.7. Угловая размерная цепь - размерная цепь, звеньями которой являются угловые размеры.
Обозначение звена угловой размерной цепи: строчная буква греческого алфавита (кроме букв α, δ, ξ, λ, ω) с индексом, соответствующим порядковому номеру звена.
Пример.
Задача: обеспечить при сборке параллельность поверхности 1 по отношению к поверхности 2
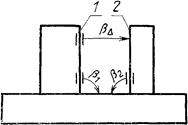
Угловая размерная цепь b, определяющая параллельность
поверхности 1 по отношению к поверхности 2.
Черт. 11
2.3.8. Плоская размерная цепь - размерная цепь, звенья которой расположены в одной или нескольких параллельных плоскостях.
2.3.9. Пространственная размерная цепь - размерная цепь, звенья которой расположены в непараллельных плоскостях.
2.3.10. Параллельно связанные размерные цепи - размерные цепи, имеющие одно или несколько общих звеньев.
Пример.
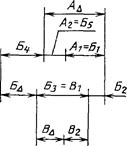
Черт. 12
2.3.11. Последовательно связанные размерные цепи - размерные цепи, из которых каждая последующая имеет одну общую базу с предыдущей.
Пример.
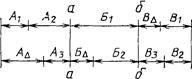
а - а, б - б - общие базы
Черт. 13
2.3.12. Размерные цепи с комбинированной связью - размерные цепи, между которыми имеются параллельные и последовательные связи.
Пример.
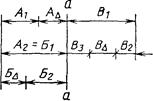
а - а - общие базы
Черт. 14
2.4. Размеры и отклонения
2.4.1. Номинальный размер - размер, относительно которого определяются предельные размеры и который служит также началом отсчета отклонений.
2.4.2. Истинный размер - размер, полученный в результате выполнения технологического процесса.
2.4.3. Измеренный размер - размер изделия, познанный в результате измерения.
Примечание. Если погрешность измерения для поставленной задачи такова, что измеренный размер может быть принят как истинный, то в соответствии с СТ СЭВ 145-75, этот измеренный размер называется действительным.
2.4.4. Предельные размеры - два предельно допустимых размера, между которыми должен находиться или которым может быть равен действительный размер.
2.4.5. Наибольший предельный размер - больший из двух предельных размеров.
2.4.6. Наименьший предельный размер - меньший из двух предельных размеров.
2.4.7. Отклонение - алгебраическая разность между размером и соответствующим номинальным размером.
2.4.8. Верхнее отклонение - алгебраическая разность между наибольшим предельным и номинальным размерами.
2.4.9. Нижнее отклонение - алгебраическая разность между наименьшим предельным и номинальным размерами.
2.4.10. Допуск - разность между наибольшим и наименьшим предельными размерами или абсолютная величина алгебраической разности между верхним и нижним отклонениями.
2.4.11. Поле допуска - поле, ограниченное верхним и нижним отклонениями или наибольшим и наименьшим предельными размерами. Для i-го звена
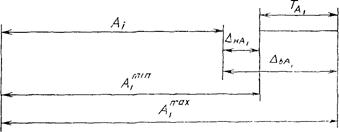
Черт 15
2.4.12. Координата середины поля допуска - координата, определяющая положение середины поля допуска относительно поминального размера
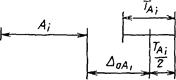
Черт. 16
2.4.13. Поле рассеяния - разность между наибольшим и наименьшим размерами в партии изделий

Черт. 17
2.4.14. Координата середины поля рассеяния - координата, определяющая положение середины поля рассеяния относительно номинального размера
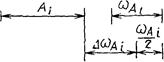
Черт. 18
2.4.15. Координата центра группирования - координата, определяющая положение центра группирования относительно поминального размера
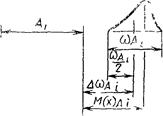
Черт. 19
2.4.16. Величина компенсации - наибольшее возможное отклонение, выходящее за пределы поля допуска замыкающего звена, подлежащее компенсации.
2.5. Расчетные коэффициенты
2.5.1. Относительное среднее квадратическое отклонение - коэффициент, характеризующий закон рассеяния размеров или их отклонений.
2.5.2. Коэффициент риска - коэффициент, характеризующий вероятность выхода отклонений замыкающего звена за пределы допуска.
2.5.3. Коэффициент относительной асимметрии - коэффициент, характеризующий асимметрию кривой рассеяния размеров.
2.5.4. Передаточное отношение составляющего звена - коэффициент, характеризующий степень влияния отклонения составляющего звена на отклонение замыкающего.
2.6. Методы достижения точности замыкающего звена
2.6.1. Метод полной взаимозаменяемости - метод, при котором требуемая точность замыкающего звена размерной цепи достигается во всех случаях ее реализации путем включения составляющих звеньев без выбора, подбора или изменения их значений.
2.6.2. Метод неполной взаимозаменяемости - метод, при котором требуемая точность замыкающего звена размерной цепи достигается с некоторым риском путем включения в нее составляющих звеньев без выбора, подбора или изменения их значений.
2.6.3. Метод групповой взаимозаменяемости - метод, при котором требуемая точность замыкающего звена размерной цепи достигается путем включения в размерную цепь составляющих звеньев, принадлежащих к соответственным группам, на которые они предварительно рассортированы.
2.6.4. Метод пригонки - метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением значения компенсирующего звена путем удаления с компенсатора определенного слоя материала.
2.6.5. Метод регулирования - метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением значения компенсирующего звена без удаления материала с компенсатора.
2.7. Задачи и способы расчета размерных цепей
2.7.1. Прямая задача - задача, при которой заданы параметры замыкающего звена (номинальное значение, допустимые отклонения и т.д.) и требуется определить параметры составляющих звеньев.
2.7.2. Обратная задача - задача, в которой известны параметры составляющих звеньев (допуски, поля рассеяния, координаты их середин и т.д.) и требуется определить параметры замыкающего звена.
2.7.3. Статическая задача - задача, решаемая без учета факторов, влияющих на изменение звеньев размерной цепи во времени.
2.7.4. Динамическая задача - задача, решаемая с учетом факторов, влияющих на изменение звеньев размерной цепи во времени.
2.7.5. Способ расчета на максимум-минимум - способ расчета, учитывающий только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания.
2.7.6. Вероятностный способ расчета - способ расчета, учитывающий рассеяние размеров и вероятность различных сочетаний отклонений составляющих звеньев размерной цепи.
3. ПОРЯДОК ПОСТРОЕНИЯ РАЗМЕРНЫХ ЦЕПЕЙ
3.1. Последовательность построения размерной цепи
В зависимости от решаемой задачи изображают схему изделия, технологической системы станок - приспособление - инструмент - деталь (СПИД), технологического процесса или измерения, на которую наносят размерную цепь или размерные цепи.
Допускается для каждой размерной цепи изображать отдельную схему.
Первым находят замыкающее звено. Далее, начиная от одной из поверхностей (осей), ограничивающих замыкающее звено, находят составляющие звенья размерной цепи, непосредственно участвующие в решении поставленной задачи, и доходят до второй поверхности (оси), ограничивающей замыкающее звено.
3.2. Нахождение замыкающего звена, его допуска и координаты середины поля допуска
Замыкающее звено размерной цепи находят, исходя из задачи, возникающей при конструировании изделия, его изготовлении или измерениях.
Поэтому вначале должна быть поставлена и четко сформулирована задача, решение которой необходимо для обеспечения соответствия конструкции изделия его служебному назначению, обеспечения требуемой точности изделия при изготовлении или оценке его точности измерением.
При конструировании изделия переход от формулировки задачи к нахождению замыкающего звена заключается в выявлении такого линейного или углового размера, от значения которого полностью зависит решение конструкторской задачи.
При изготовлении изделия замыкающим звеном размерной цепи является размер, точность которого должна быть обеспечена технологическим процессом.
При измерении замыкающим звеном является измеренный размер.
Таким образом, в замыкающем звене заключен смысл решаемой задачи, из чего следует, что каждая размерная цепь дает решение только одной задачи и может иметь одно замыкающее звено.
Допуск замыкающего звена устанавливается:
в конструкторских размерных цепях, исходя из служебного назначения изделия или его механизма;
в технологических размерных цепях в соответствии с допуском на расстояние или относительный поворот поверхностей детали (их осей) или деталей изделия, которые необходимо получать в результате осуществления технологического процесса изготовления детали или сборки изделия;
в измерительных размерных цепях, исходя из требуемой точности измерения.
Задача: обеспечить плавное (без заеданий) передвижение золотника (черт. 20).
Черт. 20
Легкость хода золотника зависит от величины зазора между золотником и отверстием в корпусе. Поэтому замыкающим звеном размерной цепи, с помощью которой решается эта задача, является зазор АD между золотником и корпусом.
Наименьшее предельное значение ![]() должно быть установлено, исходя из
условия перемещения золотника в корпусе без заеданий и обеспечения минимального
слоя смазки, и наибольшее предельное значение зазора
должно быть установлено, исходя из
условия перемещения золотника в корпусе без заеданий и обеспечения минимального
слоя смазки, и наибольшее предельное значение зазора ![]() , исходя из нормы
допустимой утечки масла в золотниковом устройстве, устанавливаемой в
соответствии с его служебным назначением.
, исходя из нормы
допустимой утечки масла в золотниковом устройстве, устанавливаемой в
соответствии с его служебным назначением.
Пример 2.
Задача: обеспечить совмещение каналов в крышке и корпусе золотникового устройства (черт. 20).
Совмещение каналов в корпусе золотника и крышке означает совпадение их осей. Поэтому замыкающим звеном размерной цепи, при помощи которой может быть решена эта задача, будет являться относительное смещение Б осей каналов. Допуск замыкающего звена БD должен быть установлен, исходя из допустимого сокращения расхода масла, проходящего через канал в единицу времени в связи с увеличением сопротивления в гидравлической цепи из-за уменьшения площади сечения канала в стыке корпуса и крышки.
Пример 3.
Задача: обеспечить присоединение крышки золотника к корпусу винтами 1 и 2 (черт. 20).
Если размеры винтов и отверстий в крышке и корпусе установлены правильно, то одним винтом, например, винтом 1, крышку всегда можно присоединить к корпусу. Присоединение крышки винтом 2 возможно лишь при том условии, если относительное смещение осей крепежных отверстий в крышке и корпусе не будет превышать половины зазора между винтом и отверстием в крышке. Поэтому замыкающим звеном В размерной цепи, при помощи которой обеспечивается присоединение крышки винтами 1 и 2, будет являться относительное смещение осей крепежных отверстий в крышке и корпусе.
При установлении допуска на замыкающее звено следует исходить из самого неблагоприятного случая и установить допуск, равный наименьшему предельному зазору между винтом и отверстием в крышке.
Пример 4.
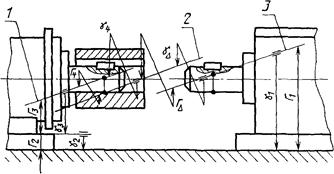
Задача: обеспечить вхождение вала К редуктора в муфту М, установленную на валу электродвигателя (черт. 21).
Черт. 21
Вхождение вала редуктора в муфту возможно, если несовпадение оси вала с осью отверстия в муфте не будет превышать зазора между ними. Так как причиной несовпадения осей является относительное смещение и поворот вала и отверстия муфты в пространстве, то в каждой из двух координатных плоскостей необходимо учесть их в виде самостоятельных замыкающих звеньев.
Например, в вертикальной плоскости (черт. 21) ими будут ГD и gD.
Прежде чем установить допуски на исходные звенья ГD и gD необходимо выявить границы допустимого зазора между валом и отверстием в муфте. Наибольший предельный зазор Smax должен быть назначен с учетом эксплуатационных требований к муфте. Наименьший предельный зазор Smin лимитируется не только условиями эксплуатации, но и трудностями изготовления деталей редуктора, двигателя, муфты и их монтажа.
Так как ![]() и
и ![]() должны быть установлены,
исходя из значения Smin, при котором
создаются самые неблагоприятные условия сборки, то сборщики изделия
заинтересованы в наибольшем приближении Smin
к Smax. Но приближение Smin к Smax сокращает допуск на зазор, а,
следовательно, допуски на диаметры валов и отверстия в муфте, и усложняет
изготовление деталей.
должны быть установлены,
исходя из значения Smin, при котором
создаются самые неблагоприятные условия сборки, то сборщики изделия
заинтересованы в наибольшем приближении Smin
к Smax. Но приближение Smin к Smax сокращает допуск на зазор, а,
следовательно, допуски на диаметры валов и отверстия в муфте, и усложняет
изготовление деталей.
Выбор значения Smin должен быть сделан с учетом сложности изготовления изделия в целом.
Переход от Smin к ![]() и
и ![]() следует произвести по схеме,
приведенной на черт. 22.
следует произвести по схеме,
приведенной на черт. 22.
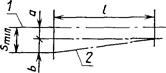
1 - ось отверстия в муфте; 2 - ось вала редуктора
Черт. 22
На схеме l - длина участка поверхности вала, на которой вал сопрягается с муфтой, а - смещение оси вала редуктора 2 относительно оси отверстия в муфте 1, b - смещение конца вала из-за поворота его относительно оси. Так как значением Smin необходимо ограничить смещение и поворот вала редуктора в пространстве, то для ограничения их только в одной координатной плоскости можно использовать лишь часть зазора. Если считать, что смещение и повороты вала в каждой из координатных плоскостей равновероятны, то
![]()
Отсюда
![]()
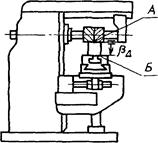
Задача: необходимо обеспечить при обработке заготовки параллельность поверхности А детали поверхности Б, которой она устанавливается на стол универсально-фрезерного станка (черт. 23).
Замыкающим звеном размерной цепи, при помощи которой решается эта задача, является относительный поворот bD поверхностей обрабатываемой детали.
Допуск замыкающего звена ![]() должен быть задан равным допуску на
относительный поворот поверхностей А к Б детали, установленному
чертежом.
должен быть задан равным допуску на
относительный поворот поверхностей А к Б детали, установленному
чертежом.
Черт. 23
3.3. Выявление составляющих звеньев размерной цепи
Выявив замыкающее звено, можно приступить к нахождению составляющих звеньев размерной цепи.
Составляющими звеньями конструкторских размерных цепей могут быть:
расстояния (относительные повороты) между поверхностями (их осями) деталей, образующих замыкающее звено, и основными базами (ГОСТ 21495-76) этих деталей;
расстояния (относительные повороты) между поверхностями вспомогательных (ГОСТ 21495-76) и основных баз деталей, непосредственно участвующих в решении поставленной задачи своп-ми размерами.
Руководствуясь этим положением, для нахождения размерной цепи следует идти от поверхностей (их осей) деталей, образующих замыкающее звено, к основным базам этих деталей, от них - к основным базам деталей, базирующих первые детали, вплоть до образования замкнутого контура. Несовпадения (зазоры, несоосности) основных и вспомогательных баз соединяемых деталей, если они возможны, учитываются отдельными звеньями.
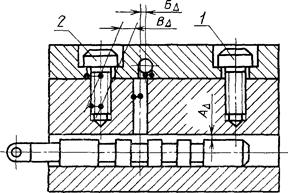
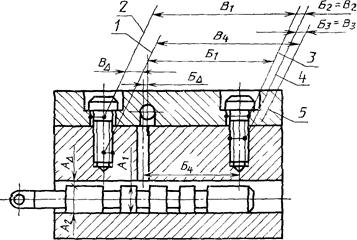
Для пояснения изложенного на черт. 24 дано схематическое изображение машины, у которой требуется обеспечить положение поверхности Б относительно поверхности А.
Черт. 24
Буквами О и В указаны соответственно основные и вспомогательные базы деталей.
В соответствии со сделанными рекомендациями построены размерные цепи Д и b, определяющие положение поверхностей А и Б.
На черт. 25 и 26 представлены размерные цепи, с помощью которых решаются задачи, рассмотренные в примерах 1 - 4, построенные по тем же правилам.
1 - ось резьбового отверстия; 2 - ось отверстия в
крышке; 3 - ось отверстия в крышке,
4 - ось винта; 5 - ось отверстия в корпусе золотника
Черт. 25
1 - ось вала двигателя; 2 - ось отверстия муфты; 3 - ось вала редуктора.
Черт. 26
По тем же правилам производится и выявление составляющих звеньев технологических размерных цепей системы СПИД и измерительных цепей (черт. 27, на котором представлена размерная цепь, относящаяся к примеру 5).
Черт. 27
Выявление технологических размерных цепей, отображающих связь операций при получении размера детали, рекомендуется начинать с последней операции, на которой получается выдерживаемый размер.
При этом могут иметь место два варианта:
а) задача обеспечения точности размера решается в пределах последней операции (в тех случаях, когда в качестве одной из технологических баз используется поверхность, от которой задан размер). В этом случае точность выдерживаемого размера достигается с помощью размерной цепи системы СПИД этой операции;
б) выдерживаемый размер будет являться замыкающим звеном трехзвенной размерной цепи, в которой одним из составляющих звеньев является расстояние (поворот) между конечным положением режущего инструмента и технологической базой детали, а другим составляющим звеном - размер, полученный на одной из предшествующих операций.
Рассматривая последний как замыкающее звено размерной цепи, возникающей на предшествующей операции, можно встретить вариант а или б. Развитие размерных связей завершается операцией, на которой размер получается как замыкающее звено размерной цепи системы СПИД.
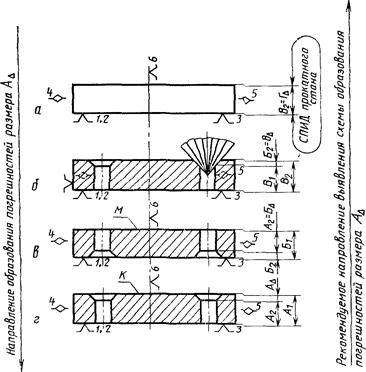
Пример 6.
Задача: выявить схему образования глубины зенковок в отверстиях пластины, обрабатываемой по следующему маршруту:
вырубка заготовки из листа (черт. 28, а);
сверление отверстий и обработка зенковок (черт. 28, б);
закалка;
шлифование поверхности М (черт. 28, в);
шлифование поверхности К (черт. 28, г).
Следуя от конечной операции, окончательно определяющей глубину зенковок, к началу технологического процесса, выявим размерные цепи, раскрывающие схему образования глубины зенковок в спроектированном (действующем) технологическом процессе.
При шлифовании на последней операции поверхности К при избранной схеме базирования заготовки будет выдерживаться размер А1 от технологической базы. Поэтому необходимая глубина зенковки будет получаться как замыкающее звено АD размерной цепи, в которой вторым составляющим звеном А2 будет размер, полученный на предшествующей операции.
Рассматривая предшествующую операцию и размер А2 как замыкающее звено БD, вновь обнаруживаем трехзвенную размерную цепь, в которой звено Б1 - размер, выдерживаемый от технологической базы, а Б2 - размер, полученный при обработке зенковки.
При обработке зенковки при избранной схеме базирования на настроенном станке выдерживается размер В1, а Б2 получается как замыкающее звено ВD размерной цепи, в которой В2 - толщина заготовки, т. е. листа, получаемого на прокатном стане, В2 = ГD - есть замыкающее звено размерной цепи системы СПИД прокатного стана.
Черт. 28
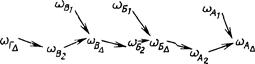
При таком построении технологического процесса поле рассеяния глубины зенковок в партии деталей образуется по следующей схеме:
4. РАСЧЕТ РАЗМЕРНЫХ ЦЕПЕЙ
В данном разделе рассматриваются методы расчета плоских размерных цепей с постоянными передаточными отношениями с использованием различных методов достижения точности.
4.1. Основные расчетные формулы
Номинальный размер замыкающего звена размерной цепи А вычисляют по формуле
где i = 1, 2, ... , m - порядковый номер звена;
![]() -
передаточное отношение i-го звена размерной
цепи.
-
передаточное отношение i-го звена размерной
цепи.
Примечание. В зависимости от вида размерной цепи передаточное отношение может иметь различное содержание и значение. Например, для линейных цепей с параллельными звеньями передаточные отношения равны:
ξi = 1 - для увеличивающих составляющих звеньев;
ξi = -1 - для уменьшающих составляющих звеньев.
Для звеньев, повернутых относительно координатных осей, роль передаточных отношений выполняют тригонометрические функции, используемые при проектировании составляющих звеньев на соответствующие координатные оси.
Таким образом, содержание передаточного отношения и его величину следует определять в соответствии с характером решаемой задачи и особенностями размерной цепи и ее составляющих звеньев.
Координату середины поля допуска ![]() замыкающего звена вычисляют по формуле:
замыкающего звена вычисляют по формуле:
где
![]()
![]()
Допуск замыкающего звена ТD вычисляют по формулам: при расчете по способу максимума-минимума:
где
![]()
![]()
при расчете по вероятностному способу:
Коэффициент риска tD выбирается из таблиц значений функции Лапласа Ф(t) в зависимости от принятого процента риска Р.
При нормальном законе распределения отклонений и равновероятном их выходе за обе границы поля допуска значение Р связано со значением Ф(t) формулой
![]()
Ряд значений коэффициента tD приведен в табл. 1.
|
Риск Р, % |
32 |
23 |
16 |
9 |
4,6 |
2,1 |
0,94 |
0,51 |
0,27 |
0,1 |
|
Коэффициент tD |
1 |
1,2 |
1,4 |
1,7 |
2 |
2,3 |
2,6 |
2,8 |
3 |
3,3 |
При нормальном законе распределения отклонений (законе
Гаусса) коэффициент ![]() .
.
При распределении отклонений по закону треугольника (закону Симпсона) ![]() .
.
При распределении отклонений по закону равной вероятности ![]() .
.
Среднее значение Tср допуска составляющих звеньев вычисляют по следующим формулам:
при расчете по способу максимума-минимума
при вероятностном способе расчета
_______________________________
* На основе аналитических расчетов, экспериментальных исследований, опыта и т. д.
Предельные отклонения i-го звена ![]() и
и ![]() вычисляют
по формулам:
вычисляют
по формулам:
Координату середины поля рассеяния замыкающего звена вычисляют по формуле:
Координату центра группирования отклонений замыкающего звена М(х)D вычисляют по формуле
Коэффициент относительной асимметрии i-го звена αi вычисляют по формуле
Поле рассеяния замыкающего звена ωD вычисляют по следующим формулам:
при расчете по способу максимума-минимума:
при вероятностном способе расчета
Относительное среднее квадратическое отклонение
где si - среднее квадратическое отклонение.
Наибольшую возможную компенсацию δк рассчитывают по формуле
Величина поправки Dк определяется по формуле:
Число ступеней неподвижных компенсаторов N рассчитывают по формуле
где Ткомп - допуск на изготовление неподвижного компенсатора.
Примеры постановки задачи, нахождения замыкающего звена и его допуска, выявления размерной цепи и расчетов допусков и предельных отклонений рассмотрены в п. 4.2.
4.2. Последовательность расчетов
Последовательность расчетов размерных цепей приведена в табл. 2.
|
Наименование этапа |
Номер формулы |
|
ПРЯМАЯ ЗАДАЧА |
|
|
1. Формулируется задача и устанавливается замыкающее звено |
- |
|
2. Исходя из поставленной задачи,
устанавливают* номинальный размер, координату середины поля допуска |
- |
|
3. Выявляют составляющие звенья и строят схему размерной цепи, составляют ее уравнение и определяют передаточные отношения |
- |
|
4. Рассчитывают номинальные размеры всех составляющих звеньев |
(1) |
|
5. Выбирают метод достижения требуемой точности замыкающего звена, экономичный в данных производственных условиях, с учетом средней величины допуска |
|
|
6. Рассчитывают и устанавливают допуски, координаты середин полей допусков и предельные отклонения: |
|
|
а) при методе полной взаимозаменяемости: |
|
|
на основе технико-экономических соображений устанавливают допуск на размер каждого из составляющих звеньев; |
|
|
проверяют правильность установленных допусков; |
(3) |
|
устанавливают координаты середин полей допусков составляющих звеньев, за исключением одного, для которого координата середины поля допуска рассчитывается решением уравнения с одним неизвестным; |
(2) |
|
рассчитывают верхнее и нижнее предельные отклонения; |
|
|
б) при методе неполной взаимозаменяемости: |
|
|
из экономических соображений принимают допустимый процент риска; |
|
|
выбирают предполагаемые законы распределения каждого из звеньев, исходя из особенностей технологического процесса изготовления деталей, и соответствующие им относительные средние квадратические отклонения; |
|
|
на основе технико-экономических соображений устанавливают допуск на размер каждого составляющего звена; |
|
|
проверяют правильность установленных допусков; |
(4) |
|
устанавливают координаты середин полей допусков для (m - 2) составляющих звеньев, недостающую координату определяют расчетом; |
(2) |
|
рассчитывают предельные отклонения; |
|
|
в) при методе групповой взаимозаменяемости: |
|
|
по технико-экономическим соображениям
устанавливают «производственный» допуск |
|
|
|
|
|
где n - число групп, на которые будут рассортированы составляющие звенья; |
|
|
рассчитывают производственные допуски |
|
|
|
(3) |
|
рассчитывают координаты середин полей допусков составляющих звеньев в каждой из групп; |
(2) |
|
на повороты и отклонения формы поверхностей деталей допуски устанавливают как при методе полной взаимозаменяемости; |
|
|
г) при методе пригонки: |
|
|
выбирают компенсирующее звено; |
|
|
устанавливают экономичные в данных производственных условиях допуски на размеры всех составляющих звеньев и координаты середин полей допусков; |
|
|
определяют производственный допуск |
(3) |
|
рассчитывают наибольшую возможную компенсацию δк; |
(15) |
|
рассчитывают величину поправки Δк; |
(16) |
|
вносят поправку в координату середины поля допуска компенсирующего звена; |
|
|
д) при методе регулирования: |
|
|
выбирают компенсирующее звено, которое конструктивно может быть оформлено в виде неподвижного или подвижного компенсатора; |
|
|
при использовании неподвижного компенсатора; |
|
|
устанавливают допуски на размеры всех
составляющих звеньев, экономически приемлемые в данных производственных
условиях и определяют «производственный» допуск |
|
|
рассчитывают наибольшую возможную компенсацию δк; |
(15) |
|
рассчитывают число ступеней неподвижных компенсаторов; |
(17) |
|
рассчитывают координаты середин полей допусков; |
|
|
рассчитывают размеры неподвижных компенсаторов; |
|
|
рассчитывают количество неподвижных компенсаторов каждой ступени |
|
|
ОБРАТНАЯ ЗАДАЧА |
|
|
1. Ставится и четко формулируется задача |
|
|
2. Рассчитывают номинальное значение размера замыкающего звена |
(1) |
|
3. Рассчитывают: |
|
|
а) при теоретических расчетах: |
|
|
координату середины поля допуска замыкающего звена; |
(2) |
|
величину поля допуска замыкающего звена и его предельные отклонения; |
|
|
при расчетах на основе теории вероятностей рассчитывают возможный риск выхода размера замыкающего звена за пределы заданного допуска; |
|
|
б) при расчетах, исходя из фактических данных, определяют поля рассеяния, координаты их середин (центров группирования) и, если необходимо, строят кривые рассеяния всех составляющих звеньев; |
|
|
определяют относительные средние квадратические отклонения и коэффициенты асимметрии кривой рассеяния каждого из составляющих звеньев; |
|
|
рассчитывают поле рассеяния замыкающего звена; |
|
|
рассчитывают возможное значение координаты середины поля рассеяния замыкающего звена; |
(9) |
|
в случае необходимости рассчитывают координату центра группирования размеров замыкающего звена; |
(10) |
|
при необходимости рассчитывают возможный выход отклонений замыкающего звена за пределы его поля допуска |
|
|
* На основе аналитических расчетов, экспериментальных исследований. |
|
4.3. Примеры расчетов допусков (прямая задача)
Пример 1.
Задача: обеспечить требуемый зазор между торцами зубчатого колеса и проставочного кольца механизма (черт. 29).
Черт. 29
Замыкающим звеном является размер АΔ, связывающий торцы зубчатого колеса и проставочного кольца. Из служебного назначения механизма следует, что минимальный зазор должен быть равен 0, а максимальный - 0,2 мм. Следовательно, поле допуска на зазор будет равно:
![]()
а координата середины поля допуска:
![]()
Уравнение размерной цепи, определяющей величину зазора, согласно черт. 29.
![]()
Задача решается пятью методами достижения требуемой точности замыкающего звена с целью их сопоставления.
1. Метод полной взаимозаменяемости
При этом методе должно быть соблюдено условие ![]() в линейной размерной
цепи
в линейной размерной
цепи ![]() .
.
Учитывая степень сложности достижения требуемой точности составляющих
звеньев, устанавливаем подбором: ![]()
![]()
![]()
Принимаем координаты середин полей допусков ![]()
![]()
Координату середины поля допуска третьего звена находим из уравнения:
![]()
![]()
Следовательно, ![]()
Правильность назначения допусков проверяем по формулам (7),
(8) настоящего пособия, представив значения ![]() и
и ![]() соответственно
через
соответственно
через ![]() и
и
![]() ,
установленные при расчете допусков:
,
установленные при расчете допусков:
![]()
![]()
Сопоставление с условиями задачи показывает, что допуски установлены верно.
2. Метод неполной взаимозаменяемости
Задаем значения коэффициента риска tΔ
и относительного среднего квадратического отклонения ![]() .
.
Допустим, что в данном случае риск Р = 1 %, при котором tΔ = 2,57, экономически оправдан.
Полагая, что условия изготовления деталей таковы, что распределение
отклонений размеров будет близким к закону Гаусса, принимаем: ![]() .
.
Учитывая трудности достижения требуемой точности каждого составляющего
звена, устанавливаем подбором следующие величины полей допусков: ![]()
![]()
![]()
Правильность подбора допусков можно проверить по формуле (4):
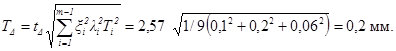
Устанавливаем следующие координаты середин полей допусков: ![]()
Значение ![]() находим из уравнения:
находим из уравнения:
![]()
![]()
Правильность установленных допусков может быть проверена по формулам:
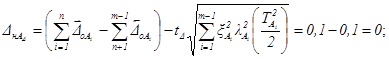
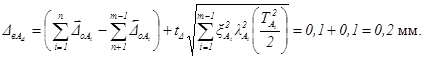
Предельные отклонения размеров составляющих звеньев: ![]() .
.
3. Метод групповой взаимозаменяемости
При решении задачи методом групповой взаимозаменяемости, прежде всего необходимо установить число групп, на которые должны быть рассортированы детали после изготовления, и значение производственного допуска замыкающего звена.
Допустим, что расширение ![]() в три раза в данном случае является
экономически обоснованным, в связи с чем число групп n
равно 3.
в три раза в данном случае является
экономически обоснованным, в связи с чем число групп n
равно 3.
Таким образом, ![]()
При расчете допусков должно быть соблюдено условие
![]()
где ![]() и
и ![]() - допуски
увеличивающих и уменьшающих звеньев. Согласно этому условию
- допуски
увеличивающих и уменьшающих звеньев. Согласно этому условию
![]()
Отсюда
![]()
и
![]()
Сообразуясь со степенью сложности изготовления деталей, установим ![]() и
и ![]() .
Устанавливаем поля допусков и координаты их середин для деталей каждой группы (табл. 3).
.
Устанавливаем поля допусков и координаты их середин для деталей каждой группы (табл. 3).
При назначении координат середин полей допусков уравнение
должно быть следующего вида ![]()
|
Группа |
|
|
|
|
|
|
|
|
|
I |
0,08 |
-0,04 |
0,1 |
+0,05 |
0,02 |
-0,01 |
0,2 |
+0,1 |
|
II |
0,08 |
+0,04 |
0,1 |
+0,15 |
0,02 |
+0,01 |
0,2 |
+0,1 |
|
III |
0,08 |
+0,12 |
0,1 |
+0,25 |
0,02 |
+0,03 |
0,2 |
+0,1 |
Две последние колонки табл. 3 показывают, что при соединении деталей в каждой из групп требуемые пределы зазора будут обеспечены.
Предельные отклонения размеров составляющих звеньев приведены в табл. 4.
|
Группа |
А1 |
А2 |
А3 |
|
I |
-0,08 |
+0,1 |
-0,02 |
|
II |
+0,08 |
+0,2 |
+0,02 |
|
+0,1 |
|||
|
III |
+0,16 |
+0,3 |
+0,04 |
|
+0,08 |
+0,2 |
+0,02 |
4. Метод пригонки
Для достижения требуемой точности зазора методом пригонки выберем в качестве компенсирующего звена размер А3 проставочного кольца, изменение которого проще всего осуществить.
Установим на составляющие звенья экономически целесообразные значения полей допусков и координаты их середин (табл. 5).
|
Звено |
|
|
|
А1 |
0,3 |
-0,15 |
|
А2 |
0,4 |
+0,2 |
|
А3 |
0,1 |
+0,25 |
Тогда производственный допуск замыкающего звена расширится до значения:
![]()
Наибольшая величина компенсации может быть равной
![]()
Для того, чтобы создать на звене A3 необходимый для пригонки слой материала, в координату середины поля допуска этого звена следует ввести поправку Dк
![]()
Поэтому следует установить
![]()
Предельные отклонения размеров составляющих звеньев:
![]()
5. Метод регулирования с применением неподвижного компенсатора
Выберем в качестве компенсатора то же звено, что было взято при решении
задачи по методу пригонки, и установим следующие допуски ![]() : 0,2 - для звена А1;
0,4 - для звена А2; 0,05 - для звена А3.
: 0,2 - для звена А1;
0,4 - для звена А2; 0,05 - для звена А3.
В размерной цепи А (черт. 29) компенсации подлежат отклонения только звеньев А1 и А2, которые в сумме могут составлять
![]()
В соответствии с этим наибольшая величина компенсации будет
![]()
Число ступеней компенсаторов вычисляют по формуле
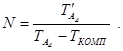
В данной задаче
![]()
С целью упрощения расчета размеров компенсаторов рекомендуется назначать координаты середин полей допусков составляющих звеньев так, чтобы совместить одну из границ расширенного поля допуска замыкающего звена с соответствующей границей его поля допуска, заданного служебным назначением изделия.
В связи с этим, при совмещении нижних границ полей допусков замыкающего звена (черт. 30), необходимо соблюсти условие:
![]()
![]()
![]()
![]()
Поскольку компенсации подлежат отклонения звеньев А1 и А2, то в расчете координат середин полей допусков компенсатор участвовать не должен.
Координата середины его поля допуска должна быть установлена независимо от координат середин полей допусков составляющих звеньев А1 и А2. С целью упрощения расчета размеров компенсаторов рекомендуется задавать координату середины поля допуска компенсирующего звена равной половине его поля допуска со знаком минус.
В данной задаче
![]()
Таким образом,
![]()
Установим
![]()
При
установленных координатах середин полей допусков звеньев А1 и
А2 поле допуска ![]() займет относительно заданного поля
допуска
займет относительно заданного поля
допуска ![]() положение,
показанное на черт. 30.
положение,
показанное на черт. 30.
При величине ступени компенсации, равной
![]()
и числе групп
компенсаторов N = 4, поле производственного допуска ![]() будет разбито на
четыре зоны с границами, показанными на черт. 30. Отклонения,
возникающие в пределах той или иной зоны, должны компенсироваться путем
постановки в изделие соответствующего проставочного кольца (компенсатора).
будет разбито на
четыре зоны с границами, показанными на черт. 30. Отклонения,
возникающие в пределах той или иной зоны, должны компенсироваться путем
постановки в изделие соответствующего проставочного кольца (компенсатора).
Размер компенсатора первой ступени равен его номинальному размеру. Размеры компенсаторов каждой следующей ступени будут отличаться от размеров компенсаторов предшествующей ступени на величину ступени компенсации.
Черт. 30
С учетом допуска на изготовление компенсаторов их размеры будут:
I ступень...![]() мм;
мм;
II ступень…![]() мм;
мм;
III ступень…![]() . мм;
. мм;
IV ступень…![]() мм.
мм.
При задании размеров компенсаторов разницу в номиналах целесообразно перенести на координаты середин полей их допусков. Тогда размеры компенсаторов должны быть равны:
![]() мм - для I ступени;
мм - для I ступени;
![]() мм- для II ступени;
мм- для II ступени;
![]() мм- для III ступени;
мм- для III ступени;
![]() мм- для IV ступени.
мм- для IV ступени.
На черт. 30 можно видеть, как осуществляется
компенсация отклонений, находящихся в различных зонах ![]() .
.
Если координаты середин полей допусков составляющих звеньев А1 и А2 установлены произвольно, то при определении размера компенсаторов первой ступени необходимо внести поправку в координату середины поля допуска компенсирующего звена
![]()
![]()
причем значения ![]() установлены произвольно.
установлены произвольно.
Если компенсатор является увеличивающим звеном, поправку ![]() вносят со
своим знаком, а если уменьшающим звеном - с противоположным знаком.
вносят со
своим знаком, а если уменьшающим звеном - с противоположным знаком.
Пример 2.
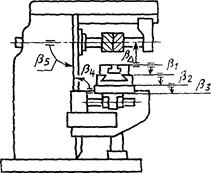
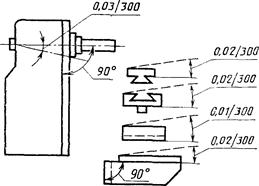
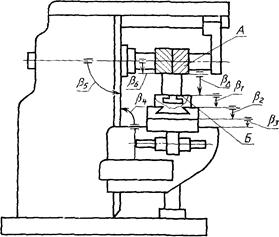
Задача: рассчитать и установить допуски на относительные повороты поверхностей деталей универсально-фрезерного станка с целью обеспечения требуемой параллельности рабочей плоскости стола оси вращения шпинделя.
Исходя из назначения станка, на замыкающее звено установлен допуск ![]() = 0,03/300
мм. При этом указано, что повороты рабочей плоскости стола и оси вращения
шпинделя могут быть направлены только в сторону оси вращения шпинделя. Считая
положительным направление поворота против часовой стрелки, согласно служебному
назначению станка следует установить
= 0,03/300
мм. При этом указано, что повороты рабочей плоскости стола и оси вращения
шпинделя могут быть направлены только в сторону оси вращения шпинделя. Считая
положительным направление поворота против часовой стрелки, согласно служебному
назначению станка следует установить ![]() = + 0,015/300 мм. Выявляем
размерную цепь, при помощи которой решается поставленная задача (черт.
31).
= + 0,015/300 мм. Выявляем
размерную цепь, при помощи которой решается поставленная задача (черт.
31).
Черт. 31
При расчетах допусков на поворот поверхностей удобно использовать следующий прием. Поскольку допуски на поворот поверхностей задают в виде линейной величины, отнесенной к соответствующей длине, их следует вначале привести к общему знаменателю. Это позволит во время расчета не учитывать его и использовать методику и формулы, служащие для расчета линейных допусков. После расчета допусков отброшенный знаменатель следует восстановить. Рассчитаем среднюю величину допуска Тср:
![]()
Полученная величина говорит о том, что детали универсально-фрезерного станка изготовить в пределах этого допуска не представляется экономически возможным.
Поэтому отказываемся от использования достижения требуемой точности методом полной взаимозаменяемости. Рассмотрим возможность использования метода неполной взаимозаменяемости.
Предварительно примем следующие исходные данные. Будем считать, что при
изготовлении станков отклонения, получаемые на деталях, будут иметь характер
рассеяния, близкий к закону Симпсона (треугольника), для которого величина
коэффициента относительного среднего квадратического отклонения ![]() . Зададимся
возможным риском Р = 10 %, чему соответствует
. Зададимся
возможным риском Р = 10 %, чему соответствует ![]() =1,65.
Подставляя перечисленные данные в формулу, получаем:
=1,65.
Подставляя перечисленные данные в формулу, получаем:
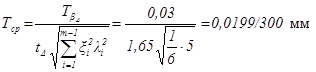
или,
округляя, будем иметь Тср »
0,02/300 мм. Считая полученное значение Тср приемлемым и
учитывая трудности изготовления и монтажа отдельных деталей, установим
следующие значения допусков: ![]() = 0,03/300 мм - на поворот
оси вращения шпинделя относительно направляющих станины (отклонение от
перпендикулярности);
= 0,03/300 мм - на поворот
оси вращения шпинделя относительно направляющих станины (отклонение от
перпендикулярности);
![]() =
0,02/300 мм - на отклонение от перпендикулярности направляющих консоли, по
которым перемещается каретка, относительно направляющих которыми консоль
скользит по станине;
=
0,02/300 мм - на отклонение от перпендикулярности направляющих консоли, по
которым перемещается каретка, относительно направляющих которыми консоль
скользит по станине;
![]() =
0,01/300 мм - на отклонение от параллельности верхней поверхности каретки
относительно ее направляющих;
=
0,01/300 мм - на отклонение от параллельности верхней поверхности каретки
относительно ее направляющих;
![]() =
0,02/300 мм и
=
0,02/300 мм и ![]() = 0,02/300 мм.
= 0,02/300 мм.
Проверим правильность установленных допусков по формуле
![]()
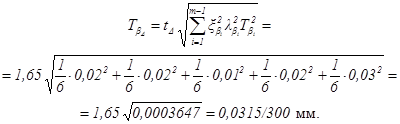
Как видно, возможные отклонения замыкающего звена несколько больше установленного допуска (0,03/300 мм). Следовательно, процент риска также будет превосходить ранее избранный (Р = 10 %).
Вычислим его:
![]()
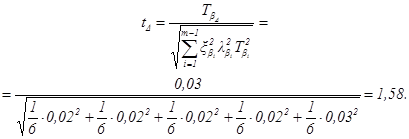
Этому значению tD соответствует возможный риск 10,5 %. Считаем, что на такой риск можно пойти, и в соответствии с этим принимаем установленные допуски.
Поскольку поворот поверхности стола должен быть направлен к оси вращения шпинделя, необходимо установить для каждого звена координату середины поля допуска и ее знак. Значения координат середин полей допусков устанавливаются с помощью уравнения.
![]()
Если принять, что оси поворота поверхностей деталей расположены слева (черт. 32), то координаты середин полей допусков звеньев b1; b2; b3; b4 будут иметь знак «+», а звена b5 - знак «-». Принимаем значения координат середин полей допусков равными:
![]() = 0,01/300;
= 0,01/300; ![]() = 0,01/300;
= 0,01/300;
![]() = 0,005/300;
= 0,005/300; ![]() = 0,01/300.
= 0,01/300.
Черт. 32
Координату середины поля допуска пятого звена находим из уравнения
![]()
![]() =
-0,02/300.
=
-0,02/300.
Для того, чтобы убедиться в правильности установленных величин допусков и координат середин их полей, проверяем верхнее и нижнее предельные отклонения замыкающего звена размерной цепи по формулам:
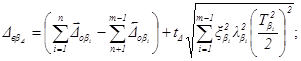
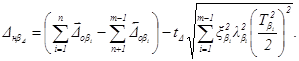
Подставляя в формулы значения установленных полей допусков: координат их середин и принятое значение tD = 1,58, получим:
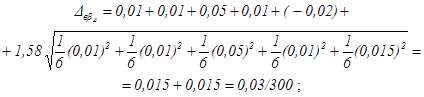
![]()
Определяем допуск замыкающего звена и координату его середины по формулам:
![]()
![]()
Сопоставляя с условиями задачи видим, что допуски и координаты середин полей допусков установлены верно.
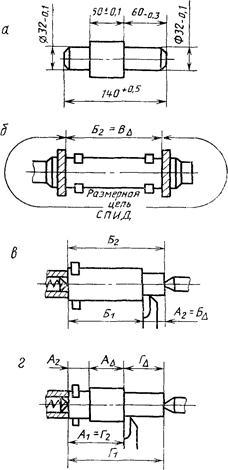
Пример 3.
Задача: установить допуски на операционные (линейные) размеры (черт. 33, а), обеспечивающие получение размеров 50 ±0,1 и 60-0,3 детали. Деталь изготовляется по следующему маршруту.
Операция 1. Подрезка торцов и зацентровка заготовки валика на фрезерно-центровальном станке (черт. 33, б).
Черт. 33
Операция 2. Токарная обработка валика с одного конца с установкой валика в центрах (передний центр-плавающий, черт. 33, в).
Операция 3. Токарная обработка валика с другого конца при аналогичной схеме базирования (черт. 33, г).
В спроектированном технологическом процессе размер 50 мм окончательно получается на третьей операции и является замыкающим звеном размерной цепи А:
АD = А1 - А2,
в которой звено А2 - размер, полученный на второй операции. Рассматривая его как замыкающее звено размерной цепи Б, имеем
А2 = БD = -Б1 + Б2,
Б2 - размер, полученный на первой операции, где он является замыкающим звеном размерной цепи В системы СПИД (Б2 = ВD). Размер 60 мм также получается на третьей операции. На черт. 33, г видно, что он является замыкающим звеном размерной цепи Г:
ГD = Г1 - Г2,
и образуется одновременно с размером АD. Так как Г1 = ВD, а Г2 = А1, то ГD = ВD - А1
Таким образом, для обеспечения требуемой точности размеров 50 и 60 мм необходимо рассмотреть систему параллельно связанных размерных цепей:
АD = А1 - А2,
А2 = БD = -Б1 + Б2,
ГD = ВD - А1
Учитывая, что более жесткие требования предъявлены к точности размера 50, установим допуски на звенья размерных цепей А и Б, применив метод неполной взаимозаменяемости и, приняв
![]() = 1/9; Р
= 0,27 %; (tD = 3).
= 1/9; Р
= 0,27 %; (tD = 3).
Исходя из значения ![]() = 0,2 мм, зададим
= 0,2 мм, зададим ![]() =
0,1 мм и
=
0,1 мм и ![]() = 0,17 мм.
= 0,17 мм.
Проверка:

Поскольку ![]() мм, установим
мм, установим ![]() мм и
мм и ![]() мм.
мм.
Проверка:
![]()
Из ранее
сказанного следует, что ![]() мм.
мм.
Проверим теперь, обеспечивают ли установленные допуски требуемую точность размера ГD
![]()
Таким
образом, принятые значения допусков надежно обеспечивают требуемую точность
размера ГD,
так как ![]() мм.
Что касается размера 140 мм, то для достижения требуемой точности АD допуск на операционный размер ВD должен быть задан более жестким,
чем это указано на чертеже детали.
мм.
Что касается размера 140 мм, то для достижения требуемой точности АD допуск на операционный размер ВD должен быть задан более жестким,
чем это указано на чертеже детали.
Приняв во внимание, что А2 = -Б1 + Б2, а Б2 = ВD, получим АD = A1 + Б1 - В1, а следовательно, для назначения координат середин полей допусков операционных размеров необходимо совместное решение уравнений координат:
Чертеж детали
требует, чтобы ![]() = 0;
= 0; ![]() = - 0,15 мм и
= - 0,15 мм и ![]() = -0,25 мм.
= -0,25 мм.
Учитывая это требование, необходимо установить:
![]()
![]()
ПРИЛОЖЕНИЕ
Принятые обозначения
|
А, Б, …, b, γ |
- |
обозначение размерной цепи; |
|
Аi, Бi, …, bi, γi |
- |
номинальный размер i-гo составляющего звена размерной цепи; |
|
АD, БD, …, bD, γD |
- |
номинальный размер замыкающего звена размерной цепи; |
|
|
- |
увеличивающее i-e составляющее звено размерной цепи; |
|
|
- |
уменьшающее i-e составляющее звено размерной цепи; |
|
|
- |
компенсирующее i-e звено размерной цепи; |
|
Аmax…bmax… |
- |
наибольший предельный размер; |
|
Аmin…bmin… |
- |
наименьший предельный размер; |
|
|
- |
верхнее предельное отклонение замыкающего звена размерной цепи А; |
|
|
- |
нижнее предельное отклонение замыкающего звена размерной цепи А; |
|
|
- |
верхнее и нижнее отклонения i-гo составляющего звена размерной цепи А; |
|
|
- |
допуск замыкающего звена размерной цепи А; |
|
|
- |
допуск i-го звена размерной цепи А; |
|
|
- |
координата середины поля допуска замыкающего звена размерной цепи А; |
|
|
- |
координата середины поля допуска i-гo составляющего звена размерной цепи А; |
|
|
- |
координата середины поля рассеяния замыкающего звена размерной цепи А; |
|
|
- |
координата середины поля рассеяния i-гo составляющего звена размерной цепи А; |
|
|
- |
координата центра группирования замыкающего звена размерной цепи А; |
|
|
- |
координата центра группирования i-гo составляющего звена размерной цепи А; |
|
δк, (Vк) |
- |
величина компенсации; |
|
λ |
- |
относительное среднее квадратическое отклонение; |
|
tD |
- |
коэффициент риска; |
|
α |
- |
коэффициент относительной асимметрии; |
|
ξA |
- |
передаточное отношение i-гo звена размерной цепи А; |
|
т |
- |
Число звеньев размерной цепи |
|
N |
- |
Число ступеней размеров неподвижного крмпенсатора |
|
P |
- |
Процент риска |
* Наряду с принятыми обозначениями, здесь и далее допускается применять обозначения, указанные в скобках.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Министерством высшего и среднего специального образования РСФСР
ИСПОЛНИТЕЛИ
И. М. Колесов, д-р техн. наук (руководитель темы); Е. И. Луцков, канд. техн. наук; В. И. Колчков, канд. техн. наук; А. И. Кубарев, канд. техн. наук; И. Л. Белкин, канд. техн. наук; И. А. Коганов, д-р техн. наук; А. В. Скворцов, канд. техн. наук; А. М. Червяков, канд. техн. наук; Г. Ф. Исьемина
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 11.05.85 № 1556
3. ВЗАМЕН ГОСТ 16319-80, ГОСТ 16320-80, ГОСТ 19415-74, ГОСТ 19416-74
4. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение документа, на который дана ссылка |
Номер пункта |
ОГЛАВЛЕНИЕ


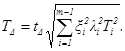 (4)
(4)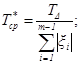 (5)
(5)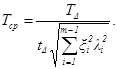 (6)
(6)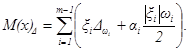 (10)
(10)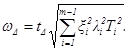 (13)
(13)