ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР
ПО УПРАВЛЕНИЮ КАЧЕСТВОМ ПРОДУКЦИИ И СТАНДАРТАМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МЕТОДИКИ РАСЧЕТА
МИКРОДОЗИМЕТРИЧЕСКИХ
ХАРАКТЕРИСТИК КОСМИЧЕСКИХ
ИЗЛУЧЕНИЙ
БЕЗОПАСНОСТЬ РАДИАЦИОННАЯ
ЭКИПАЖА КОСМИЧЕСКОГО АППАРАТА
В КОСМИЧЕСКОМ ПОЛЕТЕ
РД 50-25645.217-90
Москва
ИЗДАТЕЛЬСТВО СТАНДАРТОВ
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МЕТОДИКИ РАСЧЕТА МИКРОДОЗИМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК КОСМИЧЕСКИХ ИЗЛУЧЕНИЙ
Безопасность радиационная экипажа космического аппарата в космическом полете
Дата введения 01.07.91
Настоящие методические указания устанавливают методики расчета спектров линейной энергии для тяжелых заряженных частиц (далее - ТЗЧ) с зарядом от 1 до 32 единиц абсолютной величины заряда электрона и энергией на нуклон от 0,1 до 104 МэВ в тканеэквивалентном веществе при размерах шарового микрообъема от 0,1 до 20 мкм.
Методические указания предназначены для расчетов микродозиметрических характеристик полей ионизирующих излучений (далее - микродозиметрических характеристик), воздействующих на биологические объекты в космических полетах.
Пояснения терминов, применяемых в методических указаниях, приведены в приложении 1.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Под линейной энергией у, кэВ/мкм, понимают
относящуюся к событию поглощения стохастическую величину, равную частному от
деления фактически поглощенной в микрообъеме энергии e на среднюю длину его хорды ![]()
Для шарового микрообъема диаметром lo : l = 2lo/3.
Различают частотный и дозовый спектры линейной энергии (далее - СЛЭ). Под частотным СЛЭ f(y), мкм/кэВ, понимают относительное число событий поглощения в микрообъеме, приходящихся на элементарный интервал значений линейной энергии в окрестности у. Под дозовым СЛЭ d(y), мкм/кэВ, понимают относительную долю поглощенной дозы, приходящейся на элементарный интервал значений линейной энергии в окрестности у. Частотный и дозовый СЛЭ нормированы на единицу.
1.2. В качестве основных микродозиметрических
характеристик выбирают частотный f(у) и дозовый d(y)
СЛЭ, а также определяемые по ним частотное ![]() и
дозовое
и
дозовое ![]() средние значения линейной
энергии:
средние значения линейной
энергии:
![]() =
=
![]() ; (2)
; (2)
![]() =
= ![]() . (3)
. (3)
Другие
микродозиметрические характеристики вычисляют по f(y),
d(y), ![]() и
и ![]() с
помощью соотношений, приведенных в приложении 2.
с
помощью соотношений, приведенных в приложении 2.
1.3. Методики, представленные в разд. 2 и 3, основаны на предположениях, что при расчете СЛЭ пренебрегают:
- кривизной траекторий ТЗЧ вблизи и внутри микрообъема;
- дополнительными событиями поглощения в микрообъеме и изменением энергий заряженных частиц, обусловленными ядерными взаимодействиями и радиационными потерями вблизи и внутри микрообъема.
1.4. СЛЭ для ТЗЧ, рассчитываемые по методикам разд. 2 и 3, относятся к шаровому микрообъему, выделенному в однородном тканеэквивалентном веществе.
1.5. Методика расчета СЛЭ по методу Монте-Карло (разд. 2) установлена для случая, когда относительная
погрешность вычисления ![]() или
или ![]() ,
обусловленная пренебрежением разбросом энергетических потерь заряженных частиц
вблизи и внутри микрообъема и переносом энергии дельта-электронами, превышает 5
и 10 % соответственно. В случае непревышения этих пределов используют
аналитическую методику, установленную в разд. 3.
,
обусловленная пренебрежением разбросом энергетических потерь заряженных частиц
вблизи и внутри микрообъема и переносом энергии дельта-электронами, превышает 5
и 10 % соответственно. В случае непревышения этих пределов используют
аналитическую методику, установленную в разд. 3.
2. МЕТОДИКА РАСЧЕТА СЛЭ МЕТОДОМ МОНТЕ-КАРЛО
2.1. Настоящая методика основана на моделировании методом Монте-Карло прохождения ТЗЧ, а также возникающих под их действием дельта-электронов вблизи и внутри микрообъема и вычислении поглощенных энергий в нем, соответствующих прохождениям отдельных ТЗЧ. Считают, что центр микрообъема помещен в начало декартовой системы координат {0х1, 0х2, 0х3}, а ТЗЧ движутся в направлении оси 0х3. Изменением энергии ТЗЧ в слое вещества толщиной, достаточной для установления электронного равновесия, пренебрегают.
2.2. В качестве исходных данных для расчета частотного f(y) и дозового d(у) СЛЭ выбирают:
- энергию Е, МэВ, атомный номер Z и массовое число А ТЗЧ:
- диаметр lo, мкм, шарового микрообъема;
- значения линейной энергии yj, кэВ/мкм, определяющие интервалы Dуо = 0, Dyj = yj - yj-1 (j = 1, 2, ..., J) для усреднения значений СЛЭ. Полагают Yо = 0.
Примечание. Следует применять логарифмическую сетку, удовлетворяющую требованию, чтобы дополнительная погрешность вычисления дозового среднего значения линейной энергии по формуле
![]()
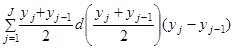 ,
(4)
,
(4)
связанная с выбором значений линейной энергии yj, не превышала 2 %.
2.3. Вычисляют параметры, используемые в дальнейших расчетах при выбранных значениях Е, Z, А, lo:
- максимальную энергию Tmax, кэВ, дельта-электрона по формулам:
b2 = (2EA + Е2А)/(1 + ЕА)2; (6)
- линейную передачу энергии LTo, кэВ/мкм, ТЗЧ в тканеэквивалентном веществе, относящуюся к немоделируемым столкновениям, по формуле
где dE/dx - ионизационные потери ТЗЧ в тканеэквивалентном веществе, кэВ/мкм;
Тo - минимальная энергия моделируемых дельта-электронов, определяемая из соотношения: To = max {0,1; 0,007lo}, кэВ;
I - средний эффективный потенциал ионизации вещества по РД 50-25645.206, кэВ;
Zэфф = Z(1 - e-125b/Z2/3); (10)
- граничную энергию Тm, кэВ, дельта-электронов, до которой учитывается пространственная корреляция траекторий дельта-электронов с траекторией ТЗЧ, по формуле
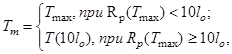 (11)
(11)
где Ro(Tmax) - практический пробег, мкм, электрона с энергией Тmax;
Т (10lo) - кинетическая энергия электрона, практический пробег которого равен 10 lo, кэВ;
- долю ионизационных потерь ТЗЧ, m(e), приходящуюся на дельта-электроны с энергией свыше Т, по формуле
- радиус dm, мкм, сечения области моделирования плоскостью, перпендикулярной траектории ТЗЧ, по формуле
где Rp(Tm) - практический пробег электрона с энергией Tm.
Примечания:
1. Значения dE/dx вычисляют при Е/А ³ 2 МэВ/нуклон по РД 50-25645.206, а при Е/А < 2 МэВ/нуклон - по данным табл. 1 и формуле (124) приложения 3. Практические пробеги электронов определяют по данным табл. 2 приложения 4.
2. Область моделирования - микрообъем и прилегающие к нему слои вещества, в пределах которых производится моделирование прохождения ТЗЧ и возникающих дельта-электронов с учетом пространственной корреляции их траекторий.
2.4. Область моделирования определяют неравенствами
![]() ;
(14)
;
(14)
![]() ;
(15)
;
(15)
![]() .
(16)
.
(16)
2.5. Алгоритм расчета СЛЭ для ТЗЧ, пересекающих область моделирования, состоит в следующем.
2.5.1. По очередному случайному числу g, равномерно распределенному в интервале (0,1) (далее - очередному g), вычисляют декартовы координаты {х1,0, х2,0, х3,0} точки входа ТЗЧ в область моделирования для очередной n-й истории по формулам:
2.5.2. Вычисляют параметры п-й истории:
- статистический вес координаты х1,0 по формуле
- координату х3,вых, соответствующую точке выхода ТЗЧ из области моделирования, по формуле
- угол jо между плоскостями, касательными к шару х21 + х22 + х23 = l2/4 и пересекающимися по линии, совпадающей с траекторией ТЗЧ, по формуле
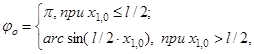 (22)
(22)
где l - свободный параметр (lo < l £ 10lo), мкм, выбираемый из условия, чтобы вероятностью попадания в микрообъем дельта-электронов с энергией менее Tm, вылетающих из точки возникновения с х1,0 ³ l в противоположном по отношению к нему направлении, можно было бы пренебречь.
2.5.3. Среднюю энергию ![]() , кэВ,
переданную ТЗЧ микрообъему в результате немоделируемых взаимодействий внутри
него, рассчитывают следующим образом
, кэВ,
переданную ТЗЧ микрообъему в результате немоделируемых взаимодействий внутри
него, рассчитывают следующим образом
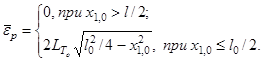 (23)
(23)
Истинное значение энергии eр, кэВ, переданной в таких взаимодействиях, рассчитывают согласно п. 2.5.4 в зависимости от значения
где sТо - макроскопическое сечение неупругих взаимодействий в тканеэквивалентном веществе с потерей энергии менее То для ТЗЧ, мкм-1, определяемое по макроскопическому сечению соответствующих неупругих взаимодействий sin для электрона одинаковой с ТЗЧ скорости по формуле
Значения sin рассчитывают по данным табл. 4 приложения 4.
2.5.4. При c = 0 полагают eр = 0.
При 0 < c £ 20 полагают
где m - целое число, удовлетворяющее, при очередном g, условиям:
![]() .
.
При 20 < c £ 400 полагают
ep = ![]() ,
,
где a - случайное число, распределенное по нормальному закону.
При c > 400 полагают ep = ![]() .
.
2.5.5. По очередному g рассчитывают координату x3,i точки i-го взаимодействия ТЗЧ с веществом, сопровождающегося испусканием дельта-электрона с энергией между ТD и Тm:
x3,i = x3,i -1 - lng/(sijo/p), (27)
где si - макроскопическое сечение ионизации с потерей энергии между ТD + I и Tm + I для ТЗЧ, проходящей на расстоянии х1, от центра микрообъема, мкм-1.
Значения si рассчитывают по формуле
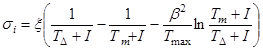 ,
(28)
,
(28)
a Tr - энергия дельта-электрона, имеющего практический пробег
Rp(Tr) = ![]() , кэВ.
, кэВ.
2.5.6. При x3,i ³ x3,вых полагают en = ei + eр и переходят к вычислениям п. 2.5.11.
При x3,i < x3,вых по очередным g¢ и g" рассчитывают энергию Ti, кэВ,
значения величин m1 и m2, характеризующих направление вылета дельта-электрона из точки {x1,0, x2,0, х3,i} относительно направления движения ТЗЧ
![]() ;
(31)
;
(31)
и статистический вес WT,i энергии Ti дельта-электрона
2.5.7. При х21,0 + х23,i £ l20/4 к текущему значению eр прибавляют I.
При х21,0 + х23,i £ l2/4 переходят к вычислениям п. 2.6.
2.5.8. Вычисляют значения D по формуле
D = l2/4 - х21,0
![]() - (х1,0 m1 - х3,i
- (х1,0 m1 - х3,i ![]() )2. (34)
)2. (34)
При D £ 0 повторяют вычисления с п. 2.5.5.
2.5.9. Расстояние S0 от точки
испускания i-го дельта-электрона до ближайшей точки пересечения
луча в направлении движения дельта-электрона с поверхностью х21
+ х22 + х23 = ![]() вычисляют
по формуле
вычисляют
по формуле
Далее переходят к п. 2.6.
2.5.10. К текущему значению ei поглощенной энергии в микрообъеме добавляют вклад от i-го дельта-электрона e*i и повторяют расчет, начиная с п. 2.5.5.
2.5.11. При en = 0 переходят к п. 2.5.1.
Значение линейной энергии уn и статистический вес Wn для n-й истории вычисляют по формулам:
где io - номер дельта-электрона последнего перед выходом ТЗЧ из области моделирования.
Находят наименьшее значение индекса jm, при котором уn £ уj, где уj - выбранные узлы разбиения шкалы линейной энергии (j = 1, 2, ..., J). (Далее j º jm).
2.5.12. В сумматоры у*F, y*D, f*(уj) и d*(уj) заносят вклады от n-й истории, равные, соответственно, ynWn, у2nWn, Wn и ynWn:
![]() (42)
(42)
2.5.13. В сумматор числа событий поглощения N заносят единицу. При N не кратном 20 повторяют вычисления по п. 2.5.1.
2.5.14. Вычисляют и запоминают оценки частотного и дозового средних значений линейной энергии для очередной серии из 20 событий поглощения:
![]() ;
(43)
;
(43)
![]() (44)
(44)
где
m - индекс, означающий, что помеченная им величина
относится к m-й серии, а также текущие значения ![]() и
и
![]() , полученные по всем N событиям поглощения:
, полученные по всем N событиям поглощения:
![]() ;
(45)
;
(45)
![]() . (46)
. (46)
2.5.15. При выполнении условия (для m > 10)
 и
и
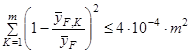 (47)
(47)
моделирование траекторий ТЗЧ прекращают, переходя к п. 2.5.16, если иначе, то продолжают расчет, начиная с п. 2.5.1.
2.5.16. Рассчитывают окончательные оценки частотного ![]() и
дозового
и
дозового ![]() средних значений линейной
энергии, частотный f(i) (у) и дозовый d{i) (у) СЛЭ для событий поглощения, обусловленных
прохождением ТЗЧ через область моделирования, по формулам:
средних значений линейной
энергии, частотный f(i) (у) и дозовый d{i) (у) СЛЭ для событий поглощения, обусловленных
прохождением ТЗЧ через область моделирования, по формулам:
![]() =
y*F/W; (48)
=
y*F/W; (48)
![]() =
y*D/y*F; (49)
=
y*D/y*F; (49)
f(i) (уj) = f* (уj)/WDyj, j = 1, 2, ..., J; (50)
d(i) (уj) = d* (уj)/W/Dyj, j = 1, 2, ..., J, (51)
Далее переходят к вычислению п. 2.7.
2.6. Траектории дельта-электронов (далее - электронов) моделируют с учетом их кривизны и возможности рождения вторичных, третичных и т. д. поколений электронов. Процедура вычисления энергии e*i, переданной электроном микрообъему, состоит в следующем.
2.6.1. Присваивают исходные значения сумматору поглощенных энергий e*i = 0, а также:
- направляющим косинусам единичного вектора wo = {w1,0, w2,0, w3,0}, задающего начальное направление движения электрона в системе координат {0х1, 0х2, 0х3},
- координатам радиуса-вектора ![]() = {x1,0, x2,0, x3,0},
задающего точку начала моделируемой траектории (j = 1, 2,
3):
= {x1,0, x2,0, x3,0},
задающего точку начала моделируемой траектории (j = 1, 2,
3):
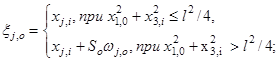 (56)
(56)
- энергии электрона t в точке ![]() :
:
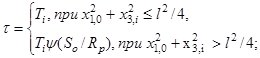 (57)
(57)
где Rp - практический пробег электрона с энергией Ti;
y(x) - энергия электрона, выраженная в единицах начальной его энергии, на глубине х, выраженной в единицах Rp.
Значения Rp и y(x) для интересующих энергий следует рассчитывать по данным табл. 2 и 3 приложения 4.
2.6.2. Ограниченные линейные передачи энергии LeD, кэВ/мкм, суммарное макроскопическое сечение ![]() ,
мкм-1, неупругих с передачей более D = 0,1 кэВ и
упругих взаимодействий, полное sеl, мкм-1, и парциальные sеl,k, мкм-1,
макроскопические сечения упругого рассеяния на элементах тканеэквивалентного
вещества для электрона с энергией t вычисляют по
данным табл. 4 и 5 приложения 4.
,
мкм-1, неупругих с передачей более D = 0,1 кэВ и
упругих взаимодействий, полное sеl, мкм-1, и парциальные sеl,k, мкм-1,
макроскопические сечения упругого рассеяния на элементах тканеэквивалентного
вещества для электрона с энергией t вычисляют по
данным табл. 4 и 5 приложения 4.
2.6.3. Длину пути l, мкм, электрона до очередного моделируемого взаимодействия рассчитывают по формуле
где у - случайное число.
Координаты радиуса-вектора ![]() = {x1, x2, x3} точки
взаимодействия вычисляют по формуле (j = 1, 2,
3):
= {x1, x2, x3} точки
взаимодействия вычисляют по формуле (j = 1, 2,
3):
2.6.4. При ![]() расчет
траектории электрона данного поколения прекращают. Проверяют, имеются ли
электроны старшего поколения. Если имеются, то координатам вектора
расчет
траектории электрона данного поколения прекращают. Проверяют, имеются ли
электроны старшего поколения. Если имеются, то координатам вектора ![]() и
направляющим косинусам
и
направляющим косинусам ![]() присваивают
ранее определенные значения, соответствующие самому младшему из нерассмотренных
поколений электронов, и переходят к п. 2.6.13, в противном случае возвращаются в п. 2.5.10.
присваивают
ранее определенные значения, соответствующие самому младшему из нерассмотренных
поколений электронов, и переходят к п. 2.6.13, в противном случае возвращаются в п. 2.5.10.
2.6.5. Длине S части отрезка ![]() ,
принадлежащей микрообъему, присваивают в зависимости от знака параметра
,
принадлежащей микрообъему, присваивают в зависимости от знака параметра
следующие значения:
при D £ 0 полагают S = 0;
при D > 0 полагают
 ,
(61)
,
(61)
и
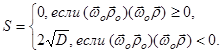 ,
(62)
,
(62)
2.6.6. Тип взаимодействия в точке ![]() определяют
по очередному у:
определяют
по очередному у:
если
у > sel/![]() , то взаимодействие неупругое. Для его
моделирования переходят к п. 2.6.10.
, то взаимодействие неупругое. Для его
моделирования переходят к п. 2.6.10.
2.6.7. Энергию электрона в точке ![]() вычисляют,
вычитая из t непрерывные
потери lLe,D. К текущему значению e*i прибавляют порцию энергии, равную S LеD.
вычисляют,
вычитая из t непрерывные
потери lLe,D. К текущему значению e*i прибавляют порцию энергии, равную S LеD.
2.6.8. Элемент, на котором произошло упругое рассеяние, определяют по очередному у путем выбора номера k, удовлетворяющего условиям
![]() .
(63)
.
(63)
2.6.9. Величины m1 = cosq и m2 = cosj, определяющие направление вылета электрона из точки упругого взаимодействия, вычисляют по формулам
m1 = 1 - 2у¢Е(t, Zk)/[1 - y¢ + E(t, Zk)]; (64)
где у¢ и у" - очередные случайные числа;
E(t, Zk) - параметр экранирования ядра электронами при энергии налетающего электрона t для ядра с атомным номером Zk, определяемый согласно приложению 4.
Далее выполняют вычисления, начиная с п. 2.6.14.
2.6.10. Потерю энергии Dt электрона с энергией t¢ = t - lLl,D в точке неупругого взаимодействия вычисляют по очередному у согласно алгоритму, изложенному в приложении 5.
Энергии электронов, покидающих точку ![]() ,
и косинусы углов q1, q2 и j1, j2,
определяющих направление вылета электронов из этой точки, рассчитывают по
формулам:
,
и косинусы углов q1, q2 и j1, j2,
определяющих направление вылета электронов из этой точки, рассчитывают по
формулам:
«е» не «эль»
где у - очередное случайное число.
2.6.11. При ![]() £ lо/2 к
текущему значению e*i прибавляют порцию энергии De, вычисляемую по формуле
£ lо/2 к
текущему значению e*i прибавляют порцию энергии De, вычисляемую по формуле
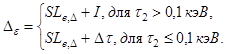 (72)
(72)
2.6.12. При t2 > 0,1 кэВ запоминают радиус-вектор ![]() ,
вектор
,
вектор ![]() и значения t1, cosq1 и cosj1, а
переменным t, m1, m2 присваивают значения, соответствующие наиболее
медленному из электронов, покидающих точку
и значения t1, cosq1 и cosj1, а
переменным t, m1, m2 присваивают значения, соответствующие наиболее
медленному из электронов, покидающих точку ![]() :
:
и переходят к п. 2.6.14.
2.6.13. Переменным t, m1 и m2 присваивают значения:
2.6.14. В случае выполнения хотя бы одного из следующих условий:
где R1(t) - длина ионизационного пробега электрона с энергией t или
моделирование
траектории электрона данного поколения прекращают. При ![]() <
lo/2 к текущему значению e*i прибавляют t. Если имеются электроны старшего поколения, то
координатам вектора
<
lo/2 к текущему значению e*i прибавляют t. Если имеются электроны старшего поколения, то
координатам вектора ![]() и направляющим косинусам
и направляющим косинусам ![]() присваивают
ранее определенные значения, соответствующие самому младшему из нерассмотренных
поколений электронов, и переходят к п. 2.6.13, в противном случае
возвращаются в п. 2.5.10.
присваивают
ранее определенные значения, соответствующие самому младшему из нерассмотренных
поколений электронов, и переходят к п. 2.6.13, в противном случае
возвращаются в п. 2.5.10.
В случае невыполнения условий (79) и (80) переходят к следующему пункту.
2.6.15. Направляющие косинусы вектора ![]() = {w1, w2, w3}, задающего
направление движения рассматриваемого электрона из точки
= {w1, w2, w3}, задающего
направление движения рассматриваемого электрона из точки ![]() ,
вычисляют по следующим формулам:
,
вычисляют по следующим формулам:
2.6.16. Координатам вектора ![]() и
направляющим косинусам вектора
и
направляющим косинусам вектора ![]() присваивают новые
значения (j = 1, 2, 3):
присваивают новые
значения (j = 1, 2, 3):
и повторяют расчеты начиная с п. 2.6.2.
2.7. При m(е) = 0 расчет завершают, полагая искомые ![]() ,
,
![]() , f(yj) и d(yj) равными
, f(yj) и d(yj) равными ![]() ,
, ![]() ,
f(i) (уj) и d(i) (уj) соответственно, а при m(е) > 0 вычисляют их по формулам:
,
f(i) (уj) и d(i) (уj) соответственно, а при m(е) > 0 вычисляют их по формулам:
![]() ; (86)
; (86)
![]() = (1 - m(e))
= (1 - m(e)) ![]() + m(e)
+ m(e) ![]() ; (87)
; (87)
f (уj) = (1 - m(e)) ![]() f(i) (уj) + m(e)
f(i) (уj) + m(e) ![]() f(e) (уj); (88)
f(e) (уj); (88)
d (уj) = (1 - m(e)) d(e) (уj) + m(e) d(e) (уj), (89)
где помеченные индексом (е) величины относятся к событиям поглощения, формируемым дельта-электронами с энергиями свыше Tm. Эти величины, одинаковые для всех ТЗЧ одной скорости, но разных зарядов, рассчитывают согласно п. 2.8.
2.8. Методика расчета ![]() ,
, ![]() ,
f(e) (уj) и d(e) (уj), основанная на использовании приближения непрерывного замедления для
вычисления дифференциального энергетического распределения электронов на
поверхности сферы х21 + х22
+ х23 = l2/4, концентричной рассматриваемому шаровому
микрообъему диаметром lо, и
моделировании прохождения электронов внутри этой сферы методом Монте-Карло
состоит в следующем.
,
f(e) (уj) и d(e) (уj), основанная на использовании приближения непрерывного замедления для
вычисления дифференциального энергетического распределения электронов на
поверхности сферы х21 + х22
+ х23 = l2/4, концентричной рассматриваемому шаровому
микрообъему диаметром lо, и
моделировании прохождения электронов внутри этой сферы методом Монте-Карло
состоит в следующем.
2.8.1. Нормированный на единицу интегральный спектр флюенса Ф(Т) у поверхности сферы диаметром l вычисляют по формулам:
 (91)
(91)
где Le (T) - линейная передача энергии, кэВ/мкм, для электрона с энергией Т в тканеэквивалентном веществе, определяемая по данным табл. 4 приложения 4.
2.8.2. Для точки вылета электрона в n-й истории принимают х1,0 = 0, х2,0 = 0, х3,i = -l/2, m2 = 1 и рассчитывают энергию Ti, кэВ, и значение величины m1, характеризующей направление вылета электрона относительно оси 0х3, по формулам:
где Ф-1(y¢) - функция, обратная Ф(Т);
у¢, у" - последовательные случайные числа.
2.8.3. Выполняют вычисления согласно п. 2.6 с той лишь разницей, что вместо предусмотренного в пп. 2.6.4, 2.6.6 и 2.6.14 перехода в п. 2.5.10, переходят в п. 2.8.4.
2.8.4. В случае e*i = 0 повторяют вычисления с п. 2.8.2, иначе полагают en = e*i, Wn = 1 и переходят к вычислениям пп. 2.5.11 - 2.5.14, минуя формулу (37). При выполнении условия (47) дальнейшее моделирование траекторий не производят, а переходят в п. 2.8.5. При невыполнении условия (47) повторяют вычисления с п. 2.8.2.
2.8.5. Окончательные оценки искомых величин для событий поглощения, формируемых дельта-электронами с энергией более Tm, рассчитывают по формулам:
![]() =
y*F/W; (94)
=
y*F/W; (94)
![]() =
y*D/y*F; (95)
=
y*D/y*F; (95)
f(e) (уj) = f* (уj)/WDyj, j = 1, 2, ..., J; (96)
d(e) (уj) = d* (уj)/W/Dyj, j = 1, 2, ..., J, (97)
3. АНАЛИТИЧЕСКАЯ МЕТОДИКА РАСЧЕТА СЛЭ
3.1. Методика основана на предположении, что разбросом энергетических потерь ТЗЧ на отрезках траекторий внутри микрообъема можно пренебречь и что вся потерянная ТЗЧ энергия поглощается в точках их взаимодействий с веществом.
3.2. В качестве исходных данных для расчетов частотного f(y) и дозового d(y) СЛЭ выбирают:
- энергию Е, МэВ, атомный номер Z и атомную массу A ТЗЧ;
- диаметр lo, мкм, микрообъема.
3.3. Линейные передачи энергии L = -dE/dx, кэВ/мкм, и ионизационные пробеги R, мкм, ТЗЧ в тканеэквивалентном веществе, используемые в расчетах, вычисляют при E/A ³ 2 МэВ/нуклон по РД 50-25645.206, а при меньших энергиях - по формулам и данным приложения 3.
3.4. В случае, когда соблюдается условие
E - 10-3loL £ 0,02E, (99)
применяют
следующие формулы для СЛЭ, частотного ![]() и дозового
и дозового ![]() средних
значений линейной энергии:
средних
значений линейной энергии:
![]() =
L; (102)
=
L; (102)
![]() =
= ![]() . (103)
. (103)
3.5. В случае, когда условие (99) не соблюдается, частотный f(y) и дозовый d(у) СЛЭ представляют в виде:
где с - постоянная величина, определяемая из условия нормировки на единицу
Физический смысл и формулы для расчета каждого слагаемого при равномерно распределенных в среде источниках ТЗЧ приведены в пп. 3.5.1 - 3.5.4.
3.5.1. Слагаемое N1(у) определяет вклад в СЛЭ от ТЗЧ, треки которых полностью принадлежат микрообъему. Значения N1(у) рассчитывают по формуле
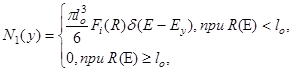 (107)
(107)
где d(Е - Еy) дельта-функция, а
![]() .
(108)
.
(108)
Здесь и далее Еу = 2×10-3 loy/3.
3.5.2. Слагаемое N2(y) определяет вклад в СЛЭ от ТЗЧ, треки которых начинаются внутри микрообъема, но заканчиваются вне его. Значения N2(y) рассчитывают по формуле
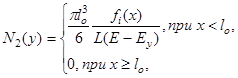 (109)
(109)
где x = R(E) - R(E - Ey),
fi(x) = 3(1 - x2/l20)/2lo. (110)
3.5.3. Слагаемое N3(y) определяет вклад в СЛЭ от ТЗЧ, треки которых начинаются вне микрообъема, но заканчиваются внутри него. Значения N3(y) рассчитывают по формуле
 (111)
(111)
где Fm(R) = 1 - R2/l20.
3.5.4. Слагаемое N4(y) определяет вклад в СЛЭ от ТЗЧ, пронизывающих микрообъем. Значения N4(y) рассчитывают по формуле
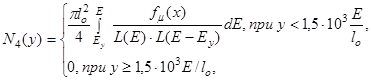 (112)
(112)
где x = R(E) - R(E - Eу),
3.5.5. Частотное ![]() и дозовое
и дозовое ![]() средние значения линейной энергии
рассчитывают по полученным f(y) и d(y) согласно формулам (2) и (3)
соответственно.
средние значения линейной энергии
рассчитывают по полученным f(y) и d(y) согласно формулам (2) и (3)
соответственно.
ПРИЛОЖЕНИЕ 1
Справочное
ПОЯСНЕНИЯ К ТЕРМИНАМ, ПРИМЕНЯЕМЫМ В МЕТОДИЧЕСКИХ УКАЗАНИЯХ
|
Пояснение |
|
|
Микрообъем |
Объем, заключающий в себе достаточно малое количество вещества, чтобы при заданных поглощенной дозе или числе событий поглощения статистическим разбросом поглощенной энергии в нем нельзя было бы пренебречь |
|
Событие поглощения |
Событие прохождения одной первичной ионизирующей частицы в рассматриваемой области вещества, приводящее к поглощению в микрообъеме отличной от нуля порции энергии |
|
Поглощенная энергия |
По ГОСТ 15484 |
|
Ионизирующая частица |
По ГОСТ 15484 |
|
Микродозиметрические характеристики поля ионизирующего излучения Микродозиметрические характеристики |
Функции и величины, характеризующие статистический разброс поглощенной энергии и других пропорциональных ей величин в микрообъемах вещества при заданных поглощенной дозе или числе событий поглощения |
|
Поглощенная доза |
По ГОСТ 15484 |
|
Дельта-электрон |
Электрон, выбиваемый из электронных оболочек атомов быстрыми заряженными частицами, движущимися через вещество |
|
Линейная передача энергии |
По ГОСТ 15484 |
|
Практический пробег электрона Практический пробег |
Точка пересечения касательной к кривой зависимости поглощенной дозы от глубины в поглотителе, построенной в точке наиболее быстрого спада поглощенной дозы, с осью глубин при нормальном падении широкого пучка электронов на поглотитель |
|
Ионизационные потери тяжелых заряженных частиц |
Средние потери тяжелых заряженных частиц на единицу пути, обусловленные их взаимодействием с электронными оболочками атомов тормозящей среды |
ПРИЛОЖЕНИЕ 2
Справочное
СВЯЗЬ ДРУГИХ МИКРОДОЗИМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СО СПЕКТРАМИ ЛИНЕЙНОЙ ЭНЕРГИИ (СЛЭ)
В микродозиметрии и ее приложениях, помимо линейной
энергии у, частотного f(y) и дозового d(y)
СЛЭ, частотного ![]() и дозового
и дозового ![]() средних
значений линейной энергии, широко используют удельную энергию z,
частотную f1(z)
и дозовую d1(z)
плотности распределения удельной энергии в одиночном событии поглощения,
частотное
средних
значений линейной энергии, широко используют удельную энергию z,
частотную f1(z)
и дозовую d1(z)
плотности распределения удельной энергии в одиночном событии поглощения,
частотное ![]() и дозовое
и дозовое ![]() средние
значения удельной энергии, а также плотность распределения fD (z) удельной энергии при заданной поглощенной дозе D.
средние
значения удельной энергии, а также плотность распределения fD (z) удельной энергии при заданной поглощенной дозе D.
Под удельной энергией z, Гр, понимают стохастическую величину, равную частному от деления фактически поглощенной в микрообъеме энергии e, Дж, на массу m, кг, содержащегося в нем вещества
При у, кэВ/мкм, z, Гр, и диаметре шарового микрообъема lo, мкм, справедливы следующие соотношения:
![]() ;
(116)
;
(116)
![]() ;
(117)
;
(117)
Для вычисления плотности распределения удельной энергии при заданной поглощенной дозе следует использовать формулу
где f(k)(z) - k-кратная свертка от f1(z), определяемая с помощью рекуррентного соотношения
При
достаточно больших (D/![]() ³ 20) и
достаточно малых (D/
³ 20) и
достаточно малых (D/![]() £ 0,01)
поглощенных дозах fD(z) вычисляют по формулам:
£ 0,01)
поглощенных дозах fD(z) вычисляют по формулам:
fD(z) = (1 -
D/![]() )d(z) + D/
)d(z) + D/![]() f1(z) (123)
f1(z) (123)
соответственно, где d(z) - дельта-функция.
ПРИЛОЖЕНИЕ 3
Справочное
ИОНИЗАЦИОННЫЕ ПОТЕРИ И ПРОБЕГИ ТЯЖЕЛЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ (ТЗЧ) С ЭНЕРГИЯМИ НА УКЛОН МЕНЕЕ 2 МЭВ
Ионизационные потери dE/dx, кэВ/мкм, в тканеэквивалентном веществе для ТЗЧ при энергиях на нуклон менее 2 МэВ следует рассчитывать по ионизационным потерям (dE/dx)p для протонов, представленным в таблице, согласно формуле:
dE/dx = (dE/dx)p×zэфф(z)2/zэфф (1)2, (124)
где zэфф(z) - эффективный заряд ТЗЧ с зарядом ядра z, определяемый формулой (10) разд. 2.
Ионизационные пробеги R(E), мкм, ТЗЧ, включая протоны, следует определять по ее ионизационным потерям согласно формуле
![]() ,
(125)
,
(125)
где Е - энергия ТЗЧ, МэВ.
Таблица 1
Ионизационные потери протонов в тканеэквивалентном веществе
|
E, МэВ |
dE/dx, кэВ/мкм |
E, МэВ |
dE/dx, кэВ/мкм |
E, МэВ |
dE/dx, кэВ/мкм |
|
0,0010 |
26 |
0,02 |
73 |
0,4 |
50 |
|
0,0015 |
27 |
0,03 |
84 |
0,5 |
44 |
|
0,0020 |
29 |
0,04 |
90 |
0,6 |
39 |
|
0,0030 |
33 |
0,05 |
95 |
0,7 |
35 |
|
0,0040 |
38 |
0,06 |
97 |
0,8 |
32 |
|
0,0050 |
41 |
0,07 |
99 |
0,9 |
29 |
|
0,0060 |
44 |
0,08 |
97 |
1,0 |
27 |
|
0,0070 |
47 |
0,09 |
97 |
1,2 |
24 |
|
0,0080 |
50 |
0,10 |
96 |
1,4 |
21 |
|
0,0090 |
52 |
0,15 |
83 |
1,6 |
19 |
|
0,1010 |
55 |
0,20 |
72 |
1,8 |
18 |
|
0,0015 |
64 |
0,30 |
59 |
2,0 |
16 |
Примечание. Для получения dE/dx при промежуточных значениях Е следует применять линейную интерполяцию в двойном логарифмическом масштабе, а при E < 0,001 МэВ/нуклон - линейную экстраполяцию в обычном масштабе.
ПРИЛОЖЕНИЕ 4
Справочное
В табл. 2 представлены значения практического пробега Rp электрона в тканеэквивалентном веществе при энергиях Т в диапазоне от 0,1 до 200 кэВ. Значения Rp для энергий этого диапазона, не представленных в табл. 2, следует вычислять методом линейной интерполяции в двойном логарифмическом масштабе.
В табл. 3 представлены значения функции y(S/Rp), определяющей зависимость энергии электрона от глубины его проникновения S, мкм, в тканеэквивалентное вещество
где T(0) - начальная энергия электрона, кэВ;
Rp - практический пробег, мкм, электрона с энергией T(0).
Значения Rр при промежуточных Т следует вычислять методом линейной интерполяции в обычном масштабе.
В табл. 4 и 5 представлены значения ионизационных пробегов Re, полных Le и ограниченных Lе,D
линейных передач энергии, а также
макроскопических сечений взаимодействия электронов в тканеэквивалентном
веществе: полного макроскопического сечения неупругих взаимодействий sin, суммы неупругих взаимодействий с передачей энергии свыше D = 0,1 кэВ и полного упругих взаимодействий ![]() ,
полного упругих взаимодействий sel и
макроскопических сечений упругих взаимодействий для отдельных элементов selk.
,
полного упругих взаимодействий sel и
макроскопических сечений упругих взаимодействий для отдельных элементов selk.
Значения представленных в табл. 4 и 5 величин при промежуточных Т следует получать методом линейной интерполяции в двойном логарифмическом масштабе.
Таблица 2
Значения практического пробега электрона в тканеэквивалентном веществе
|
Энергия T, кэВ |
Практический пробег Rp, мкм |
Энергия T, кэВ |
Практический пробег Rp, мкм |
|
0,1 |
0,008 |
10,0 |
1,74 |
|
0,2 |
0,011 |
20,0 |
6,06 |
|
0,5 |
0,020 |
50,0 |
32,4 |
|
1,0 |
0,043 |
100,0 |
116,0 |
|
2,0 |
0,115 |
200,0 |
350,0 |
|
5,0 |
0,515 |
|
|
Таблица 3
Значения функции y(x) для тканеэквивалентного вещества
|
y(x) |
x |
y(x) |
|
|
0,0 |
1,000 |
0,7 |
0,176 |
|
0,1 |
0,924 |
0,8 |
0,0944 |
|
0,2 |
0,818 |
0,9 |
0,0456 |
|
0,3 |
0,692 |
1,0 |
0,0185 |
|
0,4 |
0,554 |
1,1 |
0,0055 |
|
0,5 |
0,415 |
1,2 |
0,0011 |
|
0,6 |
0,285 |
1,3 |
0,0000 |
Таблица 4
Значения Re, Le, Le,D, sin
и ![]() для
электронов в тканеэквивалентном веществе
для
электронов в тканеэквивалентном веществе
|
Т, кэВ |
Re, мкм |
Le, кэВ/мкм |
Le,D, кэВ/мкм |
sin, мкм-1 |
|
|
0,10Е + 00 |
0,111Е - 01 |
0,297Е + 02 |
0,297Е + 02 |
0,152Е + 04 |
0,103Е + 04 |
|
0,15Е + 00 |
0,128Е - 01 |
0,307Е + 02 |
0,307Е + 02 |
0,137Е + 04 |
0,799Е + 03 |
|
0,20Е + 00 |
0,145Е - 01 |
0,282Е + 02 |
0,282Е + 02 |
0,121Е + 04 |
0,662Е + 03 |
|
0,30Е + 00 |
0,183Е - 01 |
0,248Е + 02 |
0,224Е + 02 |
0,956Е + 03 |
0,522Е + 03 |
|
0,40Е + 00 |
0,226Е - 01 |
0,220Е + 02 |
0,190Е + 02 |
0,793Е + 03 |
0,430Е + 03 |
|
0,50Е + 00 |
0,275Е - 01 |
0,186Е + 02 |
0,154Е + 02 |
0,675Е + 03 |
0,366Е + 03 |
|
0,60Е + 00 |
0,332Е - 01 |
0,166Е + 02 |
0,134Е + 02 |
0,607E + 03 |
0,320Е + 03 |
|
0,80Е + 00 |
0,465Е - 01 |
0,139Е + 02 |
0,109Е + 02 |
0,466Е + 03 |
0,256Е + 03 |
|
0,10Е + 01 |
0,620Е - 01 |
0,120Е + 02 |
0,913Е + 01 |
0,390Е + 03 |
0,217Е + 03 |
|
0,15Е + 01 |
0,110E + 00 |
0,915Е + 01 |
0,669Е + 01 |
0,283Е + 03 |
0,152Е + 03 |
|
0,20Е + 01 |
0,171Е + 00 |
0,758Е + 01 |
0,544Е + 01 |
0,224Е + 03 |
0,121Е + 03 |
|
0,30Е + 01 |
0,324Е + 00 |
0,577Е + 01 |
0,405Е + 01 |
0,161Е + 03 |
0,828Е + 02 |
|
0,40Е + 01 |
0,521Е + 00 |
0,452Е + 01 |
0,308Е + 01 |
0,126Е + 03 |
0,645Е + 02 |
|
0,50Е + 01 |
0,759Е + 00 |
0,393Е + 01 |
0,268Е + 01 |
0,106Е + 03 |
0,521Е + 02 |
|
0,60Е + 01 |
0,103Е + 01 |
0,343Е + 01 |
0,232Е + 01 |
0,905Е + 02 |
0,439Е + 02 |
|
0,80Е + 01 |
0,169Е + 01 |
0,275Е + 01 |
0,183Е + 01 |
0,707Е + 02 |
0,335Е + 02 |
|
0,10Е + 02 |
0,249Е + 01 |
0,231Е + 01 |
0,152Е + 01 |
0,584Е + 02 |
0,266Е + 02 |
|
0,15Е + 02 |
0,507Е + 01 |
0,167Е + 01 |
0,108Е + 01 |
0,413Е + 02 |
0,181Е + 02 |
|
0,20Е + 02 |
0,842Е + 01 |
0,135Е + 01 |
0,865Е + 00 |
0,322Е + 02 |
0,137Е + 02 |
|
0,30Е + 02 |
0,172Е + 02 |
0,983Е + 00 |
0,619Е + 00 |
0,229Е + 02 |
0,941Е + 01 |
|
0,40Е + 02 |
0,287Е + 02 |
0,788Е + 00 |
0,490Е + 00 |
0,182Е + 02 |
0,724Е + 01 |
|
0,50Е + 02 |
0,425Е + 02 |
0,666Е + 00 |
0,410Е + 00 |
0,152Е + 02 |
0,595Е + 01 |
|
0,60Е + 02 |
0,586Е + 02 |
0,586Е + 00 |
0,359Е + 00 |
0,133Е + 02 |
0,509Е + 01 |
|
0,80Е + 02 |
0,964Е + 02 |
0,484Е + 00 |
0,295Е + 00 |
0,107Е + 02 |
0,403E + 01 |
|
0,10Е + 03 |
0,141Е + 03 |
0,418Е + 00 |
0,253Е + 00 |
0,919Е + 01 |
0,338Е + 01 |
|
0,15Е + 03 |
0,277Е + 03 |
0,328Е + 00 |
0,196Е + 00 |
0,709Е + 01 |
0,253E + 01 |
|
0,20Е + 03 |
0,442Е + 03 |
0,284Е + 00 |
0,169Е + 00 |
0,606Е + 01 |
0,211Е + 01 |
|
0,30Е + 03 |
0,828Е + 03 |
0,239Е + 00 |
0,140Е + 00 |
0,501Е + 01 |
0,169Е + 01 |
|
0,40Е + 03 |
0,127Е + 04 |
0,217Е + 00 |
0,126Е + 00 |
0,453Е + 01 |
0,148Е + 01 |
|
0,50Е + 03 |
0,,175Е + 04 |
0,203Е + 00 |
0,116Е + 00 |
0,423E + 01 |
0,136Е + 01 |
|
0,60Е + 03 |
0,225Е + 04 |
0,197Е + 00 |
0,112Е + 00 |
0,404Е + 01 |
0,129Е + 01 |
|
0,80Е + 03 |
0,329Е + 04 |
0,188Е + 00 |
0,106Е + 00 |
0,385Е + 01 |
0,120E + 01 |
|
0,10Е + 04 |
0,437Е + 04 |
0,183Е + 00 |
0,102Е + 00 |
0,375Е + 01 |
0,115Е + 01 |
|
0,15Е + 04 |
0,711Е + 04 |
0,182Е + 00 |
0,101Е + 00 |
0,365Е + 01 |
0,109Е + 01 |
|
0,20Е + 04 |
0,985Е + 04 |
0,182Е + 00 |
0,994Е - 01 |
0,364Е + 01 |
0,106Е + 01 |
|
0,30Е + 04 |
0,153Е + 05 |
0,184Е + 00 |
0,989Е - 01 |
0,366Е + 01 |
0,104Е + 01 |
|
0,40Е + 04 |
0,207Е + 05 |
0,188Е + 00 |
0,101Е + 00 |
0,370Е + 01 |
0,103Е + 01 |
|
0,50Е + 04 |
0,259Е + 0б |
0,195Е + 00 |
0,106Е + 00 |
0,374Е + 01 |
0,103Е + 01 |
|
0,60Е + 04 |
0,309Е + 05 |
0,206Е + 00 |
0,116Е + 00 |
0,377Е + 01 |
0,102Е + 01 |
|
0,80Е + 04 |
0,405Е + 05 |
0,210Е + 00 |
0,117Е + 00 |
0,384Е + 01 |
0,102E + 01 |
|
0,10Е + 05 |
0,499Е + 05 |
0,214Е + 00 |
0,119Е + 00 |
0,387Е + 01 |
0,102Е + 01 |
|
0,15Е + 05 |
0,724Е + 05 |
0,231Е + 00 |
0,133Е + 00 |
- |
- |
|
0,20Е + 05 |
0,934Е + 05 |
0,245Е + 00 |
0,144Е + 00 |
- |
- |
|
0,30Е + 05 |
0,132Е + 06 |
0,274Е + 00 |
0,169Е + 00 |
- |
- |
|
0,40Е + 05 |
0,167Е + 06 |
0,301Е + 00 |
0,194Е + 00 |
- |
- |
|
0,50Е + 05 |
0,198Е + 06 |
0,329Е + 00 |
0,220Е + 00 |
- |
- |
|
0,60Е + 05 |
0,228Е + 06 |
0,356Е + 00 |
0,246Е + 00 |
- |
- |
|
0,80Е + 05 |
0,280Е + 06 |
0,410Е + 00 |
0,297Е + 00 |
- |
- |
|
0,10Е + 06 |
0,326Е + 06 |
0,464Е + 00 |
0,349Е + 00 |
- |
- |
|
0,15Е + 06 |
0,420Е + 06 |
0,599Е + 00 |
0,481Е + 00 |
- |
|
Таблица 5
Значения sel, sel,1, sel,2, sel,3 и sel,4 для электронов в тканеэквивалентном веществе
|
Т, кэВ |
sel, мкм-1 |
sel,1, мкм-1 |
sel,2, мкм-1 |
sel,3, мкм-1 |
sel,4, мкм-1 |
|
0,10Е + 00 |
0,103Е + 04 |
0,620Е + 03 |
0,163Е + 03 |
0,212Е + 03 |
0,314Е + 02 |
|
0,15Е + 00 |
0,799Е + 03 |
0,498Е + 03 |
0,109Е + 03 |
0,167Е + 03 |
0,251Е + 02 |
|
0,20Е + 00 |
0,662Е + 03 |
0,420Е + 03 |
0,815Е + 02 |
0,140Е + 03 |
0,210Е + 02 |
|
0,30Е + 00 |
0,503Е + 03 |
0,326Е + 03 |
0,544Е + 02 |
0,106Е + 03 |
0,163Е + 02 |
|
0,40Е + 00 |
0,409Е + 03 |
0,267Е + 03 |
0,408Е + 02 |
0,875Е + 02 |
0,133Е + 02 |
|
0,50Е + 00 |
0,345Е + 03 |
0,227Е + 03 |
0,326Е + 02 |
0,748Е + 02 |
0,113Е + 02 |
|
0,60Е + 00 |
0,301Е + 03 |
0,200Е + 03 |
0,272Е + 02 |
0,644Е + 02 |
0,984Е + 01 |
|
0,80Е + 00 |
0,239Е + 03 |
0,159Е + 03 |
0,204Е + 02 |
0,519Е + 02 |
0,788Е + 01 |
|
0,10Е + 01 |
0,202Е + 03 |
0,135Е + 03 |
0,164Е + 02 |
0,440Е + 02 |
0,667Е + 01 |
|
0,15Е + 01 |
0,141Е + 03 |
0,952Е + 02 |
0,109Е + 02 |
0,306Е + 02 |
0,469Е + 01 |
|
0,20Е + 01 |
0,112Е + 03 |
0,752Е + 02 |
0,821Е + 01 |
0,245Е + 02 |
0,372Е + 01 |
|
0,30Е + 01 |
0,766Е + 02 |
0,519Е + 02 |
0,551Е + 01 |
0,167Е + 02 |
0,256Е + 01 |
|
0,40Е + 01 |
0,597Е + 02 |
0,404Е + 02 |
0,413Е + 01 |
0,131Е + 02 |
0,201Е + 01 |
|
0,50Е + 01 |
0,481Е + 02 |
0,328Е + 02 |
0,331Е + 01 |
0,104Е + 02 |
0,163Е + 01 |
|
0,60Е + 01 |
0,405Е + 02 |
0,276Е + 02 |
0,277Е + 01 |
0,875Е + 01 |
0,135Е + 01 |
|
0,80Е + 01 |
0,309Е + 02 |
0,211Е + 02 |
0,208Е + 01 |
0,677Е + 01 |
0,104Е + 01 |
|
0,10Е + 02 |
0,245Е + 02 |
0,166Е + 02 |
0,168Е + 01 |
0,537Е + 01 |
0,821Е + 00 |
|
0,15Е + 02 |
0,166Е + 02 |
0,112Е + 02 |
0,114Е + 01 |
0,363Е + 01 |
0,555Е + 00 |
|
0,20Е + 02 |
0,126E + 02 |
0,855Е + 01 |
0,865Е + 00 |
0,277Е + 01 |
0,421Е + 00 |
|
0,30Е + 02 |
0,864Е + 01 |
0,586Е + 01 |
0,590Е + 00 |
0,190Е + 01 |
0,288Е + 00 |
|
0,40Е + 02 |
0,665Е + 01 |
0,451Е + 01 |
0,456Е + 00 |
0,146Е + 01 |
0,223Е + 00 |
|
0,50Е + 02 |
0,546Е + 01 |
0,370Е + 01 |
0,375Е + 00 |
0,120Е + 01 |
0,183Е + 00 |
|
0,60Е + 02 |
0,467Е + 01 |
0,317Е + 01 |
0,321Е + 00 |
0,102Е + 01 |
0,156Е + 00 |
|
0,80Е + 02 |
0,370Е + 01 |
0,251Е + 01 |
0,253Е + 00 |
0,810Е + 00 |
0,123Е + 00 |
|
0,10Е + 03 |
0,310Е + 01 |
0,210Е + 01 |
0,212Е + 00 |
0,680Е + 00 |
0,104Е + 00 |
|
0,15Е + 03 |
0,232Е + 01 |
0,157Е + 01 |
0,159Е + 00 |
0,508Е + 00 |
0,774Е - 01 |
|
0,20Е + 03 |
0,193Е + 01 |
0,131Е + 01 |
0,132Е + 00 |
0,423Е + 00 |
0,645Е - 01 |
|
0,30Е + 03 |
0,155Е + 01 |
0,105Е + 01 |
0,106Е + 00 |
0,339Е + 00 |
0,517Е - 01 |
|
0,40Е + 03 |
0,136Е + 01 |
0,923Е + 00 |
0,931Е - 01 |
0,298Е + 00 |
0,455Е - 01 |
|
0,50Е + 03 |
0,125Е + 01 |
0,849Е + 00 |
0,854Е - 01 |
0,275Е + 00 |
0,419Е - 01 |
|
0,60Е + 03 |
0,118Е + 01 |
0,802Е + 00 |
0,810Е - 01 |
0,259Е + 00 |
0,395Е - 01 |
|
0,80Е + 03 |
0,110Е + 01 |
0,745Е + 00 |
0,749Е - 01 |
0,241Е + 00 |
0,367Е - 01 |
|
0,10Е + 04 |
0,105Е + 01 |
0,714Е + 00 |
0,722Е - 01 |
0,231Е + 00 |
0,352Е - 01 |
|
0,15Е + 04 |
0,996Е + 00 |
0,676Е + 00 |
0,683Е - 01 |
0,219Е + 00 |
0,333Е - 01 |
|
0,20Е + 04 |
0,972Е + 00 |
0,660Е + 00 |
0,667Е - 01 |
0,213Е + 00 |
0,325Е - 01 |
|
0,30Е + 04 |
0,952Е + 00 |
0,647Е + 00 |
0,650Е - 01 |
0,209Е + 00 |
0,318Е - 01 |
|
0,40Е + 04 |
0,943Е + 00 |
0,640Е + 00 |
0,645Е - 01 |
0,207Е + 00 |
0,315Е - 01 |
|
0,50Е + 04 |
0,940Е + 00 |
0,638Е + 00 |
0,645Е - 01 |
0,206Е + 00 |
0,314Е - 01 |
|
0,60Е + 04 |
0,936Е + 00 |
0,635Е + 00 |
0,639Е - 01 |
0,206Е + 00 |
0,313Е - 01 |
|
0,80Е + 04 |
0,935Е + 00 |
0,635Е + 00 |
0,639Е - 01 |
0,205Е + 00 |
0,313Е - 01 |
|
0,10Е + 05 |
0,935Е + 00 |
0,635Е + 00 |
0,639Е - 01 |
0,205Е + 00 |
0,313Е - 01 |
Параметр экранирования ядра атомными электронами F(t, Zk) рассчитывают по формуле
F(t, Zk) = 1,70×10-5 hk
![]() , (127)
, (127)
где t - кинетическая энергия рассеиваемого электрона, выраженная в единицах энергия покоя электрона;
Zk - атомный номер k-го элемента;
hk - множитель, характеризующий k-й элемент.
Нумерация и значения параметров Zk, hk для элементов тканеэквивалентного вещества по ГОСТ 18622 представлены в табл. 6.
Таблица 6
Нумерация и значения параметров Zk, hk для элементов тканеэквивалентного вещества
|
O |
H |
С |
N |
|
|
Номер |
1 |
2 |
3 |
4 |
|
Zk |
8 |
1 |
6 |
7 |
|
hk |
1,29 |
1,13 |
1,23 |
1,26 |
ПРИЛОЖЕНИЕ 5
Справочное
АЛГОРИТМ МОДЕЛИРОВАНИЯ ПОТЕРЬ ЭНЕРГИИ ЭЛЕКТРОНОВ В НЕУПРУГИХ ВЗАИМОДЕЙСТВИЯХ
Потери энергии электронов в неупругих взаимодействиях с атомными электронами в тканиэквивалентном веществе, превышающие заданный порог Dtо, моделируют в приближении свободных электронов методом композиции. В качестве исходных данных выбирают энергию электрона t и Dt, выраженные в единицах массы покоя электрона (511 кэВ). Алгоритм моделирования потери энергии Dt, кэВ, в неупругом взаимодействии установлен в пп. 1 - 8.
1. Вычисляют параметры неупругого взаимодействия при энергии электрона t по формулам:
а2 = с1/(1 + со) - с2ln[2(1 - co)]; (132)
2. Для очередного случайного числа у, равномерно распределенного в интервале (0,1) (далее - очередного у), проверяют соблюдение условия
у < а1/aS.
Если оно выполнено, то переходят в п. 3, в противном случае - в п. 5.
3. Вычисляют потерю энергии Dt* (в единицах t), соответствующую очередному у, по формуле
4. Для очередного проверяют соблюдение условия
у > (1 - с2Dt*)/(1 - сос2). (137)
Если оно выполнено, то возвращаются в п. 3, в противном случае переходят в п. 8.
5. Для очередного у проверяют соблюдение условия
Если оно выполнено, то переходят в п. 6, в противном случае вычисляют Dt*, соответствующую очередному y, по формуле
и переходят в п. 8.
6. Вычисляют Dt*, соответствующую очередному y, по формуле
Dt* = (со + ус1)/(1 + ус1). (140
7. Для очередного у проверяют соблюдение условия
у > [1 - c2(1 - Dt*)]/(1 - с1/2). (141)
Если оно выполнено, то возвращаются в п. 6, в противном случае переходят к следующему пункту.
8. Расчет заканчивают, определяя Dt, кэВ, по формуле
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Минздравом СССР
A.С. Александров, д.-р. физ.-мат. наук; С.Г. Андреев, канд. физ.-мат. наук; П.Н. Белоногий, канд. физ.-мат. наук; B.Г. Виденский, д.-р биол. наук; А.А. Волобуев; А.И. Григорьев, д.-р мед. наук; А.Т. Губин, канд. физ.-мат. наук; А.Н. Деденков, д.-р мед. наук; В.И. Иванов, д.-р физ.-мат. наук; Е.Е. Ковалев, д.-р техн. наук; Е.Н. Лесновский, канд. техн. наук; Ю.Л. Минаев; В.А. Панин; Е.В. Пашков, канд. техн. наук; С.М. Перфильева; В.А. Питкевич, канд. физ.-мат. наук; В.А. Сакович, д.-р физ.-мат. наук
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением комитета СССР по управлению качеством продукции и стандартам от 27.03.90 № 624
3. ВВЕДЕН ВПЕРВЫЕ
4. Срок первой проверки - III кв. 1996 г.; периодичность проверки - 5 лет
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Номер пункта приложения |
|
СОДЕРЖАНИЕ
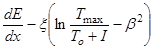 , (
, (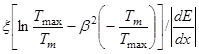 ; (
; ( (
( ], (
], (
 ;
(
;
( ; (
; ( ; (
; (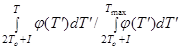 , (
, (