Системы менеджмента качества
в автомобилестроении

АНАЛИЗ ИЗМЕРИТЕЛЬНЫХ
И КОНТРОЛЬНЫХ ПРОЦЕССОВ

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о стандарте

1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции», ОАО «НИЦ КД», ОАО «АВТОВАЗ», ЗАО «АИЦ», ООО СМЦ «Приоритет»

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы управления качеством продукции»

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 мая 2005 г. № 143-ст

4 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет

Введение

В настоящее время данные измерений и контроля используют чаще и более разнообразно, не ограничиваясь проверкой только соответствия характеристик продукции установленным требованиям. В частности, решение о необходимости регулировки производственного процесса теперь обычно основывается на данных измерений (контроля), полученных в результате измерительного (контрольного) процесса. Таким образом, качество измерений влияет на достоверность принимаемых решений по управлению технологическими процессами или о соответствии продукции.

Анализ приемлемости измерительного процесса (качества измерений) представляет собой специально проводимые испытания в реальных производственных условиях (фактически произведенные образцы автомобильных компонентов, средства измерений, применяемые при контроле и испытаниях в процессе производства, операторы, проводящие измерения в реальных внешних условиях и т.д.).

Анализ приемлемости измерительной системы представляет собой специально проводимые испытания в «идеальных» условиях (эталонные образцы автомобильных компонентов, операторы высокой квалификации и т.д.). Таким образом, из анализа «искусственно» исключается большая часть реально существующей изменчивости.

Настоящий стандарт устанавливает основные принципы и методы оценки приемлемости измерительных и контрольных процессов для определения соответствия измеряемого параметра допуску на него, а также регулировки или измерения изменчивости процесса.

Применение настоящего стандарта не ограничено автомобильной отраслью. Методы, установленные в стандарте, применимы на предприятиях других отраслей, заинтересованных в развитии и непрерывном совершенствовании всех процессов системы менеджмента качества.

СОДЕРЖАНИЕ

ГОСТ Р 51814.5-2005

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Дата введения - 2005-07-01

1. Область применения

Настоящий стандарт распространяется на технические объекты автомобилестроения. В стандарте приведены общие рекомендации по применению статистических методов для анализа измерительных и контрольных процессов. Предложенные методы, прежде всего, используются для анализа приемлемости измерительных и контрольных процессов, на которые имеются ссылки в плане управления, то есть процессов определения ключевых характеристик автомобилей и автомобильных компонентов, а также ключевых параметров процессов их изготовления.

Положениями настоящего стандарта можно руководствоваться в ходе планирования качества автомобильных компонентов (APQP), а также при формировании пакета документов для одобрения производства автомобильных компонентов потребителем (РРАР).

Анализ измерительных и контрольных процессов целесообразно применять для:

- первоначального оценивания параметров статистических характеристик измерительных и контрольных процессов для параметров автомобильных компонентов, а также параметров процессов их производства на стадии подготовки производства;

- периодического подтверждения статистических характеристик измерительных и контрольных процессов между проведениями поверок/калибровок средств измерений и контроля;

- внеочередного подтверждения статистических характеристик измерительных и контрольных процессов в случаях замены, модернизации, ремонта средств измерительной техники, изменения технологического процесса, увеличения количества несоответствий измеряемого параметра и т.д.

Стандарт рекомендуется применять при разработке стандартов предприятия, руководств, методики иных документов в рамках действующей на предприятии системы менеджмента качества наряду с такими нормативными документами, как ГОСТ Р ИСО 9001, ГОСТ Р ИСО 5725-1, ГОСТ Р ИСО 5725-2, ГОСТ Р ИСО 5725-3, ГОСТ Р 51814.1, ГОСТ Р 51814.3.

2. Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие нормативные документы:

ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения

ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений

ГОСТ Р 51814.1-2004 (ИСО/ТУ 16949:2002) Системы менеджмента качества в автомобилестроении. Особые требования по применению ГОСТ Р ИСО 9001-2001 в автомобильной промышленности и организациях, производящих соответствующие запасные части

ГОСТ Р 51814.3-2001 Системы качества в автомобилестроении. Методы статистического управления процессами

ГОСТ Р ИСО 9001-2001 Системы менеджмента качества. Требования

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3. Термины, определения и обозначения

3.1. Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями:

3.1.1. средство измерительной техники: Обобщающее понятие, охватывающее технические средства, специально предназначенные для измерений [1].

Примечание - К средствам измерительной техники относят средства измерений и их совокупности, измерительные принадлежности, измерительные устройства.

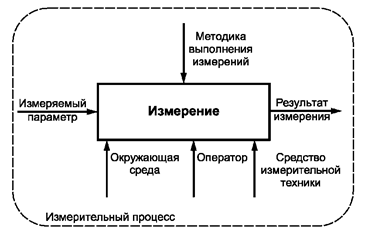
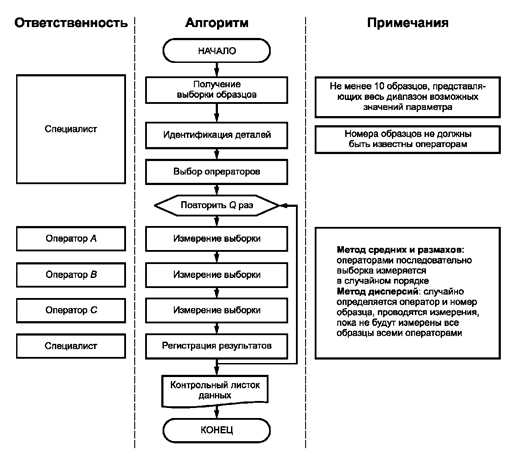
3.1.2. измерительный процесс: Процесс, преобразующий значение измеряемого параметра в результат измерений посредством использования ресурсов (средств измерительной техники и другого оборудования, оператора, окружающей среды и т.д.), регулируемый методикой выполнения измерения (рисунок 1).

3.1.3. средство контроля: Техническое устройство, применяемое для проведения проверки соответствия параметров объекта установленным техническим требованиям (например, калибр, шаблон, пробка, скоба и т.п.).

3.1.4. контрольный процесс: Процесс проверки соответствия параметров объекта установленным техническим требованиям, результатом которого являются данные, полученные по альтернативному признаку.

Рисунок 1 - Иллюстрация к термину «Измерительный процесс»

3.1.5. специалист, ответственный за оценивание статистических характеристик измерительного процесса: Лицо, имеющее квалификацию и опыт, достаточные для выполнения следующих функций:

- планирование и координирование эксперимента;

- выбор операторов;

- отбор образцов для испытания;

- предварительный анализ данных;

- составление отчета по результатам анализа.

3.1.6. оператор: Лицо, обычно выполняющее измерения в ходе процессов производства или контроля автомобильных компонентов.

3.1.7. автомобильный компонент: Комплектующее изделие или материал, используемые при производстве и сборке автомобилей.

3.1.8. образец: Измеряемая единица автомобильного компонента.

3.1.9. измеряемый параметр: Параметр образца, являющийся объектом измерения.

3.1.10. значимый цикл производства: Цикл производства длительностью от 1 до 8 ч с общим количеством последовательно произведенных автомобильных компонентов не менее 300 единиц.

3.1.11. предполагаемое истинное значение измеряемого параметра: Значение параметра детали, полученное экспериментальным путем и настолько близкое к истинному значению, что в целях анализа свойств измерительного процесса может быть использовано в качестве истинного/опорного значения [1].

Примечание - Под истинным значением параметра подразумевают значение, которое могло бы быть получено путем идеального измерения.

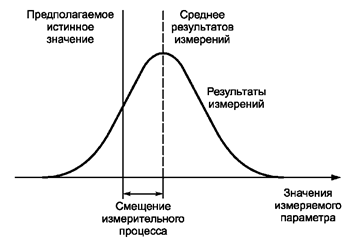
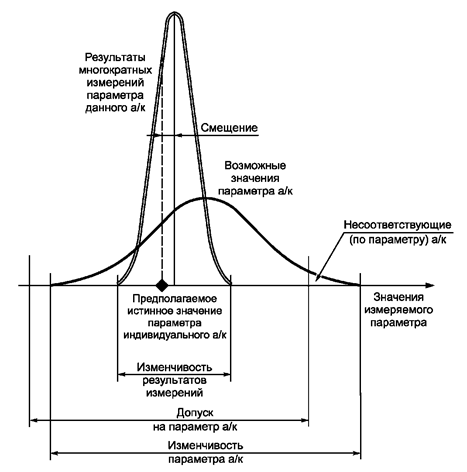
3.1.12. смещение измерительного процесса: Систематическая погрешность в результатах измерений, полученных с помощью измерительного процесса [2].

Примечание - Смещение измерительного процесса, как правило, оценивают как разность между средним значением результатов многократных измерений и предполагаемым истинным значением измеряемого параметра (см. рисунок 2).

Рисунок 2 - Смещение измерительного процесса

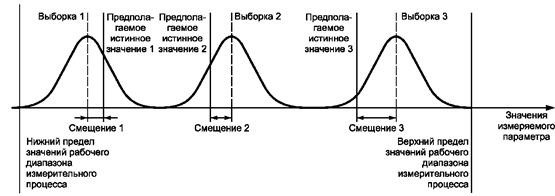
3.1.13. линейность смещения измерительного процесса: Изменение смещения измерительного процесса в диапазоне значений измеряемого параметра (рисунок 3).

Примечание - Зависимость между значениями измеряемого параметра и смещением может быть выражена в виде математического уравнения, таблицы или графика.

3.1.14. обычная причина изменчивости: Источник изменчивости, всегда влияющий на индивидуальные значения результата процесса (ГОСТ Р 51814.3).

3.1.15. особая причина изменчивости: Источник изменчивости, влияние которого на процесс может прерываться, часто непредсказуемо (ГОСТ Р 51814.3).

3.1.16. стабильность измерительного процесса (статистически управляемое состояние): Состояние измерительного процесса, при котором удалены все особые причины изменчивости, то есть наблюдаемая изменчивость может быть объяснена постоянной системой обычных причин (рисунок 4) (ГОСТ Р 51814.3).

Рисунок 3 - Линейность смещения измерительного процесса

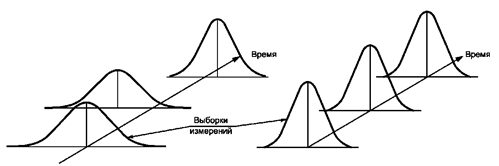
Рисунок 4 - Измерительные процессы в нестабильном (слева) и стабильном (справа) состояниях

Примечание - Стабильность измерительного процесса отражается на контрольной карте отсутствием точек за контрольными границами, трендов, неслучайного поведения в контрольных границах.

3.1.17. цикл измерений: Серия измерений параметра образца, проводимая через определенные временные интервалы (в зависимости от специфики измерительного процесса) в одинаковых условиях с целью проверки измерительного процесса на стабильность. Один цикл измерений характеризует временной «срез» измерительного процесса.

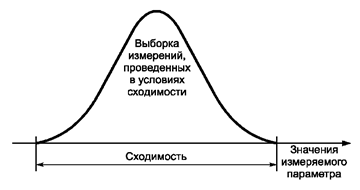
3.1.18. сходимость результатов измерений: Степень близости результатов последовательных измерений одного и того же измеряемого параметра, выполненных повторно одними и теми же средствами измерительной техники, одним и тем же методом и одним и тем же оператором (рисунок 5) [1].

Примечание - Сходимость может быть выражена количественно в виде дисперсионных характеристик результатов измерений.

Рисунок 5 - Сходимость результатов измерений

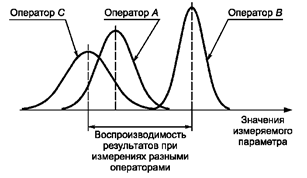
3.1.19. воспроизводимость результатов измерений: Степень близости результатов измерений одного и того же измеряемого параметра, выполненных при измененных условиях измерений (рисунок 6) [1].

Примечания

1. В настоящем стандарте измененные условия включают в себя только изменение оператора.

2. При более общем анализе воспроизводимости результатов измерений измененные условия вместо оператора могут содержать:

- методику выполнения измерений;

- средство измерительной техники;

- место проведения измерений и т.д.

Достоверное установление воспроизводимости требует констатации изменившихся условий измерения.

3. Воспроизводимость может быть выражена количественно в виде дисперсионных характеристик результатов измерений.

Рисунок 6 - Воспроизводимость результатов при измерениях разными операторами

3.1.20. ключевой параметр автомобильного компонента: Параметр автомобильного компонента, полная изменчивость которого может значительно повлиять на качество, надежность, безопасность автомобиля или соответствие автомобиля законодательным нормам.

3.1.21. допуск на параметр автомобильного компонента: Диапазон значений параметра автомобильного компонента, в пределах которого, по соглашению между поставщиком и потребителем, автомобильный компонент считают годным по данному параметру [3].

3.1.22. изменчивость параметра автомобильного компонента: Различия значений параметра индивидуальных автомобильных компонентов [3].

Примечание - Изменчивость может быть выражена количественно в виде дисперсионных характеристик распределения возможных значений параметра.

3.1.23. изменчивость результатов измерений: Различия результатов многократных измерений параметра образца.

Примечания

1. Изменчивость может быть выражена количественно в виде дисперсионных характеристик распределения возможных значений параметра.

2. Отличия между понятиями «Допуск на параметр автомобильного компонента», «Изменчивость параметра автомобильного компонента» и «Изменчивость результатов измерений» представлены на рисунке 7.

3.2. Обозначения

Т - количество циклов измерений (при исследовании измерительного процесса на стабильность);

N - количество образцов, необходимых для эксперимента;

М - количество операторов, участвующих в эксперименте;

Q - количество измерений (попыток) каждого образца каждым оператором или количество измерений в одном цикле (при исследовании измерительного процесса на стабильность);

Рисунок 7 - Изменчивость параметра автомобильного компонента (а/к) и измерительного процесса

i - номер цикла измерений от 1 до T (при исследовании измерительного процесса на стабильность) или номер образца от 1 до N (в остальных случаях);

j - номер оператора от 1 до M;

k - номер измерения (попытки) каждого образца каждым оператором или номер измерения (попытки) в цикле от 1 до Q;

X_ik - результат k-го измерения (попытки) i-го образца (при оценивании линейности смещения) или результат k-го измерения (попытки) образца в i-м цикле (при исследовании измерительного процесса на стабильность);

 - среднее значение результатов измерений для i-го цикла измерений;

R_i - размах результатов измерений для i-го цикла измерений;

 - среднее результатов всех измерений;

 - средний размах всех измерений;

 - верхняя и нижняя границы контрольной карты средних;

UCL_R, LCL_R - верхняя и нижняя границы контрольной карты размахов;

A₂, D₄, D₃ - константы для построения контрольных границ для средних и размахов, зависящие от количества измерений в одном цикле измерений;

X^ист - предполагаемое истинное значение измеряемого параметра;

X_k - результат k-го измерения (попытки) параметра образца;

 - среднее значение результатов выполненных измерений;

B - абсолютное значение смещения измерительного процесса;

% В - относительное значение смещения измерительного процесса;

USL, LSL - верхняя и нижняя границы допуска на измеряемый параметр;

 - среднее значение измеряемого параметра для каждого образца;

 - предполагаемое истинное значение измеряемого параметра i-го образца;

В_i - смещение при измерении параметра i-го образца;

R - коэффициент корреляции;

a, b - коэффициенты уравнения линии регрессии;

L - абсолютное значение линейности смещения измерительного процесса (смещение при верхней границе рабочего диапазона измерительного процесса);

UL, LL - верхняя и нижняя границы рабочего диапазона измерительного процесса;

% L - относительное значение линейности измерительного процесса;

X_ijk - результат k-го измерения (попытки) i-го образца j-м оператором;

 - среднее значение результатов измерений i-го образца j-м оператором;

R_ij - размах результатов измерений i-го образца j-м оператором;

 - среднее значение результатов измерений каждым из операторов;

 - средний размах результатов измерений каждым из операторов;

 - среднее значение результатов измерений каждого образца всеми операторами;

 - среднее значение всех результатов измерений образцов;

R_p - размах значений параметров образца;

 - средний размах всех измерений;

R_o - размах между измерениями операторов;

СКО - среднеквадратическое отклонение;

S_e - оценка СКО сходимости (повторяемости) измерительного процесса;

D₂ - константа для вычисления СКО с помощью размаха;

S_o - оценка СКО воспроизводимости (разными операторами) измерительного процесса;

S_p - оценка СКО изменчивости образца измерительного процесса;

S_m - оценка СКО сходимости (повторяемости) и воспроизводимости измерительного процесса;

S_e² - оценка дисперсии средств измерительной техники (сходимости);

S_o² - оценка дисперсии операторов (воспроизводимости);

S_р² - оценка дисперсии образцов;

S_ор² - оценка дисперсии взаимодействия операторов и образцов;

X_ij - результаты измерений для всех образцов всеми операторами;

 - среднее значение результатов измерений для каждого образца каждым из операторов;

R_i - размах результатов измерений для каждого образца каждым из операторов;

 - средний размах результатов измерений;

K_a - коэффициент, используемый при построении доверительного интервала для истинного значения измеряемого параметра образца при уровне значимости a;

EV - сходимость (повторяемость) результатов измерений;

AV - воспроизводимость (изменчивость от операторов) результатов измерений;

PV - изменчивость образцов;

INT - изменчивость, обусловленная взаимодействием операторов и образцов;

R&R - сходимость и воспроизводимость результатов измерений;

TV - полная изменчивость измерительного процесса;

% EV_SL, % AV_SL, % PV_SL, % INT_SL, % R&R_SL, % TV_SL - относительные (относительно допуска на значение измеряемого параметра образца) составляющие изменчивости;

% EV_TV, % AV_tv, % PV_tv, % INT_TV, % R&R_TV - относительные (относительно полной изменчивости измерительного процесса) составляющие изменчивости;

пр_i - количество образцов, признанных несоответствующими по результатам i-го цикла измерений;

 - среднее количество образцов, признанных несоответствующими по результатам всех циклов измерений;

UCL_np, LCL_np - верхняя и нижняя границы контрольной карты числа несоответствующих единиц в партии;

a_i - количество измерений, в которых образец был признан соответствующим, по результатам i-го цикла измерений;

a_min (a_max) - количество измерений, в которых образец, имеющий наименьшее (наибольшее) значение измеряемого параметра, был признан соответствующим;

Р (X^ист) - вероятность признания образца с известными предполагаемыми истинными значениями Х^ист соответствующим;

N(μ, s²) - нормальное распределение с параметрами (математического ожидания μ и дисперсии s²).

4. Общие положения

4.1. Целью настоящего анализа является получение заключения о приемлемости измерительного процесса при измерениях. Под измерительным процессом подразумевают не только средство измерения, но и совокупность измеряемого образца, средств измерительной техники и другого оборудования, оператора, окружающей среды и соответствующей методики выполнения измерений.

4.2. Статистический анализ измерительных процессов проводят на основании данных, полученных в результате специально проводимого исследования, заключающегося в многократном измерении образцов детали различными операторами.

4.3. Перед проведением исследования измерительного процесса все средства измерений, используемые в измерительном процессе, должны пройти поверку/калибровку.

Разрешающая способность средств измерительной техники должна быть равной, по крайней мере, одной десятой ожидаемой изменчивости характеристики процесса (или ширины поля допуска на измеряемый параметр).

При снятии показаний оборудования результаты измерений следует округлять до ближайшего числа, которое может быть получено. Например, если цена деления 0,1, то результат следует округлять до 0,05.

4.4. Образцы автомобильного компонента должны удовлетворять следующим требованиям:

- быть отобраны из значимого цикла производства;

- наиболее полно представлять весь существующий диапазон изменчивости параметра автомобильного компонента.

4.5. При выборе операторов, осуществляющих сбор данных об измерительном процессе, следует, по возможности, привлекать как операторов, имеющих большой стаж работы, так и новых операторов, чтобы при исследованиях получить наибольшую изменчивость результатов измерений разными операторами.

4.6. Заключение о приемлемости измерительного процесса выдается на основании оценивания его статистических характеристик:

- изменчивости результатов измерений (выраженной количественно через дисперсионные характеристики результатов измерений);

- изменчивости измеряемого параметра (выраженной через аналогичные дисперсионные характеристики либо через допуск на параметр).

4.7. Статистические методы анализа, изложенные в настоящем стандарте, применимы только к измерительным процессам, показания которых могут быть повторены по каждому из измеряемых параметров.

Если в процессе измерений параметр меняет свое значение или образец разрушается, то методы, изложенные в настоящем стандарте, не применимы для анализа такого процесса.

4.8. Методы статистического анализа измерительных процессов, результатами которых являются количественные данные, изложены в разделах 5 - 9.

4.9. Положения, изложенные в 4.1 - 4.6, относятся также и к контрольным процессам. Методы статистического анализа контрольных процессов, результатами которых являются данные, полученные по альтернативному признаку, изложены в разделе 10.

5. Порядок проведения анализа измерительных процессов

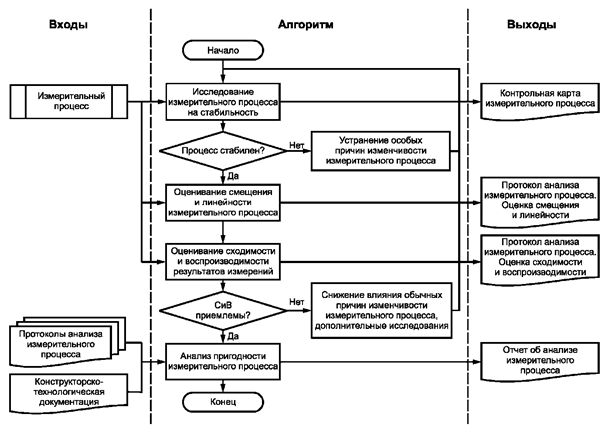
5.1. Первоначальное оценивание статистических характеристик измерительных процессов осуществляют в следующем порядке (рисунок 8):

- исследование измерительного процесса на стабильность;

- в случае нестабильного измерительного процесса - устранение особых причин изменчивости, внесение соответствующих изменений;

- оценивание смещения и линейности смещения измерительного процесса;

- оценивание сходимости и воспроизводимости результатов измерений;

- в случае неприемлемых сходимости и воспроизводимости результатов измерений - анализ причин повышенной изменчивости, проведение корректирующих действий, повторное оценивание сходимости и воспроизводимости;

- подготовка отчета об анализе измерительного процесса.

Рисунок 8 - Схема первоначального оценивания статистических характеристик

измерительных процессов

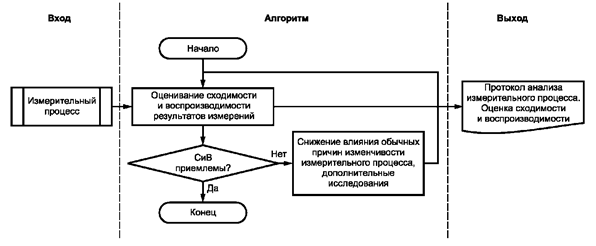
5.2. Периодическое подтверждение статистических характеристик измерительных процессов осуществляют в следующем порядке (рисунок 9):

- оценивание сходимости и воспроизводимости результатов измерений;

- в случае неприемлемых сходимости и воспроизводимости результатов измерений - анализ причин повышенной изменчивости, проведение корректирующих действий и повторное оценивание сходимости/воспроизводимости.

Подтверждение статистических характеристик измерительных процессов осуществляют в зависимости от специфики составляющих измерительного процесса, но не реже одного раза в год.

Рисунок 9 - Схема периодического оценивания сходимости и воспроизводимости

измерительных процессов

5.3. Внеочередное подтверждение статистических характеристик выполняют в случаях:

- замены, модернизации, ремонта средств измерительной техники;

- изменения технологического процесса;

- увеличения количества несоответствий измеряемого параметра и т.д.

6. Исследование измерительного процесса на стабильность

6.1. Для исследования измерительного процесса на стабильность применяют «Контрольные карты средних и размахов» (приложение А).

6.2. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, отбирает образец автомобильного компонента в соответствии со следующими требованиями:

- образец должен быть отобран из значимого цикла производства;

- значение измеряемого параметра отобранного образца должно быть близко к середине поля допуска на него.

6.3. В зависимости от специфики измерительного процесса, временных и денежных затрат специалист определяет периодичность проведения измерений параметра образца (ежедневно, ежесменно, ежечасно и т.д.), а также необходимое количество измерений Q (от трех до пяти раз) в одном цикле измерений.

Рекомендуемое число циклов измерений (для получения достоверных свидетельств стабильности измерительного процесса) Т = 25. Возможно уменьшение количества циклов (с целью сокращения времени эксперимента), но не менее чем до 10.

Указания по проведению измерений специалист заносит в «Контрольную карту средних и размахов».

6.4. Оператор в соответствии с указаниями специалиста выполняет Т циклов измерений (по Q измерений параметра образца в каждом) и заносит результаты измерений в «Контрольную карту средних и размахов».

По окончании эксперимента массив данных должен содержать ровно T циклов повторных измерений образца по Q измерений (попыток). Каждое значение массива х_ik - результат k-го измерения (попытки) образца в i-м цикле. Таким образом, индекс i обозначает номер цикла измерений от 1 до Т, k - номер измерения (попытки) образца в цикле от 1 до Q.

6.5. Для каждого i-го цикла измерений специалист рассчитывает среднее значение результатов измерений , и размах результатов измерений R_i по формулам:

                                                             (1)

                                                     (2)

Результаты расчетов , и R_i заносят в «Контрольную карту средних и размахов».

6.6. Специалист рассчитывает среднее результатов всех измерений  и средний размах  по формулам:

                                                               (3)

                                                                 (4)

Линии среднего значения измеряемого параметра и среднего размаха наносят на «Контрольную карту средних и размахов».

6.7. Специалист рассчитывает контрольные границы для средних и размахов по формулам:

                                                           (5)

                                                            (6)

                                                              (7)

                                                              (8)

где ,  - верхняя и нижняя границы контрольной карты средних соответственно;

UCL_R, LCL_R - верхняя и нижняя границы контрольной карты размахов соответственно;

А₂, D₄, D₃ - константы для построения контрольных границ для средних и размахов, зависящие от количества измерений в одном цикле измерений. Значения констант приведены в приложении Б.

Линии контрольных границ наносят на «Контрольную карту средних и размахов».

6.8. Специалист оценивает стабильность измерительного процесса.

Процесс считают нестабильным, если выполняется хотя бы одно из следующих условий:

- одна или несколько точек находятся за пределами контрольных границ;

- присутствуют серии точек - семь точек подряд находятся по одну сторону от среднего значения или семь точек подряд последовательно возрастают или убывают;

- процесс проявляет другие признаки неслучайного поведения (например, большинство точек группируется около линии среднего либо около контрольных границ и т.д.).

Подробные рекомендации по анализу контрольных карт средних и размахов приведены в ГОСТ Р 51814.3.

Заключение по результатам анализа стабильности измерительного процесса специалист регистрирует в «Контрольной карте средних и размахов».

6.9. В случае стабильности процесса проводят дальнейшие исследования измерительного процесса в соответствии с требованиями разделов 7 - 9.

6.10. В случае нестабильности процесса специалист проводит дополнительное исследование причин изменчивости измерительного процесса в соответствии с рекомендациями раздела 11.

После устранения особых причин изменчивости и снижения влияния обычных причин изменчивости исследование стабильности измерительного процесса следует повторить.

7. Оценивание смещения и линейности смещения измерительного процесса

7.1. Определение предполагаемого истинного значения измеряемого параметра образца

7.1.1. Определение предполагаемого истинного значения измеряемого параметра X^ист осуществляют в метрологическом зале с использованием средства измерительной техники наиболее высокой точности.

7.1.2. В случае, если выполнение условий 7.1.1 невозможно, рекомендуется выбрать из производства образец, значение измеряемого параметра которого попадает в середину интервала допуска, измерить этот образец 20 раз и за предполагаемое истинное значение взять среднее значение полученных измерений в условиях стабильности измерительного процесса.

7.2. Определение смещения измерительного процесса

7.2.1. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, отбирает образец (аналогично 6.2).

7.2.2. Специалист организует определение предполагаемого истинного значения измеряемого параметра X^ист в соответствии с 7.1.

7.2.3. Оператор с использованием оцениваемого средства измерительной техники под наблюдением специалиста последовательно измеряет образец Q раз. Рекомендуемое количество измерений образца Q = 10.

По окончании эксперимента массив данных должен содержать ровно Q повторных измерений образца, в котором каждое значение Х_k - результат k-го измерения (попытки) образца. Таким образом, индекс k - обозначает номер измерения (попытки) образца от 1 до Q.

7.2.4. Специалист регистрирует результаты измерений в «Контрольном листе данных для расчета смещения измерительного процесса» (приложение В).

7.2.5. Специалист рассчитывает среднее значение результатов выполненных измерений  по формуле

                                                              (9)

где Х_k - результат k-го измерения параметра образца.

7.2.6. Специалист рассчитывает абсолютное значение смещения измерительного процесса В по формуле

                                                            (10)

7.2.7. Специалист рассчитывает относительное значение смещения измерительного процесса % В по формуле

                                                      (11)

где USL, LSL - соответственно верхняя и нижняя границы допуска на измеряемый параметр.

7.2.8. Специалист анализирует относительное значение смещения. Рекомендуемое приемлемое значение % В - не более 10.

Смещение следует учитывать при дальнейших расчетах.

7.2.9. Результаты определения смещения измерительного процесса регистрируются в «Контрольном листе данных для расчета смещения измерительного процесса».

7.3. Определение линейности смещения измерительного процесса

В качестве характеристики линейности смещения измерительного процесса рассматривают величину наклона прямой, которая наилучшим образом аппроксимирует зависимость средних значений смещения для различных образцов от их предполагаемых истинных значений. Желательно, чтобы предполагаемые истинные значения испытуемых образцов представляли все возможные значения измеряемого параметра для данного измерительного процесса, а также были равномерно распределены по всему его рабочему диапазону.

7.3.1. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, отбирает N образцов автомобильных компонентов (рекомендуется N = 5), предполагаемые истинные значения измеряемого параметра которых равномерно (по возможности) распределены по всему рабочему диапазону измерительного процесса. Образцы идентифицируют таким образом, чтобы номер образца не был известен оператору.

7.3.2. Специалист организует определение предполагаемых истинных значений  измеряемых параметров каждого образца в соответствии с 7.1.

7.3.3. Оператор с использованием оцениваемого средства измерительной техники под наблюдением специалиста выполняет измерения каждого из образцов по Q раз. Рекомендуемое число измерений образца Q = 10. При измерениях рекомендуется отбирать образцы в случайном порядке.

По окончании эксперимента массив данных должен содержать ровно Q повторных измерений каждого из N образцов, в котором каждое значение X_ik - результат k-го измерения (попытки) i-го образца. Таким образом, индекс i обозначает номер образца от 1 до N, k - номер измерения (попытки) каждого образца оператором от 1 до Q.

7.3.4. Специалист регистрирует результаты измерений на «Контрольном листе данных для расчета линейности смещения измерительного процесса» (приложение Г).

7.3.5. Специалист рассчитывает среднее значение для каждого образца  по формуле

                                                            (12)

где Х_ik - результат k-го измерения параметра i-го образца.

7.3.6. Специалист рассчитывает абсолютное значение смещения измерительного процесса для каждого из образцов по формуле

                                                          (13)

где  - предполагаемое истинное значение измеряемого параметра i-го образца;

B_i - смещение при измерении параметра i-го образца.

Результаты расчета смещения заносят в «Контрольный лист данных для расчета линейности смещения измерительного процесса».

7.3.7 Специалист рассчитывает коэффициент корреляции R между предполагаемыми истинными значениями измеряемых параметров  и соответствующими смещениями B_t измерительного процесса по формуле

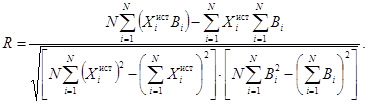                        (14)

Значение коэффициента корреляции заносят в «Контрольный лист данных для расчета линейности смещения измерительного процесса».

7.3.8. Специалист анализирует значения коэффициента корреляции.

При оценивании степени связи (качества приближения) между  и В_i рекомендуется пользоваться следующими соображениями относительно значения коэффициента корреляции. R² принимает следующие значения:

(0; 0,5) - линейная связь между величинами практически отсутствует (изменение смещения в пределах рабочего диапазона нелинейно);

(0,5; 0,75) - линейная связь между величинами слабая (изменение смещения в пределах рабочего диапазона нельзя считать линейным);

(0,75; 0,90) - линейная связь между величинами средняя (изменение смещения в пределах рабочего диапазона можно считать линейным);

(0,90; 1) - линейная связь между величинами сильная (изменение смещения в пределах рабочего диапазона линейно).

7.3.9 Специалист рассчитывает коэффициенты уравнения линии регрессии по формуле

B^* = aX^ист + b,                                                         (15)

где В^* - значение смещения, полученное с помощью уравнения регрессии;

а, b - коэффициенты уравнения линии регрессии, получаемые по формулам:

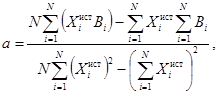                                        (16)

                                               (17)

Линию регрессии наносят на график линейности смещения «Контрольного листа данных для расчета линейности смещения измерительного процесса».

7.3.10. Специалист рассчитывает абсолютное значение линейности смещения измерительного процесса (смещение при верхней границе рабочего диапазона измерительного процесса) L по формуле

L = a · (UL - LL),                                                        (18)

где a - коэффициент уравнения линии регрессии;

UL, LL - верхняя и нижняя границы рабочего диапазона измерительного процесса соответственно.

7.3.11. Специалист рассчитывает относительное значение линейности измерительного процесса % L по формуле

                                                      (19)

При R² > 0,75 изменение смещения в пределах рабочего диапазона измерительного процесса следует учитывать при дальнейших расчетах.

Значения R² абсолютной и относительной линейности смещения измерительного процесса заносят в «Контрольный лист данных для расчета линейности смещения измерительного процесса».

8. Оценивание сходимости и воспроизводимости результатов измерений

8.1. Сбор данных для оценивания сходимости и воспроизводимости

8.1.1. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, отбирает N (рекомендуется N = 10 и N = 5 для метода размахов) образцов автомобильных компонентов (в соответствии с 4.4.).

Указанные образцы идентифицируют таким образом, чтобы номера образцов не были известны операторам.

8.1.2. Для проведения измерений специалист отбирает М операторов (рекомендуется М = 3 и М = 2 для метода размахов) из числа тех, кто обычно осуществляет измерения в процессе производства или контроля измеряемого параметра образца. Измерение выборки каждым из операторов повторяют Q раз (рекомендуется Q не менее 3 и Q = 1 для метода размахов).

8.1.3. По окончании эксперимента массив данных должен содержать ровно Q повторных измерений каждого из N образцов каждым из М операторов, в котором каждое значение X_ijk - результат k-го измерения (попытки) i-го образца j-м оператором. Таким образом, индекс i обозначает номер образца от 1 до N, индекс j - номер оператора (заметим, что в рассматриваемых далее примерах операторы идентифицируются прописными латинскими буквами) от 1 до М, k - номер измерения (попытки) каждого образца каждым оператором от 1 до Q.

Если в результате проведения эксперимента по каким-либо причинам отсутствуют некоторые измерения или присутствуют измерения, полученные при нарушениях хода эксперимента, их следует исключить из рассмотрения. Причем также следует исключить все измерения, связанные с ними, т.е. наряду с отсутствующими или некорректными измерениями нужно исключить все повторные измерения одного оператора по всем образцам или все повторные измерения всех операторов по одному образцу, или конкретное повторное измерение всех операторов по всем образцам.

8.1.4. Для оценивания сходимости и воспроизводимости измерительного процесса в настоящем стандарте изложены три метода: метод размахов (8.2), метод средних и размахов (8.3) и метод дисперсий (8.4).

При выборе метода обработки результатов измерений для оценивания сходимости и воспроизводимости измерительного процесса следует учитывать, что метод дисперсий является самым точным из представленных, однако достаточно сложен для вычисления вручную. Метод размахов самый простой для расчетов, однако не дает возможности получить полную картину изменчивости измерительного процесса и рекомендуется к применению только в условиях ограниченных временных ресурсов.

Рисунок 10 - Порядок сбора данных об измерительном процессе для оценивания его сходимости и воспроизводимости

8.1.5. Процесс сбора данных для оценивания сходимости и воспроизводимости измерительного процесса схематично представлен на рисунке 10.

8.2. Оценивание сходимости и воспроизводимости измерительного процесса методом размахов

Данный метод позволяет получить быструю аппроксимацию изменчивости измерительного процесса. Однако дает только общую картину изменчивости измерительного процесса, не позволяя разделить изменчивость на составляющие.

Обычно в методе размахов используются два оператора (М = 2) и пять образцов (N = 5). При этом каждый оператор измеряет каждый образец один раз (Q = 1). Рекомендуется использовать данный метод в случае жестких ограничений на время проведения испытаний.

8.2.1. Операторы поочередно выполняют измерения всех образцов выборки. При измерениях следует отбирать образцы в случайном порядке.

8.2.2 Специалист, ответственный за оценивание статистических характеристик измерительного процесса, регистрирует результаты измерений Х_ij для всех образцов, всеми операторами в таблице 1.

Светло-серым цветом в таблице выделено место для занесения результатов измерений.

Таблица 1

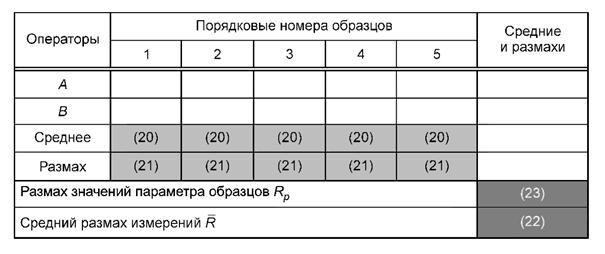
8.2.3. Специалист осуществляет предварительные расчеты для анализа сходимости и воспроизводимости (места для занесения результатов предварительных расчетов выделены серым цветом).

8.2.3.1. Для каждого образца рассчитывают среднее значение результатов его измерений каждым из операторов  и размах результатов его измерений каждым из операторов R_i по формулам:

                                                           (20)

                                                      (21)

Результаты расчетов средних и размахов заносят в соответствующие для каждого образца и каждого оператора ячейки (20) и (21) таблицы 1, обозначенные по номерам формул.

8.2.3.2. Средний размах  результатов измерений рассчитывают по формуле

                                                                (22)

Результат расчета заносят в ячейку (22) таблицы 1.

8.2.3.3. Размах R_p значений параметра образца рассчитывают по формуле

                                                   (23)

Результат расчета заносят в ячейку (23) таблицы 1.

8.2.4. Результаты измерений и предварительных расчетов специалист фиксирует в форме таблицы (аналогичной таблице 1) в «Контрольном листе данных для расчета сходимости и воспроизводимости измерительного процесса» (приложение Д). Ячейки, в которые занесены данные, необходимые для дальнейших расчетов сходимости и воспроизводимости, в таблице 1 выделены темно-серым цветом.

8.2.5. Специалист осуществляет расчет оценок среднеквадратических отклонений (СКО) составляющих изменчивости измерительного процесса.

8.2.5.1. Оценку СКО сходимости (повторяемости) и воспроизводимости измерительного процесса S_m определяют по формуле

                                                               (24)

где D₂ - константа для вычисления СКО с помощью размаха. Таблица значений константы приведена в приложении Ж. При выборе константы D₂ для расчета сходимости принимают Н = MQ = M и G = N.

8.2.5.2. Оценку СКО изменчивости образца измерительного процесса S_p рассчитывают по формуле

                                                                (25)

где D₂ - константа для вычисления СКО с помощью размаха. Таблица значений константы приведена в приложении Ж. При выборе константы D₂ для вычисления изменчивости образца принимают Н = N и G = 1.

8.2.6. Результаты расчетов изменчивости измерительного процесса специалист регистрирует в «Протоколе анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

8.3. Оценивание сходимости и воспроизводимости измерительного процесса методом средних и размахов

8.3.1. Операторы поочередно выполняют измерения всех образцов выборки. При измерениях следует отбирать образцы в случайном порядке.

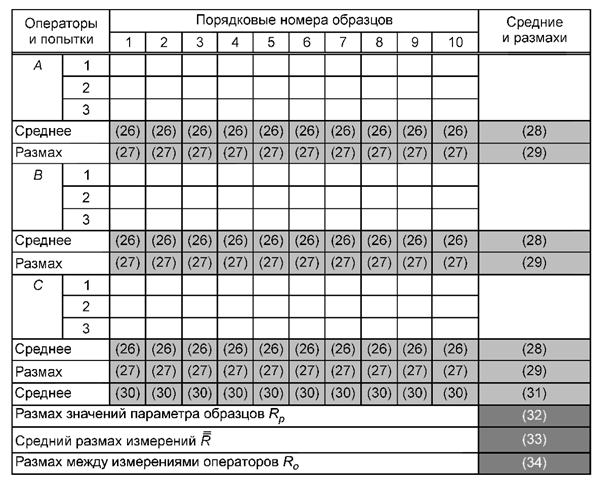
8.3.2. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, регистрируют результаты измерения X_ijk для всех образцов, операторов и попыток в таблице 2. Светло-серым цветом в таблице выделено место для занесения результатов измерений.

8.3.3. Специалист осуществляет предварительные расчеты для анализа сходимости и воспроизводимости (места для занесения результатов предварительных расчетов выделены серым цветом).

8.3.3.1. Для каждого образца рассчитывают среднее значение результатов его измерений каждым из операторов  и размах результатов его измерений каждым из операторов R_ij по формулам:

                                                           (26)

                                                   (27)

Результаты расчетов средних и размахов заносят в соответствующие для каждого образца и каждого оператора ячейки (26) и (27) таблицы 2, обозначенные по номерам формул.

8.3.3.2. Для каждого оператора рассчитывают среднее значение  и средний размах  результатов его измерений по формулам:

                                                           (28)

                                                             (29)

Результаты расчетов средних и размахов заносят в соответствующие для каждого оператора ячейки (28) и (29) таблицы 2.

8.3.3.3. Для каждого образца рассчитывают среднее значение  результатов его измерений всеми операторами по формуле

                                                           (30)

Результаты расчетов средних заносят в соответствующие для каждого образца ячейки (30) таблицы 2.

Таблица 2

8.3.3.4. Среднее значение  всех результатов измерений образцов и размах R_p значений параметра образцов рассчитывают по формулам:

                                                          (31)

                                                    (32)

Результаты расчетов средних и размахов заносят в соответствующие для каждого оператора ячейки (31) и (32) таблицы 2.

8.3.3.5. Средний размах всех измерений  рассчитывают по формуле

                                                             (33)

Результат заносят в ячейку (33) таблицы 2.

8.3.3.6. Размах между измерениями операторов R_o рассчитывают по формуле

                                                   (34)

Результат заносят в ячейку (34) таблицы 2.

8.3.4. Результаты измерений и предварительных расчетов специалист фиксирует в форме таблицы (аналогичной таблице 2) в «Контрольном листе данных для расчета сходимости и воспроизводимости измерительного процесса» (приложение Д). Ячейки, в которые занесены данные, необходимые для дальнейших расчетов сходимости и воспроизводимости, в таблице 2 выделены темно-серым цветом.

8.3.5. Специалист осуществляет расчет оценок среднеквадратических отклонений (СКО) составляющих изменчивости измерительного процесса.

8.3.5.1. Оценку СКО сходимости (повторяемости) измерительного процесса S_e определяют по формуле

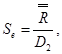                                                            (35)

где D₂ - константа для вычисления СКО с помощью размаха. Таблица значений константы приведена в приложении Ж. При выборе константы D₂ для расчета сходимости принимают Н = Q и G = MN.

8.3.5.2. Оценку СКО воспроизводимости измерительного процесса определяют по формуле

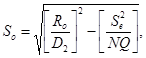                                                   (36)

где D₂ - константа для вычисления СКО с помощью размаха. Таблица значений константы приведена в приложении Ж. При выборе константы D₂ для расчета воспроизводимости принимают H = M и G = 1.

Если под радикалом окажется отрицательное число, S_o = 0.

8.3.5.3. Оценку СКО изменчивости образца измерительного процесса S_p определяют по формуле (25).

8.3.6. Результаты расчетов СКО составляющих изменчивости измерительного процесса специалист регистрирует в «Протоколе анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

8.4. Оценивание сходимости и воспроизводимости измерительного процесса методом дисперсий

8.4.1. Операторы поочередно выполняют измерения всех образцов выборки, причем следует уделить особое внимание случайному порядку сбора данных. Рекомендуется определять случайно не только номера измеряемых образцов, но и оператора, выполняющего измерения, причем этот порядок должен быть различным для различных попыток.

8.4.2. Специалист, ответственный за оценивание статистических характеристик измерительного процесса, регистрирует результаты измерений X_ijk для всех образцов, операторов и попыток в таблице 2. Светло-серым цветом в таблице выделено место для занесения результатов измерений.

8.4.3 Специалист осуществляет предварительные расчеты для анализа сходимости и воспроизводимости (место для занесения результатов предварительных расчетов выделены серым цветом).

Специалист осуществляет расчеты средних значений результатов измерений по формулам (26), (28), (30) и (31). Результаты расчетов заносят в соответствующие ячейки таблицы «Контрольного листа данных для расчета сходимости и воспроизводимости» (схема заполнения приведена в таблице 2). Ячейки, содержащие данные о размахах, не заполняют при оценивании сходимости и воспроизводимости методом дисперсий.

8.4.4. Результаты измерений и предварительные расчеты специалист регистрирует в «Контрольном листе данных для расчета сходимости и воспроизводимости измерительного процесса» (приложение Д).

8.4.5. С применением средств вычислительной техники специалист осуществляет расчет оценок дисперсий составляющих изменчивости измерительного процесса.

8.4.5.1. Оценку дисперсии S_e² средств измерительной техники (сходимости) определяют по формуле

                                  (37)

где NM(Q - 1) - число степеней свободы.

8.4.5.2 Оценку дисперсии S_o² операторов (воспроизводимости) определяют по формуле

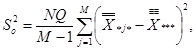                                         (38)

где М - 1 - число степеней свободы.

8.4.5.3. Оценку дисперсии S_p² образцов рассчитывают по формуле

                                         (39)

где N - 1 - число степеней свободы.

8.4.5.4. Оценку дисперсии  взаимодействия операторов и образцов рассчитывают по формуле

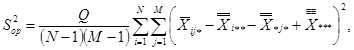                    (40)

где (N - 1)(M - 1) - число степеней свободы.

Следует заметить, что данная составляющая изменчивости не может быть оценена по методу средних и размахов.

Поскольку дисперсия выборки равна квадрату СКО этой выборки, дисперсии, полученные в 8.3.5, могут быть легко преобразованы в соответствующие СКО (для аналогии с методом средних и размахов).

8.4.6. Значимость влияния взаимодействия оператора и образца на изменчивость результатов измерений можно оценить по следующему алгоритму.

8.4.6.1. Специалист рассчитывает соотношение

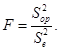                                                             (41)

8.4.6.2. По таблице F-распределения (распределения Фишера-Снедекора), приведенной в приложении И, при уровне значимости a = 0,05 определяют критическое значение распределения F_a(k₁, k₂), где k₁ - число степеней свободы большей дисперсии (из  и ), k₂ - число степеней свободы меньшей дисперсии (из  и ). Числа степеней свободы  и  равны (N - 1)(M - 1) и NM(Q - 1) соответственно.

8.4.6.3. Если F < F_a(k₁, k₂) то влияние изменчивости взаимодействия между оператором и образцом признается незначимым и в дальнейших расчетах не участвует. В противном случае влияние изменчивости взаимодействия между оператором и образцом признается значимым.

8.4.7. Результаты расчета оценок дисперсий, а также вывод о значимости изменчивости взаимодействия между оператором и образцом заносят в «Протокол анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

8.5. Оценивание приемлемости измерительного процесса

8.5.1. Изменчивость какой-либо составляющей измерительного процесса определяют как доверительный интервал при уровне значимости a (рекомендуется a = 0,99) для истинного значения измеряемого параметра образца, то есть если X - результат одного измерения параметра образца, то истинное значение измеряемого параметра с вероятностью a будет лежать в интервале

где K_a - определяют исходя из уровня значимости a и таблицы значений функции Лапласа, приведенной в приложении К. Для рекомендуемого уровня значимости a = 0,99 значение K_a = 5,15;

S_* - СКО анализируемой составляющей изменчивости.

8.5.2. Специалист рассчитывает доверительные интервалы для составляющих изменчивости измерительного процесса для заданного уровня значимости a.

8.5.2.1. Сходимость EV (повторяемость) результатов измерений рассчитывают по формуле

EV = K_a · S_e.                                                                (42)

8.5.2.2. Воспроизводимость AV (изменчивость от операторов) результатов измерений рассчитывают по формуле

AV = K_a · S_o.                                                               (43)

При анализе изменчивости по методу дисперсий в случае, если влияние взаимодействия между оператором и образцом признано значимым (8.4.6), формула для расчета воспроизводимости имеет вид

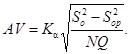                                                       (44)

8.5.2.3. Изменчивость PV образцов рассчитывают по формуле

PV = K_a · S_p.                                                             (45)

При анализе изменчивости по методу дисперсий в случае, если влияние взаимодействия между оператором и образцом признано значимым (8.4.6), формула для расчета изменчивости образцов имеет вид

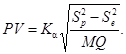                                                        (46)

8.5.2.4. Изменчивость INT, обусловленную взаимодействием операторов и образцов, рассчитывают по формуле

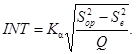                                                        (47)

Данную составляющую изменчивости измерительного процесса вычисляют только при анализе изменчивости по методу дисперсий и в случае, если влияние взаимодействия между оператором и образцом признано значимым (8.4.6).

8.5.2.5. Сходимость и воспроизводимость R&R результатов измерений рассчитывают по формуле

                                                       (48)

При анализе изменчивости методом дисперсий в случае, если влияние взаимодействия между оператором и образцом признано значимым (8.4.6), формула для расчета сходимости и воспроизводимости результатов измерений имеет вид

                                                  (49)

При анализе изменчивости по методу размахов расчет сходимости и воспроизводимости проводят по формуле

R&R = K_a · S_m.                                                               (50)

8.5.2.6. Полную изменчивость TV измерительного процесса рассчитывают по формуле

                                                        (51)

8.5.3. Результаты расчета составляющих изменчивости заносят в «Протокол анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

8.5.4. Оценивание приемлемости измерительного процесса

8.5.4.1. Оценка приемлемости измерительного процесса заключается в сравнении его сходимости и воспроизводимости с полем допуска или полной изменчивостью измеряемого параметра образца.

8.5.4.2. Приемлемость измерительного процесса для оценки соответствия допуску

8.5.4.2.1. Приемлемость измерительного процесса, применяемую для оценки соответствия измеряемого параметра образца допуску на него, определяют исходя из анализа величины относительной сходимости и воспроизводимости % R&R_SL, рассчитываемой по формуле

                                                   (52)

8.5.4.2.2. На основании величины относительной сходимости и воспроизводимости % R&R_SL и в соответствии с рекомендациями, приведенными в таблице 3, специалист делает выводы о приемлемости измерительного процесса для оценки соответствия допуску (таблица 3).

Результаты проведенных расчетов и выводы о приемлемости измерительного процесса для оценки соответствия допуску специалист регистрирует в «Протоколе анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

Таблица 3

8.5.4.3. Приемлемость измерительной системы для целей регулировки или измерения изменчивости процесса оценивают аналогично анализу приемлемости измерительного процесса для оценки соответствия допуску (8.4.4.2). Однако вместо % R&R_sl рассматривают % R&R_TV, полученную как отношение сходимости и воспроизводимости к величине полной изменчивости измерительного процесса по формуле

                                              (53)

8.5.5. Для более полного анализа измерительного процесса вычисляют относительные значения составляющих изменчивости (сходимость, воспроизводимость, изменчивость образца, взаимодействие оператора и образца) по формулам

                                                  (54)

                                                  (55)

                                                  (56)

                                                (57)

При подстановке в формулы (54) - (57) вместо полной изменчивости измерительного процесса величины допуска USL - LSL получают относительную изменчивость составляющих процесса относительно допуска.

8.5.6. Результаты вычислений заносят в «Протокол анализа сходимости и воспроизводимости измерительного процесса» (приложение Е).

8.5.7. Для определения приоритетных путей снижения изменчивости измерительного процесса относительные значения составляющих изменчивости ранжируют по убыванию. Полученная очередность составляющих изменчивости соответствует очередности применения к ним мероприятий для улучшения всего измерительного процесса.

9. Отчет об анализе измерительного процесса

В состав отчета об анализе измерительного процесса рекомендуется включать следующие результаты.

9.1. Контрольная карта средних и размахов с выводом о стабильности измерительного процесса (приложение А).

9.2. Контрольные листы данных для расчета смещения (приложение В) и линейности смещения (приложение Г) измерительного процесса.

9.3. Протокол анализа сходимости и воспроизводимости измерительного процесса (приложение Е).

9.4. Общие выводы об измерительном процессе с заключением (в произвольной форме). Возможны следующие виды заключения о приемлемости измерительного процесса:

- измерительный процесс приемлем;

- измерительный процесс может быть приемлем в зависимости от важности применения, стоимости средств измерительной техники и т.п.;

- требуются улучшения измерительного процесса.

10. Анализ контрольных процессов

10.1. Порядок проведения анализа контрольных процессов

10.1.1. Первоначальное оценивание статистических характеристик контрольных процессов для параметров автомобилей и автомобильных компонентов, а также параметров процессов их производства осуществляют в следующем порядке (рисунок 11):

- исследуют контрольный процесс на стабильность;

- в случае, если контрольный процесс нестабилен, устраняют особые причины изменчивости, вносят соответствующие изменения в операции контроля;

- оценивают смещение и сходимость результатов контроля;

- в случае, если по результатам оценивания смещения и сходимости контрольный процесс признают неприемлемым, модифицируют средства контроля, вносят соответствующие изменения в операции контроля;

- составляют отчет об анализе контрольного процесса.

10.1.2. Периодическое подтверждение статистических характеристик контрольных процессов осуществляют в следующем порядке:

- оценивают приемлемость контрольного процесса экспресс-методом;

- в случае, если контрольный процесс признан неприемлемым, модифицируют средства контроля, вносят соответствующие изменения в операции контроля и оценивают модифицированный контрольный процесс полным методом (10.1.1).

Подтверждение статистических характеристик контрольных процессов осуществляют в зависимости от специфики составляющих контрольного процесса, но не реже одного раза в год.

10.1.3. Внеочередное подтверждение статистических характеристик выполняют в случаях:

- замены, модернизации, ремонта средств контроля;

- изменения технологического процесса;

- увеличения количества несоответствий контролируемого параметра и т.д.

Рисунок 11 - Схема первоначального оценивания статистических характеристик контрольных процессов

10.2. Исследование контрольного процесса на стабильность

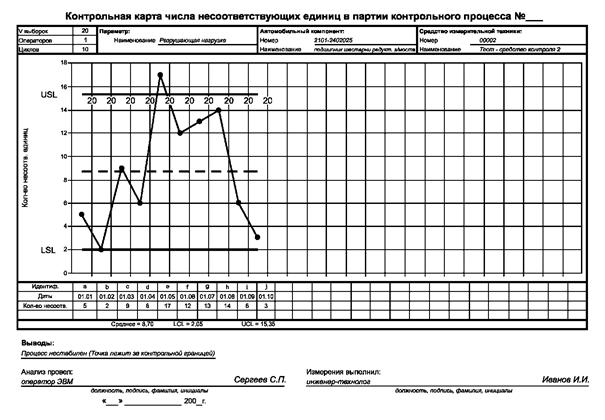
10.2.1. Анализ стабильности контрольного процесса проводят с применением «Контрольной карты числа несоответствующих единиц в партии (np-карты)» (приложение Л).

10.2.2. Специалист, ответственный за оценивание статистических характеристик контрольного процесса, с помощью универсальных средств измерений отбирает N (рекомендуется N = 25) образцов автомобильного компонента, по возможности наиболее полно представляющих весь диапазон изменения контролируемого параметра.

10.2.3. В зависимости от специфики контрольного процесса специалист определяет периодичность проведения измерений параметра образцов (ежедневно, ежесменно, ежечасно и т.д.). Указания по проведению измерений специалист заносит в «Контрольную карту числа несоответствующих единиц в партии».

10.2.4. Оператор в соответствии с указаниями специалиста выполняет Т (рекомендуется Т = 25) циклов контроля выборки образцов и заносит количество образцов np_i, признанных несоответствующими в каждом i-м цикле измерений, в «Контрольную карту числа несоответствующих единиц в партии».

10.2.5. Специалист рассчитывает среднее количество образцов  признанных несоответствующими, по формуле

                                                    (58)

где Т - количество циклов контроля;

пр_i - количество образцов, признанных несоответствующими по результатам i-го цикла контроля.

Линию среднего количества образцов, признанных несоответствующими, наносят на «Контрольную карту числа несоответствующих единиц в партии».

10.2.6. Специалист рассчитывает контрольные границы по формулам:

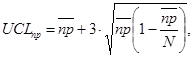                                              (59)

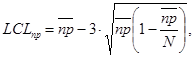                                              (60)

где UCL_np, LCL_np - соответственно верхняя и нижняя границы контрольной карты числа несоответствующих единиц в партии.

Линии контрольных границ наносят на «Контрольную карту числа несоответствующих единиц в партии».

10.2.7. Специалист оценивает стабильность контрольного процесса.

Процесс нестабилен, если выполняется хотя бы одно из следующих условий:

- одна или несколько точек находятся за пределами контрольных границ;

- присутствуют серии точек - семь точек подряд находятся по одну сторону от среднего значения или семь точек подряд последовательно возрастают или убывают;

- процесс проявляет другие признаки неслучайного поведения (например, большинство точек группируется около линии среднего либо около контрольных границ и т.д.).

Подробно рекомендации по анализу «Контрольной карты числа несоответствующих единиц в партии» приведены в ГОСТ Р 51814.3.

Заключение по результатам анализа контрольного процесса на стабильность специалист регистрирует в «Контрольной карте числа несоответствующих единиц в партии».

10.2.8. В случае, если контрольный процесс стабилен, следует оценить смещение и сходимость контрольного процесса в соответствии с требованиями 10.3.

10.2.9. В случае, если контрольный процесс нестабилен, специалист проводит дополнительное исследование причин изменчивости контрольного процесса в соответствии с рекомендациями раздела 11.

После устранения особых причин изменчивости и снижения влияния обычных причин изменчивости исследование контрольного процесса на стабильность следует повторить.

10.3. Оценивание смещения и сходимости контрольного процесса

В настоящем разделе рассматривают средство контроля, оценивающее выход параметра за нижнюю границу допуска. Рассмотренный случай легко обобщается на средство контроля, оценивающее выход параметра за верхнюю границу допуска.

10.3.1. Специалист, ответственный за оценивание контрольного процесса, совместно с оператором осуществляют отбор образцов. Отбор образцов является очень важной частью оценивания приемлемости контрольного процесса.

10.3.1.1. Специалист отбирает N (рекомендуется N = 8) образцов, по возможности, находящихся как в пределах допуска, так и выходящих за его границы. Для отобранных образцов в соответствии с требованиями 7.1 определяют предполагаемые истинные значения измеряемого параметра. Значения измеряемого параметра отобранных образцов должны быть, по возможности, равномерно распределены в пределах допуска на измеряемый параметр.

10.3.1.2. Оператор с применением исследуемого средства контроля контролирует каждый из образцов Q раз (рекомендуется Q = 20). Для каждого из образцов специалист регистрирует количество случаев a_i, в которых образец был признан соответствующим, в «Контрольном листе данных для расчета смещения и сходимости контрольного процесса» (приложение М).

10.3.1.3. Образец, имеющий наименьшее значение измеряемого параметра, по результатам измерений должен быть Q раз признан несоответствующим, то есть удовлетворять условию

a_min = 0.                                                                  (61)

Образец, имеющий наибольшее значение измеряемого параметра, по результатам измерений должен быть Q раз признан соответствующим, то есть удовлетворять условию

a_max = Q.                                                                  (62)

Для остальных (шести) образцов количество измерений, по которым образец был признан соответствующим, должно находиться в диапазоне

0 < a_i < Q.                                                                 (63)

Действия в случае несоответствия результатов контроля перечисленным критериям описаны в таблице 4. Результаты выбора и контроля образцов регистрируются в «Контрольном листе данных для расчета смещения и сходимости контрольного процесса».

Таблица 4

10.3.2. Для отобранных образцов с известными предполагаемыми истинными значениями X^ист рассчитывают вероятность признания образца соответствующим Р(Х^ист) по правилам, изложенным в таблице 5.

Таблица 5

Результаты расчета вероятностей регистрируют в «Контрольном листе данных для расчета смещения и сходимости контрольного процесса».

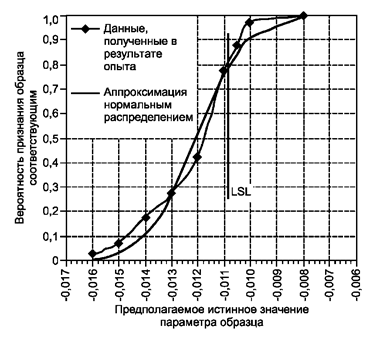
Рисунок 12 - Вид аппроксимации вероятности признания образцов соответствующими нормальным распределением

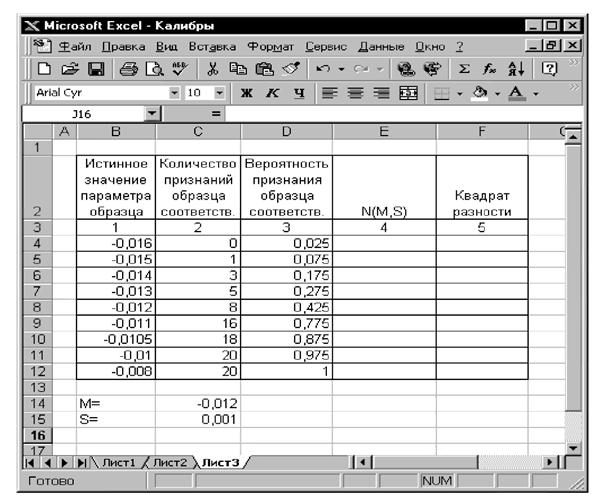
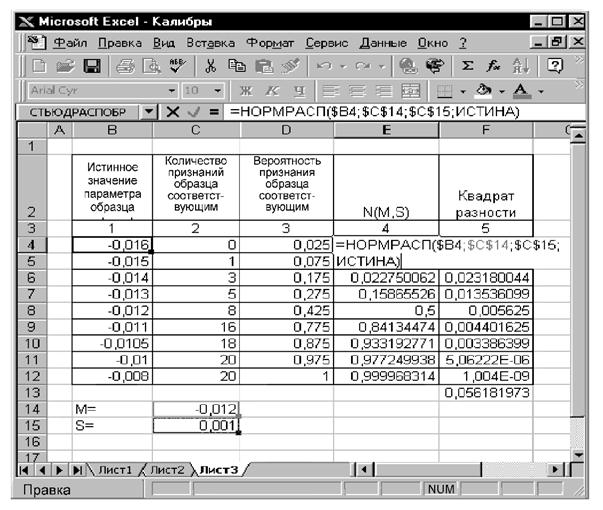
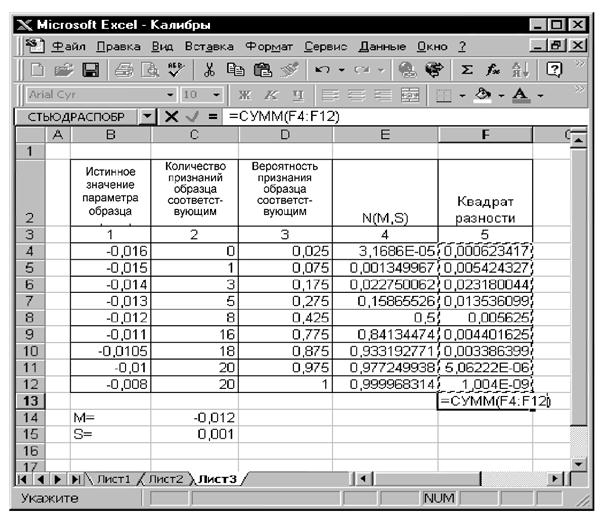
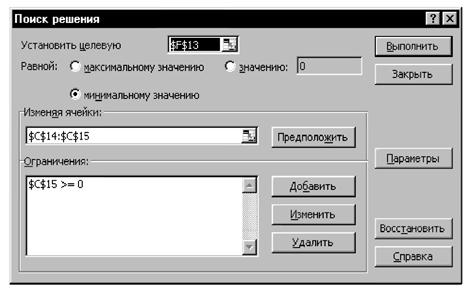
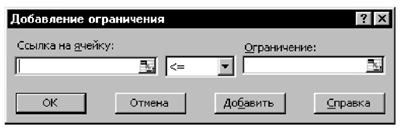
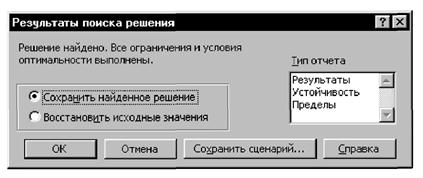
10.3.3. Предполагаемые истинные значения образцов и вероятности признания образцов соответствующими заносят в таблицу MS Excel для подбора параметров (математического ожидания μ и дисперсии s²) аппроксимирующего нормального распределения N(μ, s²) методом наименьших квадратов (рисунок 12). Инструкция по подбору параметров нормального распределения с использованием MS Excel приведена в приложении Н.

Полученные параметры аппроксимирующего распределения, а также кривую вероятности признания образца соответствующим заносят в «Протокол анализа смещения и сходимости контрольного процесса» (приложение П).

10.3.4. На основании подобранных параметров нормального распределения специалист рассчитывает предполагаемые истинные значения X^ист со следующими вероятностями признания образцов соответствующими Р(X^ист) по формулам, представленным в таблице 6.

Таблица 6

10.3.5. Специалист рассчитывает значения смещения и сходимости контрольного процесса.

10.3.5.1. Смещение контрольного процесса В рассчитывают по формуле

                                                           (72)

где LSL - нижняя граница допуска.

Для средства контроля, оценивающего выход за верхнюю границу, вместо LSL используется USL.

10.3.5.2. Сходимость контрольного процесса EV рассчитывают по формуле

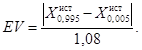                                                    (73)

Для приборов контроля сходимость нормальна и независимо распределена, и не зависит от объемов партий. Сходимость прибора смещена так, что в среднем превышает образцовую сходимость приблизительно на 8 %. Поэтому оценку сходимости, полученную по изложенному методу, нужно поделить на 1,08.

10.3.5.3. Результаты оценивания смещения В и сходимости EV контрольного процесса регистрируют в «Протоколе анализа смещения и сходимости контрольного процесса» (приложение П).

10.3.6. Анализ приемлемости контрольного процесса проводят путем проверки гипотезы о значимом отличии смещения контрольного процесса от нуля.

10.3.6.1. Специалист рассчитывает соотношение

                                                            (74)

10.3.6.2. По таблице t-распределения (распределения Стьюдента), приведенной в приложении Р, с уровнем значимости a = 0,025 для односторонней критической области определяют критическое значение распределения t, где k - число степеней свободы, равное М - 1.

10.3.6.3. Если t < t_ak, то смещение средства контроля признают незначительно отличным от нуля.

10.3.6.4. Если t ³ t_ak, то смещение средства контроля признают значительно отличным от нуля и необходима модификация средства контроля,

10.3.6.5. Вывод о значимом отличии смещения контрольного процесса от нуля регистрируют в «Протоколе анализа смещения и сходимости контрольного процесса».

10.4. Экспресс-метод оценивания приемлемости контрольного процесса

10.4.1. Для оценивания приемлемости контрольного процесса специалист отбирает N (рекомендуется N = 20) образцов автомобильного компонента. Желательно, чтобы среди образцов были как образцы со значениями измеряемого параметра выше, так и ниже контролируемой границы допуска.

10.4.2. Специалист отбирает для проведения измерений M операторов (рекомендуется М = 2) из числа тех, кто обычно осуществляет контроль автомобильных компонентов.

10.4.3. Операторы поочередно проводят контроль всех образцов. При контроле следует отбирать образцы в случайном порядке. Контроль выборки каждым из операторов повторяют Q раз (Q = 2).

10.4.4. Результаты решений операторов о соответствии/несоответствии параметра образцов специалист регистрирует в «Протоколе исследования контрольного процесса экспресс-методом» (приложение С).

10.4.5. Контрольный процесс признают приемлемым, если по каждому из образцов все решения операторов совпадают. Иначе контрольный процесс признают неприемлемым.

10.4.6. Вывод о приемлемости контрольного процесса специалист регистрирует в «Протоколе исследования контрольного процесса экспресс-методом».

10.5. Отчет об анализе контрольного процесса

В состав полного отчета об анализе контрольного процесса рекомендуется включать следующие результаты:

- контрольную карту числа несоответствующих единиц в партии с выводом о стабильности контрольного процесса (приложение Л);

- контрольные листы данных о контрольном процессе (приложение М);

- протокол анализа смещения и сходимости контрольного процесса (приложение П);

- общие выводы о контрольном процессе с заключением (в произвольной форме).

При анализе контрольного процесса экспресс-методом составление отчета не требуется.

11. Анализ причин изменчивости измерительных и контрольных процессов

11.1. Причины изменчивости результатов измерений анализируют в случае, если какую-либо из статистических характеристик измерительного или контрольного процесса по результатам измерений признают неприемлемой.

11.2. Характер влияния причины - обычная или особая причина - определяют при анализе стабильности измерительного или контрольного процесса.

Влияние особых причин изменчивости характеризуется выходом точек за контрольные границы карты, трендом, любым другим неслучайным поведением точек на контрольной карте.

Повышенное влияние обычных причин изменчивости характеризуется увеличенным (по сравнению с допуском на параметр) расстоянием между контрольными границами карты.

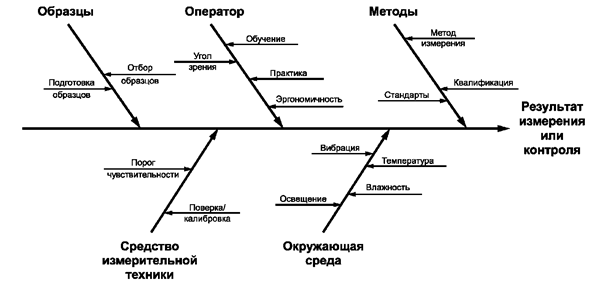
11.3. Группы причин изменчивости измерительного процесса (схематично представлены на рисунке 13):

- несоответствия образцов измерений;

- индивидуальные особенности операторов;

- несовершенство методов измерений;

- несоответствия средств измерений;

- несоответствия окружающей среды.

11.3.1. При неприемлемом значении смещения (% В > 10 %) измерительного или контрольного процесса возможными причинами могут быть:

- несоответствие параметра образца;

- износ средств измерительной техники;

- некорректная настройка средств измерительной техники;

- средство измерительной техники некорректно поверено/откалибровано;

- неправильное применение методики измерений оператором;

- неверная методика обслуживания и ремонта средств измерительной техники.

Рисунок 13 - Группы причин изменчивости измерительного или контрольного процесса

11.3.2. При нелинейном смещении измерительного процесса (R² < 0,75) возможными причинами могут быть:

- средство измерительной техники некорректно поверено/откалибровано на нижней и/или верхней границе рабочего диапазона измерительного процесса;

- несоответствия образцов на верхней/нижней границе;

- износ средств измерительной техники;

- нестабильность внутренних характеристик конструкции средств измерительной техники.

11.3.3. При неприемлемом значении сходимости результатов контроля или измерений возможными причинами могут быть:

- необходимость обслуживания/ремонта или модернизации средств измерительной техники;

- слабая фиксация средств измерительной техники;

- повышенная изменчивость измеряемых параметров образцов.

11.3.4. При неприемлемом значении воспроизводимости результатов измерений возможными причинами могут быть:

- недостаточный порог чувствительности средств измерительной техники;

- недостаточная квалификация/подготовка операторов;

- необходимость специального приспособления для операторов.

Приложение А
(рекомендуемое)

Пример заполнения «Контрольной карты средних и размахов»

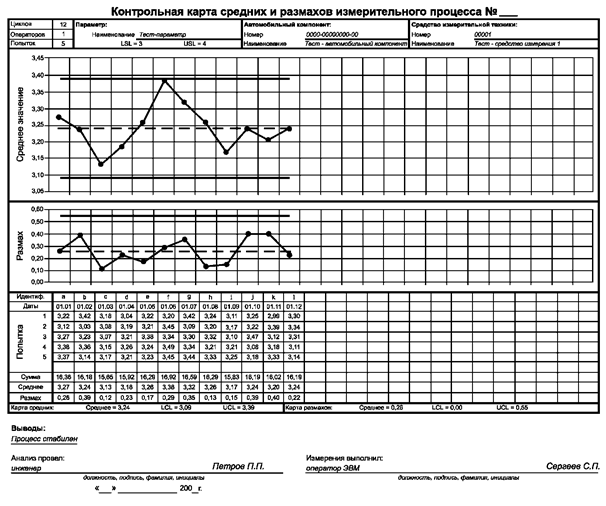
На рисунке А.1 представлен пример заполнения контрольной карты средних и размахов.

Рисунок А.1 - Пример заполнения «Контрольной карты средних и размахов»

Приложение Б
(рекомендуемое)

Константы для построения контрольных границ

Таблица Б.1

Приложение В
(обязательное)

Приложение Г
(обязательное)

Приложение Д
(обязательное)

Приложение Е
(обязательное)

Приложение Ж
(рекомендуемое)

Константы для расчета СКО

В таблице Ж.1 приведена таблица значений константы D2, используемой при расчете СКО на основе значения размаха.

Таблица Ж.1

Приложение И
(рекомендуемое)

Таблица значений распределения F-Фишера-Снедекора

В таблице И.1 приведены значения F-распределения (распределения Фишера-Снедекора) при уровне значимости a = 0,05

Таблица И.1

Примечание - k₁, k₂ - числа степеней свободы большей и меньшей дисперсии соответственно.