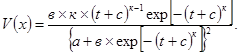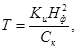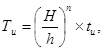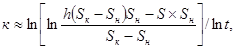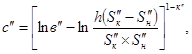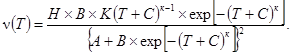|
|
Государственный дорожный научно-исследовательский институт ФГУП «СОЮЗДОРНИИ» |
УСОВЕРШЕНСТВОВАННАЯ МЕТОДИКА
РАСЧЕТА ОСАДКИ НАСЫПИ НА СЛАБЫХ
ГРУНТАХ НА ОСНОВЕ РЕАЛИЗАЦИИ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ПРОЦЕССОВ ЛАБОРАТОРНЫХ ИСПЫТАНИЙ
ОБРАЗЦОВ
Москва 2002
УСОВЕРШЕНСТВОВАННАЯ МЕТОДИКА РАСЧЕТА ОСАДКИ ДОРОЖНОЙ НАСЫПИ НА СЛАБЫХ ГРУНТАХ НА ОСНОВЕ РЕАЛИЗАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРОЦЕССОВ ЛАБОРАТОРНЫХ ИСПЫТАНИЙ ОБРАЗЦОВ. Союздорнии. М., 2002.
Отражен новый подход к решению задачи прогноза осадки насыпи на участках залегания слабых грунтов путем реализации математических корреляционных моделей процессов лабораторных компрессионных и консолидационных испытаний образцов грунта расчетного слоя. Предложены зависимости и новые схемы решения основных задач проблемы с учетом консолидационных свойств конкретных грунтов и условий их работы в конструкции.
Уточнены условия использования показателя консолидации грунтов по Н.Н. Маслову.
Предложен способ построения корреляционных моделей процессов консолидации грунта расчетного слоя по результатам лабораторных испытаний образцов разной высоты.
Разработки доведены до уровня программ для ПЭВМ. Показана высокая степень соответствия результатов расчетов и натурных наблюдений, отмечены существенные различия результатов сопоставительных расчетов, выполненных с использованием предлагаемых и традиционных представлений.
ПРЕДИСЛОВИЕ
Современные условия строительства автомобильных дорог требуют разработки индивидуальных проектов конструкции земляного полотна, обоснованных соответствующими расчетами. В большей степени это относится к условиям проектирования к строительства земляного полотна на участках залегания «слабых» грунтов, склонных к консолидационной осадке. Выбор наиболее рациональных конструкций земляного полотна во многом зависит от прогноза величины осадки и ее развития во времени под действием веса насыпи. На стадии проектирования это можно получить расчетом, поэтому развитие и совершенствование методов расчета насыпей на «слабых» грунтах является одной ил актуальных задач дорожного строительства в настоящее время.
В представленной Методике рассмотрены основные положения усовершенствованного методического подхода к расчету насыпи на «слабых» грунтах, направленные на повышение уровня соответствия расчетного аппарата реальным условиям, использование новых подходов к решению ряда задач, применение средств прикладной математики и вычислительной техники.
Высокий уровень соответствия результатов полученных расчетов и натурных наблюдений свидетельствует о перспективности предложенных разработок.
Настоящая работа выполнена канд. техн. наук Л.И. Семендяевым.
Замечания и предложения по Методике просьба направлять по адресу:
143900, Московская обл., г. Балашиха-6, ш. Энтузиастов, 79, ФГУП «Союздорнии».
Генеральный директор ФГУП «Союздорнии» В.М. Юмашев
СОСТОЯНИЕ ВОПРОСА И ПОСТАНОВКА ЗАДАЧИ
Проблема проектирования и строительства автомобильных дорог в сложных инженерно-геологических условиях Российской Федерации - одна из актуальнейших проблем отечественного дорожного строительства. Для таких условий необходимо [1] разрабатывать индивидуальные проектные решения конструкции земляного полотна на основе специальных нормативных документов и методических разработок. Они должны учитывать специфичные условия взаимодействия земляного полотна и элементов рельефа местности, особенности строительства и эксплуатации конструкции с обязательным обоснованием соответствующими расчетами, результаты которых отличаются необходимой степенью точности и надежности.
Как правило, при проектировании земляного полотна автомобильных дорог в сложных инженерно-геологических условиях, помимо обеспечения необходимой степени устойчивости откосов насыпи (выемки), необходим анализ комплекса вопросов по оценке условий взаимодействия собственно земляного полотна с элементами рельефа местности, на которых оно расположено. Так при индивидуальном проектировании земляного полотна автомобильных дорог в сложных условиях пересеченной местности следует анализировать результаты оценки устойчивости конструкции «земляное полотно-склон» [2].
Совершенно иные вопросы приходится решать при проектировании и строительстве земляного полотна на участках распространения «слабых» грунтов [3]. В этом случае необходимо учитывать особенности свойств таких грунтов (склонность к осадке под действием дополнительной нагрузки от веса насыпи), а также возможность возникновения эффекта их выдавливания из слоев основания.
В общем случае проблема расчета конструкции для таких условий предполагает рассмотрение следующих задач:
□ проведение лабораторных компрессионных и консолидационных [3] испытаний образцов «слабых» грунтов и обработка результатов, что позволит получить значения консолидационных характеристик испытываемых грунтов для расчета величины и динамики осадки конструкции;
□ оценка устойчивости основания насыпи (на выдавливание «слабого» грунта);
□ расчет конечной осадки конструкции и времени завершения требуемого уровня ее консолидации;
□ назначение (в случае необходимости) комплекса мероприятий по повышению степени устойчивости основания насыпи, уменьшению величины конечной осадки конструкции и сокращению времени завершения интенсивной части ее консолидации.
Решение каждой из перечисленных задач должно базироваться на соответствующих методических предпосылках и расчетном аппарате.
Ранее разработанные методические и нормативные документы [3, 4] ориентированы на ручной счет с использованием графиков, номограмм, упрощенных расчетных схем и представлений.
Применение средств вычислительной техники позволяет вести расчеты на современном уровне, разрабатывать и реализовывать новые методические положения, уточнять и конкретизировать расчетные схемы решения ряда задач, которые в традиционной постановке являются приближенными и субъективными.
МАТЕМАТИЧЕСКИЕ КОРРЕЛЯЦИОННЫЕ МОДЕЛИ ПРОЦЕССОВ КОМПРЕССИИ И КОНСОЛИДАЦИИ ОБРАЗЦОВ ГРУНТА, ИСПЫТЫВАЕМЫХ В ЛАБОРАТОРНЫХ УСЛОВИЯХ
Существующие методики расчета [3] земляного полотна автомобильных дорог на слабом основании базируются на результатах лабораторных компрессионных и консолидационных испытаний образцов «слабых» грунтов. С их использованием определяются расчетные консолидационные характеристики испытываемого грунта и динамика консолидации образца во времени.
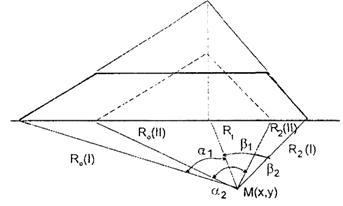
Как правило, лабораторные консолидационные испытания образцов грунта расчетного слоя конструкции осуществляются в течение длительного периода (в некоторых случаях - несколько суток). Поэтому на практике для визуальной оценки результатов лабораторных консолидационных испытаний образцов чаще используется [3, 4] полулогарифмическая система координат: на горизонтальной оси откладываются логарифмы времени в контрольных точках, а на вертикальной - соответствующие величины деформаций испытываемого образца [13]. Эта схема нередко применяется для определения времени завершения интенсивной части консолидации образца.
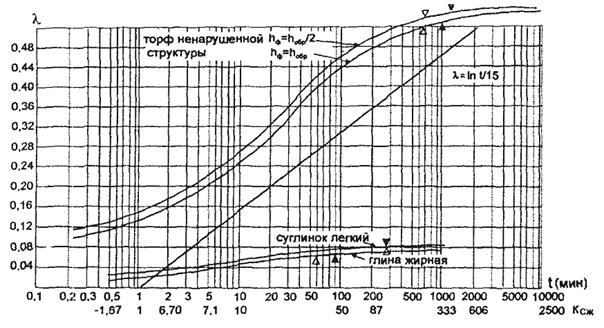
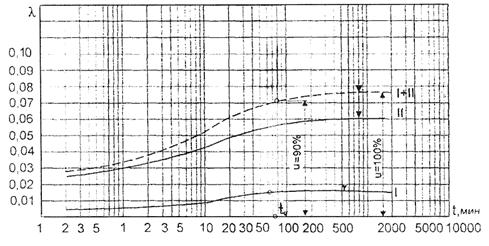
Общепринятый критериальный подход к решению указанной задачи заключается в визуальном (графический метод) поиске такой точки tк на графике (рис. 1), начиная с которой процесс консолидации образца грунта приобретает линейный (в полулогарифмической системе координат) характер.
Рис. 1. Кривые консолидации образцов. Время окончания основного этапа консолидации, полученное:
![]() - традиционным путем,
- традиционным путем,![]() - расчетным
способом
- расчетным
способом
Корректность методической обеспеченности такого подхода не является бесспорной, поскольку начиная с определенного таким образом значения tк линейно изменяется не собственно процесс консолидации образца, а некоторая его функция, представляющая исследуемый процесс в неравномерно сжатых интервалах времени. Степень (уровень) такого сжатия можно проиллюстрировать тем, что в соответствии с принятой схемой графическое отображение логарифмической функции у = аlnх будет иметь линейное представление (см. рис. 1).
Помимо этого, время завершения лабораторных консолидационных испытаний образцов грунтов в зависимости от их разновидности и состояния существенно различается: для некоторых глинистых грунтов оно составляет 100 - 1000 мин, для торфов - 5000 мин и более. При этом в соответствии с изложенным выше подходом визуально определяемое время завершения интенсивной части консолидации образца составляет для некоторых глинистых грунтов 60 - 180 мин, торфов - 600 - 1200 мин и более.
Такой широкий диапазон значений времени лишь условно вписывается в принятую схему, поскольку каждому времени соответствуют свои условия определения видимой линейности процесса (на самом деле логарифмической зависимости) консолидации. Так, для 100 мин коэффициент сжатия (Kсж = t/lgt) по горизонтальной оси графика Kсж = 50, соответственно для 1000 мин Kсж = 333, а для 10000 мин Kсж = 2500 (см. рис. 1).
Вполне возможно, что, несмотря на указанные обстоятельства, традиционный подход к определению расчетного времени завершения интенсивной части консолидации испытываемого образца может дать достаточно реальные результаты. Однако в общем случае их достоверность не может считаться обеспеченной.
Сложность проблемы расчета осадки насыпи земляного полотна автомобильных дорог на участках залегания «слабых» грунтов предопределила большое количество исследований в этом направлении [4, 8, 16 и др.]. Однако расчеты реальных конструкций осуществляются, как правило, с использованием упрощенных зависимостей и представлений, не отличающихся достаточным уровнем строгости и дающих поэтому приближенные результаты.
Повысить точность и достоверность расчетов, уровень обоснованности и степень их соответствия реальным и лабораторным процессам, уменьшить долю влияния принятых условностей и допущений и субъективного фактора, повысить уровень формализации процесса расчетов можно построением аналитических (формульных) представлений лабораторных компрессионных и консолидационных испытаний образцов грунта расчетного слоя конструкции.
Поскольку в общем случае не определена научно обоснованная физико-математическая модель таких процессов, целесообразно ориентироваться на построение корреляционной модели, учитывающей особенности проведения лабораторных экспериментов. Она должна быть достаточно универсальной, гибкой и обеспечивать выполнение следующих условий:
1) описывать с достаточной для практического использования точностью процесс лабораторных испытаний образцов грунта (от начала до завершения);
2) обеспечивать возможность аналитического описания процессов компрессии и консолидации образцов различных грунтов для разных условий проведения лабораторных экспериментов (Р, ho6p., hф);
3) позволять аналитическим путем определять основные консолидационные показатели испытываемого грунта, а также время завершения интенсивной части его консолидации исходя из условия, что при дальнейшем увеличении значений времени соответствующие приращения величины относительной осадки становятся несущественными. Основываясь на результатах лабораторных испытаний большого количества образцов различных грунтов, полученных многими исследователями в разное время, были проанализированы возможности использования для аналитического описания процессов компрессии и консолидации образцов (с учетом перечисленных условий) различных корреляционных зависимостей. В наибольшей степени соответствует предъявляемым требованиям зависимость логистического вида [17]:
на основе которой можно построить корреляционные модели процессов консолидационных и компрессионных испытаний. При обработке результатов компрессионных испытаний в качестве зависимой переменной у принимается переменная величина модуля осадки грунта е (мм/м), а независимой - изменяющаяся в процессе лабораторного эксперимента величина сжимающей нагрузки P (кгс/см2); при обработке результатов консолидационных испытаний значениями у является относительная деформация испытываемого образца, а переменной X соответствуют значения t (мин) времени контрольных замеров.
Корреляционная зависимость (1) может служить математической моделью исследуемого процесса, если зафиксированы численные значения а, в, с, к.
Сравнительно большое количество параметров зависимости (1) позволяет получить наиболее полное соответствие экспериментальных и расчетных значений уровня консолидации (осадки) образца во всем интервале изменения значений независимой переменной. Однако при такой постановке требуется разработка специальных приемов и методов, чтобы по результатам лабораторных испытаний образца грунта определить оптимальные в каждом случае значения каждого из перечисленных параметров, отражающие лабораторный процесс. Для этого необходимы современные средства вычислительной техники. Основными элементами методологической схемы решения этой задачи являются направленные итерационные циклы, уточняющие значения параметров с и к, и известный метод наименьших квадратов.
Рассчитанные таким образом значения формальных параметров корреляционного уравнения (1) могут быть использованы для определения значений основных показателей, характеризующих процесс деформирования образца в соответствии с консолидационными свойствами исследуемого грунта и условиями проведения экспериментов.
В частности, конечная (с точки зрения завершения интенсивной части консолидации) осадка образца при обработке данных его консолидационных испытаний может быть получена аналитическим путем исхода из того, что зависимость вида (1) имеет горизонтальную асимптоту, по формуле
Ук = 1/а. (2)
Начальная (условно мгновенная) осадка образца в момент нагружения расчетной нагрузкой рассчитывается аналогично:
Построенные с использованием зависимости (1) корреляционные модели лабораторных процессов позволяют усовершенствовать методики решения комплексной проблемы прогноза осадки насыпи. В частности, можно отработать единый методический подход ко всем случаям определения расчетного времени завершения интенсивной части консолидации образца.
Избежать методической неопределенности (см. рис. 1) можно, если обосновать общий критерий, имеющий вполне определенный физический смысл и позволяющий с одинаковой степенью достоверности решать задачу применительно к различным грунтам с разным временем завершения интенсивной части консолидации в лабораторных условиях и величиной осадки.
В качестве такого параметра принято использовать характеристику, независимую от свойств испытываемого грунта, например, предельно допустимую (исходя из некоторых соображений) скорость деформирования образца в направлении независимой переменной. Принято считать [3, 4], что точность результатов контрольных замеров величины осадки испытываемого образца высотой 2 см обеспечивается до тех пор, пока величина его суточных деформаций составляет не менее 0,02 мм. С учетом этого формально можно определить минимальную скорость деформирования образца, при достижении которой в соответствии с принятой масштабной системой представления результатов консолидационных испытаний образца и условиями проведения лабораторных экспериментов завершается его интенсивная часть:
Vпр = 0,00014/ho6p, (cм/мин). (4)
Определенное таким образом значение Vnp может считаться наиболее целесообразным, так как отражает реальные условия лабораторных консолидационных испытаний.
Пороговое значение скорости консолидации образцов грунта может служить критерием лишь в том случае, если реально его применение при расчетах.
В случае использования зависимости (1) в качестве корреляционной модели процесса расчетную скорость консолидации (и компрессии) образца в любой момент времени (или при любой нагрузке) можно определить аналитическим путем по формуле
Таблица 1
Результаты корреляционной обработки данных лабораторных испытаний образцов грунта
|
Параметры корреляционной модели |
Rух |
||||
|
a |
в |
с |
к |
||
|
Консолидационные испытания |
|||||
|
Суглинок легкий |
12,0188 |
119,678 |
1,9224 |
0,3528 |
0,9998 |
|
Суглинок тяжелый пылеватый |
14,1023 |
97,117 |
0,0001 |
0,384S |
0,9962 |
|
13,0987 |
65,7619 |
0 |
0,4439 |
0,9886 |
|
|
Иольдиевая глина |
31,9709 |
490,0034 |
0 |
0,2868 |
0,9970 |
|
Глина жирная |
14,3823 |
48,5145 |
0 |
0,4688 |
0,9965 |
|
Торф ненарушенной структуры |
1,8743 |
16,2619 |
0,0999 |
0,2910 |
0,9980 |
|
7,5874 |
79,4868 |
0 |
0,3678 |
0,9933 |
|
|
То же, нарушенной |
2,2260 |
19,2683 |
0,3500 |
0,9990 |
|
|
Суглинок |
20,5266 |
122,1800 |
0,3793 |
0,3698 |
0,9996 |
|
31,7887 |
60,7582 |
0,5522 |
0,2276 |
0,9991 |
|
|
20,2267 |
34,2136 |
0 |
0,3458 |
0,9988 |
|
|
13,2536 |
15,4893 |
0,0902 |
0,2773 |
0,9987 |
|
|
Компрессионные испытания |
|||||
|
Суглинок легкий |
0,0122 |
12,7154 |
3,6211 |
1,3576 |
0,9988 |
|
Глина жирная |
0,0091 |
4,2514 |
4,1676 |
1,2484 |
0,9912 |
|
То же, полутвердая |
0,0271 |
55,2842 |
4,0827 |
1,2581 |
0,9898 |
|
Торф |
0,0024 |
1,9812 |
2,9971 |
1,5476 |
0,9926 |
|
0,0016 |
5,5704 |
2,1576 |
2,4632 |
0,9925 |
|
|
Суглинок |
0,0488 |
0,0531 |
0,5792 |
0,9366 |
1,0000 |
|
0,0144 |
2,7715 |
2,3955 |
1,5943 |
0,9999 |
|
|
0,0336 |
0,0610 |
0,5616 |
2,7787 |
0,9998 |
|
|
0,0457 |
0,1315 |
0,5181 |
2,5807 |
0,9999 |
|
С помощью зависимости (5) при известном значении Vnp можно рассчитать время tnp достижения предельного значения скорости лабораторного процесса. Выбранное или определенное таким образом значение Vnp является неизменным для грунтов всех разновидностей и состояний, любых условий проведения экспериментов. Формулы (1) - (5) получены исходя из условия представления результатов в виде величин, приведенных к единичной высоте образца (l или е).
Пороговое значение скорости процесса деформирования можно выбрать исходя и из других соображений.
Практическое использование корреляционных моделей процессов консолидации образцов грунтов в лабораторных условиях уже на начальном этапе позволяет уточнить некоторые расчетные величины, которые будут определяющими при проведении дальнейших расчетов. Так, значение расчетного времени завершения интенсивной части консолидации образцов, полученное по корреляционной модели, может быть меньше соответствующего значения интенсивности, определяемого традиционным путем, в 1,5 раза (см. рис. 1). В некоторых случаях уровень различия оказывается более существенным.
Помимо этого, использование корреляционных моделей процессов лабораторных испытаний образцов грунта позволяет сгладить отдельные погрешности в исходных данных, сохраняя при этом общую тенденцию развития процесса с присущими ему особенностями.
Правомочность использования таких моделей при расчетах реальных конструкций подтверждается результатами обработки многих вариантов. Некоторые из них даны в табл. 1.
Приведенные результаты свидетельствуют о том, что корреляционная зависимость вида (1) является достаточно универсальной и может быть использована в качестве аналитического представления процессов лабораторных консолидационных и компрессионных испытаний образцов «слабых» грунтов. Уровень соответствия расчетных и экспериментальных результатов достаточно высок, что подтверждают значения оценочного параметра тесноты связи - коэффициента корреляции: практически по всем рассчитанным вариантам значения Ryx ³ 0,99. Таким образом, корреляционная зависимость вида (1) с высокой степенью достоверности отслеживает динамику развития лабораторных процессов и отражает их на всем интервале изменения независимой переменной.
ОЦЕНКА УСТОЙЧИВОСТИ ОСНОВАНИЯ ДОРОЖНОЙ НАСЫПИ
При прогнозе осадки насыпи на слабом основании расчет ее величины и динамики целесообразен при условии обеспечения необходимой степени стабильности основания дорожной насыпи. Критерием является оценка возможности выдавливания (выпора) грунта из «слабых» слоев основания насыпи под действием ее веса. Конструкция самой насыпи при этом должна отвечать требованиям по обеспечению устойчивости ее откосов [2].
Степень стабильности основания насыпи зависит от конкретных условий и определяется возможным развитием негативных проявлений, связанных с наличием в основании «слабых» слоев.
Под действием нагрузки в них возникают напряжения, которые могут стать причиной выдавливания «слабого» грунта в объемах, недопустимых для обеспечения нормального функционирования дороги. Выдавливание (или выпор) грунта может проявиться достаточно интенсивно уже в процессе сооружения насыпи. Кроме того, боковое выдавливание «слабого» грунта может произойти после значительного его уплотнения нагрузкой и носить длительный, замедленный характер.
В общем случае решение задачи по обеспечению устойчивости основания насыпи осуществляется в два этапа:
1) оценивается возможность выдавливания «слабого» грунта основания;
2) разрабатываются мероприятия для его предотвращения.
На практике оценка стабильности основания дорожной насыпи осуществляется с использованием известных представлений о его напряженном состоянии.
Как известно, напряженное состояние в произвольной точке М (х, у) основания насыпи является функцией положения расчетной точки в основании конструкции и относительно оси дороги, величины и условий распределения внешней нагрузки.
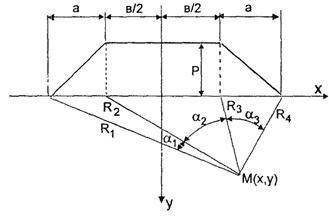
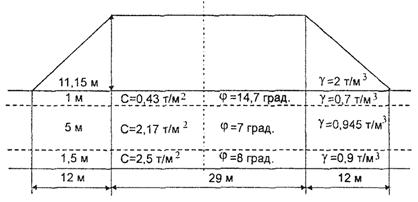
Наиболее распространенной формой конструкции насыпи является равнобочная трапеция (рис. 2). Оценка компонент напряженного состояния в расчетной точке в таком случае осуществляется [6] с использованием следующих соотношений:
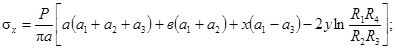
![]() (6)
(6)
![]()
Рис. 2. Оценка напряженного состояния при нагрузке в виде симметричной трапеции
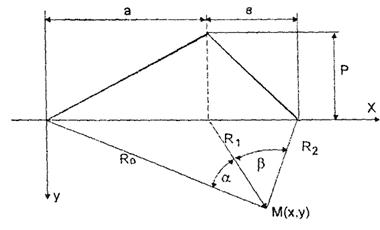
Иногда форма поперечного сечения насыпи может быть представлена несимметричной трапецией. Для такого вида нагрузки при оценке напряженного состояния в произвольной точке М (х, у) основания целесообразно использовать [6] формулы, соответствующие схеме приложения расчетной нагрузки в виде несимметричного клина (рис. 3):
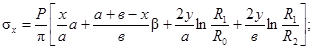
![]() (7)
(7)
![]()
Рис. 3. Оценка напряженного состояния при нагрузке в виде разностороннего треугольника (несимметричного клина)
При этом расчетные значения компонент напряженного состояния в расчетной точке основания насыпи рассчитываются как алгебраические суммы:
sх = s¢х - s²х;
sу = s¢у - s²у; (8)
tху = t¢ху - t²ху,
где s¢х, s¢у, t¢ху соответствуют расчетным значениям, полученным для нагрузки, определяемой общим треугольником;
s²х, s²у, t²ху - то же, дополнительным треугольником, условно опущенным на основание (рис. 4).
Для слоистой структуры насыпи окончательные результаты получаются суммированием sх, sу, tху, полученным последовательно для нагрузок на каждый слой.
С использованием рассчитанных таким образом значений компонент напряженного состояния могут быть определены основные напряжения, действующие в расчетной точке М (х, у):
![]()
![]() (9)
(9)
![]()
Рис. 4. Схема оценки напряженного состояния для нагрузки в виде несимметричной трапеции: общий (I) и дополнительный (II) треугольники
Принято считать, что показателем степени надежности основания в расчетной точке М (х, у) является значение коэффициента стабильности [4, 6]. При этом для его определения ученые предлагают различные подходы и соответствующие им расчетные формулы. Так Г.М. Шахунянц [6] рекомендует использовать для расчета коэффициента стабильности формулу
![]() (10)
(10)
где
А = (f ´ s1 + c)/(s1 + s2); (11)
f = tgj;
j и с - соответственно угол внутреннего трения и удельное сцепление грунта слоя, в котором расположена расчетная точка.
По В.Д. Казарновскому [4] коэффициент стабильности в расчетной точке основания определяется как отношение величины нагрузки, при которой в ней достигается предельное равновесие, к действующей нагрузке:
![]() (12)
(12)
где у ´ z - нагрузка, определяемая вышележащими слоями основания насыпи, на расчетную точку М (х, у);
z - расстояние от поверхности основания до расчетной точки.
Коэффициент стабильности для исследуемого горизонта определяется аналогично, однако в расчет берется такая точка на нем, для которой значение коэффициента стабильности будет наименьшим на горизонте. При Kст > 1 ни в одной точке на данном горизонте прочность грунта не превышена, а при Kст < 1 хотя бы в одной точке горизонта наступило запредельное состояние, что крайне нежелательно.
Наконец, величина коэффициента безопасности для всего основания определяется [4] минимальным значением коэффициента стабильности для горизонтов:
K6eз = Mин (Kcm). (13)
Теперь можно определить безопасную нагрузку как минимальную из предельных нагрузок для горизонтов или наименьшую из предельных нагрузок для точек:
Р6eз = Р0K6eз. (14)
Изложенная методика расчета K6eз и Kст в общем случае известна как метод Союздорнии [4].
Если оказывается, что K6eз < 1, то необходимо предусмотреть мероприятия по его увеличению до требуемого уровня (по крайней мере, до K6eз = 1) [3, 4].
Если K6eз ³ 1, то можно перейти к расчету величины конечной осадки конструкции и времени завершения требуемого уровня ее консолидации в зависимости от конкретных условий.
СОВЕРШЕНСТВОВАНИЕ РАСЧЕТНЫХ СХЕМ РЕШЕНИЯ ЗАДАЧИ ПРОГНОЗА ОСАДКИ СЛАБОГО ОСНОВАНИЯ ДОРОЖНОЙ НАСЫПИ
Как известно [3, 4], расчет осадки земляного полотна автомобильных дорог на слабом основании заключается в последовательном решении двух основных задач: оценка конечной осадки конструкции и определение расчетного времени завершения заданного уровня ее консолидации.
В соответствии с существующими представлениями величину конечной осадки конструкции можно получить путем дискретной оценки указанного параметра для каждого из расчетных слоев и их суммирования [3]:
![]() (15)
(15)
где k - количество расчетных слоев конструкции;
epzi - модуль осадки грунта i-гo расчетного слоя, мм/м;
Hi - толщина i-го расчетного слоя, см.
Модуль осадки грунта каждого из расчетных слоев конструкции определяется по результатам лабораторных компрессионных испытаний его образцов по формуле
epz = e¢pz - e²pz, (16)
где epz - модуль осадки при нагрузке Рz + sс.в.;
e"pz - то же, при нагрузке, отвечающей структурной прочности грунта sстр;
sс.в., Рz - расчетное напряжение соответственно от собственного веса толщи и от внешней нагрузки на данном горизонте.
Рекомендуемая [3] трактовка слагаемых формулы (16) не в полной мере соответствует реальным условиям работы конструкции, поскольку не учитывается, что условия природного равновесия основания дорожной насыпи до ее сооружения формировались под действием на расчетный горизонт бытовой нагрузки, определяемой гравитационным воздействием на горизонт вышележащих толщ основания и рядом других факторов. Поэтому использование зависимости (16) целесообразно после некоторого уточнения физического смысла и содержания ее составных частей.
С учетом известных [4] представлений значение Рz зависит от глубины расположения расчетного горизонта и величины внешней нагрузки, определяемой в данном случае весом грунта насыпи, и может быть вычислено с использованием известных методических положений:
Pz = sy, (17)
где sy - вертикальное нормальное напряжение в расчетной точке, определяемое по результатам оценки напряженного состояния основания под действием веса насыпи.
Несколько меньший уровень определенности у методики определения расчетного значения sс.в.. Этот показатель, даже рассчитанный на основе современных физических представлений, не в полной мере отражает естественные процессы, в соответствии с которыми после нагружения весом насыпи происходит консолидация грунта расчетных слоев конструкции. Условия природного равновесия основания определялись длительным действием на расчетный горизонт «бытовой» нагрузки, которая формировалась не только под гравитационным воздействием вышележащих толщ, но и рядом природных факторов (уровень подземных вод, эрозия, атмосферные осадки, хозяйственная деятельность человека и др.). В первом приближении ее расчетное значение определяют по гидростатической или геотехнической моделям, однако трудно оценить степень соответствия реальной величине.
Учесть влияние перечисленных обстоятельств и многих других на формирование величины «бытовой» нагрузки, при которой устанавливалось природное равновесие грунта на данном горизонте, исходя только из инженерных соображений невозможно. С определенной долей условности эта задача может быть решена лишь с использованием некоторых формальных приемов и представлений.
В первую очередь целесообразно предположить, что результаты лабораторных испытаний образцов, взятых на уровне горизонта, могут содержать информацию о природном состоянии грунта, в том числе о величине «бытовой» нагрузки, которую он испытывал в естественных условиях залегания.
Предварительные исследования в этом направлении в принципе не отрицают возможности извлечения такой информации из «памяти» образца. Основная методологическая концепция исследований заключалась в предположении (подтвержденном результатами многочисленных расчетов), что процесс компрессионной осадки образца может быть с достаточной для практического использования точностью описан корреляционной зависимостью вида
где е - модуль осадки грунта, мм/м;
р - переменная величина сжимающей нагрузки, кгс/см2;
а, в, с, к - параметры корреляционной модели, значения которых определяются по результатам компрессионных испытаний образца грунта расчетного слоя горизонта.
Построенные на основе зависимости (18) корреляционные модели испытаний образцов грунтов позволили отметить некоторые характерные особенности динамики изменения величины расчетной скорости процесса компрессии образцов относительно независимой переменной Р.
В большинстве рассмотренных случаев на начальном этапе отмечается нарастание скорости компрессионной осадки образцов, а начиная с некоторого (разного для различных образцов) значения нагрузки Рn процесс имеет явно выраженную тенденцию уменьшения скорости с увеличением сжимающей нагрузки Р.
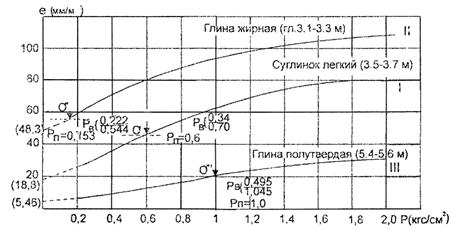
На рис. 5 приведены графики компрессионного сжатия образцов некоторых грунтов, построенные с помощью корреляционных моделей, численные значения параметров которых были определены по экспериментальным данным, представленным Э.К. Кузахметовой.
Рис. 5. Результаты компрессионных испытаний образцов грунта
Объяснить наличие точки Рп перегиба компрессионной кривой можно следующим: при извлечении монолита грунт несколько разуплотняется, поскольку снимается действующая на него в естественных условиях нагрузка. Это подтверждают и результаты экспериментов, в том числе выполненных в Союздорнии (П.А. Фонарев). В течение определенного времени после завершения компрессионных испытаний образца и снятия нагрузки происходит его частичное разуплотнение на величину, зависящую от свойств грунта и условий проведения компрессионных испытаний. Для исследуемого грунта она составила 20 % величины компрессионной осадки образца при нагрузке Р = Pz + ågН (где ågН - нагрузка на горизонт от вышележащей толщи основания; Pz - результат воздействия на расчетный горизонт веса насыпи).
Можно предположить, что при нагружении увеличивающейся нагрузкой не выше Рп, грунт образца ненарушенной структуры стремится «по памяти» восстановить природное состояние (либо собственно структуру грунта при испытаниях образцов грунта с нарушенной структурой). Только после этого появляются деформации, являющиеся реакцией на дополнительную к «бытовой» нагрузку. На этой стадии компрессионная осадка образца происходит по закономерностям, которые, как показали результаты исследований, характерны и для процесса консолидации образцов под действием расчетной нагрузки: скорость деформирования уменьшается с увеличением независимой переменной. Это обстоятельство в какой-то мере может служить косвенным подтверждением предложенной гипотезы относительно физического смысла величины Рп для испытания образцов грунта с ненарушенной структурой.
С учетом изложенного модуль осадки грунта расчетного слоя конструкции можно рассчитать по формуле (16) с несколько измененной трактовкой инженерного содержания ее слагаемых:
e¢pz - величина модуля осадки при нагрузке Р = Рz + Рп;
e"pz - то же, при Рn.
При этом значение Рn предположительно можно определить в соответствии с изложенными выше представлениями, используя компрессионную модель и полученные на ее основе дополнительные аналитические соотношения, либо исходя из других представлений.
Компрессионная модель деформирования образца грунта предполагает, таким образом, находить расчетное значение «бытовой» нагрузки Рп по состоянию грунта. Это означает, что на величину Рn в данном случае могут оказывать влияние способы отбора монолита и формирования образца. Так, если при отборе использовался ударно-канатный способ ведения буровых работ, то неизбежно возникает дополнительное обжатие образца, что отразится на рассчитанной по компрессионной модели величине Рп. Предварительные исследования показали, что ожидаемый уровень увеличения Рп в таких случаях может составить 10 - 20 %.
Помимо оценки величины конечной осадки, существенное (а иногда и определяющее) значение имеет расчетное время завершения интенсивной части ее консолидации. В соответствии с существующими положениями [3, 4] время завершения заданного уровня осадки конструкции определяется по формуле
где Ск - коэффициент консолидации, определяемый по результатам консолидационных испытаний образца грунта в соответствии с положениями теории фильтрационной консолидации [13];
Kи - коэффициент, зависящий от степени консолидации грунта и определяемый по известным таблицам или расчетным путем [13];
Нф - расчетный путь фильтрации отжимаемой из слоя воды, принимаемый равным толщине слоя при одностороннем дренировании и половине толщины - при двухстороннем.
Коэффициент консолидации грунта Ск определяется по графику процесса консолидации образца грунта, уплотненного под действием расчетной нагрузки:
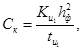 (20)
(20)
где ![]() - коэффициент, зависящий от
степени консолидации образца,
- коэффициент, зависящий от
степени консолидации образца, ![]() ;
;
![]() - время
завершения заданной степени уплотнения образца;
- время
завершения заданной степени уплотнения образца;
hф - расчетный путь фильтрации воды, отжимаемой из образца.
Многие исследователи [4, 8, 11, 12, 16 и др.] отмечают, что при традиционном подходе к решению задачи расчетные значения консолидационных характеристик конструкции (в первую очередь, времени завершения ее интенсивной части) оказываются существенно завышенными по отношению к реальным данным. Основная причина этого заключается в том, что большинство грунтов по своим деформационным свойствам не соответствуют условиям чисто фильтрационной консолидации, на основании которых построены основы существующих [3] расчетных схем. Только деформации «слабых» грунтов в состоянии избыточного увлажнения (сапропели, торф, переувлажненные глины и некоторые другие) приближенно могут быть описаны средствами теории фильтрационной консолидации. Для всех же остальных разновидностей и состояний «слабых» грунтов условия деформируемости определяются не только фильтрационным фактором, но и рядом других причин [14], иногда объединяемых термином «объемная ползучесть» [8].
Отечественная дорожная наука уделяла много внимания поиску путей решения задачи в такой постановке (С.Р. Месчян, З.Г. Тер-Мартиросян, В.Д. Казарновский, Э.К. Кузахметова и др.). Особо следует выделить исследования Н.Н. Маслова, согласно которым [10, 12] одна из основных консолидационных характеристик грунта - показатель консолидации. Он зависит от вида и состояния грунта; величины испытываемой им нагрузки как в естественных, так и в лабораторных условиях; особенностей работы грунта в конструкции. Значение показателя консолидации может изменяться в пределах 0 £ n £ 2, т.е. только в некоторых случаях соответствуя известным положениям (n = 2) теории фильтрационной консолидации.
Исходя из этого еще в 1941 г. Н.Н. Масловым [10, 12] для определения времени завершения интенсивной части осадки конструкции была предложена зависимость
где и - заданный уровень консолидации конструкции, %;
tu - время завершения требуемого уровня консолидации образца;
h - высота испытываемого образца;
H - толщина расчетного слоя;
п - показатель консолидации.
Формула (21) не предполагает использования при расчете значений традиционных характеристик, которые по отношению к реальным грунтам либо являются переменными на протяжении процесса консолидации (коэффициент консолидации Ск), либо очень приближенно отражают реальные условия деформирования конкретного грунта (Ku, n = 2 и др.).
Таким образом, использование при расчетах зависимости (21) предполагает рассмотрение только одной консолидационной характеристики - показателя консолидации п.
По результатам лабораторных испытаний образцов Н.Н. Масловым выявлены зависимости показателя консолидации от вида грунта, его консистенции, числа пластичности. Обобщение указанных зависимостей, выполненное Ле Ба Лыонгом [11], позволило предположить, что существует физическая зависимость показателя консолидации от сопротивляемости глинистых грунтов сдвигу при любых значениях плотности-влажности и нагрузках на горизонт. Она может быть описана уравнением
n = 2 - 0,73 ´ Spw, (22)
где п - показатель консолидации грунта;
Spw - сопротивляемость грунта сдвигу, кгс/см2.
Однако если учесть, что значения прочностных характеристик «слабых» грунтов мало различаются [3] при их определенном состоянии, а процессы компрессии и консолидации образцов подчиняются закономерностям, описываемым зависимостью (1), то можно предположить, что способ Н.Н. Маслова может быть отнесен с некоторой долей условности ко всем «слабым» грунтам.
Разработанный им подход (21) - (22) к решению задачи оценки времени завершения интенсивной части консолидации насыпи на слабом основании с учетом результатов теоретических исследований К. Терцаги, М.Н. Герсеванова, В.А. Флорина, Н.А. Цытовича, Н.А. Зарецкого [15], А.И. Ксенофонтова и др., позволяет рассчитывать конструкции применительно к консолидационным свойствам конкретного грунта. Это неоспоримое достоинство метода. Однако практическое использование существующих средств его реализации вызывает много вопросов.
В частности, формула (21), построенная по аналогии с выражением (19) теории фильтрационной консолидации, не имеет достаточного теоретического обоснования для реальных условий. Не совсем убедительна зависимость расчетного значения показателя консолидации в формуле (22) только от величины нагрузки и прочностных показателей грунта. Открытыми остаются вопросы о целесообразности учета при определении показателя консолидации изменений состояния (w) грунта, о возможном влиянии толщины расчетного слоя (высоты образца), уровня консолидации грунта. Ответы на перечисленные и некоторые другие вопросы могут быть получены лишь косвенным путем.
Известно, что прочностные характеристики rpунта Cw, jw определяются сдвиговыми испытаниями в лаборатории. Вместе с тем, можно предположить, что результаты деформационных испытаний содержат данные о прочностных свойствах и состоянии грунта в природных условиях, поэтому при расчете показателя консолидации грунта не требуется дополнительной информации. Анализ результатов обработки данных более 20 лабораторных испытаний образцов глинистых грунтов из реконструируемого участка автомобильной дороги МКАД-Кашира показал, что, по крайней мере, применительно к рассмотренным грунтам и условиям проведения лабораторных экспериментов полученная зависимость вида
n = 1,28 - 0,32 ´ Kконс ´ ln(Рn + sу), (23)
где п - рассчитываемое значение показателя консолидации грунта;
Kконс - величина параметра к корреляционной модели (1) процесса консолидации грунта образца высотой 2 см под расчетной нагрузкой;
Рп - расчетное значение «бытовой» нагрузки на горизонт по компрессионной модели;
sу - вертикальное нормальное напряжение в расчетной точке основания, расположенной на уровне расчетного горизонта под осевой линией дороги, от веса насыпи, позволяет в каждом случае рассчитать показатель консолидации грунта, который совпадает с определенным по формуле (22).
Максимальное отклонение сопоставляемых значений не превышает 0,26 %, а коэффициент корреляции Ryx = 0,99 свидетельствует о высоком уровне достоверности зависимости (23). Таким образом, расчетное значение показателя консолидации может быть определено с использованием Kконс, Рп, sу, которые не изменяются в процессе уплотнения грунта.
Многие исследователи [4, 8, 11, 14, 16 и др.] предполагают, что показатель консолидации зависит от уровня консолидации грунта, т.е. изменяется в процессе консолидации. Это обосновывается тем, что со временем уменьшается степени влияния на деформацию грунта фильтрационного фактора и увеличивается доля приращения деформаций, вызванных фактором объемной ползучести [8, 14], имеющих более длительный характер по сравнению с деформациями, определяемыми фильтрационным фактором. Как правило, деформации ползучести со временем убывают и, начиная с некоторого момента времени, становятся настолько малыми в сравнении с накопленными на предыдущих этапах, что ими можно пренебречь. Обычно их учитывают путем ограничения времени лабораторных компрессионных и консолидационных испытаний образцов грунта с использованием различных приемов.
Таким образом, зависимость Маслова-Лыонга отражает состояние грунта до начала лабораторных испытаний, а не его изменение в процессе уплотнения. Этот вывод может снять некоторые вопросы, возникающие при оценке условий применимости формулы (22).
Вместе с тем формулы (22) и (23) показывают, что показатель консолидации является функцией координат расчетной точки - ее расположения по глубине и относительно оси дороги.
В соответствии с известными положениями [6] в зависимости от места расчетной точки изменяется значение одной из составных частей (sу) общей нагрузки на горизонт, определяемой воздействием веса насыпи. Это обстоятельство отражается на формировании величины Р при использовании формулы (22) или величины расчетной нагрузки при лабораторных консолидационных испытаниях образцов, т.е. на их результатах и построенных корреляционных моделях.
Таким образом, проведенные исследования в определенной степени конкретизируют условия применения при расчетах реальных объектов показателя консолидации в качестве комплексной характеристики, учитывающей консолидационные свойства конкретного грунта, условия его природного залегания и работы в конструкции, а также использования формулы (22) для определения расчетного значения п. Вместе с тем остаются открытыми некоторые вопросы (предполагаемая зависимость п от толщины слоя и др.).
ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ КОРРЕЛЯЦИОННЫХ МОДЕЛЕЙ ЛАБОРАТОРНЫХ КОМПРЕССИОННЫХ И КОНСОЛИДАЦИОННЫХ ИСПЫТАНИЙ ОБРАЗЦОВ ГРУНТА
Разработанный метод прогноза осадки дорожной насыпи на участках распространения «слабых» грунтов, основанный на реализации математических корреляционных моделей, модификации и новой трактовке сущности некоторых расчетных средств, уточнении условий применения показателя консолидации по Н.Н. Маслову, позволяет получать результаты расчетов, в большей степени соответствующие реальным условиям.
Для проверки работоспособности предлагаемых методов и средств разработан комплекс программ, использование которых позволяет решить в автоматизированном и автономном режимах следующие основные задачи:
1) построение корреляционных моделей процессов лабораторных компрессионных и консолидационных испытаний образцов грунта расчетных слоев конструкции;
2) определение расчетного значения коэффициента безопасности основания насыпи, вычисляемого с использованием метода Союздорнии;
3) определение величины конечной осадки конструкции в произвольной расчетной точке, расположенной на любом участке поверхности насыпи;
4) расчет времени завершения требуемого уровня консолидации конструкции в расчетной точке.
С использованием программного комплекса были рассмотрены различные варианты с целью:
□ определить работоспособность предлагаемых разработок;
□ сопоставить получаемые результаты расчетов с аналогичными данными, полученными на основе традиционных расчетных схем;
□ выявить закономерности изменения расчетных показателей в зависимости от различных обстоятельств, в том числе и места расположения расчетной точки на поверхности земляного полотна;
□ сопоставить результаты расчетов и натурных наблюдений.
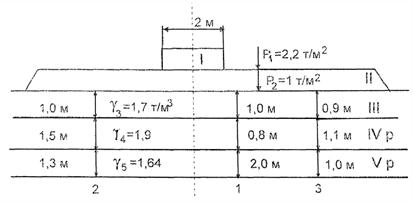
В качестве контрольной была рассмотрена конструкции земляного полотна при условии совпадения расчетного уровня грунтовых вод с поверхностью основания (рис. 6).
Рис. 6. Схема насыпи на слабом слоистом основании:
вариант I - Kбез = 0,56, S = 49,92 см, Т = 45,96 мес; вариант II - соответственно 0,56, 26,21 см, 3,40 мес
Полученные данные (см. рис. 6) свидетельствуют о том, что уровень стабильности основания насыпи явно недостаточна. Значение коэффициента безопасности Kбез = 0,56 не отрицает возможности выдавливания под действием веса насыпи грунтовой массы из «слабых» слоев основания. Отсюда первоочередная задача - увеличить значение коэффициента безопасности основания по крайней мере до Kбез = 1.
Расчетные значения конечной осадки конструкции в точке на оси дороги, полученные исходя из традиционного (вариант 1) и предлагаемого (вариант 2) методических представлений, свидетельствуют о следующем: результаты расчетов зависят от полноты учета условий залегания «слабых» грунтов и соответствия им результатов лабораторных испытаний. Для рассчитываемого объекта сопоставительные расчетные величины конечной осадки конструкции различаются почти в 2 раза. При этом значение осадки, полученное с использованием предлагаемых представлений, меньше рассчитанного традиционными методиками.
Аналогичная ситуация наблюдается при определении расчетного значения времени T завершения 90 % осадки конструкции.
Разработанный новый подход к определению модуля осадки грунта расчетного слоя конструкции построен на использовании расчетного значения Рп бытовой нагрузки, соответствующего реальным условиям залегания грунта на уровне расчетного горизонта. Расчетная схема для его определения разработана на основании реализации математических корреляционных моделей процессов компрессионного деформирования образцов грунта расчетного слоя. Как правило, традиционным аналогом бытовой нагрузки на расчетный горизонт является гравитационное воздействие на него вышележащих толщ основания.
В табл. 2 приведены результаты сопоставительных расчетов вариантов на одном из реконструируемых участков автомобильной дороги МКАД-Кашира, выполненных исходя из традиционного и предлагаемого подходов к расчету «бытовой» нагрузки.
Из табл. 2 видно, что расхождения значений величины конечной осадки S конструкции не превышают 5 %, а времени T завершения интенсивной (90 %) части консолидации (осадки) - менее 10 %.
Традиционное методическое обеспечение решения задачи прогноза осадки насыпи на слабом основании ориентировано, в первую очередь, на рассмотрение расчетных точек под осью дороги. Вместе с тем можно ожидать, что осадка поверхности насыпи земляного полотна автомобильной дороги с основанием из «слабых» грунтов будет различаться как по величине, так и по времени завершения заданного уровня консолидации в точках, расположенных на различном расстояния от оси дороги, даже при решении задачи в одномерной постановке. Причиной такой неравномерности осадки поверхности насыпи в поперечном направлении может являться переменная величина воздействия на расчетный горизонт основания распределенной на ограниченном участке внешней нагрузки - веса грунта насыпи.
Таблица 2
Результаты сопоставительных расчетов осадки конструкции
|
S, см |
Т, ч |
Отклонение, % |
||
|
S |
T |
|||
|
1 |
0,74 |
58,80 |
1,356 |
4,80 |
|
0,73 |
61,79 |
|||
|
2 |
1,48 |
25,49 |
3,38 |
9,09 |
|
1,43 |
28,04 |
|||
|
3 |
0,56 |
17,99 |
1,79 |
4,81 |
|
0,55 |
18,90 |
|||
|
4 |
0,63 |
149,15 |
4,76 |
9,02 |
|
0,60 |
163,94 |
|||
|
5 |
0,74 |
134,69 |
1,35 |
4,83 |
|
0,73 |
141,52 |
|||
|
6 |
0,74 |
23,00 |
0 |
4,84 |
|
24,17 |
||||
|
7 |
0,74 |
96,87 |
0 |
4,86 |
|
101,82 |
||||
Примечание. Над чертой - при определении Рп по компрессионной модели, под чертой - по гравитационному принципу
Не нарушая методического плана, можно рассмотреть вариант однослойной насыпи (рис. 7), поперечный разрез которой представлен неравнобочной трапецией, т.е. заложение правого и левого откосов различно.
Рис. 7. Схема расчета осадки насыпи в разных точках
В табл. 3 приведены результаты расчетов величины конечной осадки насыпи и времени завершения интенсивной (90 %) части ее консолидации (осадки) в разных точках поверхности на одном из реконструируемых участков автомобильной дороги МКАД-Кашира.
Из табл. 3 видно, что наибольшая величина S осадки наблюдается в точке под осью дороги (Хr = 0,5), наименьшая - в точках на бровках откоса. При этом она зависит и от заложения откосов: минимальное значение S соответствует бровке откоса с меньшим заложением (левый на рис. 7) (Хr = 0).
С другой стороны, расчетное время T завершения интенсивной части консолидации конструкции в точках, расположенных на некотором расстоянии от осевой линии дороги, больше, чем в точке на оси. При этом максимальное значение Т соответствует точке, расположенной под бровками более крутого откоса.
Таким образом, традиционное решение задачи, когда расчетные значения S и Т определяются для одной и той же расчетной точки на оси автомобильной дороги, не во всех случаях обеспечивает получение полной информации для принятия более обоснованных практических решений. С учетом данных табл. 3, величину конечной осадки S конструкции целесообразно, как это и принято, оценивать применительно к расчетной точке, расположенной на осевой линии дроги, а время Т завершения требуемого уровня консолидации (осадки) конструкции в целом определять как максимальное значение этого параметра в точках на бровках откоса.
Таблица 3
Результаты расчета консолидационных показателей насыпи в разных точках ее поверхности
|
S, см |
Т, ч |
Xr |
S, см |
Т, ч |
|
|
0 |
2,51 |
176,0 |
0,6 |
3,55 |
169,4 |
|
0,1 |
3,14 |
171,1 |
0,7 |
3,50 |
169,9 |
|
0,2 |
3,38 |
169,5 |
0,8 |
3,41 |
171,2 |
|
0,3 |
3,40 |
169,2 |
0,9 |
3,21 |
171,1 |
|
0,4 |
3,54 |
169,1 |
1,0 |
2,69 |
174,7 |
|
0,5 |
3,56 |
169,2 |
Примечание. Значение Хr определяется отношением расстояния расчетной точки от бровки левого откоса насыпи к ширине проезжей части дороги (см. рис. 7).
Результаты расчетов, представленные в табл. 3, получены по данным лабораторных консолидационных испытаний образцов грунта расчетного слоя основания под нагрузкой для точки на оси дороги. Учет изменения величины такой нагрузки в зависимости от удаленности расчетной точки от оси только усилит отмеченные тенденции.
Обоснованность методического обеспечения и работоспособность расчетных средств решения той или иной задачи в конечном счете могут считаться подтвержденными, если получаемые на их основе расчетные значения показателей, характеризующих исследуемый процесс, в достаточной степени корреспондируют с их реальными величинами.
С использованием предлагаемых разработок и реализующего их программного комплекса была произведена оценка осадки основания под временными технологическими опорами проектируемой эстакады через р. Ока на реконструируемом участке автомобильной дороги МКАД-Кашира. Цель расчетов - обоснование мероприятий по ускорению осадки основания в местах предполагаемого строительства временных опор, определение величины и времени действия временной пригрузки применительно к конкретным условиям. Были разработаны расчетные схемы (рис. 8), по которым в дальнейшем осуществлялся расчет конструкции (мероприятий). При этом предполагалось, что два верхних слоя конструкции условно относятся к насыпи и моделируют внешнюю нагрузку на основание. Верхний слой основания (слой III) - насыпной грунт, деформационные свойства которого можно не учитывать. Нижние слои основания - расчетные, образцы из которых были испытаны на компрессию и консолидацию для каждой контрольной точки.
Рис. 8. Расчетные схемы для контрольных точек 1, 2 и 3
По результатам расчетов в трех контрольных точках (см. рис. 8) были организованы натурные наблюдения (табл. 4).
Величина осадки конструкции по двум первым контрольным точкам (см. табл. 4) различаются в пределах натурных значений, которые фиксировались стандартной рейкой. По третьей контрольной точке уровень различия сопоставляемых значений составляет около 43 %, что объясняется, по-видимому, некоторым несоответствием толщины слоев основания, принятых в расчетной схеме, их реальным уточненным значениям.
Таблица 4
Сопоставительные результаты расчетов и натурных наблюдений
|
|
|
Т, ч |
S, мм |
|
|
1 |
- |
- |
120,27 |
13,7 |
|
48 |
14 |
88,78 |
13,2 |
|
|
2 |
74 |
12 |
284,88 |
1,62 |
|
100 |
18 |
211,69 |
16,8 |
|
|
3 |
24 |
10 |
180,87 |
16,9 |
|
66 |
12 |
113,74 |
17,1 |
* Натурные наблюдения
Примечание. Над чертой - при расчете Рп по весовому принципу, под чертой - по компрессионной модели
Расчетные значения времени Т завершения интенсивной (90 %) части осадки конструкции в принципе корреспондируют с соответствующими значениями Т2 времени проведения последних натурных замеров, после которых приращение деформаций стали настолько незначительными, что их трудно было зафиксировать примененными средствами.
В целом, можно отметить, что предложенные методические и расчетные средства решения задачи прогноза величины и динамики прохождения во времени осадки насыпи на деформируемом основании позволяют получить результаты расчетов, уровень соответствия которых реальным условиям существенно выше, чем получаемых исходя из традиционных представлений. Вместе с тем рассчитанное время завершения заданного уровня осадки конструкции может быть несколько завышенным (ориентировочно в 1,5 раза) относительно данных натурных наблюдений. Таким образом, возможно дальнейшее совершенствование методического обеспечения и расчетных схем решения комплексной задачи.
ОТРАЖЕНИЕ ХАРАКТЕРИСТИК ЛАБОРАТОРНЫХ ПРОЦЕССОВ В ЗНАЧЕНИЯХ ПАРАМЕТРОВ КОРРЕЛЯЦИОННЫХ МОДЕЛЕЙ
Использование математических корреляционных моделей вида (1) процессов компрессионных и консолидационных испытаний образцов грунта расчетного слоя конструкции предполагает необходимость формального определения численных значений параметров а, в, с, к, характеризующих изучаемый процесс. Указанные величины в каждом конкретном случае устанавливаются по результатам лабораторных экспериментов, поэтому следует ожидать, что они будут зависеть как от свойств испытываемого грунта в естественном залегании, так и от условий лабораторных испытаний.
Для выявления таких ожидаемых зависимостей значений формальных параметров корреляционных моделей от некоторых количественных характеристик процессов деформирования образцов грунта целесообразно рассматривать не величины относительных (приведенных к образцу единичной высоты) деформаций образцов (1), а их натуральные значения. В таком случае корреляционная зависимость (1) будет иметь следующий вид:
где h - высота испытываемого образца;
х - переменная величина независимой переменной - значений времени t при консолидационных испытаниях или нагрузки при компрессионных;
Y - соответствующие абсолютные значения величины деформации образца;
а, в, с, к - формальные значения параметров корреляционной модели, определяемые непосредственно по результатам лабораторных экспериментов с учетом пути фильтрации отжимаемой из образца воды.
Полученная корреляционная зависимость одинаково успешно может быть использована в качестве основы при построении и консолидационных, и компрессионных моделей лабораторных испытаний образцов грунта расчетного слоя, поэтому в рамках решаемой задачи каждую из них целесообразно рассматривать автономно.
При построении математических корреляционных консолидационных моделей вида (1) или (24) за независимую переменную х принимаются переменные значения времени t проведения лабораторных испытаний образца, а значениям у соответствуют величины S(t) осадки образца.
Согласно формуле (2) расчетная абсолютная величина конечной осадки образца может быть определена из отношения
Sк = h/а, (25)
откуда
a = h/Sк, (26)
где h - высота испытываемого образца, см;
Sк - расчетная величина консолидационной осадки образца под расчетной нагрузкой Р, см.
Поскольку значение Sк в каждом случае формируется с учетом консолидационных свойств грунта образца, его состояния, условий проведения лабораторных экспериментов, нашедших отражение в результатах лабораторных испытаний, эти же характеристики в интегральном плане учитываются в значении не только параметра а корреляционной модели, но и всех остальных.
Многочисленные корреляционные модели процессов лабораторных консолидационных испытаний образцов свидетельствуют о том, что в этом случае значение параметра с, как правило, либо равно нулю, либо близко к нему, т.е. оно несоизмеримо мало по сравнению с текущим значением времени консолидации испытываемого образца. Таким образом, в общем случае процессы консолидации образцов грунта могут быть без каких-либо ощутимых потерь описаны корреляционной моделью вида (1) или (24) при фиксированном значении с = 0.
С учетом формул (3) и (24) начальная (условно мгновенная) осадка образца при его нагружении расчетной нагрузкой может быть определена из соотношения
![]() (27)
(27)
откуда с учетом (26) для определения смыслового содержания параметра в корреляционной консолидационной модели может быть использована формула
С учетом изложенного выше при с = 0 получаем
Из выражения (29) следует, что параметр в является функцией высоты испытываемого образца и расчетных значений его конечной и начальной осадки.
В соответствии с формулой (23) расчетное значение параметра к грунта расчетного слоя конструкции является в определенном смысле аналогом показателя консолидации грунта п. Параметр к характеризует консолидационные свойства испытываемого грунта, его состояние, условия проведения лабораторных консолидационных испытаний и условия естественного залегания грунта. Способ его определения предполагает постоянство этого параметра в течение лабораторного процесса.
Формально величину к в зависимости от значений характеристик лабораторного процесса можно установить по достаточно сложному соотношению:
где t - текущее значение времени процесса консолидации образца, мин;
S - соответствующая данному моменту времени абсолютная величина осадки образца, S = S(t), см.
Из формулы (30) следует, что расчетная величина консолидационного параметра к определяет условия формирования промежуточных значений осадки образца в зависимости от времени эксперимента, увязывая его с такими характеристиками процесса консолидации образца, как Sк, Sн, h.
Таким образом, формальные параметры корреляционной модели вида (24) процесса консолидации образца грунта расчетного слоя конструкции можно определить исходя из некоторых характеристик процесса, численные значения которых рассчитываются в соответствии с консолидационными свойствами испытываемого грунта, условиями проведения консолидационных испытаний его образцов.
Помимо этого, формулы (26), (28), (30) показывают, что на формирование расчетных значений параметров а, в и к корреляционных консолидационных моделей определенное влияние оказывает и высота испытываемого образца.
Для математической обработки результатов компрессионных испытаний образцов могут быть использованы корреляционные модели (1) или (24), что и при построении моделей процессов консолидационных испытаний (см. табл. 1). Однако в этом случае зависимости, связывающие расчетные значения формальных параметров корреляционных моделей и количественные оценки характеристик лабораторных процессов компрессионных испытаний образцов грунта, имеют свои отличительные особенности. Так компрессионные модели строятся с использованием в качестве независимой переменной значений Р сжимающей нагрузки, изменяющейся в течение эксперимента, а в качестве зависимой переменной - модуля осадки.
По аналогии с формулой (26) значение параметра а корреляционной компрессионной модели может быть определено из соотношения
a² = h/S²к, (31)
где S"к - конечная величина абсолютной компрессионной осадки образца с учетом результатов воздействия последней ступени нагружения.
Кроме того, компрессионные модели характеризуются (см. табл. 1) четырьмя параметрами, которые так взаимосвязаны, что невозможно выделить какой-то из них (за исключением параметра а).
При построении компрессионных моделей значения с, как показали результаты многочисленных расчетов, в зависимости от вида испытываемого грунта соразмерны с текущими величинами сжимающей нагрузки (см. табл. 1).
В результате математической обработки данных лабораторных компрессионных испытаний образцов грунта расчетного слоя конструкции по зависимости (24) были отмечены обстоятельства, не учтенные при традиционном решении общей задачи. В первую очередь это относится к месту расположения точки перегиба графика, отражающего процесс компрессионного деформирования образца. Наличие такой точки подтверждается в большинстве рассмотренных случаев построения корреляционных моделей (см. рис. 5) процессов лабораторных компрессионных испытаний образцов грунтов ненарушенной (и нарушенной) структуры.
В рамках решаемой задачи процессы деформирования грунтов с нарушенной структурой не исследовались.
Другой отличительной особенностью является то, что модель позволяет формально вычислить некоторые условные величины осадки образцов при Р = 0 (по аналогии со значением условно мгновенной начальной осадки образца при обработке результатов его консолидационных испытаний). По традиционному подходу во всех случаях [3] величина осадки при Р = 0 принималась нулевой. Поэтому нельзя было не только определить численное значение нагрузки Рn, при котором фиксируется точка перегиба графика процесса, но и установить существование такой точки. Фиксирование же с использованием корреляционных компрессионных моделей некоторой условной величины начальной (при Р = 0) осадки образца может быть объяснено тем, что собственно процесс компрессионной осадки начинается непосредственно после приложения начальной нагрузки. В результате формируется начальная (условно мгновенная) осадка определенной величины, формальное значение которой может корректироваться результатами воздействия на образец и некоторых следующих ступеней нагружения образца. Отклик такого начального значения осадки образца, возможно, и определяет корреляционная модель при формальном значении Р = 0, не являющимся составной частью проводимых лабораторных экспериментов.
Таким образом, в значениях в, с и к через результаты лабораторных экспериментов должны найти отражение, помимо прочих, и перечисленные обстоятельства.
С точки зрения формальных математических представлений значение параметра с компрессионной модели вида (24) в некоторой степени отражает положение точки Рn (см. рис. 5) перегиба графика процесса, т.е. предположительно определяет величину естественной нагрузки на расчетный горизонт. Аналитическое выражение для определения в явном виде значения Рn в зависимости от величины с получить трудно, поэтому на практике часто используются приближенные методы, в первую очередь, итерационные с ориентацией на построенные корреляционные модели процессов.
Таким образом, положение точки перегиба графика процесса компрессионной осадки образца определяется значением параметра с корреляционной компрессионной модели, т.е.
Рn » f(c²). (32)
При известных параметрах в и к компрессионной модели значение параметра с можно установить из соотношения
где h - высота испытываемого образца;
S²к - конечная компрессионная осадка образца;
S"н - начальная компрессионная осадка образца, рассчитываемая по компрессионной модели формальным образом при Р = 0.
Смысловое содержание параметра в компрессионной модели при известных значениях с и к можно определить по формуле
Соотношения (33) и (34) показывают, что между значениями параметров в, с и к существует достаточно тесная взаимосвязь. Это обстоятельство с учетом сжимающей нагрузки Р позволяет при их неизменных на протяжении процесса компрессионной осадки грунта расчетного слоя конструкции значениях с высокой степенью точности описать процесс деформирования образца высотой h в зависимости от его деформационных свойств, условий естественного залегания грунта и особенностей проведения компрессионных испытаний образцов.
По аналогии с консолидационными моделями параметр к может являться компрессионным показателем деформирования грунта образца, значение которого определяется непосредственно по результатам компрессионных испытаний образца.
Как показали результаты расчетов, лишь часть которых отражена в табл. 1, для всех основных разновидностей «слабых» грунтов значения компрессионного показателя к превышают величину его консолидационного аналога.
РАСЧЕТ ВРЕМЕНИ ДОСТИЖЕНИЯ ТРЕБУЕМОГО УРОВНЯ ОСАДКИ НАСЫПИ НА НЕОДНОРОДНОМ ДЕФОРМИРУЕМОМ ОСНОВАНИИ
В соответствии с изложенным консолидационные испытания образцов грунта расчетного слоя основания целесообразно проводить под расчетной нагрузкой, соответствующей полной нагрузке на горизонт, определяемой как сумма бытовой нагрузки Рбыт и воздействия на горизонт веса насыпи Рвн:
Р = Р6ыт + Рвн. (35)
В реальных условиях осадка основания насыпи происходит в результате воздействия ее веса на расчетные горизонты с учетом уже сформировавшихся под действием бытовой нагрузки условий природного равновесия на каждом из них. В связи с тем, что на каждом расчетном горизонте многослойного основания насыпи такие условия (Р6ыт и Рвн) могут сильно различаться, при прогнозе осадки насыпи необходимо учитывать как условия консолидационного уплотнения каждого слоя, так и условия их совместной работы в конструкции. При этом расчет осадки насыпи на многослойном основании можно выполнять по известным [3] положениям, а существующий подход к определению времени завершения ее интенсивной части следует пересмотреть. Ориентация на значение этого параметра только для одного из расчетных слоев, для которого оно является наибольшим [3], не всегда оправдана применительно к конструкции в целом.
Нетрудно заметить, что при таком подходе не во всех случаях обеспечивается возможность решить задачу в исходной постановке. Получаемое таким образом значение Т характеризует не заданное значение уровня осадки и, а некоторое другое (неопределенное) значение Uф, которое в зависимости от конкретных условий может располагаться в интервале
U £ Uф £ 100 %. (36)
При этом условие U = Uф гарантированно выполняется лишь в тех случаях, когда в основании рассматривается только один расчетный слой либо при U = 100 %.
Задача может быть решена на основе метода суммарных представлений с оценкой последовательно уровня влияния на любой момент времени T каждого из его расчетных слоев с учетом условий их совместной работы в конструкции. Методика расчета времени Ти завершения уровня и осадки многослойного основания насыпи может быть построена на использовании математических корреляционных моделей вида (1) при с = 0.
Путем последовательной обработки результатов испытаний образцов по каждому из них может быть определена величина относительной консолидационной осадки:
![]() (37)
(37)
При этом по
соответствующей консолидационной модели расчетное значение ![]() определяется из
условия
определяется из
условия
В отличие от условия (4), зависимость (38) обеспечивает большую степень независимости контрольного параметра, поскольку такой подход устраняет необходимость учитывать специфичные условия проведения лабораторных испытаний. В качестве отправного значения выбрано t = 1 мин, поскольку на начальном этапе лабораторных испытаний (t » 1 ¸ 2 мин) на их результаты существенное влияние оказывает мгновенное приложение расчетной нагрузки.
Расчетная
скорость V (t)
процесса деформирования образца на момент времени t
рассчитывается по формуле (5), а значение ![]() - по выражению
- по выражению
![]() (39)
(39)
где аi, вi - параметры соответствующей консолидационной модели.
Полученная таким образом величина относительной осадки образца грунта i-гo расчетного слоя основания принимается за его конечную (u = 100 %) осадку. Просуммировав li по всем расчетным слоям, получим расчетную величину относительной осадки условного образца грунта основания в целом. По формуле
![]() (40)
(40)
можно рассчитать величину,
отражающую уровень U осадки
образцов грунтов основания в целом. По известному значению ![]() на основе
построенных корреляционных консолидационных моделей устанавливаем время Ти
достижения требуемого уровня и осадки многослойного основания. Решение
этой задачи достигается обычным итерационным способом. Приближенное решение
может быть получено в соответствии с разработанной методикой и графическим
способом. При этом погрешность существенно уменьшается по сравнению с
результатами, определяемыми на основе традиционных представлений.
на основе
построенных корреляционных консолидационных моделей устанавливаем время Ти
достижения требуемого уровня и осадки многослойного основания. Решение
этой задачи достигается обычным итерационным способом. Приближенное решение
может быть получено в соответствии с разработанной методикой и графическим
способом. При этом погрешность существенно уменьшается по сравнению с
результатами, определяемыми на основе традиционных представлений.
На рис. 9 представлены результаты расчетов одного из участков автомобильной дороги МКАД-Внуково, выполненных на основе изложенной методики. Насыпь высотой около 20 м расположена на деформируемом двухслойном основании. Первый (верхний) расчетный слой толщиной 1,4 м представлен глинистым грунтом: его середина расположена на глубине 3,5 м от поверхности основания. Второй слой - сапропелевый толщиной 9,1 м; расчетный горизонт (середина) заглублен примерно на 10 м.
Время достижения 90 %-го уровня осадки образцов (см. рис. 9) составляет 55 (I) и 90 (II) мин; рассчитанное время достижения того же уровня суммарной осадки - примерно 75 мин.
В соответствии с полученными таким образом результатами расчетное время Ти завершения уровня и осадки многослойного основания может быть рассчитано, как это и принято, по формуле (22). При этом за tи принимается величина tu(I + II), a n, H, h соответствуют характеристикам расчетного слоя с максимальным временем завершения этапа первичной консолидации. В рассмотренном варианте - это нижний (II) сапропелевый слой основания.
Рис. 9. Схема расчета времени завершения заданного уровня осадки многослойного основания насыпи. Пунктир - суммарный график консолидации двух образцов (I + II) из расчетных слоев основания
Для данной конструкции рассчитанное время Ти достижения уровня и = 90 % осадки слоистого основания насыпи уменьшается примерно на 15 % по сравнению с аналогичной величиной, полученной традиционным путем. В общем случае в зависимости от консолидационных особенностей грунтов «слабых» слоев и других конкретных условий различия сопоставляемых величин могут быть и более существенными.
ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ КОРРЕЛЯЦИОННЫХ МОДЕЛЕЙ ПРОЦЕССОВ КОНСОЛИДАЦИИ ГРУНТА РАСЧЕТНОГО СЛОЯ КОНСТРУКЦИИ
Использование корреляционных моделей позволяет
□ модернизировать методические аспекты решения основных задач проблемы прогноза осадки насыпи на деформируемом основании;
□ предложить новые расчетные схемы их реализации;
□ получить результаты расчетов, в наибольшей степени согласующиеся с данными натурных наблюдений, что подтверждают многочисленные примеры.
Попытки построить корреляционные консолидационные модели по результатам лабораторных испытаний образцов высотой 1,7; 2; 2,5 и 3,75 см, подтвердили высокую степень соответствия (коэффициент корреляции не ниже 0,99) аналитических представлений реальным лабораторным процессам.
Из этого следует, что и процессы консолидации грунтов расчетных слоев конструкции могут быть описаны этой корреляционной зависимостью с достаточной для практического применения точностью.
При этом возникает необходимость разработать методику определения значений параметров А, В, С и K корреляционной модели реального процесса, отражающих состояние и консолидационные свойства грунта расчетного слоя конструкции, условия его естественного залегания (толщина слоя, глубина его расположения в основании) и работы в конструкции (воздействие внешней нагрузки - веса насыпи).
Отсутствие (как правило) необходимого объема данных натурных наблюдений реально предопределяет единственную возможность решить эту задачу исходя, в первую очередь, из результатов лабораторных консолидационных и компрессионных испытаний разновысоких образцов грунта расчетного слоя конструкции. С этой целью были проанализированы данные лабораторных консолидационных испытаний разновысоких (не менее трех высот) образцов трех разновидностей торфов, полученных Э.К. Кузахметовой, и глинистых грунтов, представленных на реконструируемом участке автомобильной дороги МКАД-Кашира (П.А. Фонарев). Были построены корреляционные модели процессов консолидации образца и получены расчетные значения их формальных параметров а, в, с и к (табл. 5).
Из табл. 5 видно, что значения параметра с корреляционных моделей во всех рассмотренных случаях либо равны нулю, либо приближаются к нему и не зависят от высоты испытываемого образца, т.е. не являются в указанном смысле информационными.
Следует также отметить, что с увеличением высоты образца коэффициент корреляции, как правило, возрастает, т.е. увеличивается доля деформаций образца, определяемых собственно консолидационными свойствами грунта, и уменьшается доля деформаций, зависящих от условий отбора монолита, подготовки образца и проведения эксперимента (включая масштабный фактор). Если это так, то можно предположить, что для каждого грунта существует такое предельное значение высоты (и соответственно других габаритов) Нпр, начиная с которого на процесс консолидационного уплотнения грунта образца перестают оказывать сколько-либо существенное влияние некоторые побочные обстоятельства, определяемые регламентированными условиями проведения лабораторных экспериментов.
Таблица 5
Параметры и характеристики корреляционных моделей процессов консолидационных испытаний разновысоких образцов грунтов
|
Высота образца |
Параметры консолидационной модели |
Коэффициент корреляции |
||||
|
a |
в |
с |
к |
|||
|
Торф I |
1,70 |
3,218 |
18,379 |
0 |
0,375 |
0,9972 |
|
2,50 |
3,203 |
22,155 |
0,0002 |
0,313 |
0,9997 |
|
|
3,75 |
3,228 |
27,955 |
0,0004 |
0,281 |
0,9997 |
|
|
Торф I |
1,70 |
3,067 |
14,901 |
0 |
0,336 |
0,9981 |
|
2,50 |
3,078 |
22,022 |
0,1861 |
0,289 |
0,9990 |
|
|
3,75 |
3,175 |
26,199 |
0,0262 |
0,273 |
0,9993 |
|
|
Торф III |
1,70 |
3,753 |
13,088 |
0,0001 |
0,257 |
0,9922 |
|
2,00 |
3,841 |
16,808 |
0 |
0,271 |
0,9894 |
|
|
2,50 |
3,980 |
22,357 |
0 |
0,304 |
0,9911 |
|
|
3,75 |
4,100 |
29,702 |
0 |
0,312 |
0,9949 |
|
|
Глинистый грунт |
1,75 |
16,738 |
33,170 |
0 |
0,483 |
0,9919 |
|
2,00 |
15,861 |
40,067 |
0 |
0,476 |
0,9980 |
|
|
2,50 |
14,640 |
57,751 |
0 |
0,408 |
0,9996 |
|
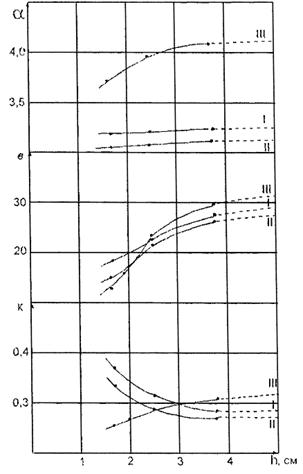
Подтверждения такого вывода могут быть получены и исходя из результатов анализа изменения значений параметров а, в и к корреляционных консолидационных моделей в зависимости от высоты испытываемого образца. В соответствии табл. 5 они заметно изменяются в зависимости от вида и состояния грунта образцов, условий проведения лабораторных экспериментов, в том числе и высоты испытываемого образца. Значения указанных параметров, таким образом, в каждом случае являются информационными.
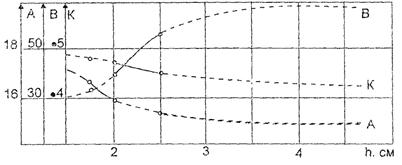
На рис. 10 представлены графики изменения значений параметров а, в, к корреляционных моделей процессов лабораторных консолидационных испытаний разновысоких образцов трех разновидностей торфов, а на рис. 11 - аналогичные графики для глинистого грунта. Из рисунков видно, что графики зависимостей имеют как индивидуальные особенности, так и некоторые общие тенденции.
Следует отметить, что во всех рассмотренных случаях расчетные значения всех параметров построенных моделей оказались неотрицательными, а скорость их изменения зависит от высоты испытываемого образца. При этом она сначала возрастает ориентировочно при h = 1,7 ¸ 2,5 см, а затем начинает убывать предположительно до нуля. Возможно, существует такая высота образца Hпр (для каждой разновидности грунта, по-видимому, своя), начиная с которой для всех значений высот больше Нпр, параметры а, в и к консолидационных корреляционных моделей могут оставаться постоянными.
Рис. 10. Зависимость а, в, к от высоты образцов торфа:
I - Карелия, влажность 600 %, II - а/д Кемь-Лоухи, 660 %, III - а/д Кривандино-Рошаль, 595 %
Рис. 11. Зависимость А, В, К от высоты образца глинистого грунта
Следует отменить и некоторые другие закономерности и тенденции. Так во всех рассмотренных случаях значения параметра в возрастают с увеличением высоты образца. Для торфяных грунтов параметр а изменяется с сохранением той же тенденции, а для глинистого грунта убывает с увеличением высоты образца.
Консолидационный параметр к глинистого грунта и некоторых разновидностей торфа (I и II) убывает с увеличением высоты образца, торфа III - возрастает, но во всех случаях он ниже I.
Дополнительно можно отметить то, что, по крайней мере, для исследуемых торфов стабильнее (для высоты образцов выше Нпр) параметры а, в и к увеличиваются с уменьшением влажности испытываемых грунтов, т.е. в соответствии с выбранным видом (1) корреляционной зависимости меньшие деформации происходят у грунтов с меньшей влажностью.
Таким образом, по рис. 9 - 10 можно определить ориентировочное значение Нпр, начиная с которого параметры корреляционных консолидационных моделей лабораторных процессов изменяются несущественно с увеличением высоты испытываемых образцов грунта. Если отмеченная тенденция имеет место, то можно сделать некоторые принципиальные выводы:
1) значения параметра к корреляционных моделей процессов лабораторных консолидационных испытаний образцов грунта высотой h ³ Hnp не изменяются с дальнейшим наращиванием значений h. Поскольку между значениями этого параметра и показателем консолидации п предположительно существует взаимосвязь (23), величина последнего будет неизменной для высоты образцов (толщины расчетных слоев) выше Hnp;
2) начиная с высот h ³ Hnp, конечная величина относительной консолидационной осадки испытываемых образцов при неизменности других условий предположительно остается постоянной;
3) с точки зрения обеспечения возможности обоснованно определять расчетные значения консолидационных характеристик грунта деформируемого слоя конструкции оптимальная высота испытываемых в лабораторных условиях образцов грунта должна быть не ниже определенной величины Hnp, которая для различных разновидностей и состояний испытываемых грунтов может быть разной.
С учетом изложенного выше по результатам лабораторных консолидационных испытаний не менее трех разновысоких образцов грунта расчетным или графическим способом по зависимостям, аналогичным представленным на рис. 10 - 11, можно установить значение Hnp, начиная с которого параметры корреляционных моделей процессов консолидации грунта образцов будут оставаться практически постоянными. В таком случае значения параметров А, В и K могут быть определены по условиям:
А = а(Нпр), (41)
В = в(Hnp), (42)
K = к(Нпр). (43)
Значение С корреляционной модели вида (1) формально можно принять равным параметру с корреляционной модели процесса лабораторных испытаний образца грунта максимальной высоты (или с = 0).
Таким образом, в общем случае корреляционную модель консолидации грунта расчетного слоя под расчетной нагрузкой, определяемой в соответствии с формулой (35), можно представить в виде:
где S - расчетная величина осадки слоя, см;
Н - толщина расчетного слоя, см;
Т - текущее значение времени консолидации грунта расчетного слоя, мин;
А, В, С, K - параметры корреляционной модели, значения которых формально определяется по результатам консолидационных испытаний не менее трех разновысоких образцов на основе соотношений (41) - (43).
Построенная таким образом корреляционная модель процесса консолидации грунта расчетного слоя конструкции под нагрузкой Р не предполагает использования при решении задачи прогноза осадки насыпи на деформируемом основании значений всех общепринятых [3] консолидационных характеристик и показателей, таких как коэффициент консолидации Ск, время завершения заданного уровня консолидации образца грунта tu, значений Ku, U1, а также показателя консолидации грунта п.
На основании выражения (44) может быть получена формула и для определения (для любого момента времени) скорости консолидации грунта расчетного слоя:
В соответствии с существующими нормативными положениями [3] на насыпях со «слабыми» грунтами капитальные покрытия можно устраивать после завершения не менее 90 % расчетной осадки или при средней интенсивности осадки за месяц, предшествующий устройству покрытия, не выше 1,5 - 2 см/год.
Для устройства облегченных покрытий - соответственно не менее 80 % конечной осадки или интенсивности не более 3 - 5 см/год.
При учете условий работы дорожных покрытий предпочтительнее рассматривать в качестве критерия скорость (или интенсивность) процесса деформирования, вернее, ее максимально допустимое значение, которое может быть поставлено с определенной долей условности в соответствие требуемому уровню расчетной осадки.
В частности, уровню и = 90 % может соответствовать предельное значение скорости (не интенсивности) процесса деформирования Vпр = 1 см/год, а для u = 80 % - соответственно Vпр = 2 см/год, что не противоречит приведенным выше нормативным условиям.
В таком случае заданному значению и допустимого уровня расчетной осадки основания конструкции формально может соответствовать скорость процесса деформирования, определяемой по формуле
![]() (46)
(46)
По определенному таким (или некоторым другим) образом значению Vnp с использованием соотношения (45) можно рассчитать значение времени Ти достижения заданного уровня консолидации грунта расчетного слоя, а по формуле (44) по известному значению Ти определить расчетную величину Su осадки конструкции.
ЛИТЕРАТУРА
1. СНиП 2.05.02-85. Автомобильные дороги. - М.: ЦИТП Госстроя СССР, 1986.
3. Пособие по проектированию земляного полотна автомобильных дорог на слабых грунтах (к СНиП 2.05.02-85). - М., Союздорнии, 1989.
5. Орнатский Н.В. Механика грунтов. - М., МГУ, 1962.
6. Шахунянц Г.М. Земляное полотно железных дорог. - М.: Трансжелдориздат, 1965.
7. Кузахметова Э.К. Современные методы прогноза осадок слабых грунтов в основании инженерных сооружений и в самих сооружениях. - Автомобильные дороги: Обзорная информация/Информавтодор, вып. 6. - М., 1994.
9. Чернявская Л.И. Исследование метода ускорения осадки насыпей на болотах временной пригрузкой. Автореф. дисс. канд. техн. наук. - М., Союздорнии, 1974.
10. Маслов Н.Н. Основы инженерной геологии и механики грунтов. - М.: Высшая школа, 1982.
12. Маслов Н.Н. Механика грунтов в практике строительства. - М.: Стройиздат, 1977.
13. Терцаги К. Теория механики грунтов. - М.: Стройиздат, 1961.
15. Зарецкий Ю.К. Вязкопластичность грунтов и расчет сооружений. - М.: Стройиздат, 1988.
18. Семендяев Л.И. Использование показателя консолидации при прогнозе осадки насыпи на слабых грунтах//Воплощение и развитие научных идей Н.Н. Маслова в практике строительства. - М., МАДИ, 1998.
СОДЕРЖАНИЕ
|
Состояние вопроса и постановка задачи. 2 Оценка устойчивости основания дорожной насыпи. 7 Отражение характеристик лабораторных процессов в значениях параметров корреляционных моделей. 20 |