МИНИСТЕРСТВО ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА СССР
ГОСУДАРСТВЕННЫЙ ВСЕСОЮЗНЫЙ ДОРОЖНЫЙ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
(СОЮЗДОРНИИ)
РЕКОМЕНДАЦИИ
ПО
ПРОЕКТИРОВАНИЮ СЕТИ
АВТОМОБИЛЬНЫХ
ДОРОГ ОБЛАСТНОГО
И
МЕСТНОГО ЗНАЧЕНИЯ
Москва - 1970
Предисловие
Совершенствование существующей сети автомобильных дорог областного и местного значения - в настоящее время одна из актуальных задач транспортного строительства. При проектировании сети должно быть обеспечено наиболее рациональное сочетание капиталовложений и транспортно-эксплуатационных затрат.
Оптимальное начертание сети дорог может быть найдено только на основе технико-экономического сопоставления многочисленных вариантов.
Успехи, достигнутые в области математики и вычислительной техники, дают возможность организовать вариантное проектирование дорожных сетей с применением быстродействующих вычислительных машин (ЭВМ).
Исследования, проведенные в Союздорнии, показали, что для определения рационального начертания сети с помощью ЭВМ может быть с успехом использован метод статистических испытаний (метод Монте-Карло), позволяющий организовать целенаправленный пересмотр вариантов дорожной сети и тем самым выявить наивыгоднейший вариант сети без перебора всех возможных решений.
Настоящие «Рекомендации» разработаны канд. техн. наук Б.А. Волковым.
Замечания и пожелания просьба присылать по адресу: Московская обл., Балашиха-6, Союздорнии.
ЗАМ. ДИРЕКТОРА СОЮЗДОРНИИ
ПО НАУЧНОЙ РАБОТЕ
кандидат технических наук Н.В. Горелышев
Общие положения
Из всех возможных вариантов развития сети следует выбирать вариант, имеющий наиболее рациональное соотношение капитальных и транспортно-эксплуатационных затрат при высоких качественных показателях.
Сравнение вариантов дорожной сети между собой - весьма трудоемкая работа. Поэтому в настоящее время, когда проектирование сетей автомобильных дорог в основном ведется с привлечением малых средств механизации, окончательное решение по развитию сети принимают, как правило, без вариантного проектирования.
Начертание сети устанавливается экспертным порядком с оптимизацией в отдельных случаях аналитическими или графоаналитическими методами локальных участков. Такой подход не дает возможности в общем случае выявить наиболее рациональное решение дорожной сети.
Быстродействующие вычислительные машины (ЭВМ) позволяют рассматривать в практически приемлемый срок большое количество вариантов дорожной сети и получать более рациональное решение сети.
Для большего эффекта целесообразно использовать методы математического программирования, что дает возможность организовать целенаправленный пересмотр вариантов сети и тем самым выявить наивыгоднейшее ее начертание без простого перебора всевозможных решений.
В настоящее время ведутся разработки по применению математических методов и ЭВМ для проектирования дорожной сети в КАДИ, ИКТП, МАДИ и других организациях. В КАДИ создана программа для ЭВМ «Минск», в основу которой положен алгоритм Р.К. Прима о построении кратчайших связывающих сетей /1/. В остальных организациях для выявления рационального начертания сети используется комбинаторный алгоритм Паршикова /2, 3/.
Указанные методики «машинного» проектирования дорожных сетей не лишены ряда существующих недостатков и на данном этапе разработки пока не могут удовлетворить запросов проектировщиков.
Исследования, проведенные в Союздорнии, показали, что для выбора наивыгоднейшего варианта сети дорог с успехом может быть использован метод статистических испытаний (известный под названием метода Монте-Карло).
Экспериментальное проектирование дорожных сетей в Омской и Волгоградской областях с помощью этого метода показало, что данная методика дает возможность уменьшить сумму приведенных строительных и транспортно-эксплуатационных затрат по дорожной сети на 10 - 12 % по сравнению с традиционным «ручным» методом проектирования сетей.
Постановка задачи
Задача определения рационального начертания дорожной сети формулируется следующим образом. Для выполнения зада того объема перевозок требуется построить (или реконструировать) сеть дорог определенных технических категорий, обеспечивающую минимальное значение критерия оптимизации при соблюдении всех строительных норм и правил. За критерий оптимизации дорожной сети на сегодняшний день целесообразно принять действующий критерий выбора проектных решений - сумму приведенных затрат /4/.
Для сетей автомобильных дорог сумма приведенных затрат может быть определена по формуле
где Сt - годовые капиталовложения в строительство и реконструкцию дорог;
Эt - годовые дорожно-эксплуатационные расходы (расходы на ремонт и содержание дорог);
Мt - годовые транспортно-эксплуатационные расходы;
ТС - срок завершения работ по приведению сети автомобильных дорог в соответствии с требованиями народного хозяйства;
ТЭ - срок службы автомобильной дороги до наступления морального износа по постоянным элементам (как правило, срок службы автомобильных дорог общей сети из условия наступления морального износа не менее 25 - 30 лет);
ЕНП - норматив для приведения разновременных затрат (в условиях действующего порядка начисления амортизации основных фондов ЕНП принимается 0,08).
В математической формулировке задача выбора оптимального варианта начертания дорожной сети может быть представлена следующим образом: найти такой вектор-решение сети - ХОПТ, который отвечал бы всем строительным нормам и правилам и максимально минимизировал критерий оптимизации К, т.е.
где X - множество векторов-решений дорожной сети.
Следует отметить, что оптимальное решение сети может быть найдено лишь при условии, что имеющаяся исходная информация (объемы перевозок между корреспондирующими пунктами, состояние существующих дорог, показатели строительной стоимости, транспортно-эксплуатационные показатели и т.д.) достоверна и достаточна для отыскания оптимума. Практически же исходная информация при проектировании сетей автомобильных дорог не полностью отвечает требованиям достаточности и достоверности. Поэтому термин «оптимальное решение» следует понимать как «близкое к оптимальному».
Выбор оптимального варианта дорожной сети методом статистических испытаний
Метод статистических испытаний (метоп Монте-Карло) позволяет найти наивыгоднейший вариант с наперед заданной вероятностью. Вероятностный подход к задаче определения рационального начертания дорожной сети вполне правомерен, ибо об объемах перевозок и их структуре на перспективу, о стоимостных оценках эксплуатационных расходов на содержание дорог, расходов на перевозку грузов и пассажиров, расходов на строительство и реконструкцию автодорог можно говорить только как о приближенных наиболее вероятностных величинах. При таком положении выбор оптимальной схемы развития сети целесообразно проводить статистическими методами с проверкой на устойчивость полученного решения в зависимости от возможного диапазона изменения исходных данных.
Выявление оптимального решения сети методом Монте-Карло заключается в следующем. Вначале разрабатываются статистические (случайные) варианты дорожной сети. Количество таких вариантов определяется по формуле
где Р - вероятность нахождения оптимального варианта сети;
Δ - точность поиска наивыгоднейшего решения.
Исследования показали, что для проектирования сетей автомобильных дорог областного и местного значения следует принять Р ≥ 0,80 и Δ ≥ 0,025. В табл. 1 приведены значения числа потребных статистических проб сети NC, найденные в соответствии с формулой (3).
Для каждого статистического варианта сети дорог определяется критерий оптимизации - сумма приведенных затрат. Тот вариант, который имеет самое минимальное значение суммы приведенных затрат, и будет оптимальным.
Построение статистических вариантов сети дорог
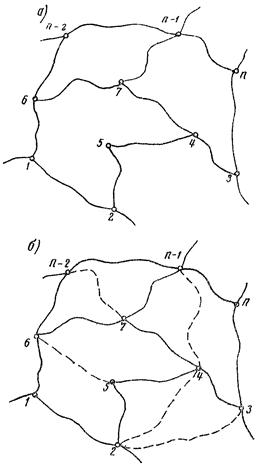
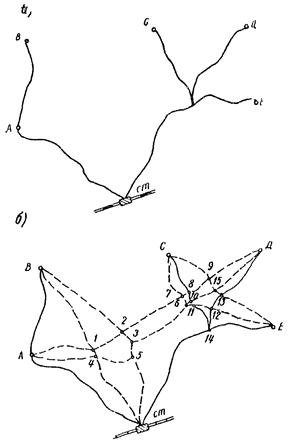
Необходимо запроектировать перспективную дорожную сеть в районе, показанном на рис. 1, а.
На существующую дорожную сеть наносим пунктиром направления новых дорог, которые могут принять участие в формировании оптимальной сети. Схему существующих дорог с нанесенными на нее направлениями новых дорог назовем исходной схемой (рис. 1, б).
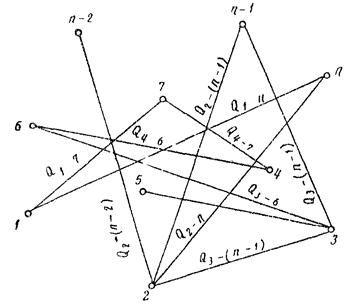
На рис. 2 приведена схема корреспондирующих связей между пунктами с указанием объемов грузовых перевозок на перспективный год.
Каждой корреспондирующей связи присвоим свой номер (табл. 2).
Порядок расположения корреспондирующих связей произвольный. Перспективная дорожная сеть должна удовлетворять всем заданным корреспондирующим связям. Под удовлетворением корреспондирующей связи понимается проведение мероприятий по реконструкции существующих или сооружение новых дорог, обеспечивающих транспортную связь между корреспондирующими пунктами. Например, связь 1 - n может быть удовлетворена за счет реконструкции существующих дорог 1 - 2 и 3 - n и сооружения новой дороги 2 - 3 (рис. 1, б).
Таблица 1
|
Δ |
0,70 |
0,75 |
0,80 |
0,85 |
0,88 |
0,90 |
0,92 |
0,95 |
0,96 |
0,97 |
0,98 |
0,99 |
|
|
|
|
|
Значения NC = f (P, ∆) |
|
|
|
|
|
|||
|
0,10 |
12 |
14 |
16 |
18 |
21 |
22 |
24 |
29 |
31 |
34 |
38 |
44 |
|
0,09 |
13 |
15 |
18 |
21 |
23 |
25 |
27 |
32 |
35 |
38 |
42 |
49 |
|
0,08 |
15 |
17 |
20 |
23 |
26 |
28 |
31 |
36 |
39 |
43 |
47 |
56 |
|
0,07 |
17 |
20 |
23 |
27 |
30 |
32 |
35 |
42 |
45 |
49 |
54 |
64 |
|
0,06 |
20 |
23 |
27 |
31 |
35 |
38 |
41 |
49 |
53 |
57 |
64 |
75 |
|
0,05 |
24 |
28 |
32 |
37 |
42 |
45 |
50 |
59 |
63 |
69 |
77 |
90 |
|
0,045 |
26 |
30 |
35 |
41 |
46 |
48 |
55 |
65 |
70 |
76 |
85 |
100 |
|
0,040 |
30 |
34 |
40 |
47 |
52 |
57 |
62 |
74 |
79 |
86 |
96 |
113 |
|
0,035 |
34 |
39 |
45 |
53 |
59 |
64 |
71 |
84 |
90 |
98 |
110 |
129 |
|
0,030 |
40 |
46 |
53 |
68 |
70 |
76 |
83 |
99 |
106 |
116 |
129 |
152 |
|
0,025 |
47 |
55 |
63 |
75 |
84 |
90 |
100 |
118 |
127 |
138 |
154 |
182 |
|
0,020 |
60 |
69 |
80 |
94 |
105 |
115 |
126 |
149 |
160 |
174 |
194 |
229 |
|
0,015 |
79 |
91 |
106 |
125 |
139 |
151 |
166 |
197 |
212 |
231 |
257 |
303 |
|
0,01 |
120 |
139 |
161 |
189 |
212 |
230 |
255 |
299 |
321 |
350 |
390 |
459 |
Рис. 1. Существующая сеть дорог (а), исходная схема (б)
Следует отметить, что перспективные объемы грузопассажирскихх) перевозок анализируемой корреспондирующей связи могут и не потребовать реконструкции существующих дорог. В этом случае связь удовлетворяется за счет использования существующих дорог без их реконструкции.
х) Объем пассажирских перевозок составляет определенный процент от грузовых.
Статистические варианты дорожной сети получаются путем удовлетворения всех корреспондирующих связей согласно исходной схеме. Закономерность удовлетворения заданных связей принимается случайной. При равномерно распределенном характере этой случайной закономерности номер очередной обеспечиваемой корреспондирующей связи NК находится по формуле:
где ξi - случайные числа, равномерно распределенные в интервале [0, 1];
nК - количество заданных корреспондирующих связей.
|
Номер связи NК |
|
|
1 - 7 |
1 |
|
1 - n |
2 |
|
2 - (n - 1)... |
3 |
|
4 - 6 |
nК - 1 |
|
4 - 7 |
nК |
Значения случайных чисел ξi могут быть получены с помощью стандартных программ на ЭВМ.
Для построения статистического варианта сети выборку случайных чисел ξi следует производить до тех пор, пока не будут удовлетворены все заданные корреспондирующие связи. При таком условии количество случайных чисел должно быть не менее числа связей.
Количество случайных чисел тогда превысит число корреспондирующих связей, когда до окончания построения варианта дорожной сети какой-либо порядковый номер связи повторится не менее двух раз. Формула (4) дает дробный результат.
Рис. 2. Схема корреспондирующих связей между пунктами 1, 2,..., n
Для получения номеров связей необходимо принять правило округления. Округлять следует так, чтобы не нарушить закона равномерного распределения. Равномерное распределение номеров корреспондирующих связей в интервале [0; 1] показано на рис. 3. Нетрудно видеть, что номеру связи NК = nК соответствует интервал [nК - 1; nК]. Следовательно, округлять дробный результат формулы (4) нужно всегда в большую сторону. В связи с этим формулу (4) целесообразно преобразовать в следующую зависимость
где Е ( ) - символ целой части. Удовлетворение i-й корреспондирующей связи производится оптимальным образом, т.е. при минимальных приведенных затратах. При этом те мероприятия по реконструкции существующих или сооружению новых дорог, которые предусматривались для наивыгоднейшего удовлетворения предшествующих i - 1 связей, считаются фиксированными. Метод оптимального обеспечения корреспондирующей связи приведен ниже.
Рис. 3. Равномерное распределение номеров корреспондирующих связей в интервале [0; 1]
Проследим построение статистического варианта дорожной сети на конкретном примере.
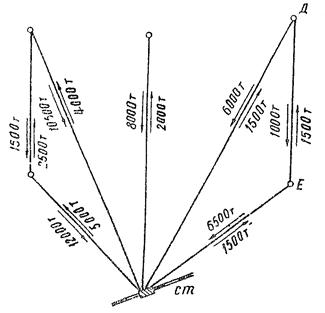
Имеется шесть грузообразующих пунктов: А, В, С, Д, Е и железнодорожная станция с определенными направлениями и объемами корреспондирующих связей на перспективный год (рис. 4).
Рис. 4. Направления и объемы грузовых перевозок на перспективный год
Каждой связи присваивается свой порядковый номер (табл. 3).
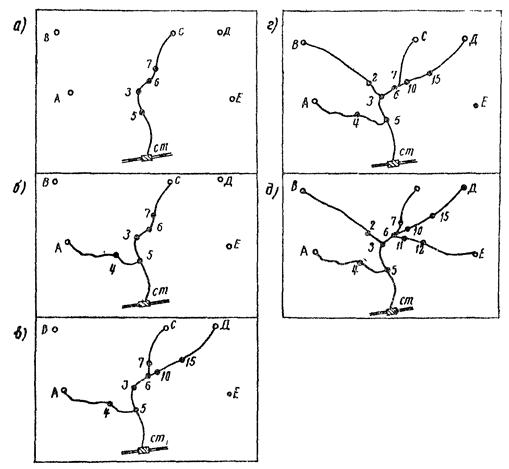
Существующая сеть дорог представлена грунтовыми дорогами, находящимися в очень плохом состоянии (рис. 5, а). Разрабатываем исходящую схему, нанося на существующую сеть направления новых дорог, которые могут принять участие в формировании оптимальной дорожной сети (рис. 5, б). При разработке исходной схемы используются ранее известные приемы оптимизации начертания дорожной сети /5 - 7/.
|
Порядковый номер связей |
|
DE |
1 |
|
AB |
2 |
|
Dcm |
3 |
|
Ecm |
4 |
|
Ccm |
5 |
|
Bcm |
6 |
|
Acm |
7 |
Направления новых дорог на исходной схеме (рис. 5, б) показаны пунктиром. Протяженность дорог по участкам приведена в табл. 4.
Рис. 5. Существующая сеть дорог (а), исходная схема оптимизации дорожной сети (б)
Статистический вариант дорожной сети строится путем оптимального удовлетворения всех заданных корреспондирующих связей. Порядок удовлетворения связей находится в соответствии с формулой (5). Пусть имеется часть равномерно распределенных случайных чисел ξ: 0,69; 0,86, 0,42; 0,86; 0,72; 0,52; 0,77; 0,05; 0,87; 0,85; 0,73, 0,24, которым соответствуют следующие номера корреспондирующих связей: 5, 7, 3, 7, 6, 4, 6, 1, 7, 6, 6, 2.
Следовательно, статистический порядок обеспечения связей такой: Сст, Аст, Дст, Вст, Ест, ДЕ, АВ.
Связь Сст обеспечивается оптимальным образом за счет сооружения наикратчайшей дороги С - 7 - 6 - 3 - 5 - станция (рис. 6, а). Для назначения оптимальных мероприятий удовлетворения связи Аст следует рассмотреть два конкретно способных варианта: 1) сооружение дороги А - станциях) и 2) сооружение дороги А - 4 - 5 и использование дороги, запроектированной для связи Сст на участке 5 - станция.
х) В данном случае речь идет не о реконструкции существующей пороги А - станция, а о строительстве новой дороги по этому же направлению, так как существующая дорога грунтовая и находится в очень плохом состоянии.
Таблица 4
|
Длина участка, км |
Участок дороги |
Длина участка, км |
Участок дороги |
Длина участка, км |
Участок дороги |
Длина участка, км |
|
|
А - В |
8,5 |
3 - 5 |
1,0 |
С - 8 |
2,5 |
3 - 6 |
3,8 |
|
А - 1 |
3,2 |
5 - ст |
5,8 |
8 - 10 |
0,5 |
6 - 10 |
1,0 |
|
А - 4 |
3,0 |
1 - 2 |
0,3 |
10 - 11 |
0,5 |
10 - 15 |
1,0 |
|
4 - 5 |
1,6 |
2 - 7 |
4,2 |
11 - 14 |
2,0 |
15 - Д |
3,0 |
|
В - 1 |
8,8 |
7 - 8 |
0,4 |
Е - 14 |
2,5 |
Ст - 14 |
8,6 |
|
В - 2 |
8,0 |
8 - 9 |
0,5 |
Е - 12 |
1,0 |
12 - 14 |
1,0 |
|
2 - 3 |
0,5 |
9 - Д |
5,0 |
11 - 12 |
1,0 |
12 - 13 |
1,0 |
|
А - ст |
7,5 |
С - 9 |
2,8 |
6 - 11 |
1,0 |
13 - Д |
3,5 |
|
1 - 4 |
0,5 |
С - 7 |
2,0 |
Е - 13 |
1,3 |
9 - 15 |
1,5 |
|
4 - ст |
4,7 |
7 - 6 |
0,8 |
9 - 13 |
3,0 |
13 - 15 |
1,5 |
Рис. 6. Построение статистического варианта порожной сети:
а - д - этапы построения
В первом варианте приведенные затраты равны:
где С - строительная стоимость 1 км дороги;
ℓА - ст - длина дороги;
SЭ - расходы на ремонт и содержание дороги, приходящиеся на 1 ткм;
Sт - транспортные расходы грузовых перевозок на 1 ткм;
![]() - годовой грузооборот корреспондирующей связи Аст приходящийся на дорогу А - станция;
- годовой грузооборот корреспондирующей связи Аст приходящийся на дорогу А - станция;
ЕН - нормативный коэффициент эффективности капитальных вложений. При С = 40 тыс. руб./км (заданный объем перевозок связи Аст требует сооружения дороги V категории) SЭ = 1,45 коп/ткм, Sт = 10,2 коп/ткм и ЕН = 0,12, К1 = 312,3 тыс. руб.
Для второго варианта.
Так как наложение дополнительного объема перевозок корреспондирующей связи Аст на ранее запроектированную дорогу 5 - станция не требует более высокой категории дороги, в формуле (7) учитываются капиталовложения лишь по сооружению дороги А - 4 - 5. Приведенные затраты по второму варианту К2 = 201,1 тыс. руб. Ввиду того, что К2 < К1 принимается второй вариант обеспечения связи Аст (рис. 6, б). Связь Дст оптимальным образом удовлетворяется с учетом ранее запроектированных дорог путем сооружения дороги Д - 15 - 10 - 6. Дорожная сеть после обеспечения связи Дст принимает вид рис. 6, в. Наивыгоднейший вариант удовлетворения следующей связи Вст - сооружение дороги В - 2 - 3 и использование ранее запроектированной дороги 3 - 5 - станция (рис. 6, г).
Связь Ест оптимально обеспечивается путем сооружения дороги Е - 12 - 11 - 6 и использованием автомобильной дороги на участке 6 - 3 - 5 - станция (рис. 6, д). Связи ДЕ и АВ обеспечиваются за счет запроектированных дорог Д - 15 - 10 - 6 - 11 - 12 - Е и А - 4 - 5 - 3 - 2 - В.
Все заданные корреспондирующие связи обеспечены. Порядок обеспечения связей статистический. Следовательно, полученный вариант дорожной сети (рис. 6, д) является статистическим.
Выборка обеспечения корреспондирующих связей
В предыдущем параграфе построение статистических вариантов сети автомобильных дорог рассматривалось при равномерном распределении сразу всех заданных корреспондирующих связей в интервале [0; 1]. В таком случае любая связь имеет равные права удовлетворения перед другими.
Практически целесообразно сгруппировать все связи по административно-территориальному признаку. Так, например, при проектировании сети областных дорог связи могут быть объединены в три группы: межобластные, межрайонные (областные) и районные.
Группа районных связей в свою очередь состоит из подгрупп, численность которых равна числу районов в области. Каждая подгруппа включает корреспондирующие связи одного района. Порядок расположения связей в группах и подгруппах произвольный. Переход от одной группы (подгруппы) к другой осуществляется после удовлетворения всех связей в рассматриваемой группе (подгруппе). Перебор групп произвольный и начинается с той, которая имеет более высокую административно-территориальную значимость.
Выборка обеспечения корреспондирующих связей в каждой группе (подгруппе) осуществляется при равномерном распределении связей группы (подгруппы) в интервале [0; 1].
Оптимальное обеспечение корреспондирующей связи методом последовательного улучшения исходного варианта
Пусть требуется найти оптимальный вариант обеспечения i-й корреспондирующей связи 1 - n (см. рис. 2). Исходная схема проектирования рациональной дорожной сети приведена выше (см. рис. 1, б).
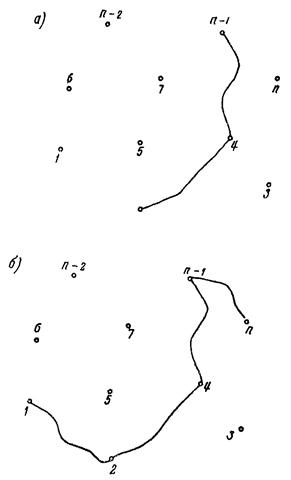
Сеть автомобильных дорог, полученная после удовлетворения предыдущих i - 1 корреспондирующих связей, дана на рис. 7, а. Допустим, имеется какой-либо вариант обеспечения i-й связи и приведенные затраты удовлетворения i-й связи по этому исходному варианту, равные Ku, больше затрат любого возможного варианта обеспечения рассматриваемой корреспондирующей связи. Такой исходный вариант является условным, ибо практически он не может существовать. Следовательно, нельзя и по нему определить значение критерия оптимизации Ku. При поиске оптимального варианта обеспечения связи на ЭВМ значение Ku принимается равным наибольшему числу, которое может поместиться в ячейку памяти машины.
Условный исходный вариант заведомо неоптимальный. Любой конкретный вариант обеспечения связи будет рациональнее исходного. Найдем этот конкретный вариант.
В ранее опубликованной работе автора /8/ приводится методика поиска оптимального обеспечения корреспондирующей связи при построении конкретных вариантов с помощью свободных правых звеньев. В той же работе показано, что такое построение вариантов не является рациональным, и приводится ряд приемов ускорения поиска наивыгоднейшего решения.
Рис. 7. Дорожная сеть после обеспечения начальных i - 1 корреспондирующих связей (а), дорожная сеть после обеспечения i-й корреспондирующей связи (б)
В настоящих «Рекомендациях» дается метод последовательного улучшения исходного варианта, в котором при построении конкретных вариантов обеспечения связи используются эти ускоряющие приемы.
Из корреспондирующего пункта 1 (см. рис. 1, б) перевозки могут осуществляться по звеньям исходной схемы 1 - 2 и 1 - 6. Условимся строить варианты удовлетворения связей с помощью свободных звеньев, имеющих наименьшее отклонение от направления на конечный корреспондирующий пункт. В данном случае таким конечным пунктом является пункт n. Свободным считается такое звено, которое, во-первых, не приводит к замкнутому контуру и, во-вторых, обеспечивает корреспондирующую связь по варианту, отличному от ранее рассмотренных.
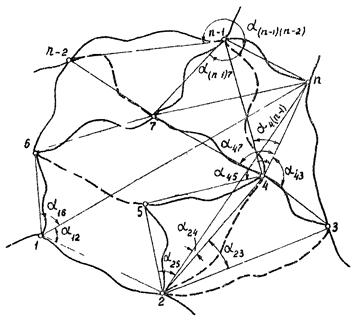
Как звено 1 - 6, так и звено 1 - 2 являются свободными. Звено 1 - 6 имеет отклонение от направления на конечный корреспондирующий пункт α16 (рис. 8), звено 1 - 2 - α12 Так как α12 > α16 принимается звено 1 - 2.
Рис. 8. Определение оптимального варианта обеспечения корреспондирующей связи 1 - n
В случае равенства углов отклонения свободных звеньев условимся принимать правое звено.
Приведенные затраты на звене 1 - 2 имеют следующий вид:
Здесь, кроме ранее названных обозначений,
![]() - затраты на реконструкцию 1 км;
- затраты на реконструкцию 1 км;
Q1-n - объем грузовых перевозок в год между корреспондирующими пунктами 1 и n;
Sa - себестоимость 1 авт/км автобусов;
Na - среднегодовая интенсивность движения автобусов в сутки;
Sл - себестоимость 1 авт/км легковых автомобилей;
Nл - среднегодовая интенсивность движения легковых автомобилей в сутки;
ℓ1-2 - длина дороги 1 - 2.
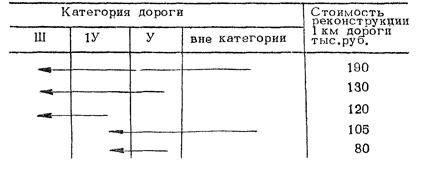
При проектировании сетей автомобильных дорог областного и местного значения капитальные затраты на реконструкцию дорог, показатели себестоимости перевозок и расходов на ремонт и текущее содержание дорог ориентировочно могут быть приняты в равнинной местности в соответствии с приведенными в табл. 5 и 6.
Таблица 5
Примечание. Стрелками обозначен переход из одной категории в другую.
Дальнейшее продолжение построения варианта, началом которого является звено 1 - 2, целесообразно лишь при условии, что приведенные затраты К1-2 меньше приведенных затрат исходного варианта. Условие
где ΣК - приведенные затраты по всем рассмотренным звеньям, должно соблюдаться на протяжении всего процесса построения варианта удовлетворения связи.
В данном случае К1-2 < Кu. Следовательно, продолжение варианта 1 - 2 рационально.
|
Тип покрытия |
Sт, коп/ткм |
SЭ, коп/ткм |
Sл, коп/авткм |
Sa, коп/авткм |
|
|
III |
Усовершенствованное капитальное |
5,3 |
0,8 |
2,2 |
9,1 |
|
Усовершенствованное облегченное |
6,0 |
0,9 |
2,3 |
10,1 |
|
|
Переходное |
6,9 |
2,2 |
2,5 |
11,8 |
|
|
IV |
Усовершенствованное облегченное |
8,3 |
2,8 |
2,5 |
11,8 |
|
Переходное |
9,4 |
3,7 |
2,7 |
14,6 |
|
|
Низшее |
11,4 |
5,0 |
2,7 |
16,9 |
|
|
V |
Переходное |
9,4 |
8,2 |
2,7 |
14,6 |
|
Низшее |
11,4 |
5,7 |
2,7 |
16,9 |
|
|
Вне категории |
Грунтовые дороги |
21,6 |
- |
5,1 |
32,1 |
Целесообразность продолжения варианта осуществляется еще проверкой невыхода его из области нахождения оптимального решения, т.е. из области Ω. Как было показано в работе /8/, область Ω представляет собой эллипс, в полюсах которого располагаются корреспондирующие пункты. Уравнение границы области Ω находят из условия
где ℓх - длина варианта удовлетворения корреспондирующей связи,
ℓ1-n - кратчайшее расстояние между корреспондирующими пунктами 1 и n,
λ - параметр эллипса.
Для того чтобы вариант удовлетворения связи не выходил за пределы области положения оптимального решения, очевидно, необходимо выполнение неравенства
Здесь ![]() - длина построенной части варианта обеспечения связи (длина от начального корреспондирующего
пункта
до конца принятого свободного звена)
- длина построенной части варианта обеспечения связи (длина от начального корреспондирующего
пункта
до конца принятого свободного звена)
![]() . (12)
. (12)
Величина параметра эллипса имеет параболическую зависимость от интенсивности движения автомобилей N на звеньях дорожной сети после обеспечения предыдущих корреспондирующих связей.
Значения параболических коэффициентов а, в, и с приведены в табл. 7 в зависимости от объемов грузовых перевозок анализируемой корреспондирующей связи Qi и от характеристики рельефа местности.
В табл. 7 приводится также потребная категория дороги для обеспечения корреспондирующей связи с объемом грузовых перевозок Qi. При определении категории дороги интенсивность движения определялась по формуле
интенсивность грузовых автомобилей
|
Объем грузовых перевозок Qi тыс. т/год |
Категория дороги |
Характеристика рельефа |
а |
в |
с |
|
|
|
Равнинный |
0,6 |
3,8·10-4 |
-3,2·10-8 |
|
230 - 670 |
III |
Пересеченный |
0,7 |
3,8·10-4 |
-3,2·10-8 |
|
|
|
Горный |
0,8 |
3,9·10-4 |
-3,3·10-8 |
|
|
|
Равнинный |
1,1 |
7,4·10-4 |
-4,2·10-8 |
|
45 - 230 |
IV |
Пересеченным |
1,2 |
8,0·10-4 |
-4,4·10-8 |
|
|
|
Горный |
1,3 |
9,0·10-4 |
-5,0·10-8 |
|
|
|
Равнинный |
2,1 |
1,2·10-3 |
-4,6·10-8 |
|
<45 |
V |
Пересеченный |
2,3 |
1,3·10-3 |
-4,8·10-8 |
|
|
|
Горный |
3,0 |
1,7·10-3 |
-6,2·10-8 |
где Кт.с. - коэффициент, учитывающий перестройку транспортных связей после сооружения дороги;
Траб - расчетное число рабочих дней в году;
g - коэффициент использования грузоподъемности автомобилей;
β - коэффициент использования пробега автомобилей;
q - грузоподъемность автомобилей.
Значения параметров, определяющих интенсивность грузовых автомобилей, были приняты следующие
Кт.с. = 1,25;
Траб = 225 дней;
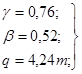 Для дорог
областного значения
Для дорог
областного значения
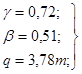 Для дорог
местного значения
Для дорог
местного значения
Состав автопарка при выявлении потребной категории автомобильной дороги и определении значений параболических коэффициентов принимался согласно табл. 8. Определение параметра эллипса λ по зависимости (13) требует однозначности значения интенсивности движения автомобилей. Практически интенсивность движения на каждом звене дорожной сети в общем случае различная. Для определения величины λ следует брать средневзвешенное значение интенсивности движения на всех звеньях, которые могут принять участие в формировании оптимального варианта обеспечения рассматриваемой корреспондирующей связи.
В случае проектирования сетей дорог областного и местного значения N может быть принято равным 1000 авт/сутки. Тогда формула (13) приобретает вид
|
Тип автомобилей |
Процент от общего числа автомобилей |
Вид автомобилей |
Процент от числа грузовых (пассажирских) автомобилей |
|
|
I |
Грузовые |
75 |
Легкие |
40 |
|
|
|
|
Средние |
45 |
|
|
|
|
Тяжелые |
15 |
|
|
Пассажирские |
25 |
Автобусы |
20 |
|
|
|
|
Легковые |
80 |
|
II |
Грузовые |
75 |
Легкие |
40 |
|
|
|
|
Средние |
50 |
|
|
|
|
Тяжелые |
10 |
|
|
Пассажирские |
25 |
Автобусы |
20 |
|
|
|
|
Легковые |
80 |
|
III |
Грузовые |
75 |
Легкие |
42 |
|
|
|
|
Средние |
55 |
|
|
|
|
Тяжелые |
3 |
|
|
Пассажирские |
25 |
Автобусы |
20 |
|
|
|
|
Легковые |
80 |
|
IV - V |
Грузовые |
90 |
Легкие |
45 |
|
|
|
|
Средние |
55 |
|
|
|
|
Тяжелые |
- |
|
|
Пассажирские |
10 |
Автобусы |
5 |
|
|
|
|
Легковые |
95 |
Значение λ при N = 1000 авт/сутки приведено в табл. 9.
Имея значение λ, можно проверить целесообразность продолжения построения варианта по условию невыхода из области Ω.
|
Объем грузовых перевозок Qi, тыс. т/год |
Категория дорог |
Характеристика рельефа |
λ |
|
|
|
Равнинный |
0,95 |
|
230 - 670 |
III |
Пересеченный |
1,05 |
|
|
|
Горный |
1,16 |
|
|
|
Равнинный |
1,80 |
|
45 - 230 |
IV |
Пересеченный |
1,96 |
|
|
|
Горный |
2,15 |
|
|
|
Равнинный |
3,25 |
|
< 45 |
V |
Пересеченный |
3,55 |
|
|
|
Горный |
4,64 |
Продолжать вариант обеспечения связи 1 - n из пункта 2 рационально при соблюдении условия (11). Величина ![]() на данном этапе поиска оптимального решения равна ℓ1-2. Произведение λℓ1-n является постоянным для корреспондирующей связи 1 - n. Возможны два случая:
на данном этапе поиска оптимального решения равна ℓ1-2. Произведение λℓ1-n является постоянным для корреспондирующей связи 1 - n. Возможны два случая:
1) ℓ1-2 < λℓ1-n и 2) ℓ1-2 ≥ λℓ1-n
В первом случае построение варианта следует продолжать, во втором - вариант отбрасывается. Для краткости изложения здесь и далее будем рассматривать только один из возможных случаев.
Допустим, что ℓ1-2 < λℓ1-n. Из точки 2 вариант следует продолжить. Свободными звеньями продолжения варианта являются звенья 2 - 3, 2 - 4 и 2 - 5. В силу того, что α24 < α23 и α24 < α25, принимается звено 2 - 4. Звено 2 - 4 ранее запроектировано при удовлетворении i - 1 начальных корреспондирующих связей (см. рис. 7, а). Приведенные затраты K2-4 в этом случае находятся по формуле
Здесь ![]() - объем грузовых перевозок на звене 2 - 4 до удовлетворения i-й корреспондирующей связи;
- объем грузовых перевозок на звене 2 - 4 до удовлетворения i-й корреспондирующей связи;
S′Э - показатель расходов на ремонт и содержание дороги, приходящихся на единицу грузооборота, который выполняется на звене 2 - 4 до обеспечения i-й корреспондирующей связи.
Следовательно, формула (17) используется для подсчета приведенных затрат при условии, что звено ранее было запроектировано для удовлетворения предыдущих корреспондирующих связей. В противном случае необходимо применять формулу (8).
Сумма приведенных затрат на участке 1 - 2 - 4, равная ΣК = К1-2 + К2-4, меньше значения приведенных затрат исходного варианта К1-2 + К2-4 < Кu. Поэтому вариант следует продолжать, если не нарушено неравенство (11). Величина ℓ′х = ℓ1-2 + ℓ2-4 < λℓ1-n. Вариант из пункта 4 продолжаем по одному из свободных звеньев 4 - 7, 4 - 5, 4 - 3 и 4 - (n - 1). Так как звено 4 - (n - 1) наименее отклонено от направления между пунктом 4 и конечным корреспондирующим пунктом n, следует принять за продолжение звено 4 - (n - 1). Проверяется выполнение условия (9). ΣК = К1-2 + К2-4 + К4-(n-1) < Кu. Условие (11) тоже выполняется, ибо ℓ′х = ℓ1-2 + ℓ2-4 + ℓ4-(n-1) < λℓ1-n. Поэтому необходимо исследовать вариант дальше. Из пункта (n - 1) выходят три свободных звена (n - 1) - 7, (n - 1) - (n - 2) и (n - 1) - n. Наименее отклоненным свободным звеном от направления (n - 1) - n является, очевидно, звено (n - 1) - n. Приняв это звено за продолжение, попадаем в конечный корреспондирующий пункт n.
Следовательно, вариант обеспечения связи 1 - n построен. Вариант проходит через пункты 1, 2, 4, (n - 1) и n. Так как ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-n < Кu, то необходимо для дальнейшего поиска более рационального решения удовлетворения связи 1 - n за исходный вариант принять вариант 1 - 2 - 4 (n - 1) - n.
В ячейку ЭВМ, где хранилось большое число, условно принятое за значение приведенных затрат первого исходного варианта, посылается значение Кu = К1-2 + К2-4 + К4-(n-1) + К(n-1)-n.
Далее отступаем от конечного корреспондирующего пункта n на одно звено по исходному варианту и попадаем в пункт (n - 1). Свободным звеном продолжения варианта 1 - 2 - 4 (n - 1), наименее отклоненным от направления (n - 1) - n, является звено (n - 1) - 7. Образуется новый вариант обеспечения связи 1 - n, началом которого служат звенья 1 - 2, 2 - 4, 4 - (n - 1) и (n - 1) - 7. Проверяем целесообразность продолжения нового варианта по условию (9). Возможны два случая:
1) ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-7 ≥ Кu;
2) ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-7 < Кu.
Условимся рассматривать только один из возможных случаев. Допустим, что имеет место второй случай. Следовательно, необходима проверка на выход варианта из области Ω. Произведение λℓ1-n > ℓ1-2 + ℓ2-4 + ℓ4-(n-1) + ℓ(n-1)-7. Из точки 7 вариант согласно ранее принятым правилам продолжаем по свободному звену 7 - (n - 2). Звено 7 - 4 не может служить продолжением, так как приводит к замкнутому контуру 4 - (n - 1) - 7, а значит звено 7 - 4 не свободное.
Приведенные затраты К7-(n-2) определяются по формуле (8) с той лишь разницей, что вместо капитальных затрат на реконструкцию в данном случае необходимо предусмотреть расходы на сооружение новой дороги 7 - (n - 2). Строительная стоимость 1 км дорог областного и местного значения в равнинной местности приведена в табл. 10.
|
Тип покрытия |
Строительная стоимость тыс. руб./км |
|
|
III |
Усовершенствованное капитальное |
160 |
|
Усовершенствованное облегченное |
140 |
|
|
Переходное |
127 |
|
|
IV |
Усовершенствованное облегченное |
95 |
|
Переходное |
80 |
|
|
Низшее |
60 |
|
|
V |
Переходное |
54 |
|
Низшее |
38 |
Так как ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-7 + К7-(n-2) > Кu, продолжать вариант 1 - 2 - 4 (n - 1) - 7 - (n - 2) нецелесообразно. Отступаем по варианту в предыдущий пункт 7. Свободным звеном для этого пункта является звено 7 - 6. В силу того, что ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-7 + К7-6 > Кu, следует, произвести проверку на выход из области Ω. ℓ1-2 + ℓ2-4 + ℓ4-(n-1) + ℓ(n-1)-7 + ℓ7-6 > λℓ1-n. т.е. продолжение по звену 7 - 6 приводит к выходу из области расположения оптимального решения. Возвращаемся в пункт 7. В пункте 7 свободных звеньев уже не осталось. Отступаем в пункт (n - 1) и исследуем возможность продолжения варианта по свободному звену (n - 1) - (n - 2). ΣК = К1-2 + К2-4 + К4-(n-1) + К(n-1)-(n-2) > Кu. Следовательно, продолжать вариант по звену (n - 1) - (n - 2) не имеет смысла. В пункте (n - 1) все свободные звенья проанализированы, отступаем в пункт 4.
Наименее отклоненным от направления 4 - n является свободное звено 4 - 7. Сумма приведенных затрат ΣК = К1-2 + К2-4 + К4-7 = Кu. Продолжать вариант не следует, ибо вариант еще не дошел до конечного корреспондирующего пункта n, а критерий оптимизации по нему уже равен сумме приведенных затрат предыдущего варианта. Возвращаемся в пункт 4. По принятому правилу продолжать можно по свободному звену 4 - 3. Но так как ΣК = К1-2 + К2-4 + К4-3 > Кu, то исследуем целесообразность продолжения по следующему свободному звену 4 - 5. Опять ΣК = К1-2 + К2-4 + К4-5 > Кu. Отступаем в пункт 2. Свободных звеньев два: 2 - 5 и 2 - 3. α23 < α25. Поэтому принимается звено 2 - 3. ΣК = К1-2 + К2-3 > Кu. Исследуем возможность продолжения начала 1 - 2 по звену 2 - 5. ΣК = К1-2 + К2-5 > Кu. Переходим в пункт 1. Из пункта 1 вариант обеспечения корреспондирующей связи может идти по свободному звену 1 - 6, В силу того, что К1-6 = Кu, продолжать этот вариант нерационально.
Таким образом, оптимальным решением обеспечения связи 1- n является вариант 1 - 2 - 4 - (n - 1) - n.
После обеспечения i-го количества корреспондирующих связей дорожная сеть принимает вид, показанный на рис. 7, б.
Использование закона распределения критерия оптимизации для уменьшения потребного количества статистических вариантов дорожной сети
Построение и обработка каждого статистического варианта сети при большом числе корреспондирующих пунктов требуют весьма больших трудозатрат. Поэтому одним из основных моментов при выборе рационального варианта сети автомобильных дорог с помощью метода Монте-Карло главное внимание уделяется разработке различных приемов уменьшения потребного числа случайных вариантов сети.
Сокращения потребного числа случайных вариантов NC можно ожидать при использовании теоретической функции распределения критерия оптимизации - суммы приведенных затрат. По данной функции можно определить такое значение приведенных затрат КОПТ, до которого следует оптимизировать дорожную сеть с заданной точностью Δ.
Статистические испытания сети в этом случае следует продолжать до случайного варианта сети, имеющего сумму приведенных затрат К менее или равной КОПТ.
Анализ показал, что КОПТ при проектировании сети автомобильных дорог областного и местного значения следует определять исходя из гипотезы о нормальности функции распределения критерия оптимизации. В этом случае КОПТ находят из равенства
где θ - математическое ожидание приведенных затрат;
σ - среднее квадратическое отклонение;
Δ - точность поиска рационального варианта дорожной сети.
КОПТ = σargф(Δ) + θ, (19)
где argф(Δ) - обратная величина нормальной функции распределения.
Для выявления значений θ и σ целесообразно использовать их доверительные интервалы, полученные в результате построения малого числа (NC ≤ 30) случайных вариантов дорожной сети.
где ![]() - минимальное граничное значение доверительного интервала математического ожидания;
- минимальное граничное значение доверительного интервала математического ожидания;
![]() ,
, ![]() - минимальное (максимальное) граничное
значение
доверительного интервала среднего квадратического отклонения.
- минимальное (максимальное) граничное
значение
доверительного интервала среднего квадратического отклонения.
где θ* - статистическая оценка математического ожидания по результатам малого числа испытаний;
σ* - то же для среднего квадратического отклонения;
tβ - параметр, определяемый в зависимости от доверительной вероятности из выражения
где Sn-1(t) - плотность закона Стьюдента.
Значения ![]() и
и ![]() соответственно находятся из условий
соответственно находятся из условий
где V - случайная величина, имеющая χ2 распределение с r = NC - 1 степенями свободы.
Статистические значения θ* и σ* при малом числе испытаний сети (NC ≤ 30) находят по формулам
Пользуясь граничными значениями доверительных интервалов, можно определить величину КОПТ. При малом числе статистических вариантов дорожной сети
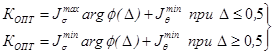 . (26)
. (26)
При определении argф(Δ), tβ, χ12, χ22 могут быть использованы таблицы, приведенные в работе Е.С. Венцеля «Теория вероятностей».
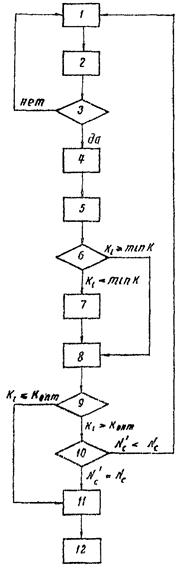
Укрупненная блок-схема выбора оптимального варианта сети дорог методом Монте-Карло
Укрупненная блок-схема выбора рационального варианта сети дорог методом Монте-Карло представлена на рис. 9. После того, как собраны исходные данные и разработана исходная схема дорожной сети, приступают к определению оптимального решения сети. Блок 1 - выявление номера корреспондирующей связи, подлежащей удовлетворению.
Номер связи выявляют в соответствии с формулой (5). Оптимальное удовлетворение связи предусмотрено блоком 2. Вариант дорожной сети считается построенным тогда, когда все заданные корреспондирующие связи обеспечены. Блок 3 предусматривает проверку перебора всех связей, т.е. осуществляет контроль окончания построения статистического варианта сети. Для построенного варианта дорожной сети определяется и запоминается критерий оптимизации - сумма приведенных затрат - Ki (блок 4). Блок 5 - добавление единицы в счетчик количества образованных статистических вариантов сети. Логический блок 6 предусматривает сравнение величины Ki, с минимальным значением приведенных затрат min K предыдущих вариантов дорожной сетиx). Если Ki < min K, то происходит запоминание построенного i-го варианта сети и посылка в ячейку, где хранилось значение min K, величины Ki (блок 7). В противном случае (Ki ≥ min K) запоминать данные i-го варианта дорожной сети не требуется.
х) Ввиду того, что при начальном цикле не имеется предыдущего варианта сети, в ячейку, в которой предусматривается хранение min K, засылается перед счетом большое число.
Использование закона распределения критерия оптимизации для уменьшения количества статистических вариантов сети предусматривается блоками 8 и 9.
Рис. 9. Укрупненная блок-схема выбора оптимального варианта сети дорог методом Монте-Карло:
блок 1 - выявление номера корреспондирующей связи; блок 2 - оптимальное обеспечение выявленной связи; блок 3 - проверка на пересмотр всех заданных корреспондирующих связей; блок 4 - определение и запоминание приведенных затрат полученного статистического варианта сети; блок 5 - добавление 1 в счетчик количества статистических вариантов; блок 6 - сравнение Ki с min K; блок 7 - запоминание варианта дорожной сети; блок 8 - определение КОПТ; блок 9 - сравнение Ki с КОПТ; блок 10 - сравнение N′C с NC; блок 11 - печать варианта с min K; блок 12 - останов
По формуле (26) определяется значение КОПТ (блок 8). При этом КОПТ уточняется после получения каждого статистического варианта сети. Если полученное значение КОПТ < Ki (блок 9), то контролем окончания поиска рационального варианта сети служит равенство N′C = NC (блок 10), где N′C - количество проанализированных статистических вариантов сети, NC - потребное количество статистических вариантов сети, определенное по формуле (3). При N′C < NC оптимизация дорожной сети продолжается. При N′C = NC печатается наивыгоднейший вариант сети из всех рассмотренных, т.е. имеющий min K (блок 11).
Если КОПТ ≥ Ki (блок 9), то оптимальный вариант дорожной сети найден. Им является i-й вариант, который печатается (блок 11). После получения окончательного решения сети происходит останов ЭВМ (блок 12).
ЛИТЕРАТУРА
1. Хомяк Я.В. Проектирование оптимальных сетей автомобильных дорог. М., «Транспорт», 1969.
2. Паршиков В.А. Выбор рационального варианта начертания дорожной сети. - «Труды ИКТП при Госплане СССР», М., «Транспорт», 1967.
3. Паршиков В.А., Полякова Г.А. Оптимальное Начертание сети дорог с помощью электронно-счетных машин. - «Автомобильные дороги», 1965, № 11.
4. «Типовая методика определения экономической эффективности капитальных вложений». М., «Экономика», 1969.
5. Андроникашвили К.И. Определение экономически наивыгоднейшего направления в зависимости от схемы транспортных связей. - «Автомобильные дороги», 1956, № 8.
6. Грибников С.М. Проектирование сетей автомобильных дорог. Киев, Госиздат УССР, 1962.
7. Замахаев М.С., Кудрявцев А.С. Экономические изыскания и проектирование дорожных сетей. М., Автотрансиздат, 1958.
8. Волков Б.А. К вопросу выбора рационального варианта дорожной сети. - «Труды Союздорнии», вып. 22, 1970.
В «Рекомендациях» приводится методика проектирования сети дорог областного и местного значения, базирующаяся на использовании методов математического программирования и быстродействующих вычислительных машин (ЭВМ). Для нахождения рационального начертания дорожной сети предлагается применять метод статистических испытаний (метод Монте-Карло). Метод Монте-Карло позволяет найти наивыгоднейшее решение с наперед заданной вероятностью Р на основании статистического анализа случайных вариантов начертания сети.
СОДЕРЖАНИЕ
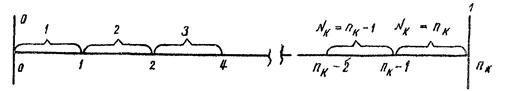
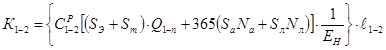 . (
. (
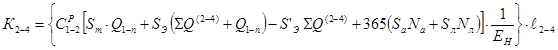 . (
. (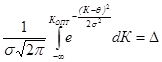 , (
, (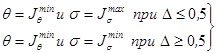 (
(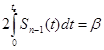 , (
, (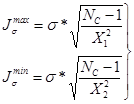 (
(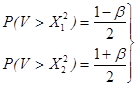 , (
, (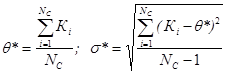 . (
. (