ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
КОЛИЧЕСТВЕННЫЕ МЕТОДЫ
ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ
СТАНДАРТИЗАЦИИ. МЕТОДЫ
ПРОГНОЗИРОВАНИЯ ПРИ ОПТИМИЗАЦИИ.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
РД 50-219-80
Москва
ИЗДАТЕЛЬСТВО СТАНДАРТОВ
1981
РАЗРАБОТАНЫ
Всесоюзным научно-исследовательским институтом стандартизации
(ВНИИС)
Директор А.В. Гличев
Зам. директора В.Н. Брюнин
Руководитель темы Е.В. Извеков
ИСПОЛНИТЕЛИ:
Д.М. Комаров, Н.Д. Алексеева, Н.И. Горшкова, С.А. Клявина, Г.В. Литманс, А.В. Матвеев, В.А. Певзнер, М.Л. Сыроватко, Г.С. Табакова
ВНЕСЕНЫ Техническим управлением Государственного комитета СССР по стандартам
Начальник Технического управления Б.Н. Лямин
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 19 декабря 1980 г. № 5897
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Количественные методы оптимизации
параметров объектов стандартизации. |
РД Введены впервые |
Утверждены Постановлением Госстандарта от 19 декабря 1980 г. № 5897, срок введения установлен с 1 января 1982 г.
Настоящие Методические указания распространяются на теоретические и экспериментальные методы оптимизации параметров объектов стандартизации (ПОС) и входят в третью группу комплекса документов «Количественные методы оптимизации ПОС» (ГОСТ 18.001-76) - «Методы обеспечения опережаемости. Основные положения».
Прогнозирование ПОС регламентируется всем комплексом документов «Количественные методы оптимизации ПОС» от [1] до [12], а также [19] и [25]. Данный документ регламентирует главным образом методы прогнозирования исходных данных, необходимых при оптимизации ПОС. Он предназначен для повышения эффективности дальнейшей работы по созданию и использованию системы оптимизации ПОС.
Необходимость данных методических указаний вызвана особенностями методов прогнозирования при оптимизации ПОС. Эти особенности связаны с тем, что значения ПОС зависят от управляющих воздействий людей, которые исходят из определенных целей и учитывают действующие ограничения.
Общие методические указания настоящего документа будут конкретизироваться в документах по базовым и рабочим методам оптимизации ПОС.
Методические указания предназначены для специалистов, разрабатывающих документы системы оптимизации ПОС и рекомендуются для разработчиков отдельных методов оптимизации.
1. ТРЕБОВАНИЯ К ТОЧНОСТИ И ПЕРИОДУ УПРЕЖДЕНИЯ ПРОГНОЗА ПРИ ОПТИМИЗАЦИИ ПОС
1.1. Требования к результатам прогноза зависят от того, для принятия каких решений они используются. Наиболее жесткие требования к результатам прогноза следует предъявить при установлении параметров объектов, записываемых в конструкторской, технологической и нормативно-технической документации, так как потери вследствие неоптимальности значений этих параметров обычно превышают потери вследствие неоптимальности других решений при стандартизации (например, потери вследствие ошибок прогноза при планировании качества).
1.2. Точность прогноза характеризуется точностью результатов прогнозирования исходных данных для оптимизации (их вероятностными характеристиками). Устанавливаемые значения параметров по результатам прогноза неизбежно отступают от абсолютно оптимальных из-за несовершенства методов прогнозирования и наличия неопределенностей.
Это приводит к некоторому снижению эффективности объекта, с другой стороны, с ростом точности прогнозирования растут расходы средств и времени на прогнозирование. Суммарные потери на разработку прогноза и потери вследствие его несовершенства имеют некоторый минимум, соответствующая точность прогноза является оптимальном (см. справочное приложение).
1.3. Период упреждения прогноза это интервал времени, на который разрабатывается прогноз.
Минимально необходимый период упреждения прогноза Tmin (в годах) для квазистатической оптимизации определяется по формуле:
Tmin = Tp + Tk,
где Tр - время разработки и внедрения нормативно-технического документа;
Тk - время от момента внедрения до момента, для которого вычисляются оптимальные параметры.
Если принять, что Тк = Tд/2, где Tд - время действия документа, то при Тр = 2 года, а Tд = 5 лет получим Tmin = 4 + 5 лет. Всегда желательно увеличить период упреждения прогноза, однако это приведет к снижению точности и подробности результатов прогноза.
2. ОСОБЕННОСТИ ПРОГНОЗИРОВАНИЯ ПРИ ОПТИМИЗАЦИИ ПОС
2.1. Будущие значения ПОС в зависимости от управляющих воздействий могут быть разными. Разумно при прогнозировании предположить, что управляющие воздействия будут оптимальными или по крайней мере близки к оптимальным. При гаком подходе нет двух отдельных задач: задачи прогнозировании и задачи оптимизации ПОС, а есть лишь одна задача прогнозирования в сочетании с оптимизацией.
Сущность такого сочетания состоит в том, что прогнозируется исходная информация, а оптимизация ПОС осуществляется по типовой схеме, регламентированной ГОСТ 18.101-76 [18], [20].
2.2. Такое сочетание прогнозирования исходной информации с оптимизацией ПОС позволяет повысить точность установления будущих ПОС за счет:
прогнозирования исходных данных (функций для эффектов, затрат и ограничений), которые, как правило, изменяются более медленно и более плавно, чем конкретные значения ПОС;
учета управляющих воздействий, которые целесообразно считать близкими к оптимальным;
широкого использования причинно-следственных математических моделей для учета связей между параметрами будущих объектов (энергетические расчеты, расчеты прочности, расчеты ускорений, скоростей, пути, расчеты точности систем управления, расчеты электрических, оптических и других характеристик для будущего времени);
более разумного использования передового опыта в области повышения качества объектов стандартизации. Этот опыт рассматривается, как возможный вариант, который корректируется в соответствии с целевой функцией и ограничениями.
2.3. Разработку нового объекта следует рассматривать как процесс прогнозирования (обоснования) ПОС. Если бы было известно, что и как следует делать для достижения заданных целей, то отпала бы необходимость разрабатывать проекты, изготовлять и испытывать опытные образцы, а можно было сразу разработать рабочие чертежи и запустить образец в массовое производство. Методы изготовления и испытания опытных образцов, применяемые при разработке новых объектов, следует включить в число основных методов прогнозирования ПОС.
2.4. Для преодоления трудностей прогнозирования параметров при разработке принципиально новых объектов, часто целесообразно использовать стратегию параллельных разработок. В этом случае с целью снижения вероятности грубых ошибок разрабатывается несколько вариантов объектов для решения одной и той же задачи, хотя достаточно создание одного варианта объекта. Разработку отдельных вариантов следует прекратить тогда, когда для этого решения имеется достоверная информация. Часто такую информацию удается получить лишь в ходе сравнительных испытаний опытных образцов.
2.5. Для оптимизации ПОС будущих объектов необходимо е общем случае прогнозировать следующие исходные данные: эффекты, затраты, ограничения, описывающие научно-технические возможности и ограничения в виде неравенств на производственные, финансовые и кадровые возможности.
Первичным для этих прогнозов при строгих методах оптимизации является прогноз научно-технических возможностей. Результаты этого прогноза являются важной основой для прогнозирования остальной исходной информации.
2.6. Прогнозирование исходной информации для оптимизации ПОС, а иногда и прогнозирование самих параметров (п. 2.10), следует производить одним из следующих методов:
изготовлением и испытанием макетов и экспериментальных образцов, а также физическим моделированием особенно при прогнозировании технических возможностей;
составлением по известным законам природы и общества причинно-следственных математических моделей и оценкой параметров этих моделей по предыстории;
составлением эмпирических зависимостей по статистике предыстории и экстраполяцией на будущее;
использованием эвристических методов.
2.7. Методы прогнозирования, основанные на составлении причинно-следственных моделей обеспечивают наибольшую точность прогноза при малых затратах. Они применимы при решении достаточно простых задач и при малых неопределенностях (например, при прогнозировании некоторых зависимостей между параметрами объектов, или прогнозировании изменений параметров в результате некоторых мероприятий). Преимущества этих методов увеличиваются с увеличением периода упреждения. При больших неопределенностях в исходной информации и численных величинах входных данных не следует усложнять модель или даже вообще ее строить.
2.8. В общем случае для построения теоретической модели, описывающей изменение параметров объектов и пригодной для их прогнозирования, целесообразно воспользоваться методами идентификации объектов управления.
Под идентификацией объектов управления понимается процедура построения оптимальной модели объекта управления по реализациям его входных и выходных сигналов с учетом общих закономерностей процессов (физических, химических и т.д.), протекающих в объекте управления. Таким образом, в результате идентификации получают математическое описание процесса, в котором учитываются как конкретные реализации так и общие закономерности процесса, т.е. для прогнозирования используется вся имеющаяся информация [31].
При непосредственной экстраполяции модель строят только по конкретным реализациям процесса в прошлом. Методы непосредственной экстраполяции при прогнозировании исходных данных также как и при прогнозировании (обосновании) ПОС находят в настоящее время широкое применение. Под непосредственной экстраполяцией при оптимизации ПОС понимается процесс определения будущих параметров объектов (зависимостей для исходных данных) по результатам наблюдения за их изменениями в прошлом. Методической основой экстраполяции является предположение о сохранении тенденций, имевших место в прошлом, и в будущем.
2.8.1. Самый простой путь использования метода непосредственной экстраполяции - это графически отобразить изменение параметров в прошлом и «на глаз» распространить тенденцию на будущее.
В общем случае необходимо подобрать аналитическую зависимость (часто используются линейная зависимость, полином, экспонента и др.) и определить коэффициенты выбранной зависимости.
2.8.2. Для определения коэффициентов выбранной зависимости целесообразно использовать:
методы, в которых все точки базового периода используются с равным весом (способ наименьших квадратов);
методы, в которых более поздние точки учитываются с большим весом.
В первом случае увеличиваются ошибки вследствие старения исходных данных. Во втором случае существует опасность принять случайные «помехи» за тенденцию. Для ослабления этого факта следует использовать, например, метод экспоненциального сглаживания, при котором веса точек экспоненциально убывают по мере учета точек, полученных в более раннее время.
2.8.3. При определении коэффициентов с использованием методов регрессионного анализа для исключения грубых ошибок необходимо, во-первых, включить в уравнения все основные факторы, во-вторых, не включать те факторы, между которыми существуют функциональные зависимости, заменив их независимыми факторами, или использовать специальные вычислительные процедуры [13], [24].
2.8.4. При использовании методов экстраполяции, для обоснования параметров, как правило, невозможно получить точность и подробность прогноза ПОС, необходимые для выполнения работ по стандартизации и управлению качеством. Последнее объясняется по крайней мере тремя причинами:
при экстраполяции считают, что объект прогнозирования является автономным, т.е. изолированным от внешней среды, или что в этой среде нет существенных изменений. Следовательно, при экстраполяции не может учитываться влияние достижений в смежных областях народного хозяйства, которое часто решающим образом сказывается на изменении ПОС;
при современном производстве ПОС изменяются во времени, как правило, скачкообразно;
в один и тот же момент имеются однородные объекты с разными параметрами.
При экстраполяции невозможно учесть результаты целенаправленной деятельности людей по совершенствованию качества продукции и прошлое слепо переносится на будущее, в том числе и ошибки прошлого.
2.8.5. Несмотря на недостатки, присущие методам экстраполяции, они могут найти применение при прогнозировании наиболее стабильной части параметров объектов. Эти методы могут найти также применение при прогнозировании исходной информации для оптимизации.
2.9. Эвристические методы прогнозирования позволяют решать сложные задачи в условиях больших неопределенностей. Из этих методов целесообразно выделить две группы:
методы прогнозирования на базе суждений экспертов (экспертные методы);
методы прогнозирования на базе результатов социологических опросов.
2.9.1. Экспертные методы прогнозирования заключаются в обработке суждений специалистов. Эти методы являются эффективными при условии, что специалисты имеют соответствующий опыт и достаточно точное представление о будущих условиях создания и использования объекта.
При разработке принципиально новых объектов и (или) новых условии их использования экспертные методы не могут обеспечить достаточную точность прогноза [7], [19].
2.9.2. Методы прогнозирования на базе социологических опросов заключаются в опросе и статистической обработке представительной группы населения. Результаты таких опросов используются с целью распространения их за пределы опрошенной группы, т.е. прогнозирования статистики мнений. Эти методы могут оказаться эффективными для прогнозирования спроса на продукцию народного потребления [21].
На следующем этапе параметры группы Б считаются заданными, а параметры группы А оптимизируются.
Если на втором этапе значения параметров группы А мало отличаются от найденных на первом этапе, то считается задача решенной, в противном случае процесс следует повторить.
3. ВЫБОР МЕТОДОВ ПРОГНОЗИРОВАНИЯ НАУЧНО-ТЕХНИЧЕСКИХ ВОЗМОЖНОСТЕЙ
3.1. Прогнозирование научно-технических возможностей заключается главным образом в определении связей между ПОС для будущего времени. Эти связи являются функциями уровня научно-технического прогресса и, следовательно, времени. Такое прогнозирование фактически производится в НИИ, КБ и на предприятиях при разработке новых моделей объектов. Особенности такого прогнозирования зависят от области науки и техники, используемой для изучения и расчета параметров будущего объекта. Эти особенности рассматриваются в соответствующих разделах курсов проектирования объектов и изучаются в технических, химических, физических и других науках. В этом главная причина невозможности разработки единой методики прогнозирования ПОС.
3.2. Закономерности, установленные в фундаментальных и прикладных науках, следует использовать для построения причинно-следственных математических моделей прогнозируемого процесса.
Решение по таким моделям для будущего времени, если они соответствуют (адекватны) реальной задаче, является научным прогнозом. Примерами применения причинно-следственных математических моделей прогнозирования являются следующие расчеты для будущих (еще не существующих) объектов:
энергетические расчеты (мощности, КПД, расхода топлива, нагрева, дальности полета и т.д.);
расчеты прочности сооружений, деталей машин;
расчеты ускорений, скоростей, пути, программ управления движением;
расчеты точности систем управления, точности механизмов и т.д.;
расчеты электрических, оптических, термодинамических и других характеристик;
расчеты надежности;
расчеты производительности;
расчеты по некоторым математическим моделям теории исследования операций.
3.3. При разработке новых объектов, как правило, целесообразно широко практиковать сочетание теоретических и экспериментальных методов прогнозирования научно-технических возможностей. При таком сочетании та часть исследуемого объекта прогноза, которая легко описывается математически, представляется в виде математической модели, другая часть, которую трудно описать математически, изготовляется и используется при прогнозировании в виде макета. Например, динамика полета летательного аппарата описывается математическими уравнениями, а система управления полетом используется в виде макета, причем предусматривается возможность варьирования характеристиками тех элементов, для которых прогнозируется влияние этих характеристик на точность полета летательного аппарата.
3.4. В тех случаях, когда составить отдельные теоретические зависимости между параметрами оптимизируемого объекта трудно или невозможно, целесообразно определить эти зависимости экспериментально, а затем прогнозировать научно-технические возможности.
При этом следует учитывать, что экспериментальные зависимости могут существенно зависеть от уровня научно-технического прогресса и, следовательно, от времени.
4. ВЫБОР МЕТОДОВ ПРОГНОЗИРОВАНИЯ ПОТРЕБНОСТЕЙ
4.1. Необходимость прогнозирования потребностей (спроса) при оптимизации ПОС возникает в следующих случаях:
когда потребности или спрос полностью удовлетворяются и принимаются за эффект, входящий в целевую функцию оптимизации (например, так поступают при оптимизации параметрических рядов);
когда удовлетворение потребностей (спроса) поставлено как ограничение;
когда потребности определяют объем продукции, входящий в выражение для затрат и (или) эффекта.
4.2. При прогнозировании потребностей следует различать особенности методов прогнозирования спроса в товарах народного потребления и потребностей продукции производственного назначения.
4.3. Спрос на товары народного потребления зависит от экономических, внеэкономических и конъюнктурных факторов.
К экономическим факторам относятся: денежный доход семьи, его дифференциация по разным группам населения, уровень и соотношение розничных цен, сбережения населения, запасы товаров и количество вновь производимых товаров. Эти факторы существенно изменяются во времени.
К внеэкономическим факторам относятся природно-климатические условия, общий уровень культуры населения, национальные особенности (привычки и традиции), половозрастной состав населения и характер его трудовой деятельности. Эти факторы в течение 5 - 6 лет могут считаться постоянными.
К конъюнктурным факторам относятся мода на товары, изменчивость погодных условий, урожайность и др. Прогнозирование этих факторов на 5 - 6 лет вперед затруднительно или невозможно.
Следует в модель прогнозирования включать только основные факторы, к которым при прогнозировании спроса на товары народного потребления, как правило, относятся доход населения и розничные цены товаров. Однако с учетом специфики товаров и оптимизируемых показателей иногда необходимо учесть и дополнительные факторы. Например, при прогнозировании спроса на предметы длительного пользования необходимо учесть наличие этих предметов у населения, при прогнозировании параметров мебели следует учесть размеры квартир и т.д.
4.5. При построении эмпирических математических моделей для прогнозирования спроса на товары народного потребления могут быть использованы следующие виды исходной информации:
данные торговой статистики;
данные демографической информации и данные о статистике бюджета населения;
сочетание первых двух видов информации [14], [15].
Данные торговой статистики позволяют выявить закономерности спроса за длительный период в зависимости от изменения доходов, розничных цен, оборота колхозного рынка, роста населения и других факторов.
Данные бюджетной статистики получают путем обследования бюджета некоторого достаточного числа семей определенных категорий населения. При таком обследовании выясняются: доход семьи, его распределение, половозрастной состав семьи, распределение дохода между разными категориями населения.
Комплексное использование торговой и бюджетной статистики позволяет повысить точность прогнозов.
4.6. Прогнозирование спроса на товары народного потребления с целью оптимизации показателей качества целесообразно проводить по поэтапной процедуре.
Вначале методами регрессионного анализа строится многофакторная математическая модель (в модель включаются базисные индексы показателей в расчете на душу населения), например, модель на всю группу непродовольственных товаров [14], [15], [22].
Чаще всего эта модель записывается в одном из следующих видов:
![]()
y = a0 + a1х1 + a2x2 + ... + аnхn,
где у - размер спроса на всю группу непродовольственных товаров;
х1, х2, ..., хп - факторы, определяющие спрос (п. 4.4);
a0, а1, ..., ап - коэффициенты модели, которые определяются по статистическим данным.
После определения спроса на всю группу непродовольственных товаров рассчитывается спрос на подгруппы товаров: предметы одежды, товары культурно-бытового назначения, предметы санитарии и гигиены и т.д.
Для оптимизации показателей качества товаров необходимо определить не только спрос на данный конкретный товар, но и на возможные его варианты, отличающиеся друг от друга значениями отдельных показателей качества. Поэтому, определив на втором этапе спрос, например, на товары культурно-бытового назначения, на третьем этапе определяют спрос на мебель, на четвертом - спрос на столовые гарнитуры, на пятом - на обеденные столы, а затем то, что нас интересует, т.е. спрос на обеденные столы разного качества.
При этом результаты прогноза на предыдущем этапе используются как факторы при прогнозировании на последующем.
После определения для разных вариантов (разных показателей качества Pi) коэффициентов aj (j = 0, 1 ...) уравнений регрессии можно получить функцию aj = f(Pi).
Полученные таким образом уравнения регрессии
y = a0(Pi) + a1(Pi)х1 + a2(Pi)x2 + ...,
![]()
следует использовать для оптимизации Рi.
4.7. Методы прогнозирования потребностей в продукции производственного назначения (сырье, материалы, топливо, комплектующие элементы, инструмент и оборудование) разделяются на три группы:
методы непосредственного счета;
нормативные методы;
методы непосредственной экстраполяции.
4.8. При использовании метода непосредственного счета производят суммирование заявок. Заявки составляются прямым подсчетом потребностей на основе первичных данных о фактических запасах, по данным проектной документации и нормативным данным.
Часто в заявках существенно завышаются потребности. Это, в частности, объясняется тем, что предприятие часто не может точно прогнозировать свои потребности из-за отсутствия необходимой информации, времени и подготовленных кадров.
4.9. При использовании нормативных методов открывается возможность учесть особенности каждого вида продукции и тех отраслей, которые являются ее основными потребителями. Нормативы устанавливаются по предыстории или на базе инженерных расчетов. (Справочное приложение 2, пример 1).
4.10. Разработанные методы прогнозирования потребностей не рассчитаны на прогнозирование дифференцированных потребностей по размерам, маркам и моделям оборудования, которые необходимы для расчета оптимальных показателей качества. Поэтому, как и для прогноза спроса на товары народного потребления, прогнозы потребностей в продукции производственного назначения следует поэтапно разукрупнить с целью получения для конкретного вида продукции зависимости потребностей от показателей качества.
5. ВЫБОР МЕТОДОВ ПРОГНОЗИРОВАНИЯ ЗАТРАТ
5.1. При прогнозировании затрат в общем случае должны учитываться следующие группы затрат: на исследования и разработку, подготовку производства, изготовление, обращение и реализацию. При этом следует учитывать разновременность затрат путем приведения затрат к одному моменту времени, использование природных ресурсов (земли, леса, воды и др.), а также затраты на охрану окружающей среды (очистка воды, воздуха и др.).
5.2. При прогнозировании затрат в зависимости от целей прогнозирования следует каждый раз выяснить необходимую и допустимую степень осреднения. Например, если необходимо прогнозировать затраты при некоторых конкретных конструкторских мероприятиях, относящихся к продукции, которая будет изготовляться на разных предприятиях, разными технологическими процессами, то следует осреднить исходные данные по затратам на изготовление в прошлом аналогичной продукции примерно на таких же предприятиях при таких же технологических процессах.
Наоборот, не следует осреднять затраты по разным хотя и близким конструкциям и моделям продукции, так как при таком осреднении теряется главное в этой задаче, а именно, влияние данного конкретного конструкторского мероприятия, по затратам на которое необходимо принять решение.
5.3. При определении затрат путем калькуляции необходимо отдельно рассчитать затраты на исследование и разработку, капитальные затраты, затраты на изготовление и затраты на эксплуатацию (использование). Расчет необходимо вести по отдельным элементам (узлам) продукции, а элементы продукции должны определяться по проектной документации или по результатам прогноза технических возможностей, которые должны включать элементы продукции (состав, узлы) и требования к ним.
5.4. При наличии статистических данных для предварительных приближенных расчетов можно использовать эмпирические зависимости вида:
З = a0 + a1P1 + a2P2 + ... + anPn
или
![]()
где ап, aп - постоянные величины, определяемые по статистике предыстории;
Р - показатель качества продукции;
п - число учитываемых факторов (показателей).
Пользоваться приведенными зависимостями следует осторожно даже для предварительных расчетов, так как коэффициенты аn и aп определяются для некоторых условий, которые часто трудно выяснить.
Составление этих зависимостей на практике связано со значительными трудностями, так как для определения коэффициентов аn и aп необходимо не менее n + 1 прототипов. Найти такое количество прототипов с одинаковым техническим уровнем, разрабатываемых, изготовляемых и применяемых при одинаковых условиях, как правило, затруднительно.
5.5. Для повышения точности прогнозирования затрат целесообразно использовать зависимости, по которым определяются только изменения затрат, связанные с изменением показателей качества:
![]() ,
,
или
![]()
где Зпр - себестоимость прототипа;
DРi - изменение показателя качества;
DЗj - изменение себестоимости j-го узла (элемента);
п - число учитываемых показателей качества;
т - число измененных узлов (элементов).
Величины ai и DЗj следует определять по выше приведенным эмпирическим зависимостям или по калькуляции после прогнозирования технических возможностей. Повышение точности прогнозирования затрат в этом случае объясняется тем, что вычисляется лишь часть себестоимости. При определении величин ai и DЗj по калькуляции точность прогнозирования затрат будет еще выше.
6. МЕТОДЫ ОЦЕНКИ ТОЧНОСТИ ПРОГНОЗОВ
6.1. Оценка точности прогнозов производится путем сравнения данных прогнозов с данными действительных реализаций или путем анализа точности математических моделей и входной информации, по которой разработан прогноз.
6.1.1. Использование первой группы методов оценки точности возможно, если известны не только данные прогноза, но и когда уже известны конкретные реализации. Такая оценка представляет интерес для определения пригодности методов прогнозирования при решении аналогичных задач.
6.1.2. При использовании второй группы методов оценки точности прогнозирования оценка производится еще до получения данных о конкретных реализациях. Методы этой группы должны применяться не только для оценки точности прогнозов исходных данных, но и для проверки всего процесса оптимизации и прежде всего для определения целесообразных границ комплексности и опережаемости. Эти методы изложены в РДМУ 119-78 [5] и поэтому здесь не рассматриваются.
6.2. При сравнении прогнозных данных с действительными реализациями оценка точности производится путем:
оценки точности только прогноза исходных данных для оптимизации ПОС;
оценки ошибки оптимизации ПОС вследствие ошибок прогнозирования исходных данных;
определения потерь из-за неточности прогнозирования.
В первом случае сравниваются полученные значения исходных данных для оптимизации (эффекты, затраты и ограничения); во втором случае сравниваются результаты оптимизации, т.е. значения ПОС и временных параметров, определяемых по прогнозным данным и фактическим реализациям; в третьем случае оцениваются потери вследствие ошибок и неполноты прогноза путем сравнения значений, например, целевых функций, определяемых по прогнозным данным и фактическим реализациям.
Наиболее ценной информацией по оценке точности прогноза является оценка потерь за счет ошибок и неполноты прогноза.
6.3. По используемым математическим процедурам следует различать вероятностные оценки точности прогнозов и оценки по теории информации. В первом случае ошибка рассматривается как случайная величина (или случайная функция времени) и задача сводится к использованию аппарата теории вероятности для определения характеристик этой величины.
Во втором случае необходимо сравнить количество информации по прогнозным данным и по реализациям. Информационные методы изложены в [19] и здесь не рассматриваются.
6.4. Оценку точности прогноза при вероятностном подходе [26] целесообразно проводить в такой последовательности.
Пусть в результате прогноза получено п значений Пi некоторой величины (непосредственно прогнозируемой величины, оптимального значения показателя качества или значения целевой функции). В действительности оказались реализованными соответственно величины Ri.
Тогда среднеквадратическая ошибка, определяемая по формуле
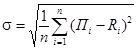
может быть принята в качестве меры точности прогноза данного параметра, при условии, что ошибка прогноза Пi - Ri являются независимыми случайными величинами.
В качестве дополнительной характеристики точности прогноза целесообразно воспользоваться математическим ожиданием, определенным по формуле
![]()
где ![]() - среднее значение по действительным реализациям;
- среднее значение по действительным реализациям; ![]() - среднее
значение по прогнозным данным.
- среднее
значение по прогнозным данным.
ПРИЛОЖЕНИЕ 1
Справочное
ОБ ОПТИМАЛЬНОЙ ТОЧНОСТИ ПРОГНОЗИРОВАНИЯ
Оптимизируемые параметры будущих объектов неизбежно отступают от абсолютно оптимальных, в частности, вследствие несовершенства методов прогнозирования и неопределенности в исходной информации для прогнозирования.
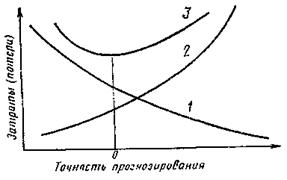
Потери вследствие отступления значений параметров от оптимальных, вызванные ошибками прогнозирования, уменьшаются с повышением точности прогнозирования (кривая 1) (чертеж). С ростом точности растут расходы средств и времени на прогнозирование (кривая 2).
Суммарные затраты на разработку прогноза и затраты, вызванные его ошибками (кривая 3) имеют, как правило, минимум (точка 0). Соответствующая точность прогноза является оптимальной.
ПРИЛОЖЕНИЕ
2
Справочное
Пример 1. Определение потребностей в электросварочном оборудовании. Рассмотрим определение потребностей народного хозяйства в электросварочном оборудовании. В [23], [24] для этого приводится зависимость:
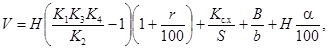
где Н - наличный парк электросварочного оборудования на конец базисного года;
K1 - коэффициент роста объема сварных металлоконструкций в плановом году по сравнению с базисным;
K2 - коэффициент изменения производительности электросварочного оборудования за этот же период;
K3 - коэффициент изменения трудоемкости производства тонны сварных металлоконструкций за тот же период;
K4 - коэффициент роста уровня механизации сварных работ за тот же период;
r - удельный вес потребления электросварочного оборудования по неучитываемым предприятиям;
Kс.х. - объем капитальных вложений на приобретение оборудования в сельском хозяйстве в планируемом периоде;
В - объем валовой продукции машиностроения и металлообработки в планируемом периоде;
S - число единиц электросварочного оборудования на 1 млн. руб. капитальных вложений на приобретение оборудования в сельском хозяйстве;
b - число единиц электросварочного оборудования на 1 млн. руб. валовой продукции;
a - показатель потребностей (в процентах) на замену парка.
В этой зависимости первое слагаемое учитывает прирост парка по всем отраслям народного хозяйства; второе слагаемое - прирост парка для сельского хозяйства; третье слагаемое - потребности машиностроения, а четвертое слагаемое - потребности в замене оборудования.
Аналогичные математические модели для прогнозирования потребностей на примере черной металлургии, по группам «топливо и электроэнергия», «транспорт» и «сельскохозяйственная продукция» даны в 22, 28.
Пример 2. Пример дезагрегирования моделей спроса на непродовольственные товары [14], [15].
Для прогноза спроса на группу непродовольственных товаров разработана эмпирическая модель (в модель включаются базисные индексы показателей в расчете на душу населения):
Iн = e-2,13 i-0,02 I0,01 D0,5 P0,02 t0,04, (1)
где Iн - размер спроса на непродовольственные товары;
i - индекс розничных цен на непродовольственные товары;
I - общий индекс розничных цен;
D - общин объем спроса населения;
Р - доля дохода колхозников во всех денежных доходах населения;
t - время.
После определения спроса на всю группу непродовольственных товаров, определяется спрос, например, на товары культурно-бытового и домашнего обихода:
Iк = 6,0 - 0,62i - 0,6Iн.п + 0,67Тн.п - 0,09P + 0,42t, (2)
где Iк - спрос на товары культурно-бытового назначения;
i - индекс розничных цен на группу товаров культурно-бытового назначения;
Iн.п. - индекс розничных цен на все непродовольственные товары;
Тн.п. - общий объем продажи непродовольственных товаров;
Р и t - обозначения прежние.
Важно заметить, что если в уравнение (1) подставляется значение всех факторов, взятых из планов, то в уравнение (2) вместо плановых значений непродовольственных товаров следует принять величины, вычисленные по уравнению (1).
Результаты вычислений по уравнению (2) совместно с соответствующими статистическими данными служат для вычисления прогноза спроса на еще более разукрупненные группы товаров.
Например, для прогноза спроса на мебель получена зависимость:
Iм = 5,52 - 0,024i - 0,01Iм.к + 1,23Тм - 0,06P + 0,06t, (3)
где Iм - объем спроса на мебель;
i - индекс розничных цен мебели;
Iм.к - групповой индекс цен на объединенную группу мебели и металлических кроватей;
Тм - объем продажи мебели и металлических кроватей.
Затем прогнозируется спрос, например, на столовые гарнитуры, затем - на обеденные столы, а затем то, что нас интересует, т.е. спрос на обеденные столы разного качества. При этой результаты прогноза на предыдущем этапе используются для последующего этапа прогноза.
СПИСОК ЛИТЕРАТУРЫ
1. ГОСТ 18.001-76. Количественные методы оптимизации параметров объектов стандартизации. Общие положения.
2. ГОСТ 18.101-76. Количественные методы оптимизации параметров объектов стандартизации. Теоретические методы. Основные положения по составлению математических моделей.
3. ГОСТ 18.301-76. Количественные методы оптимизации параметров объектов стандартизации. Методы обеспечения опережающей стандартизации. Основные положения.
4. ГОСТ 18.401-77. Количественные методы оптимизации параметров объектов стандартизации. Методы обеспечения комплексности. Основные положения.
5. Методические указания. Количественные методы оптимизации параметров объектов стандартизации. Определение целесообразных границ комплексности и целесообразного уровня опережаемости РДМУ 119-78, М.: Изд-во стандартов, 1978.
6. Методические указания. Количественные методы оптимизации параметров объектов стандартизации. Выбор методов оптимизации с использованием фонда стандартов. РДМУ 118-78, М.: Изд-во стандартов, 1978.
8. Методические рекомендации по прогнозированию при оптимизации количественных требований стандартов, М., ВНИИС, 1973.
9. Типовая методика оптимизации многомерных параметрических рядов. М.: Изд-во стандартов, 1975.
10. Типовая методика оптимизации одномерного параметрического (типоразмерного) ряда. М.: Изд-во стандартов, 1975.
11. Методика оптимизации параметров простейших последовательных комплексов объектов стандартизации. М., ВНИИС, 1978.
13. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. Вып. 1, 2, М.: Мир, 1974.
16. Гмошинский В.Г., Флиорент Г.И. Теоретические основы инженерного прогнозирования. М.: Наука, 1973.
17. Зыков Ю.А. Экономическое прогнозирование научно-технического прогресса. М.: Наука, 1975.
20. Комаров Д.М. Методы прогнозирования качества продукции. - Стандарты и качество, 1974, № 5.
21. Маслов П.П. Статистика в социологии. М.: Статистика, 1971.
23. Моисеев Н.И. Простейшие математические модели экономического прогнозирования. М.: Знание, 1975.
26. Тейл Г. Прикладное экономическое прогнозирование. М: Прогресс, 1970.
27. Фальцман В.К. Прогнозирование потребности в оборудовании. М.: Экономика, 1970.
28. Фальцман В.К. Потребность в средствах производства. М.: Мысль, 1975.
29. Ханович И.Г. Научно-техническое прогнозирование в стандартизации.- Электронная техника, сер. 8.
30. Чуев Ю.В., Михайлов Ю.Б., Кузьмин В.И. Прогнозирование количественных характеристик процессов. М.: Советское радио, 1975.
31. Энциклопедия кибернетики. Киев, 1975.
СОДЕРЖАНИЕ