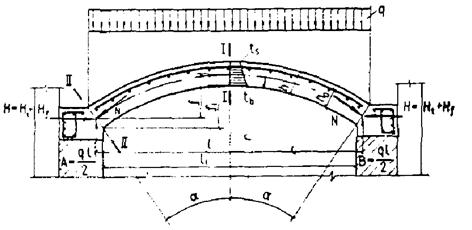
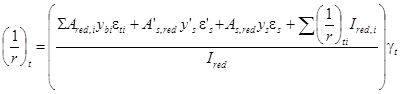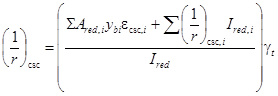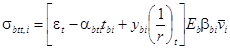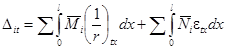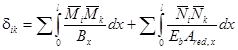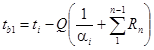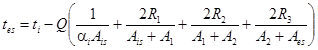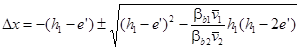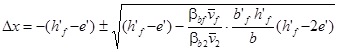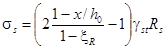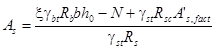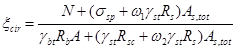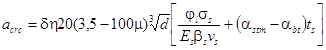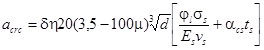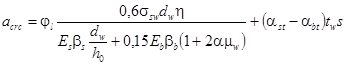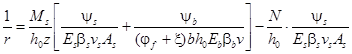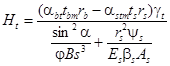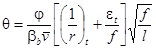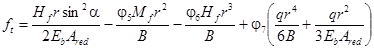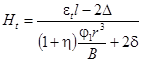ОРДЕНА
ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
БЕТОНА И ЖЕЛЕЗОБЕТОНА (НИИЖБ)
ГОССТРОЯ СССР
ПОСОБИЕ
по проектированию бетонных
и железобетонных конструкций,
предназначенных для работы
в условиях воздействия повышенных
и высоких температур
(к СНиП 2.03.04-84)
Утверждено
приказом НИИЖБ Госстроя СССР
от 25 апреля 1985 г. № 25
Москва
Центральный институт
типового проектирования
1989
Рекомендовано к изданию решением секции теории железобетона и арматуры научно-технического совета НИИЖБ Госстроя СССР.
Содержит основные положения по расчету и проектированию бетонных и железобетонных конструкций, предназначенных для работы в условиях систематического воздействия повышенных (свыше 50 до 200 °С) и высоких (свыше 200 °С) технологических температур.
Приведены примеры расчета прочности, деформаций, образования и раскрытия трещин от воздействия температуры и нагрузки.
Для инженерно-технических работников проектных организаций, научных работников, преподавателей строительных вузов, аспирантов и студентов.
При пользовании нормативным документом следует учитывать утвержденные изменения строительных норм и правил и государственных стандартов, публикуемые в журнале «Бюллетень строительной техники», «Сборнике изменений к строительным нормам и правилам» Госстроя СССР и информационном указателе «Государственные стандарты СССР» Госстандарта.
ПРЕДИСЛОВИЕ
Опыт проектирования, строительства и эксплуатации различных сооружений из обычного и жаростойкого железобетона подтверждает, что можно достигнуть длительного срока службы сооружения, если правильно будут учтены неблагоприятные влияния температуры.
Применение сборного жаростойкого бетона и железобетона в виде крупных блоков и панелей открывает широкие возможности индустриализации строительства, уменьшения трудозатрат. Кроме того, в ряде случаев значительно сокращаются сроки строительства.
В Пособии приведены требования СНиП 2.03.04-84 «Бетонные и железобетонные конструкции, предназначенные для работы в условиях воздействия повышенных и высоких температур», а также СНиП 2.03.01-84 «Бетонные и железобетонные конструкции», необходимые для проектирования. В скобках даны номера пунктов СНиП 2.03.04-84.
При составлении Пособия использованы результаты отечественных и зарубежных работ по изучению механических и реологических свойств бетона и арматуры в условиях воздействия повышенных и высоких температур, а также исследования изгибаемых, сжатых и внецентренно растянутых элементов, круглых и прямоугольных плит, элементов труб, боровов, сводов, рам и куполов из жаростойкого бетона и железобетона при воздействии температур.
На основе этих исследований разработаны общие принципы конструирования бетонных и железобетонных конструкций, работающих в условиях воздействия повышенных и высоких температур.
В Пособии детализируются отдельные положения по расчету и проектированию бетонных и железобетонных конструкций с обычной и предварительно напряженной арматурой, даются практические методы расчета прочности (проверка прочности и подбор арматуры), деформаций, образования и раскрытия трещин в железобетонных элементах при систематическом воздействии повышенных и высоких технологических температур и нагрузок, приводятся рекомендации по расчету наиболее массовых конструкций печей (сводов, куполов, фундаментов и т.д.) и других тепловых агрегатов.
В Пособии даны примеры расчета, охватывающие типичные случаи, встречающиеся в практике проектирования.
Единицы физических величин, приведенные в Пособии, соответствуют «Перечню единиц физических величин, подлежащих применению в строительстве».
В таблицах нормативные и расчетные сопротивления и модули упругости материалов приведены в МПа (кгс/см2).
В Пособии использованы буквенные обозначения и индексы к ним в соответствии с СТ СЭВ 1565-79. Основные буквенные обозначения применяемых величин приведены в приложении 6.
Разработано НИИЖБ Госстроя СССР (д-р техн. наук. проф. А. Ф. Милованов - руководитель темы; кандидаты техн. наук В. Н. Горячев, В. М. Милонов, В. Н. Самойленко; Т. Н. Малкина) с участием ВНИПИ Теплопроект Минмонтажспецстроя СССР (канд. техн. наук В. Г. Петров-Денисов; В. А. Тарасова, Е. Н. Бальных), Макеевского ИСИ Минвуза УССР (канд. техн. наук А. П. Кричевский); Харьковского Промстройниипроекта Госстроя СССР (кандидаты техн. наук И. Н. Заславский, С. Л. Фомин).
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
ОБЩИЕ УКАЗАНИЯ
1.1. Настоящее Пособие распространяется на проектирование бетонных и железобетонных конструкций, предназначенных для работы в условиях систематического воздействия повышенных (свыше 50 до 200 °С) и высоких (свыше 200 °С) технологических температур (далее - воздействие температур).
Проектирование железобетонных дымовых труб, резервуаров и фундаментов доменных печей, работающих при воздействии температуры свыше 50 °С, должно производиться с учетом дополнительных требований, предъявляемых к этим сооружениям соответствующими нормативными документами.
1.2. Выбор конструктивных решений должен производиться исходя из технико-экономической целесообразности их применения в конкретных условиях строительства с учетом максимального снижения материалоемкости, трудоемкости и стоимости строительства, достигаемого путем:
применения эффективных строительных материалов и конструкций;
снижения веса конструкций;
наиболее полного использования физико-механических свойств материалов;
использования местных строительных материалов;
соблюдения требований по экономному расходованию основных строительных материалов.
1.3. При проектировании зданий, сооружений и тепловых агрегатов должны приниматься четкие конструктивные схемы, обеспечивающие необходимую прочность, устойчивость и пространственную неизменяемость конструкции на всех стадиях возведения и при эксплуатации.
1.4. Элементы сборных конструкций должны отвечать условиям механизированного изготовления на специализированных предприятиях.
При выборе элементов сборных конструкций должны предусматриваться преимущественно предварительно напряженные конструкции из высокопрочных бетонов и арматуры, а также конструкции из легких бетонов, где их применение не ограничивается требованиями других нормативных документов.
Целесообразно укрупнять элементы сборных конструкций, насколько это позволяют грузоподъемность монтажных механизмов, условия изготовления и транспортирования.
1.5. Для монолитных конструкций следует предусматривать унифицированные размеры, позволяющие применять инвентарную опалубку, а также укрупненные унифицированные пространственные арматурные каркасы.
1.6. В сборных конструкциях особое внимание должно быть обращено на прочность и долговечность соединений.
Конструкции узлов и соединений элементов должны обеспечивать надежную передачу усилий, прочность самих элементов в зоне стыка, а также связь дополнительно уложенного бетона в стыке с бетоном конструкции.
1.7. Конструкции рассматриваются как бетонные, если их прочность в стадии эксплуатации обеспечивается одним бетоном.
1.8. Численные значения расчетных характеристик бетона и арматуры, предельных величин ширины раскрытия трещин и прогибов применяются только при проектировании; для оценки качества конструкции следует руководствоваться требованиями соответствующих стандартов и нормативных документов.
1.9 (1.1). Бетонные и железобетонные конструкции, предназначенные для работы в условиях воздействия повышенных температур, следует предусматривать, как правило, из обычного бетона.
Фундаменты, которые при эксплуатации постоянно подвергаются воздействию температуры до 250 °С включ., допускается предусматривать из обычного бетона.
Бетонные и железобетонные конструкции, предназначенные для работы в условиях воздействия высоких температур, следует предусматривать из жаростойкого бетона.
Несущие элементы конструкций тепловых агрегатов, выполняемые из жаростойкого бетона, сечение которых может нагреваться до температуры свыше 1000 °С, допускается принимать только после их опытной проверки.
Жаростойкие бетоны в элементах конструкций тепловых агрегатов следует применять согласно указаниям прил. 1.
В настоящем Пособии приняты следующие наименования бетонов: обычный (ГОСТ 25192-82); жаростойкий (ГОСТ 20910-82).
Классы по предельно допустимой температуре применения жаростойкого бетона приведены в зависимости от вида вяжущего, заполнителей, тонкомолотых добавок и отвердителя.
1.10 (1.2). Для конструкций, работающих под воздействием температуры свыше 50 °С в условиях периодического увлажнения паром, технической водой и конденсатом, необходимо соблюдать требования пп. 1.19; 2.5; 2.10; 2.11; 2.13 и 5.14.
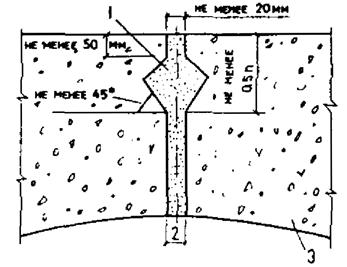
При невозможности обеспечения указанных требований расчет таких конструкций допускается производить только на воздействие температуры и нагрузки без учета периодического увлажнения. При этом в расчете сечения не должны учитываться крайние слои бетона толщиной 20 мм с каждой стороны, подвергающиеся замачиванию в течение 7 ч, и толщиной 50 мм при длительности замачивания бетона более 7 ч или должна предусматриваться защита поверхности бетона от периодического замачивания.
Окрашенная поверхность бетона или гидроизоляционные покрытия этих конструкций должны быть светлых тонов.
1.11 (1.3). Циклический нагрев - длительный температурный режим, при котором в процессе эксплуатации конструкция периодически подвергается повторяющемуся нагреву с колебаниями температуры более 30 % расчетной величины при длительности циклов от 3 ч до 30 дней.
Постоянный нагрев - длительный температурный режим, при котором в процессе эксплуатации конструкция подвергается нагреву с колебаниями температуры до 30 % расчетной величины.
1.12 (1.4). При проектировании конструкций из жаростойких бетонов по ГОСТ 20910-82 необходимо учитывать дополнительные требования «Руководства по возведению тепловых агрегатов из жаростойкого бетона» (М.: Стройиздат, 1983) к исходным материалам для жаростойких бетонов, подбору их состава и технологии приготовления, а также особенности производства работ.
ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ
1.13. Бетонные и железобетонные конструкции, работающие в условиях воздействия повышенных и высоких температур, должны удовлетворять требованиям расчета по несущей способности (предельным состояниям первой группы) и по пригодности к нормальной эксплуатации (предельным состояниям второй группы).
Расчет по предельным состояниям первой группы должен обеспечивать конструкции от:
хрупкого, вязкого или иного характера разрушения (расчет по прочности с учетом, в необходимых случаях, прогиба конструкции перед разрушением);
потери устойчивости формы конструкции (расчет на устойчивость тонкостенных конструкций и т.п.) или ее положения (расчет на опрокидывание и скольжение подпорных стен, внецентренно нагруженных высоких фундаментов, расчет на всплывание заглубленных или подземных резервуаров, насосных станций и т.п.);
усталостного разрушения (расчет на выносливость конструкций, находящихся под воздействием многократно повторяющейся нагрузки подвижной или пульсирующей; подкрановых балок, рамных фундаментов и перекрытия под некоторые неуравновешенные машины и т.п.);
разрушения под совместным воздействием силовых факторов и неблагоприятных влияний внешней среды (периодического или постоянного воздействия агрессивной среды, действия попеременного замораживания и оттаивания и т.п.).
Расчет по предельным состояниям второй группы должен обеспечивать конструкции от:
образования трещин, а также чрезмерного или длительного раскрытия (если по условиям эксплуатации образование или длительное раскрытие трещин недопустимо);
чрезмерных перемещений (прогибов, углов поворота, углов перекоса и колебаний).
1.14. Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов, как правило, производится для всех стадий: изготовления, транспортирования, возведения и эксплуатации, при этом расчетные схемы должны отвечать принятым конструктивным решениям.
1.15 (1.5). При расчете бетонных и железобетонных конструкций необходимо учитывать изменения механических и упругопластических свойств бетона и арматуры в зависимости от температуры воздействия. При этом усилия, деформации, образование, раскрытие и закрытие трещин определяют с учетом воздействия нагрузки (включая собственный вес) и температуры.
Расчетные схемы и основные предпосылки для расчета бетонных и железобетонных конструкций должны устанавливаться в соответствии с условиями их действительной работы в предельном состоянии с учетом в необходимых случаях пластических свойств бетона и арматуры, наличия трещин в растянутом бетоне, а также влияния усадки и ползучести бетона как при нормальной температуре, так и при воздействии повышенных и высоких температур.
1.16 (1.6). Расчет конструкций, работающих в условиях воздействия повышенных и высоких температур, должен производиться на все возможные неблагоприятные сочетания нагрузок от собственного веса, внешней нагрузки и температуры с учетом длительности их действия и в случае необходимости - остывания.
Расчет конструкций с учетом воздействия повышенных и высоких температур необходимо производить для следующих основных расчетных стадий работы:
кратковременный нагрев - первый разогрев конструкции до расчетной температуры;
длительный нагрев - воздействие расчетной температуры в период эксплуатации.
Расчет статически определимых конструкций по предельным состояниям первой и второй групп (за исключением расчета по образованию трещин) следует вести только для стадии длительного нагрева. Расчет по образованию трещин необходимо производить для стадий кратковременного и длительного нагрева с учетом усилий, возникающих от нелинейного распределения температуры бетона по высоте сечения элемента.
Расчет статически неопределимых конструкций и их элементов по предельным состояниям первой и второй групп должен производиться:
а) на кратковременный нагрев конструкции по режиму согласно СНиП III-15-76, когда возникают наибольшие усилия от воздействия температуры (см. п. 1.23). При этом жесткость элемента в конструкции определяется согласно указаниям пп. 4.28 - 4.30 как от кратковременного действия всех нагрузок, так и в зависимости от скорости нагрева;
б) на длительный нагрев - воздействие на конструкцию расчетной температуры в период эксплуатации, когда происходит снижение прочности и жесткости элементов в результате воздействия длительного нагрева и нагрузки.
При этом жесткость элементов определяется по указаниям пп. 4.28 - 4.30 как для длительного действия всех нагрузок.
Расчетная технологическая температура принимается равной температуре среды цеха или рабочего пространства теплового агрегата, указанной в задании на проектирование.
Расчетные усилия и деформации от кратковременного и длительного нагрева определяются по указаниям п. 1.40 с учетом коэффициента надежности по температуре.
1.17 (1.7). Величины нагрузок и воздействий, значения коэффициентов надежности, коэффициентов сочетаний, а также подразделение нагрузок на постоянные и временные длительные, кратковременные, особые следует принимать в соответствии с требованиями СНиП II-6-74 с учетом дополнительных указаний: нагрузки, учитываемые при расчете по предельным состояниям второй группы, должны приниматься согласно указаниям пп. 1.19 и 1.29. При этом к длительным нагрузкам следует относить часть полной величины кратковременных нагрузок, оговоренных в главе СНиП II-6-74, а вводимая в расчет кратковременная нагрузка принимается уменьшенной на величину, учтенную в длительной нагрузке. Коэффициенты сочетаний и другие коэффициенты снижения нагрузок относятся к полной величине кратковременных нагрузок.
Нагрузки и воздействия температуры, учитываемые при расчете конструкции по предельным состояниям первой и второй групп, следует принимать по табл. 1 и 2.
Таблица 1
|
Нагрузки и коэффициенты надежности по нагрузке γf, температурные воздействия и коэффициенты надежности по температуре γt, принимаемые при расчете |
|||
|
по прочности |
на выносливость |
по деформациям |
|
|
Статически определимые конструкции при длительном нагреве |
Постоянные, длительные и кратковременные нагрузки при γf > 1,0 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и температурные деформации при γt = 1,0 |
|
Статически неопределимые конструкции при кратковременном нагреве |
Постоянные, длительные и кратковременные нагрузки при γf > 1,0 и наибольшие усилия от воздействия температуры при γt = 1,1 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и наибольшие усилия от воздействия температуры при γt = 1,0 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и наибольшие усилия от воздействия температуры и температурные деформации при γt = 1,0 |
|
Статически неопределимые конструкции при длительном нагреве |
Постоянные, длительные и кратковременные нагрузки при γf > 1,0 и усилия от воздействия температуры при γt = 1,1 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и усилия от воздействия температуры при γt = 1,0 |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и усилия от воздействия температуры и температурные деформации при γt = 1,0 |
Примечания: 1. Бетонные конструкции рассчитываются только по прочности.
2. При расчете статически неопределимых конструкций кроме сочетаний воздействий температуры и нагрузок, указанных в настоящей таблице, в необходимых случаях следует проверить другие возможные неблагоприятные сочетания воздействий, в том числе и при остывании.
3. В статически неопределимых конструкциях допускается производить расчет:
а) при кратковременном нагреве только на наибольшие усилия от воздействия температуры, если усилия от постоянных, длительных и кратковременных нагрузок вызывают напряжения сжатия в бетоне σb ≤ 0,1 МПа;
б) при длительном нагреве свыше 700 °С - на совместное воздействие постоянных, длительных и кратковременных нагрузок без учета усилий от длительного нагрева.
4. При расчете на кратковременный нагрев длительная нагрузка учитывается как кратковременная.
5. Коэффициент надежности по температуре γt должен приниматься по указаниям п. 1.40.
6. При расчете прогибов следует учитывать указания п. 1.29.
Таблица 2
|
Категория требований к трещиностойкости железобетонных конструкций |
Нагрузки и коэффициент надежности по нагрузке γf, воздействия температуры и коэффициент надежности по температуре γt принимаемые при расчете |
|||
|
по образованию трещин |
по раскрытию трещин |
по закрытию трещин |
||
|
непродолжительному |
продолжительному |
|||
|
1-я |
Постоянные, длительные и кратковременные нагрузки при γf > 1,0* и температурные воздействия от кратковременного и длительного нагрева при γt = 1,1* |
- |
- |
- |
|
2-я |
Постоянные, длительные и кратковременные нагрузки при γf > 1,0* и температурные воздействия от кратковременного и длительного нагрева при γt = 1,1* (расчет производится для выяснения необходимости проверки по непродолжительному раскрытию трещин и по их закрытию) |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и температурные воздействия от кратковременного и длительного нагрева при γt = 1,0 |
- |
Постоянные и длительные нагрузки при γf = 1,0 и температурные воздействия от длительного нагрева при γt = 1,0 |
|
3-я |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и температурные воздействия от кратковременного и длительного нагрева при γt = 1,0 (расчет производится для выяснения необходимости проверки по раскрытию трещин) |
Постоянные, длительные и кратковременные нагрузки при γf = 1,0 и температурные воздействия от кратковременного и длительного нагрева при γt = 1,0 |
Постоянные и длительные нагрузки при γf = 1,0 и температурные воздействия от длительного нагрева при γt = 1,0 |
- |
* Коэффициент надежности по нагрузке γf и коэффициент надежности по температуре γt принимаются такими же, как при расчете по прочности.
Примечания: 1. Длительные и кратковременные нагрузки принимаются с учетом требований СНиП 2.03.01-84.
2. При расчете по образованию трещин от температурных воздействий необходимо учитывать требования п. 4.3.
3. При расчете по раскрытию трещин от температурных воздействий необходимо учитывать различие температурных деформаций бетона и арматуры по указаниям п. 4.10.
4. Коэффициент надежности по температуре γt должен приниматься по указаниям п. 1.40.
5. Особые нагрузки учитываются в расчете по образованию трещин в тех случаях, когда наличие трещин приводит к катастрофе (взрыв, пожар и т.д.).
При расчете по прочности в необходимых случаях должны учитываться особые нагрузки с коэффициентами надежности по нагрузке γf, принимаемыми по соответствующим нормативным документам. При этом усилия, вызванные воздействием температуры, не учитываются.
1.18. При расчете элементов сборных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от собственного веса элемента следует вводить в расчет с дополнительным коэффициентом динамичности, равным:
при транспортировании........................ 1,60
при подъеме и монтаже......................... 1,40
Для указанных выше коэффициентов динамичности допускается принимать более низкие значения, если это подтверждено опытом применения конструкций, но не ниже 1,25.
1.19. К трещиностойкости конструкций или их частей предъявляются требования соответствующих категорий в зависимости от условий, в которых работает конструкция, и от вида применяемой арматуры:
а) 1-я категория - не допускается образование трещин;
б) 2-я категория - допускается ограниченное по ширине непродолжительное acrc1 раскрытие трещин при условии обеспечения их последующего надежного закрытия (зажатия);
в) 3-я категория - допускается ограниченное по ширине непродолжительное acrc1 и продолжительное acrc2 раскрытие трещин.
Категории требований к трещиностойкости железобетонных конструкций в зависимости от условий их работы, вида арматуры по предельно допустимой ширине раскрытия трещин для обеспечения сохранности арматуры в элементах, эксплуатируемых в условиях неагрессивной среды, приведены в табл. 3. Нагрузки, учитываемые при расчете железобетонных конструкций по образованию трещин, их раскрытию или закрытию, должны приниматься согласно табл. 2. Если в конструкциях или их частях, к трещиностойкости которых предъявляются требования 2- и 3-й категорий, трещины не образуются при соответствующих нагрузках и температурах, указанных в табл. 3, их расчет по непродолжительному раскрытию и по закрытию трещин (для 2-й категории) или по непродолжительному и продолжительному раскрытию трещин (для 3-й категории) не производится.
Под непродолжительным раскрытием трещин понимается их раскрытие при действии постоянных длительных и кратковременных нагрузок, кратковременного нагрева, а под длительным раскрытием - только при постоянных и длительных нагрузках и длительном нагреве.
Таблица 3
|
Температура арматуры, °С |
Категория требований к трещиностойкости железобетонных конструкций и предельно допустимая ширина acrc1 и acrc2, мм, раскрытия трещин, обеспечивающие сохранность арматуры |
|||
|
стержневой классов А-I, А-II, А-III, А-IIIв и А-IV; проволочной классов B-I и Bp-I |
стержневой классов A-V и A-VI; проволочной классов B-II, Вр-II, К-7 и К-19 при диаметре проволоки 3,5 мм и более |
проволочной классов B-II, Вр-II и К-7 при диаметре проволоки 3 мм и менее |
||
|
1. В закрытом помещении |
До 100 |
3-я категория; acrc1 = 0,4; acrc2 = 0,3 |
3-я категория; acrc1 = 0,3; acrc2 = 0,2 |
3-я категория; acrc1 = 0,2; acrc2 = 0,1 |
|
100 и выше |
3-я категория; acrc1 = 0,6; acrc2 = 0,5 |
3-я категория; acrc1 = 0,5; acrc2 = 0,4 |
3-я категория; acrc1 = 0,3; acrc2 = 0,2 |
|
|
2. На открытом воздухе, а также в грунте выше уровня грунтовых вод |
До 100 |
3-я категория; acrc1 = 0,4; acrc2 = 0,3 |
3-я категория; acrc1 = 0,2; acrc2 = 0,1 |
2-я категория; acrc1 = 0,2 |
|
100 и выше |
3-я категория; acrc1 = 0,6; acrc2 = 0,5 |
3-я категория; acrc1 = 0,5; acrc2 = 0,4 |
2-я категория; acrc1 = 0,3 |
|
|
3. В грунте при переменном уровне грунтовых вод и в закрытом помещении при попеременном увлажнении |
До 100 |
3-я категория; acrc1 = 0,3; acrc2 = 0,2 |
2-я категория; acrc1 = 0,2 |
2-я категория; acrc1 = 0,1 |
Примечание. В канатах подразумевается проволока наружного слоя.
Категории требований к трещиностойкости железобетонных конструкций, а также значения предельно допустимой ширины раскрытия трещин в условиях неагрессивной среды для ограничения проницаемости конструкций принимаются по СНиП 2.03.01-84.
1.20. Для железобетонных слабоармированных элементов, характеризуемых тем, что их несущая способность исчерпывается одновременно с образованием трещин в бетоне растянутой зоны (см. п. 4.4), площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15 %.
1.21. Усилия в статически неопределимых железобетонных конструкциях от нагрузок и вынужденных перемещений (вследствие изменения температуры, влажности бетона, смещения опор и т.п.), а также усилия в статически неопределимых конструкциях при расчете их по деформированной схеме следует, как правило, определять с учетом неупругих деформаций бетона и арматуры и наличия трещин.
1.22 (1.9). Определение усилий в статически неопределимых конструкциях от внешней нагрузки, собственного веса и воздействия повышенных и высоких температур производят по правилам строительной механики методом последовательных приближений. При этом жесткость элементов определяют с учетом неупругих деформаций и наличия трещин в бетоне от одновременного действия внешней нагрузки, собственного веса и температуры.
1.23 (1.10). При кратковременном нагреве усилия от воздействия температуры в элементах статически неопределимых конструкций должны определяться в зависимости от состава бетона (см. табл. 11) и температуры нагрева, вызывающей наибольшие усилия:
а) при нагреве бетона № 1 свыше 50 до 250 °С - по расчетной температуре;
б) при нагреве бетонов № 2 - 11, 23 и 24 свыше 200 до 500 °С - по расчетной температуре; при нагреве свыше 500 °С - при 500 °С;
в) при нагреве бетонов № 12 - 21, 29 и 30 свыше 200 до 400 °С - по расчетной температуре, при нагреве свыше 400 °С - при 400 °С.
Для конструкций, находящихся на наружном воздухе, расчет наибольших усилий от воздействия температур выполняют по расчетной температуре воздуха в соответствии с требованиями п. 1.53.
При длительном нагреве усилия от воздействия температуры следует определять в зависимости от расчетной температуры согласно указаниям п. 1.16.
1.24 (1.11). При расчете по прочности, деформациям, а также раскрытию и закрытию трещин распределение температуры в сечениях конструкций определяют теплотехническим расчетом для установившегося режима теплового потока. При расчете по образованию трещин распределение температур в сечениях конструкций, нагреваемых со скоростью более 10 °С/ч, определяют для неустановившегося теплового потока по требованиям пп. 1.47 - 1.53.
1.25 (1.12). При расчете усилий, вызванных воздействием температуры, в сборных элементах конструкций жесткость сечений следует уменьшить на 20 %, если прочность на сжатие раствора в стыке минимум на 10 МПа меньше прочности бетона сборного элемента.
1.26 (1.13). Расчет элементов бетонных и железобетонных конструкций по прочности, схемы предельных состояний которых при расчете на воздействие температуры еще не установлены или условия наступления предельного состояния пока не могут быть выражены через усилия, может производиться через напряжения с учетом наличия трещин и развития неупругих деформаций бетона. При этом напряжения в бетоне и арматуре не должны превышать соответствующих расчетных сопротивлений.
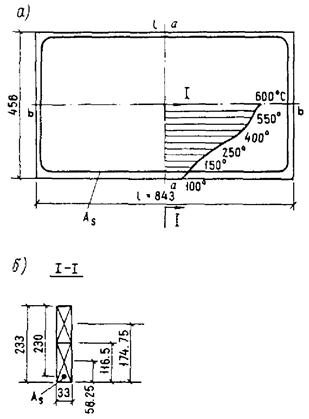
1.27 (1.14). При расчете несущих конструкций, бетон которых неравномерно нагрет по высоте сечения элемента, часть сечения, нагретую свыше 1000 °С, допускается не учитывать.
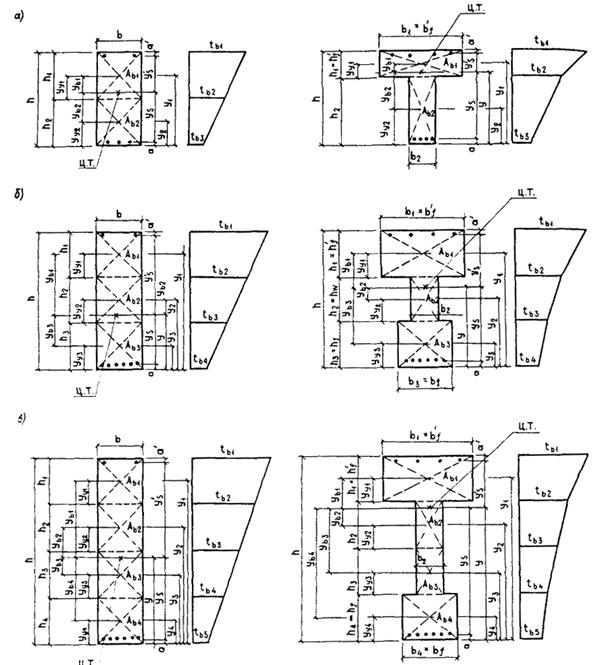
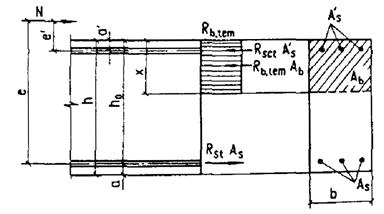
1.28 (1.15). При расчете элементов, подвергающихся нагреву, положение центра тяжести всего сечения бетона или его сжатой зоны, а также статический момент и момент инерции всего сечения следует определять, приводя все сечение к ненагретому, более прочному бетону. Для этой цели при расчете с использованием ЭВМ сечение по высоте разбивается не менее чем на четыре части.
При расчете по прочности, деформациям и раскрытию или закрытию трещин без использования ЭВМ при прямолинейном распределении температуры бетона по высоте сечения элемента допускается разбивать сечения согласно следующим указаниям:
для элемента, выполненного из одного вида бетона, если температура бетона наиболее нагретой грани не превышает 400 °С, сечение не разбивается на части и момент инерции приведенного сечения Ired относительно центра тяжести сечения принимается равным:
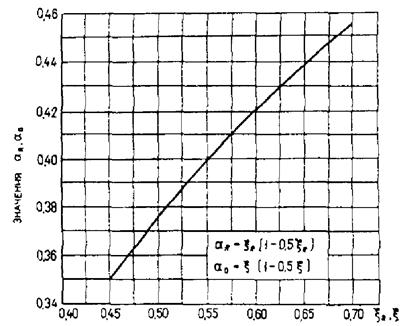
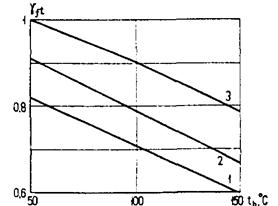
где βb - коэффициент, принимаемый в зависимости от температуры бетона в центре тяжести сечения по табл. 16;
![]() - коэффициент, принимаемый в зависимости от температуры
бетона в центре тяжести сечения для кратковременного нагрева по табл. 18;
- коэффициент, принимаемый в зависимости от температуры
бетона в центре тяжести сечения для кратковременного нагрева по табл. 18;
φb1 - коэффициент, учитывающий влияние кратковременной ползучести бетона и принимаемый для бетона составов (см. табл. 11):
№ 1 - 3, 6, 7, 10, 11, 19 - 21............... 0,85
№ 4, 5, 8, 9, 23, 24.............................. 0,80
№ 12 - 18, 29, 30................................. 0,70
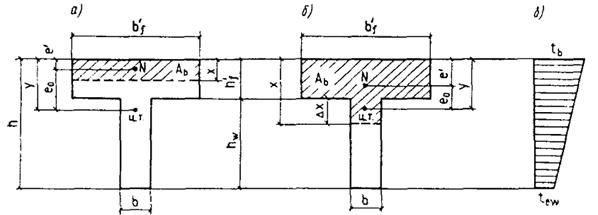
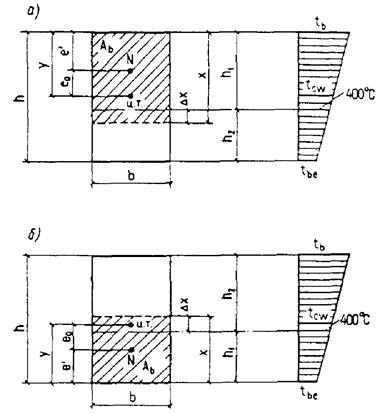
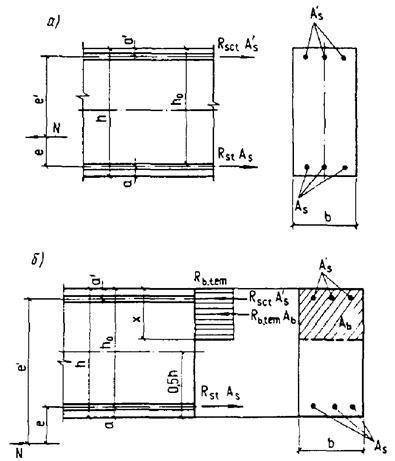
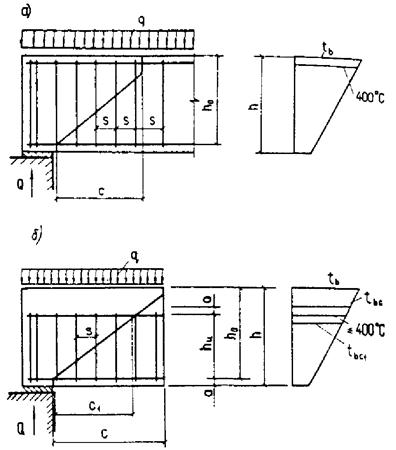
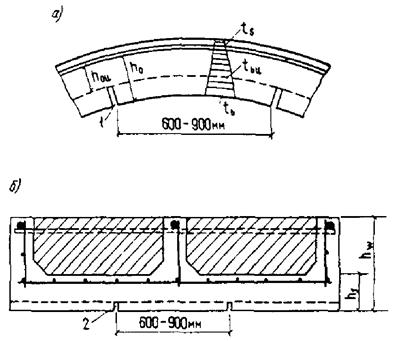
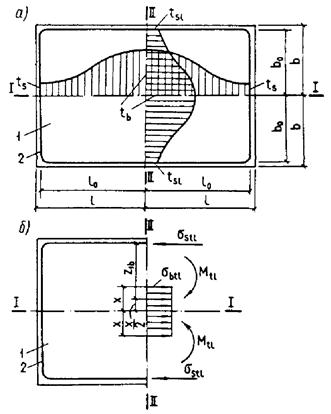
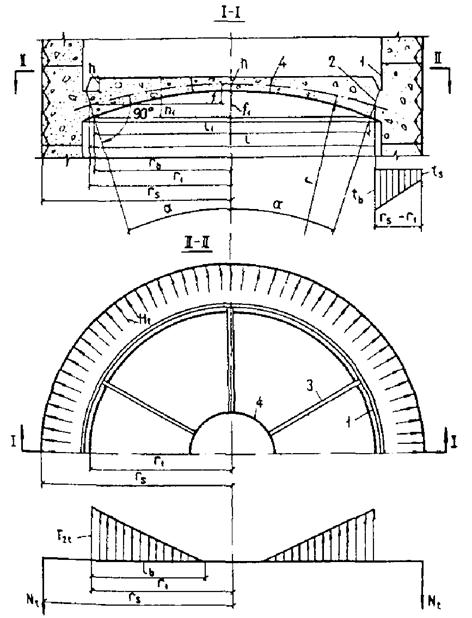
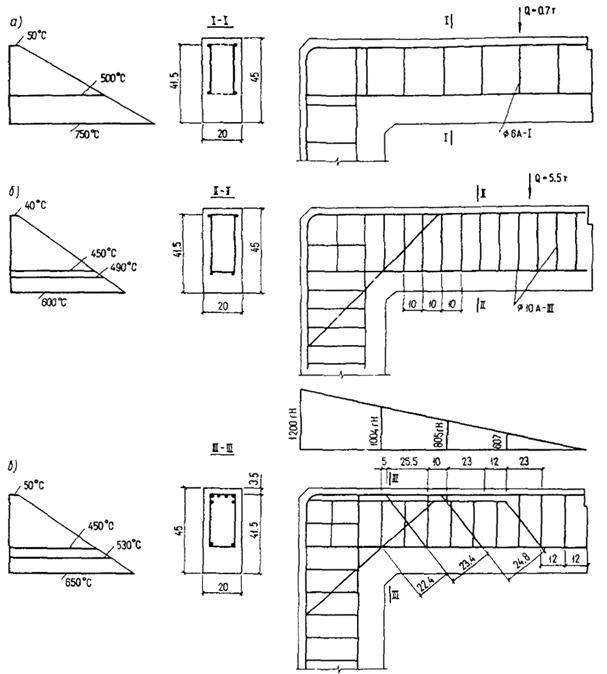
для элемента, сечение которого по высоте состоит из двух видов бетона, а также прямоугольного и таврового сечений, выполненных из одного вида бетона, если температура бетона наиболее нагретой грани превышает 400 °С, сечение разбивается по высоте на две части (черт. 1, а);
для элемента, сечение которого по высоте состоит из трех видов бетона, или двутаврового сечения, выполненного из одного вида бетона, если температура бетона наиболее нагретой грани превышает 400 °С, сечение разбивается на три части (черт. 1, б).
При расчете по образованию трещин определение напряжений от воздействия температуры производится разбивкой сечения не менее чем на четыре части независимо от температуры бетона (черт. 1, в).
В прямоугольном сечении элемента, выполненного из одного вида бетона, когда сечение по высоте разбивается на две части, линия раздела должна проходить по бетону, имеющему температуру, равную 400 °С.
В двутавровых и тавровых сечениях элементов, выполненных из одного вида бетона, линия раздела должна проходить по границе между ребром и полкой. В элементе, сечение которого по высоте состоит из различных видов бетонов, линия раздела должна проходить по границе бетонов.
Во всех случаях расчета арматура рассматривается как самостоятельная часть сечения.
Для элементов, состоящих по высоте из двух и более видов бетона, приведенная площадь Ared,i i-той части сечения, на которые разбивается все сечение элемента, определяется по формуле
где Ai - площадь i-той части сечения;
φb1, βbi и ![]() - коэффициенты,
принимаемые в зависимости от состава и
температуры бетона в центре тяжести площади i-той части сечения, как в формуле (1).
- коэффициенты,
принимаемые в зависимости от состава и
температуры бетона в центре тяжести площади i-той части сечения, как в формуле (1).
Если сечение элемента состоит из разных видов бетона, то в этой формуле правая часть умножается на отношение модуля упругости каждого вида бетона в нагретом состоянии к модулю упругости бетона, к которому приводится все сечение Еb.
При расчете без использования ЭВМ коэффициенты βbi и ![]() допускается определять в зависимости от средней
температуры бетона i-той части сечения.
допускается определять в зависимости от средней
температуры бетона i-той части сечения.
Площадь ненапрягаемой нагретой растянутой As и сжатой A′s арматуры приводится к ненагретому, более прочному бетону:
![]() , (4)
, (4)
где As,red, A′s,red - соответственно приведенная площадь растянутой и сжатой арматуры;
Es - модуль упругости арматуры, принимаемый по табл. 37;
βs - коэффициент, принимаемый в зависимости от температуры арматуры по табл. 35.
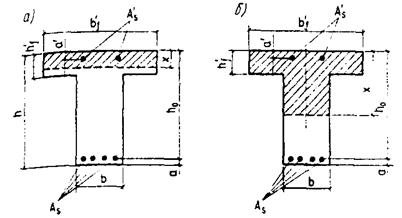
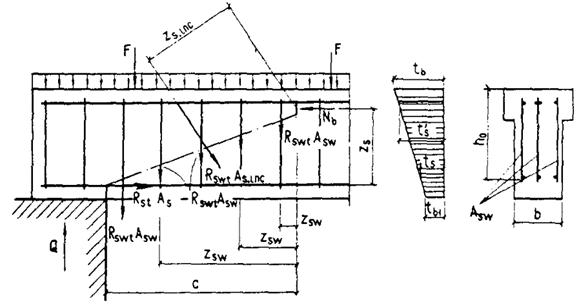
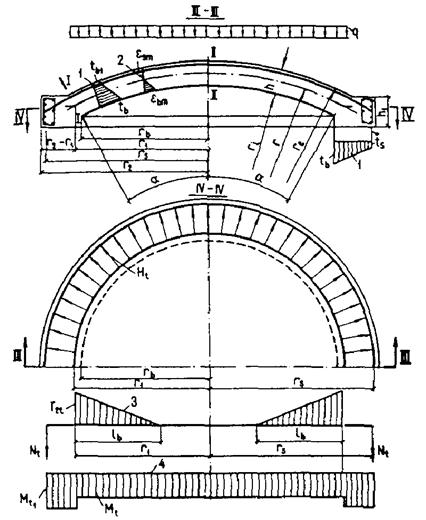
Черт. 1. Схемы разбивки на части по высоте прямоугольного, таврового и двутаврового сечения элементов
а - на 2 части; б - на 3 части; в - на 4 части; Ц. Т. - центр тяжести приведенного сечения; tb1, tb2, ..., tbi - наибольшая температура бетона 1-, 2-, ..., i-той части сечения
Расстояние от центра тяжести приведенного сечения y до наименее нагретой грани определяют по формуле
Площадь приведенного сечения элемента Ared находят по формуле
Ared = ΣAred,i + As,red + A′s,red. (6)
Статический момент площадей приведенного сечения элемента Sred относительно грани, растянутой внешней нагрузкой и воздействием температуры, определяют по формуле
Sred = ΣAred,iyi + As,reda + A′s,red (h - a′), (7)
где yi - расстояние от центра тяжести i-той части сечения бетона до наименее нагретой грани элемента, принимаемое равным
yi = h - Σhi + yyi, (8)
здесь hi - высота i-той части сечения:
При расчете без использования ЭВМ допускается принимать
yyi = 0,5hi. (10)
Момент инерции приведенного сечения элемента Ired относительно его центра тяжести определяют по формуле
Ired = ΣIred,i + ΣAred,iy2bi + As,redy2s + A′s,red(y′s)2, (11)
где Ired,i - момент инерции i-той части сечения бетона, определяемый по формуле
ybi - расстояние от центра тяжести i-той части сечения бетона до центра тяжести всего приведенного сечения, определяемое по формулам:
ybi = yi - y; (13)
ys = - (y - a); (14)
y′s = h - y - a′. (15)
1.29. Прогибы элементов железобетонных конструкций не должны превышать их предельно допустимых величин, устанавливаемых с учетом следующих требований:
технологических (условия нормальной работы кранов, технологических установок, машин и т.п.);
конструктивных (влияние соседних элементов, ограничивающих деформации; необходимость выдерживания заданных уклонов и т.п.);
эстетических.
Величины предельно допустимых прогибов приведены в табл. 4.
Расчет прогибов должен производиться:
при ограничении технологическими или конструктивными требованиями на действие постоянных, длительных и кратковременных нагрузок с учетом прогиба от кратковременного и длительного нагрева согласно указаниям пп. 4.23 - 4.27;
при ограничении эстетическими требованиями на действие постоянных и длительных нагрузок с учетом прогиба от длительного нагрева согласно указаниям пп. 4.23 - 4.27.
Таблица 4
|
Предельно допустимые прогибы |
|
|
1. Подкрановые балки при кранах: |
|
|
ручных |
l / 500 |
|
электрических |
l / 600 |
|
2. Перекрытия с плоским потолком и элементы покрытия при пролетах, м: |
|
|
l < 6 |
l / 200 |
|
6 ≤ l ≤ 7,5 |
3,0 см |
|
l > 7,5 |
l / 250 |
|
3. Перекрытия с ребристым потолком и элементы лестниц при пролетах, м: |
|
|
l < 5 |
l / 200 |
|
5 ≤ l ≤ 10 |
2,5 см |
|
l > 10 |
l / 400 |
|
4. Навесные стеновые панели (при расчете из плоскости) при пролетах, м: |
|
|
l < 6 |
l / 200 |
|
6 ≤ l ≤ 7,5 |
3,0 см |
|
l > 7,5 |
l / 250 |
Обозначения, принятые в таблице:
l - пролет балок или плит. Для консолей принимают l = 2l1, где l1 - вылет консоли.
Примечание. Предельно допустимые прогибы в поз. 1 и 4 обусловлены технологическими и конструктивными требованиями, в поз. 2 и 3 - эстетическими требованиями.
При этом коэффициент надежности по нагрузке γf и коэффициент надежности по температуре γt принимаются равными единице.
Для железобетонных элементов, выполненных со строительным подъемом, значения предельно допустимых прогибов могут быть увеличены на высоту строительного подъема, если это не ограничивается технологическими или конструктивными требованиями. Для других конструкций, не предусмотренных табл. 4, величины предельно допустимых прогибов устанавливаются по специальным требованиям, но при этом они не должны превышать 1/150 пролета и 1/75 вылета консоли.
Предельно допустимые деформации от воздействия температуры, в элементах конструкции которых требуется их ограничение при нагревании и охлаждении, должны устанавливаться нормативными документами по проектированию соответствующих конструкций, а при их отсутствии должны указываться в задании на проектирование.
Для несвязанных с соседними элементами железобетонных плит перекрытия, площадок и т.п. должна производиться дополнительная проверка по зыбкости: добавочный прогиб от кратковременно действующей сосредоточенной нагрузки 1000 Н при наиболее невыгодной схеме ее приложения должен быть не более 0,7 мм.
1.30. При расчете по прочности бетонных и железобетонных элементов на воздействие сжимающей продольной силы должен приниматься во внимание случайный эксцентриситет ea, обусловленный неучтенными в расчете факторами. Эксцентриситет ea в любом случае принимается не менее 1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения, и 1/30 высоты сечения элемента.
Кроме того, для конструкций, образуемых из сборных элементов, следует учитывать возможное взаимное смещение элементов, зависящее от вида конструкций, способа монтажа и т.п.; при отсутствии для таких конструкций экспериментально обоснованных значений случайного эксцентриситета его следует принимать не менее 1 см.
Для элементов статически неопределимых конструкций величина эксцентриситета продольной силы относительно центра тяжести приведенного сечения eo принимается равной эксцентриситету, полученному из статического расчета конструкций, но не менее ea. В элементах статически определимых конструкций эксцентриситет еo находится как сумма эксцентриситетов - определяемого из статического расчета конструкции и случайного.
При расчете по трещиностойкости и по деформациям эксцентриситет не учитывается.
В случае, если величина эксцентриситета eo, определенная в соответствии с указаниями настоящего пункта, не превышает ea = h / 30, а расчетная длина элемента прямоугольного сечения lo ≤ 20h, допускается производить его расчет согласно п. 3.37.
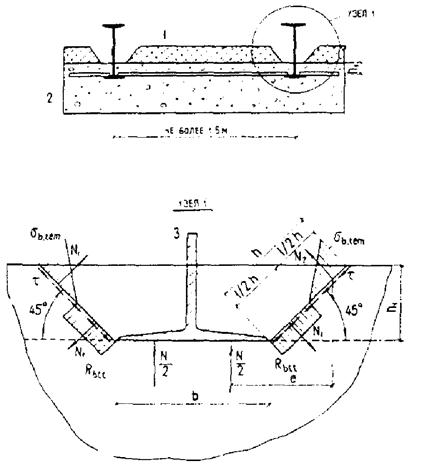
1.31. Расстояния между температурно-усадочными швами в бетонных и железобетонных конструкциях должны определяться расчетом.
Допускается указанный расчет не производить для конструкций из обычного и жаростойкого бетона, если принятое расстояние между температурно-усадочными швами не превышает величин, указанных в табл. 5, умноженных на коэффициенты δt, δe, δw и δv, принимаемые по табл. 6.
Расстояние между температурными швами в фундаментах принимается в соответствии с расположением швов в вышележащих конструкциях.
Таблица 5
|
Наибольшие расстояния между температурно-усадочными швами, м, допускаемые без расчета для конструкций, находящихся |
|||
|
внутри отапливаемых зданий или в грунте |
внутри неотапливаемых зданий |
на наружном воздухе |
|
|
1. Бетонные: |
|||
|
а) сборные |
40 |
35 |
30 |
|
б) монолитные при конструктивном армировании |
30 |
25 |
20 |
|
в) монолитные без конструктивного армирования |
20 |
15 |
10 |
|
2. Железобетонные: |
|||
|
а) сборные и сборно-каркасные одноэтажные |
72 |
60 |
48 |
|
б) сборные и сборно-каркасные многоэтажные |
60 |
50 |
40 |
|
в) сборно-блочные, сборно-панельные |
55 |
45 |
35 |
|
г) сборно-монолитные и монолитные каркасные |
50 |
40 |
30 |
|
д) сборно-монолитные и монолитные сплошные |
40 |
30 |
25 |
Примечание. Для железобетонных каркасных зданий (поз. 2а, б, г) расстояния между температурно-усадочными швами определены при отсутствии связей либо при расположении связей в середине температурного блока.
Таблица 6
|
Коэффициент |
||
|
условное обозначение |
числовое значение |
|
|
1. Расчетная температура внутри сооружений и тепловых агрегатов, °С: |
||
|
50 |
δt |
1,0 |
|
70 |
0,8 |
|
|
120 |
0,6 |
|
|
300 |
0,4 |
|
|
500 |
0,3 |
|
|
1000 и выше |
0,1 |
|
|
2. Расчетная зимняя температура воздуха (наиболее холодная пятидневка), °С: |
||
|
-40 |
δe |
1,0 |
|
-30 |
1,1 |
|
|
-20 |
1,2 |
|
|
-10 |
1,4 |
|
|
-1 |
1,6 |
|
|
3. Относительная влажность воздуха в наиболее жаркий месяц года, %: |
||
|
70 и выше |
δw |
1,0 |
|
40 |
0,8 |
|
|
20 |
0,6 |
|
|
10 |
0,4 |
|
|
4. Расстояние от верха фундамента до низа подкрановых балок, а при их отсутствии - низа ферм или балок покрытия в одноэтажных зданиях (оси балок перекрытия в многоэтажных зданиях), м: |
||
|
3 и менее |
δv |
1,0 |
|
5 |
1,2 |
|
|
7 |
1,6 |
|
|
9 и более |
2,0 |
|
Примечания: 1. При расчетной температуре внутри сооружения и тепловых агрегатов свыше 50 °С значения коэффициентов δe и δw принимаются равными единице.
2. Значения коэффициентов δt, δe, δw и δv для промежуточных значений соответственно температур и высот определяются интерполяцией.
ДОПОЛНИТЕЛЬНЫЕ УКАЗАНИЯ ПО ПРОЕКТИРОВАНИЮ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ КОНСТРУКЦИЙ
1.32. Расчет предварительно напряженных конструкций, работающих в условиях воздействия повышенных и высоких температур, должен производиться в соответствии с требованиями СНиП 2.03.01-84, Пособия по проектированию предварительно напряженных железобетонных конструкций тяжелого бетона (к СНиП 2.03.01-84) и с учетом указаний пп. 1.33 - 1.38.
1.33 (1.19). Температура нагрева предварительно напряженной арматуры не должна превышать предельно допустимой температуры ее применения, указанной в табл. 24.
1.34 (1.20). Сжимающие напряжения в бетоне σbp в стадии предварительного обжатия не должны превышать (в долях от передаточной прочности бетона Rbp):
0,70 Rbp................... при 50 °С нагрева
0,60............................ » 100 » »
0,50............................ » 150 » »
0,40............................ » 250 » »
В случае необходимости величина сжимающих напряжений в бетоне может быть повышена при обеспечении надежной работы конструкции от воздействия предварительного напряжения, нагрузки и температурных усилий.
1.35 (1.21). Полная величина потерь предварительного напряжения арматуры, учитываемая при расчете конструкций, работающих в условиях воздействия температуры выше 50 °С, определяется как сумма потерь:
основных - при нормальной температуре;
дополнительных - от воздействия температуры выше 50 °С.
Основные потери предварительного напряжения арматуры для конструкций из обычного бетона состава № 1 и жаростойкого бетона составов № 2, 3, 6, 7, 10 и 11 по табл. 11 следует определять как для тяжелого бетона по табл. 5 СНиП 2.03.01-84. Величину потерь от усадки жаростойкого бетона следует принимать на 10 МПа больше указанных в табл. 5 (поз. 8а, б, в) СНиП 2.03.01-84.
Таблица 7
|
Фактор, вызывающий дополнительные потери предварительного напряжения в арматуре при ее нагреве |
Величина дополнительных потерь предварительного напряжения, МПа |
|
Усадка обычного бетона состава № 1 и жаростойкого бетона составов № 2, 3, 6, 7, 10 и 11 по табл. 11 при нагреве: |
|
|
кратковременном |
40 |
|
длительном постоянном |
80 |
|
длительном циклическом (см. п. 1.4) |
60 |
|
Ползучесть обычного бетона состава № 1 и жаростойкого бетона составов № 2, 3, 6, 7, 10 и 11 по табл. 11: |
|
|
естественной влажности при нагреве: |
|
|
кратковременном |
10 σbp |
|
длительном постоянном |
15 σbp |
|
длительном циклическом |
18 σbp |
|
сухого при нагреве: |
|
|
кратковременном |
4 σbp |
|
длительном постоянном |
6 σbp |
|
длительном циклическом |
8 σbp |
|
Релаксация напряжений арматуры: |
|
|
проволочной классов В-II, Вр-II, К-7, К-19 |
0,0012 Δtsσsp |
|
стержневой классов A-IV, A-V, A-VI, Ат-IV, Aт-V, Aт-VI |
0,001 Δtsσsp |
|
Разность деформаций бетона и арматуры от воздействия температуры |
(αst - αbt) ΔtsEsβs |
Обозначения, принятые в таблице:
Δts - разность между температурой арматуры при эксплуатации, определяемой теплотехническим расчетом по указаниям пп. 1.47 - 1.53 и температурой арматуры при натяжении, которую допускается принимать равной 20 °С;
αbt - коэффициент, принимаемый по табл. 20 в зависимости от температуры бетона на уровне напрягаемой арматуры и длительности нагрева;
Es - модуль упругости арматуры, принимаемый по табл. 37;
αst и βs - коэффициенты, принимаемые по табл. 35 в зависимости от температуры арматуры.
Примечания: 1. Потери предварительного напряжения от релаксации напряжений арматуры принимаются для кратковременного и длительного нагрева одинаковыми и учитываются при температуре арматуры свыше 40 °С.
2. Потери предварительного напряжения арматуры от разности деформаций бетона и арматуры учитываются в элементах, выполненных из обычного бетона при нагреве арматуры свыше 100 °С и в элементах из жаростойкого бетона при нагреве арматуры свыше 70 °С.
3. Если от усилий, вызванных совместным действием нагрузки, температуры и предварительного обжатия, в бетоне на уровне арматуры в стадии эксплуатации возникают растягивающие напряжения, то дополнительные потери от ползучести бетона не учитываются.
4. Потери от ползучести бетона при натяжении в двухосном направлении следует уменьшить на 15 %.
При вычислении коэффициента φl по формуле (5) СНиП 2.03.01-84 время в сутках следует принимать: при определении потерь от ползучести - со дня обжатия бетона и от усадки - со дня окончания бетонирования до нагрева конструкции.
Дополнительные потери предварительного напряжения арматуры должны приниматься по табл. 7.
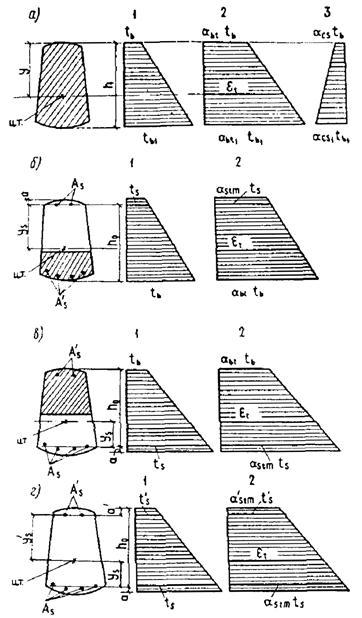
1.36 (1.22-1.23). Величины установившихся напряжений в бетоне σbp на уровне центра тяжести напрягаемой арматуры наиболее обжимаемой зоны после проявлений всех основных потерь определяются по формуле
где M - момент от собственного веса элемента;
P - усилие предварительного обжатия;
eop - эксцентриситет усилия P относительно центра тяжести приведенного сечения;
ysp - расстояние от усилия P до центра тяжести сечения.
Геометрические характеристики приведенного сечения предварительно напряженного железобетонного элемента (Ared, Sred, Ired) определяются по требованиям п. 1.28 с учетом продольной предварительно напряженной арматуры S и S′ и влияния температуры на снижение модулей упругости арматуры и бетона.
1.37 (1.24). Усилия от воздействия температуры в статически неопределимых предварительно напряженных конструкциях находят по указаниям пп. 1.45 и 1.46.
При определении усилий от воздействия температуры жесткость элемента вычисляют по указаниям пп. 4.28 и 4.29.
1.38 (1.25). При определении общего прогиба предварительно напряженного железобетонного элемента необходимо учитывать прогиб, вызванный неравномерным нагревом бетона по высоте сечения элемента, по указаниям п. 4.26.
ДЕФОРМАЦИИ И УСИЛИЯ ОТ ВОЗДЕЙСТВИЯ ТЕМПЕРАТУРЫ
1.39 (1.26). Расчет деформаций, вызванных нагреванием и охлаждением бетонных и железобетонных элементов, должен производиться в зависимости от наличия трещин в растянутой зоне бетона и распределения температуры бетона по высоте сечения элемента.
1.40 (1.27). Для участков бетонного и железобетонного элемента, где в растянутой зоне не образуются трещины, нормальные к продольной оси элемента, деформации от нагрева следует рассчитывать согласно следующим указаниям:
а) сечение элемента приводится к более прочному бетону
по указаниям п. 1.28, удлинение εt оси элемента и ее кривизну ![]() определяют по формулам:
определяют по формулам:
Удлинение εti оси i-той
части бетонного сечения и ее кривизну ![]() (черт. 2) определяют по формулам:
(черт. 2) определяют по формулам:
Удлинение εs и ε′s соответственно арматуры S и S′ находят по формулам:
В формулах (17) - (22): Ared, Ared,i, As,red, A¢s,red, ybi, ys, y′s, Ired, Ired,i, yyi принимают по указаниям п. 1.28;
αbti и αbti+1 - коэффициенты, принимаемые по табл. 20 в зависимости от температуры бетона более и менее нагретой грани i-той части сечения;
αst - коэффициент, принимаемый по табл. 35 в зависимости от температуры арматуры S и S′;
γt - коэффициент надежности по температуре, принимаемый при расчете по предельным состояниям: первой группы - 1,1; второй группы - 1,0.
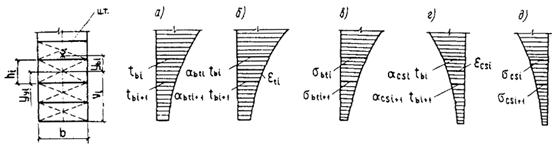
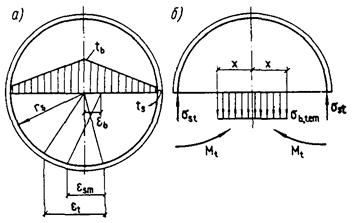
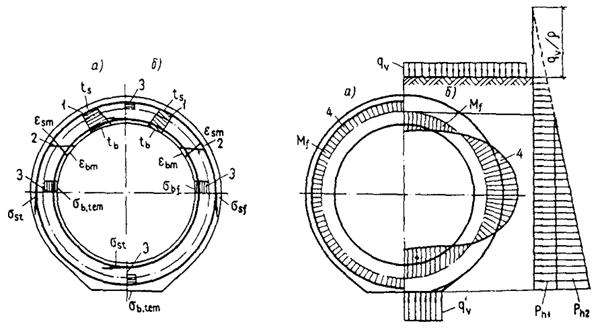
Черт. 2. Схемы распределения
а - температуры бетона; б - деформации удлинения от нагрева; в - напряжения в бетоне от нагрева; г - деформации укорочения от остывания; д - напряжения в бетоне от остывания при нелинейном изменении температур по высоте бетонного сечения элементов; Ц. Т. - центр тяжести приведенного сечения
При расчете бетонного сечения в формулах (17) и (18) удлинение арматуры εs и ε′s не учитывается;
б) при неравномерном нагреве бетона с
прямолинейным распределением температуры по высоте сечения элемента (черт. 3, а) удлинение оси элемента εt и ее кривизну ![]() допускается определять по формулам:
допускается определять по формулам:
где tb и tb1 - температура бетона менее и более нагретой грани сечения, определяемая теплотехническим расчетом согласно указаниям пп. 1.47 - 1.53;
αbt и αbt1 - коэффициенты, принимаемые в зависимости от температуры бетона менее и более нагретой грани сечения по табл. 20.
1.41 (1.28). Для участков бетонного или железобетонного элемента, где в растянутой зоне бетона не образуются трещины, нормальные к продольной оси элемента, деформации от остывания следует рассчитывать согласно следующим указаниям:
а) сечение элемента приводится к более
прочному бетону согласно указаниям п. 1.28;
от усадки и ползучести бетона укорочение εcsc оси элемента и ее кривизну ![]() определяют по
формулам:
определяют по
формулам:
Укорочение εcsc,i оси i-той части бетонного сечения и ее кривизну ![]() определяют по
формулам:
определяют по
формулам:
![]() ; (27)
; (27)
В формулах (25) - (28): Ared,i, Ared, ybi, Ired,i, Ired, hi, yyi принимают по указаниям п. 1.28.
γt - по указаниям п. 1.40;
tbi и tbi+1 - см. черт. 2;
αcs,i и αcs,i+1 - коэффициенты, принимаемые по табл. 21 в зависимости от температуры более и менее нагретой грани i-той части сечения;
εci - деформации ползучести бетона в i-той части сечения определяют по формуле (29) со знаком «минус»:
σb,tem,i и σbi - напряжения
сжатия в бетоне i-той части сечения от
усилий, вызванных температурой и нагрузкой при нагреве, определяемые по
формулам (32) и (33), в которых коэффициент ![]() принимается
по табл. 18 для кратковременного нагрева с подъемом температуры на 10 °С/ч;
принимается
по табл. 18 для кратковременного нагрева с подъемом температуры на 10 °С/ч;
βbi - коэффициент, принимаемый по табл. 16 в зависимости от температуры i-той части сечения;
![]() - коэффициент, принимаемый по табл. 18
в зависимости от температуры i-той части сечения для
длительного нагрева;
- коэффициент, принимаемый по табл. 18
в зависимости от температуры i-той части сечения для
длительного нагрева;
б) при остывании неравномерно нагретого
бетона с прямолинейным распределением температуры по высоте сечения элемента от усадки
бетона укорочение εcs оси элемента и ее кривизну ![]() допускается определять по формулам:
допускается определять по формулам:
где αcs и αcs1 - коэффициенты, принимаемые по табл. 21 в зависимости от температуры бетона менее и более нагретой грани сечения;
γt, tb, tb1 - принимают по указаниям п. 1.40.
1.42 (1.29). Для участков бетонного и железобетонного элемента, где в растянутой зоне бетона не образуются трещины, нормальные к продольной оси элемента, напряжения в бетоне грани i-той части сечения следует определять:
растяжения при нагревании от нелинейного распределения температуры по формуле
сжатия при нагревании от кратковременных усилий по формуле
растяжения при остывании от усадки и ползучести бетона по формуле
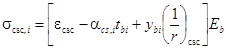 ; (34)
; (34)
где ybi, εt, ![]() - определяются соответственно по формулам (13),
(17) и (18);
- определяются соответственно по формулам (13),
(17) и (18);
αbti, tbi - принимаются по указаниям пп. 1.40 и 1.41;
Eb - принимается по табл. 17;
αcs,i, βbi и ![]() - коэффициенты, принимаемые по табл. 21, 16 и 18 в зависимости от температуры бетона
грани i-той части сечения;
- коэффициенты, принимаемые по табл. 21, 16 и 18 в зависимости от температуры бетона
грани i-той части сечения;
M и N - момент и продольная сила, приложенная к центру тяжести сечения от воздействия нагрузки и температуры;
Ared и B - принимают соответственно по указаниям пп. 1.28 и 4.28;
εcs, εcsc и ![]() - определяют соответственно по формулам (29), (25) и (26).
- определяют соответственно по формулам (29), (25) и (26).
Если в формуле (32) напряжения имеют знак «минус», то в бетоне возникают напряжения сжатия и σbtt,i заменяется σb,tem,i.
1.43 (1.30). Для участков железобетонного элемента, где в растянутой зоне образуются трещины, нормальные к продольной оси элемента, деформации от нагрева следует рассчитывать согласно следующим указаниям:
а) для железобетонного элемента с трещинами в растянутой
зоне, расположенной у менее нагретой грани сечения
(черт. 3, б), удлинение εt оси элемента и ее кривизну ![]() определяют по
формулам:
определяют по
формулам:
б) для участков железобетонного элемента с
трещинами в
растянутой зоне бетона, расположенной у более нагретой грани сечения (черт. 3, в), удлинение εt оси элемента определяется по формуле (35) и ее кривизну ![]() - по формуле
- по формуле
в) для участков железобетонного элемента с
трещинами по
всей высоте сечения (черт. 3, г)
удлинение εt оси элемента и ее кривизну ![]() определяют
по формулам:
определяют
по формулам:
![]() ; (38)
; (38)
ts, t′s - температура арматуры S и S′;
tb - температура бетона сжатой грани сечения;
αstm и α′stm - коэффициенты, определяемые по формуле (74) для арматуры S и S′;
αbt - коэффициент, принимаемый по табл. 20 в зависимости от температуры бетона более или менее нагретой грани сечения;
γt - принимается по указаниям п. 1.40;
a′ - толщина защитного слоя более нагретой грани сечения;
г) при равномерном нагреве железобетонного
элемента кривизну ![]() оси элемента допускается принимать равной
нулю. В железобетонных элементах из обычного бетона при температуре арматуры до 100 °С и из жаростойкого
бетона при температуре арматуры до 70 °С для участков с трещинами в растянутой
зоне бетона допускается определять удлинение оси элемента εt и ее кривизну
оси элемента допускается принимать равной
нулю. В железобетонных элементах из обычного бетона при температуре арматуры до 100 °С и из жаростойкого
бетона при температуре арматуры до 70 °С для участков с трещинами в растянутой
зоне бетона допускается определять удлинение оси элемента εt и ее кривизну ![]() по формулам (23) и (24) как для бетонных элементов без трещин.
по формулам (23) и (24) как для бетонных элементов без трещин.
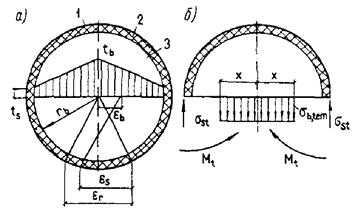
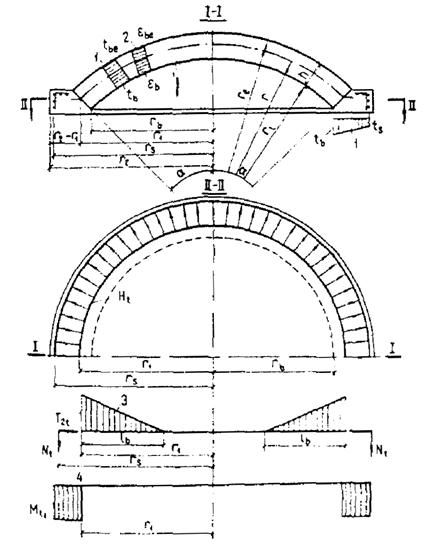
Черт. 3. Схемы распределения температур (1), деформаций от неравномерного нагрева (2) и остывания (3) при прямолинейном изменении температур по высоте сечения элементов
а - бетонного и железобетонного без трещин; б - железобетонного с трещинами в растянутой зоне, расположенной у менее нагретой грани; в - то же, у более нагретой грани; г - железобетонного с трещинами по всей высоте сечения; Ц.Т. - центр тяжести приведенного сечения
1.44 (1.31). Для участков железобетонных элементов,
где в растянутой зоне образуются трещины, нормальные к продольной оси элемента от усадки
бетона, при остывании укорочение εcs оси элемента и ее кривизну ![]() допускается
находить по формулам (30)
и (31).
допускается
находить по формулам (30)
и (31).
1.45 (1.32). Определение усилий в статически неопределимых конструкциях от воздействия температуры должно производиться по формулам строительной механики с принятием действительной жесткости сечения.
Методика определения неизвестных, составление канонических уравнений перемещений, получение окончательных эпюр такие же, как и при расчете статически неопределимых конструкций на воздействие внешней нагрузки.
Если определение усилий от воздействия температуры в плоской статически неопределимой системе производится методом сил, то канонические уравнения имеют вид
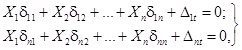 (40)
(40)
где X1, X2, ..., Xn - соответственно лишние неизвестные усилия основной системы;
δ11, δ12, δ1n - перемещение в основной системе в направлении 1, вызываемое единичной силой, действующей в направлении 1, 2 и п;
δn1, δn2, δnn - перемещения в основной системе в n-м направлении, вызываемые единичной силой, действующей в направлении 1, 2 и n;
Δ1t и Δnt - перемещение в основной системе в направлении 1 и п, вызываемое воздействием температуры.
Перемещение Δit в основной системе в i-том направлении, вызванное воздействием температуры, равно:
где ![]() ,
, ![]() - изгибающий момент и продольная сила
в сечении х элемента основной системы
от действия в i-том направлении соответствующей
единичной силы;
- изгибающий момент и продольная сила
в сечении х элемента основной системы
от действия в i-том направлении соответствующей
единичной силы;
![]() , εtx - кривизна и удлинение элемента в сечении x, вызванные воздействием температуры, определяемые согласно
указаниям пп. 1.40 и 1.43.
, εtx - кривизна и удлинение элемента в сечении x, вызванные воздействием температуры, определяемые согласно
указаниям пп. 1.40 и 1.43.
Единичное перемещение δik в направлении i, вызванное силой, равной единице, действующей в направлении k, определяется по формуле
где Bx, Ared,x - жесткость и приведенная площадь элемента в сечении x, определяемые согласно указаниям пп. 1.28, 4.28 и 4.29.
При определении жесткости сечений элемента следует учитывать усилия от нагрузки и воздействия температуры согласно требованиям табл. 1 и 2.
Удлинение εt оси элемента и ее кривизну ![]() от
воздействия температуры следует вычислять согласно указаниям пп. 1.39 - 1.43.
от
воздействия температуры следует вычислять согласно указаниям пп. 1.39 - 1.43.
При расчете железобетонных элементов, работающих на изгиб, а также на
сжатие и растяжение, когда ![]() ≥ 0,8ho, с достаточной для расчета точностью, в формулах (41) и (42)
второй интеграл можно принимать равным нулю. Для вычисления величин Δit и dik по формулам(41)
и (42) рекомендуется следующая
упрощенная методика. Элемент по длине разбивается на п участков и на каждом участке Δl определяются жесткость Вх и кривизна
≥ 0,8ho, с достаточной для расчета точностью, в формулах (41) и (42)
второй интеграл можно принимать равным нулю. Для вычисления величин Δit и dik по формулам(41)
и (42) рекомендуется следующая
упрощенная методика. Элемент по длине разбивается на п участков и на каждом участке Δl определяются жесткость Вх и кривизна ![]() в зависимости от наличия в сечении трещин и действующих
усилий:
в зависимости от наличия в сечении трещин и действующих
усилий:
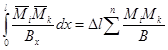 , (43)
, (43)
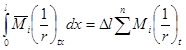 , (44)
, (44)
где Вx - жесткость посередине длины каждого участка, определяемая с учетом наличия трещин и усилий от нагрузки и температуры согласно указаниям пп. 4.28 и 4.29;
Mi и Mk - изгибающие моменты посередине длины каждого участка от действия единичной силы;
![]() - кривизна на каждом участке, определяемая согласно указаниям пп. 1.40 и 1.43.
- кривизна на каждом участке, определяемая согласно указаниям пп. 1.40 и 1.43.
Величины жесткости и кривизны зависят от усилий, вызванных температурой, поэтому расчет статически неопределимых железобетонных конструкций на воздействие температуры необходимо выполнять методом последовательных приближений до тех пор, пока величина усилия, полученная в последнем приближении, будет отличаться от усилий предыдущего приближения не более чем на 5 %.
Расчет усилий в статически неопределимых конструкциях, как
правило, следует выполнять с применением ЭВМ. При использовании малых вычислительных машин и при
ручном счете допускается принимать приведенные постоянными по длине элемента жесткость сечения Bred, удлинение оси εred,t и ее кривизну ![]() .
.
Приведенная жесткость сечения определяется по формуле
Bred = B + (B1 - B) φm. (45)
Приведенное удлинение εred,t оси
элемента и ее кривизну ![]() от нагрева определяют по формулам:
от нагрева определяют по формулам:
εred,t = εt1 + (εt2 - εt1) φm; (46)
B - жесткость сечения элемента с трещинами в растянутой зоне в месте действия наибольшего изгибающего момента M, определяемая по указаниям п. 4.29;
B1 - жесткость сечения элемента без трещин, определяемая по указаниям п. 4.28;
при M
≥ 2,5Mcrc φm = 0; Bred = B; εred,t = εt1 и ![]() ;
;
M и Mcrc - наибольший изгибающий момент и момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин, который определяется по указаниям п. 4.4;
e - основание натуральных логарифмов;
et2, ![]() - удлинение и кривизна оси элемента без
трещин от воздействия температуры, определяемые по
указаниям п. 1.40;
- удлинение и кривизна оси элемента без
трещин от воздействия температуры, определяемые по
указаниям п. 1.40;
et1, ![]() - удлинение и кривизна оси элемента с
трещинами в растянутой зоне, определяемые по указаниям п. 1.43.
- удлинение и кривизна оси элемента с
трещинами в растянутой зоне, определяемые по указаниям п. 1.43.
Расчет статически неопределимых железобетонных конструкций при температурном воздействии рекомендуется выполнять в следующем порядке:
а) составляется расчетная схема конструкции с указанием всех геометрических размеров элементов, действующих нагрузок и температур. Назначаются класс и вид бетона, класс арматуры;
б) задается минимальное армирование сечений элементов As,min конструкций по формуле
в) вычисляются моменты, которые могут воспринять различные сечения элементов конструкции при заданных размерах сечений, проценте армирования, прочности бетона и температуре;
г) определяется удлинение εt оси, кривизна ![]() элементов, вызванные
воздействием температуры.
элементов, вызванные
воздействием температуры.
Если по условию эксплуатации допускается
образование трещин в элементах, величины εt и ![]() определяют как для сечений без трещин, так
и для сечений с трещинами согласно указаниям пп. 1.40 и 1.43;
определяют как для сечений без трещин, так
и для сечений с трещинами согласно указаниям пп. 1.40 и 1.43;
д) вычисляется жесткость сечений элементов, при эксплуатации которых образование трещин маловероятно, согласно указаниям п. 4.28;
е) для элементов, при эксплуатации которых возможно образование трещин, по формулам (299) или (300) вычисляется жесткость сечения с трещинами. При вычислении жесткости предполагается, что в сечении действует момент M;
ж) для элементов, работающих с трещинами, при ручном расчете вычисляются приведенные жесткость сечения, удлинение оси и кривизна элемента по формулам (45) - (47);
з) по формулам строительной механики вычисляют коэффициенты и составляют канонические уравнения;
и) решают уравнения и находят неизвестные;
к) при различном сочетании температуры и нагрузки определяют моменты, продольные и поперечные силы в сечениях элементов конструкции;
л) полученный момент в рассматриваемом сечении элемента от действия температуры и нагрузки должен равняться или быть несколько меньше момента, который может воспринять сечение. Если полученный момент будет больше, то необходимо увеличить армирование или размеры сечения и провести повторный расчет.
1.46 (1.33). Изгибающий момент от неравномерного нагрева бетона по высоте сечения при равномерном нагреве бетона по длине элемента, заделанного на опоре от поворота, а также в замкнутых рамах кольцевого, квадратного и прямоугольного очертания, имеющих одинаковые сечения, определяют по формуле
![]() , (50)
, (50)
а изгибающий момент при остывании от усадки и ползучести бетона
![]() , (51)
, (51)
где ![]() - температурная
кривизна оси элемента от кратковременного или длительного нагрева, определяемая по указаниям пп. 1.40 и 1.43;
- температурная
кривизна оси элемента от кратковременного или длительного нагрева, определяемая по указаниям пп. 1.40 и 1.43;
![]() - кривизна оси
элемента при
остывании от
усадки и ползучести бетона, определяемая по формуле (26).
- кривизна оси
элемента при
остывании от
усадки и ползучести бетона, определяемая по формуле (26).
Допускается кривизну ![]() определять по формуле
определять по формуле
![]() , (52)
, (52)
где ![]() - кривизна оси элемента при остывании от
усадки бетона, определяемая по формуле (31);
- кривизна оси элемента при остывании от
усадки бетона, определяемая по формуле (31);
![]() - кривизна оси
элемента при остывании
от ползучести бетона, определяется по формуле (53) со знаком «минус»:
- кривизна оси
элемента при остывании
от ползучести бетона, определяется по формуле (53) со знаком «минус»:
Mt и M′t - температурные моменты соответственно для кратковременного и длительного нагрева, определяются по формуле (50), принимая температурную кривизну для кратковременного нагрева при значении αbt по табл. 20 для подъема температуры на 10 °С/ч и более независимо от длительности нагрева;
B - жесткость сечения, определяемая по указаниям пп. 4.28 и 4.29; в формуле (50) вычисляется для кратковременного и длительного нагрева, а в формулах (51) и (53) - для кратковременного нагрева со скоростью 10 °С/ч и более независимо от длительности нагрева.
ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУР В СЕЧЕНИЯХ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
1.47 (1.34). Расчет распределения температур в бетонных и железобетонных конструкциях для установившегося теплового потока следует производить, пользуясь методами расчета температур ограждающих конструкций согласно СНиП II-3-79**.
Расчет распределения температур в ограждающих конструкциях сложной конфигурации сечений элементов, в массивных конструкциях, в конструкциях, находящихся ниже уровня земли, а также при неустановившемся тепловом потоке с учетом переменной влажности бетона по сечению должен производиться методами расчета температурных полей или теории теплопроводности либо по соответствующим нормативным документам.
Расчет распределения температур в стенках боровов и каналов, расположенных под землей, допускается производить:
для кратковременного нагрева, принимая сечение по высоте стен неравномерно нагретым с прямолинейным распределением температур бетона и величину коэффициента теплоотдачи наружной поверхности стенки αe - по табл. 8;
для длительного нагрева, принимая сечение по высоте стен равномерно нагретым.
Температуру арматуры в сечениях железобетонных элементов допускается принимать равной температуре бетона в месте ее расположения.
1.48 (1.35). Для конструкций, находящихся на наружном воздухе, коэффициент теплоотдачи наружной поверхности αe, Вт/(м2 · °С), в зависимости от скорости ветра следует определять по формуле
![]() , (54)
, (54)
где v - скорость ветра, м/с.
При расчете наибольших усилий в конструкциях от воздействия температуры принимают максимальную из средних скоростей ветра по румбам за январь, повторяемость которых составляет 16 % и более, а при определении максимальной температуры нагрева бетона и арматуры принимают минимальную из средних скоростей ветра по румбам за июль, повторяемость которых составляет 16 % и более согласно СНиП 2.01.01-82, но не менее 1 м/с.
Для конструкций, находящихся в помещении или на наружном воздухе, но защищенных от воздействия ветра, коэффициент теплоотдачи наружной поверхности αe принимают по табл. 8.
Таблица 8
|
Температура наружной поверхности и воздуха, °С |
|||||||||||
|
0 |
50 |
100 |
200 |
300 |
400 |
500 |
700 |
900 |
1100 |
1200 |
|
|
αe |
8 |
12 |
14 |
20 |
26 |
- |
- |
- |
- |
- |
- |
|
αi |
- |
12 |
12 |
12 |
14 |
18 |
23 |
47 |
82 |
140 |
175 |
Примечание. Коэффициенты αe и αi для промежуточных значений температур определяют интерполяцией.
Коэффициент теплоотдачи внутренней поверхности конструкции αi следует определять, как правило, методом расчета теплопередачи как для случая сложного теплообмена. При определении распределения температуры бетона по сечению элемента допускается коэффициент αi принимать по табл. 8 в зависимости от температуры воздуха производственного помещения или рабочего пространства теплового агрегата.
1.49 (1.36). Коэффициент теплопроводности λ бетона в сухом состоянии должен приниматься по табл. 9 в зависимости от средней температуры бетона в сечении элемента. Коэффициент теплопроводности λ огнеупорных и теплоизоляционных материалов должен приниматься по табл. 10.
Термическое сопротивление невентилируемой воздушной прослойки в зависимости от температуры воздуха и независимо от ее толщины и направления следует принимать равным, м2 · °С/Вт:
0,140................................. при 50 °С
0,095.................................... » 100 »
0,035.................................... » 300 »
0,013.................................... » 500 »
Таблица 9
|
Коэффициент теплопроводности λ, Вт/(м · °С), обычного и жаростойкого бетонов в сухом состоянии при средней температуре бетона в сечении элемента, °С |
||||||
|
50 |
100 |
300 |
500 |
700 |
900 |
|
|
1 |
1,51 |
1,37 |
1,09 |
- |
- |
- |
|
20 |
2,68 |
2,43 |
1,94 |
1,39 |
1,22 |
1,19 |
|
21 |
1,49 |
1,35 |
1,37 |
1,47 |
1,57 |
1,63 |
|
2, 3, 6, 7, 13 |
1,51 |
1,37 |
1,39 |
1,51 |
1,62 |
- |
|
10, 11 |
0,93 |
0,89 |
0,84 |
0,87 |
0,93 |
1,05 |
|
14, 15, 16, 17, 18 |
0,99 |
0,95 |
0,93 |
1,01 |
1,04 |
1,28 |
|
19 |
0,87 |
0,83 |
0,78 |
0,81 |
0,87 |
0,99 |
|
4, 5, 8, 9 |
0,81 |
0,75 |
0,63 |
0,67 |
0,70 |
- |
|
12 |
0,93 |
0,88 |
0,81 |
0,90 |
- |
- |
|
23 |
0,37 0,43 |
0,39 0,45 |
0,46 0,52 |
0,52 0,58 |
0,58 0,64 |
- |
|
29 |
0,44 0,50 |
0,46 0,52 |
0,52 0,58 |
0,58 0,64 |
0,64 0,70 |
0,70 0,76 |
|
24 |
0,27 0,38 |
0,29 0,41 |
0,34 0,45 |
0,40 0,50 |
0,45 0,55 |
0,51 0,59 |
|
30 |
0,31 0,44 |
0,34 0,46 |
0,37 0,51 |
0,43 0,56 |
0,49 0,60 |
- |
|
26, 28 |
0,21 |
0,23 |
0,28 |
0,33 |
0,37 |
0,42 |
|
22, 25, 27, 31, 32, 36 |
0,29 |
0,31 |
0,36 |
0,42 |
0,48 |
0,53 |
|
33 |
0,21 |
0,22 |
0,25 |
0,29 |
0,33 |
0,37 |
|
34, 35, 37 |
0,24 |
0,27 |
0,31 |
0,37 |
0,43 |
0,49 |
Примечания: 1. Коэффициенты теплопроводности бетонов составов № 23 и № 29 приведены: над чертой для бетонов со средней плотностью 1350, под чертой 1550; для бетонов составов № 24 и № 30 соответственно 950 и 1250 кг/м3. Если средняя плотность бетона отличается от указанных значений, то коэффициент теплопроводности определяют интерполяцией.
2. Коэффициент теплопроводности λ обычного и жаростойкого бетонов с естественной влажностью после нормального твердения или тепловой обработки при атмосферном давлении при средней температуре бетона в сечении элемента до 100 °С следует принимать по данным таблицы, увеличенным на 30 %.
3. Для промежуточных значений температур коэффициент теплопроводности λ определяют интерполяцией.
Таблица 10
|
Средняя плотность в сухом состоянии, кг/м3 |
Предельно допустимая температура применения, °С |
Коэффициент теплопроводности λ, Вт/(м · °С), огнеупорных и теплоизоляционных материалов в сухом состоянии при средней температуре материала в сечении элемента, °С |
||||||
|
50 |
100 |
300 |
500 |
700 |
900 |
|||
|
1. Изделия огнеупорные шамотные, ГОСТ 390-83 |
1900 |
- |
0,73 |
0,77 |
0,88 |
1,01 |
1,14 |
1,27 |
|
7. Изделия шамотные легковесные, ГОСТ 5040-78 |
400 |
1150 |
0,13 |
0,14 |
0,17 |
0,20 |
0,23 |
0,27 |
|
3. То же |
800 |
1270 |
0,23 |
0,24 |
0,29 |
0,34 |
0,38 |
0,43 |
|
4. » |
1000 |
1300 |
0,34 |
0,35 |
0,42 |
0,49 |
0,56 |
0,63 |
|
5. » |
1300 |
1400 |
0,49 |
0,56 |
0,58 |
0,65 |
0,73 |
0,81 |
|
6. Изделия огнеупорные динасовые, ГОСТ 4157-79 |
1900 |
- |
1,60 |
1,62 |
1,70 |
1,78 |
1,85 |
1,93 |
|
7. Изделия динасовые легковесные, ГОСТ 5040-78 |
1200 - 1400 |
1550 |
0,57 |
0,58 |
0,64 |
0,70 |
0,75 |
0,81 |
|
8. Изделия каолиновые, ГОСТ 20901-75 |
2000 |
- |
1,79 |
1,80 |
1,86 |
1,90 |
1,95 |
2,01 |
|
9. Изделия высокоглиноземистые, ГОСТ 24704-81 |
2600 |
- |
1,76 |
1,74 |
1,68 |
1,65 |
1,60 |
1,55 |
|
10. Изделия огнеупорные магнезитовые, ГОСТ 4689-74 |
2700 |
- |
6,00 |
5,90 |
5,36 |
4,82 |
4,30 |
3,75 |
|
11. Изделия высокоогнеупорные периклазохромитовые, ГОСТ 10888-76 |
2800 |
- |
4,02 |
3,94 |
3,60 |
3,28 |
2,94 |
2,60 |
|
12. Изделия высокоогнеупорные хромомагнезитовые, ГОСТ 5381-72 |
2950 |
- |
2,74 |
2,71 |
2,54 |
2,36 |
2,18 |
2,01 |
|
13. Кирпич глиняный обыкновенный, ГОСТ 530-80 |
1700 |
- |
0,56 |
0,59 |
0,70 |
0,81 |
- |
- |
|
14. Изделия пенодиатомитовые теплоизоляционные, ГОСТ 2694-78 |
350 |
900 |
0,09 |
0,10 |
0,13 |
0,15 |
0,18 |
- |
|
15. То же |
400 |
900 |
0,10 |
0,11 |
0,14 |
0,16 |
0,19 |
- |
|
16. Изделия диатомитовые теплоизоляционные, ГОСТ 2694-78 |
500 |
900 |
0,12 |
0,13 |
0,19 |
0,23 |
0,28 |
- |
|
17. То же |
600 |
900 |
0,14 |
0,15 |
0,21 |
0,25 |
0,30 |
- |
|
18. Маты минераловатные прошивные на металлической сетке, ГОСТ 21880-76 |
75 - 100 |
600 |
0,05 |
0,06 |
0,11 |
0,15 |
- |
- |
|
19. Маты минераловатные прошивные, ГОСТ 21880-76 |
125 |
600 |
0,05 |
0,06 |
0,11 |
0,16 |
- |
- |
|
20. То же |
150 |
600 |
0,05 |
0,06 |
0,11 |
0,16 |
- |
- |
|
21. Плиты и маты теплоизоляционные из минеральной ваты на синтетическом связующем, ГОСТ 9573-82 |
50 - 75 |
400 |
0,05 |
0,07 |
0,13 |
- |
- |
- |
|
22. То же |
125 |
400 |
0,05 |
0,07 |
0,11 |
- |
- |
- |
|
23. » |
175 |
400 |
0,05 |
0,07 |
0,11 |
- |
- |
- |
|
24. Маты теплоизоляционные из ваты каолинового состава, ТУ 14-8-78-73 |
150 |
1100 |
0,05 |
0,06 |
0,12 |
0,18 |
0,24 |
0,31 |
|
25. То же |
300 |
1100 |
0,06 |
0,07 |
0,13 |
0,19 |
0,25 |
0,35 |
|
26. Изделия из стеклянного штапельного волокна, ГОСТ 10499-78 |
170 |
450 |
0,06 |
0,07 |
0,14 |
- |
- |
|
|
27. Перлито-фосфогелевые изделия без гидроизоляционно-упрочняющего покрытия, ГОСТ 21500-76 |
200 |
600 |
0,07 |
0,08 |
0,10 |
0,12 |
- |
- |
|
28. То же |
250 |
600 |
0,08 |
0,09 |
0,11 |
0,14 |
- |
- |
|
29. » |
300 |
600 |
0,08 |
0,09 |
0,14 |
0,16 |
- |
- |
|
30. Перлитоцементные изделия, ГОСТ 18109-80 |
250 |
600 |
0,07 |
0,09 |
0,13 |
0,16 |
- |
- |
|
31. То же |
300 |
600 |
0,08 |
0,10 |
0,14 |
0,17 |
- |
- |
|
32. » |
350 |
600 |
0,09 |
0,11 |
0,15 |
0,18 |
- |
- |
|
33. Перлитокерамические изделия, ГОСТ 21521-76 |
250 |
875 |
0,08 |
0,09 |
0,12 |
0,16 |
0,19 |
- |
|
34. То же |
300 |
875 |
0,09 |
0,10 |
0,13 |
0,17 |
0,20 |
- |
|
35. » |
350 |
875 |
0,10 |
0,11 |
0,14 |
0,1S |
0,21 |
- |
|
36. » |
400 |
875 |
0,11 |
0,12 |
0,15 |
0,19 |
0,22 |
- |
|
37. Известково-кремнеземистые изделия, ГОСТ 24748-81 |
200 |
600 |
0,07 |
0,08 |
0,10 |
0,12 |
- |
- |
|
38. Изделия на основе кремнеземного волокна, ТУ 207-67 |
120 |
1200 |
0,06 |
0,07 |
0,10 |
0,14 |
0,17 |
0,21 |
|
39. Савелитовые изделия, ГОСТ 6788-74 |
350 |
500 |
0,08 |
0,09 |
0,11 |
- |
- |
- |
|
40. Савелитовые изделия, ГОСТ 6788-74 |
400 |
500 |
0,09 |
0,10 |
0,12 |
- |
- |
- |
|
41. Вулканитовые изделия, ГОСТ 10179-74 |
300 |
600 |
0,08 |
0,09 |
0,11 |
0,13 |
- |
- |
|
42. То же |
350 |
600 |
0,08 |
0,09 |
0,11 |
0,14 |
- |
- |
|
43. » |
400 |
600 |
0,09 |
0,10 |
0,12 |
0,14 |
- |
- |
|
44. Пеностекло, СТУ 85-497-64 |
200 |
500 |
0,08 |
0,09 |
0,13 |
- |
- |
- |
|
45. Асбестовермикулитовые плиты, ГОСТ 13450-68 |
250 |
600 |
0,09 |
0,11 |
0,16 |
0,21 |
- |
- |
|
46. То же |
300 |
600 |
0,10 |
0,11 |
0,16 |
0,21 |
- |
- |
|
47. » |
350 |
600 |
0,10 |
0,12 |
0,17 |
0,22 |
- |
- |
|
48. Изделия муллитокремнеземистые огнеупорные волокнистые теплоизоляционные марки МКРВ-350, ТУ 14-8-159-75 |
350 |
1150 |
0,11 |
0,12 |
0,15 |
0,19 |
0,22 |
0,29 |
|
49. Диатомитовая крошка обожженная, ТУ 36-888-67 |
500 600 |
900 900 |
0,01 0,03 |
0,03 0,04 |
0,06 0,09 |
0,10 0,15 |
0,13 0,20 |
0,17 0,25 |
|
50. Вермикулит вспученный, ГОСТ 12865-67 |
100 |
1100 |
0,07 |
0,09 |
0,14 |
0,20 |
0,26 |
0,31 |
|
51. То же |
150 |
1100 |
0,08 |
0,09 |
0,15 |
0,21 |
0,27 |
0,32 |
|
52. » |
200 |
1100 |
0,08 |
0,10 |
0,15 |
0,21 |
0,27 |
0,33 |
|
53. Асбозурит |
600 |
900 |
0,17 |
0,18 |
0,21 |
0,24 |
- |
- |
|
54. Картон асбестовый, ГОСТ 2850-80 |
1000 - 1300 |
600 |
0,16 |
0,18 |
0,20 |
0,22 |
- |
- |
Примечания: 1. Коэффициент теплопроводности λ огнеупорных (поз. 1 - 13) и теплоизоляционных (поз. 14 - 54) материалов с естественной влажностью при средней температуре нагрева материала в сечении элемента до 100 °С следует принимать по табличным данным, увеличенным соответственно на 20 и 10 %.
2. Коэффициент теплопроводности λ для промежуточных значений температур определяют интерполяцией.
Для промежуточных температур термическое сопротивление воздушной прослойки принимается по интерполяции.
При стационарном нагреве конструкции, состоящей из п слоев, и начале отсчета слоев со стороны более нагретой поверхности температуру материала tn между слоями п - 1 и п определяют по формуле
Температура материала более нагретой поверхности tb вычисляется по формуле
а температура материала менее нагретой поверхности tes - по формуле
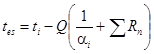 . (57)
. (57)
В трехслойной конструкции определение температуры материала между первым и вторым слоями, считая слои от более нагретой поверхности, производится по формуле
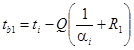 . (58)
. (58)
Температура материала между вторым и третьим слоями определяется по формуле
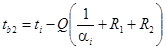 . (59)
. (59)
Температура менее нагретой поверхности третьего слоя равна
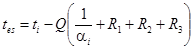 . (60)
. (60)
Тепловой поток Q, Вт/м2, определяется по формуле
где ti - температура воздуха производственного помещения или рабочего пространства теплового агрегата;
te - температура наружного воздуха.
Сопротивление теплопередаче R0, м2 · °С/Вт, многослойной конструкции следует определять по формуле
![]() , (62)
, (62)
где ![]() ;
; ![]() ; ...;
; ...; ![]() ;
; ![]() ;
;
R1, R2, ..., Rn-1, Rn - термические сопротивления материала в отдельных слоях конструкции, пронумерованные со стороны нагреваемой поверхности, м2 · °С/Вт;
t1, t2, ..., tn-1, tn - толщины отдельных слоев, м;
λ1, λ2, ..., λn-1, λn - коэффициенты теплопроводности материалов в слоях конструкции при их средней температуре, Вт/(м · °С).
1.50 (1.37). При расчете распределения температуры по толщине конструкции необходимо учитывать различие площадей теплоотдающей и тепловоспринимающей поверхностей:
при круговом очертании, если толщина стенки более 0,1 наружного диаметра;
при квадратном или прямоугольном очертании, если толщина стенки более 0,1 длины большей стороны;
при произвольном очертании, если разница в площадях теплоотдающей и тепловоспринимающей поверхностей более 10 %.
Для трехслойной конструкции ограждения с учетом различия в площадях теплоотдающих внутренней Ais и наружной Аеs поверхностей:
температура материала более нагретой поверхности
![]() ; (63)
; (63)
температура материала между первым и вторым слоями
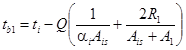 ; (64)
; (64)
температура материала между вторым и третьим слоями
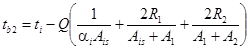 ; (65)
; (65)
Определение сопротивления теплопередачи конструкции производится по формуле
где Ais и Aes - расчетные площади теплоотдающих внутренней и наружной поверхностей;
A1 и A2 - расчетные площади конструкции на границе между первым и вторым слоями и между вторым и третьим слоями.
1.51 (1.38). В ребристых конструкциях, когда наружные поверхности бетонных ребер и тепловой изоляции совпадают, расчет температуры в бетоне должен производиться по сечению ребра. Если бетонные ребра выступают за наружную поверхность тепловой изоляции, расчет температуры в бетоне ребра должен выполняться по методам расчета температурных полей или по соответствующим нормативным документам.
При выступающей за тепловую изоляцию бетона части ребра hw (черт. 4) допускается температуру бетона менее нагретой наружной поверхности ребра tew определять по формуле
![]() ; (70)
; (70)
λ - коэффициент теплопроводности бетона при средней температуре выступающей части ребра.
Черт. 4. Схема элемента с выступающим ребром
1 - жаростойкий бетон; 2 - теплоизоляция; 3 - арматура
Величина гиперболического косинуса ch определяется по черт. 5 в зависимости от параметра mhw. Коэффициент m вычисляется по формуле (69).
Черт. 5. Значения отношения ![]() в
зависимости от параметра mhw
в
зависимости от параметра mhw
Температура бетона в ребре на уровне наружной поверхности тепловой изоляции определяется по формуле
Температура бетона более нагретой поверхности tb вычисляется по формуле (56) для сечения конструкции между ребрами.
Из совместного решения двух уравнений (68) и (71) находят температуру tew.
Температура арматуры, расположенной в ребре, определяется по формуле
Расчет ребристой конструкции с выступающими за плоскость изоляции ребрами производится в следующей последовательности.
А. При неизвестной высоте ребра
1. Задаются высотой полки h′f.
2. Теплотехническим расчетом определяют толщину эффективной теплоизоляции, укладываемой между ребрами, при заданной температуре наружной поверхности.
3. Определяют высоту ребра сечения при заданной температуре tew наружной поверхности:
а) задаются отношением hw/h′ и при известных tb и tew по формуле (71) находят температуру бетона в ребре tb1;
б) значение коэффициента m вычисляют по формуле (69), в которой αе определяют согласно указаниям п. 1.48 в зависимости от температуры наружной поверхности ограждения tes; коэффициент теплопроводности бетона λb принимают по табл. 9 в зависимости от средней температуры бетона;
в) определяют значение отношения температур (tb1 - te) / (tew - te);
г) по черт. 5 в зависимости от отношения (tb1 - te) / (tew - te) находят произведение mhw, из которого определяют высоту ребра hw и отношение hw/h′.
Если при определении температуры tb1 заданное отношение hw/h′ отличается от вычисленного, производят перерасчет. При этом отношение h′f/h должно удовлетворять данным черт. 14.
Б. При заданных размерах высоты ребра и высоты полки
1. Теплотехническим расчетом определяют толщину эффективной теплоизоляции, укладываемой между ребрами, из условия получения на ее наружной поверхности заданной температуры.
2. Задаются температурой наружной поверхности ребра tew.
3. При известных температурах tb и tew по формуле (71) находят температуру бетона в ребре tb1.
4. Вычисляют коэффициент m по формуле (69), в которой принимают αe согласно указаниям п. 1.48 в зависимости от температуры наружной поверхности ребра tew; коэффициент теплопроводности бетона λ принимают по табл. 9 в зависимости от средней температуры бетона.
5. Вычисляют величину произведения mhw и по черт. 5 определяют гиперболический косинус chmhw.
6. Из совместного решения уравнений (68) и (71) находят наружную температуру бетона ребра tew. В случае если вычисленная температура tew отличается от ранее принятой более чем на 10 %, необходимо сделать перерасчет. Теплотехническим расчетом должны быть также определены температура арматуры по формуле (72) и температура на границе полки и теплоизоляции.
1.52 (1.39). Температура бетона в сечениях конструкций от нагрева при эксплуатации должна определяться теплотехническим расчетом установившегося теплового потока при заданной по проекту расчетной температуре рабочего пространства или воздуха производственного помещения.
Для конструкций, находящихся на наружном воздухе, наибольшие температуры нагрева бетона и арматуры определяются по расчетной летней температуре наружного воздуха, принимаемой по средней максимальной температуре наружного воздуха наиболее жаркого месяца в районе строительства по СНиП 2.01.01-82. Вычисленные температуры не должны превышать предельно допустимые температуры применения бетона по ГОСТ 20910-82 и арматуры по табл. 24.
1.53 (1.40). При расчете статически неопределимых конструкций, работающих в условиях воздействия температур, теплотехнический расчет должен производиться на расчетную температуру рабочего пространства и на температуру, вызывающую наибольшие усилия, определяемые по указаниям п. 1.23.
При расчете наибольших усилий от воздействия температуры в конструкциях, находящихся на наружном воздухе, температуру бетона и арматуры вычисляют по расчетной зимней температуре наружного воздуха, принимаемой по температуре наружного воздуха наиболее холодной пятидневки с обеспеченностью 0,92 района строительства по СНиП 2.01.01-82.
1.54. Расчет температур в конструкциях с включениями из различных теплоизоляционных материалов, а также более
точный расчет ребристых конструкций из жаростойкого бетона следует производить
согласно «Указаниям по тепловому расчету конструкции тепловых агрегатов» ![]() .
.
2. МАТЕРИАЛЫ ДЛЯ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
БЕТОН
2.1 (2.1). Для бетонных и железобетонных конструкций, предназначенных для работы в условиях воздействия повышенных и высоких температур, следует предусматривать:
обычный бетон - конструкционный тяжелый бетон средней плотности 2200 до 2500 кг/м3 включ. по ГОСТ 25192-82;
жаростойкий бетон конструкционный и теплоизоляционный плотной структуры средней плотности 900 кг/м3 и более по ГОСТ 20910-82, составы которых приведены в табл. 11.
Жаростойкий бетон средней плотности до 1100 кг/м3 включ. следует предусматривать преимущественно для ненесущих ограждающих конструкций и в качестве теплоизоляционных материалов.
Жаростойкий бетон средней плотности более 1100 кг/м3 надлежит предусматривать для несущих конструкций.
Таблица 11
|
Класс бетона по предельно допустимой температуре применения |
Исходные материалы |
Наибольший класс бетона по прочности на сжатие |
Средняя плотность бетона естественной влажности, кг/м3 |
||||
|
вяжущее |
отвердитель |
тонкомолотая добавка |
заполнители |
||||
|
Обычный бетон |
|||||||
|
1 |
- |
Портландцемент, быстротвердеющий портландцемент, шлакопортландцемент |
Не применяется |
Не применяется |
Гранитовые, доломитовые, плотные известняковые, сиенитовые, плотные пески |
В50 |
2200 - 2500 |
|
Жаростойкий бетон |
|||||||
|
2 |
3 |
То же |
То же |
То же |
Андезитовые, базальтовые, диабазовые, диоритовые |
В40 |
2400 |
|
3 |
3 |
» |
» |
» |
Из доменных отвальных шлаков |
В40 |
2400 |
|
4 |
9 |
» |
» |
Из золы уноса |
Аглопоритовые. Из боя глиняного кирпича |
В15 В15 |
1800 1900 |
|
5 |
8 |
» |
» |
Из литого шлака, золы уноса, боя глиняного кирпича |
Из шлаков металлургических пористых (шлаковая пемза) |
В15 |
2000 |
|
6 |
7 |
» |
» |
Шамотная, из золы уноса, боя глиняного кирпича, из отвального и гранулированного доменного шлака |
Андезитовые, базальтовые, диабазовые, диоритовые |
В40 |
2400 |
|
7 |
7 |
» |
» |
То же |
Из доменных отвальных шлаков |
В40 |
2400 |
|
8 |
8 |
» |
» |
Из отвального и гранулированного доменного шлака, боя глиняного кирпича, золы уноса |
Из шлаков топливных, туфовые |
В15 |
1800 |
|
9 |
9 |
» |
» |
Из боя глиняного кирпича |
Из боя глиняного кирпича |
В15 |
1900 |
|
10 |
11 |
Портландцемент, быстротвердеющий портландцемент |
» |
То же, и золы уноса |
Шамотные кусковые и из боя изделий |
В35 |
2000 |
|
11 |
12 |
То же |
» |
Шамотная |
То же |
В35 |
2000 |
|
Жаростойкий бетон |
|||||||
|
12 |
8 |
Жидкое стекло |
Саморассыпающиеся шлаки |
Из шлаков ферромарганца, силикомарганца |
Из шлаков ферромарганца, силикомарганца |
В20 |
2100 |
|
13 |
6 |
То же |
Кремнефтористый натрий, нефелиновый шлам, саморассыпающиеся шлаки |
Шамотная |
Андезитовые, базальтовые, диабазовые |
В20 |
2500 |
|
14 |
10 |
» |
Кремнефтористый натрий |
Шамотная, из катализатора ИМ 2201 отработанного |
Шамотные кусковые и из боя изделий |
В20 |
2100 |
|
15 |
11 |
» |
Нефелиновый шлам, саморассыпающиеся шлаки |
Шамотная из катализатора ИМ-2201 отработанного |
Из смеси шамотных кусковых или из боя изделий и карборунда |
В20 |
2300 |
|
16 |
13 |
» |
Кремнефтористый натрий |
Магнезитовая |
Шамотные кусковые и из боя изделий |
В15 |
2100 |
|
17 |
12 |
» |
Нефелиновый шлам, саморассыпающиеся шлаки |
Шамотная, из катализатора ИМ-2201 отработанного |
То же |
В15 |
2100 |
|
18 |
13 |
» |
То же |
Магнезитовая |
» |
В15 |
2100 |
|
19 |
13 |
Глиноземистый цемент |
Не применяется |
Не применяется |
» |
В30 |
2100 |
|
20 |
12 |
То же |
То же |
То же |
Из передельного феррохрома |
В30 |
2800 |
|
21 |
14 |
» |
» |
» |
Муллитокорундовые кусковые и из боя изделий |
В35 |
2800 |
|
22 |
6 |
Портландцемент |
» |
Шамотная, из боя глиняного кирпича, золы уноса, из отвального и гранулированного доменного шлака, катализатора ИМ-2201 отработанного |
Вспученный перлит |
В5 |
1100 |
|
23 |
11 |
» |
» |
Шамотная, из катализатора ИМ-2201 отработанного |
Керамзитовые с насыпной плотностью 550 - 650 кг/м3 |
В15 |
1500 - 1700 |
|
24 |
10 |
» |
» |
То же |
Керамзитовые с насыпной плотностью 350 - 500 кг/м3 |
В5 - В10 |
1100 - 1400 |
|
25 |
10 |
» |
» |
Шамотная, из боя глиняного кирпича, из золы уноса, керамзитовая, аглопоритовая, из вулканического пепла |
Из смеси керамзита и вспученного вермикулита |
В3,5 |
1000 |
|
26 |
10 |
» |
» |
То же |
Вспученный вермикулит |
В2,5 |
1100 |
|
27 |
8 |
Жидкое стекло |
Кремнефтористый натрий |
Шамотная, из катализатора ИМ-2201 отработанного |
Из смеси керамзита и вспученного вермикулита |
В10 |
1000 |
|
28 |
8 |
То же |
То же |
То же |
Вспученный вермикулит |
В3,5 |
1100 |
|
29 |
8 |
» |
» |
» |
Керамзитовые с насыпной плотностью 550 - 650 кг/м3 |
В15 |
1500 - 1700 |
|
30 |
8 |
» |
» |
» |
Керамзитовые с насыпной плотностью 350 - 500 кг/м3 |
В5 - В10 |
1100 - 1400 |
|
31 |
8 |
» |
» |
» |
Из смеси зольного гравия и вспученного перлита |
В3,5 |
900 |
|
32 |
8 |
» |
» |
» |
Вспученный перлит |
В3,5 - В5 |
900 - 1100 |
|
33 |
11 |
Глиноземистый цемент |
Не применяется |
Не применяется |
Вспученный вермикулит |
В2,5 |
1100 |
|
34 |
11 |
То же |
То же |
То же |
Из смеси керамзита и вспученного вермикулита |
В3,5 |
1000 |
|
35 |
11 |
» |
» |
» |
Керамзитовые |
В5 |
1000 |
|
36 |
11 |
» |
» |
» |
Из смеси зольного гравия и вспученного перлита |
В5 |
1100 |
|
37 |
11 |
» |
» |
» |
Вспученный перлит |
В5 |
1000 |
Примечание. Для бетонов с отвердителем из кремнефтористого натрия классов 8 - 14 по предельно допустимой температуре применения не допускается воздействие пара и воды без предварительного нагрева до 800 °С, класса 6 - по предельно допустимой температуре применения подвергать воздействию пара не следует.
2.2 (2.2). При проектировании бетонных и железобетонных конструкций, работающих в условиях воздействия повышенных и высоких температур, в зависимости от их назначения и условий работы должны устанавливаться показатели качества бетона, основными из которых являются:
а) класс бетона по прочности на сжатие В;
б) класс обычного бетона по прочности на осевое растяжение Bt (назначается в случаях, когда эта характеристика имеет главенствующее значение и контролируется на производстве);
в) класс жаростойкого бетона по предельно допустимой температуре применения согласно ГОСТ 20910-82 (должен указываться в проекте во всех случаях);
г) марка жаростойкого бетона по термической стойкости в водных Т1 и воздушных Т2 теплосменах (назначается для конструкций, к которым предъявляются требования по термической стойкости);
д) марка по водонепроницаемости W (назначается для конструкций, к которым предъявляются требования по ограничению водопроницаемости);
е) марка по морозостойкости F (назначается для конструкций, которые в период строительства или при остановке теплового агрегата могут подвергаться эпизодическому воздействию температуры ниже 0 °С);
ж) марка по средней плотности D (назначается для конструкций, к которым кроме конструктивных предъявляются требования теплоизоляции, и контролируется при их изготовлении).
2.3 (2.3). Для бетонных и железобетонных конструкций, предназначенных для работы в условиях систематического воздействия повышенных и высоких температур, предусматривают бетоны:
а) классов по прочности на сжатие:
обычный бетон (состава № 1 по табл. 11) - по СНиП 2.03.01-84 до В50 включ.;
жаростойкий бетон (составов по табл. 11):
№ 2, 3, 6, 7 - В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30; В35; В40;
№ 10, 11, 21 - В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30; В35;
№ 19, 20 - В2,5; В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30;
№ 12, 13, 14, 15 - В2; В2,5; В5; В7,5; В10; В12,5; В15; В20;
№ 4, 5, 8, 9, 16, 17, 18, 23, 29 - В2; В2,5; В3,5; В5; В7,5; В10; В12,5; В15;
№ 24, 27, 30 - В2; В2,5; В3,5; В5; В7,5; В10;
№ 22, 24, 30, 32, 35, 36, 37 - В1; В1,5; В2; В2,5; В3,5; В5;
№ 25, 28, 31, 32, 34 - В1; В1,5; В2; В2,5; В3,5;
№ 26, 33 - В1; В1,5; В2; В2,5;
б) обычный бетон классов по прочности на осевое растяжение: (состава № 1 по табл. 11) - Вt0,8; Вt1,2; Вt1,6; Вt2; Вt2,4;
в) жаростойкий бетон марок по термической стойкости в водных теплосменах (составов № 2 - 21, 23 и 29 по табл. 11) - Т15; Т110; Т115, Т125;
в воздушных теплосменах (составов № 22, 24, 27, 30, 32, 35 - 37 по табл. 11) - Т210; T215; Т220, Т225.
Для бетона других составов марка по термической стойкости в водных и воздушных теплосменах не нормируется;
г) марок по водонепроницаемости:
обычный бетон (состава № 1) и жаростойкий бетон (составов № 2 - 21, 23 и 29 по табл. 11) - W2; W4; W6; W8.
Для бетона других составов марка по водонепроницаемости не нормируется;
д) марок по морозостойкости:
обычный бетон (состава № 1) и жаростойкий бетон (составов № 2 - 21, 23, 29 по табл. 11) - F15, F25, F35, F50, F75.
Для бетона других составов марка по морозостойкости не нормируется.
е) жаростойкий бетон марок по средней плотности составов (по табл. 11):
№ 4, 8 - D1800;
№ 23, 29 - D1700, D1600, D1500;
№ 24, 30 - D1400, D1300, D1200;
№ 22, 24, 26, 28, 30, 32, 33, 36 - D1100;
№ 25, 27, 32, 34, 35, 37 - D1000;
№ 31, 32 - D900.
Для бетона других составов марка по средней плотности не нормируется.
2.4. Возраст бетона, отвечающий его классу и марке, назначается при проектировании исходя из реальных сроков фактического загружения проектными нагрузками и нагрева конструкции, способов их возведения и условий твердения. При отсутствии этих данных класс бетона устанавливается в возрасте 28 сут.
Значение отпускной прочности бетона в элементах сборных конструкций, выполненных из обычного тяжелого бетона, устанавливается по ГОСТ 13015.0-83 и жаростойкого бетона - по ГОСТ 23521-79.
Для железобетонных конструкций из обычного тяжелого бетона, работающих в условиях воздействия повышенных температур, класс бетона по прочности на сжатие рекомендуется принимать:
для железобетонных элементов, рассчитываемых на воздействие многократно повторяющейся нагрузки, - не ниже В15;
для железобетонных сжатых стержневых элементов из тяжелого бетона - не ниже В15; то же, для сильно нагруженных сжатых стержневых элементов (например, для колонн, воспринимающих значительные крановые нагрузки, и для колонн нижних этажей многоэтажных зданий) - не ниже В25.
Для железобетонных конструкций не допускается применение обычного тяжелого бетона класса по прочности на сжатие ниже В7,5.
2.5 (2.4).Для железобетонных конструкций из жаростойкого бетона, работающих в условиях воздействия высоких температур, рекомендуется принимать класс бетона по прочности на сжатие:
для сборных несущих элементов............................................................ не ниже В7,5
для монолитных конструкций:
при постоянном нагреве (см. п. 1.11), °С:
до 500 включ.............................................................................................. не ниже В5
св. 500......................................................................................................... В7,5
при ударных и истирающих воздействиях, а также при циклическом нагреве, °С:
до 500 включ.............................................................................................. не ниже В7,5
св. 500......................................................................................................... В10
Для предварительно напряженных железобетонных конструкций из обычного и жаростойкого бетонов, работающих в условиях воздействия повышенных и высоких температур, класс бетона по прочности на сжатие должен приниматься в зависимости от вида и класса напрягаемой арматуры, ее диаметра и наличия анкерных устройств по СНиП 2.03.01-84.
Для бетонных и железобетонных конструкций, работающих в условиях воздействия высоких температур:
жаростойкие бетоны составов № 2 - 21, 23 и 29 (по табл. 11) должны иметь марку по термической стойкости в водных теплосменах, не менее, при нагреве:
постоянном.......................................................................................................... Т15
циклическом........................................................................................................ Т115
циклическом с резким охлаждением воздухом или водой............................. Т125
жаростойкие бетоны составов № 22, 24, 27, 30, 32, 35 - 37 (по табл. 11) должны иметь марку по термической стойкости в воздушных теплосменах, не менее, при нагреве:
постоянном.......................................................................................................... Т210
циклическом........................................................................................................ Т220
Для железобетонных конструкций из обычного (состава № 1) и жаростойкого бетона (составов № 2 - 21, 23 и 29 по табл. 11) марки по водонепроницаемости должны быть, не менее:
для фундаментов, боровов и других сооружений, находящихся под землей
ниже уровня грунтовых вод................................................................................... W4
для тепловых агрегатов и других сооружений, находящихся над землей
и подвергающихся атмосферным осадкам............................................................ W8
Для бетонных и железобетонных конструкций, работающих в условиях воздействия повышенных и высоких температур, которые в период строительства или при остановке теплового агрегата могут подвергаться эпизодическому воздействию температуры ниже 0 °С в условиях воздушно-влажностного состояния, обычный бетон (состава № 1) и жаростойкий бетон (составов № 2, 3, 6, 7, 13, 20 и 21 по табл. 11) должны иметь марку по морозостойкости согласно СНиП 2.03.01-84.
Требования к конструкциям и изделиям из жаростойкого бетона, предназначенным для эксплуатации в условиях воздействия агрессивной среды и высокой температуры, должны устанавливаться в соответствии с требованиями СНиП II-28-73 в зависимости от степени агрессивности среды и условий эксплуатации.
В конструкциях и изделиях, предназначенных для работы в условиях воздействия высокой температуры и агрессивной среды, должен применяться жаростойкий бетон, наиболее стойкий в агрессивной среде:
нейтральной и щелочной газовой - жаростойкий бетон на портландцементе и шлакопортландцементе;
кислой газовой и в расплавах щелочных металлов - жаростойкий бетон на жидком стекле;
углеродной и фосфорной газовой - жаростойкий бетон на высокоглиноземистом и глиноземистом цементах и фосфатных связках; на алюмосиликатных заполнителях с содержанием в них окиси железа Fe2O3 не более 1,5 % (см. п. 1.12);
водородной газовой - жаростойкий бетон на высокоглиноземистом цементе с заполнителями, содержащими окись алюминия Al2O3 не более 7 % (см. п. 1.12).
Для конструкций, работающих в условиях воздействия повышенных температур и попеременного увлажнения, рекомендуется применять обычный бетон класса по прочности на сжатие не менее В7,5 и марки по водонепроницаемости не менее W6 при нагреве до 120 °С включ. и не менее W8 при нагреве свыше 120 °С.
2.6 (2.5). При неравномерном нагреве бетона по высоте сечения элементов конструкций, в которых напряжения сжатия в бетоне от собственного веса и нагрузки составляют до 0,1 МПа включ., а также элементов конструкций, в которых усилия возникают только от воздействия температуры, предельно допустимая температура применения бетона устанавливается по ГОСТ 20910-82.
При неравномерном и равномерном нагреве по высоте сечения элементов конструкций, в которых напряжения сжатия в жаростойком бетоне от собственного веса и нагрузки составляют более 0,1 МПа, предельно допустимая температура применения бетона устанавливается расчетом.
При воздействии температур, превышающих указанные в ГОСТ 20910-82, необходимо предусматривать устройство защитных слоев (футеровок).
2.7. Для замоноличивания стыков элементов сборных железобетонных конструкций проектную марку бетона следует устанавливать в зависимости от условий работы соединяемых элементов, но принимать не ниже В7,5.
2.8. Для замоноличивания стыков элементов сборных конструкций, которые в процессе эксплуатации или монтажа на наружном воздухе могут подвергаться воздействию отрицательных температур, следует применять бетоны проектных марок по морозостойкости и водонепроницаемости не ниже принятых для стыкуемых элементов.
НОРМАТИВНЫЕ И РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ БЕТОНА
2.9. Нормативными сопротивлениями бетона являются: сопротивление осевому сжатию (призменная прочность) Rbn и сопротивление осевому растяжению Rbtn.
Расчетные сопротивления бетона для предельных состояний первой и второй групп определяются путем деления нормативных сопротивлений на соответствующие коэффициенты надежности по бетону при сжатии γbc или при растяжении γbt, принимаемые для основных видов бетона по табл. 12.
Таблица 12
|
Коэффициенты надежности по бетону при сжатии γbc и растяжении γbt для расчета конструкции по предельным состояниям |
||||
|
первой группы |
второй группы γbc и γbt |
|||
|
γbc |
γbt при назначении класса бетона по прочности |
|||
|
на сжатие |
на растяжение |
|||
|
Обычный тяжелый и жаростойкий, тяжелый и легкий бетоны |
1,3 |
1,5 |
1,3 |
1,0 |
Нормативные сопротивления бетона Rbn в зависимости от класса бетона по прочности на сжатие даны в табл. 13.
Нормативные сопротивления бетона растяжению в случаях, когда прочность бетона на растяжение не контролируется, принимаются в зависимости от класса бетона по прочности на сжатие согласно табл. 13.
Таблица 13
|
Номера составов бетона по табл. 11 |
Нормативные сопротивления Rbn, Rbtn, расчетные сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser, МПа, при классе бетона по прочности на сжатие |
|||||||||||||||
|
В2 |
В2,5 |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
||
|
Сжатие осевое (призменная прочность) Rbn и Rb,ser |
1 - 3, 6, 7, 10 - 15, 19 - 21 |
- |
- |
2,7 27,5 |
3,5 35,7 |
5,5 56,1 |
7,5 76,5 |
9,5 96,9 |
11,0 112 |
15,0 153 |
18,5 189 |
22,0 224 |
25,5 260 |
29,0 296 |
32,0 326 |
36,0 367 |
|
4, 5, 8, 9, 16 - 18, 23, 24, 29, 30 |
1,6 16,8 |
1,9 19,4 |
2,7 27,5 |
3,5 35,7 |
5,5 56,1 |
7,5 76,5 |
9,5 96,9 |
11,0 112 |
15,0 153 |
18,5 189 |
22,0 224 |
25,5 260 |
29,0 296 |
- |
- |
|
|
Растяжение осевое Rbtn и Rbt,ser |
1 - 3, 6, 7, 10 - 15, 19 - 21 |
- |
- |
0,39 4,00 |
0,55 5,61 |
0,70 7,14 |
0,85 8,67 |
1,00 10,2 |
1,15 11,7 |
1,40 14,3 |
1,60 16,3 |
1,80 18,4 |
1,95 19,9 |
2,10 21,4 |
2,20 22,4 |
2,30 23,5 |
|
4, 5, 8, 9, 16 - 18, 23, 24, 29, 30 |
0,12 1,22 |
0,29 2,96 |
0,39 4,00 |
0,55 5,61 |
0,70 7,14 |
0,85 8,67 |
1,00 10,2 |
1,15 11,7 |
1,40 14,3 |
1,60 16,3 |
1,80 18,4 |
1,95 19,9 |
2,10 21,4 |
- |
- |
|
Примечание. Над чертой указаны значения МПа, под чертой - в кгс/ см3.
При контроле класса обычного тяжелого бетона по прочности на осевое растяжение нормативные сопротивления бетона осевому растяжению Rbtn принимаются равными его гарантированной прочности (классу) на осевое растяжение.
2.10. При расчете элементов конструкций без учета воздействия температуры расчетные сопротивления бетона для предельных состояний первой группы Rb и Rbt снижаются (или повышаются) путем умножения на коэффициенты условий работы бетона γbi, учитывающие особенности свойств бетонов, длительность действия нагрузки и ее многократную повторяемость, условия и стадию работы конструкции, способ ее изготовления, размеры сечений и т.п.
Расчетные сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser вводят в расчет с коэффициентом условий работы бетона γbi = 1, за исключением случаев, указанных в пп. 4.7 и 4.9.
Значения расчетных сопротивлений основных видов бетонов в зависимости от класса бетона по прочности на сжатие приведены: для предельных состояний первой группы - в табл. 14 и для предельных состояний второй группы - в табл. 13, в зависимости от класса обычного бетона по прочности на растяжение - в табл. 14 СНиП 2.03.01-84.
Расчетные сопротивления бетона для предельных состояний первой и второй группы, приведенные в табл. 14 и 13 и в табл. 14 СНиП 2.03.01-84, в соответствующих случаях следует умножать на коэффициенты условий работы бетона согласно табл. 15.
Таблица 14
|
Номера составов бетона по табл. 11 |
Расчетные сопротивления бетона Rb и Rbt для предельных состояний первой группы при классе бетона по прочности на сжатие |
|||||||||||||||
|
В2 |
В2,5 |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
||
|
Сжатие осевое (призменная прочность) Rb |
1 - 3, 6, 7, 10 - 15, 19 - 21 |
- |
- |
2,1 21,4 |
2,80 28,6 |
4,5 45,9 |
6,0 61,2 |
7,5 76,5 |
8,5 86,7 |
11,5 117 |
14,5 148 |
17,0 173 |
19,5 199 |
22,0 224 |
25,0 255 |
27,5 280 |
|
4, 5, 8, 9, 16 - 18, 23, 24, 29, 30 |
1,25 12,8 |
1,5 15,3 |
2,1 21,4 |
2,8 28,6 |
4,5 45,9 |
6,0 61,2 |
7,5 76,5 |
8,5 86,7 |
11,5 117 |
14,5 148 |
17,0 173 |
19,5 199 |
22,0 224 |
- |
- |
|
|
Растяжение осевое Rbt |
1 - 3, 6, 7, 10 - 15, 19 - 21 |
- |
- |
0,26 2,65 |
0,37 3,77 |
0,48 4,89 |
0,57 5,81 |
0,66 6,73 |
0,75 7,65 |
0,90 9,18 |
1,05 10,7 |
1,20 12,2 |
1,30 13,3 |
1,40 14,3 |
1,45 14,8 |
1,55 15,8 |
|
4, 5, 8, 9, 16 - 18, 23, 24, 29, 30 |
0,08 0,82 |
0,20 2,04 |
0,26 2,65 |
0,37 3,77 |
0,48 4,89 |
0,57 5,81 |
0,66 6,73 |
0,74 7,55 |
0,80 8,16 |
0,90 9,18 |
1,0 10,2 |
1,10 11,2 |
1,20 12,2 |
- |
- |
|
Примечания: 1. Над чертой указаны значения в МПа, под чертой - в кгс/см2.
2. Величины Rb и Rbt в необходимых случаях должны умножаться на коэффициенты условий работы бетона согласно табл. 15 и 16.
Таблица 15
|
Факторы, обусловливающие введение коэффициента условий работы |
Коэффициент условий работы бетона |
|
|
условное обозначение |
числовое значение |
|
|
1. Многократно повторяющаяся нагрузка: |
||
|
при нормальной температуре |
γb1 |
См. табл. 22 |
|
при нагреве свыше 40 °С |
γb1t |
См. табл. 23 |
|
2. Длительность действия нагрузки: а) при учете постоянных, длительных и кратковременных нагрузок, кроме нагрузок непродолжительного действия (например, крановые нагрузки, нагрузки от транспортных средств; ветровые нагрузки; нагрузки, возникающие при изготовлении, транспортировании, возведении и т.п.), а также при учете особых нагрузок, вызванных деформациями просадочных, набухающих, вечномерзлых и других грунтов для обычного тяжелого и жаростойкого тяжелого и легкого бетонов естественного твердения и подвергнутых тепловой обработке: |
γb2 |
|
|
в условиях эксплуатации конструкций, благоприятных для нарастания прочности бетона (твердение под водой, во влажном грунте) или при влажности воздуха окружающей среды выше 75 % |
1,00 |
|
|
в остальных случаях |
0,90 |
|
|
б) при учете в рассматриваемом сочетании кратковременных (непродолжительного действия) или особых нагрузок*, указанных в поз. 2а для всех видов бетонов |
1,10 |
|
|
3. Бетонирование в вертикальном положении при высоте слоя бетонирования более 1,5 м |
γb3 |
0,85 |
|
4. Влияние двухосного сложного напряженного состояния «сжатие-растяжение» на прочность бетона |
γb4 |
См. п. 4.8 |
|
5. Бетонирование монолитных бетонных столбов и железобетонных колонн с наибольшим размером сечения менее 30 см |
γb5 |
0,35 |
|
6. Бетонные конструкции |
γb9 |
0,90 |
|
7. Нормативные и расчетные сопротивления растяжению бетона на глиноземистом цементе |
γb10 |
0,70 |
|
8. Стыки сборных элементов при толщине шва менее 1/5 наименьшего размера сечения элемента и менее 10 см. |
γb12 |
1,15 |
|
9. Воздействие повышенной и высокой температур: |
См. табл. 16 |
|
|
при сжатии |
γbt |
|
|
при растяжении |
γtt |
|
* Если при учете особых нагрузок вводится дополнительный коэффициент условий работы согласно указаниям соответствующих нормативных документов (например, при учете сейсмических нагрузок), коэффициент γb2 принимается равным единице.
Примечания: 1. Коэффициенты условий работы бетона по поз. 1, 2, 6 и 9 должны учитываться при определении расчетных сопротивлений бетона Rb и Rbt, по поз. 4 - при определении Rbr,ser, а по остальным позициям - только при определении Rb.
2. Для конструкций, находящихся под действием многократно повторяющейся нагрузки, коэффициенты γb2, γbt и γtt учитываются при расчете по прочности, a γb1 и γb1t - при расчете на выносливость и по образованию трещин.
3. Коэффициенты условий работы бетона вводятся независимо друг от друга с тем, однако, чтобы их произведение было не менее 0,45.
При расчете элементов конструкций на воздействие температуры расчетные сопротивления бетона Rb и Rb,ser необходимо дополнительно умножать на коэффициент условий работы бетона при сжатии γbt, а расчетные сопротивления бетона Rbt и Rbt,ser - на коэффициент условий работы бетона при растяжении γtt согласно табл. 16, учитывающие влияние температуры и длительность ее действия на изменение прочностных свойств бетона.
Таблица 16
|
Коэффициент |
Расчет на нагрев |
Коэффициенты условий работы бетона при сжатии γbt и растяжении γtt, коэффициент βb при температуре бетона, °С |
||||||||||
|
50 |
70 |
100 |
200 |
300 |
500 |
700 |
900 |
1000 |
1100 |
|||
|
1, 2 |
γbt |
Кратковременный |
1,00 |
0,85 |
0,90 |
0,80 |
0,65 |
- |
- |
- |
- |
- |
|
Длительный |
1,00 |
0,85 |
0,90 |
0,80 |
0,50 |
- |
- |
- |
- |
- |
||
|
Длительный с увлажнением |
1,00 |
0,65 |
0,40 |
0,60 |
- |
- |
- |
- |
- |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,70 |
0,70 |
0,60 |
0,40 |
- |
- |
- |
- |
- |
|
|
Длительный |
1,00 |
0,70 |
0,70 |
0,50 |
0,20 |
- |
- |
- |
- |
- |
||
|
Длительный с увлажнением |
1,00 |
0,50 |
0,30 |
0,40 |
- |
- |
- |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
0,90 |
0,80 |
0,60 |
0,40 |
- |
- |
- |
- |
- |
|
|
Длительный с увлажнением |
1,00 |
0,50 |
0,20 |
0,40 |
- |
- |
- |
- |
- |
- |
||
|
3 |
γbt |
Кратковременный |
1,00 |
1,00 |
1,00 |
0,90 |
0,80 |
- |
- |
- |
- |
- |
|
Длительный |
1,00 |
1,00 |
1,00 |
0,90 |
0,65 |
- |
- |
- |
- |
- |
||
|
Длительный с увлажнением |
1,00 |
0,75 |
0,50 |
0,70 |
- |
- |
- |
- |
- |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,80 |
0,75 |
0,65 |
0,50 |
- |
- |
- |
- |
- |
|
|
Длительный |
1,00 |
0,80 |
0,75 |
0,60 |
0,35 |
- |
- |
- |
- |
- |
||
|
Длительный с увлажнением |
1,00 |
0,60 |
0,40 |
0,50 |
- |
- |
- |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
1,00 |
0,90 |
0,80 |
0,60 |
- |
- |
- |
- |
- |
|
|
Длительный с увлажнением |
1,00 |
0,60 |
0,30 |
0,50 |
- |
- |
- |
- |
- |
- |
||
|
4 - 11, 23, 24 |
γbt |
Кратковременный |
1,00 |
1,00 |
1,00 |
1,10 |
1,00 |
0,90 |
0,60 |
0,30 |
0,20 |
0,10 |
|
Длительный |
1,00 |
1,00 |
1,00 |
1,00 |
0,70 |
0,40 |
0,20 |
0,06 |
0,01 |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,85 |
0,80 |
0,65 |
0,60 |
0,50 |
0,40 |
0,20 |
- |
- |
|
|
Длительный |
1,00 |
0,85 |
0,80 |
0,65 |
0,40 |
0,20 |
0,06 |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
1,00 |
1,00 |
0,90 |
0,75 |
0,50 |
0,32 |
0,22 |
0,18 |
0,15 |
|
|
12 - 15, 17, 29, 30 |
γbt |
Кратковременный |
1,00 |
1,00 |
1,10 |
1,20 |
1,20 |
1,00 |
0,75 |
0,40 |
0,20 |
- |
|
Длительный |
1,00 |
0,80 |
0,80 |
0,55 |
0,35 |
0,15 |
0,05 |
0,01 |
- |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,95 |
0,95 |
0,80 |
0,70 |
0,55 |
0,45 |
0,15 |
- |
- |
|
|
Длительный |
1,00 |
0,70 |
0,70 |
0,45 |
0,25 |
0,06 |
- |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
1,10 |
1,10 |
1,10 |
1,00 |
0,70 |
0,30 |
0,10 |
0,05 |
- |
|
|
16, 18 |
γbt |
Кратковременный |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
0,95 |
0,85 |
0,65 |
0,50 |
0,35 |
|
Длительный |
1,00 |
0,90 |
0,90 |
0,80 |
0,50 |
0,25 |
0,07 |
0,02 |
0,01 |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,95 |
0,95 |
0,80 |
0,70 |
0,55 |
0,45 |
0,35 |
- |
- |
|
|
Длительный |
1,00 |
0,80 |
0,80 |
0,70 |
0,40 |
0,12 |
0,02 |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
1,10 |
1,10 |
1,10 |
1,10 |
1,00 |
0,70 |
0,35 |
0,27 |
0,20 |
|
|
19, 20, 21 |
γbt |
Кратковременный |
1,00 |
0,90 |
0,80 |
0,70 |
0,55 |
0,45 |
0,35 |
0,30 |
0,25 |
0,20 |
|
Длительный |
1,00 |
0,90 |
0,80 |
0,70 |
0,50 |
0,25 |
0,10 |
0,05 |
0,02 |
- |
||
|
γtt |
Кратковременный |
1,00 |
0,65 |
0,55 |
0,40 |
0,45 |
0,35 |
0,25 |
0,10 |
- |
- |
|
|
Длительный |
1,00 |
0,65 |
0,55 |
0,40 |
0,30 |
0,12 |
0,02 |
- |
- |
- |
||
|
βb |
Кратковременный и длительный |
1,00 |
0,90 |
0,85 |
0,70 |
0,55 |
0,40 |
0,33 |
0,30 |
0,27 |
0,20 |
|
Примечания: 1. При расчете на длительный нагрев несущих конструкций, срок службы которых не превышает 5 лет, коэффициент γbt следует увеличить на 15 %, но он не должен превышать величины γbt при расчете на кратковременный нагрев.
2. Для конструкций, которые во время эксплуатации подвергаются циклическому нагреву, коэффициенты γbt и βb следует снизить на 15 %, коэффициент γtt - на 20 %.
3. Коэффициенты γbt, γtt и βb для промежуточных значений температур определяются интерполяцией.
4. Значения коэффициента γbt принимаются при расчете по формулам: (75), (100), (105) - (107), (109), (111), (114) - (118), (136) - (138), (140), (142) - (144), (146), (147), (161) - (163), (173), (174), (180), (181), (284) - по средней температуре бетона сжатой зоны; (82), (141) - по средней температуре бетона участков сжатой зоны; (120) - (127), (153) - (160), (186) - по средней температуре бетона сжатой зоны ребра и свесов полки; (148), (150), (187), (191), (211), (212) - по температуре бетона в центре тяжести сечения; (96), (255) - по температуре бетона в центре тяжести приведенного сечения; (221), (225), (228) - по температуре бетона в месте расположения сеток; (242) - по температуре бетона в месте расположения закладной детали.
5. Значения коэффициента γtt принимаются при растете по формулам: (198); (200) - (204), (206) - (208), (210) - по средней температуре бетона сжатой зоны; (211), (212) - по температуре бетона в центре тяжести сечения; (256), (257), (290), (302) - (304) - по температуре бетона на уровне центра тяжести растянутой арматуры; (356) - по температуре бетона у нижней полки металлической балки; (88), (89), (97) - по средней температуре бетона растянутой зоны при нагреве сжатой зоны по температуре бетона растянутой грани при нагреве растянутой зоны; (230) - по средней температуре бетона на проверяемом участке.
6. Коэффициенты γbt, γtt и βb для бетонов составов № 1 - 4 при их нагреве свыше 300 °С определяются экстраполяцией.
7. Среднюю температуру бетона сжатой зоны прямоугольных сечений при ξ < ξR допускается принимать по температуре бетона, расположенного на расстоянии 0,2ho от сжатой грани сечения; при x = ξRho и x = h - на расстоянии 0,5x от сжатой грани сечения.
2.11 (2.7). Начальный модуль упругости бетона при сжатии и растяжении Eb принимают по табл. 17.
Коэффициент βb, учитывающий снижение модуля упругости обычного и жаростойкого бетона при нагреве, следует принимать по табл. 16 в зависимости от температуры бетона.
Таблица 17
|
Номера составов и средняя плотность бетона, кг/м3 (по табл. 11) |
Начальные модули упругости бетона при сжатии и растяжении принимаются равными Eb × 103 при классе бетона по прочности на сжатие |
||||||||||||||||
|
В1 |
В1,5 |
В2 |
В2,5 |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
|
|
1 - 3, 6, 7, 13, 20, 21 естественного твердения 2200 - 2800 |
- |
- |
- |
8,5 86,7 |
9,5 96,9 |
13,0 133 |
16,0 163 |
18,0 184 |
21,0 214 |
23,0 235 |
27,0 275 |
30,0 306 |
32,5 331 |
34,5 352 |
36,0 367 |
37,5 382 |
39,0 398 |
|
1 - 3, 6, 7, 20, 21 подвергнутого тепловой обработке при атмосферном давлении 2200 - 2800 |
- |
- |
- |
8,0 82,0 |
8,5 86,7 |
11,5 117 |
14,5 148 |
16,0 163 |
19,0 194 |
20,5 209 |
24,0 245 |
27,0 275 |
29,0 296 |
31,0 316 |
32,5 332 |
34,0 347 |
35,0 357 |
|
31, 32 900 |
3,7 38,0 |
4,0 40,8 |
4,3 44,0 |
4,5 45,9 |
5,0 51,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
25, 27, 32, 34, 35, 37 1000 |
4,2 43,0 |
4,5 45,9 |
4,8 49,0 |
5,0 51,0 |
5,5 56,1 |
6,3 64,2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
22, 24, 26, 28, 30, 32, 33, 36 1100 |
4,3 44,0 |
4,6 47,0 |
4,9 49,7 |
5,5 56,1 |
6,1 62,3 |
6,9 70,7 |
7,9 81,1 |
8,7 88,7 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
24, 30 1200 - 1400 |
- |
- |
5,8 59,0 |
6,5 66,3 |
7,2 73,4 |
8,2 83,8 |
9,4 95,4 |
10,3 100,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
23, 29 1500 - 1700 |
- |
- |
7,3 75 |
8,0 82 |
9,0 91,8 |
10,0 102 |
11,5 117 |
12,5 127 |
13,2 135 |
14,0 143 |
- |
- |
- |
- |
- |
- |
- |
|
4, 8, 9 1800 - 1900 |
- |
- |
8,0 81,6 |
8,6 88 |
9,8 100 |
11,2 114 |
13,0 133 |
14,0 143 |
14,7 150 |
15,5 158 |
- |
- |
- |
- |
- |
- |
- |
|
5, 10 - 12, 14 - 19 2000 - 2300 |
- |
- |
10,0 102 |
10,5 101 |
11,5 118 |
13,0 133 |
14,5 148 |
16,0 163 |
17,0 173 |
18,0 184 |
19,5 199 |
21,0 214 |
22,0 224 |
23,0 235 |
- |
- |
- |
Примечание. Над чертой указаны значения в МПа, под чертой - в кгс/см2.
2.12. Начальный коэффициент поперечной деформации бетона (коэффициент Пуассона) v принимается равным 0,2 для всех видов бетона, а модуль сдвига G - равным 0,4 от соответствующего значения модуля упругости бетона и температур нагрева.
2.13 (2.8). Коэффициент упругости ![]() , характеризующий упруго-пластическое состояние сжатого бетона, при
определении приведенного сечения бетона, а также при расчете сводов и куполов
из жаростойкого бетона принимают по табл. 18 в зависимости от температуры и
длительности ее воздействия.
, характеризующий упруго-пластическое состояние сжатого бетона, при
определении приведенного сечения бетона, а также при расчете сводов и куполов
из жаростойкого бетона принимают по табл. 18 в зависимости от температуры и
длительности ее воздействия.
Таблица 18
|
Расчет на нагрев |
Коэффициент
упругости |
|||||||||
|
50 |
70 |
100 |
200 |
300 |
500 |
700 |
900 |
1000 |
||
|
1 - 3 |
Кратковременный Длительный |
0,85 0,30 |
0,65 0,25 |
0,70 0,25 |
0,70 0,25 |
0,65 0,20 |
- |
- |
- |
- |
|
6, 10, 11, 24 |
Кратковременный Длительный |
0,85 0,28 |
0,80 0,24 |
0,80 0,24 |
0,75 0,22 |
0,70 0,21 |
0,55 0,07 |
0,32 0,05 |
0,15 0,02 |
0,05 - |
|
4, 5, 7, 8, 9, 23 |
Кратковременный Длительный |
0,80 0,26 |
0,70 0,22 |
0,80 0,22 |
0,70 0,21 |
0,65 0,20 |
0,50 0,06 |
- |
- |
- |
|
12 - 18, 29, 30 |
Кратковременный Длительный |
0,70 0,24 |
0,70 0,20 |
0,70 0,20 |
0,65 0,20 |
0,50 0,06 |
0,35 0,02 |
0,30 - |
0,10 - |
- - |
|
19 - 21 |
Кратковременный Длительный |
0,85 0,35 |
0,80 0,30 |
0,75 0,27 |
0,60 0,25 |
0,55 0,23 |
0,45 0,03 |
0,35 0,02 |
0,20 0,01 |
0,15 - |
Примечания:
1. В таблице даны значения ![]() для
кратковременного нагрева при подъеме
температуры на 10 °С/ч и более. При подъеме
температуры менее чем на 10 °С/ч значения
для
кратковременного нагрева при подъеме
температуры на 10 °С/ч и более. При подъеме
температуры менее чем на 10 °С/ч значения ![]() = a - 0,075 (a - b)(10 - v), где a и b - значения коэффициента
= a - 0,075 (a - b)(10 - v), где a и b - значения коэффициента ![]() при кратковременном и длительном
нагреве; v - скорость подъема температуры, °С/ч.
при кратковременном и длительном
нагреве; v - скорость подъема температуры, °С/ч.
2. Коэффициент ![]() для промежуточных значений
температур определяется интерполяцией.
для промежуточных значений
температур определяется интерполяцией.
3. При длительном нагреве
50 - 200 °С и средней относительной влажности
воздуха до 40 % значение коэффициента ![]() = 0,2.
= 0,2.
4. При длительном нагреве и
увлажнении бетона составов № 1 - 3 значение коэффициента ![]() умножают на 0,5.
умножают на 0,5.
5. При двухосном напряженном состоянии значение коэффициента ![]() умножают на 1,2, но оно не должно превышать 0,85.
умножают на 1,2, но оно не должно превышать 0,85.
6. При наличии в элементе сжатой арматуры с μ′ ≥
0,7 % значение коэффициента ![]() умножают на (1 - 0,11μ′), но принимают не менее
0,5.
умножают на (1 - 0,11μ′), но принимают не менее
0,5.
Коэффициент упругости v, характеризующий упруго-пластическое состояние бетона сжатой зоны, при расчете деформаций и закладных деталей принимают по табл. 19 в зависимости от температуры и длительности ее воздействия.
Таблица 19
|
Расчет на нагрев |
Коэффициент при температуре бетона, °С |
||||||||
|
50 |
70 |
100 |
200 |
300 |
500 |
700 |
900 |
||
|
1 - 3 |
Кратковременный Длительный |
0,45 0,15 |
0,40 0,15 |
0,45 0,15 |
0,45 0,15 |
0,35 0,10 |
- |
- |
- |
|
4 - 11, 23, 24 |
Кратковременный Длительный |
0,45 0,15 |
0,43 0,15 |
0,43 0,15 |
0,40 0,10 |
0,37 0,09 |
0,28 0,05 |
0,20 0,03 |
0,10 0,01 |
|
12 - 18, 29, 30 |
Кратковременный Длительный |
0,45 0,13 |
0,43 0,13 |
0,38 0,13 |
0,35 0,10 |
0,28 0,03 |
0,20 0,01 |
0,17 - |
0,07 - |
|
19 - 21 |
Кратковременный Длительный |
0,45 0,15 |
0,43 0,15 |
0,40 0,13 |
0,33 0,13 |
0,30 0,10 |
0,25 0,03 |
0,20 0,02 |
0,15 0,01 |
Примечания: 1. В таблице даны значения v для кратковременного нагрева при подъеме температуры на 10 °С/ч и более. При подъеме температуры менее чем на 10 °С/ч значение v = a - 0,075(a - b)(10 - v), где a и b - значения коэффициента v при кратковременном и длительном нагреве; v - скорость подъема температуры, °С/ч.
2. Коэффициент v для промежуточных значений температур определяется интерполяцией.
3. При длительном нагреве 50 - 200 °С и средней относительной влажности воздуха до 40 % значение коэффициента v = 0,1.
4. При длительном нагреве и увлажнении бетона составов № 1 - 3 значение коэффициента v умножают на 0,5.
2.14 (2.9). Коэффициент линейной температурной деформации бетона αbt в зависимости от температуры и скорости подъема температуры следует принимать по табл. 20. Коэффициент αbt определен с учетом температурной усадки бетона при кратковременном и длительном его нагреве. При необходимости определения коэффициента температурного расширения бетона αtt при повторном воздействии температуры после кратковременного или длительного нагрева к коэффициенту линейной температурной деформации αbt следует прибавить абсолютное значение коэффициента температурной усадки бетона αcs соответственно для кратковременного или длительного нагрева.
Таблица 20
|
Расчет на нагрев |
Коэффициент линейной температурной деформации бетона принимают равным αbt × 10-6 град-1 при температуре бетона, °С |
||||||||
|
50 |
100 |
200 |
300 |
500 |
700 |
900 |
1100 |
||
|
1 |
Кратковременный Длительный |
10,0 4,0 |
10,0 4,5 |
9,5 7,2 |
9,0 7,5 |
- |
- |
- |
- |
|
2, 6 |
Кратковременный Длительный |
9,0 3,0 |
9,0 3,5 |
8,0 5,7 |
7,0 5,5 |
6,0 - |
5,0 - |
- |
- |
|
3, 7 |
Кратковременный Длительный |
8,5 2,5 |
8,5 3,0 |
7,5 5,2 |
7,0 5,5 |
5,5 - |
4,5 - |
4,0 - |
3,0 - |
|
8 |
Кратковременный Длительный |
9,0 2,0 |
9,0 3,0 |
8,0 5,4 |
7,0 5,3 |
6,0 5,0 |
6,0 5,0 |
- |
- |
|
4, 5, 9 - 11, 23, 24, 25 |
Кратковременный Длительный |
8,5 1,5 |
8,5 2,5 |
7,5 4,9 |
7,0 5,3 |
5,5 4,5 |
4,5 3,5 |
4,0 3,1 |
3,0 2,0 |
|
12 - 18, 27, 29, 30 |
Кратковременный Длительный |
5,0 -4,0 |
5,0 0,0 |
5,5 3,0 |
6,0 4,3 |
7,0 6,0 |
6,5 5,8 |
6,0 5,4 |
5,0 4,5 |
|
19 - 21 |
Кратковременный Длительный |
8,0 3,0 |
8,0 4,5 |
7,0 5,3 |
6,5 5,2 |
5,5 4,7 |
4,5 3,6 |
4,0 3,1 |
3,5 2,6 |
|
22 |
Кратковременный Длительный |
4,0 -3,0 |
4,0 0,0 |
3,5 1,5 |
3,0 1,5 |
2,0 1,0 |
1,0 0,0 |
- |
- |
|
26 |
Кратковременный Длительный |
4,3 -0,7 |
4,3 0,3 |
3,8 1,3 |
3,3 2,0 |
3,2 2,2 |
2,4 1,4 |
1,6 0,6 |
0,8 -0,7 |
|
28 |
Кратковременный Длительный |
5,0 -4,0 |
5,0 0,0 |
5,5 3,1 |
5,0 3,3 |
7,0 6,0 |
6,8 6,1 |
6,6 5,9 |
- |
|
31, 32 |
Кратковременный Длительный |
1,2 -7,8 |
1,2 -3,8 |
1,3 -1,1 |
1,0 -0,7 |
-1,2 -0,2 |
0,7 0,0 |
0,8 0,1 |
- |
|
33 |
Кратковременный Длительный |
-3,0 -8,0 |
-3,0 -6,5 |
-3,5 -5,3 |
-4,5 -5,8 |
-3,0 -4,5 |
-2,8 -3,7 |
-3,5 -4,5 |
-4,7 -5,7 |
|
34, 35 |
Кратковременный Длительный |
5,5 0,5 |
5,5 2,5 |
4,5 1,5 |
3,3 2,0 |
3,2 2,6 |
2,4 1,5 |
1,6 0,6 |
0,8 -0,2 |
|
36, 37 |
Кратковременный Длительный |
2,0 -3,0 |
2,0 -1,5 |
1,5 -0,8 |
1,0 -0,7 |
0,6 -1,2 |
0,4 -0,5 |
-3,7 -4,6 |
-8,6 -9,5 |
Примечания: 1. Значение коэффициента αbt для кратковременного нагрева дано при подъеме температуры на 10 °С/ч и более. Для кратковременного нагрева при подъеме температуры менее чем на 10 °С/ч от значения αbt следует отнять 0,075(a - b)(10 - v), где a и b - значения коэффициента αbt при кратковременном и длительном нагреве; v - скорость подъема температуры, °С/ч.
2. Коэффициент αbt для промежуточных значений температур определяется интерполяцией.
3. Для бетона состава № 1 с карбонатным щебнем (доломит, известняк) коэффициент αbt увеличивается на 1 · 10-6 · град-1.
Коэффициент температурной усадки бетона αcs принимают по табл. 21.
Таблица 21
|
Расчет на нагрев |
Коэффициент температурной усадки бетона принимают равным -αcs · 10-6 · град-1 при температуре бетона, °С |
||||||||
|
50 |
100 |
200 |
300 |
500 |
700 |
900 |
1100 |
||
|
1 - 4 |
Кратковременный Длительный |
0,0 6,0 |
0,0 5,5 |
0,7 3,0 |
1,0 2,5 |
- |
- |
- |
- |
|
5 - 11, 23, 24, 25 |
Кратковременный Длительный |
0,0 7,0 |
0,5 6,5 |
0,9 3,5 |
1,1 2,8 |
1,5 2,5 |
1,4 2,4 |
2,3 3,2 |
3,2 4,2 |
|
12 - 18, 27, 29, 30 |
Кратковременный Длительный |
2,0 11,0 |
3,0 8,0 |
2,5 5,0 |
2,0 3,7 |
1,3 2,3 |
1,0 1,7 |
0,8 1,4 |
0,7 1,2 |
|
19 - 21 |
Кратковременный Длительный |
0,5 5,5 |
2,0 5,5 |
1,5 3,2 |
1,3 2,6 |
1,4 2,2 |
1,6 2,5 |
2,1 3,0 |
2,3 3,2 |
|
22 |
Кратковременный Длительный |
4,0 11,0 |
5,0 9,0 |
4,7 6,7 |
4,2 5,7 |
3,7 4,7 |
3,6 4,6 |
- |
- |
|
26 |
Кратковременный Длительный |
6,6 11,6 |
7,6 11,6 |
7,1 9,1 |
7,1 8,4 |
5,5 6,5 |
4,3 5,3 |
5,0 6,0 |
6,0 7,0 |
|
28 |
Кратковременный Длительный |
4,0 13,0 |
5,0 10,0 |
4,6 7,0 |
4,1 5,8 |
1,3 2,3 |
1,2 1,9 |
1,0 1,7 |
- |
|
31, 32 |
Кратковременный Длительный |
3,0 12,0 |
4,0 9,0 |
3,6 6,0 |
3,1 4,8 |
0,3 1,3 |
0,2 0,9 |
0,0 0,7 |
- |
|
33 |
Кратковременный Длительный |
10,5 15,5 |
12,0 15,5 |
11,5 13,3 |
11,3 12,6 |
10,7 12,2 |
9,9 10,8 |
10,4 11,4 |
10,7 11,7 |
|
34, 35 |
Кратковременный Длительный |
6,3 11,3 |
7,8 10,8 |
7,3 10,3 |
7,1 8,4 |
5,5 6,1 |
4,3 5,2 |
5,0 6,0 |
5,2 6,2 |
|
36, 37 |
Кратковременный Длительный |
1,7 6,7 |
3,2 6,7 |
3,0 5,3 |
4,8 5,1 |
5,0 6,8 |
5,1 6,0 |
9,3 10,2 |
14,3 15,2 |
Примечания: 1. Значение коэффициента αcs для кратковременного нагрева дано при подъеме температуры на 10 °С/ч более. Для кратковременного нагрева при подъеме температуры менее чем на 10 °С/ч к значению αcs следует прибавить 0,075(b - a)(10 - v), где a и b - значения коэффициентов αcs для кратковременного и длительного нагрева; v - скорость подъема температуры, °С/ч.
2. Коэффициент αcs для промежуточных значений температур определяется интерполяцией.
Коэффициент температурной усадки бетона принят:
при кратковременном нагреве для подъема температуры на 10 °С/ч и более;
при длительном нагреве - в зависимости от воздействия температуры во время эксплуатации.
2.15 (2.10). Марку по средней плотности бетона естественной влажности принимают по табл. 11. Среднюю плотность бетона в сухом состоянии при его нагреве свыше 100 °С уменьшают на 150 кгс/м3. Среднюю плотность железобетона (при μ ≤ 3 %) принимают на 100 кгс/м3 больше средней плотности соответствующего состояния бетона.
2.16 (2.11). При расчете железобетонных конструкций на выносливость, а также по образованию трещин при многократно повторяющейся нагрузке в условиях воздействия температур свыше 50 °С расчетные сопротивления обычного бетона должны умножаться на коэффициенты условий его работы γb1 и γb1t, принимаемые по табл. 22 и 23.
Таблица 22
|
Состояние бетона по влажности |
Коэффициент условий работы бетона γb1 при многократно повторяющейся нагрузке и коэффициенте асимметрии цикла ρb, равном |
|||||||
|
0 - 0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
||
|
Обычный бетон состава № 1 по табл. 11 |
Естественной влажности |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
1,00 |
1,00 |
Обозначения, принятые в таблице: ![]() , где σb,min и σb,max
соответственно наименьшее и наибольшее напряжения в бетоне в пределах цикла изменения нагрузки,
определяемые согласно указаниям п. 3.71.
, где σb,min и σb,max
соответственно наименьшее и наибольшее напряжения в бетоне в пределах цикла изменения нагрузки,
определяемые согласно указаниям п. 3.71.
Таблица 23
|
Коэффициент условий работы обычного бетона γb1t при многократно повторяющейся нагрузке |
||
|
без увлажнения |
с переменным увлажнением и высыханием |
|
|
50 |
0,8 |
0,7 |
|
70 |
0,6 |
0,5 |
|
90 |
0,4 |
0,3 |
|
110 |
0,3 |
0,2 |
Примечание. Коэффициент γb1t для промежуточных значений температур определяется интерполяцией.
При применении жаростойкого бетона в железобетонных конструкциях, подвергающихся воздействию высоких температур и многократно повторяющейся нагрузки, расчетные сопротивления бетона должны быть специально обоснованы.
АРМАТУРА
2.17. Для армирования железобетонных конструкций, работающих при воздействии повышенной и высокой температур, должна приниматься арматура, отвечающая требованиям соответствующих государственных стандартов, следующих видов:
стержневая арматурная сталь:
а) горячекатаная - гладкая класса A-I; периодического профиля классов А-II, A-III, А-IV, A-V, A-VI;
б) термомеханически и термически упрочненная - периодического профиля классов Ат-III, Aт-IV, Aт-V, Aт-VI;
проволочная арматурная сталь:
в) арматурная холоднотянутая проволока:
обыкновенная - периодического профиля класса Вр-I;
высокопрочная - гладкая класса В-II; периодического профиля класса Bp-II;
г) арматурные канаты - спиральные семипроволочные класса К-7, девятнадцатипроволочные класса К-19.
Для закладных деталей и соединительных накладок применяется, как правило, прокатная углеродистая сталь марок по прил. 2 СНиП 2.03.01-84.
В железобетонных конструкциях допускается применять арматуру других видов, в том числе упрочненную вытяжкой класса А-IIIв, а также в качестве конструктивной арматуры - обыкновенную гладкую проволоку класса B-I.
Примечания: 1. Обозначения классов арматуры приняты в соответствии с СТ СЭВ 1406-78. Обозначения соответствующих классов горячекатаной арматуры, например класс A-V, используются на все виды соответствующего класса, т.е. A-V, Ат-V, Ат-VCK.
2. В обозначениях классов термически и термомеханически упрочненной стержневой арматуры добавляется индекс «С» (Ат-IVC), который указывает на возможность сваривания арматуры, а индекс «К» (Ат-IVК) - на повышенную стойкость против коррозионного растрескивания под напряжением.
3. В обозначениях горячекатаной стержневой арматуры индекс «в» употребляется для арматуры, упрочненной вытяжкой (А-IIIв), а индекс «с» - для арматуры северного исполнения (Ac-III).
4. Для краткости используются следующие термины:
«стержень» - для обозначения арматуры любого диаметра, вида и профиля независимо от того, поставляется она в прутках или мотках (бунтах);
«диаметр» (d) - если не оговорено особо, означает номинальный диаметр стержня арматурной стали.
2.18. Выбор арматурных сталей следует производить в зависимости от типа конструкции, наличия предварительного напряжения, а также от условий возведения и эксплуатации здания или сооружения в соответствии с указаниями пп. 2.19 - 2.25.
2.19. В качестве ненапрягаемой арматуры железобетонных конструкций (кроме указанных в п. 2.20) следует преимущественно применять:
а) стержневую арматуру класса A-III;
б) арматурную проволоку диаметром 3 - 5 мм класса Вр-I (в сварных сетках и каркасах);
допускается также применять:
в) стержневую арматуру классов A-II и А-I для поперечной арматуры, а также в качестве продольной рабочей арматуры, если другие виды ненапрягаемой арматуры не могут быть использованы;
г) термомеханически упрочненную стержневую арматуру класса Ат-IVC для продольной арматуры сварных каркасов и сеток;
д) стержневую арматуру классов A-IV, A-V и A-VI только для продольной рабочей арматуры, вязаных каркасов и сеток. Арматура классов A-V и A-VI в конструкциях без предварительного напряжения может применяться как сжатая арматура, а в составе предварительно напряженных - как сжатая и растянутая арматура.
Ненапрягаемую арматуру классов А-III, Вр-I, А-II и А-I рекомендуется применять в виде сварных каркасов и сварных сеток.
2.20. В конструкциях с ненапрягаемой арматурой, находящихся под давлением газов, жидкостей и сыпучих тел,
следует преимущественно применять:
стержневую арматуру классов А-II и А-I;
допускается также применять:
стержневую арматуру класса А-III;
арматурную проволоку класса Вр-I.
2.21. В качестве напрягаемой арматуры предварительно напряженных железобетонных элементов
при длине до 12 м включ.
следует преимущественно применять:
термомеханически и термически упрочненную арматуру классов Ат-VI и Ат-V;
допускается также применять:
арматурную проволоку классов В-II, Вр-II и арматурные канаты классов К-7 и К-19;
горячекатаную арматуру классов A-VI, A-V и А-IV;
стержневую арматуру класса А-IIIв;
при длине элементов свыше 12 м
следует преимущественно применять:
арматурную проволоку классов В-II, Вр-II и арматурные канаты классов К-7 и К-19;
горячекатаную арматуру классов A-V и A-VI;
допускается также применять:
горячекатаную и термомеханически упрочненную арматуру классов A-IV, Ат-IVC и А-IIIв.
2.22. В качестве напрягаемой арматуры предварительно напряженных элементов, находящихся:
под давлением газов, жидкостей и сыпучих тел
следует преимущественно применять:
арматурную проволоку классов В-II, Вр-II и арматурные канаты классов К-7 и К-19;
стержневую арматуру классов A-VI и A-V;
допускается также применять:
стержневую арматуру классов A-IV и А-IIIв;
термомеханически упрочненную арматуру классов Ат-IVC и Ат-IVК,
под воздействием агрессивной среды следует преимущественно применять горячекатаную арматуру класса А-IV и термомеханически упрочненную арматуру классов Ат-IVК, Ат-VCК и Ат-IVК.
2.23 (2.12). Для железобетонных конструкций из жаростойкого бетона при нагреве арматуры свыше 400 °С рекомендуется предусматривать стержневую арматуру и прокат:
из легированной стали марки 30ХМ по ГОСТ 4543-71;
из коррозионно-стойких, жаростойких и жаропрочных сталей марок 12X13, 20X13, 08Х17Т, 12Х18Н9Т, 20Х23Н18 и 45Х14Н14В2М по ГОСТ 5632-72 и ГОСТ 5949-75.
Предельно допустимую температуру применения арматуры и проката в железобетонных конструкциях следует принимать по табл. 24.
Таблица 24
|
Предельно допустимая температура, °С, применения арматуры и проката, установленных в железобетонных конструкциях |
||
|
по расчету |
по конструктивным соображениям |
|
|
1. Стержневая арматура классов: |
||
|
А-I и А-II |
400 |
450 |
|
A-III, Ат-III, А-IIIв, A-IV, Aт-IV, A-V, Ат-V, A-VI, Aт-VI |
450 |
500 |
|
ненапрягаемая |
450 |
- |
|
напрягаемая |
250 |
- |
|
2. Проволочная арматура классов: |
||
|
Вр-I |
400 |
450 |
|
В-II, Вр-II, К-7, К-19 |
150 |
- |
|
B-I |
- |
450 |
|
3. Прокат из стали марок: ВСт3кп2, ВСт3Гпс5, ВСт3сп5 и ВСт3пс6 |
400 |
450 |
|
4. Стержневая арматура и прокат из стали марок: |
||
|
30ХМ, 12X13 и 20X13 |
500 |
700 |
|
20Х23Н18 |
550 |
1000 |
|
12Х18Н9Т, 45Х14Н14В2М, 08Х17Т |
600 |
800 |
Примечания: 1. При циклическом нагреве предельно допустимая температура применения напрягаемой арматуры должна приниматься на 50 °С ниже указанной в таблице.
2. При многократно повторяющейся нагрузке предельно допустимая температура применения напрягаемой арматуры не должна превышать 100 °С и ненапрягаемой - 200 °С.
3. При нагреве проволоки классов В-I и Вр-I свыше 250 °С расчетные сопротивления следует принимать как для арматуры класса А-I по табл. 26 и 30.
4. Стали марок 30ХМ, 12X13 и 20X13 после сварки требуют высокотемпературного отпуска.
2.24. При выборе вида и марок стали для арматуры, устанавливаемой по расчету, а также прокатных сталей для закладных деталей должны учитываться температурные условия эксплуатации конструкций и характер их нагружения.
В климатических зонах с расчетной зимней температурой ниже минус 40 °С в случаях проведения строительно-монтажных работ в холодное время года несущая способность в стадии возведения конструкций с арматурой, допускаемой для применения только в отапливаемых зданиях, должна быть обеспечена исходя из расчетного сопротивления арматуры с понижающим коэффициентом 0,7 и расчетной нагрузки с коэффициентом надежности по нагрузке γf = 1
2.25. Для монтажных (подъемных) петель элементов сборных железобетонных и бетонных конструкций должна применяться горячекатаная арматурная сталь класса Ас-II марки 10ГТ и класса А-I марок ВСт3сп2, ВСт3пс2.
В случае, если возможен монтаж конструкций при расчетной зимней температуре ниже минус 40 °С, для монтажных петель не допускается применять сталь марки ВСт3пс2.
НОРМАТИВНЫЕ И РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ АРМАТУРЫ
2.26. За нормативные сопротивления арматуры Rsn принимаются наименьшие контролируемые значения:
для стержневой арматуры, высокопрочной проволоки и арматурных канатов - предела текучести, физического или условного (равного величине напряжений, соответствующих остаточному относительному удлинению 0,2 %);
для обыкновенной арматурной проволоки - напряжения, равного 0,75 временного сопротивления разрыву, определяемого как отношение разрывного усилия к номинальной площади сечения.
Указанные контролируемые характеристики арматуры принимаются в соответствии с государственными стандартами или техническими условиями на арматурные стали и гарантируются с вероятностью не менее 0,95.
Нормативные сопротивления Rsn для основных видов стержневой, проволочной и жаростойкой арматуры приведены соответственно в табл. 25, 26 и 27.
Таблица 25
|
Нормативные сопротивления растяжению Rsn и расчетные сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) |
|
|
А-I |
235 (2400) |
|
A-II |
295 (3000) |
|
A-III |
390 (4000) |
|
A-IV, Aт-IV |
590 (6000) |
|
A-V, Aт-V |
785 (8000) |
|
A-VI, Aт-VI |
980 (10000) |
|
А-IIIв |
540 (5500) |
Таблица 26
|
Диаметр, мм |
Нормативные сопротивления растяжению Rsn и расчетные сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) |
|
|
Вр-I |
3 |
410 (4200) |
|
4 |
405 (4150) |
|
|
5 |
395 (4050) |
|
|
B-II |
3 |
1490 (15200) |
|
4 |
1410 (14400) |
|
|
5 |
1335 (13600) |
|
|
6 |
1255 (12800) |
|
|
7 |
1175 (12000) |
|
|
8 |
1100 (11200) |
|
|
Вр-II |
3 |
1460 (14900) |
|
4 |
1370 (14000) |
|
|
5 |
1255 (12800) |
|
|
6 |
1175 (12000) |
|
|
7 |
1100 (11200) |
|
|
8 |
1020 (10400) |
|
|
К-7 |
6 |
1450 (14800) |
|
9 |
1370 (14000) |
|
|
12 |
1335 (13600) |
|
|
15 |
1295 (13200) |
|
|
К-19 |
14 |
1410 (14400) |
Таблица 27
|
Нормативные сопротивления растяжению Rsn и расчетные сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) |
|
|
30ХМ |
590 (6000) |
|
12X13 |
410 (4200) |
|
20X13 |
440 (4500) |
|
20Х23Н18, 12Х18Н9Т, 08Х17Т |
195 (2000) |
|
45Х14Н14В2М |
315 (3200) |
2.27. Расчетные сопротивления арматуры растяжению Rs для предельных состояний первой и второй групп определяются по формуле
Rs = Rsn / γs, (73)
где γs - коэффициент надежности по арматуре, принимаемый по табл. 28.
Таблица 28
|
Коэффициент надежности по арматуре γs при расчете конструкций по предельным состояниям |
||
|
первой группы |
второй группы |
|
|
Стержневая арматура классов: |
||
|
А-I, А-II |
1,05 |
1 |
|
А-III, Ат-III диаметром, мм: |
||
|
6 - 8 |
1,10 |
1 |
|
10 - 40 |
1,07 |
1 |
|
A-IV, Ат-IV, A-V, Ат-V |
1,15 |
1 |
|
A-VI, Ат-VI |
1,20 |
1 |
|
Проволочная арматура классов: |
||
|
Вр-I |
1,10 |
1 |
|
В-II и Вр-II |
1,20 |
1 |
|
К-7 и К-19 |
1,20 |
1 |
|
А-IIIв с контролем: |
||
|
удлинения и напряжения |
1,10 |
1 |
|
только удлинения |
1,20 |
1 |
|
Жаростойкая арматура марок: |
||
|
30ХМ, 12X13, 20X13, 12Х18Н9Т, 20Х23Н18, 45Х14Н14В2М, 08Х17Т |
1,30 |
1 |
Расчетные сопротивления арматуры растяжению для основных видов стержневой, проволочной и жаростойкой арматуры при расчете конструкций по предельным состояниям первой группы приведены соответственно в табл. 29, 30 и 31, а при расчете по предельным состояниям второй группы - в табл. 25, 26 и 27.
2.28. Расчетные сопротивления арматуры сжатию Rsc, принимаемые при расчете конструкций по предельным состояниям первой группы, при наличии сцепления арматуры с бетоном принимаются равными соответствующим расчетным сопротивлениям арматуры растяжению Rs, но не более 400 или 330 МПа при расчете в стадии обжатия. Для арматуры класса А-IIIв указанные значения принимаются равными соответственно 200 и 170 МПа.
Значения расчетных сопротивлений арматуры сжатию для основных видов стержневой, проволочной и жаростойкой арматуры приведены соответственно в табл. 29, 30 и 31.
Таблица 29
|
Расчетные сопротивления арматуры для предельных состояний первой группы, МПа (кгс/см2) |
|||
|
растяжению |
сжатию Rsc |
||
|
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
||
|
A-I |
225 (2300) |
175 (1800) |
225 (2300) |
|
А-II |
280 (2850) |
225 (2300) |
280 (2850) |
|
А-III диаметром, мм: |
|||
|
6 - 8 |
355 (3600) |
285 (2900)* |
355 (3600) |
|
10 - 40 |
365 (3750) |
290 (3000)* |
365 (3750) |
|
A-IV |
510 (5200) |
405 (4150) |
400 (4000) |
|
A-V, Ат-V |
680 (6950) |
545 (5550) |
400 (4000) |
|
A-VI, Ат-VI |
815 (8300) |
650 (6650) |
400 (4000) |
|
А-IIIв с контролем: |
|||
|
удлинения и напряжения |
490 (5000) |
390 (4000) |
200 (2000) |
|
только удлинения |
450 (4600) |
360 (3700) |
200 (2000) |
* В сварных каркасах для хомутов из арматуры класса А-III, диаметр которых меньше 1/3 диаметра продольных стержней, значение Rsw принимается равным 225 МПа (2600 кгс/см2).
Таблица 30
|
Диаметр, мм |
Расчетные сопротивления арматуры для предельных состояний первой группы, МПа (кгс/см2) |
|||
|
растяжению |
сжатию Rsc |
|||
|
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
|||
|
Вр-I |
3 |
375 (3850) |
270 (2750) 300 (3050)* |
375 (3850) |
|
4 |
365 (3750) |
265 (2700) 295 (3000)* |
365 (3750) |
|
|
5 |
360 (3700) |
260 (2650) 290 (2950)* |
360 (3700) |
|
|
B-II |
3 |
1240 (12650) |
990 (10100) |
400 (4000) |
|
4 |
1180 (12000) |
940 (9600) |
400 (4000) |
|
|
5 |
1110 (11300) |
890 (9000) |
400 (4000) |
|
|
6 |
1050 (10600) |
835 (8550) |
400 (4000) |
|
|
7 |
980 (10000) |
785 (8000) |
400 (4000) |
|
|
8 |
915 (9300) |
730 (7450) |
400 (4000) |
|
|
Вр-II |
3 |
1215 (12400) |
970 (9900) |
400 (4000) |
|
4 |
1145 (11700) |
915 (9350) |
400 (4000) |
|
|
5 |
1045 (10700) |
835 (8500) |
400 (4000) |
|
|
6 |
980 (10000) |
785 (8000) |
400 (4000) |
|
|
7 |
915 (9300) |
730 (7450) |
400 (4000) |
|
|
8 |
850 (8700) |
680 (6950) |
400 (4000) |
|
|
К-7 |
6 |
1210 (12300) |
965 (9850) |
400 (4000) |
|
9 |
1145 (11650) |
915 (9350) |
400 (4000) |
|
|
12 |
1110 (11300) |
890 (9050) |
400 (4000) |
|
|
15 |
1080 (11000) |
865 (8800) |
400 (4000) |
|
|
К-19 |
14 |
1175(12000) |
940(9600) |
400(4000) |
* Для случая применения в вязаных каркасах.
Таблица 31
|
Расчетные сопротивления арматуры для предельных состояний первой, группы МПа (кгс/см2) |
|||
|
растяжению |
сжатию Rsc |
||
|
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
||
|
30ХМ |
450 (4600) |
- |
400 (4000) |
|
12X13 |
325 (3300) |
260 (2650) |
325 (3300) |
|
20X13 |
345 (3500) |
275 (2800) |
345 (3500) |
|
20Х23Н18, 12Х18Н9Т, 08Х17Т |
150 (1550) |
120 (1250) |
150 (1550) |
|
45Х14Н14В2М |
245 (2500) |
195 (2000) |
245 (2500) |
При расчете конструкций из обычного и жаростойкого бетонов, для которых расчетное сопротивление бетона принято с учетом коэффициента условий работы γb2 = 0,90 (см. поз. 2 табл. 15) допускается при соблюдении соответствующих конструктивных требований п. 5.22 принимать значения Rsc равными для арматуры классов:
A-IV, Ат-IVК....................................................................................................... 450 МПа
Ат-IVC, A-V, Ат-V, A-VI, Ат-VI, В-II, Вр-II, К-7 и К-19.............................. 500 МПа
При отсутствии сцепления арматуры с бетоном значение Rsc принимается равным нулю.
2.29. Расчетные сопротивления арматуры для предельных состояний первой группы снижаются (или повышаются) путем умножения на соответствующие коэффициенты условий работы γsi, учитывающие: либо опасность усталостного разрушения, неравномерное распределение напряжений в сечении, низкую прочность окружающего бетона, условия анкеровки, либо работу арматуры при напряжениях выше условного предела текучести, либо изменение свойств стали в связи с условиями изготовления и влияния повышенной или высокой температуры и т.д.
Расчетные сопротивления арматуры для предельных состояний второй группы Rs,ser вводят в расчет с коэффициентом условий работы γs = 1.
Расчетное сопротивление поперечной арматуры (хомутов и отогнутых стержней) при расчете наклонных сечений на действие поперечных сил Rsw снижается путем умножения на коэффициенты условий работы γs1 и γs2, учитывающие особенности работы такой арматуры:
а) независимо от вида и класса арматуры - коэффициент γs1 = 0,8, учитывающий неравномерность распределения напряжений в арматуре по длине рассматриваемого сечения;
б) стержневой арматуры класса A-III и Ат-IIIС диаметром менее 1/3 диаметра продольных стержней и проволочной арматуры класса Вр-I в сварных каркасах - коэффициент γs2 = 0,9, учитывающий возможность хрупкого разрушения сварного соединения.
Расчетные сопротивления растяжению поперечной арматуры (хомутов и отогнутых стержней) Rsw с учетом указанных выше коэффициентов условий работы γs1 и γs2 арматуры приведены в табл. 29, 30 и 31.
Кроме того, расчетные сопротивления Rs, Rsw и Rsc в соответствующих случаях следует умножать на коэффициенты условий работы согласно табл. 32, 33 и 34.
Таблица 32
|
Факторы, обусловливающие введение коэффициента условий работы арматуры |
Характеристика арматуры |
Класс арматуры и марка стали |
Коэффициенты условий работы арматуры |
|
|
условное обозначение |
числовое значение |
|||
|
1. Работа арматуры на действие поперечных сил |
Поперечная |
Независимо от класса |
γs1 |
См. п. 2.29 |
|
2. Наличие сварных соединений арматуры при действии поперечных сил |
» |
A-III и Вр-I |
γs2 |
То же |
|
3. Многократно повторяющаяся нагрузка: |
||||
|
при нормальной температуре |
Продольная и поперечная |
Независимо от класса |
γs3 |
См. табл. 33 |
|
при нагреве |
То же |
То же |
γs3t |
См. п. 2.32 |
|
4. Наличие сварных соединений при многократном повторении нагрузки |
Продольная и поперечная при наличии сварных соединений |
A-I, А-II, A-III, A-IV и А-V |
γs4 |
См. табл. 34 |
|
5. Зона передачи напряжений для арматуры без анкеров и зона анкеровки ненапрягаемой арматуры |
Продольная напрягаемая |
Независимо от класса |
γs5 |
lx / lp |
|
Продольная ненапрягаемая |
То же |
lx / lan, где lx - расстояние от начала зоны передачи напряжения до рассматриваемого сечения; lp и lan - соответственно длина зоны передачи напряжений и зоны анкеровки арматуры (см. п. 5.14) |
||
|
6. Работа высокопрочной арматуры при напряжениях выше условного предела текучести |
Продольная растянутая |
A-IV, A-V, A-VI, В-II, Вр-II, К-7 и К-19 |
γs6 |
См. п. 3.14 |
|
7. Элементы из жаростойкого легкого бетона классов В7,5 и ниже |
Поперечная |
A-I, Bp-I |
γs7 |
0,8 |
|
8. Воздействие температуры свыше 50 °С |
Продольная и поперечная |
Независимо от класса и марки |
γst |
См. табл. 35 |
Примечания: 1. Коэффициенты γs3 и γs4 по поз. 3 и 4 учитываются только при расчете на выносливость; для арматуры, имеющей сварные соединения, эти коэффициенты учитываются одновременно; при нагреве арматуры свыше 100 °С дополнительно учитывается коэффициент γs3t.
2. Коэффициент γs5 по поз. 5 кроме расчетных сопротивлений Rs вводится также к предварительному натяжению арматуры σsp.
Таблица 33
|
Коэффициент условий работы арматуры γs3 при многократном повторении нагрузки и коэффициенте асимметрии цикла ρs, равном |
|||||||||
|
-1 |
-0,2 |
0 |
0,2 |
0,4 |
0,7 |
0,8 |
0,9 |
1 |
|
|
A-I |
0,41 |
0,63 |
0,70 |
0,77 |
0,90 |
1,00 |
1,00 |
1,00 |
1,00 |
|
А-II |
0,42 |
0,51 |
0,55 |
0,60 |
0,69 |
0,93 |
1,00 |
1,00 |
1,00 |
|
А-III диаметром, мм: |
|||||||||
|
6 - 8 |
0,33 |
0,38 |
0,42 |
0,47 |
0,57 |
0,85 |
0,95 |
1,00 |
1,00 |
|
10 - 40 |
0,31 |
0,36 |
0,40 |
0,45 |
0,55 |
0,81 |
0,91 |
0,95 |
1,00 |
|
А-IV |
- |
- |
- |
- |
0,38 |
0,72 |
0,91 |
0,96 |
1,00 |
|
A-V |
- |
- |
- |
- |
0,27 |
0,55 |
0,69 |
0,87 |
1,00 |
|
A-VI |
- |
- |
- |
- |
0,19 |
0,53 |
0,67 |
0,87 |
1,00 |
|
Вр-II |
- |
- |
- |
- |
- |
0,67 |
0,82 |
0,91 |
1,00 |
|
B-II |
- |
- |
- |
- |
- |
0,77 |
0,97 |
1,00 |
1,00 |
|
К-7 диаметром, мм: |
|||||||||
|
6 и 9 |
- |
- |
- |
- |
- |
0,77 |
0,92 |
1,00 |
1,00 |
|
12 и 15 |
- |
- |
- |
- |
- |
0,68 |
0,84 |
1,00 |
1,00 |
|
К-19 диаметром 14 мм |
- |
- |
- |
- |
- |
0,63 |
0,77 |
0,96 |
1,00 |
|
Вр-I |
- |
- |
0,56 |
0,71 |
0,85 |
0,94 |
1,00 |
1,00 |
1,00 |
|
А-IIIв с контролем: |
|||||||||
|
удлинений и напряжений |
- |
- |
- |
- |
0,41 |
0,66 |
0,84 |
1,00 |
1,00 |
|
только удлинений |
- |
- |
- |
- |
0,46 |
0,73 |
0,93 |
1,00 |
1,00 |
Обозначения, принятые в таблице:
![]() ,
σs,min и σs,max - соответственно наименьшее и наибольшее напряжения в растянутой арматуре в пределах цикла изменения нагрузки, определяемые
согласно указаниям п. 3.71.
,
σs,min и σs,max - соответственно наименьшее и наибольшее напряжения в растянутой арматуре в пределах цикла изменения нагрузки, определяемые
согласно указаниям п. 3.71.
Примечание. При расчете изгибаемых элементов из тяжелого бетона с ненапрягаемой арматурой значение ρs для продольной арматуры принимается:
при ![]() ρs = 0,30;
ρs = 0,30;
» ![]()
![]() ;
;
» ![]()
![]() ,
,
где Mmin и Mmax - соответственно наименьший и наибольший изгибающие моменты в расчетном сечении элемента в пределах цикла изменения нагрузки.
Таблица 34
|
Группа сварных соединений |
Коэффициент условий работы арматуры γs4 при многократном повторении нагрузки и коэффициенте асимметрии цикла ρs, равном |
|||||||
|
0,0 |
0,2 |
0,4 |
0,7 |
0,8 |
0,9 |
1,0 |
||
|
А-I, А-II |
1 |
0,90 |
0,95 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
2 |
0,65 |
0,70 |
0,75 |
0,90 |
1,00 |
1,00 |
1,00 |
|
|
3 |
0,25 |
0,30 |
0,35 |
0,50 |
0,65 |
0,85 |
1,00 |
|
|
A-III |
1 |
0,90 |
0,95 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
2 |
0,60 |
0,65 |
0,65 |
0,70 |
0,75 |
0,85 |
1,00 |
|
|
3 |
0,20 |
0,25 |
0,30 |
0,45 |
0,60 |
0,80 |
1,00 |
|
|
A-IV |
1 |
- |
- |
0,95 |
0,95 |
1,00 |
1,00 |
1,00 |
|
2 |
- |
- |
0,75 |
0,75 |
0,80 |
0,90 |
1,00 |
|
|
3 |
- |
- |
0,30 |
0,35 |
0,55 |
0,70 |
1,00 |
|
|
A-V горячекатаная |
1 |
- |
- |
0,95 |
0,95 |
1,00 |
1,00 |
1,00 |
|
2 |
- |
- |
0,75 |
0,75 |
0,80 |
0,90 |
1,00 |
|
|
3 |
- |
- |
0,35 |
0,40 |
0,50 |
0,70 |
1,00 |
|
Примечания: 1. Группы сварных соединений, приведенные в настоящей таблице, включают следующие типы соединений, допускаемые для конструкций при расчете на выносливость:
1-я - стыковое - по поз. 6 обязательного прил. 3;
2-я - крестообразное - по поз. 1, стыковые - по поз. 5, 8 и 9, а также по поз. 10 - 12 и 25 - все соединения при отношении диаметров стержней, равном 1,0 (см. обязательное прил. 3; тавровые - по поз. 5 и 7 обязательного прил. 4).
3-я - крестообразные - по поз. 2 и 4, стыковые - по поз. 13 - 26 обязательного прил. 3; тавровые - по поз. 1 - 4, 6, 8 и 9 обязательного прил. 4.
2. В таблице даны значения γs4 для арматуры диаметром до 20 мм.
3. Значения коэффициента γs4 должны быть снижены: на 5 % - при диаметре стержней 22 - 32 мм и на 10 % - при диаметре свыше 32 мм.
4. В конструкциях, рассчитываемых на выносливость, соединения по поз. 3 и 27 обязательного прил. 3, а также по поз. 10 - 14 обязательного прил. 4 применять не допускается.
При расчете элементов конструкций, предназначенных для работы в условиях воздействия повышенных и высоких температур, расчетные сопротивления арматуры необходимо, кроме того, дополнительно умножать на коэффициент условий работы γst, учитывающий изменение механических свойств арматуры в зависимости от нагрева, который принимается по табл. 35.
Таблица 35
|
Коэффициент |
Расчет на нагрев |
Коэффициенты условий работы арматуры γst, линейного температурного расширения арматуры αst и βs при температуре ее нагрева, °С |
||||||||
|
50 - 100 |
200 |
300 |
400 |
450 |
500 |
550 |
600 |
|||
|
A-I, А-II, ВСт3кп2, ВСт3Гпс5, ВСт3сп5, ВСт3пс6 |
γst |
Кратковременный |
1,00 |
0,95 |
0,90 |
0,85 |
0,75 |
0,60 |
0,45 |
0,30 |
|
Длительный |
1,00 |
0,85 |
0,65 |
0,35 |
0,15 |
- |
- |
- |
||
|
Вр-I |
Кратковременный |
1,00 |
0,90 |
0,85 |
0,60 |
0,45 |
0,25 |
0,12 |
0,05 |
|
|
Длительный |
1,00 |
0,80 |
0,60 |
0,30 |
0,10 |
- |
- |
- |
||
|
В-II, Вр-II, К-7, К-19 |
Кратковременный |
1,00 |
0,85 |
0,70 |
0,50 |
0,35 |
0,25 |
0,15 |
0,10 |
|
|
Длительный |
1,00 |
0,75 |
0,55 |
0,25 |
0,05 |
- |
- |
- |
||
|
А-I, А-II, Вр-I, В-II, Bp-II, К-7, К-19, ВСт3сп, ВСт3Гпс5, ВСт3сп5, ВСт3пс6 |
αst |
Кратковременный и длительный |
11,5 |
12,5 |
13,0 |
13,5 |
13,6 |
13,7 |
13,8 |
13,9 |
|
A-III, А-IIIв, А-IV, A-V |
γst |
Кратковременный |
1,00 |
1,00 |
0,95 |
0,85 |
0,75 |
0,60 |
0,40 |
0,30 |
|
Длительный |
1,00 |
0,90 |
0,75 |
0,40 |
0,20 |
- |
- |
- |
||
|
Aт-III, Ат-IV, AT-V |
Кратковременный |
1,00 |
1,00 |
0,90 |
0,80 |
0,65 |
0,45 |
0,30 |
0,20 |
|
|
Длительный |
1,00 |
0,85 |
0,70 |
0,35 |
0,15 |
- |
- |
- |
||
|
А-VI |
Кратковременный |
1,00 |
0,85 |
0,75 |
0,65 |
0,55 |
0,45 |
0,30 |
0,20 |
|
|
Длительный |
1,00 |
0,80 |
0,65 |
0,30 |
0,10 |
- |
- |
- |
||
|
Ат-VI |
Кратковременный |
1,00 |
0,95 |
0,85 |
0,75 |
0,50 |
0,25 |
0,22 |
0,10 |
|
|
Длительный |
1,00 |
0,85 |
0,70 |
0,35 |
0,10 |
- |
- |
- |
||
|
A-III, А-IIIв, A-IV, А-V, A-VI, Ат-III, Aт-IV, Aт-V, Aт-VI |
αst |
Кратковременный и длительный |
12,0 |
13,0 |
13,5 |
14,0 |
14,2 |
14,4 |
14,6 |
14,8 |
|
30ХМ |
γst |
Кратковременный |
1,00 |
0,90 |
0,85 |
0,78 |
0,76 |
0,74 |
0,72 |
0,70 |
|
Длительный |
1,00 |
0,85 |
0,80 |
0,25 |
0,15 |
0,08 |
- |
- |
||
|
αst |
Кратковременный и длительный |
9,5 |
10,2 |
10,7 |
11,2 |
11,5 |
11,8 |
12,1 |
12,4 |
|
|
12Х13, 20Х13 |
γst |
Кратковременный |
1,00 |
0,95 |
0,86 |
0,80 |
0,73 |
0,65 |
0,53 |
0,40 |
|
Длительный |
1,00 |
0,93 |
0,83 |
0,70 |
0,45 |
0,13 |
- |
- |
||
|
αst |
Кратковременный и длительный |
12,0 |
12,6 |
13,3 |
14,0 |
14,3 |
14,7 |
15,0 |
15,3 |
|
|
20Х23Н18 |
γst |
Кратковременный |
1,00 |
0,97 |
0,95 |
0,92 |
0,88 |
0,85 |
0,81 |
0,75 |
|
Длительный |
1,00 |
0,97 |
0,93 |
0,77 |
0,50 |
0,30 |
0,18 |
0,08 |
||
|
αst |
Кратковременный и длительный |
10,3 |
11,3 |
12,4 |
13,6 |
14,1 |
14,7 |
15,2 |
15,7 |
|
|
12Х18Н9Т, 08X17Т |
γst |
Кратковременный |
1,00 |
0,72 |
0,65 |
0,62 |
0,58 |
0,60 |
0,57 |
0,56 |
|
Длительный |
1,00 |
0,72 |
0,65 |
0,60 |
0,58 |
0,55 |
0,50 |
0,40 |
||
|
αst |
Кратковременный и длительный |
10,5 |
11,1 |
11,4 |
11,6 |
11,8 |
12,0 |
12,2 |
12,4 |
|
|
45Х14Н14В2М |
γst |
Кратковременный |
1,00 |
0,86 |
0,78 |
0,72 |
0,68 |
0,64 |
0,60 |
0,56 |
|
Длительный |
1,00 |
0,86 |
0,78 |
0,70 |
0,63 |
0,55 |
0,43 |
0,30 |
||
|
αst |
Кратковременный и длительный |
10,5 |
11,1 |
11,4 |
11,6 |
11,8 |
12,0 |
12,2 |
12,4 |
|
|
А-I, А-II, A-III, A-IV, A-V, А-VI, Вр-I, Вр-II, В-II, К-7, К-19, ВСт3кп2, ВСт3Гпс2, ВСт3сп5, ВСт3пс6, 30ХМ, 12X13, 20X13, 20Х23Н18, 08X17T, 12Х18Н9Т, 45Х14Н14В2М |
βs |
Кратковременный и длительный |
1,00 |
0,90 |
0,88 |
0,83 |
0,80 |
0,78 |
0,75 |
0,73 |
|
Ат-III, Ат-IIIв, AT-IV, AT-V |
βs |
Кратковременный и длительный |
1,00 |
0,96 |
0,92 |
0,85 |
0,78 |
0,71 |
0,55 |
0,40 |
Примечания: 1. Коэффициент линейного температурного расширения арматуры равен числовому значению, умноженному на 10-6 · град-1.
2. При расчете на длительный нагрев несущих конструкций, срок службы которых не превышает 5 лет, коэффициент γst следует увеличить на 20 %, при этом его значение должно быть не более, чем при кратковременном нагреве.
3. Коэффициенты γst, αst и βs для промежуточных значений температур определяются интерполяцией.
2.30 (2.15). Коэффициент линейного температурного расширения арматуры αst следует принимать по табл. 35.
В железобетонных элементах, имеющих трещины в растянутой зоне сечения, коэффициент температурного расширения арматуры в бетоне αstm, определяют по формуле
αstm = αbt + (αst - αbt)φα; (74)
где αbt, αst - коэффициенты, принимаемые по табл. 20 и 35 в зависимости от температуры нагрева бетона на уровне арматуры и нагрева арматуры;
φα - коэффициент, принимаемый по табл. 36 в зависимости от процента армирования сечения продольной растянутой арматурой.
Таблица 36
|
Отношение момента M1 при расчете по предельному состоянию второй группы к моменту M при расчете по предельному состоянию первой группы M1 / M |
Коэффициент φα при проценте армирования сечения продольной арматурой |
||||
|
0,2 |
0,4 |
0,7 |
1,0 |
2,0 и более |
|
|
1,0 |
0,90 |
0,95 |
1,00 |
1,00 |
1,00 |
|
0,7 |
0,75 |
0,90 |
0,95 |
1,00 |
1,00 |
|
0,5 |
0,55 |
0,80 |
0,90 |
0,95 |
1,00 |
|
0,2 |
0,20 |
0,55 |
0,70 |
0,80 |
0,95 |
Примечания: 1. Момент M принимается равным предельному моменту по прочности правой части формул (105), (107), (108), (121) и (123).
2. Момент M1 принимается равным при расчете: появления трещин Mcrc [см. формулу (245)]; деформаций M (см. п. 4.19); раскрытия трещин M [см. формулу (272)], статически неопределимых конструкций по первой группе предельных состояний M (см. примеч. 1).
3. При расчете статически
определимых элементов коэффициент φα принимается при отношении ![]() , если
наибольший изгибающий момент от всех действующих нагрузок меньше момента
появления трещин, определенного по формуле (256) при αbt =
0, а трещины в растянутой зоне появляются от
воздействия температуры (см. п. 4.3).
, если
наибольший изгибающий момент от всех действующих нагрузок меньше момента
появления трещин, определенного по формуле (256) при αbt =
0, а трещины в растянутой зоне появляются от
воздействия температуры (см. п. 4.3).
4. Коэффициент
jα
для промежуточных значений отношений моментов ![]() определяется
интерполяцией.
определяется
интерполяцией.
2.31. Модуль упругости арматуры Es для основных видов стержневой и проволочной арматуры и для арматуры и проката из жаростойкой стали принимается по табл. 37. Коэффициент βs, учитывающий снижение модуля упругости арматуры при нагреве, должен приниматься по табл. 35 в зависимости от температуры арматуры и проката.
Таблица 37
|
Модуль упругости арматуры Es, МПа (кгс/см2) |
|
|
А-I, А-II, 30ХМ |
210000 (2100000) |
|
А-III |
200000 (2000000) |
|
A-IV, А-V, А-VI, Aт-III, Aт-IV, Ат-V, Aт-VI |
190000 (1900000) |
|
B-II, Bp-II, 20Х23Н18, 08Х17Т, 12Х18Н9Т, 45Х14Н14В2М |
200000 (2000000) |
|
К-7, К-19, А-IIIв |
180000 (1800000) |
|
Вр-I |
170000 (1700000) |
|
12X13, 20X13 |
220000 (2200000) |
2.32 (2.16). При расчете на выносливость железобетонных конструкций, работающих в условиях воздействия температур свыше 50 °С, следует дополнительно вводить коэффициент условий работы арматуры γs3t, принимаемый при температуре нагрева арматуры, °С:
до 100.............................................................................. 1,00
150............................................................................... 0,80
200............................................................................... 0,65
Для промежуточных значений температур коэффициент γs3t определяется интерполяцией.
2.33 (2.17). При расчете кривизны железобетонных элементов на участках с трещинами в растянутой зоне бетона, работающих в условиях воздействия высоких температур, необходимо учитывать упруго-пластические свойства арматуры. Коэффициент упругости арматуры vs, характеризующий упруго-пластические свойства растянутой арматуры, следует принимать по табл. 38 в зависимости от величины температуры арматуры и длительности нагрева.
Таблица 38
|
Коэффициент vs при расчете на нагрев |
||
|
кратковременный |
длительный |
|
|
50 - 200 |
1,0 |
1,0 |
|
300 |
0,9 |
0,6 |
|
400 |
0,7 |
0,3 |
Примечание. Коэффициент vs для промежуточных значений температур определяется интерполяцией.
3. РАСЧЕТ ЭЛЕМЕНТОВ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
РАСЧЕТ БЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.1. Расчет по прочности элементов бетонных конструкций, подвергающихся воздействию повышенных и высоких температур, должен производиться для сечений, нормальных к их продольной оси. В зависимости от условий работы элементов они рассчитываются как без учета, так и с учетом сопротивления бетона растянутой зоны.
Без учета сопротивления бетона растянутой зоны производится расчет внецентренно сжатых элементов, принимая, что достижение предельного состояния характеризуется разрушением сжатого бетона. Сопротивление бетона сжатию условно представляется напряжениями, равными Rbγbt, равномерно распределенными по части сжатой зоны сечения - условной сжатой зоне (черт. 6), сокращенно именуемой в дальнейшем тексте сжатой зоной бетона.
Черт. 6. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно сжатого бетонного элемента, рассчитываемого без учета сопротивления бетона растянутой зоны
С учетом сопротивления бетона растянутой зоны производится расчет изгибаемых элементов, а также внецентренно сжатых элементов, в которых не допускаются трещины из условий эксплуатации конструкций (элементы, подвергающиеся давлению воды, карнизы, парапеты и др.). При этом принимается, что достижение предельного состояния характеризуется разрушением бетона растянутой зоны (появлением трещин).
Предельные усилия определяются исходя из следующих предпосылок (черт. 7):
сечения после деформаций остаются плоскими;
наибольшее относительное удлинение
крайнего растянутого волокна бетона равно ![]() ;
;
напряжения в бетоне сжатой зоны определяются с учетом упругих (а в некоторых случаях и неупругих) деформаций бетона;
напряжения в бетоне растянутой зоны распределены равномерно и равны по величине Rbtγtt.
Черт. 7. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого (внецентренно сжатого) бетонного элемента, рассчитываемого с учетом сопротивления бетона растянутой зоны
В случаях, когда вероятно образование наклонных трещин (например, элементов двутаврового и таврового сечений при наличии поперечных сил), должен производиться расчет бетонных элементов из условий (141) и (142) п. 4.11 СНиП 2.03.01-84, заменяя расчетные сопротивления бетона для предельных состояний второй группы Rb,serγbt и Rbt,serγtt соответствующими значениями расчетных сопротивлений бетона для предельных состояний первой группы Rbγbt и Rbtγtt.
Кроме того, должен производиться расчет элементов на местное действие нагрузки (смятие) согласно указаниям п. 3.63.
Внецентренно сжатые элементы
3.2. При расчете внецентренно сжатых бетонных элементов должен приниматься во внимание случайный эксцентриситет продольной силы ea, определяемый согласно указаниям п. 1.30.
Эксцентриситет продольной силы eo относительно центра тяжести однородного или приведенного сечения определяется как сумма эксцентриситетов предельной силы: определяемого из статического расчета конструкции и случайного. Следует учитывать также деформации от неравномерного нагрева бетона по высоте сечения, определяемые согласно указаниям пп. 1.39 - 1.44 и 4.26, суммируя их с эксцентриситетом продольной силы. Если деформации от нагрева уменьшают эксцентриситет продольной силы, то учет их не производится.
3.3. При гибкости элементов ![]() необходимо учитывать влияние на их несущую
способность прогибов как в плоскости
эксцентриситета продольного усилия, так и в нормальной к ней плоскости, путем
умножения значений eo на коэффициент η
(см. п. 3.7); в случае
расчета из плоскости эксцентриситета продольного усилия значение eo принимается равным величине случайного
эксцентриситета.
необходимо учитывать влияние на их несущую
способность прогибов как в плоскости
эксцентриситета продольного усилия, так и в нормальной к ней плоскости, путем
умножения значений eo на коэффициент η
(см. п. 3.7); в случае
расчета из плоскости эксцентриситета продольного усилия значение eo принимается равным величине случайного
эксцентриситета.
Применение внецентренно сжатых бетонных элементов не допускается при эксцентриситетах приложения продольной силы с учетом прогибов eoη, превышающих:
а) в зависимости от сочетания нагрузок:
при основном сочетании........................... 0,90y
» особом »................................... 0,95y
б) в зависимости от вида и класса бетона:
для тяжелого обычного бетона, тяжелого и легкого
жаростойкого бетона классов выше В7,5........................................... (y - 1) см
для других видов и классов бетона..................................................... (y - 2) »
здесь y - расстояние от центра тяжести сечения до наиболее сжатого волокна бетона (см. черт. 6).
3.4. Расчет бетонных элементов прямоугольного сечения на действие сжимающей продольной силы N при их расчетной длине lo ≤ 20h и величине эксцентриситета eo, определенной в соответствии с указаниями п. 3.2 не более ea, допускается производить из условия (148) при As = A′s = 0.
3.5. Расчет внецентренно сжатых бетонных элементов, подвергающихся равномерному и неравномерному нагреву по высоте сечения с температурой бетона наиболее нагретой грани до 400 °С, производится из условия
N ≤ RbγbtAb, (75)
где γbt - коэффициент условий работы бетона, принимаемый по табл. 16 в зависимости от средней температуры бетона сжатой зоны сечения;
Аb - площадь сечения сжатой зоны бетона, определяемая из условия, что ее центр тяжести совпадает с точкой приложения равнодействующей внешних сил.
Для элементов прямоугольного сечения (см. черт. 6) Ab определяется по формуле
Для элементов таврового сечения, если 2e′ ≤ h′f (черт. 8, а), Аb определяется по формуле (76) при b = b′f;
e′ - расстояние от точки приложения силы N до наиболее напряженной грани сечения, определяемое по формуле
e′ = y - eoη, (77)
где y - расстояние от центра тяжести приведенного сечения до его наиболее напряженной грани, определяемое согласно указаниям п. 1.28.
Черт. 8. Расчетные схемы сечений, принятые при расчете внецентренно сжатых бетонных элементов таврового сечения
а - при 2e′ ≤ h′f; б - при h′f < 2e′; в - распределения температур; Ц. Т. - центр тяжести сечения
При e′ ≤ h′f < 2e (черт. 8, б) Аb определяется по формуле
Ab = b′fh′f + bΔx, (78)
где
![]() . (79)
. (79)
3.6. Расчет внецентренно сжатых бетонных элементов, подвергающихся неравномерному нагреву по высоте сечения с температурой бетона наиболее нагретой грани более 400 °С и силе N, расположенной со стороны этой грани при 2е′ ≤ h1 для прямоугольного сечения (черт. 9, а) и 2е′ ≤ h′f для таврового сечения (см. черт. 8, а), или силе N, расположенной со стороны менее нагретой грани при 2е′ ≤ h1 (черт. 9, б), выполняется из условия (75).
Черт. 9. Расчетные схемы сечений, принятые при расчете внецентренно сжатых бетонных элементов прямоугольного сечения при его неравномерном нагреве с температурой наиболее нагретой грани сечения tb > 400 °С
а - при продольной силе N, приложенной со стороны более нагретой грани сечения; б - при продольной силе N, приложенной со стороны менее нагретой грани сечения
При этом Ab для элементов прямоугольного и таврового сечений при расположении силы N со стороны ребра (менее нагретой грани) определяется по формуле
Ab = 2bе′; (80)
для элементов таврового сечения при расположении силы со стороны полки (наиболее нагретой грани) - по формуле
Ab = 2b′fе′. (81)
Расчет прямоугольного сечения при 2е′ > h1 (см. черт. 9) выполняется из условия
При силе N, расположенной со стороны более нагретой грани (см. черт. 9, а):
Ab1 = bh1; (83)
Ab2 = bΔx; (84)
где e′ - определяется по формуле (77);
γbt, βb1, βb2, ![]() ,
, ![]() - коэффициенты, принимаемые по табл. 16 и 18 в зависимости от средней температуры бетона участков
сжатой зоны высотой соответственно h1 и Δx.
- коэффициенты, принимаемые по табл. 16 и 18 в зависимости от средней температуры бетона участков
сжатой зоны высотой соответственно h1 и Δx.
При силе N, расположенной со стороны менее нагретой грани, и обозначениях, принятых на черт. 9, б, значения Ab1, Ab2 и Δx определяются по формулам (83) - (85).
Расчет таврового сечения при силе N, расположенной со стороны полки (наиболее нагретой грани) выполняется из условия (82) при h′f < 2е′ (см. черт. 8, а):
Ab1 = b′fh′f; (86)
Ab2 - определяется по формуле (84), в которой
Здесь βbf и ![]() - коэффициенты,
принимаемые по табл. 16 и 18 в зависимости от средней температуры полки;
- коэффициенты,
принимаемые по табл. 16 и 18 в зависимости от средней температуры полки;
βb2 и
![]() - то
же, что в формуле (85).
- то
же, что в формуле (85).
При силе N, расположенной со стороны ребра, полка тавра не принимается в расчет и сечение рассчитывается как прямоугольное.
Внецентренно сжатые бетонные элементы, в которых не допускается появление трещин (см. черт. 7), независимо от расчета из условий (75) или (82) должны быть проверены с учетом сопротивления бетона растянутой зоны (см. п. 3.1) из условия
где γtt - коэффициент условий работы бетона, принимаемый по табл. 16:
при нагреве со стороны сжатой зоны - в зависимости от средней температуры бетона растянутой зоны;
при нагреве со стороны растянутой зоны - в зависимости от температуры бетона растянутой грани.
Для элементов прямоугольного сечения, подвергающихся равномерному и неравномерному нагревам по высоте сечения с температурой бетона наиболее нагретой грани до 400 °С, условие (88) имеет вид
В формулах (76), (77), (88) и (89):
η - коэффициент, определяемый по формуле (93);
r - расстояние от центра тяжести сечения до ядровой точки, наиболее удаленной от растянутой зоны, определяемое по формуле
![]() ; (90)
; (90)
φ = 1,6 - σb / Rb,ser и принимается не менее 0,7 и не более 1;
σb - максимальное напряжение сжатия, вычисляемое как для упругого тела;
Wred - момент сопротивления для растянутой грани сечения, определяемый по формуле (255);
Wpl - момент сопротивления сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый в предположении отсутствия продольной силы по формуле
где Ib0 - момент инерции сжатой зоны сечения относительно нулевой линии.
Положение нулевой линии определяется из условия
![]() , (92)
, (92)
где Sbt и Sb0 - статические моменты площади соответственно растянутой и сжатой зон сечения относительно нулевой линии;
Abt - площадь растянутой зоны сечения.
При неравномерном нагреве по высоте сечения с температурой наиболее нагретой грани свыше 400 °С положение центра тяжести сечения, а также величины Abt, Sb0, Sbt и Ib0 определяются как для приведенного сечения. Допускается Wpl определять по формуле (259).
При проверке прочности необходимо учитывать напряжения растяжения в бетоне, вызванные нелинейным распределением температуры бетона по высоте сечения элемента и определяемые по формуле (32).
Наибольшая температура бетона сжатой зоны сечения элементов не должна превышать предельно допустимую температуру применения бетона, указанную в ГОСТ 20910-82.
3.7. Значение коэффициента η, учитывающего влияние прогиба на значение эксцентриситета продольного усилия eo, следует определять по формуле
где Ncr - условная критическая сила, определяемая по формуле
В формуле (94):
φl - коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии
но не более 1 + β;
здесь β - коэффициент, принимаемый в зависимости от состава бетона и его температуры в центре тяжести сечения по табл. 39;
М - момент относительно растянутой или наименее сжатой грани сечения от действия постоянных, длительных и кратковременных нагрузок;
Ml - то же, от действия постоянных и длительных нагрузок;
l0 - определяется по табл. 40;
δe - коэффициент, принимаемый равным eo / h, но не менее величины
где γbt - принимается по табл. 16 в зависимости от температуры бетона в центре тяжести приведенного сечения;
Rb - в МПа;
Ired - момент инерции приведенного сечения относительно его центра тяжести, определяемый согласно указаниям п. 1.28.
Таблица 39
|
Коэффициент β при температуре бетона, °С, в центре тяжести сечения |
|||||||
|
50 |
100 |
200 |
300 |
500 |
700 |
900 |
|
|
1 - 3 |
1,2 |
1,4 |
1,5 |
2,0 |
- |
- |
- |
|
4 - 11, 23, 24 |
1,6 |
1,6 |
1,8 |
1,9 |
6,7 |
16,0 |
- |
|
12 - 18, 29, 30 |
1,5 |
1,5 |
2,0 |
8,0 |
33,0 |
- |
- |
|
19 - 21 |
1,2 |
1,4 |
1,5 |
2,0 |
16,0 |
25,0 |
50,0 |
Примечания: 1. Коэффициент β для промежуточных значений температур определяется интерполяцией.
2. Если температура бетона в центре тяжести внецентренно сжатого сечения превышает наибольшую температуру, для которой даны числовые значения β, то допускается расчетное сечение принимать с неполной высотой, в центре тяжести которого температура бетона не превышает наибольшую величину, указанную в таблице.
Таблица 40
|
Расчетная длина l0 внецентренно сжатых бетонных элементов |
|
|
1. Для стен и столбов с опорами, вверху и внизу: |
|
|
а) при шарнирах на двух концах, независимо от величины смещения опор |
H |
|
б) при защемлении одного из концов и возможном смещении опор: |
|
|
для многопролетных зданий |
1,25H |
|
для однопролетных зданий |
1,50H |
|
2. Для свободно стоящих стен и столбов |
2,00H |
Обозначения, принятые в таблице:
Н - высота столба или стены в пределах этажа за вычетом толщины плиты перекрытия либо высота свободно стоящей конструкции.
3.8. Расчет элементов бетонных конструкций на местное сжатие (смятие) должен производиться согласно указаниям пп. 3.63 и 3.64.
Изгибаемые элементы
3.9 (3.3). Изгибаемые бетонные элементы, подвергающиеся воздействию температуры, допускается применять только в случае, если они лежат на грунте или специальной подготовке, и, в виде исключения, в других случаях при условии, что они рассчитываются на нагрузку от собственного веса и под ними исключается возможность нахождения людей и оборудования.
Расчет изгибаемых бетонных элементов (см. черт. 7) должен производиться из условия
где γtt - коэффициент условий работы бетона, принимаемый по указаниям п. 3.6;
Wpl - определяется по формуле (91). Для элементов прямоугольного сечения подвергающихся равномерному и неравномерному нагреву по высоте сечения с температурой бетона наиболее нагретой грани до 400 °С, значение
![]() . (98)
. (98)
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.10. Расчет по прочности элементов железобетонных конструкций должен производиться для сечений, нормальных к их продольной оси, при наличии поперечных сил - также для наклонных сечений наиболее опасного направления, а при наличии крутящих моментов - также наиболее опасных пространственных сечений. Кроме того, должен производиться расчет элементов на местное действие нагрузки (смятие, продавливание, отрыв).
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.11. Определение предельных усилий в сечении, нормальном к продольной оси элемента, должно производиться исходя из следующих предпосылок:
сопротивление бетона растяжению принимается равным нулю;
сопротивление бетона сжатию представляется напряжением, равным γbtRb, равномерно распределенным по сжатой зоне бетона. Коэффициент условий работы бетона γbt, определяется по табл. 16;
для элементов прямоугольного и кольцевого сечений, а также тавровых сечений с полкой в растянутой зоне - в зависимости от средней температуры бетона сжатой зоны сечения;
для двутавровых и тавровых сечений с полкой в сжатой зоне - в зависимости от средней температуры бетона отдельно сжатой зоны ребра и сжатых свесов полки.
Среднюю температуру бетона сжатой зоны прямоугольных сечений при ξ < ξR допускается принимать по температуре бетона, расположенного на расстоянии 0,2h0 от сжатой грани сечения. Если x = ξRh0 или сечение полностью сжато (x = h), коэффициент условий работы бетона γbt допускается принимать в зависимости от температуры бетона, расположенного на расстоянии 0,5x от сжатой грани сечения.
При расчете на нагрузку наибольшая температура бетона сжатой зоны сечения элемента не должна превышать предельно допустимой температуры применения бетона, указанной в ГОСТ 20910-82. Полка, расположенная в растянутой зоне, в расчете не учитывается.
Растягивающие напряжения в арматуре принимаются не более расчетного сопротивления растяжению γstRs, a сжимающие напряжения - не более расчетного сопротивления сжатию γstRsc. Коэффициент условий работы арматуры γst определяется по табл. 35 в зависимости от температуры соответствующей арматуры. При этом температура арматуры не должна превышать предельно допустимой температуры применения арматуры, устанавливаемой по расчету согласно табл. 24.
3.12. Расчет сечений, нормальных к продольной оси элемента, когда внешняя сила действует в плоскости оси симметрии сечения и арматура сосредоточена у перпендикулярных к указанной плоскости граней элемента, должен производиться в зависимости от соотношения между величиной относительной высоты сжатой зоны бетона ξ = x / h0, определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона ξR (п. 3.13), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению γstRs. Коэффициент условий работы арматуры γst принимается по табл. 35 в зависимости от температуры арматуры.
3.13. Значение ξR определяется по формуле
где ω - характеристика сжатой зоны бетона для тяжелого обычного бетона, тяжелого и легкого жаростойкого бетона определяется по формуле
ω = α - 0,008 γbtRb, (100)
здесь α - коэффициент, принимаемый равным для бетонов составов (см. табл. 11):
1 - 3, 6, 7, 10 - 15, 19 и 21............................................... 0,85
4, 5, 8, 9, 16 - 18, 23, 24, 29 и 30..................................... 0,80
γbt - коэффициент условий работы бетона определяется по табл. 16 для кратковременного нагрева в зависимости от средней температуры бетона сжатой зоны (см. п. 3.11);
Rb - в МПа;
σsR - напряжение в арматуре, МПа, принимаемое равным:
для арматуры классов:
А-I, A-II, А-III, А-IIIв и Вр-I..................................... γstRs - σsp
А-IV, A-V, A-VI........................................................... γstRs + 400βs - σsp - Δσsp
В-II, Вр-II, К-7 и К-19................................................. γstRs + 400βs - σsp
для жаростойкой арматуры марок:
30ХМ, 12X13, 20X13, 20Х23Н18, 08Х17Т, 12Х18Н9Т и 4Х14Н14В2М................ γstRs,
здесь γst - коэффициент условий работы арматуры, который при определении σsR принимается по табл. 35 для кратковременного нагрева в зависимости от температуры арматуры;
Rs - расчетное сопротивление арматуры растяжению с учетом соответствующих коэффициентов условий работы арматуры γsi, за исключением коэффициента γs6 (см. поз. 6 табл. 32);
βs - коэффициент, принимаемый по табл. 35 в зависимости от температуры арматуры;
σsp - определяется при коэффициенте γsp меньшем единицы, и
![]() . (101)
. (101)
Значения ξR в зависимости от ξ0 при различных значениях величины σsR / σsc,uβs могут быть определены из графиков, приведенных на черт. 10.
Черт. 10. Значения ξR в зависимости от ξ0 для расчетных значений величины ![]()
σsc,u - предельное напряжение в арматуре сжатой зоны в формуле (99) принимается равным 500 МПа при расчете элементов из тяжелого обычного бетона, тяжелого и легкого жаростойкого бетона, если учитывается коэффициент условий работы бетона γb2 < 1 (см. поз. 2 табл. 15), и 400 МПа, если γb2 ≥ 1.
Если в сечении имеется растянутая арматура из сталей разных классов или с разной температурой нагрева, в формулу (99) вводится большее из значений σsR.
Статический момент площади бетона граничной сжатой зоны прямоугольной формы относительно оси, перпендикулярной к плоскости действия изгибающего момента и проходящей через центр тяжести площади сечения арматуры растянутой зоны,
SR = αRbh20, (102)
где
σR = ξR (1 - 0,5 ξR). (103)
Значения αR в зависимости от ξR приведены на черт. 11.
Черт. 11. Значения αR и α0 в зависимости от ξR и ξ
Для элементов, подвергающихся нагреву, независимо or величины температуры ξR и αR не должны превышать значений соответственно 0,70 и 0,46.
3.14. При расчете по прочности железобетонных элементов с высокопрочной арматурой классов A-IV, Aт-IV, A-V, Ат-V, Ат-VI, B-II, Вр-II, К-19 и К-7 при соблюдении условий ξ < ξR расчетное сопротивление арматуры Rs должно быть умножено на коэффициент условий работы γs6 (см. поз. 6 табл. 32), определяемый по формуле
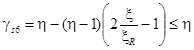 , (104)
, (104)
где η - принимается равным для арматуры классов:
A-IV.................................................................... 1,20
A-V, В-II, Вр-II, К-19 и К-7.............................. 1,15
A-VI.................................................................... 1,10
Для случая центрального растяжения, а также внецентренного растяжения продольной силой, расположенной между равнодействующими усилий в арматуре, значение γs6 принимается равным η.
При наличии сварных стыков в зоне элемента с изгибающими моментами, превышающими 0,9Mmax (где Mmax - максимальный расчетный момент), значение коэффициента γs6 для арматуры классов A-IV и A-V принимается не более 1,10, а для арматуры класса А-VI - не более 1,05.
Коэффициент условий работы γs6 не следует учитывать для арматуры элементов:
рассчитываемых на действие многократно повторяющейся нагрузки;
армированных высокопрочной проволокой, расположенной вплотную (без зазоров);
эксплуатируемых в агрессивной среде.
3.15. Для напрягаемой арматуры, расположенной в сжатой зоне при действии внешних сил или в стадии обжатия и имеющей сцепление с бетоном, расчетное сопротивление сжатию Rsc (пп. 3.17, 3.22, 3.33 и 3.46) должно быть заменено напряжением σsc, равным (σsc,u - σ′sp), МПа, но не более Rsc, где σ′sp - определяется при коэффициенте γsp, большем единицы. При расчете элементов в стадии обжатия для напрягаемой арматуры, расположенной в зоне предполагаемого разрушения бетона от сжатия, напряжение σsc,u принимается равным 330 МПа.
Изгибаемые элементы прямоугольного, таврового, двутаврового, кольцевого сечений
3.16. При расчете по прочности изгибаемых элементов рекомендуется соблюдать условие x ≤ ξRh0. В случае, когда площадь сечения растянутой арматуры по конструктивным соображениям или из расчета по предельным состояниям второй группы принята больше, чем это требуется для соблюдения условия x ≤ ξRh0, расчет следует производить по формулам для общего случая (см. пп. 3.17 и 3.28 СНиП 2.03.01-84) с учетом влияния температуры на расчетные сопротивления бетона и арматуры.
Для элементов из бетона класса В30 и ниже с ненапрягаемой арматурой классов A-I, А-II, А-III и Вр-I допускается также в случае, если полученная из расчета по формулам (106) или (122) величина x > ξRh0, расчет производить соответственно из условий (105) и (121), подставляя в них значение x = ξRh0.
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ
3.17. Расчет прямоугольных сечений, указанных в п. 3.12 (черт. 12), должен производиться:
а) при ![]()
M ≤ γbtRbbx(h0 - 0,5x) + γstRscA′s(h0 - a′); (105)
при этом высота сжатой зоны x определяется из формулы
γstRsAs - γstRscA′s = γbtRbbx; (106)
б) при ![]() прочность сечения с двойной арматурой можно проверять из условия
прочность сечения с двойной арматурой можно проверять из условия
M ≤ αRγbtRbbh20 + γstRsA′s(h0 - a′) (107)
или согласно указаниям п. 3.16;
в) при x < 2a′
M ≤ γstRsAs(h0 - a′). (108)
В формуле (107) значение αR - по указаниям п. 3.13.
Черт. 12. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого железобетонного элемента, при расчете его по прочности
3.18. При проверке прочности прямоугольных сечений с одиночной арматурой в формулах (105) - (107) принимают A′s = 0.
3.19. Подбор продольной арматуры производится следующим образом:
вычисляется значение
При отсутствии сжатой арматуры площадь сечения растянутой арматуры определяется по формуле
где v - определяется по табл. 41, где даны значения коэффициентов ξ, v и α0 для расчета по прочности железобетонных элементов;
если α0 > αR, то требуется увеличить сечение, повысить класс бетона или установить сжатую арматуру.
Таблица 41
|
v |
α0 |
ξ |
v |
α0 |
ξ |
v |
α0 |
|
|
0,01 |
0,995 |
0,010 |
0,25 |
0,875 |
0,219 |
0,49 |
0,755 |
0,370 |
|
0,02 |
0,990 |
0,020 |
0,26 |
0,870 |
0,226 |
0,50 |
0,750 |
0,375 |
|
0,03 |
0,985 |
0,030 |
0,27 |
0,865 |
0,234 |
0,51 |
0,745 |
0,380 |
|
0,04 |
0,980 |
0,039 |
0,28 |
0,860 |
0,241 |
0,52 |
0,740 |
0,385 |
|
0,05 |
0,975 |
0,049 |
0,29 |
0,855 |
0,248 |
0,53 |
0,735 |
0,390 |
|
0,06 |
0,970 |
0,058 |
0,30 |
0,850 |
0,255 |
0,54 |
0,730 |
0,394 |
|
0,07 |
0,965 |
0,068 |
0,31 |
0,845 |
0,262 |
0,55 |
0,725 |
0,399 |
|
0,08 |
0,960 |
0,077 |
0,32 |
0,840 |
0,269 |
0,56 |
0,720 |
0,403 |
|
0,09 |
0,955 |
0,086 |
0,33 |
0,835 |
0,276 |
0,57 |
0,715 |
0,408 |
|
0,10 |
0,950 |
0,095 |
0,34 |
0,830 |
0,282 |
0,58 |
0,710 |
0,412 |
|
0,11 |
0,945 |
0,104 |
0,35 |
0,825 |
0,289 |
0,59 |
0,705 |
0,416 |
|
0,12 |
0,940 |
0,113 |
0,36 |
0,820 |
0,295 |
0,60 |
0,700 |
0,420 |
|
0,13 |
0,935 |
0,122 |
0,37 |
0,815 |
0,302 |
0,61 |
0,695 |
0,424 |
|
0,14 |
0,930 |
0,130 |
0,38 |
0,810 |
0,308 |
0,62 |
0,690 |
0,428 |
|
0,15 |
0,925 |
0,139 |
0,39 |
0,805 |
0,314 |
0,63 |
0,685 |
0,432 |
|
0,16 |
0,920 |
0,147 |
0,40 |
0,800 |
0,320 |
0,64 |
0,680 |
0,435 |
|
0,17 |
0,915 |
0,156 |
0,41 |
0,795 |
0,326 |
0,65 |
0,675 |
0,439 |
|
0,18 |
0,910 |
0,164 |
0,42 |
0,790 |
0,332 |
0,66 |
0,672 |
0,442 |
|
0,19 |
0,905 |
0,172 |
0,43 |
0,785 |
0,338 |
0,67 |
0,665 |
0,446 |
|
0,20 |
0,900 |
0,180 |
0,44 |
0,780 |
0,343 |
0,68 |
0,660 |
0,449 |
|
0,21 |
0,895 |
0,188 |
0,45 |
0,775 |
0,349 |
0,69 |
0,655 |
0,452 |
|
0,22 |
0,890 |
0,196 |
0,46 |
0,770 |
0,354 |
0,70 |
0,650 |
0,455 |
|
0,23 |
0,885 |
0,203 |
0,47 |
0,765 |
0,359 |
|||
|
0,24 |
0,880 |
0,211 |
0,48 |
0,760 |
0,365 |
Примечание. Для изгибаемых элементов прямоугольного сечения
![]() ;
; ![]() .
.
При воздействии температуры, выше предельно допускаемой температуры применения бетона (см. табл. 11), сечение рассчитывается с неполной высотой.
Расчет производят следующим образом:
определяют расстояние x1 от наиболее нагретой грани до бетона, имеющего предельно допустимую температуру применения. Затем вычисляют значение α01
где γbt - принимается по табл. 16 в зависимости от средней температуры бетона сжатой зоны с укороченной высотой сечения.
Относительную высоту сжатой зоны определяют по формуле
![]() . (112)
. (112)
Для расчета принимают укороченную полезную высоту сечения
Площадь сечения растянутой арматуры определяется по формуле
Значения γbt и γst принимаются по указаниям пп. 3.11 - 3.13.
3.20. Когда требуется по расчету сжатая арматура, площадь сечения сжатой и растянутой арматуры рекомендуется определять по формулам:
![]() ; (115)
; (115)
![]() ; (116)
; (116)
Значения γbt и γst принимаются по указаниям п. 3.11, а ξR и αR - по указаниям п. 3.13.
Если принятая площадь сечения сжатой арматуры A′s значительно превышает ее величину по расчету, то площадь сечения растянутой арматуры может быть уменьшена.
Площадь сечения растянутой арматуры определяется с учетом фактической площади сечения сжатой арматуры по указаниям п. 3.21.
3.21. При наличии сжатой арматуры площадь сечения растянутой арматуры рекомендуется определять следующим образом.
Вычисляется значение
Если α0 ≤ αR, то в зависимости от значения α0
по табл. 41 находится относительная
высота сжатой зоны ![]() .
.
При ![]()
![]() . (118)
. (118)
При ![]()
![]() . (119)
. (119)
Площадь растянутой арматуры может быть снижена, если величина ξ, найденная без учета сжатой арматуры, в зависимости от значения α0 по формуле (109) оказывается менее 2a′ / h0. Тогда количество растянутой арматуры определяется без учета сжатой арматуры по формуле (110).
Если α0 > αR, то требуется увеличить сжатую арматуру. В этом случае количество сжатой и растянутой арматуры определяется по указаниям п. 3.20.
Значения γbt и γst принимаются по указаниям п. 3.11, а αR - п. 3.13.
РАСЧЕТ ТАВРОВЫХ И ДВУТАВРОВЫХ СЕЧЕНИЙ
3.22. Расчет сечений, имеющих полку в сжатой зоне, должен производиться в зависимости от положения границы сжатой зоны:
а) если граница сжатой зоны проходит в полке (черт. 13, а), т.е. соблюдается условие
γstRsAs ≤ γbtRbb′fh′f + γstRscA′s, (120)
расчет производится как для прямоугольного сечения шириной b′f в соответствии с указаниями пп. 3.17 и 3.18;
б) если граница сжатой зоны проходит в ребре (черт. 13, б), т.е. условие (120) не соблюдается:
при ![]() расчет производится из условия
расчет производится из условия
M ≤ γbtRbbx(h0 - 0,5x) + γbtRb(b′f - b)h′f ×(h0 - 0,5h′f) + γstRscA′s(h0 - a′), (121)
при этом высота сжатой зоны x определяется из формулы
γstRsAs - γstRscA′s = γbtRbbx + γbtRb(b′f - b)h′f. (122)
При x > ξRh0 можно принять x = ξRh0 и прочность сечения проверить из условия
M ≤ αRγbtRbbh20 + γbtRb(b′f - b)h′f ×(h0 - 0,5h′f) + γstRscA′s(h0 - a′) (123)
или согласно указаниям п. 3.16.
Когда в расчете учитывается арматура, расположенная в сжатой зоне, и при этом не соблюдается условие x ≥ 2a′, то следует в формулах (120) - (122) принять Rsc = 0, если это приводит к повышению прочности.
Значения γbt и γst принимаются по указаниям п. 3.11, а ξR и αR - п. 3.13.
Примечание. При переменной высоте свесов полки допускается принимать значение h′f равным средней высоте свесов.
Черт. 13. Положение границы сжатой зоны в сечении изгибаемого железобетонного элемента
а - в полке; б - в ребре
3.23. Площадь сечения сжатой арматуры определяется по формуле
где αR - определяется по указаниям п. 3.13, а γbt и γst - п. 3.11.
3.24. Площадь сечения растянутой арматуры определяется следующим образом:
а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие
M ≤ γbtRbb′fh′f (h0 - 0,5h′f) + γstRscA′s(h0 - a′), (125)
площадь сечения растянутой арматуры определяется как для прямоугольного сечения шириной b′f согласно указаниям пп. 3.19 и 3.21;
б) если граница сжатой зоны проходит в ребре, т.е. условие (125) не соблюдается, площадь сечения растянутой арматуры определяется по формуле
где ξ определяется по табл. 41 в зависимости от значения
При этом должно удовлетворяться условие α0 < αR.
Значения γbt и γst принимаются по указаниям п. 3.11, а αR - п. 3.13.
3.25. При одиночном армировании сечения продольной растянутой арматурой в формулах (120) - (123), (125) - (127) принимается Аs = 0.
Устанавливаемая в сжатой зоне конструктивная и монтажная арматура при определении прочности сечений в условиях воздействия повышенных и высоких температур не должна учитываться в расчете.
3.26. Значение b′f, вводимое в расчет по формулам (120) - (127), принимается из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) при наличии поперечных ребер или при h′f ≥ 0,1h - 1/2 расстояния в свету между ребрами;
б) при отсутствии поперечных ребер или при расстояниях между ними больших, чем расстояния между продольными ребрами, и h′f < 0,1h - 6h′f;
в) при консольных свесах полки при:
h′f ≥ 0,1h - 6h′f;
0,05h ≤ h′f < 0,1h - 3h′f;
h′f < 0,05h - свесы не учитываются, и сечение элемента рассчитывается как прямоугольное шириной b.
В ребристых конструкциях панелей, ограничивающих рабочее пространство теплового агрегата, когда невозможна установка хомутов и конструктивной арматуры в сжатой зоне бетона из-за температуры, превышающей предельно допустимую температуру применения конструктивной арматуры (см. табл. 24), рекомендуется толщину полки h′f назначать такую, чтобы отношение h′f / h таврового сечения было равно или больше, чем это указано на черт. 14.
Черт. 14. Значения отношения ![]() в зависимости от характеристики
таврового сечения
в зависимости от характеристики
таврового сечения ![]()
РАСЧЕТ КОЛЬЦЕВЫХ СЕЧЕНИЙ
3.27. Расчет изгибаемых элементов кольцевого сечения при соотношении внутреннего и наружного радиусов r1/r2 ≥ 0,5 с арматурой, равномерно распределенной по окружности (при числе продольных стержней не менее 6), должен производиться как для внецентренно сжатых элементов по указаниям п. 3.44, принимая в формулах (161) - (163) величину продольной силы N = 0 и подставляя в формулу (161) вместо Ne0 значение изгибающего момента M.
Внецентренно сжатые элементы прямоугольного, таврового, двутаврового и кольцевого сечений
3.28. При расчете внецентренно сжатых железобетонных элементов необходимо учитывать случайный начальный эксцентриситет ea согласно указаниям п. 3.3, а также влияние прогиба на их несущую способность в соответствии с требованиями пп. 3.7 и 3.29. Дополнительно должен учитываться эксцентриситет от температурного выгиба ft, вызванного неравномерным нагревом по высоте сечения элемента
e0 = e01 + еa + ft, (128)
где e01 = M / N.
Если температурный выгиб уменьшает расчетный эксцентриситет продольной силы e01, то он не учитывается.
3.29. При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкции по деформированной схеме.
Допускается производить расчет конструкции по недеформированной схеме, учитывая при гибкости l0/i > 14 влияние прогиба элемента на его прочность, путем умножения e0 на коэффициент η. При этом условная критическая сила в формуле (93) для вычисления η принимается равной
Для элементов прямоугольного сечения при равномерном и неравномерном нагреве с температурой наиболее нагретой грани до 400 °С и расположении продольной силы в плоскости симметрии
l0 - принимается по указаниям п. 3.30;
δe - коэффициент, принимаемый по указаниям п. 3.7;
φl - коэффициент, определяемый по формуле (95); при этом моменты M и Ml определяются относительно оси, параллельной линии, ограничивающей сжатую зону и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры соответственно от действия полной нагрузки и воздействия температуры и от действия постоянных и длительных нагрузок и длительного нагрева;
Ired - момент инерции приведенного бетонного сечения элемента относительно оси, проходящей через центр тяжести сечения и параллельной линии, ограничивающей сжатую зону, определяется согласно указаниям п. 1.28;
Is - момент инерции сечения всей арматуры относительно той же оси;
βs - принимается по табл. 35 в зависимости от температуры арматуры;
βb и ![]() - принимаются по табл. 16
и 18 для
кратковременного нагрева в зависимости от температуры бетона в центре тяжести
приведенного сечения;
- принимаются по табл. 16
и 18 для
кратковременного нагрева в зависимости от температуры бетона в центре тяжести
приведенного сечения;
φp - коэффициент, учитывающий влияние предварительного напряжения арматуры на жесткость элемента; при равномерном обжатии сечения напрягаемой арматурой φp определяется по формуле
![]() , (131)
, (131)
здесь σbp - определяется при коэффициенте γsp, меньшем единицы. Для элементов без предварительного напряжения арматуры φp = 1.
![]() - гибкость элемента, где i - радиус инерции сечения в плоскости изгиба.
- гибкость элемента, где i - радиус инерции сечения в плоскости изгиба.
При неравномерном нагреве по высоте сечения i определяется:
в направлении перепада температур - как для приведенного сечения (см. п. 1.28), по формуле
в направлении, перпендикулярном перепаду температур, по формуле
![]() . (133)
. (133)
Гибкость элемента прямоугольного сечения при равномерном и неравномерном нагреве по высоте сечения с температурой наиболее нагретой грани до 400 °С определяется по формуле
λ = 3,46l0 / h. (134)
Когда по условиям нагрева арматура устанавливается только у одной из граней сечения элемента, т.е. применяется одиночное армирование, в формуле (129) Is = 0 и α = 0.
При расчете из плоскости эксцентриситета продольной силы значение e0 принимается равным величине случайного эксцентриситета (см. п. 1.30).
При гибкости λ ≤ 14 допускается принимать η = 1.
При N > Ncr следует увеличить размеры сечения или уменьшить расчетную длину элемента.
3.30. Расчетные длины l0 внецентренно сжатых железобетонных элементов рекомендуется определять как для элементов рамной конструкции с учетом ее деформированного состояния при наиболее невыгодном для данного элемента расположении нагрузки, принимая во внимание неупругие деформации материалов и наличие трещин.
Для элементов наиболее часто встречающихся конструкций допускается принимать расчетные длины l0 равными:
а) для колонн многоэтажных зданий при числе пролетов не менее двух и при соединениях ригелей и колонн, рассчитываемых как жесткие:
при сборных конструкциях перекрытий................................... H
» монолитных » »........................................ 0,7H,
где H - высота этажа (расстояние между центрами узлов);
б) для колонн одноэтажных зданий с шарнирным опиранием несущих конструкций покрытий, жестких в своей плоскости (способных передавать горизонтальные усилия), а также для эстакад - по табл. 42;
в) для элементов ферм и арок - по табл. 43.
Таблица 42
|
Расчетная длина l0 колонн одноэтажных зданий при расчете их в плоскости |
||||||
|
поперечной рамы или перпендикулярной к оси эстакады |
перпендикулярной поперечной раме или параллельной оси эстакады |
|||||
|
при наличии |
при отсутствии |
|||||
|
связей в плоскости продольного ряда колонн или анкерных опор |
||||||
|
1. Здание с мостовыми кранами |
При учете нагрузки от кранов |
Подкрановая (нижняя) часть колонн при подкрановых балках |
разрезных |
1,5H1 |
0,8H1 |
1,2H1 |
|
неразрезных |
1,2H1 |
0,8H1 |
0,8H1 |
|||
|
Надкрановая (верхняя) часть колонн при подкрановых балках |
разрезных |
2,0H2 |
1,5H2 |
2,0H2 |
||
|
неразрезных |
2,0H2 |
1,5H2 |
1,5H2 |
|||
|
Без учета нагрузки от кранов |
Подкрановая (нижняя) часть колонн зданий |
однопролетных |
1,5H |
0,8H1 |
1,2H |
|
|
многопролетных |
1,2H |
0,8H1 |
1,2H |
|||
|
Надкрановая (верхняя) часть колонн при подкрановых балках |
разрезных |
2,5H2 |
1,5H2 |
2,0H2 |
||
|
неразрезных |
2,0H2 |
1,5H2 |
1,5H2 |
|||
|
2. Здания без мостовых кранов |
Колонны ступенчатые |
Нижняя часть колонн зданий |
однопролетных |
1,5H |
0,8H |
1,2H |
|
многопролетных |
1,2H |
0,8H |
1,2H |
|||
|
Верхняя часть колонн |
- |
2,5Н2 |
2,0Н2 |
2,5Н2 |
||
|
Колонны постоянного сечения |
Однопролетных зданий |
- |
1,5H |
0,8H |
1,2H |
|
|
Многопролетных зданий |
- |
1,2H |
0,8H |
1,2H |
||
|
3. Открытые крановые эстакады при подкрановых балках |
разрезных |
2,0H1 |
0,8H1 |
1,5H1 |
||
|
неразрезных |
1,5H1 |
0,8H1 |
H1 |
|||
|
4. Открытые эстакады под трубопроводы при соединении колонн с пролетным строением |
шарнирном |
2,0H |
H |
2,0H |
||
|
жестком |
1,5H |
0,7H |
1,5H |
|||
Обозначения, принятые в таблице:
H - полная высота колонны от верха фундамента до горизонтальной конструкции (стропильной или подстропильной, распорки) в соответствующей плоскости;
H1 - высота подкрановой части колонны от верха фундамента до низа подкрановой балки;
H2 - высота надкрановой части колонны от ступени колонны до горизонтальной конструкции в соответствующей плоскости.
Примечание. При наличии связей до верха колонн в зданиях с мостовыми кранами расчетная длина надкрановой части колонн в плоскости оси продольного ряда колонн принимается равной H2.
Таблица 43
|
Наименование элементов |
Расчетная длина l0 элементов ферм и арок |
|
1. Элементы ферм: |
|
|
а) верхний пояс при расчете в плоскости фермы при l0: |
|
|
< 1/8h1 |
0,9l |
|
≥ 1/8h1 |
0,8l |
|
б) то же, из плоскости фермы: |
|
|
для участка под фонарем, при ширине фонаря 12 м и более |
0,8l |
|
в остальных случаях |
0,9l |
|
в) раскосы и стойки при расчете в плоскости фермы |
0,8l |
|
г) то же, из плоскости фермы при b1/b2: |
|
|
< 1,5 |
0,9l |
|
≥ 1,5 |
0,8l |
|
2. Арки: |
|
|
а) при расчете в плоскости арки |
|
|
трехшарнирной |
0,580L |
|
двухшарнирной |
0,540L |
|
бесшарнирной |
0,365L |
|
б) при расчете из плоскости арки (любой) |
L |
Обозначения, принятые в таблице:
I - длина элемента между центрами примыкающих узлов, а для верхнего пояса фермы при расчете из плоскости фермы - расстояние между точками его закрепления;
L - длина арки вдоль ее геометрической оси; при расчете из плоскости арки - длина арки между точками ее закрепления из плоскости арки;
h1 - высота сечения верхнего пояса;
b1 и b2 - ширина сечения соответственно верхнего пояса и стойки (раскоса) фермы.
3.31. При расчете по недеформированной схеме расстояние от сжимающей продольной силы до равнодействующей усилий в арматуре в рассматриваемом сечении с учетом продольного изгиба определяется по формуле
e = e0η + ec, (135)
где e0 - расстояние от продольной силы N до центра тяжести бетонного сечения, определяемое по формуле (128);
η - коэффициент, учитывающий влияние продольного изгиба (см. пп. 3.7 и 3.29);
ec - расстояние от центра тяжести бетонного сечения до центра тяжести продольной арматуры S.
3.32. Расчет сечений внецентренно сжатых элементов при неравномерном нагреве по высоте сечения с температурой наиболее нагретой грани выше 400 °С производится с учетом следующих особенностей.
При расположении силы со стороны менее нагретой грани сечения растянутая или слабо сжатая арматура, а также свесы полки в тавровом сечении не учитываются и сечение рассчитывается как бетонное.
При расположении силы со стороны наиболее нагретой грани и наличия растянутой арматуры сжатая арматура не учитывается в расчете.
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ
3.33. Расчет прямоугольных сечений внецентренно сжатых элементов, указанных в п. 3.12, следует производить:
а) при ξ = x / h0 ≤ ξR (черт. 15) из условия
Ne ≤ γbtRbbx(h0 - 0,5x) + γstRscA′s(h0 - a′), (136)
при этом высота сжатой зоны определяется из формулы
N + γstRsAs - γstRscA′s = γbtRbbx; (137)
Черт. 15. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно сжатого железобетонного элемента, при расчете его по прочности
б) при ξ = x / h0 > ξR, равномерном и неравномерном нагревах и x ≤ h1, (см. черт. 9, а) - из условия (136); при этом высота сжатой зоны определяется:
для элементов из бетона класса В30 и ниже с ненапрягаемой арматурой классов A-I, А-II, А-III и из жаростойкой стали марок 12X13, 20X13, 20Х23Н18, 12Х18Н9Т, 08Х17Т и 4Х14Н14В2М из формулы
N + σsAs - γstRscA′s = γbtRbbx, (138)
где
для элементов из бетона класса выше В30, а также для элементов с арматурой классов выше A-III как ненапрягаемой, так и напрягаемой - из формул (66) и (67) или (68) главы СНиП 2.03.01-84 с учетом влияния температуры на расчетные сопротивления бетона и арматуры;
в) при ξ = x / h0 > ξR и неравномерном нагреве по высоте сечения с температурой наиболее нагретой грани свыше 400 °С при x > h1 (см. черт. 9, а) - из условия
Ne ≤ γbtRbbh1(h0 - 0,5h1) + γbtRbb(x - h1)(h0 - 0,5h1 - 0,5x), (140)
при этом высота сжатой зоны определяется для элементов из бетона класса В30 и ниже с ненапрягаемой арматурой классов A-I, А-II, A-III и жаростойкой стали марок 12X13, 20X13, 20Х23Н18, 12Х18Н9Т, 08Х17Т и 4Х14Н14В2М из формулы
N + σsAs = Rbb[γbth1 + γbt(x - h1)], (141)
где σs - определяется по формуле (139);
γbt - коэффициент условий работы бетона, принимаемый в зависимости от средней температуры бетона участков сжатой зоны высотой соответственно h1 и x - h1.
В формулах (136) - (139) значения γbt и γst принимаются по указаниям п. 3.11, Rs - п. 3.13, а e - п. 3.31.
3.34. При расчете прочности прямоугольных сечений с одиночной арматурой в формулах (136) - (138) принимают A′s = 0.
3.35. Площади поперечного сечения сжатой и растянутой арматуры при оптимальных их соотношениях рекомендуется определять по формулам:
Если принятая площадь поперечного сечения сжатой A′s,fact арматуры значительно превышает ее оптимальное значение A′s, определенное по формуле (142), то площадь поперечного сечения растянутой арматуры может быть уменьшена согласно формуле
где ξ - определяется по табл. 41 в зависимости от значения α0, которое определяется по формуле (142) при замене αR на α0;
а если ![]() , то площадь поперечного сечения
растянутой
арматуры определяется по формуле
, то площадь поперечного сечения
растянутой
арматуры определяется по формуле
Значения γbt и γst принимаются по указаниям п. 3.11, а ξR и αR - п. 3.13.
Если при расчете по формуле (142) величина A′s получается равной нулю или отрицательной, это означает, что сжатой арматуры по расчету не требуется и площадь растянутой арматуры As определяется по формуле (144) при A′s,fact = 0 или по формуле (145).
3.36. Площадь поперечного сечения слабосжатой или растянутой арматуры, устанавливаемой у наименее нагретой грани при одиночном армировании, неравномерно нагретого по высоте сечения до температуры наиболее нагретой грани свыше 400 °С, определяется следующим образом:
а) если удовлетворяется условие
Ne ≤ αRγbtRbbh20, (146)
где γbt - коэффициент, определяемый по указаниям п. 3.11 в зависимости от средней температуры бетона сжатой зоны высотой x = ξRh0, величину ξ находят по табл. 41 в зависимости от величины α0, определяемой из формулы (146), в которой αR заменяется на α0.
Площадь поперечного сечения арматуры вычисляют по формуле (144) при A′s,fact = 0;
б) если удовлетворяется условие
αRγbtRbbh20 < Ne ≤ 0,5γbtRbbh2, (147)
то сечение армируют конструктивно,
здесь γbt - коэффициент, определяемый по табл. 16 в зависимости от температуры бетона на расстоянии 0,5h;
в) если условие (147) не удовлетворяется, необходимо увеличить сечение элемента.
3.37. Приближенный расчет прямоугольных сечений сжатых элементов с учетом продольного изгиба, если величина эксцентриситета e0, определенная в соответствии с указаниями п. 3.28, не превышает ea, а расчетная длина элемента прямоугольного сечения l0 ≤ 20h (λ = 70), допускается производить из условия
N ≤ αγφ[γbtRbA + ΣγstRscAs], (148)
где γ - коэффициент, принимаемый равным при:
h > 20 см....................................................... 1,0
h ≤ 20 см....................................................... 0,9,
здесь h - размер сечения в плоскости наибольшей гибкости элемента;
φ - коэффициент, определяемый по формуле
φ = φb + 2(φsb - φb)Ls, (149)
но принимаемый не более φsb;
здесь φb и φsb - коэффициенты, принимаемые по табл. 44 и 45;
Таблица 44
|
Nl/N |
Коэффициент φb для бетонных элементов при l0/h |
|||||||
|
£ 6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
0,0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0,86 |
0,83 |
0,80 |
|
0,5 |
0,92 |
0,91 |
0,90 |
0,88 |
0,85 |
0,80 |
0,73 |
0,65 |
|
1,0 |
0,92 |
0,91 |
0,89 |
0,86 |
0,81 |
0,74 |
0,63 |
0,55 |
Таблица 45
|
Nl/N |
Коэффициент φsb для бетонных элементов при l0/h |
Эскиз |
|||||||
|
≤ 6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
||
|
А. При площади сечения промежуточных стержней, расположенных у граней, параллельных рассматриваемой плоскости, менее 1/3 (As + A′s) |
|
||||||||
|
0,0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0,87 |
0,84 |
0,81 |
|
|
0,5 |
0,92 |
0,92 |
0,91 |
0,90 |
0,87 |
0,84 |
0,80 |
0,75 |
|
|
1,0 |
0,92 |
0,91 |
0,90 |
0,88 |
0,86 |
0,82 |
0,77 |
0,77 |
|
|
Б. При площади сечения промежуточных стержней, расположенных у граней, параллельных рассматриваемой плоскости, равной или более 1/3 (As + A′s) |
|||||||||
|
0,0 |
0,92 |
0,92 |
0,91 |
0,89 |
0,87 |
0,84 |
0,80 |
0,75 |
|
|
0,5 |
0,92 |
0,91 |
0,90 |
0,87 |
0,83 |
0,79 |
0,72 |
0,65 |
|
|
1,0 |
0,92 |
0,91 |
0,89 |
0,86 |
0,80 |
0,74 |
0,66 |
0,58 |
|
Обозначения, принятые в таблице:
Nl - продольная сила от действия постоянных, длительных нагрузок и длительного нагрева;
N - продольная сила от действия постоянных, длительных и кратковременных нагрузок, кратковременного и длительного нагрева;
1 - 1 (см. эскиз) - рассматриваемая плоскость;
2 - (см. эскиз) - промежуточные стержни.
При промежуточных значениях l0/h и Nl/N коэффициенты φb и φsb определяются интерполяцией.
При наличии промежуточных стержней, расположенных у граней, параллельных рассматриваемой плоскости, в формуле (150) As (A′s) принимается равной половине площади сечения всей арматуры в поперечном сечении элемента.
ΣγstRscAs - сумма произведений площади арматуры, устанавливаемой по каждой из сторон сечения, на расчетное сопротивление, и коэффициент условий работы арматуры γst, который определяется по табл. 35 в зависимости от температуры арматуры.
Примечание. Если площадь сечения продольной арматуры составляет более 3 % всей площади сечения A, то в формуле (148) величина A заменяется величиной А - ΣAs.
Значение коэффициента условий работы бетона γbt принимается по табл. 16 в зависимости от температуры центра тяжести сечения.
При неравномерном нагреве по высоте сечения с температурой наиболее нагретой грани свыше 400 °С поперечное сечение элемента разбивают на две части согласно указаниям п. 1.28 и площадь бетона каждой части сечения умножается на расчетное сопротивление бетона и коэффициент условий работы бетона γbt, принимаемый по табл. 16 в зависимости от температуры бетона в центре тяжести каждой части сечения, т.е. в формуле (148) значение γbtRbA заменяется ΣγbtRbAi.
Коэффициент α учитывает влияние нагрева на продольный изгиб и определяется по формуле
где αl - принимается по табл. 46 в зависимости от температуры бетона в центре тяжести сечения;
λl = l0 / i - принимается по табл. 47. При λ ≤ 14 α = 1,0.
Таблица 46
|
Значения коэффициента αl для кратковременного и длительного нагрева при температуре бетона в центре тяжести сечения, °С |
Номера составов бетона по табл. 11 |
Значения коэффициента αl для кратковременного и длительного нагрева при температуре бетона в центре тяжести сечения, °С |
|||||||||||||||
|
50 |
100 |
200 |
300 |
500 |
700 |
900 |
1000 |
50 |
100 |
200 |
300 |
500 |
700 |
900 |
1000 |
||
|
1, 2 |
1,00 |
0,70 |
0,60 |
0,45 |
- |
- |
- |
- |
12 - 15, 17, 27, 29 |
1,00 |
0,80 |
0,70 |
0,50 |
0,25 |
0,10 |
0,03 |
- |
|
3, 4 |
1,00 |
0,75 |
0,70 |
0,55 |
- |
- |
- |
- |
16, 18 |
1,00 |
0,90 |
0,80 |
0,60 |
0,30 |
0,20 |
0,06 |
- |
|
5 - 11, 23, 24 |
1,00 |
0,90 |
0,70 |
0,60 |
0,30 |
0,20 |
0,12 |
0,05 |
19 - 21 |
1,00 |
0,85 |
0,70 |
0,60 |
0,40 |
0,20 |
0,15 |
0,10 |
Примечание. Коэффициент αl для промежуточных значений температур определяется интерполяцией.
Таблица 47
|
Предельная гибкость λl = l0/i сжатых бетонных и железобетонных элементов при температуре бетона в центре тяжести сечения, °С |
|||||
|
50 - 100 |
300 |
500 |
700 |
900 |
|
|
Бетонные |
85 |
60 |
50 |
45 |
35 |
|
Железобетонные |
125 |
90 |
55 |
- |
- |
Примечания: 1. Применение элементов конструкций, имеющих гибкость, превышающую табличные значения, должно быть специально обосновано.
2. Для железобетонных элементов с односторонним армированием предельные гибкости принимаются как для бетонных элементов.
3. Для промежуточных значений температур предельные гибкости определяются интерполяцией.
3.38. При расчете площади поперечного сечения арматуры в равномерно нагретых элементах величину Ncr разрешается определять по формулам (129) или (130), принимая площадь всей арматуры As + A′s = Aμ1. Коэффициент армирования μ1, соответствующий определенным интервалам армирования, принимается по табл. 48.
Таблица 48
|
Коэффициенты армирования μ1 для определения величины Ncr |
|
|
1. От 0,8 до 1,8 включ. |
0,01 |
|
2. Св. 1,8 » 2,8 » |
0,02 |
|
3. Св. 2,8 » 3,8 » |
0,03 |
Расчет производится следующим образом.
Задается ориентировочно армирование
элемента и по табл.
48 устанавливается коэффициент μ1,
затем вычисляются значения Ncr и η и определяется площадь поперечного
сечения арматуры по указаниям п. 3.35. В этом случае разрешается принимать значения коэффициентов βb и ![]() по температуре бетона в центре тяжести сечения.
по температуре бетона в центре тяжести сечения.
Если полученная площадь поперечного сечения арматуры As + A′s соответствует принятой, расчет считается законченным.
Если площадь арматуры As + A′s, отличается от принятой и оказывается в другом интервале армирования (см. табл. 48), следует выполнить повторный расчет, принимая коэффициент μ1 в соответствии с этим интервалом армирования. В отдельных случаях новая площадь сечения арматуры As + A′s может снова перейти в первоначальный интервал армирования, тогда площадь поперечного сечения арматуры принимается по граничным значениям.
Коэффициент армирования μ1 определяется по формуле
РАСЧЕТ ТАВРОВЫХ И ДВУТАВРОВЫХ СЕЧЕНИЙ
3.39. При расчете внецентренно сжатых железобетонных элементов таврового и двутаврового сечений должны учитываться следующие особенности:
а) ширина сжатой полки, вводимая в расчет, не должна быть больше величин, определяемых по указаниям п. 3.26. Высота сжатой полки, вводимая в расчет, при работе сечения с укороченной высотой должна соответствовать требованиям п. 3.11;
б) свесы полки, расположенные в растянутой зоне, в расчете не учитываются;
в) наиболее нагретая грань сечения совпадает со сжатой полкой.
3.40. Расчет сечений, имеющих полку в сжатой зоне, должен производиться в зависимости от положения границы сжатой зоны.
Если граница сжатой зоны проходит в полке, т.е. соблюдается условие
Ne ≤ γbtRbb′fh′f(h0 - 0,5h′f) + γstRscA′s(h0 - a′), (153)
расчет производится как для прямоугольного сечения шириной b′f в соответствии с указаниями пп. 3.33 и 3.34.
Если ξ = x / h0 ≤ ξR, граница сжатой зоны проходит в ребре, условие (153) не соблюдается, расчет производится из условия
Ne ≤ γbtRbbx(h0 - 0,5x) + γbtRb(b′f - b)h′f × (h0 - 0,5h′f) + γstRscA′s(h0 - a′), (154)
а высота сжатой зоны x определяется из формулы
N + γstRsAs - γstRscA′s = γbtRbbx + γbtRb(b′f - b)h′f. (155)
Если в расчете учитывается арматура, расположенная в сжатой зоне, и x < 2a′, то в формулах (153) - (155) принимается Rsc = 0, если это приводит к повышению прочности элемента.
Если ξ = x / h0 > ξR, граница сжатой зоны проходит в ребре и условие (153) не соблюдается, расчет сечений производится из условия (154), а высота сжатой зоны определяется:
для элементов из бетона класса В30 и ниже с ненапрягаемой арматурой классов A-I, A-II, A-III и из жаростойкой стали марок 12X13, 20X13, 20Х23Н18, 12Х18Н9Т, 08Х17Т и 4Х14Н14В2М по формуле
N + σsAs - γstRscA′s = γbtRbbx + γbtRb(b′f - b)h′f, (156)
где σs - определяется по формуле (139);
для элементов из бетона класса выше В30, а также для элементов с арматурой классов выше А-III как ненапрягаемой, так и напрягаемой - из формул (66) и (67) или (68) СНиП 2.03.01-84 с учетом влияния температуры на расчетные сопротивления бетона и арматуры.
Значения γbt и γst принимаются по указаниям п. 3.11, ξR и αR - п. 3.13 и e - п. 3.31.
3.41. Площадь поперечного сечения сжатой арматуры определяется по формуле
где αR - определяется по требованиям п. 3.13, γbt и γst - то же, п. 3.11.
3.42. Площадь поперечного сечения растянутой арматуры определяется следующим образом.
Если граница сжатой зоны проходит в полке и соблюдается условие (153), площадь поперечного сечения растянутой арматуры определяется как для прямоугольного сечения шириной b′f согласно указаниям пп. 3.36 и 3.38.
Если граница сжатой зоны проходит в ребре, условие (153) не соблюдается, и сжатая арматура вычислена по формуле (157), площадь поперечного сечения растянутой арматуры определяется по формуле
Если принятая площадь поперечного сечения сжатой арматуры A′s,fact превышает площадь A′s, определенную по формуле (158), то площадь поперечного сечения растянутой арматуры может быть принята уменьшенной согласно формуле
где ξ - определяется по табл. 41 в зависимости от значения
при этом должно удовлетворяться условие α0 < αR.
Если при расчете по формуле (157) величина A′s получается равной нулю или отрицательной, это означает, что сжатой арматуры по расчету не требуется, и площадь растянутой арматуры As определяется по формуле (159) при A′s,fact = 0.
Значения коэффициентов γbt, γst принимаются по указаниям п. 3.11, αR - п. 3.13 и e - п. 3.31.
3.43. При одиночном армировании продольной растянутой арматурой в формулах (153) - (156), (158) - (160) принимается А′s = 0.
Устанавливаемая в сжатой зоне конструктивная и монтажная арматура при определении прочности сечений в условиях воздействия повышенных и высоких температур не должна учитываться.
РАСЧЕТ ЭЛЕМЕНТОВ КОЛЬЦЕВОГО СЕЧЕНИЯ
3.44. Расчет внецентренно сжатых элементов кольцевого сечения при соотношении внутреннего и наружного радиусов r1/r2 ≥ 0,5 с арматурой, равномерно распределенной и равномерно нагретой по длине окружности (при числе продольных стержней не менее 6), должен производиться из условия
![]() , (161)
, (161)
при этом величина относительной площади сжатой зоны бетона ξcir определяется по формуле
При расчете элемента по недеформированной схеме в формуле (161) величина эксцентриситета продольного усилия относительно центра тяжести сечения e0 [см. формулу (128)] умножается на коэффициент η (см. пп. 3.7 и 3.29).
Если полученная из расчета по формуле (162) величина ξcir < 0,15, в условие (161) подставляется значение ξcir, определяемое по формуле
при этом значения φs и zs определяются по формулам (165) и (166), принимая ξcir = 0,15.
rт = (r1 + r2) / 2; (164)
rs - радиус окружности, проходящей через центры тяжести стержней рассматриваемой арматуры;
As,tot - площадь сечения всей продольной арматуры;
φs - коэффициент, определяемый по формуле
φs = ω1 - ω2ξcir; (165)
zs - расстояние от равнодействующей в арматуре растянутой зоны до центра тяжести сечения, определяемое по формуле
zs = (0,2 + 1,3ξcir)rs, (166)
но принимаемое не более rs;
σsp - определяется при коэффициенте γsp, большем единицы;
![]() ; (167)
; (167)
где ηr - коэффициент, принимаемый равным:
для арматуры классов A-I, А-II, A-III и из жаростойких сталей
марок 12Х13, 20X13, 20Х23Н18, 08Х17Т, 12Х18Н9Т и 4Х14Н14В2М.. 1,0
классов A-IV, A-V, A-VI, В-II, Вр-II, К-7 и К-19...................................... 1,1
ω2 = ω1δ, (168)
где значение δ принимается равным
δ = 1,5 + 6γstRs · 10-4, (169)
здесь Rs - в МПа.
Если вычисленное по формуле (165) значение φs ≤ 0, то в условие (161) подставляется значение φs = 0 и значение ξcir, полученное по формуле (162), при ω1 = ω2 = 0.
Значения γbt и γst принимаются по указаниям п. 3.11.
Центрально растянутые элементы
3.45. При расчете равномерно нагретых сечений центрально растянутых железобетонных элементов должно соблюдаться условие
N ≤ γstRsAs, (170)
где As - площадь сечения всей продольной арматуры.
При неравномерном нагреве по высоте сечения правая часть формулы (170) заменяется ΣγstRsAs - суммой произведений площадей арматуры, расположенной по каждой из сторон сечения, на расчетное сопротивление арматуры Rs и коэффициент условий работы γst, который принимается по табл. 35 в зависимости от температуры соответствующей арматуры.
Внецентренно растянутые элементы прямоугольного, таврового сечений
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ
3.46. Расчет прямоугольных сечений внецентренно растянутых элементов, указанных в п. 3.12, должен производиться в зависимости от положения продольной силы N:
а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S′ (черт. 16, а) - из условий
Ne ≤ γstRsA′s(h0 - a′) (171)
и
Ne′ ≤ γstRsAs(h0 - a′); (172)
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S′, т.е. e′ > h0 - a′ (черт. 16, б) - из условия
Ne ≤ γbtRbbx(h0 - 0,5x) + γstRscA′s(h0 - a′), (173)
при этом высота сжатой зоны x определяется по формуле
γstRsAs - γstRscA′s - N = γbtRbbx. (174)
Черт. 16. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно растянутого железобетонного элемента, при расчете его по прочности
а - продольная сила N приложена между равнодействующими усилий в арматуре S и S′; б - то же, за пределами расстояния между равнодействующими усилий в арматуре S и S′
Если полученная из расчета по формуле (174) величина x > ξRh0, в условие (173) подставляется значение x = ξRh0, где ξR определяется согласно указаниям п. 3.13;
если x < 2а′, то прочность сечения проверяется из условия
N[e + (h0 - a′)] ≤ γstRsAs(h0 - a′). (175)
Если высота сжатой зоны, определенная по формуле (174) без учета сжатой арматуры S, x < 2a′, то прочность сечения проверяется из условия
N(e + h0 - 0,5x′) ≤ γstRsAs(h0 - 0,5x). (176)
Если величина x, определенная без учета арматуры S′, оказывается отрицательной, то это означает, что площадь сечения арматуры S недостаточна.
Значения γbt и γst принимаются по указаниям п. 3.11, а e и e′ по указаниям п. 3.47.
3.47. Расстояние от растягивающей продольной силы до равнодействующей усилий в арматуре S в рассматриваемом сечении определяется по формулам:
а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S′
e = ec - е0, (177)
e′ = h0 - ec + e0 - a′; (178)
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S′
e = e0 - ес, (179)
где е′ - см. формулу (178);
e0 - расстояние от продольной силы N до центра тяжести бетонного сечения, определяемое по формуле (128) при ea = 0;
ec - см. п. 3.31.
3.48. Расчет продольной арматуры производится следующим образом:
а) при e′ > h0 - a′ площадь поперечного сечения сжатой арматуры определяется по формуле
![]() , (180)
, (180)
где αR - определяется по указаниям п. 3.13.
Площадь поперечного сечения растянутой арматуры определяется по формуле
где ξ - определяется по табл. 41 в зависимости от величины α0, полученной из формулы (180), в которой αR заменяется на α0, при этом должно удовлетворяться условие α0 < αR.
Если ![]() , то площадь поперечного сечения растянутой арматуры
определяется по формуле
, то площадь поперечного сечения растянутой арматуры
определяется по формуле
![]() . (182)
. (182)
Если значение ξ, определенное так
же, как и в формуле (181), без
учета арматуры S′, т.е. по значению оказывается меньше ![]() , то
, то
Коэффициент v определяется по табл. 41 в зависимости от значения α0, вычисленного без учета арматуры S′;
б) при e′ < h0 - a′ площади поперечного сечения растянутой и сжатой арматуры определяются по формулам:
Значения γbt и γst принимаются по указаниям п. 3.11, а e и e′ - п. 3.47.
При симметричном армировании равномерно нагретых сечений элемента подбор арматуры при e′ < h0 - a′ производится по формуле (184).
РАСЧЕТ ТАВРОВЫХ СЕЧЕНИЙ
3.49. Расчет тавровых сечений внецентренно растянутых элементов, указанных в п. 3.12, должен производиться в зависимости от положения продольной силы N:
а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S′ - из условий (171) и (172);
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S′, т.е. e′ > h0 - a′, и наиболее нагретая грань сечения совпадает со сжатой полкой - из условия (154); при этом высота сжатой зоны определяется из формулы
γstRsAs - γstRscA′s - N = γbtRbbx + γbtRb(b′f - b)h′f; (186)
в) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S′, т.е. e′ > h0 - a′, и наиболее нагретая грань сечения совпадает с растянутой полкой - из условий (173), (174) как для прямоугольного сечения.
Значения γbt и γst принимаются по указаниям п. 3.11.
Расчет по прочности сечений, наклонных к продольной оси элемента
3.50. Расчет железобетонных элементов по наклонным сечениям должен производиться для обеспечения прочности:
на действие поперечной силы по наклонной полосе между наклонными трещинами (п. 3.51);
на действие поперечной силы по наклонной трещине (п. 3.52);
на действие изгибающего момента по наклонной трещине (п. 3.61);
на действие поперечной силы по наклонной сжатой полосе между грузом и опорой для коротких консолей колонн (п. 3.60).
3.51. Расчет железобетонных элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия
Q ≤ 0,3φw1φb1Rbγbtbh0. (187)
Коэффициент φw1, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле
φw1 = 1 + 5αμw, (188)
но не более 1,3,
Коэффициенты βb и βs принимаются по табл. 16 и 35 в зависимости от максимальной температуры нагрева хомутов.
Коэффициент φb1 определяется по формуле
где β - коэффициент, принимаемый равным для бетона составов (см. табл. 11):
№ 1 - 3, 6, 7, 10 - 15, 19 - 21............................................ 0,01
№ 4 - 5, 8, 9, 16 - 18, 23, 24, 29 и 30............................... 0,02
Rb - в МПа;
γbt - коэффициент условий работы бетона, принимаемый по табл. 16 в зависимости от температуры бетона в центре тяжести сечения.
3.52. Расчет железобетонных элементов с поперечной арматурой (черт. 17) на действие поперечной силы для обеспечения прочности по наклонной трещине должен производиться по наиболее опасному наклонному сечению из условия
Q ≤ Qsw + Qs,inc + Qb. (192)
Поперечная сила Q определяется от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения. При расположении нагрузки по высоте сечения следует рассматривать наиболее опасное положение наклонного сечения, проходящего под местом приложения этой нагрузки.
Черт. 17. Схема усилий в сечении, наклонном к продольной оси железобетонного элемента при расчете его по прочности на действие поперечной силы
Поперечные усилия Qsw и Qs,inc определяются как сумма проекций на нормаль к продольной оси элемента предельных усилий, соответственно в хомутах и отгибах, пересекающих наклонную трещину.
Значение Qsw для хомутов, нормальных к продольной оси элемента, вычисляется по формулам:
Qsw = ΣRswγstAsw (193)
или
Qsw × qswc0 (194)
где qsw - усилие в хомутах на единицу длины элемента, определяемое по формуле
Длина c0 проекции опасной наклонной трещины на продольную ось элемента определяется из минимума правой части уравнения (192), где в значение Qb, вычисляемое по формуле (198), вместо c подставляется c0. Полученное значение c0 принимается не более 2h0 и не более значения c, а также не менее h0, если c больше h0.
В формулах (193), (194) и (195) коэффициент условий работы арматуры γst принимается по табл. 35 в зависимости от наибольшей температуры поперечной арматуры (хомутов) в рассматриваемом сечении.
Значение Qs,inc для отгибов вычисляется по формуле
Qs,inc = ΣRswγstAs,incsinα, (196)
где α - угол наклона отгибов к продольной оси элемента;
γst - коэффициент условий работы арматуры, принимаемый по табл. 35 в зависимости от наибольшей температуры отгибов в рассматриваемом сечении.
Кроме того, должна быть обеспечена прочность по наклонному сечению в пределах участков между хомутами s, между опорой и отгибом s1 и между отгибами s2.
Усилия в хомутах и отгибах учитываются по длине c не более 2h0 и не более значения c0, соответствующего условию
Qb = Qsw + Qs,inc. (197)
Поперечное усилие Qb, воспринимаемое бетоном, определяется по формуле
где γtt - коэффициент условий работы бетона, принимаемый по табл. 16 в зависимости от средней температуры бетона сжатой зоны. Среднюю температуру бетона сжатой зоны прямоугольного сечения допускается принимать по температуре бетона, расположенного на расстоянии 0,2h0 от сжатой грани сечения;
φb2 - коэффициент, принимаемый равным для бетона составов (см. табл. 11):
№ 1 - 3, 6, 7, 10 - 15, 19 - 21 при средней температуре бетона сжатой зоны сечения:
50 - 200 °С...................................................................................... 2,0
800 °С и выше............................................................................... 5,0
№ 4, 5, 8, 9, 16 - 18, 23, 24, 29 и 30 при средней температуре бетона сжатой зоны сечения:
50 - 200 °С...................................................................................... 1,5
800 °С и выше............................................................................... 4,5
Для температур между 200 и 800 °С коэффициент φb2 принимается по интерполяции;
c - длина проекции наиболее опасного наклонного сечения на продольную ось элемента;
b и h0 - принимаются в пределах наклонного сечения.
Коэффициент φf, учитывающий влияние сжатых полок в тавровых и двутавровых элементах, определяется по формуле
![]() , (199)
, (199)
но принимается не более 0,5.
При этом значение b′f принимается не более b + 3h′f. При учете свесов полки поперечная арматура должна быть надежно заанкерена в полке с μw ≥ 0,0015.
Коэффициент φп, учитывающий влияние продольных сил, определяется по формулам:
при действии продольных сжимающих сил в продольной арматуре, расположенной в растянутой зоне сечения
но принимается не более 0,5.
Для предварительно напряженных элементов в формулу (200) вместо N подставляется усилие предварительного обжатия P. Положительное влияние продольных сил не учитывается, если они создают изгибающие моменты, одинаковые по знаку с моментами от действия поперечной нагрузки;
при действии продольных растягивающих сил
но не более 0,8 по абсолютной величине. Значение 1 + φf + φn принимается во всех случаях не более 1,5.
В формулах (200) и (201) коэффициент условий работы бетона принимается таким же, как и в формуле (198).
Сила Qb в формуле (198) принимается не менее φb3(1 + φf + φn)Rbtγttbh0, где коэффициент φb3 принимается по указаниям п. 3.57, а коэффициент γtt таким же, как в формуле (198).
При расчете железобетонных элементов с поперечной арматурой должна быть обеспечена прочность по наклонному сечению в пределах между хомутами, между опорой и отгибом и между отгибами из условия (210), в котором c - длина проверяемого участка.
3.53. Для элементов с поперечной арматурой в виде хомутов, нормальных к продольной оси элемента и имеющих постоянный шаг, в пределах рассматриваемого наклонного сечения значение c0, соответствующее минимуму из выражения Qb + Qsw, определяется по формуле
При воздействии температуры, не превышающей предельно допустимую температуру применения арматуры, устанавливаемой по расчету (см. табл. 24), величина поперечной силы Qsw,b, воспринимаемой хомутами и бетоном в наклонном сечении с длиной проекции c, определяется по формуле
где φb2 - коэффициент, принимаемый согласно указаниям п. 3.52;
γtt - коэффициент, принимаемый таким же, как в формуле (198);
qsw - усилие в хомутах на единицу длины элемента, определяется по формуле (195).
В этом случае хомуты ставятся по всей высоте сечения и наклонная трещина пересекает все хомуты, определенные расчетом по формуле (195) (черт. 18)
Черт. 18. Схемы расположения поперечной арматуры при воздействии температуры
а - не превышающей предельно допустимую температуру применения арматуры; б - превышающей предельно допустимую температуру применения арматуры; c - проекция расчетного наклонного сечения элемента высотой h0; c1 - проекция расчетного наклонного сечения элемента с условно укороченной высотой hи = hw + a
При воздействии температуры, превышающей предельно допустимую температуру применения арматуры, установленной по расчету (см. табл. 24), допускается принимать поперечную арматуру, укороченную по высоте сечения элемента. Минимально допустимая длина хомутов устанавливается не менее 2/3h0 (см. черт. 18).
Величина поперечной силы, воспринимаемая укороченными хомутами и бетоном в наклонном сечении, определяется по формуле
где c - определяется по формуле (202), но не более 2h0.
Сечение элемента с укороченной поперечной арматурой необходимо проверить по формуле (203), в которой вместо h0 принимается условная рабочая высота сечения изгибаемого элемента hu, равная длине хомутов и толщине защитного слоя бетона у менее нагретой грани
hu = hw + a (см. черт. 18, б). (205)
Коэффициент условий работы бетона γtt принимается по табл. 16 в зависимости от средней температуры бетона условно сжатой зоны сечения элемента укороченной высоты, а температура бетона сжатой зоны определяется из теплотехнического расчета элемента действительной высоты. За расчетную поперечную силу принимается наименьшая величина, полученная из расчета по формуле (203) или (204).
3.54. Для хомутов, устанавливаемых по расчету в соответствии с указаниями пп. 3.52 и 3.53, должно удовлетворяться условие
Расстояние между хомутами s, между опорой и концом отгиба, ближайшего к опоре s1 (черт. 19), а также между концом предыдущего и началом последующего отгиба s2 должно быть не более величины
где φb2 - коэффициент, принимаемый согласно указаниям п. 3.52;
γtt - то же, что в формуле (198).
Черт. 19. Расстояния между хомутами и отогнутыми стержнями
Кроме того, поперечное армирование элемента, независимо от результатов расчета, должно удовлетворять конструктивным требованиям, приведенным в п. 5.26.
При воздействии температуры, не превышающей предельно допустимую температуру применения арматуры, устанавливаемой по расчету (см. табл. 24), определение усилий в хомутах на единицу длины элемента производится по формуле
где Q - поперечная сила и коэффициенты φb2 и γtt - принимается согласно указаниям п. 3.52.
3.55. Проверку прочности по поперечной силе наклонных сечений, начинающихся у опоры и у начала отгиба, допускается проводить из условия
Q ≤ Qsw,b + RswγstAs,incsinα, (209)
где Q - поперечная сила у начала рассматриваемого наклонного сечения (у опоры или у начала отгиба);
Qsw,b - поперечная сила, воспринимаемая хомутами и бетоном, определяется по формуле (203);
As,inc - площадь сечения отогнутых стержней в ближайшей за началом рассматриваемого наклонного сечения плоскости отгиба, расположенных согласно требованиям п. 3.56;
γst - коэффициент, принимаемый по указаниям п. 3.52;
α - угол наклона отогнутых стержней к продольной оси элемента в наклонном сечении.
3.56. Необходимое сечение отогнутых стержней As,inc, расположенных в одной плоскости, определяется из формулы (209). При этом поперечная сила Q принимается:
а) при расчете отогнутых стержней первой (от опоры) плоскости - равной поперечной силе у опоры;
б) при расчете отогнутых стержней в каждом из последующих плоскостей - равной поперечной силе у начала предыдущей (по отношению к опоре) плоскости отгибов (см. черт. 19).
Нижний конец наиболее удаленных от опоры отогнутых стержней должен располагаться не ближе, чем то сечение, в котором поперечная сила Q становится больше усилия, воспринимаемого бетоном и хомутами Qsw,b.
Кроме того, расположение отгибов должно удовлетворять требованиям п. 5.26.
В элементах с поперечным армированием только из отогнутых стержней расчет по поперечной силе производится из условия (192) при Qsw = 0. При этом рассчитываются наклонные сечения, начинающиеся в растянутой зоне у опоры и у начала отгибаемых стержней и заканчивающиеся в сжатой зоне в конце отгибаемых стержней каждой плоскости, а также в местах приложения сосредоточенных сил (черт. 20).
Черт. 20. Расчетная схема опасных наклонных сечений при расчете по прочности на действие поперечной силы
3.57. Расчет железобетонных элементов без поперечной арматуры на действие поперечной силы для обеспечения прочности по наклонной трещине должен производиться по наиболее опасному наклонному сечению из условия
где правая часть условия принимается не более 2,5Rbtγttbh0 и не менее φb3(1 + φn)Rbtγttbh0.
Коэффициент φn определяется по указаниям п. 3.52.
Коэффициенты φb3, φb4 принимаются по таблице:
|
Коэффициент |
Средняя температура бетона сжатой зоны сечения |
Состав бетона по табл. 11 |
|
|
φb3 |
φb4 |
||
|
0,6 |
1,5 |
50 - 200 °С 800 °С и выше |
№ 1, 3, 6, 7, 10 - 15, 19 - 21 |
|
1,3 |
3,3 |
||
|
0,4 |
1,0 |
50 - 200 °С 800 °С и выше |
№ 4, 5, 8, 9, 16 - 18, 23, 24, 29, 30 |
|
0,9 |
2,2 |
||
Для температур между 200 и 800 °С коэффициенты φb3 и φb4 принимаются по интерполяции.
В расчете рассматриваются наклонные сечения, проходящие через опору и направленные к точкам приложения сосредоточенных сил, а расчетные значения поперечных сил Q принимаются в конце рассматриваемого наклонного сечения (черт. 21).
Черт. 21. Расчетная схема опасных наклонных сечений при расчете по прочности на действие поперечной силы
1, 2 - наклонные сечения
3.58. При отсутствии нормальных трещин, т.е. если выполняется условие (247) с заменой Rbt,serγtt на Rbtγtt в рассматриваемой зоне действия поперечных сил, следует учитывать повышение прочности элемента по сравнению с формулой (210) исходя из условия
где σx и σy - нормальные напряжения в бетоне на площадке, соответственно перпендикулярной и параллельной продольной оси элемента, на уровне центра тяжести сечения от внешней нагрузки, температуры и усилия предварительного обжатия;
Ired и Sred - соответственно момент инерции сечения относительно оси, проходящей через центр тяжести сечения и статический момент части сечения, расположенного по одну сторону от оси, проходящей через центр тяжести сечения.
Значения σx, σy, Sred и Ired определяются из расчета элемента как сплошного упругого тела.
3.59. Расчет железобетонных элементов с наклонными сжатыми гранями на действие поперечной силы для обеспечения прочности по наклонной трещине производится по указаниям пп. 3.52 и 3.53, при этом в качестве рабочей высоты в пределах рассматриваемого наклонного сечения в расчет вводятся: для элементов с поперечной арматурой - наибольшее значение h0; для элементов без поперечной арматуры - среднее значение h0.
3.60. Расчет железобетонных коротких консолей колонн (lb ≤ 0,9h0, черт. 22) на действие поперечной силы для обеспечения прочности по наклонной сжатой полосе между грузом и опорой должен производиться из условия
Q ≤ 0,8φw2Rbγbtblbsinθ, (212)
где правая часть условия принимается не более 3,5Rbtγttbh0 и не менее правой части уравнения (210):
θ - угол наклона расчетной сжатой полосы к горизонтали;
lb - ширина наклонной сжатой полосы, определяется по формуле
lb = lsupsinθ, (213)
здесь lsup - длина площадки передачи нагрузки вдоль вылета консоли;
φw2 - коэффициент, учитывающий влияние поперечной арматуры, определяется по формуле
φw2 = 1 - 5αμw, (214)
здесь α и μw - см. п. 3.51;
γbt - принимается как в формуле (187).
Черт. 22. Схема для расчета коротких консолей
При расчете учитываются хомуты горизонтальные и наклонные под углом 45° к горизонтали. Поперечное армирование консолей, поддерживающих балки, фермы и т.п., независимо от результатов расчета должно удовлетворять требованиям п. 5.29.
3.61. Расчет железобетонных элементов на действие изгибающего момента для обеспечения прочности по наклонной трещине должен производиться по опасному наклонному сечению из условия (черт. 23)
M ≤ Ms + Msw + Ms,inc, (215)
Величина M определяется от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения относительно оси, перпендикулярной плоскости действия момента, и проходящей через точку приложения равнодействующей усилий Nb в сжатой зоне.
Черт. 23. Схема усилий в сечении, наклонном к продольной оси железобетонного элемента, при расчете его по прочности на действие изгибающего момента
Величины Ms, Msw и Ms,inc определяются как сумма моментов относительно той же оси от усилий в продольной арматуре, в хомутах и отогнутых стержнях, пересекающих растянутую зону наклонного сечения и вычисляются по формулам:
Ms = RsγstAszs; (216)
![]() ; (217)
; (217)
Ms,inc = ΣRswγstAs,inczs,inc, (218)
где zs, zsw, zs,inc - расстояния от плоскостей расположения соответственно продольной арматуры хомутов и отогнутых стержней до указанной выше оси;
γst - коэффициент условий работы арматуры, определяемый по табл. 35 в зависимости от наибольшей температуры продольной арматуры отогнутых стержней и хомутов;
c и qsw - определяются по формулам (202) и (195).
Высота сжатой зоны наклонного сечения (измеренная по нормали к сжатой грани элемента) определяется из условия равновесия проекций усилий в бетоне сжатой зоны и в арматуре, пересекающей растянутую зону наклонного сечения, на нормаль к продольной оси элемента.
Расчет наклонных сечений на действие момента производится в местах обрыва и отгиба продольной арматуры в пролете, а также в приопорной зоне балок у свободного края консолей. При отсутствии у арматурных стержней анкеров расчетное сопротивление арматуры растяжению в месте ее пересечения рассматриваемым наклонным сечением принимается сниженным согласно требованиям поз. 3 табл. 32. Кроме того, расчет наклонных сечений на действие момента производится в местах резкого изменения конфигурации элементов (подрезки, узлы и т.п.).
Проверка на действие изгибающего момента не производится для наклонных сечений, пересекающих растянутую грань элемента на участках, обеспеченных от образования нормальных трещин, т.е. там, где момент M от внешней нагрузки и воздействия температуры, на которую ведется расчет по прочности, меньше или равен моменту трещинообразования Mcrc, определяемому по формуле (256), принимая в ней значения Rbtγtt вместо Rbt,serγtt.
На приопорных участках элементов момент Ms, воспринимаемый продольной арматурой, пересекающей растянутую зону наклонного сечения, определяется по формуле (216).
3.62. Для обеспечения прочности наклонных сечений на действие изгибающего момента в элементах постоянной высоты продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т.е. за нормальное сечение, в котором эти стержни перестают требоваться по расчету) на длину не менее 20d и не менее величины w, определяемой по формуле
![]() , (219)
, (219)
где Q - поперечная сила в нормальном сечении, проходящем через точку теоретического отрыва стержня;
α - то же, что в п. 3.55;
qsw - усилие в хомутах на единицу длины элемента на рассматриваемом участке длиной w, определяемое по формуле (195), в которой расчетное сопротивление арматуры Rsw заменяется Rs;
d - диаметр обрываемого стержня;
γst - коэффициент условия работы арматуры принимается согласно указаниям п. 3.52.
Расчет железобетонных элементов на местное действие нагрузок
РАСЧЕТ НА МЕСТНОЕ СЖАТИЕ
3.63. При расчете на местное сжатие (смятие) элементов без косвенного армирования должно удовлетворяться условие
N ≤ ψRb,locAloc1, (220)
где N - продольная сжимающая сила от местной нагрузки;
Aloc1 - площадь смятия;
ψ - коэффициент, зависящий от характера распределения местной нагрузки по площади смятия, принимается равным: при равномерном распределении местной нагрузки на площадь смятия - 1,00;
при неравномерном распределении местной нагрузки на площадь смятия (под концами балок, прогонов, перемычек) для бетона составов № 1 - 21, 23, 29 по табл. 11 - 0,75;
Rb,loc - расчетное сопротивление бетона сжатию, определяется по формуле
Rb,loc = αφbRbγbt. (221)
Здесь α, φb ≥ 1,0.
Для бетонов классов не ниже В25 α = 1,0;
для бетонов классов В25 и выше
![]() ; (222)
; (222)
но не более:
при схеме приложения нагрузки по черт. 24, а, в, г, е, и:
для обычного и жаростойкого бетонов классов:
более 7,5.......................................................................... 2,3
В3,5; В5; В7,5................................................................. 1,5
для жаростойких бетонов классов
В2,5 и ниже.................................................................... 1,2
при схеме приложения нагрузки по черт. 24, б, д, ж независимо от вида и класса бетона 1,0
Aloc2 - расчетная площадь, определяемая по указаниям п. 3.64;
Rbt и Rb - принимается как для бетонных конструкций (см. табл. 14).
Коэффициент γbt принимается по табл. 16 в зависимости от средней температуры бетона площади смятия - при схеме приложения нагрузки по черт. 24, а, б, е, и и в зависимости от температуры наиболее нагретой грани - при схеме приложения нагрузки по черт. 24, в, г, д, ж.
Черт. 24. Схемы для расчета железобетонных элементов на местное сжатие
а - при местной нагрузке по всей ширине элемента; б - при местной краевой нагрузке по всей ширине элемента; в, г - при местной нагрузке в местах опирания прогонов и балок; д - при местной краевой нагрузке на угол элемента; е - при местной нагрузке, приложенной на части длины и ширины элемента; при местной краевой нагрузке, расположенной в пределах выступа стены или простенка; ж - при местной краевой нагрузке, расположенной в пределах выступа стены (пилястры); и - сечений сложной формы; 1 - площадь смятия; 2 - расчетная площадь смятия; 3 - минимальная зона армирования сетками, при которой косвенное армирование учитывается по формуле (225)
3.64. В расчетную площадь Aloc2 включается участок, симметричный по отношению к площади смятия (см. черт. 24). При этом должны выполняться следующие правила:
при местной нагрузке по всей ширине элемента b в расчетную площадь включается участок длиной не более b в каждую сторону от границы местной нагрузки (см. черт. 24, а);
при местной краевой нагрузке по всей ширине элемента расчетная площадь Aloc2 равна площади смятия Aloc1 (см. черт. 24, б);
при местной нагрузке в местах опирания концов прогонов и балок в расчетную площадь включается участок шириной, равной глубине заделки прогона или балки, и длиной не более расстояния между серединами примыкающих к балке пролетов (см. черт. 24, в);
если расстояние между балками превышает двойную ширину элемента, длина расчетной площади определяется как сумма ширины балки и удвоенной ширины элемента (см. черт. 24, г);
при местной краевой нагрузке на угол элемента (см. черт. 24, д) расчетная площадь Aloc2 равна площади смятия Aloc1;
при местной нагрузке, приложенной на части длины и ширины элемента, расчетная площадь принимается согласно черт. 24, е. При наличии нескольких нагрузок указанного типа расчетные площади ограничиваются линиями, проходящими через середину расстояний между точками приложения двух соседних нагрузок;
при местной краевой нагрузке, расположенной в пределах выступа стены (пилястры) или простенка таврового сечения, расчетная площадь Aloc2 равна площади смятия Aloc1 (см. черт. 24, ж);
при определении расчетной площади для сечений сложной формы не должны учитываться участки, связь которых с загруженным участком не обеспечена с необходимой надежностью (например, участок 2 на черт. 24, и).
Примечание. При местной нагрузке от балок, прогонов, перемычек и других элементов, работающих на изгиб, учитываемая в расчете глубина опоры при определении Aloc1 и Aloc2 принимается не более 20 см.
3.65. При расчете на местное сжатие равномерно нагретых элементов из тяжелого бетона с косвенным армированием в виде сварных поперечных сеток должно удовлетворяться условие
N ≤ Rb,redAloc1, (224)
где Rb,red - приведенная призменная прочность бетона, определяемая по формуле
Rb,red = γbtRbφb + φμxyγstRs,xyφs, (225)
φb - определяется по формуле (223) и принимается не более 3,5;
φs - коэффициент, учитывающий влияние косвенного армирования в зоне местного сжатия. Для схем 24, б, д, ж принимается φs = 1,0, при этом косвенное армирование учитывается в расчете при условии, что поперечные сетки установлены на площади, не менее ограниченной пунктирными линиями на соответствующих схемах черт. 24. Для схем 24, а, в, г, е, и φs определяется по формуле
![]() ; (226)
; (226)
Alf - площадь бетона, заключенного внутри контура сеток косвенного армирования, считая по их крайним стержням, для которой должно удовлетворяться условие Aloc1 < Alf £ Aloc2;
Rs,xy - расчетное сопротивление арматуры сеток;
φ - коэффициент эффективности косвенного армирования, принимаемый равным
![]() ; (227)
; (227)
μxy - коэффициент насыщения поперечной арматурой, определяемый для сварных поперечных сеток по формуле
![]() ; (229)
; (229)
здесь пх, Asx, lx - соответственно число стержней, площадь поперечного сечения и длина стержня сетки в одном направлении (считая в осях крайних стержней);
пу, Asy, ly - то же, в другом направлении;
s - расстояние между сетками;
Alf - площадь сечения бетона, заключенного внутри контура сеток (считая в осях крайних стержней).
Площади сечения стержней сетки на единицу длины в одном и другом направлениях не должны различаться более чем в 1,5 раза.
Коэффициенты γbt и γst принимаются соответственно по табл. 16 и 35 в зависимости от температуры в месте установки сеток.
РАСЧЕТ НА ПРОДАВЛИВАНИЕ
3.66. Расчет на продавливание конструкций (без поперечной арматуры) от действия сил, равномерно распределенных на ограниченной площади, должен производиться из условия
где F - продавливающая сила;
α - коэффициент, принимаемый равным для бетона составов (см. табл. 11):
№ 1 - 3, 6, 7, 10 - 15, 19 - 21....................................................... 1,0
№ 4, 5, 8, 9, 16 - 18, 23, 24, 29 и 30............................................ 0,8
um - среднеарифметическое значений периметров верхнего и нижнего оснований пирамиды, образующейся при продавливании в пределах рабочей высоты сечения h0.
При определении величин um и F предполагается, что продавливание происходит по боковой поверхности пирамиды, меньшим основанием которой служит площадь действия продавливающей силы, а боковые грани наклонены под углом 45° к горизонтали (черт. 25, а).
Значение продавливающей силы F принимается равным силе N, действующей на пирамиду продавливания, за вычетом нагрузок, приложенных к большему основанию пирамиды продавливания (считая до плоскости расположения растянутой арматуры) и сопротивляющихся продавливанию.
Если схема опирания такова, что продавливание может происходить на поверхности пирамиды с углом наклона боковых граней больше 45° (например, в свайных ростверках - черт. 25, б), правая часть условия (230) определяется для фактической пирамиды с умножением на h0/c, где c - длина горизонтальной проекции боковой грани пирамиды продавливания. При этом значение несущей способности принимается не более значения, соответствующего пирамиде с c = 0,4h0.
Черт. 25. Схемы для расчета железобетонных элементов на продавливание при угле наклона боковых граней:
а - пирамиды продавливания под углом 45°; б - то же, больше 45°
При установке в пределах пирамиды продавливания хомутов, нормальных к плоскости плиты, расчет должен производиться из условия
F ≤ Fb + 0,8Fsw, (231)
но не более 2Fb.
Усилие Fb принимается равным правой части неравенства (230), Fsw определяется как сумма всех поперечных усилий, воспринимаемых хомутами, пересекающими боковые грани расчетной пирамиды продавливания
Fsw = ΣRswγstAsw, (232)
где Asw - суммарная площадь сечения поперечной арматуры, пересекающей боковые грани пирамиды продавливания;
Rsw - не должно превышать значения, соответствующего арматуре класса A-I.
При учете поперечной арматуры значение Fsw должно быть не менее 0,5Fb.
Коэффициент γtt принимается по табл. 16 в зависимости от средней температуры бетона на проверяемом участке, γst - по табл. 35 в зависимости от наибольшей температуры поперечной арматуры в рассматриваемом сечении.
При расположении хомутов на ограниченном участке вблизи сосредоточенного груза производится дополнительный расчет на продавливание пирамиды с верхним основанием, расположенным по контуру участка с поперечной арматурой, из условия (230).
РАСЧЕТ НА ОТРЫВ
3.67. Расчет железобетонного элемента на отрыв от действия нагрузки, приложенной к его нижней части или в пределах высоты его сечения (черт. 26), должен производиться из условия
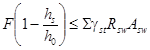 , (233)
, (233)
где F - отрывающее усилие;
ΣRswAsw - сумма поперечных усилий, воспринимаемых хомутами, устанавливаемыми дополнительно по длине зоны отрыва;
a = 2hs + b, (234)
здесь hs - расстояние от уровня передачи нагрузки до центра тяжести сечения арматуры S;
b - ширина площади передачи отрывающей силы.
Черт. 26. Схема для расчета железобетонных элементов на отрыв
Ц.Т. - центр тяжести сжатой зоны сечения примыкающего элемента
Коэффициент γst принимается по табл. 35 в зависимости от наибольшей температуры дополнительной арматуры Asw.
РАСЧЕТ ЗАКЛАДНЫХ ДЕТАЛЕЙ
3.68. Расчет анкеров, приваренных втавр к плоским элементам стальных закладных деталей, на действие изгибающих моментов, нормальных и сдвигающих сил от статической нагрузки, расположенной в одной плоскости симметрии закладной детали (черт. 27, а), должен производиться по формуле
где Аап - суммарная площадь поперечного сечения анкеров наиболее напряженного ряда;
Nan - наибольшее растягивающее усилие в одном ряду анкеров, равное
Qan - сдвигающее усилие, приходящееся на один ряд анкеров, равное
N′an - наибольшее сжимающее усилие в одном ряду анкеров, определяемое по формуле
Черт. 27. Схемы расчета закладных деталей:
а - схема усилий, действующих на закладную деталь; б - схема выкалывания бетона анкерами закладной детали с усилением на концах при N′an < 0; в - то же, без усиления на концах при N′an < 0; г - схема выкалывания бетона растянутыми анкерами закладной детали при N′an > 0; д - схема, принимаемая при расчете на откалывание бетона анкерами закладной детали; 1 - точка приложения нормальной силы N; 2 - поверхность выкалывания; 3 - проекция выкалывания на плоскость, нормальную анкерам; 4 - анкерная пластина; tan - расчетная температура нагрева анкеров
M, N и Q - соответственно момент, нормальная и сдвигающая силы, действующие на закладную деталь. Значение момента определяется относительно оси, расположенной в плоскости наружной грани пластины и проходящей через центр тяжести всех анкеров;
nan - число рядов анкеров (при определении сдвигающей силы), если не обеспечивается равномерная передача сдвигающей силы Q на все ряды анкеров, то при определении сдвигающего усилия Qan учитывается не более чем в 4 рядах;
z - расстояние между крайними рядами анкеров;
δ - коэффициент, определяемый по формуле
но принимаемый не менее 0,15;
коэффициент ω в формуле (239) принимается:
при N′an ³ 0 (имеется прижатие)
![]() ; (240)
; (240)
при N′an ≤ 0 (нет прижатия)
![]() ; (241)
; (241)
если в анкерах отсутствуют растягивающие усилия, коэффициент δ принимается равным единице;
λ - коэффициент, определяемый при анкерных стержнях диаметром 8 - 25 мм для обычного тяжелого бетона классов В12,5 - В50 и жаростойкого классов В12,5 - В30 по формуле
но принимаемый не более 0,7. Для жаростойких бетонов класса В35 и В40 коэффициент λ принимается как для класса В30.
В формуле (242):
Rb, Rs - в МПа;
Aan1 - площадь анкерного стержня наиболее напряженного ряда, см2.
Площадь сечения анкеров остальных рядов должна приниматься равной площади сечения анкеров наиболее напряженного ряда.
Коэффициент γst принимается по табл. 35 в зависимости от температуры: при нагреве со стороны закладной детали - температуры закладной детали; при нагреве со стороны, противоположной закладной детали - температуры конца анкера.
Коэффициент γbt принимается по табл. 16 в зависимости от температуры бетона в месте расположения закладной детали.
В формулах (236) и (238) нормальная сила N считается положительной, если она направлена от закладной детали, и отрицательной - если она направлена к ней. Если нормальные усилия Nan и N′an, а также сдвигающее усилие Qan при вычислении по формулам (236) - (238) получают отрицательные значения, то в формулах (235), (237) и (239) они принимаются равными нулю. Кроме того, если Nan получает отрицательное значение, то в формуле (237) принимается N′an = N (см. пример расчета 24).
При расположении закладной детали на верхней (при бетонировании) поверхности изделия коэффициент λ уменьшается на 20 %, а значение N′an принимается равным нулю.
3.69. В закладной детали с анкерами, приваренными внахлестку под углом от 15 до 30°, наклонные анкера рассчитываются на действие сдвигающей силы (при Q > N, где N - отрывающая сила) по формуле
![]() , (243)
, (243)
где Aan,inc - суммарная площадь поперечного сечения наклонных анкеров;
N′an - см. п. 3.68;
γst - то же.
При этом должны устанавливаться нормальные анкера, рассчитываемые по формуле (235) при λ = 1, Qan = 0,1 от сдвигающего усилия, определенного по формуле (237).
3.70. Конструкция сварных закладных деталей с приваренными к ним элементами, передающими нагрузку на закладные детали, должна обеспечивать включение в работу анкерных стержней в соответствии с принятой расчетной схемой. Внешние элементы закладных деталей и их сварные соединения рассчитываются согласно СНиП II-23-81. При расчете пластин и фасонного проката на отрывающую силу принимается, что они шарнирно связаны с нормальными анкерными стержнями.
Толщина пластины t расчетной закладной детали, к которой привариваются втавр анкера, должна удовлетворять условию
где dan - диаметр анкерного стержня, требуемый по расчету;
γst - см. п. 3.68;
γstRsq - расчетное сопротивление стали на срез, принимаемое согласно СНиП II-23-81, умноженное на коэффициент γst, определяемый по табл. 35 в зависимости от температуры пластины.
При применении типов сварных соединений, обеспечивающих большую зону включения пластины в работу при вырывании из нее анкерного стержня, и соответствующем экспериментальном обосновании возможна корректировка условия (244) для этих сварных соединений. Толщина пластины должна также удовлетворять технологическим требованиям по сварке.
Если на концах анкеров закладной детали имеются усиления в виде анкерных пластин или высаженных головок, бетон под этими усилениями проверяют на смятие. При этом сила смятия Nloc должна быть не больше величины αφbRbγbtAloc1; коэффициенты α и φb определяются согласно указаниям п. 3.63. Сила смятия для анкеров, приваренных втавр, при la ≥ 15d и если вдоль анкера возможно образование трещин от растяжения бетона, равна усилию в одном анкере Nan1, а если образование этих трещин невозможно, сила смятия Nloc принимается равной величине Nan1(lan - la) / lan. При длине la < 15d значение Nloc увеличивают на величину, равную Qan(15d - la) / lan. Для анкеров, приваренных внахлестку, сила смятия равна сдвигающему усилию в анкере.
Расчет железобетонных элементов на выносливость
3.71. Расчет железобетонных элементов на выносливость производится путем сравнения напряжений в бетоне и арматуре с соответствующими расчетными сопротивлениями, умноженными на коэффициенты условий работы γb1, γs3, принимаемые соответственно по табл. 22 и 33, а при наличии сварных соединений арматуры - также на коэффициент условий работы γs4 (см. табл. 34). При нагреве бетона свыше 50 °С должен учитываться коэффициент условий работы γb1t, принимаемый по табл. 23, и коэффициент условий работы арматуры γs3t, принимаемый по требованиям п. 2.32 при температурах нагрева арматуры свыше 100 °С.
Напряжения в бетоне и арматуре вычисляются как для упругого тела (по приведенным сечениям) на действие внешних нагрузок, усилий от воздействия температуры и усилия предварительного обжатия P. Неупругие деформации в сжатой зоне бетона учитываются снижением величины модуля упругости бетона, принимая коэффициенты приведения арматуры к бетону α′ равными 25, 20, 15 и 10 соответственно для бетонов классов В15, В25, В30, В40 и выше.
При воздействии температуры свыше 50 °С величины вышеприведенных коэффициентов α′ должны умножаться на отношение коэффициентов βs/βb. Значения коэффициентов βs принимаются по табл. 35 в зависимости от температуры арматуры, и βb - по табл. 16 в зависимости от средней температуры бетона сжатой зоны сечения. В случае если не соблюдаются условия п. 4.8 при замене в нем значения Rbtt,ser на Rbtt, площадь приведенного сечения растянутой зоны бетона определяется без учета растянутой зоны бетона.
3.72. Расчет на выносливость сечений, нормальных к продольной оси элемента, должен производиться из условий:
для сжатого бетона
σb,max ≤ γb1γb1tRb; (245)
для растянутой арматуры
σs,max ≤ γs3γs3tRs, (246)
где σb,max и σs,max - максимальные нормальные напряжения соответственно в сжатом бетоне и в растянутой арматуре.
При этом расчетные сопротивления бетона сжатию Rb и растяжению арматуры Rs умножаются на соответствующие коэффициенты условий работы: γb1, γb1t (см. табл. 22 и 23), принимаемые в зависимости от средней температуры бетона сжатой зоны; и γs3, γs3t, γs4 (см. табл. 33. п. 2.32 и табл. 34), принимаемые в зависимости от температуры растянутой арматуры.
В зоне, проверяемой по сжатому бетону, при действии многократно повторяющейся нагрузки появление растягивающих напряжений не допускается.
Сжатая арматура на выносливость не рассчитывается.
3.73. Расчет на выносливость сечений, наклонных к продольной оси элемента, должен производиться из условия, что равнодействующая главных растягивающих напряжений, действующих на уровне центра тяжести приведенного сечения, должна быть полностью воспринята поперечной арматурой при напряжении в ней, равном расчетному сопротивлению Rs, умноженному на коэффициенты условий работы γs3, γs4, γs3t (см. табл. 33, 34 и п. 2.32), принимаемые по наибольшей температуре нагрева поперечной арматуры.
Для элементов, в которых поперечная арматура не предусматривается, должны быть выполнены условия п. 4.11 СНиП 2.03.01-84 с введением в условия (141) и (142) вместо расчетных сопротивлений Rb,ser и Rbt,ser расчетных сопротивлений Rb и Rbt, которые умножаются на коэффициенты условий работы γb1 и γb1t (см. табл. 22 и 23).
4. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1. Железобетонные элементы, подвергаемые воздействию повышенных и высоких температур, рассчитываются по образованию трещин, нормальных и наклонных к продольной оси элемента.
Расчет по образованию трещин, нормальных к продольной оси элемента
4.2. Для изгибаемых, растянутых и внецентренно сжатых железобетонных элементов, подвергающихся воздействию повышенной и высокой температуры, усилия, воспринимаемые сечениями, нормальными к продольной оси, при образовании трещин определяются исходя из следующих положений:
сечения после деформаций остаются плоскими;
наибольшее относительное удлинение
крайнего растянутого волокна бетона равно ![]() ;
;
напряжения в бетоне сжатой зоны (если они имеются) определяются с учетом упругих или неупругих деформаций нагретого бетона, при этом наличие неупругих деформаций учитывается с уменьшением ядрового расстояния r (см. п. 4.4);
напряжения в бетоне растянутой зоны распределены равномерно и равны по величине Rbtt,ser;
напряжения в арматуре равны алгебраической сумме напряжений, отвечающих приращению деформаций окружающего нагретого бетона, и напряжений, вызванных усадкой и ползучестью бетона.
Величина коэффициента βb принимается по табл. 16 в зависимости от температуры бетона на уровне растянутой арматуры.
4.3 (4.2). Расчет железобетонных элементов по образованию трещин на усилия, вызванные воздействием температуры, следует проводить при нагреве; когда температура бетона по высоте элемента между гранями сечения отличается более чем на 30 °С в элементах статически неопределимых конструкций и более чем на 50 °С в элементах статически определимых конструкций при криволинейном распределении температуры; когда температура растянутой арматуры превышает 100 °С в конструкциях из обычного бетона и 70 °С - в конструкциях из жаростойкого бетона.
Расчет железобетонных элементов с μ ≥ 0,4 % по образованию трещин при температуре нагрева арматуры свыше 200 °С допускается не производить.
Расчет по образованию трещин в элементах конструкций производится из условия, что растягивающие напряжения бетона, вызванные распределением температуры, определяемые по формуле (32), равны или меньше величины расчетного сопротивления бетона Rbt,ser, дополнительно умноженного на коэффициент условий работы бетона γtt, принимаемый по табл. 16 в зависимости от температуры волокна бетона, для которого определяются напряжения.
4.4. Расчет изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементов по образованию трещин производится:
статически определимых конструкций из условия
Mr ≤ Mcrc; (247)
статически неопределимых конструкций из условия
(Mr ± Mt) ≤ Mcrc, (248)
где Мr - момент внешних сил, расположенных по одну сторону от рассматриваемого сечения относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;
Mt - момент, вызванный воздействием температуры, определяется согласно требованиям п. 1.46 и принимается со знаком «плюс», когда направление момента совпадает с Мr, и со знаком «минус» - когда не совпадает;
Mcrc - момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин.
Значение Mr определяется по формулам:
для изгибаемых элементов (черт. 28, а)
Mr = М; (249)
для внецентренно сжатых элементов (черт. 28, б)
Mr = N(e0 - r); (250)
для внецентренно растянутых элементов (черт. 28, в)
Mr = N(e0 + r), (251)
где r - расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Черт. 28. Схемы усилий и эпюры напряжений в поперечном сечении элемента при расчете по образованию трещин, нормальных к продольной оси элемента в зоне сечения, растянутой от действия внешних нагрузок и температуры
а - при изгибе; б - при внецентренном сжатии; в - при внецентренном растяжении; 1 - ядровая точка; 2 - центр тяжести приведенного сечения
Значение r определяется по формулам:
для внецентренно сжатых элементов
для внецентренно растянутых элементов
![]() ; (253)
; (253)
для изгибаемых элементов
но принимается не менее 0,7 и не более единицы.
Здесь σb - максимальное напряжение в сжатом бетоне от внешней нагрузки и температурных усилий, вычисляемое как для упругого тела по приведенному сечению;
Wred и Wpl - см. соответственно пп. 4.5 и 4.6.
Коэффициент α определяется по формуле (189), в которой коэффициенты βb и βs принимаются соответственно по табл. 16 и 35 в зависимости от температуры на уровне центра тяжести арматуры;
Ared - приведенная площадь нагретого элемента, определяется по формуле (6);
Mcrc - определяется по формуле
Mcrc = (Rbt,serγtt ± σbtt)Wpl, (256)
где σbtt - напряжения в бетоне на уровне растянутой арматуры, вызванные воздействием температуры, определяемые по формуле (32). Напряжения σbtt, принимаются со знаком «плюс» при сжатии и со знаком «минус» - при растяжении.
Допускается напряжения σbtt, вызванные воздействием температуры, не учитывать, если их учет увеличивает трещиностойкость сечения. Если σbtt > Rbt,serγtt, то в формуле (256) принимается σbtt = Rbt,serγtt.
При проверке возможности исчерпания несущей способности одновременно с образованием трещин (см. п. 1.20) усилие, воспринимаемое сечением при образовании трещин, определяется по формуле (256) с заменой значения Rbt,ser на 1,2Rbt,serγtt.
Расчет центрально растянутых элементов по образованию трещин производится из условия
N ≤ Rbt,serγttAred, (257)
Ared - определяется по формуле (6).
4.5. Момент сопротивления приведенного сечения элемента для крайнего растянутого волокна определяется по правилам сопротивления упругих материалов в предположении отсутствия продольных сил по формуле
где Ired - момент инерции приведенного сечения, определяемый по
формуле (11) как для упругого
материала, принимая ![]() = φb1 = 1. Расстояние от центра тяжести
приведенного сечения до крайнего растянутого волокна определяется по формуле (5).
= φb1 = 1. Расстояние от центра тяжести
приведенного сечения до крайнего растянутого волокна определяется по формуле (5).
4.6 (4.4). Момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций бетона при воздействии температуры определяется по формуле
Wpl = [0,292 + 0,75(γ1 + 2μ1α) + 0,075(γ′1 + 2μ′1α′)]bh2, (259)
где
μ1 = As / bh; (262)
μ′1 = A′s / bh. (263)
Здесь α - определяется по формуле (189), в которой коэффициент βs принимается по табл. 35 в зависимости от температуры растянутой и сжатой арматуры и коэффициент βb принимается по табл. 16 в зависимости от температуры бетона на уровне соответствующей арматуры.
Допускается при определении Wpl по формуле (259) принимать As = А′s = 0, если μ < 1,0 %.
Разрешается величину Wpl также определять по приближенной формуле
Wpl = γWred, (264)
где Wred - см. п. 4.5;
γ - коэффициент, принимаемый по табл. 49.
Таблица 49
|
Значение коэффициента γ для определения момента сопротивления Wpl |
|
|
1. Прямоугольное и тавровое с полкой, расположенной в сжатой зоне |
1,75 |
|
2. Тавровое с полкой, расположенной в растянутой зоне: |
|
|
при |
1,75 |
|
при |
1,75 |
|
при |
1,50 |
|
3. Двутавровое симметричное (коробчатое): |
|
|
при |
1,75 |
|
при 2 < |
1,50 |
|
при |
1,50 |
|
при 6 < |
1,25 |
|
4. Кольцевое и круглое |
|
Примечание. В таблице обозначения bf и hf соответствуют размерам полки, которая при расчете по образованию трещин является растянутой, a b′f и h′f - размерам полки, которая для этого случая расчета является сжатой.
При расчете элементов
с повышенной толщиной защитного слоя бетона растянутой арматуры ![]() , коэффициент
μ1 в формуле (259) умножается на величину 1
- 2δ.
, коэффициент
μ1 в формуле (259) умножается на величину 1
- 2δ.
4.7. Расчет железобетонных элементов по образованию трещин при воздействии температуры и многократно повторяющейся нагрузки производится из условия
σbt ≤ γb1γb1tRbt,ser, (265)
Максимальное нормальное растягивающее напряжение в бетоне, вызванное нагрузкой, должно суммироваться с растягивающим напряжением от воздействия температуры, определяемым по формуле (32). Коэффициенты условий работы γb1 и γb1t принимаются соответственно по табл. 22 и 23 в зависимости от температуры бетона на уровне арматуры.
Расчет по образованию трещин, наклонных к продольной оси элемента
4.8. Расчет по образованию трещин, наклонных к продольной оси элемента, при воздействии температуры производится из условия
σmt ≤ γb4Rbt,ser, (266)
где γb4 - коэффициент условий работы бетона (см. табл. 15), определяемый по формуле
![]() , но
не более 1,0;
, но
не более 1,0;
здесь α - коэффициент, принимаемый для бетонов составов (см. табл. 11):
№ 1 - 3, 6, 7, 10 - 15, 19 - 21................................................ 0,01
№ 4, 5, 8, 9, 16 - 18, 23, 24, 29 и 30.................................... 0,02
В - класс бетона по прочности на сжатие, МПа. Значение αВ следует принимать не менее 0,3. Значения главных растягивающих σmt и главных сжимающих σmc напряжений в бетоне определяются по формуле (143) СНиП 2.03.01-84.
При этом расчетные сопротивления бетона Rb,ser и Rbt,ser должны дополнительно умножаться на коэффициенты условий работы бетона соответственно γbt и γtt, принимаемые по табл. 16:
для прямоугольных элементов - в зависимости от температуры бетона центра тяжести приведенного сечения;
для элементов двутаврового и таврового сечений - в зависимости от температуры бетона в плоскости примыкания сжатых (более нагретых) полок к стенке.
4.9. При действии многократно повторяющейся нагрузки в условиях воздействия температуры расчет по образованию трещин, наклонных к продольной оси элемента, должен производиться согласно указаниям п. 4.8, при этом расчетные сопротивления бетона Rbt,ser и Rb,ser вводятся в расчет с коэффициентами условий работы γb1 и γb1t, принимаемыми по табл. 22 и 23.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
Расчет по раскрытию трещин, нормальных к продольной оси элемента
4.10 (4.8). Ширину раскрытия трещин, нормальных к продольной оси элемента, acrc, мм, при воздействии повышенных и высоких температур следует определять по формуле
после воздействия повышенных и высоких температур (в охлажденном состоянии)
δ - коэффициент, принимаемый равным: для изгибаемых и внецентренно сжатых элементов - 1; для растянутых элементов - 1,2;
η - коэффициент, принимаемый равным:
при стержневой арматуре:
периодического профиля 1,0
гладкой 1,3
при проволочной арматуре:
периодического профиля и канатах 1,2
гладкой 1,4
μ - коэффициент армирования сечения, принимаемый равным отношению площади сечения арматуры S к площади сечения бетона (при рабочей высоте h0 и без учета сжатых свесов полок), но не более 0,02;
φl - коэффициент, принимаемый равным при учете:
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок 1,00
многократно повторяющейся нагрузки, а также продолжительного действия постоянных и длительных нагрузок для конструкций из бетона составов (см. табл. 11):
№ 1 - 3, 6, 7, 13, 20, 21 естественной влажности φl = 1,60 - 15μ (269)
№ 4, 5, 8 - 12, 14 - 19, 23, 24, 29, 30......................................... 1,50
при попеременном водонасыщении и высушивании.......... 1,75
σs - напряжение в стержнях крайнего ряда арматуры S, определяемое согласно указаниям п. 4.11;
d - диаметр арматуры, мм;
βs и vs - коэффициенты, определяемые по табл. 35 и 38;
αstm - определяется по формуле (74) в зависимости от длительности нагрева;
αbt и αcs - принимаются по табл. 20 и 21 в зависимости от температуры бетона на уровне арматуры и длительности нагрева.
Дополнительное раскрытие трещин, вызванное разностью температурных деформаций бетона и арматуры, а также усадкой бетона [второй член в квадратных скобках формул (267) и (268)] допускается не учитывать: для железобетонных элементов из обычного бетона при температуре арматуры до 60 °С и из жаростойкого бетона при температуре арматуры до 50 °С.
Для элементов, к трещиностойкости которых предъявляются требования 2-й категории, ширина раскрытия трещин определяется от суммарного действия постоянных, длительных и кратковременных нагрузок, а также от действия кратковременного нагрева при коэффициенте φl = 1,0.
Для элементов, к трещиностойкости которых предъявляются требования 3-й категории, ширина продолжительного раскрытия трещин определяется от действия постоянных и длительных нагрузок и длительного нагрева при коэффициенте φl > 1,0. Ширина непродолжительного раскрытия трещин определяется как сумма ширины продолжительного раскрытия и приращения ширины раскрытия от действия кратковременных нагрузок и нагрева, определяемых при коэффициенте φl = 1,0.
Ширина раскрытия трещин, определенная по формулам (267) и (268), корректируется в следующих случаях:
а) если центр тяжести площади сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых, внецентренно растянутых при e0 ³ 0,8h0 элементов отстоит от наиболее растянутого волокна на расстоянии a2 > 0,2h, значение acrc должно быть увеличено путем умножения на коэффициент δa, равный
![]() (270)
(270)
и принимаемый не более 3;
б) для элементов из легкого жаростойкого бетона класса В7,5 и ниже значение acrc должно быть увеличено на 20 %.
4.11. Напряжения в растянутой арматуре σs должны определяться по формулам:
для центрально растянутых элементов
σs = N / As; (271)
для изгибаемых элементов
σs = M / Asz; (272)
для внецентренно сжатых, а также внецентренно растянутых при e0 ≥ 0,8h0 элементов
Для внецентренно растянутых элементов при e0 < 0,8h0 величина σs определяется по формуле (273), принимая z = zs (zs - расстояние между центрами тяжести арматуры S и S′).
В формуле (273) знак «плюс» принимается при внецентренном растяжении, а знак «минус» - при внецентренном сжатии. При расположении растягивающей продольной силы N между центрами тяжести арматуры S и S′ значение es принимается со знаком «минус».
z - расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной, определяемое согласно указаниям п. 4.20.
При расположении растянутой арматуры в несколько рядов по высоте сечения в изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементах при e0 ≥ 0,8h0 напряжения σs, подсчитанные по формулам (272) и (273), должны умножаться на коэффициент δn, равный
![]() , (274)
, (274)
где x = ξh0; значение ξ определяется по формуле (283);
a1 и a2 - расстояния от центра тяжести площади сечения соответственно всей арматуры S и крайнего ряда стержней до наиболее растянутого волокна бетона.
Значение σs не должно превышать Rst,ser.
Для изгибаемых элементов допускается определять σs по формуле
![]() . (275)
. (275)
Здесь Mu - предельный момент по прочности, равный правой части неравенств (105), (107), (108), (120), (121) и (123).
При подборе сечения арматуры
![]() , (276)
, (276)
Ms - момент от действия полной нагрузки с коэффициентом надежности по нагрузке γf > 1;
As,fact - фактическая площадь принятой арматуры;
Asd - площадь арматуры, требуемая по расчету прочности.
Расчет по раскрытию трещин, наклонных к продольной оси элемента
4.12 (4.9). Ширина раскрытия трещин, наклонных к продольной оси элементов, при воздействии повышенных и высоких температур при армировании хомутами, нормальными к продольной оси, должна определяться по формуле
где φl - коэффициент, принимаемый равным при учете:
кратковременного нагрева, кратковременных нагрузок, кратковременного нагрева и непродолжительного действия постоянных и длительных нагрузок 1,00;
многократно повторяющейся нагрузки, а также длительного нагрева, продолжительного действия постоянных и длительных нагрузок для конструкций из бетонов составов (по табл. 11):
№ 1 - 3, 6, 7, 13, 20 и 21 естественной влажности......... 1,50
№ 4, 5, 8 - 12, 14 - 19, 23, 24, 29 и 30............................... 1,50
при попеременном водонасыщении и высушивании.................................... 1,75
η - то же, что и в формуле (267);
α и μw - определяются по формулам (189) и (190), принимая коэффициенты βb и βs, соответственно по табл. 16 и 35 в зависимости от средней температуры поперечной арматуры;
dv - диаметр хомутов;
tw - температура посередине длины хомута;
αst, αbt - принимаются для арматуры хомутов по температуре середины их высоты.
Напряжение в хомутах определяется по формуле
Значение напряжений σsw, не должно превышать Rst,ser.
Здесь Q и Qb1 - соответственно левая и правая части условия (212) при замене Rbtt на Rbtt,ser; расчетные сопротивления Rbtt,ser и Rb,tem,ser не должны превышать значений, соответствующих бетону класса В30;
s - расстояние между хомутами.
При определении ширины непродолжительного и продолжительного раскрытия наклонных трещин должны учитываться указания п. 4.10 об учете длительности действия нагрузок и нагрева.
4.13. Расчет железобетонных элементов по закрытию трещин при температурном воздействии производится согласно указаниям пп. 4.18 - 4.21 СНиП 2.03.01-84, принимая расчетное сопротивление арматуры Rst,ser.
РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
4.14. Деформации (прогибы, углы поворота) элементов железобетонных конструкций, подверженных воздействию повышенных и высоких температур, должны вычисляться по формулам строительной механики, определяя входящие в них величины кривизны в соответствии с указаниями пп. 4.15 - 4.22.
4.15. Величина кривизны определяется:
а) для участков элемента, где в растянутой зоне не образуются трещины, нормальные к продольной оси элемента - как для сплошного тела;
б) для участков элемента, где в растянутой зоне имеются трещины, нормальные к продольной оси, вызванные нагрузкой и воздействием температуры - как отношение разности средних деформаций крайнего волокна сжатой зоны бетона и продольной растянутой арматуры к рабочей высоте сечения элемента.
Элементы или участки элементов рассматриваются без трещин в растянутой зоне, если трещины не образуются при действии постоянных, длительных и кратковременных нагрузок, длительного и кратковременного нагрева или если они закрыты при действии постоянных и длительных нагрузок; при этом нагрузки вводятся в расчет с коэффициентом надежности по нагрузке γf = 1, а усилия, вызванные воздействием температуры - с коэффициентом надежности по температуре γt = 1.
Определение кривизны железобетонных элементов на участках без трещин в растянутой зоне
4.16 (4.12). На участках, где не образуются нормальные к продольной оси трещины, полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов должна определяться по формуле
![]() и
и ![]() - кривизны соответственно от кратковременных нагрузок при кратковременном нагреве (определяемых
согласно указаниям п. 1.16) и от постоянных и длительных временных нагрузок
при длительном нагреве, определяемые по формулам
- кривизны соответственно от кратковременных нагрузок при кратковременном нагреве (определяемых
согласно указаниям п. 1.16) и от постоянных и длительных временных нагрузок
при длительном нагреве, определяемые по формулам
здесь M - момент соответственно от внешней нагрузки и нагрева (кратковременных и длительных) относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного сечения;
φb1 - коэффициент, учитывающий влияние кратковременной ползучести бетона, принимаемый согласно указаниям п. 1.28;
φb2 - коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин и принимаемый по табл. 50;
Ired - момент инерции приведенного сечения, определяют по указаниям п. 1.28, принимая в формуле (1) значения ![]() для
кратковременного нагрева по табл. 18
в зависимости от скорости подъема температуры и для длительного нагрева - как
при кратковременном нагреве с подъемом температуры на 10 °С/ч и более.
для
кратковременного нагрева по табл. 18
в зависимости от скорости подъема температуры и для длительного нагрева - как
при кратковременном нагреве с подъемом температуры на 10 °С/ч и более.
4.17. При определении кривизны участков элементов с начальными трещинами в
сжатой зоне, вызванными воздействием температуры, величины ![]() и
и ![]() , определяемые по формулам (280) и (281), должны быть увеличены на
15 %.
, определяемые по формулам (280) и (281), должны быть увеличены на
15 %.
Таблица 50
|
Коэффициент φb2, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин, при средней температуре бетона сжатой зоны сечения, °С |
||||||||||
|
50 |
70 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
|
|
1 - 3 |
3,0 |
4,0 |
3,5 |
4,0 |
- |
- |
- |
- |
- |
- |
|
4 - 11, 23, 24 |
3,0 |
4,0 |
3,5 |
3,5 |
3,5 |
5,0 |
7,0 |
8,0 |
10,0 |
- |
|
12 - 18, 29, 30 |
3,5 |
4,5 |
4,0 |
4,0 |
8,0 |
11,0 |
15,0 |
20,0 |
- |
- |
|
19 - 21 |
3,0 |
3,0 |
3,0 |
3,0 |
3,5 |
7,0 |
10,0 |
13,0 |
16,0 |
20,0 |
Примечания: 1. В таблице даны значения коэффициента φb2 для длительного нагрева.
2. Для кратковременного нагрева при подъеме температуры на 10 °С/ч и более и непродолжительном действии нагрузки коэффициент φb2 = 1,0.
3. Значение коэффициента φb2 для промежуточных температур принимается по интерполяции.
4. При наличии в элементе сжатой арматуры с μ′ ≥ 0,7 % значение коэффициента φb2 умножается на (1 - 0,11μ′), но не менее, чем на 0,6.
5. При двухосном напряженном состоянии значение коэффициента φb2 умножается на 0,8.
6. При попеременном увлажнении значение φb2 следует умножать на 1,2.
4.18. На участках, где образуются нормальные трещины в
растянутой зоне, но при действии рассматриваемой нагрузки обеспечено их
закрытие, значения кривизн ![]() и
и ![]() , входящие в формулу (279), увеличиваются на 20 %.
, входящие в формулу (279), увеличиваются на 20 %.
Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне
4.19. На участках, где в растянутой зоне образуются нормальные к продольной оси нагретого элемента трещины, кривизны изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементов прямоугольного, таврового и двутаврового (коробчатого) сечений при e0 ≥ 0,8h0 должны определяться по формуле
Для изгибаемых элементов последнее слагаемое правой части формулы (282) принимается равным нулю.
В формуле (282):
Ms - момент (заменяющий) относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести площади сечения арматуры S от всех внешних сил и усилий, вызванных воздействием температуры, расположенных по одну сторону от рассматриваемого сечения:
для изгибаемых элементов.................................................... Ms = M
для внецентренно сжатых и внецентренно растянутых элементов Ms = Nes
z - расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной (плечо внутренней пары сил), определяемое по указаниям п. 4.20;
ψs - коэффициент, учитывающий работу растянутого бетона на участке с трещинами и определяемый по указаниям п. 4.21;
ψb - коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами и принимаемый равным:
для обычного и жаростойкого бетонов классов выше В7,5....... 0,9
для жаростойкого бетона классов В7,5 и ниже............................ 0,7
для конструкций, рассчитываемых на действие многократно повторяющейся нагрузки, независимо от вида и класса бетона 1,0
φf - коэффициент, определяемый по формуле (286);
ξ - относительная высота сжатой зоны бетона, определяемая согласно указаниям п. 4.20;
βs - коэффициент, принимаемый по табл. 35 в зависимости от температуры растянутой арматуры;
βb - коэффициент, принимаемый по табл. 16 в зависимости от средней температуры бетона сжатой зоны;
vs - коэффициент, характеризующий упругопластическое состояние растянутой арматуры и принимаемый по табл. 38 в зависимости от температуры арматуры;
v - коэффициент, характеризующий упруго-пластическое состояние бетона сжатой зоны и принимаемый по табл. 19 для средней температуры бетона сжатой зоны;
N - продольная сила (при внецентренном растяжении сила N принимается со знаком «минус»).
Среднюю температуру бетона сжатой зоны сечения допускается принимать:
для прямоугольных сечений - по температуре бетона на расстоянии 0,2h0 от края сжатой грани сечения;
для тавровых и двутавровых сечений - по средней температуре бетона сжатой полки.
4.20. Значение ξ вычисляется по формуле
но принимается не более 1. При этом es/h0 принимается не менее 0,5.
Для второго слагаемого правой части формулы (283) верхние знаки принимаются при сжимающем, а нижние - при растягивающем усилии N (см. п. 4.19). Для изгибаемых элементов последнее слагаемое правой части формулы (283) принимается равным нулю.
В формуле (283):
![]() ; (284)
; (284)
es - эксцентриситет силы N относительно центра тяжести площади сечения арматуры S, соответствует заменяющему моменту Ms (см. п. 4.19) и определяется по формуле
Величина z вычисляется по формуле
Для внецентренно сжатых элементов величина z должна приниматься не более 0,97es.
Для элементов прямоугольного сечения и таврового с полкой в растянутой зоне в формулы (285), (286) и (288) вместо величины h′f подставляется величина 2a′ или h′f = 0 соответственно при наличии или отсутствии арматуры S′.
Расчет сечений, имеющих полку в сжатой зоне, при ![]() производится
как прямоугольных шириной b′f.
производится
как прямоугольных шириной b′f.
Расчетная ширина полки b′f определяется согласно указаниям п. 3.26.
Коэффициент γbt в формуле (284) определяется по табл. 16 в зависимости от средней температуры бетона сжатой зоны.
Коэффициент v, характеризующий упруго-пластическое состояние бетона сжатой зоны, принимается по табл. 19 в зависимости от температуры бетона на уровне сжатой арматуры.
Коэффициент α в формулах (283) и (286) определяется по формуле (189), принимая коэффициент βs по табл. 16 в зависимости от средней температуры сжатой зоны (см. п. 4.19) и коэффициент βs - по табл. 35 в зависимости от температуры растянутой арматуры в формуле (283) и сжатой арматуры в формуле (286).
4.21. Коэффициент ψs для элементов из обычного и жаростойкого бетонов определяется по формуле
но не более 1, при этом es / h0 принимается не менее 1,2/φls.
Для изгибаемых элементов последний член в правой части формулы (289) принимается равным нулю.
В формуле (289):
φls - коэффициент, учитывающий влияние длительности действия нагрузки и нагрева и принимаемый по табл. 51.
es - см. формулу (287);
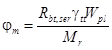 , (290)
, (290)
но не более 1.
Здесь
Wpl - см. формулу (259) или (264);
Mr - см. п. 4.4, при этом за положительные принимаются моменты, вызывающие растяжение в арматуре S.
Для конструкций, рассчитываемых на выносливость, значение коэффициента ψs принимается во всех случаях равным 1.
Таблица 51
|
Длительность действия нагрузки и нагрева и вид продольной арматуры |
Коэффициент φls при классе бетона |
|
|
свыше В7,5 |
В7,5 и ниже |
|
|
Непродолжительное действие при арматуре: |
||
|
а) стержневой гладкой |
1,0 |
0,7 |
|
б) стержневой периодического профиля |
1,1 |
0,8 |
|
в) проволочной |
1,0 |
0,7 |
|
2. Продолжительное действие (независимо от вида арматуры) |
0,8 |
0,6 |
4.22. Полное значение кривизны ![]() для участка с трещинами в растянутой зоне должно определяться по
формуле
для участка с трещинами в растянутой зоне должно определяться по
формуле
где ![]() - кривизна от
непродолжительного
действия всей нагрузки и кратковременного
нагрева, на которую производится расчет по деформациям;
- кривизна от
непродолжительного
действия всей нагрузки и кратковременного
нагрева, на которую производится расчет по деформациям;
![]() - кривизна от
непродолжительного действия постоянных и длительных
нагрузок;
- кривизна от
непродолжительного действия постоянных и длительных
нагрузок;
![]() - кривизна от продолжительного действия постоянных и длительных нагрузок
и длительного нагрева.
- кривизна от продолжительного действия постоянных и длительных нагрузок
и длительного нагрева.
Кривизны ![]() ,
, ![]() и
и ![]() определяются по формуле (282), при этом значения
определяются по формуле (282), при этом значения ![]() и
и ![]() вычисляются при
значениях ψs и
v, отвечающих непродолжительному действию нагрева и
нагрузки, а
кривизна
вычисляются при
значениях ψs и
v, отвечающих непродолжительному действию нагрева и
нагрузки, а
кривизна ![]() -
при значениях ψs и v, отвечающих продолжительному
действию нагрузки и нагрева. Если значения
-
при значениях ψs и v, отвечающих продолжительному
действию нагрузки и нагрева. Если значения ![]() и
и ![]() оказываются
отрицательными, то они принимаются равными нулю.
оказываются
отрицательными, то они принимаются равными нулю.
Определение прогибов
4.23. Полный прогиб изгибаемых элементов ftot равен сумме прогибов, обусловленных: деформацией изгиба fm, определяемой согласно указаниям п. 4.24; деформацией от воздействия температуры ft, принимаемой в соответствии с указаниями
п. 4.26; деформацией сдвига fq, учитываемой для изгибаемых элементов при
![]() согласно
указаниям п. 4.25.
согласно
указаниям п. 4.25.
Прогиб ft допускается не учитывать, если он приводит к уменьшению полного прогиба элемента.
4.24. Прогиб fm, обусловленный деформацией изгиба, определяется по формуле
где ![]() - изгибающий
момент в
сечении x от действия единичной силы,
приложенной по направлению искомого перемещения элемента в сечении x по длине пролета, для которого определяется прогиб;
- изгибающий
момент в
сечении x от действия единичной силы,
приложенной по направлению искомого перемещения элемента в сечении x по длине пролета, для которого определяется прогиб;
![]() - полная кривизна элемента в сечении x от нагрузки и усилий, вызванных температурой,
при которой определяется прогиб; значения
- полная кривизна элемента в сечении x от нагрузки и усилий, вызванных температурой,
при которой определяется прогиб; значения ![]() определяются по формулам (279) и
(291) соответственно для участков без
трещин и с трещинами; знак
определяются по формулам (279) и
(291) соответственно для участков без
трещин и с трещинами; знак ![]() принимается в соответствии с эпюрой
кривизны.
принимается в соответствии с эпюрой
кривизны.
Для изгибаемых элементов постоянного сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента (черт. 29).
Черт. 29. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения
а - схема расположения нагрузки; б - эпюра изгибающих моментов; в - эпюра кривизны
4.25. Для изгибаемых элементов при ![]() необходимо
учитывать
влияние поперечных сил на их прогиб. В этом
случае прогиб fq, обусловленный деформацией сдвига, определяется по формуле
необходимо
учитывать
влияние поперечных сил на их прогиб. В этом
случае прогиб fq, обусловленный деформацией сдвига, определяется по формуле
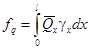 , (293)
, (293)
где ![]() - поперечная
сила в сечении x от действия по направлению искомого перемещения единичной силы, приложенной в сечении, где
определяется прогиб;
- поперечная
сила в сечении x от действия по направлению искомого перемещения единичной силы, приложенной в сечении, где
определяется прогиб;
γx - деформация сдвига, определяемая по формуле
![]() , (294)
, (294)
здесь Qx - поперечная сила в сечении x от действия внешней нагрузки;
G - модуль сдвига бетона (см. п. 2.12);
βb - коэффициент, определяемый по табл. 16 в зависимости от температуры бетона в центре тяжести сечения;
φcrc - коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:
на участках по длине элемента, где отсутствуют нормальные и наклонные к продольной оси элемента трещины, - 1,0;
на участках, где имеются только наклонные к продольной оси элемента трещины, - 4,8;
на участках, где имеются только нормальные или нормальные и наклонные к продольной оси элемента трещины, - по формуле
В формуле (295):
Mx - соответственно момент от внешней нагрузки и усилий, вызванных температурой;
![]() - см. формулу (292);
- см. формулу (292);
Ired - приведенный момент инерции сечения, определяемый согласно указаниям п. 1.28;
φb2 - коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента при нагреве, принимаемый по табл. 50.
4.26 (4.16). Прогиб ft, обусловленный деформациями от неравномерного нагрева бетона по высоте сечения элемента, определяется по формуле
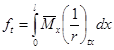 , (296)
, (296)
где ![]() - кривизна элемента в сечении x от воздействия температуры с учетом наличия в данном сечении
трещин, вызванных усилиями от действия нагрузки или температуры, определяется согласно указаниям пп. 1.40 и 1.43;
- кривизна элемента в сечении x от воздействия температуры с учетом наличия в данном сечении
трещин, вызванных усилиями от действия нагрузки или температуры, определяется согласно указаниям пп. 1.40 и 1.43;
![]() - см. п. 4.24.
- см. п. 4.24.
При расчете свободно опертой или консольной балки постоянной высоты с одинаковым распределением температуры бетона по высоте сечения на всей длине балки прогиб, вызванный воздействием температуры, определяют по формуле
где ![]() - кривизна от воздействия температуры, определяется согласно указаниям пп. 1.40 и 1.43;
- кривизна от воздействия температуры, определяется согласно указаниям пп. 1.40 и 1.43;
s - коэффициент, принимаемый равным для свободно опертых балок 1/8 и для консольных - 1/2.
Прогибы сборных элементов конструкций из жаростойкого бетона, имеющих одностороннее армирование и сварные стыки арматуры в растянутой зоне сечения, определяются с учетом повышенной деформативности стыков. При этом кривизна элемента в пределах стыка, определенная как для целого элемента, увеличивается в 5 раз при заполнении шва раствором после сварки стыковых накладок и в 50 раз при заполнении шва до сварки, осуществляемой с учетом заданной последовательности сварки, указанной в п. 5.44.
4.27. Для сплошных плит толщиной менее 25 см (кроме опертых по
контуру), армированных плоскими сетками, с
трещинами в растянутой зоне значения прогибов,
подсчитанные по формуле (292), умножаются на коэффициент 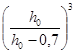 , принимаемый не более 1,5, где h0 - в см.
, принимаемый не более 1,5, где h0 - в см.
Определение жесткости сечений элементов
4.28 (4.17). На участках, где не образуются нормальные к продольной оси элемента трещины, жесткость изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяется по формуле
Величины Ired, φb1 и φb2 принимаются согласно указаниям п. 4.16.
4.29 (4.18). На участках, где образуются нормальные к продольной оси элемента трещины в растянутой зоне, жесткость определяется:
для изгибаемых элементов по формуле
для внецентренно сжатых и внецентренно растянутых при e0 ≥ 0,8h0 и приложении продольной силы в центре тяжести приведенного сечения элементов по формуле
где
![]() . (301)
. (301)
В формуле (300) знак «минус» перед z принимается при внецентренном сжатии, «плюс» - при внецентренном растяжении.
Величины, входящие в формулы (299) и (300), определяются согласно указаниям пп. 4.19 - 4.21.
Для внецентренно растянутых элементов при e0 < 0,8h0 принимается e0 = 0,8h0.
Приближенный метод расчета деформаций и жесткости элементов
4.30. Для изгибаемых элементов постоянного сечения из участках, где образуются нормальные к продольной оси элемента трещины в растянутой зоне, допускается кривизну определять по формуле
где φ1
и φ2 - коэффициенты, зависящие от формы сечения, значения ![]() и длительности действия
температуры и нагрузки, определяемые по табл. 52, в которой значения коэффициентов определяются:
и длительности действия
температуры и нагрузки, определяемые по табл. 52, в которой значения коэффициентов определяются:
φf - по формуле (286);
γ1 - по формуле (260), где вместо h принимается h0.
Значения коэффициентов βs, vs, βb принимаются согласно указаниям п. 4.19.
Таблица 52
|
γ1 |
φf |
Коэффициент φ1
при значениях |
Коэффициент φ2 при значениях |
||||||||||||||||||||||
|
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,10 |
0,13 |
0,15 |
0,17 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
< 0,04 |
0,04 - <0,08 |
0,08 - <0,15 |
0,15 - <0,30 |
0,30 - 0,50 |
|||
|
Длительные |
0,0 |
0,0 |
0,43 |
0,39 |
0,36 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,23 |
0,22 |
0,21 |
0,19 |
0,16 |
0,14 |
0,13 |
0,12 |
0,11 |
0,10 |
0,10 |
0,07 |
0,04 |
0,00 |
0,00 |
|
0,0 |
0,2 |
0,49 |
0,46 |
0,44 |
0,42 |
0,41 |
0,39 |
0,37 |
0,35 |
0,31 |
0,29 |
0,27 |
0,25 |
0,21 |
0,19 |
0,17 |
0,16 |
0,14 |
0,13 |
0,12 |
0,09 |
0,05 |
0,00 |
0,00 |
|
|
0,0 |
0,4 |
0,52 |
0,49 |
0,47 |
0,46 |
0,45 |
0,44 |
0,42 |
0,40 |
0,38 |
0,35 |
0,33 |
0,31 |
0,26 |
0,24 |
0,22 |
0,20 |
0,18 |
0,17 |
0,13 |
0,10 |
0,06 |
0,02 |
0,00 |
|
|
0,0 |
0,6 |
0,54 |
0,51 |
0,49 |
0,48 |
0,47 |
0,46 |
0,44 |
0,43 |
0,42 |
0,39 |
0,37 |
0,35 |
0,31 |
0,28 |
0,25 |
0,23 |
0,22 |
0,20 |
0,13 |
0,11 |
0,08 |
0,02 |
0,00 |
|
|
0,0 |
0,8 |
0,56 |
0,53 |
0,51 |
0,49 |
0,48 |
0,47 |
0,46 |
0,45 |
0,44 |
0,42 |
0,40 |
0,38 |
0,35 |
0,32 |
0,29 |
0,27 |
0,25 |
0,23 |
0,14 |
0,12 |
0,09 |
0,04 |
0,00 |
|
|
0,0 |
1,0 |
0,57 |
0,54 |
0,52 |
0,51 |
0,50 |
0,49 |
0,48 |
0,47 |
0,46 |
0,44 |
0,42 |
0,41 |
0,38 |
0,35 |
0,32 |
0,30 |
0,28 |
0,26 |
0,15 |
0,13 |
0,10 |
0,06 |
0,00 |
|
|
0,2 |
0,0 |
0,47 |
0,40 |
0,36 |
0,33 |
0,31 |
0,30 |
0,28 |
0,26 |
0,23 |
0,22 |
0,21 |
0,19 |
0,16 |
0,14 |
0,13 |
0,11 |
0,11 |
0,10 |
0,15 |
0,12 |
0,08 |
0,03 |
0,00 |
|
|
0,4 |
0,0 |
- |
0,42 |
0,36 |
0,33 |
0,31 |
0,30 |
0,28 |
0,26 |
0,22 |
0,21 |
0,20 |
0,19 |
0,16 |
0,14 |
0,13 |
0,11 |
0,10 |
0,10 |
0,18 |
0,16 |
0,13 |
0,06 |
0,02 |
|
|
0,6 |
0,0 |
- |
0,43 |
0,37 |
0,33 |
0,31 |
0,30 |
0,27 |
0,25 |
0,22 |
0,21 |
0,20 |
0,18 |
0,15 |
0,14 |
0,12 |
0,11 |
0,10 |
0,10 |
0,20 |
0,19 |
0,17 |
0,09 |
0,03 |
|
|
0,8 |
0,0 |
- |
- |
0,38 |
0,33 |
0,30 |
0,29 |
0,27 |
0,24 |
0,22 |
0,21 |
0,20 |
0,17 |
0,15 |
0,14 |
0,12 |
0,11 |
0,10 |
0,10 |
0,23 |
0,22 |
0,20 |
0,12 |
0,05 |
|
|
1,0 |
0,0 |
- |
- |
0,4 |
0,33 |
0,30 |
0,29 |
0,27 |
0,24 |
0,22 |
0,20 |
0,19 |
0,17 |
0,15 |
0,14 |
0,12 |
0,11 |
0,10 |
0,10 |
0,25 |
0,24 |
0,23 |
0,14 |
0,06 |
|
|
0,2 |
0,2 |
0,51 |
0,45 |
0,43 |
0,40 |
0,38 |
0,37 |
0,36 |
0,34 |
0,30 |
0,28 |
0,26 |
0,24 |
0,21 |
0,19 |
0,17 |
0,16 |
0,14 |
0,13 |
0,16 |
0,13 |
0,08 |
0,04 |
0,00 |
|
|
0,4 |
0,4 |
- |
0,53 |
0,49 |
0,47 |
0,45 |
0,43 |
0,42 |
0,39 |
0,37 |
0,35 |
0,33 |
0,30 |
0,26 |
0,23 |
0,21 |
0,20 |
0,18 |
0,17 |
0,20 |
0,19 |
0,14 |
0,07 |
0,03 |
|
|
0,6 |
0,6 |
- |
- |
0,53 |
0,50 |
0,48 |
0,46 |
0,44 |
0,41 |
0,39 |
0,38 |
0,36 |
0,34 |
0,31 |
0,28 |
0,25 |
0,23 |
0,21 |
0,20 |
0,24 |
0,22 |
0,20 |
0,12 |
0,04 |
|
|
0,8 |
0,8 |
- |
- |
- |
0,53 |
0,30 |
0,48 |
0,46 |
0,44 |
0,41 |
0,39 |
0,38 |
0,37 |
0,34 |
0,31 |
0,29 |
0,26 |
0,25 |
0,23 |
- |
0,25 |
0,24 |
0,19 |
0,08 |
|
|
1,0 |
1,0 |
- |
- |
- |
0,61 |
0,53 |
0,50 |
0,48 |
0,45 |
0,43 |
0,40 |
0,39 |
0,38 |
0,36 |
0,34 |
0,32 |
0,29 |
0,27 |
0,26 |
- |
0,26 |
0,25 |
0,20 |
0,12 |
|
|
Кратковременные |
0,0 |
0,0 |
0,64 |
0,59 |
0,56 |
0,53 |
0,51 |
0,50 |
0,49 |
0,46 |
0,43 |
0,41 |
0,40 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
0,17 |
0,14 |
0,09 |
0,02 |
0,00 |
|
0,0 |
0,2 |
0,72 |
0,66 |
0,63 |
0,61 |
0,59 |
0,58 |
0,57 |
0,56 |
0,53 |
0,51 |
0,49 |
0,46 |
0,43 |
0,40 |
0,37 |
0,35 |
0,33 |
0,31 |
0,21 |
0,18 |
0,11 |
0,03 |
0,00 |
|
|
0,0 |
0,4 |
0,76 |
0,69 |
0,66 |
0,65 |
0,63 |
0,62 |
0,61 |
0,60 |
0,59 |
0,57 |
0,56 |
0,53 |
0,49 |
0,46 |
0,44 |
0,41 |
0,39 |
0,37 |
0,23 |
0,20 |
0,14 |
0,04 |
0,00 |
|
|
0,0 |
0,6 |
0,79 |
0,71 |
0,69 |
0,67 |
0,65 |
0,64 |
0,63 |
0,63 |
0,62 |
0,61 |
0,60 |
0,58 |
0,55 |
0,52 |
0,49 |
0,56 |
0,44 |
0,42 |
0,25 |
0,21 |
0,16 |
0,05 |
0,00 |
|
|
0,0 |
0,8 |
0,82 |
0,73 |
0,70 |
0,68 |
0,67 |
0,66 |
0,65 |
0,65 |
0,64 |
0,63 |
0,63 |
0,61 |
0,58 |
0,56 |
0,53 |
0,50 |
0,48 |
0,46 |
0,26 |
0,23 |
0,17 |
0,06 |
0,00 |
|
|
0,0 |
1,0 |
0,84 |
0,74 |
0,71 |
0,69 |
0,68 |
0,67 |
0,66 |
0,66 |
0,66 |
0,65 |
0,65 |
0,63 |
0,61 |
0,59 |
0,56 |
0,54 |
0,52 |
0,50 |
0,27 |
0,24 |
0,18 |
0,07 |
0,00 |
|
|
0,2 |
0,0 |
0,74 |
0,60 |
0,56 |
0,53 |
0,51 |
0,49 |
0,47 |
0,44 |
0,42 |
0,40 |
0,39 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
0,28 |
0,23 |
0,16 |
0,07 |
0,00 |
|
|
0,4 |
0,0 |
- |
0,63 |
0,57 |
0,54 |
0,51 |
0,49 |
0,47 |
0,44 |
0,42 |
0,40 |
0,39 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
0,35 |
0,31 |
0,25 |
0,14 |
0,03 |
|
|
0,6 |
0,0 |
- |
0,81 |
0,59 |
0,54 |
0,51 |
0,49 |
0,47 |
0,44 |
0,42 |
0,40 |
0,39 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
0,36 |
0,39 |
0,32 |
0,20 |
0,08 |
|
|
0,8 |
0,0 |
- |
- |
0,63 |
0,55 |
0,51 |
0,49 |
0,47 |
0,44 |
0,42 |
0,40 |
0,39 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
0,45 |
0,40 |
0,38 |
0,25 |
0,12 |
|
|
1,0 |
0,0 |
- |
- |
0,84 |
0,57 |
0,52 |
0,49 |
0,47 |
0,44 |
0,42 |
0,40 |
0,39 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,27 |
0,25 |
0,50 |
0,46 |
0,44 |
0,29 |
0,15 |
|
|
0,2 |
0,2 |
0,79 |
0,67 |
0,63 |
0,61 |
0,59 |
0,58 |
0,56 |
0,55 |
0,52 |
0,50 |
0,48 |
0,46 |
0,42 |
0,39 |
0,37 |
0,35 |
0,33 |
0,31 |
0,27 |
0,24 |
0,17 |
0,08 |
0,00 |
|
|
0,4 |
0,4 |
- |
0,77 |
0,69 |
0,66 |
0,64 |
0,62 |
0,61 |
0,58 |
0,56 |
0,55 |
0,54 |
0,52 |
0,48 |
0,45 |
0,43 |
0,40 |
0,38 |
0,37 |
0,39 |
0,37 |
0,30 |
0,16 |
0,04 |
|
|
0,6 |
0,6 |
- |
- |
0,76 |
0,70 |
0,67 |
0,65 |
0,64 |
0,61 |
0,58 |
0,57 |
0,56 |
0,55 |
0,53 |
0,50 |
0,47 |
0,45 |
0,43 |
0,41 |
0,50 |
0,46 |
0,44 |
0,28 |
0,11 |
|
|
0,8 |
0,8 |
- |
- |
- |
0,76 |
0,71 |
0,68 |
0,66 |
0,64 |
0,61 |
0,59 |
0,58 |
0,57 |
0,56 |
0,53 |
0,51 |
0,49 |
0,47 |
0,45 |
- |
0,60 |
0,57 |
0,41 |
0,21 |
|
|
1,0 |
1,0 |
- |
- |
- |
0,92 |
0,76 |
0,71 |
0,69 |
0,66 |
0,63 |
0,61 |
0,60 |
0,58 |
0,57 |
0,56 |
0,54 |
0,52 |
0,50 |
0,48 |
- |
0,72 |
0,70 |
0,55 |
0,31 |
|
Жесткость изгибаемых элементов с трещинами в растянутой зоне допускается определять приближенным методом по формуле
Жесткость внецентренно сжатых элементов с трещинами в растянутой зоне с процентом армирования μ ≥ 0,7 % и e0 ≥ 0,8h0 допускается определять приближенным методом по формуле
где φ3 - коэффициент, принимаемый по табл. 53 для кратковременного или длительного действия нагрева и нагрузки;
r - см. п. 4.4.
Остальные обозначения величин, входящие в формулы (303) и (304), те же, что и в формуле (302).
Таблица 53
|
γ1 |
φf |
Коэффициент φ3
при значениях |
||||||||||||||||||
|
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,10 |
0,13 |
0,15 |
0,17 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
|||
|
Длительные |
0,0 |
0,0 |
1,12 |
1,08 |
0,99 |
0,91 |
0,87 |
0,83 |
0,79 |
0,75 |
0,70 |
0,66 |
0,63 |
0,59 |
0,54 |
0,50 |
0,47 |
0,45 |
0,42 |
0,41 |
|
0,0 |
0,2 |
1,19 |
1,14 |
1,07 |
0,99 |
0,95 |
0,88 |
0,84 |
0,79 |
0,74 |
0,69 |
0,66 |
0,62 |
0,57 |
0,53 |
0,50 |
0,47 |
0,44 |
0,42 |
|
|
0,0 |
0,4 |
1,25 |
1,19 |
1,15 |
1,07 |
0,99 |
0,93 |
0,89 |
0,84 |
0,79 |
0,73 |
0,69 |
0,65 |
0,61 |
0,57 |
0,54 |
0,49 |
0,46 |
0,43 |
|
|
0,0 |
0,6 |
1,29 |
1,24 |
1,20 |
1,12 |
1,05 |
0,97 |
0,93 |
0,89 |
0,83 |
0,77 |
0,73 |
0,69 |
0,65 |
0,60 |
0,57 |
0,52 |
0,47 |
0,44 |
|
|
0,0 |
0,8 |
1,32 |
1,27 |
1,23 |
1,15 |
1,09 |
1,02 |
0,97 |
0,92 |
0,87 |
0,82 |
0,77 |
0,72 |
0,68 |
0,63 |
0,59 |
0,54 |
0,49 |
0,45 |
|
|
0,0 |
1,0 |
1,34 |
1,30 |
1,25 |
1,19 |
1,13 |
1,06 |
1,00 |
0,95 |
0,90 |
0,86 |
0,80 |
0,74 |
0,70 |
0,65 |
0,61 |
0,56 |
0,51 |
0,46 |
|
|
Кратковременные |
0,0 |
0,0 |
1,15 |
1,11 |
1,07 |
1,04 |
1,01 |
0,99 |
0,97 |
0,94 |
0,90 |
0,88 |
0,86 |
0,84 |
0,81 |
0,78 |
0,75 |
0,73 |
0,70 |
0,68 |
|
0,0 |
0,2 |
1,17 |
1,14 |
1,09 |
1,06 |
1,03 |
1,01 |
0,99 |
0,96 |
0,93 |
0,91 |
0,89 |
0,87 |
0,84 |
0,82 |
0,79 |
0,77 |
0,74 |
0,72 |
|
|
0,0 |
0,4 |
1,19 |
1,16 |
1,11 |
1,08 |
1,05 |
1,03 |
1,02 |
0,98 |
0,95 |
0,94 |
0,92 |
0,90 |
0,87 |
0,85 |
0,83 |
0,80 |
0,78 |
0,76 |
|
|
0,0 |
0,6 |
1,20 |
1,17 |
1,12 |
1,09 |
1,07 |
1,05 |
1,03 |
1,00 |
0,97 |
0,96 |
0,94 |
0,92 |
0,89 |
0,87 |
0,85 |
0,83 |
0,81 |
0,79 |
|
|
0,0 |
0,8 |
1,21 |
1,18 |
1,13 |
1,10 |
1,08 |
1,06 |
1,04 |
1,02 |
0,99 |
0,97 |
0,96 |
0,94 |
0,91 |
0,89 |
0,87 |
0,85 |
0,83 |
0,81 |
|
|
0,0 |
1,0 |
1,23 |
1,19 |
1,14 |
1,11 |
1,09 |
1,07 |
1,05 |
1,03 |
1,00 |
0,98 |
0,97 |
0,95 |
0,92 |
0,90 |
0,88 |
0,86 |
0,84 |
0,83 |
|
4.31. Для свободно опертых или консольных балок постоянного
сечения при ![]() прогиб от
нагрузки определяется по формуле
прогиб от
нагрузки определяется по формуле
где ![]() - кривизна в сечении с наибольшим изгибающим моментом от нагрузки,
при которой определяется прогиб;
- кривизна в сечении с наибольшим изгибающим моментом от нагрузки,
при которой определяется прогиб;
s - коэффициент, равный:
при загружении консоли:
равномерно распределенной нагрузкой........................................... 1/4
сосредоточенной силой на конце консоли...................................... 1/3
сосредоточенной силой на расстоянии a от опоры............. ![]()
при загружении свободно опертой балки:
равномерно распределенной нагрузкой.......................................... ![]()
сосредоточенной силой по середине пролета................................. ![]()
двумя сосредоточенными силами, приложенными на расстоянии a от каждой опоры ![]() .
.
5. КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
5.1. При проектировании бетонных и железобетонных конструкций, работающих в условиях воздействия повышенных и высоких температур, для обеспечения условий их изготовления, требуемой долговечности и совместной работы арматуры и бетона следует выполнять конструктивные требования, изложенные в СНиП 2.03.01-84, а также указания пп. 5.2 - 5.63.
МИНИМАЛЬНЫЕ РАЗМЕРЫ СЕЧЕНИЯ ЭЛЕМЕНТОВ
5.2. Минимальные размеры сечения бетонных и железобетонных элементов, определяемые из расчета по действующим усилиям и соответствующим группам предельных состояний, должны назначаться с учетом экономических требований, необходимости унификации опалубочных форм и армирования, а также условий принятой технологии изготовления конструкций.
Кроме того, размеры сечения элементов железобетонных конструкций должны приниматься такими, чтобы соблюдались требования по расположению арматуры в сечении (толщины защитных слоев бетона, расстояния между стержнями и т.п.) и анкеровки арматуры.
5.3 (5.2). Минимальные размеры сечений ограждающих элементов конструкций устанавливаются теплотехническим расчетом.
Толщина монолитных сводов, куполов, плит покрытий и перекрытий из тяжелого жаростойкого бетона должна приниматься не менее 60 мм, плит из легкого жаростойкого бетона - не менее 70 мм. Минимальная толщина сборных плит должна определяться из условия обеспечения требуемой толщины защитного слоя бетона и условий расположения арматуры по толщине плиты (пп. 5.4 - 5.12).
Размеры сечений внецентренно сжатых бетонных и железобетонных элементов при воздействии повышенных и высоких температур должны приниматься такими, чтобы их гибкость l0/i не превышала предельной величины, указанной в табл. 54.
Таблица 54
|
Предельная гибкость l0/i внецентренно сжатых элементов при температуре бетона в центре тяжести сечения, °С |
||||||
|
50 - 100 |
300 |
500 |
700 |
900 |
|
|
|
Бетонные |
85 |
60 |
50 |
45 |
35 |
|
|
Железобетонные |
125 |
90 |
55 |
- |
- |
|
Примечания: 1. Для железобетонных элементов с односторонним армированием предельные гибкости принимаются как для бетонных элементов.
2. Для промежуточных значений температур предельные гибкости определяются интерполяцией.
ЗАЩИТНЫЙ СЛОЙ БЕТОНА
5.4. Защитный слой бетона для рабочей арматуры должен обеспечивать совместную работу арматуры с бетоном на всех стадиях работы конструкции, а также защиту арматуры от внешних атмосферных, температурных и тому подобных воздействий.
5.5 (5.3). Толщина защитного слоя должна составлять, как правило, не менее диаметра стержня или каната и не менее:
в конструкциях из обычного бетона для продольной рабочей арматуры (ненапрягаемой и напрягаемой, натягиваемой на упоры) при температуре арматуры до 100 °С:
в плитах и стенках толщиной до 100 мм включ........................................ 10 мм
в плитах и стенках толщиной более 100 мм, а также в балках и ребрах высотой менее 250 мм 15 мм
в балках и ребрах высотой 250 мм и более, а также в колоннах............. 20 мм
в фундаментных балках и в сборных фундаментах.................................. 30 мм
для нижней арматуры монолитных фундаментов:
при наличии бетонной подготовки............................................................ 35 мм
при отсутствии » »........................................................................ 70 мм
При температуре арматуры до 100 °С с попеременным увлажнением бетона и свыше 100 °С толщина защитного слоя должна быть увеличенной на 5 мм и быть не менее 1,5 диаметра арматуры.
В конструкциях из жаростойкого бетона толщину защитного слоя бетона для арматуры независимо от ее вида необходимо предусматривать более указанной в СНиП 2.03.01-84. При температуре арматуры, °С:
до 200 включ............................................................................................................. на 5 мм
св. 200 »................................................................................................................... » 10 »
При этом минимальная толщина защитного слоя бетона должна быть при температуре арматуры, °С:
до 100 включ..................................................................................................... 1,5d
св. 100 до 300 включ........................................................................................ 2,0d
» 300................................................................................................................. 2,5d
5.6. В конструкциях из обычного бетона толщина защитного слоя бетона для поперечной, распределительной и конструктивной арматуры должна приниматься не менее диаметра указанной арматуры и не менее:
при температуре нагрева арматуры до 100 °С:
при h < 250 мм............................................................................................... 10 мм
» h ≥ 250 »................................................................................................. 15 »
при температуре нагрева арматуры свыше 100 °С и в конструкциях из жаростойкого бетона - согласно указаниям п. 5.5.
5.7 (5.4). Толщина защитного слоя бетона у концов предварительно напряженных элементов из обычного и жаростойкого бетонов на длине зоны передачи напряжений при температуре арматуры до 100 °С должна составлять, не менее:
для стержневой арматуры классов A-IV и A-IIIв, а также для арматурных канатов 2d
для стержневой арматуры классов A-V и A-VI............................................... 3d
При более высокой температуре толщину защитного слоя бетона следует увеличивать на 0,5 диаметра анкеруемой арматуры.
Кроме того, толщина защитного слоя бетона на указанном участке длины элемента должна быть не менее 40 мм для стержневой арматуры всех классов и не менее 20 мм - для арматурных канатов.
5.8. При воздействии повышенных температур в элементах с напрягаемой продольной арматурой, натягиваемой на бетон и располагаемой в каналах, расстояние от поверхности элемента до поверхности канала должно приниматься не менее 40 мм и не менее ширины канала; указанное расстояние до боковых граней элемента должно быть, кроме того, не менее половины высоты канала.
При расположении напрягаемой арматуры в пазах или снаружи сечения элемента толщина защитного слоя бетона, образуемого последующим торкретированием или иным способом, должна приниматься не менее 20 мм.
5.9. Для возможности свободной укладки в форму цельных арматурных стержней, сеток или каркасов, идущих по всей длине или ширине изделия, концы этих стержней при их температуре до 100 °С должны отстоять от грани элемента при размере изделия: до 9 м - на 10 мм, до 12 м - на 15 мм, свыше 12 м - на 20 мм. При температуре арматуры выше 100 °С минимальное расстояние между концами арматуры и гранями элемента следует увеличивать на 5 мм.
5.10. В полых элементах кольцевого или коробчатого сечения расстояние от стержней продольной арматуры до внутренней поверхности бетона должно удовлетворять требованиям пп. 5.5 и 5.6.
МИНИМАЛЬНЫЕ РАССТОЯНИЯ МЕЖДУ СТЕРЖНЯМИ АРМАТУРЫ
5.11. Расстояния в свету между стержнями арматуры (или оболочками каналов) по высоте и ширине сечения должны обеспечивать совместную работу арматуры с бетоном и назначаться с учетом удобства укладки и уплотнения бетонной смеси; для предварительно напряженных конструкций должны также учитываться степень местного обжатия бетона и габариты натяжного оборудования (домкратов, зажимов и т.п.). В элементах, изготовляемых с применением виброштампующих машин или штыковых вибраторов, должно быть обеспечено свободное прохождение между арматурными стержнями элементов этих машин или наконечников вибраторов, уплотняющих бетонную смесь.
5.12. Расстояния в свету между отдельными стержнями продольной ненапрягаемой либо напрягаемой арматуры, натягиваемой на упоры, а также между продольными стержнями соседних плоских сварных каркасов должны приниматься не менее наибольшего диаметра стержней, а также:
если стержни при бетонировании занимают горизонтальное или наклонное положение - не менее: для нижней арматуры - 25 мм и для верхней арматуры - 30 мм; при расположении нижней арматуры более чем в два ряда по высоте расстояние между стержнями в горизонтальном направлении (кроме стержней двух нижних рядов) - не менее 50 мм;
если стержни при бетонировании занимают вертикальное положение - не менее 50 мм; при систематическом контроле фракционирования заполнителей бетона это расстояние может быть уменьшено до 35 мм, но при этом должно быть не менее полуторакратного наибольшего размера крупного заполнителя.
При стесненных условиях допускается располагать стержни арматуры попарно (без зазора между ними).
В элементах с напрягаемой арматурой, натягиваемой на бетон (за исключением непрерывно армированных конструкций), расстояние в свету между каналами для арматуры должно быть, как правило, не менее диаметра канала и не менее 50 мм.
Примечание. Расстояние в свету между стержнями периодического профиля принимается по номинальному диаметру без учета выступов и ребер.
АНКЕРОВКА НЕНАПРЯГАЕМОЙ АРМАТУРЫ
5.13. Стержни периодического профиля, а также гладкие арматурные стержни, применяемые в сварных каркасах и сетках, выполняются без крюков. Растянутые гладкие стержни вязаных каркасов и вязаных сеток должны заканчиваться крюками, лапками или петлями.
5.14 (5.7). Продольные стержни растянутой и сжатой арматуры должны быть заведены за нормальное к продольной оси элемента сечение, в котором они учитываются с полным расчетным сопротивлением, на длину не менее lan, определяемую по формуле
но не менее lan = λand,
где значения ωan, Δλan и λan, а также допускаемые минимальные величины lan определяются по табл. 55. Коэффициент условий работы арматуры γst принимается по табл. 35 в зависимости от температуры арматуры.
Таблица 55
|
Параметры для определения анкеровки ненапрягаемой арматуры |
||||||||
|
периодического профиля |
гладкой |
|||||||
|
ωan |
Δλan |
λan |
lan, мм |
ωan |
Δλan |
λan |
lan, мм |
|
|
не менее |
не менее |
|||||||
|
1. Заделка растянутой арматуры в растянутом бетоне |
0,70 |
11 |
20 |
250 |
1,20 |
11 |
20 |
250 |
|
2. Заделка сжатой или растянутой арматуры в сжатом бетоне |
0,50 |
8 |
12 |
200 |
0,80 |
8 |
15 |
200 |
|
3. Стыки арматуры внахлестку: |
||||||||
|
в растянутом бетоне |
0,90 |
11 |
20 |
250 |
1,55 |
11 |
20 |
250 |
|
в сжатом бетоне |
0,65 |
8 |
15 |
200 |
1,00 |
8 |
15 |
200 |
К величине Rb допускается введение коэффициентов условий работы бетона, кроме γb2.
Коэффициент условий работы бетона γbt принимается по табл. 16 в зависимости от температуры бетона на уровне арматуры, при этом гладкие арматурные стержни должны оканчиваться крюками или иметь приваренную поперечную арматуру по длине заделки.
Если по расчету вдоль анкеруемых стержней образуются трещины от растяжения бетона, то стержни должны быть заделаны в сжатую зону бетона на длину lan, определяемую по формуле (306).
В случае когда анкеруемые стержни поставлены с запасом по площади сечения против требуемой расчетом по прочности с полным расчетным сопротивлением, вычисленную по формуле (306) длину анкеровки lan допускается уменьшать, умножая ее на отношение необходимой по расчету и фактической площадей сечения арматуры.
При невозможности выполнения указанных выше требований должны быть приняты меры по анкеровке продольных стержней для обеспечения их работы с полным расчетным сопротивлением в рассматриваемом сечении (постановка косвенной арматуры, приварка к концам стержней анкерующих пластин или закладных деталей, отгиб анкерующих стержней). При этом величина lan должна быть не менее 10d.
При увлажнении бетона и при температуре арматуры свыше 200 °С величину lan, определяемую по формуле (306), следует увеличивать на 20 %, к каждому растянутому продольному стержню необходимо предусматривать приварку не менее двух поперечных стержней.
5.15. Для обеспечения анкеровки всех продольных стержней арматуры, заводимых за грань опоры, на крайних свободных опорах изгибаемых элементов должны выполняться следующие требования:
если соблюдаются условия п. 3.57, длина запуска растянутых стержней за внутреннюю грань свободной опоры должна составлять не менее 5d;
если условия п. 3.57 не соблюдаются, длина запуска стержней за внутреннюю грань свободной опоры должна быть не менее 10d.
Длина зоны анкеровки lan на крайней свободной опоре, на которой снижаются расчетные сопротивления арматуры, определяется согласно указаниям п. 5.14 и поз. 2 табл. 55.
При наличии косвенной арматуры длина зоны
анкеровки снижается путем деления коэффициента ωan на величину 1 + 12μv и уменьшения коэффициента Δλan на величину ![]() .
.
Здесь γbt - коэффициент условий работы бетона, принимаемый по табл. 16 в зависимости от температуры бетона на уровне арматуры;
μv - объемный коэффициент армирования, определяемый: при сварных сетках - по формуле (207); при огибающих хомутах -
![]() , (307)
, (307)
где Asw - площадь сечения огибающего хомута, расположенного у граней элемента; в любом случае значение μv принимается не более 0,06.
Напряжение сжатия бетона на опоре σb определяется делением опорной реакции на площадь опирания элемента и принимается не более 0,5Rbγbt.
Косвенное армирование распределяется по длине зоны анкеровки от торца элемента до ближайшей к опоре нормальной трещины. Длина запуска стержней за внутреннюю грань опоры уменьшается против требуемой, если величина lan < 10d, и принимается равной lan, но не менее 5d. В этом случае, а также при приварке концов стержней к надежно заанкеренным стальным закладным деталям снижение расчетного сопротивления продольной арматуры на опорном участке не производится.
ПРОДОЛЬНОЕ АРМИРОВАНИЕ ЭЛЕМЕНТОВ
5.16. Площадь сечения продольной арматуры в железобетонных элементах из обычного и жаростойкого бетона (в процентах от площади сечения бетона) должна приниматься не менее указанной в табл. 56.
Таблица 56
|
Минимальная площадь сечения продольной арматуры в железобетонных элементах из обычного и жаростойкого бетонов (% площади сечения бетона) |
|
|
1. Арматура S в изгибаемых, а также во внецентренно растянутых элементах при расположении продольной силы за пределами рабочей высоты сечения |
0,05 |
|
2. Арматура S и S′ во внецентренно растянутых элементах при расположении продольной силы между арматурой S и S′ |
0,05 |
|
3. Арматура S и S′ во внецентренно сжатых элементах при |
|
|
l0/i < 17 |
0,05 |
|
17 ≤ l0/i ≤ 35 |
0,10 |
|
35 ≤ l0/i ≤ 83 |
0,20 |
|
l0/i > 83 |
0,25 |
Примечание. Минимальная площадь сечения арматуры, приведенная в табл. 56, относится к площади сечения бетона, равной произведению ширины прямоугольного сечения либо ширины ребра таврового (двутаврового) сечения на рабочую высоту сечения h0.
В элементах с продольной арматурой, расположенной равномерно по контуру сечения, а также в центрально растянутых элементах указанная величина минимального армирования относится к полной площади сечения бетона.
В элементах с продольной арматурой, расположенной равномерно по контуру сечения, а также в центрально растянутых элементах минимальная площадь сечения всей продольной арматуры должна приниматься вдвое больше величин, указанных в табл. 56.
Минимальный процент содержания арматуры S и S′ во внецентренно сжатых элементах, несущая способность которых при расчетном эксцентриситете используется менее чем на 50 %, независимо от гибкости элементов принимается равным 0,05.
Требования табл. 56 не распространяются на армирование, определяемое расчетом элемента для стадии транспортирования и возведения; в этом случае площадь сечения арматуры определяется только расчетом по прочности.
Если расчетом установлено, что несущая способность элемента исчерпывается одновременно с образованием трещин в бетоне растянутой зоны, то должны учитываться требования п. 1.20 для слабоармированных элементов.
Требования настоящего пункта не учитываются при назначении площади сечения арматуры, устанавливаемой по контуру плит или панелей из расчета на изгиб в плоскости плиты (панели).
5.17 (5.8). Диаметр продольной рабочей арматуры не должен превышать при температуре арматуры, °С:
до 100 включ........................................................................................... 28 мм
св. 100 до 200...................................................................................... 25 »
» 200 » 300...................................................................................... 20 »
» 300 » 400...................................................................................... 16 »
» 400......................................................................................................... 12 »
Диаметр продольных стержней внецентренно сжатых элементов монолитных конструкций должен быть не менее 12 мм.
5.18. В линейных внецентренно сжатых элементах расстояния между осями стержней продольной арматуры должны приниматься в направлении, перпендикулярном плоскости изгиба, - не более 400 мм, а в направлении, параллельном плоскости изгиба, - не более 500 мм.
5.19. Во внецентренно сжатых элементах, несущая способность которых при заданном эксцентриситете продольной силы используется менее чем на 50 %, а также в элементах с гибкостью l0/i < 17 (например, подколенники), где по расчету сжатая арматура не требуется, а количество растянутой арматуры не превышает 0,3 %, допускается не устанавливать продольную и поперечную арматуру, требуемую согласно указаниям пп. 5.18, 5.22 и 5.23, по граням, параллельным плоскости изгиба. При этом армирование по граням, перпендикулярным плоскости изгиба, производится сварными каркасами и сетками с толщиной защитного слоя бетона не менее 50 мм и не менее двух диаметров продольной арматуры.
5.20. В балках шириной более 150 мм число продольных рабочих стержней, заводимых за грань опоры, должно быть не менее двух. В ребрах сборных панелей, настилов, часторебристых перекрытий и т.п. шириной 150 мм и менее допускается доведение до опоры одного продольного рабочего стержня.
В плитах расстояние между стержнями, заводимыми за грань опоры, не должно превышать 400 мм, причем площадь сечения этих стержней на 1 м ширины плиты должна составлять не менее 1/3 площади сечения стержней в пролете, определенной расчетом по наибольшему изгибающему моменту.
При армировании неразрезных плит сварными рулонными сетками допускается вблизи промежуточных опор все нижние стержни переводить в верхнюю зону.
Расстояния между осями рабочих стержней в средней части пролета плиты и над опорной (вверху) должны быть не более 200 мм при толщине плиты до 150 мм и не более 1,5h при толщине плиты более 150 мм, где h - толщина плиты.
5.21. В изгибаемых элементах при высоте сечения более 700 мм у боковых граней должны ставиться конструктивные продольные стержни с расстояниями между ними по высоте не более 400 мм и площадью сечения не менее 0,1 % площади сечения бетона с размерами, равными: по высоте элемента - расстоянию между этими стержнями и по ширине элемента - половине ширины ребра элемента, но не более 200 мм.
ПОПЕРЕЧНОЕ АРМИРОВАНИЕ ЭЛЕМЕНТОВ
5.22. У всех поверхностей железобетонных элементов, вблизи которых ставится продольная арматура, должна предусматриваться также поперечная арматура, охватывающая крайние продольные стержни. При этом расстояния между поперечными стержнями у каждой поверхности элемента должны быть не более 600 мм и не более удвоенной ширины грани элемента. Диаметр поперечной арматуры в зависимости от ее температуры не должен превышать диаметров, указанных в пп. 5.17 и 5.24.
Поперечную арматуру допускается не ставить у граней тонких ребер изгибаемых элементов (шириной 150 мм и менее), по ширине которых располагается лишь один продольный стержень или сварной каркас.
Во внецентренно сжатых линейных элементах, а также в сжатой зоне изгибаемых элементов при наличии учитываемой в расчете сжатой продольной арматуры хомуты должны ставится на расстояниях: при Rsc £ 400 МПа - не более 500 мм и при вязаных каркасах не более 15d, а при сварных - не более 20d; при Rsc ³ 450 МПа - не более 400 мм и при вязаных каркасах не более 12d, а при сварных - не более 15d (d - наименьший диаметр сжатых продольных стержней, мм). При этом конструкция поперечной арматуры должна обеспечивать закрепление сжатых стержней от их бокового выпучивания в любом направлении.
Расстояния между хомутами внецентренно сжатых элементов в местах стыкования рабочей арматуры внахлестку без сварки должны составлять не более 10d.
Если насыщение элемента требуемой по расчету сжатой продольной арматурой S′ составляет более 1,5 %, а также если все сечение элемента сжато и общее насыщение арматурой S и S′ свыше 3 %, расстояние между хомутами должно быть не более 10d и не более 300 мм.
При проверке соблюдения требований настоящего пункта продольные сжатые стержни, не учитываемые расчетом, не должны приниматься во внимание, если диаметр этих стержней не превышает 12 мм и половины толщины защитного слоя бетона.
5.23. Конструкция вязаных хомутов во внецентренно сжатых элементах должна быть такова, чтобы продольные стержни (по крайней мере через один) располагались в местах перегиба хомутов, а эти перегибы - на расстоянии не более 400 мм по ширине грани элемента. При ширине грани не более 400 мм и числе продольных стержней у этой грани не более четырех допускается охват всех продольных стержней одним хомутом.
При армировании внецентренно сжатых элементов плоскими сварными каркасами два крайних каркаса (расположенные у противоположных граней) должны быть соединены друг с другом для образования пространственного каркаса. Для этого у граней элемента, нормальных к плоскости каркасов, должны ставиться поперечные стержни, привариваемые контактной сваркой к угловым продольным стержням каркасов, или шпильки, связывающие эти стержни на тех же расстояниях, что и поперечные стержни плоских каркасов.
Если крайние плоские каркасы имеют промежуточные продольные стержни, то они не реже чем через один и не реже чем через 400 мм по ширине грани элемента должны связываться с продольными стержнями шпильками, расположенными у противоположной грани. Шпильки допускается не ставить при ширине данной грани элемента не более 500 мм, если число продольных стержней у этой грани не превышает четырех.
5.24. Диаметр хомутов в вязаных каркасах внецентренно сжатых линейных элементов должен приниматься не менее 0,25d и не менее 5 мм, где d - наибольший диаметр продольных стержней.
Диаметр хомутов в вязаных каркасах изгибаемых элементов должен приниматься не менее:
при h ≤ 800 мм.............................................................................................. 6 мм
» h > 800 »................................................................................................ 8 »
Соотношение диаметров поперечных и продольных стержней в сварных каркасах и в сварных сетках устанавливается из условий сварки по соответствующим нормативным документам.
5.25. В балочных конструкциях высотой более 150 мм, а также в многопустотных плитах (или аналогичных часторебристых конструкциях) высотой более 300 мм должна устанавливаться поперечная арматура в соответствии с указаниями п. 5.26.
В сплошных плитах независимо от высоты, в многопустотных плитах (или аналогичных часторебристых конструкциях) высотой менее 300 мм и в балочных конструкциях высотой менее 150 мм допускается поперечную арматуру не устанавливать. При этом должны быть обеспечены требования расчета согласно указаниям п. 3.57.
5.26. Поперечная арматура устанавливается на приопорных участках, равных при равномерно распределенной нагрузке 1/4 пролета, а при сосредоточенных нагрузках - расстоянию от опоры до ближайшего груза, но не менее 1/4 пролета с шагом при высоте сечения:
h ≤ 450 мм............................................................ не более h/2 и не более 150 мм
h > 450 » » » h/3 » » ».... 500 »
На остальной части пролета при высоте сечения h > 300 мм поперечная арматура устанавливается с шагом не более 3/4h и не более 500 мм.
Для колонн, а также для ребристых плит на средней части пролета при выполнении требований п. 3.57 приведенные выше указания не учитываются.
5.27. Поперечная арматура предусматривается для восприятия поперечных сил и должна иметь надежную анкеровку по концам путем приварки или охвата продольной арматуры, обеспечивающую равнопрочность соединений и хомутов.
5.28. При наличии отогнутой арматуры начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень используется по расчету, не менее чем на 0,5h, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету.
Концы отгибов должны иметь прямые участки, обеспечивающие необходимую анкеровку, согласно указаниям п. 5.14.
5.29. Поперечное армирование коротких консолей колонн выполняется горизонтальными или наклонными под углом 45° хомутами (черт. 30). Шаг хомутов должен быть не более h/4 и не более 150 мм, где h - высота консоли.
Черт. 30. Схема армирования коротких консолей
а - наклонными хомутами; б - отогнутыми стержнями и горизонтальными хомутами
СВАРНЫЕ СОЕДИНЕНИЯ АРМАТУРЫ И ЗАКЛАДНЫХ ДЕТАЛЕЙ
5.30. Арматура из горячекатаной стали гладкого и периодического профиля, термически упрочненной стали классов Ат-IIIС и Ат-IVC и обыкновенной арматурной проволоки, а также закладные детали должны, как правило, изготовляться с применением для соединения стержней между собой и с плоскими элементами проката сварки следующих видов: контактной точечной и стыковой, автоматической и полуавтоматической дуговой, а также в указанных ниже случаях ручной дуговой сварки. Стыковые соединения упрочненной вытяжкой арматуры класса А-IIIв должны свариваться до ее упрочнения.
Сварные соединения стержневой термически упрочненной арматуры классов Ат-V и Ат-VI, высокопрочной арматурной проволоки и арматурных канатов не допускаются.
5.31. Типы сварных соединений и способы сварки арматуры и закладных деталей должны назначаться с учетом условий эксплуатации и свариваемости стали, технико-экономических показателей и технологических возможностей предприятия-изготовителя в соответствии с указаниями государственных стандартов и нормативных документов на сварную арматуру и закладные детали железобетонных конструкций (см. справочные прил. 5 и 6).
5.32. В заводских условиях при изготовлении сварных арматурных сеток, каркасов и соединений по длине отдельных стержней следует применять преимущественно контактную точечную и стыковую сварку, а при изготовлении закладных деталей - автоматическую сварку под флюсом для тавровых и контактную рельефную сварку для нахлесточных соединений.
5.33. При монтаже арматурных изделий и сборных железобетонных конструкций в первую очередь должны применяться полуавтоматические способы сварки, обеспечивающие возможность контроля качества соединений.
5.34. При отсутствии необходимого сварочного оборудования допускается выполнять в заводских и монтажных условиях крестообразные, стыковые, нахлесточные и тавровые соединения арматуры и закладных деталей, применяя приведенные в справочных прил. 5 и 6 и в нормативных документах на сварочную арматуру и закладные детали способы дуговой, в том числе и ручной сварки. Не допускается применять дуговую сварку прихватами в крестообразных соединениях стержней рабочей арматуры класса A-III марки 35ГС.
Применяя ручную дуговую сварку при выполнении сварных соединений, рассчитываемых по прочности, в сетках и каркасах следует устанавливать дополнительные конструктивные элементы в местах соединения стержней продольной и поперечной арматуры (прокладки, косынки, крючки и т.д.).
СТЫКИ НЕНАПРЯГАЕМОЙ АРМАТУРЫ ВНАХЛЕСТКУ (БЕЗ СВАРКИ)
5.35. Стыки ненапрягаемой рабочей арматуры внахлестку применяются при стыковании как сварных, так и вязаных каркасов и сеток.
Стыки стержней рабочей арматуры внахлестку не рекомендуется располагать в растянутой зоне изгибаемых и внецентренно растянутых элементов в местах полного использования арматуры. Такие стыки не допускаются в линейных элементах, сечение которых полностью растянуто (например, в затяжках арок), а также во всех случаях применения стержневой арматуры классов A-IV и выше.
5.36 (5.10). Стыки растянутой или сжатой рабочей арматуры, а также сварных сеток и каркасов в рабочем направлении должны иметь длину перепуска (нахлестки) l не менее величины lan, определяемой по формуле (306) и табл. 55.
Диаметр стыкуемых стержней в зависимости от температуры арматуры следует принимать согласно требованиям пп. 5.14 и 5.17. Диаметр стыкуемых стержней из арматуры периодического профиля не должен превышать 28 мм, а из гладкой арматуры - 20 мм.
Стыки внахлестку без сварки не допускаются при циклическом нагреве и при постоянном нагреве растянутой арматуры выше 100 °С.
5.37. Стыки сварных сеток и каркасов, а также растянутых стержней вязаных каркасов и сеток внахлестку без сварки должны, как правило, располагаться вразбежку. При этом площадь сечения рабочих стержней, стыкуемых в одном месте или на расстоянии менее длины перепуска l, должна составлять не более 50 % общей площади сечения растянутой арматуры при стержнях периодического профиля и не более 25 % - при гладких стержнях.
Стыкование отдельных стержней, сварных сеток и каркасов без разбежки допускается при конструктивном армировании (без расчета), а также на тех участках, где арматура используется не более чем на 50 %.
5.38. Стыки сварных сеток в направлении рабочей арматуры из гладкой горячекатаной стали класса А-I должны выполняться таким образом, чтобы в каждой из стыкуемых в растянутой зоне сеток на длине нахлестки располагалось не менее двух поперечных стержней, приваренных ко всем продольным стержням сеток (черт. 31). Такие же типы стыков применяются и для стыкования внахлестку сварных каркасов с односторонним расположением рабочих стержней из всех видов арматуры.
Черт. 31. Стыки сварных сеток внахлестку (без сварки) в направлении рабочей арматуры, выполненной из гладких стержней
а - при поперечных стержнях, расположенных в одной плоскости; б, в - то же, в разных плоскостях
Стыки сварных сеток в направлении рабочей арматуры из классов А-II и A-III выполняются без поперечных стержней в пределах стыка в одной или обеих стыкуемых сетках (черт. 32).
Черт. 32. Стыки сварных сеток внахлестку (без сварки) в направлении рабочей арматуры, выполненной из стержней периодического профиля
а - без поперечных стержней в пределах стыка в одной из стыкуемых сеток; б - то же, в обеих стыкуемых сетках
5.39. Стыки сварных сеток в нерабочем направлении выполняются внахлестку с перепуском (считая между крайними рабочими стержнями сетки) (черт. 33, а и б):
при диаметре распределительной (поперечной) арматуры до 4 мм включ. - на 50 мм;
при диаметре распределительной арматуры более 4 мм - на 100 мм.
При диаметре рабочей арматуры 16 мм и более сварные сетки в нерабочем направлении допускается укладывать впритык друг к другу, перекрывая стык специальными стыковыми сетками, укладываемыми с перепуском в каждую сторону не менее 15 диаметров распределительной арматуры и не менее 100 мм (черт. 33, в).
Черт. 33. Стыки сварных сеток в направлении распределительной арматуры
а - стык внахлестку с расположением рабочих стержней в одной плоскости; б - то же, в разных плоскостях; в - стык впритык с наложением дополнительной стыковой сетки
Сварные сетки в нерабочем направлении допускается укладывать впритык без нахлестки и без дополнительных стыковых сеток в следующих случаях:
при укладке сварных полосовых сеток в двух взаимно перпендикулярных направлениях;
при наличии в местах стыков дополнительного конструктивного армирования в направлении распределительной арматуры.
СТЫКИ ЭЛЕМЕНТОВ СБОРНЫХ КОНСТРУКЦИЙ
5.40. При стыковании железобетонных элементов сборных конструкций усилия от одного элемента к другому передаются через стыкуемую рабочую арматуру, стальные закладные детали, заполняемые бетоном швы, бетонные шпонки или (для сжатых элементов) непосредственно через бетонные поверхности стыкуемых элементов.
5.41. Жесткие стыки сборных конструкций должны, как правило, замоноличиваться путем заполнения швов между элементами бетоном. Если при изготовлении элементов обеспечивается плотная подгонка поверхностей друг к другу (например, путем использования торца одного из стыкуемых элементов в качестве опалубки торца другого), то допускается при передаче через стык только сжимающего усилия выполнение стыков насухо.
5.42. Стыки элементов, воспринимающие растягивающие усилия, должны выполняться:
сваркой стальных закладных деталей;
сваркой выпусков арматуры;
пропуском через каналы или пазы стыкуемых элементов стержней арматуры, канатов или болтов с последующим натяжением их и заполнением пазов и каналов цементным раствором или мелкозернистым бетоном.
При проектировании стыков элементов сборных конструкций должны предусматриваться такие соединения закладных деталей, при которых не происходило бы разгибания их частей, а также выколов бетона.
5.43. Закладные детали должны быть заанкерены в бетоне с помощью анкерных стержней или приварены к рабочей арматуре элементов.
Закладные детали с анкерами должны, как правило, состоять из отдельных пластин (уголков или фасонной стали) с приваренными к ним втавр или внахлестку анкерными стержнями, преимущественно из арматуры классов А-II или A-III. Длина анкерных стержней закладных деталей при действии на них растягивающих сил должна быть не менее величины lan, определяемой согласно указаниям п. 5.14. Указанная длина анкерных стержней может быть уменьшена при условии приварки на концах стержней анкерных пластин или устройства высаженных горячим способом анкерных головок диаметром не менее 2d - для арматуры классов A-I и A-II и не менее 3d - для арматуры класса A-III. В этих случаях длина анкерного стержня определяется расчетом на выкалывание и смятие бетона и принимается не менее 10d (d - диаметр анкера, мм). При этом конец анкера должен располагаться в зоне бетона с температурой, не превышающей предельно допустимую температуру применения арматуры, указанную в табл. 24.
Если анкера, испытывающие растяжение, располагаются нормально к оси элемента, и вдоль анкеров могут образоваться трещины от основных усилий, действующих на элемент, концы анкеров должны быть усилены приваренными пластинами или высаженными головками.
Штампованные закладные детали должны состоять из полосовых анкеров, имеющих усиления (например, в виде сферических выступов), и участков, выполняющих функцию пластин (аналогично сварным деталям). Штампованные закладные детали следует, как правило, проектировать из полосовой стали толщиной 4 - 8 мм таким образом, чтобы отходы при раскрое полосы были минимальными. Деталь необходимо рассчитывать по прочности полосовых анкеров и пластин. Прочность анкеровки детали проверяется из расчета бетона на раскалывание, выкалывание и смятие.
Толщина пластин закладных деталей определяется в соответствии с указаниями п. 3.68 и требованиями сварки. В зависимости от технологии сварки отношение толщины пластины к диаметру анкерного стержня принимается в соответствии с требованиями справочного прил. 5.
5.44 (5.11). Стыки элементов сборных конструкций из жаростойкого бетона должны выполняться согласно указаниям пп. 5.40 - 5.43. Сварные соединения арматуры необходимо выполнять с соблюдением последовательности приварки стержней к накладкам. Сначала должны привариваться стержни с одной стороны, а после остывания накладки - с другой.
Стыки между стеновыми панелями из жаростойкого бетона следует предусматривать на растворе с установкой бетонного бруса размером 5 × 5 см (черт. 34, а). В стыках панелей, перекрывающих рабочее пространство теплового агрегата, бетонный брус должен устанавливаться на растворе с менее нагретой стороны ребер (черт. 34, б). Пространство между ребрами стыкуемых подвесных панелей с консольными выступами плиты следует заполнять теплоизоляционным материалом (черт. 34, в).
Стыки между панелями из легкого жаростойкого бетона следует заполнять раствором прочностью на сжатие, меньшей прочности бетона футеровки. Марка раствора принимается не ниже М15. Продольные торцевые поверхности панелей должны иметь пазы или скосы, удерживающие раствор от выпадания (черт. 34, г, д, е, ж). Толщина шва стыка между сборными элементами тепловых агрегатов должна приниматься не менее 20 мм.
Черт. 34. Стыки элементов сборных конструкций из жаростойкого бетона
а - стык ребристых панелей в стенах; б - то же, в покрытиях; в - то же, с консольными выступами; г - стык двухслойных панелей; д - стык панелей с окаймляющим арматурным каркасом; е - стык панелей с окаймляющим каркасом из тяжелого жаростойкого бетона; ж - стык панелей из легкого жаростойкого бетона; 1 - тяжелый жаростойкий бетон; 2 - арматурный каркас; 3 - легкий жаростойкий бетон с D1100 и менее; 4 - брусок сечением 50 × 50 мм из тяжелого жаростойкого бетона; 5 - стержень диаметром 6 мм; 6 - жаростойкий раствор; 7 - уголок жесткости панели; 8 - жаростойкий легкий бетон с D1200 и более; 9 - анкер; 10 - теплоизоляционная прослойка толщиной 10 - 20 мм; 11 - металлический лист; 12 - стыковая накладка
5.45 (5.12). Соединение арматуры в сборных элементах из жаростойкого бетона допускается выполнять через окаймляющие уголки, стыковые накладки или путем стыкования арматуры внахлестку (черт. 35).
Черт. 35. Соединения арматуры в стыках элементов сборных конструкций из жаростойкого бетона
а - нахлесточное соединение с металлической накладкой из листовой стали; б - стыковое соединение по ГОСТ 19292-75; в - стыковое соединение по ГОСТ 14098-68; г - нахлесточное соединение
В стыках панелей, передающих усилия от арматуры через косынку на стыковую накладку с эксцентриситетом, обязательно должны предусматриваться анкеры из арматуры периодического профиля. Длина анкерных стержней, приваренных к пластине втавр или внахлестку, должна быть не менее lan, определяемой по указаниям п. 5.14. Если необходимую расчетную длину анкеров трудно выдержать из-за температуры, превышающей предельно допустимую температуру применения арматуры, устанавливаемой по расчету (см. табл. 24), то допускается уменьшать длину анкеров с обязательной приваркой к их концам дополнительных пластин (черт. 36).
Черт. 36. Деталь стыка арматуры четырех панелей из жаростойкого железобетона
1 - арматура; 2 - косынка; 3 - стыковая накладка; 4 - сварка; 5 - анкер арматуры; 6 - анкер косынки; 7 - анкерующая пластинка
ОТДЕЛЬНЫЕ КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
5.46. Осадочные швы должны, как правило, предусматриваться в случаях возведения здания (сооружения) на неоднородных грунтах основания (просадочных и др.), в местах резкого изменения нагрузок и т.п.
Осадочные швы, а также температурно-усадочные швы в сплошных бетонных и железобетонных конструкциях должны выполняться сквозными, разрезая конструкцию до подошвы фундамента. Температурно-усадочные швы в железобетонных каркасах осуществляются посредством двойных колонн с доведением шва до верха фундамента.
Расстояния между температурно-усадочными швами в бетонных фундаментах и стенках подвалов допускается принимать в соответствии с расстояниями между швами, принятыми для вышележащих конструкций.
5.47 (5.13). Ширина температурно-усадочного шва b в зависимости от расстояния между швами l должна определяться по формуле
b = εtl. (308)
Относительное удлинение оси элемента εt следует вычислять в зависимости от вида конструкции и характера нагрева по требованиям пп. 1.39 - 1.43.
Ширину температурно-усадочного шва, вычисленную по формуле (308), следует увеличивать на 30 %, если шов заполняется асбестовермикулитовым раствором, каолиновой ватой или шнуровым асбестом, смоченным в глиняном растворе (черт. 37, а).
Температурно-усадочные швы в бетонных и железобетонных конструкциях следует принимать шириной не менее 20 мм. Когда давление в рабочем пространстве теплового агрегата не равно атмосферному, температурно-усадочный шов должен иметь уширение для установки бетонного бруса. Брус должен устанавливаться насухо без раствора. Между брусом и менее нагретой поверхностью шов следует заполнять легко деформируемым теплоизоляционным материалом (черт. 37, б).
В печах, где требуется герметичность рабочего пространства, с наружной поверхности в температурно-усадочном шве должен предусматриваться компенсатор (черт. 37, в).
Черт. 37. Температурные швы в конструкциях из жаростойкого бетона
а - шов, заполненный шнуровым асбестом; б - то же, с бетонным бруском; в - то же, с металлическим компенсатором; 1 - шнуровый асбест, смоченный в глиняном растворе; 2 - бетонный брусок; 3 - компенсатор; 4 - стальной стержень диаметром 6 мм
5.48 (5.14). Для организованного развития усадочных трещин в бетоне со стороны рабочего пространства теплового агрегата должны предусматриваться усадочные швы. Швы шириной 2 - 3 мм и глубиной, равной 1/10 высоты сечения, но не менее 20 мм, следует располагать через 60 - 90 см в двух взаимно перпендикулярных направлениях (черт. 38, б).
Черт. 38. Швы со стороны нагреваемой поверхности в конструкциях из жаростойкого бетона
а - компенсационные; б - усадочные; 1 - компенсационный шов шириной 2 - 5 мм; 2 - усадочный шов глубиной 0,1hf и шириной 2 - 3 мм
5.49. В бетонных конструкциях должно предусматриваться конструктивное армирование:
в местах резкого изменения размеров сечения элементов;
в местах изменения высоты стен (на участке не менее 1 м);
в бетонных стенах под и над проемами каждого этажа;
в конструкциях, подвергающихся воздействию динамической нагрузки;
у менее напряженной грани внецентренно сжатых элементов, если наибольшее напряжение в сечении, определяемое как для упругого тела, превышает 0,8Rbγbt, а наименьшее составляет менее 1 МПа или оказывается растягивающим; при этом коэффициент армирования μ принимается не менее 0,025 %.
Требования настоящего пункта не распространяются на элементы сборных конструкций, проверяемые в стадии транспортирования и монтажа; в этом случае необходимое армирование определяется расчетом по прочности.
Если расчетом установлено, что прочность элемента исчерпывается одновременно с образованием трещин в бетоне растянутой зоны, то следует учитывать требования п. 1.20 для слабоармированных элементов (без учета работы растянутого бетона). Если согласно расчету с учетом сопротивления растянутой зоны бетона арматура не требуется и опытом доказана возможность транспортирования и монтажа таких элементов без арматуры, конструктивная арматура не предусматривается.
5.50. Соответствие расположения арматуры ее проектному положению должно обеспечиваться специальными мероприятиями (установкой пластмассовых фиксаторов, шайб из мелкозернистого бетона и т.п.).
5.51. Отверстия значительных размеров в железобетонных плитах, панелях и т.п. должны окаймляться дополнительной арматурой сечением не менее сечения рабочей арматуры (того же напряжения), которая требуется по расчету плиты как сплошной.
5.52. При проектировании элементов сборных перекрытий должно предусматриваться устройство швов между ними, заполняемых бетоном. Ширина швов должна назначаться из условия обеспечения качественного заполнения их и должна составлять не менее 20 мм для элементов высотой сечения до 250 мм и не менее 30 мм - для элементов большей высоты.
5.53 (5.15). Усилия от неравномерного нагрева бетона по высоте сечения элемента допускается уменьшать:
устройством компенсационных швов в более нагретой сжатой зоне бетона (черт. 38, а). Компенсационные швы шириной 2 - 5 мм следует располагать через 60 - 90 см на глубину не более 0,5 высоты сечения элемента в направлении, перпендикулярном действию сжимающих усилий от воздействия температуры;
повышением температуры растянутой арматуры, расположенной у менее нагретой грани бетона, посредством увеличения толщины защитного слоя бетона или устройством наружной теплоизоляции.
5.54 (5.16). В железобетонных конструкциях из жаростойкого бетона для восприятия растягивающих усилий, как правило, следует устанавливать арматуру у менее нагретой грани сечения элемента.
Если в конструкциях от нагрузки растягивающие усилия возникают со стороны более нагретой грани сечения элемента, то арматура может воспринимать растягивающие усилия при температуре, не превышающей предельно допустимую температуру применения арматуры, устанавливаемой по расчету (см. табл. 24).
Для снижения температуры арматуры допускается увеличивать толщину защитного слоя бетона у более нагретой грани сечения элемента до 6 диаметров продольной арматуры или предусматривать теплоизоляцию из легкого жаростойкого бетона.
На границе бетонов разных видов следует устанавливать конструктивную арматуру из жаростойкой стали диаметром не более 4 мм, которая должна быть приварена к хомутам (черт. 39).
Температура нагрева конструктивной арматуры не должна превышать предельно допустимую температуру применения конструктивной арматуры, указанную в табл. 24.
Черт. 39. Конструкция изгибаемого железобетонного элемента, нагреваемого до температуры более 400 °С со стороны растянутой зоны
1 - тяжелый жаростойкий бетон; 2 - теплоизоляционный слой из легкого жаростойкого бетона; 3 - сетка из жаростойкой стали диаметром 4 мм; 4 - продольная рабочая арматура
5.55 (5.17). Несущие и ненесущие конструкции тепловых агрегатов следует выполнять из сборных однослойных или многослойных элементов. Сборные ограждающие конструкции, как правило, предусматриваются из блоков, плит и панелей.
В двухслойных панелях, проектируемых из разных видов жаростойкого бетона, теплоизоляционный легкий жаростойкий бетон может предусматриваться как со стороны рабочего пространства, так и с наружной стороны теплового агрегата.
Для улучшения совместной работы отельных слоев бетона допускается предусматривать установку конструктивной арматуры или анкеров. Арматура должна заходить в каждый слой бетона на глубину не менее 50 мм. Если в зоне сопряжения отдельных слоев бетона температура превышает предельно допустимую температуру применения конструктивной арматуры, указанную в табл. 24, то для усиления связи между слоями допускается устраивать выступы или бетонные шпонки.
В ребристых панелях плиту и ребра следует выполнять из тяжелого или легкого конструкционного жаростойкого бетона (см. черт. 38, б). В местах сопряжения ребер с плитой необходимо устраивать вуты. Между ребрами с менее нагретой стороны следует располагать тепловую изоляцию из легкого жаростойкого бетона или из теплоизоляционных материалов. В ребрах панели следует предусматривать арматурные каркасы, которые должны быть заведены в бетон плиты не менее чем на 50 мм. При необходимости снижения температуры рабочей арматуры, устанавливаемой в ребрах, ребра могут выступать за наружную поверхность тепловой изоляции. Плиту панели следует армировать конструктивной сварной сеткой из арматуры диаметром не более 4 мм с расстояниями между стержнями не менее 100 мм.
Температура нагрева сварной сетки не должна превышать предельно допустимую температуру применения конструктивной арматуры, указанную в табл. 24. Если температура нагрева плиты панели превышает предельно допустимую температуру применения конструктивной арматуры, допускается плиту не армировать.
Для ненесущих облегченных ограждающих конструкций тепловых агрегатов следует предусматривать легкие жаростойкие бетоны и эффективные теплоизоляционные материалы.
В двухслойных панелях на металлическом листе легкий жаростойкий бетон следует крепить анкерами, приваренными к листу (черт. 40, а). Анкеры должны приниматься из стержней диаметром 6 - 10 мм или полосы размером 3 × 20 мм. Длина анкера должна быть не менее половины толщины футеровки, а расстояния между ними - не более 250 мм. Металлический лист толщиной не менее 3 мм должен иметь отогнутые края или приваренные «на перо» по контуру уголки.
В панелях с окаймляющим каркасом прямоугольного или трапециевидного сечения ребра должны предусматриваться из тяжелого или легкого конструкционного жаростойкого бетона, а пространство между ребрами на всю толщину следует заполнять теплоизоляционным легким жаростойким бетоном. Ребра следует армировать плоскими каркасами, расположенными с менее нагретой стороны (черт. 40, б).
В панелях с окаймляющим арматурным каркасом сварной каркас следует располагать по периметру панели у менее нагретой стороны (черт. 40, в).
Крепление панелей к каркасу должно осуществляться так, чтобы они могли свободно перемещаться при нагреве.
В конструкциях тепловых агрегатов из монолитного железобетона со стороны рабочего пространства в углах сопряжения стен, а также стен с покрытием и перекрытием следует предусматривать вуты.
При температуре рабочего пространства тепловых агрегатов выше 800 °С ограждающую конструкцию с целью увеличения ее термического сопротивления следует решать многослойной с включением в ее состав слоев из эффективной теплоизоляции (черт. 40, г).
Черт. 40. Конструкции панелей из легкого жаростойкого бетона
а - двухслойная панель на металлическом листе; б - панель с окаймляющим каркасом из тяжелого жаростойкого бетона; в - панель с окаймляющим арматурным каркасом; г - панель со стальными анкерами и эффективной теплоизоляцией; 1 - уголок жесткости панели; 2 - металлический лист; 3 - анкер; 4 - легкий жаростойкий бетон D1100 и менее; 5 - легкий жаростойкий бетон с D1200 и более; 6 - окаймляющий каркас из тяжелого жаростойкого бетона; 7 - арматурный каркас; 8 - эффективная теплоизоляция; 9 - усадочный шов; 10 - шайба
Многослойная несущая или самонесущая конструкция со стороны рабочего пространства должна иметь футеровочную плиту из жаростойкого бетона, с ненагреваемой стороны - несущее основание в виде железобетонной плиты или металлического листа с окаймляющими уголками, а между ними слой теплоизоляции; причем волокнистые огнеупорные материалы следует применять в температурных зонах сечения конструкции, где нельзя применить более дешевые и менее дефицитные материалы, например, плиты или маты из минеральной ваты.
Для обеспечения надежного соединения несущего и футеровочного слоев многослойной футеровки рекомендуется применять пространственные анкеры в виде соединенных между собой крестообразно установленных гнутых стержней, расположенных перпендикулярно арматурной сетке (черт. 41). Пространственные анкеры устанавливают в швах плитной и минераловатной изоляции.
Черт. 41. Пространственный анкер в многослойной конструкции панели с железобетонной несущей плитой
1 - пространственный анкер; 2 - железобетонная несущая плита; 3 - минераловатная изоляция; 4 - плитная изоляция; 5 - арматурная сетка; 6 - футеровочная плита из жаростойкого бетона
Расстояние между анкерами рекомендуется принимать в пределах 0,7 - 1 м, а расстояние от краев панели до центра пространственного анкера - кратным размеру плит теплоизоляции и равным половине расстояния между анкерами. Плита из жаростойкого бетона, закрепленная с помощью анкеров, от действия собственного веса в горизонтальном положении будет работать как двухконсольная система с максимальными значениями растягивающих усилий в сечениях под пространственными анкерами, где имеются местные арматурные сетки, включенные в пространственный анкер для увеличения площади анкеровки.
Футеровочная плита из жаростойкого бетона в укрупненных монтажных элементах разрезается швами шириной 2 мм на отдельные части с таким расчетом, чтобы каждый отдельный монолитный участок бетонной футеровки крепился к основанию панели четырьмя или двумя анкерами.
5.56 (5.18). Конструкции, перекрывающие рабочее пространство теплового агрегата, могут быть свободно опертыми на стены, подвесными или монолитно связанными со стенами. Для покрытий при пролетах более 4 м должны предусматриваться преимущественно подвесные балки, плиты и панели. Расчетную схему работы подвесной конструкции следует принимать как для двухконсольной балки, при этом не допускается возникновение растягивающих напряжений в бетоне со стороны более нагретой поверхности. Подвесные конструкции не должны воспринимать никаких внешних нагрузок, кроме собственного веса, и на них не должны устраиваться мостики или настилы для хождения обслуживающего персонала.
Купола и своды должны иметь стрелу подъема не менее 1/12 пролета в свету. Нижняя криволинейная поверхность их должна сопрягаться со стенами по переходной кривой, радиус которой принимается не менее толщины стены.
Купола и своды с плоской верхней поверхностью у пяты должны иметь компенсационный шов шириной 20 - 40 мм на глубину, равную высоте сечения в замке (черт. 42). Следует предусматривать заполнение шва легко деформируемым материалом и окраску пят тонким слоем битумного лака. За осевую линию в таких куполах и сводах допускается принимать дугу окружности, проведенную через центр пяты и середину высоты сечения в центре пролета.
Черт. 42. Конструкции для круглого теплового агрегата:
а - купола перекрытия с технологическими отверстиями из жаростойкого бетона; б - железобетонного купола покрытия с плоской верхней поверхностью из жаростойкого бетона; 1 - кожух; 2 - сетка из проволоки диаметром до 6 мм; 3 - компенсационный шов шириной 20 - 40 мм, заполненный легко деформируемым материалом; 4 - купол; 5 - пята купола; 6 - теплоизоляционная прослойка толщиной 20 - 40 мм; 7 - рабочая арматура опорного кольца; 8 - то же, купола; 9 - хомут из проволоки диаметром 6 мм; 10 - опорное кольцо; 11 - шов бетонирования
В куполах и сводах с плоской верхней поверхностью при высоте сечения в замке более 250 мм кроме основной рабочей арматуры, установленной со стороны менее нагретой поверхности, необходимо предусматривать конструктивную сетку из проволоки диаметром не более 6 мм с ячейкой не менее 100 × 100 мм, которую следует располагать в бетоне с температурой, не превышающей предельно допустимую температуру применения конструктивной арматуры (см. табл. 24). Эта сетка должна соединяться хомутами с основной арматурой (см. черт. 42, б).
5.57 (5.19). Рабочую арматуру в железобетонных конструкциях, перерезаемую различными технологическими отверстиями, следует приваривать к рамкам из арматуры или проката, устанавливаемым вокруг отверстий. Размеры рамки должны приниматься такими, чтобы толщина бетона со стороны отверстия была достаточной для обеспечения температуры рамки, не превышающей предельно допустимую температуру применения арматуры, устанавливаемой расчетом по табл. 24.
Площадь сечения рамки в каждом направлении должна быть достаточной для восприятия усилий в перерезанных стержнях.
Отверстия большого размера следует окаймлять армированными бортовыми замкнутыми рамами. Сечение стенок бортовых рам определяют из расчета на усилия от воздействия температуры и нагрузки.
5.58 (5.20). Фундаменты, борова и другие сооружения, расположенные под землей и подвергающиеся нагреву, должны находиться выше наиболее возможного уровня грунтовых вод. При наличии воды следует предусматривать гидроизоляцию.
5.59 (5.21). Кожухи тепловых агрегатов из листовой стали допускается предусматривать, когда необходимо обеспечить газонепроницаемость конструкции и когда имеется большое количество отверстий или точек крепления оборудования.
Соединение кожуха с бетоном следует осуществлять арматурными сетками или анкерами, приваренными к кожуху (см. черт. 42).
5.60 (5.22). Если жаростойкий бетон подвержен сильному истирающему воздействию со стороны рабочего пространства, то его следует защищать металлической панцирной сеткой, по которой наносится слой торкретбетона, или блоками из наиболее стойкого в этих условиях жаростойкого бетона или огнеупора.
5.61. В элементах сборных конструкций должны предусматриваться мероприятия для захвата их при подъеме (инвентарные монтажные вывинчивающиеся петли, строповочные отверстия со стальными трубками, стационарные монтажные петли из арматурных стержней и т.п.). Петли для подъема должны выполняться из горячекатаной стали согласно требованиям п. 2.25.
Для подъема и монтажа жаростойких бетонных и железобетонных элементов лучше использовать цанговые или клещевые захваты.
5.62. Указания по конструированию предварительно напряженных железобетонных элементов принимаются согласно требованиям пп. 5.53 - 5.61 СНиП 2.03.01-84.
ТРЕБОВАНИЯ, УКАЗЫВАЕМЫЕ В ПРОЕКТАХ
5.63 (5.23). В рабочих чертежах конструкций или в пояснительной записке к проекту должны быть дополнительно указаны:
наибольшая температура нагрева конструкции при эксплуатации, принятая в расчете;
вид и класс бетона по предельно допустимой температуре применения;
класс бетона по прочности на сжатие и требуемая прочность бетона при температуре во время эксплуатации;
виды (классы) арматуры и марка жаростойкой стали;
вид увлажнения бетона и его периодичность при эксплуатации;
прочность бетона при отпуске сборных элементов предприятием-изготовителем;
способы обетонирования стыков и узлов, марка и состав раствора для заполнения швов в стыках элементов.
6. РАСЧЕТ И КОНСТРУИРОВАНИЕ НЕКОТОРЫХ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
В данной главе приводится расчет и конструирование некоторых элементов конструкций из обычного и жаростойкого бетона и железобетона, работающих в условиях воздействия температуры.
ФУНДАМЕНТЫ
6.1. Фундаменты под колонны и стены теплотехнических сооружений конструируют:
из сборных бетонных блоков или из монолитного бетона, если температура нагрева превышает предельно допустимую температуру применения арматуры, указанную в табл. 24;
из сборного или монолитного железобетона, если температура нагрева не превышает предельно допустимую температуру применения арматуры.
Арматура, установленная на монтажную нагрузку, не учитывается при расчете фундамента на период эксплуатации, если ее температура нагрева превышает предельно допустимую температуру применения арматуры, устанавливаемой по расчету (см. табл. 24).
6.2. Прямоугольная фундаментная плита толщиной t и размером в плане 2l × 2b, причем l ≥ b, имеет арматуру по контуру. Фундамент по высоте нагрет равномерно, а в горизонтальной плоскости - неравномерно от максимальной величины tb в центре до tsb и tsl на арматуре у короткой и длинной сторон (черт. 43, а).
Черт. 43. Расчетные схемы распределения
а - температуры; б - напряжений в прямоугольной железобетонной плите при неравномерном нагреве бетона с криволинейным распределением температуры от центра плиты до ее сторон; 1 - бетон; 2 - арматура
Плита, имеющая трещины в растянутой зоне, условно разрезается на две полуплиты по более длинной осевой линии I - I. Каждая полуплита рассчитывается как защемленная статически неопределимая балка с высотой сечения b.
Изгибающий момент в сечении II - II полуплиты от воздействия температуры определяется по формуле (50), в которой величина Mt, умножается на коэффициент φ, который
принимается по табл. 57 в
зависимости от отношения сторон плиты ![]() .
.
Таблица 57
|
Отношение сторон |
||||
|
1,0 |
1,5 |
2,0 |
4,0 и более |
|
|
φ |
0,80 |
0,90 |
0,95 |
1,00 |
|
φ1 |
1,0 |
1,5 |
1,8 |
2,0 |
Кривизна ![]() оси и жесткость B полуплиты высотой b от воздействия температуры определяются соответственно по формулам (47) и (45)
при h0 = b0.
оси и жесткость B полуплиты высотой b от воздействия температуры определяются соответственно по формулам (47) и (45)
при h0 = b0.
Расчет плиты производится методом последовательного приближения. В первом приближении для более длинной стороны 2l плиты определяем минимальное количество арматуры по формуле (49), в которой принимаем b = t, а h0 = b0.
Вычисленный момент Mtl должен удовлетворять условию прочности при изгибе согласно выражению (105). Если условие (105) не удовлетворяется, то необходим повторный расчет с увеличенным количеством арматуры.
Площадь растянутой арматуры, устанавливаемой по короткой стороне 2b плиты, определяют по формуле
![]() . (309)
. (309)
Коэффициент φ1 принимается по табл. 57.
Ширину раскрытия трещин в растянутой зоне плиты проверяют по формуле (267) при напряжении в арматуре, вычисленном по формуле (272), в которой M = Mtl, As = Аsl и z = za. Расстояние z от центра тяжести площади сечения арматуры Asb до точки приложения равнодействующей усилий в сжатой зоне бетона сечения II - II полуплиты определяется по формуле (288) при h0 = l0 (см. черт. 43). Порядок расчета прямоугольного железобетонного фундамента на воздействие температуры принимается согласно требованиям п. 6.6.
6.3. Круглая фундаментная плита армирована по периметру кольцевой арматурой. Круглая плита по толщине нагрета
равномерно, а в горизонтальной плоскости - неравномерно. Максимальная температура бетона tb в центре плиты уменьшается к ее краю до
температуры в арматуре ts (черт. 44, а). Кривизна ![]() от
воздействия температуры (т.е. относительный угол поворота вертикального сечения плиты) определяется по
формуле (36)
при h0 = rs.
от
воздействия температуры (т.е. относительный угол поворота вертикального сечения плиты) определяется по
формуле (36)
при h0 = rs.
Изгибающий момент, действующий в вертикальном сечении полуплиты на длине радиуса rs (черт. 44, б), определяют по формуле (50), в которой жесткость B вертикального сечения плиты высотой h0 = rs по растянутой зоне вычисляют по формуле (299).
Коэффициент армирования плиты принимается равным
![]() , (310)
, (310)
где t - толщина плиты.
Расчетный изгибающий момент, вычисленный по формуле (50), должен удовлетворять условию прочности плиты согласно выражению (105) при M = Mt.
Раскрытие трещин в плите проверяют по формуле (267) при напряжении в арматуре, вычисленном по формуле (272).
Порядок расчета круглого железобетонного фундамента на воздействие температуры принимается согласно требованиям п. 6.6.
Черт. 44. Расчетные схемы распределения
а - температуры и деформаций; б - напряжений в круглой железобетонной плите при неравномерном нагреве бетона с линейным распределением температуры от центра плиты до ее края
6.4. Снижение напряжений в металлическом кожухе теплового агрегата может быть достигнуто путем повышения его температуры устройством наружной теплоизоляции или прослойки между кожухом и бетоном из легко деформируемого материала.
В этом случае круглую фундаментную плиту следует рассчитывать согласно требованиям п. 6.5.
6.5. Круглая бетонная фундаментная плита имеет кожух, между кожухом и бетоном плиты положена прослойка из легко деформируемого материала: асбеста, крошки из диатомитового кирпича, углеродистой набойки и др. (черт. 45). Такую плиту рассчитывают согласно требованиям п. 6.3. При вычислении жесткости B по формуле (299) принимается коэффициент ψs = 1, ψb = 1 и вместо Esβs - условный модуль упругости стали Estc, определяемый по формуле
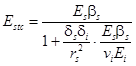 , (311)
, (311)
где δs, δi - соответственно толщина кожуха и прослойки;
rs - радиус кожуха, см;
vi - коэффициент упругости прослойки из легко деформируемого материала, принимаемый равным 0,1;
Ei - модуль упругости материала прослойки, принимаемый равным: 100 МПа для асбеста и засыпки из диатомитового кирпича, 120 МПа - для углеродистой набойки и 150 МПа - для засыпки из шамотного песка или мергеля.
Величины коэффициента упругости и модуля упругости материалов прослойки могут быть уточнены на основании опытной проверки их деформаций под нагрузкой.
Расчетный изгибающий момент, вычисленный по формуле (50), должен удовлетворять условию прочности плиты согласно выражению (105) при M = Mt. В плитах, армированных стальным кожухом, раскрытие трещин в бетоне не проверяется.
Черт. 45. Расчетные схемы распределения
а - температур и деформаций; б - напряжений в круглой бетонной плите с наружным кожухом при неравномерном нагреве бетона с линейным распределением температуры от центра плиты до кожуха; 1 - кожух; 2 - эластичная прокладка; 3 - жаростойкий бетон
6.6. Расчет конструкций фундаментов, указанных в пп. 6.1 - 6.5, производят в следующем порядке.
При принятом составе бетона и его температуре в центре плиты определяют температуру арматуры по методике расчета температур ограждающих конструкций (см. пп. 1.47 - 1.53).
Для принятых класса и состава бетона, а также класса арматуры определяют необходимые для расчета характеристики бетона и арматуры.
Задаваясь минимальным коэффициентом армирования по формуле (49) и принимая в первом приближении Mt равным правой части уравнения (105), по формуле (74) вычисляют величину коэффициента αstm.
По формуле (47) вычисляют кривизну элемента от воздействия температуры.
Относительную высоту сжатой зоны в сечении с трещиной вычисляют по формуле (283) и коэффициент ψs - по формуле (289).
Жесткость плиты с трещинами в растянутой зоне бетона вычисляют по формуле (299). В случае прямоугольной плиты жесткость определяют по сечению II - II (см. черт. 43).
Имея величины ![]() и B, по формуле (50) определяют первое значение Mt. По найденному первому значению Mt снова вычисляют ξ, ψs и B. По новому значению жесткости B определяют второе значение Mt и так далее до тех пор, пока расхождение между последним и
предыдущим значениями Mt не будет превышать ±5 %. После определения изгибающего
момента от воздействия температуры производят проверку
прочности плит и раскрытие трещин.
и B, по формуле (50) определяют первое значение Mt. По найденному первому значению Mt снова вычисляют ξ, ψs и B. По новому значению жесткости B определяют второе значение Mt и так далее до тех пор, пока расхождение между последним и
предыдущим значениями Mt не будет превышать ±5 %. После определения изгибающего
момента от воздействия температуры производят проверку
прочности плит и раскрытие трещин.
СТЕНЫ
6.7. Стены тепловых агрегатов из жаростойкого бетона и железобетона предназначаются для защиты от воздействия высокой температуры. В зависимости от схемы конструкции и условий работы теплового агрегата стены разделяются на несущие и ненесущие.
К несущим стенам относятся конструкции, в которых от собственного веса, нагрузки и неравномерного нагрева по высоте сечения возникают напряжения сжатия более 10 МПа.
К ненесущим стенам относятся конструкции, в которых отсутствуют усилия от внешней нагрузки и неравномерного нагрева по высоте сечения, а напряжения от собственного веса не превышают 10 МПа.
Толщина ненесущих стен определяется теплотехническим расчетом. Толщину несущих стен сначала определяют теплотехническим расчетом, а затем проверяют расчетом на прочность.
6.8. Стены ограждающих конструкций тепловых агрегатов проектируют:
однослойными из сборного или монолитного железобетона (черт. 46, а);
то же, с теплоизоляционной наружной штукатуркой (черт. 46, б);
то же, с теплоизоляцией и металлическим кожухом (черт. 46, в);
двухслойными и многослойными из сборного или монолитного железобетона с теплоизоляционной прослойкой (черт. 47, а);
из панелей с пустотами, которые могут быть заполнены теплоизоляцией из легкого жаростойкого бетона или другого материала (черт. 47, б);
из панелей ребристой конструкции с тепловой изоляцией, расположенной между ребрами (черт. 47, в).
Черт. 46. Железобетонные стены тепловых агрегатов
а - однослойная из сборного или монолитного железобетона; б - то же, с теплоизоляционной штукатуркой; в - то же, с теплоизоляцией и стальным кожухом; 1 -арматура; 2 - теплоизоляционная штукатурка; 3 - металлическая сетка; 4 - стальной кожух; 5 - теплоизоляция
Черт. 47. Железобетонные стены тепловых агрегатов
а - двухслойные из сборного или монолитного бетона; б - из панелей с пустотами; в - из ребристых панелей; 1 - бетон; 2 - легкий жаростойкий бетон; 3 - металлические косынки; 4 - арматура
В тепловом агрегате, имеющем в плане круглое, квадратное или прямоугольное очертание и стены одинаковой толщины, при нагреве с внутренней стороны возникает изгибающий момент, одинаковый в продольном и поперечном направлениях.
Количество горизонтальной арматуры, устанавливаемой у наружной поверхности стен, определяют по формуле (110), в которой момент M = Mt находят по формуле (50). Этот момент должен удовлетворять условию прочности вертикального сечения стены при изгибе согласно неравенству (105).
Прочность горизонтального сечения стены проверяют на совместное действие сжимающей силы от собственного веса, нагрузки и неравномерного нагрева, как это принято для сжатых элементов. Раскрытие трещин в стенах проверяют по формуле (267).
6.9. В железобетонных стенах тепловых агрегатов кольцевого или коробчатого очертаний в плане с компенсационными швами (см. п. 5.53) определение изгибающего момента от воздействия температуры производят по формуле (50). При этом в формулы для определения кривизны и жесткости сечений вместо h0 подставляют условную высоту сечения элемента h0u, вычисляемую по формуле
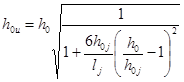 , (312)
, (312)
где lj - расстояние между компенсационными швами, которое должно удовлетворять условию
lj ≥ 6(h0 - h0j); (313)
h0j - высота сечения по шву.
ПОКРЫТИЯ
6.10. Для покрытия цехов, имеющих повышенную температуру, рекомендуется применять сборные железобетонные плиты, предварительно рассчитав их на совместное действие температуры и нагрузки.
При применении типовых сборных железобетонных предварительно напряженных плит покрытий допускается не проводить проверочного расчета. В этом случае заданную для расчета нагрузку делят на коэффициент γft, учитывающий влияние повышенной температуры на прочность и деформативность плит. Коэффициент γft принимается по черт. 48 в зависимости от температуры крайнего волокна бетона растянутой зоны.
Например, для цеха с температурой 150 °С и нормативной нагрузкой 3000 Н/м2 с учетом собственного веса плиты необходимо выбрать плиту покрытия размером 3 × 6 м.
Черт. 48. Коэффициент γft, учитывающий влияние температуры крайнего растянутого волокна бетона на величину нагрузки, принимаемой при выборе типовой плиты с арматурой класса
1 - A-IIIв, A-IV, AT-IV; 2 - A-V, Aт-V, Bp-II; 3 - Ат-VI, К-7
На черт. 48 для плиты с арматурой класса A-IV коэффициент γft при 150 °С равен 0,6. Заданную нормативную нагрузку делим на коэффициент γft (3000 : 0,6 = 5000 Н/м2) и для этой нагрузки принимаем типовую плиту с арматурой класса A-IV.
6.11. Сферический купол из жаростойкого железобетона (см. п. 5.56, черт. 49) монолитно сопряжен с опорным кольцом и подвергается воздействию равномерно распределенной вертикальной нагрузки и нагреву со стороны нижней поверхности. Купол и опорное кольцо неравномерно нагреты по высоте сечения.
Черт. 49. Расчетные схемы
1 - температур; 2 - деформаций; 3 - кольцевых усилий; 4 - моментов от неравномерного нагрева по высоте сечения купола и опорного кольца из жаростойкого железобетона
Распор от нагрева купола воспринимается арматурой опорного кольца. От неравномерного нагрева по высоте сечения купола возникают равные по величине изгибающие моменты в кольцевом и радиальном направлениях, вызывающие в кольцевой и радиальной арматуре усилия растяжения, а в бетоне со стороны более нагретой поверхности - усилия сжатия. Эти моменты в любом сечении купола, нормальном к его срединной поверхности, определяют по формуле (50).
Вследствие ограничения деформаций купола опорным кольцом при нагревании возникает распор, воспринимаемый арматурой опорного кольца. Кроме того, в бетоне краевой зоны купола возникают меридиональные T1t и кольцевые T2t усилия сжатия, которые достигают своего максимума в опорном сечении I - I (см. черт. 49) по плоскости сопряжения купола с опорным кольцом. В расчете учитывают только кольцевые усилия T2t, так как меридиональные усилия T1t по своей величине в несколько раз меньше кольцевых и они в данном случае могут не учитываться.
При высоте сечения опорного кольца h0 = (rs - r1) ≥ 0,1rs по формуле (50) определяют также изгибающий момент Mt1 от неравномерного нагрева по высоте сечения опорного кольца в радиальном направлении.
Распор от нагрузки и собственного веса, воспринимаемый арматурой опорного кольца, а также кольцевое и меридиональное усилия сжатия в куполе находят по правилам строительной механики, используя безмоментную теорию.
Усилия в опорном кольце и в куполе от воздействия температуры определяют из условия неразрывности деформаций наружной грани купола и опорного кольца. Распор от воздействия температуры на один сантиметр периметра опорного кольца определяют по формуле
где ![]() - температура бетона на уровне срединной поверхности купола;
- температура бетона на уровне срединной поверхности купола;
tb1 - температура менее нагретой поверхности купола;
ts - температура арматуры опорного кольца
rb = risinα; (315)
r - радиус срединной поверхности купола;
B - жесткость сечения шириной 1 см купола по растянутой зоне, вычисляемая по формуле (299);
γt - коэффициент перегрева, принимаемый по требованиям п. 1.39;
As - площадь арматуры опорного кольца;
ψs - коэффициент, учитывающий работу растянутого бетона в опорном кольце, определяемый по формуле (289) как для растяжения, если высота сечения опорного кольца rs - r1 < 0,1rs, и как при изгибе, если rs - r1 ≥ 0,1rs.
Коэффициент армирования принимается по площади сечения опорного кольца Ab = h1(rs - r1). При наличии в пяте купола шва опирание купола можно считать шарнирным и в знаменателе формулы (314) коэффициент φ принимается равным 2. При монолитном сопряжении купола с опорным кольцом, где арматура купола анкеруется в опорном кольце, коэффициент φ принимается равным 4.
Усилие в арматуре опорного кольца от распора, вызванного воздействием температуры, вычисляют по формуле
Nt = Htrs. (317)
Максимальное усилие T2t сжатия бетона от воздействия температуры в опорном сечении I - I шириной b = 1 см, расположенном на границе сопряжения купола с опорным кольцом, определяют по формуле
где Ebβb и ![]() - принимаются
по табл. 16, 17 и 18 при
средней температуре бетона в сечении купола, а коэффициент φ - как в формуле
(314).
- принимаются
по табл. 16, 17 и 18 при
средней температуре бетона в сечении купола, а коэффициент φ - как в формуле
(314).
Длина участка купола, на котором возникают кольцевые усилия в бетоне T2t, равна
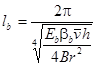 . (319)
. (319)
Распор в опорном кольце от равномерно распределенной нагрузки и собственного веса купола определяется по формуле
где q - равномерно распределенная нагрузка с учетом собственного веса купола, МПа.
Усилие в арматуре опорного кольца от нагрузки определяют по формуле
Nf = Hfr1. (321)
Кольцевое усилие сжатия в опорном сечении I - I купола шириной b = 1 см от нагрузки и собственного веса вычисляют по формуле
а максимальное меридиональное усилие сжатия - по формуле
Усилия в опорном кольце и в куполе от совместного воздействия температуры, собственного веса и нагрузки алгебраически суммируются. При высоте сечения опорного кольца (rs - r1) < 0,1rs расчетное усилие растяжения N = Nt + Nf в кольцевой арматуре должно удовлетворять условию прочности при центральном растяжении согласно формуле (170). При устройстве компенсационных швов и высоте сечения опорного кольца (rs - r1) ≥ 0,1rs или h0j > 0,1rs расчетное усилие в кольцевой арматуре N и момент Mt1 вызывают в опорном кольце внецентренное растяжение.
Эксцентриситет продольной силы N относительно центра тяжести приведенного сечения опорного кольца вычисляют по формуле
где e1 - расстояние от центра тяжести площади сечения кольцевой арматуры до центра тяжести приведенного сечения опорного кольца.
Расчет прочности и раскрытия трещин в бетоне опорного кольца с односторонним армированием с учетом Mt1 производят как для первого случая внецентренного растяжения элемента (с большим эксцентриситетом). При этом проверку прочности арматуры кольца производят согласно неравенству (173) при A′s = 0, раскрытие трещин определяют по формуле (267).
Расчет прочности и раскрытия трещин в бетоне опорного кольца с односторонним армированием без учета Mt1 производят как для центрально растянутого элемента.
Расчет прочности купола производят по
наиболее напряженному опорному сечению I - I на расчетное кольцевое усилие T2 = T2f + T2t и момент Mt от
неравномерного нагрева по высоте сечения купола. Прочность опорного сечения
купола проверяют по формуле (136)
на сжатие силой T2, приложенной с эксцентриситетом ![]() относительно центра
тяжести приведенного сечения купола.
относительно центра
тяжести приведенного сечения купола.
Раскрытие кольцевых или
меридиональных трещин в бетоне проверяют в сечении купола II - II в центре пролета при действии кольцевого
усилия ![]() и
момента Mt от неравномерного нагрева по высоте сечения как при внецентренном сжатии.
и
момента Mt от неравномерного нагрева по высоте сечения как при внецентренном сжатии.
При длительном нагреве проверяется только прочность наиболее напряженного опорного сечения купола I - I на внецентренное сжатие силой Т2 в кольцевом направлении. При этом должно также удовлетворяться условие прочности опорного сечения купола при сжатии от действия только меридионального усилия T1f, вычисленного по формуле (323).
Прогиб сферического купола в центре пролета при его загружении равномерно распределенной нагрузкой допускается вычислять по формуле
![]() , (325)
, (325)
где
![]() ;
;
![]() ;
;
φw - коэффициент, учитывающий геометрические параметры купола, принимается по табл. 58.
Значения Eb, βb и ![]() принимаются
по табл. 16, 17 и 18 при
средней температуре бетона в сечении купола.
принимаются
по табл. 16, 17 и 18 при
средней температуре бетона в сечении купола.
Таблица 58
|
Коэффициент φw · 103 в зависимости от λ, равной |
|||||
|
10 |
20 |
30 |
40 |
50 |
|
|
0,50 |
200,00 |
133,80 |
85,36 |
55,84 |
38,07 |
|
0,70 |
136,20 |
57,69 |
28,09 |
15,66 |
9,67 |
|
0,75 |
119,60 |
45,87 |
21,36 |
11,65 |
7,12 |
|
1,00 |
55,84 |
15,01 |
6,16 |
3,25 |
2,01 |
|
1,25 |
24,92 |
5,63 |
2,31 |
1,27 |
0,81 |
|
1,50 |
11,65 |
2,52 |
1,09 |
0,61 |
0,39 |
Примечание. При промежуточных значениях a и λ коэффициент φw определяется интерполяцией.
6.12. Купол из жаростойкого бетона с опорным кольцом из жаростойкого железобетона (см. п. 5.56) подвергается одностороннему нагреву и равномерно распределенной нагрузке (черт. 50).
Черт. 50. Расчетные схемы
1 - температур; 2 - деформаций; 3 - кольцевых усилий; 4 - моментов от неравномерного нагрева по высоте сечения купола из жаростойкого бетона и опорного кольца из жаростойкого железобетона; 5 - пята свода
Распор от воздействия температуры на один сантиметр периметра опорного кольца определяют по формуле (314) при φ = 2.
В формуле (314) все величины принимаются такими же, как для
железобетонного купола, кроме жесткости B. В этом случае жесткость купола вычисляют по
формуле (298), принимая Eb, βb и ![]() по табл. 16, 17 и 18 в зависимости от средней температуры бетона сечения
купола. При нагреве бетонного купола, в котором от нагрузки и собственного веса
возникают усилия до 0,1 от несущей способности купола, определение приведенного момента инерции сечения Ired производится по формуле (11). Высота сечения
купола при определении Ired по формуле (11)
принимается в зависимости от температуры наиболее нагретой грани бетона, °С:
по табл. 16, 17 и 18 в зависимости от средней температуры бетона сечения
купола. При нагреве бетонного купола, в котором от нагрузки и собственного веса
возникают усилия до 0,1 от несущей способности купола, определение приведенного момента инерции сечения Ired производится по формуле (11). Высота сечения
купола при определении Ired по формуле (11)
принимается в зависимости от температуры наиболее нагретой грани бетона, °С:
до 600................................................................................. h
1000 и более................................................................. 2/3h
Для температур бетона от 600 до 1000 °С изменение высоты сечения купола принимается по интерполяции. При усилиях в куполе более 0,1 от несущей способности независимо от температуры нагрева высота сечения принимается равной h.
Для бетонного купола момент в меридиональном и кольцевом направлениях от неравномерного нагрева по высоте сечения купола принимают равным нулю.
6.13. При монолитном сопряжении свода со стенами, когда арматура свода анкеруется в стене, своды являются элементами рамных конструкций и расчетные усилия в них определяются как для статически неопределимых конструкций (см. пп. 1.45 - 1.46).
В конструкциях тепловых агрегатов с металлическим или железобетонным каркасом передача распора от сводов на каркас осуществляется через опорные балки, имеющие наклонную пяту для опирания свода. Если температура нагрева не превышает предельно допустимую температуру применения арматуры (см. табл. 24), то применяют железобетонные своды.
6.14. Цилиндрический железобетонный свод покрытия теплового агрегата имеет одностороннее армирование, расположенное в менее нагретых слоях бетона, и неподвижные опоры (черт. 51). В зоне сопряжения свода с опорной балкой предусматривается шов. Свод подвергается неравномерному нагреву по высоте сечения со стороны нижней поверхности и действию равномерно распределенной нагрузки.
Черт. 51. Расчетная схема цилиндрического свода из жаростойкого бетона при одностороннем нагреве
Распор от воздействия температуры определяют как для свода с тремя пластическими шарнирами, расположенными в опорных сечениях и в центре пролета, по формуле
При этом наибольший распор в своде вычисляют при кратковременном нагреве с учетом указаний п. 1.23.
Продольная сила N1t в замке свода (сечение I - I) от воздействия температуры равна распору Ht, а в опорном сечении II - II она вычисляется по формуле
N2t = Htcosα. (327)
Момент в замке от воздействия температуры
M1t = - (Mt + Htlc), (328)
а в опорном сечении
M2t = Ht(f - lc) - Mt. (329)
При этом расчетный момент в опорном сечении должен удовлетворять условию
|M2t| ≤ 0,5Hthcosα. (330)
Если это условие не удовлетворяется, то момент принимается равным 0,5Hthcosα.
В формулах (326) - (330) принято:
εt - деформация оси свода в направлении пролета от нагрева, определяемая по формуле (35);
B - жесткость сечения свода в замке по растянутой зоне, определяемая по формуле (299);
η - коэффициент, учитывающий влияние продольных сил на величину распора. При температуре бетона более нагретой поверхности свода:
до 400 °С включ.
более 400 °С
где Ared и Ired - соответственно площадь и момент инерции приведенного сечения свода в замке, определяемые по формулам (6) и (11).
Для свода с высотой сечения h ≤ 0,5l, а также для свода с подъемом f ≥ 1/8l и высотой сечения h ≤ 0,1l коэффициентом η можно пренебречь.
Δ - горизонтальное перемещение конца жесткой консоли в основной системе, вызванное поворотом сечений в пластических шарнирах
Δ = fθ. (333)
где
![]() , (335)
, (335)
μ - коэффициент армирования свода, %, принимаемый не более 2,5 %; при μ = 0 φ = 50, а при μ = 2,5 % φ = 0;
![]() - кривизна железобетонного свода с трещинами в растянутой зоне, вычисляемая по формуле (36).
- кривизна железобетонного свода с трещинами в растянутой зоне, вычисляемая по формуле (36).
При определении угла θ коэффициенты βb и ![]() принимают соответственно по табл. 16 и 18 в
зависимости от средней температуры бетона в сечении
свода. Коэффициент φ1 в формуле (326) и φ2 в формулах (331) и (332)
зависят от величины центрального угла свода 2α и
принимаются по табл. 59.
принимают соответственно по табл. 16 и 18 в
зависимости от средней температуры бетона в сечении
свода. Коэффициент φ1 в формуле (326) и φ2 в формулах (331) и (332)
зависят от величины центрального угла свода 2α и
принимаются по табл. 59.
Таблица 59
|
Коэффициенты |
|||||||
|
φ1 |
φ2 |
φ3 |
φ4 |
φ5 |
φ6 |
φ7 |
|
|
35 |
0,000118 |
5019 |
1,09 |
0,0186 |
0,0463 |
0,000361 |
0,006330 |
|
40 |
0,000185 |
3700 |
1,06 |
0,0277 |
0,0603 |
0,000597 |
0,010688 |
|
45 |
0,000310 |
2500 |
1,03 |
0,0391 |
0,0766 |
0,000969 |
0,016932 |
|
50 |
0,000560 |
1295 |
1,00 |
0,0533 |
0,0937 |
0,001450 |
0,025515 |
|
60 |
0,001750 |
543 |
0,97 |
0,0906 |
0,1340 |
0,002930 |
0,051461 |
|
70 |
0,003610 |
299 |
0,94 |
0,1410 |
0,1810 |
0,005310 |
0,092155 |
|
80 |
0,006790 |
175 |
0,91 |
0,2060 |
0,2340 |
0,008830 |
0,151455 |
|
90 |
0,012300 |
105 |
0,88 |
0,2850 |
0,2930 |
0,013700 |
0,232242 |
|
100 |
0,020000 |
68 |
0,84 |
03800 |
0,3570 |
0,020200 |
0,337199 |
|
110 |
0,031900 |
45 |
0,81 |
0,4900 |
0,4260 |
0,028400 |
0,467923 |
|
120 |
0,047800 |
31 |
0,78 |
0,6140 |
0,5000 |
0,038500 |
0,625000 |
Длина жесткой консоли lc в основной системе определяется по формуле
Момент в своде от воздействия температуры определяется с учетом поворота сечений в пластических шарнирах по формуле
При действии равномерно распределенной нагрузки и собственного веса в замке и в опорном сечении свода определяют продольную силу и изгибающий момент. В замке свода продольная сила N1f равна распору Hf.
Распор от равномерно распределенной нагрузки и собственного веса определяют как для бесшарнирного свода по формуле
где q - равномерно распределенная нагрузка на 1 м пролета свода.
Изгибающий момент в замке свода
M1f = Mf - Hflk. (339)
В опорном сечении свода продольная сила
N2f = Hfcosα + 0,5qlsinα. (340)
и изгибающий момент
M2f = Mf + Hf(f - lc) - 0,5qr2sin2α. (341)
Изгибающий момент от равномерно распределенной нагрузки вычисляют по формуле
Коэффициенты φ3 и φ4 в формулах (338) и (342) принимаются по табл. 59 в зависимости от величины центрального угла свода 2α.
От совместного действия нагрузки, собственного веса и температуры изгибающие моменты и продольные силы алгебраически суммируются. Эксцентриситет продольной силы относительно оси, проходящей через центр тяжести приведенного сечения свода, определяется по формуле
![]() . (343)
. (343)
Наиболее напряженные сечения железобетонного свода в замке и на опоре рассчитывают на внецентренное сжатие при кратковременном и длительном нагреве. Сечение железобетонного свода в замке с одиночной верхней арматурой рассматривается как бетонное, если момент M1t меньше момента от собственного веса свода и нагрузки M1f. Прочность опорного сечения свода проверяется без учета арматуры по формуле (75) или (82), принимая расчетное сопротивление бетона по табл. 14, 15 и 16 как для бетонных конструкций. Коэффициент γbt принимается в зависимости от средней температуры бетона в сечении свода.
Раскрытие трещин в бетоне замка свода при внецентренном сжатии с большим эксцентриситетом и с продольной силой, расположенной со стороны более нагретой поверхности свода, определяют по формуле (267).
Выгиб железобетонного или бетонного свода в замке от воздействия температуры определяют по формуле
От равномерно распределенной нагрузки и собственного веса прогиб свода при нагреве в замке вычисляют по формуле
Hf и Mf - определяют соответственно по формулам (338) и (342);
φ5, φ6 и φ7 - коэффициенты, принимаются по табл. 59;
B - жесткость сечения в замке, вычисляют по формуле (299) для железобетонного свода и по формуле (298) - для бетонного свода;
Ared - площадь приведенного сечения свода, вычисляемая по формуле (6).
Прогиб и выгиб свода от совместного воздействия температуры, собственного веса и нагрузки алгебраически суммируются. При наличии в своде сквозных отверстий площадь сечения бетона следует уменьшать на величину площади отверстий.
6.15. Цилиндрические бетонные своды применяются при температурах нагрева, превышающих предельно допустимую температуру применения арматуры (см. табл. 24). Толщину цилиндрических бетонных сводов принимают не менее 1/20 пролета. Бетонные своды опираются на продольные балки по наклонному шву (пяте), идущему перпендикулярно к осевой линии свода.
Цилиндрический бетонный свод, очерченный по дуге круга, подвергается неравномерному нагреву по высоте сечения со стороны нижней поверхности и действию равномерно распределенной вертикальной нагрузки, включающей собственный вес свода. Свод имеет неподвижные опоры. Методика расчета бетонного свода в нагретом состоянии зависит от величины напряжения сжатия в бетоне, вызванного нагрузкой и собственным весом.
Предварительную оценку напряженного состояния производят по средним напряжениям сжатия бетона в замке, определяемым как для трехшарнирного свода (черт. 52) по формуле
где b - ширина свода.
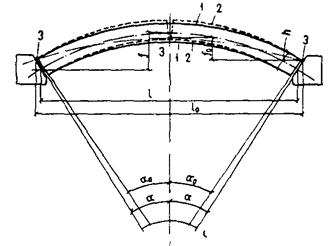
Черт. 52. Схема работы трехшарнирного свода при нагреве с напряжениями сжатия в бетоне от нагрузки и собственного веса до 0,05 МПа
1 - свод до нагрева; 2 - свод нагретый; 3 - условный шарнир
Если вычисленные по формуле (346) напряжения сжатия в бетоне замка свода σbf ≤ 0,05 МПа, то расчет прочности сечений свода можно не производить. Распор от совместного действия собственного веса, равномерно распределенной нагрузки и температуры определяют как для условного трехшарнирного свода с расчетным пролетом l0 и стрелой подъема f0 по формуле
![]() , (347)
, (347)
где
l0 = l + hsinα; (348)
![]() . (349)
. (349)
Выгиб свода в замке от воздействия температуры при σbf ≤ 0,5 МПа определяют по формуле
![]() , (350)
, (350)
где ![]() , (351)
, (351)
Δs′ = εts′; (352)
εt - деформация свода от воздействия температуры по оси в направлении пролета, вычисляемая по формуле (23).
Если вычисленные по формуле (346) напряжения сжатия в бетоне замка свода σbf > 0,05 МПа, то распор в своде от воздействия температуры
определяют по формуле (326), в которой значения εt и Δ вычисляются как для бетонного свода, а жесткость B - по формуле (298). При определении жесткости
Eb, βb и ![]() принимают по табл. 16, 17 и 18 в
зависимости от средней температуры бетона свода.
принимают по табл. 16, 17 и 18 в
зависимости от средней температуры бетона свода.
Изгибающий момент от воздействия температуры в замке свода определяют по формуле
M1t = -Htlc. (353)
В формуле (353) lc вычисляют по выражению (336).
Изгибающий момент M2t от воздействия температуры в опорном сечении свода II - II вычисляют по формуле (329). При этом расчетное значение M2t должно удовлетворять условию (330).
Распор, изгибающий момент в замке свода, продольную силу и изгибающий момент в опорном сечении свода от равномерно распределенной нагрузки и собственного веса определяют соответственно по формулам (338) - (341).
Расчетные изгибающие моменты и продольные силы в замке и в опорном сечении свода от совместного действия собственного веса, нагрузки и температуры определяют алгебраическим суммированием. После определения эксцентриситетов продольных сил в замке и в опорном сечении производят проверку прочности этих сечений на внецентренное сжатие по формуле (75) для кратковременного и длительного нагрева.
Выгиб свода в замке от воздействия температуры определяют по формуле (344), а прогиб от собственного веса и нагрузки - по формуле (345).
6.16. Для уменьшения распора и раскрытия трещин в бетоне от воздействия температуры цилиндрические своды рекомендуется проектировать с податливыми опорами. Податливые опоры при нагревании свода могут перемещаться. Перемещение опор регулируется спиральными или тарельчатыми пружинами, установленными в узлах сопряжения стоек с затяжками каркаса, или соответствующей жесткостью каркаса.
В бетонных и железобетонных сводах с податливыми опорами при расчете распора от воздействия температуры по формуле (326) необходимо учитывать перемещение опор.
При перемещении опор без их поворота определение распора от воздействия температуры в бетонном и железобетонном сводах производится по формуле
где δ - величина перемещения одной опоры свода от распора H = 10H, приложенного на уровне пересечения осевой линии свода с пятой;
φ1 - коэффициент, принимаемый по табл. 59;
εt, l, Δ, η, B - принимаются согласно требованиям пп. 6.14 и 6.15.
Для вычисления Δ по формуле (333) необходимо определить угол θ по формуле (334), в которой коэффициент φ находят по формуле
При расчете бетонных сводов с податливыми опорами, когда среднее напряжение сжатия бетона в замке от собственного веса и нагрузки, вычисленное по формуле (346), более 0,6 МПа, угол θ и величина Δ принимаются равными нулю.
Пружины или жесткость каркаса рекомендуется подбирать с таким расчетом, чтобы перемещение опоры свода от распора, равного 10 Н, находилось в пределах (0,10 ÷ 0,20) · 10-3 см.
Для обеспечения податливости опор свода при нагревании пружины предварительно должны быть поджаты с таким расчетом, чтобы уравновесить распор от собственного веса свода. При приложении нагрузки рекомендуется производить дальнейшее поджатие пружин для уравновешивания распора, создаваемого нагрузкой. При уравновешивании пружинами распора от собственного веса свода и нагрузки распор определяется по формуле (338) как для свода с неподвижными опорами.
Расчет прочности сечений свода с податливыми опорами производят на внецентренное сжатие по указаниям п. 6.15 как для сводов с неподвижными опорами.
6.17. Плоские подвесные покрытия при температурах нагрева до 800 °С могут быть выполнены из однослойных бетонных плит, подвешенных к несущим металлическим двутавровым балкам, заделанным в бетон. Плиты армируются сварными сетками (черт. 53).
Черт. 53. Расчетная схема определения прочности заделки металлической балки в бетон плиты
1 - теплоизоляция; 2 - конструктивная арматурная сетка; 3 - несущая металлическая балка
Расстояние в осях между металлическими балками должно быть не более 1,5 м, а расстояние от оси крайней балки до края плиты - не более 0,5 м. Глубина заделки металлической балки в бетон принимается не менее 50 мм. Толщина бетона плиты определяется теплотехническим расчетом из условия, что температура заделанной в бетон металлической балки не должна превышать предельно допустимую температуру применения стали согласно табл. 24. Для большей надежности заделки металлической балки в бетон рекомендуется укладывать сетку из арматуры диаметром до 6 мм с размером ячеек не менее 100 × 100 мм и приваривать ее к нижней полке.
Для образования зазоров в бетоне, компенсирующих значительное температурное расширение металла, заделываемая часть балок должна покрываться слоем выгорающей обмазки.
Прочность заделки металлической балки в бетоне определяется на основании расчета бетонного сечения, наклонного к продольной оси балки под углом 45° от нижней полки металлической балки до верхней поверхности бетона, на действие изгибающего момента от собственного веса плиты.
Нагрузка, передающаяся от плиты на единицу длины металлической балки, должна удовлетворять условию
где h1 - глубина заделки балки в бетон;
b - ширина полки балки, см;
γtt - коэффициент, принимаемый по табл. 16 в зависимости от температуры бетона на уровне нижней полки металлической балки.
6.18. Покрытия при температурах нагрева более 800 °С осуществляются из сборных подвесных железобетонных ребристых панелей (черт. 54) с окаймляющими поперечными ребрами или без них.
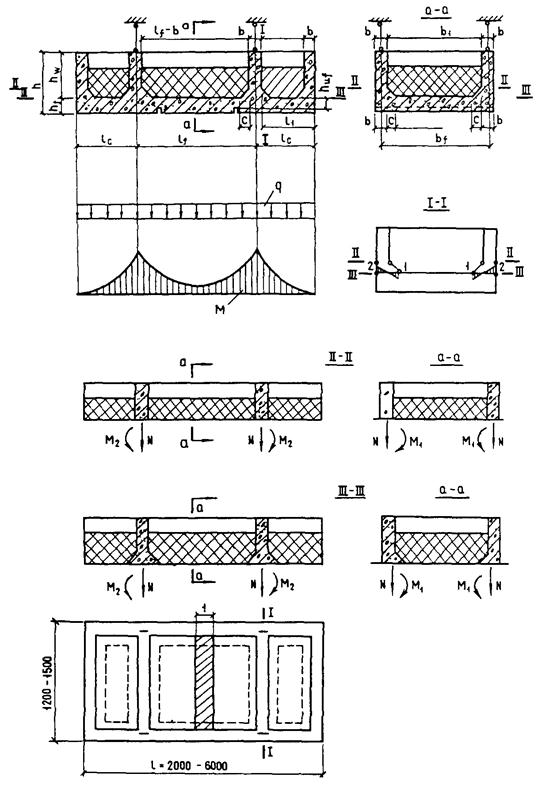
Черт. 54. Расчетная схема определения усилий в подвесной ребристой панели от собственного веса
Отношение высоты полки hf к полной высоте панели h рекомендуется принимать в соответствии с черт. 14. Расстояния между осями ребер должны приниматься: lf ≤ 150 см; bf ≤ 150 см и ширина ребра b ≥ hfj высоты полки в сечении с усадочным швом (см. черт. 54). Подвесная панель рассматривается как двухконсольная балка. Расстояния между подвесками lf и длину консоли lc следует принимать такими, чтобы в бетоне полки не возникали растягивающие напряжения. При равномерно распределенном весе q по длине панели это условие выполняется, если lc ≥ 0,5lf.
Прочность подвесных панелей, имеющих окаймляющие ребра, проверяют в наиболее напряженных местах: в вертикальном сечении I - I и в горизонтальных сечениях II - II и III - III (см. черт. 54). Расчет прочности вертикального сечения I - I производится на действие изгибающего момента от собственного веса консоли при длительном нагреве. Этот момент определяют по формуле
M = 0,5ql21, (357)
где q - расчетная нагрузка от собственного веса подвесной панели, МПа.
Расчетный изгибающий момент, вычисленный по формуле (357), должен удовлетворять условию прочности панели согласно выражению (105).
При ширине ребра b > 1,2hf или b > 1,2hfj (если есть усадочные швы в полке) расчет панели производят без учета усилий, вызванных температурой.
Расчет прочности горизонтальных сечений II - II и III - III производят на действие собственного веса полки и тепловой изоляции, расположенной между ребрами, при длительном нагреве.
Собственный вес полки и тепловой изоляции вызывает в сечениях II - II и III - III внецентренное растяжение. Напряжения растяжения в точке 1 сечения II - II ребра (см. черт. 54) вычисляют по формуле
при расчете сечения III - III в формулу (358) вместо b вводится величина b + c;
N - продольная растягивающая сила от собственного веса панели ниже рассматриваемого сечения;
M1 - изгибающий момент, определяемый как для защемленной на двух опорах бетонной балки единичной ширины:
где q1 - равномерно распределенная нагрузка от собственного веса панели ниже расчетного сечения II - II или III - III.
При расчете панели, в которой консоль не имеет окаймляющего поперечного ребра по торцу, необходимо определять также изгибающий момент в месте сопряжения полки с поперечным ребром от собственного веса консоли в сечении II - II по формуле
М2 = 0,5q1l21. (360)
При расчете сечения III - III в формулу (360) вместо l1 вводится l1 - c. При этом в формулу (358) следует подставлять наибольшее значение изгибающего момента, вычисленного по формулам (359) и (360).
Растягивающие напряжения в бетоне, вычисленные по формуле (358), должны удовлетворять условию прочности
σbt ≤ 0,7γttRbt. (361)
В неравенстве (361) коэффициент γtt принимают по табл. 16 в зависимости от температуры бетона в сечении II - II или III - III.
ПЕРЕКРЫТИЯ
6.19. Купола перекрытий часто имеют многочисленные технологические отверстия диаметром 10 - 50 мм или несколько больших отверстий. Дырчатые купола выполняют из монолитного или сборного бетона. В цилиндрических печах кипящего слоя при диаметре перекрытия до 3 м монолитный дырчатый купол целесообразно разбивать радиальными и кольцевыми швами бетонирования на 3 - 8 сегментных элемента и один центральный круглый элемент диаметром до 1 м (черт. 55). При диаметре купола перекрытия более 3 м рекомендуется увеличивать количество как радиальных, так и кольцевых швов. Купола из сборных элементов должны иметь такое же расположение швов. Максимальный размер каждого элемента, расположенного между швами, не должен превышать 1,5 м. Радиальный шов как в сборных, так и в монолитных куполах, в верхней части имеет уширение (черт. 56), которое заполняется жаростойким раствором.
Черт. 55. Расчетные схемы бетонного купола перекрытия от воздействия температуры
1 - компенсационный шов; 2 - пята купола; 3 - радиальный шов; 4 - кольцевой шов
Черт. 56. Радиальный шов в бетонном куполе
1 - жаростойкий раствор; 2 - ширина шва в сборных куполах не менее 20 мм, в монолитных - впритык; 3 - бетонный элемент
Кольцевые и радиальные стыки между сборными элементами заполняют жаростойким раствором на всю высоту сечения, а в монолитных куполах раствором заполняют только радиальные швы в их верхней части, где эти швы имеют уширение.
В монолитных бетонных куполах перекрытий без сквозных отверстий следует предусматривать радиальные и кольцевые усадочные швы со стороны нижней сферической поверхности согласно требованиям п. 5.48.
Расчет бетонного купола перекрытия с
плоской верхней поверхностью на воздействие равномерно распределенной нагрузки,
собственного веса и температуры производят согласно требованиям п. 6.12 как сферическую бетонную оболочку, геометрическая
ось которой проходит через середину высоты сечения купола в замке и в пяте (см.
черт. 55). В расчете принимается
средняя толщина оболочки ![]() с радиусом кривизны оболочки r. Собственный вес оболочки принимается по средней высоте сечения и
равномерно распределенным по длине пролета.
с радиусом кривизны оболочки r. Собственный вес оболочки принимается по средней высоте сечения и
равномерно распределенным по длине пролета.
При наличии в куполе сквозных отверстий следует учитывать ослабление сечения бетона отверстиями.
6.20. Расчет бетонных сводов с плоской верхней поверхностью и нижней цилиндрической поверхностью на воздействие равномерно распределенной нагрузки, собственного веса и температуры производят по аналогии с расчетом цилиндрических сводов, изложенным в п. 6.15. При этом распор от воздействия температуры в сводах с неподвижными опорами вычисляют по формуле (326), а в сводах с податливыми опорами - по формуле (354). Жесткость таких сводов принимается по средней высоте сечения свода, расположенного на расстоянии 1/4 пролета от опоры.
Для восприятия распора от бетонного свода устраивают добавочное армирование стенки, опорную раму или каркас.
БОРОВА
6.21. Подземные и надземные борова из жаростойкого бетона и железобетона проектируют для отвода дымовых газов. Конструкцию подземных боровов обычно принимают из сборных элементов прямоугольного, круглого, эллиптического и других видов сечения. Выбор формы сечения борова производят в зависимости от температуры отводимых газов. При температурах отводимых газов, не превышающих предельно допустимую температуру применения арматуры (см. табл. 24), борова проектируются прямоугольного или круглого сечения с передачей на арматуру больших растягивающих усилий, возникающих от внешних нагрузок и температуры. При более высоких температурах отходящих газов, при которых нельзя использовать работу арматуры на растяжение, целесообразно применять подземные борова эллиптического сечения или из жаростойких бетонных элементов с полуциркульным или лучковым сводом покрытия.
Подземный боров круглого сечения из жаростойкого железобетона (черт. 57) рассчитывается по следующим рабочим состояниям:
пуск в эксплуатацию. Действуют нагрузки, собственный вес и неравномерный нагрев по высоте сечения стенки борова. Горизонтальные и вертикальные сечения стен борова рассчитывают на внецентренное сжатие от совместного действия температуры, собственного веса и постоянной нагрузки. Внутренняя арматура в сжатой зоне стенок борова в расчете не учитывается.
Усилия от нагрузки определяются по правилам строительной механики, а изгибающий момент от неравномерного нагрева по высоте стенки борова - по формуле (50).
Расчетные сопротивления бетона и арматуры принимаются для кратковременного нагрева с учетом коэффициентов условий работы γbt и γst по табл. 16 и 35;
боров находится в эксплуатации. Стенки борова равномерно прогрелись. Горизонтальные и вертикальные сечения рассчитываются на действие нагрузки и собственного веса. Наружная арматура в сжатой зоне сечения в расчете не учитывается.
При расположении бетонного или железобетонного борова над землей или в специальном коробе, воспринимающем внешнюю нагрузку, расчет борова производят на изгибающий момент от неравномерного нагрева по высоте стенки и на собственный вес. В этом случае борова могут иметь любое очертание.
Черт. 57. Расчетные схемы
а - от воздействия температуры; б - от воздействия нагрузки; 1 - температур; 2 - деформаций; 3 - напряжений; 4 - усилий в подземном круглом железобетонном борове
6.22. При температуре дымовых газов выше предельно допустимой температуры применения арматуры (см. табл. 24) подземный боров из жаростойкого бетона должен иметь поперечное сечение в виде эллипса (черт. 58). Расчет борова производят по следующим рабочим состояниям:
боров находится в земле в ненагретом состоянии. Действуют нагрузки и собственный вес. Очертание борова подбирается таким, при котором получаются наименьшие изгибающие моменты от вертикальных и горизонтальных сил. Эллипс должен быть тем больше вытянут в вертикальном направлении, чем больше отношение между интенсивностью вертикального и бокового давления.
При равномерно распределенной внешней нагрузке отношение между вертикальным и горизонтальным диаметрами эллипса должно составлять примерно корень квадратный из отношения вертикального и бокового давления.
Усилия в сечениях стенки борова от нагрузки и собственного веса находят по формулам строительной механики;
пуск в эксплуатацию. Стенки борова неравномерно нагреты. Сечения борова рассчитываются на внецентренное сжатие продольной силой от постоянной нагрузки и собственного веса по формуле (75).
Арматуру устанавливают только у наружной стороны стенки борова из расчета на монтажные нагрузки;
боров находится в эксплуатации. Стенки равномерно прогреты. Арматура в работе не учитывается из-за высокой ее температуры. Бетонные сечения борова рассчитываются на внецентренное сжатие по формуле (75).
Расчетное сопротивление бетона на сжатие принимается с учетом коэффициента условий работы γbt по табл. 16 для длительного нагрева в зависимости от средней температуры бетона сжатой зоны.
Черт. 58. Расчетные схемы
а - температур и напряжений; б - усилий от воздействия нагрузки; 1 - температур; 2 - напряжений; 3 - усилий в подземном эллиптическом бетонном борове
При температуре отводимых газов выше предельно допустимой температуры применения арматуры (см. табл. 24) рекомендуется также применять подземные борова из жаростойких бетонных блоков с цилиндрическим полуциркульным сводом (черт. 59, а) и с лучковым сводом (черт. 59, б). Блоки для таких боровов являются наиболее простыми в изготовлении. Сводовые блоки со стороны их наружной поверхности должны иметь арматурную сетку для восприятия монтажных нагрузок. При площади проходных сечений несущих боровов от 1 до 3,5 м2 и равномерно распределенной вертикальной постоянной нагрузке до 50 кН/м2 более экономичными являются борова с полуциркульным сводом, а при площади проходных сечений 4,5; 5,5 и 6,5 м - борова с лучковым сводом, имеющим центральный угол 2α = 120° (см. черт. 59, б). При таком угле по высоте нормальных сечений своза напряжения сжатия от его собственного веса, внешней нагрузки и давления грунта распределяются наиболее равномерно. При площади проходного сечения более 6,5 м2 необходимо применять борова, расположенные в несущих железобетонных туннелях.
Черт. 59. Конструкция несущих боровов из жаростойких бетонных блоков для отвода газов с температурой до 800 °С
а - с цилиндрическим полуциркульным сводом; б - с цилиндрическим лучковым сводом
Расчет боровов из жаростойких бетонных блоков с полуциркульным или лучковым сводом производят по следующим рабочим состояниям:
боров находится в земле в ненагретом состоянии. Действуют нагрузки от давления грунта и собственный вес. Прочность сечений свода и горизонтальных сечений стен проверяют на действие изгибающего момента и продольной силы от собственного веса и симметричного бокового давления грунта до верхней поверхности свода, а также от собственного веса и давления грунта до поверхности земли. Несимметричная засыпка борова грунтом не допускается.
Расчет прочности сечений борова в пусковой период не производят;
боров находится в эксплуатации. Стенки и свод борова прогреты равномерно. Прочность сечений свода и горизонтальных сечений стен рассчитывают на внецентренное сжатие от совместного действия собственного веса и постоянной нагрузки по формуле (75) без учета усилий от воздействия температуры.
Расчетное сопротивление бетона на сжатие принимают с учетом коэффициента условий работы γbt по табл. 16 для длительного нагрева при температуре бетона в расчетном сечении.
Усилия в сечениях борова из жаростойких бетонных блоков от воздействия нагрузки, давления грунта и собственного веса определяются по черт. 60 как в однопролетной раме с криволинейным ригелем и защемленными стойками.
Для определения усилий в сечениях рамы основную систему рекомендуется принимать в виде свода и двух защемленных внизу стоек с неизвестными усилиями, приложенными в пяте (см. черт. 60).
Черт. 60. Основная система для определения усилий в сечениях несущего борова из жаростойких бетонных блоков
qv - равномерно распределенная постоянная нагрузка; pv1, pv2 и pv3 - вертикальные нагрузки от давления грунта; ph1 и ph2 - горизонтальные нагрузки от бокового давления грунта с учетом вертикальной равномерно распределенной нагрузки; ρ - плотность грунта
При симметричном загружении свода имеем два неизвестных усилия: распор X1 и изгибающий момент X3 в левом опорном сечении свода. Такие же усилия возникают и в правом опорном сечении свода. Вертикальная опорная реакция X2 равна половине всей действующей на свод вертикальной нагрузки.
Неизвестные усилия X1 и X3 определяют из условия неразрывности деформаций свода и стенки в опорном узле свода.
При этом условии линейное перемещение наклонного сечения свода Δ в направлении действия распора X1 и угол поворота этого сечения θ по направлению действия изгибающего момента X3 соответственно равны и противоположны по знаку перемещению Δ и углу поворота θ наклонного сечения в пяте.
Условие неразрывности деформаций записывается в следующих уравнениях.
Перемещение по направлению силы X1:
для сечения свода
δ11X1 + δ13X3 + Δ1g + Δ1q + Δ1pv + Δ1ph = Δ; (362)
для сечения стенки
δ′11X1 + δ′13X3 + Δ′1g + Δ′1q + Δ′1pv + Δ′1ph = -Δ. (363)
Складывая уравнения (362) и (363), получим
(δ11 + δ′11)X1 + (δ13 + δ′13)X3 + Δ1g + Δ′1g + Δ1q + Δ′1q + Δ1pv + Δ′1pv + Δ1ph + Δ′1ph = 0. (364)
Угол поворота по направлению изгибающего момента X3:
для сечения свода
δ31X1 + δ33X3 + Δ3g + Δ3q + Δ3pv + Δ3ph = φ; (365)
для сечения стенки
δ′31X1 + δ′33X3 + Δ′3g + Δ′3q + Δ′3pv + Δ′3ph = -φ. (366)
Складывая уравнения (365) и (366), получим
(δ31 + δ′31)X1 + (δ33 + δ′33)X3 + Δ3g + Δ′3g + Δ3q + Δ′3q + Δ3pv + Δ′3pv + Δ3ph + Δ′3ph = 0. (367)
Решая совместно уравнения (364) и (367), определяем распор X1 и изгибающий момент X3.
В формулах (364) - (367) принято:
δ11 и δ13 - перемещения опорного сечения
свода в основной системе по направлению силы X1
соответственно от усилий ![]() = 1 H и
= 1 H и ![]() = 1 H · см;
= 1 H · см;
Δ1g; Δ1q; Δ1pv и Δ1ph - перемещения опорного сечения свода в основной системе по направлению силы X1 соответственно от собственного веса половины свода, вертикальной внешней нагрузки, вертикального и горизонтального давления грунта только на одну половину свода;
δ′11 и δ′13 - перемещения
сечения стенки в основной системе по направлению силы X1 соответственно от усилий ![]() = 1 H и
= 1 H и ![]() = 1 H · см;
= 1 H · см;
Δ′1g; Δ′1q; Δ′1pv и Δ′1ph - перемещения сечения стенки в основной системе по направлению силы X1 соответственно от собственного веса одной стенки, вертикальной внешней нагрузки, вертикального и горизонтального давления грунта только на одну стенку. В данном случае при вертикальных стенах борова: Δ′1g = 0; Δ′1q = 0 и Δ′1pv = 1;
δ31 и δ33 - углы поворота
опорного сечения свода в основной системе по направлению изгибающего момента X3 соответственно от усилия ![]() = 1 H и
= 1 H и ![]() = 1 H · см;
= 1 H · см;
Δ3g; Δ3q; Δ3pv и Δ3ph - углы поворота опорного сечения свода в основной системе по направлению изгибающего момента X3 соответственно от собственного веса половины свода, вертикальной внешней нагрузки, вертикального и горизонтального давления грунта только на одну половину свода;
δ′31 и δ′33 - углы поворота сечения стенки в основной системе по направлению
изгибающего момента X3 соответственно от усилий ![]() = 1 H и
= 1 H и ![]() = 1 H · см;
= 1 H · см;
Δ′3g; Δ′3q; Δ′3pv и Δ′3ph - углы поворота сечения стенки в основной системе по направлению изгибающего момента X3 соответственно от собственного веса одной стенки, вертикальной внешней нагрузки, вертикального и горизонтального давления грунта только на одну стенку. В данном случае при вертикальных стенах борова Δ′3g = 0; Δ′3q = 0 и Δ′3pv = 0.
После определения неизвестных усилий X1 и X3 необходимо построить эпюры изгибающих моментов, нормальных и поперечных сил для рамной конструкции борова и вычислить расчетные усилия в наиболее напряженных сечениях свода и стен.
При передаче усилий от стен на основание необходимо, чтобы сжимающие напряжения по подошве основания не превышали расчетное сопротивление грунта при сжатии.
ПРИМЕРЫ РАСЧЕТА ЭЛЕМЕНТОВ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ В УСЛОВИЯХ ВОЗДЕЙСТВИЯ ПОВЫШЕННЫХ И ВЫСОКИХ ТЕМПЕРАТУР
ПРИМЕРЫ РАСЧЕТА ПРОЧНОСТИ ЭЛЕМЕНТОВ БЕТОННЫХ КОНСТРУКЦИЙ
Пример 1. Расчет прочности внецентренно сжатого бетонного элемента прямоугольного сечения, односторонне нагретого до 600 °С, при приложении продольной силы со стороны менее нагретой грани сечения и 2e′ < h1.
Дано: размеры сечения свободно опертого элемента: b = 500 мм, h = 500 мм; расчетная длина l0 = 4,50 м; элемент неравномерно нагрет по высоте сечения, температура наиболее нагретой грани 600 °С; бетон состава № 11 (см. табл. 11) класса В20: Rb = 11,5 МПа (см. табл. 14), Eb = 19,5 · 103 МПа (см. табл. 17); расчетные значения продольной силы: от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 600 кН, в том числе от длительно действующих нагрузок Nl = 425 кН; все нагрузки приложены со стороны менее нагретой грани сечения с эксцентриситетом, равным 100 мм.
Требуется проверить прочность сечения.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты сечения, равное 11 °С.
Прежде всего необходимо определить эксцентриситет приложения продольной силы вследствие перемещения положения центра тяжести сечения, вызванного его неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части, средняя температура бетона которых оказывается равной 225 и 500 °С, и производим приведение частей площадей к площади ненагретого бетона по формуле (2).
Линия раздела сечения проходит по бетону, имеющему температуру 400 °С, и высота каждой части сечения будет равна (см. черт. 9, б):
![]() мм
мм
h1 = 500 - h2 = 500 - 181,8 = 318,2 мм.
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
(для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
при температуре 225 °С...................................................... βb = 0,86; ![]() = 0,74
= 0,74
» » 500 °С...................................................... βb = 0,50; ![]() = 0,53
= 0,53
Для состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до грани, наиболее сжатой внешней нагрузкой (в данном случае менее нагретой грани сечения), определяем по формуле (5):
![]() мм.
мм.
Суммарный эксцентриситет продольной силы e0 относительно центра тяжести приведенного сечения определяется по формуле (128).
Значение расчетного эксцентриситета продольной силы относительно центра тяжести приведенного сечения равно e01 = 100 - (250 - 207,1) = 57,1 мм. Определяем значение случайного эксцентриситета ea согласно указаниям п. 1.30, так как свободно опертый элемент является статически определимой конструкцией
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Эксцентриситет от температурного выгиба ft, вызванного неравномерным нагревом по высоте сечения элемента, определяется по формуле (297). Для этого определяем величину кривизны оси элемента от нагрева по формуле (24).
Коэффициенты αbt и αbt1, входящие в формулу (24), принимаются в зависимости от температуры бетона менее и более нагретой грани сечения по табл. 20:
при tb = 50 °С......................................................... αbt = 1,5 · 10-6 град-1
» tb1 = 600 °С................................................... αbt1 = 4,00 · 10-6 град-1.
По формуле (24):
![]() мм-1.
мм-1.
По формуле (297):
![]() мм.
мм.
Вычисляем значение e0 по формуле (128):
e0 = 57,1 + 16,7 + 11,7 = 85,5 мм.
Для учета влияния прогиба элемента определяем его гибкость.
Момент инерции приведенного сечения Ired определяем по формуле (11):
![]() мм4.
мм4.
По формуле (132):
![]() мм;
мм;
![]() .
.
Поскольку λ = 34,47 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.3.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (94). Для этого предварительно вычисляем значение δmin по формуле (96); γbt принимаем по табл. 16 в зависимости от температуры бетона в центре тяжести приведенного сечения
![]() °C; γbt = 0,77.
°C; γbt = 0,77.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициенты γb2 = 0,85 и γb9 = 0,90, принимаемые по табл. 15.
Rb = 11,5 · 0,85 · 0,90 = 8,80 МПа.
По формуле (96):
![]() .
.
Так как ![]() < δmin = 0,34, принимаем δ = 0,34.
< δmin = 0,34, принимаем δ = 0,34.
Значение φl вычисляем по формуле (95). Значение коэффициента β по табл. 39 при tcw = 278 °С для бетона состава № 11 равно 1,88.
![]() .
.
По формуле (94):
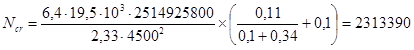 Н = 2313 кН.
Н = 2313 кН.
Коэффициент η определяем по формуле (93):
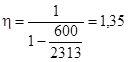 .
.
Эксцентриситет e′ с учетом прогиба вычисляем по формуле (77):
e′ = 207,1 - 85,5 · 1,35 = 91,6 мм.
Так как 2e′ = 183,2 мм < h1 = 318,2 мм, то расчет прочности элемента выполняется из условия (75).
Для этого предварительно вычисляем Ab по формуле (80):
Ab = 2 · 500 · 91,6 = 91 600 мм2
и определяем значение коэффициента γbt = 1,0 по табл. 16 в зависимости от средней температуры бетона сжатой зоны сечения:
![]() °С.
°С.
Из условия (75):
N = 600 кН < 1 · 8,8 · 91600 = 806000 Н = 806,0 кН.
Пример 2. Расчет прочности внецентренно сжатого бетонного элемента прямоугольного сечения, односторонне нагретого до 700 °С, при приложении продольной силы со стороны менее нагретой грани сечения и 2e′ > h1.
Дано: размеры сечения свободно опертого элемента - b = 500 мм, h = 500 мм; расчетная длина l0 = 4,5 м; элемент неравномерно нагрет по высоте сечения, температура наиболее нагретой грани 700 °С, наименее нагретой грани 100 °С; бетон состава № 11 (см. табл. 11) класса В20: Rb = 11,5 МПа (см. табл. 14), Eb = 19,5 · 103 МПа (см. табл. 17); расчетные значения продольной силы: от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 900 кН, в том числе от длительно действующих нагрузок Nl = 270 кН; все нагрузки приложены со стороны менее нагретой грани сечения с эксцентриситетом, равным 60 мм.
Требуется проверить прочность сечения.
Расчет. Прежде всего необходимо определить эксцентриситет приложения продольной силы вследствие перемещения центра тяжести сечения, вызванного его неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части, средняя температура которых оказывается равной 250 и 550 °С, и производим приведение площадей частей к площади ненагретого бетона по формуле (2).
Линия раздела сечения проходит по бетону, имеющему температуру 400 °С, и высота каждой части сечения будет равна: h1 = 250 мм, h2 = 250 мм.
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
(для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
при температуре 250 °С...................................................... βb = 0,82; ![]() = 0,72
= 0,72
» » 550 °С...................................................... βb = 0,45; ![]() = 0,48
= 0,48
Для состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до грани, наиболее сжатой внешней нагрузкой (в данном случае менее нагретой грани сечения), определяется по формуле (5):
![]() мм.
мм.
Величина расчетного эксцентриситета продольной силы относительно центра тяжести сечения равна
e01 = 60 - (250 - 192) = 2 мм.
Определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Эксцентриситет от температурного выгиба ft, вызванного неравномерным нагревом по высоте сечения элемента, определяется по формуле (297). Для этого определяем величину кривизны оси элемента от нагрева по формуле (24).
Коэффициенты αbt и αbt1, входящие в формулу (24), принимаются в зависимости от температуры бетона менее и более нагретой грани сечения по табл. 20:
при tb = 100 °С....................................................... αbt = 2,5 · 10-6 град-1
» tb1 = 700 °С..................................................... αbt1 = 3,5 · 10-6 град-1.
По формуле (24):
![]() мм-1.
мм-1.
По формуле (297):
![]() мм.
мм.
Вычисляем значение e0 по формуле (128):
e0 = 2 + 16,7 + 11,1 = 29,8 мм.
Для учета влияния прогиба элемента определяем его гибкость.
Момент инерции приведенного сечения Ired определяем по формуле (11):
![]() мм4.
мм4.
По формуле (132):
![]() мм;
мм;
![]() .
.
Поскольку λ = 34,09 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.3.
Для вычисления коэффициента η, на который должна быть умножена величина е0, определяем значение Ncr по формуле (94). Для этого предварительно вычисляем значение δmin по формуле (96); γbt = 0,65 принимаем по табл. 16 для состава № 11 в зависимости от температуры бетона в центре тяжести приведенного сечения
![]() °C.
°C.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициенты γb2 = 0,85 и γb9 = 0,90, принимаемые по табл. 15:
Rb = 11,5 · 0,85 · 0,90 = 8,8 МПа.
По формуле (96):
![]() .
.
Так как ![]() < δmin = 0,35, принимаем δ = 0,35.
< δmin = 0,35, принимаем δ = 0,35.
Значение φl вычисляем по формуле (95). Значение коэффициента β по табл. 39 при tcw = 330 °С для бетона состава № 11 равно 2,62.
![]() .
.
По формуле (94):
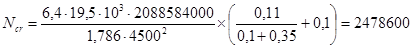 Н = 2478,6 кН.
Н = 2478,6 кН.
Коэффициент η определяем по формуле (93):
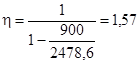 .
.
Эксцентриситет e′ с учетом прогиба вычисляем по формуле (77):
e′ = 192 - 29,8 · 1,57 = 151,6 мм.
Так как 2e′ = 303,2 мм > h1 = 250 мм, то расчет прочности элемента выполняется из условия (82).
Для этого необходимо предварительно
вычислить Δx по формуле (85). Коэффициенты βb1 и βb2, ![]() и
и ![]() (для кратковременного нагрева), входящие в эту формулу, принимаем по табл. 16 и 18 для
состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой
соответственно h1 = 250 мм и приближенно назначенной высоты
Δx = 85 мм.
(для кратковременного нагрева), входящие в эту формулу, принимаем по табл. 16 и 18 для
состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой
соответственно h1 = 250 мм и приближенно назначенной высоты
Δx = 85 мм.
Для h1 = 250 мм, tbm1 = 250 °С..................... βb1 = 0,82; ![]() = 0,72;
= 0,72;
Для Δx =
85 мм, tbm2 = 450 °С..................... βb2 = 0,56; ![]() = 0,57.
= 0,57.
По формуле (85):
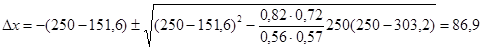 мм.
мм.
Полученное значение Δx = 86,9 мм близко по значению к заданному Δx = 85 мм, поэтому в расчете принимаем Δx = 86,9 мм.
Ab1 = 500 · 250 = 125000 мм2;
Ab2 = 500 · 86,9 = 43450 мм2.
Коэффициенты γbt определяем по табл. 16 для состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой h1 = 250 мм и Δx = 86,9 мм соответственно:
при tbm1 = 250 °С..................................................................... γbt1 = 0,85
» tbm2 = 450 °С...................................................................... γbt2 = 0,47
По условию (82):
N = 900 кН < 8,8(0,85 · 125000 + 0,47 · 43450) = 1116400 Н = 1116,4 кН,
т.е. прочность сечения обеспечена.
Пример 3. Расчет прочности внецентренно сжатого бетонного элемента прямоугольного сечения, в котором недопустимо появление трещин при его равномерном нагреве до 200 °С.
Дано: размеры сечения - b = 500 мм, h = 500 мм; расчетная длина l0 = 4 м; элемент равномерно нагрет до 200 °С; бетон состава № 1 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), естественного твердения, Eb = 30,0 · 103 МПа (см. табл. 17); расчетные значения продольной силы и изгибающего момента от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 400 кН и M = 36 кН · м от этой силы, в том числе от длительно действующих нагрузок Nl = 300 кН и Ml = 27 кН · м от этой силы.
Требуется проверить прочность сечения.
Расчет. При длительном нагреве расчетные сопротивления бетона умножаем на коэффициенты γb2 = 0,85 и γb9 = 0,90, принимаемые по табл. 15.
Rb = 14,5 · 0,85 · 0,90 = 11,1 МПа;
Rbt = 1,05 · 0,85 · 0,90 = 0,80 МПа.
Значения коэффициентов γbt, γtt и βb, ![]() принимаем соответственно по табл. 16 и 18 при t = 200 °С γbt = 0,80, γtt = 0,50 … βb = 0,60,
принимаем соответственно по табл. 16 и 18 при t = 200 °С γbt = 0,80, γtt = 0,50 … βb = 0,60, ![]() = 0,70 (для кратковременного нагрева).
= 0,70 (для кратковременного нагрева).
Расчетный элемент является элементом
статически неопределимой конструкции, поэтому случайный эксцентриситет не
учитываем, поскольку ![]() мм >
мм > ![]() мм.
мм.
Для решения вопроса об учете влияния
прогиба на прочность элемента определяем его гибкость ![]() . Для равномерно нагретого прямоугольного сечения
. Для равномерно нагретого прямоугольного сечения ![]() . В плоскости действия
изгибающего момента:
. В плоскости действия
изгибающего момента:
![]() мм;
мм;
![]() >
14.
>
14.
Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.7.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (94). Для этого предварительно вычисляем значение δmin по формуле (96):
![]() .
.
Так как ![]() < δmin = 0,33, согласно указаниям п. 3.7. принимаем δ =
0,33.
< δmin = 0,33, согласно указаниям п. 3.7. принимаем δ =
0,33.
Значение φl вычисляем по формуле (95). Значение коэффициента β по табл. 39 при t = 200 °С для бетона состава № 1 равно 1,5.
![]() .
.
Значение Ired вычисляем по формуле (1), в которой для состава № 1 φb1 = 0,85:
![]() мм4.
мм4.
По формуле (94):
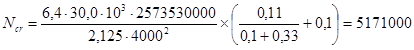 Н = 5171 кН.
Н = 5171 кН.
Коэффициент η определяем по формуле (93):
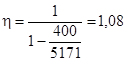 .
.
Проверку сечения производим согласно указаниям п. 3.5.
Определяем площадь сечения сжатой зоны по формуле (76):
![]() мм2.
мм2.
Из условия (75):
N = 400 кН < 0,80 · 11,1 · 151900 = 1348870 Н = 1349 кН.
В связи с тем, что по условию примера в элементе не допускается появление трещин, независимо от расчета из условия (75) необходима проверка сечения с учетом сопротивления бетона растянутой зоны.
Проверку сечения производим из условия (89):
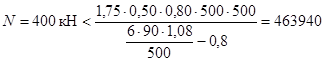 Н = 464 кН,
Н = 464 кН,
т.е. прочность сечения обеспечена.
Пример 4. Расчет прочности внецентренно сжатого бетонного элемента таврового сечения, односторонне нагретого до 300 °С, при приложении продольной силы со стороны более нагретой грани сечения (полки) и 2e′ < h′f.
Дано: размеры сечения элемента - b′f = 750 мм, h′f = 130 мм, b = 120 мм, h = 500 мм; расчетная длина l0 = 4 м; элемент неравномерно нагрет по высоте сечения, наиболее нагретая грань сжатой полки имеет расчетную температуру 300 °С, наименее нагретая наружная поверхность ребра имеет расчетную температуру 50 °С; бетон состава № 2 (см. табл. 11) класса В25, подвергнутый тепловой обработке при атмосферном давлении: Rb = 14,5 МПа (см. табл. 14), Eb = 30,0 · 103 МПа (см. табл. 17); расчетные значения продольной силы и изгибающего момента от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 1000 кН, M = 60 кН · м, в том числе от длительно действующих нагрузок Nl = 250 кН, Мl = 15 кН · м.
Требуется проверить прочность сечения.
Расчет. Определим расстояние от центра тяжести сечения до наиболее сжатой (в данном случае до более нагретой) грани сечения:
![]() мм.
мм.
Расчетный эксцентриситет продольной силы относительно центра тяжести сечения
![]() мм.
мм.
Выгиб элемента, вызванный неравномерным нагревом сечения, уменьшает расчетный эксцентриситет продольной силы e01, поэтому он не учитывается.
Поскольку расчетный элемент является элементом статически определимой конструкции, то согласно указаниям п. 1.30 учитываем величину случайного эксцентриситета
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Вычисляем значение e0 по формуле (128) при ft = 0:
e0 = 60 + 16,7 = 76,7 мм.
Для учета влияния прогиба элемента определяем его гибкость.
Определяем момент инерции I относительно центра тяжести сечения
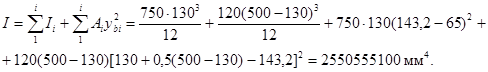
Тогда 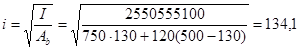 мм
мм
![]() .
.
Поскольку λ = 29,83 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.3.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем
значение Ncr по формуле (94). Величину Ired, входящую в формулу (94), определяем по формуле (1).
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18 для состава № 2 в зависимости от
температуры бетона в центре тяжести сечения:
(для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18 для состава № 2 в зависимости от
температуры бетона в центре тяжести сечения:
при ![]() °C βb = 0,54 и
°C βb = 0,54 и ![]() = 0,69.
= 0,69.
Для бетона состава № 2 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (1):
![]() мм4.
мм4.
Значение δmin вычисляем по формуле (96); γbt = 0,72 принимаем по табл. 16 для бетона состава № 2 в зависимости от температуры бетона в центре тяжести сечения, равной 228 °С.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициенты γb2 = 0,85 и γb9 = 0,90, принимаемые по табл. 15:
Rb = 14,5 · 0,85 · 0,90 = 11,1 МПа.
По формуле (96):
![]() .
.
Так как ![]() < δmin = 0,34, принимаем δ = 0,34.
< δmin = 0,34, принимаем δ = 0,34.
Значение φl вычисляем по формуле (95). Значение коэффициента β по табл. 39 для бетона состава № 2 при tcw = 228 °С равно 1,64:
![]() .
.
По формуле (94):
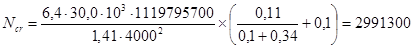 Н = 2991,3 кН.
Н = 2991,3 кН.
Коэффициент η определяем по формуле (93):
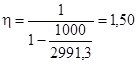 .
.
Эксцентриситет e′ с учетом прогиба вычисляем по формуле (77):
e′ = 143,2 - 76,7 · 1,50 = 28 мм.
Так как 2e′ = 56 мм < h′f = 130 мм, расчет прочности элемента выполняем из условия (75), где Ab, входящее в это условие, определяем по формуле (76) при b = b′f = 750 мм.
![]() мм2.
мм2.
Коэффициент γbt принимаем по табл. 16 для состава № 2 в зависимости от средней температуры сжатой зоны бетона Ab:
при
![]() °С … γbt = 0,54.
°С … γbt = 0,54.
По условию (75):
N = 1000 кН < 11,1 · 0,54 · 202190 = 1209682,60 Н = 1209,7 кН,
т.е. прочность сечения обеспечена.
Пример 5. Расчет прочности внецентренно сжатого бетонного элемента таврового сечения, односторонне нагретого до 700 °С, при приложении продольной силы со стороны более нагретой грани сечения (полки) и 2e′ > h′f.
Дано: размеры сечения элемента - b′f = 750 мм, h′f = 130 мм, b = 120 мм, h = 500 мм; расчетная длина l0 = 4 м; элемент неравномерно нагрет по высоте сечения, наиболее нагретая грань сжатой полки имеет расчетную температуру 700 °С, наименее нагретая наружная поверхность ребра имеет расчетную температуру 100 °С; бетон состава № 11 (см. табл. 11) класса В20: Rb = 11,5 МПа (см. табл. 14), Eb = 19,5 · 103 МПа (см. табл. 17); расчетные значения продольной силы и изгибающего момента от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 200 кН, M = 4 кН · м, в том числе от длительно действующих нагрузок Nl = 40 кн, Ml = 0,8 кН · м.
Требуется проверить прочность сечения.
Расчет. Из теплотехнического расчета получена средняя температура бетона свесов полки 670 °С, средняя температура бетона ребра 322 °С.
Определяем эксцентриситет приложения продольной силы вследствие перемещения положения центра тяжести сечения, вызванного его неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части по границе между ребром и полкой и производим приведение площадей полки и ребра к площади ненагретого бетона по формуле (2).
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем соответственно по табл. 16
и 18:
(для кратковременного нагрева) принимаем соответственно по табл. 16
и 18:
при температуре 670 °С...................................................... βb1 = 0,35; ![]() = 0,35
= 0,35
» » 322 °С...................................................... βb2 =
0,72; ![]() = 0,68
= 0,68
Для бетона состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до наиболее сжатой грани (в данном случае до более нагретой грани сечения) определяем по формуле (5):
![]() мм.
мм.
Расстояние от центра тяжести до той же грани
![]() мм.
мм.
Расчетный эксцентриситет продольной силы относительно центра тяжести приведенного сечения
![]() мм.
мм.
Выгиб элемента, вызванный неравномерным нагревом сечения, уменьшает расчетный эксцентриситет продольной силы e0, поэтому он не учитывается.
Поскольку расчетный элемент является элементом статически определимой конструкции, то согласно указаниям п. 1.30 учитываем величину случайного эксцентриситета
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Вычисляем значение e0 по формуле (128) при ft = 0:
e0 = 103,7 + 16,7 = 120,4 мм.
Для учета влияния прогиба элемента определяем его гибкость.
Момент инерции приведенного сечения Ired определяем по формуле (11):
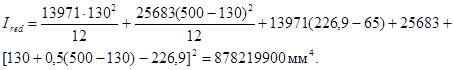
По формуле (132):
![]() мм,
мм,
![]() .
.
Поскольку λ = 26,88 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.3. Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (94). Для этого предварительно вычисляем значение δmin по формуле (96); γbt = 0,51 принимаем по табл. 16 в зависимости от температуры бетона в центре тяжести приведенного сечения, равной 428 °С.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициенты γb2 = 0,85 и γb9 = 0,90, принимаемые по табл. 15:
Rb = 11,5 · 0,85 · 0,90 = 8,8 МПа.
По формуле (96):
![]() .
.
Так как ![]() < δmin = 0,375, принимаем δ = 0,375.
< δmin = 0,375, принимаем δ = 0,375.
Значение φl вычисляем по формуле (95). Значение коэффициента β по табл. 39 при tcw = 428 °С для бетона состава № 11 равно 4,97:
![]() .
.
По формуле (94):
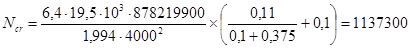 Н = 1137,3 кН.
Н = 1137,3 кН.
Коэффициент η определяем по формуле (93):
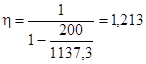 .
.
Эксцентриситет e′ с учетом прогиба вычисляем по формуле (77):
e′ = 226,9 - 120,4 · 1,213 = 80,8 мм.
Так как 2e′ = 161,6 мм > h′f = 130 мм, то расчет прочности элемента выполняется из условия (82).
Для этого необходимо предварительно
вычислить Δx по формуле (87). Коэффициенты βb1 и βb2, ![]() и
и ![]() (для кратковременного нагрева), входящие в эту формулу, принимаем по табл. 16 и 18 для
состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой
соответственно h′f = 130 мм и приближенно назначенной высоты
Δx = 60 мм.
(для кратковременного нагрева), входящие в эту формулу, принимаем по табл. 16 и 18 для
состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой
соответственно h′f = 130 мм и приближенно назначенной высоты
Δx = 60 мм.
Для h′f = 130 мм, tbm1 = 670 °С..................... βb1 = 0,35, ![]() = 0,35;
= 0,35;
Для Δx =
60 мм, tbm2 = 508 °С..................... βb2 = 0,49, ![]() = 0,52.
= 0,52.
По формуле (87):
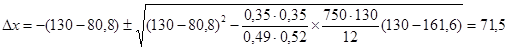 мм.
мм.
Полученное значение Δx = 71,5 мм больше заданного значения Δx = 60 мм, поэтому вторично назначим высоту
Δx = 70 мм и уточним среднюю температуру
бетона и значения
коэффициентов βb2 и ![]() для этого участка.
для этого участка.
tbm = 502 °C, βb2
= 0,50, ![]() = 0,53.
= 0,53.
По формуле (87):
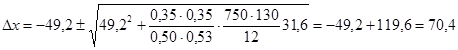 мм.
мм.
Полученное значение Δx = 70,4 мм близко по значению к повторно заданному Δx = 70 мм, поэтому в расчете принимаем Δx = 70,4 мм.
Ab1 = 750 · 130 = 97500 мм2;
Ab2 = 120 · 70,4 = 8448 мм2.
Коэффициенты γbt определяем по табл. 16 для бетона состава № 11 в зависимости от средней температуры бетона участков сжатой зоны высотой h′f = 130 мм и Δx = 70,4 мм соответственно:
для tbm1 = 670 °С....................................................................... γbt = 0,23
» tbm2 = 502 °С....................................................................... γbt = 0,40
По условию (82):
N = 200 кН < 8,8 · 0,23 · 97500 + 8,8 · 0,40 · 8448 = 226900 Н = 226,9 кН,
т.е. прочность сечения обеспечена.
ПРИМЕРЫ РАСЧЕТА ПРОЧНОСТИ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
Пример 6. Расчет прочности изгибаемого железобетонного элемента прямоугольного сечения при его равномерном нагреве до 100 °С.
Дано: размеры сечения - b = 300 мм, h = 800 мм, а = 70 мм, элемент равномерно нагрет до 100 °С; бетон состава № 1 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14); растянутая арматура из стали класса A-III: Rs = 365 МПа (см. табл. 29) с площадью поперечного сечения As = 2945 мм2 (6 Ø 25). Расчетный изгибающий момент от длительно действующей нагрузки M = 550 кН · м.
Требуется проверить прочность сечения.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15.
Rb = 14,5 · 0,85 = 12,3 МПа.
Значения коэффициентов γbt и γst, βs принимаем по таблицам соответственно 16 и 35. При температуре 100 °С γbt = 0,90, γst = 1,0, βs = 1,0;
h0 = 800 - 70 = 730 мм.
Проверку прочности сечения производим по указаниям пп. 3.17 и 3.18. Из формулы (106) при A′s = 0 определяем высоту сжатой зоны
![]() мм.
мм.
По формуле (99) определяем граничное значение относительной высоты сжатой зоны бетона ξR, вычислив предварительно значение ω по формуле (100):
ω = 0,85 - 0,008 · 0,90 · 12,3 = 0,76.
В связи с учетом коэффициента γb2 = 0,85 согласно указаниям п. 3.13 в формуле (99) вместо значения 400 принято 500:
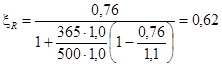 .
.
Так как х = 323,7 мм < ξRh0 = 0,62 · 730 = 452,6 мм, проверяем прочность сечения из условия (105) при A′s = 0.
M = 550 кН · м < 0,90 · 12,3 · 300 · 323,7(730 - 0,5 · 323,7) = 610765,6 Н = 610,77 кН · м,
т.е. прочность сечения обеспечена.
Пример 7. Определение площади поперечного сечения растянутой арматуры изгибаемого железобетонного элемента прямоугольного сечения, односторонне нагретого до 200 °С, при заданной площади сечения сжатой арматуры.
Дано: размеры сечения - b = 300 мм, h = 700 мм, а = 50 мм, а¢ = 30 мм; элемент неравномерно нагрет по высоте сечения; наиболее нагретая сжатая грань сечения имеет температуру 200 °С; бетон состава № 1 (см. табл. 11) класса В30: Rb = 17 МПа (см. табл. 14); вся арматура из стали класса A-III; Rs = 365 МПа (см. табл. 29), площадь сечения сжатой арматуры A′s = 942 мм2 (3 Ø 20); расчетный изгибающий момент, вызванный длительно действующими нагрузками в условиях систематического воздействия температуры, M = 450 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты сечения, равное 2,5 °С. В таком случае температура арматуры равна:
сжатой........................................................ ![]() °С
°С
растянутой................................................. ![]() °С
°С
Значения коэффициентов γst принимались по табл. 35 в зависимости от температуры арматуры:
сжатой............................................................................................ 0,91
растянутой....................................................................................... 1,0
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 17 · 0,85 = 14,45 МПа.
Согласно указаниям п. 3.11 среднюю температуру бетона сжатой зоны определяем по температуре бетона, расположенного на расстоянии 0,2h0 от сжатой грани сечения
h0 = 700 - 50 = 650 мм,
температура бетона сжатой зоны
![]() °С.
°С.
Для этой температуры бетона по табл. 16 определяем значение коэффициента γbt = 0,83.
По формуле (117) вычисляем значение α0:
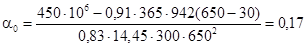 .
.
Для проверки условия α0 ≤ αR определяем значение ξR по формуле (99), предварительно вычислив значение ω по формуле (100):
ω = 0,85 - 0,008 · 0,83 · 14,45 = 0,754.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500. Значение коэффициента βs = 1,0 в зависимости от температуры растянутой арматуры принято по табл. 35:
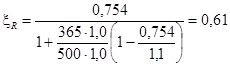 .
.
Вычисляем значение αR по формуле (103):
αR = 0,61(1 - 0,5 · 0,61) = 0,424.
Поскольку α0 = 0,17 < αR = 0,424 по табл. 41 в зависимости от значения α0 находим ξ = 0,19.
Так как ![]() , определяем необходимую площадь
растянутой арматуры по формуле (118):
, определяем необходимую площадь
растянутой арматуры по формуле (118):
![]() мм2.
мм2.
Принимаем 3 Ø 32 (As = 2413 мм2).
Пример 8. Определение площади поперечного сечения растянутой арматуры изгибаемого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 1100 °С.
Дано: размеры сечения - b = 150 мм, h = 550 мм, а = 35 мм; элемент неравномерно нагрет по высоте сечения, наиболее нагретая сжатая грань имеет температуру 1100 °С; бетон состава № 11 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14); растянутая арматура из стали класса A-III: Rs = 365 МПа (см. табл. 29). Расчетный изгибающий момент при длительном нагреве и нагрузке M = 32 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты сечения, равное 17,5 °С. В таком случае температура арматуры равна
![]() °С.
°С.
Значение коэффициента γst = 0,90 принимаем по табл. 35 в зависимости от температуры арматуры.
В связи с тем, что температура наиболее нагретой грани элемента превышает предельно допустимую температуру применения бетона, указанную в ГОСТ 20910-82, сечение согласно указаниям п. 3.19 рассчитывается с неполной высотой. Для этого определяем расстояние x1 от наиболее нагретой грани до бетона, имеющего предельно допустимую температуру применения, равную для состава № 11 - 1000 °С. Эта температура удовлетворяет требование п. 1.15:
![]() мм.
мм.
Укороченная полезная высота сечения по формуле (113) при h0 = h - a = 550 - 35 = 515 мм равна
hu = 515 - 57 = 458 мм.
Согласно указаниям п. 3.11 среднюю температуру бетона сжатой зоны в первом приближении определяем по температуре бетона, расположенного на расстоянии 0,2hu от сжатой грани сечения.
Температура бетона сжатой зоны
![]() °С.
°С.
Для этой температуры бетона по табл. 16 определяем значение коэффициента γbt = 0,10.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15.
Rb = 14,5 · 0,85 = 12,33 МПа.
Вычисляем значение α01 по формуле (111):
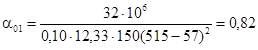 .
.
В связи с тем что α01 > αR, а следовательно и ξ > ξR, уточняем среднюю температуру бетона сжатой зоны при граничном значении высоты сжатой зоны, равном 0,7hu.
![]() °С.
°С.
Для этой же температуры бетона по табл. 16 определяем значение коэффициента γbt = 0,19.
Вычисляем новое значение коэффициента α01 по формуле (111):
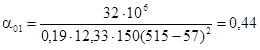 <
αR = 0,46.
<
αR = 0,46.
В зависимости от значения α01 по табл. 41 находим ξ = 0,66.
Полученное значение ξ близко к принятому граничному значению,
поэтому пересчета можно не делать. Действительно, если принять среднее значение
![]() ,
то для этой высоты сжатой зоны ее средняя температура будет равна
,
то для этой высоты сжатой зоны ее средняя температура будет равна
![]() °С;
°С;
γbt = 0,18; α01 = 0,45; ξ = 0,69.
Площадь сечения растянутой арматуры определяем по формуле (114):
![]() мм2.
мм2.
Принимаем 2 Ø 14 (As = 308 мм2).
Пример 9. Определение площади поперечного сечения арматуры изгибаемого железобетонного элемента таврового сечения при его равномерном нагреве до 100 °С.
Дано: размеры сечения - b′f = 400 мм, h′f = 120 мм, b = 200 мм, h = 600 мм, а = 60 мм; элемент равномерно нагрет до 100 °С; бетон состава № 1 (см. табл. 11) класса B15: Rb = 8,5 МПа (см. табл. 14); арматура из стали класса А-III: Rs = 365 МПа (см. табл. 29); расчетный изгибающий момент от длительного действия нагрева и нагрузки M = 250 кН · м.
Требуется определить площадь сечения арматуры.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 8,5 · 0,85 = 7,2 МПа.
Значения коэффициентов γbt и γst, βs принимаем соответственно по табл. 16 и 35. При температуре бетона 100 °C γbt = 0,90; γst = 1,0; βs = 1,0.
h0 = 600 - 60 = 540 мм.
Площадь сечения сжатой арматуры определяем по формуле (124). Для этого необходимо сначала определить значение αR. Вычисляем значение ξR по формуле (99), предварительно определив значение ω по формуле (100):
ω = 0,85 - 0,008 · 0,90 · 7,2 = 0,80.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
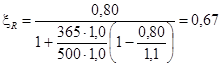 .
.
По формуле (103) определяем значение αR:
αR = 0,67(1 - 0,5 · 0,67) = 0,45;
![]() .
.
Следовательно, сжатой арматуры не требуется.
Проверяем положение границы сжатой зоны из условия (125) при А′s = 0:
M = 0,90 · 7,2 · 400 · 120(540 - 0,5 · 120) = 149,3 · 106 Н · мм = 149,3 кН · м < M = 250 кН · м.
Значит, граница сжатой зоны проходит в ребре.
Поскольку условие (125) не соблюдается, площадь сечения растянутой арматуры определяем по формуле (126) при A′s = 0. Для этого вычисляем значение α0 по формуле (127) при A′s = 0:
![]() .
.
Поскольку α0, определенное без учета сжатой арматуры, меньше αR, сжатой арматуры не требуется. Как видно, проверка этого критерия проще, чем пробное определение значения A′s.
По табл. 41 при α0 = 0,446 находим ξ = 0,67. Тогда по формуле (126) при A′s = 0
![]() мм2.
мм2.
Принимаем 4 Ø 25 (As = 1964 мм2).
Пример 10. Определение площади поперечного сечения растянутой арматуры изгибаемого железобетонного элемента таврового сечения при одностороннем нагреве до 700 °С.
Дано: размеры сечения - b′f = 700 мм, b = 130 мм, h′f = 120 мм, h = 500 мм, a = 40 мм; элемент неравномерно нагрет по высоте сечения; наиболее нагретая грань полки имеет температуру бетона 700 °С; бетон состава № 11 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14); арматура из стали класса А-III: Rs = 365 МПа (см. табл. 29); расчетный изгибающий момент, вызванный длительно действующей нагрузкой в условиях длительного нагрева М = 120 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты ребра, равное 12 °С. Средняя температура бетона свесов полки при наличии изоляции равна 650 °С, температура арматуры 100 °С.
Значение коэффициента γst = 1,0 принимаем по табл. 35 в зависимости от температуры арматуры.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Значения коэффициента условий работы бетона γbt определяем по табл. 16: для свесов полки - в зависимости от средней температуры бетона полки, равной 650 °С, для ребра - в зависимости от температуры бетона, находящегося на расстоянии 0,2h0 от сжатой грани сечения:
h0 = 500 - 40 = 460 мм.
Температура бетона сжатой зоны ребра
![]() °С.
°С.
Для свесов полки γbt = 0,25; для ребра γbt = 0,31.
Проверяем положение границы сжатой зоны из условия (125) при A′s = 0:
M = 120 кН · м > 0,25 · 12,33 · 700 · 120(460 - 0,5 · 120) = 103488000 Н · мм = 103,5 кН · м.
Поскольку условие (125) не соблюдается, граница сжатой зоны проходит в пределах ребра, площадь сечения растянутой арматуры определяем по формуле (126) при A′s = 0. Для этого вычисляем значение α0 по формуле (127) при A′s = 0:
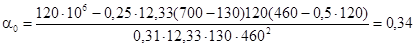 .
.
По табл. 41 при α0 = 0,34 находим ξ = 0,438. Тогда по формуле (126) при А′s = 0
![]() мм2.
мм2.
Принимаем 2 Ø 25 (As = 982 мм2).
Пример 11. Определение площади поперечного сечения растянутой арматуры изгибаемого железобетонного элемента таврового сечения при одностороннем нагреве до 1200 °С.
Дано: размеры сечения - b′f = 700 мм, b = 150 мм, h′f = 120 мм, h = 600 мм, a = 50 мм; элемент неравномерно нагрет по высоте сечения; наиболее нагретая грань полки имеет температуру бетона 1200 °С; бетон состава № 19 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), арматура из стали класса A-II: Rs = 280 МПа (см. табл. 29); расчетный изгибающий момент, вызванный длительной нагрузкой в условиях длительного нагрева M = 10 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. Из теплотехнического расчета
получено изменение температуры на 10 мм высоты свесов полки 10 °С, ребра - 18 °С. Таким
образом, средняя температура бетона полки равна ![]() °С, температура арматуры 210 °С.
°С, температура арматуры 210 °С.
Значение коэффициента γst = 0,83 принимаем по табл. 35 в зависимости от температуры арматуры.
Согласно указаниям п. 3.11, когда средняя температура бетона полки превышает предельно допустимую температуру применения бетона, указанную в ГОСТ 20910-82 (для состава № 19 - 1100 °С), сечение рассчитываем как прямоугольное без свесов полки, причем температура бетона наиболее нагретой грани этого сечения не должна превышать предельно допустимую температуру применения бетона и температуру 1000 °С согласно требованиям п. 1.15. Поэтому сечение рассчитываем с неполной высотой. Для этого определяем расстояние x1 от наиболее нагретой грани до бетона с температурой 1000 °С
![]() мм.
мм.
Укороченная полезная высота сечения по формуле (113) при h0 = 550 мм равна
hu = 550 - 111 = 439 мм.
Согласно указаниям п. 3.11 среднюю температуру бетона сжатой зоны в первом приближении определяем по температуре бетона, расположенного на расстоянии 0,2hu от сжатой грани сечения.
Температура бетона сжатой зоны
![]() °С.
°С.
Для этой температуры бетона по табл. 16 определяем значение коэффициента γbt = 0,06.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Вычисляем значение α01 по формуле (111):
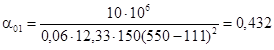 .
.
По табл. 41 находим ξ = 0,63.
Полученное значение относительной высоты сжатой зоны ξ = 0,63 значительно отличается от принятой при определении температуры бетона сжатой зоны ξ = 0,40.
Определим температуру бетона
сжатой зоны для среднего значения относительной высоты сжатой зоны ![]() .
.
При ξ = 0,51 средняя температура бетона сжатой зоны составит
![]() °С.
°С.
В соответствии с этой температурой уточняем значения γbt, α01 и ξ:
γbt = 0,08; ![]() ; ξ = 0,49.
; ξ = 0,49.
Последующее приближение при ![]() нам дает
нам дает
![]() °С;
°С;
γbt = 0,07; ![]() ; ξ = 0,50.
; ξ = 0,50.
Площадь сечения растянутой арматуры определяем по формуле (114):
![]() мм2.
мм2.
Принимаем 2 Ø 10 (As = 157 мм2).
Пример 12. Расчет прочности изгибаемого железобетонного элемента таврового сечения при одностороннем нагреве до 350 °С. Случай переармированного сечения.
Дано: размеры сечения b′f = 400 мм, h′f = 80 мм, b = 200 мм, h = 600 мм, а = 70 мм; элемент неравномерно нагрет по высоте сечения; наиболее нагретая грань полки имеет температуру бетона 350 °С; бетон состава № 2 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14); арматура из стали класса A-III: Rs = 365 МПа (см. табл. 29), площадь сечения As = 1964 мм2 (4Ø25); А′s = 0; расчетный изгибающий момент, вызванный длительно действующей нагрузкой в условиях длительного нагрева, M = 180 кН · м.
Требуется проверить прочность сечения.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты свесов полки - 4 °С, ребра - 6 °С. Таким образом, средняя температура бетона полки равна 334 °С, температура арматуры 32 °С.
Значения коэффициентов γst = 1,0 и βs = 1,0 принимаем по табл. 35 в зависимости от температуры арматуры.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Значения коэффициента условий работы бетона γbt определяем по табл. 16: для свесов полки - в зависимости от средней температуры бетона полки, равной 334 °С, для ребра - в зависимости от температуры бетона, находящегося на расстоянии 0,2h0 от сжатой грани сечения:
h0 = 600 - 70 = 530 мм.
Температура бетона сжатой зоны ребра
![]() °С.
°С.
Для свесов полки γbt = 0,37; для ребра γbt = 0,54.
Проверку прочности сечения производим согласно указаниям п. 3.22 при А′s = 0.
Поскольку γstRsAs = 1,0 · 365 · 1964 = 716860 Н = 716,9 кН больше, чем γbtRbb′fh′f = 0,37 · 12,33 · 400 · 80 = 145990 Н = 145,99 кН, т.е. условие (120) не соблюдается, граница сжатой зоны проходит в ребре. В этом случае высоту сжатой зоны определяем из формулы (122) при A′s = 0:
![]() мм.
мм.
Значение граничной относительной высоты сжатой зоны бетона ξR определяем по формуле (99), предварительно определив значение ω по формуле (100):
ω = 0,85 - 0,008 · 0,54 · 12,33 = 0,80.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
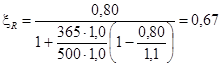 ;
;
xR = ξRh0 = 0,67 · 530 = 355,1 мм.
Полученное значение x = 483,5 мм больше xR = 355,1 мм, следовательно, сечение переармировано. В этом случае принимаем x = xR и прочность сечения проверяем из условия (123) при A′s = 0. При этом
αR = 0,67(1 - 0,5 · 0,67) = 0,446;
M = 180 кН · м < 0,446 · 0,54 · 12,33 · 200 · 5302 + 0,37 · 12,33(400 - 200)80(530 - 0,5 · 80) = 202596600 Н · мм = 202,6 кН · м
Прочность сечения обеспечена.
Пример 13. Расчет прочности внецентренно сжатого железобетонного элемента прямоугольного сечения при равномерном нагреве до 100 °С. Случай больших эксцентриситетов (ξ < ξR).
Дано: размеры сечения - b = 400 мм, h = 500 мм, а = а′ = 40 мм, расчетная длина l0 = 6 м; элемент равномерно нагрет до 100 °С; бетон состава № 1 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), подвергнутый тепловой обработке, Еb = 30,0 · 103 МПа (см. табл. 17); арматура из стали класса A-III: Rs = Rsc = 365 МПа (см. табл. 29); Еs = 0,2 · 106 МПа (см. табл. 37); площадь сечения арматуры Аs = А′s = 1232 мм2 (2Ø28); расчетные значения продольной силы и изгибающего момента: от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 700 кН, М = 213 кН · м, в том числе от длительно действующих нагрузок Nl = 650 кН, Ml = 165 кН · м.
Требуется проверить прочность сечения.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Значения коэффициентов γbt и βb, ![]() , γst и βs принимаем соответственно по табл. 16, 18 и 35. При
температуре 100 °С:
γbt =
0,90; βb =
0,80;
, γst и βs принимаем соответственно по табл. 16, 18 и 35. При
температуре 100 °С:
γbt =
0,90; βb =
0,80; ![]() =
0,70 (для кратковременного нагрева согласно указаниям п. 1.28); γst = 1,0; βs = 1,0.
=
0,70 (для кратковременного нагрева согласно указаниям п. 1.28); γst = 1,0; βs = 1,0.
Поскольку расчетный элемент является элементом статически определимой конструкции, определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Для равномерно нагретого прямоугольного сечения i = h / 3,46.
В плоскости действия изгибающего момента i = 500 / 3,46 = 144,5 мм и λ = l0 / i = 6000 / 144,5 = 41,52 > 14.
Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.29. Для этого предварительно вычисляем значение e0 по формуле (128):
![]() мм.
мм.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (130). Для этого предварительно вычисляем:
значение δmin по формуле (96):
![]() .
.
Так как e0 / h = 321 / 500 = 0,642 > δmin = 0,27, согласно указаниям п. 3.7 принимаем δ = 0,642;
значение φl по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой арматуры:
e = e0 + 0,5h - a = 321 +0,5 · 500 - 40 = 531 мм;
![]() мм.
мм.
Значение коэффициента β по табл. 39 при t = 100 °С для бетона состава № 1 равно 1,4.
![]() ;
;
![]() ;
;
h0 = 500 - 40 = 460 мм.
По формуле (130):
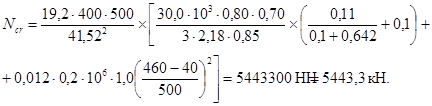
Коэффициент η определяем по формуле (93):
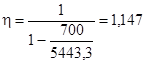 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 321 · 1,147 + 0,5 · 500 - 40 = 578,1 мм.
Проверку прочности сечения производим согласно указаниям п. 3.33. Для этого определяем высоту сжатой зоны x из формулы (137). При RstAs = RstA′s
![]() мм.
мм.
Для сравнения полученного значения x с граничным по формуле (100) определяем
ω = 0,85 - 0,008 · 0,90 · 12,33 = 0,761.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
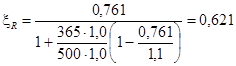 ;
;
xR = ξRh0 = 0,621 · 460 = 285,7 мм.
Поскольку x = 157,7 < xR = 285,7, прочность сечения проверяем из условия (136):
Ne = 700 · 0,58 = 406 кН · м < 0,90 · 12,33 · 400 · 157,7(460 - 0,5 · 157,7) + 1,0 · 365 · 12,32(460 - 40) = 455670130 Н · мм = 455,7 кН · м,
т.е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба
Определяем радиус инерции из плоскости изгиба
![]() мм.
мм.
Так как гибкость из плоскости изгиба λ = l0 / i = 6000 / 115,6 = 51,90 превышает гибкость в плоскости изгиба λ = 41,52, согласно указаниям п. 3.29 проверяем прочность сечения из плоскости изгиба, принимая эксцентриситет e0 равным случайному эксцентриситету ea.
Поскольку длина элемента l0 = 6 м < 20h = 20 · 0,4 = 8 м, расчет производим согласно указаниям п. 3.37 без учета арматуры.
При h > 200 мм η = 1,0.
При Nl / N = 650 / 700 = 0,93 и l0 / h = 6000 / 400 = 15 по табл. 44 находим значение коэффициента φb = 0,78.
При Аs = А′s = 0 α = 0 и φ = φb.
Для вычисления значения коэффициента α по формуле (151) по табл. 46 определяем значение αl = 0,70, а по табл. 47 значение λl = 85:
![]() .
.
Прочность сечения проверяем из условия (148) при As = 0:
N = 700 кН < 0,84 · 1,0 · 0,78(0,90 · 12,33 · 400 · 500 + 0) = 1457879 Н = 1457,9 кН,
т.е. прочность сечения из плоскости изгиба обеспечена.
Пример 14. Расчет прочности внецентренно сжатого железобетонного элемента прямоугольного сечения при равномерном нагреве до 100 °С. Случай малых эксцентриситетов (ξ > ξR).
Дано: размеры сечения - b = 400 мм, h = 500 мм, а = а′ = 40 мм, расчетная длина l0 = 6 м, элемент равномерно нагрет до 100 °С; бетон состава № 1 (см. табл. 11), подвергнутый тепловой обработке, класса В30: Rb = 17,0 МПа (см. табл. 14), Eb = 32,5 · 103 МПа (см. табл. 17); арматура из стали класса A-III: Rs = Rsc = 365 МПа (см. табл. 29), Еs = 0,2 · 106 МПа (см. табл. 37); площадь сечения арматуры As = А′s = 1473 мм2 (3Ø25); расчетные значения продольной силы и изгибающего момента: от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют), N = 2000 кН, М = 153 кН · м, в том числе от длительно действующих нагрузок Nl = 2000 кН, Мl = 50 кН · м.
Требуется проверить прочность сечения.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 17 · 0,85 = 14,45 МПа.
Значения коэффициентов γbt и βb, ![]() , γst и βs принимаем соответственно по табл.: 16, 18 и 35. При
температуре 100 °С:
γbt
= 0,90; βb = 0,80;
, γst и βs принимаем соответственно по табл.: 16, 18 и 35. При
температуре 100 °С:
γbt
= 0,90; βb = 0,80; ![]() = 0,70 (для кратковременного нагрева
согласно указаниям п. 1.28); γst = 1,0; βs = 1,0.
= 0,70 (для кратковременного нагрева
согласно указаниям п. 1.28); γst = 1,0; βs = 1,0.
Поскольку расчетный элемент является элементом статически определимой конструкции, определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Для равномерно нагретого прямоугольного сечения в плоскости действия изгибающего момента ![]() мм и
мм и ![]() > 14.
Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.29.
Для этого предварительно
вычисляем значение e0 по формуле (128):
> 14.
Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.29.
Для этого предварительно
вычисляем значение e0 по формуле (128):
![]() мм.
мм.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (130). Для этого предварительно вычисляем по формуле (96):
![]() .
.
Так как ![]() < δmin = 0,25, принимаем δ = 0,25.
< δmin = 0,25, принимаем δ = 0,25.
Значение φl вычисляем по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой арматуры:
e = e0 + 0,5h - a = 93,5 +0,5 · 500 - 40 = 303,5 мм;
![]() мм.
мм.
Значение коэффициента β по табл. 39 при t = 100 °С для бетона состава № 1 равно 1,4:
![]() ;
;
![]() ;
;
h0 = 500 - 40 = 460 мм.
По формуле (130) имеем:
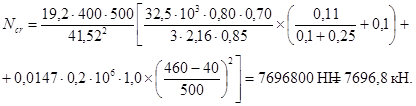
Коэффициент η определяем по формуле (93):
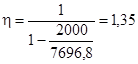 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 93,5 · 1,35 + 0,5 · 500 - 40 = 336 мм.
Проверку прочности сечения производим согласно указаниям п. 3.33. Для этого определяем высоту сжатой зоны x из формулы (137). При RsAs = RscA′s
![]() мм.
мм.
Для сравнения полученного значения x с граничным по формуле (100) определяем
ω = 0,85 - 0,008 · 0,90 · 14,45 = 0,746.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
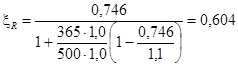 ;
;
xR = ξRh0 = 0,604 · 460 = 277,8 мм.
Поскольку x = 384,5 > xR = 277,8, прочность сечения проверяем из условия (136), определяя расчетную высоту сжатой зоны
![]() >
ξR =
0,604.
>
ξR =
0,604.
Прочность сечения проверяем из условия (136):
при ξR = 0,716, x = ξh0 = 0,716 · 460 = 329,4 мм;
Ne = 2000 · 0,336 = 672 кН · м < 0,90 · 14,45 · 400 · 329,4(460 - 0,5 · 329,4) + 1,0 · 365 · 1473(460 - 40) = 731818910 Н · мм = 731,8 кН · м,
т.е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба
Определяем радиус инерции из плоскости изгиба
![]() мм.
мм.
Так как гибкость из плоскости изгиба ![]() превышает гибкость в
плоскости изгиба λ = 41,52, согласно указаниям п. 3.29 проверяем прочность сечения из плоскости изгиба,
принимая эксцентриситет
e0 равным случайному эксцентриситету ea.
превышает гибкость в
плоскости изгиба λ = 41,52, согласно указаниям п. 3.29 проверяем прочность сечения из плоскости изгиба,
принимая эксцентриситет
e0 равным случайному эксцентриситету ea.
Поскольку длина элемента l0 = 6 м < 20h = 20 · 0,4 = 8 м, расчет производим согласно указаниям п. 3.37 без учета арматуры.
При h > 200 мм γ = 1,0.
При ![]() = 1,0 и
= 1,0 и ![]() по табл. 44 находим значение коэффициента φb = 0,77 и по табл. 45 -
значение коэффициента φsb = 0,84.
по табл. 44 находим значение коэффициента φb = 0,77 и по табл. 45 -
значение коэффициента φsb = 0,84.
По формуле (150) определяем:
![]() .
.
По формуле (149) определяем значение φ:
φ = 0,77 + 2(0,84 - 0,77)0,207 = 0,802.
Для вычисления значения коэффициента α по формуле (151) по табл. 46 определяем значение αl = 0,70, а по табл. 47 - значение λl = 85:
![]() .
.
Прочность сечения проверяем из условия (148) при As = A′s = 1473 мм2:
N = 2000 кН < 0,84 · 1,0 · 0,802 · (0,90 · 14,45 · 400 · 500 + 1,0 · 365 · 1473) = 2114440 Н = 2114,4 кН,
т.е. прочность сечения из плоскости изгиба обеспечена.
Пример 15. Расчет прочности сжатого железобетонного элемента прямоугольного сечения (e0 = ea) при равномерном нагреве до 150 °С.
Дано: размеры сечения - b = 400 мм, h = 400 мм, а = а′ = 40 мм, расчетная длина l0 = 6 м; элемент равномерно нагрет до 150 °С; бетон, подвергнутый тепловой обработке, состава № 1 (см. табл. 11), класса В25: Rb = 14,5 МПа (см. табл. 14), Еb = 30,0 · 103 МПа (см. табл. 17); арматура из стали класса A-III: Rs = Rsc = 365 МПа (см. табл. 29), Es = 0,2 · 106 МПа (см. табл. 37); площадь сечения арматуры Аs = A′s = 804 мм2 (4 Ø 16); расчетное значение продольной силы от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 1500 кН, в том числе от длительно действующих нагрузок Nl = 1300 кН.
Требуется проверить прочность сечения.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Значения коэффициентов γbt и βb, ![]() , γst и βs принимаем соответственно по табл. 16, 18 и 35. При
температуре 150 °С:
γbt
= 0,85; βb = 0,70;
, γst и βs принимаем соответственно по табл. 16, 18 и 35. При
температуре 150 °С:
γbt
= 0,85; βb = 0,70; ![]() = 0,70 (для кратковременного нагрева
согласно указаниям п. 1.28); γst = 0,95; βs = 0,98.
= 0,70 (для кратковременного нагрева
согласно указаниям п. 1.28); γst = 0,95; βs = 0,98.
Поскольку расчетный элемент является элементом статически определимой конструкции, определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм > 10 мм >
мм > 10 мм > ![]() мм.
мм.
Так как e0 = ea и l0 = 6000 < 20h = 20 · 400 = 8000 мм, производим приближенный расчет по указаниям п. 3.37. Для этого определяем значения величин, входящих в условие (148):
при h > 200 мм γ = 1,0;
при ![]() и
и ![]() ;
;
по табл. 44 находим значение коэффициента φb = 0,78, а по табл. 45 - значение коэффициента φsb = 0,84.
Определяем значение коэффициента αs по формуле (150):
![]() .
.
Значение коэффициента φ определяем по формуле (149):
φ = 0,78 + 2(0,84 - 0,78)0,333 = 0,82.
Для вычисления значения коэффициента α по формуле (151) по табл. 46 определяем значение αl = 0,65, а по табл. 47 - значение λl = 116. При
![]()
![]() .
.
Прочность сечения проверяем из условия (148):
N = 1500 кН < 0,87 · 1,0 · 0,82 · (0,85 · 12,33 · 400 · 400 + 0,95 · 365 · 1608) = 1594060 Н = 1594,1 кН,
т.е. прочность сечения обеспечена.
Проверяем прочность сечения согласно указаниям п. 3.33 с учетом влияния прогиба элемента согласно указаниям п. 3.29. Для этого определяем значение Ncr по формуле (130), предварительно вычислив значения входящих в формулу коэффициентов.
Вычисляем δmin по формуле (96):
![]() .
.
Так как ![]() < δmin = 0,245, принимаем δ = 0,245.
< δmin = 0,245, принимаем δ = 0,245.
Значение φl вычисляем по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой или слабо сжатой арматуры:
e = e0 + 0,5h - a = 13,3 +0,5 · 400 - 40 = 173,3 мм; el = e.
Значение коэффициента β по табл. 39 при t = 150 °С для бетона состава № 1 равно 1,45:
![]() ;
;
![]() ;
;
h0 = 400 - 40 = 360 мм.
По формуле (130) имеем:
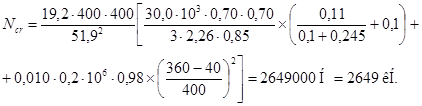
Коэффициент η определяем по формуле (93):
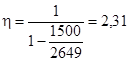 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 13,3 · 2,31 + 0,5 · 400 - 40 = 190,7 мм.
Проверку прочности сечения производим согласно указаниям п. 3.33. Для этого определяем высоту сжатой зоны x из формулы (137).
При RsAs = RscA′s
![]() мм.
мм.
Для сравнения полученного значения x с граничным по формуле (100) определяем
ω = 0,85 - 0,008 · 0,85 · 12,33 = 0,766.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
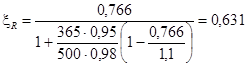 ;
;
xR = ξRh0 = 0,631 · 360 = 277,2 мм.
Поскольку x = 357,8 > xR = 227,2, прочность сечения проверяем из условия (136), определяя расчетную высоту сжатой зоны
![]() >
ξR = 0,631;
>
ξR = 0,631;
x = ξh0 = 0,812 · 360 = 292,3 мм.
Прочность сечения проверяем из условия (136) при ξ = 0,812:
Ne = 1500 · 0,191 = 286,1 кН · м < 0,85 · 12,33 · 400 · 292,3(360 - 0,5 · 292,3) + 0,95 · 365 · 804(360 - 40) = 351259400 Н · мм = 351,3 кН · м,
т.е. прочность сечения в плоскости изгиба обеспечена.
Пример 16. Определение площадей поперечного сечения растянутой и сжатой арматур внецентренно сжатого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 250 °С.
Дано: размеры сечения - b = 300 мм, h = 500 мм, a = 40 мм, a′ = 60 мм, расчетная длина l0 = 6,3 м; элемент неравномерно нагрет по высоте сечения, температура наиболее нагретой (сжатой) грани - 250 °С; бетон, подвергнутый тепловой обработке, состава № 2 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), Eb = 30,0 · 103 МПа (см. табл. 17); арматура из стали класса A-III: Rs = Rsc = 365 МПа (см. табл. 29); Es = 0,2 · 106 МПа (см. табл. 37); расчетные значения продольной силы и изгибающего момента: от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 600 кН, M = 162 кН · м, в том числе от длительно действующих нагрузок Nl = 400 кН и Ml = 100 кН · м.
Требуется определить площади сечений арматуры As и A′s.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты сечения, равное 4 °С, тогда температура растянутой арматуры As равна
![]() °С;
°С;
а температура сжатой арматуры A′s равна
![]() °С.
°С.
Значения коэффициентов γst принимаем по табл. 35 в зависимости от температуры:
для растянутой арматуры..................................................................... 1,0
» сжатой............................................................................................ 0,83
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа.
Значения коэффициентов γbt и βb, ![]() и βs принимаем по таблицам соответственно 16, 18 и 35.
и βs принимаем по таблицам соответственно 16, 18 и 35.
Согласно указаниям п. 3.11 среднюю температуру бетона сжатой зоны определяем по температуре бетона, расположенного на расстоянии 0,2h0 от сжатой грани сечения:
h0 = 500 - 40 = 460 мм.
Температура бетона сжатой зоны
![]() °С.
°С.
Для этой температуры по табл.
16
определяем значение коэффициента γbt = 0,76 в зависимости от температуры бетона
в центре тяжести сечения (см. п. 3.38), равной ![]() °С; по табл. 16 определяем значение βb = 0,70, а по табл. 18 - значение
°С; по табл. 16 определяем значение βb = 0,70, а по табл. 18 - значение ![]() = 0,70 (для кратковременного нагрева согласно
указаниям п. 1.28); для средней температуры арматуры, примерно равной
150 °С, из табл. 35 βs = 0,98.
= 0,70 (для кратковременного нагрева согласно
указаниям п. 1.28); для средней температуры арматуры, примерно равной
150 °С, из табл. 35 βs = 0,98.
Определение требуемого количества продольной арматуры производим согласно указаниям п. 3.35. Поскольку расчетный элемент является элементом статически определимой конструкции, определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм >
мм > ![]() > 10 мм.
> 10 мм.
Для неравномерно нагретого прямоугольного
сечения с температурой наиболее нагретой грани до 400 °С согласно указаниям п. 3.29 i может быть принят равным ![]() . В плоскости действия изгибающего момента
. В плоскости действия изгибающего момента
![]() мм
мм
![]() >
14. Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.29. Для этого предварительно
вычисляем значение e0 по формуле (128) при ft = 0, поскольку
температурный выгиб уменьшает расчетный эксцентриситет продольной силы:
>
14. Поэтому учитываем влияние прогиба на прочность элемента согласно указаниям п. 3.29. Для этого предварительно
вычисляем значение e0 по формуле (128) при ft = 0, поскольку
температурный выгиб уменьшает расчетный эксцентриситет продольной силы:
![]() мм.
мм.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (130). Для этого предварительно вычисляем значение δmin по формуле (96):
![]() .
.
Так как ![]() > δmin = 0,28, принимаем δ = 0,574.
> δmin = 0,28, принимаем δ = 0,574.
Значение φl вычисляем по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой арматуры:
e = e0 + 0,5h - a = 287 +0,5 · 500 - 40 = 497 мм;
![]() мм.
мм.
Значение коэффициента β по табл. 39 для температуры центра тяжести сечения (см. п. 3.7), равной 150 °С, для бетона состава № 2 равно 1,45:
![]() .
.
Согласно указаниям п. 3.38 задаемся ориентировочно, что требуемое количество арматуры As + A′s находится в первом интервале армирования (см. табл. 48), которому соответствует μ1 = 0,01. Тогда по формуле (130) имеем:
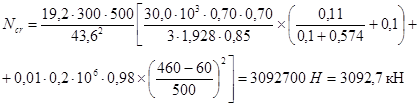
Коэффициент η определяем по формуле (93):
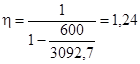 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 287 · 1,24 + 0,5 · 500 - 40 = 566 мм.
Площади сечения сжатой и растянутой арматур определяем по формулам (142) и (143):
![]() мм2;
мм2;
![]() мм2.
мм2.
Проверяем суммарный коэффициент армирования по формуле (152):
![]() %.
%.
Так как полученный коэффициент армирования соответствует принятому интервалу (от 0,8 до 1,8 % по табл. 48), то расчет считается законченным.
Принимаем: A′s = 804 мм2 (4 Ø 16), As = 1256 мм2 (4Ø20).
Пример 17. Расчет прочности внецентренно сжатого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 250 °С. Случай больших эксцентриситетов (ξ < ξR).
По данным примера 16 при A′s = 804 мм2 и As = 1256 мм2 проверить прочность сечения.
Расчет. Вычисляем значение коэффициента η согласно указаниям пп. 3.7 и 3.29. Для этого определяем Ncr по формуле (130) при
![]() ;
;
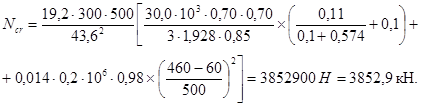
Коэффициент η определяем по формуле (93):
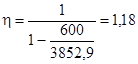 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 287 · 1,18 + 0,5 · 500 - 40 = 549 мм.
Проверку прочности сечения производим согласно указаниям п. 3.33. Для этого определяем высоту сжатой зоны x из формулы (137):
![]() мм.
мм.
Сравним полученное значение x с граничным:
xR = ξRh0 = 0,63 · 460 = 290 мм.
Так как x = 271,5 < xR = 290 мм, прочность сечения проверяем из условия (136) при x = 271,5 мм. В связи с небольшой разницей в значениях высоты сжатой зоны, принятой при определении ее средней температуры и полученной по расчету, пересчета значения x не делаем:
Ne = 600 · 0,549 = 329,2 кН · м < 0,81 · 12,33 · 300 · 271,5(460 - 0,5 · 271,5) + 0,83 · 365 · 804(460 - 60) = 361781860 Н · мм = 361,8 кН · м,
т.е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба
Определяем радиус инерции из плоскости изгиба:
![]() мм.
мм.
Так как гибкость из плоскости изгиба ![]() значительно превышает гибкость в плоскости изгиба
значительно превышает гибкость в плоскости изгиба ![]() , согласно указаниям п. 3.29 проверяем прочность сечения из
плоскости изгиба, принимая, что сечение равномерно нагрето до средней температуры 150 °С и эксцентриситет e0 равен случайному эксцентриситету ea. Поскольку
длина элемента l0 =
6,3 м > 20h = 20 · 0,3 = 6 м, расчет
производим согласно указаниям п. 3.33
без учета арматуры.
, согласно указаниям п. 3.29 проверяем прочность сечения из
плоскости изгиба, принимая, что сечение равномерно нагрето до средней температуры 150 °С и эксцентриситет e0 равен случайному эксцентриситету ea. Поскольку
длина элемента l0 =
6,3 м > 20h = 20 · 0,3 = 6 м, расчет
производим согласно указаниям п. 3.33
без учета арматуры.
Значение коэффициента γbt = 0,85 принимаем по табл. 16 для температуры бетона 150 °С.
Определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() >
> ![]() мм.
мм.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (130). Для этого предварительно вычисляем значение δmin по формуле (96):
![]() .
.
Так как ![]() < δmin = 0,185, принимаем δ = 0,185.
< δmin = 0,185, принимаем δ = 0,185.
Значение φl вычисляем по формуле (95) при β = 1,45:
![]() .
.
По формуле (130) при μ1 = 0 имеем
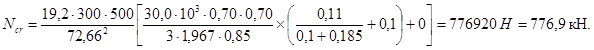
Ввиду близости значений N = 600 кН и Ncr = 776,9 кН необходимо предусмотреть конструктивное армирование длинных сторон сечения. Пусть μ1 = 0,006, тогда при h0 = 300 - 40 = 260 мм:
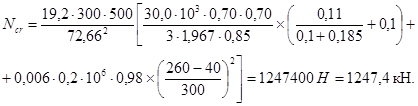
Коэффициент η определяем по формуле (93):
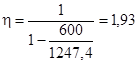 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 10,5 · 1,93 + 0,5 · 300 - 40 = 130,3 мм.
Для проверки прочности сечения определяем высоту сжатой зоны x из формулы (137), приняв As = А′s = 0,003 · 500(300 - 40) = 390 мм2 или точнее 402 мм2 (2Ø16) из стали класса А-III:
![]() мм.
мм.
Для сравнения полученного значения x с граничным определяем по формуле (100):
ω = 0,85 - 0,008 · 0,85 · 12,33 = 0,766.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500:
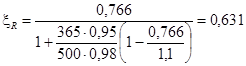 ;
;
xR = ξRh0 = 0,631 · 260 = 164,1 мм.
Так как x = 115 < xR = 164,1 мм, прочность сечения проверяем из условия (136):
Ne = 600 · 0,13 = 78 кН · м < 0,85 · 12,33 · 500 · 115(260 - 0,5 · 115) + 0,95 · 365 · 402(260 - 40) = 152698900 Н · мм = 152,7 кН · м.
Прочность сечения из плоскости изгиба обеспечена.
Пример 18. Определение площадей поперечного сечения растянутой арматуры внецентренно сжатого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 700 °С.
Дано: размеры сечения - b = 500 мм, h = 500 мм, a = 40 мм, расчетная длина l0 = 6 м; элемент неравномерно нагрет: со стороны нагрева температура 700 °С, с противоположной - 100 °С; бетон состава № 11 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14); Eb = 21,0 · 103 МПа (см. табл. 17); арматура из стали класса A-III: Rs = Rsc = 365 МПа (см. табл. 29), Es = 0,2 · 106 МПа (см. табл. 37); расчетные значения продольной силы от всех нагрузок (нагрузки, суммарная длительность действия которых мала, отсутствуют) N = 450 кН, в том числе от длительно действующих нагрузок Nl = 385 кН.
Требуется определить площадь сечения продольной арматуры.
Расчет. Прежде всего необходимо определить эксцентриситет приложения продольной силы вследствие перемещения положения центра тяжести сечения, вызванного его неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части, средняя температура которых оказывается равной 250 и 550 °С, и производим приведение площадей частей к площади ненагретого бетона по формуле (2).
Линия раздела сечения, имеющая температуру 400 °С, проходит посредине сечения, следовательно высота каждой части равна 250 мм.
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
(для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
при температуре 250 °С........................................ βb1 = 0,82, ![]() = 0,72
= 0,72
» » 550 °С....................................... βb2 = 0,45, ![]() = 0,48
= 0,48
Для бетона состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до грани, растянутой внешней нагрузкой (менее нагретой грани сечения), определяем по формуле (5):
![]() мм.
мм.
Расчетный эксцентриситет продольной силы
e01 = 250 - 192 = 58 мм.
Выгиб элемента, вызванный неравномерным нагревом сечения, уменьшает расчетный эксцентриситет продольной силы e01. Поэтому он не учитывается.
Поскольку расчетный элемент является элементом статически определимой конструкции, определяем величину случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм >
мм > ![]() мм.
мм.
Вычисляем значение e0 по формуле (128):
e0 = 58 + 17 = 75 мм.
Для учета влияния прогиба
элемента определяем его гибкость ![]() , где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0.
, где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0.
![]() мм4.
мм4.
![]() мм;
мм;
![]() <
λl = 58,
<
λl = 58,
где λl принято по табл. 47 в зависимости от температуры центра тяжести сечения;
![]() °C.
°C.
Поскольку λ = 45,45 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.29.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (129). Для этого предварительно вычисляем значение δmin по формуле (96); γbt = 0,65 принято по табл. 16 в зависимости от tcw = 330 °С.
Согласно указаниям п. 2.10 (при длительном нагреве) расчетное сопротивление бетона умножаем на коэффициенты γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа;
![]() .
.
Так как ![]() < δmin = 0,30, принимаем δ = 0,30.
< δmin = 0,30, принимаем δ = 0,30.
Значение φl вычисляем по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой арматуры:
e = 75 +0,5 · 500 - 40 = 285 мм;
el = e.
Значение коэффициента β по табл. 39 при t = 330 °С для состава № 11 равно 2,62:
![]() .
.
В связи с тем что по условиям нагрева арматура устанавливается только у одной из граней сечения элемента, в формуле (129) Is согласно указаниям п. 3.29 принимается равной нулю.
Значения βb и ![]() определяем соответственно по табл. 16 и 18 при
температуре 330 °С: βb = 0,71,
определяем соответственно по табл. 16 и 18 при
температуре 330 °С: βb = 0,71, ![]() = 0,67 (для кратковременного нагрева согласно
указаниям п. 1.28).
= 0,67 (для кратковременного нагрева согласно
указаниям п. 1.28).
По формуле (129) имеем:
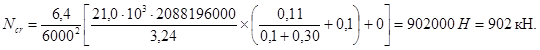
Коэффициент η определяем по формуле (93):
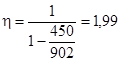 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 75 · 1,99 + 0,5 · 500 - 40 = 359 мм.
Проверяем условие (146). Для этого определяем граничное значение высоты сжатой зоны по указаниям п. 3.13. Для определения средней температуры сжатой зоны принимаем ξR = 0,70. Тогда при h0 = h - а = 500 - 40 = 460 мм
![]() °C.
°C.
По табл. 16 для этой температуры γbt = 0,39.
Температура арматуры
![]() °C.
°C.
По табл. 35 γst = 0,95, βs = 0,98.
По формуле (100) определяем значение
ω = 0,8 - 0,008 · 0,39 · 12,33 = 0,76.
В связи с учетом коэффициента γbt = 0,85 в формуле (99) вместо значения 400 принято 500:
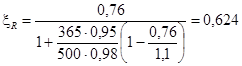 .
.
Уточняем температуру сжатой зоны при ξR = 0,624:
![]() °C;
°C;
γbt = 0,37;
ω = 0,8 - 0,008 · 0,37 · 12,33 · 0,763 = 0,77.
Следовательно, ξR может быть принято равным 0,624.
Значение αR определяем по формуле (103):
αR = 0,624(1 - 0,5 · 0,624) = 0,43.
Определяем значения величин:
αRγbtRbbh20 = 0,43 · 0,37 · 12,33 · 500 · 4602 = 208670060 Н · мм = 208,7 кН · м
и
Ne = 450 · 0,359 = 161,5 кН · м.
Поскольку удовлетворяется условие (146):
Ne = 161,5 кН · м < αRγbtRbbh20 = 208,7 кН · м,
искомую площадь поперечного сечения продольной арматуры определяем следующим образом. Из формулы (142), в которой αR заменяется на α0, находим эту величину при A′s = 0:
![]() .
.
По табл. 41 в зависимости от α0 определяем значение ξ = 0,422. Так как коэффициент γbt был определен при ξR = 0,624, уточняем температуру бетона сжатой зоны при среднем значении ξR = 0,52:
![]() °C;
°C;
γbt = 0,34;
![]() ; ξ = 0,47,
; ξ = 0,47,
что достаточно близко к заданному.
Площадь поперечного сечения растянутой арматуры определяем по формуле (144) при A′s = 0:
![]() мм2.
мм2.
Принимаем конструктивно 4 Ø 12 (As = 452 мм2).
Пример 19. Расчет прочности внецентренно сжатого железобетонного элемента таврового сечения при одностороннем нагреве до 500 °С. Случай больших эксцентриситетов (ξ < ξR).
Дано: размеры сечения элемента - b′f = 750 мм, h′f = 130 мм, b = 120 мм, h = 500 мм, a = 50 мм, счетная длина l0 = 5 м; элемент неравномерно нагрет по высоте сечения, наиболее нагретая грань сжатой полки имеет расчетную температуру 500 °С; бетон состава № 11 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), Eb = 21,0 · 103 МПа (см. табл. 17), растянутая арматура из стали класса А-III: Аs = 365 МПа (см. табл. 29), Es = 0,2 · 106 МПа (см. табл. 37); площадь сечения арматуры As = 628 мм2 (2 Ø 20), A′s = 0.
Расчетный изгибающий момент и нормативная сила, вызванные кратковременным действием температуры, Mt = 79 кН · м, Nt = 250 кН.
Требуется проверить прочность сечения.
Расчет. Из теплотехнического расчета получена температура арматуры 130 °С, наружной поверхности ребра 90 °С, средняя температура бетона свесов полки 480 °С, средняя температура бетона ребра 270 °С.
Определяем эксцентриситет приложения продольной силы вследствие перемещения положения центра тяжести сечения, вызванного его неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части по границе между ребром и полкой и производим приведение площадей полки и ребра к площади ненагретого бетона по формуле (2).
Значения коэффициентов βb и ![]() принимаем соответственно по табл. 16 и 18:
принимаем соответственно по табл. 16 и 18:
при температуре 480 °С........................................ βb1 = 0,52, ![]() = 0,55
= 0,55
» » 270 °С....................................... βb2 = 0,71, ![]() = 0,71
= 0,71
Для бетона состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до грани, растянутой внешней нагрузкой (менее нагретой грани сечения), определяем по формуле (5):
![]() мм.
мм.
Расстояние от центра тяжести сечения до той же грани
![]() мм.
мм.
Расчетный эксцентриситет продольной силы
![]() мм.
мм.
Выгиб элемента, вызванный неравномерным нагревом сечения, уменьшает расчетный эксцентриситет продольной силы e01, поэтому он не учитывается.
Поскольку расчетный элемент является элементом статически неопределимой конструкции, значение случайного эксцентриситета ea согласно указаниям п. 1.30 также не учитываем, так как
e0 =
350 мм > ![]() мм.
мм.
Для учета влияния прогиба
элемента определяем его гибкость ![]() , где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0:
, где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0:
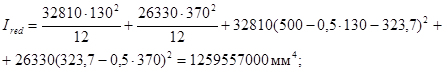
![]() мм;
мм;
![]() .
.
Поскольку λ = 34,27 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.29.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (129). Для этого предварительно вычисляем значение δmin по формуле (96); γbt = 0,97 принято по табл. 16 для кратковременного нагрева (см. условие примера) в зависимости от температуры центра тяжести приведенного сечения, равной:
![]() °C;
°C;
![]() .
.
Так как ![]() > δmin = 0,259, принимаем δ = 0,70.
> δmin = 0,259, принимаем δ = 0,70.
φl = 1,0, так как Ml = 0.
В связи с тем, что по условиям нагрева арматура устанавливается только у одной из граней сечения элемента, Is в формуле (129) согласно указаниям п. 3.29 принимается равной нулю.
Значения βb и ![]() определяем соответственно по табл. 16 и 18 при
температуре 355 °С: βb = 0,68,
определяем соответственно по табл. 16 и 18 при
температуре 355 °С: βb = 0,68, ![]() = 0,65.
= 0,65.
По формуле (129) имеем:
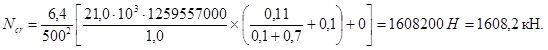
Коэффициент η определяем по формуле (93):
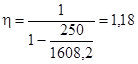 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 350 · 1,18 + 323,7 - 50 = 687 мм.
Проверку прочности сечения производим согласно указаниям п. 3.40 в зависимости от положения границы сжатой зоны.
Проверяем соблюдение условия (153) при h0 = h - а = 500 - 50 = 450 мм и A′s = 0.
Значение коэффициента γbt = 0,91 для средней температуры бетона полки 480 °С определяем по табл. 16 для кратковременного нагрева (см. условие примера):
Ne = 250 · 103 · 687 = 171675000 Н · мм = 171,7 кН · м;
γbtRbb′fh′f = 0,91 · 14,5 · 750 · 130(450 - 0,5 · 130) = 495307300 Н · мм = 495,31 кН · м.
Поскольку условие (153) соблюдается, граница сжатой зоны проходит в полке и расчет сечения производится как для прямоугольного сечения шириной b = b′f = 750 мм в соответствии с указаниями пп. 3.33 и 3.34.
Определяем значение коэффициента γst = 0,98 по табл. 35 для температуры 130 °С при кратковременном нагреве.
Вычисляем высоту сжатой зоны из формулы (137):
![]() мм < h′f = 130 мм.
мм < h′f = 130 мм.
Прочность сечения проверяем из условия (136) при A′s = 0:
Ne = 171,7 кН · м< 0,91 · 14,5 · 750 · 48(450 - 0,5 · 48) = 202756300 Н · мм = 202,8 кН · м.
Прочность сечения обеспечена.
Пример 20. Расчет прочности внецентренно сжатого железобетонного элемента таврового сечения при одностороннем нагреве до 800 °С. Случай малых эксцентриситетов (ξ < ξR).
Дано: размеры сечения элемента - b′f = 750 мм, h′f = 130 мм, b = 120 мм, h = 500 мм, а = 50 мм; расчетная длина l0 = 5 м; элемент неравномерно нагрет по высоте сечения, наиболее нагретая грань сжатой полки имеет расчетную температуру 800 °С; бетон состава № 11 (см. табл. 11) класса В25: Rb = 14,5 МПа (см. табл. 14), Eb = 21,0 · 103 МПа (см. табл. 17); растянутая арматура из стали класса А-III: Rs = 365 МПа (см. табл. 29), Еs = 0,2 · 106 (см. табл. 37); площадь сечения арматуры Аs = 628 мм (2 Ø 20), А′s = 0; расчетное значение продольной силы от всех нагрузок (кроме нагрузок, суммарная длительность действия которых мала) N = 240 кН, в том числе от длительно действующих нагрузок Nl = 40 кН.
Требуется проверить прочность сечения.
Расчет. Из теплотехнического расчета получено изменение температуры на 10 мм высоты ребра, равное 15 °С. Средняя температура бетона свесов полки при наличии изоляции равна 750 °С, температура наружной поверхности бетона ребра 50 °С, арматуры 125 °С. Средняя температура бетона ребра 330 °С.
Определяем эксцентриситет приложения продольной силы вследствие перемещения положения центра тяжести сечения, вызванного неравномерным нагревом. Для этого согласно указаниям п. 1.28 сечение разбиваем на две части по границе между ребром и полкой и производим приведение площадей полки и ребра к площади ненагретого бетона по формуле (2).
Значения коэффициентов βb и ![]() (для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
(для кратковременного нагрева) принимаем
соответственно по табл. 16 и 18:
при температуре 750 °С........................................ βb1 = 0,29, ![]() = 0,28
= 0,28
» » 330 °С....................................... βb2 = 0,71, ![]() = 0,67
= 0,67
Для бетона состава № 11 согласно указаниям п. 1.28 φb1 = 0,85.
По формуле (2):
![]() мм2;
мм2;
![]() мм2.
мм2.
Расстояние от центра тяжести приведенного сечения до грани, растянутой внешней нагрузкой (менее нагретой грани сечения), определяем по формуле (5):
![]() мм.
мм.
Расстояние от центра тяжести неприведенного сечения до той же грани
![]() мм.
мм.
Расчетный эксцентриситет продольной силы
e01 = y - yred = 357 - 253 = 104 мм.
Выгиб элемента, вызванный неравномерным нагревом сечения, уменьшает расчетный эксцентриситет продольной силы ea. Поэтому он не учитывается.
Поскольку расчетный элемент является элементом статически определимой конструкции, определяем значение случайного эксцентриситета ea согласно указаниям п. 1.30:
![]() мм >
мм > ![]() мм.
мм.
Вычисляем значение e0 по формуле (128):
e0 = 104 + 17 = 121 мм.
Для учета влияния прогиба
элемента определяем его гибкость ![]() , где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0.
, где i вычисляем по формуле (132).
Входящий в
формулу (132) момент инерции
приведенного сечения Ired определяем по формулам (11) и (12) при Areds = A′reds = 0.
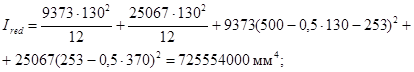
![]() мм;
мм;
![]() .
.
Поскольку λ = 34,46 > 14, учитываем при расчете влияние прогиба на прочность элемента согласно указаниям п. 3.29.
Для вычисления коэффициента η, на который должна быть умножена величина e0, определяем значение Ncr по формуле (129). Для этого предварительно вычисляем значение δmin по формуле (96); γbt = 0,50 принимаем по табл. 16 в зависимости от температуры центра тяжести приведенного сечения, равной
![]() °C.
°C.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 14,5 · 0,85 = 12,33 МПа;
![]() .
.
Так как ![]() < δmin = 0,338, принимаем δ = 0,338.
< δmin = 0,338, принимаем δ = 0,338.
Значение φl вычисляем по формуле (95), предварительно определив эксцентриситеты приложения N и Nl относительно центра тяжести площади растянутой арматуры:
e = 121 +253 - 50 = 324 мм;
el = e.
Значение коэффициента β по табл. 39 при t = 430 °С для состава № 11 равно 5,02:
![]() .
.
В связи с тем, что по условиям нагрева арматура устанавливается только у одной из граней сечения элемента, Is в формуле (129) принимается равной нулю.
Значения βb и ![]() определяем соответственно по табл. 16 и 18. При
температуре 430 °С βb = 0,59,
определяем соответственно по табл. 16 и 18. При
температуре 430 °С βb = 0,59, ![]() = 0,59 (для кратковременного нагрева)
согласно указаниям п. 1.28.
= 0,59 (для кратковременного нагрева)
согласно указаниям п. 1.28.
По формуле (129) имеем
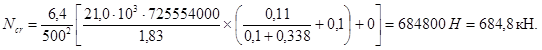
Коэффициент η определяем по формуле (93):
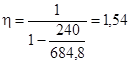 .
.
Эксцентриситет e с учетом прогиба вычисляем по формуле (135):
e = 121 · 1,54 + 253 - 50 = 389 мм.
Проверку прочности сечения производим согласно указаниям п. 3.40 в зависимости от положения границы сжатой зоны.
Проверяем соблюдение условия (153) при
h0 = h - а = 500 - 50 = 450 мм и A′s = 0.
Значение коэффициента γbt = 0,16 для средней температуры полки 750 °С определяем по табл. 16:
Ne = 240 · 0,389 = 93,4 кН · м;
γbtRbb′fh′f(h0 - 0,5h′f) = 0,16 · 12,33 · 750 · 130(450 - 0,5 · 130) = 76368200 Н · мм = 76,4 кН · м.
Поскольку условие (153) не соблюдается, расчет сечения производим как для таврового сечения в соответствии с указаниями пп. 3.40 и 3.43.
Согласно указаниям п. 3.11 значение коэффициента условий работы бетона γbt для ребра определяем по табл. 16 в зависимости от температуры бетона, находящегося на расстоянии 0,2h0 от сжатой грани сечения,
![]() °C;
°C;
γbt = 0,23.
Значение коэффициента γst = 0,97 принимаем по табл. 35 в зависимости от температуры ts = 125 °С.
Определяем высоту сжатой зоны x по формуле (155) при A′s = 0:
![]() мм.
мм.
Поскольку x > h, а следовательно и ξ > ξR, граница сжатой зоны проходит в ребре или все сечение сжато. В этом случае прочность сечения проверяем из условия (154), а высоту сжатой зоны из формулы (156).
Для определения граничного значения высоты сжатой зоны по формуле (99) определяем величину ω по формуле (100), предварительно приняв значение коэффициента γbt по табл. 16 в зависимости от средней температуры сжатой зоны при ее высоте, равной 0,7h0:
![]() °C;
°C;
γbt = 0,34;
ω = 0,8 - 0,008 · 0,34 · 12,33 = 0,767.
В связи с учетом коэффициента γb2 = 0,85 в формуле (99) вместо значения 400 принято 500.
Значение βs = 0,99 определяем по табл. 35.
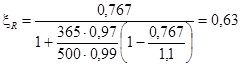 .
.
При средней температуре бетона сжатой зоны, отвечающей высоте 0,63h0,
![]() °C;
°C;
γbt = 0,31;
ω = 0,8 - 0,008 · 0,31 · 12,33 = 0,77; ξR = 0,63.
Определяем значение ξ при A′s = 0:
![]() >
ξR = 0,63.
>
ξR = 0,63.
Прочность сечения проверяем из условия (154) при A′s = 0 и x = ξh0 = 0,75 · 450 = 338 мм:
Ne = 93,4 кН · м< 0,31 · 12,33 · 120 · 338(450 - 0,5 · 338) + 0,16 · 12,33(750 - 120)130(450 - 0,5 · 130) = 108135000 Н · мм = 108,1 кН · м.
Прочность сечения обеспечена.
Пример 21. Расчет прочности внецентренно растянутого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 200 °С. Случай малых эксцентриситетов.
Дано: размеры сечения - b = 30 см, h = 25 см, a = a′ = 5 см; элемент неравномерно нагрет, при этом температура арматуры S′ равна 200 °С, арматуры S - 100 °С; бетон состава № 2 (см. табл. 11) класса В25; арматура из стали класса A-III: Rs = 365 МПа = 365 гН/см2 (см. табл. 29); площадь сечения арматуры As = A′s = 12,56 см4 (4 Ø 20); расчетное значение продольной силы N = 6000 гН, изгибающего момента М = 180 гН · м.
Требуется проверить прочность сечения.
Расчет. Определяем значения коэффициента γst по табл. 35 в зависимости от температуры соответствующей арматуры:
для арматуры S′............................................................................ γst = 0,90
» » S............................................................................ γst = 1,0
Определяем расстояния от растягивающей силы N до равнодействующих усилий в арматуре S(e) и S′(e′). Для этого предварительно определяем эксцентриситет продольной силы N при h0 = 25 - 5 = 20 см:
![]() см
< 0,5(h0 - a′) =
0,5(20 - 5) = 7,5 см.
см
< 0,5(h0 - a′) =
0,5(20 - 5) = 7,5 см.
Следовательно, продольная сила приложена между равнодействующими усилий в арматуре S и S′.
По формуле (177):
e = 0,5 · 25 - 5 - 3 = 4,5 см.
По формуле (178):
e′ = 20 - 0,5 · 25 + 5 + 3 - 5 = 10,5 см.
Проверку прочности сечения производим из условия (171):
Ne = 6000 · 4,5 = 27000 гН · см = 270 гН · м < 0,90 · 365 · 12,56(20 - 5) = 61889,4 гН · см = 619 гН · м.
и условия (172):
Ne′ = 6000 · 10,5 = 63000 гН · см = 630 гН · м < 1,0 · 365 · 12,56(20 - 5) = 68766 гН · см = 688 гН · м.
Прочность сечения обеспечена.
Пример 22. Определение площади поперечного сечения растянутой арматуры внецентренно растянутого железобетонного элемента прямоугольного сечения при одностороннем нагреве до 150 °С. Случай малых эксцентриситетов.
Дано: размеры сечения - b = 100 см, h = 50 см, a = a′ = 4 см; элемент неравномерно нагрет, при этом температура арматуры S′ равна 150 °С, арматуры S - 50 °С; бетон состава № 1 (см. табл. 11) класса В15; арматура из стали класса A-III: Rs = 365 МПа = 365 гН/см2; расчетное значение продольной силы N = 7000 гН, изгибающего момента M = 600 гН · м.
Требуется определить площадь сечения продольной рабочей арматуры.
Расчет. Определяем значение коэффициента γst по табл. 35 в зависимости от температуры соответствующей арматуры:
для арматуры S′............................................................................ γst = 0,95
» » S............................................................................ γst = 1,0
Определяем расстояния от растягивающей силы N до равнодействующих усилий в арматуре S(e) и S′(e′). Для этого предварительно определяем эксцентриситет продольной силы N при h0 = h - a = 50 - 4 = 46 см:
![]() см
< 0,5(h0 - a′) =
0,5(46 - 4) = 21 см.
см
< 0,5(h0 - a′) =
0,5(46 - 4) = 21 см.
Следовательно, продольная сила приложена между равнодействующими усилий в арматуре S и S′.
По формуле (177):
e = 0,5 · 50 - 4 - 8,57 = 12,43 см.
По формуле (178):
e′ = 46 - 0,5 · 50 + 4 + 8,57 - 4 = 29,57 см.
Так как е′ = 29,57 см < h0 - a′ = 46 - 4 = 42 см, необходимые площади сечения арматуры As и A′s определяем по формуле (184):
![]() см2;
см2;
и формуле (185)
![]() см2.
см2.
Принимаем A′s = 15,7 см2 (5Ø20) и A′s = 7,69 см2 (5 Ø 14).
Пример 23. Определение площади поперечного сечения симметричной арматуры внецентренно растянутого элемента прямоугольного сечения при его равномерном нагреве до 100 °С. Случай больших эксцентриситетов.
Дано: размеры сечения - b = 40 см, h = 20 см, a = а′ = 4 см; элемент равномерно нагрет до 100 °С; бетон состава № 1 (см. табл. 11) класса В15: Rb = 8,5 МПа = 8,5 гН/см2 (см. табл. 14); арматура из стали класса А-III: Rs = 365 МПа = 365 гН/см2 (см. табл. 29); расчетные значения от длительно действующей нагрузки: продольной силы Nl = 1700 гН, изгибающего момента Ml = 275 гН · м.
Требуется определить площадь сечения продольной симметричной арматуры.
Расчет. При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 8,5 · 0,85 = 7,2 МПа = 7,2 гН/см2.
Определяем значения коэффициентов γbt и γst соответственно по табл. 16 и 35 для температуры 100 °С: γbt = 0,90; γst = 1,0.
Определяем расстояния от растягивающей силы N до равнодействующей усилий в арматуре S(e) и S′(e′). Для этого предварительно определяем эксцентриситет продольной силы N при h0 = h - а = 20 - 4 = 16 см:
![]() см
> 0,5(h0 - a′) =
0,5(16 - 4) = 6 см.
см
> 0,5(h0 - a′) =
0,5(16 - 4) = 6 см.
Следовательно, продольная сила приложена за пределами расстояний между равнодействующими усилий в арматуре S и S′.
По формуле (179):
e = 16,2 - 0,5 · 20 + 4 = 10,2 см.
По формуле (178):
e′ = 16 - 0,5 · 20 + 4 + 16,2 - 4 = 22,2 см.
Определяем значение коэффициента α0 из формулы (180), заменив αR на α0, без учета сжатой арматуры, т.е. при A′s = 0:
![]() .
.
По табл. 41 в зависимости от полученного значения α0 определяем значение ξ = 0,31.
Так как ![]() , требуемую площадь продольной арматуры находим по формуле (183), в которой коэффициент v определяем по табл. 41: при α0 = 0,254 v = 0,85:
, требуемую площадь продольной арматуры находим по формуле (183), в которой коэффициент v определяем по табл. 41: при α0 = 0,254 v = 0,85:
![]() см2.
см2.
Принимаем As = А′s = 9,41 см2 (3 Ø 20).
Пример 24. Определение площадей поперечного сечения анкеров и пластины закладной детали колонны при ее равномерном нагреве до 100 °С и действии на закладную деталь растягивающей и сдвигающей сил и изгибающего момента.
Дано: к закладной детали колонны сечением 60 × 40 см приварены элементы стальных связей, работающие на растяжение (узел примыкания элементов и усилия в них по черт. 61); колонна и элементы связей подвергаются длительному равномерному нагреву до 100 °С; анкеры закладной детали из стали класса A-III: Rs = 365 МПа = 365 гН/см2 (см. табл. 29), бетон колонны состава № 1 (см. табл. 11) класса В30: Rb = 17,0 МПа = 17 гН/см2, Rbt = 1,2 МПа = 1,2 гН/см2 (см. табл. 14).
Требуется запроектировать анкеры закладной детали, определить толщину пластины и проверить выкалывание бетона.
Черт. 61. Закладные детали колонны при действии растягивающих и сдвигающих сил и изгибающего момента
Расчет. Принимаем расположение анкеров как показано на черт. 61. Усилие в раскосе раскладываем на нормальную силу N, приложенную к закладной детали с эксцентриситетом e0 = 5 см, и сдвигающую силу Q:
N = 1400cos43°45′ + 800 = 1810 гН;
Q = 1400sin43°45′ = 970 гН.
При z = 42 см и M = Ne = 1810 · 5 = 9050 гН · см = 90,5 гН · м определяем наибольшее растягивающее усилие в одном ряду анкеров по формуле (236):
![]() гН.
гН.
Наибольшее сжимающее усилие в одном ряду анкеров вычисляем по формуле
![]() гН
< 0.
гН
< 0.
Сдвигающее усилие Qan, приходящееся на один ряд анкеров, определяем по формуле (237), принимая N′an = 0:
![]() гН.
гН.
Так как N′an < 0,
![]() .
.
Значение коэффициента δ определяем по формуле (239):
![]() >
0,15.
>
0,15.
Для определения коэффициента λ по формуле (242) вычисляем ряд расчетных характеристик.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rb = 17 · 0,85 = 14,45 МПа = 14,45 гН/см2;
Rbt = 1,2 · 0,85 = 1,02 МПа = 1,02 гН/см2.
Значения коэффициентов принимаем по табл. 16, 18 и 35:
γbt = 0,90, γtt = 0,70, βb = 0,80, ![]() = 0,70 (для кратковременного нагрева); γst = 1,0 (для стали A-III); γst = 0,95 (для стали пластины).
= 0,70 (для кратковременного нагрева); γst = 1,0 (для стали A-III); γst = 0,95 (для стали пластины).
Задаемся площадью анкерного стержня Aan1 = 1,13 см2 (1Ø12 мм).
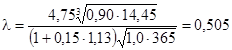 .
.
Суммарную площадь поперечного сечения анкеров определяем по формуле (235):
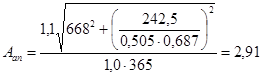 см2.
см2.
Принимаем три анкера диаметром 12 мм в каждом ряду (Аan = 3,39 см2).
Необходимая толщина пластины из условия прочности (244):
![]() см.
см.
Из условия сварки в отверстия с раззенковкой
t = 0,75dan = 0,75 · 1,2 = 0,9 см.
Принимаем t = 12 мм.
Принятые расстояния между осями анкеров вдоль и поперек сдвигающей силы, соответственно равные 14 см > 6d = 6 · 1,2 = 7,2 см и 9 см > 4d = 4 · 1,2 = 4,8 см удовлетворяют конструктивным требованиям.
Концы анкеров привариваем к аналогичной закладной детали, расположенной на противоположной грани колонны.
Поскольку N′an < 0 и концы анкеров имеют усиления, проверяем условие
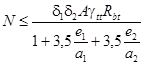 ;
;
где А - площадь проекции на плоскость, нормальную к анкерам, поверхности выкалывания, идущей от усилений анкеров (краев анкерных пластин, краев высаженных головок) под 45° к осям анкеров (см. черт. 27, б); площади анкерных пластин или высаженных головок, расположенных на поверхности выкалывания, не учитываются;
δ1 - коэффициент, принимаемый равным:
для бетонов составов (см. табл. 11):
№ 1 - 3, 6, 7, 13, 20 и 21........................................................... 0,5
№ 4, 5, 8 - 12, 14 - 19, 23 и 29.................................................. 0,4
δ2 - коэффициент, принимаемый равным:
при σbc/Rb < 0,25 или > 0,75 δ2 = 1,0
при 0,25 ≤ σbc/Rb £ 0,75 δ2 = 1,2
При этом, если часть стержня длиной a расположена в зоне бетона при 0,25 ≤ σbc/Rb ≤ 0,75, то δ2 определяется по формуле
![]() ,
,
где la - длина анкерного стержня; сжимающие напряжения в бетоне σbc, перпендикулярные к нормальному анкеру и распределенные по всей длине, определяют как для упругого материала по приведенному сечению от постоянно действующих нагрузок при коэффициенте надежности по нагрузке, равном 1;
a1 и a2 - размеры проекции поверхности выкалывания;
е1 и e2 - эксцентриситеты силы N относительно центра тяжести площади A в направлениях соответственно a1 и a2;
γtt - определяется по табл. 16 в зависимости от температуры бетона в середине длины анкера, ограниченной поверхностью выкалывания под углом 45° к осям анкеров.
Определяем площадь проекции поверхности выкалывания (см. черт. 61) за вычетом площади закладной детали, равной:
Ald = 50 · 26 = 1300 см2;
a1 = 50 + 2 · 38,8 = 127,6 см;
a2 = 60 см;
A = a1a2 - Ald = 127,6 · 60 - 1300 = 6356 см2;
e1 = e0 = 5 см; e2 = 0;
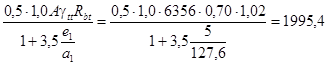 гН
> 1810 гН = N,
гН
> 1810 гН = N,
т.е. прочность бетона на выкалывание обеспечена.
Примечание. Для анкеров без усиления на концах расчет производится из условия
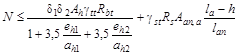 ,
,
где Аh, ah1, ah2, eh1, eh2 - то же, что и A, a1, a2, e1, e2, если поверхность выкалывания идет на расстоянии h от пластины закладной детали (см. черт. 27, в);
Aan,a - площадь сечения всех анкеров, пересекающих поверхность выкалывания;
lan - длина зоны анкеровки;
γst - определяется по табл. 35 в зависимости от наибольшей температуры анкера.
Если N′an > 0, то при наличии усиления на концах анкеров расчет бетона на выкалывание производят из условия
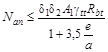 ,
,
где A1 - то же, что и А, если поверхность выкалывания начинается от места усиления анкеров наиболее растянутого ряда (см. черт. 27, г);
e - эксцентриситет усилия N относительно центра тяжести A в направлении а.
Если сдвигающая сила Q действует на закладную деталь по направлению к краю элемента (см. черт. 27, д), то при отсутствии наклонных анкеров расчет на откалывание бетона производят из условия
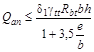 ,
,
где h - расстояние от наиболее удаленного ряда анкеров до края элемента в направлении сдвигающей силы Q, принимаемое не более толщины элемента b1 (см. черт. 27, д);
b - ширина элемента, равная b = c1 + c2 + s, где c1 и c2 - расстояния от крайних рядов анкеров до ближайших краев элемента, принимаемые не более h; s - расстояние между крайними рядами анкеров;
e - эксцентриситет силы Q относительно ширины элемента b.
Пример 25. Определение площадей поперечного сечения анкеров и пластины закладной детали колонны при ее нагреве до 300 °С со стороны, противоположной расположению закладной детали, и действии на закладную деталь сдвигающей силы и изгибающего момента.
Дано: к закладной детали колонны сечением 40 × 40 см приварен столик для опирания балки, от которой создается вертикальная нагрузка Q = 400 гН, приложенная на расстоянии 10 см от наружной поверхности колонны (закладной детали); размеры закладной детали: ширина - 15 см, высота - 28 см, колонна со стороны, противоположной расположению закладной детали, подвергается длительному нагреву до 300 °С; анкеры из стали класса A-III: Rs = 365 МПа (см. табл. 29); бетон колонны состава № 2 (см. табл. 11) класса В25: Rb = 14,5 МПа, Rbt = 1,05 МПа (см. табл. 14).
Требуется запроектировать анкеры закладной детали и определить толщину пластины.
Расчет. Из теплотехнического расчета получено изменение температуры на 1 см высоты сечения колонны, равное 5 °С.
Принимаем четыре анкера, приваренных втавр, расположенных в два ряда (nan = 2), при расстоянии между рядами анкеров z = 20 см.
Определяем наибольшие растягивающее и сжимающее усилия в одном ряду анкеров соответственно по формулам (236) и (238) при N = 0; поскольку на закладную часть действует только изгибающий момент M и сдвигающая сила Q:
![]() гН.
гН.
Сдвигающую силу, приходящуюся на один ряд анкеров, определяем по формуле (237):
![]() гН.
гН.
Значение коэффициента δ определяем по формуле (239), принимая ![]() , поскольку Nan > 0:
, поскольку Nan > 0:
![]() ;
;
![]() >
0,15.
>
0,15.
Для определения коэффициента λ по формуле (242) вычисляем ряд расчетных характеристик.
При длительном нагреве расчетное сопротивление бетона умножаем на коэффициент γb2 = 0,85, принимаемый по табл. 15:
Rbt = 14,5 · 0,85 = 12,33 МПа = 12,33 гН/см2;
Rbtt = 1,05 · 0,85 = 0,89 МПа = 0,89 гН/см2.
Значения коэффициентов γbt, βb, ![]() принимаем
соответственно по табл. 16 и 18 в зависимости от температуры бетона в месте
расположения закладной детали:
принимаем
соответственно по табл. 16 и 18 в зависимости от температуры бетона в месте
расположения закладной детали:
tld = 300 - 5 · 40 = 100 °С;
γbt = 0,90; βb = 0,80; ![]() = 0,70 (для кратковременного нагрева).
= 0,70 (для кратковременного нагрева).
Значение коэффициента γst принимаем по табл. 35 в зависимости от температуры ts конца анкера. При длине анкера, равной 300 мм:
ts = 300 - 5 · 10 = 250 °С; γst = 0,82.
Для определения коэффициента λ по формуле (242) задаемся площадью анкерного стержня Aan1 = 1,54 см2 (Ø 14 мм).
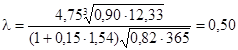 .
.
Суммарную площадь поперечного сечения анкеров определяем по формуле (235)
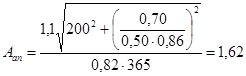 см2.
см2.
Принимаем 2 Ø 12 (As = 2,26 см2) в каждом ряду.
Из условия размещения анкеров в колонне длина анкеров принята равной 30 см, что меньше минимально допустимой длины анкеров, равной 30d = 30 · 1,2 = 36 см. Поэтому на концах анкеров привариваем круглые анкерные пластинки диаметром 50 мм и проверяем бетон на смятие под пластинками и на выкалывание. При этом длина анкера 30 см > 10d = 10 · 1,2 = 12 см, т.е. допустимо для анкеров с усилением на конце.
Расчет на смятие ведем согласно указаниям п. 3.63. Площадь смятия Aloc над анкерной пластинкой одного анкера равна
![]() см2.
см2.
Поскольку la = 30 см > 15d = 15 · 1,2 = 18 см, а в колонне в месте установки анкеров возможны растягивающие напряжения и образование трещин, Nloc определяем по формуле
![]() гН.
гН.
Проверяем условие Nloc ≤ αφbRbγbtAloc. Для этого предварительно определяем значение коэффициента γbt по табл. 16 в зависимости от температуры бетона в месте расположения анкерных пластинок, равной 250 °С:
γbt = 0,65;
αφbRbγbtAloc = 1,0 · 2,5 · 0,65 · 12,33 · 18,5 = 371 гН > Nloc = 100 гН,
т.е. прочность на смятие обеспечена.
Поскольку N′an > 0 и концы анкеров с усилением не заведены за продольную арматуру колонны, расположенную у противоположной от закладной детали грани, расчет ведем из условия Nan ≤ δ1δ2A1Rbtγtt:
![]() см2.
см2.
Значение коэффициента γtt определяем по табл. 16 в зависимости от температуры бетона в середине длины анкера, т.е. на расстоянии 25 см от наиболее нагретой грани колонны:
ts = 300 - 5 · 25 = 175 °С; γtt = 0,55;
δ1δ2A1Rbtγtt = 0,5 · 1,0 · 2561 ·0,55 · 0,89 = 627 гН > Nan = 200 гН,
т.е. прочность на выкалывание обеспечена.
Принятые расстояния между анкерами в направлениях поперек и вдоль сдвигающей силы, соответственно равные 7 см > 4d = 4 · 1,2 = 4,8 см и 20 см > 6d - 6 · 1,2 = 7,2 см, - удовлетворяют конструктивным требованиям.
Определяем необходимую толщину пластины закладной детали по формуле (244), в которой значение коэффициента γst при Rsq определяем по табл. 35 в зависимости от температуры пластины, равной 100 °С, как для арматуры класса A-I, γst = 0,95:
![]() см.
см.
Из условия сварки анкеров под слоем флюса на автоматах толщина пластины должна быть не менее 0,65d = 0,65 · 1,2 = 0,78 см. Принимаем толщину пластины t = 10 мм.
Пример 26. Расчет прочности наклонных сечений изгибаемого элемента из жаростойкого бетона без поперечной арматуры от действия поперечной силы при неравномерном нагреве до 750 °С.
Дано: ригель теплового агрегата имеет высоту h = 45 см и ширину b = 20 см. Ригель выполнен из жаростойкого бетона класса В25 на портландцементе с тонкомолотой шамотной добавкой и шамотными заполнителями (бетон состава № 11 по табл. 11). На ригель действует расчетная поперечная сила, равная 250 гН. Температура крайней грани сжатой зоны бетона ригеля равна 750 °С. Продольная рабочая арматура расположена с наружной стороны агрегата и ее температура равна 50 °С (черт. 62, а).
Необходимо проверить прочность элемента по наклонным сечениям.
h0 = 45 - 3,5 = 41,5 см.
Для жаростойкого бетона класса В25 (состав № 11) при средней температуре по высоте сечения элемента 400 °С при длительном действии нагрева по табл. 14, 15 и 16 находим Rbt = 1,05 МПа = 1,05 гН/см2, γb2 = 0,85 и γtt = 0,3.
Проверяем условие (210), обеспечивающее прочность элемента без развития наклонных трещин φb4 = 3,37 для состава № 11 при средней температуре по высоте сечения элемента 400 °С.
Для элементов без поперечной арматуры с ≤ 2,5h0, принимаем c = 2,5h0,
![]() гН.
гН.
Проверяем условия:
Q ≥ φb3Rbtγttbh0;
0,4 · 1,05 · 0,85 · 0,3 · 20 · 41,5 = 89 гН < 299 гН;
Q £ 2,5Rbtγttbh0;
2,5 · 1,05 · 0,85 · 0,3 · 20 · 41,5 = 556 гН > 299 гН.
Условия выполняются, следовательно, вся действующая поперечная сила может быть воспринята бетонным сечением элемента.
Исходя из конструктивных соображений, ставим поперечную арматуру из стали класса А-I Ø 6 мм через 200 мм в виде двух каркасов. При этом хомуты заходят в сжатую зону бетона до температуры поперечной арматуры не более 450 °С согласно табл. 24.
Черт. 62. Схема армирования поперечной арматурой
а - конструктивное армирование; б - с расчетной арматурой из хомутов; в - с расчетной арматурой из хомутов и отогнутых стержней
Пример 27. Расчет прочности наклонных сечений и ширины раскрытия наклонных трещин изгибаемого элемента из жаростойкого бетона с хомутами от действия поперечной силы при неравномерном нагреве до 600 °С.
Дано: на ригель рамы действует расчетная поперечная сила 700 гН и поперечная сила от нормативной нагрузки, равная 650 гН. Ригель теплового агрегата имеет высоту h = 45 см, ширину b = 20 см и выполняется из жаростойкого бетона класса В20 на портландцементе с тонкомолотой шамотной добавкой и шамотными заполнителями (бетон состава № 11 по табл. 11). Ригель армируется двумя сварными каркасами. Поперечные стержни выполняются из стали класса A-III периодического профиля. Температура крайней грани сжатой зоны бетона 600 °С (черт. 62, б). Температура продольной арматуры 40 °С. Максимальная температура нагрева хомутов согласно табл. 24 может быть допущена до 450 °С. Для жаростойкого бетона класса В20 для средней температуры бетона по высоте сечения ригеля, равной 320 °С, при длительном действии нагрева согласно табл. 14, 15 и 16 находим:
Rb = 11,5 МПа;
Rbt = 0,9 МПа = 0,9 гН/см2;
Rbt,ser = 1,4 МПа = 1,4 гН/см2;
γb2 = 0,85; γbt = 0,67 и γtt = 0,38.
Рабочая высота ригеля
h0 = 45 - 3,5 = 41,5 см.
Предельная поперечная сила, воспринимаемая бетоном при средней температуре бетона по высоте сечения ригеля 320 °С, c ≤ 2h0 и φb2 = 3,43.
Согласно формуле (198):
![]() гН.
гН.
Сечения бетона недостаточно. Требуется установка поперечной арматуры. Принимаем хомуты из стали класса А-III 2 Æ 10 мм, Asw =1,57 см2. Хомуты устанавливаем через 10 см. Усилие, воспринимаемое хомутами на единицу длины балки, определяют по формуле (195), в которой принимают Rsw = 290 МПа = 290 гН/см2 для максимальной температуры хомутов 450 °С, γst = 0,2 (см. табл. 29 и 35):
![]() гН/см2.
гН/см2.
Длину проекции невыгоднейшего наклонного сечения на продольную ось элемента определяем по формуле (202), в которой коэффициент условий работы γtt принимается для средней температуры сжатой зоны сечения. При неравномерном нагреве по высоте сечения среднюю температуру бетона сжатой зоны допускается принимать равной температуре бетона на расстоянии 0,2h0 от нагреваемой грани, которая равна 490 °С. Для этой температуры по табл. 16 находим γtt = 0,21. Для длительного нагрева коэффициент γb2 = 035 (см. табл. 15).
Коэффициент φb2 при температуре 490 °С принимается равным 4,34,
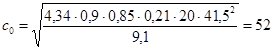 см ≤
2 · 41,4 = 83 см.
см ≤
2 · 41,4 = 83 см.
При воздействии температуры, превышающей предельно допустимую температуру применения арматуры, установленной
по расчету (см. табл. 24), допускается принимать поперечную арматуру, укороченную по
высоте сечения элемента. Минимально допустимая длина хомутов устанавливается не менее 2/3h0 и
она равна ![]() см.
Величина поперечной силы, воспринимаемая укороченными хомутами и бетоном в наклонном
сечении, определяется по формуле (204):
см.
Величина поперечной силы, воспринимаемая укороченными хомутами и бетоном в наклонном
сечении, определяется по формуле (204):
![]() гН.
гН.
Сечение элемента с укороченной поперечной арматурой необходимо проверить по формуле (203), в которой вместо h0 принимается условная рабочая высота сечения hu, равная длине хомутов и толщине защитного слоя бетона у менее нагретой грани:
hu = 27,7 + 3,5 = 31,2 см.
Температура условной сжатой зоны бетона укороченной высоты равна 380 °С. Коэффициент условий работы бетона γtt = 0,32 (см. табл. 16) и φb2 = 3,9,
![]() гН.
гН.
За расчетную поперечную силу принимается наименьшая, полученная по формуле (204), равная 780 гН, что больше действующей поперечной силы, равной 700 гН.
Наибольшее расстояние между поперечными стержнями должно быть не более величины, определенной по формуле (207), в которой для средней температуры бетона сжатой зоны 490 °С φb2 = 4,34 и γtt = 0,21:
![]() ~ 26 см.
~ 26 см.
Принятое расстояние между хомутами 10 см меньше smax = 26 см, что является вполне допустимым.
Для определения ширины раскрытия наклонных трещин от действия нормативной поперечной силы 650 гН предварительно вычислим по формуле (198) величину Qb и по формуле (278) величину σsw:
![]() гН;
гН;
![]() гН/см2.
гН/см2.
Коэффициент насыщения поперечными стержнями, нормальными к продольной оси элемента, равен
![]() .
.
Ширина раскрытия трещин, наклонных к продольной оси элемента acrc, в изгибаемых элементах, армированных поперечной арматурой, определяется по формуле (277), в которой φl = 1,5, η = 1,0; dw = 0,8 см; Es = 0,2 · 106 МПа, Eb = 18,5 · 103 МПа.
Для температуры середины высоты хомутов 250 °C βs = 0,89; βb = 0,825;
![]() ;
;
αst = 13,25 · 10-6 °С-1;
αbt = 5,1 · 10-6 °С-1;

Пример 28. Расчет прочности наклонных сечений и ширины раскрытия наклонных трещин изгибаемого элемента из жаростойкого железобетона с хомутами и отогнутой арматурой от действия поперечной силы при неравномерном нагреве до 650 °С.
Дано: на ригель теплового агрегата действует равномерно распределенная нагрузка с максимальной расчетной поперечной силой 1200 гН. Поперечная сила от нормативной нагрузки 1000 гН. Длина участка эпюры поперечных сил 200 см (черт. 62, в), размеры сечения ригеля: h = 45 см и b = 20 см.
Ригель выполнен из жаростойкого бетона класса В20 на портландцементе с тонкомолотой шамотной добавкой и шамотными заполнителями (бетон состава № 11 по табл. 11). Температура крайней грани сжатой зоны бетона равна 650 °С. Отогнутые стержни и хомуты из арматуры класса А-III. Максимальная температура применения отогнутых стержней и хомутов не должна превышать 450 °С (см. табл. 24). Температура продольной арматуры, расположенной у менее нагретой грани, равна 50 °С.
Необходимо проверить достаточность поперечного сечения изгибаемого элемента при действии поперечных сил, подобрать сечение поперечной арматуры и определить ширину раскрытия наклонных трещин в невыгоднейшем наклонном сечении от действия нормативной поперечной силы:
h0 = 45 - 3,5 = 41,5 см.
Средняя температура бетона по высоте сечения ригеля равна 350 °С. При длительном нагреве для средней температуры бетона 350 °С по табл. 14, 15 и 16 принимаем: Rb = 11,5 МПа; γb2 = 0,85; γbt = 0,625; Rbt = 0,935 МПа = 0,935 гН/см2; γtt = 0,35.
Предельная поперечная сила, воспринимаемая бетоном, определяется по формуле (198), в которой при средней температуре бетона по высоте сечения ригеля 350 °С: φb2 = 3,64, c = 2h0 = 83 см;
![]() гН,
гН,
т.е. необходим расчет поперечной арматуры.
Принимаем двухветвевые хомуты Ø 10 мм через 12 см, площадью Asw = 1,57 см2. Средняя температура сжатой зоны на расстоянии 0,2h0 равна 540 °С. Для этой температуры γtt = 0,158.
Принятое расстояние между хомутами должно быть не более максимально допустимого, определяемого по формуле (207), в которой φb2 = 4,7 согласно указаниям п. 3.52:
![]() см.
см.
Для стали класса А-III при температуре хомутов 450 °С и длительном нагреве по табл. 29 и 35 находим Rsw = 290 МПа = 290 гН/см2 и γst = 0,2.
Предельное усилие в хомутах на единицу длины элемента определяем по формуле (195):
![]() гН/см.
гН/см.
Длину проекции невыгоднейшего наклонного сечения на продольную ось элемента вычисляем по формуле (202):
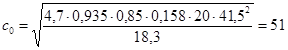 см
< 83 см.
см
< 83 см.
Поперечную силу, воспринимаемую бетоном сжатой зоны и хомутами в невыгоднейшем наклонном сечении, находим по формуле (203):
![]() гН.
гН.
Проверяем прочность наклонного сечения при укороченной высоте, равной
hw = 2/3h0 = 27,7 см,
hu = hw + a = 27,7 + 3,5 = 31,2 см.
Средняя температура бетона высоты сжатой зоны на расстоянии 0,2h0 = 41,5 - 31,2 + 0,2 · 31,2 = 16,54 см от нагреваемой грани равна 415 °С.
Rbt = 0,935 МПа = 0,935 гН/см2; γtt = 0,285 и φb2 = 4; γtt = 0,285; γb2 = 0,85.
Тогда по формуле (204):
![]() гН.
гН.
За расчетную поперечную силу принимается наименьшая поперечная сила, равная 768 гН, полученная по формуле (203). Она составляет величину, меньшую действующей поперечной силы, равной 1200 гН. Поэтому необходимо увеличить площадь сечения хомутов или поставить отогнутые стержни. Сечение отогнутых стержней арматуры определяется из формулы (209):
![]() см2.
см2.
Принимаем 2 Ø 25 A-III (As,inc1 = 9,82 см2). В конце первой плоскости отгибов находим поперечную силу Q2, приняв расстояние от грани опоры до начала первого отгиба 5 см:
![]() гН > 768 гН;
гН > 768 гН;
![]() см2.
см2.
Принимаем 2 Ø 18 A-III (As,inc2 = 5,08 см2).
![]() гН > 768 гН.
гН > 768 гН.
![]() см2.
см2.
Принимаем 2 Ø 10 A-III (As,inc3 = 1,57 см2).
![]() гН.
гН.
Эта величина поперечной силы меньше силы, воспринимаемой бетоном и хомутами.
Отогнутые стержни и хомуты должны располагаться там, где температура их нагрева не будет превышать предельно допустимую температуру применения данной марки стали.
Ширину раскрытия трещин, наклонных к продольной оси элемента acrc, в изгибаемых элементах, армированных поперечной арматурой, определяем по формуле (277). Для определения ширины раскрытия наклонных трещин в сечении с наибольшей нормативной поперечной силой Q = 1000 гН предварительно вычисляем Qb по формуле (198) и σsw по формуле (278) для первого отгиба.
Для бетона класса В20 Rbt,ser = 1,4 МПа = 1,4 гН/см2,
![]() гН;
гН;
![]() гН/см2.
гН/см2.
Коэффициент насыщения поперечными стержнями, нормальными к продольной оси элемента,
![]() .
.
Для арматуры периодического профиля η = 1. При длительно действующей нагрузке φl = 1,5.
Eb = 16,5 · 103 МПа; βb = 0,56;
Es = 0,2 · 106 МПа; βs = 0,86;
![]() .
.
При температуре середины высоты хомутов 250 °С:
αst = 13,25 · 10-6 °С-1;
αbt = 5,1 · 10-6 °С-1.
Ширина раскрытия наклонных трещин определяется по формуле (277):
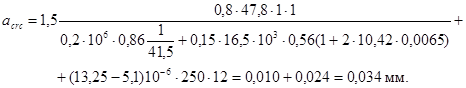
Пример 29. Расчет прогиба предварительно напряженной железобетонной плиты перекрытия, работающей при равномерном нагреве сечения при температуре 100 °С.
Дано: предварительно напряженная железобетонная ребристая плита перекрытия (черт. 63). Помещение, перекрываемое плитой, имеет нормальный влажностный режим. Класс обычного бетона В40 (состав № 1 по табл. 11). По табл. 13 и 14 определяем расчетные сопротивления бетона: Rb,ser = 29 МПа; Rbt,ser = 2,1 МПа; Rb = 22 МПа, Rbt = 1,4 МПа. По табл. 17 модуль упругости бетона Eb = 32,5 · 103 МПа.
Черт. 63. Поперечное сечение предварительно напряженной железобетонной ребристой плиты перекрытия
Предварительно напряженная арматура из стали класса A-V с Rs,ser = 785 МПа, Rs = 680 МПа (см. табл. 25 и 29); Еs = 190 · 103 МПа (см. табл. 37); ненапрягаемая арматура из горячекатаной стали класса A-III: Rs,ser = 390 МПа; Rs = 355 МПа; Es = 200 · 103 МПа; площадь сечения арматуры S: предварительно напряженной Asp = 4,91 см2 (1 Ø 25); ненапрягаемой Аs = 0,785 см2 (1 Ø 10); площадь сечения арматуры S′ А′s = 0,503 см2 (1 Ø 8); натяжение стержней осуществляется электротермическим способом.
Расчетный пролет плиты - l = 570 см.
Нормативная равномерно распределенная нагрузка длительно действующая - q = 26 кН/м.
Требуется определить прогиб плиты.
Определяем геометрические характеристики сечения без учета температуры.
Находим площадь приведенного сечения по формуле (6):
Ared = 47,5 · 5 + 30 · 9,5 + 4,91 · 5,85 + (0,785 + 0,503)6,15 = 237,5 + 285 + 28,7 + 7,9 = 559,1 см2;
![]() ;
; ![]() ;
;
Определяем статический момент относительно нижней грани ребра по формуле (7):
Sred = 237,5 · 32,5 + 285 · 15 + 4,91 · 5,85 · 4 + 0,785 · 6,15 · 2 + 0,503 · 6,15 · 32,5 = 12231 см3.
Определяем расстояние от центра тяжести приведенного сечения до нижней грани по формуле (5):
![]() см.
см.
Определяем момент инерции приведенного сечения относительно его центра тяжести по формуле (11):
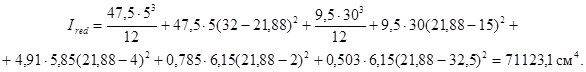
Определяем эксцентриситет усилия предварительного обжатия относительно центра тяжести приведенного сечения
eop = y - а = 21,88 - 4 = 17,88 см.
Предельно допустимое отклонение предварительного напряжения [формула (2) СНиП 2.03.01-84]:
![]() МПа.
МПа.
Величину напряжения принимаем [формула (1) СНиП 2.03.01-84]:
σsp = Rs,ser - p = 785 - 90 = 695 МПа.
Коэффициент точности предварительного напряжения арматуры [формула (6) СНиП 2.03.01-84]:
γsp = 1 + Δγsp;
где 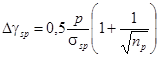 ;
;
р - предельно допустимое отклонение, МПа;
σsp - величина напряжения, МПа;
np - количество стержней напрягаемой арматуры в сечении;
![]() ;
;
γsp = 1 + 0,13 = 1,13.
Определяем потери предварительного напряжения при нормальной температуре по табл. 5 СНиП 2.03.01-84.
Первые потери, происходящие до окончания обжатия бетона:
от релаксации напряжений в арматуре
0,03σsp =0,03 · 695 = 20,85 МПа;
от деформации бетона - при быстронатекающей ползучести.
Для этого определяем напряжения в бетоне σbp на уровне центра тяжести напрягаемой арматуры от усилия предварительного обжатия с учетом влияния собственного веса элемента.
Усилие предварительного обжатия
P = γspσspAsp = 1,13 · 695 · 4,91 = 385,6 кН.
Момент от собственного веса плиты в середине пролета
![]() кН · см.
кН · см.
Усилие предварительного обжатия с учетом первых потерь
P = 1,13(695 - 20,85)4,91 = 374,0 кН;
напряжение в бетоне по формуле (16):
![]() МПа.
МПа.
Потери от деформации бетона при быстронатекающей ползучести равны:
при ![]()
и α = 0,25 + 0,0025 - 28 = 0,32;
0,85[40 · 0,32 + 85 · 1,1(0,78 - 0,32)] = 0,85(12,8 + 43,48) = 0,85 × 56,28 = 47,84 МПа.
Первые потери равны
20,85 + 47,84 = 68,69 МПа.
Определяем вторые потери, происходящие после окончания обжатия бетона:
от усадки бетона - 40,0 МПа;
потери от ползучести бетона, для чего находим
Р = 1,13(695 - 20,85 - 47,84)4,91 = 347,5 кН;
![]() МПа.
МПа.
при ![]()
потери от ползучести
0,85 · 150 · 0,72 = 92,4 МПа.
Коэффициент 0,85 в первых и вторых потерях учитывает наличие тепловлажностной обработки бетона.
Вторые потери
40 + 92,4 = 132,4 МПа.
Полные потери при нормальной температуре равны
69,69 + 132,4 = 201,09 МПа.
Находим геометрические характеристики сечения плиты с учетом температуры 100 °С.
Площадь приведенного сечения определяем по
формуле (6) при βb = 0,8; ![]() = 0,7; βs = 1 (см. табл. 16, 18, 35):
= 0,7; βs = 1 (см. табл. 16, 18, 35):
![]() см2;
см2;
![]() см2;
см2;
![]() см2;
см2;
![]() см2;
см2;
![]() см2;
см2;
Ared = 156 + 188 + 28,7 + 4,8 + 3,1 = 380,6 см2.
Статический момент относительно нижней грани ребра по формуле (7):
Sred = 156 · 32,5 + 188 · 15 + 28,7 · 4 + 4,8 · 4 + 3,1 · 32,5 = 8124,75 см3.
Расстояние от центра тяжести приведенного сечения до грани ребра определяем по формуле (5):
![]() см.
см.
Момент инерции приведенного сечения определяем по формуле (11):
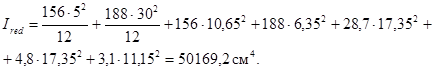
Эксцентриситет усилия обжатия
eop = у - а = 21,35 - 4 = 17,35 см.
Дополнительные потери предварительного напряжения от воздействия температуры 100 °С определяем по табл. 7, принимая βs = 1; αst = 12 · 10-6 °С-1; αbt = 10 · 10-6 °С-1 (см. табл. 20, 35):
потери от усадки - 80 МПа;
потери от релаксации напряжений в арматуре
0,001Δtsσsp = 0,001 · 80 · 695 = 55,6 МПа;
потери от разности деформаций бетона и арматуры
(αst - αbt)ΔtsEsβs = (12 - 10)10-6 · 80 · 190 · 103 · 1 = 30,4 МПа.
Дополнительные температурные потери равны
80 + 55,7 + 30,4 = 166 МПа.
Полные потери равны
201,09 + 166 = 367,09 МПа.
Усилие обжатия с учетом всех потерь
P = 4,91(695 - 367,09) - 0,785 · 367,09 - 0,503 · 367,09 = 113,7 кН.
Момент в середине пролета (для половины сечения плиты)
![]() кН
· м.
кН
· м.
Определяем момент трещинообразования Mcrc по формуле (256), для этого по формуле (259) находим Wpl, где γ′1, μ1, α - по формулам (260) - (263), (189) при βb = 0,8 и βs = 1:
![]() ; γ1 = 0;
; γ1 = 0;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Wpl = [0,292 + 0,75(2 · 0,0148 · 7,3 + 2 · 0,0024 · 7,69) + 0,075(1,143 + 2 · 0,002 · 7,69)] 9,5 · 352 = 5633 см3.
Далее определяем Mcrc, для этого находим:
по формуле (258)
![]() см3;
см3;
по формуле (255)
![]() ;
;
принимаем φ = 0,7;
по формуле (252)
![]() см;
см;
Mrp = 113700(17,35 + 4,32)1 = 2464370 Н · см = 24,64 кН · м.
Mcrc = 0,7 · 2,1 · 5633 + 2464370 = 3292441 Н · см = 32,9 кН · м < 52,8 кН · м,
т.е. трещины будут.
Следовательно, прогиб плиты определяем как для элемента с трещинами.
Определяем кривизну плиты в середине пролета от длительного действия нагрузки.
Заменяющий момент при действии внешнего момента M равен
Mr = M = 52,8 кН · м.
Определяем относительную высоту сжатой зоны бетона ξ по формуле (283), для чего находим:
по формуле (284)
![]() ;
;
по формуле (286)
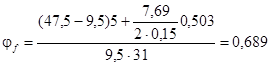 ;
;
по формуле (285)
![]() ;
;
![]() ;
;
по формуле (287)
![]() см.
см.
Относительная высота сжатой зоны [см. формулу (283)]
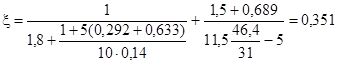 .
.
Плечо внутренней пары сил z определяем по формуле (288):
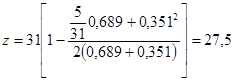 см.
см.
Затем по формуле (290) при γtt = 0,7 (см. табл. 16) находим коэффициент
![]() ;
;
по формуле (289) определяем
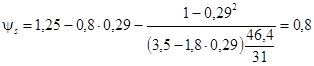 .
.
Определяем кривизну плиты в середине пролета по формуле (282):
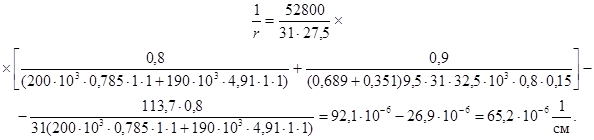
Прогиб плиты определяем по формуле (305):
![]() см < 2,5 см,
см < 2,5 см,
т.е. прогиб плиты меньше предельно допустимого и прогиб (кривизну) от выгиба можно не учитывать.
Пример 30. Расчет железобетонной плиты фундамента на неравномерный нагрев от центра к краям.
Дано: плита изготовляется из жаростойкого бетона на портландцементе с шамотными заполнителями (состав № 11 по табл. 11) класса В20 с характеристиками (см. табл. 13 и 14): Rb,ser = 15 МПа, Rbt,ser = 1,4 МПа, Rb = 11,5 МПа, Eb = 0,195 · 105 МПа. Плита армируется по контуру арматурой класса A-III: Rs = 365 МПа (см. табл. 29). Геометрические размеры плиты указаны на черт. 64, на нем же указано распределение температуры от центра плиты к периферии. Требуется определить необходимое количество арматуры для восприятия усилий от кратковременного воздействия на плиту неравномерного нагрева от центра к краям. Скорость нагрева 10 °С/ч.
Черт. 64. Прямоугольная фундаментная железобетонная плита
а - план плиты с распределением температур от центра к длинной стороне плиты; б - расчетное сечение I - I полуплиты
Наибольшие усилия от температурного перепада будут возникать в продольных сторонах плиты.
Для определения необходимого количества арматуры для восприятия этих усилий плиту мысленно разрезаем по оси b - b и ведем расчет статически неопределимой балки с сечением, указанным на черт. 64, б, загруженной по концам температурным моментом.
Определяем минимальный процент армирования продольных сторон полуплиты по формуле (49):
![]() см2.
см2.
Принимаем 4 Ø 18 A-III с Аs = 10,18 см2.
Определяем момент, который может воспринять сечение по формулам (105), (106):
![]() см;
см;
![]() Н · м = 832,7 кН · м.
Н · м = 832,7 кН · м.
Разбиваем сечение полуплиты на две части и определяем
площадь приведенного сечения по формулам (2), (3) и (6), в которых для tb = 550 и 250 °С βb = 0,46 и 0,82; ![]() = 0,48 и 0,72 (см.
табл. 16 и 18) и для ts =
150 °С βs =
0,97 (см. табл.
35):
= 0,48 и 0,72 (см.
табл. 16 и 18) и для ts =
150 °С βs =
0,97 (см. табл.
35):
![]() см2;
см2;
![]() см2;
см2;
![]() см2;
см2;
Ared = 998,7 + 2705,3 + 140,4 = 3844,4 см2.
Затем по формуле (9) определяем:
![]() см;
см;
![]() см,
см,
в которых для tb = 600, 400 и 100 °С βb = 0,41; 0,62 и 1.
По формуле (8) находим:
y1 = 0,5 · 233 + 54,22 = 170,22 см;
y2 = 53,77 см.
По формуле (7) определяем статический момент сечения
Sred = 998,7 · 170,22 + 2705,3 · 53,77 + 140,4 · 3 = 315883,9 см3.
Затем по формуле (5) определяем
![]() см.
см.
По формулам (13) и (14) находим:
yb1 = 170,22 - 82,17 = 88,05 см;
yb2 = 53,77 - 82,17 = -28,4 см;
ys = 82,17 - 3 = 79,17 см.
По формуле (11) определяем момент инерции сечения, для чего по формуле (12) находим:
![]() см4;
см4;
![]() см4;
см4;
Ired = 1129550,5 + 3059750,5 + 998,7 · 88,052 + 2705,3 · 28,42 + 140,4 · 79,162 = 14993801 см4.
По формуле (259) определяем Wpl, для чего находим величины α, μ по формулам (189), (262), в которых при tb = ts = 150 °С, βb = 0,95 и βs = 0,97 (см. табл. 16 и 35):
![]() ;
;
![]() ;
;
μα = 0,00134 · 10,53 = 0,0141;
Wpl = [0,292 + 0,75 · 2 · 0,00134 · 10,53]33 · 2332 = 561227,2 см3.
Определяем момент образования трещин по формуле (256) при σbt = 0 и γtt = 0,72 (см. табл. 16).
Mcrc = 1,4 · 0,72 · 561227,2 = 569,65 кН · м < 832,7 кН · м,
т.е. трещины будут.
Далее определяем коэффициент приведения по формуле (48)
![]() .
.
Затем определяем удлинение оси и кривизну каждого элемента сечения полуплиты по формулам (19), (20) и (21), принимая для tb = 600; 400 и 100 °С, αbt = 5; 6,25 и 8,5 · 10-6 °С-1 (см. табл. 20) и для ts = 150 °С αst = 12,5 · 10-6 °С-1 (см. табл. 35):
![]() см;
см;
![]() см;
см;
εs = 12,5 · 150 · 10-6 = 1875 · 10-6 см;
![]() ;
;
![]() .
.
Кривизна сечения без трещин по формуле (18) будет равна
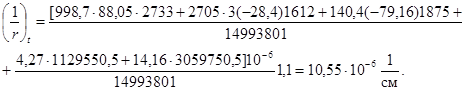 ;
;
Кривизну сечения полуплиты с трещинами находим по формуле (36), для этого определяем по формуле (74) коэффициент температурного расширения арматуры в бетоне, принимая по табл. 36:
φα = 0,9 при
![]() и μ ≤ 0,2 %;
и μ ≤ 0,2 %;
αstm = [8 + (12,5 - 8)0,9]10-6 = 12,05 · 10-6 °С-1.
Кривизна сечения полуплиты с трещинами равна [см. формулу (36)]:
![]() .
.
Приведенная кривизна сечения полуплиты по формуле (47) будет равна
![]() .
.
Жесткость сечения полуплиты без трещин по формуле (298) равна
B1 = 0,85 · 14993801 · 0,195 · 105 = 24,9 · 1010 МПа · см4.
Жесткость сечения полуплиты с трещинами определяем по формуле (303), для этого определяем
![]() .
.
Значение коэффициентов φ1 и φ2 принимаем по табл. 52:
φ1 = 0,59; φ2 = 0,17;
![]() МПа · см4.
МПа · см4.
Приведенная жесткость полуплиты по формуле (45) равна
Bred = [9,9 + (24,9 - 9,9)0,69]1010 = 20,25 · 1010 МПа · см4.
Момент от воздействия температуры по формуле (50)
Мt = 9,16 · 10-6 · 20,25 · 1010 = 1854,9 кН · м > M = 832,7 кН · м,
полученный момент больше прочности сечения, следовательно, необходимо увеличение армирования.
Принимаем 6 Ø 18 с Аs = 15,27 см2 и делаем пересчет
![]() см;
см;
![]() кН · м.
кН · м.
![]() см2;
см2;
Ared = 998,7 + 2705,3 + 245,5 = 3949,5 см2;
Sred = 998,7 · 170,22 + 2705,3 · 53,77 + 245,5 · 3 = 316199,2 см3;
![]() см;
см;
yb1 = 170,22 - 80,06 = 90,16 см;
yb2 = 53,77 - 80,06 = -26,29 см;
ys = 80,06 - 3 = 77,06 см;
Ired = 1129550,5 + 3059750,5 + 998,7 · 90,162 + 2705,3 · 26,292 + 245,5 · 77,062 = 15635205 см4.
α = 10,53;
![]() ;
;
μα = 10,53 · 0,002 = 0,0212;
Wpl = [0,292 + 0,75 · 2 · 0,00212]33 · 2332 = 580059.
Mcrc = 1,4 · 0,72 · 580059 = 588,8 кН · м.
![]() .
.
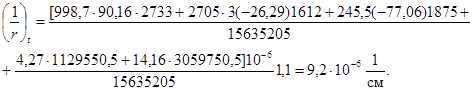 ;
;
![]() ;
;
B = 0,85IredEb;
B1 = 0,85 · 15635205 · 0,195 · 105 = 25,92 МПа · см4;
![]() ;
;
φ1 = 0,55; φ2 = 0,14;
![]() МПа · см4;
МПа · см4;
Bred = [10,92 + (25,92 - 10,92)0,42]1010 = 17,22 · 1010 МПа · см4;
Мt = 7,18 · 10-6 · 17,22
· 1010 =
1236 кН · м ![]() M = 1232
кН · м,
M = 1232
кН · м,
т.е. условие прочности соблюдается.
Далее определяем ширину раскрытия трещины, для этого находим:
по формуле (284)
![]() ;
;
φf = 0; λ = 0; μα = 0,0435;
по формуле (283)
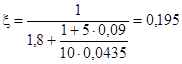 ;
;
по формуле (288)
![]() см.
см.
Напряжения в арматуре по формуле (272) будут равны
![]() МПа.
МПа.
Ширина раскрытия трещин по формуле (267) будет равна
![]() < 0,6 мм,
< 0,6 мм,
т.е. ширина раскрытия трещин вполне допустима для данной конструкции и для данных условий ее работы (см. табл. 3).
Пример 31. Расчет прочности и ширины раскрытия трещин двухшарнирной портальной рамы из жаростойкого железобетона.
Дано: пролет рамы в свету 174 см, высота стоек в свету 260 см. Сечение рамы по стойкам и ригелю одинаково.
Максимальная температура в центре рамы достигает 1000 °С.
За расчетное сечение рамы принимаем тавровый участок ребристой панели с высотой ребра h = 50 см, шириной ребра b = 12 см, ширина полки b′f = 75 см, высота полки h′f = 13 см.
Ребристые панели выполнены из жаростойкого бетона класса В25 на портландцементе с тонкомолотым шамотом и шамотным заполнителем (состав № 11 по табл. 11), арматура периодического профиля класса A-III.
Требуется определить необходимое количество арматуры, располагаемой в ребрах рамы, для восприятия температурных усилий и собственного веса конструкции, а также проверить ширину раскрытия трещин.
Расчетные размеры рамы (черт. 65):
lg = 174 + 2h′f = 174 + 26 = 200 см;
lc = 260 + h′f = 260 + 13 = 273 см.
Черт. 65. Эпюры в портальной раме
а - моментов; б - продольных сил; в - поперечных сил, вызванных единичной силой; г - моментов от собственного веса; д - моментов от воздействия температуры; е - суммарных моментов
Расчет рамы на прочность от воздействия температуры и собственного веса
Расчет производим при кратковременном нагреве до температуры 500 °С, вызывающей максимальные усилия в конструкциях из данного состава бетона (см. п. 1.23).
На основании теплотехнического расчета температура на арматуре при этих условиях будет 130 °С.
Для первого приближения армирование определяем по формуле (49):
![]() см2.
см2.
Принимаем 2 Ø 10 с As = 1,57 см2, при
этом ![]() .
.
Для определения усилий в П-образной раме воспользуемся методом сил. За расчетную схему принимаем двухшарнирную раму, являющуюся один раз статически неопределимой системой. Выбираем основную систему, отбрасывая лишнюю связь. Ее действие заменяем приложением к основной системе распора X.
Для определения неизвестного усилия X составляем каноническое уравнение перемещения
δ11X + Δit + Δig = 0,
откуда ![]() .
.
Для определения коэффициента δ11 перемещений Δit и Δig к основной системе прикладываем силу X = 1 и строим эпюры моментов и продольных сил.
Перемещение Δit определяем по формуле (41).
Предварительно определяем все величины, входящие в эту формулу, для чего находим момент, который может воспринять сечение рамы при данных температурных условиях.
Проверяем условие (120) без учета арматуры S′.
Значение коэффициента γst = 1 определяем по табл. 35 при ts = 130 °С:
γstRsAs = 1 · 365 · 1,57 = 57,3 кН.
Значение коэффициента γbt = 0,95 определяем по табл. 16 при tbc = 400 °С (на расстоянии 0,2h0 от сжатой грани сечения):
γbtRbb′fh′f = 0,95 · 14,5 · 75 · 13 = 1343,6 кН > 57,3 кН.
Усилие, которое может воспринять арматура, меньше усилия, воспринимаемого полкой сечения рамы. Следовательно, нейтральная ось проходит в полке, расчет будет производиться как для прямоугольного сечения. Из условия (106) находим высоту сжатой зоны бетона:
![]() см.
см.
По формуле (105) находим
![]() кН · м.
кН · м.
Определяем площадь приведенного сечения по формуле (6), для чего разбиваем на два элемента полку и ребро, и по формуле (2) находим:
![]() см2;
см2;
![]() см2;
см2;
![]() см2;
см2;
Ared = 440,9 + 304,6 + 15 = 760,5 см2.
В формуле (6) для tb
= 400 и 260 °С βb = 0,62 и 0,81 и ![]() = 0,61 и 0,72
(см. табл. 16 и 18).
= 0,61 и 0,72
(см. табл. 16 и 18).
Затем по формуле (9) определяем:
![]() см;
см;
![]() см,
см,
в которых для tb = 500, 400 и 100 °С βb = 0,5; 0,62 и 1.
По формуле (8) определяем:
y1 = 37 + 6,26 = 43,26 см; y2 = 17,08 см.
По формуле (7) определяем статический момент сечения
Sred = 440,9 · 43,26 + 304,6 · 17,08 + 15 · 5 = 24350,9 см3.
Затем по формуле (5) определяем
![]() см.
см.
Далее по формуле (13) определяем:
yb1 = 43,26 - 32 = 11,26 см;
yb2 = 17,08 - 32 = -14,92 см.
а по формуле (14)
ys = 32 - 5 = 27 см.
По формуле (11) определяем момент инерции сечения, для чего по формуле (12) находим:
![]() см4;
см4;
![]() см4;
см4;
Ired = 6209,3 + 34749,8 + 440,9 · 11,262 + 304,6 · 14,922 + 15 · 272 = 175600,7 см4.
По формуле (259) определяем Wpl, для чего находим величины γ′1, α, μ по формулам (261), (189) и (262), в которых при tb = ts = 130 °С βb = 0,97 и βs = 1 (см. табл. 16 и 35):
![]() ;
;
![]() ;
;
μ1 = 0,003; γ1 = 0; μ′1 = 0;
Wpl = [0,292 + 0,75 · 2 · 0,003 · 9,8 + 0,075 · 2,73] · 12 · 502 = 16226 см3.
Затем определяем момент трещинообразования по формуле (256) при σbt = 0 и γtt = 0,75 (см. табл. 16):
Mcrc = 1,6 · 0,75 · 16226 = 19,6 кН · м.
Далее определяем коэффициент приведения по формуле (48)
![]() .
.
Теперь по формуле (18) определяем кривизну сечений без трещин, для этого находим: коэффициент температурного расширения бетона, определяемый по табл. 20, при температуре нагрева крайнего волокна бетона, т.е. при tb = 500 °С αbt = 5,50 · 10-6 °С-1; при tb1 = 400 °С αbt = 6,25 · 10-6 °C-1; при tb2 = 100 °C αbt = 8,5 · 10-6 °C-1.
По формуле (19) находим удлинение оси и по формуле (20) кривизну для каждой из частей сечения:
![]() см;
см;
![]() см;
см;
εs = 12,3 · 10-6 · 130 = 1599 · 10-6;
![]() ;
;
![]() .
.
Удлинение сечения без трещин
![]() .
.
Кривизна сечения без трещин
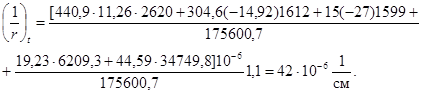 ;
;
Кривизну с трещинами определяем по формуле (36), для этого находим по формуле (74) коэффициент температурного расширения арматуры в бетоне
αstm = 8,2 · 10-6 + (12,3 - 8,2)10-6 · 0,92 = 12 · 10-6 °С-1.
Здесь коэффициенты αbt и αst определены соответственно по табл. 20 и 35 при температуре арматуры ts = 130 °С. Коэффициент φα определяем по табл. 36 при μ = 0,3 %.
Кривизна с трещинами равна
![]() .
.
Приведенная кривизна по формуле (47):
![]() .
.
Удлинение оси для сечений с трещинами определяем по формуле (35):
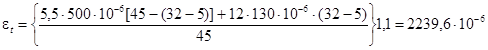 .
.
Приведенное удлинение определяем по формуле (46):
εt,red = [2239,6 + (2416 - 2239,6)0,79]10-6 = 2379 · 10-6.
Жесткость сечения определяем по формуле (45), для чего находим:
жесткость сечений без трещин по формуле (298):
B1 = 0,85 · 175600,7 · 0,21 · 105 = 0,031345 · 1010 МПа · см4;
жесткость сечений с трещинами - по формуле (299), для этого определяем:
по формуле (286)
![]() ;
;
по формуле (284)
![]() ;
;
по формуле (285)
![]() ;
;
по формуле (283)
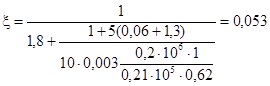 ;
;
по формуле (288)
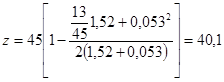 см;
см;
по формуле (289)
![]() .
.
Затем определяем жесткость сечения с трещинами
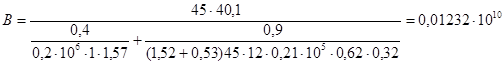 МПа · см4.
МПа · см4.
По формуле (45) определяем приведенную жесткость сечения
Bred = [0,01232 + (0,03135 - 0,01232)0,79] · 1010 = 0,02735 · 1010 МПа · см4.
Для вычисления Δit и Δig воспользуемся способом Верещагина.
В этом случае
![]() см2;
см2;
ΩN1 = 1; lg = 273 см2;
перемещение
Δit = (39,3 · 129129 + 273 · 2379)10-6 = 5,7 см;
перемещение от равномерно распределенной нагрузки (собственный вес q = 40 Н/см) равно:
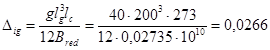 см.
см.
Значение коэффициента δ11 определяем по формуле (42) без учета продольной силы
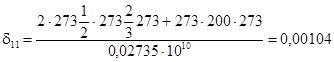 .
.
Распор будет равен
![]() кН.
кН.
Умножая единичную эпюру M (см. черт. 65, а) на X = 55, получаем эпюру момента, действующего в раме при данных температурных условиях
M = 273 · 55 = 150,2 кН · м > 25,4 кН · м.
Следовательно, условие прочности не соблюдается и двух стержней Ø 10 мм недостаточно для восприятия усилий, действующих в раме.
Принимаем 2 Ø 22 с Аs = 7,6 см2 и ![]() , и снова проводим
расчет - определяем:
, и снова проводим
расчет - определяем:
несущую способность
![]() см;
см;
![]() кН · м;
кН · м;
площадь приведенного сечения:
![]() см2;
см2;
Ared = 440,9 + 304,6 + 72,4 = 817,9 см2;
статический момент
Sred = 440,9 · 43,26 + 304,6 · 17,08 + 72,4 · 5 = 24638 см3;
![]() см;
см;
yb1 = 43,26 - 30,1 = 13,16 см;
yb2 = 17,08 - 30,1 = -13,02 см;
ys = 30,1 - 5 = 25,1 см;
момент инерции
Ired = 6209,3 + 34749,8 + 440,9 · 13,162 + 304,6 · 13,022 + 72,4 · 25,12 = 214565,3 см4.
φ1 = 2,73; α = 9,8; μ = 0,014; φ1 = 0; μ = 0;
момент сопротивления
Wpl = [0,292 + 0,75 · 2 · 0,014 · 9,8 + 0,075 · 2,73] · 12 · 502 = 21076,5 см3;
момент трещинообразования
Mcrc = 1,6 · 0,75 · 21076,5 = 25,5 кН · м;
коэффициент приведения
![]() ;
;
удлинение сечения без трещин
![]() ;
;
кривизна сечения без трещин
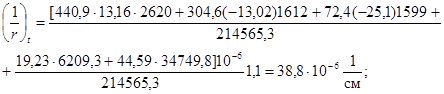 ;
;
кривизна с трещинами
αstm = 8,2 · 10-6 + (12,3 - 8,2)10-6 · 1 = 12,3 · 10-6 °С-1;
![]() ;
;
приведенная кривизна
![]() ;
;
удлинение оси сечений с трещинами
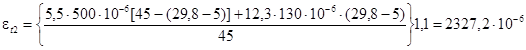 ;
;
приведенное удлинение
εt,red = [2327,2 + (2369,6 - 2327,2)0,05]10-6 = 2329,3 · 10-6;
жесткость сечений без трещин
B1 = 0,85 · 214565,3 · 0,21 · 105 = 0,0383 · 1010 МПа · см4;
жесткость сечений с трещинами
φf
= 1,52; ![]() ;
;
λ = 1,3;
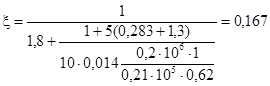 ;
;
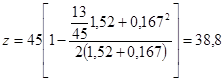 см;
см;
![]() ;
;
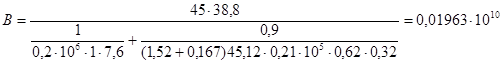 МПа · см4;
МПа · см4;
приведенная жесткость
Bred = [0,01963 + (0,0383 - 0,01963)0,05] · 1010 = 0,02056 · 1010 МПа · см4;
перемещение
Δit = (28,6 · 129129 + 273 · 2329,3)10-6 = 4,33 см;
перемещение
![]() см;
см;
коэффициент
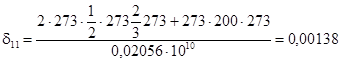 ;
;
распор
![]() кН;
кН;
момент от температурного воздействия
Mt = 273 · 31,6 = 86,3 кН · м.
Моменты от собственного веса равны (см. черт. 65, г):
в пролете рамы
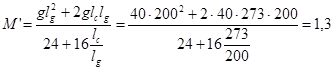 кН
· м;
кН
· м;
в углах
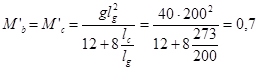 кН
· м.
кН
· м.
Суммарные моменты в раме равны (см. черт. 65, е):
в углах
Mb = Mc = Mt + M′b = 86,3 + 0,7 = 87 кН · м;
в пролете
M = Mt - M′ = 86,3 - 1,3 = 85 кН · м
Суммарный действующий в раме момент Mb = 87 кН · м меньше прочности сечения рамы M = 120,9 кН · м, следовательно, условие прочности удовлетворяется и двух стержней Ø 22 достаточно для восприятия усилий, действующих в раме.
Определяем ширину раскрытия трещин от действия момента, возникающего при нагреве внутренней поверхности рамы до 500 °С и собственного веса.
Напряжения в арматуре по формуле (272) равны
![]() кН · см2.
кН · см2.
Раскрытие трещин определяем по формуле (267):
![]() < 0,3 мм,
< 0,3 мм,
т.е. ширина раскрытия трещин находится в допустимых пределах (см. табл. 3).
Пример 32. Расчет прочности, деформаций и ширины раскрытия трещин свободно опертой плиты покрытия из жаростойкого железобетона при длительном одностороннем нагреве до 520 °С.
Дано: плита покрытия длиной 320 см с расчетным пролетом l = 290 см, шириной b = 100 см и высотой h = 35 см. Плита выполнена из жаростойкого бетона класса В25 на портландцементе с тонкомолотой шамотной добавкой и шамотными заполнителями (состав № 11 по табл. 11). Для армирования плиты используется арматура периодического профиля Ø 16 мм из горячекатаной стали класса A-III.
Продольная рабочая арматура расположена с нижней более нагретой стороны плиты с защищенным слоем 92 мм, равным примерно 6 диаметрам арматуры.
Согласно теплотехническому расчету при температуре рабочего пространства теплового агрегата ti = 550 °С и температуре наружного воздуха te = 25 °С температура арматуры равна 400 °С. Температура верхней поверхности плиты равна 90 °С, средняя температура бетона сжатой зоны, принимаемая по температуре бетона на расстоянии 0,2h0 = 5 см от верхней менее нагретой грани tbc = 162 °С, и температура более нагретой грани сечения плиты равна 520 °С.
Расчет прочности плиты производим по сечению с наибольшим изгибающим моментом в центре пролета. Нагрузка на 1 м от собственного веса плиты при средней плотности железобетона в сухом состоянии ρd = 19,5 кН/м3 и коэффициенте надежности по нагрузке γf = 1,1
g = γfbhρd = 1,1 · 1 · 0,35 · 19,5 = 7,5 кН/м.
Изгибающий момент в центре пролета свободно опертой плиты
![]() кН
· м = 790000 Н · см.
кН
· м = 790000 Н · см.
Принимаем арматуру в количестве 5 Ø 16 Аs = 10,05 см2, расположенную с шагом 200 мм по ширине плиты. При длительном нагреве по табл. 16 при tbc = 162 °С γbt = 1, а по табл. 35 при ts = 400 °С γst = 0,4. При классе бетона В25 по табл. 14 расчетное сопротивление бетона сжатию Rb = 14,5 МПа. По табл. 15 коэффициент условий работы бетона при длительном нагреве изгибаемых элементов γb2 = 0,9. Расчетное сопротивление арматуры класса A-III, согласно табл. 29, Rs = 365 МПа.
Определяем высоту сжатой зоны бетона из формулы (106):
![]() см.
см.
Условие прочности плиты с односторонним армированием проверяем по формуле (105):
![]() МПа · см3 = 4760000 Н · см.
МПа · см3 = 4760000 Н · см.
Следовательно, условие прочности плиты удовлетворяется с большим запасом.
Расчет деформаций. Проверяем возможность образования трещин в бетоне от нагрузки, вызванной собственным весом плиты. Для этой цели вычисляем момент трещинообразования Mcrc по формуле (257) при σbt = 0.
Для данной конструкции плиты при ![]() > 0,1
коэффициент армирования μ в формуле
(259) при определении Wpl необходимо умножать на φ = 1 - 2δ = 1 - 2 · 0,286 = 0,428 согласно формуле (265):
> 0,1
коэффициент армирования μ в формуле
(259) при определении Wpl необходимо умножать на φ = 1 - 2δ = 1 - 2 · 0,286 = 0,428 согласно формуле (265):
![]() ;
;
при tb = ts = 400 °С по табл. 16 γtt = 0,3, βb = 0,63, по табл. 35 βs = 0,83. Для бетона класса В25 по табл. 13 Rbt,ser = 1,5 МПа.
По формуле (189)
![]() .
.
По формуле (259)
Wpl = (0,292 + 0,75 · 2 · 0,0029 · 0,428 · 15)100 · 352 = 39418 см3.
По формуле (256)
Mcrc = WplRbt,serγtt = 39418 · 1,6 · 0,3 = 18920 МПа · см3 = 1892000 Н · см = 18,92 кН · м.
Изгибающий момент в центре пролета при нагрузке от собственного веса при коэффициенте надежности по нагрузке, равном 1:
g = bhρd = 1 · 0,35 · 19,5 = 6,8 кН · м;
![]() кН
· м.
кН
· м.
Так как M = 7,1 кН · м < Mcrc = 18,92 кН · м, то от собственного веса плиты трещины в растянутой зоне бетона не образуются.
При коэффициенте армирования плиты ![]() % и
температуре арматуры ts = 400 °С, согласно указаниям п. 4.3, плита будет работать с трещинами в бетоне растянутой
зоны, вызванными разностью коэффициентов температурного расширения арматуры и
бетона. В соответствии с этим при определении αstm коэффициент φα = 0,8. Согласно данным табл. 36
при
% и
температуре арматуры ts = 400 °С, согласно указаниям п. 4.3, плита будет работать с трещинами в бетоне растянутой
зоны, вызванными разностью коэффициентов температурного расширения арматуры и
бетона. В соответствии с этим при определении αstm коэффициент φα = 0,8. Согласно данным табл. 36
при ![]() и
μ = 0,4 %. При длительном воздействии температуры ts = 400 °С соответственно по табл. 20 и 35 имеем αbt = 4,9 · 10-6 и αst = 14 · 10-6.
и
μ = 0,4 %. При длительном воздействии температуры ts = 400 °С соответственно по табл. 20 и 35 имеем αbt = 4,9 · 10-6 и αst = 14 · 10-6.
По формуле (74)
αstm = 4,9 · 10-6 + (14 · 10-6 - 4,75 · 10-6)0,8 = 12,15 · 10-6.
Кривизну от воздействия температуры определяем по формуле (37) при коэффициенте надежности по температуре γt = 1. При tb = 90 °С по табл. 20 αbt = 2,3 · 10-6
![]() .
.
Прогиб плиты в центре пролета от неравномерного нагрева определяем по формуле (297):
![]() см = 19 мм.
см = 19 мм.
Определяем прогиб плиты в центре пролета от собственного веса.
При классе бетона В25 по табл. 13 Rb,ser = 18,5 МПа.
По формуле (284) при M = 7,1 кН · м = 7100 МПа × см3 и γbt = 1
![]() .
.
При tbc = 162 °С по табл. 16 βb = 0,94. При классе бетона В25 по табл. 17 Eb = 0,21 · 105 МПа, а по табл. 37 Es = 0,2 · 106 МПа.
По формуле (189):
![]() .
.
Относительную величину сжатой зоны бетона определяем по формуле (283):
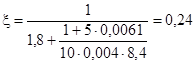 .
.
Величина z определяется по формуле (288):
z = 25(1 - 0,5 · 0,24) = 22 см.
По формуле (290) вычисляем значение φm:
![]() .
.
Так как φm = 2,67 > 1, то за расчетную величину принимаем φm = 1.
Коэффициент ψs определяем по формуле (289):
ψs = 1,25 - 0,8 · 1 = 0,45.
По формуле (282) определяем кривизну от собственного веса плиты при ψb = 0,9.
При tbc = 162 °C по табл. 19 v = 0,12, а при ts = 400 °С по табл. 38 vs = 0,3.
![]() .
.
По формуле (305) определяем прогиб от собственного веса плиты:
![]() см = 1,8 мм.
см = 1,8 мм.
Определяем полный прогиб
f = ft + fg = 19 + 1,8 = 20,8 мм.
Прогиб плиты ![]() - это незначительно отличается от допускаемого
- это незначительно отличается от допускаемого ![]() согласно п. 1.29.
согласно п. 1.29.
Расчет ширины раскрытия трещин. Ширину раскрытия трещин, нормальных к продольной оси плиты, определяем по формуле (267), в которой: φl = 1,5; δ = 1; η = 1; μ = 0,004; βs = 0,83; d = 16 мм, αstm = 12,15 · 10-6; αbt = 4,9 · 10-6.
Напряжение в арматуре σs определяем по формуле (272):
![]() кН/см2 = 32,1 МПа.
кН/см2 = 32,1 МПа.
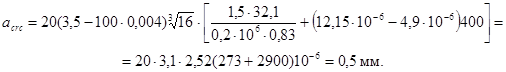
Ширина раскрытия трещин в железобетонной плите acrc = 0,5 мм не превышает допускаемую величину acrc = 0,5 мм согласно поз. 5 табл. 3 при длительном нагреве арматуры на 400 °С.
Пример 33. Расчет прочности и ширины раскрытия трещин сферического купола и опорного кольца из жаростойкого железобетона при одностороннем кратковременном нагреве.
Дано: сферический купол пролетом 5 м перекрывает рабочее пространство теплового агрегата с температурой 700 °С. Температура окружающего воздуха в зимний период равна 15 °С, а в летний - 25 °С. Подъем температуры до 700 °С производится по 10 °С/ч.
Геометрические параметры купола согласно черт. 49:
h = 240 мм; ri = 5000 мм; r = 5120 мм; re = 5240 мм, rb = 2500 мм; r1 = 2560 мм; rs = 2900 мм; r2 = 2950 мм; r2 - r1 = 390 мм; rs - r1 = 340 мм; h1 = b = 310 мм и α = 30°.
Стрела подъема срединной поверхности купола
f = r(1 - cosα) = 5120(1 - cos 30°) = 5120(1 - 0,866) = 690 мм.
Расчетный пролет купола l = 2r1 = 2 · 2560 = 5120 мм.
Для изготовления купола принимаем жаростойкий бетон состава № 11 по табл. 11 класса В20 на портландцементе с шамотным заполнителем. Для одностороннего армирования купола со стороны менее нагретой поверхности в кольцевом и радиальном направлениях и опорного кольца используется арматура диаметром соответственно 14 и 16 мм периодического профиля класса A-III.
С наружной стороны опорного кольца предусматривается тепловая изоляция в виде асбестоцементной штукатурки толщиной 20 мм для уменьшения перепада температуры по высоте сечения кольца и, следовательно, для уменьшения усилий от воздействия температуры.
Нагрузка на 1 см2 купола от его собственного веса при плотности железобетона в сухом состоянии ρd = 19,5 кН/м2 и коэффициенте надежности по нагрузке γf = 1,1 равна
g = γfρdh = 1,1 · 19,5 · 0,24 = 5,2 кН/м2 = 0,52 Н/см2.
Теплотехнический расчет купола при температуре более нагретой поверхности 500 °С в зимний период
При температуре 500 °С в статически неопределимых конструкциях из жаростойкого бетона на портландцементе согласно п. 1.23 возникают наибольшие усилия от воздействия температуры.
Принимаем температуру наружной менее
нагретой поверхности купола tbe
= 120 °С.
Средняя температура бетона ![]() °С. При tbm = 310
°С по табл. 9
коэффициент теплопроводности бетона λ1 =
0,84. При tbe = 120 °С по табл. 8 αe = 15 Вт/(м2 · °С). При высоте
сечения купола h = 24 см:
°С. При tbm = 310
°С по табл. 9
коэффициент теплопроводности бетона λ1 =
0,84. При tbe = 120 °С по табл. 8 αe = 15 Вт/(м2 · °С). При высоте
сечения купола h = 24 см:
![]() ;
; ![]() ;
;
R0 = 0,28 + 0,07 = 0,35 м2 · °С/Вт.
По формуле (61)
![]() Вт/м2;
Вт/м2;
tbe = tb - QR1 = 500 - 1385 · 0,28 = 110 °C.
Полученная температура tbe = 110 °С, что незначительно отличается от ранее принимавшейся для расчета 120 °С. Поэтому дальнейшее уточнение температуры не требуется.
Температура арматуры при защитном слое бетона, равном 30 мм, и расстоянии от центра тяжести арматуры до наружной поверхности бетона as = 44 мм равна
![]() °С.
°С.
Теплотехнический расчет опорного кольца при температуре нижней поверхности купола 500 °С в зимний период
Средняя температура бетона в куполе
![]() °С.
°С.
Принимаем температуру внутренней, более нагретой поверхности опорного кольца, равной средней температуре бетона в куполе, т.е. tb = tbm = 305 °С, температуру менее нагретой поверхности бетона tb1 = 90 °С и температуру наружной поверхности тепловой изоляции te1 = 50 °С.
Средняя температура бетона в сечении опорного кольца
![]() °С.
°С.
При tbm1 = 197 °С по табл. 9 коэффициент теплопроводности жаростойкого бетона состава № 11 λ1 = 0,87. При te1 = 50 °С по табл. 8 αе = 12 Вт/(м2 · °С). Коэффициент теплопроводности асбестоцементной штукатурки λ2 = 0,21.
При высоте сечения опорного кольца в радиальном направлении h = r2 - r1 = 39 см:
![]() ;
;
![]() ;
; ![]() ;
;
R0 = 0,45 + 0,095 + 0,085 = 0,63.
![]() Вт/м2.
Вт/м2.
tb1 = 305 - 460 · 0,45 = 99 °C;
te1 = 305 - 460(0,45 + 0,095) = 55 °C.
Полученные температуры 99 и 55 °С незначительно отличаются от ранее принимавшихся температур.
Температура кольцевой арматуры в опорном кольце при as = 50 мм
![]() °С.
°С.
Расчет прочности купола и опорного кольца при воздействии собственного веса и наибольших усилий от кратковременного нагрева до 500 °С
Кольцевую и радиальную арматуру в куполе располагаем со стороны верхней менее нагретой поверхности с шагом s = 190 мм.
Согласно указаниям п. 6.11 при расчете прочности купола от воздействия температуры определяются распор st, усилие сжатия T2t и изгибающий момент Mt в кольцевом направлении. Коэффициент армирования купола кольцевой арматурой при диаметре стержня 14 мм с площадью сечения Ar = 1,54 см2, защитным слоем 30 мм, as = 37 мм и = h - as = 24 - 3,7 = 20,3 см равен
![]() %,
%,
коэффициент
![]() %.
%.
Количество арматуры для расчетного сечения купола шириной b = 1 см равно
![]() см2.
см2.
Определяем изгибающий момент Mt в сечении купола шириной b = 1 см в кольцевом направлении, вызванный перепадом температуры по высоте сечения.
Сначала определяем среднюю температуру бетона сжатой зоны tbc = 435 °С на расстоянии 0,2h0 = 0,2 · 20,3 = 4 см от более нагретой поверхности купола согласно примеч. 7 к табл. 16.
Для бетона состава № 11 и класса В20 по табл. 13 Rbt,ser = 1,4 МПа, Rb,ser = 15 МПа; по табл. 17 Eb = 0,195 · 105 МПа и по табл. 14 Rb = 11,5 МПа.
При tb = ts = 190 °С по табл. 16 для бетона состава № 11 γtt = 0,67, βb = 0,91, а при tbc = 435 °С βb = 0,58, γbt = 0,93 и по табл. 19 v = 0,3. По табл. 20 αbt = 7,6 · 10-6 °С-1. Для арматуры класса A-III по табл. 37 Es = 0,2 · 106 МПа, а по табл. 29 Rs = 365 МПа, по табл. 35 γst = 1, αst = 12,9 · 10-6 °С-1 и βs = 0,91.
Высоту сжатой зоны бетона вычисляем из уравнения (106) при A′s = 0, b = 1 см и γst = 1:
![]() см.
см.
В первом приближении принимаем Mt равным правой части неравенства (105) при A′s = 0 и b′ = 1 см:
Мt = М = 0,93 · 11,5 · 2,7(20,3 - 0,5 · 2,7) = 528 МПа · см3 = 52800 Н · см.
Для определения жесткости сечения купола с
трещиной B и кривизны от воздействия температуры ![]() вычисляем:
вычисляем:
по формуле (189)
![]() ;
;
по формуле (259), согласно п. 4.6,
при ![]() ,
φ = 1 - 2δ = 1 - 2 · 0,15 = 0,7 и b = 1 см.
,
φ = 1 - 2δ = 1 - 2 · 0,15 = 0,7 и b = 1 см.
Wpl = (0,292 + 0,75 · 2 · 0,0034 · 0,7 · 10,2)242 = 193 см3;
по формуле (290)
![]() ;
;
по формуле (289) при φls = 1,1 и нулевом значении последнего члена
ψs = 1,25 - 1,1 · 0,34 = 1,25 - 0,37 = 0,88;
по формуле (284) при b = 1 см
![]() ;
;
по формуле (189) при tbc = 435 °C и ts = 190 °С
![]() ;
;
по формуле (283)
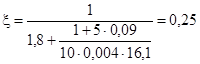 ;
;
по формуле (288)
z = 20,3(1 - 0,5 · 0,25) = 17,5 см.
по формуле (299) при vs = 1; b = 1 см и ψb = 0,9
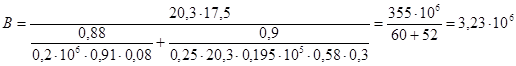 МПа · см4 = 323 · 106 Н · см.
МПа · см4 = 323 · 106 Н · см.
Для определения αstm коэффициент φα принимаем в первом приближении по табл. 36 при ![]() и μ = 0,4 равным 0,95;
и μ = 0,4 равным 0,95;
по формуле (74)
αstm = 7,6 · 10-6 + (12,9 · 10-6 - 7,6 · 10-6)0,95 = 12,6 · 10-6 °С-1;
по формуле (36) при αbt = 5,5 · 10-6 °С-1 и коэффициенте надежности по температуре γbt = 1,1
![]() ;
;
по формуле (50)
Мt = 19,5 · 10-6 · 323 · 106 = 6300 Н · см.
Полученный момент значительно отличается
от момента 52800 Н · см, принимавшегося для первого приближения. Для второго
приближения принимаем среднее значение ![]() Н · см. Опуская
промежуточные расчеты, для третьего приближения принимаем Mt = 20000 Н · см = 200 МПа
· см3. В
этом случае:
Н · см. Опуская
промежуточные расчеты, для третьего приближения принимаем Mt = 20000 Н · см = 200 МПа
· см3. В
этом случае:
по формуле (290)
![]() ;
;
по формуле (289)
ψs = 1,25 - 1,1 · 0,9 = 0,26;
по формуле (284)
![]() ;
;
по формуле (283)
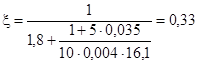 ;
;
по формуле (288)
z = 20,3(1 - 0,5 · 0,33) = 17 см;
по формуле (299)
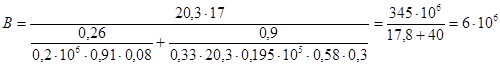 МПа · см4 = 600 · 106 Н · см2.
МПа · см4 = 600 · 106 Н · см2.
При ![]() и μ = 0,4 % по табл. 36 φα
= 0,68.
и μ = 0,4 % по табл. 36 φα
= 0,68.
По формуле (74)
αstm = 7,6 · 10-6 + (12,9 · 10-6 - 7,6 · 10-6)0,68 = 11,2 · 10-6;
![]() .
.
Мt = 33,7 · 10-6 · 600 · 106 = 20200 Н · см.
Полученный момент незначительно отличается от принимавшегося ранее для расчета в третьем приближении.
Переходим к определению распора Ht от воздействия температуры.
Кольцевую арматуру опорного кольца принимаем в количестве пяти стержней диаметром 16 мм. Площадь сечения арматуры As = 5 · 2,01 = 10,05 см2. При расстоянии от центра тяжести арматуры до наружной поверхности опорного кольца as = 50 мм, высота сечения h0 = (r2 - r1) - as = 39 - 5 = 34 см и b = h1 = 31 см.
Коэффициент армирования равен:
![]() %;
%;
![]() %.
%.
При высоте сечения опорного кольца в радиальном направлении h0 = 34 см > 0,1rs = 0,1 · 290 = 20 см, согласно п. 6.11, необходимо определять изгибающий момент Mt1 в опорном кольце.
Принимаем для первого приближения ![]() и ψs = 0,7.
и ψs = 0,7.
При ![]() и μ
= 0,95 % по табл. 36 φα = 1 и αstm = αst.
и μ
= 0,95 % по табл. 36 φα = 1 и αstm = αst.
При ts = 125 °С по табл. 35 αst = 12,25 · 10-6 °С-1, a βs = 0,98.
При классе бетона В20 для состава № 11 по табл. 17 Eb = 0,195
· 105 МПа, а при температуре бетона 305 °С по табл. 16
βb
= 0,75, а по
табл. 18 ![]() = 0,7; по табл. 20 αbt = 7 · 10-6 °С-1.
= 0,7; по табл. 20 αbt = 7 · 10-6 °С-1.
По формуле (316) определяем значение s при жесткости купола B = 6 · 106 МПа · см4 = 600 · 106 Н · см2:
![]() .
.
Распор от воздействия температуры на 1 см периметра опорного кольца определяем по формуле (314) при γt = 1,1:
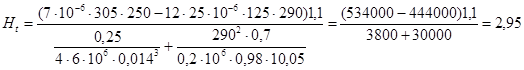 МПа
· см2 = 295 Н.
МПа
· см2 = 295 Н.
Усилие сжатия бетона в кольцевом направлении от воздействия температуры в опорном сечении I - I (см. черт. 49) шириной 1 см определяем по формуле (318):
![]() МПа
· см2 = 1100 Н.
МПа
· см2 = 1100 Н.
Кольцевое усилие сжатия в опорном сечении I - I шириной 1 см от собственного веса купола вычисляем по формуле (322) при cosα = cos 30° = 0,866 и cos2 30° = 0,75
![]() Н.
Н.
Расчетная сжимающая сила от воздействия температуры и собственного веса в опорном сечении I - I купола
T2 = T2t + T2f = 1100 + 88 = 1188 Н.
Проверка прочности опорного сечения купола I - I при внецентренном сжатии.
При температуре более нагретой грани
сечения I - I, равной в данном случае 500 °С, разбиваем
сечение, согласно указаниям п. 1.28,
на две площади с линией раздела, проходящей по бетону с температурой 400 °С. Для первой площади высотой h1 =
18 см при средней температуре бетона tbm1 = 255 °С βb = 0,83 и ![]() = 0,725. Для второй площади высотой h2 = 6 см при средней температуре бетона tbm2 = 450 °С βb = 0,56 и
= 0,725. Для второй площади высотой h2 = 6 см при средней температуре бетона tbm2 = 450 °С βb = 0,56 и ![]() = 0,57.
= 0,57.
При ширине сечения b = 1 см A1 = bh1 = 18 см, а A2 = bh2 = 6 см2.
Для бетона состава № 11, согласно указаниям п. 1.28, φb1 = 0,85. Площади бетона, приведенные к ненагретому бетону, по формуле (2):
![]() см2;
см2;
![]() см2.
см2.
Площадь сечения I - I, приведенная к ненагретому бетону, по формуле (6)
Ared = 10,83 + 2,25 = 13,08 см2.
При расстояниях центров тяжести площадей до наименее нагретой грани сечения y1 = 9 см и y2 = 21 см, пренебрегая растянутой арматурой, по формуле (7) определяем статический момент
Sred = 10,83 · 9 + 2,25 · 21 = 97,5 + 47 = 144,5 см3.
Расстояние от центра тяжести приведенного сечения до наименее нагретой грани по формуле (5)
![]() см.
см.
Эксцентриситет сжимающей силы T2 в опорном сечении I - I относительно центра тяжести приведенного сечения
![]() см.
см.
Эксцентриситет силы T2 в опорном сечении I - I относительно центра тяжести растянутой кольцевой арматуры купола по формуле (135) при η = 1 и ec = y - as = 11 - 4,4 = 6,6 см:
e = 17 + 6,6 = 23,6 см.
Высоту сжатой зоны бетона определяем из формулы (137) при T2 = 11,88 МПа · см2, Rs = 365 МПа, b = 1 см и A′s = 0:
![]() см.
см.
По формуле (100) при α = 0,85 для состава бетона № 11
ξ = 0,85 - 0,008 · 0,93 · 11,5 = 0,85 - 0,09 = 0,76.
По формуле (99) при σs = γstRs = 1 · 365 = 365 МПа, согласно п. 3.13 и βs = 0,91
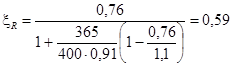 .
.
В данном случае при ![]() < ξR = 0,59 прочность сечения I - I в куполе при внецентренном сжатии должна
удовлетворять условию (136) при
А′s = 0 и b = 1 см, т.е.
< ξR = 0,59 прочность сечения I - I в куполе при внецентренном сжатии должна
удовлетворять условию (136) при
А′s = 0 и b = 1 см, т.е.
T2е = 1188 · 23,6 = 28000 Н · см < 0,93 · 11,5 · 3,8(20,3 - 0,5 · 3,8) = 750 МПа · см3 = 75000 Н · см.
Следовательно, условие прочности опорного сечения купола I - I при внецентренном сжатии удовлетворяется с большим запасом.
Расчет прочности опорного кольца
Усилие растяжения в арматуре опорного кольца от распора, вызванного воздействием температуры, вычисляем по формуле (317)
Nt = 295 · 290 = 85600 Н.
Распор в опорном кольце от собственного веса купола определяем по формуле (320):
![]() Н.
Н.
Усилие растяжения в арматуре опорного кольца от собственного веса купола определяем по формуле (321):
Nf = 123,6 · 256 = 31600 Н.
Расчетное усилие растяжения в опорном кольце от воздействия температуры и собственного веса купола
N = Nt + Nf = 85600 + 31600 = 117200 Н.
В данном случае при высоте сечения опорного кольца h0 = rs - r1 = 340 мм > 0,1rs = 290 мм, согласно указаниям п. 6.11, по формуле (50) определяем также изгибающий момент Mt1 от неравномерного нагрева по высоте сечения опорного кольца в радиальном направлении:
при ts = 125 °C γst = 1, βs = 0,99,
αst = 12,25 · 10-6 °С-1, γtt = 0,76 и vs = 1;
при tb = 305 °С по табл. 20 αbt = 7 · 10-6 °С-1;
при tb = ts = 125 °С, βb = 0,98 и αbt = 8,25 · 10-6 °С-1.
При средней температуре бетона сжатой зоны, принимаемой, согласно примеч. 7 к табл. 16, на расстоянии 0,2h0 = 0,2 · 34 = 6,8 см от внутренней поверхности опорного кольца и равной tbc = 264 °С γbt = 1,04, βb = 0,8 и v = 0,38.
Определяем высоту сжатой зоны x при внецентренном растяжении опорного кольца из формулы (174):
![]() см.
см.
Определяем значение правой части выражения (173)
M = Ne = 1,04 · 11,5 · 31 · 6,6(34 - 0,5 · 6,6) = 75123 МПа · см3 = 7512300 Н · см.
При расчете для первого приближения принимаем
Mt1 = 0,7М = 0,7 · 7512300 = 5258600 Н · см = 52586 МПа · см3.
По формуле (324) при l1 = 0,5h - as = 0,5 · 39 = 14,5 см
![]() см.
см.
По формуле (189) при ts = tb = 125 °С
![]() .
.
По формуле (259)
Wpl = (0,292 + 0,75 · 2 · 0,0083 · 10,3)31 · 392 = 19800 см3.
По формуле (254) А = 31 · 39 = 1209 см2,
![]() см.
см.
По формуле (251)
Mr = 117200(59,4 + 14) = 8600000 Н · см = 86000 МПа · см3.
По формуле (290)
![]() .
.
![]() см.
см.
По формуле (289) определяем коэффициент ψs:
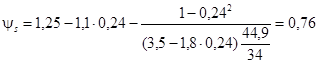 .
.
По формуле (189) при tbc = 264 °C и βb = 0,8
![]() .
.
По формуле (284) при γbt = 1,04
![]() .
.
По формуле (283)
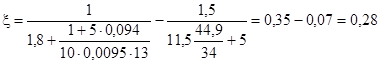 .
.
По формуле (288)
z = 34(1 - 0,5 · 0,28) = 29 см.
По формуле (300) определяем жесткость опорного кольца по сечению с трещиной при vs = 1:
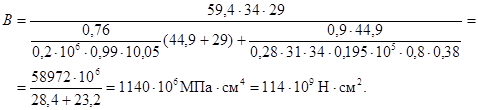
При ![]() и μ = 0,95 % по табл. 36 φα
= 0,99.
и μ = 0,95 % по табл. 36 φα
= 0,99.
По формуле (74)
αstm = 8,25 · 10-6 + (12,25 · 10-6 - 8,25 · 10-6)0,99 = 12,2 · 10-6 °С-1.
По формуле (36) при γt = 1,1
![]() .
.
По формуле (50)
Мt1 = 19,7 · 10-6 · 114 · 109 = 2240000 Н · см.
Полученное значение Mt1 = 2240000 Н · см значительно отличается от ранее принимавшегося для расчета 5258600 Н · см, поэтому производим дальнейшее уточнение Мt1.
Опуская промежуточные расчеты, для третьего приближения принимаем
Mt1 = 2700000 Н · см = 27000 МПа · см3;
![]() см;
см;
![]() см.
см.
Mr = 117200(37,5 + 14) = 6100000 Н · см = 61000 МПа · см3.
![]() .
.
При ![]() принимаем
принимаем ![]() согласно п. 4.21;
согласно п. 4.21;
![]() ;
;
![]() ;
;
 ;
;
z = 34(1 - 0,5 · 0,23) = 30 см.
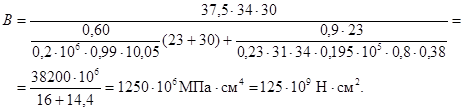
При ![]() и μ = 0,95 % по табл. 36 φα
= 0,88;
и μ = 0,95 % по табл. 36 φα
= 0,88;
αstm = 8,25 · 10-6 + (12,25 · 10-6 - 8,25 · 10-6)0,88 = 11,5 · 10-6 °С-1.
![]() .
.
Мt1 = 22,6 · 10-6 · 125 · 109 = 28000000 Н · см.
Разница между полученным моментом и моментом, принимавшимся ранее для третьего приближения, составляет
![]() %,
%,
т.е. меньше ±5 %, поэтому дальнейшее уточнение Mt1 не требуется.
Прочность сечения опорного кольца при внецентренном растяжении должна удовлетворять условию (173) при x = 6,6 см и γbt = 1,04.
Ne = Mt1 = 2800000 Н · см < 1,04 · 11,5 · 31 · 6,6(34 - 0,5 · 6,6) = 75120 МПа · см3 = 7512000 Н · см.
Следовательно, условие прочности опорного кольца при внецентренном растяжении удовлетворяется с большим запасом.
Расчет ширины раскрытия трещин в куполе
Ширину раскрытия трещин в куполе acrc определяем в сечении II - II в центре пролета только от действия Mt; усилиями от собственного веса купола пренебрегаем вследствие их малой величины.
Расчетные данные, согласно указаниям п. 4.10: δ = 1 как для изгибаемых элементов; η = 1; φe = 1; d = 14 мм; μ = 0,004; βs = 0,96; αstm = 11,2 · 10-6 °C-1, αbt = 7,6 · 10-6 °С-1 и z = 17 см.
Напряжение растяжения в арматуре определяем по формуле (272) при расчетном моменте Mt = 20200 Н · см:
![]() Н/см2 = 148 МПа.
Н/см2 = 148 МПа.
По формуле (267)
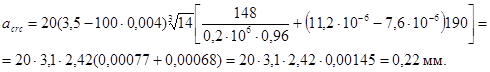
Расчет ширины раскрытия трещин в опорном кольце
Расчетные данные согласно п. 4.10: δ = 1,2 как для внецентренно растянутых элементов; η = 1; φl = 1; d = 16 мм; μ = 0,0095; βs = 0,99; αstm = 11,5 · 10-6 °С-1; αbt = 8,25 · 10-6 °С-1; es = 23 см и z = 30 см.
Напряжение в арматуре по формуле (273)
![]() Н/см2 = 206 МПа.
Н/см2 = 206 МПа.
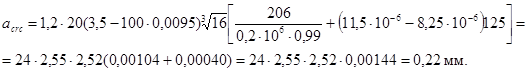
Ширина раскрытия трещин в куполе и кольце не превышает допускаемого значения, согласно табл. 3, при кратковременном нагреве элементов конструкций третьей категории трещиностойкости, эксплуатирующихся в закрытом помещении при температуре нагрева арматуры выше 100 °С.
Пример 34. Расчет прочности и прогиба цилиндрического свода из жаростойкого бетона с податливыми опорами при одностороннем нагреве до 1080 °С.
Дано: свод пролетом 6 м перекрывает рабочее пространство теплового агрегата с температурой 1100 °С. Скорость нагрева свода 10 °С/ч. Температура окружающего воздуха в зимний период равна 15 °С, а в летний 30 °С. Геометрические параметры свода в соответствии с черт. 51:
l1 = 6000 мм, f1 = 800 мм, rb = 6000 мм, α = 30°; l = 6175 мм, f = 830 мм, r = 6175 мм, h = 350 мм.
В расчете рассматривается участок свода шириной b = 1000 мм. На свод сверху действует постоянная равномерно распределенная по поверхности свода расчетная внешняя нагрузка 6 кН/м2. Для изготовления свода принят жаростойкий бетон состава № 18 по табл. 11, класса В15 на жидком стекле тонкомолотым магнезитом и заполнителем из шамота. Плотность бетона с естественной влажностью (по табл. 11) ρw = 2100 кг/м3, а в сухом состоянии с учетом удаленной влаги весом 150 кг/м3, согласно указаниям п. 2.15, ρd = 1950 кг/м3.
Податливость каждой опоры в горизонтальном направлении при нагреве свода от распора в 1 Н равна δ = 0,1 · 10-4 см.
Требуется произвести теплотехнический расчет свода и определить:
1) прочность свода в момент пуска теплового агрегата в зимний период при скорости подъема температуры по 10 °С/ч;
2) прочность свода при длительном воздействии температуры, собственного веса и внешней нагрузки в летний период;
3) перемещение свода в центре пролета при его длительной эксплуатации.
Теплотехнический расчет свода
ПРИ ТЕМПЕРАТУРЕ БОЛЕЕ НАГРЕТОЙ ПОВЕРХНОСТИ СВОДА 400 °С В ЗИМНИЙ ПЕРИОД
При температуре 400 °С в статически неопределимых конструкциях из жаростойкого бетона на жидом стекле, согласно указаниям п. 1.23, возникают наибольшие усилия от кратковременного воздействия температуры при первом нагреве теплового агрегата.
Задаемся температурой менее нагретой поверхности свода tbe = 80 °С.
Средняя температура бетона
![]() °С.
°С.
При tbm = 240 °С коэффициент теплопроводности бетона по табл. 9 λ = 0,94 Вт/(м · °С).
При tbe = 80 °С по табл. 8 αe = 13 Вт/(м2 · °С);
![]() ;
;
![]() ;
;
![]() м2 · °С/Вт.
м2 · °С/Вт.
По формуле (61)
![]() Вт/м2;
Вт/м2;
tbe = tb - QR = 400 - 856 · 0,37 = 400 - 317 = 83 °C;
![]() °С.
°С.
ПРИ РАБОЧЕЙ ТЕМПЕРАТУРЕ СРЕДЫ В ПОДСВОДОВОМ ПРОСТРАНСТВЕ ti = 1100 °С В ЛЕТНИЙ ПЕРИОД
Задаемся температурой верхней менее нагретой поверхности свода tbe = 180 °С и температурой более нагретой поверхности свода tb = 1080 °С.
![]() °С;
°С;
при tbm = 630 °С λ = 1,03 Вт/(м · °С);
» ti = 1100 °С αi = 140 Вт/(м2 · °С) - по табл. 8;
» tbe = 180 °С αe = 18,5 Вт/(м2 · °С);
![]() ;
;
![]() ;
;
![]() .
.
R0 = 0,007 + 0,32 + 0,054 = 0,381 м2 · °С/Вт.
![]() Вт/м2.
Вт/м2.
По формуле (55)
tb = 1100 - 2810 · 0,007 = 1080 °C;
tbe = 1100 - 2810(0,007 + 0,32) = 180 °C.
Расчет прочности свода при кратковременном нагреве до 400 °С
Определяем распор, продольные силы и изгибающие моменты от воздействия температуры.
По табл. 20
при tb = 400 °С αbt = 6,5 · 10-6 °С-1;
» tbe = 107 °С αbt = 5 · 10-6 °С-1.
По формуле (23) при y = 0,5 и γt = 1,1
![]() .
.
По формуле (24) при γt = 1,1
![]() .
.
При средней температуре бетона в сечении tbm = 241 °С по табл. 16 βb = 1,1, а по табл. 18 ![]() = 0,59.
= 0,59.
По формуле (334) вычисляем угол θ при φ = 20 согласно формуле (355):
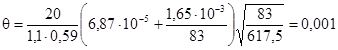 .
.
По формуле (333) Δ = fθ = 83 · 0,001 = 0,08 см.
По табл. 59 при 2α = 60° φ1 = 0,00175 и φ2 = 543.
Момент инерции расчетного сечения шириной b = 100 см и высотой h = 35 см:
![]() см4.
см4.
Согласно указаниям п. 1.28 для бетона состава № 18 φb1 = 0,7.
Момент инерции приведенного сечения по формуле (1)
![]() см4.
см4.
Жесткость приведенного сечения по формуле (298) при Eb = 18000 МПа, φb1 = 0,7 и φb2 = 1
B = 0,7 · 18000 · 331000 = 4,16 · 109 МПа · см4 = 41,6 · 1010 Н · см2.
Коэффициент η по формуле (331)
![]() .
.
Распор от воздействия температуры по формуле (354):
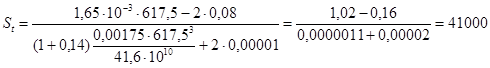 Н.
Н.
Продольная сила:
в замке свода (в сечении I - I, см. черт. 51)
N1t = St = 41000 Н = 41 кН;
в опорном сечении II - II по формуле (327)
N2t = 41000 · 0,866 = 355000 Н = 35,5 кН.
Изгибающий момент по формуле (337)
![]() Н ·
см.
Н ·
см.
Длина жесткой консоли lc в основной системе по формуле (336):
![]() см.
см.
Изгибающий момент в сечении I - I по формуле (353)
M1t = -41000 · 30 = -1230000 Н · см = -12,3 кН · м.
Изгибающий момент в опорном сечении II - II (см. черт. 51) по формуле (329)
M2t = 41000(83 - 30) - 27,2 · 106 = 2,17 · 106 - 27,2 · 106 = -25,03 · 106 Н · см.
Изгибающий момент M2t должен удовлетворять условию (330).
В данном случае при
|M2t| = 25,03 · 106 Н · см > 0,5 · 41000 · 35 · 0,866 = 0,62 · 106 Н · см
это условие не удовлетворяется. Следовательно, согласно п. 6.14, расчетное значение M2t в этом случае следует принимать равным правой части неравенства (330) только со знаком «минус», т.е.
M2t = -0,62 · 106 Н · см = -6,2 кН · м.
РАСПОР, ПРОДОЛЬНЫЕ СИЛЫ И ИЗГИБАЮЩИЕ МОМЕНТЫ ОТ СОБСТВЕННОГО ВЕСА СВОДА И ВНЕШНЕЙ НАГРУЗКИ
Расчетная нагрузка от собственного веса свода на 1 м с коэффициентом надежности по нагрузке γf = 1,1 и b = 1 м
g′ = γfρdhb = 1,1 · 19,5 · 0,35 = 7,51 кН/м
или, приводя нагрузку к горизонтальной проекции свода, получаем
![]() кН/м.
кН/м.
Расчетная равномерно распределенная внешняя нагрузка g2 = 6 кН/м.
Полная расчетная нагрузка
g = g1 + g2 = 7,87 + 6 = 13,87 кН/м = 138,7 Н/см.
Распор в своде от нагрузки определяем по формуле (338). По табл. 59 при 2α = 60° φ3 = 0,97.
Радиус кривизны принимаем по средней оси действительного сечения свода:
![]() Н = 72,7 кН.
Н = 72,7 кН.
Продольная сила:
в сечении I - I
N1f = Hf = 72,7 кН,
в опорном сечении II - II по формуле (340)
N2f = 72,7 · 0,866 + 0,5 · 13,87 · 6,175 · 0,5 = 84,4 кН.
Изгибающий момент по формуле (342) при φ4 = 0,0906:
![]() кН · м.
кН · м.
Изгибающий момент в сечении I - I по формуле (339)
M1f = 22,88 · 72,7 · 0,3 = 1,07 кН · м.
Изгибающий момент в опорном сечении II - II по формуле (341)
M2f = 22,88 + 72,7(0,83 - 0,3) - 0,5 · 13,87 · 6,1752 · 0,25 = 22,88 + 38,5 - 66,11 = -4,73 кН · м.
Расчетные продольные силы и изгибающие моменты от совместного действия температуры, собственного веса и нагрузки:
в сечении I - I (в замке)
N = N1t + N1f = 41 + 72,7 = 113,7 кН;
M = M1t + M1f = -12,3 + 1,07 = -11,23 кН · м.
в опорном сечении II - II
N = 35,5 + 84,4 = 119,9 кН;
M = -6,2 - 4,73 = -10,93 кН · м.
Расчет прочности сечения I - I в замке (см. черт. 51).
Прочность сечения проверяем на внецентренное сжатие силой N = 113,7 кН по формуле (75).
Эксцентриситет продольной силы относительно центра тяжести сечения
![]() см.
см.
Знак «минус» означает, что продольная сила приложена ниже центра тяжести сечения со стороны более нагретой грани. При кратковременном действии нагрузки по формуле (95) коэффициент φl = 1.
Расчетную длину свода определяем как для бесшарнирной арки по табл. 33 главы СНиП 2.03.01-84.
![]() см.
см.
![]() .
.
При температуре бетона в центре тяжести сечения 241 °С по табл. 16 γbt = 1. Для бетона класса В15 по табл. 14 Rb = 8,5 МПа.
По формуле (96)
![]() .
.
Так как α = 0,29 < δ = 0,35, то согласно указаниям п. 3.7 принимаем δ = δmin = 0,35, φl = 1.
По формуле (94)
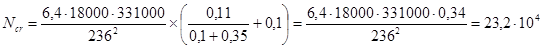 МПа · см = 23,2
· 106 Н.
МПа · см = 23,2
· 106 Н.
По формуле (93)
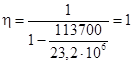 .
.
По формуле (76)
![]() см2.
см2.
Проверяем условие прочности сечения I - I свода в замке по формуле (75) с учетом γb9 = 0,9 согласно табл. 15
N = 113,7 кН < 0,9 · 8,45 · 1500 = 11400 МПа · см2 = 1140 кН.
Таким образом, условие прочности сечения свода в замке удовлетворяется с большим запасом.
Продольная сила в опорном сечении II - II от совместного действия собственного веса свода, нагрузки и температуры по своей величине незначительно превышает продольную силу в замке и приложена с меньшим эксцентриситетом e0 = 9 см также со стороны более нагретой грани сечения. Учитывая большой запас прочности, полученный для сечения I - I в замке, прочность опорного сечения II - II при кратковременном действии нагрузки и температуры с учетом собственного веса свода можно не проверять.
Расчет прочности свода при длительном нагреве
Определяем распор в своде от действия температуры.
При tb = 1080 °С αbt = 4,6 · 106 °С-1, при tbe = 180 °С αbt = 2,8 · 10-6 °С-1.
![]() ;
;
![]() .
.
При средней температуре бетона в сечении tbm = 630 °С βb = 0,80 и ![]() = 0,32 вычисляем угол θ по формуле (334):
= 0,32 вычисляем угол θ по формуле (334):
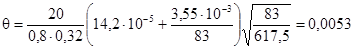 .
.
Δ = fθ = 83 · 0,0053 = 0,44 см.
При определении жесткости свода без трещин его неравномерно нагретое сечение приводим к ненагретому бетону. Для этого сечение свода разбиваем на две площади с зоной раздела по температуре бетона 400 °С.
Первая площадь имеет высоту h1 = 26,5 см и среднюю температуру бетона ![]() °С. Вторая площадь
имеет высоту h2 =
8,5 см и среднюю температуру
бетона
°С. Вторая площадь
имеет высоту h2 =
8,5 см и среднюю температуру
бетона ![]() °С;
°С;
при tbm = 740 °С βb = 0,63 и ![]() = 0,26;
= 0,26;
» tbm = 290 °С βb = 1,1 и ![]() = 0,56;
= 0,56;
А1 = bh1 = 100 · 26,5 = 2650 см2;
А2 = bh2 = 100 · 8,5 = 850 см2.
Площади бетона, приведенные к ненагретому бетону:
![]() см2;
см2;
![]() см2;
см2;
Ared = Ared1 + Ared2 = 620 + 680 = 1300 см2.
При расстояниях центров тяжести площадей до менее нагретой грани сечения y1 = 21,75 см и y2 = 4,25 см определяем статический момент приведенного сечения:
Sred = 620 · 21,75 + 680 · 4,25 = 16390 см3.
Расстояние от центра тяжести приведенного сечения до менее нагретой грани по формуле (5):
![]() см;
см;
yb1 = y1 - y = 21,75 - 12,6 = 9,15 см;
yb2 = y - 0,5h2 = 12,6 - 0,5 · 8,5 = 8,35 см;
![]() см4;
см4;
![]() см4;
см4;
Ired = 36300 + 4100 + 620 · 9,152 + 680 · 8,352 = 139800 см4.
При средней температуре бетона в сечении tbm = 630 °С по экстраполяции данных табл. 50 коэффициент φb2 можно принять равным 21,5. Жесткость приведенного сечения по формуле (298)
![]() МПа · см4 = 8,4 · 109 Н · см2.
МПа · см4 = 8,4 · 109 Н · см2.
![]() .
.
Распор от воздействия температуры
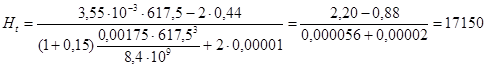 Н;
Н;
N1t = Ht = 17150 Н = 17,15 кН;
M1t = -17150 · 30 = -514500 Н · см = -5,145 кН · м.
Расчетные усилия в сечении I - I (в замке)
N = N1t + N1f = 17,5 + 73,52 = 90,67 кН = 90670 Н.
M = M1t + M1f = -5,145 + 0,82 = -4,325 кН · м = -432500 Н · см.
![]() см.
см.
При температуре бетона в центре тяжести приведенного сечения, равной 566 °С для жаростойкого бетона состава № 18 в табл. 39, нет данных для определения коэффициента β, входящего в формулу (95). В этом случае при расчете прочности свода, согласно примеч. 2 к табл. 39, необходимо отбросить часть сечения с температурой бетона выше 800 °С с таким расчетом, чтобы получить температуру бетона в центре тяжести оставшейся приведенной части сечения, не превышающую 500 °С. При этом расчетная высота сечения свода с температурой бетона от 180 до 800 °С h′ = 24 см.
При делении расчетного сечения высотой 24 см на две площади с зоной раздела по температуре бетона 400 °С получаем для первой площади h1 = 15,5 см и среднюю температуру бетона ![]() °С и для второй площади h2 = 8,5 см и
°С и для второй площади h2 = 8,5 см и ![]() °С.
°С.
При tbm1 = 600 °С, βb = 0,85 и
![]() =
0,325
=
0,325
А1 = bh1 = 100 · 15,5 = 1550 см2;
![]() см2.
см2.
Согласно ранее сделанному приведению сечения с полной высотой Ared2 = 680 см2 при h2 = 8,5 см и tbm2 = 290 °С
Ared = Ared1 + Ared2 = 610 + 680 = 1290 см2.
Для приведенного сечения с h′ = 24 см, y1 = 16,25 см и y2 = 4,25 см
Sred = 610 · 16,25 + 680 · 4,25 = 9913 + 2890 = 12803 см3.
Расстояние от центра тяжести приведенного сечения с h′ = 24 см до менее нагретой грани
![]() см.
см.
При температуре бетона в центре тяжести приведенного сечения свода высотой h′ = 24 см, tbw = 464 °С по табл. 39 для бетона состава № 18 коэффициент β = 28,5.
По формуле (95) Мl = М:
φl = 1 + 28,5 = 29,5;
![]() .
.
При температуре бетона в центре тяжести приведенного сечения 464 °С γbt = 0,29.
По формуле (96)
![]() .
.
По формуле (94)
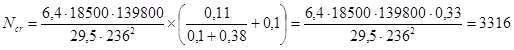 МПа · см2 = 331600 Н.
МПа · см2 = 331600 Н.
По формуле (93)
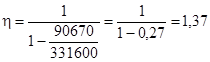 .
.
В данном случае расстояние от центра тяжести приведенного сечения до его наиболее напряженной грани, согласно черт. 9, а, при рабочей высоте сечения h′ = 24 см y = 24 - 10 = 14 см.
По формуле (77)
e′ = 14 - 4,8 · 1,37 = 7,4 см.
В данном случае 2e′ = 2 · 7,4 = 14,8 см < h1 = 15,5 см.
По формуле (80)
Ab = 2 · 100 · 7,4 = 1480 см2.
Температура бетона в центре тяжести сжатой зоны на расстоянии e′ = 7,4 см от более нагретой грани сечения высотой h′ = 24 см равна 609 °С. При tb = 609 °C по табл. 16 γbt = 0,15.
Проверяем условие прочности сечения I - I свода (в замке) высотой h′ = 24 см, согласно выражению (75), с учетом по табл. 15 γb2 = 0,9 и γb9 = 0,9:
N = 90,67 кН < 0,9 · 0,9 · 8,45 · 0,15 · 1480 = 1520 МПа · см2 = 152 кН.
Таким образом, условие прочности сечения свода в замке при длительном воздействии собственного веса, нагрузки и высокой температуры удовлетворяется.
Условие прочности опорного сечения II - II свода, как показали аналогичные расчеты, также удовлетворяется.
Расчет прогиба свода в центре пролета при длительном действии собственного веса, нагрузки и температуры
Выгиб свода в центре пролета от воздействия температуры по формуле (344)
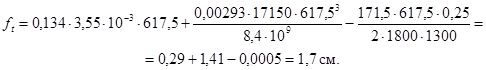 .
.
Прогиб свода от равномерно распределенной нагрузки q = 13,87 кН/м, с учетом собственного веса по формуле (345)
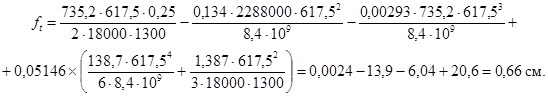 .
.
Суммарный прогиб свода от длительного воздействия собственного веса, нагрузки и температуры
f = ft - ff = 1,7 - 0,66 = 1,04 см,
т.е. свод будет иметь выгиб вверх, равный 1,04 см.
ПРИЛОЖЕНИЕ 1
Рекомендуемое
УКАЗАНИЯ ПО ПРИМЕНЕНИЮ ЖАРОСТОЙКОГО БЕТОНА В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
|
Тепловой агрегат |
Элементы из жаростойкого бетона |
Температура рабочего пространства печи, °С |
Рекомендуемый состав бетона по табл. 11, № |
|
I. В черной металлургии |
|||
|
Доменная печь |
Фурменные приборы |
1300 |
16, 19 |
|
Шахта, пень, лещади, борова |
1200 |
11 |
|
|
Газоотводы и наклонный газопровод, пылеуловитель |
800 |
23, 24 |
|
|
Вагранки для плавки чугуна |
Стены колосника и плавильного пояса |
1300 |
19 |
|
Воздухонагреватели |
Стены (нижняя часть), днище |
1200 |
11 |
|
Борова |
800 |
23, 24 |
|
|
Обжиговые машины агломерационного производства |
Нижний и верхний коллекторы и газоотводы |
800 |
23, 24 |
|
Нагревательные колодцы |
Стены рабочих ячеек, под, крышка |
1300 |
19, 21 |
|
Методические нагревательные печи |
Изоляция глиссажных труб и стены на высоту 1 м |
1200 |
19 |
|
Ямные печи для замедленного охлаждения |
Стены |
800 |
23, 24 |
|
Коксовые батареи |
Фундаменты и борова |
600 |
23, 24 |
|
II. В цветной металлургии |
|||
|
Графитировочные печи |
Стены |
1200 |
11 |
|
Печи кипящего слоя |
Своды и решетка |
1100 |
11, 15 |
|
Алюминиевые и магниевые электролизеры |
Днища |
1000 |
10, 11 |
|
Электролизеры сверхчистого алюминия |
То же |
1000 |
10, 11 |
|
Термические нагревательные, отжигательные печи |
Стены, свод и под |
1200 |
11, 19 |
|
Пылевые камеры |
Стены и покрытие |
800 |
15 |
|
Печи для оплавления лома алюминия |
Стены и свод |
1000 |
15 |
|
Надземные газоходы или подземные в галереях |
Днище, стены и свод |
1100 |
11, 15 |
|
Фосфорные электропечи |
Свод |
1100 |
15 |
|
Ферросплавные печи |
Днище и стены |
1000 |
10, 11 |
|
Камерные печи |
Свод, стены, под |
1200 |
19 |
|
Электролитические ванны цветной металлургии |
Стены |
1000 |
10, 11 |
|
III. В нефтеперерабатывающей и нефтехимической промышленности |
|||
|
Трубчатые печи |
Стены и своды камеры радиации |
1000 |
31 |
|
Стены и своды камеры конвекции |
1000 |
23, 24, 25, 26 |
|
|
Вертикально-секционные печи |
Стены камеры радиации |
900 |
31 |
|
Трубчатые печи беспламенного горения типа Б |
Фундаменты, стены, свод, под, перевальные стенки |
800 |
10, 11 |
|
Трубчатые печи беспламенного горения типа 3Р |
Стены, свод, под |
850 - 1100 |
23 - 30 |
|
Трубчатые печи настильные типа 3Д |
Стены, свод, под |
900 - 1100 |
23 - 30 |
|
Трубчатые печи секционные типа В |
То же |
800 |
22 |
|
Вертикально-факельные типа ГС |
Стены камер конвекции и радиации, свод, подовая часть |
900 |
23 - 26 |
|
Объемно-настильные печи с разделительной стенкой типа ГН |
То же |
900 - 1100 |
23 - 26 |
|
Цилиндрические, факельные типа ЦС |
Стены камер конвекции и радиации, свод, подовая часть |
800 - 1100 |
23 - 30 |
|
Цилиндрические печи типа ЦД настильные с дифференцированным подводом воздуха |
То же |
800 - 1100 |
23 - 30 |
|
Каталитического риформинга и гидроочистки типа Р многокамерные |
Стены, свод, подовая часть |
1250 |
23 - 26 |
|
Надземные газоходы трубчатых печей |
Все элементы |
600 |
23 - 26 |
|
Подземные газоходы трубчатых печей |
То же |
800 |
10, 11 |
|
IV. В промышленности строительных материалов |
|||
|
Туннельные печи для обжига обыкновенного глиняного кирпича |
Стены и своды зон подогрева и охлаждения, подины вагонеток |
1000 |
10, 11 |
|
Стены и своды зоны обжига |
1300 |
19, 21 |
|
|
Вращающаяся печь для обжига цемента |
Зона цепной завесы и откатная головка |
1000 |
10, 11 |
|
Туннельные печи для обжига эмальизделий |
Стены и свод |
1200 |
19 |
|
Кольцевые печи для обжига кирпича |
Покрытие, стены, днище |
1100 |
10, 11 |
|
V. В разных отраслях промышленности |
|||
|
Борова и газоходы для температур до 350 °С |
Стены, свод |
350 |
2 - 4 |
|
Борова и газоходы для температур выше 350, но не более 800 °С |
То же |
800 |
6 - 9 |
|
Паровые котлы, экономайзеры, котлы-утилизаторы |
Футеровка стен |
800 |
10, 11 |
|
Фундаменты тепловых агрегатов |
Элементы, нагревающиеся до температур выше 200, но не более 800 °С |
800 |
6 - 9 |
|
Полы горячих цехов |
- |
7 - 8 |
|
|
Колпаковые печи для обжига металла |
- |
800 |
10, 11 |
|
Обжиговые печи электродной промышленности |
- |
1400 |
20, 21 |
|
Сушильные печи |
Покрытие, стены, под |
1000 |
10, 11 |
|
Котлы различного назначения |
Футеровка экранированных стен |
800 |
23 - 30 |
|
Нагревательные прокатные, кузнечные и конвейерные печи |
Стены, под, глиссажные и опорные трубы |
1200 |
19, 21 |
|
Печи для обжига сернистых материалов |
Стены, свод, под |
1000 |
15 - 18 |
|
Печи для обжига сантехоборудования |
Свод |
1100 |
19 |
ПРИЛОЖЕНИЕ 2
Справочное
СОКРАЩЕННЫЙ СОРТАМЕНТ АРМАТУРНОЙ СТАЛИ ДЛЯ ПРОЕКТИРОВАНИЯ И ИЗГОТОВЛЕНИЯ СБОРНЫХ, СБОРНО-МОНОЛИТНЫХ И МОНОЛИТНЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
|
Вид арматуры и документы, регламентирующие ее качество |
Класс арматуры |
Диаметр арматуры, мм |
|||||||||||||||||||||
|
3 |
4 |
4,5 |
5 |
6 |
7 |
7,5 |
8 |
9 |
10 |
12 |
14 |
15 |
16 |
18 |
20 |
22 |
25 |
28 |
32 |
36 |
40 |
||
|
Стержневая горячекатаная гладкая, ГОСТ 5781-82 |
А-I |
+ |
- |
+ |
+ |
+ |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
- |
- |
|||||||
|
Стержневая горячекатаная периодического профиля, ГОСТ 5781-82 |
А-II |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
||||||||||
|
A-III, Ат-III |
+ |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||||||||
|
А-IIIв |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
||||||||
|
Стержневая термически упрочненная периодического профиля, ГОСТ 10884-81 |
A-IV, Aт-IVC |
+ |
+ |
+ |
+ |
+ |
0 |
0 |
0 |
0 |
0 |
||||||||||||
|
Ат-IV |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
||||||||||||
|
A-V, Ат-V |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
0 |
0 |
0 |
|||||||||||||
|
A-VI, Ат-VI |
+ |
+ |
+ |
+ |
+ |
0 |
0 |
0 |
0 |
0 |
|||||||||||||
|
Обыкновенная арматурная проволока гладкая, ГОСТ 6727-80 |
B-I |
- |
- |
- |
|||||||||||||||||||
|
То же, периодического профиля, ГОСТ 6727-80 |
Вр-I |
+ |
+ |
+ |
|||||||||||||||||||
|
Высокопрочная арматурная проволока гладкая, ГОСТ 7348-81 |
B-II |
+ |
+ |
+ |
0 |
0 |
|||||||||||||||||
|
То же, периодического профиля, ГОСТ 7348-81 |
Вр-II |
+ |
0 |
0 |
0 |
||||||||||||||||||
|
Арматурные канаты, ГОСТ 13840-68 |
К-7 |
+ |
+ |
+ |
+ |
||||||||||||||||||
|
Арматурные канаты, ТУ 14-4-22-71 |
К-19 |
0 |
|||||||||||||||||||||
Примечания: 1. Диаметры арматуры приняты согласно сортаменту по соответствующим ГОСТ или ТУ с учетом указаний по области применения различных классов арматурных сталей СНиП 2.03.01-84.
2. Знаком «+» обозначены рекомендуемые к использованию диаметры и классы арматурной стали; знаком «-» - исключенные из сортамента диаметры и классы арматурной стали; знаком «0» - обозначен сортамент эффективной стали.
3. Сталь класса А-IIIв диаметрами более 20 мм, упрочненная вытяжкой на предприятиях стройиндустрии, допускается к применению в качестве напрягаемой арматуры при отсутствии арматурной стали более высоких классов.
4. При изготовлении конструкций допускается замена проволоки класса Вр-I на имеющуюся в наличии проволоку класса В-I.
ПРИЛОЖЕНИЕ 3
Обязательное
ОСНОВНЫЕ ТИПЫ СВАРНЫХ СОЕДИНЕНИЙ АРМАТУРЫ
|
Тип соединений, способ сварки и схема конструкции |
Положение стержней при сварке |
Диаметр стержней, мм |
Класс и марка арматурной стали |
Дополнительные указания |
|
|
I. Крестообразное |
|||||
|
Сварка |
|||||
|
1. Контактная точечная двух стержней |
|
Горизонтальное (возможно вертикальное в кондукторах) |
6 - 40 10 - 50 6 - 40 10 - 22 10 - 28 3 - 5 3 - 5 |
А-I A-II A-III Aт-IIIC Aт-IVC В-I Вр-I |
Отношение меньшего диаметра стержня к большему составляет 0,25-1,00 |
|
2. Контактная точечная трех стержней |
|
Горизонтальное (возможно вертикальное в кондукторах) |
6 - 40 10 - 50 6 - 40 10 - 22 10 - 28 |
А-I А-II A-III Aт-IIIC Aт-IVC |
Отношение диаметра среднего стержня к одному из одинаковых крайних стержней большого диаметра должно быть не менее 0,5 |
|
3. Ручная дуговая точечными прихватками |
|
Горизонтальное и вертикальное |
10 - 40 10 - 28 10 - 18 10 - 32 10 - 28 10 - 22 10 - 18 |
А-I А-II (ВСт5сп2) А-II (ВСт5пс2) Ас-II А-III(25Г2С) Ат-IIIС Aт-IVC |
В условиях отрицательных температур допускается применять сварные соединения только из арматурной стали классов А-I и Ас-II |
|
4. Ручная дуговая с принудительным формированием шва |
|
Вертикальное |
14 - 40 |
А-I; А-II; A-III |
Положение сварных швов вертикальное. Сварка выполняется в инвентарных фермах |
|
II. Стыковое |
|||||
|
Сварка |
|||||
|
5. Контактная стыковая |
|
Горизонтальное |
10 - 40 10 - 80 10 - 40 10 - 22 10 - 22 10 - 28 10 - 22 10 - 14 |
А-I А-II A-III Aт-IIIC A-IV Aт-IVC A-V A-VI |
Отношение меньшего диаметра стержня к большему составляет 0,85 - 1,00. Допускается отношение диаметров стержней не менее 0,30 при применении специального устройства, обеспечивающего предварительный нагрев стержня большего диаметра |
|
6. То же, с последующей механической обработкой |
|
» |
10 - 80 10 - 40 10 - 22 10 - 22 10 - 28 10 - 22 |
А-II А-III Ат-IIIС A-IV Ат-IVC A-V |
- |
|
7. Ванная полуавтоматическая под флюсом 8. Ванная одноэлектродная 9. Полуавтоматическая порошковой проволокой |
|
» |
20 - 40 |
А-I А-II А-III |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,00. Сварка выполняется в инвентарных формах |
|
10. Ванная полуавтоматическая под флюсом 11. Ванная одноэлектродная 12. Полуавтоматическая порошковой проволокой |
|
Вертикальное |
20 - 40 |
А-I А-II A-III |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0. Сварка выполняется в инвентарных формах. Стержень меньшего диаметра сверху |
|
13. Ванная полуавтоматическая под флюсом 14. Полуавтоматическая порошковой проволокой 15. Ванная одноэлектродная |
|
Горизонтальное |
32 - 40 |
A-III |
Сварка выполняется в инвентарных формах |
|
16. Полуавтоматическая порошковой проволокой 17. Ванная одноэлектродная |
|
» |
32 - 40 |
A-III |
Сварка выполняется в инвентарных формах |
|
18. Ванная полуавтоматическая порошковой проволокой на стальной скобе-подкладке 19. Ванная одноэлектродная на стальной скобе-подкладке |
|
» |
20 - 32 |
A-I А-II A-III |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0 |
|
20. Полуавтоматическая открытой дугой голой легированной проволокой (СОДГП) на стальной скобе-накладке 21. Ванно-шовная на стальной скобе-накладке |
|
» |
20 - 40 20 - 80 20 - 40 20 - 22 20 - 28 36 - 40 36 - 80 36 - 40 20 - 22 20 - 28 |
A-I А-II A-III Ат-IIIС Ат-IVC A-I А-II А-III Ат-IIIС Ат-IVC |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0. Термически и термомеханически упрочненная арматура должна свариваться на удлиненной до 4d стальной скобе-накладке |
|
22. Полуавтоматическая порошковой проволокой многослойными швами на стальной скобе-подкладке 23. Ручная дуговая многослойными швами на стальной, скобе-подкладке |
|
Вертикальное |
20 - 40 20 - 80 20 - 40 20 - 22 20 - 28 |
A-I А-II А-III Ат-IIIС Ат-IVC |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0. Ручную дуговую сварку соединений стержней диаметрами 36 - 80 мм следует выполнять на стальной скобе-накладке, а термически и термомеханически упрочненная арматура должна свариваться на удлиненной до 4d стальной скобе-накладке |
|
24. Полуавтоматическая СОДГП на стальной скобе-накладке |
|
» |
20 - 40 20 - 80 20 - 40 20 - 22 20 - 28 |
А-I А-II А-III Ат-IIIС Ат-IVC |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0. Термически и термомеханически упрочненная сталь должна свариваться на удлиненной до 4d стальной скобе-накладке |
|
25. Ручная дуговая многослойными швами без дополнительных технологических элементов |
|
Вертикальное |
20 - 40 20 - 80 20 - 40 |
A-I А-II A-III |
Отношение меньшего диаметра стержня к большему составляет 0,5 - 1,0 |
|
26. Ручная дуговая протяженными швами с круглыми накладками |
|
Горизонтальное и вертикальное |
10 - 40 10 - 80 10 - 40 10 - 22 10 - 22 10 - 28 10 - 22 |
А-I А-II А-III Ат-IIIС А-IV Aт-IVC A-V |
Соединения арматуры классов A-IV и A-V следует выполнять со смешенными накладками. Допускается применять соединения с двухсторонними швами для арматуры классов A-I, A-II, A-III |
|
III. Нахлесточное |
|||||
|
Сварка |
|||||
|
27. Ручная дуговая протяженными швами |
|
То же |
10 - 40 10 - 25 10 - 25 10 - 22 |
A-I А-II A-III Ат-IIIС |
Допускается применять двухсторонние швы для соединений стержней классов A-I и Ас-II марки 10ГТ |
ПРИЛОЖЕНИЕ 4
Обязательное
ОСНОВНЫЕ ТИПЫ СВАРНЫХ СОЕДИНЕНИЙ СТЕРЖНЕВОЙ АРМАТУРЫ С ПЛОСКИМИ ЭЛЕМЕНТАМИ СОРТОВОГО ПРОКАТА
|
Тип соединения, способ сварки и схема конструкции |
Положение стержня при сварке |
Минимальное отношение толщины плоского элемента сортового проката к диаметру стержня |
Диаметр стержня, мм |
Класс арматуры |
Дополнительные указания |
|
|
I. Тавровое |
||||||
|
Сварка |
||||||
|
1. Автоматическая под флюсом без присадочного электродного материала |
|
Вертикальное |
0,50 0,55 0,65 0,65 0,75 0,65 |
8 - 40 10 - 25 28 - 40 8 - 25 28 - 40 10 - 18 |
А-I А-II А-III Ат-IIIС |
- |
|
2. Ручная под флюсом без присадочного электродного материала |
» |
0,75 |
8 - 16 10 - 16 8 - 16 |
А-I А-II A-III |
- |
|
|
3. Полуавтоматическая в среде CO2 |
|
» |
0,50 0,50 0,55 0,55 |
12 - 25 12 - 25 12 - 25 12 - 18 |
А-I А-II А-III Ат-IIIС |
Сварку полуавтоматическую в среде CO2 и ручную валиковыми швами применять в основном для изготовления закладных деталей типа «закрытый столик» |
|
4. Ручная валиковыми швами |
» |
0,50 0,65 0,75 0,75 |
8 - 40 10 - 40 8 - 40 10 - 18 |
А-I А-II А-III Ат-IIIС |
||
|
5. Контактная рельефная |
|
Вертикальное |
0,40 0,50 |
10 - 20 10 - 20 |
А-I; А-II A-III |
При минимальном отношении толщины плоского элемента сортового проката к диаметру стержня, равному 0,40 и 0,50, толщина элемента должна быть не менее 4 мм |
|
6. Полуавтоматическая в среде CO2 в глубоко в выштампованном отверстии |
|
» |
0,30 0,40 0,40 |
10 - 36 10 - 36 10 - 18 |
А-I; А-II A-III Ат-IIIС |
То же, при отношении, равном 0,30 и 0,40 |
|
7. Автоматическая под флюсом без присадочного материала по элементу жесткости (рельефу) |
|
» |
0,40 0,40 0,50 0,50 |
8 - 25 10 - 25 8 - 25 10 - 18 |
А-I А-II А-III Ат-IIIС |
То же, при отношении, равном 0,40 и 0,50 |
|
8. Ванная одноэлектродная |
|
Горизонтальное |
0,50 |
16 - 40 |
А-I А-II А-III |
Сварка выполняется в инвентарных формах |
|
9. Ручная дуговая многослойными швами |
|
Горизонтальное (оба стержня расположены в одной горизонтальной плоскости) |
0,50 |
32 - 40 |
А-III |
То же |
|
10. Автоматическая под флюсом без присадочного материала под углом к плоскому элементу сортового проката |
|
Вертикальное (α = 25-85 °) |
0,50 0,55 0,65 0,65 |
8 - 16 10 - 16 8 - 16 10 - 16 |
А-I А-II А-III Ат-IIIС |
- |
|
Вертикальное (α = 60-85°) |
0,50 0,55 0,65 |
18 - 25 18 - 25 18 - 25 |
А-I А-II А-III |
|||
|
11. То же, под углом к торцу плоского элемента сортового проката |
|
Вертикальное (α = 5-25°) |
0,50 0,55 0,65 0,65 |
8 - 16 10 - 16 8 - 16 10 - 16 |
А-I А-II А-III Ат-IIIС |
- |
|
II. Нахлесточное |
||||||
|
Сварка |
||||||
|
12. Контактная по одному рельефу |
|
Горизонтальное |
0,30 |
6 - 14 10 - 14 6 - 14 10 - 14 |
А-I А-II А-III Ат-IIIС |
При отношении, равном 0,30, толщина плоского элемента сортового проката должна быть не менее 4 мм |
|
13. Контактная по двум рельефам |
|
Горизонтальное |
0,30 |
6 - 16 10 - 16 6 - 16 10 - 16 |
A-I A-II А-III Aт-IIIC |
То же. Сварные соединения, выполняемые по двум рельефам, при d < 14 мм следует применять, когда не исключено воздействие на сварное соединение случайных моментов |
|
14. Ручная дуговая фланговыми швами |
|
Горизонтальное и вертикальное |
0,30 |
10 - 40 10 - 22 10 - 28 10 - 22 |
А-I; А-II; А-III Aт-IIIC; A-IV Aт-IVC A-V |
При отношении, равном 0,30, толщина плоского элемента сортового проката должна быть не менее 4 мм |
ПРИЛОЖЕНИЕ 5
Справочное
СОРТАМЕНТ АРМАТУРНОЙ СТАЛИ
СОРТАМЕНТ СТЕРЖНЕВОЙ АРМАТУРЫ
|
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
|
6 |
0,283 |
0,222 |
18 |
2,54 |
2 |
|
7 |
0,385 |
0,302 |
20 |
3,14 |
2,47 |
|
8 |
0,503 |
0,395 |
22 |
3,8 |
2,98 |
|
9 |
0,636 |
0,499 |
25 |
4,91 |
3,85 |
|
10 |
0,785 |
0,617 |
28 |
6,15 |
4,83 |
|
12 |
1,131 |
0,888 |
- |
- |
- |
|
14 |
1,54 |
1,21 |
- |
- |
- |
|
16 |
2,01 |
1,58 |
- |
- |
- |
СОРТАМЕНТ АРМАТУРНОЙ ПРОВОЛОКИ
|
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
||
|
классов B-I, B-II и Вр-II |
класса Вр-I |
классов В-I, В-II и Вр-II |
класса Вр-I |
||||
|
3 |
0,071 |
0,055 |
0,051 |
6 |
0,283 |
0,222 |
- |
|
4 |
0,126 |
0,099 |
0,090 |
7 |
0,385 |
0,302 |
- |
|
5 |
0,196 |
0,154 |
0,139 |
8 |
0,503 |
0,395 |
- |
СОРТАМЕНТ АРМАТУРНЫХ КАНАТОВ К-7
|
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
Номинальный диаметр, мм |
Расчетная площадь поперечного сечения, см2 |
Теоретический вес 1 м, кг |
|
4,5 |
0,127 |
0,100 |
9 |
0,510 |
0,402 |
|
6 |
0,227 |
0,173 |
12 |
0,906 |
0,714 |
|
7,5 |
0,354 |
0,279 |
15 |
1,416 |
1,116 |
Примечание. Номинальный диаметр арматуры (номер сечения) соответствует: для горячекатаной и термически упрочненной арматурной стали периодического профиля - номинальному диаметру равновеликих по площади поперечного сечения гладких стержней; для обыкновенной и высокопрочной арматурной проволоки периодического профиля - номинальному диаметру проволоки до придания ей периодического профиля; для арматурных канатов - диаметру их описанных окружностей.
ПРИЛОЖЕНИЕ 6
Справочное
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ ВЕЛИЧИН
УСИЛИЯ ОТ ВОЗДЕЙСТВИЯ НАГРУЗКИ И ТЕМПЕРАТУРЫ В ПОПЕРЕЧНОМ СЕЧЕНИИ ЭЛЕМЕНТА
Mtot и Ntot - изгибающий момент и продольная сила от совместного действия усилий, вызванных температурой и нагрузкой;
M и Mt - изгибающий момент соответственно от воздействия внешней нагрузки и температуры;
N и Nt - продольная сила соответственно от воздействия нагрузки и температуры;
Q и Qt - поперечная сила соответственно от воздействия нагрузки и температуры.
ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ ПРИ ВОЗДЕЙСТВИИ ТЕМПЕРАТУРЫ
Rb,tem = Rbγbt; Rbtt = Rbtγtt - расчетное сопротивление бетона сжатию и растяжению для предельных состояний первой группы;
Rb,tem,ser и Rbtt,ser - расчетные сопротивления бетона сжатию и растяжению для предельных состояний второй группы;
Rst = Rsγst и Rst,ser - расчетные сопротивления арматуры растяжению для предельных состояний соответственно первой и второй групп;
Rb,los - расчетное сопротивление бетона смятию, определяемое по формуле (221);
Rswt - расчетное сопротивление поперечной арматуры растяжению для предельных состояний первой группы при расчете сечений, наклонных к продольной оси элемента, на действие поперечной силы;
Rsct - расчетное сопротивление арматуры сжатию для предельных состояний первой группы;
Eb - начальный модуль упругости бетона при сжатии и растяжении;
Еbt - модуль упругости бетона при воздействии температуры;
Es - модуль упругости арматуры при нормальной температуре;
Est - модуль упругости арматуры при воздействии температуры;
βb и βs - коэффициенты, учитывающие снижение модуля упругости бетона и арматуры при воздействии температуры;
σs и σb - напряжения в растянутой арматуре и в сжатой зоне бетона в сечении с трещиной;
σsm и σbm - средние напряжения в арматуре и в бетоне сжатой зоны на участках между трещинами;
σst, σbtt и σb,tem - напряжения в растянутой арматуре, в растянутом бетоне и сжатом бетоне в сечении с трещиной от воздействия температуры;
σs, σbt и σb - то же, от нагрузки;
σs,tot, σbt,tot и σb,tot - то же, от суммарного воздействия температуры и нагрузки;
αtt, αcs, αbt - коэффициент линейного температурного расширения, температурной усадки и температурной деформации бетона;
αst - коэффициент линейного температурного расширения арматуры;
αstm - коэффициент температурного расширения растянутой арматуры в бетоне с учетом влияния работы бетона между трещинами, определяемый по формуле (74).
ХАРАКТЕРИСТИКИ ПОЛОЖЕНИЯ ПРОДОЛЬНОЙ АРМАТУРЫ В ПОПЕРЕЧНОМ СЕЧЕНИИ ЭЛЕМЕНТА
S - обозначение продольной арматуры:
а) при наличии сжатой и растянутой, от действия внешней нагрузки зон сечения - расположенной в растянутой зоне;
б) при полностью сжатом от действия внешней нагрузки сечении - расположенной у менее сжатой грани сечения;
в) при полностью растянутом от действия внешней нагрузки сечении для внецентренно растянутых элементов - расположенной у более растянутой грани сечения, для центрально растянутых элементов - всей в поперечном сечении элемента;
S′ - обозначение продольной арматуры:
а) при наличии сжатой и растянутой от действия внешней нагрузки зон сечения - расположенной в сжатой зоне;
б) при полностью сжатом от действия внешней нагрузки сечении - расположенной у более сжатой грани сечения;
в) при полностью растянутом от действия внешней нагрузки сечении внецентренно растянутых элементов - расположенной у менее растянутой грани сечения;
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
![]() и
и ![]() - кривизны осей элементов от воздействия
температуры при нагреве и остывании;
- кривизны осей элементов от воздействия
температуры при нагреве и остывании;
b - ширина прямоугольного сечения, ширина ребра таврового и двутаврового сечений;
bf и b′f - ширина полки таврового или двутаврового сечения соответственно в растянутой и сжатой зоне;
h - высота прямоугольного, таврового или двутаврового сечения;
a и a′ - расстояния от равнодействующей усилий соответственно в арматуре S и S′ до ближайшей грани сечения;
h0 и h′0 - рабочие высоты сечения, равные соответственно h - a и h - a′;
hu - рабочая высота сечения у шва, равная hw - a;
hf и h′f - высоты полки таврового или двутаврового сечения соответственно в растянутой и сжатой зоне;
e0p - эксцентриситет усилия предварительного обжатия P относительно центра тяжести приведенного сечения, определяемый в соответствии с указаниями СНиП 2.03.01-84;
e0 - эксцентриситет продольной силы N относительно центра тяжести приведенного сечения, определяемый в соответствии с указаниями п. 1.30;
es - расстояние от точки приложения продольной силы N до центра тяжести площади сечения арматуры S;
l - пролет элемента;
l0 - расчетная длина элемента, подвергающаяся действию сжимающей продольной силы; величина l0 принимается по табл. 42, 43 и указаниям п. 3.30;
i - радиус инерции поперечного сечения элемента относительно центра тяжести сечения;
d - номинальный диаметр стержней арматурной стали;
A - площадь всего бетона с поперечном сечении;
Ab - площадь сечения сжатой зоны бетона;
Abt - площадь сечения растянутой зоны бетона;
Ared - площадь приведенного сечения элемента, определяемая в соответствии с указаниями п. 1.28;
Aloc - площадь смятия бетона;
e и e′ - расстояния от точки приложения продольной силы N до равнодействующей усилий соответственно в арматуре S и S′;
As и A′s - площади сечения ненапрягаемой арматуры соответственно S и S′;
Asw - площадь сечения хомутов, расположенных в одной нормальной к продольной оси элемента плоскости, пересекающее наклонное сечение;
x - высота сжатой зоны бетона;
ξ - относительная высота сжатой зоны бетона равна x/h0;
μ - коэффициент армирования, определяемый как отношение площади сечения арматуры S к площади поперечного сечения элемента bh0 без учета сжатых и растянутых полок;
S′b0 и Sb0 - статические моменты площадей сечения соответственно сжатой и растянутой зоны бетона относительно нулевой линии;
Ss0 и S′s0 - статические моменты площадей сечения соответственно арматуры S и S′ относительно нулевой линии;
I - момент инерции сечения бетона относительно центра тяжести сечения элемента, вычисляемый без учета температуры как для ненагретого бетона;
Ired - момент инерции приведенного сечения элемента относительно его центра тяжести, определяемый в соответствии с указаниями п. 1.28;
Is - момент инерции площади сечения арматуры относительно центра тяжести сечения элемента;
Ib0 - момент инерции площади сечения сжатой зоны бетона относительно нулевой линии;
Is0 и I′s0 - моменты инерции площадей сечения соответственно арматуры S и S′ относительно нулевой линии;
y - расстояние от центра тяжести приведенного сечения до растянутой грани в формулах (5) до волокна бетона, в котором определяется напряжение, в формуле (16) и до менее нагретой грани в формулах (23), (30);
ys и y′s - расстояния от центра тяжести приведенного сечения элемента до равнодействующей усилий в арматуре S и S′ [в формулах (14) и (15)];
ft, εt и εcs - расчетные величины прогиба, удлинения и укорочения элемента от воздействия температуры;
acrc - средняя расчетная величина раскрытия трещин;
As,inc - площадь сечения отогнутых стержней, расположенных в одной наклонной и продольной оси элемента плоскости, пересекающей наклонное сечение;
sinc - расстояние между плоскостями отогнутых стержней, измеренное по нормали к ним;
s - расстояние между хомутами, измеренное по длине элемента;
tb - температура бетона;
tbm - средняя температура бетона;
ts и t′s - температуры арматуры S и S′;
ti - температура среды со стороны источника тепла;
te - температура воздуха с наружной стороны элемента;
tbw - температура бетона в центре тяжести приведенного сечения;
tbc - средняя температура бетона сжатой зоны сечения.
СОДЕРЖАНИЕ