|
ФЕДЕРАЛЬНАЯ
СЛУЖБА ПО ЭКОЛОГИЧЕСКОМУ, |
|
УТВЕРЖДЕНО приказом Федеральной службы по экологическому, технологическому и атомному надзору от 14 сентября 2011 г. № 535 |
ПОЛОЖЕНИЕ
О ПРИМЕНЕНИИ МЕТОДОВ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
ДЛЯ УЧЕТА И КОНТРОЛЯ ЯДЕРНЫХ МАТЕРИАЛОВ
(РБ-066-11)
|
Введено
в действие |
Москва 2011
Положение о применении методов математической статистики для учета и контроля ядерных материалов носит рекомендательный характер и не является нормативным правовым актом.
Настоящее Положение содержит рекомендации Федеральной службы по экологическому, технологическому и атомному надзору по применению методов математической статистики в целях учета и контроля ЯМ.
Выпускается впервые*
_____________
* Разработано коллективом авторов в составе Д.А. Боков, B.C. Кирсанов, Л.Н. Кушневский, О.В. Сопов (ФБУ «НТЦ ЯРБ»).
Список сокращений
В настоящем документе используются следующие сокращения:
МБП - межбалансовый период
МВИ - методика выполнения измерений
ЗБМ - зона баланса материалов
ИР - инвентаризационная разница
КТИ - ключевая точка измерений
СКД - средство контроля доступа
СКО - среднее квадратическое отклонение
СФНК - список фактически наличного количества
ТВС - тепловыделяющая сборка
ТВЭЛ - тепловыделяющий элемент
УЕ - учетная единица
ФИ - физическая инвентаризация
ЯМ - ядерный материал
I. Общие положения
1. Положение о применении методов математической статистики для учета и контроля ядерных материалов (далее - Положение) входит в число руководств по безопасности, носит рекомендательный характер и не является нормативным правовым актом.
2. Настоящее Положение содержит рекомендации Федеральной службы по экологическому, технологическому и атомному надзору по применению методов математической статистики в целях учета и контроля ЯМ.
3. Настоящее Положение рекомендуется использовать при разработке документов организации по статистической обработке результатов измерения количества и состава ЯМ в каждой ЗБМ, количества и состава ЯМ при передачах между ЗБМ, а также при подведении баланса ЯМ в ЗБМ.
4. Содержание настоящего Положения не охватывает всех существующих методов математической статистики. В нем представлены методы математической статистики, которые наиболее применимы в практике учета и контроля ЯМ, а также рекомендации по их применению для решения таких задач учета и контроля ЯМ как:
установление соответствия фактических параметров УЕ учетным данным;
определение объема подтверждающих измерений и анализ разницы между результатами учетных и подтверждающих измерений количественных параметров ЯМ, УЕ, продуктов;
определение объема случайной выборки при проверке пломб;
анализ расхождения данных по ЯМ организации-отправителя и организации-получателя;
проведение учетных и подтверждающих измерений фактически наличного количества ЯМ с учетом погрешностей измерений;
оценка величины неизмеренных потерь ЯМ и ее погрешности;
определение погрешности ИР, статистический анализ значимости ИР.
5. Рекомендации настоящего Положения касаются только ЯМ, учет и контроль которых осуществляется в форме УЕ.
6. Настоящее Положение содержит практические примеры возможного применения методов математической статистики.
II. Рекомендации по установлению соответствия фактических параметров УЕ существующим учетным данным
7. Определение соответствия фактических параметров УЕ существующим учетным данным в организациях рекомендуется проводить путем сопоставления результатов измерений параметров УЕ с учетными данными. Например, при установлении несоответствия результатов измерений параметров УЕ учетным данным, а также в организациях, в которых формируются новые УЕ. Учетные измерения рекомендуется осуществлять в соответствии со специально разрабатываемыми МВИ, предусматривающими либо однократное измерение параметра проверяемой УЕ, либо выполнение нескольких одновременных измерений этого параметра. В случае, когда МВИ предусматривает однократные измерения параметра проверяемых УЕ, в ней определяется и порядок получения гарантированных границ погрешности измерения. Совпадение результата измерения с учетными данными в пределах этих границ рекомендуется рассматривать как соответствие фактического значения характеристики УЕ существующим учетным данным.
8. Статистическую обработку результатов однократных измерений для подтверждения количества ЯМ в выборке УЕ рекомендуется осуществлять на основе определенных характеристик.
Так, например, в случае определения массы ЯМ среднее значение массы ЯМ в выборке однородных (изготовленных по одним техническим условиям) УЕ рекомендуется вычислять по формуле:
 (1)
(1)
где mi - значение массы ЯМ в отдельных УЕ выборки;
n - число УЕ в выборке.
Для определения значений mi с помощью прямых или косвенных методов рекомендуется использовать аттестованные МВИ, определяющие порядок проведения измерений и гарантированную погрешность результата.
Выборочную дисперсию массы ЯМ в УЕ рекомендуется определять в соответствии с выражениями:
![]() (2)
(2)
или:
 (21)
(21)
СКО и коэффициент вариации по выборке рекомендуется определять по формулам:
![]() (3)
(3)
и
![]() (4)
(4)
Расчет перечисленных характеристик рекомендуется выполнять с использованием интегрированных статистических пакетов. В случаях, когда при проведении измерений количества ЯМ в продуктах с использованием имеющихся МВИ обнаружено значимое расхождение с учетными данными рекомендуется убедиться в целесообразности дальнейшего использования перечисленных характеристик.
Для этого рекомендуется выполнить проверку соответствующих статистических гипотез.
9. Для проверки гипотез рекомендуется подход, основанный на формировании статистического вывода о количестве ЯМ в УЕ с использованием двух типов гипотез: нулевой гипотезы, заключающейся в том, что действительное количество ЯМ равно заявленному и альтернативной гипотезы, заключающейся в том, что количество ЯМ в УЕ отличается от заявленного.
При проверке гипотез возможны ошибка, состоящая в отклонении нулевой гипотезы, когда она истинна (ошибка 1-го рода), и ошибка, состоящая в принятии нулевой гипотезы, когда истинной является альтернативная гипотеза (ошибка 2-го рода).
Вероятности возникновения ошибок 1-го рода и ошибок 2-го рода соответственно обозначаются, как α и β.
10. Проверку согласия опытного распределения с нормальным законом рекомендуется проводить в соответствии с Правилами проверки, согласия опытного распределения с теоретическим (рекомендации по стандартизации Р 50.1.037-2002). При этом в зависимости от числа проводимых измерений рекомендуется использовать различные критерии.
Например, при числе измерений, превышающем пятьдесят, рекомендуется использовать критерий ω2.
При расчете ω2
рекомендуется табличный метод отображения, при котором значения, например,
содержания каждого изотопа хi (i = 1, ..., n) располагаются
в порядке их возрастания и результаты упорядочения (xj, j = 1, ..., n) заносятся
в первый столбец таблиц. Во второй столбец таблиц записываются значения функции
распределения проверяемого теоретического распределения F(xj), j = 1,
..., п. В третий столбец таблиц записываются значения ln F(xj), j =
1, ..., п.
В четвертый - значения (2j - 1)/(2n), j = 1, ..., n. В пятый - произведения значений в столбцах (3) и (4) для j = 1,
..., п. В шестой - разность
единицы и значений в столбце (4) для j = 1,
..., п. В седьмой - разность единицы и значений в столбце (2) для j = 1,
..., п. В восьмой столбец записываются значения ln [1 - F(xj)], j = 1, ..., п. В девятый - произведения
значений в столбцах (6) и (8) для j = 1,
..., п. В десятый - сумма значений в столбцах (5) и (9) для j = 1,
..., п. По таблицам рассчитываются значения ![]() Здесь суммирование по j =
1, ..., n. Рассчитанные значения
Здесь суммирование по j =
1, ..., n. Рассчитанные значения ![]() сравниваются с критическим
для уровня значимости 0,05 значением, приведенным в Правилах проверки согласия
опытного распределения с теоретическим (рекомендации по стандартизации Р
50.1.037-2002).
сравниваются с критическим
для уровня значимости 0,05 значением, приведенным в Правилах проверки согласия
опытного распределения с теоретическим (рекомендации по стандартизации Р
50.1.037-2002).
11. Проверку стохастической независимости результатов параллельных определений рекомендуется проводить на основе критерия отношений квадратов последовательных разностей. Для этого для каждых n одновременных измерений рассчитывается значение:
y(n) = g2(n)/s2(n), (5)
где ![]()
![]()
![]()
В случае у(п) > у'0,05(п),
где ![]() , а и0,05 - табулированное значение, гипотеза о стохастической
независимости результатов параллельных определений не отвергается.
, а и0,05 - табулированное значение, гипотеза о стохастической
независимости результатов параллельных определений не отвергается.
12. Проверку незначимости расхождения результатов параллельных определений (хi, i = 1, ..., n) для каждой серии из п измерений при доверительной вероятности 0,95 рекомендуется оценивать с помощью неравенства:
![]() (6)
(6)
где верхняя граница относительного СКО результатов измерений ![]() доверительные границы (интервал)
случайной погрешности результата измерений
доверительные границы (интервал)
случайной погрешности результата измерений ![]() среднее
арифметическое
среднее
арифметическое ![]() СКО
СКО  t(n-1);0,95 - значение
коэффициента Стьюдента с (п - 1) степенями свободы при доверительной вероятности 0,95. При
определении значения коэффициента β используются
существующие в этой области стандарты и рекомендации. В случае выполнения
неравенства оснований для исключения из анализа i-го
значения как аномального нет.
t(n-1);0,95 - значение
коэффициента Стьюдента с (п - 1) степенями свободы при доверительной вероятности 0,95. При
определении значения коэффициента β используются
существующие в этой области стандарты и рекомендации. В случае выполнения
неравенства оснований для исключения из анализа i-го
значения как аномального нет.
13. Для проверки незначимости различия дисперсий по критерию Кохрена для каждого изотопа (элемента) образцов каждого содержания рекомендуется рассчитывать значения
![]() (7)
(7)
Здесь ![]() a
a ![]() - наибольшее из
- наибольшее из ![]() Расчет
Расчет
![]() производится
по формуле:
производится
по формуле: ![]() N - число параллельных определений содержания каждого изотопа (элемента) в
каждом образце, а
m - количество образцов каждого содержания.
N - число параллельных определений содержания каждого изотопа (элемента) в
каждом образце, а
m - количество образцов каждого содержания.
Для проверки незначимости различия дисперсий, рассчитанные значения Gmax сравниваются с критическим для уровня значимости 0,05 значением Gкр(N - 1, m), которое определяется в соответствии с существующими в этой области стандартами и рекомендациями.
14. При исследовании однородности образцов содержания элемента
(изотопа) для каждого содержания по каждому элементу (изотопу) рассчитывается
сумма квадратов отклонений результатов определений внутри проб (под пробами
здесь понимаются образцы одного содержания) ![]() и между средними
арифметическими по пробам
и между средними
арифметическими по пробам ![]() Здесь
Здесь
![]() -
среднее арифметическое значение J параллельных определений (xnj, j = 1, ..., J) каждого
элемента (изотопа) в n-ом
образце исследуемого содержания, а
-
среднее арифметическое значение J параллельных определений (xnj, j = 1, ..., J) каждого
элемента (изотопа) в n-ом
образце исследуемого содержания, а ![]() - среднее
арифметическое значение всех NJ определений xnj. Затем
вычисляются выборочные средние квадраты отклонений результатов внутри проб
- среднее
арифметическое значение всех NJ определений xnj. Затем
вычисляются выборочные средние квадраты отклонений результатов внутри проб ![]() и между
пробами
и между
пробами ![]() Для неделимых образцов
СКО, характеризующие неоднородность материала по содержанию каждого элемента
(изотопа) в образцах каждого содержания элемента (изотопа), рассчитываются по
формуле:
Для неделимых образцов
СКО, характеризующие неоднородность материала по содержанию каждого элемента
(изотопа) в образцах каждого содержания элемента (изотопа), рассчитываются по
формуле: ![]()
Пример сравнения двух алгоритмов обработки спектров приведен в Приложении № 1 к настоящему Положению.
III. Определение объема подтверждающих измерений и УЕ для измерений. Анализ разницы между результатами учетных и подтверждающих измерений
15. При наличии возможностей рекомендуется проводить подтверждающие измерения всего ЯМ, находящегося в ЗБМ. В противном случае рекомендуется проводить измерения УЕ, случайным образом выбираемых из общего их количества в ЗБМ. При этом рекомендуется применять дифференцированный подход, учитывающий влияние трех факторов: категории ЯМ, объема применения к нему СКД и массы ЯМ в УЕ.
16. При осуществлении дифференцированного подхода к выбору УЕ для проведения подтверждающих измерений рекомендуется распределить их по стратам (совокупностям отдельных УЕ с одинаковыми или близкими физическими характеристиками и химическим составом ЯМ), и составить перечень УЕ, входящих в каждую страту. При этом объем выборки задается двумя величинами: G - пороговым количеством ЯМ в единицах массы и Р - вероятностью обнаружения недостачи/излишка порогового количества ЯМ.
17. Пороговое количество G рекомендуется определять в зависимости от категории ЯМ.
18. Вероятность обнаружения недостачи/излишка Р рекомендуется определять в соответствии с таблицей 1.
Таблица 1
Вероятность обнаружения недостачи/излишка порогового количества ЯМ для расчета объема выборки подтверждающих измерений
|
Объем применения СКД к ЯМ |
Вероятность обнаружения Р, %, не менее |
|
|
Для категорий 1, 2, 3 |
Для категории 4 |
|
|
Только пломбы |
50 |
30 |
|
Только система наблюдения |
50 |
30 |
|
Одновременно два вида разнообразных СКД |
25 |
9 |
|
Одновременно m видов разнообразных СКД |
100 ∙ (0,5)m |
100 ∙ (0,3)m |
19. Если ЯМ представлены в форме УЕ, целостность которых при нахождении в ЗБМ в МБП обеспечена их конструкцией (например, неразборные тепловыделяющие сборки или диски, блочки, изделия с ЯМ, покрытые оболочками, в результате чего ЯМ не могут быть извлечены из них без нарушения целостности оболочек) и может быть подтверждена (например, визуальным осмотром, сравнением образов гамма- или ультразвукового сканирования швов сварки), то для этих ЯМ при расчете объема выборки подтверждающих измерений рекомендуется использовать значения вероятностей обнаружения, аналогичные применяемым к ЯМ с пломбами. При этом рекомендуется принимать во внимание наличие документального подтверждения целостности неразборных УЕ и отсутствия несанкционированного доступа, а также фактической проверки СКД при проведении ФИ.
20. Расчет объема выборки (n) рекомендуется осуществлять в соответствии с Приложением № 2 к настоящему Положению, по формуле:
![]() (8)
(8)
N - количество УЕ в страте;
х - средняя масса ЯМ в одной УЕ;
[ ]+ - в формуле означает округление до ближайшего большего целого числа.
21. Номера подлежащих измерению УЕ рекомендуется выбирать случайным образом из перечня проверяемых УЕ каждой страты.
22. Случайный выбор рекомендуется проводить с помощью генератора случайных чисел с предварительным присвоением каждой УЕ проверяемой страты порядкового номера от 1 до N.
23. После измерения количественных параметров ЯМ, УЕ, продуктов рекомендуется проводить анализ разницы между результатами учетных и подтверждающих измерений.
Для этого рекомендуется рассчитать значение контрольного допуска по формуле:
![]() (9)
(9)
Здесь σподтв. - СКО подтверждающих измерений, а σучетн. - СКО учетных измерений.
24. При проведении измерений УЕ нескольких страт в случае необходимости объединения результатов измерений рекомендуется для нормально распределенных случайных величин выполнять проверку гипотез о равенстве средних значений и дисперсий. Это может потребоваться в задачах объединения нескольких страт, либо в задачах разбиения одной страты на несколько для получения представительных результатов. Пример практического решения такой задачи приведен в Приложении № 3 настоящего Положения.
Две выборочные дисперсии рекомендуется сравнивать с помощью критерия Фишера F. Для этого вычисляют отношение большей выборочной дисперсии к меньшей.
Если отношение выборочных дисперсий ![]() при
при
![]() больше
или равно
больше
или равно ![]() с
числом степеней свободы п1 - 1 и п2 -
1, где п1, п2 -
объемы выборок, а α - уровень
значимости, то рекомендуется принять гипотезу о неравенстве двух генеральных дисперсий
и, следовательно, нельзя объединять выборки. В случае соблюдения условия
с
числом степеней свободы п1 - 1 и п2 -
1, где п1, п2 -
объемы выборок, а α - уровень
значимости, то рекомендуется принять гипотезу о неравенстве двух генеральных дисперсий
и, следовательно, нельзя объединять выборки. В случае соблюдения условия ![]() рекомендуется
принять гипотезу о равенстве генеральных дисперсий, и переходят к проверке
равенства выборочных средних значений.
рекомендуется
принять гипотезу о равенстве генеральных дисперсий, и переходят к проверке
равенства выборочных средних значений.
Средние значения нормально распределенных случайных величин рекомендуется сравнивать с помощью t- критерия Стьюдента, значения которого приведены в анализе характеристик выборочного распределения (Приложение № 3 настоящего Положения). Для этого, в случае доказанного равенства выборочных дисперсий, вычисляют сводную дисперсию в соответствии с выражением:
![]() (10)
(10)
и значение t согласно выражению:
 (11)
(11)
Если ![]() то рекомендуется принять гипотезу о
равенстве средних. Здесь α - уровень
значимости, а k - число
степеней свободы, определяемое выражением k = n1 + п2 -
2. В случае
то рекомендуется принять гипотезу о
равенстве средних. Здесь α - уровень
значимости, а k - число
степеней свободы, определяемое выражением k = n1 + п2 -
2. В случае ![]()
Рекомендуемый порядок применения контрольного допуска, а также примеры сравнения двух выборочных дисперсий и средних приведены в Приложении № 4 к настоящему Положению.
IV. Определение объема случайной выборки при проверке пломб
25. Для определения объема выборки проверяемых пломб рекомендуется
рассчитать значение ![]() где N - количество установленных
пломб в ЗБМ. Здесь []+ также означает округление до
ближайшего большего целого числа. Значения объема выборки для различных
значений N приведены в Приложении №2 к
настоящему Положению.
где N - количество установленных
пломб в ЗБМ. Здесь []+ также означает округление до
ближайшего большего целого числа. Значения объема выборки для различных
значений N приведены в Приложении №2 к
настоящему Положению.
26. Номера подлежащих проверке пломб рекомендуется выбирать случайным образом.
V. Анализ расхождения данных организации-отправителя и организации - получателя
27. Для анализа расхождения данных по ЯМ организации-отправителя и организации-получателя рекомендуется определить допустимые границы такого расхождения:
![]() (12)
(12)
где -σo-n СКО результатов измерений массы с помощью весов отправителя и получателя. В общем случае:
![]() (13)
(13)
где ![]() и
и ![]() - значения
случайных составляющих погрешностей весов отправителя и получателя
соответственно, a
- значения
случайных составляющих погрешностей весов отправителя и получателя
соответственно, a ![]() и
и ![]() -
значения систематических составляющих погрешностей весов отправителя и
получателя соответственно.
-
значения систематических составляющих погрешностей весов отправителя и
получателя соответственно.
На практике в технической документации на весы, как правило, указана полная погрешность, приведенная к доверительному интервалу 0,99, уже включающая в себя как систематическую так и случайную составляющие погрешности (например: в абсолютных единицах Δ = ±0,1 г или в относительных δ = ±0,1 %). В этом случае расчет ведется по формуле:
![]() (14)
(14)
Или
![]() (15)
(15)
В случае отсутствия данных по весам отправителя соответствующие погрешности принимаются равными нулю и соответственно допустимые границы расхождения данных по ЯМ организации-отправителя и организации-получателя будут более «жесткими». Примеры расчета, а также алгоритм оценки значимости систематических расхождений σo-n приведены в Приложении № 5 к настоящему Положению.
28. Если расхождение данных по ЯМ организации-отправителя и
организации-получателя ![]() , (здесь mпол -
масса ЯМ по данным организации-отправителя, а mпол - масса
ЯМ по данным организации-получателя), то ЯМ рекомендуется ставить на учет в
организации-получателе по данным организации-отправителя.
, (здесь mпол -
масса ЯМ по данным организации-отправителя, а mпол - масса
ЯМ по данным организации-получателя), то ЯМ рекомендуется ставить на учет в
организации-получателе по данным организации-отправителя.
VI. Проведение учетных и подтверждающих измерений фактически наличного количества ЯМ с учетом погрешностей измерений
29. В учете и контроле ЯМ наиболее распространена задача сопоставления результатов подтверждающих измерений ЯМ с учетными данными. Эта задача описана в разделе 111 настоящего Положения. Однако иногда возникает необходимость проанализировать данные по партии ЯМ (раздел V настоящего Положения), стратам ЯМ. Фактически наличное количество ЯМ в страте из N УЕ, имеющих массу Mk, k = 1, ..., N рекомендуется определять следующим образом:
![]() (16)
(16)
где ![]() - среднее
учетное значение массы УЕ.
- среднее
учетное значение массы УЕ.
30. При оценке фактически наличного количества ЯМ по выборке {![]() , i = 1, ..., n} из
ограниченной совокупности, где
, i = 1, ..., n} из
ограниченной совокупности, где ![]() mi - истинное значение массы ЯМ для i-ой УЕ, a Δmi -
неопределенность этого значения, рекомендуется рассматривать, по крайней мере,
три компоненты Δm:
mi - истинное значение массы ЯМ для i-ой УЕ, a Δmi -
неопределенность этого значения, рекомендуется рассматривать, по крайней мере,
три компоненты Δm:
- первая из них (δ) является функцией измеряемой массы, характеристик образца, влияющих на калибровку, метода измерения (при повторных измерениях δ ведет себя как систематическая погрешность). Влияние δ на измеряемые значения минимизируется путем построения калибровочных кривых. В действительности полностью исключить эту составляющую не удается, каждое измерение имеет систематическое отклонение, зависящее от массы, а также от других факторов, влияющих на результат измерения. В идеальном случае эта составляющая уже включена в дисперсию;
- вторая: η - функция оценок калибровочной кривой, причем коэффициенты последней обычно зависят от измеряемой массы. При измерении двух разных УЕ η каждой из них является причиной ковариации измерений, а ковариация в свою очередь зависит от масс этих УЕ;
- третья: ε - случайная погрешность, связанная со статистикой счета. Она принимает независимые значения при повторных измерениях одной УЕ, а также для разных УЕ. В общем случае ε является функцией измеряемой массы.
Выборки из страты обычно являются бесповторными. Случайные величины {mi, I = 1, ..., n} одинаково распределены, но в отличие от случая выборки из бесконечной генеральной совокупности не являются независимыми. Эта зависимость определяется ковариацией, которая в рассматриваемом случае равна: cov(mi, mj) = -σ2/(N - 1). Здесь
![]() (17)
(17)
Связь характеристик выборки с характеристиками страты без учета погрешности измерения рекомендуется описывать следующим образом:
![]()
![]()
![]()
Здесь Е(х) и Var(x) - математическое ожидание и дисперсия величины x соответственно.
31. Оценка фактически наличного количества ЯМ стремится к истинному значению при уменьшении суммы систематических отклонений, которые вносило бы измерение каждой УЕ страты:
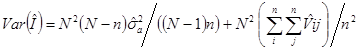 - дисперсия оценки.
- дисперсия оценки.
Здесь  где
<m> - среднее значение
где
<m> - среднее значение ![]() i = 1,
..., n, a
i = 1,
..., n, a ![]() - оценки элементов
матрицы дисперсий погрешности измерений. Такие оценки условных значений
дисперсии и ковариации зависят от массы и служат оценками математических
ожиданий для выборки этих значений дисперсии и ковариации. Последнее позволяет
работать с выборками из конечной совокупности с учетом погрешностей измерений,
не ограничивая себя конфетной моделью погрешности. Условные значения дисперсии
и ковариации обычно содержатся в описании и программном обеспечении большинства
современных измерительных систем.
- оценки элементов
матрицы дисперсий погрешности измерений. Такие оценки условных значений
дисперсии и ковариации зависят от массы и служат оценками математических
ожиданий для выборки этих значений дисперсии и ковариации. Последнее позволяет
работать с выборками из конечной совокупности с учетом погрешностей измерений,
не ограничивая себя конфетной моделью погрешности. Условные значения дисперсии
и ковариации обычно содержатся в описании и программном обеспечении большинства
современных измерительных систем.
Оценка фактически наличного количества ЯМ в УЕ страты стремится к истинному значению при уменьшении суммы систематических отклонений, которые вносило бы измерение каждой УЕ страты. Для минимизации суммы систематических отклонений рекомендуется проведение более тщательной калибровки, учитывающей зависимость систематических отклонений от измеряемой массы, а также других влияющих на измерение факторов.
Указанное выше справедливо при наличии достаточно близких параметров УЕ. При наличии значительных различий параметров УЕ рекомендуется использовать не абсолютные значения массы, а расхождения этих значений, полученных в результате учетных и подтверждающих измерений. В этом случае оценивается общая величина расхождения данных.
VII. Определение погрешности ИР. Статистический анализ значимости ИР
32. ИР рекомендуется вычислять по элементу и по изотопу для каждого ЯМ:
ИР = ФК - ДК = ФК - (НК + УВ - УМ), (18)
где ФК - фактически наличное количество ЯМ в ЗБМ, определенное в результате данной ФИ;
ДК - документально зарегистрированное количество ЯМ в ЗБМ на начало ФИ (конец данного МБП);
УВ - документально зарегистрированное увеличение количества ЯМ в ЗБМ за данный МБП в результате всех поступлений, наработок и т.д.;
УМ - документально зарегистрированное уменьшение количества ЯМ в ЗБМ за данный МБП в результате всех отправок из ЗБМ, ядерных превращений, потерь и т.д.;
НК - документально зарегистрированное количество ЯМ в ЗБМ на начало данного МБП.
Уравнение ИР можно представить как сумму ЯМ (элемента или изотопа).
![]() (19)
(19)
где: N1 - количество УЕ в НК
N2 - количество УЕ в УВ
N3 - количество УЕ в УМ
N4 - количество УЕ в ФК
mi - масса элемента при определении ИР по элементу (массовая доля С):
mi = mнiCi, (20)
где: mнi - масса нетто;
mi - масса изотопа при определении ИР по изотопу (массовая доля Си):
mi = mнiCiCиi, (21)
33. Для оценки погрешности ИР рекомендуется использовать метод переноса погрешности измерений.
34. В связи с тем, что измерения количеств ЯМ, как правило, являются косвенными, то дисперсию ИР рекомендуется в общем случае представлять квадратной диагональной матрицей дисперсий и ковариаций результатов измерений, которая, исходя из числа компонент уравнения баланса материалов, содержит по 4 строки и столбца и имеет вид:
С учетом (22) выражение для определения погрешности ИР может быть представлено в следующем виде:
![]() (23)
(23)
где i - индекс строки матрицы дисперсий и ковариаций;
j - индекс столбца матрицы дисперсий и ковариаций;
σi - погрешность результатов измерения количества ЯМ в компоненте уравнения баланса с индексом i;
σj - погрешность результатов измерения количества ЯМ в компоненте уравнения баланса с индексом j;
ρij - коэффициент корреляции между компонентами уравнения баланса с индексами i и j.
Структура погрешности результатов измерения ЯМ рассмотрена в разделе VI настоящего Положения. В этом же разделе приведены аналитические выражения для расчета дисперсий и ковариаций. В таких расчетах рекомендуется использовать данные, содержащиеся в документации на средства измерения, в МВИ.
Причиной корреляции между компонентами уравнения баланса может служить использование при проведении учетных измерений ЯМ одних и тех же средств измерения.
35. Для вычисления СКО величин каждого из компонентов уравнения
баланса все УЕ, которые подвергаются измерениям, рекомендуется разбить на
несколько (К) независимых друг от друга (некоррелированных) страт. Дисперсия
результатов измерений ЯМ в УЕ k-ой
страты ![]() в
общем случае с учетом возможных корреляций определения параметров ЯМ в УЕ,
составляющих данную страту, может быть вычислена по формуле:
в
общем случае с учетом возможных корреляций определения параметров ЯМ в УЕ,
составляющих данную страту, может быть вычислена по формуле:
![]() (24)
(24)
где ![]() - дисперсия определения массы ЯМ l-ой УЕ,
входящей в k-ую страту, содержащую Nk УЕ,
с учетом случайной и систематической составляющих погрешности определения величины
массы ЯМ в l-ой УЕ - Mkl;
- дисперсия определения массы ЯМ l-ой УЕ,
входящей в k-ую страту, содержащую Nk УЕ,
с учетом случайной и систематической составляющих погрешности определения величины
массы ЯМ в l-ой УЕ - Mkl;
индексы l и m соответствуют порядковым номерам УЕ, входящих в k-ую страту;
ρ(Mkl, Mkm) - коэффициент корреляции между значениями масс ЯМ в l-ой УЕ - Mkl и в m-ой УЕ - Mkm, входящих в k-ую страту.
Величина коэффициентов корреляции может изменяться в пределах от -1 до +1.
Для независимых величин коэффициент корреляции между ними равен нулю.
Определение значения величины коэффициента корреляции при анализе
результатов измерений является достаточно трудоемкой задачей. Поэтому в
большинстве случаев для упрощения обработки результатов измерений и вычисления
величины σИР возможными
корреляциями между компонентами уравнения баланса, а также между результатами измерений
параметров ЯМ в стратах УЕ рекомендуется пренебречь. При этом значения σИР, ![]() определяются
в соответствии с выражениями:
определяются
в соответствии с выражениями:
![]() (25)
(25)
![]() (26)
(26)
Это в конечном итоге приведет к некоторому уменьшению найденного
значения σИР и,
следовательно, повышению риска ошибки первого рода (фиксации аномалии в учете и
контроле при фактическом ее отсутствии). Однако, следует полагать, что при
правильной организации учета и контроля ЯМ в ЗБМ данное явление будет
происходить достаточно редко, что обусловливает приемлемость допущения об
отсутствии корреляций между соответствующими величинами при определении σИР, ![]() в
практических задачах.
в
практических задачах.
Если все же существуют веские причины необходимости учета корреляций, то для определения соответствующих коэффициентов корреляции рекомендуется в организации разработать необходимые для этого методики.
36. Для определения дисперсий масс ЯМ в УЕ в организации рекомендуется разработать методики определения массы ЯМ и ее погрешности с учетом оснащения ЗБМ техническими средствами для проведения учетных измерений, МВИ, особенностей технологических процессов.
37. При расчете погрешности определения массы рекомендуется учитывать такие источники погрешности как: статистическая погрешность отбора УЕ, погрешность балк - измерения, погрешность пробоотбора материала, погрешность химического анализа материала и другие в зависимости от особенностей технологических процессов.
38. Для тех страт УЕ с ЯМ в ЗБМ, которые не подвергались каким-либо превращениям в течение МБП, при вычислении ИР и σИР рекомендуется использовать учетные данные, полученные ранее для входящих в их состав УЕ. При этом такие данные какого-либо влияния на величину σИР не оказывают.
39. Для вычисления σИР и анализа результатов на наличие возможных аномалий в учете и контроле ЯМ рекомендуется порядок, изложенный в Стандарте корпорации ОАО «ТВЭЛ». «Система учета и контроля ядерных материалов», в соответствии с которым производится:
установление СКО систематических (σs) и случайных (σR) составляющих погрешностей всех методов измерений ЯМ в ЗБМ;
подготовка данных регистрации движения ЯМ для вычисления ИР и σИР выделение групп (страт) ЯМ;
вычисление ИР по элементу и по изотопу для каждого ЯМ в ЗБМ;
исключение из расчета σИР «парных учетных записей», которые не должны влиять на σИР;
вычисление ![]() (дисперсий ИР);
(дисперсий ИР);
проверка по критериям обнаружения аномалий в учете и контроле ЯМ.
40. При определении характеристик погрешностей измерений (СКО систематических и случайных составляющих) рекомендуется:
установить на основании МВИ ЯМ случайные и систематические составляющие характеристики погрешностей измерения ЯМ в ЗБМ;
для вычисления σИР вычислить СКО для каждой случайной и систематической составляющей погрешности всех методов измерения ЯМ в ЗБМ. Если погрешность МВИ регламентируется в абсолютной форме - Δ, то рекомендуется следовать аддитивной модели погрешности. Если погрешность МВИ регламентируется в относительной форме - δ, то рекомендуется следовать мультипликативной модели. Описание аддитивной и мультипликативной моделей погрешности измерения, а также связь с абсолютной и относительной погрешностями измерения приведены в Приложении № 6 к настоящему Положению.
Переход от интервальных характеристик погрешности к СКО (σ) при Р = 0,95 рекомендуется осуществлять следующим образом:
![]() - СКО случайной составляющей для
абсолютной погрешности (аддитивная модель);
- СКО случайной составляющей для
абсолютной погрешности (аддитивная модель);
![]() - СКО случайной
составляющей для относительной погрешности (мультипликативная модель);
- СКО случайной
составляющей для относительной погрешности (мультипликативная модель);
где: ΔR , δR - интервальные характеристики случайной составляющей погрешности измерения при Р = 0,95;
![]() - СКО систематической составляющей для абсолютной
погрешности (аддитивная модель);
- СКО систематической составляющей для абсолютной
погрешности (аддитивная модель);
![]() - СКО систематической составляющей для относительной
погрешности (мультипликативная модель);
- СКО систематической составляющей для относительной
погрешности (мультипликативная модель);
где: Θ(Δ)S, Θ(δ)S - интервальные характеристики систематической составляющей погрешности измерения при Р = 0,95.
Для процедур взвешивания в расчетах рекомендуется использовать паспортизованные значения погрешностей при Р = 1.
После определения всех характеристик погрешностей измерения рекомендуется разработать итоговый отчет (справку) соответствующий документам предприятия.
Пример рекомендуемой формы представления итоговых результатов определения СКО составляющих погрешностей измерения представлен в Приложении № 7 к настоящему Положению.
41. При подготовке данных регистрации движения ЯМ к вычислению ИР и σИР, при выделении групп (страт) ЯМ рекомендуется:
все поступления и другие увеличения ЯМ в ЗБМ, отправления и другие уменьшения ЯМ (например, образование отходов) из ЗБМ, результаты предыдущей и текущей ФИ зафиксировать в отчетных документах в соответствии с документами предприятия по учету и контролю ЯМ. Пример регистрации движения ЯМ для ЗБМ производства ТВЭЛ представлен в таблице П8.1 Приложения № 8 к настоящему Положению;
выделить группы (страты) ЯМ. Каждая группа (страта) характеризуется набором одних и тех же методов измерений (например: взвешивание на одних и тех же весах, определение массовой доли элемента по одной и той же МВИ, определение массовой доли изотопа по одной и той же МВИ) и соответствующими характеристиками погрешности (пример в таблице П8.1 Приложения № 8 к настоящему Положению).
В каждой группе (страте) содержится информация о движении ЯМ в ЗБМ за МБП. Пример выделения групп (страт) для ЗБМ производства ТВЭЛ представлен в таблицах П8.2, П8.3, П8.4 Приложения № 8 к настоящему Положению.
42. При вычислении ИР рекомендуется пользоваться формулой (20). Вычисления проводятся для каждого ЯМ (элемента и изотопа).
43. Для исключения из расчета σИР «парных учетных записей» рекомендуется:
при анализе таблицы регистрации движения ЯМ (пример - таблица П8.1 Приложения № 8 к настоящему Положению выделить такие учетные записи, которым соответствует одна и та же УЕ (с одним и тем же идентификационным номером), которая осталась без изменения и работы с ней за МБП не выполнялись, а достоверность учетных данных для этой УЕ с момента их определения до момента использования подтверждена надлежащим состоянием примененных СКД;
если для каждой такой УЕ существуют две учетные записи, соответствующие разным членам уравнения ИР с разными знаками, то такие «парные учетные записи» необходимо исключить из расчета σИР, чтобы не допустить необоснованного увеличения σИР. Например, возможны следующие типы «парных учетных записей»:
Члены уравнения инвентаризационной разницы УВ и ФК.
Поступившие в ЗБМ УЕ (УВ), которые зарегистрированы в соответствии с данными отправителя, затем при проведении ФИ эти же УЕ были занесены в инвентаризационную ведомость (ФК).
Члены уравнения инвентаризационной разницы УВ и УМ.
Поступившие в ЗБМ УЕ (УВ), которые затем были отправлены из ЗБМ (УМ).
Члены уравнения инвентаризационной разницы НК и УМ.
Часть УЕ из предыдущей ФИ (НК) были отправлены из ЗБМ (УМ).
Члены уравнения инвентаризационной разницы НК и ФК.
Часть УЕ из предыдущей ФИ (НК) вошли в список УЕ текущей инвентаризации (ФК).
Пример исключения парных записей приведен в Приложении № 9 к настоящему Положению.
44. Вычисление σИР рекомендуется проводить как с усреднением так и без усреднения по потоку.
Подход с использованием усреднения по потоку заключается в предположении, что в среднем все учетные массы в партии ЯМ являются примерно одинаковыми и масса одной УЕ равна средней массе УЕ по партии. При использовании этого подхода получаемое значение σИР, как правило, определяет целесообразность применения более «жестких» критериев обнаружения аномалий, чем при вычислении без усреднения по потоку.
Подход к вычислению ![]() без усреднения по потоку состоит в том,
что используются индивидуальные учетные массы ЯМ по каждой УЕ. Для реализации
этого подхода рекомендуется разработать специальное программное обеспечение.
без усреднения по потоку состоит в том,
что используются индивидуальные учетные массы ЯМ по каждой УЕ. Для реализации
этого подхода рекомендуется разработать специальное программное обеспечение.
Общая последовательность вычисления σИР и проверки гипотезы об отсутствии аномалий остается одинаковой для этих двух способов.
При принятии решения об использовании того или иного метода
рекомендуется сделать оценку величины, на которую уменьшается вычисляемая ![]() с усреднением
по потоку (Приложение № 10 к
настоящему Положению).
с усреднением
по потоку (Приложение № 10 к
настоящему Положению).
45. При вычислении ![]() (с усреднением по
потоку) рекомендуются аналитические выражения для относительных погрешностей
измерения как наиболее часто применяемых в практике при вычислении дисперсии ИР
(мультипликативная модель).
(с усреднением по
потоку) рекомендуются аналитические выражения для относительных погрешностей
измерения как наиболее часто применяемых в практике при вычислении дисперсии ИР
(мультипликативная модель).
При этом вклад систематической составляющей погрешности по одному из методов измерения (взвешивание, измерение объема, других МВИ) в дисперсию ИР для j-той группы (страты) рекомендуется определять с помощью выражения:
где σsj - СКО систематической составляющей погрешности одного из методов измерения,
sgn(mi) = +1 для mi из НК, УВ - членов уравнения ИР,
sgn(mi) = -1 для тi из ФК, УМ - членов уравнения ИР. Этот подход справедлив, например, при взвешивании всего ЯМ, составляющего члены уравнения ИР, на одних и тех же весах без перекалибровки.
При проведении взвешиваний и определении массовой доли элемента (изотопа) рекомендуется следующий подход.
При вычислении ИР по элементу:
mЯМi = (mбi - mтi)Ci, (29)
где mбi - масса брутто;
mтi - масса тары;
Q - массовая доля элемента.
При вычислении ИР по изотопу:
mЯМi = (mбi - mтi)СiCиi, (30)
где: Сиi - массовая доля изотопа.
При вычислении вклада систематической составляющей погрешности в ![]() определяется
общая сумма масс ЯМ в группе (страте) с учетом их знака в уравнении ИР. В связи
с тем, что результаты суммы масс как для метода с усреднением по потоку, так и
для метода без усреднения, являются одинаковыми, то эти два подхода дают
эквивалентные результаты. Порядок вычисления суммарной массы МЯМj j-той группы
(страты) для определения вклада систематических и случайных составляющих
погрешностей в
определяется
общая сумма масс ЯМ в группе (страте) с учетом их знака в уравнении ИР. В связи
с тем, что результаты суммы масс как для метода с усреднением по потоку, так и
для метода без усреднения, являются одинаковыми, то эти два подхода дают
эквивалентные результаты. Порядок вычисления суммарной массы МЯМj j-той группы
(страты) для определения вклада систематических и случайных составляющих
погрешностей в ![]() приведен ниже.
приведен ниже.
Вклад случайной составляющей погрешности по одному из методов
измерения (взвешивание, измерение объема, МВИ разрушающих и неразрушающих
методов анализа) в ![]() для j-той
группы (страты) рекомендуется вычислять с использованием выражения:
для j-той
группы (страты) рекомендуется вычислять с использованием выражения:
 (31)
(31)
где ![]() -
суммарная масса элемента (изотопа) j-той
группы (страты);
-
суммарная масса элемента (изотопа) j-той
группы (страты);
Nj - число измерений в j-той группе (страте);
σRj - случайная составляющая погрешности одного из методов измерения j-той группы (страты).
Суммарная масса элемента (изотопа) j-той группы (страты):
![]() (32)
(32)
где R - число партий в j-той группе (страте);
МЯМi - суммарная масса элемента (изотопа) в i-той партии.
Общее число взвешиваний (измерений объема и т.п.) в j-той группе (страте):
![]() (33)
(33)
где R - число партий в j-той группе (страте);
Ni - число контейнеров (измерений объема) в i-той партии.
Общее число анализов по МВИ одним из разрушающих (неразрушающих) методов анализа в j-той группе (страте):
Nj = R ∙ pi, (34)
где R - число партий ЯМ, в которых определяется массовая доля элемента (изотопа) по МВИ для j-той группы (страты);
pi - число проб на партию.
Аналитические выражения для вычисления ![]() без усреднения по
потоку рассмотрены в Приложении № 11
к настоящему Положению.
без усреднения по
потоку рассмотрены в Приложении № 11
к настоящему Положению.
При вычислении суммарной массы MЯМj в j-той группе (страте) для
определения вклада систематических и случайных составляющих погрешностей в ![]() (с
усреднением по потоку) к его началу рекомендуется провести процедуру исключения
«парных учетных записей».
(с
усреднением по потоку) к его началу рекомендуется провести процедуру исключения
«парных учетных записей».
Для вычисления вклада в ![]() систематических составляющих
погрешностей рекомендуется суммировать массы элемента (изотопа) с учетом знака
уравнения ИР для случая, когда при взвешивании всего ЯМ, составляющего члены
уравнения ИР используются одни и те же средства измерения без перекалибровки. В
примере исключения парных записей, представленном в Приложении № 9 к настоящему Положению суммируются
суммы масс элемента (изотопа) и записываются в строку MЯМS(сист)
по элементу и изотопу:
систематических составляющих
погрешностей рекомендуется суммировать массы элемента (изотопа) с учетом знака
уравнения ИР для случая, когда при взвешивании всего ЯМ, составляющего члены
уравнения ИР используются одни и те же средства измерения без перекалибровки. В
примере исключения парных записей, представленном в Приложении № 9 к настоящему Положению суммируются
суммы масс элемента (изотопа) и записываются в строку MЯМS(сист)
по элементу и изотопу:
MЯМS(сист) = Сумма(НК) + Сумма(УВ) - Сумма(ФК) - Сумма(УМ). (35)
Для вычисления вклада в ![]() случайных составляющих погрешностей
рекомендуется суммировать массы элемента (изотопа) без учета знака уравнения ИР
для случая, когда при взвешивании всего ЯМ, составляющего члены уравнения ИР,
используются одни и те же средства измерения без перекалибровки. В примере
исключения парных записей, представленном в Приложении № 9 к настоящему Положению суммируются суммы масс
элемента (изотопа) и записываются в строку MЯМR(случ)
по элементу и изотопу:
случайных составляющих погрешностей
рекомендуется суммировать массы элемента (изотопа) без учета знака уравнения ИР
для случая, когда при взвешивании всего ЯМ, составляющего члены уравнения ИР,
используются одни и те же средства измерения без перекалибровки. В примере
исключения парных записей, представленном в Приложении № 9 к настоящему Положению суммируются суммы масс
элемента (изотопа) и записываются в строку MЯМR(случ)
по элементу и изотопу:
MЯМR(случ) = Сумма(НК) + Сумма(УВ) + Сумма(ФК) + Сумма(УМ). (36)
Пример вычисления суммарной массы материала приведен в Приложении № 12 к настоящему Положению.
При вычислении значения ![]() рекомендуется использовать следующие
данные:
рекомендуется использовать следующие
данные:
- характеристики погрешностей (σR и σS);
- количество измерений (количество контейнеров при однократном взвешивании);
- количество проб, которые были взяты из партии ЯМ для определения массовой доли элемента и изотопа.
В Приложении № 13 к
настоящему Положению приведен пример вычисления вклада систематических и
случайных составляющих погрешностей j-ой
группы (страты) в ![]() .
.
Для вычисления вклада в ![]() систематических составляющих
погрешностей для тех методов измерения, которые выполнялись в j-ой группе (страте) рекомендуется использовать выражение (27). Определяется суммарный вклад
систематических составляющих погрешностей j-ой
группы (страты) в
систематических составляющих
погрешностей для тех методов измерения, которые выполнялись в j-ой группе (страте) рекомендуется использовать выражение (27). Определяется суммарный вклад
систематических составляющих погрешностей j-ой
группы (страты) в ![]() .
.
Например:
- VSMj - вклад
систематической составляющей погрешности взвешивания j-ой группы (страты) в ![]() ;
;
- VSAj - вклад
систематической составляющей погрешности разрушающего анализа (по элементу и по
изотопу) j-ой группы (страты) в ![]() .
.
Определяется общий вклад в ![]() систематических составляющих
погрешностей как сумма отдельных вкладов (взвешивание и анализ):
систематических составляющих
погрешностей как сумма отдельных вкладов (взвешивание и анализ):
VSΣj = VSMj + VSAj. (37)
Для вычисления вклада в ![]() случайных составляющих погрешностей для
тех методов измерения, которые выполнялись в j-ой
группе (страте) рекомендуется использовать выражение (28). Определяется суммарный вклад случайных
составляющих погрешностей
j-ой группы (страты) в
случайных составляющих погрешностей для
тех методов измерения, которые выполнялись в j-ой
группе (страте) рекомендуется использовать выражение (28). Определяется суммарный вклад случайных
составляющих погрешностей
j-ой группы (страты) в ![]() .
.
Например:
- VRM - вклад
случайной составляющей погрешности взвешивания j-ой
группы (страты) в ![]() ;
;
- VRA -
вклад случайной составляющей погрешности разрушающего анализа (по элементу и по
изотопу) j-ой
группы (страты) в ![]() .
.
Определяется общий вклад в ![]() случайных составляющих погрешностей как
сумма отдельных вкладов (взвешивание и анализ):
случайных составляющих погрешностей как
сумма отдельных вкладов (взвешивание и анализ):
VRΣj = VRMj + VRAj. (38)
Суммируются вклады в ![]() систематических составляющих
погрешностей всех групп (страт):
систематических составляющих
погрешностей всех групп (страт):
![]() (39)
(39)
где: VSΣj -
вклад систематических составляющих погрешностей в ![]() j-ой
группы (страты);
j-ой
группы (страты);
K - число групп (страт).
Суммируются вклады в ![]() случайных составляющих погрешностей
всех групп (страт):
случайных составляющих погрешностей
всех групп (страт):
![]() (40)
(40)
где: ![]() - вклад случайных
составляющих погрешностей в
- вклад случайных
составляющих погрешностей в ![]() j-ой
группы (страты).
j-ой
группы (страты).
Рекомендуется провести сравнительный анализ вносимой доли каждой
из составляющих погрешности в ![]() .
.
Суммарная ![]() складывается из систематических и
случайных составляющих погрешностей измерений всех групп (страт):
складывается из систематических и
случайных составляющих погрешностей измерений всех групп (страт):
![]() (41)
(41)
СКО инвентаризационной разницы:
![]() (42)
(42)
46. В качестве критерия обнаружения аномалий в учете и контроле ЯМ за МБП рекомендуется использовать выполнение хотя бы одного из неравенств следующей системы:
Числовые значения в третьем и четвертом неравенствах системы (43) определяют критические доли от общего количества данного ЯМ, преобразованного и подвергшегося учетным измерениям в данный МБП или в процессе ФИ.
Проверку выполнения второго неравенства системы рекомендуется проводить только в отношении ЯМ, для которых пороговые значения G установлены.
Проверку выполнения третьего и четвертого неравенств рекомендуется проводить отдельно для каждого ЯМ в ЗБМ по элементу и по изотопу.
Приложение № 1
к Положению по применению
методов математической
статистики для учета и контроля
ядерных материалов,
утвержденному приказом
Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Пример сравнения двух алгоритмов обработки спектров
При разработке стандартных образцов содержания плутония для инспекционных измерений эти образцы измерялись с помощью инспекционной гамма спектрометрической станции U-Pu Inspector с низкоэнергетическим германиевым детектором (LEGe) активной площадью 5 см2. Для получения данных об изотопном составе использовалось программное обеспечение MGA. Результаты измерения были обработаны с целью их сопоставления с данными, полученными с помощью разрушающего анализа проб материала, а также для сопоставления двух предусмотренных программным обеспечением станции алгоритмов: с декларацией содержания Pu-242 до измерения образца и без таковой.
Измерениям подверглись 11 комплектов стандартных образцов, в каждый из которых входило по четыре образца разного изотопного состава. Данные о составе были получены с помощью разрушающих методов анализа проб материала до изготовления образцов и представлены до проведения инспекционных измерений. Так, например, процентное содержание Pu-239 в образцах состава № 1 было равно 94,176 ± 0,020, для состава № 2 - 90,034 ± 0,026, для состава № 3 - 85,06 ± 0,06, а для состава № 4 - 79,24 ± 0,02. Для каждого из 44 образцов было выполнено 8 параллельных определений изотопного состава с обработкой спектра по алгоритму, предусматривающему декларацию содержания Pu-242 до измерения образца. Для обработки каждого девятого спектра использовался алгоритм, не требующий декларировать содержание Pu-242. Разрешение на 122 кэВ при измерениях составляло (590 - 600) эВ (ПШПВ). Время набора каждого спектра составляло 1000 с. Путем изменения расстояния между детектором и образцом, а также подбором толщины фильтра для снижения интенсивности низкоэнергетических фотонов «мертвое» время для образцов разного содержания регулировалось в диапазоне (18 - 22) %. При этом общее за время набора каждого спектра число отсчетов составляло (6 - 8)×106, а в энергетических областях при (59,54; 129,29; 208,00) кэВ - не менее 105 при сопоставимых значениях. Смещение центроид, соответствующих перечисленным энергиям, находилось при измерениях в пределах пяти каналов. Необходимости коррекции смещения усиления в период измерений не возникало. Коэффициент, соответствующий усилению в уравнении калибровки, составлял ~ 0,075 кэВ.
На этапе предварительного анализа для каждого образца по 8 параллельным определениям содержания каждого изотопа с использованием действующих методик выполнялись следующие проверки:
согласия опытного распределения с теоретическим;
стохастической независимости результатов параллельных определений;
незначимости расхождения результатов параллельных определений;
незначимости различия дисперсий по критерию Кохрена; однородности.
Для проверки согласия опытного распределения с нормальным законом значение критерия для малых объемов выборки сравнивалось с критическим для уровня значимости 0,05. В ходе такой проверки несоответствия данных параллельных определений нормальному закону для уровня значимости 0,05 установлено не было.
Стохастическая независимость результатов параллельных определений проверялась с помощью критерия отношений квадратов последовательных разностей. В ходе такой проверки случаев невыполнения неравенства для уровня значимости 0,05 установлено не было.
Проверка незначимости расхождения результатов (xi, i = 1, ..., n) для каждой серии из n = 8 параллельных определений для доверительной вероятности 0,95 аномальных значений в экспериментальных данных не выявила.
Проверка дисперсий для каждого изотопа образцов каждого содержания значимых различий дисперсий не выявила.
При исследовании однородности стандартных образцов содержания плутония для каждого содержания по каждому изотопу были рассчитаны СКО, характеризующие неоднородность материала по содержанию каждого изотопа в образцах каждого содержания плутония, σn.
После того, как значимых различий между параллельными определениями содержания каждого анализируемого изотопа в стандартных образцах одного содержания плутония установлено не было, данные по таким образцам были объединены.
При проверке согласия опытных распределений объединенных данных с нормальным законом (число измерений превышает пятьдесят) по критерию ω2 доказательств несоответствия для уровня значимости 0,05 опытного распределения нормальному закону установлено не было.
На следующем этапе по каждому изотопу формировались таблицы, в
каждый из четырех столбцов которых записывались результаты измерения образцов
одного содержания плутония. Для анализа таблиц использовался обычный
интегрированный статистический пакет, позволяющий, не углубляясь в теорию,
выполнить стандартные статистические расчеты. Для таблицы по анализируемому
изотопу рассчитывались арифметические средние и дисперсии измерений четырех
стандартных образцов содержания плутония, дисперсии сравнивались по критерию
Фишера, определялся вид модели погрешностей измерения. Затем с использованием однофакторного
дисперсионного анализа определялись случайная и систематическая составляющие
погрешностей измерения по следующему алгоритму. Если в ![]() ввести
следующие обозначения:
ввести
следующие обозначения: ![]()
![]() и считать,
что
и считать,
что ![]() -
распределено по нормальному закону (индекс «R»
относится к случайной составляющей погрешностей измерения, a «S» - к систематической), то
получим:
-
распределено по нормальному закону (индекс «R»
относится к случайной составляющей погрешностей измерения, a «S» - к систематической), то
получим:
![]()
![]()
![]()
Здесь k = 4 - число стандартных образцов в комплекте; n = 88 - количество измерений образцов одного содержания плутония;
![]() -
для i-го образца j-го содержания разность между измеренным с помощью U-Pu Inspector значением и значением,
полученным в аналитической лаборатории;
-
для i-го образца j-го содержания разность между измеренным с помощью U-Pu Inspector значением и значением,
полученным в аналитической лаборатории; ![]()
![]()
Аналогично обрабатывались результаты измерений без декларации содержания Pu-242. Только в этом случае анализировались таблицы размером 11×4.
Результаты обработки приведены в таблицах ниже (в каждой ячейке таблицы последовательно записаны данные для образцов состава № 1, № 2, № 3 и № 4).
Таблица П1.1
Результаты анализа измерений с декларацией содержания Pu-242
|
Изотоп Характеристика |
Pu-238 |
Pu-239 |
Pu-240 |
Pu-241 |
Am-241 |
|
Среднее квадратическое отклонение, характеризующее неоднородность материала стандартного образца σн - по каждому изотопу для образцов одного содержания плутония. |
1,44 ∙ 10-4 |
1,49 ∙ 10-2 |
1,48 ∙ 10-2 |
1,59 ∙ 10-4 |
1,05 ∙ 10-4 |
|
1,65 ∙ 10-4 |
0,93 ∙ 102 |
0,94 ∙ 10-2 |
2,49 ∙ 10-4 |
0,96 ∙ 10-4 |
|
|
2,37 ∙ 10-4 |
2,13 ∙ 10-2 |
2,00 ∙ 10-2 |
1,98 ∙ 10-4 |
1,57 ∙ 10-4 |
|
|
1,76 ∙ 10-4 |
1,56 ∙ 10-2 |
1,47 ∙ 10-2 |
3,66 ∙ 10-4 |
1,43 ∙ 10-4 |
|
|
Случайная составляющая погрешностей измерения по каждому изотопу для образцов одного содержания плутония. |
3,81 ∙ 10-4 |
3,33 ∙ 10-2 |
3,33 ∙ 10-2 |
3,94 ∙ 10-4 |
2,9 ∙ 10-4 |
|
5,36 ∙ 10-4 |
3,61 ∙ 10-2 |
3,58 ∙ 10-2 |
6,63 ∙ 10-4 |
3,4 ∙ 10-4 |
|
|
6,21 ∙ 10-4 |
5,29 ∙ 10-2 |
5,22 ∙ 10-2 |
8,24 ∙ 10-4 |
3,3 ∙ 10-4 |
|
|
6,00 ∙ 10-4 |
5,35 ∙ 10-2 |
5,27 ∙ 10-2 |
9,15 ∙ 10-4 |
3,3 ∙ 10-4 |
|
|
Систематическая составляющая погрешностей измерения по каждому изотопу для образцов одного содержания плутония. |
4,11 ∙ 10-4 |
3,94 ∙ 10-3 |
3,85 ∙ 10-3 |
2,50 ∙ 10-4 |
3,05 ∙ 10-5 |
|
2,18 ∙ 10-4 |
2,75 ∙ 10-3 |
2,75 ∙ 10-3 |
1,39 ∙ 10-4 |
1,80 ∙ 10-5 |
|
|
2,84 ∙ 10-4 |
2,61 ∙ 10-3 |
2,56 ∙ 10-3 |
1,62 ∙ 10-4 |
2,60 ∙ 10-5 |
|
|
2,32 ∙ 10-4 |
4,23 ∙ 10-3 |
4,22 ∙ 10-3 |
2,03 ∙ 10-4 |
2,05 ∙ 10-5 |
|
|
Доверительные границы (интервал) случайной погрешности результата измерений δ по каждому изотопу для образцов одного содержания плутония. |
0,83 ∙ 10-4 |
0,72 ∙ 10-2 |
3,72 ∙ 10-2 |
0,83 ∙ 10-4 |
6,2 ∙ 10-5 |
|
1,17 ∙ 10-4 |
0,77 ∙ 10-2 |
0,77 ∙ 10-2 |
1,40 ∙ 10-4 |
7,2 ∙ 10-5 |
|
|
1,35 ∙ 10-4 |
1,14 ∙ 10-2 |
1,12 ∙ 10-2 |
1,74 ∙ 10-4 |
7,1 ∙ 10-5 |
|
|
1,31 ∙ 10-4 |
1,15 ∙ 10-2 |
1,13 ∙ 10-2 |
1,93 ∙ 10-4 |
7,0 ∙ 10-5 |
|
|
Верхняя граница относительного среднего квадратического отклонения результатов определений BSr по каждому изотопу для образцов одного содержания плутония. |
1,01 ∙ 10-2 |
3,56 ∙ 10-4 |
0,59 ∙ 10-2 |
0,41 ∙ 10-2 |
3,76 ∙ 10-2 |
|
0,32 ∙ 10-2 |
4,03 ∙ 10-4 |
0,38 ∙ 10-2 |
0,32 ∙ 10-2 |
5,56 ∙ 10-2 |
|
|
0,29 ∙ 10-2 |
6,27 ∙ 10-4 |
0,37 ∙ 10-2 |
0,29 ∙ 10-2 |
8,51 ∙ 10-2 |
|
|
0,32 ∙ 10-2 |
6,81 × 10-4 |
0,26 ∙ 10-2 |
0,28 ∙ 10-2 |
7,08 ∙ 10-2 |
|
|
Доверительные границы погрешности результата анализа ΔАсо по каждому изотопу для образцов одного содержания плутония. |
4,19 ∙ 10-4 |
8,21 ∙ 10-3 |
8,17 ∙ 10-3 |
2,63 ∙ 10-4 |
6,91 ∙ 10-5 |
|
2,47 ∙ 10-4 |
8,18 ∙ 10-3 |
8,18 ∙ 10-3 |
1,97 ∙ 10-4 |
7,42 ∙ 10-5 |
|
|
3,14 ∙ 10-4 |
11,70 ∙ 10-3 |
11,49 ∙ 10-3 |
2,38 ∙ 10-4 |
7,56 ∙ 10-5 |
|
|
2,66 ∙ 10-4 |
12,25 ∙ 10-3 |
12,06 ∙ 10-3 |
2,80 ∙ 10-4 |
7,29 ∙ 10-5 |
|
|
Доверительные границы погрешности с учетом неоднородности образцов Δсо по каждому изотопу для образцов одного содержания плутония. |
5,05 ∙ 10-4 |
3,03 ∙ 10-2 |
3,01 ∙ 10-2 |
4,08 ∙ 10-4 |
2,17 ∙ 10-4 |
|
4,07 ∙ 10-4 |
2,00 ∙ 10-2 |
2,02 ∙ 10-2 |
5,26 ∙ 10-4 |
2,02 ∙ 10-4 |
|
|
5,61 ∙ 10-4 |
4,34 ∙ 10-2 |
4,08 ∙ 10-2 |
4,55 ∙ 10-4 |
3,17 ∙ 10-4 |
|
|
4,36 ∙ 10-4 |
3,29 ∙ 10-2 |
3,12 ∙ 10-2 |
7,70 ∙ 10-4 |
2,90 ∙ 10-4 |
Таблица П1.2
Результаты анализа измерений без декларации содержания Pu-242
|
Изотоп Характеристика |
Pu-238 |
Pu-239 |
Pu-240 |
Pu-241 |
Pu-242 |
Am-241 |
|
Среднее квадратическое отклонение, характеризующее неоднородность материала стандартного образца σн - по каждому изотопу для образцов одного содержания плутония. |
3,30 ∙ 10-4 |
2,17 ∙ 10-2 |
2,16 ∙ 10-2 |
3,82 ∙ 10-4 |
0,99 ∙ 10-4 |
2,10 ∙ 10-4 |
|
6,17 ∙ 10-4 |
2,19 ∙ 10-2 |
2,15 ∙ 10-2 |
6,58 ∙ 10-4 |
1,04 ∙ 10-4 |
3,52 ∙ 10-4 |
|
|
5,05 ∙ 10-4 |
6,20 ∙ 10-2 |
6,12 ∙ 10-2 |
5,43 ∙ 10-4 |
7,70 ∙ 10-4 |
3,33 ∙ 10-4 |
|
|
3,81 ∙ 10-4 |
5,09 ∙ 10-2 |
4,78 ∙ 10-2 |
10,13 ∙ 10-4 |
32,62 ∙ 10-4 |
3,85 ∙ 10-4 |
|
|
Случайная составляющая погрешностей измерения по каждому изотопу для образцов одного содержания плутония. |
3,23 ∙ 10-4 |
2,10 ∙ 10-2 |
2,16 ∙ 10-2 |
3,87 ∙ 10-4 |
0,44 ∙ 10-4 |
5,26 ∙ 10-3 |
|
6,04 ∙ 10-4 |
2,12 ∙ 10-2 |
2,15 ∙ 10-2 |
6,67 ∙ 10-4 |
0,46 ∙ 10-4 |
8,81 ∙ 10-3 |
|
|
4,95 ∙ 10-4 |
6,00 ∙ 10-2 |
6,11 ∙ 10-2 |
5,50 ∙ 10-4 |
3,41 ∙ 10-4 |
8,34 ∙ 10-3 |
|
|
3,73 ∙ 10-4 |
4,92 ∙ 10-2 |
4,77 ∙ 10-2 |
10,27 ∙ 10-4 |
14,44 ∙ 10-4 |
9,63 ∙ 10-3 |
|
|
Систематическая составляющая погрешностей измерения по каждому изотопу для образцов одного содержания плутония. |
1,07 ∙ 10-3 |
2,48 ∙ 10-2 |
1,08 ∙ 10-2 |
6,76 ∙ 10-4 |
2,29 ∙ 10-2 |
6,36 ∙ 10-3 |
|
0,57 ∙ 10-3 |
1,70 ∙ 10-2 |
0,77 ∙ 10-2 |
3,77 ∙ 10-4 |
1,22 ∙ 10-2 |
3,61 ∙ 10-3 |
|
|
0,74 ∙ 10-3 |
1,61 ∙ 10-2 |
0,72 ∙ 10-2 |
4,38 ∙ 10-4 |
1,63 ∙ 10-2 |
3,73 ∙ 10-3 |
|
|
0,60 ∙ 10-3 |
2,61 ∙ 10-2 |
1,18 ∙ 10-2 |
5,50 ∙ 10-4 |
1,54 ∙ 10-2 |
3,68 ∙ 10-3 |
|
|
Доверительные границы (интервал) случайной погрешности результата измерений ε по каждому изотопу для образцов одного содержания плутония. |
2,33 ∙ 10-4 |
1,53 ∙ 10-2 |
1,52 ∙ 10-2 |
2,69 ∙ 10-4 |
0,70 ∙ 10-4 |
1,48 ∙ 10-4 |
|
4,34 ∙ 10-4 |
1,54 ∙ 10-2 |
1,57 ∙ 10-2 |
4,64 ∙ 10-4 |
0,74 ∙ 10-4 |
2,48 ∙ 10-4 |
|
|
3,56 ∙ 10-4 |
4,37 ∙ 10-2 |
4,31 ∙ 10-2 |
3,83 ∙ 10-4 |
5,43 ∙ 10-4 |
2,35 ∙ 10-4 |
|
|
2,68 ∙ 10-4 |
3,59 ∙ 10-2 |
3,37 ∙ 10-2 |
7,14 ∙ 10-4 |
22,99 ∙ 10-4 |
2,71 ∙ 10-4 |
|
|
Верхняя граница относительного среднего квадратического отклонения результатов определений BSr по каждому изотопу для образцов одного содержания плутония. |
1,00 ∙ 10-2 |
2,69 ∙ 10-4 |
4,48 ∙ 10-3 |
4,62 ∙ 10-3 |
6,59 ∙ 10-3 |
3,14 ∙ 10-2 |
|
0,42 ∙ 10-2 |
2,83 ∙ 10-4 |
2,66 ∙ 10-3 |
3,77 ∙ 10-3 |
3,25 ∙ 10-3 |
6,71 ∙ 10-2 |
|
|
0,27 ∙ 10-2 |
8,52 ∙ 10-4 |
5,02 ∙ 10-3 |
2,29 ∙ 10-3 |
3,18 ∙ 10-3 |
9,97 ∙ 10-2 |
|
|
0,23 ∙ 10-2 |
7,55 ∙ 10-4 |
2,79 ∙ 10-3 |
3,69 ∙ 10-3 |
5,87 ∙ 10-3 |
9,47 ∙ 10-2 |
|
|
Доверительные границы погрешности результата анализа ΔАсо по каждому изотопу для образцов одного содержания плутония. |
1,10 ∙ 10-3 |
2,91 ∙ 10-2 |
1,86 ∙ 10-2 |
7,28 ∙ 10-4 |
2,29 ∙ 10-2 |
6,36 ∙ 10-3 |
|
0,72 ∙ 10-3 |
2,29 ∙ 10-2 |
1,75 ∙ 10-2 |
5,98 ∙ 10-4 |
1,22 ∙ 10-2 |
3,62 ∙ 10-3 |
|
|
0,82 ∙ 10-3 |
4,66 ∙ 10-2 |
4,37 ∙ 10-2 |
5,82 ∙ 10-4 |
1,63 ∙ 10-2 |
3,74 ∙ 10-3 |
|
|
0,66 ∙ 10-3 |
4,44 ∙ 10-2 |
3,57 ∙ 10-2 |
9,01 ∙ 10-4 |
1,56 ∙ 10-2 |
3,69 ∙ 10-3 |
|
|
Доверительные границы погрешности с учетом неоднородности образцов Δсо по каждому изотопу для образцов одного содержания плутония. |
1,27 ∙ 10-3 |
5,16 ∙ 10-2 |
4,63 ∙ 10-2 |
1,04 ∙ 10-3 |
2,29 ∙ 10-2 |
6,38 ∙ 10-3 |
|
1,41 ∙ 10-3 |
4,87 ∙ 10-2 |
4,56 ∙ 10-2 |
1,42 ∙ 10-3 |
1,22 ∙ 10-2 |
3,68 ∙ 10-3 |
|
|
1,29 ∙ 10-3 |
13,01 ∙ 10-2 |
12,77 ∙ 10-2 |
1,21 ∙ 10-3 |
1,64 ∙ 10-2 |
3,79 ∙ 10-3 |
|
|
1,00 ∙ 10-3 |
10,92 ∙ 10-2 |
10,03 ∙ 10-2 |
2,18 ∙ 10-3 |
1,68 ∙ 10-2 |
3,77 ∙ 10-3 |
Рассчитанные значения параметров калибровочных характеристик y = ах + b, где у - измеряемое значение содержания изотопа Pu, a x - полученное в аналитической лаборатории, приведены в таблицах ниже.
Таблица П1.3
Характеристики статистических моделей для измерений с декларацией содержания Pu-242
|
Изотоп Характеристика |
Pu-238 |
Pu-239 |
Pu-240 |
Pu-241 |
|
Параметр а (стандартная ошибка параметра). |
1,023 (3,13 ∙ 10-3) |
1,007 (0,44 ∙ 10-3) |
1,007 (0,45 ∙ 10-3) |
0,992 (1,58 ∙ 10-3) |
|
Параметр b (стандартная ошибка параметра). |
-4,97 ∙ 10-3 (5,37 ∙ 10-4) |
-6,99 ∙ 10-1 (3,85 ∙ 10-2) |
-2,86 ∙ 10-2 (6,08 ∙ 10-3) |
-8,72 ∙ 10-3 (3,95 ∙ 10-4) |
|
Обусловленная регрессией сумма квадратов SSD. |
1,72 |
1,11 ∙ 104 |
1,03 ∙ 104 |
2,56 |
|
Остаточная сумма квадратов SSR. |
5,65 ∙ 10-3 |
0,746 |
0,730 |
2,26 ∙ 10-3 |
|
Коэффициент корреляции r. |
0,998 |
0,999 |
0,999 |
0,999 |
Таблица П1.4
Характеристики статистических моделей для измерений без декларации содержания Pu-242
|
Изотоп Характеристика |
Pu-238 |
Pu-239 |
Pu-240 |
Pu-241 |
Pu-242 |
|
Параметр а (стандартная ошибка параметра). |
1,021 (8,14 ∙ 10-3) |
1,034 (2,79 ∙ 10-3) |
1,002 (1,26 ∙ 10-3) |
0,987 (4,25 ∙ 10-3) |
2,259 (0,338) |
|
Параметр b (стандартная ошибка параметра). |
-4,98 ∙ 10-3 (1,40 ∙ 10-3) |
-3,032 (0,244) |
0,017 (0,017) |
-7,76 ∙ 10-3 (1,07 ∙ 10-3) |
-0,152 (0,066) |
|
Обусловленная регрессией сумма квадратов SSD. |
0,214 |
1465 |
1278 |
0,316 |
1,473 |
|
Остаточная сумма квадратов SSR. |
5,72 ∙ 10-4 |
0,449 |
0,085 |
2,46 ∙ 10-4 |
1,386 |
|
Коэффициент корреляции r. |
0,999 |
0,999 |
0,999 |
0,999 |
0,718 |
На рассмотренном примере продемонстрировано как по экспериментальным данным путем их обработки рассчитать характеристики погрешности результатов определения содержания изотопов в образцах; оценить параметры калибровочных характеристик для различных алгоритмов обработки спектров: когда содержание Pu-242 декларируется до начала измерения, а также для случая без такой декларации.
При сопоставлении характеристик погрешности результатов определения содержания изотопов в стандартных образцах отмечается ухудшение большинства этих характеристик при использовании алгоритма без декларации содержания Pu-242. Это наиболее заметно для Am-241.
Для всех изотопов Pu регрессионные модели для уровня значимости 0,05 оказались адекватны экспериментальным данным как в случае декларации содержания Pu-242, так и без таковой. Для Pu-242 качество регрессионной модели оказалось ниже, чем для других изотопов Pu. Угол наклона калибровочной характеристики для Pu-242 существенно отличается от 45°, а для Pu-239 эта характеристика существенно смещается вниз для случая программного определения содержания Pu-242 в образцах.
При анализе составляющих погрешностей измерения отмечается тенденция к уменьшению систематической составляющей для Pu-238 с увеличением содержания этого изотопа при использовании обоих алгоритмов обработки спектров. Случайная составляющая для Pu-239 уменьшается, а для остальных изотопов Pu увеличивается с увеличением содержания соответствующего изотопа в случае использования алгоритма обработки спектров с декларацией содержания Pu-242. Других тенденций к увеличению (уменьшению) составляющих погрешностей для уровня значимости 0,05 не выявлено.
Характеристики погрешности результатов определения содержания изотопов Pu, приведенные в настоящем приложении, а также выявленные особенности предлагаемых разработчиками программного обеспечения алгоритмов обработки спектров целесообразно учитывать при решении задач учета и контроля ЯМ.
Приложение № 2
к Положению по применению
методов математической
статистики для учета и контроля
ядерных материалов,
утвержденному приказом
Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Порядок расчета объема выборок
Объем выборки задается двумя величинами: пороговым количеством ЯМ в единицах массы (G) и вероятностью обнаружения недостачи/излишка порогового количества ЯМ в безотносительных единицах (Р). Эти величины определяются в соответствии с Основными правилами учета и контроля ядерных материалов (НП-030-11). Результаты проверки целостности неразборных УЕ, а также состояния СКД документируются на предмет документального подтверждения отсутствия несанкционированного доступа.
Перед расчетом объема выборки определяется отношение G/x.
Расчет объема выборки (n) осуществляется следующим образом:
при величине G/x ≤ N, объем выборки (n)
рассчитывается по формуле
![]() (П2.1)
(П2.1)
N - количество УЕ в страте;
х - средняя масса ЯМ в одной УЕ;
[ ]+ - в формуле означает округление до ближайшего большего целого числа.
при величине G/x > N проверке подлежат все учетные единицы.
Определение объема выборки проверяемых пломб согласно пункту 25 настоящего Положения осуществляется с помощью уравнения n = [N(1 - (1 - 0,95)1/(0,05N))]+; где N - количество установленных пломб в ЗБМ. Здесь [ ]+ также означает округление до ближайшего большего целого числа. Ниже приведены результаты такого расчета для нескольких значений N.
|
Всего пломб, штук |
Число пломб, работоспособность и состояние которых проверяется |
|
10 |
10 |
|
20 |
19 |
|
50 |
35 |
|
100 |
46 |
|
1000 |
59 |
|
10000 |
60 |
Пример расчета объема выборки
Пусть в ЗБМ находятся три страты ЯМ, в каждой из которых содержится 1000 УЕ. Под стратой понимается совокупность отдельных УЕ с одинаковыми или близкими физическими характеристиками и химическим составом ЯМ для осуществления статистической выборки. На практике, в страты обычно выделяют: ТВС одной партии, либо однотипные ТВС; одинаковые в пределах технических условий УЕ для формирования критических (подкритических) сборок; партии одинаковых продуктов, на которые оформляется общий паспорт и т.д. В научно-исследовательских организациях, а также в организациях, где номенклатура используемых ЯМ велика, количество таких страт может оказаться значительным.
Пусть в нашем примере первая и вторая страты представлены одинаковыми УЕ, содержащими металлический высокообогащенный уран в алюминиевой оболочке с номерами, выполненными электроискровым карандашом. Подобным образом выполнены УЕ третьей страты, содержащие металлический низкообогащенный уран. В каждой из УЕ, содержащих высокообогащенный и низкообогащенный уран, находится по 1000 г 235U. Пусть УЕ первой страты в данный МБП после использования в эксперименте были извлечены из критсборки, помещены в трубы как в контейнеры, трубы опечатаны после регистрации соответствующих учетных данных, а УЕ второй и третьей страт в данный МБП не использовались, и находились в опечатанных трубах с момента предыдущей инвентаризации. Таким образом, для первой страты вероятность обнаружения недостачи/излишка порогового количества ЯМ принимается равной 0,5, а для второй и третьей страт - равной 0,25, так как материалы второй и третьей страт находились еще и под системой наблюдения. Такой выбор вероятности обнаружения для каждой из страт рекомендуется делать при условии, что результаты проверки целостности неразборных УЕ, а также состояния СКД документируются на предмет документального подтверждения отсутствия несанкционированного доступа.
Поскольку отношение G/x для первой и второй страт 8000/1000 = 8, а для третьей 70000/1000 = 70 и во всех случаях G/x ≤ N (значение N для каждой из страт равно 1000), то для расчета объема выборки во всех случаях используем формулу (П2.1).
В соответствии с формулой (П2.1) и параметрами G и Р для первой страты объем выборки составит:
n1 = 1000[1 - (1 - 0,5)1000/8000] = 1000[1 - (0,5)1/81 = 1000 ∙ 0,0830 = 83,0.
Для второй страты:
n2 = 1000[1 - (1 - 0,25)1000/8000] = 1000[1 - (0,75)1/8] = 1000 ∙ 0,0353 = 35,3, но, округляя n2 до ближайшего большего целого, получаем n2 = 36,0.
Для третьей страты:
n3 = 1000[1 - (1 - 0,25)1000/70000] = 1000[1 - (0,75)1/70] = 1000 ∙ 0,0041 = 0,4, но, округляя n3 до ближайшего большего целого, получаем n3 = 1,0.
Таким образом, всего должно быть подвергнуто измерениям:
83 + 36 + 1 = 120 учетных единиц.
Приложение № 3
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Анализ характеристик выборочного распределения
В табл. П3.1 приведены значения tk,1-α коэффициента для уровня значимости α и различных степеней свободы k.
Если случайная величина х распределена нормально с
математическим ожиданием α, то
по выборке объема и (х1, х2, ..., хп) можно найти доверительные границы для α следующим образом: ![]() где k = п - 1.
где k = п - 1.
Таблица П3.1
Значения коэффициента Стьюдента ta,k
|
1 - α k |
0,80 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,999 |
|
2 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
14,09 |
31,60 |
|
3 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
7,453 |
12,92 |
|
4 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
5,598 |
8,610 |
|
5 |
1,476 |
2,015 |
2,571 |
3,365 |
4,032 |
4,773 |
6,869 |
|
6 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
4,317 |
5,959 |
|
7 |
1,415 |
1,895 |
2,365 |
2,998 |
3,500 |
4,029 |
5,408 |
|
8 |
1,397 |
1,860 |
2,306 |
2,897 |
3,355 |
3,833 |
5,041 |
|
9 |
1,383 |
1,833 |
2,262 |
2,821 |
3,325 |
3,690 |
4,781 |
|
10 |
1,372 |
1,813 |
2,228 |
2,764 |
3,169 |
3,581 |
4,587 |
|
11 |
1,363 |
1,796 |
2,201 |
2,718 |
3,106 |
3,497 |
4,437 |
|
12 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
3,423 |
4,318 |
|
13 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
3,373 |
4,221 |
|
14 |
1,345 |
1,761 |
2,145 |
2,625 |
2,977 |
3,326 |
4,141 |
|
15 |
1,341 |
1,753 |
2,131 |
2,603 |
2,947 |
3,286 |
4,073 |
|
16 |
1,337 |
1,746 |
2,120 |
2,584 |
2,921 |
3,252 |
4,015 |
|
17 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,222 |
3,965 |
|
18 |
1,330 |
1,734 |
2,101 |
2,552 |
2,878 |
3,197 |
3,922 |
|
19 |
1,328 |
1,729 |
2,093 |
2,540 |
2,861 |
3,174 |
3,883 |
|
20 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,153 |
3,850 |
|
22 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,119 |
3,792 |
|
24 |
1,318 |
1,711 |
2,064 |
2,492 |
2,797 |
3,091 |
3,745 |
|
26 |
1,315 |
1,706 |
2,056 |
2,479 |
2,770 |
3,067 |
3,707 |
|
28 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,047 |
3,674 |
|
30 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,030 |
3,646 |
|
40 |
1,303 |
1,684 |
2,021 |
2,423 |
2,705 |
2,971 |
3,551 |
|
50 |
1,299 |
1,676 |
2,009 |
2,403 |
2,678 |
2,937 |
3,496 |
|
60 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
2,915 |
3,460 |
|
80 |
1,292 |
1,664 |
1,990 |
2,374 |
2,639 |
2,887 |
3,416 |
|
100 |
1,290 |
1,660 |
1,984 |
2,364 |
2,626 |
2,871 |
3,391 |
|
150 |
1,287 |
1,655 |
1,976 |
2,352 |
2,609 |
2,849 |
3,357 |
|
200 |
1,286 |
1,653 |
1,972 |
2,345 |
2,601 |
2,839 |
3,340 |
|
300 |
1,284 |
1,650 |
1,968 |
2,339 |
2,592 |
2,828 |
3,323 |
|
500 |
1,283 |
1,648 |
1,965 |
2,334 |
2,586 |
2,820 |
3,310 |
|
¥ |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
2,807 |
3,291 |
Пример.
Масса изделий подчиняется нормальному закону. Имеется
статистический материал для n = 25
образцов, по которым найдено ![]() a s = 600 г.
Найти для α = 0,9 доверительные границы для математического ожидания массы
генеральной совокупности образцов.
a s = 600 г.
Найти для α = 0,9 доверительные границы для математического ожидания массы
генеральной совокупности образцов.
Решение. По табл. П3.1 для α = 0,90 и k = п - 1 = 24 находим tα,k = 1,711, и определяем доверительные границы для математического ожидания следующим образом:
![]()
Таким образом, образцы, результаты измерения которых находятся в пределах рассчитанных доверительных границ, могут быть объединены при α = 0,9 в одну страту для проведения выборочных измерений с целью уменьшения объема измерений при проверке страты.
Приложение № 4
Положению по применению
методов математической
статистики для учета и контроля
ядерных материалов,
утвержденному приказом
Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Рекомендуемый порядок применения контрольного допуска
С помощью гамма-спектрометрической станции U-Pu Inspector с низкоэнергетическим германиевым детектором измерен образец с процентным содержанием Pu-239, равным по данным разрушающего анализа 85,06 ± 0,06 (учетные данные). Для получения учетных данных согласно требованию Основных правил учета и контроля ядерных материалов (НП-030-11), методики выполнения измерений должны быть метрологически аттестованы в соответствии с требованиями документов в области стандартизации (границы погрешности измерений устанавливаются для доверительной вероятности 95 %).
Для получения данных об изотопном составе с помощью гамма - спектрометрической станции U-Pu Inspector с низкоэнергетическим германиевым детектором спектр обрабатывается с помощью программного обеспечения станции MGA. Для определения границ погрешности измерения использовалась методика: Плутоний и его соединения. Методика выполнения измерений массовых долей изотопов плутония и изотопа америций-241 в плутонии гамма-спектрометрическим методом с использованием гамма-спектрометра U-Pu Inspector. МВИ 223.13.17.104/2006 (границы погрешности измерений по этой методике устанавливаются для доверительной вероятности 95 %). Результат, полученный с использованием названной методики, оказался равным: 85,05 ± 0,05.
Поскольку все погрешности документируются и рассчитываются при 95 % доверительной вероятности, то для получения среднеквадратических погрешностей значения 0,06 и 0,05 должны быть уменьшены в 1,96 раза. Таким образом,
![]()
Расхождение учетных данных и результата подтверждающих измерений составляет 0,01 и находится в пределах контрольного допуска 0,10.
Примеры сравнения двух выборочных дисперсий и средних
При необходимости объединения данных по двум или нескольким
партиям ЯМ рекомендуется проводить сравнение выборочных дисперсий и средних.
Случай двух партий рассмотрен ниже. В результате проведения учетных измерений
двух партий, в состав которых входят n1 = 30
и n2 = 20
УЕ, найдены выборочные значения математического ожидания и дисперсии массы
учитываемого нуклида в этих УЕ. Значения этих величин составили: ![]()
![]()
![]()
![]() Требуется
оценить значимость расхождения выборочных дисперсий.
Требуется
оценить значимость расхождения выборочных дисперсий.
В рассматриваемом примере ![]() при числе степеней свободы 29 и 19. Это
говорит об отсутствии значимого различия в дисперсиях массы учитываемого
нуклида в УЕ первой и второй выборок. То есть можно принять, что данные выборки
могут быть объединены по критерию равенства дисперсий после проверки равенства
средних.
при числе степеней свободы 29 и 19. Это
говорит об отсутствии значимого различия в дисперсиях массы учитываемого
нуклида в УЕ первой и второй выборок. То есть можно принять, что данные выборки
могут быть объединены по критерию равенства дисперсий после проверки равенства
средних.
Для этого определим объединенную оценку выборочной дисперсии:
![]()
и значение t статистики:

Т.к. ![]() при числе степеней свободы 48, то можно принять, что
при числе степеней свободы 48, то можно принять, что ![]() а значение объединенной
оценки выборочного среднего равно:
а значение объединенной
оценки выборочного среднего равно:
![]()
Приложение № 5
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Примеры расчета σо-п, а также алгоритм оценки значимости систематических расхождений.
Примеры расчета σo-n:
Допустим, полные погрешности весов, приведенные к доверительной вероятности 0,99 составляют:
а) отправителя ±75 г, получателя ±50 г; тогда
![]()
б) отправителя ±0,2 %, получателя ±0,3 %, а измеряемая масса 25 кг; тогда
![]()
в) отправителя ±0,075 кг, получателя ±0,3 %, а измеряемая масса 25 кг; тогда
![]()
Алгоритм оценки значимости систематических расхождений
Для проверки значимости систематических расхождений между данными отправителя mотп и получателя mпол рекомендуется пользоваться парным критерием Стьюдента. Для этого вычислить:
- наблюдаемые парные разности di = (mотп)i - (mпол)i
- среднее значение парных разностей ![]() где n - количество пар (mотп)i,
(mпол)i
где n - количество пар (mотп)i,
(mпол)i
- среднее квадратическое отклонение среднего значения парных
разностей 
- наблюдаемый критерий ![]()
При выполнении условия tн > t(P, f), где t(P, f) - табличное значения коэффициента Стьюдента при доверительной вероятности Р и числе степеней свободы f = n - 1, нулевая гипотеза H0:тотп = тпол отвергается.
Пример. В таблице ниже приведены данные масс брутто отправителя и получателя пятнадцати контейнеров с ЯМ. Допустимые расхождения, вычисленные по паспортным данным, не должны превышать 15 условных единиц.
Таблица
|
№ п/п |
momn |
mпол |
d = momn - mпол |
|
|
Z |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
282 |
290 |
-8 |
-0,3 |
0,09 |
286,0 |
|
2 |
347 |
350 |
-3 |
4,7 |
22,09 |
348,5 |
|
3 |
286 |
296 |
-10 |
-2,3 |
5,29 |
291,0 |
|
4 |
319 |
326 |
-7 |
0,7 |
0,49 |
322,5 |
|
5 |
337 |
346 |
-9 |
-1,3 |
1,69 |
341,5 |
|
6 |
290 |
300 |
-10 |
-2,3 |
5,29 |
295,0 |
|
7 |
301 |
300 |
1 |
8,7 |
75,69 |
300,5 |
|
8 |
314 |
323 |
-9 |
-1,3 |
1,69 |
318,5 |
|
9 |
373 |
380 |
-7 |
0,7 |
0,49 |
376,5 |
|
10 |
236 |
246 |
-10 |
-2,3 |
5,29 |
241,0 |
|
11 |
361 |
370 |
-9 |
-1,3 |
1,69 |
365,5 |
|
12 |
333 |
340 |
-7 |
0,7 |
0,49 |
336,5 |
|
13 |
292 |
302 |
-10 |
-2,3 |
5,29 |
297,0 |
|
14 |
340 |
347 |
-7 |
0,7 |
0,49 |
343,5 |
|
15 |
320 |
330 |
-10 |
-2,3 |
5,29 |
325,0 |
|
Σ |
4731 |
4846 |
-115 |
0,5 |
131,35 |
4788,5 |
Из таблицы видно, что все наблюдаемые расхождения не превышают величину допустимых расхождений, но почти все расхождения имеют один знак, что свидетельствует о наличии не исключенных систематических погрешностей в данных отправителя или (и) получателя.
Проверим значимость систематических расхождений.
По данным столбцов 2 и 3 вычисляем d1 = (mотп)i - (mпол)i, и заполняем столбец 5.
По данным столбца 4 вычисляем
![]()
По данным столбца 4 вычисляем ![]() и
и ![]() заполняем столбцы 5
и 6 и вычисляем
заполняем столбцы 5
и 6 и вычисляем 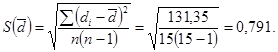
Вычисляем наблюдаемый критерий
![]()
Критическое значение коэффициента Стьюдента при доверительной вероятности 0,99 и числе степеней свободы 14 равно 2,9768.
Так как условие tн = 9,7362 > t(0,99, 14) = 2,9768 соблюдается, то нулевая гипотеза Н0:тотп = тпол отвергается. Следовательно, между данными отправителя и получателя наблюдаются значимые систематические расхождения, и до выяснения причин расхождений взаиморасчеты рекомендуется проводить по средним значениям Z, значения которых приведены в столбце 7 таблицы.
Приложение № 6
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
П6.1 Абсолютная погрешность измерения
По определению абсолютная погрешность есть
Δ = Хизм - Хист, (П6.1)
где: Хизм - измеренная величина;
Хист - истинное значение.
Абсолютная погрешность Δ выражается в единицах измеряемой величины. Значение установленной погрешности Δ для МВИ или средств измерений является неизменной во всем измеряемом (установленном) диапазоне. Например, Δ = 0,25 грамм для весов означает, что во всем измеряемом диапазоне эта декларируемая погрешность остается постоянной.
Взвешивание 1 кг осуществляется с погрешностью 0,25 г, взвешивание 10 кг также осуществляется с погрешностью 0,25 г.
График зависимости погрешности измерения от измеряемой величины показан на рис. П6.1.

Рис. П6.1. Зависимость погрешности измерения от измеряемой величины.
В общем случае значение абсолютной погрешности не зависит от значения измеряемой величины (свойство аддитивности). На практике производитель средства измерения может определить различные значения абсолютной погрешности для разных диапазонов измеряемых значений (например: от 1 до 100 грамм - 0,5 грамм, а от 100 до 500 грамм - 1 грамм).
П6.2 Относительная погрешность измерения
По определению относительная погрешность есть
![]() (П6.2)
(П6.2)
Относительная погрешность является безразмерной величиной, допускается запись ее значений в процентах.
Значение установленной погрешности δ для МВИ или средства измерений является неизменной во всем измеряемом (установленном) диапазоне. Например, δ = 0,05 % для весов означает, что во всем измеряемом диапазоне эта декларируемая погрешность остается постоянной. Взвешивание 1 кг осуществляется с погрешностью 0,05 %, что составляет 0,5 г, взвешивание 10 кг также осуществляется с погрешностью 0,05 %, что составляет 5 г. В данном случае значение абсолютной погрешности прямо пропорционально измеряемой величине (свойство мультипликативности).
График зависимости погрешности измерения от измеряемой величины показан на рис. П6.2.
Рис. П6.2. Зависимость погрешности измерения от измеряемой величины.
П6.3 Аддитивная модель погрешности измерения, связь с абсолютной погрешностью измерения
Абсолютная погрешность измерения структурируется и представляется как сумма систематической и случайной составляющих погрешности
Δ = S + R, (П6.3)
где: S - систематическая составляющая погрешности, имеет размерность измеряемой величины;
R - случайная составляющая погрешности, имеет размерность измеряемой величины.
Подставив правую часть выражения (П6.3) в (П6.1) и сделав преобразования, получим:
Xизм = Xист + S + R. (П6.4)
Выражение (П6.4) есть аддитивная модель погрешности измерения. Это есть другая запись абсолютной погрешности измерения с учетом выделения систематической и случайной составляющих.
Свойство модели (П6.4) со статистической точки зрения:
Хист - детерминированная величина;
S - случайная величина, как правило подчиняющаяся нормальному закону распределения N(0, σS);
R - случайная величина, как правило подчиняющаяся нормальному закону распределения N(0, σR);
Дисперсия погрешности из (П6.4) будет:
σ2(Хизм - Хист) = ![]() (П6.5)
(П6.5)
где: σS - СКО систематической составляющей погрешности (имеет размерность измеряемой величины);
σR - СКО случайной составляющей погрешности (имеет размерность измеряемой величины).
Значения σS и σR
необходимо вычислить по известным интервальным оценкам погрешности. Значения
σS и σR
будут использоваться при вычислении ![]()
П6.4 Мультипликативная модель погрешности измерения, связь с относительной погрешностью измерения.
Относительная погрешность измерения структурируется и представляется как сумма систематической и случайной составляющих погрешности:
δ = S + R, (П6.6)
где: S - систематическая составляющая погрешности, безразмерная величина;
R - случайная составляющая погрешности, безразмерная величина.
Подставив правую часть выражения (П6.6) в (П6.2) и сделав преобразования, получим:
Xизм = Xист(1 + S + R). (П6.7)
Выражение (П6.7) есть мультипликативная модель погрешности измерения. Это есть другая запись относительной погрешности измерения с учетом выделения систематической и случайной составляющих.
Свойство модели (П6.7) со статистической точки зрения:
Хист - детерминированная величина;
S - случайная величина, как правило подчиняющаяся нормальному закону распределения N(0,σS);
R - случайная величина, как правило подчиняющаяся нормальному закону распределения N(0,σR).
Дисперсия погрешности из (П6.7) будет:
![]() (П6.8)
(П6.8)
где: σS - СКО систематической составляющей погрешности (безразмерная величина);
σR - СКО случайной составляющей погрешности (безразмерная величина).
Значения σS и σR
необходимо вычислить по известным интервальным оценкам погрешности. Значения
σS и σR будут использоваться при вычислении ![]()
П6.5 Смешанная модель и приведенная погрешность.
Нередко реальные погрешности не описываются ни аддитивной, ни мультипликативной моделями. В одних участках диапазона измерения модель может быть одна, в других - другая. В этих случаях применяют смешанную модель погрешности. Для средств измерения модель погрешности устанавливают при метрологической аттестации.
Принято считать, что для средства измерения на участке диапазона протяженностью до 1 % от его предела модель погрешности можно считать аддитивной. Это допущение позволяет существенно упростить оценки погрешностей с достаточной степенью корректности.
Часто для описания погрешности средства измерения применяют приведенную погрешность, которая равна максимальному значению погрешности по диапазону, отнесенному к пределу измерения (верхнему пределу шкалы). По приведенной погрешности можно оценить максимальную погрешность в диапазоне независимо от ее модели.
Приложение № 7
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Характеристики погрешности измерений*
Таблица № П7.1 - Характеристики погрешности измерений ЯМ
Название ЗБМ: Производство таблеток
|
Группа (страта) ЯМ |
Метод измерения |
Случайная составляющая погрешности |
Систематическая составляющая погрешности |
||||
|
ΔR |
δR |
σR |
Θ (Δ)S |
Θ (δ)S |
σS |
||
|
1 Порошок двуокиси урана 4,4 % |
1 Взвешивание Mettler KE 1500 |
- |
- |
0,0005 отн. ед. |
- |
0,0005 отн. ед. |
|
|
2 Масс. доля U ОСТ 95 175-90 |
- |
0,0014 |
0,00071 отн. ед. |
0,0016 |
0,0008 отн. ед. |
||
|
3 Масс доля U235 ОСТ 95 446-84 |
- |
0,0075 |
0,0038 отн. ед. |
0,0042 |
0,0021 отн. ед. |
||
|
2 Шлиф. отходы 4,4 % |
1 Взвешивание Mettler KB-60s |
- |
- |
0,0005 отн. ед. |
- |
- |
0,0005 отн. ед. |
|
2 Масс. доля U ТУ 002.46-82 |
- |
0,0071 |
0,0036 отн. ед. |
- |
0,0081 |
0,0041 отн. ед. |
|
|
3 Масс доля U235 ОСТ 95 446-84 |
- |
0,0075 |
0,0038 отн. ед. |
- |
0,0042 |
0,0021 отн. ед. |
|
|
3 Таблетки 4,4 % |
1 Взвешивание Mettler KB-32S |
- |
- |
0,0005 отн. ед. |
- |
- |
0,0005 отн. ед. |
|
2 Масс. доля U ОСТ 95 175-90 |
- |
0,0014 |
0,00071 отн. ед. |
- |
0,0016 |
0,0008 отн. ед. |
|
|
3 Масс доля U235 ОСТ 95 446-84 |
- |
0,0075 |
0,0038 отн. ед. |
- |
0,0042 |
0,0021 отн. ед. |
|
|
4 Отходы спеченные 4,4 % |
1 Взвешивание Mettler KB-60s |
- |
- |
0,0005 отн. ед. |
- |
- |
0,0005 отн. ед. |
|
2 Масс. доля U ОСТ 95 175-90 |
- |
0,0014 |
0,00071 отн. ед. |
- |
0,0016 |
0,0008 отн. ед. |
|
|
3 Масс доля U235 ОСТ 95 446-84 |
- |
0,0075 |
0,0038 отн. ед. |
- |
0,0042 |
0,0021 отн. ед. |
|
_____________
* Статистические методы для контроля качества измерений и анализа инвентаризационной разницы. Методические материалы курса. Учебно-методический центр по учету и контролю ядерных материалов. Обнинск, ГНЦ РФ-ФЭИ, 2010.
Приложение № 8
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Таблицы движения материалов в ЗБМ
Таблица П8.1 - Таблица движения материалов в ЗБМ производства ТВЭЛ
|
Наименование материала |
Номер партии |
Кол-во УЕ |
Масса брутто |
Масса тары |
Масса нетто |
Масс. доля эл-та |
Масс. эл-та |
Масс. доля изотопа |
Масса изотопа |
|
Предыдущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
Таб05 |
75 |
|||||||
|
Таб07 |
39 |
||||||||
|
Таб10 |
17 |
||||||||
|
Таб12 |
45 |
||||||||
|
Таб15 |
53 |
||||||||
|
ТВЭЛ |
ТВ07 |
135 |
|||||||
|
ТВ09 |
85 |
||||||||
|
ТВ11 |
37 |
||||||||
|
Брак (таблетки) |
Taб07d |
2 |
|||||||
|
Taб10d |
3 |
||||||||
|
Сметки |
См01 |
2 |
|||||||
|
Поступления и др. увеличения ЯМ в ЗБМ (УВ) |
|||||||||
|
Таблетки UO2 |
Таб16 |
205 |
|||||||
|
Таб17 |
203 |
||||||||
|
Таб18 |
200 |
||||||||
|
Таб19 |
203 |
||||||||
|
Таб20 |
229 |
||||||||
|
Таб21 |
211 |
||||||||
|
Таб22 |
201 |
||||||||
|
Отправления и др. уменьшения ЯМ из ЗБМ (УМ) |
|||||||||
|
Брак (таблетки) |
Taб07d |
2 |
|||||||
|
Taб10d |
3 |
||||||||
|
Taб35d |
5 |
||||||||
|
Taб36d |
7 |
||||||||
|
Taб37d |
3 |
||||||||
|
ТВЭЛ |
TB07 |
120 |
|||||||
|
TB09 |
83 |
||||||||
|
TB11 |
37 |
||||||||
|
TB15 |
58 |
||||||||
|
TB17 |
115 |
||||||||
|
Сметки |
См01 |
2 |
|||||||
|
См02 |
4 |
||||||||
|
Текущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
Таб12 |
45 |
|||||||
|
Таб17 |
53 |
||||||||
|
Таб20 |
29 |
||||||||
|
Таб22 |
51 |
||||||||
|
ТВЭЛ |
ТВ07 |
15 |
|||||||
|
ТВ09 |
2 |
||||||||
|
ТВ15 |
35 |
||||||||
|
Брак.-табл. |
- |
0 |
|||||||
|
Сметки |
См03 |
2 |
|||||||
Таблица П8.2 - Группа (страта) ТВЭЛ
Название ЗБМ: Производство ТВЭЛ
|
Наименование материала |
Номер партии |
Кол-во УЕ |
Масса брутто |
Масса тары |
Масса нетто |
Масс. доля эл-та |
Масса эл-та |
Масс. доля изотопа |
Масса изотопа |
|
Предыдущая ФИ (СФНК) |
|||||||||
|
ТВЭЛ |
ТВ07 |
135 |
|||||||
|
ТВ09 |
85 |
||||||||
|
ТВ11 |
37 |
||||||||
|
Поступления и др. увеличения ЯМ в ЗБМ(УВ) |
|||||||||
|
ТВЭЛ |
= |
0 |
|||||||
|
Отправления и др. уменьшения ЯМ из ЗБМ(УМ) |
|||||||||
|
ТВЭЛ |
ТВ07 |
120 |
|||||||
|
ТВ09 |
83 |
||||||||
|
ТВ11 |
37 |
||||||||
|
ТВ15 |
58 |
||||||||
|
ТВ17 |
115 |
||||||||
|
Текущая ФИ (СФНК) |
|||||||||
|
ТВЭЛ |
ТВ07 |
15 |
|||||||
|
ТВ09 |
2 |
||||||||
|
ТВ15 |
35 |
||||||||
Таблица П8.3 - Группа (страта) сметок
Название ЗБМ: Производство ТВЭЛ
|
Наименование материала |
Номер партии |
Кол-во УЕ |
Масса брутто |
Масса тары |
Масса нетто |
Масс. доля |
Масса эл-та |
М.Д. изотопа |
Масса изотопа |
|
Предыдущая ФИ (СФНК) |
|||||||||
|
Сметки |
См01 |
2 |
|||||||
|
Поступления и др. увеличения ЯМ в ЗБМ (УВ) |
|||||||||
|
Сметки |
0 |
||||||||
|
Отправления и др. уменьшения ЯМ из ЗБМ (УМ) |
|||||||||
|
Сметки |
См01 |
2 |
|||||||
|
См02 |
4 |
||||||||
|
Текущая ФИ (СФНК) |
|||||||||
|
Сметки |
См03 |
2 |
|||||||
Таблица П8.4 - Группа (страта) таблеток (бракованных)
Название ЗБМ: Производство ТВЭЛ
|
Наименование материала |
Номер партии |
Кол-во УЕ |
Масса брутто |
Масса |
Масса нетто |
М.Д. эл-та |
Масса эл-та |
М.Д. изотопа |
Масса изотопа |
|
Предыдущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
Таб05 |
75 |
|||||||
|
Таб07 |
39 |
||||||||
|
Таб10 |
17 |
||||||||
|
Таб12 |
45 |
||||||||
|
Таб15 |
53 |
||||||||
|
Брак (таблетки) |
Taб07d |
2 |
|||||||
|
Taб10d |
3 |
||||||||
|
Поступления и др. увеличения ЯМ в ЗБМ (УВ) |
|||||||||
|
Таблетки UO2 |
Таб16 |
205 |
|||||||
|
Таб17 |
203 |
||||||||
|
Таб18 |
200 |
||||||||
|
Таб19 |
203 |
||||||||
|
Таб20 |
229 |
||||||||
|
Таб21 |
211 |
||||||||
|
Таб22 |
201 |
||||||||
|
Отправления и др. уменьшения ЯМ из ЗБМ (УМ) |
|||||||||
|
Брак (таблетки) |
Taб07d |
2 |
|||||||
|
Taб10d |
3 |
||||||||
|
Taб35d |
5 |
||||||||
|
Taб36d |
7 |
||||||||
|
Taб37d |
3 |
||||||||
|
Текущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
Таб12 |
45 |
|||||||
|
Таб17 |
53 |
||||||||
|
Таб20 |
29 |
||||||||
|
Таб22 |
51 |
||||||||
|
Брак.-табл. |
- |
0 |
|||||||
Приложение № 9
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Пример исключения парных записей
Группа (страта) таблеток производство ТВЭЛ представлена в таблице П8.4 приложения № 8 к настоящему Положению.
В данном примере партия Таб12 (45 контейнеров) присутствует в предыдущей (НК) и текущей инвентаризации (ФК), партии Таб17, Таб20, Таб22 поступили в ЗБМ (УВ) и частично были переработаны - собраны в ТВЭЛы, оставшиеся контейнеры из этих партий присутствуют в текущей инвентаризации (ФК). Данные по контейнерам в этих партиях представляют собой «парные учетные записи». Остальные партии таблеток были собраны в ТВЭЛы.
Партии Taб07d, Таб10 (бракованные таблетки), из предыдущей (НК) инвентаризации были отправлены из ЗБМ (УМ). УЕ данных партий представляют собой «парные учетные записи».
После исключения «парных учетных записей» данная группа (страта) представлена в таблице № П9.1.
Таблица П9.1 - Группа (страта) таблеток (исключены «парные учетные записи»)
Название ЗБМ: Производство ТВЭЛ
|
Наименование материала |
Номер партии/ |
Кол-во УЕ |
Масса брутто |
Масса тары |
Масса нетто |
Масс. доля |
Масса эл-та |
Масс. доля |
Масса изотопа |
|
Предыдущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
Таб05 |
75 |
|||||||
|
Таб07 |
39 |
||||||||
|
Таб10 |
17 |
||||||||
|
Таб15 |
53 |
||||||||
|
Поступления и др. увеличения ЯМ в ЗБМ (УВ) |
|||||||||
|
Таблетки UO2 |
Таб16 |
205 |
|||||||
|
Таб17 |
150 |
||||||||
|
Таб18 |
200 |
||||||||
|
Таб19 |
203 |
||||||||
|
Таб20 |
200 |
||||||||
|
Таб21 |
211 |
||||||||
|
Таб22 |
150 |
||||||||
|
Отправления и др. уменьшения ЯМ из ЗБМ (УМ) |
|||||||||
|
Брак (таблетки) |
|||||||||
|
Таб35d |
5 |
||||||||
|
Таб36d |
7 |
||||||||
|
Таб37d |
3 |
||||||||
|
Текущая ФИ (СФНК) |
|||||||||
|
Таблетки UO2 |
|||||||||
Приложение № 10
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Оценка
составляющей дисперсии, на которую уменьшается вычисляемая ![]() по способу с
усреднением по потоку
по способу с
усреднением по потоку
Если обозначить сумму массы элемента (изотопа) в п. УЕ партии как
МЯМ, то средняя масса ЯМ одной
УЕ будет ![]()
Для определения ![]() под знак суммы подставляется эта
средняя масса и в аналитических выражениях будет стоять масса всей партии, что
позволяет уменьшить объем вычислений.
под знак суммы подставляется эта
средняя масса и в аналитических выражениях будет стоять масса всей партии, что
позволяет уменьшить объем вычислений.
Если найти разность между аналитическими выражениями вычисления ![]() по
способу без усреднения по потоку и по способу с усреднением по потоку (для
мультипликативных моделей погрешности измерения), то составляющая, на которую
уменьшается оценка
по
способу без усреднения по потоку и по способу с усреднением по потоку (для
мультипликативных моделей погрешности измерения), то составляющая, на которую
уменьшается оценка ![]() по методу усреднения по потоку,
есть:
по методу усреднения по потоку,
есть:
 (П10.1)
(П10.1)
где: mЯМi - масса ЯМ каждой УЕ партии;
МЯМ - масса ЯМ всей партии;
n - число УЕ в партии;
σRM - СКО случайной составляющей погрешности взвешивания;
σRA - СКО случайной составляющей погрешности МВИ разрушающего метода анализа.
Пример:
Пусть имеется партия ЯМ состоящая из 50 УЕ, измеренные массы которых представлены ниже. Погрешности измерений: σRM = 0,05 %, σRA = 0,1 %.
41.3940.9640.6640.7441.6 40.8741.2641.4640.7741.29
41.8541.2240.8340.4441.2440.9641.3 41.8741.3241.09
42.3340.9941.5 41.0241.8240.3640.9 41.0440.8541.34
41.7241.6241.9239.7441.3641.0841.1440.8841.6241.12
40.9342.2 41.1441.3340.7 41.3541.2 41.1 41.3141.58
Средняя масса ЯМ одной УЕ = 41,206
Составляющая, на которую уменьшается оценка а по методу усреднения по потоку, есть:
V(-) = 1,3 ∙ 10-5
Приложение № 11
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Аналитические
выражения для вычисления ![]() без усреднения по потоку
без усреднения по потоку
Рассматриваются аналитические выражения для мультипликативных
моделей погрешностей измерения как наиболее часто применяемых в международной
практике при вычислении ![]() .
.
П11.1 Вклад систематических составляющих погрешностей в ![]() .
.
Вклад систематической составляющей погрешности измерения по одному
из методов измерения (взвешивания, измерения объема, МВИ разрушающих и
неразрушающих методов анализа) в ![]() в одной из групп (страт) STRj вычисляется (без усреднения
по потоку):
в одной из групп (страт) STRj вычисляется (без усреднения
по потоку):
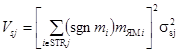 , (П11.1)
, (П11.1)
где: sgn(mi) = +1 для mi из НК, УВ - членов уравнения ИР;
sgn(mi) = -1 для mi из ФК, УМ - членов уравнения ИР;
σsj - СКО систематической составляющей погрешности одного из методов измерения.
Этот подход справедлив, например, при взвешивании всего ЯМ, составляющего члены уравнения баланса, на одних и тех же весах без перекалибровки.
Вклад в дисперсию систематической составляющей погрешности взвешивания будем обозначать с индексом «М»: VSMj и σSMj. При измерении объема в обозначениях вместо «М» следует подставить «V». Вклад в дисперсию систематической составляющей погрешности МВИ разрушающих и неразрушающих методов анализа будем обозначать с индексом «A»: VSAj и σSAj.
При проведении взвешиваний и определении массовой доли элемента (изотопа) рекомендуется следующий подход.
При вычислении ИР по элементу:
![]() (П11.2)
(П11.2)
где: mбi - масса брутто;
mтi - масса тары;
Сi - массовая доля элемента.
При вычислении ИР по изотопу:
![]() , (П11.3)
, (П11.3)
где: Сиi - массовая доля изотопа.
П11.2 Вклад случайных составляющих погрешностей в ![]()
П11.2.1 Вклад случайной составляющей погрешности взвешивания в
![]() в
одной из групп (страт) STRj
(без усреднения по потоку):
в
одной из групп (страт) STRj
(без усреднения по потоку):
![]() (П11.4)
(П11.4)
где: ni - количество взвешиваний i-го контейнера в j-той группе (страте) (требование записи среднего результата измерений по ni взвешиваниям одного и того же контейнера определяется инструкциями предприятия), в большинстве случаев ni = 1;
σRMj - СКО случайной составляющей погрешности взвешивания в j-той группе (страте);
Ci - массовая доля элемента.
При вычислении ![]() по изотопу вместо Ci
необходимо в (П11.4) подставить Ci ∙ Cиi.
по изотопу вместо Ci
необходимо в (П11.4) подставить Ci ∙ Cиi.
Выражение (П11.4) используется при способе расчета ![]() без усреднения по потоку, в котором mбi, mтi индивидуальные
массы брутто и тары i-го контейнера в j-той
группе (страте).
без усреднения по потоку, в котором mбi, mтi индивидуальные
массы брутто и тары i-го контейнера в j-той
группе (страте).
П11.2.2 Вклад случайной составляющей погрешности измерения
объема в ![]() в
одной из групп (страт) (без усреднения по потоку):
в
одной из групп (страт) (без усреднения по потоку):
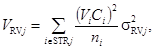 (П11.5)
(П11.5)
где: ni - количество измерений i-ого объема (требование записи среднего результата измерений по ni результатам измерения одного и того же объема определяется инструкциями предприятия), в большинстве случаев ni = 1;
σRVj - СКО случайной составляющей погрешности измерения объема в j-той группе (страте);
Сi - массовая доля элемента.
При вычислении ![]() по изотопу вместо Ci
необходимо в (П11.5) подставить Ci ∙ Cиi.
по изотопу вместо Ci
необходимо в (П11.5) подставить Ci ∙ Cиi.
Выражение (П11.5) используется при способе расчета ![]() без усреднения по
потоку, в котором Vj
индивидуальные измерения объема в j-той
группе (страте).
без усреднения по
потоку, в котором Vj
индивидуальные измерения объема в j-той
группе (страте).
П11.2.3 Вклад в ![]() случайной составляющей погрешности МВИ
одного из методов разрушающего и неразрушающего анализа в j-той группе (страте) (без усреднения по потоку):
случайной составляющей погрешности МВИ
одного из методов разрушающего и неразрушающего анализа в j-той группе (страте) (без усреднения по потоку):
![]() (П11.6)
(П11.6)
где: R - количество партий ЯМ, в которых определяется массовая доля элемента (изотопа) по МВИ (для j-той группы (страты);
Ni - число контейнеров в партии;
mбik, mтik - массы брутто, тары k-го контейнера из i-той партии;
pi - число проб на партию;
Сi - массовая доля элемента;
σRAj - СКО случайной составляющей погрешности МВИ для j-той группы (страты).
При вычислении ![]() по изотопу вместо Ci
необходимо в (П11.6) подставить Ci ∙ Cиi.
по изотопу вместо Ci
необходимо в (П11.6) подставить Ci ∙ Cиi.
Приложение № 12
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Пример вычисления суммарной массы материала
В таблице П12.1 представлены учетные данные предыдущего примера по партиям таблеток производства ТВЭЛ и результаты вычислений суммарной массы MЯМj.
МЯМS (сист) = 6356,6793 + 47892,794 - 0 - 456,18745 = 53793,286 кг (для элемента)
МЯМS (сист) = 185,63364 + 1413,7849 - 0 - 13,463192 = 1585,9553 кг (для изотопа)
МЯМR (случ) = 6356,6793 + 47892,794 + 0 + 456,18745 = 54705,661 кг (для элемента)
МЯМR (случ) = 185,63364 + 1413,7849 + 0 + 13,463192 = 1612,8817 кг (для изотопа)
Таблица П12.1 - Суммарные массы МЯМS (сист) и МЯМR (случ), исключены «парные учетные записи»
Название ЗБМ: Производство ТВЭЛ
|
Группа (страта) таблеток (исключены «парные учетные записи») |
|||||||
|
Член ур-я ИР |
Партия |
Кол-во УЕ |
Масса нетто кг |
м.д. U % |
Масса MU кг |
м.д. U235 % |
Масса МU239 кг |
|
Таб05 |
75 |
3098,25 |
87,3 |
2704,7723 |
2,91 |
78,708874 |
|
|
Таб07 |
39 |
1615,38 |
87,5 |
1413,4575 |
2,87 |
40,56623 |
|
|
НК |
Таб10 |
17 |
706,01 |
87,4 |
617,05274 |
2,95 |
18,203056 |
|
Таб15 |
53 |
1859,40 |
87,2 |
1621,3968 |
2,97 |
48,155485 |
|
|
Сумма |
6356,6793 |
185,63364 |
|||||
|
Таб16 |
205 |
8513,65 |
87,6 |
7457,9574 |
2,94 |
219,26395 |
|
|
Таб17 |
150 |
6202,50 |
87,7 |
5439,5925 |
2,95 |
160,46798 |
|
|
Таб18 |
200 |
8286,00 |
87,5 |
7250,25 |
2,98 |
216,05745 |
|
|
УВ |
Таб19 |
203 |
8426,53 |
87,4 |
7364,7872 |
2,93 |
215,78826 |
|
Таб20 |
200 |
8284,45 |
87,3 |
7232,3249 |
2,95 |
213,35358 |
|
|
Таб21 |
211 |
8754,39 |
87,8 |
7686,3544 |
2,97 |
228,28473 |
|
|
Таб22 |
150 |
6234,62 |
87,6 |
5461,5271 |
2,94 |
160,5689 |
|
|
Сумма |
47892,794 |
1413,7849 |
|||||
|
УМ |
Таб35d |
5 |
172,85 |
87,5 |
151,24375 |
2.98 |
4,5070637 |
|
Таб36d |
7 |
242,9 |
87,6 |
212,7804 |
2,94 |
6,2557438 |
|
|
Таб37d |
3 |
105,45 |
87,4 |
92,1633 |
2,93 |
2,7003847 |
|
|
Сумма |
0 |
456,18745 |
13,463192 |
||||
|
ФК |
- |
0 |
0 |
0 |
|||
|
Сумма |
0 |
0 |
0 |
||||
|
МЯМS (сист) |
53793,286 |
1585,9553 |
|||||
|
MЯMR (случ) |
54705,661 |
1612,8817 |
|||||
Приложение № 13
к Положению по
применению методов
математической статистики для
учета и контроля ядерных
материалов, утвержденному
приказом Федеральной службы по
экологическому, технологическому
и атомному надзору
от 14 сентября 2011 г. № 535
Пример
вычисления вклада в ![]() систематических и случайных
составляющих погрешностей группы (страты).
систематических и случайных
составляющих погрешностей группы (страты).
В таблице П13.1 представлены результаты вычисления по данным
приложения № 12 настоящего
Положения вклада в ![]() систематических и случайных
составляющих погрешностей группы (страты).
систематических и случайных
составляющих погрешностей группы (страты).
Для рассматриваемого примера выполняется однократное взвешивание каждого контейнера, поэтому Nj соответствует суммарному числу контейнеров (1518). Массовая доля элемента и изотопа определялась в другой ЗБМ. В среднем отбирались 2 пробы на 200 кг ЯМ для определения массовой доли элемента и 2 пробы на 300 кг ЯМ для определения массовой доли изотопа. Каждая проба анализировалась один раз, поэтому число анализов для определения массовой доли элемента есть (54705,661/200) ∙ 2 = 547, число анализов для определения массовой доли изотопа есть (1612,8817/300) ∙ 2 = 11.
Для взвешивания СКО систематической составляющей погрешности σSM = 0,05 % (соответствует международным целевым значениям ITV - 2000). Для МВИ разрушающего анализа СКО систематической составляющей погрешности определения массовой доли элемента σSA = 0,1 %, определения массовой доли изотопа σSA = 0,08 %.
Вклад систематических составляющих погрешностей в ![]() :
:
- VSM - взвешивание (723,4294 кг2 - по элементу, 0,62881 кг2 - по изотопу);
- VSA - разрушающий анализ (2893,7176 кг2 - по элементу, 1,60976 кг2 - по изотопу);
- VSΣj - общий вклад систематических составляющих погрешностей в σИР j-ой группы (страты) (3617,147 кг2 - по элементу, 2,23857 кг2 - по изотопу).
Для взвешивания случайная составляющая погрешности σRM = 0,05 % (соответствует международным целевым значениям ITV - 2000).
Для МВИ разрушающего анализа случайная составляющая погрешности определения массовой доли элемента σRA = 0,15 %, определения массовой доли изотопа σRA = 0,1 %.
Вклад случайных составляющих погрешностей в ![]() :
:
- VRM - взвешивание (0,966 кг2 - по элементу; 0,00084 кг2 - по изотопу);
- VRA - разрушающий анализ (12,31005 кг2 - по элементу; 1,60976 кг2 - по изотопу);
- VRΣj - общий вклад систематических составляющих погрешностей j-ой группы (страты) в ![]() (3617,147
кг2 - по элементу; 0,23649 кг2 - по изотопу).
(3617,147
кг2 - по элементу; 0,23649 кг2 - по изотопу).
Таблица
П13.1 - Вклад систематических и
случайных составляющих группы (страты) таблеток в ![]() .
.
Название ЗБМ: Производство ТВЭЛ
|
Группа (страта) таблеток (исключены «парные учетные записи») |
|||||||
|
Член ур-я ИР |
Партия |
Кол-во УЕ |
Масса нетто кг |
м.д. U % |
Масса МU кг |
м.д. U235 % |
Масса MU235 кг |
|
НК |
Таб05 |
75 |
3098,25 |
87,3 |
2704,7723 |
2,91 |
78,708874 |
|
Таб07 |
39 |
1615,38 |
87,5 |
1413,4575 |
2,87 |
40,56623 |
|
|
Таб10 |
17 |
706,01 |
87,4 |
617,05274 |
2,95 |
18,203056 |
|
|
Таб15 |
53 |
1859,40 |
87,2 |
1621,3968 |
2,97 |
48,155485 |
|
|
Сумма |
6356,6793 |
185,63364 |
|||||
|
УВ |
Таб16 |
205 |
8513,65 |
87,6 |
7457,9574 |
2,94 |
219,26395 |
|
Таб17 |
150 |
6202,50 |
87,7 |
5439,5925 |
2,95 |
160,46798 |
|
|
Таб18 |
200 |
8286,00 |
87,5 |
7250,25 |
2,98 |
216,05745 |
|
|
Таб19 |
203 |
8426,53 |
87,4 |
7364,7872 |
2,93 |
215,78826 |
|
|
Таб20 |
200 |
8284,45 |
87,3 |
7232,3249 |
2,95 |
213,35358 |
|
|
Таб21 |
211 |
8754,39 |
87,8 |
7686,3544 |
2,97 |
228,28473 |
|
|
Таб22 |
150 |
6234,62 |
87,6 |
5461,5271 |
2,94 |
160,5689 |
|
|
Сумма |
47892,794 |
1413,7849 |
|||||
|
ФК |
0 |
0 |
0 |
||||
|
Сумма |
0 |
0 |
|||||
|
УМ |
Таб35d |
5 |
172,85 |
87,5 |
151,24375 |
2,98 |
4,5070637 |
|
Таб36d |
7 |
242,9 |
87,6 |
212,7804 |
2,94 |
6,2557438 |
|
|
Таб37d |
3 |
105,45 |
87,4 |
92,1633 |
2,93 |
2,7003847 |
|
|
Сумма |
0 |
456,18745 |
13,463192 |
||||
|
Определение вклада
систематических составляющих погрешностей в |
|||||||
|
Элемент |
Изотоп |
||||||
|
МЯМS (сист) |
53793,286 |
1585,9553 |
|||||
|
Взвешивание σS |
0,05 % |
0,05 % |
|||||
|
VMS |
723,4294 |
0,62881 |
|||||
|
Анализ σS |
0,1 % |
0,08 % |
|||||
|
VAS |
2893,7176 |
1,60976 |
|||||
|
VSΣ = VMS + VAS |
3617,147 |
2,23857 |
|||||
|
Определение вклада
случайных составляющих погрешностей в |
|||||||
|
МЯМR (случ) |
54705,661 |
1612,8817 |
|||||
|
Взвешивание σMR |
0,07 % |
0,07 % |
|||||
|
Число контейнеров |
1518 |
1518 |
|||||
|
VMR |
0,966 |
0,00084 |
|||||
|
Анализ σAR |
0,15 % |
0,1 % |
|||||
|
Число анализов |
547 |
11 |
|||||
|
VAR |
12,31005 |
0,23649 |
|||||
|
VRΣ - VMR + VAR |
13,27605 |
0,23733 |
|||||
СОДЕРЖАНИЕ

 (43)
(43)