РЕКОМЕНДАЦИЯ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
ОБЩИЕ ТРЕБОВАНИЯ
МИ 2091-90
Москва
КОМИТЕТ СТАНДАРТИЗАЦИИ
И МЕТРОЛОГИИ СССР
1991
РЕКОМЕНДАЦИЯ
|
ГСИ. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН Общие требования |
МИ 2091-90 |
Дата введения 01.01.92
Настоящая рекомендация распространяется на нормативно-технические и методические документы, регламентирующие правила выполнения как однократных, так и многократных измерений, и устанавливает общие требования к этим измерениям.
Положения настоящей рекомендации могут быть основой при подготовке программ для автоматизированного процесса измерений или автоматизации обработки результатов измерений.
Настоящая рекомендация не регламентирует общие требования, к разработке методик выполнения измерений, установленные в ГОСТ 8.010-90.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Целью измерений является получение объективной информации о значениях физических величин.
1.2. Результаты измерений должны выражаться в единицах физических величин, соответствующих требованиям ГОСТ 8.417-81.
1.3. Все измерения должны выполняться средствами измерений, прошедшими государственные испытания или метрологическую аттестацию и (или) поверку.
1.4. Правила выполнения наиболее ответственных, повторяющихся и сложных измерений (прямых многократных, косвенных, совокупных, совместных, имеющих существенные методические составляющие, требующих обработки измерительной информации и др.) рекомендуется регламентировать методиками выполнения измерения.
1.5. При планировании измерений необходимо проанализировать правильность постановки измерительной задачи, установить требования к погрешности измерений, числу измерений, квалификации оператора, форме представления результатов измерений и предусмотреть мероприятия, обеспечивающие их выполнение.
2. АНАЛИЗ ПРАВИЛЬНОСТИ ПОСТАНОВКИ ИЗМЕРИТЕЛЬНОЙ ЗАДАЧИ
2.1. При постановке измерительной задачи следует:
выбрать модель, измеряемые параметры которой соответствуют свойствам объекта, информацию о которых следует получить в результате измерений;
оценить предполагаемую точность результата измерений и формы его представления.
2.2. При проведении анализа правильности постановки измерительной задачи следует уточнить принятую модель объекта измерений (процесса, явления), параметры которой являются величинами, подлежащими измерению, и проверить ее соответствие объекту измерений; оценить, удовлетворяет ли предполагаемая точность результата измерений и форма его представления цели измерительной задачи.
Примечание. С целью проведения анализа правильности постановки измерительной задачи в случае необходимости выполняют предварительные измерения.
2.2.1. Модель объекта измерения должна удовлетворять следующим основным требованиям:
погрешность, обусловленная несоответствием модели объекту измерений, не должна превышать 10 % от предела допускаемой погрешности измерений;
составляющая погрешности измерений, обусловленная нестабильностью измеряемых физических величин в течение времени, необходимого для проведения измерения, не должна превышать 10 % от предела допускаемой погрешности измерений.
2.2.2. Если выбранная модель не удовлетворяет требованиям п. 2.2.1, то следует перейти к другой модели объекта измерений или спланировать измерительный процесс таким образом, чтобы уменьшить указанные погрешности. Подробнее о выборе измеряемой модели изложено в МИ 1967-89.
2.3. Требования к погрешности результата измерений должны соответствовать цели измерительной задачи. Эту погрешность целесообразно оценить предварительно с учетом ее предполагаемых источников.
2.3.1. Предварительную оценку погрешности измерений определяют путем суммирования всех составляющих погрешностей, возникновение которых предполагается при выполнении измерений.
2.3.2. Если предварительная оценка погрешности не соответствует требованиям точности измерительной задачи, следует проанализировать предполагаемые источники погрешности и осуществить мероприятия по их уменьшению (выбрать более точное средство измерений, изменить метод измерений, поручить измерения более квалифицированному оператору, уточнить влияющие величины и уменьшить их воздействие и т.д.).
2.4. Результат измерений обычно сопровождается указанием погрешности, с которой выполнено измерение. В зависимости от цели измерительной задачи погрешность результата измерений может быть представлена своими составляющими или суммарной погрешностью с указанием доверительной вероятности. Характеристики погрешности измерений, формы их представления и способы использования при испытаниях изложены в МИ 1317-86.
3. ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ИЗМЕРЕНИЙ
3.1. Точным измерениям присущи отсутствие промахов и малость систематических и случайных погрешностей.
3.2. Промахи исключают из результатов измерений.
3.2.1. При однократных измерениях обнаружить промах не представляется возможным. Чтобы уменьшить вероятность получения промаха в результате измерений, необходимо повторить измерения 2 - 3 раза, а за результат измерений принять среднее арифметическое полученных отсчетов.
3.2.2. При многократных измерениях для обнаружения промахов используют статистические критерии [1]. Предварительно должно быть проверено, какому виду распределения соответствует распределение результатов измерений в соответствии с требованиями НТМ СЭВ 1-84. Для результатов измерений, распределенных нормально, наибольшее (наименьшее) значение λi является промахом, если удовлетворяется неравенство [1]
где ![]() - среднее
арифметическое группы результатов измерений;
- среднее
арифметическое группы результатов измерений;
 -
смещенное среднее квадратическое отклонение группы результатов измерений;
-
смещенное среднее квадратическое отклонение группы результатов измерений;
Т(q, h) - квантиль распределения, соответствующий уровню значимости q и числу измерений n в группе (см. приложение 1);
n - число измерений в группе.
3.3. Обнаруженные систематические погрешности должны быть устранены из результатов измерений путем введения поправок.
Неисключенные остатки систематических погрешностей, границы, которых обозначены Θ, оцениваются нестатистическими методами в соответствии с требованиями МИ 1552-86 и ГОСТ 8.207-76.
3.3.1. Постоянно возрастающую или постоянно убывающую систематическую погрешность можно обнаружить по одной группе результатов измерений посредством критерия Аббе (см. приложение 2) [3].
3.3.2. Неизменяющуюся в процессе измерений систематическую погрешность не представляется возможным обнаружить по одной группе многократных измерений.
При наличии двух или более групп результатов измерений физической величины одного и того же значения, полученных различными методами или средствами измерений, различными операторами либо отличающиеся условиями или методикой выполнения измерений, возникающую при этом неизменяющуюся систематическую погрешность или различия систематических погрешностей в группах можно обнаружить посредством нижеизложенных статистических критериев.
3.3.2.1. При наличии, двух групп
результатов измерений одной и той же физической величины, имеющих нормальное
распределение с однородными (![]() ) средними квадратическими отклонениями,
неизменяющуюся систематическую погрешность или различия систематических
погрешностей в группах можно обнаружить посредством критерия Стьюдента.
Систематическая погрешность присутствует в одной из групп или они различны в группах, если выполняется неравенство
) средними квадратическими отклонениями,
неизменяющуюся систематическую погрешность или различия систематических
погрешностей в группах можно обнаружить посредством критерия Стьюдента.
Систематическая погрешность присутствует в одной из групп или они различны в группах, если выполняется неравенство
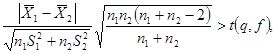 (2)
(2)
где ![]() ,
,
![]() - средние арифметические значения, соответственно,
первой и второй групп результатов измерений;
- средние арифметические значения, соответственно,
первой и второй групп результатов измерений;
![]()
![]() -
средние квадратические отклонения первой и второй групп, соответственно;
-
средние квадратические отклонения первой и второй групп, соответственно;
n1, n2 - число измерений в первой и второй группах, соответственно;
t(q, f) - квантиль распределения Стьюдента, соответствующий уровню значимости q и числу степеней свободы f = n1 + n2 - 2.
Квантили распределения Стьюдента в зависимости от уровня значимости q и числа степеней свободы f представлены в приложении 3.
Примечание. Однородность средних квадратических отклонений проверяют посредством критериев, изложенных в пп. 3.4.2.4, 3.4.2.5.
3.3.2.2. Если средние квадратические отклонения не однородны, то вместо неравенства (4) используют неравенство
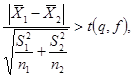 (3)
(3)
где f - число степеней свободы является наибольшим целым числом, не превосходящим
3.3.3. При нормальном распределении нескольких групп (L ³ 3) результатов измерений одной и той же физической величины для обнаружения систематической погрешности или различия систематических погрешностей в группах применяют критерий Фишера. Систематические погрешности различны в группах или присутствуют в одной из групп, если выполняется неравенство [1]
 (5)
(5)
где ![]()
![]()
![]()
L - число групп результатов измерений;
ni - число измерений в i-й группе;
F(q, f1, f2) - квантиль распределения Фишера, соответствующий уровню значимости q и числу результатов измерений в группах f1 = L - l, f2 = N - L (см. приложение 4).
3.3.4. При неизвестном распределении результатов измерений групп для обнаружения систематической погрешности или различия систематических погрешностей в группах применяют статистический критерий Вилкоксона (см. приложение 5).
3.4. По значениям случайных погрешностей измерений могут оцениваться сходимость измерений (т.е. близость друг к другу результатов измерений, выполняемых в одинаковых условиях) и воспроизводимость измерений (т.е. близость друг к другу результатов измерений, выполненных в различное время, в разных местах, разными методами и средствами измерений, но приведенных к одним и тем же условиям - температура, давление, влажность и т.д.).
3.4.1. Сходимость группы результатов измерений характеризуют средним квадратическим отклонением результата группы или его доверительной случайной погрешностью.
3.4.2. Воспроизводимость нескольких групп результатов измерений характеризуют близостью результатов измерений групп и характеристик их случайных погрешностей.
3.4.2.1. При нормальном распределении результатов измерений для проверки близости (допустимости различия) результатов измерений групп следует пользоваться статистическими критериями, изложенными в пп. 3.3.1, 3.3.3.
3.4.2.2. Для проверки допустимости различия средних квадратических отклонений двух групп результатов измерений (близости средних квадратических отклонений) используют критерий Фишера, для числа групп более двух - критерий Бартлетта [5].
3.4.2.3. Различие средних квадратических отклонений S1 и S2 двух групп результатов измерений с числом измерений n1 и n2 допустимо, если выполняется неравенство
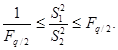 (6)
(6)
Значение критических значений Fq/2 в зависимости от числа степеней свободы f1 = n1 - 1 и f2 = n2 - 1 для уровней значимости 0,05 и 0,01 приведены в таблицах приложения 4.
3.4.2.4. Различие средних квадратических отклонений S1, S2, ..., SL групп результатов измерений допустимо, если выполняется неравенство
![]() (7)
(7)
где 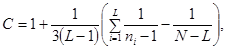
![]()
![]()
ni - число результатов измерений в i-й группе,
X2(q, f) - квантиль распределения X2, соответствующий уровню значимости q и числу степеней свободы f = L - 1 (см. приложение 6).
3.4.2.5. При неизвестном распределении результатов измерений для проверки близости результатов измерений групп применяют статистический критерий Вилкоксона, а для проверки допустимости различия средних квадратических отклонений - критерий Сиджела-Тьюки (см. приложение 5).
3.5. Указание о том, на каких этапах оценивания погрешности измерений целесообразны указанные критерии и их влияние на последующий ход оценивания погрешностей, должно быть рекомендовано НТД, регламентирующими методы обработки результатов конкретных измерений.
3.6. Ввиду разнообразия причин, вызывающих систематические погрешности, невозможно во всех случаях дать исчерпывающие правила их исключения. В ряде случаев можно выполнить работы по выявлению и устранению этих погрешностей [7]:
при подготовке к выполнению измерений - это поверка применяемых СИ с целью определения действительного значения их погрешностей, предварительный анализ методической погрешности с целью введения поправок, фиксация измерений влияющих величин, поддержание стабильности условий измерений;
при выполнении измерений - это использование метода замещения, устранения влияния вариации, исключение погрешности от мертвого хода, измерения одной величины несколькими независимыми методами, несколькими СИ, уравновешивание результатов измерений, связанных известным условием.
3.7. Точность полученных при измерении отсчетов и последующих вычислений при их обработке должна соответствовать требуемой точности результата измерений, обусловленной измерительной задачей.
Число разрядов при отсчете и в промежуточных вычислениях должно быть на единицу или две больше, чем в окончательном результате.
4. УСЛОВИЯ ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ
4.1. В зависимости от требований измерительной задачи измерения могут выполняться как в нормальных, так и в рабочих условиях.
4.2. При выполнении измерений в нормальных условиях должно быть выделено рабочее пространство, действием влияющих величин внутри которого можно пренебречь.
4.3. При выборе номинальных значений и пределов допускаемых значений влияющих величин для нормальных условий следует руководствоваться ГОСТ 8.395-80 «ГСИ. Нормальные условия измерений при поверке. Общие требования», МИ 1888-88 «ГСИ. Нормальные условия измерений в ГПС. Общие положения».
4.4. Если действием влияющих величин внутри рабочего пространства нельзя пренебречь, следует их фиксировать с целью расчета и последующего введения поправок в результаты измерений или с целью расчета дополнительных погрешностей.
4.5. Погрешность средств измерений, применяемых для контроля влияющих величин, должна составлять не более 25 % от изменения влияющей величины.
4.6. При необходимости сопоставления результатов измерений они должны выполняться в одинаковых условиях или их результаты должны приводиться к одинаковым условиям, чаще всего к нормальным.
5. ВЫБОР МЕТОДА И СРЕДСТВА ИЗМЕРЕНИЙ
5.1. Метод и средство измерений должны обеспечить выполнение измерительной задачи и в основном требуемую измерительной задачей точность измерений в данных условиях измерений.
5.2. При выборе средства измерений следует учитывать принцип его действия, приемы применения, метрологические характеристики, характеристики надежности, стойкость к внешним воздействиям. Рекомендации по выбору методов и средств измерений с учетом факторов, характерных для технических измерений, изложены в МИ 1967-89.
5.3. Метод измерений должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу систематических погрешностей в разряд случайных погрешностей (рандомизация систематических погрешностей). Например, с целью исключения систематических погрешностей из-за неадекватности модели измеряемому объекту намечают выполнение измерений в нескольких точках; для исключения систематических погрешностей от вариации, гистерезиса, мертвого хода измерения выполняют при подходе к определенной точке шкалы слева и справа.
5.4. По выбранному методу и средству измерений целесообразно предварительно определить погрешность измерений DΣ, включающую погрешность предполагаемых средств измерений, метода, оператора и погрешности, обусловленные внешними воздействиями, и сравнить ее с пределом допускаемой погрешности измерений Dр.
5.4.1. Если DΣ < Dр, выбранные метод и средства измерений обеспечивают получение результата с требуемой погрешностью.
5.4.2. Если DΣ > Dр, уточняют правильность выбранного метода, условий выполнения измерений или выбирают более точное средство измерений.
Если не удается обеспечить выполнение требований п. 5.4.1, следует проанализировать требования измерительной задачи к погрешности результата измерений.
5.5. При выборе средств и методов измерений для контроля следует учитывать влияние погрешности измерений на брак контроля. Функциональные зависимости между пределом допускаемой погрешности измерений и показателями брака контроля приведены в приложении 5 к МИ 1317-86 и при контроле линейных размеров - в приложении 1 к ГОСТ 8.051-81.
5.6. Для выполнения однократных измерений следует выбирать средство измерений с возможно меньшей случайной погрешностью.
5.7. При выборе средств измерений следует учитывать, что в нормальных условиях их применения допустимо изменение их погрешности до 35 % (см. ГОСТ 8.395-80). Следовательно, если погрешность выбираемого средства измерений DСИ должна быть не более Dр, то рекомендуется выбирать средство измерений с погрешностью
![]() (8)
(8)
6. ЧИСЛО ИЗМЕРЕНИЙ
6.1. Число измерений n зависит как от требований к точности результата измерений, так и от реальной возможности выполнять повторные измерения.
6.1.1. Число измерений n определяется значимостью случайных погрешностей по сравнению с пределом допускаемой погрешности предполагаемого результата
![]() (9)
(9)
где t(q, n) - коэффициент Стьюдента (см. приложение 3),
S - среднее квадратическое отклонение группы результатов измерений.
6.1.2. Число измерений увеличивают при наличии существенных систематических погрешностей (метода, средства измерений, оператора) с целью их перевода в случайные (рандомизация систематических погрешностей, см. п. 5.3).
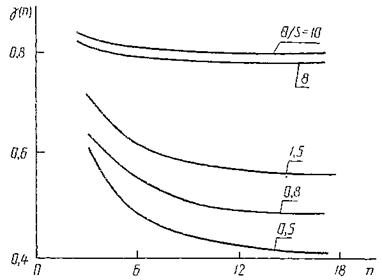
6.2. При наличии случайных S и неисключенных систематических погрешностей Θ число измерений n определяется их соотношением Θ/S и требованием к точности результата измерений.
На графике приведена зависимость n от отношений Θ/S и относительного изменения погрешности результата измерений g(n) при увеличении числа измерений [6].
7. ОБЯЗАННОСТИ ОПЕРАТОРА
7.1. Оператор должен изучить методику выполнения измерений, последовательность их выполнения. Перед измерениями он должен убедиться в том, что основные и вспомогательные средства измерений имеют действующие свидетельства о поверке (поверительное клеймо) или свидетельство о метрологической аттестации.
7.2. Перед проведением измерений с помощью автоматизированных средств измерений необходимо пропустить определенный тест через измерительную систему и сопоставить результат, полученный на выходе системы, с ожидаемым результатом.
7.3. С целью уменьшения субъективных погрешностей оператора наиболее ответственные, высокоточные измерения допускается выполнять несколькими операторами, а за результат измерений принять среднее арифметическое их показаний. Автоматизация процесса измерений позволяет исключить возможность появления подобных погрешностей.
7.4. Погрешность округления при снятии отсчетов оператором не должна влиять на последнюю значащую цифру погрешности окончательного результата измерения, т.е. она не должна превышать 10 % от предела допускаемой погрешности результата измерений Dр (D0 £ 0,1 · Dр). Если это неравенство не выполняется, число отсчетов необходимо увеличить настолько, чтобы D0 удовлетворяло указанному требованию или учитывать эту составляющую погрешности результата измерений.
8. ОБРАБОТКА И ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
8.1. Обработке результатов измерений предшествует этап их анализа.
8.1.1. Если при анализе процесса измерений удалось установить источник появления промахов (неверное действие оператора, падение напряжения в электрической сети, магнитные бури и др. причины), то их исключают перед обработкой результатов измерений.
8.1.2. Если причины появления промахов неизвестны, для решения вопроса возможности их исключения используют статистические критерии (см. пп. 3.2.2, 3.2.3).
8.1.3. Обнаруженные систематические погрешности измерения (систематические погрешности средств измерений, метода, оператора, из-за воздействия влияющих факторов) вносят в результаты измерений в виде поправок, а неисключенные систематические и случайные погрешности составляют погрешность результата измерений.
8.2. Обработка прямых однократных измерений проводится в соответствии с МИ 1552-86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений». Обработка прямых многократных измерений - в соответствии с ГОСТ 8.207-76. Обработка косвенных измерений - в соответствии с МИ 2083-90 «Измерения косвенные. Определение результатов измерений и оценивание их погрешностей». Обработка результатов сличений при совокупных измерениях изложена в МИ 1832-88 «ГСИ. Сличения групп средств поверки одинакового уровня точности. Основные правила».
8.3. Результаты измерений в зависимости от цели измерительной задачи могут быть представлены числом, в виде таблицы, графика и другом виде.
Формы представления результатов измерений и их погрешностей должны соответствовать МИ 1317-86 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроля их параметров».
8.4. Погрешность результата измерений выражают, как правило, одной значащей цифрой. Две значащие цифры в погрешности результата измерения сохраняют: при точных измерениях; если первая значащая цифра не более трех; если предел допускаемой погрешности задан двумя значащими цифрами.
ПРИЛОЖЕНИЕ 1
Справочное
Квантили распределения Т(q, n).
|
п |
q |
|||
|
0,01 |
0,02 |
0,05 |
0,10 |
|
|
4 |
1,73 |
1,72 |
1,71 |
1,69 |
|
5 |
1,97 |
1,96 |
1,92 |
1,87 |
|
6 |
2,16 |
2,13 |
2,07 |
2,00 |
|
7 |
2,31 |
2,26 |
2,18 |
2,09 |
|
8 |
2,43 |
2,37 |
2,27 |
2,17 |
|
9 |
2,53 |
2,46 |
2,35 |
2,24 |
|
10 |
2,62 |
2,54 |
2,41 |
2,29 |
|
12 |
2,75 |
2,66 |
2,52 |
2,39 |
|
14 |
2,86 |
2,76 |
2,60 |
2,46 |
|
16 |
2,95 |
2,84 |
2,67 |
2,52 |
|
18 |
3,02 |
2,90 |
2,73 |
2,58 |
|
20 |
3,08 |
2,96 |
2,78 |
2,62 |
|
22 |
3,13 |
3,01 |
2,82 |
2,66 |
|
24 |
3,18 |
3,05 |
2,86 |
2,70 |
|
26 |
3,22 |
3,09 |
2,90 |
2,73 |
|
28 |
3,26 |
3,12 |
2,93 |
2,76 |
|
30 |
3,29 |
3,16 |
2,96 |
2,79 |
|
40 |
3,42 |
3,28 |
3,08 |
2,90 |
|
50 |
3,52 |
3,37 |
3,16 |
2,99 |
ПРИЛОЖЕНИЕ 2
Справочное
Группа результатов измерений содержит постоянно возрастающую или постоянно убывающую систематическую погрешность, если выполняется неравенство
![]()
где Sd - среднее квадратическое отклонение группы результатов измерений, вычисленное по формуле
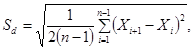
S - среднее квадратическое отклонение группы результатов измерений, вычисленное по формуле
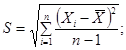
n - число измерений в группе;
Xi - i-й результат измерений группы;
vt(q, n) - квантиль распределения, соответствующий уровню значимости q и числу измерений n в группе.
Значения vt(q, n) в зависимости от уровня значимости q и числа измерений n представлены в таблице.
Квантили распределения vt(q, n)
|
Число измерений, n |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
30 |
35 |
40 |
50 |
60 |
|
|
Уровень значимости, q |
0,01 |
0,31 |
0,28 |
0,33 |
0,37 |
0,41 |
0,45 |
0,47 |
0,50 |
0,52 |
0,54 |
0,56 |
0,60 |
0,62 |
0,65 |
0,68 |
0,71 |
|
0,05 |
0,39 |
0,44 |
0,49 |
0,53 |
0,56 |
0,59 |
0,61 |
0,63 |
0,65 |
0,66 |
0,68 |
0,71 |
0,73 |
0,75 |
0,77 |
0,79 |
|
ПРИЛОЖЕНИЕ 3
Справочное
Квантили распределения Стьюдента t(q, f)
|
Число степеней свободы, f |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
40 |
60 |
|
|
Уровень значимости, q |
0,050 |
2,4 |
2,1 |
2,0 |
1,9 |
1,9 |
1,9 |
1,8 |
1,8 |
1,8 |
1,8 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
1,7 |
|
0,025 |
3,2 |
2,8 |
2,6 |
2,4 |
2,4 |
2,3 |
2,3 |
2,2 |
2,2 |
2,1 |
2,1 |
2,1 |
2,1 |
2,1 |
2,1 |
2,1 |
2,0 |
2,0 |
2,0 |
2,0 |
|
|
0,005 |
5,8 |
4,6 |
4,0 |
3,7 |
3,5 |
3,4 |
3,2 |
3,2 |
3,1 |
3,0 |
2,9 |
2,9 |
2,8 |
2,8 |
2,8 |
2,8 |
2,8 |
2,8 |
2,7 |
2,7 |
|
ПРИЛОЖЕНИЕ 4
Справочное
Таблица 1
Квантили распределения F0,05
|
Число степеней свободы f2 |
Число степеней свободы f1 |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
8 |
12 |
16 |
50 |
∞ |
|
|
2 |
19,0 |
19,2 |
19,2 |
19,3 |
19,3 |
19,4 |
19,4 |
19,4 |
19,5 |
19,5 |
|
3 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,85 |
8,74 |
8,69 |
8,58 |
8,53 |
|
4 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,84 |
5,70 |
5,63 |
|
5 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,60 |
4,44 |
4,37 |
|
6 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,92 |
3,75 |
3,67 |
|
7 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,49 |
3,32 |
3,23 |
|
8 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,20 |
3,02 |
2,93 |
|
9 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
2,99 |
2,80 |
2,71 |
|
10 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,83 |
2,64 |
2,54 |
|
15 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,38 |
2,18 |
2,07 |
|
20 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,45 |
2,28 |
2,18 |
1,97 |
1,84 |
|
25 |
3,39 |
2,99 |
2,76 |
2,60 |
2,49 |
2,34 |
2,16 |
2,07 |
1,84 |
1,71 |
|
30 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,27 |
2,09 |
1,99 |
1,76 |
1,62 |
|
35 |
3,26 |
2,87 |
2,64 |
2,48 |
2,37 |
2,22 |
2,04 |
1,94 |
1,70 |
1,57 |
|
40 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,18 |
2,00 |
1,90 |
1,66 |
1,51 |
|
45 |
3,21 |
2,81 |
2,58 |
2,42 |
2,31 |
2,15 |
1,97 |
1,87 |
1,63 |
1,48 |
|
50 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,13 |
1,95 |
1,85 |
1,60 |
1,44 |
|
∞ |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
1,94 |
1,75 |
1,64 |
1,35 |
1,00 |
Таблица 2
Квантили распределения F0,01
|
Число степеней свободы f2 |
Число степенен свободы f1 |
||||||||||
|
2 |
3 |
4 |
5 |
6 |
8 |
12 |
16 |
24 |
50 |
∞ |
|
|
2 |
99,0 |
99,2 |
99,2 |
99,3 |
99,3 |
99,4 |
99,4 |
99,4 |
99,5 |
99,5 |
99,5 |
|
3 |
30,8 |
29,4 |
28,7 |
28,2 |
27,9 |
27,5 |
27,1 |
26,8 |
26,6 |
26,4 |
26,1 |
|
4 |
18,0 |
16,7 |
16,0 |
15,5 |
15,2 |
14,8 |
14,4 |
14,2 |
13,9 |
13,7 |
13,5 |
|
5 |
13,3 |
12,1 |
11,4 |
11,0 |
10,7 |
10,3 |
9,89 |
9,68 |
9,47 |
9,24 |
9,02 |
|
6 |
10,9 |
9,78 |
9,15 |
8,75 |
8,47 |
8,10 |
7,72 |
7,52 |
7,31 |
7,09 |
6,88 |
|
7 |
9,55 |
8,45 |
7,85 |
7,46 |
7,19 |
6,84 |
6,47 |
6,28 |
6,07 |
5,86 |
5,65 |
|
8 |
8,65 |
7,59 |
7,01 |
6,63 |
6,37 |
6,03 |
5,67 |
5,48 |
5,28 |
5,07 |
4,86 |
|
9 |
8,02 |
6,99 |
6,42 |
6,06 |
5,80 |
5,47 |
5,11 |
4,92 |
4,73 |
4,52 |
4,31 |
|
10 |
7,56 |
6,55 |
5,99 |
5,64 |
5,39 |
5,06 |
4,71 |
4,52 |
4,33 |
4,12 |
3,91 |
|
15 |
6,36 |
5,42 |
4,89 |
4,56 |
4,32 |
4,00 |
3,67 |
3,49 |
3,29 |
3,08 |
2,87 |
|
20 |
5,85 |
4,94 |
4,43 |
4,10 |
3,87 |
3,56 |
3,23 |
3,05 |
2,86 |
2,64 |
2,42 |
|
25 |
5,57 |
4,68 |
4,18 |
3,85 |
3,63 |
3,32 |
2,99 |
2,81 |
2,62 |
2,40 |
2,17 |
|
30 |
5,39 |
4,51 |
4,02 |
3,70 |
3,47 |
3,17 |
2,84 |
2,66 |
2,47 |
2,25 |
2,01 |
|
35 |
5,27 |
4,40 |
3,91 |
3,59 |
3,37 |
3,07 |
2,74 |
2,56 |
2,37 |
2,13 |
1,90 |
|
40 |
5,18 |
4,31 |
3,83 |
3,51 |
3,29 |
2,99 |
2,66 |
2,48 |
2,29 |
2,06 |
1,80 |
|
45 |
5,11 |
4,25 |
3,77 |
3,45 |
3,23 |
2,94 |
2,61 |
2,43 |
2,23 |
1,99 |
1,75 |
|
50 |
5,06 |
4,20 |
3,72 |
3,41 |
3,19 |
2,89 |
2,56 |
2,38 |
2,18 |
1,95 |
1,68 |
|
∞ |
4,61 |
3,78 |
3,32 |
3,02 |
2,80 |
2,51 |
2,18 |
2,00 |
1,79 |
1,52 |
1,00 |
ПРИЛОЖЕНИЕ 5
Справочное
Из двух групп результатов измерений: x1, ..., xn; y1, ..., ym, n ³ m ³ 5 составляют вариационный ряд, в котором все п + т значений x1, ..., xn; y1, ..., ym располагают в порядке их возрастания и приписывают им ранги - порядковые номера членов вариационного ряда. Различие средних допустимо, если выполняется неравенство
![]()
где Ri - ранг xi, равный его номеру в вариационном ряду;
![]() ,
, ![]() - нижнее
и верхнее критические значения для выбранного уровня q.
- нижнее
и верхнее критические значения для выбранного уровня q.
При т £ 15 критические значения ![]() и
и ![]() определяют
по таблице. При m > 15 критические значения
определяют
по таблице. При m > 15 критические значения ![]() ,
, ![]() вычисляют
по формулам:
вычисляют
по формулам:
![]()
![]()
где zр/2 - квантиль нормированной функции Лапласа.
КРИТЕРИЙ СИДЖЕЛА-ТЬЮКИ
Рассеивание средних квадратических отклонений групп допустимо, если выполняется неравенство
![]()
где Ri - ранг хi,
определяемый следующим образом. В вариационном ряду из (п + m) значений x и y
(n ³
m ³ 5)
приписывают ранг 1 наименьшему значению, ранг 2 - наибольшему, ранг 3 -
предыдущему наибольшему значению, ранг 4 - второму после наименьшего значению,
ранг 5 - третьему после наименьшего значению, ранг 6 - третьему перед
наибольшим значению и т.д. Критические значения ![]() ,
, ![]() определяют
по таблице.
определяют
по таблице.
Критические значения ![]() ,
, ![]() и
и![]() ,
, ![]()
|
п |
5 |
7 |
8 |
9 |
10 |
12 |
14 |
15 |
||||||||||||
|
m |
5 |
7 |
10 |
15 |
7 |
10 |
15 |
8 |
10 |
15 |
9 |
15 |
10 |
15 |
12 |
15 |
14 |
15 |
15 |
|
|
5 % |
|
17 |
20 |
23 |
29 |
36 |
42 |
52 |
49 |
53 |
65 |
62 |
79 |
78 |
94 |
115 |
127 |
160 |
164 |
184 |
|
|
38 |
45 |
57 |
76 |
69 |
84 |
109 |
87 |
99 |
127 |
109 |
146 |
132 |
166 |
185 |
209 |
246 |
256 |
281 |
|
|
1 % |
|
15 |
16 |
19 |
23 |
32 |
37 |
44 |
43 |
47 |
56 |
56 |
69 |
71 |
84 |
105 |
115 |
147 |
151 |
171 |
|
|
40 |
49 |
61 |
82 |
73 |
89 |
117 |
93 |
105 |
136 |
115 |
156 |
139 |
176 |
195 |
221 |
259 |
268 |
294 |
|
ПРИЛОЖЕНИЕ 6.
Справочное
Квантили распределения X2(q, f)
|
Число степеней свободы, f = L - 1 |
3 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
30 |
35 |
40 |
45 |
50 |
|
|
Уровень значимости, q |
0,01 |
11,3 |
13,3 |
16,8 |
20,1 |
23,2 |
26,2 |
29,1 |
32,0 |
34,8 |
37,6 |
40,3 |
43,0 |
45,6 |
50,9 |
57,3 |
63,7 |
70,0 |
76,1 |
|
0,05 |
7,8 |
9,5 |
12,6 |
15,5 |
18,3 |
21,0 |
23,7 |
26,3 |
28,9 |
31,4 |
33,9 |
36,4 |
38,9 |
43,8 |
49,8 |
55,8 |
61,7 |
67,5 |
|
|
0,10 |
6,2 |
7,8 |
10,6 |
13,4 |
16,0 |
18,5 |
21,1 |
23,5 |
26,0 |
28,4 |
30,8 |
33,2 |
35,6 |
40,3 |
46,1 |
51,8 |
57,5 |
63,2 |
|
ЛИТЕРАТУРА
2. НТМ СЭВ 1-84. Методы обработки результатов прямых измерений с многократными наблюдениями.
4. Welch В.L. The generalization of Student's problem when several different population variances are involved. Biometrika, 34, 1947, 28 - 35.
5. Хальд А. Математическая статистика c техническими приложениями. - M. 1956.
7. Труды метрологических институтов СССР. Выпуск 134 (194). - М.: Изд-во стандартов, 1972.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНА НПО «ВНИИМ им. Д.И. Менделеева»
ИСПОЛНИТЕЛИ
М.Н. Селиванов, канд. техн. наук; Ж.Ф. Кудряшова, канд. техн. наук; И.А. Евреинов.
2. УТВЕРЖДЕНА НПО «ВНИИМ им. Д.И. Менделеева» 25.12.89 г.
3. ЗАРЕГИСТРИРОВАНА ВНИИМС в ноябре 1990 г.
СОДЕРЖАНИЕ
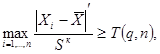 (1)
(1)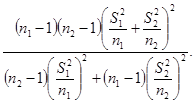 (4)
(4)