межгосударственный совет по стандартизации, метрологии
и сертификации
(МГС)
INTERSTATE COUNCIL FOR STANDARDIZATION, METROLOGY AND
CERTIFICATION
(ISC)
|
МЕЖГОСУДАРСТВЕННЫЙ |
ГОСТ |
Государственная
система обеспечения
единства измерений
ЭТАЛОНЫ
Способы выражения точности
|
|
Москва Стандартинформ 2012 |
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2009 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, применения, обновления и отмены»
Сведения о стандарте
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ им. Д.И. Менделеева») Федерального агентства по техническому регулированию и метрологии
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 10 ноября 2009 г. № 36-2009)
За принятие проголосовали:
|
Краткое наименование страны по MK (ИСО 3166) 004-97 |
Код страны по MK (ИСО 3166) 004-97 |
Сокращенное наименование национального органа по стандартизации |
|
Армения |
AM |
Минэкономики Республики Армения |
|
Азербайджан |
AZ |
Азгосстандарт |
|
Казахстан |
KZ |
Госстандарт Республики Казахстан |
|
Кыргызстан |
KG |
Кыргызстандарт |
|
Молдова |
MD |
Молдова-Стандарт |
|
Российская Федерация |
RU |
Ростехрегулирование |
|
Таджикистан |
TJ |
Таджикстандарт |
|
Узбекистан |
UZ |
Узстандарт |
(Поправка).
4 Приказом Федерального агентства по техническому регулированию и метрологии от 30 ноября 2010 г. № 769-ст межгосударственный стандарт ГОСТ 8.381-2009 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2012 г.
5 ВЗАМЕН ГОСТ 8.381-80
6 ПЕРЕИЗДАНИЕ. Декабрь 2011 г.
Информация о введении в действие (прекращении действия) настоящего стандарта и изменений к нему на территории указанных выше государств публикуется в указателях национальных стандартов, издаваемых в этих государствах.
Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст изменений - в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»
СОДЕРЖАНИЕ
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Государственная система обеспечения единства измерений
ЭТАЛОНЫ
Способы выражения точности
State system for ensuring the uniformity of measurements. Standards. Ways for expressing the accuracy
Дата введения - 2012-01-01
1 Область применения
Настоящий стандарт распространяется на государственные первичные, в том числе первичные специальные (далее - первичные) эталоны и вторичные эталоны единиц величин (далее - эталоны) и устанавливает способы выражения точности эталонов (погрешности и/или неопределенности измерений) в нормативных документах по обеспечению единства измерений в стране.
Формулы для оценивания точности эталонов приведены в приложении А.
Примеры оценивания точности эталонов приведены в приложении Б.
(Поправка).
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ 8.207-76* Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения
________
* На территории Российской Федерации действует ГОСТ Р 8.736-2011 «Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения»
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочного стандарта на территории государства по соответствующему указателю стандартов, составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
(Поправка).
3 Термины, определения и сокращения
3.1 В настоящем стандарте применены термины по [1], а также следующие термины с соответствующими определениями:
3.1.1 погрешность передачи размера единицы величины: Погрешность, представляющая собой результат суммирования случайных и неисключенных систематических погрешностей метода и средств измерений, используемых при передаче размера единицы величины.
3.1.2 нестабильность эталона: Изменение размера единицы величины, воспроизводимой эталоном, за установленный интервал времени.
3.1.3 точность эталона: Характеристика качества эталона, отражающая близость воспроизводимого им значения величины к истинному (опорному) значению.
3.2 В настоящем стандарте применены следующие сокращения:
СИ - средство измерений;
СКО - среднее квадратическое отклонение;
НСП - неисключенная систематическая погрешность.
4 Общие положения
4.1 Погрешность и неопределенность измерений, выполняемых при воспроизведении единицы величины или при передаче ее размера вторичным эталонам, указывают либо в абсолютной форме (в единицах измеряемой величины), либо в относительной форме.
Примечание - Если зависимость погрешности (неопределенности измерений) от значения величины, воспроизводимой эталоном, отличается от линейной, то погрешность (неопределенность измерений) может быть указана в виде таблицы по выбранным диапазонам измерений или в виде функциональной зависимости погрешности (неопределенности измерений) от значений измеряемой величины.
4.2 При оценивании доверительных границ погрешности (расширенной неопределенности измерений при воспроизведении единицы величины) первичных эталонов рекомендуется принимать доверительную вероятность (уровень доверия), равную 0,99.
При оценивании доверительных границ погрешности (расширенной неопределенности измерений при передаче размера единицы величины) вторичных эталонов рекомендуется принимать доверительную вероятность (уровень доверия), равную 0,95.
4.3 Для первичных и вторичных эталонов указывают все источники погрешностей и оценки этих погрешностей, способы их вычисления и суммирования.
Выражая точность эталонов неопределенностью измерений при воспроизведении единицы величины и передаче ее размера, указывают стандартную неопределенность, оцениваемую по типу А, стандартную неопределенность, оцениваемую по типу В, а также, при необходимости, суммарную стандартную неопределенность или расширенную неопределенность измерений.
5 Способы выражения точности первичных эталонов
5.1 Способы выражения погрешности первичных эталонов
- случайные погрешности;
- неисключенные систематические погрешности.
При необходимости указывают нестабильность эталона во времени.
5.1.1.1 Случайную погрешность первичного эталона характеризуют СКО
среднего арифметического результатов измерений ![]() при воспроизведении единицы
величины в условиях сходимости с указанием числа измерений.
при воспроизведении единицы
величины в условиях сходимости с указанием числа измерений.
Примечание - СКО случайной погрешности первичного эталона определяют на основе результатов измерений, полученных при исследовании эталона, учитывая при этом результаты анализа влияющих величин.
5.1.1.2 Неисключенные систематические погрешности первичного эталона представляют границами, доверительными границами.
Примечание - НСП первичного эталона в зависимости от числа ее составляющих выражают границами или доверительными границами:
границами ±|Θ| - при числе составляющих N ≤ 3, доверительными границами ±Θ(P) - при числе составляющих более трех.
5.1.1.3 Нестабильность v первичного эталона следует характеризовать изменением размера воспроизводимой единицы за установленный интервал времени. Нестабильность эталона определяют в процессе его создания или эксплуатации.
5.1.2 Допускается указывать доверительные границы суммарной погрешности первичного эталона.
5.2 Способы выражения неопределенности измерений при воспроизведении единицы величины первичным эталоном
5.2.1 Неопределенность измерений при воспроизведении единицы величины первичным эталоном характеризуют:
- стандартными неопределенностями, оцениваемыми по типу А [2] - [4];
- стандартными неопределенностями, оцениваемыми по типу В [2] - [4].
При необходимости указывают нестабильность эталона во времени.
5.2.1.1 Стандартные неопределенности, оцениваемые по типу А, ![]() характеризуют
СКО среднего арифметического результатов измерений при воспроизведении единицы
величины в условиях сходимости с указанием числа измерений.
характеризуют
СКО среднего арифметического результатов измерений при воспроизведении единицы
величины в условиях сходимости с указанием числа измерений.
5.2.1.2 Стандартные неопределенности, оцениваемые по типу В, иB при воспроизведении единицы величины определяют на основе теоретических (аналитических) исследований комплекса СИ и других технических средств, входящих в состав эталона, знаний о поведении и свойствах соответствующих материалов и средств их измерений, условий измерений, влияющих факторов, возникающих при измерении, справочных данных о составляющих, участвующих в измерениях.
5.2.1.3 Нестабильность первичного эталона определяют в соответствии с 5.1.1.3.
5.2.2 Допускается указывать суммарную стандартную неопределенность или расширенную неопределенность измерений при воспроизведении единицы величины первичным эталоном.
6 Способы выражения точности вторичных эталонов
6.1 Способы выражения погрешности вторичных эталонов
6.1.1 Для вторичного эталона указывают суммарную погрешность, образованную случайными погрешностями и НСП первичного и вторичного эталонов при передаче размера единицы величины от первичного эталона, погрешностью передачи размера единицы величины от первичного вторичному эталону, а также нестабильностью вторичного эталона.
6.1.2 Допускается указывать отдельно суммарное СКО, обусловленное влиянием случайных погрешностей, НСП вторичного эталона и нестабильность вторичного эталона.
Примечание - НСП вторичного эталона учитывает НСП передачи размера единицы величины.
6.1.3 Суммарную погрешность вторичного эталона характеризуют:
- суммарным СКО SΣ, обусловленным влиянием случайных погрешностей и НСП первичного и вторичного эталонов, методов и средств передачи размера единицы величины от первичного эталона, а также нестабильностью эталонов;
- доверительными границами суммарной погрешности ∆(Р), вычисленными с вероятностью, равной 0,95, и нестабильностью эталонов.
6.1.4 Если случайную погрешность, НСП, учитывающую НСП передачи размера единицы величины, нестабильность вторичного эталона указывают отдельно, то их выражают в виде, принятом для первичного эталона (5.1.1).
6.2 Способы выражения неопределенностей измерений при передаче размера единицы величины вторичным эталонам
6.2.1 Неопределенности измерений при передаче размера единицы величины вторичным эталонам характеризуют:
- или суммарной стандартной неопределенностью uc, обусловленной стандартными неопределенностями измерений при передаче размера единицы величины от первичного вторичному эталону, оцениваемыми по типу А и по типу В, а также нестабильностью эталонов,
- или расширенной неопределенностью измерений при передаче размера единицы величины от первичного эталона U(0,95) для уровня доверия 0,95 и нестабильностью эталонов.
6.2.2 Если стандартные неопределенности измерений при передаче размера единицы величины от первичного эталона, оцениваемые по типу А и по типу В, и нестабильность вторичного эталона указывают отдельно, то их выражают в виде, принятом для первичного эталона (5.1.1).
6.2.3 Нестабильность вторичного эталона за установленный интервал времени оценивают при передаче размера единицы величины от первичного эталона.
7 Способы выражения точности групповых эталонов
7.1 За значение величины, приписанное групповому эталону, принимают среднее арифметическое значение результатов сличений мер, входящих в состав группового эталона, если различия СКО результатов сличений мер, а также их НСП незначительны.
Если различия СКО результатов сличений мер или их НСП существенны, за значение величины, приписанное групповому эталону, принимают среднее взвешенное значение результатов сличений мер, входящих в состав группового эталона.
7.2 Способы выражения погрешностей групповых эталонов
7.2.1 СКО группового эталона ![]() определяют как СКО среднего арифметического значения результатов
сличений мер или как
СКО среднего взвешенного значения результатов
сличений мер, входящих в состав группового эталона, в зависимости от того, какое
значение величины приписано групповому эталону.
определяют как СКО среднего арифметического значения результатов
сличений мер или как
СКО среднего взвешенного значения результатов
сличений мер, входящих в состав группового эталона, в зависимости от того, какое
значение величины приписано групповому эталону.
7.2.2 За границы Θ (доверительные границы Θ(Р)) НСП группового эталона принимают границы (доверительные границы) НСП меры, входящей в состав группового эталона, если НСП этих мер пренебрежимо мало различаются между собой. Если различия НСП мер существенны, за границы Θ (доверительные границы Θ(Р)) НСП группового эталона принимают границы (доверительные границы) НСП меры, входящей в состав группового эталона, у которой она наибольшая.
7.3 Способы выражения неопределенностей измерений при определении точности групповых эталонов
7.3.1 Стандартную неопределенность типа А uA
группового эталона выражают стандартной неопределенностью среднего
арифметического значения результатов сличений мер ![]() или стандартной неопределенностью среднего взвешенного
значения результатов сличений мер
или стандартной неопределенностью среднего взвешенного
значения результатов сличений мер ![]() , входящих в состав группового эталона,
в зависимости от того, какое значение величины приписано групповому эталону.
, входящих в состав группового эталона,
в зависимости от того, какое значение величины приписано групповому эталону.
7.3.2 Стандартную неопределенность типа В uB группового эталона выражают стандартной неопределенностью меры, входящей в состав группового эталона, если стандартные неопределенности типа В этих мер пренебрежимо мало различаются между собой. Если различия стандартных неопределенностей мер существенны, за стандартную неопределенность типа В uB группового эталона принимают стандартную неопределенность той меры, входящей в состав группового эталона, у которой она наибольшая.
7.3.3 Нестабильность v группового эталона оценивают в соответствии с 7.2.3.
Приложение А
(справочное)
Формулы для оценивания точности эталонов
А.1 Формулы для оценивания погрешности эталонов
А.1.1 Воспроизводимая единица величины Y в большинстве случаев зависит от других измеряемых входных величин Х1, Х2, ..., Хт
Y = f(X1, X2, ..., Xm), (A.1)
где Х1, Х2, ..., Хт - непосредственно измеряемые входные величины, влияющие на размер единицы эталона;
m - число этих величин;
f - вид функциональной зависимости.
Примечание - Входные величины также могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические погрешности, поэтому функциональная зависимость f может быть сложной и определяемой экспериментально.
А.1.2 Многократные измерения входных величин х11, х12, ..., х1n1; ...; хi1, хi2, ..., хin1; ...; хm1, хm2, ..., хтп (i = 1, 2, ..., т) позволяют вычислить оценки входных величин, равные
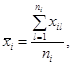 (А.2)
(А.2)
где ![]() - оценка i-й входной величины;
- оценка i-й входной величины;
xil - l-й результат измерений i-й входной величины;
ni - число измерений i-й входной величины.
А.1.3 Воспроизводимую единицу величины
![]() вычисляют как функцию оценок входных величин
вычисляют как функцию оценок входных величин ![]() ,
, ![]() , ...,
, ..., ![]() после
внесения в показания средств измерений поправок на все известные источники
погрешностей, имеющих систематический характер
после
внесения в показания средств измерений поправок на все известные источники
погрешностей, имеющих систематический характер
![]() (А.3)
(А.3)
А.1.4 Оценивание случайной составляющей погрешности
А.1.4.1 Средние квадратические отклонения вычисляют по формулам:
- для ряда результатов измерений входных величин
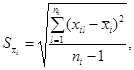 (А.4)
(А.4)
- для оценок измеряемых входных величин
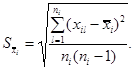 (А.5)
(А.5)
А.1.4.2 В случае
некоррелированных оценок ![]() ,
, ![]() , ...,
, ..., ![]() среднее
квадратическое отклонение
воспроизводимой единицы величины вычисляют по формуле
среднее
квадратическое отклонение
воспроизводимой единицы величины вычисляют по формуле
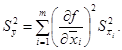 (A.6)
(A.6)
А.1.4.3 В случае коррелированных оценок ![]() ,
, ![]() , ...,
, ..., ![]() среднее квадратическое отклонение
оценки воспроизводимой
единицы величины вычисляют по формуле
среднее квадратическое отклонение
оценки воспроизводимой
единицы величины вычисляют по формуле
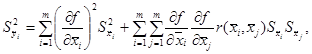 (A.7)
(A.7)
где r(![]() ,
,![]() ) - коэффициент корреляции.
) - коэффициент корреляции.
А.1.4.4 Коэффициент корреляции для согласованных пар измерений входных величин (хil, хjl) (l = 1, 2, ..., nij) вычисляют по формуле
где nij - число согласованных пар результатов измерений.
А.1.5 Оценивание неисключенной систематической погрешности
Границу (доверительную границу) НСП оценки воспроизводимой единицы
величины ![]() вычисляют
в зависимости
от числа оценок входных величин
вычисляют
в зависимости
от числа оценок входных величин ![]() ,
, ![]() , ...,
, ..., ![]() , содержащих НСП, и в зависимости от того, представлены ли НСП границами или доверительными границами.
, содержащих НСП, и в зависимости от того, представлены ли НСП границами или доверительными границами.
А.1.5.1 Если только одна оценка входной величины ![]() из всех оценок входных величин
из всех оценок входных величин ![]() ,
, ![]() , ...,
, ..., ![]() содержит НСП, представленную границами
содержит НСП, представленную границами ![]() , границу НСП
воспроизводимой единицы величины
, границу НСП
воспроизводимой единицы величины ![]() оценивают по формуле
оценивают по формуле
А.1.5.2 Если оценки входных
величин ![]() ,
,
![]() , ...,
, ..., ![]() содержат НСП, каждая из которых представлена
границами
содержат НСП, каждая из которых представлена
границами ![]() ,
границу (доверительную границу)
,
границу (доверительную границу) ![]() , (
, (![]() , (Р)) НСП
воспроизводимой единицы величины оценивают, соответственно, по формулам
, (Р)) НСП
воспроизводимой единицы величины оценивают, соответственно, по формулам
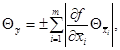 если m ≤
3; (А.10)
если m ≤
3; (А.10)
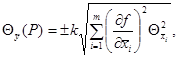 если m ≥
4, (А.11)
если m ≥
4, (А.11)
где k - коэффициент, определяемый выбранной доверительной вероятностью Р, числом составляющих НСП и их соотношением.
А.1.5.3 Значение коэффициента k для доверительной вероятности Р, равной 0,99, при числе НСП больше четырех (т > 4) принимают равным 1,4 (k0,99 = 1,4), при меньшем числе НСП (т ≤ 4) значение коэффициента определяют по графику, приведенному в ГОСТ 8.207.
Для доверительной вероятности Р, равной 0,95, значение коэффициента k равно 1,1 (k0,95 = 1,1).
А.1.5.4 Если оценки l
входных величин содержат НСП, представленные границами ![]() , а оценки т -
l входных величин содержат
НСП, представленные доверительными границами, то доверительные границы НСП
воспроизводимой единицы величины
, а оценки т -
l входных величин содержат
НСП, представленные доверительными границами, то доверительные границы НСП
воспроизводимой единицы величины ![]() оценивают по формуле
оценивают по формуле
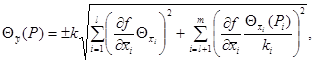 (A.12)
(A.12)
где l - число входных величин, НСП которых представлена границами;
![]() - доверительная
граница НСП оценки i-й
входной величины, вычисленная для доверительной вероятности Рi;
- доверительная
граница НСП оценки i-й
входной величины, вычисленная для доверительной вероятности Рi;
k, ki - коэффициенты, соответствующие доверительным вероятностям Р и Рi.
А.1.6 Оценивание доверительных границ суммарной погрешности эталона
А.1.6.1 Доверительные границы суммарной погрешности
воспроизводимой единицы величины ![]() вычисляют по формуле
вычисляют по формуле
![]() (A.13)
(A.13)
где KS - коэффициент, определяемый доверительной вероятностью Р и отношением случайных погрешностей и НСП;
![]() - суммарное СКО воспроизводимой единицы величины, обусловленное
воздействием случайных погрешностей и НСП.
- суммарное СКО воспроизводимой единицы величины, обусловленное
воздействием случайных погрешностей и НСП.
А.1.6.2 Значение коэффициента KS вычисляют по формуле
где t - коэффициент Стьюдента, соответствующий доверительной вероятности Р и эффективному числу степеней свободы veff, вычисляемому по формуле
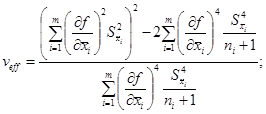
![]() вычисляют по формуле (А.9)
или (А.10), или (А.11), или (А.12) в зависимости от числа составляющих и формы
представления НСП оценок входных величин;
вычисляют по формуле (А.9)
или (А.10), или (А.11), или (А.12) в зависимости от числа составляющих и формы
представления НСП оценок входных величин;
![]() -
среднее квадратическое отклонение НСП воспроизводимой единицы величины.
-
среднее квадратическое отклонение НСП воспроизводимой единицы величины.
А.1.6.3 Среднее квадратическое отклонение НСП вычисляют, соответственно, по формулам
если составляющие НСП представлены границами по формуле (А.9) или (А.10);
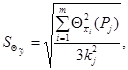 (А.16)
(А.16)
если составляющие НСП представлены доверительными границами по формуле (А.11);
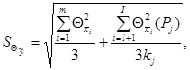 (А.17)
(А.17)
если часть составляющих НСП представлена границами, а часть составляющих НСП - доверительными границами по формуле (А.12),
где kj - коэффициент, соответствующий доверительной вероятности Рj при вычислении доверительных границ НСП.
А.1.6.4 Суммарное СКО воспроизводимой единицы величины ![]() , обусловленное воздействием случайных
погрешностей и НСП, вычисляют по формуле
, обусловленное воздействием случайных
погрешностей и НСП, вычисляют по формуле
А.1.7 Значения величин, приписываемых групповому эталону
А.1.7.1 Если различия СКО результатов сличений мер, а также их
НСП незначительны, среднее арифметическое значение результатов сличений мер ![]() , входящих в
состав группового эталона, вычисляют по формуле
, входящих в
состав группового эталона, вычисляют по формуле
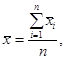 (А.19)
(А.19)
где ![]() - результат сличений i-й
меры группового эталона;
- результат сличений i-й
меры группового эталона;
п - число мер, входящих в состав группового эталона.
А.1.7.2 При значительном
различии СКО результатов сличений мер и пренебрежимо малом различии их НСП
среднее взвешенное значение результатов сличений мер ![]() , входящих в состав
группового эталона, вычисляют по формуле
, входящих в состав
группового эталона, вычисляют по формуле
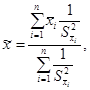 (А.20)
(А.20)
где ![]() - СКО
результата сличений i-й
меры группового эталона.
- СКО
результата сличений i-й
меры группового эталона.
А.1.7.3 Если различия СКО, а также НСП результатов сличений
мер, входящих в состав группового эталона, существенны, то среднее взвешенное
значение результатов сличений мер ![]() вычисляют по формуле
вычисляют по формуле
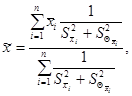 (А.21)
(А.21)
где ![]() - СКО
результата сличений i-й меры группового эталона;
- СКО
результата сличений i-й меры группового эталона;
![]() -
СКО НСП результата сличений i-й меры группового эталона.
-
СКО НСП результата сличений i-й меры группового эталона.
А.1.8 Оценивание погрешностей группового эталона
А.1.8.1 Если за значение величины, приписываемое групповому эталону, принимают среднее арифметическое значение мер, входящих в состав группового эталона, то СКО группового эталона вычисляют по формуле
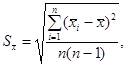 (А.22)
(А.22)
где ![]() - результат
сличений i-й меры группового эталона.
- результат
сличений i-й меры группового эталона.
А.1.8.2 Если за значение
величины, приписываемое групповому эталону, принимают среднее взвешенное
значение мер, входящих в его состав, то СКО группового эталона ![]() вычисляют по следующим формулам.
вычисляют по следующим формулам.
Если различия СКО результатов сличений мер существенны, а различия
НСП мер пренебрежимо малы, то формула для расчета ![]() имеет
вид
имеет
вид
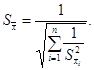 А.23)
А.23)
Если различия СКО результатов сличений мер, а также их НСП
существенны, то СКО группового эталона ![]() вычисляют по формуле
вычисляют по формуле
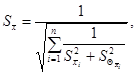 (А.24)
(А.24)
где ![]() -
СКО НСП результата сличений i-й
меры группового эталона.
-
СКО НСП результата сличений i-й
меры группового эталона.
А.2 Оценивание погрешностей воспроизведения производной единицы величины эталоном
А.2.1 Воспроизводимая производная единица величины Y зависит от единиц Y1, Y2, ..., Ym, воспроизводимых эталонами, входящими в состав эталона производной единицы величины
Y = F[Y1(X11, X12, ..., X1l), Y2(X21, X22, .. , Х2k), ..., Ym(Xm1, Xm2, ..., Xmh)]. (A.25)
А.2.2 Воспроизводимая единица величины каждого из эталонов, входящих в состав эталона производной единицы, может зависеть от величин, оказывающих влияние на воспроизводимую единицу и тем самым на производную единицу.
А.2.3 Погрешность воспроизведения производной единицы величины
оценивают в соответствии с А.1.4 - А.1.6, где
вместо погрешностей оценок входных величин ![]() ,
, ![]() , ...,
, ..., ![]() будут погрешности
воспроизводимой производной единицы величины Y1, Y2,
..., Ym.
будут погрешности
воспроизводимой производной единицы величины Y1, Y2,
..., Ym.
А.3 Формулы для оценивания неопределенности измерений при воспроизведении единицы величины эталоном
А.3.1 Воспроизводимая единица величины Y в большинстве случаев зависит от других измеряемых входных величин X1, X2, ..., Хm в соответствии с А.1.1. Воспроизводимую эталоном единицу величины вычисляют в соответствии с А.1.3.
А.3.2 Стандартная неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемая по типу А
Стандартную неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемую по типу А, вычисляют по формуле
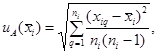 (A.26)
(A.26)
где xiq - q-й результат измерений i-й входной величины;
пi - число результатов измерений;
![]() - среднее арифметическое
значение результатов измерений i-й
входной величины.
- среднее арифметическое
значение результатов измерений i-й
входной величины.
Примечание - При многократных измерениях должна быть обеспечена взаимная независимость отдельных измерений.
А.3.3 Стандартная неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемая по типу В, uB
А.3.3.1 Исходные данные для вычисления:
- данные об измерении величин, влияющих на результат измерений входных величин, и данные о зависимости результатов измерений входных величин;
- данные, полученные в результате опыта о поведении и свойствах приборов и материалов;
- данные о калибровке, поверке, сведения изготовителя о приборе и другие сведения о приборе;
- неопределенности справочных данных, используемых констант.
А.3.3.2 Неопределенности для указанных в А.3.3.1 исходных данных возможно представить только границами (нижней а- и верхней а+), в которых находятся значения измеряемой величины. В случае отсутствия любой информации о значении величины предполагают равномерное распределение возможных ее значений внутри указанного интервала. Например, для i-й измеряемой величины нижняя и верхняя границы соответственно равны аi- и аi+.
Стандартную неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемую по типу В, в подобной ситуации вычисляют по формуле
![]() где
где
![]() (A.27)
(A.27)
А.3.3.3 Если интервал от аi до bi, несимметричен, то стандартную неопределенность измерений, оцениваемую по типу В, вычисляют по формуле
![]() (A.28)
(A.28)
А.3.3.4 Суммарную стандартную
неопределенность измерений ![]() при воспроизведении единицы величины в
случае некоррелированных оценок
при воспроизведении единицы величины в
случае некоррелированных оценок ![]() ,
, ![]() , ...,
, ..., ![]() вычисляют по формуле
вычисляют по формуле
где ![]() -
стандартная неопределенность измерений i-й
входной величины, вычисленная по типу А или по типу В.
-
стандартная неопределенность измерений i-й
входной величины, вычисленная по типу А или по типу В.
А.3.3.5 Суммарную стандартную
неопределенность измерений ![]() в случае коррелированных оценок
в случае коррелированных оценок ![]() ,
, ![]() , ...,
, ..., ![]() вычисляют по формуле
вычисляют по формуле
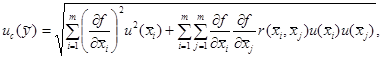 (A.30)
(A.30)
где ![]() -
стандартная неопределенность измерений i-й
входной величины, вычисленная по типу А или по типу В.
-
стандартная неопределенность измерений i-й
входной величины, вычисленная по типу А или по типу В.
Коэффициент корреляции ![]() вычисляют в соответствии с А.1.4.4 по формуле (А.8).
вычисляют в соответствии с А.1.4.4 по формуле (А.8).
А.3.3.6 Расширенную неопределенность измерений U c выбранным уровнем доверия Р вычисляют по формуле
где kP - коэффициент охвата, соответствующий выбранному уровню значимости Р;
![]() - суммарная стандартная
неопределенность измерений при воспроизведении единицы величины, вычисленная в
соответствии с А.3.3.4 или А.3.3.5.
- суммарная стандартная
неопределенность измерений при воспроизведении единицы величины, вычисленная в
соответствии с А.3.3.4 или А.3.3.5.
А.3.3.7 Выбор коэффициента
охвата kP требует полного знания распределения вероятностей, которое
характеризуется результатом измерений ![]() и его суммарной стандартной
неопределенностью измерений
и его суммарной стандартной
неопределенностью измерений ![]() .
.
А.3.3.8 В общем случае коэффициент охвата выбирают в соответствии с формулой
kP = tP(veff), (A.32)
где tP(veff) - квантиль распределения Стьюдента с эффективным числом степеней свободы veff и уровнем доверия Р.
Число степеней свободы veff определяют по формуле
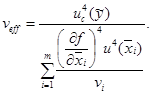 (А.33)
(А.33)
где vi - число степеней свободы:
vi = ni - 1 для вычисления неопределенностей измерений по типу А;
пi = ¥ для вычисления неопределенностей измерений по типу В.
А.3.3.9 В случае когда распределение результатов измерений не противоречит нормальному, для расчета коэффициента охвата kР используют квантили нормального распределения:
Расширенную неопределенность измерений при воспроизведении единицы величины эталона U(0,99) для уровня доверия 0,99 вычисляют по формуле
![]() (А.34)
(А.34)
Расширенную неопределенность измерений при воспроизведении единицы величины эталона U(0,95) для уровня доверия 0,95 вычисляют по формуле
![]() (А.35)
(А.35)
А.4 Значение величины, приписываемое групповому эталону
А.4.1 Если различия стандартных неопределенностей типа А ![]() результатов
сличений мер, а также их стандартных неопределенностей типа В
результатов
сличений мер, а также их стандартных неопределенностей типа В ![]() несущественны,
за значение величины, приписываемое групповому
эталону, принимают среднее арифметическое значение результатов сличений мер
несущественны,
за значение величины, приписываемое групповому
эталону, принимают среднее арифметическое значение результатов сличений мер ![]() , которое
вычисляют по формуле
, которое
вычисляют по формуле
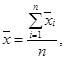 (А.36)
(А.36)
где ![]() -
результат сличений i-й
меры группового эталона;
-
результат сличений i-й
меры группового эталона;
п - число мер, входящих в состав группового эталона.
А.4.2 При значительном различии стандартных неопределенностей
типа А ![]() результатов
сличений мер и пренебрежимо малом различии их стандартных неопределенностей
типа В
результатов
сличений мер и пренебрежимо малом различии их стандартных неопределенностей
типа В ![]() среднее
взвешенное значение результатов сличений мер
среднее
взвешенное значение результатов сличений мер ![]() , входящих в состав группового
эталона, вычисляют по формуле
, входящих в состав группового
эталона, вычисляют по формуле
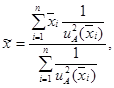 (А.37)
(А.37)
где ![]() -
стандартная неопределенность типа А результата сличений i-й меры группового эталона.
-
стандартная неопределенность типа А результата сличений i-й меры группового эталона.
А.4.3 Если различия стандартных неопределенностей типа А ![]() результатов
сличений мер, а также их стандартных неопределенностей типа В
результатов
сличений мер, а также их стандартных неопределенностей типа В ![]() существенны,
за значение величины, приписанное групповому эталону, принимают среднее
взвешенное значение результатов сличений мер
существенны,
за значение величины, приписанное групповому эталону, принимают среднее
взвешенное значение результатов сличений мер ![]() , которое вычисляют по формуле
, которое вычисляют по формуле
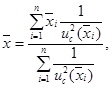 (А.38)
(А.38)
где ![]() - суммарное
стандартное отклонение i-й
меры группового эталона.
- суммарное
стандартное отклонение i-й
меры группового эталона.
А.4.4 Если за значение величины, приписываемое групповому
эталону, принимают среднее арифметическое значение мер, входящих в состав
группового эталона, то стандартную неопределенность типа А ![]() результатов сличений мер группового эталона вычисляют по формуле
результатов сличений мер группового эталона вычисляют по формуле
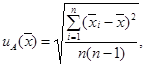 (A.39)
(A.39)
где ![]() -
результат сличений i-й
меры группового эталона.
-
результат сличений i-й
меры группового эталона.
А.4.5 Если за значение
величины, приписываемое групповому эталону, принимают среднее взвешенное
значение мер, входящих в его состав, то стандартную неопределенность группового
эталона типа А ![]() вычисляют по следующим формулам.
вычисляют по следующим формулам.
Если различия стандартных неопределенностей типа А ![]() результатов сличений мер существенны, а
различия стандартных неопределенностей типа В
результатов сличений мер существенны, а
различия стандартных неопределенностей типа В ![]() результатов сличений мер
пренебрежимо малы, то формула для расчета
результатов сличений мер
пренебрежимо малы, то формула для расчета ![]() имеет вид
имеет вид
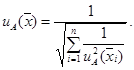 (А.40)
(А.40)
Если различия стандартных неопределенностей типа А ![]() результатов сличений мер, а также их
стандартных неопределенностей типа В
результатов сличений мер, а также их
стандартных неопределенностей типа В ![]() существенны, то
существенны, то ![]() группового эталона
вычисляют по формуле
группового эталона
вычисляют по формуле
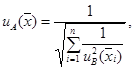 (А.41)
(А.41)
где ![]() -
стандартная неопределенность типа В результата сличений i-й
меры группового эталона.
-
стандартная неопределенность типа В результата сличений i-й
меры группового эталона.
Приложение Б
(справочное)
Примеры оценивания точности эталонов
Б.1 Пример вычисления погрешности при передаче размера единицы величины вторичному эталону
Б.1.1 Размер единицы вторичного эталона единицы длины - штрихового метра получают от первичного эталона в результате прямых измерений
Х = Х(Y1, Y2, Y3, Y4), (Б.1)
где Y1, Y2, Y3, Y4 - влияющие величины.
Число измерений равно десяти (n = 10):
Результат измерений ![]() = 1,00000147
м.
= 1,00000147
м.
СКО результата измерений S = 0,023 мкм.
Б.1.2 НСП представлены
границами с учетом числовых значениq частных
производных
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Это позволяет оценить
как доверительные границы суммарной
погрешности вторичного эталона, так и представить отдельно случайную погрешность, НСП и
нестабильность вторичного эталона.
. Это позволяет оценить
как доверительные границы суммарной
погрешности вторичного эталона, так и представить отдельно случайную погрешность, НСП и
нестабильность вторичного эталона.
Б.1.3 Вычисленные границы НСП из-за неточного:
- определения показателя преломления воздуха Θ1 = 0,030 мкм;
- значения длин волн Θ2 = 0,016 мкм;
- знания температуры Θ3 = 0,026 мкм;
- определения поправок на размер коллиматорной щели Θ4 = 0,002 мкм.
Б.1.4 Суммарная погрешность вторичного эталона
Б.1.4.1 Суммарное CKO SΣ, обусловленное влиянием случайных погрешностей и НСП, сличаемых эталонов, методов и средств передачи размера единицы от первичного эталона, вычисляют по формуле (А.18)
![]()
Из исследований платиноиридиевой штриховой меры (вторичный эталон) за ряд лет установлено, что его максимальная нестабильность не превышает 0,10 мкм в год, т.е. v = 0,10 мкм/год.
Б.1.4.2 Форма представления результата:
![]() = 1,00000147 м; SΣ = 0,000000034 м; п = 10.
= 1,00000147 м; SΣ = 0,000000034 м; п = 10.
Нестабильность эталона v = 0,10 мкм/год.
Б.1.4.3 Доверительные границы суммарной погрешности вторичного эталона
Б.1.4.3.1 Доверительные
границы суммарной погрешности ![]() , полагая распределение случайных
погрешностей нормальным, вычисляют по формуле (А.13)
, полагая распределение случайных
погрешностей нормальным, вычисляют по формуле (А.13)
![]()
Б.1.4.3.2 Среднее квадратическое отклонение НСП (без учета знака) вычисляют по формуле (А.15)
![]()
Б.1.4.3.3 Суммарное среднее квадратическое отклонение SΣ суммы случайных погрешностей и НСП вычисляют по формуле (А.18)
![]()
Б.1.4.3.4 Коэффициент KΣ вычисляют по формуле (А.14), выбрав из таблиц коэффициент Стьюдента t0,95 (n = 10) = 2,26,
![]()
Б.1.4.3.5 Доверительные границы суммарной погрешности вторичного эталона для вероятности 0,95 (без учета знака) равны при вычислении по формуле (А.13)
ΔΣ(0,95) = 2,1 ∙ 0,034 мкм = 0,0713 мкм ≈ 0,07 мкм.
Б.1.4.3.6 Из исследований платиноиридиевой штриховой меры (вторичный эталон) за ряд лет установлено, что его максимальная нестабильность не превышает 0,10 мкм в год, т.е. v = 0,10 мкм/год.
Б.1.4.3.7 Форма представления результата:
![]() =
1,00000147 м; Δ(0,95) = ±0,00000007 м; n = 10;
=
1,00000147 м; Δ(0,95) = ±0,00000007 м; n = 10;
![]() = 1,00000147 ± 0,00000007 м; n =
10.
= 1,00000147 ± 0,00000007 м; n =
10.
Нестабильность эталона v = 0,10 мкм/год.
Б.1.5 Составляющие погрешности вторичного эталона
Б.1.5.1 Среднее квадратическое отклонение среднего
арифметического значения ![]() = 0,023 мкм.
= 0,023 мкм.
Б.1.5.2 Доверительные границы неисключенной систематической погрешности (без учета знака)
![]()
Б.1.5.3 Форма представления результата:
![]() =
1,00000147 m;
=
1,00000147 m; ![]() = 0,000000023
м; n = 10; Θ(0,95) = 0,00000005 м.
= 0,000000023
м; n = 10; Θ(0,95) = 0,00000005 м.
Нестабильность эталона v = 0,10 мкм/год.
Б.2 Оценивание неопределенности измерений при передаче размера единицы величины вторичному эталону
Б.2.1 Размер единицы вторичного эталона единицы длины - штрихового метра получают от первичного эталона в результате прямых измерений
Х = Х(Y1, Y2, Y3, Y4), (Б.2)
где Y1, Y2, Y3, Y4 - влияющие величины.
Число измерений равно десяти (n = 10).
Результат измерений ![]() = 1,00000147 м.
= 1,00000147 м.
Б.2.2 Бюджет стандартных
неопределенностей представлен в таблице Б.1
с учетом коэффициентов влияния ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таблица Б.1 - Бюджет стандартных неопределенностей
|
Значение, мкм |
|
|
Стандартная неопределенность измерений, оцениваемая по типу А, возникающая из-за выполнения повторных измерений (n = 10) |
|
|
Стандартная неопределенность измерений, оцениваемая по типу В, возникающая из-за неточного определения показателя преломления воздуха Y1, uB(y1) |
|
|
Стандартная неопределенность измерений, оцениваемая по типу В, возникающая из-за неточного значения длин волн Y2, uB(у2) |
|
|
Стандартная неопределенность измерений, оцениваемая по типу В, возникающая из-за неточного знания температуры Y3, uB(у3) |
|
|
Стандартная неопределенность измерений, оцениваемая по типу В, возникающая из-за неточного определения поправок на размер коллиматорной щели Y4, uB(у4) |
|
Б.2.3 Суммарная стандартная неопределенность измерений
Б.2.3.1 Суммарную стандартную неопределенность измерений вычисляют по формуле (А.29)
![]()
Б.2.3.2 Форма представления результата:
![]() =
1,00000147
м; uс = 0,000000034 м; n =
10.
=
1,00000147
м; uс = 0,000000034 м; n =
10.
Нестабильность эталона v = 0,10 мкм/год.
Б.2.4 Расширенная неопределенность измерений
Б.2.4.1 Расширенную неопределенность измерений для уровня доверия Р = 0,95 вычисляют по формуле (А.31)
U(0,95) = 2 ∙ 0,034 = 0,068 ≈ 0,07 мкм.
Б.2.4.2 Форма представления результата:
![]() =
1,00000147 м; U(0,95) = ±0,00000007 м; n =
10.
=
1,00000147 м; U(0,95) = ±0,00000007 м; n =
10.
Нестабильность эталона v = 0,10 мкм/год.
Б.2.5 Составляющие неопределенности измерений при передаче размера единицы величины вторичному эталону
Б.2.5.1 Неопределенность измерений при передаче размера единицы величины вторичному эталону, оцениваемая по типу А,
uА = 0,023 мкм.
Б.2.5.2 Неопределенность измерений при передаче размера единицы величины вторичному эталону, оцениваемую по типу В, вычисляют по формуле
![]() 0,0247 мкм
≈
0,025 мкм.
0,0247 мкм
≈
0,025 мкм.
Б.2.5.3 Форма представления результата:
![]() =
1,00000147
м; uA =
0,000000023
м; uB = 0,000000025; n =
10.
=
1,00000147
м; uA =
0,000000023
м; uB = 0,000000025; n =
10.
Нестабильность эталона v = 0,10 мкм/год.
Б.3 Пример вычисления погрешности и неопределенности измерений при воспроизведении единицы электрического напряжения государственным первичным эталоном
Б.3.1 Эталон единицы электрического напряжения (далее - эталон) основан на эффекте Джозефсона, в соответствии с которым напряжение UJ определяют согласно уравнению
где n - номер ступени вольтамперной характеристики (ВАХ) перехода Джозефсона;
KJ = 483597,9 ГГц/В - константа Джозефсона;
f - частота облучения перехода Джозефсона.
Б.3.2 Исследование погрешностей эталона
Аппаратурная реализация эффекта Джозефсона приводит к необходимости учета различных влияющих факторов, включая эффект Зеебека, действие на микросхему, содержащую набор переходов Джозефсона (далее - МД), внешних факторов, вызывающих появление «замороженных» магнитных потоков и изменение ширины рабочей области ступеней напряжения, а также дефектов в МД, таких как наличие резистивности, неустойчивость ступеней и детектирование мощности облучения. В общем случае воспроизводимое напряжение на выходе эталона Uэ определяют согласно уравнению
Uэ = UJ + ΔU, (Б.4)
где UJ - напряжение, определяемое соотношением (Б.3);
![]() - инструментальная погрешность,
- инструментальная погрешность,
где Δf - погрешность частоты облучения МД;
EТЭДС - термоЭДС в выходной цепи эталона;
Rц - сопротивление выходной цепи эталона;
Rу - сопротивление утечек в выходной цепи эталона;
UR - дополнительное напряжение от наклона ступени ВАХ МД;
UP - дополнительное напряжение от детектирования мощности облучения;
Uп - дополнительное напряжение от «перескоков» ступеней на ВАХ МД.
Влияние замороженных магнитных потоков и внешних наводок заключается в уменьшении критического тока и рабочей области ступеней напряжения, что ухудшает метрологические параметры МД вплоть до потери ее работоспособности.
Для снижения действия постоянных составляющих на результат воспроизведения методика воспроизведения постоянного напряжения предусматривает усреднение абсолютного значения при отрицательном и положительном значениях воспроизводимого напряжения. В этом случае уравнение (Б.4) записывают в виде
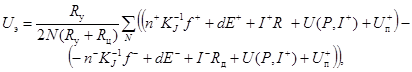
где Rу - сопротивление утечек в выходной цепи эталона;
Rц - сопротивление выходной цепи эталона;
N - число циклов измерений, заключенных под знаком суммы Σ;
f - частота облучения переходов Джозефсона;
п+ и п- - номер квантованной ступени при положительном и отрицательном выходном напряжении;
KJ - константа Джозефсона;
dE+ и dE- - значение термоЭДС выходной цепи эталона при положительном и отрицательном выходном напряжении;
I+ и I- - ток через переход Джозефсона при положительном и отрицательном выходном напряжении;
Rд - динамическое сопротивление МД;
U(P, I+) и U(P, I-) - значение детектируемого напряжения в зависимости от подаваемой на МД мощности и полярности протекающего тока.
Исходя из вышеизложенного погрешность эталона включает в себя составляющие, обусловленные:
- погрешностями стандарта частоты, синтезатора и системы фазовой автоподстройки частоты СВЧ-генератора;
- сопротивлением выходной цепи эталона и сопротивлением утечек выходной цепи эталона;
- наличием дефектов в МД, которые вызывают появление:
дополнительного напряжения от наклона ступени на ВАХ МД,
дополнительного напряжения из-за детектирования СВЧ-сигнала,
дополнительного напряжения из-за «перескоков» между ступенями ВАХ МД;
- наличием термоЭДС в выходной цепи эталона.
Оценка СКО SO случайной погрешности проведена в соответствии с рекомендациями рабочей группы Международного Бюро мер и весов (МБМВ) расчетным путем на основе исследования влияющих факторов, перечисленных выше, по формуле
![]()
где Si - оценка СКО i-й составляющей погрешности.
Оценки составляющих случайной погрешности приведены в таблице Б.2. В таблице Б.2 также приведены источники НСП и границы составляющих НСП.
Таблица Б.2 - Оценки составляющих НСП и случайных погрешностей
|
Эталон 1 В |
Эталон 10 В |
|||
|
Si |
Θi |
Si |
Θi |
|
|
Дрейф и флуктуации частоты |
0,04 ∙ 10-9 |
0,06 ∙ 10-9 |
0,04 ∙ 10-9 |
0,06 ∙ 10-9 |
|
Утечки сопротивлений |
0,1 ∙ 10-9 |
0,1 ∙ 10-9 |
||
|
Наклон ступени ВАХ |
0,1 ∙ 10-9 |
0,01 ∙ 10-9 |
||
|
Детектирование СВЧ-мощности |
0,1 ∙ 10-9 |
0,01 ∙ 10-9 |
||
|
«Перескоки» на ВАХ |
0,1 ∙ 10-9 |
0,1 ∙ 10-9 |
0,2 ∙ 10-9 |
0,2 ∙ 10-9 |
|
Дрейф и флуктуации термоЭДС |
0,5 ∙ 10-9 |
0,1 ∙ 10-9 |
0,05 ∙ 10-9 |
0,01 ∙ 10-9 |
Б.3.3 Оценивание погрешности для эталона 1 В
Б.3.3.1 Среднее квадратическое отклонение для эталона 1 В
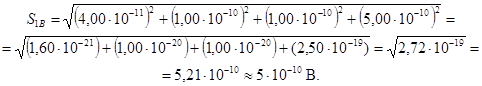
Б.3.3.2 Доверительные границы неисключенной систематической погрешности для эталона 1 В Оценку границы НСП вычисляют по формуле (А.11)
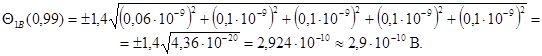
Б.3.3.3 Форма представления результата может быть следующей:
![]() = 1 B; SIB = 5
∙ 10-10 B; ΘIB(0,99)
= 2,9 ∙ 10-10 В.
= 1 B; SIB = 5
∙ 10-10 B; ΘIB(0,99)
= 2,9 ∙ 10-10 В.
Б.3.4 Оценивание погрешности для эталона 10 В
Оценки составляющих случайной погрешности и границы составляющих НСП приведены в таблице Б.2.
Б.3.4.1 Среднее квадратическое отклонение
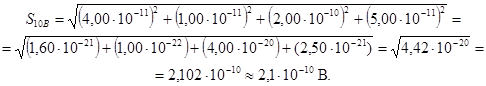
Б.3.4.2 Доверительные границы НСП вычисляют по формуле (А.11)
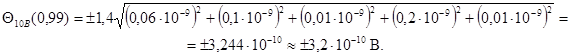
Б.3.4.3 Форма представления результата может быть следующей:
![]() = 10
В; S10B =
2,1 ∙ 10-10 В;
Θ10В(0,99)
= 3,2 ∙ 10-10 В.
= 10
В; S10B =
2,1 ∙ 10-10 В;
Θ10В(0,99)
= 3,2 ∙ 10-10 В.
Б.3.5 Оценивание неопределенности измерений при воспроизведении единицы величины для эталона 1 В
Б.3.5.1 Стандартная неопределенность, оцениваемая по типу А,
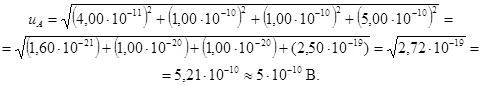
Б.3.5.2 Стандартную неопределенность, оцениваемую по типу В, вычисляют по формуле
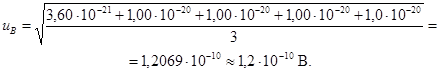
Б.3.5.3 Форма представления результата может быть следующей:
![]() = 1
В; uА = 5
∙ 10-10 В; uB =
1,2 ∙ 10-10 В.
= 1
В; uА = 5
∙ 10-10 В; uB =
1,2 ∙ 10-10 В.
Б.3.6 Оценивание неопределенности измерений при воспроизведении единицы величины для эталона 10 В
Б.3.6.1 Стандартная неопределенность, оцениваемая по типу А,
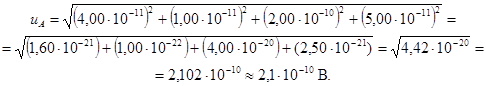
Б.3.6.2 Стандартная неопределенность измерений, оцениваемая по типу В,
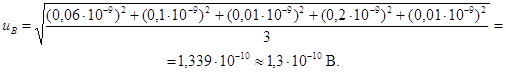
Б.3.6.3 Форма представления результата может быть следующей:
![]() = 1
В; uА =
2,1 ∙ 10-10 В; uB =
1,3 ∙ 10-10 В.
= 1
В; uА =
2,1 ∙ 10-10 В; uB =
1,3 ∙ 10-10 В.
Библиография
|
[1] |
Рекомендации по межгосударственной стандартизации |
Государственная система обеспечения единства измерений. Метрология. Основные термины и определения |
|
[2] |
Рекомендации по межгосударственной стандартизации |
Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений» |
|
[3] |
Руководство по выражению неопределенности измерения/Под ред. В.А. Слаева. - СПб, 1999. - (В пер. ВНИИМ им. Д.И. Менделеева) |
|
|
Guide to the Expression of Uncertainty in Measurement: First edition. - ISO, Switzerland, 1993. - (Текст находится во ФГУП «СТАНДАРТИНФОРМ») |
||
Ключевые слова: государственный первичный эталон; вторичный эталон; рабочий эталон; групповой эталон; эталонный набор; погрешность измерений при воспроизведении единицы величины; среднее квадратическое отклонение; неисключенная систематическая погрешность; нестабильность эталона; неопределенности измерений при воспроизведении единицы величины эталоном; стандартная неопределенность измерений, оцениваемая по типу А; стандартная неопределенность измерений, оцениваемая по типу В; суммарная стандартная неопределенность измерений; расширенная неопределенность измерений
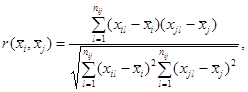
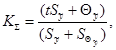
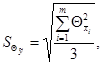
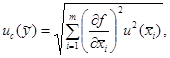 (А.29)
(А.29)