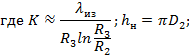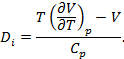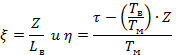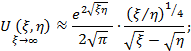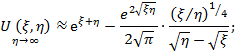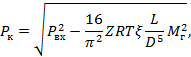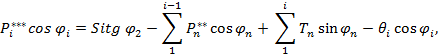МИНИСТЕРСТВО СТРОИТЕЛЬСТВА ПРЕДПРИЯТИЙ
НЕФТЯНОЙ И ГАЗОВОЙ ПРОМЫШЛЕННОСТИ

Всесоюзный научно-исследовательский институт
по строительству магистральных трубопроводов

«ВНИИСТ»

РЕКОМЕНДАЦИИ
ПО ПРОЕКТИРОВАНИЮ
ГАЗОПРОВОДОВ,
ТРАНСПОРТИРУЮЩИХ
ОХЛАЖДЕННЫЙ ГАЗ

Р 585-85

Москва 1986

Настоящий документ устанавливает принципиальные расчетные соотношения при проектировании трубопроводов, транспортирующих охлажденный газ.

Рекомендации предназначены для проектирования линейной части опытно-промышленных трубопроводов для транспорта природного газа в охлажденном состоянии.

Рекомендации разработаны ВНИИCToM, лабораторией исследования эксплуатационных нагрузок и воздействий на трубопроводы (ЛИЭНТ): кандидатами техн. наук А.Д. Двоирисом, Г.М. Чичко, инженерами О.Е. Ганиной, А.К. Малышевой, М.А. Салуцкой, В.П. Ханкиным.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Рекомендации по проектированию газопроводов, транспортирующих охлажденный газ, предназначены для проектирования линейной части экспериментальных трубопроводов для транспорта природного газа в охлажденном и сжиженном состоянии (сокращенно - трубопроводов ОПГ и СПГ или низкотемпературных трубопроводов - НТТ).

1.2. Проектирование НТТ следует выполнять, включая определение общестроительных нагрузок и воздействий, по главам СНиП 2.05.06-85.

1.3. В Рекомендациях рассмотрены специальные технологические нагрузки, возникающие при запуске и эксплуатации НТТ, а также природно-климатические воздействия, которые согласно СНиП II-6-76 относятся к «прочим» и не входят в главы общестроительных СНиПов.

В настоящих Рекомендациях рассмотрен режим стационарной эксплуатации НТТ, а также некоторые вопросы режима пуска, именуемого режимом захолаживания. В дальнейшем будут рассмотрены нагрузки и воздействия в периоды аварийных и плановых остановок и пусков.

К воздействиям отнесены силы и перемещения на поверхностях контакта трубопроводов с грунтовым массивом, а также на поверхностях и в сечениях отдельных узлов и конструкций трубопровода.

1.4. Данные Рекомендации составлены применительно к конструкции трубопровода, состоящего из стальной трубы (в основном диаметром 1220 или 1420 мм), слоя тепловой изоляции на наружной поверхности трубы (в дальнейшем названного теплоизоляционным слоем), гидроизоляционного покрытия на наружной поверхности теплоизоляционного слоя и наружного железобетонного защитного покрытия (из кольцевых элементов или сегментов) или без защитного кожуха.

Внесены ОПН ВНИИСТа

Утверждены ВНИИСТом 25 сентября 1985 г.

Срок введения в действие 1 июля 1986 г.

Теплогидроизоляционные защитные слои и покрытия в совокупности с окружающим грунтом подземных трубопроводов в дальнейшем названы изоляционно-грунтовым массивом.

2. КЛАССИФИКАЦИЯ НИЗКОТЕМПЕРАТУРНЫХ ТРУБОПРОВОДОВ ПО ТЕХНОЛОГИЧЕСКИМ ПАРАМЕТРАМ

2.1. Низкотемпературные трубопроводы применяются для магистральной транспортировки природного газа в охлажденном или сжиженном состоянии от месторождений или хранилищ к потребителям. В комплекс низкотемпературных трубопроводов входят:

установки первоначального охлаждения (сжижения), располагаемые на головных сооружениях (головные заводы охлаждения или сжижения);

компрессорные (насосные) станции;

промежуточные станции охлаждения;

непосредственно трубопровод, при необходимости с тепловой изоляцией (в зависимости от уровня охлаждения) с линейной и запорной арматурой;

установки регазификации для подачи газа потребителям.

В настоящих Рекомендациях рассмотрены только магистральные газопроводы больших диаметров (1020, 1220 и 1420 мм), для которых транспорт охлажденного газа экономически оправдан [1].

2.2. Низкотемпературные газопроводы (НТГ) транспортируют природный газ при температурах эксплуатации, равных или ниже температуры окружающей среды. Предполагается, что такой температурный режим поддерживается круглогодично, независимо от сезона, что требует применения специальных средств охлаждения газа^*.

_______________

^* В отличие от систем охлаждения современных газопроводов, где охлаждение газа на компрессорных станциях осуществляется в аппаратах воздушного охлаждения (АВО) за счет естественного холода. Температура газа после АВО не может быть ниже температуры окружающего воздуха; обычно Т_г = Т_в + (10 - 15), где Т_г - температура газа после АВО; Т_в - температура окружающего воздуха.

Охлаждение газа предусмотрено на компрессорных станциях (при транспорте охлажденного газа) или насосных станциях (при транспорте сжиженного газа). Станции охлаждения могут быть расположены на каждой КС (или НС), через несколько КС (или НС) или по обоим вариантам.

2.3. Различаются три основных уровня (режима) температур охлаждения транспортируемого газа.

I уровень - охлаждение газа до температур, близких к температурам грунта при подземной прокладке трубопровода (от 278 до 283 К на участках с водонасыщенными грунтами и от 271 до 263 К на участках с вечномерзлыми грунтами). Этот режим не требует тепловой изоляции трубопровода.

II уровень - охлаждение до температур, близких к критической температуре природного газа (от 213 до 208 К). В этом случае на трубопровод предусмотрено нанесение тепловой изоляции.

III уровень - первоначальное охлаждение до температур ниже критической, перевод газа в сжиженное состояние и поддержание этого температурного режима на всей трассе (охлаждение от 163 до 153 K). В этом случае также необходимо применять теплоизоляционные трубы.

Для двух первых режимов максимальное рабочее давление в газопроводе составляет от 7,3 до 10,0 МПа, для третьего - 5,5 МПа. Все другие предлагаемые уровни охлаждения транспортируемого газа (охлаждение от 240 до 260 К и т.д.) являются промежуточными между указанными.

2.4. Охлаждение до температур, близких к температуре грунта (ОТГ), позволяет уменьшить осевые сжимающие усилия в трубопроводе и снизить степень его напряженного состояния.

При прокладке трубопроводов в водонасыщенных грунтах с малой защемляющей способностью ОТГ позволяет повысить устойчивость на выпуклых кривых и в целом надежность эксплуатации.

При подземной прокладке на вечномерзлых участках ОТГ технологически необходимо для предотвращения протаивания и вызываемых им неконтролируемых перемещений трубопровода.

Классификация низкотемпературных газопроводов и их характерные технологические параметры приведены в табл. 1.

Таблица 1

Классификация и параметры низкотемпературных газопроводов

3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ТРАНСПОРТИРОВКИ ОПГ И СПГ ТРУБОПРОВОДА ПРИ СТАЦИОНАРНЫХ РЕЖИМАХ ПЕРЕКАЧКИ

3.1. Для определения параметров транспортировки охлажденного и сжиженного природного газа (ОПГ и СПГ) в стационарных условиях необходимо решить следующую систему дифференциальных уравнений:

 

а при граничных условиях

 

 

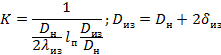
В формулах (1) и (2) использованы следующие условные обозначения, символы, единицы и термины:

Р - давление, мПа;

V - удельный объем, м³/кг;

T - температура, К;

Z - коэффициент сжимаемости;

R - газовая постоянная, Дж/кг ∙ К, для метана R = 518,271 Дж/кг ∙ К;

ρ - плотность, кг/м³;

С_р, С_v - теплоемкости при постоянном давлении при объеме, кДж/кг ∙ К;

 - теплоемкости идеального газа при P → 0, кДж/кг ∙ К;

D_i - дифференциальный дроссель-эффект, К/мПа;

ξ - коэффициент гидравлического сопротивления;

D_н, D_вн, D_из - соответственно, наружный и внутренний диаметры трубопровода, м;

F - живое сечение трубопровода, м²;

ε - степень сжатия газа на КС;

G - весовой расход, кг/с;

K - коэффициент теплопередачи от трубопровода в грунт, Вт/м ∙ К;

a - скорость распространения звука в среде, м/с;

k - показатель адиабаты Пуассона.

Индексы:

н, к - соответственно, начальный и конечный;

кр. - критические параметры;

T - текущая температура газа, К;

T_тр - температура грунта, К;

δ_из - толщина слоя изоляции, м;

λ_из - теплопроводность изоляции, Вт/м ∙ К.

Систему дифференциальных уравнений (1) - (2) замыкаем уравнением состояния вида φ(Р, V, T) = 0. Эта система является нелинейной и ее решают численно, а функция φ(Р, V, T) = 0 может быть задана таблично.

3.2. Выбор уравнения состояния является определяющим. На основе анализа известных уравнений состояния и табличных данных, приведенных в работе [2], рекомендуется для трубопроводов ОПГ применять уравнение Редлиха-Квонга, имеющее аналитическое решение; для трубопроводов СПГ рекомендуется использовать табличные данные [3], так как они убедительно подкреплены экспериментальными измерениями.

Выборка необходимых термодинамических данных для расчета параметров транспортировки СПГ приведена в табл. 2. В пределах этой таблицы величины ρ, D_i, С_р могут быть при необходимости линейно интерполированы.

3.3. Был разработан алгоритм и программа численного решения уравнений (1) - (2) на ЭВМ ЕС 1022. Программа включает следующие данные:

1) при заданных начальных значениях Р_н и Т_н определяют величины V, С_р, D_i. В случае применения уравнения Редлиха-Квонга величину ρ определяют на основании аналитического решения, а С_р и D_i рассчитывают на основе имеющихся термодинамических соотношений. При использовании табличных данных работы [3] эти величины находят на основе линейной интерполяции;

Таблица 2

Термодинамические параметры СПГ

Примечание. В таблице приняты следующие величины: плотность ρ - кг/м³; теплоемкость С_р - кДж/кг ∙ К; дроссель-эффект D_i - К/мПа.

2) определяют начальное значение массового расхода по формуле

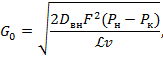
где ℒ - длина участка трубопровода, м,

причем краевая задача, описываемая уравнениями (1) и (2), переходит в задачу Коши, которую решают методом Рунге-Кутта;

3) методом деления отрезка пополам с заданной точностью определяют величину G. Для этого на i-шаге находят значения и , так что вычисленные значения  и  удовлетворяют условию . Тогда на следующем i + 1 шаге задают значение  и вычисляют значение P_кi+1, после чего определяют новые границы:

 

Процедуру вычислений продолжают до тех пор, пока не будет выполнено условие

Результаты численного расчета в виде зависимости температуры ОПГ и СПГ по длине участка трубопровода представлены в приложении 1, рекомендуемом.

4. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПУСКОВЫХ РЕЖИМОВ НИЗКОТЕМПЕРАТУРНЫХ ТРУБОПРОВОДОВ

Математическая модель процесса захолаживания

4.1. Для пуска трубопровода в эксплуатацию предполагается в основном газовый режим захолаживания:

для трубопроводов ОПГ необходимо захолаживание до 200 К;

для трубопроводов СПГ - захолаживание до температуры 150 К.

Предполагается, что для обоих режимов имеется возможность подачи в начальный участок трубопровода холодного газа с головного завода охлаждения (сжижения) в количестве, определяемом проектными параметрами и технологическим регламентом захолаживания.

4.2. Процесс захолаживания участка теплоизолированного трубопровода характеризуется следующей системой дифференциальных уравнений [1, 3]:

 

 

 

 

Уравнения (3) - (7) замыкают уравнением состояния, позволяющим получить зависимости

и

Система (3) - (9) имеет следующие начальные и граничные условия

 

 

 

 

где R₁, R₂, R₃ - радиусы внутренней поверхности трубы, внутреннего и наружного слоев изоляции;

r и Z - координаты по радиусу и вдоль трубы;

T, θ и t - температура изоляции, стенки трубопровода и охлаждающей среды, К;

ξ - коэффициент гидравлического сопротивления;

λ_из, λ_w - теплопроводность изоляции и стенки;

K - коэффициент, характеризующий термическое сопротивление окружающего трубопровод массива грунта;

T_гр - естественная температура грунта на глубине и заложения трубопровода;

a_из, a_w - соответственно, коэффициенты температуропроводности изоляции и стенки трубопровода;

h_в - внутренний периметр трубопровода (h_в = πD₁);

f - площадь сечения трубопровода (h_в = πD₁);

i - энтальпия;

D_i - дроссель-эффект;

C_р - теплоемкость газа;

α_в - коэффициент теплоотдачи от газа к стенке трубопровода;

ω - скорость потока, м/с;

τ - время, с.

4.3. Система уравнений (3) - (9) нелинейная, с дифференциальными уравнениями в частных производных и может быть упрощена введением имеющихся физических и расчетных предпосылок, а именно путем:

исключения влияния нестационарности - на распределение температур в слое теплоизоляции вследствие незначительности этого эффекта;

пренебрежения радиальными потоками тепла через стенку трубопровода, что соответствует достаточно высокой теплопроводности металла трубы и относительно малому значению ее толщины.

На основе указанных допущений система уравнений (3) - (9) имеет следующий вид;

 

 

 

 

при граничных условиях:

 

 

 

 

ρ_w - удельная масса металла трубы, кг/м³.

Здесь  - масса единицы длины трубопровода;

C_w - теплоемкость металла;

q_н; q_в - тепловые потоки от грунта к стенке и от стенки к газу на единицу длины трубопровода;

P_вх, t_вх - соответственно начальные значения давления и температуры газа на входе в трубопровод (Z = 0);

P_к - давление в конце участка трубопровода (Z = l);

P_н - начальное давление заполненного газом трубопровода

Р_к < Р_н < P_вх

4.4. Система уравнений (15) - (19) при краевых условиях (20) - (24) является квазилинейной гиперболической системой и решается численно на основе имеющихся уравнений состояния. В процессе решения можно получить распределение температур, давлений охлаждающей среды по длине трубопровода и во времени, и соответственно определить требуемое для захолаживания участка длины ℒ за время τ (имеется в виду заранее указанную малую разность температур охлаждающей среды и стенки трубопровода в его концевом сечении).

4.5. Для определения входящих в (20) - (21) термодинамических свойств охлаждающей среды при режиме захолаживания природным газом (ρ, С_р, D_i) предложено использовать уравнение состояния Редлиха-Квонга (Р-К):

где a = 0,427

P_кр = 4,626 МПа;

T_кр = 190,77 К;

R = 518,271 Дж/кг ∙ К.

Уравнение РК имеет аналитические решения для V. Теплоемкость С_р и дифференциальный дроссель-эффект D_i рассчитывают по термодинамическим соотношениям:

 

 

 

 

4.6. Коэффициент теплоотдачи от газа к стенке трубопровода определяют по уравнению

 

где число Рейнольда

а число Прандгля

μ, λ - соответственно вязкость и теплопроводность газового потока.

Уравнение (31) справедливо при Re > 10⁴.

4.7. Для практических оценок распределения температуры и времени захолаживания используют линейную систему уравнений вида [3]:

 

при T_w (Z, 0) = t(Z, 0) = T₀; t (0, τ) = t_вх.

Уравнения (33) - (34) предполагают отсутствие потоков тепла через изоляцию.

Коэффициенты L_b, T_в и Т_м определяют как

 

 

где c_w, δ, ρ_w - теплоемкость, толщина стенки трубопровода и плотность металла, соответственно.

Решение (29) - (30) получено в работе [3] путем введения новых переменных

в виде

 

где

 

Значения ρW, С_р и ρ предполагают равными средним между их стационарными значениями и значениями после изменения параметров потока на входе в трубопровод.

Функция является решением гиперболического уравнения второго порядка типа

с краевыми условиями

U (0, η) = eη; U (ξ, 0) = 1.

4.8. Величины ξ и η затабулированы в работе [3] в диапазоне 0 ≤ ξ ≤ 50 и 0 ≤ η ≤ 100.

Для больших значений ξ и η характерных для протяженных трубопроводов (например, для трубопровода диаметром 1420 мм при длине 25 - 30 км), можно использовать приближенные уравнения:

а) при больших ξ:

б) при больших η:

в) при больших ξ и η:

Для более точных расчетов рекомендуется следующее уравнение для U(ξ, η):

где

R - очень малый остаток;

модифицированные функции Бесселя полуцелого индекса выражены через гиперболические функции

 

 

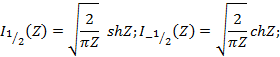
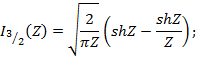
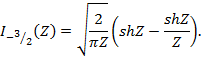
Для функции Бесселя целого порядка имеется уравнение

4.9. Для определения возможности реализации принятых температурных и расходных показателей процесса захолаживания уравнения (39) - (45) дополняют квазистационарным приближением уравнения движения (18), которое при ρw ≈ const и заданном начальном давлении P_вх позволяет рассчитать конечное давление в трубопроводе P_к по уравнению

 

k = 0,03 мм;

Величины ρ и Т в уравнениях (48) - (50) могут быть приняты при начальном давлении и минимальной температуре, до которой захолаживается участок трубопровода.

Режимы захолаживания и распределение температуры на участке трубопровода

4.10. Предполагается, что перед началом захолаживания проведено заполнение участка «теплым» газом с начальным давлением Р_н.

В дальнейшем в трубопровод начинает поступать «холодный» газ с давлением Р_вх > Р_н, постепенно вытесняя содержащийся в трубопроводе объем теплого газа в соседний участок.

Для более эффективного вытеснения «теплого» газа целесообразно использовать поршень-разделитель. После окончания вытеснения в конечном сечении трубопровода устанавливается и поддерживается определенное давление.

4.11. В процессе захолаживания наблюдается продвижение фронта захолаживания от начального к конечному сечениям участка.

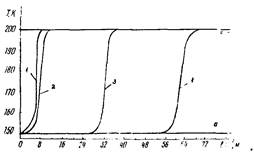
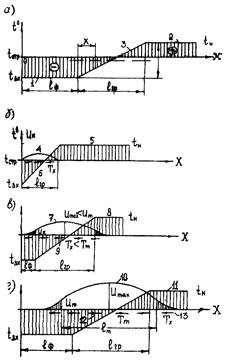
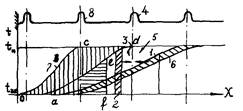
Температура стенки трубопровода Т_w изменяется по длине и во времени от Т₀ до t_вх , как это показано на рис. 1 и 2 (для режима захолаживания до температуры 200 К участка диаметром 1420 мм и протяженностью l = 100 км при Р_вх = 2,0 мПа и начальной скорости w = 5 м/с).

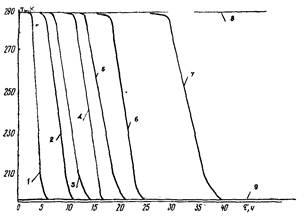
Рис. 1. Изменение температуры стенки трубопровода диаметром 1420 мм во времени при захолаживании его газовым потоком с T_вх = 200 К, массовой скоростью ρw = 69,15 кг/м² ∙ с:

1- l = 10 км; 2 - l = 20 км; 3 - l = 30 км; 4 - l = 40 км; 5 - l = 50 км; 6 - l = 70 км; 7 - l = 100 км; 8 - T_w = T₀ = 290 К; 9 - I_w = Т_вх = 200 К (где T_w - температура стенки трубопровода; Т₀ - начальная температура; Т_вх - входная температура охлаждающей среды; l - расстояние)

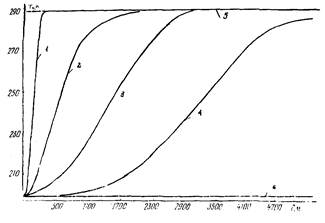
Рис. 2. Изменение температуры стенки Т_w трубопровода диаметром 1420 мм по длине с T_вх = 200 К, массовая скорость ρw = 69,15 кг/м² ∙ с:

1 - τ = 0,1 ч; 2 - τ = 0,25 ч; 3 - τ = 0,5 ч; 4 - τ = 1 ч; 5 - T_w = T₀ = 290 К; 6 - T_w = T_вх = 200 К

Максимальные продольные градиенты температуры стенки трубопровода образуются в первоначальный период (от 10 до 20 мм); по мере продвижения фронта захолаживания длина переходной зоны увеличивается, а продольные градиенты температуры - снижаются. Скорость продвижения фронта существенно зависит от технологических параметров процесса захолаживания и увеличивается с увеличением начального давления и расхода охлаждающей среды.

4.12. При принятых толщинах стенки трубопроводов диаметрами 1020, 1220 и 1420 мм температура стенки в поперечном направлении (по радиусу) остается практически неизменной на весь период захолаживания, т.е. поперечные градиенты температуры стенки трубопровода отсутствуют.

4.13. Характеристикой процесса захолаживания является период (время захолаживания), в течение которого температурный перепад между стенкой трубопровода T_w и входной температурой охлаждающей среды t становится близким к 0. Для заданного сечения время захолаживания определяют из условия, когда

 

а для участка трубопровода в целом

 

 

4.14. Время захолаживания участка трубопровода характеризуется степенью приближения температурного перепада в конечном сечении к исходному температурному перепаду.

В настоящих Рекомендациях в соответствии с работой [3] это приближение оценено от 0,02 до 0,2 %. При захолаживании участка с начальной температурой Т₀ = 290 К природным газом температура стенки в концевом сечении будет отличаться от t_вх примерно на 0,2 К при t_вх = 200 К и на 0,3 К при t_вх = 150 К.

4.15. Расчетные параметры процесса захолаживания участка трубопровода диаметром 1420 мм протяженностью l = 100 км представлены в табл. 3, 4.

Таблица 3

Параметры процесса захолаживания участка теплоизолированного трубопровода диаметром 1420 мм до Т = 200 К

Рн, кгс/см2	ρ, кг/м3	M, кг/c	αв, ккал	ξ	η	ΔP, кгс/см2	τ, ч
			м2 ∙ ч ∙ К
1	2	3	4	5	6	7	8
L = 100 км, w = 5 м/с
20	13,83	104	166	332	405	1,4	38
25	17,45	131,8	201,49	326	382	1,5	30
30	21,15	160	225,8	343	420	1,94	26
40	32,66	246	348,2	286	368	3,0	19
50	36,64	276,7	383,9	268	337	3,1	17
75	57,605	435	571,15	234	287	-5,4	12
100	79,93	603,8	796,7	214	276,6	6,4	10
L = 100 км, w = 10 м/с
20	13,83	208	290,46	329	441	5,4	19
30	21,15	320	414,12	270	331	8,15	13
40	28,75	434,17	622,75	290	349	11,1	10
50	36,64	553,32	738,79	260	363	15	9
75	57,61	870	1141,3	234	320	23	б
100	79,93	1207	1581,8	169	219	31,46	5
L = 100 км, w = 12 м/с
20	13,83	249,6	335,86	279	373	8,51	18
30	21,15	384,0	479,69	261	350	13,5	12
40	28,75	521	700,01	271	364	17,4	9
50	36,64	664,3	781,3	229	336	22,5	8
75	57,61	1044,5	1163,9	198	238	34,7	5
100	79,93	1449,2	1605	179	273	50,0	4,5

Таблица 4

Параметры процесса захолаживания участка теплоизолированного трубопровода диаметром 1420 мм до Т = 150 К сжиженным природным газом при Р_н = 5,0 мПа

Примечание

Расчеты проводили на основании таблиц и по уравнениям (56) - (60) работы [3] применительно к трубопроводам ОПГ (t_вх = 200 К, максимальное рабочее давление в трубопроводе 10,0 мПа) и трубопроводам СПГ (t_вх = 150 К, максимальное рабочее давление 5,5 мПа) при фиксированных начальных давлениях и скоростях газового потока. Начальная температура участка трубопровода принята T₀ = 290 К. При расчетах время захолаживания τ_* определено при ξ и η, соответствующих V₁ → 1 и V₀ → 0.

4.16. Для трубопроводов СПГ захолаживание проводят в два этапа:

1) участок трубопровода захолаживают в газовом режиме до температуры 200 К, давление на входе в трубопровод поддерживают в пределах от 3,0 до 4,0 мПа;

2) в трубопровод через поршень-разделитель подают СПГ при начальном давлении 5,5 мПа так, чтобы на выходе участка давление не было ниже 2,5 - 3 мПа. Такой режим обеспечивает практически однофазный процесс захолаживания участка.

Распределение температур в период второго этапа захолаживания показано на рис. 3, 4.

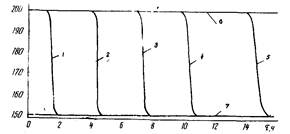
Рис. 3. Изменение температуры стенки трубопровода диаметром 1420 мм во времени при захолаживании его от 200 К до 150 К сжиженным природным газом (второй этап захолаживания)

Р_н = 5,5 МПа, ρw = 734 кг/м² ∙ с:
1 - l = 10 км; 2 - l = 30 км; 3 - l = 50 км; 4 - l = 70 К; 5 - l = 100 км; 6 - T_w = T_вх = 150 К; 7 - T_w = T_n = 200 К

Рис. 4. Изменение температуры стенки трубопровода диаметром 1420 мм по длине при захолаживании его от 200 К до 150 К (второй этап захолаживания):

Р_н = 5,5 МПа, ρw = 69,15 кг/м² ∙ c), 1 - τ = 0,1 ч; 2 - τ = 0,25 ч; 3 - τ = 0,5 ч; 4 - τ = 1 ч; 5 - T_w = T₀ = 200 К; 6 - T_w = T_вх = 150 К

Приближенная методика расчета времени захолаживания

4.17. Для определения времени захолаживания τ_* используем зависимость η = η (ξ), полученную при расчетах по уравнениям (43) - (46) из условий, что V₁ → 1 и V₀→ 0.

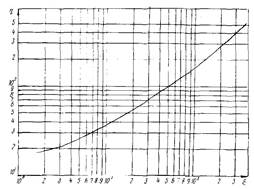
Зависимость η = η(ξ) приведена на рис. 5 и аппроксимирована эмпирическим уравнением вида

где А, m - числовые коэффициенты, представленные в табл. 5.

Рис. 5. Зависимость η от ξ при V₁ - V₀ → 1 (полное захолаживание участка трубопровода)

Таблица 5

Значения констант в уравнении (56)

4.18. Время захолаживания определяем из формулы (38) при подстановке вместо ητ_* в формуле (56). В этом случае τ_* будет

или

где

4.19. Коэффициент теплоотдачи α_в определяем по уравнению (31). Для P_r ≃ 0,75 и примерно постоянных значениях теплофизических свойств газа (λ, μ) для определения α_в получим приближенное уравнение

или α_в ≃ 5,522 (ρw)^0,8 при D₁ ≃ 1,387.

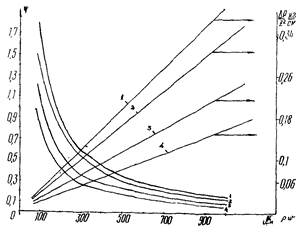
4.20. Величина  в уравнении (57) - (58) характеризует время прохождения газом рассматриваемого участка длиной l. Функцию f определяем в соответствии с (59). Для упрощения расчетов построены диаграммы на рис. 6 - 8 (где f и τ_* определяем в зависимости от массовой скорости ρw, средней плотности газа и величины τ₀). На этих же графиках показана зависимость удельного перепада давлений от параметров его движения (массовой линейной скорости), что характеризует возможность реализации принятого режима захолаживания.

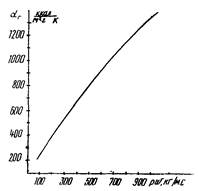
Рис. 6. Значения α_r в зависимости от массовой скорости (ρw) в процессе захолаживания участка трубопровода диаметром 1420 мм

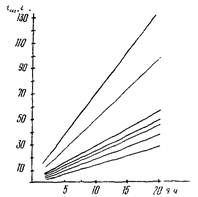
Рис. 7. Диаграмма для приближенной оценки времени захолаживания участка трубопровода диаметром 1420 мм протяженностью Z при средней скорости газа w для разных значений f:

1 - f = 1,5; 2 - f = 1; 3 - f = 0,5; 4 - f = 0,4; 5 - f = 0,3; 6 - f = 0,2; 7 - f = 0,1

Рис. 8. Значения f и в зависимости от ρw и w:

1 - w = 12 м/с; 2 - w = 10 м/с; 3 - w = 7 м/с; 4 - w = 5 м/с

5. РАСЧЕТ НА ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ НИЗКОТЕМПЕРАТУРНЫХ ТРУБОПРОВОДОВ

5.1. Расчет низкотемпературных (н.т.) трубопроводов на прочность, деформативность (перемещения) и устойчивость выполняются в основном по СНиП 2.05.06-85 и правилам строительной механики [6]. Данные Рекомендации содержат дополнительные требования к расчету и конструированию н.т. трубопроводов, отражающие особые условия их работы.

5.2. Подземные и надземные (в насыпи) н.т. трубопроводы необходимо конструировать и рассчитывать по принципу ограничения в пределах деформации грунта и материала тепловой изоляции, которую можно считать обратимой в течение всего срока эксплуатации.

5.3. Продольные перемещения должны быть исключены с помощью технических средств или отрегулированы в допустимых пределах компенсацией термоупругого изменения длины трубопровода.

5.4. Состояние равновесия участка подземного трубопровода, при котором грунт и средства балластировки достигли предельного сопротивления поперечным перемещениям, направленным вверх, следует рассматривать как предельное для данного участка и его нельзя допускать.

Нарушение статического равновесия системы труба - изоляция - грунт следует рассматривать как потерю устойчивости. Запас равновесия от потери устойчивости следует принимать П_у ≥ 2.

5.5. Толщина стенки н.т. трубопроводов (номинальная) должна быть определена по формуле

где D_н - наружный диаметр трубы;

P - рабочее (нормативное) давление в трубопроводе;

n - коэффициент перегрузки рабочего давления в трубопроводе, принимаемый по СНиП 2.05.06-85;

R₁ - расчетное сопротивление

где m, K₁, K_н - коэффициенты, принимаемые по СНиП II-45-75;

 - нормативное сопротивление растяжению (сжатию) металла труб и сварных соединений, принимаемое равным минимальным значениям временного сопротивления σ_вр по государственным стандартам и техническим условиям на трубы;

f₁ - коэффициент, учитывающий двухосное напряженное состояние труб, определяют по формуле

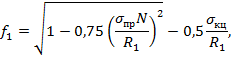
где σ_прN - абсолютное значение продольного осевого сжимающего напряжения, определяемое от расчетных нагрузок и воздействий.

5.6. При растягивающем осевом напряжении σ_прN коэффициент f₁ принимают равным единице.

5.7. Проверку прочности подземных и наземных (в насыпи) н.т. трубопроводов следует выполнять по условию

где R₁ - расчетное сопротивление, определяемое по формуле (62);

f₂ - коэффициент, учитывающий двухосное напряженное состояние металла труб:

при растягивающих осевых продольных напряжениях (σ_прN ≥ 0) принимают равным единице;

при сжимающих напряжениях (σ_прN < 0) определяют по формуле

где σ_кц - кольцевое напряжение от расчетного внутреннего давления находят по формуле

5.8. Для прямолинейных и упругоизогнутых участков подземных и наземных (в насыпи) трубопроводов с охлаждением газа до температуры грунта при ограничении поперечных перемещений упругими деформациями и при отсутствии продольных перемещений осевые напряжения от воздействия температуры и внутреннего давления определяют с учетом упруго-пластической работы металла трубы по формуле

5.9. Для подземных и наземных (в насыпи) трубопроводов ОПГ и СПГ при ограничении поперечных перемещений в пределах обратимых деформаций грунта и тепловой изоляции и при исключении продольных перемещений осевое напряжение от воздействия температуры и внутреннего давления следует определять по стадии упругой работы материала стенки стальной трубы по формуле

В формулах (66) и (67) величина Δt представляет собой расчетный температурный перепад, который находят согласно пп. 5.10 - 5.12 настоящих Рекомендаций и принимают положительными, если температура стенки трубы при эксплуатации превышает температуру, при которой части трубопровода соединены в непрерывную нитку (в расчете на отсутствие начальных напряжений).

5.10. Нормативный температурный перепад Δt_н следует принимать равным разнице между максимально или минимально возможной температурой стенок в процессе эксплуатации и наименьшей или наибольшей температурой, при которой осуществляется соединение всех частей трубопровода в непрерывную нитку без начальных продольных осевых напряжений.

Если в процессе соединения частей появляются начальные напряжения, то необходимо выполнить пересчет температуры замыкания на условие отсутствия начальных напряжений.

5.11. Расчетный температурный перепад определяют из условия

где n_t ≥ 1 - коэффициент перегрузки температурного перепада, принимаемый по специальному обоснованию.

5.12. Расчетный температурный перепад н.т. трубопроводов (см. пп. 5.8 и 5.9) должен соответствовать условиям прочности, которые с учетом формул (63) и (64) приводят к ограничениям вида:

а) при Δt > 0:

б) при Δt < 0 для абсолютного значения перепада:

В условиях (69) и (70) следует принимать:

а) для газопроводов с охлаждением до температуры грунта коэффициент η = 0,25;

б) для трубопроводов ОПГ и СПГ η = 0,15.

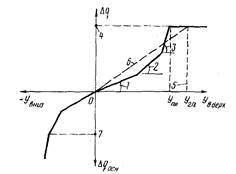
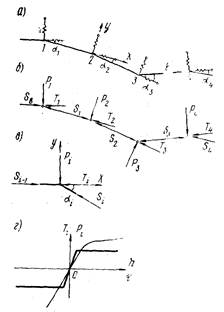
5.13. Взаимодействие участков трубопровода с грунтом и изоляционным покрытием допускается моделировать двусторонними продольными и поперечными связями и аппроксимировать фазы упругой и пластической работы диаграммой из отрезков прямых линий рис. 9.

Рис. 9. Диаграмма сопротивления грунта и изоляции поперечным перемещениям трубы:

1 - ; 2 - ; 3 - ; 4 - Δq = Δq_пр.гр
5 - y = y_пр - предельное перемещение; 6 - «секущая» характеристика; y_зп - запредельное перемещение

5.14. Сопротивление Δq грунта основания, засыпки и слоя изоляций в стадии упругой работы при вертикальном перемещении у, можно определять по зависимости

где  - коэффициенты нормального сопротивления, аналогичные коэффициенту постели основания Винклера.

Каждое из слагаемых в (71) «выключается» из суммы по мере исчерпания упругих свойств соответствующего слоя грунта. Суммарный эффект можно учитывать «секущим» коэффициентом нормального сопротивления , если поперечные перемещения не превосходят продольные более чем на 10 - 20 % (пунктирная прямая на рис. 9).

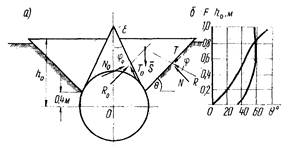
5.15. Предельное сопротивление грунта засыпки вертикальным перемещениям трубопровода следует определять по формуле (72), учитывающей образование над трубой грунтовой призмы выпирания треугольного сечения рис. 10.

где угол 𝜃 определяется из соотношения cos(φ + ε)cos ε = sin 𝜃 sin (𝜃 + φ).

График функции F = sin 𝜃 sin (𝜃 + φ) при φ₀ = φ = 19° приведен на рис. 10.

Последнее слагаемое (72) отражает структурное сцепление, которое можно учитывать при соответствующей обработке грунта засыпки (битумизация, уплотнение и т.д.).

Рис. 10. Состояние предельного сопротивления грунта засыпки с образованием призм выпирания треугольного сечения (а) и графики зависимости (б):

1 - график зависимости F = sin 𝜃 sin (𝜃 + φ] при φ (угол внутреннего трения) = 19°;
2 - график зависимости h₀ от 𝜃 (h₀ - расстояние от середины трубы до плоскости выпирания, Q - угол).

Полное предельное сопротивление q_пр поперечным перемещениям складывают из сопротивления грунта засыпки и собственной массы трубопровода с изоляцией и продуктом.

В случае применения железобетонных грузов (без засыпки) q_пр равно сумме собственной массы грузов, трубы, изоляции и продукта, т.е.

5.16. Предельное поперечное перемещение, соответствующее переходу в состояние предельного равновесия, определяют из зависимости:

5.17. Предельную осевую сжимающую силу в стенке трубы от полного предельного сопротивления (названной граничной) вычисляют по формуле

здесь ρ₀ - осредненное значение радиуса кривизны выпуклой части подземного трубопровода, принимаемое с учетом п. 6.24.

5.18. Предельный эквивалентный температурный перепад с учетом температуры и давления связан с граничной снимающей силой зависимостью

где

5.19. Возможность потери устойчивости подземного трубопровода наступает после перехода в стадию предельного сопротивления грунта и балласта. При параметре выпуклой части изогнутого участка K > 1 по [4] потеря устойчивости имеет форму многократного увеличения начального прогиба и происходит внезапно (проскоком):

где

l - длина полухорды выпуклой части волны (78).

5.20. Потеря устойчивости проскоком при температурном перепаде Δt < Δt_пр происходит с преодолением порога устойчивости.

5.21. При K < 1 и Δt > Δt_пр выпуклые участки находятся в состоянии неустойчивого равновесия, нарушение которого сопровождается прогрессивным нарастанием прогиба.

5.22. С учетом пп. 5.19 - 5.21 допустимый температурный перепад и интенсивность пригрузки от потери устойчивости следует определять по формуле

где S - продольная осевая сила сжатия:

где F - площадь поперечного сечения стенки трубы;

σ_кц - кольцевое напряжение от внутреннего давления, определяемое по формуле (65);

m - коэффициент условий работы участка трубопровода;

K_в - коэффициент запаса устойчивости, формирующий необходимый порог устойчивости, приближенно можно принимать K_в = 1,8.

5.23. Пригрузку от потери устойчивости, исходя из расчетного температурного перепада, определяют в последовательности по формулам (79), (78), (75), исходя из условия

где n_бл - коэффициент условий работы балласта:

для грунтовой засыпки n_бл = n_гр = 0,8;

для бетонных пригрузов n_бл = n_б = 0,95.

5.24. Пригрузку q_уст необходимо размещать в пределах всей выпуклой части изогнутого участка трубопровода и не меньше чем на длине 2l_on,

где

где t_m - сопротивление грунта продольным перемещениям, кгc/см;

J - момент сопротивления поперечного сечения трубы, см⁴.

5.25. При переменной кривизне участка плавного очертания (дуга окружности, полуволна, синусоиды, парабола) допускается в расчете пригрузки применять осредненный радиус начального изгиба кривизны, равный

где l - длина полухорды;

f₀ - стрела начального изгиба выпуклой части участка трубопровода.

5.26. Угловое соединение двух прямых участков при определении пригрузки от потери устойчивости не допускается заменять участками плавного очертания. Устойчивость участков с угловым соединением обеспечивает пригрузка, сосредоточенная в области углового соединения.

5.27. Для подземных трубопроводов с отрицательным температурным перепадом изменений проектного положения подвержены вогнутые участки. Пригрузку вогнутых участков подземных трубопроводов для ориентировочных расчетов можно определять по зависимости

Зависимость (81) аналогична зависимостям (75), (78) и (79), но не содержит коэффициента запаса устойчивости. Потеря устойчивости проскоком растянутых участков трубопроводов маловероятна.

5.28. Инженерная методика расчета перемещений низкотемпературных трубопроводов приведена в разделе 16 настоящих Рекомендаций. Расчеты н.т. трубопроводов с помощью ЭВМ должны получить максимальное применение, так как они дают возможность:

учитывать многообразие и изменения условий расчета по длине трассы и с течением времени;

учитывать совместную работу участков, узлов, грунта и балласта;

осуществлять оптимизацию параметров технических решений и экономических показателей.

6. ТЕХНИЧЕСКИЕ РЕШЕНИЯ ПО СТРОИТЕЛЬСТВУ ТРУБОПРОВОДА

6.1. В комплекс технических решений по строительству трубопроводов должны быть включены:

схемы прокладок и их геометрические параметры;

схемы конструкции теплоизолированных труб, узлов их опирания, закрепления и компенсации;

технологические принципы строительства.

Необходимо обеспечить возможность заводского и базового изготовления теплоизолированных труб и осуществить поточную технологию строительства магистральных трубопроводов с максимальным использованием современной трубопроводной строительной техники и освоенной технологии строительства.

6.2. Выбор трассы н.т. трубопровода следует выполнять методом оптимизации [9] одновременно с выбором способов прокладки и основных конструктивных решений с учетом природно-климатических, геологических и географо-экономических условий районов строительства.

6.3. Для трубопроводов СПГ способы прокладки в значительной степени определяются конструктивными и эксплуатационными особенностями теплоизолированных труб.

6.4. Подземная и наземная (в насыпи) прокладка защищает теплоизолированный трубопровод от непосредственного влияния солнечной радиации, атмосферы и механических повреждений.

Трубопровод на значительной своей длине может быть собран, сварен и уложен в траншею поточными методами строительства, но требует применения высоконадежной гидроизоляции, что вызывает промерзание окружающего грунта, требует создания комплексов гидротехнических и мелиоративных объектов и систем, предупреждающих экологически недопустимые последствия промерзания грунта и нарушения режима поверхностных стоков.

Технические характеристики подземных и наземных (в насыпи) трубопроводов СПГ позволяют рекомендовать их применение в населенных и промышленных районах на трассах с низким расположением уровня грунтовой воды.

6.5. Надземная прокладка упрощает конструкцию труб в связи с меньшей толщиной теплоизоляционного слоя, но требует большого числа опор и устройств для компенсации термоупругого изменения длины трубопровода, ограничивает возможности поточного строительства.

Применение надземной прокладки целесообразно в малонаселенных районах на трассах с малосвязными, просадочными и пучинистыми грунтами при высоком уровне грунтовых вод, на переходах через болота и поймы рек.

7. ТРУБЫ И ТРУБНАЯ СТАЛЬ

7.1. Для трубопроводов СПГ применяются трубы диаметром 1020, 1220 и 1420 нм. Основным следует считать диаметр 1220 мм, так как при этом диаметре существенно упрощается конструкция теплогидроизоляции трубопровода и строительно-монтажные работы на трассе с сохранением достаточно высокого экономического эффекта от магистрального транспорта повышенных объемов газа (до 70 млрд. м³ в год).

7.2. При производстве труб для линейной части магистральных трубопроводов СПГ можно ориентироваться на разработанные ВНИИСТом следующие технические требования к механическим свойствам стали:

7.3.Указанным требованиям удовлетворяет разработанная ВНИИСТом с Центральным научно-исследовательским институтом черной металлургии (ЦНИИЧМ) и Институтом электросварки им. О.Е. Патона экономнолегированная малоперлитная дисперсионно-твердеющая сталь 10ХГНМАЮ. Сталь 10ХГНМАЮ содержит в качестве легирующих элементов от 1,3 до 1,6 % Ni и 0,2 - 0,3 M₀, эту сталь выплавляют в электродуговых печах. Сталь 10ХГНМАЮ рекомендуется для прямых неизгибаемых участков.

Химический состав стали 10ХГНМАЮ (в %):

Свойства труб для трубопроводов СПГ из стали марки 10ХГНМАЮ:

7.4. Для получения аустенитных швов с высокой хладостойкостью в заводских условиях при сварке труб из стали 10ХГНМАЮ рекомендуется применять среднелегированную сварочную проволоку (3 - 5 %) типа СВ-06НЗ в сочетании с низкокремнистыми флюсами AH-15M, АН-20 или АН-60, с последующей обязательной термообработкой швов (закалка + отпуск).

7.5. Поворотную и неповоротную сварку труб из стали 10ХГНМАЮ в монтажных и трассовых условиях осуществляют по технологии, разработанной ВНИИСТом.

7.6. Для изогнутых компенсационных участков, включая фасонные детали, рекомендуется применять экономнолегированную никелем нержавеющую аустенитную сталь 10Х14Г14Н4Т (ЭИ711).

Химический состав стали 10Х14Г14Н4Т по ГОСТ 5632-72 (%):

Сталь зарегистрирована в Госгортехнадзоре СССР в качестве материала для труб и листового материала для сосудов, работающих под давлением. Сталь имеет высокую пластичность и ударную вязкость при низких температурах.

Сталь удовлетворительно деформируется в горячем и холодном состоянии, хорошо сваривается. Рекомендуемые присадочные материалы: электроды типа АНВ-24 и сварочная проволока С_в - 04Х19H9. Термообработка сварных швов не требуется.

Стандартизованные механические свойства стали 10Х14Г14Н4Т по ГОСТ 7350-70:

7.7. В связи с высокой стоимостью и дефицитностью аустенитной нержавеющей стали 10Х14Г14Н4Т количество ее при строительстве трубопроводов СПГ должно быть сведено к минимуму.

8. КОНСТРУКЦИЯ НИЗКОТЕМПЕРАТУРНЫХ ТРУБ

8.1. Конструкция теплоизолированной трубы для надземного трубопровода СПГ в принципиальной схеме состоит из стальной трубы диаметром 1220 мм или 1420 мм с учетом требований раздела 7 настоящих Рекомендаций, кольцевого слоя теплоизоляционного материала на наружной поверхности трубы (в дальнейшем - теплоизоляционный слой) и гидроизоляционного покрытия на наружной поверхности теплоизоляционного слоя.

8.2. Для подземной прокладки теплоизолированная труба должна иметь утяжеляющее бетонное покрытие, одновременно защищающее теплоизоляционный слой от механического воздействия захватных устройств при такелажных работах, сосредоточенного давления опор на бровке и неравномерного отпора грунтового основания в траншее, динамического воздействия грунта при засыпке траншеи (рис. 11).

8.3. В качестве теплоизоляционного материала для трубопроводов СПГ по данным исследований ВНИИСТа и СФ ВНИИСТа [7] и на основании опыта криогенной техники можно применять пенополиуретан (предпочтительно), пенополистирол, ФРП, ПСФ - ВНИИСТа, маты из минеральной ваты или стекловолокна.

Технические характеристики теплоизоляционных материалов приведены в табл. 6.

8.4. Толщина теплоизоляционного слоя из пенополиуретана для надземных трубопроводов СПГ составляет 100 - 150 мм, для подземных и наземных (в насыпи) 300 - 400 мм.

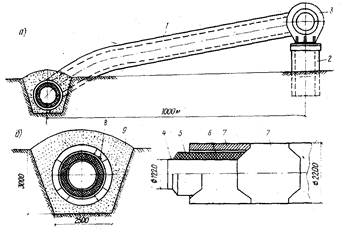
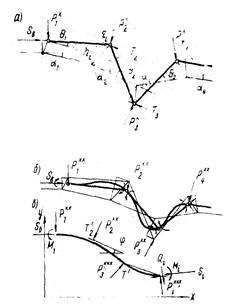
Рис. 11. Узлы подземного трубопровода СПГ:

а - надземный компенсатор; б - подземная теплогидроизоляционная труба; 1 - теплоизолированное плечо компенсатора; 2 - основание неподвижной опоры типа сваи-оболочки; 3 - опорное кольцо на стенке стальной трубы; 4 - стальная труба; 5 - теплоизоляционный слой; 6 - гидроизоляционное покрытие; 7 - сборное железобетонное защитное покрытие типа УКС; 8 - вкладыши центрирующие и антифрикционные из фторопласта - 4; 9 - засыпка из гидрофобизированного грунта

8.5. Поризованные пластические материалы наносят на поверхность трубы напылением, вспениванием или вспучиванием в кольцевом пространстве между трубой и цилиндрическим кожухом. Кожухом может служить гидроизоляционное покрытие (см. п. 8.1), установленное на трубу с кольцевым зазором и закрепленное прокладками из жесткого теплоизоляционного материала.

8.6. Требованиям гидроизоляции теплоизоляционного слоя отвечает листовой полимерный материал (например, из полиэтилена толщиной 4 - 8 мм).

Таблица 6

Технические характеристики теплоизоляционных материалов

8.7. Соединение листов из полимерного материала выполняют сваркой встык с помощью горячего воздуха и применением присадочного прутка из того же материала.

8.8. Механизация процесса обертки и закрепления листового полимера на поверхности теплоизоляционного слоя возможна с применением компрессионной автоматической сварки или методом спиральной намотки в сочетании с автоматической сваркой, рис. 12.

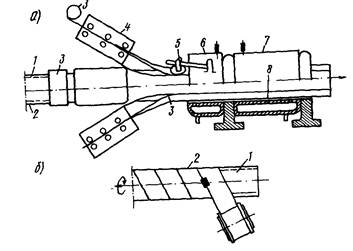
Рис. 12. Технологические схемы механизации нанесения гидроизоляции из полимерного листового пластика на трубу с тепловой изоляцией:

a - методом компрессионной сварки; б - методом спиральной навивки с автоматической сваркой; 1 - стальная труба; 2 - теплоизоляционный слой с фольговым покрытием; 3 - лента полимерного покрытия; 4 - печь; 5 - сварочная головка; 6 - камера предварительного охлаждения; 7 - камера интенсивного охлаждения; 8 - формующая втулка

Нанесение полимерного гидроизолирующего покрытия на теплоизоляционный слой напылением также может служить основой механизации.

8.9. Темпы и эффективность поточного строительства трубопроводов СПГ могут быть достигнуты путем поставки на трассу теплогидроизолированных плетей не менее чем из двух стальных труб, т.е. длиной не менее 20 м.

Технические характеристики и технологические свойства выпускаемых промышленностью поризованных и монолитных полимерных материалов позволяют создать заводскую и базовую технологию механизированного изготовления теплогидроизолированных плетей необходимой длины.

8.10. Для тепловой изоляции трубопроводов СПГ можно применять жесткие теплоизоляционные изделия в виде сегментов или полуколец из пенополистирола ПСВ-С, фенольных пенопластов ФРП, ПСФ-ВНИИСТ и пенополиуретана ППУ различных марок.

Жесткие теплоизоляционные изделия можно изготавливать в заводских или базовых условиях.

8.11. Мягкие теплоизоляционные изделия для трубопроводов СПГ изготавливают в виде матов из минеральной ваты с ориентированными волокнами или стекловолокна. Маты обертывают полиэтиленовой пленкой или фольгой.

Мягкие теплоизоляционные изделия должны быть уложены на трубы при подземной и надземной прокладках только между кольцами из жесткого теплоизоляционного материала. Назначение колец - предохранить от смятия гидроизоляционное покрытие и теплоизоляционные мягкие изделия при складировании, транспортировке и подземной прокладке.

8.12. Опирание теплоизоляционных труб в условиях складирования, транспортировки и монтажа следует осуществлять на участках с жестким теплоизоляционным материалом с учетом допустимого опорного давления на сжатие теплоизоляционного материала.

Пределу прочности на сжатие, приведенному в табл. 6, должно соответствовать допустимое опорное давление не более 0,1 МПа при конструктивном обеспечении его распределения.

8.13. Давление неподвижных и подвижных опор надземных трубопроводов должно передаваться на стенку стальной трубы через опорные кольца, ребра, пластины, минуя теплоизоляционный слой.

При подземной или наземной (в насыпи) прокладке теплоизоляционный слой следует ограждать от механического воздействия грунта жестким защитным покрытием. Целесообразно для этой цели применять изделия из бетона (кольца, сегменты, колпаки, сплошное покрытие), используя их одновременно как утяжелители, предохраняющие от всплытия и как защиту от повреждений гидроизоляционного покрытия, рис. 13.

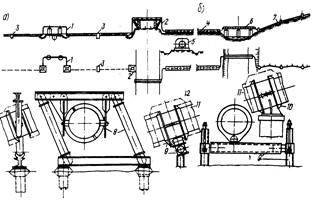
Рис. 13. Схемы узлов подземного и надземного способов прокладки трубопровода СПГ:

а - участок подземной прокладки; б - участок надземной прокладки; 1 - надземный компенсационный участок на пересечении с водоводом; 2 - надземный компенсационный участок на пересечении с транспортной магистралью; 3 - разделительный подземный упор; 4 - прямолинейная прокладка, ограждающая теплоизоляционная конструкция из седловидных блоков и плит; 5 - поперечное сечение ограждающей теплоизоляционной конструкции; 6 - переход через водную преграду, совмещенный с компенсатором; 7 - прокладка змейкой по наклонному участку трассы; 8 - шарнирнобалансирная опора змейки; 9 - катковая свободноподвижная опора змейки; 10 - угловая неподвижная опора змейки; 11 - теплоизолированная труба; 12 - кожух с засыпкой порошковой изоляцией

9. ПОДЗЕМНАЯ ПРОКЛАДКА

9.1. Рекомендуемые условия на проектирование подземного магистрального трубопровода СПГ опытно-промышленного назначения:

диаметр стальной трубы на основной части трассы - 1220 мм и, возможно, на части трассы - 1420 мм;

материал труб согласно разделу 7 для линейной части трубопровода - 10ХГ;

рабочее (нормативное) давление продукта Р = 5,5 МПа;

температура продукта и стенки труб 153 К;

возможная наибольшая температура соединения участков в нитку между НС плюс 283 К;

нормативный температурный перепад минус 130 К;

температурный режим - стабильный, температура стенки стальной трубы изменяется во время пуска при захолаживании трубопровода на 20 - 30° в сутки и при вынужденных остановках на участках с продуктом температура изменяется на 2 - 3° в сутки;

толщина слоя теплоизоляции из пенополиуретана по данным теплофизического расчета 300 - 400 мм и для надземных компенсационных участков 100 - 150 мм или в случае применения другого материала с эквивалентной толщиной слоя следует руководствоваться разделом 8, табл. 6.

9.2. Результаты расчетного определения основных параметров конструкции подземного трубопровода СПГ по зависимости раздела 5 приведены в табл. 7.

9.3. Из данных табл. 7 можно заключить, что при полном защемлении трубопровода (если предположить эту возможность) продольные осевые напряжения растяжения от воздействия нормативного температурного перепада и давления по формуле (67) достигают 420 МПа, это превышает расчетное сопротивление для материалов труб и определяет необходимость частичной компенсации термоупругого сокращения длины подземного трубопровода от расчетного температурного перепада.

Таблица 7

Технические характеристики надземных и подземных теплоизолированных труб СПГ

Примечание. В таблице принято следующее обозначение: n - коэффициент перегрузки по давлению.

9.4. Пригрузка q, удерживающая от «выдергивания» трубопровода из траншей под воздействием растягивающей осевой силы, необходима на вогнутых кривых, что характерно для трубопровода СПГ. В предположении полного защемления при начальном радиусе кривизны ρ₀ ≥ 10⁴ пригрузка q достигает 18 т/м (см. табл. 7), что превышает возможности конструктивного и экономически приемлемого решения пригрузки и также ориентирует на компенсацию термоупругого изменения длины.

9.5. Пригрузка, локализующая выталкивающее действие воды на случай затопления траншей и насыщения грунта засыпки водой в предпусковой период с учетом балластирующего действия грунта, составляет примерно 2 т/м, что вполне доступно для практического осуществления.

9.6. Подземный трубопровод СПГ, отвечающий требованиям настоящего раздела, возможен в варианте конструктивной схемы, приведенной на рис. 11 и 13:

а) трубопровод состоит из прямолинейных в плане подземных участков длиной 2 - 3 км, между которыми расположены надземные компенсационные участки П-образной формы с радиусом кривизны отводов не менее 7 м для обеспечения пропуска поршня.

Для расположения компенсационных участков используют по возможности понижения рельефа местности: переходы через поймы рек, болота, пересечения с инженерными сетями, углы поворота трассы;

б) прямолинейные участки монтируют из теплоизолированных плетей и сваривают в нитку на бровке с последующей изоляцией монтажных стыков;

в) устанавливают бетонные утяжеляющие пригрузы типа УКС, как показано на рис. 11 (они же являются защитой для теплогидроизоляции) с зазором в 4 - 5 см относительно гидроизолирующего покрытия. На внутренней поверхности сегментов УКС при их изготовлении устанавливают центрирующие вкладыши из антифрикционного материала (например, фторопласта - 4);

г) в качестве утяжеляющего покрытия можно применить заводское обетонирование теплогидроизолированной трубы или плети с кольцевой разрезкой по схеме рис. 14. Для обеспечения свободы продольного перемещения трубы относительно бетонного покрытия до обетонирования на гидроизоляционное покрытие следует нанести антифрикционный слой в 0,02 - 0,025 м (например, из асбеста с графитом);

д) масса и гибкость теплоизолированных труб с конструкцией бетонного покрытия (по пп. в, г) позволяет осуществить укладку нитки в траншею несколькими трубоукладчиками по технологической схеме, аналогичной укладке обетонированных обычных труб.

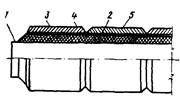
Рис. 14. Теплогидроизолированная труба СПГ с заводским обетонированном:

1 - стальная труба; 2 - теплоизоляционный слой; 3 - гидроизоляционное покрытие; 4 - антифрикционный слой из асбеста с графитом; 5 - защитное покрытие заводского обетонирования

9.7. Для засыпки траншей трубопроводов СПГ следует применять гидрофобный минеральный грунт - песок, сунель, суглинок, перемешанный с 7 - 8 % битумовидных остатков крекинга нефти. Такая грунтовая масса имеет начальное структурное сцепление, что увеличивает ее балластирующее действие сразу же после засыпки, особенно при послойном или, хотя бы, при поверхностном уплотнении (см. рис. 13).

Для подземных трубопроводов СПГ засыпка из гидрофобного грунта улучшает гидрозащиту теплоизоляционного материала.

9.8. Гидрофобный грунт имеет повышенное и более устойчивое во времени тепловое сопротивление в сравнении с естественным грунтом, коэффициент теплопроводности битумизированного песчаного грунта составляет λ = 0,46 до 0,7 Вт/(м ∙ к), битумизированного суглинка λ = от 0,23 до 0,35 Вт/(м ∙ к).

9.9. Компенсация термоупругого изменения длины подземного трубопровода с конструктивной схемой по п. 9.7 происходит путем изгиба надземных компенсационных участков и сопровождается преодолением сил трения на поверхности раздела гидроизоляционного покрытия и наружной бетонной (сборной или монолитной) пригружающей и ограждающей конструкции.

9.10. Участки между компенсаторами не должны иметь начального изгиба радиусом ρ₀ < 10⁵. При несоблюдении этого условия пригрузка q_выд, удерживающая трубопровод от выдергивания, значительно превышает собственную массу q_с.в и силы трения теплогидроизолированного трубопровода по бетонной ограждающей конструкции возрастают.

9.11. В качестве опорных конструкций для неподвижных опор компенсационных участков (см. рис. 11 и 13) могут быть применены железобетонные кольца (типа водопроводных колодцев), опускаемые в грунт методом гравитационного «задавливания» или вибрационного погружения с извлечением керна (на плотных грунтах) или без извлечения керна (на торфе).

9.12. Конструкция теплогидроизолироваиных труб для надземных компенсаторов определяется условиями п. 8.13. Теплоизолированные трубы не допускается опирать на опорные конструкции посредством сжатия теплоизоляционного слоя. Для этой цели следует применять опорные элементы из стали или железобетона, передающие давление опоры стенке стальной трубы согласно рис. 13.

10. НАДЗЕМНАЯ ПРОКЛАДКА

10.1. В зависимости от местных условий для надземных н.т. трубопроводов можно применять следующие схемы прокладки: змейкой относительно коротких прямых участков, плавно сопряженных между собой, прямолинейную в плане с компенсационными участками и параллельную прокладку (см. рис. 13).

10.2. Техническая характеристика схем надземной прокладки приведена в табл. 8.

10.3. Для одного трубопровода можно применять различные схемы прокладки, характеристики должны соответствовать местным условиям строительства и эксплуатации.

10.4. Прокладку змейкой целесообразно использовать на повышенных участках трассы и на уклонах в связи с умеренностью снегового покрова и возможностью закрепления трубопровода от осевых перемещений на уклонах с помощью большого числа неподвижных опор (см. рис. 14).

Таблица 8

Техническая характеристика схем надземной прокладки низкотемпературных трубопроводов

10.5. В условиях тундрового ландшафта при малых уклонах местности и низкой несущей способности грунтов прокладка змейкой имеет следующие преимущества: меньшая нагруженность неподвижных опор, отпадает влияние топографических условий на расположение большеразмерных компенсационных участков сосредоточенного действия, необходимых для прямолинейной прокладки.

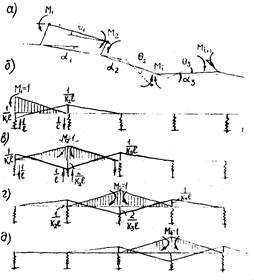
10.6. Прокладку змейкой следует применять в конструктивном варианте, отличающемся тем, что неподвижные опоры располагают в углах змейки по одну сторону от воздушной оси трассы, а не в середине плеч, как обычно принято. При таком решении в несколько раз уменьшается горизонтальная сила от ветровой нагрузки, действующей на неподвижную опору.

На неподвижной опоре, размещенной в середине плеча, распоры от ветровой нагрузки смежных пролетов совпадают по направлению и арифметически складывают. При размещении опоры в вершине компенсационного участка распоры направлены в противоположные стороны под небольшим углом одна к другой и их равнодействующая меньше каждого из слагаемых.

10.7. Выбор геометрических параметров и расчет компенсирующей способности н.т. трубопроводов с прокладкой по системе змейки следует выполнять с учетом геометрической нелинейности расчетной схемы в упругой стадии работы материала труб при минимальных начальных прогибах f₀ , такой принцип:

уменьшает дополнительный расход труб на искривлении оси трубопровода от оси трассы;

упрощает конструкцию ригелей;

упрощает разбивку опор, которые могут быть ориентированы перпендикулярно к оси трассы;

дает возможность применить упрощенную конструкцию подвижных опор, например однороликовых (рис. 14).

10.8. Ориентировочные значения геометрических параметров надземных н.т. трубопроводов при прокладке змейкой приведены в табл. 9.

Таблица 9

Значения геометрических параметров надземных н.т. трубопроводов при прокладке змейкой

10.9. Прямолинейную прокладку с П-образым или трапециевидным компенсатором, располагая над зеркалам прямой участок пролета или компенсатора, целесообразно применять на пониженных участках и переходах через постоянные и сезонные водотоки доемы.

10.10. В освоенных населенных районах с большим числом пересечений трассы, кроме подземной прокладки с надземными компенсаторами, возможно применение надземной прямолинейной прокладки с компенсационными участками. Этот вид прокладки отличается тем, что прямые участки располагают на сплошном основании и ограждают железобетонными конструкциями, например, в форме пригрузов, (см. рис. 12). Принцип действия такого трубопровода по компенсации изменения длины тот же, что и указано в разделе 9.

10.11. Ограждающие конструкции трубопровода для СПГ могут быть выполнены из поризованного или ячеистого бетона и иметь назначение ограждающей и теплоизоляционной конструкции. Для этой цели может быть использован стиролпорбетон (полистиролбетон) объемной массой γ = 500 - 800 марки М 50-75, с коэффициентом теплопроводности λ = 0,086 - 0,129 ВТ/(м ∙ К).

Применение такого теплоизоляционного ограждения (оно также является защитным) позволяет значительно уменьшить толщину эффективной тепловой изоляции стенки трубопровода из дефицитных материалов типа пенополиуретана, а в некоторых случаях исключить ее применение.

10.12. Конструкция строительной части опор трубопроводов может быть свайной или плитной на подсыпках из местного дренирующего грунта, можно применять опускные колодцы (сваи-оболочки) с погружением статической или динамической нагрузкой.

10.13. Подвижные части опор трубопроводов СПГ должны иметь конструкцию, обеспечивающую постоянную готовность к перемещениям в условиях кратковременного изменения нагрузки при обледенении, в связи с чем целесообразно применять опоры балансирного типа.

10.14. Для подвижных опор н.т. газопроводов также следует применять подвижные части роликового и каткового типа.

Работа опорных частей фрикционного действия с применением фторопласта, маслянитов и графитополистирола (как показано в работе [3]) характеризуется неравномерностью хода, чередованием коротких перемещений с остановками, преодолением регулярных силовых барьеров, резким динамическим эффектом типа ударов, что влияет на прочность конструкции опор и трубы.

10.15. В строительной части конструкции опор необходимо предусмотреть возможность регулировки их высоты в ходе монтажа и при эксплуатации, если возникнут недопустимые просадки и перекосы.

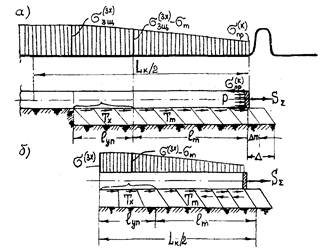
11. ТЕМПЕРАТУРНЫЕ ВОЗДЕЙСТВИЯ В ПЕРИОД ЗАХОЛАЖИВАНИЯ ТРУБОПРОВОДА

11.1. К специальным нагрузкам и воздействиям на трубопроводы ОПГ и СПГ относятся силы и перемещения, которые развиваются в результате формирования нестационарных температурных полей в конструкции трубопровода и в прилегающих массивах грунта.

11.2. Распределение температуры стенки стальной трубы в составе теплоизолированного подземного трубопровода в пролете между Н.С. (в продольном направлении) можно аппроксимировать диаграммой рис. 15, а, диаграмма состоит из:

горизонтального участка 1 длиной l_ф с постоянной температурой заболачивания t_зх, равной температуре захолаживающей среды;

горизонтального участка 2 с начальной температурой стенки t_н, равной температуре окружающего грунта или содержащейся в трубе среды до захолаживания;

наклонного участка 3 длиной l_гр, называемого переходным, с температурой, изменяющейся по линейному закону от t_зх до t_н.

11.3. За температуру строительства t_стр принимают температуру стальной трубы, при которой осуществляют соединение всех ее частей в непрерывную нитку без начальных продольных осевых напряжений или температуру, приведенную к этим условиям.

11.4. Начальным температурным перепадом Δt_н целесообразно назвать разность начальной температуры t_стр стенки и температуры строительства

11.5. Температурным перепадом захолаживания можно именовать разность температуры строительства t_стр и температуры захолаживания t_зх:

11.6. Градиент температуры стальной трубы в продольном направлении на переходном участке для расчетов на прочность и деформативность допускается определять по упрощенной зависимости согласно рис. 15, а

11.7. Фронтом захолаживания в дальнейшем принимают границу участка захолаживания (длиной l_ф) и переходного участка (длиной l_гр).

Рис. 15. Температурные изменения стенки и продольные перемещения трубопровода при захолаживании:

а - температура стенки и продольные перемещения трубопровода при захолаживании; б - продольные перемещения в начале захолаживания; в - продольные перемещения в допредельной стадии сопротивления; г - продольные перемещения в предельной стадии сопротивления; U_max - максимально-поперечное перемещение; U_m - перемещение в предельной стадии; T_к - касательная сила сопротивления продольному перемещению в допредельной стадии; Т_m - касательная cила сопротивления продольному перемещению в предельной стадии; 1 - температура на захоложенном участке; 2 - температура на незахоложенном участке; 3 - температура на участке градиента; 4 - продольные перемещения в начале захолаживания; 5 - температура стенки; 6 - переменные по длине силы сопротивления Т_x; 10 - прододьные перемещения в допредельной стадии сопротивления; 11 - температура стенки; 12 - постоянные силы зоны предельного сопротивления Т, переменные силы сопротивления T_x; 13 - силы трения

11.8. Скоростью захолаживания V_зх будем считать как скорость перемещения фронта захолаживания.

12. СОПРОТИВЛЕНИЕ ИЗОЛЯЦИОННО-ГРУНТОВОГО МАССИВА ПРОДОЛЬНЫМ ПЕРЕМЕЩЕНИЯМ

12.1. Силы сопротивления τ_х осевому перемещению стальной трубы на поверхности контакта стальной трубы и теплоизоляционного слоя можно определять расчетом как краевые напряжения сдвига элементарного слоя изоляционно-грунтового массива, выделенного параллельными плоскостями, перпендикулярными к оси трубопровода.

12.2. Примем, что напряжения сдвига τ_х в элементарном ортогональном слое изоляционно-грунтового массива подчиняются закону парности и изменяются обратно пропорционально радиусу в пределах изоляционных слоев и в грунтовом слое толщиной порядка 0,25 D_н.

12.3. Осевое перемещение внутренней поверхности теплоизоляционного слоя радиусом R₁ (и стальной трубы при сохранении с ней контакта) относительно произвольной цилиндрической поверхности радиуса R₂ этого слоя определяем формулой

где G - модуль сдвига материала слоя;

τ_х - напряжение сдвига на наружной поверхности стальной трубы.

12.4. Для изоляционно-грунтового массива перемещение внутренней поверхности теплоизоляционного слоя (и стальной трубы при сохранении сплошности) относительно наружной поверхности произвольного n-го слоя определяем согласно рис. 16 зависимостью

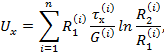
здесь  - напряжение сдвига на внутренней поверхности i-го слоя, причем

12.5. Закономерность (84) сохраняется в допредельном состоянии, т.е. до появления предельного значения  в одном из слоев. Дальнейшее перемещение U_x происходит путем взаимного скольжения слоев по поверхности нарушенного контакта.

12.6. Для ориентировочной оценки механических свойств пластических масс в табл. 10 приведены результаты испытаний некоторых видов конструктивных полимерных материалов при нормальных условиях и кратковременном нагружении.

Таблица 10

Механические свойства пластических масс

Модуль сдвига G для пластмасс и металла можно определить исходя из величины модуля деформации при растяжении по зависимости

Предел прочности теплоизоляционного материала при вдвиге τ_m можно оценивать, исходя из предела прочности при растяжении по зависимости

которая следует из выражения для эквивалентного напряжения при чистом сдвиге по энергетической теории.

Нормативные и расчетные характеристики грунтов определяют экспериментальным путем или по нормативным значениям физических характеристик согласно СНиП II-15-74 «Основания зданий и сооружений».

Модуль сдвига и коэффициент поперечной деформации грунтов не имеют однозначного физического смысла и обычно не нормируются. Для оценки явлений сдвига в расчетах низкотемпературных трубопроводов можно исходить из нормированных значений модуля деформации E и принимать в формуле (85) ориентировочные значения порядка μ = 0,1 - 0,2.

12.7. В грунтовом массиве поверхность скольжения образуется при соотношении между нормальными Р и предельными касательными напряжениями μ_m по всей поверхности скольжения, которое соответствует предельному состоянию грунта и подчиняется зависимости

где φ₁ и C₁ - расчетные значения угла внутреннего трения и удельного сцепления (в деформационных расчетах принимаются равными нормативным).

Для медленно уплотняющихся водонасыщенных глинистых и заторфованных грунтов (при степени влажности G ≥ 0,85 и коэффициенте консолидации G_v ≤ I ∙ 10⁷ см²/год) следует учитывать уменьшение касательного напряжения τ_m по поверхности скольжения за счет образования избыточного давления поровой воды по зависимости

12.8. Нормативные и расчетные характеристики грунтов, входящие в формулы (85) - (89), вычисляют по результатам инженерно-геологических изысканий.

Для расчетов деформаций допускается определять нормативные характеристики грунтов по их физическим характеристикам: углу внутреннего трения φ, удельному сцеплению С и модулю деформации E, приведенным в нормативных документах.

Для трубопроводов независимо от их диаметра в первом приближении можно определять Р в формулах (87) и (88) на уровне оси трубопровода по зависимости

Исследования [5] показывают, что прочность породы при промерзании возрастает как в талой зоне (в 2 - 3 раза) в результате уменьшения влажности и уплотнения, так и в мерзлой зоне (в 30 - 40 раз). Наибольшие напряжения усадки возникают в глинах коалинового состава (0,08 - 0,2 МПа), наименьшие - в супеси (менее 0,04 МПа), в суглинках и глинах полиминерального состава они занимают среднее значение.

С уменьшением скорости промерзания величина напряжения возрастает, а их градиенты - уменьшаются.

Когда напряжения достигают критических величин, близких к прочности породы, происходит разрыв структурных связей и нарушение сплошности, что выражается в преобразовании не только структуры, но и текстуры породы.

Структурообразование сопровождается как увеличением, так и уменьшением напряжений и деформаций.

При текстурообразовании происходит снятие напряжений в результате деформаций и разрывов структурных связей.

12.9. Касательную силу сопротивления продольному перемещению трубы в допредельной стадии выражаем зависимостями

где обобщенный коэффициент сопротивления изоляционно-грунтового массива продольным перемещениям равен

где K_пр - коэффициент, учитывающий нелинейность и неравномерность распределения τ_x по окружности, равный ориентировочно 0,5 - 0,3.

12.10. Касательную силу сопротивления продольному перемещению в предельной стадии определяют зависимостью

где τ_m - предельное касательное напряжение, определяемое по (86),(87), (88);

D_ск - диаметр поверхности скольжения.

12.11. Для сохранения прочности изоляционного слоя при захолаживании грунтовый материал засыпки трубопроводов следует подбирать так, чтобы поверхность скольжения образовывалась в грунтовом массиве, т.е. при условии

Условие (93) можно обеспечить применением торфа, гидрофобного грунта и пластифицирующих добавок в минеральные грунты, а также поддерживающих давление поровой воды.

12.12. Для вариантов прокладки теплогидроизолированного трубопровода с конструктивным зазором относительно жесткого защитного покрытия или с опиранием на сплошную жесткую плиту предельную силу сопротивления продольному перемещению учитывают по зависимости для «кулоновской» силы трения

где q_c.в - собственный вес единицы длины теплогидроизолированной трубы (с продуктом или без продукта в зависимости от условий расчета);

μ - коэффициент трения в зависимости от конструкции и состояния трущихся поверхностей;

K_т - коэффициент перегрузки сил трения, назначаемый в зависимости от конструкции трубопровода и очертания его оси.

13. СИЛОВЫЕ ВОЗДЕЙСТВИЯ И ПЕРЕМЕЩЕНИЯ ОТ ПРОДОЛЬНОГО ТЕМПЕРАТУРНОГО ГРАДИЕНТА НА ПОДЗЕМНЫЙ ТРУБОПРОВОД БЕЗ КОМПЕНСАТОРОВ (АНАЛИТИЧЕСКОЕ РЕШЕНИЕ)

13.1. Осевое напряжение растяжения при захолаживании от воздействия температуры и внутреннего давления на участке (включая его границы), где нет продольных перемещений или они пренебрежимо малы, именуют напряжением защемления и их необходимо определять с учетом упругой работы материала стенки стальной трубы по формуле

где Р_зх - давление внутри трубопровода при захолаживании (здесь Δt_зх - положительная величина).

13.2. Продольную осевую силу растяжения на защемленных участках при захолаживании следует определять по формуле

где F - площадь сечения стенки стальной трубы;

Е - модуль упругости ее материала.

13.3. Дифференциальное уравнение продольных перемещений стальной трубы теплогидроизолированного подземного трубопровода при допредельном сопротивлении перемещениям грунтоизоляционного массива с учетом градиента температуры стенки в продольном направлении имеет вид

γ - принимаем за постоянный коэффициент (квадрат коэффициента затухания)

α - коэффициент температурного удлинения;

F - площадь поперечного сечения стенки трубы;

С_ох - обобщенный коэффициент сопротивления изоляционно-грунтового массива, определяемый по (91).

13.4. Решение уравнения (97) состоит из общего интеграла однородного уравнения без правой части (т.е. без учета градиента) и частного интеграла неоднородного уравнения.

13.5. Общий интеграл однородного уравнения (97) для случаев, когда по физической сущности задачи перемещения затухают по направлению от граничного сечения, имеет вид

Нормальные напряжения, которые развиваются от продольного перемещения (99) определяют по зависимости

и они равны

,

где краевое значение нормального напряжения

σ_x = EγU_к.

Касательные силы сопротивления (83) продольному перемещению связаны с формулой (99) и (100) зависимостями

(101)

13.6. Особенность функций (99) - (101) в том, что они затухают теоретически «на бесконечности», что является следствием линейной зависимости (85) и (88) между продольными перемещениями и силами сопротивления.

В практике расчетов [10] считают, что затухание происходит на длине l_уп до сечения, где теоретическое значение напряжения или перемещения составляет 5 % от начального значения. Из формулы (99), также как из (100) и (101), следует, что

(102)

13.7. Перемещение U_к отражает краевые условия задач, решаемых уравнением (97).

13.8. Действие градиента на участке l_гр выражено частным решением неоднородного уравнения (97), которое вместе с общим решением однородного уравнения должно удовлетворять граничным условиям.

13.9. Продольные перемещения от градиента можно определить численным методом (см. раздел 16). При умеренной длине участка градиента l_гр в первом приближении можно пренебречь упругими измерениями длины стальной трубы от сил сопротивления в сравнении с температурными изменениями длины.

Примечание. Возможность такого допущения проверена путем сравнения перемещений от изменения температуры с перемещениями от пропорциональных им сил сопротивления.

13.10. Изменение температурного перепада в предположении линейного закона по графику (см. рис. 15, а) в пределах участка l_гр относительно среднего значения перепада выразим формулой

(103)

чему соответствует дифференциал продольного перемещения

откуда после интегрирования следует выражение для продольного перемещения в пределах участка градиента

(104)

где U_к - перемещение в начале участка l_гр.

Перепад Δt_зх по графику (см. рис. 15, а) следует считать отрицательным. Знак минус при U_x означает направление перемещения в сторону, противоположную оси X. Функция (104) имеет максимум, равный

в сечении с координатой

Перемещение в конце участка l_гр равно перемещению в его начале, т.е.

U_{l гр} = U_к.

13.11. Решение уравнений (99) - (101) и (104) однородного и неоднородного уравнения (97) дают возможность найти перемещения на участках 1 - 3 (см. рис. 15, а) - фронт захолаживания, участок градиента и участок за их пределами по ходу газа при различных последовательно сменяющихся этапах захолаживания, характерными из которых служат следующие стадии:

допредельного сопротивления, когда l_ф практически равен нулю, соответственно U_к = 0 (см. рис. 15, б);

допредельного сопротивления, когда

U_max < U_m; τ_{x max} < τ_m;

допредельного сопротивления, когда , максимальное перемещение U_{х max} и сопротивление сдвигу T_{x max} достигают предельных значений (см. рис. 15, в), т.е.

U_{x max} >> U_m; T_{x max} = T_m;

предельного сопротивления, когда на всем участке образуется поверхность сдвига (см. рис. 15, г), т.е.

U_{x max} >> U_m; T_x = T_m = const.

13.12. Продольное перемещение стальной трубы U_m, превышение которого приводит к образованию поверхности скольжения, согласно (90) равно

и с учетом

13.13. Анализ зависимостей (103) и (104) показывает, что волна продольных перемещений стальной трубы, вызванная градиентом температуры, совпадает с температурной волной.

На участке l_ф (перед участком градиента l_гр) после прохождения температурной и упругой волны устанавливается состояние защемления при температуре захолаживания.

13.14. После образования поверхности сдвига ее длину определяют по формуле

где

14. НАГРУЗКИ НА КОМПЕНСАТОРЫ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ ПРИ ЗАХОЛАЖИВАНИИ И ЭКСПЛУАТАЦИИ

14.1. Необходимость применения компенсаторов на подземных трубопроводах ОПГ и СПГ определяется повышенным влиянием температурного перепада и давления при захолаживании и эксплуатации на продольное напряжение растяжения. Согласно формуле (95) напряжения от этих факторов суммируют, тогда как для трубопроводов теплого газа, осуществляемых строительством в зимних условиях, - вычитают.

14.2. Компенсаторы необходимы для обеспечения условия прочности стенки стальной трубы

здесь R₁ - расчетное сопротивление, определяемое по СНиП 2.05.06-85;

f₂ - коэффициент, учитывающий двухосное напряженное состояние металла труб:

при растягивающих осевых продольных напряжениях (σ_{пр N} ≥ 0) принимают f₂ = 1;

при сжимающих напряжениях (σ_{пр N} < 0) определяют по формуле

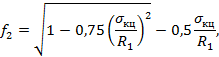
где σ_кц - кольцевое напряжение от расчетного внутреннего давления находят по формуле

В дальнейшем формулу (95) используют в виде

14.3. Продольное напряжение (108) развивается при захолаживании и эксплуатации подземного трубопровода без компенсаторов или в средней части пролета между компенсаторами при условии, что расстояние между ними отвечает условию

При условии (109) силы на стальную трубу распределены по схеме (рис. 16).

14.4. Длина участка предельного сопротивления изоляционно-грунтового массива при условии (110) равна

где S_зщ - определяют по формуле (96);

S_Σ - упругое сопротивление компенсатора.

Рис. 16. Схема сил, действующих на подземный трубопровод с компенсаторами:

а - распределение сил, действующих на трубу при расстановке компенсаторов, по условию ℒ_x ≥ 2(l_m - l_ул)
б - распределение сил, действующих на трубу по условию ℒ_к < 2(l_m + l_уп)

14.5. Длина участка допредельного сопротивления изоляционно-грунтового массива равна

14.6. Перемещение конца компенсатора выражено формулой

14.7. Продольные перемещения развиваются на всем пролете между компенсаторами при условии, что

где l_m - определяют по формуле (111).

Неподвижным остается сечение, которое при однородном изоляционно-грунтовом массиве располагается в середине пролета на расстоянии.

Равенство (114) сохраняется и при ассиметричном нагружении компенсаторов по пп. 14.10 и 14.11.

Длину участка предельного сопротивления l^*_m определяют из равенства (115),

где

Распределение силовых воздействий характеризуется схемой рис. 16.

14.8. Наибольшее напряжение растяжения при условии (113) развивается в среднем сечении и равно

14.9. Перемещение, передающееся компенсатору при условии (113), равно

14.10. Движение температурной волны захолаживания сопровождается последовательным включением в работу и неравномерным нагружением компенсаторов по схеме (рис. 17), что характеризуется следующими положениями:

1) компенсатор вступает в действие после того, как его пересечет S-образная кривая температуры захолаживания (в дальнейшем - начальная кривая захолаживания);

2) перемещения, передающиеся компенсатору, увеличиваются по мере прохождения начальной кривой захолаживания через место, где он расположен;

3) в начале цикла нагружения компенсатора преобладают перемещения со стороны входного патрубка, в конце - со стороны выходного;

4) полное перемещение, воспринимаемое компенсатором, пропорционально части площади графика захолаживания, ограниченной двумя начальными кривыми захолаживания последовательно распределенных компенсаторов и вертикальными прямыми, средними между компенсаторами (см. рис. 17) (для компенсатора 8 это площадь а, b, c, d, e, f); при однородном изоляционно-грунтовом массиве располагать компенсаторы целесообразно, соблюдая равенство упомянутых площадей.

Рис. 17. Схема нагружения компенсаторов подземного трубопровода продольными перемещениями при захолаживании:

1 - кривая температуры стенки на участке градиента (кривая захолаживания); 2 - дифференциал площади графика захолаживания; 3 - площадь градиента захолаживания, пропорциональная полному перемещению входного патрубка компенсатора 4; 4 и 8 - компенсаторы; 5 - площадь графика захолаживания, пропорциональная перемещению выходного патрубка компенсатора 4; 6 - полный дифференциал площади графика захолаживания; 7 - нагрузка перемещением компенсатора 8 до вступления в работу компенсатора 4

14.11. Асимметричность нагружения компенсаторов перемещениями необходимо учитывать при его конструировании и расчете.

14.12. Первый компенсатор следует располагать в начале перегона между н.с., чтобы избежать образования зоны защемления головного участка в результате промерзания изоляционно-грунтового массива.

15. УЧЕТ СКОРОСТЕЙ ЗАХОЛАЖИВАНИЯ И ПРОМЕРЗАНИЯ

15.1. Теплотехнические расчеты раздела 4 показывают, что скорость движения фронта захолаживания на 2 - 5 порядка более высокая, чем скорость промерзания изоляционно-грунтового массива. Такое соотношение скоростей дает возможность рассматривать ряд процессов и явлений в работе трубопровода независимо один от другого.

15.2. При первом цикле захолаживания перемещения и напряжения трубопровода можно определять исходя из физических характеристик и состояния изоляционно-грунтового массива, которые предшествуют захолаживанию, и не учитывать промерзания, связанного с захолаживанием.

15.3. Перемещения и напряжения при повторном цикле захолаживания следует определять с учетом промерзания за время между циклами.

15.4. Промерзание грунта в процессе эксплуатации и связанные с ним пучение, усадку, морозобойные трещины и т.д., следует рассматривать при эксплуатационных режимах работы трубопровода в переменных природно-климатических условиях.

15.5. Поперечные перемещения трубопровода в связи с пучением грунтового массива рекомендуется определять методом последовательных приближений в такой последовательности:

в первом приближении можно пренебречь изгибной жесткостью трубопровода и считать, что упругая ось трубопровода следует перемещениям грунтового массива;

во втором приближении определить силы взаимодействия трубопровода с грунтом путем дифференцирования аналитических выражений перемещений упругой линии, полученных в первом приближении и найти перемещения грунтового массива второго приближения с учетом сил взаимодействия.

Предлагаемая последовательность может быть продолжена до получения практически приемлемой погрешности.

16. ПРОГРАММА РАСЧЕТА ПОДЗЕМНЫХ НИЗКОТЕМПЕРАТУРНЫХ ТРУБОПРОВОДОВ МЕТОДОМ «КИНЕМАТИЧЕСКАЯ ЦЕПЬ» С ПРИМЕНЕНИЕМ МИКРОКАЛЬКУЛЯТОРОВ ТИПА МК-54, МК-56

16.1. Программа расчета предназначена для определения перемещений предварительно изогнутых участков низкотемпературных трубопроводов и сопутствующих факторов напряженного состояния (внутренних сил, реакций окружающей среды и т.д.) при следующих условиях:

нагрузкой служит внутреннее давление среды и температура, стенки трубопровода, действие этих факторов учитывается эквивалентным перепадом Δt_э;

тепловую изоляцию подземного трубопровода рассматривают, как часть внешней среды, в связи с этим внешнюю среду называют изоляционно-грунтовым массивом;

силы сопротивления изоляционно-грунтового массива поперечным и продольным перемещениям развиваются непропорционально соответствующим перемещениям трубопровода;

перемещения трубопровода (особенно поперечные) достигают значений, соизмеримых с диаметром трубопровода, поэтому сопровождаются существенным изменением очертания его оси. Трубопровод в целом представляет собой физически и геометрически нелинейную систему;

сложность статического расчета трубопроводов преодолевают применением алгоритмов и программ для ЭВМ на основе численных методов;

методика и алгоритмы известных программ «Дога», «Шаг - лента», и другие являются разновидностями метода конечных элементов [10] в сочетании с методом сил.

16.2. Метод сил применим к линейно-деформируемым системам. Понятие о «секущих» коэффициентах сопротивления окружающего грунта продольным и поперечным перемещениям открывают возможность расчета подземных трубопроводов методом сил.

16.3. Алгоритм строят по принципу последовательных приближений за несколько этапов;

определяют положение трубопровода на проектных отметках;

находят перемещения первого приближения при действии всего расчетного температурного перепада и внутреннего давления;

После каждого цикла итерации изменяют величину секущих коэффициентов согласно перемещениям, найденным в предыдущих циклах до получения результатов, совпадающих с заданной степенью приближения.

В практике проектирования трубопроводов приведенные программы реализуются на ЭВМ ЕС.

ХАРАКТЕРИСТИКА МЕТОДА И АЛГОРИТМА «КИНЕМАТИЧЕСКАЯ ЦЕПЬ»

16.4 Предлагаемый метод и алгоритм расчета нелинейно-деформируемых трубопроводов по рекурентным зависимостям в отличие от итерационной последовательности дает возможность построить алгоритмы для микро-ЭВМ со средним объемом памяти (например, типа «Искра» 226 и для микрокалькуляторов МК-56 и МК-54), представляет собой разновидность метода сил и отличается от традиционных вариантов тем, что основной системой служит кинематическая цепь (сокращенно КЦ).

16.5. Данный метод может быть применен для разработки алгоритмов расчета трубопроводов без ограничения их назначения.

Кинематической цепью (КЦ) будем называть систему коротких (l ≅ 2 - 3 D_н) прямолинейных участков трубопровода (звеньев), последовательно соединенных между собой шарнирами, которые располагаются на упругой оси трубопровода.

16.6. Сопротивление изоляционно-грунтового массива поперечным и продольным перемещениям моделируется дискретными нелинейно-податливыми внешними связями, присоединенными к шарнирам КЦ.

16.7. От аналогичных известных в строительной механике методов предлагаемый метод отличается тем, что очертание КЦ формируется последовательно в ходе поэтапного расчёта заданной системы.

Расчет подземных низкотемпературных трубопроводов состоит из трех этапов.

Первый этап, названный безмоментным расчетом,- шарниры КЦ до нагружения располагают на проектных отметках оси трубопровода. Внутренние продольные силы в звеньях и реакции внешних связей определяют по полному температурному перепаду последовательно от узла к узлу по рекурентным зависимостям, выражающим условия равновесия узлов, т.е. как для статически определимой сжато-растянутой шарнирно-стержневой системы.

Перемещения узлов и звеньев КЦ определяют по величине реакций внешних связей согласно их деформационным характеристикам при соблюдении условия неразрывности продольных, поперечных и угловых перемещений.

На этом этапе используют свойство инвариантности внутренних сил и реакций внешних связей статически определимой шарнирно-стержневой системы к деформационным характеристикам внешних связей, что максимально упрощает учет физической и геометрической нелинейности заданной системы: определяют внутренние силы и реакции связей, после чего находят перемещения узлов и звеньев согласно характеристикам податливости связей.

Первый этап дает первое приближение для величин перемещений, внутренних и внешних сил, причем звенья линейно-напряженной КЦ получают взаимные повороты Δ𝜃_i.

16.8. Второй этап включает определение следующих параметров:

внутренних изгибающих моментов, которые необходимо приложить к концам звеньев, соединенных шарнирами, чтобы ликвидировать взаимные повороты звеньев, возникшие на первом этапе;

дополнительных поперечных перемещений от изгибающих моментов;

суммарных поперечных перемещений первого и второго этапа и соответствующих им реакций поперечных связей (второе приближение поперечных перемещений и реакций).

Перемещения от изгибающих моментов, как правило, на порядок меньше наибольших перемещений от продольных сил, определенных на первом этапе^*. В связи с этим геометрическая и физическая нелинейность на втором этапе проявляется слабо, ее можно не учитывать и выполнять расчет, как для линейно деформируемой системы при соответствующем постоянном значении коэффициента поперечного сопротивления K_п.изг.

_______________

^* Это положение имеет общетеоретические основы, наиболее полно разработанные трудам.: В.З. Власова [8].

16.9. Третий этап - трубопровод рассматривают с плавно очерченной осью, получившей суммарные перемещения первого и второго этапов.

Из условия равновесия конечной части трубопровода от начального поперечного сечения в вершине изогнутого участка до произвольного - текущего находят внутренние осевые силы, продольные перемещения и реакции продольных внешний связей второго приближения.

16.10. Программа составлена применительно к участкам с начальными искривлениями в вертикальной плоскости. Одновременно работу изогнутых и прямых последовательно расположенных участков можно исследовать данным методом, задаваясь соответствующими граничными условиями.

Программа состоит из нескольких подпрограмм, соответствующих этапам расчета, применительно к микрокалькуляторам МК-56 и МК-54.

16.11. Подпрограммы не связаны переходами в автоматическом режиме вычислений. Такую связь не позволяет осуществить объем памяти используемых микрокалькуляторов. Однако подпрограммы могут быть объединены в единую программу при использовании мини-ЭВМ типа «Искра» 226.

ПОДПРОГРАММА ПЕРВОГО ЭТАПА (ВЕЗМОМЕНТНЫЙ РАСЧЕТ)

16.12. Расчетная схема подпрограммы первого этапа - это кинематическая цепь шарнирно соединенных прямолинейных элементов-звеньев с внешними продольными и поперечными дискретными нелинейно податливыми связями (рис. 18, а).

Внешние связи расположены вдоль и перпендикулярно к концу каждого звена. Реакции связей Т_i и Р_i имеют порядковый номер шарнира, к которому присоединены связи. Звено и продольная сила в нем имеют номер предыдущего узла. Положительными считаются продольные силы сжатия.

Зависимость между реакциями связей и составляющими перемещений в общем виде можно выразить формулами

где множители K_ni и K_τi сами являются функциями перемещений и могут изменяться вдоль трубопровода (при переходе от узла к узлу) как показано на рис. 18, г.

Функциональные множители K_ni и К_τi названы в дальнейшем коэффициентами сопротивления поперечным и продольным перемещениям.

Шарниры цепи до нагружения расположены на проектных отметках оси трубопровода.

Рис. 18. Расчетная схема безмоментного расчета кинематической цепи:

а - кинематическая цепь с внешними продольными и поперечными дискретными связями; б - план сил; в - план сил в произвольном узле; г - диаграммы податливости продольных и поперечных связей

Рис. 19. Схема расчета на изгиб:

а - продольная напряженная кинематическая цепь; б - план сил при одновременном действии продольного напряжения и изгиба кинематической цепи; в - план сил третьего этапа расчета

Углы исходной взаимной ориентации звеньев α_i считаются положительными при «повороте» последующего звена относительно предыдущего по часовой стрелке.

В результате нагружения КЦ полным эквивалентным перепадом шарниры получают линейные перемещения h_i и τ_i положительные - в направлении осей xy при этом звенья поворачиваются относительно исходного положения на угол 𝜃_i. Повороты на угол 𝜃_i считаются положительными, если они происходят по часовой стрелке.

Продольные силы S_i в звеньях и реакции связей определяют последовательно от узла к узлу по рекурентным зависимостям, выражающим условия равновесия узлов и условия неразрывности линейных и угловых перемещений звеньев.

Условия равновесия произвольного узла «i» (рис. 18, б, в) приводят к зависимостям

 

Изменение расстояния между смежными узлами τ_i определяют следующими факторами:

увеличением продольной силы растяжения (S_в - S_i);

поворотом звена на угол 𝜃_i и дополнительным удлинением от нагрева звена ;

зависимостью

где S_в - сила продольного растяжения (отрицательная) или сжатия (положительная) при полном защемлении;

l_i - длина звена;

F - площадь поперечного сечения стенки трубы;

Е - модуль упругости материала стенки трубы.

В формулу (117) входит выражение суммарного продольного перемещения, равного

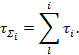
Поворот звена на угол 𝜃_i происходит в основном в связи с разностью поперечных перемещений узловых шарниров (продольные перемещения имеют второстепенное влияние) и с достаточной точностью можно выразить формулой

Взаимный поворот смежных звеньев приводит к значительному (в отдельных узлах) изменению реакции (рис. 19, а) по сравнению с вычисленной по формуле (118) до величины

В этом изменении реакции проявляется геометрическая нелинейность системы, свидетельствующая о том, что равновесие кинематической цепи при перемещениях, определенных на первом этапе, требует приложения дополнительных сил, равных . Однако необходимость в приложении этих сил отпадает после «сращивания» звеньев на втором этапе расчета.

16.13. Подпрограмма КЦ-ПI последовательного решения уравнений (118) - (122) с помощью микрокалькуляторов типа МК-54 и МК-56 приведена в приложении 2, рекомендуемом.

Расчет изогнутого участка (например вогнутого) следует начинать с его вершины (наиболее низкая точка оси). Если соответствующее сечение не смещается в продольном направлении (например, участок симметричный или имеется анкер), то τ₁ = 0.

Начальную сжимающую силу следует положить равной

S_в = Δt_эквαEF,

тогда

P₁ = S_в tg α₁ и S₁ = S_b / cos α₁.

Далее вычисления выполняют последовательно по формулам (118) - (122) путем перехода от узла к узлу.

Подпрограмма КЦ-П1 предусматривает ввод с пульта исходных расчетных параметров, в том числе углов взаимной ориентации звеньев α_i и коэффициентов сопротивления поперечным и продольным перемещениям  для первого звена (первого цикла), а также ввод значений этих параметров при переходе к последующим узлам, если они изменяются.

Если коэффициенты сопротивлений являются функциями перемещений, то следует подготовить данные по этим зависимостям в виде графиков, таблиц или составить подпрограммы их вычислениям на том же или дополнительном калькуляторе.

АЛГОРИТМ И ПОДПРОГРАММЫ ВТОРОГО ЭТАПА (УЧЕТ ИЗГИБА)

16.14. В результате перемещений шарниров звенья цепи располагаются под углами 𝜃_i к исходному (проектному) положению и соответственно получают взаимный поворот на угол

На втором этапе находят внутренние изгибающие моменты, которые необходимо приложить к концам звеньев в шарнирах цепи так, чтобы углы взаимного поворота звеньев были равными нулю. Для решения этой задачи рекомендуется применять метод сил.

Основной системой второго этапа служит кинематическая цепь, получившая перемещения от действия продольных сил при полном эквивалентном перепаде (см. рис. 20, а).

Для пологих участков с отношением стрелы прогиба к хорде не более 1:10 можно пренебречь расположением поперечных опор, под углом одна к другой, т.е. свести задачу к рассмотрению неразрезного прямолинейного упругого стержня на податливых опорах.

Единичные состояния для пологого участка представлены на рис. 20. Единичные перемещения - коэффициенты податливости определяют «перемножением» эпюр и исходя из геометрических соотношений. Матрица податливости поперечного изгиба (табл. 11) имеет диагональную симметричную структуру.

16.15. Подпрограммы решения системы пятичленных уравнений составлены на основе метода Гаусса, т.е. последовательным исключением неизвестных. Диагонально-симметричную матрицу предварительно приводят к треугольному виду (подпрограмма КЦ-П2, приложение 2, рекомендуемое). Для этого первые слагаемые смежных уравнений приводят к единице и проводят их последовательное вычитание.

В результате n-е пятичленное уравнение принимает вид:

и последнее m - е:

M_m + Δp^*_m = 0.

Обратным ходом подстановкой находят все неизвестные моменты по зависимости

Подпрограмма нахождения моментов по зависимости (123) КЦ-П3 приведена в приложении 2, рекомендуемом.

Рис. 20. Основная система и единичные состояния расчета кинематической цепи на изгиб на разных этапах итерационного расчета:

а - первый этап;
б - второй этап;
в - третий этап;
г - четвертый этап

По изгибающим моментам в узлах определяют перемещения узлов от изгиба, которые связаны с моментами зависимостью (см. эпюру в КЦ-П4)

Подпрограмма КЗ-P4 приведена в приложении 2, рекомендуемом.

16.16. Краевые условия решения системы пятичленных уравнений моментов сводятся к заданию угловых перемещений на концах участка.

Таблица 11

Матрица податливости поперечного изгиба

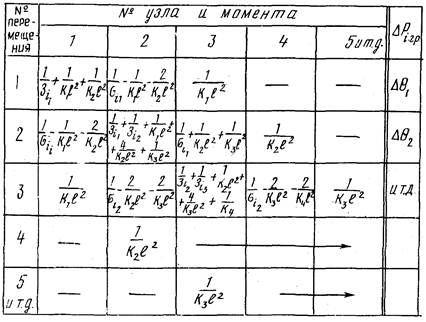
В частности, поперечная сила Р_к на конце участка в основной системе, т.е. в кинематической цепи, создает угол наклона первого звена:

что служит одним из краевых условий.

Для случаев расчета, когда коэффициенты сопротивления K_ni могут считаться одинаковыми для ряда узлов, исходная матрица податливости упрощается умножением каждой строки и соответствующего грузового члена на Kl². Тогда первый и пятый элементы строки будут равны единице.

Подпрограммы КЦ-П2 и КЦ-П3 составлены применительно к исходной матрице с единичными крайними членами.

ПОДПРОГРАММА ТРЕТЬЕГО ЭТАПА (ДЕЙСТВИЕ ПРОДОЛЬНЫХ СИЛ И ИЗГИБА)

16.17. Задача третьего этапа - найти второе приближение для продольных сил и продольных перемещений с учетом плавного очерчения оси и соответствующих реакций внешних связей (см. рис. 20, б и в), определенных на втором этапе. Третий этап состоит из следующих операций:

1) вводят общую систему координат с горизонтальной x и вертикальной осью у;

2) составляют условие равновесия конечной части трубопровода от начального поперечного сечения в вершине изогнутого участка до произвольного сечения с текущей координатой x;

3) по вспомогательным подпрограммам^* определяют:

________________

^* Вспомогательные подпрограммы не приведены в настоящих Рекомендациях.

суммарные поперечные перемещения первого и второго этапов ;

реакции поперечных связей , исходя из h_Σi их нелинейных характеристик (см. рис. 19, г);

углы наклона звеньев в общих осях xy т.е. ;

углы наклона касательной к упругой линии в ее исходном положении , если они не заданы в другой форме;

углы поворота звеньев от суммарных поперечных перемещений шарниров  и их среднее значение -

углы наклона касательной к упругой оси -  поперечные силы от изгиба 𝜃_i = 0,5(M_i+1 - M_i) : K_изгl.

16.18. Условия равновесия конечной части трубопровода в виде суммы проекций внешних и внутренних сил на общие координатные оси xy дают возможность найти продольные силы и продольные перемещения второго приближения.

По сумме проекций на горизонтальную ось получают

В формулу не включены проекции сил сопротивления поперечным перемещениям, как пренебрежимо малые.

Сумма проекций на вертикальную ось дает возможность вывести зависимость

где изменение расстояния между узлами составляет:

а сила сопротивления продольному перемещению в пределах звена:

Подпрограмма КЦ-П5 вычислений по рекурентным зависимостям (125) - (128) приведена в приложении 2, рекомендуемом.

Третий этап вычислений может состоять из нескольких циклов. Первый цикл вычислений может быть заключительным, если р^*** по формуле (126) отличается от Р^** на допустимо малую величину.

При необходимости этапы расчета повторяют во втором, третьем и т.д. циклах до заданной точности совпадения результатов последовательных вычислений.

ПРИНЦИПЫ ПОСТАНОВКИ КРАЕВЫХ УСЛОВИЙ

16.19. Определение перемещений подземного трубопровода методом кинематической цепи, как и другими методами, требует выполнения краевых условий на границах рассматриваемого участка (например, как расчета изгиба балок методом начальных параметров).

Специфика постановки краевых условий в аналогичных задачах заключается в том, что хотя бы одно из граничных сечений должно находиться в зоне интенсивной деформации. Краевые условия должны быть достаточно «жесткими», иначе задача становится неопределенной.

В случае применения моментных фокусных отношений к расчету многопролетных балок при учете условий закрепления одного из концов («левые» или «правые» фокусные отношения) необходимо учитывать опорные моменты загруженного пролета.

16.20. При расчете подземных трубопроводов часто необходимо знать поперечные и продольные перемещения вершины изогнутого участка.

В определении поперечного перемещения вершины помогает свойство ее элементарной части (рис. 21, а), которую можно считать находящейся в состоянии чистого изгиба моментом M_в и осевого сжатия силой S_в. Если радиус кривизны элемента ρ₀, то он будет находиться в состоянии равновесия независимо от величины момента M_в, при сопротивлении поперечному перемещению

Величина q_в однозначно определяет поперечное перемещение согласно нелинейной характеристике податливости изоляционно-грунтового массива.

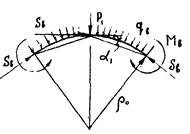
Рис. 21. Расчетные схемы постановки краевых условий при распределенной реакции  и при дискретной связи p₁ = q₁l, p₁ = S_вt₂α₁

В данной методике это свойство использовано для вершины кинематической цепи при дискретном приложении сил сопротивления к узловым шарнирам.

Для граничного сечения, удаленного от вершины, могут приниматься закрепления в виде подвижных или неподвижных заделок или шарниров в зависимости от конкретных конструктивных решений трубопровода.

При расчете двух смежных участков целесообразно предварительно ввести вертикально подвижную заделку и выполнить расчет участков независимо один от другого. Взаимодействие участков устанавливают путем «удаления» заделки и решения соответствующих уравнений неразрывности перемещений концов смежных участков.

Пример расчетного определения перемещений, внутренних сил и реакции изоляционно-грунтового массива изогнутого участка трубопровода приведен в приложении 3, рекомендуемом.

ПРИЛОЖЕНИЯ

Приложение 1
Рекомендуемое

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РАСЧЁТА ПАРАМЕТРОВ ТРАНСПОРТИРОВКИ ОПГ И СПГ

На рис. 1 - 4 приведены результаты расчета температур ОПГ и СПГ на участке трубопровода диаметром 1420 мм, протяженностью 100 км по различным уравнениям, а также представлена зависимость производительности трубопроводов ОПГ и СПГ в конце участка от конечного давления.

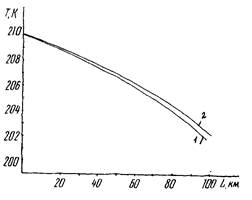
Рис. 1. Профиль температур (T) ОПГ на участке трубопровода диаметром 1420 мм протяженностью (L) 100 км при Р = 9,806 МПа; Р_к = 6,763 МПа, Т_н = 210 К; K = 0,43 Вт/м² ∙ К:

1 - расчет по уравнению Редлиха-Квонга (РК) Q = 82,6 млрд.м³/г; 2 - расчет по уравнению Старлинга-Хана (СХ) Q = 81,1 млрд.м³/г

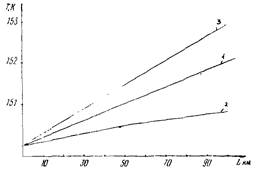
Рис. 2. Профиль температур СПГ (Т) на участке трубопровода диаметром 1420 мм, протяженностью (L) 100 км при P_н = 5,393 МПа; Р_к = 2,942 МПа; Т_н = 150 К; K = 0,43 Вт/м² ∙ К:

1 - расчет по уравнению Редлиха-Квонга Q = 101,2 млрд.м³/г;
2 - расчет по уравнению Старлинга-Хана Q = 94,6 млрд. м³/г;
3 - расчет по данным работы [2] Q = 102,5 млрд.м³/г

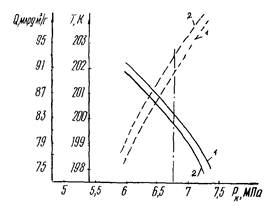
Рис. 3. Зависимость производительности трубопровода ОПГ (Q) и температуры ОПГ (Т) в конце участка от конечного давления Р_к = 6,763 МПа; Р_н = 9,806 МПа; Т_н = 210 К; K = 0,43 Вт/м² ∙ К

Рис. 4. Зависимость производительности трубопровода СПГ (Q) и температуры СПГ в конце участка от конечного давления Р_к = 2,942 МПа; P_н = 5,393 МПа; T_н = 150 К; K = 0,43 Вт/м² ∙ К

Приложение 2
Рекомендуемое

ПРОГРАММЫ ЭТАПОВ РАСЧЕТА НИЗКОТЕМПЕРАТУРНЫХ ТРУБОПРОВОДОВ МЕТОДОМ «КИНЕМАТИЧЕСКАЯ ЦЕПЬ»

Продолжение приложения 2

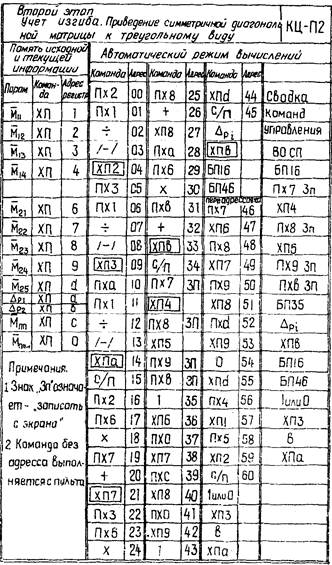
Продолжение приложения 2

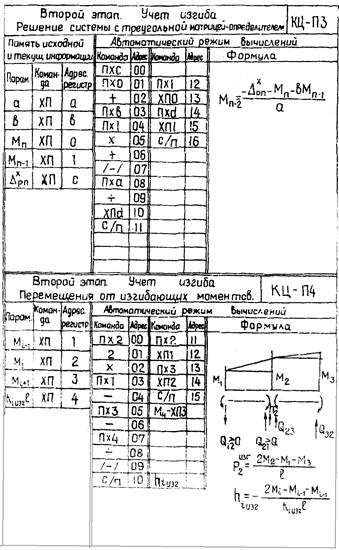
Окончание приложения 2

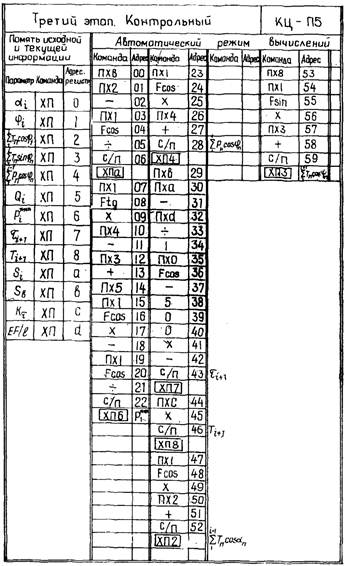
Приложение 3
Рекомендуемое

ПРИМЕР РАСЧЕТНОГО ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ, ВНУТРЕННИХ СИЛ И РЕАКЦИИ ИЗОЛЯЦИОННО-ГРУНТОВОГО МАССИВА ИЗОГНУТОГО УЧАСТКА ТРУБОПРОВОДА

1. Необходимо рассчитать симметричный подземный переход через овраг.

2. Проектный профиль симметричной половины участка приведен на рис. 1.

Ось трубопровода в проектном ненагруженном положении (после строительства) задана углами α_i взаимной ориентации хорд, длиною l = 500 см. Величины углов α_i внесены в строку памяти исходных данных с адресом ХПО.

Стальная труба имеет наружный диаметр 1420 мм: момент инерции поперечного сечения J = 1,83 ∙ 10⁶ см⁴, площадь поперечного сечения 729 см².

3. Сопротивление изоляционно-грунтового массива продольным перемещениям изменяется по схеме вида диаграммы Прандтля (см. рис. 19). Распределенное по поверхности трубы сопротивление в зоне линейной обратимой деформации задано коэффициентом  кгс/см³, что соответствует сопротивлению дискретной связи K_τ = 66916 кгс/см.

4. Сопротивление изоляционно-грунтового массива поперечным перемещениям задано графиком (рис. 2). Расчетные дискретные поперечные связи характеризуются следующими характеристиками для перемещений вверх:

в зоне обратимой деформации коэффициент сопротивления K_n = 2500 кгс/см;

в зоне необратимой деформации (запредельной)  кгс/см;

сила предельного сопротивления - Р_пр = 10000 кгс;

предельное поперечное перемещение h_пр = 4 см;

сила запредельного сопротивления определяется по зависимости

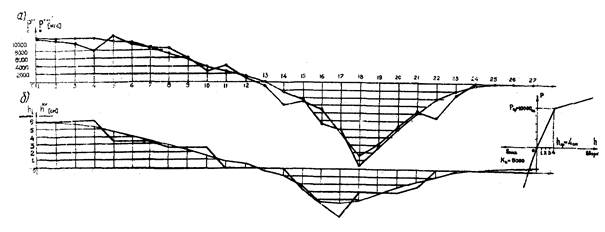
Рис. 1. Профиль участка трубопровода в проектном положении и после нагружения (а) и эпюра изгибающих моментов (б)

Рис. 2. Поперечные перемещения и реакции грунта на поперечные перемещения:

а - поперечные перемещения; б - реакции поперечных связей;
в - характеристика деформационно-силовых свойств грунта

Поперечное перемещение в запредельной области соответственно равно

5. Принимаем, что перемещение вниз сопровождается увеличением сопротивления по линейному закону во всем возможном диапазоне изменения перемещений при  = 5000 кгс/см.

Нагрузкой служит эквивалентный температурный перепад охлаждения трубопровода относительно температуры строительства на Δt = -119,75 °С.

Соответственно S_в = - EFΔtα - 2199981,7 кгс.

6. Исходные данные занесены в таблицы памяти соответствующих подпрограмм, где помещены также результаты вычислений предыдущих подпрограмм, которые служат исходными параметрами для последующих подпрограмм.

7. Поперечные перемещения кинематической цепи даны на графике рис. 2, а «расчетные» точки отмечены кружками.

Суммарные перемещения КЦ от продольных сил и от изгиба изображены графически на рис. 2, а (отмечены знаком «^**»). Этот график имеет плавное очертание, он как бы осредняет перемещения КЦ от продольных сил.

Сопоставление сил поперечного сопротивления по итогу первого и второго этапа Р^** c силами сопротивления третьего P^*** выполнено на рис. 2, б. Если отклонения Р^** от P^*** можно считать допустимыми, то третий этап является заключительным в первом цикле расчетов.

Разница между Р^** и Р^*** может быть уменьшена последующими циклами итерации, для каждого из которых P^*** будут служить исходными параметрами для второго этапа.

ЛИТЕРАТУРА

1. О.М. Иванцов, А.Д. Двойрис. Низкотемпературные трубопроводы. - М.: Недра, 1980.

2. В.В. Сычев, А.А. Вассерман, В.А. Загорученко и др. Термодинамические свойства метана, ГСССД. -: Изд-во стандартов, М., 1979.

3. Е.П. Серов, Б.П. Корольков. Динамика парогенераторов. - М.: Энергия, 1972.

4. Г.И. Чичко. Исследование устойчивости подземных трубопроводов. Сб. трудов ВНИИСТа. - М.: ВНИИСТ, 1983.

5. Э.Д. Ершов, Ю.П. Лебеденко и др. Структурообразование и деформирование пород при промерзании и оттаивании. Мерзлотные исследования. Выпуск XXI. - М.: Изд-во Московского университета, 1983.

6. А.Б. Айнбиндер, А.Г. Камерштейн. Расчет магистральных трубопроводов на прочность и устойчивость. - М.: Недра, 1982.

7. А.Е. Полозов. Магистральные трубопроводы для транспорта сжиженного природного газа. «Строительство трубопроводов». - М.: 1981, № 2.

8. В.З. Власов. Общая теория оболочек. - Л.: Изд-во научно-технической литературы, 1949.

9. П.П. Бородавкин, В.Л. Березин. Сооружение магистральных трубопроводов. - М.: Недра, 1977.

10. И.П. Петров, С.К. Гильзин. Руководство по конструкции и прочностному расчету низкотемпературных теплоизолированных трубопроводов охлажденного и сжиженного природного газа (применительно к опытному участку). - М.: ВНИИСТ, 1976.

СОДЕРЖАНИЕ