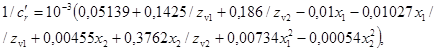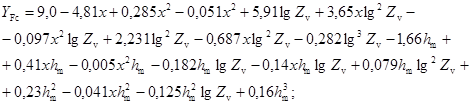РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
НА ПРОЧНОСТЬ

Руководство
Р.007-2004

Москва
2004

Утверждено приказом Российского Речного Регистра № 32-п от 24.12.2004 г.

Введено в действие с 07.02.2005 г.

Издание 1

Ответственный за выпуск - В.Ю. Иванова

СОДЕРЖАНИЕ

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. ОБЛАСТЬ РАСПРОСТРАНЕНИЯ

1.1.1. Требования настоящего руководства предназначены для работников Речного Регистра и проектантов (изготовителей) главных и ответственных вспомогательных зубчатых передач с цилиндрическими и коническими колесами, а также планетарных передач, предназначенных для применения на судах с классом Речного Регистра. Они распространяются на изготовленные из стали со степенью точности изготовления 5 - 9 в соответствии с ГОСТ 1643-81 внешние и внутренние эвольвентные зацепления с прямыми, косыми или шевронными зубьями с линейным или точечным контактом, а также конические эвольвентные поверхности с прямыми, тангенциальными или круговыми зубьями, работающие со смазкой маслом и окружными скоростями не более 70 м/с.

1.1.2. Передачи могут быть спроектированы в соответствии с методиками организации-проектанта. Если эти методики и программные продукты согласованы Речным Регистром, представление расчета главных и ответственных вспомогательных зубчатых передач на прочность в составе технической документации не требуется. В противном случае для каждого зубчатого зацепления рассматриваемых передач организация-проектант должна представить список исходных данных установленного Речным Регистром образца или результаты расчета по методике, изложенной в настоящем руководстве.

1.2. ТРЕБОВАНИЯ К ПРОЧНОСТИ

Зубчатые передачи должны быть признаны удовлетворяющими условиям прочности, если одновременно выполняются следующие требования:

поверхностные контактные напряжения s_НР меньше допускаемых ст_НР или, по меньшей мере, равны им;

запас прочности по отношению к глубинным разрушениям  больше допускаемого S_НРгл или равен ему;

запас прочности при перегрузках  по отношению к глубинным разрушениям больше единицы, но не менее ;

напряжения s_F у основания зуба (на изгиб) меньше допускаемых s_FP или, по меньшей мере, равны им;

запас прочности при изгибе максимальной нагрузкой  больше предельно допускаемого S_FP или равен ему;

запас стойкости против заедания S_S больше допускаемого S_SP или равен ему.

1.3. ПЕРЕЧЕНЬ ТРЕБУЕМЫХ РАСЧЕТОВ

Если в соответствии с 1.1.2 организация-проектант представляет Речному Регистру результаты расчета зубчатых зацеплений на прочность, то этот расчет должен включать в себя следующие разделы [1 - 6]:

.1. проверочный расчет зубьев на поверхностную контактную прочность;

.2. проверочный расчет зубьев на глубинную контактную прочность, в том числе и при перегрузках;

.3. проверочный расчет зубьев на выносливость при изгибе, в том числе максимальной нагрузкой;

.4. расчет зубьев на заедание.

2. ОПРЕДЕЛЕНИЯ, ПОЯСНЕНИЯ И ОБОЗНАЧЕНИЯ

2.1. ОПРЕДЕЛЕНИЯ И ПОЯСНЕНИЯ

Все термины, встречающиеся в тексте руководства, отвечают требованиям стандартов. Ниже приведены определения наиболее часто используемых терминов и пояснения к ним.

Зубчатое зацепление - кинематическая пара, образованная зубчатыми колесами передачи.

Шестерня - зубчатое колесо с меньшим числом зубьев. При одинаковом числе зубьев зубчатых колес шестерней называется ведущее зубчатое колесо. Параметры шестерни помечаются нижним индексом «1».

Колесо - зубчатое колесо с большим числом зубьев. При одинаковом числе зубьев зубчатых колес колесом называется ведомое зубчатое колесо. Параметры колеса помечаются нижним индексом «2».

Прямозубое зубчатое колесо - зубчатое колесо с прямыми зубьями.

Косозубое зубчатое колесо - цилиндрическое зубчатое колесо с винтовыми зубьями, теоретические линии которых эквидистантны и на развертке соосной цилиндрической поверхности являются параллельными прямыми.

Прямой зуб - зуб, делительная теоретическая линия которого лежит в плоскости осевого сечения зубчатого колеса.

Винтовой зуб - зуб, теоретическая линия которого образована сложным движением точки по соосной поверхности: равномерным движением по линии пересечения этой поверхности с плоскостью осевого сечения зубчатого колеса и равномерным вращением вокруг его оси.

Начальная поверхность зубчатого колеса - соосная поверхность зубчатого колеса, в любой точке касания которой с соосной поверхностью другого зубчатого колеса передачи проходящие через нее линии зубьев или идентичные им линии имеют общую касательную, и вектор скорости относительного движения зубчатых колес направлен вдоль нее или равен нулю.

Начальная окружность зубчатого колеса - каждая из взаимокасающихся концентрических окружностей зубчатых колес передачи, принадлежащая начальной поверхности данного зубчатого колеса.

Полюсная линия - линия касания начальных поверхностей.

Полюс зацепления - точка или одна из точек начальных поверхностей зубчатых колес.

Модификация поверхности зуба (модификация) - преднамеренное отклонение поверхности зуба от главной поверхности, осуществляемое для компенсации действия факторов, отрицательно влияющих на работу зубчатой передачи.

Продольная модификация зуба - модификация поверхности зуба по линии зуба.

Делительная поверхность зубчатого колеса - соосная поверхность зубчатого колеса, которая является базой для определения элементов зубьев и их размеров.

Соосная поверхность зубчатого колеса - поверхность вращения, ось которой совпадает с осью зубчатого колеса.

Делительная окружность - окружность с центром на оси зубчатого колеса, лежащая в торцовом сечении и принадлежащая делительной поверхности зубчатого колеса.

Шевронное цилиндрическое зубчатое колесо - цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями.

Правый (левый) зуб - зуб, имеющий теоретические линии, точки на которых движутся по часовой стрелке (против часовой стрелки) при удалении от наблюдателя, смотрящего со стороны выбранного торца.

Коническая зубчатая передача - зубчатая передача с пересекающимися осями, у зубчатых колес которой аксоидные, начальные и делительные поверхности конические.

Аксоидная поверхность зубчатого колеса передачи - каждая из поверхностей, описываемых мгновенной осью относительного движения зубчатых колес передачи, относящаяся к данному зубчатому колесу.

Мгновенная ось в зубчатой передаче с пересекающимися осями - воображаемая линия, вокруг которой происходит мгновенное вращение зубчатого колеса относительно его сопряженного зубчатого колеса.

Ортогональная зубчатая передача - зубчатая передача, межосевой угол которой равен 90°.

Делительный конус - коническая поверхность производящего конического зубчатого колеса, т.е. плоскость, которая вместе с делительным конусом является базовой для определения элементов зубьев и их геометрических размеров.

Эквивалентная цилиндрическая передача - передача, которой при расчете прочности условно заменяют коническую передачу с прямыми зубьями и колеса которой имеют в главном сечении шаги, размеры и форму зубьев, идентичные размерам и форме прямых зубьев колес конической передачи.

Биэквивалентная цилиндрическая передача - передача, которой при расчете прочности условно заменяют коническую передачу с непрямыми зубьями и колеса которой имеют размеры и форму зубьев, идентичные размерам и форме зубьев конических колес с непрямыми зубьями в сечении, нормальном к средней линии зубьев.

Планетарная передача - планетарный механизм, состоящий из зубчатых колес, в котором геометрическая ось хотя бы одного из колес подвижна.

Водило - звено планетарного механизма, в котором установлены зубчатые колеса с подвижными осями - сателлиты.

2.2. ОБОЗНАЧЕНИЯ

В руководстве приняты следующие обозначения:

A_j - коэффициент приведенных глубинных касательных напряжений в соответствии с заданным сроком службы;

а_C - отношение коэффициентов жесткости;

a_M - отношение приведенных масс;

a_w - межосевое расстояние, мм;

a - угол профиля исходного контура, град;

a_е - коэффициент градиента напряжений;

a_n - угол зацепления в нормальном сечении, град;

a_t - угол зацепления в торцевом сечении, град;

a_w - угол зацепления в полюсе в торцевой плоскости на начальном цилиндре, град;

a_s - теоретический коэффициент концентрации напряжений, используется при расчете концентрации напряжений  изгиба максимальной нагрузкой;

B - рабочая ширина зубчатого венца, мм (обобщенный параметр);

b_w - рабочая ширина зубчатого венца, мм;

b - делительный угол наклона линии зуба, град;

b_b - угол наклона зубьев на основном цилиндре, град;

b_n - угол наклона зубьев конических зубчатых колес в нормальном сечении, град;

с - коэффициент удельной жесткости пары зубьев передачи, МПа;

C_T - степень точности изготовления по нормам плавности в соответствии с ГОСТ 1643-81;

c_m1 - коэффициент удельной нормальной жесткости пары зубьев, МПа;

d - диаметр делительной окружности, мм;

d_m - средний делительный диаметр конического зубчатого колеса, мм;

d_w - диаметр начальной окружности, мм;

d_wе - внешний начальный диаметр конического зубчатого колеса, мм;

D - ошибка окружного шага или профиля, мкм;

δ - угол начального конуса, град;

δ_Н - коэффициент, учитывающий жесткость зубьев и особенности работы передачи с непрямыми зубьями;

Е₁, Е₂ - модули упругости первого рода материалов шестерни и колеса соответственно, МПа;

e_a - коэффициент торцового перекрытия;

e_b - коэффициент осевого перекрытия;

f_kv - фактическое отклонение положения контактных линий, мм;

f₁ - коэффициент перекрытия профиля;

f₂ - коэффициент, учитывающий точность изготовления передачи;

j - параметр толщины упрочненного слоя;

g₀ - коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса;

g_h - коэффициент, учитывающий глубину азотирования;

g_А - коэффициент, учитывающий влияние амплитуд напряжений противоположного знака;

h_а - высота делительной головки зуба, мм;

h_t - толщина упрочненного слоя, расстояние от поверхности до точки, в которой твердость упрочненного слоя равна твердости сердцевины, мм;

H⁰ - твердость поверхности зуба, НВ, HV или HRC_Э;

Н^K - твердость сердцевины зуба, НВ, HV или HRC_Э;

i - передаточное отношение между ведущим и ведомым валами;

K_А - коэффициент внешней динамической нагрузки, передаваемой от двигателя на зубчатую передачу;

K_П - коэффициент распределения нагрузки между параллельными потоками мощности;

K_c - коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами;

K_Ш - коэффициент неравномерности распределения нагрузки между полушевронами;

K_be - коэффициент ширины зубчатого венца;

K_Fd - коэффициент, учитывающий влияние деформационного упрочнения;

К_Fg - коэффициент, учитывающий влияние шлифования переходной поверхности зуба;

K_Fa, K_Fb, K_Fv - аналоги коэффициентов K_Ha, K_Hb, K_Hv при расчете на выносливость при изгибе;

K_Fx - коэффициент, учитывающий размеры зубчатого колеса;

K_Ha - коэффициент, учитывающий распределение нагрузки между парами зубьев;

K_Hb - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

K_Hv - коэффициент, учитывающий «внутреннюю» динамическую нагрузку в зацеплении;

K_δ - коэффициент, учитывающий отклонение суммарной длины контактных линий от их среднего значения;

L_h - требуемый ресурс передачи, ч;

m - модуль, мм;

m_n - модуль нормальный, мм;

µ_T - коэффициент, учитывающий возможность возникновения трещины в упрочненном слое ранее, чем в сердцевине зуба;

n - частота вращения, мин^-1;

N_KП - номер конструкции передачи с коническими колесами;

n_c - число сателлитов;

N_HE - эквивалентное число циклов перемены напряжений;

N_{H lim} - базовое число циклов напряжений;

N_k - число циклов напряжений в соответствии с заданным сроком службы;

v_F - коэффициент понижения несущей способности конических колес по сравнению с цилиндрическими;

v₁, v₂ - коэффициенты Пуассона материалов шестерни и колеса соответственно;

P - мощность, кВт;

R_a - среднее арифметическое отклонение профиля шероховатости по ГОСТ 2789-73*, мкм;

R_e - внешнее делительное (начальное) конусное расстояние, мм;

R_eH - предел текучести материала, МПа;

R_m - временное сопротивление материала на растяжение, МПа;

R_z - высота неровностей профиля шероховатости по ГОСТ 2789-73*, мкм;

ρ_a - радиус профиля головки, мм;

ρ_fn - радиус кривизны переходной кривой в опасном сечении, мм;

ρ_v - приведенный радиус кривизны сопряженных профилей зубьев в полюсе зацепления, мм;

S_F - запас прочности при изгибе;

 - запас прочности при изгибе максимальной нагрузкой;

S_Hгл - запас прочности по отношению к глубинным разрушениям;

 - запас прочности по отношению к глубинным разрушениям при перегрузках;

S_S - запас стойкости против заедания;

s_y - коэффициент безопасности;

s_F - напряжения изгиба у основания зуба, МПа;

s_FP - допускаемые напряжения изгиба у основания зуба, МПа;

s_H - поверхностные контактные напряжения, МПа;

s_НР - допускаемые контактные напряжения, МПа;

Σ - межосевой угол конических зубчатых колес, град;

T_F - расчетный вращающий момент для определения напряжений изгиба, Н · мм;

T_H - расчетный вращающий момент для определения контактных напряжений зуба, Н · мм;

T_max - максимальный вращающий момент, Н · мм;

U - передаточное число, равное отношению числа z₁ зубьев колеса к числу z₂ зубьев шестерни;

V - окружная скорость, м/с;

V_m - окружная скорость по средней делительной окружности конического колеса, м/с;

V_Σ - суммарная скорость качения, м/с;

w_Hv - удельная окружная динамическая сила, Н/мм;

х - коэффициент осевого смещения зубчатого колеса;

Y_T - коэффициент, учитывающий технологию изготовления;

Y_F - коэффициент, учитывающий форму зуба;

Y_FL - коэффициент долговечности (числа циклов);

Y_k - коэффициент пространственного изменения напряжений;

Y_N - коэффициент числа циклов;

Y_R - коэффициент, учитывающий шероховатость переходной поверхности;

Y_Z - коэффициент, учитывающий способ получения заготовки зубчатого колеса;

у_a - износ зубьев в результате приработки, мм;

Y_b - коэффициент, учитывающий наклон зубьев;

Y_e - коэффициент, учитывающий перекрытие зубьев;

Y_s - коэффициент, учитывающий градиент напряжений и чувствительность материала к концентрации напряжений;

z - число зубьев;

Z_E - коэффициент, учитывающий механические свойства материала, МПа;

Z_H - коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;

Z_k - коэффициент, учитывающий длину условной линии контакта по высоте зуба в зацеплении Новикова;

Z_L - коэффициент смазки;

Z_M - коэффициент материала;

Z_N - коэффициент долговечности;

Z_R - коэффициент, учитывающий шероховатость поверхностей зубьев;

Z_V - коэффициент, учитывающий окружную скорость;

Z_b - коэффициент, учитывающий действительную площадь контакта в зацеплении Новикова;

Z_e - коэффициент, учитывающий суммарную длину контактных линий;

Z_v - эквивалентное число зубьев;

Z_vt - эквивалентное число зубьев конического зубчатого колеса.

2.3. ОСОБЕННОСТИ ЗАПИСИ НЕКОТОРЫХ ФОРМУЛ

Отдельные формулы в настоящем руководстве заканчиваются в правой части неравенством типа Y = .......... ³ 1.

Это означает, что если в результате расчета значение определяемого параметра не отвечает поставленному условию, следует принимать его равным значению, указанному в неравенстве. Например, если расчет дает Y < 1, то следует принимать Y = 1.

3. ПРОВЕРОЧНЫЙ РАСЧЕТ ЗУБЬЕВ НА ПОВЕРХНОСТНУЮ КОНТАКТНУЮ ПРОЧНОСТЬ

3.1. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ КОЛЕСА

Расчет необходим для проверки устойчивости профиля зубьев к износу и питтингу. Методика основана на расчете контактных напряжений s_H по Герцу с помощью следующих формул:

                                       (3.1-1)

где Z - коэффициент:

Z = Z_H · Z_E · Z_ε,                                                                (3.1-2)

Z_H - коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления:

                                         (3.1-3)

b_b - угол наклона зубьев на основном цилиндре; для прямозубых передач b_b = 0;

a_tw - угол зацепления в полюсе в торцовой плоскости на начальном цилиндре; в проектировочном расчете a_tw можно определить из выражения:

                           (3.1-4)

z₁, z₂ - число зубьев шестерни и колеса соответственно;

x₁, х₂ - коэффициенты осевого смещения шестерни и колеса соответственно;

a - угол профиля исходного контура;

a_t - угол зацепления в торцевом сечении:

a_t = arctg(tga/cosb), inva_t = tga_t - a_t, inva_tw =tga_tw - a_tw;   (3.1-5)

b - делительный угол наклона линии зуба.

В проверочном расчете

a_tw = arccos[m_n(z₁ + z₂)cosa_t/(2a_wcosb)],                         (3.1-6)

где m_n - модуль нормальный, мм;

a_w - межосевое расстояние, мм.

В формулах (3.1-1) и (3.1-4) знак «плюс» выбирают для внешнего зацепления, знак «минус» - для внутреннего;

Z_E - коэффициент, учитывающий механические свойства материала, Н^0,5/мм (МПа^0,5):

                               (3.1-7)

v₁, v₂ - коэффициенты Пуассона материалов шестерни и колеса;

Е₁, Е₂ - модули упругости I рода материалов шестерни и колеса, МПа. Для стальных зубчатых колес Z_E = 190 МПа^0,5;

Z_e - коэффициент, учитывающий суммарную длину контактных линий. Коэффициент Z_e, который иногда называют коэффициентом перекрытия, описывает те же параметры, что и коэффициент K_Нa распределения нагрузки между парами зубьев. При представлении коэффициента K_Нa как доли нагрузки на рассчитываемую пару зубьев [см. уравнения (3.1-26) и (3.1-35)] Z_E = 1. При расчете прямозубых передач (e_b = 0) внешнего зацепления с помощью коэффициента Z_e можно учесть благоприятное воздействие коэффициента e_a торцового перекрытия на контактную прочность и при K_Нa = 1 принять

                                                 (3.1-8)

e_a - торцовый коэффициент перекрытия:

e_a = e_a1 + e_a2;                                                                    (3.1-9)

e_a1, e_a2 - коэффициенты перекрытия соответственно шестерни и колеса, определяемые высотой головок зубьев:

                                             (3.1-10)

d_a1, d_a2 - диаметр окружности вершин зубьев шестерни и колеса соответственно:

для внешнего зацепления

                                      (3.1-11)

для внутреннего зацепления:

без учета конкретного зуборезного инструмента

                                    (3.1-12)

при окончательной обработке колеса зуборезным долбяком

                             (3.1-13)

где Dy - коэффициент уравнительного смещения:

Dy = (x₂ ± x₁) - y;                                                              (3.1-14)

y - коэффициент воспринимаемого смещения:

y = (a_w - а)/m_n;                                                                  (3.1-15)

a - делительное межосевое расстояние:

                                                               (3.1-16)

h_а - коэффициент головки зубьев;

Dy₀₂ - коэффициент уравнительного смещения для станочного зацепления колеса с внутренними зубьями и долбяка:

Dy₀₂ = x₂ - х₀ - y₀₂;                                                             (3.1-17)

x₀ - коэффициент смещения долбяка;

y₀₂ - коэффициент воспринимаемого смещения станочного зацепления долбяка с колесом:

                     (3.1-18)

z₀ - число зубьев долбяка;

m_t - модуль торцовый: m_t = m/cosb;

a - угол профиля исходного контура;

k₂ - коэффициент:

при x₂ < 2k₂ = 0,25 - 0,125x₂,

при x₂ ³ 2k₂ = 0;

d_b1, d_b2 - основной диаметр шестерни и колеса соответственно:

d_b1 = d₁cosa_t; d_b2 = d₂cosa_t;                                             (3.1-19)

d₁, d₂ - делительный диаметр шестерни и колеса соответственно:

d₁ = m_nz₁/cosb, d₂ = m_nz₂/cosb;                                         (3.1-20)

e_b - коэффициент осевого перекрытия:

                                                                 (3.1-21)

f₁ - коэффициент перекрытия профиля; для главных передач f₁ = 1,0, для передач якорных лебедок f₁ = 0,90, для зубчатых приводов баллера руля f₁ = 0,75.

Для косозубых передач при e_b < 1 и K_Ha = 1,0

                                (3.1-22)

а при e_b ³ 1

                                                                   (3.1-23)

B - рабочая ширина зубчатого венца колеса, мм; для нешевронных колес при e_b £ e_a В = b_w, при e_b > e_a В = b_we_a/e_b, для шевронных колес B = 2b_w;

d_w - диаметр начальной окружности, мм;

T_H - расчетный вращающий момент при определении контактной выносливости в полюсе зацепления, Н · мм.

В случае постоянной нагрузки (постоянной передаваемой мощности Р, кВт) T_H определяют с помощью формулы:

T_H = 9,554 · 10⁶Р/n,                                                         (3.1-24)

где n - частота вращения, мин^-1.

В случае переменной нагрузки T_H определяют по действующим стандартам с использованием методов эквивалентного числа циклов, эквивалентных моментов и эквивалентных напряжений. При этом необходимо учитывать вид циклограммы, режим нагружения и представлять кривую усталости двумя наклонными участками. При проведении традиционных инженерных расчетов чаще используют метод эквивалентного числа циклов, который обеспечивает более высокие значения T_H, чем метод эквивалентных напряжений. Вместе с этим, при автоматизированном проектировании и организации вероятностных расчетов более предпочтительным считается метод эквивалентных напряжений;

K_Н - коэффициент:

K_Н = K_АK_ПK_ШK_НaK_НbK_Нv;                                                (3.1-25)

K_А - коэффициент внешней динамической нагрузки, передаваемой от двигателя на зубчатую передачу, зависит от типа двигателя и соединения между двигателем и передачей. Коэффициент K_А должен быть указан в техническом задании на проектирование. Если внешние динамические нагрузки учтены циклограммой нагружения, и следовательно, при определении T_H, то K_A = 1,0. В противном случае:

для турбинных электрических и дизельных приводов с гидравлической или электромагнитной муфтой скольжения между двигателем и передачей K_A = 1,0;

для дизельных приводов с высокоупругой муфтой между двигателем и передачей K_A = 1,25;

для дизельных приводов, не имеющих в своем составе высокоупругих муфт K_A = 1,4.

Допускается принимать значения коэффициента K_A по итогам расчета крутильных колебаний энергетической установки с последующим подтверждением этого значения результатами экспериментального исследования головного судна (тензометрирование, торсиографирование);

K_П - коэффициент неравномерности распределения нагрузки между параллельными потоками мощности в многопоточных редукторах или между сателлитами в планетарных передачах. В передачах с раздвоением потока мощности K_П = 1,1. В однопоточных передачах K_П = 1,0. Для планетарных передач коэффициент K_П зависит от числа сателлитов, точности изготовления и жесткости деталей редуктора и должен быть задан по результатам специального расчета;

K_Ш - коэффициент неравномерности распределения нагрузки между полушевронами. Устанавливается в зависимости от типа опор плавающих валов, расстояния между полушевронами и кинематической точности передачи и для расчета на прочность задается в явном виде. Для нешевронных зубчатых колес K_Ш = 1,0;

K_Нa - коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых передач при e_a < 2 коэффициент K_Нa = 1.

В случае, когда обеспечено двухпарное зацепление при выполнении условия отсутствия интерференции продольной кромки внешнего зуба с главной поверхностью внутреннего, приводящей к заклиниванию при упоре вершин зубьев (см. [1]), или имеет место E_a - парное зацепление (E_a - целая часть e_a) при e_a > 2, для прямозубых передач с целью расчета K_Нa может быть использована формула, справедливая также для косозубых передач при e_a ³ e_b;

  (3.1-26)

где K_e - коэффициент, учитывающий отклонение суммарной длины контактных линий от их среднего значения b_we_a/cosb_b:

                                         (3.1-27)

Первое уравнение (3.1-27) справедливо при n_a + n_b £ 1, второе - при b = 0, третье - при n_a + n_b > 1;

n_a, n_b - дробные части e_a и e_b;

E_a1, Е_a2 - целые части e_a1, e_a2 (см. выше);

а_н - коэффициент, при b = 0 а_н = 1, в остальных случаях а_н = 0,9;

b_b - основной угол наклона: b_b = arcsin(sinbcosa);

K_Hv - коэффициент, учитывающий динамическую нагрузку в зацеплении; определяется в дорезонансной зоне в соответствии с ГОСТ 21354-87, а в резонансной и зарезонансной зонах - согласно рекомендациям ISO/DIN 6336/1 (см. также номограммы [1]);

с' - коэффициент удельной жесткости пары зубьев, Н/мм² (МПа); для передач с исходным контуром по ГОСТ 13755-81 :

     (3.1-28)

где z_v - эквивалентное число зубьев:

z_v1 = z₁/[cosbcos(2b_b)], z_v2 = z₂z_v1/z₁;                                (3.1-29)

для передач с внутренним зацеплением z_v2 = ∞;

для передач с исходным контуром, отличающимся от контура по ГОСТ 13755-81, и при внутреннем зацеплении косозубых колес для определения с' может быть использована методика [1], в соответствии с которой для внешнего зацепления , где K_B - коэффициент, учитывающий отличие коэффициента податливости  при отклонении параметров  и a соответственно от  и a = 20°:

     (3.1-30)

где a - в радианах (a_рад = a°p/180);

при a = 0,35 рад (20°) и  следует принимать K_B = 1,0.

Для внутреннего зацепления см. формулы и табл. [1];

g_fΣ - разность погрешностей основных шагов смежных пар зубьев передачи, мм:

                                                  (3.1-31)

e - погрешность в долях среднего квадратического отклонения, определяемая по задаваемой доверительной вероятности Р с использованием функции Лапласа:

при Р = 0,8e = 0,842,

при Р = 0,95e = 1,645,

при Р = 0,99e = 2,326,

при Р = 0,99999e = 4,265;

s_g0 - параметр, для поверхностно упрочненных зубьев s_g0 = 0,2;

f_pb1, f_pb2 - погрешности шагов зубьев шестерни и колеса соответственно, определяются по ГОСТ 1643-81;

y_a - износ зубьев в результате приработки, мм:

для колес с однородной структурой

y_a = 160f_pb/s_{H lim b};                                                            (3.1-32)

для зубьев с поверхностным упрочнением

y_a = 0,075f_pb,                                                                     (3.1-33)

                                                   (3.1-34)

s_{H lim b} - предел длительной контактной поверхностной выносливости, МПа.

Для косозубых передач при e_b > e_a

(3.1-35)

В уравнениях (3.1-26) и (3.1-35) не указаны индексы (1 или 2) у параметров Т_H, d, что соответствует тенденции перехода на вероятностные расчеты, предполагающие, помимо прочего, определение напряжений как в шестерне, так и в колесе;

K_Hb - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:

                             (3.1-36)

e_bb - отношение коэффициентов перекрытий:

e_bb = e_b/e_a £ 0,7;                                                                (3.1-37)

f_KУ - фактическое отклонение положения контактных линий, мм:

f_KУ = f_KE + f_KZ - y_b;                                                             (3.1-38)

f_KE - суммарная погрешность контакта, вызываемая деформацией деталей передачи, мм:

f_KE = |f_sh + f_sr + f_sb|;                                                             (3.1-39)

f_sh - суммарная погрешность контакта зубьев при изгибе валов, мм, зависит от кинематической схемы передачи, нагрузки, отношений рабочей ширины венца, диаметра вала к делительному диаметру, размеров пролетов, коэффициентов K_А и K_Hv. Рекомендуется определять по методикам СТ СЭВ 5744-86 или [1];

f_sr - суммарная погрешность контакта при кручении, мм, см. [1];

f_sb - погрешность контакта, вызываемая деформациями подшипников, мм, см. [1];

f_KZ - отклонение положения контактных линий вследствие погрешностей изготовления, мм:

f_KZ = 0,38eF_b cosa_twcosb_b;                                                (3.1-40)

F_b - допуск на погрешность направления зубьев, определяется по ГОСТ 1643-81 для принятой степени точности по нормам контакта в зависимости от ширины зубчатого венца;

y_b - износ контактирующих поверхностей зубьев в результате приработки, мм;

для зубчатых колес с однородной структурой материала:

y_b = 160(f_КЕ + f_KZ)/s_{H lim b};                                                 (3.1-41)

для зубчатых колес с поверхностным упрочнением зубьев:

y_b = 0,075(f_KE + f_KZ);                                                         (3.1-42)

c_mi - коэффициент удельной нормальной жесткости пары зубьев, Н/мм² (МПа), определяется с учетом их положения в расчетный момент зацепления. Для косозубых и шевронных передач c_mi = c'.

При выполнении приближенных оценок K_Hb или первой итерации расчетов можно использовать также следующие уравнения:

для пары «шестерня - колесо» без коррекции распределения нагрузки по ширине зубчатого венца:

K_Hb = 1,05 + 0,0044(e_a - 0,2)[(l_K/d_w)⁴ + 10(b_w/d_w)²]f₂,      (3.1-43)

где l_K - максимальная длина контактной линии:

при e_b £ e_a

l_K = b_w/cosb_b;                                                                    (3.1-44)

при e_b > e_a

l_K = b_we_b/(e_bcosb_b);                                                            (3.1-45)

d_w - диаметр начальной окружности:

d_w1 = 2a_w/(U + 1), d_w2 = 2a_wU/(U + 1);                            (3.1-46)

с коррекцией распределения этой нагрузки

K_Hb = 1,0 + 0,0026(e_a - 0,2)[(l_K/d_w)⁴ + 10(b_w/d_w)²]f₂;        (3.1-47)

для ступеней, в которых шестерня образует зацепление с несколькими колесами:

без коррекции распределения нагрузки по ширине зубчатого венца

K_Hb = 1,05 + 0,044(e_a - 0,2)(b_w/d_w)²f₂;                              (3.1-48)

с коррекцией распределения нагрузки

K_Hb = 1,0 + 0,026(e_a - 0,2)(b_w/d_w)²f₂;                                (3.1-49)

В формулах (3.1-43) - (3.1-49) f₂ - коэффициент, учитывающий точность изготовления передачи; для высокоточных главных передач f₂ = 1,0. В остальных случаях можно использовать следующие данные, указанные в табл. 3.1-1.

Таблица 3.1-1

В случае, когда имеет место зацепление нескольких зубьев на зубчатом колесе с внутренними зубьями, значение f₂ должно быть увеличено на 15 %, а когда имеет место зацепление нескольких зубьев на солнечной шестерне планетарной передачи - на 20 %.

Не менее важным по сравнению с K_Hb параметром является уже использовавшийся в уравнениях (3.1-26), (3.1-28), (3.1-35) и (3.1-36) коэффициент K_Hv, учитывающий динамические нагрузки, возникающие в результате ошибок зацепления и пересопряжения зубьев.

В дорезонансной зоне при выполнении условий VZ/1000 < 1 для прямозубых и VZ/1000 < 1,4 для косозубых передач:

K_Нv = 1 + w_Hv · b_wd_w/(2T_HK_АK_ПK_ШK_НaK_Нb).                    (3.1-50)

При невыполнении условий применимости уравнения (3.1-50) в случае, когда частота вращения шестерни составляет более 85 % резонансной в резонансной, промежуточной и закритической зонах коэффициент K_Hv определяют по приложению 5 ГОСТ 21354-87.

В уравнении (3.1-50) w_Hv - удельная окружная динамическая сила, Н/мм, которую можно определить с помощью уравнения:

                          (3.1-51)

где δ_Н - коэффициент, учитывающий жесткость зубьев и особенность работы передачи с косыми зубьями, определяется с помощью табл. 3.1-2;

Таблица 3.1-2

Значения коэффициентов δ_Н и δ_F

g₀ - коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется с помощью табл. 3.1-3;

Таблица 3.1-3

Значения коэффициента g₀

V - окружная скорость, м/с:

V = (pn/60)d_w/1000;                                                         (3.1-52)

а_с - отношение коэффициентов жесткости c_m колес рассматриваемой передачи заданного исходного контура и такой же передачи с исходным контуром по ГОСТ 13755-81; если рассматриваемая передача имеет исходный контур по ГОСТ 13755-81, то а_с = 1. Для косозубой передачи c_m = c';

a_M - отношение приведенных масс: a_M = ,

где M_ΣΠ - действительная приведенная масса, кг;

M_Σ - приведенная масса зубчатых колес передачи, кг.

В тех случаях, когда с шестерней связана массивная деталь с моментом инерции в g раз большим, чем у шестерни, полученное по формуле (3.1-51) значение w_Hv следует увеличить в  раз.

Полученное в итоге значение w_Hv не должно превышать предельного значения w_Hvmax, приведенного в табл. 3.1-4. Если w_Hv > w_Hvmax, то следует принимать w_Hv = w_Hvmax.

Таблица 3.1-4

Предельные значения w_Нvmax и w_Fvmax, Н/мм

3.2. КОНИЧЕСКИЕ ЗУБЧАТЫЕ КОЛЕСА

3.2.1. Прямозубые колеса

Методика основана на использовании расчетных формул для прямозубых цилиндрических зубчатых колес благодаря введению дополнительных конусов в среднем сечении зуба и эквивалентных зубчатых колес.

Расчетное контактное напряжение в полюсе зацепления

    (3.2.1-1)

где

Z = Z_H · Z_E · Z_e,                                                                (3.2.1-2)

Z_H - коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления:

Z_H = 70,97 - 148,95(1 - f_x) + 79,75(l - f_x)²,                        (3.2.1-3)

где f_x - параметр:

f_x = x₁ + x₂/(Z_vt1 + Z_vt2);                                                    (3.2.1-4)

х₁, x₂ - коэффициенты осевого смещения шестерни и колеса;

Z_vt1, Z_vt2 - эквивалентное число зубьев шестерни и колеса:

Z_vt1 = Z₁/ cosδ₁, Z_vt2 = Z₂/cosδ₂;                                        (3.2.1-5)

для ортогональных (Σ = 90°) конических передач

                                                        (3.2.1-6)

Z_E - коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес:

                          (3.2.1-7)

Z_e - коэффициент, учитывающий суммарную длину контактных линий. Поскольку здесь K_Нa = 1, то Z_e £ 1. Тогда коэффициент Z_e можно рассчитать с помощью формулы (3.1-8), предварительно определив коэффициент торцового перекрытия для эквивалентной цилиндрической передачи в зависимости от параметров Z_vt1, Z_vt2, высоты головок зубьев h_ae1, h_ae2, модуля m_c и угла зацепления α (см., например, [3]).

Для приближенных оценок (с запасом) может быть использована формула

                           (3.2.1-8)

Σ - межосевой угол зубчатых колес;

K_be = b_w/R_e - коэффициент ширины зубчатого венца;

R_e - внешнее делительное (начальное) конусное расстояние (рис. 3.2.1);

Рис. 3.2.1

d_we - внешний начальный диаметр, мм;

δ₁, δ₂ - углы начальных конусов шестерни и колец, град; для нулевых или равносмещенных передач δ₁ + δ₂ = Σ;

T_H - расчетный вращающий момент, Н · мм (см. 3.1);

 - коэффициент:

K_Hb - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:

                                                                  (3.2.1-9)

 - параметр:

                                                             (3.2.1-10)

N_KП - номер передачи с коническими колесами. Если оба колеса расположены консольно, опоры - на шариковых подшипниках, то N_KП = 1. Если оба колеса расположены консольно, опоры - на роликовых подшипниках, то N_KП = 2. Если одно колесо расположено консольно, другое в пролете, опоры - на шариковых подшипниках, то N_KП = 3. Если одно колесо расположено консольно, другое в пролете, опоры - на роликовых подшипниках, то N_KП = 4. Если колеса расположены в пролете между опорами на шариковых подшипниках, то N_KП = 5. Если колеса расположены в пролете между опорами на роликовых подшипниках, N_KП = 6;

П_НВ - признак, указывающий на твердость поверхности зубьев колеса; если , П_НВ = 1, если , П_НВ = 2;

C_b - коэффициент; для прямозубых конических передач C_b = 1,14;

K_Hv - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении:

K_Hv = 1 + w_Hvb_wd_m/(2T_HK_АK_Hb);                                       (3.2.1-11)

d_m - средний делительный диаметр, мм;

w_Hv - удельная окружная динамическая сила рассматриваемого колеса, Н/мм:

                                                     (3.2.1-12)

V_m - окружная скорость по средней делительной окружности рассматриваемого колеса:

V_m = pd_mn/60000;                                                            (3.2.1-13)

δ_Н, g₀ - см. табл. 3.1-2 и 3.1-3 соответственно.

Полученное значение w_Hv не должно превышать предельного значения w_Hvmax, определенного с помощью табл. 3.1-4. В случае, если w_Hv > w_Hvmax, следует принимать w_Hv = w_Hvmax.

3.2.2. Колеса с непрямыми зубьями

Введение понятия биэквивалентных зубчатых колес позволяет свести расчет конических зубчатых передач с непрямыми, в том числе с круговыми, зубьями к расчету цилиндрических зубчатых передач.

Расчет базируется на использовании формулы (3.2.1-1). При этом отличия касаются расчета Z_H, Z_e, , K_Hb, K_Hv.

Коэффициент Z_H, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, определяют в зависимости от b_n и z = (x₁ + x₂)/(z₁ + z₂) с помощью следующей аппроксимации:

(3.2.2-1)

Коэффициент Z_e, учитывающий суммарную длину контактных линий, для передач с тангенциальными зубьями может быть рассчитан с помощью уравнения:

                 (3.2.2-2)

где b_n - средний угол наклона зубьев.

Для передач с круговыми зубьями

                                                       (3.2.2-3)

где v_H - коэффициент: при твердости рабочих поверхностей зубьев шестерни и колеса 350 НВ и менее

v_H = 1,22 + 0,21U;                                                            (3.2.2-4)

при твердости шестерни более 45 HRC_Э и колеса 350 НВ и менее

v_H = l,13 + 0,13U;                                                             (3.2.2-5)

при твердости рабочих поверхностей зубьев шестерни и колеса 45 HRC_Э и более

v_H = 0,81 + 0,15U;                                                            (3.2.2-6)

 - коэффициент:

                                                       (3.2.2-7)

K_Ha - коэффициент, учитывающий распределение нагрузки между зубьями, имеет другой физический смысл по сравнению с K_Нa, определяемым по формулам (3.1-26), (3.1-35):

K_Нa = 1 + 0,0025(0,17C_T)⁴V_m + 0,02(C_T - 6)^1,35;              (3.2.2-8)

K_Hb - см. формулы (3.2.1-9) и (3.2.1-10), при этом для передач с круговыми зубьями следует принимать C_b = 1,07;

K_Hv - коэффициент, учитывающий динамические нагрузки, возникающие в результате ошибок зацепления и пересопряжения зубьев:

K_Hv = 1 + w_Hvb_wd_m/(2Т_HK_AK_HaK_Hb),                                 (3.2.2-9)

w_Hv - см. формулу (3.2.1-12).

Все проверочные расчеты заканчиваются проверкой условия прочности.

3.3. ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ КОНТАКТНЫХ НАПРЯЖЕНИЙ

3.3.1. Цилиндрические зубчатые колеса

Предельные напряжения по Герцу  при оценке поверхностной контактной прочности не поддаются точному расчету и их определяют путем прямых экспериментов на роликовых моделях и зубчатых передачах. Наиболее достоверные значения  приведены в табл. 3.3-1, при этом пересчет твердости в HV и HRC_Э в единицы твердости по Бринеллю может быть осуществлен с помощью корреляций

НВ = -1,674 + l,1025HV - 0,402 · 10^-3HV²;                   (3.3.1-1)

                                          (3.3.1-2)

Экспериментальные проверки (см., например, [2]), однако, показывают, что значения  практически не зависят от химического состава материала. Для стальных косозубых и шевронных зубчатых колес с модулем 2 ... 8 мм при определении  может быть использовано уравнение [2]

                                                        (3.3.1-3)

где V_Σ - суммарная скорость качения:

V_Σ = 2Vsina_tw.                                                                  (3.3.1-4)

Для планетарных передач V_Σ - окружная скорость в движении относительно водила.

Формула (3.3.1-3) проверена опытным путем в диапазоне 10 £ V_Σ £ 120 м/с и справедлива при V_Σ < 70 м/с. При V_Σ > 70 м/с следует принимать значение , рассчитанные по формуле (3.3.1-3) при V_Σ = 70 м/с. Формулу (3.3.1-3) в [2] рекомендуют использовать и при расчетах зубьев с химико-термическим упрочнением, причем, если твердость рабочих поверхностей более 550 НВ, то следует принимать 550 НВ. Одновременно следует проверить значения  с помощью данных табл. 3.3-1 и в дальнейшем использовать меньшие значения . При окружных скоростях V < 12,5 м/с рекомендации табл. 3.3-1 более надежны.

Таблица 3.3-1

Расчетные формулы для определения , МПа

Предел контактной выносливости

                                           (3.3.1-5)

где Z_R - коэффициент, учитывающий шероховатость поверхностей зубьев; определяется по тому из сопряженных колес, зубья которого имеют более грубые поверхности. Значения этого коэффициента в зависимости от шероховатости поверхности зубьев выбирают так:

если R_a = 0,63 ... 1,25 мкм, то Z_R = 1;

если R_a = 1,25 ... 2,5 мкм, то Z_R = 0,95;

если R_z = 10 ... 40 мкм, то Z_r = 0,9;

Z_V - коэффициент, учитывающий окружную скорость:

при H⁰ £ 350 HB

Z_V = 0,85V^0,1 ³ 1;                                                             (3.3.1-6)

при Н⁰ > 350 НВ

Z_V = 0,925V^0,05 ³ 1.                                                          (3.3.1-7)

Формулы (3.3.1-6) и (3.3.1-7) справедливы при окружной скорости V £ 25 м/с. При большей окружной скорости

при H⁰ < 350 НВ

Z_V = 1,17Z_V1 · Z_V2;                                                           (3.3.1-8)

при H⁰ > 350 НВ

Z_V = 1,08Z_V1 · Z_V2,                                                            (3.3.1-9)

где

Z_V1 = [V_Σ/(50sina_tw)]^0,21 ³ 1;                                             (3.3.1-10)

Z_V2 = (30/V_Σ)^0,15 £ 1;                                                         (3.3.1-11)

Формулы (3.3.1-8) - (3.3.1-11) справедливы при V_Σ £ 70 м/с. Если V_Σ > 70 м/с, то в формулы (3.3.1-10) - (3.3.1-11) подставляют значения V_Σ = 70 м/с;

Z_L - коэффициент смазки, учитывает влияние вязкости и качества смазочного материала. Это влияние недостаточно изучено, поэтому можно принимать Z_L = 1,0.

Для высокоскоростных передач (V > 25 м/с)

при  £ 850 МПа

Z_L = 0,68V_f + 0,83,                                                           (3.3.1-12)

где

V_f = (1,2 + 80/v₅₀)^-2;                                                          (3.3.1-13)

при 850 <  £ 1200 МПа

Z_L = C_ZL + 4(1 - C_ZL)V_f,                                                    (3.3.1-14)

где

C_ZL = /4375 + 1,024;                                              (3.3.1-15)

при  > 1200 МПа

Z_L = 0,36V_f + 0,91;                                                           (3.3.1-16)

Z_X - коэффициент, учитывающий размеры колеса. Предполагается, что с ростом диаметра колеса d контактная выносливость снижается, поэтому при изучении этого вопроса экспериментально влияние размеров колеса на контактную выносливость обнаруживается не всегда, в связи с чем при d < 700 мм следует принимать Z_X = 1,0;

при d > 700 мм

                                                   (3.3.1-17)

Z_N - коэффициент долговечности, зависящий от числа циклов нагружения. Метод определения Z_N зависит от метода учета переменных режимов нагружения.

При постоянной нагрузке или переменных режимах нагружения, учитываемых по методу эквивалентной нагрузки,

                                               (3.3.1-18)

При переменных режимах нагружения, учитываемых по методу эквивалентного числа циклов напряжений,

                                               (3.3.1-19)

где N_{H lim} - базовое число циклов напряжений, соответствующее точке перегиба кривой усталости; при любых видах нагрузок

                                          (3.3.1-20)

N_K - число циклов напряжений в соответствии с заданным сроком службы, при постоянной нагрузке

N_K = N_Σ = 60nL_h;                                                              (3.3.1-21)

L_h - ресурс, ч;

N_HE - эквивалентное число циклов напряжений;

q_H - показатель степени кривой усталости; если N_{H lim} ³ N_K, то q_H = 6, если N_K > N_{H lim}, то q_H = 20.

Параметры N_K, N_HE определяют путем специального расчета (см., например, [1]) по формулам, вид которых зависит от учета одного наклонного участка кривой усталости (для стальных зубчатых колес q_H = 6) или обоих ( = 6,  = 20). Для колес из нормализованной и улучшенной сталей максимальное значение коэффициента долговечности ; для колес из цементированной и нитроцементированной сталей, а также из стали, подвергнутой поверхностной закалке, ; для колес из стали, подвергнутой газовому азотированию, . Минимальное значение коэффициента . Для режимов заднего хода и других режимов работы с небольшим числом циклов нагружения рекомендуется принимать Z_N = 1,15.

Допускаемые контактные напряжения

s_НР = s_{H lim b}/S_НР,                                                              (3.3.1-22)

где S_НР - допустимый запас прочности; следует принимать S_НР не менее S_НР = 1,2. Для передач, выход из строя которых связан с тяжелыми последствиями, рекомендуется увеличивать S_НР до 1,25 ... 1,30.

При расчете на контактную выносливость прямозубой передачи в качестве допускаемого контактного напряжения используют меньшее из сопоставленных значений s_НР1 и s_НР2, то есть

                                                               (3.3.1-23)

при скорости V до 20 м/с для косозубых передач

                                                  (3.3.1-24)

при этом s_НР не должно выходить из диапазона

s_{HP min} < s_HР £ l,25 s_{HP min}.                                              (3.3.1-25)

При больших окружных скоростях V следует использовать условие (3.3.1-23).

В случае выполнения условия s_НР < l,25s_{HP min} для косозубых и шевронных передач может быть использована формула

s_НР = 0,45(s_НР1 + s_НР2) ³ s_{НР min}.                                    (3.3.1-26)

В [3] и приложении 7 ГОСТ 21354-87 приводится уточненная методика расчета допускаемых напряжений для косозубых и шевронных передач, учитывающая геометрические параметры зацепления, от которых зависит нагрузочная способность передач в зоне I, в которой головки зубьев шестерни зацепляются с ножками зубьев колеса, и в зоне II, в которой головки зубьев колеса зацепляются с ножками зубьев шестерни. Там же приведены все необходимые графики и номограммы. Эта методика дает значения s_НР, которые ниже, чем определенные с помощью формулы (3.3.1-24).

3.3.2. Прямозубые конические колеса

Для расчета s_НР1 и s_НР2 применяют формулы (3.3.1-22) - (3.3.1-26) с заменой V на V_m и использованием условия (3.3.1-23), однако значения s_НР1 и s_НР2 находят по формулам:

s_HP1 = 0,9s_{H lim bl}/S_HP;                                                       (3.3.2-1)

s_HP2 = 0,9s_{H lim b2}/S_HP.                                                      (3.3.2-2)

3.3.3. Конические колеса с непрямыми зубьями

Для расчета s_НР1 и s_НР2 применяют формулы (3.3.1-22) - (3.3.1-26) с заменой V на V_m. Значение s_НР рассчитывают с помощью формулы:

s_HP = (s_HP1 + s_HP2)/2;                                                       (3.3.3-1)

при этом должно выполняться неравенство

s_HP < 1,15s_{HP min}                                                                                   (3.3.3-2)

Если условие (3.3.3-2) не выполняется, то принимают s_НР = 1,15s_{HP min}, где s_{НР min} - наименьшее из значений s_HP1 и s_HP.

4. РАСЧЕТ ЗУБЬЕВ НА ГЛУБИННУЮ КОНТАКТНУЮ ПРОЧНОСТЬ

4.1. Расчет производят для азотированных, цементированных и нитроцементированных (цианированных) цилиндрических зубчатых колес с малой толщиной упрочненного слоя в тех случаях, когда полученное в результате расчета зубьев на поверхностную контактную прочность значение напряжений s_H превышает значение  контактных напряжений, определенных для сердцевины зубьев.

4.2. Расчет сводится к определению запаса прочности по отношению к глубинным разрушениям:

                                              (4.2-1)

где  - предельное глубинное напряжение по Герцу, МПа;

для высокопрочных сталей с твердостью сердцевины

                                             (4.2-2)

A_j - коэффициент приведения глубинных касательных напряжений к предельным глубинным напряжениям:

при 0,1 < j < 0,45 A_j = 5,1;                                            (4.2-3)

при 0,45 £ j < 6A_j = 5,1 + a_j,                                        (4.2-4)

где a_j = 1,1(j - 0,4/j) ³ 0;                                              (4.2-5)

j - параметр толщины упрочненного слоя:

                                                          (4.2-6)

h_t - расстояние от поверхности до той точки, в которой твердость упрочненного слоя равна твердости сердцевины, мм, для азотированного слоя h_t = 0,6 ... 0,8 мм;

 - твердость сердцевины по Виккерсу;

 - то же для поверхности упрочненного слоя;

ρ_g - приведенный радиус кривизны сопряженных профилей зубьев в полюсе зацепления:

                                                           (4.2-7)

где d_b - основной диаметр колеса;

µ_T - коэффициент, учитывающий возможность возникновения трещин в упрочненном слое ранее, чем в сердцевине зуба:

для азотированных сталей

                      (4.2-8)

для цементированных и нитроцементированных сталей

                        (4.2-9)

Формулами (4.2-8) и (4.2-9) можно пользоваться, если распределение твердости по толщине поверхностного слоя не хуже, чем описываемое зависимостями:

для азотированных поверхностей

(4.2-10)

для цементированных и нитроцементированных поверхностей

                     (4.2-11)

, H_HV(z),  - значения микротвердости в единицах HV на поверхности слоя в точке с координатой z, мм, отсчитываемой от поверхности к сердцевине, и в сердцевине материала соответственно.

При отклонении распределения твердости от описываемого формулами (4.2-10) и (4.2-11) возможны погрешности в определении µ_T, особенно для случая цементирования (например, сталь 20Х2Н4А). Во всех таких случаях Речной Регистр вправе потребовать указания в технической документации значения µ_T;

 - коэффициент, учитывающий число циклов напряжений рассчитываемого зубчатого колеса:

                                                      (4.2-12)

где  - базовое число циклов глубинных напряжений:

                                                            (4.2-13)

 - эквивалентное число циклов нагружения, зависит от метода учета переменных режимов нагружения, определяется так же, как и при работе на поверхностную контактную прочность (см. 3.3.1), но q_H = 18. В случае учета переменных режимов нагружения по методу эквивалентных нагрузок

 - твердость сердцевины по Бринеллю.

Минимальные допустимые значения запасов по глубинной контактной прочности можно принимать по стандарту. При отсутствии статистических данных для случаев, когда разрушение может развиваться под слоем, , а для случаев, когда имеется вероятность появления разрушений в пределах упрочненного слоя .

5. ЗАПАС ПРОЧНОСТИ ПРИ ПЕРЕГРУЗКАХ

5.1. Расчет необходим для предотвращения остаточной деформации или хрупкого разрушения поверхностного слоя и выполняется в случае, когда расчетная нагрузка T_H, определенная с учетом всех возможных режимов нагружения, меньше максимально возможной T_max.

5.2. Запас по глубинной контактной прочности при перегрузках может быть рассчитан с помощью следующей формулы:

                 (5.2-1)

где  - коэффициент приведения глубинных касательных напряжений к предельным глубинным напряжениям, определенный по формулам (4.2-3) - (4.2-4) при

                                                         (5.2-2)

µ_Т - коэффициент, учитывающий возможность возникновения трещин в упрочненном слое ранее, чем в сердцевине зуба, рассчитывается с помощью формул (4.2-8) или (4.2-9) при j';

 - базовое число циклов нагружения:

                                            (5.2-3)

N_c - число циклов действия перегрузок за весь период работы передачи.

Запас по поверхностной контактной прочности при перегрузках для азотированных зубчатых колес может быть рассчитан с помощью формулы

                                              (5.2-4)

где N_lim - базовое число циклов; можно принимать N_lim = 10 · 10⁷.

При использовании формул (5.2-1) и (5.2-4) возможны ситуации, когда при перегрузке запас прочности по отношению к поверхностным разрушениям возрастает, а по отношению к глубинным - падает.

Значения  для передач, выход из строя которых связан с тяжелыми последствиями, не должны быть менее 1,4 в случае, когда разрушение может развиваться под слоем, и менее 1,5 для случая, когда разрушение может иметь место в пределах упрочненного слоя. Для передач вспомогательных технических средств в некоторых случаях Речным Регистром в результате специального рассмотрения может быть допущено соотношение

Значения  должны быть не менее 1,2, а для передач, выход из строя которых связан с тяжелыми последствиями, - не менее 1,25 ... 1,3.

Взамен пересчета запаса прочности при перегрузках можно выполнить расчет зубьев на поверхностную и глубинную контактную прочность (см. 3.1, 3.2, 4.2) при T_H = T_max и сопоставить полученные значения максимальных напряжений s_Нmax со следующими допускаемыми контактными напряжениями s_Нmax при максимальной нагрузке:

s_НРmax = 2,8R_eH;                                                                                     (5.2-6)

цементации или поверхностной закалке

                                                             (5.2-7)

азотированию

                                                                 (5.2-8)

При этом должно выполняться условие s_{H max} < s_{HP max}.

Здесь R_eH - предел текучести материала зубчатого колеса, МПа.

6. РАСЧЕТ ЗУБЬЕВ НА ВЫНОСЛИВОСТЬ ПРИ ИЗГИБЕ

6.1. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ КОЛЕСА

Расчет несущей способности ножки зуба необходим для оценки вероятности предотвращения усталостного излома зубьев.

Расчетное напряжение изгиба зубьев каждого зубчатого колеса рассчитывают с помощью следующего выражения:

                                                      (6.1-1)

где F_Ft - окружная сила на делительном цилиндре, Н:

при постоянной нагрузке

F_Ft = 2T₁/d₁ = 2T₂/d₂;                                                        (6.1-2)

при переменных режимах нагружения

F_Ft = 2T_F1/d₁ = 2T_F2/d₂.                                                     (6.1-3)

Окружные силы на делительных цилиндрах неравносмещенных шестерни и колеса неодинаковы, поэтому равенство (6.1-3) для таких передач является приближенным;

m - модуль, мм;

T₁, Т₂ - постоянный вращающий момент шестерни и колеса, Н · мм;

T_F1, Т_F2 - расчетный вращающий момент, Н · мм. Значения Т_F зависят от метода учета переменного режима нагружения, самого режима нагружения (тяжелого, среднего равновероятного, среднего нормального и т.д.) и суммарного числа циклов нагружения;

В - см. 3.1;

K_F - коэффициент:

K_F = K_AK_ПK_ШK_FaK_FbK_Fv,                                                 (6.1-4)

K_A, K_П, K_Ш - см. 3.1;

K_Fb - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий

K_Fb = 0,95 + (K_Hb - 1)(1 - 1,4m_n/l_K)/(1 + 1,4m_n/l_K);           (6.1-5)

K_Hb, l_K - см. (3.1-25), (3.1-43), (3.1-44);

K_Fa - коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых колес при e_a < 2, K_Fa = 1, при e_a ³ 2, K_Fa = K_Ha,

для косозубых и шевронных колес при e_b £ e_a

   (6.1-6)

при e_b > e_a

   (6.1-7)

K_eb - коэффициент:

K_eb = (n_ab - n_an_b)/(eb);                                                      (6.1-8)

n_a, n_b - дробные части e_a, e_b;

n_ab - меньшее из n_a и n_b;

K_Fv - коэффициент, учитывающий динамическую нагрузку в зацеплении:

K_Fv = 1 + d_ww_FvВ/(2T_FK_AK_ПK_ШK_FaК_Fb);                          (6.1-9)

                              (6.1-10)

a_с, a_M - см. уравнение (3.1-50);

δ_F - коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев, см. табл. 3.1-2;

g₀ - коэффициент, см. табл. 3.1-3;

В тех случаях, когда с шестерней связана массивная деталь с моментом инерции в g раз большим, чем у шестерни, то полученное с помощью формулы (6.1-10) значение w_Fv следует увеличить в  раз.

Найденное по уравнению (6.1-10) или с учетом g значение w_Fv не должно превышать предельного значения, приведенного в табл. 3.1-4;

Y_F - коэффициент, учитывающий форму зуба; для зубьев с внешним зацеплением:

Y_F = Y_FcB_Y,                                                                        (6.1-11)

где Y_Fc - коэффициент формы зубьев со стандартным профилем по ГОСТ 13755-81:

    (6.1-12)

для зубьев с модификацией ножек при с^* = 0,4, р^* = 0,05 (параметр протуберанца) и

(6.1-13)

Z_v - коэффициент: Z_v = Z/cos³b;

h_m - расстояние по радиусу зубчатого колеса от вершины зуба до точки приложения силы на профиле зуба; можно принимать h_m = h/m, где h_w - высота головки зуба от начальной окружности. При Z= Z₁, х = х₁, h_m = 0;

B_Y - коэффициент, учитывающий колебания Y_Fc при отклонениях угла a профиля основного контура и коэффициента  высоты головки от значений 20° и 1° соответственно:

    (6.1-14)

Корреляции (6.1-12) и (6.1-14) достоверны для зубчатых колес с числом зубьев Z = 10 ... 500, коэффициентом смещения х = -0,6 ... 1,2 при следующих параметрах исходного контура: a = 15 ... 30°, ; с^* = 0,25 (с^* - коэффициент радиального зазора, с^* = с/т),  ( - коэффициент радиуса переходной кривой исходного контура).

Коэффициент формы зуба Y_F для внутреннего зацепления допускается определять по ISO 63330, методике Российского Морского Регистра судоходства или по номограммам и графикам [1]. Ориентировочные значения этого коэффициента: для внешнего зацепления Y_F = 4,5, для внутреннего Y_F = 5,8.

Для внешних зубьев с исходным контуром по ГОСТ 13755-81 при расчете Y_F можно использовать более простые зависимости:

применительно к зубьям без профилей модификации:

Y_Fc = 3,47 + 13,2/Z_v - 29,7x/Z_v + 0,092x²;                        (6.1-15)

применительно к зубьям, изготовленным с применением червячной фрезы или зубострогальной гребенки с протуберанцем при р^* = 0,05, , с^* = 0,4, a = 20°, a_M = 6°, :

Y_Fc = 3,69 + 0,05х² + 11,4/Z_v - 30,4x/Z_v.                          (6.1-16)

Рекомендуется рассчитать Y_Fc с помощью уравнений (6.1-12), (6.1-13), (6.1-15) и (6.1-16) и в дальнейшем расчете использовать наибольшие из полученных значений Y_Fc.

g_b - коэффициент, учитывающий наклон зубьев:

                                                 (6.1-17)

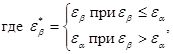
Для прямозубых колес Y_b = 1;

Y_e - коэффициент, учитывающий перекрытие зубьев. Поскольку коэффициент K_Fa представлен как доля нагрузки на рассчитываемый зуб, то Y_e = 1. Для косозубых передач при K_Fa = 1 и e_b ³ 1 Y_e = 1/e_a;

Y_FL - коэффициент числа циклов, учитывающий повышенную прочность ножки зуба колес с ограниченным сроком службы: для главных передач, привода генераторов, рулевых машин и подруливающих устройств Y_FL = 1, для остальных случаев

при N_Σ = 60nL_n £ 10⁴ Y_FL = 0,4;

при 10⁴ < N_Σ £ 4 · 10⁶

                                                  (6.1-18)

где:

для конструкционных и улучшаемых сталей c_FL = 0,16;

для цементированных и нитроцементированных сталей c_FL = 0,12;

для азотируемых сталей c_FL = 0,059.

При N_Σ > 4 · 10⁶ Y_FL = 1.

6.2. КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

6.2.1. Прямозубые колеса

Расчетное напряжение изгиба на переходной поверхности зуба определяют с помощью формулы:

            (6.2.1-1)

где Y_F - коэффициент, учитывающий форму зуба; определяется с помощью формул (6.1-11) - (6.1-14) при условии замены Z₁ или Z₂ на Z_vt1 = Z₁/cosδ₁ или Z_vt2 = Z₂/cosδ₂;

F_Ft - см. уравнения (6.1-2), (6.1-3);

δ₁, K_be, b_w - см. 3.2.1;

m - расчетный модуль зубчатого колеса, мм;

K_Fb - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:

                                                                (6.2.1-2)

     (6.2.1-3)

где , N_KП, П_HB - см. уравнение (3.2.1-10);

c_Fb - коэффициент, учитывающий погрешность определения ; для прямозубых колес c_Fb = 1,17;

K_Fv - коэффициент, учитывающий динамическую нагрузку в зацеплении:

K_Fv = l + w_Fb_w/(F_FtK_Fb);                                                    (6.2.1-4)

w_Fv - удельная окружная динамическая сила:

                                                   (6.2.1-5)

g₀ - см. табл. 3.1-3;

V_m - см. уравнение (3.2.1-13);

R_e - см. рис. 3.2.1.

6.2.2. Конические колеса с непрямыми зубьями

Расчетное напряжение изгиба определяется с помощью формулы:

                                  (6.2.2-1)

где F_Ft - см. уравнения (6.1-2), (6.1-3);

δ₁, K_be - см. 3.2.1;

K_Fb - см. уравнение (6.2.1-2), при этом значение c_Fb следует принимать равным 1,13;

Y_F - коэффициент, учитывающий форму зуба; определяется с помощью формул (6.1-11) - (6.1-14) при условии замены Z₁ или Z₂ (Z_v1 или Z_v2) на число зубьев биэквивалентных зубчатых колес:

Z_vn1 = Z₁/(cosδ₁cos³b_n); Z_vn2 = Z₂/(cosδ₂cos³b_n);               (6.2.2-2)

Y_b - коэффициент, учитывающий наклон зубьев:

Y_b = 1 - 0,0073b_n;                                                             (6.2.2-3)

K_Fv - коэффициент, учитывающий динамическую нагрузку в зацеплении; определяется с помощью формул (6.2.1-4) и (6.2.1-5) с заменой коэффициента 0,15 на 0,07;

v_F - коэффициент понижения несущей способности конических колес по сравнению с цилиндрическими; для колес с тангенциальными зубьями v_F = 0,85, а для колес с круговыми зубьями:

при H₁ и Н₂ £ 350 НВ                        v_F = 0,94 + 0,08U;                                            (6.2.2-4)

при H₁ ³ 45 HRC_Э и Н₂ £ 350 НВ     v_F = 0,85 + 0,043U;                                          (6.2.2-5)

при H₁ и H₂ ³ 45 HRC_Э                       v_F = 0,65 + 0,11U.                                           (6.2.2-6)

Для расчета s_H и s_F конических колес с круговыми зубьями могут быть использованы специальные методики, признанные Речным Регистром.

6.3. ОПРЕДЕЛЕНИЕ ДОПУСКАЕМОГО НАПРЯЖЕНИЯ ИЗГИБА ЗУБЬЕВ

6.3.1. Цилиндрические зубчатые колеса

Расчетный передел выносливости зубьев при изгибе может быть определен с помощью следующего уравнения:

                                  (6.3.1-1)

где  - базовый предел выносливости при изгибе; определяется при вероятности неразрушения 0,99 с помощью данных табл. 6.3.1-1 - 6.3.1-4;

K_Fg - коэффициент, учитывающий влияние шлифования переходной поверхности зуба, определяется с помощью данных табл. 6.3.1-1 - 6.3.1-4 в зависимости от способа химико-термической обработки. Для зубчатых колес с нешлифованной переходной поверхностью зубьев принимают K_Fg = 1,0;

Таблица 6.3.1-1

Параметры , K_Fg, K_Fd и S_F для цементированных зубчатых колес

Таблица 6.3.1-2

Параметры , K_Fg, K_Fd для нитроцементированных зубчатых колес

Таблица 6.3.1-3

Параметры , K_Fg, K_Fd для зубчатых колес из отожженной, нормализованной и улучшенной стали

K_Fd - коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности, определяется с помощью данных таблиц 6.3.1-1 - 6.3.1-4. Если зубчатые колеса не подвергаются указанным видам обработки, K_Fd = 1,0;

Y_N - коэффициент долговечности (числа циклов):

                                                      (6.3.1-2)

где q_F - параметр; для зубчатых колес из материала с однородной структурой, включая закаленные при нагреве ТВЧ со сквозной закалкой, и для зубчатых колес со шлифованной переходной поверхностью, независимо от твердости и термообработки их зубьев, q_F = 6. Для азотированных, цементированных и нитроцементированных зубчатых колес с нешлифованной поверхностью q_F = 9;

Таблица 6.3.1-4

Параметры , K_Fg, K_Fd для зубчатых колес, закаленных при нагреве токами высокой частоты

N_Flim - базовое число циклов напряжений: N_Flim = 4 · 10⁶;

N_K - см. уравнения (3.3.1-18) и (3.3.1-19); подставляется в уравнение (6.3.1-2) при использовании метода эквивалентных нагрузок. В случае учета переменности режимов нагружения с помощью метода эквивалентного числа циклов в формулу (6.3.1-2) вместо N_K подставляется значение N_FE, которое определяют по результатам специального расчета (см., например, [1]).

Максимальные значения коэффициента Y_N:

при q_F = 6,

при q_F = 9,

Y_s - коэффициент, учитывающий градиент напряжений и чувствительность материала к концентрации напряжений (опорный коэффициент); для колес с внешним зацеплением при радиусе p_fn кривизны переходной кривой в опасном сечении ρ_fn £ 7 мм

Y_s = 1,082 - 0,172lgm.                                                     (6.3.1-3)

Для уточненных расчетов при ρ_fn > 7 мм для зубчатых колес с внешним зацеплением, изготовленных из нормализованной улучшенной стали и с поверхностной закалкой без охвата основания зуба:

               (6.3.1-4)

где R_eH - см. уравнение (5.2-6);

х - относительный градиент напряжений, мм^-1:

х = 2,3/ρ_fn;                                                                         (6.3.1-5)

для цементированных, нитроцементированных зубчатых колес и с поверхностной закалкой, кроме закалки без охвата основания зуба:

                                              (6.3.1-6)

Радиус кривизны переходной кривой зубьев с исходным контуром по ГОСТ 13755-81:

            (6.3.1-7)

для зубьев, нарезаемых зуборезным инструментом с протуберанцем:

   (6.3.1-8)

для колес с внутренним зацеплением и ρ_fn > 7 мм при изготовлении из нормализованной, улучшенной стали и с поверхностной закалкой без охвата основания зубьев:

                                           (6.3.1-9)

где χ_s - относительный градиент напряжений, мм^-1:

χ_s = a_G/m;                                                                         (6.3.1-10)

а_G - коэффициент градиента напряжений, определяемый по формулам (6.1-12) и (6.1-13) или (6.1-15), в которых Y_F заменяют на а_G, или по таблицам, номограммам (графикам) [1] при внутреннем зацеплении;

для цементированных, нитроцементированных колес с поверхностной закалкой

Y_s = 1 + χ ⁰⁵ · 10^-1,3;                                                          (6.3.1-11)

Y_R - коэффициент, учитывающий шероховатость переходной поверхности. Для шлифованных и зубофрезерованных поверхностей с шероховатостью R_Z £ 40 мкм Y_R = 1,0. Для полированных поверхностей в зависимости от способа термического упрочнения принимают: при цементации, нитроцементации, азотировании (полирование до химико-термической обработки) Y_R = 1,05; при нормализации и улучшении Y_R = 1,20; при закалке с нагревом ТВЧ, когда закаленный слой повторяет очертания впадины между зубьями, Y_R = 1,05; при закалке с нагревом ТВЧ, когда закаленный слой распределяется по всему сечению зуба, а также по части ступицы под основанием зуба и впадины или обрывается к переходной кривой, Y_R = 1,20;

K_FX - коэффициент, учитывающий размеры зубчатого колеса;

K_FX = 1,05 - 0,000125d,                                                   (6.3.1-12)

g_h - коэффициент, учитывающий глубину азотирования:

g_h = b₀/1,2;                                                                        (6.3.1-13)

при отсутствии азотирования g_h = 1,0;

b₀ - параметр глубины:

b₀ = fh_t/m;                                                                         (6.3.1-14)

h_t - глубина азотирования - замеренное на травленом шлифе под микроскопом расстояние от поверхности до границы видимой упрочненной зоны.

Значения b₀ приведены в табл. 6.3.1-5.

Таблица 6.3.1-5

Допускаемое напряжение изгиба зубьев

s_FP = s_{F lim b}K_FCY_TY_z/S_F,                                                   (6.3.1-15)

где K_FC - коэффициент, учитывающий влияние двухстороннего приложения нагрузки, для нереверсивных передач K_FC = 1,0. При двухстороннем приложении нагрузки

K_FC = 1 - g_Ag_TFYNmin/g_TFYNmax.                                                          (6.3.1-16)

Здесь g_А - коэффициент, учитывающий влияние амплитуд напряжений противоположного знака; для зубчатых колес из отожженной, нормализованной и термоулучшенной стали g_А = 0,35, для колес с твердостью зубьев более 45 HRC_Э, за исключением азотированных, g_А = 0,25, для азотированных зубчатых колес g_А = 0,1;

g_TFYNmin, g_TFYNmax - отношения:

                                                     (6.3.1-17)

                                                    (6.3.1-18)

,  - нагрузка и коэффициент долговечности (числа циклов) применительно к противоположной стороне зуба. Эти параметры определяют по той же методике, что и T_F и Y_N. При Т_F < 0,6Т_F можно принимать K_FC = 1;

Y_T - коэффициент, учитывающий технологию изготовления. Если при изготовлении выполнены условия, указанные в табл. 6.3.1-1 - 6.3.1-4, то Y_T = 1; в противном случае Y_T < 1 и его значение должно быть указано в документации, представляемой Речному Регистру;

Y_Z - коэффициент, учитывающий способ получения заготовки зубчатого колеса. Для поковок и штамповок Y_Z = 1,0, для проката Y_Z = 0,9, для литых заготовок Y_Z = 0,8;

S_F - запас прочности (безопасности), определяется с помощью данных, приведенных в табл. 6.3.1-1 - 6.3.1-4. При отсутствии необходимых сведений можно принимать S_F = 1,7.

6.3.2. Конические колеса с прямыми зубьями

Допускаемое напряжение изгиба определяют с помощью следующей зависимости:

                                  (6.3.2)

где  - предел выносливости материала при изгибе, соответствующий базовому числу циклов изменения напряжений; определяют с помощью табл. 6.3.1-1 - 6.3.1-4;

Y_s, Y_R, Y_Fx, K_Fg, K_Fd, K_Fc - коэффициенты, определяют в соответствии с 6.3.1;

S_F - запас прочности при изгибе, определяют с помощью данных табл. 6.3.1-1 - 6.3.1-4 и приложений к ним.

6.3.3. Конические колеса с непрямыми зубьями

Допускаемые напряжения изгиба определяют с помощью формулы (6.3.2).

6.4. Запас прочности при изгибе максимальной нагрузкой

Расчетное напряжение изгиба определяют с помощью следующей зависимости

        (6.4-1)

где T_{F mах} - максимальный вращающий момент, Н · мм;

(K_AK_FaK_FbK_Fv) - произведение коэффициентов, определяемых по методикам, описанным в 6.1 и 6.2 при действии максимального вращающего момента.

Допускаемые напряжения изгиба максимальной нагрузкой определяют с помощью следующей формулы:

                                   (6.4-2)

где  - предельное напряжение при изгибе зубьев максимальной нагрузкой:

                                                                        (6.4-3)

 - базовое значение предельного напряжения зубьев; определяют с помощью данных табл. 6.4-1;

 - коэффициент, учитывающий влияние шлифования переходной поверхности зуба. Для зубчатых колес с переходной поверхностью, подвергнутой шлифованию после сквозной закалки с нагревом ТВЧ и объемной закалки,  = 0,95 при черновом режиме и  = 1,1 при чистовом режиме зубошлифования; цементации с закалкой - соответственно  = 1,0 и 1,05; нитроцементации с закалкой -  = 0,90 и 0,95;

 - коэффициент, учитывающий влияние деформационного упрочнения. При деформационном упрочнении нешлифованной переходной поверхности  = 0,95, шлифованной -  = 1,00, без деформационного упрочнения  = 1,00;

 - коэффициент, учитывающий шероховатость переходной поверхности, при использовании данных табл. 6.4-1  = 1,0;

K_Fx - коэффициент, учитывающий размеры зубчатого колеса; определяют так же, как и при расчете допускаемого напряжения для оценки длительной выносливости (см. 6.3.1);

 - опорные коэффициенты при максимальной нагрузке. Для передач с внешним зацеплением при учете данных табл. 6.4-1  = 1,0. Во всех остальных случаях эти коэффициенты определяют с помощью табл. 6.4-2.

В табл. 6.4-2 a_s - теоретический коэффициент концентрации напряжений, определяют по методике [1] расчета коэффициента формы Y_F для внутреннего зацепления, заменив Y_F на a_s, а коэффициенты уравнения - на соответствующие коэффициенты табл. 5.2, 5.3 и 5.4 [1].

Таблица 6.4-1

Значения  при изгибе максимальной нагрузкой

Для зубьев с исходным контуром по ГОСТ 13755-81 и протуберанцем при a_M = 6° (угол профиля модифицированного участка исходного контура), р^* = 0,05 (параметр протуберанца),   [см. формулы (6.1-12) - (6.1-14)]:

а_s = 1,67 + 0,13х - 5,1/Z_V + 4,12x/Z_v;                              (6.4-4)

Таблица 6.4-2

Опорные коэффициенты при изгибе максимальной нагрузкой

S_FP - коэффициент запаса прочности:

S_FP = Y_zS_y,                                                                         (6.4-5)

где Y_z - см. 6.3.1;

S_y - коэффициент безопасности, при доверительной вероятности неразрушения 0,95 S_у = 1,75.

Таким образом, запас прочности при изгибе максимальной нагрузкой

                                                                     (6.4-6)

должен быть не менее запаса прочности S_F, значения которого приведены в табл. 6.3.1-1 - 6.3.1-4. В отдельных случаях по согласованию с Речным Регистром допускается принимать

                                                                       (6.4-7)

но при этом значение  не должно быть меньше S_FP.

7. РАСЧЕТ ЗУБЬЕВ НА ЗАЕДАНИЕ

Несмотря на то, что до настоящего времени не разработаны надежные и универсальные расчетные методики, на утверждение Речному Регистру должен быть представлен расчет зубьев на заедание, в котором должны быть определены расчетная нагрузка W_str в наиболее опасной точке на участке линии зацепления от полюса до точки конца зацепления и предельная по заеданию нагрузка W_{s lim r} расчетной точке.

Запас стойкости зубьев на заедание

S_si = W_{s lim i}/W_sti,

должен быть не менее предельно допускаемого запаса стойкости S_SP = 1,3.

Для косозубых и шевронных цилиндрических колес при расчетах может быть использована методика [2].

8. ОСОБЕННОСТИ РАСЧЕТА НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ НОВИКОВА

8.1. КОНТАКТНЫЕ НАПРЯЖЕНИЯ

Расчетное контактное напряжение по Герцу:

    (8.1-1)

где Z_M - коэффициент материала:

                            (8.1-2)

v₁, v₂, E₁, E₂ - см. формулу (3.1-7);

Z_b - коэффициент, учитывающий действительную площадь контакта; в диапазоне b = 5 ... 45°

Z_b = 0,12 + 0,013b - 3,34 · 10^-20ехрb + 0,379/b - 0,417/b²;  (8.1-3)

Z_K - коэффициент, учитывающий длину условной линии контакта по высоте зуба:

                                                  (8.1-4)

 - параметр радиуса ρ_а профиля головки:

a₁, a₂ - предельные углы давления на линии контакта, рад.

Для исходных контуров по ГОСТ 15326-76 Z_k = 0,8, для контуров ДЛЗ-1,0 ... 0,15 Z_k = 0,95 и ДЛЗ-0,7 ... 0,15 Z_k = 1,22;

d₁ - диаметр делительной окружности шестерни, мм;

K_Ha - коэффициент неравномерности распределения нагрузки между головкой и ножкой зуба:

                                              (8.1-5)

 - параметр головки зуба:

K_Hv - коэффициент, учитывающий динамичность нагрузки, см. формулы (3.1-50) и (3.1-50);

K_e - коэффициент распределения нагрузки по площадкам контакта, для передач с двумя линиями зацепления (ДЛЗ) при e_b > 1

K_e = 2E_b + n_b/(2E_b);                                                          (8.1-6)

E_b, n_b - целая и дробная части значения коэффициента e_b осевого перекрытия:

e_b = b_w/p_x = E_b + n_b;                                                          (8.1-7)

р_х - осевой шаг.

Коэффициенты 2 в уравнении (8.1-6) учитывают две линии зацепления.

8.2. НАПРЯЖЕНИЯ ИЗГИБА

Расчетное напряжение изгиба зубьев под действием нагрузки, распределенной на площадках контакта равномерно по высоте зуба и по эллиптическому закону вдоль зуба для менее прочного колеса пары:

s_F = Y_FY_bY_K2T_FK_FaK_Fv/(m³ZK_e),                                      (8.2-1)

где Y_F - коэффициент формы зуба; определяется с помощью корреляции, справедливой для диапазона Z_v = 5 ... 300 (Z_v - эквивалентное число зубьев: Z_v = Z/cos³b):

        (8.2-2)

Для исходных контуров по ГОСТ 15023-76 коэффициенты уравнения (8.2-2) равны: b₀ = 4,706; b₁ = 0,0017; b₂ = -0,0645; b₃ = 83,71; b₄ = 1237,44;

для контура ДЗЛ-1,0 ... 0,15 - b₀ = 3,237; b₁ = 0,00155; b₂ = -0,0398; b₃ = 71,57; b₄ = 1111,6;

для контура ДЗЛ-0,7 ... 0,15 - b₀ = 2,681; b₁ = 0,0006; b₂ = -0,0207; b₃ = 49,15; b₄ = 238,02;

Y_b - коэффициент, учитывающий влияние угла b наклона зубьев и отличие действительной площадки контакта от принятых в расчетной схеме; в диапазоне b = 5 ... 45°

Y_b = -0,105 + 0,0089b + 5,29 · 10^-20 · ехрb + 0,929/b - 2,23/b²;    (8.2-3)

Y_K - коэффициент пространственного изменения напряжений вследствие перемещения площадки контакта по длине зуба; для диапазона n_b = 0 ... 0,5

                                          (8.2-4)

где коэффициенты c₀, c₁, c₂, c₃ равны:

при минимальном числе K_min площадок контакта (K_min = 1 - одна линия зацепления):

с₀ = 2,211; с₁ = -1,269; с₂ = 2,777; c₃ = -1,275;

при K_min = 2

с₀ = 1,399; с₁ = 0,339; с₂ = 0,000381; с₃ = -0,744;

при K_min = 3

с₀ = 1,12; c₁ = -0,112; c₂ = 0,167; c₃ = -0,103;

при K_min = 4

c₀ = 1,05; c₁ = 0,0374; с₂ = 0,0882; c₃ = -0,09;

K_Fa - коэффициент неравномерности распределения нагрузки между головкой и ножкой зуба:

                                             (8.2-5)

Для передач ДЛЗ с твердостью 350 НВ и менее при Z₁ ³ 20 и U £ 4 можно принимать K_Fa = 1;

K_Fv - коэффициент, учитывающий динамичность нагрузки, см. формулу (6.1-10);

K_e - коэффициент распределения нагрузки по площадкам контакта, см. формулу (8.1-6).

8.3. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ

Выбор допускаемых напряжений для передач Новикова проводят так же, как и для эвольвентных (см. 3.3.1 и 6.3.1).

9. ОСОБЕННОСТИ РАСЧЕТА НА ПРОЧНОСТЬ ПЛАНЕТАРНЫХ ПЕРЕДАЧ

Расчет планетарных передач на контактную прочность и выносливость при изгибе ведут с помощью тех же самых формул, которые используют для цилиндрических зубчатых колес, но при этом учитывают следующее.

При использовании записи «±» знак «+» принимают для наружного зацепления, а знак «-» - для внутреннего. Расчетный момент для каждой кинематической пары определяется с помощью выражений, справедливых для конкретных кинематических схем планетарных редукторов, в которые входят: расчетный вращающий момент на ведомом валу T_рн на водиле или Т_р1 на колесе и передаточное отношение i (отношение угловых скоростей или моментов), а в некоторых случаях и передаточное число U.

Неравномерность распределения нагрузки между сателлитами учитывают путем введения к расчетному моменту на центральном (солнечном) колесе сомножителя K_c/n_c, где K_с - коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами, для приближенных оценок можно принимать: при отсутствии связей, например, при плавающем солнечном колесе K_с = 1,15 ... 1,20; при отсутствии выравнивания нагрузки K_c = 2; n_c - число сателлитов.

Более точно расчетный вращающий момент можно рассчитать по следующей методике.

Для зацепления I (рис. 9.1):

при Z_g ³ Z_a

                                                                 (9-1)

при Z_a > Z_g

                                                                        (9-2)

Здесь и далее индексы «a», «g», «b», «f» в обозначениях моментов T и числа зубьев Z соответствуют обозначению колес планетарной передачи на рис. 9.1. Для схем А и Б с плавающей подвеской центральных колес  = 1,1; для схемы В при n_c > 1 и плавающем центральном колесе  = 1,25, а при n_c > 1 и неплавающем центральном колесе  = 2;

Рис. 9.1

для зацепления II:

                                                                       (9-3)

для зацепления III:

                                                                       (9-4)

где для схем А и Б с плавающей подвеской центральных колес  = 1,1, для схемы В с плавающей подвеской колеса b  = 1,0, для схем А и Б без плавающей подвески

   (9-5)

d_b - диаметр колеса b, мм.

При s_НР > 900 МПа следует принимать s_НР = 900 МПа;

для схемы В при плавающем колесе е  = 1,0;

                                                              (9-6)

i - передаточное отношение между ведущим и ведомым валами;

для схемы В с плавающей подвеской колеса b

                                               (9-7)

В случае, когда имеет место зацепление нескольких зубьев на солнечном колесе, то при использовании для расчета K_Hb уравнений (3.1-36) в их второй член правой части нужно ввести сомножитель 1,2, а при использовании уравнений (3.1-43), (3.1-47) - (3.1-49) - увеличить коэффициент f₂ на 20 %. Таким образом, учитывается увеличение неравномерности распределения нагрузки по длине контактных линий (увеличение K_Hb влечет за собой и увеличение K_Fb).

Коэффициенты K_Hv и K_Fv, учитывающие динамическую нагрузку в зацеплении, следует определять для скорости относительно водила.

При определении эквивалентного числа N_E циклов нагружения количество зацеплений для центральных колес учитывают умножением на n_с.

Допускаемое напряжение изгиба зубьев сателлитов [см. уравнение (6.3.1-15)] рекомендуется определять при увеличении запаса S_F прочности (безопасности) на 50 % по сравнению с непланетарными передачами, учитывая таким путем влияние тонких ободов сателлитов и корончатых колес на изломную прочность зубьев.

Расчеты планетарных передач на прочность допускается выполнять с помощью методики [6].

10. ВЕРОЯТНОСТНЫЕ РАСЧЕТЫ НА ПРОЧНОСТЬ ЗУБЧАТЫХ ПЕРЕДАЧ

Целью вероятностного расчета является определение вероятности безотказной работы (сохранения работоспособности) по сопротивлению контактной усталости и усталости по изгибу. Эти расчеты выполняют отдельно для шестерни и колеса.

Обязательность выполнения вероятностных расчетов настоящим руководством не регламентируется.

Для выполнения вероятностных расчетов могут быть рекомендованы методики [1] или [5], а в случае расчетов с помощью компьютерных приложений - методика, основывающаяся на вычислительном эксперименте, проводимом с целью учета рассеяния следующих факторов:

K_А - коэффициента внешней динамической нагрузки (х₁);

K_v - коэффициента внутренней динамической нагрузки через коэффициент g₀, учитывающий влияние разности шагов зацепления (x₂);

K_a - коэффициента распределения нагрузки между зубьями через параметр g_fΣ, представляющий собой разность погрешностей основных шагов смежных пар зубьев передачи (х₃);

K_b - коэффициента концентрации нагрузки через параметр f_ку, учитывающий фактическое отклонение положения контактных линий (х₄).

Используемое компьютерное приложение должно быть адаптировано к вычислительному эксперименту, то есть оно должно позволять варьировать значениями K_А, g₀, g_fΣ и f_ку перед каждым вычислительным опытом (расчетом). В случае, если в данном варианте расчета g₀, g_fΣ или f_ку не используется, то варьироваться могут, помимо K_А, сами значения K_v, K_a, K_b.

Рекомендуемый план вычислительного эксперимента (план Хартли-Коно) приведен в табл. 10-4.

Кодированные значения факторов обозначают следующее:

1 - в опыте используется максимально возможное значение фактора, например, при х₁ = 1 K_А = 1,4;

Таблица 10-4

План вычислительного эксперимента

0 - в опыте используется среднее значение фактора, например, при x₁ = 0, K_А = 1,2;

-1 - в опыте используется минимально возможное значение фактора, например, при х₁ = -1 K_А = 1,0.

По итогам вычислительного эксперимента для каждого колеса передачи получают четыре массива значений

s_Нi, n_Hi = s_{H lim b}/s_Hi, s_Fi, n_Fi = s_{F lim b}/s_Fi,

где i - номер элементов массивов, i = 1, 2, ..., 18.

Далее элементы каждого массива (будем обозначать их у_ij, где j = 1, 2, 3, 4) обрабатываются в следующей последовательности.

Рассчитывается выборочное среднее:

Определяется среднее квадратическое отклонение от среднего (только для s):

Вычисляется коэффициент вариации (только для s):

Имея полученные таким образом значения v_sH и v_sF, определяют квантили распределения:

где v_{H lim}, v_{F lim} - коэффициенты вариации пределов выносливости; для улучшенных, нормальных и нормализованных колес v_Hlim = 0,07 ... 0,09; v_{F lim}= 0,08 ... 0,1; для колес, зубья которых имеют поверхностное упрочнение v_{H lim} = 0,085 ... 0,13; v_{F lim} = 0,1 ... 0,14.

Затем по таблицам нормированного нормального распределения с использованием значений u_рН и u_рF находят вероятности Р(Н) и P(F) безотказной работы по сопротивлению контактной усталости и усталости по изгибу.

11. РАСЧЕТ НАПРЯЖЕННОГО СОСТОЯНИЯ ЗУБЧАТЫХ КОЛЕС С ПРИМЕНЕНИЕМ ДИСКРЕТНЫХ МОДЕЛЕЙ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

11.1. ЦЕЛЬ РАСЧЕТА

Обязательность выполнения расчета напряженного состояния зубчатых колес с применением дискретных моделей метода конечных элементов (МКЭ) настоящим руководством не регламентируется.

Целью расчета являются определение напряженно-деформированного состояния зубчатых колес как объемной конструкции с учетом пространственного приложения нагрузки и оценка статической и усталостной прочности зубьев.

При реализации цели последовательно решаются следующие задачи:

расчет параметров, необходимых для построения трехмерных (3D) моделей зубчатых колес, в том числе профилей зубьев, и зубчатого зацепления (фактически создается виртуальный зуборезный инструмент, с помощью которого инженер-расчетчик «нарезает» на экране зубья требуемой конструкции), выбор схемы приложения нагрузок к поверхности зубьев, идеализация нагрузок применительно к конечно-элементной модели;

построение 3D модели с учетом всех конструктивно-технологических особенностей зубчатых колес;

построение конечно-элементной модели каждого зубчатого колеса зацепления и расчет напряженного состояния конструкции;

расчет зубьев на усталостную прочность по результатам определения напряжений в элементах конструкции.

11.2. ОСОБЕННОСТИ ПОДХОДА К РАСЧЕТУ ПРОЧНОСТИ

Зубчатое колесо рассматривается как объемная конструкция с учетом всех особенностей геометрии, пространственного приложения нагрузок и схемы поддержки с помощью опор. Для реализации таких представлений разрабатывается трехмерная модель зубчатого колеса и зацепления в целом с применением интегрированных CAD/CAM/CAE систем. Для разработки 3D моделей и последующего определения напряженно-деформированного состояния зубьев могут быть использованы любые вычислительные системы (программные продукты), признанные Речным Регистром.

Крутящий момент считается приложенным к ведущему валу (валу колеса 1). Собственные инерционные нагрузки колеса рассчитываются в большинстве интегрированных CAD/CAM/CAE систем путем задания углов скорости и оси вращения вала: система автоматически вычисляет массовые нагрузки в конечных элементах и приводит их к узловым инерционным силам. Контактные пары между валом и подшипниками на опорах также создаются самой системой. В случае проработки CAD-модели опор и подшипников можно проанализировать процесс деформации вала с учетом податливости опорных узлов и подшипников

Следует, однако, указать, что с усложнением CAD-модели зубчатого зацепления вместе с опорами и подшипниками увеличивается время расчета и повышаются требования к быстродействию и возможностям вычислительной техники (платформе), которую используют при проведении расчетов.

Расчет напряженного состояния для каждого варианта конструкции включает в себя глобальный анализ, то есть решение конкретной задачи взаимодействия зубчатых колес между собой и определение напряженного состояния конструкции на «грубой» сетке, и локальный анализ с целью уточнения результатов глобального анализа для элементов с повышенным уровнем напряжений на мелкой сетке.

11.3. СВОЙСТВА ПРИМЕНЯЕМЫХ МАТЕРИАЛОВ

Для моделирования напряженно-деформированного состояния зубчатых колес необходимо задать следующие свойства материалов зубьев:

модуль упругости Е, МПа;

коэффициент Пуассона µ;

плотность ρ, кг/м³;

временное сопротивление на растяжение R_m, МПа;

предел выносливости симметричного цикла s_-1, МПа;

предел текучести R_eH, МПа.

11.4. РАСЧЕТ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

Расчет зубчатого зацепления выполняют для заданной частоты вращения колеса 1 (шестерни) и передаваемого вращающего момента.

Определяют нагрузочные диаграммы и составляют блоки нагрузок в зависимости от угла поворота ведущего вала через каждые 1 - 3 град. Таким образом, рассчитывается несколько вариантов напряженно-деформированного состояния зубчатых колес. Уточнение напряжений и определение коэффициентов концентрации напряжений производят в каждом нагруженном элементе конструкции, определяющих в конечном итоге усталостную прочность зубьев.

Для каждой зоны с повышенным уровнем напряжений фиксируются максимальные и минимальный компоненты тензора напряжений, с помощью которых определяют запас прочности по усталостным напряжениям на основе диаграммы предельных состояний. Полный тензор напряжений во всех точках конструкции вычисляется интегрированной CAD/CAM/CAE системой автоматически и выдается в табличном виде и в виде трехмерных цветных графических изображений конструкции, при этом красным цветом помечаются элементы, напряжения в которых имеют максимальные значения.

12. РАСЧЕТ ЗУБЬЕВ НА УСТАЛОСТНУЮ ПРОЧНОСТЬ ПРИ ИСПОЛЬЗОВАНИИ ДИСКРЕТНЫХ МОДЕЛЕЙ МКЭ

12.1. ОБЩИЕ ЗАМЕЧАНИЯ

Изложенные в разд. 2 - 10 методы расчета на прочность зубчатых колес создавались эмпирически по результатам анализа испытаний, опыта проектирования, изготовления и эксплуатации зубчатых зацеплений в различных областях техники. Достоверное определение напряженного состояния зубьев с помощью этих методов возможно, но осложняется необходимостью использования эмпирических коэффициентов, которые применяют также и при вычислении допускаемых напряжений.

Метод конечных элементов (при условии точного воспроизведения в 3D-модели геометрии зубьев, взаимного расположения колес в паре, жесткости колес, валов и опор) позволяет с большой достоверностью определить опасные напряжения в зубе при статическом приложении нагрузки. Однако, по результатам сопоставления смоделированных напряжений с предельно допустимыми напряжениями, определенными как функция от условного предела текучести материала, делать вывод о выносливости зубьев было бы преждевременно.

Зубчатые колеса судовых передач работают в условиях приложения знакопеременных нагрузок, при этом напряжения в элементах конструкции редко достигают опасных значений, даже в зонах с повышенным уровнем напряжений. Однако, после приложения определенного числа циклов нагружения возможны повреждения зубьев даже в тех случаях, когда напряжения в 2 - 3 раза ниже предельно допускаемых, то есть возможные отказы зубчатых колес, удовлетворяющих критерию статической прочности, могут иметь усталостный характер. Поэтому проверка элементов конструкции зубчатых колес, напряженно-деформированное состояние которых определено с помощью дискретных моделей МКЭ, по критериям усталостной прочности обязательна.

Несмотря на то, что большинство интегрированных CAD/CAM/CAE систем позволяет выполнять оценки по критериям усталостной прочности, Речной Регистр регламентирует применение изложенной ниже методики расчета, выдержавшей многочисленные экспериментальные проверки.

12.2. МЕТОДИКА РАСЧЕТА

Условие усталостной прочности имеет вид:

s_y = k_ss_a/(e_sb_s) + ψ_ss_m = s_-1,                                          (12.2-1)

где s_у - амплитуда эквивалентных напряжений, приведенная к симметричному циклу;

k_s - эффективный коэффициент концентрации напряжений. Поскольку напряженное состояние конструкции определено с учетом концентрации напряжений, а эффективный коэффициент концентрации всегда меньше теоретического, то принимают k_s = 1;

e_s - масштабный коэффициент, учитывающий влияние абсолютных размеров детали на усталостную прочность, определяется по формуле

                                                       (12.2-2)

где e_∞ - базовый масштабный коэффициент: e_∞ = 0,5 для сталей;

λ - масштабный фактор; можно принимать λ = 0,02 мм^-1;

d - характерный диаметр, мм;

b_s - коэффициент, учитывающий влияние состояния поверхности детали на усталостную прочность; определяется по формуле:

b_s = b_Tb_корb_уп;                                                                  (12.2-3)

b_T - отражает влияние шероховатости; для полированной поверхности зубьев b_T = 0,85, для шлифования b_T = 1,1 ÷ 1,2, для цементации поверхностей зубьев b_T = 1,2 ÷ 1,3, для азотирования поверхностей зубьев b_T = 1,3 ÷ 1,5;

b_кор - отражает влияние коррозионной среды; при отсутствии коррозионной среды b_кор = 1;

b_уп - отражает влияние упрочняющих технологий; значения b_уп приведены в табл. 12.2;

Таблица 12.2

s_а - интенсивность переменных напряжений, определяется по формуле:

                                                              (12.2-4)

где а = (s_xa - s_ya)² + (s_ya - s_za)²,

s_za ... t_zxa - амплитуды компонент переменных напряжений, определяемые по формулам:

s_xa = (s_xmax - s_xmin)/2;                                                        (12.2-5)

s_ya = (s_ymax - s_ymin)/2;                                                        (12.2-6)

s_za = (s_zmax - s_zmin)/2;                                                        (12.2-7)

t_xya = (t_xymax - t_xymin)/2;                                                       (12.2-8)

t_yza = (t_yzmax - t_yzmin)/2;                                                       (12.2-9)

t_zxa = (t_zxmax - t_zxmin)/2;                                                       (12.2-10)

s_xmax ... t_zxmin, s_xmin ... t_zxmin - соответственно максимальные и минимальные компоненты тензора напряжений;

s_m - интенсивность средних напряжений, определяется как наибольшее главное напряжение из решения характеристического уравнения

                                                       (12.2-11)

где s_xm ... t_zxm - компоненты средних напряжений, определяемые по формулам:

s_xа = (s_xmax + s_xmin)/2;                                                       (12.2-12)

s_yа = (s_ymax + s_ymin)/2;                                                       (12.2-13)

s_zа = (s_zmax + s_zmin)/2;                                                       (12.2-14)

t_xyа = (t_xymax + t_xymin)/2;                                                      (12.2-15)

t_yzа = (t_yzmax + t_yzmin)/2;                                                      (12.2-16)

t_zxа = (t_zxmax + t_zxmin)/2;                                                      (12.2-17)

s_xmax ... t_zxmax, s_xmin ... t_zxmin - максимальные и минимальные компоненты тензора напряжений соответственно;

ψ_s - коэффициент; отражает зависимость предела выносливости по амплитуде при асимметричном цикле от среднего (статистического) напряжения, действующего в той же точке сечения, определяется по формулам:

ψ_s = 0 при s_HI < 0;                                                           (12.2-18)

 при s_m > 0.                      (12.2-19)

12.3. ОЦЕНКА БЕЗОПАСНОСТИ ПО КРИТЕРИЯМ СТАТИЧЕСКОЙ И УСТАЛОСТНОЙ ПРОЧНОСТИ

Коэффициент запаса прочности по подобному циклу (при одновременном увеличении амплитуды и средних напряжений) определяется по формуле:

n = s_-1/s_y.                                                                         (12.3-1)

Коэффициент запаса прочности по переменным напряжениям (увеличение амплитуды при постоянных средних напряжениях) определяется по формуле:

n_a = (s_-1 - ψ_ss_m)e_sb_s/(s_aK_s)                                             (12.3-2)

Коэффициент запаса прочности по пределу текучести определяется по формуле:

n_T = R_eH/s_экв.                                                                     (12.3-3)

Коэффициент запаса прочности по пределу прочности определяется с помощью зависимости

n_B = R_m/s_экв.                                                                     (12.3-4)

Коэффициент запаса прочности по контактной выносливости определяется по формуле:

n_H = s_HP/s_H,                                                                      (12.3-5)

где s_н - наибольшие контактные напряжения в зубе;

Результаты расчета по приведенной методике для всех элементов конструкции зуба сводят в таблицу, анализ данных которой позволяет судить о том, что конструкция зубьев удовлетворяет или не удовлетворяет критериям статической и усталостной прочности.

ПРИЛОЖЕНИЕ

ПРИМЕРЫ РАСЧЕТА ЗУБЧАТЫХ ПЕРЕДАЧ НА ПРОЧНОСТЬ

Пример 1. Выполнить расчет передачи с коническими зубчатыми колесами и круговыми зубьями для СПК типа «Ласточка» (проект № 03525). Исходные данные приведены в табл. А1.

Таблица А1

Поскольку расчет прочности выполнялся на компьютере, промежуточные результаты не представлены, а рассчитанные напряжения и коэффициенты запаса прочности приведены в табл. А2.

Таблица А2

Анализ данных табл. А2 показывает, что поверхностная контактная прочность зубьев не обеспечивается.

Пример 2. Выполнить расчет на прочность передачи с цилиндрическими зубчатыми колесами (первая ступень редуктора Г81). Зацепление - внешнее, косозубое, зубья нешевронные без модификации, термическая обработка - цементация. Исходные данные приведены в табл. А3.

Таблица A3

Поскольку расчет выполнен на компьютере, то промежуточные результаты не приведены. Итоговые результаты сведены в табл. А4.

Таблица А4

Пример 3. Выполнить расчет передачи с коническими зубчатыми колесами и круговыми зубьями для СПК типа «Ласточка» (проект 03525) методом конечных элементов в CAD/CAM/CAE системе I-DEAS фирмы CDRC (США). Исходные данные принять такими же, что и в примере 1 (см. табл. А1).

Созданное в системе CAD 3D изображение конструкции на основании чертежей № 021110037, 021110038 приведено на рис. А1, а конечно-элементная модель зацепления - на рис. А2.

Рис. А1

Рис. А2

Расчет напряженного состояния (контактная задача) выполнен в линейной постановке с использованием объемных конечных элементов для относительного положения колеса и шестерни, при котором возникают максимальные напряжения в шестерне, как наиболее слабом элементе конструкции.

Расчетная нагрузка реализует максимальный крутящий момент на ведущее колесо, составляющий 4680 Н · м.

Материал конструкции - сталь 18Х2Н4МА со следующими характеристиками при твердости HRC_Э = 58:

Е = 210000 МПа - модуль нормальной упругости;

µ = 0,3 - коэффициент Пуассона;

R_m = 1180 МПа - временное сопротивление;

R_eH = 980 МПа - предел текучести;

s_-1 = 510 МПа - предел выносливости симметричного цикла;

s_НР = 1090 МПа - предел контактной выносливости.

На рис. А3 приведено распределение эквивалентных напряжений, а на рис. А4 - контактных напряжений в зубе шестерни, МПа.

В табл. А5 приведены компоненты тензора напряжений, характеризующие амплитуду пульсирующего цикла в наиболее опасном с точки зрения усталостной прочности районе (район действия максимальных напряжений растяжения), а также максимальное эквивалентное и максимальное контактное напряжение в зубе шестерни.

Таблица А5

Результаты расчета по приведенной методике для конструкции зуба ведомой шестерни приведены в табл. А6.

Анализ результатов показывает, что конструкция зубчатых колес углового редуктора удовлетворяет критериям статической и усталостной прочности, за исключением поверхностной контактной выносливости. Поэтому при изготовлении зубьев требуется усиленный контроль механических свойств материала и технологии изготовления. Если этот контроль не может быть обеспечен в должном объеме, зацепление должно быть забраковано.

Таблица А6

Рис. A3

Рис. А4

Пример 4. Выполнить расчет на прочность передачи с цилиндрическими зубчатыми колесами (первая ступень редуктора Г81) методом конечных элементов в системе I-DEAS. Исходные данные принять такими же, что и в примере 2 (см. табл. А3).

Расчет напряженного состояния (контактная задача) выполнен в линейной постановке с использованием объемных конечных элементов для относительного положения колеса и шестерни, при котором возникают максимальные напряжения в шестерне, как наиболее слабом элементе конструкции.

3D модель конструкции построена на основании чертежей Г81-240105, Г81-250106 (рис. А5).

Конечно-элементная модель приведена на рис. А6 и ограничена зубьями колеса и шестерни, образующими зацепление, вместе с прилегающими к зубьям участками обода колеса и шестерни с соответствующими граничными условиями.

Рис. А5

Рис. А6

Рис. А7

Расчетная нагрузка создает максимальный вращающий момент на ведущей шестерне, составляющий 21020 Н · м.

Материал конструкции - сталь 18Х2Н4ВА со следующими характеристиками:

Е = 210000 МПа - модуль нормальной упругости;

µ = 0,3 - коэффициент Пуассона;

R_m = 1010 Мпа - временное сопротивление;

R_eH = 834 МПа - предел текучести;

s_-1 = 450 МПа - предел выносливости симметричного цикла;

s_HP = 955 МПа - предел контактной выносливости.

Таблица А7

Таблица А8

На рис. А7 показано распределение в зубе шестерни контактных напряжений. В таблице А7 приведены компоненты тензора напряжений, характеризующие амплитуду пульсирующего цикла в наиболее опасном с точки зрения усталостной прочности районе (район действия максимальных напряжений растяжения), а также максимальное эквивалентное и максимальное контактное напряжение в зубе шестерни (колеса 2).

Результаты расчета по приведенной методике для конструкции зуба шестерни приведены в табл. А8.

Анализ результатов показывает, что конструкция зубчатых колес судового редуктора Г81 удовлетворяет критериям статической и усталостной прочности.

ЛИТЕРАТУРА

1. Брагин В.В., Решетов Д.Н. Проектирование высоконапряженных цилиндрических зубчатых передач. - М.: Машиностроение, 1991. - 224 с.

2. Редукторы энергетических машин: Справочник / Б.А. Балашов, Р.Р. Гальпер, Л.М. Гаркави и др.; под общей редакцией Ю.А. Державца. - Л.: Машиностроение, Ленингр. отделение, 1985. - 232 с.

3. Зубчатые передачи: Справочник / Е.Г. Гинзбург, Н.Ф. Голованов, Н.Б. Фи-рун, Н.Т. Халебский; под общей редакцией Е.Г. Гинзбурга. - Л.: Машиностроение. Ленингр. отделение, 1980. - 416 с.

4. Проектирование механических передач / С.А. Чернявский, Г.А. Снесарев, Б.С. Козинцев и др. - М.: Машиностроение, 1984. - 560 с.

5. Решетов Д.Н. Детали машин. - М.: Машиностроение, 1989. - 496 с.

6. Планетарные передачи: Справочник / В.Н. Кудрявцев, Ю.Н. Кирдяшев, Е.Г. Гинзбург и др. Под ред. В.Н. Кудрявцева и Ю.Н. Кирдяшева. - Л.: Машиностроение, Ленингр. отделение, 1977. - 536 с.

7. Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. Расчет на прочность деталей машин: Справочник - М.: Машиностроение, 1979. - 702 с.