Государственный ордена Трудового
Красного Знамени
проектный институт
«ПРОЕКТМОНТАЖАВТОМАТИКА»
РУКОВОДЯЩИЙ МАТЕРИАЛ
СИСТЕМЫ АВТОМАТИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ
ПРОЦЕССОВ
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ИСПОЛНИТЕЛЬНЫХ
МЕХАНИЗМОВ ПРИ ПРОЕКТИРОВАНИИ
РМ 4-173-79
Срок введения
1 декабря 1979 г.
Главный инженер Антонов
Начальник отдела Хакимов
Гл. специалист Абросимов
1979
Настоящий руководящий материал (РМ) предназначен для ориентировочного определения необходимых крутящих моментов (усилий) и времен полного хода электрических исполнительных механизмов (ЭИМ) постоянной скорости, поставляемых отдельно от регулирующих органов, с которыми они сочленяются по чертежам сочленений. Расчет ЭИМ является логическим продолжением расчета регулирующего органа, с которым он образует исполнительное устройство. В расчете ЭИМ используются те же исходные данные, что и при расчете регулирующих органов по ГОСТ 16443-70 «Устройства исполнительные. Методы расчета пропускной способности, выбора условного прохода и пропускной характеристики». Результаты расчета регулирующего органа также необходимы для расчета ЭИМ. Вследствие такой взаимосвязи расчета ЭИМ с расчетом регулирующего органа в данном РМ использованы те же единица измерении, что и в действующем в настоящее время ГОСТ 16443-70.
Настоящий РМ не заменяет собой каталогов, нормативных и информационных материалов, содержащих указания по применению ЭИМ. Поэтому при выполнении расчетов и выборе ЭИМ в каждом конкретном случае необходимо выяснять по указанным документам возможность применения выбираемого в процессе расчета ЭИМ.
СОДЕРЖАНИЕ
1. НАЗНАЧЕНИЕ
Настоящий руководящий материал является руководством по расчету электрических исполнительных механизмов (ЭИМ) постоянной скорости на этапе численных оценок параметров звеньев системы регулирования, электрическая схема которой принята на предшествующих этапах проектирования.
Выбор нужного ЭИМ по нагрузке и быстродействие производится в процессе расчета необходимого крутящего момента (усилия) и времени полного хода из ряда серийно изготавливаемых ЭИМ, совместимых (сопрягаемых) с принятой электрической схемой регулирования. Выбирается конкретный типономинал, имеющий необходимый крутящий момент в приемлемое время полного хода выходного органа.
Теоретически, определение этих параметров ЭИМ является частью полного динамического расчета или моделирования системы автоматического регулирования (САР). Выполнение таких полных расчетов, как правило, целесообразно лишь для объектов, по которым отсутствует опыт эксплуатации. Так как при выполнении полных динамических расчетов САР необходимо предварительно принимать конкретные значения параметров ЭИМ, то методика определения этих параметров необходима независимо от того, будет ли в дальнейшем производиться полный (уточняющий) расчет или нет.
Пригодность принимаемого ЭИМ по другим характеристикам (выбег и люфт выходного органа, возможность и необходимость работы ЭИМ в стопорном режиме и т.п.) должны выявляться в процессе проработки основных проектных решений по каталогам, правилам и информационным материалам. Определенные по данному материалу параметры ЭИМ могут быть уточнены при моделировании или выполнении более полных динамических расчетов системы автоматического регулирования.
Данный материал не распространяется на расчет специальных и уникальных ЭИМ и ЭИМ большой мощности, для расчета которых необходимо и экономически оправдано применение более точных и трудоемких методов, требующих дополнительных затрат на получение большего количества уточненных экспериментальным путем исходных данных. Этот материал также не регламентирует объем в формы исполнения расчетов, так как они определяются особенностями проектируемых систем автоматизации, достоверностью и полнотой исходных данных, доступных проектировщику.
В руководящем материале приняты следующие условные обозначения
|
Наименование величины |
Условное обозначение |
|
Коэффициент, зависящий от угла поворота затвора |
a |
|
Плечо силы |
b |
|
Внутренний диаметр трубопровода |
D |
|
Присоединительный (условный) диаметр регулирующего органа |
d |
|
Диаметр прохода седла |
dc |
|
Диаметр поперечного сечения штока |
dш |
|
Основание натуральных логарифмов |
e |
|
Площадь |
F |
|
Коэффициент трения |
f |
|
Ускорение свободного падения |
g |
|
Коэффициент передачи объекта |
kоб |
|
Коэффициент передачи регулятора |
kp |
|
Коэффициент передачи системы |
kc |
|
Отношение пускового крутящего момента к номинальному |
k |
|
Длина трубопровода |
L |
|
Длина тяги сочленения |
l |
|
Крутящий момент (общее обозначение) |
M |
|
Гидродинамический момент |
Mg |
|
Момент трения |
Mтр |
|
Коэффициент гидродинамического момента |
m |
|
Сила (общее обозначение) |
N |
|
Сила давления среды на затвор |
Nз |
|
Перестановочное усилие на штоке регулирующего органа |
Nпс |
|
Сила трения штока в сальнике |
Nтр |
|
Сила давления среды на шток |
Nш |
|
Сила уплотнительного контакта |
Nуп |
|
Коэффициент запаса |
n |
|
Коэффициент ослабления |
no |
|
Давление (общее обозначение) |
P |
|
Давление перед регулирующим органом |
P1 |
|
Давление после регулирующего органа |
P2 |
|
Перепад давления |
ΔP |
|
Располагаемый напор гидравлической цепи |
ΔPc |
|
Расход (общее обозначение) |
Q |
|
Длина ведущего рычага сочленения |
R |
|
Длина ведомого рычага сочленения |
r |
|
Радиус шейки вала (цапфы) затвора |
rш |
|
Площадь (общее обозначение) |
S |
|
Комплексная переменная преобразования Лапласа |
s |
|
Постоянная времени объекта |
T |
|
Время изодрома |
Tи |
|
Время (общее обозначение) |
t |
|
Время полного хода ЭИМ |
Tc |
|
Скорость (общее обозначение) |
V |
|
Передаточная функция объекта |
Wоб(s) |
|
Передаточная функция регулятора |
Wp(s) |
|
Выходная величина объекта (в замкнутой системе - регулируемая переменная) |
x |
|
Входная величина объекта (в замкнутой системе - регулирующее воздействие) |
y |
|
Возмущающее воздействие |
yв |
|
Задающее воздействие |
yз |
|
Коэффициент затухания |
z |
|
Отклонение |
ε |
|
Параметр |
λ |
|
Плотность (общее обозначение) |
ρ |
|
Время запаздывания объекта регулирования |
τ |
|
Перемещение затвора регулирующего органа, считая от положения «закрыто» |
φ |
|
Перемещение выходного органа ЭИМ, считая от положения «закрыто» |
ф |
|
Угловая частота (общее обозначение) |
ω |
|
Собственная частота |
ωc |
|
Частота незатухающих колебаний |
ωn |
2. ЗАДАЧА РАСЧЕТА ЭЛЕКТРИЧЕСКОГО ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА (ЭИМ)
Электрический исполнительный механизм является силовым звеном системы регулирования и должен быть совместимым как с регулятором, так и с регулирующим органом. В системах автоматизации технологических процессов, как правило, применяются серийно изготавливаемые ЭИМ. Соответствие выбираемого ЭИМ регулятору выявляется при разработке электрической схемы регулирования и уточняется по каталогам и другим информационным материалам. Выбор наиболее подходящего типономинала ЭИМ из серии ЭИМ, сопряжимых с регулятором, используемым в принятой электрической схеме, производится по необходимому крутящему моменту, или усилию, необходимому для перемещения затвора регулирующего органа в рабочих условиях и с необходимой скоростью. Поэтому ЭИМ должен с некоторым запасом развивать крутящий момент (усилие), необходимый для преодоления момента (усилия) на затворе регулирующего органа в рабочих условиях. Скорость движения выходного органа ЭИМ, определяемая временем его полного хода, должна быть достаточной для того, чтобы затвор регулирующего органа своевременно, без существенного отставания, принимал бы положения, соответствующие управляющему сигналу регулятора.
Из вышеизложенного следует, что ЭИМ является динамическим звеном, выбираемым в процессе расчета системы регулирования с учетом статических и динамических свойств, как объекта регулирования, так и других звеньев системы регулирования.
Теоретически прямой и логичный путь определения необходимых параметров ЭИМ системы регулирования состоит в составлении системы дифференциальных уравнений, описывающих поведение системы «объект - система регулирования», из решения которой можно было бы найти необходимый крутящий момент и время полного хода ЭИМ. Сложность и трудность составления этих уравнений, недостаточная изученность динамики многих технологических процессов и отсутствие достаточно достоверных исходных данных препятствуют широкому применению такого подхода при расчете ЭИМ систем автоматизации технологических процессов.
Более простой и менее трудоемкий способ определения необходимого крутящего момента ЭИМ состоит в составлении и решении системы статических уравнений равновесия сил и моментов, действующих в подсистеме «ЭИМ - регулирующий орган», и определение из этих уравнений величин крутящих моментов на выходном органе ЭИМ для крайних и нескольких промежуточных положений регулирующего органа. Необходимый крутящий момент ЭИМ определится наибольшей из найденных величин крутящего момента, взятого с некоторым запасом, для компенсации погрешностей исходных данных для расчета и неучета применяемыми уравнениями динамических свойств подсистемы «ЭИМ - регулирующий орган».
В большинстве практических случаев и этот упрощенный способ применить возможно лишь в редких случаях, вследствие отсутствия возможности получить расчетным путем достоверные зависимости между расходом, перепадом давления и положением затвора регулирующего органа в рабочих условиях. Поэтому в большинстве случаев при определении необходимого крутящего момента ЭИМ приходится ограничиться оценкой только одного значения перепада давления для самого неблагоприятного и не всегда реального условия работы регулирующего органа. Поскольку такая оценка производится на основании ориентировочных исходных данных, то ее приходиться принимать с некоторым страхующим коэффициентом запаса.
Так как время полного хода ЭИМ является динамическим параметром, то для определения этой величины все равно необходимо хотя бы простейшее математическое описание динамики объекта регулирования и регулятора.
В данном руководящем материале используется метод статических уравнений для определения крутящего момента ЭИМ и упрощенная динамическая модель объекта регулирования для оценки величины времени полного хода выходного органа ЭИМ.
3. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО КРУТЯЩЕГО МОМЕНТА ЭИМ
3.1. Общие положения
Для перемещения затвора регулирующего органа в рабочих условиях ЭИМ должен преодолеть силу инерции и иные силы, действующие на затвор и прочие подвижные элементы регулирующего органа.
В зависимости от вида регулирующего органа, его конструктивных особенностей и условий работы на затвор, шток или вал регулирующего органа могут воздействовать следующие силы или крутящие моменты:
сила или момент на затворе от воздействия перепада давления;
гидродинамическая сила или момент на затворе;
силы трения в опорах затвора и уплотнениях вала или штока;
вес затвора и других подвижных элементов регулирующего органа;
сила инерции массы затвора и других подвижных элементов регулирующего органа и т.п.
Для достоверной оценки этих сил и моментов расчетным путем необходимы экспериментально подтвержденные технические характеристики и параметры конкретных типономиналов серийно изготавливаемых регулирующих органов. Для большинства серийных регулирующих органов такие данные известны лишь ориентировочно. Поэтому выполнение уточненных расчетов сил и крутящих моментов, действующих в регулирующих органах в рабочих условиях, как правило, не представляется возможным. В данном руководящем материале производится оценка наиболее существенных сил и моментов, а остальные учитываются некоторым коэффициентом запаса. Для сил и моментов, изменяющихся по величине и направлению, приходится оценивать их максимальные значения и наиболее неблагоприятные направления. Значения коэффициента запаса n можно принимать по табл. 1, если нет важных причин принять иные значения.
Таблица 1
|
Коэффициент запаса n |
|
|
Плавное управление расходом среды, протекающей через регулирующий орган |
2 |
|
Быстрое и прецизионное управление положением затвора регулирующего органа |
3 |
3.2. Нагрузка на заслоночном регулирующем органе
Крутящий момент на валу заслоночного регулирующего органа (поворотной заслонки) представляет собой алгебраическую сумму следующих основных крутящих моментов:
- гидродинамический момент, всегда стремящийся закрыть регулирующий орган;
- момент сил трения в опорах вала, действующий при движении затвора и направленный в сторону, противоположную направлению движения.
Кроме указанных моментов к валу заслоночного органа могут быть приложены следующие моменты:
- момент сил трения в уплотнениях и опорах вала;
- момент сил трения в седле;
- гидростатический момент, действующий на закрытый регулирующий орган, когда трубопровод заполнен средой только с одной стороны регулирующего органа (предпусковое положение). Эти моменты сил трения зависят от конструкции, материала и состояния уплотнений и седел и обычно учитываются коэффициентом запаса к моменту сил трения в опорах.
Гидростатический момент действует только в положении «закрыто», когда трубопровод с одной стороны регулирующего органа опорожнен. Так как, как правило, регулирующие органы не предназначены для эксплуатации в качестве запорных, то этот режим использования регулирующих органов в данном материале не рассматривается.
Потребный крутящий момент на валу заслоночного регулирующего органа, развиваемый ЭИМ, будет равен
где n - коэффициент запаса, учитывающий условия и режим работы регулирующего органа, затяжку сальников и т.п. Этот коэффициент можно принимать по табл. 1;
Mg - гидродинамический момент на валу регулирующего органа, кгс · м;
Mтр - момент трения в опорах регулирующего органа, кгс · м.
Гидродинамический момент является следствием несимметричности сил воздействия протекающей среды относительно оси вращения (вала) затвора.
Величина гидродинамического момента может быть выражена следующим образом
где N - равнодействующая гидродинамических сил, действующих на затвор;
b - плечо силы N.
Величина силы N зависит от угла поворота затвора φ, площади прохода или квадрата присоединительного (условного) диаметра регулирующего органа d, перепада давления на регулирующем органе ΔP и может быть выражена следующей формулой
N = ad2ΔP, (3)
где a - коэффициент, зависящий от угла поворота затвора.
Величина плеча b силы N для данного положения затвора зависит от диаметра d
b = a'd, (4)
где a' - коэффициент, зависящий от угла поворота затвора φ, считая от положения «закрыто».
Подставив выражения (3) и (4) в (2), получим
Mg = md3ΔP, кгс · м (5)
где m = aa' - коэффициент гидродинамического момента (величина безразмерная);
d - присоединительный (условный) диаметр заслоночного регулирующего органа, м;
ΔP - перепад давления на регулирующем органе, кгс/м2.
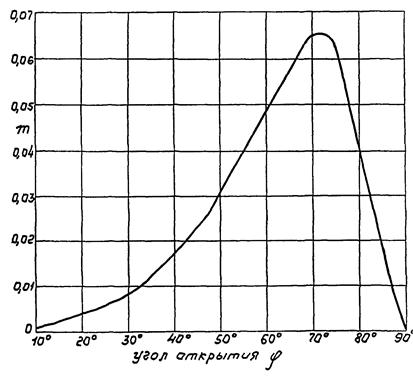
Коэффициент m определяется экспериментально и зависит от формы и конструкции затвора. В приложении данного материала показана осредненная зависимость коэффициента гидродинамического момента m от угла поворота затвора φ для заслоночных регулирующих органов с плоским затвором. Этим приложением можно пользоваться при отсутствии данных по коэффициентам m для конкретных применяемых типов заслоночных регулирующих органов.
Из графика приложения видно, что коэффициент m имеет максимум при φ ≈ 73°. Так как в большинстве случаев регулирующий орган работает при переменном перепаде давления ΔP, то максимальное значение Mg не соответствует максимуму коэффициента m, то есть при пользовании формулой (5) для выявления максимального гидродинамического момента необходимо определить величину Mg для ряда значений ΔP и φ в рассматриваемом диапазоне изменения расхода в рабочих условиях.
Такой способ определения максимальной величины гидродинамического момента Mg слишком трудоемок, что делает его применение целесообразным лишь при расчете ЭИМ на ЭВМ для специальных и уникальных регулирующих органов и в случае использования ЭИМ большой мощности, когда большие дополнительные трудозатраты экономически оправданы. В остальных случаях, как правило, при оценке максимального значения Mg в формулу (5) приходится подставлять максимальное значение перепада давления на регулирующем органе ΔP, соответствующее положению регулирующего органа «закрыто». При этом в формулу (5) также подставляется максимальное значение коэффициента гидродинамического момента m.
Из приложения к данному материалу следует, что максимальное ориентировочное значение коэффициента гидродинамического момента m заслоночного регулирующего органа с плоским затвором m = 0,0654. Поэтому оценку максимального значения гидродинамического момента заслоночного регулирующего органа с плоским затвором можно получить, придав формуле (5) следующий вид
Mg = 0,0654d3ΔPm, кгс · м (6)
где d - присоединительный (условный) диаметр заслоночного регулирующего органа с плоским затвором, м;
ΔPm - перепад давления на регулирующем органе при максимальном значении гидродинамического момента, кгс/м2.
В качестве приемлемого значения ΔPm при ориентировочном определении Mg можно принимать величину перепада давления на регулирующем органе при среднем расходе, равном половине максимального расхода через регулирующий орган. Перепад давления, соответствующий этому расходу, может быть вычислен по формулам раздела 4 руководящего материала РМ 4-163-77.
Величина момента сил трения в опорах вала заслоночного регулирующего органа определяется следующим выражением
Так как нас интересует оценка максимальной величины Mтр, имеющей место в положении «закрыто», то в уравнение (7) следует подставлять ΔP, равное избыточному давлению перед регулирующим органом
ΔP = P1. (8)
Таким образом, максимальный момент трения будет равен
Mтр = 0,785d2rшfP1, кгс · м (9)
где d - присоединительный (условный) диаметр регулирующего органа, м;
rш - радиус шейки вала (цапфа) затвора, м;
f - коэффициент трения в опорах (величина безразмерная, принимается равной 0,15 - 0,25);
P1 - избыточное давление перед закрытым регулирующим органом, кгс/м2.
3.3. Нагрузка на односедельном регулирующем органе
Перестановочное усилие на штоке односедельного регулирующего органа равно
Nпс = ±Nз ± Nш + Nтр + Nут, кгс/см2 (10)
где Nз - сила давления среды на затвор, кгс;
Nш - сила давления среды на шток, кгс;
Nтр - сила трения штока в сальнике, кгс;
Nут - сила, необходимая для создания уплотнительного контакта затвора с седлом, кгс.
Сила давления среды на затвор равна
Nз = FсΔP = Fc(P1 - P2), кгс (11)
где Fc - площадь прохода в седле, см2;
ΔP - перепад давленая на регулирующем органе, кгс/см2;
P1 - давление перед регулирующем органом, кгс/см2;
P2 - давление после регулирующего органа, кгс/см2.
При разгруженном затворе при определении Fc принимается в расчет разность площадей поршня и седла.
Сила давления среды на шток равна
Nш = 0,785d2шP2, кгс/см2 (12)
где dш - диаметр поперечного сечения штока в сальнике, см;
P2 - давление среды после регулирующего органа, кгс/см2.
Знаки перед Nз и Nш в уравнении (10) принимаются в зависимости от направления этих сил. Если направление соответствующей силы противоположно направлению усилия от ЭИМ, то она принимается со знаком плюс, в ином случае - со знаком минус.
Сила трения штока в сальнике с асбографитовой набивкой может быть определена по следующей формуле
Nтр = 1,1dш + 0,02dшP, кгс (13)
где dш - диаметр штока, мм;
P - давление среды под сальниковой камерой, кгс/см2.
В односедельных регулирующих органах с разгруженными затворами следует дополнительно учитывать трение, создаваемое уплотнением в направляющей втулке. Эта сила трения может быть ориентировочно подсчитана по формуле
Nтр = 0,4dш + 0,01dнΔP, кгс (14)
где dн - диаметр направляющей части затвора, мм;
ΔP - максимальный передал давления при закрытом проходе, кгс/см2.
Сила, необходимая для создания уплотнительного контакта в жесткой запорной паре, может быть ориентировочно подсчитана по следующим формулам:
при условном давлении Ру < 100 кгс/см2
Nуп ≈ 0,75pdc, кгс; (15)
при условном давлении Ру > 100 кгс/см2
Nуп ≈ 0,75pdcPy/100, кгс; (16)
где dc - диаметр прохода седла, мм;
Py - условное давление, кгс/см2.
3.4. Нагрузка на двухседельном регулирующем органе
Перестановочное усилие на штоке двухседельного регулирующего органа, работающего без плотной посадки затвора на седло, то есть без учета силы, необходимой для создания уплотнительного контакта затвора с седлом, равно
где Nз - сила давления среды на затвор, кгс;
Nш - сила давления среды на шток, кгс;
Nтр - сила трения штока в сальнике, кгс.
Сила давления среды на затвор Nз равна
Nз = ΔPc(P1 - P2) = ΔPcΔP, кгс (18)
где ΔFc - разность площадей проходов большого Fсб и малого Fсм седел, см2;
P1 - давление перед регулирующим органом, кгс/см2;
P2 - давление после регулирующего органа, кгс/см2;
ΔP - перепад давления на регулирующем органе, кгс/см2.
Сила давления среды на шток равна
Nш = 0,785d2шP2, кгс/см2 (19)
где dш - диаметр сечения штока в сальнике, см2;
P2 - давление среды после регулирующего органа, кгс/см2.
Знак перед Nш в уравнении (17) принимается в зависимости от направления этой силы. Если направление Nш совпадает с направлением силы Nз, то Nш принимается со знаком плюс, в противном случае - со знаком минус.
Сила трения штока в сальнике может быть определена по следующим формулам:
для сальников с фторопластовыми кольцами и штока, обработанного по 11-му классу шероховатости
Nтр = 0,6dш + 0,01dшP, кгс (20)
для сальников с другими набивочными материалами
Nтр = 1,1dш + 0,02dшP, кгс (21)
где dш - диаметр штока в сальнике, мм;
P - давление среды под сальниковой камерой, кгс/см2.
3.5. Крутящий момент на рычаге регулирующего органа
Поворотное перемещение вала затвора заслоночного регулирующего органа удобно сочетается с поворотным движением выходного рычага ЭИМ при их сочленении шарнирным четырехзвенником.
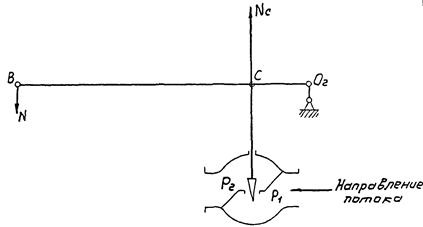
Регулирующие органы с поступательным движением затвора также удобно сочленять с ЭИМ посредством шарнирного четырехзвенника, однако в этом случае они должны иметь рычажный привод, как это показано на рис. 1. Тяга шарнирного четырехзвенника сочленения, соединяющая ведущий рычаг ЭИМ с точкой В рычага регулирующего органа, передает усилие N, с которым ЭИМ удерживает рычаг ВO2 = r. Сила на штоке регулирующего органа Nc стремится повернуть рычаг BO2 по часовой стрелке около оси О2. Обозначив длину плеча CO2 = b, найдем необходимый крутящий момент на рычаге регулирующего органа
где n - коэффициент запаса, учитывающий условия и режим работы регулирующего органа, затяжку сальников и т.п., принимается по табл. 1;
b - плечо силы на штоке регулирующего органа, м;
Nпс - необходимое усилие на штоке регулирующего органа, определяемое по формуле (10) или (17), кгс.
Рис. 1. Односедельный регулирующий орган с рычажным приводом:
ВО2 = r - рычаг регулирующего органа; CO2 = b - плечо силы на штоке; Nc - сила на штоке регулирующего органа; N - сила на рычаге регулирующего органа; P1 - давление перед регулирующим органом; P2 - давление после регулирующего органа.
3.6. Нагрузка на выходном органе ЭИМ
Для того, чтобы выбрать конкретный типономинал ЭИМ необходимо знать нагрузку не на валу или штоке регулирующего органа, а на выходном органе ЭИМ.
Для приведения нагрузки на валу или штоке регулирующего органа к выходному органу ЭИМ необходим учет влияния кинематической схемы сочленения на передаваемую ей нагрузку. Поскольку выбор типономинала ЭИМ предшествует разработке чертежей сочленения, то возникает необходимость в предварительной оценке влияния сочленения на передаваемый им крутящий момент или усилие.
Поставляемые без ЭИМ регулирующие органы, как правило, сочленяются с ними посредством шарнирного четырехзвенника. Такое сочленение изменяет передаваемый крутящий момент, который становится зависимым от положения рычагов сочленения. При этом возможно весьма существенное уменьшение крутящего момента, особенно в одном или обоих крайних положениях затвора регулирующего органа. Уменьшение крутящего момента сочленением удобно учитывать коэффициентом ослабления крутящего момента no.
При определении необходимого крутящего момента на выходном органе ЭИМ необходимо также учитывать величину отношения пускового крутящего момента выбираемого ЭИМ к его номинальному крутящему моменту k.
Необходимый крутящий момент ЭИМ, сочленяемого с регулирующим органом, будет равен
где М - необходимый крутящий момент на валу или рычаге регулирующего органа, кгс · м;
no - коэффициент ослабления крутящего момента механизмом сочленения (величина безразмерная);
k - отношение пускового крутящего момента ЭИМ к номинальному (величина безразмерная).
Подставив в уравнение (23), значение M из уравнения (1) подраздела 3.2, получим формулу необходимого крутящего момента ЭИМ, сочленяемого с заслоночным регулирующим органом
где n - коэффициент запаса (величина безразмерная, принимается по табл. 1);
no - коэффициент ослабления крутящего момента сочленением (величина безразмерная);
k - отношение пускового крутящего момента ЭИМ к номинальному крутящему моменту (величина безразмерная);
Mg - гидродинамический момент на валу регулирующего органа, кгс · м;
Mтр - момент трения в опорах регулирующего органа, кгс · м.
Моменты Mg и Mтр определяются по формулам (5), (6) и (9) подраздела 3.2.
Подставив в уравнение (23) значение M, определяемое уравнением (22), получим формулу необходимого крутящего момента ЭИМ, сочленяемого с регулирующим органом, имеющим рычажный привод
где n - коэффициент запаса (величина безразмерная, принимаемая по табл. 1);
no - коэффициент ослабления крутящего момента сочленением (величина безразмерная);
k - отношение пускового крутящего момента ЭИМ к номинальному крутящему моменту (величина безразмерная);
b - плечо силы на штоке регулирующего органа, м;
Nпс - необходимое усилие на штоке регулирующего органа, определяемое по формуле (10) или (17), кгс.
Величина коэффициента ослабления крутящего момента механизмом сочленения зависит от кинематической схемы сочленения. Так как в большинстве случаев всегда имеется вероятность того, что в процессе наладки системы регулирования может возникнуть необходимость корректировки расходной характеристики регулирующего органа за счет сочленения, то величину коэффициента ослабления целесообразно принимать с некоторым запасом, что обеспечивается при n = 4.
Необходимый крутящий момент Mc, найденный по формулам (24) и (25), не должен быть больше максимального допускаемого крутящего момента Mgn, определяемого условиями прочности регулирующего органа. Если в информационных материалах на принимаемый заслоночный регулирующий орган нет указаний о величине максимального допускаемого крутящего момента на валу регулирующего органа, то эта величина может быть вычислена по известной формуле сопротивления материалов
Mgn = τgnWp, кгс · см (26)
где τgn - допускаемое касательное напряжение для материала вала, кгс/см2;
Wp - момент сопротивления наиболее слабого сечения вала при кручении, см3.
Номинальный крутящий момент Mн выбранного ЭИМ должен быть равен или больше величины Mc, найденной по формулам (24) и (25).
4. СОЧЛЕНЕНИЕ ЭИМ С РЕГУЛИРУЮЩИМ ОРГАНОМ
4.1. Общие положения
Электрический исполнительный механизм, воздействующий на регулирующий орган, размещается на некотором расстоянии от этого органа и сочленяется с ним посредством механизма сочленения.
Работа механизма сочленения описывается характеристикой сочленения, имеющей следующий вид
где φ - ход затвора регулирующего органа;
kсв(φ) - коэффициент передачи сочленения (связи);
ф - ход выходного органа ЭИМ.
Как правило, во избежание перенастройки регулятора при существенном изменении нагрузки объекта целесообразно приблизительно соблюдать постоянство коэффициента передачи разомкнутого контура системы kc. Этот коэффициент равен
где kp - коэффициент передачи регулятора вместе с ЭИМ;
kсв - коэффициент передачи связи (сочленения) между ЭИМ и регулирующим органом;
kр.о. - коэффициент передачи регулирующего органа;
kоб - коэффициент передачи объекта регулирования.
Коэффициент передачи регулятора kp является настроечным параметром, который в процессе эксплуатации системы регулирования желательно иметь неизменным. Коэффициент передачи объекта kоб, в общем случае, есть величина переменная, зависящая от нагрузки объекта, характеризуемой положением затвора регулирующего органа φ. Следовательно, kоб есть функция
kоб = kоб(φ). (29)
Коэффициент передачи регулирующего органа kр.о. численно равен угловому коэффициенту касательной в рабочей точке расходной характеристики Q = ψ(φ) регулирующего органа. Так как в общем случае, при переменном перепаде давления на регулирующем органе, расходная характеристика нелинейна, то коэффициент kр.о. также непостоянен и зависит от положения затвора регулирующего органа, то есть
kр.о. = kр.о.(φ). (30)
С учетом вышеизложенного уравнение (28) примет вид
kc = kpkсвkр.о.(φ)kоб(φ), (31)
где величину коэффициента передачи сочленения целесообразно сделать переменной, зависящей от φ таким образом, чтобы kc ≈ const.
Коэффициент передачи объекта kоб численно равен угловому коэффициенту касательной в рабочей точке статической характеристики объекта.
Из уравнения (31) коэффициент передачи сочленения будет равен
Из уравнения (32) следует, что для выявления потребной характеристики сочленения (27) необходимы статическая характеристика объекта и расходная характеристика регулирующего органа. Статическую характеристику объекта получить расчетным путем на стадии проектирования очень сложно. Несколько проще получить расчетным путем расходную характеристику регулирующего органа. Однако необходимый для определения расходной характеристики регулирующего органа объем вычислений, как правило, слишком велик, а получаемая точность результатов мала вследствие недостаточной достоверности исходных данных и методических погрешностей формул гидравлики. Поэтому на стадии проектирования приходится условно полагать kоб ≈ const и ограничиться приближенным постоянством произведения kсвkр.о.(φ) ≈ const.
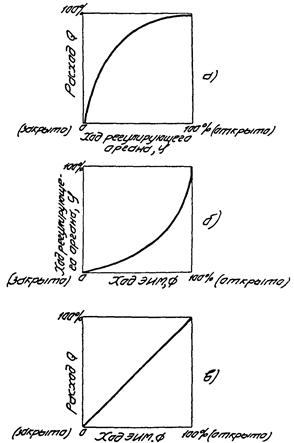
На рис. 2а показана расходная характеристика регулирующего органа в рабочих условиях, то есть при непостоянном перепаде давления на нем. Расходная характеристика, в отличие от пропускной характеристики, при ΔP ≠ const всегда более выпукла.
Из рис. 2б видно, что для компенсации выпуклости расходной характеристики, характеристика сочленения должна быть вогнутой, в результате чего характеристика исполнительного устройства может стать линейной (рис. 2в).
Во избежание внесения вредных нелинейностей в контур регулирования, при разработке чертежей сочленения необходимо обеспечить достаточную жесткость звеньев сочленения и свести к минимуму люфты в кинематических парах (шарнирах).
При построении кинематической схемы сочленения для ЭИМ с органом ручного управления (ручным дублером) необходимо обеспечить ожидаемое соответствие между направлением вращения дублера и результатом этого воздействия. Если результат вращения дублера будет контролироваться по положению затвора регулирующего органа, то при построении кинематической схемы сочленения целесообразно обеспечить традиционное соответствие «вращение по часовой стрелке закрывает». Если же ЭИМ размещается таким образом, что обеспечивается пользование прибором, отражающим результат ручного воздействия (регулируемую переменную), то сочленением следует обеспечить соответствие «вращение по часовой стрелке увеличивает регулируемую переменную».
Рис. 2. Характеристики исполнительного устройства и его частей:
а - расходная характеристика регулирующего органа; б - характеристика сочленения; в - характеристика исполнительного устройства в рабочих условиях.
4.2. Выбор характеристики сочленения
Из изложенного в подразделе 4.1 следует, что необходимая форма характеристики сочленения зависит от расходной характеристики регулирующего органа, которая определяется формой пропускной характеристики регулирующего органа и отношением перепада давления на регулирующем органе ΔP к общему располагаемому напору ΔPc гидравлической цепи, в которой установлен регулирующий орган (РМ 4-163-77).
Заслоночные регулирующие органы имеют приблизительно равнопроцентную пропускную характеристику, которая при ΔP ≠ const стремится стать выпуклой и может создать приблизительно линейную или выпуклую расходную характеристику. Применительно к заслоночным органам и другим регулирующим органам с равнопроцентной характеристикой таблице выбора характеристик исполнительных устройств (раздел 13 РМ 4-163-77) целесообразно придать следующий вид:
Таблица 2
|
Характеристика сочленения ЭИМ с заслонкой |
||
|
ΔP/ΔPc ≥ 0,25 |
0,06 < ΔP/ΔPc < 0,25 |
|
|
Регулирование расхода газа или жидкости; расход измеряется сужающим устройством, |
линейная |
линейная |
|
расход измеряется ротаметром (или сужающим устройством и устройством извлечения квадратного корня) |
линейная |
вогнутая |
|
Регулирование уровня в емкости |
линейная |
вогнутая |
Из табл. 2 следует, что почти во всех случаях на стадии проектирования при ΔP/ΔPc < 0,25 предпочтение следует отдавать вогнутой характеристике сочленения ЭИМ с заслоночным регулирующим органом.
Регулирующие органы других типов, поставляемые без исполнительных механизмов, имеют различные пропускные характеристики, пересчет которых в расходные характеристики не целесообразен вследствие низкой точности исходных данных и большого объема вычислений. Для таких органов на стадии проектирования целесообразно предусматривать линейную характеристику сочленения, которая может быть скорректирована при наладке системы регулирования по фактическим данным на объекте.
4.3. Сочленение ЭИМ с заслоночным регулирующим органом
Шарнирный четырехзвенник, сочленяющий ЭИМ с заслоночным регулирующим органом, должен строиться с соблюдением следующих ограничивающих условий:
а) ведущий рычаг R и тяга l могут располагаться на одной прямой линии только в положении «закрыто»;
б) ведомый рычаг r и тяга l не должны располагаться на одной прямой во всех допустимых положениях, включая положения «открыто» и «закрыто»;
в) в крайних положениях механизма сочленения плечо силы, приложенной к ведомому рычагу r, не должно быть меньше 0,25r;
г) расстояние между осями ЭИМ и регулирующего органа, как правило, должно быть не менее 2,5R;
д) во избежание поломки регулирующего органа и сочленения и для предотвращения перемещения затвора вне предусмотренных пределов угол поворота рычага ЭИМ должен быть ограничен механическими упорами в положениях «закрыто» и «открыто».
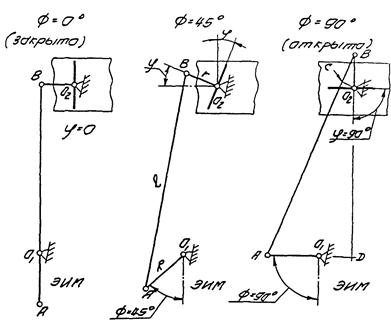
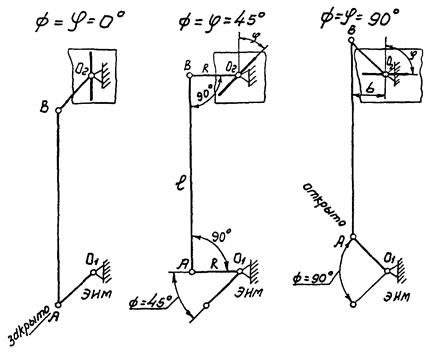
Рис. 3. Сочленение ЭИМ с заслоночным регулирующим органом (вогнутая характеристика):
O1A = R - рычаг ЭИМ; AB = l - тяга сочленения; BO2 = r - рычаг регулирующего органа; ф - угол поворота рычага ЭИМ, считая от положения «закрыто»; φ - угол поворота рычага регулирующего органа, считая от положения «закрыто».
На рис. 3 показано сочленение ЭИМ с заслоночным регулирующим органом посредством шарнирного четырехзвенника. Из этого рисунка следует, что для получения вогнутой характеристики необходимо, чтобы в начале открытия точка А перемещалась бы в поперечном направлении относительно прямой О1О2, а в конце открытия - продольно этой прямой.
Эти соображения реализуются при совпадении следующих требований:
- в положении «закрыто» тяга l и ведущий рычаг R расположены на одной прямой и являются продолжением друг друга, а ведомый рычаг r перпендикулярен тяге l;
- для установки в положение «открыто» ведомый рычаг повертывается на 90° при соблюдении условия
![]() (33)
(33)
где O2C - перпендикуляр к тяге l.
Для того, чтобы при повороте ведущего рычага R на 90°, ведомый рычаг r также повернулся на 90°, необходима определенная длина этого рычага.
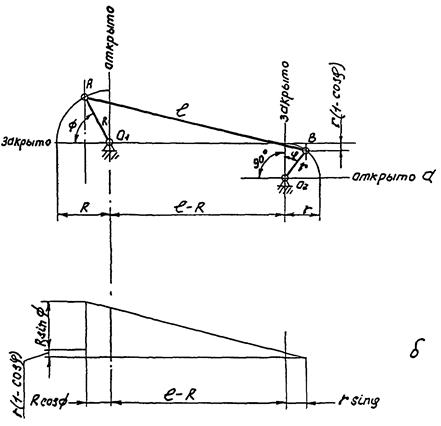
На рис. 4 показано сочленение в некотором промежуточном положении, из которого видно, что этому положению соответствует прямоугольный треугольник, высота которого равна
Rsinф + r(1 - cosφ),
а основание
Rcosф + (l - R) + rsinφ.
Гипотенуза этого треугольника равна длине тяги l.
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов
l2 = [Rsinφ + r(1 - cosφ)]2 + [R(cosф - 1) + l + rsinφ]2. (34)
Выражение (34) справедливо также и для положения «открыто», когда
ф = 90º; φ = 90º;
cosф = 0; cosφ = 0.
Рис. 4. Шарнирный четырехзвенник сочленения в промежуточном положении
а - схема сочленения; б - прямоугольный треугольник.
Подставив в выражение (34) значения тригонометрических функций (35) и выполнив необходимые преобразования, получим
Решение уравнения (36) дает искомую длину ведомого рычага
В формуле (37) величины l, R и r должны иметь одинаковую размерность, например, мм.
Из рис. 3 видно, что наименьшая длина плеча O2C силы, передаваемой тягой AB, имеет место в положении «открыто». Из подобия прямоугольных треугольников ABD и CBO2 следует
![]()
или, приняв CO2 = b, получим
Из выражения (38) плечо b равно
Приняв коэффициент ослабления крутящего момента no равным отношению длины ведомого рычага r к наименьшей длине плеча b, из выражения (39) получим формулу коэффициента ослабления крутящего момента ЭИМ шарнирным четырехзвенником сочленения, реализующего вогнутую характеристику
Как правило, при определении необходимого крутящего момента на выходном органе ЭИМ следует задаваться
no = 4. (41)
Величина no спроектированного сочленения, определяемая формулой (40), не должна быть больше четырех.
Изложенные в начале данного раздела ограничивающие условия являются общими для шарнирных четырехзвенников с любой формой характеристики. Задача построения сочленения шарнирным четырехзвенником с линейной характеристикой значительно упрощается тем, что в этом случае
r = R и l = O1O2 (42)
и, следовательно, четырехзвенник образует параллелограмм. При проектировании сочленения с линейной характеристикой в качестве исходного положения построения удобно принять не ф = φ = 0, а ф = φ = 45°, так как в этом положении четырехзвенник образует прямоугольник и рычаги R и r будут перпендикулярны тяге l (рис. 4).
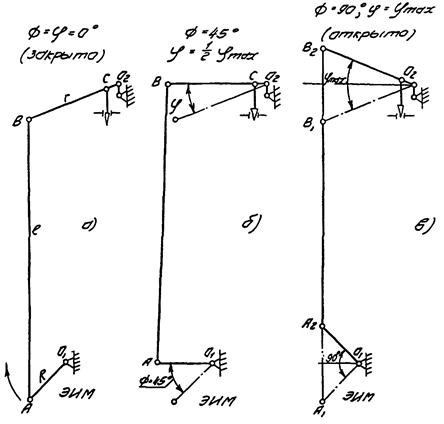
Из рис. 5 видно, что наименьшая величина плеча силы, передаваемой тягой l, имеет место в крайних положениях «открыто» и «закрыто».
Это плечо b равно
![]() (43)
(43)
Приняв коэффициент ослабления крутящего момента равным отношению длины ведущего рычага R к наименьшей длине плеча b найдем этот коэффициент
![]() (44)
(44)
Так как при наладке системы регулирования может возникнуть необходимость изменения кинематической схемы сочленения, то, как правило, коэффициент ослабления следует принимать
no = 4. (41)
Рис. 5. Сочленение ЭИМ с заслоночным регулирующим органом (линейная характеристика):
O1A = R - рычаг ЭИМ; AB = l - тяга сочленения; BO2 = r - рычаг регулирующего органа; ф - угол поворота рычага ЭИМ, считая от положения «закрыто»; φ - угол поворота рычага регулирующего органа, считая от положения «закрыто».
4.4. Сочленение ЭИМ с регулирующими органами, имеющими рычажный привод
Регулирующие органы (клапаны) с рычажным приводом обычно сочленяются с ЭИМ так же, как и заслоночные регулирующие органы, то есть с помощью шарнирного четырехзвенника. В качестве ведомого рычага сочленения используется рычаг привода регулирующего органа, рабочая длина которого (расстояние от оси вращения рычага до оси тяги) определяется при расчете сочленения. При расчете сочленения ЭИМ с рычажным регулирующим органом необходимо учитывать, что угол полного хода ведомого рычага сочленения в данном случае, как правило, меньше 90°.
В отличие от заслоночных регулирующих органов, пропускные характеристики которых всегда приблизительно равнопроцентны, регулирующие клапаны изготавливаются с разными пропускными характеристиками, что достигается применением затворов различного профиля. Поэтому регулирующие клапаны, как правило, целесообразно заказывать с нужной пропускной характеристикой (раздел 13 РМ 4-163-77), что позволяет сочленять эти клапаны с ЭИМ посредством кинематических схем с линейной характеристикой.
В данном руководящем материале мы изложим построение схем сочленения с линейной характеристикой.
Построение кинематических схем сочленений с нелинейной характеристикой для регулирующих органов с углом поворота ведомого рычага φ ≠ 90º, весьма сложно и трудоемко. По этой причине проектирование таких сочленений целесообразно лишь при наличии достаточно достоверных исходных данных (расходной характеристики регулирующего органа, полученной опытным путем), то есть, как правило, реализация сочленений с нелинейной характеристикой для регулирующих клапанов должна осуществляться на этапе наладки системы регулирования, если возникнет в этом необходимость.
Методика построения кинематических схем сочленений с заданной формой нелинейной характеристики изложена в книге «Наладка промышленных систем автоматического регулирования. Руководство. ЦБТИ Минмонтажспецстроя СССР, 1966».
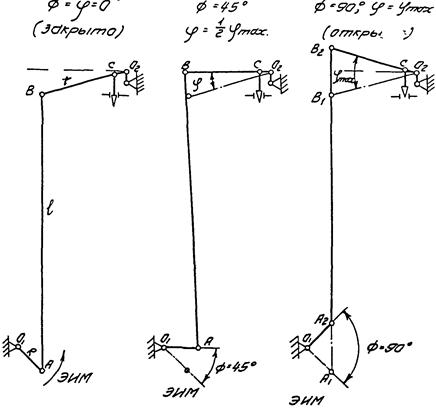
На рис. 6 показано сочленение, реализующее линейную характеристику, в начальном («закрыто»), среднем (ф = φ = 45°) и конечном («открыто») положениях. С учетом конструктивных соображений ЭИМ размещается относительно регулирующего органа таким образом, чтобы в среднем положении рычагов AO1 и BO2 они были бы параллельны, а тяга AB в крайних положениях была бы перпендикулярна этим средним положениям рычагов AO1 и BO2.
Так как ведущий рычаг AO1 обычно поставляется в комплекте ЭИМ, то его длина R является заданной величиной. Длина тяги AB = l принимается из конструктивных соображений при выборе положения ЭИМ относительно регулирующего органа. Таким образом, необходимый угол полного хода φmax ведомого рычага BO2 удобно обеспечить за счет его длины r.
Определим длину ведомого рычага BO = r, необходимую для его поворота на угол φmax, при повороте ведущего рычага AO1 = R на угол ф = 90°.
Из рис. 6в следует, что
A1A2 = B1B2 = b. (45)
Из равнобедренного треугольника A1A2O1 имеем
H = A1A2 = 2Rsin(ф/2). (46)
Аналогично, из равнобедренного треугольника B1B2O2 получим
H = B1B2 = 2rsin(φmax/2). (47)
Приравняв выражения (46) и (47), получим
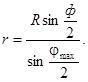 (48)
(48)
Рис. 6. Сочленение ЭИМ с рычажным регулирующим клапаном (прямого типа, линейная характеристика сочленения):
O1A = R - рычаг ЭИМ; AB = l - тяга сочленения; BO2 = r - рычаг регулирующего клапана; ф - угол поворота рычага ЭИМ, считая от положения «закрыто»; φ - угол поворота рычага регулирующего клапана, считая от положения «закрыто»
Искомое выражение для r получим, приняв ф = 90°,
На рис. 7 показана кинематическая схема сочленения обратного типа, когда регулирующий орган открывается при вращении ведущего рычага против часовой стрелки. Формула (49) пригодна для определения r и для этой схемы.
Схемы, показанные на рис. 6 и 7, могут быть использованы и для сочленения регулирующего органа с выходным штоком прямоходного ЭИМ типа МЭП по ГОСТ 7192-74. В этом случае номинальный полный ход выходного штока ЭИМ должен быть равен отрезкам A1A2 = B1B2 = b' и расчет кинематической схемы ведется по формуле (47), из которой определяется величина r.
Рис. 7. Сочленение ЭИМ с рычажным регулирующим клапаном (обратного типа, линейная характеристика сочленения):
O1A = R - рычаг ЭИМ; AB = l - тяга сочленения; BO2 = r - рычаг регулирующего клапана; ф - угол поворота рычага ЭИМ, считая от положения «закрыто»; φ - угол поворота рычага регулирующего клапана, считая от положения «закрыто»
5. ОЦЕНКА НЕОБХОДИМОГО ВРЕМЕНИ ПОЛНОГО ХОДА ВЫХОДНОГО ОРГАНА ЭИМ
5.1. Общие положения
Электрический исполнительный механизм является силовым элементом системы регулирования и от развиваемого им крутящего момента и угловой скорости зависят работоспособность и качество работы системы регулирования. Чрезмерно большое время полного хода (малая угловая скорость) выходного органа ЭИМ при значительных возмущающих воздействиях на объект будет сопровождаться длительным и большим несоответствием между выходным сигналом регулятора и соответствующим этому сигналу, положением затвора регулирующего органа, т.е. будет иметь место отставание расхода регулирующего агента от величины, требуемой регулятором.
При длительно приложенных возмущающих воздействиях это будет сопровождаться насыщением регулятора. Регулятор будет работать при предельном значении проходящего через него сигнала, т.е. в нелинейной области. При наличии в законе регулирования И-компоненты указанное насыщение может быть устранено лишь при изменении знака разности между заданным и текущим значениями регулируемой переменной, на что потребуется некоторое довольно большое время и что будет сопровождаться большими отклонениями регулируемой величины от заданного значения, т.е. низким качеством регулирования.
При слишком малом времени полного хода (большой угловой скорости) возрастет частота включения ЭИМ, уменьшится длительность каждого включения и, следовательно, возрастет вредное влияние выбега исполнительного механизма.
Из вышеизложенного следует, что задача определения потребного времени полного хода ЭИМ является динамической задачей, аналогичной задаче определения настроечных параметров регулятора, так как время полного хода ЭИМ в сочетании с динамическими характеристиками объекта и настроечными параметрами регулятора определяет качество регулирования. Для конкретного объекта регулирования величина необходимого времени полного хода ЭИМ, т.е. скорость перемещения затвора регулирующего органа, в конечном счете, определяется величиной, формой, местом приложения и длительностью возмущающего воздействия, прикладываемого к объекту регулирования.
Эти характеристики возмущающего воздействия, как правило, являются случайными и, следовательно, они проектировщику неизвестны.
Таким образом, основной функцией ЭИМ вместе с регулирующим органом является своевременное изменение количества вещества или энергии, вводимой в объект или отводимой из объекта таким образом, чтобы этим компенсировать возмущающие воздействия на объект, что и определяет необходимый крутящий момент (усилие) и (угловую) скорость (время полного хода) выходного органа ЭИМ. В соответствии с вышеизложенным следует признать, что теоретически для выбора времени полного хода ЭИМ необходим полный динамический расчет или моделирование всей системы регулирования. Однако и при выполнении полного (детального) расчета или моделирования системы регулирования необходимо предварительно выбирать конкретное время полного хода ЭИМ с последующим уточнением его по результатам расчета или моделирования. Поэтому методика ориентировочного определения времени полного хода ЭИМ необходима независимо от того, будет ли в дальнейшем производиться уточненный расчет или моделирование или нет.
5.2. Время полного хода ЭИМ
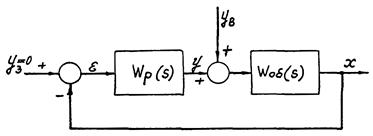
На рис. 8 показана упрощенная структурная схема одноконтурного регулирования, которую мы используем при выводе формулы оценки необходимого времени полного хода ЭИМ. Мы будем полагать, что динамические свойства ЭИМ учтены в передаточной функции регулятора Wp(s), а расходная характеристика регулирующего органа - в передаточной функции объекта Wоб(s). Таким образом раздел между регулятором и объектом будет проходить по сочленению ЭИМ с регулирующим органом, характеристику которого ради простоты будем считать линейной.
Вывод необходимого выражения для времени полного хода ЭИМ будем выполнять в следующей последовательности:
- в качестве упрощенной модели объекта примем передаточную функцию звена первого порядка с запаздыванием;
- аппроксимируем изображение Лапласа запаздывания объекта приближением Падэ первого порядка;
- в качестве регулятора примем ПИ-регулятор;
- в качестве критерия качества регулирования примем процент перерегулирования при ступенчатом возмущающем воздействии;
- определим коэффициент передачи системы kc для принятого процента перерегулирования;
- определим частоту незатухающих колебаний системы ωn и коэффициент затухания z;
- для найденных kc, ωn и z найдем выражение для скорости перемещения ЭИМ при ступенчатом возмущающем воздействии;
- из полученного выражения для скорости ЭИМ найдем максимальную скорость ЭИМ;
- по найденной максимальной скорости ЭИМ найдем оценку времени полного хода ЭИМ.
Рис. 8. Упрощенная структурная схема одноконтурного регулирования:
Wp(s) - передаточная функция регулятора; Wоб(s) - передаточная функция объекта; x - регулируемая переменная; yв - возмущающее воздействие; уз - задающее воздействие; ε - отклонение.
Передаточная функция ПИ-регулятора имеет вид
где kp - коэффициент передачи регулятора;
Tи - время изодрома;
s - комплексная переменная преобразования Лапласа.
Из выражения (50) следует, что для определения скорости перемещения ЭИМ необходимо оценить настроечные параметры ПИ-регулятора. Из большого разнообразия описанных в литературе методик определения настроечных параметров ПИ-регулятора нам целесообразно принять такую, использование которой существенно упростило бы вывод искомой формулы и саму формулу. В данном случае удобно воспользоваться методом определения настроечных параметров, предложенный Мартином, Коррипо и Смитом. Согласно этому методу настроечные параметры ПИ-регулятора для объекта первого порядка с запаздыванием определяются следующими выражениями
Tи = T, (51)
![]() (52)
(52)
где Tи - время изодрома;
T - постоянная времени объекта;
kp - коэффициент передачи регулятора;
kоб - коэффициент передачи объекта;
τ - время запаздывания объекта;
λ - параметр, определяющий величину перерегулирования.
Величина параметра λ определяется следующим выражением
где с = 0,78 при 1 %-ом перерегулировании;
с = 1,1 при 5 %-ом перерегулировании.
Заметим, что значения параметров kp и Tи по формулам (51) и (52) приняты лишь для вывода формулы оценки времени полного хода ЭИМ и не должны рассматриваться как обязательные для настройки проектируемой системы регулирования.
Подставив выражение (53) в (52), получим
С учетом выражения (54), коэффициент передачи системы будет равен
Передаточная функция объекта, звена первого порядка с запаздыванием, будет иметь вид
Аппроксимировав запаздывание объекта приближением Падэ первого порядка
и подставив выражение (57) в (56), получим приближенное выражение для передаточной функции объекта
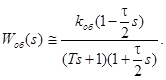 (58)
(58)
Передаточная функция показанной на рис. 8 структурной схемы регулирования будет равна
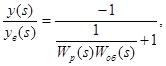 (59)
(59)
где y(s) - изображение регулирующего воздействия (преобразование Лапласа);
yв(s) - изображение возмущающего воздействия (преобразование Лапласа);
Wр(s) - передаточная функция регулятора;
Wоб(s) - передаточная функция объекта.
Передаточная функция разомкнутого контура с учетом выражений (50), (51), (52) и (55) будет иметь вид
Из выражения (60), имеем
Подставив выражение (61) в (59), получим
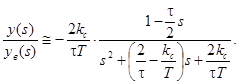 (62)
(62)
Приняв
получим
где ωn - частота незатухающих колебаний;
z - коэффициент затухания.
Примем для ступенчатого возмущающего воздействия
![]() (66)
(66)
где ф - ступенчатое изменение положения выходного органа ЭИМ.
Из выражения (65) найдем изображение Лапласа регулирующего воздействия
Умножив выражение (67) на s, найдем изображение Лапласа скорости регулирующего воздействия
Для того чтобы по изображению (68) найти скорость регулирующего воздействия V(t), необходимо оценить величину коэффициента демпфирования z.
Из выражения (64) найдем коэффициент затухания
Подставив выражение (55) в (69) и (63), получим
По формулам (70) и (71) определим коэффициент затухания при 1 %-ом перерегулировании, c = 0,78
Выполнив аналогичный расчет для 5 %-го перерегулирования, c = 1,1 получим
z5 = 0,72. (75)
Из выражений (73) и (75) следует, что в данном случае z < 1. Выполнив обратное преобразование Лапласа выражения (68) для z < 1 найдем скорость регулирующего воздействия
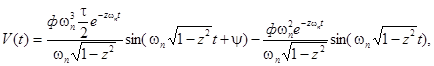 (76)
(76)
где 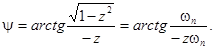 (77)
(77)
Приняв
получим следующее выражение
Подставив тождество
![]()
в выражение (79), получим
![]() (80)
(80)
Применив подстановку
![]()
![]()
после приведения подобных членов, получим
В полученном выражении член перед квадратной скобкой монотонно убывает, приближаясь к нулю при t → ∞ и, следовательно, имеет единственный максимум при t = 0. Постоянная времени этой экспоненты равна
Выразим TЭ через время запаздывания объекта τ. Подставив в формулу (82) значения z и ωn из выражений (72) ÷ (75), получим для 1 %-го перерегулирования
TЭ1 ≈ 1,29τ, (83)
а для 5 %-ого перерегулирования
TЭ5 ≈ 1,36τ. (84)
Из выражения (81) следует, что период гармонических колебаний Tг, равен
Выразим период Tг через время запаздывания объекта τ. Подставив в выражение (85) значение ωс, вычисленное по формуле (78), найдем для 1 %-ого перерегулирования
Tг1 = 12τ, (86)
а для 5 %-ого перерегулирования
Tг5 = 8,8τ. (87)
Следовательно, длительность первой четверти периода гармонических колебаний при 1 %-ом перерегулировании будет равна 3τ. Таким образом, при 1 %-ном перерегулировании, по крайней мере, на интервале времени 0 < t < 3τ скорость регулирующего воздействия будет монотонно убывать. Выразив это время в долях ТЭ1, получим
![]()
За время, равное 2,3TЭ1 экспонента уменьшается до 0,1 первоначального значения при t = 0. Положив в выражении (81) t = 0, найдем выражение для оценки максимальной скорости движения выходного органа ЭИМ
Подставив значения ωn2 из выражений (72) и (74) в выражение (88), получим для 1 %-ого перерегулирования
а для 5 %-ого перерегулирования
Наименьшее время полного хода ЭИМ равно
где фmax - величина полного хода выходного органа ЭИМ.
Подставив в выражение (91) величину Vmax из выражений (89) и (90), получим для 1 %-ого перерегулирования
и для 5 %-го перерегулирования
Если принять максимальное возмущающее воздействие равным половине полного хода ЭИМ
![]()
то формулы (92) и (93) примут вид:
для 1 %-го перерегулирования
Tc ≈ 4,6τ, (94)
а для 5 %-ого перерегулирования
Tc ≈ 3,8τ. (95)
Вывод формул (94) и (95) построен на оценке максимальной скорости регулирующего воздействия непрерывной (неимпульсной) системы регулирования.
В системе регулирования ВТИ (МЭТА) исполнительные механизмы постоянной скорости работают в пульсирующем режиме. Так как в таких системах работа ЭИМ в режиме постоянной скорости нецелесообразна, то в них следует применять ЭИМ с большей скоростью регулирующего воздействия (меньшими Tc), чем это необходимо в системах, использующих ЭИМ в режиме постоянной скорости.
В книге Стефани Е.П. «Основы расчета настройки регуляторов теплотехнических процессов, М., 1972» рекомендуются следующие зависимости для определения времени полного хода ЭИМ, работающих в пульсирующем режиме:
для П- и ПИ-регуляторов
Tc ≈ 2τ, (96)
с допустимым отклонением в пределах
Tc ≈ (1 ÷ 4)τ, (97)
для ПИД-регуляторов
Tc ≈ τ, (98)
с допустимым отклонением в пределах
Tc ≈ (0,75 ÷ 2)τ. (99)
Из сравнения формул (94) и (95) следует, что время полного хода Tc уменьшается с ростом процента перерегулирования и приближается к значениям Tc, даваемым формулами (96) и (98).
Из вышеизложенного следует, что время полного хода ЭИМ постоянной скорости можно ориентировочно принимать по формулам (97) и (99).
При этом меньшие значения Tc следует принимать для систем регулирования, в которых ЭИМ работают в пульсирующем режиме, а большие значения - при работе ЭИМ в режиме постоянной скорости.
5.3. Проверка на гидравлический удар
В тех случаях, когда регулирующий орган управляет потоком жидкости и сочленен с ЭИМ, имеющим малое время полного хода, возможно возникновение ситуаций, когда система регулирования быстро закроет регулирующий орган, что может сопровождаться резким повышением давления в трубопроводе.
Это явление, именуемое гидравлическим ударом, может стать причиной разрушения трубопровода, регулирующего органа и других элементов объекта регулирования. Во избежание возникновения гидравлических ударов время закрытия регулирующего органа обычно ограничивается условием
Tзmin = 0,2d, с (100)
где Tзmin - наименьшее время перемещения затвора регулирующего органа из положения «открыто» в положение «закрыто», с;
d - присоединительный (условный) диаметр регулирующего органа, мм.
Если полный ход затвора регулирующего органа с поступательным движением затвора меньше величины присоединительного диаметра d, то в формулу (100) вместо d следует подставлять величину этого полного хода, в мм. Для регулирующих органов с тарельчатым затвором величину полного хода следует принимать равной 0,25d.
Во избежание гидравлического удара необходимо соблюдать условие
Tc ≥ Tзmin, (101)
где Tc - время полного хода принятого типономинала ЭИМ;
Tзmin - время, вычисленное по формуле (100).
Из нарушения условия (101) следует необходимость выполнения проектировщиками технологической части проекта специальных расчетов гидравлического удара для уточнения режимов работы технологического объекта и проверки совпадения условий прочности объекта и регулирующего органа.
6. РЕКОМЕНДУЕМЫЙ ПОРЯДОК РАСЧЕТА
6.1. Исходные данные
Так как определение расчетным путем крутящего момента и времени полного хода ЭИМ представляет собой логическое продолжение расчета регулирующего органа, то для расчета ЭИМ необходимы все исходные данные, предусмотренные в разделе 14 РМ 4-163-77 «Расчет и применение регулирующих органов в системах автоматизации технологических процессов», а также результаты расчета регулирующего органа, с которым сочленяется ЭИМ. Кроме этого также необходимо знать усредненное значение времени запаздывания объекта τ (среднее τ для нескольких нагрузок объекта). Величина запаздывания может быть получена, например, по методике, изложенной в книге: Копелович А.П. Инженерные методы расчета при выборе автоматических регуляторов, М., 1960.
6.2. Порядок расчета
Определение нужного номинального крутящего момента и времени полного хода ЭИМ целесообразно выполнять в следующем порядке:
- определить недостающие данные, необходимые для выполнения расчета (диаметр вала или штока регулирующего органа, диаметр седла и т.п.);
- определить максимальный перепад давления на регулирующем органе и силы (крутящие моменты), действующие на шток (вал) регулирующего органа;
- определить необходимый крутящий момент на рычаге регулирующего органа;
- определить необходимый крутящий момент на выходном органе ЭИМ и выбрать номинальный крутящий момент ЭИМ;
- определить необходимое время полного хода ЭИМ и выбрать его номинальную величину;
- рассчитать кинематическую схему сочленения.
7. ПРИМЕР РАСЧЕТА И СОЧЛЕНЕНИЯ ЭИМ С ЗАСЛОНОЧНЫМ РЕГУЛИРУЮЩИМ ОРГАНОМ
В этом примере производится расчет ЭИМ к регулирующему органу, расчет пропускной способности которого приведен в разделе 22 руководящего материала РМ 4-163-77.
Данные для расчета
1. Абсолютное давление газа перед регулирующим органом Р1 = 2,1 кгс/см2
2. Абсолютное давление газа после регулирующего органа при максимальном расходе P2 = 1,2 кгс/см2
3. Присоединительный (условный) диаметр регулирующего органа d = 0,4 м
4. Радиус шейки вала заслоночного регулирующего органа rш = 0,035 м
5. Коэффициент трения в опорах f = 0,15
6. Время запаздывания объекта τ = 36 с
7. Закон регулирования ПИ
8. Отношение пускового крутящего момента ЭИМ к номинальному k = 1,7
9. Необходимая характеристика сочленения - вогнутая
Расчет
1. Данный регулирующий орган работает при критическом истечении газа через него при всех значениях протекающего через него расхода. При максимальном расходе перепад давления равен
ΔP'm = P1 - P2 = 2,1 - 1,2 = 0,9 кгс/см2.
В положении «закрыто» перепад давления будет равен избыточному давлению перед регулирующим органом
ΔР'o = Р1 - Ратм = 2,1 - 1,0 = 1,1 кгс/см2 = 1,1 · 104 кгс/м2.
Поскольку перепад давления на регулирующем органе изменяется сравнительно немного, то не будет чрезмерной ошибкой, если в качестве перепада давления, соответствующего максимуму гидродинамического момента, принять ΔР'o.
2. Оценим максимальный гидродинамический момент на валу регулирующего органа
Mg = 0,654d3ΔРo = 0,0654 · 0,43 · 1,1 · 104 = 46 кгс · м.
3. Определим максимальный момент трения в опорах вала регулирующего органа
Mтр =0,785d2rшfΔP = 0,785 · 0,42 · 0,035 · 0,15 · 1,1 · 104 = 6,6 кгс · м.
4. Определим необходимые крутящий момент на валу регулирующего органа
M = n(Mg + 1,2Mтр) = 2(46 +1,2 · 6,6) = 108 кгс · м,
где n = 2, коэффициент запаса, учитывающий условия и режим работы регулирующего органа, затяжку сальников и т.п. (см. табл. 1).
5. Определим необходимый крутящий момент на выходном органе ЭИМ
![]()
По ГОСТ 7192-74 примем номинальный момент исполнительного механизма
Mн = 400 кгс · м.
6. Определим необходимое время полного хода ЭИМ
Tc ≈ (1 ÷ 4)τ = 36 ÷ 144 с.
По ГОСТ 7192-74 примем Tc = 63 с.
Длина выходного рычага этого исполнительного механизма R = 360 мм.
7. Из конструктивных (компоновочных) соображений примем расстояние по вертикали между уровнем оси заслоночного регулирующего органа и уровнем, на котором находится ось вала ЭИМ, равным H = 2 м.
Тогда из рис. 3 следует, что длина тяги l будет равна
l = H + R = 2 + 0,36 = 2,36 м.
8. Определим необходимую длину рычага заслоночного регулирующего органа
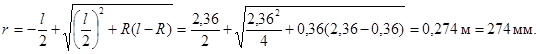
Схема сочленения аналогична показанной на рис. 3.
Длину рычага r целесообразно округлить до r = 280 мм. Округление делаем в сторону увеличения длины рычага, так как этому соответствует уменьшение угла полного хода регулирующего органа.
Этот угол будет немного меньше 90°,что приемлемо, так как необходимая максимальная пропускная способность регулирующего органа обеспечена его расчетом при φ ≈ 60° (раздел 22 РМ 4-163-77).
9. Определим получившееся значение коэффициента ослабления крутящего момента ЭИМ сочленением
![]()
что меньше исходного значения no = 4 и, следовательно, допустимо.
Из этого примера видно, что ориентировочное значение no = 4 не является чрезмерно завышенной величиной. Можно убедиться расчетом, что при l = 3 м no = 4,6, что вынудит уменьшить l м, приблизив ЭИМ к регулирующему органу.
8. ПРИМЕР РАСЧЕТА И СОЧЛЕНЕНИЯ ЭИМ С ОДНОСЕДЕЛЬНЫМ РЕГУЛИРУЮЩИМ ОРГАНОМ, ИМЕЮЩИМ РЫЧАЖНЫЙ ПРИВОД
Определить номинальный крутящий момент и время полного хода ЭИМ и рассчитать кинематическую схему сочленения его с односедельным регулирующим органом с рычажным приводом, управляющим потоком воды.
Данные для расчета
1. Давление воды перед регулирующим органом Р1 = 60 кгс/см2
2. Присоединительный (условный) диаметр регулирующего органа d = 20 мм
3. Диаметр седла dc = 18 мм
4. Диаметр штока dш = 20 мм
5. Ход штока hш = 22 мм
6. Плечо силы на штоке b = 45 мм
7. Длина рычага регулирующего органа r1 = 440 мм
8. Время запаздывания объекта τ = 36 с
9. Необходимая характеристика сочленения - линейная
10. Отношение пускового крутящего момента ЭИМ к номинальному k = 1,7
Расчет
1. Определим максимальную силу давления среды на затвор и шток. Так как dш > dc, то наибольшая сила давления среды на шток будет в положении «открыто», когда перепад давления минимален.
Пренебрегая величиной этого перепада, найдем
(Nз + Nш)max = 0,785 · 22 · 60 = 189 кгс.
2. Определим силу трения штока в сальнике
Mтр = 1,1dш + 0,02dшP1 = 1,1 · 20 + 0,02 · 20 · 60 = 46 кгс.
3. Так как односедельный регулирующий орган может быть запорным, то оценим силу, необходимую для создания уплотнительного контакта в жесткой запорной паре «седло-плунжер»
Nуп = 0,75pdc = 0,75 · 3,14 · 18 = 42 кгс.
5. Определим максимальное перестановочное усилие на штоке
Nпс = (Nз + Nш)max + Nтр + Nуп = 189 + 46 + 42 = 277 кгс.
6. Приняв по табл. 1 коэффициент запаса n = 2, определим необходимый момент на рычаге регулирующего органа
M = nb · Nпс = 2 · 0,045 · 277 = 25 кгс · м.
7. Определим необходимый крутящий момент на выходном органе ЭИМ
![]()
где no = 4 коэффициент ослабления крутящего момента сочленением.
По ГОСТ 7192-74 примем номинальный крутящий момент Mн = 63 кгс · м.
8. Определим номинальное время полного хода ЭИМ
Тс = (1 ÷ 4)τ = 36 ÷ 144 с.
Примем номинальное время по ГОСТ 7192-74 равным Тс = 63 с.
Так как Тс > 0,2d = 4 с, то гидравлического удара при внезапном закрытии регулирующего органа не будет.
9. Из показанных на рис. 6 и 7 кинематических схем сочленения следует, что в данном случае расчетом определяется только длина рычага регулирующего органа r. Выбранный нами ЭИМ имеет длину рычага r = 250 мм.
Определим синус половины угла поворота рычага r из положения «закрыто» в положение «открыто»
![]()
10. Определим длину рычага, обеспечивающую ход штока hш = 22 мм
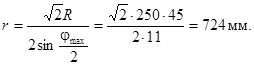
Схема сочленения аналогична показанной на рис. 6 или 7.
Для реализации полученного сочленения необходимо удлинение имеющегося на регулирующем органе рычага длиной 440 мм до длины 724 мм. Такое удлинение сделает сочленение очень громоздким и затруднит обеспечение жесткости рычага.
Поэтому целесообразно рассмотреть возможность применения ЭИМ прямоходного типа, типа МЭП по ГОСТ 7192-74.
11. Определим необходимое усилие на конце рычага r1 = 440 мм
![]()
12. Определим необходимое усилие на штоке ЭИМ
![]()
13. Примем ближайшее по ГОСТ 7192-74 номинальное усилие ЭИМ
Nн = 250 кгс.
14. Определим полный ход H конца рычага регулирующего органа при его длине r1 = 440 мм
![]()
![]()
Примем наиболее близкое к H значение номинального хода выходного штока ЭИМ по ГОСТ 7192-74, равное Hн = 160 мм.
15. Определим необходимую длину рычага регулирующего органа r при сочленении его с прямоходным ЭИМ, имеющим номинальное усилие 250 кгс и номинальный ход выходного штока 160 мм
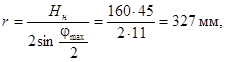 что меньше r1 = 440
мм и вполне приемлемо.
что меньше r1 = 440
мм и вполне приемлемо.
16. Определим необходимое усилие на рычаге регулирующего органа длиной r = 327 мм
![]()
17. Определим необходимое усилие на штоке ЭИМ
![]() что приемлемо, так как меньше Nн = 250 кгс.
что приемлемо, так как меньше Nн = 250 кгс.
Окончательно примем прямоходный ЭИМ по ГОСТ 7192-74 типа МЭП, имеющий номинальное усилие на выходном штоке 250 кгс, ход штока 160 мм и время полного хода 63 с. При этом длину рычага регулирующего органа r округлим до 330 мм. Характеристика сочленения линейная, аналогичная показанной на рис. 6, где B1B2 = A1A2 = 160 мм и выходной шток ЭИМ шарнирно соединен в точке А с тягой AB, а BO2 = 330 мм.
Приложение
Ориентировочные значения коэффициента гидродинамического момента m для заслоночного регулирующего органа с плоским затвором.
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННЫХ ДОКУМЕНТОВ И ЛИТЕРАТУРЫ
1. Технические документы
ГОСТ 7192-74. Механизмы исполнительные электрические постоянной скорости ГСП.
ГОСТ 14691-69. Устройства исполнительные для систем автоматического регулирования. Термины
РМ 4-163-77. Расчет и применение регулирующих органов в системах автоматизации технологических процессов (ГПИ ПМА, 1977)
2. Литература
1. Агейкин Д.И. и др. Руководство до проектированию элементов и систем автоматики. Пособие по курсовому проектированию. Выпуск 2. М., 1959.
2. Бельтюков В.П. Определение моментных коэффициентов центрально расположенных дроссельных заслонок, «Известия вузов. Машиностроение», № 2, 1975.
3. Гуревич Д.Ф. Расчет и конструирование трубопроводной арматуры, М., 1964.
4. Емельянов А.И., Емельянов В.А. Исполнительные устройства промышленных регуляторов. М., 1975.
5. Казинер Ю.Я., Слободкин М.С. Арматура систем автоматического управления, М., 1977.
6. Копелович А.П. Инженерные методы расчета при выборе автоматических регуляторов. М., 1960.
7. Макаров А.Н., Шерман М.Я. Расчет дроссельных устройств. М., 1953.
8. Стефани Е.П. Основы расчета настройки регуляторов теплотехнических процессов. М., 1972.
9. Шабленко Б.И., Земницкий А.А. Выбор исполнительных механизмов для воздушных клапанов центральных кондиционеров. Водоснабжение и санитарная техника. № 5, 1970.
10. Шегал Г.П., Коробков Г.С. Электрические исполнительные механизмы в системах управления. М., 1968.
11. Яковлев Ю.С. и др. Технические средства локальных САР. Чебоксары, 1973.
12. Яньшин Б.И. Затворы и переходы трубопроводов. М., 1962.
13. Benjes H.H. Operator torques for butterfly valves, Journal of American Water Works Association, vol. 53, No. 3, 1965, pp. 1139 - 1144.
14. Hanssen A.J. Butterfly valves, Power, January, 1966, pp. 62 - 65.
15. Hatch A.E., Chamberlian W.H. Torque characteristics of butterfly valves. Water and Sewage Works, February, 1958, pp. 67 - 69.
16. Guins V.J. Flow characteristics of butterfly and spherical valves. Proceedings of the American Society of Civil Engineers, Journal of the Hydraulic Division, May, 1968.
17. Manifold G.O. Automatic control for power and process. N.Y., 1964.
18. Martin Jr.J., Corripio A.B., Smith C.L. How to select controller modes and tuning parameters from simple process model, ISA Transactions, vol. 15, No. 4, 1976, pp. 314 - 319.
19. Roth G.L. Modifying valves characteristics to fit the process. Control Engineering, January, 1957, pp. 69 - 72.
20. Schuder C.B. Understanding fluid forces in control valves, Instrumentation technology, May, 1971, pp. 48 - 52.
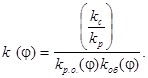 (32)
(32)
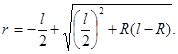 (37)
(37)
 (49)
(49)
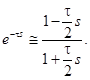 (57)
(57)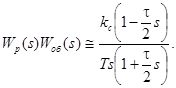 (60)
(60)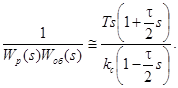 (61)
(61)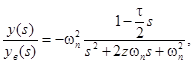 (65)
(65)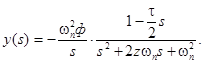
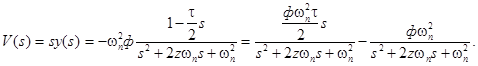
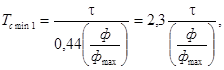 (92)
(92)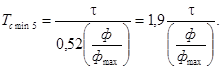 (93)
(93)