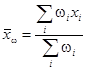ФЕДЕРАЛЬНОЕ
АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р ИСО |
Качество воздуха
ОЦЕНКА
НЕОПРЕДЕЛЕННОСТИ
МЕТОДА ИЗМЕРЕНИЙ
В УСЛОВИЯХ ПРИМЕНЕНИЯ
С ИСПОЛЬЗОВАНИЕМ РЕФЕРЕНТНОГО
МЕТОДА
ISO
13752:1998
Air quality - Assessment of uncertainty of a measurement
method under field conditions
using a second method as reference
(IDT)
![]()
Москва
Стандартинформ
2006
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1. ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2. ВНЕСЕН Техническим комитетом по стандартизации ТК 457 «Качество воздуха»
3. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 22 декабря 2005 г. № 321-ст
4. Настоящий стандарт идентичен международному стандарту ИСО 13752:1998 «Качество воздуха. Оценка неопределенности метода измерений в условиях применения с использованием второго метода в качестве референтного» (ISO 13752:1998 «Air quality - Assessment of uncertainty of a measurement method under field conditions using a second method as reference»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении C
5. ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет
Введение
Характеристики методов измерений качества воздуха установлены ИСО 6879. Соответствующие процедуры их определения приведены в ИСО 9169, за исключением точности, в настоящем стандарте рассматриваемой как неопределенность измерений в соответствии с требованиями «Руководства по выражению неопределенности измерений».
Неопределенность измерений в условиях применения рассматривается также в стандартах ИСО 7935:1992 «Выбросы стационарных источников - Определение массовой концентрации диоксида серы - Параметры автоматических методов измерений» и ИСО 10849:1996 «Выбросы стационарных источников - Определение массовой концентрации оксидов азота - Рабочие характеристики автоматических измерительных систем». Однако процедуры, приведенные в этих стандартах, ограничиваются определением либо независимой от концентрации систематической погрешности при допущении независимой от концентрации дисперсии, либо пропорциональной концентрации систематической погрешности при допущении относительно пропорциональной концентрации дисперсии.
СОДЕРЖАНИЕ
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Качество воздуха ОЦЕНКА
НЕОПРЕДЕЛЕННОСТИ МЕТОДА ИЗМЕРЕНИЙ Air quality. |
Дата введения - 2006-06-01
1 Область применения
Настоящий стандарт устанавливает процедуру оценки неопределенности измерений, выполняемых «полевым»1) методом, подлежащим проверке (далее - проверяемый метод), по другому (референтному) методу. Используемый референтный метод не обязательно должен быть стандартизован.
1) Метод измерений в реальных условиях применения (далее - условия применения).
Неопределенность измерений оценивают сравнением результатов измерений, полученных одновременно на реальных пробах проверяемым и референтным методами. Оценка неопределенности относится только к диапазону измерений, в котором она была получена.
Настоящая процедура разработана специально для оценки пригодности (валидации) проверяемого метода.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 6879:1995 Качество воздуха - Характеристики и соответствующие им понятия, относящиеся к методам измерений качества воздуха
ИСО 9169:1994 Качество воздуха - Определение характеристик методов измерений
3 Обозначения и сокращения
В настоящем стандарте применены следующие обозначения и сокращения2):
2) Определения применяемых терминов можно найти в [1] и [2].
a0, а1 а2 - коэффициенты функции дисперсии.
ХКВ - характеристика качества воздуха (обычно концентрация).
b0, b1 - коэффициенты функции линейной регрессии или градуировочной функции.
F - F-статистика.
k - коэффициент охвата.
L - функция правдоподобия.
l - логарифм функции правдоподобия.
N, N1 N2 - число пар (хi, yi) и число пар подсовокупностей 1 и 2 соответственно.
Р(уi) - вероятность yi.
ri - остаток при xi.
s, si - стандартное отклонение как функция ХКВ и при значении ХКВ, равном xi, соответственно.
s′ - преобразованное стандартное отклонение как функция ХКВ.
sao, sa1, sa2 - стандартное отклонение а0, а1 и а2 соответственно3.
3) Данные обозначения в тексте стандарта не употребляются, приведены для сохранения идентичности ИСО 13752:1998.
sb0, sb1 - стандартное отклонение b0 и b1 соответственно.
sx, sy - стандартное отклонение значений хi и yi соответственно1).
![]() - стандартное
отклонение измеренного значения у после введения поправки на
систематическую погрешность.
- стандартное
отклонение измеренного значения у после введения поправки на
систематическую погрешность.
sDy - стандартное отклонение (неопределенность) систематической погрешности.
U - расширенная неопределенность (коэффициент охвата k = 2) как мера неопределенности измерений.
X - переменная величина х-метода.
x, xi - значение ХКВ и i-е значение ХКВ соответственно.
![]() -
преобразованное значение хi.
-
преобразованное значение хi.
![]() - среднее и
средневзвешенное всех значений xi и среднее всех
значений yi
соответственно.
- среднее и
средневзвешенное всех значений xi и среднее всех
значений yi
соответственно.
Y - переменная величина у-метода.
yi - результат измерений у-методом при xi или значение выходного сигнала у-метода при xi
![]() -
преобразованное значение yi.
-
преобразованное значение yi.
![]() - оценка Y при значении
ХКВ, равном x.
- оценка Y при значении
ХКВ, равном x.
![]() - оценка Y при значении
ХКВ, равном xi.
- оценка Y при значении
ХКВ, равном xi.
ycor - результат измерений, полученный у-методом после введения поправки на систематическую погрешность.
Dу - систематическая погрешность (смещение) проверяемого метода при значении ХКВ, равном X = х.
e - случайное число из нормального распределения с центральным значением 0 и стандартным отклонением 11).
1) Данные обозначения в тексте стандарта не употребляются, приведены для сохранения идентичности ИСО 13752:1998.
ωi - весовой коэффициент при xi.
е - 2,718.
4 Основные принципы
На основе параллельных измерений в условиях применения получают N пар результатов измерений [(x1 y1), ..., (xN, yN)]. Результаты измерений, полученные референтным методом (х-методом), рассматривают как истинные. Разность результатов измерений в паре приписывают отклонению результата измерений, полученному проверяемым методом (у-методом).
При выборе модели зависимости между переменными величинами Х и Y принимают допущение об их линейной зависимости:
Коэффициенты функции линейной регрессии b0 и b1 оценивают исходя из следующих допущений относительно дисперсии результатов измерений, полученных у-методом:
- стандартное отклонение проверяемого метода не зависит от х (т.е. стандартное отклонение является постоянным) и задается формулой
![]() (2)
(2)
- стандартное отклонение проверяемого метода пропорционально х (т.е. коэффициент вариации постоянен) и задается формулой
![]() или s = а2х.
(3)
или s = а2х.
(3)
Примечание 1 - Первое допущение рассматривает флуктуации фона или значения коэффициента b0 (свободного члена - отсекаемого отрезка2)) без учета флуктуации коэффициента Ь1 (коэффициента наклона); второе - флуктуации коэффициента наклона без учета флуктуации фона или свободного члена.
2) См. ИСО 6879.
Примечание 2 - Значения коэффициентов функции линейной регрессии (оценка систематической погрешности) слабо зависят от отклонений, принятых в допущении о стандартном отклонении проверяемого метода. Однако оцененная случайная составляющая неопределенности измерений сильно зависит от данного допущения.
Функция дисперсии общего вида, используемая в настоящем стандарте, позволяет учитывать не только изменчивость коэффициентов наклона и значений свободных членов, но также статистический шум, стандартное отклонение которого пропорционально квадратному корню из значения х (приблизительно пропорционально квадратному корню из х). Функцию дисперсии общего вида рассчитывают по формуле
Примечание 3 - Коэффициенты возведены в квадрат, т.к. коэффициент в большей мере, чем его квадрат, отражает физический смысл.
Примечание 4 - Процедура вычисления функции дисперсии общего вида, представленная в ИСО 9169, не может быть использована, т.к. отсутствует возможность проведения измерений в условиях повторяемости.
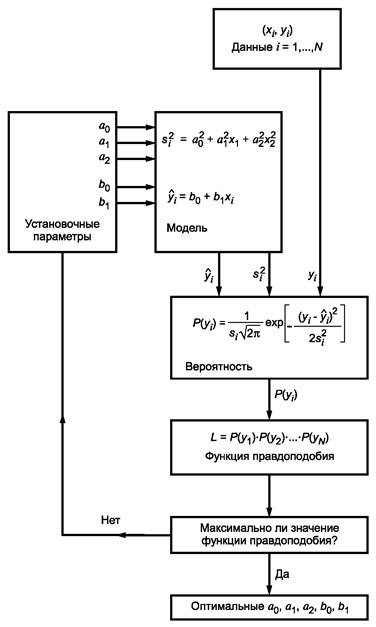
Значения коэффициентов принятой модели дисперсии общего вида [b0 и b1 в формуле (1) и a0, a1, и a2 в формуле (4)] не могут быть рассчитаны. Их подбирают на основе критерия максимального правдоподобия итеративным методом. Блок-схема вычисления коэффициентов функции линейной регрессии методом максимального правдоподобия приведена на рисунке 1. После выбора начальных значений коэффициентов, при использовании допущения о нормальности закона распределения, вычисляют вероятность Р(уi) в каждой точке, отвечающей результатам измерений (xi, yi) и принадлежащей линии регрессии, по формуле
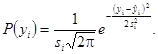 (5)
(5)
Функцию правдоподобия L, являющуюся произведением отдельных вероятностей результатов измерений, полученных у-методом, вычисляют по формуле
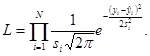 (6)
(6)
Варьируя коэффициенты, вычисляют значения функции правдоподобия вплоть до максимального. Соответствующие коэффициенты являются коэффициентами максимального правдоподобия регрессионной модели. Для определения этого значения применяют компьютерную обработку данных.
Неопределенность измерений, соответствующую любому полученному значению ХКВ, оценивают по функции регрессии и функции дисперсии.
Рисунок 1 - Блок-схема вычисления коэффициентов функции линейной регрессии методом максимального правдоподобия
5 Требования
5.1 Общие положения
Процедуру, установленную настоящим стандартом, применяют при выполнении следующих условий:
- существует линейная зависимость между сравниваемыми переменными; если зависимость нелинейна, но известно ее математическое выражение, процедура может быть адаптирована;
- погрешности измерений проверяемого метода подчиняются нормальному закону распределения;
- неопределенность измерений, присущая референтному методу, незначительна по сравнению с неопределенностью измерений проверяемого метода; в противном случае она будет ошибочно приписана проверяемому методу, что приведет к завышению неопределенности измерений;
- влияние различий в составе проб воздуха, отобранных двумя методами, незначительно по сравнению с ожидаемой неопределенностью измерений проверяемого метода; в противном случае данная составляющая погрешности будет ошибочно приписана проверяемому методу, что приведет к завышению неопределенности измерений.
Неопределенность коэффициентов, оцененных в соответствии с настоящим стандартом, может быть снижена путем увеличения числа пар измерений. Поэтому рекомендуется проводить по крайней мере 30 пар измерений, если применяют модель дисперсии общего вида, принятую настоящим стандартом.
5.2 Проверяемый метод (y-метод)
Выполняют все операции, предусмотренные методом измерений, который подлежит оценке.
5.3 Референтный метод (х-метод)
Проверяют допущение о незначительности неопределенности х-метода по сравнению с у-методом с учетом условий проведения измерений (в том числе условий окружающей среды), ожидаемых на месте проведения проверки, например наличия мешающих веществ, температуры и т.д. Проверку допущения о неопределенности х-метода проводят на основе анализа принципа измерений, литературных данных или результатов испытаний в лабораторных условиях или в условиях применения. Ориентируясь на детальное описание х-метода, выполняют соответствующие измерения.
5.4 Условия проведения измерений
Условия проведения измерений должны соответствовать условиям, в которых планируют использовать проверяемый метод (продолжительность измерений, диапазон изменений ХКВ, диапазон изменений физических и химических влияющих величин и условия работы). Фиксируют условия, в том числе окружающей среды, на месте проведения измерений.
Средства измерений, используемые в обоих методах, должны быть установлены так, чтобы:
- различия в составе параллельных проб были незначительны;
- средства измерений одного метода не влияли на средства измерений другого метода.
5.5 Обработка данных
При использовании модели дисперсии общего вида для нахождения функции максимального соответствия (правдоподобия) путем подбора значений а0, а1, а2, b0 и b1 применяют компьютерную обработку данных.
6 Параллельные измерения
Проводят параллельные измерения, являющиеся представительными для условий, в которых планируют применение проверяемого метода. Фиксируют результаты параллельных измерений.
7 Графический анализ дисперсии
Дисперсия результатов измерений может быть постоянной или увеличиваться при увеличении значения ХКВ. Зависимость дисперсии от значения ХКВ может быть представлена графически путем построения для всех пар результатов измерений (хi, yi) абсолютных разностей |ri| в зависимости от хi, где ri = yi - ŷi a ŷi - предсказанное значение, полученное оценкой регрессии обычным методом наименьших квадратов:
- если значения разностей не зависят от хi, см. 8.2;
- если значения разностей являются пропорциональными хi, см. 8.3;
- если значения разностей не являются ни независимыми, ни пропорциональными хi, см. 8.4.
В тех случаях, когда первое или второе условие применимо только для части диапазона измерений, диапазон измерений должен быть соответственно уменьшен1).
1) Диапазон измерений может быть разбит на поддиапазоны, в каждом из которых должно быть выполнено конкретное условие из перечисленных.
Коэффициенты функции регрессии и функции дисперсии в соответствии с 8.2 и 8.3 могут быть рассчитаны (простая модель дисперсии). Коэффициенты в соответствии с 8.4 определяют итеративным методом, что требует многократных расчетов, возможных лишь при использовании компьютера (модель дисперсии общего вида).
Подразделы 8.2 и 8.3 содержат процедуры проверки, позволяющие выяснить, подтверждается или нет допущение относительно принятой модели дисперсии.
8 Оценка коэффициентов функции линейной регрессии
8.1 Общие положения
Принятая линейная зависимость между переменными Х и Y описывается уравнением линейной регрессии
Если дисперсия результатов измерений относительно линии регрессии не зависит от значения ХКВ (см. 8.2), ее определяют по формуле
![]() (8)
(8)
Если дисперсия относительно линии регрессии пропорциональна значению ХКВ (см. 8.3), ее определяют по формуле
![]() (9)
(9)
В общем случае, если дисперсия относительно линии регрессии является монотонной функцией значения ХКВ (см. 8.4), ее определяют по формуле
Выбирают одну из указанных выше моделей дисперсии.
8.2 Стандартное отклонение постоянно
Коэффициенты функции линейной регрессии b1 и b0 вычисляют по формулам:
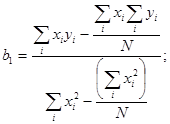 (11)
(11)
![]() (12)
(12)
Проверяют, подтверждается или нет допущение относительно постоянства дисперсии:
- выбирают N1 пар результатов измерений вблизи верхнего предела диапазона измерений и N2 пар вблизи нижнего предела при условии N1 = N2 = N/3;
- не используют среднюю часть диапазона измерений;
- рассчитывают статистику F формуле
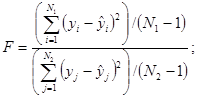 (13)
(13)
- если F не превышает
табулированное значение ![]() для -распределения в случае одностороннего
критерия для уровня значимости a
= 0,05, принятое за критическое значение, дисперсию считают постоянной;
для -распределения в случае одностороннего
критерия для уровня значимости a
= 0,05, принятое за критическое значение, дисперсию считают постоянной;
- если превышает табулированное значение F, см. 8.3 или 8.4.
Дисперсию s2 вычисляют по формуле
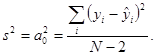 (14)
(14)
Стандартные
отклонения ![]() и
и ![]() коэффициентов b0 и b1 вычисляют по
формулам:
коэффициентов b0 и b1 вычисляют по
формулам:
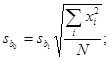 (15)
(15)
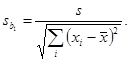 (16)
(16)
8.3 Коэффициент вариации постоянен
Для получения
линейного соотношения с постоянной дисперсией исходный набор данных (xi,yi) преобразуют в
новый набор данных ![]() по формулам:
по формулам:
![]() (17)
(17)
![]() (18)
(18)
Коэффициенты
функции линейной регрессии ![]() и
и ![]() вычисляют по формулам:
вычисляют по формулам:
 (19)
(19)
![]() (20)
(20)
Проверяют, подтверждается или нет допущение относительно постоянства дисперсии для преобразованных переменных:
- выбирают N1, пар результатов измерений в области верхней границы диапазона измерений и N2 пар в области нижней границы с условием N1 = N2 = N/3;
- не используют среднюю часть диапазона;
- статистику F вычисляют по формуле
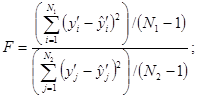 (21)
(21)
- если F не превышает
табулированное значение ![]() для F-распределения в
случае одностороннего
критерия для уровня значимости a
= 0,05, принятое за критическое значение, дисперсию считают постоянной;
для F-распределения в
случае одностороннего
критерия для уровня значимости a
= 0,05, принятое за критическое значение, дисперсию считают постоянной;
- если превышает табулированное значение F, см. 8.2 или 8.4.
функцию дисперсии s′2 вычисляют по формуле
 (22)
(22)
Проводят обратное преобразование полученных значений по формулам:
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
Стандартные
отклонения ![]() и
и ![]() коэффициентов b0 и b1 вычисляют по
формулам:
коэффициентов b0 и b1 вычисляют по
формулам:
 (26)
(26)
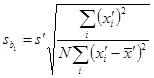 (27)
(27)
8.4 Модель дисперсии общего вида
Выбирают начальные значения коэффициентов модели b0 и b1 [формула (7)] и а0, а1, а2 [формула (10)], где a0 ≠ 0.
Для каждой пары
результатов измерений (xi, уi) вычисляют ![]() и
и ![]() :
:
![]() (29)
(29)
Логарифм функции правдоподобия l вычисляют по формуле
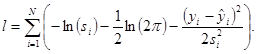 (30)
(30)
Находят максимальное значение l путем многократных вычислений b0, b1, а0, a1 и a2 с использованием процедуры оптимизации расчетов, например градиентного метода. Поскольку в уравнения входят квадраты коэффициентов a0, a1, и a2, их значения могут быть положительными и отрицательными. Сохраняют положительные значения:
a0 = |a0|; (31а)
a1 = |a1|; (31b)
а2 = |а2|. (31c)
Используют
значения коэффициентов b0, b1, a0, а1
и a2,
соответствующие максимальному L. Стандартные
отклонения ![]() и
и ![]() коэффициентов b0 и b1 вычисляют по
формулам:
коэффициентов b0 и b1 вычисляют по
формулам:
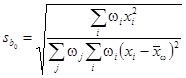 (32)
(32)
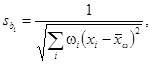 (33)
(33)
где
Образец крупноформатной таблицы для расчета коэффициентов функции регрессии и функции дисперсии приведен в приложении А, а соответствующий пример крупноформатной таблицы - в приложении В.
Примечания
1 Члены ![]() и/или
и/или ![]() в выражении
для функции дисперсии могут быть незначительны. Это проверяют, полагая равными
нулю коэффициенты а1 и/или а2 и повторяя
процедуру расчета соответствующего максимума l. Если абсолютная разность двух
значений l меньше 2, существенной разницы
между моделями нет. Сохраняют более простую модель.
в выражении
для функции дисперсии могут быть незначительны. Это проверяют, полагая равными
нулю коэффициенты а1 и/или а2 и повторяя
процедуру расчета соответствующего максимума l. Если абсолютная разность двух
значений l меньше 2, существенной разницы
между моделями нет. Сохраняют более простую модель.
2 Обычно функция дисперсии имеет
вид ![]() .
Эта функция отражает стремление дисперсии к константе в области нижней границы
диапазона измерений и пропорциональность дисперсии значению ХКВ в области
верхней границы диапазона измерений. Три члена в выражение для функции
дисперсии вводят только при большом числе пар измерений.
.
Эта функция отражает стремление дисперсии к константе в области нижней границы
диапазона измерений и пропорциональность дисперсии значению ХКВ в области
верхней границы диапазона измерений. Три члена в выражение для функции
дисперсии вводят только при большом числе пар измерений.
3 Если зависимость у = f(x) является нелинейной, но ее математический вид известен, формула (28) может быть заменена соответствующей математической функцией, а коэффициенты регрессии определены аналогично методом максимального правдоподобия.
9 Оценка неопределенности измерений
Значения коэффициентов b0 и b1 существенно отличаются от идеальных значений 0 и 1 соответственно, если:
и
Если формулы (36) и (37) показывают значимость поправок, систематическая погрешность при X = х может быть рассчитана в пределах диапазона измерений по формуле
Dy = b0 + (b1 - 1) · x. (38)
В соответствии с процедурами, указанными в [3], систематическая погрешность, возникающая в результате выявленного эффекта, может быть компенсирована путем введения поправки. Поправки могут быть введены, только если значения влияющих переменных, ответственных за эту систематическую погрешность, представительные. Однако неопределенность поправок, приравниваемая к неопределенности систематической погрешности, остается:
![]() (39)
(39)
где ![]() :
:
а) при модели дисперсии 8.2:
![]() (40)
(40)
b) при модели дисперсии 8.3:
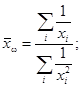 (41)
(41)
c) при модели дисперсии 8.4: см. формулы (34) и (35).
При Х = х вычисляют стандартное отклонение результата измерений в условиях применения на основе функции дисперсии по формуле
![]() (42)
(42)
Предполагая, что может быть введена поправка на систематическую погрешность Dу, вычисляют стандартное отклонение исправленного значения уcor по формуле
var(ycor) = var(y) + var(Dy), (43a)
т.е.
![]() (43б)
(43б)
Неопределенность единичного результата измерений при Х = x с коэффициентом охвата k = 2 определяют по формуле
![]() (44)
(44)
Коэффициент охвата k = 2 соответствует коэффициенту Стьюдента для доверительного интервала 95 % и нормального распределения.
В [3] рекомендуется всегда вводить поправку на систематическую погрешность. Обычно в инструкциях по оценке неопределенности измерений не приводят способы определения и введения поправок на систематические погрешности. Если введение поправки на систематические погрешности не является частью у-метода, эти погрешности включают в неопределенность измерений. Применяя согласно [3] принцип выражения погрешностей в показателях дисперсии, неопределенность измерений вычисляют по формуле
![]() (45)
(45)
Числовые значения неопределенности измерений всегда должны сопровождаться записью условий, в том числе условий окружающей среды, в которых они были получены.
Приложение А
(справочное)
Образец крупноформатной таблицы для расчета регрессии и функции дисперсии
В настоящем приложении приведен пример расчета коэффициентов функции регрессии и функции дисперсии с помощью программы табличных вычислений Microsoft Excel ® Версия 5.01). Вводят формулы из таблицы А.1 в соответствующие ячейки пустой формы таблицы А.2.
1) Excel® - торговое наименование программы, предоставляемой Microsoft. Возможно использование других программ, приводящее к получению аналогичных результатов.
Таблица А.1 - Формулы для введения в пустую форму
|
Содержание |
|
|
Е5 |
=С5 |
|
Е6 |
=С6 |
|
Е7 |
=С7 |
|
Е8 |
=С8 |
|
Е9 |
=С9 |
|
Е12 |
=SUM(G19:INDIRECT(ADDRESS(J3+18.7))) |
|
F5 |
=SQRT((J5+J4^2)/(J5*J7)) |
|
F6 |
=SQRT(1/(J5*J7)) |
|
J3 |
=COUNT(B19:B2018) |
|
J4 |
=SUMPRODUCT((B19:INDIRECT (J8))/(F19: INDIRECT(J10)))/J7 |
|
J5 |
=SUMPRODUCT(((B19:INDIRECT(J8))-J4)^2/(F19:INDIRECT(J10)))/J7 |
|
J6 |
=SUMPRODUCT((E19:INDIRECT(J9))^2/(F19:INDIRECT(J10)))/J7 |
|
J7 |
=SUMPRODUCT(1/(F19:INDIRECT(J10))) |
|
J8 |
=ADDRESS(J3+18,2) |
|
J9 |
=ADDRESS(J3+18,5) |
|
j10 |
=ADDRESS(J3+18,6) |
|
D19 |
=IF(ISNUMBER(C19),$E$5+$E$6*B19,«-») |
|
Е19 |
=IF(ISNUMBER(C19),C19-D19,«-») |
|
F19 |
=IF(ISNUMBER(C19),$E$7^2+$E$8^2*B19+$E$9^2*B19^2, «-») |
|
G19 |
=IF(ISNUMBER(C19),-(E19^2/F19)/2-LN(2.5066*SQRT(F19)), «-») |
Таблица А.2 - Незаполненная форма крупноформатной таблицы
|
А |
В |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|||||
|
1 |
|
Версия 1.2 |
|||||||||||||
|
|
|
Результаты расчета по модели |
|
Вспомогательные переменные |
|
|
|||||||||
|
3 |
Число измерений |
|
|||||||||||||
|
4 |
Стартовые значения |
Коэффициенты |
Значение |
Стандартное отклонение |
|
Взвешенное среднее х |
|
||||||||
|
5 |
b0 = |
0,0000 |
b0 = |
|
|
|
Взвешенная дисперсия х |
|
|||||||
|
6 |
b1 = |
1,0000 |
b1 = |
|
|
|
Остатки взвешенной дисперсии |
|
|||||||
|
7 |
а0 = |
1,0000 |
а0 = |
|
|
|
Сумма весов |
|
|||||||
|
8 |
а1 = |
0,0000 |
а1 = |
|
(сохранить абсолютное значение) |
Адрес ссылки |
|
||||||||
|
9 |
а2 = |
0,10000 |
а2 = |
|
(сохранить абсолютное значение) |
|
|
||||||||
|
10 |
|
|
|
|
|
|
|
||||||||
|
11 |
|
|
|
|
|
|
Модель регрессии |
|
|||||||
|
12 |
|
|
ln(L) |
-105,18 |
|
|
^Y = b0 + b1х |
||||||||
|
13 |
|
|
|
|
|
|
s^2 = а0^2 + а1^2х + а2^2х^2 |
||||||||
|
14 |
|
|
|||||||||||||
|
15 |
Пары результатов измерений |
Значения вероятности |
|
Инструкции/рекомендации |
|||||||||||
|
16 |
Референтный метод |
Проверяемый метод |
Модель y |
Остаток |
Модель дисперсии |
In (вероятность) |
1) Убедиться в том, что установлена дополнительная программа <Solver> (программа-решатель) 2) Всегда используют пустую форму таблицы (ячейки с $Е$5 по $Е$9 будут перезаписаны) 3) Вводят N пар результатов измерений (xi, yi) в ячейки с В19, С19 по B(N + 18), C(N + 18) 4) Копируют формулу D19 - G19 вниз от D(N + 18) до G(N + 18) 5) Проверяют/модифицируют стартовые значения. Если N > 2000, корректируют J3 6) Выбирают сервисную команду <Solver>. Ожидают появления окна <Solver parameters> (Параметры программы-решателя) 7) Параметры установки программы-решателя (по умолчанию) Установить целевую ячейку $Е$12 Равно Макс Путем замены ячеек SE$5 : $E$9 Ограничения $Е$7 > = 0,0000001 Необязательные ограничения $Е$8= 0 и/или $Е$9 = 0 (упрощения модели) 8) Возобновить работу <Solve> (решить) |
||||||||
|
17 |
X |
Y |
^y |
у - ^у |
S^2 |
|
|||||||||
|
18 |
|||||||||||||||
|
19 |
1 |
|
|
|
|
|
|
||||||||
|
20 |
2 |
|
|
|
|
|
|
||||||||
|
21 |
3 |
|
|
|
|
|
|
||||||||
|
22 |
4 |
|
|
|
|
|
|
||||||||
|
23 |
5 |
|
|
|
|
|
|
||||||||
|
24 |
6 |
|
|
|
|
|
|
||||||||
|
25 |
7 |
|
|
|
|
|
|
||||||||
|
26 |
8 |
|
|
|
|
|
|
||||||||
|
27 |
9 |
|
|
|
|
|
|
||||||||
|
28 |
10 |
|
|
|
|
|
|
||||||||
|
29 |
11 |
|
|
|
|
|
|
||||||||
|
30 |
12 |
|
|
|
|
|
|
9) Если значения модели для а1 или а2 отрицательные, сохраняют абсолютное значение |
|||||||
Приложение В
(справочное)
Пример крупноформатной таблицы для расчета регрессии и функции дисперсии
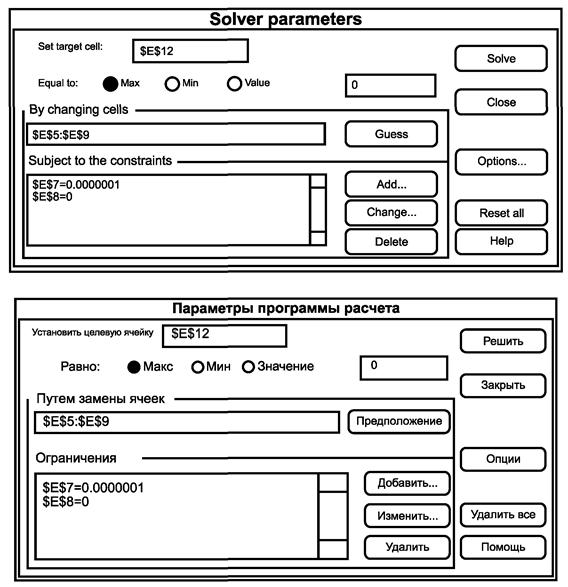
Рисунок В.1 - Пример окна параметров программы-решателя1)
1) Программа-решатель на русском языке приведена для удобства пользователей настоящего стандарта.
Таблица В.1 - Пример крупноформатной таблицы
|
|
А |
в |
с |
D |
Е |
F |
G |
H |
I |
J |
K |
|
1 |
|
Версия 1.2 |
|||||||||
|
2 |
Результаты расчетов по модели |
|
Вспомогательные переменные |
|
|
||||||
|
3 |
Число измерений |
30 |
|||||||||
|
4 |
Стартовые значения |
Коэффициенты |
Значение |
Стандартное отклонение |
|
Взвешенное среднее х |
43,309 |
||||
|
5 |
b0 = |
0,0000 |
b0 = |
- 0,846 |
1,212 |
|
Взвешенная дисперсия х |
3970,171 |
|||
|
6 |
b1 = |
1,0000 |
b1 = |
0,925 |
0,016 |
|
Остатки взвешенной дисперсии |
29,935 |
|||
|
7 |
а0 = |
1,0000 |
а0 = |
3,755 |
|
|
Сумма весов |
1,002 |
|||
|
8 |
а1 = |
0,0000 |
а1 = |
0,0000 |
(сохранить абсолютное значение) |
Адрес ссылки |
$В$48 |
||||
|
9 |
а2 = |
0,10000 |
а2 = |
0,05204 |
(сохранить абсолютное значение) |
|
$Е$48 |
||||
|
10 |
|
|
|
|
|
|
$F$48 |
||||
|
11 |
|
|
|
|
|
|
Модель регрессии |
|
|
||
|
12 |
|
|
In(L) |
- 105,18 |
|
|
^У = b0 + b1 · х |
|
|||
|
13 |
|
|
|
|
|
|
s^2 = a0^2 + а1^2х + а2^2х^2 |
||||
|
14 |
|
Инструкции/рекомендации |
|||||||||
|
15 |
Пары результатов измерений |
|
Значения вероятности |
|
|
1) Убедиться в том, что установлена дополнительная программа <Solver> (программа-решатель) 2) Всегда используют пустую форму таблицы (ячейки с $Е$5 по $Е$9 будут перезаписаны) 3) Вводят N пар результатов измерений (xi, yi) в ячейки с В19, С19 по B(N + 18), C(N + 18) 4) Копируют формулу D19 - G19 вниз от D(N + 18) до G(N + 18) 5) Проверяют/модифицируют стартовые значения. Если N > 2000, корректируют J3 6) Выбирают сервисную команду <Solver>. Ожидают появления окна <Solver parameters> (Параметры программы-решателя) 7) Параметры установки программы-решателя (по умолчанию) Установить целевую ячейку $Е$12 Равно Макс Путем замены ячеек SE$5 : $E$9 Ограничения $Е$7 > = 0,0000001 Необязательные ограничения $Е$8 = 0 и/или $Е$9 = 0 (упрощения модели) 8) Возобновить работу программы: <Solve> (решить) 9) Если значения модели для а1 или а2 отрицательные, сохраняют абсолютное значение |
|||||
|
16 |
Референтный метод |
Проверяемый метод |
Модель у |
Остаток |
Модель дисперсии |
In (вероятность) |
|||||
|
17 |
X |
Y |
^y |
y - ^y |
S^2 |
|
|||||
|
18 |
|||||||||||
|
19 |
1 |
11 |
6 |
9,33 |
- 3,33 |
14,43 |
- 2,64 |
||||
|
20 |
2 |
11 |
15 |
9,33 |
5,67 |
14,43 |
- 3,37 |
||||
|
21 |
3 |
12 |
14 |
10,25 |
3,75 |
14,49 |
- 2,74 |
||||
|
22 |
4 |
13 |
6 |
11,17 |
- 5,17 |
14,56 |
- 3,18 |
||||
|
23 |
5 |
17 |
22 |
14,87 |
7,13 |
14,89 |
- 3,98 |
||||
|
24 |
6 |
19 |
15 |
16,72 |
- 1,72 |
15,08 |
- 2,37 |
||||
|
25 |
7 |
20 |
17 |
17,65 |
- 0,65 |
15,19 |
- 2,29 |
||||
|
26 |
8 |
22 |
14 |
19,50 |
- 5,50 |
15,41 |
- 3,27 |
||||
|
27 |
9 |
23 |
22 |
20,42 |
1,58 |
15,54 |
- 2,37 |
||||
|
28 |
10 |
29 |
25 |
25,97 |
- 0,97 |
16,38 |
- 2,35 |
||||
|
29 |
11 |
39 |
39 |
35,21 |
3,79 |
18,22 |
- 2,76 |
||||
|
30 |
12 |
50 |
50 |
45,39 |
4,61 |
20,87 |
- 2,95 |
|
|||
|
31 |
13 |
51 |
47 |
46,31 |
0,69 |
21,15 |
- 2,46 |
||||
|
32 |
14 |
52 |
43 |
47,29 |
- 4,23 |
21,43 |
- 2,87 |
||||
|
33 |
15 |
79 |
71 |
72,20 |
- 1,20 |
31,01 |
- 2,66 |
||||
|
34 |
16 |
104 |
91 |
95,31 |
- 4,31 |
43,40 |
- 3,02 |
||||
|
35 |
17 |
105 |
88 |
96,24 |
- 8,24 |
43,96 |
- 3,58 |
||||
|
36 |
18 |
173 |
180 |
159,11 |
0,89 |
95,16 |
- 3,20 |
||||
|
37 |
19 |
196 |
185 |
180,38 |
4,62 |
118,14 |
- 3,40 |
||||
|
38 |
20 |
197 |
173 |
181,30 |
- 8,30 |
119,21 |
- 3,60 |
||||
|
39 |
21 |
211 |
188 |
194,25 |
- 6,25 |
134,68 |
- 3,52 |
||||
|
40 |
22 |
221 |
196 |
203,49 |
- 7,49 |
146,38 |
- 3,60 |
||||
|
41 |
23 |
230 |
203 |
211,62 |
- 8,82 |
157,37 |
- 3,70 |
||||
|
42 |
24 |
295 |
305 |
271,92 |
33,08 |
249,79 |
- 5,87 |
||||
|
43 |
25 |
328 |
306 |
302,43 |
5,57 |
305,47 |
- 3,83 |
||||
|
44 |
26 |
328 |
295 |
302,43 |
- 7,43 |
305,47 |
- 3,87 |
||||
|
45 |
27 |
577 |
556 |
532,66 |
23,34 |
915,76 |
- 4,83 |
||||
|
46 |
28 |
676 |
586 |
624,20 |
- 38,20 |
1251,71 |
- 5,07 |
||||
|
47 |
29 |
793 |
825 |
732,38 |
92,62 |
1717,18 |
- 7,14 |
||||
|
48 |
30 |
862 |
770 |
796,17 |
- 26,17 |
2026,45 |
- 4,89 |
||||
Приложение C
(справочное)
Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным (региональным) стандартам
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта Российской Федерации |
|
ИСО 6879:1995 |
* |
|
ИСО 9169:1994 |
* |
|
ИСО 3534-1:1993 |
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения |
|
ИСО 4225:1994 |
* |
|
ИСО 7935:1992 |
* |
|
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. |
|
Библиография
[2] ИСО 4225:1994 Качество воздуха - Общие аспекты (положения) - Словарь
1) Руководство по выражению неопределенности измерения: Аутентичный перевод с англ. /Под ред. проф. Слаева В.А. - СПб.: Изд-во ВНИИМ им. Д.И. Менделеева, 1999.
ИСО 7935:1992 Выбросы стационарных источников - Определение массовой концентрации диоксида серы - Параметры автоматических методов измерений
ИСО 10849:1996 Выбросы стационарных источников - Определение массовой концентрации оксидов азота - Рабочие характеристики автоматических измерительных систем
|
Ключевые слова: качество воздуха, метод измерений, референтный метод, параллельные измерения, оценка неопределенности измерений |