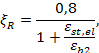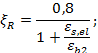МИНИСТЕРСТВО
СТРОИТЕЛЬСТВА
И ЖИЛИЩНО-КОММУНАЛЬНОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
АВТОНОМНОЕ УЧРЕЖДЕНИЕ
«ФЕДЕРАЛЬНЫЙ ЦЕНТР НОРМИРОВАНИЯ,
СТАНДАРТИЗАЦИИ И ТЕХНИЧЕСКОЙ ОЦЕНКИ
СООТВЕТСТВИЯ В СТРОИТЕЛЬСТВЕ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО РАСЧЕТУ И ПРОЕКТИРОВАНИЮ
СТАЛЕЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
С ЖЕСТКОЙ АРМАТУРОЙ
Москва 2019
Содержание
Введение
Настоящее методическое пособие разработано в развитие положений СП 266.1325800.2016 «Конструкции сталежелезобетонные. Правила проектирования» для правильного применения проектировщиками и разработчиками расчетных комплексов требований, заложенных в сводах правил, и выполнения грамотного и рационального проектирования сталежелезобетонных конструкций с жесткой арматурой, подверженных внецентренному сжатию. В методическом пособии приведены рекомендации по назначению нагрузок и воздействий, дополнительные положения по расчетам (учет неточностей монтажа, расчет на устойчивость к прогрессирующему обрушению всей конструктивной системы и устойчивости отдельных элементов). Приведены рекомендации по учету ползучести и усадки бетона, назначению характеристик материалов, к расчету по линейным и нелинейным диаграммам работы стали и бетона, расчету по трещиностойкости, приведены рекомендации по определению высоты сжатой зоны, рекомендован сортамент металлопроката.
Методическое пособие разработано в развитие положений СП 266.1325800.2016 (разделы 4, 5, подраздел 7.1), СП 16.13330.2017 (пункт 4.2.4), СП 63.13330.2018 (пункт 8.1.6), СП 20.13330.2016 (разделы 10 и 14), не распространяется на трубобетонные конструкции и конструкции, подверженные изгибу.
Методическое пособие составлено с учетом требований Федеральных законов от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», от 22 июня 2008 г. № 123-ФЗ «Технический регламент о требованиях пожарной безопасности», от 30 декабря 2009 г. № 384-ФЗ «Технический регламент о безопасности зданий и сооружений».
Методическое пособие разработано авторским коллективом АО «НИЦ «Строительство» (д-р техн. наук И.И. Ведяков - руководитель работы, канд. техн. наук Д.В. Конин, инженеры А.С. Крылов, Л.С. Рожкова (ЦНИИСК им. В.А. Кучеренко); д-р техн. наук С.Б. Крылов (НИИЖБ им. А.А. Гвоздева).
1 Область применения
Настоящее методическое пособие (далее - пособие) разработано в развитие положений СП 266.1325800.2016 и содержит рекомендации для расчета конструкций с жесткой арматурой, подверженных внецентренному сжатию. Область применения настоящего пособия ограничивается областью применения сталежелезобетонных конструкций, приведенной в СП 266.1325800.2016 (раздел 1).
2 Нормативные ссылки
В настоящем пособии использованы нормативные ссылки на следующие документы:
ГОСТ Р 57837-2017 Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия
ГОСТ 27751-2014 Надежность строительных конструкций и оснований. Основные положения
ГОСТ 27772-2015 Прокат для строительных стальных конструкций. Общие технические условия
СП 14.13330.2014 «СНиП II-7-81* Строительство в сейсмических районах» (с изменением № 1)
СП 16.13330.2017 «СНиП II-23-81* Стальные конструкции» (с изменением № 1)
СП 20.13330.2016 «СНиП 2.01.07-85* Нагрузки и воздействия» (с изменениями № 1, № 2)
СП 63.13330.2018 «СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения»
СП 70.13330.2012 «СНиП 3.03.01-87 Несущие и ограждающие конструкции» (с изменениями № 1, № 3)
СП 266.1325800.2016 Конструкции сталежелезобетонные. Правила проектирования (с изменением № 1)
СП 267.1325800.2016 Здания и комплексы высотные. Правила проектирования
СП 294.1325800.2017 Конструкции стальные. Правила проектирования (с изменением № 1)
Примечание - При пользовании настоящим сводом правил целесообразно проверить действие ссылочных документов в информационной системе общего пользования - на официальном сайте федерального органа исполнительной власти в сфере стандартизации в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего свода правил в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде стандартов.
3 Термины и определения
В настоящем пособии применяются термины по ГОСТ 27751, СП 16.13330, СП 63.13330, СП 266.1325800.
4 Общие положения
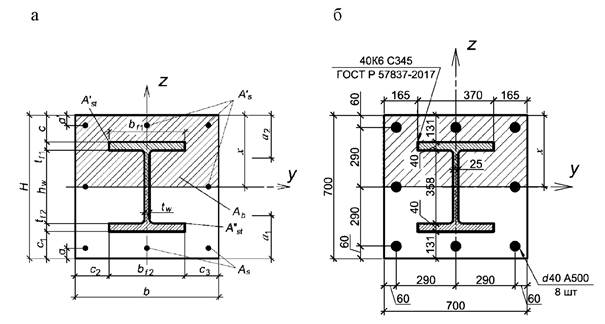
4.1 Типы сечений сталежелезобетонных конструкций с жесткой арматурой
По типу бетонирования сечения делятся на:
- полностью обетонированные;
- частично обетонированные.
Жесткая арматура может быть различного очертания: сплошного, замкнутого, разомкнутого и других видов сечений. Типовые поперечные сечения приведены на рисунке 4.1.
Сталежелезобетонные конструкции - оптимальный вид конструкций при проектировании и возведении многоэтажных, высотных зданий, конструкций зрелищных сооружений и сооружений, где требуется повышенная прочность конструкций, малые габариты в плане для колонн, а также высокая огнестойкость [1], [2]. Наибольшей технологичностью изготовления и монтажа отличаются поперечные сечения, без замкнутых полостей (рисунок 4.1 а, б, г, д).
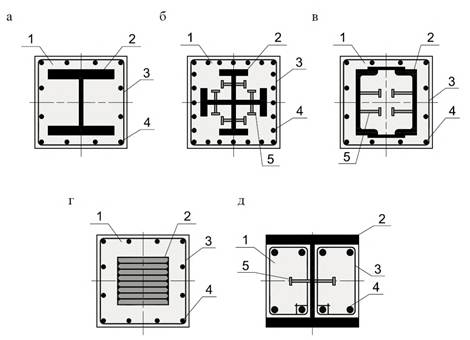
а - жесткая арматура в форме двутавра; б - жесткая
арматура в форме крестообразного сечения;
в - жесткая арматура коробчатого сечения, образованного швеллерами,
объединенными планками;
г - жесткая арматура в виде «сердечника», «сляба» сплошного сечения; д -
сечение с частичным
обетонированием жесткой арматуры;
1 - бетон; 2 - жесткая
арматура; 3 - поперечная гибкая арматура;
4 - продольная гибкая арматура; 5 - упор
Рисунок 4.1 - Типовые поперечные сечения железобетонных
конструкций с жесткой арматурой
4.2 Нагрузки и воздействия
4.2.1 Нагрузки и воздействия следует принимать согласно требованиям СП 20.13330, в соответствии заданием на проектирование, учитывающим специфические виды нагрузок, а также со специальными техническими условиями на проектирование конкретного объекта, если таковые разработаны. Для климатических нагрузок (снеговых и ветровых) могут применяться результаты численного моделирования и продувок в аэродинамических трубах и расчетов нагрузок с использованием специализированных компьютерных программ.
4.2.2 Сочетания нагрузок следует принимать согласно требованиям СП 20.13330.2016 (раздел 6).
4.2.3 Сейсмическое воздействие следует учитывать согласно требованиям СП 14.13330.
4.2.4 Этапы монтажа необходимо учитывать для определения перераспределения усилий и деформаций между элементами конструкции в процессе ее возведения. Это перераспределение усилий влияет на напряженно-деформированное состояние здания (сооружения) и после его возведения, а также на запас устойчивости конструкций. Особенно сильно это влияние проявляется в высотных зданиях и большепролетных сооружениях, а также в зданиях и сооружениях, расчетная схема которых изменяется в процессе возведения из-за использования временных связей, опор и т.д.
Наиболее точно этапы монтажа могут быть учтены с помощью специальных модулей расчетных программных комплексов.
4.2.5 Нагрузки, действующие на конструкцию при монтаже (собственный вес, вес подмостей, кранов, работающих людей, инструментов, мелкого оборудования, односторонний распор и др.), а также при изготовлении и транспортировании элементов, следует принимать по проектным данным с учетом предусматриваемых условий производства работ и требований СП 70.13330.
4.3 Материалы и номенклатура металлопродукции
4.3.1 Для сталежелезобетонных конструкций с жесткой арматурой рекомендуется назначать бетон класса по прочности не ниже В20, сталь по ГОСТ 27772 от С255 до С440, продольную гибкую арматуру класса не ниже А400. Эффективность применения указанных материалов подтверждена экспериментальными данными [2], [3], [4].
4.3.2 Характеристики материалов следует принимать согласно СП 266.1325800.2016 (раздел 5) с учетом 4.3.3 и 4.5.4.
4.3.3 Расчет по линейным и нелинейным диаграммам работы стали и бетона
4.3.3.1 Диаграммы состояния (деформирования) бетона, арматуры и стали применяются при расчете сталежелезобетонных элементов по нелинейной деформационной модели.
4.3.3.2 Диаграмма состояния сжатого бетона принимается по СП 63.13330.2018 (6.1.19 - 6.1.26). Рекомендуется использование трехлинейной диаграммы. Возможно применение и апробированных диаграмм, приведенных в работах [5], [6] и других.
4.3.3.3 Диаграмма состояния арматуры принимается по СП 63.13330.2018 (6.2.13 - 6.2.15).
4.3.3.4 Диаграмма состояния конструкционной стали принимается по СП 16.13330.2017 (4.2.4, рисунок В.1). Рекомендуется использование двухлинейной диаграммы по точкам OBD (или OACD - с моделированием упругопластического перехода) с обязательным ограничением деформаций текучести. Использование «бесконечной» диаграммы Прандтля, в которой деформации текучести не имеют ограничений, при моделировании сталежелезобетонных конструкций не допускается.
4.3.4 Номенклатура металлопродукции
В качестве жесткой арматуры следует использовать прокатные профили по ГОСТ Р 57837 или другим нормативным документам (НД), а также составного сечения из листового и фасонного проката.
При проектировании сжатых элементов следует использовать двутавры типов К (колонные), ДК (колонные дополнительных серий), С (свайные) (обозначения по ГОСТ Р 57837) или их сварные аналоги.
При проектировании элементов, подверженных сжатию и значительной изгибающей нагрузке, рационально использовать поперечные сечения, развитые в направлении изгибающего момента (например, типов Ш, Б, ДБ по ГОСТ Р 57837 или их сварных аналогов).
4.4 Общие положения по проектированию
Сталежелезобетонные конструкции с жесткой арматурой должны удовлетворять требованиям СП 266.1325800.2016 (подраздел 4.2).
Конструктивные требования к железобетонным конструкциям с жесткой арматурой должны удовлетворять СП 266.1325800.2016 (подраздел 8.3).
4.5 Общие положения по расчетам
4.5.1 Для сталежелезобетонных конструкций с жесткой арматурой в дополнение требованиям, приведенным в СП 266.1325800.2016 (подразделы 4.3, пункты 4.4.1 - 4.4.3), должны соблюдаться дополнительные требования 4.5.2, а также рекомендации 4.5.3.
Расчеты выполняются методами предельных усилий [7] или по нелинейной деформационной модели [8], [9]. Выбор конкретного способа расчета осуществляется проектировщиком для получения достоверных результатов расчетов.
4.5.2 Дополнительные требования к расчету сталежелезобетонных конструкций с жесткой арматурой
4.5.2.1 Неточности монтажа вертикальных конструкций учитываются с помощью задания случайных эксцентриситетов продольных сил. Значения эксцентриситетов следует принимать в соответствии с СП 266.1325800.2016 (подпункты 7.1.1.5 - 7.1.1.7). При расчете уже возведенных конструкций значения эксцентриситетов принимаются равными фактическим значениям, но не меньше значений случайных эксцентриситетов. Фактические значения эксцентриситетов определяются путем обработки результатов геодезической съемки.
В расчетных схемах фактические эксцентриситеты, не предусмотренные проектом, моделируются с помощью смещения элементов относительно их проектных положений с помощью введения жестких вставок или с помощью задания дополнительных изгибающих моментов в качестве внешней нагрузки в местах эксцентриситетов. Правила моделирования смещений в расчетных схемах следует принимать с учетом СП 294.1235800.2017 (пункт 25.3.4).
4.5.2.2 При проектировании конструкций в соответствии с требованиями НД должна быть предусмотрена конструктивная схема, не допускающая возможности прогрессирующего (лавинообразного) обрушения в случае локального разрушения несущих конструкций или их элементов, при аварийных воздействиях, не предусмотренных условиями нормальной эксплуатации зданий (пожары, взрывы, ударные воздействия транспортных средств, несанкционированная перепланировка и т.п.).
Требования по учету особых нагрузок и воздействий при аварийных ситуациях природного, техногенного и антропогенного характеров следует принимать в соответствии с СП 296.1325800.
Соответствующие расчеты конструкций и их элементов следует проводить при учете постоянных и длительных нагрузок и воздействий (при коэффициентах надежности по нагрузке γf = 1). Расчетные прочностные и деформационные характеристики материалов следует принимать равными их нормативным значениям. В случае необходимости учет кратковременных нагрузок и воздействий следует предусматривать в задании на проектирование.
Расчет, в случае локального разрушения конструкций, проводят только по предельным состояниям первой группы. Развитие неупругих деформаций, перемещения конструкций и раскрытие в них трещин в рассматриваемой чрезвычайной ситуации не ограничивают, если иное не предусмотрено в задании на проектирование.
4.5.2.3 Устойчивость сжатого или сжато-изогнутого сталежелезобетонного элемента проверяется в ходе прочностного расчета. При приближении нагрузки к критическому значению, увеличиваются прогибы элементов и, соответственно, изгибающие моменты. Такой расчет допускается проводить по деформированной или не деформированной схеме.
При расчете по недеформированной схеме следует руководствоваться СП 266.1325800.2016 (подпункт 7.1.2.5).
При расчете по деформированной схеме выполняется расчет упругой конструкции по правилам строительной механики (в т.ч. методом конечных элементов в виде геометрически нелинейной задачи). При выполнении такого расчета следует учитывать проявление ползучести в бетоне при длительно действующих и постоянных нагрузках. Ползучесть бетона учитывается с помощью снижения его модуля упругости в соответствии с методикой СП 63.13330. При назначении жесткости сечения используется приведенная изгибная жесткость, полученная суммированием изгибной жесткости бетонной части сечения с (учетом ползучести) и стальной части. Если в ходе расчета выявляется, что в бетоне возникают трещины, то для уточнения результатов выполняется повторный расчет, в котором жесткость бетонной части дополнительно умножается на коэффициент 0,667 (2/3).
При расчете на устойчивость всей конструкции здания или сооружения следует также руководствоваться изложенными выше правилами.
Для многоэтажных и высотных зданий общая устойчивость должна быть обеспечена в соответствии с требованиями СП 267.1325800.
Помимо расчета на устойчивость, как части расчета на прочность, должна выполняться проверка устойчивости системы. В этом случае отношение критических нагрузок к расчетным должно быть не менее коэффициента надежности по устойчивости системы γstab, значения которого указаны в СП 266.1325800.2016 (пункт 4.3.6).
4.5.3 Рекомендации по учету ползучести, усадки и образованию трещин при назначении модуля упругости бетона
4.5.3.1 При выполнении расчетов учет ползучести, усадки и образования трещин осуществляется в зависимости от методики расчета и возможностей используемой компьютерной программы. Современное состояние вопроса нелинейных расчетов железобетонных конструкций изложено в [11].
4.5.3.2 Расчеты с использованием диаграмм деформирования материалов выполняются, как правило, в расчетных программных комплексах. Если программный комплекс позволяет непосредственно учесть ползучесть бетона, то допускается использовать диаграмму деформирования бетона для кратковременных нагрузок, а ползучесть учитывается заданием соответствующих параметров расчета. При этом, не зависимо от результатов расчета, все проверки прочности, предусмотренные СП 266.1325800, должны быть выполнены.
Если при расчете с использованием диаграмм деформирования материалов программа не допускает учет ползучести в явном виде, то для расчета следует использовать диаграммы состояния сжатого бетона, соответствующие длительной нагрузке [12].
При использовании расчетных программных комплексов, ориентированных на зарубежные нормы проектирования, следует иметь в виду, что развитие ползучести в них отличается от отечественных норм. Разница с Еврокодами, например, во времени развития процесса ползучести приблизительно 10-кратная. Это следует иметь в виду при выборе того или иного способа учета ползучести бетона.
4.5.3.3 Если конструкция рассчитывается как линейно-упругая, то ползучесть и нелинейность работы бетона учитывается снижением модуля упругости бетона. Снижение модуля упругости определяется по методике СП 63.13330. Если в результате расчета выявляется, что бетон работает с трещинами, то для уточнения результатов выполняется повторный расчет с дополнительным снижением модуля упругости бетона с помощью умножения на коэффициент 0,667 (2/3).
4.5.3.4 Усадка бетона создает в конструкциях напряжения, которые со временем релаксируют в значительной степени. При расчете усадка учитывается по методике [10]. Учет усадки необходим только в случаях, когда она происходит в условиях стеснения деформаций и только в протяженных конструкциях. При использовании программных расчетных комплексов усадку следует учитывать непосредственно (задавая соответствующий параметр счета) или моделировать ее с помощью температурного воздействия, исходя из значений коэффициентов температурного расширения материалов.
5 Рекомендации к проектированию и расчетам сталежелезобетонных конструкций с жесткой арматурой
5.1 Расчет по прочности на внецентренное сжатие следует проводить из условия равновесия по СП 266.1325800.2016 (подпункт 7.1.2.1 и формула (7.1)). Эксцентриситет приложения продольной силы е1 принимается по правилам СП 266.1325800.2016 (подпункт 7.1.2.4 и формула (7.5)) с учетом влияния продольного изгиба стержня, учитываемого коэффициентом η, определяемого по СП 266.1325800.2016 (подпункт 7.1.2.5, формулы (7.6) и (7.7)), и эксцентриситетов продольной силы относительно центра тяжести поперечного сечения е0 и случайного еа, определяемых по СП 266.1325800.2016 (подпункты 7.1.1.5, 7.1.1.6).
В соответствии с СП 266.1325800.2016 (подпункты 7.1.1.7) расчет внецентренно сжатых элементов проводится как в плоскости расчетного эксцентриситета продольного усилия, так и в нормальной к ней плоскости, в которой эксцентриситет е0 принимается равным случайному еа. При этом в обоих плоскостях учитывается влияние прогиба посредством коэффициента η.
Расчет по прочности сечения при приложении продольной силы с эксцентриситетом в двух плоскостях (косой изгиб со сжатием) выполняется по СП 266.1325800.2016 (подраздел 7.3).
5.2 Высота сжатой зоны бетона определяется из условий равновесия усилий, действующих в рассматриваемом нормальном сечении элемента. В общем виде это условие приведено в СП 266.1325800.2016 (формула (7.2)).
В общем случае высота сжатой зоны бетона определяется методом последовательных приближений. При этом, на каждом этапе расчета назначается положение границы сжатой зоны, затем проверяется выполнение условий равновесия. Если относительная погрешность выполнения условий равновесия велика, то уточняется положение границы сжатой зоны и повторяется расчет.
5.3 Наиболее точные результаты дает расчет с применением диаграмм деформирования бетона, стального сердечника и стержневой арматуры. При выполнении расчета в стали жесткой и в стали стержневой арматуры допускаются пластические деформации, не превышающие предельные значения, приведенные в СП 16.13330, СП 63.13330 и СП 266.1325800. Работа растянутого бетона, как правило, не учитывается. Работу растянутого бетона допускается учитывать при использовании фибробетонов. При учете работы растянутого бетона формулы, приведенные в 5.7, следует корректировать, вводя дополнительное слагаемое RbtAb, где Rbt - прочность бетона на растяжение, Abt - площадь сечения растянутого бетона.
5.4 При определении высоты сжатой зоны допускается вводить следующие расчетные допущения:
- Эпюра напряжений в сжатой зоне бетона принимается постоянной (прямоугольной) с ординатой, равной значению расчетного сопротивления бетона;
- Эпюры напряжений в стальном сердечнике в сжатой и растянутой его частях принимаются постоянными (прямоугольными) с ординатами, равными значениям расчетных сопротивлений стали при растяжении и сжатии;
- Напряжения в сжатой части стального сердечника и в сжатой стержневой арматуре принимаются не больше значения, соответствующего условиям совместной работы стали и бетона;
- Если по результатам расчета граница сжатой зоны располагается в пределах полки (при рассмотрении изгиба в плоскости наибольшей жесткости) или стенки (при рассмотрении изгиба в плоскости наименьшей жесткости) стального сердечника, то в запас прочности работа этой полки или стенки не учитывается.
5.5 Рассчитывать по прочности нормальные сечения следует в
зависимости от соотношения между значением относительной высоты сжатой зоны
бетона ![]() , определяемым из соответствующих
условий равновесия, и значением граничной относительной высоты сжатой зоны ξR,
при котором предельное состояние элемента наступает одновременно с достижением
в растянутой арматуре напряжения, равного расчетным сопротивлениям Rs
и Ry.
, определяемым из соответствующих
условий равновесия, и значением граничной относительной высоты сжатой зоны ξR,
при котором предельное состояние элемента наступает одновременно с достижением
в растянутой арматуре напряжения, равного расчетным сопротивлениям Rs
и Ry.
5.6 Значения ξR определяются по формуле
- для жесткой арматуры:
|
|
(5.1) |
где εst,el - относительная деформация растянутой арматуры определяется по формуле
|
εst,el = Ry/Est, |
εb2 - относительная деформация сжатого бетона при напряжениях, равных Rb, принимаемая в соответствии с СП 63.13330.2018 (пункт 6.1.20);
- для стержневой арматуры:
|
|
(5.3) |
|
εs,el = Rs/Es. |
(5.4) |
Для тяжелого бетона классов В70 - В100 и для мелкозернистого бетона в числителе формул (5.1), (5.3) вместо 0,8 следует принимать 0,7.
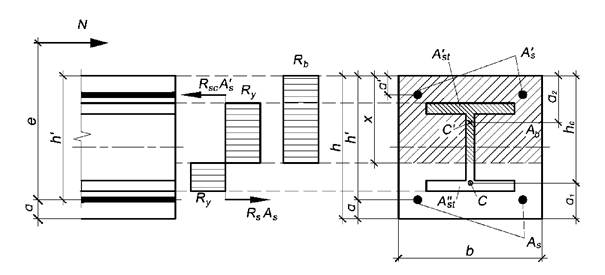
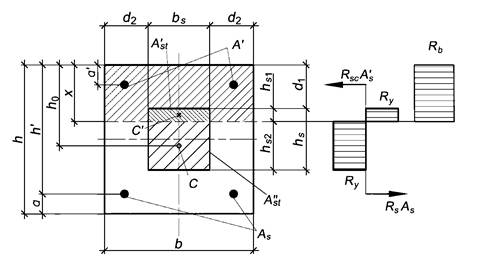
5.7 Высоту сжатой зоны х определяют:
- при ![]() (рисунок 5.1) по формуле
(рисунок 5.1) по формуле
|
|
(5.5) |
- при ![]() по формуле
по формуле
|
|
(5.6) |
Рисунок 5.1 - Схема усилий и эпюры напряжений в сечении,
нормальном
к продольной оси внецентренно сжатого сталежелезобетонного элемента
5.8 Расчет сечения сжато-изогнутого элемента по трещиностойкости
Расчет по образованию и раскрытию трещин, нормальных к продольной оси элемента, выполняется согласно СП 63.13330.2018 (пункты 8.2.14, 8.2.15).
Изгибающие моменты при образовании трещин определяются по предельному состоянию растянутого бетона. Допускается изгибающий момент приводить к эксцентрично приложенной продольной силе.
Расчет проводится на основе нелинейной деформационной модели. Изгибающие моменты Му,сrс и Mz,crc при образовании трещин, а также напряжения в растянутой арматуре после образования трещин σs и σs,crc, входящие в формулы (8.128) и (8.137) СП 63.13330.2018, вычисляются на основе диаграмм состояния бетона, арматуры и конструкционной стали. Площади сечения растянутого бетона Abt и сечения растянутой арматуры As, через которые по формуле (8.136) СП 63.13330.2018 вычисляется базовое расстояние между трещинами ls, определяются непосредственно перед образованием трещин. Значение Abt определяется при следующих ограничениях на высоту растянутой зоны: xt ≥ 2а, xt ≤ h/2, где а - расстояние от наиболее растянутой арматуры до ближайшей границы железобетонной части сечения, h - сумма высот растянутой и сжатой зон железобетонной части сечения. Значение As определяется суммой площадей Asi арматурных слоев с учетом средних по слою деформаций растяжения εi по формуле As = ΣiAsi(εi/εmax), где εmах - деформация наиболее растянутой арматуры.
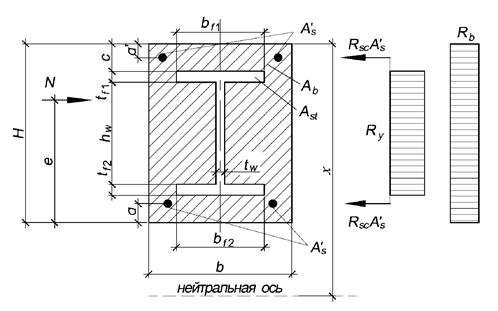
6 Определение высоты сжатой зоны прямоугольных сечений с жесткой арматурой в виде двутавра
В настоящем разделе приведены расчеты высоты сжатой зоны сечений колонн (или любых других внецентренно сжатых элементов) с жесткой арматурой в виде двутавра. Для стальной части сечения использована диаграмма работы как для идеального жескопластического материала по СП 266.1325800.2016 (подпункты 6.2.1.6 и 6.2.1.10).
В 6.1 - 6.13
приводятся формулы расчета высоты сжатой зоны внецентренно сжатых элементов при
![]() . В приложении А приведены примеры расчета сталежелезобетонных
конструкций с жесткой арматурой.
. В приложении А приведены примеры расчета сталежелезобетонных
конструкций с жесткой арматурой.
6.1 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось лежит за пределами поперечного сечения (сжатие с малым эксцентриситетом), всё поперечное сечение сжато
Расчет положения границы сжатой зоны (рисунок 6.1) выполняется по формуле
|
|
(6.1) |
Рисунок 6.1 - Сжатие с изгибом (сила ≤ показана условно)
6.2 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось не пересекает двутавр и лежит между гибкой арматурой и полкой двутавра
Расчет положения границы сжатой зоны выполняется по формуле
|
|
(6.2) |
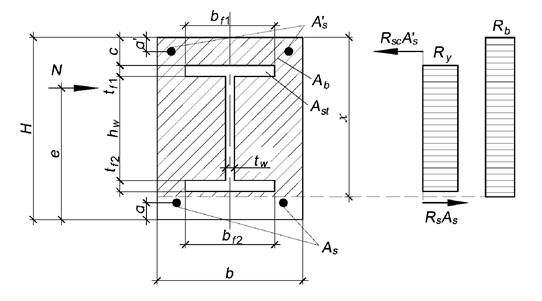
Рисунок 6.2 - Сжатие с изгибом (сила N показана условно)
6.3 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось пересекает полку двутавра, сечение двутавра работает как внецентренно сжатый тавр
Такой случай - наиболее предпочтителен при подборе поперечного сечения сталежелезобетонного элемента. В результате его реализации проектируемое сечение получается наиболее экономичным.
Если при определении значения х по формуле (6.2) окажется, что нейтральная ось пересекает профиль жесткой арматуры, а при проверке по формуле (6.3) - не пересекает профиль (весь профиль находится в сжатой зоне), то расчет следует проводить, полагая, что нейтральная ось проходит в пределах толщины нижней полки профиля жесткой арматуры (рисунок 6.3).
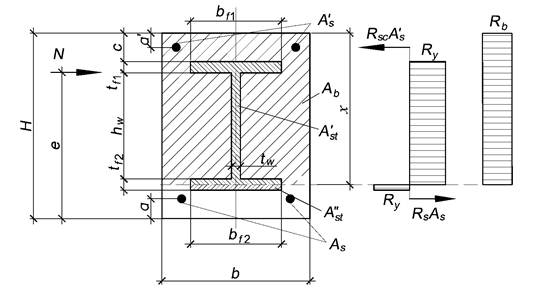
Рисунок 6.3 - Сжатие с изгибом (сила N показана условно)
6.4 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось пересекает стенку двутавра
Расчет положения границы сжатой зоны (на рисунке 6.4) выполняется по формуле
|
|
|
|
|
|
Рисунок 6.4 - Сжатие с изгибом (сила N показана условно)
6.5 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось пересекает полку двутавра, а сечение двутавра работает как внецентренно растянутый тавр
Такой случай соответствует значительным эксцентриситетам и работа сечения не может считаться оптимальной, поскольку площадь растянутого бетона значительно превышает площадь сжатого и в расчете не учитывается. Если в результате расчета расположение сжатой зоны поперечного сечения соответствует рисунку 6.5 или её высота еще меньше, следует изменить поперечное сечение элемента (развить его размер в направлении, соответствующем действию изгибающего момента, увеличить размер двутавра жесткой арматуры и т.д.).
Если при определении значения х по формуле (6.3) окажется, что нейтральная ось не пересекает профиль жесткой арматуры (весь профиль находится в растянутой зоне), а при проверке по формуле (6.4) - пересекает стенку профиля, то расчет следует производить, полагая, что нейтральная ось проходит в пределах толщины верхней (на рисунке 6.5) полки профиля жесткой арматуры.
Рисунок 6.5 - Сжатие с изгибом (сила N показана условно)
6.6 Сжатие с изгибом в плоскости стенки двутавра, когда нейтральная ось не пересекает двутавр и расположена между гибкой арматурой и полкой двутавра, весь двутавр находится в растянутой зоне
Такой случай также, как и указанный в 6.5, соответствует значительным эксцентриситетам, и работа сечения не оптимальная, поскольку площадь растянутого бетона значительно превышает площадь сжатого и в расчете не учитывается. Если в результате расчета расположение сжатой зоны поперечного сечения соответствует рисунку 6.6 или её высота еще меньше, следует изменить поперечное сечение элемента (развить его размер в направлении, соответствующем действию изгибающего момента, увеличить размер двутавра жесткой арматуры и т.д.).
Расчет положения границы сжатой зоны выполняется по формуле
|
|
(6.4) |
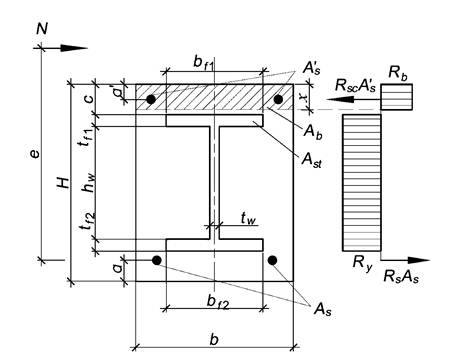
Рисунок 6.6 - Сжатие с изгибом (сила N показана условно)
6.7 Сжатие с изгибом в плоскости полок двутавра, когда нейтральная ось лежит за пределами поперечного сечения (сжатие с малым эксцентриситетом), всё поперечное сечение сжато
Расчет положения границы сжатой зоны (рисунок 6.7) выполняется по формуле (6.1).
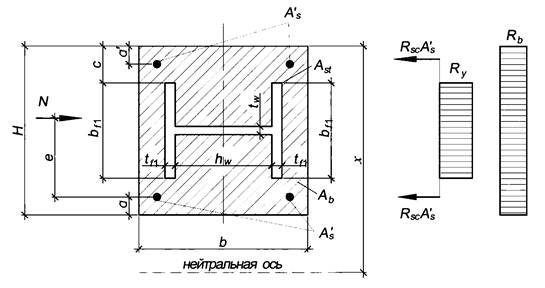
Рисунок 6.7 - Сжатие с изгибом (сила N показана условно)
6.8 Сжатие с изгибом в плоскости полок двутавра, когда нейтральная ось не пересекает двутавр и лежит между гибкой арматурой и полкой двутавра
Расчет положения границы сжатой зоны (рисунок 6.8) выполняется по формуле (6.2).
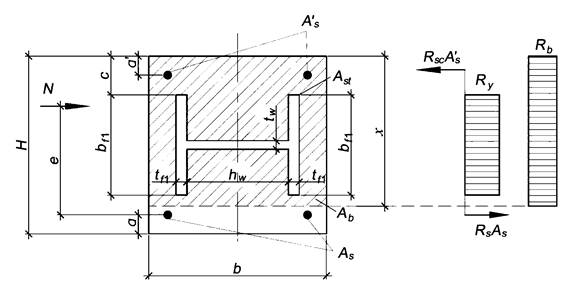
Рисунок 6.8 - Сжатие с изгибом (сила N показана условно)
6.9 Сжатие с изгибом в плоскости полок двутавра, когда нейтральная ось пересекает полки двутавра, стенка и более половины ширины полок сжаты
Этот случай (рисунок 6.9) является наиболее предпочтительным при подборе поперечного сечения сталежелезобетонного элемента. В результате его реализации проектируемое сечение получается наиболее экономичным.
Расчет положения границы сжатой зоны выполняется по формуле
|
|
(6.5) |
Рисунок 6.9 - Сжатие с изгибом (сила N показана условно)
6.10 Сжатие с изгибом в плоскости полок двутавра, когда нейтральная ось пересекает стенку двутавра, половина ширины полок сжата, половина ширины полок - растянута (стенка в работе сечения не участвует)
Если при определении величины х по формуле (6.5) окажется, что стенка профиля и большая часть полок находятся в растянутой зоне, а при проверке по формуле (6.6) - находятся в сжатой зоне, то расчет следует производить, полагая, что нейтральная ось проходит в пределах толщины стенки профиля жесткой арматуры (рисунок 6.10).
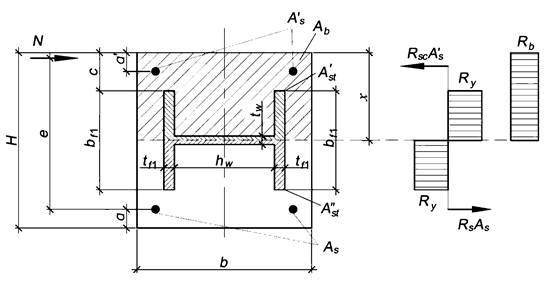
Рисунок 6.10 - Сжатие с изгибом (сила N показана условно)
6.11 Сжатие с изгибом в плоскости полок двутавра, когда нейтральная ось пересекает полки двутавра, менее половины ширины полок сжата, более половины ширины полок и стенка - растянуты
Такой случай соответствует значительным эксцентриситетам и работа сечения не может считаться оптимальной, так как растянутый бетон, занимающий большую часть поперечного сечения, не работает и не учитывается расчетом. Если по расчетам сжатая зона поперечного сечения соответствует рисунку 6.11 или еще меньше, следует изменить поперечное сечение элемента (изменить ориентацию двутавра в поперечном сечении, развить его размер в направлении, соответствующим действию изгибающего момента, увеличить номер двутавра жесткой арматуры и т.д.). Расчет положения границы сжатой зоны выполняется по формуле
|
|
(6.6) |
Рисунок 6.11 - Сжатие с изгибом (сила N показана условно)
6.12 Во всех рассмотренных случаях при конструктивном армировании As и A's значения RbAs и RbA's допускается не учитывать.
6.13 Для поперечных сечений, у которых ![]() высоту сжатой зоны следует определять
по формуле (5.6).
высоту сжатой зоны следует определять
по формуле (5.6).
7 Узлы сопряжения стальных балок с колоннами с жесткой арматурой
Опирание стальной балки на колонну с жесткой арматурой может осуществляться путем организации узла соединения с бетонной частью колонны через закладную деталь (рисунок 7.1) либо непосредственно с жесткой арматурой через стальные элементы (рисунок 7.2).
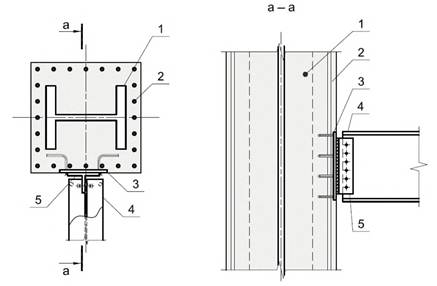
1 - жесткая арматура, 2 -
гибкая арматура,
3 - закладная деталь, 4 - стальная балка, 5 - флажок
Рисунок 7.1 - Узел соединения стальной балки с бетонной частью
сталежелезобетонной колонны через закладную деталь
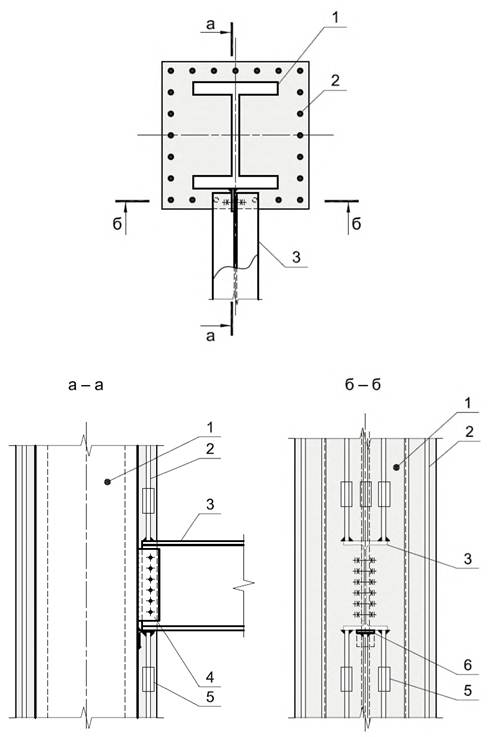
1 - жесткая арматура, 2 -
гибкая арматура, 3 - стальная балка, 4 - флажок,
5 - соединительная муфта гибкой арматуры, 6 - монтажный столик
Рисунок 7.2 - Узел соединения стальной балки с жесткой
арматурой
сталежелезобетонной колонны через стальной флажок
(хомуты и шпильки условно не показаны)
Приложение А
Примеры расчетов сталежелезобетонных конструкций с жесткой арматурой
Пример 1. Жесткая арматура в виде двутавра
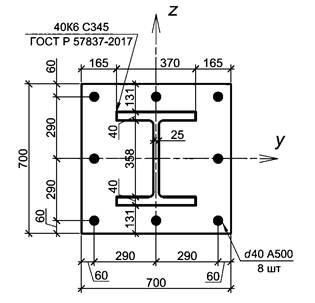
Дано: сталежелезобетонная колонна среднего этажа рамного каркаса квадратного поперечного сечения с размерами по рисунку А.1. Длина колонны - 3,0 м, опирание шарнирное несмещаемое на одном конце и жесткое на другом. Бетон класса по прочности на сжатие В30. Жесткая арматура - двутавр 40К6 по ГОСТ Р 57837-2017 из стали С345. Стержневая арматура расположена по контуру согласно рисунку А.1 - 8 шт. d40А500. Строительство в г. Москве.
Нагрузки:
- изгибающий момент в плоскости наибольшей жесткости двутавра
Му = 490,5 кНм;
- изгибающий момент в плоскости наименьшей жесткости двутавра
Mz = 196,2 кНм;
- продольная сила N = 7700,0 кН.
Все нагрузки длительные.
Требуется проверить прочность поперечного сечения.
Рисунок А.1 - Геометрические размеры поперечного сечения колонны
Записываем геометрические и прочностные характеристики элементов, формирующих поперечное сечение сталежелезобетонной колонны:
|
Rs = 435 МПа, |
εb2 = 0,0048, |
|
Rsc = 435 МПа, |
Ast = 38965 мм2, |
|
Rb = 17,0 МПа, |
bf1 = bf2 = 370 мм, |
|
Ry = 310 МПа, |
tf1 = tf2 = 40 мм, |
|
Es = 2,0·105 МПа, |
tw = 25 мм, |
|
Est = 2,06·105 МПа, |
hw = 358 мм. |
|
Eb = 32500 МПа. |
|
Площадь поперечного сечения одного стержня продольной арматуры равна 1256,1 мм2.
Момент инерции одного стержня продольной арматуры относительно собственной оси Is1 = 1,257·105 мм4.
Моменты инерции стального сердечника относительно собственной оси:
Iy,st = 128432,3·104 мм4, Iz,st = 33828,6·104 мм4.
С учетом длительности действия нагрузок расчетное сопротивление бетона осевому сжатию Rb = γb1Rb = 0,9·17,0 = 15,3 МПа.
Модуль деформации бетона с учетом длительности действия нагрузки определяем по формуле (Г.13) СП 266.1325800.2016
|
|
|
Определяем коэффициенты приведения к бетону для жесткой и гибкой арматуры по формуле (Г.18) СП 266.1325800.2016:
|
|
|
|
|
|
Выполняем проверку условия подпункта 7.1.1.3 СП
266.1325800.2016 ![]()
Радиус инерции приведенного сечения определяется по СП 266.1325800.2016 (формула (Г.15))
|
|
|
Вычисляем моменты инерции приведенного сечения элемента относительно его центра тяжести по формуле (Г.16) СП 266.1325800.2016. В рассматриваемом примере центр тяжести приведенного сечения совпадает с центром тяжести бетонной части и жесткой арматуры в связи с их симметричным расположением:
![]()
= 18089179963,6 + 128432,3·104·20,92 + 634833369,6·20,31 = 57845203347,3 мм4,
![]()
= 19035219963,6 + 33828,6·104·20,92 + 634833369,6·20,31 = 39002997439,6 мм4,
где Iу,s, Iz,s - моменты инерции стержневой арматуры относительно центра тяжести приведенного сечения, определяемые по формуле
![]()
= 8·1,257·105 + 6·1256,1·((700 - 60 - 60)/2)2 =
= 634833369,6 мм4,
Iy, Iz - моменты инерции бетонной части относительно центра тяжести приведенного сечения (с учетом вытеснения бетона арматурой), определяемые по формулам:
![]()
![]()
![]()
![]()
Определяем площадь приведенного поперечного сечения по СП 266.1325800.20 (формула (Г.17))
Ared = Ab + Astαst + (As + A's)αs =
= (b·h - Ast - As - A's) + Astαst + (As + A's)αs =
= (700·700 - 38965 - 1256,1·8) + 38965·20,92 + 1256,1·8·20,31 = 1409065,1 мм2.
Радиусы инерции приведенного сечения определяем по формулам:
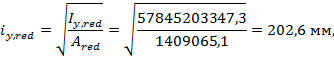
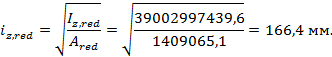
Расчетную длину элемента определяем по СП 63.13330.2018 (пункт 8.1.17)
l0 = 0,7L = 0,7·3000 = 2100 мм.
Тогда:
![]()
![]()
Согласно СП 266.1325800.2016 (подпункт 7.1.1.3), влияние прогиба на значение эксцентриситета не учитывается и коэффициент η = 1.
Определение эксцентриситетов
Определяем случайный эксцентриситет еа по СП 266.1325800.2016 (подпункт 7.1.1.5):
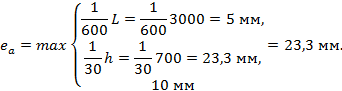
Определяем эксцентриситет е0 продольной силы для плоскостей у и z:
![]()
![]()
Будем считать, что рассматриваемая конструкция статически неопределимая, поэтому, согласно СП 266.1325800.2016 (раздел 7), полученный выше расчетным путем эксцентриситет приложения продольной силы со случайным эксцентриситетом не суммируется.
Определяем эксцентриситет приложения продольной силы относительно центра тяжести сечения растянутого стержня гибкой арматуры с учетом случайного эксцентриситета и влияния продольного изгиба согласно СП 266.1325800.2016 (подпункт 7.1.2.4):
![]()
![]()
Проверка прочности поперечного сечения элемента в плоскости наибольшей жесткости z
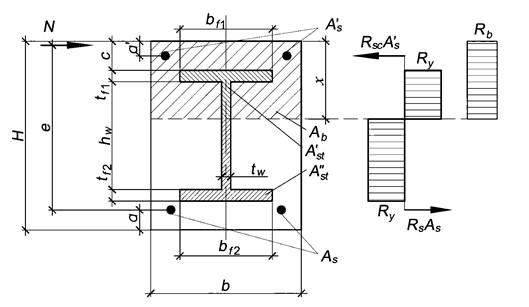
Общий вид поперечного сечения элемента при проверке прочности в плоскости наибольшей жесткости приведен на рисунке А.2.
Определяем граничную относительную высоту сжатой зоны для стального сердечника и стержневой арматуры согласно 5.6:
- для стального сердечника:
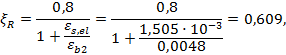
где ![]()
а - общий вид поперечного сечения; б - поперечное сечение - размеры и материалы
Рисунок А.2 - Проверка прочности поперечного сечения элемента
в плоскости наибольшей жесткости z
- для стержневой арматуры:
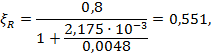
где ![]()
В качестве рабочего значения принимаем меньшее, как наиболее опасное ξR = 0,551.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.4 по формуле (6.3)
х = (N + RsAs + RbA's - RscA's - (Rb - Ry)[tw(tf1 + с) - bf1tf1] +
+ Ry[tw(hw + tf1 + c) + bf2tf2])/(Rbb + Rytw - tw(Rb - Ry)) =
= (7700·103 + 435·1256,1·3 + 15,3·1256,1·3 - 435·1256,1·3 -
- (15,3 - 310)[25·(40 + 131) - 370·40] + 310[25(358 + 40 + 131) +
+ 370·40])/(15,3·700 + 310·25 - 25·(15,3 - 310) = 516,6 мм.
Определяем расстояние от центра тяжести растянутой арматуры до растянутой грани сечения
a1 = (tw(hw + tf1 + c - x)((hw + tf1 + c - x)/2 + c1 + tf2)Ry + bf2tf2(tf2/2 +
+ c1)Ry + RsAsa)/(A"stRy + RsAs) =
= (25(358 + 40 + 131 - 516,6) (((358 + 40 + 131 - 516,6))/2 + 131 +
+ 40) 310 + 370·40(40/2 + 131)310 + 435·1256,1·3·60)/(15108,8·
·310 + 435·1256,1·3) = 128 мм,
где A"st = tw(hw + tf1 + c - x) + bf2tf2 =
= 25·(358 + 40 + 131 - 516,6) + 370·40 = 15108,8 мм2.
Рабочая высота сечения h0 = Н - а1 = 700 - 127,8 = 572,2 мм.
Определяем относительную высоту сжатой зоны
![]()
ξ = 0,903 > ξR = 0,551.
Условие ξ < ξR не выполнено, поэтому расчет высоты сжатой зоны необходимо выполнить по формуле (5.6).
Определяем высоту сжатой зоны сечения для случая ξ > ξR.
В качестве исходного значения высоты сжатой зоны будем использовать значение, полученное выше. Рабочую высоту сечения, площади сжатой и растянутой частей стального сердечника также принимаем по результатам выполненного выше расчета:
Высота сжатой зоны х определяется по формуле
![]()
= 572,2·([7700·103 - (310 - 15,3)·23856,2 - 435·1256,1·3]·
·(1 - 0,551) + (310·15108,8 + 435·1256,1·3)(1 + 0,551)))/15,3·
·700·572,2·(1 - 0,551) + 2·(310·15108,8 + 435·1256,1·3) = 348,1 мм,
где A'st = Ast - A"st = 38966 - 15108 = 23856 мм2.
Полученное значение х значительно отличается от вычисленного ранее. Соответственно отличаются и остальные параметры, используемые в качестве исходных данных при записи уравнения. Необходимо выполнить дополнительную итерацию по корректировке значения высоты сжатой зоны.
Расстояние от центра тяжести растянутой арматуры до растянутой грани сечения а1 вычисляем по формуле
a1 = tw(hw + tf1 + c - x)((hw + tf1 + c - x)/2 + c1 + tf2)Ry +
+ bf2tf2(tf2/2 + c1)Ry + RsAsa/(A"stRy + RsAs) =
= (25(358 + 40 + 131 - 348,1)((358 + 40 + 131 - 348,1)/2 + 131 + 40)310 +
+ 370·40(40/2 + 131)310 + 435·1256,1·3·60)/(19323,2·310 + 435·1256,1·3) = 151,8 мм,
где A"st = tw(hw + tf1 + c - x) + bf2tf2 =
= 25·(358 + 40 + 131 - 348,1) + 370·40 = 19323,2 мм2.
Рабочая высота сечения h0 = Н - a1 = 700 - 151,8 = 548,2 мм.
Площадь сжатой части жесткой арматуры
A'st = Ast - A"st = 38966 - 19323,2 = 19641,8 мм2
Высота сжатой зоны х определяется по формуле:
![]()
= 548,2·([7700·103 - (310 - 15,3)·19641,8 - 435·1256,1·3]·
·(1 - 0,551) + (310·19323,2 + 435·1256,1·3)(1 + 0,551)))/15,3·
·700·548,2·(1 - 0,551) + 2·(310·19323,2 + 435·1256,1·3) = 366,1 мм.
Для полученной высоты сжатой зоны определяем площади растянутой и сжатой частей жесткой арматуры:
A"st = tw(hw + tf1 + с - х) + bf2tf2 =
= 25·(358 + 40 + 131 - 366,1) + 370·40 = 18872,1 мм2.
A'st = Ast - A"st = 38966 - 18872,1 = 20092,9 мм2
Полученное значение высоты сжатой зоны близко к значению, полученному на предыдущем этапе расчета (отличие 5 %). Принимаем вычисленное значение х для дальнейших расчетов. В случае значительного отличия необходимо выполнить дополнительную итерацию по корректировке значения высоты сжатой зоны.
Определяем центр тяжести сжатого бетона относительно наиболее сжатой точки поперечного сечения
![]()
![]()
![]()
![]()
Определяем предельный момент, который может быть воспринят сечением элемента, относительно наиболее растянутого стержня гибкой арматуры
![]()
![]()
![]()
![]()
= 15,3(700·366,1 - 1256,1·3 - 20092,9)(640 - 185,6) + 435·1256,1·3·
·(640 - 60) + 310[370·40(640 - 131 - 40/2) + 25(366,1 - 131 -
- 40)(640 - 131 - 40 - (366,1 - 131 - 4)/2)] - 310[370·40·(131 +
+ 40/2 - 60) + 25(358 + 40 + 131 - 366,1)((358 + 40 + 131 - 366,l)/2 +
+ 40 + 131 - 60)] = 4711277656,5 H·мм.
Отсюда предельная продольная сила, которая может быть воспринята сечением элемента при заданном эксцентриситете
![]()
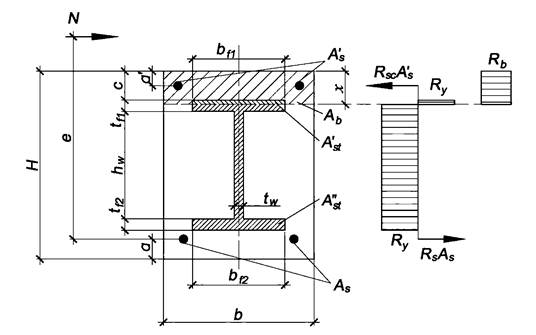
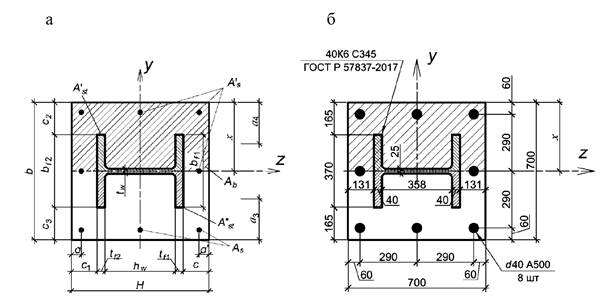
Проверка прочности поперечного сечения элемента в плоскости наименьшей жесткости у
Общий вид поперечного сечения элемента при проверке прочности в плоскости наименьшей жесткости приведен на рисунке А.3.
а - общий вид поперечного сечения; б - поперечное сечение - размеры и материалы
Рисунок А.3 - Проверка прочности поперечного сечения элемента
в плоскости наименьшей жесткости у
Определяем высоту сжатой зоны сечения применительно к случаю расчета 6.9 по формуле (6.5)
![]()
= (7700·103 + 435·1256,1·3 + 15,3·1256,1·5 - 435·1256,1·5 + 2·
·310·40·(370 + 2·165) - 2·15,3·40·165 + 358·25·(15,3 -
- 310))/(15,3·700 + 2·40·(2·310 - 15,3) = 359,2 мм.
Полученный результат свидетельствует о том, что нейтральная ось пересекает стенку двутавра, что не соответствует принятой схеме расположения нейтральной оси в поперечном сечении. Необходимо выполнить перерасчет и уточнить значение высоты сжатой зоны. Теперь, при записи уравнения равновесия полагаем, что стенка находится в растянутой зоне.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.11 по формуле (6.6)
![]()
= (7700·103 + 435·1256,1·5 + 15,3·1256,1·3 - 435·1256,1·3 +
+ 310(2·370·40 + 4·165·40 + 358·25) - 2·15,3·40·165)/(15,3·
·700 + 2·40·(2·310 - 15,3)) = 487,1 мм.
Полученный результат свидетельствует о том, что стенка двутавра находится в сжатой зоне, что не соответствует принятой схеме расположения нейтральной оси в поперечном сечении. Согласно 6.10 считаем, что нейтральная ось проходит в пределах толщины стенки профиля жесткой арматуры.
Принимаем х = 350 мм.
Центр тяжести растянутой арматуры а3 относительно растянутой грани сечения определяется по формуле
![]()
= (2·40·(370 + 165 - 350)·310·((370 + 165 - 350)/2 + 165) +
+ 435·1256,1·3·60)(2·40·(370 + 165 - 350)·310 + 435·1256,1·3) =
= 205,5 мм.
Рабочая высота сечения h0 = Н - а3 = 700 - 205,5 = 494,5 мм.
Определяем относительную высоту сжатой зоны ![]() .
.
ξ = 0,708 > ξR = 0,551.
Условие ξ < ξR не выполнено, поэтому расчет высоты сжатой зоны необходимо выполнить по формуле (5.6).
Определяем высоту сжатой зоны сечения для случая ξ > ξR.
Рассмотрим случай, когда нейтральная ось пересекает полки двутавра, стенку и более половины ширины полок сжаты по 6.13.
Высоту сжатой зоны примем равной х = 400 мм.
Центр тяжести растянутой арматуры относительно растянутой грани сечения
![]()
= (2·40·(370 + 165 - 400)((370 + 165 - 400)/2 + 165)·310 +
+ 435·1256,1·3·6)/(2·40·(370 + 165 - 400)·310 +
+ 435·1256,1·3) = 175,8 мм.
Рабочая высота сечения h0 = Н - а3 = 700 - 175,8 = 524,2 мм.
Площади сжатой и растянутой частей жесткой арматуры:
A"st = 2·tf1·(bf1 + с2 - х) = 2·40·(370 + 165 - 400) = 10800 мм2.
A'st = Ast - A"st = 38965 - 10800 = 28165 мм2.
Высота сжатой зоны
![]()
= 524,2([7700·103 - (310 - 15,3)·28165 - 435·1256,1·5](1 - 0,551) +
+ (310·10800 + 435·1256,1·3)(1 + 0,551))/(15,3·700·524,2·
·(1 - 0,551) + 2·(310·10800 + 435·1256,1·3)) = 261,5 мм.
Полученный результат свидетельствует о том, что стенка двутавра находится в растянутой зоне, что не соответствует принятой схеме расположения нейтральной оси в поперечном сечении. Необходимо выполнить перерасчет и уточнить значение высоты сжатой зоны. Теперь, при записи уравнения равновесия будем полагать, что стенка находится в растянутой зоне.
Рассмотрим случай, когда нейтральная ось пересекает полки двутавра, менее половины ширины полок сжата, более половины ширины полок и стенка - растянуты (6.11).
Высоту сжатой зоны принимаем равной значению, вычисленному на предыдущем этапе расчета х = 261,5 мм.
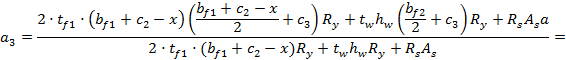
= (2·40·(370 + 165 - 261,5)((370 + 165 - 261,5)/2 + 165)·310 +
+ 25·358·(370/2 + 165)·310 + 435·1256,1·5·60)/(2·40·(370 + 165 -
- 261,5)·310 + 25·358·310 + 435·1256,1·5) = 258,9 мм,
где As = 1256,1·5 = 6280,5 мм2.
Рабочая высота сечения h0 = Н - а3 = 700 - 258,9 = 441,1 мм.
Площади сжатой и растянутой частей жесткой арматуры:
A'st = 2tf1(x - с2) = 2·40·(261,5 - 165) = 7721,8 мм2,
A"st = Ast - A'st = 38965 - 7721,8 = 31243,2 мм2.
Высота сжатой зоны
![]()
= 441,1([7700·103 - (310 - 15,3)·7721,8 - 435·1256,1·3](1 - 0,551) +
+ (310·31243,2 + 435·1256,1·5)(1 + 0,551))/(15,3·700·441,1·
·(1 - 0,551) + 2·(310·31243,2 + 435·1256,1·3)) = 497,7 мм.
Полученный результат свидетельствует о том, что стенка двутавра находится в сжатой зоне, что не соответствует принятой схеме расположения нейтральной оси в поперечном сечении. Принимаем, что нейтральная ось проходит в пределах толщины стенки профиля жесткой арматуры.
Принимаем х = 350 мм.
Определяем центр тяжести сжатого бетона относительно наиболее сжатой точки поперечного сечения
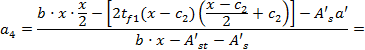
= (700·350·350/2 - [2·40·(350 - 165)((350 - 165)/2 + 165)] -
- 1256,1·3·60)/(700·350 - 14800 - 1256,1·3) = 171,5 мм.
где A'st = 2tf1(x - с2) = 2·40·(350 - 165) = 14800 мм2.
Определяем предельный момент, который может быть воспринят сечением элемента, относительно наиболее растянутого стержня гибкой арматуры
![]()
![]()
= 15,3(700·350 - 1256,1·3 - 14800)(640 - 171,5) +
+435·1256,1·3(640 - 60) + 310·[2·40·(350 - 165)(640 - 165 -
- (350 - 165)/2)] - 310·[2·40(370 + 165 - 350)(640 - 350 -
- (370 + 165 - 350)/2)] = 3422521395,8 Н·мм.
Отсюда предельная продольная сила, которая может быть воспринята сечением элемента при заданном эксцентриситете
![]()
Определяем предельное значение продольной силы, которое может быть воспринято элементом по СП 266.1325800.2016 (формуле (7.4))
![]()
![]()
где φ = 0,92 согласно СП 266.1325800.2016 (таблица 7.1);
Ab = bh - Ast - As,tot = 700·700 - 38965 - 8·1256,1 = 440986,2 мм2.
Выполняем проверку прочности по формуле (7.3) СП 266.1325800.2016:
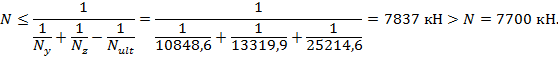
Прочность поперечного сечения колонны обеспечена.
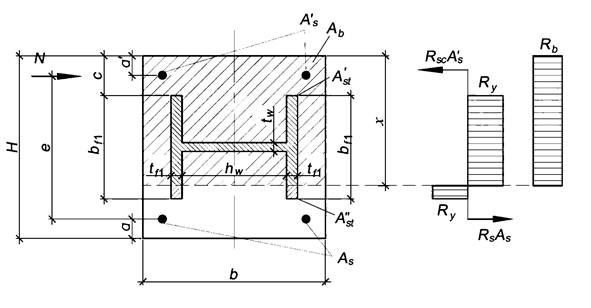
Пример 2. Жесткая арматура в виде сердечника сплошного сечения
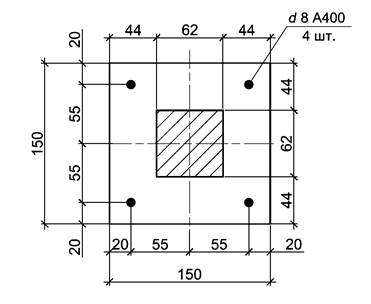
Дано: сталежелезобетонная колонна среднего этажа рамного каркаса квадратного поперечного сечения с размерами по рисунку А.4. Длина колонны - 0,6 м, шарнирное опирание на двух концах. Бетон класса по прочности на сжатие В80. Жесткая арматура - стальной сердечник квадратного сечения 62×62 мм из стали С255. Стержневая арматура - 4 шт. d8А400. Строительство в г. Москве.
Нагрузки:
- изгибающий момент
Му = 14 кНм;
- продольная сила N = 650 кН.
Все нагрузки длительные.
Требуется проверить прочность поперечного сечения.
Рисунок А.4 - Геометрические размеры поперечного сечения колонны
Записываем геометрические и прочностные характеристики элементов, формирующих поперечное сечение сталежелезобетонной колонны:
Rs = 400 МПа,
Rsc = 400 МПа,
Rb = 57,0 МПа,
Ry = 245 МПа,
Es = 2,0·105 МПа,
Est = 2,06·105 МПа,
Eb = 42000 МПа,
Ast = 3844 мм2.
Значение относительной деформации εb2 для высокопрочного бетона В80 определяем по 6.1.20 СП 63.13330.2018
![]()
Площадь поперечного сечения растянутой арматуры
As = 50,3·2 = 100,6 мм2.
Площадь поперечного сечения сжатой арматуры
A's = 50,3·2 = 100,6 мм2.
Момент инерции одного стержня продольной арматуры относительно собственной оси Is1 = 201,0 мм4.
Моменты инерции стального сердечника относительно собственной оси:
Iу,st = Iz,st = 1231361,3 мм4.
С учетом длительности действия нагрузок расчетное сопротивление бетона осевому сжатию Rb = γb1Rb = 0,9·57 = 51,3 МПа.
Модуль деформации бетона с учетом длительности действия нагрузки определяем по формуле (Г.13) СП 266.1325800.2016
![]()
Определим коэффициенты приведения к бетону для жесткой и гибкой арматуры по формуле (Г.18) СП 266.1325800.2016:
![]()
![]()
Выполняем проверку условия подпункта 7.1.1.3 СП
266.1325800.2016 ![]()
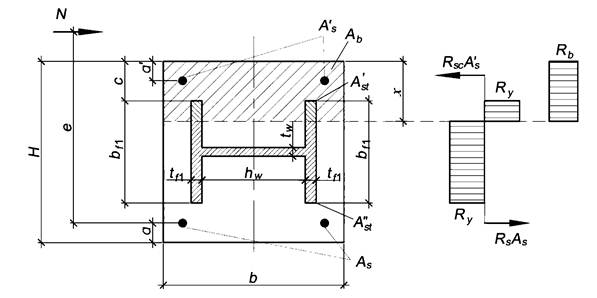
Условные обозначения геометрических размеров приведены на рисунке А.5.
Радиус инерции приведенного сечения определяется по СП 266.1325800.2016 (формуле (Г.15))
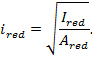
Вычисляем моменты инерции приведенного сечения элемента относительно его центра тяжести по СП 266.1325800.2016 (формула (Г.16)). В рассматриваемом примере центр тяжести приведенного сечения совпадает с центром тяжести бетонной части и жесткой арматуры в связи с их симметричным расположением, моменты инерции равны):
Iy,red = Iz,red = I + Istαst + Is αs =
= 40346704,4 + 1231361,3·11,77 + 609434,3·11,43 = 61805661 мм4,
где Is - моменты инерции стержневой арматуры относительно центра тяжести приведенного сечения:
![]()
![]()
I - момент инерции бетонной части относительно центра тяжести приведенного сечения (с учетом вытеснения бетона арматурой)
![]()
Определяем площадь приведенного поперечного сечения по СП 266.1325800.20 (формула (Г.17)):
Ared = Ab + Astαst + (As +A's)αs =
= (b·h - Ast - As - A's) + Astαst + (As + A's)αs =
= (150·150 - 3844 - 100,6·2) + 3844·11,77 + 100,6·2·11,43 =
= 65998 мм2.
Рисунок A.5 - Проверка прочности поперечного сечения элемента
Радиус инерции приведенного сечения
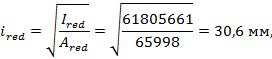
Расчетную длину элемента определяем по СП 63.13330.2018 (пункт 8.1.17)
l0 = 1L = 1·600 = 600 мм.
Тогда:
![]()
Согласно СП 266.1325800.2016 (подпункт 7.1.1.3), влияние прогиба на значение эксцентриситета следует учитывать.
Определение эксцентриситетов
Определим случайный эксцентриситет еа согласно СП 266.1325800.2016 (подпункт 7.1.1.5):
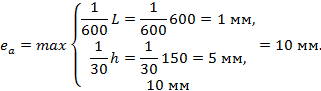
Определяем эксцентриситет е0 продольной силы для плоскостей у и z:
![]()
ey = ea = 10,0 мм.
Для вычисления коэффициента, учитывающего влияние продольного изгиба элемента на его несущую способность η, необходимо определить характеристики приведенного сечения по Г.2 СП 266.1325800.2016.
Коэффициенты:
- δе - относительное значение эксцентриситета продольной силы вычисляем по формуле
![]()
- φl - коэффициент, учитывающий влияние длительности действия нагрузки определяем по формуле
![]()
- ![]()
- ks = 0,7.
Определяем жесткость сталежелезобетонного элемента в предельной по прочности стадии по СП 266.1325800.2016 (формула (Г.11)):
D = kbEb1I + ks(EsIs + EstIst) =
= 0,167·17500·40346704 + 0,7(200000·609434 + 206010·1231361) =
= 380569606365 Н·мм2.
Условная критическая сила согласно СП 266.1325800.2016 (формула (7.7))
![]()
Коэффициент, учитывающий влияние продольного изгиба элемента на его несущую способность η, и определяемый по СП 266.1325800.2016 (подпункт 7.1.2.5)
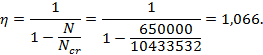
Определяем эксцентриситет приложения продольной силы относительно центра тяжести сечения растянутого стержня гибкой арматуры с учетом случайного эксцентриситета и влияния продольного изгиба согласно СП 266.1325800.2016 (подпункт 7.1.2.4):
![]()
![]()
Проверка прочности поперечного сечения элемента в плоскости наибольшей жесткости z
Определяем граничную относительную высоту сжатой зоны для стального сердечника и стержневой арматуры по формулам (5.1) и (5.2):
- для стального сердечника:
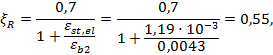
где ![]()
- для стержневой арматуры:
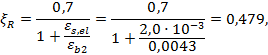
где ![]()
В качестве рабочего значения принимаем меньшее, как наиболее опасное ξR = 0,479.
Определяем высоту сжатой зоны сечения, предполагая, что часть сердечника сжата, часть растянута на основании СП 266.1325800.2016 (подпункт 7.1.2.2):
N = Rb(b·d1 + 2d2(x - d1) - A's) + Rybs(x - d1) - Rybs(hs - (x - d1) + RscA's - RsAs,
![]()
= (650000 - 51,3(150·44 - 2·44·44 - 100,6) + 245·62(2·44 + 62) -
- 400·100,6 + 400·100,6)/(2(51,3·44 + 245·62) = 80,0 мм.
Определяем относительную высоту сжатой зоны. Влиянием продольной арматуры на конечный результат пренебрежем, т.к. ее площадь мала по отношению к площади жесткой арматуры. Расстояние до центра тяжести растянутого волокна стального сечения:
![]()
![]() .
.
ξ = 0,86 > ξR = 0,479.
Тогда, согласно формуле (5.6)
![]()
![]()
x = ([650000 - (245 - 51,3)(x - 44)62 - 400·100,6](1 - 0,479) +
+ (245·62(44 + 62 - x) + 400·100,6)(1 + 0,479))/(51,3·150(1 + 0,479) +
+ (x + 44 + 62)(51,3·62(44 + 62 - x) + 400·100,6).
Решением данного уравнения является х = 60,1 мм.
Сжатая зона находится внутри сердечника.
Расстояние до центра тяжести растянутого волокна стального сечения:
![]()
Определяем предельный момент, который может быть воспринят сечением элемента, относительно центра тяжести растянутого сечения жесткой арматуры
My.ult = Rbbd1(h0 - d1/2) + Rb(b - bs)(x - d1)(h0 - (x + d1)/2) + RscA's(h0 - d1) + Rybs(x - d1)hs/2) =
= 51,3·150·44(83,05 - 44/2) + 51,3(150 - 62)(60,1 - 44)·
·(83,05 - (60,1 + 44)/2) + 400·100,6(83,05 - 44) + 245·62·(60,1 - 44)62/2 = 33026148 H·мм.
Так как сечение симметричное, предельный момент Mz,ult = My,ult.
Уточняем эксцентриситет приложения продольной силы
ez1 = е0η + (h0 - h/2) = 21,5·1,066 + 83,05 - 75 = 31,0 мм,
еу1 = 10·1,066 + 83,05 - 75 = 18,7 мм.
Отсюда предельная продольная сила, которая может быть воспринята сечением элемента при заданном эксцентриситете:
![]()
![]()
Определяем предельное значение продольной силы, которая может быть воспринята элементом по СП 266.1325800.2016 (формула (7.4)):
![]()
![]()
+ 400(100,6 + 100,6) + 245·62·62) = 2140 кH,
где φ = 0,92 согласно СП 266.1325800.2016 (таблица 7.1) φ = 0,92.
Выполняем проверку прочности по СП 266.1325800.2016 (формула (7.3)):
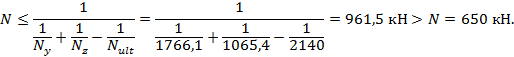
Прочность поперечного сечения колонны обеспечена.
Библиография
[1] Травуш В.И. Отечественный и зарубежный опыт исследований работы сталежелезобетоных конструкций на внецентренное сжатие. - Травуш В.И., Конин Д.В., Рожкова Л.С., Крылов А.С. // Строительство и реконструкция. - Орел, 2016. - № 5 (67). С. 31 - 44.
[2] Травуш В.И. Экспериментальные исследования сталежелезобетонных конструкций, работающих на внецентренное сжатие. Травуш В.И., Конин Д.В., Рожкова Л.С., Крылов А.С., Каприелов С.С., Чилин И.А., Мартиросян А.С., Фимкин А.И. // Academia. Архитектура и строительство. - Москва, 2016. - № 3. С. 127 - 135.
[3] Травуш В.И. Экспериментальные исследования сталежелезобетонных конструкций, работающих на изгиб. Травуш В.И., Конин Д.В., Крылов А.С., Каприелов С.С., Чилин И.А. // Строительство и реконструкция. - Орел. 2017. - № 4 (72). С. 63 - 71.
[4] Травуш В.И. Определение несущей способности на сдвиг контактной поверхности «сталь-бетон» в сталежелезобетонных конструкциях для бетонов различной прочности на сжатие и фибробетона. Травуш В.И., Каприелов С.С., Конин Д.В., Крылов А.С., Кашеварова Г.Г., Чилин И.А. //Строительство и реконструкция. - Орел, 2016. - № 4 (66). С. 45 - 55.
[5] Карпенко Н.И. Общие модели механики железобетона. - Карпенко Н.И. - М.: Стройиздат. - 1996. - 416 с.
[6] Мурашкин Г.В. Моделирование диаграммы деформирования бетона и схемы напряженно-деформированного состояния. - Мурашкин Г.В., Мурашкин В.Г. - Известия высших учебных заведений. Строительство. - 1997. № 10. - С. 4 - 6.
[7] Десяткин М.А. Расчет сталежелезобетонной колонны высотного дома на косое внецентренное сжатие. - Десяткин М.А., Конин Д.В., Мартиросян А.С., Травуш В.И. // Жилищное строительство. - Москва: 2015. - № 5. С. 92 - 95.
[8] Мухамедиев Т.А. Расчет прочности сталежелезобетонных колонн с использованием деформационной модели. - Мухамедиев Т.А., Старчикова О.И. - Бетон и железобетон. - 2006. № 4. - С. 18 - 21.
[9] Карпенко Н.И. К расчёту прочности, жёсткости и трещиностойкости внецентренно сжатых железобетонных элементов с применением нелинейной деформационной модели. - Карпенко Н.И., Соколов Б.С., Радайкин О.В. - Известия Казанского государственного архитектурно-строительного университета. - 2013. № 4(26). - С. 113 - 120.
[10] Рекомендации по учёту ползучести и усадки бетона при расчёте бетонных и железобетонных конструкций. НИИЖБ Госстроя СССР, Москва, Стройиздат, 1988, 120 с.
[11] Арленинов, П.Д. Крылов С.Б. Современное состояние нелинейных расчетов железобетонных конструкций // Сейсмостойкое строительство. Безопасность сооружений. - № 3, - 2017 - С. 50 - 53.
[12] Арленинов, П.Д. Крылов С.Б. Опыт совместного использования уравнений теории ползучести и современных программных расчетных комплексов // Бетон и железобетон. - № 3. - 2013 - С. 9 - 10.
|
Ключевые слова: конструкции сталежелезобетонные, жесткая арматура, расчет сталежелезобетонных конструкций, надежность, прочность, трещиностойкость, колонны, устойчивость, стальной сердечник, внецентренное сжатие, косой изгиб, сжатие |