ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ
СОВЕТА МИНИСТРОВ СССР
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МЕТОДИКА ВЫБОРА И ОПТИМИЗАЦИИ
КОНТРОЛИРУЕМЫХ ПАРАМЕТРОВ
ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
РДМУ 109-77
МОСКВА ИЗДАТЕЛЬСТВО СТАНДАРТОВ
1978
РАЗРАБОТАНА Горьковским филиалом Всесоюзного научно-исследовательского института по нормализации в машиностроении (Гф ВНИИНМАШ)
Директор филиала канд. техн. наук Скворцов Т.П.
Зам. директора по научной работе Шолкин В.Г.
Нач. отдела Данилов Н.Г.
Руководитель темы ответственный исполнитель мл. науч. сотрудник Белов Л.П.
ПРИ УЧАСТИИ Всесоюзного научно-исследовательского института по нормализации в машиностроении (ВНИИНМАШ)
Директор института канд. техн. наук Грешников В.А.
Зам. директора по научной работе канд. техн. наук Герасимов Н.Н.
Зав. отделом канд. техн. наук Амиров Ю.Д.
Зам. зав. отделом Яновский Г.А.
ВНЕСЕНА Горьковским филиалом Всесоюзного научно-исследовательского института по нормализации в машиностроении (Гф ВНИИНМАШ)
Директор филиала канд. техн. наук Скворцов Т.П.
ПОДГОТОВЛЕНА К УТВЕРЖДЕНИЮ Техническим Управлением Государственного комитета стандартов Совета Министров СССР
Начальник Технического управления Лямин Б.Н.
Гл. технолог Технического управления Башкирова Н.Т.
УТВЕРЖДЕНА И ВВЕДЕНА В ДЕЙСТВИЕ Постановлением Государственного комитета стандартов Совета Министров СССР от 19 декабря 1977 г. № 2928. Срок введения 1 июля 1978 г.
В настоящей методике рассматривается применение метода планирования активного эксперимента для построения математической модели при выборе контролируемых параметров технологических процессов независимо от их физической природы.
Методология эксперимента позволяет успешно решать наиболее важные для исследователя вопросы: определять количество опытов, которые следует провести, каким образом обрабатывать их результаты, чтобы решить поставленную задачу при минимальном числе опытов.
Методика устанавливает правила выбора контролируемых параметров технологических процессов при их разработке и оптимизации действующих процессов.
Методика предназначена для работников научно-исследовательских институтов, конструкторских бюро и инженеров-технологов предприятий, занимающихся разработкой, исследованием и совершенствованием действующих технологических процессов.
ВВЕДЕНИЕ
В современных условиях машиностроение играет решающую роль в развитии экономики страны (его продукция - более 50 тыс. наименований машин, аппаратов, приборов, оборудования для всего народного хозяйства). В отрасли сконцентрированы огромные ресурсы: пятая часть основных фондов всей промышленности, более трети рабочих, около 25 % объема валовой продукции. Затраты на развитие и внедрение мероприятий по новой технике составляют 35 % соответствующих затрат всей промышленности. Ежегодно в машиностроении разрабатываются десятки тысяч различных конструкций. Разработка конструкций важный, но лишь первый шаг в создании изделий. Реализация идей, заложенных в проекте, зависит от уровня технологии производства. Поиск путей осуществления проекта - главная задача технологической подготовки производства. При этом перед коллективом каждого машиностроительного и приборостроительного завода стоят следующие задачи:
обеспечение выпуска качественной продукции, соответствующей утвержденным чертежам и техническим условиям;
выявление и предупреждение брака;
разработка и внедрение мероприятий, направленных на улучшение качества продукции.
Для решения этих взаимосвязанных задач следует повысить роль технического контроля при создании изделий. Если учесть, что в стране в течение года появляется около 150 тыс. видов новой продукции, то можно представить масштабы трудовых затрат на разработку технологических процессов, в том числе технического контроля.
Известно, что 60 % затрат на освоение новых изделий связано с проектированием и изготовлением технологической оснастки, а трудоемкость разработки процессов технического контроля составляет до 25 % от общей трудоемкости разработки технологического процесса.
В настоящее время в народном хозяйстве в эксплуатации находится около 800 млн. средств измерений. Ежегодно на измерения затрачивается около 20 млрд. руб. Как подсказывает практика, необходимо внедрять более эффективные методы измерения и контроля качества продукции. Повышение эффективности контроля заключается в увеличении его надежности и производительности труда при контрольных работах, а также при снижении их себестоимости. Большое значение при этом играет правильный выбор контролируемых параметров, особенно для контроля сложных технологических процессов сложных видов изделий.
В настоящей методике устанавливают правила, необходимые для обоснованного выбора контролируемых параметров при разработке и совершенствовании действующих технологических процессов в машиностроении и приборостроении на основе методов планирования эксперимента.
Внедрение статистических методов планирования эксперимента позволяет в значительной степени исключить интуитивный подход, заменить его научно обоснованной программой проведения экспериментального исследования, включающей объективную оценку результатов эксперимента на всех последовательных этапах исследования.
Основная задача исследования при планировании эксперимента - оптимизация, заключающаяся в нахождении совокупности варьируемых факторов, при которых выбранная целевая функция (параметр оптимизации) принимает экстремальное значение, решается оптимальным образом. При этом осуществляется минимальное число опытов, позволяющее произвести на каждом этапе надежную статистическую оценку.
Даже при неполном знании механизма изучаемого процесса направленным экспериментом можно получить математическую модель, включающую наиболее значимые факторы технологического процесса независимо от их физической природы. Такая модель может быть с успехом применена для нахождения необходимых режимов работы процесса и управления им.
Цель настоящей методики - применение на практике инженерами-технологами методов планирования экспериментов для получения линейной математической модели при определении контролируемых параметров сложных технологических процессов.
Задача выбора контролируемых параметров состоит в определении значимых факторов, определяющих ход технологического процесса, с целью последующего систематического контроля. При решении поставленной задачи необходимы следующие условия:
решения должны иметь определенные ограничения, так как они допускают оптимизацию только одного параметра детали, сборочной единицы или процесса;
процесс должен быть задан множеством факторов;
каждый фактор должен быть управляем;
результаты опытов должны воспроизводиться;
опыты равноценны, т.е. различием в стоимости можно пренебречь;
математическая модель заранее неизвестна.
По данной методике могут быть решены задачи с числом факторов от двух до тридцати одного. Для построения математических моделей применяют полный или дробный факторный план эксперимента, обладающий оптимальной матрицей планирования.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Настоящая методика устанавливает:
правила построения линейной и неполной квадратичной математической модели технологических процессов и проверки ее адекватности, т.е. пригодности;
правила выбора контролируемых параметров технологических процессов.
1.2. Настоящая методика обеспечивает объективный выбор контролируемых параметров технологических процессов в предположении справедливости линейной и неполной квадратичной модели процесса (отсутствие квадратичных эффектов) при определенных пределах изменения параметров, влияющих на показатель параметра оптимизации.
1.3. Методика определяет выбор контролируемых параметров, которые входят в общую оценку эффективности функционирования технологического процесса, в соответствии с техническими условиями, в заданный период времени, при заданных условиях эксплуатации.
1.4. Выбранные в соответствии с настоящей методикой контролируемые параметры являются исходными данными для выбора методов и средств контроля.
1.5. Полученная совокупность контролируемых параметров вносится в соответствующую нормативно-техническую документацию и после этого технологический процесс контролируют по всем внесенным показателям.
1.6. Кроме контролируемых параметров, выбранных в соответствии с настоящей методикой, допускается, при необходимости, включать в нормативно-техническую документацию дополнительные параметры.
1.6.1. Выбор дополнительных параметров обусловливается более полной характеристикой технологического процесса.
1.6.2. Номенклатура дополнительных параметров определяется спецификой технологических процессов каждой отрасли.
1.7. Настоящей методикой можно пользоваться при разработке технологических процессов и оптимизации действующих технологических процессов серийного и массового производства.
1.8. Термины и определения понятий, применяемых в настоящей методике, приведены в приложении 1.
2. ЦЕЛИ И ЗАДАЧИ ПРИМЕНЕНИЯ МЕТОДА
2.1. Цели применения метода
2.1.1. Основная цель метода - обеспечить объективный выбор контролируемых параметров технологического процесса.
2.1.2. Цель выбора контролируемых параметров - сократить до минимума контролируемые параметры при обеспечении высокого качества выпускаемой продукции. Это достигается за счет определения коэффициентов влияния факторов исследуемого процесса.
2.2. Задачи применения метода
2.2.1. Выбор контролируемых параметров определен как разработка метода определения коэффициентов влияния параметров на показатель параметра оптимизации.
2.2.2. Вычисление коэффициентов влияния процесса связано с построением линейной математической модели и проверкой ее адекватности. Эту задачу решают на основе теории планирования эксперимента.
2.2.3. Построение математической модели технологического процесса в зависимости от поставленной задачи, кроме выбора контролируемых параметров, может преследовать следующие цели:
по входу процесса: минимизировать расход материалов на единицу выпускаемой продукции при сохранении качества выпускаемой продукции, т.е. произвести замену дорогостоящих материалов на недорогостоящие или дефицитных на распространенные;
по процессу: при сохранении качества выпускаемой продукции сократить время обработки в целом или на отдельных операциях, перевести отдельные режимы в некритические зоны, повысить производительность труда, т.е. снизить трудовые затраты на единицу продукции и т.д.;
по показателю параметра оптимизации: улучшить частные показатели и общее количество готовой продукции, повысить однородность качества и надежности деталей, сборочных единиц;
по процессу управления: увеличить надежность и быстродействие управления; снизить ошибки контроля за счет внедрения новых методов и средств контроля.
3. ПРАВИЛА ВЫБОРА КОНТРОЛИРУЕМЫХ ПАРАМЕТРОВ ПРИ РАЗРАБОТКЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
3.1. Выбор параметров оптимизации
3.1.1. За параметр оптимизации принимают показатель качества детали, сборочной единицы или технологического процесса по каждой операции отдельно.
Например, при термической обработке распределительного вала за параметр оптимизации принимают твердость поверхности термически обработанного вала.
3.1.2. Параметр оптимизации должен соответствовать следующим требованиям:
параметр должен измеряться при любом изменении (комбинации) режима технологического процесса, т.е. показатель параметра должен находиться опытным путем в виде некоторого числа принятых для данной величины единиц измерения;
параметр должен быть статистически эффективным, т.е. измеряться с наибольшей точностью, что позволяет сократить до минимума дублирование опытов;
параметр должен быть информационным, т.е. всесторонне характеризовать технологический процесс;
параметр должен иметь физический смысл, т.е. должна быть возможность достижения полезных результатов определенного свойства детали, сборочной единицы в соответствующих условиях процесса;
параметр должен быть однозначным, т.е. должно максимизироваться либо минимизироваться только одно свойство детали, сборочной единицы или процесса.
3.1.3. Параметры оптимизации в зависимости от типа контролируемых параметров и признаков качества деталей, сборочных единиц или технологического процесса могут быть:
пространства и времени (длина, время, площадь, объем, линейная скорость, угловая скорость, линейное ускорение и т.д.);
механические [масса, плотность, сила, момент силы (пары сил), работа, энергия, мощность, давление, удельный, вес, динамическая вязкость, кинематическая вязкость и т.д.];
электрические и магнитные (количество электричества, электрический заряд, плотность электрического тока, линейная плотность электрического тока, объемная плотность электрического заряда, удельное электрическое сопротивление, напряженность магнитного поля, магнитный поток и т.д.);
тепловые (температура, количество теплоты, тепловой поток, теплоемкость и энтропия, удельные теплоемкость и энтропия, поверхностная плотность теплового потока, коэффициенты теплообмена и т.д.);
акустические (звуковое давление, объемная скорость, акустическое сопротивление, интенсивность звука и т.д.);
световые величины энергетической фотометрии (световой поток, световая энергия, светимость, освещение, яркость и т.д.);
радиоактивности и ионизирующих излучений (поглощенная доза излучения, мощность поглощенной дозы излучения, интенсивность излучения и т.д.);
качественные (внешний вид детали, сборочной единицы и т.д.).
3.1.4. Любой параметр должен быть ограничен пределами допусков, в которых проводится оптимизация.
3.1.5. Параметры оптимизации обозначают символом Y, в действительности соответствующие определенному показателю детали, сборочной единицы или технологического процесса, узаконенных единиц измерений.
3.2. Выбор фактов процесса, влияющих на показатель параметра оптимизации
3.2.1. За фактор принимают контролируемую переменную объекта, т.е. величину, характеризующую то или иное свойство процесса или режим работы какого-либо устройства, установки и являющуюся основным показателем этого устройства. Эта величина, числовое значение которой измеряется в пределах (границах) изменения, должна влиять на параметр оптимизации.
3.2.2. При определении величин количественных оценок во внимание должны приниматься только те факторы, которые имеют четкий метрологический смысл.*
* Под метрологическим смыслом следует иметь в виду: возможность измерения фактора с определенной точностью конкретным измерительным прибором; возможность изменения фактора в конкретных условиях в пределах его допуска.
3.2.3. Состав факторов технологического процесса определяется разработчиком или действующим технологическим процессом.
3.2.4. Факторы технологического процесса обозначают символом X.
3.2.5. Границы изменения факторов объекта определяют так, чтобы обеспечить условия физической реализации переменных факторов, т.е. нормальный ход технологического процесса с ожидаемым показателем параметра оптимизации. Связь параметра оптимизации Y с технологическими факторами процесса Х1, Х2, ..., Хк в общем виде можно записать:
Y = f(Х1, Х2, ..., Хк).
3.2.6. Факторы технологического процесса должны соответствовать следующим требованиям:
факторы должны быть управляемыми, т.е. позволяющими экспериментатору устанавливать требуемое значение фактора и поддерживать постоянным это значение в течение опыта;
для любой пары факторов должно выполняться условие совместимости, т.е. такое условие, при котором возможное взаимное влияние факторов не должно вызывать нарушение технологического процесса или качества конечного продукта;
факторы должны быть независимыми, т.е. должна быть возможность установления фактора на любом уровне независимо от уровней других факторов;
факторы должны быть однозначны, т.е. не являться функцией других факторов;
факторы должны непосредственно воздействовать на параметр оптимизации;
факторы должны быть определены операционально, т.е. должна быть определена последовательность действий (операций), при помощи которых устанавливаются действительные значения уровней факторов;
точность установления граничных значений факторов должна быть максимально высокой, т.е. отклонение действительного значения фактора от заданного номинального значения не должно превышать погрешности прибора.
3.2.7. Факторы технологического процесса так же, как и параметры оптимизации могут быть пространства и времени, механические, электрические, магнитные, тепловые, акустические, световые величины энергетической фотометрии, радиоактивности и ионизирующих излучений, качественные.
3.2.8. После выбора управляемых факторов технологического процесса и параметра оптимизации детали или сборочной единицы проводят подготовку к проведению полного факторного эксперимента (см. подраздел п. 3.3) или дробного факторного эксперимента (см. подраздел п. 3.4).
3.3. Полный факторный эксперимент (ПФЭ), равный 2k
3.3.1. Полный факторный эксперимент целесообразно проводить в том случае, если он по времени непродолжителен и требует небольших затрат.
3.3.2. В эксперимент включают Х1, Х2, ..., Хк или K - факторов, для каждого из которых следует установить только два уровня: верхний и нижний, например фактор Х1 - температура заливки металла в форму равна 1600 - 1750°, фактор Х2 - выдержка отливки в форме в течение 15 - 20 мин и т.д. У фактора Х1 нижний уровень равен 1600 °С, верхний уровень - 1750 °С, всего два уровня и т.д.
3.3.3. Поскольку факторы процесса неоднородны и имеют различные единицы измерения, а числа, выражающие величины факторов, имеют различные порядки, их следует привести к единой системе счисления путем перехода от действительных значений факторов к кодированным по формулам:
![]() (1)
(1)
где Xi осн - основной уровень (определенный для каждого фактора),
Xi max - верхний уровень (определенный для каждого фактора),
Xi min - нижний уровень (определенный для каждого фактора),
2 - число уровней,
i - номер фактора;
![]() (2)
(2)
где DХi - интервал варьирования (определенный для каждого фактора),
![]() (3)
(3)
где ![]() - кодированное значение
фактора, вычисляемое по формуле.
- кодированное значение
фактора, вычисляемое по формуле.
3.3.4. Рассчитанные значения действительных значений факторов процесса, вычисленные по формулам (1 - 3), записывают в табл. 1.
Таблица 1
Исследуемые факторы в действительных значениях
|
Факторы процесса в единицах измерения |
|||||
|
t, °С |
мин |
|
|
|
|
|
Верхний |
1750 |
20 |
|
|
|
|
Нижний |
1600 |
15 |
|
|
|
|
Основной |
1675 |
17,5 |
|
|
|
|
Интервал варьирования |
75 |
2,5 |
|
|
|
|
Кодовые обозначения |
Х1 |
Х2 |
Х3 |
... |
Xk |
3.3.5. Вводят условное обозначение верхнего, нижнего и основного уровней фактора соответственно +1, -1, 0. При построении планов матриц планирования эксперимента цифры (единицы) следует опускать и писать только их знаки «+» или «-».
3.3.6. Затем строят план матрицы планирования эксперимента. Построение плана матрицы сводится к стандартной форме записи условий проведения экспериментов в виде таблицы, в строках которой записывают данные опытов, в столбцах - факторы (в кодах «+» и «-») с реализацией всех возможных сочетаний упорядоченных комбинаций факторов.
В первом столбце таблицы следует менять знаки поочередно, во втором столбце чередовать их через два, в третьем - через четыре, в четвертом - через восемь и т.д. по степеням двойки. Все точки плана для реализации всех возможных сочетаний уровней факторов определяют по формуле
где N - общее число различных точек в плане;
2 - число уровней;
K - общее число факторов.
Например, имеется два фактора Х1, Х2 тогда, придавая каждому фактору два значения (верхний «+» и нижний «-»), получим всевозможные сочетания уровней для двух факторов неполного плана матрицы планирования 22 (табл. 2). В этом случае больше четырех комбинаций сделать невозможно. Для записи плана матриц в одну строчку вводят специальные обозначения: строку, состоящую из одних минусов, всегда обозначают (0), в остальных строчках вводят обозначения цифрами натурального ряда с апострофом (‘), только тех факторов, которые находятся на верхнем уровне «+», например, фактору Х1 соответствует цифра (1‘), фактору Х2 - цифра (2‘) и т.д. в порядке чисел натурального ряда. План матрицы задается перечислением строк. Некоторые планы матриц планирования эксперимента в кодовых обозначениях строк приведены в приложении 2. Таблица примет вид (табл. 2).
Таблица 2
Неполный план матрицы планирования 22
|
Факторы |
Кодовые обозначения строк |
||
|
X1 |
X2 |
||
|
1 |
- |
- |
(0) |
|
2 |
+ |
- |
(1‘) |
|
3 |
- |
+ |
(2‘) |
|
4 |
+ |
+ |
(1‘2‘) |
Для составления плана матрицы для трех факторов матрицу планирования (см. табл. 2) повторяют дважды: один раз при значениях Х3, находящихся на нижнем уровне, второй раз - при значениях X3, находящихся на верхнем уровне. Чтобы получить кодовую запись плана матрицы, следует кодовые обозначения строк умножить один раз на единицу, второй - на 3 (табл. 3).
Таблица 3
Неполный план матрицы планирования 23
|
Факторы |
Кодовые обозначения строк |
|||
|
Х1 |
Х2 |
Х3 |
||
|
1 |
- |
- |
- |
(0) |
|
2 |
+ |
- |
- |
(1‘) |
|
3 |
- |
+ |
- |
(2‘) |
|
4 |
+ |
+ |
- |
(1‘2‘) |
|
5 |
- |
- |
+ |
(3‘) |
|
6 |
+ |
- |
+ |
(1‘3‘) |
|
7 |
- |
+ |
+ |
(2‘3‘) |
|
8 |
+ |
+ |
+ |
(1‘2‘3‘) |
Если же будет рассмотрен четвертый фактор Х4, то аналогичным образом будет повторено планирование для трех переменных (табл. 3): один раз - для фактора Х4, находящегося на нижнем уровне, второй раз - для фактора Х4, находящегося на верхнем уровне.
Аналогично получается план матрицы планирования для пяти, десяти и т.д. факторов, т.е. для любого числа факторов.
Табл. 3 представляет план матрицы планирования эксперимента, реализовав который, можно подсчитать коэффициенты факторов процесса (или параметров модели) b1 ® Х1, b2 ® Х2, b3 ® Х3, однако этих коэффициентов недостаточно, чтобы получить уравнение регрессии вида Y = b0 + blXl + b2X2 + b3X3 + b1,2XlX2 + b1,3XlX3 + b1,2,3XlX2X3.
3.3.7. Чтобы получить любой полный план матрицы планирования для подсчета всех коэффициентов, необходимо (например, для неполного плана 23) добавить в табл. 3 еще один столбец - фиктивную переменную Х0 для оценки свободного члена b0. Значение Х0 всегда одинаково во всех строках и равно +1.
3.3.8. Для оценки коэффициентов взаимодействия факторов в табл. 3 вводят столбцы со всевозможными комбинациями произведений факторов: Х1Х2; Х1Х3; Х2Х3; Х1Х2Х3, которые позволяют оценить эффекты взаимодействия факторов. Поскольку переменные Х1, Х2, Х3 принимают значения «+1» и «-1», то произведения переменных примут те же значения «+1» и «-1». Тогда с учетом требований, указанных в пп. 3.3.7 и 3.3.8, табл. 3 примет следующий вид (табл. 4).
Таблица 4
Полный план матрицы планирования 23
|
Значения факторов в кодовых обозначениях |
Комбинации произведений факторов в кодовых обозначениях |
Действительное значение показателя параметра оптимизации по реализации эксперимента |
|||||||||
|
X0 |
X1 |
X2 |
X3 |
X1X2 |
X1X3 |
X2X3 |
X1X2X3 |
Y1 |
Y2 |
|
|
|
1 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
Y1 |
Y2,1 |
Y1 |
|
2 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
Y2 |
Y2,2 |
Y2 |
|
3 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
Y3 |
Y2,3 |
Y3 |
|
4 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
Y4 |
Y2,4 |
Y4 |
|
5 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
Y5 |
Y2,5 |
Y5 |
|
6 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |
Y6 |
Y2,6 |
Y6 |
|
7 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
Y7 |
Y2,7 |
Y7 |
|
8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
Y8 |
Y2,8 |
Y8 |
Примечание.
В рамке, обведенной полужирными линиями, показан план эксперимента, остальные
данные необходимы для подсчета коэффициентов. Пользуясь такой матрицей
планирования, можно приступать к эксперименту, при этом следует иметь в виду,
что значения «+» и «-» факторов соответствуют верхнему и нижнему уровню в
действительных значениях факторов процесса, например, см. табл. 1. Если
параллельных опытов два, то фиксируется среднее значение ![]() .
.
3.4. Дробный факторный эксперимент (ДФЭ), равный 2k-p
3.4.1. Дробный факторный эксперимент следует проводить при числе факторов процесса или операции от двух и более при условии, если полный эксперимент по экономическим соображениям проводить невыгодно.
3.4.2. От действительных значений факторов к кодированным переходят так же, как при ПФЭ 2k.
3.4.3. Дробные факторные эксперименты следует условно обозначать 2k-p, где р - число линейных эффектов, приравненных к эффектам взаимодействия. При р = 1 получают 1/4 ПФЭ, при р = 2 получают 1/4 ПФЭ, при р = 3 получают 1/8 ПФЭ и т.д. по степени двойки.
3.4.4. При построении любых планов матриц планирования ДФЭ произведения комбинаций факторов можно приравнять к новым факторам, если известно, что между факторами отсутствует эффект взаимодействия. Тогда значения нового фактора в условиях опытов определяют по знакам, указанным в этом столбце. При этом сокращается число опытов, например, факторы операции токарной обработки не взаимодействуют с факторами операции шлифовки и т.п.
Если в ПФЭ (табл. 4) один из эффектов взаимодействия (Х1Х2, Х1Х3, Х2Х3, Х1Х2Х3) заменить четвертым фактором Х4, то получим половину 24-1 от ПФЭ. Если два эффекта взаимодействия заменить факторами Х4 и X5, то получим 1/4 25-2 от ПФЭ 25.
Можно получить 1/8 от ПФЭ 26, заменив три эффекта взаимодействия факторами Х4, Х5, Х6.
Если заменить четыре эффекта взаимодействия факторами Х4, Х5, Х6 и Х7, то получим 1/16 27-4 от ПФЭ.
3.4.5. В качестве подходящего ДФЭ следует брать ближайший полный факторный эксперимент, число опытов в котором больше, чем число факторов в исследуемом процессе, операции.
3.4.6. Часть от полного факторного эксперимента, т.е. дробного факторного эксперимента должна состоять из данных в строках плана матрицы планирования с четным или нечетным числом цифр, например, матрица планирования 23-1 (табл. 5) может быть представлена двумя частями при Х3 = Х1Х2 и при Х3 = Х1Х2.
Таблица 5
Две части плана матрицы планирования 23-1
|
Матрица I |
Матрица II |
||||||||||
|
Номер точки плана |
X0 |
X1 |
X2 |
(X3) = Х1X2 |
Кодовые обозначения строк |
Номер точки плана |
X0 |
X1 |
X2 |
(X3) = Х1X2 |
Кодовые обозначения строк |
|
1 |
+ |
- |
- |
+ |
(3‘) |
1 |
+ |
- |
- |
- |
(0) |
|
2 |
+ |
+ |
- |
- |
(1‘) |
2 |
+ |
+ |
- |
+ |
(1‘3‘) |
|
3 |
+ |
- |
+ |
- |
(2‘) |
3 |
+ |
- |
+ |
+ |
(2‘3‘) |
|
4 |
+ |
+ |
+ |
+ |
(1‘2‘3) |
4 |
+ |
+ |
+ |
- |
(1‘2‘) |
В табл. 5 в первой части плана матрицы (кодовые обозначения) в строках (3‘), (1‘), (2‘), (1‘2‘3‘) нечетные числа, а во второй части плана матрицы (кодовые обозначения) в строках (1‘3‘), (2‘3‘), (1‘2‘) четные числа, считая строку (0) четной.
Примечание. В рамках, обведенных полужирными линиями, приведены планы эксперимента, т.е. эксперимент можно ставить по данным любой части табл. 5.
3.5. Разрешающая способность дробных экспериментов
3.5.1. При отсутствии априорной информации об эффектах взаимодействия следует брать часть от ПФЭ с наибольшей разрешающей способностью. Если существует информация об эффектах взаимодействия, то ими следует пользоваться при выборе ДФЭ. Раздельные оценки несмешанных линейных эффектов и различных взаимодействий ДФЭ определяют его разрешающую способность.
3.5.2. Затем следует определить генерирующие соотношения, которые для любой матрицы планирования показывают, какое из взаимодействий принято незначимым и заменено новым фактором, например, Х3 = ±Х1Х2 (табл. 5).
3.5.3. После этого находят определяющий контраст, т.е. соотношения произведений факторов, задающие элементы столбца, состоящего только из плюсов или минусов для любой матрицы планирования, например, определить определяющий контраст у двух частей матриц планирования 23-1 (табл. 6).
Таблица 6
Две части плана матрицы планирования 23-1
|
Матрица I |
Матрица II |
||||||||||
|
Номер точки плана |
Х0 |
Х1 |
Х2 |
Х3 |
Х1Х2Х3 |
Номер точки плана |
Х0 |
Х1 |
Х2 |
Х3 |
Х1Х2Х3 |
|
1 |
+ |
- |
- |
+ |
+ |
1 |
+ |
- |
- |
- |
- |
|
2 |
+ |
+ |
- |
- |
+ |
2 |
+ |
+ |
- |
+ |
- |
|
3 |
+ |
- |
+ |
- |
+ |
3 |
+ |
- |
+ |
+ |
- |
|
4 |
+ |
+ |
+ |
+ |
+ |
4 |
+ |
+ |
+ |
- |
- |
Произведение данных, приведенных в трех столбцах (матрица I), вычисляют по соотношению 1 = Х1Х2Х3, а для матрицы II - по соотношению 1 = Х1Х2Х3. В столбцах находят одинаковые знаки: в первом случае их элементы равны +1, во втором - -1. Условное (кодовое) обозначение произведений столбцов, в которых имеются только «+» или «-» (кроме столбца Х0), следует называть определяющим контрастом и обозначать 1. Контраст помогает определить совместные оценки факторов.
3.5.4. Затем определяют совместные оценки факторов, т.е. всегда для любой матрицы планирования надо последовательно перемножить графы независимых переменных Х1, Х2, Х3 и т.д. на определяющий контраст и учесть, что Xi2 = 1 или 12 = 1. В примере, приведенном в табл. 6, совместные оценки задаются соотношениями:
Для матрицы I Для матрицы II
Х1 = Х2Х3 Х1 = -Х2Х3
Х2 = Х1Х3 Х2 = -Х1Х3
Х3 = Х1Х2 Х3 = -Х1Х2
Это значит, что коэффициенты факторов или параметров двух частей плана матрицы планирования будут совместными оценками:
b1 ® b1 + b2,3 b1 ® b1 - b2,3
b2 ® b2 + b1,3 b2 ® b2 - b1,3
b3 ® b3 + b1,2 b3 ® b3 - b1,2
3.5.5. Для оценки разрешающей способности ДФЭ большой дробности (l/4, l/8, l/16 и т.д.) необходимо пользоваться обобщенным определяющим контрастом.
3.5.6. Строят матрицу планирования ДФЭ большой дробности, например, l/16 ПФЭ 27 - в виде 27-4, т.е. получится 23 ПФЭ.
Для этого необходимо:
построить матрицу планирования 23 (см. пп. 3.3.6, 3.3.8 в результате получается табл. 7);
комбинации произведений факторов Х1Х2, Х1Х3, Х2Х3, которые позволяют оценить двойные взаимодействия факторов, предположить незначимыми или равными нулю;
приравнять комбинации произведений факторов новым факторам Х4 = Х1Х2, X5 = Х1Х3, Х6 = Х2Х3, X7 = X1X2X3.
Таблица 7
План матрицы планирования 27-4
|
Значения факторов в кодовых обозначениях |
Действительное значение показателя параметра оптимизации по реализации эксперимента |
||||||||||
|
Х0 |
Х1 |
Х2 |
Х3 |
Х4 = Х1Х2 |
Х5 = Х2Х3 |
Х6 = Х2Х3 |
Х7 = Х1Х2Х3 |
Y1 |
Y2 |
|
|
|
1 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
Y1 |
Y2,1 |
Y1 |
|
2 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
Y2 |
Y2,2 |
Y2 |
|
3 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
Y3 |
Y2,3 |
Y3 |
|
4 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
Y4 |
Y2,4 |
Y4 |
|
5 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
Y5 |
Y2,5 |
Y5 |
|
6 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |
Y6 |
Y2,6 |
Y6 |
|
7 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
Y7 |
Y2,7 |
Y7 |
|
8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
Y8 |
Y2,8 |
Y8 |
В табл. 7 число опытов больше, чем число факторов, в исследуемом процессе. План экспериментов заключен в рамку. Пользуясь таким планированием и проведя эксперимент, можно вычислить коэффициенты факторов или параметров уравнения регрессии (модели)
Y = b0 + blX1 + b2X3 + b2X3 + b4X4 + b5X5 + b6X6 + b7X7.
3.5.7. Затем определяют генерирующие соотношения матрицы планирования 27-4 (табл. 7), которые показывают, какое взаимодействие принято незначимым, т.е. Х4 = Х1Х2; X5 = Х1Х3; Х6 = Х2Х3; X7 = X1X2X3.
3.5.8. Находят определяющий контраст, т.е. соотношения, задающие элементы, указанные в столбце Х0. Определяющими контрастами для плана 27-4 являются соотношения:
1) 1 = X1X2X4; 2) 1 = X1X3X5;
3) 1 = X2X3X6; 4) 1 = X1X2X3X7.
Если попарно перемножить эти определяющие контрасты 1 ´ 2; 1 ´ 3; 1 ´ 4; 2 ´ 3; 2 ´ 4; 3 ´ 4, то получим элементы первого столбца 1 = X2X3X4X5; 1 = X1X3X4X6; 1 = X3X4X7; 1 = X1X2X5X6; 1 = X2X5X7; 1 = X1X6X7.
Если перемножить определяющие контрасты по три: 1 ´ 2 ´ 3; 1 ´ 2 ´ 4; 1 ´ 3 ´ 4, то получим соотношения 1 = X4X5X6 = X1X4X7 = X3X5X6X7.
3.5.9. Определяют обобщающий определяющий контраст, т.е. произведения высшего порядка определяющих контрастов, чтобы полностью охарактеризовать разрешающую способность ДФЭ. Обобщающий определяющий контраст записывают в следующем виде:
1 = X1X2X4 = X1X3X5 = X2X3X6 = X1X2X3X7 = X2X3X4X5 = X1X3X4X6 = X3X4X7 = = X1X2X5X6 = X2X5X7 = X1X6X7 = X4X5X6 = X1X4X5X7 = X2X4X6X7 = X3X5X6X7.
Умножая определяющие контрасты по четыре, получают обобщающий определяющий контраст
1 = X1X2X3X4Х5Х6Х7.
3.5.10. Охарактеризовывают разрешающую способность ДФЭ умножением обобщающего определяющего контраста последовательно на Х1, Х2, Х3, ..., и т.д.
3.5.11. Если всеми эффектами взаимодействия, начиная с тройных, пренебречь, то коэффициенты параметров регрессии будут совместными оценками:
b1 ® b1 + b2,4 + b3,5 + b6,7
b2 ® b2 + b1,4 + b3,6 + b5,7
b3 ® b3 + b1,5 + b2,6 + b4,7
b4 ® b4 + b1,2 + b5,6 + b3,7
b5 ® b5 + b1,3 + b4,6 + b2,7
b6 ® b6 + b2,3 + b4,5 + b1,7
b7 ® b7 + b3,4 + b2,5 + b1,6
Таким образом, все линейные эффекты оказались смешанными с несколькими парными взаимодействиями, поэтому разрешающая способность ДФЭ низкая.
3.5.12. Для планов матриц планирования экспериментов рекомендуется выбирать дробные факторные планы с возможно большей разрешающей способностью, т.е. ДФЭ, у которых линейные эффекты, смешанные с эффектами взаимодействия, должны быть близки к нулю.
3.6. Проверка свойств планов матриц планирования ПФЭ = 2k и ДФЭ = 2k-p
3.6.1. После построения плана матрицы планирования необходимо проверить ее свойства:
симметричность относительно центра эксперимента - алгебраическая сумма элементов столбца каждого фактора должна быть равна нулю, кроме столбца, отвечающего свободному члену, b0, т.е.
где v - номер точки опыта;
i - номер фактора;
N - число различных точек плана матрицы;
нормировку - сумма квадратов элементов каждого столбца равна числу точек плана матрицы, т.е.
![]() (6)
(6)
ортогональность - сумма построчных произведений плана матрицы любых двух столбцов равна нулю, т.е.
![]() (7)
(7)
где j - комбинация факторов в v-й точке, i ¹ j.
Ортогональность матрицы позволяет оценить все коэффициенты регрессии независимо друг от друга, т.е. величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты.
3.6.2. Если план матрицы планирования отвечает свойствам, указанным в п. 3.6.1, то он соответствует свойству ротатабельности, т.е. математическая модель, полученная в результате эксперимента, способна предсказать значение показателя параметра оптимизации с одинаковой точностью в любых направлениях на равных расстояниях от центра эксперимента или плана матрицы.
3.7. Проведение эксперимента ПФЭ или ДФЭ
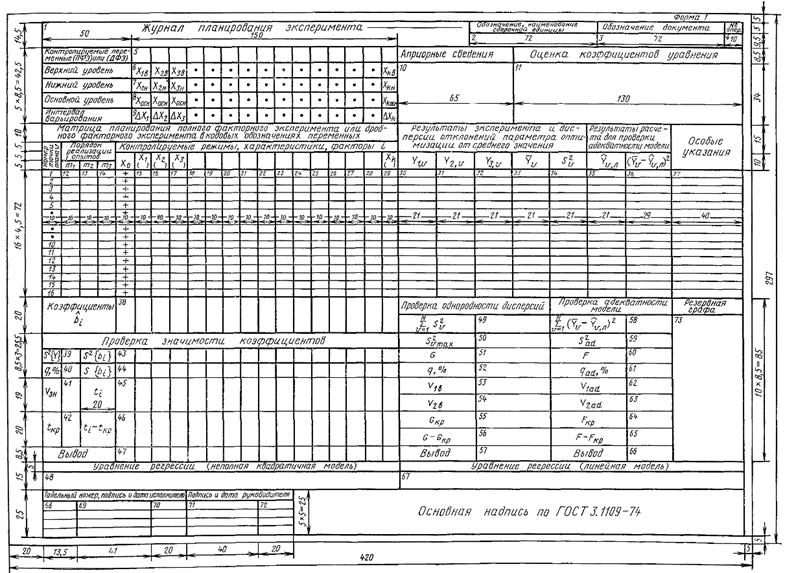
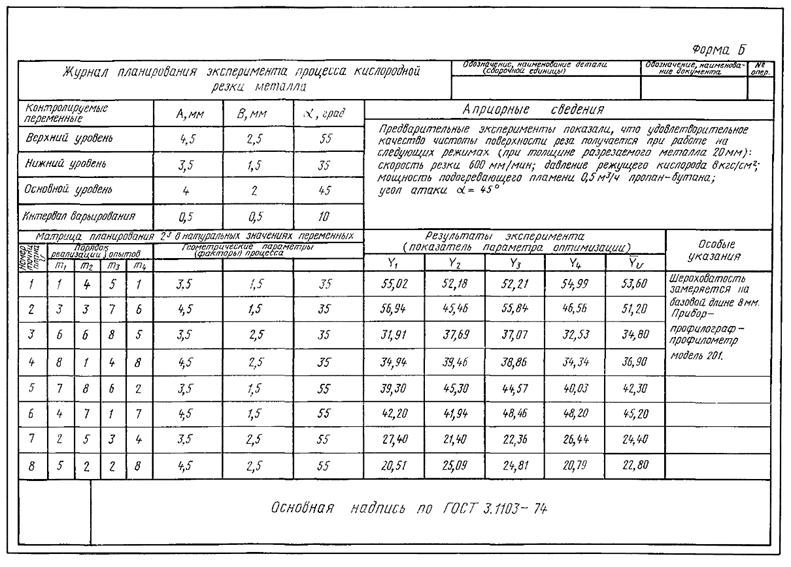
3.7.1. Для записи априорных сведений о факторах процесса, записи верхних, нижних и основных уровней факторов, интервалов варьирования, плана матрицы планирования, результатов эксперимента, промежуточных и конечных результатов расчета, для поверки воспроизводимости эксперимента, значимости коэффициентов, проверки адекватного описания процесса подготавливают к заполнению журналы планирования эксперимента (формы 1 и 2 приложения 3).
3.7.2. Перед реализацией плана эксперимента на объекте опыты, предусмотренные в плане матрицы планирования, следует рандомизировать, т.е. проводить в случайной последовательности. Порядок проведения опытов в случайной последовательности следует выбирать по таблице равномерно распределенных случайных чисел (приложение 4). Например, если требуется провести восемь опытов, то из случайного места таблицы необходимо последовательно выписать числа, лежащие в интервале от 1 до 8, при этом надо отбросить уже выписанные числа, превышающие восемь. Так, например, начиная с числа 09 (второй столбец таблицы приложения 4), получаем следующую последовательность реализации опытов:
номер точки в плане матрицы - 1, 2, 3, 4, 5, 6, 7, 8
порядок реализации опытов - 1, 6, 5, 8, 2, 7, 4, 3
Порядок реализации опытов записывают в графу 12 (в форме 1 - графа 12, в форме 2 - графа 11) форм 1 и 2 приложения 3 (значения m1).
Аналогично определяют поочередно порядок реализации опытов во второй и третьей сериях. Эти сведения так же записывают в соответствующие графы форм 1 и 2 приложения 3 (значения m2, m3).
3.7.3. По каждой точке плана матрицы планирования устанавливают действительные значения факторов, верхний или нижний уровень, в порядке реализации опытов первой серии эксперимента. Требуемые фактические значения факторов следует поддерживать постоянными в течение опыта.
3.7.4. Получают действительные значения ожидаемого показателя параметра оптимизации по всем точкам плана матрицы планирования. Эти значения замеряют одним и тем же прибором и данные замеров записывают в графу 30 и 32 соответственно форм 1 и 2 приложения 3 (значения Y1,v)
3.7.5. Нужные значения факторов устанавливают по каждой точке плана матрицы планирования поочередно второй и третьей серии эксперимента (см. пп. 3.7.3, 3.7.4) и полученные результаты замеров ожидаемого показателя параметра оптимизации записывают в графы 31, 32 и 33, 34 соответственно форм 1 и 2 приложения 3 (значения Y2,v; Y3,v).
3.7.6. Объем выборки, т.е. количество единиц штучной продукции, составляющих выборку, в каждой точке плана эксперимента (1, 2, ..., n) должен быть постоянным. В графах 30, 31, 32 и 32, 33, 34 форм 1 и 2 соответственно приложения 3 (значения Y1,v; Y2,v; Y3,v) записывают среднее значение объема выборки, если в опыте взято несколько измерений детали или сборочной единицы.
3.7.7. Среднее значение показателя параметра оптимизации определяют по реализации параллельных наблюдений по формуле
 (8)
(8)
где ![]() - среднее арифметическое по m опытам в точке с номером v;
- среднее арифметическое по m опытам в точке с номером v;
v - строчка плана матрицы планирования или номер опыта;
Yv,j - действительное значение показателя параметра оптимизации;
m - число параллельных наблюдений в каждой точке.
Результаты
среднего значения ![]() записывают в графы 33 и 37,
соответственно форм 1 и 2
приложения 3
(значение
записывают в графы 33 и 37,
соответственно форм 1 и 2
приложения 3
(значение ![]() ).
).
3.8. Обработка результатов эксперимента
3.8.1. Для оценки отклонения показателя параметра оптимизации от среднего значения следует вычислить дисперсию воспроизводимости по данным т параллельных наблюдений плана матрицы планирования в каждой точке по формуле
 (9)
(9)
где Sv2 - дисперсия в v-й точке;
j - порядковый номер параллельного опыта в данной точке плана матрицы;
![]() - среднее
арифметическое значение показателя параметра оптимизации в m
параллельных опытах в точке v;
- среднее
арифметическое значение показателя параметра оптимизации в m
параллельных опытах в точке v;
Yv,j - значение параметра оптимизации в v-й точке;
m - 1 - число параллельных наблюдений в точках плана матрицы.
Значения Sv2, вычисленные для всех точек плана матрицы, записывают в графу 34 формы 1 (приложение 3).
3.8.2. Дисперсии в графе 34 формы 1 приложения 3, суммируют по текущим номерам точек или строк плана матрицы и записывают в графу 49 формы 1 приложения 3.
3.8.3. Находят максимальную дисперсию в графе 34 формы 1 и записывают в графу 50 формы 1 приложения 3.
3.8.4. Затем проверяют однородность дисперсий.
Для проверки гипотезы однородности дисперсий следует пользоваться критерием Кохрена, который основан на законе распределения отношения максимальной дисперсии к сумме всех дисперсий, т.е.
 (10)
(10)
где G - критерий Кохрена;
![]() -
максимальная дисперсия в v-й точке;
-
максимальная дисперсия в v-й точке;
![]() - сумма
всех дисперсий.
- сумма
всех дисперсий.
3.8.5. Проверяют гипотезу о воспроизводимости измерений, заключающуюся в определении того факта, при котором выборочные дисперсии для каждой точки плана матрицы однородны.
Для этого следует задать уровень значимости q = 5 %, определить число степеней свободы V1, в max = m - 1 и V2, в = N, найти табличное значение критерия Кохрена Gкр в табл. 1 приложения 5 при соответствующих степенях свободы. Если расчетное значение G, определенное по формуле (10), окажется меньше найденного в табл. 1 приложения 5, то гипотеза об однородности дисперсий и воспроизводимости результатов принимается. Если проверка дала отрицательный результат, то следует увеличить число параллельных опытов.
Примечание. Следует выбирать уровень значимости по всем критериям (Кохрена, Стъюдента, Фишера), одинаковым при решении поставленной задачи. Здесь и далее по тексту для примера установлен уровень значимости, равный 5 %.
3.8.6. Находят разность между расчетным значением эксперимента G, определенным по формуле (10), и Gкр, найденным в табл. 1 приложения 5. Этот результат записывают в графу 56 формы 1 приложения 3.
3.8.7. Для контроля расчетов проверки однородности дисперсии в форму 1 приложения 3 записывают следующие значения: G - в графу 51, q в процентах - в графу 52, V1, в - в графу 53, V2, в - в графу 54, Gкр - в графу 55. В графу 57 записывают вывод: дисперсии однородны или неоднородны.
3.8.8. Если дисперсии однородны, то их следует усреднить, т.е. найти дисперсию параметра оптимизации по формуле
где S2{Y} - средняя арифметическая дисперсий всех различных точек плана матрицы или дисперсия параметра оптимизации;
v - дисперсия в v-й точке;
![]() - сумма
всех дисперсий;
- сумма
всех дисперсий;
N - общее число различных точек в плане матрицы планирования.
Вычисленное значение S2{Y} записывают в графу 39 формы 1 приложения 3.
3.9. Построение математической модели процесса
3.9.1. Как указывалось выше, пользуясь
методом ПФЭ или ДФЭ, можно получить описание изучаемого процесса в виде ![]() , где
выборочные коэффициенты параметров модели процесса b0,
b1, b2
и т.д. являются лишь оценками для теоретических коэфициентов b0, b1,
b2, b3, и т.д., а
, где
выборочные коэффициенты параметров модели процесса b0,
b1, b2
и т.д. являются лишь оценками для теоретических коэфициентов b0, b1,
b2, b3, и т.д., а ![]() - оценка математического ожидания
показателя параметра оптимизации процесса.
- оценка математического ожидания
показателя параметра оптимизации процесса.
3.9.2. Определение параметров модели процесса или коэффициентов регрессии
Коэффициенты
регрессии определяют (одинаково, независимо от проведения ПФЭ или ДФЭ)
умножением данных ![]() на данные Хi, v
в кодовых обозначениях с последующим делением полученного произведения на общее
число точек в плане матрицы, т.е. по формуле
на данные Хi, v
в кодовых обозначениях с последующим делением полученного произведения на общее
число точек в плане матрицы, т.е. по формуле
где bi - коэффициенты регрессии 0, 1, 2, ..., k;
Хi, v - номер (фактора в кодовых обозначениях) столбца в плане матрицы 0, 1, 2, ..., k;
![]() - среднее
арифметическое по m опытам в точке с номером v;
- среднее
арифметическое по m опытам в точке с номером v;
N - общее число различных точек в плане матрицы.
Вычисленные значения bi записывают в графу 38 формы 1 приложения 3.
3.9.3. Нахождение дисперсии ошибки определения коэффициента регрессии
При равном числе параллельных опытов (m0) во всех точках плана матрицы дисперсию ошибки определения коэффициента регрессии определяют по формуле
![]() (13)
(13)
где S2{bi} - дисперсия ошибки определения коэффициента;
S2{Y} - дисперсия показателя параметра оптимизации;
N - общее число различных точек в плане матрицы;
m - число параллельных наблюдений в каждой точке.
Вычисленное значение S2{bi} записывают в графу 43 формы 1 приложения 3. Значение S2{bi} для всех коэффициентов одинаковое.
3.9.4. Среднеквадратическое отклонение дисперсии ошибки определения коэффициента регрессии bi определяют по формуле
![]() (14)
(14)
Вычисленное значение S{bi} записывают в графу 44 формы 1 приложения 3.
Найденное значение S{bi} для всех коэффициентов одинаковое.
3.9.5. Значимость коэффициентов регрессии определяют по t - критерию Стьюдента. Для каждого коэффициента вычисляют значения ti - критерия по формуле
где ti - критерий Стьюдента;
|bi| - рассчитанные коэффициенты регрессии;
S{bi} - среднеквадратическое отклонение дисперсий коэффициента регрессии.
Полученные значения ti записывают в графу 42 формы 1 приложения 3.
3.9.6. Затем проверяют гипотезу о значимости коэффициента bi. Для этого следует задать уровень значимости q = 5 % и определить число степеней свободы Vзн =N(m - 1), найти критическое значение tкр в табл. 3 приложения 5 для определенного числа степеней свободы. Если расчетное значение ti, определенное по формуле (15), окажется больше значения tкр, найденного в табл. 3 приложения 5, то гипотеза отвергается и коэффициент bi признается значимым. В противном случае bi, считается статистически незначимым, т.е. bi = 0.
Если какой-либо коэффициент окажется статистически незначимым, то он может быть отброшен без пересчета остальных коэффициентов.
3.9.7. Находят разность между расчетными значениями эксперимента ti, определенными по формуле (15), и tкр, найденным в табл. 3 приложения 5. Результат записывают в графу 46 формы 1 приложения 3.
3.9.8. Для контроля расчетов проверки значимости коэффициентов регрессии в форму 1 приложения 3 записывают следующие значения: q = 5 % - в графу 40, Vзн - в графу 41, tкр - в графу 42. В графу 47 записывают вывод: коэффициенты значимые или незначимые.
3.9.9. В графу 48 формы 1 приложения 3 следует записывать предполагаемую модель технологического процесса или операции со всеми коэффициентами (значимыми и незначимыми).
3.9.10. Статистическая незначимость коэффициента bi может быть обусловлена следующими причинами:
а) основной уровень режима фактора Xi осн близок к точке частного экстремума, т.е. bi @ 0
б) интервал варьирования фактора DХi выбран малым;
в) данная
переменная (произведение переменных) не имеет статистической связи с
показателем параметра оптимизации ![]() ;
;
г) велика ошибка эксперимента вследствие наличия неуправляемых и неконтролируемых факторов. Если имеют место причины, указанные в подпунктах а и b, то значение фактора следует стабилизировать на определенном уровне (не выходя за пределы варьирования), если имеет место причина, указанная в подпункте б, то следует увеличить интервал варьирования на величину, равную 0,05 ¸ 0,3 от интервала варьирования фактора, т.е. область варьирования должна составлять 10 - 60 % от размаха варьирования фактора. Если имеет место причина, указанная в подпункте г, то следует принять меры к уменьшению ошибки эксперимента.
3.9.11. В математическую модель технологического процесса включают только значимые коэффициенты.
Получают
уравнение регрессии в виде ![]() , где
, где ![]() - математическое ожидание
показателя параметра оптимизации;
- математическое ожидание
показателя параметра оптимизации;
![]() -
коэффициенты параметров модели;
-
коэффициенты параметров модели;
Хi - факторы процесса.
3.10. Проверка адекватности модели
3.10.1. По уравнению регрессии
определяют величину ![]() для каждой точки плана матрицы, т.е.
для каждой строчки, с учетом знака фактора в плане матрицы найти алгебраическую
сумму коэффициентов уравнения.
для каждой точки плана матрицы, т.е.
для каждой строчки, с учетом знака фактора в плане матрицы найти алгебраическую
сумму коэффициентов уравнения.
Вычисленное
значение ![]() записывают
в графу 35 формы 1 приложения 3.
записывают
в графу 35 формы 1 приложения 3.
3.10.2. Находят разность между средним
значением ![]() (графа
33 формы 1 приложения 3) показателя параметра оптимизации процесса для каждой
точки плана матрицы, полученным экспериментально, и значением
(графа
33 формы 1 приложения 3) показателя параметра оптимизации процесса для каждой
точки плана матрицы, полученным экспериментально, и значением ![]() (графа 35
формы 1 приложения 3), подсчитанным по уравнению регрессии. Эту разность
возводят в квадрат. Полученные результаты
(графа 35
формы 1 приложения 3), подсчитанным по уравнению регрессии. Эту разность
возводят в квадрат. Полученные результаты ![]() записывают в графу 36,
формы 1 приложения 3 и суммируют. Результат суммирования
записывают в графу 36,
формы 1 приложения 3 и суммируют. Результат суммирования ![]() записывают
в графу 58 формы 1 приложения 3.
записывают
в графу 58 формы 1 приложения 3.
3.10.3. Оценку дисперсии адекватности модели определяют по формуле.
![]() (16)
(16)
где S2ad - оценка дисперсии адекватности модели;
т - число параллельных наблюдений в точках плана матрицы;
N - общее число различных точек в плане матрицы;
l - число значимых коэффициентов (включая b0);
![]() - среднее
арифметическое по m опытам в точке с номером v;
- среднее
арифметическое по m опытам в точке с номером v;
![]() -
математическое ожидание параметра оптимизации, подсчитанное по уравнению
регрессии.
-
математическое ожидание параметра оптимизации, подсчитанное по уравнению
регрессии.
Примечание. Формула справедлива лишь при равном числе параллельных опытов во всех точках плана матрицы.
Найденное значение S2ad записывают в графу 59 формы 1 приложения 3.
3.10.4. Адекватность модели проверяют по формуле
где F - критерий Фишера;
S2ad - оценка дисперсии адекватности;
S2{Y} - дисперсия параметра оптимизации.
Полученное значение критерия F записывают в графу 60 формы 1 приложения 3.
3.10.5. Для проверки гипотезы адекватности модели следует задать уровень значимости q = 5 %, определить число степеней свободы V1, ad = N - l и V2, ad = N(m - 1), найти табличное значение критерия Фишера Fкр для определенного числа степеней свободы в табл. 4 приложения 5. Если расчетное значение критерия F, определенное по формуле (17), окажется меньше значения Fкp, определенного в табл. 4 приложения 5, то гипотеза адекватности модели принимается.
Примечание. Проверка адекватности модели возможна лишь при V1, ad > 0, т.е. число оцениваемых коэффициентов l не должно быть равно числу точек N в плане матрицы.
3.10.6. Находят разность между расчетным значением эксперимента критерием F, определенным по формуле (17), и Fкp, найденным в табл. 4 приложения 5. Результат записывают в графу 65 формы 1 приложения 3.
3.10.7. Для контроля расчетов проверки адекватности модели в форму 1 приложения 3 записывают следующие значения: 5 % - в графу 61, V1, ad - в графу 62, V2, ad - в графу 63, Fкp - в графу 64. В графу 66 записывают вывод: уравнение адекватно или неадекватно.
3.10.8. В графу 67 формы 1 приложения 3 следует записывать уравнение регрессии (линейная модель), т.е. математическую модель технологического процесса, включая только значимые коэффициенты.
3.10.9. Если гипотеза адекватности отвергается, то возможны следующие приемы получения адекватной модели:
увеличение интервалов варьирования факторов (см. п. 3.9.10), этот прием может привести к цели, если решается задача оптимизации;
выделение (если возможно) фактора, порождающего неадекватность, и реализация для оставшихся k - 1 факторов новых планов, при этом выделенный фактор зафиксирован на определенном уровне;
преобразование контролируемых переменных (факторов), т.е. переход к новым факторам, статистически связанным со старыми.
3.11. Выбор контролируемых параметров по реальной модели технологического процесса или операции
3.11.1. При выборе контролируемых параметров возможны три варианта:
все коэффициенты регрессии значимы;
часть коэффициентов регрессии значима, часть незначима;
все коэффициенты регрессии незначимы.
3.11.2. Поскольку выбор контролируемых параметров технологического процесса осуществляется на основании требований к конечному продукту при учете вклада каждого выделенного фактора, то следует оценить коэффициенты влияния (чувствительности) в действительных значениях по формуле
где Ai - коэффициент чувствительности параметра процесса в действительных значениях;
bi - рассчитанные коэффициенты регрессии;
DХi - интервал варьирования фактора.
Вычисление коэффициента чувствительности в безразмерном масштабе производят по формуле
где ai - коэффициент чувствительности в безразмерном масштабе;
Хi осн - основной уровень фактора процесса.
Коэффициент влияния Ai - мера чувствительности процесса к изменению интервала варьирования факторов служит для определения допусков факторов.
3.11.3. Если для коэффициентов влияния необходимо определить допуски, то в процессе функционирования реального технологического процесса соответствующие приращения можно определить, вводя искусственно, если они незначительно изменят выход процесса и не вызовут появление бракованной продукции.
3.11.4. Если все коэффициенты регрессии значимы, то все факторы (параметры) технологического процесса следует контролировать.
3.11.5. Если часть коэффициентов значима, а часть незначима, то следует контролировать только факторы (параметры) технологического процесса при значимых коэффициентах.
3.11.6. Если все коэффициенты регрессии незначимы, то следует увеличить интервалы варьирования (см. п. 3.9.10) факторов (параметров) и провести дополнительный эксперимент. После этого поступают так же, как указано в пп. 3.11.4 или 3.11.5.
3.11.7. Выбранные контролируемые параметры вносят в соответствующую нормативно-техническую документацию с учетом следующих свойств коэффициентов:
чем больше абсолютная величина коэффициента фактора (параметра) технологического процесса, тем большее влияние оказывает фактор (параметр) на показатель параметра оптимизации;
если коэффициент регрессии отрицателен, то для увеличения показателя параметра оптимизации надо уменьшить значение фактора (параметра) технологического процесса, если положителен - увеличивать;
при минимизации показателя параметра оптимизации можно изменить знаки коэффициентов, кроме b0, на обратные и далее поступать так же как указано в предыдущем случае;
если эффект взаимодействия факторов (параметров) технологического процесса имеет отрицательный знак, то для увеличения показателя параметра оптимизации факторы (параметры) должны одновременно изменяться в разных направлениях, например, Х1 = +1, Х2 = -1, или Х1 = -1, Х2 = +1.
Пример разработки процесса и выбора контролируемых параметров приведен в приложении 6.
4. МЕТОД КРУТОГО ВОСХОЖДЕНИЯ
4.1. Проведение эксперимента ПФЭ или ДФЭ
4.1.1. Обрабатывают результаты эксперимента и, в частности, вычисляют оценки факторов, т.е. коэффициенты регрессии.
4.1.2. Определяют значимые факторы, определяющие показатель параметра оптимизации процесса.
4.1.3. Строят модель технологического процесса или операции.
4.1.4. Проверяют адекватность модели.
4.2. Крутое восхождение
4.2.1. Крутое восхождение следует применять при оптимизации и прогнозировании процесса или операции.
4.2.2. Подготовить журнал проведения эксперимента методом крутого восхождения (см. форму 3 приложения 3).
4.2.3. Крутое восхождение следует начинать от основных уровней значимых факторов, т.е. Хосн1, Xосн2, ..., Хоснk.
4.2.4. При крутом восхождении факторы изменяют пропорционально величинам коэффициентов регрессии и с учетом их знаков плюс или минус.
4.2.5. Вычисляют произведения biDXi однозначно по каждому фактору, т.е. следует умножить коэффициент регрессии на интервал варьирования фактора. Результаты вычислений записывают в графу 11 формы 3 приложения 3.
4.2.6. Находят фактор, для которого произведение biDXi является наибольшим по абсолютной величине. Следует именовать этот фактор базовым, т.е. max (bi × DХi) = bб × DХб.
4.2.7. Выбирают сдвиг в направлении крутого восхождения по базовому фактору от основного уровня, который может быть равен DХб или части этого интервала, т.е. mDХб (0 £ m < 1) или m = 0,1; 0,2; 0,3; 0,4 и т.д. до 1.
4.2.8. Определяют величину первого шага эксперимента l, для этого необходимо величину сдвига разделить на коэффициент базового фактора, т.е.
4.2.9. Вычисляют шаги первой точки крутого восхождения эксперимента по формуле Xhl(biDXi) + Xi осн, где i =1,2, ..., k - факторы процесса или операции:
Xi осн - основной уровень фактора процесса или операции, т.е. интервал варьирования умножить на коэффициент фактора и величину l, а полученное произведение сложить с основным уровнем фактора. При необходимости численное значение величины шага Xhi округляют.
Результаты вычислений записывают в графу 12, формы 3 приложения 3.
4.2.10. Далее следует последовательно прибавлять к предыдущей точке шаг соответствующего фактора l(biDXi). Количество шагов определяют полным или дробным экспериментом. Результаты вычислений записывают в графы 20 - 34 формы 3 приложения 3.
4.2.11. Проводят ПФЭ или ДФЭ, устанавливая действительные значения факторов процесса или операции в каждой точке плана матрицы в соответствии с условиями шагов факторов. Незначимые факторы устанавливают на любом удобном уровне в интервале ±1. Если нет специальных соображений, то выбирают средний уровень фактора. Если же по экономическим соображениям, например, выгодно поддерживать нижний уровень фактора, то выбирают его.
4.2.12. Обрабатывают результаты эксперимента.
4.3. Принятие решений после крутого восхождения
4.3.1. При эффективном крутом восхождении возможны два исхода:
оптимум достигнут;
оптимум не достигнут.
4.3.2. Если оптимум не достигнут, то необходимо построить линейный план нового цикла. Из реализованных опытов следует выбрать наилучший по результатам показателя параметра оптимизации процесса или операции и принять его за базовый, чтобы продолжить цикл крутого восхождения.
4.3.3. Если оптимум достигнут, то необходимо прекратить цикл крутого восхождения.
4.3.4. При неэффективном крутом восхождении возможна ситуация, при которой все коэффициенты регрессии получились незначимыми (модель неадекватна), но оптимум не достигнут, следует поставить опыт в центре плана эксперимента, для грубой оценки квадратичных членов уравнения регрессии.
4.3.5. Если сумма квадратичных членов уравнения регрессии значима, то это свидетельствует о близости оптимума.
4.3.6. Если, многократно реализовав шаговую процедуру, получен наилучший результат, который, однако, хуже требуемого, то это значит, что достигнут предел возможностей данной операции или процесса и предъявленным требованиям операция или процесс не могут удовлетворять. Требуется модернизация процесса, операции или их замена.
4.3.7. Если модель неадекватна, то возможны следующие ситуации:
интервалы варьирования выбраны неудачно;
исходную модель строили по части полного факторного эксперимента;
исходную модель строили от полного факторного эксперимента 2k-p, где p > 1.
4.3.8. Увеличивают вдвое интервал варьирования у незначимых факторов и проводят дополнительный эксперимент.
4.3.9. Если модель строилась по части полного факторного эксперимента, то следует достроить часть эксперимента до полного факторного эксперимента, провести эксперимент по новому плану матрицы, получить раздельные оценки для всех коэффициентов и совершить новое крутое восхождение.
4.3.10. Если модель строилась по части полного факторного эксперимента 2k-p, то следует применить метод «перевала», т.е. построить план матрицы второй серии опытов, изменив все знаки на обратные. Это дает возможность освободить линейные эффекты от совместных оценок с парными взаимодействиями. Положение не изменится, если значимыми являются взаимодействия более высокого порядка.
4.4. Реализация «мысленных опытов»
4.4.1. Если опыты очень дороги или известна математическая модель, то следует оценивать показатель параметра оптимизации в «мысленных опытах».
4.4.2. При реализации «мысленных опытов» по плану матрицы эксперимента существует две возможные ситуации:
одновременно могут ставиться все мысленные опыты через один, через два в плане матрицы эксперимента и т.д.;
реализуются два крайних «мысленных опыта» плана матрицы эксперимента, а затем «прощупывается» пространство внутри этого интервала. Минимальное число опытов - три, так как оптимум необходимо «захватить в вилку».
4.4.3. Для оценки показателя параметра оптимизации при «мысленных опытах» следует действительные значения факторов перевести в кодированные по формуле
где ![]() - кодовое обозначение
действительного значения фактора;
- кодовое обозначение
действительного значения фактора;
Хi осн- действительное значение i-гo фактора на основном уровне;
DXi - интервал варьирования i-гo фактора.
4.4.4. Умножают кодовые значения факторов на коэффициенты уравнения регрессии.
4.4.5. По уравнению регрессии (включая
только значимые факторы) определяют величину ![]() для каждой точки плана
матрицы, т.е. для каждой строчки, с учетом знака фактора находят алгебраическую
сумму коэффициентов уравнения.
для каждой точки плана
матрицы, т.е. для каждой строчки, с учетом знака фактора находят алгебраическую
сумму коэффициентов уравнения.
4.4.6. В «мысленных опытах» исследователь часто выходит далеко за ту область, для которой находилось линейное приближение, что приводит к большому расхождению между наблюдениями и вычисленными значениями показателя параметра оптимизации. Это обстоятельство не должно вызывать недоумение - линейным приближением в этих случаях пользуются не для предсказания выхода процесса, а для определения направления движения.
4.4.7. После получения выхода процесса принимают решение, как указано в пп. 4.3., 4.4 и 3.11.
ПРИЛОЖЕНИЕ 1
ТЕРМИНЫ, ПРИМЕНЯЕМЫЕ В МЕТОДИКЕ И ИХ ОПРЕДЕЛЕНИЯ
|
Определение |
|
|
|
ОСНОВНЫЕ ПОНЯТИЯ |
|
|
|
1. Технологический процесс |
По ГОСТ 3.1109-73 |
|
|
2. Технологическая операция |
По ГОСТ 3.1109-73 |
|
|
3. Технологический режим |
Условия выполнения определенной части технологического процесса, характеризуемые значениями эксплуатационных параметров применяемых средств технологического оснащения |
|
|
4. Эксперимент |
Система операций и, в случае необходимости, воздействий, выполняемых для получения информации об объекте на основе результатов наблюдений |
|
|
5. План эксперимента |
Правила проведения эксперимента, устанавливающие объем, условие и порядок реализации опытов |
|
|
6. Планирование эксперимента |
Выбор плана эксперимента |
|
|
7. Математическая модель Модель |
Система соотношений между параметром оптимизации и факторами, а также ограничениями, накладываемыми на них |
|
|
8. Параметр оптимизации |
Показатель качества детали, сборочной единицы или технологического процесса, для определения наилучшего значения которого проводится эксперимент |
|
|
9. Фактор Ндп. Входная переменная, вход, параметр |
Контролируемая переменная объекта, которая влияет на параметр оптимизации |
|
|
10. Уровень фактора |
Фиксированное значение фактора, соответствующее границе поля допуска |
|
|
11. Действительное значение фактора |
Количественная характеристика фактора, полученная в результате измерений с допустимой погрешностью |
|
|
12. Безразмерный масштаб фактора |
Отношение действительного значения фактора к условно принятому |
|
|
13. Кодирование факторов |
Обозначение действительных значений факторов в безразмерном масштабе |
|
|
14. Основной уровень фактора Ндп. Базовый уровень |
Действительное значение фактора, соответствующее середине поля допуска и нулю в безразмерном масштабе |
|
|
15. Верхний уровень фактора |
Допустимое максимальное отклонение фактора от основного уровня, соответствующее плюс единице в безразмерной шкале |
|
|
16. Нижний уровень фактора |
Допустимое минимальное отклонение фактора от основного уровня, соответствующее минус единице в безразмерной шкале |
|
|
17. Размах варьирования фактора |
Разность между максимальным и минимальным действительными значениями фактора в данном плане |
|
|
18. Интервал варьирования фактора |
Предельно допустимые отклонения действительного значения фактора от основного уровня, соответствующие плюс и минус единице по безразмерной шкале |
|
|
19. Операциональность факторов |
Последовательность операций, при помощи которых устанавливают действительные значения уровней факторов |
|
|
20. Установ фактора |
Выполнение действий по достижению и закреплению определенного значения фактора |
|
|
2:1. Позиция фактора |
Каждое из различных значений, которое может принимать фактор в пределах размаха варьирования |
|
|
22. Переход фактора |
Изменение действительного значения фактора от верхнего до нижнего или от нижнего до верхнего уровня. Примечание. Переход может быть разделен на проходы |
|
|
23. Проход фактора |
Часть перехода фактора, обусловленная изменением значения фактора в пределах размаха варьирования. Примечание. Примером прохода фактора является установление фактора на основном уровне |
|
|
24. Прием установки режима |
Совокупность воздействий, обусловленных установлением действительных значений факторов по условиям плана эксперимента |
|
|
25. Управляемость факторов |
Возможность осуществления совокупности воздействий, выбранных из множества возможных для корректировки отклонений факторов от заданных действительных значений |
|
|
26. Точность установки фактора |
Отклонение действительного значения фактора от заданного номинального значения |
|
|
27. Независимость фактора |
Возможность установления фактора на любом уровне независимо от уровней других факторов |
|
|
28. Совместимость факторов |
Условие, при котором возможное взаимное влияние факторов не должно вызывать нарушение технологического процесса или качества конечного продукта |
|
|
29. Рандомизация |
Случайный порядок проведения опытов |
|
|
30. Параллельные опыты |
Рандомизированные во времени опыты, в которых уровни всех факторов одинаковы |
|
|
31. Параметр модели |
Константа, входящая в математическую модель |
|
|
МОДЕЛИ, ПЛАНЫ, МЕТОДЫ ПЛАНИРОВАНИЯ |
|
|
|
32. Модель регрессионного анализа |
Модель, отражающая зависимость математического ожидания параметра оптимизации от непрерывных контролируемых факторов |
|
|
33. Полиноминальная модель регрессионного анализа Полиноминальная модель |
Модель регрессионного анализа линейная по параметрам, задаваемая полиномом по факторам |
|
|
34. Модель регрессионного анализа первого порядка Линейная модель |
Модель регрессионного анализа, задаваемая полиномом первого порядка по факторам |
|
|
35. Коэффициент регрессии |
Параметр модели регрессионного анализа |
|
|
36. Блок плана |
Часть плана, на которую не накладываются ограничения по рандомизации |
|
|
37. Точка плана |
Упорядоченная совокупность численных значений факторов, соответствующая условиям проведения опыта |
|
|
38. Центральная точка плана |
Точка плана, соответствующая нулям безразмерного масштаба по всем факторам |
|
|
39. Матрица плана |
Стандартная форма записи условий проведения экспериментов в виде таблицы, данные расположенные в строках соответствуют опытным, в столбцах - факторам |
|
|
40. Матрица дублирования |
Диагональная матрица плана, элементы которой равны числам параллельных, опытов в соответствующих точках плана |
|
|
41. Полный факторный план |
План, содержащий все возможные комбинации факторов, каждый из которых принудительно варьируется на двух уровнях равное число раз |
|
|
42. Дробный факторный план Дробная реплика полного факторного плана |
План, содержащий часть возможных комбинаций полного факторного плана |
|
|
43. Генератор плана |
Алгебраическое выражение, используемое при построении дробного факторного плана с заданными свойствами |
|
|
44. План эксперимента первого порядка Линейный план |
План, при котором возможны раздельные оценки параметров регрессионной модели первого порядка |
|
|
45. Разрешающая способность дробного плана |
Раздельные оценки несмешанных линейных эффектов и различных взаимодействий |
|
|
46. Генерирующее соотношение дробного факторного плана |
Соотношение, при помощи которого определяется, какой ид взаимодействующих факторов отсутствует и какой фактор вместо него используется в плане матрицы |
|
|
47. Определяющий контраст дробного факторного плана |
Соотношения произведений факторов, задающие элементы столбца, состоящего только из плюсов или минусов |
|
|
48. Обобщающий определяющий контраст дробного факторного плана |
Произведения высшего порядка определяющих контрастов |
|
|
49. Симметричность плана |
Свойство плана, при котором в матрице алгебраическая сумма элементов столбца каждого фактора равна нулю |
|
|
50. Нормирование плана |
Свойство плана, при котором в матрице сумма квадратов элементов каждого столбца равна числу точек плана матрицы |
|
|
51. Ортогональность плана |
Свойство плана, при котором в матрице сумма построчных произведений любых двух столбцов равна нулю |
|
|
52. Ротатабельность плана |
Свойство плана, обеспечивающее возможность предсказывать значения параметра оптимизации с одинаковой точностью в любых направлениях от центра эксперимента |
|
|
53. Насыщенность плана |
Мера близости между числом точек матрицы плана и числом параметров в модели |
|
|
54. Метод крутого восхождения Метод Бокса-Уилсона |
Метод планирования эксперимента, обеспечивающий возможность проведения полного или дробного факторного эксперимента с приближением значений параметров технологического процесса к оптимальным |
|
|
ЭКСПЕРИМЕНТ |
|
|
|
55. Активный эксперимент |
Эксперимент, в котором уровни факторов для каждого опыта задает исследователь |
|
|
56. Пассивный эксперимент |
Эксперимент, при котором уровни факторов в каждом опыте регистрируются исследователем, но не задаются |
|
|
57. Последовательный эксперимент Ндп. Шаговый эксперимент |
Эксперимент, реализуемый в виде серий, при этом условия проведения каждой последующей серии определяются результатами предыдущей серии |
|
|
АНАЛИЗ ЭКСПЕРИМЕНТА |
|
|
|
58. Регрессионный анализ |
Статистический метод анализа и обработки экспериментальных данных, основанный на оценке параметров заданной модели и проверке гипотез о ее статистических свойствах |
|
|
59. Выборка |
По ГОСТ 15895-70 |
|
|
60. Объем выборки |
По ГОСТ 15895-70 |
|
|
61. Воспроизводимость результатов |
Мера разброса результатов в параллельных опытах |
|
|
62. Проверка гипотезы |
Вероятное предположение соответствия определенной совокупности явлений их действительности |
|
|
63. Критерий для проверки гипотезы |
Правило, согласно которому гипотеза принимается или отвергается |
|
|
64. Критическая область |
Область, содержащая множество значений, при которых проверяемая гипотеза отвергается |
|
|
65. Информационная матрица |
Нормированная матрица моментов Примечание. Матрица моментов, каждый элемент которой поделен на число точек в плане матрицы |
|
|
66. Оценочная функция отклика |
Функция отклика, в которой неизвестные значения параметров заменены их оценками |
|
|
67. Эффект взаимодействия факторов |
Зависимость изменения уровня одного фактора от уровней других факторов |
|
|
68. Линейный эффект параметра оптимизации |
Зависимость параметра оптимизации от соответствующего фактора |
|
|
69. Смешанная оценка параметров модели |
Оценка, в которой невозможно отделить линейный эффект параметра модели от эффекта взаимодействия факторов |
|
|
70. Дисперсия оценки функции отклика |
Дисперсия оценки математического ожидания отклика в некоторой данной точке плана |
|
|
71. Оценка числа степеней свободы |
Оценка, в которой учитывается статистическая ситуация связи, ограничивающая свободу изменения случайных величин |
|
|
72. Область оптимума |
Область контролируемых переменных, отвечающая оптимальным результатам и условиям эксперимента |
|
|
73. Адекватность модели |
Соответствие модели с экспериментальными данными по выбранному параметру оптимизации с требуемой степенью точности |
|
ПРИЛОЖЕНИЕ 2
МАТРИЦЫ ПЛАНИРОВАНИЯ
В приложении приведены некоторые простейшие матрицы полных и дробных факторных планов. Для упрощения записи приняты специальные обозначения: строка, состоящая из одних минусов, обозначается (0), в остальных строках приводятся цифровые обозначения только тех факторов, которые находятся на верхнем уровне «+», например, фактору Х1 соответствует цифра 1, фактору Х2 - цифра 2 и т.д. в порядке чисел натурального ряда. План матрицы задается перечислением строк.
|
Обозначение строки матрицы |
Смешанные эффекты |
Определяющий контраст |
||
|
линейные |
взаимодействия |
|||
|
ПФЭ 22 |
(0), (1‘), (2‘), (1‘2‘) |
Не смешаны |
Не смешаны |
1 = Х1Х2Х3 |
|
ПФЭ 23 |
(0), (1‘), (2‘), (1‘2‘), (3‘), (1‘3‘), (2‘3‘), (1‘2‘3‘) |
Не смешаны |
Не смешаны |
1 = Х1Х2Х3Х4 |
|
1/2 от ПФЭ2 или 23-1 |
(1‘), (2‘), (3‘), (1‘2‘3‘) |
b1 ® b1 + b2,3 |
Не определяют |
1 = Х1Х2Х3 |
|
b2 ® b2 + b1,3 |
||||
|
b3 ® b3 + b1,2 |
||||
|
ПФЭ4 |
(0), (1‘), (2‘), (3‘), (4‘), (1‘2‘), (1‘3‘), (1‘4‘), (2‘3‘), (2‘4‘), (3‘4‘), (1‘2‘3‘), (1‘2‘4‘), (1‘3‘4‘), (2‘3‘4‘), (1‘2‘3‘4) |
Не смешаны |
Не смешаны |
1 = Х1Х2Х3Х4Х5 |
|
1/2 от ПФЭ 24 или 24-1 |
(0), (1‘2‘), (1‘3‘), (1‘4‘), (2‘4‘), (3‘4‘), (1‘2‘3‘4‘) |
Не смешаны |
b1,2 ® b1,2 + b3,4 |
1 = Х1Х2Х3Х4 |
|
b1,3 ® b1,3 + b2,4 |
||||
|
b1,4 ® b1,4 + b2,3 |
||||
|
ПФЭ 25 |
(0), (1‘), (2‘), (3‘), (4‘), (1‘2‘), (1‘3‘), (1‘4‘), (2‘3‘), (2‘4‘), (3‘4‘), (1‘2‘3‘), (1‘2‘4‘), (1‘3‘4‘), (2‘3‘4‘), (1‘2‘3‘4), (5‘), (1‘5‘), (2‘5‘), (3‘5‘), (4‘5‘), (1‘2‘5‘), (1‘3‘5‘), (1‘4‘5‘), (2‘3‘5), (2‘4‘5‘), (3‘4‘5‘), (1‘2‘3‘5‘), (1‘2‘4‘5), (1‘3‘4‘5‘), (2‘3‘4‘5‘), (1‘2‘3‘4‘5‘) |
Не смешаны |
Не смешаны |
1 = Х1Х2Х3Х4Х5Х6 |
|
1/2 от ПФЭ 25 или 25-1 |
(0), (1‘2‘), (1‘3‘4‘5‘), (2‘3‘4‘5‘), (1‘3‘), (2‘3‘), (4‘5‘), (1‘2‘3‘5‘), (1‘5‘), (2‘5‘), (3‘4‘), (1‘2‘3‘4‘), (1‘4‘), (2‘4‘), (3‘5‘), (1‘2‘3‘5‘) |
Не смешаны |
He смешаны |
1 = Х1Х2Х3Х4Х5 |
|
1/4 от ПФЭ 25 или 25-2 |
(0), (1‘3‘5‘), (2‘3‘5‘), (1‘4‘5‘), (2‘4‘5‘), (1‘2‘), (3‘4‘), (1‘2‘3‘4‘) |
b1 ® b1 + b2,5 |
b1,3 ® b1,3 + b1,4 |
1 = Х1Х2Х5 = Х3Х4Х5 = Х1Х2Х3X4 |
|
b2 ® b2 + b1,5 |
b1,4 ® b1,4 + b2,3 |
|||
|
b3 ® b3 + b4,5 |
|
|||
|
b4 ® b4 + b3,5 |
||||
|
b5 ® b5 + b1,2 + b3,4 |
||||
|
1/8 от ПФЭ 25 или 26-3 |
(0), (1‘3‘6‘), (1‘4‘5‘), (2‘3‘5‘), (2‘4‘6‘), (1‘2‘3‘4‘), (1‘2‘5‘6‘), (3‘4‘5‘6‘) |
b1 ® b1 + b3,5 + b4,5 |
b1,2 ® b1,2 + b3,4 + b3,6 |
1 = Х1Х3Х5 = Х1Х4Х6 = Х2Х3Х6 = Х2Х4Х5 = Х1Х2Х3X4 = Х1Х2Х5X6 = Х3Х4Х5X6 |
|
b2 ® b2 + b3,6 + b4,6 |
||||
|
b3 ® b3 + b1,5 + b2,6 |
||||
|
b4 ® b4 + b1,6 + b2,5 |
||||
|
b5 ® b5 + b1,3 + b2,4 |
||||
|
b6 ® b6 + b1,4 + b2,3 |
||||
|
1/16 от ПФЭ 27 или 27-4 |
(0), (1‘2‘3‘4‘), (1‘2‘5‘6‘), (1‘3‘6‘7‘), (2‘4‘6‘7‘), (3‘4‘5‘7‘), (1‘2‘5‘7‘) |
b1 ® b1 + b2,7 + b3,5 + b4,6 |
He определяют |
1 = Х1Х2Х7 = Х1Х3Х5 = Х1Х4Х6 = Х2Х3Х6 = Х2Х4X5 = Х3Х4X7 = Х1Х2X5Х6 = Х1Х3Х6Х7 = Х1Х4Х5Х6 = Х2Х3Х5Х7 = Х2Х4Х6Х7 = Х3Х4Х5X6 = Х1Х2Х3X4Х5Х6Х7 |
|
b2 ® b2 + b1,7 + b3,6 + b4,5 |
||||
|
b3 ® b3 + b1,5 + b2,6 + b4,7 |
||||
|
b4 ® b4 + b1,6 + b2,5 + b3,7 |
||||
|
b5 ® b5 + b1,3 + b2,4 + b6,7 |
||||
|
b6 ® b6 + b1,4 + b2,3 + b1,4 |
||||
|
b7 ® b7 + b1,2 + b3,4 + b3,6 |
||||
ПРИЛОЖЕНИЕ 3
ФОРМЫ ЖУРНАЛОВ ПЛАНИРОВАНИЯ И ПРАВИЛА ИХ ЗАПОЛНЕНИЯ
В настоящем приложении устанавливают правила оформления документов по проведению эксперимента:
журнала планирования эксперимента (форма 1 - см. бандероль);
журнала планирования (операционного) эксперимента (форма 2 - см. бандероль);
журнала планирования эксперимента методом крутого восхождения (операционного) (форма 3 - см. бандероль).
1. ПРАВИЛА ОФОРМЛЕНИЯ ЖУРНАЛА ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
1.1. Журнал планирования эксперимента предназначен для записи априорных сведений о факторах (параметрах) процесса, записи верхних, нижних и средних уровней факторов, интервалов варьирования, плана матрицы планирования, результатов эксперимента, промежуточных и конечных результатов расчета, для проверки воспроизводимости эксперимента, значимости коэффициентов, проверки адекватного описания процесса, а также для указания подписей исполнителя технологического процесса (операции), руководителя участка и контролирующего лица.
1.2. Журнал планирования эксперимента следует оформлять при изготовлении первых деталей (сборочных единиц) или при запуске технологического процесса для определения номенклатуры контролируемых параметров. Журналом планирования эксперимента можно пользоваться и после внедрения технологических процессов для оформления результатов операционного контроля.
1.3. Учет и хранение журналов планирования эксперимента должны соответствовать правилам, установленным на предприятии.
1.4. Журнал планирования эксперимента ПФЭ или ДФЭ соответствующего технологического процесса или операции следует оформлять по форме 1.
Пример заполнения формы 1 указан в приложении 6 (форма А).
1.5. Графы формы следует заполнять в соответствии с табл. 1.
Таблица 1
|
Содержание графы |
|
|
1 |
Наименование журнала |
|
2 |
Обозначение и наименование детали (сборочной единицы) по конструкторскому документу |
|
3 |
Обозначение документа, содержащего описание технологического процесса операции. Допускается, при необходимости, в графу записывать наименование предприятия |
|
4 |
Номер операции технологического процесса |
|
5 |
Условные обозначения и единицы измерения характеристик, параметров (факторов) |
|
6 |
Количественные значения характеристик, параметров на верхнем допусковом уровне |
|
7 |
Количественные значения характеристик, параметров на нижнем допусковом уровне |
|
8 |
Количественные значения характеристики, параметров на основном уровне |
|
9 |
Количественные значения интервалов варьирования характеристик, параметров |
|
10 |
Априорные сведения о технологическом процессе или операции, условия и результаты, достигнутые при изучении аналогичных процессов, результаты предварительного эксперимента или данные из литературных источников, а также данные о взаимодействии параметров (факторов) |
|
11 |
Оценка коэффициентов уравнения. В графу следует записывать сведения о линейных оценках коэффициентов и коэффициенты, у которых невозможно различить линейный эффект и эффект взаимодействия в зависимости от выбранного плана матрицы |
|
12 - 14 |
В графах записывают числа, обозначающие порядок (номер) опыта, определяемые по таблице нормально распределенных случайных чисел. Количество этих граф допускается увеличивать за счет графы «Особые указания» |
|
15 - 29 |
Контролируемые параметры, характеристики, режимы технологического процесса или операции. В этих графах запись производят в кодовых обозначениях «+» и «-». Допускается в заголовках этих граф, кроме обозначений Х1, Х2, ..., Xk, при необходимости, проставлять условные обозначения характеристик, параметров, соответствующие указанным в графе 5. Примечания: 1. Количество граф допускается изменять в зависимости от количества контролируемых переменных технологического процесса или операции, включаемых в эксперимент. 2. Количество номеров точек плана матрицы для полного факторного эксперимента определяют по формуле 2k, а для дробного факторного эксперимента - по формуле 2k-p |
|
30 - 32 |
В графах записывают количественные значения функциональных характеристик величины показателя параметра оптимизации (детали, сборочной единицы), получаемые замером при реализации серии (m1, m2, m3) параллельных опытов для конкретной точки плана матрицы |
|
33 |
Результаты расчетов среднего значения показателя параметра оптимизации по реализации серии параллельных опытов |
|
34 |
Дисперсия отклонений показателя параметра оптимизации от среднего |
|
35 |
Результаты расчетов показателя параметра оптимизации по линейному уравнению регрессии |
|
36 |
Квадрат разности между средним (см. графу 33) и рассчитанным по уравнению регрессии (см. графу 35) значениями показателя параметра оптимизации процесса (операции) |
|
37 |
Особые указания Графу следует заполнять по усмотрению предприятия. В этой графе допускается давать ссылки на документы, разрешающие отступления от утвержденной технологии, замечания и т.д. |
|
38 |
Коэффициенты уравнения репрессии и получаемые расчетным путем |
|
39 |
Сумма всех дисперсий (см. графу 34), деленная на количество точек в плане матрицы |
|
40 |
Заданный уровень значимости в процентах, определяемый по таблице Стьюдента при проверке значимости коэффициентов репрессии |
|
41 |
Число степеней свободы при проверке значимости коэффициентов регрессии |
|
42 |
Критическое значение коэффициента регрессии, определяемое по таблице Стьюдента при соответствующих степенях свободы и заданном уровне значимости |
|
43 |
Дисперсия коэффициентов репрессии при проверке значимости коэффициентов регрессии, получаемая расчетным путем |
|
44 |
Среднеквадратическое отклонение дисперсии коэффициентов регрессии (см. графу 43) при проверке значимости коэффициентов регрессии |
|
45 |
Расчетное значение критерия Стьюдента для каждого коэффициента регрессии |
|
46 |
Разность между расчетными (см. графу 45) и табличным (см. графу 48) значениями критерия Стьюдента при проверке коэффициентов регрессии |
|
47 |
О значимости или незначимости коэффициента регрессии следует условно писать «ЗН» или «НЕЗН» |
|
48 |
Модель технологического процесса или операции со всеми значимыми и незначимыми коэффициентами |
|
49 |
Сумма всех дисперсий (см. графу 34) |
|
50 |
Максимальная дисперсия, выбранная из графы S2v (см. графу 34) |
|
51 |
Отношение максимальной дисперсии к сумме всех дисперсий |
|
52 |
Заданный уровень значимости в процентах по таблице Кохрена при проверке однородности дисперсий |
|
53 |
Число степеней свободы максимальной дисперсии при проверке однородности дисперсии |
|
54 |
Число степеней свободы суммы всех дисперсий |
|
55 |
Критическое значение дисперсии, определяемое по таблице Кохрена при соответствующих степенях свободы и заданном уровне значимости |
|
56 |
Разность между расчетным (см. графу 51) и табличным значениями критерия Кохрена при проверке однородности дисперсий |
|
57 |
Об однородности или неоднородности дисперсий следует указывать словом |
|
58 |
Сумма
|
|
59 |
Дисперсия адекватности при проверке адекватности модели |
|
60 |
Отношение дисперсии адекватности (см. графу 59) к дисперсии параметра оптимизации (см. графу 39) |
|
61 |
Заданный уровень значимости в процентах по таблице Фишера при проверке адекватности модели |
|
62 |
Число степеней свободы для дисперсии адекватности при проверке адекватности модели |
|
63 |
Число степеней свободы для дисперсии параметра оптимизация при проверке адекватности модели |
|
64 |
Критическое значение равенства двух генеральных дисперсий, определяемое по таблице Фишера при соответствующих степенях свободы и заданном уровне значимости |
|
65 |
Разность между расчетным (см. графу 60) и табличными значениями критерия Фишера при проверке адекватности модели |
|
66 |
Об адекватности или неадекватности модели следует писать словом |
|
67 |
Модель технологического процесса (операции), включая только значимые коэффициенты регрессии |
|
68 |
Табельный номер исполнителя технологического процесса (рабочего, бригадира, испытателя) |
|
69 |
Подпись исполнителя технологического процесса (рабочего, бригадира, испытателя) |
|
70 |
Дата исполнения технологического процесса |
|
71 |
Подпись руководителя участка (мастера, инженера-испытателя, старшего мастера) |
|
72 |
Дата подписи руководителя участка (мастера, инженера-испытателя, старшего мастера) |
|
73 |
Резервная графа. Заполняют по усмотрению разработчика |
2. ПРАВИЛА ОФОРМЛЕНИЯ (ОПЕРАЦИОННОГО) ЖУРНАЛА ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
2.1. Журнал планирования эксперимента (операционный) предназначен для записи уровней контролируемых характеристик, факторов (параметров) технологического процесса в действительных значениях по условиям плана эксперимента. Этот журнал следует применять в комплекте с формой 1 (см. бандероль).
2.2. Журналом планирования эксперимента пользуются при проведении эксперимента для осуществления последовательности: действий (операций), с помощью которых устанавливаются конкретные уровни факторов (параметров) в действительных значениях.
2.3. Журнал планирования эксперимента соответствующего технологического процесса следует оформлять по форме 2 (см. бандероль).
Пример заполнения формы 2 указан в приложении 6 (форма Б).
2.4. Графы формы следует заполнять в соответствии с табл. 2.
Таблица 2
|
Содержание графы |
|
|
1 |
Наименование журнала |
|
2 - 10 |
Следует заполнять так же, как графы 2 - 10 формы 1 |
|
11 - 16 |
Следует заполнять так же, как графы 12 - 14 формы 1. Количество граф в данной форме должно быть не менее трех. Количество граф допускается увеличивать при неадекватности модели или невоспроизводимости результатов измерений |
|
17 - 31 |
Контролируемые параметры, характеристики, технологического процесса или операции в действительных значениях переменных. Допускается в заголовках этих граф, кроме Х1, Х2, ..., Xk, при необходимости, проставлять условные обозначения характеристик, параметров, соответствующие указанным в графе 5 |
|
32 - 37 |
Следует заполнять так же, как графы 30 - 32 формы 1. Количество граф зависит от числа параллельных опытов |
|
38 |
Результаты расчетов среднего значения показателя параметра оптимизации по реализации серии параллельных опытов |
|
39 - 44 |
Следует заполнять так же, как графы 37, 68, 69, 70, 71, 72 формы 1 соответственно |
3. ПРАВИЛА ОФОРМЛЕНИЯ ЖУРНАЛА ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА МЕТОДОМ КРУТОГО ВОСХОЖДЕНИЯ (ОПЕРАЦИОННОГО)
3.1. Журнал планирования эксперимента методом крутого восхождения (операционный) предназначен для записи величин контролируемых характеристик, факторов (параметров) технологического процесса или операции в действительных значениях по условиям плана эксперимента. Этот журнал следует применять в комплекте с формами 1 и 2.
3.2. Журналом планирования эксперимента методом крутого восхождения (операционный) пользуются при оптимизации технологического процесса (операции) или при его (ее) прогнозировании.
3.3. Журнал планирования эксперимента методом крутого восхождения ПФЭ или ДФЭ соответствующего технологического процесса или операции следует оформлять по форме 3 (см. бандероль).
Пример заполнения формы 3 указан в приложении 6 (форма В).
3.4. Графы следует заполнять в соответствии с табл. 3.
Таблица 3
|
Содержание графы |
|
|
1 - 9 |
Следует заполнять так же, как соответствующие графы формы 1 |
|
10 |
Коэффициенты регрессии переносят из формы 1, графа 38 |
|
11 |
Результаты
произведения |
|
12 |
Шаг крутого восхождения, получаемый расчетным путем |
|
13 |
Следует заполнять так же, как графу 10 формы 1 |
|
14 - 19 |
Следует заполнять так же, как графы 11 - 16 формы 2 |
|
20 - 34 |
Контролируемые параметры, характеристики технологического процесса или операции в натуральных значениях переменных, соответствующих шагу крутого восхождения. Допускается в заголовках этих граф, кроме Х1, Х2, ..., Xk, при необходимости, проставлять условные обозначения характеристики параметров, соответствующих указанным в графе 5 |
|
35 - 40 |
Следует заполнять так же, как графы 30 - 32 формы 1. Количество граф зависит от числа параллельных опытов |
|
41 |
Результаты расчетов среднего значения показателя параметра оптимизации по реализации серии параллельных опытов |
|
42 - 47 |
Следует заполнять так же, как графы 37, 68, 69, 70, 71, 72 формы 1 соответственно |
ПРИЛОЖЕНИЕ 4
ТАБЛИЦА
РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ЧИСЕЛ
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
|
10 |
09 |
73 |
25 |
33 |
76 |
52 |
01 |
35 |
86 |
34 |
67 |
35 |
48 |
76 |
80 |
95 |
90 |
91 |
17 |
39 |
29 |
27 |
49 |
45 |
|
37 |
54 |
20 |
48 |
05 |
67 |
89 |
47 |
42 |
96 |
24 |
80 |
52 |
40 |
37 |
20 |
63 |
62 |
04 |
02 |
00 |
82 |
29 |
16 |
65 |
|
08 |
42 |
26 |
89 |
53 |
19 |
64 |
50 |
97 |
03 |
23 |
20 |
90 |
25 |
60 |
15 |
95 |
33 |
47 |
64 |
35 |
08 |
03 |
36 |
06 |
|
99 |
01 |
90 |
25 |
29 |
09 |
37 |
67 |
07 |
15 |
33 |
31 |
13 |
11 |
65 |
88 |
67 |
67 |
43 |
97 |
04 |
43 |
62 |
76 |
59 |
|
12 |
80 |
79 |
99 |
70 |
80 |
15 |
73 |
61 |
47 |
64 |
03 |
23 |
66 |
53 |
98 |
95 |
11 |
68 |
77 |
12 |
17 |
17 |
68 |
33 |
|
66 |
06 |
57 |
47 |
17 |
34 |
07 |
27 |
68 |
50 |
36 |
69 |
73 |
61 |
70 |
65 |
81 |
33 |
98 |
85 |
11 |
19 |
92 |
91 |
70 |
|
31 |
06 |
01 |
08 |
05 |
45 |
57 |
18 |
24 |
26 |
35 |
30 |
34 |
26 |
14 |
86 |
79 |
90 |
74 |
39 |
23 |
40 |
30 |
97 |
32 |
|
85 |
26 |
97 |
76 |
02 |
02 |
05 |
16 |
56 |
92 |
68 |
66 |
57 |
48 |
18 |
73 |
05 |
38 |
52 |
47 |
18 |
62 |
38 |
85 |
79 |
|
63 |
57 |
33 |
21 |
35 |
05 |
32 |
54 |
70 |
48 |
90 |
55 |
35 |
75 |
48 |
28 |
46 |
82 |
87 |
09 |
83 |
49 |
12 |
56 |
24 |
|
73 |
79 |
64 |
57 |
53 |
03 |
52 |
96 |
47 |
73 |
35 |
80 |
83 |
42 |
82 |
60 |
93 |
52 |
03 |
44 |
35 |
27 |
38 |
84 |
35 |
|
98 |
52 |
01 |
77 |
67 |
14 |
90 |
56 |
86 |
07 |
22 |
10 |
94 |
05 |
58 |
60 |
97 |
09 |
34 |
33 |
50 |
50 |
07 |
87 |
98 |
|
11 |
80 |
50 |
54 |
31 |
39 |
80 |
82 |
77 |
32 |
50 |
72 |
56 |
82 |
48 |
29 |
40 |
52 |
42 |
01 |
52 |
77 |
56 |
78 |
51 |
|
83 |
45 |
20 |
96 |
34 |
06 |
28 |
89 |
80 |
83 |
13 |
74 |
67 |
00 |
78 |
18 |
47 |
54 |
06 |
10 |
68 |
71 |
17 |
78 |
17 |
|
88 |
68 |
54 |
02 |
00 |
86 |
50 |
75 |
84 |
01 |
36 |
76 |
66 |
79 |
51 |
90 |
36 |
47 |
64 |
93 |
29 |
60 |
91 |
10 |
62 |
|
99 |
59 |
46 |
73 |
48 |
37 |
51 |
76 |
49 |
69 |
91 |
82 |
60 |
89 |
28 |
93 |
78 |
56 |
13 |
68 |
23 |
47 |
83 |
41 |
13 |
|
65 |
48 |
11 |
76 |
74 |
17 |
46 |
85 |
09 |
50 |
58 |
04 |
77 |
69 |
74 |
73 |
03 |
95 |
71 |
86 |
40 |
31 |
81 |
65 |
44 |
|
80 |
12 |
43 |
56 |
35 |
17 |
72 |
70 |
70 |
15 |
45 |
31 |
82 |
23 |
74 |
21 |
11 |
57 |
82 |
53 |
14 |
38 |
55 |
37 |
63 |
|
74 |
35 |
09 |
98 |
17 |
77 |
45 |
27 |
72 |
14 |
43 |
23 |
60 |
02 |
10 |
45 |
52 |
16 |
42 |
37 |
96 |
28 |
60 |
26 |
55 |
|
69 |
91 |
62 |
68 |
03 |
66 |
25 |
22 |
91 |
48 |
36 |
93 |
68 |
72 |
03 |
76 |
62 |
11 |
39 |
90 |
94 |
40 |
05 |
64 |
18 |
|
09 |
89 |
32 |
05 |
05 |
14 |
22 |
56 |
85 |
14 |
46 |
42 |
75 |
67 |
88 |
96 |
29 |
77 |
88 |
22 |
54 |
38 |
21 |
45 |
98 |
|
91 |
49 |
91 |
45 |
23 |
68 |
47 |
92 |
76 |
86 |
46 |
16 |
28 |
35 |
54 |
94 |
75 |
08 |
99 |
23 |
37 |
08 |
92 |
00 |
48 |
|
80 |
33 |
69 |
45 |
98 |
26 |
94 |
03 |
68 |
58 |
70 |
29 |
73 |
41 |
35 |
53 |
14 |
03 |
33 |
40 |
42 |
05 |
08 |
23 |
41 |
|
42 |
10 |
48 |
19 |
49 |
85 |
15 |
74 |
79 |
54 |
32 |
97 |
92 |
65 |
37 |
57 |
60 |
04 |
08 |
81 |
22 |
22 |
20 |
64 |
13 |
|
12 |
55 |
07 |
37 |
42 |
11 |
10 |
00 |
20 |
40 |
12 |
86 |
07 |
46 |
97 |
96 |
64 |
48 |
94 |
39 |
28 |
70 |
72 |
58 |
15 |
|
63 |
60 |
64 |
93 |
29 |
16 |
50 |
53 |
44 |
84 |
40 |
21 |
95 |
25 |
63 |
43 |
64 |
17 |
70 |
82 |
07 |
20 |
73 |
17 |
90 |
|
61 |
19 |
69 |
04 |
46 |
26 |
45 |
74 |
77 |
74 |
61 |
92 |
43 |
37 |
29 |
65 |
39 |
45 |
95 |
93 |
42 |
58 |
26 |
05 |
27 |
|
15 |
47 |
44 |
52 |
66 |
95 |
27 |
07 |
99 |
53 |
59 |
36 |
78 |
38 |
48 |
82 |
39 |
61 |
01 |
18 |
33 |
21 |
15 |
94 |
66 |
|
94 |
55 |
72 |
85 |
73 |
67 |
89 |
75 |
43 |
87 |
54 |
62 |
24 |
44 |
31 |
91 |
19 |
04 |
25 |
92 |
92 |
92 |
74 |
59 |
73 |
|
42 |
48 |
11 |
62 |
13 |
97 |
34 |
40 |
87 |
21 |
16 |
86 |
84 |
87 |
67 |
03 |
07 |
11 |
20 |
59 |
25 |
70 |
14 |
66 |
70 |
|
23 |
52 |
37 |
83 |
18 |
73 |
20 |
88 |
98 |
37 |
68 |
93 |
69 |
14 |
16 |
26 |
25 |
22 |
96 |
65 |
05 |
52 |
28 |
25 |
62 |
|
04 |
49 |
35 |
24 |
94 |
75 |
24 |
63 |
38 |
24 |
45 |
86 |
25 |
10 |
25 |
61 |
96 |
27 |
93 |
35 |
68 |
73 |
71 |
24 |
72 |
|
00 |
54 |
99 |
76 |
54 |
64 |
05 |
18 |
81 |
69 |
96 |
11 |
96 |
38 |
96 |
54 |
69 |
28 |
23 |
91 |
23 |
28 |
72 |
95 |
29 |
|
35 |
96 |
31 |
53 |
07 |
26 |
89 |
30 |
93 |
64 |
33 |
35 |
13 |
54 |
52 |
77 |
97 |
45 |
00 |
24 |
90 |
10 |
33 |
93 |
33 |
|
50 |
80 |
80 |
83 |
91 |
45 |
42 |
72 |
68 |
42 |
83 |
60 |
94 |
97 |
00 |
13 |
02 |
12 |
48 |
92 |
78 |
56 |
52 |
01 |
06 |
|
46 |
05 |
88 |
52 |
36 |
01 |
39 |
09 |
22 |
86 |
77 |
28 |
14 |
40 |
77 |
93 |
91 |
08 |
36 |
47 |
70 |
61 |
74 |
29 |
41 |
|
32 |
17 |
90 |
05 |
97 |
87 |
37 |
92 |
52 |
41 |
05 |
56 |
70 |
70 |
07 |
86 |
74 |
31 |
71 |
57 |
95 |
39 |
41 |
18 |
38 |
|
69 |
23 |
46 |
14 |
06 |
20 |
11 |
74 |
52 |
04 |
15 |
95 |
66 |
00 |
00 |
18 |
74 |
39 |
24 |
23 |
97 |
11 |
89 |
63 |
38 |
|
19 |
56 |
54 |
14 |
30 |
01 |
75 |
87 |
53 |
79 |
40 |
41 |
52 |
15 |
85 |
66 |
67 |
43 |
68 |
06 |
84 |
96 |
28 |
52 |
07 |
|
45 |
15 |
51 |
49 |
38 |
19 |
47 |
60 |
72 |
46 |
43 |
66 |
79 |
45 |
43 |
59 |
04 |
79 |
00 |
33 |
20 |
82 |
66 |
95 |
41 |
|
94 |
86 |
43 |
19 |
94 |
36 |
16 |
81 |
08 |
51 |
34 |
88 |
88 |
15 |
53 |
01 |
54 |
03 |
54 |
56 |
05 |
51 |
45 |
11 |
76 |
|
98 |
08 |
62 |
48 |
26 |
45 |
24 |
02 |
84 |
04 |
44 |
99 |
90 |
88 |
96 |
39 |
09 |
47 |
31 |
07 |
35 |
44 |
13 |
18 |
80 |
|
33 |
18 |
51 |
62 |
32 |
41 |
94 |
15 |
09 |
49 |
89 |
43 |
54 |
85 |
81 |
88 |
69 |
54 |
19 |
94 |
37 |
54 |
87 |
30 |
43 |
|
80 |
95 |
10 |
04 |
06 |
96 |
38 |
27 |
07 |
74 |
20 |
15 |
12 |
33 |
87 |
25 |
01 |
62 |
52 |
98 |
94 |
62 |
46 |
11 |
71 |
|
79 |
75 |
24 |
91 |
40 |
71 |
96 |
12 |
82 |
96 |
69 |
86 |
10 |
25 |
91 |
74 |
85 |
22 |
05 |
39 |
00 |
38 |
75 |
95 |
79 |
|
18 |
63 |
33 |
25 |
37 |
98 |
14 |
50 |
65 |
71 |
31 |
01 |
02 |
46 |
74 |
05 |
45 |
56 |
14 |
27 |
77 |
83 |
89 |
19 |
39 |
|
74 |
02 |
94 |
39 |
02 |
77 |
55 |
73 |
22 |
70 |
97 |
79 |
01 |
71 |
19 |
52 |
62 |
75 |
80 |
21 |
80 |
81 |
45 |
17 |
48 |
|
54 |
17 |
84 |
56 |
11 |
80 |
99 |
33 |
71 |
43 |
05 |
33 |
51 |
29 |
69 |
56 |
12 |
71 |
92 |
55 |
36 |
04 |
09 |
53 |
24 |
|
11 |
66 |
44 |
98 |
83 |
52 |
07 |
98 |
48 |
27 |
59 |
38 |
17 |
15 |
39 |
09 |
97 |
33 |
34 |
40 |
88 |
46 |
12 |
33 |
56 |
|
48 |
32 |
47 |
79 |
28 |
31 |
24 |
96 |
47 |
10 |
42 |
29 |
53 |
68 |
70 |
32 |
30 |
75 |
75 |
46 |
15 |
02 |
00 |
99 |
94 |
|
69 |
07 |
49 |
41 |
38 |
87 |
63 |
79 |
19 |
76 |
35 |
58 |
40 |
44 |
01 |
10 |
51 |
82 |
16 |
15 |
01 |
84 |
87 |
69 |
38 |
|
09 |
18 |
82 |
00 |
97 |
32 |
82 |
53 |
95 |
27 |
04 |
22 |
08 |
63 |
04 |
83 |
38 |
98 |
73 |
74 |
64 |
27 |
85 |
80 |
44 |
|
90 |
04 |
58 |
54 |
97 |
51 |
58 |
15 |
06 |
54 |
94 |
93 |
88 |
19 |
97 |
91 |
87 |
07 |
61 |
60 |
68 |
47 |
66 |
46 |
59 |
|
73 |
18 |
95 |
02 |
07 |
47 |
67 |
72 |
62 |
69 |
52 |
29 |
06 |
46 |
64 |
27 |
12 |
46 |
70 |
18 |
41 |
36 |
18 |
27 |
60 |
|
75 |
76 |
87 |
64 |
90 |
20 |
97 |
18 |
17 |
49 |
90 |
42 |
91 |
22 |
72 |
95 |
37 |
50 |
58 |
71 |
93 |
82 |
34 |
31 |
78 |
|
54 |
01 |
64 |
40 |
66 |
66 |
28 |
13 |
10 |
03 |
00 |
68 |
22 |
73 |
98 |
20 |
71 |
45 |
32 |
95 |
07 |
70 |
61 |
78 |
13 |
|
08 |
35 |
86 |
99 |
10 |
73 |
64 |
24 |
27 |
85 |
13 |
66 |
15 |
88 |
73 |
04 |
61 |
68 |
75 |
53 |
31 |
22 |
30 |
84 |
20 |
|
28 |
30 |
60 |
32 |
64 |
81 |
33 |
31 |
05 |
91 |
40 |
51 |
00 |
78 |
93 |
32 |
60 |
46 |
04 |
75 |
94 |
11 |
90 |
18 |
40 |
|
53 |
84 |
08 |
62 |
33 |
81 |
59 |
41 |
36 |
28 |
51 |
21 |
59 |
02 |
90 |
28 |
46 |
66 |
87 |
95 |
77 |
76 |
22 |
07 |
91 |
|
91 |
75 |
75 |
77 |
41 |
61 |
61 |
32 |
22 |
69 |
50 |
26 |
39 |
02 |
14 |
65 |
78 |
17 |
65 |
14 |
83 |
48 |
34 |
70 |
65 |
|
89 |
41 |
59 |
26 |
94 |
90 |
39 |
75 |
83 |
91 |
12 |
60 |
71 |
76 |
46 |
48 |
94 |
97 |
93 |
06 |
94 |
54 |
13 |
74 |
08 |
|
77 |
51 |
30 |
38 |
22 |
86 |
83 |
42 |
89 |
01 |
58 |
41 |
48 |
27 |
74 |
51 |
90 |
81 |
39 |
80 |
72 |
89 |
35 |
57 |
07 |
|
19 |
50 |
23 |
71 |
74 |
69 |
97 |
92 |
02 |
88 |
55 |
21 |
02 |
97 |
73 |
74 |
28 |
77 |
52 |
51 |
65 |
34 |
46 |
75 |
15 |
|
21 |
81 |
85 |
99 |
13 |
93 |
27 |
88 |
17 |
67 |
05 |
68 |
67 |
31 |
56 |
07 |
08 |
28 |
50 |
46 |
31 |
85 |
33 |
84 |
52 |
|
51 |
47 |
46 |
64 |
99 |
68 |
10 |
72 |
36 |
21 |
94 |
04 |
99 |
13 |
45 |
42 |
83 |
60 |
91 |
91 |
08 |
00 |
74 |
64 |
49 |
|
99 |
65 |
96 |
83 |
31 |
62 |
53 |
52 |
41 |
70 |
69 |
77 |
71 |
28 |
30 |
74 |
81 |
97 |
81 |
42 |
43 |
86 |
07 |
28 |
34 |
|
33 |
71 |
34 |
80 |
07 |
93 |
68 |
47 |
28 |
69 |
51 |
92 |
66 |
47 |
21 |
58 |
30 |
32 |
98 |
22 |
93 |
17 |
49 |
39 |
72 |
|
85 |
27 |
49 |
68 |
93 |
11 |
30 |
32 |
92 |
70 |
28 |
83 |
43 |
41 |
37 |
73 |
51 |
59 |
04 |
00 |
71 |
14 |
84 |
36 |
43 |
|
84 |
13 |
38 |
96 |
40 |
33 |
03 |
55 |
21 |
66 |
73 |
85 |
27 |
00 |
91 |
61 |
22 |
26 |
05 |
61 |
66 |
32 |
71 |
84 |
23 |
|
56 |
73 |
21 |
62 |
34 |
17 |
39 |
59 |
61 |
31 |
10 |
12 |
39 |
16 |
22 |
85 |
49 |
65 |
75 |
66 |
81 |
60 |
41 |
88 |
80 |
|
65 |
13 |
85 |
68 |
06 |
87 |
64 |
88 |
52 |
61 |
34 |
31 |
36 |
58 |
61 |
45 |
87 |
52 |
10 |
68 |
85 |
64 |
44 |
72 |
77 |
|
38 |
00 |
10 |
21 |
76 |
81 |
71 |
91 |
17 |
11 |
71 |
60 |
29 |
29 |
37 |
74 |
21 |
96 |
40 |
49 |
65 |
58 |
44 |
96 |
98 |
|
37 |
40 |
29 |
63 |
97 |
01 |
31 |
47 |
75 |
86 |
56 |
27 |
11 |
00 |
86 |
47 |
32 |
46 |
26 |
05 |
40 |
03 |
03 |
74 |
38 |
|
97 |
12 |
54 |
03 |
48 |
87 |
08 |
33 |
14 |
17 |
21 |
81 |
53 |
92 |
60 |
75 |
23 |
79 |
20 |
47 |
15 |
50 |
12 |
95 |
78 |
|
21 |
82 |
64 |
11 |
84 |
47 |
14 |
33 |
40 |
72 |
64 |
53 |
88 |
59 |
02 |
59 |
13 |
90 |
64 |
41 |
03 |
85 |
65 |
45 |
59 |
|
73 |
13 |
54 |
27 |
42 |
95 |
71 |
90 |
90 |
35 |
85 |
79 |
47 |
42 |
96 |
08 |
79 |
98 |
81 |
17 |
64 |
69 |
11 |
92 |
02 |
|
07 |
63 |
87 |
79 |
29 |
03 |
06 |
11 |
80 |
73 |
96 |
20 |
74 |
41 |
56 |
23 |
82 |
19 |
95 |
38 |
04 |
71 |
76 |
69 |
94 |
|
60 |
52 |
88 |
74 |
41 |
07 |
95 |
41 |
98 |
14 |
59 |
17 |
52 |
06 |
95 |
05 |
53 |
35 |
21 |
99 |
61 |
21 |
20 |
44 |
55 |
|
83 |
59 |
53 |
56 |
55 |
06 |
95 |
89 |
29 |
83 |
05 |
12 |
80 |
97 |
19 |
77 |
49 |
35 |
37 |
83 |
92 |
30 |
15 |
04 |
98 |
|
39 |
82 |
09 |
89 |
52 |
43 |
62 |
26 |
31 |
47 |
64 |
42 |
18 |
08 |
14 |
43 |
80 |
00 |
93 |
51 |
31 |
02 |
47 |
31 |
67 |
|
10 |
85 |
06 |
26 |
46 |
99 |
59 |
91 |
05 |
47 |
13 |
49 |
90 |
63 |
19 |
53 |
07 |
57 |
18 |
39 |
06 |
41 |
01 |
93 |
62 |
|
59 |
58 |
00 |
64 |
78 |
75 |
56 |
97 |
88 |
00 |
88 |
83 |
55 |
44 |
86 |
23 |
76 |
80 |
61 |
56 |
04 |
11 |
10 |
34 |
08 |
|
38 |
50 |
80 |
73 |
41 |
23 |
79 |
34 |
87 |
63 |
90 |
82 |
29 |
70 |
22 |
17 |
71 |
90 |
42 |
07 |
95 |
95 |
04 |
99 |
53 |
|
30 |
69 |
27 |
06 |
68 |
94 |
68 |
81 |
61 |
27 |
56 |
19 |
68 |
00 |
91 |
82 |
06 |
76 |
34 |
00 |
05 |
46 |
26 |
92 |
00 |
|
65 |
44 |
39 |
56 |
59 |
18 |
28 |
82 |
74 |
37 |
49 |
63 |
22 |
40 |
41 |
08 |
33 |
76 |
56 |
76 |
96 |
29 |
99 |
08 |
36 |
|
27 |
26 |
75 |
02 |
64 |
13 |
19 |
27 |
22 |
94 |
07 |
47 |
74 |
46 |
06 |
17 |
98 |
34 |
89 |
11 |
97 |
34 |
13 |
03 |
58 |
|
91 |
30 |
70 |
69 |
91 |
19 |
07 |
22 |
42 |
10 |
36 |
69 |
95 |
37 |
28 |
28 |
82 |
53 |
57 |
93 |
28 |
97 |
66 |
62 |
52 |
|
68 |
43 |
49 |
46 |
88 |
84 |
47 |
31 |
36 |
25 |
62 |
12 |
69 |
84 |
08 |
12 |
84 |
38 |
25 |
90 |
09 |
81 |
59 |
31 |
46 |
|
48 |
90 |
81 |
58 |
77 |
54 |
74 |
52 |
45 |
91 |
35 |
70 |
00 |
47 |
54 |
83 |
82 |
45 |
26 |
92 |
54 |
13 |
05 |
51 |
60 |
|
06 |
91 |
34 |
51 |
97 |
42 |
67 |
27 |
86 |
01 |
11 |
88 |
30 |
95 |
28 |
63 |
01 |
19 |
89 |
01 |
14 |
87 |
44 |
03 |
44 |
|
10 |
45 |
51 |
60 |
19 |
14 |
21 |
03 |
37 |
12 |
91 |
34 |
23 |
78 |
21 |
88 |
32 |
68 |
08 |
51 |
43 |
66 |
77 |
08 |
83 |
|
12 |
38 |
39 |
73 |
43 |
65 |
02 |
76 |
11 |
84 |
04 |
28 |
50 |
13 |
92 |
17 |
97 |
41 |
50 |
77 |
90 |
71 |
22 |
67 |
69 |
|
21 |
77 |
83 |
09 |
76 |
38 |
80 |
73 |
69 |
61 |
31 |
64 |
94 |
20 |
96 |
63 |
28 |
10 |
20 |
23 |
08 |
81 |
64 |
74 |
49 |
|
19 |
52 |
85 |
95 |
15 |
65 |
12 |
25 |
96 |
59 |
86 |
28 |
36 |
82 |
58 |
69 |
59 |
21 |
37 |
98 |
16 |
43 |
59 |
15 |
29 |
|
67 |
24 |
55 |
26 |
70 |
35 |
58 |
31 |
65 |
63 |
79 |
24 |
68 |
66 |
86 |
76 |
46 |
33 |
42 |
22 |
26 |
65 |
59 |
08 |
02 |
|
60 |
58 |
44 |
73 |
77 |
67 |
50 |
03 |
79 |
92 |
45 |
13 |
42 |
65 |
29 |
26 |
76 |
68 |
36 |
37 |
41 |
32 |
64 |
43 |
44 |
|
53 |
85 |
34 |
13 |
17 |
36 |
06 |
69 |
48 |
50 |
58 |
83 |
87 |
38 |
59 |
49 |
36 |
47 |
33 |
31 |
96 |
24 |
04 |
36 |
42 |
|
24 |
63 |
73 |
87 |
36 |
74 |
38 |
48 |
93 |
42 |
52 |
62 |
30 |
79 |
92 |
12 |
36 |
91 |
86 |
01 |
03 |
74 |
28 |
38 |
73 |
|
83 |
08 |
01 |
24 |
51 |
38 |
99 |
22 |
28 |
25 |
07 |
75 |
95 |
17 |
77 |
97 |
37 |
72 |
75 |
85 |
51 |
97 |
23 |
78 |
67 |
|
16 |
44 |
42 |
43 |
34 |
36 |
15 |
19 |
20 |
73 |
27 |
49 |
37 |
09 |
39 |
85 |
13 |
03 |
25 |
52 |
54 |
84 |
65 |
47 |
59 |
ПРИЛОЖЕНИЕ 5
ТАБЛИЦЫ КРИТЕРИЕВ КОХРЕНА, СТЬЮДЕНТА, ФИШЕРА
Таблица 1
ТАБЛИЦЫ КРИТЕРИЕВ КОХРЕНА
Пятипроцентные пределы для отношения Gmax наибольшей эмпирической дисперсии к сумме N эмпирических дисперсий, полученных из независимых выборок с одинаковым числом степеней N1, в и числом степеней свободы суммы всех дисперсий N2, в = N.
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
N2,в = N |
N1,в max = m - 1 |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
141 |
¥ |
|
|
2 |
0,9985 |
0,9750 |
0,9392 |
0,9057 |
0,8772 |
0,8534 |
0,8332 |
0,8159 |
0,8010 |
0,7880 |
0,7341 |
0,6602 |
0,5813 |
0,5000 |
|
3 |
9669 |
8709 |
7977 |
7457 |
7071 |
6771 |
6530 |
6333 |
6167 |
6025 |
5466 |
4748 |
4031 |
3333 |
|
4 |
9065 |
7679 |
6841 |
6287 |
5895 |
5598 |
5365 |
5175 |
5017 |
4884 |
4366 |
3720 |
3093 |
2500 |
|
5 |
0,8412 |
0,6838 |
0,5981 |
0,5440 |
0,5063 |
0,4783 |
0,4564 |
0,4387 |
0,4241 |
0,4118 |
0,3645 |
0,3066 |
0,2513 |
0,2000 |
|
6 |
7808 |
6161 |
5321 |
4803 |
4447 |
4148 |
3980 |
3817 |
3682 |
3568 |
3135 |
2612 |
2119 |
1667 |
|
7 |
7271 |
5612 |
4800 |
4307 |
3974 |
3726 |
3555 |
3384 |
3254 |
3154 |
2756 |
2273 |
1833 |
1429 |
|
8 |
0,6798 |
0,5157 |
0,4377 |
0,3910 |
0,3595 |
0,3362 |
0,3185 |
0,3043 |
0,2926 |
0,2829 |
0,2462 |
0,2020 |
0,1516 |
0,1250 |
|
9 |
6385 |
4775 |
4027 |
3584 |
3286 |
3067 |
2901 |
2768 |
2659 |
2568 |
2226 |
1820 |
1446 |
1111 |
|
10 |
6020 |
4450 |
3733 |
3311 |
3029 |
2823 |
2666 |
2541 |
2439 |
2353 |
2032 |
1655 |
1308 |
1000 |
|
12 |
0,5410 |
0,3924 |
0,3264 |
0,2880 |
0,2624 |
0,2439 |
0,2299 |
0,2187 |
0,2098 |
0,2020 |
0,1737 |
0,1403 |
0,1100 |
0,0833 |
|
15 |
4709 |
3346 |
2758 |
2419 |
2195 |
2034 |
1911 |
1815 |
1736 |
1671 |
1429 |
1144 |
0889 |
0667 |
|
20 |
3894 |
2705 |
2205 |
1921 |
1735 |
1002 |
1601 |
1422 |
1357 |
1303 |
1108 |
0879 |
0,675 |
0500 |
|
24 |
0,3434 |
0,2354 |
0,1907 |
0,1656 |
0,1493 |
0,1374 |
0,1286 |
0,1216 |
0,1160 |
0,1113 |
0,0942 |
0,0743 |
0,0567 |
0,0417 |
|
30 |
2929 |
1980 |
1593 |
1377 |
1237 |
1137 |
1061 |
1002 |
0958 |
0921 |
0771 |
0604 |
0457 |
0333 |
|
40 |
2370 |
1576 |
1259 |
1082 |
0968 |
0887 |
0827 |
0780 |
0745 |
0713 |
0595 |
0462 |
0347 |
0250 |
|
60 |
0,1737 |
0,1131 |
0,0895 |
0,0765 |
0,0682 |
0,0623 |
0,0583 |
0,0552 |
0,0520 |
0,0497 |
0,0411 |
0,0316 |
0,0234 |
0,0167 |
|
120 |
0998 |
0632 |
0495 |
0419 |
0371 |
0337 |
0312 |
0292 |
0279 |
0266 |
0218 |
0165 |
0120 |
0083 |
|
¥ |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
Таблица 2
Однопроцентные пределы для отношения Gmax наибольшей эмпирической дисперсии к сумме N1,в эмпирических дисперсий, полученных из независимых выборок с одинаковым числом степеней свободы N1, в и числом степеней свободы суммы всех дисперсий N2, в = N.
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
N2, в = N |
N1, в max = m - 1 |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
141 |
¥ |
|
|
2 |
0,9999 |
0,9950 |
0,9794 |
0,9586 |
0,9373 |
0,9172 |
0,8988 |
0,8223 |
0,8674 |
0,8539 |
0,7949 |
0,7067 |
0,6062 |
0,5000 |
|
3 |
9933 |
9423 |
8831 |
8355 |
7933 |
7606 |
7335 |
7107 |
6912 |
6743 |
6059 |
5153 |
4230 |
3333 |
|
4 |
9676 |
8643 |
7814 |
7212 |
6761 |
6410 |
6129 |
6897 |
6702 |
5536 |
4884 |
4057 |
3451 |
2500 |
|
5 |
0,9279 |
0,7885 |
0,6957 |
0,6329 |
0,5875 |
0,5531 |
0,5259 |
0,5037 |
0,4854 |
0,4697 |
0,4090 |
0,3361 |
0,2644 |
0,2500 |
|
6 |
8828 |
7218 |
6258 |
5635 |
5195 |
4866 |
4608 |
4401 |
4229 |
4084 |
3529 |
2858 |
2229 |
1667 |
|
7 |
8376 |
6644 |
5685 |
5080 |
4659 |
4347 |
4105 |
3911 |
3751 |
3616 |
3105 |
2494 |
1929 |
1429 |
|
8 |
0,7945 |
0,6162 |
0,5209 |
0,4627 |
0,4226 |
0,3932 |
0,3704 |
0,3522 |
0,3373 |
3248 |
0,2779 |
0,2214 |
0,1700 |
0,1260 |
|
9 |
7544 |
5727 |
4810 |
4251 |
3870 |
3592 |
3378 |
3207 |
3067 |
2950 |
2511 |
1992 |
1521 |
1111 |
|
10 |
7175 |
5358 |
4469 |
3934 |
3572 |
3308 |
3106 |
2945 |
2813 |
2704 |
2297 |
1811 |
1376 |
1000 |
|
12 |
0,6528 |
0,4751 |
0,3919 |
0,3428 |
0,3099 |
0,2861 |
0,2680 |
0,2535 |
0,2419 |
0,2320 |
0,1961 |
0,1535 |
0,1157 |
0,0839 |
|
15 |
5747 |
4069 |
3317 |
2882 |
2593 |
2386 |
2228 |
2104 |
2002 |
1918 |
1612 |
1251 |
0934 |
0667 |
|
20 |
4799 |
3297 |
2654 |
2288 |
2048 |
1877 |
1748 |
1646 |
1567 |
1501 |
1248 |
0960 |
0709 |
0500 |
|
24 |
0,4247 |
0,2871 |
0,2295 |
0,1970 |
0,1759 |
0,1608 |
0,1495 |
0,1406 |
0,1338 |
0,1283 |
0,1060 |
0,0810 |
0,0595 |
0,0417 |
|
30 |
3632 |
2412 |
1913 |
1635 |
1454 |
1327 |
1232 |
1157 |
1100 |
1054 |
0867 |
0659 |
0480 |
0333 |
|
40 |
2910 |
1915 |
1508 |
1281 |
1135 |
1033 |
0957 |
0898 |
0853 |
0816 |
0668 |
0503 |
0368 |
0250 |
|
60 |
0,2151 |
0,1371 |
0,1069 |
0,0902 |
0,0796 |
0,0722 |
0,0668 |
0,0625 |
0,0594 |
0,0567 |
0,0461 |
0,0344 |
0,0245 |
0,0167 |
|
120 |
1252 |
0759 |
0585 |
0189 |
0429 |
0387 |
0337 |
0334 |
0316 |
0302 |
0242 |
0178 |
0125 |
0083 |
|
¥ |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
Таблица 3
ТАБЛИЦА КРИТЕРИЕВ СТЬЮДЕНТА
Значения t критерия Стьюдента при различных уровнях значимости.
Столбцы соответствуют q в процентах различным степеням свободы.
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
NЗН = N(m - 1) |
tкр при q в процентах |
|||||||
|
20 |
10 |
5 |
2 |
1 |
0,5 |
0,2 |
0,1 |
|
|
1 |
3,0770 |
6,3130 |
12,7060 |
31,820 |
63,656 |
127,656 |
318,306 |
636,619 |
|
2 |
1,8850 |
2,9200 |
4,3020 |
6,964 |
9,924 |
14,089 |
22,327 |
31,599 |
|
3 |
6377 |
35340 |
3,182 |
4,540 |
5,840 |
7,458 |
10,214 |
12,924 |
|
4 |
5332 |
13180 |
2,776 |
3,746 |
4,604 |
5,597 |
7,173 |
8,610 |
|
5 |
4759 |
01500 |
2,570 |
3,649 |
0321 |
4,773 |
5,893 |
6,863 |
|
6 |
1,4390 |
1,943 |
2,4460 |
3,1420 |
3,7070 |
4,316 |
5,2070 |
5,958 |
|
7 |
4149 |
8946 |
3646 |
2,998 |
4995 |
2293 |
4,785 |
4079 |
|
8 |
3968 |
8596 |
3060 |
8965 |
3554 |
3,832 |
5008 |
0413 |
|
9 |
3830 |
8331 |
2622 |
8214 |
2498 |
6897 |
2968 |
4,780 |
|
10 |
3720 |
8125 |
2281 |
7638 |
1693 |
5814 |
1437 |
5869 |
|
11 |
1,363 |
1,795 |
2,201 |
2,718 |
3,105 |
3,496 |
4,024 |
4,437 |
|
12 |
3562 |
7823 |
1788 |
6810 |
0845 |
4284 |
3,929 |
3178 |
|
13 |
3502 |
7709 |
1604 |
6503 |
1123 |
3725 |
3,852 |
2208 |
|
14 |
3450 |
7613 |
1448 |
6245 |
2,976 |
3257 |
3,787 |
1405 |
|
15 |
3406 |
7530 |
1314 |
6025 |
9467 |
2860 |
3,732 |
0728 |
|
16 |
1,3360 |
1,7450 |
2,1190 |
2,5830 |
2,9200 |
3,2520 |
3,6860 |
4,0150 |
|
17 |
3334 |
7396 |
1098 |
5668 |
8982 |
2224 |
6458 |
3,965 |
|
18 |
3304 |
7341 |
1009 |
5514 |
8784 |
1966 |
6105 |
9216 |
|
19 |
3277 |
7291 |
0930 |
5395 |
8609 |
1737 |
5794 |
8834 |
|
20 |
3253 |
7247 |
08600 |
5280 |
8453 |
1534 |
5518 |
8495 |
|
21 |
1,3230 |
1,7200 |
2,0790 |
2,5170 |
2,8310 |
3,1350 |
3,5270 |
3,8190 |
|
22 |
3212 |
7117 |
0739 |
5083 |
8188 |
1188 |
5050 |
7921 |
|
23 |
3195 |
7139 |
0687 |
4999 |
8073 |
1040 |
4850 |
7676 |
|
24 |
1378 |
7109 |
0639 |
4922 |
7969 |
0905 |
4668 |
7454 |
|
25 |
3163 |
7081 |
0595 |
4851 |
7874 |
0782 |
4502 |
7251 |
|
26 |
1,315 |
1,705 |
2,059 |
2,478 |
2,778 |
3,0660 |
3,4360 |
3,7060 |
|
27 |
3137 |
7033 |
0518 |
4727 |
7707 |
0565 |
4210 |
6896 |
|
28 |
3125 |
7011 |
0484 |
4671 |
7633 |
0469 |
4082 |
6739 |
|
29 |
3114 |
6991 |
0452 |
4620 |
7564 |
0360 |
3962 |
8494 |
|
30 |
3104 |
6973 |
0423 |
4573 |
7500 |
0298 |
3852 |
6460 |
|
32 |
1,3080 |
1,6930 |
2,0360 |
2,4480 |
2,7380 |
3,0140 |
3,3650 |
3,6210 |
|
34 |
3070 |
6909 |
0322 |
4411 |
7284 |
9520 |
3479 |
6007 |
|
36 |
3050 |
6883 |
0281 |
4345 |
7195 |
9,490 |
3326 |
5821 |
|
38 |
3042 |
6860 |
0244 |
4286 |
7116 |
9808 |
3190 |
5657 |
|
40 |
3031 |
6839 |
0211 |
4233 |
7045 |
9712 |
3069 |
5510 |
|
42 |
1,320 |
1,682 |
2,018 |
2,418 |
2,6980 |
2,6930 |
3,2960 |
3,5370 |
|
44 |
3011 |
6802 |
0154 |
4141 |
6923 |
9555 |
2861 |
5258 |
|
46 |
3002 |
6767 |
0129 |
4102 |
6870 |
9488 |
2771 |
5150 |
|
48 |
2994 |
6772 |
0106 |
4056 |
6822 |
9426 |
2689 |
5051 |
|
50 |
2987 |
6759 |
0086 |
4033 |
6778 |
9370 |
2614 |
4060 |
|
55 |
1,997 |
1,673 |
2,0040 |
2,3960 |
2,6680 |
2,9240 |
3,2560 |
3,4760 |
|
60 |
2958 |
6706 |
0003 |
3901 |
6603 |
9146 |
2317 |
4602 |
|
65 |
2947 |
6686 |
1,997 |
3851 |
6536 |
9060 |
2204 |
4466 |
|
70 |
2938 |
6689 |
9944 |
3808 |
6479 |
8987 |
2108 |
4350 |
|
80 |
1,2820 |
1,6640 |
1,9900 |
2,3730 |
2,6380 |
2,8870 |
3,1950 |
3,4160 |
|
90 |
2910 |
6620 |
9867 |
3885 |
6316 |
8779 |
1833 |
4019 |
|
100 |
2901 |
6602 |
9840 |
3642 |
6259 |
8707 |
1737 |
3905 |
|
120 |
2888 |
6577 |
9799 |
3578 |
6174 |
8598 |
1595 |
3735 |
|
150 |
2872 |
6551 |
9759 |
3515 |
6090 |
8482 |
1455 |
3566 |
|
200 |
2858 |
6525 |
9719 |
3451 |
6006 |
8385 |
1315 |
3398 |
|
250 |
2849 |
6510 |
9695 |
3414 |
5966 |
8222 |
1232 |
3299 |
|
300 |
2844 |
6499 |
9679 |
3388 |
5923 |
8279 |
1176 |
3233 |
|
400 |
2837 |
6487 |
9659 |
3357 |
5882 |
8227 |
1107 |
3150 |
|
500 |
1,2830 |
1,6470 |
1,9640 |
2,3330 |
2,7850 |
2,8190 |
3,1060 |
3,3100 |
Таблица 4
ТАБЛИЦЫ КРИТЕРИЯ ФИШЕРА
Пятипроцентные верхние пределы для величины F в зависимости от числа степеней свободы N1 и N2
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
N2ad = N(m - 1) = S2{Y} |
Fкр при N1,ad = S2ad = N - l |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
13 |
16 |
20 |
24 |
30 |
10 |
75 |
100 |
¥ |
|
|
1 |
161 |
200 |
216 |
225 |
230 |
234 |
237 |
239 |
241 |
242 |
244 |
246 |
248 |
249 |
250 |
251 |
253 |
253 |
254 |
|
2 |
18,51 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,36 |
19,37 |
19,38 |
19,39 |
19,41 |
19,43 |
19,44 |
19,45 |
19,46 |
19,47 |
19,48 |
19,49 |
19,50 |
|
3 |
10,13 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,88 |
8,84 |
8,81 |
8,78 |
8,74 |
8,69 |
8,66 |
8,64 |
8,62 |
8,60 |
8,57 |
8,56 |
8,53 |
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,000 |
5,96 |
5,91 |
5,84 |
5,80 |
5,77 |
5,74 |
5,71 |
5,68 |
5,66 |
5,63 |
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,78 |
4,74 |
4,68 |
4,60 |
4,56 |
4,53 |
4,50 |
4,46 |
4,42 |
4,40 |
4,36 |
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
4,00 |
3,92 |
3,87 |
3,64 |
3,81 |
3,77 |
3,72 |
3,71 |
3,67 |
|
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,63 |
3,57 |
3,49 |
3,44 |
3,41 |
3,38 |
3,34 |
3,29 |
3,28 |
3,23 |
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,34 |
3,28 |
3,20 |
3,15 |
3,12 |
3,08 |
3,05 |
3,00 |
2,98 |
2,93 |
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,13 |
3,07 |
2,98 |
2,93 |
2,90 |
2,86 |
2,82 |
2,77 |
2,76 |
2,71 |
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,97 |
2,91 |
2,82 |
2,77 |
2,74 |
2,70 |
2,67 |
2,61 |
2,59 |
2,54 |
|
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
3,01 |
2,95 |
2,90 |
2,86 |
2,79 |
2,70 |
2,65 |
2,61 |
2,57 |
2,58 |
2,47 |
2,45 |
2,40 |
|
12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,92 |
2,85 |
2,80 |
2,76 |
2,69 |
2,60 |
2,54 |
2,50 |
2,46 |
2,42 |
2,36 |
2,35 |
2,30 |
|
13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,84 |
2,77 |
2,72 |
2,67 |
2,60 |
2,51 |
2,46 |
2,42 |
2,38 |
2,34 |
2,28 |
2,26 |
2,21 |
|
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,77 |
2,70 |
2,65 |
2,60 |
2,53 |
2,44 |
2,39 |
2,35 |
2,31 |
2,27 |
2,21 |
2,19 |
2,13 |
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,70 |
2,64 |
2,59 |
2,55 |
2,48 |
2,39 |
2,33 |
2,29 |
2,25 |
2,21 |
2,15 |
2,12 |
2,07 |
|
16 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,66 |
2,59 |
2,54 |
2,49 |
2,42 |
2,33 |
2,28 |
2,24 |
2,20 |
2,16 |
2,09 |
2,07 |
2,01 |
|
17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,62 |
2,55 |
2,50 |
2,45 |
2,38 |
2,29 |
2,23 |
2,19 |
2,15 |
2,11 |
2,04 |
2,02 |
1,96 |
|
18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,58 |
2,51 |
2,46 |
2,41 |
2,34 |
2,25 |
2,19 |
2,15 |
2,11 |
2,07 |
2,00 |
1,98 |
1,92 |
|
19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,55 |
2,48 |
2,43 |
2,38 |
2,31 |
2,21 |
2,15 |
2,11 |
2,07 |
2,02 |
1,96 |
1,94 |
1,88 |
|
20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,52 |
2,45 |
2,40 |
2,35 |
2,28 |
2,18 |
2,12 |
2,08 |
2,04 |
1,89 |
1,92 |
1,90 |
1,84 |
|
21 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,49 |
2,42 |
2,37 |
2,32 |
2,25 |
2,15 |
2,09 |
2,05 |
2,00 |
1,96 |
1,89 |
1,87 |
1,81 |
|
22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,47 |
2,40 |
2,35 |
2,20 |
2,23 |
2,13 |
2,07 |
2,03 |
1,98 |
1,93 |
1,87 |
1,84 |
1,78 |
|
23 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,45 |
2,38 |
2,32 |
2,28 |
2,20 |
2,10 |
2,04 |
2,00 |
1,96 |
1,91 |
1,84 |
1,82 |
1,76 |
|
24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,43 |
2,36 |
2,30 |
2,26 |
2,18 |
2,09 |
2,02 |
1,98 |
1,94 |
1,89 |
1,82 |
1,80 |
1,73 |
|
25 |
4,26 |
3,38 |
2,99 |
2,76 |
2,60 |
2,49 |
2,41 |
2,34 |
2,28 |
2,24 |
2,16 |
2,06 |
2,00 |
1,96 |
1,92 |
1,87 |
1,80 |
1,77 |
1,71 |
|
26 |
4,22 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,39 |
2,32 |
2,27 |
2,22 |
2,15 |
2,05 |
1,99 |
1,90 |
1,95 |
1,85 |
1,78 |
1,76 |
1,69 |
|
27 |
4,21 |
3,35 |
2,96 |
2,73 |
2,57 |
2,46 |
2,37 |
2,30 |
2,25 |
2,20 |
2,13 |
2,03 |
1,97 |
1,93 |
1,88 |
1,84 |
1,76 |
1,74 |
1,67 |
|
28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,44 |
2,36 |
2,29 |
2,24 |
2,19 |
2,12 |
2,02 |
1,96 |
1,91 |
1,87 |
1,81 |
1,75 |
1,72 |
1,65 |
|
29 |
4,18 |
3,33 |
2,93 |
2,70 |
2,54 |
2,43 |
2,35 |
2,28 |
2,22 |
2,18 |
2,10 |
2,00 |
1,94 |
1,90 |
1,85 |
1,80 |
1,73 |
1,71 |
1,64 |
|
30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,34 |
2,27 |
2,21 |
2,16 |
2,09 |
1,99 |
1,93 |
1,89 |
1,64 |
1,79 |
1,62 |
1,72 |
1,69 |
|
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,07 |
2,00 |
1,90 |
1,84 |
1,79 |
1,74 |
1,69 |
1,51 |
1,61 |
1,59 |
|
60 |
4,00 |
3,15 |
2,76 |
2,52 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1,92 |
1,81 |
1,75 |
1,70 |
1,65 |
1,59 |
1,39 |
1,50 |
1,48 |
|
125 |
3,92 |
3,07 |
2,68 |
2,44 |
2,29 |
2,17 |
2,08 |
2,01 |
1,95 |
1,90 |
1,85 |
1,72 |
1,65 |
1,60 |
1,65 |
1,55 |
1,25 |
1,49 |
1,36 |
|
¥ |
3,84 |
2,99 |
2,60 |
2,37 |
2,21 |
2,09 |
2,01 |
1,94 |
1,88 |
1,83 |
1,75 |
1,64 |
1,57 |
1,52 |
1,46 |
1,40 |
1,00 |
1,28 |
1,24 |
Таблица 5
2,5-процентные верхние пределы для величины F в зависимости от числа степеней свободы V1 и V2.
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
N2ad = N(m - 1) = S2{Y} |
Fкр при V1,ad = S2ad = N - l |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
647,7 |
799,5 |
864,1 |
899,5 |
921,8 |
937,1 |
948,2 |
956,6 |
963,2 |
968,6 |
976,6 |
984,8 |
993,1 |
987,2 |
1001,4 |
1005,6 |
1009,8 |
1014,0 |
1018,3 |
|
2 |
38,50 |
39,00 |
39,16 |
39,24 |
39,29 |
39,33 |
39,35 |
39,37 |
38,38 |
39,39 |
39,41 |
39,48 |
39,44 |
39,45 |
39,46 |
37,47 |
39,48 |
39,49 |
39,49 |
|
3 |
17,44 |
16,04 |
15,13 |
15,10 |
14,88 |
14,73 |
14,62 |
14,57 |
14,47 |
14,41 |
14,33 |
14,25 |
14,16 |
14,12 |
14,00 |
14,03 |
13,99 |
13,94 |
13,90 |
|
4 |
12,21 |
10,64 |
9,979 |
9,604 |
9,364 |
9,197 |
9,074 |
8,979 |
8,904 |
8,843 |
8,751 |
8,636 |
8,559 |
8,510 |
8,461 |
8,411 |
8,360 |
8,309 |
8,257 |
|
5 |
10,00 |
8,433 |
7,763 |
7,387 |
7,146 |
6,977 |
6,853 |
6,757 |
6,681 |
6,619 |
6,524 |
6,422 |
6,328 |
6,278 |
6,226 |
6,175 |
6,122 |
6,069 |
6,015 |
|
6 |
8,813 |
7,259 |
6,598 |
6,227 |
6,987 |
5,819 |
5,595 |
5,599 |
5,523 |
5,461 |
5,366 |
5,288 |
5,168 |
5,117 |
5,065 |
5,012 |
4,958 |
4,904 |
4,849 |
|
7 |
8,072 |
6,541 |
5,889 |
5,522 |
5,285 |
5,418 |
4,994 |
4,899 |
4,823 |
4,761 |
4,666 |
4,567 |
4,466 |
4,415 |
4,382 |
4,308 |
4,254 |
4,198 |
4,142 |
|
8 |
7,570 |
6,059 |
5,416 |
5,052 |
4,817 |
4,651 |
4,528 |
4,433 |
1,357 |
4,295 |
4,199 |
4,101 |
3,999 |
3,947 |
3,894 |
3,839 |
3,784 |
3,727 |
3,670 |
|
9 |
7,209 |
5,714 |
5,078 |
4,718 |
4,184 |
4,319 |
4,197 |
4,102 |
4,026 |
3,963 |
3,868 |
3,769 |
3,666 |
3,614 |
3,560 |
3,505 |
3,449 |
3,391 |
3,332 |
|
10 |
6,936 |
5,456 |
4,825 |
4,468 |
4,236 |
4,072 |
3,949 |
3,854 |
3,779 |
3,716 |
3,620 |
3,521 |
3,418 |
3,365 |
3,311 |
3,255 |
3,198 |
3,139 |
3,079 |
|
11 |
6,724 |
5,255 |
4,630 |
4,275 |
4,044 |
3,880 |
3,758 |
3,663 |
3,587 |
3,525 |
3,429 |
3,329 |
3,226 |
3,172 |
3,117 |
3,061 |
3,003 |
2,944 |
2,882 |
|
12 |
6,553 |
5,095 |
4,474 |
4,12 |
3,891 |
3,728 |
3,606 |
3,511 |
3,435 |
3,373 |
3,277 |
3,177 |
3,072 |
3,018 |
2,963 |
2,006 |
2,847 |
2,787 |
2,724 |
|
13 |
6,414 |
4,965 |
4,347 |
3,995 |
3,766 |
3,614 |
3,482 |
3,388 |
3,312 |
3,249 |
3,153 |
3,052 |
2,947 |
2,893 |
2,837 |
2,779 |
2,720 |
2,659 |
2,595 |
|
14 |
6,297 |
4,856 |
4,241 |
3,891 |
3,663 |
3,501 |
3,379 |
3,285 |
3,209 |
3,146 |
3,050 |
2,949 |
2,843 |
2,788 |
2,732 |
2,674 |
2,614 |
2,651 |
2,487 |
|
15 |
6,199 |
4,765 |
4,152 |
3,804 |
3,576 |
3,414 |
3,293 |
3,198 |
3,122 |
3,050 |
2,963 |
2,882 |
2,755 |
2,700 |
2,643 |
2,585 |
2,524 |
2,461 |
2,395 |
|
16 |
6,155 |
4,686 |
4,976 |
3,729 |
3,502 |
3,340 |
2,129 |
3,124 |
3,048 |
2,936 |
2,889 |
2,787 |
2,680 |
2,625 |
2,567 |
2,508 |
2,447 |
2,383 |
2,316 |
|
17 |
6,042 |
4,618 |
4,012 |
3,661 |
3,437 |
3,276 |
3,155 |
3,081 |
2,284 |
2,922 |
2,824 |
2,723 |
2,615 |
2,559 |
2,502 |
2,442 |
2,380 |
2,315 |
2,247 |
|
18 |
5,978 |
4,559 |
3,953 |
3,608 |
3,382 |
3,220 |
3,009 |
3,005 |
2,929 |
2,866 |
2,768 |
2,666 |
2,559 |
2,502 |
2,444 |
2,384 |
2,321 |
2,255 |
2,185 |
|
19 |
5,921 |
4,507 |
3,903 |
3,558 |
3,332 |
3,171 |
3,050 |
2,956 |
2,880 |
2,817 |
2,179 |
2,617 |
2,508 |
2,452 |
2,383 |
2,332 |
2,269 |
2,203 |
2,133 |
|
20 |
5,871 |
4,461 |
3,858 |
3,514 |
3,289 |
3,128 |
3,007 |
3,912 |
2,836 |
2,773 |
2,875 |
2,573 |
2,464 |
2,407 |
2,348 |
2,287 |
2,223 |
2,156 |
2,085 |
|
21 |
5,826 |
4,419 |
3,818 |
3,474 |
3,250 |
3,089 |
2,968 |
2,974 |
2,797 |
2,734 |
2,636 |
2,533 |
2,424 |
2,367 |
2,306 |
2,246 |
2,181 |
2,114 |
2,042 |
|
22 |
5,786 |
3,382 |
3,782 |
3,440 |
3,125 |
3,054 |
2,933 |
2,839 |
2,762 |
2,699 |
2,601 |
2,498 |
2,389 |
2,331 |
2,271 |
2,209 |
2,144 |
2,076 |
2,038 |
|
23 |
5,749 |
3,349 |
3,750 |
3,408 |
3,183 |
3,023 |
3,902 |
2,807 |
2,731 |
2,668 |
2,569 |
2,466 |
2,356 |
2,298 |
2,238 |
2,176 |
2,110 |
2,041 |
2,967 |
|
24 |
5,716 |
4,318 |
3,721 |
3,379 |
3,154 |
2,994 |
2,873 |
2,779 |
2,702 |
2,630 |
2,541 |
2,437 |
2,327 |
2,269 |
2,209 |
2,146 |
2,079 |
2,009 |
1,936 |
|
25 |
5,686 |
4,290 |
3,694 |
3,363 |
3,128 |
2,968 |
2,846 |
2,753 |
2,676 |
2,613 |
2,514 |
2,411 |
2,360 |
2,242 |
2,181 |
2,118 |
2,051 |
1,981 |
1,905 |
|
26 |
2,658 |
4,285 |
3,669 |
3,328 |
3,104 |
2,944 |
2,884 |
2,824 |
2,729 |
2,509 |
3,490 |
2,386 |
2,275 |
2,217 |
2,156 |
2,092 |
2,025 |
1,954 |
1,878 |
|
27 |
5,633 |
4,242 |
3,647 |
3,306 |
3,082 |
2,922 |
2,802 |
2,707 |
2,630 |
2,567 |
2,468 |
2,344 |
2,253 |
2,194 |
2,130 |
2,060 |
2,001 |
1,929 |
1,852 |
|
28 |
5,609 |
4,220 |
3,626 |
3,286 |
3,062 |
2,902 |
3,782 |
2,687 |
2,610 |
2,547 |
2,446 |
2,343 |
2,232 |
2,173 |
2,112 |
2,047 |
2,979 |
1,907 |
1,829 |
|
29 |
5,587 |
4,200 |
3,607 |
3,267 |
3,043 |
2,884 |
2,763 |
2,668 |
2,591 |
2,528 |
2,429 |
2,324 |
2,213 |
2,154 |
2,092 |
2,027 |
1,959 |
1,886 |
1,907 |
|
30 |
5,567 |
4,182 |
3,589 |
3,249 |
3,026 |
2,866 |
2,746 |
2,651 |
2,574 |
2,511 |
2,412 |
2,307 |
2,195 |
2,135 |
2,073 |
2,009 |
2,940 |
1,856 |
1,786 |
|
40 |
5,423 |
4,051 |
3,463 |
3,126 |
2,903 |
2,744 |
2,623 |
2,528 |
2,451 |
2,382 |
2,288 |
2,181 |
2,067 |
2,006 |
1,942 |
1,875 |
1,802 |
1,724 |
1,737 |
|
60 |
5,285 |
3,825 |
3,342 |
3,007 |
2,786 |
2,627 |
2,506 |
2,411 |
4,334 |
2,270 |
2,160 |
1,061 |
1,944 |
1,881 |
1,815 |
1,744 |
1,666 |
1,581 |
1,482 |
|
120 |
5,152 |
3,804 |
3,227 |
2,894 |
2,515 |
2,394 |
2,299 |
2,299 |
2,221 |
2,157 |
2,054 |
1,945 |
1,824 |
1,759 |
1,689 |
1,614 |
1,529 |
1,432 |
1,310 |
|
¥ |
5,023 |
3,688 |
3,116 |
2,786 |
2,566 |
2,408 |
2,237 |
2,191 |
2,223 |
2,048 |
1,944 |
1,832 |
1,708 |
1,640 |
1,566 |
1,483 |
1,383 |
1,268 |
1,000 |
Таблица 6
Однопроцентные верхние пределы для величины F в зависимости от числа степеней свободы V1 и V2
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
N2ad = N(m - 1) = S2{Y} |
Fкр при V1,ad = S2ad = N - l |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
16 |
20 |
24 |
30 |
40 |
45 |
100 |
¥ |
|
|
1 |
4052 |
4999 |
5403 |
5625 |
5764 |
5889 |
5928 |
5981 |
6022 |
6056 |
6106 |
6169 |
6208 |
6334 |
3258 |
6286 |
3323 |
6334 |
6366 |
|
2 |
98,49 |
99,05 |
99,17 |
99,25 |
99,30 |
99,33 |
99,34 |
99,36 |
99,38 |
99,40 |
99,42 |
99,44 |
99,45 |
99,47 |
99,47 |
99,48 |
99,49 |
99,49 |
99,50 |
|
3 |
23,12 |
38,81 |
29,46 |
28,71 |
28,24 |
27,91 |
26,67 |
27,49 |
27,34 |
27,23 |
27,05 |
26,83 |
26,69 |
26,60 |
26,50 |
26,41 |
26,27 |
26,23 |
26,12 |
|
4 |
21,20 |
18,00 |
1,69 |
15,28 |
15,52 |
15,21 |
14,90 |
14,80 |
14,66 |
14,54 |
14,37 |
14,15 |
14,02 |
13,93 |
13,83 |
13,74 |
13,61 |
13,57 |
13,46 |
|
5 |
16,28 |
13,27 |
12,06 |
11,39 |
10,97 |
10,67 |
10,45 |
10,27 |
10,15 |
10,05 |
9,89 |
9,68 |
9,55 |
9,47 |
9,38 |
9,29 |
9,17 |
9,13 |
9,02 |
|
6 |
13,74 |
10,92 |
9,78 |
9,15 |
8,75 |
8,47 |
8,26 |
8,10 |
7,98 |
7,87 |
7,52 |
7,52 |
7,39 |
7,31 |
7,23 |
7,14 |
7,02 |
6,69 |
6,88 |
|
7 |
12,25 |
9,55 |
8,45 |
7,85 |
7,46 |
7,19 |
7,00 |
6,84 |
6,71 |
6,82 |
6,47 |
6,27 |
6,15 |
6,07 |
5,98 |
5,90 |
5,78 |
5,75 |
5,65 |
|
8 |
11,26 |
8,65 |
7,59 |
7,01 |
6,63 |
6,37 |
6,19 |
6,03 |
5,91 |
5,82 |
5,67 |
5,48 |
5,36 |
5,28 |
5,20 |
5,11 |
5,00 |
4,96 |
4,86 |
|
9 |
10,56 |
8,02 |
6,99 |
6,42 |
6,06 |
5,80 |
5,62 |
5,47 |
5,35 |
5,26 |
5,11 |
4,92 |
4,80 |
4,73 |
4,64 |
4,66 |
4,45 |
4,41 |
4,31 |
|
10 |
10,04 |
7,56 |
6,55 |
5,99 |
5,64 |
5,39 |
5,21 |
5,06 |
4,95 |
4,85 |
4,71 |
4,52 |
4,41 |
4,33 |
4,25 |
4,17 |
4,05 |
4,01 |
3,91 |
|
11 |
9,35 |
7,20 |
6,22 |
5,67 |
5,32 |
5,07 |
4,88 |
4,74 |
4,63 |
4,54 |
4,40 |
4,21 |
4,10 |
4,02 |
3,94 |
3,86 |
3,74 |
3,70 |
3,60 |
|
12 |
9,33 |
6,93 |
5,95 |
5,41 |
5,06 |
4,82 |
4,65 |
4,50 |
4,39 |
4,30 |
4,16 |
4,98 |
3,86 |
3,70 |
3,70 |
3,61 |
3,49 |
3,46 |
3,36 |
|
13 |
9,07 |
6,70 |
5,74 |
5,20 |
4,86 |
4,62 |
4,44 |
4,30 |
4,19 |
4,10 |
3,96 |
3,78 |
3,67 |
3,59 |
5,51 |
3,42 |
3,30 |
3,27 |
3,16 |
|
14 |
8,86 |
6,51 |
5,56 |
5,03 |
4,69 |
4,46 |
4,28 |
4,14 |
4,03 |
3,94 |
3,80 |
3,62 |
3,51 |
3,43 |
3,34 |
3,26 |
3,14 |
3,11 |
3,00 |
|
15 |
8,68 |
6,38 |
5,42 |
4,89 |
4,56 |
4,32 |
4,14 |
4,00 |
3,89 |
3,80 |
3,67 |
3,48 |
3,36 |
3,29 |
3,20 |
3,12 |
3,00 |
2,97 |
2,87 |
|
16 |
8,53 |
6,23 |
5,29 |
4,47 |
4,44 |
4,29 |
2,03 |
3,89 |
3,78 |
3,69 |
3,55 |
3,37 |
3,25 |
3,18 |
3,10 |
3,01 |
2,89 |
2,86 |
2,75 |
|
17 |
8,40 |
6,11 |
5,18 |
4,67 |
4,34 |
4,10 |
3,93 |
3,79 |
3,68 |
3,59 |
3,45 |
3,27 |
3,16 |
3,08 |
3,00 |
2,92 |
2,79 |
2,76 |
2,65 |
|
18 |
8,28 |
6,01 |
5,09 |
4,58 |
4,25 |
4,01 |
3,85 |
3,71 |
3,60 |
3,51 |
3,37 |
3,19 |
3,07 |
3,00 |
2,91 |
2,83 |
2,71 |
2,78 |
2,57 |
|
19 |
8,18 |
5,93 |
5,01 |
4,50 |
4,17 |
3,94 |
3,77 |
3,63 |
3,52 |
3,43 |
3,20 |
3,12 |
3,00 |
3,92 |
2,84 |
2,76 |
2,68 |
2,60 |
2,49 |
|
20 |
8,10 |
5,85 |
4,94 |
4,43 |
4,10 |
3,87 |
3,71 |
3,56 |
3,45 |
3,37 |
3,23 |
3,05 |
2,94 |
2,86 |
2,77 |
2,68 |
2,56 |
2,53 |
2,42 |
|
21 |
8,02 |
5,78 |
4,87 |
4,37 |
4,04 |
3,81 |
3,65 |
3,51 |
3,40 |
3,31 |
3,17 |
2,99 |
2,88 |
2,80 |
2,72 |
2,63 |
2,51 |
2,47 |
2,36 |
|
22 |
7,94 |
5,72 |
4,82 |
4,31 |
3,99 |
3,76 |
3,59 |
3,45 |
3,35 |
3,26 |
3,12 |
2,94 |
2,83 |
2,45 |
2,67 |
2,58 |
2,46 |
2,42 |
2,31 |
|
23 |
7,88 |
5,66 |
4,76 |
4,26 |
3,94 |
3,71 |
3,54 |
3,41 |
3,30 |
3,22 |
2,07 |
2,89 |
2,78 |
2,70 |
2,62 |
2,53 |
2,41 |
2,37 |
2,26 |
|
24 |
7,82 |
5,61 |
4,72 |
4,22 |
3,90 |
3,67 |
3,50 |
3,36 |
3,25 |
3,17 |
3,03 |
2,85 |
2,74 |
2,66 |
2,58 |
2,49 |
2,36 |
2,33 |
2,21 |
|
25 |
7,77 |
5,57 |
4,68 |
4,68 |
3,86 |
3,63 |
3,46 |
3,32 |
3,31 |
3,13 |
2,99 |
2,81 |
2,70 |
2,62 |
2,64 |
2,45 |
2,32 |
2,29 |
2,17 |
|
26 |
7,72 |
5,53 |
4,64 |
4,14 |
3,82 |
3,59 |
3,42 |
3,29 |
3,17 |
3,09 |
2,96 |
2,77 |
2,66 |
2,68 |
2,50 |
2,41 |
2,28 |
2,25 |
2,13 |
|
27 |
7,68 |
5,49 |
4,60 |
4,11 |
3,79 |
3,56 |
3,39 |
3,26 |
3,14 |
3,06 |
2,93 |
2,74 |
2,63 |
2,55 |
2,47 |
2,38 |
2,25 |
2,21 |
2,10 |
|
28 |
7,64 |
5,45 |
4,57 |
4,07 |
3,76 |
3,53 |
3,36 |
3,23 |
3,11 |
3,03 |
2,90 |
2,71 |
2,60 |
2,52 |
2,44 |
2,35 |
2,22 |
2,18 |
2,06 |
|
29 |
7,60 |
5,42 |
4,54 |
4,04 |
3,73 |
3,50 |
3,33 |
3,20 |
3,08 |
3,03 |
2,87 |
2,68 |
2,57 |
2,49 |
2,41 |
2,32 |
2,19 |
2,15 |
2,03 |
|
30 |
7,56 |
5,39 |
4,51 |
4,02 |
3,70 |
3,47 |
3,30 |
3,17 |
3,06 |
2,98 |
2,84 |
2,66 |
2,55 |
2,47 |
2,38 |
2,29 |
2,16 |
2,13 |
2,01 |
|
40 |
7,31 |
5,18 |
4,31 |
3,83 |
3,51 |
3,29 |
3,12 |
2,99 |
2,88 |
2,80 |
2,66 |
2,49 |
2,37 |
2,29 |
2,20 |
2,11 |
1,91 |
1,94 |
1,81 |
|
60 |
7,08 |
4,08 |
4,13 |
3,65 |
3,34 |
3,12 |
2,95 |
2,82 |
2,72 |
2,67 |
2,50 |
2,32 |
2,20 |
2,12 |
2,03 |
1,93 |
1,97 |
1,74 |
1,60 |
|
125 |
6,84 |
4,78 |
3,94 |
3,47 |
3,17 |
2,95 |
2,79 |
2,65 |
2,65 |
2,47 |
2,33 |
2,15 |
2,03 |
1,94 |
1,85 |
1,75 |
1,59 |
1,54 |
1,37 |
|
¥ |
6,64 |
4,60 |
3,78 |
3,32 |
3,02 |
2,80 |
2,64 |
2,51 |
2,41 |
2,32 |
2,18 |
1,99 |
1,87 |
1,79 |
1,69 |
1,59 |
1,41 |
1,36 |
1,09 |
Таблица 7
0,5-процентные верхние пределы для величины F в зависимости от числа степеней свободы V1 и V2.
На пересечении соответствующих столбца и строки находится критическое значение критерия
|
V1,ad = N(m - 1) = S2{Y} |
Fкр при V1,ad = S2ad = N - l |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
¥ |
|
|
1 |
16211 |
20000 |
21615 |
22500 |
23056 |
23437 |
23715 |
23925 |
24091 |
24224 |
24426 |
24630 |
24836 |
24940 |
25014 |
25148 |
25253 |
25359 |
25465 |
|
2 |
198,5 |
199,0 |
199,1 |
199,2 |
199,3 |
199,3 |
199,3 |
199,3 |
199,3 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
199,4 |
|
3 |
55,55 |
49,79 |
47,46 |
46,19 |
45,89 |
44,83 |
41,43 |
44,12 |
43,88 |
43,68 |
43,38 |
43,09 |
42,77 |
42,62 |
42,48 |
42,30 |
42,14 |
41,98 |
41,82 |
|
4 |
31,33 |
26,28 |
24,25 |
23,25 |
22,45 |
21,97 |
21,62 |
21,35 |
21,13 |
20,96 |
20,70 |
20,43 |
20,16 |
20,03 |
19,98 |
19,75 |
19,61 |
19,46 |
19,32 |
|
5 |
22,78 |
18,31 |
16,53 |
15,55 |
14,91 |
14,51 |
13,20 |
13,96 |
13,77 |
13,61 |
13,38 |
13,14 |
12,90 |
12,78 |
12,65 |
12,23 |
12,40 |
12,27 |
12,14 |
|
6 |
18,63 |
14,54 |
12,91 |
12,07 |
11,46 |
11,07 |
10,78 |
10,56 |
10,39 |
10,25 |
10,08 |
9,814 |
9,589 |
9,474 |
9,358 |
9,240 |
2,121 |
9,001 |
8,879 |
|
7 |
16,23 |
12,40 |
10,88 |
10,05 |
9,522 |
9,155 |
8,885 |
8,678 |
8,513 |
8,380 |
8,176 |
7,967 |
7,754 |
7,645 |
7,534 |
7,422 |
7,308 |
7,193 |
7,076 |
|
8 |
14,68 |
11,04 |
9,596 |
8,805 |
8,301 |
7,952 |
7,691 |
7,496 |
7,338 |
7,210 |
7,014 |
6,814 |
6,608 |
6,502 |
6,396 |
6,287 |
6,177 |
8,064 |
5,950 |
|
9 |
13,61 |
10,10 |
8,717 |
7,955 |
7,471 |
7,133 |
6,884 |
6,693 |
6,541 |
6,417 |
6,227 |
6,032 |
5,831 |
5,729 |
5,524 |
5,518 |
5,410 |
5,300 |
5,187 |
|
10 |
12,82 |
9,427 |
8,080 |
7,342 |
6,872 |
6,514 |
6,302 |
6,115 |
5,967 |
5,86 |
5,661 |
5,470 |
5,274 |
5,173 |
5,070 |
4,965 |
4,856 |
4,750 |
4,638 |
|
11 |
12,22 |
8,912 |
7,600 |
6,880 |
6,421 |
6,101 |
5,864 |
5,682 |
5,336 |
5,418 |
5,236 |
5,048 |
4,855 |
4,755 |
4,654 |
4,550 |
4,445 |
4,336 |
4,225 |
|
12 |
11,75 |
8,509 |
7,225 |
6,521 |
6,071 |
5,757 |
5,524 |
5,345 |
5,202 |
5,085 |
4,906 |
4,721 |
4,529 |
4,431 |
4,330 |
4,228 |
4,122 |
4,014 |
3,903 |
|
13 |
11,37 |
8,186 |
6,925 |
6,233 |
5,791 |
5,481 |
5,252 |
5,076 |
4,935 |
4,819 |
4,642 |
4,460 |
4,270 |
4,172 |
3,970 |
3,865 |
3,75 |
3,757 |
3,646 |
|
14 |
11,06 |
7,921 |
6,680 |
5,998 |
5,562 |
5,257 |
5,031 |
4,856 |
4,717 |
4,603 |
4,428 |
4,246 |
4,058 |
3,961 |
3,861 |
3,760 |
3,655 |
3,547 |
3,435 |
|
15 |
10,79 |
7,700 |
6,476 |
6,802 |
5,972 |
5,078 |
5,847 |
4,674 |
4,536 |
4,423 |
4,249 |
4,069 |
3,882 |
3,785 |
3,686 |
3,585 |
3,480 |
3,372 |
3,260 |
|
16 |
10,57 |
7,513 |
6,303 |
5,537 |
5,211 |
4,913 |
4,092 |
4,520 |
3,383 |
4,271 |
4,099 |
3,920 |
3,734 |
3,637 |
3,538 |
3,437 |
3,332 |
3,224 |
3,111 |
|
17 |
10,38 |
7,353 |
6,155 |
5,496 |
5,074 |
4,778 |
4,559 |
4,389 |
4,253 |
4,142 |
3,970 |
3,792 |
3,607 |
3,511 |
3,412 |
3,310 |
3,205 |
3,097 |
2,283 |
|
18 |
10,21 |
7,214 |
6,027 |
5,374 |
4,956 |
4,662 |
4,441 |
4,275 |
4,141 |
4,030 |
3,859 |
3,682 |
3,497 |
3,401 |
3,303 |
2,201 |
3,096 |
2,987 |
2,873 |
|
19 |
10,07 |
7,095 |
5,916 |
5,268 |
4,852 |
4,561 |
4,344 |
4,177 |
4,042 |
3,932 |
3,763 |
3,586 |
3,402 |
3,306 |
3,207 |
3,105 |
3,000 |
2,890 |
2,776 |
|
20 |
9,943 |
6,986 |
5,817 |
5,174 |
4,761 |
4,472 |
4,256 |
4,090 |
3,956 |
3,847 |
3,677 |
3,502 |
3,317 |
3,222 |
3,123 |
3,021 |
2,915 |
2,805 |
2,690 |
|
21 |
9,829 |
6,891 |
5,730 |
5,091 |
4,680 |
4,393 |
4,178 |
4,012 |
3,879 |
3,770 |
3,602 |
3,427 |
3,243 |
3,147 |
3,048 |
2,946 |
2,840 |
2,730 |
2,614 |
|
22 |
9,727 |
6,806 |
5,652 |
5,016 |
4,608 |
4,322 |
4,109 |
3,344 |
3,811 |
3,703 |
3,535 |
3,360 |
3,176 |
3,080 |
2,982 |
2,879 |
2,773 |
2,661 |
2,545 |
|
23 |
9,634 |
6,730 |
5,582 |
4,950 |
4,544 |
4,259 |
4,046 |
3,882 |
3,750 |
3,642 |
3,474 |
2,299 |
3,116 |
3,020 |
2,922 |
2,819 |
2,713 |
2,601 |
2,483 |
|
24 |
9,551 |
6,661 |
5,519 |
4,889 |
4,485 |
4,201 |
3,990 |
3,826 |
3,694 |
3,587 |
3,419 |
3,245 |
3,062 |
2,966 |
2,867 |
2,765 |
2,656 |
2,546 |
2,427 |
|
25 |
9,475 |
6,598 |
5,461 |
4,836 |
4,432 |
4,150 |
3,939 |
3,755 |
3,644 |
3,637 |
3,370 |
3,196 |
3,013 |
2,917 |
2,818 |
2,716 |
2,608 |
2,496 |
2,376 |
|
26 |
9,405 |
6,540 |
5,409 |
4,785 |
4,384 |
4,102 |
3,892 |
3,729 |
3,598 |
3,491 |
3,325 |
3,151 |
2,968 |
2,872 |
2,773 |
2,670 |
2,563 |
2,450 |
2,329 |
|
27 |
9,342 |
6,488 |
5,361 |
4,739 |
4,340 |
4,059 |
3,350 |
3,685 |
3,657 |
3,449 |
3,283 |
3,110 |
2,927 |
2,831 |
2,732 |
2,629 |
2,521 |
2,407 |
2,286 |
|
28 |
9,283 |
6,440 |
5,317 |
4,607 |
4,299 |
4,019 |
3,811 |
3,648 |
3,518 |
3,411 |
3,246 |
3,072 |
2,889 |
2,794 |
2,694 |
2,591 |
2,433 |
2,369 |
2,246 |
|
29 |
9,229 |
6,395 |
5,276 |
4,659 |
4,252 |
3,983 |
3,774 |
3,612 |
3,483 |
3,376 |
3,211 |
3,037 |
2,855 |
2,759 |
2,660 |
2,556 |
2,447 |
2,333 |
2,210 |
|
30 |
9,179 |
6,354 |
5,238 |
4,623 |
4,227 |
3,949 |
3,741 |
3,530 |
3,450 |
3,344 |
3,178 |
3,005 |
2,823 |
2,727 |
2,627 |
2,594 |
2,415 |
2,229 |
2,176 |
|
40 |
8,827 |
6,066 |
4,975 |
4,373 |
3,986 |
3,712 |
3,508 |
3,349 |
3,222 |
3,116 |
2,953 |
2,781 |
2,593 |
2,502 |
2,401 |
2,295 |
2,183 |
2,063 |
1,981 |
|
60 |
8,484 |
5,795 |
4,729 |
4,139 |
3,760 |
3,491 |
3,291 |
3,134 |
3,008 |
2,904 |
2,741 |
2,570 |
2,387 |
2,289 |
2,187 |
2,078 |
1,962 |
1,834 |
1,688 |
|
120 |
8,179 |
5,539 |
4,497 |
3,920 |
3,548 |
3,284 |
3,087 |
2,933 |
2,808 |
2,705 |
2,543 |
2,372 |
2,188 |
2,089 |
1,983 |
1,870 |
1,746 |
1,605 |
1,431 |
|
¥ |
8,879 |
5,298 |
4,279 |
3,715 |
3,349 |
3,091 |
2,896 |
2,744 |
2,621 |
2,513 |
2,358 |
2,186 |
1,999 |
1,898 |
1,789 |
1,669 |
1,532 |
1,363 |
1,000 |
ПРИЛОЖЕНИЕ 6
ПРИМЕР РАЗРАБОТКИ ПРОЦЕССА И ВЫБОРА КОНТРОЛИРУЕМЫХ ПАРАМЕТРОВ ЧИСТОВОЙ КИСЛОРОДНОЙ РЕЗКИ МЕТАЛЛА [37]
1. АПРИОРНЫЕ СВЕДЕНИЯ О ПРОЦЕССЕ
Во многих случаях механизированная разделительная кислородная резка не обеспечивает требуемых механических свойств металла свободных кромок, в первую очередь усталостную прочность. Это вынуждает производить механическую обработку кромок.
Снижение механических свойств обусловлено в основном образующимися на поверхности реза характерными бороздами (надрезами), являющимися концентраторами напряжений. При этом качество обработанной поверхности можно рассматривать как шероховатость.
Шероховатость поверхности в соответствии с требованиями, установленными в ГОСТ 2789-73, оценивают по среднему арифметическому отклонению профиля и высоте неровностей профиля в десяти точках Rz. При механизированной кислородной резке металла шероховатость обработанной поверхности обычно характеризуется классом шероховатости первой группы (1 - 5), а числовые значения параметров шероховатости оцениваются Rz 50 ± 15 мкм.
В настоящем примере показана последовательность разработки процесса и выбора контролируемых параметров чистовой кислородной резки металла, обеспечивающих высокую чистоту поверхности, а, следовательно, и улучшение механических свойств.
Для разработки процесса применен ПФЭ, позволяющий получить математическую модель, выбрать контролируемые параметры и определить движение по градиенту, т.е. направление, при движении по которому параметр оптимизации (шероховатость поверхности) уменьшается быстрее, чем в любом другом направлении.
В качестве априорных сведений был выбран процесс скоростной кислородной резки [37]. Предварительные эксперименты показали, что удовлетворительное качество чистоты поверхности реза получается при работе на следующих режимах (при толщине разрезаемого металла 20 мм): скорость резки 0,01 м/с, давление режущего кислорода 784532 Н/м2, мощность подогревающего пламени 0,14 × 10-3 м3/с пропан-бутана, угол атаки a = 45°. Схема газовой резки показана на чертеже.
В качестве параметра оптимизации Y была выбрана шероховатость поверхности. Ее замеряли на профилографе-профилометре модели 201 в соответствии с требованиями ГОСТ 2789-73 на базовой длине 8 мм. В качестве независимых переменных (факторов) были выбраны следующие геометрические параметры процесса (см. чертеж): расстояние А между осям дополнительных струй (верхний уровень 4,5 мм, нижний уровень 3,5 мм), расстояние В между осями основной и дополнительных струй режущего кислорода (верхний уровень 2,5 мм, нижний 1,5 мм) и угол атаки a струй режущего кислорода к поверхности листа (верхний уровень 55°, нижний 35°).
Для предсказания направления градиента была выбрана линейная модель (неполная квадратичная модель) уравнения регрессии
Y = b0 + b1X1 + b2X2 + b1,2X1X2 + b1,3X1X2 + b2,3X2X3 + b1,2,3X1Х2Х3,
где Y - параметр оптимизации;
bi - параметры модели;
Xi - факторы процесса.
Факторы, их уровни и интервалы варьирования приведены в форме А. Расчеты произведены по формулам (1, 3) настоящей методики, например определяют основной уровень по формуле (1)
![]()
и интервал варьирования по формуле (2)
![]() и т.д.
и т.д.
Вводят специальные обозначения, чтобы верхний уровень фактора соответствовал +1, нижний -1, а основной 0. Как видно из формы А, все факторы варьировали на двух уровнях. В плане матрицы планирования эксперимента цифры (единицы) опускают и пишут только их знаки «+» или «-».
2. ПЛАНИРОВАНИЕ И ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА
2.1. Для записи априорных сведений о факторах процесса, записи верхних и нижних уровней, интервалов варьирования, плана матрицы планирования, результатов эксперимента, промежуточных и конечных результатов расчета для проверки воспроизводимости эксперимента, проверки значимости коэффициентов проверки адекватного описания процесса был составлен журнал планирования эксперимента (форма А - см. бандероль).
2.2. Построили план матрицы планирования полного фактора эксперимента типа 2k, где k - число факторов (форма А). При k = 3 число точек плана N = 8.
Матрица планирования отражает последовательность реализации всех возможных комбинаций факторов (графы Х1, Х2, Х3). Кроме того, для обеспечения расчетов ввели графу фиктивной переменной Х0, которая принимает во всех опытах значения +1, и графы взаимодействия факторов. В графах факторов знак «+» означает, что в данном опыте данный фактор должен находиться на верхнем уровне: соответственно знак «-» означает, что фактор должен находиться на нижнем уровне. Для удобства и исключения ошибок установления уровней факторов матрица в кодовых обозначениях факторов (для плана эксперимента, показанного в рамке, обведенной полужирными линиями в форме А) составлена в действительных значениях факторов (форма Б).
2.3. Перед реализацией плана эксперимента на объекте опыты, предусмотренные планом матрицы, проводились в случайной последовательности. Порядок реализации опытов (графы m1, m2, m3 форма А и форма Б - см. бандероль) в случайной последовательности выбирали по таблице равномерно распределенных случайных чисел (таблица приложения 4).
2.4. Устанавливали нужное значение факторов поочередно в каждой точке плана матрицы в порядке реализации каждой серии эксперимента (геометрические параметры в форме Б приведены в действительных значениях факторов) в соответствии с реализацией плана матрицы планирования и поддерживали эти значения постоянными в течение опыта Полученные действительные значения ожидаемого параметра оптимизации замеряли соответствующим прибором и результаты записывали в графы Y1, Y2, Y3, Y4 форм А и Б.
3. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Воспроизводимость измерений проверяли следующим образом.
3.1. Подсчитали средний показатель
параметра оптимизации процесса по реализации параллельных наблюдений по формуле
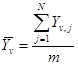 .
.
Например, по
реализации первой точки плана матрицы ![]()
![]() и т.д.
и т.д.
Результаты
вычислений записали в графу ![]() форм А и Б.
форм А и Б.
3.2. Подсчитали выборочную дисперсию воспроизводимости параллельных наблюдений для каждой точки плана матрицы по формуле

Например, по реализации первой точки плана матрицы
![]()
Результаты вычислений для всех точек плана матрицы записали в графу S2v формы А.
3.3. Однородность дисперсий проверили по формуле

В табл. 1 приложения 5 нашли для V1, в max = 3 и V2, в = 8 степеням свободы и уровню значимости q = 5 % критическое значение Кохрена равно 0,44. Расчетное значение - 0,41 критерия меньше табличного. Гипотеза однородности дисперсий принимается.
3.4. Для контроля расчетов
однородности дисперсий записали следующие значения в соответствующие графы
формы, А: 88,43 - в графу ![]() ; 36,33 - в графу S2max; 0,41
- в графу G; q = 5 % - в графу q; 3 - в
графу V1, в; 8 - в графу V2, в; 0,44 - в графу Gкp - 0,03 - в графу G - Gкp; в
графе «вывод» записали: дисперсии однородны.
; 36,33 - в графу S2max; 0,41
- в графу G; q = 5 % - в графу q; 3 - в
графу V1, в; 8 - в графу V2, в; 0,44 - в графу Gкp - 0,03 - в графу G - Gкp; в
графе «вывод» записали: дисперсии однородны.
3.5. Подсчитали дисперсию воспроизводимости измерений или дисперсию параметра оптимизации по формуле

Расчетное значение 11,05 записали в графу S2{Y} формы А.
4. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОЦЕССА
4.1. Подсчитали коэффициенты репрессии по формуле

Например, для определения
коэффициента b1 необходимо: умножить
комбинации факторов, приведенные в графе Х1, на данные,
приведенные в графе ![]() (форма А), затем
нашли алгебраическую сумму полученного произведения и разделили на число точек
в плане матрицы
(форма А), затем
нашли алгебраическую сумму полученного произведения и разделили на число точек
в плане матрицы

Рассчитанные значения коэффициентов записали в графу bi формы А.
4.2. Подсчитали дисперсии ошибки определения коэффициента регрессии по формуле
![]()
Расчетное значение 0,34 записали в графу S2{bi} формы А.
4.3. Для определения значимых коэффициентов репрессии из полученного результата S2{bi} извлекли квадратный корень по формуле
![]()
Расчетное значение 0,18 записали в графу S{bi} формы А.
4.4. Определили значимость коэффициентов регрессии по критерию Стьюдента по формуле
![]()
где ti - критерий Стьюдента;
|bi| - рассчитанные коэффициенты регрессии (см. форму А);
S{bi} - дисперсия коэффициента регрессии.
Получили значения
![]()
![]()
![]()
![]() t4 = 0;
t4 = 0; ![]()
![]()
![]()
Критическое
значение tкр нашли в табл. 3
приложения 5
для числа степеней свободы Vзн = N(m - 1) = 24 и на данном
уровне значимости q = 5
%. Критическое значение tкр = 2,06.
Если ti > tкр,
то коэффициент ![]() признается значимым. В нашем примере
значимым оказались следующие коэффициенты: b0,
b2, b3.
признается значимым. В нашем примере
значимым оказались следующие коэффициенты: b0,
b2, b3.
Расчетные значения занесли в графу ti формы А.
4.5. В математическую модель процесса включили только значимые коэффициенты. Получили уравнение репрессии в виде
![]()
4.6. Для контроля расчетов значимости коэффициентов уравнения репрессии записали следующие значения в соответствующие графы формы А: 5 % - в графу q %; 24 - в графу Vзн; 2,06 - в графу tкр; (216; 0,7; 51; 29; 01; 0,5; 0,6) в графу ti; (+2,13; -1,98; +48; +26; -1,96; -1,56; -1,46) - в графу ti - tкр; в графе «Вывод» записали: коэффициент значим, нет.
5. ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ
5.1. По уравнению регрессии подсчитали
величину ![]() для
каждой точки плана матрицы, т.е. по каждой строчке с учетом знака фактора в
плане матрицы нашли алгебраическую сумму коэффициентов уравнения поскольку |Х0|
= |Х1| = |Х2| = |Х3| =
|1|, например, по реализации первого опыта, умножив знаки коэффициентов на
знаки факторов, получим
для
каждой точки плана матрицы, т.е. по каждой строчке с учетом знака фактора в
плане матрицы нашли алгебраическую сумму коэффициентов уравнения поскольку |Х0|
= |Х1| = |Х2| = |Х3| =
|1|, например, по реализации первого опыта, умножив знаки коэффициентов на
знаки факторов, получим
![]() и т.д.
и т.д.
Полученные
результаты записали в графу ![]() формы А.
формы А.
5.2. Нашли разность между средним
значением ![]() показателя
параметра оптимизации процесса для каждой точки плана матрицы, полученным
экспериментально, и значением, полученным по уравнению регрессии
показателя
параметра оптимизации процесса для каждой точки плана матрицы, полученным
экспериментально, и значением, полученным по уравнению регрессии ![]() ; затем эту разность
возвели в квадрат.
; затем эту разность
возвели в квадрат.
Полученные
результаты записали в графу (![]() -
- ![]() ) формы А
и просуммировали.
) формы А
и просуммировали.
5.3. Нашли оценку дисперсии адекватности по формуле
![]()
где l - число значимых коэффициентов (включая b0).
Полученный результат записали в графу S2ad формы А.
5.4. Адекватность модели проверили по формуле
![]()
В табл. 4 приложения 5 нашли для V1, ad = N - l = 5 и V2, ad = N (m - 1) = 24 степеней свободы при заданном уровне значимости. Расчетное значение F = 1,1, приведенное в табл. 4, - 2,62. Гипотеза адекватности модели принимается.
5.5. Для контроля расчетов
адекватности модели записали следующие значения в соответствующие графы формы А; 17,179 - в графу ![]() ; 13,74 - в графу S2ad; 1,1 - в графу F;
5 % - в графу q %; 5 - в графу V1, ad;
24 - в графу V2, ad; 2,62 - в графу Fкp; - 1,52 - в графу F - Fкp; в
графе «Вывод» записали: модель адекватна.
; 13,74 - в графу S2ad; 1,1 - в графу F;
5 % - в графу q %; 5 - в графу V1, ad;
24 - в графу V2, ad; 2,62 - в графу Fкp; - 1,52 - в графу F - Fкp; в
графе «Вывод» записали: модель адекватна.
5.6. Поскольку выбор контролируемых параметров процесса осуществляется на основе требований к конечному продукту или к параметру оптимизации с учетом вклада каждого из выделенных параметров (факторов), то были оценены коэффициенты влияния (чувствительности) по формуле
![]()
для
коэффициента ![]() ;
;
для
коэффициента ![]() .
.
Фактор Х2 оказывает большее влияние на показатель параметра оптимизации по сравнению с фактором Х3. Это следует учитывать при контроле процесса.
5.7. Следовательно, следует контролировать геометрические параметры процесса: расстояние между осями основной и дополнительных струй режущего кислорода (фактор Х2) и угол атаки (фактор Х3).
В то же время нет необходимости контролировать расстояние между осями дополнительных струй (фактор X1). При этом необходимо при контроле больше внимания уделять фактору Х2, так как он более чувствителен к изменению хода процесса.
6. КРУТОЕ ВОСХОЖДЕНИЕ
6.1. Полученные данные о процессе в виде уравнения регрессии первой степени позволили перейти к его оптимизации.
6.2. Для записи априорных сведений о факторах процесса, верхних и нижних уровней, основных уровней, интервалов варьирования факторов, плана крутого восхождения, результатов эксперимента, промежуточных и конечных результатов расчета, для проверки воспроизводимости эксперимента, значимости коэффициентов, адекватного описания процесса был составлен журнал планирования эксперимента метода крутого восхождения (форма В - см. бандероль).
6.3. Крутое восхождение начинали от основных уровней значимых факторов: Х2 осн, Х3 осн, т.е. от нулевых уровней факторов в безразмерном масштабе.
6.4. Факторы изменены пропорционально величинам коэффициентов регрессии с учетом их знаков.
6.5. Вычислили произведения ![]() однозначно
по каждому фактору, т.е. умножили коэффициент репрессии факторов на их интервалы
варьирования, например, для фактора Х1 = 9,18 ´ 0,5 = 4,59 и т.д. (см. форму В, графа
однозначно
по каждому фактору, т.е. умножили коэффициент репрессии факторов на их интервалы
варьирования, например, для фактора Х1 = 9,18 ´ 0,5 = 4,59 и т.д. (см. форму В, графа ![]() ) - интервал варьирования.
) - интервал варьирования.
6.6. Нашли базовый фактор, для
которого произведение оказалось наибольшим по абсолютной величине, т.е. для
фактора Х2 величина равна 52,3 (см. форму В,
графа ![]() )
- интервал варьирования.
)
- интервал варьирования.
6.7. Выбрали сдвиг направления крутого восхождения по базовому фактору, равному 0,55.
6.8. Определили величину l первого шага эксперимента, т.е.
величину сдвига разделили на коэффициент базового фактора: ![]() .
.
6.9. Вычислили шаги первой точки крутого восхождения для факторов Х2 в Х3 по формуле Хh = l(biDXi) + Хi осн. При этом округлили расчетные значения для Х2 = -0,439 для Х3 = -5.
6.10. Серию последующих шагов рассчитывали последовательно, прибавляя к предыдущей точке шаг фактора l(biDXi) (см. форму В) номера точек плана 10 - 13.
6.11. Провели эксперимент, устанавливая факторы процесса в действительных значениях в соответствии с условиями шага. При этом незначимый фактор X1 стабилизировали на основном уровне. Ввиду того, что определялся минимум шероховатости, знаки коэффициентов регрессии были заменены на обратные. Реализация 10 - 13 опытов крутого восхождения (см. форму В - среднее четырех параллельных опытов позволила получить высокое качество поверхности реза Rz 7,3 мкм по ГОСТ 2789-73). Поэтому в дальнейших исследованиях применяли геометрические параметры процесса, соответствующие опыту 12 см, форму В (А = 4 мм; В = 3,8 мм; a = 25°), которые обеспечили указанное качество поверхности при резке стальных листов толщиной 6 - 50 мм в режимах, приведенных в форме В графе «Особые указания». Расчеты по проверке адекватности модели крутого восхождения не приведены, они аналогичны ПФЭ.
Рассмотрен метод полного факторного эксперимента. Обратимся к матрице планирования 23 (форма А). Она позволяет нам построить неполную квадратичную модель с взаимодействиями, т.е. рассчитать восемь коэффициентов. Если бы перед опытом были основания считать, что в выбранных интервалах варьирования процесс описывается линейной моделью, то достаточно было бы определить четыре коэффициента b0, b1, b2, b3. Именно так и обстоит дело, поскольку коэффициенты при взаимодействиях оказались статистически незначительными. Тогда у нас остается еще четыре степени свободы, которые можно использовать для минимизации числа опытов, т.е. в нашем примере мы могли проводить не восемь опытов, а всего четыре, при этом расчетные значения коэффициентов изменились бы несущественно.
Сравнение ДФЭ и ПФЭ по числу опытов в аналогичных ситуациях приведены в таблице приложения 7.
ПРИЛОЖЕНИЕ 7
ТАБЛИЦА
сравнения ДФЭ и ПФЭ по числу опытов
|
ДФЭ |
Условное обозначение |
Число опытов для |
||
|
ДФЭ |
ПФЭ |
|||
|
3 |
1/2 от ПФЭ 23 |
23-1 |
4 |
8 |
|
4 |
1/2 от ПФЭ 24 |
24-1 |
8 |
16 |
|
5 |
1/4 от ПФЭ 25 |
25-2 |
8 |
32 |
|
6 |
1/8 от ПФЭ 26 |
26-3 |
8 |
64 |
|
7 |
1/16 от ПФЭ 27 |
27-4 |
8 |
128 |
|
5 |
1/2 от ПФЭ 25 |
25-1 |
16 |
32 |
|
6 |
1/4 от ПФЭ 26 |
26-2 |
16 |
64 |
|
7 |
1/8 от ПФЭ 27 |
27-3 |
16 |
128 |
|
8 |
1/16 от ПФЭ 28 |
28-4 |
16 |
256 |
|
9 |
1/32 от ПФЭ 29 |
29-5 |
16 |
512 |
|
10 |
1/64 от ПФЭ 210 |
210-6 |
16 |
1024 |
|
11 |
1/128 от ПФЭ 211 |
211-7 |
16 |
2048 |
|
12 |
1/256 от ПФЭ 212 |
212-8 |
16 |
4096 |
|
13 |
1/512 от ПФЭ 213 |
213-9 |
16 |
8192 |
|
14 |
1/1024 от ПФЭ 214 |
214-10 |
16 |
16384 |
|
15 |
1/2048 от ПФЭ 215 |
215-11 |
16 |
32768 |
|
16 |
1/4096 от ПФЭ 216 |
216-11 |
32 |
65536 |
|
17 |
1/8192 от ПФЭ 217 |
217-12 |
32 |
131072 |
|
18 |
1/16384 от ПФЭ 218 |
218-13 |
32 |
262144 |
|
19 |
1/32768 от ПФЭ 219 |
219-14 |
32 |
524288 |
|
20 |
1/65536 от ПФЭ 220 |
220-15 |
32 |
1048576 |
|
21 |
1/131072 от ПФЭ 221 |
221-16 |
32 |
2097152 |
|
22 |
1/262144 от ПФЭ 222 |
222-17 |
32 |
4194304 |
|
23 |
1/524288 от ПФЭ 223 |
223-18 |
32 |
8388608 |
|
24 |
1/1048576 от ПФЭ 224 |
224-19 |
32 |
16777216 |
|
25 |
1/2097152 от ПФЭ 225 |
225-20 |
32 |
33554432 |
|
26 |
1/4194304 от ПФЭ 226 |
226-21 |
32 |
67108864 |
|
27 |
1/8388608 от ПФЭ 227 |
227-22 |
32 |
134217728 |
|
28 |
1/16777216 от ПФЭ 228 |
228-23 |
32 |
268435456 |
|
29 |
1/335544432 от ПФЭ 229 |
229-24 |
32 |
536870912 |
|
30 |
1/67108864 от ПФЭ 230° |
230-25 |
32 |
1073741824 |
|
31 |
1/134217728 от ПФЭ 231 |
231-26 |
32 |
2147483648 |
ЛИТЕРАТУРА
1. ГОСТ 14.301-73 - ГОСТ 14.317-75.
2. ГОСТ 9867-61. Международная система единиц.
3. ГОСТ 7663-55. Образование кратных и дольных единиц измерений.
4. ГОСТ 7664-61. Механические единицы.
5. ГОСТ 8033-56. Электрические и магнитные единицы.
6. ГОСТ 8550-61. Тепловые единицы.
7. ГОСТ 7932-56. Световые единицы.
8. ГОСТ 8849-58. Акустические единицы.
9. ГОСТ 8848-63. Единицы радиоактивности и ионизирующих излучений.
10. ГОСТ 1493-62. Обозначение основных общетехнических величин.
11. Единицы физических величин (проект стандарта).
12. Адлер Ю.П. Введение в планирование эксперимента. М., «Металлургия», 1969.
13. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М., «Наука», 1975.
14. Адлер Ю.П., Грановский Ю.В. Обзор прикладных работ по планированию эксперимента. М., Изд-во МГУ, 1972.
15 Бойцов В.В. Комплексная нормализация элементов производственного процесса - основа дальнейшего совершенствования авиационного производства. М., «Оборонгиз», 1958.
16. Бойцов В.В. Рекомендации по технологичности самолетных конструкций. М., «Оборонгиз», 1963.
17. Бойцов В.В. Механизация и автоматизация в мелкосерийном и серийном производствах. М., «Машиностроение», 1971.
18. Бородюк В.П., Круг Г.К. Некоторые вопросы организации эксперимента по сбору статистического материала, Труды МЭИ, выпуск 51, 1963.
19. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М., «Наука», 1965.
20. Бородюк В.П., Лецкий Э.К. Статистическое описание промышленных объектов. М., «Энергия», 1971.
21. Вознесенский В.А. Статистические решения в технологических задачах. Кишинев, «Картя молдовеняске», 1968.
22. Вознесенский В.А. Статистические методы планирования эксперимента в технико-экономических исследованиях. М., «Статистика», 1974.
23. Гинберг А.М. и др. Оптимизация технологических процессов в гальванотехнике. М., «Машиностроение», 1972.
24. Гитман А.С., Гитман Е.С. Поиск оптимальных параметров феррорезонансного стабилизатора методом крутого восхождения «Известия Томского политехнического института», т. 172, 1967.
25. Зайдель А.Н. Ошибки измерений физических величин. Л., «Наука», 1974.
26. Ивоботенко Б.А. и др. Планирование эксперимента в электромеханике. М., «Энергия». 1975.
27. Круг Г.К. Теоретические основы планирования экстремальных исследований. М., Изд-во МЭИ. 1969.
28. Кацев П.Г. Статистические методы исследования режущими инструментами. М., «Машиностроение», 1974.
29. Лабораторный практикум по курсу: «Теоретические основы планирования экспериментальных исследований». Под ред. Г.К. Круга. М., МЭИ, 1969.
30. Морозов В.П. Стандартизация как фактор совершенствования технологии машиностроительного производства. «Плановое хозяйство», 1975, № 12.
31. Налимов В.В., Чернова Н.А. Статистические методы экстремальных экспериментов. М., «Наука», 1965.
32. Налимов В.В., Голикова Т.П. Логические основания планирования эксперимента. М., Изд-во МГУ, 1972.
33. Новик В.С. Математические методы планирования экспериментов в металловедении (Московский институт стали и сплавов). М., выпуск I - 1969, вып. II - 1970, вып. III - IV - 1971.
34. Некоторые вопросы математического описания и оптимизации многофакторных процессов. Под ред. Круга Г.К. Труды МЭИ, 1963.
35. Рузинов Л.П. Статистические методы оптимизации химических процессов. М., «Химия», 1972.
36. Федоров В.В. Теория оптимального эксперимента. М., «Наука», 1971.
37. Шиловский В.Н. Разработка параметров чистовой кислородной резки с применением математических методов. «Сварочное производство», 1974, № 6.
38. Ткаченко В.В. Основы стандартизации контроля качества. М., Изд-во стандартов, 1973.
39. Точность производства в машиностроении и приборостроении. Под ред. А.Н. Гаврилова. М., «Машиностроение», 1973.
40. Якушев А.И. Взаимозаменяемость, стандартизация и технические измерения. Изд. 3-е. М., «Машиностроение», 1974.
СОДЕРЖАНИЕ
 (
( (
(